- 1WSL Institute for Snow and Avalanche Research SLF, Davos, Switzerland
- 2Institute of Meteorology and Climate Research, Atmospheric Environmental Research (KIT/IMK-IFU), Garmisch-Partenkirchen, Germany
- 3Centre for Hydrology, University of Saskatchewan, Saskatoon, SK, Canada
The temporal evolution of seasonal snow cover and its spatial variability in environments such as mountains, prairies or polar regions is strongly influenced by the interactions between the atmospheric boundary layer and the snow cover. Wind-driven coupling processes affect both mass and energy fluxes at the snow surface with consequences on snow hydrology, avalanche hazard, and ecosystem development. This paper proposes a review on these processes and combines the more recent findings obtained from observations and modeling. The spatial variability of snow accumulation across multiple scales can be associated to wind-driven processes ranging from orographic precipitation at large scale to preferential-deposition of snowfall and wind-induced transport of snow on the ground at smaller scales. An overview of models of varying complexity developed to simulate these processes is proposed in this paper. Snow ablation is also affected by wind-driven processes. Over continuous snow covers, turbulent fluxes of latent and sensible heat, as well as blowing snow sublimation, modify the mass, and energy balance of the snowpack and their representation in numerical models is associated with many uncertainties. As soon as the snow cover becomes patchy in spring local heat advection induces the development of stable internal boundary layers changing heat exchange toward the snow. Overall, wind-driven processes play a key role in all the different stages of the evolution of seasonal snow. Improvements in process understanding particularly at the mountain-ridge and the slope scale, and processes representations in models at scales up to the mountain range scale, will be the basis for improved short-term forecast and climate projections in snow-covered regions.
Introduction
The strong interaction between atmospheric boundary layer and land-surface via energy and mass exchange processes makes the distribution of snow a key element of the Earth system (Roesch et al., 2001; Vaughan et al., 2013) with crucial consequences for the hydrological cycle (Lehning, 2013) and the climate of cold regions (Beniston et al., 2018). In many regions of the world, seasonal snow cover provides the dominant source of drinking water supply (Sturm et al., 2017). A change in this seasonal water resource is of strong importance for economies (Beniston, 2012; Sturm et al., 2017), ecosystem function (Allan and Castillo, 2007; Wheeler et al., 2016), flood hazard (Hamlet and Lettenmaier, 2007), and winter tourism (Abegg et al., 2007; Grünewald et al., 2018).
Snow accumulation reveals strong variability across multiple temporal and spatial scales. Timing and magnitude of snow melt are strongly influenced by inter-annual variability in weather and by climate change impact (Grundstein and Leathers, 1999; Pedersen et al., 2013). Warmer temperatures reduce snowfall and snow cover duration (Barnett et al., 2005; Mote, 2006; Brown and Mote, 2009; Magnusson et al., 2010; Bavay et al., 2013) and lead to earlier onset of snow melt (López-Moreno et al., 2013). Musselman et al. (2017) even claim that lower net radiation earlier in the melt season might decrease snow melt in a warmer climate.
At smaller temporal and spatial scales, snow accumulation and ablation are highly variable in space and time, mainly a result of the complexity of snow processes across multiple scales (Blöschl, 1999; Clark et al., 2011). The final snow cover variability at the end of a snow accumualtion season has shown to be critical for capturing timing and magnitude of hydrological response in alpine catchments (Luce et al., 1998; Warscher et al., 2013; Winstral et al., 2013). Increased heterogenity of snow depth at the beginning of the melt period, results in much more differential melt over time and space, a faster runoff generation at the beginning of a melting period from shallow snowpacks and a prolonged melting season because of the delayed melt from deeper snow accumualtion areas (Brauchli et al., 2017). The change in melt dynamics of spatially variable snow covers strongly impacts the mass balance of glaciers (Mott et al., 2008; Dadic et al., 2010a) and run-off dynamics in alpine and glaciated catchements (Freudiger et al., 2017).
The spatial variability of snow at the catchment scale and at smaller scales is mainly the result of wind-driven processes driving mass and energy fluxes between the snow cover and the overlying atmosphere. The interaction between the wind field, snowfall and the snow surface governs the spatial variability in winter snow accumulation via pre- and post-depositional snow transport processes. Wind further plays an important role in the mass and energy balance of the snow cover, driving the turbulent energy exchange between the snow cover and the atmosphere via sensible and latent heat and due to blowing snow sublimation. Furthermore, complex boundary layer flows over heterogenous land-covers in spring strongly affect snow melt patterns (Mott et al., 2017).
The key to predicting seasonal snow cover dynamics and run-off generation during spring time is to adequately describe the complex snow-atmosphere interactions with wind as the main driver, provoking mass and energy fluxes to and from the snow cover. In the following, we provide an overview of the current state of knowledge on wind-driven coupling processes between the snow cover and the atmosphere governing seasonal snow cover dynamics, with a special focus on mountaineous regions. The review is meant to primarily discuss more recent research advances in this scientific field, particularly highlighting studies of the last 10 years. Earlier studies are referenced where required. In section Wind-driven Processes Driving Snow Accumulation Patterns at Different Scales, we discuss winter snow cover variability at different scales and related wind-driven snow processes shaping snow accumulation patterns. Here we distinguish between current knowledge on pre-depositional and post-depositional accumulation processes as well as sublimation of drifting and blowing snow. In section Heat Exchange Processes Driving Snow Melt Patterns, we first give an overview over scientific progress investigating heat exchange processes that are dominant over continuous snow covers (turbulent fluxes of latent/sensible heat and surface). Second, we discuss atmospheric boundary layer processes that become important over patchy snow covers, changing the energy balance during the later stages of the melting period when the land-surface becomes very heterogeneous.
Snow Energy and Mass Balance
Typically, the snowpack energy balance can be written, assuming a continuous snow cover, as (Armstrong and Brun, 2008):
where is the net change rate of the snowpack internal energy per unit area. At the snow-atmosphere interface the following fluxes determine the energy balance: QS is net shortwave radiation (incoming minus reflected shortwave radiation); QL is the net longwave radiation (downward and upward component of longwave radiation); Qh is the turbulent flux of sensible heat exchanged at the surface due to the temperature gradient between snow surface and atmosphere; Qe is the turbulent flux of latent heat exchanged between the surface and the overlying atmosphere due to water vapor pressure differences; it represents the sublimation and evaporation from and the condensation to the snow surface and is thus directly connected with the mass balance of the snow cover; Qa is the flux of energy advected via precipitation or blowing snow. Finally, QG is the ground heat flux due to conduction.
The mass balance of the snow cover including blowing snow can be written as (Armstrong and Brun, 2008):
where is the snowpack mass change rate; P is the precipitation rate. Dbs is the horizontal blowing snow transport due to redistribution of surface snow (mass per unit length per unit time) and Ebs the rate of sublimation of blowing snow. E is the sum of sublimation or evaporation (loss of mass) or condensation (gain of mass) rates at the surface. R is the runoff rate (liquid water leaving the bottom of the snowpack) and negatively contributes to the mass balance.
Wind-Driven Processes Driving Snow Accumulation Patterns at Different Scales
Large snow depth variability in winter can be observed over a range of scales (Figures 1, 2) and is controlled by different processes (Blöschl, 1999). We thus discuss wind-driven snow processes shaping the snow accumulation patterns at different scales of a mountainous area (Figure 2): (1) The Mountain range-scale, ranging from kilometers (mountain massifs; e.g., Coastal Mountains, Dolomites, Mont Blanc massif) to thousands of kilometers (e.g., Alps, Pyrenees, North American Rockies, Himalaya) (Figure 2A). (2) The mountain-ridge scale ranging from hundreds to thousands of meters depending on the size of an individual mountain. It comprises all processes that act over the full length of a mountain ridge, including slopes of different aspects (windward and leeward slopes) and the mountain crest area (Figure 2B) (3) The slope scale, ranging from few meters to hundreds of meters, deals with local crests and single mountain slopes, which can be either windward or leeward slopes, or nearly flat areas characterized by small-scale topography (bumps, depressions, gullies) (Figure 2C). In the following the discussion on snow processes is strongly focussed on the mountain-ridge and the slope scale as the spatial variability of the snow cover is strongest at these scales (see discussion below). Many snow processes shape the mountain snow cover at the mountain-ridge and the mountain-slope scale at the same time. We therefore discuss the spatial variability and the governing processes of these two scales in one subsection.
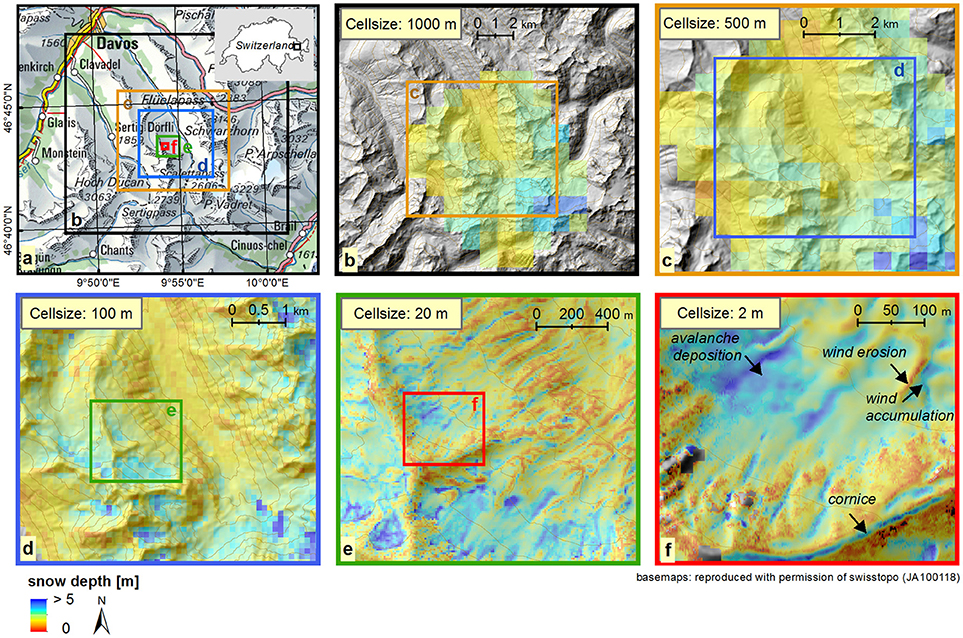
Figure 1. Snow depth variability represented by different measurement resolutions: 1,000 m (b), 500 m (c), 100 m (d), 20 m (e), and 2 m (f). An overview of the different domains is provided in (a). Same data set as used in Grünewald et al. (2014).
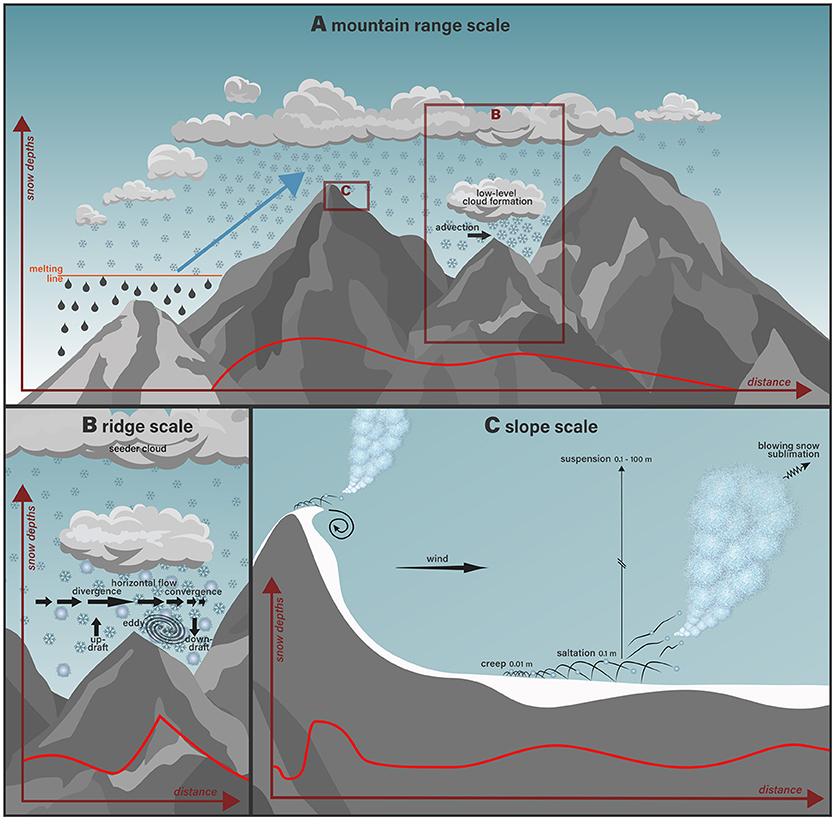
Figure 2. Schematic description of snow accumulation processes acting on different scales: the Mountain range scale (A), the ridge scale (B), and the slope scale (C).
The Mountain-Range Scale
At the mountain-range scale (Figures 1B,C, 2A), snow accumulation depends on climate, elevation and vegetation (Roe, 2005; López-Moreno et al., 2008; Clark et al., 2011; Anderson et al., 2014). Mountain-range scale precipitation patterns are mainly driven by orographic precipitation, which summarizes all processes that are related to regional precipitation patterns in mountainous terrain where the interaction of the ambient atmospheric flow with the underlying orography results in regions of enhanced or reduced snowfall (Colle et al., 2013). Roe (2005), Smith and Evans (2007), and Houze (2012) provide comprehensive reviews on regional-scale orographic precipitation. The main driving process is the forced dynamical lifting of air masses leading to cooling of the air column and resulting in condensation and precipitation (e.g., Smith et al., 2003) and a phase change from rain to snow above the zero-degree elevation band. Dynamical and cloud micro-physical trends tend to make leeward slopes drier than windward slopes (Houze, 2012). Such regional trends of decreasing precipitation are typically aligned with the prevailing synoptic wind direction (Gerber et al., 2018a). Most numerical studies on orographic precipitation over mountain ranges are restricted to model resolutions of ≥1 km (e.g., Rasmussen et al., 2011; Silverman et al., 2013; Pontoppidan et al., 2017).
Many studies based on high-resolution area wide snow depth data (Lehning et al., 2011; Grünewald et al., 2013, 2014; Kirchner et al., 2014; Zheng et al., 2016) show that elevation is the most important variable for precipitation patterns at the mountain range scale. Zheng et al. (2016) further highlighted the strong dependency on the defined grid resolution (Figure 1), when determining snow depth variability in both, forested and open terrain. Similarly, Tennant et al. (2017) explained snow depth variability at the regional scale by aspect, elevation, and vegetation height, but identified elevation as the dominant factor at all investigated regions. Very recently, Fayad et al. (2017) reviewed literature on snow hydrology in the Mediterranean mountains and concluded that, although the snow cover is highly variable in space and time, the persistence of the snow cover is mainly controlled by the interaction between elevation and precipitation. Other studies, however, showed that such elevation based precipitation gradients can significantly change over a specific elevation range. Analyzing high-resolution snow depth data for different regions, Grünewald and Lehning (2011), Grünewald et al. (2014), and Kirchner et al. (2014) evidenced a flattening or even decrease in the snow depth gradient above a certain elevation. These studies were confirmed by a very recent study of Collados-Lara et al. (2018) analyzing station data in the Mediterranean mountains. Similar to the other studies, they observed inverse snow depth gradients at higher elevations. There are two explanations for the non-linearity of precipitation at higher elevation. First, a precipitation maximum might be reached above a certain elevation (Blanchet et al., 2009), because decreasing air density in higher elevations reduce the amount of moisture available for condensation. Similarly, Kirchner et al. (2014) argued that the decline of snow depths at high elevations might be caused by depletion of orographic precipitation. However, no measurements are available that verify such a precipitation maxima above a certain height. Second, high elevations are usually steeper resulting in stronger gravitational and wind-induced snow redistribution (Winstral and Marks, 2002; Winstral et al., 2002; Bernhardt et al., 2010) from higher to lower elevations. Grünewald et al. (2014) attributed the spatial trends of decreasing snow depths at higher elevation sites to the dominance of steep, rocky exposures above a certain elevation. Lehning et al. (2011) explained the spatial variability of snow only by altitude and land surface roughness. They statistically showed that rougher terrain holds less snow than smooth terrain. Similarly, Grünewald et al. (2013) claimed that the major part of snow depth variability can be predicted by four topographic parameters: elevation gradient, slope, aspect, and wind-sheltering. They could also show that the application of a global model is limited because the relationship between snow and topography appeared to be not universal for all landscapes.
The Mountain-Ridge and Slope Scale
Spatial Variability of Snow Accumulation
Contrary to what is observed for large mountain ranges, ridge-scale snow accumulation patterns (hundreds to thousands of meters) (Figures 1D,E, 2B) typically reveal much larger spatial variability of snow and enhanced snow deposition over leeward slopes of single mountain peaks (Lehning et al., 2008; Zängl et al., 2008; Mott et al., 2010, 2014; Vionnet et al., 2017).
Describing the spatial structure of measured snowfall fields (horizontal resolution of 75 m) with fractal analysis, Scipión et al. (2013) found coherent patterns up to scales of 2 km (scale break). Similar scale breaks were found by Gerber et al. (2018a) who concluded that precpitation patterns at the mountain-ridge scale are dominated by smaller-scale precipitation processes that are mainly terrain and wind-driven. Gerber et al. (2018a) highlight the importance of using horizontal model resolutions up to 50 m in order to capture spatial variability of precipitation at the mountain-ridge scale. Scipión et al. (2013) showed that snow deposition at the ground revealed much larger spatial variability than snowfall variability measured several hundreds of meters above ground. This large difference in the spatial structure was mainly attributed to the interaction between the near-surface flow field and snow particles, which is also known as preferential deposition of snowfall. This process is active in the lowest hundreds of meters above ground and not fully captured by radars.
Following Mott et al. (2014) and Vionnet et al. (2017) snow deposition at the mountain ridge scale, is caused by three processes: (i) snowfall enhancement caused by the interaction of the local flow field and local cloud formation processes, such as seeder-feeder mechanisms, (ii) pure particle flow interaction (preferential deposition of snowfall) and (iii) snow redistribution by saltation and suspension. Preferential deposition of snowfall (Lehning et al., 2008) is active in all cases with sufficient wind. Contrary, snowfall enhancement is limited by temperature and moisture fields and sufficiently strong updrafts allowing condensation to take place, provoking local feeder clouds over single peaks and ridges (Mott et al., 2014).
The relative importance of these processes for the spatial variability of snow accumulation appear to be scale-dependent. Gerber et al. (2018b) applied the COSMO-WRF model chain to simulate winter precipitation on a grid resolution of 50 m. They showed that the combined effect of cloud-dynamical effects and particle-flow interaction at heights above 100 m above ground may alter precipitation by 20% of mean precipitation. Pure particle-flow interaction very close to the ground (lowest 100 m above ground) appear to alter precipitation by 10% of mean precipitation. Vionnet et al. (2017) applied the fully coupled snowpack/atmosphere model Meso-NH/Crocus (Vionnet et al., 2014) which allows the investigation of micro-physical processes, such as snowfall enhancement, and preferential deposition at the same time. Similar to Gerber et al. (2018b) their numerical results (also 50-m resolution) indicate that spatial variability of precipitation is more dominated by micro-physical processes such as riming of snow particles than by the pure particle flow interaction. The effect of model resolution on the process representation is, however, in question. Gerber et al. (2018a) and Roth et al. (2018) show that model resolution not only affects precipitation amount, but also the spatial structure of snowfall. Especially, the overstimation of updrafts over windward side of steep mountain ridges may lead to an overprediction of riming intensity. Gerber et al. (2018b) demonstrates that lee-side flow separation and ridge-scale snowfall enhancement starts to develop at a model resolution of 50 m, indicating a strong need for higher resolution precipitation modeling in complex terrain, possibly even at resolutions higher than 50 m.
Applying higher model resolutions (20 m and less), Mott and Lehning (2010) and Gerber et al. (2017) suggest that preferential deposition of snowfall mainly drive spatial variability of snow depths at the ridge scale (hundreds to thousands of meters), causing snow loading on leeward slopes of mountain ridges and reduced snow deposition on the windward slopes (slope scale, Figure 2C). Snow accumulation patterns at the ridge scale (Figure 2B), driven by preferential deposition, are super-imposed by snow drift processes (acting on the scales of a few to hundreds of meters) and snow avalanches (Gerber et al., 2017). Grünewald et al. (2014) and Kirchner et al. (2014) pointed to the challenges in distinguishing between these different physical processes acting at the mountain ridge scale in the area-wide snow depth dataset available in the community.
Snow redistribution processes, such as saltation and turbulent suspension, are dominant drivers for snow deposition patterns at the slope scale and the lower range of the ridge scale shaping snow deposition patterns in a wide scale range of a few meters to hundreds of meters across different environments (alpine, artic, prairies; Shook and Gray, 1996; Sturm et al., 2001; Essery and Pomeroy, 2004; Fang and Pomeroy, 2009; Mott et al., 2010; Dadic et al., 2013a; Schön et al., 2015). Preferred loading of snow on leeward slopes leads to more homogenous snow depth distributions (Mott and Lehning, 2010). Contrary, snow erosion by wind is mainly detected at flat areas such as in the prairies or over frozen lakes where an adequate fetch to establish wind erosion exists (Sturm and Liston, 2003; Iacozza and Barber, 2010; Dadic et al., 2013a), or at wind-exposed areas of various size (from local bumps to large ridge crests). Snow tends to be deposited preferentially in the lee of topographic disturbances such as ridges or in local depressions, leading to local snow deposition features such as snow dunes, drifts, cornices and filling of troughs (Figures 1F, 2C).
Wind-driven snow redistribution processes result in a smoothing of land-surface roughness (Mott et al., 2011b; Schirmer and Lehning, 2011). Studies analyzing the fractal behavior of snow depths at the ridge scale found scale-breaks in the order of tens of meters, with a stronger autocorrelation before the scale break than beyond (Shook and Gray, 1996; Deems et al., 2006; Trujillo et al., 2007; Mott et al., 2011b; Schirmer and Lehning, 2011). This scale break was clearly attributed to wind-driven snow accumulation features. The interaction of wind with vegetation leads to similar spatial variability, with even smaller scale breaks of a few meters (Trujillo et al., 2012; Deems et al., 2013; Tedesche et al., 2017; Webb et al., 2017). Schirmer and Lehning (2011) even demonstrated that fractal parameters of snow depths were able to distinguish between wind-protected and wind-exposed areas and to describe the structure of snow depth change during more and less wind-influenced snowfall periods. Mott et al. (2011b) demonstrated that preferential deposition of snowfall and the small-scale redistribution processes, saltation and suspension, drive the spatial structure of snow depths, explaining the stronger autocorrelation of snow depths at the scale of tens of meters. The scaling analysis performed by Mott et al. (2011b) showed that a model resolution of 5 m is still insufficient to capture the whole range of scales where driving processes are active. In Arctic environment, vegetation such as shrubs and local topography strongly influenced snow redistribution (Essery and Pomeroy, 2004). While snow tends to be deposited on slopes in the lee of prevailing wind directions over bare soil or tundra, shrubs act as snow trap both on the leeward and windward slopes.
Moreover, surface roughness has strong implications for snow accumulation even at steep rock faces allowing more snow to accumulate than expected by most models that assume no snow accumulation at steep slopes (>60°) (Blöschl and Kirnbauer, 1992). Typically, hydrological models tend to underestimate snow accumulation in rock walls due to the strong dependency of gravitational snow transport models on the slope, not considering small-scale surface roughness (Bernhardt and Schultz, 2010; Dadic et al., 2010a; Warscher et al., 2013). However, several studies demonstrated high spatial variability of snow depths in very steep rock faces and very rough rock walls with rock ledges (Wirz et al., 2011; Haberkorn et al., 2015, 2017; Sommer et al., 2015).
The strong relation of slope-scale and ridge-scale snow deposition patterns to the local flow field modified by complex topography (Helbig et al., 2017), is reflected in a high intra- and inter-annual persistence of snow depth distribution (Deems et al., 2008; Mott et al., 2010; Schirmer et al., 2011; Grünewald et al., 2013; Helfricht et al., 2014; Revuelto et al., 2014; Winstral and Marks, 2014; López-Moreno et al., 2017). Contrary, in case of strong shift of major wind directions from year to year, such inter-annual persistency was not observed (MacDonald et al., 2009). Moreover, López-Moreno et al., 2013) showed that the statistical relationship between terrain parameters and snow depth distribution is not transferable between different regions.
Pre-depositional Processes: Orographic Effects on Snowfall Deposition
Snowfall enhancement
Orographically-induced ascend of the near-surface airflow can change the local condensation regime leading to low-level cloud formation above the ridge crest. Such low-level clouds provide an additional moisture source for the growth of snow crystals falling from clouds advected at higher levels, promoting local enhancement of snowfall (e.g., Choularton and Perry, 1986; Dore and Choularton, 1992; Minder et al., 2008). The so-called seeder-feeder mechanism was first proposed by Bergeron (1965) to explain orographic precipitation enhancement. Analyzing a specific snowfall event in the Swiss Alps, Mott et al. (2014) demonstrated that such local cloud formation processes, in the presence of a larger-scale seeding cloud aloft, typically form small scale patterns of snowfall enhancement in the downwind region of summits. During the seeder-feeder process, crystals typically grow by riming and aggregation. If the particle distribution is dominated by the seeder-feeder mechanism, rimed and aggregated snow particles are more likely to get deposited than non-aggregated and unrimed crystals owing to their higher terminal velocities (Houze and Medina, 2005). Due to higher snowfall production and higher terminal velocities, low-level clouds can promote strong snowfall over mountain ridges.
Preferential deposition of snowfall
Downstream advection of falling snow particles by high horizontal wind velocities at mountain crests play a decisive role in the final distribution of snowfall and snow deposition (Colle, 2004; Zängl, 2008; Mott et al., 2014). This effect of the atmospheric boundary layer flow on falling snow particle trajectories is known as preferential deposition of snow (Lehning et al., 2008). In the last decade, several studies confirmed this concept to drive snow depth distribution after snowfall events in alpine catchments (Mott and Lehning, 2010; Mott et al., 2010, 2014; Warscher et al., 2013; Vionnet et al., 2017; Wang and Huang, 2017) and to control seasonal snow cover dynamics over glaciers (Mott et al., 2008; Dadic et al., 2010a,b). Following Mott et al. (2014) snow concentration fields in the atmosphere and final snow deposition at the ground can directly be linked to the near-surface flow field (Figure 3). In case of weakly stable atmospheric conditions (Figure 3), streamwise flow divergence cause strong advection of particles in downwind direction, reducing snow deposition over windward slopes (Choularton and Perry, 1986; Colle, 2004; Lehning et al., 2008; Zängl et al., 2008; Winstral et al., 2013). The peak particle concentration in the atmosphere is typically found at the ridge crest, at the transition between streamwise flow divergence and convergence, which is also the transition between updrafts (reduced snow deposition) on the windward and downdrafts (enhanced snow deposition) on leeward side of a mountain crest. Over the leeward slope streamwise flow convergence typically coincide with downdrafts resulting in converging particle trajectories and thus enhanced snow deposition in this area (Figure 2B). As the effect of near-surface flow fields on the falling particles increase with decreasing distance to the surface, the resulting snow deposition at the ground shows below average snow deposition on the windward slope and an amplification of snow accumulation on the leeward slope (Figures 2B, 3). This process description as presented by Mott et al. (2014), is especially valid for weak atmospheric stabilities and flow separation forming over lee-side slopes of mountain ridges (Gerber et al., 2018b).
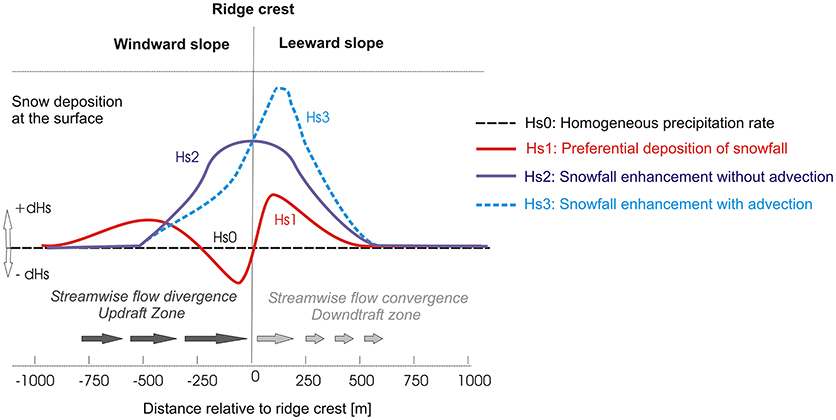
Figure 3. Schematic description of final snow deposition around a ridge crest driven by homogenous precipitation rate (Hs0), preferential deposition of snowfall (Hs1), snowfall enhancement without advection by the mean wind (seeder-feeder mechanism only) (Hs2) and the combined effect of snowfall enhancement and preferential deposition of snowfall (Hs3) (Modified after Mott et al., 2014).
Gerber et al. (2017) pointed to strong effects of the complex nature of lee-side eddy structures and corresponding flow separation types on small-scale precipitation distribution. Several studies (e.g., Gerber et al., 2017; Wang and Huang, 2017) highlight the strong dependency of preferential deposition of snowfall to atmospheric stability and related changes in the local flow field. Wang and Huang (2017) investigated snowfall deposition for stronger atmospheric stabilities and found strong snowfall deposition over windward slopes due to flow blocking, but report a shift of precipitation peaks from the windward to the leeward slope for strong adjective winds. However, similar to what has been observed for post-depositional processes (e.g., Aksamit and Pomeroy, 2016, 2018a; Paterna et al., 2017), the coupling of coherent turbulent structures and snow transport in the air is still not fully understood.
Post-depositional Processes
Drifting and blowing snow
The final pattern of snow accumulation on the ground is strongly influenced by post-depositional processes, especially at the slope scale (Figures 1F, 2C). This includes wind-induced snow transport during drifting and blowing snow events and redistribution by avalanches that may occur in steep slopes (e.g., Bernhardt and Schultz, 2010). In this section, we restrict our presentation to physical processes during wind-induced snow transport (see Equation 2). Traditionally and similarly to sand transport (e.g., Bagnold, 1941; Kok et al., 2012), wind-induced snow transport has been divided in three main transport modes: creep, saltation and suspension (e.g., Pomeroy and Gray, 1995). Creep (or reptation) is defined as the rolling of the largest snow particles on the snow surface never rising more than a grain diameter in height above the surface. Saltation corresponds to the transport of snow crystals in a layer close to the ground (typical thickness: 5–10 cm). These crystals follow ballistic trajectories influenced by wind drag and gravity with frequent rebounds from the snow surface (Figure 2C). Finally, smaller snow particles in suspension are lifted up above the saltation layer by vertical gusts and can be transported in a deep layer (from a few meters up to a few hundred meters) over large distances of tens to hundreds of meters without contact with the surface (Figure 2C). Mass loss of snow particles in saltation and in suspension occurs due to blowing snow sublimation (see section Snow Sublimation: Mass Loss and Atmospheric Feedback).
Two main modes have been traditionally identified for the transport of snow particles in the saltation layer and its initiation: aerodynamic and splash entrainment (e.g., Nishimura and Hunt, 2000; Doorschot and Lehning, 2002). Aerodynamic entrainment occurs when the wind flow has sufficient momentum to entrain snow crystals from the surface. Splash entrainment corresponds to the movement of incoming grains already in transport impacting the snow surface, rebounding and/or projecting additional grains in the saltation layer. Recent studies have improved our understanding of the coupling between the near-surface atmospheric turbulence and the saltation dynamics and the unsteadiness of these processes (Naaim-Bouvet et al., 2011). Based on wind tunnel measurements over natural snow cover, Paterna et al. (2016) revealed the presence of two saltation regimes: a “weak” saltation where the turbulence influences the saltation dynamics and a turbulence-independent “strong” saltation. A refined analysis of these experiments showed that the “weak” saltation can be associated with aerodynamic entrainment and the “strong” saltation with splash entrainment (Paterna et al., 2017). Using laser-illuminated high-speed camera deployed in natural environment, Askamit Aksamit and Pomeroy (2016) identified an additional initiation mode for moderate wind speed and intermittent transport and showed the importance of creep to the initiation of transport by saltation. Particles in an active creep layer appear as an efficient source of saltation particles since they are already moving without cohesive bonds with the snow surface, lowering the forces required for aerodynamic or splash entrainment. These experiments carried out in a mountainous environment with fully-developed atmospheric turbulence allowed the identification of turbulent structures responsible for saltation dynamics (Aksamit and Pomeroy, 2018a). Sweeps, wind motions with greater than average streamwise and less than average vertical velocities, were the dominant motion for both initiating blowing-snow transport, and increasing concentration and particle number flux near the surface. Ejections, wind motions with less than average streamwise and greater than average vertical velocities, were not effective in initiating snow particle motion and mainly sustained transport, through vertical transport. In addition, large scale turbulent motions generated by the surrounding topography modulate the local saltation dynamics (Aksamit and Pomeroy, 2018b).
Blowing snow and the snow surface properties are strongly coupled and influence each other. Indeed, the dynamics and the initiation of the transport in saltation, and ultimately in turbulent suspension, depend on the properties of the snow surface (type of crystals, cohesion, and roughness). Schmidt (1980), Lehning et al. (2000) and He and Ohara (2017) have proposed formulations for the threshold wind speed of snow transport accounting for cohesion due to sintering between snow grains at the surface. The lowest threshold wind speeds are found for fresh-fallen dendritic snow characterized by low cohesion (Guyomarc'h and Merindol, 1998). Field work by Doorschot et al. (2004) and wind tunnel experiments by Clifton et al. (2006) showed that the threshold wind speed increased with increasing snow grain size and increasing snow density. Li and Pomeroy (1997) found that the threshold wind speeds for wet snow are significantly higher than those for dry snow due to viscous forces associated with thin layers of liquid water between snow grains in wet snow. The snow surface hardness and cohesion modify the ability of the snow surface to absorb wind and particle momentum (Aksamit and Pomeroy, 2016; Comola and Lehning, 2017) and influence the saltation dynamics. In return, wind-driven snow transport modifies the physical properties and roughness of surface snow. For snowfall with moderate wind, measurements by Sato et al. (2008) showed that snowflakes break upon collisions with the surface and that the number of fragments increases with impact velocity. Comola et al. (2017) developed a model to represent the fragmentation of wind-blown snow crystals and concluded that this process is responsible for the transformation from large dendritic snowflakes following an exponential distribution into small wind-blown particle following a gamma distribution (e.g., Nishimura and Nemoto, 2005; Naaim-Bouvet et al., 2011; Gromke et al., 2014). Because of this fragmentation, deposited snow crystals are made of fine grains which quickly gains cohesion due to sintering increasing the hardness of surface snow. Using wind-tunnels experiments, Sommer et al. (2017, 2018) showed that the formation of wind-packed snow at the surface is only observed when saltation occurs. Wind hardening does not occur in erosion zones and is found preferentially in wind-exposed deposition zones. Vionnet et al. (2013) showed that the wind-dependance of snow crystal properties during snowfall and the packing and fragmentation of surface snow during snow transport needs to be taken into account to properly simulate the occurrence of blowing snow at an alpine site. Blowing snow modifies also surface roughness of the snow cover creating a large variety of shapes such as ripples, sastrugis, or snow dunes (Filhol and Sturm, 2015). These modifications alter the generation of atmospheric turbulence and thus modify the wind field and the blowing snow fluxes (Amory et al., 2017). Once emitted, wind-blown snow particles in the suspension layer are transported without contact with the snow surface. A strong near-surface gradient of particle concentration is found with roughly an order-in-magnitude decrease between 0.1 and 1 m and another one between 1 and 10 m (e.g., Schmidt, 1982; Gordon et al., 2010; Naaim-Bouvet et al., 2010). The snow particle speed was always found 1 to 2 m s−1 less than the wind speed in an observation dataset collected in alpine terrain between 0.1 and 1 m above the snow surface (Nishimura et al., 2014).
Snow sublimation: mass loss and atmospheric feedback
Snow sublimation is defined as the transfer of water directly from the snow to the atmosphere through phase change. It corresponds to a mass loss for the snowpack (Equation 2) and an energy loss due to the associated negative latent heat flux (Equation 1). Snow sublimation is made of three components: (i) ground snow sublimation, (ii) sublimation of snow intercepted by the vegetation and (iii) blowing snow sublimation (e.g., Pomeroy et al., 1998b; Molotch et al., 2007; Strasser et al., 2008; Reba et al., 2012; Sexstone et al., 2018). The intensity of surface sublimation varies as a function of wind speed, net radiation, air temperature, and relative humidity (e.g., Hood et al., 1999; Jackson and Prowse, 2009; Reba et al., 2012; MacDonell et al., 2013; Sexstone et al., 2016). The diurnal cycle of these radiative and meteorological drivers creates a strong diurnal cycle of surface sublimation rate which tends to peak in early afternoon (e.g., Reba et al., 2012; Sexstone et al., 2016). In addition to these drivers, sublimation of snow intercepted by the vegetation depends on the canopy structure (Pomeroy et al., 1998b; Svoma, 2017). During blowing snow events, part of the transported snow is lost due to sublimation of airborne snow particles, reducing the amount of deposited snow and modifying the overall snowpack mass balance (e.g., Pomeroy and Gray, 1995). The intensity of blowing snow sublimation is influenced by the snow surface conditions that impact the occurrence of blowing snow (see section Drifting and Blowing Snow) and on the total amount of snow particles transported in the atmosphere, their size distribution and the associated ventilation speeds (Thorpe and Mason, 1966; Schmidt, 1982; Wever et al., 2009).
Sublimation rates for surface snow and snow intercepted by the canopy have been quantified at many experimental sites around the world. Jackson and Prowse (2009) and Svoma (2016) summarized the findings of these studies and showed that the large variability of measured sublimation rates not only depends on the local meteorological conditions but also on the different methods used to estimate these fluxes (eddy covariance, bulk aerodynamic flux, aerodynamic profile; see section The Spatial Variability of Energy Balance and snow Melt Processes). On the contrary, only few field measurements or estimations of blowing snow sublimation intensity over seasonal snow cover are available in the literature. Using eddy covariance techniques, Pomeroy and Essery (1999) measured sublimations rates between −1.2 and −1.8 mmSWE day−1 during a blowing snow event in the Prairies of Central Canada. These measurements also include the contribution of snow surface sublimation. Schmidt (1982) measured the vertical profiles of wind speed, humidity, and blowing snow mass at an experimental site located over gentle terrain in south-eastern Wyoming (USA) and derived estimates of blowing snow sublimation rates ranging from −0.5 to −5.3 mmSWE day−1. All these field measurements or estimations of snow sublimation rates were obtained at single sites. Numerical models have been used to quantify mass loss due to sublimation at large scales, especially over complex terrain, where the intensity of snow sublimation varies greatly in time and space due to complex boundary layer flows (Strasser et al., 2008; Groot Zwaaftink et al., 2011; Vionnet et al., 2014).
Table 1 summarizes different estimations of mass loss due to snow sublimation for several regions of the world. These results concern single events or the entire winter season and are restricted to surface and blowing snow sublimation. The estimations vary greatly from one study to another, especially at the seasonal scale. These differences of estimations arise from three main reasons: (i) meteorological conditions, (ii) topography, and (iii) model configuration and complexity. For example, the dryer conditions in the Andes can favor larger sublimation rates than in the Europeans Alps (Bernhardt et al., 2012; Gascoin et al., 2013; Groot Zwaaftink et al., 2013). Reba et al. (2012) and Sexstone et al. (2016) showed also that the relative importance of snow sublimation strongly depends on the total amount of snowfall in a given year. The large spatial variability of sublimation rates in alpine terrain also explains the different estimations reported in the literature. Strasser et al. (2008); Groot Zwaaftink et al. (2011) and Vionnet et al. (2014) showed that maximal sublimation losses are found nearby wind-exposed crest where blowing snow intensity is larger. This can explain the differences between estimation for a single crest as in MacDonald et al. (2010) and for larger catchments as in Strasser et al. (2008) and Bernhardt et al. (2012). Alpine terrain is also characterized by shorter fetches compared to more gentle terrain like the Canadian Prairies (Pomeroy and Gray, 1995) or the Arctic (Pomeroy et al., 1997; Liston and Sturm, 1998; Liston et al., 2002). Finally, the models used in these studies differ in terms of configuration and complexity. For example, model resolution has an impact on the simulated sublimations rates since crests where high sublimations rates are simulated have a smaller spatial extent at finer resolution (Bernhardt et al., 2010). In addition, recent works by Huang and Shi (2017) and Sharma et al. (2018) have suggested that blowing snow models should not neglect sublimation in the saltation layer which can lead to an underestimation of the importance of blowing snow sublimation by the models.
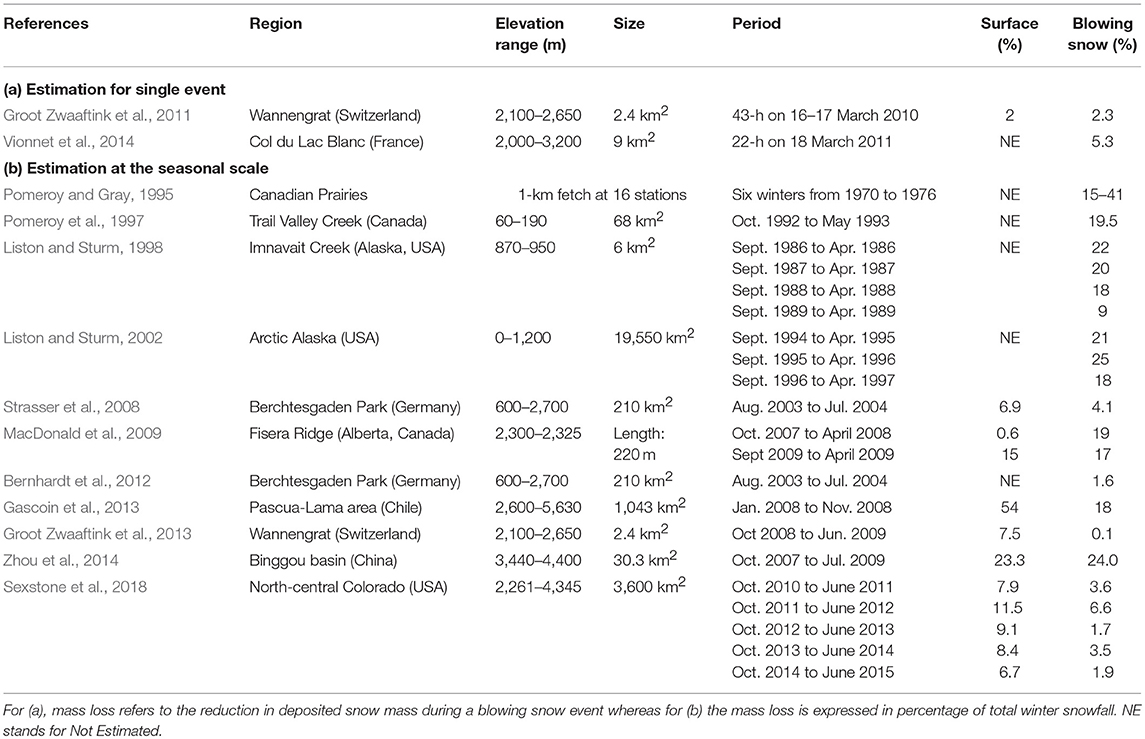
Table 1. Estimation of mass loss due to surface and blowing snow sublimation for (a) single events and (b) at the seasonal scale reported in different studies.
Snow sublimation (surface and blowing snow) also influences the atmospheric conditions in the surface boundary layer and leads to an increase in relative humidity and a decrease in air temperature. Eventually, sublimation rates can decrease and specific and latent turbulent fluxes between the snow surface and the atmosphere are modified (Taylor, 1998; Bintanja, 2001; Wever et al., 2009). During blowing snow events, these feedbacks can lead to saturation of the near-surface boundary layer as observed in Antarctica (Mann et al., 2000; Barral et al., 2014). In mountainous regions and in the prairies, Musselman et al. (2015) and Pomeroy and Li (2000) showed that air humidity did not reach saturation or even decreased due to entrainment of dry air from layers aloft. Groot Zwaaftink et al. (2011) and Vionnet et al. (2014) have estimated the effects of the thermodynamics feedbacks of blowing snow sublimation on mass and energy exchanges in alpine terrain using numerical models accounting for these feedbacks. They found that the increase in relative humidity due to blowing sublimation is limited (9–15%) without saturation of the near surface layer. Accounting for the feedbacks limits blowing snow sublimation, resulted in a 2% difference in deposition reduction in a lee slope (Groot Zwaaftink et al., 2011). Vionnet et al. (2014) showed that surface sublimation is also reduced by 30% due to the feedbacks but total sublimation (surface + blowing snow) is three times higher when accounting for blowing snow sublimation which is the main source of transfer of water vapor to the atmosphere (78% of total sublimation).
Modeling Approaches of Snow Accumulation Processes
A large variety of models have been developed to simulate and better understand snow accumulation processes in different environments seasonally covered by snow (e.g., alpine, arctic, prairies). Accounting for wind-induced snow transport is required to capture the small-scale pattern of snow accumulation. Table 2 gives the main characteristics of models capable of simulating snow variability influenced by wind redistribution. These models can be divided in two main categories: (i) models based on semi-empirical parameterizations of the physics of snow transport and (ii) models resolving the 3D turbulent-diffusion equation for blown snow particles in the atmosphere. Models in the first category rely on vertically-integrated transport rates in the saltation and the suspension layer (Pomeroy et al., 1993; Liston and Sturm, 1998; Durand et al., 2005; Liston et al., 2007). Due to their relatively low computational costs, these models were applied with certain success to simulate entire snow seasons in the Canadian Prairies and the Arctic (e.g., Pomeroy and Li, 2000) or in mountainous terrain (e.g., MacDonald et al., 2010; Gascoin et al., 2013). Bernhardt et al. (2009) and Musselman et al. (2015) have shown that these models are very sensitive to the driving wind field, especially in alpine terrain. Improved modeling of snow accumulation requires a consideration of atmospheric turbulence. Therefore, for the second category of models, computational fluid dynamics (CFD; Naaim et al., 1998; Gauer, 2001; Schneiderbauer and Prokop, 2011) and atmospheric models in Large Eddy Simulations (LES) mode providing libraries of flow fields as input for snow cover process models (Lehning et al., 2008; Mott et al., 2010) or fully coupled to a snow cover process model (Vionnet et al., 2014) have been used. Because of their complexity, these models are usually focusing on single blowing snow events but can be occasionally used over an entire snow season (Groot Zwaaftink et al., 2013). The 3D turbulent-diffusion equation for snow particles in the suspension layer is solved with different assumptions on the particle size distributions (fixed or non-uniform). Description of the saltation layer varies from semi-empirical relationships (Pomeroy and Gray, 1990; Sørensen, 2004) to more advanced models representing the essential characteristics of saltating snow particles (aerodynamic entrainment, splash) (Gauer, 2001; Doorschot and Lehning, 2002). In these models, the 3D wind field is obtained from a library of pre-computed situations (Raderschall et al., 2008; Mott et al., 2010) or downscaled from meteorological analysis or forecast using a grid nesting approach (Vionnet et al., 2017). Preferential deposition can also be explicitly simulated. An alternative method to study terrain-flow-particles interactions more in detail relies on Lagrangian-tracking of falling snow particles as in Wang and Huang (2017). In addition, the coupled snow-atmosphere modeling approach proposed by Vionnet et al. (2014) allows to explicitly simulate local cloud dynamical effect and to discuss the relative importance of the different processes influencing the variability of snow accumulation in alpine terrain (Vionnet et al., 2017). But this approach is still restricted to intermediate resolutions (50 m) due computational costs and numerical stability in steep terrain and cannot be used to explore patterns of snow accumulation at very high resolution (Mott and Lehning, 2010).
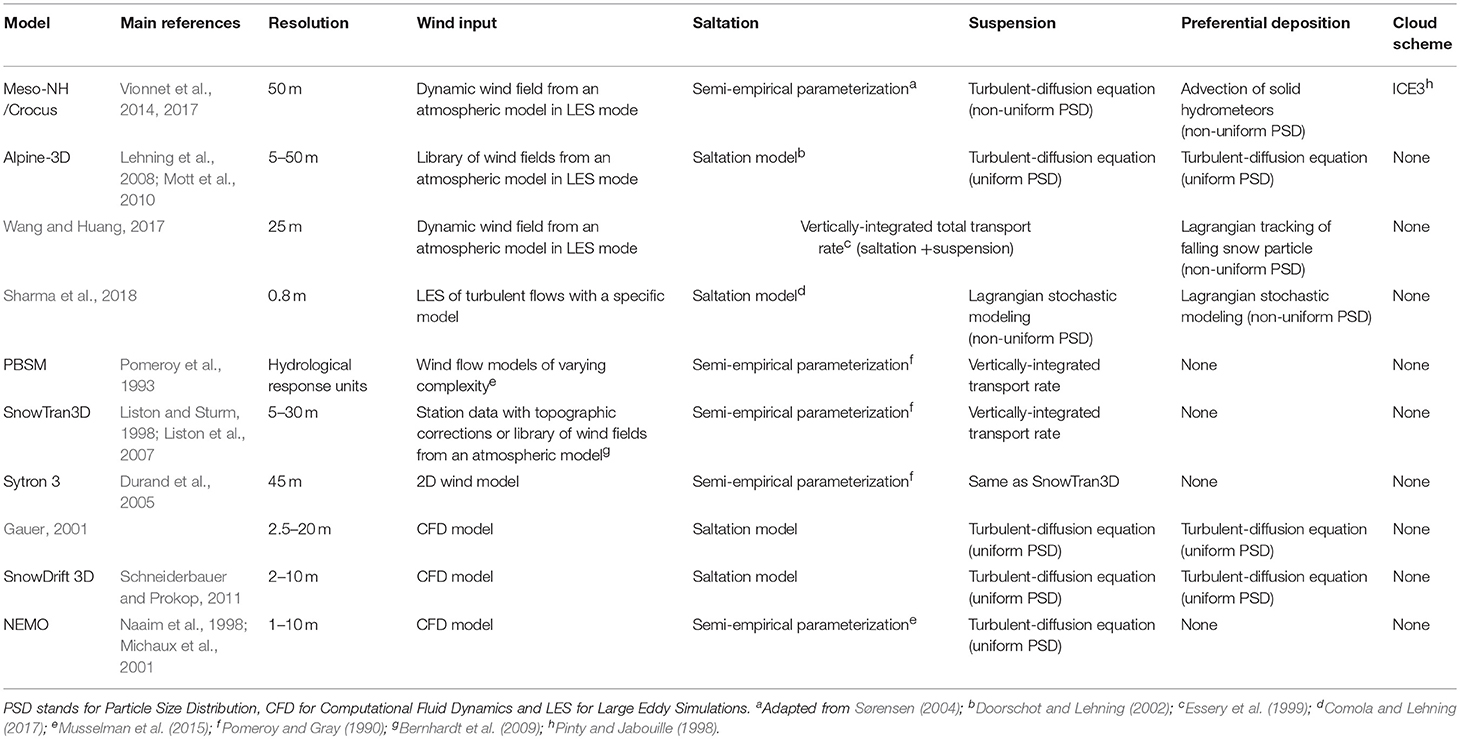
Table 2. Main characteristics of the different numerical models capable of simulating snow variability influenced by wind redistribution.
Modeling snow accumulation processes at various time and spatial scales remains a great challenge and existing models require improvements in many ways. In particular, the physical parameterizations used in numerical modeling of blowing snow do not include the latest findings in the complex coupling between turbulence and snow transport (see section Modeling Approaches of Snow Accumulation Processes; Aksamit and Pomeroy, 2016, 2018a; Paterna et al., 2016, 2017). In alpine environments, real case simulations of wind-induced snow transport will require a modeling approach that can combine LESs in the atmosphere (Vionnet et al., 2017; Wang and Huang, 2017) to capture the complexity of the atmospheric flow with advanced particle motion models representing the interactions between turbulence, grain dynamics and snow surface (Nemoto and Nishimura, 2004; Groot Zwaaftink et al., 2014; Comola and Lehning, 2017; Comola et al., 2017). In addition, atmospheric models in LES mode present a large potential to study local snowfall processes and their contribution to the variability of snow accumulation (Vionnet et al., 2017; Gerber et al., 2018a,b). Overall, the main challenge in the future will be to develop a model or a combination of models that can simulate the inherently turbulent nature of the different processes driving the spatial variability of snow accumulation across a large range of scales.
Heat-Exchange Processes Driving Snow Melt Patterns
The Spatial Variability of Energy Balance and Snow Melt Processes
Complex snow-atmosphere interactions drive snow ablation at multiple temporal and spatial scales (Dornes et al., 2008a,b; Mott et al., 2011a; Helbig et al., 2015; DeBeer and Pomeroy, 2017; Hock et al., 2017). The spatio-temporal ablation patterns in mountainous terrain are controlled by spatially variable shortwave radiation (governed by terrain slope, aspect, shading) (Figure 4a), longwave radiation (local cloud formation) and turbulent heat exchange (Pohl et al., 2006; Grünewald et al., 2010; Mott et al., 2011a). Many hydrological studies, however, have used spatially uniform melt applied to basin snow water equivalent (SWE) distributions or snow cover depletion parametrizations (Liston, 1999, 2004; Luce and Tarboton, 2004; Egli et al., 2012; Helbig et al., 2015). Egli et al. (2012) for instance argued that the spatially variable snow melt rates caused by spatial differences in the surface energy balance, are less important than the heterogeneity in SWE caused by snow accumulation processes. Following this argumentation, Egli et al. (2012) proposed that for sites with similar meteorological and topographical conditions snow volume and snow covered area can be well-simulated with spatially uniform melt rates if the SWE distribution at time of peak accumulation is known.
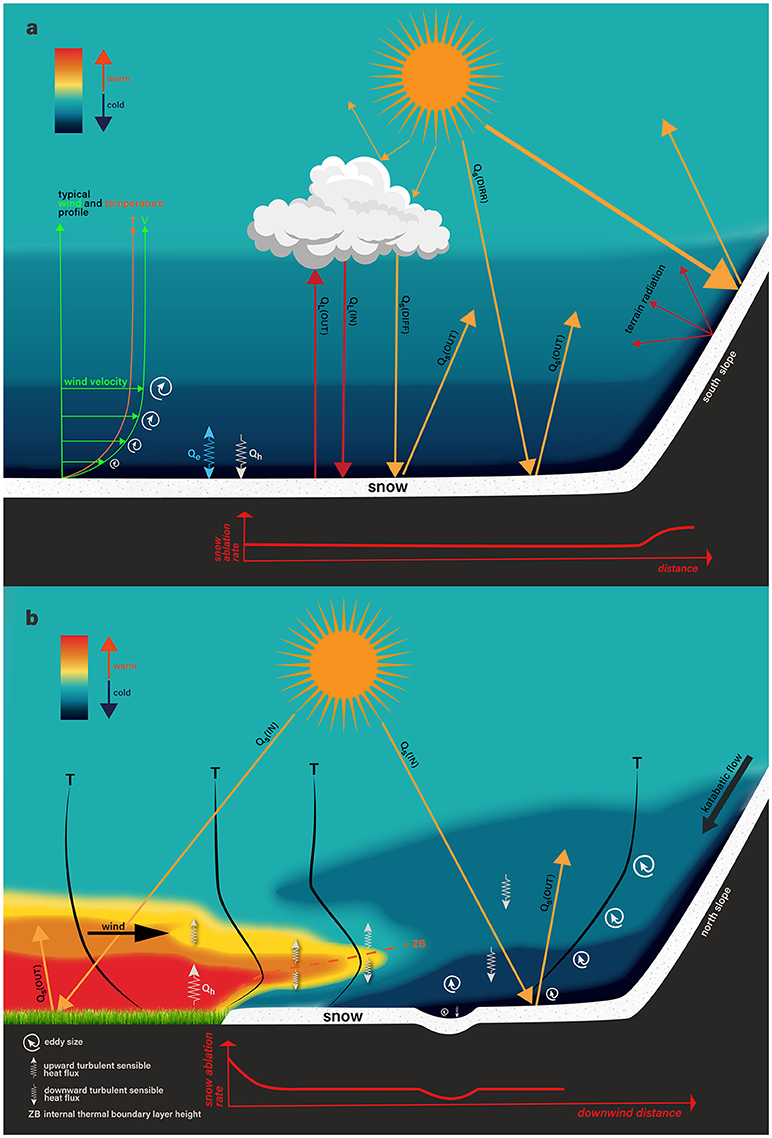
Figure 4. Schematic description of energy exchange processes over a continuous snow cover (a) and additional processes acting over a patchy snow cover (b). For the continuous snow cover incoming and outgoing longwave radiation (QLin, QLout), incoming and reflected shortwave radiation (QSin, QSout), terrain radiation, turbulent sensible and latent heat fluxes (Qh, Qe) are presented. Typical profiles of wind, air temperatures and turbulence evolving during stable atmospheric conditions over snow are shown as well. For the patchy snow cover case, the boundary layer development (air temperature, turbulence, sensible heat fluxes) over snow induced by local advection of heat from snow-free toward the snow-covered area is presented.
There are, however, multiple studies demonstrating the importance of the consideration of spatially variable snow melt in mountainous terrain. At basin scale, (Dornes et al., 2008a,b) found that missing representation of spatial differences in snow-melt rates and runoff among slopes of different aspects led to poor representation of snow cover ablation and basin runoff. Hock et al. (2017) emphasized the importance of the boundary layer feedback and representativeness of the spatial variability of meteorological input variables (Schlögl et al., 2016) for accurate snow melt modeling. DeBeer and Pomeroy (2017) argue that uniform melt rate approaches might produce reasonable results in certain topographic settings and climatic conditions, but especially for cold regions, windy conditions, increasingly complex terrain and large model domains the consideration of the spatial variability in the snowpack energy balance should not be ignored. Pohl et al. (2006) demonstrated the high spatial variability of turbulent fluxes in mountainous terrain. They showed that, due to the high spatial variability of the near-surface wind velocities, turbulent fluxes within the investigation area varied by as much as 20% from the mean, leading to large differences in potential snowmelt over the entire melt period.
Schlögl et al. (2017) particularly pointed to the high spatial variability of melt rates during the later stages of the melt periods, when turbulent fluxes are most sensitive to wind velocity and air temperature variations within the lowest atmospheric boundary layer. There are several studies showing that the turbulent flux contribution becomes particularly important late in the season (Essery et al., 2006; Mott et al., 2011a, 2017; Harder et al., 2017) when the blanket of snow gradually thins and exposes bare ground involving a high spatio-temporal variability of albedo and surface temperature, thus, energy balance, and melt processes (DeBeer and Pomeroy, 2009). Pohl and Marsh (2006) illustrated that the consideration of end of winter snow cover, the spatial variability of turbulent fluxes and local advection processes were crucial for an accurate determination of the location and timing of melt-water release. Additionally, several studies demonstrated the increase in spatial energy balance variation by local flow systems suppressing or fostering heat exchange processes at the snow cover (e.g., Shea and Moore, 2010; Mott et al., 2015; Sauter and Galos, 2016). Several studies pointed to the importance of land-surface heterogeneity induced by patchy snow covers in spring evolving high complexity in boundary layer dynamics and exchange processes (Figure 4b) between the land-surface and the near-surface atmosphere (Liston, 1995; Essery et al., 2006; Pohl and Marsh, 2006; Harder et al., 2017; Mott et al., 2017). Information on snow-covered area (SCA) and the effect of land-surface heterogeneity on surface energy fluxes remains a challenging part in Earth system modeling (Liston, 2004; de Vrese et al., 2016). Essery and Pomeroy (2004) pointed to the necessity of the representation of sub-grid snow cover in surface schemes used in atmospheric and hydrological models, especially when calculating snow cover depletion curves. There are several hydrological models and land-surface schemes that parameterize sub-grid fractional snow cover as simplified functions of mean SWE, accumulated depth of snowmelt over time, roughness lengths and sub-grid orography (Roesch et al., 2001; Takata et al., 2003; Liston, 2004; Essery, 2008; Dutra et al., 2010; Best et al., 2011; Nitta et al., 2014). The interaction between the fractional snow cover and the overlying atmosphere is highly simplified in such models and the variability of relevant sub-grid processes is hard to be captured (DeBeer and Pomeroy, 2009). Experiments on snow melt dynamics conducted by Mott et al. (2017) demonstrated that insufficient representation of sub-grid snow cover fractions on the regional scale and simple gradient-flux relationships at the same time lead to large biases in flux estimates that need to be addressed in atmospheric and hydrological models in future.
Heat Exchange Processes Over a Continuous Snow Covers
Turbulent fluxes of sensible and latent heat (see Equation 1) are typically small in winter, especially when averaged over periods of weeks or months (Willis et al., 2002; Hock, 2005) but they can exceed the radiation fluxes over short time intervals of hours or days (Anderson et al., 2010). Often the radiative losses over snow in winter can be compensated by the turbulent sensible heat flux, which has been observed to be of equal magnitude to net longwave radiation in winter (e.g., Cullen and Conway, 2015). In spring, net radiation is still the main driver for snowmelt, especially during the early to mid-melt period (DeBeer and Pomeroy, 2017; Fitzpatrick et al., 2017) and for sunny conditions (Figure 5). In mid-winter, snow mass can be lost via turbulent energy exchange at the snow surface via sublimation (Marks and Dozier, 1992; Marks and Winstral, 2001). Also highest melt rates often coincide with high values of turbulent sensible and latent heat fluxes (Hay and Fitzharris, 1988; Gillett and Cullen, 2011). In arid environments turbulent fluxes can dominate the energy balance, especially in early spring before shortwave radiation increases in magnitude (Hawkins and Ellis, 2007; Stoy et al., 2018). The contribution of turbulent heat fluxes can reach and sometimes exceed 50% of the melt energy, especially in regions with generally high wind speeds (Funk, 1985; Pohl et al., 2006), during cloudy conditions when the advection of warm and moisture-laden air is enhanced (Cullen and Conway, 2015; Conway and Cullen, 2016) or when local wind systems change the local temperature fields and the associated heat exchange between snow and the atmosphere (Greuell and Böhm, 1998; Shea and Moore, 2010; Mott et al., 2015). In maritime environments, melt is observed to be quite similar during clear-sky and overcast conditions as positive net longwave radiation and latent heat fluxes allow melt to be maintained over a greater length of time compared to clear-sky conditions (Conway and Cullen, 2016). Furthermore, turbulent fluxes become important during rain-on-snow events due to saturated conditions and dew point temperatures above 0°C (Dyer and Mote, 2002; Dadic et al., 2013b; Pomeroy et al., 2016; Würzer et al., 2016), accounting 60–90% of energy available for snow melt at open test sites (Marks et al., 1999, 2001; Garvelmann et al., 2014).
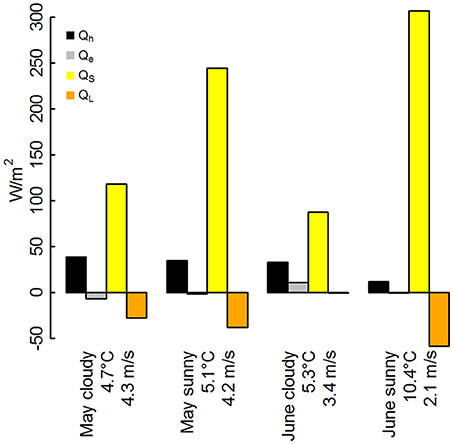
Figure 5. Twelve hourly-mean of daytime energy fluxes (06:00 a.m.−06:00 p.m.) modeled with SNOWPACK for the Weissfluhjoch test site (Swiss Alps, 2560 m ASL) for typical cloudy and sunny days in May and June. Air temperatures and wind velocities are mean values for the given time period of 12 h. QS is net shortwave radiation (yellow). QL is net longwave radiation (orange). Black and gray colors indicate turbulent exchange of sensible (Qh) and latent heat (Qe).
While direct measurements of energy balance components typically exist only for shortwave and longwave radiation, turbulent heat fluxes can only be measured directly using eddy covariance that requires advanced and careful data processing, especially in complex terrain (e.g., Reba et al., 2011). Therefore, the most common approach to parameterize the turbulent energy exchange from measured meteorological variables is the bulk approach. This approach is based on Monin–Obukhov theory and involves large uncertainties. For parametrizing turbulent heat fluxes, the bulk aerodynamic method employs an integrated form of the gradient transport (Stull, 1988) assuming constant flux layer, stationarity, and negligible advection (Prandtl, 1934; Sverdrup, 1936; Obukhov, 1946). The turbulent energy fluxes are proportional to the time-averaged gradients of potential air temperature (turbulent energy flux of sensible heat) and specific humidity (turbulent energy flux of latent heat) between the snow surface and the surface boundary layer. Exchange coefficients are calculated as a function of roughness lengths for momentum, temperature and water vapor, and atmospheric stability based either on Monin–Obukhov lengths (e.g., Dyer, 1974; Beljaars and Holtslag, 1991; Stearns and Weidner, 1993; Van den Broeke et al., 2005) or Richardson number (e.g., Webb, 1970; Sicart et al., 2005; Brock et al., 2010; Grachev et al., 2013; Sorbjan, 2016; Schlögl et al., 2017). Many different forms of stability corrections have been published, but often show poor performance over snow in different environments (alpine, acrtic, glacierized) when compared to measured turbulent fluxes (Andreas, 2002; Radić et al., 2017; Schlögl et al., 2017). The simplest form excludes a stability function (assuming neutral stability) and applies a logarithmic wind profile (e.g., Conway and Cullen, 2013).
The prediction of the exchange coefficient over snow is challenging due to multiple factors (Pomeroy et al., 1998a) including the violation of constant flux layer assumption in complex terrain (Dadic et al., 2013b; Schlögl et al., 2017), often very high stabilities over snow (Male, 1980; Forrer and Rotach, 1997; Fitzpatrick et al., 2017), low turbulence level over the smooth snow surface (Yen, 1995) and uncertainties in surface roughness variability and the invalid assumption of equal roughness lengths for momentum, heat and water vapor (Smeets and van den Broeke, 2008; Anderson et al., 2010; Conway and Cullen, 2016; Fitzpatrick et al., 2017).
Fitzpatrick et al. (2017) assessed the performance of most commonly used bulk methods to calculate turbulent heat fluxes on a mid-latitude glacier over one melt season. They showed that functions based on Monin-Obukhov lengths returned smallest errors in the mean daily flux values but also displayed poor performance on hourly time-scales, especially for periods characterized by an overestimation of downward turbulent sensible heat fluxes. Schlögl et al. (2017) assessed sensible heat flux parametrizations in stable conditions over snow by analyzing a wide range of stability correction functions for two alpine and two polar test sites. They confirmed that stability correction in particular need improvements for periods of overestimation, in particular for large temperature differences and large wind speeds. The study of Schlögl et al. (2017) emphasized that differences between stability corrections are, however, of the same order of magnitude as the error, which is introduced by the Monin–Obukhov bulk formation itself. Both recent studies assessing turbulent flux parametrizations on surface energy balance models (Fitzpatrick et al., 2017; Schlögl et al., 2017) pointed to the violation of the mandatory assumptions of stationarity and horizontal homogeneity, which are rarely fulfilled at test sites in complex terrain.
Heat Exchange Processes Over a Patchy Snow Cover
Surface Fluxes and Flow Development Driven by Snow Cover Fraction
In spring, surface energy, mass, and momentum fluxes are strongly linked to horizontally heterogeneous land surfaces (Cohen and Rind, 1991). The spatial variability in surface energetics gets especially large as soon as snow cover becomes patchy in the course of an ablation season. Strong differences in surface albedo and surface emissivity between snow-free and SCAs induce a high spatial variability in net radiation, even over small distances of a few meters (Figure 4b). The spatial variability in surface energetics is enhanced by the limitation of snow surface temperatures to a maximum of 0°C, resulting in large surface temperature gradients. The high spatial variability in surface characteristics coincide with significantly different fluxes of longwave radiation and of turbulent sensible and latent heat. Typical atmospheric processes acting over patchy snow covers are summarized in Figure 4b.
The decrease in SCA during springtime and shorter snow-cover duration can result in significant local atmospheric heating (Chapin et al., 2005). The importance of sub-grid snow distribution for snow-melt modeling has been demonstrated by studies investigating the feedback between the heterogeneous land-surface and overlying atmosphere (Ménard et al., 2014; Letcher and Minder, 2015; Mott et al., 2015; Harder et al., 2017; Schlögl et al., 2018a). Considering snow and snow-free cells (including vegetation), Ménard et al. (2014) calculated energy fluxes in vertical and horizontal direction and found a significant warming feedback through reduction in albedo for decreasing snow-cover fractions. Also Letcher and Minder (2015) emphasized that snow albedo feedbacks enhance large-scale variability of atmospheric warming and even change diurnal wind systems. Similarly, Mott et al. (2015) showed that for small snow-cover fractions, the dominance of upward heat fluxes over snow-free areas result in a net warming of near-surface atmosphere, enhancing the downward heat flux over still SCAs. Numerical simulations performed by Schlögl et al. (2018b) for an idealized flat test site, confirmed earlier results from Mott et al. (2015) and Ménard et al. (2014), revealing 22–40% larger daily snow depth depletion rates when considering the warming feedback of patchy snow on the atmosphere.
In flat terrain, strong thermal contrasts between bare and snow-covered ground induce snow-breeze type of circulation (Johnson et al., 1984; Taylor et al., 1998). In mountainous terrain snow-breeze circulations and diurnal mountain wind systems interact (Letcher and Minder, 2017). The presence of snow at higher elevations can even counteract the diurnal upslope flow, changing the thermal wind system of a valley (Segal et al., 1991). Recent numerical results presented by Mott et al. (2015) demonstrated that large patches of snow can also have an impact on the local wind system, similar to wind systems typically found at mountain glaciers (Shea and Moore, 2010). Simulating the boundary-layer flow field over patchy snow covers, Mott et al. (2015) showed that katabatic wind systems can develop over large snow fields located on slopes, exerting a major control on the local energy balance. While the atmosphere adjacent to the snow cover is decoupled (isolated) from the ambient warmer air temperature (Mott et al., 2015), strong katabatic winds drive heat exchange toward the snow cover, cooling the near-surface atmospheric layers (Greuell and Böhm, 1998; Strasser et al., 2004; Shea and Moore, 2010). Similarly, Sauter and Galos (2016) concluded that katabatic flows at lower elevated zones of glaciers prevent warm air advection from the surroundings prohibiting local warming. Numerical finding of Mott et al. (2015) and Sauter and Galos (2016) were confirmed by turbulence measurements conducted by Mott et al. (2017) over three melting periods. Experimental results evidenced the formation of katabatic flows over long-lasting snow patches strongly affecting the temporal evolution of snow surface temperature patterns. The influence of such wind systems on the mean melt rates of snow at glaciers or alpine catchments has not been quantified yet, but studies point to the strong effect on local ablation rates estimates and wrong estimations of temperature lapse rates depending on measurement locations (Sauter and Galos, 2016).
Local Heat Advection of Sensible Heat
Internal boundary layer development
Air flow over the extremely heterogeneous land surface of patchy snow induces the development of dynamic and thermal internal boundary layers downwind of the transition of abrupt changes of surface temperature, humidity and roughness (Garratt, 1990; Savelyev and Taylor, 2005). The coexistence of stable and unstable internal boundary layers even leads to mass and energy fluxes with a high spatial variability not only in the horizontal but also in the vertical direction (Essery et al., 1999, 2006; Granger et al., 2006; Mott et al., 2013; Harder et al., 2017). Based on profile measurements, Granger et al. (2006) and Takahara and Higuchi (1985) suggested describing boundary-layer growth by a power law function of the fetch distance. The boundary-layer growth was shown to be mainly affected by the upwind surface roughness and the change of stability from upwind to downwind conditions.
Performing turbulence measurements over three melting periods in an alpine field site, Mott et al. (2017) identified three stages of snow cover distribution considerably driving the frequency of internal boundary layer development: continuous snow cover, presence of a distinct snow-line, and patchy snow cover distribution. In case of internal stable boundary layer development, typically found during snow line and patchy snow cover stage, the local stratification is typically enhanced close to the snow surfaces resulting in atmospheric decoupling of the air adjacent to the snow cover from the warm air above. This subsequently limits the amount of senible and latent heat than can be transmitted from the atmosphere to the snow. There are mainly two factors causing such a strong atmospheric stability (Mott et al., 2016): (i) temperature difference between melting snow surface and air temperature and (ii) cold-air pooling in topographic depressions. The collapse of turbulence close to the melting snow is, thus, especially supported by sheltering effects in complex terrain (Fujita et al., 2010; Mott et al., 2016) leading to high differences in aerial ablation rates of neighboring snow patches (Eveland et al., 2013) or local decrease in snow ablation across single patches (Figure 4b).
Different models have been developed during the last decades accounting for the effect of local advection of sensible heat in snow melt modeling (Table 3). One approach to resolve boundary layer development over patchy snow covers is applying atmospheric boundary layer models (Liston, 1995) or large-eddy simulations (Mott et al., 2015; Sauter and Galos, 2016). Such model approaches are, however, computational expensive. Weisman (1977) applied mixing length theory to estimate advection of heat to snow patches. This early work showed that the efficiency of local advection of sensible heat appears to be a function of snow cover fraction. Marsh and Pomeroy (1996) developed a simple model, using an empirically developed efficiency parameter to transfer heat from snow-free toward snow-covered ground as a function of snow-cover fraction. Similarly, Neumann and Marsh (1998) introduced an advection efficiency term quantifying the fraction of sensible heat originating from bare ground areas advected to adjacent snow patches. More recently, Pohl and Marsh (2006) applied this concept for an arctic catchment using a regression equation relating the efficiency term to percentage snow-free area determined from a combination of field measurements (Neumann and Marsh, 1998) and model data (Liston, 1995; Marsh et al., 1999). The resulting advected energy was uniformly distributed over SCAs, not accounting for the observed fetch distance dependency of local heat advection (Essery et al., 2006; Mott et al., 2011a). Despite the simple approach, they showed that the contribution of local heat advection to the snow-melt energy was small early in the ablation season but strongly increased late in the ablation season, contributing about 28% to the overall melt energy.
Areal average estimates of advection have been provided by a more complex boundary layer integration approach applied by Essery et al. (2006) and Granger et al. (2002). Essery et al. (2006) applied boundary layer principles to estimate the net flux gained from advective heat as a function of fetch distance and boundary layer depth, using model parameters which depend on surface roughness and atmospheric stability. Based on a parametrized temperature profile and a flux-gradient relationship, the horizontal advection of heat was integrated through the depth of the stable internal boundary layer to find the net advection and an average flux into the snow cover. Their results showed that the standard deviation and average flux decrease with increasing patch lengths. Although the approach allowed a better representation of local surface fluxes at some point of a snow patch, the approach is highly sensitive to accurate information on atmospheric conditions and accurate representation of roughness lengths. An alternative approach has been developed by Schlögl et al. (2018a). They developed a temperature footprint approach to resolve the spatial variability of air temperature due to warm air advection by calculating the fetch dependent near-surface air temperatures very close to the snow surface. A prerequisite for this approach is accurate information on the spatial distribution of snow cover at time of peak accumulation.
Enhanced snow melt at leading edge of snow patches
The horizontal transport of sensible and latent heat with the mean flow across a step change in surface temperatures (Figure 4b) and moisture is called local advection of sensible and latent heat. Snow hydrologists have been attracted by the advective energy transport for decades, trying to quantify the enhancing effect of local heat advection on snow melt on the local but also on the catchment scale. While local heat advection has long been recognized to be an important driver for snow melt in the mid and later stage of a melting period, the advection of latent heat has been widely ignored or assumed to be negligible.
A number of studies tried to experimentally investigate the effect of local advection of sensible heat on snow melt. Measuring snow ablation in very high resolution with a terrestrial laser scanner (TLS), Mott et al. (2011a) and Schlögl et al. (2018a) demonstrated the effect of local heat advection on snow melt rates as a function of the distance to the leading edge of snow patches, both quantifying an increase in snow ablation at the upwind edges of snow patches by 25–30% (Table 4). Schlögl et al. (2018a) estimated an increase in daily snow ablation rates accounts 4–6% on a catchment scale (Table 4). Considering the process to become more important toward the late stage of the ablation season when the snow over becomes patchy, the pure effect of local heat advection increases the total seasonal snow ablation by ~1–5%. Even larger estimates for the contribution of advection of latent and sensible heat are suggested for the Canadian Prairies (Harder et al., 2017), where the snow cover is characterized by a higher frequency of small snow patches and the presence of upwind wetted surfaces making the advection of latent heat an additionally important process. Based on direct measurements of the effect of local heat advection on snow-melt rates by temperature, humidity and wind profile, their experimental results reveal local heat advection driven by surface temperature heterogeneity as a large source of energy available for snow-melt. They showed that sensible heat advection accounted for 31% (Table 4) of the net available melt energy at the leading edge of a snow patch. Harder et al. (2017) showed that latent heat advection can also be a substantial source of energy for snow-melt but is conditional upon the presence of upwind ponded water or wet exposed soils. Under conditions with wet upwind surfaces, the local advection of latent heat was estimated to account for another 33% (Table 4) of the net energy available for melt at the leading edge of a snow patch.
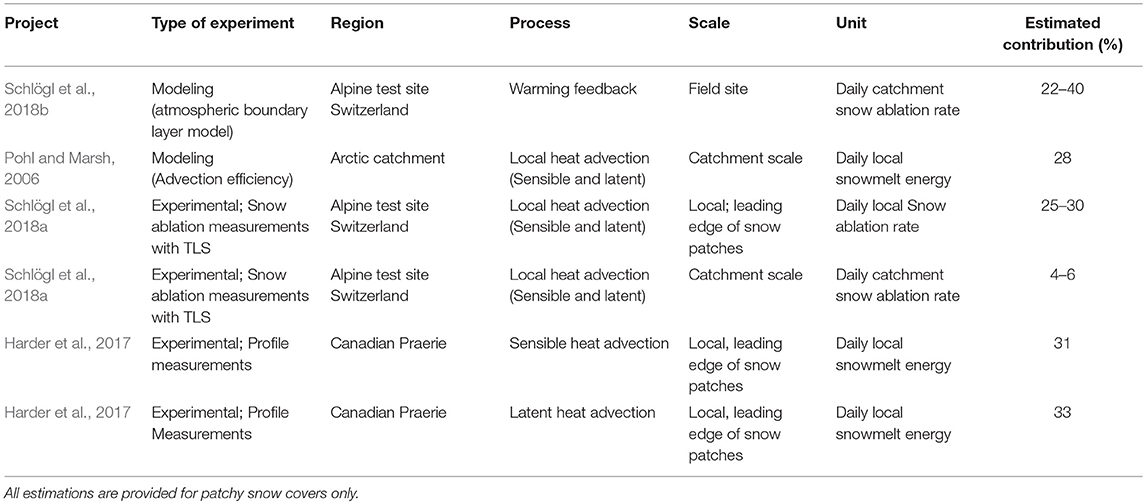
Table 4. Comparison of estimated maximum contributions of local heat advection and warming feedback on snow melt rates or net available energy melt on the local scale (leading edge of snow patches) and on the catchments scale.
Conclusion and Outlook
Wind-driven coupling processes between the snow cover and the atmosphere govern snow accumulation and ablation via mass and energy fluxes. In this review, we have addressed the current state of knowledge on wind-driven snow transport, interactions between snowfall and atmospheric flow, snow-mass loss and feedbacks on the atmosphere due to sublimation (surface and blowing snow), and heat exchange processes over continuous and patchy snow covers.
We have pointed to the strong scale dependency of snow-depth variability and dominant wind-driven processes affecting snow accumulation. On the mountain-range scale, snow depth patterns can be mainly attributed to orographic precipitation patterns with elevation as the most dominant factor. Snow patterns on the ridge-scale are mainly driven by the local wind interacting with snowfall and the snow surface. Small-scale updrafts can produce local cloud-formation processes, typically forming distinct patterns of snowfall enhancement in the summit region. Downstream advection of snow particles further causes preferential deposition of snowfall over leeward slopes of mountains where streamwise flow convergence and enhanced snow deposition velocities result in enhanced snow-deposition rates. Finally, local strong winds cause redistribution of snow via saltation and suspension leading to distinct snow erosion and deposition patterns shaping the snow cover at the ridge scale and the slope scale. Wind-induced snow transport also strongly influences the physical properties of the surface snow and its surface roughness.
There are different attempts to model snow accumulation on various scales. At the regional scale (mountain-range scale) most precipitation studies reproduce precipitation patterns using horizontal grid resolutions of 1 km and coarser. Other studies, however, showed that resolving ridge-scale precipitation and accumulation patterns, require higher model resolutions of 50 m or less to capture the effect of local flow fields on precipitation patterns. Even higher model resolutions of 5 m and less are needed to resolve wind-induced snow-redistribution processes. Different model approaches exist to simulate snow-depth variability at the ridge scale and slope scale, which can be divided in two main categories: models relying on vertically-integrated snow-transport rates and models resolving 3D turbulent-diffusion equations for blown snow particles in the atmosphere. Future efforts are required to combine LESs to capture the complexity of the atmospheric flow with advanced particle-motion models to account for the inherent turbulent nature of physical processes driving the variability of snow deposition at the ridge scale and the slope scale. Applying such models over large temporal and spatial scales will be one of the major challenge in the near future to improve snow prediction in complex terrain. Furthermore, extensive measurement campaigns are required to measure flow-precipitation interactions within the near-surface atmospheric boundary layer. Although different measurement devices exist to measure flow field and snow particle distribution in the air, such as weather radars (X-band) or Doppler Wind Lidars, the strong interferences of measurements with the solid earth surface make measurements close to the surface difficult.
In this review, we have also summarized ablation processes that are directly linked to the effect of the local wind field. The estimation of mass loss due to snow sublimation at the surface and by blowing snow is shown to be challenging. Specific measurements can be used at local sites but models are required to provide estimations for larger areas. The thermo-dynamical feedback of blowing snow sublimation on the surface boundary layer, in particular, has been discussed by several studies, and can lead to near-surface saturation as found in Antarctica. On the other hand, no saturation is found over seasonal snow in mountains and in the prairies, potentially due to shorter fetch distances over snow and entrainment of dry air from layer aloft.
This review has also discussed the complex nature of heat-exchange processes over continuous and patchy snow covers. While turbulent heat fluxes have been shown to considerably contribute to the energy balance over snow, especially on shorter temporal scales, turbulent heat flux parameterizations in stable conditions over snow involve large uncertainties, mainly related to errors in stability correction functions and the violation of Monin–Obukhov similarity theory assumptions. The bulk approach, however, leads to significant errors of the turbulent heat flux estimation over snow even if necessary assumptions are met. The uncertainty in turbulent heat flux predictions dramatically increases as soon as the snow cover gets patchy. Changes in the local wind system can enhance or suppress heat exchange over remaining SCAs. Some studies even hint to a suppression of turbulence due to atmospheric decoupling of the air adjacent to the snow cover from the warm air above, strongly limiting the heat exchange toward the snow cover. There are many open questions regarding boundary layer development, local heat advection and associated heat-exchange processes over patchy snow covers. Although, some of the processes are acting on a very small scale, these processes also affect snow ablation at the catchment scale as decreasing SCA results in a net near-surface atmospheric warming. While this effect has been recognized by many studies, the SCA is still not satisfactorily accounted for in most hydrological models. Also, considering glaciers as very large snow and ice patches, similar processes such as local heat advection are assumed to also affect snow and ice ablation. More measurement campaigns with dense networks of energy balance stations including near-surface turbulence measurements are required to provide new insight into the feedback between the glacier katabatic wind system and the lateral advection of heat from the glacier boundary areas during the course of an ablation season. A measurement campaign conducted in summer 2018 at the glacier Hintereisferner, running four complete energy balance stations, however, highlighted the challenges and strong efforts associated with the maintenance of a dense network of such stations at the typically rough glacier surface facing strong ice melt. New measurement strategies in the field using laser technology combined with further wind tunnel experiments in controlled environments (e.g., Mott et al., 2016) need to be developed to better understand how much energy is transported toward the SCAs and when boundary layer decoupling is more dominant than the local heat advection. Only a profound understanding will allow a good parameterization of these processes in larger-scale hydrological and land surface models.
By highlighting the impact of wind-driven processes on snow accumulation and snow ablation, this review has attempted to emphasize the central role of wind-driven coupling processes in the seasonal snow dynamics across different temporal and spatial scales. Although research on some of these processes has a long tradition, there are still many open questions that need to be addressed in future. Not only the observation of processes at small scales is essential for improved knowledge on seasonal snow cover dynamics, but also further efforts are required to implement small-scale processes, such as wind-induced snow transport, preferential deposition of snowfall and energy advection in large scale and operational models with variable model resolutions. Indeed, operational snowpack and hydrological models are reaching resolutions where wind-driven coupling processes need to be explicitly represented. This process representation is not applicable to all scales so that a scaling of process representations in different models is strongly required. There is certainly a further need for improvements in coupling advanced snowpack models with atmospheric models, but also in dynamical downscaling using multi-scale atmospheric models including snow drift resolving scales. Such efforts, however, strongly rely on advances in computational power allowing for more complex simulations also for longer time periods, larger areas and higher resolution.
Fast advances in remote sensing techniques will provide more improved model input (e.g., SCA, SWE, and albedo) on higher temporal and spatial resolution. Limits of data availability, related to limited temporal and spatial coverage as well as restricted access to data is claimed by several scientific communities and will require substantial efforts in future. Improvements in process understanding, processes representations at different scales and model input will be the basis for meaningful climate change scenario runs for mountainous regions, where local climate extremes are often connected to micrometeorlogy.
Author Contributions
RM, VV, and TG wrote the manuscript and prepared figures and tables under the guidance of RM.
Funding
The work was funded by Swiss National Science Foundation (Project: The sensitivity of very small glaciers to micrometeorology. P300P2_164644). Funding from the Commission for Technology and Innovation CTI (grant 2013.0288). NSERC Discovery Grant RGPIN-2014-06543.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor declared a past supervisory role with the authors RM and TG.
Acknowledgments
We thank nuance mediadesign for creating Figures 2, 4 describing snow-atmosphere processes. We gratefully appreciate the proof reading of Michael Lehning and his valuable suggestions.
References
Abegg, B., Agrawala, S., Crick, F., and de Montfalcon, A. (2007). “Climate change impacts and adaptation in winter tourism,” in Climate Change in the European Alps: Adapting Winter Tourism and Natural Hazards Management, ed S. Agrawala (Paris: OECD Publishing), 25–60.
Aksamit, N. O., and Pomeroy, J. W. (2016). Near-surface snow particle dynamics from particle tracking velocimetry and turbulence measurements during alpine blowing snow storms. Cryosphere 10:3043. doi: 10.5194/tc-10-3043-2016
Aksamit, N. O., and Pomeroy, J. W. (2018a). The effect of coherent structures in the atmospheric surface layer on blowing-snow transport. Boundary Layer Meteorol. 167, 211–233. doi: 10.1007/s10546-017-0318-2
Aksamit, N. O., and Pomeroy, J. W. (2018b). Scale interactions in turbulence for mountain blowing snow. J. Hydrometeorol. 19, 305–320. doi: 10.1175/JHM-D-17-0179.1
Allan, J. D., and Castillo, M. M. (2007). Stream Ecology: Structure and Function of Running Waters, 2nd Edn. New York, NY: Chapman and Hall. doi: 10.1007/978-1-4020-5583-6
Amory, C., Gallée, H., Naaim-Bouvet, F., Favier, V., Vignon, E., Picard, G., et al. (2017). Seasonal variations in drag coefficient over a sastrugi-covered snowfield in coastal East Antarctica. Boundary Layer Meteorol. 164, 107–133. doi: 10.1007/s10546-017-0242-5
Anderson, B., Mackintosh, A., Stumm, D., and Fitzsimons, S. J. (2010). Climate sensitivity of a high-precipitation glacier in New Zealand. J. Glaciol. 56, 114–128. doi: 10.3189/002214310791190929
Anderson, B. T., McNamara, J. P., Marshall, H.-P., and Flores, A. N. (2014). Insights into the physical processes controlling correlations between snow distribution and terrain properties. Water Resour. Res. 50, 4545–4563. doi: 10.1002/2013WR013714
Andreas, E. L. (2002). Parameterizing scalar transfer over snow and ice: a review. J. Hydrometeorol. 3, 417–432. doi: 10.1175/1525-7541(2002)003<0417:PSTOSA>2.0.CO;2
Armstrong, R. L., and Brun, E. (eds.). (2008). Snow and Climate: Physical Processes, Surface Energy Exchange and Modeling (Cambridge: Cambridge University Press), 256.
Barnett, T. P., Adam, J. C., and Lettenmaier, D. P. (2005). Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 438, 303–309. doi: 10.1038/nature04141
Barral, H., Genthon, C., Trouvilliez, A., Brun, C., and Amory, C. (2014). Blowing snow in coastal Adélie Land, Antarctica: three atmospheric-moisture issues. Cryosphere 8, 1905–1919. doi: 10.5194/tc-8-1905-2014
Bavay, M., Grünewald, T., and Lehning, M. (2013). Response of snow cover and runoff to climate change in high Alpine catchments of Eastern Switzerland. Adv. Water Resour. 55, 4–16. doi: 10.1016/j.advwatres.2012.12.009
Beljaars, A. C. M., and Holtslag, A. A. M. (1991). Flux parametrization over land surfaces for atmospheric models. J. Appl. Meteorol. 30, 327–341.
Beniston, M. (2012). Is snow in the Alps receding or disappearing? WIRES Climate Change 3, 349–358. doi: 10.1002/wcc.179
Beniston, M., Farinotti, D., Stoffel, M., Andreassen, L. M., Coppola, E., Eckert, N., et al. (2018). The European mountain cryosphere: a review of its current state, trends, and future challenges. Cryosphere 12, 759–794. doi: 10.5194/tc-12-759-2018
Bergeron, T. (1965). “On the low-level redistribution of atmospheric water caused by orography,” in Paper Presented at International Conference on Cloud Physics (Tokyo).
Bernhardt, M., Liston, G. E., Strasser, U., Zängl, G., and Schulz, K. (2010). High resolution modelling of snow transport in complex terrain using downscaled MM5 wind fields. Cryosphere 4, 99–113. doi: 10.5194/tc-4-99-2010
Bernhardt, M., and Schultz, K. (2010). SnowSlide: a simple routine for calculating gravitational snow transport. Geophys. Res. Lett. 37:L11502. doi: 10.1029/2010GL043086
Bernhardt, M., Schulz, K., Liston, G. E., and Zängl, G. (2012). The influence of lateral snow redistribution processes on snow melt and sublimation in alpine regions. J. Hydrol. 424, 196–206. doi: 10.1016/j.jhydrol.2012.01.001
Bernhardt, M., Zängl, G., Liston, G. E., Strasser, U., and Mauser, W. (2009). Using wind fields from a high-resolution atmospheric model for simulating snow dynamics in mountainous terrain. Hydrol. Process. 23, 1064–1075. doi: 10.1002/hyp.7208
Best, M. J., Pryor, M., Clark, D. B., Rooney, G. G., Essery, R. L. H., Menard, C. B., et al. (2011). The Joint UK Land Environment Simulator (JULES), model description—Part 1: energy and water fluxes. Geosci. Model Dev. 4, 677–699. doi: 10.5194/gmd-4-677-2011
Bintanja, R. (2001). Modelling snowdrift sublimation and its effect on the moisture budget of the atmospheric boundary layer. Tellus A Dyn. Meteorol. Oceanogr. 53, 215–232. doi: 10.3402/tellusa.v53i2.12189
Blanchet, J., Marty, C., and Lehning, M. (2009). Extreme value statistics of snowfall in the Swiss Alpine region. Water Resour. Res. 45:W05424. doi: 10.1029/2009WR007916
Blöschl, G., and Kirnbauer, R. (1992). An analysis of snow cover patterns in a small Alpine catchment. Hydrol. Process. 6, 99–109. doi: 10.1002/hyp.3360060109
Brauchli, T., Trujillo, E., Huwald, H., and Lehning, M. (2017). Influence of slopescale snowmelt on catchment response simulated with the Alpine3D model. Water Res. Res. 53, 10723–10739. doi: 10.1002/2017WR021278
Brock, B. W., Mihalcea, C., Kirkbride, M. P., Diolaiuti, G., Cutler, M. E. J., and Smiraglia, C. (2010). Meteorology and surface energy fluxes in the 2005–2007 ablation seasons at the Miage debris-covered glacier. Mont Blanc Massif, Italian Alps. J. Geophys. Res. 115:D09106. doi: 10.1029/2009JD013224
Brown, R. D., and Mote, P. W. (2009). The response of northern hemisphere snow cover to a changing climate. Climate J. 22, 2124–2145 doi: 10.1175/2008JCLI2665.1
Chapin, F. S. III, Sturm, M., Serreze, M. C., McFadden, J. P., Key, J. R., Lloyd, A. H., et al. (2005). Role of land-surface changes in arctic summer warming. Science 310, 657–660. doi: 10.1126/science.1117368
Choularton, T. W., and Perry, S. J. (1986). A model of the orographic enhancement of snowfall by the seeder-feeder mechanism. Q. J. R. Meteorol. Soc. 112, 335–345. doi: 10.1002/qj.49711247204
Clark, M. P., Hendrikx, J., Slater, A. G., Kavetski, D., Anderson, B., Cullen, N. J., et al. (2011). Representing spatial variability of snow water equivalent in hydrologic and land-surface models: A review. Water Res. Res. 47:W07539. doi: 10.1029/2011WR010745
Clifton, A., Rüedi, J. D., and Lehning, M. (2006). Snow saltation threshold measurements in a drifting-snow wind tunnel. J. Glaciol. 52, 585–596. doi: 10.3189/172756506781828430
Collados-Lara, A.-J., Pardo-Igúzquiza, E., Pulido-Velazquez, D., and Jiménez-Sánchez, J. (2018). Precipitation fields in an alpine Mediterranean catchment: Inversion of precipitation gradient with elevation or undercatch of snowfall? Int. J. Climatol. 38, 3565–3578. doi: 10.1002/joc.5517
Colle, B. (2004). Sensitivity of orographic precipitation to changing ambient conditions and terrain geometries: An idealized modeling perspective. J. Atmos. Sci. 61, 588–606. doi: 10.1175/1520-0469(2004)061<0588:SOOPTC>2.0.CO;2
Colle, B. A., Smith, R. B., and Wesley, D. A. (2013). “Theory, observations, and predictions of orographic precipitation,” in Mountain Weather Research and Forecasting, Springer Atmospheric Sciences, ed F. Chow, S. F. J. De Wekker, and B. J. Snyder (Springer Atmospheric Sciences), 291–344. doi: 10.1007/978-94-007-4098-3_6
Comola, F., Kok, J. F., Gaume, J., Paterna, E., and Lehning, M. (2017). Fragmentation of wind-blown snow crystals. Geophys. Res. Lett. 44, 4195–4203. doi: 10.1002/2017GL073039
Comola, F., and Lehning, M. (2017). Energy-and momentum-conserving model of splash entrainment in sand and snow saltation. Geophys. Res. Lett. 44, 1601–1609. doi: 10.1002/2016GL071822
Conway, J. P., and Cullen, N. J. (2013). Constraining turbulent heat flux parameterization over a temperate maritime glacier in New Zealand. Annal. Glaciol. 54, 41–51. doi: 10.3189/2013AoG63A604
Conway, J. P., and Cullen, N. J. (2016). Cloud effects on surface energy and mass balance in the ablation area of Brewster Glacier, New Zealand. Cryosphere 10, 313–328. doi: 10.5194/tc-10-313-2016
Cullen, N. J., and Conway, J. P. (2015). A 22-month record of surface meteorology and energy balance from the ablation zone of Brewster Glacier, New Zealand. J. Glaciol. 61, 931–946. doi: 10.3189/2015JoG15J004
Dadic, R., Mott, R., Horgan, H. J., and Lehning, M. (2013a). Observations, theory, and modeling of the differential accumulation of Antarctic megadunes. J. Geophys. Res. Earth Surf. 118, 2343–2353 doi: 10.1002/2013JF002844
Dadic, R., Mott, R., Lehning, M., and Burlando, P. (2010a). Wind influence on snow depth distribution and accumulation over glaciers. J. Geophys. Res. 115:F01012 doi: 10.1029/2009JF001261
Dadic, R., Mott, R., Lehning, M., and Burlando, P. (2010b). Parameterization for wind-induced preferential deposition of snow. J. Hydrol. Process. 24, 1994–2006. doi: 10.1002/hyp.7776
Dadic, R., Mott, R., Lehning, M., Carenzo, M., Anderson, B., and Mackintosh, A. (2013b). Sensitivity of turbulent fluxes to wind speed over snow surfaces in different climatic settings. Adv. Water Resour. 55, 178–189. doi: 10.1016/j.advwatres.2012.06.010
de Vrese, P., Schulz, J.-P., and Hagemann, S. (2016). On the representation of heterogeneity in land-surface–atmosphere coupling. Bound. Layer Meteor. 160, 157–183. doi: 10.1007/s10546-016-0133-1
DeBeer, C. M., and Pomeroy, J. W. (2009). Modelling snow melt and snow- cover depletion in a small alpine cirque, Canadian Rocky Mountains. Hydrol. Process. 23, 2584–2599. doi: 10.1002/hyp.7346
DeBeer, C. M., and Pomeroy, J. W. (2017). Influence of snowpack and melt energy heterogeneity on snow cover depletion and snowmelt runoff simulation in a cold mountain environment. J. Hydrol. 553, 199–213. doi: 10.1016/j.jhydrol.2017.07.051
Deems, J. S., Fassnacht, S. R., and Elder, K. J. (2006). Fractal distribution of snow depth from lidar data. J. Hydrometeor. 7, 285–297. doi: 10.1175/JHM487.1
Deems, J. S., Fassnacht, S. R., and Elder, K. J. (2008). Interannual consistency in fractal snow depth patterns at two colorado mountain sites. J. Hydrometeor. 9, 977–988. doi: 10.1175/2008JHM901.1
Deems, J. S., Painter, T. H., and Finnegan, D. C. (2013). Lidar measurement of snow depth: a review. J. Glaciol. 59, 467–479. doi: 10.3189/2013JoG12J154
Doorschot, J. J., and Lehning, M. (2002). Equilibrium saltation: mass fluxes, aerodynamic entrainment, and dependence on grain properties. Boundary Layer Meteorol. 104, 111–130. doi: 10.1023/A:1015516420286
Doorschot, J. J., Lehning, M., and Vrouwe, A. (2004). Field measurements of snow-drift threshold and mass fluxes, and related model simulations. Boundary Layer Meteorol. 113, 347–368. doi: 10.1007/s10546-004-8659-z
Dore, A. J., and Choularton, T. W. (1992). Orographic enhancement of snowfall. Environ. Pollut. 75, 175–179. doi: 10.1016/0269-7491(92)90037-B
Dornes, P. F., Pomeroy, J. W., Pietroniro, A., Carey, S. K., and Quinton, W. L. (2008a). Influence of landscape aggregation in modelling snow-cover ablation and snowmelt runoff in a sub-arctic mountainous environment. Hydrol. Sci. J. 53, 725–740. doi: 10.1623/hysj.53.4.725
Dornes, P. F., Pomeroy, J. W., Pietroniro, A., and Verseghy, D. L. (2008b). Effects of spatial aggregation of initial conditions and forcing data on modeling snowmelt using a land surface scheme. J. Hydrometeorol. 9, 789–803. doi: 10.1175/2007JHM958.1
Durand, Y., Guyomarc'h, G., Mérindol, L., and Corripio, J. G. (2005). Improvement of a numerical snow drift model and field validation. Cold Regions Sci. Technol. 43, 93–103. doi: 10.1016/j.coldregions.2005.05.008
Dutra, E., Balsamo, G., Viterbo, P., Miranda, P. M. A., Beljaars, A., Schär, C., et al. (2010). An improved snow scheme for the ECMWF land surface model: description and offline validation. J. Hydrometeor. 11, 899–916. doi: 10.1175/2010JHM1249.1
Dyer, A. J. (1974). A review of flux-profile relationships. Boundary Layer Meteorol. 7, 363–372. doi: 10.1007/BF00240838
Dyer, J. L., and Mote, T. L. (2002). Role of energy budget components on snow ablation from a mid-latitude prairie snowpack. Polar Geogr. 26, 87–115. doi: 10.1080/789610133
Egli, L., Jonas, T., Grünewald, T., Schirmer, M., and Burlando, P. (2012). Dynamics of snow ablation in a small Alpine catchment observed by repeated terrestrial laser scans. Hydrol. Process. 26, 1574– 1585. doi: 10.1002/hyp.8244
Essery, R. (2008). “Snow parameterization in GCMs,” in Snow and Climate: Physical Processes, Surface Energy Exchange and Modeling, eds R. L. Armstrong and E. Brun (Cambridge: Cambridge University Press), 145–156.
Essery, R., Granger, R., and Pomeroy, J. W. (2006). Boundary-layer growth and advection of heat over snow and soil patches: Modelling and parameterization. Hydrol. Process. 20, 953–967. doi: 10.1002/hyp.6122
Essery, R., Li, L., and Pomeroy, J. (1999). A distributed model of blowing snow over complex terrain. Hydrol. Process. 13, 2423–2438.
Essery, R., and Pomeroy, J. (2004). Vegetation and topographic control of wind-blown snow distributions in distributed and aggregated simulations for an Arctic tundra basin. J. Hydrometeorol. 5, 735–744. doi: 10.1175/1525-7541(2004)005<0735:VATCOW>2.0.CO;2
Eveland, J. W., Gooseff, M. N., Lampkin, D. J., Barrett, J. E., and Takacs-Vesbach, C. D. (2013). Seasonal controls on snow distribution and aerial ablation at the snow-patch and landscape scales, McMurdo Dry Valleys, Antarctica. Cryosphere 7, 917–931. doi: 10.5194/tc-7-917-2013
Fang, X., and Pomeroy, J. (2009). Modelling blowing snow redistribution to prairie wetlands. Hydrol. Process. 23, 2557–2569. doi: 10.1002/hyp.7348
Fayad, A., Gascoin, S., Faour, G., López-Moreno, J., Drapeau, L., Le Page, M., et al. (2017). Snow hydrology in Mediterranean mountain regions: a review. J. Hydrol. 551, 374–396. doi: 10.1016/j.jhydrol.2017.05.063
Filhol, S., and Sturm, M. (2015). Snow bedforms: a review, new data, and a formation model. J. Geophys. Res. Earth Surf. 120, 1645–1669. doi: 10.1002/2015JF003529
Fitzpatrick, N., Radic, V., and Menounos, B. (2017). Surface energy balance closure and turbulent flux parameterization on a mid-latitude mountain glacier, Purcell Mountains, Canada. Front. Earth Sci. 5:67. doi: 10.3389/feart.2017.00067
Forrer, J., and Rotach, M. (1997). On the turbulence structure in the stable boundary layer over the Greenland ice sheet. Boundary Layer Meteorol. 85:111. doi: 10.1023/A:1000466827210
Freudiger, D., Kohn, I., Seibert, J., Stahl, K., and Weiler, M. (2017). Snow redistribution for the hydrological modeling of alpine catchments. WIREs Water 4:e1232. doi: 10.1002/wat2.1232
Fujita, K., Hiyama, K., Iida, H., and Ageta, Y. (2010). Self-regulated fluctuations in the ablation of a snow patch over four decades. Water Resour. Res. 46:W11541. doi: 10.1029/2009WR008383
Funk, M. (1985). Räumliche Verteilung der Massenbihmz auf dem Rhonegletscher und ihre Beziehung zu Klimaelementen. Zürcher Geogr. Sehr. 24.
Garratt, J. R. (1990). The internal boundary layer-A review. Boundary Layer Meteorol. 50, 171–203. doi: 10.1007/BF00120524
Garvelmann, J., Pohl, S., and Weiler, M. (2014). Variability of observed energy fluxes during rain-on-snow and clear sky snowmelt in a midlatitude mountain environment. J. Hydrometeor. 15, 1220–1237. doi: 10.1175/JHM-D-13-0187.1
Gascoin, S., Lhermitte, S., Kinnard, C., Bortels, K., and Liston, G. E. (2013). Wind effects on snow cover in Pascua-Lama, Dry Andes of Chile. Adv. Water Resour. 55, 25–39. doi: 10.1016/j.advwatres.2012.11.013
Gauer, P. (2001). Numerical modeling of blowing and drifting snow in Alpine terrain. J. Glaciol. 47, 97–110. doi: 10.3189/172756501781832476
Gerber, F., Besic, N., Sharma, V., Mott, R., Daniels, M., Gabella, M., et al. (2018a). Spatial variability of snow precipitation and accumulation in COSM–WRF simulations and radar estimations over complex terrain. Cryosphere, 12, 3137–3160. doi: 10.5194/tc-12-3137-2018
Gerber, F., Lehning, M., Hoch, S. W., and Mott, R. (2017). A close-ridge small-scale atmospheric flow field and its influence on snow accumulation. J. Geophys. Res. Atmos. 122, 7737–7754. doi: 10.1002/2016JD026258
Gerber, F., Mott, R., and Lehning, M. (2018b). The importance of near-surface winter precipitation processes in complex alpine terrain. J. Hydromet. doi: 10.1175/JHM-D-18-0055.1. [Epub ahead of print].
Gillett, S., and Cullen, N. J. (2011). Atmospheric controls on summer ablation over Brewster Glacier, New Zealand. Int. J. Climatol. 31, 2033–2048. doi: 10.1002/joc.2216
Gordon, M., Biswas, S., Taylor, P. A., Hanesiak, J., Albarran-Melzer, M., and Fargey, S. (2010). Measurements of drifting and blowing snow at Iqaluit, Nunavut, Canada during the star project. Atmos. Ocean 48, 81–100. doi: 10.3137/AO1105.2010
Grachev, A. A., Andreas, E. L., Fairall, C. W., Guest, P. S., and Persson, P. O. G. (2013). The critical Richardson number and limits of applicability of local similarity theory in the stable boundary layer. Boundary Layer Meteorol. 147, 51–82. doi: 10.1007/s10546-012-9771-0
Granger, R. J., Essery, R., and Pomeroy, J. W. (2006). Boundary-layer growth over snow and soil patches: Field observations. Hydrol. Process. 20, 943–951. doi: 10.1002/hyp.6123
Granger, R. J., Pomeroy, J. W., and Parviainen, J. (2002). Boundary-layer integration approach to advection of sensible heat to a patchy snow cover. Hydrol. Process. 16, 3559–3569. doi: 10.1002/hyp.1227
Greuell, W., and Böhm, R. (1998). 2m temperatures along melting midlatitude glaciers, and implications for the sensitivity of the mass balance to variations in temperature. J. Glaciol. 44, 9–20. doi: 10.1017/S0022143000002306
Gromke, C., Horender, S., Walter, B., and Lehning, M. (2014). Snow particle characteristics in the saltation layer. J. Glaciol. 60, 431–439. doi: 10.3189/2014JoG13J079
Groot Zwaaftink, C., Diebold, M., Horender, S., Overney, J., Lieberherr, G., Parlange, M. B., et al. (2014). Modelling small-scale drifting snow with a Lagrangian stochastic model based on large-eddy simulations. Boundary Layer Meteorol. 153, 117–139. doi: 10.1007/s10546-014-9934-2
Groot Zwaaftink, C. D., Löwe, H., Mott, R., Bavay, M., and Lehning, M. (2011). Drifting snow sublimation: a high-resolution 3D model with temperature and moisture feedbacks. J. Geophys. Res. Atmos. 116:D16107. doi: 10.1029/2011JD015754
Groot Zwaaftink, C. D., Mott, R., and Lehning, M. (2013). Seasonal simulation of drifting snow sublimation in Alpine terrain. Water Resour. Res. 49, 1581–1590. doi: 10.1002/wrcr.20137
Grundstein, A. J., and Leathers, D. J. (1999). A spatial analysis of snow-surface energy exchanges over the northern Great Plains of the United States in relation to synoptic scale forcing mechanisms. Int. J. Climatol. 19, 489–511.
Grünewald, T., Buhler, Y., and Lehning, M. (2014). Elevation dependency of mountain snow depth. Cryosphere 8, 2381–2394. doi: 10.5194/tc-8-2381-2014
Grünewald, T., and Lehning, M. (2011). Altitudinal dependency of snow amounts in two small alpine catchments: Can catchment-wide snow amounts be estimated via single snow or precipitation stations. Ann. Glaciol. 52, 153–158. doi: 10.3189/172756411797252248
Grünewald, T., Schirmer, M., Mott, R., and Lehning, M. (2010). Spatial and temporal variability of snow depth and ablation rates in a small mountain catchment. Cryosphere 4, 215–225 doi: 10.5194/tc-4-215-2010
Grünewald, T., Stotter, J., Pomeroy, J. W., Dadic, R., Banos, I. M., Lehning, M., et al. (2013). Statistical modelling of the snow depth distribution in open alpine terrain. Hydrol. Earth Syst. Sci. 17, 3005–3021. doi: 10.5194/hess-17-3005-2013
Grünewald, T., Wolfsperger, F., and Lehning, M. (2018). Snow farming: conserving snow over the summer season. Cryosphere 12, 385–400. doi: 10.5194/tc-12-385-2018
Guyomarc'h, G., and Merindol, L. (1998). Validation of an application for forecasting blowing snow. Ann. Glacial. 26, 138–143.
Haberkorn, A., Hoelzle, M., Phillips, M., and Kenner, R. (2015). Snow as a driving factor of rock surface temperatures in steep rough rock walls. Cold Regions Sci. Technol. 118, 64–75. doi: 10.1016/j.coldregions.2015.06.013
Haberkorn, A., Wever, N., Hoelzle, M., Phillips, M., Kenner, R., Bavay, M., et al. (2017). Distributed snow and rock temperature modelling in steep rock walls using Alpine3D. Cryosphere 11, 585–607. doi: 10.5194/tc-11-585-2017
Hamlet, A. F., and Lettenmaier, D. P. (2007). Effects of 20th century warming and climate variability on flood risk in the western US. Water Resour. Res. 43:W06427. doi: 10.1029/2006WR005099
Harder, P., Pomeroy, J. W., and Helgason, W. (2017). Local scale advection of sensible and latent heat during snowmelt. Geophys. Res. Lett. 44, 9769–9777. doi: 10.1002/2017GL074394
Hawkins, T. W., and Ellis, A. W. (2007). A case study of the energy budget of a snowpack in the arid, subtropical climate of the southwestern United States. J. Arizona Nevada Acad. Sci. 39, 1–13. doi: 10.2181/1533-6085(2007)39[1:ACSOTE]2.0.CO;2
Hay, J. E., and Fitzharris, B. B. (1988). A comparison of energy balance and bulk aerodynamic approaches for estimating glacier melt. J. Glaciol. 34, 145–153. doi: 10.1017/S0022143000032172
He, S., and Ohara, N. (2017). A new formula for estimating the threshold wind speed for snow movement. J. Adv. Model. Earth Syst. 9, 2514–2525. doi: 10.1002/2017MS000982
Helbig, N., Mott, R., van Herwijnen, A., Winstral, A., and Jonas, T. (2017). Parameterizing surface wind speed over complex topography. J. Geophys. Res. Atmos. 122, 651–667. doi: 10.1002/2016JD025593
Helbig, N., van Herwijnen, A., Magnusson, J., and Jonas, T. (2015). Fractional snow-covered area parameterization over complex topography. Hydrol. Earth Syst. Sci. 19, 1339–1351. doi: 10.5194/hess-19-1339-2015
Helfricht, K., Söber, J., Schneider, K., Sailer, R., and Kuhn, M. (2014). Interannual persistence of the seasonal snow cover in a glacierized catchment. J. Glaciol. 60, 889–904. doi: 10.3189/2014JoG13J197
Hock, R. (2005). Glacier melt: a review of processes and their modelling. Prog. Phys. Geogr. 29, 362–391. doi: 10.1191/0309133305pp453ra
Hock, R., Hutchings, J. K., and Lehning, M. (2017). Grand challenges in cryospheric sciences: toward better predictability of glaciers, snow and sea ice. Front. Earth Sci. 5:64. doi: 10.3389/feart.2017.00064
Hood, E., Williams, M., and Cline, D. (1999). Sublimation from a seasonal snowpack at a continental, mid-latitude alpine site. Hydrol. Process. 13, 1781–1797.
Houze, R. A., and Medina, S. (2005). Turbulence as a mechanism of orographic precipitation enhancement. J. Atmos. Sci. 62, 3599–3623. doi: 10.1175/JAS3555.1
Houze, R. A. Jr. (2012). Orographic effects on precipitating clouds. Rev. Geophys. 50:RG1001. doi: 10.1029/2011RG000365
Huang, N., and Shi, G. (2017). The significance of vertical moisture diffusion on drifting snow sublimation near snow surface. Cryosphere 11:3011. doi: 10.5194/tc-11-3011-2017
Iacozza, J., and Barber, D. G. (2010). An examination of snow redistribution over smooth land-fast sea ice. Hydrol. Process. 24, 850–865. doi: 10.1002/hyp.7526
Jackson, S. I., and Prowse, T. D. (2009). Spatial variation of snowmelt and sublimation in a high-elevation semi-desert basin of western Canada. Hydrol. Process. 23, 2611–2627. doi: 10.1002/hyp.7320
Johnson, R. H., Young, G. S., and Toth, J. J. (1984). Mesoscale weather effects of variable snow cover over northeast Colorado. Mon. Wea. Rev. 112, 1141–1152.
Kirchner, P. B., Bales, R. C., Molotch, N. P., Flanagan, J., and Guo, Q. (2014). LiDAR measurement of seasonal snow accumulation along an elevation gradient in the southern Sierra Nevada, California. Hydrol. Earth Syst. Sci. 18, 4261–4275. doi: 10.5194/hess-18-4261-2014
Kok, J. F., Parteli, E. J., Michaels, T. I., and Karam, D. B. (2012). The physics of wind-blown sand and dust. Rep. Progr. Phys. 75:106901. doi: 10.1088/0034-4885/75/10/106901
Lehning, M. (2013). Snow-atmosphere interactions and hydrological consequences. [Editorial]. Adv. Water Resour. 55, 1–3. doi: 10.1016/j.advwatres.2013.02.001
Lehning, M., Doorschot, J., and Bartelt, P. (2000). A snowdrift index based on SNOWPACK model calculations. Ann. Glaciol. 31, 382–386. doi: 10.3189/172756400781819770
Lehning, M., Grünewald, T., and Schirmer, M. (2011). Mountain snow distribution governed by an altitudinal gradient and terrain roughness. Geophys. Res. Lett. 38:L19504. doi: 10.1029/2011GL048927
Lehning, M., Löwe, H., Ryser, M., and Raderschall, N. (2008). Inhomogeneous precipitation distribution and snow transport in steep terrain. Water Resour. Res. 44:W07404. doi: 10.1029/2007WR006545
Letcher, T. W., and Minder, J. R. (2015). Characterization of the simulated regional snow albedo feedback using a regional climate model over complex terrain. Climate J. 28, 7576–7595. doi: 10.1175/JCLI-D-15-0166.1
Letcher, T. W., and Minder, J. R. (2017). The simulated response of diurnal mountain winds to regionally enhanced warming caused by the snow albedo feedback. J. Atmos. Sci. 74, 49–67. doi: 10.1175/JAS-D-16-0158.1
Li, L., and Pomeroy, J. W. (1997). Estimates of threshold wind speeds for snow transport using meteorological data. J. Appl. Meteorol. 36, 205–213.
Liston, G. E. (1995). Local advection of momentum, heat and moisture during the melt of patchy snow covers. J. Appl. Meteorol. 34, 1705–1715. doi: 10.1175/1520-0450-34.7.1705
Liston, G. E. (1999). Interrelationships among snow distribution, snowmelt, and snow cover depletion: implications for atmospheric, hydrologic, and ecologic modeling. J. Appl. Meteor. 38, 1474–1487.
Liston, G. E. (2004). Representing subgrid snow cover heterogeneities in regional and global models. Climate J. 17, 1381–1397. doi: 10.1175/1520-0442(2004)017<1381:RSSCHI>2.0.CO;2
Liston, G. E., Haehnel, R. B., Sturm, M., Hiemstra, C. A., Berezovskaya, S., and Tabler, R. D. (2007). Simulating complex snow distributions in windy environments using SnowTran-3D. J. Glaciol. 53, 241–256. doi: 10.3189/172756507782202865
Liston, G. E., McFadden, J. P., Sturm, M., and Pielke Sr, R. A. (2002). Modeled changes in arctic tundra snow, energy, and moisture fluxes due to increased shrubs. Global Change Biol. 8, 17–32. doi: 10.1046/j.1354-1013.2001.00416.x
Liston, G. E., and Sturm, M. (1998). A snow-transport model for complex terrain. J. Glaciol. 44, 498–516. doi: 10.1017/S0022143000002021
Liston, G. E., and Sturm, M. (2002). Winter precipitation patterns in arctic Alaska determined from a blowing-snow model and snow-depth observations. J. Hydrometeorol. 3, 646–659. doi: 10.1175/1525-7541(2002)003<0646:WPPIAA>2.0.CO;2
López-Moreno, J. I., Gascoin, S., Herrero, J., Sproles, E. A., Pons, M., Alonso-González, E., et al. (2017). Different sensitivities of snowpacks to warming in Mediterranean climate mountain areas. Environ. Res. Lett. 12:074006. doi: 10.1088/1748-9326/aa70cb
López-Moreno, J. I., Goyette, S., Beniston, M., and Alvera, B. (2008). Sensitivity of the snow energy balance to climatic changes: implications for the evolution of snowpack in the Pyrenees in the 21st century. Climate Res. 36, 206–217. doi: 10.3354/cr00747
López-Moreno, J. I., Pomeroy, J., Revuelto, J., and Vicente-Serrano, S. M. (2013). Response of snow processes to climate change: spatial variability in a small basin in the Spanish Pyre- nees. Hydrol. Process. 27, 2637–2650. doi: 10.1002/hyp.9408
Luce, C. H., and Tarboton, D. G. (2004). The application of depletion curves for parameterization of subgrid variability of snow. Hydrol. Process. 18, 1409–1422. doi: 10.1002/hyp.1420
Luce, C. H., Tarboton, D. G., and Cooley, K. R. (1998). The influence of the spatial distribution of snow on basin-averaged snowmelt. Hydrol. Process. 12, 1671–1683.
MacDonald, M. K., Pomeroy, J. W., and Pietroniro, A. (2009). Parameterizing redistribution and sublimation of blowing snow for hydrological models: tests in a mountainous subarctic catchment. Hydrol. Process. 23, 2570–2583. doi: 10.1002/hyp.7356
MacDonald, M. K., Pomeroy, J. W., and Pietroniro, A. (2010). On the importance of sublimation to an alpine snow mass balance in the Canadian Rocky Mountains. Hydrol. Earth Syst. Sci. 14, 1401–1415. doi: 10.5194/hess-14-1401-2010
MacDonell, S., Kinnard, C., Mölg, T., Nicholson, L., and Abermann, J. (2013). Meteorological drivers of ablation processes on a cold glacier in the semi-arid Andes of Chile. Cryosphere 7, 1513–1526. doi: 10.5194/tc-7-1513-2013
Magnusson, J., Jonas, T., López-Moreno, I., and Lehning, M. (2010). Snow cover response to climate change in a high alpine and half-glacierized basin in Switzerland. Hydrol. Res. 41, 230–240. doi: 10.2166/nh.2010.115
Male, D. H. (1980). “The seasonal snowcover,” in Dynamics of Snow and Ice Masses, ed S. Colbeck (Toronto, ON: Academic Press), 305–395. doi: 10.1016/B978-0-12-179450-7.50011-5
Mann, G. W., Anderson, P. S., and Mobbs, S. D. (2000). Profile measurements of blowing snow at Halley, Antarctica. J. Geophys. Res. Atmos. 105, 24491–24508. doi: 10.1029/2000JD900247
Marks, D., Domingo, J., Susong, D., Link, T., and Garen, D. (1999). A spatially distributed energy balance snowmelt model for application in mountain basins. Hydrol. Process. 13, 1935–1959.
Marks, D., and Dozier, J. (1992). Climate and energy exchange at the snow surface in the Alpine Region of the Sierra Nevada: 2. Snow cover energy balance. Water Resour. Res. 28, 3043–3054. doi: 10.1029/92WR01483
Marks, D., Link, T., Winstral, A., and Garen, D. (2001). Simulating snowmelt processes during rain-on-snow over a semi-arid mountain basin. Ann. Glaciol. 32, 195–202. doi: 10.3189/172756401781819751
Marks, D., and Winstral, A. (2001). “The effect of variable patterns of snow deposition and drifting on snowmelt, runoff, and stream discharge in a semi-arid mountain basin,” in Proc. 69th Western Snow Conf. (Sun Valley, ID), 127–130.
Marsh, P., Essery, R., Neumann, N., and Pomeroy, J. W. (1999). “Model estimates of local advection of sensible heat over a patchy snow cover,” in Interactions between the Cryosphere, Climate and Greenhouse Gases, Vol 256, ed M. Tranter (Burmingham: IAHS Publ.), 103–110.
Marsh, P., and Pomeroy, J. W. (1996). Meltwater fuxes at an arctic forest tundra site. Hydrol. Process. 10, 1383–1400.
Ménard, C. B., Essery, R., and Pomeroy, J. (2014). Modelled sensitivity of the snow regime to topography, shrub fraction and shrub height. Hydrol. Earth Syst. Sci. 18, 2375–2392. doi: 10.5194/hess-18-2375-2014
Michaux, J. L., Naaim-Bouvet, F., and Naaim, M. (2001). Drifting-snow studies over an instrumented mountainous site: II. Measurements and numerical model at small scale. Ann. Glaciol. 32, 175–181. doi: 10.3189/172756401781819364
Minder, J. R., Durran, D. R., Roe, G. H., and Anders, A. M. (2008). The climatology of small-scale orographic precipitation over the Olympic mountains: Patterns and processes. Q. J. R. Meteorol. Soc. 134, 817–839. doi: 10.1002/qj.258
Molotch, N. P., Blanken, P. D., Williams, M. W., Turnipseed, A. A., Monson, R. K., and Margulis, S. A. (2007). Estimating sublimation of intercepted and sub-canopy snow using eddy covariance systems. Hydrol. Process. 21, 1567–1575. doi: 10.1002/hyp.6719
Mote, P. W. (2006). Climate-driven variability and trends in mountain snowpack in Western North America. J. Clim. 19, 6209–6220. doi: 10.1175/JCLI3971.1
Mott, R., Daniels, M., and Lehning, M. (2015). Atmospheric flow development and associated changes in turbulent sensible heat flux over a patchy mountain snow cover. J. Hydrometeor. 16, 1315–1340. doi: 10.1175/JHM-D-14-0036.1
Mott, R., Egli, L. T., Grünewald, Dawes, N., Manes, C., Bavay, M., et al. (2011a). Micrometeorological processes driving snow ablation in an Alpine catchment. Cryosphere 5, 1083–1098. doi: 10.5194/tc-5-1083-2011
Mott, R., Faure, F., Lehning, M., Löwe, H., Michlmayr, G., Hynek, B., et al. (2008). Simulation of seasonal snow cover development and seasonal snow cover distribution for glaciated sites (Sonnblick, Austrian Alps) with the ALPINE3D model. Ann. Glaciol. 49, 155–160. doi: 10.3189/172756408787814924
Mott, R., Gromke, C. T., and Grünewald, Lehning, M. (2013). Relative importance of advective heat transport and boundary layer decoupling in the melt dynamics of a patchy snow cover. Adv. Water Resour. 55, 88–97. doi: 10.1016/j.advwatres.2012.03.001
Mott, R., and Lehning, M. (2010). Meteorological modeling of very high resolution wind fields and snow deposition for mountains. J. Hydromet. 11, 934–949. doi: 10.1175/2010JHM1216.1
Mott, R., Paterna, E., Horender, S., Crivelli, P., and Lehning, M. (2016). Wind tunnel experiments: cold-air pooling and atmospheric decoupling above a melting snow patch. Cryosphere 10, 445–458. doi: 10.5194/tc-10-445-2016
Mott, R., Schirmer, M., Bavay, M., Grünewald, T., and Lehning, M. (2010). Understanding snow-transport processes shaping the mountain snow-cover. Cryosphere 4, 545–559. doi: 10.5194/tc-4-545-2010
Mott, R., Schirmer, M., and Lehning, M. (2011b). Scaling properties of wind and snow depth distribution in an Alpine catchment. J. Geophys. Res. 116:D0616. doi: 10.1029/2010JD014886
Mott, R., Schlögl, S., Dirks, L., and Lehning, M. (2017). Impact of extreme land surface heterogeneity on micrometeorology over spring snow cover. J. Hydrometeor. 18, 2705–2722. doi: 10.1175/JHM-D-17-0074.1
Mott, R., Scipión, D. E., Schneebeli, M., Dawes, N., Berne, A., and Lehning, M. (2014). Orographic effects on snow deposition patterns in mountainous terrain. J. Geophys. Res. Atmos. 119, 1419–1439. doi: 10.1002/2013JD019880
Musselman, K. N., Clark, M. P., Liu, C., Ikeda, K., and Rasmussen, R. (2017). Slower snowmelt in a warmer world. Nat. Clim. Change 7, 214–219. doi: 10.1038/nclimate3225
Musselman, K. N., Pomeroy, J. W., Essery, R. L., and Leroux, N. (2015). Impact of windflow calculations on simulations of alpine snow accumulation, redistribution and ablation. Hydrol. Process. 29, 3983–3999. doi: 10.1002/hyp.10595
Naaim, M., Naaim-Bouvet, F., and Martinez, H. (1998). Numerical simulation of drifting snow: erosion and deposition models. Ann. Glaciol. 26, 191–196. doi: 10.1017/S0260305500014798
Naaim-Bouvet, F., Bellot, H., and Naaim, M. (2010). Back analysis of drifting-snow measurements over an instrumented mountainous site. Ann. Glaciol. 51, 207–217. doi: 10.3189/172756410791386661
Naaim-Bouvet, F., Naaim, M., Bellot, H., and Nishimura, K. (2011). Wind and drifting-snow gust factor in an Alpine context. Ann. Glaciol. 52, 223–230. doi: 10.3189/172756411797252112
Nemoto, M., and Nishimura, K. (2004). Numerical simulation of snow saltation and suspension in a turbulent boundary layer. J. Geophys. Res. 109:D18206. doi: 10.1029/2004JD004657
Neumann, N., and Marsh, P. (1998). Local advection of sensible heat in the snowmelt landscape of Arctic tundra. Hydrol. Process. 12, 1547–1560.
Nishimura, K., and Hunt, J. C. R. (2000). Saltation and incipient suspension above a flat particle bed below a turbulent boundary layer. J. Fluid Mech. 417, 77–102. doi: 10.1017/S0022112000001014
Nishimura, K., and Nemoto, M. (2005). Blowing snow at Mizuho station, Antarctica. Philos. Trans. R. Soc. Lond. A 363, 1647–1662. doi: 10.1098/rsta.2005.1599
Nishimura, K., Yokoyama, C., Ito, Y., Nemoto, M., Naaim-Bouvet, F., Bellot, H., et al. (2014). Snow particle speeds in drifting snow. J. Geophys. Res. Atmos. 119, 9901–9913. doi: 10.1002/2014JD021686
Nitta, T., Yoshimura, K., Takata, K., O'ishi, R., Sueyoshi, T., Kanae, T., et al. (2014). Representing variability in subgrid snow cover and snow depth in a global land model: Offline validation. Climate J. 27, 3318–3330. doi: 10.1175/JCLI-D-13-00310.1
Obukhov, A. M. (1946). Turbulence in an atmosphere with a non-uniform temperature. Boundary Layer Meteorol. 2, 7–29.
Paterna, E., Crivelli, P., and Lehning, M. (2016). Decoupling of mass flux and turbulent wind fluctuations in drifting snow. Geophys. Res. Lett. 43, 4441–4447. doi: 10.1002/2016GL068171
Paterna, E., Crivelli, P., and Lehning, M. (2017). Wind tunnel observations of weak and strong snow saltation dynamics. J. Geophys. Res. Earth Surf. 122, 1589–1604. doi: 10.1002/2016JF004111
Pedersen, A. Ø., Speed, J. D. M., and Tombre, I. M. (2013). Prevalence of grubbing in the arctic tundra increases with the pink- footed goose population expansion. Polar Biol. 36, 1569–1575. doi: 10.1007/s00300-013-1374-9
Pinty, J. P., and Jabouille, P. (1998). “A mixed-phased cloud parameterization for use in a mesoscale non-hydrostatic model: simulations of a squall line and of orographic precipitation,” in Conference on Cloud Physics: 14th Conference on Planned and Inadvertent Weather Modification (Everett, WA), 217–220.
Pohl, S., and Marsh, P. (2006). Small-scale modelling of spatially variable snowmelt in an arctic catchment. Hydrol. Process. 20, 1773–1792. doi: 10.1002/hyp.5955
Pohl, S., Marsh, P., and Liston, G. E. (2006). Spatial-temporal variability in turbulent fluxes during spring snowmelt. Arct. Antarct. Alp. Res. 38, 136–146. doi: 10.1657/1523-0430(2006)038[0136:SVITFD]2.0.CO;2
Pomeroy, J. W., and Essery, R. L. (1999). Turbulent fluxes during blowing snow: field tests of model sublimation predictions. Hydrol. Process. 13, 2963–2975.
Pomeroy, J. W., Fang, X., and Marks, G. (2016). The cold rain-on-snow event of June 2013 in the Canadian Rockies — characteristics and diagnosis. Hydrol. Process. 30, 2899–2914. doi: 10.1002/hyp.10905
Pomeroy, J. W., and Gray, D. M. (1990). Saltation of snow. Water Resour. Res. 26, 1583–1594. doi: 10.1029/WR026i007p01583
Pomeroy, J. W., and Gray, D. M. (1995). Snowcover accumulation, relocation and management. Bull. Int. Soc. Soil Sci. 88.
Pomeroy, J. W., Gray, D. M., and Landine, P. G. (1993). The prairie blowing snow model: characteristics, validation, operation. J. Hydrol. 144, 165–192. doi: 10.1016/0022-1694(93)90171-5
Pomeroy, J. W., Gray, D. M., Shook, K., Toth, B., Essery, R. L. H., Pietroniro, A., et al. (1998a). An evaluation of snow accumulation and ablation processes for land surface modelling. Hydrol. Process. 12, 2339–2367.
Pomeroy, J. W., and Li, L. (2000). Prairie and arctic areal snow cover mass balance using a blowing snow model. J. Geophys. Res. Atmos. 105, 26619–26634. doi: 10.1029/2000JD900149
Pomeroy, J. W., Marsh, P., and Gray, D. M. (1997). Application of a distributed blowing snow model to the Arctic. Hydrol. Process. 11, 1451–1464.
Pomeroy, J. W., Parviainen, J., Hedstrom, N., and Gray, D. M. (1998b). Coupled modelling of forest snow interception and sublimation. Hydrol. Process. 12, 2317–2337.
Pontoppidan, M., Reuder, J., Mayer, S., and Kolstad, E. W. (2017). Downscaling an intense precipitation event in complex terrain: the importance of high grid resolution. Tellus A Dyn. Meteorol. Oceanogr. 69:1271561. doi: 10.1080/16000870.2016.1271561
Prandtl, L. (1934). “Aerodynamic theory,” in A General Review of Progress Under a Grant of the Guggenheim Fund for the Promotion of Aeronautics, ed W. F. Durand (Berlin: Springer).
Raderschall, N., Lehning, M., and Schär, C. (2008). Fine-scale modeling of the boundary layer wind field over steep topography. Water Resour. Res. 44:W09425. doi: 10.1029/2007WR006544
Radić, V., Menounos, B., Shea, J., Fitzpatrick, N., Tessema, M. A., and Déry, S. J. (2017). Evaluation of different methods to model near-surface turbulent fluxes for a mountain glacier in the Cariboo Mountains, BC, Canada. Cryosphere 11, 2897–2918. doi: 10.5194/tc-11-2897-2017
Rasmussen, R., Liu, C., Ikeda, K., Gochis, D., Yates, D., Chen, F., et al. (2011). High-resolution coupled climate runoff simulations of seasonal snowfall over Colorado: a process study of current and warmer climate. Climate J. 24, 3015–3048. doi: 10.1175/2010JCLI3985.1
Reba, M. L., Marks, D., Seyfried, M., Winstral, A., Kumar, M., and Flerchinger, G. (2011). A long-term data set for hydrologic modeling in a snow-dominated mountain catchment. Water Resour. Res. 47:W07702. doi: 10.1029/2010WR010030
Reba, M. L., Pomeroy, J., Marks, D., and Link, T. E. (2012). Estimating surface sublimation losses from snowpacks in a mountain catchment using eddy covariance and turbulent transfer calculations. Hydrol. Process. 26, 3699–3711. doi: 10.1002/hyp.8372
Revuelto, J., López-Moreno, J. I., Azorin-Molina, C., and Vicente-Serrano, S. M. (2014)., Topographic control of snowpack distribution in a small catchment in the central Spanish Pyrenees: intra- and inter-annual persistence. Cryosphere 8, 1989–2006. doi: 10.5194/tc-8-1989-2014
Roe, G. H. (2005). Orographic precipitation. Annu. Rev. Earth Planet. Sci. 33, 645–671. doi: 10.1146/annurev.earth.33.092203.122541
Roesch, A., Wild, M., Gilgen, H., and Ohmura, A. (2001). A new snow cover fraction parametrization for the ECHAM4 GCM. Climate Dyn. 17, 933–946. doi: 10.1007/s003820100153
Roth, A., Hock, R., Schuler, T. V., Bieniek, P. A., Pelto, M., and Aschwanden, A. (2018). Modeling winter precipitation over the Juneau Icefield, Alaska, using a linear model of orographic precipitation. Front. Earth Sci. 6:20. doi: 10.3389/feart.2018.00020
Sato, T., Kosugi, K., Mochizuki, S., and Nemoto, M. (2008). Wind speed dependences of fracture and accumulation of snowflakes on snow surface. Cold Regions Sci. Technol. 51, 229–239. doi: 10.1016/j.coldregions.2007.05.004
Sauter, T., and Galos, S. P. (2016). Effects of local advection on the spatial sensible heat flux variation on a mountain glacier. Cryosphere 10, 2887–2905. doi: 10.5194/tc-10-2887-2016
Savelyev, S. A., and Taylor, P. A. (2005). Internal boundary layers: I. height formulae for neutral and diabatic flows. Boundary Layer Meteorol. 115, 1–25. doi: 10.1007/s10546-004-2122-z
Schirmer, M., and Lehning, M. (2011). Persistence in intra-annual snow depth distribution: 2. Fractal analysis of snow depth development. Water Resour. Res. 47:W09517. doi: 10.1029/2010WR009429
Schirmer, M., Wirz, V., Clifton, A., and Lehning, M. (2011). Persistence in intra-annual snow depth distribution: 1. Measurements and topographic control. Water Resour. Res. 47:W09516. doi: 10.1029/2010WR009426
Schlögl, S., Lehning, M., and Mott, R. (2018a). How are turbulent heat fluxes and snow melt rates affected by a changing snow cover fraction? Front. Earth Sci. 6:154. doi: 10.3389/feart.2018.00154
Schlögl, S., Lehning, M., and Mott, R. (2018b). Representation of horizontal transport processes in snow melt modelling by applying a footprint approach. Front. Earth Sci. 6:120. doi: 10.3389/feart.2018.00120
Schlögl, S., Lehning, M., Nishimura, K., Huwald, H., Cullen, N. J., and Mott, R. (2017). How do stability corrections perform in the stable boundary layer over snow? Boundary Layer Meteorol. 165, 161–180. doi: 10.1007/s10546-017-0262-1
Schlögl, S., Marty, C., Bavay, M., and Lehning, M. (2016). Sensitivity of Alpine3D modeled snow cover to modifications in DEM resolution, station coverage and meteorological input quantities. Environ. Model. Softw. 83, 387–396. doi: 10.1016/j.envsoft.2016.02.017
Schmidt, R. A. (1980). Threshold wind-speeds and elastic impact in snow transport. J. Glaciol. 26, 453–467. doi: 10.1017/S0022143000010972
Schmidt, R. A. (1982). Vertical profiles of wind speed, snow concentration, and humidity in blowing snow. Boundary Layer Meteorol. 23, 223–246. doi: 10.1007/BF00123299
Schneiderbauer, S., and Prokop, A. (2011). The atmospheric snow-transport model: SnowDrift3D. J. Glaciol. 57, 526–542. doi: 10.3189/002214311796905677
Schön, P., Prokop, A., Vionnet, V., Guyomarc'h, G., Naaim-Bouvet, F., and Heiser, M. (2015). Improving a terrain-based parameter for the assessment of snow depths with TLS data in the Col du Lac Blanc area. Cold Regions Sci. Technol. 114, 15–26. doi: 10.1016/j.coldregions.2015.02.005
Scipión, D. E., Mott, R., Lehning, M., Schneebeli, M., and Berne, A. (2013). Seasonal small-scale spatial variability in alpine snowfall and snow accumulation. Water Resour. Res. 49, 1446–1457. doi: 10.1002/wrcr.20135
Segal, M., Garrat, J. R., Pielke, R. A., and Ye, Z. (1991). Scaling and numerical model evaluation of snow-cover effects on the generation and modification of daytime mesoscale circulations. J. Atmos. Sci. 48, 1024–1041.
Sexstone, G. A., Clow, D. W., Fassnacht, S. R., Liston, G. E., Hiemstra, C. A., Knowles, J. F., et al. (2018). Snow sublimation in mountain environments and its sensitivity to forest disturbance and climate warming. Water Resour. Res. 54, 1191–1211. doi: 10.1002/2017WR021172
Sexstone, G. A., Clow, D. W., Stannard, D. I., and Fassnacht, S. R. (2016). Comparison of methods for quantifying surface sublimation over seasonally snow-covered terrain. Hydrol. Process. 30, 3373–3389. doi: 10.1002/hyp.10864
Sharma, V., Comola, F., and Lehning, M. (2018). On the suitability of the Thorpe-Mason model for calculating sublimation of saltating snow. Cryosphere Discuss. 12, 3137–3160. doi: 10.5194/tc-2018-33
Shea, J., and Moore, R. (2010). Prediction of spatially distributed regional-scale fields of air temperature and vapor pressure over mountain glaciers. 113:D23107. doi: 10.1029/2010JD014351
Shook, K., and Gray, D. M. (1996). Small-scale spatial structure of shallow snowcovers. Hydrol. Process. 10, 1283–1292.
Sicart, J. E., Wagon, P., and Ribstein, P. (2005). Atmospheric controls of the heat balance of Zongo Glacier (16°S, Bolivia). J. Geophys. Res. 110:D12106. doi: 10.1029/2004JD005732
Silverman, N. L., Maneta, M. P., Chen, S.-H., and Harper, J. T. (2013). Dynamically downscaled winter precipitation over complex terrain of the Central Rockies of Western Montana, USA. Water Resour. Res. 49, 458–470. doi: 10.1029/2012WR012874
Smeets, C. J. P. P., and van den Broeke, M. R. (2008). The parameterization of scalar transfer over rough ice. Boundary Layer Meteorol. 128, 339–355. doi: 10.1007/s10546-008-9292-z
Smith, R. B., and Evans, J. P. (2007). Orographic precipitation and water vapor fractionation over the Southern Andes. J. Hydrometeor. 8, 3–19. doi: 10.1175/JHM555.1
Smith, R. B., Jiang, Q., Fearon, M., Tabary, P., Dorninger, M., Doyle, J., et al. (2003). Orographic precipitation and airmass transformation: an Alpine example. Q. J. Roy. Meteor. Soc. 129B, 433–454. doi: 10.1256/qj.01.212
Sommer, C. G., Lehning, M., and Fierz, C. (2017). Wind tunnel experiments: saltation is necessary for wind-packing. J. Glaciol. 63, 950–958. doi: 10.1017/jog.2017.53
Sommer, C. G., Lehning, M., and Fierz, C. (2018). Wind tunnel experiments: influence of erosion and deposition on wind-packing of new snow. Front. Earth Sci. 6:4. doi: 10.3389/feart.2018.00004
Sommer, C. G., Lehning, M., and Mott, R. (2015). Snow in a very steep rock face: accumulation and redistribution during and after a snowfall event. Front. Earth Sci. 3:73. doi: 10.3389/feart.2015.00073
Sorbjan, Z. (2016). Similarity scaling systems for stably stratified turbulent flows. Q. J. R. Meteorol. Soc. 142, 805–810. doi: 10.1002/qj.2682
Sørensen, M. (2004). On the rate of aeolian sand transport. Geomorphology 59, 53–62. doi: 10.1016/j.geomorph.2003.09.005
Stearns, C. R., and Weidner, G. A. (1993). Sensible and Latent heat flux estimates in Antarctica. Antarctic Res. Ser. 61, 109–138. doi: 10.1029/AR061p0109
Stoy, P. C., Peitzsch, E., Wood, D., Rottinghaus, D., Wohlfahrt, G., Goulden, M., et al. (2018). On the exchange of sensible and latent heat between the atmosphere and melting snow. Agric. Forest Meteorol. 252, 167–174. doi: 10.1016/j.agrformet.2018.01.028
Strasser, U., Bernhardt, M., Weber, M., Liston, G. E., and Mauser, W. (2008). Is snow sublimation important in the alpine water balance? Cryosphere 2, 53. doi: 10.5194/tc-2-53-2008
Strasser, U., Corripio, J., Pellicciotti, F., Burlando, P., Brock, B., and Funk, M. (2004). Spatial and temporal variability of meteorological variables at Haut Glacier d'Arolla, Switzerland, during the ablation season 2001: measurements and simulations. J. Geophys. Res. 109:D03103. doi: 10.1029/2003JD003973
Stull, R. B. (1988). An Introduction to Boundary Layer Meteorology. Dordrecht: Kluwer Academic Publishers. doi: 10.1007/978-94-009-3027-8
Sturm, M., Goldstein, M. A., and Parr, C. (2017). Water and life from snow: a trillion dollar science question. Water Resour. Res. 53, 3534–3544. doi: 10.1002/2017WR020840
Sturm, M., and Liston, G. E. (2003). The snow cover on lakes of the Arctic Coastal Plain of Alaska, USA. J. Glaciol. 49, 370–380. doi: 10.3189/172756503781830539
Sturm, M., Liston, G. E., Benson, C. S., and Holmgren, J. (2001). Characteristics and growth of a snowdrift in Arctic Alaska, Arctic, USA. Antarctic Alpine Res. 33, 319–329. doi: 10.1080/15230430.2001.12003436
Sverdrup, H. H. (1936). The eddy conductivity of the air over a smooth snowfield. Geophys. Publ. 11, 5–49.
Svoma, B. M. (2016). Difficulties in determining snowpack sublimation in complex terrain at the macroscale. Adv. Meteorol. 2016:9695757. doi: 10.1155/2016/9695757
Svoma, B. M. (2017). Canopy effects on snow sublimation from a central Arizona Basin. J. Geophys. Res. Atmos. 122, 20–46. doi: 10.1002/2016JD025184
Takahara, H., and Higuchi, K. (1985). Thermal modification of air moving over melting snow surfaces. Ann. Glaciol. 6, 235–237. doi: 10.1017/S0260305500010442
Takata, K., Emori, S., and Watanabe, T. (2003). Development of the minimal advanced treatments of surface interaction and runoff. Global Planet. Change 38, 209–222. doi: 10.1016/S0921-8181(03)00030-4
Taylor, C. M., Harding, R. J., Pielke Sr, R. A., Vidale, P. L., Walko, R. L., and Pomeroy, J. W. (1998). Snow breezes in the boreal forest. J. Geophys. Res. 103, 23087–23101.
Taylor, P. (1998). The thermodynamic effects of sublimating, blowing snow in the atmospheric boundary layer. Boundary Layer Meteorol. 89, 251–283. doi: 10.1023/A:1001712111718
Tedesche, M. E., Fassnacht, S. R., and Meiman, P. J. (2017). Scales of snow depth variability in high elevation rangeland sagebrush. Front. Earth Sci. 11:469. doi: 10.1007/s11707-017-0662-z
Tennant, C. J., Harpold, A. A., Lohse, K. A., Godsey, S. E., Crosby, B. T., Glenn, N. F., et al. (2017). Regional sensitivities of seasonal snowpack to elevation, aspect, and vegetation cover in western North America. Water Resour. Res. 53, 6908–6926. doi: 10.1002/2016WR019374
Thorpe, A. D., and Mason, B. J. (1966). The evaporation of ice spheres and ice crystals. Brit. J. Appl. Phys. 17, 541. doi: 10.1088/0508-3443/17/4/316
Trujillo, E., Molotch, N. P., Goulden, M. L., Kelly, A. E., and Bales, R. C. (2012). Elevation-dependent influence of snow accumulation on forest greening. Nat. Geosci. 5, 705–709. doi: 10.1038/ngeo1571
Trujillo, E., Ramirez, J. A., and Elder, K. J. (2007). Topographic,meteorologic,andcanopycontrolsonthescaling characteristics of the spatial distribution of snow depth fields. Water Resour. Res. 43:W07409. doi: 10.1029/2006WR005317
Van den Broeke, M., Reijmer, C., van As, D., van de Wal, R., and Oerlemans, J. (2005). Seasonal cycles of Antarctic surface energy balance from automatic weather stations. Ann. Glaciol. 41, 131–139. doi: 10.3189/172756405781813168
Vaughan, D. G., Comiso, J. C., Allison, I., Carrasco, J., Kaser, G., Kwok, R., et al. (2013). “Observations: cryosphere,” in Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, eds T. F. Stocker, D. Qin, D., G.-K. Plattner, M. Tignor, S. K. Allen, J. Boschung, A. Nauels, Y. Xia, V. Bex, and P. M. Midgley (Cambridge, UK; New York, NY: Cambridge University Press).
Vionnet, V., Guyomarc'h, G., Bouvet, F. N., Martin, E., Durand, Y., Bellot, H., et al. (2013). Occurrence of blowing snow events at an alpine site over a 10-year period: observations and modelling. Adv. Water Resour. 55, 53–63. doi: 10.1016/j.advwatres.2012.05.004
Vionnet, V., Martin, E., Masson, V., Guyomarc'h, G., Bouvet, F. N., Prokop, A., et al. (2014). Simulation of wind-induced snow transport and sublimation in alpine terrain using a fully coupled snowpack/atmosphere model. Cryosphere 8, 395. doi: 10.5194/tc-8-395-2014
Vionnet, V., Martin, E., Masson, V., Lac, C., Naaim Bouvet, F., and Guyomarc'h, G. (2017). High-resolution large eddy simulation of snow accumulation in Alpine Terrain. J. Geophys. Res. Atmos. 122, 11005–11021. doi: 10.1002/2017JD026947
Wang, Z., and Huang, N. (2017). Numerical simulation of the falling snow deposition over complex terrain. J. Geophys. Res. Atmos. 122, 980–1000. doi: 10.1002/2016JD025316
Warscher, M., Strasser, U., Kraller, G., Marke, T., Franz, H., and Kunstmann, H. (2013). Performance of complex snow cover descriptions in a distributed hydrological model system: a case study for the high Alpine terrain of the Berchtesgaden Alps. Water Resour. Res. 49, 2619–2637. doi: 10.1002/wrcr.20219
Webb, E. K. (1970). Profile relationships the log-linear range and extension to strong stability. Q. J. R. Meteorol. Soc. 96, 67–90. doi: 10.1002/qj.49709640708
Webb, R. W., Fassnacht, S. R., and Gooseff, M. N. (2017). Defining the diurnal pattern of snowmelt using a beta distribution function. J. Am. Water Resour. Assoc. 53, 684–696. doi: 10.1111/1752-1688.12522
Weisman, R. N. (1977). Snowmelt: A two-dimensional turbulent diffusion model. Water Resour. Res. 13, 337–342. doi: 10.1029/WR013i002p00337
Wever, N., Lehning, M., Clifton, A., Rüedi, J. D., Nishimura, K., Nemoto, M., et al. (2009). Verification of moisture budgets during drifting snow conditions in a cold wind tunnel. Water Resour. Res. 45. doi: 10.1029/2008WR007522
Wheeler, J. A., Cortés, A. J., Sedlacek, J.;, Karrenberg, S., Van Kleunen, M., Wipf, S., et al. (2016). The snow and the willows: earlier spring snowmelt reduces performance in the low-lying alpine shrub Salix herbacea. J. Ecol. 104, 1041–1050. doi: 10.1111/1365-2745.12579
Willis, I. C., Arnold, N. S., and Brock, B. W. (2002). Effect of snowpack removal on energy balance, melt and runoff in a small supraglacial catchment. Hydrol. Process. 16, 2721–2749. doi: 10.1002/hyp.1067
Winstral, A., Elder, K., and Davis, R. E. (2002). Spatial snow modeling of wind-redistributed snow using terrain-based parameters. J. Hydrometeor. 3, 524–538. doi: 10.1175/1525-7541(2002)003<0524:SSMOWR>2.0.CO;2
Winstral, A., and Marks, D. (2002). Simulating wind fields and snow redistribution using terrain-based parameters to model snow accumulation and melt over a semi-arid mountain catchment. Hydrol. Process. 16, 3585–3603. doi: 10.1002/hyp.1238
Winstral, A., and Marks, D. (2014). Long-term snow distribution observations in a mountain catchment: assessing variability, time stability, and the representativeness of an index site. Water Resour. Res. 50, 293–305. doi: 10.1002/2012WR013038
Winstral, A., Marks, D., and Gurney, R. (2013). Simulating wind-affected snow accumulations at catchment to basin scales. Adv. Water Resour. 55, 64–79. doi: 10.1016/j.advwatres.2012.08.011
Wirz, V., Schirmer, M., Gruber, S., and Lehning, M. (2011). Spatio-temporal measurements and analysis of snow depth in a rock face. Cryosphere 5, 893–905. doi: 10.5194/tc-5-893-2011
Würzer, S., Jonas, T., Wever, N., and Lehning, M. (2016). Influence of initial snowpack properties on runoff formation during rain-on-snow events. J. Hydrometeor. 17, 1801–1815. doi: 10.1175/JHM-D-15-0181.1
Yen, Y.-C. (1995). Sensible heat flux measurements near a cold surface. US Army Cold Regions Research and Engineering Laboratory Report (Hanover, NH).
Zängl, G. (2008). The temperature dependence of small-scale orographic precipitation enhancement. Q. J. R. Meteorol. Soc. 134, 1167–1181. doi: 10.1002/qj.267
Zängl, G., Aulehner, D., Wastl, C., and Pfeiffer, A. (2008). Small-scale precipitation variability in the Alps: climatology in comparison with semi-idealized numerical simulations. Q. J. R. Meteorol. Soc. 134, 1865–1880. doi: 10.1002/qj.311
Zheng, Z., Kirchner, P. B., and Bales, R. C. (2016). Topographic and vegetation effects on snow accumulation in the southern Sierra Nevada: a statistical summary from lidar data. Cryosphere 10, 257–269. doi: 10.5194/tc-10-257-2016
Keywords: seasonal snow, mountains, snow-atmosphere interactions, wind, snowfall, snow drift, turbulent fluxes
Citation: Mott R, Vionnet V and Grünewald T (2018) The Seasonal Snow Cover Dynamics: Review on Wind-Driven Coupling Processes. Front. Earth Sci. 6:197. doi: 10.3389/feart.2018.00197
Received: 21 June 2018; Accepted: 22 October 2018;
Published: 03 December 2018.
Edited by:
Alun Hubbard, UiT The Arctic University of Norway, NorwayReviewed by:
David F. Porter, Columbia University, United StatesNicolas Cullen, University of Otago, New Zealand
Copyright © 2018 Mott, Vionnet and Grünewald. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rebecca Mott, bW90dEBzbGYuY2g=
 Rebecca Mott
Rebecca Mott Vincent Vionnet
Vincent Vionnet Thomas Grünewald
Thomas Grünewald