Impurity Resistivity of fcc and hcp Fe-Based Alloys: Thermal Stratification at the Top of the Core of Super-Earths

Introduction

Because the electrical current and the heat are mainly transported by mobile electrons in the metallic core, it is important to understand the electron scattering mechanisms in Fe-based alloys at high pressure and temperature to estimate the thermal conductivity and the electrical resistivity. Gomi et al. (2013) proposed the core resistivity model that the resistivity saturation was firstly taken into account. Later, many studies (Kiarasi and Secco, 2015; Gomi et al., 2016; Ohta et al., 2016, 2018; Pozzo and Alfè, 2016a,b; Wagle et al., 2018; Xu et al., 2018) investigated the resistivity saturation. Because of its universality, we expect that the resistivity saturation model is applicable to metallic cores of terrestrial planets with various pressure, temperature and compositions. In order to improve our previous model, we address the following two topics in this study.

The first topic of this study is the compositional effect on the electrical resistivity of cores, namely impurity resistivity. On the one hand, first-principles molecular dynamics (FPMD) studies computed the effects of alloying Si, O, and S (de Koker et al., 2012; Pozzo et al., 2013, 2014; Wagle et al., 2018). On the other hand, high pressure experimental works investigated the impurity resistivities of Si, Ni, S and C (Matassov, 1977; Gomi et al., 2013, 2016; Seagle et al., 2013; Gomi and Hirose, 2015; Kiarasi and Secco, 2015; Suehiro et al., 2017; Ohta et al., 2018; Zhang et al., 2018). In order to understand the relative importance of light elements, Gomi et al. (2013) calculated the impurity resistivities of C, S, and O from the impurity resistivity of silicon by using the Linde's rule (Norbury, 1921; Linde, 1932). However, Suehiro et al. (2017) demonstrated the violation of the Linde's rule from measurements on Fe-Si-S ternary alloys. The Linde's rule is known as a model for impurity resistivity in noble metal hosts, which predicts a parabolic dependence as a function of valence difference Z between impurity element and the host metal. The Linde's rule is valid for impurity elements located at the right hand side of the host noble metal in the periodic table, however, it is strongly violated for magnetic transition metal impurity. Therefore, application to transition metal hosts is indeed questionable. Instead of the Linde's rule, we will show the relative importance of the impurity resistivity of light alloying elements in fcc and hcp Fe by means of the Korringa-Kohn-Rostoker method combined with the coherent potential approximation (KKR-CPA) (Oshita et al., 2009; Kou and Akai, 2018), which successfully reproduces the impurity resistivities of Si and Ni in hcp Fe (Gomi et al., 2016).

The second topic of this study is the validity of the Widemann-Franz law. The Widemann-Franz law predicts the thermal conductivity from the electrical resistivity as:

$\begin{array}{ll}k=\frac{LT}{\rho }& (1)\end{array}$

where k is the thermal conductivity, L is the Lorenz number, T is the absolute temperature and ρ is the electrical resistivity. The Lorenz number is almost independent of temperature and common for almost all metals. The Sommerfeld value $L_{Somm}=\frac{1}{3}\frac{{\pi }^2{k}_B^2}{e^2}=2.445\times 10^{-8}$ WΩ/K² is widely used as the Lorenz number, where k_B is the Boltzmann's constant and e is electronic charge (e.g., Anderson, 1998; Poirier, 2000; see also Appendix of Gomi and Hirose, 2015). However, FPMD studies predict the deviation of the Lorenz number from the Sommerfeld value (de Koker et al., 2012; Pozzo et al., 2012, 2013, 2014; Pozzo and Alfè, 2016b). More importantly, the experimentally determined Lorenz number of hcp Fe, which is calculated from recent laser heated diamond-anvil cell (LHDAC) measurements on the electrical resistivity (Ohta et al., 2016) and the thermal conductivity (Konôpková et al., 2016), exhibit substantially smaller than the Sommerfeld value. Even though these LHDAC results may have large uncertainty (Dobson, 2016), this fact suggests potential violation of the Widemann-Franz law. Gomi and Hirose (2015) pointed out three important approximations, which potentially violate the Wiedemann-Franz law: omitting the additional contribution from lattice or ionic conductivity, neglecting the anelastic scattering, and the application of the Sommerfeld expansion. Additionally, electron-electron scattering may affect the Lorenz number (Pourovskii et al., 2017). Among them, the violation of the Sommerfeld expansion may cause 2–43% deviation from the Sommerfeld value of the Lorenz number, if we adopt the calculated electron density of states (DOS) of fcc and hcp Fe reported by Boness et al. (1986). However, this argument is limited to pure Fe. As well as the impurity resistivity calculation, the KKR-CPA method can easily simulate the DOS of disordered alloys (Gomi et al., 2016, 2018).

This paper is organized as follows. In the section Methods, the first-principles methods were described. The impurity resistivities of various impurities in fcc Au were first calculated to examine the validity and the physical origin of the violation of the Linde's rule (section Dilute Alloys). Then, impurity resistivities in fcc and hcp Fe-based alloys were simulated at high pressure (sections Dilute Alloys and Concentrated Alloys). Simultaneously, electron DOS were computed. The electronic specific heat was then estimated by numerical integration based on the DOS. The numerically-calculated specific heat values were compared with that was obtained by the Sommerfeld expansion to discuss the possible deviation of the Lorenz number from its Sommerfeld value (section Electronic Specific Heat and Wiedemann-Franz Law). Combined with the present impurity resistivity and the Lorenz number, we revised our thermal conductivity model (Gomi et al., 2016) (section Electrical Resistivity and Thermal Conductivity of the Earth's Core). Finally, the model was applied to the planetary cores with various planetary mass from 0.1 to 10 times Earth mass (section Heat Flux at the CMB of Super-Earths).

Methods

We carried out the first-principles electronic band structure calculation of fcc Au-, hcp and fcc Fe-based alloys. For fcc Au alloys, the lattice parameters are set to a = 7.71 Bohr, which correspond the ambient pressure value. For hcp Fe alloys, the lattice volumes are set to 19.10, 16.27, and 9.80 ų. These values correspond to 40, 120, and 1,000 GPa pressure at ambient temperature (Dewaele et al., 2006). The axial ratio was set to the ideal value (c/a = 1.633). For fcc Fe alloys, we used the same atomic volumes as for hcp Fe alloys. The Kohn-Sham equation was solved by means of Korringa-Kohn-Rostoker (KKR) Green function method, which implemented in AkaiKKR package (Akai, 1989). The local density approximation (LDA) was adapted to exchange-correlation potential (Moruzzi et al., 1978); the specific choice of the exchange-correlation functional may not significantly affect the resistivity value (see Supplementary Figure S1 of Gomi et al., 2016). The crystal potential was approximated by using the atomic spherical approximation (ASA). The maximum angular momentum quantum number was set to l = 3. Relativistic effects are considered in the scalar relativistic approximation. The substitutional chemical disorder is described in the coherent potential approximation (CPA). The electrical resistivity is calculated from the Kubo-Greenwood formula with the vertex correction (Butler, 1985; Oshita et al., 2009; Gomi et al., 2016; Kou and Akai, 2018). The hcp Fe-alloys have two independent resistivity components with respect to crystallographic orientation; ρ_|| and ρ_⊥ are the resistivities calculated parallel and perpendicular to the c-axis, respectively. The resistivities of polycrystalline hcp Fe-alloys are calculated as ρ_poly = (2ρ_⊥ +ρ_||)/3 (Alstad et al., 1961).

Dilute Alloys

Norbury (1921) conducted systematic measurements of impurity resistivity of dilute alloys, and found that the impurity resistivity is enhanced with increasing horizontal distance between the positions of impurity element and host metal in the periodic table. Linde (1932) reported that impurity resistivity of noble metal-based alloys is proportional to Z², where Z is the difference in valence between impurity element and host metal. This relationship is observed in the noble metal alloyed with the impurity element located at the right hand side of the noble metal in the periodic table, and is so-called the Linde's rule. Mott (1936) provided an interpretation for Linde's rule, assuming the impurity atom to be a point charge Z × e, where e is the elementary electrical charge. This approximation successfully explained the Z² dependence of the impurity resistivity. However, impurity elements on the left hand side of the noble metal exhibit complicated behavior. This is reasonably explained by Friedel model with the idea of the virtual bond state (VBS) (Friedel, 1956).

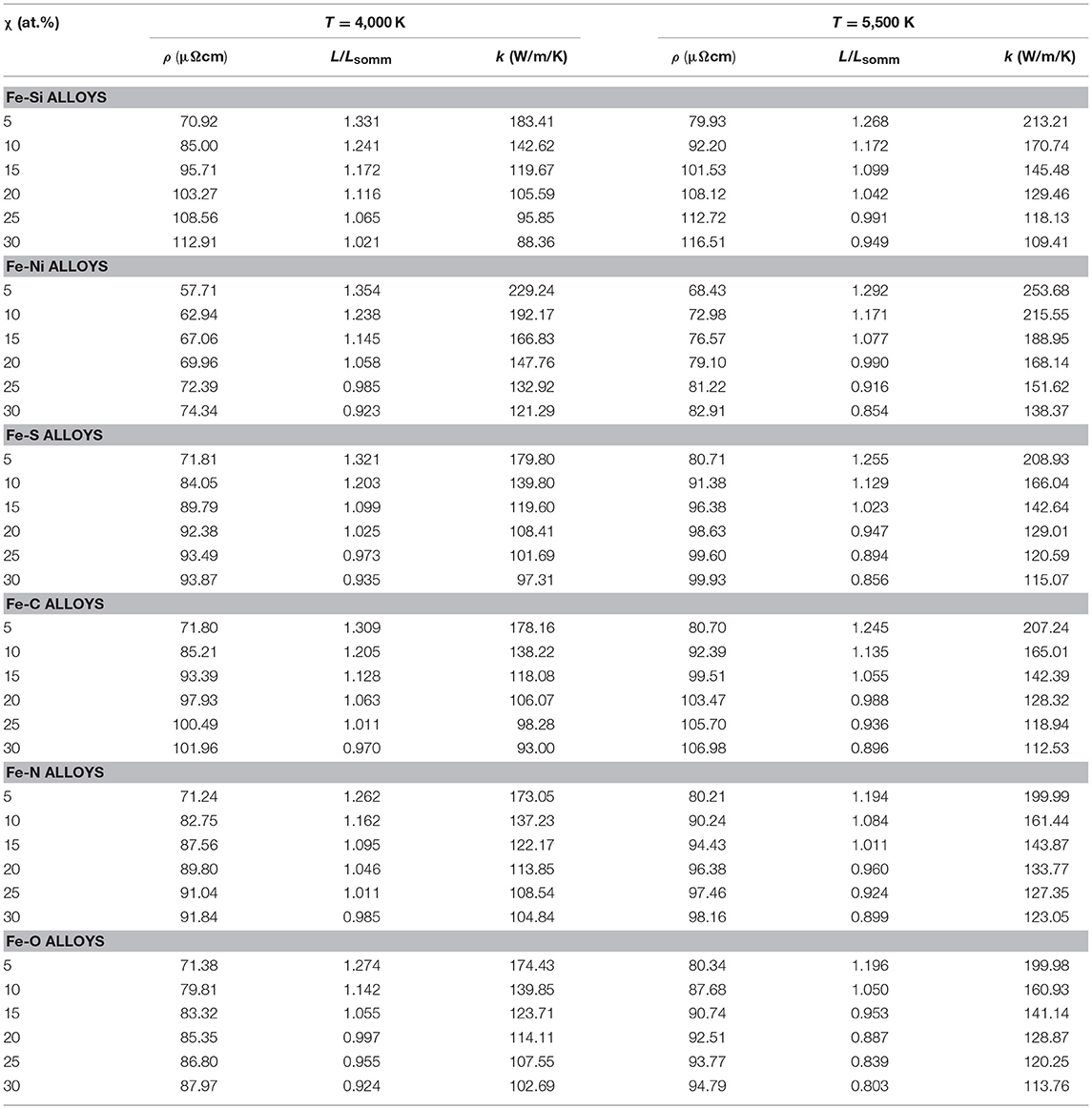
Figure 1A shows the impurity resistivities of impurity elements with the atomic numbers from 1 (H) to 18 (Kr) in fcc Au host. We tried to simulate both of non-magnetic and local magnetic disorder (LMD) state for all these impurity elements, and the LMD solution was obtained only for V, Cr, Mn, Fe, Co, and Ni impurity. For these six impurity elements, the impurity resistivity value is largely different between the non-magnetic state and the LMD state, and the LMD results are consistent with previous experimental results. The impurity resistivities of the other 12 elements without local magnetic moments show good agreement with previous experimental results (Friedel, 1956).

FIGURE 1

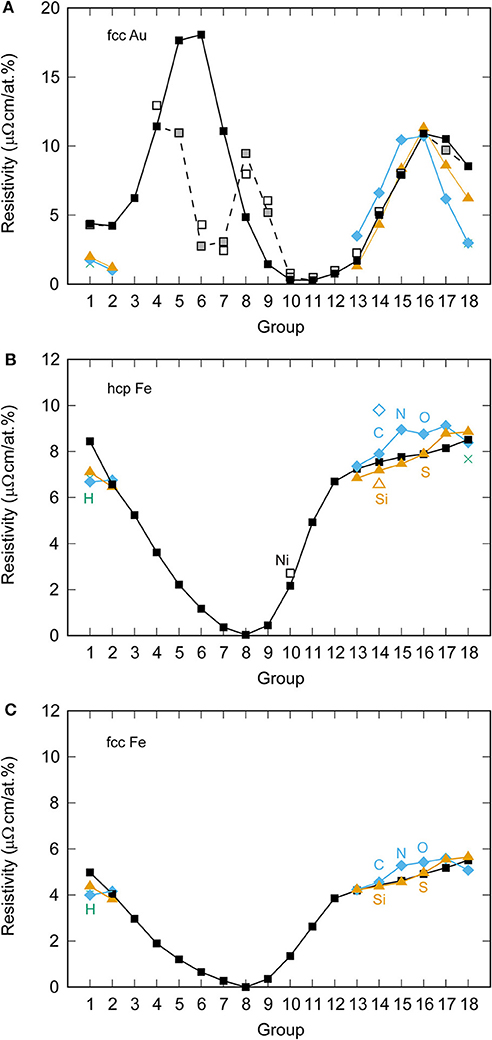
Figure 1. Impurity resistivities of 1st (green cross; H and He), 2nd (blue diamond; Li, Be, B, C, N, O, F and Ne), 3rd (orange triangle; Na, Mg, Al, Si, P, S, Cl, and Ar) and 4th (black square; K, Ca, Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, Ga, Ge, As, Se, Br and Kr) period elements. (A) fcc Au-alloys at 1 bar compared with literature values (Friedel, 1956). (B) hcp Fe-alloys at 40 GPa compared with previous DAC experiments (Ni: Gomi and Hirose, 2015; Si: Gomi et al., 2016; C: Zhang et al., 2018). (C) fcc Fe-alloys at 40 GPa. In common, solid symbols with solid lines are present nonmagnetic calculations, gray square symbols with broken line are obtained from present LMD calculations and open symbols represent previous experiments.

For 3rd period impurity elements located at the right hand side of Cu in the periodic table, namely Zn, Ga, Ge and As, are known to follow the Linde's rule (Norbury, 1921; Linde, 1932), and our first-principles calculations without local magnetic moment well reproduce previous experimental results (Friedel, 1956). Our calculations on 13 to 15 group of 2nd and 3rd period elements, which include the possible candidates of the light elements alloying with planetary cores (C, N, O, Si, S), also show the similar trend predicted by the Linde's rule.

In the Figure 1A, filled squares are present first-principles calculation without spin-polarization, which show parabola dependence. Open squares indicate present first-principles with local magnetic disorder (LMD), which reproduce previous experimental results (Friedel, 1956). To discuss the Friedel mode, we computed the partial density of states (PDOS) of impurity elements in fcc Au (Figure 2). Figure 2A shows the non-magnetic PDOS of Ti, V, Cr, Mn, Fe, Co, and Ni. In fcc Au, PDOS of these transition impurities have a sharp peak at the vicinity of the Fermi level, which is so-called virtual bond state (VBS) (Friedel, 1956; Mertig, 1999). The peak position shifts from high energy to low energy with increasing the atomic number. The impurity resistivities of non-magnetic fcc Au-based alloys exhibit the maximum coincidence with the VBS peak across the Fermi energy. Experimental and LMD impurity resistivity can also be explained by the peak position relevant to the Fermi energy. Figure 2B represents the PDOS of Cr with non-magnetic (solid line) and LMD (broken lines). The impurity resistivity of non-magnetic Cr is predicted to be 1.0 × 10⁻⁷ Ωm, which is larger than the experimental value of 4.0 × 10⁻⁸ Ωm. In an opposite manner, non-magnetic Co impurity resistivity is larger than experimental and LMD impurity resistivity. The VBS of non-magnetic Co is a little bit shifted to lower energy compared with the Fermi energy, but, in LMD state, the VBS split and the up spin peak move to the Fermi level. This causes the strong scattering.

FIGURE 2

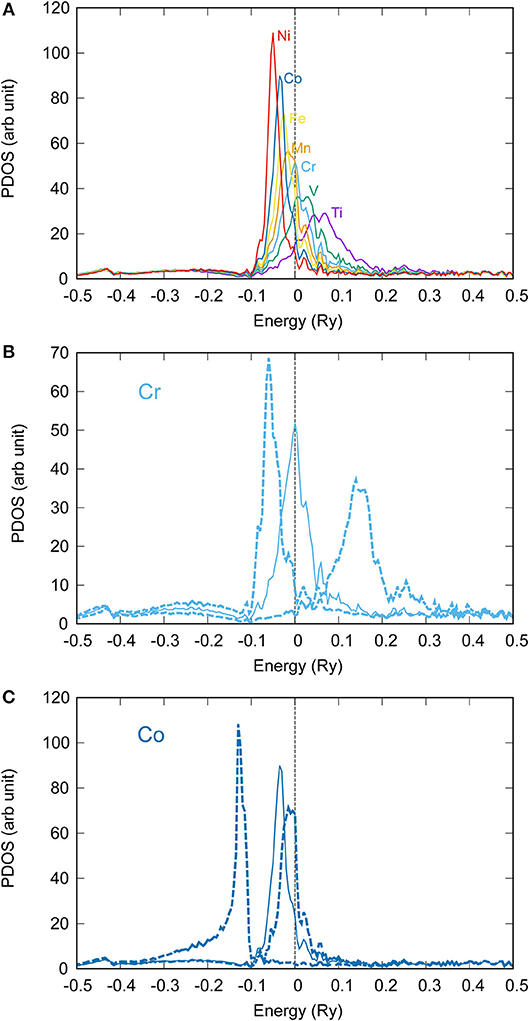
Figure 2. Partial density of states (PDOS) of impurity elements in fcc Au. (A) PDOS of Ti (purple), V (green), Cr (cyan), Mn (orange), Fe (yellow), Co (blue), and Ni (red) without local magnetic moment. (B) PDOS of Cr with (broken lines) and without (solid line) local magnetic moment. (C) PDOS of Co with (broken line) and without (solid line) local magnetic moment.

Figure 1B shows the impurity resistivities of hcp Fe-based alloys at the volume of 19.1 ų, which corresponds to the pressure of 40 GPa for pure hcp Fe at 300 K (Dewaele et al., 2006). Experimentally determined impurity resistivities of Ni, Si, and C are also plotted, which is interpolated between binary alloys (Gomi and Hirose, 2015; Gomi et al., 2016; Zhang et al., 2018) and pure Fe (Gomi et al., 2013) at ambient temperature. The present calculations of impurity resistivities of light element candidates (C, N, O, Si, and S) are almost identical and larger than Ni impurity resistivity. It is well-known that the impurity resistivity of 3d transition metal impurity in 3d transition metal host is small, in general (Tsiovkin et al., 2005, 2006). Among the light element candidates, the impurity resistivity increases with increasing atomic number in the same period. Also, in the same group, the second period atoms show higher impurity resistivity than third period atoms, which is consistent with the experimental fact that the impurity resistivity of C (Zhang et al., 2018) is higher than that of Si (Gomi et al., 2016). This trend is also observed for fcc Fe-based alloys (Figure 1C). Impurity resistivity of H seems comparable to the other light elements, however, it may be overestimate. In this study, we assumed that the all impurity elements substitute the Fe sites. But H is known to enter the interstitial sites (Antonov et al., 2002; Fukai, 2006). The partial density of states (PDOS) of interstitial H in hcp and double hexagonal close-packed (dhcp) Fe is located at far below the Fermi energy (e.g., Tsumuraya et al., 2012; Gomi et al., 2018). Therefore, Gomi et al. (2018) argued that the impurity resistivity of interstitial hydrogen is negligibly small. This is consistent with recent DAC experiments on fcc FeH_x alloys (Ohta et al., 2018).

Concentrated Alloys

In the previous section, we discussed dilute alloys, however, the Earth's core should have a large amount of impurity elements (e.g., Hirose et al., 2013). Gomi et al. (2016) reported the resistivity calculation of Fe-Si and Fe-Ni alloys by using the KKR-CPA method, as well as DAC experiments of Fe-Si alloys. Here, we show the systematic survey of impurity resistivity of light element candidates (C, N, O, Si, and S) and Ni in Fe-based high concentration alloys at zero Kelvin (Figure 3 and Table 1). Basically, impurity resistivity of light element candidates is larger than Ni, which agree with dilute alloy results. This can qualitatively be understood in terms of the broadening of energy dispersion via the uncertainty relationship between energy and time; ΔEΔt ≥ ℏ/2, where ΔE is the uncertainty in energy, Δt is electron life time, and ℏ is the reduced Planck's constant (the Dirac's constant) (Gomi et al., 2016). Figure 4 shows the Bloch spectral function along with the path, which connects the high symmetry points in the Brillouin zone of the hexagonal lattice. If there is no scattering, the Bloch spectral function is equivalent to the band structure of perfectly ordered crystal. Indeed, the broadening features of Fe-Ni alloys are weaker than that of other Fe-light elements alloys. At 19.10 ų (~40 GPa), Si shows the largest impurity resistivity, followed by C, S, and N. The smallest impurity resistivity is obtained from O impurity among the light element candidates. Note that this sequential order is completely different from that of dilute alloys (Figure 1).

FIGURE 3

Figure 3. Impurity resistivities of concentrated Fe based alloys (A) hcp at 40 GPa, (B) fcc at 40 GPa, (C) hcp at 120 GPa, (D) fcc at 120 GPa, (E) hcp at 1000 GPa, (F) fcc at 1000 GPa. The alloying elements are Si (purple), Ni (green), S (cyan), C (orange), N (yellow) and O (blue).

TABLE 1

Table 1. Impurity resistivity of Fe-alloys at zero Kelvin.

FIGURE 4

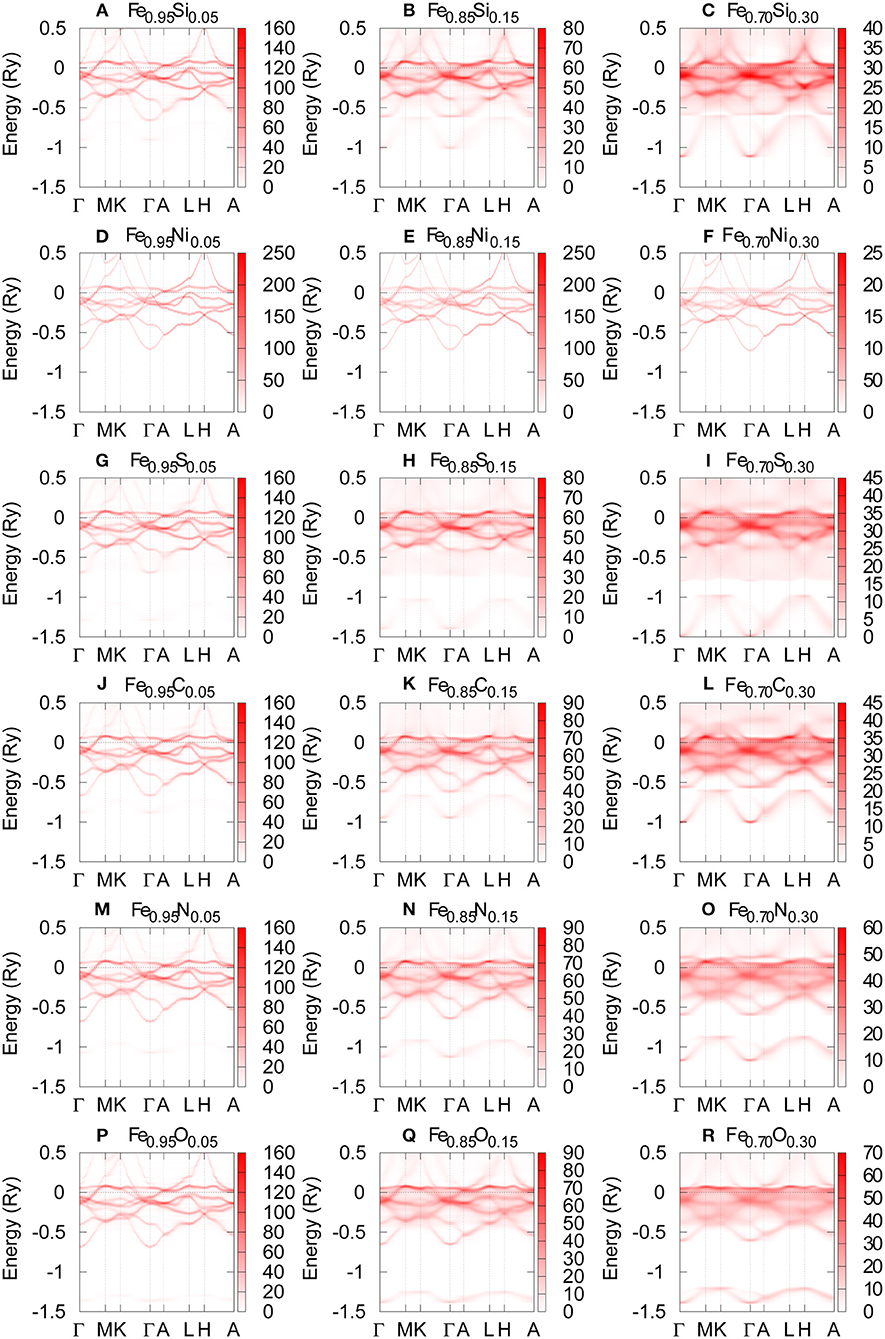
Figure 4. The band structure of hcp Fe-based alloys with the volume of 19.10 ų (~40 GPa). The Fermi energy is set to be 0 Ry. The compositions are (A) Fe_0.95Si_0.05, (B) Fe_0.85Si_0.15, (C) Fe_0.70Si0.30, (D) Fe_0.95Ni_0.05, (E) Fe_0.85Ni_0.15, (F) Fe_0.70Ni_0.30, (G) Fe_0.95S_0.05, (H) Fe_0.85S_0.15, (I) Fe_0.70Si_0.30, (J) Fe_0.95C_0.05, (K) Fe_0.85C_0.15, (L) Fe_0.70C_0.30, (M) Fe_0.95N_0.05, (N) Fe_0.85N_0.15, (O) Fe_0.70N_0.30, (P) Fe_0.95O_0.05, (Q) Fe_0.85O_0.15 and (R) Fe_0.70O_0.30.

This is potentially explained by the variation of the saturation resistivity due to the chemical composition. The electrical resistivity of transition metals and alloys tends to saturate at high resistivity (Mooij, 1973; Bohnenkamp et al., 2002). This resistivity saturation is observed when the mean free path of conduction electrons becomes comparable to the inter-atomic distance; this condition is so-called the Mott-Ioffe-Regel criteria (Mott, 1972; Gurvitch, 1981). This condition may be graphically identified from the cross sections of the Bloch spectral function at the Fermi energy (Figure 5), because the inverse of the mean free path is proportional to the width of the Fermi surface broadening, and the boundary of the first Brillouin zone is proportional to the inverse of the lattice parameter (Butler and Stocks, 1984; Butler, 1985; Banhart et al., 1989; Glasbrenner et al., 2014; Gomi et al., 2016). Gomi et al. (2016) compared the cross section of Fe-Si and Fe-Ni alloys, and argued that the non-linear concentration-resistivity relationship observed in Fe-Ni alloys is explained by the Nordheim's rule, whereas that of Fe-Si alloys is due to the resistivity saturation. Interestingly, the broadening feature of S, C, N and O impurity alloys are similar to the Si alloy. Especially, the O alloy's width seems even larger than that of Si alloy. This suggests that the high-concentration Fe-O alloys satisfies the Mott-Ioffe-Regel criteria, even though the impurity resistivity is smaller than Fe-Si alloy.

FIGURE 5

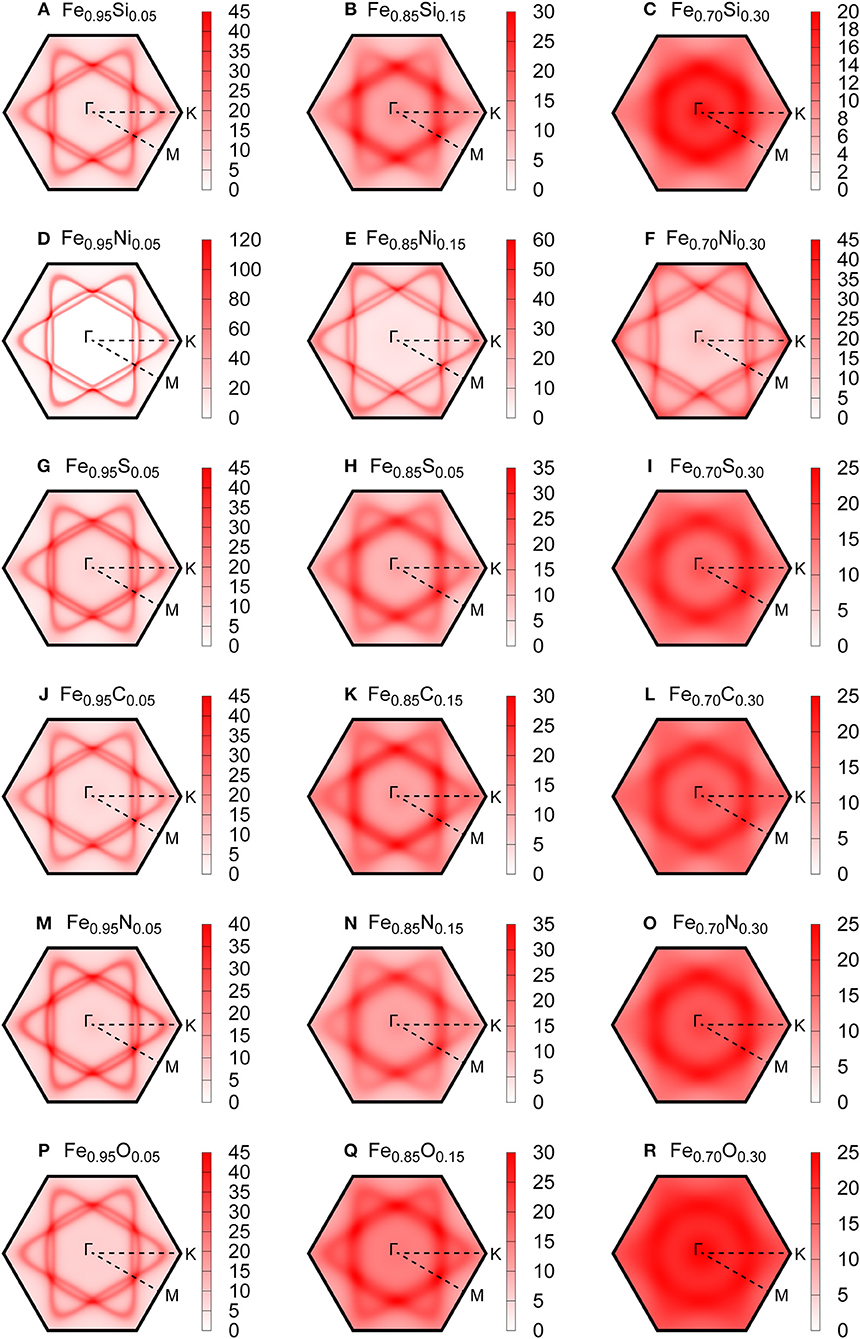
Figure 5. The cross section of the Bloch spectral function at the Fermi energy (Fermi surface) of hcp Fe-based alloys with the volume of 19.10 ų (~40 GPa). The compositions are (A) Fe_0.95Si_0.05, (B) Fe_0.85Si_0.15, (C) Fe_0.70Si_0.30, (D) Fe_0.95Ni_0.05, (E) Fe_0.85Ni_0.15, (F) Fe_0.70Ni_0.30, (G) Fe_0.95S_0.05, (H) Fe_0.85S_0.15, (I) Fe_0.70Si_0.30, (J) Fe_0.95C_0.05, (K) Fe_0.85C_0.15, (L) Fe_0.70C_0.30, (M) Fe_0.95N_0.05, (N) Fe_0.85N_0.15, (O) Fe_0.70N_0.30, (P) Fe_0.95O_0.05, (Q) Fe_0.85O_0.15 and (R) Fe_0.70O_0.30.

We also calculated the impurity resistivity of Fe-Si-S ternary alloys (Figure 6). The results are consistent with the DAC measurements by Suehiro et al. (2017). Figure 6 also implies the violation of the Matthiessen's rule, which is a simple sum rule of resistivity of all the scattering terms. The violation of the Matthiessen's rule is already reported by previous calculations (Glasbrenner et al., 2014; Gomi et al., 2016; Drchal et al., 2017).

FIGURE 6

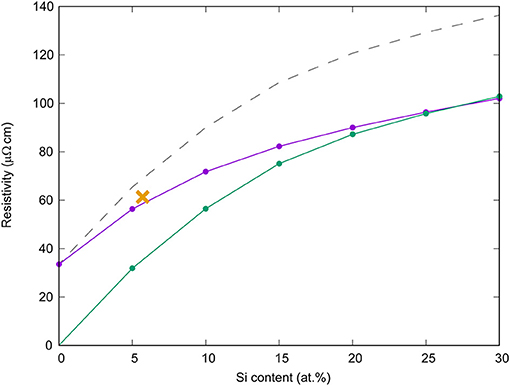
Figure 6. Impurity resistivity of hcp Fe_100−xSi_x binary (green) and Fe_95−xSi_xS₅ ternary (purple) alloys as a function of silicon content at the volume of 19.10 Å (~40 GPa) and zero Kelvin. Gray broken line shows the sum of the resistivity of Fe₉₅S₅ and Fe_100−xSi_x (the Matthiessen's rule). The orange cross represents the resistivity of hcp Fe_89.3Si_5.7S_5.0 alloy measured at ~40 GPa and ambient temperature (Suehiro et al., 2017).

Electronic Specific Heat and Wiedemann-Franz Law

Only a few direct thermal conductivity measurements at high pressure and temperature have been reported (Konôpková et al., 2011, 2016; McWilliams et al., 2015). Even though the thermal conductivity can directly be calculated from first-principles calculations (Sha and Cohen, 2011; de Koker et al., 2012; Pozzo et al., 2012, 2013, 2014; Pozzo and Alfè, 2016b; Pourovskii et al., 2017; Wagle et al., 2018; Xu et al., 2018; Yue and Hu, 2018), the Wiedemann-Franz law has been widely used to estimate the thermal conductivity of the Earth's core from the electrical resistivity measurements (Anderson, 1998; Stacey and Anderson, 2001; Stacey and Loper, 2007; Deng et al., 2013; Gomi et al., 2013, 2016; Seagle et al., 2013; Gomi and Hirose, 2015; Ohta et al., 2016, 2018; Hieu et al., 2017; Suehiro et al., 2017; Pommier, 2018; Silber et al., 2018; Zhang et al., 2018) (see Williams, 2018 for a recent review). The Lorenz number is related to the electronic band structure (Vafayi et al., 2006; Gomi and Hirose, 2015; Secco, 2017). Gomi and Hirose (2015) mentioned that the Lorenz number may have up to ~40 % uncertainty, based on the first-principles calculations on the electronic specific heat reported by Boness et al. (1986). However, this value was calculated only for pure Fe. Therefore, in this section, we investigated how the specific heat deviates from its Sommerfeld value for Fe-based alloys.

At around the ambient temperature, the electronic specific heat can be estimated based on the Sommerfeld expansion,

$\begin{array}{ll}{c}_{ve}\left(T\right)=\frac{{\pi }^2}{3}{k}_B^{2}D\left({\epsilon }_F\right)T& (2)\end{array}$

where c_ve is the electronic specific heat, k_B is the Boltzmann constant, ε_F is the Fermi energy, D(ε) is the DOS, and T is temperature. However, this relation is violated at high temperatures, as in terrestrial planetary cores (Boness et al., 1986; Boness and Brown, 1990; Tsuchiya and Kawamura, 2002; Lin et al., 2008). The exact values can be calculated from numerical integration with the electronic density of state. Following Boness et al. (1986), we calculated the electronic specific heat from its definition:

$\begin{array}{ll}{c}_{ve}\left(T\right)={\left(\frac{\partial u_e}{\partial T}\right)}_v,& (3)\end{array}$

where u_e is the internal energy of electrons, which can be obtained from electron density of state D(ε),

$\begin{array}{ll}{u}_e\left(T\right)={\displaystyle \int }\epsilon f\left(\epsilon ,T\right)D\left(\epsilon \right)\text{d}\epsilon & (4)\end{array}$

and f (ε, T) is the Fermi-Dirac distribution function,

$\begin{array}{ll}f\left(\epsilon ,T\right)=\frac{1}{exp\left\{\frac{ϵ-\mu \left(T\right)}{k_{B}T}\right\}+1}.& (5)\end{array}$

The chemical potential μ(T) is obtained from conservation of number of electrons (n_e),

$\begin{array}{ll}{n}_e={\displaystyle \int }f\left(\epsilon ,T\right)D\left(\epsilon \right)\text{d}\epsilon .& (6)\end{array}$

Figure 7 shows the electron DOS of Fe-Si alloys and the corresponding electronic specific heat. In the DOSs of pure Fe, sharp peaks are observed around the Fermi level. However, these sharp peaks are broaden by the effect of alloying of impurity elements (Gomi et al., 2016). In the temperature dependence of the electronic specific heat of Fe and Fe-Si alloys (Figures 7B,D,F,H), the solid lines are obtained from numerical calculation (Equations 3–6), whereas the broken lines are calculated based on the Sommerfeld expansion (Equation 2). Boness et al. (1986) and Boness and Brown (1990) argued that both numerical and Sommerfeld values of the electronic specific heat show linear temperature dependences for hcp Fe for temperatures below ~2,000 K. However, at higher than ~2,000 K, the numerical value increases more rapidly than the Sommerfeld value, which indicates the violation of the Sommerfeld expansion. Our calculations for pure Fe broadly reproduce this temperature dependence (Figure 7B). Such a violation is widely observed in many metals at extremely high temperature (e.g., Tsuchiya and Kawamura, 2002; Lin et al., 2008). On the other hand, as Si content increases, the deviation from the Sommerfeld expansion becomes small (Figure 7). This trend is also found in other Fe-light element alloys. Boness et al. (1986) argued that the relation between the deviation and the location of the Fermi level is within the sharp peaks of the DOS. In this sense, in highly concentrated alloys, these sharp peaks are smeared out because of impurity scattering. This is the reason why the deviation from the Sommerfeld expansion is relatively small in highly concentrated alloys. The Wiedemann-Franz law is based on the fact that the carrier of both of electric current and heat is conduction electrons. The pre-factor of linear temperature dependence attributed to the result of the Sommerfeld expansion, thus, Gomi and Hirose (2015) pointed out the deviation of the Lorenz number from its Sommerfeld value.

FIGURE 7

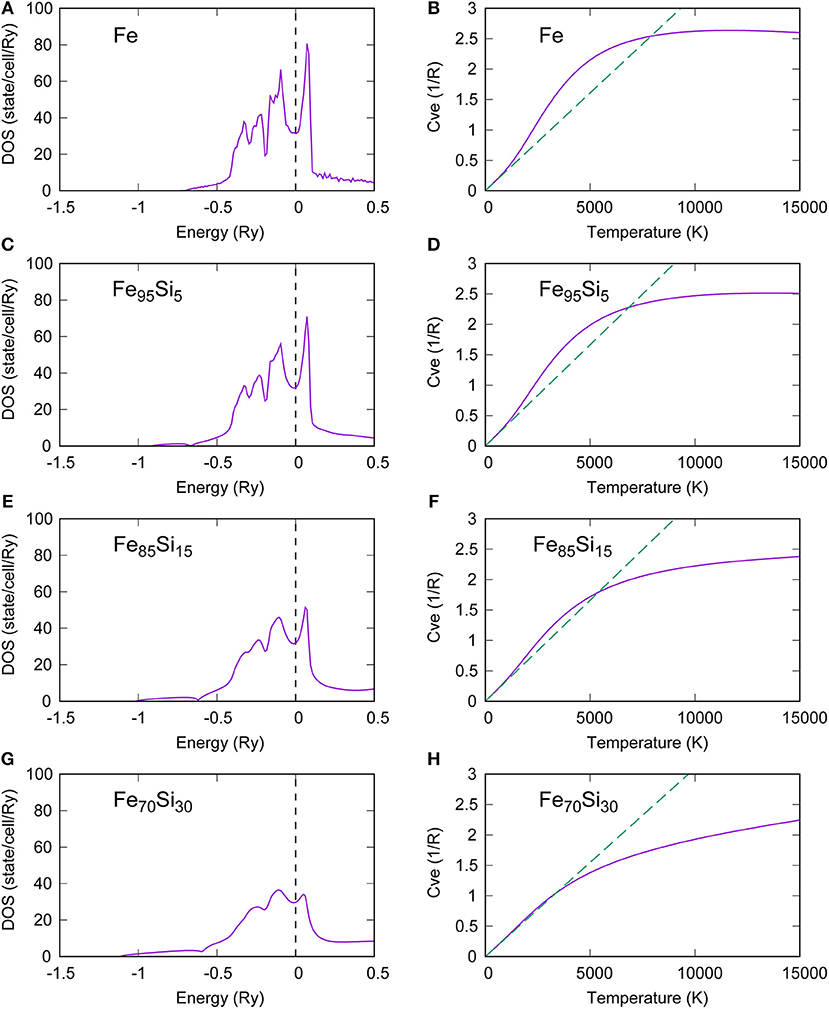
Figure 7. Density of states (DOS) (A,C,E,G) and corresponding electronic specific heat (B,D,F,H). Green broken lines represent the electronic specific heat obtained from the Sommerfeld expansion.

Figure 8 represents the deviation of the Lorenz number of Fe alloyed with Ni or light element candidates as function of temperature. The representative values at V = 16.27 ų and T = 4,000 K or 5,500 K are summarized in the Table 2. Broadly speaking, Fe-Si alloys show relatively large Lorenz number, whereas the alloying O tend to decrease the Lorenz number. Also, the Lorenz number decreases with increasing impurity concentration and/or temperature. These trends are consistent with previous first-principles molecular dynamics calculation (de Koker et al., 2012).

FIGURE 8

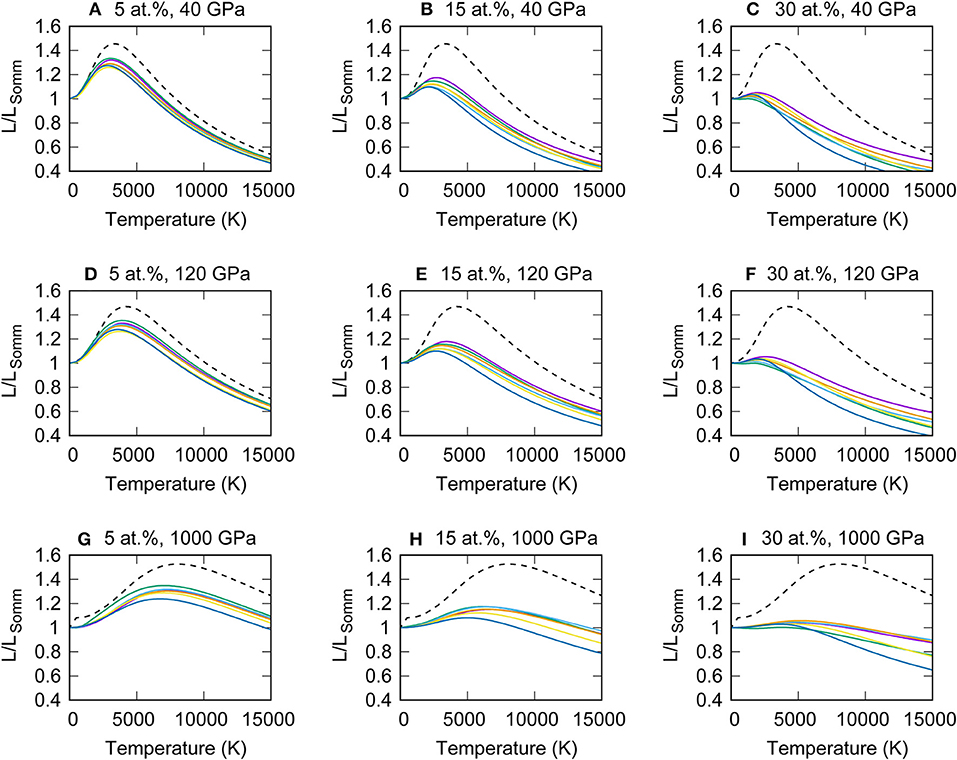
Figure 8. The deviation of the Lorenz number from the Sommerfeld value predicted by the electronic specific heat of hcp Fe_0.95X_0.05, Fe_0.85X_0.15 and Fe_0.70X_0.30, where X is Si (purple), Ni (green), S (cyan), C (orange), N (yellow) and O (blue) at the volume of V = 19.10 ų (P ~ 40 GPa at 300 K) (A–C), 16.27 ų (P~120 GPa at 300 K) (D–F) and 9.80 ų (P~1,000 GPa at 300 K) (G–I). Black broken lines are pure Fe for comparison.

TABLE 2

Table 2. Transport properties of Fe-alloys at the Earth's outer core (V = 16.27 ų).

It is worth mentioning about the relationship between energy-dependent conductivity σ(ε) and the Lorenz number. The thermal conductivity of metals is represented by using the Onsager's kinetic coefficient,

$\begin{array}{ll}{K}_n={\displaystyle \int }\sigma \left(\epsilon \right){\left(\epsilon -\mu \right)}^n\left(-\frac{\partial f}{\partial \epsilon }\right)\text{d}\epsilon ,& (7)\end{array}$

the electrical resistivity can be described as

$\begin{array}{ll}\sigma =K_0,& (8)\end{array}$

and the thermal conductivity is

$\begin{array}{ll}k=\frac{1}{e^{2}T}\left(K_2-\frac{K_1^2}{K_0}\right)& (9)\end{array}$

Applying the relaxation time approximation, the energy-dependent conductivity function can be expressed as

$\begin{array}{ll}\sigma \left(\epsilon \right)=\frac{e^2}{3}D\left(\epsilon \right){\left\{v\left(\epsilon \right)\right\}}^2\tau \left(\epsilon \right)& (10)\end{array}$

where D(ε) is the density of states, v(ε) is the group velocity and τ(ε) is the relaxation-time. Pourovskii et al. (2017) focused on the energy dependence of the relaxation-time of electron-electron scattering. They conducted the dynamical mean-field theory (DMFT) calculations to incorporate the electron correlation effects and found that the hcp Fe exhibits a nearly perfect Fermi liquid (FL) behavior, which strongly decrease the Lorenz number and hence the thermal conductivity. Xu et al. (2018) also carried out DMFT calculations. Although they did not observe FL behavior at high temperature, the energy dependence of the relaxation-time reduced the Lorenz number by 20–45% of the Sommerfeld value. Yue and Hu (2018) calculated the thermal conductivity of hcp Fe based on the non-equilibrium ab initio molecular dynamics (NEAIMD) simulation, which simultaneously incorporates the electron-phonon and electron-electron scattering. On the other hand, the present study focused on the energy dependence of the DOS, via the electronic specific heat, which also relates to the energy dependent conductivity as Equation (10). These recent theoretical assessments on the Lorenz number have been partly motivated by the inconsistency of experimental results between the electrical resistivity measurement by Ohta et al. (2016) and the thermal conductivity measurements by Konôpková et al. (2016) (see also Dobson, 2016). The theoretical works are broadly consistent with the experimental result of low resistivity (Ohta et al., 2016), however, failed to reproduce the low thermal conductivity (Konôpková et al., 2016). Pourovskii et al. (2017) reported k = 190 W/m/K for hcp Fe at the inner core boundary (ICB) condition. Xu et al. (2018) suggested k = 97 W/m/K for hcp Fe at the CMB. Yue and Hu (2018) obtained k ~ 190 W/m/K for hcp Fe at both of the CMB and ICB. These values are significantly higher than k = 33 and 46 W/m/K at the CMB and ICB, respectively (Konôpková et al., 2016). This situation is not altered by considering the effect of alloying on the energy dependence of DOS obtained by this study, and the uncertainties due to the deviation from the Sommerfeld value may be smaller than 30% for the Earth's core (see Table 2). Therefore, we conclude that, even though it is a not good approximation for pure Fe, the Sommerfeld value is a good proxy of the Lorenz number of the planetary cores.

Electrical Resistivity and Thermal Conductivity of the Earth's Core

In the section Concentrated Alloys, we computed the impurity resistivity of Ni and light element candidates (C, N, O, Si, and S). In the section Electronic Specific Heat and Wiedemann-Franz Law, we computed the electron DOS of Fe-based alloys to estimate the Lorenz number, which varies with pressure, temperature, impurity species and concentration. In this section, we first calculated the total resistivity of the Earth's core by combining the impurity resistivity and phonon-contributed resistivity following Gomi et al. (2016). Then, we estimated the thermal conductivity via the Wiedemann-Franz law (Equation 1) using the present resistivity and the Lorenz number.

The total electrical resistivity was calculated from the Cote and Meisel (1978) model combined with the present impurity resistivity and the phonon-contributed resistivity modeled by Gomi et al. (2013, 2016, 2018).

$\begin{array}{l}{\rho }_{\text{tot}}\left(V,T\right)=\left(1-\frac{{\rho }_{\text{tot}}\left(V,T\right)}{{\rho }_{\text{sat}}\left(V\right)}\right){\rho }_{\text{ph},\text{ideal}}\left(V,T\right)\\ +{\rho }_{\text{imp}}\left(V\right)exp\left(-2W\left(V,T\right)\right)& (11)\end{array}$

where ρ_tot(V, T) is the total electrical resistivity, ρ_sat(V) is the saturation resistivity, ρ_ph,ideal(V, T) is the “ideal” phonon-contributed resistivity, which neglects the effect of the resistivity saturation, ρ_imp(V) is the impurity resistivity, and exp(−2W(V, T)) is the Debye Waller factor, which gives the temperature dependence of the impurity resistivity. Because the resistivity saturation phenomena occurs when the mean free path becomes comparable to the inter atomic distance, the saturation resistivity may scale by V^1/3 (Gomi et al., 2013)

$\begin{array}{ll}{\rho }_{\text{sat}}\left(V\right)={\rho }_{\text{sat}}\left(V_0\right){\left(\frac{V}{V_0}\right)}^{\frac{1}{3}}& (12)\end{array}$

where ρ_sat(V₀) = 1.68 × 10⁻⁶ Ωm is the saturation resistivity of bcc and fcc Fe-based alloys (Bohnenkamp et al., 2002). The phonon-contributed resistivity of hcp Fe at ambient temperature was obtained from previous measurement (Gomi et al., 2013) as

$\begin{array}{ll}\rho \left(V,300K\right)=5.26\times 10^{-9}\times {\left(1.24-\frac{V}{V_0}\right)}^{-3.21}\Omega m& (13)\end{array}$

The “ideal” phonon-contributed resistivity can be extrapolated from the ambient temperature resistivity by using the Bloch-Grüneisen formula,

$\begin{array}{ll}{\rho }_{\text{ph},\text{ideal}}\left(V,T\right)=B\left(V\right){\left(\frac{T}{{\Theta }_D\left(V\right)}\right)}^5{\displaystyle {{\displaystyle \int }}_0^{\frac{{\Theta }_D\left(V\right)}{T}}}\frac{x^5\text{d}x}{\left(exp\left(x\right)-1\right)\left(1-exp\left(-x\right)\right)}& (14)\end{array}$

where B(V) is the material constant, which can be obtained from Equation (13), and Θ_D(V) is the Debye temperature (Dewaele et al., 2006). Assuming the Debye model, W(V, T) can be calculated as Markowitz (1977)

$\begin{array}{ll}W\left(V,T\right)=\frac{3{\hslash }^2{K}^2{T}^2}{2m{k}_B{\Theta }_D^3}{\displaystyle {{\displaystyle \int }}_0^{\frac{{\Theta }_D}{T}}}\left(\frac{1}{exp\left(x\right)-1}+\frac{1}{2}\right)x\text{d}x& (15)\end{array}$

where h is the reduced Planck's constant (the Dirac's constant), m is the atomic mass, K(V) ~ π/a is the electronic wave vector transfer, where a is the lattice parameter. The impurity resistivity ρ_imp(V) is obtained from the present DFT calculations of hcp Fe-based alloys. The resistivity of the solid Fe alloy depends on the crystal structure (Figures 1, 3). The crystal structure of Fe at the Earth's core pressure is known to be hcp (Tateno et al., 2010; Smith et al., 2018). However, its stability field may be influenced by further compression (Stixrude, 2012). Alloying elements also affect the crystal structure: Ni extends the stability field of fcc phase (Kuwayama et al., 2008), H stabilizes dhcp structure (Gomi et al., 2018) and Si favors B2 or body-centered cubic (bcc) structure (Tateno et al., 2015; Ozawa et al., 2016). Recent shock compression experiments on Fe with 15 wt.% Si suggest that bcc structure is stable at the center of super-Earth with three times Earth mass (Wicks et al., 2018). Although the solid phase crystal structure is important, we simply assumed that the hcp Fe alloys are good proxy. The spin disorder scattering is potentially important (Drchal et al., 2017), especially for small planets with hydrogen containing core (Gomi et al., 2018). But in this study, we neglect this effect. It is known that the resistivity change upon melting is very small for transition metals at 1 bar (e.g., Van Zytveld, 1980). Van Zytveld (1980) reported that the resistivity increase upon melting is ~8% for Fe. The ratio of resistivity between liquid and solid phase at the melting temperature, ρ_L/ρ_S, is generally very close to unity for transition metals, but it is also known to be ~1.5 for alkali metals and ~2 for noble metals (Mott, 1934; Cusack and Enderby, 1960; Faber, 1972). This systematic trend was also confirmed by Secco and co-workers at high pressure (Ezenwa and Secco, 2017a,b,c; Ezenwa et al., 2017; Silber et al., 2017, 2018). Mott (1934) considered that the resistivity change upon melting is related to the entropy of fusion, and semi-empirically formulated as follows:

$\begin{array}{ll}\frac{{\rho }_L}{{\rho }_S}=exp\left(\frac{2S_m}{3R}\right)& (16)\end{array}$

where S_m is the entropy of fusion and R is the gas constant. This model shows good agreement with large resistivity ratio observed in alkali and noble metals, however, it cannot account the small degree of the resistivity jump of transition metals. One possible modification of this model is the incorporation of the effect of the resistivity saturation (Mott, 1972); the solid transition metals exhibit already large electrical resistivity at the melting temperature, which is comparable to the saturation resistivity. As a result the saturation suppresses the resistivity jump upon melting. The other model was proposed by Wagle and Steinle-Neumann (2018) based on the Ziman approximation (Ziman, 1961), which yields the following equation

$\begin{array}{ll}\frac{{\rho }_L}{{\rho }_S}={\left(\frac{K_{T,L}}{K_{T,S}}\right)}^{-1}{\left(\frac{{\rho }_L^{\text{den}}}{{\rho }_S^{\text{den}}}\right)}^{-2}& (17)\end{array}$

where K_{T, L} and K_{T, S} are the isothermal bulk modulus, ${\rho }_L^{\text{den}}$ and ${\rho }_S^{\text{den}}$ are the density of liquid and solid metal, respectively. This model can reasonably reproduce the small jump of transition metals, as well as the large contrast of simple metals (e.g., Na and Al). However, it systematically underestimates the resistivity ratio of closed d-shell metals (Zn and noble metals). These two models may be verified by investigating the pressure dependence of the resistivity ratio. If the former model is correct, the resistivity ratio may increase with increasing pressure, because the resistivity of hcp Fe decreases faster than the V^1/3 dependence of the saturation resistivity (Gomi et al., 2013). On the other hands, if the latter model is correct, the resistivity ratio may not significantly change (Wagle and Steinle-Neumann, 2018). The results of high-pressure melting experiments are still controversial. Secco and Schloessin (1989), Silber et al. (2018), and Ezenwa and Secco (2017c) measured the resistivity of Fe and Co, respectively. These measurements on transition metals verified the small degree of the resistivity jump upon melting even at high pressure 12 GPa. Deng et al. (2013) also measured the resistivity of Fe, but their results seem to have large resistivity enhancement upon melting at the identical pressure. Pommier (2018) reproduced the Deng et al. (2013)'s results at 4.5 GPa. Ohta et al. (2016) carried out the melting experiments in a laser-heated diamond-anvil cell showing ~20% increase upon melting at 51 GPa. Bi et al. (2002) measured the electrical resistivity of shock induced melting of Fe with melt fraction of 0.7 at 208 GPa. The resultant resistivity values follow the general trend obtained in the solid phase region along the Hugoniot, which suggests the absence of large resistivity change upon melting. In this study, we assume that the resistivity difference between liquid and solid Fe-alloys is very small. This may be good approximation, because, even if the former model is correct, the total core resistivity may be close to the saturation resistivity because of large impurity resistivity. Finally, the thermal conductivity is calculated via the Wiedemann-Franz law (Equation 1) with the predicted Lorenz number from the electronic specific heat (see section Electronic Specific Heat and Wiedemann-Franz Law).

Figure 9 illustrates the electrical resistivity of Fe alloyed with 5, 15, or 30 atomic % impurity elements at the volume of 19.10, 16.27, and 9.80 ų. The electrical resistivity increases with increasing impurity concentration. The impurity resistivity of Si is the largest and that of Ni is the smallest, as already discussed in the section Concentrated Alloys. The electrical resistivity is also enhanced at high temperatures following the Bloch-Grüneisen formula (Equation 14). At high resistivity ~100 μΩcm, the total resistivity saturates. The saturation resistivity decreases with increasing pressure via the Equation (12). Figure 10 represents the thermal conductivity of Fe alloyed with 5, 15, or 30 atomic % impurity elements at the volume of 19.10, 16.27, and 9.80 ų. The temperature and impurity concentration dependences of the thermal conductivity are more complicated compared with the electrical resistivity. At low temperatures smaller than ~5,000 K, the thermal conductivities of Fe based alloys have positive temperature coefficient because of the following reason. First, it should be noted that the Wiedemann-Franz law (Equation 1) predicts the linear temperature dependence, if the electrical resistivity and the Lorenz number are independent of temperature. This condition is nearly satisfied for the electrical resistivity of Fe-light element alloys because, at low temperatures, the impurity resistivity is predominant. Also, as shown in Figure 8, the Lorenz number exhibits positive temperature coefficient. Combining these two temperature effects, the thermal conductivity initially increases with increasing temperature. Above 5,000 K, the thermal conductivity becomes insensitive to temperature. The temperature coefficient of the resistivity becomes small due to the resistivity saturation (Figure 9), whereas the Lorenz number tends to decrease with increasing temperature (Figure 8). Therefore, the effects of temperature on the Lorenz number and the linear temperature factor in the Wiedemann-Franz law are canceled out, which result in the nearly constant thermal conductivity at high temperature. Table 2 summarized the electrical resistivity, the Lorenz number and the thermal conductivity of Fe alloys at V = 16.27 ų and T = 4,000 or 5,500 K, which correspond to the Earth's outer core conditions. Considering the compositional effects, our preferred thermal conductivity is higher than ~90 W/m/K.

FIGURE 9

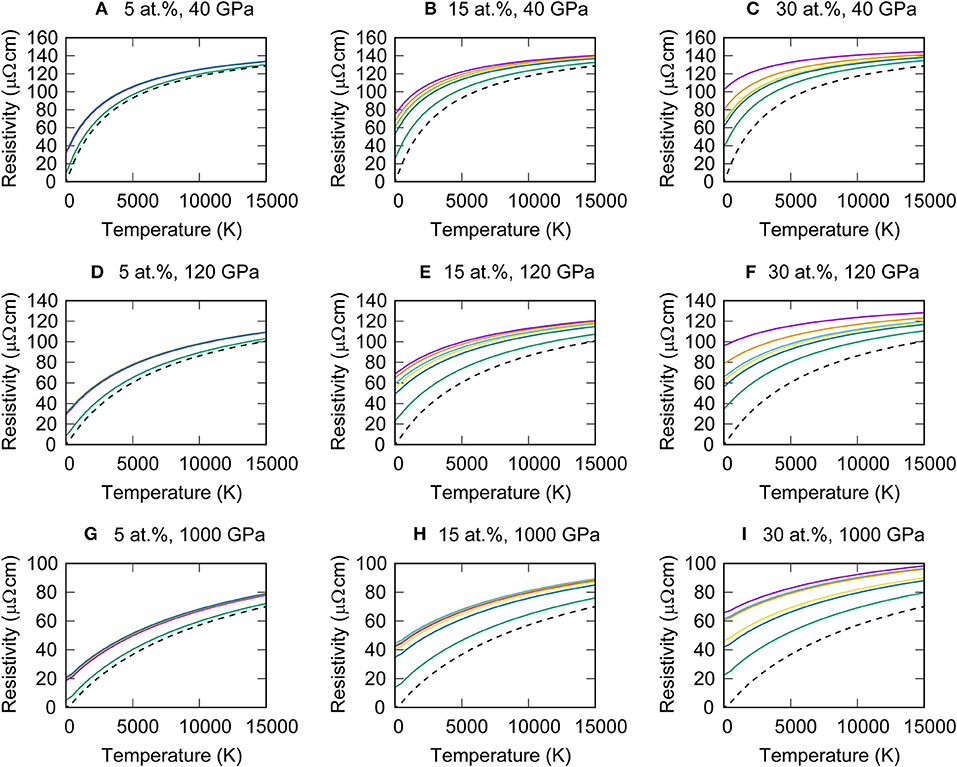
Figure 9. Electrical resistivity of hcp Fe_0.95X_0.05, Fe_0.85X_0.15, and Fe_0.70X_0.30, where X is Si (purple), Ni (green), S (cyan), C (orange), N (yellow), and O (blue) at the volume of V = 19.10 ų (P~40 GPa at 300 K) (A–C), 16.27 ų (P ~ 120 GPa at 300 K) (D–F), and 9.80 ų (P ~ 1,000 GPa at 300 K) (G–I). Black broken lines are pure Fe for comparison.

FIGURE 10

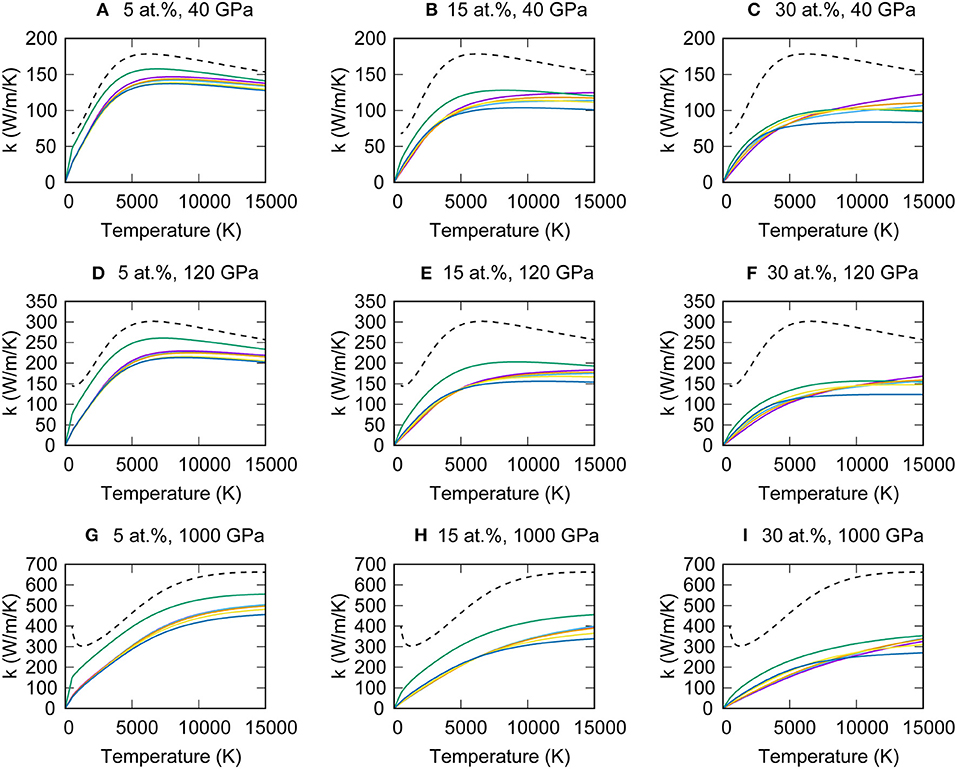
Figure 10. Thermal conductivity of hcp Fe_0.95X_0.05, Fe_0.85X_0.15, and Fe_0.70X_0.30, where X is Si (purple), Ni (green), S (cyan), C (orange), N (yellow), and O (blue) at the volume of V = 19.10 ų (P~40 GPa at 300 K) (A–C), 16.27 ų (P~120 GPa at 300 K) (D–F), and 9.80 ų (P~1,000 GPa at 300 K) (G–I). Black broken lines are pure Fe for comparison.

Heat Flux at the CMB of Super-Earths

The recent developments of astronomical observation can allow to find many terrestrial exoplanets. The exoplanets with the masses of <10 times the Earth's mass (M_E) are so-called super-Earths (e.g., Valencia et al., 2007; Charbonneau et al., 2009). Some of these planets locate within the habitable zone, suggesting the presence of liquid water at the surface of the planet (e.g., Anglada-Escudé et al., 2012; Gillon et al., 2017). In term of the surface habitability, the existence of the global magnetic fields is a necessary condition. The planetary magnetic field is generated via the geodynamo driven by thermal and/or chemical convective motion in the liquid outer core. If super-Earths have thermally driven geodynamo, the heat flux through the bottom of mantle, q_CMB, must be higher than the conductive heat flux along the adiabatic temperature gradient at the top of their core

$\begin{array}{ll}{q}_s=k{\left(\frac{\partial T}{\partial r}\right)}_S=k\frac{{\rho }^{\text{den}}g\gamma }{K_S}T& (18)\end{array}$

where k is the thermal conductivity, ρ^den is the density, g is the gravity, γ is the Grüneisen parameter and K_S is the adiabatic bulk modulus. Morard et al. (2011) suggested the absence of liquid core in the super Earth from the first-principles calculation of melting temperature of Fe. Many studies investigated the mantle convection in the super-Earths with varying physical quantities. The effects of depth increasing mantle viscosity (Tackley et al., 2013), thermal conductivity (Kameyama and Yamamoto, 2018) and compressibility (CíŽková et al., 2017) suppress the mantle convection in the deep portion of the super-Earths. The phase transitions of mantle materials with negative Clapeyron slope also contribute as a stratification of the mantle (Umemoto et al., 2006; Tsuchiya and Tsuchiya, 2011; McWilliams et al., 2012). On the other hand, Stixrude (2014) argued the energetics of accretion, giant impact and core formation events of the super-Earths, and concluded that the mantle convection is sufficiently vigorous to sustain the geodynamo. Miyagoshi et al. (2017) demonstrated the occurrence of thermal convection in the mantle of super-Earth from numerical mantle convection simulations with initially hot shallow mantle conditions, which is expected due to giant impacts. Tachinami et al. (2011) calculated the thermal evolution of the cores of super-Earths coupled with the mixing-length theory for the mantle convective heat transfer, in order to discuss the possibility of the thermally driven geodynamo. However, they adopted the core thermal conductivity of k = 40 W/m/K, which is one order smaller than the present estimate for the 10 Earth mass planet. The purpose of this section is to calculate the conductive heat flux at the top of the liquid core of super-Earths with high thermal conductivity inferred from the previous sections.

To calculate the energy balance in the super-Earths, one-dimensional density and temperature model is required (e.g., Valencia et al., 2006; Papuc and Davies, 2008; Tachinami et al., 2011). In this study, we read the density profile of super-Earths from Figure 1 of Tachinami et al. (2011). Hence, the planetary masses of our model are 0.1, 0.2, 0.5, 1, 2, 5, and 10 times to the Earth's mass (M_E). The gravity profile can be calculated from

$\begin{array}{ll}g\left(r\right)=G\frac{M\left(r\right)}{r^2}& (19)\end{array}$

where G = 6.67408 × 10⁻¹¹ m³/kg/s² is the gravitational constant, M(r) is the inner mass of the radial position r. The mass of the inner core M_c is assumed to be 30% of the planetary mass M_p. The pressure-density relation at the reference temperature T₀ = 300 K is given by the Vinet equation of state (EOS):

$\begin{array}{l}P({\rho }^{\text{den}},T_0)=3K_0{\left(\frac{{\rho }_0^{\text{den}}}{{\rho }^{\text{den}}}\right)}^{-\frac{2}{3}}\left\{1-{\left(\frac{{\rho }_0^{\text{den}}}{{\rho }^{\text{den}}}\right)}^{\frac{1}{3}}\right\}\\ \exp \left[\frac{3}{2}\left(K_0\prime -1\right)\left\{1-{\left(\frac{{\rho }_0^{\text{den}}}{{\rho }^{\text{den}}}\right)}^{\frac{1}{3}}\right\}\right]& (20)\end{array}$

where ${\rho }_0^{\text{den}}$, K₀ and K′₀ are density, bulk modulus and its pressure differentiation at zero pressure, respectively. These parameters are given as ${\rho }_{0,Fe}^{\text{den}}$ = 8,300 kg/m³, K_0,Fe = 164.8 GPa and K′_0,Fe = 5.33 for Fe liquid, whereas ${\rho }_{0,\text{FeS}}^{\text{den}}$ = 5,330 kg/m³, K_0,FeS = 126 GPa and K′_0,FeS = 4.8 for FeS liquid (see Tachinami et al., 2011 and references therein). The EOS parameters for the outer core of Fe-FeS liquid mixture are given as function of mass fraction of S as

$\begin{array}{ll}{x}_{\text{FeS}}=x_S\frac{Z_{\text{Fe}}+Z_S}{Z_S}& (21)\end{array}$

$\begin{array}{ll}{\rho }_{0,\text{OC}}^{\text{den}}={\left(\frac{1-x_{\text{FeS}}}{{\rho }_{0,\text{Fe}}^{\text{den}}}+\frac{x_{\text{FeS}}}{{\rho }_{0,\text{FeS}}^{\text{den}}}\right)}^{-1}& (22)\end{array}$

$\begin{array}{ll}{K}_{0,\text{OC}}=\frac{1}{{\rho }_{0,\text{OC}}^{\text{den}}}\frac{1}{\frac{1-x_{\text{FeS}}}{{\rho }_{0,\text{Fe}}^{\text{den}}}\frac{1}{K_{0,\text{Fe}}}+\frac{x_{\text{FeS}}}{{\rho }_{0,\text{FeS}}^{\text{den}}}\frac{1}{K_{\text{FeS}}}}& (23)\end{array}$

$\begin{array}{ll}K{\prime }_{\text{0},\text{OC}}=-1+{\rho }_{\text{0},\text{Fe}}^{\text{den}}{K}_{\text{0},\text{OC}}^2\left(\frac{1-x_{\text{FeS}}}{{\rho }_{\text{0},\text{Fe}}^{\text{den}}}\frac{1+K{\prime }_{\text{0},\text{Fe}}}{K_{\text{0},\text{Fe}}^2}+\frac{x_{\text{FeS}}}{{\rho }_{\text{0},\text{FeS}}^{\text{den}}}\frac{1+K{\prime }_{\text{0},\text{FeS}}}{K_{\text{0},\text{FeS}}^2}\right)& (24)\end{array}$

where x_Fe, x_FeS are mass fractions of Fe and FeS, Z_Fe = 55.845 and Z_S = 32.065 are mass of Fe and S. Following Tachinami et al. (2011), we assumed the bulk S content is set to be x_0S = 0.1 and also assumed that S completely partition into the outer core, the mass fraction of S can be calculated as

$\begin{array}{ll}{x}_S=x_{0S}\frac{M_c}{M_c-M_{ic}}& (25)\end{array}$

where M_c and M_ic are the mass of bulk and inner core, respectively. In this study, we only considered the situation that M_ic = 0.06 M_c, which is close to the present Earth's value. This leads x_S = 0.10638. Our assumption of pure Fe inner core may look unrealistic, however, note that the present heat flux calculation does not refer the chemical composition of the inner core. The isothermal bulk modulus at the reference temperature is obtained by differentiation of the Vinet density-pressure equation of states:

$\begin{array}{l}{K}_T\left({\rho }^{\text{den}},T_0\right)=\{2K_0\left[1-{\left(\frac{{\rho }_0^{\text{den}}}{{\rho }^{\text{den}}}\right)}^{\frac{1}{3}}\right]{\left(\frac{{\rho }^{\text{den}}}{{\rho }_0^{\text{den}}}\right)}^{\frac{2}{3}}\\ +\frac{3}{2}\left(K\prime -1\right)K_0\left[1-{\left(\frac{{\rho }_0^{\text{den}}}{{\rho }^{\text{den}}}\right)}^{\frac{1}{3}}\right]{\left(\frac{{\rho }^{\text{den}}}{{\rho }_0^{\text{den}}}\right)}^{\frac{1}{3}}\\ +K_0{\left(\frac{{\rho }^{\text{den}}}{{\rho }_0^{\text{den}}}\right)}^{\frac{1}{3}}\}\exp \left\{\frac{3}{2}\left(K\prime -1\right)\left[1-{\left(\frac{{\rho }_0^{\text{den}}}{{\rho }^{\text{den}}}\right)}^{\frac{1}{3}}\right]\right\}& (26)\end{array}$

The thermal effect on the equation of states is incorporated as the thermal corrections by the Mie-Grüneisen equation with the Debye model as:

$\begin{array}{ll}P\left({\rho }^{\text{den}},T\right)=P\left({\rho }^{\text{den}},T_0\right)+\Delta P_{\text{th}}\left({\rho }^{\text{den}},T\right)& (27)\end{array}$

$\begin{array}{ll}\Delta P_{\text{th}}\left({\rho }^{\text{den}},T\right)=\left(\frac{\gamma }{V}\right)\left(E_{th}\left({\rho }^{\text{den}},T\right)-E_{th}\left({\rho }^{\text{den}},T_0\right)\right)& (28)\end{array}$

Similarly, the thermal effect on the isothermal bulk modulus is represented as follows (Stixrude and Lithgow-Bertelloni, 2005):

$\begin{array}{ll}{K}_T\left({\rho }^{\text{den}},T\right)=K_T\left({\rho }^{\text{den}},T_0\right)+\Delta K_T\left({\rho }^{\text{den}},T\right)& (29)\end{array}$

$\begin{array}{l}\Delta K_T\left({\rho }^{\text{den}},T\right)=\left(\gamma +1-q\right)\frac{\gamma }{V}(E_{th}\left({\rho }^{\text{den}},T\right)\\ -E_{th}\left({\rho }^{\text{den}},T_0\right))-\frac{{\gamma }^2}{V}(T{C}_v\left({\rho }^{\text{den}},T\right)\\ -T_0{C}_v\left({\rho }^{\text{den}},T_0\right))& (30)\end{array}$

$\begin{array}{ll}{E}_{th}\left({\rho }^{\text{den}},T\right)=9n{k}_{B}T{\left(\frac{T}{{\Theta }_D}\right)}^3{\displaystyle {{\displaystyle \int }}_0^{\frac{{\Theta }_D}{T}}}\frac{x^3}{exp\left(x\right)-1}\text{d}x& (31)\end{array}$

$\begin{array}{ll}{C}_v\left({\rho }^{\text{den}},T\right)=9n{k}_B{\left(\frac{T}{{\Theta }_D}\right)}^3{\displaystyle {{\displaystyle \int }}_0^{\frac{{\Theta }_D}{T}}}\frac{x^{4}exp\left(x\right)}{{\left(exp\left(x\right)-1\right)}^2}\text{d}x& (32)\end{array}$

where V is the molar volume (1/V = ρ^den/V₀${\rho }_0^{\text{den}}$).

$\begin{array}{ll}{K}_S=K_T\left(1+1\alpha \gamma T\right)& (33)\end{array}$

$\begin{array}{ll}\alpha =\frac{\gamma C_v}{V{K}_T}& (34)\end{array}$

The Grüneisen parameter can be calculated as follows:

$\begin{array}{ll}\gamma ={\gamma }_0{\left(\frac{{\rho }_0^{\text{den}}}{{\rho }^{\text{den}}}\right)}^q& (35)\end{array}$

with the parameter values of γ₀ = 1.36 and q = 0.91 for the outer core liquid (see Tachinami et al., 2011 and references therein). The melting temperature of Fe at the ICB is estimated based on Anzellini et al. (2013) as

$\begin{array}{ll}{T}_{\text{m},\text{Fe}}=T_{\text{TP}}{\left(\frac{P-P_{\text{TP}}}{161.2}+1\right)}^{\frac{1}{1.72}}& (36)\end{array}$

where P_TP = 98.5 GPa and T_TP = 3,712 K. This extrapolation is same as the first-principles calculation (Morard et al., 2011). The ICB temperature should be equal to the melting temperature of Fe-S alloy at the ICB pressure, which may be lower than the melting temperature of pure Fe. Such melting temperature depression is expressed as T_ICB = (1 – χ_S)T_m,Fe (Usselman, 1975; Stevenson et al., 1983). Assuming the adiabatic temperature gradient, the temperature profile can be calculated by solving the following ordinary differential equation:

$\begin{array}{ll}\frac{\text{d}T}{\text{d}r}=-\frac{{\rho }^{\text{den}}g\gamma }{K_S}T& (37)\end{array}$

We estimated the thermal conductivity of the top of the core of super-Earths from KKR-CPA calculation of Fe_82.83S_37.13 alloys combined with phonon scattering (see section Electrical Resistivity and Thermal Conductivity of the Earth's Core) (Figure 11A). The thermal conductivity of 1 M_E planet is calculated to be k = 124 W/m/K. The thermal conductivity increases with increasing planetary mass, and is k = 361 W/m/K for the 10 M_E planet. Stixrude (2014) extrapolate the thermal conductivity from Pozzo et al. (2012), which yields $k\propto M_p^{\frac{1}{2}}$. Our thermal conductivity values are basically consistent with Stixrude (2014). The actual heat flux across the CMB is regulated by the thermal conduction at the thermal boundary layer (TBL) located at the bottom of the mantle.

$\begin{array}{ll}{q}_{\text{TBL}}=k_{\text{TBL}}\frac{\Delta T_{\text{TBL}}}{\delta }& (38)\end{array}$

where k_TBL = 10 W/m/K is the thermal conductivity of the TBL, ΔT_TBL is the temperature difference between top and bottom of the TBL, and δ is the thickness of the TBL. To discuss the thermal convection in the mantle, a dimensionless number, Ra, which is so-called the Rayleigh number, is usually used.

$\begin{array}{ll}\text{Ra}=\frac{{\rho }^{\text{den}}g\alpha \Delta T{d}^3}{\kappa \eta }& (39)\end{array}$

where ΔT and d are the temperature difference and thickness between top and bottom of the layer, respectively, κ is the thermal diffusivity, and η is the viscosity. Note that

$\begin{array}{ll}\kappa =\frac{k}{{\rho }^{\text{den}}{C}_p}& (40)\end{array}$

where C_P is the isobaric specific heat. According to the thermal boundary layer theory, the thickness of the TBL can be estimated from the condition that the local Rayleigh number of the TBL, Ra_l is nearly equal to the critical Rayleigh number Ra_c, which is ~650 for thermal convection.

$\begin{array}{ll}{\text{Ra}}_l={\left(\frac{\rho g\alpha }{\kappa \eta }\right)}_l{\delta }^3\Delta T_{\text{TBL}}~{\text{Ra}}_{\text{c}}~650& (41)\end{array}$

The temperature profile of the mantle is calculated from the adiabatic temperature gradient with assumed potential temperature to be 1,600 K. Figure 11B plots the conductive heat flux at the top of the liquid core as function of the planetary mass normalized by the Earth's mass (Equation 18). The conductive flux increases rapidly with increasing the planetary mass, mainly because of the internal temperature. The green broken lines indicate the total core cooling across the CMB (Equation 38), which strongly depends on the mantle viscosity. The calculated TBL heat flux values are q_TBL = 111, 54 and 26 mW/m² for M_p = 1 M_E planet with the viscosity values of η = 10²², 10²³, and 10²⁴ Pa·s, respectively. These values correspond to the Earth's CMB heat flux, which is ranging from 33 to 99 mW/m² (5–15 TW) (e.g., Lay et al., 2008). At 1 M_E, the core conductive heat flux is comparable or larger than the thermal boundary layer heat flux. In this case, the liquid core may partly stratify (Labrosse et al., 1997; Lister and Buffett, 1998; Pozzo et al., 2012; Gomi et al., 2013; Labrosse, 2015; Nakagawa, 2017), which is consistent with seismic observation (Tanaka, 2007; Helffrich and Kaneshima, 2010). Considering increase of core thermal conductivity with depth, before the onset of the inner core growth, the fluid core tends to be stratified from the bottom (Gomi et al., 2013). This in turn means that purely thermal buoyancy cannot drive the convection, if the top of the core is subisentropic. Hence, additional chemical buoyancies are necessary to maintain the geodynamo. In our Earth, the chemical buoyancy arising from the growing inner core contributes large portion of geodynamo efficiency (e.g., Lister and Buffett, 1995; Labrosse, 2015). Recently, MgO or SiO₂ precipitation is proposed for another source of chemical buoyancy (O'rourke and Stevenson, 2016; Hirose et al., 2017). Assuming that the mantle viscosity is independent of the planetary mass, the magnitude relation between the core adiabatic heat flux and the TBL heat flux of M_p > 1 M_E is similar to that of M_p = 1 M_E, which suggests that the similar situation is predicted in the super-Earths: thermally stratified layer at the top of the liquid core and a requirement of chemical buoyancies for geodynamo.

FIGURE 11

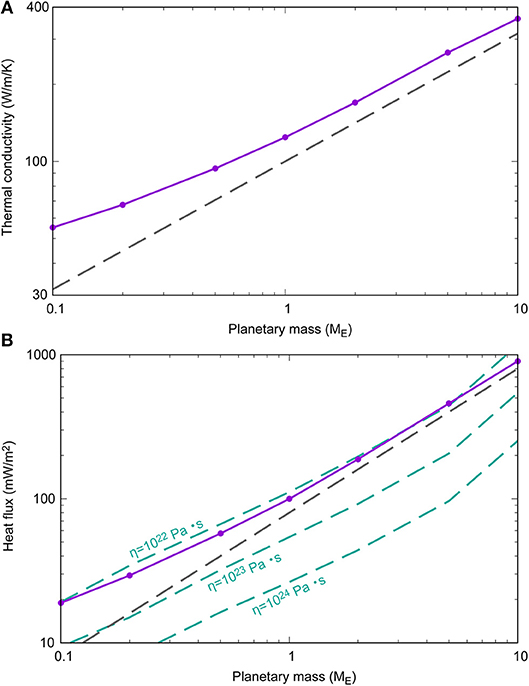
Figure 11. (A) Thermal conductivity of terrestrial planets at the top of the core as functions of planetary mass normalized to the Earth's mass (M_E). Purple line with circles indicates present estimate. Gray broken line represents previous scaling (Stixrude, 2014). (B) The heat flux at the CMB as a function of planetary mass. Purple solid line with circles indicates conductive heat flux along the isentropic temperature gradient at the top of the core. Green broken lines indicate the calculated heat flux across the thermal boundary layer (TBL) at the bottom of the mantle with assumed viscosity (see text). Gray broken line shows the previous estimate of the heat flux across the TBL (Stixrude, 2014).

In this study, we considered only one specific scenario with many assumptions, however, many scenarios should be considered because of large uncertainties of material properties other than the thermal conductivity of the core. One of the most important uncertainty may be caused by viscosity of the mantle (Tachinami et al., 2011; Tackley et al., 2013). Experimental and theoretical studies suggested that the lattice thermal conductivity of the mantle strongly depends on pressure, temperature and phase transitions (Manthilake et al., 2011; Ohta et al., 2012; Dekura et al., 2013). In addition to the lattice thermal conductivity, the radiative conductivity may become important because it is expected to enhance with temperature, although the value is controversial (Goncharov et al., 2008; Keppler et al., 2008). Since we are interested in the super-Earth located within the habitable zone that have the surface liquid water, we assumed that the mantle potential temperature may be comparable to that of the Earth T = 1,600 K. On the other hand, Stixrude (2014) suggests a higher mantle potential temperature due to accretion. Miyagoshi et al. (2017) concluded that if shallow part of the mantle was hotter than the adiabatic temperature extrapolated from the deeper mantle at the initial stage of mantle convection, such layered structure continues more than several billion years. Furthermore, if the temperature is sufficiently high to melt the mantle material, dynamo process in the magma ocean can also be possible due to high electrical conductivity of melt (McWilliams et al., 2012; Soubiran and Militzer, 2018). Similarly, the core temperature is also uncertain. We just assumed the inner core radius to determine the core adiabat, however, Morard et al. (2011) suggested that the core temperature is too low to melt the metallic core. The internal temperature should vary with time. Therefore, simulations of coevolution of thermally coupled mantle and core are needed for the future work.

Summary

We conducted KKR-CPA-DFT calculations of impurity resistivity of Fe-based light elements (C, N, O, Si, S) or Ni alloys, which is consistent with recent diamond-anvil cell experiments (Gomi and Hirose, 2015; Gomi et al., 2016; Suehiro et al., 2017; Zhang et al., 2018). The results suggest that impurity resistivity of Si is the largest among the light elements candidates, followed by C, S, N, and O (Figure 3). This may be due to the variation of the saturation resistivity on composition (Figure 5). The impurity resistivity of Ni is smaller than that of five light elements candidates. The resistivity calculation on Fe-Si-S ternary alloys suggests the violation of the Matthiessen's rule (Figure 6). We also computed the electronic specific heat of Fe alloys, which show the violation of the Sommerfeld expansion (Boness et al., 1986) with low impurity concentration. However, the degree of deviation becomes smaller with increasing impurity concentration (Figures 7, 8), which suggests that the Sommerfeld value of the Lorenz number may be good approximation at the terrestrial cores. The implausibility of geodynamo motion in the super-Earths has been discussed in terms of the absence of mantle convection (Tachinami et al., 2011; CíŽková et al., 2017; Kameyama and Yamamoto, 2018). The present study, on the other hand, focused on the thermal conductivity of the core. We modeled the thermal conductivity to be higher than ~90 W/m/K for the Earth's outer core (Table 2). For the super-Earth with 10 M_E, the thermal conductivity of the top of the core is estimated to be 361 W/m/K (Figure 11A), which is one order higher than the value of k = 40 W/m/K, which adopted previous thermal evolution calculation (Tachinami et al., 2011) and is consistent with result from recent scaling calculation (Stixrude, 2014). The resultant conductive heat flux at the top of the liquid core of terrestrial planets as function of planetary mass is compared with the heat flux across the thermal boundary layer (TBL) at the bottom of mantle (Figure 11B). The present result suggests the absence of the thermal convection in the core, which predicts the presence of the thermally stratified layer at the top of the core of super-Earths, similar to the Earth. In order to sustain the geodynamo motion in the liquid core, chemical convection is required, which associates with the inner core growth or precipitation of MgO and/or SiO₂ (O'rourke and Stevenson, 2016; Hirose et al., 2017).

Author Contributions

HG conducted the calculations. HG and TY wrote the manuscript.

Funding

This work was supported by JSPS MEXT/KAKENHI Grant Number JP15H05827.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank Hisazumi Akai for providing the conductivity calculation code implemented in the AkaiKKR package. The authors also thank to Sonju Kou for fruitful discussion. This work was supported by JSPS MEXT/KAKENHI Grant Number JP15H05827. We are grateful to the two reviewers for their comments.

References

Akai, H. (1989). Fast Korringa-Kohn-Rostoker coherent potential approximation and its application to FCC Ni-Fe systems. J Phys. 1, 8045. doi: 10.1088/0953-8984/1/43/006

CrossRef Full Text | Google Scholar

Alstad, J., Colvin, R., and Legvold, S. (1961). Single-crystal and polycrystal resistivity relationships for yttrium. Phys. Rev. 123, 418–419. doi: 10.1103/PhysRev.123.418

CrossRef Full Text | Google Scholar

Anderson, O. L. (1998). The Grüneisen parameter for iron at outer core conditions and the resulting conductive heat and power in the core. Phys. Earth Planet. Inter. 109, 179–197. doi: 10.1016/S0031-9201(98)00123-X

CrossRef Full Text | Google Scholar

Anglada-Escudé, G., Arriagada, P., Vogt, S. S., Rivera, E. J., Butler, R. P., Crane, J. D., et al. (2012). A planetary system around the nearby M dwarf GJ 667C with at least one super-Earth in its habitable zone. Astrophys. J. Lett. 751, L16. doi: 10.1088/2041-8205/751/1/L16

CrossRef Full Text | Google Scholar

Antonov, V. E., Baier, M., Dorner, B., Fedotov, V. K., Grosse, G., Kolesnikov, A. I., et al. (2002). High-pressure hydrides of iron and its alloys. J. Phys. 14, 6427. doi: 10.1088/0953-8984/14/25/311

CrossRef Full Text | Google Scholar

Anzellini, S., Dewaele, A., Mezouar, M., Loubeyre, P., and Morard, G. (2013). Melting of iron at Earth's inner core boundary based on fast X-ray diffraction. Science 340, 464–466. doi: 10.1126/science.1233514

PubMed Abstract | CrossRef Full Text | Google Scholar

Banhart, J., Weinberger, P., and Voitlander, J. (1989). Fermi surface and electrical resistivity of Cu-Pt alloys: a relativistic calculation. J. Phys. 1, 7013. doi: 10.1088/0953-8984/1/39/012

CrossRef Full Text | Google Scholar

Bi, Y., Tan, H., and Jing, F. (2002). Electrical conductivity of iron under shock compression up to 200 GPa. J. Phys. 14, 10849. doi: 10.1088/0953-8984/14/44/389

CrossRef Full Text | Google Scholar

Bohnenkamp, U., Sandström, R., and Grimvall, G. (2002). Electrical resistivity of steels and face-centered-cubic iron. J. Appl. Phys. 92, 4402–4407. doi: 10.1063/1.1502182

CrossRef Full Text | Google Scholar

Boness, D. A., and Brown, J. M. (1990). The electronic band structures of iron, sulfur, and oxygen at high pressures and the Earth's core. J. Geophys. Res. 95, 21721–21730. doi: 10.1029/JB095iB13p21721

CrossRef Full Text | Google Scholar

Boness, D. A., Brown, J. M., and McMahan, A. K. (1986). The electronic thermodynamics of iron under Earth core conditions. Phys. Earth Planet. Inter. 42, 227–240. doi: 10.1016/0031-9201(86)90025-7

CrossRef Full Text | Google Scholar

Butler, W. H. (1985). Theory of electronic transport in random alloys: Korringa-Kohn-Rostoker coherent-potential approximation. Phys. Rev. B 31:3260. doi: 10.1103/PhysRevB.31.3260

PubMed Abstract | CrossRef Full Text | Google Scholar

Butler, W. H., and Stocks, G. M. (1984). Calculated electrical conductivity and thermopower of silver-palladium alloys. Phys. Rev. B 29, 4217. doi: 10.1103/PhysRevB.29.4217

CrossRef Full Text | Google Scholar

Charbonneau, D., Berta, Z. K., Irwin, J., Burke, C. J., Nutzman, P., Buchhave, L. A., et al. (2009). A super-Earth transiting a nearby low-mass star. Nature 462, 891. doi: 10.1038/nature08679

PubMed Abstract | CrossRef Full Text | Google Scholar

CíŽková, H., van den Berg, A., and Jacobs, M. (2017). Impact of compressibility on heat transport characteristics of large terrestrial planets. Phys. Earth Planet. Inter. 268, 65–77. doi: 10.1016/j.pepi.2017.04.007

CrossRef Full Text | Google Scholar

Cote, P. J., and Meisel, L. V. (1978). Origin of saturation effects in electron transport. Phys. Rev. Lett. 40, 1586–1589. doi: 10.1103/PhysRevLett.40.1586

CrossRef Full Text | Google Scholar

Cusack, N., and Enderby, J. E. (1960). A note on the resistivity of liquid alkali and noble metals. Proc. Phys. Soc. 75, 395. doi: 10.1088/0370-1328/75/3/310

CrossRef Full Text | Google Scholar

de Koker, N., Steinle-Neumann, G., and Vlček, V. (2012). Electrical resistivity and thermal conductivity of liquid Fe alloys at high P and T, and heat flux in Earth's core. Proc. Natl. Acad. Sci. U.S.A. 109, 4070–4073. doi: 10.1073/pnas.1111841109

PubMed Abstract | CrossRef Full Text | Google Scholar

Dekura, H., Tsuchiya, T., and Tsuchiya, J. (2013). Ab initio lattice thermal conductivity of MgSiO₃ perovskite as found in Earth's lower mantle. Phys. Rev. Lett. 110:025904. doi: 10.1103/PhysRevLett.110.025904

PubMed Abstract | CrossRef Full Text | Google Scholar

Deng, L., Seagle, C., Fei, Y., and Shahar, A. (2013). High pressure and temperature electrical resistivity of iron and implications for planetary cores. Geophys. Res. Lett. 40, 33–37. doi: 10.1029/2012GL054347

CrossRef Full Text | Google Scholar

Dewaele, A., Loubeyre, P., Occelli, F., Mezouar, M., Dorogokupets, P. I., and Torrent, M. (2006). Quasihydrostatic equation of state of iron above 2 Mbar. Phys. Rev. Lett. 97:215504. doi: 10.1103/PhysRevLett.97.215504

PubMed Abstract | CrossRef Full Text | Google Scholar

Dobson, D. (2016). Geophysics: earth's core problem. Nature 534, 45. doi: 10.1038/534045a

PubMed Abstract | CrossRef Full Text | Google Scholar

Drchal, V., Kudrnovský, J., Wagenknecht, D., Turek, I., and Khmelevskyi, S. (2017). Transport properties of iron at Earth's core conditions: the effect of spin disorder. Phys. Rev. B 96:024432. doi: 10.1103/PhysRevB.96.024432

CrossRef Full Text | Google Scholar

Ezenwa, I. C., and Secco, R. A. (2017a). Constant electrical resistivity of Zn along the melting boundary up to 5 GPa. High Press. Res. 37, 319–333. doi: 10.1080/08957959.2017.1340473

CrossRef Full Text | Google Scholar

Ezenwa, I. C., and Secco, R. A. (2017b). Electronic transition in solid Nb at high pressure and temperature. J. Appl. Phys. 121, 225903. doi: 10.1063/1.4985548

CrossRef Full Text | Google Scholar

Ezenwa, I. C., and Secco, R. A. (2017c). Invariant electrical resistivity of Co along the melting boundary. Earth Planet. Sci. Lett. 474, 120–127. doi: 10.1016/j.epsl.2017.06.032

CrossRef Full Text | Google Scholar

Ezenwa, I. C., Secco, R. A., Yong, W., Pozzo, M., and Alfè, D. (2017). Electrical resistivity of solid and liquid Cu up to 5 GPa: decrease along the melting boundary. J. Phys. Chem. Solids 110, 386–393. doi: 10.1016/j.jpcs.2017.06.030

CrossRef Full Text | Google Scholar

Faber, T. E. (1972). An Introduction to the Theory of Liquid Metals. Cambridge: Cambridge University Press.

Google Scholar

Friedel, J. (1956). On some electrical and magnetic properties of metallic solid solutions. Can. J. Phys. 34, 1190–1211. doi: 10.1139/p56-134

CrossRef Full Text | Google Scholar

Fukai, Y. (2006). The Metal-Hydrogen System: Basic Bulk Properties, Vol. 21. Berlin; Heidelberg; New York, NY: Springer Science & Business Media.

Google Scholar

Gillon, M., Triaud, A. H., Demory, B. O., Jehin, E., Agol, E., Deck, K. M., et al. (2017). Seven temperate terrestrial planets around the nearby ultracool dwarf star TRAPPIST-1. Nature 542, 456. doi: 10.1038/nature21360

PubMed Abstract | CrossRef Full Text | Google Scholar

Glasbrenner, J. K., Pujari, B. S., and Belashchenko, K. D. (2014). Deviations from Matthiessen's rule and resistivity saturation effects in Gd and Fe from first principles. Phys. Rev. B 89:174408. doi: 10.1103/PhysRevB.89.174408

CrossRef Full Text | Google Scholar

Gomi, H., Fei, Y., and Yoshino, T. (2018). The effects of ferromagnetism and interstitial hydrogen on the equation of states of hcp and dhcp FeH_x: implications for the Earth's inner core age. Am. Mineral. 103, 1271–1281. doi: 10.2138/am-2018-6295

CrossRef Full Text | Google Scholar

Gomi, H., and Hirose, K. (2015). Electrical resistivity and thermal conductivity of hcp Fe–Ni alloys under high pressure: implications for thermal convection in the Earth's core. Phys. Earth Planet. Inter. 247, 2–10. doi: 10.1016/j.pepi.2015.04.003

CrossRef Full Text | Google Scholar

Gomi, H., Hirose, K., Akai, H., and Fei, Y. (2016). Electrical resistivity of substitutionally disordered hcp Fe–Si and Fe–Ni alloys: chemically-induced resistivity saturation in the Earth's core. Eart Planet. Sci. Lett. 451, 51–61. doi: 10.1016/j.epsl.2016.07.011

CrossRef Full Text | Google Scholar

Gomi, H., Ohta, K., Hirose, K., Labrosse, S., Caracas, R., Verstraete, M. J., et al. (2013). The high conductivity of iron and thermal evolution of the Earth's core. Phys. Earth Planet. Inter. 224, 88–103. doi: 10.1016/j.pepi.2013.07.010

CrossRef Full Text | Google Scholar

Goncharov, A. F., Haugen, B. D., Struzhkin, V. V., Beck, P., and Jacobsen, S. D. (2008). Radiative conductivity in the Earth's lower mantle. Nature 456, 231. doi: 10.1038/nature07412

PubMed Abstract | CrossRef Full Text | Google Scholar

Gurvitch, M. (1981). Ioffe-Regel criterion and resistivity of metals. Phys. Rev. B 24:7404. doi: 10.1103/PhysRevB.24.7404

CrossRef Full Text | Google Scholar

Helffrich, G., and Kaneshima, S. (2010). Outer-core compositional stratification from observed core wave speed profiles. Nature 468, 807. doi: 10.1038/nature09636

PubMed Abstract | CrossRef Full Text | Google Scholar

Hieu, H. K., Hai, T. T., Hong, N. T., Sang, N. D., and Tuyen, N. V. (2017). Electrical resistivity and thermodynamic properties of iron under high pressure. J. Electr. Mater. 46, 3702–3706. doi: 10.1007/s11664-017-5411-2

CrossRef Full Text | Google Scholar

Hirose, K., Labrosse, S., and Hernlund, J. (2013). Composition and state of the core. Annu. Rev. Earth Planet. Sci. 41, 657–691. doi: 10.1146/annurev-earth-050212-124007

CrossRef Full Text | Google Scholar

Hirose, K., Morard, G., Sinmyo, R., Umemoto, K., Hernlund, J., Helffrich, G., et al. (2017). Crystallization of silicon dioxide and compositional evolution of the Earth's core. Nature 543, 99. doi: 10.1038/nature21367

PubMed Abstract | CrossRef Full Text | Google Scholar

Kameyama, M., and Yamamoto, M. (2018). Numerical experiments on thermal convection of highly compressible fluids with variable viscosity and thermal conductivity: implications for mantle convection of super-Earths. Phys. Earth Planet. Inter. 274, 23–36. doi: 10.1016/j.pepi.2017.11.001

CrossRef Full Text | Google Scholar

Keppler, H., Dubrovinsky, L. S., Narygina, O., and Kantor, I. (2008). Optical absorption and radiative thermal conductivity of silicate perovskite to 125 gigapascals. Science 322, 1529–1532. doi: 10.1126/science.1164609

PubMed Abstract | CrossRef Full Text | Google Scholar

Kiarasi, S., and Secco, R. A. (2015). Pressure-induced electrical resistivity saturation of Fe17Si. Phys. Status Solidi (b) 252, 2034–2042. doi: 10.1002/pssb.201552029

CrossRef Full Text | Google Scholar

Konôpková, Z., Lazor, P., Goncharov, A. F., and Struzhkin, V. V. (2011). Thermal conductivity of hcp iron at high pressure and temperature. High Press. Res. 31, 228–236. doi: 10.1080/08957959.2010.545059

CrossRef Full Text | Google Scholar

Konôpková, Z., McWilliams, R. S., Gómez-Pérez, N., and Goncharov, A. F. (2016). Direct measurement of thermal conductivity in solid iron at planetary core conditions. Nature 534, 99. doi: 10.1038/nature18009

PubMed Abstract | CrossRef Full Text | Google Scholar

Kou, S., and Akai, H. (2018). First-principles calculation of transition-metal Seebeck coefficients. Solid State Commun. 276, 1–4. doi: 10.1016/j.ssc.2018.02.018

CrossRef Full Text | Google Scholar

Kuwayama, Y., Hirose, K., Sata, N., and Ohishi, Y. (2008). Phase relations of iron and iron-nickel alloys up to 300 GPa: implications for composition and structure of the Earth's inner core. Earth Planet. Sci. Lett. 273, 379–385. doi: 10.1016/j.epsl.2008.07.001

CrossRef Full Text | Google Scholar

Labrosse, S. (2015). Thermal evolution of the core with a high thermal conductivity. Phys. Earth Planet. Inter. 247, 36–55. doi: 10.1016/j.pepi.2015.02.002

CrossRef Full Text | Google Scholar

Labrosse, S., Poirier, J. P., and Le Mouël, J. L. (1997). On cooling of the Earth's core. Phys. Earth Planet. Inter. 99, 1–17. doi: 10.1016/S0031-9201(96)03207-4

CrossRef Full Text | Google Scholar

Lay, T., Hernlund, J., and Buffett, B. A. (2008). Core–mantle boundary heat flow. Nat. Geosci. 1, 25. doi: 10.1038/ngeo.2007.44

CrossRef Full Text | Google Scholar

Lin, Z., Zhigilei, L. V., and Celli, V. (2008). Electron-phonon coupling and electron heat capacity of metals under conditions of strong electron-phonon nonequilibrium. Phys. Rev. B 77:075133. doi: 10.1103/PhysRevB.77.075133

CrossRef Full Text | Google Scholar

Linde, J. O. (1932). Elektrische Eigenschaften verdünnter Mischkristallegierungen III. Widerstand von Kupfer-und Goldlegierungen. Gesetzmäßigkeiten der Widerstandserhöhungen. Ann. Phys. 407, 219–248. doi: 10.1002/andp.19324070206

CrossRef Full Text | Google Scholar

Lister, J. R., and Buffett, B. A. (1995). The strength and efficiency of thermal and compositional convection in the geodynamo. Phys. Earth Planet. Inter. 91, 17–30. doi: 10.1016/0031-9201(95)03042-U

CrossRef Full Text | Google Scholar

Lister, J. R., and Buffett, B. A. (1998). Stratification of the outer core at the core-mantle boundary. Phys. Earth Planet. Inter. 105, 5–19. doi: 10.1016/S0031-9201(97)00082-4

CrossRef Full Text | Google Scholar

Manthilake, G. M., de Koker, N., Frost, D. J., and McCammon, C. A. (2011). Lattice thermal conductivity of lower mantle minerals and heat flux from Earth's core. Proc. Natl. Acad. Sci. U.S.A. 108, 17901–17904. doi: 10.1073/pnas.1110594108

PubMed Abstract | CrossRef Full Text | Google Scholar

Markowitz, D. (1977). Calculation of electrical resistivity of highly resistive metallic alloys. Phys. Rev. B 15:3617. doi: 10.1103/PhysRevB.15.3617

CrossRef Full Text | Google Scholar

Matassov, G. (1977). The Electrical Conductivity of Iron-Silicon Alloys at High Pressures and the Earth's Core. Ph.D. thesis, Lawrence Livermore Laboratory, University of California.

McWilliams, R. S., Konôpková, Z., and Goncharov, A. F. (2015). A flash heating method for measuring thermal conductivity at high pressure and temperature: application to Pt. Phys. Earth Planet. Inter. 247, 17–26. doi: 10.1016/j.pepi.2015.06.002

CrossRef Full Text | Google Scholar

McWilliams, R. S., Spaulding, D. K., Eggert, J. H., Celliers, P. M., Hicks, D. G., Smith, R. F., et al. (2012). Phase transformations and metallization of magnesium oxide at high pressure and temperature. Science 338, 1330–1333. doi: 10.1126/science.1229450

PubMed Abstract | CrossRef Full Text | Google Scholar

Mertig, I. (1999). Transport properties of dilute alloys. Rep. Prog. Phys. 62, 237. doi: 10.1088/0034-4885/62/2/004

CrossRef Full Text | Google Scholar

Miyagoshi, T., Kameyama, M., and Ogawa, M. (2017). Extremely long transition phase of thermal convection in the mantle of massive super-Earths. Earth Planets Space 69, 46. doi: 10.1186/s40623-017-0630-6

CrossRef Full Text | Google Scholar

Mooij, J. H. (1973). Electrical conduction in concentrated disordered transition metal alloys. Phys. Status Solidi 17, 521–530. doi: 10.1002/pssa.2210170217

CrossRef Full Text | Google Scholar

Morard, G., Bouchet, J., Valencia, D., Mazevet, S., and Guyot, F. (2011). The melting curve of iron at extreme pressures: implications for planetary cores. High Energy Density Phys. 7, 141–144. doi: 10.1016/j.hedp.2011.02.001

CrossRef Full Text | Google Scholar

Moruzzi, V. L., Janak, J. F., and Williams, A. R. (1978). Calculated Electronic Properties of Metals. New York, NY: Pergamon Press Inc.

Google Scholar

Mott, N. F. (1934). The resistance of liquid metals. Proc. R. Soc. Lond. A 146, 465–472. doi: 10.1098/rspa.1934.0166

CrossRef Full Text | Google Scholar

Mott, N. F. (1936). “The electrical resistance of dilute solid solutions,” in Mathematical Proceedings of the Cambridge Philosophical Society, Vol. 32 (Cambridge: Cambridge University Press), 281–290.

Google Scholar

Mott, N. F. (1972). The electrical resistivity of liquid transition metals. Philos. Mag. 26, 1249–1261. doi: 10.1080/14786437208220339

CrossRef Full Text | Google Scholar

Nakagawa, T. (2017). On the thermo-chemical origin of the stratified region at the top of the Earth's core. Phys. Earth Planet. Inter. 276, 172–181. doi: 10.1016/j.pepi.2017.05.011

CrossRef Full Text | Google Scholar

Norbury, A. L. (1921). The electrical resistivity of dilute metallic solid solutions. Trans. Faraday Soc. 16, 570–596. doi: 10.1039/tf9211600570

CrossRef Full Text | Google Scholar

Ohta, K., Kuwayama, Y., Hirose, K., Shimizu, K., and Ohishi, Y. (2016). Experimental determination of the electrical resistivity of iron at Earth's core conditions. Nature 534, 95. doi: 10.1038/nature17957

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohta, K., Suehiro, S., Hirose, K., and Ohishi, Y. (2018). Electrical resistivity of fcc phase iron hydrides at high pressure and temperatures. Comptes Rendus Geosci. doi: 10.1016/j.crte.2018.05.004. [Epub ahead of print].

CrossRef Full Text | Google Scholar

Ohta, K., Yagi, T., Taketoshi, N., Hirose, K., Komabayashi, T., Baba, T., et al. (2012). Lattice thermal conductivity of MgSiO₃ perovskite and post-perovskite at the core–mantle boundary. Earth Planet. Sci. Lett. 349, 109–115. doi: 10.1016/j.epsl.2012.06.043

CrossRef Full Text | Google Scholar

O'rourke, J. G., and Stevenson, D. J. (2016). Powering Earth's dynamo with magnesium precipitation from the core. Nature 529, 387. doi: 10.1038/nature16495

PubMed Abstract | CrossRef Full Text | Google Scholar

Oshita, M., Yotsuhashi, S., Adachi, H., and Akai, H. (2009). Seebeck coefficient calculated by kubo–greenwood formula on the basis of density functional theory. J. Phys. Soc. Jpn. 78:024708. doi: 10.1143/JPSJ.78.024708

CrossRef Full Text | Google Scholar

Ozawa, H., Hirose, K., Yonemitsu, K., and Ohishi, Y. (2016). High-pressure melting experiments on Fe-Si alloys and implications for silicon as a light element in the core. Earth Planet. Sci. Lett. 456, 47–54. doi: 10.1016/j.epsl.2016.08.042

CrossRef Full Text | Google Scholar

Papuc, A. M., and Davies, G. F. (2008). The internal activity and thermal evolution of Earth-like planets. Icarus 195, 447–458. doi: 10.1016/j.icarus.2007.12.016

CrossRef Full Text | Google Scholar

Poirier, J. P. (2000). Introduction to the Physics of the Earth's Interior. Cambridge: Cambridge University Press.

Google Scholar

Pommier, A. (2018). Influence of sulfur on the electrical resistivity of a crystallizing core in small terrestrial bodies. Earth Planet. Sci. Lett. 496, 37–46. doi: 10.1016/j.epsl.2018.05.032

CrossRef Full Text | Google Scholar

Pourovskii, L. V., Mravlje, J., Georges, A., Simak, S. I., and Abrikosov, I. A. (2017). Electron–electron scattering and thermal conductivity of ϵfnduc at Earth's core conditions. New J. Phys. 19, 073022. doi: 10.1088/1367-2630/aa76c9

CrossRef Full Text | Google Scholar

Pozzo, M., and Alfè, D. (2016a). Saturation of electrical resistivity of solid iron at Earth's core conditions. Springerplus 5, 256. doi: 10.1186/s40064-016-1829-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Pozzo, M., and Alfè, D. (2016b). “Electrical resistivity saturation of solid iron at Earth's core conditions from density functional theory,” in AGU Abstract DI13A-2356, AGU Fall Meeting (San Fransisco, CA).

Google Scholar

Pozzo, M., Davies, C., Gubbins, D., and Alfè, D. (2012). Thermal and electrical conductivity of iron at Earth's core conditions. Nature 485, 355. doi: 10.1038/nature11031

PubMed Abstract | CrossRef Full Text | Google Scholar

Pozzo, M., Davies, C., Gubbins, D., and Alfè, D. (2013). Transport properties for liquid silicon-oxygen-iron mixtures at Earth's core conditions. Phys. Rev. B 87:014110. doi: 10.1103/PhysRevB.87.014110

CrossRef Full Text | Google Scholar

Pozzo, M., Davies, C., Gubbins, D., and Alfè, D. (2014). Thermal and electrical conductivity of solid iron and iron–silicon mixtures at Earth's core conditions. Earth Planet. Sci. Lett. 393, 159–164. doi: 10.1016/j.epsl.2014.02.047

CrossRef Full Text | Google Scholar

Seagle, C. T., Cottrell, E., Fei, Y., Hummer, D. R., and Prakapenka, V. B. (2013). Electrical and thermal transport properties of iron and iron-silicon alloy at high pressure. Geophys. Res. Lett. 40, 5377–5381. doi: 10.1002/2013GL057930

CrossRef Full Text | Google Scholar

Secco, R. A. (2017). Thermal conductivity and Seebeck coefficient of Fe and Fe-Si alloys: implications for variable Lorenz number. Phys. Earth Planet. Inter. 265, 23–34. doi: 10.1016/j.pepi.2017.01.005

CrossRef Full Text | Google Scholar

Secco, R. A., and Schloessin, H. H. (1989). The electrical resistivity of solid and liquid Fe at pressures up to 7 GPa. J. Geophys. Res. 94, 5887–5894. doi: 10.1029/JB094iB05p05887

CrossRef Full Text | Google Scholar

Sha, X., and Cohen, R. E. (2011). First-principles studies of electrical resistivity of iron under pressure. J. Phys. 23:075401. doi: 10.1088/0953-8984/23/7/075401

PubMed Abstract | CrossRef Full Text | Google Scholar

Silber, R. E., Secco, R. A., and Yong, W. (2017). Constant electrical resistivity of Ni along the melting boundary up to 9 GPa. J. Geophys. Res.122, 5064–5081. doi: 10.1002/2017JB014259

CrossRef Full Text | Google Scholar

Silber, R. E., Secco, R. A., Yong, W., and Littleton, J. A. (2018). Electrical resistivity of liquid Fe to 12 GPa: implications for heat flow in cores of terrestrial bodies. Sci. Rep. 8, 10758. doi: 10.1038/s41598-018-28921-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, R. F., Fratanduono, D. E., Braun, D. G., Duffy, T. S., Wicks, J. K., Celliers, P. M., et al. (2018). Equation of state of iron under core conditions of large rocky exoplanets. Nat. Astron. 2, 452–458. doi: 10.1038/s41550-018-0437-9

CrossRef Full Text | Google Scholar

Soubiran, F., and Militzer, B. (2018). Electrical conductivity and magnetic dynamos in magma oceans of Super-Earths. Nat. Commun. 9, 3883. doi: 10.1038/s41467-018-06432-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Stacey, F. D., and Anderson, O. L. (2001). Electrical and thermal conductivities of Fe–Ni–Si alloy under core conditions. Phys. Earth Planet. Inter. 124, 153–162. doi: 10.1016/S0031-9201(01)00186-8

CrossRef Full Text | Google Scholar

Stacey, F. D., and Loper, D. E. (2007). A revised estimate of the conductivity of iron alloy at high pressure and implications for the core energy balance. Phys. Earth Planet. Inter. 161, 13–18. doi: 10.1016/j.pepi.2006.12.001

CrossRef Full Text | Google Scholar

Stevenson, D. J., Spohn, T., and Schubert, G. (1983). Magnetism and thermal evolution of the terrestrial planets. Icarus 54, 466–489. doi: 10.1016/0019-1035(83)90241-5

CrossRef Full Text | Google Scholar

Stixrude, L. (2012). Structure of Iron to 1 Gbar and 40 000 K. Phys. Rev. Lett. 108:055505. doi: 10.1103/PhysRevLett.108.055505

PubMed Abstract | CrossRef Full Text | Google Scholar

Stixrude, L. (2014). Melting in super-earths. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 372, 20130076. doi: 10.1098/rsta.2013.0076

PubMed Abstract | CrossRef Full Text | Google Scholar

Stixrude, L., and Lithgow-Bertelloni, C. (2005). Thermodynamics of mantle minerals—I. Physical properties. Geophys. J. Int. 162, 610–632. doi: 10.1111/j.1365-246X.2005.02642.x

CrossRef Full Text | Google Scholar

Suehiro, S., Ohta, K., Hirose, K., Morard, G., and Ohishi, Y. (2017). The influence of sulfur on the electrical resistivity of hcp iron: implications for the core conductivity of Mars and Earth. Geophys. Res. Lett. 44, 8254–8259. doi: 10.1002/2017GL074021

CrossRef Full Text | Google Scholar

Tachinami, C., Senshu, H., and Ida, S. (2011). Thermal evolution and lifetime of intrinsic magnetic fields of super-Earths in habitable zones. Astrophys. J. 726:70. doi: 10.1088/0004-637X/726/2/70

CrossRef Full Text | Google Scholar

Tackley, P. J., Ammann, M., Brodholt, J. P., Dobson, D. P., and Valencia, D. (2013). Mantle dynamics in super-Earths: post-perovskite rheology and self-regulation of viscosity. Icarus 225, 50–61. doi: 10.1016/j.icarus.2013.03.013

CrossRef Full Text | Google Scholar

Tanaka, S. (2007). Possibility of a low P-wave velocity layer in the outermost core from global SmKS waveforms. Earth Planet. Sci. Lett. 259, 486–499. doi: 10.1016/j.epsl.2007.05.007

CrossRef Full Text | Google Scholar

Tateno, S., Hirose, K., Ohishi, Y., and Tatsumi, Y. (2010). The structure of iron in Earth's inner core. Science 330, 359–361. doi: 10.1126/science.1194662

PubMed Abstract | CrossRef Full Text | Google Scholar

Tateno, S., Kuwayama, Y., Hirose, K., and Ohishi, Y. (2015). The structure of Fe-Si alloy in Earth's inner core. Earth Planet. Sci. Lett. 418, 11–19. doi: 10.1016/j.epsl.2015.02.008

CrossRef Full Text | Google Scholar

Tsiovkin, Y. Y., Voloshinskii, A. N., Gapontsev, V. V., and Ustinov, V. V. (2005). Residual electrical resistivity in dilute nonmagnetic alloys of transition metals. Phys. Rev. B 71:184206. doi: 10.1103/PhysRevB.71.184206

CrossRef Full Text | Google Scholar

Tsiovkin, Y. Y., Voloshinskii, A. N., Gapontsev, V. V., and Ustinov, V. V. (2006). Theory of the residual resistivity of dilute alloys of nonmagnetic 3 d−5 d transition metals. Low Temp. Phys. 32, 863–867. doi: 10.1063/1.2356843

CrossRef Full Text | Google Scholar

Tsuchiya, T., and Kawamura, K. (2002). First-principles electronic thermal pressure of metal Au and Pt. Phys. Rev. B 66:094115. doi: 10.1103/PhysRevB.66.094115

CrossRef Full Text | Google Scholar

Tsuchiya, T., and Tsuchiya, J. (2011). Prediction of a hexagonal SiO2 phase affecting stabilities of MgSiO₃ and CaSiO₃ at multimegabar pressures. Proc. Natl. Acad. Sci. U.S.A. 108, 1252–1255. doi: 10.1073/pnas.1013594108

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsumuraya, T., Matsuura, Y., Shishidou, T., and Oguchi, T. (2012). First-principles study on the structural and magnetic properties of iron hydride. J. Phys. Soc. Jpn. 81:064707. doi: 10.1143/JPSJ.81.064707

CrossRef Full Text | Google Scholar

Umemoto, K., Wentzcovitch, R. M., and Allen, P. B. (2006). Dissociation of MgSiO₃ in the cores of gas giants and terrestrial exoplanets. Science 311, 983–986. doi: 10.1126/science.1120865

PubMed Abstract | CrossRef Full Text | Google Scholar

Usselman, T. M. (1975). Experimental approach to the state of the core; Part I, The liquidus relations of the Fe-rich portion of the Fe-Ni-S system from 30 to 100 kb. Am. J. Sci. 275, 278–290. doi: 10.2475/ajs.275.3.278

CrossRef Full Text | Google Scholar

Vafayi, K., Calandra, M., and Gunnarsson, O. (2006). Electronic thermal conductivity at high temperatures: violation of the Wiedemann-Franz law in narrow-band metals. Phys. Rev. B 74:235116. doi: 10.1103/PhysRevB.74.235116

CrossRef Full Text | Google Scholar

Valencia, D., O'Connell, R. J., and Saselov, D. (2006). Internal structure of massive terrestrial planets. Icarus 181, 545–554. doi: 10.1016/j.icarus.2005.11.021

CrossRef Full Text | Google Scholar

Valencia, D., Sasselov, D. D., and O'Connell, R. J. (2007). Radius and structure models of the first super-Earth planet. Astrophys. J. 656, 545. doi: 10.1086/509800

CrossRef Full Text | Google Scholar

Van Zytveld, J. B. (1980). Electrical resistivities of liquid transition metals. Le J. Phys. Colloques 41, C8–C503. doi: 10.1051/jphyscol:19808126

CrossRef Full Text

Wagle, F., and Steinle-Neumann, G. (2018). Electrical resistivity discontinuity of iron along the melting curve. Geophys. J. Int. 213, 237–243. doi: 10.1093/gji/ggx526

CrossRef Full Text | Google Scholar

Wagle, F., Steinle-Neumann, G., and de Koker, N. (2018). Saturation and negative temperature coefficient of electrical resistivity in liquid iron-sulfur alloys at high densities from first principles calculations. Phys. Rev. B 97:094307. doi: 10.1103/PhysRevB.97.094307

CrossRef Full Text | Google Scholar

Wicks, J. K., Smith, R. F., Fratanduono, D. E., Coppari, F., Kraus, R. G., Newman, M. G., et al. (2018). Crystal structure and equation of state of Fe-Si alloys at super-Earth core conditions. Sci. Adv. 4:eaao5864. doi: 10.1126/sciadv.aao5864

PubMed Abstract | CrossRef Full Text | Google Scholar

Williams, Q. (2018). The thermal conductivity of Earth's core: a key geophysical parameter's constraints and uncertainties. Annu. Rev. Earth Planet. Sci. 46, 47–66. doi: 10.1146/annurev-earth-082517-010154

CrossRef Full Text | Google Scholar

Xu, J., Zhang, P., Haule, K., Minar, J., Wimmer, S., Ebert, H., et al. (2018). Thermal conductivity and electrical resistivity of solid iron at Earth's core conditions from first principles. Phys. Rev. Lett. 121:096601. doi: 10.1103/PhysRevLett.121.096601

PubMed Abstract | CrossRef Full Text | Google Scholar

Yue, S. Y., and Hu, M. (2018). Insight of the thermal conductivity of ε iron at Earth's core conditions from the newly developed direct ab initio methodology. arXiv:1808.10860 [Preprint].

Google Scholar

Zhang, C., Lin, J. F., Liu, Y., Feng, S., Jin, C., Hou, M., et al. (2018). Electrical resistivity of Fe-C alloy at high pressure: effects of carbon as a light element on the thermal conductivity of the Earth's core. J. Geophys. Res. 123, 3564–3577. doi: 10.1029/2017JB015260

CrossRef Full Text | Google Scholar

Ziman, J. M. (1961). A theory of the electrical properties of liquid metals. I: the monovalent metals. Philos. Mag. 6, 1013–1034. doi: 10.1080/14786436108243361

CrossRef Full Text | Google Scholar