Measuring Coseismic Deformation With Spaceborne Synthetic Aperture Radar: A Review

In the past 25 years, space-borne Synthetic Aperture Radar imagery has become an increasingly available data source for the study of crustal deformation associated with moderate to large earthquakes (M > 4.0). Coseismic surface deformation can be measured with several well-established techniques, the applicability of which depends on the ground displacement pattern, on several radar parameters, and on the surface properties at the time of the radar acquisitions. The state-of-the-art concerning the measurement techniques is reviewed, and their application to over 100 case-studies since the launch of the Sentinel-1a satellite is discussed, including the performance of the different methods and the data processing aspects, which still constitute topics of ongoing research.

Introduction

Coseismic deformation measurements based on spaceborne SAR sensors have been carried out since 25 years (Massonnet et al., 1993). Furthermore, high-quality SAR data suitable for crustal deformation studies, in particular with low spatial and temporal baselines and precise orbital and timing control, has never been so abundant since the launch of the Sentinel-1a and Sentinel-1b satellites in Apr. 2014 and 2016 respectively, and of ALOS-2 in May 2014.

The maturity of the processing techniques together with the quality and availability of SAR data have contributed to the standardization of several processing steps and to the development of automated processing chains for Sentinel-1 data (Feng et al., 2016; Li et al., 2016b). However, a given application and/or dataset can still present some challenges for the current state-of-the-art processing techniques, or require ad-hoc decisions on behalf of the image analyst. Furthermore, some specific properties as well as the wide-area coverage of the main Sentinel-1 and ALOS-2 acquisition modes, and the free and open data policy of the Sentinel-1 missions, has stimulated new algorithmic developments, which are partially still ongoing.

The measurement principles and state of the art of current SAR-based measurement techniques used for coseismic deformation applications are discussed in section SAR Deformation Measurements. A review of coseismic deformation studies concerning earthquakes, which occurred after the launch of Sentinel-1, is then carried out, discussing the performance of the measurement techniques (section Technique Application) as well as the data processing aspects, which are still challenging and not fully standardized (section Current Challenges). Finally, future developments are discussed in section Future Developments.

SAR Deformation Measurements

Sensitivity to Motion

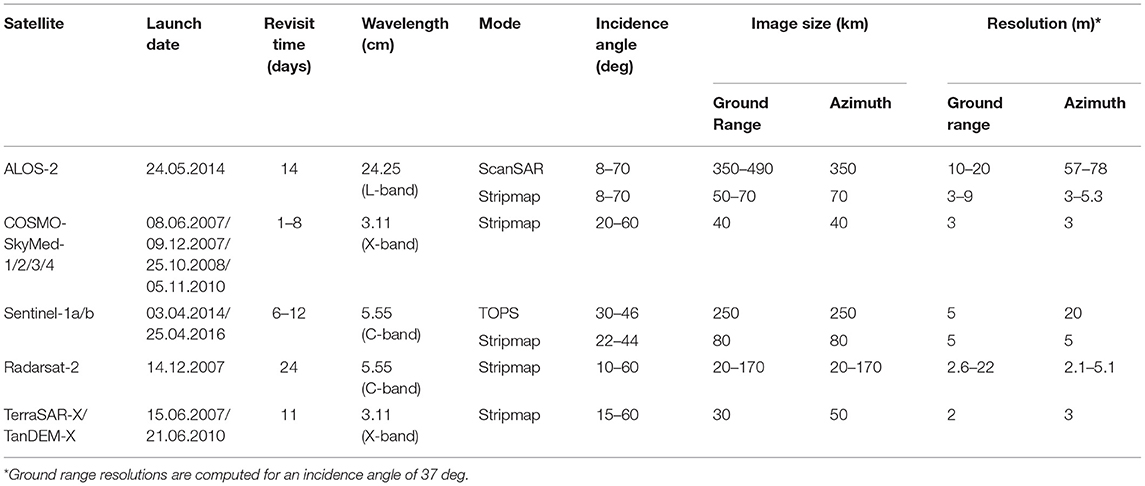
SAR-based ground deformation measurements rely on repeat-pass acquisitions carried out by C-, L-, and X-band microwave SAR sensors operating in Stripmap and ScanSAR acquisition modes (Cumming and Wong, 2005) and, since the launch of Sentinel-1a, also on imagery acquired in Terrain Observation with Progressive Scans (TOPS) mode (De Zan and Monti Guarnieri, 2006). An overview of spaceborne SAR sensors and modes, which have been used for coseiemic deformation measurements since the launch of Sentinel-1a is provided in Table 1. The properties of other sensors and acquisition modes are reviewed in Sansosti et al. (2014).

TABLE 1

Table 1. Properties of SAR sensors and modes currently used for coseismic deformation measurements.

A schematic of the above-mentioned acquisition modes is shown in Figure 1. In Stripmap mode, the SAR maintains a fixed side-looking beam pointing throughout a data take, yielding spatial resolutions in the order of a few meters and image sizes of tens of km in both ground range and azimuth (Table 1). ScanSAR and TOPS modes trade-off azimuth resolution, which is degraded to tens of meters, for an increased range coverage, which can reach several hundreds of km (Table 1). This is achieved by illuminating the ground with a fixed antenna beam orientation only for the duration of a so called data burst, after which the beam is electronically steered in range to cover an adjacent sub-swath. In the TOPS case the antenna is also steered in the azimuth direction within each burst, mainly to reduce an undesired intensity modulation known as image scalloping (Meta et al., 2008). In the ScanSAR case, and to a lesser extent also in the TOPS case, an azimuth overlap exists between consecutive bursts of the same swath, which can be exploited for deformation measurements as discussed in section Split-Bandwidth Interferometry.

FIGURE 1

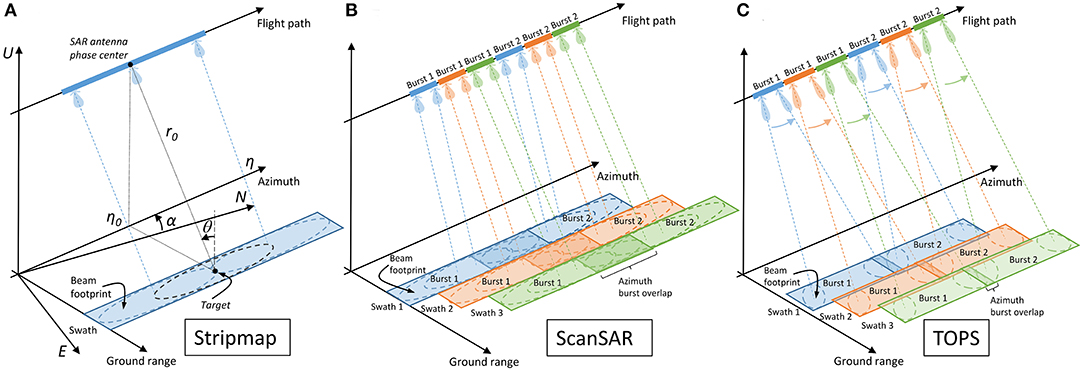
Figure 1. SAR acquisition geometries. (A) Stripmap (B) ScanSAR with three range swaths and two azimuth looks (C) TOPS with three range swaths, such as the Sentinel-1a/b Interferometric Wideswath (IW) mode. The symbols which appear in (A) are described in section Sensitivity to Motion.

For all acquisition modes sensitivity to motion arises from the positioning information contained in the amplitude and phase of focused SAR imagery. The data of current spaceborne sensors is distributed in zero-Doppler geometry, implying that a point on ground is positioned about its zero-Doppler coordinates (η₀, τ₀) in the SAR image. Coordinate η₀ represents the time at which the derivative of the azimuth phase modulation between consecutive pulses backscattered from the same object on ground is zero, whereas τ₀ represents the two-way range-delay at time η₀. In an ideal scenario, and in particular neglecting the atmospheric effects discussed in sections Tropospheric Propagation and Ionospheric Propagation, the Doppler coordinates have a geometric interpretation shown in Figure 1A, in which η₀ represents the azimuth time of closest approach between a point on ground and the SAR antenna phase center (IEEE Standard Definitions of Terms for Antennas, 1993) and τ₀ = 2r₀/c, where r₀ is the one-way range of closest approach and c is the speed of light.

Due to the finite resolution of the SAR in both the range and azimuth dimensions, a point on ground (target) actually covers a two-dimensional locus h(τ,η) in the SAR image, which for low-squint systems can be written as Holzner and Bamler (2002); Cumming and Wong (2005), and De Zan et al. (2014):

$\begin{array}{l}h(\tau ,\eta ;{\tau }_0,{\eta }_0)=A·exp\left(j\text{ψ}\right)·p_r\left(\tau -{\tau }_0\right)·p_a(\eta -{\eta }_0)·\\ \exp \left(-j2\pi f_c{\tau }_0^{phase}\right)·\exp \left[j2\pi f_{dc}·\left(\eta -{\eta }_0\right)\right]& (1)\end{array}$

$\begin{array}{cc}{f}_{dc}=f_{dc}({\tau }_0,{\eta }_0)\text{ for Stripmap}& (2)\end{array}$

$\begin{array}{cc}{f}_{dc}=f_{dc}({\tau }_0,T_c-{\eta }_0)\text{ for ScanSAR},\text{ TOPS}& (3)\end{array}$

where τ and η represent the slant-range delay and azimuth time variables, A and ψ are amplitude and phase terms related to the electromagnetic properties of the target, p_r() and p_a() represent sharply peaked (sinc-like) functions, f_c is the carrier frequency of the radar, ${\tau }_0^{phase}$ is the range phase delay which differs slightly from the range group delay τ₀ due to ionospheric propagation (section Ionospheric Propagation), and f_dc is the instantaneous Doppler centroid. The latter is a slowly varying function of (η₀, τ₀) in the Stripmap case, whose values are typically <100 Hz in magnitude for current systems. For a single ScanSAR burst (Holzner and Bamler, 2002) and for TOPS acquisitions (De Zan et al., 2014) the Doppler centroid also depends on the azimuth time distance from the burst center (T_c). In the ScanSAR case values in the order of 1 KHz in magnitude can be reached, whereas for Sentinel-1 TOPS the maximum instantaneous Doppler centroid magnitude is around 2.6 KHz (Yague-Martinez et al., 2016).

Considering now two SAR images acquired respectively before and after an earthquake, based on Figure 1A, a 3D coseismic deformation, represented by its components (Δe, Δn, Δu) in a local East-North-Up Cartesian system, will cause the following zero-Doppler deformations in the range and azimuth directions (Δr_defo, Δa_defo), counted positive respectively away from the radar and along the flight path:

$\begin{array}{cc}\left(\begin{array}{c}\Delta r_{defo}\\ \Delta a_{defo}\end{array}\right)=\left(\begin{array}{ccc}\text{cos }\alpha \text{ sin }\theta & \text{sin }\alpha \text{ sin }\theta & -\text{cos }\theta \\ -\text{sin }\alpha & \text{cos }\alpha & 0\end{array}\right)\left(\begin{array}{c}\Delta e\\ \Delta n\\ \Delta u\end{array}\right)& (4)\end{array}$

where θ is the local incidence angle counted positive from the vertical (U), and α is the angle between North (N) and the ground-projection of the flight direction, counted positive counter-clockwise. Typical incidence angle values are between 20 deg and 50 deg (Table 1), whereas α is in the order of 10 deg to 15 deg at mid-latitudes.

Δr_defo is more commonly referred to in literature as the line-of-sight (LoS) deformation. For a given point, such deformation components will contribute to the following zero-Doppler time coordinate variations between the pre- and post-event image:

$\begin{array}{cc}\left(\begin{array}{c}\Delta {\tau }_{defo}\\ \Delta {\eta }_{defo}\end{array}\right)=\left(\begin{array}{c}2\Delta r_{defo}/c\\ \Delta a_{defo}/V_r\end{array}\right)& (5)\end{array}$

where V_r is an effective rectilinear velocity (Cumming and Wong, 2005), which is in the order of 7100 m/s for remote sensing satellites in near-polar orbit.

Measurement Techniques

Three SAR-based techniques are currently used for coseismic deformation measurement, namely Differential SAR Interferometry (DInSAR), which measures the LoS deformation component, offset-tracking, which provides both the LoS and the azimuth components, and Split-bandwidth Interferometry (SBI), which can be separately applied to the range and azimuth dimensions to yield respectively the LoS and the azimuth deformation. These methods, which are detailed in the following sub-sections, measure the displacement occurred between two SAR acquisitions, and the permanent coseismic deformation is typically obtained by applying these techniques to a single image pair spanning the earthquake. Methods based on a redundant network of acquisition pairs, namely Multi-Temporal DInSAR (MT-DInSAR) techniques, have been used in a limited amount of cases to reduce measurement noise (e.g. Fattahi et al., 2015; Fielding et al., 2017; Grandin et al., 2017; Lee et al., 2017). In section Recovering the 3D Deformation Field methods to obtain the 3D deformation field from suitable LoS and azimuth measurements are discussed.

Differential SAR Interferometry

DInSAR exploits the range-dependent phase term in (1) to measure the LoS deformation component. Its application to Stripmap SAR imagery has been the topic of several review papers (Bamler and Hartl, 1998; Massonnet and Feigl, 1998; Bürgmann et al., 2000; Rosen et al., 2000; Zhou et al., 2009; Simons and Rosen, 2015). The main processing steps, based on developments of the original two-pass approach proposed by Massonnet et al. (1993), are shared by virtually all processing chains (cfr. Figure 2 in Bürgmann et al., 2000). These include image co-registration, interferogram formation and filtering, removal of the topographic phase contribution using an external Digital Elevation Model (DEM), 2D phase unwrapping and conversion to displacement. The latter step may optionally preceded by a calibration procedure to estimate and remove image-wide error trends and refer the measurements to a reference point or set of points of known motion (e.g., GPS stations or areas which are assumed to be stationary).

Considering a pixel located at zero-Doppler coordinates $({\tau }_0^1,{\eta }_0^1)$ in image 1, and whose corresponding position in image 2 is$({\tau }_0^2,{\eta }_0^2)$, orbital and timing uncertainties, as well as ionospheric propagation effects discussed in section Ionospheric Propagation, will allow only estimates of these quantities to be determined, namely $(\widehat{{\tau }_0^1},\widehat{{\eta }_0^1})$and $(\widehat{{\tau }_0^2},\widehat{{\eta }_0^2})$. If a deformation in the LoS and azimuth directions (Δτ_defo, Δη_defo) has caused the actual location in image 2 to be $({\tau }_0^2+{\Delta \tau }_{defo},{\eta }_0^2+{\Delta \eta }_{defo})$, the DInSAR interferogram pixel value I_DinSAR will be:

$\begin{array}{l}{I}_{DInSAR}=h\left(\widehat{{\tau }_0^1},\widehat{{\eta }_0^1};{\tau }_0^1,{\eta }_0^1\right)·conj\left(h\left(\widehat{{\tau }_0^2},\widehat{{\eta }_0^2};{\tau }_0^2+\Delta {\tau }_{defo},{\eta }_0^2+\Delta {\eta }_{defo}\right)\right)\\ \propto \exp \left(j\Delta \psi \right)·\exp (j2\pi f_c\Delta {\tau }^{phase})·\exp \left[j2\pi f_{dc}\left(\Delta \eta \right)\right]& (6)\end{array}$

in which: conj() represents complex conjugation; Δτ^phase is the range phase delay difference (7), due to deformation Δτ_defo, tropospheric propagation τ_tropo, and ionospheric propagation ${\Delta \tau }_{iono}^{phase}(f_c)$; η is the azimuth position difference (8), due to the underlying deformation Δη_defo, and to the orbital uncertainty (Δη_orb) and ionospheric propagation contributions (η_iono) to the overall azimuth co-registration error Δη_coreg, which is given by (9). It is further assumed that in the differential interferogram formation process the flat earth and topographic contributions were perfectly removed. Any residual errors would appear as additional error terms in (7).

$\begin{array}{cc}\Delta {\tau }^{phase}=\Delta {\tau }_{defo}+\Delta {\tau }_{tropo}+\Delta {\tau }_{iono}^{phase}\left(f_c\right)& (7)\end{array}$

$\begin{array}{cc}\Delta \eta =\Delta {\eta }_{defo}+\Delta {\eta }_{coreg}=\Delta {\eta }_{defo}+\Delta {\eta }_{orb}+\Delta {\eta }_{iono}& (8)\end{array}$

$\begin{array}{cc}\Delta {\eta }_{coreg}=\widehat{{\eta }_0^1}-\widehat{{\eta }_0^2}-\left({\eta }_0^1-{\eta }_0^2\right)& (9)\end{array}$

The prerequisite for DInSAR is interferometric coherence, which occurs when the target-dependent amplitude and phase terms, namely A and ψ in (1), are statistically similar in the two acquisitions. In this case the corresponding phase difference Δψ can be considered a random variable with a distribution, which is sharply peaked around a null mean value (Bamler and Hartl, 1998), so that in the error-free case, the LoS deformation Δr_defo can be related to the phase of a DInSAR interferogram as follows:

$\begin{array}{cc}\Delta r_{defo}=\frac{c}{2}\Delta {\tau }_{defo}\simeq \frac{c}{2}\Delta {\tau }^{phase}\simeq \frac{\lambda }{4\pi }·unwrap\left(\arg \left(I_{DInSAR}\right)\right)& (10)\end{array}$

where λ is the radar wavelength, arg() is a function returning the argument of a complex number in the (-π,π] interval and unwrap() is a function performing phase unwrapping. The last equality in (10) holds only if the Doppler-centroid dependent phase term in (6) is negligible, which is always the case for Stripmap imagery, whereas as discussed below, this assumption may not hold for pixels at the edge of TOPS bursts (large f_dc) in the presence of significant horizontal deformation, particularly in the north-south direction [large Δη based on (4) and (5)].

DInSAR application to burst-mode and full-aperture ScanSAR image pairs (Holzner and Bamler, 2002) as well as to ScanSAR-Stripmap imagery (Bertan-Ortiz and Zebker, 2007), was successfully demonstrated for several past missions, such as Radarsat-1, ENVISAT, and ALOS-1 (Bamler and Holzner, 2004; Guccione, 2006; Motagh et al., 2008; Tong et al., 2010; Xu et al., 2011; Fielding et al., 2013), even though these had not been originally designed to support ScanSAR interferometry. Currently ScanSAR DInSAR is highly relevant for coseismic applications, in particular due to the routine observations carried out by the ALOS-2 sensor, which maintains a high level of burst alignment since Feb. 2015 (Natsuaki et al., 2017). Specific DInSAR processing issues related to the full-aperture product of this sensor are discussed in Liang and Fielding (2017a).

In recent years further algorithmic developments were required to apply DInSAR to the Interferometric Wideswath (IW) TOPS imaging mode of the Sentinel-1a and Sentinel-1b sensors, for which the azimuth beam steering introduces a significant coupling between azimuth image registration and interferometric phase (Prats-Iraola et al., 2012) through the azimuth-dependent phase term in (6). Methods have been developed to meet the much more stringent azimuth co-registration requirements compared to the Stripmap case (Yague-Martinez et al., 2016) and adaptations have been proposed to handle spatially varying azimuth co-registration errors related to orbital/timing uncertainties over long data takes (Xu et al., 2016) and (presumably) ionospheric propagation effects (Wang et al., 2017c). As previously mentioned, the TOPS DInSAR phase is also sensitive to azimuth motion, through the Δη_defo and Δη terms in (8) and (6) respectively. While on one side it has rightly been observed that this sensitivity is just a property of the TOPS acquisition mode (De Zan et al., 2014), in the presence of significant azimuth motion it may cause phase discontinuities at the burst boundaries due to the change of sign of and f_dc in (6), which in turn complicates the phase unwrapping step (González et al., 2015; Scheiber et al., 2015). However, as reviewed in section 3, so far this did not prevent application of TOPS imagery also to very large earthquakes.

For each imaging mode, namely Stripmap, ScanSAR and TOPS, DInSAR is the measurement technique, which typically provides the highest accuracy, which can reach a fraction of the centimetric SAR wavelength, provided interferometric coherence between the two acquisitions is retained and the error sources discussed in section Current Challenges are not dominant compared to the deformation. Concerning coherence, for current sensors the main limitations for coseismic applications are often surface changes due to land cover (e.g., vegetation and water bodies) and weather (e.g., snow in mountainous regions), geometric distortions (radar layover and shadow) due to topographic relief, as well as high strain rates, such as those typically observed close to fault surface ruptures (Massonnet and Feigl, 1998; Bürgmann et al., 2000). In particular if the strain rate exceeds a deformation of λ/4 within a SAR resolution element, either in the range or in the azimuth dimension, coherence will be completely lost.

The achievable spatial resolution of DInSAR LoS measurements in each image dimension is in the order of several radar resolution cells, which in turn are between 2 and 80 m in each image dimension for current SAR acquisition modes relevant for coseismic studies (Table 1). Finally, an important property of DInSAR measurements, regardless of the imaging mode, is that they are spatially relative. Depending on the processing approach, the output deformation map is either referred to a reference pixel with respect to which the phase gradients were unwrapped, or to the average motion of the tie-points used to calibrate the measurements after the phase unwrapping step.

A first DInSAR application example is shown in Figure 2, where two Stripmap InSAR pairs are considered, namely a descending one acquired by COSMO-SkyMed-1/2 on 02 Feb. 2014 and 10. Feb. 2014 respectively, and an ascending image pair acquired by the TanDEM-X satellite on 28 Jan. 2014 and 08. Feb. 2014. Both pairs span the Mw 5.9 Feb 3rd, 2014 Cephalonia, Greece, earthquake (Merryman Boncori et al., 2014). Considering the descending dataset, Figure 2A shows a coherence map prior to phase filtering, in which low coherence levels correspond to vegetated and cultivated areas, to surface ruptures in the northern part of the Paliki peninsula, and of course to water bodies. Figure 2B shows the wrapped and filtered DInSAR phase, in which each phase cycle represents a LoS deformation of half a radar wavelength based on (10), which amounts to 1.55 cm for the X-band COSMO-SkyMed radars (Table 1). Figure 2E shows the unwrapped LoS DInSAR deformation, in which data gaps are present for areas whose phase noise levels are too high even after phase filtering, and which can therefore not be reliably unwrapped. In this particular case, the coseismic deformation field causes a DInSAR phase discontinuity of several cycles in the northern part of the Paliki peninsula, so that phase unwrapping had to be performed separately for the western and eastern sectors of the image, using respectively R1 and R2 as spatial references. As detailed further in section 4.3, offset-tracking results were then used to recover the deformation gradients between these reference points and generate the LoS deformation map shown in Figure 2E.

FIGURE 2

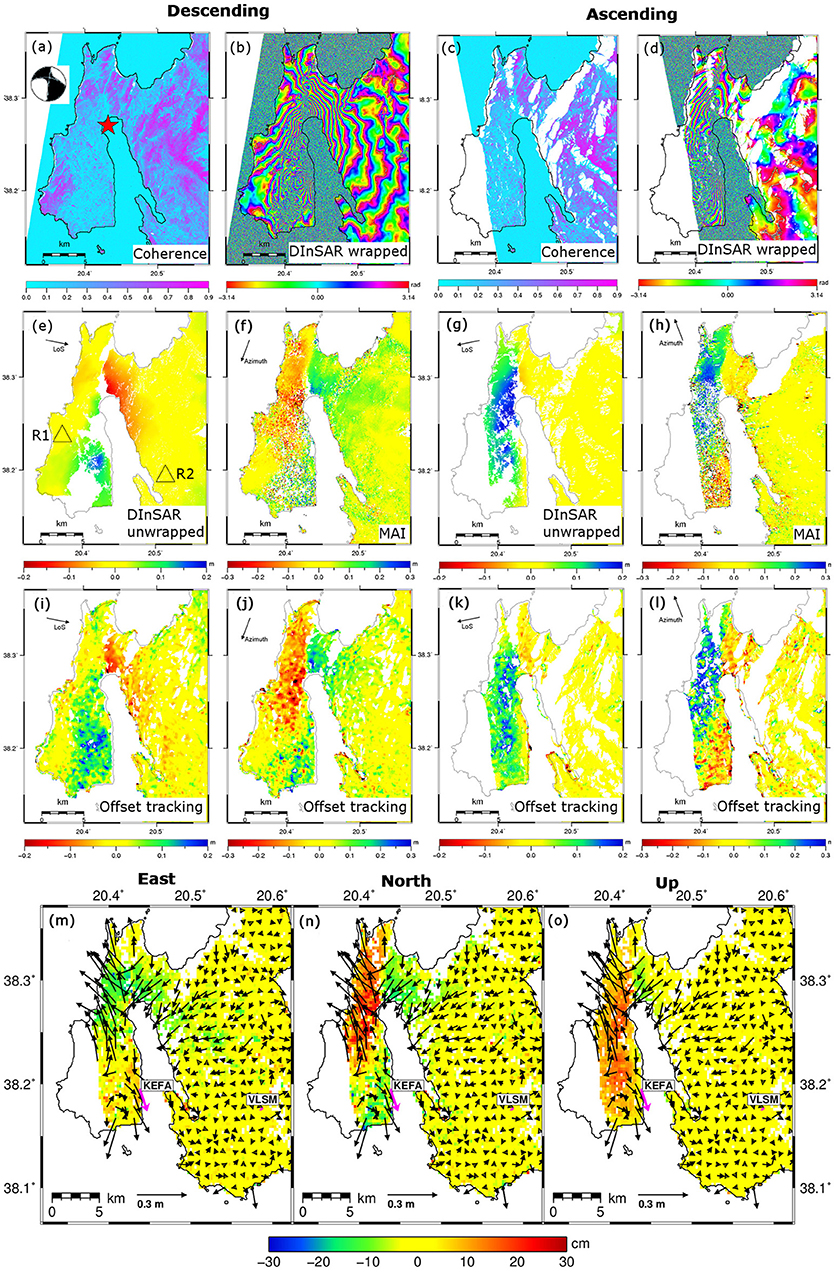
Figure 2. (A,C) Interferometric coherence. (B,D) Wrapped DInSAR phase spanning the Mw 5.9 February 3rd, 2014 Cephalonia, Greece, earthquake. Each phase cycle represents 1.55 cm of deformation. (E,G) DInSAR LoS deformation (positive toward the satellite). (F,H) Azimuth split-bandwidth InSAR (MAI) deformation (positive in the flight direction). (I,K) Offset-tracking LoS deformation. (J,L) Offset-tracking azimuth deformation (M–O) East, North, Up deformation. Descending image pair, panels (A,B,E,F,I,J): COSMO-SkyMed-1/2 Stripmap, 02 February 2014 and 10 February 2014. Ascending image pair, panels (C,D,G,H,K,L): TanDEM-X Stripmap, 28 January 2014 and 08 February 2014. Panel (A) also shows the focal mechanism at the location of the earthquake epicenter. Copyright Seismological Society of America. Adapted from Figure 3, Figures S1–S6 in Merryman Boncori et al. (2014).

Further examples of DInSAR interferograms at are shown in Figures 3A,E, 4A for the C-band Sentinel-1a sensor, operating in TOPS mode, and in Figures 5B,D for L-band ALOS-1 PALSAR sensor, acquiring in Stripmap mode. These examples will be referred to further in the following sections. At this stage it is just worth noting that the phase cycles (fringes) represent half a wavelength of LoS deformation (or more in general phase delay), which amounts to 1.55 cm for Figures 3B,D (X-band), to 2.8 cm for Figure 4A (C-band) and to 11.8 cm for Figures 5B,D.

FIGURE 3

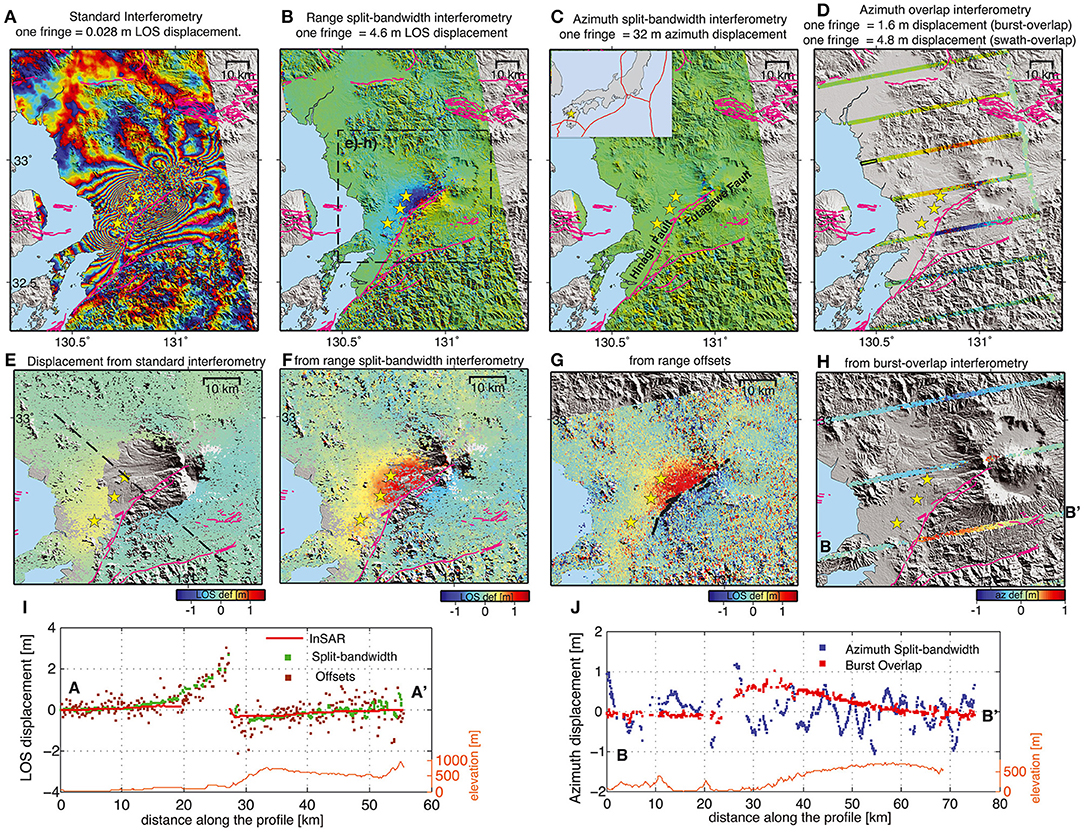
Figure 3. Coseismic deformation of the Mw 7.1 April 16, 2016 Kumamoto, Japan, earthquake based on ascending Sentinel-1a TOPS imagery acquired on 08 April 2016 and 20 April 2016. (A) Wrapped DInSAR phase. (B) Range split-bandwidth InSAR phase. (C) Azimuth split-bandwidth InSAR (MAI) phase. (D) Burst Overlap MAI phase. (E) DInSAR LoS deformation (positive away from the satellite). (F) Range-SBI LoS deformation. (G) Offset-tracking LoS deformation, (H) Burst Overlap MAI azimuth deformation (positive opposite to the azimuth direction). (I) LoS deformation profiles along the dashed line in panel (E) taken from the deformation maps in panels (E–G). (J) Azimuth deformation profiles between points B and B' in panel (H) based on panels (C,H). The earthquake locations (yellow stars) are from the Global Centroid Moment Tensor project. The mapped faults are indicated as magenta lines. Reproduced with permission from Figure 2 in Jiang et al. (2017a). ©2017. American Geophysical Union. All rights reserved.

FIGURE 4

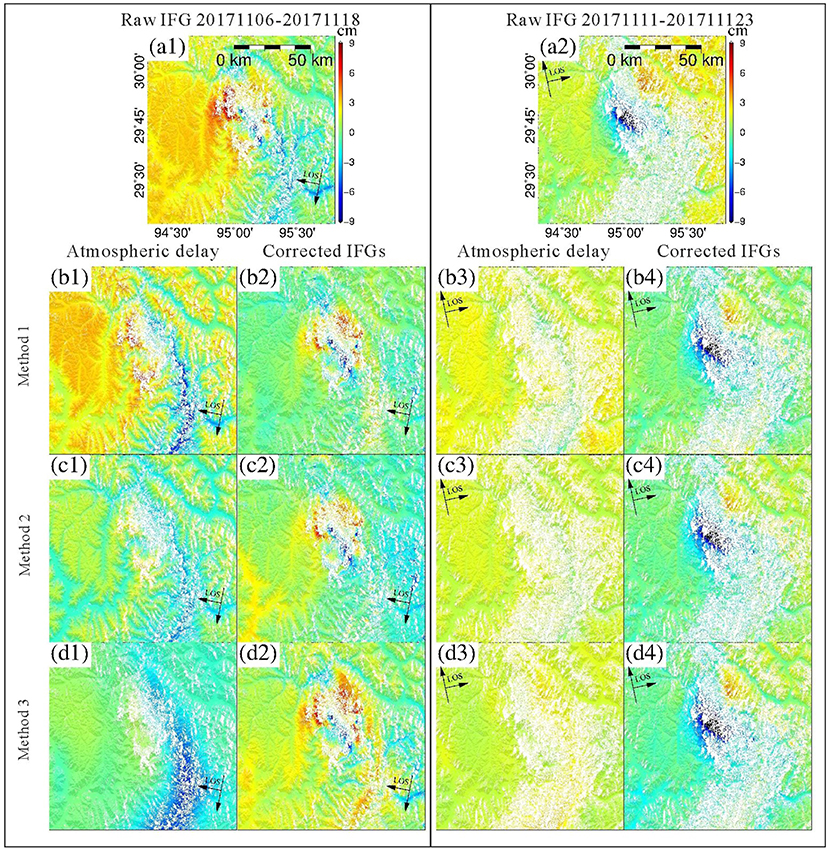
Figure 4. (A1,A2) Uncorrected DInSAR LoS deformation (positive away from the radar) spanning the Mw 6.4 November 17, 2017 Nyingchi, China, earthquake. The descending pass image pair was acquired by Sentinel-1a on November 6th, 2017 and November 18th 2017. The ascending pass image pair was acquired by Sentinel-1a on November 11th, 2017 and November 23rd, 2017. (B–D) Estimated tropospheric delay and corrected LoS deformation using different data and methods: (B1–B4) HRES-ECMWF data interpolated with the Iterative Tropospheric Decomposition model (Yu et al., 2018). (C1–C4) Exponential model fitted to far-field DInSAR phase values. (D1–D4) HRES-ECMWF interpolated bilinearly. Reproduced from Figure 2 in Yu et al. (2018), distributed under the CC BY 4.0 license (https://creativecommons.org/licenses/by/4.0/).

FIGURE 5

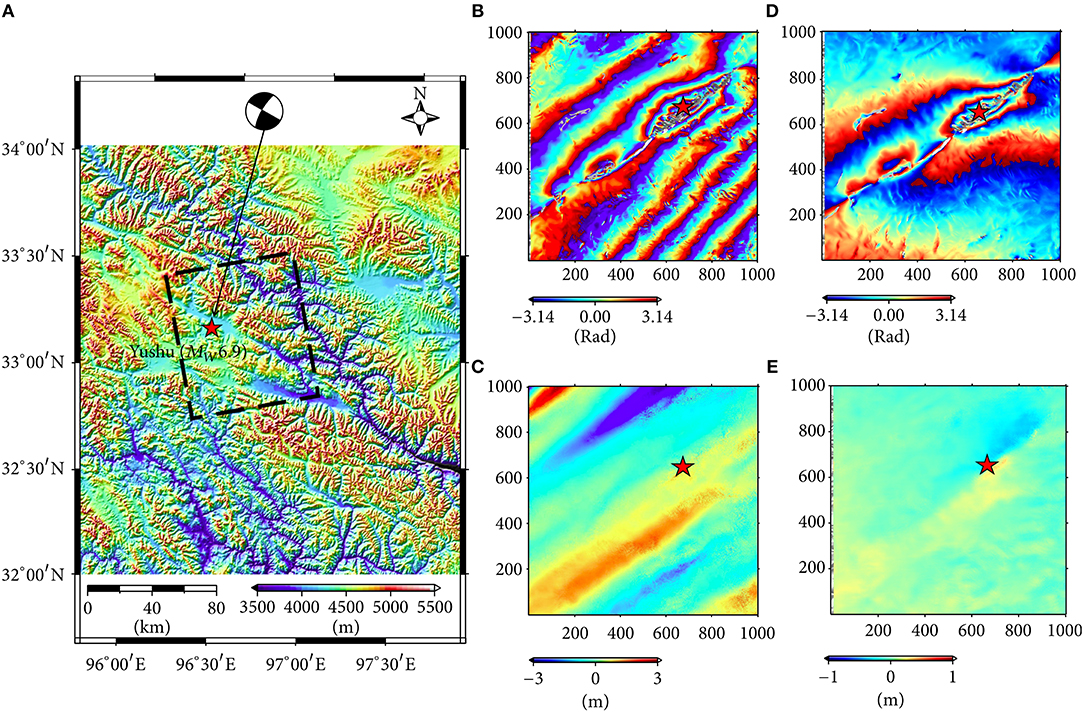
Figure 5. (A) Topographic map of the area of the Mw 6.9 April 13th, 2010 Yushu, China, earthquake (epicenter shown with a red star). The black rectangle indicates the coverage of the ALOS-1 PALSAR Stripmap data (B,C) Wrapped DInSAR phase and offset tracking azimuth displacement for the January 15, 2010 – July 18, 2010 image pair. (D,E) Wrapped DInSAR phase and offset tracking azimuth displacement for the January 15, 2010 – April 17, 2010 image pair. Reproduced from Figure 4 in Zhu et al. (2017), distributed under the CC BY 4.0 license (https://creativecommons.org/licenses/by/4.0/).

Offset Tracking

Offset-tracking methods, also referred to as pixel-offset or pixel-tracking techniques, exploit the range- and azimuth-dependent amplitude terms in (1) to measure both the LoS and the azimuth displacement components between two SAR acquisitions. This is done by estimating the 2D mis-registration (i.e., group delay change) of corresponding pixels by applying several image matching techniques (Brown, 1992) to track amplitude (or intensity) features and/or coherent SAR speckle. Gray et al. (1998) first demonstrated the use of amplitude cross-correlation for ice velocity measurements, whereas Michel et al. (1999) and Peltzer et al. (1999) first carried out coseismic deformation measurements with phase correlation and normalized cross-correlation respectively. These latter techniques are still currently the most widely used, although recently some algorithmic variations have also been proposed (e.g., Wang and Jónsson, 2015).

An offset tracking measurement can be considered the result of a search of the registration shifts, which maximize a similarity parameter, e.g., Normalized Cross Correlation (NCC):

$\begin{array}{l}\left(\Delta {\tau }^{group},\Delta \eta \right)=\\ \arg \underset{\delta \tau ,\delta \eta }{max}NCC\left(\left|h\left(\tau ,\eta ;{\tau }_0^1,{\eta }_0^1\right)\right|,\left|h\left(\tau ,\eta ;\widehat{{\tau }_0^2}+\delta \tau ,\widehat{{\eta }_0^2}+\delta \eta \right)\right|\right)& (11)\end{array}$

Compared to the differential phase delay in (7), the group delay has an inverted ionospheric contribution (section Ionospheric Propagation), and an additional term related to LoS position uncertainties (τ_orb), due to orbit inaccuracies:

$\begin{array}{cc}\Delta {\tau }^{group}=\Delta {\tau }_{defo}+\Delta {\tau }_{orb}+\Delta {\tau }_{tropo}-\Delta {\tau }_{iono}^{phase}\left(f_c\right)& (12)\end{array}$

The azimuth mis-registration Δη is the same as in (8). Based on (5), in the error-free case the LoS deformation Δr_defo and azimuth deformation Δa_defo can be related to the respective range and azimuth mis-registration as follows:

$\begin{array}{cc}\Delta r_{defo}=\frac{c}{2}\Delta {\tau }_{defo}\simeq \frac{c}{2}\Delta {\tau }^{group}& (13)\end{array}$

$\begin{array}{cc}\Delta a_{defo}=V_r·\Delta {\eta }_{defo}\simeq V_r·\Delta \eta & (14)\end{array}$

The achievable accuracy of offset-tracking techniques is typically between 1/10th and 1/100th of the spatial resolution in each SAR image dimension, and thus at least an order of magnitude worse than for DInSAR. Accuracy depends on interferometric coherence, if coherent speckle is being tracked, or on the prominence of common features if these are present (Bamler and Eineder, 2005). The spatial resolution of the measurements is in the worst case equal to twice the matching window size, which is typically tens of radar resolution cells in each image dimension, and in the best case equal to the distance (posting) between neighboring measurements, which is typically chosen to be a fraction of the matching window size (Pritchard et al., 2005). Thus, compared to DInSAR, also the spatial resolution of the measurements is at least an order of magnitude worse.

Despite the above mentioned drawbacks, offset tracking also offers some advantages and complementarities with respect to DInSAR: the measurement of the azimuth deformation component; the possibility of succeeding also in the absence of interferometric coherence, provided trackable amplitude features are present; a greater algorithmic robustness, due to the fact of not requiring co-registration nor phase unwrapping, which may be delicate processing steps for specific sites and datasets (section Phase Unwrapping).

An example of the complementarities of offset-tracking with respect to DInSAR is shown in Figure 2 for the Mw 5.9 Cephalonia, Greece, event. Concerning the LoS measurements, the coarse spatial resolution and higher noise level of offset tracking compared to DInSAR is apparent comparing Figure 2I with Figures 2E,K with Figure 2G. For these Stripmap datasets (Table 1) the spatial resolutions of DInSAR measurements after phase averaging are between 10 and 30 m for the descending and ascending datasets respectively, and between 100 and 800 m for the offset-tracking measurements. However, offset-tracking also provides LoS measurements where the DInSAR phase cannot be unwrapped, since amplitude features provide cross-correlation peaks in (11), even in the absence of interferometric coherence. Furthermore, offset tracking provides also the azimuth motion components (Figures 2J,L), which in this case are essential to reveal the complexity of the fault geometry (Merryman Boncori et al., 2014).

Finally, it should be noted that although co-registration is not required by offset-tracking, any image-wide co-registration errors, e.g., due to orbital and timing uncertainties and/or atmospheric propagation, will translate directly into a bias in the measurements. As for DInSAR, a tie-point calibration procedure based on points of known motion or areas assumed to be stationary can be used to compensate such effects.

Split-Bandwidth Interferometry

Split-bandwidth Interferometry techniques measure displacement in each dimension through a double difference interferometric procedure. Interferograms between corresponding upper and lower spectral sub-bands in each image are formed (I^u and I^l), followed by a second difference interferogram, the unwrapped phase of which is proportional to the sought displacement. For the TOPS mode case, the images should be deramped to remove the phase modulation due to the azimuth antenna scanning before forming the sub-band interferograms (I^u and I^l).

In the azimuth dimension, assuming an upper and a lower Doppler frequency sub-bands centered about $f_{dc}^u$ and $f_{dc}^l$ respectively, the following relations hold:

$\begin{array}{cc}{I}_a^u=\exp \left(j\Delta {\psi }^u\right)·exp(j2\pi f_c\Delta {\tau }^{phase})·\exp (j2\pi f_{dc}^u\Delta \eta )& (15)\end{array}$

$\begin{array}{cc}{I}_a^l=\exp \left(j\Delta {\psi }^l\right)·exp(j2\pi f_c{\tau }^{phase})·\exp (j2\pi f_{dc}^l\Delta \eta )& (16)\end{array}$

from which the azimuth deformation is obtained in the error free case as:

$\begin{array}{l}\Delta a_{defo}=V_r·\Delta {\eta }_{defo}\simeq V_r·\Delta \eta \\ =\frac{V_r}{2\pi (f_{dc}^u-f_{dc}^l)}·unwrap\left(\arg \left(I_a^u·conj\left(I_a^l\right)\right)\right)& (17)\end{array}$

In the range dimension, assuming upper and lower range-frequency sub-bands centered around $f_c^u$ and $f_c^l$ respectively, the corresponding split-bandwidth interferograms are given by:

$\begin{array}{l}{I}_r^u=\exp \left(j\Delta {\psi }^u\right)·exp\left[j2\pi f_c^u\left(\Delta {\tau }_{defo}+\Delta {\tau }_{tropo}+\Delta {\tau }_{iono}^{ph}\left(f_c^u\right)\right)\right]\\ ·\exp (j2\pi f_{dc}\Delta \eta )& (18)\end{array}$

$\begin{array}{l}{I}_r^l=\exp \left(j\Delta {\psi }^l\right)·exp\left[j2\pi f_c^l\left(\Delta {\tau }_{defo}+\Delta {\tau }_{tropo}+{\tau }_{iono}^{ph}\left(f_c^l\right)\right)\right]\\ ·\exp (j2\pi f_{dc}\Delta \eta )& (19)\end{array}$

For TOPS imagery, unlike the azimuth-SBI case, it is not necessary to deramp the input images before forming the sub-band interferograms in (18) and (19). Neglecting ionospheric propagation effects (section Ionospheric Propagation), the LoS deformation is given by:

$\begin{array}{cc}\Delta r_{defo}=\frac{c}{2}\Delta {\tau }_{defo}\simeq \frac{c}{4\pi (f_c^u-f_c^l)}·unwrap\left(\arg \left(I_r^u·conj\left(I_r^l\right)\right)\right)& (20)\end{array}$

SBI was originally proposed in the range dimension for absolute phase estimation (Madsen and Zebker, 1992) and later both in the range and in the azimuth dimensions for Stripmap image co-registration (Scheiber and Moreira, 2000), where it was named Spectral Diversity. Its potential for geophysical applications, was recognized following the work of Bechor and Zebker (2006), who reformulated azimuth Spectral Diversity in terms of squint angle rather than of Doppler frequency, dubbing their method Multi Aperture Interferometry (MAI), and applying it to the Mw 7.1 1999 Hector Mine event. In the latter study, the azimuth sub-bands were obtained by dedicated raw data focusing steps, whereas the same method was applied to conventionally focused Stripmap imagery by Barbot et al. (2008) and used to study the Mw 7.2, 2003 Altai event. Further developments of MAI were proposed by Jung et al. (2009), who among other contributions, included the use of an adaptive phase filtering algorithm widely used for DInSAR (Goldstein and Werner, 1998). Bamler and Eineder (2005) derived theoretical upper bound and empirical curves for the accuracy of the technique as a function of coherence and phase estimation window size (multi-looking factors), as well as the optimum frequency separation between sub-bands. De Zan et al. (2015) discussed the effects of multi-looking the sub-band interferograms prior to formation of the final difference interferogram (referred to as early multi-looking) as opposed to forming the sub-band interferograms at a full resolution and averaging only the final difference interferogram (referred to as late multi-looking).

Recent developments of azimuth split-bandwidth interferometry addressed its application to Sentinel-1 TOPS and ALOS-2 ScanSAR imagery. Concerning Sentinel-1, spatially discontinuous measurements were obtained by applying the method to the burst-overlap regions (Grandin et al., 2016; Jiang et al., 2017a,b), which have a “naturally” large Doppler frequency separation due to the azimuth antenna steering, and thus a high motion sensitivity (10). This method will be referred to as Burst-Overlap MAI (BO-MAI) in the following. Jiang et al. (2017a) also reported the first application, to the author's best knowledge, of range-SBI, which was demonstrated for the 2016 Kumamoto sequence on Sentinel-1 TOPS data, the large range bandwidth of which allows a high sub-band frequency separation and thus good motion sensitivity (20). Concerning ALOS-2 ScanSAR, Liang and Fielding (2017b) applied azimuth SBI to data acquired from different bursts [with Doppler frequency separation given by (3)], after extracting these from the full-aperture product, to obtain a continuous azimuth deformation map for the 2015 Mw 7.8 Gorkha event. This technique can be considered the ScanSAR equivalent of BO-MAI, and will be referred to as such in the following.

From the performance point of view, SBI shares the same interferometric coherence requirements as DInSAR, being itself an interferometric method, including the limitations due to the maximum observable strain rates. However, when applied to Stripmap images or single ScanSAR or TOPS bursts, phase unwrapping is almost never required due to the limited frequency separations in (19) and (20), which in turn can lead to improved spatial coverages compared to DInSAR. Compared to offset-tracking, SBI typically provides greater accuracies and spatial resolutions in coherent areas, whereas being a phase-based method it cannot carry out measurements in completely decorrelated areas.

For the azimuth-SBI case (MAI), an example of these considerations is shown in Figure 2. The spatial coverage of the MAI measurements (Figures 2F,H) has less data voids compared to their DInSAR counterparts (Figures 2E,G), since some areas had to be masked out to avoid phase unwrapping errors. Compared to offset-tracking (Figures 2J,L), an increase in spatial resolution can be noticed. The latter is about 60 m for MAI compared to 100–800 m for offset-tracking as mentioned in section Offset tracking. The lower noise level compared to offset-tracking is also apparent.

Concerning the range-SBI case, an application example is shown in Figure 3 for a Sentinel-1a TOPS image pair used to study the Mw 7.1 2016 Kumamoto, Japan, event. The coverage difference with respect to DInSAR is very significant in this case (cfr. Figures 2F,E), given the fringe density close to the fault (Figure 2A), which causes the phase unwrapping to be problematic. In contrast, where DInSAR is applicable, its significantly higher spatial resolution and reduced noise level compared to range SBI is obvious. Compared to LoS offset-tracking, Figure 2G, range-SBI provides an increased spatial resolution as well as a reduced noise level. However, offset-tracking provides an even better coverage close to the fault, since range-SBI fails where coherence is lost, e.g., due to the above-mentioned maximum strain-rate constraints.

Finally, an example of TOPS BO-MAI is shown in Figures 3D,H. The spatial coverage is discontinuous, although compared to conventional MAI applied to each TOPS burst (Figure 2C), higher accuracies and resolutions can be achieved due to the much higher Doppler frequency separation (17), which is between 4.4 and 5.2 KHz in the BO-MAI case and at most 150 Hz in the conventional MAI.

Recovering the 3D Deformation Field

Based on (4), each LoS and azimuth deformation measurement provides one equation in 3 unknowns, namely the Cartesian components of the underlying 3D deformation. Provided at least 3 linearly independent LoS and/or azimuth components are available, a Weighted Least Squares (WLS) problem may be formulated and solved (Wright et al., 2004), in which the weights are typically based on the variance of the measurements in the deformation far-field (Funning et al., 2005). Improvements to the WLS approach to account for the spatial correlation among measurements have been recently proposed (Liu et al., 2018a). Regardless of the inversion approach, observables are provided either by LoS and azimuth observations on ascending and descending passes of right-looking acquisitions (e.g., Jo et al., 2017; Morishita et al., 2018; Wang et al., 2018b; Xu et al., 2018b), or by LoS observations alone, taken from left- and right-looking acquisitions (Liu et al., 2018a).

An application example of the WLS method is shown in Figure 2, where LoS and azimuth measurements available from DInSAR, MAI and offset-tracking (Figures 2E–L) are jointly inverted to solve for the Cartesian deformation components (Figures 2M–O).

For cases in which only DInSAR observations of the LoS deformation Δr_defo are carried out from ascending and descending passes, which is often the case (e.g., Huang et al., 2016; Solaro et al., 2016; Wen et al., 2016; Cheloni et al., 2017), the so-called 2.5D deformation field can be computed, which consists in the east and vertical deformation components, respectively Δe and Δu, computed by assuming no north contribution (Δn = 0). This assumption is motivated by the lower sensitivity of LoS measurements to the north motion component due to the near-polar satellite orbit, which can be quantified for a given SAR image pixel using (4). Assuming a mid-latitude value of α = 10°, and θ = 38° as in the center of a Sentinel-1 IW2 swath, the following relations hold:

$\begin{array}{cc}\left(\begin{array}{c}\Delta r_{defo}\\ \Delta a_{defo}\end{array}\right)=\left(\begin{array}{ccc}0.61& 0.11& -0.79\\ -0.17& 0.98& 0\end{array}\right)\left(\begin{array}{c}\Delta e\\ \Delta n\\ \Delta u\end{array}\right)& (21)\end{array}$

From (21) it is seen that LoS measurements are 6 to 7 times more sensitive to east and vertical motion respectively, compared to the north direction.

Technique Application

Weston et al. (2012) and Weston et al. (2011) compiled an InSAR Centroid Moment Tensor catalog based on 67 earthquakes occurred between 1992 and 2010, covered by about 80 SAR-based coseismic deformation studies. More recently, since the launch of the Sentinel-1a satellite in April 2014, 34 SAR-based coseismic deformation studies have been described in about 115 publications to the author's best knowledge (Supplementary Table 1). The resulting deformation fields span spatial gradients of ~3 cm in the radar LoS over spatial scales of a few km (e.g., the 2017 Mw 3.9 Ischia, Italy and the 2017 Mw 5.9 Pawnee, Oklahoma events) to gradients of several meters in the LoS and/or azimuth components, spanning several hundreds of km (e.g., the 2015 Mw 7.8 Gorkha, Nepal, the 2015 Mw 8.3 Illapel, Chile, and the 2016 Mw 7.8 Kaikōura, New Zealand events).

Coseismic studies in the past 4 years have mainly relied on Sentinel-1 TOPS Interferometric Wideswath (IW) data and/or on ALOS-2 ScanSAR Wide Beam (WB) or Stripmap acquisitions, with occasional contributions from COSMO-SkyMed and Radarsat-2 Stripmap imagery (Table 1). From the measurement technique point of view, DInSAR is by far the most extensively applied (Supplementary Table 1), mainly owing to its higher accuracy and spatial resolution, and thus broader application range, compared to offset-tracking and split-bandwidth techniques. Such differences are enhanced for TOPS and ScanSAR-based measurements, compared to the Stripmap case, since these acquisition modes are designed to trade-off in particular azimuth spatial resolution in favor of swath (range) coverage. Of course DInSAR requires a sufficient level of interferometric coherence to be applied, and if this requirement is not met, e.g., due to dense vegetation, earthquakes may be undetected (Funning and Garcia, 2019).

The possibility of complementing DInSAR LoS measurements with azimuth deformation components derived with offset-tracking and/or MAI depends on the fault mechanism of the earthquake as well as on the coherence and spatial resolution of the SAR images. Concerning Sentinel-1 IW and ALOS-2 WB modes, azimuth offset-tracking and direct application of MAI by splitting the azimuth bandwidth available within a single burst, restricts the application of these techniques to events associated with large azimuth deformations (>1 m). Successful examples include the 2015 Mw 7.2 Murghab, Tajikistan (Metzger et al., 2017), the 2015 Mw 7.8 Gorkha, Nepal (Grandin et al., 2015; Elliott et al., 2016; Wei et al., 2018) and the 2016 Mw 7.8 Kaikōura, New Zealand events (Hamling et al., 2017; Wang et al., 2018b, Xu et al., 2018b). BO-MAI provides an increased sensitivity to azimuth motion, and has been applied to the Illapel (Grandin et al., 2016), Gorkha (Jiang et al., 2017b) and Kumamoto events (Jiang et al., 2017a) concerning Sentinel-1 TOPS, and to the Gorkha (Liang and Fielding, 2017b) and Kaikōura events (Hamling et al., 2017), concerning ALOS-2 ScanSAR. A limitation in the Sentinel-1 case, is the spatial discontinuity of the azimuth measurements, which can be derived in 1.5 km bands spaced 20 km apart (Jiang et al., 2017a).

For higher resolution Stripmap acquisitions, such as those provided by the ALOS-2 Ultrafine 3 m resolution modes (UBS/UBD), azimuth deformation gradients of 20 to 30 cm can be easily measured in coherent imagery, as demonstrated for the 2014 Mw 6.2 Nagano, Japan event (Kobayashi et al., 2018) and for the 2016 Mw 6.0 and Mw 6.2 foreshocks of the Kumamoto, Japan sequence (Kobayashi, 2017). A similar performance can be expected also from Sentinel-1 Stripmap mode data, which, although not routinely acquired, has been successfully used to derive azimuth measurements for the 2014 Mw 6.0 South Napa, USA event (Jo et al., 2017).

Another complementarity among measurement techniques, which has long been exploited (Peltzer et al., 1999), concerns the potential of offset-tracking measurements to provide LoS measurements closer to fault ruptures, where high strain rates often make DInSAR phase unwrapping unfeasible or cause loss of coherence as mentioned in section Differential SAR Interferometry and shown in Figure 3 for the 2016 Mw 7.1 Kumamoto, Japan earthquake. For Sentinel-1 IW and ALOS-2 WB acquisitions offset-tracking was carried out for events associated with large (>1 m) surface displacements, Examples include the 2015 Mw 7.2 Murghab, Tajikistan event (Metzger et al., 2017), the 2015 Mw 7.8 Gorkha, Nepal event (Elliott et al., 2016) and the 2016 Mw 7.8 Kaikōura, New Zealand event (Hamling et al., 2017).

For large-deformation applications/areas where sufficient coherence levels are retained, an even better complement to DInSAR may be represented by split-bandwidth methods, which can provide higher spatial resolutions and accuracy compared to offset tracking, with greatly reduced phase unwrapping requirements (if any) compared to DInSAR. An example concerning the LoS deformation component is given by Jiang et al. (2017a), in which DInSAR, offset-tracking, and range-SBI are applied to Sentinel-1 TOPS data covering the 2016 Mw 7.0 Kumamoto, Japan mainshock and foreshocks. In the azimuth dimension, the effects of ALOS-2 ScanSAR BO-MAI for the aforementioned Kaikōura event (Hamling et al., 2017), based on the approach of Liang and Fielding (2017b), can be compared to the ScanSAR azimuth offset-tracking results of Xu et al. (2018b). It should be noted however, that in cases/areas where interferometric coherence is lost, split-bandwidth methods, like DInSAR, will not yield useful results, whereas offset-tracking of intensity features might still succeed. An example of this is provided by the above-mentioned Gorkha event, comparing the azimuth offset-tracking results of Elliott et al. (2016) with the MAI results of Jiang et al. (2017b), the coverage of which is limited by loss of coherence due to snow in the Himalayas.

Current Challenges

The processing methods described in section Measurement Techniques are implemented in several commercial and freely available software packages, and, as mentioned in section Introduction, there are several existing systems, which carry out DInSAR processing of Sentinel-1 data in an automated fashion. On the other hand only few of the coseismic deformation studies in recent literature (Supplementary Table 1) are based on automated processing chains. For a given earthquake, area of interest and available SAR data, an image analyst must typically take some ad-hoc decisions. These include what techniques to apply, and assessing whether the results elicit additional processing steps, in particular concerning the mitigation of tropospheric and ionospheric propagation effects and, in the case of, also phase unwrapping errors.

Tropospheric Propagation

Tropospheric propagation affects all LoS measurement techniques, namely DInSAR, offset-tracking (range offsets only) and range-SBI, by introducing a spatially varying differential range delay:

$\begin{array}{cc}\Delta {\tau }_{tropo}=f(P_d\left(z\right),T\left(z\right),e\left(z\right),z_0,\theta )& (22)\end{array}$

which depends on the vertical profiles of partial pressure of dry air, P_d(z), Temperature, T(z), and partial pressure of water vapor, e(z), as well as on topographic height, z₀, and local incidence angle, θ (Hanssen, 2001). In particular (13) can be considered the sum of turbulent component, uncorrelated with topography and characterized by significant horizontal spatial variability, and of a stratified delay component, strongly correlated with topography and slowly varying horizontally (Doin et al., 2009). Tropospheric propagation can be comparable in magnitude to the coseismic deformation and make it difficult or impossible to detect the deformation pattern (Funning and Garcia, 2019). An example is shown in Figure 4A for the 2017 Mw 6.4 Nyingchi, China, earthquake.

The effects of tropospheric propagation on azimuth measurements are instead negligible due to the low height of the troposphere compared to the satellite orbit, which implies that different radar pulses backscattered from a same resolution cell traverse virtually the same troposphere (Meyer et al., 2006).

An extensive literature exists concerning both error characterization and mitigation strategies for DInSAR (e.g., Scott and Lohman, 2016; Yu et al., 2018, and references therein), whereas for offset-tracking (and the seldom applied range-SBI) tropospheric propagation effects often lie below the measurement noise floor and are therefore ignored. In recent coseismic deformation studies (Supplementary Table 1) three different approaches are followed to deal with this error source in DInSAR: no action is taken; an empirical model correction is applied; a correction based on a numerical weather model is applied.

Empirical model corrections address topography correlated tropospheric delays. The simplest models are based on the estimation of a linear phase-elevation relation in the far-field, where no deformation is assumed (Wicks et al., 2002), possibly coupled with the estimation of the parameters of a conic to model image-wide error trends, due to atmospheric propagation and/or orbit uncertainties (Cavalié et al., 2007). More general approaches to improve the robustness of stratified delay estimation in the presence of deformation, turbulence, and/or image-wide errors due to orbital uncertainties (Lin et al., 2010; Shirzaei and Bürgmann, 2012; Bekaert et al., 2015). In recent coseismic literature (Supplementary Table 1), linear phase-elevation correction models are applied by Feng et al. (2018), Xu et al. (2018a), Yi et al. (2018), Wang et al. (2017a), Metzger et al. (2017), Xu et al. (2017), Wen et al. (2016), Motagh et al. (2015), Copley et al. (2015). Ganas et al. (2016) analyze the effects of different linear corrections and conclude that they have no impact for that specific deformation study (2015 Mw 6.5 Lefkada, Greece). Non-linear phase-elevation models are applied by Yang et al. (2018a) and Nocquet et al. (2016).

Numerical weather prediction models provide estimates of atmospheric parameters, including those in (13), at a set of pressure levels, several times per day. Correction procedures have been proposed based on global reanalysis data, such as ERA-Interim and MERRA (Doin et al., 2009; Jolivet et al., 2011, 2014), on operational analysis models such as HRES-ECMWF (Yu et al., 2018), and on meso-scale models (Foster et al., 2006; Puyssegur et al., 2007; Wadge et al., 2010; Kinoshita et al., 2013; Jung et al., 2014). In recent coseismic studies, Jiang et al. (2018) tested the application of ERA-Interim corrections based on the interpolation approach of Jolivet et al. (2011) and of the HRES-ECMWF global model, based on the Iterative Tropospheric Decomposition model of Yu et al. (2017), provided through the Generic Atmospheric Correction Online Service for InSAR (GACOS). The latter was also used by Albano et al. (2018). Feng et al. (2017a) tested the application of ERA-Interim and MERRA global models (Jolivet et al., 2011) as well as empirical corrections (Bekaert et al., 2015). Finally, meso-scale models were used by Kobayashi et al. (2018) and Ozawa et al. (2016).

Although there is clearly not a consensus on the best tropospheric correction approach for a given area of interest, nor on whether corrections should be applied systematically, there is a good agreement in literature concerning the pros and cons of the above-mentioned methods. Empirical approaches may outperform weather models in situations where stratified delays prevail (Kinoshita et al., 2013; Bekaert et al., 2015), but are more limited in dealing with spatial variability of both the turbulent and stratified components, and cannot resolve a potential correlation of deformation with height. Global atmospheric models are readily available, also in near real time if operational models are used (Li et al., 2016b), and have been proved successful in many cases (Jolivet et al., 2014). However, there may be areas and/or conditions under which they do not perform satisfactorily (Walters et al., 2013). Meso-scale models provide the highest spatial resolutions and have been proved very effective (Wadge et al., 2010), but also require expertise in numerical weather modeling to be exploited successfully.

An example of weather-model and empirical corrections is shown in Figure 4. Comparing the correction based on a simple exponential delay vs. elevation model, Figure 4C2, to that based on Iterative Tropospheric Decomposition interpolation of HRES-ECMWF profiles, Figure 4B2, it is clear that the horizontal variability plays an important role for this dataset and in this case it is well-captured by weather model data, provided this more complex interpolation scheme is used to separate the turbulent and stratified delay contributions, rather than performing a more simple bilinear interpolation (Figure 4D2).

Ionospheric Propagation

Ionospheric propagation affects both LoS and azimuth deformation measurements, regardless of which technique is applied. In the range dimension, a differential phase and group delay with opposite signs are introduced (Meyer et al., 2006):

$\begin{array}{cc}\Delta {\tau }_{iono}^{phase}\propto \frac{\Delta TEC\left(\eta \right)}{\text{cos }\theta ·f_c^2}{|}_{\eta ={\eta }_0}& (23)\end{array}$

$\begin{array}{cc}{\tau }_{iono}^{group}=-\Delta {\tau }_{iono}^{phase}& (24)\end{array}$

where ΔTEC is the Total Electron Content (TEC) difference between the two acquisitions, f_c is the carrier frequency of the radar, and θ the local incidence angle. Azimuth variations of ΔTEC in (22) on spatial scales smaller than the synthetic aperture length (~1 to 20 km depending on acquisition mode and carrier frequency) also cause a local shift in the temporal azimuth zero-Doppler coordinates given by Gray et al. (2000) and Liang and Fielding (2017b):

$\begin{array}{cc}\Delta {\eta }_{iono}\propto \frac{\partial {\tau }_{iono}^{phase}}{\partial \eta }{|}_{\eta ={\eta }_0}& (25)\end{array}$

Such shifts are spatially correlated in the range direction, and appear as “azimuth-streaks” of variable orientation in the azimuth measurements carried out with offset-tracking (13) and MAI (16), (e.g., Gray et al., 2000; Raucoules and De Michele, 2010; Jung et al., 2013).

An example of the phase delay (22) and azimuth streak effects (24) is shown in Figure 5, in which L-band ALOS-1 Stripmap data pairs spanning the Mw 6.9 Apr. 13th 2010 Yushu, China, earthquake are analyzed. Figures 5B,C show the DInSAR phase and azimuth offset-tracking results for an image pair in which the coseismic deformation patterns are visible, alongside severe ionospheric effects, which amount to several tens of cm in terms of DInSAR LoS deformation (Figure 5B) and several meters in terms of apparent azimuth deformation (Figure 5C). In this case the azimuth streak orientation is actually parallel to the fault. Figures 5D,E show the DInSAR phase and azimuth offset-tracking results for an image pair with less ionospheric propagation effects, in which the coseismic deformation patterns are predominant.

Ionospheric propagation effects received an increased interest in recent years, due to the abundance of data acquired with wide-area acquisitions modes, in particular Sentinel-1 TOPS and ALOS-2 ScanSAR, in which the effects of ionospheric phase delay (22) can be better appreciated, even at C-band where they were previously considered negligible (Gomba et al., 2017). In recent coseismic deformation studies (Supplementary Table 1) three different approaches are followed to deal with this error source, both concerning the LoS and the azimuth measurements: no action is taken; empirical model corrections are applied; corrections based on the split-spectrum approach are applied (Brcic et al., 2010; Rosen et al., 2010; Gomba et al., 2016, 2017). Although not applied in recent literature, other correction methods for the ionospheric phase delay (22) have been proposed, and are reviewed in Gomba and De Zan (2017).

Empirical corrections for the range phase delay (22) are considered only for DInSAR, since such effects can seldom be appreciated by offset-tracking (or range-SBI) measurements, due to the higher measurement noise floors. The parameters of a low-order polynomial are typically estimated in the far field of the coseismic deformation, possibly at the locations of GPS stations, and the derived error model is then removed from the entire interferogram. In recent studies, first or second-order polynomial calibrations are applied to DInSAR measurements by Wei et al. (2018), Xu et al. (2018b), Yang et al. (2018a), Castaldo et al. (2017), Feng et al. (2017a), Wang et al. (2017d), Zuo et al. (2016), Sreejith et al. (2016), Diao et al. (2015), Feng et al. (2015a), Ge et al. (2015), Galetzka et al. (2015), Kobayashi et al. (2015). DInSAR measurements are instead fitted to GPS data by Morishita et al. (2018) and Kobayashi (2017).

Empirical azimuth offset-tracking corrections to reduce the effects of azimuth streaks (24) consist in directional spatial filtering (Raucoules and De Michele, 2010; Chae et al., 2017) or band-pass filtering (Kobayashi et al., 2009). These approaches are equally applicable to MAI.

The split-spectrum approach conceptually consists in solving Equations (17,18) for Δτ_defo and ΔTEC, using the known frequency dependence of ionospheric delay (22) (Brcic et al., 2010; Rosen et al., 2010). Stripmap and TOPS split-spectrum algorithms are detailed in Gomba et al. (2016, 2017), whereas ALOS-2 ScanSAR application is discussed in Liang and Fielding (2017b). In recent literature split-spectrum corrections were applied by Hamling et al. (2017), Yue et al. (2017b), and Liang and Fielding (2017b). In the latter study, BO-MAI ionospheric corrections are also derived based on (24), using the ionospheric phase isolated with the split-spectrum technique.

Phase Unwrapping

Two-dimensional phase unwrapping is a processing step required by DInSAR and, in general, by range and azimuth split-bandwidth methods, as discussed in section Measurement Techniques. Errors occur locally due to phase variations greater than π in magnitude between adjacent pixels. If such variations occur for most of the paths connecting two regions, due to loss of coherence (e.g., due to water bodies, permanent snow cover, vegetation, radar layover/shadow) or discontinuity of the underlying deformation, then a phase jump of one or several multiples of 2π between all pixels in these regions is likely to arise.

In recent coseismic literature (Supplementary Table 1), ad-hoc phase unwrapping strategies include: manually preventing error-prone integration paths, e.g., across fault ruptures (Yue et al., 2017b) or high fringe-rate areas (Wang et al., 2018b); manual phase-jump corrections,.between mainland and islands (Moreno et al., 2018) or across coherence gaps (Lindsey et al., 2015; Nocquet et al., 2016; Bie et al., 2018; Wei et al., 2018); use of offset-tracking range offsets, either to support manual correction of phase jumps (Xu, 2017) or to reduce (“flatten”) the phase-gradients prior to DInSAR phase unwrapping (Baek et al., 2018).

An example in which an ad-hoc phase unwrapping approach was used is shown in Figure 3E, in which the presence of water and of an east-west phase discontinuity due to the coseismic deformation pattern would made it impossible to unwrap the phase without violating the assumption that phase variations greater than π radians do not occur between adjacent pixels. Thus, unwrapping was performed separately for the western and eastern sectors of the wrapped interferogram in Figure 2B, with respect to reference points R1 and R2 in Figure 2E. The deformation of the reference points was inferred from the local median of the LoS offset-tracking measurements in Figure 2J.

Future Developments

The long-term commitment of the Sentinel-1 missions up to at least 2030, together with its free and open data policy, implies that such data will continue to be among the main source for coseismic deformation studies for many years to come. Full exploitation of the properties of its main acquisition mode over land, namely the TOPS IW mode, is unlikely to have been reached by the current state of the art. Concerning the measurement techniques, application of range-SBI and BO-MAI are still rightly considered innovative (Jiang et al., 2017a), and their use can expected to become more systematic in the future. It has also been pointed out in section Differential SAR Interferometry, that the effects of azimuth motion on the DInSAR phase have not been a limitation for recent coseismic studies, although theoretically they could be relevant (González et al., 2015). It could therefore not be excluded that applications will arise, which elicit a better procedure to account for this property of TOPS acquisition, either in the generation or in the subsequent interpretation/modeling of Sentinel-based deformation maps (De Zan et al., 2014).

Concerning the error sources, as reviewed in section Current Challenges, it is not seldom that an image analyst processing a given site and dataset is faced with measurement challenges, which require ad-hoc solutions. Concerning tropospheric propagation effects, new strategies are still being proposed (Yu et al., 2018) and still do not appear solve all the observed problems, as discussed in section Tropospheric Propagation. Regarding ionospheric propagation effects, the split-spectrum approach, the application of which to Sentinel-1 and ALOS-2 ScanSAR modes is also recent (Gomba et al., 2017), could be used systematically to avoid ad-hoc calibration of so called “long-wavelength” errors, and could also be systematically exploited for azimuth-streak corrections of offset-tracking results in coherent areas and MAI results (Liang and Fielding, 2017b). Concerning phase unwrapping errors, a more systematic comparison with offset-tracking and range-SBI results could provide an additional tool to make decisions less subjective, in particular for Sentinel-1 TOPS IW data, which provides a large range bandwidth and is less sensitive to ionospheric propagation effects compared to L-band systems.

Finally, in a context of standardization of the processing algorithms and increased data availability, in particular in connection with the systematic wide-area products which will be provided openly by the NASA-ISRO SAR (NISAR) mission, the appeal of higher-level products (e.g., interferometric) generated by automated state-of-the-art cloud-based processing systems such as those described in Feng et al. (2016) and Li et al. (2016b) can be expected to increase significantly.

Author Contributions

JM carried out the review of processing techniques and applications described in this paper and wrote all parts of the manuscript.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2019.00016/full#supplementary-material

References

Ainscoe, E. A., Elliott, J. R., Copley, A., Craig, T. J., Li, T., Parsons, B. E., et al. (2017). Blind thrusting, surface folding, and the development of geological structure in the Mw 6.3 2015 Pishan (China) earthquake. J. Geophys. Res. Solid Earth 122, 9359–9382. doi: 10.1002/2017JB014268

CrossRef Full Text | Google Scholar

Albano, M., Saroli, M., Montuori, A., Bignami, C., Tolomei, C., Polcari, M., et al. (2018). The relationship between InSAR coseismic deformation and earthquake-induced landslides associated with the 2017 Mw 3.9 Ischia (Italy) earthquake. Geosciences 8:303. doi: 10.3390/geosciences8080303

CrossRef Full Text | Google Scholar

Ando, R., Imanishi, K., Panayotopoulos, Y., and Kobayashi, T. (2017). Dynamic rupture propagation on geometrically complex fault with along-strike variation of fault maturity: insights from the 2014 northern Nagano earthquake. Earth Planets Space 69:130. doi: 10.1186/s40623-017-0715-2

CrossRef Full Text | Google Scholar

Avallone, A., Cirella, A., Cheloni, D., Tolomei, C., Theodoulis, N., Piatanesi, A., et al. (2017). Near-source high-rate GPS, strong motion and InSAR observations to image the 2015 Lefkada (Greece) earthquake rupture history. Sci. Rep. 7:10358. doi: 10.1038/s41598-017-10431-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Avouac, J.-P., Meng, L., Wei, S., Wang, T., and Ampuero, J.-P. (2015). Lower edge of locked main Himalayan thrust unzipped by the 2015 Gorkha earthquake. Nat. Geosci. 8:708. doi: 10.1038/ngeo2518

CrossRef Full Text | Google Scholar

Baek, W.-K., Jung, H.-S., and Chae, S.-H. (2018). Feasibility of ALOS2 PALSAR2 offset-based phase unwrapping of SAR interferogram in large and complex surface deformations. IEEE Access 6, 45951–45960. doi: 10.1109/ACCESS.2018.2865799

CrossRef Full Text | Google Scholar

Bamler, R., and Eineder, M. (2005). Accuracy of differential shift estimation by correlation and split-bandwidth interferometry for wideband and delta-k SAR systems. IEEE Geosc. Rem. Sens. Lett. 2, 151–155. doi: 10.1109/LGRS.2004.843203

CrossRef Full Text | Google Scholar

Bamler, R., and Hartl, P. (1998). Synthetic aperture radar interferometry. Inverse Probl. 14:R1–R54. doi: 10.1088/0266-5611/14/4/001

CrossRef Full Text | Google Scholar

Bamler, R., and Holzner, J. (2004). ScanSAR interferometry for RADARSAT-2 and RADARSAT-3. Can. J. Remote Sens. 30, 437–447. doi: 10.5589/m03-070

CrossRef Full Text | Google Scholar

Barbot, S., Hamiel, Y., and Fialko, Y. (2008). Space geodetic investigation of the coseismic and postseismic deformation due to the 2003 Mw 7.2 Altai earthquake: implications for the local lithospheric rheology. J. Geophys. Res. 113:B03403. doi: 10.1029/2007JB005063

CrossRef Full Text | Google Scholar

Barnhart, W. D., Brengman, C. M. J., Li, S., and Peterson, K. E. (2018). Ramp-flat basement structures of the Zagros mountains inferred from co-seismic slip and afterslip of the 2017 Mw7.3 Darbandikhan, Iran/Iraq earthquake. Earth Planet. Sci. Lett. 496, 96–107. doi: 10.1016/j.epsl.2018.05.036

CrossRef Full Text | Google Scholar

Barnhart, W. D., Murray, J. R., Briggs, R. W., Gomez, F., Miles, C. P. J., Svarc, J., et al. (2016). Coseismic slip and early afterslip of the 2015 Illapel, Chile, earthquake: implications for frictional heterogeneity and coastal uplift, J. Geophys. Res. Solid Earth 121, 6172–6191. doi: 10.1002/2016JB013124

CrossRef Full Text | Google Scholar

Barnhart, W. D., Murray, J. R., Yun, S.-H., Svarc, J. L., Samsonov, S. V., Fielding, E. J., et al. (2015). Geodetic constraints on the 2014 M 6.0 South Napa earthquake. Seis. Res. Lett. 86, 335–343. doi: 10.1785/0220140210

CrossRef Full Text | Google Scholar

Bechor, N. B. D., and Zebker, H. A. (2006). Measuring two-dimensional movements using a single InSAR pair. Geophys. Res. Lett. 33:L16311. doi: 10.1029/2006GL026883

CrossRef Full Text | Google Scholar

Béjar-Pizarro, M., Álvarez Gómez, J. A., Staller, A., Luna, M. P., Pérez-López, R., Monserrat, O., et al. (2018). InSAR-based mapping to support decision-making after an earthquake. Remote Sens. 10:899. doi: 10.3390/rs10060899

CrossRef Full Text | Google Scholar

Bekaert, D. P. S., Walters, R. J., Wright, T. J., Hooper, A. J., and Parker, D. J. (2015). Statistical comparison of InSAR tropospheric correction techniques. Remote Sens. Environ. 170, 40–47. doi: 10.1016/j.rse.2015.08.035

CrossRef Full Text | Google Scholar

Bertan-Ortiz, A., and Zebker, H. (2007). ScanSAR-to-Stripmap mode interferometry processing using ENVISAT/ASAR data. IEEE Trans. Geosci. Remote Sens. 45, 3468–3480. doi: 10.1109/TGRS.2007.895970

CrossRef Full Text | Google Scholar

Bie, L., González, P. J., and Rietbrock, A. (2017). Slip distribution of the 2015 Lefkada earthquake and its implications for fault segmentation. Geophys. J. Int. 210, 420–427. doi: 10.1093/gji/ggx171

CrossRef Full Text | Google Scholar

Bie, L., Hicks, S., Garth, T., Gonzalez, P., and Rietbrock, A. (2018). ‘Two go together’: near-simultaneous moment release of two asperities during the 2016 M_w6.6 Muji, China earthquake. Earth Planet. Sci. Lett. 491, 34–42. doi: 10.1016/j.epsl.2018.03.033

CrossRef Full Text | Google Scholar

Bignami, C., Tolomei, C., Pezzo, G., Guglielmino, F., Atzori, S., Trasatti, E., et al. (2016). Source identification for situational awareness of the August 24th 2016 central Italy event. Ann. Geophys. 47, 1723–1742. doi: 10.4401/AG-7233

CrossRef Full Text | Google Scholar

Brcic, R., Parizzi, A., Eineder, M., Bamler, R., and Meyer, F. (2010). “Estimation and compensation of ionospheric delay for SAR interferometry,” in Proceedings of Geoscience and Remote Sensing Symposium (IGARSS), 2010 IEEE International (Honolulu, HI), 2908–2911. doi: 10.1109/IGARSS.2010.5652231

CrossRef Full Text | Google Scholar

Brown, L. G. (1992). A survey of image registration techniques. Comput. Surv. 24, 325–376. doi: 10.1145/146370.146374

CrossRef Full Text | Google Scholar

Bürgmann, R., Rosen, P. A., and Fielding, E. J. (2000). Synthetic aperture radar interferometry to measure Earth's surface topography and its deformation. Annu. Rev. Earth Planet. Sci. 28, 169–209. doi: 10.1146/annurev.earth.28.1.169

CrossRef Full Text | Google Scholar

Castaldo, R., De Novellis, V., Solaro, G., Pepe, S., Tizzani, P., De Luca, C., et al. (2017). Finite element modelling of the 2015 Gorkha earthquake through the joint exploitation of DInSAR measurements and geologic-structural information. Tectonophysics 714–715, 125–132. doi: 10.1016/j.tecto.2016.06.037

CrossRef Full Text | Google Scholar

Cavalié, O., Doin, M. P., Lasserre, C., and Briole, P. (2007). Ground motion measurement in the Lake Mead area, Nevada, by differential synthetic aperture radar interferometry time series analysis: probing the lithosphere rheological structure. J. Geophys. Res. 112:B03403. doi: 10.1029/2006JB004344

CrossRef Full Text | Google Scholar

Cesca, S., Zhang, Y., Mouslopoulou, V., Wang, R., Saul, J., Savage, M., et al. (2017). Complex rupture process of the Mw 7.8, 2016, Kaikoura earthquake, New Zealand, and its aftershock sequence. Earth Planet. Sci. Lett. 478, 110–120. doi: 10.1016/j.epsl.2017.08.024

CrossRef Full Text | Google Scholar

Chae, S.-H., Lee, W.-J., Jung, H.-S., and Zhang, L. (2017). Ionospheric correction of L-Band SAR offset measurements for the precise observation of glacier velocity variations on Novaya Zemlya. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 10, 3591–3602. doi: 10.1109/JSTARS.2017.2690799

CrossRef Full Text | Google Scholar

Cheloni, D., De Novellis, V., Albano, M., Antonioli, A., Anzidei, M., Atzori, S., et al. (2017). Geodetic model of the 2016 central Italy earthquake sequence inferred from InSAR and GPS data. Geophys. Res. Lett. 44, 6778–6787. doi: 10.1002/2017GL073580

CrossRef Full Text | Google Scholar

Chen, K., Feng, W., Liu, Z., and Song, Y. T. (2018). 2017 Mw 8.1 Tehuantepec earthquake: deep slip and rupture directivity enhance ground shaking but weaken the Tsunami. Seis. Res. Lett. 89, 1314–1322. doi: 10.1785/0220170277

CrossRef Full Text | Google Scholar

Copley, A., Karasozen, E., Oveisi, B., Elliott, J., Samsonov, S., and Nissen, E. (2015). Seismogenic faulting of the sedimentary sequence and laterally variable material properties in the Zagros Mountains (Iran) revealed by the August 2014 Murmuri (E. Dehloran) earthquake sequence. Geophys. J. Int. 203, 1436–1459. doi: 10.1093/gji/ggv365

CrossRef Full Text | Google Scholar

Cumming, I. G., and Wong, F. H. (2005). Digital Processing of Synthetic Aperture Radar Data. Norwood, MA: Artech House.

Google Scholar

De Novellis, V., Carlino, S., Castaldo, R., Tramelli, A., De Luca, C., Pino, N. A., et al. (2018). The 21 August 2017 Ischia (Italy) earthquake source model inferred from seismological, GPS, and DInSAR measurements. Geophys. Res. Lett. 45, 2193–2202. doi: 10.1002/2017GL076336

CrossRef Full Text | Google Scholar

De Zan, F., and Monti Guarnieri, A. (2006). TOPSAR: terrain observation by progressive scans. IEEE Trans. Geosci. Remote Sens. 44, 2352–2360. doi: 10.1109/TGRS.2006.873853

CrossRef Full Text | Google Scholar

De Zan, F., Prats-Iraola, P., and Rodriguez-Cassola, M. (2015). On the dependence of delta-k efficiency on multilooking. IEEE Geosci. Remote Sens. Lett. 12, 1745–1749. doi: 10.1109/LGRS.2015.2424272

CrossRef Full Text | Google Scholar

De Zan, F., Prats-Iraola, P., Scheiber, R., and Rucci, A. (2014). “Interferometry with TOPS: coregistration and azimuth shifts,” in Conference: European Conference on Synthetic Aperture Radar (EUSAR) (Berlin).

Google Scholar

Diao, F., Walter, T. R., Motagh, M., Prats-Iraola, P., Wang, R., and Samsonov, S. (2015). The 2015 Gorkha earthquake investigated from radar satellites: slip and stress modeling along the MHT. Front. Earth Sci. 3:65. doi: 10.3389/feart.2015.00065

CrossRef Full Text | Google Scholar

Doin, M. P., Lasserre, C., Peltzer, G., Cavalié, O., and Doubre, C. (2009). Corrections of stratified tropospheric delays in SAR interferometry: validation with global atmospheric models. J. Appl. Geophys. 69, 35–50. doi: 10.1016/j.jappgeo.2009.03.010

CrossRef Full Text | Google Scholar

Dreger, D., Huang, M.-H., Rodgers, A., Taira, T., and Wooddell, K. (2015). Kinematic finite-source model for the 24 August 2014 South Napa, California, earthquake from joint inversion of seismic, GPS, and InSAR data. Seis. Res. Lett. 86, 327–334. doi: 10.1785/0220140244

CrossRef Full Text | Google Scholar

Du, H.-L., Zhang, X., Xu, L.-S., Feng, W., Yi, L., and Li, P. (2018). Source complexity of the 2016 Mw7.8 Kaikoura (New Zealand) earthquake revealed from teleseismic and InSAR data. Earth Planet. Phys. 2, 1–17. doi: 10.26464/epp2018029

CrossRef Full Text | Google Scholar

Elliott, J. R., Jolivet, R., Gonzalez, P. J., Avouac, J.-P., Hollingsworth, J., Searle, M. P., et al. (2016). Himalayan megathrust geometry and relation to topography revealed by the Gorkha earthquake. Nat. Geosci. 9:174. doi: 10.1038/ngeo2623

CrossRef Full Text | Google Scholar

Fattahi, H., Amelung, F., Chaussard, E., and Wdowinski, S. (2015). Coseismic and postseismic deformation due to the 2007 M5.5 Ghazaband fault earthquake, Balochistan, Pakistan. Geophys. Res. Lett. 42, 3305–3312. doi: 10.1002/2015GL063686

CrossRef Full Text | Google Scholar

Feng, G., Li, Z., Shan, X., Xu, B., and Du, Y. (2015b). Source parameters of the Mw 6.1 South Napa earthquake estimated from the Sentinel 1A, COSMO-SkyMed and GPS data. Tectonophysics 655, 139–146. doi: 10.1016/j.tecto.2015.05.018

CrossRef Full Text | Google Scholar

Feng, G., Li, Z., Shan, X., Zhang, L., Zhang, G., and Zhu, J. (2015a). Geodetic model of the 2015 April 25 Mw 7.8 Gorkha Nepal Earthquake and Mw 7.3 aftershock estimated from InSAR and GPS data. Geophys. J. Int. 2, 896–900. doi: 10.1093/gji/ggv335

CrossRef Full Text | Google Scholar

Feng, G., Li, Z., Xu, B., Shan, X., Zhang, L., and Zhu, J. (2016). Coseismic deformation of the 2015 Mw 6.4 Pishan, China, earthquake estimated from Sentinel-1A and ALOS2 data. Seis. Res. Lett. 87, 800–806. doi: 10.1785/0220150264

CrossRef Full Text | Google Scholar

Feng, W., Lindsey, E., Barbot, S., Samsonov, S., Dai, K., Li, P., et al. (2017b). Source characteristics of the 2015 Mw 7.8 Gorkha (Nepal) earthquake and its Mw 7.2 aftershock from space geodesy. Tectonophysics 712–713, 746–758. doi: 10.1016/j.tecto.2016.02.029

CrossRef Full Text | Google Scholar

Feng, W., Samsonov, S., Almeida, R., Yassaghi, A., Li, J., Qiu, Q., et al. (2018). Geodetic constraints of the 2017 Mw7.3 Sarpol Zahab, Iran earthquake, and its implications on the structure and mechanics of the northwest Zagros thrust-fold belt. Geophys. Res. Lett. 45, 6853–6861. doi: 10.1029/2018GL078577

CrossRef Full Text | Google Scholar

Feng, W., Samsonov, S., Tian, Y., Qiu, Q., Li, P., Zhang, Y., et al. (2017a). Surface deformation associated with the 2015 Mw8.3 Illapel earthquake revealed by satellite-based geodetic observations and its implications for the seismic cycle. Earth Planet. Sci. Lett. 460, 222–233. doi: 10.1016/j.epsl.2016.11.018

CrossRef Full Text | Google Scholar

Feng, W., Tian, Y., Zhang, Y., Samsonov, S., Almeida, R., and Liu, P. (2017c). A slip gap of the 2016 Mw 6.6 Muji, Xinjiang, China, earthquake inferred from Sentinel-1 TOPS interferometry. Seis. Res. Lett. 88, 1054–1064. doi: 10.1785/0220170019

CrossRef Full Text | Google Scholar

Fielding, E. J., Sangha, S. S., Bekaert, D. P. S., Samsonov, S. V., and Chang, J. C. (2017). Surface deformation of north-central Oklahoma related to the 2016 Mw 5.8 Pawnee earthquake from SAR interferometry time series. Seis. Res. Lett. 88, 971–982. doi: 10.1785/0220170010

CrossRef Full Text | Google Scholar

Fielding, E. J., Sladen, A., Li, Z., Avouac, J.-P., Bürgmann, R., and Ryder, I. (2013). Kinematic fault slip evolution source models of the 2008 M7.9 Wenchuan earthquake in China from SAR interferometry, GPS, and teleseismic analysis and implications for Longmen Shan tectonics. Geophys. J. Int. 194, 1138–1166. doi: 10.1093/gji/ggt155

CrossRef Full Text | Google Scholar

Foster, J., Brooks, B., Cherubini, T., Shacat, C., Businger, S., and Werner, C. L. (2006). Mitigating the atmospheric noise for InSAR using a high resolution weather model. Geophys. Res. Lett. 33:L16304. doi: 10.1029/2006GL026781

CrossRef Full Text | Google Scholar

Fujiwara, S., Yarai, H., Kobayashi, T., Morishita, Y., Nakano, T., Miyahara, B., et al. (2016). Small-displacement linear surface ruptures of the 2016 Kumamoto earthquake sequence detected by ALOS-2 SAR interferometry. Earth Planets Space 68:160. doi: 10.1186/s40623-016-0534-x

CrossRef Full Text | Google Scholar

Fukahata, Y., and Hashimoto, M. (2016). Simultaneous estimation of the dip angles and slip distribution on the faults of the 2016 Kumamoto earthquake through a weak nonlinear inversion of InSAR data. Earth Planets Space 68:204. doi: 10.1186/s40623-016-0580-4

CrossRef Full Text | Google Scholar

Funning, G. J., and Garcia, A. (2019). A systematic study of earthquake detectability using Sentinel-1 interferometric wide-swath data. Geophys. J. Int. 216, 332–349. doi: 10.1093/gji/ggy426

CrossRef Full Text | Google Scholar

Funning, G. J., Parsons, B., Wright, T. J., and Fielding, E. J. (2005). Surface displacements and source parameters of the 2003 Bam (Iran) earthquake from Envisat advanced synthetic aperture radar imagery. J. Geophys. Res. 110:B09406. doi: 10.1029/2004JB003338

CrossRef Full Text | Google Scholar

Galetzka, J., Melgar, D., Genrich, J. F., Geng, J., Owen, S., Lindsey, E. O., et al. (2015). Slip pulse and resonance of the Kathmandu basin during the 2015 Gorkha earthquake, Nepal. Science 349, 1091–1095. doi: 10.1126/science.aac6383

PubMed Abstract | CrossRef Full Text | Google Scholar

Ganas, A., Elias, P., Bozionelos, G., Papathanassiou, G., Avallone, A., Papastergios, A., et al. (2016). Coseismic deformation, field observations and seismic fault of the 17 November 2015 M = 6.5, Lefkada Island, Greece earthquake. Tectonophysics 687, 210–222. doi: 10.1016/j.tecto.2016.08.012

CrossRef Full Text | Google Scholar

Ganas, A., Kourkouli, P., Briole, P., Moshou, A., Elias, P., and Parcharidis, I. (2018). Coseismic displacements from moderate-size earthquakes mapped by Sentinel-1 differential interferometry: the case of February 2017 Gulpinar earthquake sequence (Biga peninsula, Turkey). Remote Sens. 10:1089. doi: 10.3390/rs10071089

CrossRef Full Text | Google Scholar

Ge, L., Ng, A. H.-M., Li, X., Liu, Y., Du, Z., and Liu, Q. (2015). Near real-time satellite mapping of the 2015 Gorkha earthquake, Nepal. Ann. GIS 21, 175–190. doi: 10.1080/19475683.2015.1068221

CrossRef Full Text | Google Scholar

Goldstein, R. M., and Werner, C. L. (1998). Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 25, 4035–4038. doi: 10.1029/1998GL900033

CrossRef Full Text | Google Scholar

Gomba, G., and De Zan, F. (2017). Bayesian data combination for the estimation of ionospheric effects in SAR interferograms. IEEE Trans. Geosci. Remote Sens. 55, 6582–6592. doi: 10.1109/TGRS.2017.2730438

CrossRef Full Text | Google Scholar

Gomba, G., Parizzi, A., De Zan, F., Eineder, M., and Bamler, R. (2016). Toward operational compensation of ionospheric effects in SAR interferograms: the split-spectrum method. IEEE Trans. Geosci. Remote Sens. 54, 1446–1461. doi: 10.1109/TGRS.2015.2481079

CrossRef Full Text | Google Scholar

Gomba, G., Rodríguez González, F., and De Zan, F. (2017). Ionospheric phase screen compensation for the Sentinel-1 TOPS and ALOS-2 ScanSAR modes. IEEE Trans. Geosci. Remote Sens. 55, 223–235. doi: 10.1109/TGRS.2016.2604461

CrossRef Full Text | Google Scholar

González, P. J., Bagnardi, M., Hooper, A. J., Larsen, Y., Marinkovic, P., Samsonov, S. V., et al. (2015). The 2014–2015 eruption of Fogo volcano: geodetic modeling of Sentinel-1 TOPS interferometry. Geophys. Res. Lett. 42, 9239–9246. doi: 10.1002/2015GL066003

CrossRef Full Text | Google Scholar

Grandin, R., Klein, E., Métois, M., and Vigny, C (2016), Three-dimensional displacement field of the 2015 Mw8.3 Illapel earthquake (Chile) from across- along-track Sentinel-1 TOPS interferometry. Geophys. Res. Lett. 43, 2552–2561. doi: 10.1002/2016GL067954

CrossRef Full Text | Google Scholar

Grandin, R., Vallée, M., and Lacassin, R. (2017). Rupture process of the Mw 5.8 Pawnee, Oklahoma, earthquake from Sentinel-1 InSAR and seismological data. Seis. Res. Lett. 88, 994–1004. doi: 10.1785/0220160226

CrossRef Full Text | Google Scholar

Grandin, R., Vallée, M., Satriano, C., Lacassin, R., Klinger, Y., Simoes, M., et al. (2015). Rupture process of the Mw = 7.9 2015 Gorkha earthquake (Nepal): insights into himalayan megathrust segmentation. Geophys. Res. Lett. 42, 8373–8382 doi: 10.1002/2015GL066044

CrossRef Full Text | Google Scholar

Gray, A. L., Mattar, K. E., and Sofko, G. (2000). Influence of ionospheric electron density fluctuations on satellite radar interferometry. Geophys. Res. Lett. 27, 1451–1454. doi: 10.1029/2000GL000016

CrossRef Full Text | Google Scholar

Gray, A. L., Mattar, K. E., and Vachon, P. W. (1998). “InSAR results from the RADARSAT Antarctic mapping mission data: estimation of glacier motion using a simple registration procedure,” in Geoscience and Remote Sensing Symposium Proceedings, 1998. IGARSS '98. 1998 IEEE International (Seattle, WA).

Google Scholar

Guccione, P. (2006). Interferometry with ENVISAT wide swath ScanSAR data. IEEE Geosci. Remote Sens. Lett. 3, 377–381. doi: 10.1109/LGRS.2006.873876

CrossRef Full Text | Google Scholar

Hamling, I. J., Hreinsdottir, S., Clark, K., Elliott, J., Liang, C., Fielding, E., et al. (2017). Complex multifault rupture during the 2016 Mw 7.8 Kaikoura earthquake, New Zealand. Science 356:eaam7194. doi: 10.1126/science.aam7194

PubMed Abstract | CrossRef Full Text | Google Scholar

Hanssen, R. F. (2001). Radar Interferometry: Data Interpretation and Error Analysis. Dordrecht: Kluwer.

Google Scholar

Hayes, G. P., Briggs, R. W., Barnhart, W. D., Yeck, W. L., McNamara, D. E., Wald, D. J., et al. (2015). Rapid characterization of the 2015 Mw 7.8 Gorkha, Nepal, earthquake sequence and its seismotectonic context. Seis. Res. Lett. 86, 1557–1567. doi: 10.1785/0220150145

CrossRef Full Text | Google Scholar

He, P., Ding, K., and Xu, C. (2018b). The 2016 Mw 6.7 Aketao earthquake in Muji range, northern Pamir: rupture on a strike-slip fault constrained by Sentinel-1 radar interferometry and GPS. Int. J. Appl. Earth Obs. Geoinform. 73, 99–106. doi: 10.1016/j.jag.2018.06.001

CrossRef Full Text | Google Scholar

He, P., Hetland, E. A., Niemi, N. A., Wang, Q., Wen, Y., and Ding, K. (2018a). The 2016 Mw 6.5 Nura earthquake in the Trans Alai range, northern Pamir: possible rupture on a back-thrust fault constrained by Sentinel-1A radar interferometry. Tectonophysics 749, 62–71. doi: 10.1016/j.tecto.2018.10.025

CrossRef Full Text | Google Scholar

He, P., Hetland, E. A., Wang, Q., Ding, K., Wen, Y., and Zou, R. (2017). Coseismic slip in the 2016 Mw 7.8 Ecuador earthquake imaged from Sentinel-1A radar interferometry. Seis. Res. Lett. 88, 277–286. doi: 10.1785/0220160151

CrossRef Full Text | Google Scholar

He, P., Wang, Q., Ding, K., Wang, M., Qiao, X., Li, J., et al. (2016). Source model of the 2015 Mw 6.4 Pishan earthquake constrained by interferometric synthetic aperture radar and GPS: insight into blind rupture in the western Kunlun Shan. (2016). Geophys. Res. Lett. 43, 1511–1519. doi: 10.1002/2015GL067140

CrossRef Full Text | Google Scholar

Holzner, J., and Bamler, R. (2002). Burst-mode and ScanSAR interferometry. IEEE Trans. Geosci. Remote Sens. 40, 1917–1934. doi: 10.1109/TGRS.2002.803848

CrossRef Full Text | Google Scholar

Huang, M.-H., Fielding, E. J., Liang, C., Milillo, P., Bekaert, D., Dreger, D., et al. (2017). Coseismic deformation and triggered landslides of the 2016 Mw 6.2 Amatrice earthquake in Italy. Geophys. Res. Lett. 44, 1266–1274. doi: 10.1002/2016GL071687

CrossRef Full Text | Google Scholar

Huang, M.-H., Tung, H., Fielding, E. J., Huang, H.-H., Liang, C., Huang, C., et al. (2016), Multiple fault slip triggered above the 2016 Mw 6.4 MeiNong earthquake in Taiwan. Geophys. Res. Lett. 43, 7459–7467. doi: 10.1002/2016GL069351

CrossRef Full Text | Google Scholar

IEEE Standard Definitions of Terms for Antennas, IEEE Std 145-1993. (1993). Antenna Standards Committee of the IEEE Antennas and Propagation Society, IEEE Standards Board.

Jiang, G., Wen, Y., Li, K., Fang, L., Xu, C., Zhang, Y., et al. (2018). A NE-trending oblique-slip fault responsible for the 2016 Zaduo earthquake (Qinghai, China) revealed by InSAR Data. Pure Appl. Geophys. 175, 4275–4288. doi: 10.1007/s00024-018-1948-0

CrossRef Full Text | Google Scholar

Jiang, G., Wen, Y., Liu, Y., Xu, X., Fang, L., Chen, G., et al. (2015). Joint analysis of the 2014 Kangding, southwestChina, earthquake sequence with seismicity relocation and InSAR inversion. Geophys. Res. Lett. 42, 3273–3281. doi: 10.1002/2015GL063750

CrossRef Full Text | Google Scholar

Jiang, H., Feng, G., Wang, T., and Bürgmann, R. (2017a). Toward full exploitation of coherent and incoherent information in Sentinel-1 TOPS data for retrieving surface displacement: application to the 2016 Kumamoto (Japan) earthquake. Geophys. Res. Lett. 44, 1758–1767. doi: 10.1002/2016GL072253

CrossRef Full Text | Google Scholar

Jiang, H. J., Pei, Y. Y., and Li, J. (2017b). Sentinel-1 TOPS interferometry for along-track displacement measurement. IOP Conf. Ser. Earth Environ. Sci. 57:012019. doi: 10.1088/1755-1315/57/1/012019

CrossRef Full Text | Google Scholar

Jo, M. J., Jung, H. S., and Yun, S. H. (2017). Retrieving precise three-dimensional deformation on the 2014 M6.0 South Napa earthquake by joint inversion of multi-sensor SAR. Sci. Rep. 7:5485. doi: 10.1038/s41598-017-06018-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Jolivet, R., Agram, P. S., Lin, N. Y., Simons, M., Doin, M.-P., Peltzer, G., et al. (2014). Improving InSAR geodesy using global atmospheric models. J. Geophys. Res. Solid Earth 119, 2324–2341. doi: 10.1002/2013JB010588

CrossRef Full Text | Google Scholar

Jolivet, R., Grandin, R., Lasserre, C., Doin, M. P., and Peltzer, G. (2011). Systematic InSAR tropospheric phase delay corrections from global meteorological reanalysis data. Geophys. Res. Lett. 38:L17311. doi: 10.1029/2011GL048757

CrossRef Full Text | Google Scholar

Jung, H.-S., Lee, D.-T., Lu, Z., and Won, J.-S. (2013). Ionospheric correction of SAR interferograms by multiple-aperture interferometry. IEEE Trans. Geosci. Remote Sens. 51, 3191–3198. doi: 10.1109/TGRS.2012.2218660

CrossRef Full Text | Google Scholar

Jung, H. S., Won, J. S., and Kim, S. W. (2009). An improvement of the performance of multiple-aperture SAR interferometry (MAI). IEEE Trans. Geosci. Remote Sens. 47, 2859–2869. doi: 10.1109/TGRS.2009.2016554

CrossRef Full Text | Google Scholar

Jung, J., Kim, D.-J., and Park, S.-E. (2014). Correction of atmospheric phase screen in time series InSAR Using WRF model for monitoring volcanic activities. IEEE Trans. Geosci. Remote Sens. 52, 2678–2689. doi: 10.1109/TGRS.2013.2264532

CrossRef Full Text | Google Scholar

Kinoshita, Y., Furuya, M., Hobiger, T., and Ichikawa, R. (2013). Are numerical weather model outputs helpful to reduce tropospheric delay signals in InSAR data?. J. Geod. 87, 267–277. doi: 10.1007/s00190-012-0596-x

CrossRef Full Text | Google Scholar

Kobayashi, T. (2017). Earthquake rupture properties of the 2016 Kumamoto earthquake foreshocks (M-j 6.5 and M-j 6.4) revealed by conventional and multiple-aperture InSAR. Earth Planets Space 69:7. doi: 10.1186/s40623-016-0594-y

CrossRef Full Text | Google Scholar

Kobayashi, T., Morishita, Y., and Yarai, H. (2015). Detailed crustal deformation and fault rupture of the 2015 Gorkha earthquake, Nepal, revealed from ScanSAR-based interferograms of ALOS-2. Earth Planets Space 67:201. doi: 10.1186/s40623-015-0359-z

CrossRef Full Text | Google Scholar

Kobayashi, T., Morishita, Y., and Yarai, H. (2018). SAR-revealed slip partitioning on a bending fault plane for the 2014 northern Nagano earthquake at the northern Itoigawa-Shizuoka tectonic line. Tectonophysics 722, 85–99. doi: 10.1016/j.tecto.2017.12.001

CrossRef Full Text | Google Scholar

Kobayashi, T., Takada, Y., Furuya, M., and Murakami, M. (2009). Locations and types of ruptures involved in the 2008 Sichuan earthquake inferred from SAR image matching. Geophys. Res. Lett. 36:L07302. doi: 10.1029/2008GL036907

CrossRef Full Text | Google Scholar

Lavecchia, G., Castaldo, R., De Nardis, R., De Novellis, V., Ferrarini, F., Pepe, S., et al. (2016). Ground deformation and source geometry of the 24 August 2016 Amatrice earthquake (Central Italy) investigated through analytical and numerical modeling of DInSAR measurements and structural-geological data. Geophys. Res. Lett. 43, 12389–12398. doi: 10.1002/2016GL071723

CrossRef Full Text | Google Scholar

Lee, W. J., Lu, Z., Jung, H. S., and Ji, L. (2017). Measurement of small co-seismic deformation field from multi-temporal SAR interferometry: application to the 19 September 2004 Huntoon Valley earthquake. Geom. Nat. Haz. Risk 8, 1241–1257. doi: 10.1080/19475705.2017.1310764

CrossRef Full Text | Google Scholar

Li, Y., Jiang, W., Zhang, J., and Luo, Y. (2016a). Space geodetic observations and modeling of 2016 Mw 5.9 Menyuan earthquake: implications on seismogenic tectonic motion. Remote Sens. 8:519. doi: 10.3390/rs8060519

CrossRef Full Text | Google Scholar

Li, Y., Luo, Y., Zhang, J., and Jiang, W. (2018). The 2015 Mw 6.4 Pishan earthquake, China: geodetic modelling inferred from Sentinel-1A TOPS interferometry. Surv. Rev. 50, 522–530. doi: 10.1080/00396265.2017.1335381

CrossRef Full Text | Google Scholar

Li, Z., Wright, T., Hooper, A., Crippa, P., Gonzalez, P., Walters, R., et al. (2016b). “Towards INSAR everywhere, all the time, with Sentinel-1,” in Proceedings of XXIII ISPRS Congress (Prague) 763–766.

Google Scholar

Liang, C., and Fielding, E. J. (2017a). Interferometry with ALOS-2 full-aperture ScanSAR data. IEEE Trans. Geosci. Remote Sens. 55, 2739–2750. doi: 10.1109/TGRS.2017.2653190

CrossRef Full Text | Google Scholar

Liang, C., and Fielding, E. J. (2017b). Measuring azimuth deformation with L-band ALOS-2 ScanSAR interferometry. IEEE Trans. Geosci. Remote Sens. 55, 2725–2738. doi: 10.1109/TGRS.2017.2653186

CrossRef Full Text | Google Scholar

Lin, Y. N., Simons, M., Hetland, E. A., Muse, P., and Di Caprio, C. J. (2010). A multiscale approach to estimating topographically correlated propagation delays in radar interferograms. Geochem. Geophys. Geosyst. 11, 1–17. doi: 10.1029/2010GC003228

CrossRef Full Text | Google Scholar

Lindsey, E. O., Natsuaki, R., Xu, X., Shimada, M., Hashimoto, M., Melgar, D., et al. (2015), Line-of-sight displacement from ALOS-2 interferometry: Mw 7.8 Gorkha earthquake Mw 7.3 aftershock. Geophys. Res. Lett. 42, 6655–6661. doi: 10.1002/2015GL065385

CrossRef Full Text | Google Scholar

Liu, J.-H., Hu, J., Li, Z.-W., Zhu, J.-J., Sun, Q., and Gan, J. (2018a). A method for measuring 3-D surface deformations with InSAR based on strain model and variance component estimation. IEEE Trans. Geosci. Remote Sens. 56, 239–250. doi: 10.1109/TGRS.2017.2745576

CrossRef Full Text | Google Scholar

Liu, J. H., Hu, J., and Li, Z. W. (2018b). “Extracting 3-D deformation fields from left- and right-looking InSAR with SM-VCE method: a case study of October 21, 2016 central Tottori earthquake,” in 2018 ISPRS TC III Mid-Term Symposium on Developments, Technologies and Applications in Remote Sensing (Beijing), 42, 1065–1067.

Google Scholar

Liu, Y., Zhang, G., Zhang, Y., and Shan, X. (2018c). Source parameters of the 2016 Menyuan earthquake in the northeastern Tibetan Plateau determined from regional seismic waveforms and InSAR measurements. J. Asian Earth Sci. 158, 103–111. doi: 10.1016/j.jseaes.2018.02.009

CrossRef Full Text | Google Scholar

Ma, Y., Qiao, X., Chen, W., and Zhou, Y. (2018). Source model of 2016 Mw6.6 Aketao earthquake, Xinjiang derived from Sentinel-1 InSAR observation. Geodesy. Geodyn. 9, 372–377. doi: 10.1016/j.geog.2018.05.001

CrossRef Full Text | Google Scholar

Madsen, S. N., and Zebker, H. A. (1992). “Automated absolute phase retrieval in across-track interferometry,” in Proceedings of IGARSS'92 (Houston, TX).

Google Scholar

Massonnet, D., and Feigl, K. L. (1998). Radar interferometry and its application to changes in the Earth's surface. Rev. Geophys. 36, 441–500. doi: 10.1029/97RG03139

CrossRef Full Text | Google Scholar

Massonnet, D., Rossi, M., Carmona, C., Adragna, F., Peltzer, G., Feigl, K., et al. (1993). The displacement field of the Landers earthquake mapped by radar interferometry. Nature 364, 138–142. doi: 10.1038/364138a0

CrossRef Full Text | Google Scholar

Melgar, D., Fan, D., Riquelme, S., Geng, J., Liang, C., Fuentes, M., et al. (2016). Slip segmentation and slow rupture to the trench during the 2015, Mw8.3 Illapel, Chile earthquake. Geophys. Res. Lett. 43, 961–966. doi: 10.1002/2015GL067369

CrossRef Full Text | Google Scholar

Melgar, D., Ganas, A., Geng, J., Liang, C., Fielding, E. J., and Kassaras, I. (2017a). Source characteristics of the 2015 Mw6.5 Lefkada, Greece, strike.slip earthquake. J. Geophys. Res. Solid Earth 122, 2260–2273. doi: 10.1002/2016JB013452

CrossRef Full Text | Google Scholar

Melgar, D., Riquelme, S., Xu, X., Baez, J. C., Geng, J., and Moreno, M. (2017b). The first since 1960: a large event in the Valdivia segment of the Chilean subduction zone, the 2016 M7.6 Melinka earthquake. Earth Planet. Sci. Lett. 474, 68–75. doi: 10.1016/j.epsl.2017.06.026

CrossRef Full Text | Google Scholar

Merryman Boncori, J. P., Papoutsis, I., Pezzo, G., Tolomei, C., Atzori, S., Ganas, A., et al. (2014). The February 2014 Cephalonia earthquake (Greece): 3D deformation field and source modeling from multiple SAR techniques. Seis. Res. Lett. 86, 124–137. doi: 10.1785/0220140126

CrossRef Full Text | Google Scholar

Meta, A., Prats, P., Steinbrecher, U., Mittermayer, J., and Scheiber, R. (2008). “TerraSAR-X TOPSAR and ScanSAR comparison,” in Proceedings of EUSAR 2008 (Friedrichshafen).

Google Scholar

Metzger, S., Schurr, B., Ratschbacher, L., Sudhaus, H., Kufner, S.-K., Schöne, T., et al. (2017). The 2015 Mw7.2 Sarez strike-slip earthquake in the Pamir interior: response to the underthrusting of India's western promontory. Tectonics 36, 2407–2421. doi: 10.1002/2017TC004581

CrossRef Full Text | Google Scholar

Meyer, F., Bamler, R., Jakowski, N., and Fritz, T. (2006). The potential of low-frequency SAR systems for mapping ionospheric TEC distributions. IEEE Trans. Geosci. Remote Sens. 3, 560–564. doi: 10.1109/LGRS.2006.882148

CrossRef Full Text | Google Scholar

Michel, R., Avouac, J. P., and Taboury, J. (1999). Measuring ground displacements from SAR amplitude images: application to the Landers earthquake. Geophys. Res. Lett. 26, 875–878. doi: 10.1029/1999GL900138

CrossRef Full Text | Google Scholar

Moreno, M., Li, S., Melnick, D., Bedford, J. R., Baez, J. C., Motagh, M., et al. (2018). Chilean megathrust earthquake recurrence linked to frictional contrast at depth. Nat. Geosci. 11, 285–290. doi: 10.1038/s41561-018-0089-5

CrossRef Full Text | Google Scholar

Morishita, Y., Kobayashi, T., Fujiwara, S., and Yarai, H. (2018). Complex crustal deformation of the 2016 Kaikoura, New Zealand, earthquake revealed by ALOS-2. Bull. Seis. Soc. Am. 108, 1746–1756. doi: 10.1785/0120180070

CrossRef Full Text | Google Scholar

Motagh, M., Bahroudi, A., Haghshenas Haghighi, M., Samsonov, S., Fielding, E., and Wetzel, H.-U. (2015). The 18 August 2014 Mw 6.2 Mormori, Iran, earthquake: a thin-skinned faulting in the Zagros mountain inferred from InSAR measurements. Seis. Res. Lett. 86, 775–782. doi: 10.1785/0220140222

CrossRef Full Text | Google Scholar

Motagh, M., Wang, R., Walter, T. R., Bürgmann, R., Fielding, E., Anderssohn, J., et al. (2008). Coseismic slip model of the 2007 August Pisco earthquake (Peru) as constrained by wide swath radar observations. Geophys. J. Int. 174, 842–848. doi: 10.1111/j.1365-246X.2008.03852.x

CrossRef Full Text | Google Scholar

Natsuaki, R., Motohka, T., Shimada, M., and Suzuki, S. (2017). Burst misalignment evaluation for ALOS-2 PALSAR-2 ScanSAR-ScanSAR interferometry. Remote Sens. 9:216. doi: 10.3390/rs9030216

CrossRef Full Text | Google Scholar

Nie, Z., Wang, D.-J., Jia, Z., Yu, P., and Li, L. (2018). Fault model of the 2017 Jiuzhaigou Mw 6.5 earthquake estimated from coseismic deformation observed using global positioning system and interferometric synthetic aperture radar data. Earth Planets Space 70:55. doi: 10.1186/s40623-018-0826-4

CrossRef Full Text | Google Scholar

Nocquet, J.-M., Jarrin, P., Vallée, M., Mothes, P. A., Grandin, R., Rolandone, F., et al. (2016). Supercycle at the Ecuadorian subduction zone revealed after the 2016 Pedernales earthquake. Nat. Geosci. 10:145. doi: 10.1038/ngeo2864

CrossRef Full Text | Google Scholar

Ozawa, T., Fujita, E., and Ueda, H. (2016). Crustal deformation associated with the 2016 Kumamoto Earthquake and its effect on the magma system of Aso volcano. Earth Planets Space 68:186. doi: 10.1186/s40623-016-0563-5

CrossRef Full Text | Google Scholar

Papadopoulos, G. A., Ganas, A., Agalos, A., Papageorgiou, A., Triantafyllou, I., Kontoes, C.h., et al. (2017). Earthquake triggering inferred from rupture histories, DInSAR ground deformation and stress-transfer modelling: the case of central Italy during August 2016-January 2017. Pure Appl. Geophys. 174, 3689–3711. doi: 10.1007/s00024-017-1609-8

CrossRef Full Text | Google Scholar

Peltzer, G., Crampé, F., and King, G. (1999). Evidence of nonlinear elasticity of the crust from the Mw 7.6 Manyi (Tibet) earthquake. Science 286, 272–276. doi: 10.1126/science.286.5438.272

CrossRef Full Text | Google Scholar

Polcari, M., Albano, M., Atzori, S., Bignami, C., and Stramondo, S. (2018). The causative fault of the 2016 Mwp 6.1 Petermann ranges intraplate earthquake (Central Australia) retrieved by C- and L-band InSAR data. Remote Sens. 10:1311. doi: 10.3390/rs10081311

CrossRef Full Text | Google Scholar

Polcari, M., Fernández, J., Albano, M., Bignami, C., Palano, M., and Stramondo, S. (2017). An improved data integration algorithm to constrain the 3D displacement field induced by fast deformation phenomena tested on the Napa Valley earthquake. Comput. Geosci. 109, 206–215. doi: 10.1016/j.cageo.2017.09.002

CrossRef Full Text | Google Scholar

Prats-Iraola, P., Scheiber, R., Marotti, L., Wollstadt, S., and Reigber, A. (2012). TOPS interferometry with TerraSAR-X. IEEE Trans. Geosci. Remote Sens. 50, 3179–3188. doi: 10.1109/TGRS.2011.2178247

CrossRef Full Text | Google Scholar

Pritchard, H., Murray, T., Luckman, A., Strozzi, T., and Barr, S. (2005). Glacier surge dynamics of Sortebræ, east Greenland, from synthetic aperture radar feature tracking. J. Geophys. Res. 110:F03005. doi: 10.1029/2004JF000233

CrossRef Full Text | Google Scholar

Puyssegur, B., Michel, R., and Avouac, J. P. (2007). Tropospheric phase delay in InSAR estimated from meteorological model and multispectral imagery. J. Geophys. Res. 112:B05419. doi: 10.1029/2006JB004352

CrossRef Full Text | Google Scholar

Qiu, J., and Qiao, X. (2017). A study on the seismogenic structure of the 2016 Zaduo, Qinghai Ms6.2 earthquake using InSAR technology. Geodesy. Geodyn. 8, 342–346. doi: 10.1016/j.geog.2017.04.008

CrossRef Full Text | Google Scholar

Qu, C., Zuo, R., Shan, X., Hu, J.-C., and Zhang, G. (2017a). Coseismic deformation of the 2016 Taiwan Mw6.3 earthquake using InSAR data and source slop inversion. J. Asian Earth Sci. 148, 96–104. doi: 10.1016/j.jseaes.2017.08.027

CrossRef Full Text | Google Scholar

Qu, C., Zuo, R., Shan, X., Zhang, G., Zhang, Y., Song, X., et al. (2017b). Coseismic and post-seismic deformation fields mapped using satellite radar interferometry and fault slip inversion of the Mw8.3 Illapel earthquake, Chile. J. Geodyn. 104, 36–48. doi: 10.1016/j.jog.2016.10.004

CrossRef Full Text | Google Scholar

Raucoules, D., and De Michele, M. (2010). Assessing ionospheric influence on L-Band SAR data: implications on coseismic displacement measurements of the 2008 Sichuan earthquake. IEEE Geosci. Remote Sens. Lett. 7, 286–290. doi: 10.1109/LGRS.2009.2033317

CrossRef Full Text | Google Scholar

Rosen, P., Hensley, S., and Chen, C. (2010). “Measurement and mitigation of the ionosphere in L-band interferometric SAR data,” in Proceedings of IEEE Radar Conference May 2010 (Arlington, VA) 1459–1463. doi: 10.1109/RADAR.2010.5494385

CrossRef Full Text | Google Scholar

Rosen, P. A., Hensley, S., Joughin, I. R., Li, F. K., Madsen, S. N., Rodriguez, E., et al. (2000). Synthetic aperture radar interferometry. Proc. IEEE 88, 333–382. doi: 10.1109/5.838084

CrossRef Full Text | Google Scholar

Sangha, S., Peltzer, G., Zhang, A., Meng, L., Liang, C., Lundgren, P., et al. (2017). Fault geometry of 2015, Mw7.2 Murghab, Tajikistan earthquake controls rupture propagation: insights from InSAR and seismological data. Earth Planet. Sci. Lett. 462, 132–141. doi: 10.1016/j.epsl.2017.01.018

CrossRef Full Text | Google Scholar

Sansosti, E., Berardino, P., Bonano, M., Calo', F., Castaldo, R., Casu, F., et al. (2014). How second generation SAR systems are impacting the analysis of ground deformation. Intl. J. Appl. Earth Obs. Geoinform. 28, 1–11. doi: 10.1016/j.jag.2013.10.007

CrossRef Full Text | Google Scholar

Scheiber, R., Jager, M., Prats-Iraola, P., De Zan, F., and Geudtner, D. (2015). Speckle tracking and interferometric processing of TerraSAR-X TOPS data for mapping nonstationary scenarios. IEEE Trans. Geosci. Remote Sens. 8, 1709–1719. doi: 10.1109/JSTARS.2014.2360237

CrossRef Full Text | Google Scholar

Scheiber, R., and Moreira, A. (2000). Coregistration of interferometric SAR images using spectral diversity. IEEE Trans. Geosci. Remote Sens. 38, 2179–2191. doi: 10.1109/36.868876

CrossRef Full Text | Google Scholar

Scott, C., and Lohman, R. (2016). Sensitivity of earthquake source inversions to atmospheric noise and corrections of InSAR data. J. Geophys. Res. Solid Earth 121, 4031–4044 doi: 10.1002/2016JB012969

CrossRef Full Text | Google Scholar

Shen, W., Li, Y., and Zhang, J. (2017). Hybrid stochastic ground motion modeling of the Mw 7.8 Gorkha, Nepal earthquake of 2015 based on InSAR inversion. J. Asian Earth Sci. 141, 268–278. doi: 10.1016/j.jseaes.2016.12.004

CrossRef Full Text | Google Scholar

Shirzaei, M., and Bürgmann, R. (2012). Topography correlated atmospheric delay correction in radar interferometry using wavelet transforms. Geophys. Res. Lett. 39:L01305. doi: 10.1029/2011GL049971

CrossRef Full Text | Google Scholar

Simons, M., and Rosen, P. A. (2015). “Interferometric synthetic aperture radar geodesy,” in Treatise on Geophysics, 2nd Edn, ed. G. Schubert (Oxford: Elsevier), 339–385.

Google Scholar

Solaro, G., De Novellis, V., Castaldo, R., De Luca, C., Lanari, R., Manunta, M., et al. (2016). Coseismic fault model of Mw 8.3 2015 Illapel earthquake (Chile) retrieved from multi-orbit Sentinel1-A DInSAR measurements. Remote Sens. 8:323. doi: 10.3390/rs8040323

CrossRef Full Text | Google Scholar

Sreejith, K. M., Sunil, P. S., Agrawal, R., Saji, A. P., Ramesh, D. S., and Rajawat, A. S (2016), Coseismic early postseismic deformation due to the 25 April 2015, Mw 7.8 Gorkha, Nepal, earthquake from InSAR GPS measurements, Geophys. Res. Lett. 43, 3160–3168. doi: 10.1002/2016GL067907

CrossRef Full Text | Google Scholar

Su, Z., Yang, Y.-H., Li, Y.-S., Lu, X.-W., Zhang, J., Zhou, X., et al. (2019). Coseismic displacement of the 5 april 2017 Mashhad earthquake (Mw 6.1) in NE Iran through Sentinel-1A TOPS data: new implications for the strain partitioning in the southern Binalud mountains. J. Asian Earth Sci. 169, 244–256. doi: 10.1016/j.jseaes.2018.08.010

CrossRef Full Text | Google Scholar

Sun, J., Shen, Z.-K., Li, T., and Chen, J. (2016). Thrust faulting and 3D ground deformation of the 3 July 2015 Mw 6.4 Pishan, China earthquake from Sentinel-1A radar interferometry. Tectonophysics 683, 77–85. doi: 10.1016/j.tecto.2016.05.051

CrossRef Full Text | Google Scholar

Tilmann, F., Zhang, Y., Moreno, M., Saul, J., Eckelmann, F., Palo, M., et al. (2016). The 2015 Illapel earthquake, central Chile: a type case for a characteristic earthquake?. Geopyhs. Res. Lett. 43, 574–583. doi: 10.1002/2015GL066963

CrossRef Full Text | Google Scholar

Tong, X., Sandwell, D., Luttrell, K., Brooks, B., Bevis, M., Shimada, M., et al. (2010). The 2010 Maule, Chile earthquake: downdip rupture limit revealed by space geodesy. Geophys. Res. Lett. 37:L24311. doi: 10.1029/2010GL045805

CrossRef Full Text | Google Scholar

Vajedian, S., Motagh, M., Mousavi, Z., Motaghi, K., Fielding, E. J., Akbari, B., et al. (2018). Coseismic deformation field of the Mw 7.3 12 November 2017 Sarpol-e Zahab (Iran) earthquake: a decoupling horizon in the northern Zagros mountains inferred from InSAR observations. Remote Sens. 10:1589. doi: 10.3390/rs10101589

CrossRef Full Text | Google Scholar

Wadge, G., Zhu, M., Holley, R. J., James, I. N., Clark, P. A., Wang, C., et al. (2010). Correction of atmospheric delay effects in radar interferometry using a nested mesoscale atmospheric model. J Appl. Geophys. 72, 141–149. doi: 10.1016/j.jappgeo.2010.08.005

CrossRef Full Text | Google Scholar

Walters, R. J., Elliott, J. R., Li, Z., and Parsons, B. (2013). Rapid strain accumulation on the Ashkabad fault (Turkmenistan) from atmosphere-corrected InSAR. J. Geophys. Res. Solid Earth 118, 3674–3690. doi: 10.1002/jgrb.50236

CrossRef Full Text | Google Scholar

Wang, H., Liu-Zeng, J., Ng, A. H.-M., Ge, L., Javed, F., Long, F., et al. (2017a). Sentinel-1 observations of the 2016 Menyuan earthquake: a buried reverse event linked to the left-lateral Haiyuan fault. Int J. Appl. Earth Obs. Geoinform. 61, 14–21. doi: 10.1016/j.jag.2017.04.011

CrossRef Full Text | Google Scholar

Wang, K., and Fialko, Y. (2015). Slip model of the 2015 Mw 7.8 Gorkha (Nepal) earthquake from inversions of ALOS-2 and GPS data. Geophys. Res. Lett. 42, 7452–7458. doi: 10.1002/2015GL065201

CrossRef Full Text | Google Scholar

Wang, K., Xu, X., and Fialko, Y. (2017c). Improving burst alignment in TOPS interferometry with bivariate enhanced spectral diversity. IEEE Geosci. Remote Sens. Lett. 14, 2423–2427. doi: 10.1109/LGRS.2017.2767575

CrossRef Full Text | Google Scholar

Wang, L., Gao, H., Feng, G., and Xu, W. (2018c). Source parameters and triggering links of the earthquake sequence in central Italy from 2009 to 2016 analyzed with GPS and InSAR data. Tectonophysics 744, 285–295. doi: 10.1016/j.tecto.2018.07.013

CrossRef Full Text | Google Scholar

Wang, L.-H., Gao, H., and Feng, G.-C. (2017b). InSAR and GPS earthquake source parameter inversion for the 2016 Mw6.4 Meinong, Taiwan earthquake. Chin. J. Geophys. 60, 346–357. doi: 10.1002/cjg2.30051

CrossRef Full Text | Google Scholar

Wang, S., Xu, C., Wen, Y., Yin, Z., Jiang, G., and Fang, L. (2017d). Slip model for the 25 November 2016 Mw 6.6 Aketao earthquake, western China, revealed by Sentinel-1 and ALOS-2 observations. Remote Sens. 9:325. doi: 10.3390/rs9040325

CrossRef Full Text | Google Scholar

Wang, T., and Jónsson, S. (2015). Improved SAR amplitude image offset measurements for deriving three-dimensional coseismic displacements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 8, 3271–3278. doi: 10.1109/JSTARS.2014.2387865

CrossRef Full Text | Google Scholar

Wang, T., Wei, S., Shi, X., Qiu, Q., Li, L., Peng, D., et al. (2018b). The 2016 Kaikoura earthquake: simultaneous rupture of the subduction interface and overlying faults. Earth Planet. Sci. Lett. 482, 44–51. doi: 10.1016/j.epsl.2017.10.056

CrossRef Full Text | Google Scholar

Wang, Z., Zhang, R., Wang, X., and Liu, G. (2018a). Retrieving three-dimensional co-seismic deformation of the 2017 Mw7.3 Iraq earthquake by multi-sensor SAR images. Remote Sens. 10:857. doi: 10.3390/rs10060857

CrossRef Full Text | Google Scholar

Wei, S., Chen, M., Wang, X., Graves, R., Lindsey, E., Wang, T., et al. (2018). The 2015 Gorkha (Nepal) earthquake sequence: I. Source modeling and deterministic 3D ground shaking. Tectonophysics 722, 447–461. doi: 10.1016/j.tecto.2017.11.024

CrossRef Full Text | Google Scholar

Wen, Y., Xu, C., Liu, Y., and Jiang, G. (2016). Deformation and source parameters of the 2015 Mw 6.5 earthquake in Pishan, western China, from Sentinel-1A and ALOS-2 data. Remote Sens. 8:134. doi: 10.3390/rs8020134

CrossRef Full Text | Google Scholar

Weston, J., Ferreira, A. M. G., and Funning, G. J. (2011). Global compilation of interferometric synthetic aperture radar earthquake source models: 1. Comparisons with seismic catalogs. J. Geophys. Res. 116:B08408. doi: 10.1029/2010JB008131

CrossRef Full Text | Google Scholar

Weston, J., Ferreira, A. M. G., and Funning, G. J. (2012). Systematic comparisons of earthquake source models determined using InSAR and seismic data. Tectonophysics 532–535, 61–81. doi: 10.1016/j.tecto.2012.02.001

CrossRef Full Text | Google Scholar

Wicks Jr, C. W., Dzurisin, D., Ingebritsen, S., Thatcher, W., Lu, Z., and Iverson, J. (2002). Magmatic activity beneath the quiescent Three Sisters volcanic center central Oregon Cascade Range, USA. Geophys. Res. Lett. 29:1122. doi: 10.1029/2001GL014205

CrossRef Full Text | Google Scholar

Wright, T. J., Parsons, B. E., and Lu, Z. (2004). Toward mapping surface deformation in three dimensions using InSAR. Geophys. Res. Lett. 31:L01607. doi: 10.1029/2003GL018827

CrossRef Full Text | Google Scholar

Xu, B., Li, Z., Feng, G., Zhang, Z., Wang, Q., Hu, J., et al. (2016). Continent-wide 2-D co-seismic deformation of the 2015 Mw 8.3 Illapel, Chile earthquake derived from Sentinel-1A data: correction of Azimuth co-registration error. Remote Sens. 8:376. doi: 10.3390/rs8050376

CrossRef Full Text | Google Scholar

Xu, C., Wang, H., and Jiang, G. (2011). Study on crustal deformation of Wenchuan Ms8.0 earthquake using wide-swath ScanSAR and MODIS. Geodesy. Geodyn. 2, 1–6. doi: 10.3724/SP.J.1246.2011.00001.1

CrossRef Full Text | Google Scholar

Xu, G., Xu, C., and Wen, Y. (2018a). Sentinel-1 observation of the 2017 Sangsefid earthquake, northeastern Iran: Rupture of a blind reserve-slip fault near the Eastern Kopeh Dagh. Tectonophysics 731–732, 131–138. doi: 10.1016/j.tecto.2018.03.009

CrossRef Full Text | Google Scholar

Xu, G., Xu, C., Wen, Y., and Jiang, G. (2017). Source parameters of the 2016–2017 central Italy earthquake sequence from the Sentinel-1, ALOS-2 and GPS data. Remote Sens. 9:1182. doi: 10.3390/rs9111182

CrossRef Full Text | Google Scholar

Xu, W. (2017). Finite-fault slip model of the 2016 Mw 7.5 Chiloé earthquake, southern Chile, estimated from Sentinel-1 data, Geophys. Res. Lett. 44, 4774–4780. doi: 10.1002/2017GL073560

CrossRef Full Text | Google Scholar

Xu, W., Feng, G., Meng, L., Zhang, A., Ampuero, J. P., Bürgmann, R., et al. (2018b). Transpressional rupture cascade of the 2016 Mw 7.8 Kaikoura earthquake, New Zealand. J. Geophys. Res. Solid Earth 123, 2396–2409. doi: 10.1002/2017JB015168

CrossRef Full Text | Google Scholar

Yague-Martinez, N., Prats-Iraola, P., Rodriguez Gonzalez, F., Brcic, R., Shau, R., Geudtner, D., et al. (2016). Interferometric processing of Sentinel-1 TOPS data. IEEE Trans. Geosci. Remote Sens. 54, 2220–2234. doi: 10.1109/TGRS.2015.2497902

CrossRef Full Text | Google Scholar

Yang, Y., Chen, Q., Xu, Q., Liu, G., and Hu, J. C. (2018a). Source model and Coulomb stress change of the 2015 Mw 7.8 Gorkha earthquake determined from improved inversion of geodetic surface deformation observations. J. Geodesy. 1–19. doi: 10.1007/s00190-018-1164-9

CrossRef Full Text | Google Scholar

Yang, Y., Chen, Q., Xu, Q., Zhang, Y., Yong, Q., and Liu, G. (2017). Coseismic surface deformation of the 2014 Napa earthquake mapped by Sentinel-1A SAR and accuracy assessment with COSMO-SkyMed and GPS data as cross validation. Int J. Digital Earth 10, 1197–1213. doi: 10.1080/17538947.2017.1299806

CrossRef Full Text | Google Scholar

Yang, Y.-H., Hu, J.-C., Tung, H., Tsai, M.-C., Chen, Q., Xu, Q., et al. (2018b). Co-seismic and postseismic fault models of the 2018 Mw 6.4 Hualien earthquake occurred in the junction of collision and subduction boundaries offshore eastern Taiwan. Remote Sens. 10:1372. doi: 10.3390/rs10091372

CrossRef Full Text | Google Scholar

Yi, L., Xu, C., Wen, Y., Zhang, X., and Jiang, G. (2018). Rupture process of the 2016 Mw 7.8 Ecuador earthquake from joint inversion of InSAR data and teleseismic P waveforms. Tectonophysics 722, 163–174. doi: 10.1016/j.tecto.2017.10.028

CrossRef Full Text | Google Scholar

Yu, C., Li, Z., Chen, J., and Hu, J.-C. (2018). Small magnitude co-seismic deformation of the 2017 Mw 6.4 Nyingchi earthquake revealed by InSAR measurements with atmospheric correction. Remote Sens. 10:684. doi: 10.3390/rs10050684

CrossRef Full Text | Google Scholar

Yu, C., Li, Z., and Penna, N. T. (2017). Interferometric synthetic aperture radar atmospheric correction using a GPS-based iterative tropospheric decomposition model. Remote Sens. Environ. 204, 109–121. doi: 10.1016/j.rse.2017.10.038

CrossRef Full Text | Google Scholar

Yue, H., Ross, Z. E., Liang, C., Michel, S., Fattahi, H., Fielding, E., et al. (2017b). The 2016 Kumamoto Mw = 7.0 earthquake: a significant event in a fault–volcano system. J. Geophys. Res. Solid Earth 122, 9166–9183. doi: 10.1002/2017JB014525

CrossRef Full Text | Google Scholar

Yue, H., Simons, M., Duputel, Z., Jiang, J., Fielding, E., Liang, C., et al. (2017a). Depth varying rupture properties during the 2015 Mw 7.8 Gorkha (Nepal) earthquake. Tectonophysics 714–715, 44–54. doi: 10.1016/j.tecto.2016.07.005

CrossRef Full Text | Google Scholar

Zhang, Y., Shan, X., Zhang, G., Gong, W., Liu, X., Yin, H., et al. (2018b). Source model of the 2016 Kumamoto, Japan, earthquake constrained by InSAR, GPS, and strong-motion data: fault slip under extensional stress. Bull. Seis. Soc. Am. 108, 2675–2686. doi: 10.1785/0120180023

CrossRef Full Text | Google Scholar

Zhang, Y., Zhang, G., Hetland, E. A., Shan, X., Wen, S., and Zuo, R. (2016). Coseismic fault slip of the September 16, 2015 Mw 8.3 Illapel, Chile earthquake estimated from InSAR data. Pure Appl. Geophys. 173, 1029–1038. doi: 10.1007/s00024-016-1266-3

CrossRef Full Text | Google Scholar

Zhang, Y., Zhang, G., Hetland, E. A., Shan, X., Zhang, H., Zhao, D., et al. (2018a). Source fault and slip distribution of the 2017 Mw 6.5 Jiuzhaigou, China, earthquake and its tectonic implications. Seis. Res. Lett. 89, 1345–1345. doi: 10.1785/0220170255

CrossRef Full Text | Google Scholar

Zhao, D., Qu, C., Shan, X., Gong, W., Zhang, Y., and Zhang, G. (2018). InSAR and GPS derived coseismic deformation and fault model of the 2017 Ms7.0 Jiuzhaigou earthquake in the northeast Bayanhar block. Tectonophysics 726, 86–99. doi: 10.1016/j.tecto.2018.01.026

CrossRef Full Text | Google Scholar

Zhou, X., Chang, N. B., and Li, S. (2009). Applications of SAR interferometry in Earth and environmental science research. Sensors 9, 1876–1912. doi: 10.3390/s90301876

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, W., Zhang, W.-T., He, Y.-F., and Qu, W. (2017). Performance evaluation of azimuth offset method for mitigating the ionospheric effect on SAR interferometry. J. Sensors 2017:4587475. doi: 10.1155/2017/4587475

CrossRef Full Text | Google Scholar

Zuo, R., Qu, C., Shan, X., Zhang, G., and Song, X. (2016). Coseismic deformation fields and a fault slip model for the Mw7.8 mainshock and Mw7.3 aftershock of the Gorkha-Nepal 2015 earthquake derived from Sentinel-1A SAR interferometry. Tectonophysics 686, 158–169. doi: 10.1016/j.tecto.2016.07.032

CrossRef Full Text | Google Scholar