The Influence of Microporous Cements on the Pore Network Geometry of Natural Sedimentary Rocks

We investigate the pore network geometry and permeability of six natural sandstones and carbonate rocks. Using 3D microtomographic images, we segment each rock sample into three phases: Solid matrix of grains, macropores containing void spaces, and a third microporous phase containing nanometer-sized pores beyond the resolution of the image. In the majority of our samples, the microporosity exists inside cements deposited as a secondary phase along the surface of grains. Within the macropores, the pore radius, coordination number, throat radius, and throat length display a power law relation with porosity. We also find that the permeability of the aggregate depends on the porosity following the relation $k=k_0{\varphi }^{3.32}$, where log k₀ = 5.52 (mD). The fraction of connected porosity shows a strongly non-linear reduction with an increase in the volume fraction of microporous cement.

1. Introduction

Carbonates and sandstones form important reservoirs for hydrocarbons and can act as potential sinks for the future storage of anthropogenic green-house gases by carbon capture and sequestration. The nature of the pore space in these rock types can be complex, often resulting from a combination of depositional and diagenetic processes. The pore geometry of carbonates is commonly more tortuous due to millimeter scale macroporosity, which may include interparticle, intercrystal, moldic and vuggy porosity (Choquette and Pray, 1970), and microporosity (submicron porosity), typically intraparticle, including partially dissolved bioclastic and/or grain material, and cementation found along the pore and throat grain contacts. Clean sandstones display a simplistic pore geometry, with macroporosity forming a more uniform intergranular network and microporosity forming from detrital and authigenic clays (Pittman, 1979). “Tight” (low porosity) sandstones, however, can demonstrate characteristics that lead to a more complicated pore network. Such features include variable grain size, grain packing, sorting, clay distribution and after burial compaction (Marquez et al., 2014; Teles et al., 2016). Additionally, primary pore geometry in these sandstones can be reduced by cementation, rendering them “tight.” Consequently, determination of petrophysical properties of these sandstones are often as challenging as carbonate rocks.

Conventional relationships used to predict petrophysical properties are restricted by the presence of microporosity found in many carbonates and tight sandstones. Such relationships include Archie's law for resistivity, the Carman–Kozeny permeability estimate and the Brooks–Corey parameterization of relative permeability, which were all originally designed for more simplistic rocks with intergranular pores. When considering these classic models for complex carbonates and tight sandstones, the results are inaccurate due to the greater range in pore-size distributions and interconnectivity of different pore types (Jennings and Jerry Lucia, 2003).

The use of X-ray computed microtomography (micro CT), high resolution, three-dimensional (3D) images of porous geological media have become greatly popular over the past two decades (Valvatne and Blunt, 2004; Andrä et al., 2013a,b; Madonna et al., 2013; Prodanović et al., 2014; Bultreys et al., 2016a). This non-invasive technique allows 3D pore geometries to be evaluated quantitatively, whilst preserving the integrity of the original sample. The other great advantage of a digitized pore space network reconstruction is the ability to simulate a multitude of different transport properties. Porous flow, in particular, has several applications to many important geological fields, including hydrology, the recovery of oil and gas, and carbon sequestration. Recent studies related to the storage of anthropogenic CO₂ in the subsurface highlight the in situ process of dissolution and its effects on porosity and permeability of different carbonates by means of experiment performed with lab-based micro CT scanner visualization (Menke et al., 2015, 2016). Numerical models of single and multiphase fluid flow have also been used to predict absolute and relative permeability for a variety of different rock type. The use of traditional computation fluid dynamics, which incorporates finite difference, finite volume and finite element (Mostaghimi et al., 2013; Raeini et al., 2014), and the lattice-Boltzmann method (Ramstad et al., 2010; Shah et al., 2016) have proven popular in recent years. For more detail on the use of micro CT and its applications to geoscience, the reader is referred to a number of recent review papers (Cnudde and Boone, 2013; Bultreys et al., 2016a; Berg et al., 2017).

Other studies have shown that micro CT can provide useful insights into the key processes occurring at the pore scale within unconventional resources such as shale oil and shale gas. Ma et al. (2016) successfully combined micro CT and scanning electron microscopy (SEM) to identify and quantify four different types of porosity within the Bowland Shale, UK. Their results indicated that porosity was unconnected at scales greater than 20 nm, whilst organic matter and clay minerals at scales of less than 20 nm was found to be connected and offered potential diffusion transport pathways for gas. A similar study by Saif et al. (2017) on the Green River oil shale (USA) highlighted the evolution of an interconnected fracture network and increased porosity due to the breakdown of kerogen into hydrocarbon fluids during pyrolysis. Such insights are powerful tools which can be used to estimate the petrophysical properties of many rocks for modeling and designing production processes.

Microporosity typically exists at a resolution below that from which clear segmentation can not be achieved. This results in an intermediate phase, that can neither be assigned to void space nor solid in conventional micro CT. To accurately visualize and represent microporosity in 3D it is possible to combine SEM with various reconstruction techniques (Øren and Bakke, 2003; Okabe and Blunt, 2005), or more recently, with the use of focused ion beam scanning electron microscopy (FIB-SEM) (Bera et al., 2011; Jiao et al., 2014). The variation in pore sizes between micro and macroporosity means that not all pores can be incorporated in one single imaging experiment. It remains challenging to combine data from multiple experiments because the necessary resolution of such a model is influenced by the finest pores, while the minimal size of the model is controlled by the representative elementary volume of the sample (Bultreys et al., 2016a). The joint modeling of such different scales results in a difference of several orders of magnitude, which often presents computational limitations. The use of a pore network model (PNM) reduces the computational expense, which at present are probably the best suited technique for dual scale porosity simulations (Jiang et al., 2012, 2013; Mehmani and Prodanović, 2014; Bultreys et al., 2015).

Despite the challenges in identifying and quantifying microporosity, their presence can provide an insight into the nature of fluid flow through a connected, intergranular macroporous network. In this article, we distinguish microporosity arising from two different sources: microporosity in primary rock-forming grains and microporosity within secondary phases. An example of the former includes fossils in carbonate rocks while an example of the latter includes microporous cement deposited as secondary phases along the walls of a pore network. Recent work by Bultreys et al. (2015) discussed the effective transport properties combining imaged macroporosity and models of microporosity. We refer the reader to this work for physical properties involving microporosity and focus on (a) the pore network geometry of the connected macro pore space, macroporosity, and (b) the way development of secondary microporosity, or cement, affect the connectivity of the primary porosity.

We segment and analyze the micro CT images of six natural sandstones and carbonates into three phases (microporosity, macroporosity and matrix) to quantify their volume fraction and to evaluate the nature of their pores and throats using pore network models. We further analyze each rock type by selecting one or more smaller regions of interest (ROI) to assess sample heterogeneity and perform error analysis. We compare the results between three different sandstones, the Doddington, Knorringfjellet, and Wilcox, and three different carbonates, the Estaillades, Massangis Jaune, and Savonnières. The characteristics of the raw data for all six samples is summarized in Table 1.

TABLE 1

Table 1. Characteristics of raw data.

2. Methods

All data used in this work was sourced externally. The Doddington and Wilcox sandstone data sets were acquired online from the British Geological Society's (BGS) National Geoscience Data Centre (Shah et al., 2016) and the Digital Rocks Portal (Mehmani and Prodanović, 2014; Prodanović et al., 2014), respectively. Images for the Knorringfjellet sandstone and three carbonate samples, Estaillades, Massangis Jaune (Boone et al., 2014), and Savonnières were kindly provided by Tom Bultreys (Bultreys et al., 2016b) (Imperial College London).

We filtered the gray scale images to reduce noise and remove unwanted artifacts. We then segmented the filtered image into microporosity, macroporosity and matrix by thresholding. Next, we analyzed the proportion of microporosity and macroporosity in each sample, using a series of ROI to assess the influence of sample heterogeneity. Pore network modeling and absolute permeability simulations were then carried out to characterize the nature of the pore geometries in all samples and to quantify the effect of microporosity on single phase fluid flow. We used the commercial software PerGeos, from Thermo Fisher Scientific, to prepare images, to perform network modeling, and to simulate fluid flow through the segmented 3D images.

2.1. Image Processing

We filtered the micro CT images to reduce spurious features that occur from the image acquisition process (Ketcham and Carlson, 2001; Wildenschild et al., 2002) and to amplify the contrast between key phases. Firstly, we extracted a subvolume from the original raw data for computational efficiency in filtering and simulations at a later stage. The sub volume characteristics are highlighted in Table 1. Next, we applied various filters including anisotropic diffusion, non-local means, and despeckle to reduce salt and pepper noise at the center of grains, whilst maintaining detail at the boundaries between pores and solid matrix.

The process of segmentation in micro CT images is a crucial step which can induce operator bias and subsequently affect the quality of all other image analyses (Wildenschild and Sheppard, 2013; Schlüter et al., 2014). A wide variety of segmentation techniques exist, which can broadly be separated into two groups. Global thresholding includes all methods where labels are assigned to voxels by histogram evaluation only, without thought for how the gray values are spatially arranged in the image. Such techniques have been reviewed extensively in the past by many authors (Pal and Pal, 1993; Trier and Jain, 1995; Sezgin and Sankur, 2004; Iassonov et al., 2009), only to conclude that none of the methods are particularly good for all segmentation challenges. Local segmentation techniques make up the other popular class and these take account of neighborhood statistics enabling smoother boundaries, avoidance of noise objects, and compensation for local intensity changes. This greater flexibility and often more satisfying segmentation results is what differentiates the local segmentation methods from global thresholding (Iassonov et al., 2009; Wang et al., 2011).

In this work we used manual thresholding to segment the volume into three phases: microporosity, macroporosity and matrix. Whilst the classification for labeling the macroporosity and matrix were fairly simple, the microporosity existed as an intermediate phase, which created a more challenging interpretation. This intermediate phase included voxels of a particular gray scale that could often be identified in contact with macroporosity at the edges of grains (cementation), and sometimes occurring as whole or part of grains. This observation suggests that some microporosity exists as partially dissolved grains and/or bioclastic material in most of the samples. Although our chosen technique was user dependent and was likely to result in a certain degree of uncertainty, we manually adjusted the thresholds to produce results that we considered visually correct. To further reduce this uncertainty we benchmarked our results where possible with those found in previous studies (Boone et al., 2014; Derluyn et al., 2014; Mehmani and Prodanović, 2014; Alyafei and Blunt, 2016; Bultreys et al., 2016b). The micrographs in Figure 1 show the segmented gray scale images from the six samples analyzed in this study.

FIGURE 1

Figure 1. From top, left to right: (a) Doddington sandstone, (b) Knorringfjellet sandstone, (c) Wilcox sandstone, (d) Estaillades limestone, (e) Massangis Jaune limestone, and (f) Savonnières limestone. Single slice view of each sample. A quarter of the image is represented in gray scale only. The remaining voxels display macroporosity in red, and microporosity in blue.

2.2. Pore Network Model (PNM)

Following segmentation, pore-based PNM are extracted using a hybrid method described in Youssef et al. (2007). This method employs a medial-axis algorithm guided by a distance map which progressively erodes the pore-grain interface until a one-voxel thick skeleton of the entire pore space is achieved. The algorithm then calculates the length and connectivity of each line and designates each one as either pore or throat based on a known extreme radius. The intersection between two or more lines is marked as a node. A segment of the skeleton is marked as a pore if the extreme radius of the segment is larger than its length, whilst throats are classified as segments with length that do not exceed their extreme radius. The subsequent expansion of the one-voxel thick skeleton in these pores and throats allows the calculation of the radius of sphere (able to fit in each pore) and the length and equivalent hydraulic radius of each throat. The output of this algorithm results in the coordination number (number of throats connected to each pore), radius, area and volume of every pore, and the radius and length of each throat.

We test a simple model to evaluate the effects of microporosity on the pore geometry using two different scenarios. Initially, we generate the PNM using only the connected pore space (where possible) of macroporosity. Following this, we generate a second PNM where we assume that microporosity is made up of 100% void space, thus describing the pore network prior to cementation. To do this, we simply created a separate binary image for the total porosity case which incorporated both the microporosity and macroporosity. In samples where microporosity occurs within the cement, this step allows us to compare the reduction of pore connectivity and permeability due to cementation. All PNM simulations reported here are derived only from the macropores. The PNM analysis of micropores is an interesting topic for research involving high resolution nano-CT.

2.2.1. Porosity

Using the smaller sub-sampled volumes of each rock, we generated new label fields for microporosity and macroporosity in each volume. Microporosity was assigned to the voxels deemed to be associated with the primary rock-forming material (e.g., fossils in carbonates that may have been affected by secondary dissolution) and cement phases found along the walls of the pores. Typically these phases appear as a lighter shade of gray compared to macroporosity. The macroporosity was assigned with much less difficulty based on a dark black or gray color (Figure 1). The volume fraction of porosity was calculated in each of these by measuring the number of voxels assigned to the void space, compared to those making up the remaining background voxels in each sub-sample. The macroporosity and microporosity proportion was calculated for each of the different samples by using the phase segmented data and calculating the volume of the total number of macroporosity and microporosity voxels to the total number of voxels in the complete sample. The total porosity was simply calculated by adding the macroporosity and microporosity. The volumes used for the calculations of the entire sample are highlighted in Table 1, whilst the volume fraction of porosity is summarized in Table 2.

TABLE 2

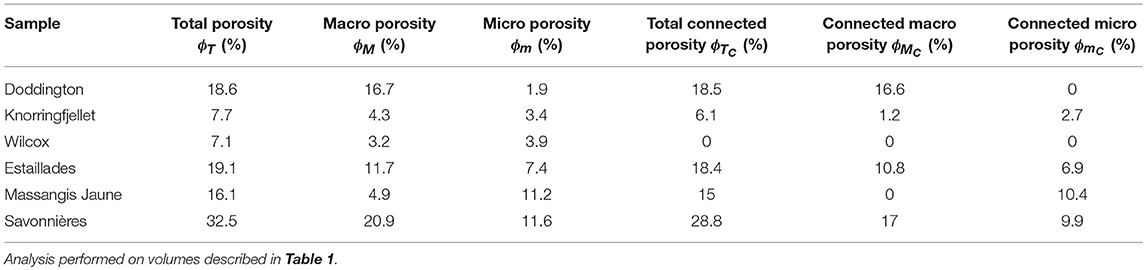
Table 2. Volume fraction of total porosity (ϕ_T), macroporosity (ϕ_M), microporosity (ϕ_m), total connected porosity (ϕ_TC), connected macroporosity (ϕ_MC), and connected microporosity (ϕ_mC) of total smple volumes.

We took the porosity analysis a step further and separated each sample down into further divisions to assess the heterogeneity at this scale. All samples were subsampled along the Z-axis into divisions of three, with the exception of the Knorringfjellet sandstone (8 subvolumes). Figure 2 shows a volume rendering representation of each sample and their subdivisions. The data from this analysis is summarized in the Supplementary Material.

FIGURE 2

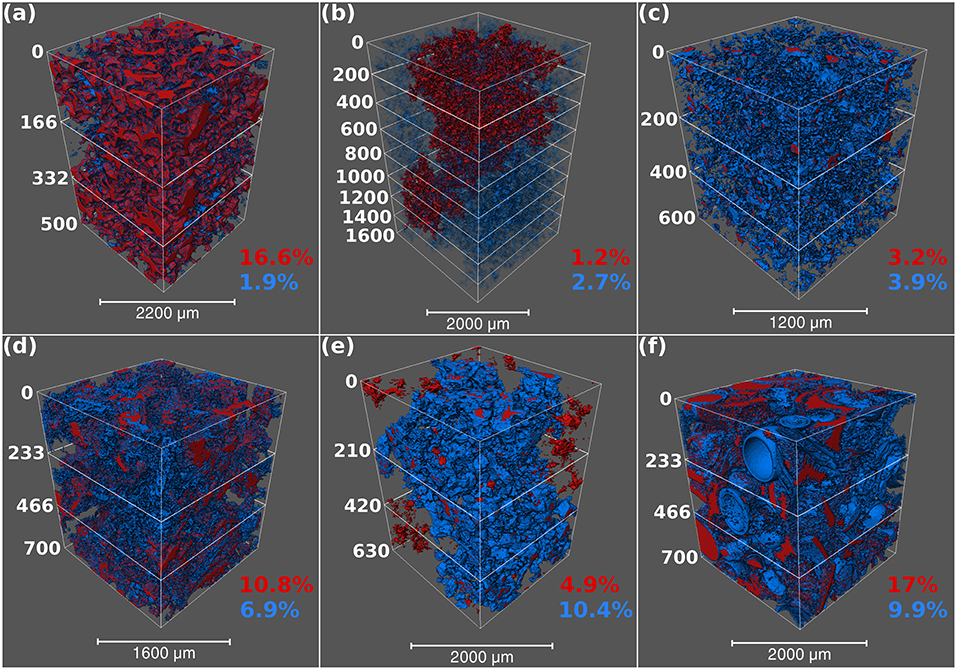
Figure 2. Volume rendering visualization of the six different samples. From top, left to right: (a) Doddington sandstone showing connected macroporosity and total microporosity, (b) Knorringfjellet sandstone showing connected macroporosity and connected microporosity, (c) Wilcox sandstone showing total macroporosity and total microporosity, (d) Estaillades limestone showing connected macroporosity and connected microporosity, (e) Massangis Jaune limestone showing total macroporosity and connected microporosity, and (f) Savonnières limestone showing connected macroporosity and connected microporosity. For each volume the macroporosity is shown in red and microporosity in blue. Table 2 summarizes the volume fractions of porosity observed in all samples. Subdivisions are also shown here, from which the subvolume porosity analysis was performed.

It is important to note that microfractures can contribute toward the connectivity of pores in many rocks. These microfractures may be natural or induced during the sample preparation stage. With the images used in this study we found no evidence to suggest the presence of microfractures, so focus on the primary porosity that can be observed in all images. The connectivity of the macroporosity in each subsample volume was assessed along the Z-axis. Volumes found to have a connected network that passes a percolation threshold from top to bottom were classified as having a connected porosity. Voxels that belong to the initial porosity but do not make up part of the connected network are determined as isolated pores and are removed from the resulting binary image. To fully evaluate the heterogeneity of each rock we generated a combined (microporosity and macroporosity) label field to test the total porosity case and assess whether or not the microporosity had any effect on the connectivity of each sub-sample volume.

2.2.2. Permeability Simulation

We performed absolute permeability simulations on each rock to calculate the flow of fluid directly through the connected pore space of the 3D micro CT images. We used a finite volume solver in the petrophysics module of PerGeos to calculate the flow of water given by Stokes equation,

$\begin{array}{ll}\nabla ·u=0,& (1)\end{array}$

$\begin{array}{ll}-\nabla P+\mu {\nabla }^{2}u=0,& (2)\end{array}$

where u is the fluid velocity vector, P is the pressure and μ = 1 × 10⁻³ Pa.s is viscosity of water. Each simulation was set up with a series of specified boundary conditions described in Thomson et al. (2018). Parameters were kept constant for all simulations, with the exception of the 3D micro CT input image.

We carried out numerical simulations on the connected pore network derived from both the total pore space and the macro pore space for all samples except for the Wilcox sandstone and Massangis Jaune carbonate. In the former, a connected pore network could not be established using the method described above. In the latter, a connected network was absent in macropores, but existed in micropore and total pore space. Samples in which micropores occur within the cement phase, we define the normalized permeability $k^{*}=k_M/k_T$, where k_M is the permeability derived from the macro pore network and k_T is the permeability derived from the total pore space (e.g., both macro and micro pores combined together). In section 4 we show the variations in k* with cement volume fraction (volume fraction of micropores).

We first carried out permeability simulations in samples with a connected porosity across the entire volume, evaluating both k_M and k_T, to assess the changes to permeability with the addition of microporosity permitting total flow. Next, we followed a similar approach to assess the influence of heterogeneity within the microtomographic images. We selected small regions of interest in each volume along their Z-axis. Each subvolume was 200 slices (voxels) in length. We then calculated the total porosity and connected porosity, when possible, in each sub-sample. Volumes found to have connected porosity were used to simulate permeability. Variations in porosity within the small subvolumes are shown in Figures 3B,D for Doddington and Knoringfjellet sandstones.

FIGURE 3

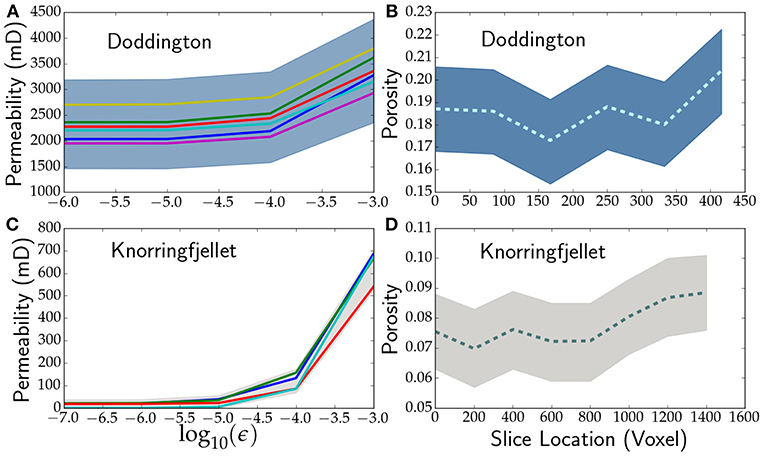
Figure 3. (A) Plot of calculated permeability as a function of the residual from permeability simulations in Doddington Sandstone. (B) Variation of porosity measured within subvolumes of a sample of Doddington. (C,D) Same as in panels (A,B) respectively, from Knorringfjellet. The shaded region indicates the maximum and minimum values obtained from each subvolume.

The numerical value of permeability, determined from the simulations, depends strongly on the convergence criterion for the simulation. The convergence criterion or error, ϵ, is defined as the maximum change in the value of an unknown variable (e.g., velocity and pressure) per time step. Equations (1) and (2) describe a steady-state, i.e., the calculates values of x, y, and z components of velocity and pressure should not change on subsequent iterations. As a result, we can define,

$\begin{array}{ll}ϵ=max( \frac{v_x(n)-v_x(n-1)}{\delta t},\frac{v_y(n)-v_y(n-1)}{\delta t},\frac{v_z(n)-v_z(n-1)}{\delta t},\frac{P(n)-P(n-1)}{c^2\delta t} )& (3)\end{array}$

where n is the current iteration, v_i are components of the velocity vector, P is the pressure, t is the time step and c² is a compressibility coefficient used in the simulation.

We carried out a series of numerical experiments (Figures 3A,C), by terminating the simulations when a prescribed value of ϵ is reached. The results in Figures 3A,C) show the sensitivity of the permeability to the value of ϵ. While a high value of ϵ, such as 10⁻³, reduces the computation time, the computed permeability is significantly higher than those obtained for a lower value of ϵ. For example, in Figures 3A,C, the calculated permeability remained nearly constant for ϵ ≤ 10⁻⁵. After performing this initial series of sensitivity tests on Doddington and Knoringfjellet sandstones, we set the value of ϵ between 10⁻⁵ and 10⁻⁶ for the remaining permeability simulations.

3. Results

For each sample we compare the porosity, PNM characteristics and permeability. We show the total porosity, the proportion of macroporosity and microporosity, and the volume of connected (effective) porosity for each of these. The PNM attributes highlight the variation in the characteristics of pores and throats. Lastly, we compare the results of permeability simulations using a macroporosity only model and a total porosity (micro and macro) model through the samples.

3.1. Porosity Analysis

The Doddington and Knorringfjellet sandstones are both potential CO₂ sequestration target reservoirs with quite different porosity characteristics. The Doddington sandstone has a higher total porosity of 18.6%, which is largely shared by macroporosity, contributing to 89.8% of the pore space, whilst only a small fraction of microporosity makes up the remaining network. Overall, the Doddington sandstone has good effective porosity with total connected porosity at 18.5% and connected macroporosity at 16.6%. Conversely, the Knorringfjellet sandstone has a much lower total porosity of 7.7%. The macroporosity and microporosity in this sample are 4.3 and 3.4%, respectively, indicating that the microporosity occupies a larger proportion (44.2%) of the total pore network compared to that observed in the Doddington sandstone (10.2%). The total connected porosity observed in the Knorringfjellet sandstone is 20% reduced compared to its overall total porosity, significantly more compared to that seen in the Doddington sandstone.

The unconventional Wilcox sandstone is a tight gas target with similar porosity characteristics to the Knorringfjellet sandstone. The Wilcox also has a low total porosity of only 7.1%, separated by 3.2% macroporosity and 3.9% microporosity. In this sample the microporosity contributes toward 54.9% of the total pore space, providing the highest proportion of microporosity observed in all the sandstone samples that we analyzed. As indicated in the data in Table 2, we failed to detect an interconnected pore network in this sample.

The Doddington sandstone shows very minimal variation across the three volumes with a range in total porosity from 18 to 19.2%. The total porosity is reduced by an average of 0.7% when assessing the connectivity of the total pore volume. The Knorringfjellet sandstone however, shows greater variation across the eight volumes that were analyzed. This sample has a range in total porosity from 7 to 8.8%, whilst the proportion of connected total porosity is reduced by 20% on average. The Wilcox sandstone follows a similar trend with increasing heterogeneity. This sample has a total porosity range from 6.6 to 7.4%, and a significant reduction in the proportion of the total porosity when considering the connectivity of the network. On average, the total connected porosity is reduced by 66%. Interestingly, this is only observed in the sub-volume analysis, whilst zero connected porosity was identified using the whole volume.

The three limestone samples are from outcrop in France. The Estaillades limestone has a total porosity of 19.1%, which is largely occupied by macroporosity, 61.3% of the total pore volume. The microporosity makes up only 7.4% of the total sample volume, the lowest proportion observed in all three of the carbonates analyzed. The connectivity of the total porosity is high, with only a 3.7% reduction compared to the total pore volume. The Massangis Jaune carbonate has the lowest total porosity of all three carbonates, with 16.1% total pore volume. Of this, the macroporosity makes up only 30.4%, the lowest proportion observed in the carbonates. This sample is also the only one to have a microporosity fraction that exceeds that of the macroporosity. The total porosity is well-connected, with microporosity seemingly contributing almost entirely toward this. The complete absence of connectivity in macroporosity supports this observation. The Savonnières carbonate is composed largely of ooliths and some complete and partial shell fragments. This composition provides the highest total porosity observed in all of the samples (32.5%). The macroporosity has a 64.3% share of the total pore volume, which appears as intergranular and moldic porosity. Microporosity fulfills the remaining pore space as partially dissolved ooliths and shell material. The total porosity is well-connected, represented by 28.8% of total sample volume.

The Estaillades limestone shows the widest range in total porosity, with values from 18.6 to 22.7%. This porosity is reduced by an average of 3.9% when we take the connectivity of each pore volume. This is the lowest reduction in porosity observed between the three carbonate samples. The Massangis Jaune sample had a range in total porosity from 15.2 to 17.2% across the sub-volumes. The total connected porosity was 9.7% less on average compared to the total pore volume when analyzed. This sample has a huge variation in the connectivity of the macroporosity, with a range from 47.8 to 93.8%. This is interesting as zero connected macroporosity is observed when considering the whole sample volume. The Savonnières limestone has a total porosity range from 31.7 to 33.2%. The connected proportion of this porosity is reduced by 12.6% on average.

3.2. Pore Network Model Characteristics

The PNM uses the macroporosity of each sample to generate an idealized network of pores and throats, represented by red spheres and gray cylinders, respectively (Figure 4). The visualizations shown in Figures 4a–f highlight the contrast between the nature of the pore networks when the models have been scaled to show the same characteristics (pore and throat radius).

FIGURE 4

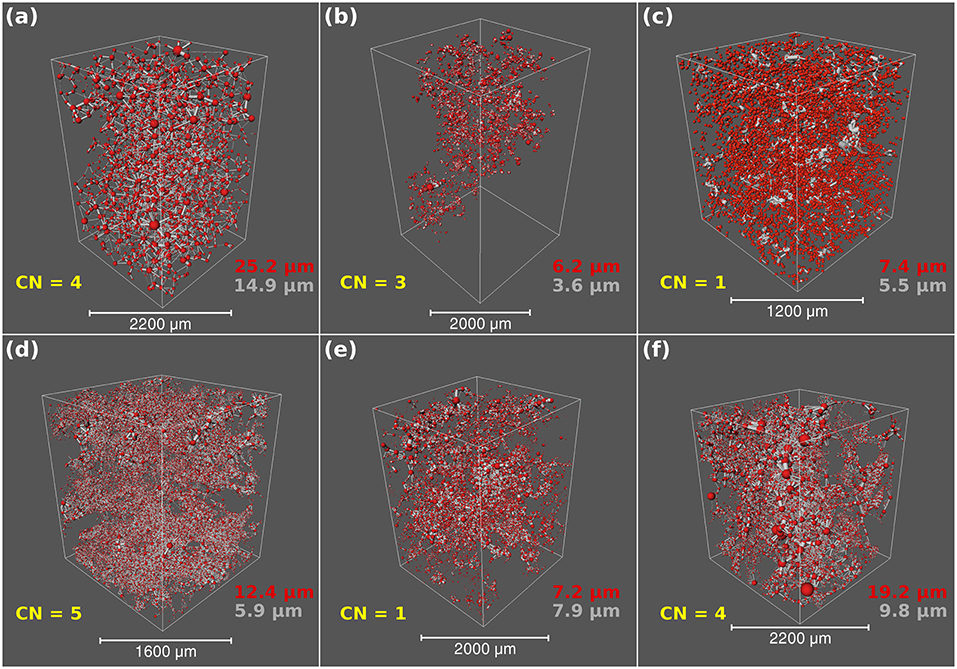
Figure 4. Pore network model visualization of the six samples using the macroporosity network only. From top, left to right: (a) Doddington sandstone, (b) Knorringfjellet sandstone, (c) Wilcox sandstone, (d) Estaillades limestone, (e) Massangis Jaune limestone, and (f) Savonnières limestone. In this schematic the pores are displayed as red spheres and the throats are gray cylinders. CN = mean coordination number, whilst the red text represents the median pore radius and the gray text represents the median throat radius.

We compare the characteristics of the macropore geometry for the three different sandstone samples: Doddington, Knorringfjellet, and Wilcox in Figures 4a–c. The pore network of Doddington sandstone (Figure 4a) is dense and well-connected, due to higher porosity and generally larger pores and throats. The mean coordination number for pores is 4, whilst the median pore radius, throat radius and throat length is 25.2, 14.9, and 158.6 μm, respectively. The pore network shown in the Knorringfjellet sandstone (Figure 4b) is significantly less dense, and appears to have a more isolated confined nature compared to the other two sandstones. The mean coordination number is 3, whilst the dimensions of the network in the Knorringfjellet sandstone are the smallest observed in all three sandstones, with median pore radius of 6.2 μm, throats of radius 3.6 μm and throat length of 33.8 μm. The Wilcox sandstone (Figure 4c) has the lowest connectivity with a mean pore coordination number of 1. The low connectivity of the pore network in Wilcox can be visualized in Figure 4c by the relatively high abundance of red, spherical pores and low abundance of gray, cylindrical throats compared to the Doddington network in Figure 4a, which shows a high abundance of throats connecting the pores. In Wilcox, pores have a median radius of 7.4 μm, whilst the median throat radius is 5.5 μm and the median throat length is 37.1 μm.

The macropore network characteristics of the three different carbonates: Estaillades, Massangis Jaune, and Savonnières are compared in Figures 4d–f. The Estaillades limestone (Figure 4d) has the highest density of small, gray, and cylindrical throats, reflected by a pore coordination number of 5, the highest value observed in all samples. The median pore radius, throat radius and throat length is 12.4, 5.9, and 40.4 μm, respectively. The pore geometry observed in the Massangis Jaune limestone (Figure 4e) is the least well-connected, highlighted by a mean pore coordination number of 1. This sample has median pore radius of 7.2 μm, median throat radius of 7.9 μm, and median throat length of 53.4 μm. The Savonnières limestone network (Figure 4f) also consists of high throat density, reflected by a pore coordination number of 4. The pores in Savonnières have a median radius of 19.2 μm, whilst the throats have a median radius of 9.8 μm, the highest values observed in all three carbonates. The same can be said for the median throat length, calculated at 66.7 μm.

The log normal plots in Figure 5 show the distributions of pore and throat geometries in sandstones (Figures 5A,B) and carbonates (Figures 5C,D). We also report the mean coordination number, median pore and throat radius, and median throat length values in Table 3. In Figures 5A,B, we included published data from Fontainebleau and Berea Sandstones (Thomson et al., 2018) for comparison. The high coordination number and connectivity in the Doddington sandstone is clearly demonstrated by the peaks in the histograms in Figures 5A,B. The distribution of pore radius in all three carbonates in Figure 5C are asymmetric with a skewness toward the right. In comparison, distribution of throat radii in the carbonates in Figure 5D is nearly symmetric.

FIGURE 5

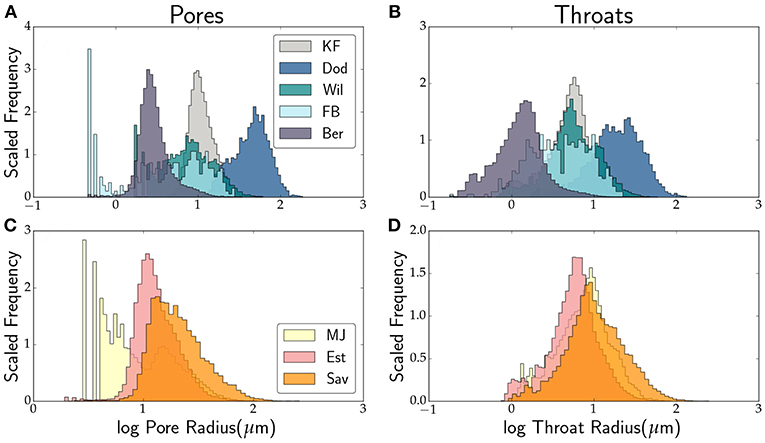
Figure 5. Log normal distribution of the pore and throat geometry in sandstones (A,B) and limestones (C,D). The left column illustrate the distribution of pore radii, while the right column displays the distribution of throat radii. Six samples from this study (KF, Knorringfjellet; Wil, Wilcox; Dod, Doddington; MJ, Massangis Jaune; Sav, Savonnières; Est, Estaillades) and two samples (FB, Fontainebleau; Ber, Berea) from Thomson et al. (2018).

TABLE 3

Table 3. Pore network model characteristics for the macroporosity and permeability results.

The main attributes of the pore network display a power law relationship with porosity. The data in these plots involve only the macroporosity. The plots shown in Figure 6 demonstrate the relationship between porosity and pore radius, throat radius and throat length in all six samples, with the addition of two sandstones used in a similar study by Thomson et al. (2018). We also plot the porosity-coordination number relation for comparison. In the log-log plots, we overlay fits of the form y = aϕⁿ, in each plot with the value of n annotated in the plots.

FIGURE 6

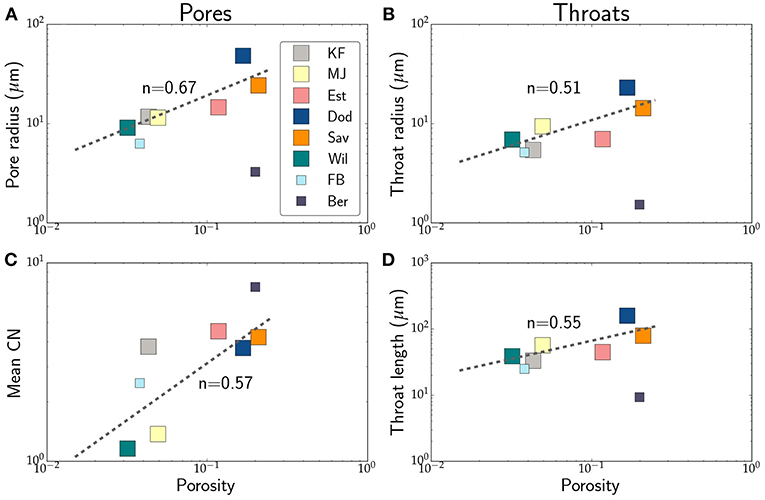
Figure 6. Macropore network characteristics of the six samples from this study (KF, Knorringfjellet; Wil, Wilcox; Dod, Doddington; MJ, Massangis Jaune; Sav, Savonnières; Est, Estaillades) and 2 samples (FB, Fontainebleau; Ber, Berea) from Thomson et al. (2018). The panels display log-log plots of (A) pore radius, (B) throat radius, (C) mean coordination number, and (D) throat length as a function of macroporosity. The broken line indicates a power law fit through the six data points from this study. The power law exponent for each fit is annotated in the plot. The two samples with smaller symbol size are from higher resolution images with smaller voxel dimensions.

Among the PNM attributes considered here, the pore radius displays the strongest dependence on porosity. From the porosity-pore radius plot in Figure 6A we observe that the pore radius varies with porosity with an exponent of 2/3. Both the radius and length of the throats in panels (B) and (D) show a near square-root variation with porosity. Coordination number of the pores also increase with the porosity with an exponent of 0.57.

3.3. Absolute Permeability Simulation

We modeled the single phase flow of water directly through the pore space images of the macroporosity and total porosity cases along the Z-axis only. Results of each simulation have been summarized in Table 3. In the Doddington sandstone, permeability measured through macroporosity has a value of 3,013 mD, which increases by 24% to 3,725 mD when the simulation is computed considering the total porosity. These are the highest values of permeability observed in the three sandstone samples. The Knorringfjellet sandstone shows a dramatic increase in permeability when considering the macroporosity and total porosity scenarios. The connected porosity proportion has a permeability of 7 mD. The total porosity provided a value of 60 mD, which is 760% increase compared to the macroporosity only simulation. The Wilcox sandstone has zero connected porosity when analyzing the entire volume in this study, and therefore could not be used to simulate flow. As such, no permeability measurements were acquired. The Estaillades limestone allowed flow through its macroporosity at 259 mD. Compared to the total porosity model, this value increased by 132% to 601 mD. Similarly to the Wilcox sandstone, the Massangis Jaune limestone has zero connected porosity in the macroporosity case, meaning that no permeability simulation could be modeled. However, in the total porosity case the connectivity across the Z-axis permitted flow and a permeability measure was obtained at 612 mD. The Savonnières limestone has the most efficient network for fluid flow, with a macroporosity permeability value at 1408 mD. The total porosity simulation provided an increased permeability at 3,990 mD, 183% more.

We display the combined porosity and permeability data in Figure 7. Where applicable, the plot displays data from both the macropore network (filled squares) and total pore network (filled circles). Also added in the plot are data from Fontainebleau and Berea sandstones from Thomson et al. (2018). We fit the data with an equation of the form $k=k_0{\varphi }^n$. Values of both parameters are annotated in the plot. The exponent of n = 3.32 from our data is higher than the theoretical value of n = 2 of throats with a circular cross section, but is slightly lower than the value of 3.8–4.5 obtained from experimental measurements (Doyen, 1988; Bernabé et al., 2010; Revil et al., 2014).

FIGURE 7

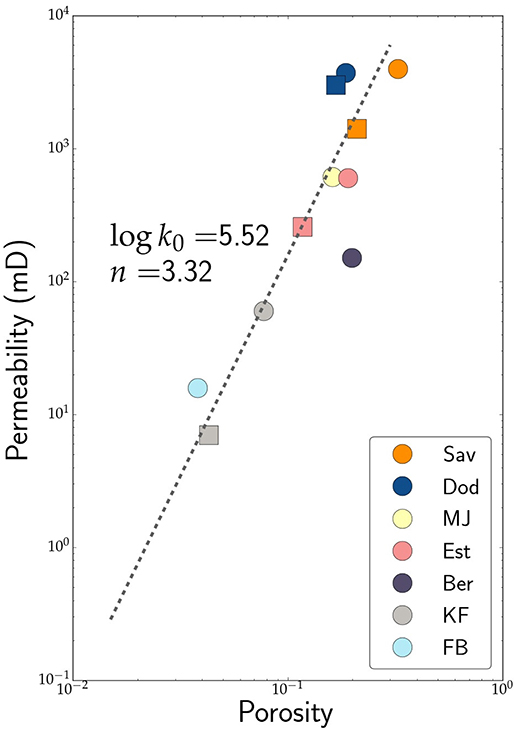
Figure 7. Plot of porosity and permeability from our samples and Fontainebleau (FB) and Berea (B) sandstones from Thomson et al. (2018). Filled circles represent data from total porosity while filled squares represent data from macroporosity alone. The broken line is a fit to the data of the form $k=k_0{\varphi }^n$. The fit parameters are annotated in the plot.

4. Discussion

4.1. Micropermeability

As discussed in the introduction, dimension of the micropores in our samples are beyond the limit of detection and analysis in this study. As a result, certain assumptions must be made regarding the geometry and connectivity of micropores Bultreys et al. (2015). We chose to select two end member cases. In one case, the microporosity is considered impermeable, thus the permeability of the rock is determined only by the macroporosity. In the other case, we consider the microporosity consists essentially of void space and the effective permeability of the rock is given by the total permeability. In reality, the microporous phase may have a non-zero permeability, rendering the effective permeability somewhere between these two cases. To rigorously address the issue of micropermeability two issues need to be addressed in future work.

First, the 3D microtomographic images of the pore network can be supplemented by additional, higher resolution 3D images, possibly obtained by techniques such as FIB electron microscopic tomography. These two different scales will provide two values of permeability through the macro and micro pore spaces, which then need to be averaged using some weighting formula.

Secondly, the nature of flow through nanometer-sized pores can be fundamentally different from the classic Darcy flow model. At such small pore dimensions, the ratio between surface area to volume of pores increase substantially (Israelachvili, 1991; Chen et al., 2004), rendering surface tension at the grain-fluid interface as a strong retarding force to fluid percolation. Thus, evaluation of permeability from these pore spaces need to use a modified form of Stokes flow, taking into account the surface tension (Hier-Majumder et al., 2006; Takei and Hier-Majumder, 2009; Hier-Majumder and Abbott, 2010).

Despite these uncertainties, the end member approach taken in this study can be extremely useful in identifying the role of cementation in reducing permeability during reactive porous flow. In the following section, we discuss the implications of our results on such flows.

4.2. Effect of Cementation on Fluid Transport

Cementation during reactive porous flow leads to the deposition of secondary phases along the initially interconnected pore network, reducing the effective transport properties of the network. Using the results of our pore network models and permeability simulations, we can quantify the influence of cement volume fraction on two important parameters, the fraction of connected pore space and the ratio between permeability after and before cementation.

The 3D image of Knoringfjellet sandstone in Figure 8 demonstrates the way cement, identified as the microporous phase, influences the pore space. The grain matrix is shown in gray scale, while the macroporosity (labeled “pore”) and microporosity (labeled “cement”) are identified in cyan and red, respectively. As the colored image on the right demonstrates, the cement fills up several channels essentially disconnecting the top and the bottom sections of the image. The presence of this cement has important consequences on the connectivity of the pore network.

FIGURE 8

Figure 8. 3D visualization of gray scale and segmented images of a subvolume in the Knorringfjellet sandstone. The micrograph in the middle overlaps the gray scale image on the segmented phases, whereas the micrograph on the right shows only the macropore and the microporous cement.

For example, the Doddington sandstone has a total porosity of 18.6%, of which only 1.9% resides in microporosity (Table 2). As a result, 16.6% of the total volume of the Doddington sample resides in connected macropores. In contrast, Massangis Jaune carbonate shows a comparable total porosity of 16.1%, the majority of which (11.2% of total volume) resides in microporosity in the cement. In this sample, no connected macroporosity was detected due to cementation. The plot in Figure 9A plots the fraction of interconnected macropores as a function of cement volume fraction. As the plot depicts, the interconnectivity of the pore network is substantially reduced at cement volume fractions greater than 4 vol%. This result implies that the connectivity of a pore network will decline with time as precipitation occurs during reactive porous flow, until this threshold value is reached at which majority of the network will be cut-off from pervasive percolation of pore fluid.

FIGURE 9

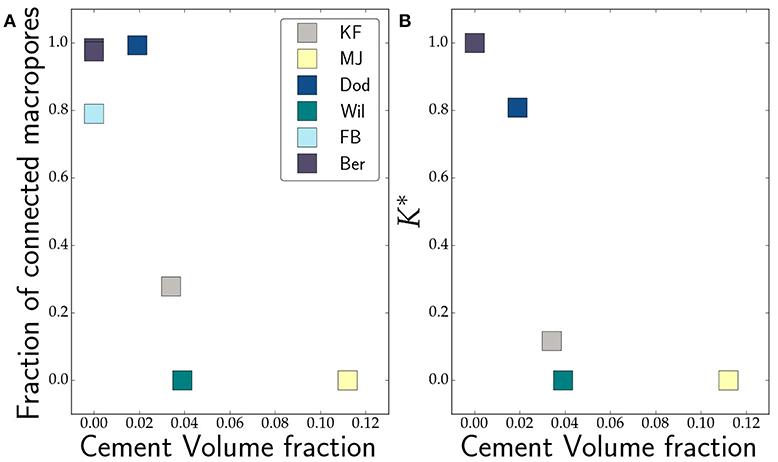
Figure 9. Plots of fraction of (A) interconnected macroporosity and (B) the ratio between macro permeability and total permeability as a function of cement volume fraction.

The effect of cementation is also observed directly on the effective permeability. Since the segmentation allows us to evaluate the pore space before (total porosity) and after (macroporosity) cementation, the ratio of permeability between these two networks can be quite useful. The plot in Figure 9B illustrates this behavior in the plot of $k^{*}=k_M/k_T$ as a function of cement volume fraction. As before, we notice that the permeability declines sharply with an increase in cement volume fraction, eventually becoming zero for cement volume fractions greater than 4 vol%. The permeability values are reported in Table 3.

As permeability is progressively reduced by cement deposition, the fluid flux through a pore network will decrease with time. A number of recent studies on reactive porous flow during carbon capture and sequestration (Ghesmat et al., 2011; Unwin et al., 2016) and reaction infiltration instability (Takei and Hier-Majumder, 2009; Kelemen et al., 2011; Szymczak and Ladd, 2013) detailed the way in which development of reaction fronts play an important role in sequestering dissolved chemical components in the fluid. None of these studies, however, take into account the way permeability changes during the progression of reactive porous flow. As discussed above, the flux of porous flow will diminish with time due to permeability reduction, thus reducing the efficiency of carbon sequestration over the life time of an operation. The reduction in flux of porous flow can also be seen as a positive, particularly in the upper regions of carbon sequestration reservoirs where the sealing capacity may increase with time due to cementation and clogging of pores. This can enhance reservoir storage and reduce unwanted leakage. Future models incorporating the influence of cementation will provide more accurate and realistic estimates of the amount of carbon that can be stored in subsurface reservoirs.

5. Conclusions

• We analyzed 6 natural rocks, most containing a microporous cement phase. We consider the microporosity as void space to capture the pore network prior to cementation and solid to capture the pore geometry after cementation.

• In the macropore space, the pore radius varies with porosity with an exponent of 2/3, while mean coordination number, throat radius, and throat length all vary with a porosity exponent close to 1/2. Our results indicate a porosity exponent of 3.3 for permeability.

• We find that, within the sample set used in this study and the resolution of our images, the fraction of connected pores and permeability decrease sharply with cement volume fraction and the connectivity of macropores is cut off near a cement volume fraction of 4%.

Data Availability

The results from PNM model are available through Figshare: Hier-Majumder, Saswata; Thomson, Paul-Ross; Hazel, Alexander (2019): Data for “The Influence of Microporous Cements on the Pore Network Geometry of Natural Sedimentary Rocks.” figshare. Fileset. https://doi.org/10.17637/rh.7667642.

Author Contributions

P-RT carried out the image segmentation and permeability simulations in all samples. AH carried out the analysis and permeability simulations on Doddington and Knorringfjellet sandstones. SH-M and P-RT jointly carried out the final pore-network modeling and statistical analysis. All three authors contributed to writing and revision of the manuscript.

Funding

This research was also supported by the grant EAR125880 from the US National Science Foundation.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors acknowledge insightful suggestions from Yiqiao Wu on the pore network models of the carbonate rocks. The raw 3D Images used in this work were kindly provided by Tom Bultreys. P-RT acknowledges support from a NERC Oil and Gas CDT graduate fellowship (grant number NE/M00578X/1).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2019.00048/full#supplementary-material

References

Alyafei, N., and Blunt, M. J. (2016). The effect of wettability on capillary trapping in carbonates. Adv. Water Resour. 90, 36–50. doi: 10.1016/j.advwatres.2016.02.001

CrossRef Full Text | Google Scholar

Andrä, H., Combaret, N., Dvorkin, J., Glatt, E., Han, J., Kabel, M., et al. (2013a). Digital rock physics benchmarks-Part I: imaging and segmentation. Comput. Geosci. 50, 25–32. doi: 10.1016/j.cageo.2012.09.005

CrossRef Full Text | Google Scholar

Andrä, H., Combaret, N., Dvorkin, J., Glatt, E., Han, J., Kabel, M., et al. (2013b). Digital rock physics benchmarks-part II: Computing effective properties. Comput. Geosci. 50, 33–43. doi: 10.1016/j.cageo.2012.09.008

CrossRef Full Text | Google Scholar

Bera, B., Mitra, S. K., and Vick, D. (2011). Understanding the micro structure of Berea Sandstone by the simultaneous use of micro-computed tomography (micro-CT) and focused ion beam-scanning electron microscopy (FIB-SEM). Micron 42, 412–418. doi: 10.1016/j.micron.2010.12.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Berg, C. F., Lopez, O., and Berland, H. (2017). Industrial applications of digital rock technology. J. Petrol. Sci. Eng. 157, 131–147. doi: 10.1016/j.petrol.2017.06.074

CrossRef Full Text | Google Scholar

Bernabé, Y., Li, M., and Maineult, A. (2010). Permeability and pore connectivity: a new model based on network simulations. J. Geophys. Res. Solid Earth 115, 1–14. doi: 10.1029/2010JB007444

CrossRef Full Text

Boone, M. A., De Kock, T., Bultreys, T., De Schutter, G., Vontobel, P., Van Hoorebeke, L., et al. (2014). 3D mapping of water in oolithic limestone at atmospheric and vacuum saturation using X-ray micro-CT differential imaging. Mater. Character. 97, 150–160. doi: 10.1016/j.matchar.2014.09.010

CrossRef Full Text | Google Scholar

Bultreys, T., De Boever, W., and Cnudde, V. (2016a). Imaging and image-based fluid transport modeling at the pore scale in geological materials: a practical introduction to the current state-of-the-art. Earth Sci. Rev. 155, 93–128. doi: 10.1016/j.earscirev.2016.02.001

CrossRef Full Text | Google Scholar

Bultreys, T., Stappen, J. V., Kock, T. D., Boever, W. D., Boone, M. A., Hoorebeke, L. V., et al. (2016b). Investigating the relative permeability behavior of microporosity-rich carbonates and tight sandstones with multiscale pore network models. J. Geophys. Res. Solid Earth 121, 7929–7945. doi: 10.1002/2016JB013328

CrossRef Full Text | Google Scholar

Bultreys, T., Van Hoorebeke, L., and Cnudde, V. (2015). Multi-scale, micro-computed tomography-based pore network models to simulate drainage in heterogeneous rocks. Adv. Water Resour. 78, 36–49. doi: 10.1016/j.advwatres.2015.02.003

CrossRef Full Text | Google Scholar

Chen, N., Kuhl, T., Tadmor, R., Lin, Q., and Israelachvili, J. (2004). Large deformation during coalescence of fluid interfaces. Phys. Rev. Lett. 92:024501. doi: 10.1103/PhysRevLett.92.024501

CrossRef Full Text | Google Scholar

Choquette, P. W., and Pray, L. C. (1970). Geologic nomenclature and classification of porosity in sedimentary carbonates. AAPG Bull. 54, 207–250.

Google Scholar

Cnudde, V., and Boone, M. N. (2013). High-resolution X-ray computed tomography in geosciences: a review of the current technology and applications. Earth Sci. Rev. 123, 1–17. doi: 10.1016/j.earscirev.2013.04.003

CrossRef Full Text | Google Scholar

Derluyn, H., Dewanckele, J., Boone, M. N., Cnudde, V., Derome, D., and Carmeliet, J. (2014). Crystallization of hydrated and anhydrous salts in porous limestone resolved by synchrotron X-ray microtomography. Nuclear Instrum. Methods Phys. Res. B 324, 102–112. doi: 10.1016/j.nimb.2013.08.065

CrossRef Full Text | Google Scholar

Doyen, P. M. (1988). Permeability, conductivity, and pore geometry of sandstone. J. Geophys. Res. 93:7729.

Google Scholar

Ghesmat, K., Hassanzadeh, H., and Abedi, J. (2011). The impact of geochemistry on convective mixing in a gravitationally unstable diffusive boundary layer in porous media: CO2storage in saline aquifers. J. Fluid Mech. 673, 480–512. doi: 10.1017/S0022112010006282

CrossRef Full Text | Google Scholar

Hier-Majumder, S., and Abbott, M. E. (2010). Influence of dihedral angle on the seismic velocities in partially molten rocks. Earth Planet. Sci. Lett. 299, 23–32. doi: 10.1016/j.epsl.2010.08.007

CrossRef Full Text | Google Scholar

Hier-Majumder, S., Ricard, Y., and Bercovici, D. Role of grain boundaries in magma migration storage. (2006). Earth Planet. Sci. Lett. 248, 735–749. doi: 10.1016/j.epsl.2006.06.015

CrossRef Full Text

Iassonov, P., Gebrenegus, T., and Tuller, M. (2009). Segmentation of x-ray computed tomography images of porous materials: a crucial step for characterization and quantitative analysis of pore structures. Water Resour. Res. 45:W09415. doi: 10.1029/2009WR008087

CrossRef Full Text | Google Scholar

Israelachvili, J. N. (1991). Intermolecular and Surface Forces, 2 Edn. London; San Diego, CA: Academic Press.

Jennings, J. W., and Lucia, F. J. (2003). Predicting Permeability From Well Logs in Carbonates With a Link to Geology for Interwell Permeability Mapping. SPE Reservoir Evaluation & Engineering. Vol. 6. Society of Petroleum Engineers. doi: 10.2118/84942-PA

CrossRef Full Text

Jiang, Z., Van Dijke, M. I., Sorbie, K. S., and Couples, G. D. (2013). Representation of multiscale heterogeneity via multiscale pore networks. Water Resour. Res. 49, 5437–5449. doi: 10.1002/wrcr.20304

CrossRef Full Text | Google Scholar

Jiang, Z., van Dijke, M. I., Wu, K., Couples, G. D., Sorbie, K. S., and Ma, J. (2012). Stochastic pore network generation from 3D rock images. Transport Porous Media 94, 571–593. doi: 10.1007/s11242-011-9792-z

CrossRef Full Text | Google Scholar

Jiao, K., Yao, S., Liu, C., Gao, Y., Wu, H., Li, M., and Tang, Z. (2014). The characterization and quantitative analysis of nanopores in unconventional gas reservoirs utilizing FESEM-FIB and image processing: an example from the lower Silurian Longmaxi Shale, upper Yangtze region, China. Int. J. Coal Geol. 128-129, 1–11. doi: 10.1016/j.coal.2014.03.004

CrossRef Full Text | Google Scholar

Kelemen, P. B., Matter, J., Streit, E. E., Rudge, J. F., Curry, W. B., and Blusztajn, J. (2011). Rates and mechanisms of mineral carbonation in peridotite: natural processes and recipes for enhanced, in situ CO2 capture and storage. Annu. Rev. Earth Planet. Sci 39 545–576. doi: 10.1146/annurev-earth-092010-152509

CrossRef Full Text | Google Scholar

Ketcham, R. A., and Carlson, W. D. (2001). Acquisition, optimization and interpretation of x-ray computed tomographic imagery: applications to the geosciences. Comput. Geosci. 27, 381–400. doi: 10.1016/S0098-3004(00)00116-3

CrossRef Full Text | Google Scholar

Ma, L., Taylor, K. G., Lee, P. D., Dobson, K. J., Dowey, P. J., and Courtois, L. (2016). Novel 3D centimetre-to nano-scale quantification of an organic-rich mudstone: The Carboniferous Bowland Shale, Northern England. Mar. Petrol. Geol. 72, 193–205. doi: 10.1016/j.marpetgeo.2016.02.008

CrossRef Full Text | Google Scholar

Madonna, C., Quintal, B., Frehner, M., Almqvist, B. S. G., Tisato, N., Pistone, M., et al. (2013). Synchrotron-based X-ray tomographic microscopy for rock physics investigations. Geophysics 78, D53–D64. doi: 10.1190/geo2012-0113.1

CrossRef Full Text | Google Scholar

Marquez, X., Solling, T., Finlay, S., Bounoua, N., and Gagigi, T. (2014). 3D imaging of porosity modifying phases in Shuaiba Reservoir, Al Shaheen Field. International Petroleum Technology Conference (Doha), 16.

Google Scholar

Mehmani, A., and Prodanović, M. (2014). The effect of microporosity on transport properties in porous media. Adv. Water Resour. 63, 104–119. doi: 10.1016/j.advwatres.2013.10.009

CrossRef Full Text | Google Scholar

Menke, H., Andrew, M., Blunt, M., and Bijeljic, B. (2016). Reservoir condition imaging of reactive transport in heterogeneous carbonates using fast synchrotron tomography—effect of initial pore structure and flow conditions. Chem. Geol. 428, 15–26. doi: 10.1016/j.chemgeo.2016.02.030

CrossRef Full Text | Google Scholar

Menke, H. P., Bijeljic, B., Andrew, M. G., and Blunt, M. J. (2015). Dynamic three-dimensional pore-scale imaging of reaction in a carbonate at reservoir conditions. Environ. Sci. Technol. 49, 4407–4414. doi: 10.1021/es505789f

PubMed Abstract | CrossRef Full Text | Google Scholar

Mostaghimi, P., Blunt, M. J., and Bijeljic, B. (2013). Computations of absolute permeability on micro-CT images. Math. Geosci. 45, 103–125.

Google Scholar

Okabe, H., and Blunt, M. J. (2005). Pore space reconstruction using multiple-point statistics. J. Petrol. Sci. Eng. 46, 121–137. doi: 10.1007/s11004-012-9431-4

CrossRef Full Text | Google Scholar

Øren, P.-E., and Bakke, S. (2003). Reconstruction of berea sandstone and pore-scale modelling of wettability effects. J. Petrol. Sci. Eng. 39, 177–199. doi: 10.1016/j.petrol.2004.08.002

CrossRef Full Text | Google Scholar

Pal, N. R., and Pal, S. K. (1993). A review on image segmentation techniques. Pattern Recogn. 26, 1277–1294. doi: 10.1016/S0920-4105(03)00062-7

CrossRef Full Text | Google Scholar

Pittman, E. D. (1979). “Porosity, diagenesis and productive capability of sandstone reservoirs,” in ‘Aspects of Diagenesis’, (SEPM Society for Sedimentary Geology). doi: 10.2110/pec.79.26.0159

CrossRef Full Text | Google Scholar

Prodanović, M., Mehmani, A., and Sheppard, A. P. (2014). Imaged-based multiscale network modelling of microporosity in carbonates. Geol. Soc. Lond. 406, SP406–SP409. doi: 10.1016/0031-3203(93)90135-J

CrossRef Full Text

Raeini, A. Q., Blunt, M. J., and Bijeljic, B. (2014). Direct simulations of two-phase flow on micro-CT images of porous media and upscaling of pore-scale forces. Adv. Water Resour. 74, 116–126. doi: 10.1016/j.advwatres.2014.08.012

CrossRef Full Text | Google Scholar

Ramstad, T., Øren, P.-E., Bakke, S., et al. (2010). Simulation of two-phase flow in reservoir rocks using a lattice boltzmann method. SPE J. 15, 917–927. doi: 10.2118/124617-PA

CrossRef Full Text | Google Scholar

Revil, A., Kessouri, P., and Torres-Verdín, C. (2014). Electrical conductivity, induced polarization, and permeability of the Fontainebleau sandstone. Geophysics 79, D301–D318. doi: 10.1190/geo2014-0036.1

CrossRef Full Text | Google Scholar

Saif, T., Lin, Q., Butcher, A. R., Bijeljic, B., and Blunt, M. J. (2017). Multi-scale multi-dimensional microstructure imaging of oil shale pyrolysis using X-ray micro-tomography, automated ultra-high resolution SEM, MAPS Mineralogy and FIB-SEM. Appl. Ener. 202, 628–647. doi: 10.1016/j.apenergy.2017.05.039

CrossRef Full Text | Google Scholar

Schlüter, S., Sheppard, A., Brown, K., and Wildenschild, D. (2014). Image processing of multiphase images obtained via X-ray microtomography: a review. Water Resour. Res. 50, 3615–3639. doi: 10.1002/2014WR015256

CrossRef Full Text | Google Scholar

Sezgin, M., and Sankur, B. (2004). Survey over image thresholding techniques and quantitative performance evaluation. J. Electron. Imaging 13, 146–166. doi: 10.1117/1.1631315

CrossRef Full Text | Google Scholar

Shah, S., Gray, F., Crawshaw, J., and Boek, E. (2016). Micro-computed tomography pore-scale study of flow in porous media: Effect of voxel resolution. Adv. Water Resour. 95, 276–287. doi: 10.1016/j.advwatres.2015.07.012

CrossRef Full Text | Google Scholar

Szymczak, P., and Ladd, A. J. C. (2013). Interacting length scales in the reactive-infiltration instability. Geophys. Res. Lett. 40, 3036–3041. doi: 10.1002/grl.50564

CrossRef Full Text | Google Scholar

Takei, Y., and Hier-Majumder, S. (2009). A generalized formulation of interfacial tension driven fluid migration with dissolution/precipitation. Earth Planet. Sci. Lett. 288, 138–148. doi: 10.1016/j.epsl.2009.09.016

CrossRef Full Text | Google Scholar

Teles, A. P., Lima, I., and Lopes, R. T. (2016). Rock porosity quantification by dual-energy X-ray computed microtomography. Micron 83, 72–78. doi: 10.1016/j.micron.2016.02.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Thomson, P.-r., Aituar-zhakupova, A., and Hier-majumder, S. (2018). Image segmentation and analysis of pore network geometry in two natural sandstones. Front. Earth Sci. 6:58. doi: 10.3389/feart.2018.00058

CrossRef Full Text | Google Scholar

Trier, Ø. D., and Jain, A. K. (1995). Goal-directed evaluation of binarization methods. IEEE Trans. Patt. Anal. Mach. Intelligence, 12, 1191–1201.

Google Scholar

Unwin, H. J. T., Wells, G. N., and Woods, A. W. (2016). CO2 dissolution in a background hydrological flow. J. Fluid Mech. 789, 768–784. doi: 10.1017/jfm.2015.752

CrossRef Full Text | Google Scholar

Valvatne, P. H., and Blunt, M. J. (2004). Predictive pore-scale modeling of two-phase flow in mixed wet media. Water Resour. Res. 40:W07406. doi: 10.1029/2003WR002627

CrossRef Full Text | Google Scholar

Wang, W., Kravchenko, A., Smucker, A., and Rivers, M. (2011). Comparison of image segmentation methods in simulated 2d and 3d microtomographic images of soil aggregates. Geoderma 162, 231–241. doi: 10.1016/j.geoderma.2011.01.006

CrossRef Full Text | Google Scholar

Wildenschild, D., and Sheppard, A. P. (2013). X-ray imaging and analysis techniques for quantifying pore-scale structure and processes in subsurface porous medium systems. Adv. Water Resour. 51, 217–246. doi: 10.1016/j.advwatres.2012.07.018

CrossRef Full Text | Google Scholar

Wildenschild, D., Vaz, C., Rivers, M., Rikard, D., and Christensen, B. (2002). Using x-ray computed tomography in hydrology: systems, resolutions, and limitations. J. Hydrol. 267, 285–297. doi: 10.1016/S0022-1694(02)00157-9

CrossRef Full Text | Google Scholar

Youssef, S., Rosenberg, E., Gland, N. F., Kenter, J. A., Skalinski, M., and Vizika, O. (2007). “High resolution CT and pore-network models to assess petrophysical properties of homogeneous and heterogeneous carbonates,” in SPE/EAGE Reservoir Characterization and Simulation Conference, 28–31 October (Abu Dhabi: Society of Petroleum Engineers), 28-31. doi: 10.2118/111427-MS

CrossRef Full Text | Google Scholar