Elemental Uptake by Calcite Slowly Grown From Seawater Solution: An in-situ Study via Depth Profiling

Crystal growth rate has not been sufficiently explored to understand element partitioning between calcite and seawater solutions. We investigated the uptake of Li, B, Mg, Sr, and Ba by Mg-bearing calcite slowly grown on a calcite cleavage fragment. Experiments were conducted by elevating the alkalinity of an artificial seawater solution. Growth rates were evaluated by addition of lanthanum spike. At the end of each experiment, cleavage fragments were extracted and examined with micro-Raman spectroscopy, scanning electron microscopy (SEM), electron backscattered diffraction (EBSD), and laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) using depth profiling technique. Distribution of Li, B, Mg, Sr, and Ba in calcite overgrowth as well as partition coefficients of those elements were evaluated.

Introduction

Uptake of trace elements by calcite (one the most abundant marine and terrestrial minerals) has a variety of applications in climate and environmental sciences. For example, element/Ca ratios (E/Ca) as measured in the calcite shell of foraminifera are widely used proxies to reconstruct the environmental conditions at the time the calcite was precipitated by the organism. Reconstructing of seawater temperature and composition in the past (paleoenvironmental proxies) through E/Ca in carbonate minerals is among of them (e.g., Elderfield et al., 1996; Nürnberg et al., 1996; Lea, 2003; Katz et al., 2010). Despite a wide use of trace element signatures in biogenic and abiogenic calcite, some complications are associated with the interpretation of calcite elemental composition. It was found that crystal growth rate (V) plays an important role in elemental uptake and the relationship between E/Ca and V is not universal (e.g., Lorens, 1981; Tesoriero and Pankow, 1996; Huang and Fairchild, 2001; Stoll et al., 2002; Nehrke et al., 2007; Tang et al., 2008; Mavromatis et al., 2013; Gabitov et al., 2014a). Furthermore, fluid chemistry sometimes affects elemental incorporation into calcite, as shown by the apparent partition coefficient of Mg between calcite and fluid (K^Mg = (Mg/Ca)_calcite/(Mg/Ca)_fluid), which decreases with increasing Mg/Ca in the solution (Mucci and Morse, 1983). In this scenario, it appears evident that studies with goals to decouple the effects of growth rate and fluid content on the elemental uptake by calcite, are of fundamental importance to improve our interpretation of palaeoceanographic proxies and our understanding of mineralization processes. In this study, we present microscale analyses on the uptake of Li, B, Mg, Sr, and Ba by Mg-bearing calcite grown slowly from artificial seawater (ASW) solution at laboratory conditions. This slow rate is lower than typical extension rates of coccolithophores and foraminifera, and therefore, should represent calcite growth conditions that are closer to equilibrium compared to many marine biominerals. Although physiological effect can play an important role in elemental uptake during calcite biomineralization, it is not discussed in this study as we focused on an inorganic system, which is far from being completely understood.

Materials and Methods

Precipitation Experiments

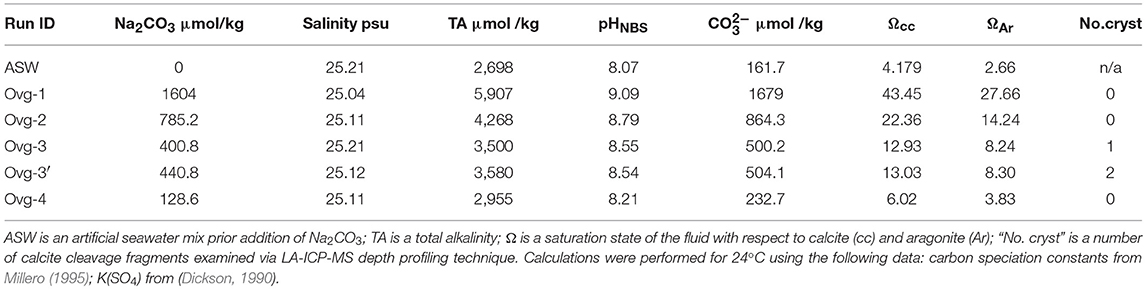
Five experiments were conducted in plastic containers at room temperature at different saturation states of the fluids (Ω). Cleavage fragments of calcite (substrates) were cleaned with 5% HCl (except calcite in the run OVG-3′) and reverse osmosis (RO) H₂O. Those calcite fragments were placed in each container. 100 g of seawater salt mix (Instant Ocean) were dissolved in 3.33 l of RO water. This solution was pumped through 0.2 μm Nalgene filter to remove organic molecules and fluid portions of ~850 ml was placed in each container (Table 1). In order to promote calcite growth, aliquots of 0.1 M Na₂CO₃ were added to each container while ASW was stirred to avoid rapid nucleation. Amounts of 0.1 M Na₂CO₃ were varied from 3.4 to 13.5 ml to achieve different fluid saturation states with respect to calcite and aragonite (Ω) (Table 1). pH and salinity were measured in those “initial” experimental fluids using Hana Instrument meter and electrodes. Total alkalinity (TA) of ASW was determined using titration system in Keck Water Research Laboratory at Rensselaer Polytechnic Institute (Lab ID#11879). TA after addition of Na₂CO₃ aliquots (TA_initial, in μmol/kg) was calculated as TA_initial = TA_ASW+2·Na₂CO₃. Initial Ω values were calculated for each of the runs using initial values of pH and TA with an Excel implementation of CO2SYS (Lewis and Wallace, 1998). Calculations were performed for 24°C using the following data: carbon speciation constants from Millero (1995); K(SO₄) from Dickson (1990); total boron content was automatically set to the value from Uppstrom (1974). Containers were closed with plastic lids and experiments remained unstirred during precipitation. One hundred sixty-nine days after beginning of experiments a small aliquot of 1 ppm of La was introduced to each container in order to mark calcite overgrowth. Experiments were stopped within 244 days after addition of Na₂CO₃ aliquot.

TABLE 1

Table 1. Experimental parameters and calculated parameters.

Analytical Techniques

SEM (BSE, EDS, EBSD) and Micro-Raman

The mineralogy and major chemical composition of calcite overgrowth were characterized with electron microscopy and micro-Raman spectroscopy techniques in Lomonosov Moscow State University (Moscow, Russia). Cleavage fragments of calcite were embedded into epoxy mounts (Buehler EpoxyCure) in order to expose new formed CaCO₃ crystals grew outward from the surface of the substrate. Samples were polished with Buehler 400, 600, 800, 1,200 grit SiC paper and 1 μm alumina on the polish cloth. Scanning electron microscope (SEM JSM-6480LV, Jeol) equipped with energy dispersive X-ray (EDS) spectrometer (X-Maxⁿ, Oxford Instrument) and electron backscattered diffraction (EBSD) system (NordlysMax²) was used to characterize calcite overgrowth and other precipitated crystals. Polished samples were coated with 35 nm of carbon. Analyses were conducted at 20 kV accelerating voltage, 0.7 nA probe current and count rate about 17 kcps (with dead time about 22–25 %) during 100 s live time. Program INCA (version 21b, “Oxford Instruments”) with XPP-correction model was used for processing of EDS measurement results. Identification of the space group of carbonates was conducted using EBSD. For the analysis of the diffraction patterns and processing the results software HKL (Oxford Instruments) and Inorganic Crystal Structure Database (ICSD) were used.

ICP-MS and LA-ICP-MS

Analysis of the initial experimental fluids (dissolved Instant Ocean salt mix) was conducted on a quadrupole ICP-MS (Agilent 7900), at the Department of Earth and Environmental Sciences, University of Rochester (Rochester, NY, USA). Prior analysis, samples were diluted, acidified with 2% HNO₃, and spiked with an internal standard (¹¹⁵In) to a final concentration of 2 ppb. All samples were analyzed in 1 day using an autosampler (ASX-520; Agilent). Analysis of ⁷Li, ¹¹B, ²⁴Mg, ⁴³Ca, ⁸⁸Sr, ¹¹⁵In, and ¹³⁸Ba was conducted using a glass nebulizer. Prior to analysis, the instrument was tuned using a 1 ppb Li, Mg, Co, Y, Ce, Tl tuning solution (Agilent). After tuning, the instrument was calibrated using a 5-point calibration curve composed by a blank (2% HNO₃) and four standards. The standards were prepared using different dilutions of the seawater standard CRW-SW (High Purity Standard). Blanks and standards were spiked with ¹¹⁵In, as well. At the end of the calibration, the correlation coefficient was 0.996 or better for every element analyzed. Argon was used as the carrier gas and its flow set at 1.15 L/min (Table 2). The nebulizer pump was set at 0.5 rps. Integration times were as follows: 0.99 s for ⁷Li and ¹¹B; 0.30 s for ²⁴Mg; and 0.12 s for ⁴³Ca, ⁸⁸Sr, and ¹³⁸Ba. The acquisition method included 3 points/peak, 3 replicates, and 100 sweeps/replicate. ²⁴Mg, ⁴³Ca, ⁸⁸Sr, and ¹³⁸Ba were measured using a helium flow of 4.2 mL/min in the collision reaction cell (He mode). This helium flow was turned off to analyze ⁷Li and ¹¹B (no gas mode). The internal standard (¹¹⁵In) was analyzed in both no gas mode and He mode and the integration times were 0.21 s and 0.30 s, respectively. After the initial tuning of the instrument, oxides interferences were below 2.3% in no gas mode and 0.7% in He mode. Doubly-charged ion interferences were below 1.4% in both no gas mode and He mode. Concentration data were obtained using the software MassHunter 4.1 Workstation Software for 7900 ICPMS (Agilent). Instrumental error for the analyzed elements is within 5% (relative standard deviation). Fluids collected at the end of experiments (final fluids) were analyzed via ICP-MS (ElementXR, Sector Field ICP-MS) at the University of Western Australia. LA-ICP-MS analyses were performed at Cambridge University (Cambridge, UK). Calcite cleavage fragments (not imbedded into the epoxy) with sufficiently thick overgrowth (runs OVG-3 and OVG-3′) were examined via depth profiling (163 cycles each profile) with ablation rate of ~0.2 μm per second. This high-resolution depth profiling technique employs Analyte G2 excimer laser (Teledyne Photon Machines Inc., Omaha, NE, USA) coupled with Thermo i-CapQ ICP-MS to measure the trace metal elemental profiles in calcium carbonates. The isotopes ⁷Li, ¹¹B, ²⁵Mg, ⁴³Ca, ⁸⁸Sr, ¹³⁷Ba, and ¹³⁹La. The Laser Ablation system was optimized for high spatial resolution using a 40 μm × 40 spot measurements μm and 2 Hz laser frequency with a 1.8 J/cm² laser fluence. Approximately the top 1 μm of the crystal calcite was removed using preablation, with a 60 × 60 μm laser spot to avoid any potential surface contamination. The ICP-MS sensitivity was optimized using NIST-SRM612 reference glass material for maximum sensitivity across the Mg–U mass range and maintaining ThO/Th < 0.5% and a Th/U ratio of ~1. Data reduction involved the initial screening of spectra for outliers, subtraction of the mean background intensities (measured with the laser turned off) from the analyzed isotope intensities, internal standardization to ⁴³Ca, and external standardization using the NIST-SRM612 glass reference material. In-house OKA calcite standards (collected at Oka carbonatite complex Quebec, Canada) and NIST-SRM614 were used to monitor long-term the reproducibility of the standards, which were below 1.5 RSD % (relative standard deviation).

TABLE 2

Table 2. Summary of the ICP-MS operating conditions.

Results

In the experiment with high initial saturation state (Ω_cc = 43.45, run OVG-1) abundant nucleation on the walls and the bottom of the containers were observed with naked eye and pH (NBS scale) decreased from 9.09 to 7.96 during experiment. The degree of visible nucleation decreased with decreasing of Ω values between experiments. Thus, only small amount of crystals (other than cleavage fragments) were observed in the runs OVG-3 (Ω_cc = 12.93) and OVG-3′ (Ω_cc = 13.03) where pH decreased from 8.55 to 7.95 (OVG-3) and from 8.54 to 8.13 (OVG-3′). Despite decrease of pH from 8.21 to 7.98, run OVG-4 (Ω_cc = 6.02) did not yield visible crystallization. Obtained crystals and cleavage fragments were examined with electron microscopy and Raman spectroscopy techniques.

SEM (BSE, EDS, EBSD) and Raman

Three morphological types of new formed crystals were identified: (1) acicular crystals radiating away from the substrate in two experiment (OVG-1 and OVG-2; Figures 1A–E); (2) monocrystals grown on the substrate in one experiment (OVG-3; Figure 1F); (3) thin (2 μm of thickness) overgrowth layer of likely new formed material in one experiment (OVG-3; Figure 1F). Raman spectroscopy analyses demonstrated that the first two types of crystals (acicular and monocrystal fragments) are aragonites. This observation was confirmed by EBSD, which also revealed that thin overgrowth layer (the third type) is a calcite. SEM BSE imaging identified crystals grown at the rim of the substrate (Figure 1). EDS spot analyses yielded that both types of aragonite crystals contained similar amount of Ca, but elevated amount of Na (0.4 wt%) and Sr (1 wt%) compared to the substrate, where no Na and Sr were detected. The thin layer of calcite overgrowth has similar amount of Ca, but higher concentration of Mg (up to 1.5 wt%) compared to all other examined crystals. EDS maps of the crystals from experiment OVG-3 confirmed EDS spot analyses by visualizing aragonite crystals fragments enriched in Na and Sr and calcite overgrowth layer in enriched in Mg (Figure 2). EDS imaging also yielded that sulfur is enriched in newly formed crystals compared to the substrate; however, we are not discussing this element in our study because EDS analyses were not optimized for sulfur.

FIGURE 1

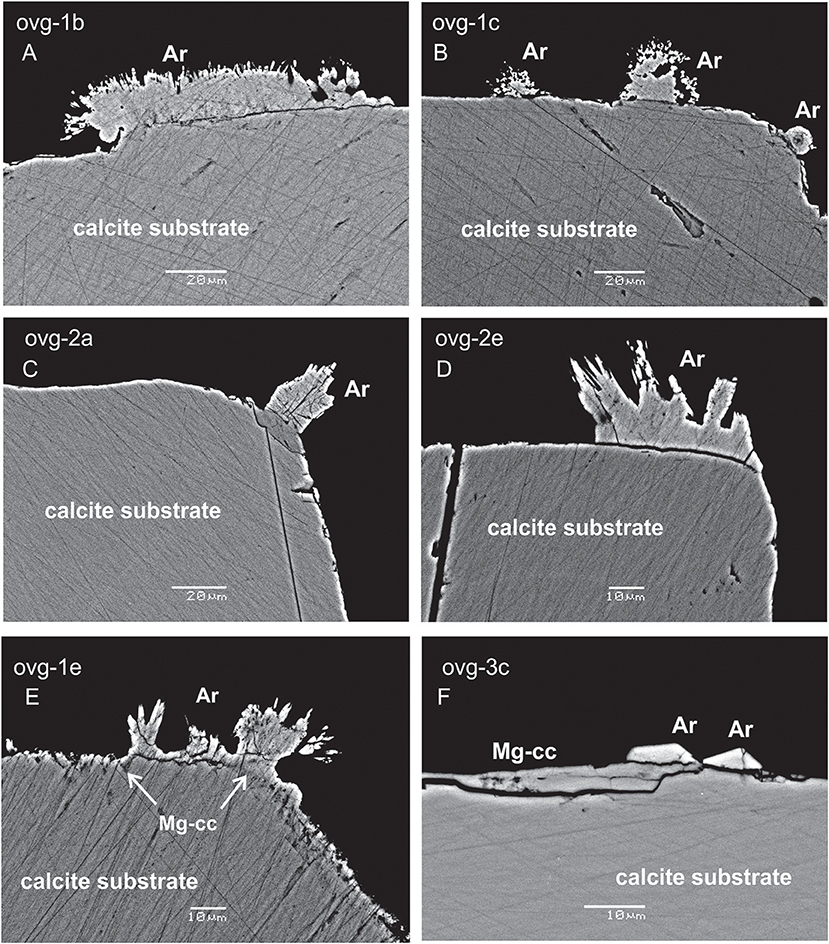
Figure 1. SEM BSE images of calcite substrate and new formed crystals. Acicular crystals of aragonite (Ar) are radiating away from the substrate in the experiments ovg-1 and ovg-2 (A–E); aragonite monocrystals and thin layer of new-formed calcite (Mg-cc) are growing on the substrate in ovg-3 experiment (F). Scale bars are 20μm in (A–C) and 10 μm in (D–F).

FIGURE 2

Figure 2. SE image and EDS elemental maps of Ca, Mg, Sr, Na, and S.

EDS results are consistent with many of previous studies, which showed that Mg and Sr preferentially incorporate into calcite and aragonite, respectively. Overall, combination of SEM EDS and EBSD techniques proves that newly formed calcite overgrowth occurred in the experiments (OVG-3 and OVG-3′), where the largest overgrowth thickness was detected. Further in the text, only those experiments will be discussed as the other experiments yielded calcite overgrowth of the thickness insufficient for LA-ICP-MS depth profiling.

ICP-MS Data of Experimental Fluids and LA-ICP-MS Data of Calcite Overgrowth

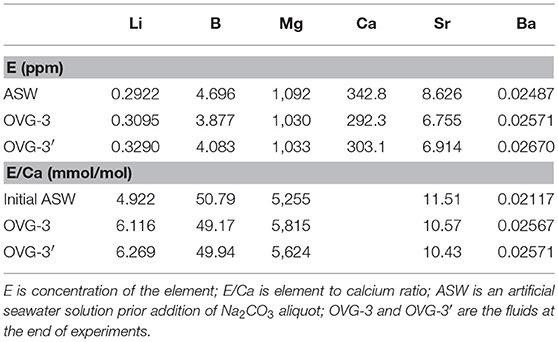
Elemental concentrations and E/Ca in initial and final fluids of the experiments OVG-3 and OVG-3′ are presented in Table 3. It is shown that concentrations of B, Mg, Ca, and Sr decreased during the experiments. The change in fluid B/Ca during experiment was insignificant considering the analytical error of 5%. Sr/Ca decreased by <10% and Mg/Ca increased by <11% during experiments. Lithium and barium, the most unabundant among measured elements, slightly increased during crystallization likely due to contamination of the growth media; Li/Ca increased by <28%, Ba/Ca increased by <8%. The evolution of the fluid composition was included into calculation of partition coefficients and presented further in the text.

TABLE 3

Table 3. Elemental composition of artificial seawater (Instant Ocean) and final fluids.

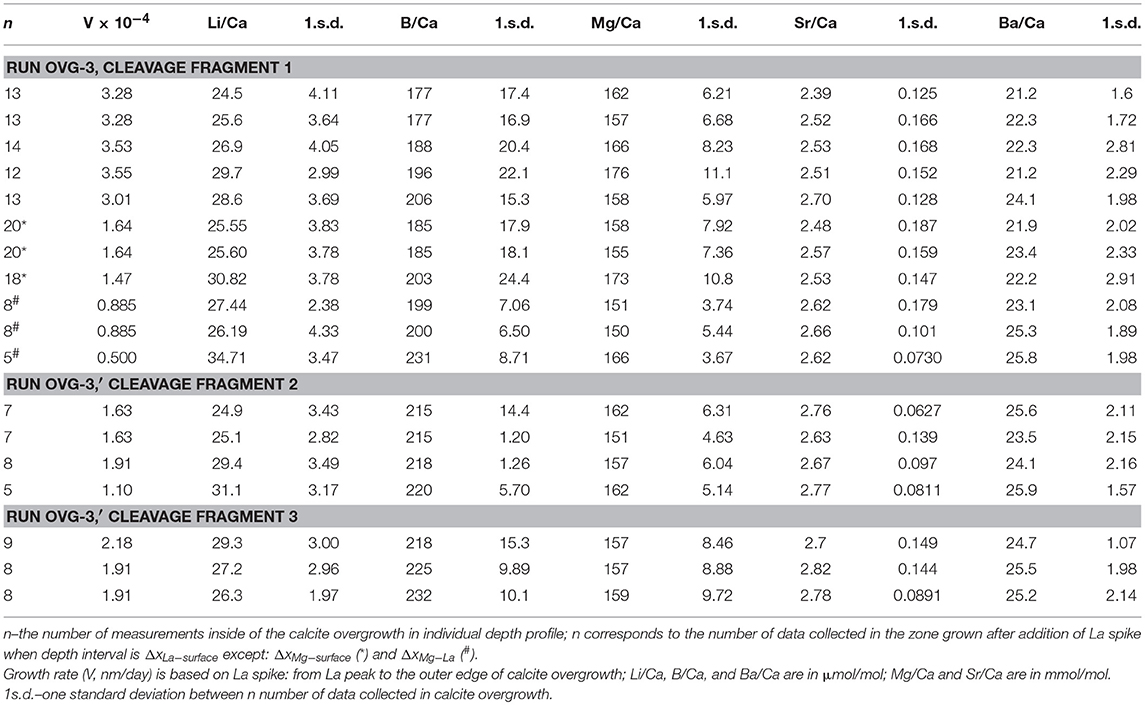
Only two experiments (OVG-3 and OVG-3′) yielded calcite overgrowth thick enough (1–3 μm thickness) for depth profiling analysis by LA-ICP-MS. In particular, 12 profiles were successfully conducted on the three cleavage fragments (one from OVG-3 and two from OVG-3′) in the areas where no aragonite was detected (Table 4). Overgrowth contained higher amount Li, B, Mg, Sr, and Ba compared to the concentrations of these elements in the calcite substrate. Example of E/Ca from one of the profiles is shown on Figure 3. The maximum in La/Ca corresponds to the time when La was added into solution and captured by calcite growing layer followed by the rapid decrease of La/Ca toward calcite surface (zero distance). This rapid decrease in La/Ca is due to the strong affinity of La in coprecipitating with calcite (Terakado and Masuda, 1988; Zhong and Mucci, 1995; Toyama and Terakado, 2014; Voigt et al., 2017; Gabitov et al., 2017). The plots of Sr/Ca vs. Mg/Ca show three data groups collected in the calcite overgrowth, calcite substrate, and mixing zone (probably formed due to micro-asperities on the boundary between substrate and overgrowth) (Figure 3A). The all LA-ICP-MS data are presented in the Table S1.

TABLE 4

Table 4. Element to calcium ratios in calcite overgrowth.

FIGURE 3

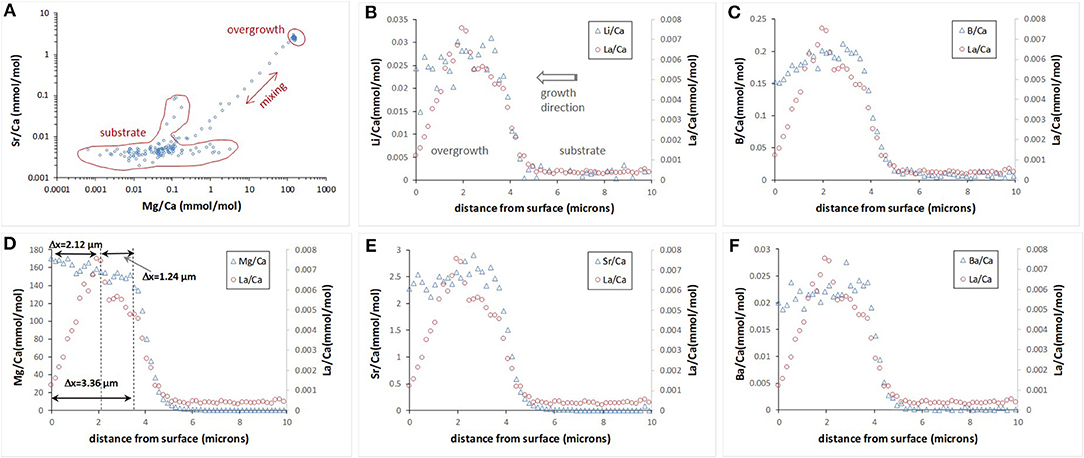
Figure 3. Example of E/Ca depth profile evaluated by LA-ICP-MS. Sr/Ca vs. Mg/Ca collected in the 163 depth steps (0–29 μm) show distinct chemical composition of the calcite substrate, new formed calcite overgrowth, and mixing zone (A). E/Ca profiles for the top 10 μm (B–F); zero distance is an outer edge of the overgrowth.

Depth profiling data showed E/Ca distribution was not entirely homogeneous in the calcite overgrowth. Certain trends were observed in the relatively thick (2–3 μm) overgrowth layers. In particular, Li/Ca, B/Ca, Sr/Ca, and Ba/Ca decreased toward the outer edge (i.e., cleavage fragment surface at 0 μm) of the overgrowth layer, (i.e., decreased with growth time), whereas Mg/Ca increased with the growth of calcite. Example of 10 μm portion of 29 μm deep profile for each E/Ca is shown on the Figures 3B–F.

Evaluation of Growth Rate

Extension rate of the calcite overgrowth in the direction perpendicular to the substrate surface was evaluated using depth profiling data of Mg/Ca (Mg is the most abundant element in the overgrowth) and La/Ca (La was added as a marker). Figure 3D contains an example of the profile where Mg and La marked zones are labeled. The increase in Mg/Ca corresponds to initiation of the growth at the time (t) of 7 days considering that Na₂CO₃ aliquot was added at t = 0 days. This consideration is based on the observations in the other similar runs by monitoring of pH and assuming that decrease in pH corresponds to the onset of formation of the overgrowth layer of calcite. The increase in La/Ca corresponds to its addition into growth media at 169 days. Another assumption is that growth of calcite stopped at the end of experiment at 244 days after crystallization was initiated by addition of Na₂CO₃ aliquot.

The interval between the maximum value of La and the sample surface (Δx_La−surface = 2.12 μm) was divided by the time interval between the La addition and the end of experiment (Δt = 244–169 = 75 days) and yielded growth rate (V) of 0.0283 μm/day or 3.27·10⁻⁴ nm/s. The other intervals could potentially be used for growth rate calculation and examples are shown on Figure 3D: (1) Δx_Mg−La of 1.24 μm between increase of seawater elements (e.g., Mg) and La and corresponded Δt = 169–7 = 162 days yielded V = 0.0142 μm/day; (2) Δx_Mg−surface of 3.36 μm between increase of seawater elements (e.g. Mg) and the end of experiment and corresponded Δt = 244–7 = 237 days yielded V of 0.0142 μm/day. The Δx_Mg−La was distinct from zero in three depth profiles collected on the cleavage fragment from the run OVG-3. In other profiles the maximum amount of La often overlaps with a rapid increase of Mg suggesting that overgrowth started to form around time of La additions into growth solution, i.e., 169 days after the beginning of the experiment (Table S1). Such long delay in growth initiation is in agreement with variation of overgrowth thickness (from 0.71 to 3.36 μm), which indicates the non-uniform growth of new calcite layer.

Discussion

Decrease in uptake of Li/Ca, B/Ca, Sr/Ca, and Ba/Ca by calcite overgrowth (Figure 3, distance from 3 to 0 μm) cannot entirely be explained by evolution of E/Ca in experimental fluid where Li/Ca, Mg/Ca, and Ba/Ca increased with time, Sr/Ca decreased with time, and B/Ca decrease is insignificant (Table 3). Similar trends for B/Ca and Sr/Ca were observed at large scales where those ratios decreased from the fast growth core (nucleation site) to the slow grown rim of crystals with the sizes of up to 1,500 μm (Gabitov and Watson, 2006; Gabitov et al., 2014a,b). Bulk precipitation experiments of calcite also found strong growth rate effect on Sr, Ba, and B uptake (e.g., Tesoriero and Pankow, 1996; Uchikawa et al., 2015; Mavromatis et al., 2018). In our study, growth rate can potentially control B, Sr, and Ba uptake because decrease in Ω with experimental duration should cause a decrease in growth rate (e.g., Zhong and Mucci, 1989) however, this was not confirmed by the growths rate calculated from LA-ICP-MS depth profiles. Therefore, the reason for decrease in Sr/Ca and Ba/Ca is not entirely clear. B/Ca trend could be caused by pH drop by 0.6 units during experiment OVG-3, however the observed decrease in calcite B/Ca (25%) is much smaller than B/Ca decrease (by a factor of 100) observed by Uchikawa et al. (2015) for pH decrease from 8.5 to 8.0. Observed trend in Li/Ca is much less pronounced due to larger scattering, which resulted from low concentration of Li.

Mg/Ca is the only ratio in the overgrowth that often correlates with evolution of fluid Mg/Ca, i.e., Mg/Ca increases in both calcite and fluid with the time of calcite growth. On the other hand, an increase of calcite Mg/Ca with time can be related to slow dehydration of Mg²⁺(H₂O)₆ compare to Ca²⁺(H₂O)₆ at the calcite surface (Pavlov et al., 1998; Rodriguez-Cruz et al., 1999a,b).

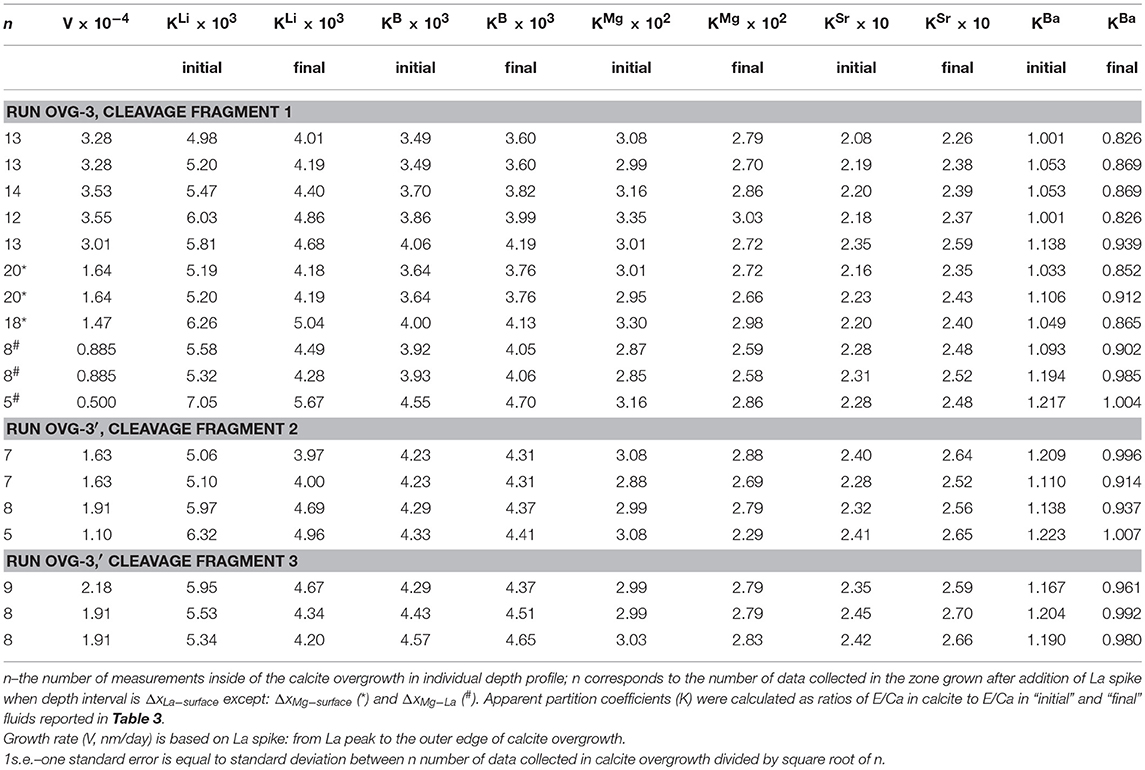
Pairs of apparent partition coefficients (K) were calculated for each element in the newly formed calcite overgrowth as E/Ca ratios between calcite and solutions (initial and final) (Table 5). Depth profiling data for calcite precipitated between the addition of La and the end of experiment (Δx_La−surface) were used in the calculation of K values as an average E/Ca for Δx_La−surface layer (Figure 3D). In the three profiles (run OVG-3), where locations of the increase in Mg/Ca were distinct from the increase in La/Ca, K were also calculated for Δx_La−surface and Δx_Mg−La. In the run OVG-3′ the width of calcite overgrowth was thinner that the overgrowth width in the run OVG-3, showing slower growth in the run OVG-3′. The small difference in saturation states (Ω_cc = 12.93 and 13.03) unlikely can explain this inconsistency. The most reasonable explanation is the difference between cleaning treatments of calcite cleavage fragments. The quick rinse of calcite with HCl caused surface etching and created higher potential for nucleation on the cleavage fragment in the run OVG-3 in comparison to the run OVG-3′ where calcite was rinsed with H₂O only.

TABLE 5

Table 5. Apparent partition coefficients.

K-values vs. calcite growth rate are plotted together with those from previous studies (Figure 4). There, most of the growth rates were originally reported as bulk precipitation rates (R) (amount of CaCO₃ precipitated per calcite area per time); except studies of Gabitov et al. (2014a,b), where velocities of advancing crystal surface (V) were evaluated (extension per time). Bulk precipitation rates were converted to extension rates using molar volume of calcite (V_m = 3.69·10⁻⁵ m³/mol); for example: V = R·V_m = 3.98·10⁻⁹ mol/(m²·s)·3.69·10⁻⁵ m³/mol = 1.47·10⁻⁴ nm/s.

FIGURE 4

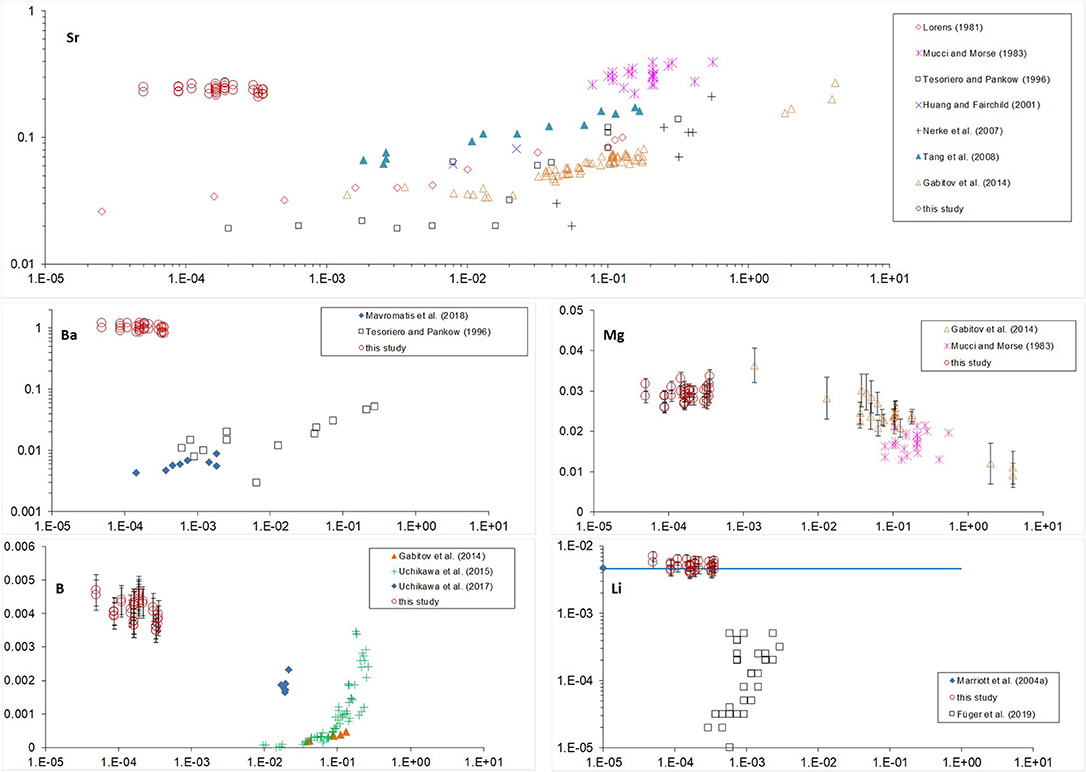
Figure 4. Partition coefficients of Sr, Ba, Mg, B, and Li vs. crystal growth rate. Standard error bars of our data are not presented on the plot if smaller than size of the marker.

All of the data shown on Figure 4 are for low-Mg and Mg-free calcite except for the data from Mucci and Morse (1983) and our study. It was found that high Mg content of the fluid affects incorporation of elements into calcite. The strongest effect was observed for Sr and Ba (Figure 4), where K^Sr and especially K^Ba of Mg-bearing calcite are much higher than those of low-Mg or Mg-free calcite precipitated at similar rates (see Lorens, 1981; Tesoriero and Pankow, 1996). This effect was explained previously by coupled substitution of Ca in calcite due to the differences in ion radii of Mg, Ca, Sr, Ba (r_Mg < r_Ca < r_Sr < r_Ba), where the distortion of crystal lattice due to incorporation of small Mg (relative to Ca) is compensated by involvement of large Sr (e.g., Mucci and Morse, 1983). This explanation is consistent with our data where deviation of K^Ba (Ba is the largest cation) from the literature data is stronger than of K^Sr: K^Ba of Mg-bearing calcite is two orders of magnitude higher than K^Ba of Mg-free calcite precipitated at similar rates (10⁻⁴-10⁻³ nm/s) whereas our K^Sr is higher than literature values by one order of magnitude (Lorens, 1981; Tesoriero and Pankow, 1996; Mavromatis et al., 2018). Sr incorporation into Mg-bearing calcite demonstrates much lower dependence on growth rate in comparison to Sr in low-Mg or Mg-free calcite, which corroborate the dominance of substitution of Ca with Mg and Sr over the growth rate of Mg-bearing calcite.

In contrast to K^Sr and K^Ba, K^Mg is similar to previously reported data for slowly grown low-Mg calcite (Gabitov et al., 2014a) demonstrating near-equilibrium partitioning of Mg in our study. The similarity between K^Mg values from our study (where Mg/Ca_fluid = 5.2–5.8 mol/mol) and those reported by Gabitov et al. (2014a) (where Mg/Ca_fluid = 0.08–0.2 mol/mol) suggest that fluid Mg/Ca does not significantly affect K^Mg at growth rates between 10⁻⁴ and 0.1 nm/s (Figure 4). The potential explanation is that at a slow growth rate, Mg incorporation is not limited by its dehydration rate of hydrated Mg molecules. K^B is much higher than previously reported data for calcite slowly grown from solutions having pH values within the range of pH in our experiments. Our partition coefficients overlap only with those for calcite grown at higher rates from the study of Uchikawa et al. (2015). We hesitate to interpret obtained data as boron incorporation into calcite is different from divalent cations and strongly depends on pH and carbonate chemistry of the solution (e.g., Uchikawa et al., 2017). Lithium unlikely substitutes Ca in calcite lattice as was considered for divalent cations, but rather incorporates interstitially (discussed in Marriott et al., 2004a). The recent study shows increase of KLi with increasing of growth rate (Füger et al., 2019). However, even at relatively high growth rates their K^Li are lower than ours by an order of magnitude, whereas our data partially overlaps with the data of Marriott et al. (2004a) for calcite precipitated at unknown rate. It was shown that salinity has positive effect on K^Li (Marriott et al., 2004b), however it is cannot entirely explain the difference between our data (salinity ~25 psu) and those of Füger et al. (2019) (salinity ~18 psu).

This study shows that elemental entrapment by Mg-bearing calcite could be very different from entrapment by low-Mg calcite, suggesting non-equilibrium elemental partitioning between calcite and seawater even when crystal growth rate is very slow. This finding corroborates an importance in the development of empirical K-V relationships for calcite precipitated from seawater and suggests that existed K-V trends for B, Sr, Ba, and possibly Li in low-Mg and Mg-free calcite cannot be directly applied for growth rate correction in geochemical proxies based on marine Mg-bearing calcite samples.

The recent study shows increase of K^Li with increasing of growth rate and decreasing of pH (Füger et al., 2019). However, even at relatively high growth rates their K^Li are lower than ours by an order of magnitude (at similar pH range), whereas our data partially overlaps with the data of Marriott et al. (2004a) for calcite precipitated at unknown rate. It was shown that salinity has positive effect on K^Li (Marriott et al., 2004b), however the higher salinity in our experiments cannot entirely explain the difference between our data (salinity ~25 psu) and those of Füger et al. (2019) (salinity ~18 psu).

Conclusions

• High fluid Mg/Ca strongly promotes incorporation of Sr and Ba into calcite probably due to the ion size compensation.

• Growth rate effect on Sr incorporation into Mg-bearing calcite is much smaller compare to low-Mg and Mg-free calcite.

• At slow growth (10⁻⁴-0.1 nm/s), K^Mg of Mg-bearing calcite is close to K^Mg of low-Mg calcite suggesting near-equilibrium Mg uptake, which is not limited by Mg dehydration.

Author Contributions

RG and AS conceived the project. RG conducted experiments with assistance of KS. VY, AB, and RG collected the SEM data. AS collected LA-ICP-MS and ICP-MS data on calcite and final fluids. CB conducted ICP-MS analysis of initial fluid. RG wrote the first draft of the manuscript. RG, CB, AP-H, VY, AB, AS, and KS participated to the interpretation of the data and participated to the subsequent stages of preparation of the manuscript.

Funding

Experiments were supported by Mississippi State University funds issued to RG. Raman, SEM EDS and EBSD analysis was supported by funds from the Program of the Development of the Lomonosov Moscow State University. Analysis of fluids were supported by C-DEBI grant issued to RG, Australian Research Council through the Centre of Excellence for Coral Reef Studies (CE140100020), and ICP-MS laboratory at the University of Rochester. The ICP-MS laboratory at the University of Rochester is partially supported by the NSF grant EAR-1545637 to Dustin Trail. LA-ICP-MS analyses were covered with ERC grant 2010- NEWLOG ADG-267931 to Harry Elderfield.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2019.00051/full#supplementary-material

Table S1. OVG-3 and OVG-3' are two experiments; CF is a cleavage fragment; Pr is a profile. “ElapsedTime_s” can be converted to ablation rate via multiplying by 0.2 micron/s.

References

Dickson, A. G. (1990). Thermodynamics of the dissociation of boric acid in synthetic seawater from 273.15 to 318.15 K. Deep Sea Res. 37, 755–766. doi: 10.1016/0198-0149(90)90004-F

CrossRef Full Text | Google Scholar

Elderfield, H., Bertram, C. J., and Erez, J. (1996). A biomineralization model for the incorporation of trace elements into foraminiferal calcium carbonate. Earth Planet. Sci. Lett. 142, 409–423. doi: 10.1016/0012-821X(96)00105-7

CrossRef Full Text | Google Scholar

Füger, A., Konrad, F., Leis, A., Dietzel, M., and Mavromatis, V. (2019). Effect of growth rate and pH on lithium incorporation in calcite. Geochim. Cosmochim. Acta 248, 14–24. doi: 10.1016/j.gca.2018.12.040

CrossRef Full Text | Google Scholar

Gabitov, R. I., Rollion-Bard, C., Tripati, A., and Sadekov, A. (2014b). In situ study of boron partitioning between calcite and fluid at different crystal growth rates. Geochim. Cosmochim. Acta 137, 81–92. doi: 10.1016/j.gca.2014.04.014

CrossRef Full Text | Google Scholar

Gabitov, R. I., Sadekov, A., and Leinweber, A. (2014a). Crystal growth rate effect on Mg/Ca and Sr/Ca partitioning between calcite and fluid: an in-situ approach. Chem. Geol. 367, 70–82. doi: 10.1016/j.chemgeo.2013.12.019

CrossRef Full Text | Google Scholar

Gabitov, R. I., Sadekov, A., and Migdisov, A. (2017). REE incorporation into calcite individual crystals as one time spike addition. Minerals (INVITED) 7, 204. doi: 10.3390/min7110204

CrossRef Full Text | Google Scholar

Gabitov, R. I., and Watson, E. B. (2006). Partitioning of strontium between calcite and fluid. Geochem. Geophys. Geosyst. 7, Q11004. doi: 10.1029/2005GC001216

CrossRef Full Text | Google Scholar

Huang, Y., and Fairchild, I. J. (2001). Partition of Sr²⁺ and Mg²⁺ into calcite under karst-analogue experimental conditions. Geochim. Cosmochim. Acta 65, 47–62. doi: 10.1016/S0016-7037(00)00513-5

CrossRef Full Text | Google Scholar

Katz, M. E., Cramer, B. S., Franzese, A., Hönisch, B., Miller, K. G., Rosenthal, Y., et al. (2010). Traditional and emerging geochemical proxies in foraminifera. J. Foramin. Res. 40, 165–192, doi: 10.2113/gsjfr.40.2.165

CrossRef Full Text | Google Scholar

Lea, D. W. (2003). “Trace elements in foraminiferal calcite,” in Modern Foraminifera, ed B. K. Sen Gupta (Dordrecht: Kluwer Academic Publishers), 259–277.

Google Scholar

Lewis, E., and Wallace, D. W. R. (1998). Program Developed for CO₂ System Calculations. ORNL/CDIAC-105 carbon dioxide information analysis center, Oak Ridge National Laboratory, U.S. Department of Energy, Oak Ridge, TN.

Lorens, R. B. (1981). Sr, Cd, Mn, and Co distribution coefficients in calcite as a function of calcite precipitation rate. Geochim. Cosmochim. Acta 45, 553–561. doi: 10.1016/0016-7037(81)90188-5

CrossRef Full Text | Google Scholar

Marriott, C. S., Henderson, G. M., Belshaw, N. S., and Tudhope, A. W. (2004a). Temperature dependence of δ⁷Li, δ⁴⁴Ca and Li/Ca during growth of calcium carbonate. Earth Planet. Sci. Lett. 222, 615–624. doi: 10.1016/j.epsl.2004.02.031

CrossRef Full Text | Google Scholar

Marriott, C. S., Henderson, G. M., Crompton, R., Staubwasser, M., and Shaw, S. (2004b). Effect of mineralogy, salinity, and temperature on Li/ Ca and Li isotope composition of calcium carbonate. Chem. Geol. 212, 5–15. doi: 10.1016/j.chemgeo.2004.08.002

CrossRef Full Text | Google Scholar

Mavromatis, V., Gautier, Q., Bosc, O., and Schott, J. (2013). Kinetics of Mg partition and Mg stable isotope fractionation during its incorporation in calcite. Geochim. Cosmochim. Acta 114, 188–203. doi: 10.1016/j.gca.2013.03.024

CrossRef Full Text | Google Scholar

Mavromatis, V., Goetschl, K. E., Grengg, C., Konrad, F., Purgstaller, B., and Dietzel, M. (2018). Barium partitioning in calcite and aragonite as a function of growth rate. Geochim. Cosmochim. Acta 237, 65–78. doi: 10.1016/j.gca.2018.06.018

CrossRef Full Text | Google Scholar

Millero, F. J. (1995). Thermodynamics of the carbon dioxide system in the oceans. Geochim. Cosmochim. Acta 59, 661–677.

Google Scholar

Mucci, A., and Morse, J. W. (1983). The incorporation of Mg²⁺ and Sr²⁺ into calcite overgrowths: influences of growth rate and solution composition. Geochim. Cosmochim. Acta 47, 217–233. doi: 10.1016/0016-7037(83)90135-7

CrossRef Full Text | Google Scholar

Nehrke, G., Reichart, G. J., Van Cappellen, P., Meile, C., and Bijma, J. (2007). Dependence of calcite growth rate and Sr partitioning on solution stoichiometry: Non-Kossel crystal growth. Geochim. Cosmochim. Acta 71, 2240–2249. doi: 10.1016/j.gca.2007.02.002

CrossRef Full Text | Google Scholar

Nürnberg, D., Bijma, J., and Hemleben, C. (1996). Assessing the reliability of magnesium in foraminiferal calcite as a proxy for water mass temperature. Geochim. Cosmochim. Acta 60, 803–814. doi: 10.1016/0016-7037(95)00446-7

CrossRef Full Text | Google Scholar

Pavlov, M., Siegbahn, P. E. M., and Sandstro, M. (1998). Hydration of beryllium, magnesium, calcium, and zinc ions using density functional theory. J. Phys. Chem. A 102, 219–228. doi: 10.1021/jp972072r

CrossRef Full Text | Google Scholar

Rodriguez-Cruz, S. E., Jockusch, R. A., and Williams, E. R. (1999a). Binding energies of hexahydrated alkaline earth metal ions, M²⁺(H₂O)₆, M = Mg, Ca, Sr, Ba: evidence of isomeric structures for magnesium. J. Am. Chem. Soc. 121, 1986–1987. doi: 10.1021/ja983232v

PubMed Abstract | CrossRef Full Text | Google Scholar

Rodriguez-Cruz, S. E., Jockusch, R. A., and Williams, E. R. (1999b). Hydration energies and structures of alkaline earth metal ions, M²⁺(H₂O)_n, n = 5–7, M = Mg, Ca, Sr, and Ba. J. Am. Chem. Soc. 121, 8898–8906. doi: 10.1021/ja9911871

PubMed Abstract | CrossRef Full Text | Google Scholar

Stoll, H. M., Rosenthal, Y., and Falkowski, P. (2002). Climate proxies from Sr/Ca of coccolith calcite: calibrations from continuous culture of Emiliania huxleyi. Geochim. Cosmochim. Acta 66, 927–936. doi: 10.1016/S0016-7037(01)00836-5

CrossRef Full Text | Google Scholar

Tang, J., Köhler, S. J., and Dietzel, M. (2008). Sr²⁺/Ca²⁺ and 44Ca/40Ca fractionation during inorganic calcite formation: I. Sr incorporation. Geochim. Cosmochim. Acta 72, 3718–3732. doi: 10.1016/j.gca.2008.05.031

CrossRef Full Text | Google Scholar

Terakado, Y., and Masuda, A. (1988). The coprecipitation of rare-earth elements with calcite and aragonite. Chem. Geol. 69, 103–110. doi: 10.1016/0009-2541(88)90162-3

CrossRef Full Text | Google Scholar

Tesoriero, A. J., and Pankow, J. F. (1996). Solid solution partition of Sr²⁺, Ba²⁺, and Cd²⁺ to calcite. Geochim. Cosmochim. Acta 60, 1053–1063. doi: 10.1016/0016-7037(95)00449-1

CrossRef Full Text | Google Scholar

Toyama, K., and Terakado, Y. (2014). Experimental study of rare earth element partitioning between calcite and sodium chloride solution at room temperature and pressure. Geochem. J. 48, 463–477. doi: 10.2343/geochemj.2.0322

CrossRef Full Text | Google Scholar

Uchikawa, J., Harper, D. T., Penman, D. E., Zachos, J. C., and Zeebe, R. E. (2017). Influence of solution chemistry on the boron content in inorganic calcite grown in artificial seawater. Geochim. Cosmochim. Acta 218, 291–307. doi: 10.1016/j.gca.2017.09.016

CrossRef Full Text | Google Scholar

Uchikawa, J., Penman, D. E., Zachos, J. C., and Zeebe, R. E. (2015). Experimental evidence for kinetic effects on B/Ca in synthetic calcite: implications for potential B(OH)4– and B(OH)3 incorporation. Geochim. Cosmochim. Acta 150, 171–191. doi: 10.1016/j.gca.2014.11.022

CrossRef Full Text | Google Scholar

Uppstrom, L. R. (1974). The boron/chlorinity ratio of deep-sea water from the Pacific ocean. Deep Sea Res. 21, 161–162. doi: 10.1016/0011-7471(74)90074-6

CrossRef Full Text | Google Scholar

Voigt, M., Mavromatis, V., and Oelkers, E. H. (2017). The experimental determination of REE partition coefficients in the water calcite system. Chem. Geol. 462, 30–43. doi: 10.1016/j.chemgeo.2017.04.024

CrossRef Full Text | Google Scholar

Zhong, S., and Mucci, A. (1989). Cacite and aragonite precipitation from seawater of various salinities: precipitation rates and overgrowth compositions. Chem. Geol. 78, 283–299. doi: 10.1016/0009-2541(89)90064-8

CrossRef Full Text | Google Scholar

Zhong, S., and Mucci, A. (1995). Partitioning of rare earth elements (REEs) between calcite and seawater solutions at 25°C and 1 atm, and high dissolved REE concentrations, Geochim. Cosmochim. Acta 59, 443–453. doi: 10.1016/0016-7037(94)00381-U

CrossRef Full Text | Google Scholar