Multiband Atmospheric Correction Algorithm for Ocean Color Retrievals

Introduction

Ocean color retrieval algorithms require an atmospheric correction (AC) process to separate the radiometric contribution of the atmosphere from the ocean, given the radiance measured at the top of atmosphere (TOA). The National Aeronautics and Space Administration (NASA) standard approach to the AC is a two-step process: the atmosphere and surface contributions are first removed using minimal assumptions about the water optical properties (Gordon and Wang, 1994; Franz et al., 2007; Ahmad et al., 2010; Bailey et al., 2010; Mobley et al., 2016), and the resulting spectral water-leaving radiances are then used to infer water column optical properties and constituent concentrations (e.g., Gordon et al., 1988; O'Reilly et al., 1998; Morel and Maritorena, 2001; Hu et al., 2012; Werdell et al., 2013). AC involves finding a solution to a set of deterministic models, enabling the removal of atmospheric path and surface effects from the TOA signal. The primary challenge is determining the contribution of aerosols (a primary source of uncertainty in the AC) to the atmospheric path radiance, which is highly variable and, thus, must be inferred from observation. This approach takes advantage of the strong absorption of water in the Near Infrared to Shortwave Infrared (NIR-SWIR) (longward of 700 nm) to separate the atmospheric and oceanic signals (Gordon and Wang, 1994; Wang et al., 2009; Ahmad et al., 2010). This AC process aims for retrievals that meet ocean color requirements (i.e., 5% uncertainty on water-leaving radiance at 443 nm) over the open ocean and in the absence of strongly absorbing aerosols (i.e., dust, organic, and black carbon) (Gordon and Wang, 1994; Mobley et al., 2016). In coastal and optically complex waters, the water-leaving radiance retrievals often fail in meeting that requirement due to non-negligible water-leaving radiance in the NIR bands used for the AC, with water-leaving radiance often underestimated or even negative in value. Iterative AC techniques have been developed to model the ocean reflectance in the NIR, which mitigate the problem effectively in moderately turbid and productive waters (Siegel et al., 2000; Bailey et al., 2010). Although this iterative approach has been used in the NASA standard processing (Bailey et al., 2010), it has been shown that such methods can fail in highly turbid waters (Wang et al., 2012; Goyens et al., 2013). Other methods, based on the SWIR bands, have been shown effective in separating the aerosol signal from the TOA signal over highly turbid waters, due to the increased water absorption at these longer wavelengths (Shi and Wang, 2007; Wang and Shi, 2007, 2012; Jiang and Wang, 2014; Vanhellemont and Ruddick, 2015; Pahlevan et al., 2017). The SWIR-based methods has limitations, however, for two reasons: (1) the signal-to-noise ratio (SNR) on SWIR bands is low for current ocean color sensors [i.e., MODIS (Moderate Resolution Imaging Spectroradiometer) and VIIRS (Visible Infrared Imaging Radiometer Suite)] and (2) the approach generally requires discrete switching from the NIR AC bands to SWIR bands over coastal waters, thus producing spatial inconsistency or artifacts in the retrievals. For example, Shi and Wang (2007) utilized 1,240 and 2,130 nm for MODIS to perform the AC using the 2-band Gordon and Wang (1994) AC approach. The algorithm switches from NIR to SWIR based on a turbidity index threshold (Shi and Wang, 2007; Wang and Shi, 2007; Wang et al., 2009). Werdell et al. (2010) have shown the effectiveness of the 2-band SWIR AC approach, but with increased uncertainties in the ocean color retrievals due to low SWIR SNR of MODIS-Aqua. Still, other studies have shown failure in the NIR-SWIR switching method due to the NIR sensor saturation at moderate to high turbidity (i.e., >35 g m⁻³) where the NIR bands on MODIS-Aqua saturate at TOA radiances >2.8–3.45 mW cm⁻² μm⁻¹ sr⁻¹ for 748 nm and >1.9–2.45 mW cm⁻² μm⁻¹ sr⁻¹ for 869 nm and improper cloud masking (Aurin et al., 2013). A recent study by Liu et al. (2019) indicated that the turbidity index, responsible for the switching, varies with the aerosol size distribution, optical depth, and observing geometry, thus rendering the effectiveness of the NIR-SWIR switching questionable.

One way for reducing the uncertainty in ocean color retrievals using the SWIR bands is to use more spectral information to reduce sensor random noise impact produced by low SNR. Gao et al. (2000, 2007) used a spectral matching technique to fit the measured TOA signal with an aerosol lookup table (LUT) for bands >860 nm and demonstrated improved retrieval of ocean reflectance in turbid and shallow waters from MODIS-Aqua and Airborne Visible/Infrared Imaging Spectrometer (AVIRIS). They also showed a sensitivity study indicating that SWIR bands are sensitive to variations in aerosol size distributions including some fine-mode dominant types, although the sensitivity is weaker than that of the visible–NIR spectral regime. Other methods that utilize more spectral information for the AC, such as machine learning techniques (i.e., neural network) and coupled atmosphere–ocean simultaneous retrievals, have shown promising results (Gordon et al., 1997; Chomko and Gordon, 1998, 2001; Chomko et al., 2003; Stamnes et al., 2003; Jamet et al., 2005; Brajard et al., 2006; Schroeder et al., 2007; Spurr et al., 2007; Kuchinke et al., 2009; Steinmetz et al., 2011; He et al., 2012; Frouin and Gross-Colzy, 2016; Fan et al., 2017; Gossn et al., 2019). Some of these algorithms were more successful over the open ocean, while others were specifically tuned for coastal cases, and they often require the use of a bio-optical ocean model with inherent assumptions about the marine optical properties.

Cloud detection and masking in turbid waters can also be challenging. Extremely turbid waters are masked as clouds when a simple NIR threshold technique is used, as is the case for the standard NASA processing. Wang and Shi (2006) proposed an improved cloud masking in coastal regions using SWIR channels. Other cloud masking methods that utilize more spectral bands have shown improved discrimination between clouds and water in highly turbid conditions (Nordkvist et al., 2009).

NASA is planning to launch the Plankton, Aerosol, Cloud, and ocean Ecosystem (PACE) satellite in 2022. The PACE satellite will host a state-of-the-art hyperspectral ocean color sensor (the Ocean Color Instrument, OCI). OCI will measure the hyperspectral radiance at the TOA from 340 to 890 nm at 5-nm spectral resolution and at seven discrete channels in the SWIR: 940, 1,038, 1,250, 1,378, 1,615, 2,130, and 2,260 nm, of which two are water vapor bands (940 and 1,378 nm) and five are window bands (i.e., no major gas absorption features). In fact, OCI will host the first instrument with a set of SWIR bands primarily designed for the ocean AC. The SWIR bands will have sufficient radiometric performance (i.e., high SNR with low systematic bias) to enable their use for AC over open oceans as well as coastal water conditions (Ibrahim and McKinna, 2018). The analysis throughout the manuscript assumed the following SNRs for OCI (420 at 1,038 nm, 280 at 1,250 nm, 220 at 1,615 nm, and 76 at 2,260 nm, excluding 2,130 nm as cloud band), for the typical ocean scene, which are based on current best estimates since the design is currently subject to slight changes. The AC algorithm proposed here attempts to exploit the unprecedented capabilities of OCI to improve the quality of ocean color retrievals from the PACE mission.

Multiband AC Algorithm

The heritage aerosol correction algorithm utilizes two bands either in the NIR or SWIR spectral range by calculating a band ratio of the Rayleigh (+ surface) and gas corrected reflectance, namely, epsilon, as follows:

$\begin{array}{ll}\epsilon =\frac{{\rho }_a({\lambda }_s)}{{\rho }_a({\lambda }_l)},& (1)\end{array}$

where λ_s and λ_l correspond to the short and long wavelength either in the NIR or SWIR range (e.g., for MODIS, λ_s = 748 nm and λ_l = 869 nm) and ρ_a(λ) is the aerosol reflectance defined as:

$\begin{array}{ll}{\rho }_a(\lambda )=\frac{\pi \times \left[L_a(\lambda )+L_{ra}(\lambda )\right]}{F_0\times {\mu }_0},& (2)\end{array}$

F₀ is the extraterrestrial solar irradiance and μ₀ is the cosine of the solar zenith angle. Since the aerosol radiance term is a strong function of the viewing/illumination geometry, the LUT is generated as a function of the solar and sensor zenith angle and relative azimuth angle. NASA's current approach to estimate the aerosol reflectance term is by finding the best match of the observed single scattering epsilon value to the model single scattering epsilon value. Since the LUT is calculated for a set of deterministic aerosol models based on Ahmad et al. (2010), the algorithm interpolates the single scattering aerosol reflectance from the LUT to match the observed reflectance. Accounting for multiple scattering interactions between the aerosol and molecules, is crucial when extrapolating the reflectance to shorter wavelengths. Given the aerosol type estimated from the single scattering epsilon in the longer wavelengths, the multiple scattered aerosol radiance is then estimated through a polynomial relationship derived through vector radiative transfer simulations (Gordon and Wang, 1994), and this multi-scattering estimate of aerosol path reflectance is then used in the aerosol correction.

The process of deriving single scattering epsilon and then converting it into multiple scattering radiance is unnecessary since currently computationally feasible multiple scattering tables can be easily generated and irreversible since there is no 1–1 relationship between multiple and single scattering when different aerosol types are mixed. Ahmad and Franz (2018) proposed an alternative approach, where the aerosol model and optical properties determination is done in multiple scattering space. It is based on the Ahmad et al. (2010) aerosol models, for which the TOA reflectance due to aerosols can be described by three parameters: relative humidity (RH), Angstrom exponent (α), or the analogous fine-mode fraction (f), and optical thickness of the aerosols (τ) in the model atmosphere. Briefly, for any relative humidity suite, the dependence of multiple-scattering epsilon $\epsilon (\lambda )=\frac{\rho (\lambda )}{\rho (869)}$ on ρ(869) would look like the x–y plot shown in Figure 1. Here, ρ refers to TOA aerosol reflectance and the subscript numbers refer to wavelength bands.

FIGURE 1

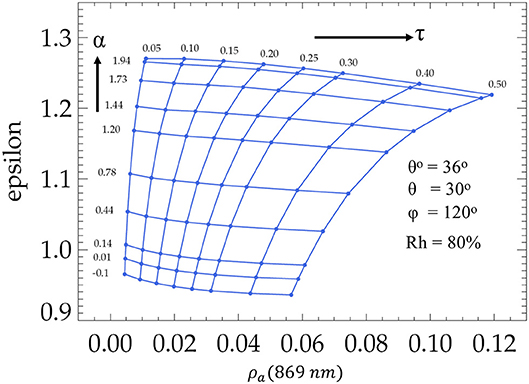
Figure 1. A graph of multiple-scattering epsilon (ε₇₄₈ = ρ₇₄₈/ρ₈₆₉) vs. ρ₈₆₉ for solar zenith, θ₀ = 36°, view zenith, θ = 30°, relative azimuth angle, φ = 120°, and relative humidity (RH) = 80% from MODIS LUT (Ahmad and Franz, 2018).

In Figure 1, the aerosol optical depth (τ) varies along the “horizontal” axis, and the Angstrom exponent (α) and extinction coefficients (ξ) vary along the “vertical” axis. This parametrization of the LUT allows one to readily calculate the aerosol reflectance at any grid point. One advantage of this approach over the current NASA standard algorithm is that it provides a mathematical framework for the aerosol reflectance determination that facilitates the application of standard error propagation techniques.

The multiband AC (MBAC) algorithm is based on this multi-scattering epsilon approach by Ahmad and Franz (2018), but it utilizes all the spectral window channels (i.e., not affected by strongly absorbing gases such as water vapor, oxygen, and carbon dioxide) available at which the water absorption is high to separate the aerosol signal (i.e., black-pixel). MBAC determines the best aerosol model by fitting the magnitude and the spectrum of the aerosol reflectance at all window NIR to SWIR bands (e.g., excluding 940- and 1,378-nm channels for OCI). The aerosol reflectance at each wavelength is stored in a LUT as a polynomial function of the geometry (not shown in Equation 3 for simplicity), aerosol optical depth, relative humidity, and fine-mode fraction:

$\begin{array}{l}{\rho }_a(\lambda ,{\tau }_a,RH,f)=a(\lambda ,RH,f)+b(\lambda ,RH,f)\times {\tau }_a\\ +c(\lambda ,RH,f)\times {{\tau }_a}^2,& (3)\end{array}$

where a, b, and c are the fitting coefficients stored in the aerosol LUT. For any spectral band in the NIR-SWIR range at which the water-leaving radiance can be assumed negligible, the atmospheric path radiance can be derived from the observed TOA radiance. Assuming a proper correction for absorbing gases (discussed in the section Correction for Absorbing Gases) and Rayleigh scattering has been done, aerosol reflectance can be determined and the aerosol optical depth can then be estimated by solving the quadratic equation, as

$\begin{array}{ll}{\tau }_a\left(\lambda =869nm,RH,f\right)=\frac{-b\left({\lambda }_{869},RH,f\right)+\sqrt{{b\left({\lambda }_{869},RH,f\right)}^2-4\times c\left({\lambda }_{869},RH,f\right)\times \left(a\left({\lambda }_{869},RH,f\right)-{\rho }_a^{obs}\left({\lambda }_{869}\right)\right)}}{2\times c\left({\lambda }_{869},RH,f\right)},& (4)\end{array}$

For consistency with the system vicarious calibration procedure, which is performed relative to one wavelength in the NIR (e.g., 869 nm for MODIS), the optical depth is estimated at that wavelength.

For an observed aerosol reflectance, the optical depth can be calculated for each aerosol model set (RH, f) as shown in Figure 2.

FIGURE 2

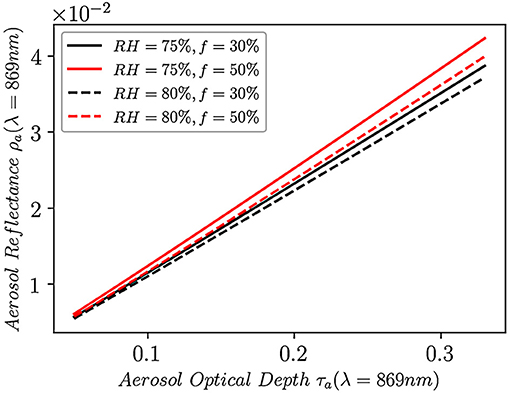
Figure 2. The aerosol reflectance as a function of the aerosol optical depth at 869 nm for aerosol models with relative humidity RH = 75% and 80% and for fine-mode fraction f = 30% and 50%.

The algorithm then calculates the aerosol optical depth and reflectance spectrally for all aerosol models as:

$\begin{array}{ll}{\tau }_a(\lambda ,RH,f)=\frac{\xi (\lambda ,RH,f)}{\xi ({\lambda }_{869},RH,f)}\times {\tau }_a({\lambda }_{869},RH,f),& (5)\end{array}$

where ξ(λ, RH, f) is the aerosol extinction coefficient for each aerosol model. Then, the spectral aerosol reflectance for each aerosol model set (RH, f) is recalculated from the polynomial equation.

The MBAC algorithm fits the aerosol reflectance in the NIR and SWIR for all models calculated in the previous step. However, since multiple solutions can exist, especially at low optical depth over the open ocean, we constrain the model selection to consider only those models with the two relative humidities bracketing the observed RH (as obtained from ancillary meteorological data). The maximum likelihood method is used to find the closest solution by minimizing the cost function:

$\begin{array}{ll}{\chi }^2(RH,f)=\frac{1}{DOF}\times {\displaystyle \sum _{\lambda ={\lambda }_s}^{{\lambda }_l}}\frac{{\left[{\rho }_{obs}(\lambda )-{\rho }_a(\lambda ,RH,f)\right]}^2}{{\sigma }^2(\lambda )}\times SW(\lambda ),& (6)\end{array}$

where ρ_obs(λ) is the observed aerosol reflectance and ρ_a(λ, RH, f) is the aerosol reflectance from the LUT for each relative humidity and fine-mode fraction. Note that the geometry is omitted from Equation 6 for simplicity; however, it depends on the solar and viewing zenith and relative azimuth angles. DOF is the degree of freedom of the observed signal. Assuming each band in the NIR and SWIR is an independent observations, DOF is the number of bands from the shortest band in the NIR, λ_s, to the longest band in the SWIR, λ_l. σ²(λ) is the squared measurement uncertainty (variance assuming gaussian random noise) of the sensor, as determined from the sensor-specific noise model for a given radiance level.

SW(λ) is a spectral weight (SW) that is set to change the relative weighting in the cost function for the spectral bands in different environmental conditions. For example, setting SW(λ) to 1 in all bands will minimize the cost function to fit the aerosol reflectance to all NIR/SWIR bands. The method will then be skewed to bands with better radiometric performance (i.e., the NIR). And when the weight is set 0 for NIR bands, the cost function will be skewed toward longer wavelengths in the SWIR, where the ocean signal is still negligible. In this implementation, we vary the SW, adaptively, as a function of the number of iterations in the iterative scheme of Bailey et al. (2010), which is currently used in the standard NASA AC algorithm to estimate any non-negligible water-leaving reflectance contribution in the NIR bands. The Bailey algorithm works by modeling the ocean reflectance in the NIR based on a bio-optical model for productive waters. The algorithm is initiated by a first guess of the NIR ocean reflectance [i.e., R_rs(NIR) = 0], where the AC is performed, and then the R_rs(NIR) is estimated based on a bio-optical model that is propagated to the TOA to perform another AC and this process is repeated until the changes in the retrieved ocean reflectance is <2%. Similarly, the MBAC algorithm performs the AC at every iteration while bio-optical model parameters and the SW are tuned until the convergence criterion of 2% change in ocean reflectance is met. Thus, more iterations indicate more difficulty in fitting the bio-optical model possibly due to a higher optical complexity in turbid waters. The SW is then calculated as $SW(\lambda )=exp(-\tilde{\beta }(\lambda )\times \frac{\left[i-2\right]}{\left[i_{max}-2\right]})$, where i is the number of iterations in the current step and i_max is the maximum number of iterations set in the Bailey algorithm (operationally i_max = 11). Note that the actual number of iterations is reduced by 2 since the algorithm always performs at least two iterations in the AC: the first one with Rayleigh correction only (to estimate glint), and the second one for the aerosol correction. $\tilde{\beta }(\lambda )$ is an empirically estimated value that determines the slope of the exponential function for a given sensor by processing various scenes to inspect for image artifacts. We adopted an exponential function for the SW to ensure a quick transition toward the SWIR bands once non-negligible NIR ocean signal is detected since the SWIR bands will have an effect only when the weight on the NIR bands is largely reduced. This is because measurement uncertainty on the NIR is nearly an order of magnitude lower than the SWIR bands (at least for MODIS and VIIRS sensors). Higher value of the slope $\tilde{\beta }(\lambda )$ > 10 leads to a quick switching to the SWIR bands in coastal waters, including for low/moderate turbidity, while smaller values < 5 give more dependence on the NIR AC in the same water conditions. For MODISA, $\tilde{\beta }(\lambda )=7$ for NIR bands and 0 for SWIR bands, as this provides for a smooth transition from open ocean AC, where we want an equal SW on all bands to a smaller weight on the NIR in more turbid waters. In the open ocean, NIR bands will dominate the cost function; thus, the AC will be similar to the standard approach, while in turbid waters, the AC will depend more on the SWIR bands. The slope $\tilde{\beta }(\lambda )$ will primarily impact the number of iterations required in the convergence; thus, it is not critically important to have an exact optimal value. What really matters is the bio-optical model used in the R_rs convergence in the first few iterations where the AC is affected by the modeled NIR reflectance. After three or four iterations, the bio-optical model becomes irrelevant since the cost function will be mostly skewed toward the SWIR bands. With every iteration, a new cost function will be calculated with new aerosol models, and the NIR-SWIR ocean radiance will be estimated until the convergence criteria in Bailey et al. (2010) is met. If the bio-optical model does not converge in sediment-dominant waters, the SW in those cases will skew all of the cost function toward the SWIR bands, thus improving the AC.

At each iteration of the AC, the following steps are performed.

Assuming a smooth unimodal shape to the cost function χ²(RH, f), the minimum of the function at which the best solution exists can be calculated as:

$\begin{array}{ll}\nabla {\chi }^2(RH,f)=0& (7)\end{array}$

For the sake of simplicity in the operational code implementation, the 2-d partial derivate can be converted into 1-d minimization problem by finding the minimum of the cost function for a given RH set (i.e., RH₁) from National Centers for Environmental Prediction (NCEP). However, ideally, the cost function minimization could be done for optical depth, fine-mode fraction, and relative humidity [i.e., ∇χ²(τ, RH, f) = 0]. The cost function will be minimized for a set of fine-mode fractions of aerosols. The smallest two χ² values in the set will be:

$\begin{array}{ll}{{\chi }^2}_{\text{min }1}(f)=min:\{{\chi }^2(f)\}& (8)\end{array}$

$\begin{array}{ll}{{\chi }^2}_{\text{min }2}(f)=min:\{{\chi }^2(f)~({\chi }_{\text{min }1}^2\in {\chi }^2)\}& (9)\end{array}$

The observed aerosol reflectance typically falls in-between the two closest aerosol reflectance, ρ_a(λ, RH₁, f_{min 1}) and ρ_a(λ, RH₁, f_{min 2}) from the model set, and are chosen based on the ${{\chi }^2}_{\text{min }1}(f)$ and ${{\chi }^2}_{\text{min }2}(f)$, similar to the current operational algorithm. Since the fine-mode fractions in the table are discrete values with a relatively coarse step, an interpolation or a smoothing scheme of the aerosol reflectance is necessary. One way of doing this is to weight all of the aerosol models within the set for all fine-mode fractions with the χ².

$\begin{array}{ll}{\rho }_a(\lambda ,R{H}_1,f_{mix})=\frac{{\displaystyle {\sum }_{n=1}^{max}}1/{{\chi }^2}_n\times {\rho }_a(\lambda ,R{H}_1,f_n)}{{\displaystyle {\sum }_{n=1}^{max}}1/{{\chi }^2}_n},& (10)\end{array}$

where n is the number of models to be mixed such that n starts from minimum χ² and ends with the maximum χ². However, there is no strong justification to mix all models since a mixture of all the models is not what happens in the atmosphere. A more physical description is to find the most immediate models around the observations, of which ${{\chi }^2}_{\text{min }1}$ and ${{\chi }^2}_{\text{min }2}$ can be used as a weight to the aerosol reflectance, where n is 2.

This process is repeated for the second set of RH in the case that the ancillary RH falls between two values in the aerosol LUT to estimate ρ_a(λ, RH₂, f_mix). Finally, a linear interpolation of the two estimated aerosol reflectance is calculated as follows:

$\begin{array}{l}{\rho }_a(\lambda ,R{H}_{obs},f_{mix})={(1-w_{RH})\times \rho }_a(\lambda ,R{H}_1,f_{mix})\\ +{w_{RH}\times \rho }_a(\lambda ,R{H}_2,f_{mix})& (11)\end{array}$

The final ρ_a(λ, RH_obs, f_mix) should fit through the observed aerosol reflectance in the NIR and SWIR channels, while the extrapolated reflectance to the visible channels based on the model mixtures are used for the aerosol correction.

To demonstrate how the fitting of the spectral information improves the determination of the aerosol spectral dependence, we show in Figure 3 an example of two retrievals of the aerosol reflectance for a 50% fine-mode fraction case and coarse-mode dominant aerosol case, 10% fine-mode fraction, at 77.5% RH, using the 2-band and the 6-band MBAC algorithms. The analysis is done by propagating an assumed ocean reflectance for Chlor-a = 0.03 mg m⁻³, from The International Ocean-Color Coordinating Group (IOCCG) report 10 for MODIS bands, to the TOA and adding the Rayleigh (+ glint) and the aerosol reflectance at one geometry (solar zenith θ₀ = 25°, view zenith, θ = 26°, relative azimuth angle, φ = 90°) (IOCCG, 2010). We assume an optical depth of 0.2 at 869 nm for the two aerosol cases. The summation of all these signals at TOA is the total radiance (reflectance), of which we add sensor random + systematic noise (as described in the section Error Assessment). This would simulate the expected measurement uncertainty for these specific observations. The Rayleigh (+ glint) reflectance is then removed from the total signal, and the resultant signal is the noised observed TOA reflectance (blue curve), which is the summation of the water and aerosol reflectance at TOA needed for the aerosol correction algorithms. We also show the true (input) aerosol reflectance that we aim to retrieve, shown as the black curve. The red and green curves show the retrieved aerosol reflectance from the observed (noised) reflectance, for the 2-band standard AC and the 6-band MBAC algorithm, respectively.

FIGURE 3

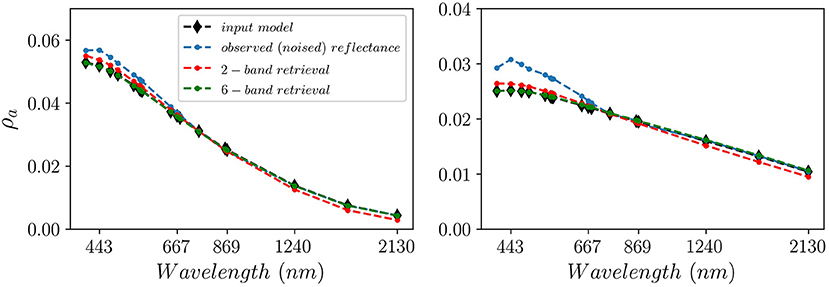
Figure 3. Example to demonstrate the aerosol reflectance retrievals for MODISA using the 2-band (red curve) and 6-band (green curve) algorithms. The input model reflectance (black curve) is before adding noise; meanwhile, the observed reflectance (blue curve) is the noised reflectance after removing the Rayleigh + glint reflectance (i.e., the observed reflectance is the aerosol + water signal). The left panel is for aerosol with 50% fine-mode fraction and the right panel is for 10% fine-mode fraction, and in both cases for 0.2 optical depth at 869 nm. Solar zenith θ₀ = 25°, view zenith, θ = 26°, relative azimuth angle, φ = 90°.

Since the 2-band algorithm aims to match the spectral dependence of the aerosol as a two-band ratio in the NIR, extrapolating that information to the visible (and SWIR) will depend on the radiometric quality of these two NIR bands and the linear mixing of the aerosol types in the LUT necessary for the visible correction. As can be seen from Figure 3, the spectral dependence of the retrieved aerosol reflectance using the 2-band algorithm (red curve) is similar to the observed reflectance (blue curve) within the NIR range, which is expected. However, that does not necessarily retrieve the correct reflectance in the visible and SWIR, of which the retrieval departs from the input reference reflectance (black curve) in both fine-mode fraction cases. On the other hand, the 6-band algorithm fits the spectral information for the whole NIR-SWIR range and thus is less affected by the sensor noise as more spectral information improves the chance to fit the right model. This is also demonstrated as the 6-band algorithm retrievals (green curve) overlap with the input reference model reflectance (black curve) throughout the whole spectrum. This demonstration, however, is qualitative; thus, a more thorough analysis is shown in the section Error Assessment, including the method to add noise to the reflectance.

Correction for Absorbing Gases

Ocean color bands are designed to avoid detection in spectral regions contaminated by strongly absorbing gases such as water vapor, oxygen, methane, and carbon dioxide. However, due to the imperfect spectral response of the detectors (i.e., broad bandwidth and out-of-band response), the measured TOA radiance is modulated by strongly absorbing gases. AC requires a correction for strongly absorbing gases as well as broadly absorbing gases, such as ozone and nitrogen dioxide that mostly absorb in the visible. The current NASA algorithm uses the method of Gordon (1995) that was implemented for SeaWiFS and then extended to all ocean color sensors. The method corrects for strongly absorbing gases, primarily for water vapor, by correcting the epsilon ratio using an empirical polynomial function for a given column gas (water vapor) concentration and air mass. To avoid this step in our proposed AC algorithm, we generate a LUT of transmittances of all strongly absorbing gases that include oxygen, water vapor, methane, and carbon dioxide using HITRAN 2012 LBL absorption database (Rothman et al., 2013; Ibrahim et al., 2018). The water vapor LUT is a function of column water vapor following the ATREM method of Gao et al. (2000). The other gases are corrected based on ancillary or climatology column concentrations, while the transmittance is adjusted for air mass per pixel. MODIS and VIIRS sensors have strong out-of-band effects from absorbing gases in the SWIR range; thus, the LUT correction method allows for a proper correction to utilize all window SWIR bands (i.e., excluding water vapor bands) in the MBAC algorithm.

Error Assessment

Algorithm

The aerosol LUT in the MBAC algorithm is pre-computed at discretized optical properties of the aerosols; thus, the interpolation step between different fine-mode fractions and relative humidity increases the uncertainty in the retrieval of the remote sensing reflectance. To assess the algorithm error, we introduce a set of aerosol optical properties that are not part of the discretized LUT. We do so by simulating the aerosol reflectance set for an RH of 77.5%, which falls between the 75% and 80% RH in the operational LUT. The aerosol properties and reflectance are then calculated using the model set of Ahmad et al. (2010) (i.e., 10 fine-mode fractions), but with an RH of 77.5%. To define the uncertainty in the AC, we estimate the root mean squared error (RMSE) in Δρ_w for the normalized water-leaving radiance. We do so by assuming a reference ocean reflectance from IOCCG report 10 for case I clear waters with chlorophyll concentration, Chlor-a, 0.03 mg m⁻³ (IOCCG, 2010). That reference reflectance is then propagated to the TOA assuming different aerosol types and optical thicknesses for different geometries to perform the uncertainty analysis. The aerosol models are based on Ahmad et al. (2010) operational LUTs. Figure 4 shows the polar plot of Δρ_w at 443 nm for all view geometries in the LUT, where 0° relative azimuth is specular reflection plane, and for three solar angles, 10, 20, 30, and 60°.

FIGURE 4

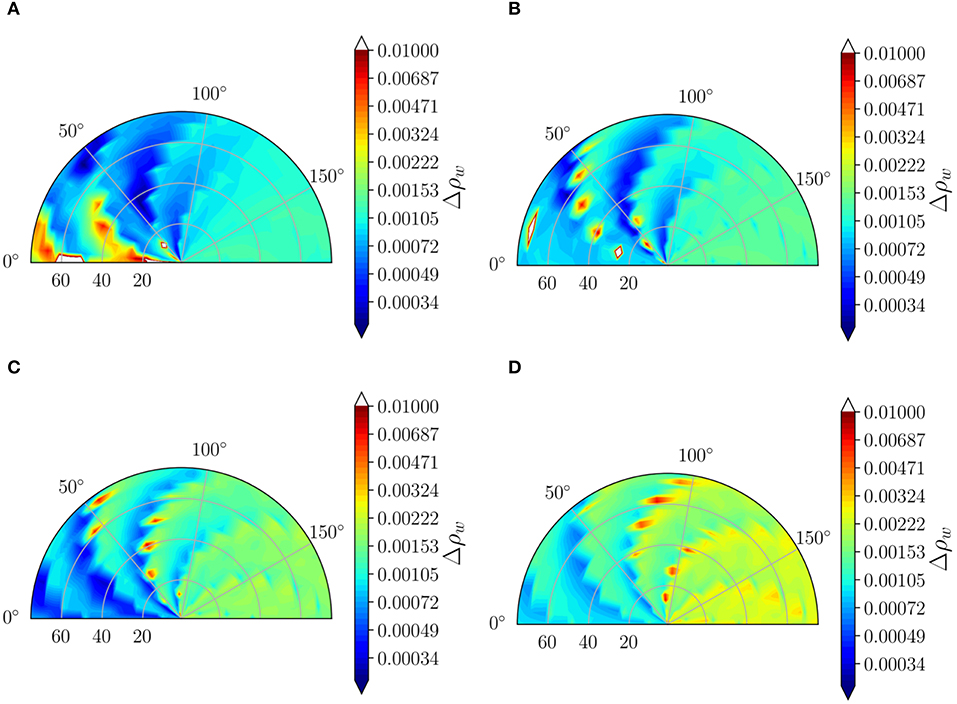
Figure 4. (A–D) are the algorithm uncertainty in water reflectance, Δρ_w, at 443 nm as a function of the viewing geometry for solar zenith angles of 10, 20, 30, and 60°, respectively. The simulations are done for all aerosol models with relative humidity RH = 77.5% at optical depth at 869 nm from 0.05 to 0.35, and the retrieval is done using models with RH = 75% and 80%.

The aerosol models encompass all aerosol types, as defined in Ahmad et al. (2010), from fine-mode to coarse-mode dominant cases with equal weights, and the aerosol reflectances were calculated for optical depth ranging from 0.05 to 0.35 at 869 nm. The uncertainty level in the retrievals is generally smaller than the scale midpoint at 0.0015 and increases with increasing solar angle from 10 to 60°. There are some hotspots in the geometry plot that indicated a higher uncertainty in the retrievals. These regions could be due to the decreased sensitivity of the aerosol models, where the algorithm finds it difficult to determine the type due to the ambiguity in the phase function of aerosols at certain scattering angles, or geometry midpoint interpolation errors, but further analysis is needed. The uncertainty in the aerosol reflectance at 443 nm, optical depth retrievals at 869 nm, and the Angstrom coefficient expressed as a percent difference are shown in Figure 5 for all simulated cases of 1,037,400 (i.e., 12 solar angle × 35 sensor angle × 19 azimuth angle × 10 models × 13 optical depth).

FIGURE 5

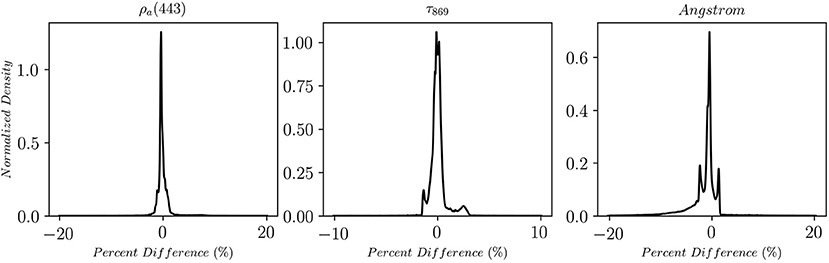
Figure 5. The normalized density histogram of the percentage difference for the aerosol reflectance and optical depth retrievals at 443 and 869 nm, respectively, and the Angstrom coefficient for all cases of different aerosol types, optical depths, and geometries.

The mean bias in the aerosol reflectance at 443 nm is −0.04% and the standard deviation is 3.5%, while optical depth retrieval is 0.05% with a standard deviation of 1.35%, and the Angstrom coefficient retrieval shows a mean bias of −1.9% with a standard deviation of 15%. The small bias and standard deviation indicate that the algorithm can well-retrieve the optical depth; however, there is a more significant uncertainty in the Angstrom coefficient retrievals with tendency to retrieve coarser aerosol types than the input data. This could be an inherent error due to the definition of the Angstrom coefficient that assumes a power law relationship of the aerosol spectral dependence from 443 to 869 nm. Since we are including all cases of aerosol types with equal representation, the uncertainty is overestimated. In the cases at the extreme ends of the aerosol's LUT, there could be large errors in the retrievals because of the necessity to extrapolate to models that are not in the table. However, these extreme ends of the LUT are intentionally added to reduce that necessity for the extrapolation since these aerosol conditions are rarely observed based on AERONET data (Ahmad et al., 2010). Finally, note that the uncertainty increases at the highest two values of fine-mode fractions (i.e., f = 0.95 and f = 0.80). Since most of the aerosol absorption is in the fine-mode aerosols, these two models are more absorbing than others; thus, the difference in the single scattering albedo is >0.05 in the blue wavelengths, which can induce more than 3% errors in the aerosol reflectance at TOA by linear mixing (Abdou et al., 1997; Ahmad et al., 2010). Additionally, NIR and SWIR bands used in the cost function are less sensitive to fine-mode aerosols; thus, fine-mode dominant cases will be erroneously observed as coarser aerosols, which is the case for the operational algorithm. The only method to reduce that uncertainty is by inferring the aerosol properties at shorter wavelengths while minimizing the impact of the marine reflectance. For example, observations in the UV could improve the MBAC algorithm when non-absorbing fine-mode aerosols are present over coastal (absorbing) waters where the UV signal is negligible. OCI will measure in the UV, which will be a subject of future work.

Random Noise

The uncertainty in the TOA radiance measurements due to sensor random noise will impact the retrieval uncertainty of the ocean reflectance through influence on the AC process. The uncertainty propagation of the sensor noise is simulated here using the Monte Carlo method, where the sensor noise at a given SNR value is generated for 300 iterations for all aerosol model sets mentioned above. We performed the sensitivity analysis using the NIR 2-band AC (standard approach) and a 6-band MBAC (i.e., for MODIS 748, 859, 869, 1,240, 1,640, and 2,130 nm). The theoretical analysis for MODIS-Aqua is done for the six bands; however, we drop 1,640 nm in our real retrievals because of defective detectors at that band. The noise model here is based on the MODIS model with the noise-equivalent radiance of:

$\begin{array}{ll}NE\Delta L(\lambda )=\left[C_0(\lambda )+C_1(\lambda )\times L_t(\lambda )\right]\times S(\lambda ),& (12)\end{array}$

where C₀(λ) and C₁(λ) are linear fit coefficients of the noise model from Xiong et al. (2010), and S(λ) is the spectral-dependent spatial weight to bring all bands to a common spatial resolution since MODIS land bands have finer spatial resolution than ocean bands. We also performed an analysis at PACE-OCI radiometric performance levels, where the MODIS noise model was scaled to OCI noise levels such that the noise equivalent radiance, NEΔL, response to the dynamic range is consistent for both instruments.

The random noise for each iteration is generated as follows:

$\begin{array}{ll}\sigma =\frac{NE\Delta L(\lambda )}{L_t(\lambda )},& (13)\end{array}$

and the Gaussian random noise is generated as:

$\begin{array}{ll}{L}_{noise}={N}(0,\sigma ),& (14)\end{array}$

The result of the analysis shown in Figures 6A,B indicates that the geometrically averaged uncertainty in reflectance, Δρ_w, is closer to 0.0016 levels for the 6-band MBAC algorithm, while it is slightly higher near 0.0021 levels for the 2-band AC for MODIS-Aqua noise levels. The improvement in the uncertainty between the two algorithms is shown in Figure 6C as the ratio of Δρ_w(6 − band) to the Δρ_w(2 − band) AC. The average reduction in uncertainty is nearly 24% using the 6-band MBAC for the MODIS-Aqua sensor; however, when the same analysis for the 6-band MBAC is done using the expected OCI performance, the average reduction in the uncertainty approaches 29% as shown in Figure 6D. The relatively modest improvement for MODIS-Aqua using the MBAC algorithm is attributed to the reduced performance of the SWIR radiometric detection. The high NEL(λ) for MODIS SWIR channels reduces the weight in the cost function in determining the best aerosol models, relative to the higher radiometric quality of the NIR bands. The MBAC algorithm, however, shows more improvement for the OCI type of radiometric performance due to the increased SNR of the SWIR detectors relative to its NIR channels, although the visible performance is kept the same as MODIS for relative comparison. It is apparent that the merit of the MBAC algorithm will prevail when the estimated aerosol reflectance at the NIR bands is compromised. In fact, that is the case for nearly 10% of the global ocean, where the non-negligible reflectance from the turbid/coastal ocean leads to systematic underestimation and often negative reflectance retrievals due to overcorrection for aerosols. More details will be discussed in the section Application to Ocean Color Instrument.

FIGURE 6

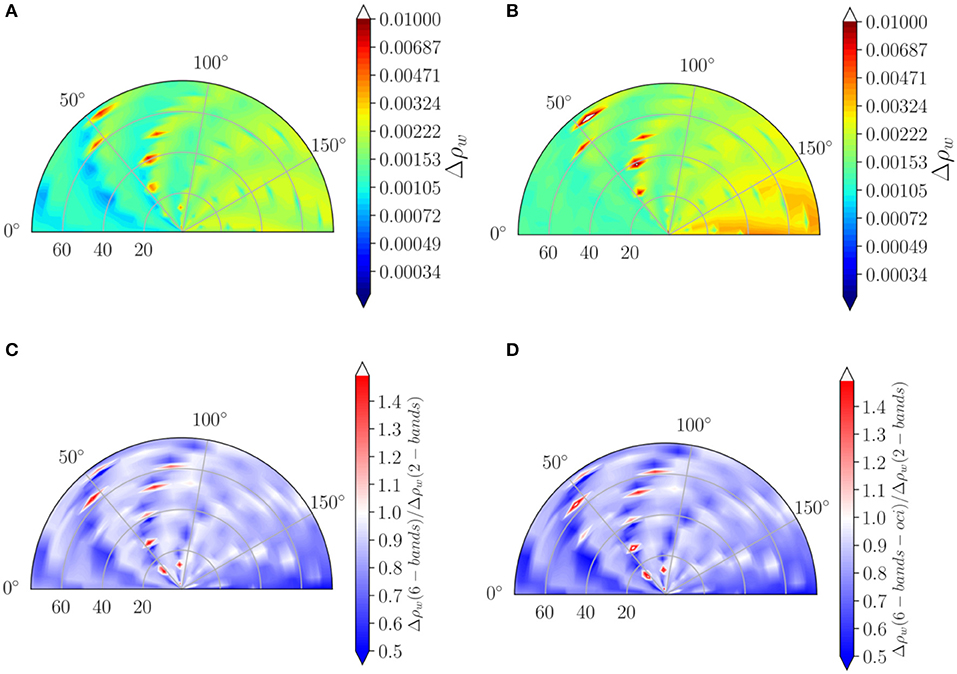
Figure 6. (A,B) are the algorithm + random uncertainty in water reflectance, Δρ_w, at 443 nm as a function of the viewing geometry for solar zenith angles of 30°, using six bands MBAC and two NIR bands AC, respectively. (C,D) are the ratio between the reflectance uncertainty using six bands AC with MODIS-Aqua noise levels, and PACE OCI noise levels. The simulations are done for all aerosol models with relative humidity RH = 77.5% at optical depth at 869 nm from 0.05 to 0.35, and the retrieval is done using models with RH = 75 and 80%.

Systematic Errors

To have a complete understanding of the potential sources of uncertainty for the MBAC algorithm, we also performed an analysis to understand the impact of systematic uncertainty on the retrievals. Systematic errors in measurements are very difficult to characterize post-launch due to the lack of an accurate absolute calibration apparatus on-orbit. Typically, a solar diffuser is used as a calibration reference; however, due to the immediate degradation of the diffuser, the absolute calibration with a high degree of certainty cannot generally be achieved. Thus, the ocean color community depends on a system vicarious calibration, which aims to remove any systematic bias due to the sensor or algorithm errors. For all ocean color sensors processed by NASA GSFC, we use the vicarious calibration method by Franz et al. (2007) using the MOBY in situ measurements as ground truth. The vicarious calibration procedure reduces the systematic uncertainty to 0.5% for all bands relative to the 869-nm band for MODIS sensors. However, the absolute calibration at 869 nm and SWIR bands is assumed to be 2%. Typically, systematic errors will depend on the environment and geometry at which the instrument is observing the Earth. Systematic bias can be influenced by various observing conditions and sensor characteristics, such as the operating temperature, instrument polarization sensitivity, stray light, and optical or electronic cross-talk. The behavior of the errors on a per-pixel basis cannot be easily predicted; thus, it remains unknown; however, the bias can be reduced through prelaunch characterization and derived correction algorithms (e.g., polarization correction of the instrument, correction for out-of-band response, estimation, and correction for straylight). The spectral correlation of systematic bias can play an important role in determining the uncertainty of the retrievals. For example, the spectral correlation of the two-band ratio algorithm will suffer when the systematic bias is random and independent at the two bands. Since such a spectral covariance in bias cannot be directly measured on-orbit, we assume a conservative scenario in our analysis by assuming a 10% correlation inter-bands, although the spectral correlation between bands could increase/decrease depending on the spectral distance. We ran the MC analysis assuming a random bias at the levels mentioned above for MODIS-Aqua observations. The covariance matrix, Cov(λ_n, λ_m), of the system errors is equal to 0.1 for off-diagonal elements and 1 for diagonal ones. The correlated random bias is then calculated as follows:

$\begin{array}{ll}Bias(iterations,\lambda )={U}(-1,1)·L({\lambda }_n,{\lambda }_m)& (15)\end{array}$

The bias is generated for the number of iterations in the MC analysis for each band. ${U}$(−1, 1) is uniform distribution of random numbers from −1 to 1, while L(λ_n, λ_m) is Lower Cholesky factorization of the covariance matrix such that:

$\begin{array}{ll}Cov\left({\lambda }_n,{\lambda }_m\right)=L\left({\lambda }_n,{\lambda }_m\right)D\left({\lambda }_n,{\lambda }_m\right)L^{\ast }\left({\lambda }_n,{\lambda }_m\right)& (16)\end{array}$

${\mathit{\text{L}}}^{*}({\lambda }_n,{\lambda }_m)$ is the conjugate value of the matrix and D(λ_n, λ_m) is the diagonal matrix. The Cholesky matrix allows the generation of random errors with inter-bands correlation specified in the covariance matrix. The bias levels are then re-adjusted to match the level of the instrument.

In Figures 7A,B, the uncertainty, Δρ_w, at 443 nm is due to algorithm + random + systematic errors for the 6-band MBAC and NIR 2-band AC, respectively. The average uncertainty for the 2-band AC is 0.0036, while for the 6-band MBAC algorithm, the average uncertainty is 0.0024, with an improvement of 33% over the 2-band standard algorithm as shown in Figure 7C. For the OCI configuration, at higher SNRs, the improvement is only slight at 37% relative to the MODIS-Aqua configuration in Figure 7D. This can be attributed to the dominant impact of systematic uncertainty over random noise; however, in practice, OCI is expected to have lower systematic errors at 1.6% levels, which is not simulated here. Additionally, the high SNR on OCI's SWIR will have a more significant impact when retrieving in coastal waters, when the NIR signal is contaminated by non-negligible water-leaving radiance.

FIGURE 7

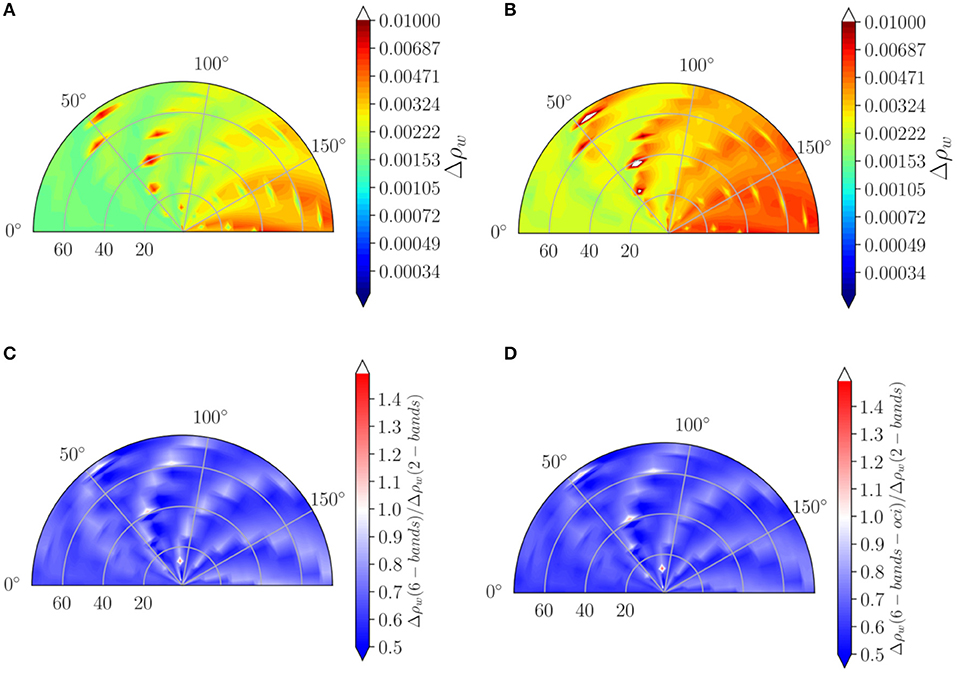
Figure 7. (A,B) are the algorithm + random + systematic uncertainty in water reflectance, Δρ_w, at 443 nm as a function of the viewing geometry for solar zenith angles of 30°, using six bands MBAC and NIR two bands AC, respectively. (C,D) are the ratio between the reflectance uncertainty using 6-bands AC with MODIS-Aqua noise levels and PACE OCI noise levels. The simulations are done for all aerosol models with relative humidity RH = 77.5% at optical depth at 869 nm from 0.05 to 0.35, and the retrieval is done using models with RH = 75 and 80%.

Application to Ocean Color Instrument

Unlike MODIS or VIIRS, the SWIR detection assembly on OCI will include channels specifically tuned for good radiometric performance over the relatively dark ocean. This significant advancement will provide an opportunity to improve ocean color observations in complex water environments (i.e., coastal ocean) due to the increased sensitivity to the aerosols and less to the water signal. With the MBAC algorithm, the combined utilization of all SWIR channels (excluding water vapor bands) and NIR channels will offer an improved AC over coastal waters and open ocean by utilizing more spectral bands to reduce the effect of sensor noise and with adaptive weighting toward the bands that are less influenced by non-negligible water-leaving radiance.

Figure 8 shows the spectral uncertainty, Δρ_w, for proxy OCI wavelengths from the UV to red wavelengths for open ocean and coastal turbid waters (with high total suspended material, TSM). The open ocean reflectance was simulated with Hydrolight assuming Chlor-a = 0.03 mg/m³ and TSM = 0 g m⁻³ while turbid waters assume TSM = 10 g m⁻³ that has been propagated to the TOA for each atmospheric composition and geometry [more details are in Ibrahim and McKinna (2018)]. The retrieval was done with the 2-band NIR-only algorithm and the SWIR-only MBAC algorithm. The uncertainty is calculated for the aerosol set as in the section Error Assessment except for one specific geometry in the operational LUTs (i.e., solar zenith, θ₀ = 25°, view zenith, θ = 26°, relative azimuth angle, φ = 90°). For an OCI-like instrument, the SWIR MBAC algorithm shows a slight reduction in the uncertainty as compared to the 2-band NIR AC over open ocean conditions. In contrast, over turbid waters, the non-negligible water-leaving radiance at the NIR bands shows a large uncertainty (systematic bias) in the reflectance retrievals from the 2-band NIR AC, which is substantially reduced using the SWIR MBAC algorithm. As previously discussed, the SW, SW(λ), in the cost function is based on the NIR iteration scheme of Bailey et al. (2010) to reduce the impact of contaminated NIR bands in the AC over productive waters. The algorithm sequentially iterates over a bio-optical model until a convergence criterion is met. The SW is directly dependent on the convergence process such that the weight on the contaminated NIR bands is quickly (exponentially) reduced with increasing difficulty in the bio-optical model fit. The SW is proportional to the number of iterations; thus, it translates linearly. At the maximum of the iterations range, the SW is set to zero on the NIR bands; thus, the algorithm transitions into a full SWIR MBAC. This adaptive weight allows for a smooth transition in the processing between clear waters and productive waters; thus, it does not require switching between two or more algorithms. This allows for producing more consistent products, while maximizing the information content from all observations at all bands.

FIGURE 8

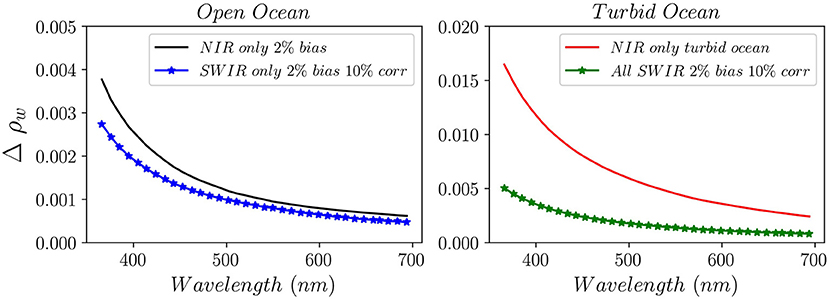
Figure 8. The spectral uncertainty, Δρ_w, for a proxy OCI wavelengths from the UV to red wavelengths for open ocean and coastal turbid waters. The uncertainty is calculated at one specific geometry (i.e., solar zenith θ₀ = 25°, view zenith, θ = 26°, relative azimuth angle, φ = 90°). The analysis assumes a 2% systematic bias at NIR and SWIR bands.

Application to MODIS Retrievals

The MBAC algorithm has been implemented into NASA's L2gen processing code. L2gen (Level-2 generator) within the SeaDAS software package is the multi-sensor Level-1 to Level-2 processing code developed and maintained by NASA's Ocean Biology Processing Group (OBPG) that is capable of retrieving ocean color products from TOA radiances for a host of sensors. L2gen supports multiple AC methods and variations that can be applied to a variety of ocean color sensors (Gordon and Wang, 1994; Ruddick et al., 2000; Wang et al., 2009; Ahmad et al., 2010; Bailey et al., 2010; Ibrahim et al., 2018).

Figure 9 shows the Chlor-a retrieval from MODISA observations for both the operational algorithm and the MBAC algorithm (748, 859, 869, 1,240, and 2,130 nm, excluding 1,640 nm for Aqua because of bad detectors), the average percent difference (APD), and the SW at NIR over the East Coast of the United States. Qualitatively, there is general agreement between the two algorithms for the Chlor-a product and through the APD histogram. This agreement confirms the feasibility of implementation in an operational environment. Differences are evident, however, in coastal waters such as the turbid Chesapeake Bay (39.5°-37° N, 75.5°-76° W) or the shallow Pamlico Sound (35° N, 76° W) as shown in the APD figure. There are some apparent artifacts in the upper part of the scene from the MBAC retrievals that could be due to strong NIR/SWIR calibration artifacts at the edge of the scan; however, a further assessment of SWIR calibration for MODIS is necessary for reliable retrievals. The SW map shows lower values (i.e., closer to 0) near the coast where the Bailey NIR iterative algorithm was triggered, thus relying more on the SWIR bands with each increased iteration. The SW is, however, higher over more clear water over the open Atlantic waters; thus, the algorithm relies on both the NIR and SWIR bands. We believe that the MBAC algorithm should be validated in the more common moderate turbid waters and highly productive waters. That scene includes regions with high turbidity such as the upper bay regions and inland rivers as well as shallow water regions such as Pamlico Sound, highly productive waters such as middle Chesapeake Bay region, highly absorbing waters such as Long Island Sound, and the less productive to more clear waters in the open Atlantic waters. Testing the MBAC algorithm over a large dynamic range of water conditions and more complex atmospheric conditions (i.e., including the large range of Angstrom coefficients from coarse to fine aerosols) provides more insight.

FIGURE 9

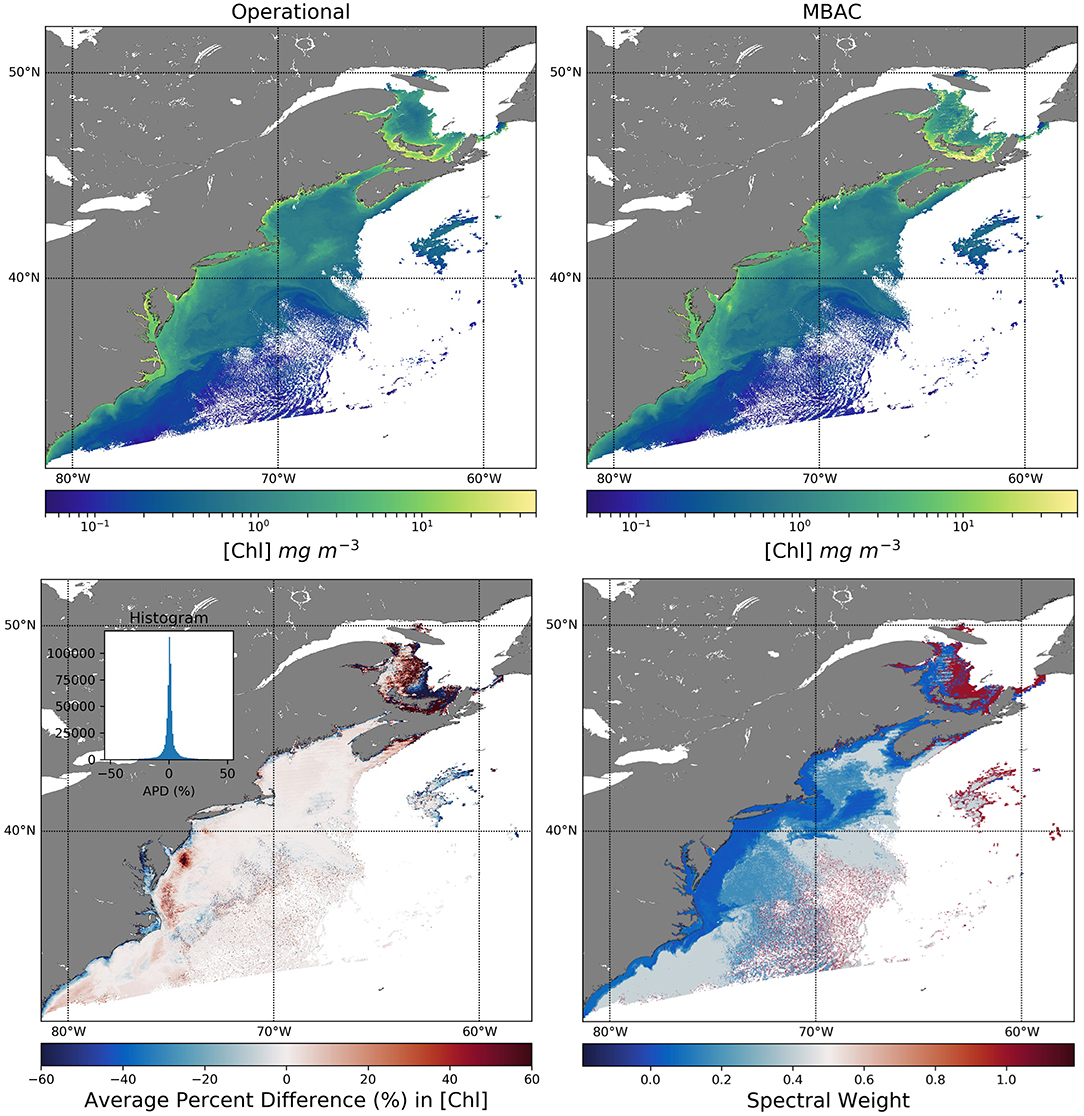
Figure 9. MODISA chlor-a retrieval of a scene over the east coast of the US using the operational 2-bands and the MBAC algorithm, the average percent difference (APD), and the NIR Spectral Weight (SW) map used in the MBAC retrievals.

We also show in Figure 10 the aerosol's Angstrom coefficient retrieval over these coastal regions for both the operational and the MBAC algorithm.

FIGURE 10

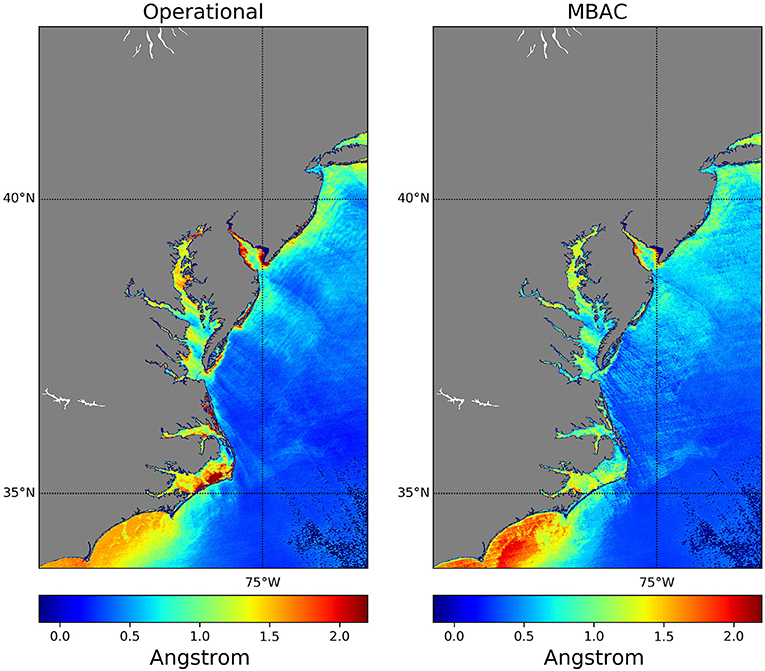
Figure 10. MODISA retrieval of the aerosols' Angstrom coefficient of a scene over the east coast of the US using the operational 2-band and the MBAC algorithm.

The operational algorithm shows an increased Angstrom over turbid or shallow regions near the coast that can be attributed to the failure in the NIR iterative algorithm to mitigate the non-negligible water-leaving radiance in the NIR bands. This artifact in the aerosol properties typically leads to the overcorrection of aerosol radiance and the potential retrieval of negative radiances. However, using the adaptive SW in the MBAC algorithm, it quickly damps that NIR contamination by decreasing the weight of the NIR bands in the cost function, and thus, the Angstrom coefficient is reduced to a range that agrees better with the surrounding pixels. Notice that the southwesternmost part of the scene shows an increase in the Angstrom coefficient with the MBAC algorithm, which could be a more realistic retrieval or an artifact due to a bias in the SWIR calibration. However, this could indicate that the MBAC algorithm is sensitive to fine-mode as much as coarse-mode aerosols. Better quantitative evidence is further discussed in the next section.

Validation

Using NASA's SeaBASS dataset of in situ R_rs measurements, we performed match-up to MODIS retrievals at eight bands in the visible spectral range near 412, 443, 488, 531, 547, 555, 667, and 678 nm, using both the 2-band operation algorithm and the MBAC algorithm for MODIS-Aqua. Many of the SeaBASS data points are coastal, however less frequent than AERONET-OC data. Table 1 below shows the spectral uncertainty, ΔR_rs(λ), R², and the mean bias in the retrievals compared to in situ observations for MODISA for both the operational and the MBAC algorithm. The retrieval uncertainty, ΔR_rs(λ), for the 6-band MBAC algorithm is reduced as compared to the operational algorithm, especially in the green wavelengths at 531, 547, and 555 nm, where the uncertainty is reduced by 52, 55, and 29%, respectively. There is a slight increase in uncertainty at 678 nm, which could be due to the lack of high-quality in situ observations at longer wavelengths. The coefficient of determination, however, is slightly lower for 412 and 443 for the MBAC algorithm relative to the operational one. There is a more significant correlation for the green channels, 531, 547, and 555, using the MBAC algorithm. Overall, the uncertainty is reduced using the MBAC algorithm due to the decreased mean bias in retrievals. Because of the extrapolation of the aerosol information from the NIR/SWIR to the visible, at shorter wavelengths, the retrievals uncertainty will increase specifically in coastal waters where the ocean blue reflectance is small. Thus, retrievals in the blue bands are slightly noisier due to the impact of low-SNR SWIR bands due to the spectral extrapolation of the selected aerosol models.

TABLE 1

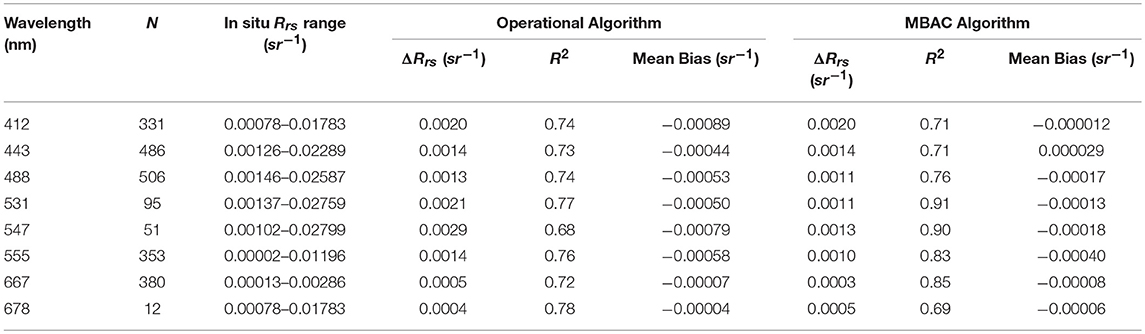
Table 1. A summary of statistical indicators to match-ups of MODISA retrievals with in situ R_rs from the SeaBASS dataset.

A further investigation into a proper estimation of systematic uncertainty and its spectral correlation is necessary to provide uncertainties that are similar to in situ validation. It is important to note that the validation analysis has been done with an initial SWIR vicarious calibration following Franz et al. (2007). The reduction of systematic bias is essential to provide reliable MBAC retrievals, which will require a thorough assessment of the SWIR calibration in a future study.

Conclusion

The MBAC algorithm shows several potential merits over NASA's current operational Gordon and Wang (1994) 2-band ratio aerosols correction algorithm. The utilization of multibands from the NIR to SWIR in the AC reduces the uncertainty in the retrieval of ocean color reflectance due to sensor random and systematic noise. The adaptive SW reduces the weight on the NIR bands over turbid or highly productive waters; thus, the contamination from bright ocean signal in the NIR is reduced. This algorithm enables the production of spatially consistent ocean color data in turbid and open ocean conditions. The limitations of the algorithm are mainly tied to the radiometric performance in the SWIR bands. A significantly decreased performance in the SWIR for some sensors leads to noisy retrievals in the coastal regions. For the OCI on PACE, the SWIR bands are expected to have a much higher SNR compared to MODISA within the radiance range observed over oceans; thus, a significant improvement using the MBAC algorithm is expected, especially in coastal regions. The sensitivity analysis shows an overall reduction in the reflectance uncertainty by 33% over open ocean conditions and over 300% over turbid water conditions in the blue spectral region. In addition, the SeaBASS in situ match-ups show an improvement in the retrievals using the MBAC algorithm relative to the 2-band algorithm, especially in the green spectral range where the reduction in the uncertainty is nearly 50% at 531 nm. An improvement in the system vicarious calibration of the SWIR bands for current ocean color sensors shall increase the value of the MBAC algorithm in producing more consistent products.

Author Contributions

AI performed the analysis in the manuscript for the sections Error Assessment, Application to Ocean Color Instrument, Application to MODIS Retrievals, and Validation. BF contributed to editing and guiding the manuscript discussion. ZA provided Figure 1 and the aerosol LUTs. SB provided the SWIR vicarious calibration gains necessary for the MBAC algorithm.

Funding

Support for this work was provided by a NASA Ocean Biology and Biogeochemistry PACE Science Team and Aqua, Terra, and Sumi-NPP Science Team award.

Conflict of Interest Statement

AI was employed by Science Systems and Applications Inc. and ZA was employed by Science Application International Corp. when this manuscript was being prepared.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We acknowledge the MOBY team of NOAA for providing the in situ MOBY radiometry, Chris Proctor for providing the SeaBASS dataset, and other OBPG team members for their valuable input.

References

Abdou, W. A., Martonchik, J. V., Kahn, R. A., West, R. A., and Diner, D. J. (1997). A modified linear-mixing method for calculating atmospheric path radiances of aerosol mixtures. J .Geophys. Res. Atmos. 102, 16883–16888. doi: 10.1029/96JD03434

CrossRef Full Text | Google Scholar

Ahmad, Z., and Franz, B. A. (2018). “Uncertainty in aerosol model characterization and its impact on ocean color retrievals,” in PACE Technical Report Series, Volume 6: Data Product Requirements and Error Budgets, eds I. Cetinić, C. R. McClain, and P. J. Werdell (Greenbelt, MD: NASA Goddard Space Flight Space Center), 45–55.

Google Scholar

Ahmad, Z., Franz, B. A., McClain, C. R., Kwiatkowska, E. J., Werdell, J., Shettle, E. P., et al. (2010). New aerosol models for the retrieval of aerosol optical thickness and normalized water-leaving radiances from the SeaWiFS and MODIS sensors over coastal regions and open oceans. Appl. Opt. 49:5545. doi: 10.1364/AO.49.005545

PubMed Abstract | CrossRef Full Text | Google Scholar

Aurin, D., Mannino, A., and Franz, B. (2013). Spatially resolving ocean color and sediment dispersion in river plumes, coastal systems, and continental shelf waters. Remote Sens. Environ. 137, 212–225. doi: 10.1016/j.rse.2013.06.018

CrossRef Full Text | Google Scholar

Bailey, S. W., Franz, B. A., and Werdell, P. J. (2010). Estimation of near-infrared water-leaving reflectance for satellite ocean color data processing. Opt. Express 18, 7521. doi: 10.1364/OE.18.007521

PubMed Abstract | CrossRef Full Text | Google Scholar

Brajard, J., Jamet, C., Moulin, C., and Thiria, S. (2006). Use of a neuro-variational inversion for retrieving oceanic and atmospheric constituents from satellite ocean colour sensor: application to absorbing aerosols. Neural Networks 19, 178–185. doi: 10.1016/j.neunet.2006.01.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Chomko, R. M., and Gordon, H. R. (1998). Atmospheric correction of ocean color imagery: use of the Junge power-law aerosol size distribution with variable refractive index to handle aerosol absorption. Appl. Opt. 37, 5560–5572. doi: 10.1364/AO.37.005560

PubMed Abstract | CrossRef Full Text | Google Scholar

Chomko, R. M., and Gordon, H. R. (2001). Atmospheric correction of ocean color imagery: test of the spectral optimization algorithm with the sea-viewing wide field-of-view sensor. Appl. Opt. 40, 2973–2984. doi: 10.1364/AO.40.002973

PubMed Abstract | CrossRef Full Text | Google Scholar

Chomko, R. M., Gordon, H. R., Maritorena, S., and Siegel, D. A. (2003). Simultaneous retrieval of oceanic and atmospheric parameters for ocean color imagery by spectral optimization: a validation. Remote Sens. Environ. 84, 208–220. doi: 10.1016/S0034-4257(02)00108-6

CrossRef Full Text | Google Scholar

Fan, Y., Li, W., Gatebe, C. K., Jamet, C., Zibordi, G., Schroeder, T., et al. (2017). Atmospheric correction over coastal waters using multilayer neural networks. Remote Sens. Environ. 199, 218–240. doi: 10.1016/j.rse.2017.07.016

CrossRef Full Text | Google Scholar

Franz, B. A., Bailey, S. W., Werdell, P. J., and McClain, C. R. (2007). Sensor-independent approach to the vicarious calibration of satellite ocean color radiometry. Appl. Opt. 46, 5068. doi: 10.1364/AO.46.005068

PubMed Abstract | CrossRef Full Text | Google Scholar

Frouin, R. J., and Gross-Colzy, L. S. (2016). Contribution of Ultraviolet and Shortwave Infrared Observations to Atmospheric Correction of PACE Ocean-Color Imagery. eds R. J. Frouin, S. C. Shenoi, K. H. Rao. New Delhi, SPIE.

Google Scholar

Gao, B., Montes, M. J., Li, R., Dierssen, H. M., and Davis, C. O. (2007). An atmospheric correction algorithm for remote sensing of bright coastal waters using MODIS land and ocean channels in the solar spectral region. IEEE Trans. Geosci. Remote Sens. 45, 1835–1843. doi: 10.1109/TGRS.2007.895949

CrossRef Full Text | Google Scholar

Gao, B.-C, Montes, M. J., Ahmad, Z., and Davis, C. O. (2000). Atmospheric correction algorithm for hyperspectral remote sensing of ocean color from space. Appl. Opt. 39, 887. doi: 10.1364/AO.39.000887

PubMed Abstract | CrossRef Full Text | Google Scholar

Gordon, H. R. (1995). Remote sensing of ocean color: a methodology for dealing with broad spectral bands and significant out-of-band response. Appl. Opt. 34, 8363–8374. doi: 10.1364/AO.34.008363

PubMed Abstract | CrossRef Full Text | Google Scholar

Gordon, H. R., Brown, O. B., Evans, R. H., Brown, J. W., Smith, R. C., Baker, K. S., et al. (1988). A semianalytic radiance model of ocean color. J .Geophys. Res. Atmos. 93, 10909–10924. doi: 10.1029/JD093iD09p10909

CrossRef Full Text | Google Scholar

Gordon, H. R., Du, T., and Zhang, T. (1997). Remote sensing of ocean color and aerosol properties: resolving the issue of aerosol absorption. Appl. Opt. 36, 8670–8684. doi: 10.1364/AO.36.008670

PubMed Abstract | CrossRef Full Text | Google Scholar

Gordon, H. R., and Wang, M. (1994). Retrieval of water-leaving radiance and aerosol optical thickness over the oceans with SeaWiFS: a preliminary algorithm. Appl. Opt. 33, 443. doi: 10.1364/AO.33.000443

PubMed Abstract | CrossRef Full Text | Google Scholar

Gossn, J. I., Ruddick, K. G., and Dogliotti, A. I. (2019). Atmospheric correction of OLCI imagery over extremely turbid waters based on the red, NIR and 1016 nm bands and a new baseline residual technique. Rem. Sensing. 11:220. doi: 10.3390/rs11030220

CrossRef Full Text | Google Scholar

Goyens, C., Jamet, C., and Schroeder, T. (2013). Evaluation of four atmospheric correction algorithms for MODIS-aqua images over contrasted coastal waters. Remote Sens. Environ. 131, 63–75. doi: 10.1016/j.rse.2012.12.006

CrossRef Full Text | Google Scholar

He, X., Bai, Y., Pan, D., Tang, J., and Wang, D. (2012). Atmospheric correction of satellite ocean color imagery using the ultraviolet wavelength for highly turbid waters. Opt. Express 20, 20754–20770. doi: 10.1364/OE.20.020754

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, C., Lee, Z., and Franz, B. (2012). Chlorophyll A algorithms for oligotrophic oceans: a novel approach based on three-band reflectance difference. J. Geophys. Res. Oceans 117, C01011. doi: 10.1029/2011JC007395

CrossRef Full Text | Google Scholar

Ibrahim, A., Franz, B., Ahmad, Z., Healy, R., Knobelspiesse, K., Gao, B., et al. (2018). Atmospheric correction for hyperspectral ocean color retrieval with application to the Hyperspectral Imager for the Coastal Ocean (HICO). Remote Sens. Environ. 204, 60–75. doi: 10.1016/j.rse.2017.10.041

CrossRef Full Text | Google Scholar

Ibrahim, A., and McKinna, L. (2018). “Uncertainty in aerosol model characterization and its impact on ocean color retrievals,” in PACE Technical Report Series, Volume 6: Data Product Requirements and Error Budgets, eds I. Cetinić, C. R. McClain, and P. J. Werdell (NASA Goddard Space Flight Space Center). Available online at: https://pace.oceansciences.org/docs/TM2018219027Vol.7.pdf (accessed November 2018).

Google Scholar

IOCCG (2010). Atmospheric Correction for Remotely-Sensed Ocean-Colour Products. Dartmouth, NS: The International Ocean-Colour Coordinating Group.

Google Scholar

Jamet, C., Thiria, S., Moulin, C., and Crepon, M. (2005). Use of a neurovariational inversion for retrieving oceanic and atmospheric constituents from ocean color imagery: a feasibility study. J. Atmos. Oceanic Technol. 22, 460–475. doi: 10.1175/JTECH1688.1

CrossRef Full Text | Google Scholar

Jiang, L., and Wang, M. (2014). Improved near-infrared ocean reflectance correction algorithm for satellite ocean color data processing. Opt. Express 22, 21657–21678. doi: 10.1364/OE.22.021657

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuchinke, C. P., Gordon, H. R., and Franz, B. A. (2009). Spectral optimization for constituent retrieval in case 2 waters I: implementation and performance. Remote Sens. Environ. 113, 571–587. doi: 10.1016/j.rse.2008.11.001

CrossRef Full Text | Google Scholar

Liu, H., Hu, S., Zhou, Q., Li, Q., and Wu, G. (2019). Revisiting effectiveness of turbidity index for the switching scheme of NIR-SWIR combined ocean color atmospheric correction algorithm. Int. J. Appl. Earth Obs. Geoinf. 76, 1–9. doi: 10.1016/j.jag.2018.10.010

CrossRef Full Text | Google Scholar

Mobley, C., Werdell, J., Franz, B., Ahmad, Z., and Bailey, S. (2016). Atmospheric Correction for Satellite Ocean Color Radiometry. Available online at: https://oceancolor.gsfc.nasa.gov/docs/technical/NASA-TM-2016-217551.pdf (accessed November 2018).

Google Scholar

Morel, A., and Maritorena, S. (2001). Bio-optical properties of oceanic waters: a reappraisal. J. Geophys. Res. Oceans 106, 7163–7180. doi: 10.1029/2000JC000319

CrossRef Full Text | Google Scholar

Nordkvist, K., Loisel, H., and Gaurier, L. D. (2009). Cloud masking of SeaWiFS images over coastal waters using spectral variability. Opt. Express 17, 12246–12258. doi: 10.1364/OE.17.012246

PubMed Abstract | CrossRef Full Text | Google Scholar

O'Reilly, J. E., Maritorena, S., Mitchell, B., Greg, S., David, A., Carder, K. L., et al. (1998). Ocean color chlorophyll algorithms for SeaWiFS. J. Geophys. Res. Oceans 103, 24937–24953. doi: 10.1029/98JC02160

CrossRef Full Text | Google Scholar

Pahlevan, N., Roger, J.-C., and Ahmad, Z. (2017). Revisiting short-wave-infrared (SWIR) bands for atmospheric correction in coastal waters. Opt. Express 25, 6015–6035. doi: 10.1364/OE.25.006015

PubMed Abstract | CrossRef Full Text | Google Scholar

Rothman, L. S., Gordon, I. E., Babikov, Y., Barbe, A., Chris Benner, D., Bernath, P. F., et al. (2013). The HITRAN2012 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transfer 130, 4–50. doi: 10.1016/j.jqsrt.2013.07.002

CrossRef Full Text | Google Scholar

Ruddick, K., Ovidio, F., and Rijkeboer, M. (2000). Atmospheric correction of SeaWiFS imagery for turbid coastal and inland waters. Appl. Opt. 39:897. doi: 10.1364/AO.39.000897

PubMed Abstract | CrossRef Full Text | Google Scholar

Schroeder, T.h, Behnert, I., Schaale, M., Fischer, J., and Doerffer, R. (2007). Atmospheric correction algorithm for MERIS above case-2 waters. Int. J. Remote Sens. 28, 1469–86. doi: 10.1080/01431160600962574

CrossRef Full Text | Google Scholar

Shi, W., and Wang, M. (2007). Detection of turbid waters and absorbing aerosols for the MODIS ocean color data processing. Remote Sens. Environ. 110, 149–161. doi: 10.1016/j.rse.2007.02.013

CrossRef Full Text | Google Scholar

Siegel, D. A., Wang, M., Maritorena, S., and Robinson, W. (2000). Atmospheric correction of satellite ocean color imagery: the black pixel assumption. Appl. Opt. 39, 3582–3591. doi: 10.1364/AO.39.003582

PubMed Abstract | CrossRef Full Text | Google Scholar

Spurr, R., Stamnes, K., Eide, H., Li, W., Zhang, K., and Stamnes, J. (2007). Simultaneous retrieval of aerosols and ocean properties: a classic inverse modeling approach. I. Analytic Jacobians from the linearized CAO-DISORT model. J. Quant. Spectrosc. Radiat. Transfer 104, 428–449. doi: 10.1016/j.jqsrt.2006.09.009

CrossRef Full Text | Google Scholar

Stamnes, K., Li, W., Yan, B., Eide, H., Barnard, A., Pegau, W. S., et al. (2003). Accurate and self-consistent ocean color algorithm: simultaneous retrieval of aerosol optical properties and chlorophyll concentrations. Appl. Opt. 42, 939–951. doi: 10.1364/AO.42.000939

PubMed Abstract | CrossRef Full Text | Google Scholar

Steinmetz, F., Deschamps, P.-Y., and Ramon, D. (2011). Atmospheric correction in presence of sun glint: application to MERIS. Opt. Express 19, 9783–9800. doi: 10.1364/OE.19.009783

PubMed Abstract | CrossRef Full Text | Google Scholar

Vanhellemont, Q., and Ruddick, K. (2015). Advantages of high quality SWIR bands for ocean colour processing: examples from Landsat-8. Remote Sens. Environ. 161, 89–106. doi: 10.1016/j.rse.2015.02.007

CrossRef Full Text | Google Scholar

Wang, M., and Shi, W. (2006). Cloud masking for ocean color data processing in the coastal regions. IEEE Trans. Geosci. Remote Sens. 44, 3196–3105. doi: 10.1109/TGRS.2006.876293

CrossRef Full Text | Google Scholar

Wang, M., and Shi, W. (2007). The NIR-SWIR combined atmospheric correction approach for MODIS ocean color data processing. Opt. Express 15, 15722–15733. doi: 10.1364/OE.15.015722

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, M., and Shi, W. (2012). Sensor noise effects of the SWIR bands on MODIS-derived ocean color products. IEEE Trans. Geosci. Remote Sens. 50, 3280–3292. doi: 10.1109/TGRS.2012.2183376

CrossRef Full Text | Google Scholar

Wang, M., Shi, W., and Jiang, L. (2012). Atmospheric correction using near-infrared bands for satellite ocean color data processing in the turbid western Pacific region. Opt. Express 20, 741–753. doi: 10.1364/OE.20.000741

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, M., Son, S., and Shi, W. (2009). Evaluation of MODIS SWIR and NIR-SWIR atmospheric correction algorithms using SeaBASS data. Remote Sens. Environ. 113, 635–644. doi: 10.1016/j.rse.2008.11.005

CrossRef Full Text | Google Scholar

Werdell, P. J., Franz, B. A., and Bailey, S. W. (2010). Evaluation of shortwave infrared atmospheric correction for ocean color remote sensing of Chesapeake Bay. Remote Sens. Environ. 114, 2238–2247. doi: 10.1016/j.rse.2010.04.027

CrossRef Full Text | Google Scholar

Werdell, P. J., Franz, B. A., Bailey, S. W., Feldman, G. C., Boss, E., Brando, V. E., et al. (2013). Generalized ocean color inversion model for retrieving marine inherent optical properties. Appl. Opt. 52, 2019–2037. doi: 10.1364/AO.52.002019

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiong, X., Sun, J., Xie, X., Barnes, W. L., and Salomonson, V. V. (2010). On-orbit calibration and performance of aqua MODIS reflective solar bands. IEEE Trans. Geosci. Remote Sens. 48, 535–546. doi: 10.1109/TGRS.2009.2024307

CrossRef Full Text | Google Scholar