- 1Department of Earth, Environmental and Planetary Sciences, Rice University, Houston, TX, United States
- 2Department of Earth, Ocean and Atmospheric Sciences, University of British Columbia, Vancouver, BC, Canada
Kimberlite magmas transport cratonic mantle xenoliths and diamonds to the Earth's surface. However, the mechanisms supporting the successful and efficient ascent of these cargo-laden magmas remains enigmatic due to the absence of historic eruptions, uncertainties in melt composition, and questions concerning their rheology. Mantle-derived xenocrystic olivine is the most abundant component in kimberlite and is uniquely rounded and ellipsoidal in shape. Here, we present data from a series of attrition experiments designed to inform on the transport of low-viscosity melts through the mantle lithosphere. The experimental data suggest that the textural properties of the mantle-derived olivine are records of the flow regime, particle concentration, and transport duration of ascent for kimberlitic magmas. Specifically, our results provide evidence for the rapid and turbulent ascent of kimberlite during their transit through the lithosphere; this transport regime creates mechanical particle-particle interactions that, in combination with chemical processes, continually modify the mantle cargo and facilitate mineral assimilation.
Introduction
Magmas erupt as a complex mixture of melt, solids, and volatile-rich fluid, thus the properties of these components, where preserved, inform on magma source, and ascent conditions. The solid fraction in magmas can include both phenocrysts crystallized from the melt, and xenoliths, and xenocrysts of foreign lithospheric material sampled and entrained during transport. In most systems, the volume fractions of melt, solids, and fluid evolve during transport in response to cooling and crystallization, fluid exsolution and expansion, and to entrainment or settling of foreign cargo (Wilson and Head, 2007; Russell et al., 2012; Cashman et al., 2017). Under certain conditions, the solids in the ascending magma are subject to mechanical modification driven by particle-particle interactions termed, herein, as attrition (Dufek et al., 2012; Jones and Russell, 2017). Attrition has been shown to be a dominant and pervasive process in a variety of volcanic systems, including: within-conduit rounding of accessory lithics (Campbell et al., 2013); milling of pumice during conduit transport and pyroclastic flow (Dufek and Manga, 2008; Dufek et al., 2012; Kueppers et al., 2012; Jones et al., 2016); secondary production of fine ash (Engwell and Eychenne, 2016; Jones and Russell, 2017), and the transport of mantle xenoliths (Barton and Gerya, 2003; Arndt et al., 2010). These volcanological studies illustrate how the properties of the attritted cargo inform on the physical conditions attending transport, eruption and deposition—where attrition is linked to rapid, transitional to turbulent transport conditions.
Kimberlites are volcanic rock bodies distributed mainly across the Earth's cratons and preserved as low volume pipes, dykes, sheets, and sills (Dawson and Hawthorne, 1973; Brown et al., 2007; Kavanagh and Sparks, 2011; Brown and Valentine, 2013). The parental magmas source from depths in excess of 150 km, transit relatively cool cratonic mantle, and have ascent rates in excess of other magma types (McGetchin et al., 1973; Eggler, 1989; Sparks et al., 2006; Wilson and Head, 2007; Arndt et al., 2010; Russell et al., 2012). Although volumetrically insignificant, kimberlite is notable because it is the single largest natural source of diamond. Kimberlite magmas also entrain, transport and erupt anomalously large volumes of mantle-derived xenoliths and xenocrysts which inform on the structure, stability, composition, thermal state, age, and origin of the Earth's cratonic mantle. However, the mechanisms, styles, and rates of kimberlite ascent remain subjects of debate (Sparks, 2013).
Within kimberlite's mantle-derived cargo, olivine grains, derived from disaggregation of cratonic mantle peridotite, dominate volumetrically, and can comprise 25–50% (Smith, 2008); 20–40% (Field et al., 2009); 40–50% (Brett et al., 2009; Moss et al., 2010) or 40–60% (Giuliani, 2018) of the final rock. The olivine xenocrysts within kimberlite are commonly rounded and ellipsoidal in shape (Mitchell, 1986; Arndt et al., 2010; Jones et al., 2014). Importantly, the size distributions, shapes, and surfaces of kimberlitic olivine are distinctly different from the olivine originally released from parental peridotite xenoliths (Jones et al., 2014; Brett et al., 2015). This mechanical (Arndt et al., 2006, 2010; Russell et al., 2012; Jones et al., 2014; Brett et al., 2015) and/or chemical (Kamenetsky et al., 2008; Pilbeam et al., 2013) modification of the xenocrystic cargo takes place during the kimberlite's ascent through the mantle and crustal lithosphere. Hence, the resulting textural properties of the mantle cargo are embedded with information that strongly informs on the mechanisms, styles and rates of kimberlite ascent.
Here, we present data from a new series of analog experiments designed to explore attrition driven by particle-particle interactions in a fluidized system. We build on the previous experimental work of Jones and Russell (2018) who compared two different environments hosting particle interaction—a fluidized bed and a tumbling mill. In this study we investigate olivine attrition (scaled for an ascending cargo-laden kimberlite dyke) as a function of particle concentration, time, and energy. We use our experimental results to discuss the conditions attending kimberlite ascent and the relative timings of mechanical vs. chemical modification of the mantle cargo.
Methods
Pre-experiment Sample Characterization
For this study, olivine derived from crushed mantle dunite was obtained from Luossavaara-Kiirunavaara Aktiebolag (LKAB). The olivine grains were washed with deionized water to remove adhering fines and manually sieved to a restricted grain size (250–500 μm) using a standard stack of Tyler sieves. The grain size distribution of this starting, or feeding, material was measured using a Malvern Mastersizer 2000 laser diffraction device with a hydro 2000 Mu water dispersion module attached. Using a pump speed of 2,100 rpm, an absorption coefficient of 0.1 and a refractive index of 1.7, an aliquot of the sample was added to the dispersion module and measured three times. An ultrasonic pulse was applied to the sample for 2 s immediately before measurement to prevent particle aggregation. This method was repeated three times to give a total of nine measurements which were then averaged to obtain the final mean grain size distribution. The olivine density was calculated using an analytical balance to measure mass of an aliquot of grains and a Micrometrics Accuppyc II 1340 Helium Pycnometer to measure sample volume. This technique produced a density value of 3,305 kg m−3. The chemical composition of the washed olivine was measured using X-Ray Fluorescence by ALS Chemex on the author's behalf (Table S1).
Attrition Experiments
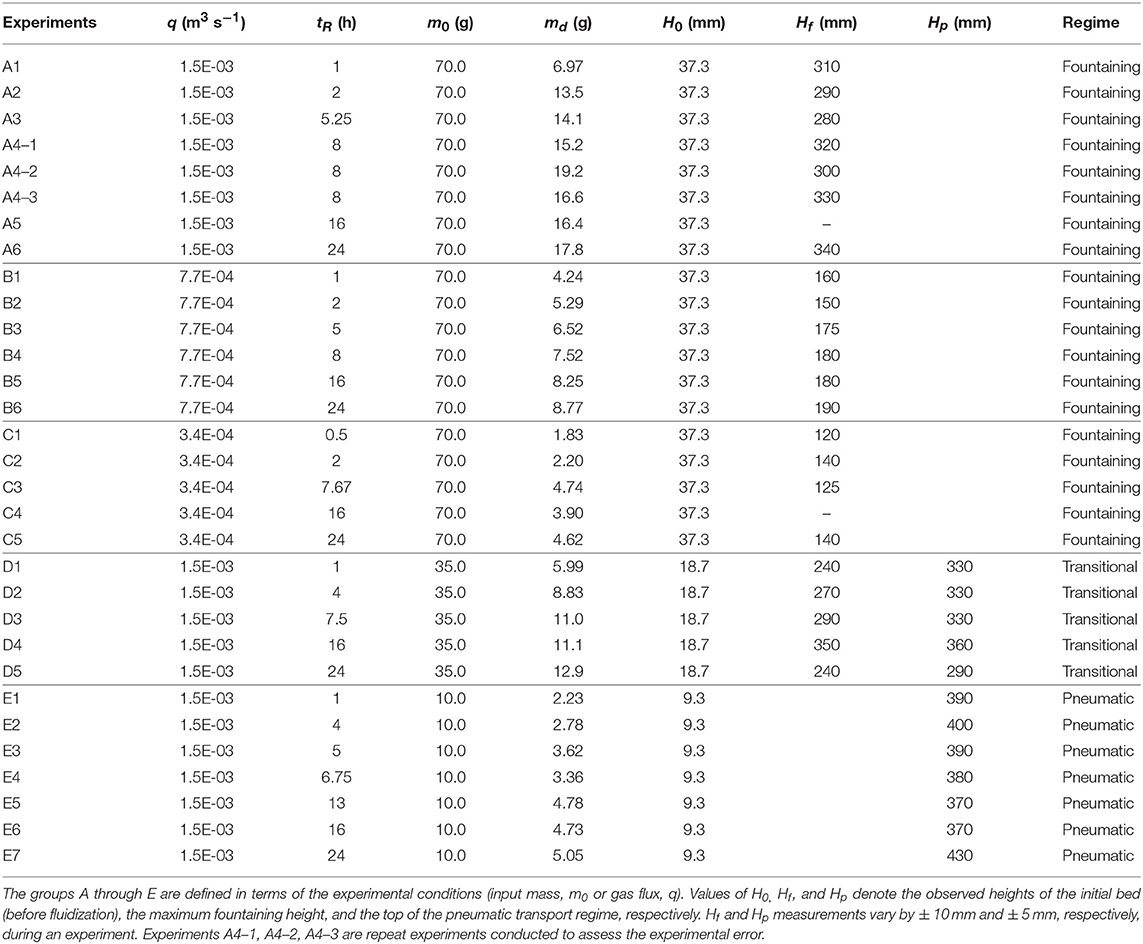
All experiments were performed at standard laboratory conditions in a fluidized bed apparatus wherein particles of the mineral olivine were suspended by an air-jet (Figure 1). These conditions were selected in order to scale our experiments to the natural system—see the following section. The three experimental variables were: (i) residence time in the tube (tR), (ii) the input mass of particles (m0), and (iii) the gas flux (q). Time series experiments were performed under fixed conditions (e.g., flux, input mass) and are grouped accordingly as A-E in Table 1. The experimental apparatus (Figure 1) consisted of a compressed air feed which supplied air to the base of a vertical attrition tube. During an experiment the olivine was suspended within the first 3.5 cm diameter, 120 cm long tube. The other tubes and connectors ensured the complete recovery of all experimental products. The duration of each experiment was set arbitrarily, and our experiments spanned 0.5–24 h. The specific flow rate was set and monitored using a calibrated FMA5526 Omega gas flow meter.
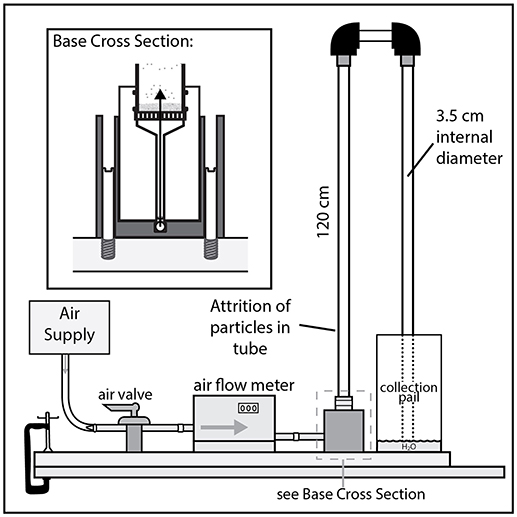
Figure 1. A schematic diagram of the experimental apparatus used in this study. A fluidized bed where gas is supplied from a compressed air supply through a calibrated flow meter, at a user-determined flow rate, into the attrition tube where the particle collisions take place. A series of tubes, connectors, and a water reservoir ensure the successful recovery of all the products. Figure modified from Jones and Russell (2018).
A measured mass of 10, 35, or 70 g of olivine grains was poured into the base of the attrition tube and allowed to rest on the distributor. This distributor plate featured ~40 evenly spaced holes to ensure an equally distributed gas flux to suspend the particles. After the particles were loaded onto the distributor plate, their fill height above the base of the distributor plate (H0) was recorded. A controlled gas feed of 20, 45, or 85.5 L min−1 was applied to fluidize the olivine particles. These gas fluxes were chosen such that the Reynolds Numbers (Re) in our experiments cover the same range as expected during kimberlite magma ascent (see following section). During each experiment, measurements were taken to document the nature of the suspended load including: the maximum height achieved where the fountain exhibited pulsating behavior (Hf) and/or the top of a stable region where a low concentration of particles (~50–100) was constantly suspended (Hp) (Table 1; Figure 2). As particle interactions occur within the attrition tube, fine particles are elutriated from the bed, passing up the attrition tube, along an elbow joint and down a tube submersed ~0.5 cm in a 500 mL water reservoir to ensure that no fine particles are lost from the system. A cellulose fabric (Kimwipe) by Kimtech Science was used to seal the collection bucket to prevent any sample loss. Furthermore, to document particle interactions a select number of experiments (A4–1, E4; Table 1), were recorded using a Chronos 1.4 high-speed camera at 1,000 frames per second. Videos S1, S2 can be found in the online supplementary information.
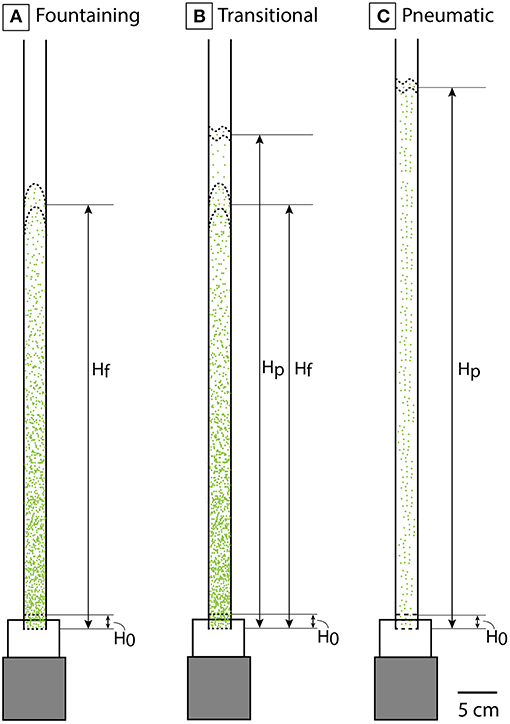
Figure 2. Scaled diagrams of the fluidized regimes observed in this study. (A) Fountaining regime in which bed height (Hf) pulsates (±10 mm) and an average bed height is measured. H0 is the initial height of the particle bed before air is fluxed through the system. (B) Transitional regime in which a fountaining bed height is present in addition to a pneumatic regime enclosed by Hp in which a stable low particle concentration area exists. (C) Pneumatic regime in which particle concentrations are low and particles are homogeneously distributed within the column.
Scaling Experiments to Kimberlite Ascent
Our experimental conditions (i.e., gas flux and host fluid) were chosen to ensure that the dynamical regime (turbulent flow) and parameter space cover a similar range as expected during kimberlite magma ascent (Re ~102-105). Specifically, as conservative estimates we use a magma density ρm of 2,800 kg m−3, a magma viscosity μ range of 0.1–50 Pa s (Sparks et al., 2006; Moss and Russell, 2011), a dyke width x of 1 m (Sparks et al., 2006), and an ascent velocity υ of 4 m s−1 (Sparks et al., 2006), to estimate the Reynolds number of kimberlite ascent by: Re = .
The Reynolds number range expected for natural systems (2 × 102 to 1 × 105) matches our experimental conditions (8 × 102 < Re < 4 × 103). We can therefore confirm that the relationships quantified in this study parallel those attending the ascent of kimberlite magma (Merle, 2015). However, it should be noted that the natural estimates are based upon minimum values; at shallower crustal depths where CO2 is liberated as a supercritical fluid and later a gaseous phase, the kimberlite density will decrease, and ascent velocity will increase (e.g., Russell et al., 2012; Stone and Luth, 2016), further supporting attrition.
Post-experiment Sample Characterization
After each experiment the entire apparatus was carefully disassembled and washed with deionized water into a 500 mL collection flask. The particle size distributions of the run products suspended in deionized water were measured using the laser diffraction methods (as previously described in “Pre-experiment sample characterization”). Grain morphology and surface textures of both experimental and natural olivine grains were assessed at various magnifications using a Philips XL30 scanning electron microscope (SEM) in scanning electron mode with a 15 kV accelerating voltage, an 11 mm working distance, and a 35 μA beam current. To prepare the natural olivine for SEM observations, fresh (i.e., unaltered) grains of natural xenocrystic olivine were disaggregated from coherent (hypabyssal) kimberlite drill core of the Diavik A154N pipe. This was done in two stages. Firstly, by using a diamond drill tip to remove each olivine grain encased by a layer of groundmass. Then, secondly, carefully rinsed with water to remove the attached groundmass coating.
Results
Experimental Observations
A stream of compressed gas fed into the vertical attrition tube system (Figure 1) fluidizes the particle bed of olivine of original height H0. The extent and nature of the fluidization varied as a function of experimental conditions (Table 1) and we identified two end member regimes (fountaining and pneumatic) corresponding to the experiments that use the highest (70 g) and lowest (10 g) initial particle feeds. Experiments in series A, B, and C used a common 70 g of input material and varied gas velocities. These experiments showed fountaining behavior in which the bed moves coherently, but the bed height fluctuates or pulsates with time. For these experiments, we recorded the average height sustained by the fountain, Hf. Under this fountaining regime, particle collisions are frequent, but via visual inspection of high-speed videos (Video S1), differential velocities are low. The mean fountain height decreases steadily between experiments A (310 mm), B (173 mm), and C (131 mm) in response to a decreasing gas flux of: 1.5 × 10−3 m3 s−1; 7.7 × 10−4 m3 s−1, and 3.4 × 10−4 m3 s−1, respectively (Table 1; Figure 2).
The other end member regime was identified in the series E experiments which fluidize a lower mass (10 g) of olivine grains. In these experiments, the fluidized column features lower particle concentrations wherein particles are uniformly distributed (Video S2). The particles are able to move more freely in comparison to experiments A–C. Particle collisions are less frequent in this regime but are observed to collide at greater velocities in the high-speed videography (Video S2). We refer to the type of behavior observed in this study as pneumatic transport. Within this regime, fountaining behavior is absent, so we do not report measurements of Hf; instead we measure the height to the top of the dilute column (Hp).
Experiments in series D which fluidize an intermediate mass (35 g) are transitional in style showing elements of both fountaining and pneumatic behavior. There is a discrete fountain surface (Hf), as well as a distinct region above the fountain where particles are homogenously suspended (Hp). Particle concentrations in this upper region (i.e., pneumatic behavior) are higher than in experiment group E. Values of Hf and Hp are recorded for experiment D because both end member flow behaviors are observed. Hf measurements for D (278 mm) are comparable to values for group A (310 mm; Table 1; Figure 2). The effect of initial mass (m0) on pneumatic column height is seen by comparing mean Hp values from D (m0 = 35 g) and E (m0 = 10 g); group D had a mean value of 328 mm compared with 386 mm for group E.
Scanning Electron Microscopy
The attritted olivine grains observed under the SEM reveal striking textural features. The original, highly irregular morphology of the input, or parent grains become highly rounded at the grain-scale and their original faceted surfaces become rough and pitted (Figure 3). The particle surfaces contain numerous (hemi-spherical) pits creating a micro-flaked surface texture. These textural features on the experimental products are extremely similar to observations made on olivine extracted from natural kimberlite deposits. Olivine derived from coherent kimberlite at Diavik diamond mine (this study; bottom of Figure 3) and from lava flows at the Igwisi Hills Volcano (Jones et al., 2014), both, show rough, pitted surfaces. Such surfaces have been inferred to result from abrasion during ascent (Peltonen et al., 2002; Arndt et al., 2010; Jones et al., 2014; Brett et al., 2015). The daughter particles formed by the attrition of the parent particles again show distinctive textural features (Figure 4). Their surfaces have less pitting and their shapes are more angular. The very fine particles measuring only a few microns can be seen in aggregates that adhere to larger olivine grains. Given that all these daughter particles deviate in shape from a sphere, any grain size measurement technique, including laser diffraction as used here, will introduce uncertainty to the measured grain diameter.

Figure 3. Scanning electron microscope images of parent particles olivine recovered from our experimental run products (top row; Experiment A6) and compared to olivine from samples of coherent kimberlite (bottom row).

Figure 4. Scanning electron microscope images of daughter olivine particles of varying size fractions recovered from our experimental run products (Experiment A2). Smaller size fractions show less pitted surfaces and more angularity compared to the parent particles. Very fine surface derived chips produced by abrasion are observed adhering to larger particles within each size fraction.
Total Grain-Size Distributions
The total grain size distributions (TGSD) of the run products directly reflect the changing experimental conditions (Table 1; Figure 5). In all experimental data sets, the mass of the parent grain size population is reduced with increased residence time (Figure 5A). As commonly observed in these types of experimental studies, the decrease occurs in a non-linear manner with attrition most successful at early residence times (Xiao et al., 2014; Jones and Russell, 2017, 2018; Jones et al., 2017). The effect of varying the flux (and velocity) of the gas feed is also important. Figure 5B shows the TGSD derived from three experiments performed at three different gas fluxes after a 24 h residence time (i.e., constant tR). As expected, higher gas fluxes increase the efficiency of attrition; the parent particle abundance is decreased by the creation of daughter particles (Figure 5B). In contrast to the other experiments, experiments conducted at a lower gas flux (q ~ 3.4 × 10−4 m3 s−1) did not produce any daughter particles measuring between 30 and 80 μm in size. We also ran experiments with different input masses. Whilst holding all other variables constant, decreasing m0 increases the amount of attrition and increases the amount of fine daughter products measuring <20 μm in size (Figure 5C).
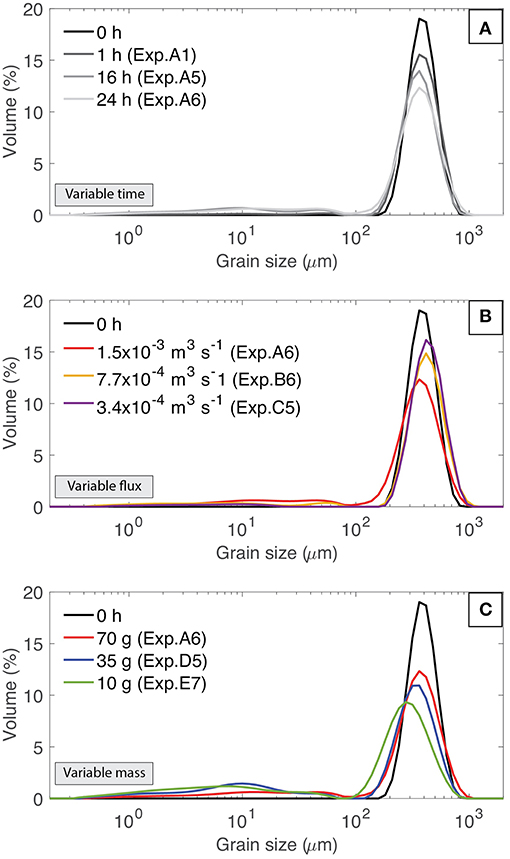
Figure 5. Total grain size distributions of run products from a select number of experiments illustrating the effects of: (A) changing residence time (tR), (B) changing input gas flux (constant tR = 24 h; m0 = 70 g) and of (C) changing the input mass (constant tR = 24 h; gas flux = 1.5 × 10−3 m3 s−1).
Analysis
Fines Production Modeling
The production of daughter particles serves as a simple and effective metric for quantifying attrition (Gwyn, 1969; Jones et al., 2017). On that basis we plotted the mass of daughter particles (md) normalized to the initial, feeding mass (m0) as a function of tR (Table S2; Figure 6). Each dataset shows an initial period of rapid, attrition where daughter particles are produced very efficiently over the first <10 h. This is followed by a plateau where the mass of daughter particles becomes relatively stable and does not significantly increase with increased residence time (Figures 6A,B). This limit has been observed in previous attrition studies (Knight et al., 2014; Jones et al., 2017) and is thought to represent the stable state at a given energy condition, where only minor daughter production occurs through repeated impacts. Such properties of the time-dependent datasets suggest an empirical, descriptive model having the form:
after Jones et al. (2017). Where a is the dimensionless infinite-time attrition limit, b [h−1] is the attrition rate constant, and tR [h] is the residence time. The models fitted to the experimental data (solid lines) for each of the five experimental datasets are shown on Figures 6A,B. Increasing the gas flux increases both the attrition rate (Figure 6A) and maximum amount of daughter particles produced. Conversely, decreasing the initial mass of particles (m0) decreases the attrition rate but, increases the maximum proportion of daughter particles produced (Figure 6B). These relationships are clearly shown in Figure 6C where the optimal model parameters, a and b are plotted, with reference to the experimental conditions. The ellipses denote the 95% confidence limits on the estimated values of the model parameters a and b and their covariance.
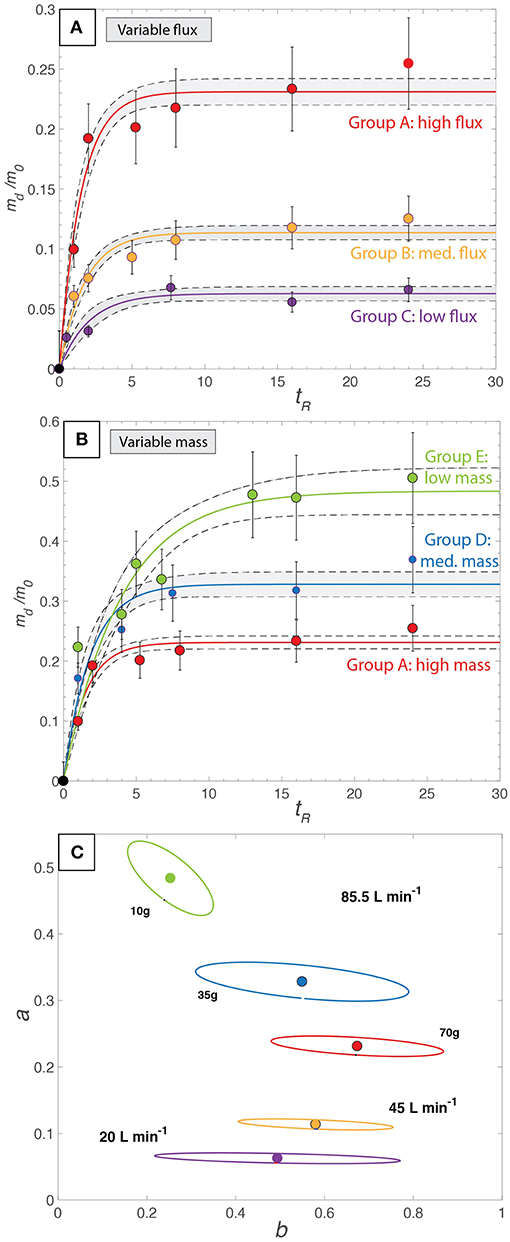
Figure 6. Results of attrition experiments. Mass of the daughter products (md) produced by attrition normalized to the initial mass (m0) as a function of residence time (tR) for experiments using different (A) gas fluxes, and (B) input masses. Solid curves are modeled using the empirical relationship: md/m0 = a(1-e)−bt after Jones et al. (2017). (C) The model values of infinite time production limit, a, and the attrition rate constant, b for all experiments. The ellipses represent a 95% confidence envelope based on the fit of Equation 1 to our data. Color coding is consistent with Figure 5.
Model Grain Size Distributions
Each experiment generates a unique distribution of particle grain sizes relative to the starting material (Figure 7A). Our analysis of the grain size datasets begins by modeling the TGSD of the run products using a linear combination of normalized log-normal distributions (Costa et al., 2016; Jones and Russell, 2017). The TGSD's are modeled using Gaussian distributions fitted to the natural logarithm of particle size (d) and feature a maximum of four modes corresponding to: (1) a parent mode initially at 474 μm that is reduced with increasing attrition; (2) a D1 daughter population at d ~57 μm; (3) a D2 daughter population at d ~11 μm; and (4) a D3 daughter population with a prescribed modal grain size of 2.0 μm. The n normalized log normal distributions are fitted to the TGSD's (Figure 7A) as:
Where Vol is the volume particle distribution; xi, and σi are adjustable parameters for the model distributions and represent the median particle size and standard deviation of each distribution, respectively. The third adjustable parameter, pi, is the weighting or abundance of each subpopulation and the sum of pi's is required to equal 1.
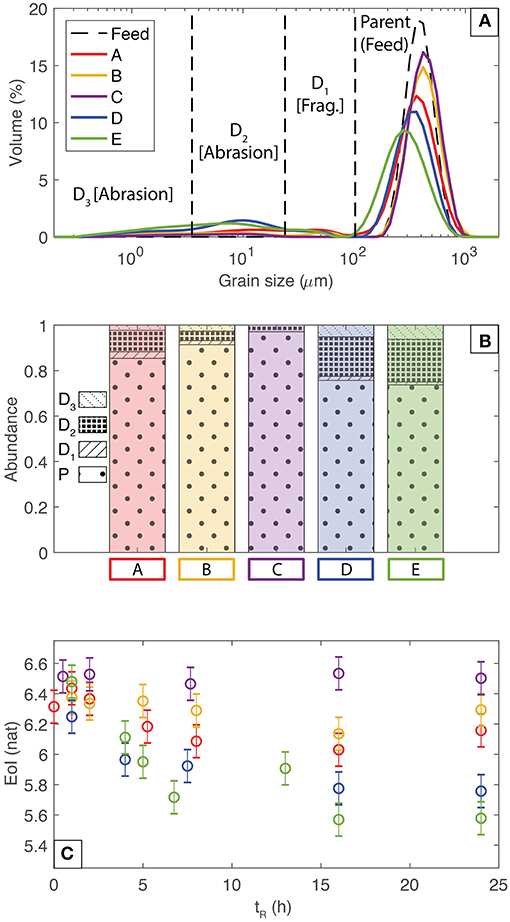
Figure 7. (A) Total grain size distributions for the longest duration (24 h) experiment from each series (A through E; see Table 1). Subpopulations of grains (parent, daughter 1, daughter 2, and daughter 3) are denoted by the vertical dashed lines. Corresponding curve fitting data can be found in Table S3. (B) The proportions of parent (P) and different daughter particles (D1, D2, and D3) for the experimental series A–E after 24 h. (C) Calculated values of the weighted or combined entropy of information (EoI) for the total grain size distribution for each experimental series (Table S3). Colors in all parts of this figure are consistent with the legend in part (A).
The relative abundance of these grain size populations can be tracked as a function of experimental conditions (Figure 7B). The time series data are reported in Table S3 for reference. For all experimental series (Table 1; A–E), the abundance of the parent population systematically decreases with increased residence time. The D1 abundance shows an initial increase to ~0.025 for early (<5 h) residence times and then becomes near constant for experiment groups A, D and E (highest gas flux, variable mass input). However, experiments in group B (medium gas flux of 7.7 × 10−4 m3 s−1, highest mass input) show no D1 population at early residence times; only after an 8 h residence time can a D1 population be observed. The experiments with the lowest gas flux (group C) never develop a D1 population (Figure 7B). The D2 population increases with increased residence time for all experiments. The experiments in groups E (highest gas flux, lowest mass input) and C (lowest flux, highest mass input) have the highest and lowest D2 abundance values, respectively (Figure 7B). Lastly, the D3 population abundance increases with increased residence time except in the group C experiments (lowest gas flux) in which no D3 population is observed (Figure 7B).
This complex and transient evolution in attrition-modified grain size data can be encapsulated by the Entropy of Information (EoI) which is a measure of the disorder associated with a random variable (Jones and Russell, 2017). EoI has previously been used to quantify the attrition potential of a grain size distribution—where high values of EoI have a greater attrition potential (Xiao et al., 2014; Jones and Russell, 2017). Here, EoI values for each mode were calculated using the respective median particle size (xi) and standard distribution (σi) of log normal distributions (Table S3) fitted to the grain size data (Xiao et al., 2014):
The model values of pi allow for a weighted value of EoI representing the total grain size distribution (Figure 7C). In all of our experimental runs, the starting material has a weighted EoI of ~6.3 ± 0.1. After short residence times exceeding ~2 h, the weighted values of EoI decrease corresponding to the increased attrition. The experiments conducted at the lowest gas flux do not show this progressive reduction in EoI (Series C), rather, EoI remains near-constant at ~6.5. This is because, as outlined in Figure 7B, these experiments do not create any D1 or D3 sub-populations and only a very small amount (~0.04) of D2 particles. Attrition is largely unsuccessful, such that the population remains disordered and remains susceptible to attrition under different conditions. For all other experimental series, EoI quantifies the reduction in disorder due to sustained particle attrition—a process that strives to reduce particle populations to a uniform grain size.
Attrition Energetics
Previous work (e.g., Gwyn, 1969; Bemrose and Bridgwater, 1987) has shown that attrition is dependent on a minimum of four governing parameters: concentration of suspended particles; feed particle size distribution; particle/gas velocity; and particle residence time. Attrition is typically promoted by high particle concentrations, poorly sorted feed distributions, high differential velocities, and long residences times (e.g., Bemrose and Bridgwater, 1987; Jones and Russell, 2018). The question now is, how can we relate the attrition model parameters (i.e., a and b) to physical quantities relevant to kimberlite ascent? In a fluidized system the infinite time attrition limit, a, depends on the amount of energy that the suspended particles have. Here, we quantify this by calculating an average kinetic energy available. Specifically, the kinetic energy supplied to the particles per second [J s−1] was approximated by firstly calculating the mass (m) of air (with density 1.225 kg m−3) supplied to the apparatus at a superficial gas velocity (v). Then using kinetic energy, KE , the total KE supplied to the particles per second was calculated. The number of input particles in each experiment was calculated using the mean parent particle diameter of 474 μm. Finally, the KE of the feeding gas was divided by the total number of parent particles to give an approximation of the KE supplied to each particle, per second—the metric used in this study.
Our data show that there is a strong non-linear positive correlation between the KE supplied to the particles and the infinite time attrition limit (Figure 8A). Increasing the amount of KE supplied to the particles increases a. This quantification supports previous models wherein the extent of fines-production is directly related to the energy available (Kueppers et al., 2006; Jones and Russell, 2017).
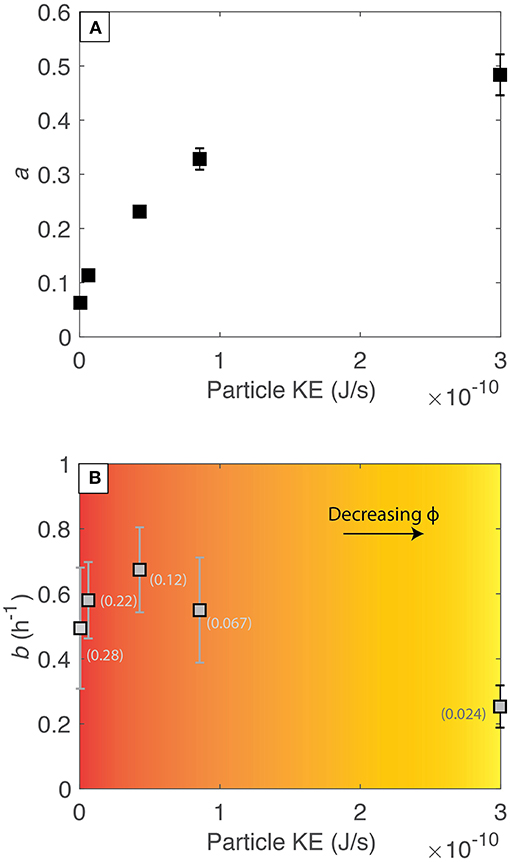
Figure 8. (A) The infinite time production limit, a for all experiments as a function of the amount of kinetic energy (KE) supplied to each particle per second. (B) The attrition rate constant, b for all experiments as a function of the KE supplied to each particle per second. Color shading denotes the decreasing dimensionless particle concentration (ϕ) with increasing KE. The numbers adjacent to the data points correspond to the specific ϕ for each experiment. Error bars denote one standard deviation.
The attrition rate constant, b depends on both the probability for a collision to occur and the likelihood that collisions are at, or above, the threshold velocity for breakage. The latter can again be quantified by KE whereas the former can be quantified by the concentration of particles in the fluidized system. Specifically, we calculate the dimensionless particle concentrations as: and for the experiments that showed fountaining or pneumatic behavior, respectively. Group D experiments that showed transitional behavior were calculated using Hf because this is where most of the particles reside. In general, the attrition rate (b) is expected to increase with increasing ϕ and increasing KE (Bemrose and Bridgwater, 1987; Jones and Russell, 2018). However, in our experiments we show that these simple general expectations are not always valid; rather, there is a clear “trade-off” between these parameters (Figure 8B). At relatively low KE, the effect of increasing KE dominates over the reduction in ϕ. However, as KE is increased the effect of decreasing the particle concentration becomes dominant resulting in a reduced attrition rate. This is important for systems, such as kimberlite magmas, where particle load and velocity are highly transient during ascent.
Attrition Mechanics
The two main modes of attrition that contribute to grain size reduction and creation of sub-populations are fragmentation and abrasion. Fragmentation is a relatively high-energy process involving wholesale fracturing of parent particles to form smaller, often similarly sized, daughter particles (e.g., Bemrose and Bridgwater, 1987; Jones et al., 2017). Abrasion is a less energetic mode of attrition wherein the rough edges or asperities of the parent (and daughter) particles are removed and particles become rounded. Importantly, abrasion is accompanied by the production of very fine particles—commonly chips (Figure 4) derived from the surficial asperities on the parent grains (Bemrose and Bridgwater, 1987; Kueppers et al., 2012; Jones et al., 2017; Jones and Russell, 2018).
Firstly, we consider the energetics that support olivine fragmentation during the attrition experiments. From the Griffith's criterion the critical stress required to fragment, σf can be calculated as Ball and Payne (1976):
where E is the Young's modulus [Pa] of the material, γ is the fracture surface energy [J m−2] and l is the crack/flaw length [m]. Grain fragmentation occurs when the impacting stress (σim) is equal to or exceeds the critical stress: σim ≥ σf. For an equant shaped particle with dimension l, the stress upon impact with a planar surface can be approximated by:
where V is the impacting velocity [m s−1] and ρ is the particle density [kg m−3]. Equating Equations 4 and 5, using a crack length, l of 474 μm (the average parent grain size), an E of 1.95 × 1011 Pa and a γ of 1 J m−2 (Swain and Atkinson, 1978), we find that the critical velocity required for fragmentation (Vf) of the parent grains is 0.65 m s−1 (see Supplementary Information for detailed methods). Assuming that the particles and gas feed are fully coupled this critical velocity corresponds to an average gas flux of 6.2 × 10−4 m3 s−1. This is in excellent agreement with our experimental data: experiment groups A, B, D, and E were performed above this threshold gas flux and in each case produced a D1 peak. In contrast, experiment group C used a gas flux ~50% lower than the threshold Vf value and hence the grain size distributions for these experiments do not show a D1 peak. We therefore interpret the D1 sub-population to be caused by fragmentation of parent olivine grains.
The energetics driving attrition of olivine grains by abrasion are different. The SEM images of olivine both from our experiments and from kimberlite (Figures 3, 4) show that abrasion occurs through the production of hemi-spherical surface derived chips. The threshold velocity for chipping/abrasion Va is lower than Vf and is met or exceeded in all of our experiments (Table 1). From indentation mechanics, a dimensionless parameter ψ, describing abrasion propensity can be directly related to the fractional loss per impact and is given by Ghadiri and Zhang (2002):
where d is the particle dimension [mm], H is the particle hardness [Pa] and Kc is the fracture toughness [N m−3/2]. This relationship implies that collisions at higher velocities (V), but below the threshold velocity for fragmentation (Vf), will markedly increase abrasion success (i.e., ψ).
Discussion
Kimberlite, the rock, is a product of many complex processes that attend the magma's ascent through the cratonic mantle lithosphere. During kimberlite ascent, mechanical (abrasion and fragmentation) and chemical (dissolution and crystallization) processes operate concurrently (Arndt et al., 2010) allowing for grain shape, surface, and size modifications (Figure 9). As kimberlite dykes transit the cratonic mantle lithosphere mantle-derived xenoliths are sampled and entrained. Rapid depressurization during ascent promotes decompression and disaggregation of these xenoliths, liberating mantle minerals as xenocrysts to the melt (Brett et al., 2015). The liberated xenocryst size distribution will directly reflect that of the mantle source region and be on the order of 0.1−10 mm (e.g., Drury and van Roermund, 1989). Initially, mantle silicate minerals are out of equilibrium with the melt which supports chemical dissolution; olivine xenocrysts commonly have strongly corroded cores and melt embayments consistent with early (potentially even pre-ascent) dissolution (Arndt et al., 2006, 2010; Kamenetsky et al., 2008; Brett et al., 2009; Giuliani, 2018). We suggest that at these early ascent stages mechanical cargo modifications are trivial and chemical processes dominate.
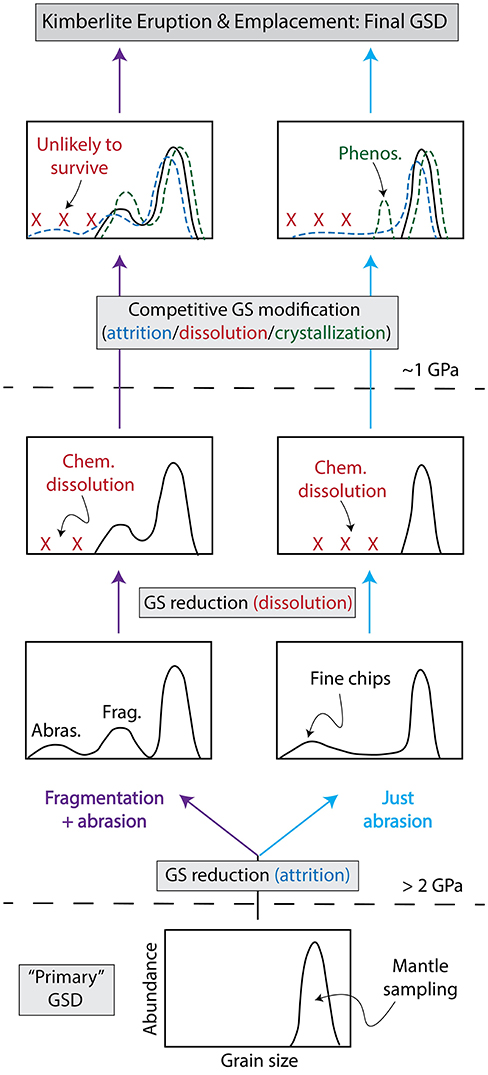
Figure 9. Conceptual model for the mechanical and chemical modification of mantle-derived minerals during magma transport. Xenocrysts of minerals (i.e., olivine) are liberated from mantle xenoliths by decompression, thereby, creating a primary grain size distribution (GSD). During ascent from the deep mantle (lower portion of diagram) to the surface (upper part of diagram) the xenocrysts are modified by mechanical (fragmentation and abrasion) and chemical (dissolution and crystallization) processes. The relative importance of each process varies during ascent. Olivine grain size distributions recovered from surface kimberlite deposits inform on subsurface ascent dynamics.
Carbonate-rich kimberlite parental melts can be induced to exsolve a CO2 dominated fluid phase in the mantle (~3.5 and 2.5 GPa) by assimilation of mantle silicate minerals, especially orthopyroxene (Russell et al., 2012, 2013; Stone and Luth, 2016). Importantly, the production of a CO2 fluid continually increases the melt's rise velocity (Russell et al., 2012). A velocity threshold (Dufek et al., 2012; Jones and Russell, 2018) will then be reached above which abrasion (Va) or fragmentation and abrasion (Vf) can occur (Figure 9). This is the conservative beginning of mechanical modification and we suggest that once an exsolved fluid phase (supercritical fluid or gas depending on depth) develops the attrition of mantle cargo becomes an important and ubiquitous process. However, the process is not continuous or constant—dykes are known to propagate in pulses related to overpressure build up at the crack tip (Wilson and Head, 2007; Kavanagh and Sparks, 2011; Brett et al., 2015) and the particle load will be variable; xenoliths and xenocrysts will settle out (Sparks et al., 1977) whilst new mantle cargo is periodically supplied from the damage zone at the crack tip (Brett et al., 2015).
Chemical processes (dissolution or crystallization) can continue to operate during kimberlite transport and modify the crystal cargo (Mitchell, 1986; Kamenetsky et al., 2008; Moore, 2012; Pilbeam et al., 2013). The small flakes and chips of olivine produced by attrition would be particularly susceptible to rapid and complete chemical dissolution (Figure 9). Conversely, there is strong evidence for olivine crystallization in kimberlites at lower pressures ( ≤ 1 GPa; Mitchell, 1986; Scott Smith, 1992; Canil and Bellis, 2008). Texturally olivine crystallization is expressed by compositionally distinct rims on cores of olivine xenocrysts or in the form of smaller sized “true” phenocrysts (Mitchell, 1986; Scott Smith, 1992; Kamenetsky et al., 2008; Brett et al., 2009; Bussweiler et al., 2015; Giuliani, 2018) (Figure 9). The exact transition depth where olivine begins to crystallize (rather than dissolve) is controlled by a number of factors. Temperature and volatile contents of the kimberlite magma are important but are secondary to the composition of the melt—more efficient assimilation of the mantle cargo will drive the system to earlier olivine saturation. Interestingly, mechanical rounding and pitting has been observed on phenocrystic overgrowths demonstrating that attrition post-dates or, at a minimum, is synchronous with olivine saturation (Arndt et al., 2010; Jones et al., 2014).
The modification of mantle cargo during transport has several implications. Firstly, the size distributions, shapes, and relative proportions of mantle minerals in kimberlite need not be representative of the original mantle material sampled (Jerram et al., 2009; Moss et al., 2010). Secondly, fresh fracture surfaces with sharp edges (fragmentation) and rounded particles with microscopically rough surfaces (abrasion) yield ideal surfaces for supporting heterogeneous bubble nucleation (Edwards and Russell, 2009). Thirdly, surface-derived chips are highly amenable to rapid dissolution into the melt which facilitates an assimilation-induced transition in melt composition from more carbonatitic to kimberlitic and enhances the opportunity for early exsolution of a fluid phase (Russell et al., 2012, 2013; Stone and Luth, 2016). Lastly, textural observations on the solid cargo (i.e., crystals, xenoliths, xenocrysts) can inform on their transport and eruption history (Campbell et al., 2013; Jones et al., 2014; Brett et al., 2015) including estimates on ascent velocities (>4 m s−1; Sparks et al., 2006), style of flow (turbulent or transitional), transit times (10's of h), and average concentrations of solid particles.
Olivine, the most abundant component in kimberlite, has features that relate to the dynamics attending magma ascent. Modified grain size distributions (Jerram et al., 2009; Moss et al., 2010), rounded to ellipsoidal shapes (Arndt et al., 2006, 2010; Brett et al., 2009), and the pitted olivine surfaces (Jones et al., 2014; Brett et al., 2015; Jones and Russell, 2018) are all indicative of attrition driven by particle-particle collisions, in a high velocity (1–10's m s−1; Sparks, 2013), fluidized (Russell et al., 2012; Brett et al., 2015), solid-rich suspension of kimberlite magma. Thus, where these features are observed (e.g., Diavik Diamond Mine, Northwest Territories, Canada, Brett et al., 2015; Igwisi Hills Volcanoes, Tanzania, Jones et al., 2014), kimberlite ascent (Figure 10) is identified as rapid, cargo-laden and volatile-rich. Conversely, a lack of evidence for mechanical modification (intrusive kimberlite and other related alkaline magmas) may indicate slower ascent rate of a less fluidized, cargo-poor magma and may, in fact, point to lower potential diamond grades (i.e., lack of deep-seated mantle cargo). The transport distance also matters—off-craton kimberlites or related alkalic magmas that ascend short distances relative to their on-craton equivalents have less opportunity for cargo modification. Furthermore, mantle cargo that is entrained at shallow depths, above the diamond window, for example, are less likely to be heavily abraded. However, irrespective of the ascent pathway, we take the pervasive textures of attrition recorded by the olivine cargo in many kimberlites as direct unequivocal evidence for the vigorous, turbulent ascent of kimberlite through the mantle lithosphere.
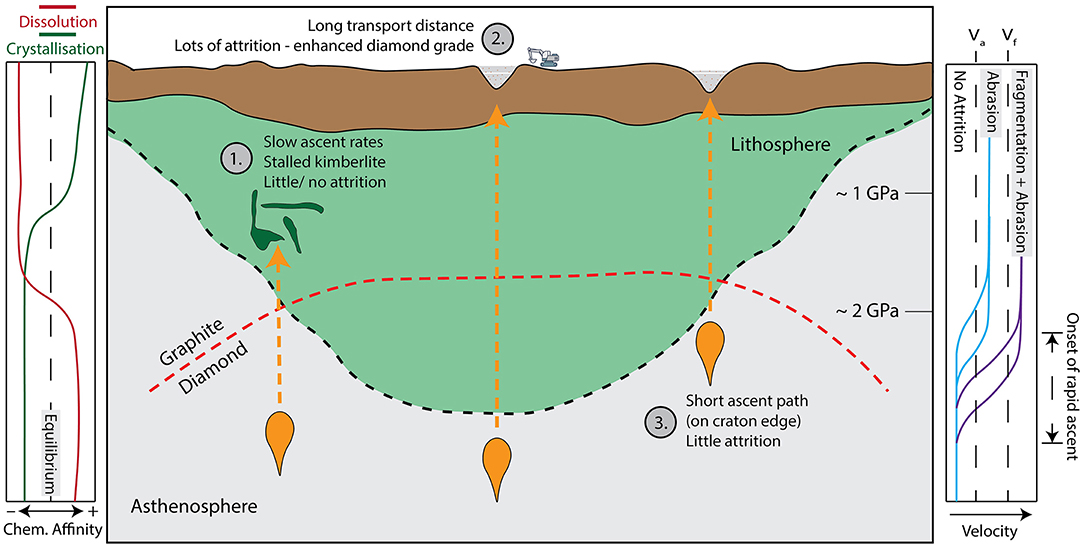
Figure 10. Schematic representation of three different kimberlite ascent paths: (1) Slow ascent leads to the stalling and eventual cooling of the kimberlite. Attrition plays little role in these magmas due to low energy and short residence times. The resulting deposits will show little modification of mantle cargo. (2) Deep-seated melt accumulation followed by early and sustained rapid ascent supports pervasive attrition due to a high energy environment and a long residence time. Resulting deposits will contain heavily rounded olivine grains and potentially an enhanced diamond grade. (3) Shallow-seated melt accumulation and relatively late onset of rapid ascent—attrition occurs only over a short distance. Resulting deposits have olivine (and other indicator minerals) that are less rounded than those observed in deposit 2.
Conclusion
The mechanical modification of the mineral olivine has been explored to constrain the physical conditions of kimberlite ascent. We use a purpose-built experimental apparatus designed to fluidize a known mass of olivine particles at a controlled velocity for a specified time. We use SEM imagery and grain size distributions to document the physical processes that occur (e.g., fragmentation and abrasion) and model our data using the attrition model of Jones et al. (2017). This yields two parameters: (a) a stable mass reduction limit, and (b) an attrition rate. For the first time we relate these parameters (a and b) to the particle concentration and the particle kinetic energy—intrinsic variables that can be directly applied to kimberlite magma ascent. Lastly, we contextualize these insights provided by the attrition energetics into our evolving understanding of subsurface kimberlite ascent. Our demonstration of mechanical modification of the xenocrystic cargo during ascent has implications for bubble nucleation, chemical evolution of the kimberlite melts, and the interpretation of componentry and size distributions within natural deposits. Furthermore, we propose that by comparing xenocryst size and shape between deposits their relative ascent rates and transport distances can be determined.
Data Availability
All datasets generated for this study are included in the manuscript and/or the Supplementary Files.
Author Contributions
TJJ designed the study with support from JKR. DS performed the experiments with the support of TJJ. JKR performed the EoI modeling. TJJ conducted all other data analysis. All authors contributed to the editing of the manuscript after an initial draft was prepared by TJJ.
Funding
For this work TJJ was supported by a Rice Academy Research Fellowship at Rice University and JKR was supported by the Natural Sciences and Engineering Research Council of Canada through the Discovery Grants program. DS was funded by the NSERC CREATE program (University of Alberta and the University of British Columbia): Diamond Exploration and Research Training School (DERTS).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2019.00134/full#supplementary-material
References
Arndt, N. T., Boullier, A.-M., Clément, J.-P., Dubois, M., and Schissel, D. (2006). What olivine, the neglected mineral, tells us about kimberlite petrogenesis. eEarth Discuss. 1, 37–50. doi: 10.5194/eed-1-37-2006
Arndt, N. T., Guitreau, M., Boullier, A.-M., Le Roex, A., Tommasi, A., Cordier, P., et al. (2010). Olivine, and the origin of kimberlite. J. Petrol. 51, 573–602. doi: 10.1093/petrology/egp080
Ball, A., and Payne, B. W. (1976). The tensile fracture of quartz crystals. J. Mater. Sci. 11, 731–740. doi: 10.1007/BF01209461
Barton, J. M. Jr, and Gerya, T. V. (2003). Mylonitization and decomposition of garnet: evidence for rapid deformation and entrainment of mantle garnet-harzburgite by kimberlite magma, K1 Pipe, Venetia Mine, South Africa. South Afr. J. Geol. 106, 231–242. doi: 10.2113/106.2-3.231
Bemrose, C. R., and Bridgwater, J. (1987). A review of attrition and attrition test methods. Powder Technol. 49, 97–126. doi: 10.1016/0032-5910(87)80054-2
Brett, R. C., Russell, J. K., Andrews, G. D. M., and Jones, T. J. (2015). The ascent of kimberlite: insights from olivine. Earth Planet. Sci. Lett. 424, 119–131. doi: 10.1016/j.epsl.2015.05.024
Brett, R. C., Russell, J. K., and Moss, S. (2009). Origin of olivine in kimberlite: phenocryst or impostor? Lithos 112, 201–212. doi: 10.1016/j.lithos.2009.04.030
Brown, R. J., Kavanagh, J., Sparks, R. S. J., Tait, M., and Field, M. (2007). Mechanically disrupted and chemically weakened zones in segmented dike systems cause vent localization: evidence from kimberlite volcanic systems. Geology 35, 815–818. doi: 10.1130/G23670A.1
Brown, R. J., and Valentine, G. A. (2013). Physical characteristics of kimberlite and basaltic intraplate volcanism and implications of a biased kimberlite record. Bulletin 125, 1224–1238. doi: 10.1130/B30749.1
Bussweiler, Y., Foley, S. F., Prelević, D., and Jacob, D. E. (2015). The olivine macrocryst problem: new insights from minor and trace element compositions of olivine from Lac de Gras kimberlites, Canada. Lithos 220, 238–252. doi: 10.1016/j.lithos.2015.02.016
Campbell, M. E., Russell, J. K., and Porritt, L. A. (2013). Thermomechanical milling of accessory lithics in volcanic conduits. Earth Planet. Sci. Lett. 377, 276–286. doi: 10.1016/j.epsl.2013.07.008
Canil, D., and Bellis, A. J. (2008). Phase equilibria in a volatile-free kimberlite at 0.1 MPa and the search for primary kimberlite magma. Lithos 105, 111–117. doi: 10.1016/j.lithos.2008.02.011
Cashman, K. V., Sparks, R. S. J., and Blundy, J. D. (2017). Vertically extensive and unstable magmatic systems: a unified view of igneous processes. Science 355:eaag3055. doi: 10.1126/science.aag3055
Costa, A., Pioli, L., and Bonadonna, C. (2016). Assessing tephra total grain-size distribution: insights from field data analysis. Earth Planet. Sci. Lett. 443, 90–107. doi: 10.1016/j.epsl.2016.02.040
Dawson, J. B., and Hawthorne, J. B. (1973). Magmatic sedimentation and carbonatitic differentiation in kimberlite sills at Benfontein, South Africa. J. Geol. Soc. Lond. 129, 61–85. doi: 10.1144/gsjgs.129.1.0061
Drury, M. R., and van Roermund, H. L. M. (1989). Fluid assisted recrystallization in upper mantle peridotite xenoliths from kimberlites. J. Petrol. 30, 133–152. doi: 10.1093/petrology/30.1.133
Dufek, J., and Manga, M. (2008). In situ production of ash in pyroclastic flows. J. Geophys. Res. Solid Earth 113, 2156–2202. doi: 10.1029/2007JB005555
Dufek, J., Manga, M., and Patel, A. (2012). Granular disruption during explosive volcanic eruptions. Nat. Geosci. 5, 561–564. doi: 10.1038/ngeo1524
Edwards, B. R., and Russell, J. K. (2009). “Xenoliths as magmatic'menthos,” in AGU Spring Meeting Abstracts. Vancouver, BC. Available online at: http://adsabs.harvard.edu/abs/2009AGUSM.V22A.06E
Engwell, S., and Eychenne, J. (2016). “Chapter 4. contribution of fine ash to the atmosphere from plumes associated with pyroclastic density currents,” in Volcanic Ash, 1st Edn. (Elsevier), 67–85. doi: 10.1016/B978-0-08-100405-0.00007-0
Field, M., Gernon, T. M., Mock, A., Walters, A., Sparks, R. S. J., and Jerram, D. A. (2009). Variations of olivine abundance and grain size in the Snap Lake kimberlite intrusion, Northwest Territories, Canada: a possible proxy for diamonds. Lithos 112, 23–35. doi: 10.1016/j.lithos.2009.04.019
Ghadiri, M., and Zhang, Z. (2002). Impact attrition of particulate solids. Part 1: a theoretical model of chipping. Chem. Eng. Sci. 57, 3659–3669. doi: 10.1016/S0009-2509(02)00240-3
Giuliani, A. (2018). Insights into kimberlite petrogenesis and mantle metasomatism from a review of the compositional zoning of olivine in kimberlites worldwide. Lithos 312–313, 322–342. doi: 10.1016/j.lithos.2018.04.029
Gwyn, J. E. (1969). On the particle size distribution function and the attrition of cracking catalysts. AIChE J. 15, 35–39. doi: 10.1002/aic.690150112
Jerram, D. A., Mock, A., Davis, G. R., Field, M., and Brown, R. J. (2009). 3D crystal size distributions: a case study on quantifying olivine populations in kimberlites. Lithos 112, 223–235. doi: 10.1016/j.lithos.2009.05.042
Jones, T. J., McNamara, K., Eychenne, J., Rust, A. C., Cashman, K. V., Scheu, B., et al. (2016). Primary and secondary fragmentation of crystal-bearing intermediate magma. J. Volcanol. Geotherm. Res. 327, 70–83. doi: 10.1016/j.jvolgeores.2016.06.022
Jones, T. J., and Russell, J. K. (2017). Ash production by attrition in volcanic conduits and plumes. Sci. Rep. 7:5538. doi: 10.1038/s41598-017-05450-6
Jones, T. J., and Russell, J. K. (2018). Attrition in the kimberlite system. Mineral. Petrol. 112(Suppl. 2), 491–501. doi: 10.1007/s00710-018-0580-0
Jones, T. J., Russell, J. K., Lim, C. J., Ellis, N., and Grace, J. R. (2017). Pumice attrition in an air-jet. Powder Technol. 308, 298–305. doi: 10.1016/j.powtec.2016.11.051
Jones, T. J., Russell, J. K., Porritt, L. A., and Brown, R. J. (2014). Morphology and surface features of olivine in kimberlite: implications for ascent processes. Solid Earth 5:313. doi: 10.5194/se-5-313-2014
Kamenetsky, V. S., Kamenetsky, M. B., Sobolev, A. V., Golovin, A. V., Demouchy, S., Faure, K., et al. (2008). Olivine in the Udachnaya-East kimberlite (Yakutia, Russia): types, compositions and origins. J. Petrol. 49, 823–839. doi: 10.1093/petrology/egm033
Kavanagh, J. L., and Sparks, R. S. J. (2011). Insights of dyke emplacement mechanics from detailed 3D dyke thickness datasets. J. Geol. Soc. Lond. 168, 965–978. doi: 10.1144/0016-76492010-137
Knight, A., Ellis, N., Grace, J. R., and Lim, C. J. (2014). CO2 sorbent attrition testing for fluidized bed systems. Powder Technol. 266, 412–423. doi: 10.1016/j.powtec.2014.06.013
Kueppers, U., Perugini, D., and Dingwell, D. B. (2006). “Explosive energy” during volcanic eruptions from fractal analysis of pyroclasts. Earth Planet. Sci. Lett. 248, 800–807. doi: 10.1016/j.epsl.2006.06.033
Kueppers, U., Putz, C., Spieler, O., and Dingwell, D. B. (2012). Abrasion in pyroclastic density currents: insights from tumbling experiments. Phys. Chem. Earth, Parts A B C 45, 33–39. doi: 10.1016/j.pce.2011.09.002
McGetchin, T. R., Nikhanj, Y. S., and Chodos, A. A. (1973). Carbonatite-kimberlite relations in the Cane Valley Diatreme, San Juan County, Utah. J. Geophys. Res. 78, 1854–1869. doi: 10.1029/JB078i011p01854
Merle, O. (2015). The scaling of experiments on volcanic systems. Front. Earth Sci. 3:26. doi: 10.3389/feart.2015.00026
Mitchell, R. H. (1986). Kimberlites: Petrology, Mineralogy and Geochemistry, 1st Edn. Springer Science and Business Media. doi: 10.1007/978-1-4899-0568-0
Moore, A. E. (2012). The case for a cognate, polybaric origin for kimberlitic olivines. Lithos 128, 1–10. doi: 10.1016/j.lithos.2011.11.002
Moss, S., and Russell, J. K. (2011). Fragmentation in kimberlite: products and intensity of explosive eruption. Bull. Volcanol. 73, 983–1003. doi: 10.1007/s00445-011-0504-x
Moss, S., Russell, J. K., Smith, B. H. S., and Brett, R. C. (2010). Olivine crystal size distributions in kimberlite. Am. Mineral. 95, 527–536. doi: 10.2138/am.2010.3277
Peltonen, P., Kinnunen, K. A., and Huhma, H. (2002). Petrology of two diamondiferous eclogite xenoliths from the Lahtojoki kimberlite pipe, eastern Finland. Lithos 63, 151–164. doi: 10.1016/S0024-4937(02)00119-6
Pilbeam, L. H., Nielsen, T. F. D., and Waight, T. E. (2013). Digestion fractional crystallization (DFC): an important process in the genesis of kimberlites. Evidence from olivine in the Majuagaa kimberlite, southern West Greenland. J. Petrol. 54, 1399–1425. doi: 10.1093/petrology/egt016
Russell, J. K., Porritt, L. A., and Hilchie, L. (2013). “Kimberlite: rapid ascent of lithospherically modified carbonatitic melts,” in Proceedings of 10th International Kimberlite Conference. New Delhi: Springer, 195–210. doi: 10.1007/978-81-322-1170-9_12
Russell, J. K., Porritt, L. A., Lavallée, Y., and Dingwell, D. B. (2012). Kimberlite ascent by assimilation-fuelled buoyancy. Nature 481, 352–356. doi: 10.1038/nature10740
Smith, B. H. S. (2008). Canadian kimberlites: geological characteristics relevant to emplacement. J. Volcanol. Geotherm. Res. 174, 9–19. doi: 10.1016/j.jvolgeores.2007.12.023
Sparks, R. S. J. (2013). Kimberlite volcanism. Annu. Rev. Earth Planet. Sci. 41, 497–528. doi: 10.1146/annurev-earth-042711-105252
Sparks, R. S. J., Baker, L., Brown, R. J., Field, M., Schumacher, J., Stripp, G., et al. (2006). Dynamical constraints on kimberlite volcanism. J. Volcanol. Geotherm. Res. 155, 18–48. doi: 10.1016/j.jvolgeores.2006.02.010
Sparks, R. S. J., Pinkerton, H., and Macdonald, R. (1977). The transport of xenoliths in magmas. Earth Planet. Sci. Lett. 35, 234–238. doi: 10.1016/0012-821X(77)90126-1
Stone, R. S., and Luth, R. W. (2016). Orthopyroxene survival in deep carbonatite melts: implications for kimberlites. Contrib. Mineral. Petrol. 171, 1–9. doi: 10.1007/s00410-016-1276-2
Swain, M. V., and Atkinson, B. K. (1978). Fracture surface energy of olivine. Pure Appl. Geophys. 116, 866–872. doi: 10.1007/BF00876542
Wilson, L., and Head, J. W. (2007). An integrated model of kimberlite ascent and eruption. Nature 447, 53–57. doi: 10.1038/nature05692
Keywords: attrition, olivine, grain size distribution, milling, abrasion, kimberlite ascent
Citation: Jones TJ, Russell JK and Sasse D (2019) Modification of Mantle Cargo by Turbulent Ascent of Kimberlite. Front. Earth Sci. 7:134. doi: 10.3389/feart.2019.00134
Received: 18 February 2019; Accepted: 14 May 2019;
Published: 07 June 2019.
Edited by:
Shanaka L. de Silva, Oregon State University, United StatesReviewed by:
Raymond A. F. Cas, Monash University, AustraliaGeoff Kilgour, GNS Science, New Zealand
Copyright © 2019 Jones, Russell and Sasse. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Thomas J. Jones, dGhvbWFzLmpvbmVzQHJpY2UuZWR1
 Thomas J. Jones
Thomas J. Jones James K. Russell
James K. Russell David Sasse
David Sasse