- 1Department of Earth Sciences, University of Southern California, Los Angeles, CA, United States
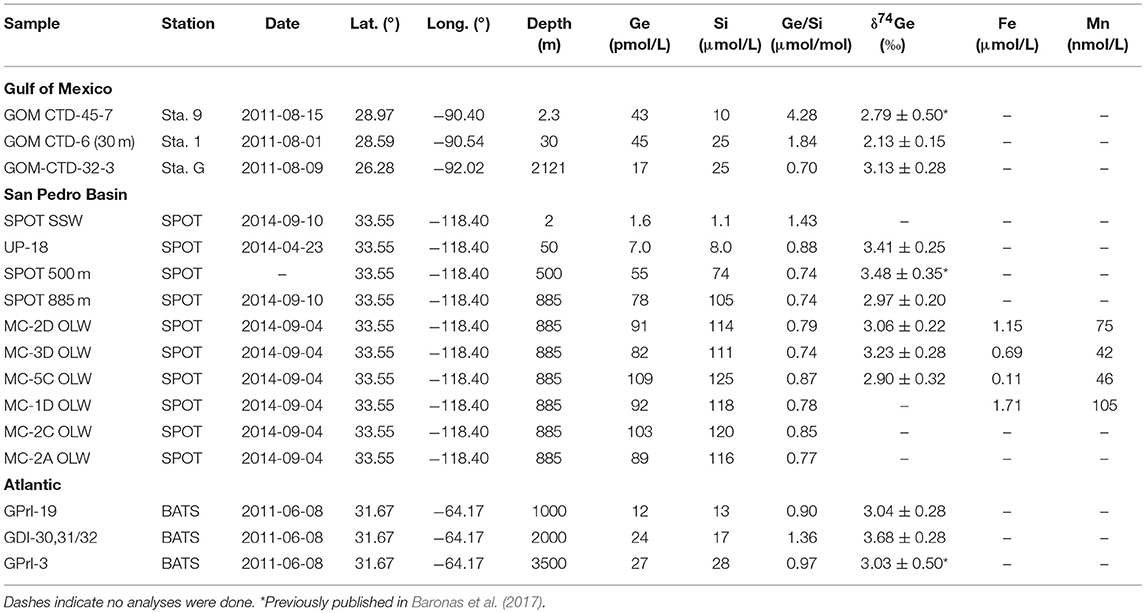
- 2IFREMER, Centre de Brest, Unité Géosciences Marines, Plouzané, France
The removal of chemical species from seawater during the precipitation of authigenic minerals is difficult to constrain but may play a major role in the global biogeochemical cycles of some elements, including silicon (Si) and germanium (Ge). Here, we present Ge/Si, δ74Ge, and supporting chemical data of pore waters and core incubations at three continental margin sites in California and the Gulf of Mexico. We used these data to partition Ge release and uptake by the various allogenic (delivered via sedimentation) and authigenic (formed in situ) phases in these sediments. About half of the pore water Ge (δ74Gepw = 1.3–2.4‰) is supplied by biogenic silica dissolution (δ74Ge ~ 3‰), with the other half contributed by lithogenic particulates (δ74Ge ~ 0.6‰). The highest Ge/Si (~3μmol/mol) and lowest δ74Ge (1.3–1.9‰) are observed at the Fe redox horizon, suggesting a supply from detrital Ge-rich Fe oxides. The precipitation of authigenic phases (most likely aluminosilicate clays) in deeper sediments preferentially incorporates Ge over Si, resulting in low pore water Ge/Si (~0.3μmol/mol). The lack of corresponding δ74Gepw trend indicates negligible Ge isotope fractionation during this process. Ge fluxes measured via core incubations were variable and appeared strongly controlled by Fe redox behavior near the sediment-water interface. In some cases, reductive Fe oxide dissolution appeared to enhance the benthic Ge flux by over 100% and released fractionated low δ74Ge of ~−0.7‰, resulting in overall benthic δ74Geinc between –0.2 and 3.6‰, depending on Fe oxide contribution to Ge flux. We estimate that detrital inputs supply 12–31% of total dissolved Ge to continental margin pore fluids globally, resulting in an average pore water and benthic flux δ74Ge between 2.2 and 2.7‰. Assuming 10-60% of pore water Ge is captured by the authigenic aluminosilicate sink, the dissolved Ge flux to the ocean derived from terrigenous inputs should be roughly 2.5–6.6 Mmol/y, much higher than previously estimated. Our results imply that authigenic Si burial in continental margins should be in the range of 1–8 Tmol/y (best estimate 3.1 Tmol/y), sufficient to close the global marine Si budget.
1. Introduction
Silicon (Si) is a major constituent of Earth's silicate crust that is released to solution during rock weathering and delivered to the ocean by rivers, where it sustains the productivity of marine biosilicifying organisms (Tréguer and De La Rocha, 2013). Oceanic Si concentrations also determine the rate of authigenic clay formation in sediments, which has been proposed to influence global climate through its effects on the marine carbonate balance (Mackenzie and Garrels, 1966). Silicon isotope ratio (30Si/28Si, expressed as δ30Si) and the germanium-to-silicon (Ge/Si) ratio have been developed as proxies tracing the biogeochemical cycling of Si (e.g., Froelich et al., 1985; Murnane and Stallard, 1990; De La Rocha et al., 2000; Ziegler et al., 2005). Recently, the stable isotope composition of Ge (74Ge/70Ge ratio, expressed as δ74Ge) has been measured in the major Earth surface reservoirs and proposed as an additional proxy helping to constrain the coupled biogeochemical cycles of Ge and Si (Rouxel et al., 2006; Escoube et al., 2012, 2015; Baronas et al., 2017, 2018; Rouxel and Luais, 2017). Germanium is a useful tracer of the Si cycle due to its prevalence in silicate rocks and the similar atomic properties and chemical behavior of the two elements (Burton et al., 1959; Froelich and Andreae, 1981; Rouxel and Luais, 2017). The ranges of Ge/Si and especially δ74Ge signatures in silicate rocks are relatively narrow (Mortlock and Froelich, 1987; Escoube et al., 2012; Rouxel and Luais, 2017). During continental weathering processes, the precipitation of secondary weathering products such as Al- and Fe-oxides and aluminosilicate clays preferentially incorporates Ge relative to Si (Froelich et al., 1992; Kurtz et al., 2002) and light Ge isotopes preferentially relative to heavy ones, resulting in dissolved river composition that has lower Ge/Si but higher δ74Ge relative to silicate rocks (Baronas et al., 2018).
The seawater Ge/Si and δ74Ge composition is primarily controlled by a balance of riverine and hydrothermal inputs and biogenic and authigenic outputs (Elderfield and Schultz, 1996; Hammond et al., 2000; Escoube et al., 2015; Baronas et al., 2017). Although biological Ge/Si fractionation is variable, most diatoms appear to discriminate against Ge only when dissolved Si is depleted below ~ 10 μmol/L (Sutton et al., 2010; Baronas et al., 2016). Ge/Si ratios are relatively invariable in deep seawater and in diatom biogenic silica (bSi) because nearly all dissolved Ge and Si upwelled to the photic zone is exported by diatom growth and settling, and most of this export dissolves congruently in deep water (Froelich et al., 1985, 1992; Ellwood and Maher, 2003; Baronas et al., 2016; Guillermic et al., 2017).
The Ge isotopic composition appears to be unfractionated during Ge incorporation into diatom bSi, although some fractionation may occur during Ge incorporation into the organic cellular material (Mantoura, 2006; Guillermic et al., 2017; Rouxel and Luais, 2017). Because most organic matter is rapidly remineralized in the upper water column, this secondary fractionation should have little effect on sedimentary δ74Ge dynamics. In contrast, all siliceous sponge spicules analyzed to date exhibit Ge/Si and δ74Ge signatures significantly lower than seawater, indicating strong vital effects (Ellwood et al., 2006, 2010; Rouxel et al., 2006; Guillermic et al., 2017). The magnitude of sponge bSi production and burial is not well-known, although it is likely small relative to diatoms (Van Cappellen, 2003), limiting the influence of biological fractionation on global seawater Ge/Si and δ74Ge composition.
While the burial of diatom bSi has little or no effect on the seawater δ74Ge composition, a large portion of bSi reaching the seafloor dissolves at or just below the water-sediment interface, releasing Ge and Si into marine pore waters. A range of complex diagenetic reactions take place in marine sediments, including the precipitation of various authigenic clay minerals (e.g., Aller, 2014). These authigenic minerals incorporate Ge and Si, affecting pore water Ge/Si (Hammond et al., 2000; King et al., 2000; Baronas et al., 2016), δ30Si (Ehlert et al., 2016), and possibly δ74Ge signatures. Recent studies have suggested that authigenic (“non-opal”) burial plays a major role in the global marine cycles of Ge and Si (Baronas et al., 2016, 2017; Rahman et al., 2016, 2017). Indeed, variations in authigenic Ge burial fluxes are likely responsible for the large seawater Ge/Si fluctuations over glacial-interglacial cycles (Mortlock et al., 1991; Hammond et al., 2004b; Baronas et al., 2016). A fully constrained global Ge isotope budget and unambiguous interpretation of past δ74Ge variations in seawater therefore require knowledge of the chemical and isotopic Ge behavior during marine sediment authigenesis.
Here, we present dissolved Ge/Si, δ74Ge, and various other solute concentration data at three different continental margin sites. Sediment pore water signatures were used to track the potential isotopic fractionation with progressing sediment diagenesis and authigenesis, while sediment core incubation data were used to constrain the net effect of these processes on the benthic flux. Ultimately, Ge isotopes have allowed us to put preliminary quantitative constraints on Ge partitioning between different sources and sinks in the studied sediments.
2. Study Sites
San Pedro and Santa Monica basins are located in the Southern California continental margin, ~20 and ~40 km offshore from Los Angeles, respectively. A detailed description of the geological and oceanographic setting of the Southern California Bight can be found elsewhere (Gorsline, 1992; Hickey, 1992). San Pedro basin has an area of 819 km2 and is 900 m deep. The Santa Monica basin is 2,225 km2 large and 925 m deep. Both basins are silled below 725 m depth, restricting the circulation of bottom water, with periodic flushing every few years (Berelson, 1991). Organic matter remineralization renders the restricted bottom water suboxic in both basins, typically <9 μM O2 in San Pedro basin and <4 μM O2 in Santa Monica basin, resulting in reducing sediment pore waters and limited macrofaunal activity in the benthos (Berelson et al., 1987; Leslie et al., 1990; Gorsline, 1992). In San Pedro basin, minor sediment irrigation and bioturbation may occur at times, whereas Santa Monica basin sediments are finely laminated, indicating lack of macrofaunal activity. Material is supplied to both basins primarily through particle infall from the overlying water column and through nepheloid plume transport (e.g., Collins et al., 2011). The sediments are comprised of 1–4% bSi, 8–10% CaCO3, and ~ 4% organic matter, with the remainder being lithogenic particles (Gorsline, 1992; Cheng et al., 2009).
Additional data are presented from the continental Gulf of Mexico shelf, close to the Mississippi River delta. Ge cycling in the area has been described in detail by Baronas et al. (2016), showing that Ge/Si ratios in the region are generally elevated due to contamination from coal ash (Froelich et al., 1985) and that authigenic Ge accounts for about 50% of total Ge burial in the Gulf of Mexico shelf sediments. In this study, new δ74Ge data from the two regions are presented and analyzed in the context of previously published pore water concentrations and core incubation results.
3. Methods
3.1. Sample Collection
San Pedro basin (SPB) sediment cores were collected on 2014-09-04 aboard the R/V Yellowfin at the San Pedro Ocean Timeseries (SPOT) study site. SPOT is the site of a multi-year monthly water column sampling campaign (https://dornsife.usc.edu/spot/). Santa Monica basin (SMB) cores were collected on 2012-03-08 aboard the R/V Yellowfin in the central part of the basin (Table 1). The cores were kept on ice before being placed in a 5°C cold room within 8 h from retrieval. For half of the cores, the overlying water was siphoned off while avoiding disturbance of the sediment surface. Then, pore waters were sampled using Rhizons (0.2 μm membrane; Rhizosphere Research Products, The Netherlands). The suction was applied at all depth horizons simultaneously to minimize vertical pore water advection during sampling. The pore waters were collected for up to 24 h. All samples were acidified to 0.1 vol% with Teflon-distilled conc. HNO3 inside the sampling syringe. Another set of cores with overlying water were incubated for several days as described below.
Additional water column samples were collected at SPB and in the Atlantic Ocean in 2014 and previously (Table 1). The SPB samples were collected in Niskin bottles on a CTD rosette aboard R/V Yellowfin, filtered through a 0.2 μm pore size filter within 10 h from retrieval, and acidified prior to analyses. The Atlantic Ocean samples were collected at the Bermuda Atlantic Time Series (BATS) station during the June 2008 GEOTRACES intercalibration cruise aboard the R/V Knorr. Further details are given in Baronas et al. (2017).
The Gulf of Mexico (GoMex) samples were collected in August 2011 during cruise EN-494 aboard the R/V Endeavor. Sediment cores were collected using a multi-corer and seawater samples using Niskin bottles. Pore waters were collected via sectioning under N2 atmosphere and centrifugation. All samples were filtered through 0.2 μm membrane and acidified prior to analysis. A detailed description of the GoMex methods is given in Baronas et al. (2016).
3.2. Core Incubations
Core incubations were carried out using the method described by Hammond et al. (2004a). Briefly, within 6–8 h of retrieval, sediment cores with 1–1.5 L of overlying water were capped, placed in a 5°C cold room and the water slowly stirred (20–30 rpm) using a suspended magnetic stir bar. During incubations, 10–20 mL of overlying water was periodically sampled for Ge and Si concentration analyses using a plastic syringe, while the piston was advanced to keep air out. Although care was taken to avoid air contact during core retrieval and incubations, in some cases a bubble of air was introduced to the overlying water, either during capping or via leakage around piston o-rings during sampling. The samples were immediately filtered through a 0.2 μm membrane and acidified prior to analysis. After the incubation was completed, the remaining overlying water was collected via siphoning, filtered through a 0.2 μm membrane and acidified prior to δ74Ge analyses.
3.3. Solute Concentration Analyses
Silicic acid and ammonia concentrations were measured using standard colorimetric techniques (Mullin and Riley, 1955; Bower and Holm-Hansen, 1980) with a precision better than 5%. Ammonia analyses were carried out within 24 h of sample collection to minimize degassing. Iron and manganese concentrations were analyzed by ICP-MS on a Thermo Scientific Element2 with a precision of ~ 10%. Sulfate concentrations were measured on a Metrohm Ion Chromatograph. Germanium concentrations were measured using isotope-dilution-hydride-generation-ICP-MS on a Thermo Scientific Element2, using the method developed by Mortlock and Froelich (1996) and modified by Baronas et al. (2016).
3.4. Ge Isotope Analyses
3.4.1. Ge Co-precipitation
Filtered and acidified samples of pore water from similar depths of multiple cores were combined to obtain larger composite samples required for δ74Ge analyses. Ge concentrations of individual aliquots were analyzed beforehand to ensure that all cores had similar Ge and Si concentration profiles. Pore water, incubation, and seawater samples ranging from 100 mL to 9 L and containing 4–13 ng of Ge were then spiked with a Ge isotope double spike (73Ge/70Ge ≈ 1, previously calibrated and used by Escoube et al., 2012, 2015; Baronas et al., 2018) in a spike/sample Ge mass ratio of 1–2 and a purified FeCl3 solution to obtain a Fe concentration of ~0.2 mmol/L. The samples were well mixed, and allowed to equilibrate for at least 16 h. Next, Fe(OH)3 flock was precipitated by bubbling pure NH3 gas through the sample until the solution reached a pH of 8–10. The flock was collected by settling and centrifugation, redissolved in 2 mL concentrated Teflon-distilled HNO3 and diluted to 10 mL with ultrapure (18 MΩ) H2O. The samples were then dried down, redissolved in 1 mL concentrated Optima-grade HF and diluted to 30 mL with ultrapure H2O to obtain a final 1 M HF solution. They were then purified through anion exchange columns as described below. The procedural blank was determined by processing spiked ultrapure H2O and ranged from 0.01 to 0.3 ng Ge.
3.4.2. Anion-Exchange Chromatographic Separation
A procedure adapted from Rouxel et al. (2006) and described in detail by Guillermic et al. (2017) and Baronas et al. (2018) was used. All reagents used were either in-house Teflon-distilled or Optima-grade. A 10 mL column was loaded with 1.8 mL (wet volume) of BioRad AG1-X8 resin, washed with 10 mL of 3 M HNO3, 0.28 M HNO3, and ultrapure H2O in sequence and conditioned with 5 mL 1 M HF. Samples in 1 M HF solution as prepared above were centrifuged to separate insoluble fluorides and 10–29 mL of the solution was carefully added to columns. The presence or the amount of insoluble fluorides at this stage did not appear to affect the final Ge recovery. The remaining matrix was eluted with 5 mL of 1 M HF followed by 3 mL of ultrapure H2O, leaving fluorinated Ge retained on the column. Ge was then eluted with 10 mL 0.28 M HNO3. If required, the solution was dried down and redissolved in a smaller volume of 0.28 M HNO3 to obtain the 0.5–10 ppb Ge concentration required for isotope measurements. Each column was reused 4–5 times, except when retention of DOC from the previous sample was observed based on the color, in which case the resin was replaced. Ge blanks from reused resin were below detection limit.
Ge recovery ranged from 20 to 90%, with one sample being as low as 8%. Incomplete recovery was most likely due to variable Ge co-precipitation efficiency with Fe(OH)3 (resulting from variable precipitation rates, final pH, and variable sample matrices, especially DOC concentrations in pore waters), as well as some loss during co-precipitate recovery from the solution. Importantly, incomplete recovery did not affect the measured δ74Ge values, as all samples were double-spiked prior to sample preparation.
Seawater contains relatively high concentrations of methylated Ge, which does not participate in the inorganic Ge cycle (Lewis et al., 1985, 1988, 1989). It is therefore important to separate the inorganic and the methylated species prior to δ74Ge analysis. Baronas et al. (2017) achieved this via chromatographic separation of the methylated and inorganic Ge hydrides. In this study, separation was achieved during both Fe co-precipitation and anion column chromatography, and is confirmed by the agreement of seawater δ74Ge determined via both methods (Table 1).
3.4.3. HG-MC-ICP-MS
Ge isotope analyses were performed on a Thermo Neptune multi-collector ICP-MS at Ifremer in Brest, France, using the method of Rouxel et al. (2006) as adapted by Escoube et al. (2015), Guillermic et al. (2017), and Baronas et al. (2018). Sample solutions of 0.5–10 ppb natural Ge in 0.28 M HNO3 were introduced into an online hydride generation system (CETAC HGX-200) at a rate of 150 μL/min where they were mixed with 0.25 M NaBH4 solution (in 1.5 M NaOH) introduced at an equal rate. The dissolved Ge(OH)4 species were reduced to gaseous GeH4 and transported into the ICP-MS torch using Ar carrier gas. The Neptune MC-ICP-MS was operated in low mass resolution mode, measuring 70Ge, 72Ge, 73Ge, and 74Ge in L2, C, H1 and H2 cups, respectively. In addition, L4, L3, L1, and H4 cups were also monitored for 68Zn (possible interference as 70Zn), 69Ga, 71Ga (possible interferences at m/z 70), and 77Se (possible interference as 74Se), respectively. No interferences were detected in any of the runs. The samples were bracketed using a NIST-3120a standard solution that had a total Ge concentration generally within ~20% of the bracketed sample, and was double-spiked to have a spike/sample ratio within ~ 20% of the bracketed sample. Each sample or standard run consisted of 6 measurement blocks each lasting 2 min (30 cycles of 4 s each), and in most cases 4–5 blocks displaying the most stable signal were retained. Therefore, each measurement consisted of 8–10 min of counting statistics at signal intensities ranging from 0.4 to 6 V (4-60 pA) at 74Ge (depending on Ge concentration in sample solution and instrument tuning). Instrumental blank measurements were generally below 2% of measured sample and standard intensities, suggesting that a wash-out time of 8 min was sufficient to avoid significant memory effects. The δ74Ge values were calculated for each block using the double-spike data reduction routine of Siebert et al. (2001) and are reported in ‰ as 74Ge/70Ge sample ratio normalized to the average 74Ge/70Ge ratio of bracketing measurements of Ge isotope standard NIST 3120a. This method also yields Ge concentration values based on the measured spike/sample ratio. Several different reference materials were analyzed multiple times, interspersed with the samples, and all agreed well with values previously reported by Baronas et al. (2018). The measurement uncertainty is reported as the internal 2σ standard error of the used sample blocks, or 2σ standard deviation of all NIST 3120a bracketing standard measurements within a given analytical session, whichever is higher.
4. Results
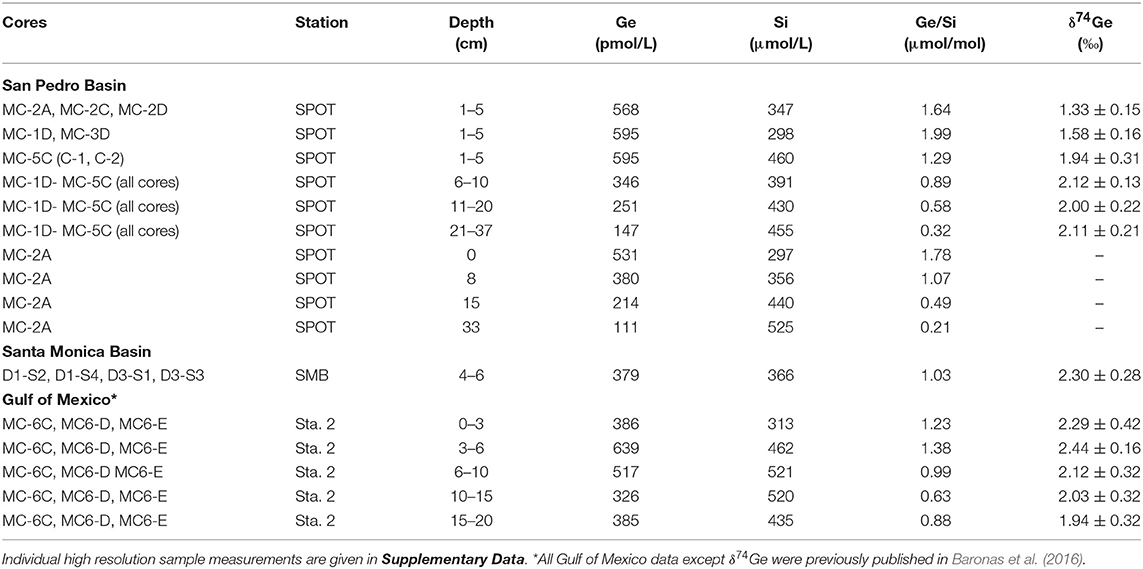
All of the Gulf of Mexico (GoMex) data, with the exception of δ74Ge, were previously reported and discussed by Baronas et al. (2016). This section therefore focuses on the newly acquired data from San Pedro and Santa Monica basins.
4.1. Seawater
Seawater data are reported in Table 1. Several samples were previously analyzed for δ74Ge by Baronas et al. (2017) and re-analyzed in this study, yielding identical values within analytical uncertainty.
The Ge/Si value determined for SPB bottom seawater (885 m depth) was 0.74 μmol/mol, close to the global ocean value of 0.76 μmol/mol (Froelich et al., 1985; Sutton et al., 2010). Core top water collected up to 8 h after core retrieval exhibited slightly elevated Ge and Si concentrations, with Ge/Si up to 0.87 μmol/mol. These were likely affected by benthic flux and disturbance during transport. SPB bottom seawater δ74Ge ranged from 2.9 to 3.2‰, slightly lighter than the 3.4–3.5‰ determined higher in the water column (Table 1; Baronas et al., 2017), which is indistinguishable from deep seawater δ74Ge values in other oceanic basins (Guillermic et al., 2017).
4.2. Pore Waters
The pore water solute concentrations were similar in each individual core. Ge concentrations ranged from 90 to 1,200 pmol/L (Supplementary Data) and showed a maximum at 2–3 cm depth, decreasing monotonically below (Figure 1). In contrast, Si concentrations were lowest at the sediment-water interface and increased from ~250 to ~400 μmol/L within the top 10 cm, with a continued slow increase to ~500 μmol/L by 35 cm depth (Figure 1). Pore water Ge/Si ranged from a high of 2–3 μmol/mol at 2–3 cm depth to a low of 0.2–0.4 μmol/mol at the bottom of the cores. δ74Ge values in pore water were lighter than in the water column, ranging from 1.3 to 2.3‰ in SPB and SMB and from 1.9 to 2.4‰ in GoMex sediments (Table 2). Pore water δ74Ge showed little variation with depth.
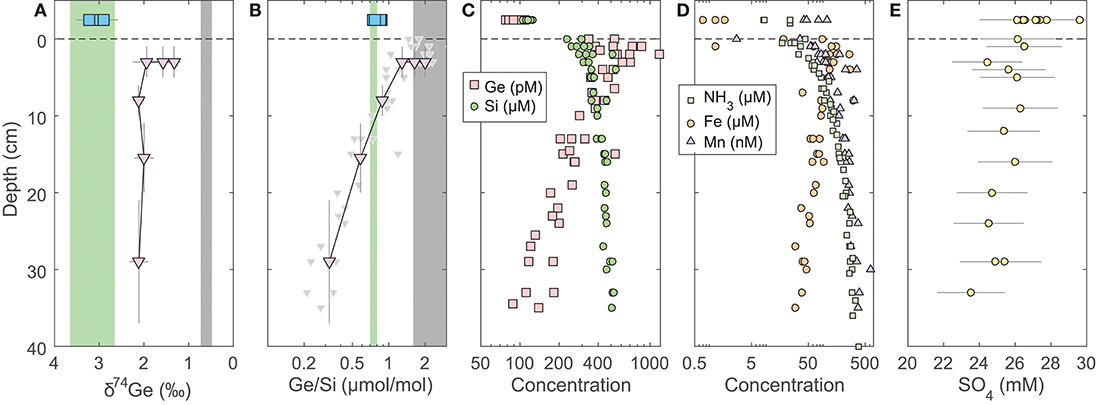
Figure 1. Pore water profiles of San Pedro Basin (SPB) sediments collected from five cores. Bottom seawater and initial core top overlying water data are plotted at an arbitrary depth above the sediment-water interface as blue squares. (A) Ge isotope composition of composite samples; vertical error bars show the depth range of combined samples. Three different composites were measured at the 1–5 cm horizon (see Table 2). Note the reverse x-axis; (B) Ge/Si of composite samples as in (A); also shown are individual sample Ge/Si ratios as small gray triangles. Note the log scale of x-axis. The green band shows the estimated δ74Ge and the measured Ge/Si composition of bSi (Baronas et al., 2016), equivalent to seawater. The gray bands show the typical composition of lithogenic silicates (Escoube et al., 2012; Rouxel and Luais, 2017); (C) Ge and Si concentrations; (D) NH3, Fe, and Mn concentrations; (E) Sulfate concentrations from cores MC-1D and MC-2A (Supplementary Data), uncorrected for potential variations in salinity.
Fe, Mn, NH3, and SO4 concentrations in SPB pore waters are reported in Figure 1 and Supplementary Data. Fe concentrations ranged from 1 to 300 μmol/L, with a maximum at 2–3 cm depth. Mn and NH3 concentrations ranged from 0 to 600 nmol/L and from 20 to 400 μmol/L, respectively, and both increased monotonically with depth. Fe and Mn concentrations reported here are in good agreement with recently published profiles from ancillary cores collected during this cruise (Monteverde et al., 2018). Sulfate concentrations were in 24–26 mmol/L range and appeared to slightly decrease with depth in SPB sediments (previously published by Monteverde et al., 2018).
4.3. Core Incubations
Core incubations were performed with core-top water present for up to 6 days, to constrain the net effect of sediment diagenetic processes on the benthic Ge and Si fluxes and the δ74Ge composition of the benthic flux. Throughout the incubations, Ge concentrations increased from 70–80 to 80–120 pmol/L in SPB overlying water and from 90–100 to 120–150 pmol/L in SMB overlying water. Si concentrations increased from ~100 to 130–150 μmol/L in SPB and from ~130 to 150–190 μmol/L in SMB (Figure 3; Supplementary Data). Table 3 summarizes the chemical and isotopic composition of the post-incubation overlying water and the calculated benthic fluxes. The Ge benthic fluxes were calculated to range from ~0 to 1.8 nmol m−2 d−1 at SPB and from 0.9 to 1.5 nmol m−2 d−1 at SMB. The Si benthic fluxes ranged from 0.7 to 1.6 mmol m−2 d−1 at SPB and from 0.5 to 1.4 mmol m−2 d−1 at SMB, in good agreement with previous measurements (e.g., Hammond et al., 2000; McManus et al., 2003; Baronas et al., 2016). As a result, the benthic flux Ge/Si ratios exhibited a wide range at both sites (0.03–1.1 μmol/mol at SPB and 0.9–1.8 μmol/mol at SMB). The post-incubation δ74Ge was in the 2.9–3.5‰ range, similar to the initial overlying composition (2.9–3.2‰), with the exception of one SPB incubation (MC-3A; 2.07 ± 0.71‰) that showed the highest Ge flux.
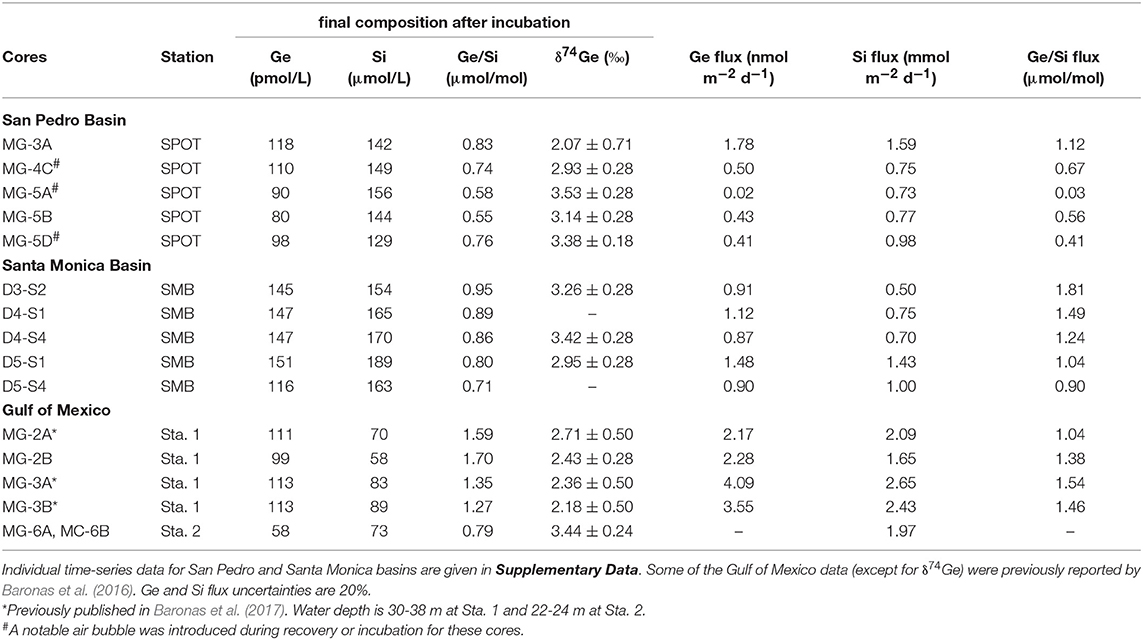
Table 3. Summary of core incubation data, showing the final post-incubation composition of the overlying water, as well as the calculated Ge and Si fluxes.
In the Gulf of Mexico, the δ74Ge composition of two post-incubation overlying water samples was determined in addition to previous data reported by Baronas et al. (2017) (Table 3). At Station 1, which is located close to the Mississippi River delta, post-incubation δ74Ge was determined to be 2.4‰ (bottom seawater at this site was 2.1‰), in agreement with data from other cores of Baronas et al. (2017). At Station 2, which was located several hundred kilometers away from the river delta, δ74Ge was determined to be 3.4‰, similar to the deep seawater in the Gulf of Mexico and other oceanic basins (Table 1; Guillermic et al., 2017).
5. Discussion
5.1. Pore Waters
Broadly, the δ74Ge and Ge/Si composition of fluids within and above sediments is controlled by (1) mixing of various solute sources (dissolution of bSi vs. lithogenic particles, as well as trapped/diffusing bottom water); and (2) solute removal via precipitation of authigenic phases (Fe oxides and authigenic aluminosilicates), and associated elemental or isotopic fractionation. Pore water δ74Ge measured in SPB and SMB sediments was 1–2‰ lighter than the expected composition of the dissolving diatom bSi, which is likely to be similar to the overlying seawater (Figure 1A). Therefore, the low δ74Gepw composition must reflect either a significant contribution from an isotopically lighter source, or fractionation during Ge incorporation into precipitating authigenic phases. Previous studies have shown that various lithogenic silicates, including marine sediments, exhibit a narrow δ74Ge range of 0.4–0.8‰(Rouxel and Luais, 2017). Secondary terrestrial weathering products, for example Fe oxides, are known to be enriched in Ge (Kurtz et al., 2002) and to preferentially incorporate light Ge isotopes during formation (Pokrovsky et al., 2014). The δ74Ge signature of lithogenic material delivered to the sediments should therefore be close to (potentially slightly lower than) the Bulk Silicate Earth value of 0.58 ± 0.21‰(Rouxel and Luais, 2017).
In SPB pore waters, the lowest δ74Gepw values are found in the 1–5 cm depth horizon, coinciding with the highest Ge/Si ratios and highest Fe concentrations in pore waters (Figure 1). Pore water composition in this zone is therefore most likely controlled by mixing of three sources: dissolution of bSi (Ge/Si = 0.7 μmol/mol; δ74Ge = 3–3.5‰), dissolution or desorption of Ge from lithogenic particles (Ge/Si⩾1.5 μmol/mol; δ74Ge ⩽ 0.6‰), and the reductive dissolution of authigenic Fe oxides that precipitate at the sediment-water interface (Figure 1). Germanium is well-known to adsorb or co-precipitate with Fe (oxy)hydroxides (e.g., Pokrovsky et al., 2006). Indeed, Fe (oxy)hydroxide (abbreviated as FeOx from here on) co-precipitation is used to pre-concentrate Ge from dissolved samples during sample preparation (see section 3). This scenario might involve non-steady state Fe redox dynamics in these sediments, which is possible, given the occasional re-oxygenation of bottom waters (Berelson, 1991) and the possible introduction of oxygen during core retrieval (see section 5.2). For this reason, further pore water discussion focuses on deeper (>10 cm) pore waters, which are unaffected by Fe redox dynamics. We will return to the coupling of Ge to Fe redox in the discussion of core incubation data (section 5.2).
5.1.1. Effect of Authigenic Clay Precipitation on Ge Isotope Composition
Pore water Ge/Si values decrease with depth (Figure 1B), indicating that dissolved Ge is being removed from pore water via the precipitation of authigenic (non-opal) phases, which has previously been observed in SPB (Hammond et al., 2000; King et al., 2000; McManus et al., 2003). Although the stoichiometry and the mineralogy of the precipitating phases are poorly constrained, the tight coupling of Ge and Fe concentrations (Figures 1C,D) suggests it could be Fe-rich aluminosilicate clays. Such clays have been shown to form rapidly in continental margin environments, including GoMex sediments (Michalopoulos and Aller, 1995; Presti and Michalopoulos, 2008; Rahman et al., 2017). The formation of aluminosilicate clays is also suggested by the asymptotic increase in Si concentrations to ~400–500 μmol/L at 30–40 cm depth (Table 2, Figures 1; 2; see also Murnane et al., 1989), which are significantly lower than the solubility of bSi, the latter ranging from 600 to 1,000 μmol/L, depending on bSi age and the degree of surface passivation by authigenic coatings (e.g., McManus et al., 1995). Very similar dissolved Si profiles have been observed in other regions with high rates of authigenic clay formation (e.g., Michalopoulos and Aller, 1995, 2004; Ehlert et al., 2016).
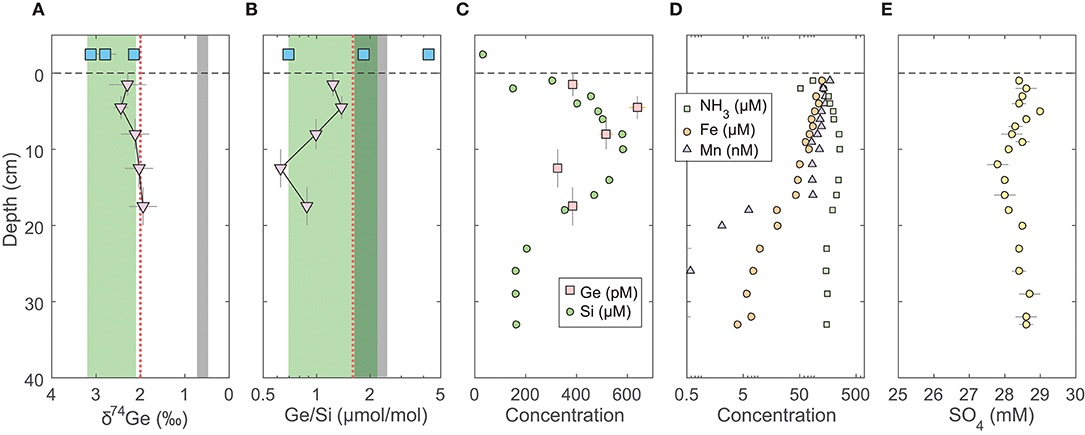
Figure 2. Pore water profiles of Gulf of Mexico (GoMex) sediments collected from three cores at Sta. 2 (Table 2; Baronas et al., 2016). GoMex seawater data are plotted at an arbitrary depth above the sediment-water interface. (A) Ge isotope composition of composite samples; vertical error bars show the depth range of combined samples. Note the reverse x-axis; (B) Ge/Si of composite samples as in (A). Note the log scale of x-axis. The green band shows the estimated δ74Ge and Ge/Si composition of bSi in GoMex shelf area affected by the Mississippi River (pink dotted line; see text). The gray bands show the typical composition of lithogenic silicates (Escoube et al., 2012; Rouxel and Luais, 2017); (C) Ge and Si concentrations, including additional Si data from a separate core MC-5; (D) NH3, Fe, and Mn concentrations in MC-5; (E) Sulfate concentrations in MC-5, corrected for salinity. All the data except for δ74Ge were previously published in Baronas et al. (2016).
Isotopically light Ge is also readily incorporated into sulfide minerals that precipitate in hydrothermal settings, e.g., sphalerite (ZnS) (Luais, 2007, 2012; Escoube et al., 2012, 2015; Belissont et al., 2014; Meng et al., 2015) and possibly during sulfate reduction in marine sediments (Murnane et al., 1989), although the latter has not been clearly demonstrated. Sulfate concentration in SPB pore waters decreases slightly with depth (Figure 1E), indicating likely sulfate reduction. Leslie et al. (1990) previously argued that sulfate reduction and pyrite precipitation rates decrease with depth in SPB sediments. Therefore, if pyrite precipitation fractionates δ74Ge while sequestering a significant fraction of Ge, we would expect to see a strong δ74Gepw gradient. Such a gradient is not observed (Figure 1A). Overall, authigenic Ge sequestration appears to be independent of sulfide precipitation in this and other continental margins (Hammond et al., 2000; Baronas et al., 2016), which might be due to a low Ge partitioning coefficient into iron sulfides, as suggested by relatively low, sub-ppm Ge concentrations in such minerals (Burton et al., 1959). Pyrite formation is therefore unlikely to be a major factor regulating dissolved Ge dynamics in the sediments studied here.
Regardless of the exact phase, the fraction of dissolved Ge removed from pore waters via authigenesis can be calculated from the change in pore water Ge/Si composition with depth. Given that in SPB about half of Ge is supplied via bSi and the other half by lithogenic particles (see section 5.2.2), the Ge/Si signature supplied to pore waters should be within 1.0–1.8 μmol/mol. Therefore, ~80–90% of the pore water Ge has to be precipitated to achieve the measured Ge/Sipw of 0.2–0.3 μmol/mol by 30 cm depth. This fraction is slightly higher than previously estimated values of 50–60% which had not accounted for lithogenic Ge supply (Hammond et al., 2000; Baronas et al., 2016). Note that a significant portion of dissolved Ge diffuses back into overlying water, and therefore the fraction of the total Ge rain to the sediments captured by the authigenic phase is lower (see section 5.2.2). A key take-away from pore water data is that although 80–90% of dissolved Ge is precipitated by 30 cm depth, the δ74Gepw composition remains constant, indicating that any isotopic fractionation during this process is small (–0.3 < <0.3‰).
Although the geochemical setting is more complicated and there are fewer data available, the same conclusion can be drawn from the GoMex pore waters (Figure 2). Here, δ74Gepw is also relatively constant in the 1.9–2.4‰ range, whereas Ge/Si varies between 1.4 and 0.6 μmol/mol, generally decreasing with depth. The Mississippi River supplies a large amount of Ge and Si to the studied area, partly due to contamination by anthropogenic activity (Mississippi Ge/Si = 1.6 μmol/mol; δ74Ge = 2.0‰; Baronas et al., 2017). Its discharge and possibly chemical and isotopic composition varies temporally, as a result variably affecting the elemental and isotopic composition of diatom bSi that is supplied to and dissolves in the GoMex shelf sediments. Despite the uncertainty of the bSi end-member, the large decrease in pore water Ge/Si can only be explained by authigenic Ge precipitation (Baronas et al., 2016). Yet, similarly to SPB sediments, no detectable variation of δ74Gepw with depth is observed at GoMex (Figure 2A).
We do acknowledge the possibility that the dissolution of several phases (bSi, detrital oxides and silicates) and the precipitation of several others (FeSx, FeOx, authigenic silicates) could fractionate δ74Gepw in opposite directions, theoretically resulting in the relatively constant δ74Gepw of about 2‰. Assessing this possibility is, however, outside of the scope of this paper and we therefore argue that the simplest explanation—no δ74Ge fractionation during authigenic phase precipitation—is most likely to be the correct one, especially given the consistency of δ74Gepw across both (SPB and GoMex) study sites.
Given that secondary clay formation during terrestrial weathering fractionates δ74Ge (Baronas et al., 2018; Qi et al., 2019), it is somewhat surprising that authigenic clay formation in continental margin sediments studied here does not appear to do so. Additional studies are needed to investigate Ge fractionation in these environments in detail; at the moment we can only speculate on the cause of this distinction. Possible reasons include the likely differences in mineralogy of the clays forming in terrestrial and marine environments (e.g., kaolinite vs. glauconite) and the redox conditions (oxic in saprolite, reducing in continental margin sediments), given that Fe oxides are known to strongly fractionate δ74Ge (Pokrovsky et al., 2014, also see discussion below). Another possibility is that Ge isotope fractionation by clays is dominantly kinetic, and in the diffusion-dominated reducing sediments, authigenic clays are able to isotopically re-equilibrate with pore waters, erasing any such kinetic fractionation. In contrast, during continental weathering solute transport is dominated by advection (percolation of rain water through soil and saprolite), which limits the time for potential isotopic equilibration between secondary clays and dissolved Ge. Future studies are needed to test these hypotheses.
5.2. Core Incubations
Benthic flux measurements reflect the composition of solutes diffusing into the overlying water column, integrating the net effect of all sedimentary processes. Core incubation data can therefore be used to more quantitatively assess the various sources of dissolved Ge to pore waters and the potential isotopic fractionation associated with authigenic phase formation.
5.2.1. Ge and Si Benthic Fluxes
The benthic Si fluxes were similar at SPB and SMB sites and individual core experiments agreed well with each other at a given site (relative standard deviation of ~40%; Table 3; Figure 3). In contrast, Ge fluxes differed significantly between the two sites and were especially variable within SPB, spanning two orders of magnitude and resulting in a wide range of observed benthic flux Ge/Si ratios. We propose that Ge fluxes in these experiments were affected by variable redox conditions in the sediments that were perturbed during retrieval, transportation, and incubation.
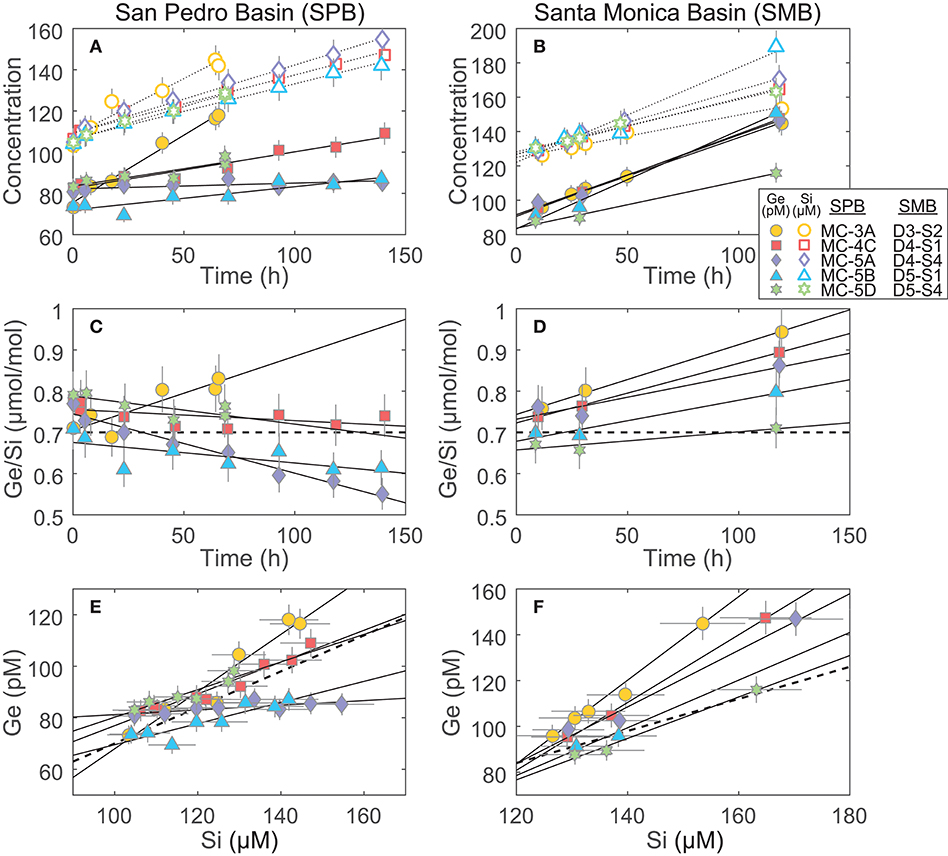
Figure 3. Incubation results of cores from San Pedro and Santa Monica basins (SPB and SMB, respectively): (A,B) The increase of Ge and Si concentrations in the incubated overlying water. These slopes, once corrected for water loss via sampling (see Supplementary Data), were used to determine the benthic Ge and Si fluxes reported in Table 3; (C,D) The change in the Ge/Si ratio of the overlying water. The thick dashed line shows the Ge/Si of biogenic silica in the SPB and SMB sediments (0.7 μmol/mol; Baronas et al., 2016); (E,F) plots showing Ge vs. Si concentration over the course of the incubations. These slopes were used to calculate the benthic flux Ge/Si ratio (Table 3). The thick dashed line shows Ge/Si of biogenic silica (0.7 μmol/mol).
Santa Monica basin bottom waters and sediments are known to be consistently anoxic, exhibiting high benthic Fe flux and dissolved Fe2+ up to (or nearly up to) the sediment-water interface (McManus et al., 1997; Elrod, 2004; Severmann et al., 2010). The Ge/Si flux at SMB was significantly higher than the 0.7 μmol/mol of dissolving bSi in all cases (Figure 3; Table 3), consistent with the dissolution of Ge-enriched Fe oxides.
At SPB, benthic Ge fluxes and Ge/Si ratios varied widely, the latter ranging from ~0.03 to 1.12 μmol/mol (Figure 3; Table 3). Considering that all cores were collected in close proximity (cores MC-5A, -5B, and -5D were collected during a single multi-corer deployment), this variability is unlikely to be caused by spatial heterogeneity in surface sediment composition. The wide range of observed fluxes therefore probably results from the perturbation of bottom redox conditions during core recovery and incubation. It is unavoidable that some oxygen is introduced during sampling. As a result, dissolved Fe2+ in the overlying water and the surficial pore water can be oxidized, capturing a portion (or all, in the case of MC-5A) of the potential Ge benthic flux. Orange, most likely FeOx, flock was observed on sediment surface of most cores. In addition, core MC-5A, which had negligible benthic Ge flux, also had a large burrow at the sediment water interface and seemed the most disturbed during recovery, including air bubbles trapped in the core liner. In support of this hypothesis, the benthic dissolved Fe flux at SPB was previously determined by in-situ incubations and water column measurements to often be 1–2 orders of magnitude lower than that based on pore water Fe gradients, suggesting that a large fraction of dissolved Fe is captured near the water-sediment interface (Elrod, 2004; Severmann et al., 2010; John et al., 2012).
In summary, the core incubations performed on SPB and SMB sediments together represent a range of bottom redox conditions. Such sampling-induced perturbation provides an independent test of any δ74Ge fractionation potentially associated with Fe oxide precipitation in marine sediments. Below, we perform some simple mass balance modeling to determine benthic flux δ74Ge signature of each core and the fraction of Ge released or sequestered by the various solid phases.
5.2.2. Modeling Ge Isotope Mass Balance During Core Incubations
Although the large amount of seawater needed for δ74Ge analyses prevents the collection of δ74Ge time-series data during core incubations, the final post-incubation δ74Ge signature () can be used to assess the isotopic composition of Ge flux that has been affected by non-opal phases. To do this, a simple mass balance model was built, partitioning Ge amounts dissolved and sequestered by the various phases, and their associated Ge isotope signatures (Figure 4). The model was implemented using MATLAB R2018b, and the source code is given in the Supplementary Material.
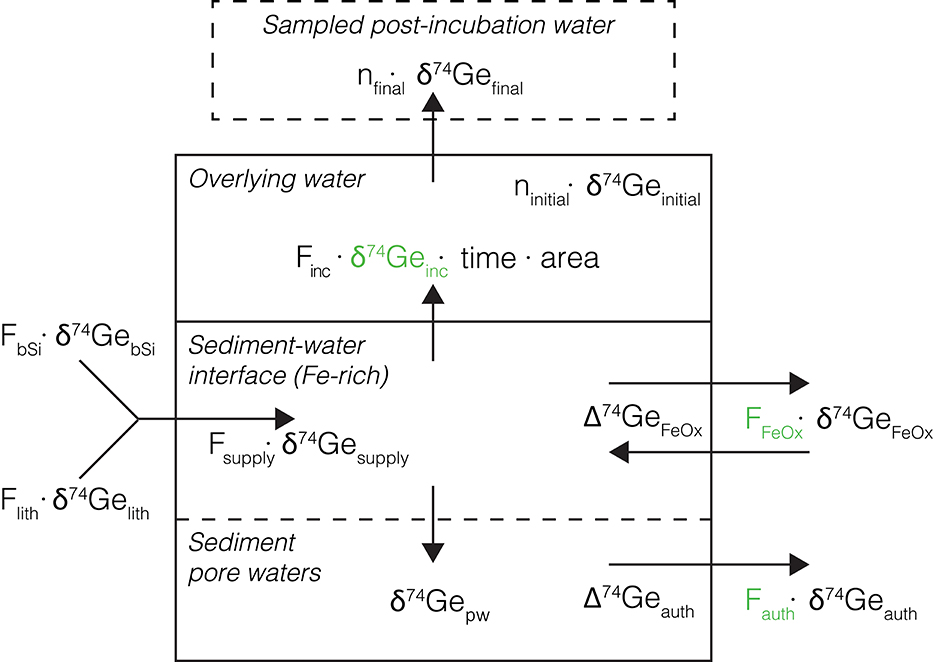
Figure 4. Schematic representation of the Ge isotope mass balance model used to interpret core incubation data. The main model-calculated parameters (namely δ74Geinc, Fauth, and FFeOx) are shown in green. Other values are either measured or calculated as described in text. Back-diffusion of Ge from overlying water into the sediments is assumed to be small and is ignored.
For each incubated sediment core, the amount of Ge (ni, in mol) in the overlying post-incubation water is the sum of Ge initially present prior to the incubation and the net added via the benthic flux during incubation:
where [Ge]initial and Vinitial are the measured Ge concentration and volume of the pre-incubation overlying water. Finc is the measured Ge incubation flux given in Table 3 (in mol m−2 time−1), t is incubation time and A is the core sediment surface area (in m2). The Ge isotope composition in the final post-incubation overlying water is then
Having measured all the other parameters, Equation (4) can be used to calculate δ74Geinc, the isotopic composition of Ge released into the overlying water during the incubation. Using a number of additional observations and assumptions (see below), we can quantify the different processes controlling the dissolved Ge isotope mass balance in these sediments: (1) Ge release from bSi and lithogenic particle dissolution (Flith and FbSi, respectively), followed by (2) the removal or addition of Ge by Fe redox reactions near the sediment-water interface (FFeOx), and (3) continued removal of Ge by other authigenic phases in deeper sediments (Fauth), as observed in the pore water profiles (Figure 4). A Monte Carlo approach (running the model 1 million times for each incubated core) was utilized to assess the full range of uncertainty associated with all the input parameters, yielding probability distributions of the calculated values.
A detailed description of model equations and input parameters is given in section 5.2.2.1. The model results for each individual core are given in Supplementary Material. Here we provide a summary of the overall results.
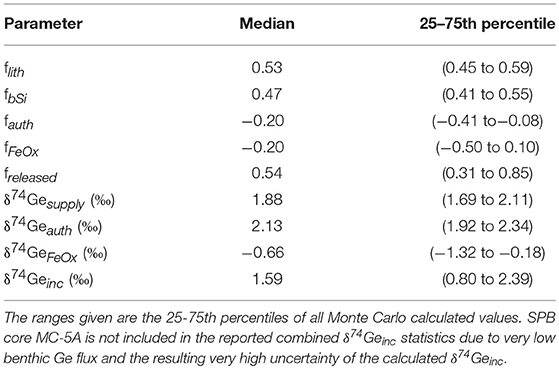
The combined model results of all eight incubated SPB and SMB cores are given in Table 4 and Figure 5. Based on the measured benthic Si flux (combined with diatom Ge/Si ratio) and lithogenic FeOx input flux (Leslie et al., 1990) we show that the biogenic and lithogenic Ge input fluxes are roughly similar (Figure 5E). Using the fractionation factors reported by Pokrovsky et al. (2014) along with the δ74Gepw data reported here, we calculate that on average, authigenic Ge sequestration takes up between 8 and 41% of the total allogenic supply (fauth between −0.08 and −0.41; Table 4; Figure 5C), whereas iron (oxy)hydroxides in most cases sequester a similar proportion of Ge (fFeOx down to −0.5) but in some cases can also release authigenic Ge during dissimilatory Fe reduction (fFeOx > 0). This variability in fFeOx is consistent with the qualitative discussion of variable Fe redox dynamics and their perturbation during recovery and is discussed in more detail below.
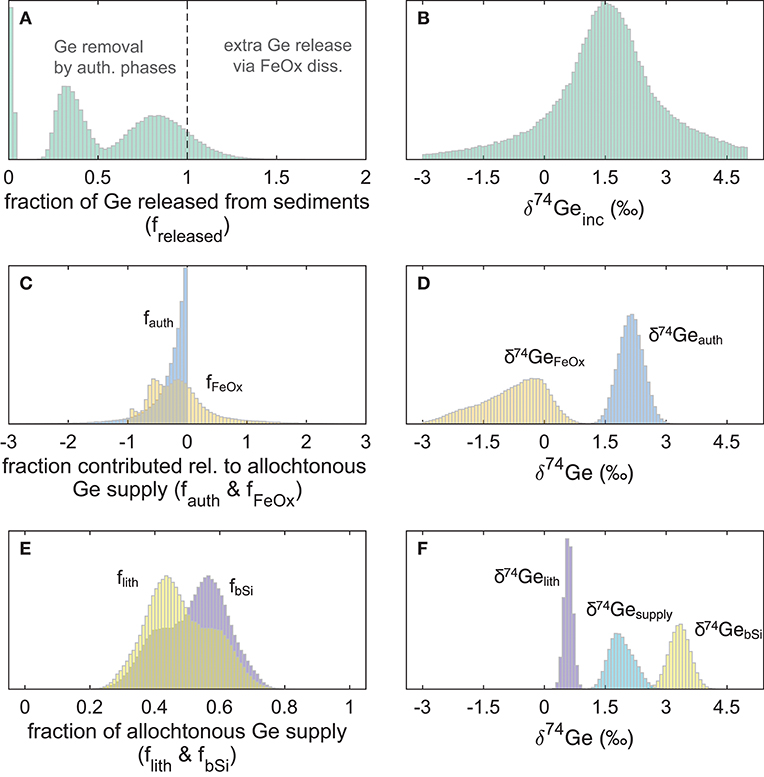
Figure 5. Probability distributions of the fraction of Ge released or consumed by different phases (relative to the allogenic supply from bSi and lithogenic inputs) during San Pedro and Santa Monica basin core incubation experiments, and their isotopic compositions: (A) freleased values <1 indicate net Ge sequestration in sediments, and values >1 indicate additional Ge release from authigenic Fe oxide reduction; (B) the combined probability distribution of δ74Ge released during all eight core incubations; (C) fraction of Ge consumed (<0) or released (>0) from the deep authigenic (possibly clay) phase (fauth) and authigenic Fe oxides (fFeOx); (D) the calculated Ge isotope composition of the two authigenic phases; (E) the calculated fraction of allogenic Ge supply by lithogenic particles and bSi; (F) the assigned Ge isotope composition of lithogenic and bSi phases, and the calculated composition of total allogenic Ge input ().
For SMB cores, the fraction of allogenic Ge input that is captured by authigenic phases is relatively constant, ranging from 14 to 29% (median freleased between 0.71 and 0.86; Supplementary Material). Our modeling indicates that authigenic phases play a relatively minor role in SMB sediments (−0.19 < fauth < −0.1 and −0.17 < fFeOx < 0.07). While SPB sediments exhibited similar Ge sequestration by the deep (possibly clay) authigenic phase (−0.23 < fauth < −0.16 with the exception of MC-3A where median fauth = −0.81), dissolved Ge uptake or release by authigenic Fe oxides was much more variable (−0.75 < fFeOx < 0.80) at SPB, likely caused by perturbations and variable oxygen introduction during core retrieval and incubation (Table 3). As a result, the net fraction of dissolved Ge released back into overlying waters, varied widely among SPB core incubations (freleased = 0.02–0.98). Below we give a detailed description of how these different estimates were calculated.
5.2.2.1. Detailed core incubation model description
Having measured the pre- and post-incubation overlying water δ74Ge, Equation (4) allows the calculation of δ74Geinc, or the Ge isotope composition of the incubation flux. Here we describe the subsequent calculations used to partition this flux between the different Ge sources and sinks in the incubated sediments. All input parameter values and their uncertainty ranges are given in Supplementary Material.
First, the Ge benthic flux expected from bSi dissolution was calculated simply as
which assumes that the amount of the benthic Si flux () captured by sediment authigenesis is negligible (e.g. less than 10%). This assumption is validated by the good agreement between the average annual measured flux of 1.2±0.3 mmol m−2 d−1 during 2004–2006 (Hammond et al., unpub. data) and the bSi rain to the seafloor of 1.3±0.2 mmol m−2 d−1 during this time, measured using sediment traps (Collins et al., 2011). Ge/SibSi is taken to be equivalent to deep Ge/Sisw in the California Margin, as confirmed by a bSi-targeting weak alkaline leach of the trap material of Collins et al. (2011) [Supplementary Material of Baronas et al. (2016)].
The detrital Ge flux can be estimated from the external Fe (oxy)hydroxide input to SPB sediments, which was previously calculated by Leslie et al. (1990) as the flux required to sustain the pyrite burial flux, equal to 26 Fe μmol m−2 d−1. Making the simplifying assumption that reducible Fe oxides are the dominant lithogenic source of dissolved Ge in these sediments, the detrital Ge flux can be calculated from the Ge/Fe ratio of these oxides. Given that both Ge and Fe are highly immobile and mostly retained in the solid phases during weathering (Gaillardet et al., 2014; Baronas et al., 2018), detrital Fe oxides should have Ge/Fe that is similar to continental crust, i.e., around 27 μmol/mol (Rudnick and Gao, 2014). Using Ge/Fe = 27±10 μmol/mol yields a lithogenic-derived Ge contribution to pore waters (Flith) of 0.70±0.26 nmol m−2 d−1. The isotopic composition of this detrital flux should be close to the crustal value, given that more than 95% of river-delivered Ge is retained in the solid phase and that riverine suspended sediment δ74Ge composition is for the most part indistinguishable from primary igneous rock values (Baronas et al., 2018).
The allogenic supply of dissolved Ge to the sediments is therefore:
and its isotopic composition:
Finally, the measured incubation flux (Finc) is affected by the sequestration or release of Ge by authigenic phases, which we here separate into iron oxides (FeOx; note that these are authigenic oxides that precipitate and dissolve within sediments, distinct from the detrital rain-delivered Fe oxides denoted above as lith) and other authigenic phases, such as authigenic clays (auth):
where positive F values indicate Ge release into dissolved phase, and negative F values indicate Ge sequestration into solid phase. The isotopic composition of FeOx is simply
where is assigned the experimentally determined range between −1.6 and −4.6‰(Pokrovsky et al., 2014). In the case of downcore authigenic phases, no experimental or theoretical values are available. However, the lack of pore water δ74Gepw gradient observed at SPB (Figure 1) limits to 0 ± 0.3‰. The isotopic composition of this downcore authigenic phase is then
Using δ74Gepw instead of for the initial value is necessary in this case, to allow for the potential influence of isotopically distinct Ge released from reductive FeOx dissolution higher in the sediment column.
Equations (8–11) can be combined to solve for FFeOx and Fauth.
The fractions of Ge supplied or consumed by different phases are defined as fractions of the allogenic supply:
Given that ninc for the incubated cores ranged between 1 and 35% of nfinal, and the similar values between and , the calculated δ74Geinc can be sensitive to analytical and experimental uncertainty. We used a Monte Carlo approach to fully assess this uncertainty and to further deconvolve the various factors influencing δ74Geinc. The above set of calculations is performed a large number of times (n = 1,000,000), each time randomly selecting from within the uncertainty range of each given parameter (see Supplementary Material). Finally, the following boundary conditions are applied to remove physically impossible results and very long probability distribution tails that can arise from certain combinations of input parameter values:
The model results for each individual core are given in Supplementary Material.
5.3. Implications for the Global Ge Isotope Budget
Across all incubated cores, the probability distribution of δ74Geinc is centered around 1.6‰ (25-75th percentile range 0.8–2.4‰; Table 4; Figure 5B), possibly slightly lighter than the allogenic Ge supply (1.9±0.6‰; a mixture of isotopically light lithogenic- and isotopically heavy biogenic-sourced Ge) but essentially indistinguishable within uncertainty. In long-term mass balance terms, the isotopic composition of Ge released to pore waters (input) is expected to equal the output, i.e., the combined composition of authigenic phases and the benthic flux. Given that there is no detectable Ge isotope fractionation during authigenic Ge uptake at depth (i.e. ‰; see discussion above), the allogenic input and the benthic flux should be isotopically indistinguishable. Any natural Fe redox-induced perturbations, much like the ones observed during our incubation experiments, reflect a non-steady state process and ultimately should have little effect on Ge benthic flux or authigenic composition. The latter should therefore primarily depend on the ratio of Ge supplied from terrigenous vs. biogenic inputs.
Assuming that the observations at San Pedro Basin are applicable to continental margin sediments in general and making a number of additional simplifying assumptions, we can construct a rough Ge budget for the global continental shelf sediments. All the input parameters used in the following calculations and their range of uncertainties are summarized in Supplementary Material. Using a Monte Carlo approach, the calculations were performed 1 million times, sampling randomly from within the uncertainty of all input parameters. All results below are reported as the 25–75% confidence interval of the 1 million Monte Carlo calculations. The calculations were performed using MATLAB R2018b, and the source code is given in the Supplementary Material.
Here, we use our data from the San Pedro Basin to determine the fraction of lithogenic particulate Ge that gets released into pore waters () and, in the absence of similar data from other sites, apply this value globally. First, the total lithogenic Ge flux to SPB sediments is calculated as:
where is the detrital flux measured via sediment traps (Collins et al., 2011), [Ge]UCC = 1.4±0.2 ppm is Ge concentration of average upper continental crust (Rudnick and Gao, 2014), and Mw = 72.6 g/mol is the atomic mass of germanium, yielding of 6.4–7.1 nmol m−2 d−1.
The net supply of dissolved Ge released to pore waters from detrital particles () can be estimated from the amount of detrital Fe input required to sustain long-term pyrite burial in SPB sediments (, calculated to be 26 μmol m−2 d−1; Leslie et al., 1990):
where Ge/FeUCC = 25−30 μmol/mol (Rudnick and Gao, 2014). Equation (18) yields , which is the value used in the core incubation model described above. We acknowledge the possibility that Ge and Fe release from detrital particles may not be stoichiometric but we deem it a reasonable assumption at this stage, given the absence of any data regarding this question.
The fraction of lithogenic Ge that dissolves, i.e., is released to the pore waters is thus:
yielding flith−released = 9.9−11.5%. The global biogenic silica flux to shelf sediments was previously estimated as 16–87 Tmol/y, with about 3 Tmol/y buried and the rest dissolving (Tréguer and De La Rocha, 2013). Using a Ge/SibSi ratio of 0.5–0.7 μmol/mol (to account for potential inputs of low-Ge/Si bSi from sponges and radiolarians, e.g., Rouxel and Luais, 2017) yields a biogenic Ge flux of 18-39 Mmol/y to the shelf sediments (Equation 20).
The total detrital Ge supply to the ocean can be estimated from the total riverine sediment flux (19100 Mt/y; Milliman and Farnsworth, 2011) and [Ge]UCC (given that globally >95% of riverine Ge is transported in the solid phase; Gaillardet et al., 2014), yielding roughly 370 Mmol Ge/y. Assuming all this detrital material settles on continental shelves and using calculated above gives 37 Mmol/y flux of lithogenic Ge that is released to shelf pore waters globally. This value, however, is bound to be strongly over-estimated, since it is much higher than any of the other fluxes in the global marine Ge budget (Baronas et al., 2017). Indeed, most detrital Ge is locked in primary and secondary silicate phases (Mortlock and Froelich, 1987) that are thermodynamically stable in most marine pore waters (e.g., Helgeson et al., 1969). Therefore, most of the pore water Ge of lithogenic origin is likely derived from the reduction of amorphous secondary Fe (oxy)hydroxides (Poulton and Raiswell, 2002). Baronas et al. (2018) calculated that for various global rivers, the fraction of dissolved Ge released during weathering that remains in solution () ranges between 1 and 10% and therefore Ge uptake into terrestrial secondary phases is between 90 and 99%. Using a global riverine dissolved Ge flux () of 3.2±1.2 Mmol/y (Baronas et al., 2017) yields a total secondary detrital Ge flux to continental margin sediments of 38–95 Mmol/y (Equation 21), 4–10 Mmol/y of which is then released to pore waters (Equation 22).
Using the value calculated here and assuming a dissolved Ge sequestration efficiency between 10 and 60% (Table 4; Baronas et al., 2016) yields a total shelf authigenic Ge burial flux of 7–18 Mmol/y. The uncertainty of this value is now significantly lower compared to the previous 3–27 Mmol/y estimate of Baronas et al. (2016), demonstrating the power of isotopic mass balance constraints in refining global elemental budgets. Importantly, if 10–60% of lithogenic-derived Ge is captured in shelf sediments, the remaining 40-90% escapes back into the water column, contributing 2.5–6.6 Mmol/y Ge to seawater. This flux is significantly higher than the previous Si budget-based estimate of detrital Ge input to the ocean, 1.6±1.5 Mmol/y (Baronas et al., 2017).
The isotopic composition of the allogenic supply to global shelf sediment pore waters is then simply a mixture of the biogenic and the detrital inputs:
Using ‰ and of 2.5–3.5‰ (to account for the potential contribution of isotopically lighter sponges; Guillermic et al., 2017), Equation (23) yields = 2.2–2.7‰. Reassuringly, this value is similar to the pore water compositions reported for the Southern California and Gulf of Mexico margins here (Table 2). In summary, continental margin sediments are expected to exhibit lower pore water δ74Ge relative to open ocean sediments, due to an estimated 12–31% contribution of dissolved Ge from isotopically light lithogenic particles. Importantly, our observations at San Pedro Basin imply that the shelf pore water δ74Ge composition is translated to the deep authigenic Ge sink (likely, aluminosilicate clays) without significant fractionation. Therefore, δ74Ge of the long-term benthic flux out of shelf sediments should also equal approximately 2.2–2.7‰.
Finally, we can use the refined authigenic Ge burial flux value to estimate the equivalent burial flux of Si. Rahman et al. (2017) showed that anywhere from 50 to 75% of biogenic Si is typically converted to authigenic clays in continental margin settings. Using previously measured bSi burial rates in San Pedro Basin sediments (Hammond et al., 2000; McManus et al., 2003; Baronas et al., 2016) and assuming that authigenic clay Si burial is three times higher, we can estimate authigenic Si burial rates of about 0.16 mmol m−2 d−1. Combining this value with independent estimates of authigenic Ge burial (Baronas et al., 2016) yields authigenic clay Ge/Si values between 2.2 and 7.6 μmol/mol. Assuming these Ge/Si values are applicable to margin sediments globally, the authigenic Si burial in continental margins should be in the range of 1–8 Tmol/y (best estimate of 3.1 Tmol/y), in good agreement with recent 32Si-based estimates of 4.5–4.9 Tmol/y (Rahman et al., 2017), and sufficient to close the global marine Si budget.
6. Conclusions
We have presented Ge/Si, δ74Ge, and supporting chemical data from seawater, pore waters, and core incubations at three continental margin sites in the Southern California Bight and the Gulf of Mexico. During core incubations the flux of dissolved Ge from sediments was highly variable, likely due to variable oxygenation of the cores, perturbing the Fe redox conditions in shallow sediments. The incubation results demonstrate the strong coupling between Ge and Fe in reducing continental margin sediments. Below the very shallow Fe redox boundary, pore water δ74Ge is a mixture of Ge released via dissolution of isotopically heavier biogenic silica and isotopically lighter lithogenic particles (possibly reducible Fe oxides). With depth, the precipitation of a Ge/Si-enriched authigenic phase (possibly aluminosilicate clays) results in up to 90% depletion of dissolved Ge. Pore water δ74Ge signatures remain constant with depth, suggesting negligible fractionation during this process. Therefore, the pore waters, the authigenic clays, and the long-term benthic flux should all have identical δ74Ge signatures within uncertainty. Using global estimates of biogenic and lithogenic Ge input to global continental shelf sediments, we calculate an average lithogenic Ge contribution of 12–31%, with the resulting average dissolved δ74Ge of 2.2–2.7‰ in the continental margin.
Data Availability
All data discussed in this study is supplied in the main text and Supplementary Tables.
Author Contributions
JB and DH designed the study. JB and DM collected the samples. JB and OR performed Ge isotope analyses. JB performed the experiments and modeling and wrote the article, with input from all co-authors.
Funding
Financial support for the SPB cruise was provided by US National Science Foundation (NSF) grant OCE-1260692 to DH. SMB cruise was supported by US NSF grants OCE-0962209 to Sergio Sañudo-Wilhelmy, OCE-0934073 to Douglas Capone, and PLR-1029878 to William Berelson. Additional support was provided by US NSF grant OCE-1061700 to DH. JB was also supported by a CUAHSI Pathfinder graduate student fellowship, an InterRidge research fellowship, and a John Montagne Award from GSA Quaternary Geology and Geomorphology Division. Support for OR was provided by the Institut Carnot Ifremer EDROME and the LabexMer ANR-10-LABX-19-01.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank the crew of R/V Yellowfin, Nick Rollins, Elias Karkabi, Brian Seegers, and Will Berelson for their assistance with sample collection and processing. We also thank Emmanuel Ponzevera for assistance with Ge isotope measurements at Ifremer. Two reviewers are thanked for their constructive comments that helped improve the manuscript.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2019.00162/full#supplementary-material
References
Aller, R. C. (2014). “Sedimentary Diagenesis, Depositional Environments, and Benthic Fluxes,” in Treatise on Geochemistry, 2nd Edn, eds H. D. Holland and K. K. Turekian (Amsterdam: Elsevier), 293–334.
Baronas, J. J., Hammond, D. E., Berelson, W. M., McManus, J., and Severmann, S. (2016). Germanium-silicon fractionation in a river-influenced continental margin: The Northern Gulf of Mexico. Geochim. Cosmochim. Acta 178, 124–142. doi: 10.1016/j.gca.2016.01.028
Baronas, J. J., Hammond, D. E., McManus, J., Wheat, C. G., and Siebert, C. (2017). A global Ge isotope budget. Geochim. Cosmochim. Acta 203, 265–283. doi: 10.1016/j.gca.2017.01.008
Baronas, J. J., Torres, M. A., West, A. J., Rouxel, O., Georg, B., Bouchez, J., et al. (2018). Ge and Si isotope signatures in rivers: a quantitative multi-proxy approach. Earth Planet. Sci. Lett. 503, 194–215. doi: 10.1016/j.epsl.2018.09.022
Belissont, R., Boiron, M.-C., Luais, B., and Cathelineau, M. (2014). LA-ICP-MS analyses of minor and trace elements and bulk Ge isotopes in zoned Ge-rich sphalerites from the Noailhac Saint-Salvy deposit (France): insights into incorporation mechanisms and ore deposition processes. Geochim. Cosmochim. Acta 126, 518–540. doi: 10.1016/j.gca.2013.10.052
Berelson, W. M. (1991). The flushing of two deep-sea basins, southern California borderland. Limnol. Oceanogr. 36, 1150–1166.
Berelson, W. M., Hammond, D. E., and Johnson, K. (1987). Benthic fluxes and the cycling of biogenic silica and carbon in two southern California borderland basins. Geochim. Cosmochim. Acta 51, 1345–1363. doi: 10.1016/0016-7037(87)90320-6
Bower, C., and Holm-Hansen, T. (1980). A salicylate-hypochlorite method for determining ammonia in seawater. Can. J. Fish. Aquat. Sci. 37, 794–798.
Burton, J., Culkin, F., and Riley, J. (1959). The abundances of gallium and germanium in terrestrial materials. Geochim. Cosmochim. Acta 16, 151–180.
Cheng, T., Hammond, D. E., Berelson, W. M., Hering, J. G., and Dixit, S. (2009). Dissolution kinetics of biogenic silica collected from the water column and sediments of three Southern California borderland basins. Mar. Chem. 113, 41–49. doi: 10.1016/j.marchem.2008.12.001
Collins, L. E., Berelson, W. M., Hammond, D. E., Knapp, A., Schwartz, R., and Capone, D. (2011). Particle fluxes in San Pedro Basin, California: a four-year record of sedimentation and physical forcing. Deep Sea Res. I 58, 898–914. doi: 10.1016/j.dsr.2011.06.008
De La Rocha, C. L., Brzezinski, M. A., and DeNiro, M. J. (2000). A first look at the distribution of the stable isotopes of silicon in natural waters. Geochim. Cosmochim. Acta 64, 2467–2477. doi: 10.1016/S0016-7037(00)00373-2
Ehlert, C., Doering, K., Wallmann, K., Scholz, F., Sommer, S., Grasse, P., et al. (2016). Stable silicon isotope signatures of marine pore waters–biogenic opal dissolution versus authigenic clay mineral formation. Geochim. Cosmochim. Acta 191, 102–117. doi: 10.1016/j.gca.2016.07.022
Elderfield, H., and Schultz, A. (1996). Mid-ocean ridge hydrothermal fluxes and the chemical composition of the ocean. Annu. Rev. Earth Planet. Sci. 24, 191–224.
Ellwood, M. J., Kelly, M., Maher, W. A., and De Deckker, P. (2006). Germanium incorporation into sponge spicules: development of a proxy for reconstructing inorganic germanium and silicon concentrations in seawater. Earth Planet. Sci. Lett. 243, 749–759. doi: 10.1016/j.epsl.2006.01.016
Ellwood, M. J., and Maher, W. A. (2003). Germanium cycling in the waters across a frontal zone: the Chatham Rise, New Zealand. Mar. Chem. 80, 145–159. doi: 10.1016/S0304-4203(02)00115-9
Ellwood, M. J., Wille, M., and Maher, W. (2010). Glacial silicic acid concentrations in the Southern Ocean. Science 330, 1088–1091. doi: 10.1126/science.1194614
Elrod, V. A. (2004). The flux of iron from continental shelf sediments: a missing source for global budgets. Geophys. Res. Lett. 31:L12307. doi: 10.1029/2004GL020216
Escoube, R., Rouxel, O. J., Edwards, K., Glazer, B., and Donard, O. F. X. (2015). Coupled Ge/Si and Ge isotope ratios as geochemical tracers of seafloor hydrothermal systems: Case studies at Loihi Seamount and East Pacific Rise 9°50′N. Geochim. Cosmochim. Acta 167, 93–112. doi: 10.1016/j.gca.2015.06.025
Escoube, R., Rouxel, O. J., Luais, B., Ponzevera, E., and Donard, O. F. (2012). An intercomparison study of the Germanium isotope composition of geological reference materials. Geostand. Geoanal. Res. 36, 149–159. doi: 10.1111/j.1751-908X.2011.00135.x
Froelich, P., and Andreae, M. (1981). The marine geochemistry of germanium: Ekasilicon. Science 213, 205–207.
Froelich, P., Blanc, V., Mortlock, R., Chillrud, S., Dunstan, W., Udomkit, A., et al. (1992). River fluxes of dissolved silica to the ocean were higher during glacials: Ge/Si in diatoms, rivers, and oceans. Paleoceanography 7, 739–767.
Froelich, P., Hambrick, G., Andreae, M., Mortlock, R., and Edmond, J. (1985). The geochemistry of inorganic germanium in natural waters. J. Geophys. Res. 90, 1133–1141.
Gaillardet, J., Viers, J., and Dupré, B. (2014). “Chapter 7.7: Trace Elements in River Waters,” in Treatise on Geochemistry, 2nd Edn, eds H. D. Holland and K. K. Turekian (Amsterdam: Elsevier), 195–235.
Gorsline, D. (1992). The geological setting of Santa Monica and San Pedro Basins, California Continental Borderland. Prog. Oceanogr. 30, 1–36.
Guillermic, M., Lalonde, S. V., Hendry, K. R., and Rouxel, O. J. (2017). The isotope composition of inorganic germanium in seawater and deep sea sponges. Geochim. Cosmochim. Acta 212, 99–118. doi: 10.1016/j.gca.2017.06.011
Hammond, D. E., Cummins, K. M., McManus, J., Berelson, W. M., Smith, G., and Spagnoli, F. (2004a). Methods for measuring benthic nutrient flux on the California Margin: comparing shipboard core incubations to in situ lander results. Limnol. Oceanogr. Methods 2, 146–159. doi: 10.4319/lom.2004.2.146
Hammond, D. E., McManus, J., and Berelson, W. M. (2004b). Oceanic germanium/silicon ratios: evaluation of the potential overprint of temperature on weathering signals. Paleoceanography 19:PA2016. doi: 10.1029/2003PA000940
Hammond, D. E., McManus, J., Berelson, W. M., Meredith, C., Klinkhammer, P., and Coale, K. (2000). Diagenetic fractionation of Ge and Si in reducing sediments: the missing Ge sink and a possible mechanism to cause glacial/interglacial variations in oceanic Ge/Si. Geochim. Cosmochim. Acta 64, 2453–2465. doi: 10.1016/S0016-7037(00)00362-8
Helgeson, H. C., Garrels, R. M., and MacKenzie, F. T. (1969). Evaluation of irreversible reactions in geochemical processes involving minerals and aqueous solutions–II. Applications. Geochim. Cosmochim. Acta 33, 455–481. doi: 10.1016/0016-7037(69)90127-6
Hickey, B. M. (1992). Circulation over the Santa Monica-San Pedro Basin and Shelf. Prog. Oceanogr. 30, 37–115. doi: 10.1016/0079-6611(92)90009-O
John, S. G., Mendez, J., Moffett, J., and Adkins, J. (2012). The flux of iron and iron isotopes from San Pedro Basin sediments. Geochim. Cosmochim. Acta 93, 14–29. doi: 10.1016/j.gca.2012.06.003
King, S., Froelich, P., and Jahnke, R. (2000). Early diagenesis of germanium in sediments of the Antarctic South Atlantic: in search of the missing Ge sink. Geochim. Cosmochim. Acta 64, 1375–1390. doi: 10.1016/S0016-7037(99)00406-8
Kurtz, A., Derry, L., and Chadwick, O. (2002). Germanium-silicon fractionation in the weathering environment. Geochim. Cosmochim. Acta 66, 1525–1537. doi: 10.1016/S0016-7037(01)00869-9
Leslie, B. W., Hammond, D. E., Berelson, W. M., and Lund, S. P. (1990). Diagenesis in anoxic sediments from the California continental borderland and its influence on iron, sulfur, and magnetite behavior. J. Geophys. Res. 95:4453. doi: 10.1029/JB095iB04p04453
Lewis, B., Andreae, M., and Froelich, P. (1989). Sources and sinks of methylgermanium in natural waters. Mar. Chem. 27, 179–200.
Lewis, B., Andreae, M., Froelich, P. N., and Mortlocka, R. A. (1988). A review of the biogeochemistry of germanium in natural waters. Sci. Total Environ. 73, 107–120.
Lewis, B., Froelich, P., and Andreae, M. (1985). Methylgermanium in natural waters. Nature 313, 303–305.
Luais, B. (2007). Isotopic fractionation of germanium in iron meteorites: significance for nebular condensation, core formation and impact processes. Earth Planet. Sci. Lett. 262, 21–36. doi: 10.1016/j.epsl.2007.06.031
Luais, B. (2012). Germanium chemistry and MC-ICPMS isotopic measurements of Fe–Ni, Zn alloys and silicate matrices: insights into deep Earth processes. Chem. Geol. 334, 295–311. doi: 10.1016/j.chemgeo.2012.10.017
Mackenzie, F. T., and Garrels, R. M. (1966). Chemical mass balance between rivers and oceans. Am. J. Sci. 264, 507–525. doi: 10.2475/ajs.264.7.507
Mantoura, S. C. (2006). Development and Application of Opal Based Paleoceanographic Proxies (PhD thesis). University of Cambridge.
McManus, J., Berelson, W. M., Coale, K. H., Johnson, K. S., and Kilgore, T. E. (1997). Phosphorus regeneration in continental margin sediments. Geochim. Cosmochim. Acta 61, 2891–2907. doi: 10.1016/S0016-7037(97)00138-5
McManus, J., Hammond, D. E., Berelson, W. M., Kilgore, T. E., Demaster, D. J., Ragueneau, O. G., et al. (1995). Early diagenesis of biogenic opal: dissolution rates, kinetics, and paleoceanographic implications. Deep Sea Res. II 42, 871–903.
McManus, J., Hammond, D. E., Cummins, K., Klinkhammer, G. P., and Berelson, W. M. (2003). Diagenetic Ge-Si fractionation in continental margin environments: further evidence for a nonopal Ge sink. Geochim. Cosmochim. Acta 67, 4545–4557. doi: 10.1016/S0016-7037(03)00385-5
Meng, Y. M., Qi, H. W., and Hu, R. Z. (2015). Determination of germanium isotopic compositions of sulfides by hydride generation MC-ICP-MS and its application to the Pb-Zn deposits in SW China. Ore Geol. Rev. 65, 1095–1109. doi: 10.1016/j.oregeorev.2014.04.008
Michalopoulos, P., and Aller, R. C. (1995). Rapid clay mineral formation in Amazon delta sediments: reverse weathering and oceanic elemental cycles. Science 270, 614–617.
Michalopoulos, P., and Aller, R. C. (2004). Early diagenesis of biogenic silica in the Amazon delta: alteration, authigenic clay formation, and storage. Geochim. Cosmochim. Acta 68, 1061–1085. doi: 10.1016/j.gca.2003.07.018
Milliman, J. D., and Farnsworth, K. L. (eds.). (2011). “Oceania,” in River Discharge to the Coastal Ocean (Cambridge: Cambridge University Press), 13–69.
Monteverde, D. R., Sylvan, J. B., Suffridge, C., Baronas, J. J., Fichot, E., Fuhrman, J., et al. (2018). Distribution of extracellular flavins in a coastal marine basin and their relationship to redox gradients and microbial community members. Environ. Sci. Technol. 52, 12265–12274. doi: 10.1021/acs.est.8b02822
Mortlock, R., Charles, C., Froelich, P., Zibello, M., Saltzman, J., Hays, J., et al. (1991). Evidence for lower productivity in the Antarctic Ocean during the last glaciation. Nature 351, 220–223.
Mortlock, R., and Froelich, P. (1987). Continental weathering of germanium: Ge/Si in the global river discharge. Geochim. Cosmochim. Acta 51, 2075–2082.
Mortlock, R., and Froelich, P. (1996). Determination of germanium by isotope dilution-hydride generation inductively coupled plasma mass spectrometry. Anal. Chim. Acta 332, 277–284.
Mullin, J., and Riley, J. (1955). The colorimetric determination of silicate with special reference to sea and natural waters. Anal. Chim. Acta 12, 162–175.
Murnane, R., and Stallard, R. (1990). Germanium and silicon in rivers of the Orinoco drainage basin. Nature 344, 749–752.
Murnane, R. J., Leslie, B., Hammond, D. E., and Stallard, R. F. (1989). Germanium geochemistry in the Southern California Borderlands. Geochim. Cosmochim. Acta 53, 2873–2882.
Pokrovsky, O., Pokrovski, G., Schott, J., and Galy, A. (2006). Experimental study of germanium adsorption on goethite and germanium coprecipitation with iron hydroxide: X-ray absorption fine structure and macroscopic characterization. Geochim. Cosmochim. Acta 70, 3325–3341. doi: 10.1016/j.gca.2006.04.012
Pokrovsky, O. S., Galy, A., Schott, J., Pokrovski, G. S., and Mantoura, S. (2014). Germanium isotope fractionation during Ge adsorption on goethite and its coprecipitation with Fe oxy(hydr)oxides. Geochim. Cosmochim. Acta 131, 138–149. doi: 10.1016/j.gca.2014.01.023
Poulton, S. W., and Raiswell, R. (2002). The low-temperature geochemical cycle of iron: from continental fluxes to marine sediment deposition. Am. J. Sci. 302, 774–805. doi: 10.2475/ajs.302.9.774
Presti, M., and Michalopoulos, P. (2008). Estimating the contribution of the authigenic mineral component to the long-term reactive silica accumulation on the western shelf of the Mississippi River Delta. Continent. Shelf Res. 28, 823–838. doi: 10.1016/j.csr.2007.12.015
Qi, H. W., Hu, R. Z., Jiang, K., Zhou, T., Liu, Y. F., and Xiong, Y. W. (2019). Germanium isotopes and Ge/Si fractionation under extreme tropical weathering of basalts from the Hainan Island, South China. Geochim. Cosmochim. Acta 253, 249–266. doi: 10.1016/j.gca.2019.03.022
Rahman, S., Aller, R. C., and Cochran, J. K. (2016). Cosmogenic 32 Si as a tracer of biogenic silica burial and diagenesis: Major deltaic sinks in the silica cycle. Geophys. Res. Lett. 43, 7124–7132. doi: 10.1002/2016GL069929
Rahman, S., Aller, R. C., and Cochran, J. K. (2017). The missing silica sink: revisiting the marine sedimentary Si cycle using cosmogenic 32 Si. Glob. Biogeochem. Cycles 31, 1559–1578. doi: 10.1002/2017GB005746
Rouxel, O., Galy, A., and Elderfield, H. (2006). Germanium isotopic variations in igneous rocks and marine sediments. Geochim. Cosmochim. Acta 70, 3387–3400. doi: 10.1016/j.gca.2006.04.025
Rouxel, O. J., and Luais, B. (2017). Germanium isotope geochemistry. Rev. Mineral. Geochem. 82, 601–656. doi: 10.2138/rmg.2017.82.14
Rudnick, R., and Gao, S. (2014). “Composition of the continental crust,” in Treatise on Geochemistry, 2 Edn, eds H. D. Holland and K. K. Turekian (Amsterdam: Elsevier), 1–51.
Severmann, S., McManus, J., Berelson, W. M., and Hammond, D. E. (2010). The continental shelf benthic iron flux and its isotope composition. Geochim. Cosmochim. Acta 74, 3984–4004. doi: 10.1016/j.gca.2010.04.022
Siebert, C., Nägler, T., and Kramers, J. (2001). Determination of molybdenum isotope fractionation by double-spike multicollector inductively coupled plasma mass spectrometry. Geochem. Geophys. Geosyst. 2, 1–16. doi: 10.1029/2000GC000124
Sutton, J., Ellwood, M. J., Maher, W. A., and Croot, P. L. (2010). Oceanic distribution of inorganic germanium relative to silicon: Germanium discrimination by diatoms. Glob. Biogeochem. Cycles 24:GB2017. doi: 10.1029/2009GB003689
Tréguer, P. J., and De La Rocha, C. L. (2013). The world ocean silica cycle. Annu. Rev. Mar. Sci. 5, 477–501. doi: 10.1146/annurev-marine-121211-172346
Van Cappellen, P. (2003). Biomineralization and global biogeochemical cycles. Rev. Mineral. Geochem. 54, 357–381. doi: 10.2113/0540357
Keywords: germanium, biogenic silica, authigenesis, Fe oxides, isotope fractionation, continental margin
Citation: Baronas JJ, Hammond DE, Rouxel OJ and Monteverde DR (2019) A First Look at Dissolved Ge Isotopes in Marine Sediments. Front. Earth Sci. 7:162. doi: 10.3389/feart.2019.00162
Received: 14 April 2019; Accepted: 06 June 2019;
Published: 21 June 2019.
Edited by:
Gilad Antler, Ben-Gurion University of the Negev, IsraelReviewed by:
Claudia Ehlert, University of Oldenburg, GermanyAlbert Galy, Université de Lorraine, France
Copyright © 2019 Baronas, Hammond, Rouxel and Monteverde. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: J. Jotautas Baronas, am90YXV0YXMuYmFyb25hc0BnbWFpbC5jb20=
†Present Address: J. Jotautas Baronas, Department of Earth Sciences, University of Cambridge, Cambridge, United Kingdom
Danielle R. Monteverde, Division of Geology and Planetary Sciences, California Institute of Technology, Pasadena, CA, United States
 J. Jotautas Baronas
J. Jotautas Baronas Douglas E. Hammond
Douglas E. Hammond Olivier J. Rouxel
Olivier J. Rouxel Danielle R. Monteverde
Danielle R. Monteverde