Pursuit of Optimal Design for Winter-Balance Surveys of Valley-Glacier Ablation Areas

1. Introduction

Spatially distributed glacier-wide estimates of seasonal snow accumulation are critical for understanding glacier mass balance and for predicting the availability and timing of surface runoff, especially in mountainous regions (e.g., Kaser et al., 2010; Huss and Hock, 2018). The net accumulation of snow on a glacier over a winter season is known as the winter surface mass balance, or “winter balance” and is typically reported in metres of water equivalent (m w.e.) (e.g., Østrem and Brugman, 1991; Cogley et al., 2011). Winter balance accounts for half of the seasonally resolved mass balance, initialises ablation conditions and affects energy and mass exchange between the land and atmosphere (e.g., Hock, 2005; Réveillet et al., 2016).

Snow surveys on glaciers are conducted to estimate winter balance, with multi-year sampling programs established to monitor temporal changes in winter balance (e.g., Andreassen et al., 2016). Depending on the application, winter balance may refer to the point balance b_w or the glacier-wide specific balance B_w (Cogley et al., 2011). Although some studies have documented interannual variability in the spatial patterns of winter balance (e.g., Björnsson et al., 1998; Hodgkins et al., 2005), there is a mounting literature that documents quasi-stationarity of interannual patterns of both snow distribution on ice-free landscapes (e.g., Deems et al., 2008; Sturm and Wagner, 2010; Schirmer et al., 2011) and winter balance on glaciers (e.g., Taurisano et al., 2007; Sold et al., 2016; McGrath et al., 2018). This persistence in spatial patterns is attributed to persistence of synoptic scale weather patterns including the prevailing winds (e.g., Winstral and Marks, 2002), topography (e.g., Erickson et al., 2005) and its associated roughness (e.g., Lehning et al., 2011), and in the case of ice-free landscapes, vegetation (e.g., Sturm and Wagner, 2010).

Optimal survey designs for snow depth are central to estimating snow distribution and mass balance from in situ measurements (e.g., Watson et al., 2006). Measuring snow depth and travelling between measurement locations is both time consuming and can disturb the snow, so care must be taken to choose a survey design that avoids bias, allows for the greatest variability to be measured and minimises distance travelled (e.g., Shea and Jamieson, 2010; Kinar and Pomeroy, 2015). Moreover, the period of seasonal maximum snow depth can be brief, and even difficult to pinpoint for glaciers with a large range in elevation, further motivating the need for time-efficient surveys.

There are a number of different survey designs that have been employed to obtain point measurements of snow depth, including pure random (e.g., Elder et al., 1991), linear random (e.g., Shea and Jamieson, 2010), nested (e.g., Schweizer et al., 2008), gridded random (e.g., Bellaire and Schweizer, 2008; Elder et al., 2009; Bellaire and Schweizer, 2011) and gridded (e.g., Molotch and Bales, 2005; Kronholm and Birkeland, 2007; López-Moreno et al., 2011). Sampling schemes that incorporate randomness limit sampling bias by varying sample spacing and direction. However, they are less efficient than designs that incorporate grids. Grid-based designs minimise travel distance but measurements are biased by regularly spaced intervals and linear orientations which can result in an under-representation of snow-depth variability (Kronholm and Birkeland, 2007).

An optimal survey requires (1) a spatial sampling scheme (survey design) that captures snow-depth variability and minimises travel distance and (2) identification of the minimum number of measurement locations needed to estimate winter balance to the desired precision or accuracy. The optimal design also requires temporal consistency in sampling locations (e.g., McGrath et al., 2018) in order that interannual spatial variability in sampling locations does not confound the determination of interannual variability in the winter-balance field (e.g., Escher-Vetter et al., 2009). This consistency is important both for calibration of geodetic mass-balance measurements and for in-situ measurements alone. Optimisation of winter-balance surveys is rarely investigated because the locations of snow-depth measurements are often dictated by some combination of resources, logistics, safety and precedent. Of the few studies that have investigated the number of measurement locations needed to effectively sample mass-balance distributions (c.f. Cogley, 1999; Fountain and Vecchia, 1999; Pelto, 2000; Walmsley, 2015; Surjanovic, 2016), some have found errors to decline sharply with as few as 4–5 measurements (e.g., Fountain and Vecchia, 1999).

The optimal survey design would sample every unique region of the field of interest, thus requiring a priori knowledge of the field itself. A logical approach to discovering this field would be through high-density sampling using a space-filling design such as a regular grid or Voronoi polygons, but such an approach is rarely feasible. Centreline profiles, alone or combined with transverse profiles, comprise the most common survey designs used in winter-balance studies (e.g., Kaser et al., 2002; Machguth et al., 2006; Escher-Vetter et al., 2009; Möller and Möller, 2019). The centreline profile aims to capture changes in winter balance with elevation and may capture expected orographic effects (e.g., Grünewald et al., 2014). However, centreline profiles are known to increase the correlation between winter balance and elevation compared to other survey designs (e.g., Escher-Vetter et al., 2009), and may therefore lead to under- or overestimation of glacier-wide winter balance. Transverse profiles are therefore often added to improve the reliability of the sampling scheme (e.g., Walmsley, 2015). An hourglass with an inscribed circle (personal communication from C. Parr, 2016) is an alternative sampling scheme that captures changes in winter balance with elevation while avoiding the centreline bias. To our knowledge, no study has yet compared the performance of these different sampling schemes in estimating winter balance.

The goal of this work is to evaluate different survey designs and sample sizes used to estimate winter balance in the ablation areas of three valley glaciers in the St. Elias Mountains of Yukon, Canada, using in-situ measurements. Our specific objectives are to (1) determine how to accurately estimate winter balance, including its potential interannual variability, with the fewest possible measurements, (2) examine the relationship between optimal design and topographic controls on winter balance, and (3) provide a modular template for other studies that may seek to apply principles of experimental design to new or existing mass-balance programs. We focus primarily on the winter-balance field b_w(x, y), as our data best address this variable, but we also consider the specific winter balance B_w as the most commonly targeted variable by mass-balance programs.

2. Study Site

We investigate winter-balance survey design for the ablation areas of three unnamed glaciers in the Donjek Range of southwest Yukon, Canada (Figure 1). Our study is restricted to the ablation areas due to low data density in the accumulation areas (see Pulwicki et al., 2018). Monitoring snow distribution and glacier mass balance in the St. Elias Mountains began in the 1950s and 1960s with a series of research programs, including Project “Snow Cornice” and the Icefield Ranges Research Project (Wood, 1948; Danby et al., 2003). More recent studies have focused on individual glaciers (e.g., Clarke, 2014; Flowers et al., 2014) as well as regional glacier mass balance and dynamics (e.g., Arendt et al., 2008; Burgess et al., 2013; Larsen et al., 2015; Waechter et al., 2015).

FIGURE 1

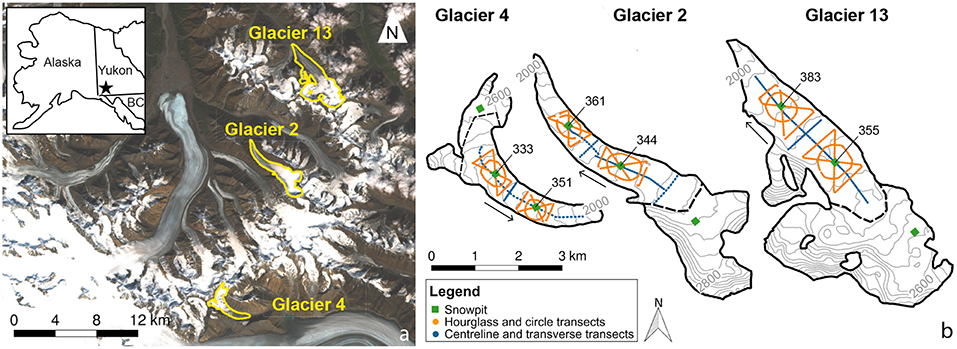
Figure 1. Study area and measurement locations on Glaciers 4, 2 and 13. (a) Donjek Range of the St. Elias Mountains, Yukon, Canada (star in inset). Imagery from Sentinel-2A (29 August 2013, Copernicus Sentinel data 2013, processed by ESA). (b) Snow-depth survey designs: centreline and transverse profiles (blue dots), hourglass with inscribed circle (orange dots). Also shown are locations of snow-pit density measurements (green squares with densities given in kg m⁻³), ice-flow directions (arrows), approximate location of ELA on each glacier (black dashed lines) and elevation contours (grey) at 50 m intervals. Data from the accumulation area are omitted.

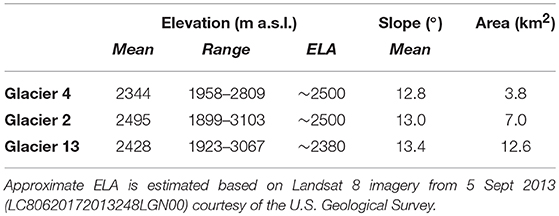
Situated on the northern flanks of the St. Elias Mountains, which rise sharply from the Pacific Ocean, the Donjek Range experiences a continental climate (Taylor-Barge, 1969). Glacier 4, Glacier 2, and Glacier 13 (labelling adopted from Crompton and Flowers, 2016) are small alpine glaciers (3.8–12.6 km²) (see Figure 1, Table 1) that lie along a transect roughly perpendicular to this major regional orographic barrier (to the southwest in Figure 1). Within the L-shaped Donjek Range itself, Glacier 4 and Glacier 2 are, respectively, situated on the southeast and northwest sides of the same limb of the divide, while Glacier 13 is situated on the northeast side of the other limb. Glaciers 2 and 13 flow dominantly northwest, while Glacier 4 flows dominantly southeast. The elevation of these glaciers ranges from ~1,900 to ~3,100 m a.s.l., with Equilibrium Line Altitudes (ELAs) located between ~2,300 and ~2,500 m a.s.l.

TABLE 1

Table 1. Physical characteristics of the study glaciers.

All three glaciers inhabit steep-walled valleys, with Glaciers 2 and 13 having steep and somewhat complex headwalls. This complexity in the upper accumulation area is typical of many alpine glaciers, and is one of many hindrances to spatially comprehensive in-situ measurements of mass balance. We expect that all three glaciers are polythermal, based on a targeted study of Glacier 2 (Wilson et al., 2013) and related theoretical modelling (Wilson and Flowers, 2013). These glaciers were chosen specifically in 2016 to study winter-balance estimation and uncertainty, a detailed analysis of which forms the basis of the present study (Pulwicki, 2017; Pulwicki et al., 2018).

3. Methods

Below we outline the process of determining point-scale and grid-scale values of winter balance from snow depth and density measurements. We then present our strategy for evaluating survey designs with real and synthetic data.

3.1. Field Measurements

Point-scale values of winter balance are obtained from direct measurements of snow depth and density (Figure 1). Snow depth was measured using 3.2 m graduated aluminium avalanche probes. Measurement locations followed linear and curvilinear profiles in various survey designs termed “centreline” and “transverse” profiles, “hourglass” and “circle.” Sampling was similar between study glaciers, with a sample spacing of 10–60 m dictated by protocols for safe glacier travel. Each observer made 3–4 individual depth measurements within ~1 m at each survey location; these measurements were averaged to obtain a single value. Geolocation was obtained based on single-frequency GPS measurements. Snow-depth measurements were largely restricted to the ablation area, where the clear distinction between snow and ice ensures that only snow from the most recent accumulation season is measured. In total, we collected more than 9,000 snow-depth measurements throughout the study area from 4 to 15 May 2016.

Snowpit-density profiles were measured using a wedge cutter and spring scale in at least three locations on each glacier, including at least two locations in the ablation area (see Figure 1). Snow density is often assumed to vary with elevation (e.g., Sold et al., 2013), but such a relationship is not always observed (e.g., Möller and Möller, 2019). In our case, only two of three glaciers clearly exhibit an elevation-dependent density as measured in the snow pits (Pulwicki, 2017). Based on a detailed analysis of density estimation and the comparatively modest uncertainty it introduces in estimates of winter balance for these glaciers (Pulwicki et al., 2018), we take the simple and common approach of using a mean density calculated for each glacier (e.g., Escher-Vetter et al., 2009; McGrath et al., 2015; Cullen et al., 2017; McGrath et al., 2018) to convert snow depth at all measurement locations in the ablation area to values of point-scale winter balance. The mean ablation-area snow densities are 342 kg m⁻³ for Glacier 4, 353 kg m⁻³ for Glacier 2 and 369 kg m⁻³ for Glacier 13.

All point-scale values of winter balance (up to six, average two) located within a single 40 × 40 m gridcell of a SPIRIT SPOT-5 digital elevation model (DEM) (Korona et al., 2009) are averaged to obtain a single value of winter balance in each sampled gridcell (Pulwicki, 2017). The use of “samples” henceforth refers to grid-scale, rather than point-scale, values of winter balance; we omit any further discussion of how to obtain accurate and representative estimates of grid-scale winter balance. In a detailed analysis of winter-balance estimation for the study glaciers, Pulwicki et al. (2018) found both sub-grid snow-depth variability and treatment of snow density to be less important as sources of uncertainty than the method of interpolation/extrapolation.

3.2. Analysis

Below we give an overview of the structure of, and rationale for, our methods of analysis. In statistical experimental design, the objective is often to obtain a design that is optimal in some sense over the plausible, or expected, range of possible configurations of the field of interest, rather than simply optimal for a single realisation of this field (Dean et al., 2017). Similarly, in pursuing optimal designs for winter-balance surveys, we seek a more general result than can be obtained by using a single realisation of the winter balance. We therefore complement our real datasets with synthetic datasets, of which we can generate an arbitrary number.

Beginning with the real data, we select subsets of the grid-scale values of winter balance (samples described in section 3.1) from which we estimate winter balance across the ablation area. We then evaluate the quality of this estimate against the measured values for each survey design. Quality is assessed primarily based on the root mean squared error (RMSE) of the estimated winter-balance field b_w(x, y), though we also consider the specific balance B_w. To complement the real data, which represent a single realisation of the winter-balance field for each glacier, we generate synthetic data using a topographic regression model. From the numerous synthetic realisations of the winter-balance field, which we refer to as “synthetic winter-balance fields,” we can extract “synthetic samples.” The synthetic data ideally represent the sort of variability in winter balance that we expect to see in practice. With these samples, we again estimate the winter balance field b_w(x, y) as well as B_w, both of which can be evaluated against the synthetic data for each survey design. Figure 3 shows the procedures described in this section for real and synthetic data.

3.2.1. Real Data

Using the real data, we extract subsets of N samples of the gridcell-averaged winter balance from six possible survey designs: centreline (CL), centreline and transverse profiles (CT), circle (CR), hourglass (HG), hourglass with inscribed circle (HC), and random (RN) (Figure 2). All designs were used in the field (Figure 1) except random, which permits sampling anywhere deemed safely accessible in the ablation area. These designs remain fixed in size and space to match the actual designs used in the field. For each survey design we investigate the effect of sample size N, where N ranges from a minimum of six to a maximum determined by the number of gridcells actually sampled (57 to 228 depending on the survey design). We adopt a regression model where winter balance is related to topographic parameters (e.g., McGrath et al., 2015):

$\begin{array}{ll}{b}_{\text{w}}(x,y)={\beta }_0+{\displaystyle \sum _i}{\beta }_i{X}_i(x,y)+ϵ,& (1)\end{array}$

with β₀ the intercept, β_i the coefficients, X_i the topographic regressors, and ϵ the random error. The regressors are topographic parameters derived from the above-mentioned 40 × 40 m SPIRIT SPOT-5 DEM (Korona et al., 2009) and include only the four found to have some explanatory power in our datasets (Pulwicki et al., 2018): elevation, slope, curvature and S_x. S_x is a wind parameter that describes terrain exposure to (negative values) or shelter from (positive values) the prevailing wind, and depends on local topography and wind direction (Winstral et al., 2002). Estimates of the expected value of b_w are determined by least-squares regression using the Matlab function regress and denoted ${\widehat{b}}_{\text{w}}$.

FIGURE 2

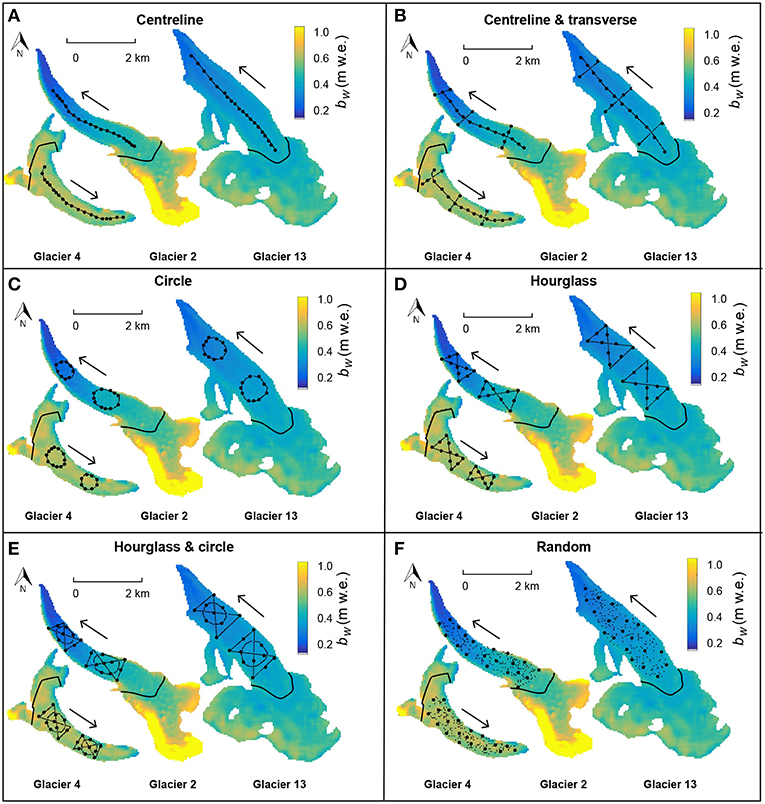
Figure 2. Survey designs on the three study glaciers. (A) Centreline. (B) Centreline and transverse. (C) Circle. (D) Hourglass. (E) Hourglass and Circle. (F) Random. Filled circles show N = 20 possible sampling locations amongst many in the ablation area (along lines for all designs but Random, where dots show 200 possible sampling locations). Solid black line indicates approximate ELA. The reference winter-balance field (b_w), shown in colour, is derived from linear topographic regression of the real data. Across the ablation area, b_w averages to 0.59 m w.e., 0.34 m w.e. and 0.27 m w.e. for Glaciers 4, 2 and 13, respectively. When the accumulation area is included, B_w is estimated to be 0.59 m w.e., 0.57 m w.e. and 0.38 m w.e.

For each survey design, a set of N irregularly spaced samples is chosen by first randomly selecting N sampling locations 100–1,000 times and choosing the set from 100 to 1,000 that maximises the minimum distance between samples (an approximate “maximin” distance design; Johnson et al., 1990). We do this 200 times. This approach avoids a degree of irregularity in sampling schemes, arising from purely randomly selected sampling locations, that we deem unrealistic for field practice. For each of the 200 subsets of irregularly spaced samples of size N, we use a linear regression to obtain ${\widehat{b}}_{\text{w}}$. RMSE is then computed between estimated (${\widehat{b}}_{\text{w}}$) and observed (b_w) winter balance at all measurement locations on a gridcell-by-gridcell basis:

$\begin{array}{ll}\text{RMSE}=\sqrt{\frac{1}{N_{\text{T}}}{\displaystyle \sum _{j=1}^{N_{\text{T}}}}{\left({\widehat{b}}_{{\text{w}}_j}-b_{{\text{w}}_j}\right)}^2},& (2)\end{array}$

where N_T is the total number of measured gridcells. The performance of designs associated with lower RMSEs, on average, is considered better than those associated with higher RMSEs. By repeating the steps above 200 times (see Figure 3), we can assess the sensitivity of RMSE to differences in sampling locations for a given survey design and sample size. While the RMSE is an assessment of the winter-balance field b_w(x, y), compensating spatial errors could result in simultaneously poor estimation of b_w(x, y) (high RMSE) and good estimation of the specific balance B_w. We cannot, however, compute a metric of accuracy for B_w, because we do not know the true value of B_w, even in the ablation area. Instead, we compare B_w estimated with sample subsets to that estimated with the full set of measurements.

FIGURE 3

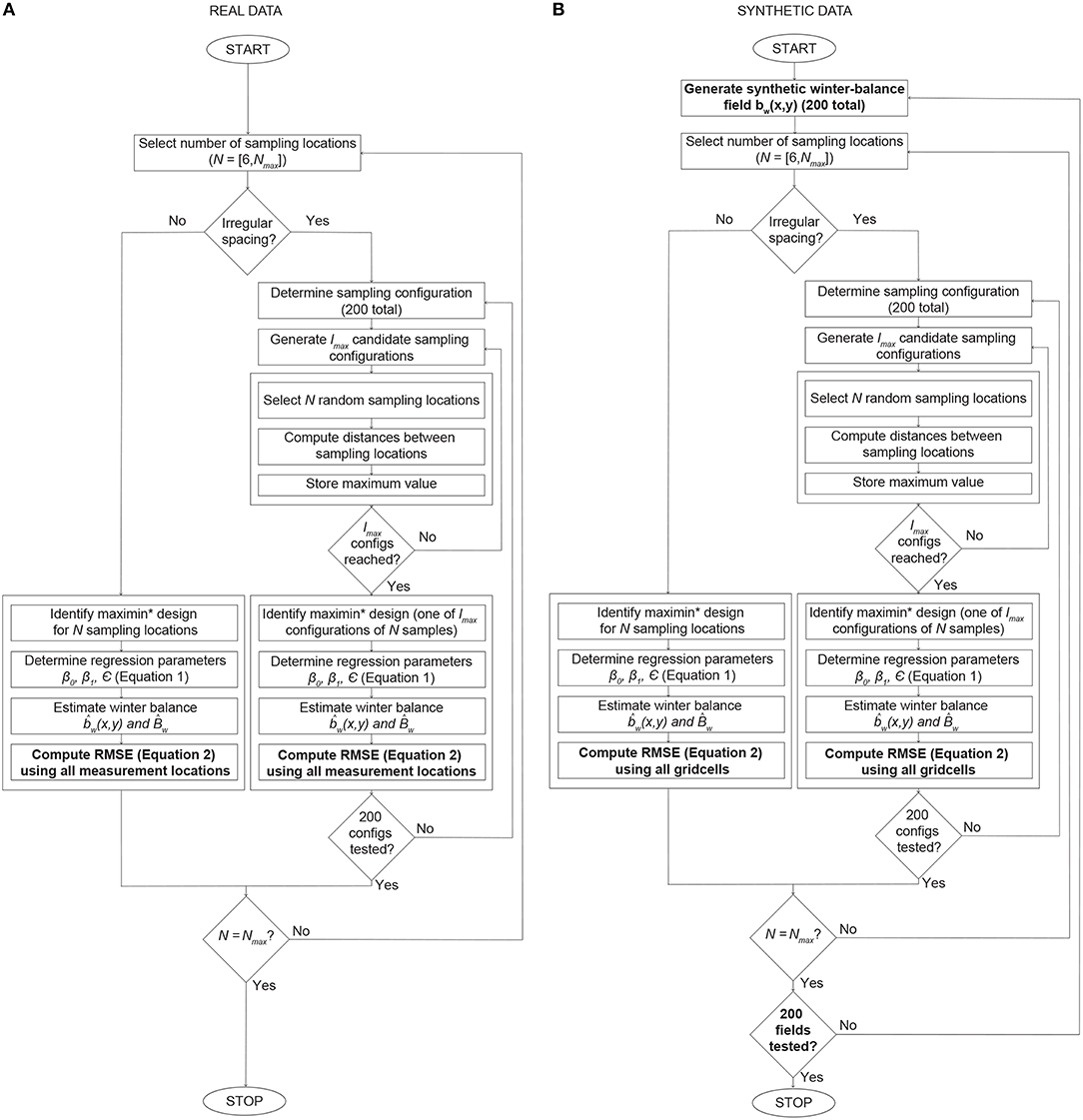
Figure 3. Algorithm used for (A) real and (B) synthetic data with loops over the three glaciers and six survey designs omitted. Differences are shown in bold. l_max ranges from 100 to 1,000. N_max is the number of measured gridcells and depends on the survey design. *The “maximin” design maximises the minimum distance between samples (Johnson et al., 1990). See Supplementary Material for corresponding pseudocode.

We also perform one additional simulation for each survey design and sample size N using quasi-regularly spaced samples that are intended to represent a plausible expert design. In this case, sampling always begins at the location of the first field measurement (e.g., at the corner or end of a profile) and subsequent sampling locations are again chosen to maximise the minimum distance between samples (Johnson et al., 1990). Sampling locations thus remain fixed as N increases and the survey design fills in.

3.2.2. Synthetic Data

While any number of models could be used to generate synthetic data, we use a topographic regression both for its simplicity and for its demonstrated potential to generate realistic distributions of winter balance. This approach has the added benefit of allowing us to evaluate survey designs on winter-balance distributions that are purely related to topographic parameters. The regressors are again elevation, slope, curvature and S_x. We use the results of McGrath et al. (2015) to define normal distributions for the coefficients β_i (Equation 1) in standardised form from which we can randomly sample (see Supplementary Material). Normal distributions for β₀ and ϵ are defined based on our data, out of necessity, and are glacier-specific. Random error ϵ is assumed to have zero mean and a standard deviation equal to that of the glacier-specific subgrid variability of winter balance determined by Pulwicki et al. (2018). By using distributions for β_i from McGrath et al. (2015) and topographic parameters X_i from the study glaciers, we generate synthetic distributions of winter balance that are largely independent of our measurements but adjusted to local terrain. This approach allows us to evaluate the quality of designs over any number of potentially plausible winter-balance fields. We perform a similar set of tests with β_i from Pulwicki et al. (2018) for comparison (Supplementary Material).

We use the above procedure to generate 200 synthetic distributions of winter balance (see Figure 3 and Supplementary Material). Tests with larger numbers of synthetic b_w distributions showed little change in the results. In order to make results between different winter-balance fields for a given glacier comparable, the magnitudes of the synthetic winter balances are scaled such that the specific balance B_w remains constant and equal to the reference value obtained when all real data are used in the linear regression. For the ablation area only, B_w is 0.59 m w.e. for Glacier 4, 0.34 m w.e. for Glacier 2 and 0.27 m w.e. for Glacier 13 (see Figure 2). When the accumulation area is included, B_w becomes 0.59 m w.e. for Glacier 4, 0.57 m w.e. for Glacier 2 and 0.38 m w.e. for Glacier 13. Prior to this scaling, the raw synthetic winter balance is shifted upward by a constant to remove any negative values generated by the regression.

To evaluate survey designs, as in the case with real data, we extract 200 subsets of N samples within a given design (CL, CT, CR, HG, HC, RN) from each synthetic distribution of winter balance. With each subset of N samples, we again estimate the winter-balance field using new values of β₀ and β_i determined by least-squares regression. Although the form of the model (linear regression on topographic parameters) used to generate the synthetic data here is the same as that used to estimate winter balance, this need not be the case. For example, one could use a linear or non-linear statistical model that does not explicitly incorporate topography (e.g., Lliboutry, 1974) or that instead specifies spatial covariance characteristics. Using the same form of the model to generate and estimate winter balance offers a less challenging test than using different models, because it eliminates error due to mismatch in model form (known as model-form error).

We again compute the RMSE between the estimated and known (synthetic) winter balance on a gridcell-by-gridcell basis across the entire domain (either the ablation area or the entire glacier) to assess the performance of each survey design and sample size. We also consider the quality of the estimated values of B_w, both across the ablation area and glacier wide. In this case, N_T (Equation 2) is the total number of gridcells in the domain, rather than the total number of measured gridcells. With the synthetic data, results for each survey design and sample size reflect 40,000 simulations: 200 winter-balance distributions ×200 subsets of N samples. As for the real data, we perform one additional simulation for each survey design, sample size N and winter-balance field using quasi-regularly spaced samples; since there are 200 winter-balance fields in this case (compared to one in the real-data case), we have 200 additional simulations for each survey design and sample size.

4. Results

Below we describe the performance of the different survey designs and sample sizes for each glacier, and rank each survey design based on the RMSE.

4.1. Real Data

The mean RMSE between estimated and measured winter balance decreases markedly with sample size N for all survey designs on all glaciers (solid coloured lines, Figure 4), with inflection points between N ≈ 10–15 in most cases. In several cases, mean RMSE reaches the target (dashed horizontal lines, Figure 4) with N < 45. At low N, individual simulations sometimes yield RMSE below the target (coloured swaths dipping below horizontal dashed lines) due to fortuitous sampling locations. The individual simulations with quasi-regularly spaced samples (dotted lines, Figure 4) produce RMSEs that are sometimes, but not always, lower than the mean RMSEs with irregularly spaced samples (coloured lines, Figure 4). The general decline in RMSE with N in the simulations with quasi-regularly spaced samples is not usually monotonic.

FIGURE 4

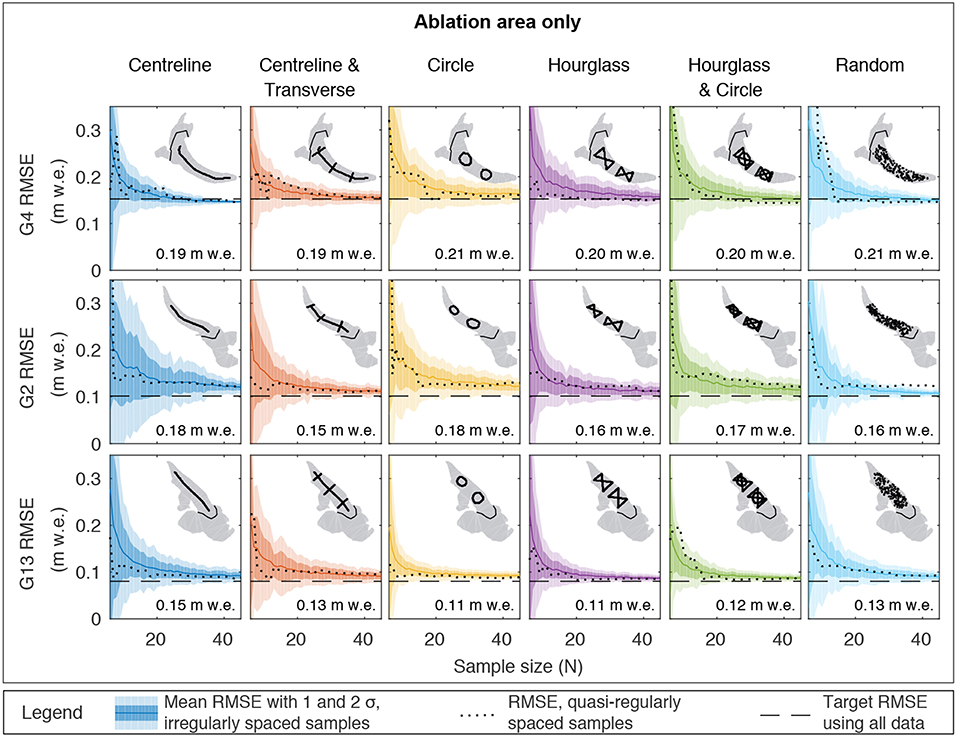
Figure 4. RMSEs for real data computed on a gridcell-by-gridcell basis between measured winter balance and co-located estimates of winter balance using subsets of the data in a linear topographic regression (Equation 1) for various survey designs (columns) and sample sizes N (x-axes) for Glacier 4 (top row), Glacier 2 (middle row), and Glacier 13 (bottom row). Insets show example sampling configurations. Bold coloured lines are mean values of RMSE from 200 estimates of the winter-balance field using different configurations of irregularly spaced samples; values are given for N = 10. Dark and light shading, respectively, indicate one and two standard deviations arising from different sampling configurations. Horizontal dashed lines are the target RMSEs when all data are used to estimate winter balance. Dotted lines represent individual simulations with quasi-regularly spaced samples. The proximity of the RMSE to the dashed line is a measure of precision, while its proximity to zero is a measure of accuracy.

Survey design can be assessed by averaging RMSEs over various ranges of N, both for glaciers individually and in combination (Figure 5). Three ranges of N were chosen, as RMSE can exhibit somewhat different behaviour at low and high N. N = 10–15 (Figure 5A) is around the inflection point of most curves in Figure 4, while the performance ranking of survey designs for a given glacier does not usually change beyond N = 35–40 (Figure 5C); N = 6–45 (Figure 5B) represents the full range of N presented in Figure 4. Aggregated results (rows labelled “ALL” and “G2 & G13” in Figure 5) are obtained by averaging the ranks for each glacier and each value of N (e.g., N = 10–15) to obtain a more representative result than averaging the integer ranks 1–6 reported for the glaciers individually. The rank of the RN survey design can vary with each trial due to its random nature and has therefore been excluded from Figure 5.

FIGURE 5

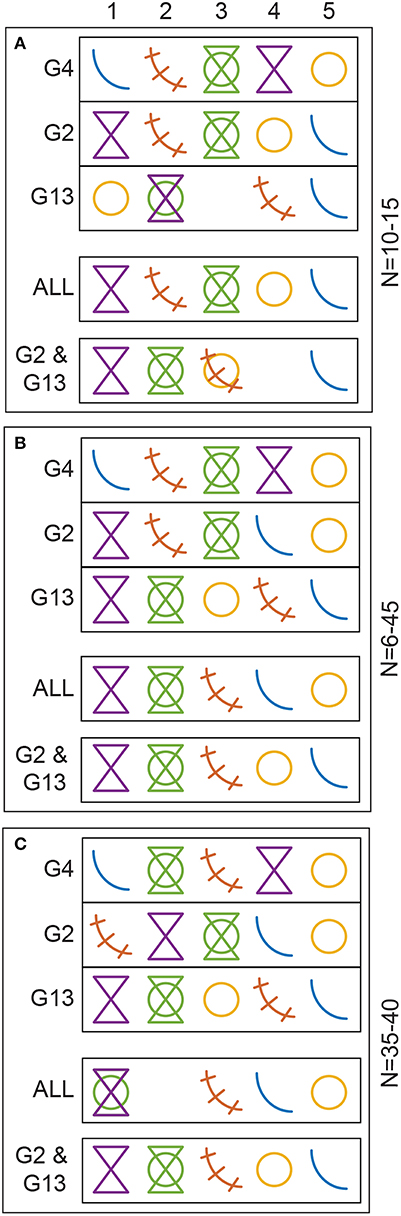
Figure 5. Ranking of survey designs from 1 to 5 (best to worst, left to right) using real data for (A) low N (10–15 sampling locations), (B) wide range of N (6–45 sampling locations), and (C) high N (35–40 sampling locations). Rankings are based on RMSE for b_w for a given survey design averaged over the specified range of N. Results are shown for Glaciers 4, 2, 13 individually (G4, G2, G13), together (ALL) and for Glaciers 2 and 13 combined (G2 & G13). From left to right in top row, symbols represent CL, CT, HC, HG, CR. RN is excluded. Overlapping symbols indicate a tie.

Design rankings differ between glaciers (rows labelled “G4,” “G2,” “G13” in Figure 5). Only HC ranks in the top three for all glaciers for all ranges of N. HG is always in the top two and CL in the bottom two for G2 and G13. Across all glaciers, CT is never worst, and only once best (G2, N = 35–40). In assessing the results aggregated across glaciers (rows labelled “ALL” in Figure 5), HG is first, HC and CT are in the top three, and CL and CR in the bottom two for all ranges of N. Only minor changes in the rankings occur when Glacier 4 is excluded (rows labelled “G2 & G13” in Figure 5).

Estimates of B_w using the different survey designs (Figure 6) have an inflection point at lower N than in the case for b_w (RMSEs in Figure 4). The implication is that fewer measurements are needed to achieve a substantial reduction in error of B_w, as compared to b_w. The variance is higher, as expected, for glacier-wide estimates of B_w (Figure 6B) as compared to estimates for the ablation area only (Figure 6A). In both cases, compared to b_w, estimates of B_w with quasi-regularly spaced samples (dotted lines in Figure 6) are highly non-monotonic with N. Some designs systematically under- or overestimate B_w relative to the value obtained when samples from all measurement locations are used; for a given design, whether B_w is higher or lower than the target depends on the glacier.

FIGURE 6

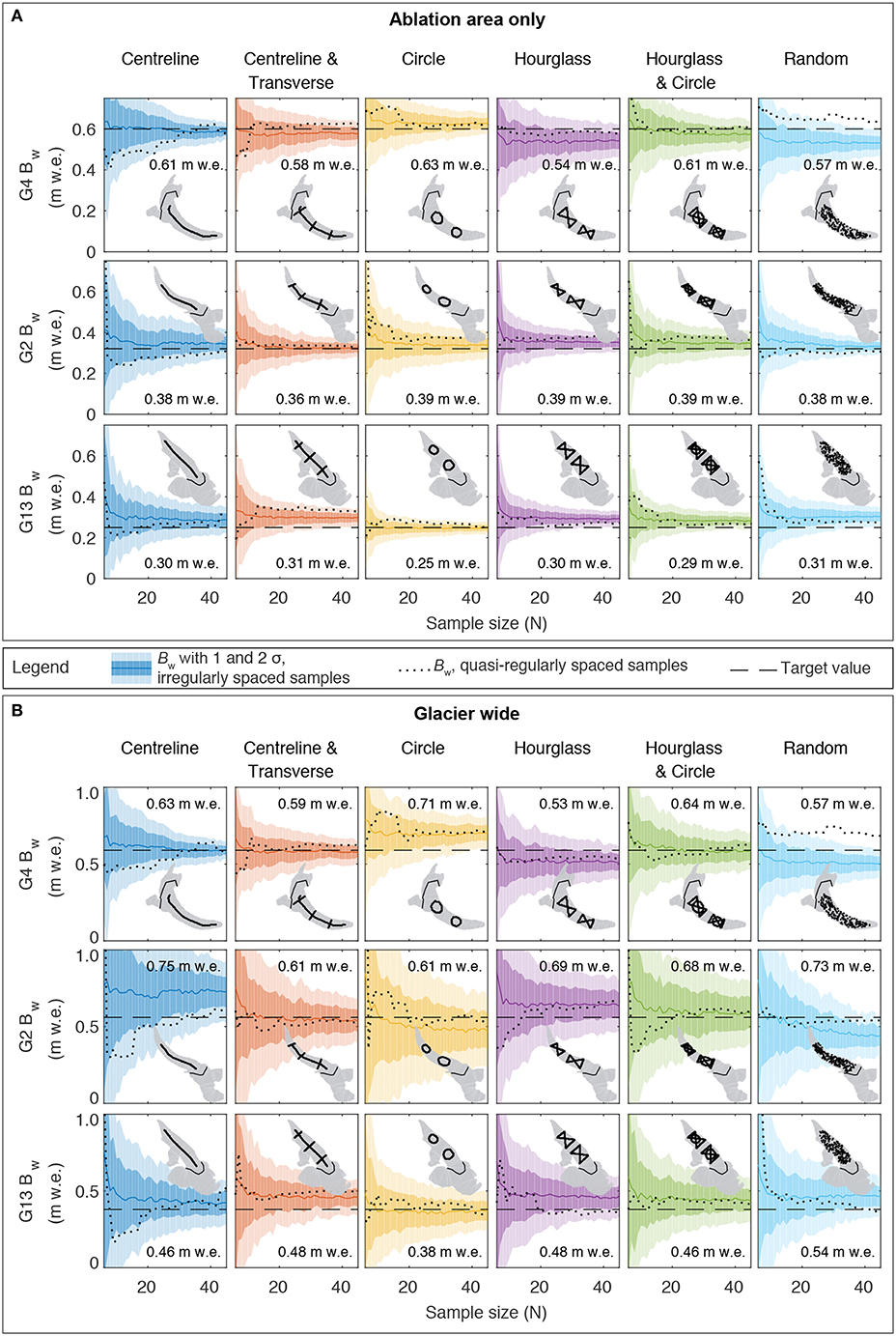
Figure 6. Ablation-area-wide (A) and glacier-wide (B) winter balance B_w estimated using real data in a linear topographic regression for various survey designs (columns) and sample sizes N (x-axes) for Glacier 4 (top rows), Glacier 2 (middle rows) and Glacier 13 (bottom rows). Insets show example sampling configurations. Bold coloured lines are mean values of 200 estimates of B_w using different configurations of irregularly spaced samples; values are given for N = 10. Dark and light shading, respectively, indicate one and two standard deviations arising from different sampling configurations. Horizontal dashed lines are the target values of B_w estimated using all data. Dotted lines represent individual simulations with quasi-regularly spaced samples.

4.2. Synthetic Data

RMSE again declines rapidly with sample size N, whether considering just the ablation area (Figure 7A) or the glacier as a whole (Figure 7B) this time. Although we have restricted our sampling designs to the ablation area for comparability with the real data, the synthetic data allow us to evaluate design performance for glacier-wide estimation of winter balance. RMSE evaluated in the ablation area (Figure 7A) comes closer to the target value (horizontal dashed line) by N = 45 than RMSE evaluated glacier wide (Figure 7B). Unlike the real-data case, the standard deviation of the RMSE in Figure 7 (shading) arises primarily from the 200 different realisations of winter balance (see Supplementary Material). The additional variability contributed by the irregular sampling locations (light shading) is small. Model fits with quasi-regularly spaced samples (dotted lines, Figure 7) are similar to those with real data: RMSEs are often, but not always, lower than those obtained on average with the irregularly spaced samples. Qualitatively similar results are obtained for synthetic data based on Pulwicki et al. (2018) instead of McGrath et al. (2015) (Supplementary Material).

FIGURE 7

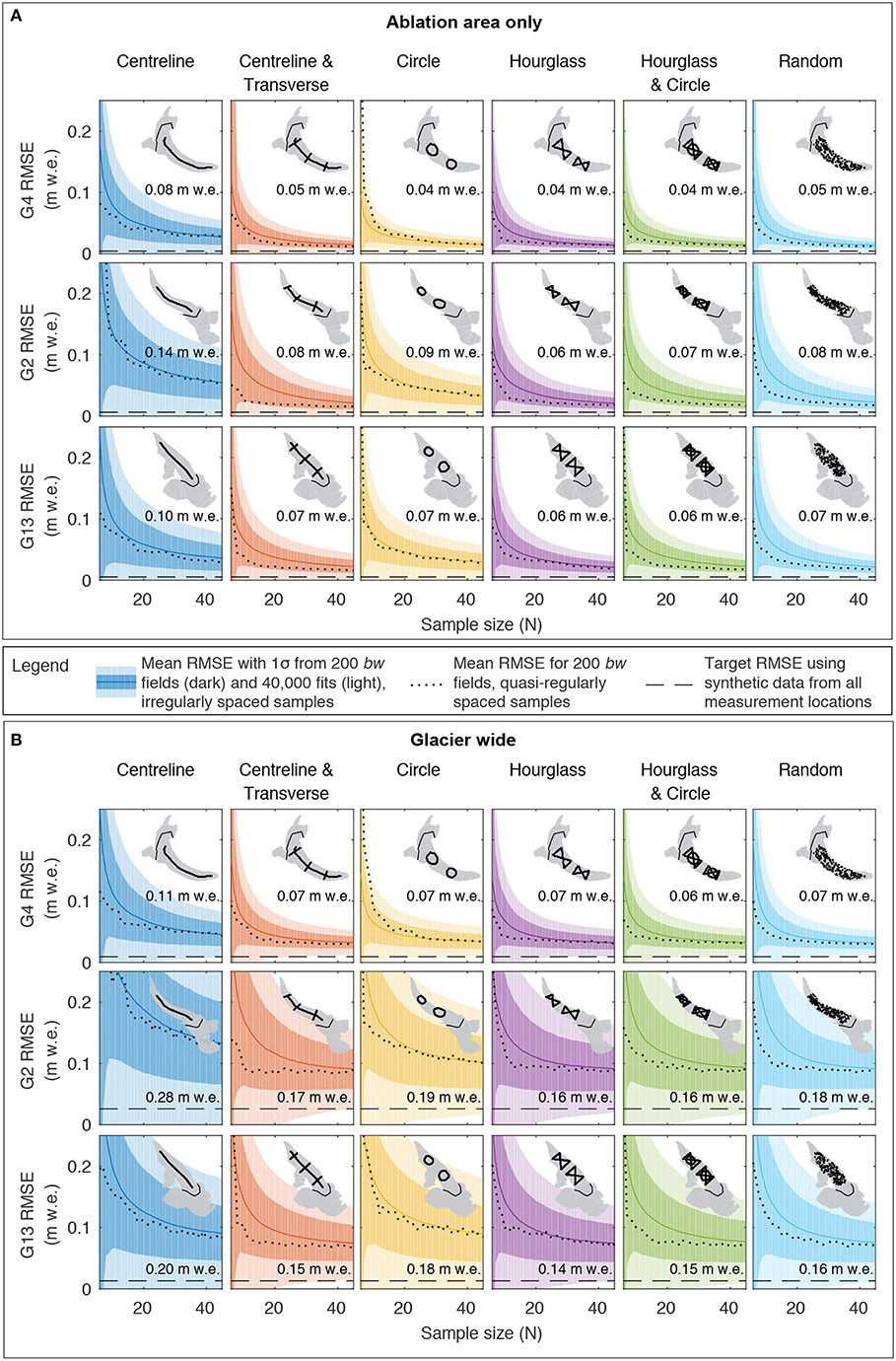
Figure 7. RMSEs for synthetic data (based on McGrath et al., 2015) computed on a gridcell-by-gridcell basis across the ablation area (A) and glacier wide (B) between known (synthetic) winter balance and that estimated using subsets of the synthetic data in a linear topographic regression (Equation 1) for various survey designs (columns) and sample sizes N (x-axes) for Glacier 4 (top rows), Glacier 2 (middle rows) and Glacier 13 (bottom rows). Insets show example sampling configurations. Bold coloured lines are mean values of RMSE from 200 estimates of each of the 200 synthetic winter-balance fields using different configurations of irregularly spaced synthetic samples (40,000 model fits); values are given for N = 10. Light shading indicates the standard deviation arising from the 40,000 fits. Dotted lines are mean values of RMSE from estimates of each of the 200 synthetic winter-balance fields using quasi-regularly spaced synthetic samples. Dark shading indicates the standard deviation arising from the 200 different winter-balance fields. Horizontal dashed lines are the RMSEs when synthetic data from all measurement locations are used to estimate winter balance.

Survey-design rankings present a similar but cleaner picture for the synthetic data (Figure 8) than for the real data (Figure 5). HG always ranks in the top two, with one exception. CL ranks last without exception. CR ranks in the bottom three with one exception. CT is never best, but never worst. RN improves with N, and is included here because the 40,000 simulations in each design assessment for each N make its rank more stable. Rankings for G2 and G13 bear more similarity to each other than to those for G4, indicating that there is something topographically distinct about G4. Design rankings differ only slightly when using RMSE evaluated glacier wide (not shown) as compared to RMSE evaluated only in the ablation area (Figure 8). They are also similar for synthetic data based on Pulwicki et al. (2018) instead of McGrath et al. (2015) (Supplementary Material).

FIGURE 8

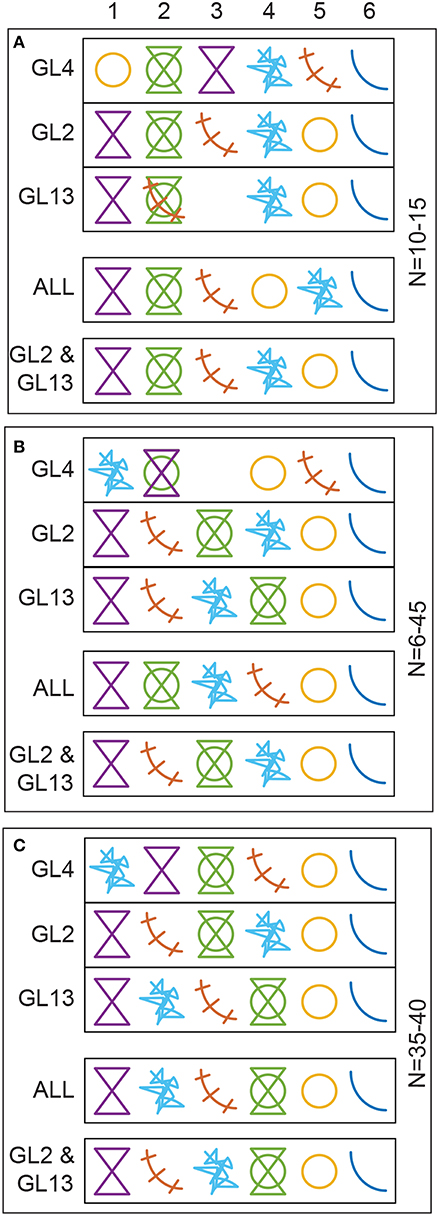
Figure 8. Ranking of survey designs from 1 to 6 (best to worst, left to right) using synthetic data (based on McGrath et al., 2015) for (A) low N (10–15 sampling locations), (B) wide range of N (6–45 sampling locations), and (C) high N (35–40 sampling locations). Rankings are based on RMSE for b_w across the ablation area for a given survey design averaged over the specified range of N. Results are shown for Glaciers 4, 2, 13 individually (G4, G2, G13), together (ALL) and for Glaciers 2 and 13 combined (G2 & G13). From left to right in top row, symbols represent CR, HC, HG, RN, CT, CL.

The idealised nature of the synthetic data is evident in estimates of the specific balance B_w (Figure 9) where the true values of B_w are easily achieved. Such a result is unsurprising given that misfit arises only from the random error added to the samples which averages to zero. Errors in estimating B_w are sufficiently small (Figure 9) that design rankings are not meaningful, with the exception that CL is consistently worst. Unlike in the real-data case, quasi-regularly spaced samples perform almost identically to the mean of the irregularly spaced samples.

FIGURE 9

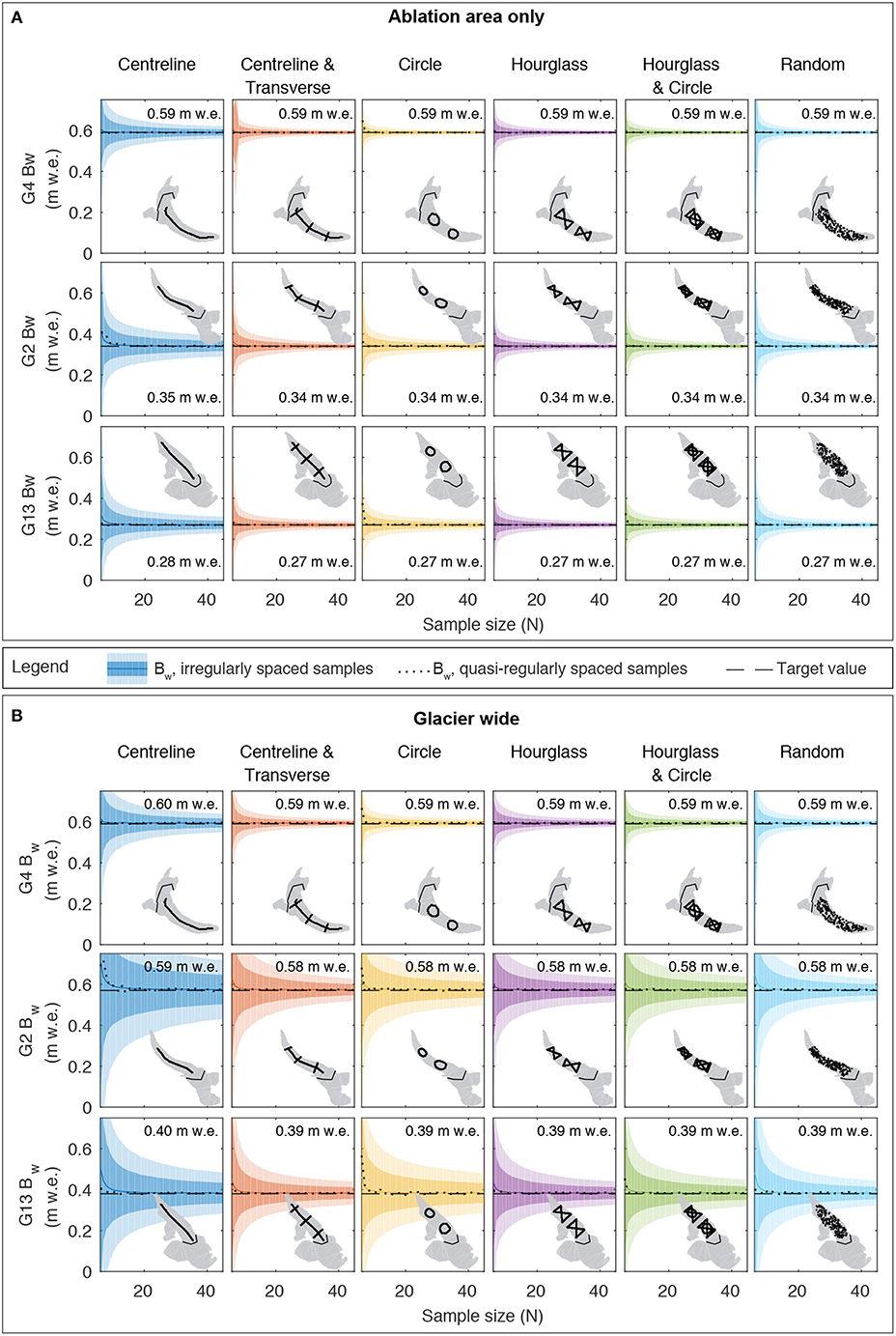
Figure 9. Ablation-area-wide (A) and glacier-wide (B) winter balance B_w estimated using synthetic data (based on McGrath et al., 2015) in a linear topographic regression for various survey designs (columns) and sample sizes N (x-axes) for Glacier 4 (top rows), Glacier 2 (middle rows) and Glacier 13 (bottom rows). Insets show example sampling configurations. Bold coloured lines are mean values of 200 estimates of B_w from each of the 200 synthetic winter-balance fields using different configurations of irregularly spaced synthetic samples (40,000 model fits); values are given for N = 10. Light shading indicates the standard deviation arising from the 40,000 fits. Dark shading indicates the standard deviation arising from the 200 different winter-balance fields. Horizontal dashed lines are the true values of B_w. Dotted lines are mean values of B_w from estimates of each of the 200 synthetic winter-balance fields using quasi-regularly spaced synthetic samples.

5. Synthesis and Discussion

Below we provide a brief synthesis of results, consolidate what we have learned about survey design, discuss discrepancies between results with real and synthetic data, comment on differences between glaciers and highlight both the limitations and wider implications of the study.

5.1. Survey Design

A robust result of this study is the decline in mean RMSE of the estimated winter-balance field b_w with sample size N for every survey design considered. Whether or not RMSE closely approaches the value obtained by using data from all measurement locations, a distinct inflection point in RMSE is apparent between N≈ 10–15. Results thus improve quickly up to N≈15 and more slowly thereafter. This inflection point occurs at even lower N when considering the specific balance B_w. There have been previous studies (e.g., Cogley, 1999; Fountain and Vecchia, 1999; Pelto, 2000) to suggest that low sample sizes may be sufficient to estimate the annual mass balance. An important caveat to our study is that each sample represents the mean winter balance within a 40 × 40 m gridcell, rather than an individual point measurement. Furthermore, even for a given sample size N, we find that estimates of b_w and B_w can vary significantly depending on sampling locations. Oversampling is therefore always recommended.

Notable differences emerge between quasi-regularly and irregularly spaced sampling in some cases (dotted lines vs coloured lines in Figures 4–7). The former often produces lower RMSE on the winter-balance field b_w for a given N than the mean RMSE of 200 trials with irregularly spaced samples (see Figure 4 for real data and Figure 7 for synthetic data). Further improvement, including a more monotonic decline in RMSE with N, would be expected if the survey were entirely redesigned with each additional sampling location, such that samples were truly regularly spaced. Our methodology, while failing to seek the globally optimal design, mimics the field situation of adding to or pruning an existing measurement network. The superior performance of more regularly spaced sampling schemes is particularly evident in comparisons with truly random sampling schemes (not shown). The same is not true for estimates of B_w using real data (Figure 6), where quasi-regularly spaced sampling is no guarantee of improved performance over irregularly spaced sampling. In contrast, there is almost no difference between sampling schemes in estimating B_w using synthetic data (Figure 9).

Although there is visual similarity in the performance of different survey designs (e.g., Figures 4, 7), both real and synthetic data point to a broadly consistent ranking (Figures 5, 8) evaluated on the basis of RMSE on the winter-balance field b_w. HG is often best, CL often worst, CT and HG somewhere in the middle and CR near the bottom. The best survey designs sample the glacier margins even at low N (e.g., HG), while the worst undersample the margins even at high N (e.g., CL, CR). Intermediate designs, though they extend to the glacier margins in principle (e.g., CT), may not adequately sample the margins at low N. Some designs (e.g., HC) have many possible sampling locations, such that samples may or may not land near the margins. The propensity for the best designs to sample away from the centreline also explains why the relative performance of RN improves with N (Figure 8).

Design rankings based on the specific balance B_w are less meaningful and were therefore not shown. For the synthetic data, all designs but CL perform similarly well when evaluated using B_w. For the real data, using B_w effectively compares the precision (not the accuracy) of an extrapolation to unmeasured areas. Furthermore, compensating spatial errors can lead to changes in design rankings from those based on accurately capturing the field b_w. Designs HG, CR and CL for G13 present an interesting case study: they are ranked 1, 3, and 5, respectively, based on the accuracy of estimating b_w in Figures 5B,C, but the values of B_w estimated by CR and CL are closer to the value estimated using the full dataset than that estimated by HG (Figure 6). This upset can be explained by considering the similarity of the regression coefficients determined using the individual designs and those determined using the full dataset. Averaged over the 200 model fits, CL best estimates the coefficient of the most important regressor (elevation) determined using the full dataset, while CR best estimates the intercept of the linear regression. HG is second best in both cases, but on average, best samples the regressor (elevation) compared to the full dataset. The combination of slopes and intercepts arising from model fits with each of the designs leads to estimates of winter balance using HG that compare more favourably with observations than those with CR or CL over the range of topographic parameters present in the data. When these regression coefficients are applied to topographic parameters beyond those sampled by the full dataset (e.g., across the entire ablation area or glacier wide), the extrapolated winter balance estimated with CR or CL is closer to that estimated using the full data set. Since this is an extrapolation without data for comparison, it is not possible to determine whether design performance based on B_w using the real data is meaningful.

The data suggest that sampling away from the glacier centreline provides a significant improvement in winter-balance estimation, even though elevation remains the dominant topographic control for two of the three glaciers (Pulwicki et al., 2018). In a study of two Norwegian glaciers with mass-balance records exceeding 40 years, Walmsley (2015) also identified shortcomings in the CL design, in that case leading to systematic underestimation of winter balance. Berthier et al. (2010) hypothesised that extrapolation from centreline repeat-altimetry profiles can lead to overestimation of regional glacier mass loss. The performance of any design, including CL, is linked to how well it samples the winter-balance distribution, and in our case, the topographic parameters with the most explanatory power. CL typically samples elevation well, but fails to sample the glacier margins where snow accumulation and persistence can be greater than along the centreline (e.g., Machguth et al., 2006; Walmsley, 2015).

Other studies of survey design for summer or annual (summer + winter) balance find that relatively few measurements along the centreline may be sufficient for accurate balance estimates. For example, Surjanovic (2016) finds that a CL design performs well in some ablation regimes. Fountain and Vecchia (1999) find that as few as five stakes are needed to estimate the annual balances of two small glaciers in the western continental United States. Fountain and Vecchia (1999) emphasise that there is little transverse variation in annual balance and that elevation is the dominant control on annual balance. Our results are not necessarily inconsistent with those of Fountain and Vecchia (1999) if annual balance correlates more strongly with summer- rather than winter balance.

5.2. Real vs. Synthetic Data

Though the results for real and synthetic data point to some robust conclusions (see above), there are informative differences between them. The target RMSEs are lower for the synthetic data (horizontal dashed lines in Figure 7 compared to Figure 4), because the synthetic winter-balance fields, generated with a linear regression model, can be precisely estimated with that same model in the absence of noise. The values of the target RMSEs for the synthetic data therefore isolate the performance of the survey design, or more precisely, the ability of the design to capture variation in the topographic parameters correlated with winter balance. With real data, the values of the target RMSEs combine the performance of the survey design and the performance of the linear regression in representing the observed winter-balance field. The most notable contrast between the design rankings with real (Figure 5) and synthetic data (Figure 8) is the greater consistency present for the synthetic data, owing to its idealised nature. While the optimal survey design depends on the nature of the field being measured (e.g., Escher-Vetter et al., 2009), the broad similarity of results across real and synthetic datasets, including hundreds of realisations of the winter balance field in the synthetic case, demonstrates some underlying robustness of the different survey designs.

5.3. Differences Between Glaciers

Results for Glacier 4 are often different than for Glaciers 2 and 13: (1) G4 has the highest target RMSE for the real data (~ 0.15 m w.e., Figure 4); (2) errors in estimating both b_w and B_w with the synthetic data are the lowest for G4 of all glaciers (Figures 7, 9); (3) B_w evaluated across the ablation area is the same as that evaluated glacier wide (0.59 m w.e.) for G4; (4) CL ranks as the best design for G4 for all ranges of N for the real data (Figure 5); (5) G4 is the only glacier for which HG is not ranked first for the synthetic data (Figure 8). The first of these differences means that the winter-balance estimates for G4 are less accurate. Based strictly on our measurements, G4 had the highest mean snow depth and the highest proportion of outliers (Pulwicki et al., 2018). The linear regression explains little of the variance in the real data for G4 (Pulwicki et al., 2018), with regression coefficients often taking on signs opposite to those of coefficients for G2 and G13 (Pulwicki, 2017). Notably, elevation explains the most variance in winter balance for G2 and G13, but almost none of the variance for G4 (Pulwicki et al., 2018). While the real data were demonstrably unrelated to topographic parameters for G4 (Pulwicki et al., 2018), the synthetic data, which are unambiguously a function of topography, require another explanation. Compared to G2 and G13, G4 is small, spans about half the elevation range, and has few steep slopes, a near absence of positive surface curvature, and a lower accumulation area ratio (AAR). It is thus topographically distinct from G2 and G13 which may explain observations (4) and (5) above, and in combination with G4's low AAR, observation (3). These differences highlight the value of including multiple glaciers in this study.

5.4. Study Limitations and Wider Implications

The dataset we exploited for this study was not collected with an interrogation of optimal design in mind, and thus imposes significant limitations. The most glaring among them is the omission of the accumulation area, which was vastly under-sampled (Pulwicki et al., 2018). Reliable in-situ measurements of snow depth in the accumulation area are time-consuming, as detection of the snow–firn interface by probing can be difficult (e.g., Østrem and Brugman, 1991) and must often be replaced by the excavation of snow pits. Such limitations can be overcome with alternative methods of measuring snow depth, such as ground-penetrating radar (GPR) (e.g., Machguth et al., 2006; Gusmeroli et al., 2014; McGrath et al., 2015, 2018) and repeat lidar surveys (e.g., Sold et al., 2013). Nevertheless, limitations will always remain that will introduce sampling bias. Ground-based measurements will undersample areas that are difficult to navigate or unsafe (e.g., icefalls), while remote methods are subject to other limitations such as fixed orbits, restricted aircraft heights or flight patterns and incomplete sensor viewsheds.

Even in the presence of sparse measurements in the accumulation area, we are often tasked with estimating the glacier-wide winter balance. RMSEs increase when winter-balance data from the ablation area are extrapolated into the accumulation area, even in the idealised case of synthetic data where the relationship between topography and winter balance is the same in the ablation and accumulation areas. Other studies have observed accumulation to increase to some elevation below the maximum elevation of the glacier and either decreases or exhibit no relationship thereafter (Machguth et al., 2006; Helfricht et al., 2012; Sold et al., 2013). To evaluate the consequences of spatially variable relationships between winter balance and topographic variables would require a more complete dataset with good coverage of the accumulation area. Though less grievous than the spatial limitations of our data, our work is also limited by the data being restricted to a single accumulation season. Inter-annual variability in snow distribution has been observed (e.g., Crochet et al., 2007), but numerous studies document a spatial stationarity that can be exploited once it is characterised (e.g., Pelto, 2000; Sturm and Wagner, 2010; McGrath et al., 2018). A final limitation imposed by our original dataset is the fixed nature of the sampling locations. Our data do not permit us to answer questions such as: What is the optimal placement of a given survey design (e.g., CR)? Are fewer large CR/HG/HC better than a greater number of small ones? Does a regular grid of N samples outperform the tested designs with N samples? What is the global optimum survey design? Such questions represent worthwhile research directions, ideally pursued with a more complete dataset.

Despite these limitations, our analysis suggests that sampling away from the centreline is usually important, even in the ablation area and even in cases where elevation is the dominant topographic control on winter balance. Any plausible alternative design will capture variation with elevation at the same time it captures variation with other topographic parameters such as slope and curvature. Off-centreline sampling likely becomes more important in the accumulation area, where the relationship between winter balance and elevation in the ablation area may break down. A space-filling hourglass might be a reasonable design to attempt in the accumulation area if little is known about the structure of the winter-balance field. Our analysis shows that although RMSEs decline sharply at low N (< 15) when averaged over hundreds of realisations of a given survey design, any individual survey may require a much larger N to reliably achieve the same error reduction. We have also documented differences among glaciers within the same small mountain range subject to the same synoptic weather patterns, cautioning against extrapolation of topographic relationships between sites. In establishing a new mass-balance program it would be wise to invest initially in dense spatial sampling to determine the structure of the winter-balance field (e.g., Van Beusekom et al., 2010), with the expectation that N could be substantially reduced over time (e.g., Pelto, 2000).

6. Conclusion

Using in-situ snow-depth and density measurements from three glaciers in the St. Elias Mountains of Yukon, Canada, we investigate the problem of optimal survey design for estimating winter balance with a focus on the ablation area. We consider six survey designs and the full range of sample sizes permitted by our methodology and dataset. Quantitative criteria allow us to rank each design by performance for each glacier using real- and synthetic data. Mean RMSE between estimated and observed winter-balance fields b_w declines rapidly, over all designs, for samples sizes up to N≈10–15, with little improvement thereafter. This decline occurs at even lower N for the specific winter balance B_w. For a given survey design, RMSE is generally found to be lower when samples are more regularly spaced. For both real- and synthetic data, the traditional centreline profile performed poorly, even in cases where elevation is the dominant topographic control on winter balance. An unconventional design termed the “hourglass” performed best overall; survey designs that sample the glacier margins even at low N were favoured by both the real and synthetic data. Whether our results are generalisable depends on their robustness to different glacier hypsometries, climate settings, terrain model resolutions, methods of interpolation/extrapolation and winter-balance sampling schemes that include the accumulation area. While our study is most limited by the dearth of data from the accumulation area, it does provide a methodological template that can be applied to existing datasets to evaluate survey design, or to new sites where digital terrain models exist but mass balance has not yet been measured.

Data Availability

The datasets analysed in this study can be downloaded from https://github.com/apulwicki/SnowDepth/tree/Density/Raw%20Data.

Author Contributions

AP planned and executed the data collection, developed the code, carried out all simulations and preliminary analyses, made the figures and wrote an initial draft of the manuscript. GF conceived of the study based on discussions and collaboration with DB, contributed to field planning and data collection, oversaw all aspects of the research, interpreted the results, and revised the manuscript. DB consulted on the statistical methods and interpretation of results, and edited the submitted draft of the manuscript.

Funding

Financial support was provided by the Natural Sciences and Engineering Research Council of Canada (Discovery Grant, Northern Research Supplement), Polar Knowledge Canada (Northern Scientific Training Program), and Simon Fraser University (Graduate Fellowship, KEY Big Data Scholarship).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgements

We thank the Kluane First Nation (KFN), Parks Canada and the Yukon Territorial Government for granting us permission to work in KFN Traditional Territory and Kluane National Park and Reserve. We are grateful for financial support provided by the Natural Sciences and Engineering Research Council of Canada, Simon Fraser University (including the KEY Big Data Initiative) and the Northern Scientific Training Program. We kindly acknowledge research station managers Sian Williams and Lance Goodwin, and Trans North pilot Dion Parker for facilitating field logistics. We are grateful to Alison Criscitiello and Coline Ariagno for all aspects of field assistance, and to Sarah Furney for assistance with data entry. Thank you to Etienne Berthier for providing us with the SPIRIT SPOT-5 DEM and for assistance in DEM correction. Reviewers SO'N and MP and Editor MH are credited with critical comments that helped reshape the analysis and improve the manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2019.00199/full#supplementary-material

References

Andreassen, L. M., Elvehøy, H., Kjøllmoen, B., and Engeset, R. V. (2016). Reanalysis of long-term series of glaciological and geodetic mass balance for 10 norwegian glaciers. Cryosphere 10, 535–552. doi: 10.5194/tc-10-535-2016

CrossRef Full Text | Google Scholar

Arendt, A. A., Luthcke, S. B., Larsen, C. F., Abdalati, W., Krabill, W. B., and Beedle, M. J. (2008). Validation of high-resolution GRACE mascon estimates of glacier mass changes in the St. Elias Mountains, Alaska, USA, using aircraft laser altimetry. J. Glaciol. 54, 778–787. doi: 10.3189/002214308787780067

CrossRef Full Text | Google Scholar

Bellaire, S., and Schweizer, J. (2008). “Deriving spatial stability variations from penetration resistance measurements,” in Proceedings ISSW (Whistler, BC), 188–194.

Google Scholar

Bellaire, S., and Schweizer, J. (2011). Measuring spatial variations of weak layer and slab properties with regard to snow slope stability. Cold Regions Sci. Technol. 65, 234–241. doi: 10.1016/j.coldregions.2010.08.013

CrossRef Full Text | Google Scholar

Berthier, E., Schiefer, E., Clarke, G. K., Menounos, B., and Rémy, F. (2010). Contribution of Alaskan glaciers to sea-level rise derived from satellite imagery. Nat. Geosci. 3, 92–95. doi: 10.1038/ngeo737

CrossRef Full Text | Google Scholar

Björnsson, H., Pálsson, F., Gudmundsson, M. T., and Haraldsson, H. H. (1998). Mass balance of western and northern vatnajökull, Iceland, 1991–1995. Jökull 45, 35–58.

Burgess, E. W., Forster, R. R., and Larsen, C. F. (2013). Flow velocities of Alaskan glaciers. Nat. Commun. 4, 2146–2154. doi: 10.1038/ncomms3146

PubMed Abstract | CrossRef Full Text | Google Scholar

Clarke, G. K. C. (2014). A short and somewhat personal history of Yukon glacier studies in the Twentieth Century. Arctic 37, 1–21. doi: 10.14430/arctic4355

CrossRef Full Text | Google Scholar

Cogley, J., Hock, R., Rasmussen, L., Arendt, A., Bauder, A., Braithwaite, R., et al. (2011). Glossary of Glacier Mass Balance and Related Terms. Paris: UNESCO-IHP.

Cogley, J. G. (1999). Effective sample size for glacier mass balance. Geografiska Ann. Ser. A Phys. Geogr. 81, 497–507. doi: 10.1111/j.0435-3676.1999.00079.x

CrossRef Full Text | Google Scholar

Crochet, P., Jóhannesson, T., Jónsson, T., Sigurdsson, O., Björnsson, H., Pálsson, F., et al. (2007). Estimating the spatial distribution of precipitation in Iceland using a linear model of orographic precipitation. J. Hydrometeorol. 8, 1285–1306. doi: 10.1175/2007JHM795.1

CrossRef Full Text | Google Scholar

Crompton, J. W., and Flowers, G. E. (2016). Correlations of suspended sediment size with bedrock lithology and glacier dynamics. Ann. Glaciol. 57, 1–9. doi: 10.1017/aog.2016.6

CrossRef Full Text | Google Scholar

Cullen, N. J., Anderson, B., Sirguey, P., Stumm, D., Mackintosh, A., Conway, J. P., et al. (2017). An 11-year record of mass balance of Brewster Glacier, New Zealand, determined using a geostatistical approach. J. Glaciol. 63, 199–217. doi: 10.1017/jog.2016.128

CrossRef Full Text | Google Scholar

Danby, R. K., Hik, D. S., Slocombe, D. S., and Williams, A. (2003). Science and the St. Elias: an evolving framework for sustainability in North America's highest mountains. Geogr. J. 169, 191–204. doi: 10.1111/1475-4959.00084

CrossRef Full Text | Google Scholar

Dean, A., Voss, D., and Draguljic, D. (2017). Design and Analysis of Experiments, 2nd Edn. New York, NY: Springer.

Deems, J. S., Fassnacht, S. R., and Elder, K. J. (2008). Interannual consistency in fractal snow depth patterns at two Colorado mountain sites. J. Hydrometeorol. 9, 977–988. doi: 10.1175/2008JHM901.1

CrossRef Full Text | Google Scholar

Elder, K., Cline, D., Liston, G. E., and Armstrong, R. (2009). NASA Cold Land Processes Experiment (CLPX 2002/03): field measurements of snowpack properties and soil moisture. J. Hydrometeorol. 10, 320–329. doi: 10.1175/2008JHM877.1

CrossRef Full Text | Google Scholar

Elder, K., Dozier, J., and Michaelsen, J. (1991). Snow accumulation and distribution in an alpine watershed. Water Resour. Res. 27, 1541–1552. doi: 10.1029/91WR00506

CrossRef Full Text | Google Scholar

Erickson, T. A., Williams, M. W., and Winstral, A. (2005). Persistence of topographic controls on the spatial distribution of snow in rugged mountain terrain, Colorado, United States. Water Resour. Res. 41:W04014. doi: 10.1029/2003WR002973

CrossRef Full Text | Google Scholar

Escher-Vetter, H., Kuhn, M., and Weber, M. (2009). Four decades of winter mass balance of Vernagtferner and Hintereisferner, Austria: methodology and results. Ann. Glaciol. 50, 87–95. doi: 10.3189/172756409787769672

CrossRef Full Text | Google Scholar

Flowers, G. E., Copland, L., and Schoof, C. G. (2014). Contemporary Glacier Processes and Global Change: recent Observations from Kaskawulsh Glacier and the Donjek Range, St. Elias Mountains. Arctic 67, 22–34. doi: 10.14430/arctic4356

CrossRef Full Text | Google Scholar

Fountain, A. G., and Vecchia, A. (1999). How many stakes are required to measure the mass balance of a glacier? Geografiska Ann. Ser. A Phys. Geogr. 81, 563–573. doi: 10.1111/1468-0459.00084

CrossRef Full Text | Google Scholar

Grünewald, T., Bühler, Y., and Lehning, M. (2014). Elevation dependency of mountain snow depth. Cryosphere 8, 2381–2394. doi: 10.5194/tc-8-2381-2014

CrossRef Full Text | Google Scholar

Gusmeroli, A., Wolken, G. J., and Arendt, A. A. (2014). Helicopter-borne radar imaging of snow cover on and around glaciers in Alaska. Ann. Glaciol. 55, 78–88. doi: 10.3189/2014AoG67A029

CrossRef Full Text | Google Scholar

Helfricht, K., Schöber, J., Seiser, B., Fischer, A., Stötter, J., and Kuhn, M. (2012). Snow accumulation of a high alpine catchment derived from lidar measurements. Adv. Geosci. 32, 31–39. doi: 10.5194/adgeo-32-31-2012

CrossRef Full Text | Google Scholar

Hock, R. (2005). Glacier melt: a review of processes and their modelling. Prog. Phys. Geogr. 29, 362–391. doi: 10.1191/0309133305pp453ra

CrossRef Full Text | Google Scholar

Hodgkins, R., Cooper, R., Wadham, J., and Tranter, M. (2005). Interannual variability in the spatial distribution of winter accumulation at a high-Arctic glacier (Finsterwalderbreen, Svalbard), and its relationship with topography. Ann. Glaciol. 42, 243–248. doi: 10.3189/172756405781812718

CrossRef Full Text | Google Scholar

Huss, M., and Hock, R. (2018). Global-scale hydrological response to future glacier mass loss. Nat. Clim. Change 8:135. doi: 10.1038/s41558-017-0049-x

CrossRef Full Text | Google Scholar

Johnson, M., Moore, L., and Ylvisaker, D. (1990). Minimax and maximin distance designs. J. Stat. Plan. Inference 26, 131–148. doi: 10.1016/0378-3758(90)90122-B

CrossRef Full Text | Google Scholar

Kaser, G., Fountain, A., and Jansson, P. (2002). A Manual for Monitoring the Mass Balance of Mountain Glaciers. IHP-VI- Technical documents in hydrology.

Google Scholar

Kaser, G., Großhauser, M., and Marzeion, B. (2010). Contribution potential of glaciers to water availability in different climate regimes. Proc. Natl. Acad. Sci. U.S.A. 107, 20223–20227. doi: 10.1073/pnas.1008162107

PubMed Abstract | CrossRef Full Text | Google Scholar

Kinar, N., and Pomeroy, J. (2015). Measurement of the physical properties of the snowpack. Rev. Geophys. 53, 481–544. doi: 10.1002/2015RG000481

CrossRef Full Text | Google Scholar

Korona, J., Berthier, E., Bernard, M., Rémy, F., and Thouvenot, E. (2009). SPIRIT SPOT 5 stereoscopic survey of Polar Ice: reference images and topographies during the fourth International Polar Year (2007–2009). ISPRS J. Photogrammetr. Remote Sens. 64, 204–212. doi: 10.1016/j.isprsjprs.2008.10.005

CrossRef Full Text | Google Scholar

Kronholm, K., and Birkeland, K. W. (2007). Reliability of sampling designs for spatial snow surveys. Comput. Geosci. 33, 1097–1110. doi: 10.1016/j.cageo.2006.10.004

CrossRef Full Text | Google Scholar

Larsen, C., Burgess, E., Arendt, A., O'Neel, S., Johnson, A., and Kienholz, C. (2015). Surface melt dominates Alaska glacier mass balance. Geophys. Res. Lett. 42, 5902–5908. doi: 10.1002/2015GL064349

CrossRef Full Text | Google Scholar

Lehning, M., Grünewald, T., and Schirmer, M. (2011). Mountain snow distribution governed by an altitudinal gradient and terrain roughness. Geophys. Res. Lett. 38:L19504. doi: 10.1029/2011GL048927

CrossRef Full Text | Google Scholar

Lliboutry, L. (1974). Multivariate statistical analysis of glacier annual balances. J. Glaciol. 13, 371–392. doi: 10.3189/S0022143000023169

CrossRef Full Text | Google Scholar

López-Moreno, J. I., Fassnacht, S., Beguería, S., and Latron, J. (2011). Variability of snow depth at the plot scale: implications for mean depth estimation and sampling strategies. Cryosphere 5, 617–629. doi: 10.5194/tc-5-617-2011

CrossRef Full Text | Google Scholar

Machguth, H., Eisen, O., Paul, F., and Hoelzle, M. (2006). Strong spatial variability of snow accumulation observed with helicopter-borne GPR on two adjacent alpine glaciers. Geophys. Res. Lett. 33, 1–5. doi: 10.1029/2006GL026576

CrossRef Full Text | Google Scholar

McGrath, D., Sass, L., O'Neel, S., Arendt, A., Wolken, G., Gusmeroli, A., et al. (2015). End-of-winter snow depth variability on glaciers in Alaska. J. Geophys. Res. Earth Surf. 120, 1530–1550. doi: 10.1002/2015JF003539

CrossRef Full Text | Google Scholar

McGrath, D., Sass, L., O'Neel, S., McNeil, C., Candela, S. G., Baker, E. H., et al. (2018). Interannual snow accumulation variability on glaciers derived from repeat, spatially extensive ground-penetrating radar surveys. Cryosphere 12, 3617–3633. doi: 10.5194/tc-12-3617-2018

CrossRef Full Text | Google Scholar

Möller, M., and Möller, R. (2019). Snow cover variability across glaciers in nordenskiöldland (svalbard) from point measurements in 2014–2016. Earth Syst. Sci. Data Discuss. 2019, 1–16. doi: 10.5194/essd-2018-158

CrossRef Full Text | Google Scholar

Molotch, N. P., and Bales, R. C. (2005). Scaling snow observations from the point to the grid element: implications for observation network design. Water Resour. Res. 41:W11421. doi: 10.1029/2005WR004229

CrossRef Full Text | Google Scholar

Østrem, G., and Brugman, M. (1991). Mass Balance Measurement Techniques. A manual for field and office work. National Hydrology Research Institute (NHRI) Science Report.

Pelto, M. S. (2000). The impact of sampling density on glacier mass balance determination. Hydrol. Process. 14, 3215–3225. doi: 10.1002/1099-1085(20001230)14:18<3215::AID-HYP197>3.0.CO;2-E

CrossRef Full Text | Google Scholar

Pulwicki, A. (2017). Multi-scale investigation of winter balance on alpine glaciers (Master's thesis). Simon Fraser University, Burnaby, BC, Canada.

Google Scholar

Pulwicki, A., Flowers, G. E., Radić, V., and Bingham, D. (2018). Estimating winter balance and its uncertainty from direct measurements of snow depth and density on alpine glaciers. J. Glaciol. 64, 781–795. doi: 10.1017/jog.2018.68

CrossRef Full Text | Google Scholar

Réveillet, M., Vincent, C., Six, D., and Rabatel, A. (2016). Which empirical model is best suited to simulate glacier mass balances? J. Glaciol. 63, 1–16. doi: 10.1017/jog.2016.110

CrossRef Full Text | Google Scholar

Schirmer, M., Wirz, V., Clifton, A., and Lehning, M. (2011). Persistence in intra-annual snow depth distribution: 1. Measurements and topographic control. Water Resour. Res. 47:W09516. doi: 10.1029/2010WR009426

CrossRef Full Text | Google Scholar

Schweizer, J., Heilig, A., Bellaire, S., and Fierz, C. (2008). Variations in snow surface properties at the snowpack-depth, the slope and the basin scale. J. Glaciol. 54, 846–856. doi: 10.3189/002214308787780058

CrossRef Full Text | Google Scholar

Shea, C., and Jamieson, B. (2010). Star: an efficient snow point-sampling method. Ann. Glaciol. 51, 64–72. doi: 10.3189/172756410791386463

CrossRef Full Text | Google Scholar

Sold, L., Huss, M., Hoelzle, M., Andereggen, H., Joerg, P. C., and Zemp, M. (2013). Methodological approaches to infer end-of-winter snow distribution on alpine glaciers. J. Glaciol. 59, 1047–1059. doi: 10.3189/2013JoG13J015

CrossRef Full Text | Google Scholar

Sold, L., Huss, M., Machguth, H., Joerg, P. C., Leysinger Vieli, G., Linsbauer, A., et al. (2016). Mass balance re-analysis of Findelengletscher, Switzerland; benefits of extensive snow accumulation measurements. Front. Earth Sci. 4:18. doi: 10.3389/feart.2016.00018

CrossRef Full Text | Google Scholar

Sturm, M., and Wagner, A. M. (2010). Using repeated patterns in snow distribution modeling: an Arctic example. Water Resour. Res. 46:W12549. doi: 10.1029/2010WR009434

CrossRef Full Text | Google Scholar

Surjanovic, S. (2016). Using computer model uncertainty to inform the design of physical experiments: an application in glaciology (Master's thesis). Simon Fraser University, Burnaby, BC, Canada.

Google Scholar

Taurisano, A., Schuler, T. V., Ove Hagen, J., Eiken, T., Loe, E., Melvold, K., et al. (2007). The distribution of snow accumulation across the austfonna ice cap, svalbard: direct measurements and modelling. Polar Res. 26, 7–13. doi: 10.1111/j.1751-8369.2007.00004.x

CrossRef Full Text | Google Scholar

Taylor-Barge, B. (1969). The Summer Climate of the St. Elias Mountain Region. Montreal, QC: Arctic Institute of North America, Research Paper No. 53.

Google Scholar

Van Beusekom, A. E., O'Neel, S. R., March, R. S., Sass, L. C., and Cox, L. H. (2010). Re-analysis of Alaskan Benchmark Glacier Mass-Balance Data Using the Index Method. Technical Report 2010–5247, US Geological Survey.

Google Scholar

Waechter, A., Copland, L., and Herdes, E. (2015). Modern glacier velocities across the Icefield Ranges, St. Elias Mountains, and variability at selected glaciers from 1959 to 2012. J. Glaciol. 61, 624–634. doi: 10.3189/2015JoG14J147

CrossRef Full Text | Google Scholar

Walmsley, A. P. U. (2015). Long-term observations of snow spatial distributions at Hellstugubreen and Gråsubreen, Norway (Master's thesis). University of Oslo, Oslo, Norway.

Google Scholar

Watson, F. G., Anderson, T. N., Newman, W. B., Alexander, S. E., and Garrott, R. A. (2006). Optimal sampling schemes for estimating mean snow water equivalents in stratified heterogeneous landscapes. J. Hydrol. 328, 432–452. doi: 10.1016/j.jhydrol.2005.12.032

CrossRef Full Text | Google Scholar

Wilson, N., and Flowers, G. (2013). Environmental controls on the thermal structure of alpine glaciers. Cryosphere 7, 167–182. doi: 10.5194/tc-7-167-2013

CrossRef Full Text | Google Scholar

Wilson, N. J., Flowers, G. E., and Mingo, L. (2013). Comparison of thermal structure and evolution between neighboring subarctic glaciers. J. Geophys. Res. Earth Surf. 118, 1443–1459. doi: 10.1002/jgrf.20096

CrossRef Full Text | Google Scholar

Winstral, A., Elder, K., and Davis, R. E. (2002). Spatial snow modeling of wind-redistributed snow using terrain-based parameters. J. Hydrometeorol. 3, 524–538. doi: 10.1175/1525-7541(2002)003<0524:SSMOWR>2.0.CO;2

CrossRef Full Text | Google Scholar

Winstral, A., and Marks, D. (2002). Simulating wind fields and snow redistribution using terrain-based parameters to model snow accumulation and melt over a semi-arid mountain catchment. Hydrol. Process. 16, 3585–3603. doi: 10.1002/hyp.1238

CrossRef Full Text | Google Scholar

Wood, W. A. (1948). Project “Snow Cornice": the establishment of the Seward Glacial research station. Arctic 1, 107–112. doi: 10.14430/arctic4005

CrossRef Full Text | Google Scholar