Storm Surge and Extreme River Discharge: A Compound Event Analysis Using Ensemble Impact Modeling

Introduction

Floods are a major cause of casualties due to natural disasters, with over 6.8 million deaths globally during the 20^th century (Doocy et al., 2013), and an annual average loss of 104 billion US$ (Blöschl et al., 2017). Rivers floods are the result of a complex chain of atmospheric and surface hydrological processes (Hall et al., 2014; Merz et al., 2014). Atmospheric circulation patterns distribute the necessary precipitation on a variety of spatial scales and intensities (Prudhomme and Genevier, 2011). Following the characteristics of the local hydrology the water then aggregates into streams and rivers, ultimately transporting river runoff to coastal estuaries. On its way to the sea, the main river is fed from several sub-catchments and receives input from reservoirs that act on longer time scales than runoff routing processes. These long time scales introduce a dependence on antecedent conditions, for example ice and snowmelt from high-altitude glaciers and/or snow reserves located in the headwaters, soil moisture retention, and baseflow processes. In low-lying countries like the Netherlands, flood defense infrastructure protects the densely populated hinterland. Risk of river flooding therefore typically only occurs in the winter season when deep Atlantic low-pressure systems (extratropical cyclones) precipitate large amounts of water over the European Alps and Central Europe.

Traditionally floods are defined by a set of correlated random variables like flood peak, flood volume, and duration (Chebana and Ouarda, 2009; Brunner et al., 2016). However, in the assessment of flood events this univariate approach to discharge is only suitable when dependencies between the contributing variables are known or absent (Yue and Rasmussen, 2002; Serinaldi et al., 2015). Ignoring the dependencies may lead to severe over or under estimation of the flood risk (De Michele et al., 2005).

Coastal regions are threatened not only by river flooding. Storm surges and sea-level rise provide additional risk to flooding (Olbert et al., 2017; Wahl et al., 2017). Atlantic cyclones are prime candidates to cause both storm surges and large-scale precipitation over western and central Europe (Ulbrich et al., 2009; Hawcroft et al., 2012). Since storm surges find their origin in the very same Atlantic winter storms that also bring large amounts of precipitation, possible relations between the two factors play a major role in the assessment of flood risks. If high coastal water levels occur simultaneously with extreme river discharge events, flood risk increases as the river is not able to discharge its water at the outlet, eventually causing river water levels to rise (van den Hurk et al., 2015). Further, projected sea-level rise will strongly amplify this risk (van den Hurk et al., 2014; Vries et al., 2014; Wahl et al., 2015). Previous studies investigated the probability of joint occurrence of storm surge and precipitation/river floods based on observed data along the British, Australian, and United States coasts and Dutch coasts (Svensson and Jones, 2004; Geerse, 2013; Zheng et al., 2013; Wahl et al., 2017). In literature, these sets of joint extreme events are categorized as compound events. Their societal importance and association to risk are well discussed by Seneviratne et al. (2012), Leonard et al. (2014), and Hazeleger et al. (2015).

Inclusion of tail dependence, i.e., the probability that a given variable exceeds a certain threshold given the exceedance probability of a threshold by another variable, is necessary for the investigation of joint extremes events (Joe, 1997). Poulin et al. (2007), who used families of copulas to study the joint behavior of river flood peaks and flood volumes, demonstrated that resulting joint return periods are significantly sensitive to the choice of the copula model and inclusion of tail dependence in the analysis. Recent studies, such as Bevacqua et al. (2017) and Moftakhari et al. (2017) for the Italy and United States coasts, respectively, further explored the importance of multivariate (copula) analysis of compound events related to coastal flooding including sea water level and river discharge. Also, these studies confirmed a substantial decrease in return periods if the compound occurrence probability of related events was considered.

For the Rhine river catchment, previous studies have investigated those compound events based on observations, reanalysis products and model simulations. By using a coarse-resolution global climate model ensemble, Kew et al. (2013) showed that low pressure systems over the North Sea can lead to compound occurrence of extreme storm surges and precipitation affecting the Dutch coast. Proxies for storm surge and river runoff were used, namely north-westerly winds and multi-day precipitation sums. In an attempt to use more realistic data to assess the statistical relationship between surge and river discharge, Klerk et al. (2015) subsequently used variables diagnosed from hydrological, hydraulic and storm surge models. In their coarse-resolution dataset covering the relatively short historical period from 1981 to 2010 they found a clear correlation between the two variables, but only when a substantial time lag of 6 days was taken into account. This is the time scale needed to transport excess precipitation peak in the Rhine catchment to the river outlet. Accordingly, they conclude that there is no increased risk at simultaneous occurrence (zero lag). However, an in-depth investigation of the uncertainty introduced by the hydrological and storm surge model to the time dependence correlation was not performed.

Here, we build on the findings of the previous studies and extend them by including the application of (a) a fine resolution climate model, (b) a large sample of data (800 years) obtained from a climate model ensemble, and (c) two different regimes of hydrological models. The use of large sample of data obtained from a fine resolution climate model ensemble provides a better insight into the statistical connection between the two variables (Wahl et al., 2015; Wu et al., 2018) than possible in previous assessments in Rhine which used either samples from observations limited to the past 30–40 years or used coarse resolution climate model simulations. Furthermore, by applying two hydrological models, we demonstrate the importance of proper physical model configurations to correctly assess the lag time correlation for compounding high coastal water level and high discharge events. Using a methodology developed by van den Hurk et al. (2015), we force three impact models (one storm surge model and two hydrological models) with output from a large ensemble of a high-resolution regional climate model (RCM) avoiding the necessity of proxies as applied in some of the previous assessments. Further, this approach provides us with a large dataset ensuring a solid statistical assessment of the problem. The combination of these improvements, i.e., the use of real impact variables rather than proxies, different regimes of discharge models and a longer timeseries obtained from a high-resolution climate model ensemble, improve our ability to draw more consistent conclusions than possible in previous studies.

Data and Methods

Study Area

The Rhine basin covers an area of 185,000 km² and runs over 1320 km from its source in the Alps to the North Sea. The streamflow in the Rhine is mainly dominated by snowmelt and rainfall-runoff from the Alps during summer for the upper part of Rhine (Viviroli et al., 2003). However, for lower parts at Lobith, streamflow is mostly dominated by rainfall resulting in streamflow peaks during winter. A peak-shift in the average annual hydrograph is observed from summer to winter from the upper Rhine at Basel (50 km downstream of Untersiggenthal as shown in Figure 1) and lower Rhine at Lobith (Engel and Disse, 2001; Photiadou et al., 2011). The snowmelt contribution to the streamflow at Lobith is significant and total annual contribution to streamflow is around 30% (Stahl et al., 2016). The area upstream of Basel produces almost 50% of the discharge despite only covering around 20% of the total area of the Rhine catchment (Kwadijk and Deursen, 1999). The flood wave travel time from Basel to Lobith is around 5 days (Hegnauer et al., 2014). Further, the slow melt from snow and glaciers would require an additional day or two to reach Basel.

FIGURE 1

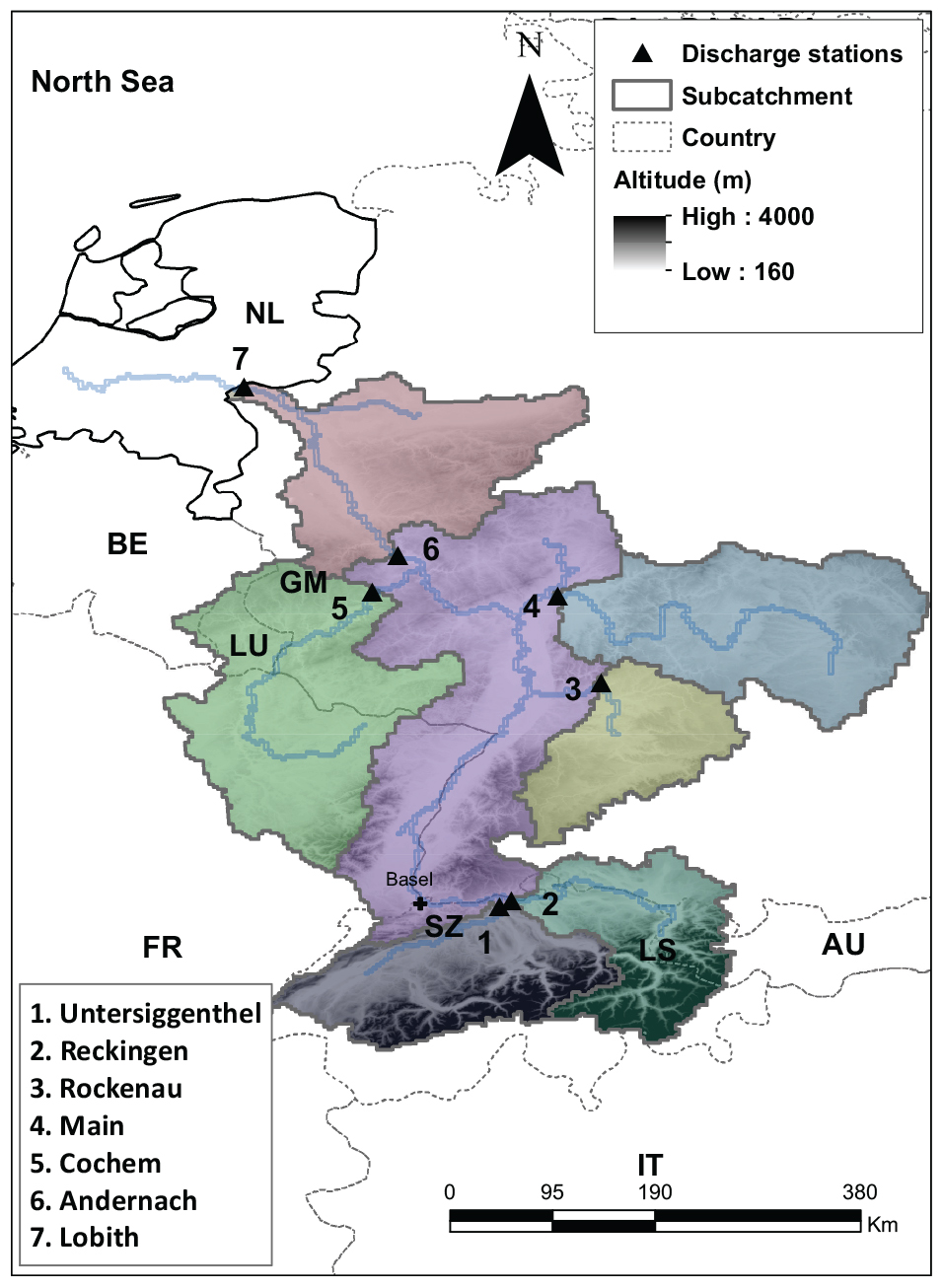
Figure 1. The Rhine basin, with seven sub catchments used for the calibration in the study. The triangles (black) represents the outlet of sub-basin used for the calibration. The two letter abbreviations are used to denote the countries. The blue line represents the Rhine and the tributaries. The black boundary represents the Netherlands outline.

The storm surges along the Dutch coasts are driven by meteorological conditions (Ridder et al., 2018a). In general, the most extreme storm surges are associated with low pressure systems in the North Eastern Atlantic area, depression trajectories with a south-east direction, along the jet stream over the North Sea results in the development of persistent strong north-westerly winds and related surge conditions at the Dutch coast (van den Hurk et al., 2015). These stormy conditions in the North Sea area mainly develop during the winter season from October to March. Every year on average two strong storm events (winds higher than 19–20 m/s) are recorded at Hoek van Holland (Smits et al., 2005). Further, these depression systems are also characterized by humid Atlantic moisture conditions and primarily transport the moisture toward the Netherlands (Khanal et al., 2019).

Observations and Climate Model Data

We use data from a 16-member ensemble obtained with the Global Climate Model (GCM) EC-Earth (Hazeleger et al., 2012), created using a perturbed atmospheric initial-state approach (start in 1850). Each of the ensemble member is a plausible representation of possible climate states and differs from each other in their initial atmospheric conditions and model internal variability. The internal variability of the climate system is highly non-linear, which causes significant variability between model runs. Thus, each of the ensemble member represents how climate can vary due to chaotic internal variability (Deser et al., 2012).

This study focuses on the period from 1951 to 2000. The GCM ensemble is dynamically downscaled using the RCM RACMO2 at 12-km resolution (van Meijgaard et al., 2008). Daily precipitation output from RACMO2 is subsequently bias-corrected using gridded E-OBS V14 data at a 0.25°resolution (Haylock et al., 2008). The downscaled temperatures are further adjusted with a temperature lapse correction rate of −6.5°C/km. The dynamically downscaled and bias-corrected data serves as input for two conceptually different hydrological models for the Rhine basin (a) SPHY (Terink et al., 2015) (b) HBV-96 (Bergström, 1976) and a storm surge model; WAQUA/DCSMv5 (Gerritsen et al., 2013). The performance of the hydrological models is tested against observed mean daily Rhine river discharge at Lobith, where the Rhine enters the Netherlands and daily mean total water levels (the sum of the tidal contribution and the non-tidal residual including the meteorological effect referred to as TWL i.e., total water level) at Hoek van Holland (HvH) for the period 1951–2000 provided by Rijkswaterstaat and are available online¹. The overall modeling framework of this study is presented in Figure 2.

FIGURE 2

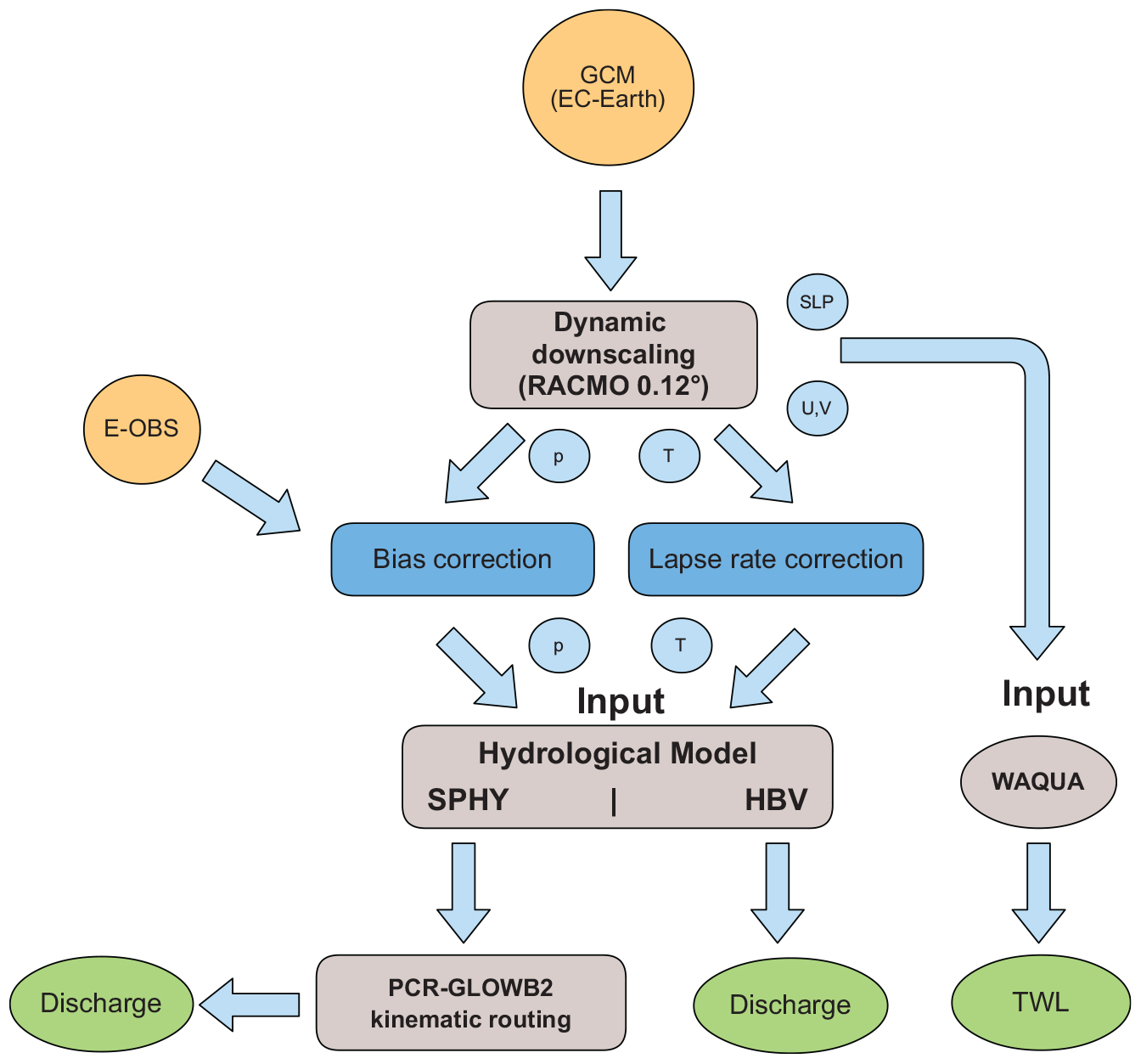
Figure 2. The research framework used in this study. The orange, green and gray color represents the input, output and the model used in the study, respectively. The P, T, SLP, U and V represents the precipitation, temperature, sea level pressure, zonal and meridional wind components, respectively. The blue color represents the intermediate steps followed like bias correction of precipitation and lapse rate correction of temperature obtained from downscaling EC-Earth.

Hydrological Modeling of Rhine River Discharge Using SPHY and HBV-96

The application of two hydrological models allows the assessment of model-uncertainty in simulating discharge waves in relation to the natural variability due to e.g., dominant precipitation regions, and the sensitivity of different routing methods. To this end, we use different hydrological models to simulate the daily discharge of the river Rhine at Lobith. From this point on the flow of the river is highly regulated with the main part of the river discharge being directed to the coastal outlet at HvH. Since snowmelt runoff plays a significant role in defining the hydrological regime and annual cycle along the Rhine (Stahl et al., 2016), we use models that explicitly account for this process.

The Spatial Processes in HYdrology model (SPHY) is a spatially distributed, physically based “leaky-bucket” type model, which operates on a gridpoint basis. It integrates parameterizations of the dominant hydrological processes: (i) rainfall–runoff; (ii) lake/reservoir outflow, (iii) cryospheric processes (snow, ice, glaciers), (iv) dynamic vegetation, (v) evapotranspiration, and (vi) root-zone moisture content. It contains sub-grid variability (e.g., cells can be glacier-free or partially to fully covered with glaciers) and is based on the widely-used degree-day melt modeling approach (Hock, 2003). SPHY requires daily precipitation, and daily maximum, minimum and average temperature as forcing input. SPHY was calibrated against observed time-series of daily discharge (Obs), obtained from the Global Runoff Data Centre², at seven locations along the Rhine for the period of 1989–2000. The calibration was performed sequentially; initially for five independent upstream (U/S) locations and subsequently for the two downstream (D/S) locations Andernach and Lobith. We used the mean square error (MSE) as the objective function and maximum likelihood estimation (MLE) criteria to calibrate the model parameters. SPHY uses a simple flow recession coefficient (kx) to simulate the delay between generation of specific runoff within the catchment and reaching the outlet. The recession coefficient is used as a weighting parameter to calculate the routed flow at each pixel, which in SPHY is calculated as weighted average inflow of the current and previous day (Terink et al., 2015). The averaging used in SPHY causes the attenuation and delay of the floodwaves in the model. A simple accumulation of the fluxes over the drainage network is used to calculate the flow. This method is typically suitable when aggregation time period (month, year) is larger than the travel times of water along the longest river length. To simulate the realistic flood wave propagation, we use the stand-alone version of PCR-GLOBWB2 kinematic wave routing scheme (here after referred to as routing model). SPHY is coupled one-way to the routing model as the outputs from SPHY serve as input for the routing model. More detail about routing model can be found in Sutanudjaja et al. (2018). The routing model is calibrated for Manning’s n for the same time period as SPHY. The daily flux in mm/day generated by SPHY model is routed with the calibrated routing model to get the discharge. From now onward the discharge or floods from SPHY mentioned in this study will refer to the routed discharge after the use of routing model. Calibration and performance of the upstream sub basins are provided in the Supplementary Material (Supplementary Figures S1–S3). The extreme flooding events of 1993/1994 and 1995, dominated by precipitation and snowmelt, respectively (Engel, 1997), are included in the calibration period.

The second hydrological model is HBV-96 (hereafter referred to as HBV) originally developed by Swedish Meteorological and Hydrological Institute (SMHI, Bergström, 1976) and updated to version used here by Lindström et al. (1997). HBV is a “semi-distributed” conceptual model and, similar to SPHY, also includes parameterizations for processes such as snow accumulation and melt, evapotranspiration, soil moisture and runoff. Unlike SPHY, HBV contains a detailed routing procedure to model flow between sub-basins and through lakes. In this study, we use the version of HBV calibrated by Deltares (Kramer et al., 2008). The final discharge series at Lobith for both the calibration run and the 16-member ensemble were provided by Deltares.

Storm Surge Modeling of the North Sea Using WAQUA/DCSMv5

The storm-surge model used in this study is WAQUA/DCSMv5 (hereafter referred to as WAQUA). WAQUA solves the two-dimensional shallow water equations on a (1/8)°× (1/12)° grid to simulate water levels for the North Sea and its coastal areas. For this, the model takes into account the astronomical tide, the wind-induced movement of water and the barometric effect (Olbert and Hartnett, 2010) associated with the locally prevailing sea level pressure. Therefore, when a low-pressure system travels over the North Sea, WAQUA responds to the main meteorological forcing components that affect shallow seas during such an event. Tidal effects, modified in amplitude and timing by geometry of the coast and the underlying bathymetry, are calculated separately to this meteorological forcing. To obtain the TWL, WAQUA is first run using only the harmonic components at the domain boundaries, while the meteorological forcing is neglected. In a second step, WAQUA uses the calculated tidal level from the previous step and applies the meteorological forcing to calculate TWL. The non-tidal residual (hereafter referred to as surge) is then derived by subtracting the tidal level from the TWL.

A detailed description of how surge and tides are computed in WAQUA can be found in Gerritsen et al. (2013). The model sensitivity and capability to represent relevant air-sea momentum transfer processes and annual extreme water levels is described in Ridder et al., 2018b. For the study presented here, the daily mean TWL (tide plus surge) at HvH is used.

Performance of the Surge and Discharge Models

It is important to assess the basic quality of the surge and discharge models. For a validation of the storm surge model WAQUA the reader is referred to previous studies that present this assessment in detail (van Meijgaard et al., 2008; Ridder et al., 2018b). Since the aim of this study is the exploration of relations between river discharge at Lobith and coastal water level at HvH, the amplitude, timing and duration of (extreme) discharge events are particularly critical.

Hydrological Models (SPHY and HBV)

To assess the performance of the two hydrological models, both HBV and SPHY (together with routing model) were forced with bias-corrected E-OBS daily precipitation and temperature data for the period 1951–2000. The output of both models thus produced (hereafter referred to as EOBS runs) is compared to the observed discharge at Lobith. The assessment focuses on the ability of the models to reproduce discharge amounts, duration of the flood wave (see section “Flood Wave Duration Distribution”) and timing of flood peaks (see section “Timing of Onset and Peak”). For this we use a simplified threshold approach to identify the flood waves in the discharge time series. In this study, a flood wave event is defined as a series of consecutive days with daily discharge exceeding the 95^th quantile of the annual distribution. The length of each flood wave (in days) is calculated as the time difference between the onset (flow exceeds threshold) and offset (flow falls below threshold). The 95^th quantiles are computed independently for the observations and the models based on the respective full-time series to account for model biases.

Basic Metrics and Distribution

Figure 3 shows the daily Rhine river discharge for the entire period 1951–2000 as modeled by HBV and SPHY compared to observations. HBV tends to slightly overestimate observed high peaks (flow greater than 95^th quantile) by up to 420 m³s^–1 on average (> 3500 m³s^–1 in some cases). Similarly, SPHY overestimates the discharge by up to 390 m³s^–1 on average (>8000 m³s^–1 in some cases). Modeled discharge in SPHY exceeds 16,600 m³s^–1 as compared to the observed discharge around 11,885 m³s^–1, making it unsuitable as a forecast model for the Rhine river’s discharge extremes without additional statistical post-processing (such as quantile correction). Nevertheless, both models show the ability to represent observed discharge values fairly well with an overall bias and Nash Sutcliffe Efficiency (NSE, Nash and Sutcliffe (1970) see supplementary SE1 for the equation) of 0.3% and 0.69 for SPHY, and −10.3% and 0.87 for HBV (Table 1). HBV thus outperforms SPHY at all metrics except bias.

FIGURE 3

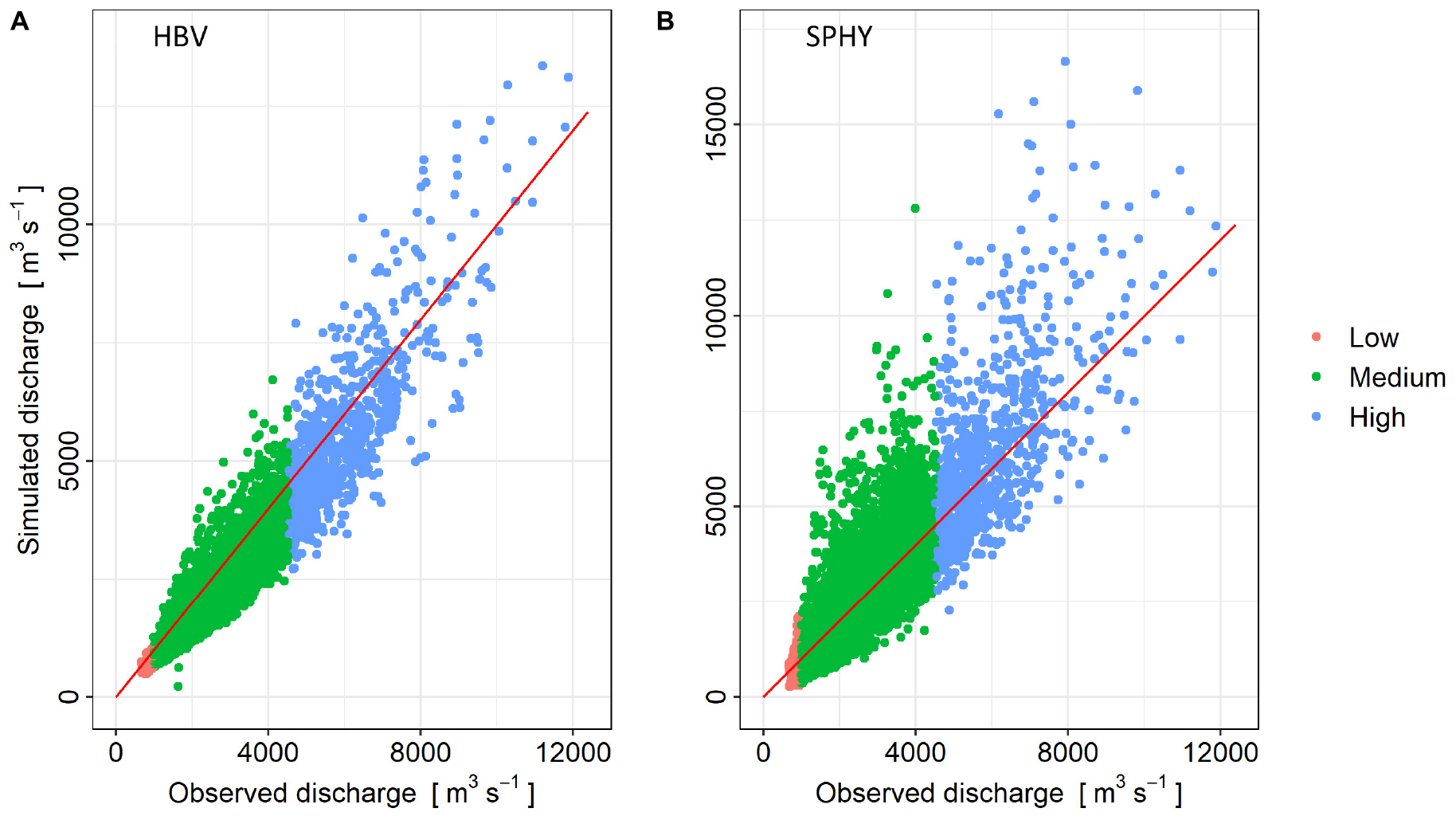
Figure 3. Observed versus modeled daily discharge at Lobith (A) HBV and (B) SPHY for the period between 1951 and 2000. Colors indicate three ranges based on observed quantiles: “Low” (<5%, red), “Medium” (5–95%, green), and “High” (>95%). The solid red line represents the 1:1 slope.

TABLE 1

Table 1. Performance index for HBV and SPHY model on a daily time scale.

The normal quantile-quantile plot using observed and modeled discharge (Figure 4) shows that both HBV and SPHY overestimate the observed flow at low discharge values. At intermediate values (ranging from ±1.5 standard deviation of mean discharge) SPHY reproduces observations fairly well, while HBV clearly outperforms SPHY for values above 2 standard deviations. At the highest discharge extremes, observations lie below the discharges of HBV and SPHY with HBV following observations more closely.

FIGURE 4

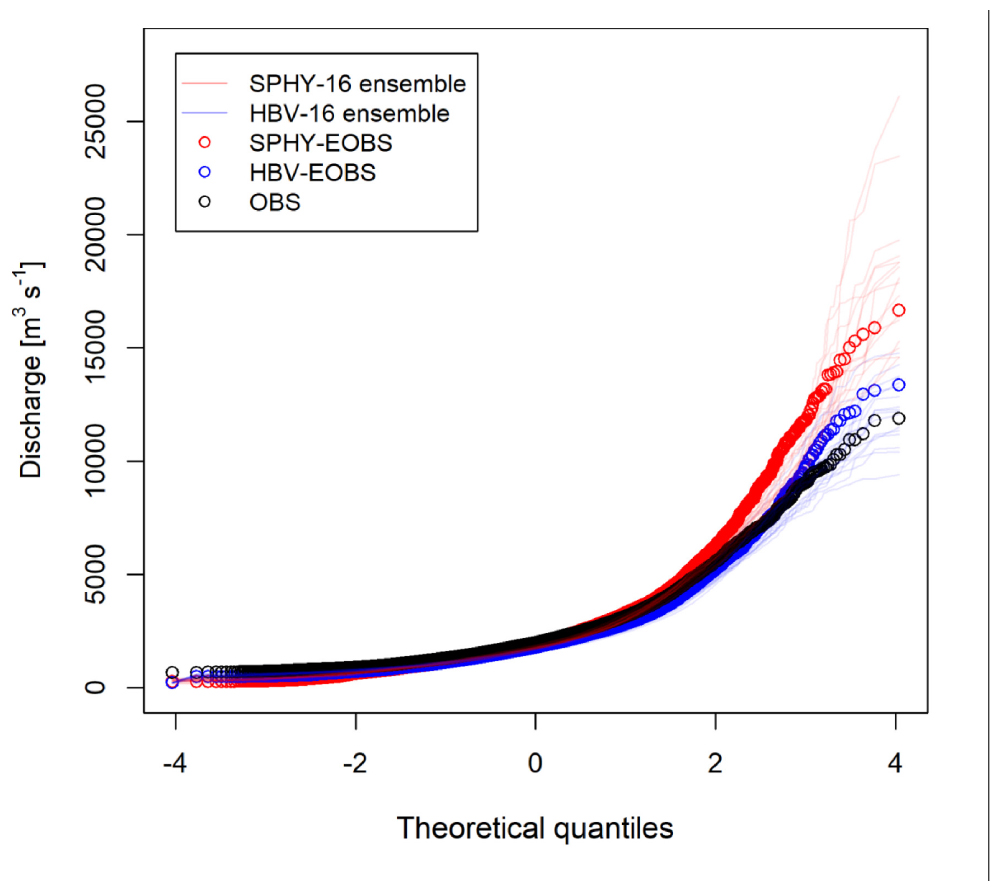
Figure 4. Normal quantile plot for HBV (blue), SPHY (red) and Observation (black). On the horizontal axis, the distributions are centered and scaled (divided by the standard deviation). The light blue and red lines represent 16 ensemble members for HBV and SPHY.

Flood Wave Duration Distribution

Using the definition of a flood wave event described in section “Hydrological Models (SPHY and HBV)”, i.e., flows higher than the 95^th quantile of the respective dataset, we find 92 (SPHY), 113 (HBV) and 116 (observations) flood waves in the 50 years between 1951 and 2000, just under two per year on average. Most of these events have occurred in the winter half year (October to March). Their duration ranges from one to up to 35 (in HBV), 40 (in Obs), and 50 (in SPHY) days (Figure 5A). As a result, HBV reproduces the observed mean flood wave length of approximately eight days fairly well while SPHY overestimates the mean duration. Note that the calculation of the mean flood wave length is based on the number of flood waves in the respective dataset. Therefore, in SPHY fewer occasions of overestimated flood durations affect the mean of the flood wave length more strongly than in HBV where a higher total number of flood waves can mask the effect of prolonged flood waves. This can be seen in the empirical cumulative distributions (ECDFs) of the flood duration for the hydrological models and observation (Figure 5B). The ECDFs of the two models show that half of the events (ranging from a probability of 0.25–0.75) last between 4–9 days in HBV and 2–9 days in SPHY (Figure 5B). Hence, there is no consistent overestimation of flood wave duration in SPHY but the overestimation of the mean is highly biased by a few long flood waves.

FIGURE 5

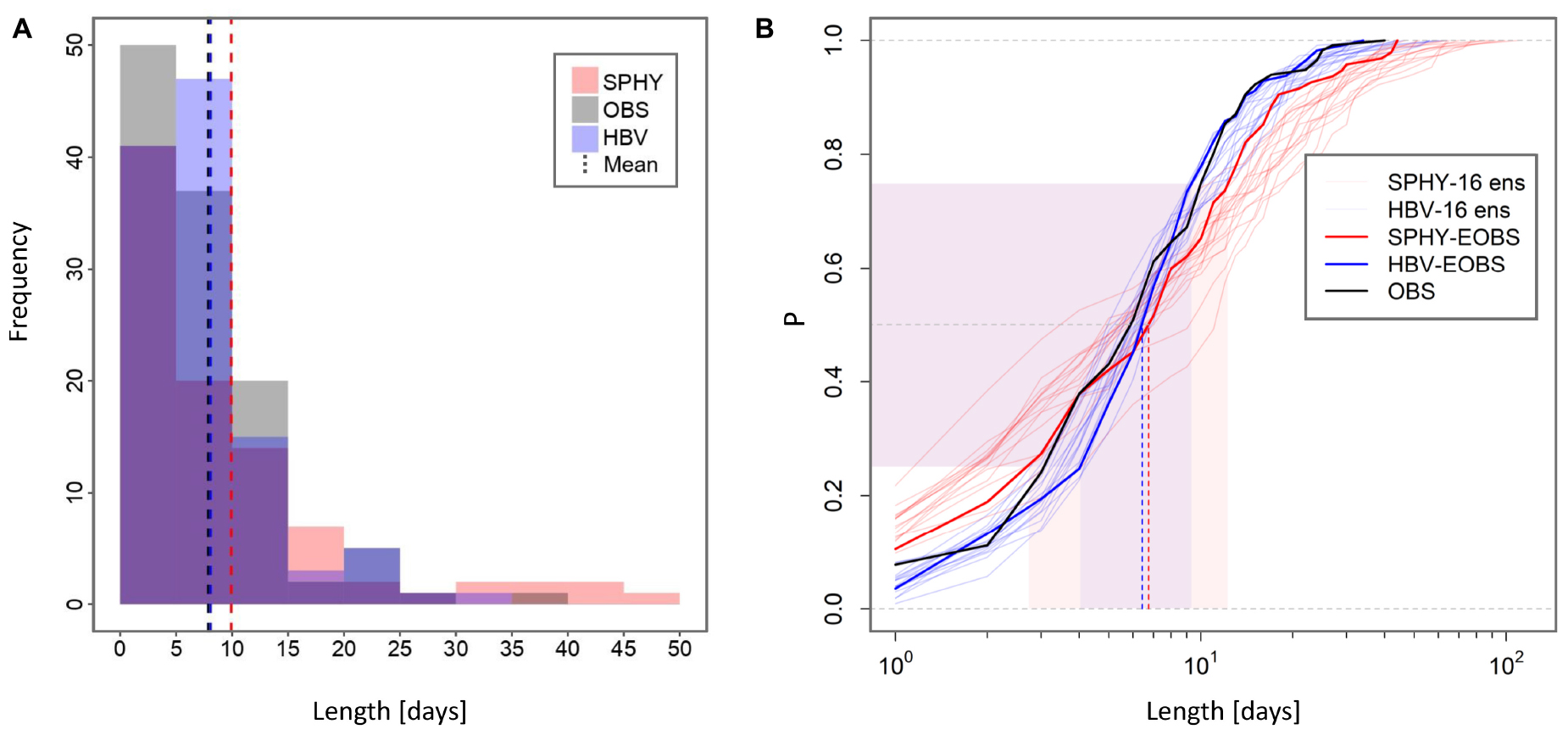
Figure 5. (A) Frequency plot for the flood wave length above 95^th quantile threshold of discharge. The dash vertical lines show the mean of the flood waves for SPHY (red), HBV (black) and HBV (blue). (B) The Empirical cumulative distribution function (ECDF) plot for the floodwave length above 95^th quantile threshold of individual time series discharge. The light red and the blue shaded area represents the 0.25 and 0.75 for SPHY and HBV, respectively.

Adding the ECDFs of the different RACMO2 ensemble members (light blue and red lines) highlights the range of uncertainties in flood wave length. A comparison between ensemble members and observations is of course not possible. However, adding them alongside the ECDFs of the two EOBS runs (blue and red solid lines) gives an indication of the influence of random internal variations (see section “Observations and Climate Model Data”) and highlights that the results of both models fall within the physically plausible flood wave durations.

Timing of Onset and Peak

In compound events, two or more variables reach high quantiles of their distribution simultaneously, or in rapid succession. Therefore, the ability of hydrological models to reproduce the timing of events in impact-parameter space (TWLs and discharge) is crucial. However, neither SPHY nor HBV are able to reproduce all observed flood peaks. Out of the 200 highest maximum discharge dates in the observations, 141 are realized in HBV, but only 115 in SPHY. A better match is reached if we allow for some flexibility in the timing, accounting for random errors in the meteorological forcing or runoff generation process. The modeled arrival time of the peak of a flood wave is sensitive to many parameters, including intensity, duration and frequency of precipitation, soil moisture, the existence of basal flow (e.g., due to snow/ice melt upstream), river bathymetry and topography. Modeling and representation errors in each of these processes can explain part of the large difference in observed and modeled peak-flow days.

Here, we use the exact matching of the peak timing of the flood waves in observations and the models. The dates corresponding to local maxima within the onset and offset of the flood waves in the impact models are then compared with the observed peak dates allowing for a difference of ± 5 days to match. Since taking longer than ±5 days might result in matching the flood peaks entirely from different events, we chose to use ±5 days here. From 116 floodwaves in total, the peaks that lie outside (2 in HBV and 8 in SPHY) of the ±5 days range, are discarded. Figure 6 shows the distribution of arrival-time differences in peak timings of flood. Both models mostly have a negative time lag (implying that most peaks arrive earlier than in the observations) but in HBV the negative time lag (about 1 day) is larger than the value in SPHY (almost zero). This suggest that both the models have errors in estimating the timings of flood waves and HBV being the worst of two. Half of the data points lie between −1 and 1 for HBV and SPHY. The presence of positive values in the distribution indicate the models waves sometimes occur too late. The broad shape of the distribution of both HBV and SPHY reflects the complex interaction of the climatic and hydrologic processes. This wide distribution is a result of multiple drivers of flood rather than a single flood generation mechanism. The climatic mechanism includes persistent synoptic weather conditions favoring a very extreme event or episodes of moderate precipitation events resulting in a multiple day extreme event or extreme positive temperature anomaly causing a quick melt of snow in the catchment (Prudhomme and Genevier, 2011; Gaál et al., 2012; Nied et al., 2014). The hydrological processes such as antecedent soil moisture conditions, snow and ice storage in the catchment, rain on snow mechanisms, and antecedent ground water level play an important role in defining the magnitude and length of the flood wave (Merz and Blöschl, 2003, 2008). Further, the superposition of flood waves from different tributaries of the river also contributes toward the increased length and magnitude of the flood wave. Moreover, coincidence of any of the extremes from the climatic and hydrological processes results in amplification of the flooding magnitude and extent.

FIGURE 6

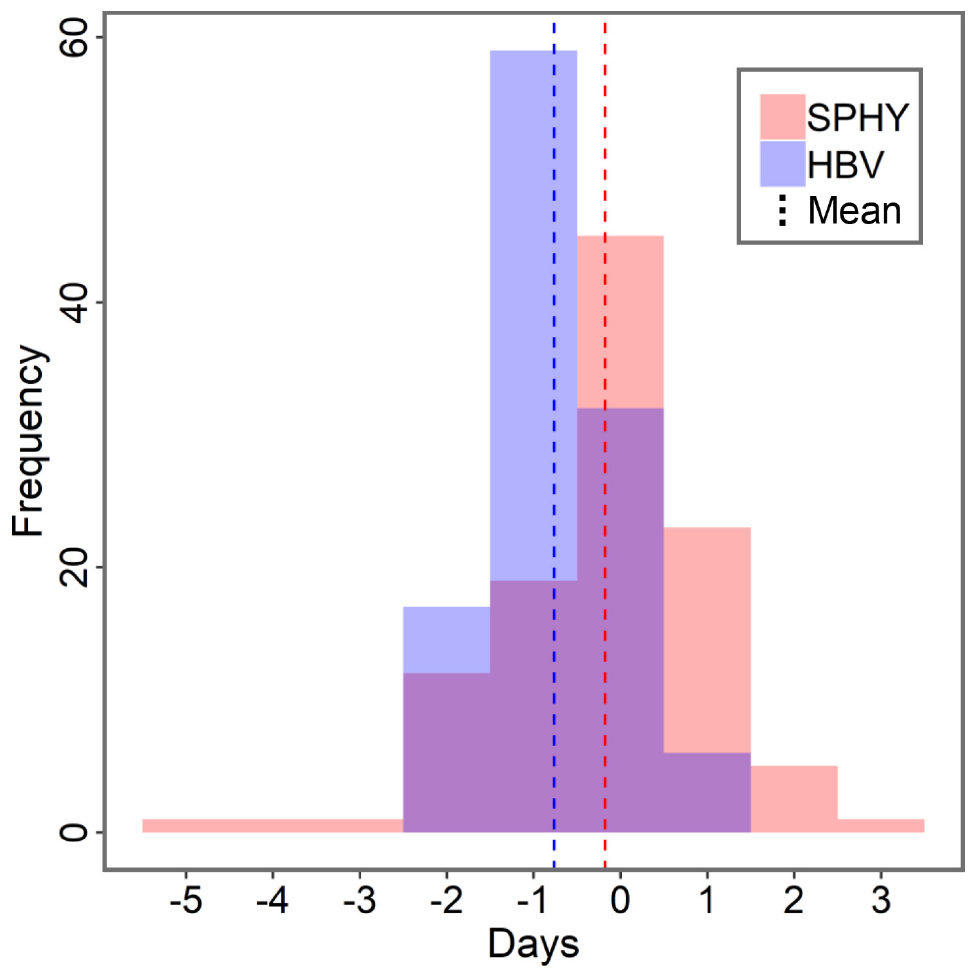
Figure 6. The frequency plot for the peak of the floodwave models compared with the observation. The X axis represent the lag in the peak of the wave as compared to the observed peak. The negative and positive value represents the peak of the modeled waves are earlier and later than the peak of observed floodwaves. The dash line (blue and red) represent the weighted mean of the distribution (HBV and SPHY).

In summary, SPHY overestimates the peaks, while the flood waves in HBV reach the outlet earlier than observed flood waves. Both models have difficulties in reproducing the exact flood timing, and HBV generates flood waves that occur systematically too early. However, the distribution of timing errors is quite broad which makes correcting for this error difficult.

Dependencies Between Storm Surge and River Discharge

In this section, we assess the dependence between Rhine river discharge at Lobith (modeled by SPHY and HBV) and TWL at HvH (modeled by WAQUA). Since most storm driven high water levels and discharge events occur in winter, we focus our analysis on the winter half year only (October–March). Here we repeat the earlier analyses of Geerse (2013) and Klerk et al. (2015), but account for a range of both positive (discharge event succeeded by TWL event) and negative (discharge event preceded by the TWL event) time lags in our assessment. A positive lag can account for the time required for the weather system to move inland including hydrological responses of the catchment. A negative lag may result from an unusual track of the passing weather system, or from natural variability where the events are shaped by a sequence of storms. The use of a range of time lags allows also to account for the inherent model uncertainty in reproducing the correct wave travel speed (Figure 6). To analyze the influence of the choice of time lag on the dependence structure of high discharges and high TWL, we base our assessment on extreme values in TWL. We use daily mean TWL instead of the maximum TWL to eliminate any possibilities of extreme sea levels driven by the astronomical tide. By using the daily mean TWL the effect of astronomical tide on total water level is neglected focusing our analysis on the meteorological driver only. Thus, we define a high/extreme water level event as a day where the daily mean TWL at HvH exceeds the 90^th quantile of its distribution. Figure 7 shows this composite for the RACMO based ensemble of WAQUA-HBV and WAQUA-SPHY. In absence of any correlation between TWL and Rhine discharge, the 90%-confidence bands of the percentiles of the lagged time series around a high-water event (shaded area) would overlap with the unconditional discharge percentiles. This is not the case. Depending on the hydrological model, and more importantly, depending on the discharge quantile considered, the composite shows elevated discharge levels for a range of lags. For the 90^th quantile the discharge levels are significantly elevated at lags ranging from −2 days to >10 days. This indicates that there is dependence between the two variables starting 2 days before a high water (90^th quantile) event and lasting up to 10 days after the event. The elevated conditional discharge 2 days before a high TWL event possibly due to the twin or series of storm surge where the water level is already elevated by the first storm event. These ranges of lag are consistent with the time (i) the low-pressure system causing the conditions in both variables requires to move over the catchment area, affecting the fetch for surge and precipitation starting locally and moving further upstream, and (ii) the transformation of rainfall to runoff and the propagation of the runoff waves to the downstream location of Lobith, and (iii) natural variability in the dependence of discharge and TWL. The relationship between the discharge and TWL is not linear as the conditional discharge starts to rise with the positive lag and attains a maximum value around positive lag of 6 days (Figure 6). The dependence ceases afterward with increase in the positive lag days ultimately leveling off with the climatology. Both HBV and SPHY show significantly elevated discharges at the 99^th quantile for a lag of four to 8 days. The 90^th, 95^th, and 99^th quantiles show a clear deviation from the climatology in both models.

FIGURE 7

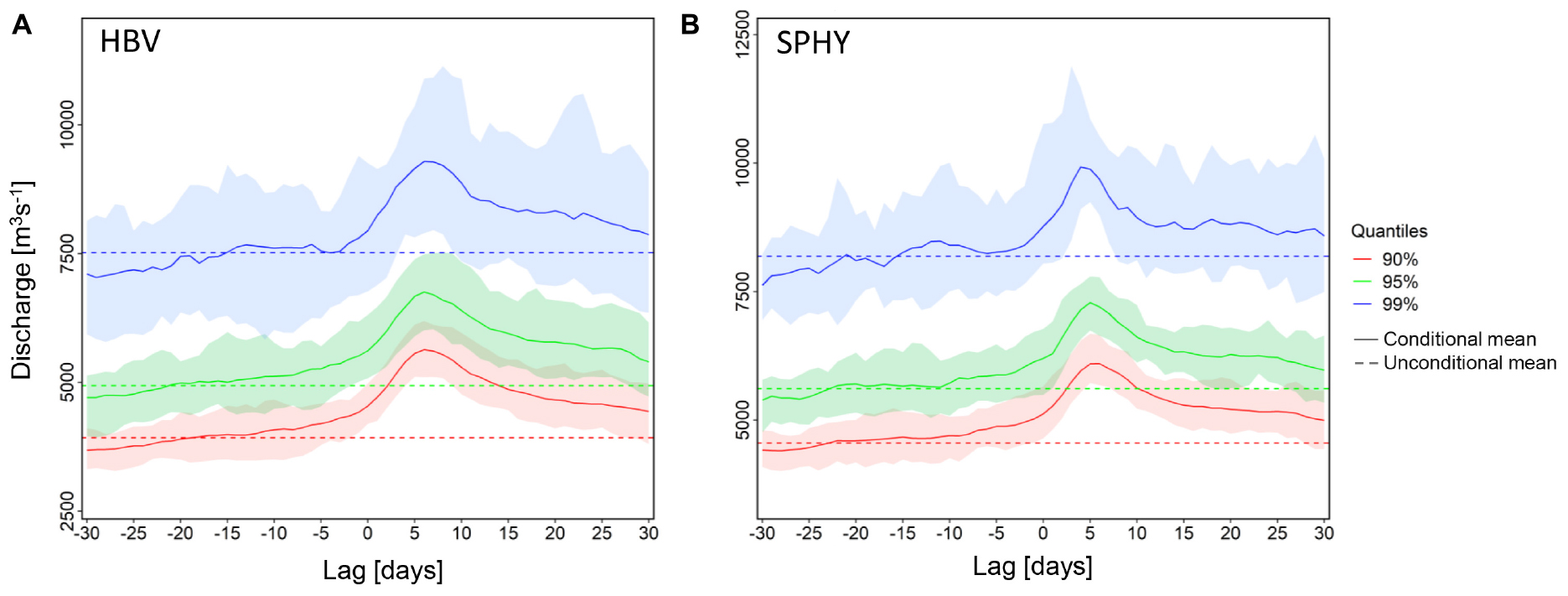
Figure 7. Mean temporal evolution of the 90^th (red), 95^th (green) and 99^th (blue) quantile of discharge at Lobith for total water level events exceeding the 90^th quantile at HvH in WAQUA as modeled by HBV (A) and SPHY (B). The lag in discharge at Lobith is relative to the peak in total sea water level at HvH. Negative and positive lag days indicate that the discharge peak occurs before and after the day of the high sea water event. The dashed lines are the unconditional discharge quantiles, i.e. discharge quantiles independent of water level; solid lines are the ensemble mean of the conditional quantiles. The shaded area represents 16 different lines for each ensemble and we only took the 5^th and 95^th quantile of those 16 lines to show spread of 16 ensemble members.

Dependence in the Tail of the Distributions

In this section, we examine how the upper tails of these two distributions are related. As mentioned in the introduction, tail dependence has been shown to be of particular importance for the influence of compound events on flood risk. Since tail dependence describes the degree of dependence in the tails of a multivariate distribution, we investigate the tail of the discharge distribution conditioned on the distribution of total water level and compare it with the unconditional tail of the discharge distribution. The result of this analysis determines whether or not there is any underlying correlation in the tails of the discharge and TWL distributions. The availability of 800 years of data provides us with sufficient confidence in analyzing the extremes in the tail of the distributions.

Having determined the correlation for a range of time lags in discharge and TWL (Figure 7), we now examine the dependence in the tail of the distribution for a lag of 3 days, i.e., with a water level event at HvH occurring 3 days before the discharge peak at Lobith. This is a shorter time lag than applied by Klerk et al. (2015), who presented the dependence in the tail for a lag of 6 days. Despite this shorter time lag we find a similar relation between the two variables as Klerk et al. (2015) (Figures 8A,C). For this, we test the 50^th and 90^th quantile of the discharge distribution conditional on TWL and compare it to the respective unconditional discharge. We use seven different quantile of the full water level distribution to determine the conditional discharge (50, 60, 70, 80, 90, 95, and 99). The conditional discharge values lie above the unconditional discharge. This suggests that the two variables show some correlation in the tail of their distribution even at a lag shorter than the 6 days. The background scatter points only serve as an illustration of the joint distribution of the two variables. Presence of red scatter points on the top right corner implies that two variables are dependent. However, discharge and TWL do not show any strong dependence, especially for very large values.

FIGURE 8

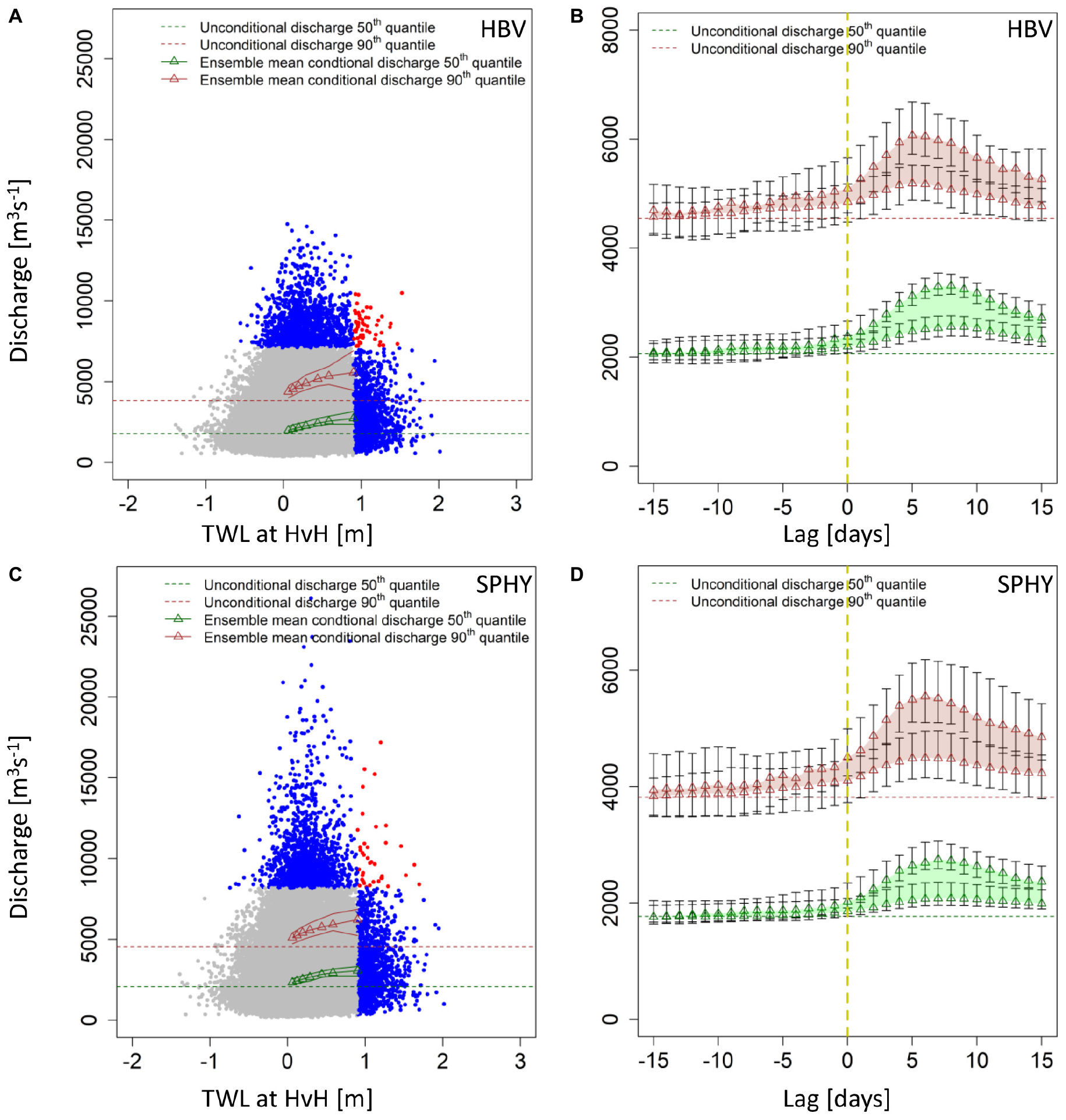
Figure 8. Scatter plot of coastal water levels and discharge for a lag of 3 days (A) HBV and (C) SPHY) and 16 ensemble members. Events exceeding the 99^th quantile of either of the variables are marked in blue. Events exceeding the 99^th quantile of both variables are marked in red. The triangles (green/brown) represent the ensemble mean of the conditional discharge (50^th and 90^th). The green solid lines represent the spread of ensemble i.e., 5^th and 95^th quantiles of the conditional discharge (50^th quantile). Similarly, the brown solid lines represent the 5^th and 95^th quantiles of the conditional discharge (90^th quantile). Conditional discharge plot for 50^th and 95^th quantile of surge [(B) HBV and (D) SPHY]. The green band, represents the conditional discharge distribution i.e., the discharge distribution between the 50^th and 90^th quantile only for the cases where the total water level is above 50^th quantile. Similarly, the brown band represents the conditional discharge distribution i.e., the discharge distribution between the 50^th and 90^th quantile only for the cases where the total water level is above 90^th quantile. The upper and lower green triangle represent the mean of the 50^th and 90^th quantile of discharge conditioned on 50^th quantile of TWL. Similarly, the upper and lower brown triangle represent the mean of the 50^th and 90^th quantile of discharge conditioned on 90^th quantile of TWL. The vertical yellow dash line indicates the time lag zero. The error bar on triangle represent the confidence interval estimates of the mean (5^th and 95^th quantiles) from 16 ensemble members.

Since the dependency in tail of these two-distribution is already realized at a lag of 3 days, we also assess if the correlation still holds for other choices of lag duration. For this, we investigate the discharge distribution conditioned on specific (50^th and 90^th) quantiles of TWL. We find that, due to the longevity of floodwaves and the natural variability within the system, this tail dependency can be shown to hold for a range of lags. To illustrate this, we chose the 50^th and 90^th quantile of TWL and again determined the part of the discharge distribution between 50^th and 90^th quantiles, i.e., the high tail of the conditional discharge distribution. Figures 8B,D show the discharge conditioned on the 50^th and 90^th quantile value of TWL as function of time lags varying from −15 to 15 days. Two important aspects can be seen in this figure: (1) the width of the band increases with time lag, and (2) the timescales at which the band approaches the climatology, i.e., none of the ensemble members shows a correlation between discharge and TWL. The band width (brown and green area) represents the conditional discharge distribution (part of distribution between the 50^th and 90^th quantiles) for the respective TWL quantile. The increasing band width suggests a large variation in the distribution (between 50^th and 90^th quantiles) and vice versa. The band width is decreasing with increasingly negative lag days and approaches its climatological value quickly. This implies that discharge and TWL before a high coastal water level event are uncorrelated and their connection is not different than during normal climatological conditions. For positive lags the band width increases with increasing number of lag days and attains a maximum deviation from climatology around 4–8 days. This variability in bandwidth could be explained by the connection between TWL and river discharge for positive lags and indicates that both variables have the same origin, i.e., winter storms building high surge levels at the coast and dropping large amounts of precipitation to the catchment resulting in high river discharge levels after few days. The 90% confidence interval within the ensemble (i.e., 5^th and 95^th quantiles) in bandwidth and are calculated from the ensemble. The ensemble confidence is larger in estimating the bandwidth for 90^th quantile (brown band) than the 50^th quantile (green band). Like bandwidth, ensemble spread (bars) increases for 4–8 days positive lag, but are still higher than climatology. Conversely, at negative lags the uncertainties overlap with climatological values. The uncertainty bands are higher than climatology only after positive lag of 2 days for both HBV and SPHY.

Other than for negative lags, the bandwidth for large positive values does not reach the climatological values. This is mainly imposed due to the slow hydrological response of the catchment and large duration of the river floods. This means that local precipitation at the discharge location occurs within hours, while the precipitation over the upper regions of the catchment takes several days to be transformed into river discharge and travel downstream. Furthermore, a second low pressure system closely following the previous system can cause the initial increase in river flow by precipitating in the same local downstream region and later accumulating with the upstream precipitation from the previous system.

Joint Distribution

In order to discard the possibility that the joint occurrence of high discharge and water level (red dots in Figures 8A,C) are just based on coincidence, we follow the method applied in Kew et al. (2013) and van den Hurk et al. (2015). For this, the probability density function (PDF) of the full, physically related ensemble is compared to a “randomized version” where the statistical relation between the two variables is removed by combining random pairs of variables (Figure 9). Results are shown for a 3-day lag, but similar results are found for all lags where tail-dependence was shown (see section “Dependence in the Tail of the Distributions”).

FIGURE 9

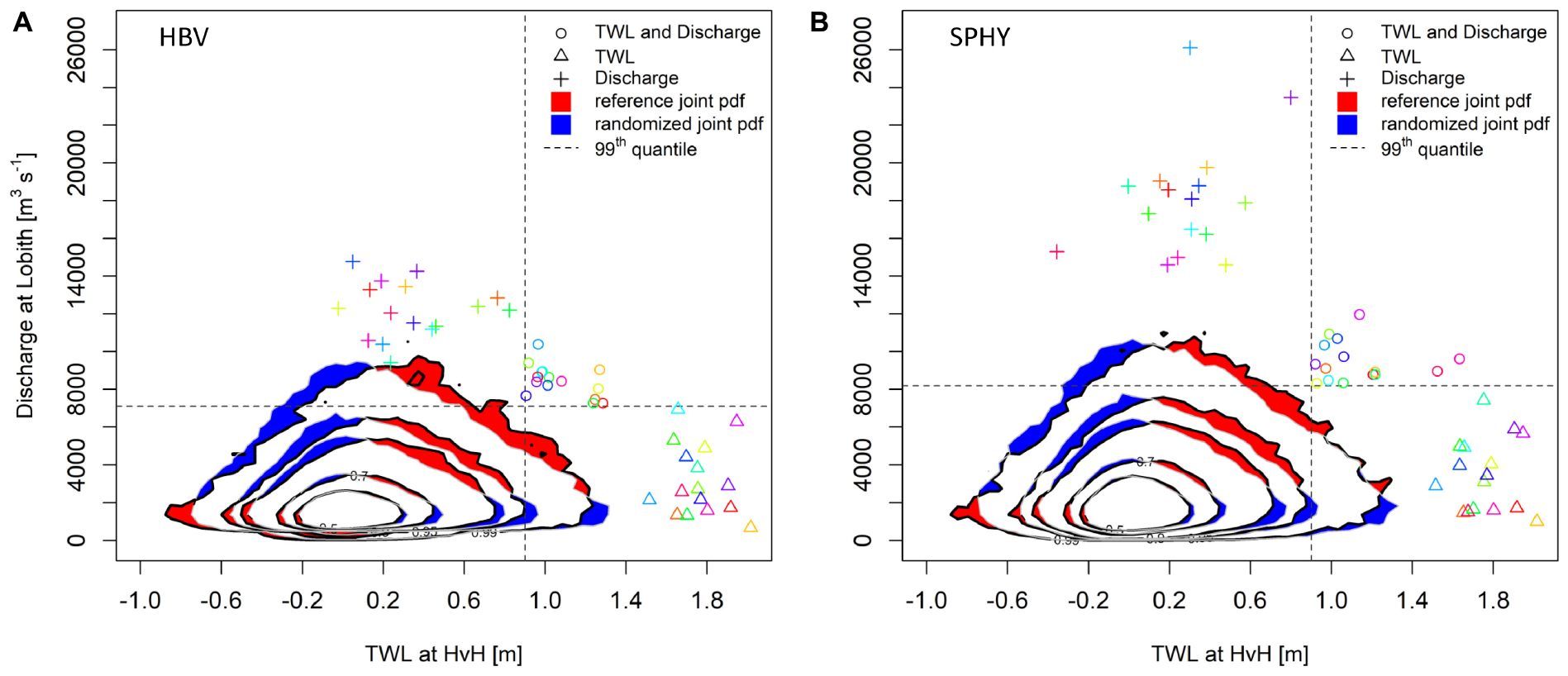
Figure 9. Joint probability density for total water level at HvH and discharge at Lobith (3-day lagged) for winter 6 months period (A) HBV and (B) SPHY). The contours show different quantiles of the joint distribution (50^th, 70^th, 90^th, 95^th, and 99^th). Shading is used to contrast density estimates from direct model output and randomized (shuffled) data, where correlations have been artificially removed. Red/blue shading indicates regions where model data is more/less populated than the shuffled data. The thin dashed lines show the 99^th quantiles of each variable in the respective dataset. The colored points correspond to the highest TWL (Δ), discharge (+) and compound events (o) for individual ensemble members.

The shuffled dataset is derived from the original data in the following way. First, the 16 discharge ensemble members were shuffled (changing the order of ensemble randomly). Then this new data is paired with the TWL data from all other ensemble members. In this way fifteen shuffled sets of 800 years (16 ensembles × 50 years) of paired data were created. The reference data set, in which the physical between the two variables is retained, links TWL to the discharge 3 days later. Maximum discharge from the reference and shuffled data sets are shown in Figure 9. Each ensemble member is shown using a different color. Both hydrological models show similar joint distribution patterns for the reference dataset. However, SPHY reaches further into the high discharge area of the distribution than HBV. This is to be expected due to overestimation of high discharge events by SPHY (see section “Basic Metrics and Distribution”).

The area of interest for the assessment of the connection between coastal water level and discharge is the area between quantile contours of the reference and randomized joint probability distributions. Consistently probabilities of joint occurrence of high TWL and discharge levels are found in the reference data set exceed randomized joint probability density in the diagonal top direction, which indicates an increasing dependence with increasing return period. Conversely, combinations of high TWL/low discharge and vice versa are less likely than randomized joint probability density (diagonal perpendicular to the previous diagonal). This elongated shape of the joint distribution of the reference data along the diagonal indicates a positive correlation between the TWL and discharge volumes 3 days later. The same diagram for other lag days shows similar features suggesting that this correlation is not limited to one fixed choice of lag but exists over a range of time scales. The main differences between the different distributions depending on lag day is that the correlation is stronger for lag days around 6 days with the regions only covered by the reference distribution being bigger than for shorter time lags (Supplementary Figure S4).

Compound Probabilities

Up to now we have shown several aspects of the relation between lagged extremes in TWL and Rhine river discharge at Lobith. In this final section we compare the probability of Rhine discharge exceeding a certain level, given that TWL at HvH is also high. The unconditional probabilities here are referred to as “random chance” as these are not dependent on any pre-requisite threshold of TWL. The metric of interest is the conditional probability scaled with its random chance. For example, if TWL and discharge were completely uncorrelated, we expect a random probability x × y that TWL >x^th quantile and discharge >y^th quantile of their respective distributions. We calculate the random chance for different quantiles purely from the reference winter discharge distribution. The conditional discharge probability only for TWL higher than 97.5^th quantile is then calculated for same quantiles again for winter discharge distribution. By scaling the conditional probabilities by the random chance, the inflation factor due to the tail-dependence is quantified. Figure 10 shows these scaled probabilities for TWL >97.5^th quantile of the winter distribution, and a range of discharge exceedance probabilities. Results are shown for various time lags. A value till one implies scaled probabilities do not exceed the random chance probability. These values near unity are found at all lags for the lowest discharge percentiles. However, for increasingly rare conditions (higher discharge percentiles), the scaled probabilities strongly increase. For HBV up to 2–5 times higher values are found for the higher discharge percentiles, for a broad range of time lags. This implies that it is 2–5 times more likely to get a high discharge once TWL is high. SPHY shows qualitatively the same result. Although its peaks reach lower values, the levels remain elevated for longer positive lags than in HBV. This is clearly related the generally longer duration of the floodwaves in SPHY.

FIGURE 10

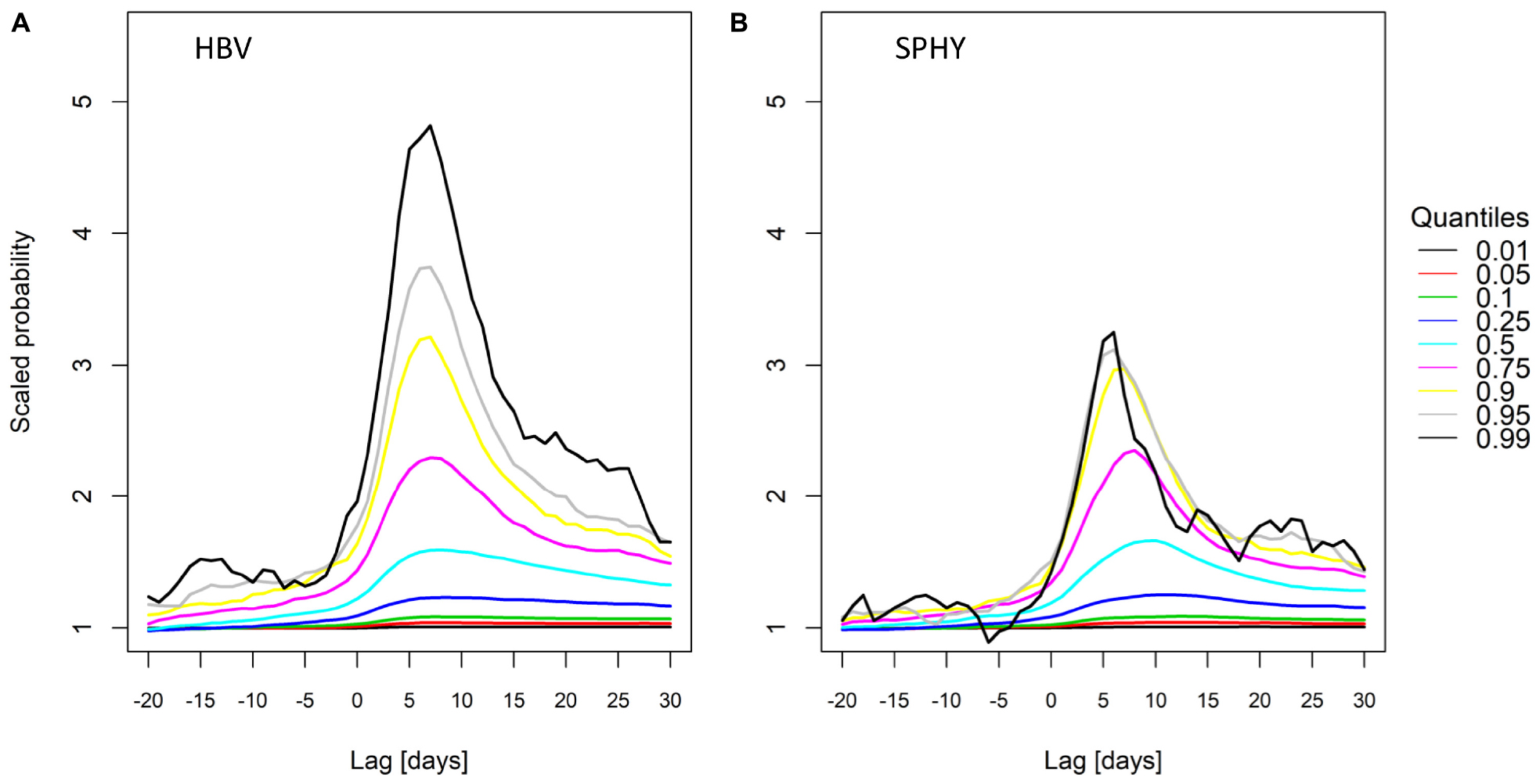
Figure 10. Probability for getting river discharge above a certain quantile (A) HBV and (B) SPHY, given that total water levels also exceed the 97.5^th quantile. For each discharge quantile, the probability is scaled by the random probability of the event.

Discussion

Using the dynamically downscaled output of the EC-Earth ensemble, we obtain coastal water levels and associated river discharge from one state-of-the-art storm surge model (WAQUA/DCSMv5) and two hydrological river-discharge models (SPHY with routing model and HBV). The use of a physically related 16-member ensemble provides us with a larger sample size (800 years), allowing a solid statistical assessment of physical relationship that cannot be carried out with observations alone, as applied in previous studies. The increased sample size is particularly important for the assessment of the high tails of the tail of two distributions and their joint distribution.

This study is limited by the performance of the applied models. The results presented here carry the bias of the meteorological and hydrological models. For instance, both hydrological models show discrepancies to observed high discharges. Both HBV and SPHY overestimates the discharge at high values. These large biases mainly emerge in the peak discharge events, characterized as multi-day events occurring roughly twice every year. The same is valid for the storm surge model WAQUA, which has been shown to reproduce observed coastal water levels and their extremes fairly well (Ridder et al., 2018b). Since the results presented here are based on quantile thresholds relative to the respective dataset, the biases in the model results do impact the findings concerning the statistical relation between the variables water level and river discharge. The results of two hydrological models with different bias allows evaluation of the impact of these bias on the correlation characteristics, and gives an indication of the contribution of model bias to uncertainty of this joint correlation.

The presented results are based on daily values, both in the analysis of the relevant variables as well as in the forcing of the hydrological models. Consequently, the data does not contain any diurnal variations in river discharge and surge/TWL. Averaging to daily values leads to smoothening of the response and to additional uncertainty in the timing of the peak onset and duration. Moreover, the effect of two or more consecutive precipitation events within a couple of days (analogous to two or more small depression passing over in quick succession) could be considered as one. This would result in underestimation of extreme events frequency, particularly in hydrological sense. Since with the current threshold approach to identify the flood wave, differentiation between the flood wave generated separately from multiple precipitation event in quick succession is not possible. More importantly, two storms in quick succession (“twin storms”) where the second storm coincides with delayed high runoff could not be resolved completely and considered as one in the present setup. Although, the elevated conditional discharge 2 days before a high TWL event, to some extent, is explained by “twin storms” still it is not completely understood in this study. While it is unlikely that this has a significant impact on the probabilities of occurrence of compounding events it should be highlighted as it may lead to a (small) underestimation of the number of these events.

The impact models, especially HBV, are unable to resolve the exact timing of the observed floodwaves. SPHY tends to overestimate the flood peaks making it unsuitable to use for the forecasting purposes unless additional post processing is considered. To avoid a large mismatch of timing of floods peaks, we chose to define the peak as the local maxima between the onset and offset of the floodwaves. We found that both hydrological models are unable to simulate the correct timing of the flood peaks, but flood durations are well represented in both models.

The uncertainty due to downscaling from RACMO may introduce spurious biases in the results presented here. RACMO is known to release precipitation too close to the coastline (van Meijgaard et al., 2012) which makes it difficult to estimate the basin scale hydrological responses of the synoptic scale circulation pattern. This may lead to an overestimation of the local flood magnitude near coastal areas. Additionally, the most extreme wind speeds can only be generated at scales that are finer than those resolved by RACMO. Consequently, the modeled TWL may display a bias as well. The statistical bias correction methods do not always accurately preserve the properties of extremes and associated signals (Christensen et al., 2008; Ehret et al., 2012; Sippel et al., 2016). The possible alteration in extreme precipitation signals, due to bias correction of downscaled EC-Earth ensemble, may affect the results presented here.

Copula models, though rely on many assumptions, are very useful and powerful tools in simulating the dependence of variables in a multivariate environment. However, these statistical models rely on many assumptions to simulate the joint behavior or distribution. The joint distribution of the variables is difficult to estimate beforehand and a physical modeling framework that represents the physical correlations directly is needed. Our approach is focused on addressing the correlation using a physical model setup to generate the long time series. This indeed introduces model error. On the other hand, fitting distributions through the sparse number of observations lead to a large error, in particular for the tails of the distributions, i.e., the very extremes, which we are particularly interested in for this study. To this end, we adopt a methodology that directly assesses the compound nature of coastal water level and discharge, rather than indirect proxies. By using multiple hydrological models and fine resolution gridded climate data in ensemble mode, we ensure that the heterogenous variation of meteo-hydrological processes and the memory components of the system are well captured in this study while they were missing in earlier studies for the Rhine. We used a complete physical approach to investigate the joint occurrence of high discharge and water level to show that the correlations are not just by a chance. We conceptually show that a strong storm whose winds set up a storm surge will need time to reach the Rhine headwaters where heavy rainfall will find its way to the river mouth after multiple days of travel time. However, in reality this simple rationale is blurred by natural variability where multiple storms and anomalous travel times may lead to very different correlation lag times. Our ensemble high-resolution model set-up allows diagnosing this correlation range much better than studies that rely on observational records. Fitting distributions through the sparse number of observations leads to a large error, in particular for the tails of the distributions, i.e., the very extremes, which we are particularly interested in for this study. We believe a multivariate statistical fit on the model output data set will give more robust results but pretty similar to the current findings Nonetheless, we show that the compound events, consisting of high discharges and high TWLs, are physically related to each other. This is an important finding to improve assessments of coastal flood risks.

Conclusion and Recommendation

The temporal dependence structure of compounding extreme coastal water level and river discharge events has been analyzed. Taking into account model uncertainty, natural variability and duration of flood peaks, we find that correlation between the discharge at Lobith and coastal water levels at Hoek van Holland occur at a range of time lags. Other than previous studies, which are based on historical observations, we find model uncertainties make it necessary to consider a range of lag days rather than a fixed time lag of 6 days. Thus, considering these uncertainties, the impact of co-occurring high river discharges and coastal surge levels cannot be neglected for large catchment areas as the Rhine basin, as was suggested in earlier studies. Our results show that even shorter time lags show significantly increased probabilities of joint occurrence. Neglecting these short time lags can lead to significant underestimations in return periods and thus flood risk. Finally, this study illustrates the importance of good physical models in compounding event analysis framework to allow for solid and reliable assessments of the events.

It is possible that the temporal dependence structure will be significantly altered when different subcomponents of discharge such as rain, snow melt and baseflow are considered separately. While we did not assess this in the present study, we believe it to be a valuable assessment and plan to follow up this line of investigation in a future study.

Data Availability

The code of the SPHY model is publicly available at https://github.com/FutureWater/SPHY. The PCR-GLOBWB2 source code is publicly available at https://github.com/UU-Hydro/PCR-GLOBWB_model. The WAQUA model codes are available upon request. The datasets that are produced in this study are available upon request.

Author Contributions

BH, HV, NR, SK, and WT designed the study. SK and WT ran the SPHY model. SK and HV performed the results analyses with the support of NR. SK, NR, and HV prepared the manuscript. SK prepared the figures. All authors performed the proofreading.

Funding

This project has received funding from the European Union’s Horizon 2020 Research and Innovation Program under the Marie Skłodowska-Curie grant agreement no. 676027. This study was also partly funded by the Netherlands Organisation for Scientific Research (NWO) as part of the project “Impacted by Coincident Weather Extremes” (ICOWEX; Grant Number 869.15.017).

Conflict of Interest Statement

SK was employed by company FutureWater, Wageningen, Netherlands.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank the IMPREX project, in particular Femke Davids and Erik van Meijgaard, for providing the data from two of the impact models. We would also like to thank Ferdinand Diermanse, Arthur Lutz, and Walter Immerzeel for their valuable comments and expert advice during the data analysis for this study.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2019.00224/full#supplementary-material

Footnotes

1. ^ www.rijkswaterstaat.nl/
2. ^ http://grdc.bafg.de/

References

Bergström, S. (1976). Development and application of a conceptual runoff model for Scandinavian catchments. Bull. Ser. A 52, 128–134.

Google Scholar

Bevacqua, E., Maraun, D., Hobaek Haff, I., Widmann, M., and Vrac, M. (2017). Multivariate statistical modelling of compound events via pair-copula constructions: analysis of floods in Ravenna (Italy). Hydrol. Earth Syst. Sci. 21, 2701–2723. doi: 10.5194/hess-21-2701-2017

CrossRef Full Text | Google Scholar

Blöschl, G., Hall, J., Parajka, J., Perdigão, R. A. P., Merz, B., Arheimer, B., et al. (2017). Changing climate shifts timing of European floods. Science 357, 588–590. doi: 10.1126/science.aan2506

PubMed Abstract | CrossRef Full Text | Google Scholar

Brunner, M. I., Seibert, J., and Favre, A.-C. (2016). Bivariate return periods and their importance for flood peak and volume estimation. Wiley Interdiscip. Rev. Water 3, 819–833. doi: 10.1002/wat2.1173

CrossRef Full Text | Google Scholar

Chebana, F., and Ouarda, T. B. M. J. (2009). Index flood-based multivariate regional frequency analysis. Water Resour. Res. 45, 1–15. doi: 10.1029/2008WR007490

CrossRef Full Text | Google Scholar

Christensen, J. H., Boberg, F., Christensen, O. B., and Lucas-Picher, P. (2008). On the need for bias correction of regional climate change projections of temperature and precipitation. Geophys. Res. Lett. 35:L20709. doi: 10.1029/2008GL035694

CrossRef Full Text | Google Scholar

De Michele, C., Salvadori, G., Canossi, M., Petaccia, A., and Rosso, R. (2005). Bivariate statistical approach to check adequacy of Dam Spillway. J. Hydrol. Eng. 10, 50–57. doi: 10.1061/(ASCE)1084-0699200510:1(50)

CrossRef Full Text | Google Scholar

Deser, C., Knutti, R., Solomon, S., and Phillips, A. S. (2012). Communication of the role of natural variability in future North American climate. Nat. Clim. Change 2, 775–779. doi: 10.1038/nclimate1562

CrossRef Full Text | Google Scholar

Doocy, S., Daniels, A., Murray, S., and Kirsch, T. D. (2013). The human impact: a historical review of events and systematic literature review. PLoS Curr. Disaster 1:ecurrents.dis.f4deb457904936b07c09daa98ee8171a. doi: 10.1371/currents.dis.f4deb457904936b07c09daa98ee8171a

PubMed Abstract | CrossRef Full Text | Google Scholar

Ehret, U., Zehe, E., Wulfmeyer, V., Warrach-Sagi, K., and Liebert, J. (2012). HESS opinions “should we apply bias correction to global and regional climate model data?” Hydrol. Earth Syst. Sci. 16, 3391–3404. doi: 10.5194/hess-16-3391-2012

CrossRef Full Text | Google Scholar

Engel, H. (1997). “The flood events of 1993/1994 and 1995 in the Rhine River basin,” in Destructive Water: Water-caused natural Disasters, Their Abatement and Control, IAHS Publication no 239, eds F. H. M. Leavesly, G. H., Lins, H. F., Nobilis, F., Parker, R. S. Schneider, V. R. Van de Ven, 21–32. (Wallingford: IAHS Press).

Google Scholar

Engel, H., and Disse, M. (2001). Flood events in the rhine basin: genesis, influences and mitigation. Nat. Hazards 23, 271–290.

Google Scholar

Gaál, L., Szolgay, J., Kohnová, S., Parajka, J., Merz, R., Viglione, A., et al. (2012). Flood timescales: understanding the interplay of climate and catchment processes through comparative hydrology. Water Resour. Res. 48, 1–21. doi: 10.1029/2011WR011509

CrossRef Full Text | Google Scholar

Geerse, C. (2013). Correlatie Tussen Stormvloeden en Afvoeren Voor de Benedenrivieren, Mate Van Correlatie en Geschatte Invloed op de Toetspeilen, Report PR2442.10. Lelystad: HKV Lijn in Water.

Google Scholar

Gerritsen, H., de Vries, H., and Philippart, M. (2013). “The Dutch continental shelf model TT,” in Quantitative Skill Assessment for Coastal Ocean Models eds D. R. Lynch, A. M. Davies (Washington, DC: American Geophysical Union?). 425–467.

Google Scholar

Hall, J., Arheimer, B., Borga, M., Brázdil, R., Claps, P., Kiss, A., et al. (2014). Understanding flood regime changes in Europe: a state-of-the-art assessment. Hydrol. Earth Syst. Sci. 18, 2735–2772. doi: 10.5194/hess-18-2735-2014

CrossRef Full Text | Google Scholar

Hawcroft, M. K., Shaffrey, L. C., Hodges, K. I., and Dacre, H. F. (2012) How much Northern Hemisphere precipitation is associated with extratropical cyclones? Geophys. Res. Lett. 39, 1–7. doi: 10.1029/2012GL053866

CrossRef Full Text | Google Scholar

Haylock, M. R., Hofstra, N., Klein Tank, A. M. G., Klok, E. J., Jones, P. D., and New, M. (2008). A European daily high-resolution gridded data set of surface temperature and precipitation for 1950-2006. J. Geophys. Res. Atmos. 113:d20119. doi: 10.1029/2008JD010201

CrossRef Full Text | Google Scholar

Hazeleger, W., van den Hurk, B. J. J. M., Min, E., van Oldenborgh, G. J., Petersen, A. C., Stainforth, D. A., et al. (2015). Tales of future weather. Nat. Clim. Change 5, 107–113. doi: 10.1038/nclimate2450

CrossRef Full Text | Google Scholar

Hazeleger, W., Wang, X., Severijns, C., Ştefǎnescu, S., Bintanja, R., Sterl, A., et al. (2012). EC-Earth V2.2: description and validation of a new seamless earth system prediction model. Clim. Dyn. 39, 2611–2629. doi: 10.1007/s00382-011-1228-5.

CrossRef Full Text | Google Scholar

Hegnauer, M., Beersma, J. J., van den Boogaard, H. F. P., Buishand, T. A., and Passchier, R. H. (2014). Generator of Rainfall and Discharge Extremes (GRADE) for the Rhine and Meuse basins. Final report of GRADE 2.0. Delft: Deltares.

Google Scholar

Hock, R. (2003). Temperature index melt modelling in mountain areas. J. Hydrol. 282, 104–115. doi: 10.1016/S0022-1694(03)00257-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Joe, H. (1997). Multivariate Models and Multivariate Dependence Concepts. Abingdon: Taylor & Francis.

Google Scholar

Kew, S. F., Selten, F. M., Lenderink, G., and Hazeleger, W. (2013). The simultaneous occurrence of surge and discharge extremes for the Rhine delta. Nat. Hazards Earth Syst. Sci. 13, 2017–2029. doi: 10.5194/nhess-13-2017-3

CrossRef Full Text | Google Scholar

Khanal, S., Lutz, A. F., Immerzeel, W. W., de Vries, H., Wanders, N., and van den Hurk, B. (2019). The impact of meteorological and hydrological memory on compound peak flows in the Rhine River basin. Atmosphere 10, 1–19. doi: 10.3390/atmos10040171

CrossRef Full Text | Google Scholar

Klerk, W. J., Winsemius, H. C., van Verseveld, W. J., Bakker, A. M. R., and Diermanse, F. L. M. (2015). The co-incidence of storm surges and extreme discharges within the Rhine–Meuse Delta. Environ. Res. Lett. 10:035005. doi: 10.1088/1748-9326/10/3/035005

CrossRef Full Text | Google Scholar

Kramer, N., Beckers, J., and Weerts, A. (2008). Generator of Rainfall and Discharge Extremes (GRADE) - Part D & E, Deltares report Q4424. Delft: Deltares.

Google Scholar

Kwadijk, J., and Deursen, W. (1999). Development and Testing of a GIS Based Water Balance Model for the Rhine Drainage Basin. Utrecht University: Utrecht.

Google Scholar

Leonard, M., Westra, S., Phatak, A., Lambert, M., van den Hurk, B., Mcinnes, K., et al. (2014). A compound event framework for understanding extreme impacts. Wiley Interdiscip. Rev. Clim. Change 5, 113–128. doi: 10.1002/wcc.252

CrossRef Full Text | Google Scholar

Lindström, G., Johansson, B., Persson, M., Gardelin, M., and Bergström, S. (1997). Development and test of the distributed HBV-96 hydrological model. J. Hydrol. 201, 272–288. doi: 10.1016/S0022-1694(97)00041-3

CrossRef Full Text | Google Scholar

Merz, B., Aerts, J., Arnbjerg-Nielsen, K., Baldi, M., Becker, A., Bichet, A., et al. (2014). Floods and climate: emerging perspectives for flood risk assessment and management. Nat. Hazards Earth Syst. Sci. 14, 1921–1942. doi: 10.5194/nhess-14-1921-2014.

CrossRef Full Text | Google Scholar

Merz, R., and Blöschl, G. (2003). A process typology of regional floods. Water Resour. Res. 39, 1–20. doi: 10.1029/2002WR001952

CrossRef Full Text | Google Scholar

Merz, R., and Blöschl, G. (2008). Flood frequency hydrology: 1. Temporal, spatial, and causal expansion of information. Water Resour. Res. 44, 1–17. doi: 10.1029/2007WR006744

CrossRef Full Text | Google Scholar

Moftakhari, H. R., Salvadori, G., AghaKouchak, A., Sanders, B. F., and Matthew, R. A. (2017). Compounding effects of sea level rise and fluvial flooding. Proc. Natl. Acad. Sci. U.S.A. 114, 9785–9790. doi: 10.1073/pnas.1620325114

PubMed Abstract | CrossRef Full Text | Google Scholar

Nash, J. E., and Sutcliffe, J. V. (1970). River flow forecasting through conceptual models part I-a discussion of principles. J. Hydrol. 10, 282–290. doi: 10.1016/0022-1694(70)90255-6

CrossRef Full Text | Google Scholar

Nied, M., Pardowitz, T., Nissen, K., Ulbrich, U., Hundecha, Y., and Merz, B. (2014). On the relationship between hydro-meteorological patterns and flood types. J. Hydrol. 519, 3249–3262. doi: 10.1016/j.jhydrol.2014.09.089

CrossRef Full Text | Google Scholar

Olbert, A. I., Comer, J., Nash, S., and Hartnett, M. (2017). High-resolution multi-scale modelling of coastal flooding due to tides, storm surges and rivers inflows. A Cork City example. Coast. Eng. 121, 278–296. doi: 10.1016/j.coastaleng.2016.12.006

CrossRef Full Text | Google Scholar

Olbert, A. I., and Hartnett, M. (2010). Storms and surges in Irish coastal waters. Ocean Model. 34, 50–62. doi: 10.1016/j.ocemod.2010.04.004

CrossRef Full Text | Google Scholar

Photiadou, C. S., Weerts, A. H., and Van Den Hurk, B. J. J. M. (2011). Evaluation of two precipitation data sets for the Rhine River using streamflow simulations. Hydrol. Earth Syst. Sci. 15, 3355–3366. doi: 10.5194/hess-15-3355-2011

CrossRef Full Text | Google Scholar

Poulin, A., Huard, D., Favre, A.-C., and Pugin, S. (2007). Importance of tail dependence in bivariate frequency analysis. J. Hydrol. Eng. 12, 394–403. doi: 10.1061/(ASCE)1084-0699200712:4(394)

CrossRef Full Text | Google Scholar

Prudhomme, C., and Genevier, M. (2011). Can atmospheric circulation be linked to flooding in Europe? Hydrol. Process. 25, 1180–1190. doi: 10.1002/hyp.7879.

CrossRef Full Text | Google Scholar

Ridder, N., De Vries, H., and Drijfhout, S. (2018a). The role of atmospheric rivers in compound events consisting of heavy precipitation and high storm surges along the Dutch coast. Nat. Hazards Earth Syst. Sci. 18, 3311–3326. doi: 10.5194/nhess-18-3311-2018

CrossRef Full Text | Google Scholar

Ridder, N., De Vries, H., Drijfhout, S., Van Den Brink, H., Van Meijgaard, E., and De Vries, H. (2018b). Extreme storm surge modelling in the North Sea The role of the sea state, forcing frequency and spatial forcing resolution. Ocean Dyn. 68, 255–272. doi: 10.1007/s10236-018-1133-0

CrossRef Full Text | Google Scholar

Seneviratne, S., Nicholls, N., Easterling, D., Goodess, C., Kanae, S., Kossin, J., et al. (2012). “Changes in climate extremes and their impacts on the natural physical environment,” in Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation, eds C. B. Field, V. Barros, T. F. Stocker, D. Qin, D. J. Dokken, K. L. Ebi et al. (Cambridge: Cambridge University Press), 109–230.

Google Scholar

Serinaldi, F., Bárdossy, A., and Kilsby, C. G. (2015). Upper tail dependence in rainfall extremes: would we know it if we saw it? Stoch. Environ. Res. Risk Assess. 29, 1211–1233. doi: 10.1007/s00477-014-0946-8

CrossRef Full Text | Google Scholar

Sippel, S., Otto, F. E. L., Forkel, M., Allen, M. R., Guillod, B. P., Heimann, M., et al. (2016). A novel bias correction methodology for climate impact simulations. Earth Syst. Dyn. 7, 71–88. doi: 10.5194/esd-7-71-2016

CrossRef Full Text | Google Scholar

Smits, A., Tank, A. M. G. K., and Onnen, G. P. K. (2005). Trends in storminess over The Netherlands, 1962–2002. Int. J. Climatol. 25, 1331–1344. doi: 10.1002/joc.1195

CrossRef Full Text | Google Scholar

Stahl, K., Weiler, M., Kohn, I., Freudiger, D., Seibert, J., Vis, M. et al. (2016). The Snow and Glacier Melt Components of Streamflow of the River Rhine and its Tributaries Considering the Influence of Climate Change. Available at: www.chr-khr.org/en/publications (accessed March 30, 1989).

Google Scholar

Sutanudjaja, E. H., Van Beek, R., Wanders, N., Wada, Y., Bosmans, J. H. C., Drost, N., et al. (2018). A 5 arcmin global hydrological and water resources model. Geosci. Model. Dev. 11, 2429–2453. doi: 10.5194/gmd-11-2429-2018

CrossRef Full Text | Google Scholar

Svensson, C., and Jones, D. A. (2004). Dependence between sea surge, river flow and precipitation in south and west Britain. Hydrol. Earth Syst. Sci. 8, 973–992. doi: 10.5194/hess-8-973-2004

CrossRef Full Text | Google Scholar

Terink, W., Lutz, A. F., Simons, G. W. H., Immerzeel, W. W., and Droogers, P. (2015). SPHY: spatial processes in hydrology. Geosci. Model. Dev. Discuss. 8, 1687–1748. doi: 10.5194/gmdd-8-1687-2015

CrossRef Full Text | Google Scholar

Ulbrich, U., Leckebusch, G. C., and Pinto, J. G. (2009). Extra-tropical cyclones in the present and future climate: a review. Theor. Appl. Climatol. 96, 117–131. doi: 10.1007/s00704-008-0083-8

CrossRef Full Text | Google Scholar

van den Hurk, B., Siegmund, P., Klein Tank, A., Attema, J., Bakker, A., Beersma, J., et al. (2014). KNMI’14: Climate Change Scenarios for the 21st Century – A Netherlands Perspective. Scienticfic Report WR2014-01. KNMI: De Bilt

Google Scholar

van den Hurk, B., van Meijgaard, E., de Valk, P., van Heeringen, K.-J., and Gooijer, J. (2015). Analysis of a compounding surge and precipitation event in the Netherlands. Environ. Res. Lett. 10:035001. doi: 10.1088/1748-9326/10/3/035001

CrossRef Full Text | Google Scholar

van Meijgaard, E., Van Ulft, L. H., Bosveld, F. C., Lenderink, G., and Siebesma, A P. (2008). The KNMI Regional Atmospheric Climate Model RACMO Version 2.1.

Google Scholar

van Meijgaard, E., van Ulft, L. H., Lenderink, G., de Roode, S. R., and Timmermans, R. M. A. (2012). Refinement and Application of a Regional Atmospheric Model for Climate Scenario Calculations of Western Europe. De Bilt: KNMI.

Google Scholar

Viviroli, D., Weingartner, R., and Messerli, B. (2003). Assessing the hydrological significance of the World’s Mountains. Mt. Res. Dev. 23, 369–375. doi: 10.1659/0276-47412003023

CrossRef Full Text | Google Scholar

Vries, H. D., Katsman, C., and Drijfhout, S. (2014). Constructing scenarios of regional sea level change using global temperature pathways. Environ. Res. Lett. 9:115007. doi: 10.1088/1748-9326/9/11/115007

CrossRef Full Text | Google Scholar

Wahl, T., Haigh, I. D., Nicholls, R. J., Arns, A., Dangendorf, S., Hinkel, J., et al. (2017). Understanding extreme sea levels for broad-scale coastal impact and adaptation analysis. Nat. Commun. 8:16075. doi: 10.1038/ncomms16075

PubMed Abstract | CrossRef Full Text | Google Scholar

Wahl, T., Jain, S., Bender, J., Meyers, S. D., and Luther, M. E. (2015). Increasing risk of compound flooding from storm surge and rainfall for major US cities. Nat. Clim. Change 5, 1093–1097. doi: 10.1038/nclimate2736

CrossRef Full Text | Google Scholar

Wu, W., McInnes, K., O’Grady, J., Hoeke, R., Leonard, M., and Westra, S. (2018). Mapping dependence between extreme rainfall and storm surge. J. Geophys. Res. Ocean 123, 2461–2474. doi: 10.1002/2017JC013472

CrossRef Full Text | Google Scholar

Yue, S., and Rasmussen, P. (2002). Bivariate frequency analysis: discussion of some useful concepts in hydrological application. Hydrol. Process. 16, 2881–2898. doi: 10.1002/hyp.1185

CrossRef Full Text | Google Scholar

Zheng, F., Westra, S., and Sisson, S. A. (2013). Quantifying the dependence between extreme rainfall and storm surge in the coastal zone. J. Hydrol. 505, 172–187. doi: 10.1016/j.jhydrol.2013.09.054

CrossRef Full Text | Google Scholar