High Resolution Attenuation Images From Active Seismic Data: The Case Study of Solfatara Volcano (Southern Italy)

Introduction

Fluids play a key role in controlling and governing the evolution of magmatic processes and eruptions. A reliable imaging of fluid storage areas and an accurate tracking of their movements within the crust is therefore critical in evaluating the actual state and future evolution of volcanic activity. On these grounds, an efficient strategy of monitoring and hazard assessment should be addressed. For this purpose, seismic velocity tomography is commonly used to image volumes of active faults and magmatic structures (Toomey and Foulger, 1989; Judenherc and Zollo, 2004; Battaglia et al., 2008; Dawson et al., 2016; De Landro et al., 2017; Amoroso et al., 2018; Gammaldi et al., 2018). However, due to the geological heterogeneity of volcanic media, a simple description of the subsoil in terms of elastic properties may be not sufficient for a thorough understanding of volcanic dynamics. The body wave quality factor Q, describing the anelastic attenuation of the medium, is more sensitive to the rock’s physical properties such as temperature, porosity, permeability, and degree of fluid saturation than elastic parameters (Sanders et al., 1995; de Lorenzo et al., 2001; Serlenga et al., 2016; Amoroso et al., 2017). Therefore, especially for volcanic areas, it is very useful to integrate the information provided by elastic imaging with that coming from an anelastic attenuation model.

A common way to obtain a 3-D seismic attenuation model for P-waves is to invert the linear relation between the quality factor Q_P, which is defined as the relative energy per cycle lost by a wave during its travel path, and the t${}_P^{*}$, the ratio between the P-travel time and the quality factor. The inversion can be performed by using, for example, a tomographic method. This strategy is usually adopted when the velocity model is known and, consequently, the ray-paths are fixed (Schurr et al., 2003; Martinez-Arevalo et al., 2005, Serlenga et al., 2016; Amoroso et al., 2017).

The measurement of t^∗ parameter is a crucial operation. In most cases t^∗ measurements are obtained by modeling the far-field displacement spectrum of earthquake signals. A drawback arising from this analysis is the trade-off between the quality factor Q and other source-dependent parameters, such as the corner frequency and the high-frequency spectral fall-off (Zollo et al., 2014). This issue may lead to an intrinsic ambiguity of the t^∗ measurements retrieved from the signals in the frequency domain.

This problem can be avoided when data from active sources are available. When the source time function is known, its contribution can be removed from the records by extracting the Green’s function of the medium, which only contains information on the wave path, including anelastic attenuation.

Another critical issue in imaging the elastic and anelastic properties of the subsoil is the choice of the initial model for the tomographic inversion. It is well known that the initial guess affects the final solution retrieved by a linearized inversion method (Kissling et al., 1994). In the anelastic attenuation tomography, a homogenous attenuation model is commonly used as the initial model (De Gori et al., 2005; Bisrat et al., 2013; Serlenga et al., 2016). Thus, an intermediate step between the t^∗ estimations and their inversion is required to obtain a reference Q model to be used as the starting point for the inversion.

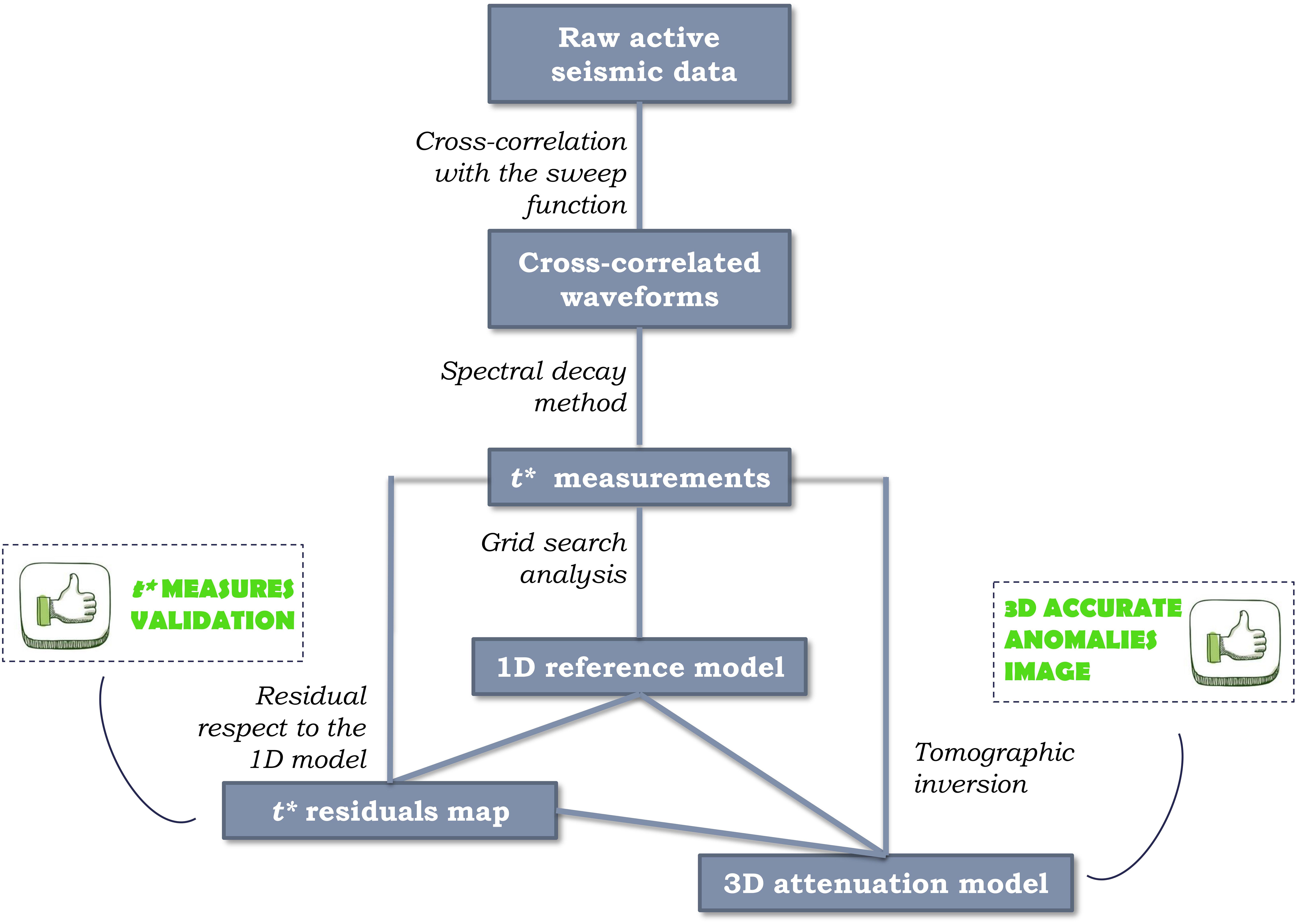
Here, we present a methodology that allows to obtain highly accurate 1-D and 3-D attenuation models from active seismic data (Figure 1). The procedure of retrieving 3-D Q_P image starts from the t^∗ measurement. In this step, in order to remove the source effect from data, the signal is cross-correlated with the sweep function (Brittle et al., 2001). Then, the t^∗ are used to obtain a reference 1-D attenuation model for the area. We proposed a grid search analysis to retrieve a three-gradient 1-D Q_P model to be used as starting attenuation model. A preliminary analysis aimed to validate the t^∗ catalog has been performed by mapping the average t^∗ residuals over all the stations and sources. If the t^∗ data set is reliable, due to the dense geometry of sources and stations located on the surface, we expect a spatial coherence of the residues associated with neighboring points. Finally, in order to retrieve the 3-D attenuation tomographic model, the t^∗ are inverted through an iterative tomographic inversion procedure (Latorre et al., 2004; Amoroso et al., 2017).

FIGURE 1

Figure 1. Schematic representation of procedure applied in order to obtain the attenuation images.

We applied the described methodology to the data collected during the active seismic experiment RICEN (Repeated InduCed Earthquake and Noise, Serra et al., 2016), performed within the MED-SUV project at the Solfatara Crater. It is located within the Campi Flegrei caldera, 1.5 km North-East of the town of Pozzuoli and about 10 km West of Naples, in Southern Italy. The dynamics of the Campi Flegrei caldera is controlled by a deep magmatic source, at about 8 km depth (Zollo et al., 2008), which provides repeated injections of magmatic fluids into a shallower source at 4 km depth and then into the hydrothermal system (Chiodini et al., 2016). The Solfatara is considered as the top of a hydrothermal plume with large episodes of hydrothermal-magmatic gas emission (Chiodini et al., 2001). The energy released here by degassing is nowadays much higher than the energy released within the whole caldera through other processes such as thermal conduction, earthquakes, and ground deformation. The crater, with a diameter of about 600 m, has been investigated by diverse multidisciplinary campaigns, that include active seismic (Bruno et al., 2007, 2017; Serra et al., 2016; Gammaldi et al., 2018; Scala et al., 2019), magnetotelluric (Siniscalchi et al., 2019), and geochemical (Chiodini et al., 2001) surveys and resistivity surveys (Byrdina et al., 2014; Gresse et al., 2017). The velocity tomographic images (Serra et al., 2016; De Landro et al., 2017, Gammaldi et al., 2018) reveal a complex structure with an alternation of water-rich and gas-rich rocks. The images also delineate conduits that culminate with a strong gas emission at the Bocca Grande and Bocca Nuova main fumaroles (De Landro et al., 2017). In this framework, the present study will provide complementary information on the complex hydrothermal system by obtaining models of the attenuation parameter, very fluid-sensitive, at the small unexplored scale of shallow crater.

Data and Method

In the frame of the RICEN experiment, three one-week-long geophysical surveys were carried out at Solfatara volcano on September 2013, May and November 2014. Each experiment allowed to collect recordings of active seismic data and of continuous ambient noise. The active seismic part consisted of the acquisition of more than 75,000 seismograms. Active seismic data were recorded using a single 6400 kg IVI-MINIVIB^® vibroseis truck, which delivers a maximum theoretical peak force of ∼ 27 kN at each sweep and which operated in the frequency range 5–125 Hz. The Vibroseis source behaves as a high-pass filter with a cut-off frequency of 40 Hz and a ratio of about 4:1 between its flat level and its spectral amplitude at 7 Hz (Serra et al., 2016). Seismic waveforms were recorded by 4.5 Hz vertical component geophones (GS-11-D).

In this study, the data collected during the first active seismic experiment were used. The geometry of the stations allowed to sample an area of 90 × 115 m² by the deployment of a regular grid of 240 vertical sensors at the crater surface (Figures 2B,C). In detail, the network was set up according to a two-dimensional (2-D) grid with 10 lines of 24 sensors, having a spatial step of 5 m (i.e., in-line distance). The distance between two adjacent lines (i.e., cross-line distance) was 10 m. About 100 shot-points were energized on a staggered grid relatively to the receiver grid. In order to have a regular and dense sampling for the vibrational sources too, the shots were performed by maintaining both the in-line and cross-line inter-distances of 10 m. For each shot position, three consecutive energizations were performed and waveforms at each site were stacked with the aim of increasing the signal-to-noise ratio.

FIGURE 2

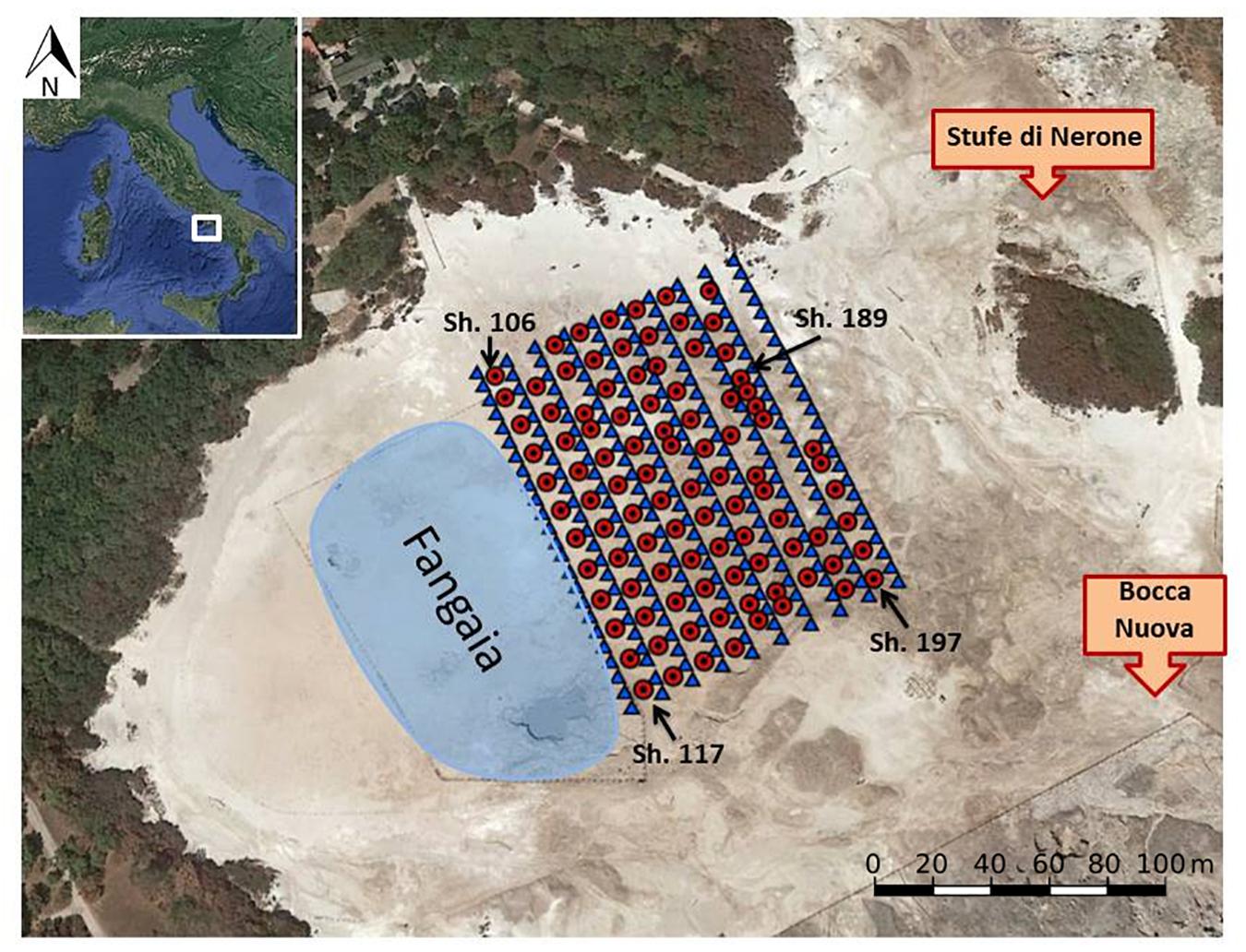
Figure 2. RICEN experiment layout: the red dots represent the shots, the blue triangles the stations. The arrows indicate the shots analyzed in Figure 2. The maps has been obtained with Google Maps 9.38.1 2019 (Map data: Google, DigitalGlobe): Solfatara, Pozzuoli, Metropolitan City of Naples, Italy retrieved from https://www.google.com/maps/@40.8174278,14.1393587,1292a,20y,41.32t/data=!3~m1!1e3.

Data Analysis: t^∗ Measurement

The data analysis of this work mainly consisted of measuring the t^∗ parameter for all the possible source-receiver couples of the seismic experiment.

The displacement spectrum A_ij(f) of the i-th energization recorded at the j-th station at distance x from the source is:

$$A_{i,j}\left(f\right)=G(f,x)S_i\left(f\right)C_j\left(f\right)I\left(f\right)(1)$$

where the function S_i(f) represents the source term, whereas the frequency-dependent site effects are described by C_j(f). The term I(f) is the instrumental response, while the function G(f,x) accounts for the geometrical spreading, radiation pattern and anelastic body wave attenuation along the travel path. The latter term may be expressed as follows:

$$G(f,x)=C_s^{\prime }\exp \left(-\mathrm{\pi }{t}^{*}f\right)(2)$$

where a distance-dependent term C’_S accounts for direct P- and S-wave amplitude variations due to geometrical spreading, vertically varying velocity structure and free-surface effects (Aki and Richards, 1980).

The t^∗ operator is:

$$t_{i,j}^{*}=\underset{ray}{\int }\frac{ds}{V\left(s\right)Q(s)}(3)$$

In the previous equation, the term ds describes the ray path infinitesimal element. Q(s) and V(s) represent the quality factor and velocity along the ray-path, respectively. Since the ray-paths depend only on the velocity structure of the medium, which is assumed to be known, the mathematical relation between the t^∗ operator and Q(s) is fully linear.

The instrumental response, I(f), may be easily known from additional sources. Therefore, the main remaining problem for extracting information on the anelastic properties of the medium is the knowledge and the removal of source contribution and site effects.

Concerning the removal of source signal from the spectra, one of the most common adopted techniques in scientific literature is the spectral ratio method (Teng, 1968). In a common source configuration, the computation of the ratio between two spectra recorded at two different receivers allows to cancel out the same, unknown, source contribution from the signals. It is always true in the case the two receivers are at the same azimuth with respect to an earthquake source, for which the effects of radiation pattern have to be taken into account. In particular, spectral ratio method is a very useful technique in processing and analysis of signals generated by natural seismic sources. Due to some complications related to the application of this method (Sams and Goldberg, 1990; Serlenga et al., 2016) and since an active seismic dataset was used for our purposes, we proceeded in a different way. Actually, in this case, the source contribution is known. In particular, a well-known method applied in the processing of active seismic data has been adopted, that is the cross-correlation of the recorded trace with the sweep. The latter represents the Vibroseis source, that is an oscillating signal with its frequency monotonically increasing with time. The cross-correlation technique is the industry standard for removing an embedded sweep from a signal. Brittle et al. (2001) demonstrated that in order to remove the effect of the source in vibroseis recordings, for a linear sweep, its cross-correlation with the signal provides equivalent results with respect to those obtained by a frequency-domain sweep deconvolution (FDSD) (Figure 3). The latter consists of removing in the frequency domain the sweep function through a simple division of the signal and the source spectra.

FIGURE 3

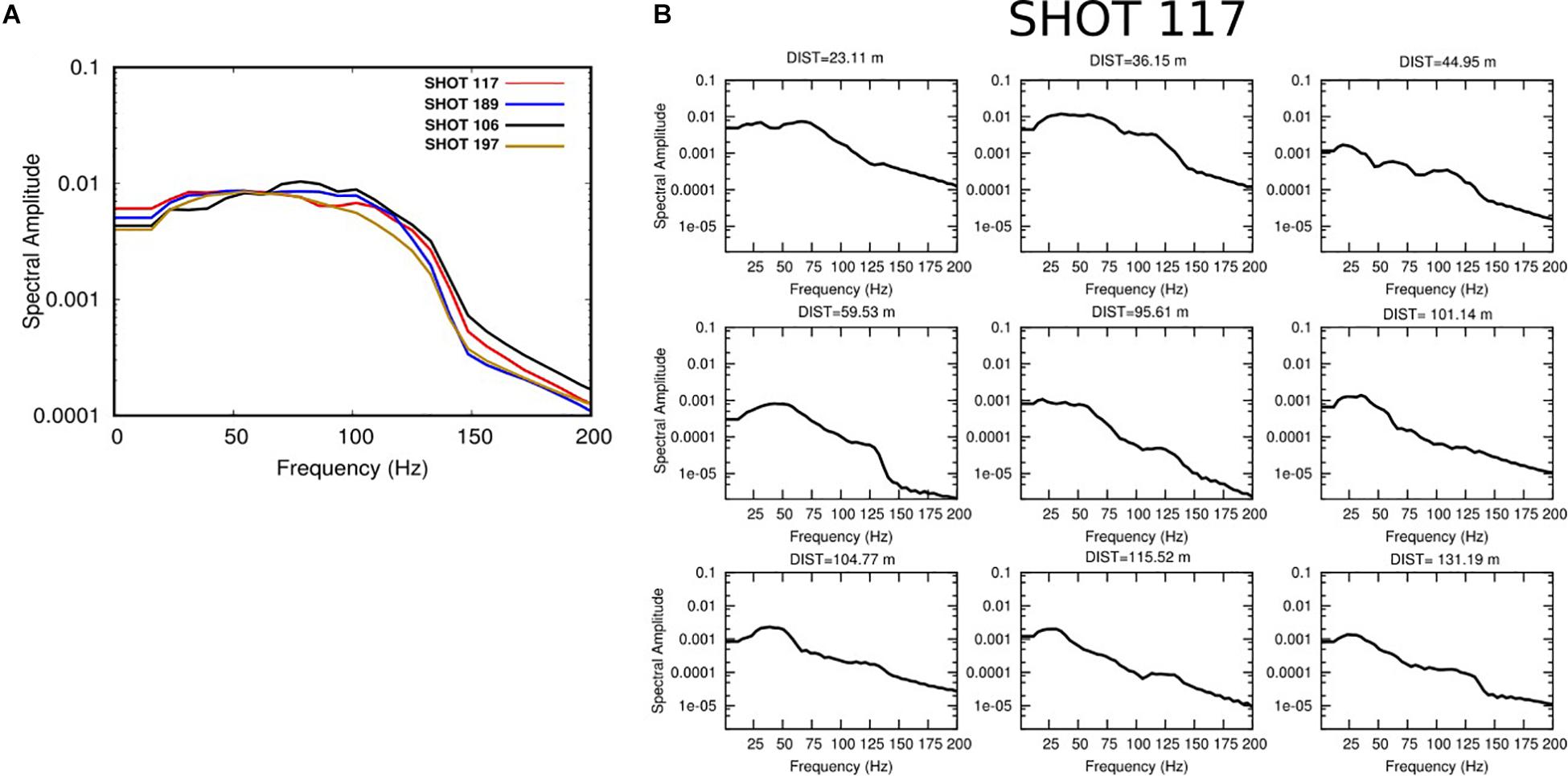
Figure 3. (A) Displacement spectra computed as the average of spectra recorded at the four closest receivers to each of the four selected shots. Each curve represents the average displacement spectrum for different source, following the color legend in figure. Spectra were computed in a 0.128 s long time window. The position of shots on the field is represented in Figure 2. (B) Spectra computed at increasing distances from the shot 117. The effect of anelastic absorption on high frequencies is clear, in particular if we compare these to the “source” spectra.

In order to preserve the causality in the data, an additional minimum phase filter was applied after cross-correlation (Gibson and Larner, 1984; Serra et al., 2016). A comparison of the signals before and after the processing is shown in Supplementary Figure S2.

Regarding the site effect contribution, on the other hand, it may distort the seismic spectrum in a remarkable way, also in volcanic environments, as pointed out by Galluzzo et al. (2009). Anyway, the common practice of spectral smoothing may greatly contribute to mitigate the possible site effects on it. Indeed, the site effect can generate wide band amplification/attenuation and/or typically multi-peak amplifications on the signal spectrum (Kanamori, 1967a, b; Der and McElfresh, 1976).

Then, for data analysis and t^∗ measurements we selected only signal recordings with a signal-to-noise ratio higher than 2 (cfr Supplementary Figure S1 by De Landro et al., 2017). The cross-correlated signals were cut in a 0.126 s wide time window around the P-wave arrival time. Afterward, a 5% cosine taper was applied. The selected time window represented a very good compromise between two different necessities: (1) exclusion of arrivals of surfaces waves from the spectrum computation; (2) accurate estimation of the spectrum, with a proper frequency resolution for our further analyses. We checked that, even if at very short distances a small portion of surface waves may be included in the selected time window, this did not greatly affect t^∗ measurements (see Supplementary Text S1 and Supplementary Figure S1). The signals, furthermore, were zero-padded up to 0.256 s to increase their spectral resolution without adding further phases to the analyzed signal. We verified that this procedure allowed to obtain a spectrum almost completely equivalent to the one retrieved by a simple resampling of a spectrum retrieved in a 0.126 s wide time window. Then, the velocity seismograms were integrated in the time domain, and the displacement spectra were computed. A five-points-wide averaging moving window was used to smooth the amplitude spectra. This way allowed to mitigate both the possible site effects on amplitude spectra and the undesired effects related to zero-padding. Finally, a linear fit of the natural logarithm of the spectral amplitudes in the sense of least-squares was carried out in the range 40–125 Hz (Figure 4A). In this frequency interval the instrumental response and the source spectrum are flat.

FIGURE 4

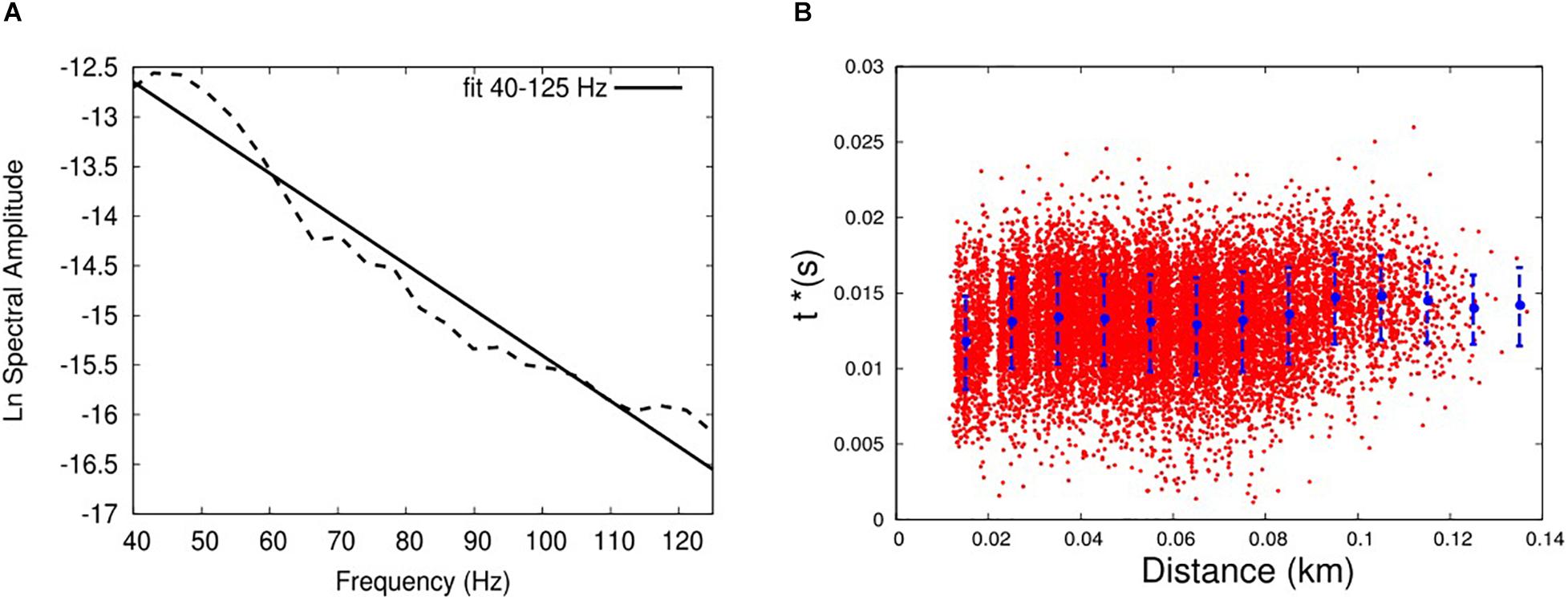
Figure 4. (A) Example of a displacement spectrum (dashed line) fitted in the least-squares sense in the frequency range 40–125 Hz. (B) final t^∗ dataset, with average values (blue points), with standard deviation associated (dashed blue lines) computed in interval of distances of 10 m.

As a consequence of the applied processing on seismic signals and on displacement spectra, the logarithmic form of equation (1) may be approximated as follows:

$$ln{A}_{i,j}\left(f\right)=ln{C}_S^{\prime }-\mathrm{\pi }{t}^{*}f(4)$$

with a linear slope equal to π t^∗. Only displacement spectra and their respective t^∗ values showing a linear correlation coefficient |R| > 0.9 were selected. In that way, we chose only data showing a strictly linear decreasing trend. Therefore, we discarded other signals characterized by strong deviations from linearity, which might be caused by unmodeled site and/or multipath effects. A final dataset of 15,297 t^∗ measurements was collected and used for further analyses and attenuation tomography (Figure 4B).

Determination of 1-D Attenuation Model and Residual Mapping

Although the mathematical problem of attenuation tomography is fully linear, data are still affected by errors and uncertainties. Furthermore, the seismic tomographic inversion, independently of the target physical parameter, is a typical example of mixed-determined problem. It is an inverse problem neither completely over-determined nor completely underdetermined, because of inhomogeneous distribution of seismic rays in the investigated Earth volume (Menke, 1989). Thus, in spite of its mathematical linearity, this geophysical inverse problem is usually solved through an iterative scheme. As a consequence, the final results of a tomographic inversion may strongly depend on the starting solution, which has to be carefully chosen and needs to be as close as possible to the true, unknown, attenuation model. Usually, in attenuation tomography the homogeneous model which minimizes the RMS of residuals between observed and theoretical t^∗ is adopted as starting solution.

In this case we propose a more robust approach driven by the t^∗ measurements distribution as a function of distance. As shown in Figure 4B by the binned distribution of measured t^∗, these values exhibit an almost constant average trend with increasing distances. Taking into account that: (1) in the acquisition layout the sources and receivers are located at very similar elevations; (2) the elastic properties of the medium guide the ray paths connecting sources and receivers; and (3) the elastic properties of the medium may be described on average by an increasing P-wave velocity with depth (see the following section) we explain the constant trend of t^∗ = $\frac{T}{Q}$ vs. distance as due to the compensating effect of increasing travel time with distance and ray deepening and the increase of the quality factor Q with depth. In order to validate this hypothesis, we performed several tests with synthetic data using the real source-receiver configuration. The steps below were followed in our analyses:

– We implemented the 3-D P-wave velocity model by De Landro et al. (2017) in the adopted tomographic code.

– We manually built three different categories of 1-D Q_P models: (1) single linear gradient of variation of Q_P as a function of depth; (2) Q_P models described as piecewise linear profiles composed of two different gradients of variation of Q_P as a function of depth; (3) Q_P models described as piecewise linear profiles composed of three different gradients of variation of Q_P as a function of depth.

– For each category, several 1-D models were manually created in a sort of trial and error procedure and synthetic t${}_P^{*}$ were computed. The same source-receiver couples for which we measured t${}_{P,}^{*}$ were used for the synthetic computation.

For the computation of synthetic t${}_P^{*}$, we used the forward part of the inversion code described in the section “Discussion”. Then, the binned t${}_P^{*}$ vs. distance distribution was retrieved.

After a simple, visual, comparison of measured and synthetic binned t${}_P^{*}$ distribution, a 3-gradients Q_P model was chosen as the simplest solution which reproduced at best the distribution of t^∗ as a function of the distance. Indeed, we observed that both 1- and 2-gradients Q_P models were not able to fit the average t${}_P^{*}$ distribution as a function of distance (Supplementary Figures S3, S4). The 3-gradients 1-D Q_P model can be described, from a mathematical point of view, in this way:

$$\{\begin{array}{cc}Q(z)=Q_0+\alpha z\mathit{\hspace{1em}}\hfill & z<h_1\hfill \\ Q(z)=Q_{h_1}+\beta \left(z-h_1\right)\mathit{\hspace{1em}}\hfill & h_1<z<h_2\hfill \\ Q(z)=Q_{h_2}+\gamma \left(z-h_2\right)\mathit{\hspace{1em}}\hfill & z>h_2\hfill \end{array}(5)$$

where Q₀ represents the quality factor value at the surface, the term Q_h1 the quality factor value at depth h₁ from the bottom of the synthetic tomographic grid. The term Q_h2 describes the quality factor value at depth h₂. The terms α, β, and γ represent the three different linear increases of quality factor with depth, respectively. The terms h₁ and h₂ describe the depths where the transition between the linear gradients α - β and β - γ occurs, respectively.

Therefore, in order to retrieve the final, preliminary 1-D attenuation model, a grid-search procedure was carried out. In particular, a systematic exploration of Q₀, h₁, h₂, α, β, and γ parameters was performed. Each parameter was allowed to vary in the following ranges:

$$\{\begin{array}{c}5<Q_0<6\hfill \\ 5m<h_1<10m\hfill \\ 10m<h_2<15m\hfill \\ 0.1/m<\alpha <0.3/m\hfill \\ 0.4/m<\beta <0.9/m\hfill \\ 1/m<\gamma <1.5/m\hfill \end{array}$$

The “grid-spacing” for each parameter was set up as follows:

$$\{\begin{array}{cc}d{Q}_0=1\mathit{\hspace{1em}}\hfill & \\ d{h}_1=1m\mathit{\hspace{1em}}\hfill & \\ d{h}_2=1m\mathit{\hspace{1em}}\hfill & \\ d\alpha =0.1/m\mathit{\hspace{1em}}\hfill & \\ d\beta =0.1/m\mathit{\hspace{1em}}\hfill & \\ d\gamma =0.1/m\mathit{\hspace{1em}}\hfill & \end{array}$$

The Q_{h_1} and Q_{h_2} parameters were not explored, since they are function of the combination of α–h₁ and β–h₂ parameters, respectively.

A total number of 12,960 mono-dimensional three-gradients Q_P models was created and synthetic t${}_P^{*}$ were computed for each model. The model that provided the best agreement between the observed and synthetic t${}_P^{*}$ and that minimized the RMS of binned t^∗ residuals was chosen as representative of the final 1-D Q_P attenuation model (Figures 5A–C).

FIGURE 5

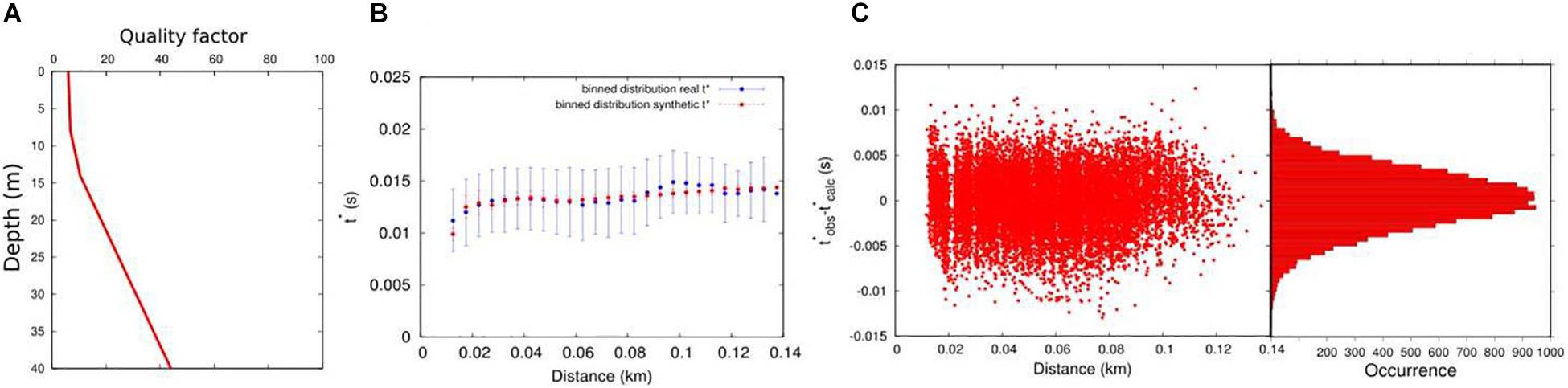
Figure 5. (A) Final 1-D attenuation model retrieved at the end of grid-search procedure. (B) Real and synthetic t^∗ distribution. The blue points represent the binned distribution of measured t^∗. The red points represent the binned distribution of synthetic ^∗, relative to the represented 1-D Q_P and 3-D V_P models. (C) Representation of residuals between observed and synthetic t^∗ as a function of distance. The right figure represents the histogram of residuals.

The retrieved 1-D attenuation model was used to validate the t^∗ catalog. Based on the general criteria of the lateral coherency of residuals, we underweighted for the final inversion the data from stations/sources showing isolated picks in the residual map.

Moreover, the areas characterized by a spatial coherence of t^∗ residual values, i.e., the northeast and central negative t^∗-residual anomalies and the southwest positive t^∗- residual anomaly, are well correlated to the Q_P anomalies of the first 15–20 m of depth in the 3-D attenuation model. Clearly, the tomography allows to better reconstruct in terms of amplitude and location the attenuation anomalies roughly imaged by the t^∗ residual map.

For each source-receiver couple the t^∗ residuals (t^∗_obs – t^∗_calc) with respect to the obtained 1-D Q_P model and the 3-D V_P model were computed. In Figure 6 we mapped the average residuals for all stations and sources (Achauer et al., 1986; Dawson et al., 1992, 2016). In particular, we introduced two different variables, R_i and R_j, that represent the average residuals for each station i and for each source j, respectively. These were defined as follows:

$$R_i=\frac{{\sum }_{j=1}^{N_j}{R}_{ij}}{N_j}(6)$$

$$R_j=\frac{{\sum }_{i=1}^{N_i}{R}_{ij}}{N_i}(7)$$

FIGURE 6

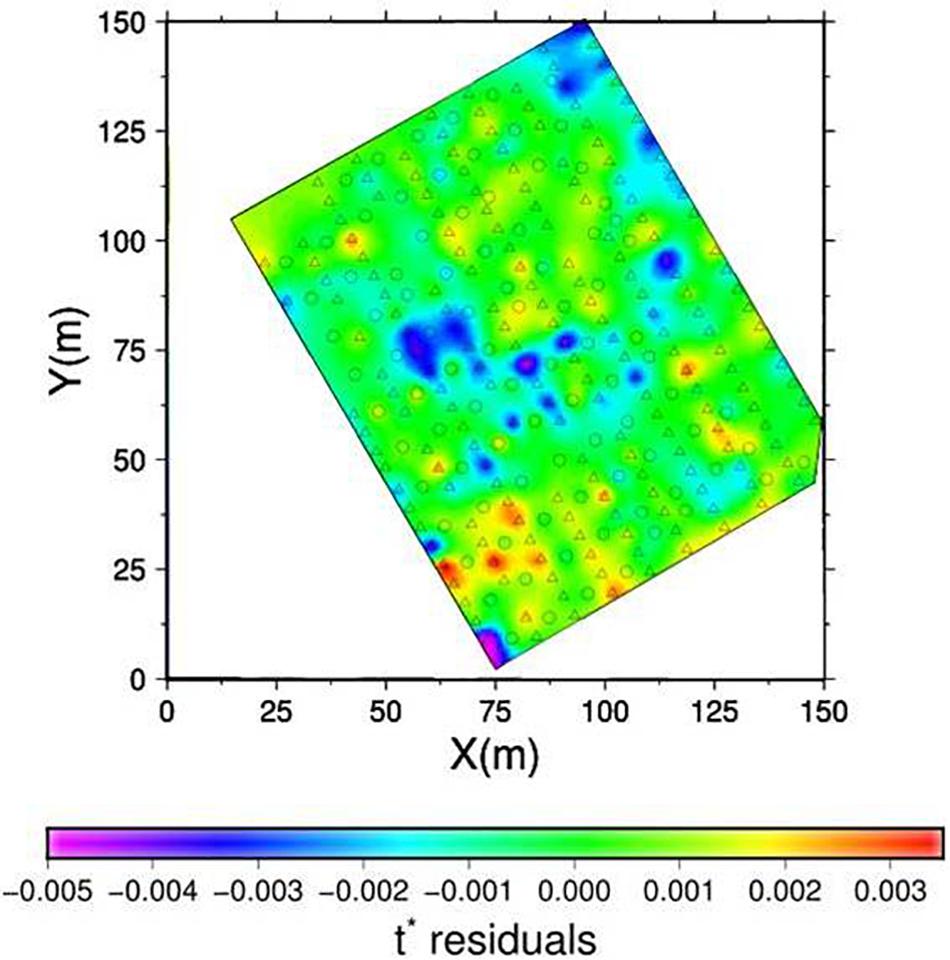
Figure 6. Map of average t^∗ residual with respect to the average 1-D Q_P model retrieved from the grid search procedure, computed over all stations and sources. The circles and the triangles represent the position of sources and stations, respectively.

The average residual value for the i-th station was computed over N_j sources for which a t^∗ measurement relative to that station was selected. On the other hand, the average residual value for the j-th source was computed over a number of stations N_i for which a t^∗ measurement relative to that source was selected. Due to the high density of stations and sources and to their homogeneous distribution in the investigated domain no azimuthal biases are present in equations (6) and (7), differently from Achauer et al. (1986).

3-D Attenuation Tomography and Inversion Strategy

To perform the 3-D tomographic inversion we used a code originally implemented for the velocity tomography and developed with the contribution of several authors and for which a complete description of the theoretical basis can be found in Latorre et al. (2004). The tomographic code has been used for several applications both in tectonic and volcanic environment considering either passive or active dataset (e.g., Vanorio et al., 2005; Battaglia et al., 2008; Amoroso et al., 2014). A recent version, modified to perform the 3-D attenuation tomography, was developed by Amoroso et al. (2017). The inversion is performed through a linearized, perturbative approach. In particular, a solution in the sense of damped least-squares is searched, by minimizing the following function:

$$\phi (m)={(d-Gm)}^T(d-Gm)+{\epsilon }^2{\left(m-m_0\right)}^T\left(m-m_0\right)$$

$$+L{m}^T{D}^{T}Dm(8)$$

The term m₀ represents the vector of initial model parameters, whereas the term D represents the second derivative smoothing operator. In equation (5), two weighting, regularization, dimensionless-factors ε² and L (damping and smoothing parameter, respectively) are present. These constraints are fundamental in order to avoid that instabilities emerge in the final solution. In particular, the use of smoothing allows us to limit possible artifacts in poorly sampled regions with respect to the use of the sole damping parameter. On the other hand, the use of smoothing makes more difficult the imaging of sharp anomalies in the model (Thurber and Ritsema, 2007).

With the aim of obtaining the attenuation model, the code was modified by considering that the residual of t^∗ (δt^∗) can be expressed as a function of partial derivatives with respect to the velocity v and attenuation Q parameters:

$$\delta t^{*}=\frac{\partial t^{*}}{\partial (u)}\delta u+\frac{\partial t^{*}}{\partial (\eta )}\delta \eta (9)$$

where u and η represent the slowness, the reciprocal of velocity V, and the reciprocal of quality factor Q, respectively. Since in the attenuation tomography the velocity model is fixed, the term du is zero. Therefore, the t^∗ variation is linearly related to the variation of the attenuation factor η via the Fréchet derivative matrix. In this way, the inversion steps are, as in the original code:

a. Ray-tracing in the velocity model (a priori known from previous analyses) for all the available station-event couples.

b. Calculation of the theoretical t^∗, and residuals Δt^∗ = t^∗_obs− t^∗_cal.

c. Set up of the system of equations to be solved by matrix inversion.

d. Smoothing and preconditioning of the matrix; matrix inversion performed using the LSQR method.

e. Once the attenuation model is obtained, the RMS of residuals is evaluated. If its value is below a given threshold, iteration is stopped; otherwise the procedure is re-iterated from step b.

We used the P-wave velocity model retrieved by De Landro et al. (2017, Figure 7) using the same dataset of this study. Analogously to the velocity model, a volume of 160 × 160 × 45 m³ was investigated, the top being at 100 m a.s.l., due to the source-receiver configuration. The attenuation model parameterization is the one of the fixed velocity model, i.e., 10 × 10 × 5 m³.

FIGURE 7

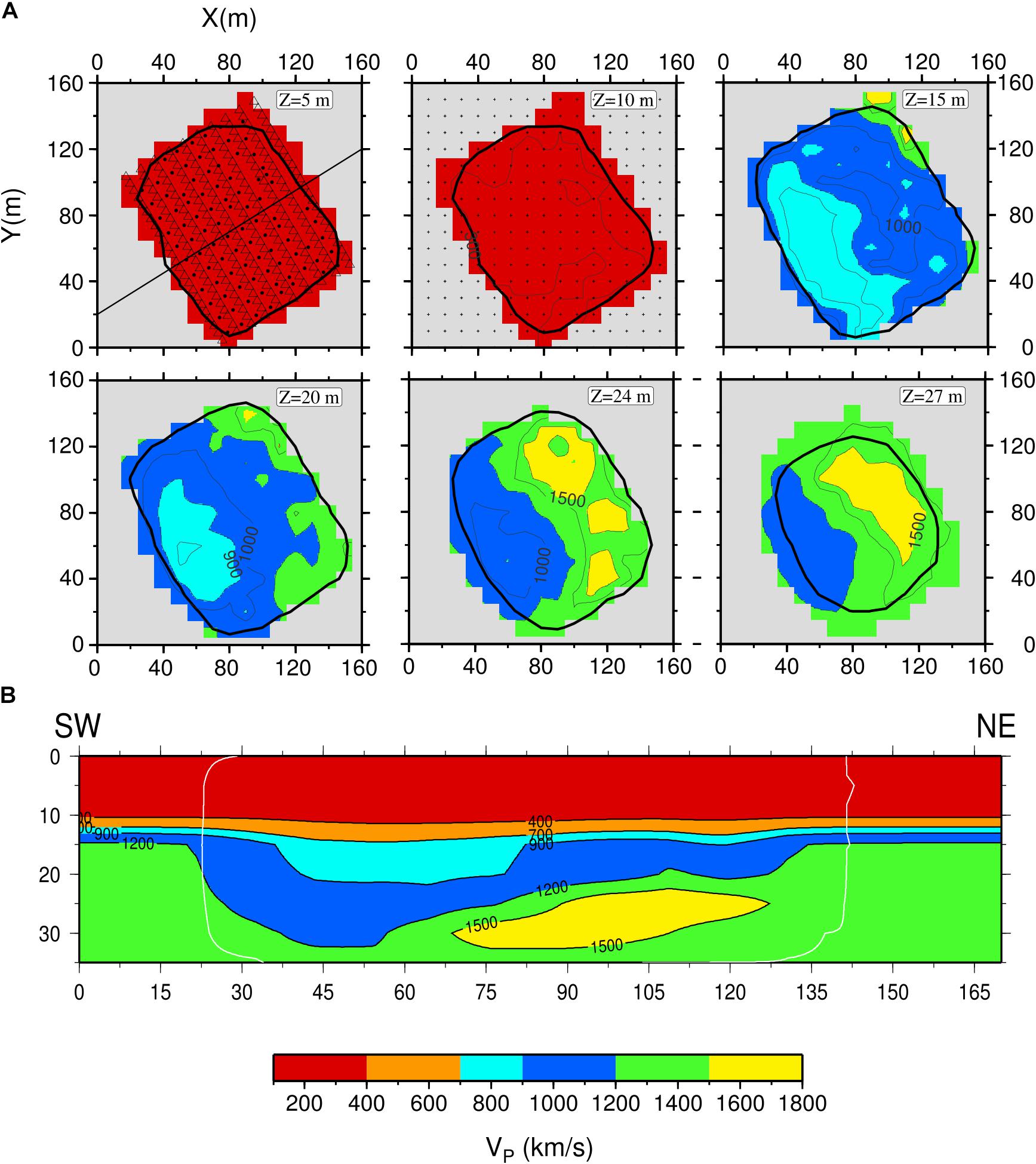
Figure 7. P-wave velocity model. (A) Horizontal slice of P-wave velocity model at different depths. The black contour delimitates the resolved area, i.e., the area for which the three resolution parameters (RDE, Sj, and DWS) are included in a threshold value. The threshold values of S _j and DWS are chosen in order to obtain a similar contour, binding the RDE to be higher than 0.9. The gray regions in each slice represent areas not covered by rays. (B) P-wave velocity model projected onto the NE-SW cross-section located in (A). The white contour delimitates the resolved area. Modified after De Landro et al. (2017).

We performed a preliminary analysis with the aim of choosing the optimal values of inversion parameters, which are the damping, the hard bound and smoothing. Hard bounds represent the maximum allowed model variation for each iteration. In order to find the best combination between regularization parameters and hard bounds, a recursive procedure was adopted (Rawlinson et al., 2006). The best combination of damping and hard bound parameters was chosen by analyzing the L-curve that describes the reduction of variance of residuals as a function of the increase of solution variance, and the curves of RMS vs. number of iterations. Then, several one-step inversions with different combinations of smoothing parameters were carried out, by keeping fixed the selected hard bound and damping value. The best combination of smoothing parameters in the three dimensions was found by looking at trade-off curves between variance of residuals and model roughness. The combination providing the best compromise between reduction of residual variance and increase of model roughness was chosen. This procedure was repeated until the best combination of damping and smoothing parameters did not change anymore.

At the end, final values of ε²=1.5, hard bound = 1.0 and Lx = Ly = 0.1; Lz = 0.5 were chosen and used for the final inversion of t^∗ data (see Supplementary Figures S5, S6).

To identify the well resolved model regions, we calculated the Derivative Weight Sum (DWS, Toomey and Foulger, 1989), which measures the ray density in the neighborhood of every node, and the resolution matrix, represented in terms of its diagonal elements (RDE) and the spread function S_j (Michelini and McEvilly, 1991) related to off-diagonal elements. In that way we take into account both the resolution of single node (RDE and DWS) and the associated possible smearing effect (Sj). Therefore, for small to medium-sized linear or linearizable inverse problems, the calculation of resolution matrix is relatively straight forward, and has been frequently used as a measure of solution reliability in elastic and anelastic tomography (Rietbrock, 2001; Bisrat et al., 2013; Amoroso et al., 2014; Improta et al., 2017). Moreover, Rawlinson and Spakman (2016) clearly underlined that methods that quantify solution reliability explicitly, like calculation of full resolution matrix, should be preferred to sensitivity analysis in resolution assessment of a tomographic image.

The full resolution matrix was calculated starting from the tomographic matrix and it was represented in terms of its resolution diagonal elements RDE and the spread function S_j (Michelini and McEvilly, 1991) related to off-diagonal elements. In particular, the S_j is defined as:

$$S_j=\log \left({\left|s_j\right|}^{-1}\sum _{k=1}^N{\left(\frac{s_{kj}}{s_j}\right)}^2{D}_{jk}\right)(10)$$

where s_j is the L₂ norm of diagonal j element of resolution matrix, and can be interpreted as a weighting factor that takes into account the value of the resolution kernel for each parameter, s_kj is the elements of j-th row of resolution matrix, and D_jk is the distance between model parameter j and k. So, S_j is calculated by compressing each row of the resolution matrix into a single number, that describes how peaked is the resolution for the corresponding diagonal element. The lower the S_j the more peaked is the resolution.

Concerning the ray coverage evaluation, we computed the derivative weight sum (DWS), which measures the ray density in the neighborhood of every node of the tomographic grid (Toomey and Foulger, 1989). The DWS of the n-th V parameters is defined as:

$$DWS\left(V_n\right)=N\sum _i\sum _j\left\{{\int }_{L_{ij}}{\omega }_n(x)\mathit{d}s\right\}(11)$$

where i and j are indices for event and station, ω is the linear interpolation weight that depends on coordinate position, L_ij is the ray path from i to j, and N is the normalization for the volume influenced by V_n. The ray-path L_ij is computed in final model obtained by observation, and takes into account the real ray-path geometry.

For each of the resolution parameters, it is possible to define a threshold value that can be used to delimit the model regions that are considered well-resolved. The threshold values of S_j and DWS are chosen in order to obtain a similar contour, binding the RDE to be higher than 0.85 (see Figure 8 and Supplementary Figures S8, S9). The resolution matrix and the spread function allow to state that the final model is well resolved down to 30 m depth.

FIGURE 8

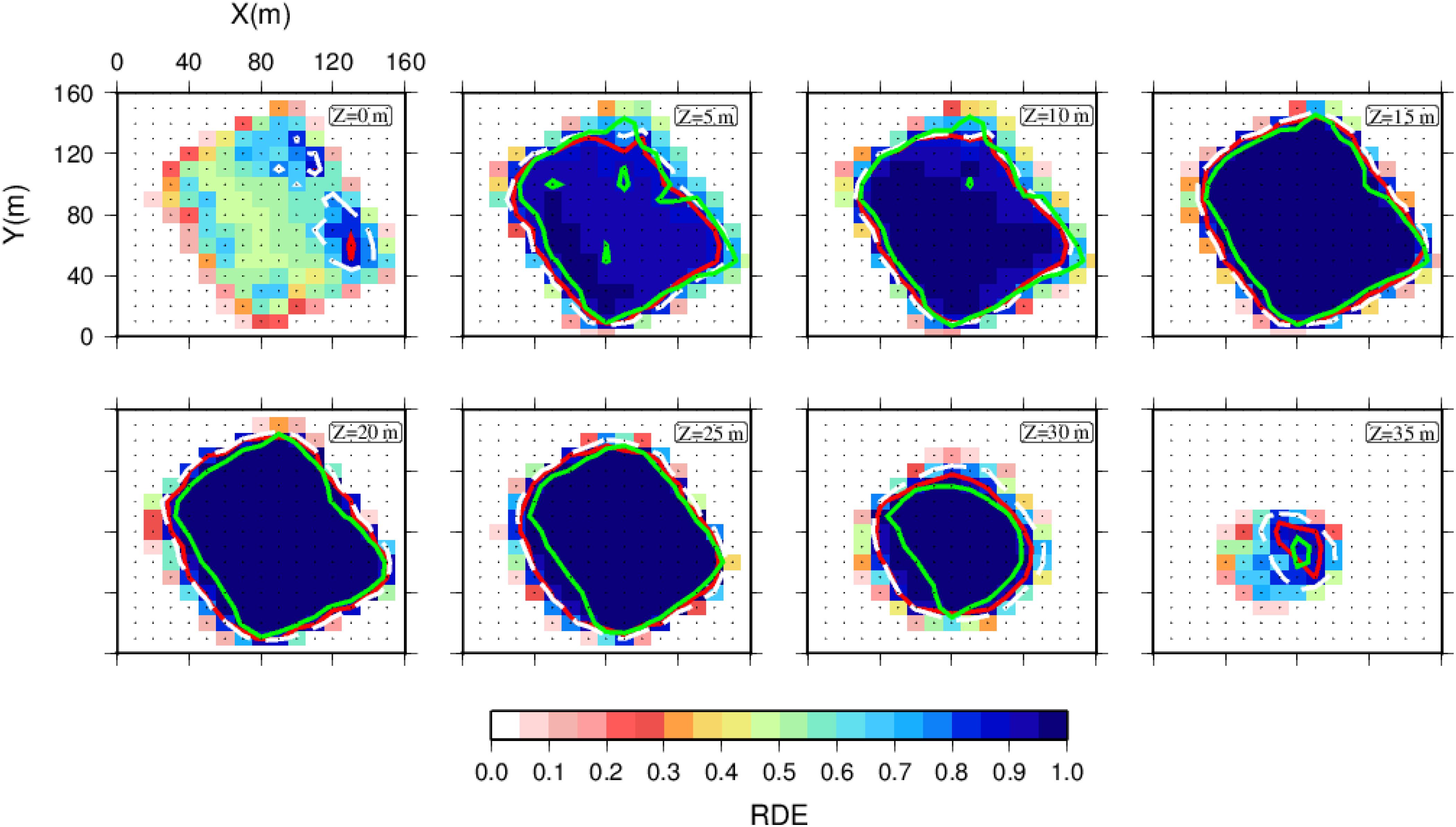
Figure 8. Diagonal elements of the resolution matrix (RDE) of the 3D attenuation model obtained with the parameterization 10 m³ × 10 m³ × 5 m³. The RDE is represented at each inverted depth. The contours represents the threshold values of RDE (red) Sj (white) and DWS (green) chosen in order to obtain a similar contour, binding the RDE to be higher than 0.85 (see Supplementary Figures S8, S9).

Results

In Figure 9, we show the 3-D final attenuation model, retrieved from the tomographic inversion of t^∗ in horizontal (Figure 9A) and vertical (Figure 9B) slices. The vertical slices represent the Q_P variations in six SW-NE sections (the black lines in Figure 9A) crossing the tomographic model from NW to SE. The RMS value of retrieved model residuals shows a reduction of about 15% for the Q_P inversion, with a final RMS of 2.8 ms (see Supplementary Figure S7). The results of the resolution analysis allowed us to state that the final model is well resolved down to about 30 m depth (for further details see Figure 8 and Supplementary Figures S8, S9). The Q_P retrieved values range between 5 and 40.

FIGURE 9

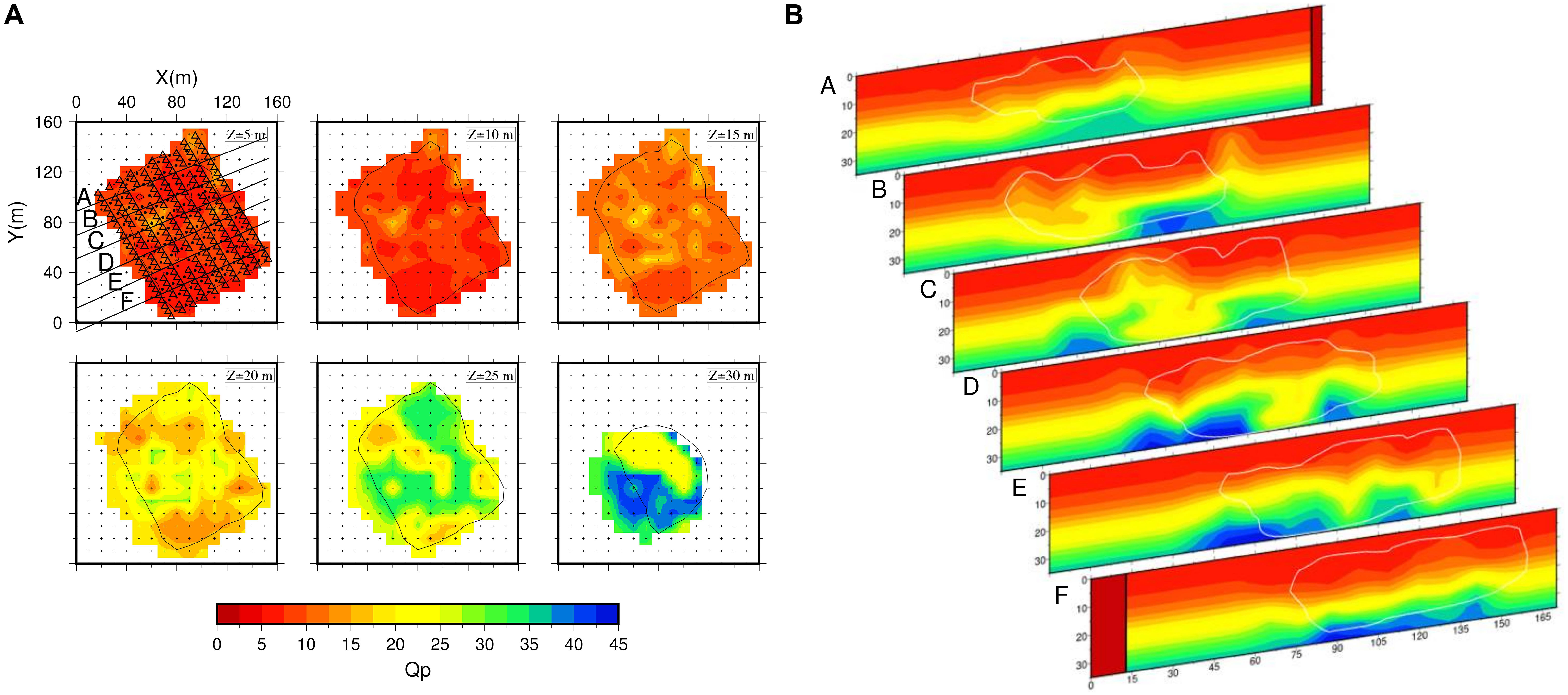
Figure 9. 3-D Q_P attenuation model. (A) Horizontal slice of P-wave attenuation model at different depths. The black contour delimitates the resolved area, i.e., the area for which the DWS is higher than the threshold value (see Figure 8). This threshold value is chosen binding the RDE to be higher than 0.85 (see Supplementary Figures S8, S9). The white regions in each slice represent areas not covered by rays. (B) P-wave attenuation model projected onto the NE-SW cross-sections located in A. The black contoured regions in each slice represent resolved areas.

The model shows a heterogeneous image of the shallow Solfatara crater. In the first 15 m of depth, the Q_P ranges between 5 and 10 with some small (15–20 m) higher Q_P anomalies (Q_P values up to 20). Then, from 20 to 25 m of depth the Q_P has a constant background value of 20 with two extended high Q_P anomalies in the NE and SW part of the model. Finally, at 30 m of depth, where the resolved area is smaller, a higher Q_P value (35–40) is clearly visible in the SW direction. These features are clearly imaged in the vertical slices too (Figure 9B), where it is possible to appreciate the geometries of the anomalies and their extension. In particular, the NE–SW sections show a sharp vertical contrast in the attenuation values at about 20 m of depth. Furthermore, at greater depths, a heterogeneity in the attenuation structure, higher than that at shallower depths, was retrieved.

Discussion

The low Qp values describe a high attenuating medium, in agreement with the results of Calò and Tramelli (2018) who obtained large-scale models of elastic and anelastic properties of Campi Flegrei volcanic system. In the Solfatara area they found Q_P values lower than 50. Furthermore, these Q_P values are consistent with those retrieved by other studies in different volcanic environments and with different techniques: Pujol and Smithson (1991) analyzed the seismic attenuation of the Snake River Volcanic Plain (ID, United States) using vertical seismic profiling; De Gori et al. (2005) obtained the three−dimensional Q_P structure of the Mount Etna volcano (Italy) by using local earthquake data retrieving at very shallow depths Q_P values also lower than 40; Lin et al. (2015) provided the attenuation structure of Kilauea volcano by inverting earthquake data, highlighting the presence of very attenuating bodies (Q_P lower than 30) down to 3 km depth.

The retrieved 3-D attenuation model (Figure 9) exhibits somehow different geometries and positions of the anomalies with respect to the 3-D P-wave velocity model (De Landro et al., 2017; Figure 7) which was kept fixed during the inversion of the t^∗. The differences between elastic and anelastic models could be explained as the evidence that attenuation mechanisms are related to the rock’s physical property changes in a different way than the one expected for the elastic constants. Concerning the attenuation mechanism in porous saturated rocks, Johnston et al. (1979) showed that friction on thin cracks, and grain boundaries is the dominant attenuation mechanism for consolidated rocks under most conditions in the Earth’s upper crust. Increasing pressure decreases the number of cracks contributing to attenuation by friction, thus decreasing the attenuation. Water wetting of cracks and pores reduces the friction coefficient, facilitating the sliding, and thus increasing the attenuation. So, the attenuation in rocks strongly depends on the fluid physical state and rock saturation conditions, and it generally varies much more than the seismic velocities as a result of the changes in the physical state of materials (Toksöz et al., 1979).

The 3-D attenuation model images the shallow Solfatara crater as a very complex volume. The Solfatara crater is mainly composed by volcanic sediments more or less consolidated and saturated by the hydrothermal fluids (Isaia et al., 2015; De Landro et al., 2017).

The retrieved very low Q_P values, which are usually interpreted, in a volcanic environment, as the effect of loose and very porous volcanic sediments (Clawson et al., 1989; Gudmundsson et al., 2004; De Gori et al., 2005) well fit with the expected low degree of consolidation of the shallowest materials. This is confirmed by the very low Vp values obtained by De Landro et al. (2017) and Gammaldi et al. (2018) at the very shallow depths of the Solfatara crater. In this case, both the velocity and attenuation parameters are mainly affected by the lithology.

Concerning the presence of hydrothermal fluids, the NE part of the investigated area, characterized by with high P-wave velocity values, can be associated to the shallow release of the CO₂ plume through the main fumaroles (see Stufe di Nerone in Figure 2; De Landro et al., 2017; Gresse et al., 2017). The observed presence of low attenuating bodies, mainly at about 30 m of depth, but also at middle depths, is in agreement with this interpretation (Ito et al., 1979).

The SW part of the investigated medium is located very close the Fangaia area (Figure 2), water-saturated and replenished from deep aquifers (Gresse et al., 2017). In spite of a well-defined V_P anomaly, mainly at depths greater than 15 m (Figure 7), in this work we retrieved a more heterogeneous distribution of attenuation bodies. This may be related to different conditions of saturation of volcanic sediments in that subsoil volume (Winkler and Nur, 1979).

Then, the results provided by our methodology fit well with the knowledge of the area arising from the previous geophysical studies, allowing us to be more confident about the robustness of methodology.

Conclusion

Our work describes a methodology that can be applied on active seismic data-sets acquired in complex geological volumes, in order to infer a complete description of the anelastic properties of the investigated medium. The methodology has been applied to the shallow Solfatara crater (Southern Italy).

First, we obtained new t^∗ measurements from the most recent active seismic survey at the Solfatara crater by applying the spectral decay method in the frequency domain. In order to correct the source effect on the recorded signal, the cross-correlation of the time series with the sweep function was performed. Then, we determined a 1-D Q_P model by applying a grid-search technique aimed at finding the 3-gradient 1-D Q_P model which greatly minimized the misfit between the observed and the theoretical t^∗. By mapping the t^∗ residual with respect to the 1-D average Q_P optimized model, and by averaging them over all the stations and sources, we were able to validate the t^∗ measurements by verifying the lateral coherence of residual values and, so, identifying outliers as data associated to incoherent t^∗ residuals. Then, we obtained a 3-D high-resolution Q_P attenuation model for the Solfatara crater, with an unprecedented spatial resolution, by inverting the t^∗ measurements and starting from the 1-D Q_P optimized model.

In that way, we were able to image the anelastic properties of the shallowest depths of the Solfatara crater, down to about 30 m obtaining results consistent with the previous knowledge of the area.

In summary:

1. The Q_P retrieved values, ranging between 5 and 40, are in agreement with previous results obtained at the Campi Flegrei larger scale and in other volcanic environments (Pujol and Smithson, 1991; De Gori et al., 2005; Lin et al., 2015; Calò and Tramelli, 2018);

2. The shallow low Q_P values well correlate with the low Vp values at the same depth, indicating the low degree of consolidation of the shallowest crater materials, in accordance with other studies in volcanic environments (Clawson et al., 1989; Gudmundsson et al., 2004; De Gori et al., 2005);

3. The NE part of the investigated area is characterized by higher Q_P values than the average ones and high Vp bodies in agreement with the interpretation of an area of shallow release of the CO₂ plume through the main fumaroles (Isaia et al., 2015; Gresse et al., 2017).

The reliability of the obtained attenuation images of such heterogeneous, geologically complex and small-scale volcanic area like Solfatara crater makes us confident about the robustness of the proposed technique.

As shown by Amoroso et al. (2017), the attenuation images are complementary to the velocity ones and allow to better constrain the quantitative determination of rock micro-parameters (porosity, degree of saturation, type of permeating fluids) through a rock physical modeling. This procedure will provide more comprehensive information about fluid circulation in the subsoil, that is of great importance not only in volcanic areas, but also in tectonic and underground exploitation ones (i.e., hydrocarbon extraction and storage, hydraulic fracturing, stimulation of geothermal fields, etc.).

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

VS worked at the t^∗ measurements and the 1D reference model obtainment. GR and GD worked at the inversions obtaining the 3D tomographic model. OA, GD, VS, GR, and AZ were involved in the discussion of the different phases of the data analysis and inversion. GD, VS, GR, OA, GF, and AZ were involved in model analysis and interpretation of results. GD and VS wrote the manuscript and prepared the figures. All co-authors were involved in the review of the manuscript.

Funding

This work has been a part of the MED-SUV project. MED-SUV has received funding from the European Union’s Seventh Program for research, technological development, and demonstration under the grant agreement no. 308665.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors wish to thank the editor, reviewers, and Valerio Acocella for their valuable comments, which have contributed to improve the quality of the manuscript. The authors also thank all the members of the RISSC-Lab of the Department of Physics (University of Naples Federico II) who have taken part in the RICEN experiment. The authors would like to acknowledge the CNR- IAMC for providing instrumentation and personnel for the survey.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2019.00295/full#supplementary-material

References

Achauer, U., Greene, L., Evans, J. R., and Iyer, H. M. (1986). Nature of the magma chamber underlying the mono craters area, Eastern California, as determined from Teleseismic travel time residuals. J. Geophys. Res. 91, 13873–13891.

Google Scholar

Aki, K., and Richards, P. G. (1980). Quantitative Seismology, Theory and Methods. San Francisco: W. H. Freeman.

Google Scholar

Amoroso, O., Ascione, A., Mazzoli, S., Virieux, J., and Zollo, A. (2014). Seismic imaging of a fluid storage in the actively extending Apennine mountain belt, southern Italy. Geophys. Res. Lett. 41, 3802–3809. doi: 10.1002/2014GL060070

CrossRef Full Text | Google Scholar

Amoroso, O., Festa, G., Bruno, P. P., D’Auria, L., De Landro, G., Di Fiore, V., et al. (2018). Integrated tomographic methods for seismic imaging and monitoring of volcanic caldera structures and geothermal areas. J. Appl. Geophys. 156, 16–30. doi: 10.1016/j.jappgeo.2017.11.012

CrossRef Full Text | Google Scholar

Amoroso, O., Russo, G., De Landro, G., Garambois, S., Mazzoli, S., Parente, M., et al. (2017). From velocity and attenuation tomography to rock physical modeling: inferences on fluid driven earthquake processes at the Irpinia fault system in southern Italy. Geophys. Res. Lett. 44, 6752–6760. doi: 10.1002/2016gl072346

CrossRef Full Text | Google Scholar

Battaglia, J., Zollo, A., Virieux, J., and Dello Iacono, D. (2008). Merging active and passive data sets in travel time tomography: the case study of Campi Flegrei caldera (southern Italy). Geophys. Prospect. 56, 555–573. doi: 10.1111/j.1365-2478.2007.00687.x

CrossRef Full Text | Google Scholar

Bisrat, S. T., DeShon, H. R., Pesicek, J., and Thurber, C. (2013). High-resolution 3-D P wave attenuation structure of the new madrid seismic zone using local earthquake tomography. J. Geophys. Res. 119, 409–424. doi: 10.1002/2013JB010555

CrossRef Full Text | Google Scholar

Brittle, K. F., Lines, L. R., and Dey, A. K. (2001). Vibroseis deconvolution: a comparison of crosscorrelation and frequency-domain sweep deconvolution. Geophys. Prospect. 49, 675–686. doi: 10.1046/j.1365-2478.2001.00291.x

CrossRef Full Text | Google Scholar

Bruno, P. P. G., Maraio, S., and Festa, G. (2017). The shallow structure of Solfatara Volcano, Italy, revealed by dense, wide-aperture seismic profiling. Sci. Rep. 7:17386. doi: 10.1038/s41598-017-17589-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Bruno, P. P. G., Ricciardi, G. P., Petrillo, Z., Di Fiore, V., Troiano, A., and Chiodini, G. (2007). Geophysical and hydrogeological experiments from a shallow hydrothermal system at solfatara volcano, campi flegrei, italy: response to caldera unrest. J. Geophys. Res. 112, 17386.

Google Scholar

Byrdina, S., Vandemeulebrouck, J., Cardellini, C., Legaz, A., Camerlynck, C., Chiodini, G., et al. (2014). Relations between electrical resistivity, carbon dioxide flux, and self-potential in the shallow hydrothermal system of Solfatara (Phlegrean Fields, Italy). J. Volcanol. Geother. Res. 283, 172–182. doi: 10.1016/j.jvolgeores.2014.07.010

CrossRef Full Text | Google Scholar

Calò, M., and Tramelli, A. (2018). Anatomy of the campi flegrei caldera using enhanced seismic tomography models. Sci. Rep. 8:16254. doi: 10.1038/s41598-018-34456-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Chiodini, G., Frondini, F., Cardellini, C., Granieri, D., Marini, L., and Ventura, G. (2001). CO2 degassing and energy release at solfatara volcano, phlegraean fields, Italy. J. Geophys. Res. 106, 16213–16221. doi: 10.1029/2001jb000246

CrossRef Full Text | Google Scholar

Chiodini, G., Paonita, A., Aiuppa, A., Costa, A., Caliro, S., De Martino, P., et al. (2016). Magmas near the critical degassing pressure drive volcanic unrest towards a critical state. Nat. Commun. 7:13712. doi: 10.1038/ncomms13712

PubMed Abstract | CrossRef Full Text | Google Scholar

Clawson, S. R., Smith, R. B., and Benz, H. M. (1989). P wave attenuation of the Yellowstone Caldera from three-dimensional inversion of spectral decay using explosion source seismic data. J. Geophys. Res. Solid Earth 94, 7205–7222. doi: 10.1029/JB094iB06p07205

CrossRef Full Text | Google Scholar

Dawson, P., Chouet, B., and Pitt, A. (2016). Tomographic image of a seismically active volcano: mammoth mountain, California. J. Geophys. Res. Solid Earth 121, 114–133. doi: 10.1002/2015JB012537

CrossRef Full Text | Google Scholar

Dawson, P. B., Iyer, H. M., and Evans, J. R. (1992). “Three-dimensional Imaging of the crust and upper mantle in the long Valley-mono craters region, California, Using teleseismic P-wave residuals,” in Proceedings of the IAVCEI, Volcanology, Volcanic seismology, eds R. Scarpa, P. Gasparini, and K. Aki (Heidelberg: Springer-Verlag Berlin), 3, 339–358. doi: 10.1007/978-3-642-77008-1_23

CrossRef Full Text | Google Scholar

De Gori, P., Chiarabba, C., and Patan, E. D. (2005). QP structure of mount etna: constraints for the physics of the plumbing system. J. Geophys. Res. 110:B05303. doi: 10.1029/2003JB002875

CrossRef Full Text | Google Scholar

De Landro, G., Serlenga, V., Russo, G., Amoroso, O., Festa, G., Bruno, P. P., et al. (2017). 3-D ultra-high resolution seismic imaging of shallow solfatara crater in campi flegrei (Italy): new insights on deep hydrothermal fluid circulation processes. Sci. Rep. 7:3412. doi: 10.1038/s41598-017-03604-3600

CrossRef Full Text | Google Scholar

de Lorenzo, S., Zollo, A., and Mongelli, F. (2001). Source parameters and three-dimensional attenuation structure from the inversion of microearthquake pulse width data: QP imaging and inferences on the thermal state of campi flegrei caldera (Southern Italy). J. Geophys. Res. 106, 265–286. doi: 10.1029/2000JB900462

CrossRef Full Text | Google Scholar

Der, Z. A., and McElfresh, T. W. (1976). Short-period P-wave attenuation along various paths in North America as determined from P-wave spectra of the salmon nuclear explosion. Bull. Seism. Soc. Am. 66, 1609–1622.

Google Scholar

Galluzzo, D., Del Pezzo, E., la Rocca, M., Castellano, M., and Bianco, F. (2009). Source scaling and site effects at vesuvius Volcano. Bull. Seism. Soc. Am. 99, 1705–1719. doi: 10.1785/0120080142

CrossRef Full Text | Google Scholar

Gammaldi, S., Amoroso, O., D’Auria, L., and Zollo, A. (2018). High resolution, multi-2D seismic imaging of solfatara crater (campi flegrei caldera, southern Italy) from active seismic data. J. Volcanol. Geother. Res. 357, 177–185. doi: 10.1016/j.volgeores.2018.03.025

CrossRef Full Text | Google Scholar

Gibson, B., and Larner, K. (1984). Predictive deconvolution and the zero-phase source. Geophysics 49, 379–397. doi: 10.1190/1.1441674

CrossRef Full Text | Google Scholar

Gresse, M., Vandemeulebrouck, J., Byrdina, S., Chiodini, G., Revil, A., Johnson, T. C., et al. (2017). Three -dimensional electrical resistivity tomography of the solfatara crater (italy): implication for the multiphase flow structure of the shallow hydrothermal system. J. Geophys. Res. 122, 8749–8768. doi: 10.1002/2017jb014389

CrossRef Full Text | Google Scholar

Gudmundsson, O., Finlayson, D. M., Itikarai, I., Nishimura, Y., and Johnson, J. R. (2004). Seismic attenuation at rabaul volcano, Papua New Guinea. J. Volcanol. Geother. Res. 130, 77–92. doi: 10.1016/S0377-0273(03)00282-288

CrossRef Full Text | Google Scholar

Improta, L., Bagh, S., De Gori, P., Valoroso, L., Pastori, M., Piccinini, D., et al. (2017). Reservoir structure and wastewater-induced seismicity at the Val d’Agri oilfield (Italy) shown by three-dimensional Vp and Vp/Vs local earthquake tomography. J. Geophys. Res. Solid Earth 122, 9050–9082. doi: 10.002/2017JB014725

CrossRef Full Text | Google Scholar

Isaia, R., Vitale, S., Di Giuseppe, M. G., Iannuzzi, E., Assisi Tramparulo, F. D., and Troiano, A. (2015). Stratigraphy, structure, and volcano-tectonic evolution of Solfatara maar-diatreme (Campi Flegrei, Italy). Geol. Soc. Am. Bull. 127, 1485–1504. doi: 10.1130/B31183.1

CrossRef Full Text | Google Scholar

Ito, H., DeVilbiss, J., and Nur, A. (1979). Compressional and shear waves in saturated rock during water-steam transition. J. Geophys. Res. 84, 4731–4735. doi: 10.1029/JB084iB09p04731

CrossRef Full Text | Google Scholar

Johnston, D. H., Toksöz, M. N., and Timur, A. (1979). Attenuation of seismic waves in dry and saturated rocks: II. Mechanisms. Geophysics 44, 691–711. doi: 10.1190/1.1440970

CrossRef Full Text | Google Scholar

Judenherc, S., and Zollo, A. (2004). The bay of naples (southern Italy): constraints on the volcanic structure inferred from a dense seismic survey. J. Geophys. Res. 109:B10312. doi: 10.1029/2003JB002876

CrossRef Full Text | Google Scholar

Kanamori, H. (1967a). Spectrum of P and PcP in relation to the mantle-core boundary and attenuation in the mantle. J. Geophys. Res. 72, 559–571. doi: 10.1029/JZ072i002p00559

CrossRef Full Text | Google Scholar

Kanamori, H. (1967b). Spectrum of short-period core phases in relation to the attenuation in the mantle. J. Geophys. Res. 72, 2182–2186. doi: 10.1029/JZ072i008p02181

CrossRef Full Text | Google Scholar

Kissling, E., Ellsworth, W. L., Eberhart-Phillips, D., and Kradolfer, U. (1994). Initial reference models in local earthquake tomography. J. Geophys. Res. 99, 19635–19646. doi: 10.1029/93jb03138

CrossRef Full Text | Google Scholar

Latorre, D., Virieux, J., Monfret, T., Monteiller, V., Vanorio, T., Got, J. L., et al. (2004). A new seismic tomography of aigion area (Gulf of Corinth, Greece) from the 1991 data set. Geophys. J. Int. 159, 1013–1031. doi: 10.1111/j.1365-246x.2004.02412.x

CrossRef Full Text | Google Scholar

Lin, G., Shearer, P. M., Amelung, F., and Okubo, P. G. (2015). Seismic tomography of compressional wave attenuation structure for kilauea volcano, Hawai’i. J. Geophys. Res. Solid Earth 120, 2510–2524. doi: 10.1002/2014JB011594

CrossRef Full Text | Google Scholar

Martinez-Arevalo, C., Patan, E. D., Rietbrock, A., and Ibanez, J. M. (2005). The intrusive process leading to the Mt. Etna 2001 flank eruption: constraints from 3-D attenuation tomography. Geophys. Res. Lett. 32:L21309. doi: 10.1029/2005GL023736

CrossRef Full Text | Google Scholar

Menke, W. (1989). Geophysical Data Analysis: Discrete Inverse Theory. New York, NY: Academic Press, Inc.

Google Scholar

Michelini, A., and McEvilly, T. V. (1991). Seismological studies at Parkfield. I. Simultaneous inversion for velocity structure and hypocenters using cubic B-splines parameterization. Bull. Seismol. Soc. Am. 81, 524–552.

Google Scholar

Pujol, J., and Smithson, S. (1991). Seismic attenuation in volcanic rocks from VSP experiments. Geophysics 56, 1441–1455. doi: 10.1190/1.1443164

CrossRef Full Text | Google Scholar

Rawlinson, N., Reading, A. M., and Kennet, B. L. N. (2006). Litospheric structure of Tasmania from a novel form of teleseismic tomography. J. Geophys. Res. 111:B02301. doi: 10.1029/2005JB/2005JB003803

CrossRef Full Text | Google Scholar

Rawlinson, N., and Spakman, W. (2016). On the use of sensitivity tests in seismic tomography. Geophys. J. Int. 205, 1221–1243. doi: 10.1093/gji/ggw084

CrossRef Full Text | Google Scholar

Rietbrock, A. (2001). P wave attenuation structure in the fault area of the 1995 Kobe earthquake. J. Geophys. Res. 106, 4141–4154. doi: 10.1029/2000jb900234

CrossRef Full Text | Google Scholar

Sams, M., and Goldberg, D. (1990). The validity of Q estimates from borehole data using spectral ratios. Geophysics 55, 97–101. doi: 10.1190/1.1442776

CrossRef Full Text | Google Scholar

Sanders, C. O., Ponko, S. C., Nixon, L. D., and Schwarts, E. A. (1995). Seismological evidence for magmatic and hydrothermal structure in Long Valley caldera from local earthquake attenuation and velocity tomography. J. Geophys. Res. 100, 8311–8326. doi: 10.1029/95jb00152

CrossRef Full Text | Google Scholar

Scala, A., Serra, M., Festa, G., and Roux, P. (2019). Insight into the wave scattering properties of the Solfatara Volcano. Front. Earth Sci. 14:56. doi: 10.3389/feart.2019.00307

CrossRef Full Text | Google Scholar

Schurr, B., Asch, G., Rietbrock, A., Trumbull, R., and Haberland, C. (2003). Complex patterns of fuid and melt transport in the central andean subduction zone revealed by attenuation tomography. Earth Planet. Sci. Lett. 205, 105–119. doi: 10.1016/s0012-821x(03)00441-2

CrossRef Full Text | Google Scholar

Serlenga, V., de Lorenzo, S., Russo, G., Amoroso, O., Garambois, S., Virieux, J., et al. (2016). A three-dimensional QP imaging of the shallowest subsurface of Campi Flegrei offshore caldera, southern Italy. Geophys. Res. Lett. 43:218. doi: 10.1002/2016GL071140

CrossRef Full Text | Google Scholar

Serra, M., Festa, G., Roux, P., Gresse, M., Vandemeulebrouck, J., and Zollo, A. (2016). A strongly heterogeneous hydrothermal area imaged by surface waves: the case of Solfatara, Campi Flegrei, Italy. Geophys. J. Int. 205, 1813–1822. doi: 10.1093/gji/ggw119

CrossRef Full Text | Google Scholar

Siniscalchi, A., Tripaldi, S., Romano, G., Chiodini, G., Improta, L., Petrillo, Z., et al. (2019). Reservoir structure and hydraulic properties of the campi flegrei geothermal system inferred by audiomagnetotelluric, geochemical and seismicity study. J. Geophys. Res. 124, 5336–5356. doi: 10.1029/2018JB016514

CrossRef Full Text | Google Scholar

Teng, T. (1968). Attenuation of body waves and the Q structure of the mantle. J. Geophys. Res. 73, 2195–2208. doi: 10.1029/JB073i006p02195

CrossRef Full Text | Google Scholar

Thurber, C., and Ritsema, J. (2007). “Theory and observations – seismic tomography and inverse methods,” in Treatise on Geophysics, ed. G. Schubert, (Amsterdam: Elsevier).

Google Scholar

Toksöz, M. N., Johnston, D. H., and Timur, A. (1979). Attenuation of seismic waves in dry and saturated rocks: I. Laboratory measurements. Geophysics 44, 681–690. doi: 10.1190/1.1440969

PubMed Abstract | CrossRef Full Text | Google Scholar

Toomey, D. R., and Foulger, G. R. (1989). Tomographic inversion of local earthquake data from the hengill-grensdalur central volcano complex, Iceland. J. Geophys. Res. 94, 497–517. doi: 10.1029/JB094iB12p17497

CrossRef Full Text | Google Scholar

Vanorio, T., Virieux, J., Capuano, P., and Russo, G. (2005). Three-dimensional seismic tomography from P wave and S wave microearthquake travel times and rock physics characterization of the Campi Fields Caldera. J. Geophys. Res. 110:B03201. doi: 10.1029/2004JB003102

CrossRef Full Text | Google Scholar

Winkler, K., and Nur, A. (1979). Pore fluids and seismic attenuation in rocks. Geophys. Res. Lett. 6, 1–4. doi: 10.1029/GL006i001p00001

PubMed Abstract | CrossRef Full Text | Google Scholar

Zollo, A., Maercklin, N., Vassallo, M., Dello Iacono, D., Virieux, J., and Gasparini, P. (2008). Seismic reflections reveal a massive melt layer feeding campi flegrei caldera. J. Geophys. Res. 35:L12306. doi: 10.1029/2008GL034242

CrossRef Full Text | Google Scholar

Zollo, A., Orefice, A., and Convertito, V. (2014). Source parameter scaling and radiation efficiency of microearthquakes along the irpinia fault zone in southern apennines. Italy. J. Geophys. Res. 119, 3256–3275. doi: 10.1002/2013JB010116

CrossRef Full Text | Google Scholar