- 1COMET, School of Earth and Environment, University of Leeds, Leeds, United Kingdom
- 2Department of Hydrology and Atmospheric Science, The University of Arizona, Tucson, AZ, United States
- 3Planetary Science Institute, Tucson, AZ, United States
- 4Water, Sediment, Hazards, and Earth-surface Dynamics (waterSHED) Lab, Department of Geoscience, University of Calgary, Calgary, AB, Canada
- 5Department of Geology, College of Arts and Sciences, University of Dayton, Dayton, OH, United States
- 6Department of System and Industrial Engineering, College of Engineering, The University of Arizona, Tucson, AZ, United States
- 7Department of Aerospace and Mechanical Engineering, College of Engineering, The University of Arizona, Tucson, AZ, United States
The formation and expansion of Himalayan glacial lakes has implications for glacier dynamics, mass balance and glacial lake outburst floods (GLOFs). Subaerial and subaqueous calving is an important component of glacier mass loss but they have been difficult to track due to spatiotemporal resolution limitations in remote sensing data and few field observations. In this study, we used near-daily 3 m resolution PlanetScope imagery in conjunction with an uncrewed aerial vehicle (UAV) survey to quantify calving events and derive an empirical area–volume relationship to estimate calved glacier volume from planimetric iceberg areas. A calving event at Thulagi Glacier in 2017 was observed by satellite from before and during the event to nearly complete melting of the icebergs, and was observed in situ midway through the melting period, thus giving insights into the melting processes. In situ measurements of Thulagi Lake’s surface and water column indicate that daytime sunlight absorption heats mainly just the top metre of water, but this heat is efficiently mixed downwards through the top tens of metres due to forced convection by wind-blown icebergs; this heat then is retained by the lake and is available to melt the icebergs. Using satellite data, we assess seasonal glacier velocities, lake thermal regime and glacier surface elevation change for Thulagi, Lower Barun and Lhotse Shar glaciers and their associated lakes. The data reveal widely varying trends, likely signifying divergent future evolution. Glacier velocities derived from 1960/70s declassified Corona satellite imagery revealed evidence of glacier deceleration for Thulagi and Lhotse Shar glaciers, but acceleration at Lower Barun Glacier following lake development. We used published modelled ice thickness data to show that upon reaching their maximum extents, Imja, Lower Barun and Thulagi lakes will contain, respectively, about 90 × 106, 62 × 106 and 5 × 106 m3 of additional water compared to their 2018 volumes. Understanding lake–glacier interactions is essential to predict future glacier mass loss, lake formation and associated hazards.
Introduction
Many ice-contact proglacial and supraglacial lakes are expanding across the central and eastern Himalaya in response to prevailing negative glacier mass balance conditions (Bolch et al., 2012; Brun et al., 2017a; Nie et al., 2017; Song et al., 2017). Proglacial lakes can form when supraglacial ponds begin to coalesce on low-gradient debris-covered glacier termini (Reynolds, 2000; Quincey et al., 2007; Benn et al., 2012). An enlarged supraglacial lake can initiate rapid calving retreat at ice cliffs (Sakai et al., 2009), expand across the width of the glacier and melt through to the glacier bed. This process can isolate the debris-covered glacier terminus, which typically remains as a stagnant (non-flowing) ice-cored moraine dam. The ice-cored moraine normally melts slowly due to the insulating debris cover (Pickard, 1983; Richardson and Reynolds, 2000b). Calving retreat of the active glacier on the up-valley side of the lake then may lead to lake expansion, until the valley floor intersects the lake level (Chinn et al., 2014), at which time the glacier physically detaches from the lake (Warren, 1991; Kirkbride, 1993; Sakai et al., 2009; Somos-Valenzuela et al., 2014; Haritashya et al., 2018). An ice-cored moraine of such a lake can erode thermally, thereby lowering and shrinking the lake. While the ice-cored moraine dam is in substantial direct contact with the lake, the system is metastable and some can be so unstable that a glacial lake outburst flood (GLOF) may occur due to dam breakup or overtopping and rapid erosional incision (Richardson and Reynolds, 2000a; ICIMOD, 2011; Rounce et al., 2017). GLOFs have large socioeconomic impacts in many regions of the world, including the Himalaya (Carrivick and Tweed, 2016), and are expected to increase in frequency in coming decades (Harrison et al., 2018), although GLOF reporting bias complicates historical trend analysis (Veh et al., 2019). Nonetheless, the physics and consequence of glacier-lake thermal and physical interactions are important to document and understand.
The glacial lake calving regime responds to lakebed topography at the calving front; water temperature, depth, their seasonal fluctuations and circulation patterns; air temperature, solar insolation, glacier debris cover and melting and glacier velocity and ice thickness at the calving front (Kirkbride and Warren, 1997; Rohl, 2006; Benn et al., 2007; Sakai et al., 2009). Calving can become an important component of mass loss for glaciers terminating into proglacial lakes (Sakai et al., 2009; Carrivick and Tweed, 2013; Maurer et al., 2016) and can decouple glacier mass loss from climate forcing due to heat absorption by the lake (Bolch et al., 2012). Glaciers typically exhibit high rates of mass loss close to the glacier terminus due to direct melting and thinning at the lower elevations, but for non-calving debris-covered glaciers the maximum ablation rates are commonly shifted up-glacier due to the influence of the thickest insulating debris near the terminus (Reznichenko et al., 2010; Benn et al., 2012). When calving into a proglacial lake is involved, mass loss is shifted dramatically to the calving front (Bolch et al., 2011; Thakuri et al., 2016; King et al., 2018). However, rates of mass loss are spatially variable on both calving and non-calving glaciers due to variable debris thickness and the distribution of supraglacial ponds and ice cliffs (Nicholson and Benn, 2013; Immerzeel et al., 2014; Buri et al., 2016; Miles et al., 2017; Watson et al., 2017b), and variations in microclimate parameters, such as due to radiative and climatic orography (Heynen et al., 2016). Recently, it was shown that Himalayan glaciers connecting with larger proglacial lakes are shrinking more rapidly than glaciers lacking them (Maurer et al., 2019). That finding is consistent with limnological control of glacier dynamics adding to or sometimes exceeding climatic control (Haritashya et al., 2018), as first conceived for Tasman Glacier and its lake (Kirkbride and Warren, 1997), which evolved much as predicted by Kirkbride and Warren (Chinn et al., 2014).
Observations of calving and the presence of icebergs in Himalayan glacial lakes have received little attention due to infrequent satellite observations capable of resolving the icebergs and difficult field access. However, icebergs and ice rafted debris hinder glacial lake classification when misclassified as glacier or land (Strozzi et al., 2012). Deriving the volume of floating ice could be used to infer subaerial or subaqueous calved volume, the latter of which cannot be discerned by differencing digital elevation models (DEMs). Multitemporal DEMs were used to derive iceberg volume change and an empirical relationship between iceberg area and volume for Greenland icebergs, allowing volume to be estimated using only a satellite-derived iceberg area (Enderlin and Hamilton, 2014; Sulak et al., 2017). A similar approach could be valuable for assessing calving events at Himalayan glacial lakes. Additionally, satellite-derived water temperatures were used to discriminate the hydrological connectivity of Himalayan supraglacial lakes and the available energy to melt additional glacier ice during lake expansion or drainage (Wessels et al., 2002). However, the time series of satellite-derived thermal data from the ASTER and Landsat programmes has not yet been exploited to explore water temperatures and seasonal variation affecting the lake–glacier interface.
In this study, we used optical and thermal satellite data and field surveys to quantify calving, thermal regime and calving events at the proglacial Thulagi Lake in Nepal. We then compare Thulagi to two rapidly expanding proglacial lakes at higher altitude (Imja and Lower Barun) (Figure 1). Our objectives are to: (1) quantify the areal evolution of icebergs at Thulagi Lake following multiple calving events in 2017; (2) assess the utility of deriving area-volume relationships for icebergs using DEMs of their above-surface topography and (3) investigate the role of calving and lake thermal regimes on glacier dynamics and future lake expansion.
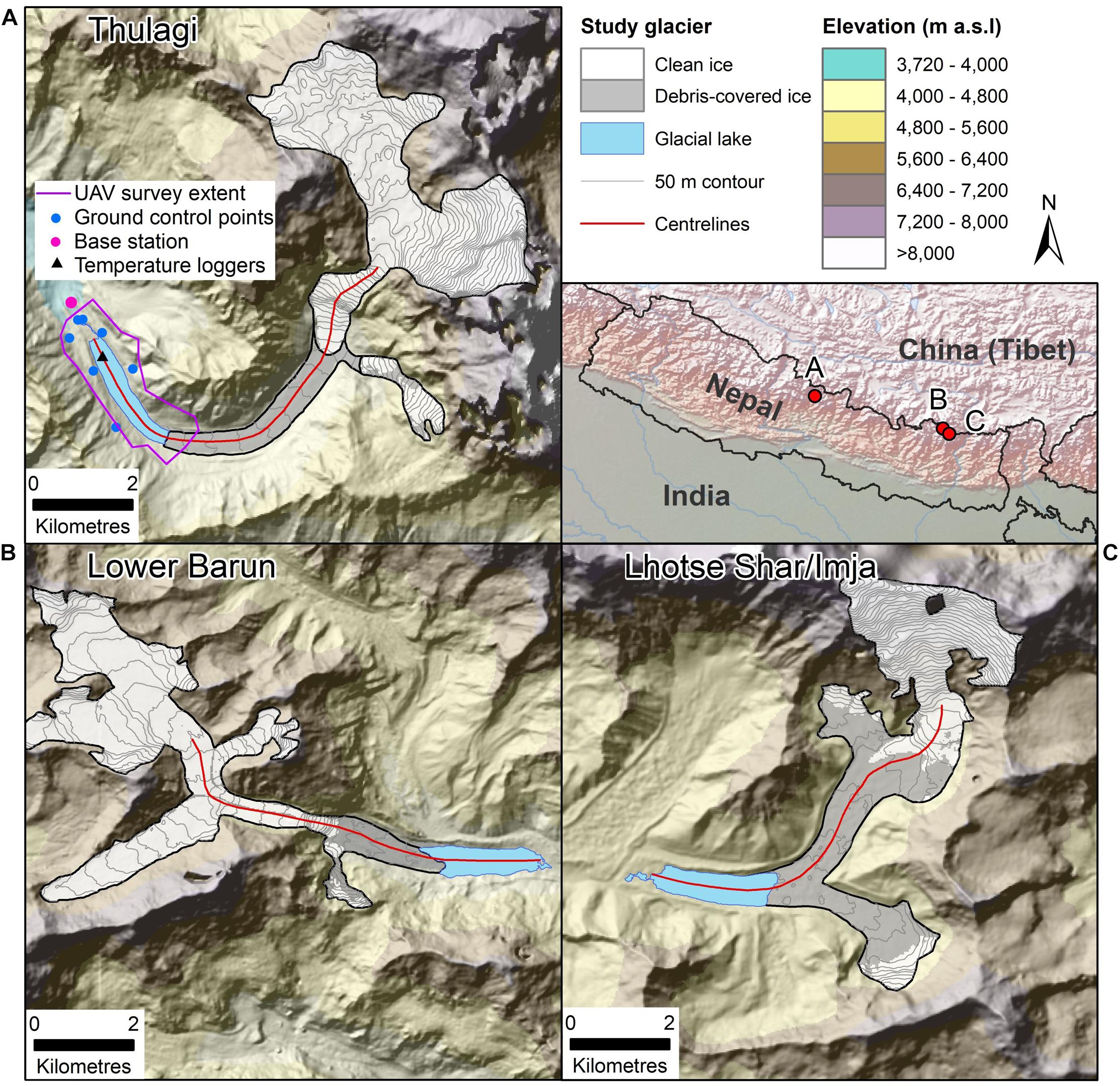
Figure 1. Location of the study glaciers and lakes in Nepal. (A–C) Elevations and hillshades are from the AW3D30 DEM. Debris-covered extents are shown from Kraaijenbrink et al. (2017). The inset has a Natural Earth shaded relief background.
study Sites and Methods
Study Sites
Thulagi, Lower Barun and Imja glacial lakes are located at altitudes of ∼4045, 4538 and 5005 m a.s.l., with maximum observed depths of 76 m (October 2017), 205 m (October 2015) and 150 m (October 2014), respectively (Table 1) (Haritashya et al., 2018). ICIMOD (2011) classified all three lakes as Category 1 high priority lakes for extensive field investigation and mapping due to their high potential GLOF hazard. Rounce et al. (2017) classified Thulagi and Imja lakes as moderate hazards due to the lack of avalanche trajectories that could enter the lakes, whereas Lower Barun was classified as a high hazard. Along the glacier centreline, Thulagi Lake expanded by 203 m (2008–2018) compared to 614 m for Lower Barun and 729 m for Imja (Haritashya et al., 2018). Imja Lake was reportedly lowered by 3 m in 2016 to reduce its hazard but a corresponding change in lake area was unclear (Lala et al., 2018).
Thulagi Lake Field Surveys
An uncrewed aerial vehicle (UAV) survey was flown at Thulagi Lake on 27 October 2017 using a DJI Phantom 4 Pro + operated from the lake shore. The UAV collected still images every 2 s with an oblique viewing angle, which were processed following a structure from motion with multi-view stereo (hereafter SfM) workflow to generate topography and an orthophoto (e.g. James and Robson, 2012; Westoby et al., 2012; Smith et al., 2015) (section ‘Structure-From-Motion Model Generation and Iceberg Volume’). Ground control points (G) were collected around the lake on lateral moraines and stable ground in October 2018 using Emlid Reach RS L1 Global Navigation Satellite System (GNSS) receivers (Figure 1A). GCPs were collected on large boulders that were occupied with a receiver for approximately 10 min at each point. A second receiver was used as a temporary base station.
The vertical water temperature profile was measured at Thulagi Lake using six temperature sensors on a rope that were set to log with a 10-min interval (28–30 October 2017). The rope was suspended by buoys at the lake surface and anchored by a rock on the lakebed, and contained one sensor slightly submerged (a few centimetres deep) near the lake surface and at depths of 1, 2, 5, 10 and 55 m (on the lakebed). Except for the sensor on the lakebed, the sensors (TinyTag TGC-0020) were rated to 15 m maximum depth with a manufacturer stated accuracy of ∼0.5°C. The temperature sensor on the lakebed (TinyTag Aquatic 2) was rated to 500 m maximum depth with an accuracy of 0.5°C. Temperature sensor calibration in a controlled temperature environment (4.5°C) indicated a relative accuracy (precision) of ± 0.04°C. A HOBO Onset MX2001 (accuracy ± 0.44°C) was used to measure the water temperature at ∼1 m depth in the outlet of Thulagi Lake.
The downwelling panchromatic light intensity in the water column, integrated over nearly a hemisphere, was measured using a Li-Cor sensor down to about four metres depth. The light field also must involve upwelling light, but this is a small fraction of the downwelling beam and was not measured. The measurements were recorded as a function of time, and depth was reconstructed based on the deployment geometry of the cable connected to the sensor and the known distance interval as the sensor was increasingly submerged to record light intensity. Several profiles were taken, but we use only the highest quality profile; the others were disturbed by the passage of clouds, the accidental movement of the kayak over the light sensor, instability of the deployment geometry and so on. With the best quality profile, the light sensor was deployed in such a way as to minimise the interference by the kayak, from which the sensor was deployed. The sky was slightly hazy but gave uniform incident solar radiation, with no dense clouds or clearings passing by during the measurements. The light field was first measured just above and just beneath the water surface. Then the sensor cable, to which we had applied length markings to provide submergence information, was extended by fixed increments to the best of our ability to maintain steady manual deployment and for kayak station keeping relative to the cable deployment point. The deployment methodology allowed the vertical depth of the sensor, hence the vertical profile of downwelling light intensity, to be reconstructed. The water was optically thick (deep), such that no bottom reflectance was sensed.
Iceberg Calving
Iceberg Delineation
The areal extent of glacier calving and icebergs were derived using 35 PlanetScope satellite images collected 16 April 2017–28 November 2017 with acquisition times ranging from 10:01 AM Nepal Time (NPT) to 11:12 AM (Supplementary Table S1). The imagery were acquired at ∼3.7 m resolution but delivered at 3 m resolution after orthorectification and processing to surface reflectance (Planet Team, 2019). Icebergs were semi-automatically classified in cloud-free satellite imagery using manually determined thresholds (t) applied to a normalised difference water index (NDWI) band ratio of near-infrared (NIR) and green 3 m resolution PlanetScope bands (Eq. 1) (Figure 2A).
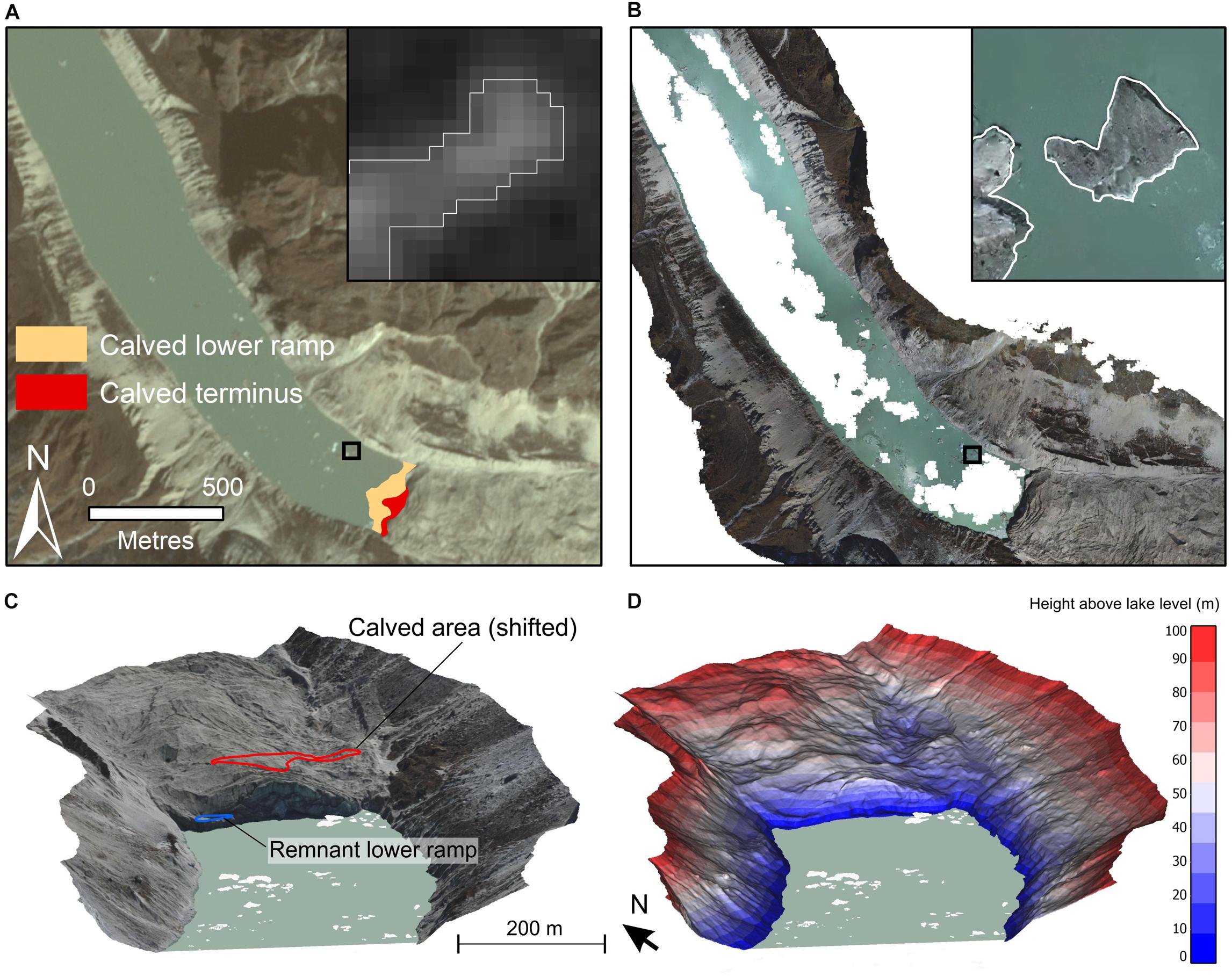
Figure 2. (A) Calved area of Thulagi Glacier shown on a PlanetScope satellite image (27 October 2017). Inset shows iceberg classification (white polygon) on an NDWI image. (B) Orthophoto generated from UAV flights on 27 October 2017. Inset shows the same icebergs as A. (C) Oblique view of the structure-from-motion model showing icebergs (white) and the calved area shifted up-glacier in order to estimate the calving event volume. (D) Height above lake level used to estimate the volume of the calved area.
NDWIIceberg thresholds ranged from −0.23 to 0.01 and were determined through manual inspection of iceberg classification with NIR, blue and red band false colour composites. The thresholded band ratio image was masked to the lake boundary and was used to extract the area and number of icebergs in each image (e.g. Figure 2A). Manual adjustment of the iceberg polygons was required in several cases to remove areas of brash ice or of shadow at the calving front in some images. Uncertainty in the iceberg delineation was estimated using a ± 0.5 pixel boundary to account for systematic over- or under-estimation of iceberg area due to the use of variable band ratio thresholds. The relative precision of image-to-image area measurements is better than the absolute accuracy; hence, we also report the random uncertainty following Krumwiede et al. (2014).
Structure-From-Motion Model Generation and Iceberg Volume
Images from the UAV survey (n = 431) were processed in Agisoft Photoscan 1.3.5 following an SfM workflow with ‘high’ quality settings. Points with a reprojection error > 0.6 pixels and clear outliers were excluded from the sparse point clouds. Dense point clouds were used to generate a DEM and orthophoto at 0.5 and 0.2 m resolution, respectively. Seven GCPs within the UAV survey extent were used to georeference the model. GNSS data were processed using RTKLIB (RTKPOST v.2.4.3. Emlid b28) using precise global positioning system (GPS) and global navigation satellite system (GLONASS) ephemeris data. First, the temporary base station data were processed against the UNAVCO permanent base station at Lamjung (∼38 km away). Second, the mobile rover data were processed against the corrected temporary base station location to extract GCPs for use in the SfM model. The final model had a root-mean-square error (RMSE) of 0.56 m.
Icebergs were manually digitised in Photoscan using the generated orthophoto (Figure 2B). We could not use the spectral ratio above to delineate icebergs in the UAV imagery since the onboard camera only had RGB bands. The iceberg polygons were used to clip the dense point cloud, which was then rasterised at 0.5 m resolution in CloudCompare using the mean point elevation in each cell. Above-surface iceberg volumes were calculated using the iceberg elevation above the lake level, which was derived through inspection of the shoreline elevation in the SfM model. Two example iceberg profiles are shown in Supplementary Figure S1. The model RMSE (0.56 m) was used to derive upper and lower bounds of the lake level, which affects the relative iceberg height. Total iceberg volume was calculated assuming 91.7% of the iceberg lies beneath the water line (from an ice density of 917 kg m3).
Iceberg volumes at Lower Barun Lake were derived using a 2 m resolution DEM (15 January 2015) (Shean, 2017). The mean lake elevation respective to the DEM (4503.59 m ellipsoid), and one standard deviation (0.13 m) was calculated using a 0.3 km2 iceberg-free patch of the lake. The lake was frozen at the time of DEM acquisition, so we used a minimum elevation of 0.5 m above the lake surface to separate icebergs from the frozen and snow-covered lake surface. Icebergs were converted to polygons and manually edited where required. The total iceberg volume at Lower Barun was derived following the method applied at Thulagi Lake, but using ± 0.13 m as the lake level uncertainty, which was equal to one standard deviation of the mean lake surface elevation.
Calving Volume
The total area change at the glacier terminus due to two calving events was estimated using PlanetScope images from 16 April 2017 and 9 September 2017, which extended across both calving events (Figure 3). The glacier terminus, split into a lower ice ledge and the main glacier, was manually digitised in each image (Figure 2A). The post-calving terminus location was converted to points at 1 m intervals, which were shifted up-glacier using the summer velocity raster (section ‘Satellite Measurements of Glacier Velocity’) and a 146-day separation period to remove the effect of glacier displacement (mean of ∼7 m across the calving front). The calved area was then delineated as the area between the two terminus lines. Since pre- and post-calving DEMs were not available, we estimated the above lake height of the calved glacier using the SfM model (27 October 2017) (Figure 2D). The area of the calved glacier was manually translated up-glacier and the height values were used to calculate the above-lake volume (Figures 2C,D). Here we assume that the contemporary glacier surface was similar in morphology to the area that calved. The below-surface calved volume was estimated using lake bathymetry from Haritashya et al. (2018) within the calved area. Since the bathymetry survey did not extend fully into the calved area, we allocated depth values to NoData areas using the values of the nearest neighbour. The total calving volume was estimated as the sum of the above- and below-surface volumes for the area of calved terminus. We did not attempt to estimate the volume of the lower ledge since the height and below-surface characteristics were unknown. None of the glaciers are expected to have large sectors of their tongues in flotation except for thinned areas near the margins of the tongue (Haritashya et al., 2018) and some sections where thermal undercutting occurs (see section ‘Discussion’).
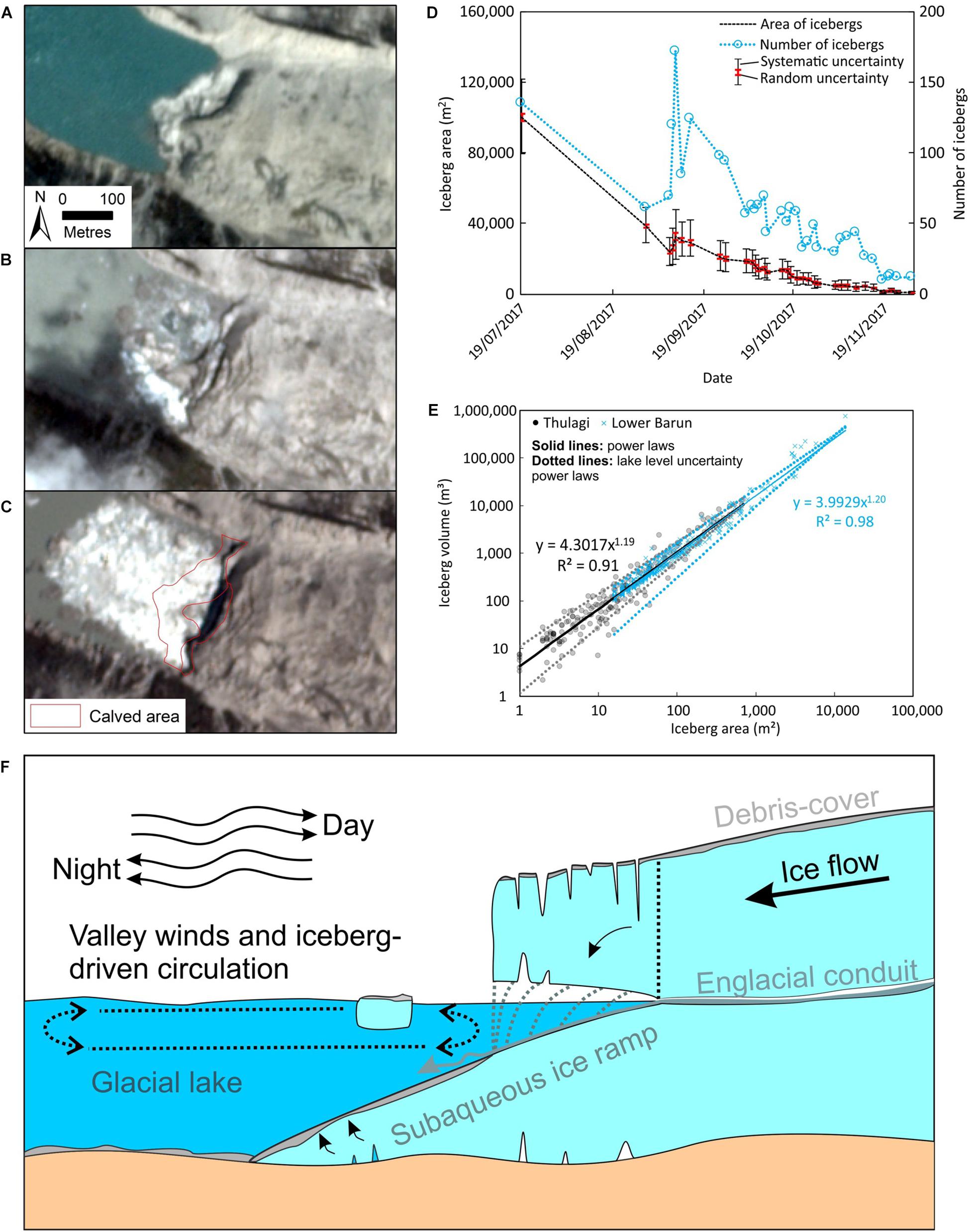
Figure 3. PlanetScope satellite image showing (A) the calving front of Thulagi Glacier on 16 April 2017, (B) 7 September 2017 and (C) post-calving (second event) 9 September 2017. (D) Area and number of icebergs on Thulagi Lake classified using PlanetScope imagery. (E) The relationship between planimetric iceberg area and total iceberg volume derived at Thulagi (n = 181) and Lower Barun (n = 389) lakes. (F) Conceptual diagram of glacier calving.
Satellite Measurements of Lake Temperature
ASTER L2 Surface Kinetic Temperature images collected 17 February 2001–27 October 2017 (10:38–11:09 NPT) were used to quantify seasonal lake temperature (Supplementary Table S2). The data are delivered at ∼100 m resolution; however, the thermal signature of each pixel is influenced by the neighbouring ∼2 pixels (Ramachandran et al., 2014). To calculate the mean lake temperature for each image, we applied an internal buffer of 150 m to the lake boundaries and used the remaining pixels in the lake interior to derive the lake temperature, excluding any pixels containing icebergs. We also used the thermal infrared bands of Landsat 5, 7 and 8, which generally had a slightly earlier acquisition time compared to ASTER (∼30 min earlier), to derive lake temperatures 2000–2018 using the Google Earth Engine (GEE)-based Landsat Land Surface Temperature tool (Parastatidis et al., 2017). The tool used a single channel algorithm applied to thermal infrared data and includes atmospheric and emissivity corrections, and the application of a cloud mask. We removed observations with a standard deviation greater than 2°C, which can signal thermal contamination from icebergs, including possible debris. The Landsat thermal observations are much more abundant than ASTER, although their spatial resolution is lower than ASTER and more model-dependent and perhaps less accurate due to having fewer bands (one band Landsat 5 and 7, two bands Landsat 8, five bands ASTER), and Landsat probably has a similar adjacency effect as ASTER.
Satellite Measurements of Glacier Velocity
Corona Pre-processing
Several studies have shown that subsets of declassified stereo Corona satellite imagery (<5 m spatial resolution, available from https://earthexplorer.usgs.gov/) can be processed using photogrammtery software packages without knowledge of the panoramic distortion model present in the imagery (Altmaier and Kany, 2002; Casana and Cothren, 2007; Watanabe et al., 2017). Here, we follow Casana and Cothren (2007) to process subsets of the imagery (∼4000 × 4000 pixels) for each glacier in Agisoft Metashape 1.5.1 by treating images as a frame camera. Ground control points were added using a Pléiades DEM and orthoimage of Imja/Lhotse Shar, and GoogleEarth for Thulagi and Lower Barun. Control point RMSE (XYZ) for the models was 5 m at Lhotse Shar, 12 m at Thulagi and 19 m at Lower Barun. We follow a similar method to that recently proposed by Cook and Dietze (2019) to align the Corona images by initially processing the images from different years in the same chunk during the image alignment step, which permits matching of stable ground but does not match the dynamic glacier surface. The images from the two time periods are then separated before processing the dense cloud, DEM and co-registered orthophotos. In the case of Thulagi and Lower Barun where suitable stereo imagery was not available for multiple time periods, we orthorectify images using a single DEM.
Feature Tracking
The ENVI software add-on Cosi-Corr (Leprince et al., 2007) was used to derive glacier velocity for pairs of Sentinel-2 (10 m resolution) and PlanetScope (3 m resolution) satellite images (2016–2018) applied to the near infrared bands (Table 2). We selected images to cover annual, summer and winter periods; however, the presence of snow and cloud cover dictated the image availability for the summer and winter comparisons. We used a correlation window of 64 to 16 pixels with a step size of four pixels for the Sentinel-2 imagery, 128 to 16 pixels with a step size of 4 pixels for the PlanetScope imagery and 64 to 16 (Thulagi and Lhotse Shar) and 128 to 32 (Lower Barun) pixels for Corona imagery. Post-processing of the data included a signal-to-noise threshold of > 0.95, a displacement direction filter to exclude pixels deviating more than 45° from the median direction within a circle of radius nine pixels, and a focal mean of 3 × 3 pixels was used to fill small gaps. Off-glacier displacement was calculated on slopes < 20° to estimate the velocity uncertainty in the Sentinel-2 and PlanetScope correlations (e.g. Quincey et al., 2009). Corona uncertainties were assessed using the mean off-glacier displacement in a manually defined 9 km2 area of stable ground adjacent to the glaciers, which was required to exclude areas of poor correlation due to image contrast and shadows.
Glacier and Lake Characteristics
Ice cliffs, supraglacial ponds, supraglacial streams, crevasses and lateral moraines of the three study glaciers were manually digitised using fine-resolution satellite imagery in Google Earth from 2015. The ice cliff and supraglacial ponds data of Watson et al. (2017a) for 2015 were combined and used for Imja and Lhotse Shar glaciers. Lake depth and glacier ice thickness at the calving front were derived for each glacier (Supplementary Figure S2). Here, the raw bathymetry data points of Haritashya et al. (2018) were used to derive the lake depth. Ice thickness was derived from the modelled ice thickness data of Farinotti et al. (2019), which is an ensemble of model outputs used to improve overall robustness (Farinotti et al., 2017). The ice thickness dataset was also used to identify glacier bed overdeepenings in conjunction with glacier surface topography from the ALOS World 3D–30 m (AW3D30) DEM. Mean lake expansion rates 2008–2018 (Haritashya et al., 2018) were used to approximate future lake expansion (e.g. Rounce et al., 2016), although the assumption of a constant expansion rate and uncertainties in modelled ice thickness data (e.g. Farinotti et al., 2019) mean that the predictions should be revised through time. Glacier mass balance was derived using the surface elevation change and uncertainty data of Brun et al. (2017b), which was gap-filled using the median elevation change in each 100 m elevation band (e.g. Ragettli et al., 2016).
We use the flotation thickness hf to determine how close the glacier termini are to flotation (Boyce et al., 2007):
where d is the water depth, ρw is the density of water (1000 kg m3) and ρi is the density of ice (917 kg m3) (e.g. Carrivick et al., 2017).
Results
Thulagi Lake Iceberg Production and Evolution
We observed two iceberg production events in 2017. The first occurred 30 June–14 July 2017; however, the exact date is unknown due to cloud cover in the satellite imagery. This first event did not appear linked to subaerial glacier calving and an ice ledge appeared, suggesting flotation of subaqueous ice occured, probably from a submerged part of an ice ramp (Supplementary Figure S3b). The second event began with crevasse expansion at the glacier terminus, which was visible on 30 August 2017, and calving occurred 7–8 September 2017 (Figure 3). The total calved area was comprised of a lower ramp (17,100 m2) and the main icewall-fronted glacier terminus (6800 m2). We estimated the calved area of the glacier terminus to have an above-lake volume of 307,000 m3 and a submerged volume of 180,000 m3, suggesting that this sector of the glacier was grounded. The volume of the lower ledge could not be calculated; therefore, the total calved volume of 487,000 m3 is likely a lower bound.
The area and number of icebergs (n = 135) produced in the first calving event decreased over the summer, before increasing during the second event to an area of 32,600 m2 on 9 September 2017 (Figure 3D). Notably, the areal increase of icebergs associated with the second event was small, despite a large number of icebergs (n = 172 on 9 September 2017). The rate of iceberg shrinkage slowed throughout the year, but the iceberg area decreased until November 2017 when most icebergs had melted. Icebergs were wind-drifted across the lake over the study period and collected preferentially at the glacier terminus and the lake outlet, as observed by a compilation of positions of icebergs in the morning satellite imagery acquisitions (Supplementary Figure S4). Satellite imagery show that icebergs shifted back and forth across the length of the lake, but the period was not possible to rigorously estimate by satellite because the imaging times lacked coverage through the day and night (cf section ‘Lake Surface Temperature Depression Due to the September 2017 Calving Event’).
Iceberg Areas, Heights and Volumes
Icebergs in Thulagi Lake (27 October 2017) had a mean planimetric area of 55 m2 and a maximum area and height of 710 m2 and 4 m. By comparison, icebergs in Lower Barun Lake (15 January 2015) had a mean planimetric area of 270 m2 and a maximum area and height of 13,800 m2 and 11 m. The difference may relate to the differing thicknesses of the two glaciers, different ice wall heights and differing lake depths and ability to float icebergs. The iceberg heights imply submerged depths that extend 10–11 times deeper than their heights, so up to a maximum of around 40 m below-water roots for Thulagi’s biggest icebergs and 110 m for Lower Barun’s. These are both well within flotation over much of the lakes’ areas.
Icebergs displayed a similar area-volume relationship for both Thulagi and Lower Barun Lakes (Figure 3E). The total above-surface volume of Thulagi icebergs (27 October 2017) was 11,500 ± 5400 m3, which suggests a total iceberg volume of 139,000 ± 65,000 m3 assuming that 91.7% of the iceberg volume was below the waterline. The volumes of course would be lower if a lower iceberg mean density was adopted. Using the derived area–volume equations for either Thulagi or Lower Barun (Figure 3E), approximately 80% of the total iceberg volume was predicted using the planimetric iceberg areas from 27 October 2017. Approximately 70% of the iceberg volume at Lower Barun Lake was predicted using the same equations applied to the iceberg areas dataset from 15 January 2015.
Lake Temperature and Other Water Conditions
Satellite Surface Temperature Measurements
As expected, lake surface temperatures follow a seasonal cycle related to spring thawing of the lakes’ surfaces, a peak temperature during or shortly after the summer monsoon, followed by decreasing temperatures until the lakes freeze when approaching winter (Figures 4A,B). The warmest mean lake temperatures observed with ASTER and Landsat thermal imagery were 10.7 and 10.8°C for Thulagi Lake on 29 September 2015 and 30 September 2016; 4.2 and 7.2°C at Lower Barun Lake on 9 October 2004 and 30 September 2015 and 8.6 and 9.6°C for Imja Lake on 9 October 2004. When interpreting Figure 4, we should recall the RMSE evaluated for Landsat 8 surface temperatures of + −1.6–2 K (García-Santos et al., 2018) and ASTER (about + −0.8 K, Ramachandran et al., 2014), and the temperature bias of + 0.8 K for ASTER (Ramachandran et al., 2014). Considering these errors, it may be seen that Thulagi Lake well exceeds the 4°C density-maximum temperature of water, but for Lower Barun, it did not clearly ever exceed that temperature. Imja Lake might significantly exceed the 4° threshold in some September and early October measurements, but for the most part it also remains near or below 4°C. Satellite-based observations were sparse during the summer monsoon due to the presence of cloud cover but generally show a plateau or depression of temperatures during the monsoon (Figure 4B). Lake temperature comparisons between ASTER and Landsat thermal data had an RMSE (mean difference) of 1.1°C (Figure 4D), which is comparable to the RMSE of 1.52°C (between ASTER and Landsat sensors) found by Parastatidis et al. (2017) for land surfaces. ASTER might be more accurate as temperature is derived from five bands, instead of two for Landsat 8, but Landsat 8 gives a much better frequency of measurements.
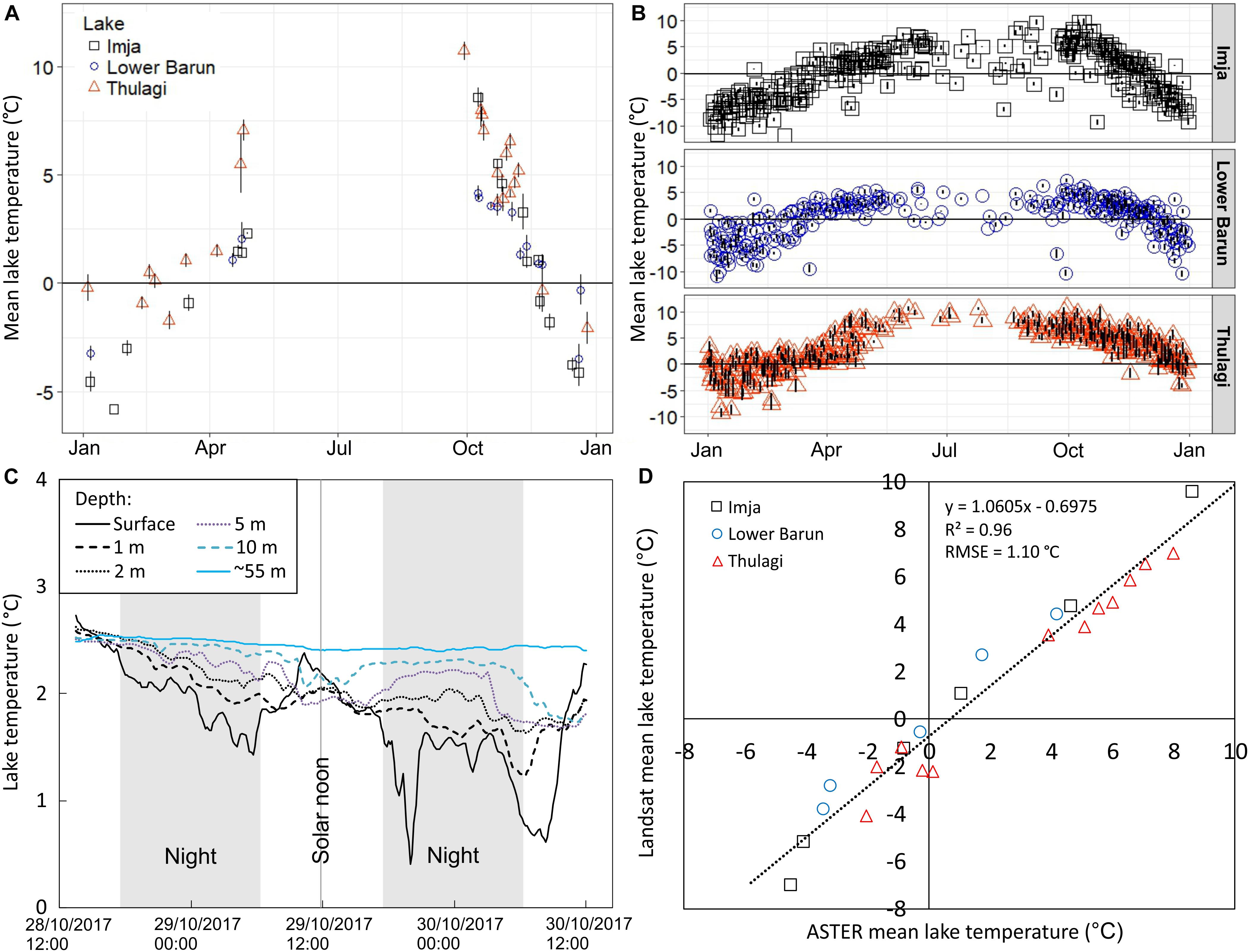
Figure 4. (A) Mean lake temperature derived from ASTER L2 Surface Kinetic Temperature data (n = 17, 14 and 21, for Imja, Lower Barun and Thulagi, respectively). Error bars indicate one standard deviation. (B) Mean lake temperature from Landsat thermal data (n = 300, 291 and 338, for Imja, Lower Barun and Thulagi, respectively). (C) Vertical temperature profile at Thulagi Lake (28–30 October 2017). (D) Comparison of coincident ASTER- and Landsat-derived lake temperatures (n = 24).
Satellite thermometry and imaging shows that Thulagi Lake is likely dimictic (two distinct convective mixings per year and intervening periods of thermally density stratified conditions)—with formation of lake ice in the winter, and surface temperatures exceeding 4°C in summer and early autumn. We infer that spring and autumn temperature-driven convective overturning likely occurs—in accordance with the lake classification by Lewis (1983). Calculations of lake overturning are complicated by the presence of a high suspended sediment load and forced convection driven by wind and iceberg drift (see Supplementary Figure S5). However, as considered below, the lake appears to be very well mixed in suspended load at least in the upper few metres and across the whole lake surface, so the 4°C maximum density of pure water still likely controls density stratification and lake overturning by thermal convection, but forced convection is a different matter. The depths, elevations and latitudes of Lower Barun and Imja Lake also place them firmly into a region where dominantly monomict behaviour (one overturning per year) and temperatures attaining a maximum of 4°C or less are expected (Lewis, 1983).
Lake Surface Temperature Depression Due to the September 2017 Calving Event
Supplementary Figure S6 is the same multi-year compiled lake surface data from Landsat 8 shown in Figure 4B for Thulagi Lake. As mentioned, there is a plateau of temperatures related to the monsoon. The 2017 data show what appears to be a strong temperature depression starting at the time of the September calving event, and cold-water conditions continued while iceberg melting was in progress. The thermal influence of icebergs is likely caused by iceberg generation of meltwater. A mechanism to cool the lake quickly: The meltwater does not initially mix, and 0°C water is buoyant relative to warmer underlying ambient lake water (up to 8°C if pure water, or up to almost 12°C if underlying lake water contains 500 mg/l suspended sediment). So the meltwater spreads over the lake quickly. However, thermal convection and forced convection must mix this water over the upper 30–40 m of the lake (section ‘Iceberg Areas, Heights and Volumes’).
The depression of temperatures by roughly 2°C in the first several days relative to the seasonal normal (running average in Supplementary Figure S6) represents a lot of rapidly lost energy which most likely went into melting of ice. If this temperature depression occurred throughout the upper 40 m—a volume of roughly 3.2 × 107 m3 of water—implies a thermal energy loss during those days of about 2.7 × 1014 J as calculated from the heat capacity of liquid water. When calculated as a volume of ice that must melt in order to drive that much cooling (the enthalpy of melting—rendered as per cubic metre of ice— is 3.06 × 108 J/m3), we find that about 880,000 m3 of ice must have melted in the first days of the calving event to drive temperatures that low, assuming the cooled water was mixed over the top 40 m of the lake. This is about double the lower limit of the amount of calved ice as calculated in Section ‘Thulagi Lake Iceberg Production and Evolution’. The numbers may be brought into alignment if mixing was not initially thorough through the upper 40 m. However, certainly by some weeks into the event, the upper 40 m would have become well mixed, and still temperatures were depressed by roughly 2°C. It is possible that the autumn was colder than normal, thus explaining the temperature depression. However, seeing the number of record-cold and near-record cold lake temperature measurements during that period, we think melting ice is the cause, and that the amount is roughly as estimated—880,000 m3. In turn, this implies that much of the ice came from the submerged ice ramp, as that volume was not determined in Section ‘Thulagi Lake Iceberg Production and Evolution’.
In situ Temperature Measurements and Weather Conditions of Thulagi Lake
During our bathymetry surveys, we visually observed icebergs drifting each afternoon at estimated speeds of a few hundred metres per hour as katabatic breezes blew up the valley. The afternoon winds generally brought clouds, falling temperatures and then rain or snow by midafternoon, when icebergs also converged near the upstream end of the lake. Each night icebergs tended to shift down the lake, converging by morning near the downstream end, completing a daily cycle.
We measured the temperature of the water column in Thulagi Lake for just over 48 h, 28–30 October 2017 using six thermistors at one site (Figure 4C). At that time, nightly lake ice was forming over part of the lake surface and melting by mid-morning. Icebergs were plying the lake surface as driven by daily reversing katabatic winds and the lake water currents (section ‘Thulagi Lake Iceberg Production and Evolution’), which also are mostly wind driven. Most of the large icebergs had surface elevations about 2–3 m above lake surface, implying depths extending to 20–30 m, and deeper for the very largest icebergs. Direct comparisons between satellite- and field-derived water temperatures were only available on 4th and 5th November at ∼10:30 NPT. The mean field-derived temperature (2.6°C) was 0.6°C lower than the satellite-derived temperature (3.2°C) but the measurements had overlapping error bars (Supplementary Figure S7).
The surface water had the largest thermal cycling, as one would expect from solar heating and nightly cooling. Convection—both free thermal convection and forced wind- and iceberg-drift-driven—was also clearly affecting the surface water and down to 10 m depth (Figure 4C). Thermal oscillations decreased in magnitude with depth down to 10 m. In general, the surface water was the coldest, and the deepest water the warmest during the period of measurement, implying an overall stable density stratification at that time in the year. However, with the daily cycle of solar heating, the surface warmed briefly to become the warmest measured. Since all the in situ measured temperatures were below 4°C, and since turbidity was nearly constant close to the surface both across the lake and with depth in the upper few metres [hence, the effect of suspended sediment on density was constant, section ‘In situ Light Level (Turbidity) Measurements of the Water Column’] (Supplementary Figure S8), we conclude that thermal convection must have been occurring in the upper metre during those warmest parts of the mid-day. Otherwise, all indications of convection must involve forced convection by either wind-driven currents and wind-driven iceberg ploughing of the water column.
At the lake bottom, the measured temperature at 55 m depth was steady and so was not mixing with shallow water. Clearly, there was a thermocline somewhere between 10 and 55 m depth, and we surmise that it was likely around 30–40 m deep, where forced convection by passing icebergs probably became minimal. Excluding only the bottom thermistor (55 m deep), the temperatures at all depths from near surface to 10 m almost converged for each of 3 days roughly mid-day. We believe this was due to nearly thorough mixing of at least the upper 10 m caused by a combination of daytime warming of the lake surface layer by solar heating, thermal convection and forced convection by wind-driven currents and drifting icebergs. A similar convergence did not occur at night, when instead the surface water plunged in temperature. However, the surface temperature showed short-term thermal oscillations that were sympathetic with measurements made at 1, 2 and 5 m, again indicating that convection was occurring in the upper water column during the night also. Such convection must be forced, not free thermally driven convection.
In situ Light Level (Turbidity) Measurements of the Water Column
Measurements of downwelling panchromatic light intensity show a monotonic log-linear (exponential) decrease in light intensity (Supplementary Figure S8). The implications are that: (a) The turbidity of the water column in the upper four metres is uniform, hence suggesting thorough mixing on time scales that are short compared to expected seasonally variable inputs, settling and stream discharge of suspended sediment. (b) Solar heating is primarily in the upper metre of the lake, and almost all the rest is absorbed in the next few metres. The measured local solar absorption rate in the visible wavelengths, recalculated for the sun at zenth, is a factor of two for every 71 cm increase of depth. (c) Since thermal conduction is not significant on time scales of days and distances of metres, we also infer any changes of temperature beneath of a few metres (Figure 4C) is due to convection, either forced or free, or due to uptake of heat by melting of passing icebergs.
Glacier Dynamics
Thulagi Glacier is heavily crevassed in the lower 500 m (Figure 5A). Ice cliffs are prevalent farther up-glacier and supraglacial ponds only have sporadic coverage. A network of supraglacial streams was present, which appear to transition englacially upon their termination. Lower Barun Glacier was comparable to Thulagi Glacier for the size of debris-covered area, supraglacial pond coverage and ice cliff density (Table 3). Thulagi and Lower Barun glaciers also had a similar mass balance of −0.21 ± 0.38 and −0.20 ± 0.31 m.w.e. a–1, respectively (2000–2016) (Table 1). Imja/Lhotse Shar Glacier had a three times larger debris-covered area (6 vs. 2 km2) and percentage pond coverage compared to Thulagi and Lower Barun Glaciers but a similar ice cliff density (Table 3). All three glaciers display high rates of surface lowering in their debris-covered areas (Figure 6).
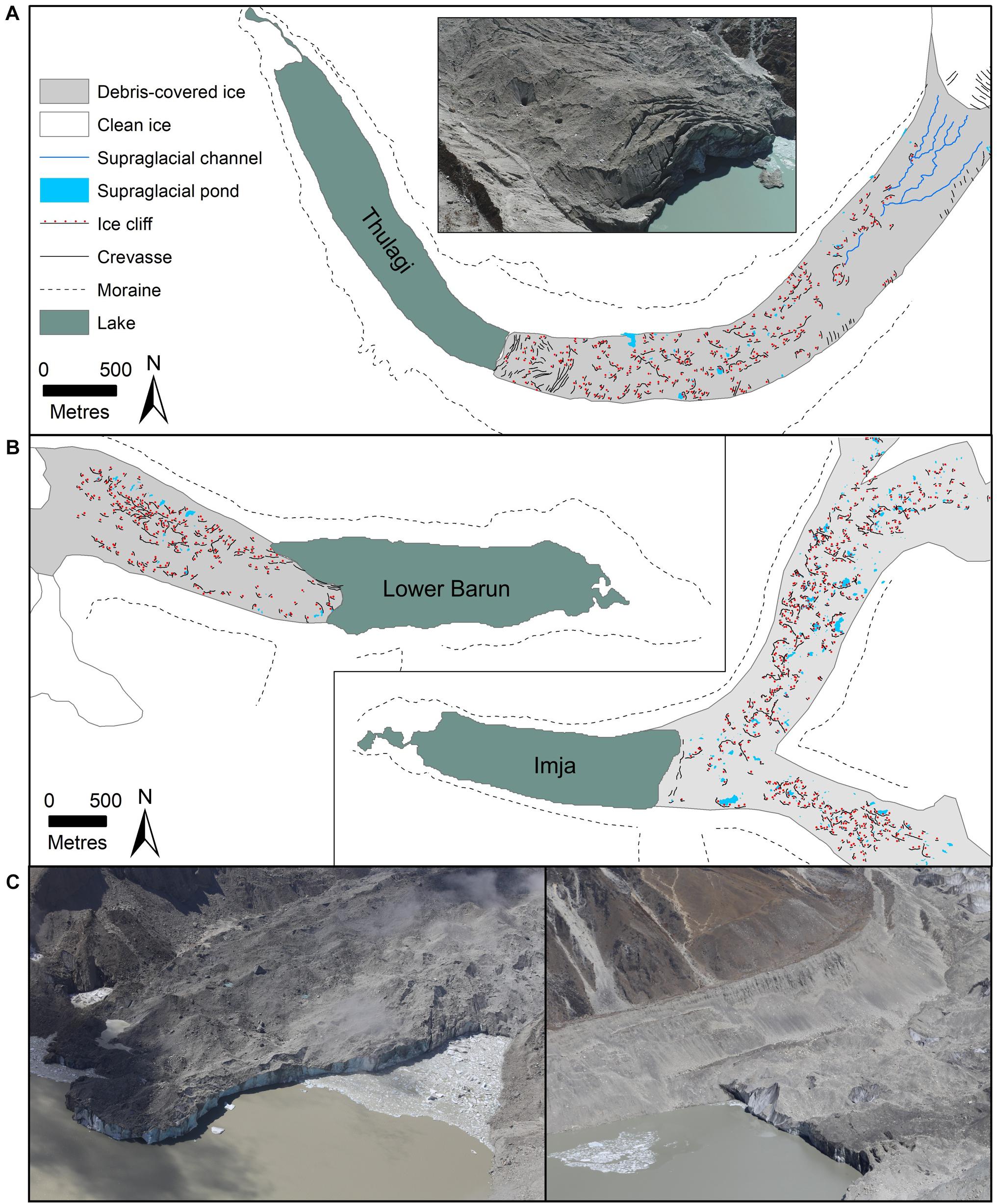
Figure 5. Surface morphology of (A) Thulagi Glacier (inset is a terminus photo from October 2017) and (B) Lower Barun and Lhotse Shar/Imja glaciers. (C) Aerial photographs of the calving fronts of Lower Barun (left) and Lhotse Shar Glacier (right) taken October 2015.
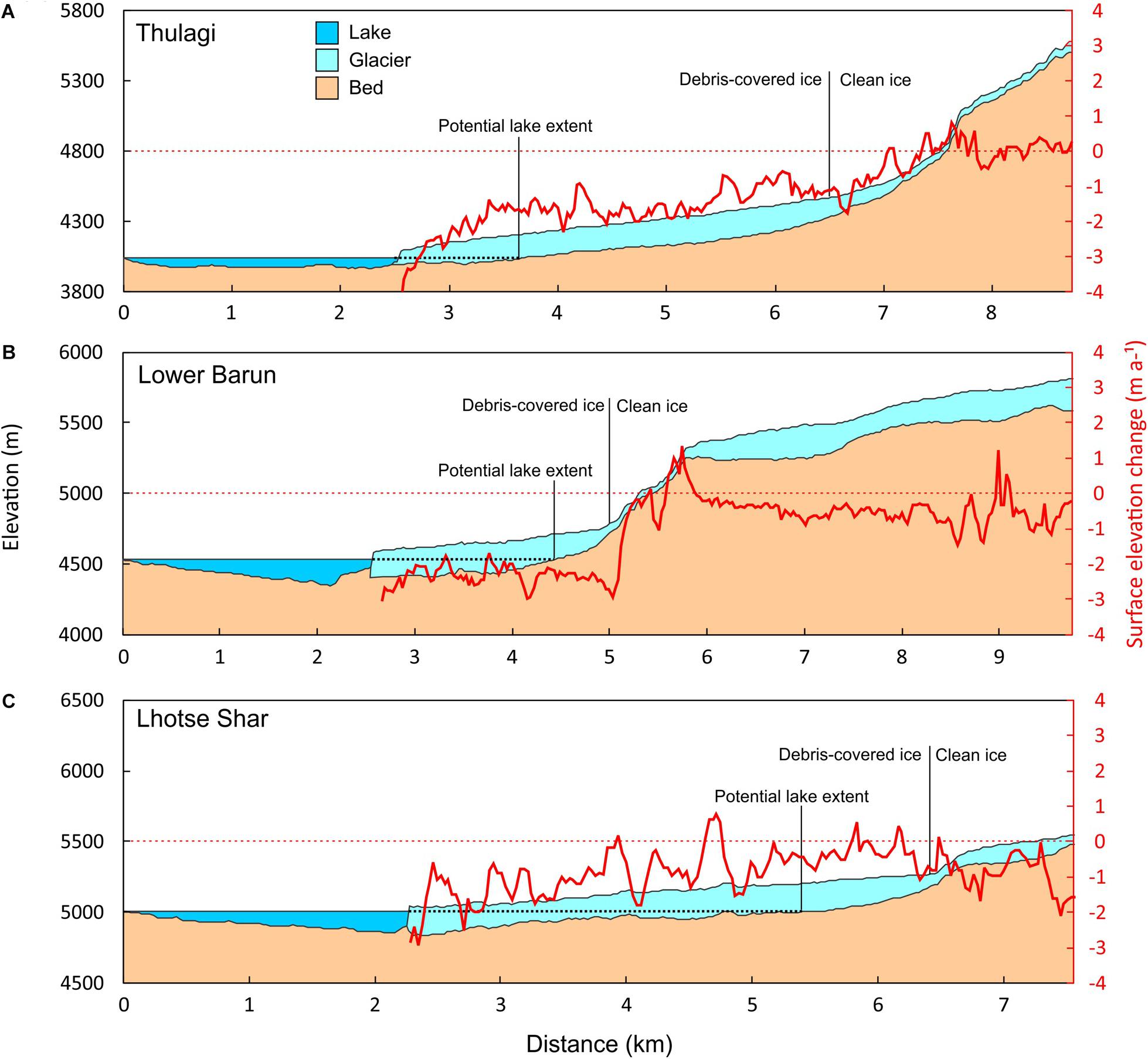
Figure 6. Centreline profiles (shown in Figure 1) for (A) Thulagi, (B) Lower Barun and (C) Lhotse Shar/Imja Lake. Lake bathymetry data are from Haritashya et al. (2018), surface elevation change data are from Brun et al. (2017b), ice thickness data are from Farinotti et al. (2019) and glacier topography from the AW3D30 DEM. Note that the exact nature of the lake–glacier interface is not known for the three lakes.
All glaciers in the current study exhibit active flow in their debris-covered ablation areas (Figure 7); however, velocities were lowest for Imja and Lower Barun Glaciers, and highest for Thulagi Glacier, which had increasing velocities with distance up-glacier. Thulagi Glacier displayed summer velocity acceleration within ∼1 km of the terminus and at ∼5 km, with summer velocities at the terminus of ∼0.07 m d–1 compared to 0.02 m d–1 in winter (Figure 7). There was not a clear seasonal trend on Lower Barun Glacier; however, winter velocities marginally exceeded summer velocities. On Imja Glacier, there was evidence of localised acceleration within 1 km of the glacier calving front with mean summer velocities of 0.04 m d–1 compared to 0.02 m d–1 in winter. Similar to Thulagi, higher summer velocities were observed at the transition from clean to debris-covered ice on Imja glacier. Velocity change from the 1960s to present day was most apparent on Lower Barun Glacier, where velocities in the vicinity of the present day calving front (< 3.5 km up-glacier) increased from ∼0.03 m d–1 (1962–64) to ∼0.08 m d–1 (2016–2018) (Figure 7B). On Thulagi and Lhotse Shar Glaciers, 1960s velocities were comparable to the present day summer velocities.
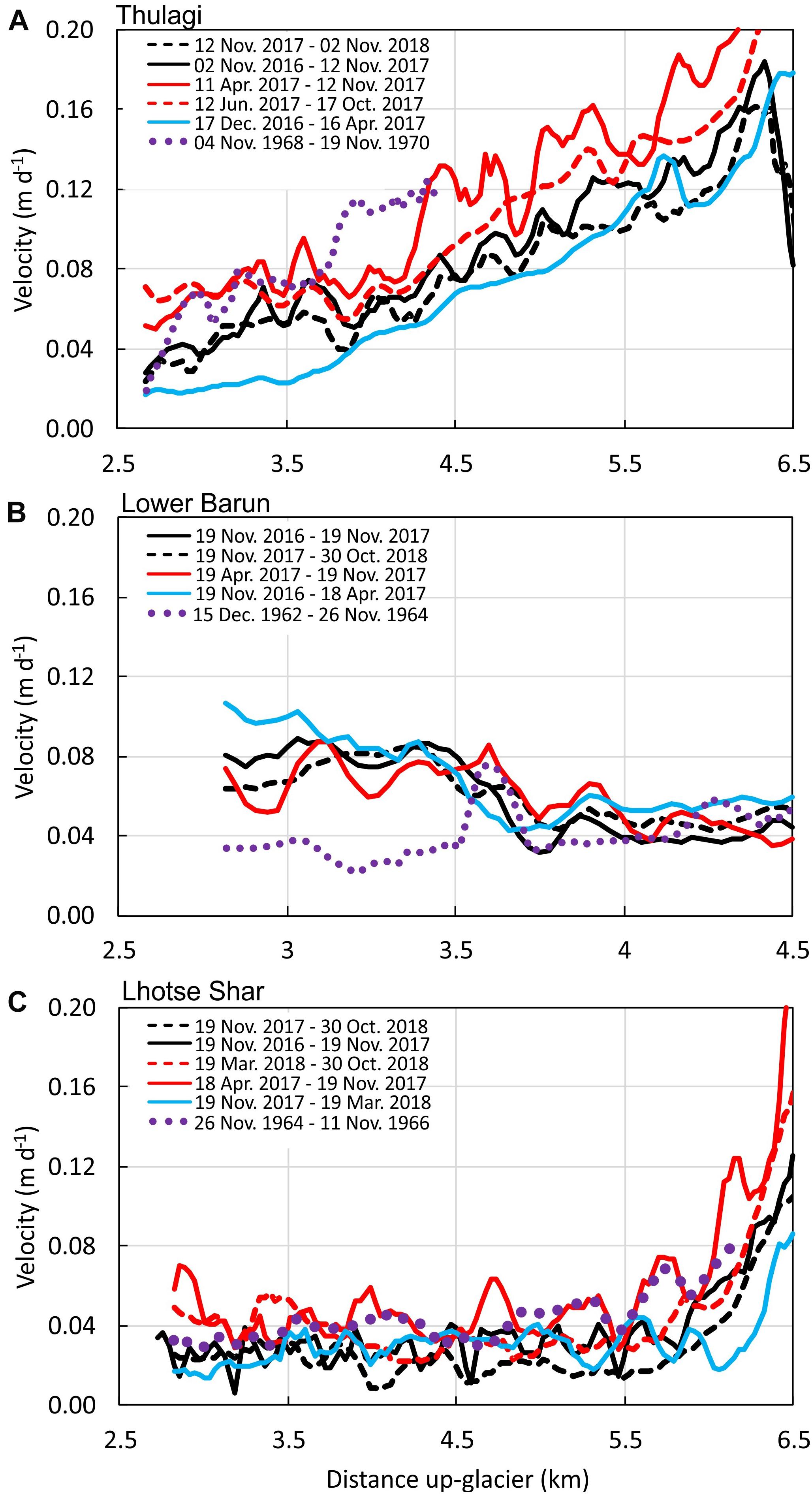
Figure 7. Centreline glacier velocity for (A) Thulagi, (B) Lower Barun and (C) Lhotse Shar glaciers. Data are 150 m moving averages. Velocities for annual image pairs are coloured back, those spanning the melt season are red, those spanning winter are blue and those from Corona imagery (1960s) are dotted purple. Distances up-glacier are measured from the lake terminus corresponding to Figure 6.
Meltwater was observed emerging from Thulagi Glacier terminus over a lower ledge that appeared grounded on the lakebed and covered in fine sediment in September 2013 (Figure 8C). In contrast, the terminus had receded > 100 m by October 2017 and the ledge was replaced with an undercut terminus ∼10 m high (Figure 8D). Thulagi Lake had a mean depth of 58 m in the vicinity of the glacier calving front, compared to 145 m for Lower Barun and Imja lakes (Table 4). However, bathymetry data close to the calving front are lacking; hence, the exact nature of the glacier–lake transition zone is unknown.

Figure 8. (A) Photograph of Thulagi Glacier terminus from a helicopter flight in May 2013 and (B) the same view from a textured SfM model (27 October 2017). Red dots indicate stable features for image registration. (C) Calving front and ice ledge in September 2013 (see also Supplementary Figure S3). (D) The calving front and portal in October 2017.

Table 4. Calving front characteristics that correspond to the lake and calving front zones shown in Supplementary Figure S2.
All three lakes are apt to continue expanding as their parent glaciers retreat and this is most rapid for Imja Lake, followed by Lower Barun and Thulagi (Figures 6, 9 and Table 1). Upon reaching the maximum modelled lake extents, Imja, Lower Barun and Thulagi lakes would contain an additional 90 × 106, 62 × 106 and 5 × 106 m3 of water, respectively, compared to their 2018 volumes. However, there are large unquantified uncertainties present in modelled ice thickness data used to determine these volumes, which would benefit from field-derived ice thickness observations.

Figure 9. Projected glacial lake expansion for (a) Thulagi, (b) Lower Barun and (c) Imja, using mean expansion rates (2008–2019) (Haritashya et al., 2018) and modelled ice thickness data (Farinotti et al., 2019). Colour bands are 5-year intervals. Background: Sentinel-2 Nir, red, blue composites from 2018.
Discussion
Glacier Calving and Iceberg Production
The presence of icebergs in Himalayan glacial lakes is problematic for automated lake classification relying on infrequent satellite overpasses (Bolch et al., 2008b; Strozzi et al., 2012). Previously, it was not possible to observe related calving events with any useful temporal resolution; however, with the availability of daily < 4 m resolution imagery from Planet Labs, the presence and persistence of icebergs can be quantified through time. Icebergs reveal insights into subaerial and subaqueous glacier calving and act to mix the water as they drift around the lake.
The first iceberg production event observed in this study at Thulagi Lake (30 June–14 July 2017) did not appear to be linked to subaerial glacier calving and appeared to be of subaqueous origin. The icebergs could have originated from calving of a submerged ice ramp extending from the terminus of Thulagi Glacier or dead ice on the lakebed, similar to observations at Imja Lake (Somos-Valenzuela et al., 2014) (Figure 3F). The appearance of a sediment-covered ice ledge over the monsoon of 2013 (Figure 8C) also indicates the presence of subaqueous ice. Sediment deposition as glacier meltwater enters the lake was the likely source of sediment observed to partly blanket the ledge, which was elevated to the surface when the submerged ice became detached, but still partially grounded. The second event was linked to crevasse development and undercutting at the glacier terminus (Figure 3). The total calved volume (16 April 2017–9 September 2017) was estimated as 487,000 m3; however, this is assumed to be a lower bound since it did not include the submerged ledge of ice. Nonetheless, using the empirical area-volume relationship (Figure 3E), the predicted iceberg volume on 9 September 2017 of 538,500 m3 suggests our estimate was reasonable. The thermal analysis of the lake surface temperature anomaly seemingly caused by this calving event suggests that a larger volume of submerged ice was involved (section ‘Lake Surface Temperature Depression due to the September 2017 Calving Event’).
The number and area of icebergs declined in the weeks and months following the 7–9 September calving event, and the rate of change slowed approaching winter (Figure 3), which corresponds with decreasing lake temperatures (Figure 4) and lower air temperatures and solar radiation receipt. Wind and water current drifting of icebergs was prevalent across the study period and was also observed in the field. Katabatic breezes—blowing upvalley and accompanied by intrusion of afternoon cloud cover and usually rain or snow, and anabatic breezes blowing downvalley and accompanied by night-time clearing of clouds—were an every-day occurrence during 2013 and 2017 field work at Thulagi Lake. Such breezes and wind-driven surface and deep return water currents and Ekman flow (Shulman and Bryson, 1961) are enough to move the icebergs completely down and across and back up the lake on a daily basis. The observed accumulation of icebergs at the outlet of the lake did not cause any channel blockages, though icebergs were seen to be breaking up and leaving the lake in small bergy bits through the outlet complex. The accumulation of icebergs at the glacier terminus likely contributed to localised cooling of the lake surface and made it more susceptible to night-time freezing here, which impedes thermo-erosional undercutting of the glacier. The seasonal variation in glacial lake temperature was captured using satellite data for all three lakes; however, in situ validation data are lacking and should be collected for comparison with satellite-derived temperature measurements. Coincident field-based and satellite temperature measurements (4–5 November 2017) revealed that field temperatures were 0.6°C lower than those from the satellite data, although the measurements had overlapping error bars.
The measured positive temperature bias of satellite vs. in situ measurements is consistent with previous calibrations/validations of ASTER kinetic surface temperatures (Tonooka and Palluconi, 2005) and our own ASTER thermal validations at an iceberg-choked lake and on melting snow and glacier clean-ice fields (Ramachandran et al., 2014). Validations of Landsat 8 temperatures have involved radiometrically very different types of surfaces (urban buildings, asphalt and orchards for instance) but have also shown biases and RMSEs similar to those of ASTER (García-Santos et al., 2018) and have revealed algorithm-dependent and humidity-dependent biases. Li and Jiang (2018) found a negative bias of about −0.49 K between Landsat 8 temperatures (cooler) compared to MODIS MOD11, which is roughly consistent with the Landsat 8/ASTER bias since ASTER temperatures were partly calibrated using MODIS (Arai, 1996). In general, the temperature dispersion we measured by satellite on Thulagi Lake in a given weekly period (same year and different years) exceeds the biases and RMS errors reported in these other studies; hence, they are tending to show actual temperature differences due presumably to: (i) weather variations on daily/weekly time frames and between years and (ii) variations in ice conditions on daily/weekly time frames and between years. We cannot definitively isolate weather vs. ice disturbances, but given that we observed the iceberg calving event in 2017, that seems the most likely explanation for anomalously cold lake temperatures and then recovery to ‘normal’ a few months later. The influence of calving on lake thermal regime is a desirable focus of future work and should include in situ monitoring of lake temperature.
Although the volume of calved ice is not easily or accurately discernible using optical imagery, empirical relationships between the area and volume of icebergs, similar to those derived for Greenland icebergs (Enderlin and Hamilton, 2014; Sulak et al., 2017), could be used to estimate the calved volume of glacier ice in the absence of DEMs. The derived area–volume relationships can be used to predict iceberg volume using satellite-derived area measurements (Figure 3), but should be explored for other glacial lakes that exhibit different calving regimes due to the inherent variability in iceberg morphology. Complexities also exist due to the autocorrelation of area and volume similar to relationships applied to derive glacial lake volume from area (e.g. Cook and Quincey, 2015; Haeberli, 2015). Nonetheless, empirical area–volume relationships could be particularly valuable for estimating the volume of subaqueous calving events (e.g. Somos-Valenzuela et al., 2014), which unlike glacier calving, cannot be resolved using DEMs of difference. Glacial lakes that are rapidly deepening and expanding, such as Lower Barun and Imja lakes in the Everest region of Nepal, could be expected to produce larger icebergs due to greater calving activity. By contrast, our observations at Thulagi Lake likely capture smaller icebergs associated with slower rates of lake expansion (ICIMOD, 2011; Rounce et al., 2016; Haritashya et al., 2018; Robson et al., 2018).
Lake Thermal Regime and Glacier Dynamics
Thulagi Lake is free-draining through an outlet complex; hence, the water level should be relatively stable, which promotes thermo-erosional undercutting of the glacier terminus and overhanging ice (Benn et al., 2007). Thermo-erosional undercutting promotes a tensional regime on the terminus of Thulagi Glacier, which is expressed through the prevalence of crevasses (Figure 5A). Since the glacier still terminates in Thulagi Lake and is actively flowing at the terminus, calving is likely to continue in spite of the current limited lake expansion. The glacier is grounded in water < 60 m deep and future lake expansion was expected to be limited (e.g. Robson et al., 2018). However, Thulagi Glacier retreated 200 m (2008–2018) (Table 1) and modelled ice thickness suggests that subsequent glacier retreat would continue to allow lake expansion for another ∼1 km up-valley (Figures 6A, 9). The lake level was reported to be dropping by 0.3–0.5 m a–1 (1996–2009), which was in excess of base level (moraine dam) lowering (ICIMOD, 2011). However, observations of a higher water level in 2013 compared to 2017 (Figure 8) suggested this had at least temporarily reversed.
Moraine dam degradation or engineering interventions will determine the future extent of each lake by changing the lake level. It is clear that Imja Lake has the largest potential to expand and is doing so at the fastest rate (Figure 9), which could increase the future hazard due to the potential for avalanches to directly impact the lake (Rounce et al., 2016, 2017). The role of engineering works to lower the lake level by 3 m is not clear and requires further investigation (Lala et al., 2018). Consideration of glacier flotation is critical when considering GLOF mitigation measures such as lake lowering, since loss of hydraulic support for the glacier terminus can lead to large calving events and displacement waves (Reynolds, 1998). None of the three study glaciers are in full flotation, though Lhotse Shar and Lower Barun likely have areas of the calving front in partial flotation (Haritashya et al., 2018) (Table 4).
Velocities on Lhotse Shar Glacier have recently increased close to the lake terminus, reflecting a more dynamic lake–glacier interaction (2013–2015 vs. 1999–2003) (King et al., 2018) and show evidence of seasonal variation similar to Thulagi Glacier (Figure 7). The seasonal speedup of Thulagi Glacier could be linked to the englacial termination of meltwater streams that route water to lubricate the bed (Figure 5), whereas the high lake depth (mean of 145 m, Table 4) adjacent to the terminus of Lhotse Shar Glacier likely induce meltwater intrusion from the lake under the glacier. The impact of the glacial lakes on glacier velocity is most apparent on Lower Barun Glacier, which has highest velocities close to the calving front, which is likely in partial flotation. The present day velocities also contrast with those derived from Corona imagery (1962–1964) where velocities have accelerated by ∼0.5 m d–1 after the formation of Lower Barun Lake (Figure 7B). Several studies have used Corona imagery for DEM generation to assess glacier surface elevation change (e.g. Bolch et al., 2008a; Lamsal et al., 2016). However, to our knowledge, none have utilised the archive to derive glacier velocities in the Himalaya. In this study, we have shown that even over large image separations (> 700 days), automated feature tracking is able to produce useable (but incomplete) velocity fields using Corona imagery. Further use of the archive would help reveal the onset of a general trend of glacier slowdown (e.g. Dehecq et al., 2019) in the context of accelerating glacier mass loss over the last 40 years (Maurer et al., 2019), and also the impact of lakes on glacier dynamics.
Conclusion
In this study, we have shown the utility of fine-resolution satellite imagery with a short revisit period for monitoring glacier calving events and capturing events of subaqueous origin. We derived iceberg topography using imagery from a UAV survey and show that empirical relationships between iceberg area and volume could be used to estimate the volume of calving events in the absence of corresponding DEMs, which could be particularly useful when investigating subaqueous calving. The equations should be evaluated for other glacial lakes with different calving regimes. Nonetheless, we show that the relationship derived at Thulagi Lake was able to predict 70% of the iceberg volume at Lower Barun Lake. We observed via satellite and with in situ measurements the effects of a large, discrete iceberg calving event on Thulagi Lake’s thermal structure, including the effects of iceberg drifting and the dynamic melting of icebergs and bergy bits as the lake interacted thermally with the calved ice. This event afforded new insights into glacial lake assisted melting of glaciers. We used published modelled ice thickness data to show that upon reaching their maximum extents, Imja, Lower Barun and Thulagi lakes would contain an estimated 90 × 106, 62 × 106 and 5 × 106 m3 of additional water, respectively, compared to their 2018 volumes. These maximum extents could be reached by 2040, 2060 and 2070 for Lower Barun, Lhotse Shar and Thulagi glaciers, respectively, due to the variable expansion rates. Understanding lake–glacier interactions is essential to predict future glacier mass loss, lake formation and associated outburst flood hazards. However, uncertainties exist in modelled ice thickness data, lake expansion rates and our understanding of moraine dam degradation that are all required to project lake evolution. Utilising declassified spy satellite data as presented in this study offers one means of deriving historic glacier velocities to assess lake–glacier interactions. Application of ice thickness models to the respective pre-lake DEMs derived from declassified stereo imagery could also offer insights into the reliability of the ice thickness estimates by making comparisons with observations of contemporary lake bathymetry. Further validation of in situ and satellite-derived lake temperatures is also a priority.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
CW performed the satellite remote sensing and UAV data analysis and drafted the manuscript. JK developed the iceberg melt analysis and light level/turbidity analysis. CW and JK conducted the fieldwork. All authors edited the manuscript and interpreted the results.
Funding
All authors were funded under NASA High Mountain Asia grants NNX16AQ62G and 80NSSC19K0653.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Dan Jantzen for flying the UAV survey, and Bob Yoder and Dan Spare for collecting the ground control points and providing the lake outlet temperature data. The Planet Labs Education and Research Program are thanked for providing access to PlanetScope imagery. CloudCompare (version 2.8, 2016) is GPL software retrieved from http://www.cloudcompare.org/. We thank David Parastatidis for providing Landsat-derived lake temperature data. We thank the Nepal Department of National Parks and Wildlife Conservation, and the Himalayan Research Centre for facilitating a research permit for fieldwork. The AW3D30 DEM is provided by the Japan Aerospace Exploration Agency (http://www.eorc.jaxa.jp/ALOS/en/aw3d30/index.htm) ©JAXA. Pléiades images used in DEM generation were supplied by Airbus Defence and Space through a Category-1 agreement with the European Space Agency (ID No. 32600). We thank the two reviewers for suggestions that helped improve this study.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2019.00342/full#supplementary-material
References
Altmaier, A., and Kany, C. (2002). Digital surface model generation from CORONA satellite images. ISPRS J. Photogram. Remote Sens. 56, 221–235. doi: 10.1016/s0924-2716(02)00046-1
Arai, K. (1996). Interactive calibration of the sensors onboard the same platform. Adv. Space Res. 17, 21–28. doi: 10.1016/0273-1177(95)00440-p
Benn, D. I., Bolch, T., Hands, K., Gulley, J., Luckman, A., Nicholson, L. I., et al. (2012). Response of debris-covered glaciers in the Mount Everest region to recent warming, and implications for outburst flood hazards. Earth Sci. Rev. 114, 156–174. doi: 10.1016/j.earscirev.2012.03.008
Benn, D. I., Warren, C. R., and Mottram, R. H. (2007). Calving processes and the dynamics of calving glaciers. Earth Sci. Rev. 82, 143–179. doi: 10.1016/j.earscirev.2007.02.002
Bolch, T., Buchroithner, M., Pieczonka, T., and Kunert, A. (2008a). Planimetric and volumetric glacier changes in the Khumbu Himal, Nepal, since 1962 using Corona, Landsat TM and ASTER data. J. Glaciol. 54, 592–600. doi: 10.3189/002214308786570782
Bolch, T., Buchroithner, M. F., Peters, J., Baessler, M., and Bajracharya, S. (2008b). Identification of glacier motion and potentially dangerous glacial lakes in the Mt. Everest region/Nepal using spaceborne imagery. Nat. Hazards Earth Syst. Sci. 8, 1329–1340. doi: 10.5194/nhess-8-1329-2008
Bolch, T., Kulkarni, A., Kääb, A., Huggel, C., Paul, F., Cogley, J. G., et al. (2012). The state and fate of himalayan glaciers. Science 336, 310–314. doi: 10.1126/science.1215828
Bolch, T., Pieczonka, T., and Benn, D. I. (2011). Multi-decadal mass loss of glaciers in the Everest area (Nepal Himalaya) derived from stereo imagery. Cryosphere 5, 349–358. doi: 10.5194/tc-5-349-2011
Boyce, E. S., Motyka, R. J., and Truffer, M. (2007). Flotation and retreat of a lake-calving terminus, Mendenhall Glacier, southeast Alaska, USA. J. Glaciol. 53, 211–224. doi: 10.3189/172756507782202928
Brun, F., Berthier, E., Wagnon, P., Kaab, A., and Treichler, D. (2017a). A spatially resolved estimate of High Mountain Asia glacier mass balances from 2000 to 2016. Nat. Geosci. 10, 668–673. doi: 10.1038/NGEO2999
Brun, F., Berthier, E., Wagnon, P., Kääb, A., and Treichler, D. (2017b). “Elevation changes of High Mountain Asia from 2000 to 2016, links to GeoTIFFs”, in: supplement to: Brun, F et al. (2017): a spatially resolved estimate of High Mountain Asia glacier mass balances from 2000 to 2016. Nat. Geosci. 10, 668–673. doi: 10.1038/ngeo2999
Buri, P., Pellicciotti, F., Steiner, J. F., Miles, E. S., and Immerzeel, W. W. (2016). A grid-based model of backwasting of supraglacial ice cliffs on debris-covered glaciers. Ann. Glaciol. 57, 199–211. doi: 10.3189/2016aog71a059
Carrivick, J. L., and Tweed, F. S. (2013). Proglacial lakes: character, behaviour and geological importance. Q. Sci. Rev. 78, 34–52. doi: 10.1016/j.quascirev.2013.07.028
Carrivick, J. L., and Tweed, F. S. (2016). A global assessment of the societal impacts of glacier outburst floods. Glob. Planet. Change 144, 1–16. doi: 10.1016/j.gloplacha.2016.07.001
Carrivick, J. L., Tweed, F. S., Ng, F., Quincey, D. J., Mallalieu, J., Ingeman-Nielsen, T., et al. (2017). Ice-dammed lake drainage evolution at russell glacier, West Greenland. Front. Earth Sci. 5:100. doi: 10.3389/feart.2017.00100
Casana, J., and Cothren, J. (2007). Stereo analysis, DEM extraction and orthorectification of CORONA satellite imagery: archaeological applications from the Near East. Antiquity 82, 732–749. doi: 10.1017/s0003598x00097349
Chinn, T. J., Kargel, J. S., Leonard, G. J., Haritashya, U. K., and Pleasants, M. (2014). “New Zealand’s Glaciers,” in Global Land Ice Measurements from Space, eds J. S. Kargel, G. J. Leonard, M. P. Bishop, A. Kääb, and B. H. Raup (Berlin: Springer), 675–715.
Cook, K. L., and Dietze, M. (2019). Short communication: a simple workflow for robust low-cost UAV-derived change detection without ground control points. Earth Surf. Dynam. Discuss. 2019, 1–15.
Cook, S. J., and Quincey, D. J. (2015). Estimating the volume of Alpine glacial lakes. Earth Surf. Dynam. 3, 559–575. doi: 10.5194/esurf-3-559-2015
Dehecq, A., Gourmelen, N., Gardner, A. S., Brun, F., Goldberg, D., Nienow, P. W., et al. (2019). Twenty-first century glacier slowdown driven by mass loss in High Mountain Asia. Nat. Geosci. 12, 22–27. doi: 10.1038/s41561-018-0271-9
Enderlin, E. M., and Hamilton, G. S. (2014). Estimates of iceberg submarine melting from high-resolution digital elevation models: application to Sermilik Fjord, East Greenland. J. Glaciol. 60, 1084–1092. doi: 10.3189/2014jog14j085
Farinotti, D., Brinkerhoff, D. J., Clarke, G. K. C., Fürst, J. J., Frey, H., Gantayat, P., et al. (2017). How accurate are estimates of glacier ice thickness? results from ITMIX, the Ice Thickness Models Intercomparison eXperiment. Cryosphere 11, 949–970.
Farinotti, D., Huss, M., Fürst, J. J., Landmann, J., Machguth, H., Maussion, F., et al. (2019). A consensus estimate for the ice thickness distribution of all glaciers on Earth. Nat. Geosci. 12, 168–173. doi: 10.1038/s41561-019-0300-3
García-Santos, V., Cuxart, J., Martínez-Villagrasa, D., Jiménez, M. A., and Simó, G. (2018). Comparison of three methods for estimating land surface temperature from Landsat 8-TIRS Sensor Data. Remote Sens. 10:1450. doi: 10.3390/rs10091450
Haeberli, W. (2015). Interactive comment on “Estimating the volume of Alpine glacial lakes” by Cook, S. J. and Quincey. Earth Surf. Dynam. Discuss. 3, C342–C343.
Haritashya, U., Kargel, J., Shugar, D., Leonard, G., Strattman, K., Watson, C., et al. (2018). Evolution and Controls Of Large Glacial Lakes In the Nepal Himalaya. Remote Sens. 10:798. doi: 10.3390/rs10050798
Harrison, S., Kargel, J. S., Huggel, C., Reynolds, J., Shugar, D. H., Betts, R. A., et al. (2018). Climate change and the global pattern of moraine-dammed glacial lake outburst floods. Cryosphere 12, 1195–1209. doi: 10.5194/tc-12-1195-2018
Heynen, M., Miles, E. S., Ragettli, S., Buri, P., Immerzeel, W. W., and Pellicciotti, F. (2016). Air temperature variability in a high elevation Himalayan catchment. Ann. Glaciol. 57, 212–222. doi: 10.3189/2016aog71a076
ICIMOD, (2011). Glacial Lakes and Glacial Lake Outburst Floods in Nepal. Available from: http://www.icimod.org/dvds/201104_GLOF/reports/final_report.pdf (accessed February 2, 2015).
Immerzeel, W. W., Kraaijenbrink, P. D. A., Shea, J. M., Shrestha, A. B., Pellicciotti, F., Bierkens, M. F. P., et al. (2014). High-resolution monitoring of Himalayan glacier dynamics using unmanned aerial vehicles. Remote Sens. Environ. 150, 93–103. doi: 10.1016/j.rse.2014.04.025
James, M. R., and Robson, S. (2012). Straightforward reconstruction of 3D surfaces and topography with a camera: accuracy and geoscience application. J. Geophys. Res. 117, 1–17.
King, O., Dehecq, A., Quincey, D., and Carrivick, J. (2018). Contrasting geometric and dynamic evolution of lake and land-terminating glaciers in the central Himalaya. Glob. Planet. Change 167, 46–60. doi: 10.1016/j.gloplacha.2018.05.006
Kirkbride, M. P. (1993). The temporal significance of transitions from melting to calving termini at glaciers in the central Southern Alps of New Zealand. Holocene 3, 232–240. doi: 10.1177/095968369300300305
Kirkbride, M. P., and Warren, C. R. (1997). Calving processes at a grounded ice cliff. Ann. Glaciol. 24, 116–121. doi: 10.1017/s0260305500012039
Kraaijenbrink, P. D. A., Bierkens, M. F. P., Lutz, A. F., and Immerzeel, W. W. (2017). Impact of a global temperature rise of 1.5 degrees Celsius on Asia’s glaciers. Nature 549, 257–260. doi: 10.1038/nature23878
Krumwiede, B. S., Kamp, U., Leonard, G. J., Kargel, J. S., Dashtseren, A., and Walther, M. (2014). “Recent glacier changes in the mongolian Altai Mountains: case studies from Munkh Khairkhan and Tavan Bogd,” in Global Land Ice Measurements from Space, eds J. S. Kargel, G. J. Leonard, M. P. Bishop, A. Kääb, and B. H. Raup (Berlin: Springer), 481–508. doi: 10.1007/978-3-540-79818-7_22
Lala, J. M., Rounce, D. R., and Mckinney, D. C. (2018). Modeling the glacial lake outburst flood process chain in the Nepal Himalaya: reassessing Imja Tsho’s hazard. Hydrol. Earth Syst. Sci. 22, 3721–3737. doi: 10.5194/hess-22-3721-2018
Lamsal, D., Sawagaki, T., Watanabe, T., and Byers, A. C. (2016). Assessment of glacial lake development and prospects of outburst susceptibility: chamlang South Glacier, eastern Nepal Himalaya. Geomatics. Nat. Hazards Risk 7, 403–423. doi: 10.1080/19475705.2014.931306
Leprince, S., Barbot, S., Ayoub, F., and Avouac, J. P. (2007). Automatic and Precise Orthorectification, Coregistration, and Subpixel Correlation of Satellite Images, Application to Ground Deformation Measurements. IEEE Trans. Geosci. Remote Sens. 45, 1529–1558. doi: 10.1109/tgrs.2006.888937
Lewis, W. M. Jr. (1983). A revised classification of Lakes Based on Mixing. Can. J. Fish. Aqua. Sci. 40, 1779–1787. doi: 10.1139/f83-207
Li, S., and Jiang, G. (2018). Land surface temperature retrieval from Landsat-8 data with the generalized Split-Window Algorithm. IEEE Access. 6, 18149–18162. doi: 10.1109/access.2018.2818741
Maurer, J. M., Rupper, S. B., and Schaefer, J. M. (2016). Quantifying ice loss in the eastern Himalayas since 1974 using declassified spy satellite imagery. Cryosphere 10, 2203–2215. doi: 10.5194/tc-10-2203-2016
Maurer, J. M., Schaefer, J. M., Rupper, S., and Corley, A. (2019). Acceleration of ice loss across the Himalayas over the past 40 years. Sci. Adv. 5:eaav7266. doi: 10.1126/sciadv.aav7266
Miles, E. S., Steiner, J., Willis, I., Buri, P., Immerzeel, W. W., Chesnokova, A., et al. (2017). Pond dynamics and supraglacial-englacial connectivity on debris-covered Lirung Glacier, Nepal. Front. Earth Sci. 5:69. doi: 10.3389/feart.2017.00069
Nicholson, L., and Benn, D. I. (2013). Properties of natural supraglacial debris in relation to modelling sub-debris ice ablation. Earth Surf. Process. Landforms 38, 490–501. doi: 10.1002/esp.3299
Nie, Y., Sheng, Y., Liu, Q., Liu, L., Liu, S., Zhang, Y., et al. (2017). A regional-scale assessment of Himalayan glacial lake changes using satellite observations from 1990 to 2015. Remote Sens. Environ. 189, 1–13. doi: 10.1016/j.rse.2016.11.008
Parastatidis, D., Mitraka, Z., Chrysoulakis, N., and Abrams, M. (2017). Online global land surface temperature estimation from Landsat. Remote Sens. 9:1208. doi: 10.3390/rs9121208
Pickard, J. (1983). Surface lowering of ice-cored moraine by wandering lakes. J. Glaciol. 29, 338–342. doi: 10.1017/s0022143000008388
Planet Team, (2019). Planet Application Program Interface: in Space for Life on Earth. San Francisco, CA: Planet Team.
Quincey, D. J., Luckman, A., and Benn, D. (2009). Quantification of everest region glacier velocities between 1992 and 2002, using satellite radar interferometry and feature tracking. J. Glaciol. 55, 596–606. doi: 10.3189/002214309789470987
Quincey, D. J., Richardson, S. D., Luckman, A., Lucas, R. M., Reynolds, J. M., Hambrey, M. J., et al. (2007). Early recognition of glacial lake hazards in the Himalaya using remote sensing datasets. Glob. Planet. Change 56, 137–152. doi: 10.1016/j.gloplacha.2006.07.013
Ragettli, S., Bolch, T., and Pellicciotti, F. (2016). Heterogeneous glacier thinning patterns over the last 40 years in Langtang Himal, Nepal. Cryosphere 10, 2075–2097. doi: 10.5194/tc-10-2075-2016
Ramachandran, B., Dwyer, J., Raup, B. H., and Kargel, J. S. (2014). “ASTER datasets and derived products for global glacier monitoring,” in Global Land Ice Measurements From Space, eds J. S. Kargel, G. J. Leonard, M. P. Bishop, A. Kääb, and B. H. Raup (Berlin: Springer), 145–162. doi: 10.1007/978-3-540-79818-7_6
Reynolds, J. M. (1998). Managing the risks of glacial flooding at hydro plants. Hydro Rev Worldwide 62, 2–6.
Reynolds, J. M. (2000). “On the formation of supraglacial lakes on debris-covered glaciers,” in IAHS Publ. 264 (Symposium at Seattle 2000 – Debris-Covered Glaciers), eds M. Nakawo, C. F. Raymond, and A. Fountain (Seattle, WA: IAHS Publishing).
Reznichenko, N., Davies, T., Shulmeister, J., and Mcsaveney, M. (2010). Effects of debris on ice-surface melting rates: an experimental study. J. Glaciol. 56, 384–394. doi: 10.3189/002214310792447725
Richardson, S. D., and Reynolds, J. M. (2000b). “Degradation of ice-cored moraine dams: implications for hazard development,” in Proceedings of a Workshop Held at Seattle, Seattle, WA.
Richardson, S. D., and Reynolds, J. M. (2000a). An overview of glacial hazards in the Himalayas. Q. Int. 65–66, 31–47. doi: 10.1016/s1040-6182(99)00035-x
Robson, B. A., Nuth, C., Nielsen, P. R., Girod, L., Hendrickx, M., and Dahl, S. O. (2018). Spatial variability in patterns of glacier change across the manaslu range, Central Himalaya. Front. Earth Science 6:12. doi: 10.3389/feart.2018.00012
Rohl, K. (2006). Thermo-erosional notch development at fresh-water-calving Tasman Glacier, New Zealand. J. Glaciol. 52, 203–213. doi: 10.3189/172756506781828773
Rounce, D., Watson, C., and Mckinney, D. (2017). Identification of hazard and risk for glacial lakes in the Nepal Himalaya using satellite imagery from 2000–2015. Remote Sens. 9:654. doi: 10.3390/rs9070654
Rounce, D. R., Mckinney, D. C., Lala, J. M., Byers, A. C., and Watson, C. S. (2016). A new remote hazard and risk assessment framework for glacial lakes in the Nepal Himalaya. Hydrol. Earth Syst. Sci. 20, 3455–3475. doi: 10.5194/hess-20-3455-2016
Sakai, A., Nishimura, K., Kadota, T., and Takeuchi, N. (2009). Onset of calving at supraglacial lakes on debris-covered glaciers of the Nepal Himalaya. J. Glaciol. 55, 909–917. doi: 10.3189/002214309790152555
Shean, D. (2017). High Mountain Asia 8-meter DEM Mosaics Derived from Optical Imagery, Version 1. Boulder, CO: NASA National Snow and Ice Data Center Distributed Active Archive Center. doi: 10.3189/002214309790152555
Shulman, M. D., and Bryson, R. A. (1961). The vertical variation of wind-driven currents in Lake Mendota. Limnol. Oceanogr. 6, 347–355. doi: 10.4319/lo.1961.6.3.0347
Smith, M. W., Carrivick, J. L., and Quincey, D. J. (2015). Structure from motion photogrammetry in physical geography. Prog. Phys. Geography 40, 1–29. doi: 10.1016/j.scitotenv.2016.09.036
Somos-Valenzuela, M. A., Mckinney, D. C., Rounce, D. R., and Byers, A. C. (2014). Changes in Imja Tsho in the Mount Everest region of Nepal. Cryosphere 8, 1661–1671. doi: 10.5194/tc-8-1661-2014
Song, C., Sheng, Y., Wang, J., Ke, L., Madson, A., and Nie, Y. (2017). Heterogeneous glacial lake changes and links of lake expansions to the rapid thinning of adjacent glacier termini in the Himalayas. Geomorphology 280, 30–38. doi: 10.1016/j.geomorph.2016.12.002
Strozzi, T., Wiesmann, A., Kääb, A., Joshi, S., and Mool, P. (2012). Glacial lake mapping with very high resolution satellite SAR data. Nat. Hazards Earth Syst. Sci. 12, 2487–2498. doi: 10.5194/nhess-12-2487-2012
Sulak, D. J., Sutherland, D. A., Enderlin, E. M., Stearns, L. A., and Hamilton, G. S. (2017). Iceberg properties and distributions in three Greenlandic fjords using satellite imagery. Ann. Glaciol. 58, 92–106. doi: 10.1017/aog.2017.5
Thakuri, S., Salerno, F., Bolch, T., Guyennon, N., and Tartari, G. (2016). Factors controlling the accelerated expansion of Imja Lake, Mount Everest region, Nepal. Ann. Glaciol. 57, 245–257. doi: 10.3189/2016aog71a063
Tonooka, H., and Palluconi, F. D. (2005). Validation of ASTER/TIR standard atmospheric correction using water surfaces. IEEE Trans. Geosci. Remote Sens. 43, 2769–2777. doi: 10.1109/tgrs.2005.857883
Veh, G., Korup, O., Von Specht, S., Roessner, S., and Walz, A. (2019). Unchanged frequency of moraine-dammed glacial lake outburst floods in the Himalaya. Nat. Clim. Change 9, 379–383. doi: 10.1038/s41558-019-0437-5
Warren, C. R. (1991). Terminal environment, topographic control and fluctuations of West Greenland glaciers. Boreas 20, 1–15. doi: 10.1111/j.1502-3885.1991.tb00453.x
Watanabe, N., Nakamura, S., Liu, B., and Wang, N. (2017). Utilization of Structure from Motion for processing CORONA satellite images: application to mapping and interpretation of archaeological features in Liangzhu Culture, China. Archaeol. Res. Asia 11, 38–50. doi: 10.1016/j.ara.2017.06.001
Watson, C. S., Quincey, D. J., Carrivick, J. L., and Smith, M. W. (2017a). Ice cliff dynamics in the everest region of the Central Himalaya. Geomorphology 278, 238–251. doi: 10.1016/j.geomorph.2016.11.017
Watson, C. S., Quincey, D. J., Smith, M. W., Carrivick, J. L., Rowan, A. V., and James, M. (2017b). Quantifying ice cliff evolution with multi-temporal point clouds on the debris-covered Khumbu Glacier, Nepal. J. Glaciol. 63, 823–837. doi: 10.1017/jog.2017.47
Wessels, R. L., Kargel, J. S., and Kieffer, H. H. (2002). ASTER measurement of supraglacial lakes in the Mount Everest region of the Himalaya. Ann. Glaciol. 34, 399–408. doi: 10.3189/172756402781817545
Keywords: glacial lake, calving, lake temperature, icebergs, NDWI, Corona, structure from motion, glacier velocity
Citation: Watson CS, Kargel JS, Shugar DH, Haritashya UK, Schiassi E and Furfaro R (2020) Mass Loss From Calving in Himalayan Proglacial Lakes. Front. Earth Sci. 7:342. doi: 10.3389/feart.2019.00342
Received: 26 June 2019; Accepted: 06 December 2019;
Published: 08 January 2020.
Edited by:
Sujay V. Kumar, National Aeronautics and Space Administration, United StatesReviewed by:
Qiao Liu, Institute of Mountain Hazards and Environment (CAS), ChinaShun Tsutaki, National Institute of Polar Research, Japan
Copyright © 2020 Watson, Kargel, Shugar, Haritashya, Schiassi and Furfaro. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: C. Scott Watson, c2NvdHRAcm9ja3lnbGFjaWVycy5vcmc=
 C. Scott Watson
C. Scott Watson Jeffrey S. Kargel
Jeffrey S. Kargel Dan H. Shugar
Dan H. Shugar Umesh K. Haritashya
Umesh K. Haritashya Enrico Schiassi
Enrico Schiassi Roberto Furfaro
Roberto Furfaro