PyTrx: A Python-Based Monoscopic Terrestrial Photogrammetry Toolset for Glaciology

1. Introduction

Terrestrial photogrammetry is a rapidly growing technique in glaciology as a result of its expanding capabilities in the digital computing era, with applications in monitoring change in glacier terminus position (e.g., Kick, 1966), glacier surface conditions (e.g., Parajka et al., 2012; Huss et al., 2013), supraglacial lakes (e.g., Danielson and Sharp, 2013), meltwater plume activity (e.g., Schild et al., 2016; How et al., 2017; Slater et al., 2017), and calving dynamics (e.g., Kaufmann and Ladstädter, 2008; Ahn and Box, 2010; James et al., 2014; Whitehead et al., 2014; Pȩtlicki et al., 2015; Medrzycka et al., 2016; Mallalieu et al., 2017; How et al., 2019). It provides adequate spatial resolution and a temporal resolution that can surpass airborne and satellite-derived measurements, with flexible data-capture that is relatively easy to control.

A prevailing application has been in deriving glacier surface velocity from sequential monoscopic imagery using a displacement technique called feature-tracking, which offers highly detailed (both spatially and temporally) records (e.g., Finsterwalder, 1954; Fox et al., 1997; Maas et al., 2006; Dietrich et al., 2007; Eiken and Sund, 2012; Heid and Kääb, 2012; Rosenau et al., 2013). However, other than for glacier surface velocity measurements, monoscopic time-lapse photogrammetry remains an under-used technique in glaciology. This is because there are few publicly-available toolsets, and an increasing demand for efficient photogrammetry tools that can execute large-batch processing quickly. The majority of monoscopic photogrammetry toolsets are either distributed as programming scripts or with graphical user interfaces, and for those without prior knowledge in photogrammetry and computer coding, their applications are largely limited to calculating glacier surface velocities (e.g., Kääb and Vollmer, 2000; Messerli and Grinsted, 2015; James et al., 2016; Schwalbe and Maas, 2017). The future of glacial photogrammetry lies in its valuable ability to examine different aspects of the glacier system simultaneously, such as glacier velocity, fjord dynamics, surface lake drainage and calving dynamics. These can be studied using different image capture frequencies and over different lengths of time. To achieve this though, there needs to be greater focus on expanding the capabilities of existing toolsets, and a marked effort to develop new toolsets which widens the range of data products that can be obtained from time-lapse imagery.

PyTrx (short for “Python Tracking”) is a new toolset, which is presented here to widen the range of monoscopic photogrammetry toolsets on offer to the glaciology community, and expand the types of measurements that can be derived from time-lapse imagery. The toolset is coded in Python, an open-source computing language, and the PyTrx toolset is freely available and easily accessible to beginners in programming (available at https://github.com/PennyHow/PyTrx). PyTrx has been developed with glaciological applications in mind, with functions for deriving surface velocities via two feature-tracking approaches, surface areas (e.g., supraglacial lakes and meltwater plume expressions) with automated area detection, and line profiles (e.g., glacier terminus position) with a manual point selection method.

The common photogrammetry methods used in glaciology will be outlined subsequently, followed by PyTrx's key features and unique characteristics compared to existing toolsets. PyTrx's capabilities will be demonstrated and evaluated using time-lapse imagery from Kronebreen and Tunabreen, two tidewater glaciers in Svalbard.

2. Common Photogrammetric Methods in Glaciology

Current photogrammetry tools for monoscopic approaches with glacial imagery can generally be divided into those that perform feature-tracking algorithms such as IMCORR (Scambos et al., 1992), COSI-Corr (Leprince et al., 2007), and CIAS (Kääb and Vollmer, 2000; Heid and Kääb, 2012); and those that perform image transformation functions such as Photogeoref (Corripio, 2004) and PRACTISE (Härer et al., 2016). A common limitation is that few tools unite all the photogrammetry processes needed to compute real world measurements from monoscopic time-lapse imagery (i.e., distance, area, and velocity). There are a handful of toolsets that provide functions for all of these processes, such as the Computer Vision System toolbox for Matlab and the OpenCV toolbox for C++ and Python. However, these are merely distributed as algorithms and a significant amount of time and knowledge is needed to produce the desired measurements and information.

ImGRAFT (available at imgraft.glaciology.net), Pointcatcher (available at lancaster.ac.uk/…pointcatcher.htm) and Environmental Motion Tracking (EMT) (available at tu-dresden.de/geo/emt/) were the first toolsets made publicly available that contain the processes needed to obtain velocities from monoscopic time-lapse set-ups in glacial environments (Messerli and Grinsted, 2015; James et al., 2016; Schwalbe and Maas, 2017). These toolsets have been developed specifically for glaciological applications, either distributed as programming scripts (in the case of ImGRAFT) or with a graphical user interface (in the case of Pointcatcher and EMT). These toolsets have similar workflows and the steps involved will be outlined subsequently.

2.1. Displacement Analysis

Displacements are measured through a sequence of images using feature-tracking, by which pixel intensity features are matched from one image to another with a cross-correlation technique (Ahn and Howat, 2011). Pixel-intensity features are typically defined in the image plane as templates, creating a grid for feature-tracking and producing continuous surface measurements (also referred to as dense feature-tracking) (e.g., Ahn and Box, 2010). Feature-tracking can be conducted by creating and matching templates exclusively between each image pair in an image set (e.g., Messerli and Grinsted, 2015), or by matching the same templates through an entire image set (e.g., James et al., 2016).

When template matching between an image pair, the two images have been referred to in many ways, such as “image A” and “image B” (e.g., Messerli and Grinsted, 2015), the “reference” and “destination” images (e.g., James et al., 2016), and the “reference” and “search” images (e.g., Ahn and Box, 2010). The terms reference image and destination image will be used subsequently; the reference image being the image in which the templates are defined, and the destination image being the image in which the templates are matched. Normalized cross-correlation is a common approach for automated feature-tracking, with cross-correlation referring to the correlation between two signals (i.e., the pixel intensity distribution in two images) (Zhao et al., 2006). This technique is applied using the pixel intensity distribution in a window within a given template in the reference image (T) (Solem, 2012):

$\begin{array}{ll}R(x,y)=\frac{{\displaystyle {\sum }_{x^{\prime },y^{\prime }}\left(T\left(x^{\prime },y^{\prime }\right)·I\left(x+x^{\prime },y+y^{\prime }\right)\right)}}{\sqrt{{\displaystyle {\sum }_{x^{\prime },y^{\prime }}T{\left(x^{\prime },y^{\prime }\right)}^2·{\displaystyle {\sum }_{x^{\prime },y^{\prime }}I}{\left(x+x^{\prime },y+y^{\prime }\right)}^2}}}& (1)\end{array}$

Where R is the correlation between the reference template and the destination image, and I is the destination image. The function is applied to each possible position in the image (x, y), thus defining the correlation for every template (x′, y′). The highest correlation is defined as the best match between the reference template and the destination image. The correlation for each template in the image can also be determined using different correlation methods such as the normalized square difference, the least square sum and the least difference methods (e.g., Lowe, 1999). Matching coherence through long-duration sequences is frequently subject to severe lighting discrepancies and shadowing, which cause false motion. In such cases, image selection is of prime importance. Images with similar lighting and limited shadowing variation must be selected, which may limit the temporal resolution of the collected data.

2.2. Motion Correction

During image acquisition, the time-lapse camera platform is often subject to movement caused by wind, ground heave, thermal expansion of the tripod, and animal/human intervention. This introduces false motion to the measurements derived from an image sequence, which needs to be corrected for in order to make accurate measurements through sequential imagery. This process is referred to as image registration.

Feature-based registration methods are more commonly used for glacial environments due to large variations in lighting and glacier surface evolution over time, especially over long-duration sequences (Eiken and Sund, 2012). Feature-based registration aligns the images by matching templates containing static features. These can be natural features, such as mountain peaks (e.g., James et al., 2016), or man-made targets (e.g., Dietrich et al., 2007). Observed movement of these templates signify false motion. Ideally, static feature templates would be distributed evenly across the image plane. Static features in the foreground of an image are more sensitive and can be better for constraining camera rotation angles (Eiken and Sund, 2012), but equally heavy reliance on these can introduce false motion from image noise, which can be produced by the image sensor and manifests as imperceptible specks on the image (James et al., 2016).

The two-dimensional pixel displacements between template pairs are subsequently used to align the image pair using a transformation model, effectively mapping one image plane to another. A planar projective transformation model is typically used for time-lapse photogrammetry in glaciology because it utilizes homogeneous coordinates, and transform an original image planar surface to a continuous surface:

$\begin{array}{ll}\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ w^{\prime }\end{array}\right]=\left[\begin{array}{ccc}{h}_1& h_2& h_3\\ h_4& h_5& h_6\\ h_7& h_8& h_9\end{array}\right]\left[\begin{array}{c}x\\ y\\ w\end{array}\right]or{x}^{\prime }=Hx& (2)\end{array}$

Where H is the homography matrix that represents the transformation from one plane to another, and the h values correspond to the homogeneous transformation of each point within the planar surface, which is used to translate coordinates from the original image (x, y, w) to the destination image (x′, y′, w′). In other words, coordinates in the destination (x′) are represented by the homography and the corresponding coordinates in the reference image (Hx) (Hartley and Zisserman, 2004). The homography matrix can be applied to correct false motion from subsequent measurements, which will improve the signal-to-noise ratio of displacement information derived from feature-tracking. Motion that cannot be accounted for from the two-dimensional displacements is represented as a root-mean-square (RMS) residual pixel value, which is used as a measure of uncertainty.

2.3. Image Transformation

Image transformation is the process by which measurements in the image plane are translated to 3D measurements. A popular approach to image transformation is image georectification, where the image plane is mapped directly to a 3D coordinate system and measurements can be transformed even when defined at an angle to the camera (e.g., James et al., 2016). The planar projective transformation technique described previously (Equation 2) is also used in georectification. A homography model is calculated that represents the translation from the 3D scene to the image plane (i.e., a projection), which can also be used to create an inverse projection matrix that maps the image plane to the 3D scene (Hartley and Zisserman, 2004). This is determined using an assortment of information about the 3D scene and how the camera captures this. A Digital Elevation Model (DEM) is typically used to represent the 3D scene, along with a camera model to represent the image acquisition through the camera. The camera model commonly used in glaciology utilizes the extrinsic (R, t) and intrinsic (K) information about the camera (Xu and Zhang, 1996):

$\begin{array}{ll}P=\left[\begin{array}{c}R\\ t\end{array}\right]K& (3)\end{array}$

Where P is the camera model that mathematically represents the transformation between the three-dimensional world scene and the two-dimensional image; R, t are the extrinsic camera parameters that represent the location of the camera in three-dimensional space; and K are the intrinsic camera parameters that represent the conversion from three-dimensional space to a two-dimensional image plane.

The extrinsic and intrinsic camera parameters can be considered as separate matrices. The extrinsic camera matrix consists of a rotation matrix (r) representing the camera pose with three degrees of movement, and a translation (t) vector that describes the position of the origin of the world coordinate system in image space (Zhang, 2000):

$\begin{array}{ll}\left[R|T\right]=\left[\begin{array}{ccc}{r}_{1,1}& r_{1,2}& r_{1,3}\\ r_{2,1}& r_{2,2}& r_{2,3}\\ r_{3,1}& r_{3,2}& r_{3,3}\end{array}|\begin{array}{c}{t}_1\\ t_2\\ t_3\end{array}\right]& (4)\end{array}$

The location of the camera and its pose are needed to accurately define this rotation and translation. Pose can be encapsulated as yaw, pitch and roll, which defines the camera position around its horizontal, vertical and optic axes (Eiken and Sund, 2012).

The intrinsic camera matrix (K) is a 3 × 3 matrix that contains information about the focal length of the camera in pixels (f_x, f_y), the principal point in the image (c_x, c_y) and the camera skew (s) (Heikkila and Silven, 1997):

$\begin{array}{ll}K=\left[\begin{array}{ccc}{f}_x& 0& 0\\ s& f_y& 0\\ cx& cy& 1\end{array}\right]& (5)\end{array}$

The focal length (in millimeters) is usually included in the EXIF information for an image, but it is advised to calculate the focal length for zoom lenses and compact cameras for greater accuracy. The principal point is also referred to as the optical center of an image, and describes the intersection of the optical axis and the image plane. Its position is not always the physical center of the image due to imperfections produced in the camera manufacturing process; this difference is known as the principal point offset (Hartley and Zisserman, 2004). The skew coefficient is the measure of the angle between the xy pixel axes, and is a non-zero value if the image axes are not perpendicular (i.e., a “skewed” pixel grid).

The intrinsic camera matrix (K) assumes that the system is a pinhole camera model and does not use a lens to gather and focus light to the camera sensor (Xu and Zhang, 1996). Camera systems that include a lens introduce distortions to the image plane. These distortions are a deviation from a rectilinear projection, in which straight lines in the real world remain straight in an image. These distortions ineffectively represent the target object in the real world, and therefore distortion coefficients (k₁, k₂, p₁, p₂, k₃…k₅) are needed to correct for this. These coefficient values correct for radial (k₁, k₂, k₃…k₅) and tangential (p₁, p₂) distortions (Zhang, 2000):

$\begin{array}{ll}\begin{array}{l}{x}_{corrected}=x^{\prime }\left(1+k_1{r}^2+k_2{r}^4+k_3{r}^6+k_4{r}^8+k_5{r}^{10}\right)\\ y_{corrected}=y^{\prime }\left(1+k_1{r}^2+k_2{r}^4+k_3{r}^6+k_4{r}^8+k_5{r}^{10}\right)\end{array}& (6)\end{array}$

$\begin{array}{ll}\begin{array}{l}{x}_{corrected}=x^{\prime }+\left[2p_{1}xy+p_2\left(r^2+2x^2\right)\right]\\ y_{corrected}=y^{\prime }+\left[p_1\left(r^2+2y^2\right)+2p_{2}xy\right]\end{array}& (7)\end{array}$

Where x′, y′ are the uncorrected pixel locations in an image, and x_corrected, y_corrected are their corrected counterparts. Radial distortion arises from the symmetry of the camera lens, whilst tangential distortion is caused by misalignment of the camera lens and the camera sensor. Radial distortion is the more apparent type of distortion in images, especially in wide angle images, and those containing straight lines (e.g., skyscraper landscapes) which appear curved. Severe tangential distortion can visibly alter the depth perception in images.

The camera model and distortion coefficients can be computed using geometric calibration, whereby images of an object with a known and precise geometry are used to estimate each intrinsic and extrinsic parameter (Heikkila and Silven, 1997; Zhang, 2000). A commonly used object is a black and white chessboard, with the positioning and distance between the corners used as the x′, y′ coordinates. Other objects which can be used are grids of symmetrical circles (with the center of each circle forming the x′, y′ coordinates), and targets which are specified by programs that perform camera calibration. However, some parameters of the camera model are challenging to define prior to installing the camera in the field, such as the camera pose (yaw, pitch and roll). In such circumstances, parameters in the camera model can be determined using an optimization routine which estimates and refines them based on the known parameters and a set of ground control points (GCPs). GCPs are point locations in the image plane with corresponding 3D coordinates, typically located on stable, non-moving features (e.g., mountain peaks), or features on the glacier whose positions have been accurately measured at the time of image acquisition (e.g., with GNSS). The positions of the GCPs in the image plane and projected from the 3D scene are used in the optimization routine to refine the camera model, minimising differences between the image and projected GCP positions (e.g., Messerli and Grinsted, 2015).

3. Structure of PyTrx

PyTrx (available at https://github.com/PennyHow/PyTrx) has been developed to further terrestrial time-lapse photogrammetry techniques in glaciology, and offer an alternative to the monoscopic toolsets currently available. Specifically, PyTrx has achieved this with the following key features:

1. Two feature-tracking approaches, which compute accurate velocities either as a set of discrete measurements using Optical Flow approximation, or as a continuous surface using cross-correlation template matching;

2. Approaches for deriving areal and line measurements from oblique images, with automated and manual detection methods;

3. Camera calibration and optimization functionality to calculate and refine the camera model;

4. Written in Python, a free and open-source coding language, and provided with simple example applications for easy use;

5. Engineered with object-oriented design for efficient handling of large data sets;

6. Core methods designed as stand-alone functions which can be used independent of the class objects, making it flexible for users to adapt accordingly.

PyTrx is aimed at users with all levels of programming experience. The rigid structure of the class objects is ideal for beginners in programming who have little need to change the scripts, whilst advanced users can use and adapt the stand-alone functions for more complex applications.

PyTrx is compatible with Python 3 and largely utilizes the OpenCV (Open Source Computer Vision) toolbox (v3.4 and upwards), which is a free library designed to provide computer vision and machine learning tools that are computationally efficient and operational in real-time applications. The library has over 2500 optimized algorithms including those for monoscopic photogrammetry and camera calibration (Solem, 2012). A number of other packages are also used by PyTrx, notably GDAL, Glob, Matplotlib, NumPy, PIL, and SciPy; and these come pre-installed with most Python distributions such as PythonXY and Anaconda.

PyTrx is distributed as a series of files, which requires a driver script to run. The toolset consists of eight Python files, which handle the main classes and functions:

1. CamEnv.py – Handles the objects and functions associated with the camera environment;

2. DEM.py – Handles the DEM and associated functions;

3. Images.py – Handles the objects and functions associated with the image sequence and the individual images within that sequence;

4. Velocity.py – Handles the Velocity and Homography objects, and functions for correcting for camera motion, and deriving velocity measurements;

5. Area.py – Handles the Area object and functions for deriving areal measurements;

6. Line.py – Handles the Line objects and functions for deriving line;

7. FileHandler.py – Contains the functions for importing and exporting data;

8. Utilities.py – Contains the functions for plotting and presenting data.

Within these files, ten class objects perform the core photogrammetry processes that were outlined in the previous section: GCPs, DEM, CamCalib, CamImage, ImageSequence, Homography, Velocity, Area, Length, and CamEnv. They operate according to the workflow presented in Figure 1.

FIGURE 1

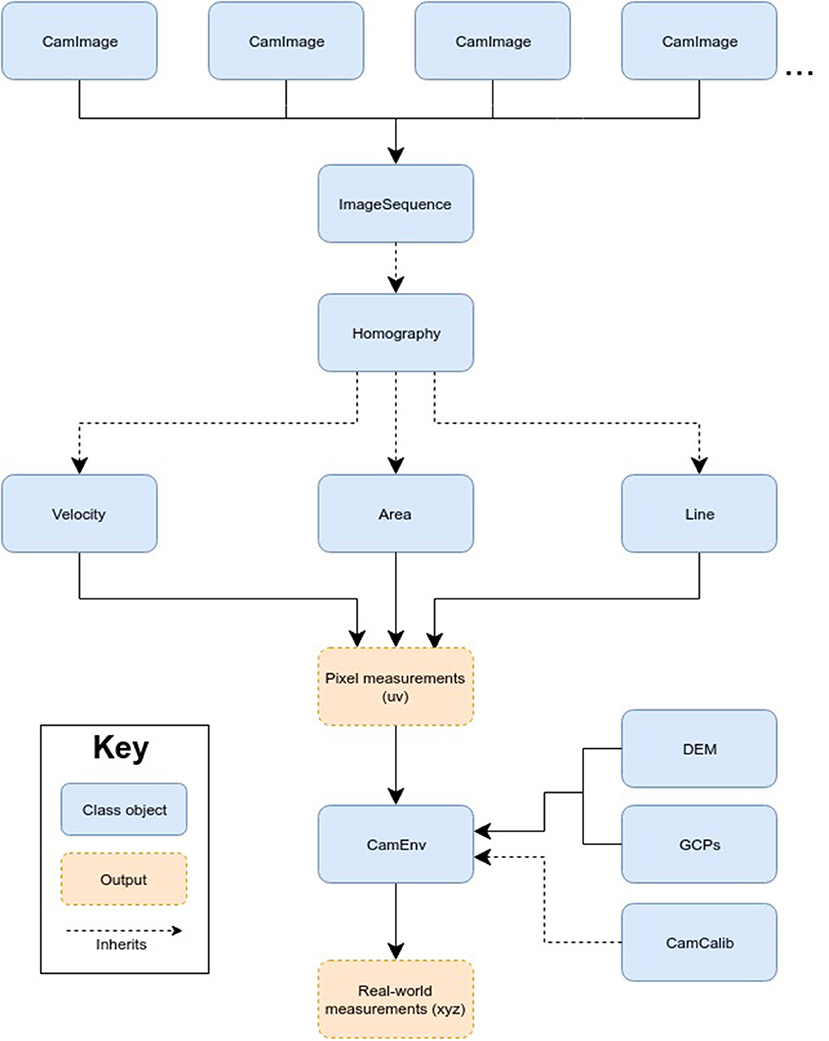
Figure 1. PyTrx's workflow, showing how each of the class objects interact with one another. An image and its associated information is encapsulated as a CamImage object, with multiple CamImage objects compiled together as an ImageSequence object. The Homography, Velocity, Area, and Line objects inherit the attributes of the ImageSequence object, thereby measurements can be computed through a series of images. The CamEnv object is composed of the DEM, GCPs and CamCalib objects, which represents the camera model and used to transform measurements between the image plane and the 3D scene.

The key features of PyTrx, which are different from the general techniques discussed previously, will be outlined comprehensively in the subsequent sections with reference to PyTrx's object-oriented workflow. Class objects, functions and input variables in PyTrx will be highlighted in italics.

4. Features and Applications of PyTrx

4.1. Field Set-Up

Examples are given throughout which demonstrate the capabilities of PyTrx and its applications in glaciology. These examples use time-lapse imagery collected from Kronebreen (78.8°N, 12.7°E, Figure 2B) and Tunabreen (78.3^oN, 12.3^oE, Figure 2C), which are two tidewater glaciers in Svalbard (Figure 2A). These time-lapse camera systems consisted of a Canon 600D/700D camera body and a Harbortronics Digisnap 2700 intervalometer, powered by a 12 V DC battery and a 10 W solar panel. The field of view from each camera is shown in Figure 3, acquired through the use of EF 20 mm f/2.8 USM prime lenses for the Kronebreen cameras (Figures 3A–C) and an EF 50 mm f/1.8 II prime lens for the Tunabreen camera (Figure 3D). The cameras were enclosed in waterproof Peli Case boxes, modified with a porthole that could hold a sheet of optical glass between two steel frames. Each box was fixed on a tripod, anchored by digging the tripod legs into the ground, burying the tripod legs with stones, and/or drilling guide wires into the surrounding bedrock. An example of one of these set-ups is shown in Figure 2D.

FIGURE 2

Figure 2. Maps showing the Svalbard archipelago (A), Kronebreen (B), and Tunabreen (C) with numbered camera sites installed over the 2014 and 2015 melt seasons; and an example of one of the time-lapse camera installations in the field (D).

FIGURE 3

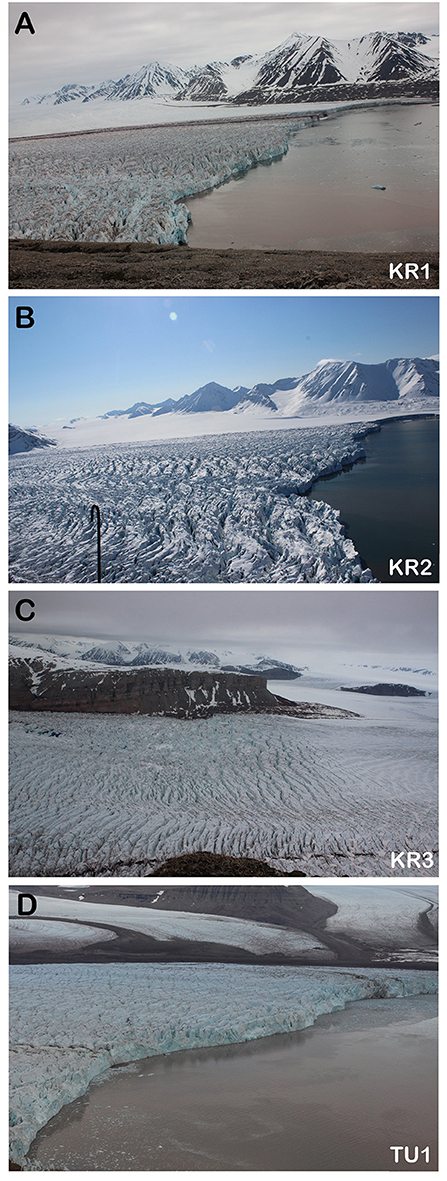
Figure 3. Examples of images taken from each time-lapse camera used in this study. The camera names correspond to those used in the examples presented from PyTrx, and those in Figure 2. (A) shows the viewpoint from KR1 of the terminus and proglacial area of Kronebreen, which is ideal for examining processes at the ice-ocean interface. (B) shows the viewpoint from KR2 of the terminus and near-terminus area of Kronebreen, which can be used to measure near-terminus glacier dynamics such as glacier surface velocity. (C) shows the viewpoint from KR3 of the upper glacier region of Kronebreen, where supraglacial lakes can be identified and monitored. (D) shows the viewpoint from TU1 of the terminus and proglacial area of Tunabreen, which is optimum for examining terminus dynamics.

Accurate locations for the time-lapse cameras were measured using a Trimble GeoXR GPS rover to a SPS855 base station, which was positioned ~15 km away. Positions were differentially post-processed in a kinematic mode using the Trimble Business Centre software, with an average horizontal positional accuracy of 1.15 m and an average vertical positional accuracy of 1.92 m. GCPs were determined for each camera set-up from known locations that were visible in the field of view of each camera. Each camera (and lens) was calibrated using the camera calibration functions in PyTrx to obtain intrinsic camera matrices and lens distortion coefficient values. The GCPs and intrinsic camera matrices were then used to optimize the camera pose, as part of the optimization functionality within PyTrx.

The DEM of the Kongsfjorden area originates from a freely available DEM dataset provided by the Norwegian Polar Institute, which was obtained from airborne photogrammetric surveying in 2009 (Norwegian Polar Institute, 2014). This DEM was chosen because of its higher accuracy over those closer to the acquisition of the time-lapse imagery. The DEM of the Tempelfjorden area originates from ArcticDEM, Scene ID WV01-20130714-1020010 (14 July 2013). These DEMs are distributed with PyTrx in a modified form, with each scene clipped to the area of interest, downgraded to 20 m resolution, and smoothed using a 3×3 low-pass filter in order to eliminate artifacts that do not reflect the surface at the time of image acquisition. For measurements derived at sea level (e.g., meltwater plume extent and terminus profile), we transformed all low-lying elevations (below 150 m) to 0 m a.s.l. in order to project them to a flat, homogeneous surface.

4.2. Image Enhancement

An image is passed into PyTrx as an array, either using the readImg function found in Filehandler.py or when initialising the CamImage object which is in Images.py. Image enhancement processes are executed by modifying the array that represents the image. The image enhancement methods that are available in PyTrx are histogram equalization, the extraction of information from a single image band or grayscale, and simple arithmetic manipulations on an image's pixel values. Histogram equalization is a point operator manipulation, used to achieve suitable pixel contrast for distinguishing features for reliable matching (Soha and Schwartz, 1978; Akcay and Avsar, 2017). An intensity mapping function is calculated by computing the cumulative distribution function (c(I)) with an integrated distribution (h(I)) and the known number of pixels (N) in the image (I) (Solem, 2012):

$\begin{array}{ll}c\left(I\right)=\frac{1}{N}{\displaystyle \sum _{i=0}^{I}h}(I)=c(I-1)+\frac{1}{N}h(I)& (8)\end{array}$

This reduces the range of pixel values in an image, and smooths drastic changes in lighting and color.

Grayscale, equalized images are used commonly in photogrammetric processing in order to reduce processing time (e.g., James et al., 2016). This means that the three color channels (RGB) are reassigned to one, and each pixel represents one single grayscale value. However, this can alter the image and its uses for extracting measurements from. PyTrx has been designed to overcome this limitation by providing a method for extracting information from a specified band of an image. An image can be passed either in grayscale, or with one of the RGB bands. Although this is executed in the readImg function or the CamImage object, it can also be defined in the Velocity, Area, and Line objects with the band variable. The string inputs r, g, b, and l denote whether the red, green, blue, or grayscale bands should be retained. This does not affect the processing time drastically, and enables effective detection of areas of interest in images, such as meltwater plumes and supraglacial lakes. The example in Figure 4 demonstrates how each selected band affects the pixel intensity range associated with a cluster of supraglacial lakes. These surface areas have been detected automatically based on pixel intensity. Ideally, regions of interest in an image are effectively detected when they are represented by the smallest range in pixel intensity (i.e., a homogeneous surface). In the example presented in Figure 4, the red band of the image (Figure 4C) offers the smallest pixel intensity range and thus the lakes are represented as a homogeneous surface. This proves easiest to define on an automated basis.

FIGURE 4

Figure 4. An example of PyTrx's ability to the extract pixel information from a specified image band using an example image from Kronebreen. The image shows a cluster of supraglacial lakes, which were monitored through the 2015 melt season. (A) shows the original time-lapse image. The yellow box denotes the subset from which pixel information is extracted from and displayed in the subsequent images: grayscale (B), the red image band (C), the green image band (D), and the blue image band (E). The white plotted lines in these subsets show attempts to automatically detect the lake extent. The red image band yields the best detection as it closely follows the lake extent.

PyTrx offers an additional enhancement process to improve the ability to detect areas of interest in an image automatically. The enhanceImg function in Images.py uses simple arithmetic to manipulate image brightness and contrast. This enhancement method uses three variables to change the intensity and range of the image array:

1. diff : Changes the intensity range of the image pixels. This has two outcomes. Either it changes dark pixels to become much brighter and bright pixels become slightly brighter, or it changes dark pixels to become much darker and bright pixels become slightly darker.

2. phi: Multiplies the intensity of all pixel values.

3. theta: Defines the number of “colors” in the image by grouping pixel intensity regions together, also known as image segmentation.

The result better distinguishes areas of interest, and makes it easier for the subsequent detection. See Section 4.4 for more information on how areal measurements are derived from images using PyTrx.

4.3. Deriving Velocities From Feature-Tracking

As previously outlined, a dense feature-tracking approach computes glacier velocities over a grid of templates, which can be interpolated to create a continuous surface of measurements. However, this approach can limit the spatial resolution of velocity measurements to the template size, and is also difficult to perform on large datasets because matching is based on the correlation between relative pixel differences which is a computationally inefficient method. For this reason, PyTrx offers two feature-tracking approaches: (1) a dense feature-tracking approach similar to those outlined previously which computes glacier velocities via template matching over a regular grid; and (2) a sparse feature-tracking approach which computes glacier velocities as a set of discrete measurements using a corner feature detection method to define templates and Optical Flow to match templates. The sparse feature-tracking approach serves as an alternative method to dense feature-tracking, with an efficient matching method that produces spatially detailed velocities.

The dense feature-tracking approach offered in PyTrx first generates templates as a gridded array based on a defined spacing and size, and then uses OpenCV's matchTemplate algorithm to match each template between an image pair. Dense feature-tracking with PyTrx can be used to generate sequential velocity maps over short time windows, as illustrated in Figure 5 where an early season speed-up at the terminus of Kronebreen is observed across image pairs spanning 14 June to 7 July 2014. PyTrx's template matching can be performed using one of six correlation methods offered in PyTrx's calcDenseVelocity function—cross-coefficient, normalized cross-coefficient, cross correlation, normalized cross-correlation, square difference, and normalized square difference. Templates can be generated and matched through a series of images by calling each one-by-one through the ImageSequence object (found in Images.py). An ImageSequence object holds the information about a series of CamImage objects (as shown in Figure 1). It references the CamImage objects sequentially (sorted alphabetically based on file name) so that they can be called easily in subsequent processing, such as the selection of single images and image pairs.

FIGURE 5

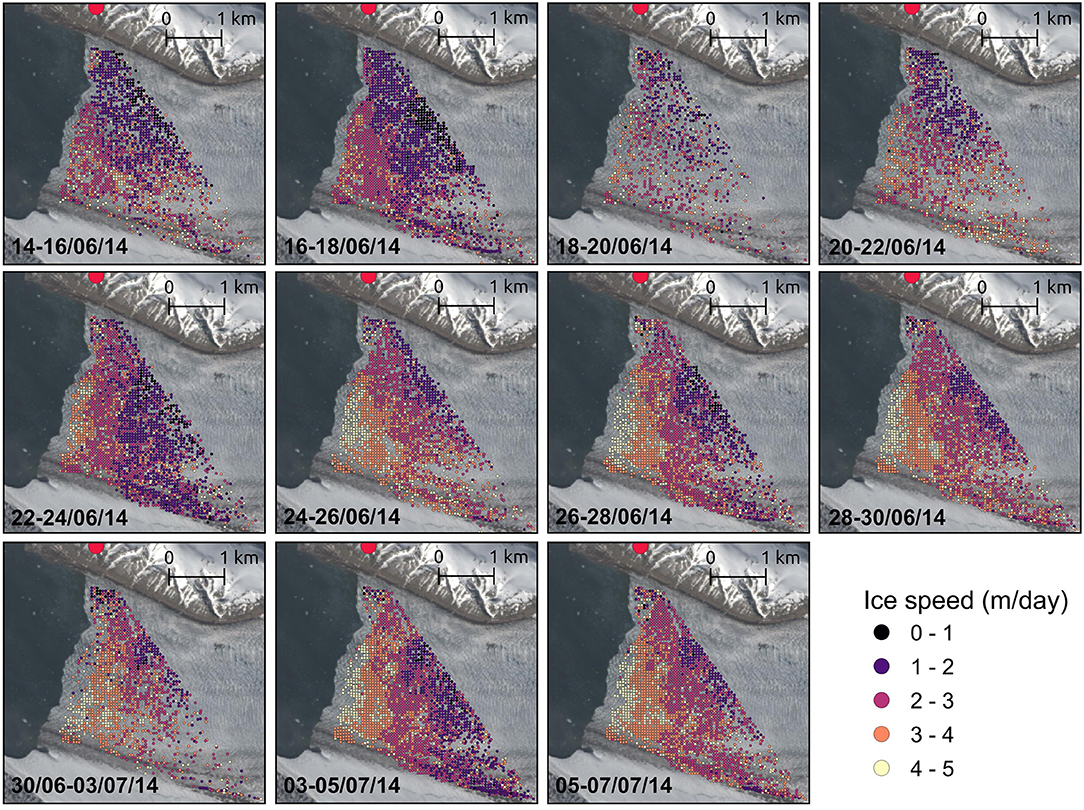
Figure 5. An example of PyTrx's dense feature-tracking and georectification functionality, with velocities determined from oblique time-lapse image pairs between 14 June and 7 July 2014 at Kronebreen camera KR2. Templates (represented here as points) were defined over a 50 × 50 m grid, which were matched between image pairs using normalized cross-correlation and filtered by correlation (i.e., templates were retained where the correlation of the match was above 0.8). The results have been plotted onto a coinciding Landsat 8 satellite image, with the red point denoting the location of the time-lapse camera (Kronebreen camera KR2). The sequence shows an early season speed-up at the terminus of the glacier, where velocities increase from an average of 2.5 m/day (14–16 June, first panel) to 4.7 m/day (5–7 July, last panel). A subset of this example (28 June to 7 July) is provided with PyTrx at https://github.com/PennyHow/PyTrx.

In the sparse feature-tracking approach, templates are first defined in the image plane by identifying corner features which provide distinctive pixel-intensity distributions that can be matched easily between an image pair (Harris and Stephens, 1988). Corner templates are generated in PyTrx's calcSparseVelocity function using the Shi-Tomasi Corner Detection method (Shi and Tomasi, 1994). This is based on the Harris Corner Detection method, which evaluates the difference in intensity for a displacement of (u, v) in all directions for a given region of an image (E) (Harris and Stephens, 1988). Templates are selected based on the largest intensity differences:

$\begin{array}{ll}E(u,v)={\displaystyle \sum _{x,y}w}(x,y){\left[I\left(x+u,y+v\right)-I\left(x,y\right)\right]}^2& (9)\end{array}$

Where w is the window function (rectangular or Gaussian) defined as a width and height (x, y) and I is pixel intensity. The first term within the square brackets, (I(x+u, y+v)) defines the shifted intensity, and the second part (I(x, y)) calculates the intensity at the center origin. A scoring function (R) is subsequently used to define whether the pixel-intensity signature in the template represents a corner, a flat area or an edge:

$\begin{array}{ll}R=min\left({\lambda }_1{\lambda }_2\right)& (10)\end{array}$

Where λ₁ and λ₂ are the eigen values in the horizontal and vertical axes of a given symmetric matrix (Shi and Tomasi, 1994). This forms a descriptor for the matrix, which can be used to evaluate the template:

1. A homogeneous (“flat”) region of the image is present if λ₁ ≈ λ₂ ≈ 0 (e.g., Figure 6A);

2. An edge is present if one of the eigenvalues is large and the other is approximately zero (e.g., λ₁ > 0 and λ₂ ≈ 0) (e.g., Figure 6B);

3. A corner is present if λ₁ and λ₂ are both large positive values (e.g., Figure 6C).

PyTrx's featureTrack function returns the strongest corner templates, as defined by the quality level which denotes the minimum quality of a corner, measured as a value between 0 and 1. The function attempts to generate 50,000 templates with a quality level of 0.1 and a minimum Euclidean distance of three pixels in an image. These default settings produce a heavily populated sparse template set in the image plane.

FIGURE 6

Figure 6. Corner feature coherency demonstrated using regions of a time-lapse image of a crevasse field. The crevasse field (top image) is a subset of a time-lapse image from Kronebreen, Svalbard. The regions highlighted from this subset are examples of a homogeneous area (A), an edge feature (B), and a corner feature (C). At the red point in (A), there is an indistinctive pixel pattern that could not be matched from image to image. The red point in (B) has a distinct boundary between different pixel intensities, but tracking may drift along the boundary over time. The red point in (C) is a very distinctive pixel pattern with a defined corner feature that is easy to track.

The set of sparse corner templates are matched between image pairs in PyTrx's calcSparseVelocity function using the Lucas Kanade Optical Flow Approximation method (Lucas and Kanade, 1981). Optical Flow is the pattern of apparent motion of an object between two images, caused by the movement of the object or the camera. It is a concept readily employed in video processing to distinguish motion and has been used in motion detection applications to predict the trajectory and velocity of objects (e.g., Baker et al., 2011; Vogel et al., 2012). It is represented as a two-dimensional vector field, working on the assumptions that the pixel-intensity distribution of an object does not change between the image pair, and the neighbouring pixels display similar motion (Tomasi and Kanade, 1991). Between two images, the position of a pixel (I) will change (δx, δy) over time (δt), assuming that the pixel intensity is unchanging (Zhang and Chanson, 2018):

$\begin{array}{ll}I(x,y,t)=I\left(x+\delta x,y+\delta y,t+\delta t\right)& (11)\end{array}$

The Lucas-Kanade algorithm approximates Optical Flow between an image pair using a template window, assuming all pixels in the template display the same motion (Lucas and Kanade, 1981). The Lucas Kanade Optical Flow approximation algorithm is available in the calcOpticalFlowPyrLK function in the OpenCV library, which is employed in PyTrx's calcSparseVelocity function because of its computational efficiency.

Back-tracking verification (Kalal et al., 2010) is used subsequently to assess matching coherency by matching templates back from the destination image to the reference image (e.g., Scambos et al., 1992; Jeong et al., 2017). This generates two sets of templates in the reference image, the original template and the corresponding back-tracked template. If a back-tracked template is within a given distance of the original template then it is deemed accurate and retained. Templates which exceed this distance threshold are discarded, and the distance between the original template and the back-tracked template can be used as a reliable measure of error. An example of this sparse feature-tracking functionality is shown in Figure 7, with a comparison to the dense feature-tracking method.

FIGURE 7

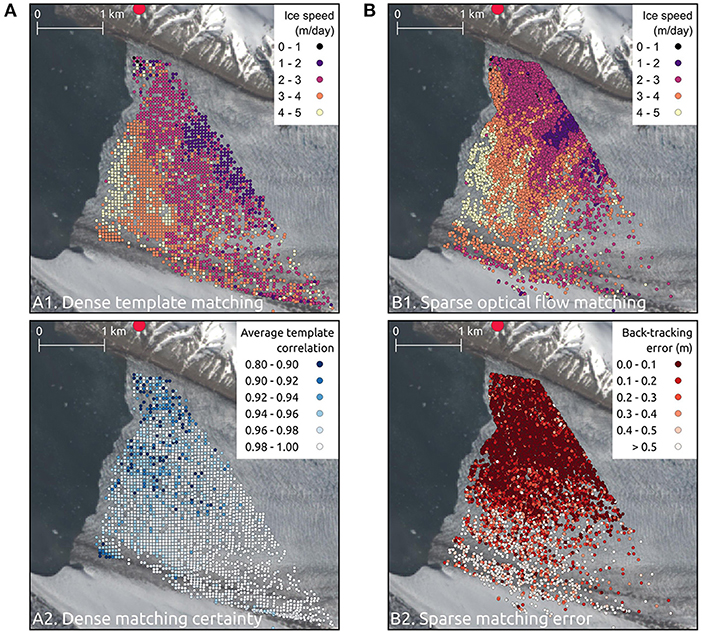
Figure 7. PyTrx's dense template matching method (A) and sparse Optical Flow matching method (B) implemented on an image pair (28–30 June) from Kronebreen camera KR2 (A1,B1), including measures of error for each approach (A2,B2). The velocities derived from these two methods are plotted onto a coinciding Landsat 8 satellite image. Velocities are calculated over a regular grid using the template matching method, providing a good basis for subsequent operations such as interpolation (A1). 2,826 of 2,854 templates were successfully matched between the image pair in this example. The correlation of each template matched between an image pair is a reliable measure of certainty (A2); in this example, the average template correlation between the image pair was 0.97. The Optical Flow method produces a high concentration of velocity measurements in areas of high corner coherency. 16,181 templates were matched in the example in (B1), with a high concentration of corner templates generated across the crevasse field nearest to the camera (B1). Matching errors are identified using back-tracking verification, where the difference between an original template and its back-tracked position provides an absolute error value. In (B2), the average difference between the position of a template and its back-tracked position is 0.15 m.

Velocity.py contains all the processing steps for PyTrx's dense and sparse feature-tracking approaches. The stand-alone functions calculate this information for an image pair (i.e., calcDenseVelocity and calcSparseVelocity), and the Velocity object can be used to iterate these functions across a sequence of images (i.e., calcVelocities). The dense feature-tracking method offered in PyTrx is suitable for calculating glacier velocity as regional averages, ensuring displacement measurements are conducted at regular intervals and matched using a correlation method impervious to illumination change (Figure 7A). The sparse feature-tracking method is effective at measuring displacements as a detailed point set, suitable for measuring surface changes over short time steps or for collecting intensive measurements over a small area (Figure 7B).

4.4. Deriving Area and Line Objects

Current photogrammetric toolsets focus on deriving velocities from time-lapse sequences, such as ImGRAFT (Messerli and Grinsted, 2015), Pointcatcher (James et al., 2016) and EMT (Schwalbe and Maas, 2017). Other measures of the glacial system would be valuable, such as changes in the area of supraglacial lakes, the expression of a meltwater plume, and glacier terminus position. PyTrx has been developed to offer area and line/distance measurements, in addition to velocities, from image sequences. The Area and Length class objects contain all of the processing steps to obtain these measurements, which can be found in the Areas.py and Line.py scripts, respectively. Both class objects inherit from the ImageSequence class object.

The Area.py script contains all the processing steps for deriving area measurements from imagery, in both an automated and manual manner. The stand-alone functions provide methods for measuring areas from a single image, whilst the Area object can be used to measure areas across a series of images. The automated detection of areas is based on changes in pixel intensity, from which edges are derived using OpenCV's findContours function which is a border-following algorithm. The Line.py script contains all the processing steps for manually deriving line measurements from imagery, with stand-alone functions for making measurements from a single image and the Line object for making measurements across a series of images. The area and line features defined in both these scripts are transformed to real-world measurements using the georectification functions in CamEnv.py, in a similar fashion to the approach in Velocity.py.

Areal features have been constructed from the distinguished surface expression of meltwater plumes and overlaid onto a satellite scene in the example presented in Figure 8. Meltwater plumes are the main sources of outflow from a tidewater glacier, and tracking their surface area can be used to infer changes in discharge (e.g., How et al., 2017). The steady recession of the meltwater plume extents shown in Figure 8 is linked to diurnal fluctuations in melt production.

FIGURE 8

Figure 8. Changes in meltwater plume extent distinguished from time-lapse imagery of Kronebreen camera KR1. The surface expression of the meltwater plume has been tracked through images captured on 05 July 2014 at 18:00 (A), 20:00 (B), and 22:00 (C) to demonstrate part of its diurnal recession. Each plot shows the plume definition in the image plane (top) and its translation to real-world coordinates and plotted onto a coinciding Landsat 8 satellite image (bottom). A similar example of this is provided with PyTrx at https://github.com/PennyHow/PyTrx.

4.4.1. Automated Detection

Areas are automatically computed using the calcAutoArea function and the Area object's calcAutoAreas function in Area.py. These are automatically detected based on pixel intensity within the image plane. This entails several key steps and functions to ensure adequate detection in each image. The image is masked to the area of interest firstly, thus reducing processing time and limiting the chance of false detection. The mask can be defined or read from file using the readMask function, which is within the FileHandler.py script. This masking is also used for defining templates in a given region of an image (as part of the feature-tracking and image registration functionality).

The image is next subjected to the simple arithmetic enhancement method outlined in section 4.2 to better distinguish the target area. The pixel intensities associated with the target area are defined subsequently as a range of the lowest and highest values. This range can either be pre-defined, or manually defined on a point-and-click basis (using the defineColourrange function). Pixels within this intensity range are distinguished and grouped using the OpenCV function inRange. The grouped pixels form regions which are transformed into polygons using the OpenCV function contour. Each point within the polygon(s) is defined by coordinates within the image plane.

Often this results in many polygons being created. The number of points in each polygon is used to filter out noise and falsely-detected areas, with small polygons (e.g., constructed with under 40 points) discarded. In addition, the user can define a threshold for the number of polygons retained (i.e., if the threshold is defined as 4, then the 4 largest polygons are retained). There is the additional option to manually verify the detected areas after these steps. This can be defined in the Area object's calcAutoAreas function with the boolean variable verify. This calls on the Area object's verifyExtents function, which cycles through all the detected area features in all the images and allows the user to manually verify each one based on a click-by-click basis. This can be a time-consuming process with long image sequences, but ensures that falsely-detected areas are discarded.

4.4.2. Manual Detection

Area and line features can also be defined manually in the image plane. This requires the user to click around the area of interest, which creates a set of points from which a polygon/line object is formed. The user input is facilitated by the ginput plotting available in Matplotlib. The polygon/line object can subsequently be georectified to create an object with real-world coordinates.

An example of PyTrx's manual definition of line features is displayed in Figure 9. Sequential terminus positions were defined within the image plane on a click-by-click basis, from which line objects were constructed and projected. Terminus profiles have been plotted between 20 August and 5 September 2015 (every 5 days), providing a detailed record of changes in terminus position over time. This shows a gradual retreat in terminus position over a peak period in the melt season.

FIGURE 9

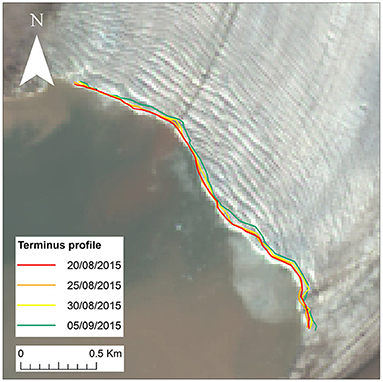
Figure 9. An example of PyTrx's ability to the extract sequential terminus profiles from Tunabreen camera TU1. The terminus profiles have subsequently been plotted onto a Landsat 8 satellite image, captured on 17 August 2015. A similar example of this is provided with PyTrx at https://github.com/PennyHow/PyTrx.

Currently, lines are limited to being manually defined, and only one line can be defined within a given image plane. Automated line detection would be a valuable addition in the future for detecting terminus profiles in sequential imagery of calving glacier fronts. However, attempts to detect terminus profiles from oblique time-lapse imagery have proved problematic due to reflections from the adjacent fjord water, tidal fluctuation, and changes in lighting and shadowing. With future development, it is hoped that these limitations can be overcome.

4.5. Image Registration and Georectification

The CamEnv.py script handles all information concerning the camera environment, including functionality for determining the camera model, either from a text file of raw information or a set of calibration images. Calibration using inputted chessboard images is carried out in the calibrateImages function, based on the approach available in the OpenCV toolbox. Camera calibration is automatically conducted during the initialization of the CamEnv object when the input directory is defined as a folder containing a set of calibration chessboard images.

The corners of the chessboard are first detected in each image (using OpenCV's findChessboardCorners algorithm), based on the inputted chessboard corner dimensions defined by the user. If all corners of the chessboard are found, the locations of these corners are then defined in the image plane to sub-pixel accuracy (using OpenCV's drawChessboardCorners and cornerSubPix algorithms). Image plane coordinates for the detected chessboard corners from all of the images are subsequently used to calculate the intrinsic camera matrix and lens distortion coefficients (using OpenCV's calibrateCamera algorithm). A rough camera matrix and distortion coefficients is initially computed using the raw inputted coordinates. These are then refined with a second calibration run, whereby the principal point (calculated initially) remains fixed. PyTrx returns the intrinsic camera matrix (as shown in Equation 4), the lens disortion coefficients (k₁, k₂, p₁, p₂, k₃), and the calibration error estimate, which are used subsequently in PyTrx's image correction and georectification processes.

The camera model can be optimized using PyTrx's optimiseCamera function, which adopts SciPy's least_squares function for optimising variables in a given function. Residuals between the positions of image GCPs and projected GCPs are first computed based on an initial camera model, and refined over iterations by adjusting the tuneable parameters. PyTrx's optimiseCamera offers optimization of the camera pose, the intrinsic matrix (i.e., focal length, principal point, skew, and distortion coefficients), and the extrinsic matrix (i.e., camera location and pose). Optimization can be carried out with a choice of three algorithms: (1) the Trust Region Reflective algorithm, which is ideal for optimising many parameters; (2) the Dogleg algorithm, suited for optimising one or two parameters; and (3) the Levenberg-Margquardt algorithm which is a popular and familiar method that has been implemented in other glacial photogrammetry toolsets such as ImGRAFT (Messerli and Grinsted, 2015).

For image registration, PyTrx encapsulates the relationship between two image planes as a homography matrix based on a set of matched templates that represent stable features. These templates can be determined and matched between an image pair either through PyTrx's dense feature-tracking approach (calcDenseHomography) or the sparse feature-tracking approach (calcSparseHomography) outlined previously. These matched templates compute the homography matrix using OpenCV's findHomography function. Homography matrices can also be determined through a series of images using the calcHomographies function within the Homography object.

The georectification method follows a similar workflow to the ImGRAFT toolset (Messerli and Grinsted, 2015). The homography model is calculated based on a camera model (i.e., extrinsic and intrinsic parameters, and distortion coefficients), which is used to compute the inverse projection variables. These variables are either defined by the user in the stand-alone functions, or compiled and stored in the CamEnv object, and subsequently called upon by the Velocity, Area, and Line objects. An example of PyTrx's georectification capabilities, using images from Tunabreen (TU1, Figure 2C), is shown in Figure 10. Point locations in Figure 10A denote the position of observed calving events (i.e., the break-off of ice from the glacier terminus), which were detected manually in the image plane (How et al., 2019). The color of each point denotes the style of calving, ranging from small break-offs (i.e., waterline and ice fall events) to large collapses (i.e., sheet and stack collapses), and detachments that occur below the waterline (i.e., subaqueous events). These xy point locations have been transformed to real-world coordinates using the georectification functions available in PyTrx (Figure 10B).

FIGURE 10

Figure 10. Calving events observed from Tunabreen camera TU1 in the image plane (A) and georectified (B), with the color of the point denoting the style of calving. Events were manually detected, from which the style of calving was interpreted. The oblique image (A) is taken from a sequence captured between 7 and 8 August 2015. The underlying satellite image (B) is a Landsat 8 image, captured on 17 August 2015. Figure adapted from How et al. (2019). This example is provided with PyTrx at https://github.com/PennyHow/PyTrx.

The point locations are overlain onto a satellite scene of the glacier terminus, which was captured as close as possible to the time of the time-lapse image acquisition (Figure 10B). The point locations tightly follow the terminus position, demonstrating good accuracy in the georectification technique and the given information about the camera environment. However, points tend to deviate from the terminus position on the eastern side of the terminus, which is further away from the camera. Similar deviation is evident in Figure 9 also. This may indicate a degree of distance decay that is difficult to correct in the homography model. Distance decay is evident in other georectification methods, especially when performing georectification from monoscopic set-ups (James et al., 2016).

5. Evaluation of PyTrx

5.1. Feature-Tracking Capabilities

Velocities are derived using a robust template matching approach, and an alternative approach utilizing an Optical Flow approximation that proves effective and computationally-efficient. The comparison presented in Figure 7 show good coherency between the two methods. Both methods capture the general spatial pattern in velocities, with faster velocities (4–5 m/day) in the central region of the glacier terminus and slower velocities (1–3 m/day) upglacier and nearer the north margin.

Velocities from the dense template matching method (Figure 7A, panel 1) appear relatively smooth compared to the sparse Optical Flow matching method (Figure 7B, panel 1), most likely because of the selection of templates based on the gridded and corner feature approaches. For the dense matching method, the correlation of each matched template provides a relatively good measure of certainty, with Figure 7A (panel 2), showing correlations of above 0.8 across the entire scene. The back-tracking evaluation provided with the sparse matching method can be used as an absolute measure of error, with all back-tracking error constrained to under 1 m; and back-tracking error in the foreground part of the image limited to an average of 0.15 m.

5.2. Error Estimation

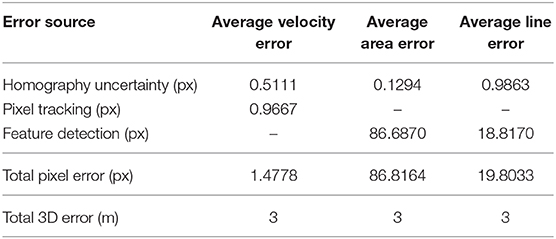
Errors have been determined for the examples presented previously, as summarized in Table 1. These errors are divided into pixel errors that are introduced during the measurements in the image plane, and those associated with the georectification process (Schwalbe and Maas, 2017). Homography uncertainty is defined as motion in the camera platform that is not resolved by the homography model. In all cases, this is constrained to less than one pixel (Table 1). When deriving velocities, matching error can either be defined by the average correlation (Figure 7A, panel 2), or the difference between the original template and the back-tracked template from the destination image to the reference image (Figure 7B, panel 2). This error can be adequately constrained using the back-tracking threshold, which is defined by the user and effectively removes template matches that are uncertain as specified by a user-defined threshold. Human error from area and line feature detection were determined based on sensitivity testing, whereby area and line features from the examples provided were delineated manually over 10 simulations to produce the average variation in pixel measurements. These can vary significantly based on the feature, as demonstrated in Table 1, and therefore it is advised to perform this sensitivity test when carrying out this approach in PyTrx (e.g., How et al., 2017). Toolsets such as ImGRAFT and Pointcatcher have adopted the Monte Carlo method to indicate the sensitivity of the image registration process, using random repeated sampling to simulate variation in the static template displacements (Messerli and Grinsted, 2015; James et al., 2016). PyTrx could benefit from such error analysis in future releases.

TABLE 1

Table 1. Error estimations for deriving velocity, area and line measurements using PyTrx.

Errors in the camera model have been constrained through the optimization routine available in PyTrx, which refines the projection of the 3D scene to the image plane based on the positions of a set of GCPs. Remaining differences between the positions of the image GCPs and the corresponding projected GCPs represent residuals in the camera model, which are used as a measure of error. Discrepancies in the camera model used to derive the velocities presented in Figure 5 were reduced by 140 pixels following the optimization of the camera pose, leaving a residual of 5 pixels. The effect of this remaining residual on the overall error of the georectification process has been defined previously using general estimates (e.g., Messerli and Grinsted, 2015), or distance-based approximations (whereby error is determined as a function of distance from the camera, e.g., Schwalbe and Maas, 2017). In PyTrx, we introduce a direct approach to determine error from the georectification process, by calculating the difference between the 3D GCP positions and their corresponding reprojected positions from the image. This is similar to the optimization routine, where differences in the GCP positions are used as the measure of pixel error to aid in refining the camera model. By reprojecting the image GCPs to the 3D scene and comparing them to the 3D GCPs, we calculate an absolute error for the georectification process. In the examples presented in this manuscript, the difference in GCP positions was 3 m on average, and therefore the overall error from the georectification process is also 3 m. This error is a conservative estimate though, as all GCPs in these examples were defined in the far-ground of the images and it is generally understood that the errors in georectification propagate with distance from the camera. This error estimate will be more representative of measurements in the near-ground of the image in cases where GCPs can be defined closer to the camera.

6. Conclusions

PyTrx (programmed in Python, an open-source programming language) and its modular object-oriented design make it an accessible toolset for deriving measurements from oblique terrestrial imagery. PyTrx offers flexible functionality and can be adapted easily for the user's requirements, as it is distributed as a set of files with simple example drivers. The examples shown throughout demonstrate PyTrx's specific applications in deriving ice flow velocities, surface areas of supraglacial lakes and meltwater plumes, georectified point locations denoting the position of calving events, and glacier terminus profiles. Velocities can be derived using a robust template matching approach that is suitable for deriving velocity time-series, such as those presented from Kronebreen, showing spatial variability in surface velocity over the course of a melt season. An alternative feature-tracking approach is also introduced in PyTrx, which utilizes an Optical Flow approximation approach and shows good correspondence to the results from the template matching method. Comparison of the reuslts from these two feature-tracking methods show good coherency, both capturing the general spatial pattern in velocities ranging between 1 and 5 m/day.

The area and line measurement capabilities in PyTrx can be used and adapted to identify a range of glacial features. Image segmentation methods are implemented to aid in the automated detection of areas, as shown by the example of detecting supraglacial lake extents from Kronebreen. Features can also be identified manually from image-to-image on a point and click basis, and subsequently georectified to the 3D scene; which proves suitable for the classification of meltwater plume surface extent (as shown by the example from Kronebreen), and terminus position (as shown by the example from Tunabreen).

Overall, the glacial photogrammetry toolsets currently available have aspects and functionality that make them unique and beneficial to use. For instance, ImGRAFT contains sophisticated error refinement functionality to produce accurate projections (Messerli and Grinsted, 2015), multiple DEMs can be inputted into Pointcatcher to derive well-constrained vertical and horizontal displacements (James et al., 2016), and shadowing effects can be reduced in EMT (Schwalbe and Maas, 2017). PyTrx offers new progressions in glacial photogrammetry with its new functionality, such as its automated and manual methods for deriving area and line measurements, the incorporation of camera calibration in the camera model definition, and the option of two feature-tracking approaches for deriving velocities. Users therefore have a greater range of toolsets to choose from when embarking on glacial photogrammetry.

Data Availability Statement

The PyTrx toolset is available on GitHub at https://github.com/PennyHow/PyTrx (431 MB), which is compatible with Windows, Linux, and Apple operating systems and requires no additional licenses to run. The repository includes driver scripts for the specified examples in this paper, along with the accompanying data and time-lapse imagery.

Author Contributions

PH developed the PyTrx algorithms for dense feature-tracking, geometric measurements (i.e. areas and lines), camera calibration, camera optimisation, and revised the pre-existing functions to produce a coherent, fully documented toolset. In addition, PH led the writing of the paper and produced all example applications of PyTrx presented. NH developed the homography and georectification functions in PyTrx and supervised LB (née Addison) in developing the image handling and feature-tracking functionality. LB produced the initial skeleton of PyTrx and its work flow as part of her M.Sc. dissertation in Geographical Information Science, at the University of Edinburgh (Addison, 2015). DB aided in the structuring and writing of the manuscript.

Funding

This work was affiliated with the CRIOS project (Calving Rates and Impact On Sea Level), which was supported by the Conoco Phillips-Lundin Northern Area Program. PH was funded by a NERC Ph.D. studentship (reference number 1396698).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

A pre-print of this paper is available as How et al. (2018). The DEM of Kongsfjorden was provided by the Norwegian Polar Institute under the CC BY 4.0 license. The DEM of Tempelfjorden was provided by ArcticDEM (DigitalGlobe, Inc.) and funded under National Science Foundation awards 1043681, 1559691, and 1542736. We would like to thank the University of Edinburgh GeoSciences Mechanical Workshop for manufacturing the camera enclosures, Adrian Luckman for his feedback on the manuscript, and Timothy C. Bartholomaus (scientific editor), Andrew J. Sole and Robert McNabb (reviewers) for their constructive comments throughout the review process.

References

Addison, L. (2015). PyTrx: Feature Tracking Software for Automated Production of Glacier Velocity. (M.Sc. Thesis). University of Edinburgh, Edinburgh, UK.

Google Scholar

Ahn, Y., and Box, A. (2010). Glacier velocities from time-lapse photos: technique development and first results from the Extreme Ice Survey (EIS) in Greenland. J. Glaciol. 56, 723–734. doi: 10.3189/002214310793146313

CrossRef Full Text | Google Scholar

Ahn, Y., and Howat, I. (2011). Efficient automated Glacier surface velocity measurement from repeat images using multi-image/multichip and null exclusion feature tracking. IEEE Trans. Geosci. Remote Sens. 49, 2838–2846. doi: 10.1109/TGRS.2011.2114891

CrossRef Full Text | Google Scholar

Akcay, O., and Avsar, E. O. (2017). The effect of image enhancement methods during feature detection and matching of thermal images. IAPRS Spatial Inform. Sci. 42, 575–578. doi: 10.5194/isprs-archives-XLII-1-W1-575-2017

CrossRef Full Text | Google Scholar

Baker, S., Scharstein, D., Lewis, J. P., Roth, S., Black, M. J., and Szeliski, R. (2011). A database and evaluation methodology for optical flow. Int. J. Comp. Vis. 92, 1–31. doi: 10.1007/s11263-010-0390-2

CrossRef Full Text | Google Scholar

Corripio, J. G. (2004). Snow surface albedo estimation using terrestrial photography. Int. J. Comp. Vis. 25, 5705–5729. doi: 10.1080/01431160410001709002

CrossRef Full Text | Google Scholar

Danielson, B., and Sharp, M. (2013). Development and application of a time-lapse photograph analysis method to investigate the link between tidewater glacier flow variation and supraglacial lake drainage events. J. Glaciol. 59, 287–302. doi: 10.3189/2013JoG12J108

CrossRef Full Text | Google Scholar

Dietrich, R., Maas, H.-G., Baessler, M., Rülke, A., Richter, A., Schwalbe, E., et al. (2007). Jakobshavn Isbræ, West Greenland: flow velocities and tidal interaction of the front area from 2004 field observations. J. Geophys. Res. Earth Surf. 112:F03S21. doi: 10.1029/2006JF000601

CrossRef Full Text | Google Scholar

Eiken, T., and Sund, M. (2012). Photogrammetric methods applied to Svalbard glaciers: accuracies and challenges. Polar Res. 31:18671. doi: 10.3402/polar.v31i0.18671

CrossRef Full Text | Google Scholar

Finsterwalder, R. (1954). Photogrammetry and Glacier research with special reference to Glacier retreat in the Eastern alps. J. Glaciol. 2, 306–315. doi: 10.1017/S0022143000025119

CrossRef Full Text | Google Scholar

Fox, A. J., and Nuttall, A. M. (1997). Photogrammetry as a research tool for Glaciology. Photogramm. Rec. 15, 725–737. doi: 10.1111/0031-868X.00081

CrossRef Full Text | Google Scholar

Härer, S., Bernhardt, M., and Schulz, K. (2016). PRACTISE – Photo Rectification And ClassificaTIon SoftwarE (V.2.1). Geosci. Model Develop. 9, 307–321. doi: 10.5194/gmd-9-307-2016

CrossRef Full Text | Google Scholar

Harris, C., and Stephens, M. (1988). A combined corner and edge detector. Proceed. Alvey Vis. Conf. 23, 147–151. doi: 10.5244/C.2.23

CrossRef Full Text | Google Scholar

Hartley, R. I., and Zisserman, A. (2004). Multiple View Geometry in Computer Vision, 2nd Edn. Cambridge: Cambridge University Press.

Google Scholar

Heid, T., and Kääb, A. (2012). Evaluation of existing image matching methods of deriving glacier surface displacements globally from optical satellite imagery. Remote Sens. Environ. 118, 339–355. doi: 10.1016/j.rse.2011.11.024

CrossRef Full Text | Google Scholar

Heikkila, J., and Silven, O. (1997). “A four-step camera calibration procedure with implicit image correction,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (San Juan: Puerto Rico), 1106–1112. doi: 10.1109/CVPR.1997.609468

CrossRef Full Text | Google Scholar

How, P., Benn, D. I., Hulton, N. R. J., Hubbard, B., Luckman, A., Sevestre, H., et al. (2017). Rapidly changing subglacial hydrological pathways at a tidewater glacier revealed through simultaneous observations of water pressure, supraglacial lakes, meltwater plumes and surface velocities. Cryosphere 11, 2691–2710. doi: 10.5194/tc-11-2691-2017. [Epub ahead of print].

CrossRef Full Text | Google Scholar

How, P., Hulton, N. R. J., and Buie, L. (2018). PyTrx: a Python toolbox for deriving velocities, surface areas and line measurements from oblique imagery in glacial environments. Geosci. Instrum. Methods Data Syst. Discuss. doi: 10.5194/gi-2018-28

CrossRef Full Text | Google Scholar

How, P., Schild, K. M., Benn, D. I., Noormets, R., Kirchner, N., Luckman, A., et al. (2019). Calving controlled by melt-under-cutting: detailed mechanisms revealed through time-lapse observations. Ann. Glaciol. 60, 20–31. doi: 10.1017/aog.2018.28

CrossRef Full Text | Google Scholar

Huss, M., Sold, L., Hoelzle, M., Stokvis, M., Salzmann, N., Daniel, F., et al. (2013). Towards remote monitoring of sub-seasonal glacier mass balance. Ann. Glaciol. 54, 75–83. doi: 10.3189/2013AoG63A427

CrossRef Full Text | Google Scholar

James, M. R., How, P., and Wynn, P. (2016). Pointcatcher software: analysis of glacial time-lapse photography and integration with multitemporal digital elevation models. J. Glaciol. 62, 159–169. doi: 10.1017/jog.2016.27

CrossRef Full Text | Google Scholar

James, T. D., Murray, T., Selmes, N., Scharrer, K., and O'Leary, M. (2014). Buoyant flexure and basal crevassing in dynamic mass loss at Helheim Glacier. Nat. Geosci. 7, 593–596. doi: 10.1038/ngeo2204

CrossRef Full Text | Google Scholar

Jeong, S., Howat, I. M., and Ahn, Y. (2017). Improved multiple matching method for observing glacier motion with repeat image feature tracking. IEEE Trans. Geosci. Remote Sens. 55, 2431–2441. doi: 10.1109/TGRS.2016.2643699

PubMed Abstract | CrossRef Full Text | Google Scholar

Kääb, A., and Vollmer, M. (2000). Surface geometry, thickness changes and flow fields on creeping mountain permafrost: automatic extraction by digital image analysis. Permafrost Periglac. 11, 315–326.

Google Scholar

Kalal, Z., Mikolajczyk, K., and Matas, J. (2010). “Forward-backward error: automatic detection of tracking failures,” in 20th International Conference on Pattern Recognition, 2756–2759. doi: 10.1109/ICPR.2010.675

CrossRef Full Text | Google Scholar

Kaufmann, V., and Ladstädter, R. (2008). Application of terrestrial photogrammetry for glacier monitoring in Alpine environments. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 37, 813–818.

Google Scholar

Kick, W. (1966). Long-term glacier variations measured by photogrammetry. A re-survey of Tunsbergdalsbreen after 24 years. J. Glaciol. 6, 3–18. doi: 10.1017/S002214300001902X

CrossRef Full Text | Google Scholar

Leprince, S., Barbot, S., Ayoub, F., and Avouac, J. P. (2007). Automatic and precise orthorectification, coregistration, and subpixel correlation of satellite images, application to ground deformation measurements. IEEE Trans. Geosci. Remote Sens. 45, 1529–1558. doi: 10.1109/TGRS.2006.888937

CrossRef Full Text | Google Scholar

Lowe, D. G. (1999). “Object recognition from local scale-invariant features,” in IEEE Proceedings of the Seventh IEEE International Conference on Computer Vision (Kerkyra), 1150–1157. doi: 10.1109/ICCV.1999.790410

CrossRef Full Text | Google Scholar

Lucas, B. D., and Kanade, T. (1981). “An iterative image registration technique with an application to stereo vision,” in Proceedings of the Seventh International Joint Conference on Artificial Intelligence, Vol. 2 (San Francisco, CA), 674–679.

Google Scholar

Maas, H.-G., Dietrich, R., Schwalbe, E., Bässler, M., and Westfield, P. (2006). Analysis of the motion behaviour of Jakobshavn Isbræglacier in Greenland by monocular image sequence analysis. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 36, 179–183.

Google Scholar

Mallalieu, J., Carrivick, J. L., Quincey, D. J., Smith, M. W., and James, W. H. M. (2017). An integrated Structure-from-Motion and time-lapse technique for quantifying ice-margin dynamics. J. Glaciol. 63, 937–949. doi: 10.1017/jog.2017.48

CrossRef Full Text | Google Scholar

Medrzycka, D., Benn, D. I., Box, J. E., Copland, L., and Balog, J. (2016). Calving behavior at Rink Isbræ, West Greenland, from time-lapse photos. Arct. Antarct. Alp. Res. 48, 263–277. doi: 10.1657/AAAR0015-059

CrossRef Full Text | Google Scholar

Messerli, A., and Grinsted, A. (2015). Image GeoRectification and feature tracking toolbox: ImGRAFT. Geosci. Instrum. Method. Data Syst. 4, 23–34. doi: 10.5194/gi-4-23-2015

CrossRef Full Text | Google Scholar

Norwegian Polar Institute (2014). Terrengmodell Svalbard (S0 Terrengmodell) [Data set]. Tromsø: Norwegian Polar Institute. doi: 10.21334/npolar.2014.dce53a47

CrossRef Full Text | Google Scholar

Parajka, J., Haas, P., Kirnbauer, R., Jansa, J., and Blöschl, G. (2012). Potential of time-lapse photography of snow for hydrological purposes at the small catchment scale. Hydrol. Process. 26, 3327–3337. doi: 10.1002/hyp.8389

CrossRef Full Text | Google Scholar

Pȩtlicki, M., Ciepły, M., Jania, J. A., Promińska, A., and Kinnard, C. (2015). Calving of a tidewater glacier driven by melting at the waterline. J. Glaciol. 61, 851–863. doi: 10.3189/2015JoG15J062

CrossRef Full Text | Google Scholar

Rosenau, R., Schwalbe, E., Maas, H.-G., Baessler, M., and Dietrich, R. (2013). Grounding line migration and high-resolution calving dynamics of Jakobshavn Isbræ, West Greenland. J. Geophys. Res. Earth Surf. 118, 382–395. doi: 10.1029/2012JF002515

CrossRef Full Text | Google Scholar

Scambos, T. A., Dutkiewicz, M. J., Wilson, J. C., and Bindschadler, R. A. (1992). Application of image cross-correlation to the measurement of glacier velocity using satellite image data. Remote Sens. Environ. 42, 177–186. doi: 10.1016/0034-4257(92)90101-O

CrossRef Full Text | Google Scholar

Schild, K. M., Hawley, R. L., and Morriss, B. F. (2016). Subglacial hydrology at Rink Isbræ, West Greenland inferred from sediment plume appearance. Ann. Glaciol. 57, 118–127. doi: 10.1017/aog.2016.1

CrossRef Full Text | Google Scholar

Schwalbe, E., and Maas, H.-G. (2017). The determination of high-resolution spatio-temporal glacier motion fields from time-lapse sequences. Earth Surf. Dynam. 5, 861–879. doi: 10.5194/esurf-5-861-2017

CrossRef Full Text | Google Scholar

Shi, J., and Tomasi, C. (1994). “Good features to track,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Seattle, WA), 593–600. doi: 10.1109/CVPR.1994.323794

CrossRef Full Text | Google Scholar

Slater, D., Nienow, P., Sole, A., Cowton, T., Mottram, R., Langen, P., et al. (2017). Spatially distributed runoff at the grounding line of a Greenlandic tidewater glacier inferred from plume modelling. J. Glaciol. 63, 309–323. doi: 10.1017/jog.2016.139

CrossRef Full Text | Google Scholar

Soha, J. M., and Schwartz, A. A. (1978). “Multidimensional histogram normalization contrast enhancement,” in Proceedings of the 5th Canadian Symposium on Remote Sensing (Victoria, BC), 86–93.

Google Scholar

Solem, J. E. (2012). Programming Computer Vision with Python: Tools and Algorithms for Analyzing Images, 1st Edn. Sebastopol, CA: O'Reilly Media.

Google Scholar

Tomasi, C., and Kanade, T. (1991). Detection and Tracking of Point Features. International Journal of Computer Vision Technical Report.

Google Scholar

Vogel, C., Bauder, A., and Schindler, K. (2012). “Optical flow for glacier motion estimation,” in ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Vol. 3 (Melbourne, VIC), 359–364. doi: 10.5194/isprsannals-I-3-359-2012

CrossRef Full Text | Google Scholar

Whitehead, K., Moorman, B., and Wainstein, P. (2014). Measuring daily surface elevation and velocity variations across a polythermal arctic glacier using ground-based photogrammetry. J. Glaciol. 60, 1208–1220. doi: 10.3189/2014JoG14J080

CrossRef Full Text | Google Scholar

Xu, G., and Zhang, Z. (1996). Epipolar Geometry in Stereo, Motion and Object Recognition: A Unified Approach. Dordrecht: Kluwer Academic Publishers.

Google Scholar

Zhang, G., and Chanson, H. (2018). Application of local optical flow methods to high-velocity free-surface flows: validation and application to stepped chutes. Exp. Therm. Fluid Sci. 90, 186–199. doi: 10.1016/j.expthermflusci.2017.09.010

CrossRef Full Text | Google Scholar

Zhang, Z. (2000). A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Machine Intell. 22, 1330–1334. doi: 10.1109/34.888718

CrossRef Full Text | Google Scholar

Zhao, F., Huang, Q., and Gao, W. (2006). “Image matching by normalized cross-correlation,” in Proceedings of the IEEE International Conference on Acoustics Speech and Signal Processing II-II (Toulouse).

Google Scholar