Multi-Stage Magma Evolution in Intra-Plate Volcanoes: Insights From Combined in situ Li and Mg–Fe Chemical and Isotopic Diffusion Profiles in Olivine

Introduction

In principle, chemically zoned crystals can be the result of crystal growth in an evolving melt (growth zoning) or of chemical diffusion, as the result of disequilibrium, between minerals and the surrounding melt (diffusion zoning) (Costa et al., 2008). In the case of Li, this can be caused either by an increase in Li concentration in the magma, typically either due to magma mixing or crystal fractionation, or, due to a decrease in Li concentration in the melt, e.g., during degassing (Vlastélic et al., 2011; Lynn et al., 2018). The resulting zoning can be used to reconstruct the migration of crystals through dynamic plumbing systems with several reservoirs of compositionally different melts (Kahl et al., 2013, 2015). Olivine and clinopyroxene, as early forming crystals, are the most likely minerals to accept Li in their structure due to similar ionic radii of Mg and Fe in the octahedrally coordinated sites (Shannon, 1976). Nevertheless, Li behaves incompatibly during magma differentiation, with typical concentration levels of 3 to 8 μg/g in basalts and of ∼20 μg/g in rhyolites (Ryan and Langmuir, 1987; Ryan and Kyle, 2004) and with olivine/melt distribution coefficients of 0.2–0.35 (Ryan and Langmuir, 1987; Brenan et al., 1998). As olivine is a very abundant mineral in primitive basalts and chemical diffusion in olivine is well characterized, e.g., for Fe–Mg exchange (Dohmen and Chakraborty, 2007; Dohmen et al., 2007) or for Li (Dohmen et al., 2010; Richter et al., 2017), it frequently serves for diffusion studies (e.g., Lynn et al., 2018; Oeser et al., 2018). However, growth and diffusive origins of zoning cannot easily be distinguished by the investigation of chemical zoning alone and, notably, only the latter bears timescale information.

At magmatic temperatures, diffusion results in large isotope fractionation, e.g., of Li, Fe, and Mg, which may be recorded as isotopic zoning (e.g., Richter et al., 2003). Isotopic zoning coupled with chemical zoning is a strong indicator for a diffusive origin of the zoning because high-temperature equilibrium isotope fractionation is very limited, e.g., for Li (Tomascak et al., 1999b; Jeffcoate et al., 2007; Parkinson et al., 2007), Fe (Weyer and Ionov, 2007), and Mg (Teng et al., 2007; Liu et al., 2011). The combined information of chemical and isotopic zoning of Fe and Mg were successfully used in a number of recent studies to investigate complex magmatic evolution processes, such as magmatic differentiation and magma mixing, in a variety of different settings and to evaluate the effects of the end member processes of crystal growth and pure diffusion on the development of compositional zoning (Teng et al., 2011; Sio et al., 2013; Oeser et al., 2015, 2018; Collinet et al., 2017). Lithium is the lightest alkali metal and has two stable isotopes with a relative mass difference of ∼17%. Accordingly, large isotopic fractionations are observed between different geochemical reservoirs (see compilation in Penniston-Dorland et al., 2017 and references therein). Large Li isotope fractionations have also been observed on the mineral scale, e.g., up to 29‰ in a clinopyroxene from the Solomon Islands volcanic rocks (Parkinson et al., 2007), 29‰ in San Carlos olivine and 38‰ for an orthopyroxene crystal (Jeffcoate et al., 2007), which is thought to be mainly caused by chemical diffusion. However, the origin of the low δ⁷Li-values in olivines remain debated. They may be directly caused by subduction-derived metasomatized material, such as isotopically light lower crust (Hamelin et al., 2009) or the ingress of light subduction-derived fluids in the mantle (Gu et al., 2016). On the other hand, they are assumed to be the result of Li diffusion in the mantle or during magmatic processes such as subduction or magma differentiation (Marschall et al., 2007a, b; Magna et al., 2008).

Here, we explore the suitability of using Li and Li isotope profiles recorded by chemically and isotopically zoned magmatic olivine to unravel magmatic processes and timescales of magmatic events. As Li is thought to diffuse faster than the Fe–Mg diffusion couple and also has specific physiochemical properties in melts such as volatility, it may record short magmatic processes which occur just before (or even after) eruption, and which are not otherwise recorded. The aim of this study is to investigate if the fast-diffusing Li isotope system is coupled with or decoupled from Mg–Fe exchange diffusion (Weyer and Seitz, 2012). We focus on chemically zoned magmatic olivine crystals from the Massif Central continental intra-plate volcanic system, which were previously investigated for Fe–Mg inter-diffusion processes and diffusion-driven Fe–Mg isotopic zoning of olivine (Oeser et al., 2015), thus providing a framework for investigating Li in this study. Li concentrations and isotope ratios of olivine are analyzed by a newly developed matrix independent measurement method by femtosecond-laser ablation-MC-ICP-MS (Steinmann et al., 2019). By combining diffusion profiles of Fe–Mg and Li, we intend to decipher complex magma evolution scenarios, including cooling, magma mixing and degassing.

Materials and Methods

Samples and Geological Setting

Samples from two locations [Roche Sauterre (N45°54.858′, E02°55.674′) and Banne D’Ordanche (N45°36.671′, E02°46.355′)] in the continental intra-plate volcanic setting Massif Central (France) were investigated in this study. Olivine-phyric basanites from Roche Sauterre may originate from a large lava flow that merged into a small lava lake in a paleo-topographic low during the late Miocene to early Pliocene (Nehlig et al., 2001; Lorand et al., 2003; Richet, 2003). At the summit of the Banne D’Ordanche, an olivine- and clinopyroxene-bearing ∼710,000-year-old basanite from the north-west slope of a former strato-volcano was sampled (Richet, 2003). The samples were characterized regarding their major and trace element composition by Oeser et al. (2015). All investigated olivines are normally zoned with respect to Mg# (Mg# = [Mg]/([Mg] + [Fe])) with high Mg# (0.86 to 0.90) in their cores and low Mg# (0.74 to 0.8) in their rims. Nickel concentrations follow this trend. The width of Mg# zoning reaches up to 400 μm into the up-to-2 mm in diameter olivine crystals. Mg# zoning is accompanied by inversely correlated Mg and Fe isotopic signatures underlining a diffusive origin of the zoning. The inter-correlation indicates an inter-diffusion process with Mg diffusing out of the olivine and Fe diffusing into the olivine (Oeser et al., 2015). Lithium concentrations and Mg# are summarized in Supplementary Table S1 and backscattered electron images of the investigated crystals are displayed in Supplementary Figure S1.

Methods

Bulk Li Isotope Analyses With Solution Nebulization MC-ICP-MS

Two rock samples from Roche Sauterre (St6 and St3) were ground to a fine powder in order to perform whole rock δ⁷Li analyses. Sample dissolution and chromatographic Li purification was conducted as described in detail in Tomascak et al. (1999a), Bouman et al. (2004), and Seitz et al. (2004). Analyses of the purified Li fraction were conducted on a Thermo-Scientific Neptune Plus MC-ICP-MS for the simultaneous measurement of ⁶Li and ⁷Li. Following Seitz et al. (2004), a Cetac Aridus II desolvation unit equipped with a pneumatic nebulizer with an uptake rate of ca. 50 μl/min fitted into a PFA spray chamber was used. Sample analysis was performed sequentially, applying sample-standard-bracketing with the IRMM-16 Li reference solution. The reference material JB-2 (basalt powder, Geological survey of Japan) was measured relative to IRMM-16 with 3.2 ± 1.2‰ (2 SD) which agrees within uncertainties to the compiled literature values of 3.5–4.9‰ (Brant et al., 2012; Dellinger et al., 2014; Coogan et al., 2017).

Lithium Isotope Analyses With fs-LA-MC-ICP-MS

For in situ Li isotope analyses, a femtosecond laser ablation system (Spectra-Physics Solstice) was coupled to a multi collector inductively coupled plasma mass spectrometer (MC-ICP-MS, Thermo-Scientific Neptune Plus). The ablation beam has a pulse duration of ∼100 fs and a wavelength of 194 nm which is generated via frequency conversion from an infrared beam with 775 nm wavelength in a mirror and lens system and focused on the sample surface via a modified in-house built New Wave (ESI) stage combined with an optical microscope (Horn et al., 2006; Horn and von Blanckenburg, 2007). The laser spot size of ∼26 μm on the bracketing standard GOR132-G (Gorgona Island komatiite) allows for sufficient spatial resolution to resolve diffusion profiles. The protocol for Li isotope measurement was applied as described in detail by Steinmann et al. (2019). In brief, measurements were performed at relatively cool plasma conditions (900 W) in order to avoid matrix ionization in the plasma. In situ Li isotope ratio measurements were performed in static mode at low mass resolution which is sufficient to resolve atomic interferences. In order to keep background Li signals low, the measurements were performed under dry plasma conditions. The sample was mixed in a homogenization device to increase signal stability (Steinmann et al., 2019). For the detection of ⁷Li a 10¹³ Ω amplifier coupled to a faraday cup was deployed, while a secondary ion multiplier was used for the detection of the less abundant ⁶Li. Due to the slower signal response of the 10¹³ Ω amplifiers (as compared to 10¹¹ Ω amplifiers) a tau correction (Kimura et al., 2016) was applied during data reduction. All measurements were performed using standard-sample-bracketing with the komatiitic MPI DING reference glass GOR132-G as bracketing standard according to Eq. (1):

$${\mathrm{\delta }}^{7}Li=\left[\frac{{\left(\frac{{}^{7}Li}{{}^{6}Li}\right)}_{sample}}{{\left(\frac{{}^{7}Li}{{}^{6}Li}\right)}_{GOR132-G}}-1\right]\times 1000(1)$$

Subsequently, all data were converted relative to the internationally used Li isotope standard IRMM-16 (with δ⁷Li_IRMM–16 = δ⁷Li_GOR132–G + 8.6; Jochum et al., 2006; Steinmann et al., 2019). Measurements of the bracketing standard GOR132-G were performed in raster ablation mode with a scan speed of 20 μm/s; the olivine profiles were measured in line ablation mode with lines arranged parallel to the crystal rim so that each line accounts for one measured δ⁷Li-value. Individual measurements consist of 180 cycles, each with an integration time of 1.049 s. The first ∼35 cycles were used for background correction, measuring only the gas blank without a laser ablation signal. This was followed by ∼130 cycles of sample ablation. As internal control for the accuracy of the method, the MPI DING reference glass T1-G [δ⁷Li = 1.6–2.4‰, (Jochum et al., 2006; Le Roux, 2010; Xu et al., 2013)] was measured and yielded a long term value of 2.1‰ (δ⁷Li = 0.4‰, 2 SD for n = 64 in 16 sessions throughout 22 months) in agreement with Steinmann et al. (2019). All individual data points along the profiles were conducted as ∼100 μm long line scans parallel to the crystal rim [similar to trace element and Fe- and Mg isotope analyses (Oeser et al., 2015) (Figure 1)]. This was necessary to detect a sufficient number of Li ions in order to satisfy counting statistics due to the low concentration of Li in the samples, and in order to achieve a stable signal over the duration of the measurement. One crystal (St6-2b_ol4b, displayed in Figure 1) was analyzed across the whole crystal; all other crystals were analyzed from rim to core.

FIGURE 1

Figure 1. Photomicrograph (reflected light) of sample St6-2b_ol4b showing the positions for major and trace element and isotope analyses. Black dots are from laser ablation for trace element analyses (indicated by the red arrow), which were conducted exactly along the profile previously analyzed for major elements with EMPA (not visible). Short black lines are from laser ablation for isotope analyses, which was conducted from both rims toward the core of the olivine grain (indicated by blue arrows).

FIGURE 2

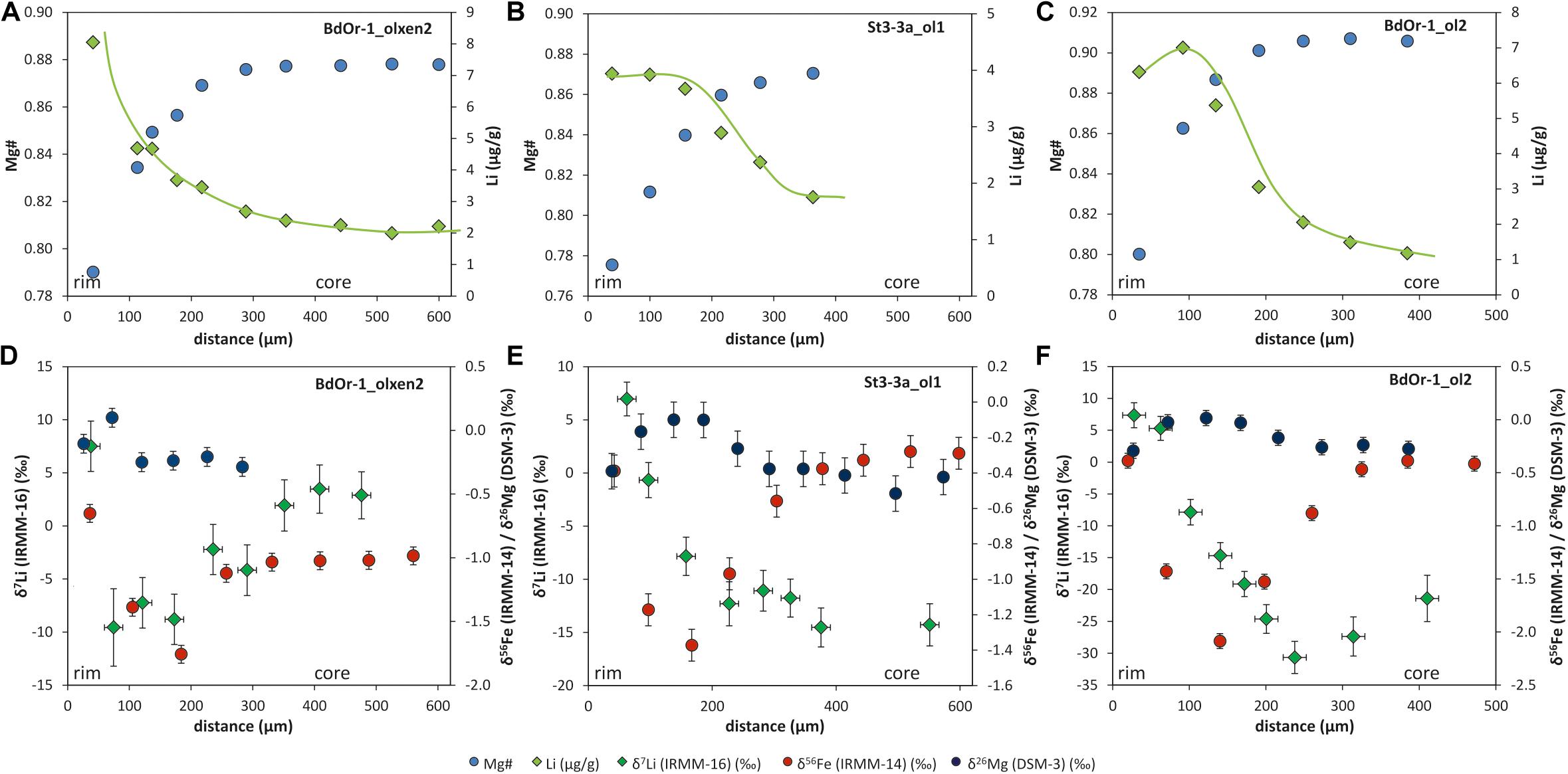
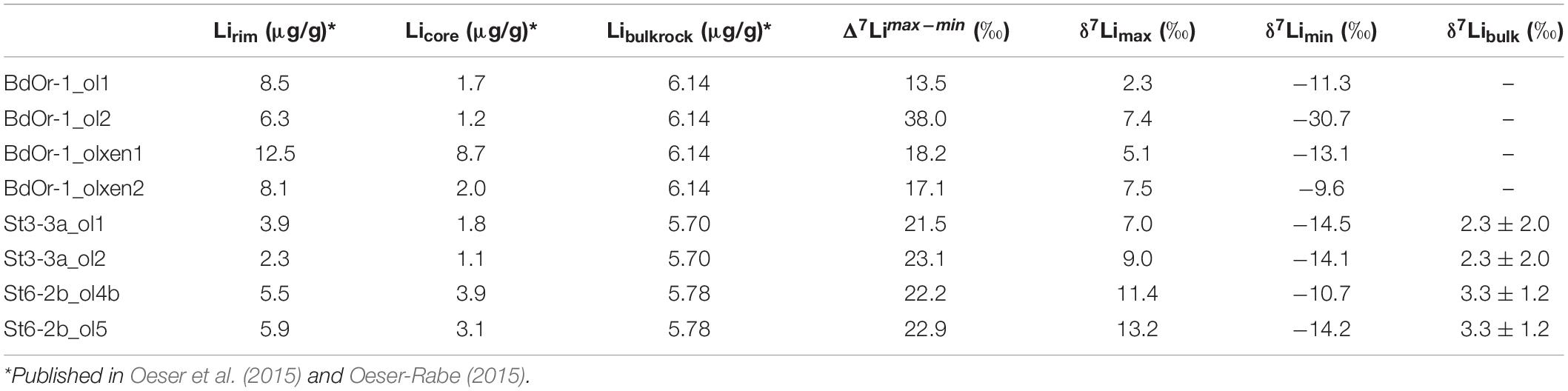
Figure 2. Mg–Fe and Li concentration zoning for (A) BdOr1_olxen2, (B) St3-3a_ol1, and (C) BdOr-1_ol2. Li concentration zoning with best-fit shape of the concentration profile (green lines) and Mg# are reversely correlated Mg, Fe, and Li isotope profiles for (D) BdOr1_olxen2, (E) St3-3a_ol1, and (F) BdOr-1_ol2. The isotope profiles show a coupling between Li and Mg–Fe diffusion, however, with an offset toward a wider zoning for Li for most olivines. Horizontal error bars display the spot size for laser ablation (∼30 μm) and vertical error bars represent the analytical uncertainty (2σ) during one sample-standard-bracketing for Li and 2SD during one analytical session for Mg and Fe [values for Mg and Fe isotopes are taken from Oeser et al. (2015)].

Diffusion Models

Diffusion has been modeled in several studies by applying an analytical or numerical approach to solve Fick’s second law of diffusion with the aim of equilibrating an initially homogeneous olivine with new boundary conditions, e.g., by changing the conditions and concentration in the surrounding melt (Costa et al., 2008). Most of the investigated olivine crystals have an elongated shape and we always analyzed the short distance to the core of those crystals (i.e., vertically to the long side, see Figure 1). For this purpose, a one-dimensional expression for the diffusion equation in a plane sheet (rather than a spherical) geometry in Eq. (2) has been solved for diffusion modeling with analytical and numerical calculations (see Supplementary Material for equations).

$$\frac{\partial C(x,t)}{\partial t}=\text{D}\frac{{\partial }^{2}C(x,t)}{\partial x^2}(2)$$

This equation is valid for diffusive processes, which are not dependent on concentration, which was used for modeling Li diffusion in this study. The diffusivity of Li in olivine has been investigated in several studies following different approaches, either based on laboratory experiments at defined conditions or based on the analyses of natural samples.

(1) An experimental study performed by Dohmen et al. (2010) found two diffusion mechanisms for Li in olivine: one “fast” diffusion mechanism, operating at interstitial sites in the olivine structure and one “slow,” metal vacancy-controlled diffusion mechanism, operating at octahedral sites. The existence of these mechanisms was later confirmed by Richter et al. (2017). In natural systems, the slower mechanism, Li diffusion via octahedral sites, is assumed to dominate (Dohmen et al., 2010). From their experiments, conducted at 800 to 1200°C and at controlled fO₂ (≈ WM buffer), Dohmen et al. (2010) have developed an equation from an approximated Arrhenius relation to determine the diffusivity of the “slow” diffusion mechanism in olivine as a function of temperature:

$$\log \left(D_{Li}\right)=-5.92\left(\pm 1.0\right)-1.2847\times {10}^4/T(K)(3)$$

The resulting diffusion coefficients are still about an order of magnitude faster than those of most divalent cations, such as Mg, Fe, or Ni.

(2) Several other studies investigated the diffusivity of Li relative to that of other cations and observed an interdependence of the diffusivities of e.g., Fe, Mg, Ni, Mn, Li, and other trace elements (Qian et al., 2010; Spandler and O’Neill, 2010; Oeser-Rabe, 2015). The diffusivity of Li was determined relative to that of Mg–Fe exchange diffusion as given in Eq. (4). The factor Γ denotes the product of diffusion coefficient and duration which equals the diffusive flux (Γ = D⋅t; e.g., Ganguly, 2002). For this purpose the concentration profiles of Li and Mg# (recalculated from MgO and FeO concentrations) are analyzed and Mg# is fitted with Eqs. (S.1) and (S.2). The concentration profile of Li is fitted by adjusting Γ, which gives the relative diffusivity of Li depending on Mg–Fe. Eq. (4) is valid under the assumption that the diffusion time t is the same or very similar for all elements.

$$\frac{{\text{Γ}}_{Li}}{{\text{Γ}}_{Mg-Fe}}\cong \frac{{\text{D}}_{Li}}{{\text{D}}_{Mg-Fe}}(4)$$

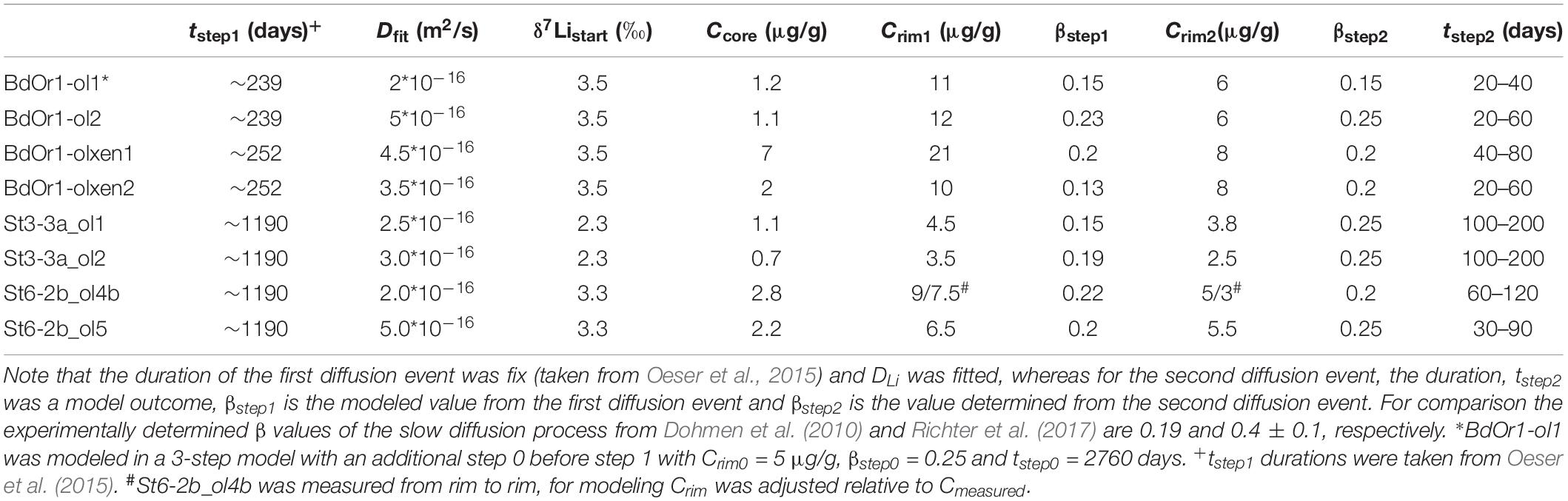
(3) We applied an approach similar to approach (2) for the olivine investigated in this study. As all olivine crystals, analyzed for their Li isotope composition in this study, were previously analyzed for their major and trace element compositions, including Fe, Mg, and Li, as well as for their Fe–Mg isotope compositions, we were able to determine Li diffusivity data relative to those of the well-determined Fe–Mg exchange diffusion. In detail, we used the timescales, as determined by Oeser et al. (2015), by modeling chemical and isotopic Mg and Fe inter-diffusion, which were interpreted to represent the residence of the olivine crystals in a magma between crystal formation for phenocrysts and the entrainment of xenocrysts in the host magma and eruption of the magma. Based on these time scales (fixed parameter t), the Li concentration and isotope profiles were fitted by adjusting D_Li in order to determine the diffusivity of Li. Thus, the resulting Li diffusivity is based on modeling of two Li profiles, i.e., the concentration and isotope profiles. To be consistent with modeling by Oeser et al. (2015) for the same samples we applied constant temperature conditions for the system. We decided to assume a temperature of 1250°C, as this was shown to be best suited for the investigated samples (Oeser et al., 2015). We are aware that a rim Mg# of 0.8 indicates lower temperatures around 1200°C (Roeder and Emslie, 1970). However, Costa et al. (2008) demonstrated that modeling with an integrated cooling rate does not affect the modeled time scales significantly as most of the diffusive flux occurs in the highest temperature regime of the system. In contrast to Fe–Mg diffusion, Li diffusion was generally modeled from both sides of the crystal, even if the profile was not measured as a complete transect. This was necessary because, due to the relatively fast diffusive character of Li, the crystal core composition was affected by diffusion from both of the opposite crystal rims, in several cases. For all crystals measured as half transects, boundary conditions for the unknown crystal rim are assumed to be in accordance with those of the measured rim. For St6-2b_ol4b, a complete transect was measured, and hence the measured values were applied in the model.

From the samples described above, olivine crystals with high Li concentrations and with the largest variations in Li concentrations from rim to core were selected for Li isotope analysis and modeling of profiles. For approach (1) the diffusivity is calculated according to Eq. (3), as the diffusivity depends on the temperature T. For approach (2) an analytical solution [Eq. (S.1) and Eq. (S.2) in Supplementary Table S1] of Eq. (2) is applied and for approach (3) a numerical solution by the method of finite differences of the diffusion equation in Eq. (2) (Eq. (S.3) in Supplementary Table S1 is applied.

The relation between the diffusion coefficients of the two isotopes of Li can be described by the empirical formula of Richter et al. (1999):

$$\frac{D_{{}^{6}Li}}{D_{{}^{7}Li}}={\left(\frac{m_{{}^{7}Li}}{m_{{}^{6}Li}}\right)}^{\mathrm{\beta }}(5)$$

Where D values are the diffusion coefficients of ⁶Li and ⁷Li, m values are the atomic masses of ⁶Li and ⁷Li in Dalton and the β-value describes the diffusion-driven isotope fractionation. β is an empirical constant which depends on the diffusion medium and is smaller than 0.5 (Richter et al., 1999). A β-value of 0.5 is the factor for a non-uniform gas (Chapman and Cowling, 1953), and the maximum value achievable. The β-value for Li has been determined experimentally and can be fitted by values of β = 0.4 ± 0.1 for the crystallographic a- and c-axis whereas the fractionation along the b-axis appears to be slightly lower (Richter et al., 2017). Transferring the relative difference in the diffusivities of the two Li isotopes, determined by Dohmen et al. (2010) to a β-value, a β_Li of 0.19 may be assumed for the slow diffusion mechanism (⁶Li diffuses 3% faster than ⁷Li) and of 0.32 for the fast diffusion mechanism (⁶Li is 5% faster than ⁷Li). Compared to Richter et al. (2017), these values are slightly lower but comparable to Li diffusivity in molten oxides (Richter et al., 2003).

Results

Four olivines from Banne D’Ordanche (BdOr-1_ol1, BdOr-1_ol2, BdOr-1_olxen1, and BdOr-1_olxen2) were analyzed regarding their Li isotope composition. Major- and trace element concentration data were taken from Oeser-Rabe (2015). The investigated olivine grains display Li concentrations varying from ∼8 to 9 μg/g at their rims to 1–2 μg/g in their core regions. The lava lake of Roche Sauterre was been sampled at two positions. Two olivines from one sample (St6-2b_ol4b and St6-2b_ol5) display concentrations varying from 7 μg/g at their rims to 3 μg/g in their cores. Two olivines in the other sample (St3-3a_ol1 and St3_3a_ol2) have somewhat lower Li concentrations ranging from 4 μg/g at their rims to 1 μg/g in their cores. All investigated grains display the lowest Li concentrations in their cores. Nevertheless, Li concentration profiles show different shapes (Figures 2A–C), i.e., some of them show a slight decrease of Li toward the very rim. Lithium concentrations and isotope compositions for all investigated samples are compiled in Table 1.

TABLE 1

Table 1. Lithium rim and core compositions of investigated olivines.

Lithium isotope profiles of all measured olivines display elevated δ⁷Li-values at the crystal rims and significantly lower values in the core regions (Figure 2) with a Li isotope fractionation between rim and core ranging from Δ⁷Li^rim–core = 21.5‰ to 27.3‰ for Roche Sauterre and Δ⁷Li^rim–core = 13.5‰ to 38‰ for Banne D’Ordanche. In most cases Δ⁷Li^rim–core is equal- or close to the largest Li isotope fractionation Δ⁷Li^min–max observed for each grain, which indicates that the cores are strongly affected by diffusion and have not preserved their original Li isotopic composition. The δ⁷Li-values in the cores (−9.6 to −14.5‰ and −30.7‰ for one crystal) are clearly lower than δ⁷Li-values of ∼4‰ of volcanic bulk rock (Seitz et al., 2004; Magna et al., 2006; Jeffcoate et al., 2007). Similar low δ⁷Li–δ⁷Li values in natural olivines were observed for other olivines from the Massif Central (Gu et al., 2016) and for San Carlos olivine xenoliths (Jeffcoate et al., 2007). Lithium concentration and isotope profiles are broadly correlated, with high Li concentration and high δ⁷Li-values at the rim and decreasing Li concentrations and low δ⁷Li-values toward the core (Figure 2). The shape of the Li isotope profiles is consistent with the shape that would be expected from diffusion-driven isotope fractionation (Parkinson et al., 2007). Iron and magnesium isotope profiles, displaying diffusion-driven zoning of δ⁵⁶Fe and δ²⁶Mg are shown for comparison in Figures 2D–F (taken from Oeser et al., 2015). The width of Li isotopic zoning slightly exceeds that of Fe and Mg isotopic zoning, in most cases. All measured Li concentration and isotope ratios (this study) are listed in Supplementary Tables S2, S3 together with the Mg and Fe isotope compositions determined by Oeser et al. (2015).

Discussion and Modeling of Diffusion Events

Boundary Conditions of the System

Coupled Li concentration and isotope profiles from the rims of the crystals toward their cores, and the extremely light isotopic composition of the olivine cores (δ⁷Li_min-values down to −30.7‰, Table 1) strongly indicate a diffusive origin of the zoning caused by faster diffusion of ⁶Li into the crystal compared to ⁷Li. The coupled zoning profiles for Li concentrations and isotope compositions are similar, though not identical in scale and magnitude, to previously investigated Fe concentration and isotope profiles (and anti-correlated Mg concentration and isotope profiles), which were generated by Fe–Mg exchange diffusion (Oeser et al., 2015; Figure 2). The Li concentration profile shapes observed for olivine from the Massif Central can be distinguished into three types (indicated by the green lines in Figures 2A–C, which represent best fits through the data), with always higher Li concentrations in the rims and lower concentrations in the cores. Type I (Figure 2A) shows decreasing Li concentrations toward the cores which is a typical profile for diffusion into the crystals. Type II (Figure 2B) consists of two compositional plateaux with constant Li concentrations at outermost rims and cores and gradually decreasing Li concentrations in transition zones. Type III (Figure 2C) exhibits maximum Li concentrations at some distance from rims (∼100 μm) and then decreases of Li concentrations toward cores. These latter profiles may indicate two diffusion events with a first event of Li diffusion into the crystals and a second event causing Li diffusion out of the crystals. While the differences between the three types of Li concentration profiles are striking, the corresponding isotope profiles cannot be distinguished as clearly.

Before diffusion models can be established, the boundary conditions of the system at the start of diffusion have to be evaluated (Costa et al., 2008). These include the Li concentration (profile) before diffusion started and here also the initial isotope composition (or isotope profile). Here, we assume that the crystals were initially homogeneous and grew in equilibrium with the melt. Assuming that the melt initially had a similar Li concentration to that analyzed for whole rock samples [BdOr1 = 6.14 μg/g, St3-3a = 5.7 μg/g, and St6-2b = 5.78 μg/g (Oeser et al., 2015)] and applying the Li olivine/melt partition coefficient determined by Brenan et al. (1998) for olivine with high Mg# (of ∼0.2), this results in equilibrium concentrations for olivine of 1.16 to 1.47 μg/g (see also Supplementary Figure S2). Lithium concentrations in the olivine cores range from 1 to 2 μg/g for the two olivine crystals from sample St3a from Roche Sauterre, as well as for three out of four Banne D’Ordanche olivines. The other two Roche Sauterre crystals (from St6) exhibit higher Li concentrations of 3.1 μg/g and 3.9 μg/g (Table 1). Only one crystal from Banne D’Ordanche displays a Li_core concentration of 8.7 μg/g, likely indicating significant Li diffusion into this core. Two of the crystals are found in a glomerocryst and hence are described as xenocrysts by Oeser et al. (2015). The initial concentration of such crystals is difficult to constrain. Notably, the rim Li concentration of most olivine grains is on the order of 4 to 8 μg/g and difficult to explain with olivine/melt partition coefficient on the order of 0.2 (Brenan et al., 1998), as this would indicate extremely high Li concentrations (on the order of 20 to 40 μg/g) in the melt at the time when diffusion ceased, i.e., at the end of fractional crystallization. Such high Li concentrations were not observed for any of the investigated basalts (Oeser et al., 2015). However, although Brenan et al. (1998) suggested low olivine/melt partition coefficient on the order of ∼0.2, those were essentially determined for extremely forsterite-rich olivine (Mg# = 99 to 100), while a higher olivine/melt partition coefficient (of ∼0.35) was observed for an olivine with a slightly lower Mg# (of 92). Other authors have observed higher partition coefficients, between 0.21 and 0.56 (Taura et al., 1998; McDade et al., 2003; Ottolini et al., 2009), which are always in combination with lower Mg# than the forsterite-rich olivines form Brenan et al. (1998). Ottolini et al. (2009) have interpreted, that there might be an influence of the melt composition on the partition coefficient, and Taura et al. (1998) supposed a pressure dependence. Thus, Li partitioning into olivine potentially increases with decreasing Mg#. If so, the high Li contents, observed in the olivine rims, may primarily be driven by increasing Li partitioning into olivine during fractional crystallization, rather than by increasing Li contents in the melt, though Li concentrations in the melt at the end of fractional crystallization may also have been slightly higher than those observed in the sampled basalts.

Similar to the Li concentrations, the measured δ⁷Li_bulk of the basalts may be assumed as the initial Li isotope composition of the olivine crystals before diffusion started. The isotopic composition of fresh basalts varies from +2‰ to +5‰ and does not appear to change significantly during fractional crystallization (Chan et al., 1992; Elliott et al., 2006; Tomascak et al., 2008). The degassing of a melt causes a transition of Li from the melt or crystal to a vapor phase and a decrease in δ⁷Li to lower values (Vlastélic et al., 2011). For Roche Sauterre St6 and St3 a δ⁷Li_bulk of 3.3 ± 1.3‰ and 2.3 ± 2.0‰ were determined, respectively. For Banne D’Ordanche, no δ⁷Li_bulk is available and a mean basaltic δ⁷Li value of 3.5‰ was assumed as the initial value for the modeling. Furthermore, the initial isotopic composition of the crystals is assumed to be homogeneous and the isotopic composition of the melt to be constant during fractional crystallization (e.g., Tomascak et al., 1999b). The initial Li isotope composition of the potential xenocrysts is uncertain and may as well be different from that of basalts. Mantle olivine may have heterogeneous δ⁷Li, which is ascribed to metasomatic overprinting (e.g., Nishio et al., 2004; Tang et al., 2012; Ackerman et al., 2013; Su et al., 2016) or diffusion in the mantle (e.g., Marschall et al., 2007a, b; Magna et al., 2008).

The First Diffusion Event: Constraints on Li Diffusion Coefficients and β Values

For the model applied here, an open system is assumed due to the quasi-infinite supply of Li from the surrounding melt. This quasi-infinite supply of Li also justifies the use of a fixed boundary concentration. As outlined above, a variety of Li diffusion coefficients, determined with different approaches, are available in the literature for modeling the observed chemical and isotopic zoning of Li. As will be shown below, the choice of Li diffusion coefficients is critical for the determination of diffusion timescales. We considered the Mg–Fe diffusion time determined by Oeser et al. (2015) as a fixed diffusion event to determine Li diffusivity. For this purpose we applied a combined approach of chemical and isotopic modeling of Mg–Fe exchange diffusion, because the diffusivity of Li in olivine is less well constrained than that of Mg–Fe (Dohmen et al., 2007). This event was interpreted as the residence time of the olivine crystals in a magma reservoir. Iron–Mg exchange diffusion was driven by the chemical evolution of the magma, as a result of fractional crystallization, which generated a chemical gradient between the melt and previously formed olivine crystals (Oeser et al., 2015). This chemical evolution would have also generated a chemical gradient in Li between olivine and surrounding melt (and as described above, likely also a change in Li partitioning), forcing Li diffusion. This scenario is consistent with increasing Li concentrations toward olivine rims and decreasing δ⁷Li values toward the olivine cores, indicating diffusion of Li (and preferentially of isotopically light Li) into olivine, as would be expected during magma differentiation. We therefore assume that the light Li and Fe isotope- (and heavy Mg isotope) signatures were generated by the same event.

Based on this assumption, Li diffusion into olivine was modeled using the timescales given by Oeser et al. (2015) for the same samples (for BdOr1_ol2 = 239 days, for BdOr1_olxen2 = 252 days and for St3-3a_ol1 = 3.26 years) and fitting the measured Li concentration and isotope profiles. The initial concentration calculated above was assumed as the Li core concentration (C_core) and in some cases it was adapted to fit the measured profile. In the first modeled event a Li rim concentration (C_rim1) of 3.5 to 21 μg/g was applied in order to match the slope of the measured profiles (Table 2). Notably, all crystals were modeled assuming equivalent diffusion and C_rim from both crystal rims toward the core. The only exception was St6-2b_ol 4b, because the crystal was measured as a whole transect, and hence both measured rim concentrations were modeled. As mentioned above, the investigated olivines display three different types of Li zoning (Figure 2) and the shapes with constant or decreasing Li concentrations at the very rim (type II and III, Figures 2B,C) cannot have formed during a single diffusion event, but rather indicate a second diffusion event (with Li diffusion in opposite direction). For those olivines, including BdOr1_ol2, BdOr1_olxen1, St3-3a_ol1, and St6-2b_ol4b, the Li concentration and isotope composition measured at the very rim was excluded when modeling the olivine core composition and the slope of the core-rim transition during the first diffusion event. As will be shown below, the very rim composition of such olivines can be modeled with a second diffusion event.

TABLE 2

Table 2. Modeling parameters of the first and second diffusion event.

Our results show that the initial concentration in crystal cores (C_core) changed during the course of diffusion for several grains, as a result of the faster diffusion of Li, as compared to that of Fe and Mg. Assuming a fixed diffusion timescale from Fe–Mg diffusion, the diffusion coefficient D_Li was fitted to obtain congruent modeled and measured zoning profiles, for both, the Li concentration and Li isotope profiles, with a particular focus on Li core compositions. Another important variable for modeling the isotopic profiles of Li is the β-value, which describes isotope fractionation during diffusion. It also has to be fitted in order to match the amplitude of the measured isotope profiles. β-values were determined in this study by fitting the modeled isotope profiles to the measured ones (as done for Fe and Mg in previous studies, e.g., Sio et al., 2013; Oeser et al., 2015 and others). With this approach, β-values determined in this study do not exceed 0.25 which is lower than the β-values of 0.4 ± 0.1 determined by Richter et al. (2017) for the crystallographic a- and c-axes, (for the b-axis somewhat lower β-values were determined), and also lower than that those that have been modeled by the same authors for a natural olivine (β = 0.30–0.36). The β-values obtained here indicate a 1.6% (β = 0.1) to 3.9% (β = 0.25) higher relative diffusivity of ⁶Li as compared to ⁷Li. This is similar to the results of Dohmen et al. (2010), who determined a ∼3% faster diffusivity of ⁶Li relative to ⁷Li in their experiments, which corresponds to β = 0.19. These findings imply, that β-values for Li may depend on intensive thermodynamic variables which have not yet been explored in detail. As the zoning profiles of several of the investigated olivines indicate a second diffusion event (see below), a slightly lower β value (than required for a perfect match of the core composition in only one diffusion step) was generally assumed for modeling of the first event, in order to match the measured isotopic zoning with a combined model of both diffusion events. Thus, the final β-value for the first diffusion event could only be determined after modeling both diffusion events. This is described in more detail below. Notably, assuming that some of the olivine grains (type I, Figure 2A) were unaffected by the second diffusion event would result in a slight underestimation of the β value for those samples. For example, olivine grain BdOr1-olxen2 was modeled with both one and two diffusion events. This revealed β-values of 0.16 for one diffusion event (Figure 3) and 0.13 for the first of two diffusion events (Supplementary Figure S3F), respectively. However, the assumption of a second diffusion event had no effect on the modeled values for D_fit. All modeled D_Li and β-values are listed in Table 2.

FIGURE 3

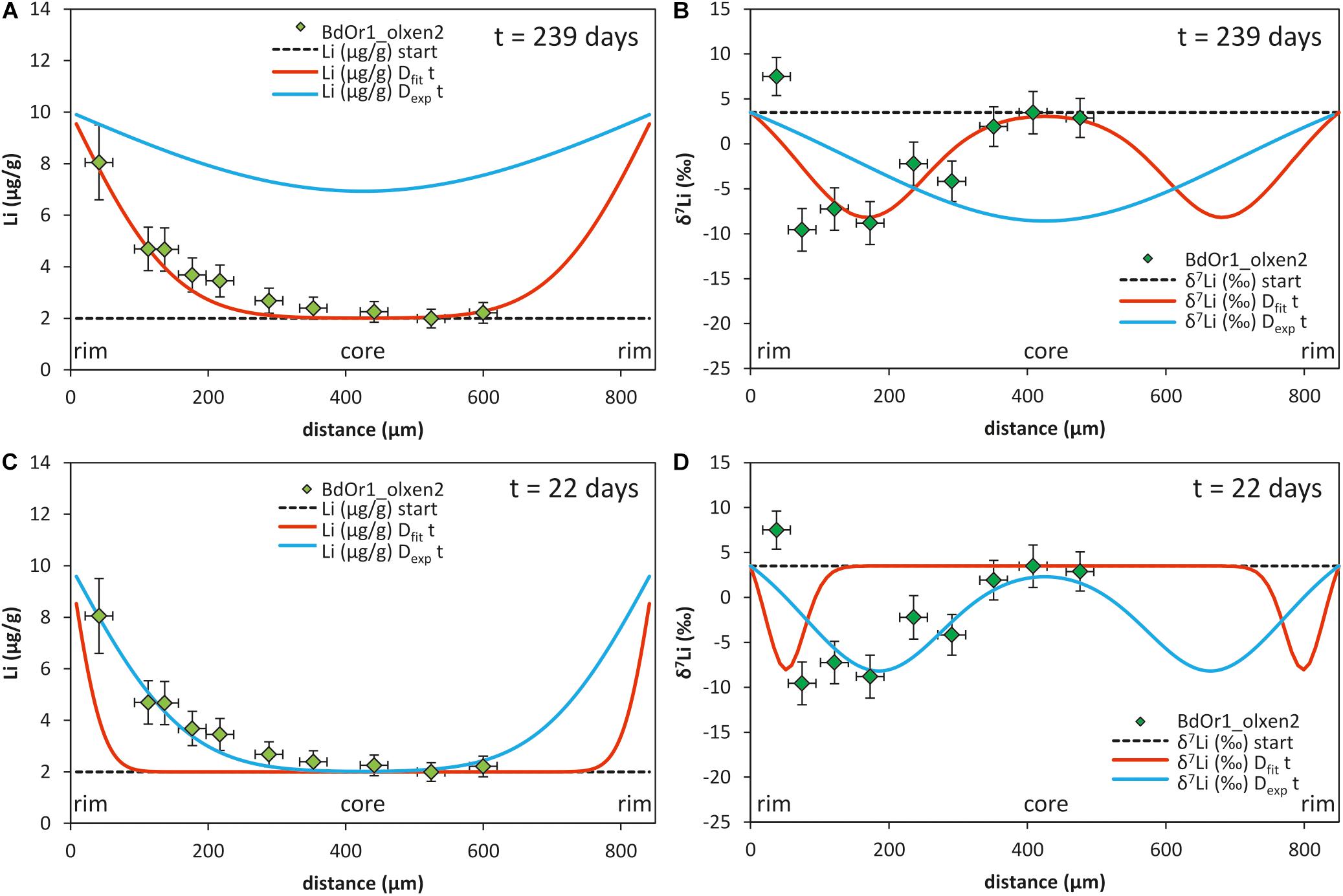
Figure 3. Modeling of the observed Li concentration and isotope composition profiles of olivine grain BdOr1 olxen2 with a 1-step diffusion model; A,B) by using the times scale as determined by Fe–Mg modeling (t = 239 days, taken from Oeser et al., 2015) and fitting the Li diffusivity (D_fit) to the measured profiles (red line); for comparison the same model (with t = 239 days) is shown using D_exp of Dohmen et al. (2010) which does not match the observed Li concentration and isotope profiles (blue lines). (C,D) the same model is shown using the diffusivity D_exp (Dohmen et al., 2010) and fitting the time scale to match the Li concentration and isotope profiles yields a diffusion time of t = 22 days (blue line); for comparison the profile is also modeled with the same time applying the fitted diffusivity from (A,B) (red line). All fits were modeled assuming a diffusivity D_exp = 4.42*10^{– 15} m²/s according to a temperature of 1250°C and D_fit = 3.5*10^{– 16} m²/s.

Diffusivities of Li relative to the diffusion couple Mg–Fe were obtained from the equations for the analytical solution in Supplementary Table S1 and yield D_Li/D_Mg–Fe ratios of ∼2 for BdOr1, which means the diffusivity of Li is twice as fast as the diffusivity of Mg–Fe in BdOr1. For St3-3a and St6-2b the diffusivity of Li is ∼1.5 times faster than the diffusivity of Mg–Fe (Figure 4). These results are similar to previous findings by Qian et al. (2010) and Spandler and O’Neill (2010). The parametrization for the determination of the diffusion coefficient of Mg–Fe diffusion in olivine by Dohmen and Chakraborty (2007) depends on temperature (T), pressure (P), oxygen fugacity (fO₂), the mole fraction of the fayalite component (X_Fe), and the crystallographic orientation of the measured profile. With Eq. (4) and the relative diffusivities of Mg–Fe and Li and the absolute calculated diffusion coefficients for Mg–Fe (D_Mg–Fe) the diffusion coefficient for Li (D_Li) is obtained (Table 3).

FIGURE 4

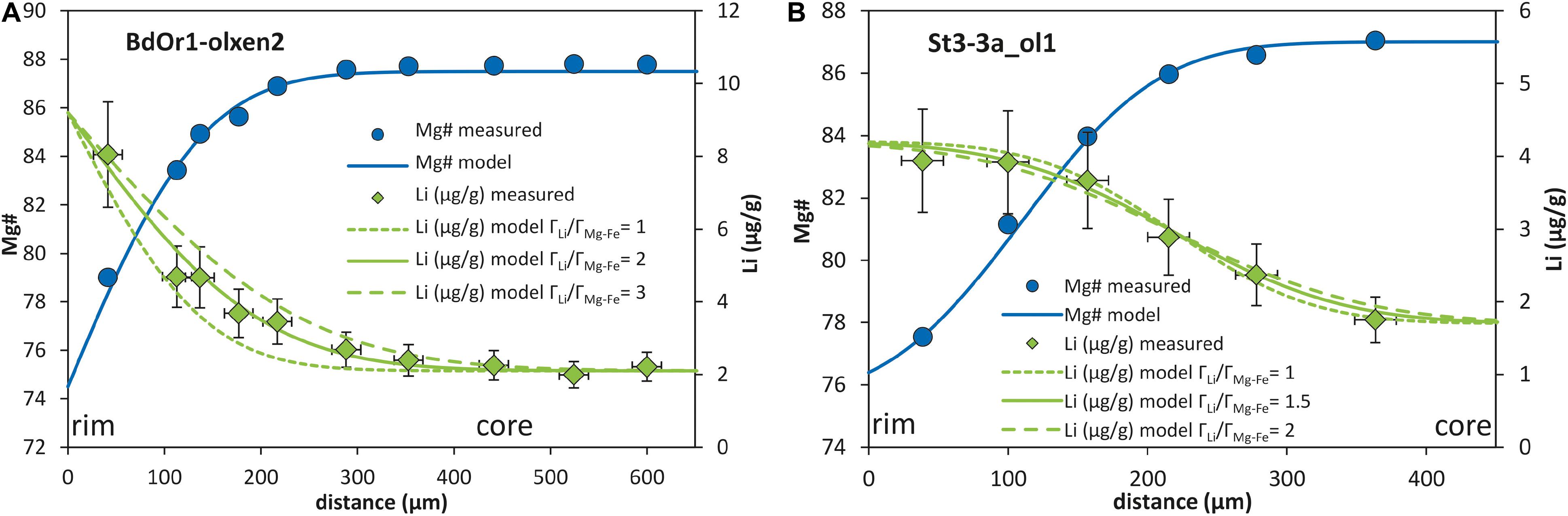
Figure 4. Relative modeling of Mg# and Li (μg/g). The Mg# and Li profiles are fitted by adjusting Ã_Mg–Fe, and Ã_Li, respectively. The ratio of the Ã-values is calculated giving the relative diffusivity of Li relative to Mg–Fe, various curves for the Li profile show the variability and uncertainty in the modeled factor for relative diffusities. (A) BdOr1-olxen2 is modeled with an infinite analytical approach assuming a fixed rim concentration. The modeled profile for Li yields a factor for the Li diffusivity relative to that of the Fe–Mg exchange (indicated by Mg#) Ã_Li/Ã_Mg–Fe from 1 to 3, which may be considered as the uncertainty of this approach. (B) St3-3a_ol1 is modeled with a semi-infinite analytical approach assuming the equilibration of two chemically distinct layers of the crystal over time, yielding a relative diffusivity factor within an uncertainty of Ã_Li/Ã_Mg–Fe from 1 to 2.

The effect of using different Li diffusion coefficients was evaluated, by comparatively modeling Li diffusion with the experimentally determined diffusion coefficient (D_exp) (for this comparison, we used the slower diffusion mechanism of Dohmen et al., 2010) and the fitted diffusion coefficient from this study (D_fit). In Figure 3 the effect of both models on the shape of the chemical and isotopic diffusion profiles is compared (for sample BdOr1_olxen2). For the comparison in Figure 3, a crystal was selected, for which the effect of a potential second diffusion event was negligible. The experimentally determined diffusion coefficient for Li from Dohmen et al. (2010) was adjusted to a temperature of 1250°C (Oeser et al., 2015), according to Eq. (3), although, experimental diffusion coefficients were only determined in the temperature range between 800°C and 1200°C. This comparison reveals that applying the experimentally determined diffusivity of Li, the modeled Li concentrations and isotope compositions do not match the observed profiles when assuming a diffusion time from Oeser et al. (2015) (Figures 4A,B). In turn, applying D_exp and fitting the modeled Li and δ⁷Li to the measured profile would indicate a significantly shorter diffusion time scale than that determined by modeling Mg–Fe exchange diffusion (Figures 3C,D). This would imply, however, that the development of Li concentration gradients was entirely decoupled from the development of Fe–Mg concentration gradients for all investigated samples, i.e., was generated by a much later event. Exchange diffusion between Fe and Mg was likely driven by the chemical differentiation of the melt in the magma chamber. Thus, this scenario would imply that both Li concentration in the melt, as well as Li partitioning between olivine and melt, which itself is dependent on Mg# of the olivine, remained about constant for most of the time and then only changed at the end of magma differentiation. In contrast, assuming the time scales for the individual samples, given by modeling of Fe–Mg diffusion (Oeser et al., 2015) and fitting the Li diffusivity to the measured profiles, a narrow range of D_fit does acceptably fit to all analyzed Li concentration- and Li isotope profiles. We therefore conclude that diffusion timescales for Li were likely similar to those for Fe–Mg and that Li diffusivities in the investigated olivines are likely more similar to those suggested by Qian et al. (2010); Spandler and O’Neill (2010) and Oeser-Rabe (2015), rather than to those determined by Dohmen et al. (2010) (here labeled as D_exp). These findings demonstrate that additional experimental investigations on Li diffusivity at lower concentration levels are urgently demanded.

Differences between experimentally determined and fitted diffusion coefficients may arise from differences in the initial and boundary conditions between those imposed in experiments and those assumed for the investigated natural samples, e.g., Li concentration in the melt (or in the powder of the experiments) surrounding the olivine crystals. In the investigated samples, the melt Li concentrations were estimated (from bulk rocks and model fits), between 5.7 and 6.14 μg/g. In contrast, the powder mixture of 90% San Carlos olivine and Li₂SiO₃, used in the experimental setup of Dohmen et al. (2010), had significantly higher Li concentrations. Notably, it was observed by Dohmen et al. (2010) that Li diffusivity in olivine depends on the Li concentration and appears to decrease with decreasing Li concentrations.

Furthermore, other intensive thermodynamic variables of the system, including the chemical composition of the crystals and melt and fO₂, which may not have yet been investigated in sufficient detail, may affect Li diffusion in olivine. In a recent experimental study, Richter et al. (2014) demonstrated a strong sensitivity of Li diffusion in clinopyroxene to fO₂. Also the experiments of Dohmen et al. (2010) imply that the diffusion mechanism of Li in olivine depends on environmental variables, such as fO₂ and aSiO₂ (amongst other factors). These parameters affect the vacancy concentrations in olivine which control the diffusion mechanism (Dohmen et al., 2010). For a series of trace elements in olivine, including Al, Cr and Be, several studies observed a dependence of the diffusivity on factors, such as silica activity (aSiO₂) and oxygen fugacity (fO₂) (Jollands et al., 2016a, b; Zhukova et al., 2017). The diffusivity of Al in forsterite at low aSiO₂ for example is up to three orders of magnitude slower than at high aSiO₂ (Zhukova et al., 2017). These studies show that diffusion in olivine may depends on parameters involving the activity of SiO₂ and fO₂.

The Second Diffusion Event

While our models broadly reproduce the low Li isotope compositions observed in olivine cores, modeled Li concentrations do not match the rim areas of several of the olivine grains investigated (e.g., BdOr1_ol2; BdOr1_olxen1; St3-3a_ol1). Similarly, the Li isotope composition does not match the observed δ⁷Li profiles for these olivine grains. Rather, the change in slope of the Li concentration profile in Figure 2C indicates that the flux of Li into the crystal (assumed in the first diffusion event) changed to a flux of Li out of the crystal during a second diffusion event at a later stage (Figure 5). The latter is not visible in all Li concentration profiles and potentially has not affected all olivine crystals to the same extent.

FIGURE 5

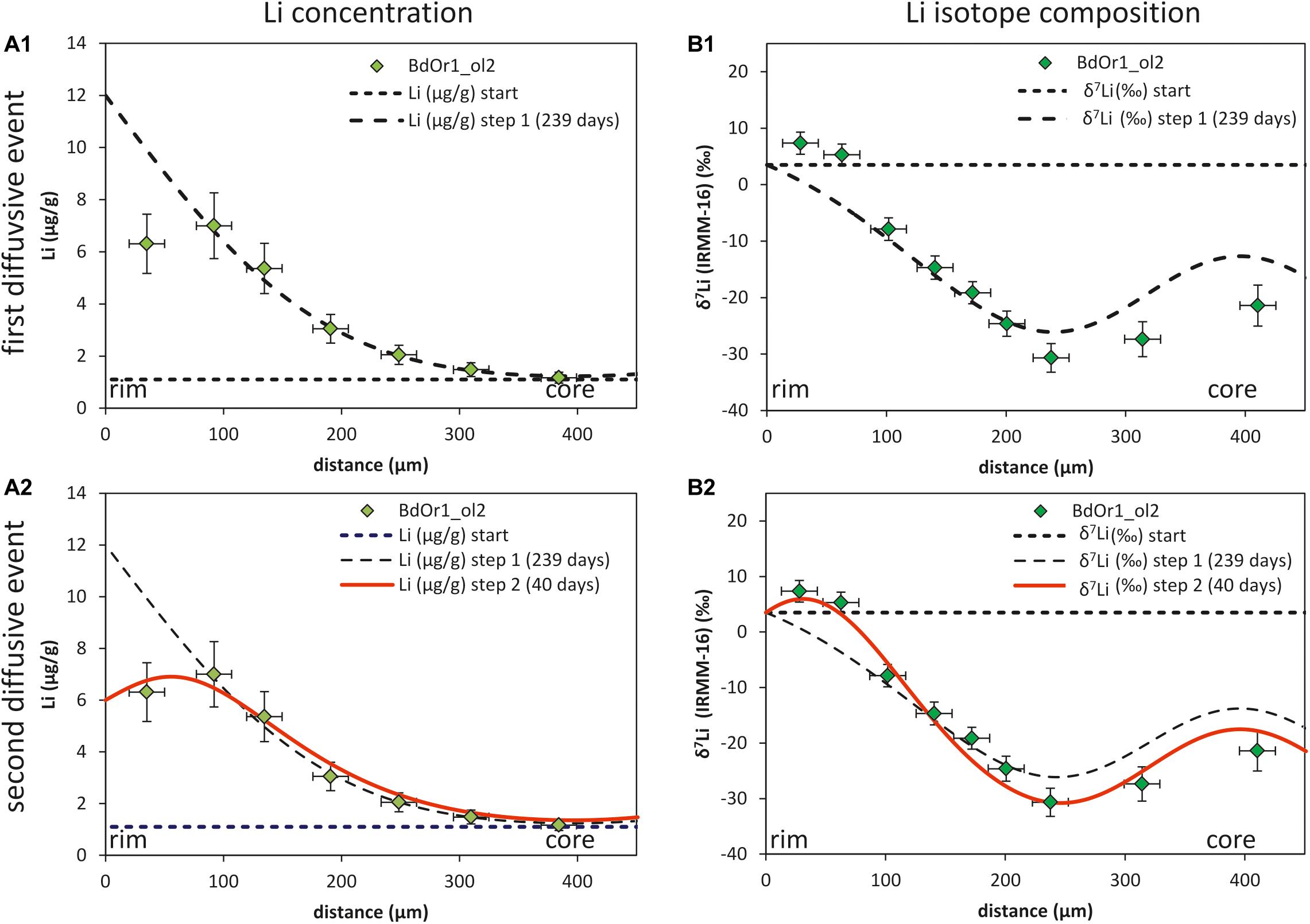
Figure 5. (A1) and (B1) show the Li concentration and isotopic composition of the first diffusion event for BdOr1_ol2 with a duration of t = 239 days, C_core = 1.1 μg/g, C_rim1 = 12 μg/g and β = 0.25. (A2) and (B2) show the model for the second diffusion event (which is based on the first diffusion event) with t = 40 days, C_rim2 = 6 μg/g and β = 0.2, the Li diffusion coefficient was determined by fitting the observed Li concentrations and isotope compositions to 5.5*10^{– 16} m²/s. Core Li concentrations and isotope compositions are marked by a dashed line.

Such a second diffusion step was modeled using the Li diffusivity that was determined by modeling the first diffusion event, but assuming a different Li rim concentration (C_rim2; Figure 5). C_rim2 was estimated based on the bulk rock Li concentration of the samples [5.78 μg/g for St6-2b, 5.7 μg/g for St3-3a and 6.14 μg/g for BdOr-1; Oeser et al. (2015)] and slightly adapted to better fit the observed Li concentrations (Table 2). This second diffusion event was modeled by fitting the Li isotope and concentration profiles to those observed at the crystal rims. As the diffusivity of Li was assumed to be given by the results of the first diffusion step, the modeled profiles were fitted by adjusting the duration of diffusion, which was unknown for this second event. Applying such a model, yields durations of 20 to 80 days for Banne D’Ordanche, 100 to 200 days for St3-3a from Roche Sauterre and 30 to 120 days for St6-2b from Roche Sauterre for this event (Figure 6). For the second modeling step the β-value was readjusted in order to fit the amplitude of the Li isotope diffusion profile. As described above, modeling of the second diffusion event also has an effect on the amplitude of the isotope profiles modeled in the first diffusion event. Best fit modeling of the olivine core- (first diffusion event) and rim (second diffusion event) isotope compositions furthermore, resulted in different β-values for the first and second diffusion event (Table 2).

FIGURE 6

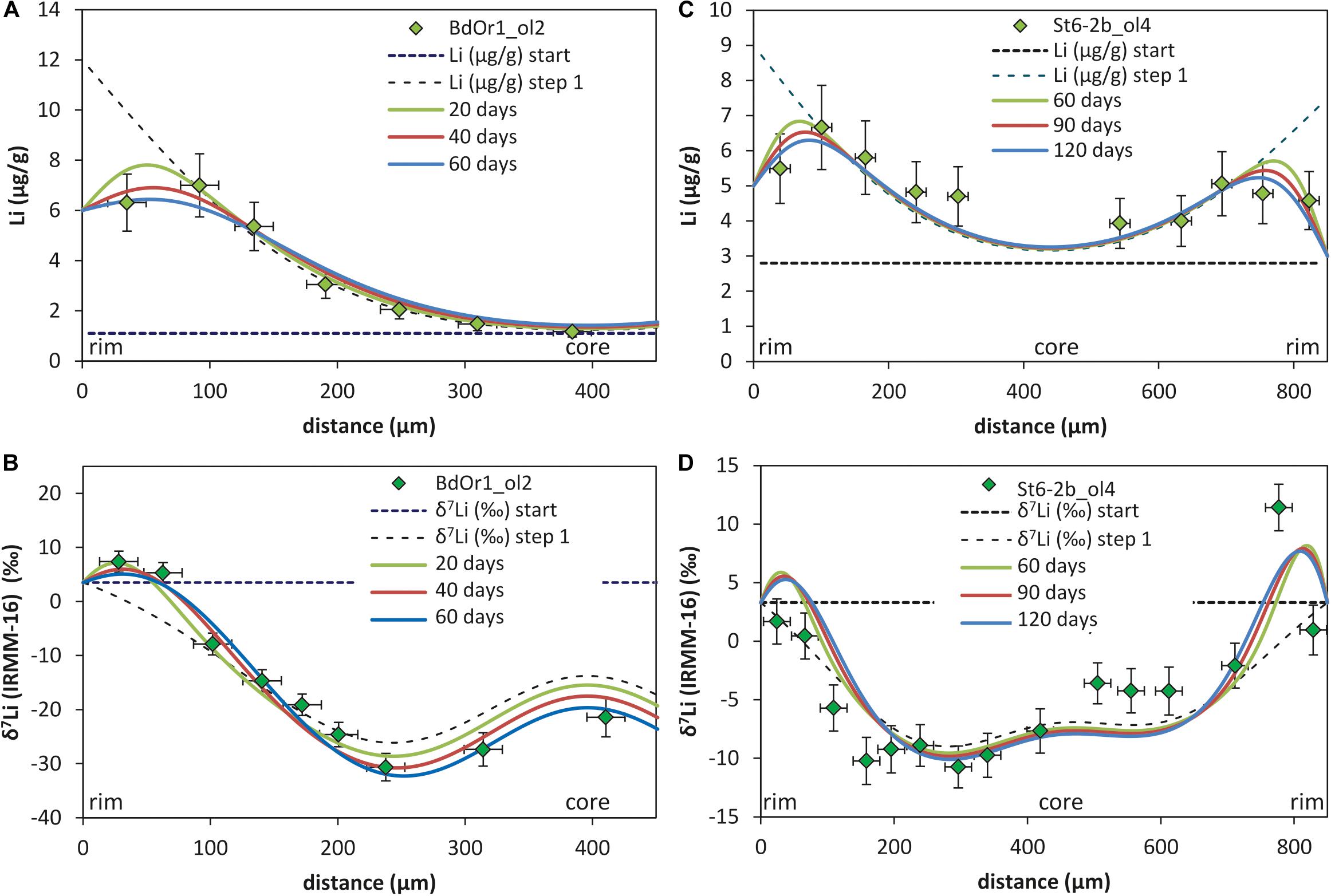
Figure 6. Two step model of Li concentration (A,C) and Li isotope profiles (B,D) fitted with t = 239–252 days for Banne D’Ordanche (BdOr1_ol2) and t = 3.26 years for Roche Sauterre (St6-2b_ol4b) for the first diffusion event (dashed lines, time scales are taken from Oeser et al., 2015). The time scales for the second diffusion event are modeled be fitting the observed Li concentrations and isotope compositions at the rims of the olivines are indicated by the solid lines. The models of all other investigated samples can be found in Supplementary Figure S.3.

The second diffusion event of Li diffusion out of the olivine crystals indicates a decrease of the Li concentration in the melt, which may be associated to the ascent of the melt, or even have occurred after the emplacement of the lava. During the exsolution of H₂O-rich vapor in the course of decompression Li is largely mobilized in magmatic systems (Sakuyama and Kushiro, 1979). For example, Neukampf et al. (2019) observed a significant decrease in Li concentrations in plagioclase, which they interpreted to be driven by a Li loss in the melt during degassing of the magma. The low Li concentrations in the melt caused Li diffusion out of the crystals. Similarly (though to a lower extent than observed by Neukampf et al., 2019), decreasing or constant Li concentrations at the olivine rims, observed in this study, may be related to degassing-driven Li loss in the melt during magma ascent or emplacement, resulting in Li diffusion out of the olivine crystals. Notably, the second event, which operated in an opposite direction to the first diffusion event, is not visible in the Mg–Fe chemical or isotopic zoning. This finding may support degassing as the driving force for diffusion during the final melt evolution, which would have affected fluid mobile elements, such as Li, but not refractory elements, such as Fe and Mg. Hence, though Li and Fe–Mg diffusion were likely coupled during the first diffusion event, they were apparently decoupled during the second event. This final decoupling was likely the result of the different physiochemical properties and diffusivity of Li, as compared to Fe–Mg. Accordingly, Li concentrations and isotopes may unravel processes which cannot be seen with Mg–Fe isotopes alone.

Some profiles are not matched perfectly by modeled curves (e.g., Figure 6D and Supplementary Figure S3B) which may be the result of cutting effects during the preparation of the sections. That is some sections probably do not sample the core of the crystals, which would result in an underestimation of the diffusive mass flux and isotope fractionation (Weyrauch et al., 2019). Furthermore, some sections were probably not cut perpendicularly to crystal rims, which may be indicated by asymmetric zoning (e.g., crystal St6-2b1_ol4) in the case of rim-to-rim profiles. This effect would result in artificially elongated Li diffusion profiles. For Mg and Fe diffusion modeling, the orientation of the crystallographic axes was determined by Oeser et al. (2015) by electron backscatter diffraction analyses. This is necessary due to the difference in diffusivities along the crystallographic axes (Dohmen et al., 2007). However, crystallographic orientation does not seem to have a large effect on Li diffusivity in olivine (Dohmen et al., 2010) and thus was not considered.

The time scales of the second diffusion event determined by Li diffusion modeling are 20–80 days for Banne D’Ordanche and 30–200 days for Roche Sauterre which is longer than the time scales obtained by Lynn et al. (2018) for the Keanakâko’i Tephra (Kîlauea Volcano, Hawai’i), also using Li diffusion modeling (only Li concentrations). The authors conclude a similar process of syn-eruptive degassing in their study with time scales of only hours to days which is 1–2 orders of magnitude faster than that estimated with the fitted D_Li values of this study. The difference in the determined time scales of the degassing process is essentially the result of the different diffusion coefficients used in the studies. In this study, the same diffusion coefficient, as determined from the first diffusion event (Table 3, derived from the comparison of Li- with Fe–Mg diffusion profiles) has been assumed for both diffusion events. However, as the diffusion coefficient may depend on temperature, fO₂ and the fluid content of the melt (Coogan et al., 2005; Dohmen et al., 2007) it may have changed during the second diffusion event, at which the melt may have become water saturated during degassing. Accordingly, it cannot be excluded that Li diffusion was faster during the second diffusion event and the modeled time scales overestimate the duration of a potential degassing process.

TABLE 3

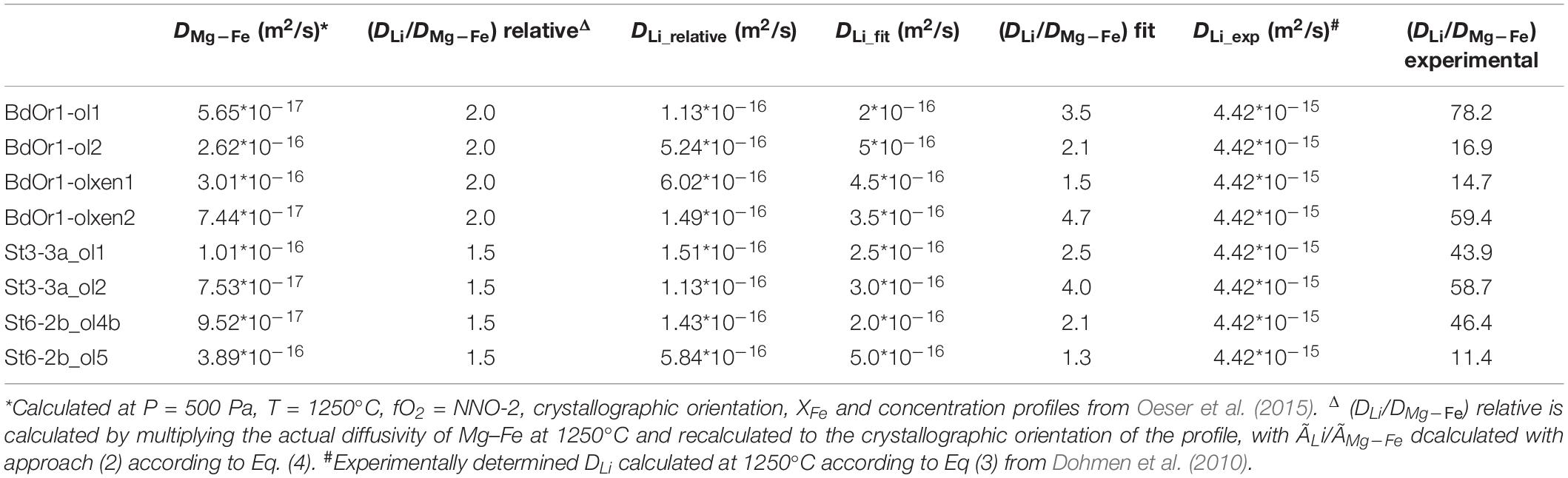
Table 3. Comparison of the Li diffusion coefficients, as determined (1) relative to the diffusivity of Mg–Fe exchange diffusion (D_{Li relative}), (2) by fitting D_Li to the observed Li concentration and isotope profiles assuming the time scales from Fe–Mg exchange diffusion modeling (Oeser et al., 2015), and (3) the experimentally determined D_Li and D_Mg–Fe (Dohmen et al., 2007, 2010) calculated for 1250°C.

Notably, however, the basalts investigated in this study, originate from massive flows, or in the case of Roche Sauterre, even from a small lava lake (Nehlig et al., 2001; Lorand et al., 2003; Richet, 2003). Thus degassing, as recorded by Li diffusion, may have occurred mostly during cooling of the magma after lava emplacement and thus lasted much longer than timescales typically expected for magma ascent. Assuming the outcrop of Roche Sauterre samples represents a small lava lake, this scenario would explain the longer degassing timescales for samples from this locality as compared to those from Banne D’Ordanche. It may also explain that some samples appear to be more affected by degassing than others, as degassing rates would depend on the position of the samples in the lava flow/lake.

Conclusion

Combined in situ Li concentration and isotope analyses were performed on zoned olivines from the Massif Central volcanic region. A diffusive origin for Li concentration and isotope profiles was deducted from correlations with Mg–Fe isotopic inter-diffusion. However, in contrast to Fe and Mg, Li indicates two diffusion episodes. The first likely represents the residence time of olivine in a (deeper) part of the plumbing system, as implied by Mg–Fe isotope diffusion modeling (Oeser et al., 2015). This diffusion event is likely driven by an increase in Li concentration in the melt and, likely also, by an increased partitioning of Li into olivine, driven by decreasing Mg# in olivine during fractional crystallization. Lithium diffusion into the olivines generated low δ⁷Li-values in the cores of the crystals. A second and shorter diffusion event, recorded by several of the investigated olivine grains resulted in Li diffusion out of olivine crystals, indicating a Li decrease in the melt. This second event is likely related to degassing of the melt during its ascent and after lava emplacement, resulting in the mobilization of Li into a vapor phase. Such a diffusion event can be deduced by modeling Li concentration and Li isotope profiles simultaneously. The second diffusion episode is not recorded in Mg–Fe profiles, which highlights that Li profiles can preserve information about magmatic evolution that is not recorded by Mg–Fe zoning, potentially due to the volatile character of Li in magmatic fluids. These findings demonstrate that combining information from chemical and isotopic zoning of Li with those from Fe–Mg is a very powerful tool for unraveling the timing of complex magma evolution scenarios, such as commonly observed in magma plumbing systems.

Data Availability Statement

All datasets generated for this study are included in the article/Supplementary Material.

Author Contributions

LS contributed to the analyses of Li isotope profiles with femtosecond-laser ablation-MC-ICP-MS, solution nebulization isotope analyses with MC-ICP-MS and proceeding Li column chromatography, and data processing and interpretation, diffusion modeling, and writing the manuscript. MO contributed to the project design, analytical support with fs-LA-MC-ICP-MS, support with diffusion modeling, and data interpretation, support with manuscript writing. IH contributed to the analytical support with fs-LA-MC-ICP-MS and support with manuscript writing. SW contributed to the project design, support with data interpretation, and support with manuscript writing.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling Editor declared a past co-authorship with the authors MO, SW.

Acknowledgments

This study was supported by the Deutsche Forschungsgemein-schaft (grant # OE 653/1-1) which is gratefully acknowledged. We are grateful for the reviews of TK and IP and editorial handling by DN, whose constructive comments significantly helped to improve this paper.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2020.00201/full#supplementary-material

References

Ackerman, L., Špaček, P., Magna, T., Ulrych, J., Svojtka, M., Hegner, E., et al. (2013). Alkaline and carbonate-rich melt metasomatism and melting of subcontinental lithospheric mantle: evidence from mantle xenoliths, NE Bavaria, Bohemian Massif. J. Petrol. 54, 2597–2633. doi: 10.1093/petrology/egt059

CrossRef Full Text | Google Scholar

Bouman, C., Elliott, T., and Vroon, P. Z. (2004). Lithium inputs to subduction zones. Chem. Geol. 212, 59–79. doi: 10.1016/j.chemgeo.2004.08.004

CrossRef Full Text | Google Scholar

Brant, C., Coogan, L. A., Gillis, K. M., Seyfried, W. E., Pester, N. J., and Spence, J. (2012). Lithium and Li-isotopes in young altered upper oceanic crust from the East Pacific Rise. Geochim. Cosmochim. Acta 96, 272–293. doi: 10.1016/j.gca.2012.08.025

CrossRef Full Text | Google Scholar

Brenan, J. M., Neroda, E., Lundstrom, C. C., Shaw, H. F., Rverson, F. J., and Phinney, D. L. (1998). Behaviour of boron, beryllium, and lithium during melting and crystallization: constraints from mineral-melt partitioning experiments. Geochim. Cosmochim. Acta 62, 2129–2141. doi: 10.1016/S0016-7037(98)00131-8

CrossRef Full Text | Google Scholar

Chan, L. H., Edmond, J. M., Thompson, G., and Gillis, K. (1992). Lithium isotopic composition of submarine basalts: implications for the lithium cycle in the oceans. Earth Planet. Sci. Lett. 108, 151–160. doi: 10.1016/0012-821X(92)90067-6

CrossRef Full Text | Google Scholar

Chapman, S., and Cowling, T. G. (1953). Mathematical Theory of Non-uniform Gases - An account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in GASES, 3rd Edn. Cambridge: Cambridge Mathematical Library.

Google Scholar

Collinet, M., Charlier, B., Namur, O., Oeser, M., Médard, E., Vander Auwera, J., et al. (2014). Fe and Mg Isotope Fractionation in Olivine from the NWA 1068 Shergottite. Sacramento, CA: Goldschmidt california.

Google Scholar

Collinet, M., Charlier, B., Namur, O., Oeser, M., Médard, E., and Weyer, S. (2017). Crystallization history of enriched shergottites from Fe and Mg isotope fractionation in olivine megacrysts. Geochim. Cosmochim. Acta 207, 277–297. doi: 10.1016/j.gca.2017.03.029

CrossRef Full Text | Google Scholar

Coogan, L. A., Gillis, K. M., Pope, M., and Spence, J. (2017). The role of low-temperature (off-axis) alteration of the oceanic crust in the global Li-cycle: insights from the Troodos ophiolite. Geochim. Cosmochim. Acta 203, 201–215. doi: 10.1016/j.gca.2017/01.002

CrossRef Full Text | Google Scholar

Coogan, L. A., Kasemann, S. A., and Chakraborty, S. (2005). Rates of hydrothermal cooling of new oceanic upper crust derived from lithium-geospeedometry. Earth Planet. Sci. Lett. 240, 415–424. doi: 10.1016/j.epsl.2005.09.020

CrossRef Full Text | Google Scholar

Costa, F., Dohmen, R., and Chakraborty, S. (2008). Time scales of magmatic processes from modeling the zoning patterns of crystals. Rev. Mineral. Geochemistry 69, 545–594. doi: 10.2138/rmg.2008.69.14

CrossRef Full Text | Google Scholar

Dellinger, M., Gaillardet, J. Ô, Bouchez, J., Calmels, D., Galy, V., Hilton, R. G., et al. (2014). Lithium isotopes in large rivers reveal the cannibalistic nature of modern continental weathering and erosion. Earth Planet. Sci. Lett. 401, 359–372. doi: 10.1016/j.epsl.2014.05.061

CrossRef Full Text | Google Scholar

Dohmen, R., Becker, H. W., and Chakraborty, S. (2007). Fe-Mg diffusion in olivine I: experimental determination between 700 and 1,200°C as a function of composition, crystal orientation and oxygen fugacity. Phys. Chem. Miner. 34, 389–407. doi: 10.1007/s00269-007-0157-7

CrossRef Full Text | Google Scholar

Dohmen, R., and Chakraborty, S. (2007). Fe-Mg diffusion in olivine II: point defect chemistry, change of diffusion mechanisms and a model for calculation of diffusion coefficients in natural olivine. Phys. Chem. Miner. 34, 409–430. doi: 10.1007/s00269-007-0158-6

CrossRef Full Text | Google Scholar

Dohmen, R., Kasemann, S. A., Coogan, L., and Chakraborty, S. (2010). Diffusion of Li in olivine. Part I: experimental observations and a multi species diffusion model. Geochim. Cosmochim. Acta 74, 274–292.

Google Scholar

Elliott, T., Thomas, A., Jeffcoate, A., and Niu, Y. (2006). Lithium isotope evidence for subduction-enriched mantle in the source of mid-ocean-ridge basalts. Nature 443, 565–568. doi: 10.1038/nature05144

CrossRef Full Text | Google Scholar

Ganguly, J. (2002). Diffusion kinetics in minerals: principles and applications to tectono-metamorphic processes. EMU Notes Mineral. Energy Model. Miner. 4, 271–309.

Google Scholar

Gu, X., Deloule, E., France, L., and Ingrin, J. (2016). Multi-stage metasomatism revealed by trace element and Li isotope distributions in minerals of peridotite xenoliths from Allègre volcano (French Massif Central). Lithos 264, 158–174. doi: 10.1016/j.lithos.2016.07.019

CrossRef Full Text | Google Scholar

Hamelin, C., Seitz, H. M., Barrat, J. A., Dosso, L., Maury, R. C., and Chaussidon, M. (2009). A low δ7Li lower crustal component: evidence from an alkalic intraplate volcanic series (Chaîne des Puys, French Massif Central). Chem. Geol. 266, 205–217.

Google Scholar

Horn, I., and von Blanckenburg, F. (2007). Investigation on elemental and isotopic fractionation during 196 nm femtosecond laser ablation multiple collector inductively coupled plasma mass spectrometry. Spectrochim. Acta B At. Spectrosc. 62, 410–422. doi: 10.1016/j.sab.2007.03.034

CrossRef Full Text | Google Scholar

Horn, I., von Blanckenburg, F., Schoenberg, R., Steinhoefel, G., and Markl, G. (2006). In situ iron isotope ratio determination using UV-femtosecond laser ablation with application to hydrothermal ore formation processes. Geochim. Cosmochim. Acta 70, 3677–3688. doi: 10.1016/j.gca.2006.05.002

CrossRef Full Text | Google Scholar

Jeffcoate, A. B., Elliott, T., Kasemann, S. A., Ionov, D., Cooper, K., and Brooker, R. (2007). Li isotope fractionation in peridotites and mafic melts. Geochim. Cosmochim. Acta 71, 202–218. doi: 10.1016/j.gca.2006.06.1611

CrossRef Full Text | Google Scholar

Jochum, K. P., Stoll, B., Herwig, K., Willbold, M., Hofmann, A. W., Amini, M., et al. (2006). MPI-DING reference glasses for in situ microanalysis: new reference values for element concentrations and isotope ratios. Geochem. Geophys. Geosyst. 7, 1–44. doi: 10.1029/2005GC001060

CrossRef Full Text | Google Scholar

Jollands, M. C., Burnham, A. D., O’Neill, H. S. C., Hermann, J., and Qian, Q. (2016a). Beryllium diffusion in olivine: a new tool to investigate timescales of magmatic processes. Earth Planet. Sci. Lett. 450, 71–82. doi: 10.1016/j.epsl.2016.06.028

CrossRef Full Text | Google Scholar

Jollands, M. C., Hermann, J., St. O’Neill, H. C., Spandler, C., and Padrón-Navarta, J. A. (2016b). Diffusion of Ti and some divalent cations in olivine as a function of temperature, oxygen fugacity, chemical potentials and crystal orientation. J. Petrol. 57, 1983–2010. doi: 10.1093/petrology/egw067

CrossRef Full Text | Google Scholar

Kahl, M., Chakraborty, S., Costa, F., Pompilio, M., Liuzzo, M., and Viccaro, M. (2013). Compositionally zoned crystals and real-time degassing data reveal changes in magma transfer dynamics during the 2006 summit eruptive episodes of Mt. Etna. Bull. Volcanol. 75, 1–14. doi: 10.1007/s00445-013-0692-7

CrossRef Full Text | Google Scholar

Kahl, M., Chakraborty, S., Pompilio, M., and Costa, F. (2015). Constraints on the nature and evolution of the magma plumbing system of Mt. Etna volcano (1991-2008) from a combined thermodynamic and kinetic modelling of the compositional record of minerals. J. Petrol. 56, 2025–2068. doi: 10.1093/petrology/egv063

CrossRef Full Text | Google Scholar

Kimura, J.-I., Chang, Q., Kanazawa, N., Sasaki, S., and Vaglarov, B. S. (2016). High-precision in situ analysis of Pb isotopes in glasses using 1013 Ω resistor high gain amplifiers with ultraviolet femtosecond laser ablation multiple Faraday collector inductively coupled plasma mass spectrometry. J. Anal. At. Spectrom. 31, 790–800. doi: 10.1039/C5JA00374A

CrossRef Full Text | Google Scholar

Le Roux, P. J. (2010). Lithium isotope analysis of natural and synthetic glass by laser ablation MC-ICP-MS. J. Anal. At. Spectrom. 25, 1033–1038. doi: 10.1039/b920341a

CrossRef Full Text | Google Scholar

Liu, S. A., Teng, F. Z., Yang, W., and Wu, F. Y. (2011). High-temperature inter-mineral magnesium isotope fractionation in mantle xenoliths from the North China craton. Earth Planet. Sci. Lett. 308, 131–140. doi: 10.1016/j.epsl.2011.05.047

CrossRef Full Text | Google Scholar

Lorand, J. P., Alard, O., Luguet, A., and Keays, R. R. (2003). Sulfur and selenium systematics of the subcontinental lithospheric mantle: inferences from the Massif Central xenolith suite (France). Geochim. Cosmochim. Acta 67, 4137–4151. doi: 10.1016/S0016-7037(03)00305-3

CrossRef Full Text | Google Scholar

Lynn, K. J., Shea, T., Garcia, M. O., Costa, F., and Norman, M. D. (2018). Lithium diffusion in olivine records magmatic priming of explosive basaltic eruptions. Earth Planet. Sci. Lett. 500, 127–135. doi: 10.1016/j.epsl.2018.08.002

CrossRef Full Text | Google Scholar

Magna, T., Ionov, D. A., Oberli, F., and Wiechert, U. (2008). Links between mantle metasomatism and lithium isotopes: evidence from glass-bearing and cryptically metasomatized xenoliths from Mongolia. Earth Planet. Sci. Lett. 276, 214–222. doi: 10.1016/j.epsl.2008.09.027

CrossRef Full Text | Google Scholar

Magna, T., Wiechert, U., and Halliday, A. N. (2006). New constraints on the lithium isotope compositions of the Moon and terrestrial planets. Earth Planet. Sci. Lett. 243, 336–353. doi: 10.1016/j.epsl.2006.01.005

CrossRef Full Text | Google Scholar

Marschall, H. R., Altherr, R., and Rüpke, L. (2007a). Squeezing out the slab - modelling the release of Li, Be and B during progressive high-pressure metamorphism. Chem. Geol. 239, 323–335. doi: 10.1016/j.chemgeo.2006.08.008

CrossRef Full Text | Google Scholar

Marschall, H. R., Pogge von Strandmann, P. A. E., Seitz, H. M., Elliott, T., and Niu, Y. (2007b). The lithium isotopic composition of orogenic eclogites and deep subducted slabs. Earth Planet. Sci. Lett. 262, 563–580. doi: 10.1016/j.epsl.2007.08.005

CrossRef Full Text | Google Scholar

McDade, P., Blundy, J. D., and Wood, B. J. (2003). Trace element partitioning on the Tinaquillo solidus at 1.5 GPa. Phys. Earth Planet. Inter. 139, 129–147. doi: 10.1016/S0031-9201(03)00149-3

CrossRef Full Text | Google Scholar

Nehlig, P., Boivin, P., de Goër, A., Mergoil, J., Poutrau, G., Sustrac, G., et al. (2001). Les volcans du Massif Central. Géologues 130/131, 66–91.

Google Scholar

Neukampf, J., Ellis, B. S., Laurent, O., Steinmann, L. K., Dohmen, R., Ubide, T., et al. (2019). Timescales of Degassing in Rhyolitic Magmas Tracked by Li in Plagioclase. Italy: University of Palermo.

Google Scholar

Nishio, Y., Nakai, S., Yamamoto, J., Sumino, H., Matsumoto, T., Prikhod’ko, V. S., et al. (2004). Lithium isotopic systematics of the mantle-derived ultramafic xenoliths: implications for EM1 origin. Earth Planet. Sci. Lett. 217, 245–261. doi: 10.1016/S0012-821X(03)00606-X

CrossRef Full Text | Google Scholar

Oeser, M., Dohmen, R., Horn, I., Schuth, S., and Weyer, S. (2015). Processes and time scales of magmatic evolution as revealed by Fe–Mg chemical and isotopic zoning in natural olivines. Geochim. Cosmochim. Acta 154, 130–150. doi: 10.1016/j.gca.2015.01.025

CrossRef Full Text | Google Scholar

Oeser, M., Ruprecht, P., and Weyer, S. (2018). Combined Fe-Mg chemical and isotopic zoning in olivine constraining magma mixing-to-eruption timescales for the continental arc volcano Irazú (Costa Rica) and Cr diffusion in olivine. Am. Mineral. 103, 582–599. doi: 10.2138/am-2018-6258

CrossRef Full Text | Google Scholar

Oeser-Rabe, M. (2015). Constraints on the Evolution of Magmas from Diffusion-driven Chemical and Fe-Mg Isotopic Zoning in Natural Olivines analyzed by Femtosecond-LA-ICP-MS. Ph.D. thesis, Universitätsbibliothek Hannover, Hannover.

Google Scholar

Ottolini, L., Laporte, D., Raffone, N., Devidal, J.-L., and Le Fèvre, B. (2009). New experimental determination of Li and B partition coefficients during upper mantle partial melting. Contrib. Mineral. Petrol. 157, 313–325. doi: 10.1007/s00410-008-0336-7

CrossRef Full Text | Google Scholar

Parkinson, I. J., Hammond, S. J., James, R. H., and Rogers, N. W. (2007). High-temperature lithium i fractionation: insights from lithium isotope diffusion in magmatic systems. Earth Planet. Sci. Lett. 257, 609–621. doi: 10.1016/j.epsl.2007.03.023

CrossRef Full Text | Google Scholar

Penniston-Dorland, S., Liu, X.-M., and Rudnick, R. L. (2017). Lithium isotope geochemistry. Rev. Mineral. Geochemistry 82, 165–217. doi: 10.2138/rmg.2017.82.6

CrossRef Full Text | Google Scholar

Qian, Q., O’Neill, H. S. C., and Hermann, J. (2010). Comparative diffusion coefficients of major and trace elements in olivine at ~950 °C from a xenocryst included in dioritic magma. Geology 38, 331–334. doi: 10.1130/G30788.1

CrossRef Full Text | Google Scholar

Richet, P. (2003). Guide des volcans de France. 1st ed., BRGM. Paris: Belin.

Google Scholar

Richter, F., Chaussidon, M., Bruce Watson, E., Mendybaev, R., and Homolova, V. (2017). Lithium isotope fractionation by diffusion in minerals Part 2: olivine. Geochim. Cosmochim. Acta 219, 124–142. doi: 10.1016/j.gca.2017.09.001

CrossRef Full Text | Google Scholar

Richter, F., Watson, B., Chaussidon, M., Mendybaev, R., and Ruscitto, D. (2014). Lithium isotope fractionation by diffusion in minerals. Part 1: pyroxenes. Geochim. Cosmochim. Acta 126, 352–370. doi: 10.1016/j.gca.2013.11.008

CrossRef Full Text | Google Scholar

Richter, F. M., Davis, A. M., DePaolo, D. J., and Watson, E. B. (2003). Isotope fractionation by chemical diffusion between molten basalt and rhyolite. Geochim. Cosmochim. Acta 67, 3905–3923. doi: 10.1016/S0016-7037(03)00174-1

CrossRef Full Text | Google Scholar

Richter, F. M., Liang, Y., and Davis, A. M. (1999). Isotope fractionation by diffusion in molten oxides. Geochim. Cosmochim. Acta 63, 2853–2861. doi: 10.1016/S0016-7037(99)00164-7

CrossRef Full Text | Google Scholar

Roeder, P. L., and Emslie, R. F. (1970). Olivine-liquid equilibrium. Contr. Mineral. Petrol. 29, 275-289. doi: 10.1007/BF00371276

CrossRef Full Text | Google Scholar

Ryan, J. G., and Kyle, P. R. (2004). Lithium abundance and lithium isotope variations in mantle sources: insights from intraplate volcanic rocks from Ross Island and Marie Byrd Land (Antarctica) and other oceanic islands. Chem. Geol. 212, 125–142. doi: 10.1016/j.chemgeo.2004.08.006

CrossRef Full Text | Google Scholar

Ryan, J. G., and Langmuir, C. H. (1987). The systematics of lithium abundances in young volcanic rocks. Geochim. Cosmochim. Acta 51, 1727–1741. doi: 10.1016/0016-7037(87)90351-6

CrossRef Full Text | Google Scholar

Sakuyama, M., and Kushiro, I. (1979). Vesiculation of hydrous andesitic melt and transport of alkalies by separated vapor phase. Contrib. Mineral. Petrol. 71, 61–66. doi: 10.1007/BF00371881

CrossRef Full Text | Google Scholar

Seitz, H.-M., Brey, G. P., Lahaye, Y., Durali, S., and Weyer, S. (2004). Lithium isotopic signatures of peridotite xenoliths and isotopic fractionation at high temperature between olivine and pyroxenes. Chem. Geol. 212, 163–177. doi: 10.1016/j.chemgeo.2004.08.009

CrossRef Full Text | Google Scholar

Shannon, R. D. (1976). Revised effective ionic radii in halides and chalcogenides. Acta Crystallogr. A 32, 751–767. doi: 10.1107/S0567739476001551

CrossRef Full Text | Google Scholar

Sio, C. K. I., Dauphas, N., Teng, F. Z., Chaussidon, M., Helz, R. T., and Roskosz, M. (2013). Discerning crystal growth from diffusion profiles in zoned olivine by in situ Mg-Fe isotopic analyses. Geochim. Cosmochim. Acta 123, 302–321. doi: 10.1016/j.gca.2013.06.008

CrossRef Full Text | Google Scholar

Spandler, C., and O’Neill, H. S. C. (2010). Diffusion and partition coefficients of minor and trace elements in San Carlos olivine at 1,300°C with some geochemical implications. Contrib. Mineral. Petrol. 159, 1–28. doi: 10.1007/s00410-009-0456-8

CrossRef Full Text | Google Scholar

Steinmann, L. K., Oeser, M., Horn, I., Seitz, H.-M., and Weyer, S. (2019). In situ high-precision lithium isotope analyses at low concentration levels with femtosecond-LA-MC-ICP-MS. J. Anal. At. Spectrom. 34, 1447–1458. doi: 10.1039/C9JA00088G

CrossRef Full Text | Google Scholar

Su, B. X., Zhou, M. F., and Robinson, P. T. (2016). Extremely large fractionation of Li isotopes in a chromitite-bearing mantle sequence. Sci. Rep. 6, 1–9. doi: 10.1038/srep22370

CrossRef Full Text | Google Scholar

Tang, Y. J., Zhang, H. F., Deloule, E., Su, B. X., Ying, J. F., Xiao, Y., et al. (2012). Slab-derived lithium isotopic signatures in mantle xenoliths from northeastern North China Craton. Lithos 149, 79–90. doi: 10.1016/j.lithos.2011.12.001

CrossRef Full Text | Google Scholar

Taura, H., Yurimoto, H., Kurita, K., and Sueno, S. (1998). Pressure dependence on partition coefficients for trace elements between olivine and the coexisting melts. Phys. Chem. Miner. 25, 469–484. doi: 10.1007/s002690050138

CrossRef Full Text | Google Scholar

Teng, F. Z., Dauphas, N., Helz, R. T., Gao, S., and Huang, S. (2011). Diffusion-driven magnesium and iron isotope fractionation in Hawaiian olivine. Earth Planet. Sci. Lett. 308, 317–324. doi: 10.1016/j.epsl.2011.06.003

CrossRef Full Text | Google Scholar

Teng, F. Z., Wadhwa, M., and Helz, R. T. (2007). Investigation of magnesium isotope fractionation during basalt differentiation: implications for a chondritic composition of the terrestrial mantle. Earth Planet. Sci. Lett. 261, 84–92. doi: 10.1016/j.epsl.2007.06.004

CrossRef Full Text | Google Scholar

Teng, F. Z., Yang, W., Rudnick, R. L., and Hu, Y. (2013). Heterogeneous magnesium isotopic composition of the lower continental crust: a xenolith perspective. Geochem. Geophys. Geosyst. 14, 3844–3856. doi: 10.1002/ggge.20238

CrossRef Full Text | Google Scholar

Tomascak, P. B., Carlson, R. W., and Shirey, S. B. (1999a). Accurate and precise determination of Li isotopic compositions by multi-collector sector ICP-MS. Chem. Geol. 158, 145–154. doi: 10.1016/S0009-2541(99)00022-4

CrossRef Full Text | Google Scholar

Tomascak, P. B., Langmuir, C. H., Le Roux, P. J., and Shirey, S. B. (2008). Lithium isotopes in global mid-ocean ridge basalts. Geochim. Cosmochim. Acta 72, 1626–1637. doi: 10.1016/j.gca.2007.12.021

CrossRef Full Text | Google Scholar

Tomascak, P. B., Tera, F., Helz, R. T., and Walker, R. J. (1999b). The absence of lithium isotope fractionation during basalt differentiation: new measurements by multicollector sector ICP-MS. Geochim. Cosmochim. Acta 63, 907–910.

Google Scholar

Vlastélic, I., Staudacher, T., Bachèlery, P., Télouk, P., Neuville, D., and Benbakkar, M. (2011). Lithium isotope fractionation during magma degassing: constraints from silicic differentiates and natural gas condensates from Piton de la Fournaise volcano (Réunion Island). Chem. Geol. 284, 26–34. doi: 10.1016/j.chemgeo.2011.02.002

CrossRef Full Text | Google Scholar

Weyer, S., and Ionov, D. A. (2007). Partial melting and melt percolation in the mantle: the message from Fe isotopes. Earth Planet. Sci. Lett. 259, 119–133. doi: 10.1016/j.epsl.2007.04.033

CrossRef Full Text | Google Scholar

Weyer, S., and Seitz, H.-M. (2012). Coupled lithium- and iron isotope fractionation during magmatic differentiation. Chem. Geol. 29, 42–50. doi: 10.1016/j.chemgeo.2011.11.020

CrossRef Full Text | Google Scholar

Weyrauch, M., Zipfel, J., and Weyer, S. (2019). Origin of metal from CB chondrites in an impact plume – A combined study of Fe and Ni isotope composition and trace element abundances. Geochim. Cosmochim. Acta 246, 123–137. doi: 10.1016/j.gca.2018.11.022

CrossRef Full Text | Google Scholar

Xu, R., Liu, Y., Tong, X., Hu, Z., Zong, K., and Gao, S. (2013). In-situ trace elements and Li and Sr isotopes in peridotite xenoliths from Kuandian, North China Craton: insights into Pacific slab subduction-related mantle modification. Chem. Geol. 354, 107–123. doi: 10.1016/j.chemgeo.2013.06.022

CrossRef Full Text | Google Scholar

Zhukova, I., O’Neill, H., and Campbell, I. H. (2017). A subsidiary fast-diffusing substitution mechanism of Al in forsterite investigated using diffusion experiments under controlled thermodynamic conditions. Contrib. Mineral. Petrol. 172, 1–12. doi: 10.1007/s00410-017-1365-x

CrossRef Full Text | Google Scholar