- 1Centre for Hydrogeology and Geothermics (CHYN), University of Neuchâtel, Neuchâtel, Switzerland
- 2French National Radioactive Waste Management Agency (ANDRA), Châtenay-Malabry, France
Over the last decade, data assimilation methods based on the ensemble Kalman filter (EnKF) have been particularly explored in various geoscience fields to solve inverse problems. Although this type of ensemble methods can handle high-dimensional systems, they assume that the errors coming from whether the observations or the numerical model are multivariate Gaussian. To handle existing non-linearities between the observations and the variables to estimate, iterative methods have been proposed. In this paper, we investigate the feasibility of using the ensemble smoother and two iterative variants for the calibration of a synthetic 2D groundwater model inspired by a real nuclear storage problem in France. Using the same set of sparse and transient flow data, we compare the results of each method when employing them to condition an ensemble of multi-Gaussian groundwater flow parameter fields. In particular, we explore the benefit of transforming the state observations to improve the parameter identification performed by one of the two iterative algorithms tested. Despite the favorable case of a multi-Gaussian parameter distribution addressed, we show the importance of defining an ensemble size of at least 200 to obtain sufficiently accurate parameter and uncertainty estimates for the groundwater flow inverse problem considered.
1. Introduction
Since the ensemble Kalman filter (EnKF) (Evensen, 1994) has been introduced as a computationally efficient Monte Carlo approximation of the Kalman filter (Kalman, 1960; Anderson, 2003), ensemble methods for data assimilation have been widely used for high-dimensional estimation problems in geosciences (Evensen, 2009b). In all these methods, an initial ensemble of realizations which should capture the initial uncertainty of the state or parameter variables of interest is first generated. Then, thanks to the assimilation of available uncertain observations, an updated ensemble of realizations that are conditioned by the observations is obtained. However, a main limitation is that ensemble Kalman methods assume multivariate Gaussian error statistics in the distributions involved in the computation of the update. As a result, departures from this multi-Gaussian assumption can lead to an important loss of optimality in the estimated ensemble mean and variance.
EnKF is for example extensively applied in meteorology in order to estimate the current state of the atmosphere in real time (Anderson, 2009). In such atmospheric applications, newly obtained observations of the atmosphere are assimilated sequentially in order to update the initial conditions of weather predictions models. In reservoir modeling, ensemble methods have also become a standard tool with the use, more particularly, of smoother algorithms for inverse modeling (Evensen, 2018). Still with the aim of improving model forecasts, time series of state observations collected during the production of a reservoir are with smoother methods processed all simultaneously in order to update the static parameters of reservoir simulation models.
EnKF has also been applied in surface and groundwater hydrology for the estimation of both the parameter and state variables of a system (Moradkhani et al., 2005; Hendricks Franssen and Kinzelbach, 2008). In particular, it has been shown that the increased degree of freedom introduced by the larger number of unknowns can make the estimation of EnKF particularly unstable, especially in the presence of non-linear dynamics (Moradkhani et al., 2005). When the problem is non-linear, such joint estimation can also result in inconsistent predicted data after the update and physical inconsistencies between the updated states and parameters (Gu and Oliver, 2007; Chen et al., 2009). These issues have particularly motivated the development of iterative EnKF methods based on the iterative minimization of a cost function for each iteration of the standard EnKF (Gu and Oliver, 2007; Emerick and Reynolds, 2012b).
Because of the need of restarting the dynamic model multiple times in the context of non-linear parameter estimation with EnKF, the simultaneous assimilation of all the data set in the ensemble smoother method (van Leeuwen and Evensen, 1996) has been considered a suitable alternative to EnKF in reservoir applications. Instead of having to update the variables at each assimilation time step, the ensemble smoother can process all the data of the time series in one single update step. Similarly to the iterative EnKF, successive updates can also be applied using iterative forms of the ensemble smoother in order to improve the data fit in non-linear problems (Chen and Oliver, 2012; Emerick and Reynolds, 2012a; Luo et al., 2015). (Chen and Oliver, 2012; Emerick and Reynolds, 2012a; Luo et al., 2015).
This paper focuses on the performance of two existing iterative forms of ensemble smoother for a synthetic groundwater flow application. Although the model is synthetic, it is inspired by the real hydraulic perturbation observed at the Andra's Meuse/Haute-Marne site since the construction and operation of the Underground Research Laboratory (Benabderrahmane et al., 2014; Kerrou et al., 2017). In particular, the problem considers a transient flow induced by one vertical shaft, and transient observations at points located in a restricted region of the model. Note that these situations of sparse and unevenly distributed data are very common in real groundwater modeling studies and makes the problem of subsurface characterization by inverse modeling more difficult.
The main objective of this synthetic application is to assess the benefit of assimilating different types of flow data, namely hydraulic heads and flow rates, for the identification of multi-Gaussian log hydraulic conductivity (log K) fields. In particular, the effects of increasing the ensemble size on the accuracy of the mean estimate and its associated uncertainty captured by the ensemble will be compared for both methods. In addition, similarly to the work of Schoniger et al. (2012) which introduced the benefit of using a normal-score transform on the state variables prior to updating multi-Gaussian log K fields with EnKF, we will also assess in this study the benefit of using a similar transformation approach but in the specific context of one of the tested smoother algorithms. Indeed, it has been shown that such state transformations could improve the accuracy of the updates computed by EnKF thanks to a pseudolinearization between the multi-Gaussian parameter field and the transformed states variables (Schoniger et al., 2012). As a matter of fact, the normal-score transform approach has already been applied in the context of iterative ensemble smoothing in the recent work of Li et al. (2018). However, in that study, the proposed approach specifically aimed at addressing the problem of identifying non-Gaussian parameter fields. Hence the approach required transforming not only the state variables but also the parameters in order to perform the update in both the transformed parameter and data spaces. The main motivation for the normal-score transform in that particular context was to get closer to the assumption of multi-Gaussian variables which underlie ensemble Kalman methods. However, unlike the normal-score transform approach introduced by Schoniger et al. (2012), one main drawback of transforming both the parameter and state variables is that it can actually increase the non-linearity between those variables (Zhou et al., 2011).
Hereinafater, we first present in section 2 the ensemble smoother and the two iterative ensemble smoother considered in this study: LM-EnRML (Chen and Oliver, 2013) and ES-MDA (Emerick and Reynolds, 2012a). Both are the main iterative variants currently used for inverse modeling in reservoir applications (Evensen, 2018). The synthetic case including the model set up and the generation of the initial ensemble are presented in section 3. The performance used to analyze our results on the synthetic case are presented in section 4. Finally, the results are discussed in section 5.
2. General Background on the Ensemble Smoother and Iterative
The ensemble smoother (ES) introduced by van Leeuwen and Evensen (1996) is an extension of the ensemble Kalman filter. Both are similar in that a set of N realizations is used to represent a presumed multi-Gaussian distribution, and is updated by the assimilation of measurements in order to form a new conditional distribution. When using either ES or EnKF for the inverse modeling of parameters based on observations of state variables, each conditioned parameter realization of the ensemble is calculated from the unconditioned realization according to the following equation
with
The matrix K represents an approximation of the so-called “Kalman gain” in the Kalman filter update equation, derived so as to minimize the error covariance of the posterior estimate. It is here computed based on approximations from the ensemble of the cross-covariance matrix between the vector of prior parameters and the vector of predicted data, noted , the auto-covariance matrix of predicted data , and the covariance matrix of observed data measurement errors Cerr. By evaluating the relative uncertainty of the measurements and prior estimate, the Kalman gain weights the contribution of each conditioning observation relatively to the prior estimate for the computation of the update. More precisely, it weights the contribution from each component of the mismatch between the vector of perturbed observations dobs,i, i.e., the observations corrupted with noise zobs,i ~ N(0, Cerr), and the corresponding vector of predicted states using the forward operator g.
Unlike EnKF however, ES does not assimilate the data sequentially in time. Instead, it assimilates all the available observations simultaneously in a single conditioning step. Hence the prediction step in ES prior to the single update will be longer than each recursive one in EnKF since the ensemble of prior realizations need to be forwarded in time until the time of the last conditioning observation. Evensen and van Leeuwen (2002) showed that when the prior realizations are multi-Gaussian and the forward model is linear, ES and EnKF at the last data assimilation will give the same result. In this special case, they will converge to the exact solution in the Bayesian sense as the ensemble size increases to infinity (hence the subscripts pr and post used in the previous equations to denote the unconditioned and conditioned realizations respectively). In non-linear cases, EnKF has been shown to outperform ES (Crestani et al., 2013). Indeed, the sequential processing of fewer data in EnKF effectively allows the computation of smaller updates than the single global update of ES. This fact particularly allows EnKF to better match the measurements than ES in non-linear problems.
Even so, if the whole data set for the parameter estimation is already acquired, the assimilation with ES of the whole set of data in a global update step may seem more convenient to implement. Indeed, the additional computations of intermediate conditional ensembles over time with EnKF can be avoided. For non-linear problems, iterative versions of the ES have been especially developed in order to improve the insufficient data match obtained with ES. Like ES, these iterative variants assimilate the complete data set during the conditioning step. However, the assimilation is performed multiple times on the same data set in order to reach the final solution. In the following sections, we introduce two existing iterative ensemble smoother algorithms which are particularly used in reservoir applications (Evensen, 2018), namely the simplified version of the Levenberg-Marquardt Ensemble Randomized Maximum Likelihood (LM-EnRML) of Chen and Oliver (2013) and the Ensemble smoother with Multiple Data Assimilation (ES-MDA) of Emerick and Reynolds (2012a).
2.1. Levenberg–Marquardt Ensemble Randomized Likelihood (LM-EnRML)
LM-EnRML is an iterative ensemble smoother based on a modified form of the Levenberg-Marquardt algorithm (Chen and Oliver, 2013). By modifying the Hessian term, LM-EnRML avoids the explicit computation of the sensitivity matrix of the predicted data to the model parameters using the ensemble at each iteration as in the original LM-EnRML formulation. This allows LM-EnRML to reduce the numerical instability usually observed with the original method for large-scale problems where the ensemble size becomes smaller than the number of parameters to estimate (Chen and Oliver, 2013). For our study, we will use a simplified version of LM-EnRML referred as LM-EnRML (approx.) in Chen and Oliver (2013) which neglects the contribution to the update of the mismatch between the updated and the prior realization. Indeed, Chen and Oliver (2013) showed that using this simpler variant did not significantly affect the results obtained with an ensemble of 104 realizations for a large-scale estimation problem involving 165000 parameters and 4000 observations.
Assuming a prior multi-Gaussian distribution of realizations with i = 1, …, N, the algorithm aims to generate a posterior ensemble of N realizations mi that each individually minimizes an objective function
which measures the distance between mi and the realization sampled from a prior distribution and the distance between the noisy observations dobs,i and the corresponding vector of predictions, noted g(mi), which results from the application of the forward operator g to mi.
Each minimization of the ensemble of objective functions is performed iteratively, so that for each ensemble member, the updated realization at iteration k + 1 is computed using the results of the previous iteration k as follows
where Cerr is the covariance of measurement errors, Csc, a scaling matrix for the model parameters. Although Csc is typically defined diagonal with its diagonal elements equal to the variance of the prior distribution in the general form of LM-EnRML, Csc can simply be the identity matrix in the approximate version LM-EnRML as it allows the algorithm to converge more quickly (Chen and Oliver, 2013). Δme represents an ensemble of deviations from the mean of the parameters vectors, computed as
with me the ensemble of N parameter vectors and the ensemble mean. As for the terms , , and , they result from the truncated singular value decomposition, based on a number PD of singular values, of the ensemble of deviations from the mean of the vectors of predictions, noted Δde, so that . This ensemble of predicted data deviations is calculated as
with de the ensemble of N prediction vectors and the ensemble mean. Finally, λ is a damping parameter, also known as the Levenberg-Marquardt regularization parameter (Chen and Oliver, 2013), and is adjusted by the algorithm. This parameter is critical for the convergence of the algorithm as it affects the search direction and length of each update step. The LM-EnRML algorithm as proposed by Chen and Oliver (2013) adjusts λ after each parameter update computation according to whether the updated parameters lead to a decrease or increase of the objective function. If the objective function is decreased, the update is accepted and the parameter search continues with a decreased λ. Otherwise, λ is increased until an update that decreases the objective function is found. LM-EnRML will stop iterating either after a maximum number of iterations allowed is reached, or the relative decrease of the objective function or the magnitude of the realization update falls below a defined threshold. To allow a convergence toward a sufficiently low value of the objective function, we set for our synthetic problem the initial value of λ to 100 and defined a factor for either decreasing or increasing the damping parameter equal to 4. Indeed, after testing different initial values of λ, we found that lower values such as 1 × 10−3 did not allow a significant change of the results in terms of convergence and final data match. However, we noticed that values larger than 1 × 105 could result to very small changes in the objective function and consequently to the termination of the algorithm before a good data match could be reached.
2.2. Ensemble Smoother With Multiple Data Assimilation (ES-MDA)
Thanks to its simple formulation, ES-MDA of Emerick and Reynolds (2012a) is perhaps the most used iterative form of the ensemble smoother in geoscience applications. The standard algorithm consists simply in repeating a predefined number of times the standard ensemble smoother (ES) (Emerick and Reynolds, 2012a). However, unlike in the ES update, the covariance of the measurement errors in ES-MDA is inflated so that each realization mi of the ensemble of size N at iteration k + 1 is updated as follows
where with zd,i ~ N(0, Id).
The purpose of inflating the Gaussian noise, sampled at every iteration, via the coefficient α > 1 is to limit the confidence given to the data as they will be assimilated multiple times (Emerick and Reynolds, 2012a). In so doing, the parameter covariance reduction which occurs after each data assimilation is also limited. The inflation factors used to inflate the covariance matrix of the measurement errors need to satisfy the following condition
where Na is the number of times we repeat the data assimilation. Indeed, this condition has been derived in order to make the single update by ES and multiple data assimilation by ES-MDA equivalent for the linear Gaussian case. For all our tests using ES-MDA, we set for simplicity the inflation coefficients equal to the predefined number of assimilations, as varying them in a decreased order do not lead to a significant improvement of the data match (Emerick, 2016).
ES-MDA effectively improves the data fit obtained by ES in the non-linear case because ES is in fact equivalent to one single iteration of the Gauss-Newton procedure to minimize the objective function (2) when using a full step length and an average sensitivity matrix calculated from the ensemble (Emerick and Reynolds, 2012a; Le et al., 2016). The motivation for applying ES-MDA in non-linear problems is that it would be comparable to several Gauss-Newton iterations with an average sensitivity matrix which is updated after each new data assimilation. By calculating smaller updates than one single potentially large ES update, ES-MDA is expected to lead to better results than ES.
The quality of the final data fit achieved with ES-MDA will particularly depend on the predefined number of data assimilations. The standard ES-MDA algorithm is therefore not an optimized procedure as it requires some amount of trial before finding a number of iterations which allows an acceptable match. Although we did not consider them in this synthetic study, implementations of ES-MDA which allow to adapt the inflation coefficients and the number of iterations as the history match proceeds have been proposed (Emerick, 2016; Le et al., 2016).
2.3. Normal-Score Transform of State Variables With ES-MDA
Considering that the forward model g can be non-linear due to the physical process being modeled and/or the influence of imposed boundary conditions on the predicted states, the assumption of multi-Gaussian dependence among state variables in ensemble Kalman methods is generally not justified in subsurface flow modeling even in the case of multi-Gaussian log hydraulic conductivity fields (Schoniger et al., 2012). In addition to the linearization around the ensemble mean introduced by the use of an ensemble gradient, the derivation of the ES update equation (6) particularly involves a linearization of the forward model around the local estimate (Luo et al., 2015; Evensen, 2018). Hence ES-MDA, which is based on the repeated application of ES using inflated measurement errors, also applies such a local linearization at each update step (Evensen, 2018).
Because of this aforementioned local linearization in the update step, we are here interested in assessing the effects of a normal-score transform in order to apply the ES-MDA update to locally Gaussian state distributions. In a previous study, (Schoniger et al., 2012) observed an improved performance of EnKF for the identification of multi-Gaussian log hydraulic conductivity fields when assimilating normal-score transformed state variables such as hydraulic heads. They attributed this improvement to an “implicit pseudolinearization” of the relationship between the multi-Gaussian log hydraulic fields and the transformed predicted data which benefited the “linear updating step” of EnKF. In addition to this statement, we conjecture here that it is more specifically the local linearization highlighted by Evensen (2018), rather than the linearization around the ensemble mean introduced by the approximated gradient, which will benefit from such a normal-score transform performed locally at the data points. The “pseudolinearization” observed by Schoniger et al. (2012) would then allow a better approximation of the forward model from the local linearization applied at each update step, thereby yielding more accurate updates.
The effects of the ES-MDA update in the transformed space will be tested as follows
where
with
where the hat indicates either transformed variables or covariances calculated based on transformed variables. A normal-score transform (NST) function denoted ψk, for each data type, is calculated based on the time series of state variables predicted at each one of the k observation locations (Figure 1) which we perturb with noise beforehand. Indeed, we perturb the predicted data using the same inflated measurement errors added to the observations dobs in (8). This NST function maps the p-quantile of the ensemble distribution of original perturbed predicted values at one location to the p-quantile of a standard normal distribution. In order to evaluate properly the data mismatch in the transformed space, the predicted data without added noise and the perturbed observations are transformed using the same NST functions defined depending on the location of the data. Note that is the cross-covariance between the parameters and the normal-score transform of the predicted data without added measurement errors.
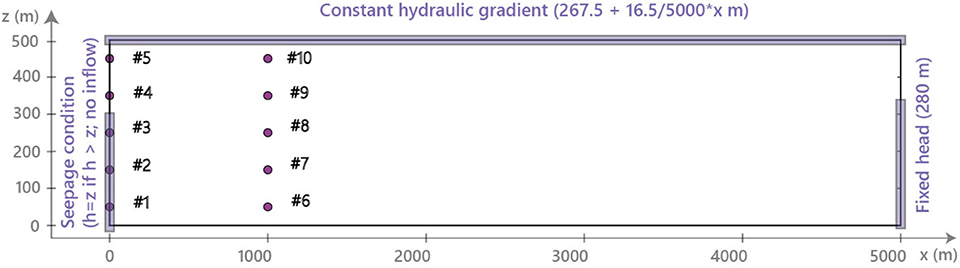
Figure 1. The two-dimensional vertical domain modeled of 5,000 m length and 500m depth. The thin rectangles indicates the location of nodes with a boundary condition applied. The dots indicates the head observation nodes. Not shown here, the seepage boundary is divided into 5 zones where the produced flowrates are measured. Reprinted from Lam et al. (2020) with permission.
To transform the term , Schoniger et al. (2012) suggested to calculate the covariance using directly the transformed perturbed predicted data from which we built the NST functions. In this way, the terms and Cerr don't need to be transformed separately. However, unlike in EnKF where the inversion of the matrix is fast thanks to the generally small number of data at each observation time (Liu and Oliver, 2005), the assimilation of a large data set here with ES-MDA will require the use of the subspace inversion procedure of Evensen (2004). Consequently, the calculation of the transformed terms and will be needed in any case to compute the pseudo-inverse of in (8). In the end, can be calculated simply on the basis of the normal-score transform of the predicted data without added measurement errors, while the transformed measurement error covariance will be determined so as to respect the following ratio
where Cerr is the untransformed measurement error covariance which is often assumed diagonal, is the diagonal matrix constructed from the diagonal elements of the covariance of the transformed perturbed predicted data, and is the untransformed equivalent. It is worth pointing out that transforming properly the measurement error covariance is particularly critical in this proposed application of ES-MDA in the transformed space as the data mismatch reduction with ES-MDA will rely on the inflation of . Moreover, to better taking into account the data of different orders of magnitude in the update, Emerick (2016) suggested using the measurement error covariance to rescale the predicted data before calculating the truncated singular value decomposition (SVD) in the subspace inversion procedure.
3. A Synthetic Inverse Problem Inspired by the Andra's Site
A synthetic case inspired by the hydraulic situation encountered at the Andra's Meuse/Haute-Marne site during the construction and the operation of the Underground Research Laboratory (Benabderrahmane et al., 2014; Kerrou et al., 2017) was created. The model represents a two-dimensional vertical cross-section of a multilayered aquifer system and is inspired by previous modeling studies on the Andra's site (Bourgeat et al., 2004; Deman et al., 2015). The model was designed to mimic the hydraulic behavior of the Oxfordian limestone multi-layered aquifer above the Callovo-Oxfordian clay host formation which is not included in the model. It will be used to analyze the performance of the ensemble smoother and the two iterative ensemble smoother algorithms presented previously for the identification of multi-Gaussian parameter fields. We present hereinafter the inverse problem set up, the assumptions for the application of the methods, and the performance criteria.
3.1. Model Set Up
The synthetic model is two-dimensional over a vertical domain of 5,000 m along the west-east direction and 500m in depth. In order to solve the groundwater flow equation, the domain is discretized by 50 × 500 square elements of 10m wide. Along the top boundary, constant heads are imposed. The head values vary from 267.5m on the west side to 284m on the east side according to a small hydraulic gradient observed in the shallow aquifers which we did not represent in our model. At depth, between 150 and 500m, a constant head of 280m is imposed on the east side to maintain a continuous east-west flow in the system (Figure 1). To mimic the hydraulic perturbation created by one vertical shaft to the underground research laboratory at the Andra's site, a subsequent transient flow simulation is calculated by adding from time zero a seepage condition over the nodes corresponding to the first 300 m of the western boundary starting from the bottom (Figure 1). The nodes over the remaining 200m toward the surface do not contribute to the production of water as they model the isolated upper part of the shaft as in the real case. Since the produced flowrates at the shaft are unknown prior to the computed head solution at each time step, using a seepage boundary condition instead of a pumping well with a prescribed extraction rate seems indeed more appropriate here. Note that in exploratory simulations, a sensitivity analysis was carried out on different levels of the finite element mesh refinement and the solver parameters, as well as on various types of flow boundary conditions and hydraulic property values. This was in order to ensure robust numerical solutions and optimized CPU time, and also to avoid bias from boundary effects.
For simplicity, the groundwater flow equation was solved numerically under saturated conditions. All the groundwater flow simulations in the framework of this study were performed with the simulator GroundWater (GW) (Cornaton, 2014). This numerical code uses the standard Galerkin Finite Element and the Control Volume Finite Element methods, and has been validated on the basis of a series of standard benchmarks by comparison with analytical solutions as well as with commercial numerical simulators.
3.2. Synthetic Data Set
Since we intend in this synthetic study to apply ensemble Kalman methods to an initial ensemble of multi-Gaussian parameter realizations, a reference field of values of decimal logarithm of hydraulic conductivity (log K) with mean −5 and variance 0.49 was generated with a multi-Gaussian simulation technique (Figure 2). To generate the synthetic data set of the inverse problem, a steady state groundwater flow was first simulated prior to the activation of the seepage boundary condition. The computed heads were then used as initial conditions for a subsequent transient flow simulation after the activation of the seepage condition at time zero. A constant specific storage value of 10−6 m−1 was assumed over the whole domain as they will not be considered in the inverse modeling. In the end, the data set for the inversion is composed of simulated heads collected every 1,200 s from t = 0 to t = 43, 200s, hence at 37 time steps, at the ten observation points shown in Figure 1, and of the flowrates produced every 300s in five defined zones of nodes spread along the seepage boundary during the first 6,000 s of the time series. As a result, the data set will be composed of at most 570 observations in our experiments. Note that the final time step of the flow simulation was chosen so as to capture approximatively the drawdown before its stabilization, similarly to the situation observed at the Andra's site in Meuse/Haute Marne (Kerrou et al., 2017).
3.3. Initial Ensemble of Parameters and Assumptions for the Update Step
In this synthetic case, an initial multi-Gaussian distribution of the variables to condition was considered to respect the underlying multivariate Gaussian assumption of ensemble Kalman methods. The initial ensemble is composed of multi-Gaussian realizations of mean −5 of log hydraulic conductivity (log K) values generated using a fast Fourier transform method. This mean corresponds to the one used for the reference field as we assume this value to be known in our case. Although different variogram models could have been considered for the generation of the initial ensemble, Wen and Chen (2005) showed that the covariance model was not critically important to reproduce the main heterogeneity features from the assimilation of flow data with an ensemble Kalman method. Interestingly, Jafarpour and Khodabakhshi (2011) concluded in a study which addressed variogram uncertainty that the direct estimation of the variogram model parameters with an ensemble Kalman method was made difficult due to an insufficient strength of the linear correlation between the flow data and those parameters. Ultimately, we chose to simply assume a known variogram and hence used the same variogram model as the one used for the reference to describe the spatial variability of the ensemble of log K fields, i.e., an exponential variogram of variance 0.49 and correlation lengths of 120 gridblocks in the horizontal direction and 10 gridblocks in the vertical direction. We assumed longer ranges in the horizontal direction to mimic the presence of the elongated porous horizons “HP” observed in the real field case. In the vertical direction, we assumed the existence of five horizons, hence a correlation length was set to one fifth of the vertical dimension of the model. The realizations generated are considered quite heterogeneous since the correlation lengths are shorter with respect to the domain size, namely about one fifth of each dimension.
One practical issue of ensemble methods is that the finite number of members, usually no more than O(100) in applications (Wen and Chen, 2005; Gillijns et al., 2006; Anderson, 2009; Evensen, 2009a), can cause spurious covariances between widely separated components of the parameter vector and between components of the vector of parameters and vector of predicted data. Since these long-range spurious correlations are non-physical, they can bring an undesirable response in the update computed. In general, they cause an underestimation of the ensemble variance which can potentially lead to “filter divergence” (Evensen, 2009a). This term refers to the situation where the assimilation of new measurements stops being effective because the spread of the ensemble has overly reduced or has “collapsed” to take them into account.
Considering that the observations are spatially restricted to the modeled domain (Figure 1) and that the hydraulic perturbation from the shaft is local relatively to the horizontal extension of the model, such long range correlations will be inevitable in this synthetic case. Therefore, it is necessary to try to filter them out as much as possible before computing the update. To this end, we will use a simple approach which consists in “localizing” the Kalman gain matrix so that only the parameters located within a certain distance of an observation will be influenced by this observation during the update (Chen and Oliver, 2017). We will multiply the Kalman gain element-wisely with a “localization matrix” of the same size, i.e., number of parameters by number of data, which each entry will be a factor between 0 and 1 calculated by the correlation function defined by Gaspari and Cohn (1999)
where δ denotes the distance between each couple of parameter and data variable and L is a predefined “critical length” beyond which the contribution of the data to the parameter update will be negligible. In this way, long-range spurious correlations will be partly removed from the Kalman gain and the performance of the ensemble method will be improved. To avoid potential discontinuities in the localized parameter update between the two columns of data points (Figure 1), we set L to 1,600 m, hence over a little larger distance than the distance separating the points horizontally, in all tests. In this synthetic case, this distance is consistent with the domain of the model that is identifiable given our data set, namely the region influenced by the observed hydraulic perturbation.
The ensemble smoother, LM-EnRML and ES-MDA all consider the vector of observations in their update equation as a random vector with the addition of a random noise vector sampled from the measurement error covariance Cerr. For all tests performed, we assumed a diagonal covariance matrix of independent measurement errors of 0.05m2 for every head observation. When flowrate data were assimilated in addition to the hydraulic heads, Cerr also included independent flowrate measurement errors set equal to the square of 20% of the flowrate value. For the application of ES-MDA with transformed state variables, Cerr was transformed as described in section 2.3.
4. Performance Criteria
Ideally, the application of ensemble Kalman methods for our parameter estimation problem aims to satisfy the following two criteria: (1) to reproduce the dynamic observations of state variables with the final ensemble of conditioned realizations, and (2) to obtain a final ensemble of conditional realizations which variations around the mean correctly quantify the uncertainty. As we assumed in this synthetic case no model errors or errors in the choice of the prior distribution used to sample the parameter space, meeting both these criteria should ensure that the ensemble-based uncertainty in the model predictions will be well-represented.
To assess the quality of the fit between the simulated g(mi) and observed data dobs using either LM-EnRML or ES-MDA with or without transformed data, we will consider the evolution of the sum of squared errors
Note that this sum of squared errors does not correspond to the data mismatch term of the objective function which is actually minimized by each algorithm considered (cf. section 2). Indeed, dobs here denotes the vector of the original observations even in the case of ES-MDA when considering transformed data. In this manner, we will be able to more easily compare the data mismatch results obtained using LM-EnRML, ES-MDA with or without transformed data. Note also that in this defined sum of squared residuals, no normalization by the observation error is considered. Therefore, when assimilating both heads and flowrates, this sum will be dominated by the head data.
In addition, to compare the efficiency of ES-MDA when using transformed vs. untransformed data, we will also compute for each case the data mismatch term of the different cost functions being minimized at each iteration. Indeed, Evensen (2018) noted that each updated estimate of ES-MDA actually corresponds to an estimation of the minimum of a cost function written as
where and with the prior model covariance approximated from the ensemble around the prior ensemble mean .
Once an acceptable data match has been reached during the conditioning procedure, the uncertainty based on the variability of the final ensemble of conditioned realizations can be assessed. In practice, ensemble-based Kalman methods are known to particularly overestimate the uncertainty reduction when they are not applied in sufficiently optimal conditions. In particular, the use of a finite ensemble inevitably introduces sampling errors in the approximated covariances which can lead to an overly reduced variance of the conditioned ensemble. Moreover, the solution space spanned by the ensemble when computing the update will likely be under-sampled (Evensen, 2009a) and the estimated uncertainty will not be reliable. To reduce these sampling errors, a natural solution is to increase the ensemble size. However, because the Monte Carlo sampling errors decrease proportionally to , with N the ensemble size, the improved performance of the ensemble method can come at a significant computational cost. For example, Chen and Zhang (2006) noted that an ensemble size of 1,000 allowed EnKF to obtain an accurate uncertainty estimation for their synthetic case, but ultimately concluded that an ensemble size of 200 was sufficient to achieve results with both accuracy and efficiency. When applying iterative ensemble smoothers, the choice of the ensemble size will be particularly constrained by the time needed to run all the forward predictions of the ensemble during one iteration. Consequently, larger ensemble sizes than O(100) are generally not affordable if the available computational resources are not sufficient to efficiently parallelize the prediction step of every ensemble member. For these practical reasons, we will discuss the performance of the different ensemble methods based on tests involving ensemble sizes of the order of O(102) at most.
To assess the accuracy of the uncertainty captured by the final conditioned ensemble, a common approach consists in comparing the error between the ensemble mean of log K realizations and the known reference to the ensemble mean error that was obtained by the ensemble method, also called the “ensemble spread” (Houtekamer and Mitchell, 1998). For the first error mentioned, we will simply compute the root-mean-squared error (RMSE) as follows
where Nm is the number of gridblocks, mtrue is the reference log K field, and me stands for the mean of the ensemble of log hydraulic conductivity fields.
The ensemble spread, here noted Sens, corresponds to an average uncertainty on the log K property calculated from the ensemble
where corresponds to the variance estimated from the ensemble of log K realizations at one gridblock i. For our uncertainty analysis, we will systematically evaluate these average errors by considering the gridblocks of the model located within a certain distance from the seepage boundary which includes all the data points. In particular, we will set this distance equal to the “critical length” used for the localization of the update (cf. section 3.3). In this way, the comparison between the RMSE and the ensemble spread will be based on the set of parameters which are the most informed by the observations and hence which uncertainty will decrease the most during the assimilation.
One goal of this analysis will be to illustrate how the spread between ensemble members updated using either LM-EnRML, ES-MDA with or without transformed data is representative of the difference between the ensemble mean and the reference (RMSE) depending on the ensemble size. Indeed, as the size of the ensemble increases, the discrepancy between the final conditioned ensemble and the RMSE should reduce thanks to the reduced sampling errors. However as previously mentioned, a trade-off between accuracy of the uncertainty and computational efficiency will need to be found. In the end, if the ensemble spread is not overly underestimating the RMSE, we will consider that the ensemble method has performed correctly given its intrinsic limitations. In addition, although the inverse problem is ill-posed, i.e., there are more parameters to infer than data to inform them in a unique way, we expect for this synthetic case that the information contained in the data set (i.e., hydraulic heads and flowrates) is sufficient in order to yield after the data assimilation estimates that are closer to the reference than initially in the most updated region of parameters. Therefore, the performance of the smoother will also be assessed in its ability to decrease the RMSE value.
5. Results and Discussion
5.1. Ensemble Smoother and Benefit of Data Transformation
As expected in a non-linear case, the application of a non-iterative ensemble method such as the ensemble smoother (ES) results in an insufficient match between the final ensemble of predicted data, i.e., computed from the ensemble of updated realizations, and the observations. Figure 3 shows for three locations at different depths 1 km away from the producing shaft the simulated heads before and after the update of 100 realizations with ES. By using the same initial ensemble, the evolution of the data mismatch obtained from the assimilation of the head data only and both the head and flowrate data simultaneously are shown respectively in Figures 4A,C. Because the represented data mismatch does not include the inflated measurement error in the observed data and hence the normalization by the error variance, as defined in section 4, the additional contribution to the mismatch from the flowrates in Figure 4C is not visible. Even so, compared to Figure 4A), we can observe that the assimilation of the flowrates in addition to the heads allows the data mismatch to decrease thanks to a better match of the head data.
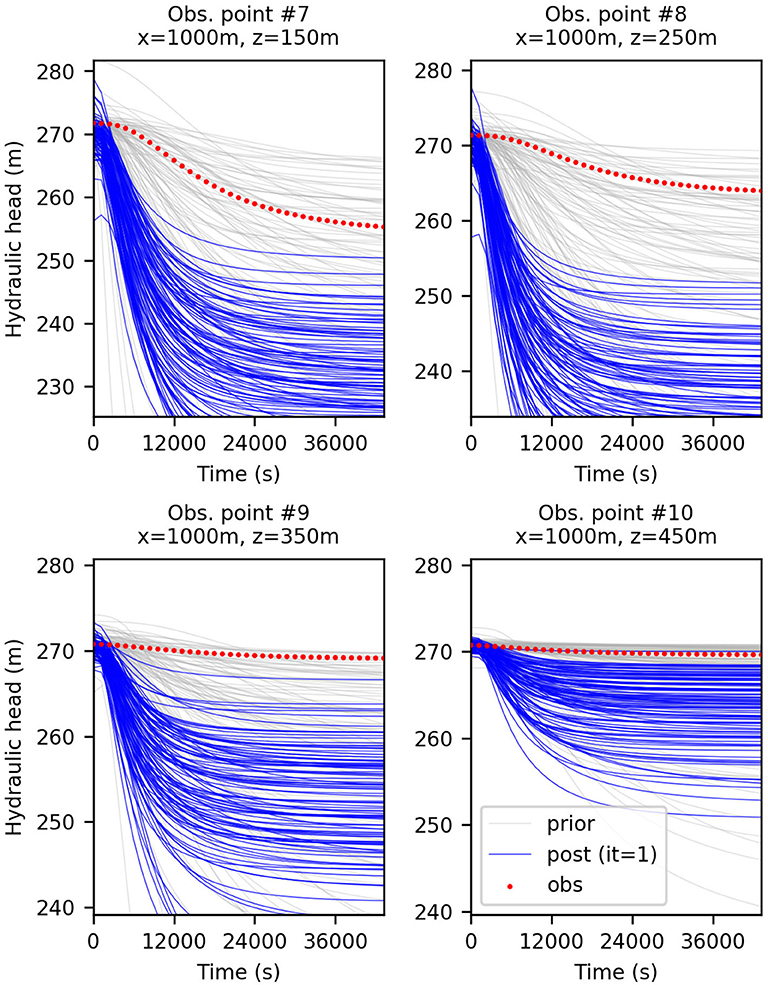
Figure 3. Predicted hydraulic head at four different locations, before (in gray) and after (in blue) the assimilation with ES of the head data without normal-score transform. The red dots are the observed data; The ensemble size is 100.
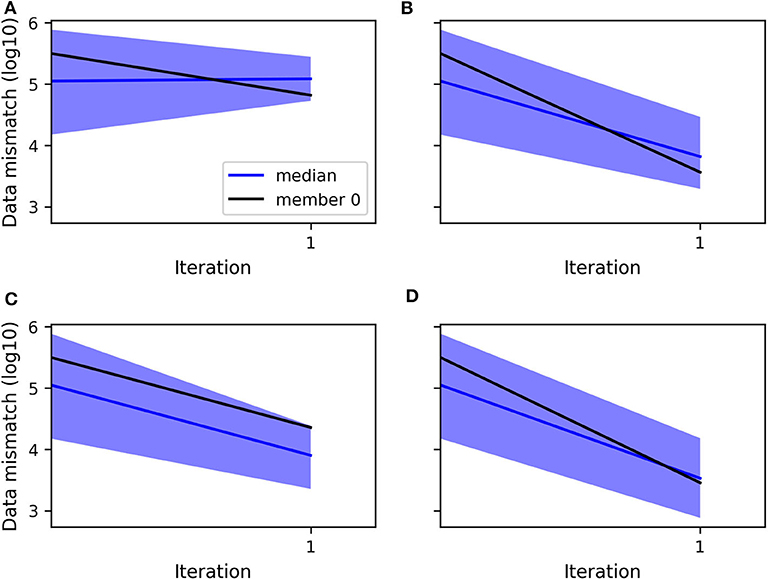
Figure 4. Evolution of the decimal logarithm of the data mismatch when assimilating with ES: (A) the head data, (B) the transformed head data, (C) both the head and flowrate data, (D) both the transformed head and transformed flowrate data. The blue curve is the median, the blue area corresponds to the region between the percentiles P5 and P95 of the ensemble of values, and the black curve is the values computed for the ensemble member no. 0.
The strategy of transforming the data prior to each update of ES-MDA, as described in section 2.3, was also tested here with ES using the same initial ensemble. Indeed, ES is equivalent to ES-MDA with only one iteration and hence applies once a local linearization of the model around the initial parameter estimate to compute its single update. As shown in Figures 4B,D, whether only the head data are assimilated or both the head and flowrate data, the data mismatch is reduced in both cases with a slightly lower mismatch in the case mentioned last. Therefore, compared to the case where only untransformed head are assimilated (Figure 4A), the data transformation seems to have a positive impact on the decreased data mismatch which, we remind, considers the original data even for the transformed case. The improved history match can be observed for example by comparing Figure 3 with Figure 5. In particular, we note that when data transformation is used, the ensemble of predicted values better tracks the observations, most certainly as a result of a more accurate update of each ensemble member. Indeed, the comparison of the RMSE and the ensemble spread in Table 1 for each one of the cases considered in Figure 4 shows that the assimilation of the transformed heads instead of the original data results in a more accurate estimation of the ensemble mean and spread thanks to a decrease of the RMSE which reduces the discrepancy with the reduced ensemble spread. As for the assimilation of both the head and flowrate data simultaneously, we can see that compared to when the data are transformed, the assimilation is less efficient with a less reduced ensemble spread and a RMSE that has almost not reduced. Based on both the evolution of the RMSE and the “coverage”, which we defined as the percentage of true values of the reference captured by the final ensemble spread in the most updated region of the model, we can conclude from Table 1 that transforming the data clearly benefits the performance of ES. However, we note that the assimilation of both the transformed head and flowrate data with ES does not allow to further reduce the RMSE compared to when using the transformed heads only, although the ensemble spread is further reduced.
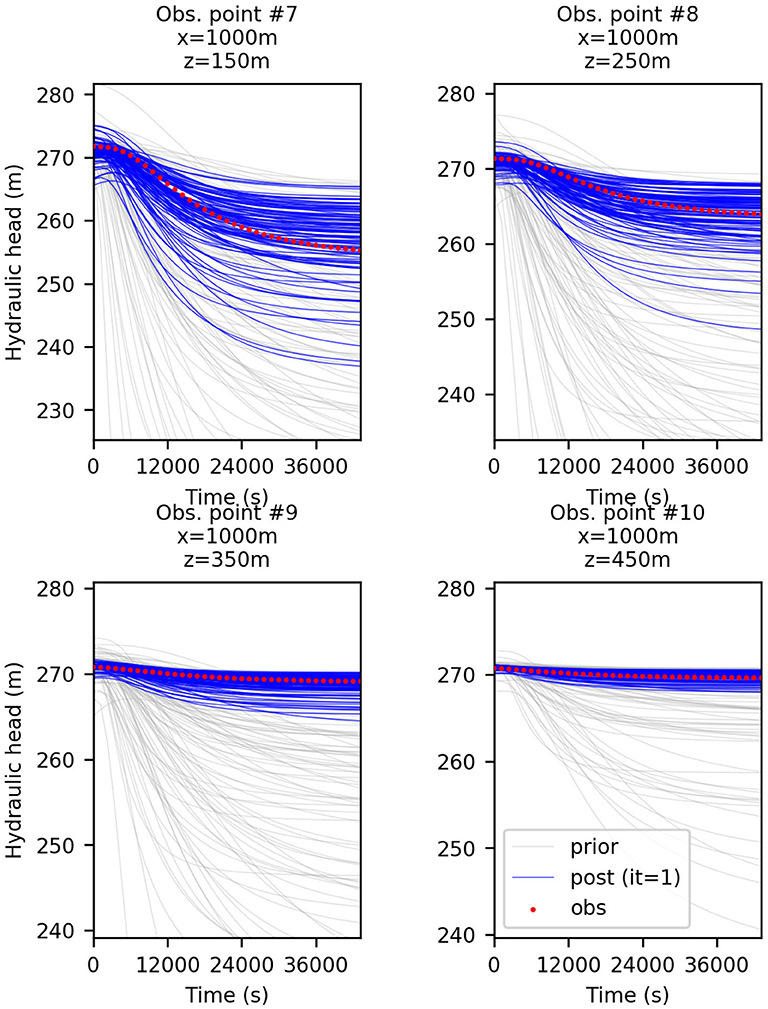
Figure 5. Predicted hydraulic head at four different locations, before (in gray) and after (in blue) the assimilation with ES of normal-score transformed head data. The red dots are the observed data; The ensemble size is 100.
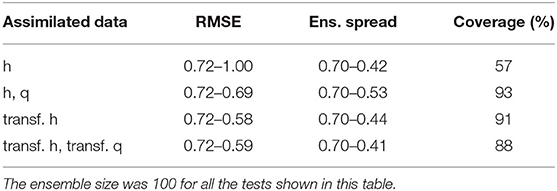
Table 1. Influence of different types of data assimilated (transformed or not) on the RMSE, ensemble spread, and coverage calculated with ES.
5.2. Comparing the Accuracy of LM-EnRML and ES-MDA Estimates
Although ES-MDA and the LM-EnRML were developed with the aim of improving the data match obtained with ES in the non-linear case, the iterative updates will likely cause a more important underestimation of the uncertainty than with ES. Indeed, at each iteration, the sampling errors in the approximated covariances of the Kalman gain will affect the estimates of the method, and more particularly the ensemble uncertainty. Seeing as how the Monte Carlo sampling errors decrease according to where N is the ensemble size (Evensen, 2009a), we tested for our synthetic case the effect of increasing N on the performance of ES-MDA and LM-EnRML when only assimilating the head data. Table 2 shows the evolution of the RMSE and the ensemble spread when applying ES-MDA with 4 arbitrarily defined iterations. Whether we consider an ensemble of 100, 200, or 400, hence of the order of O(102) to remain computationally efficient, we note that starting from the first update, the ensemble spread measuring the variability between the ensemble members systematically underestimates the RMSE which measures the error between the reference and the ensemble mean. This discrepancy with the RMSE further increases with each iteration as the spread keeps decreasing while the RMSE remains higher. Although we do not show it here, not localizing the update resulted in a larger discrepancy between the RMSE and ensemble spread for the different ensemble sizes tested.
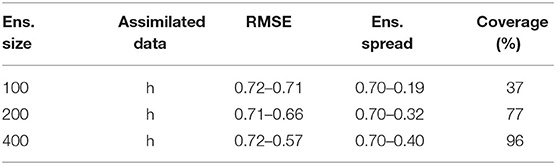
Table 2. Effect of increasing the ensemble size on the RMSE, ensemble spread, and coverage after 4 predefined ES-MDA iterations.
Nevertheless, we note that the larger the ensemble size, the more reduced the gap between the RMSE and the ensemble spread becomes. As expected, the estimated uncertainty gains in accuracy with the ensemble size. We note however that the most significant improvement occurs when increasing the ensemble from 100 to 200 realizations for both algorithms (Tables 2, 3). Indeed, as indicated for ES-MDA in Table 2, the coverage, defined as the proportion of reference values that are within the ensemble range in the most updated region of the model, has more than doubled with a final value of 77% after the same number of iterations. In a similar manner, the coverage also doubled with LM-EnRML (Table 3). Moreover, when using an ensemble size of 100, we can see that the evolution of the RMSE is particularly unstable for both LM-EnRML and ES-MDA. The ensemble means estimated with LM-EnRML even lead to a final RMSE value which is much higher than initially. In contrast, an ensemble size of 200 allows LM-EnRML to provide a more accurate estimation of the true uncertainty than with ES-MDA. The results shown in Table 3 were all calculated based on the estimates of LM-EnRML obtained after 8 iterations when the reduction of the objective function seemed to have decreased to a sufficiently low data mismatch value as shown in Figure 6A. We note also from Figure 6, however, that it seems to take more iterations for LM-EnRML to converge to the same level of data match achieved by ES-MDA using 6 predefined iterations.
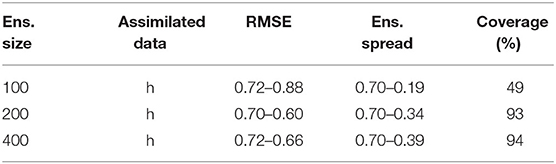
Table 3. Effect of increasing the ensemble size on the RMSE, ensemble spread, and coverage with LM-EnRML at iteration 8.
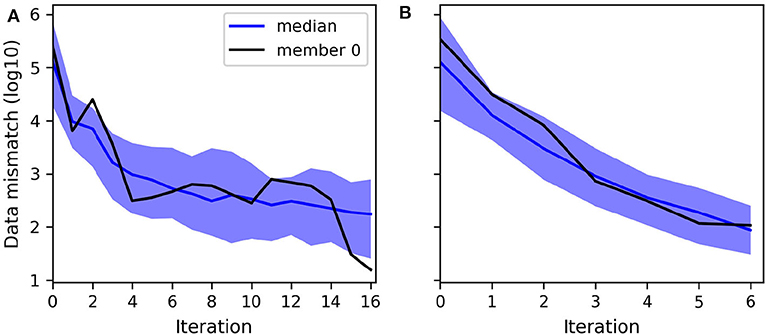
Figure 6. Evolution of the decimal logarithm of the data mismatch when assimilating head data with: (A) LM-EnRML, (B) ES-MDA (×6). The ensemble size is 200.
From all these tests, it is clear that the larger the size, the more accurate the uncertainty estimated by LM-EnRML or ES-MDA will be. However, as can be observed in Table 2, this improvement in the estimates comes at an increased computational cost. For our synthetic problem, we note that an ensemble of 400 realizations would still not allow the ensemble to represent correctly the true error on the ensemble mean. Since increasing the ensemble size does not seem to be a reasonable option computationally, it seems that the application of such ensemble methods necessarily requires to achieve a balance between accuracy and computational efficiency. This computational efficiency is of even more importance for large-scale problems since the biggest constraint would often be the long flow simulation time required to run the prediction step for each ensemble member. Hence the larger the ensemble, the longer it will take to complete all the predictions of the ensemble before being able to start the update step. Indeed, we remind that the update of each member is based on the same ensemble-based Kalman gain matrix. It is worth mentioning that this matter of efficiency also concerns the case where the ensemble of predictions steps is parallelized. Indeed, it would still require to have enough resources to efficiently run the whole ensemble of forward simulations simultaneously after each update step.
From Tables 2, 3, it is clear that the improvement on both the ensemble mean and spread is very significant when increasing the size from 100 to 200 with either LM-EnRML and ES-MDA. However, the differences in the estimated ensemble mean fields shown in Figure 7 suggest that the two methods converge toward different solutions. This is confirmed by the fact that when increasing the ensemble size from 200 to 400, the accuracy of both the error and uncertainty estimated with ES-MDA keeps increasing whereas for LM-EnMRL, no visible improvement is observed as if an optimal ensemble size has been reached around 200.
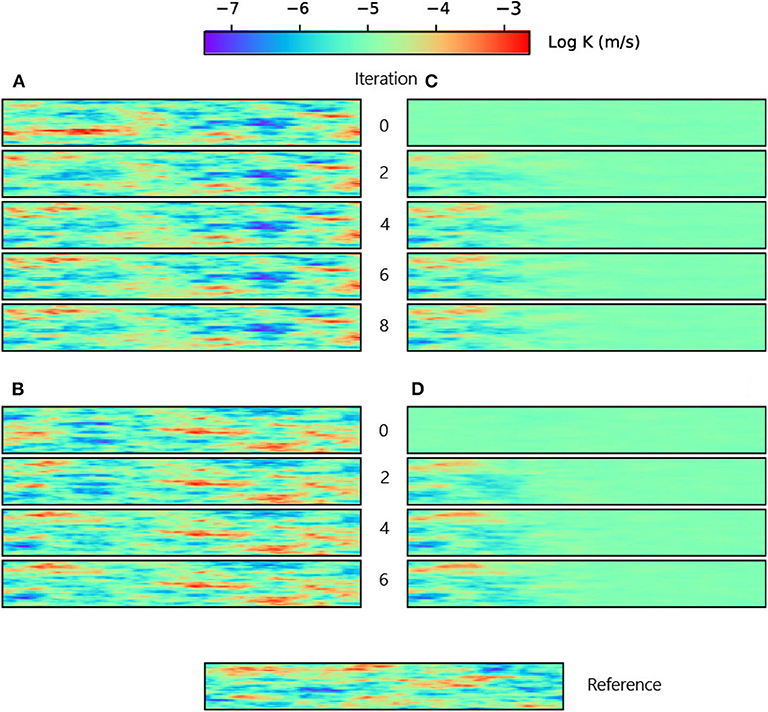
Figure 7. Two initial different realizations of log hydraulic conductivity being updated, respectively, with LM-EnRML (A) and ES-MDA (B) throughout the iterations. Panels (C,D) show the corresponding ensemble mean fields at each iteration. The ensemble size is 200.
Although LM-EnRML provides the more accurate estimation of the uncertainty compared to ES-MDA for any of the tested ensemble sizes, ES-MDA seems to converge faster, as shown in Figure 6. Indeed, it takes more iterations with LM-EnRML to reach the same mismatch value which corresponds to a good match as obtained with ES-MDA using 6 iterations. In the end, although the estimates of ES-MDA definitely improve with an ensemble size of 400, we will consider that using an ensemble of size 200 with either ES-MDA or LM-EnRML in our case is acceptable in order to achieve both accuracy and efficiency.
5.3. Assimilating Both Hydraulic Head and Flowrate Data With LM-EnRML and ES-MDA
As shown in Table 4, the assimilation of both head and flowrate data with LM-EnRML yields estimates of similar accuracy to when only the heads are assimilated. Neither the larger number of observations nor the higher “weights” of the flowrates in the objective function, given their much lower magnitudes, seem to have affected the minimization process. Figure 8A shows in fact that the mismatch associated to the flowrate data in the objective function, i.e., the sum of squared residuals weighted by the inverse of the measurement variance, is mostly reduced after the first iteration so that ultimately the remaining of the optimization deals with the reduction of the mismatch associated to the head data (Figure 8B). Although the convergence of LM-EnRML seems effective when assimilating different data types, we note that the accuracy of the estimates does not improve with the additional information coming from the assimilated flowrates. This lack of improvement could be related to possible over-corrections of the parameters during the first iteration as often observed with gradient-based methods. One way to reduce such over-corrections would be to artificially increase the measurement errors. We did not try that however since the parameter estimates obtained seem sufficiently accurate in terms of the estimated uncertainty.
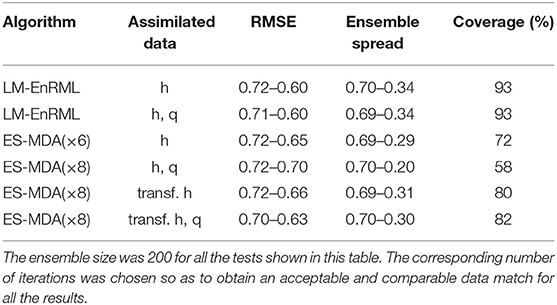
Table 4. Effect of assimilating the flowrate data in addition to the hydraulic heads on the RMSE, ensemble spread, and coverage with LM-EnRML and ES-MDA with or without transformed data.
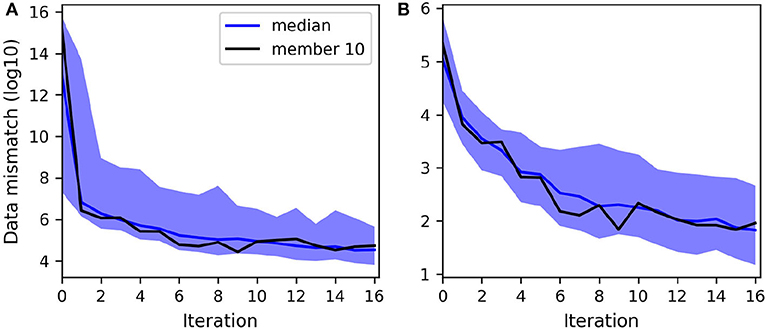
Figure 8. Evolution of the decimal logarithm of the data mismatch when assimilating both head and flowrate data with LM-EnRML: (A) With the normalization of the residuals by their variance (as minimized by the objective function). (B) Without normalization, hence the values reflect the head data mismatch reduction mainly. The ensemble size is 200.
For the assimilation of both data types, we first note that ES-MDA converged more rapidly, i.e., in 8 iterations, to the same level of data match achieved with LM-EnRML after 16 iterations (Figures 8A, 9A). For brevity, we do not show the associated good match of the head and flowrate observations obtained with both methods. However, unlike previously with LM-EnRML, the mean and variance estimates obtained with ES-MDA are less accurate than those obtained by the assimilation of head data only (Table 4). This illustrates that the different data types are not properly taken into account with ES-MDA during the multiple assimilations compared to LM-EnRML.
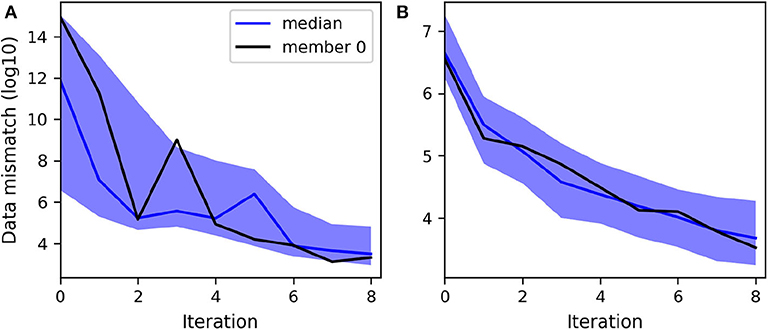
Figure 9. Evolution of the decimal logarithm of the data mismatch term of the cost function minimized at each iteration when assimilating both head and flowrate data with ES-MDA: (A) Without transformed data. (B) With transformed data. The ensemble size is 200.
As done previously with ES in order to mitigate the effects of non-Gaussianity on the performance of the method, we applied a normal-score transform on the data so as to obtain ensemble distributions of predicted variables which are locally Gaussian, for each data type, before performing each update step of ES-MDA in the transformed data space. As shown in Figure 10, the proposed state transformation allows ES-MDA to achieve an acceptable match of the head and flowrate observations after 8 iterations. Table 4 shows the estimates obtained after assimilating only the transformed heads resulted in a slight improvement. The coverage has slightly increased, which indicates that the estimated uncertainty, although still underestimated, has improved a little. A much more significant improvement, however, can be observed when both the head and flowrate data are assimilated in the transformed space. Compared to when no transformation is applied, the assimilation of both transformed data types is much more efficient given the larger variability of the ensemble and the smaller RMSE.
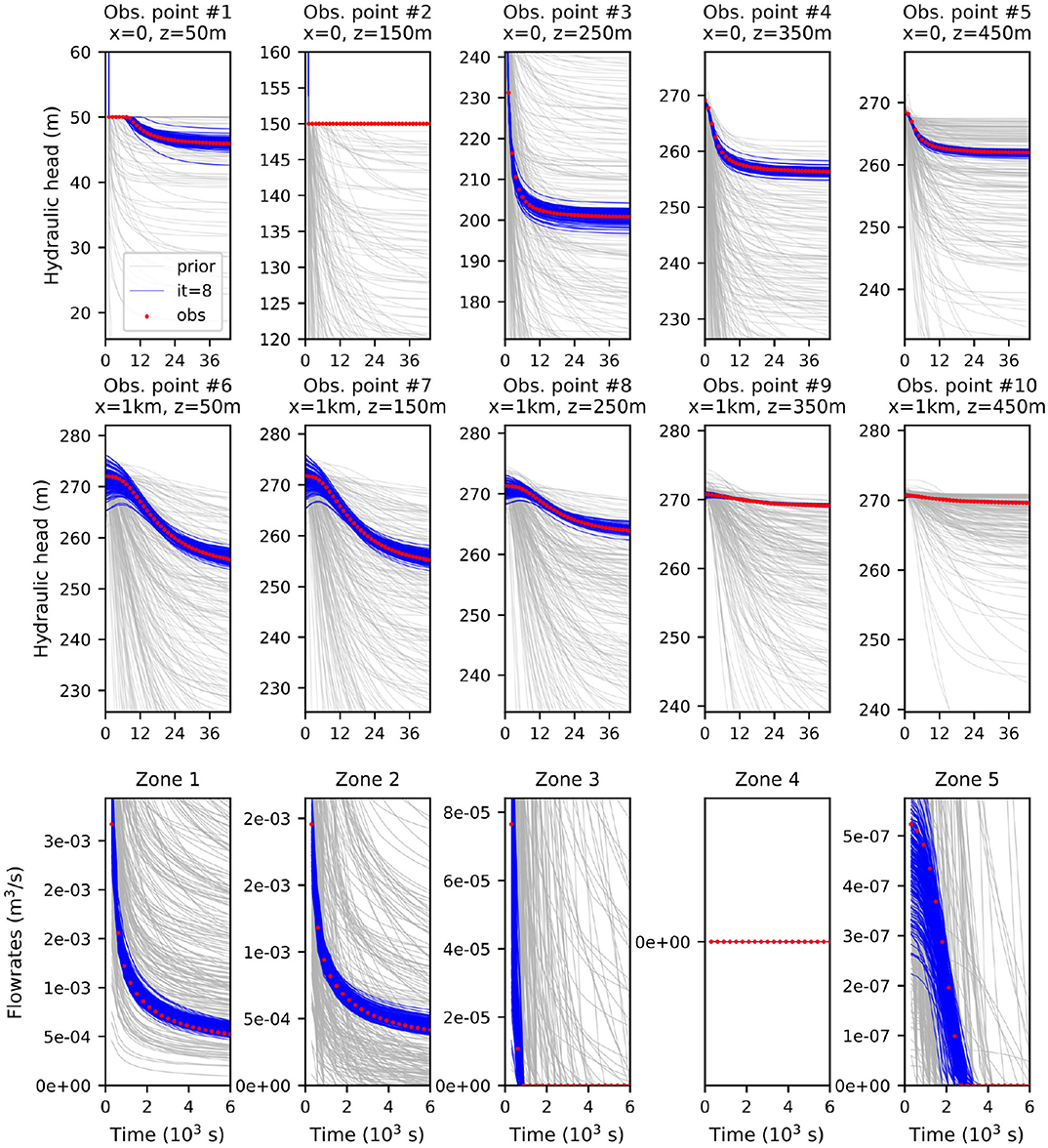
Figure 10. Predicted hydraulic head and flowrate data at the observation locations, before (in gray) and after (in blue) the assimilation of both the transformed hydraulic heads and transformed flowrate data with ES-MDA. The red dots are the observed data; the ensemble size is 200.
Figure 9 shows that when both data types are transformed, the decrease of the cost functions minimized for each iteration of ES-MDA (Evensen, 2018) is more stable than when no transformation is applied. In the case without transformation, the larger range of the initial ensemble of values reflects the differences of magnitude of the mismatch associated to the flowrate data on the one hand, and the one associated to the heads on the other hand. As shown in Figure 11A, the distribution is spread around two distinct modes. Hence the less stable reduction observed is probably related to the contribution of the flowrate data which dominates the cost function to minimize because of their much more smaller measurement errors. In contrast, the initial ensemble of mismatch values resulting from the transformed data (Figure 9B) is much less spread and resembles a Gaussian distribution (Figure 11). By making Gaussian the distribution of all mismatch values defining the first cost function to be minimized with ES-MDA, the normal-score transform applied to each data type seems to have benefited the data assimilation with ES-MDA. Since a new cost function is minimized after each ES-MDA iteration, we suppose that the initial Gaussian distribution of all the data mismatch values resulting from the transformation contributes to make the minimization more efficient by allowing to take equally account of each data type in the assimilation from the start of the assimilation. However, as discussed by Schoniger et al. (2012), it is important to note that such local transformation of the state variables would not have led to a successful application of ES-MDA if the multivariate dependence of the state variables was not sufficiently Gaussian in the first place. Indeed, since the proposed transformation only affects the marginal distribution, it is essential that the multivariate structure of the state variables is near-Gaussian in order to really observe an improvement of the performance of the ensemble Kalman method. Crestani et al. (2013) illustrated this point by observing that similar local transformation performed on concentration data can deteriorate the performance of EnKF because of an insufficient dependence between the multi-Gaussian log hydraulic conductivity parameters and the concentrations.
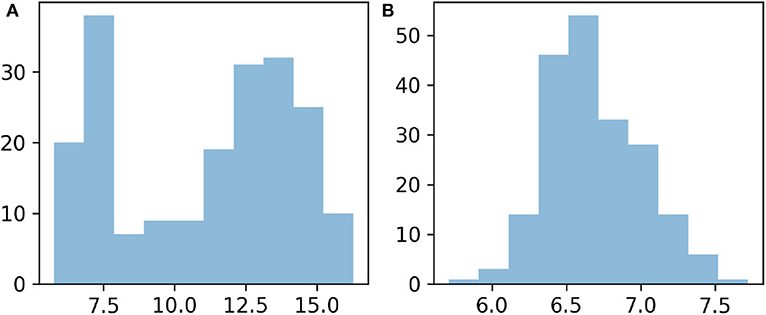
Figure 11. Distribution of the decimal logarithm of the sum of weighted squared errors prior to the assimilation of head and flowrate data with ES-MDA: (A) Without transformation. (B) With transformation.
It could be argued that equal contributions from both the heads and flowrate data to the first cost function could also have been obtained in the case without transformation by decreasing the measurement variance of the head measurements. However, the use of very small values of measurement errors can cause problems during the data assimilation as it may lead to severe underestimations of the parameter uncertainty due to the overconfidence in the assimilated data.
6. Conclusion
In this synthetic study, two iterative forms of ensemble smoother, LM-EnRML (Chen and Oliver, 2013) and ES-MDA (Emerick and Reynolds, 2012a), were applied and compared. They were both used to condition an ensemble of multi-Gaussian log hydraulic conductivity fields to transient hydraulic data. Given the non-linear dynamics of the groundwater flow problem inspired by a real hydraulic situation, the results show the necessity of using an iterative instead of non-iterative ensemble smoother in order to obtain an ensemble of hydraulic conductivity fields which all match properly the data.
Despite the multi-Gaussian log K distribution considered, the repeated assimilations of the data set have highlighted the known tendency of ensemble Kalman methods to underestimate the true error due to the finite ensemble size. A trade-off between accuracy of the estimation and computational efficiency hence needs to be found when applying such methods. Our uncertainty analysis based on the comparison between the ensemble spread and the true error, here accessible in this synthetic study, clearly indicated the existence of a threshold ensemble size below which the updated mean and variance are not reliable. For our case, we found that the final estimates using an ensemble of 100 were not acceptable whereas increasing the ensemble to a still reasonable size of 200 improved significantly the accuracy of the updated mean and spread of the ensemble for both algorithms. Because determining this threshold ensemble size a priori is not possible, it seems all the more important before tackling large-scale applications to try to estimate this threshold size on a smaller-sized problem but which will take into account the main characteristics of the real inverse problem.
Although LM-EnRML outperforms ES-MDA in terms of the accuracy of the estimated uncertainty when using an ensemble size of 200, the performance of ES-MDA seems to improve steadily with the ensemble size while LM-EnRML does not. In particular, the RMSE of the ES-MDA estimates keeps decreasing. This particularly underlines that both algorithms do not converge to the same solution. It is not so surprising considering that LM-EnRML was derived so as to minimize an objective function using a gradient-based approach while ES-MDA was derived to minimize the variance of the error (Chen and Oliver, 2013; Evensen, 2018).
The benefit of transforming the state variables with ES-MDA was mainly observed when assimilating the hydraulic head and flowrate data simultaneously. Indeed, the normal-score transform of the state variables allowed a normalization of the magnitudes of all data types to values drawn from a standard normal distribution. Consequently, both data types could be more equally taken into account during the data assimilation as shown by the more stable reduction of the cost functions compared to the application of ES-MDA without transformation. However, as commented in previous studies (Schoniger et al., 2012; Crestani et al., 2013), the applicability of such state transformation could be questioned in cases where the multi-Gaussian dependence of the state variables is not as strong as in this multi-Gaussian log K case, either as a result of the non-linearity of the model and/or because of an initial non-multi-Gaussian parameter distribution.
Although this paper focused on the performance of iterative ensemble smoothers in the specific case of multi-Gaussian distributions, their application to condition non-Gaussian distributions is of special interest for many real field applications. For a case such as the one of the ANDRA where the built groundwater model is very high-dimensional, the observed efficiency of iterative ensemble smoothers to decrease the data mismatch in the multi-Gaussian case is very interesting. However, as summarized by Zhou et al. (2014), one main issue when conditioning directly non-multi-Gaussian distributions using ensemble Kalman methods is that the consistency of the initial geological structures is lost. A relevant future perspective for the case of the ANDRA will hence to consider an appropriate parameterization for the application of iterative ensemble smoother methods to non-Gaussian heterogeneous fields such as when generated with truncated Gaussian or multiple-point statistics simulation techniques.
Data Availability Statement
A repository with the data set used in this paper is published on Zenodo (https://doi.org/10.5281/zenodo.3878820).
Author Contributions
D-TL implemented, tested, and analyzed the methods presented and wrote the article. JK helped in the set up of the synthetic groundwater flow model and supervised the work. PR gave critical feedback on the intermediary results which helped improving the final manuscript. HB gave important information of the real problem which inspired the addressed synthetic case. PP commented on the progress of the project and manuscript. All authors contributed to the article and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors thank the University of Neuchâtel for funding this work and for providing the necessary computational resources.
References
Anderson, J. L. (2003). An ensemble adjustment Kalman filter for data assimilation. Mthly. Weather Rev. 129, 2894–2903. doi: 10.1175/1520-0493(2001)129<2884:AEAKFF>2.0.CO;2
Anderson, J. L. (2009). Ensemble Kalman filters for large geophysical applications: adaptive algorithms for improving ensemble filter performance. IEEE Control Syst. 29, 66–82. doi: 10.1109/MCS.2009.932222
Benabderrahmane, H., Kerrou, J., Tacher, L., Deman, G., and Perrochet, P. (2014). Modelling of predictive hydraulic impacts of a potential radioactive waste geological repository on the Meuse/Haute-Marne multilayered aquifer system (France). J. Appl. Math. Phys. 02, 1085–1090. doi: 10.4236/jamp.2014.212125
Bourgeat, A., Kern, M., Schumacher, S., and Talandier, J. (2004). The COUPLEX test cases: nuclear waste disposal simulation. Comput. Geosci. 8, 83–98. doi: 10.1023/B:COMG.0000035073.03009.5d
Chen, Y., and Oliver, D. S. (2012). Ensemble randomized maximum likelihood method as an iterative ensemble smoother. Math. Geosci. 44, 1–26. doi: 10.1007/s11004-011-9376-z
Chen, Y., and Oliver, D. S. (2013). Levenberg-Marquardt forms of the iterative ensemble smoother for efficient history matching and uncertainty quantification. Comput. Geosci. 17, 689–703. doi: 10.1007/s10596-013-9351-5
Chen, Y., and Oliver, D. S. (2017). Localization and regularization for iterative ensemble smoothers. Comput. Geosci. 21, 13–30. doi: 10.1007/s10596-016-9599-7
Chen, Y., Oliver, D. S., and Zhang, D. (2009). Data assimilation for nonlinear problems by ensemble Kalman filter with reparameterization. J. Petrol. Sci. Eng. 66, 1–14. doi: 10.1016/j.petrol.2008.12.002
Chen, Y., and Zhang, D. (2006). Data assimilation for transient flow in geologic formations via ensemble Kalman filter. Adv. Water Resour. 29, 1107–1122. doi: 10.1016/j.advwatres.2005.09.007
Cornaton, F. (2014). GroundWater (GW) A 3-D GroundWater and SurfaceWater Flow, Mass Transport and Heat Transfer Finite Element Simulator. Technical report. University of Neuchâtel.
Crestani, E., Camporese, M., Baú, D., and Salandin, P. (2013). Ensemble Kalman filter versus ensemble smoother for assessing hydraulic conductivity via tracer test data assimilation. Hydrol. Earth Syst. Sci. 17, 1517–1531. doi: 10.5194/hess-17-1517-2013
Deman, G., Konakli, K., Sudret, B., Kerrou, J., Perrochet, P., and Benabderrahmane, H. (2015). Using sparse polynomial chaos expansions for the global sensitivity analysis of groundwater lifetime expectancy in a multi-layered hydrogeological model. Reliabil. Eng. Syst. Saf. 147, 156–169. doi: 10.1016/j.ress.2015.11.005
Emerick, A. A. (2016). Analysis of the performance of ensemble-based assimilation of production and seismic data. J. Petrol. Sci. Eng. 139, 219–239. doi: 10.1016/j.petrol.2016.01.029
Emerick, A. A., and Reynolds, A. C. (2012a). Ensemble smoother with multiple data assimilation. Comput. Geosci. 55, 3–15. doi: 10.1016/j.cageo.2012.03.011
Emerick, A. A., and Reynolds, A. C. (2012b). History matching time-lapse seismic data using the ensemble Kalman filter with multiple data assimilations. Comput. Geosci. 16, 639–659. doi: 10.1007/s10596-012-9275-5
Evensen, G. (1994). Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. 99:10143. doi: 10.1029/94JC00572
Evensen, G. (2004). Sampling strategies and square root analysis schemes for the EnKF. Ocean Dyn. 54, 539–560. doi: 10.1007/s10236-004-0099-2
Evensen, G. (2009b). The ensemble Kalman filter for combined state and parameter estimation: Monte Carlo techniques for data assimilation in large systems. IEEE Control Syst. 29, 83–104. doi: 10.1109/MCS.2009.932223
Evensen, G. (2018). Analysis of iterative ensemble smoothers for solving inverse problems. Comput. Geosci. 22, 885–908. doi: 10.1007/s10596-018-9731-y
Evensen, G., and van Leeuwen, P. J. (2002). An ensemble Kalman smoother for nonlinear dynamics. Mthly. Weather Rev. 128, 1852–1867. doi: 10.1175/1520-0493(2000)128<1852:AEKSFN>2.0.CO;2
Gaspari, G., and Cohn, S. E. (1999). Construction of correlation functions in two and three dimensions. Q. J. R. Meteorol. Soc. 125, 723–757. doi: 10.1002/qj.49712555417
Gillijns, S., Mendoza, O., Chandrasekar, J., De Moor, B., Bernstein, D., and Ridley, A. (2006). “What is the ensemble Kalman filter and how well does it work?” in American Control Conference, 2006 (IEEE), 4448–4453. doi: 10.1109/ACC.2006.1657419
Gu, Y., and Oliver, D. S. (2007). An iterative ensemble Kalman filter for multiphase fluid flow data assimilation. SPE J. 12, 438–446. doi: 10.2118/108438-PA
Hendricks Franssen, H. J., and Kinzelbach, W. (2008). Real-time groundwater flow modeling with the Ensemble Kalman Filter: Joint estimation of states and parameters and the filter inbreeding problem. Water Resour. Res. 44:W09408. doi: 10.1029/2007WR006505
Houtekamer, P. L., and Mitchell, H. L. (1998). Data assimilation using an ensemble Kalman filter technique. Mthly. Weather Rev. 126, 796–811. doi: 10.1175/1520-0493(1998)126<0796:DAUAEK>2.0.CO;2
Jafarpour, B., and Khodabakhshi, M. (2011). A probability conditioning method (PCM) for nonlinear flow data integration into multipoint statistical facies simulation. Math. Geosci. 43, 133–164. doi: 10.1007/s11004-011-9316-y
Kalman, R. E. (1960). A new approach to linear filtering and prediction problems. J. Basic Eng. 82:35. doi: 10.1115/1.3662552
Kerrou, J., Deman, G., Tacher, L., Benabderrahmane, H., and Perrochet, P. (2017). Numerical and polynomial modelling to assess environmental and hydraulic impacts of the future geological radwaste repository in Meuse site (France). Environ. Modell. Softw. 97, 157–170. doi: 10.1016/j.envsoft.2017.07.018
Lam, D.-T., Renard, P., Straubhaar, J., and Kerrou, J. (2020). Multiresolution approach to condition categorical multiple-point realizations to dynamic data with iterative ensemble smoothing. Water Resour. Res. 56:e2019WR025875. doi: 10.1029/2019WR025875
Le, D. H., Emerick, A. A., and Reynolds, A. C. (2016). An adaptive ensemble smoother with multiple data assimilation for assisted history matching. SPE J. 21, 2195–2207. doi: 10.2118/173214-PA
Li, L., Stetler, L., Cao, Z., and Davis, A. (2018). An iterative normal-score ensemble smoother for dealing with non-Gaussianity in data assimilation. J. Hydrol. 567, 759–766. doi: 10.1016/j.jhydrol.2018.01.038
Liu, N., and Oliver, D. S. (2005). Ensemble Kalman filter for automatic history matching of geologic facies. J. Petrol. Sci. Eng. 47, 147–161. doi: 10.1016/j.petrol.2005.03.006
Luo, X., Stordal, A. S., Lorentzen, R. J., and Nævdal, G. (2015). Iterative ensemble smoother as an approximate solution to a regularized minimum-average-cost problem: theory and applications. SPE J. 20, 962–982. doi: 10.2118/176023-PA
Moradkhani, H., Sorooshian, S., Gupta, H. V., and Houser, P. R. (2005). Dual state-parameter estimation of hydrological models using ensemble Kalman filter. Adv. Water Resour. 28, 135–147. doi: 10.1016/j.advwatres.2004.09.002
Schoniger, A., Nowak, W., and Hendricks Franssen, H. J. (2012). Parameter estimation by ensemble Kalman filters with transformed data: approach and application to hydraulic tomography. Water Resour. Res. 48, 1–18. doi: 10.1029/2011WR010462
van Leeuwen, P. J., and Evensen, G. (1996). Data assimilation and inverse methods in terms of a probabilistic formulation. Mthly. Weather Rev. 124, 2898–2913. doi: 10.1175/1520-0493(1996)124<2898:DAAIMI>2.0.CO;2
Wen, X. H., and Chen, W. (2005). “Real-time reservoir model updating using ensemble Kalman filter,” in SPE Reservoir Simulation Symposium (Houston, TX), 1–14. doi: 10.2118/92991-MS
Zhou, H., Gómez-Hernández, J. J., Hendricks Franssen, H. J., and Li, L. (2011). An approach to handling non-Gaussianity of parameters and state variables in ensemble Kalman filtering. Adv. Water Resour. 34, 844–864. doi: 10.1016/j.advwatres.2011.04.014
Keywords: inverse problem, transient groundwater flow, parameter identification, iterative ensemble smoother, data assimilation, uncertainty
Citation: Lam D-T, Kerrou J, Renard P, Benabderrahmane H and Perrochet P (2020) Conditioning Multi-Gaussian Groundwater Flow Parameters to Transient Hydraulic Head and Flowrate Data With Iterative Ensemble Smoothers: A Synthetic Case Study. Front. Earth Sci. 8:202. doi: 10.3389/feart.2020.00202
Received: 03 February 2020; Accepted: 18 May 2020;
Published: 16 June 2020.
Edited by:
Teng Xu, Hohai University, ChinaReviewed by:
Xiaodong Luo, Norwegian Research Institute (NORCE), NorwayAndrea Zanini, University of Parma, Italy
Copyright © 2020 Lam, Kerrou, Renard, Benabderrahmane and Perrochet. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dan-Thuy Lam, ZGFuLXRodXkubGFtQG91dGxvb2suZnI=
 Dan-Thuy Lam
Dan-Thuy Lam Jaouher Kerrou
Jaouher Kerrou Philippe Renard
Philippe Renard Hakim Benabderrahmane2
Hakim Benabderrahmane2