Modeling δD-δ18O Steady-State of Well-Sealed Perennially Ice-Covered Lakes and Their Recharge Source: Examples From Lake Untersee and Lake Vostok, Antarctica

Introduction

In Antarctica, several hundred lakes have been identified and classified according to their ice cover regime (Figure 1A; Morgan et al., 2007; Vincent et al., 2008). Seasonally ice-covered lakes are found along the warmer Antarctic Peninsula and other coastal regions. These lakes lose their ice cover in austral summer and are typically recharged by a combination of local precipitation and glacial meltwater (e.g., Gibson, 1999; Lyons et al., 2013). Perennially ice-covered lakes are found in polar desert regions and exist as two main types: those that develop moats in summer and are fed by glacial melt streams, and those that are tightly sealed from the atmosphere and solely fed by subaqueous glacial melt and groundwater (e.g., Priscu, 1998; Faucher et al., 2019). Further, many subglacial lakes are found beneath the Antarctic ice sheet and are recharged by a combination of subglacial and englacial waters (e.g., Wingham et al., 2006; Priscu and Foreman, 2009; Wright and Siegert, 2012).

FIGURE 1

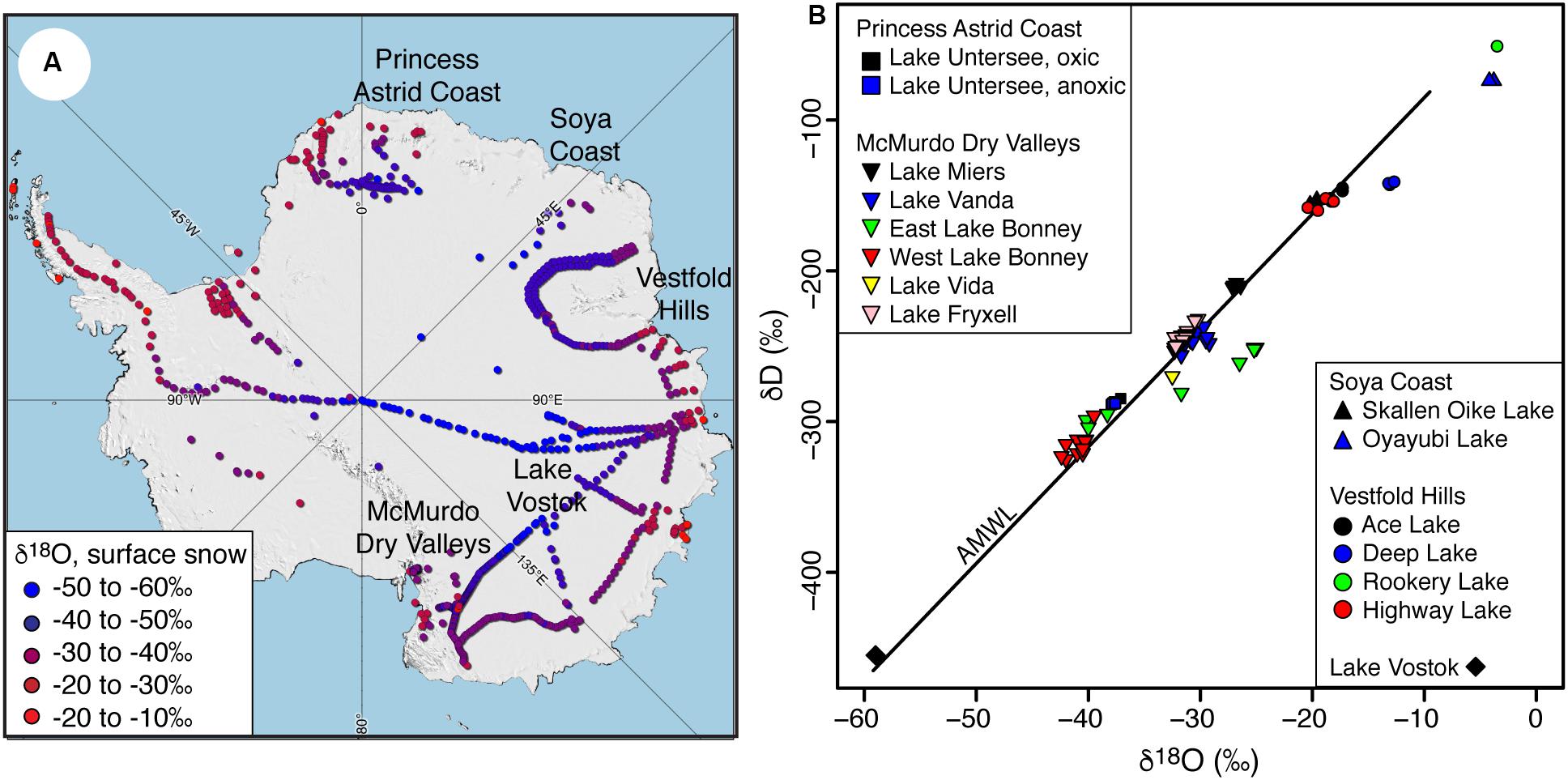
Figure 1. (A) Distribution of surface snow δ¹⁸O values across Antarctica (data from Touzeau et al., 2016). (B) Stable water isotope (δD-δ¹⁸O) ratios of perennially ice-covered lakes in the Antarctic: Princess Astrid Coast (Lake Untersee), Southern Victoria land region (Lake Miers, Lake Vanda, Lake Bonney, Lake Fryxell, Lake Vida) (Matsubaya et al., 1979; Miller and Aiken, 1996; Dugan et al., 2015) and Soya Coast (Skallen Oike) (Matsubaya et al., 1979). AMWL, Antarctic Meteoric Water line from Masson-Delmotte et al. (2008) (δD = 7.75 δ¹⁸O – 4.93; r² = 0.99; Masson-Delmotte et al., 2008).

The source of water recharging the various types of Antarctic lakes and its evolution can influence key physicochemical conditions, the composition of microbial communities and biogeochemical cycling (e.g., Lyons and Finlay, 2008; Wand et al., 2006). The analysis of the δD-δ¹⁸O composition of polar lakes has proven to be a reliable tool to determine the source of water, the process that evolved the lake chemistry, and water balance parameters, such as the amount of evaporation (Jeffries et al., 1984; Gibson, 1999; Gooseff et al., 2006; Horita, 2009). In Antarctica, the δ¹⁸O values of lake waters range from c. 0 to −60‰ (Figure 1B), a range that reflects the main sources of water recharging the lakes. Lakes with δ¹⁸O values near 0‰ are a heritage of isostatic rebound and their formation is attributed to the freezing of trapped seawater following decrease in sea level (Bird et al., 1991). Lakes with δ¹⁸O values near −15 to −10‰ have been attributed to mixing of seawater and local coastal precipitation (Matsubaya et al., 1979; Richter and Strauch, 1983; Bird et al., 1991). Finally, lakes with δ¹⁸O values <−25‰ are recharged mainly from glacial meltwater, with those with very low δ¹⁸O composition likely receiving input from late Pleistocene meltwater (Matsubaya et al., 1979; Richter and Strauch, 1983; Bird et al., 1991). The ice-cover regime of the lake (i.e., seasonally or perennially ice-covered) determines whether evaporation or freezing then drives the evolution of the lake isotope chemistry (Miller and Aiken, 1996). Both seasonally ice-covered lakes and perennially ice-covered lakes that develop summer moats have lake waters with δD-δ¹⁸O composition that are typically distributed below the Antarctic Meteoric Water Line (AMWL) (Figure 1B). The isotopic behavior of these lakes is strongly influenced by evaporation that enriches the residual water and distributes it along an evaporative line with lower slope than the AMWL. The δ¹⁸O composition of evaporative lakes is determined by atmospheric parameters such as humidity and isotopic composition of the water vapor, and numerical models of the evolving salinity in the water column have been developed to estimate a lake’s δD-δ¹⁸O steady-state (i.e., Gibson, 1999; Horita, 2009).

A few Antarctic lakes have δD-δ¹⁸O values distributed above the AMWL (Figure 1B): two of these are Lake Untersee, a well-sealed perennially ice-covered lake, and Lake Vostok, a subglacial lake beneath the East Antarctic Ice Sheet. Consequently, the water columns of these lakes do not interact with the atmosphere (i.e., no fractionation due to evaporation) and the δD-δ¹⁸O evolution of each water column is controlled by recharge and the freezing at the bottom of the ice cover. In the case of Lake Vostok, the recharge water source, the freezing process and its isotopic steady-state are well established (e.g., Royston-Bishop et al., 2004; Souchez et al., 2004; Ekaykin et al., 2010). However, the isotopic mass-balance of Lake Untersee remains unknown. In addition, unlike evaporative lakes (i.e., Gibson, 1999; Horita, 2009), no studies have yet developed a model capable of predicting the δD-δ¹⁸O steady-state of the water column that includes the evolution of the ice-water isotope fractionation factor as freezing changes the salinity of the residual water and recursive recharge that mixes with the residual lake water.

The objective of this study is to develop a model of δD-δ¹⁸O evolution of well-sealed perennial ice-covered lakes that accounts for changing chemistry in the residual water and annual recharge that mixes with residual water. This objective was achieved by using FREEZCH5, an isotope-augmented version of the FREZCHEM low temperature geochemistry model (Marion et al., 2010; Fisher et al., 2020) and making the model recursive. The model is tested against datasets from Lake Vostok and is then used to assess the δD-δ¹⁸O mass balance of Lake Untersee and evaluate if the lake is in isotopic steady-state. The results are presented in terms of residence times of water with different mixing scenarios, which allow to apply the findings to other well-sealed perennial ice-covered lakes or subglacial lakes.

Materials and Methods

Background on Water-Ice Fractionation During Freezing

The freezing of water under equilibrium condition follows a Rayleigh-type fractionation:

$$R=R_0{f}^{(\mathrm{\alpha }\text{i-w}-1)}(1)$$

where R is the isotope ratio of ¹⁸O/¹⁶O or D/H and of α_i–w is the water-ice fractionation factor with two distinct sets of α_i–w for ¹⁸O/¹⁶O and D/H reported in the literature: 1.0031 and 1.0193, respectively (O’Neil, 1968); 1.0028 and 1.0206, respectively (Suzuoki and Kimura, 1973).

During freezing, the forming ice is ¹⁸O enriched but the residual water is progressively depleted and evolves above the Global Meteoric Water Line (GMWL) because the freezing line has a lower slope (Horita, 2009; Lacelle, 2011). Freezing of water also imparts an ionic segregation that increases the solute content in the residual water (Terwilliger and Dizio, 1970; Killawee et al., 1998). Because freezing reduces the water activity, a correction to the D/H and ¹⁸O/¹⁶O water-ice fractionation factors should be applied, especially at higher salinities where solutes may bind water molecules in hydration spheres around the cations and following the precipitation of hydrated salts (i.e., NaCl⋅2H₂O, MgCl₂⋅12H₂O, CaCl₂⋅6H₂O). The theory of changing ice-water isotope fractionation under changing water salinities was described in Sofer and Gat (1972, 1975) and Stewart and Friedman (1975) and they showed that the isotopic salt effect is linearly correlated for different salt solutions at varying concentrations.

In addition to evolving isotope salt effect, Jouzel and Souchez (1982) observed that the initial isotope composition of water also affects the isotope composition of ice during freezing. Consequently, Souchez and Jouzel (1984) suggested that the influence of the initial isotope composition of water on the water-ice fractionation factor (α_δO) could be estimated from:

$${\mathrm{\alpha }}_{\mathrm{\delta }O}=({\mathrm{\alpha }}_{i-w}-1)(1000+{\mathrm{\delta }}_O)/1000+1(2)$$

where δ_O is the initial isotope composition of water, α_i–w is the equilibrium fractionation factor. The equation shows that α_δO is reduced with decreasing initial isotope composition of water; for most waters, this correction can be ignored as it only exceeds the analytical error when δ¹⁸O < −40‰.

Finally, the water-ice isotope fractionation during freezing is also dependent on the kinetics of the reaction, which includes the freezing rate, boundary-layer thickness and isotope diffusion at the ice-water interface. The kinetic water-ice isotope fractionation factor (α_FR) can be approximated by a modified version of Burton et al.’s (1953) equation for solute segregation:

$${\mathrm{\alpha }}_{FR}=\left(\frac{{\mathrm{\alpha }}_{i-w}}{{\mathrm{\alpha }}_{i-w}-({\mathrm{\alpha }}_{i-w}-1)e^{\frac{-hv}{D*}}}\right)(3)$$

where h is the thickness of the boundary layer (cm), v is the freezing rate (cm s^–1), D^∗ is the diffusion coefficient in water. At 0C, D^∗ values for H₂¹⁸O and HDO are 1.1 10^–5 cm² s^–1 and 1.33 10^–5 cm² s^–1, respectively (Wang et al., 1953).

When the freezing rate is slower than the diffusion coefficient, α_FR approximates the equilibrium fractionation factor, but under increasing freezing rate, α_FR is reduced towards unity (i.e., Lacelle, 2011).

Description of FREEZCH5 (Isotope-Augmented FREZCHEM)

The core of the FREEZCH5 model is FREZCHEMv15, an equilibrium chemical thermodynamic model over the temperature range of −73 to 25${}^{\circ }$C (Marion and Kargel, 2008; Fisher et al., 2020). FREZCHEM simulates the freezing of water by decreasing the temperature in fixed steps and determines the presence of residual water if the water activity calculated from the Pitzer equations is less than the equilibrium constant for water-ice. At each decreasing temperature step (“i”), the model provides: (1) the amount of residual water (in g; WAT_LIQ); (2) the amount of ice formed (in g; Δ_ICE); (3) the molalities of the major cations (Na⁺, Ca²⁺, Mg²⁺, K⁺) and anions (Cl^–, NO₃^–, SO₄^2–); (4) the amount of hydrated salts that precipitates (in g; ΔWATNa, ΔWATMg, and ΔWATCa); and (5) the total ionic strength of the solution (proportional to conductivity and salinity of the residual water). FREZCHEM completely segregates the solutes in the residual water and none are incorporated as inclusions in the ice lattice or along grain boundaries and likely over-estimates the salinity in the residual water (i.e., Killawee et al., 1998; Petrenko and Whitworth, 1999). However, properly accounting for ionic segregation in equilibrium modeling is challenging as it was found that the concentration factor (or the segregation coefficient) is dependent on initial water chemistry and freezing rates (Santibáñez et al., 2019).

The evolution of δ¹⁸O of the residual water (δ¹⁸Orw) and for the incremental ice that forms at each decreasing temperature step was added to FREZCHEM in a routine called FREEZCH5, where the initial δ¹⁸O composition of the water and the α_i–w is specified by the user:

$${\mathrm{\delta }}^{18}{\text{O}}_{\text{rw}}(\text{i})={\mathrm{\delta }}^{18}{\text{O}}_{\text{rw}}\left(\text{i}-1\right)+\mathrm{\Delta }{\mathrm{\delta }}^{18}{\text{O}}_{\text{rw}}(4)$$

where Δδ¹⁸O_rw is given by:

$$\begin{array}{c}\begin{array}{cc}\hfill \mathrm{\Delta }{\mathrm{\delta }}^{18}{\text{O}}_{\text{rw}}\hfill & \hfill =-(1000+{\mathrm{\delta }}^{18}{\text{O}}_{\text{rw}}(\text{i}-1))[({\mathrm{\alpha }}_{18\mathrm{O}-\text{i}-\text{w}}-1)\mathrm{\Delta }\text{ICE}/\text{WATLIQ}\hfill \\ & \hfill +({\mathrm{\alpha }}_{18\mathrm{O}-\text{w}-\text{Naprecip}}-1)\mathrm{\Delta }\text{WATNa}/\text{WATLIQ}\hfill \\ & \hfill +({\mathrm{\alpha }}_{18\mathrm{O}-\text{w}-\text{Mgprecip}}-1)\mathrm{\Delta }\text{WATMg}/\text{WATLIQ}\hfill \\ & \hfill +({\mathrm{\alpha }}_{18\mathrm{O}-\text{w}-\text{Caprecip}}-1)\mathrm{\Delta }\text{WATCa}/\text{WATLIQ}]\hfill \end{array}\hfill \end{array}(5)$$

where α_18O–i–w is the ice-water fractionation factor (corrected for initial isotopic composition using equation 1), α¹⁸O_w–Naprecip is the water-NaCl⋅2H₂O precipitate fractionation coefficient; α¹⁸O_w–Mgprecip is that for water-MgCl₂⋅12H₂O; and α¹⁸O_w–Caprecip is CaCl₂⋅6H₂O. Note that δ¹⁸O_rw is the isotopic composition for the total water in the solution (free water and the water attached in the hydration spheres around the positive ions).

The various hydrated salts do not have reported water-precipitate fractionation factors and we assume that they are unity or as defined by Sofer and Gat (1972, 1975) for the cations-hydration spheres within the liquid solution. Since FREZCHEM is an equilibrium model, the effect of freezing rates on water-ice fractionation factors are not included, but these should have little effect on the freezing of perennially ice-covered lakes where freezing takes place near 0°C at the ice-water boundary.

With δ¹⁸O_rw, we can use the Sofer and Gat (1972, 1975) isotope salt effects correction to determine the δ¹⁸O offset between the δ¹⁸O total water (free and hydration sphere waters) and δ¹⁸O free water only (i.e., water activity), a correction that depends on the molality of each cation (Na⁺, Ca²⁺, Mg²⁺, K⁺):

$$({\mathrm{\delta }}^{18}{\text{O}}_{\text{rw}}-{\mathrm{\delta }}^{18}{\text{O}}_{\text{activty}})=\mathrm{\Delta }{\mathrm{\delta }}^{18}{\text{O}}_{\text{Na}+}+\mathrm{\Delta }{\mathrm{\delta }}^{18}{\text{O}}_{\mathrm{Mg2}+}+\mathrm{\Delta }\mathrm{\delta }{1}^8{\text{O}}_{\mathrm{Ca2}+}+\mathrm{\Delta }{\mathrm{\delta }}^{18}{\text{O}}_{\text{K}+}(6)$$

where Δδ¹⁸Ocations are functions of the remaining liquid water molality, which are calculated at each temperature step. The FREEZCH5 model is described in detail in Supplementary Appendix A of Fisher et al. (2020).

Description of FREEZCH9 (a Recursive FREEZCH5)

For perennially ice-covered lakes under hydrological steady-state condition, the annual rate of water freezing at the bottom of the ice cover equals the annual ablation rate at the ice surface (Wilson and Wellman, 1962; McKay et al., 1985). This implies that to maintain the lake water volume constant (ΔV = 0), the annual accretion and ablation rates of the ice cover must be equal. We developed a recursive version of FREEZCH5 (FREEZCH9) that maintains ΔV = 0 by mixing the evolved chemistry and δD-δ¹⁸O composition of the residual water with an input of water of fixed chemistry and δD-δ¹⁸O composition, which then produces the new input chemistry and δD-δ¹⁸O for the next loop. The hydrated precipitates that may form are accumulated in the series. Supplementary Appendix A provides details of FREEZCH9.

Field Sampling and Laboratory Analysis

The water column in the oxic basin of Lake Untersee was sampled in December 2016 at 10-m depth interval using a 2.2-L acrylic Kemmerer bottle content and samples were stored in sealed 20 ml high density polyethylene bottles (HDPE) bottles. The ice cover was sampled at the same location in December 2017 with a Cold Regions Research and Engineering Laboratory coring kit to a depth of c. 2 m to prevent mixing with lake water. Surface samples from the Anuchin Glacier were collected with a Kovacs ice corer powered by a Bosch Hammer GBH 36V-LI PLUS electrical drill, to a depth of 50 cm (e.g., Weisleitner et al., 2019). Samples from the Anuchin Glacier and the ice cover of Lake Untersee (sliced at 2 cm intervals) were melted in sealed Ziploc bags, transferred in HDPE bottles and shipped in coolers to the University of Ottawa where they were stored at 4°C until analyzed for stable water isotopes.

The ¹⁸O/¹⁶O and D/H ratios of lake water and melted ice samples were analyzed using a Los Gatos Research liquid water analyzer coupled to a CTC LC-PAL auto sampler and verified for spectral interference contamination. The results are presented using the δ-notation (δ¹⁸O and δD), where δ represents the parts per thousand differences for ¹⁸O/¹⁶O or D/H in a sample with respect to Vienna Standard Mean Ocean Water (VSMOW). Analytical reproducibility for δ¹⁸O and δD was ±0.3‰ and ±1‰, respectively. Deuterium-excess (d) was then calculated using the following equation (d = δD – 8 δ¹⁸O; Dansgaard, 1964).

Results

Modeling the Freezing of Low to High Salinity Waters

The freezing point of water is determined by the chemical composition of the solution and ranges from 0°C for pure water to −2.3°C for sea water (Figure 2A). Freezing under equilibrium conditions progressively decreases the amount of residual water while increasing the concentration of solutes in the residual water. This cryo-concentration of solutes on decreasing residual water is dependent on the initial chemical composition of the solution where for nearly pure water the bulk of the water is frozen over the 0 to −4°C range, but for more saline waters, c. 15–20% of residual water may occur over the −5 to −20°C range (Figure 3A). For brackish to saline waters, hydrated salts can precipitate (NaCl⋅2H₂O at −23°C, MgCl₂⋅12H₂0 at −36°C) and the formation of these precipitates further reduces the amount of residual water (Figure 2A).

FIGURE 2

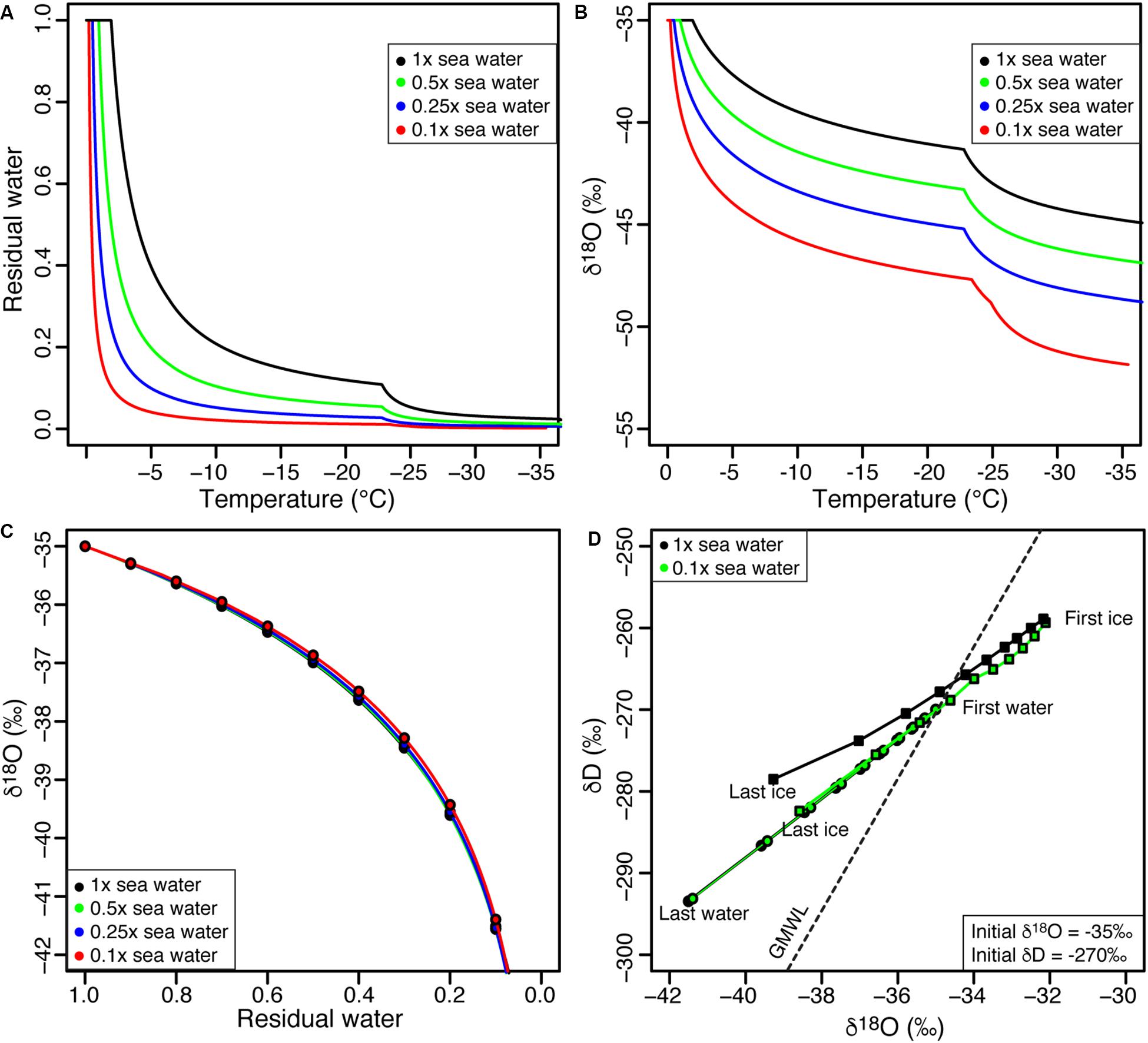
Figure 2. Evolution of (A) residual water fraction and (B) δ¹⁸O of residual water during freezing as a function of various molalities of sea water; (C) relation between δ¹⁸O and residual water for various molalities of sea water; and (D) δD-δ¹⁸O evolution of liquid water and ice during freezing, using 100 and 10% sea water salinity solutions (circles = water; squares = ice). See Table 1 for values of input parameters used in modeling.

FIGURE 3

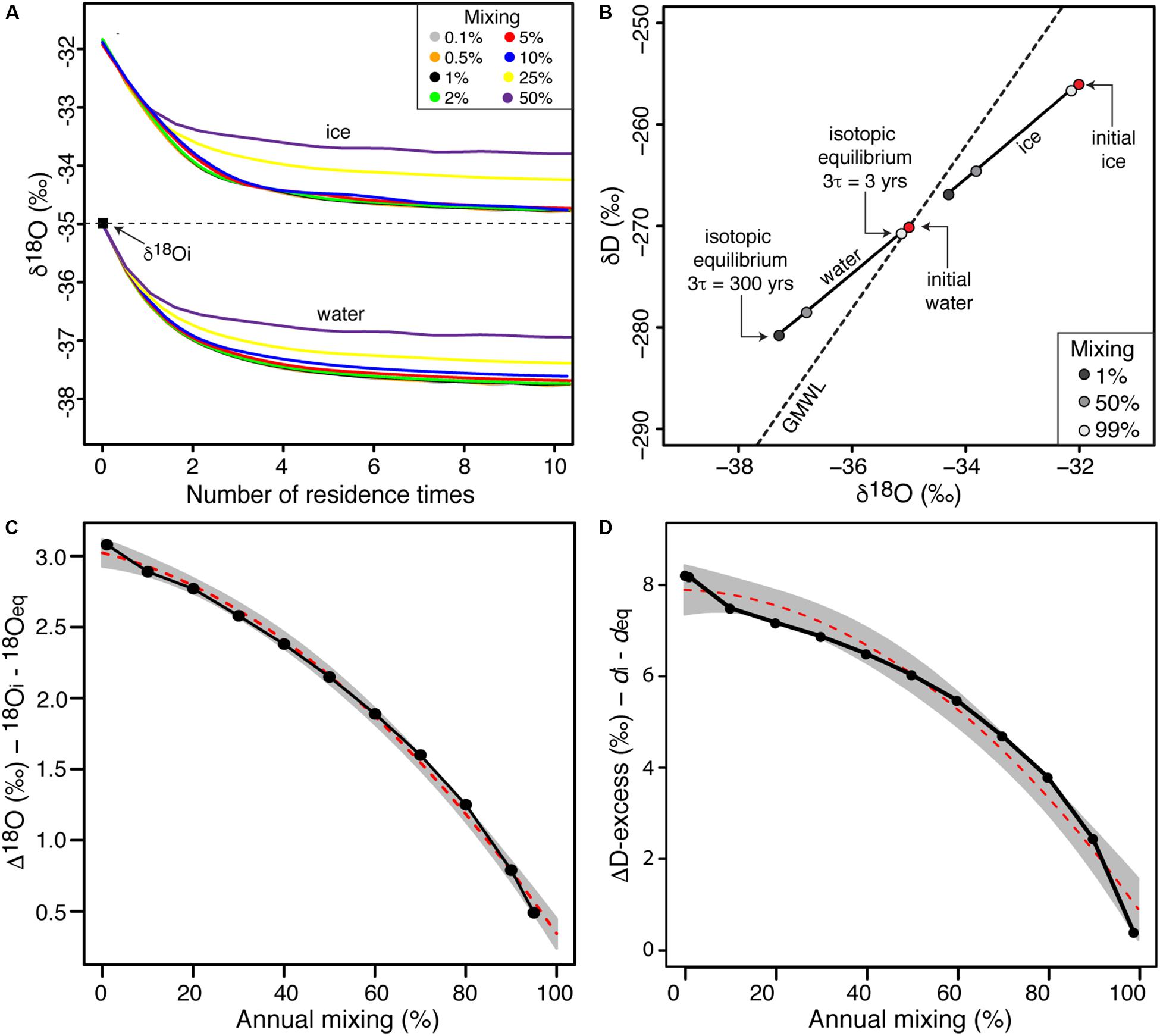
Figure 3. (A) δ¹⁸O evolution of lake water and forming ice for various annual mixing scenarios as a function of number of residence time (initial δD-δ¹⁸O values are –270 and –35‰, respectively). The colored lines represent different annual mixing rate scenarios (0.1–50%); (B) δD-δ¹⁸O plot of evolving lake water and ice as a function of the annual mixing rates of well-sealed perennially ice-covered lakes. The red dots indicate the δD-δ¹⁸O values of initial waters and accreted ice; (C) effect of annual mixing rates in perennially ice-covered lakes on the difference between the initial and steady-state δ¹⁸O values of lake water; and (D) effect of annual mixing rates in perenially ice-covered lakes on the difference between the initial and steady-state D-excess values of lake water.

TABLE 1

Table 1. Initial hydrochemical parameters for the mixing simulations.

The dependence of the initial chemical composition of the solutions on the amount residual water is reflected in the δ¹⁸O of the residual water (Figure 2B). For nearly pure waters, the δ¹⁸O of the residual water rapidly decreases as most of the water freezes over a narrow temperature range. For example, the freezing of nearly pure water with an initial δ¹⁸O composition of −35‰ over the temperature range of 0 to −4°C will cause the δ¹⁸O of the residual water to rapidly decrease to value of −45‰ (when residual water fraction is 0.05). In contrast, the freezing of sea water with the same initial δ¹⁸O composition over the temperature range of 0 to −4°C will cause the δ¹⁸O of the residual water to decreases to −37‰ (when residual water fraction is 0.85). A value of −45‰ in the residual water of sea water would only be reached following the precipitation of NaCl⋅2H₂0.

These numerical simulations allow us to explore the effect of temperature on residual water content and its δ¹⁸O composition during equilibrium freezing of solutions with varied salinities. However, exploring the evolution of δ¹⁸O of residual water as a function of decreasing fractions of residual water revealed no significant differences between solutions of varying salinities (Figure 2C). As such, a Rayleigh-type isotope fractionation during equilibrium freezing of liquid water with varied salinities using FREEZCH5 shows that, as freezing begins, the first ice to form will be enriched in δ¹⁸O by about 3% (and about 20% in δD), but as freezing continues, the δ¹⁸O composition of the ice formed progressively becomes depleted as the δ¹⁸O composition of the residual water trends toward lower value. The extent of δ¹⁸O depletion of the residual water during freezing is constrained by the evolving eutectic temperature of the residual water and temperature at the ice-water interface. Despite little differences in the evolving δD-δ¹⁸O of residual waters of varied salinities, a difference is observed in the δD-δ¹⁸O composition of the forming ice following the precipitation of hydrated minerals (Figure 2D).

For perennially ice-covered lakes under hydrological steady-state, the evolution of δ¹⁸O in lake water and ice during equilibrium freezing was explored using FREEZCH9 for a range of recharge and mixing scenarios (Figure 3). The results are expressed in terms of residence times instead of annual loops to facilitate comparison. For all mixing scenarios, the results show that isotopic equilibrium (steady-state) in the lake water and ice is reached after more than three residence times. However, the difference between δ¹⁸O of input water and that of isotopic equilibrium decreases under increasing mixing scenarios. For mixing scenarios <∼5%, the Δδ¹⁸O input and equilibrium approaches ln(α¹⁸O_i–w); however, as the amount of annual mixing approaches 95%, the Δδ¹⁸O input and equilibrium approaches 0.

Testing FREEZCH9 With Lake Vostok, East Antarctic Plateau

Lake Vostok is a large subglacial lake located beneath c. 4 km of ice on the east Antarctic plateau (Lyons et al., 2016). The lake is about 250 km long and 80 km wide, has a surface area of ∼13,000 km² and a water volume of 4658–6350 km³ depending on the estimation method (e.g., Studinger et al., 2004; Siegert et al., 2011; Li et al., 2019). Lake Vostok is recharged from the melting of the overlying East Antarctic Ice Sheet in the northern basin (incoming rate of c. 4 cm yr^–1) and loses ice via ice accretion at the ice-water interface in the southern and central basins (freezing rate of c. 2 cm yr^–1) (Siegert et al., 2000; Bell et al., 2002; Studinger et al., 2004). The annual input of water is estimated at 0.19 km³ yr^–1, which translates to a residence time equivalent to c. 28,000 years or an annual mixing rate of c. 0.0037% (Royston-Bishop et al., 2004).

Based on the average of δ¹⁸O time-series during the last four glacial cycles in the Dome B record, Royston-Bishop et al. (2004) first estimated the δD-δ¹⁸O of input water to Lake Vostok to be −442.2 and −56.7‰, respectively. Lipenkov et al. (2016) later revised the δD-δ¹⁸O composition of input water, based on data from the overlying accreted ice, to be −442.4‰ and −56.2‰, respectively, with D-excess = 7.2‰. Based on a closed-system isotopic equilibrium model using the δD-δ¹⁸O data of re-frozen lake water in borehole, Ekaykin et al. (2016) estimated the average δD and δ¹⁸O composition of the Lake Vostok to be −455 ± 1‰ and −59.0 ± 0.3‰, respectively (D-excess of 17 ± 1‰).

FREEZCH9 was used with input parameters defined as 0.0037% annual mixing (e.g., Royston-Bishop et al., 2004), the average major ions concentrations in the Vostok ice core which extends to 160 kyr BP (Legrand et al., 1988), and the equilibrium factors (α_i–w) of O’Neil (1968) and Suzuoki and Kimura (1973) also corrected for initial isotope composition of water. When using the δD-δ¹⁸O of the input water estimated by Royston-Bishop et al. (2004) (−442.2 and −56.7‰, respectively), the model does not perfectly match the measurements in the accreted ice (Figure 4). However, if we use the α_i–w corrected for initial isotope composition of water and adjust the δD-δ¹⁸O of input water to match the measurements in the accreted ice, we find input values for δD-δ¹⁸O of −443.5 and −56.4‰, respectively. With 0.0037% annual mixing, the time for the water column to reach isotopic equilibrium is in the order of c. 2–3 residence times and the δD-δ¹⁸O of Lake Vostok is estimated to be −453.5 and −59.1‰, within error of the values reported by Ekaykin et al. (2016).

FIGURE 4

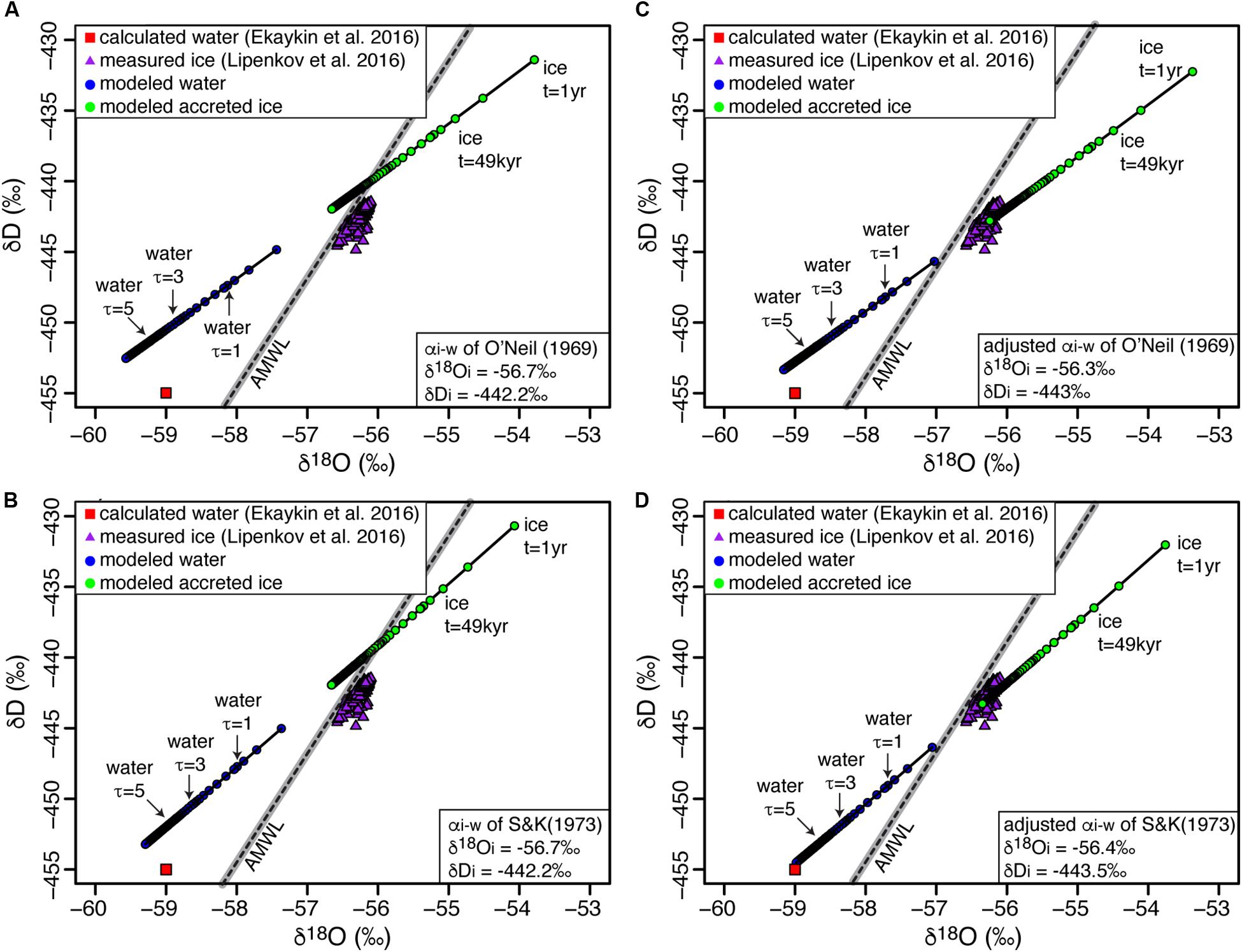
Figure 4. Modeled δD-δ¹⁸O composition of Lake Vostok’s upper water column and accreted ice using the initial δD-δ¹⁸O input values of Royston-Bishop et al. (2004) with (A) O’Neil’s (1968) and (B) Suzuoki and Kimura’s (1973) fractionation factors. Modeled δD-δ¹⁸O composition of Lake Vostok’s upper water column and accreted ice but adjusting δD-δ¹⁸O inputs to fit measured accreted lake values by Lipenkov et al. (2016) using (C) O’Neil’s (1968) and (D) Suzuoki and Kimura’s (1973) fractionation factors, respectively. AMWL, Antarctic Meteoric Water Line (δ D = 7.75 δ¹⁸O – 4.93; r² = 0.99); gray bar represents 99% confidence interval. See Table 1 for values of input parameters used in modeling.

FREEZCH9 and Lake Untersee, Dronning Maud Land, Antarctica

Lake Untersee is a perennially ice-covered lake located in the Gruber Mountains of central Dronning Maud Land, approximately 90 km southeast of the Schirmacher Oasis. The 6.5 km long and 1.5 km wide lake (surface area = 8.73 km²), with a water volume of 5.21 × 10⁸ m³, is located in a closed-basin dammed at its northern end by the Anuchin Glacier (Faucher et al., 2019). Lake Untersee has two sub-basins: (1) a large well-mixed oxic basin at the northern and central section with a maximum depth of 169 m; and (2) a shallower basin at its southern section with a maximum depth of 100 m depth (Wand et al., 1997; Andersen et al., 2011). Unlike most perennially ice-covered lakes, Lake Untersee does not develop a summer moat. Loss of water is entirely through the sublimation of the ice cover (61 ± 11 cm yr^–1) with annual loss of 4.90 ± 0.8 × 10⁶ m³ of water (or 0.94 ± 0.17% of total lake water volume) (Faucher et al., 2019). To maintain hydrological steady-state, Lake Untersee receives an equal volume of inflow sourced from the subaqueous melting of the Anuchin Glacier (40–45% of annual contribution) and from subglacial meltwater (55–60% of annual input) (Faucher et al., 2019).

The oxic water column of Lake Untersee has a narrow δD-δ¹⁸O composition, from −288.4 to −287.3‰ and from −37.9 to −37.6‰, respectively (Figure 5). With D-excess ranging from 12.8 to 14.7‰, the water samples are distributed above the AMWL (Figure 5). The ice cover sampled at the same location has higher δD-δ¹⁸O values varying from −279.5 to −268.5‰ and from −36.2 to −33.55‰, respectively, with lower D-excess ranging from −8.8 to 11.4‰ (Figure 5). FREEZCH9 was used with input parameters defined as 1% annual mixing (Faucher et al., 2019), α_i–w of O’Neil’s (1968) and Suzuoki and Kimura’s (1973) corrected for initial isotope composition of water and the δD-δ¹⁸O of input water was adjusted to match the δD-δ¹⁸O measurements in the oxic water column. The initial chemistry of the input water was based on data from nearby shallow firn core (Isaksson et al., 1996). The FREEZCH9 modeling indicates that the measured δD-δ¹⁸O values in the water column is in isotopic equilibrium with initial input water having δD-δ¹⁸O values of −275.0 and −35.0‰, respectively. With 1% annual mixing, the time to reach isotopic equilibrium in the water column is in the order of c. 300–500 years.

FIGURE 5

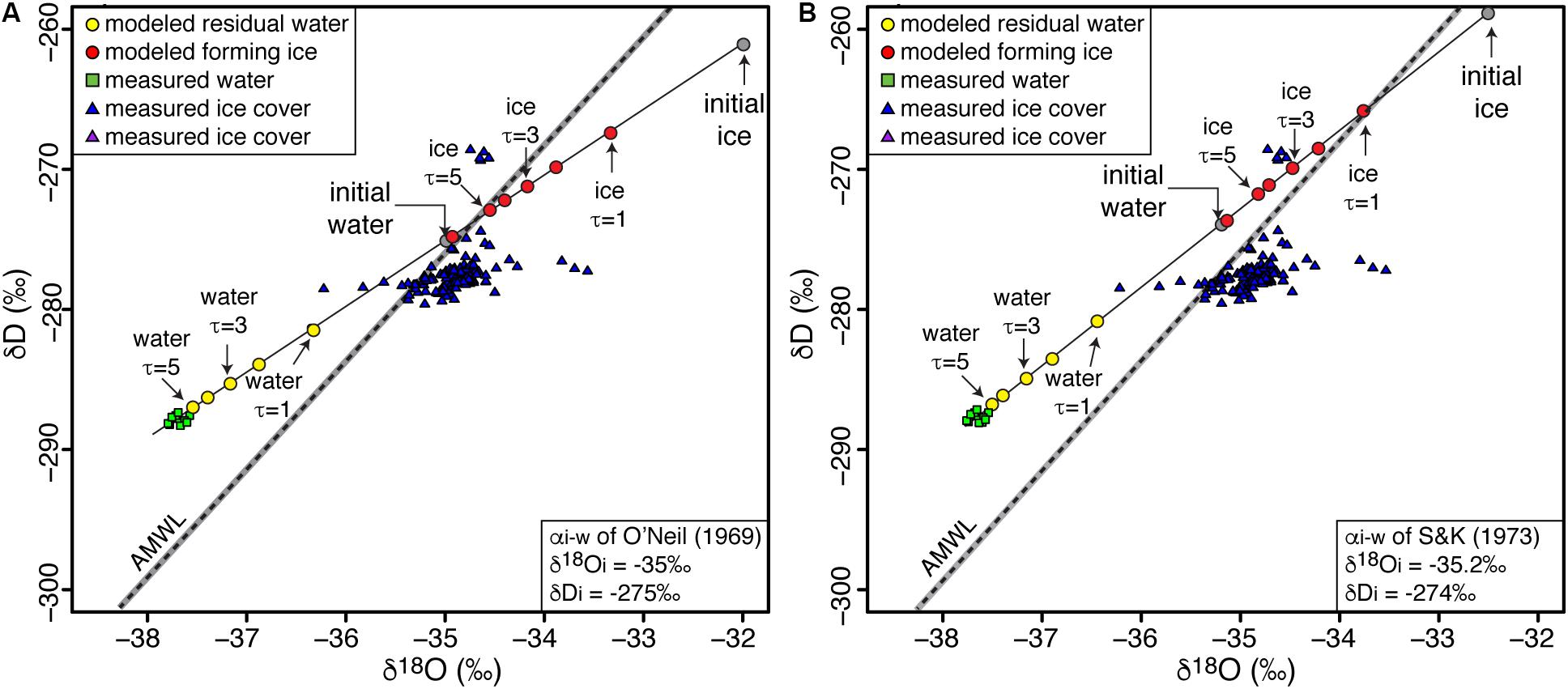
Figure 5. Modeled δD-δ¹⁸O composition of Lake Untersee and its ice cover using (A) O’Neil’s (1968) and (B) Suzuoki and Kimura’s (1973) fractionation factors. AMWL, Antarctic Meteoric Water Line (δ D = 7.75 δ¹⁸O – 4.93; r² = 0.99); gray bar represents 99% confidence interval. See Table 1 for values of input parameters used in modeling.

Discussion

δD-δ¹⁸O Composition of Input Waters to Lake Untersee

Based on a hydrological and energy mass balance, it was suggested that the well-sealed perennially ice-covered Lake Untersee is recharged by two sources: subaqueous terminus melting of the Anuchin Glacier (40–45% of annual contribution) and from subglacial meltwater and/or from groundwater (55–60% of annual input) (Faucher et al., 2019). The FREEZCH9 modeling using 1% annual recharge and mixing with lake water suggests that the δ¹⁸O composition of Lake Untersee (−37.9 to −37.6‰) is in equilibrium with source waters having an average δ¹⁸O composition of −35.0‰. The δ¹⁸O composition of the contribution from the subaqueous melting of the Anuchin Glacier can be estimated from the thickness of the glacier at the lake-glacier interface (c. 160 m) and the age-depth relation from the Dome Fuji, Dome C, and Taylor Dome ice cores (Lorius et al., 1979; Steig et al., 2000; Uemura et al., 2012). The age of the ice in the uppermost c. 160 m at these three sites varies from 0 to 3000–4500 years (Figure 6A); assuming a similar age-depth relation applies for the Dronning Maud Land region, the average age of the subaqueous meltwater recharging Lake Untersee is estimated at c. 1800 years. The δ¹⁸O composition of a series of shallow ice cores (uppermost 50 cm) of a 3.2 km long transect on both sides of the medial moraine on the Anuchin Glacier ranged from −36.4 to −30.8‰ (average of −34.2 ± 1‰). Given that over the past 3000–5000 years, the δ¹⁸O time-series of deep ice cores showed fluctuations in the order of 0.5‰ (Figure 6B), the average δ¹⁸O of near-surface ice of the Anuchin Glacier likely reflects that over a 160 m thick section (or past c. 1800 years). Therefore, the δ¹⁸O of Lake Untersee water is in equilibrium with subaqueous melting of the Anuchin Glacier having an average δ¹⁸O composition of −34.2 ± 1‰ and to obtain the calculated δ¹⁸O of input water of −35.0‰, a two-component mixing model indicates that the subglacial meltwater has an average δ¹⁸O composition of −35.8 ± 1‰ (δD: −280‰; D-excess: 6‰). Considering that the Δδ¹⁸O of last glacial maximum to Holocene age glacial ice is in the order of 6–8‰, the subglacial meltwater recharging Lake Untersee is likely of similar age (late Holocene) to that of the Anuchin Glacier and does not reflect subglacial meltwater sourced during the last glacial period or far in the Antarctic interior.

FIGURE 6

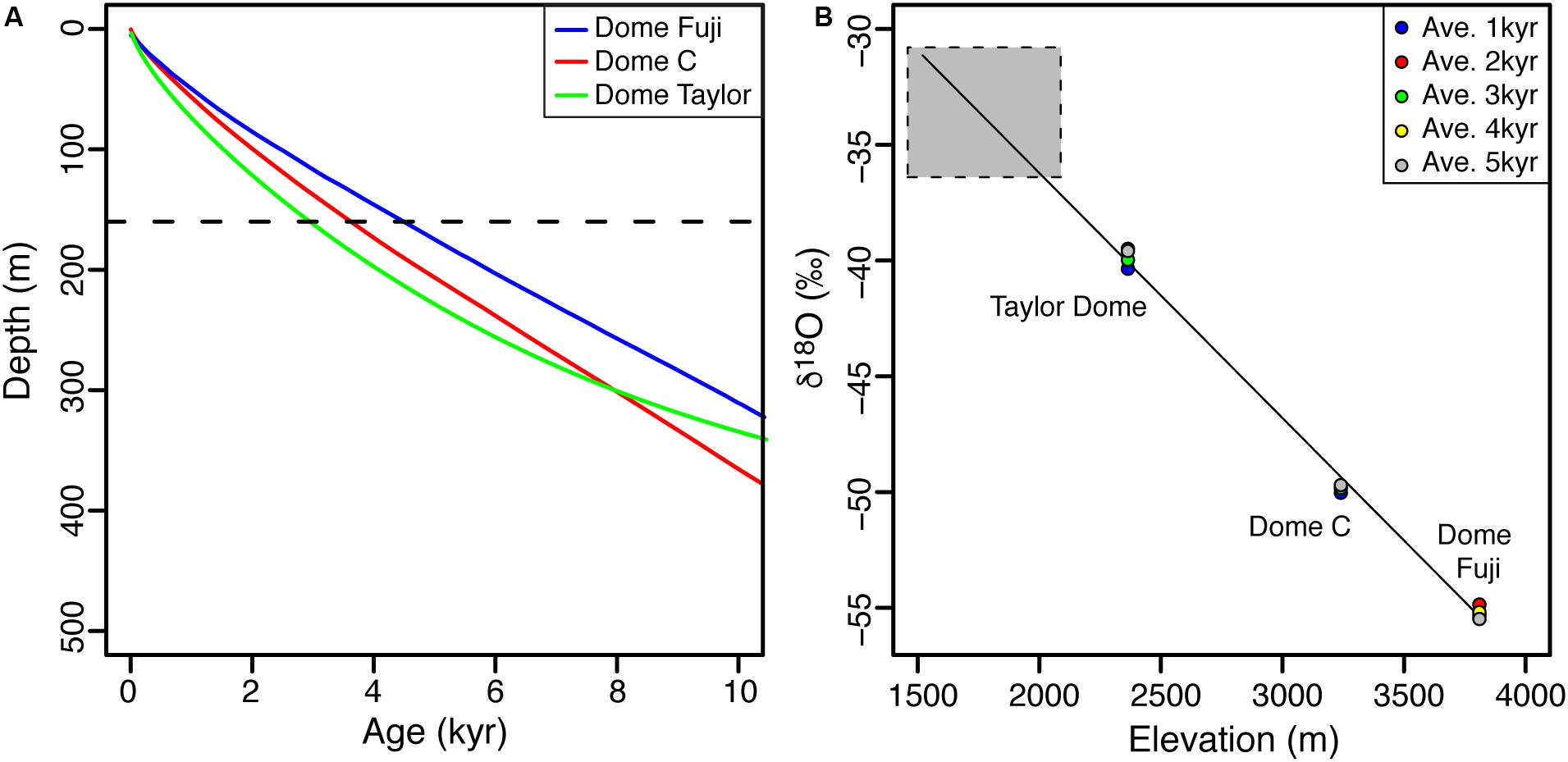
Figure 6. (A) Ice cores age-depth relations for the Dome Fuji (Uemura et al., 2012), Dome C (Lorius et al., 1979) and Taylor Dome (Steig et al., 2000). The dotted line indicates the thickness of the Anuchin glacier at the lake-glacier interface (160 m). (B) δ¹⁸O composition of Dome Fuji (3810 m.a.s.l.), Dome C (3240 m.a.s.l.) and Taylor Dome (2365 m.a.s.l.) ice cores averaged over 1–5 ka. Gray box represents δ¹⁸O measurements for the Anuchin Glacier.

The oxic water column of Lake Untersee is well-mixed as a result of buoyancy-driven convection which allows for effective mixing within a time-scale of one month (Steel et al., 2015). Based on the volume of water in the lake, its surface area and ablation rate, the residence time of water in the lake was estimated at c. 100 years (Faucher et al., 2019) and δ¹⁸O steady-state is achieved within 300–500 years (3–5 residence times). Considering that the 2016 water samples in Lake Untersee plot above the AMWL with D-excess of 14‰, this suggest that for at least the past 300–500 years: (1) subaqueous melting of the Anuchin Glacier and subglacial meltwater were the only sources of water recharging the lake (i.e., no to very little recharge from surface streams with an evaporated δ¹⁸O signature); (2) the δD-δ¹⁸O composition of the subglacial meltwater is likely distributed on the AMWL and does not reflect a subglacial meltwater that has evolved under cryo-freezing; and (3) the ice cover has remained well-sealed to atmospheric exchange (i.e., no evaporative loss of the water column). These conditions were likely made possible by the cooler air temperatures in the region since the 1800s (Isaksson et al., 1996).

Despite generally cooler temperatures over the past few hundred years, we can test for the effect of an anomalous warm summer on the potential contribution of surface stream to the δD-δ¹⁸O composition on Lake Untersee. As a hypothetical scenario, we mixed 5–10% input of stream having a δD = −233.0‰ and δ¹⁸O = −23‰ (a scenario that represents the Anuchin Glacier δD-δ¹⁸O composition that evaporated 40% under relative humidity of 50%) with Lake Untersee and the δD-δ¹⁸O composition of the lake evolved outside the range measured in the oxic water column (10%mix: δD = −281.5‰δ¹⁸O = −36.4‰; 5%mix: δD = −284.7‰δ¹⁸O = −37.1‰). If Lake Untersee then continues to be under hydrological steady-state and keeps being recharged by subaqueous melting and subglacial meltwater sources having an average δ¹⁸O composition of −35.0‰, the δD-δ¹⁸O of Lake Untersee will evolve to the isotopic steady-state determined by input and recharge over a period of 200–300 years. Therefore, this modeling exercise shows that Lake Untersee most likely did not receive additional input from streams under an anomalous warm summer as its δD-δ¹⁸O composition would be distributed closer to the AMWL.

Application of FREEZCH9

This study developed an isotope-augmented version of FREZCHEM (FREEZCH5) and made it recursive (FREEZCH9) to predict the δD-δ¹⁸O evolution and isotopic steady-state of well-sealed perennially ice-covered lakes and subglacial lakes. The model accounts for changes in the ice-water isotope fractionation factor as freezing increases the salinity of the residual water and, to maintain the lake volume in equilibrium, mixes some input water of fixed chemistry and δD-δ¹⁸O composition to the residual water in the lake. Lerman (1979) suggested that the δD-δ¹⁸O steady-state of freezing lakes is reached after more than three residence times. Although the modeling reaches the same conclusion, the δD-δ¹⁸O composition of freezing lakes is not only determined by the residence time of water but also by the volume of ice that freezes annually which determines the volume of water that is added and mixes in the lake to maintain hydrological equilibrium. For mixing scenarios <∼5%, the difference between δ¹⁸O input and equilibrium in the lake water approaches ln(α¹⁸O_i–w); however, as the amount of annual mixing approaches 95%, the δ¹⁸O input and equilibrium approaches 0. In terms of deviation from the GMWL, the difference between D-excess of input and equilibrium in the lake water approaches 8‰ for annual mixing scenarios <5% and is reduced to near 0 as the amount of annual mixing approaches 95% (Figure 3D).

FREEZCH9 allows one to test for the effects of input water with differing isotopic signatures (i.e., evaporated water, meteoric water, cryo-freezing water) on the distribution of lake water isotopic composition in δD-δ¹⁸O space (Figure 7). Horita (2009) suggested that lakes with δD-δ¹⁸O composition plotting above the GMWL are reflective of being affected by the freezing process. The residual waters in well-sealed ice-covered lakes and subglacial lakes that are recharged by meteoric-like waters (i.e., plotting along the GMWL) should plot above the GMWL, regardless of their annual mixing rate. The extent to which the D-excess of these lakes will deviate from the GMWL will be a function of their annual mixing rate. This is the case for Lake Vostok (0.0037% annual mixing) where the δ¹⁸O of recharge water (−56.7‰) approximates that in the accreted ice (−56.2‰) and the water column is depleted by c. 3‰ (−59.0 ± 0.3‰) but with D-excess (17 ± 1‰) c. 10‰ higher than estimated for the input water (7.2‰).

FIGURE 7

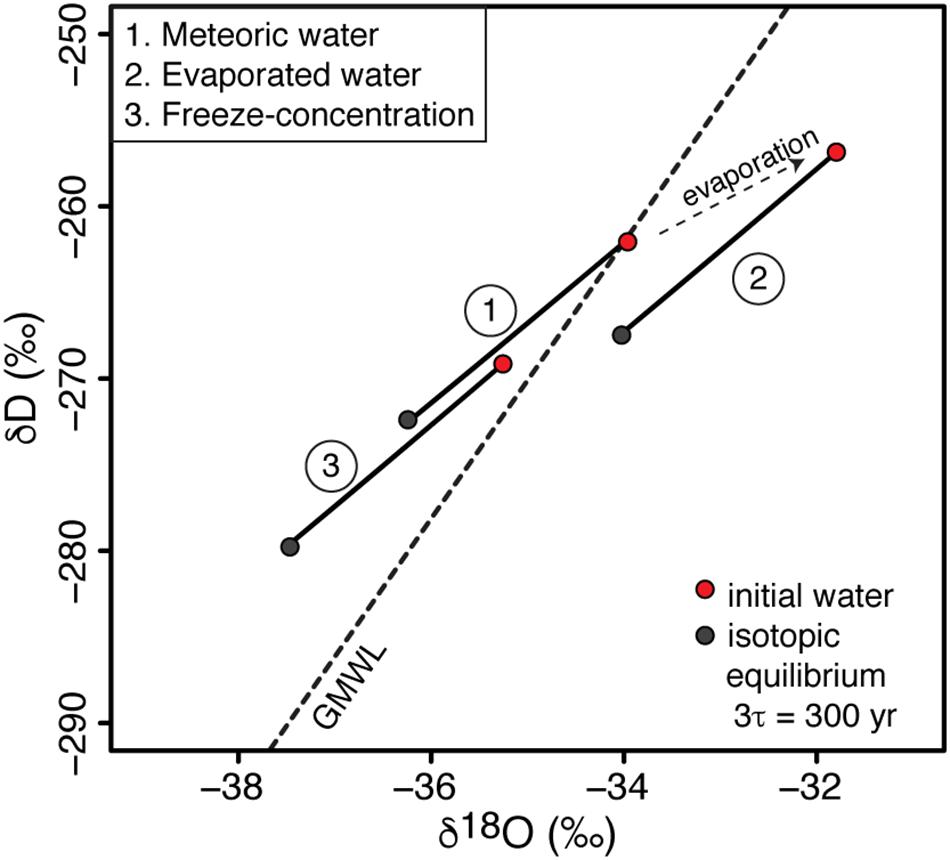
Figure 7. Effects of water input with various δD-δ¹⁸O signatures (i.e., evaporated water, meteoric water, cryo-freezing water) on the δD-δ¹⁸O composition of well-sealed ice-covered lakes. For this example, the mixing rate is 1% and isotopic steady-state is reached in c. 300 years.

In the case of well-sealed perennially ice-covered lakes or subglacial lakes recharged by surface or soil waters (e.g., ephemeral streams) and whose δD-δ¹⁸O composition is shifted below the GMWL due to evaporation, the δD-δ¹⁸O of the water column may not be shifted above the GMWL following the freezing process (Figure 7). The latter would be dependent on the extent of evaporation and mixing condition in the lake.

Finally, in the case of well-sealed perennially ice-covered lakes or subglacial lakes recharged by subglacial waters that have experienced freeze-concentration, the δD-δ¹⁸O of these lakes will strongly deviate above the GMWL for any mixing scenarios. That is because the recharge waters will have δD-δ¹⁸O composition plotting above the GMWL and the freezing process taking place in the lake will shift the δD-δ¹⁸O of the lake water further above the GMWL (but within the limits shown in Figures 3C,D). Such lakes may have D-excess that evolved to values greater than 17‰. It has been suggested that there might exist a regional groundwater system beneath the Antarctic Ice Sheet, as inferred for Lake Bonney in the McMurdo Dry Valleys from airborne transient electromagnetic sensor (i.e., Mikucki et al., 2015). If this regional groundwater system includes circulation through subglacial lakes, this isotopic signature could be used to infer the source of water (largely from basal melting or multiple freeze-concentration).

Conclusion

In this study, we developed an isotope-augmented version of FREZCHEM (FREEZCH5) and made it recursive (FREEZCH9) to predict the δD-δ¹⁸O evolution and isotopic steady-state while accounting for changes in the ice-water isotope fractionation factor as freezing increases the salinity of the residual water. The following conclusions can be drawn from our results:

1. Unlike previous models, FREEZCH9 takes into consideration the combined effects of residual water mixing with incoming waters and evolving geochemistry on the stable water isotopic composition of well-sealed ice-covered lakes; it can be a tool to estimate the annual mixing fraction and residence time of the lake.

2. FREEZCH9 modeling of Lake Vostok suggests that the δD-δ¹⁸O composition of the upper water column should be −453.5 and −59.1‰, respectively; these are within error of the calculations of Ekaykin et al. (2016) (−455 ± 1‰ and −59.0 ± 0.3‰ for δD-δ¹⁸O, respectively).

3. FREEZCH9 modeling of Lake Untersee using 1% annual recharge and mixing with lake water suggests that the δ¹⁸O composition (−37.9 to −37.6‰) is in equilibrium with source waters having an average δ¹⁸O composition of −35.0‰. The lake is recharged from subaqueous melting of the Anuchin Glacier and subglacial meltwater. Based on the δ¹⁸O age-depth relation, the δ¹⁸O of the subaqueous melting of the Anuchin Glacier is estimated at −34.2‰ and two-component mixing indicates that the δ¹⁸O of subglacial meltwater is −35.8‰. The distribution of δD-δ¹⁸O of the oxic water above the AMWL with D-excess of 14‰ suggest that the lake has been well-sealed for the last 300–500 years and not been fed by surface waters (recharged only by subaqueous melting of the Anuchin Glacier and from subglacial meltwater).

4. The distribution of well-sealed ice-covered lakes in δD-δ¹⁸O space depends on the input water (i.e., evaporated water, meteoric water, cryo-freezing water) having different D-excess signatures. Hence, FREEZCH9 may be also used to determine if the hypothetical groundwater systems of the McMurdo Dry Valleys (i.e., Mikucki et al., 2015) are fully or partially recharged by subglacial lakes.

Data Availability Statement

All datasets generated for this study are included in the article/Supplementary Material.

Author Contributions

BF: manuscript writing (main contributor), data collection, data analysis and interpretation, and editing prior to manuscript’s submission. DL: manuscript writing, data collection, data interpretation, and editing prior to manuscript’s submission. DF: model development and editing prior to manuscript’s submission. KW and DA: data collection and editing prior to manuscript’s submission.

Funding

This work was supported by the TAWANI Foundation, the Trottier Family Foundation, the Natural Sciences and Engineering Research Council of Canada (NSERC) Discovery Grant, Polar Knowledge Canada (POLAR), NASA’s Astrobiology Program and the Arctic and Antarctic Research Institute/Russian Antarctic Expedition. A NSERC Alexander Graham Bell Canada Graduate Scholarship provided financial support to BF. Logistical support was provided by the Antarctic Logistics Centre International, Cape Town, South Africa.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We are grateful to Colonel (IL) J.N. Pritzker, IL ARNG (retired), of the TAWANI Foundation, the Trottier Family Foundation and fellow field team members for their support during the expeditions. We would also like to extend our gratitude to Dr. Lipenkov and Dr. Ekaykin from Russia’s Arctic and Antarctic Research Institute (AARI) for providing δD values from their Lake Vostok accreted ice core sampled during the 2012–2013 period. We thank the two reviewers and the editor for their constructive comments.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2020.00220/full#supplementary-material

References

Andersen, D. T., Sumner, D. Y., Hawes, I., Webster-Brown, J., and McKay, C. P. (2011). Discovery of large conical stromatolites in Lake Untersee, Antarctica. Geobiology 9, 280–293. doi: 10.1111/j.1472-4669.2011.00279.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Bell, R. E., Studinger, M., Tikku, A. A., Clarke, G. K., Gunter, M. M., and Meertens, C. (2002). Origin and fate of Lake Vostok water frozen to the base of the East Antarctic ice sheet. Nature 416, 307–310. doi: 10.1038/416307a

PubMed Abstract | CrossRef Full Text | Google Scholar

Bird, M. I., Chivas, A. R., Radnell, C. J., and Burton, H. R. (1991). Sedimentological and stable-isotope evolution of lakes in the Vestfold Hills, Antarctica. Palaeogeogr. Palaeoclimatol. Palaeoecol. 84, 109–130. doi: 10.1016/0031-0182(91)90039-T

CrossRef Full Text | Google Scholar

Burton, J. A., Prim, R. C., and Slichter, W. P. (1953). The distribution of solute in crystals grown from the Melt. Part I. theoretical. J. Chem. Phys. 21, 1987–1991. doi: 10.1063/1.1698728

CrossRef Full Text | Google Scholar

Dansgaard, W. (1964). Stable isotopes in precipitation. Tellus 16, 436–468. doi: 10.1111/j.2153-3490.1964.tb00181.x

CrossRef Full Text | Google Scholar

Dugan, H. A., Doran, P. T., Wagner, B., Kenig, F., Fritsen, C. H., Arcone, S. A., et al. (2015). Stratigraphy of Lake Vida, Antarctica: hydrologic implications of 27 m of ice. Cryosphere 9, 439–450. doi: 10.5194/tc-9-439-2015

CrossRef Full Text | Google Scholar

Ekaykin, A. A., Lipenkov, V. Y., Kozachek, A. V., and Vladimirova, D. O. (2016). Stable water isotopic composition of the Antarctic subglacial lake vostok: implications for understanding the lake’s hydrology. Isot. Environ. Health Stud. 52, 1–9. doi: 10.1080/10256016.2015.1129327

PubMed Abstract | CrossRef Full Text | Google Scholar

Ekaykin, A. A., Lipenkov, V. Y., Petit, J. R., Johnsen, S., Jouzel, J., and Masson-Delmotte, V. (2010). Insights into hydrological regime of Lake Vostok from differential behavior of deuterium and oxygen-18 in accreted ice. J. Geophys. Res. 115:C05003. doi: 10.1029/2009JC005329

CrossRef Full Text | Google Scholar

Faucher, B., Lacelle, D., Fisher, D. A., Andersen, D. T., and McKay, C. P. (2019). Energy and water mass balance of Lake Untersee and its perennial ice cover, east Antarctica. Antarct. Sci. 31, 271–285. doi: 10.1017/S0954102019000270

CrossRef Full Text | Google Scholar

Fisher, D. A., Lacelle, D., Pollard, W., and Faucher, B. (2020). A model for stable isotopes of residual water and ice in permafrost soils using arbitrary water chemistries and soil specific empirical residual water functions. Permafrost Periglacial Process. (accepted).

Google Scholar

Gibson, J. A. E. (1999). The meromictic lakes and stratified marine basins of the Vestfold Hills, East Antarctica. Antarct. Sci. 11, 175–192. doi: 10.1017/S0954102099000243

CrossRef Full Text | Google Scholar

Gooseff, M. N., Lyons, W. B., McKnight, D. M., Vaughn, B. H., Fountain, A. G., and Dowling, C. (2006). A stable isotopic investigation of a polar desert hydrologic system, McMurdo Dry Valleys, Antarctica. Arct. Antarct. Alp. Res. 38, 60–71.

Google Scholar

Horita, J. (2009). Isotopic evolution of saline lakes in the low-latitude and polar regions. Aquat. Geochem. 15, 43–69. doi: 10.1007/s10498-008-9050-3

CrossRef Full Text | Google Scholar

Isaksson, E., Karlen, W., Gundestrup, N., Mayewski, P., Whitlow, S., and Twickler, M. (1996). A century of accumulation and temperature changes in Dronning Maud Land, Antarctica. J. Geophys. Res. 101, 7085–7094. doi: 10.1029/95JD03232

CrossRef Full Text | Google Scholar

Jeffries, M. O., Krouse, H. R., Shakur, M. A., and Harris, S. A. (1984). Isotope geochemistry of stratified Lake’ A’, Ellesmere Island, N.W.T., Canada. Can. J. Earth Sci. 21, 1008–1017. doi: 10.1139/e84-105

CrossRef Full Text | Google Scholar

Jouzel, J., and Souchez, R. A. (1982). Melting-refreezing at the glacier sole and the isotopic composition of the ice. J. Glaciol. 28, 35–42. doi: 10.3189/s0022143000011771

CrossRef Full Text | Google Scholar

Killawee, J. A., Fairchild, I. J., Tison, J. L., Janssens, L., and Lorrain, R. (1998). Segregation of solutes and gases in experimental freezing of dilute solutions: implications for natural glacial systems. Geochim. Cosmochim. Acta 62, 3637–3655. doi: 10.1016/S0016-7037(98)00268-3

CrossRef Full Text | Google Scholar

Lacelle, D. (2011). On the δ18O, δD and D-excess relation in meteoric precipitation and during equilibrium freezing: theoretical approach and field examples. Permafrost Periglacial Process. 22, 13–25. doi: 10.1002/ppp.712

CrossRef Full Text | Google Scholar

Legrand, M., Lorius, C., Barkov, N. I., and Petrov, V. N. (1988). Vostok (Antarctica) ice core: atmospheric chemistry changes over the last climatic cycle (160,000 years). Atmos. Environ. 22, 317–331. doi: 10.1016/0004-6981(88)90037-6

CrossRef Full Text | Google Scholar

Lerman, A. (1979). Geochemical Processes: Water and Sediment Environments. New York: Wiley-Interscience.

Google Scholar

Li, Y., Lu, Y., Zhang, Z. Z., Shi, H., and Xi, H. (2019). Characterizing three-dimensional features of Antarctic subglacial lakes from the inversion of hydraulic potential—Lake Vostok as a case study. Adv. Polar Sci. 30, 70–75. doi: 10.13679/j.advps.2019.1.00070

CrossRef Full Text | Google Scholar

Lipenkov, V. Y., Ekaykin, A. A., Polyakova, E. V., and Raynaud, D. (2016). Characterization of subglacial Lake Vostok as seen from physical and isotope properties of accreted ice. Philos. Trans. A Math. Phys. Eng. Sci. 374:20140303. doi: 10.1098/rsta.2014.0303

PubMed Abstract | CrossRef Full Text | Google Scholar

Lorius, C., Merlivat, L., Jouzel, J., and Pourchet, M. (1979). A 30,000 yr isotope climatic record from Antarctic ice. Nature 280, 644–648. doi: 10.1038/280644a0

CrossRef Full Text | Google Scholar

Lyons, W. B., and Finlay, J. C. (2008). “Biogeochemical processes in high-latitude lakes and rivers,” in Polar Lakes and Rivers: Limnology of Arctic and Antarctic Aquatic Ecosystems, eds W. F. Vincent and J. Laybourn-Parry (New York: Oxford University Press), 137–156. doi: 10.1093/acprof:oso/9780199213887.003.0008

CrossRef Full Text | Google Scholar

Lyons, W. B., Welch, K. A., Priscu, J. C., Tranter, M., and Royston-Bishop, G. (2016). Source of Lake Vostok cations constrained with strontium isotopes. Front. Earth Sci. 4:78. doi: 10.3389/feart.2016.00078

CrossRef Full Text | Google Scholar

Lyons, W. B., Welch, K. A., Welch, S. A., Camacho, A., Rochera, C., Michaud, L., et al. (2013). Geochemistry of streams from Byers Peninsula, Livingston Island. Antarct. Sci. 25, 181–190. doi: 10.1017/S0954102012000776

CrossRef Full Text | Google Scholar

Masson-Delmotte, V., Hou, S., Ekaykin, A., Jouzel, J., Aristarain, A., Bernardo, T. A., et al. (2008). A review of Antarctic surface snow isotopic composition: observations, atmospheric circulation, and isotopic modeling. J. Clim. 21, 3359–3387. doi: 10.1175/2007JCLI2139.1

CrossRef Full Text | Google Scholar

Marion, G. M., and Kargel, J. S. (2008). Cold Aqueous Planetary Geochemistry with FREZCHEM: From Modeling to the Search for Life at the Limits. Heidelberg: Springer.

Google Scholar

Marion, G. M., Mironenko, M. V., and Roberts, M. W. (2010). FREZCHEM: a geochemical model for cold aqueous solutions. Comput. Geosci. 36, 10–15. doi: 10.1016/j.cageo.2009.06.004

CrossRef Full Text | Google Scholar

Matsubaya, O., Sakai, H., Torii, T., Burton, H., and Knowles, K. (1979). Antarctic saline lakes stable isotopic ratios, chemical compositions and evolution. Geochim. Cosmochim. Acta 43, 7–25. doi: 10.1016/0016-7037(79)90042-5

CrossRef Full Text | Google Scholar

McKay, C. P., Clow, G., Wharton, R. A. Jr., and Squyres, S. W. (1985). Thickness of ice on perennially frozen lakes. Nature 313, 561–562. doi: 10.1038/313561a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Mikucki, G., Auken, E., Tulaczyk, S., Virginia, R. A., Schamper, C., Sørensen, K. I., et al. (2015). Deep groundwater and potential subsurface habitats beneath an Antarctic Dry Valley. Nat. Commun. 6:6831. doi: 10.1038/ncomms7831

PubMed Abstract | CrossRef Full Text | Google Scholar

Miller, L. G., and Aiken, G. R. (1996). Effects of glacial meltwater inflows and moat freezing on mixing in an ice-covered Antarctic lake as interpreted from stable isotope and tritium distributions. Limnol. Oceanogr. 41, 966–976. doi: 10.4319/lo.1996.41.5.0966

CrossRef Full Text | Google Scholar

Morgan, F., Barker, G., Briggs, C., Price, R., and Keys, H. (2007). Environmental Domains Analysis for the Antarctic Continent: Version 2.0 Final Report. Landcare Research Report LC0708/055 for Antarctica. Lincoln, NZ: New Zealand and Department of Conservation.

Google Scholar

O’Neil, J. R. (1968). Hydrogen and oxygen isotope fractionation between ice and water. J. Phys. Chem. 72, 3683–3684. doi: 10.1021/j100856a060

CrossRef Full Text | Google Scholar

Petrenko, V. F., and Whitworth, R. W. (1999). Physics of Ice. Oxford: Oxford University Press.

Google Scholar

Priscu J. C. (ed.) (1998). Ecosystem (dynamics)in a Polar Desert: The McMurdo Dry Valleys, Antarctica. Antarctic Research Series. Washington DC: American Geophysical Union.

Google Scholar

Priscu, J. C., and Foreman, C. M. (2009). “Lakes of Antarctica,” in Encyclopedia of Inland Waters, ed. G. E. Likens (Oxford: Elsevier), 555–566. doi: 10.1016/b978-012370626-3.00038-7

CrossRef Full Text | Google Scholar

Richter, W., and Strauch, G. (1983). Deuterium and O-18 variations in lakes of the Schirmacher Oasis (East-Antarctica). Isotopenpraxis 19, 145–153. doi: 10.1080/10256018308544867

CrossRef Full Text | Google Scholar

Royston-Bishop, G., Tranter, M., Siegert, M. J., Lee, V., and Bates, P. D. (2004). Is Vostok lake in steady state? Ann. Glaciol. 39, 490–494. doi: 10.3189/172756404781813853

CrossRef Full Text | Google Scholar

Santibáñez, P. A., Michaud, A. B., Vick-Majors, T. J., D’Andrilli, J., Chiuchiolo, A., Hand, K. P., et al. (2019). Differential incorporation of bacteria, organic matter, and inorganic ions into lake ice during ice formation. J. Geophys. Res. Biogeosci. 124, 585–600. doi: 10.1029/2018JG004825

CrossRef Full Text | Google Scholar

Siegert, M. J., Kwok, R., Mayer, C., and Hubbard, B. (2000). Water exchange between the subglacial Lake Vostok and the overlying ice sheet. Nature 403, 643–646. doi: 10.1038/35001049

PubMed Abstract | CrossRef Full Text | Google Scholar

Siegert, M. J., Popov, S., and Studinger, M. (2011). “Vostok Subglacial Lake: a review of geophysical data regarding its discovery and topographic setting,” in Antarctic Subglacial Aquatic Environments, eds M. J. Siegert and M. C. Kennicutt II R. A. Bindschadler (Washington, DC: American Geophysical Union), 45–60. doi: 10.1029/2010gm000934

CrossRef Full Text | Google Scholar

Sofer, Z., and Gat, J. R. (1972). Activities and concentrations of oxygen-I8 in concentrated aqueous salt solutions: analytical and geophysical implications. Earth Planet. Sci. Lett. 15, 232–238. doi: 10.1016/0012-821X(72)90168-9

CrossRef Full Text | Google Scholar

Sofer, Z., and Gat, J. R. (1975). The isotope composition of evaporating brines: effect of the isotopic activity ratio in saline solutions. Earth Planet. Sci. Lett. 26, 179–186. doi: 10.1016/0012-821X(75)90085-0

CrossRef Full Text | Google Scholar

Souchez, R., Petit, J., Jouzel, J., de Angelis, M., and Tison, J. (2004). Reassesing Lake Vostok’s behaviour from existing and new ice core data. Earth Planet. Sci. Lett. 217, 163–170. doi: 10.1016/S0012-821X(03)00588-0

CrossRef Full Text | Google Scholar

Souchez, R. A., and Jouzel, J. (1984). On the isotopic composition in delta D and delta18O of water and ice during freezing. J. Glaciol. 30, 369–372. doi: 10.3189/s0022143000006249

CrossRef Full Text | Google Scholar

Steel, H. C. B., McKay, C. P., and Andersen, D. T. (2015). Modeling circulation and seasonal fluctuations in perennially ice-covered and ice-walled Lake Untersee, Antarctica. Limnol. Oceanogr. 60, 1139–1155. doi: 10.1002/lno.10086

CrossRef Full Text | Google Scholar

Steig, E. J., Morse, D. L., Waddington, E. D., Stuiver, M., Grootes, P. M., Mayewski, P. A., et al. (2000). Wisconsinan and Holocene climate from an ice core at Taylor Dome, western Ross Embayment, Antarctica. Geogr. Ann. 82, 213–225. doi: 10.1111/j.0435-3676.2000.00122.x

CrossRef Full Text | Google Scholar

Stewart, M. K., and Friedman, I. (1975). Deuterium fractionation between aqueous salt solutions and water vapor. J. Geophys. Res. 80, 3812–3818. doi: 10.1029/JC080i027p03812

CrossRef Full Text | Google Scholar

Studinger, M., Bell, R. E., Buck, R. W., Karner, G. D., and Blankenship, D. D. (2004). Sub-ice geology inland of the Transantarctic Mountains in light of new aerogeophysical data. Earth Planet Sc. Lett. 20, 391–408. doi: 10.1016/s0012-821x(04)00066-4

CrossRef Full Text | Google Scholar

Suzuoki, T., and Kimura, T. (1973). D/H and 18O/16O fractionation in ice-water system. Mass Spectrom 21, 229–233. doi: 10.5702/massspec1953.21.229

CrossRef Full Text | Google Scholar

Terwilliger, K. P., and Dizio, S. F. (1970). Salt rejection phenomena in the freezing of saline solutions. Chem. Eng. Sci. 25, 1331–1349. doi: 10.1016/0009-2509(70)80010-0

CrossRef Full Text | Google Scholar

Touzeau, A., Landais, A., Stenni, B., Uemura, R., Fukui, K., Fujita, S., et al. (2016). Acquisition of isotopic composition for surface snow in East Antarctica and the links to climatic parameters. Cryosphere 10, 837–852. doi: 10.5194/tc-10-837-2016

CrossRef Full Text | Google Scholar

Uemura, R., Masson-Delmotte, V., Jouzel, J., Landais, A., Motoyama, H., and Stenni, B. (2012). Ranges of moisture-source temperature estimated from Antarctic ice cores stable isotope records over glacial–interglacial cycles. Clim. Past. 8, 1109–1125. doi: 10.5194/cp-8-1109-2012

CrossRef Full Text | Google Scholar

Vincent, W. F., Hobbie, J. E., and Laybourn-Parry, J. (2008). “Introduction to the limnology of high-latitude lake and river ecosystems,” in Polar Lakes and Rivers: Limnology of Arctic and Antarctic Aquatic Ecosystems Oxford, etc, eds W. F. Vincent and J. Laybourn-Parry (Oxford: Oxford University Press), 1–23.

Google Scholar

Wand, U., Samarkin, V. A., Nitzsche, H. M., and Hubberten, H. W. (2006). Biogeochemistry of methane in the permanently ice-covered Lake Untersee, central Dronning Maud Land, East Antarctica. Limnol. Oceanogr. 51, 1180–1194. doi: 10.4319/lo.2006.51.2.1180

CrossRef Full Text | Google Scholar

Wand, U., Schwarz, G., Brüggemann, E., and Bräuer, K. (1997). Evidence for physical and chemical stratification in Lake Untersee (central Dronning Maud Land, East Antarctica). Antarct. Sci. 9, 43–45. doi: 10.1017/S0954102097000060

CrossRef Full Text | Google Scholar

Wang, J. H., Robinson, C. B., and Edelman, I. S. (1953). Self-diffusion and structure of liquid water, III, Measurement of the self-diffusion of liquid water with H2, H3, and O18 as tracers. J. Am. Chern. Soc. 75, 466–470. doi: 10.1021/ja01098a061

CrossRef Full Text | Google Scholar

Weisleitner, K., Perras, A., Moissl-Eichinger, C., Andersen, D. T., and Sattler, B. (2019). Source environments of the microbiome in perennially ice-covered Lake Untersee, Antarctica. Front. Microbiol. 10:1019. doi: 10.3389/fmicb.2019.01019

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, A. T., and Wellman, H. W. (1962). Lake Vanda: an Antarctic Lake: lake Vanda as a Solar Energy Trap. Nature 196, 1171–1173. doi: 10.1038/1961171a0

CrossRef Full Text | Google Scholar

Wingham, D. J., Siegert, M. J., Shepherd, A., and Muir, A. S. (2006). Rapid discharge connects Antarctic subglacial lakes. Nature 440, 1033–1036. doi: 10.1038/nature04660

PubMed Abstract | CrossRef Full Text | Google Scholar

Wright, A., and Siegert, M. A. (2012). Fourth inventory of Antarctic subglacial lakes. Antarct. Sci. 24, 659–664. doi: 10.1017/S095410201200048X

CrossRef Full Text | Google Scholar