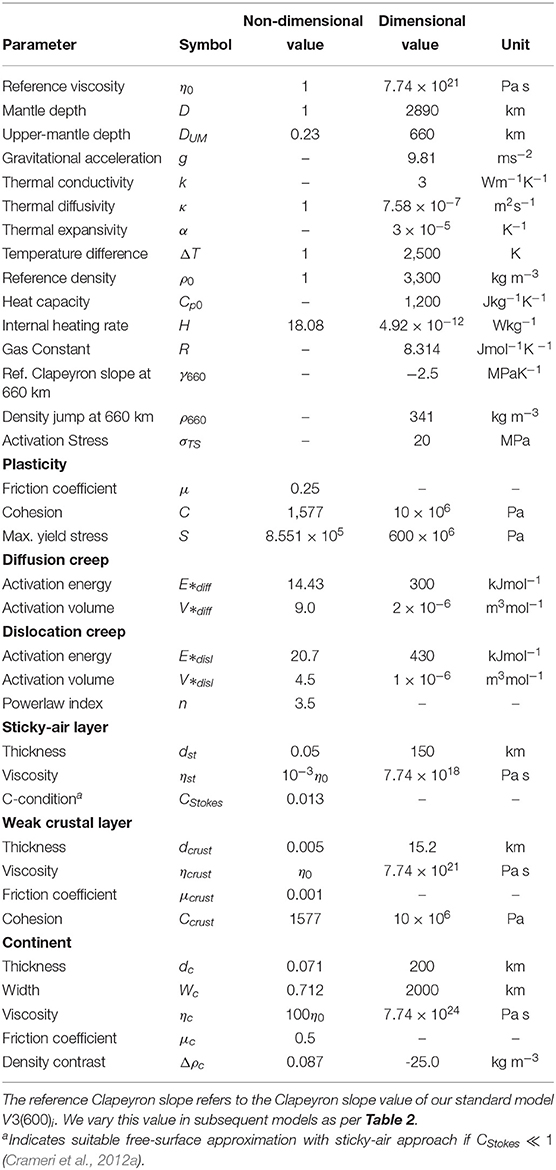
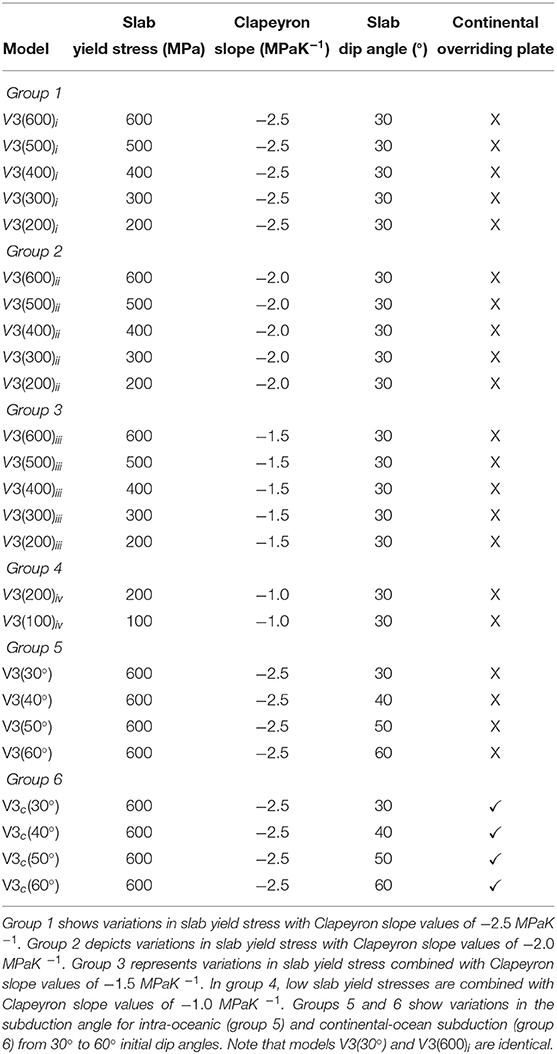
- 1Earth Sciences Department, University College London, London, United Kingdom
- 2Department of Earth, Planetary, and Space Sciences, University of California, Los Angeles, Los Angeles, CA, United States
- 3Center for Earth Evolution and Dynamics, University of Oslo, Oslo, Norway
Slab orphaning is a newly discovered phenomenological behavior, where the slab tip breaks off at the top of the lower mantle (~660 km depth) and is abandoned by its parent slab. Upon orphaning, subduction continues uninterrupted through the lateral motion of the parent slab above 660 km depth. In this work, we present a regime diagram for the range of conditions under which slabs can orphan at the top of the lower mantle. Our models show that a viscosity jump at 1,000 km depth not coincident with the endothermic phase change responsible for the 660 km seismic discontinuity, is necessary for orphaning as is the presence of a low viscosity channel between 660 and 1,000 km depth. We show that orphan slabs, similar to other deep slab morphologies, can be the end result for a wide range of physical parameters governing slab dynamics: slab orphaning persists across wide variations in slab dip, slab yield stress/strength, Clapeyron slope values, and overriding plate nature. The diversity in orphan slab sizes and orphaning periods is tied to the orphaning regime space, which describes a hitherto unexplored region between deflected and penetrating deep-subduction modes. Orphaning provides a simple dynamic link between the well-known deflection and penetration, and provides one possible way for slabs to switch from direct penetration to deflection, littering the mantle with abandoned fragments. Orphan slabs are therefore the intermediary between these two extensively studied slab morphologies.
1. Introduction
Upper-lower mantle slab morphology and dynamics are currently described in terms of slab deflection and flattening or direct penetration (e.g., Christensen and Yuen, 1984; Christensen, 1996; Fukao et al., 2001, 2009; Čížková et al., 2002; Yoshioka et al., 2010; Yoshida et al., 2012; Fukao and Obayashi, 2013; Garel et al., 2014; Goes et al., 2017; Yoshida, 2017; Čížková and Bina, 2019). Despite the well-entrenched presence of these key terms in the literature, the debate is still out on what leads a slab to adopt one behavior over the other at any point throughout its evolutionary history. Many previous studies have hypothesized that the age, and hence the strength of the slab is the determining factor that shapes its behavior (e.g., Garel et al., 2014; Goes et al., 2017). This would suggest that older, colder and therefore stronger slabs should always penetrate into the lower mantle while younger, warmer slabs should deflect and flatten at the top of the lower mantle. However, as attested by the slabs of the Pacific this does not always hold true (e.g., Yoshioka et al., 2010; Goes et al., 2017).
What ultimately controls the slab behavior is the relationship between the buoyancy and strength of the slab with respect to the surrounding ambient mantle. Understanding the nuances of this relationship depends on our knowledge of the mantle viscosity structure. Previous work based on inversions of post-glacial rebound and the gravity field has extensively explored the effects of a viscosity increase at 660 km depth (e.g., Hager and Richards, 1984, 1989; Hager et al., 1985; Čížková et al., 2002; Funiciello et al., 2003; Billen and Hirth, 2007; Billen, 2010; Garel et al., 2014). However, when the viscosity jump is not prescribed to occur at 660 km depth, the increase in viscosity occurs much closer to ~ 900–1,200 km depth (King and Masters, 1992; Forte and Mitrovica, 2001; Mitrovica and Forte, 2004; Rudolph et al., 2015). New geophysical evidence from trans-dimensional, trans-hierarchical Bayesian inversions of the geoid, which do not prescribe the number or depth of viscosity jumps show both the deeper viscosity increase (~ 1,000 km) and a low viscosity layer of moderate contrast above it (~ 10 times less viscous than the upper mantle). It is not uncommon for a low viscosity layer (LVL) to emerge from geoid inversions for the radial viscosity structure of the mantle. In previous work this has often been prescribed to be in the transition zone (Hager and Richards, 1984, 1989; Hager et al., 1985). Our recent inversions suggest it is not (Rudolph et al., 2015). Recent mineral physics studies aimed at understanding the flattening of slabs at a 1,000 km in the absence of known phase transitions suggest mechanisms for a viscosity jump at 1,000 km rather than 660 km depth related to changes in strength in ferropericlase (Marquardt and Miyagi, 2015). Karato et al. (1995, 2001) have shown evidence for a superplastic layer below 660 km depth, though thinner and much less viscous that what is seen in the geoid inversion. This difference can be understood in terms of the Cathles parameter—a ratio of the thickness of the layer and the flow wavelength cubed multiplied by the viscosity contrast of the layer (Richards and Lenardic, 2018). At long wavelengths, such as those appropriate to infer the radial viscosity structure of the mantle, the Cathles parameter shows that a thick, moderately low viscosity layer is equivalent to a thin, very low viscosity layer. New evidence from Mohiuddin et al. (2020) also suggests that cold slabs undergo extensive weakening due to the grain size reduction in ringwoodite. A significant reduction in the slab strength at the top of the lower mantle would be seen as a moderate reduction in viscosity in the spherical average to which the geoid is sensitive. Both the new geophysical constraints and the mineral physics studies suggest it is worth revisiting the traditional viscosity structure used to understand the controls on slab morphology. In this study we add to the existing body of work on slab behavior by exploring the effects of this new viscosity structure. The results are significant, as we find a new morphological feature with implications for the interpretation of the slabs observed in seismic tomography.
We term this new morphological feature slab orphaning (Grima et al., submitted). Orphaning enables a penetrative slab to split in to separate orphan and parent slabs at upper-lower mantle depths. Upon the abandonment of its orphan the parent slab deflects at the top of the upper-lower mantle. The flattened parent slab travels laterally across the top of the lower mantle and its negative buoyancy sustains the ongoing, continuous, and uninterrupted, subduction and plate convergence at the trench. Meanwhile the abandoned orphan slowly sinks under its own weight toward the core-mantle boundary (CMB) (see Videos S1, S2).
Slab orphaning results from intrinsic buoyancy changes within the slab at the depth of the perovskite forming reaction at 660 km depth and is an expression of an opposing force balance within the slab at the top of the lower mantle (Figure 1, step 1). Key to orphaning is the temperature dependence of the phase boundary depth associated with the transition. At 660 km depth the anomalously buoyant, untransformed material within cold slab core resists subduction into the lower mantle (Figures 2a,b). Contrary to Yoshioka et al. (2010), we find that the presence of an LVL encourages faster slab sinking speeds in the proto-orphan, leading to a proto-orphan in tension down-dip and a proto-parent in compression up-dip (Figure 1, step 2a,b). Higher slab sinking velocities in the LVL translate to higher strain rates for the proto-orphan (Figures 2d–f), which as the slab is at its maximum stress, decrease the viscosity of proto-orphan, weakening it (Figure 1, step 3, Figure 2g). The presence of a viscosity increase at the bottom of the LVL mainly confines the induced slab-mantle coupled viscous flow to the mantle above 1,000 km depth (e.g., Dal Zilio et al., 2018), and forces flow that was predominantly vertically oriented in the upper mantle, to switch to predominantly horizontal between 660 and 1,000 km depth (Figure 1, step 4, Figures 2g–i). The change in flow direction contributes to the slab shearing that takes place around the lens of anomalously buoyant material within the slab (Figure 1, step 5). Contemporaneous to the shearing of the proto-orphan, the increase in the lateral extent of the low density lens (due to continued subduction and hence accumulation of cold slab material at this depth) encourages the deflection of the proto-parent slab until it flattens at the top of the lower mantle (Figures 2a–c,f,i). Contrary to shallow slab tearing which is typically caused by extrinsic changes in the slab buoyancy (e.g., Yoshioka et al., 1995; Buiter et al., 2002; Burkett and Billen, 2009, 2010; Duretz et al., 2011, 2012; van Hunen and Allen, 2011), slab orphaning occurs independently of any external forces and is entirely a slab intrinsic process. The slab weakening at depth is also independent of the bending and unbending of the slab at the trench (e.g., Čížková et al., 2007). As we do not implement damage rheology the slab heals “instantly” from the increase in strain rates at shallow depths due to the slab bending at the trench, which hence does not influence orphaning at depth. For further in-detail discussions and descriptions of orphaning we refer the reader to Grima et al. (submitted).
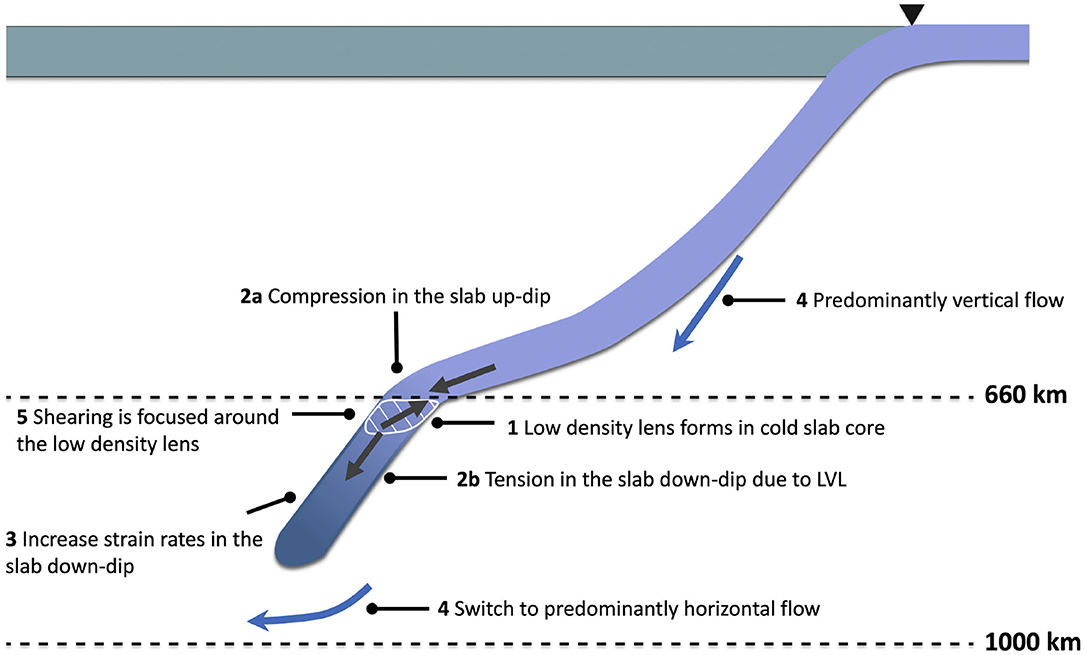
Figure 1. Schematic showing the slab orphaning process. A lens of anomalously buoyant material forms within the cold slab core due to the temperature dependence of the phase boundary depth of the phase change (1). The anomalously buoyant material resists subduction and compresses the slab up-dip (2a). Faster sinking speeds in the LVL result in a proto-orphan in tension (2b) and give rise to an opposing force balance up and down-dip of the phase change. Faster slab sinking speeds in the LVL increase the strain rates in the proto-orphan and reduce its viscosity resulting in weakening (3). An increase in viscosity at 1,000 km mainly confines the induced slab-mantle viscous flow to the mantle above 1,000 km depth, forcing a switch in predominantly vertical flow above 660 km depth to predominantly horizontal flow in the LVL (4). Horizontal flow in the LVL increases the shearing and stretching of the slab around the low density lens (5) until the slab splits into separate flattened parent slab and a quasi-vertical orphan slab. The flattened parent slab travels laterally on top of the lower mantle sustaining subduction at the trench as the orphan slowly sinks toward the CMB.

Figure 2. Each panel represents a time slice in the evolution of our standard model V3(600)i. (a–c) (Density) The temperature dependence of the phase boundary depth introduces a low density lens within the cold slab core at 660 km depth and resists the slab's penetration into the lower mantle. Continued subduction increases the lateral extent of the lens and encourages the flattening of the proto-parent (d–f) (Strain Rate) Higher slab sinking velocities in the LVL increase the strain rates within the proto-orphan. As the slab and proto-orphan have reached their maximum stress, the higher strain-rates are accommodated by a decrease in viscosity of the proto-orphan, weakening it. (g–i) (Viscosity) The change in flow direction from predominantly vertical in the upper mantle to horizontal in the LVL encourages the shearing of the proto-orphan from its parent.
A key question that naturally follows on from the observed diversity in slab morphologies, is the link that connects penetrative, flattened and orphaned slabs. Can slabs switch from one mode to another (and possibly back again) over time. If so, how? Mode switching has been proposed as a viable interpretation for the observed morphology in tomographic models of slabs such as those in the Tethys, Japan, and Tonga subduction zones (e.g., Hafkenscheid et al., 2006; Agrusta et al., 2017; Yoshida, 2017). Plate reconstruction models often require slabs to switch from one behavior to the other to fit the geological observations at the surface (e.g., van der Hilst, 1995). Previous studies have suggested that one way slabs could mode switch, from flattening to penetrating, is through slab avalanching, where slab material piles up within the mantle transition zone until it avalanches, or flushes, downwards into the lower mantle (e.g., Machetel and Weber, 1991; Tackley et al., 1993; Zhong and Gurnis, 1995; Yoshioka et al., 2010; Yoshida, 2017). It has also been suggested that a flattened slab could switch to a penetrative mode if its viscosity is reduced through heating over time (Nakakuki et al., 2010). Agrusta et al. (2017) have proposed that mode switching is linked to factors such as the presence of phase transitions, slab age, changing upper plate forcing and changes in Clapeyron slope values due to slab dehydration. We propose that slabs can also mode switch from penetration to flattening, through slab orphaning (Grima et al., submitted). We suggest that slab break-off at the top of the lower mantle can split the previously penetrative slab into a separate flattened parent slab at the upper-mantle lower-mantle interface and an abandoned orphan that slowly sinks downwards toward the core mantle boundary. Similar to slab avalanching, slab orphaning is entirely independent of extrinsic surface plate dynamics and hence different from shallow slab break-off. Orphaning introduces the idea that slab fragmentation does not require major shifts in surface plate kinematics, nor the cessation of subduction, which are both often a staple in previous interpretations of slab break-off (e.g., Wortel, 2000; Sigloch et al., 2008; van der Meer et al., 2010, 2012, 2017; Richards et al., 2011; Sigloch, 2011; Schellart and Spakman, 2012; Sigloch and Mihalynuk, 2013; Honda, 2014, 2016).
We illustrate below with a regime diagram how slab orphaning links the two previously described archetypal slab morphologies observed in seismic tomography models, and how it is possible for a slab to dynamically transition from an initially penetrative mode dominated by vertical sinking to a flattened mode dominated by lateral motion above 660 km depth. The abundant abandoned orphans observed in the present-day Earth at upper-lower mantle depths and deeper (e.g., Hafkenscheid et al., 2006; Sigloch et al., 2008; Sigloch, 2011; Honda, 2014; van der Meer et al., 2017) are therefore both a consequence and a testament to the penetrative-to-flattened mode switch itself (Grima et al., submitted).
Subduction dynamics within the traditional viscosity structure for the mantle have been explored extensively, but slab orphaning occurs within a hitherto overlooked region in the regime space between slab penetration and flattening. Similar to flattening and penetration, orphaning can occur for a wide variety of slab yield stresses, and therefore slab strengths and slab ages, initial subduction angles, overriding plate types, and Clapeyron slopes. We show that slab orphaning persists across various model setups, initial conditions and model resolutions, indicating that orphaning is a robust dynamical phenomenon. Slab orphaning also introduces an additional, intermediary mode to our previous binary understanding of slab dynamics. Not only can slabs flatten or penetrate but they can also adjust dynamically to changes in the relative strength of slab vs. mantle as a function of depth, giving rise to a new slab mode that is slab orphaning (Grima et al., submitted). Our results highlight the fundamental importance of the radial viscosity structure of the background mantle for slab morphology. For an extended discussion on the effects of different viscosity structures on deep slab morphology we refer the reader to the Supplementary Section 1.4 and Figures S15, S16.
2. Materials and Methods
2.1. Physical Model
Similar to previous work (e.g., Tackley, 2011; Crameri et al., 2012b; Garel et al., 2014; Crameri and Lithgow-Bertelloni, 2018; Čížková and Bina, 2019), we model an incompressible mantle by solving the non-dimensional equations for the conservation of mass (Equation 1), momentum (Equation 2), and energy (Equation 3) in the Boussinesq approximation, using the multi-grid finite difference/volume code StagYY (Tackley, 2008):
where v is the velocity, σij is the deviatoric stress tensor, p the pressure, Ra the Rayleigh number, PB, the phase buoyancy parameter, Γ the phase function, π the excess pressure, T the temperature, the vertical unit vector, t the time and H the non-dimensional internal heating rate.
The Rayleigh number (Ra) (see e.g., Turcotte and Schubert, 2014) can be expressed in terms of density (ρ), gravitational acceleration (g), the thermal expansivity (α), temperature scale (ΔT), mantle depth (D), thermal diffusivity (κ), and reference viscosity (η0) as
The Rayleigh number is 107 and the internal heating rate has a value of 4.92 × 10−12 Wkg−1 which is equivalent to a non-dimensional value of 18.08, giving an internal heating-based Rayleigh number of 1.8 × 108 (see e.g., Turcotte and Schubert, 2014).
PB (Christensen, 1995) is given by:
where γ is the Clapeyron slope, Γ is a phase function (0 ≤ Γ ≤ 1) indicating the relative portion of the dense phase and π is the excess pressure (Christensen and Yuen, 1985), defined as:
where P is the hydrostatic pressure, p0 is the transition pressure at 0 K.
We use a fixed depth discontinuous phase mode implemented as a sheet mass anomaly (Tackley, 1994, 1996) where the buoyancy deflection associated with the phase change is concentrated into one cell to represent an infinitely sharp transition rather than one with a finite width (Christensen and Yuen, 1984; Christensen, 1995). This method is equivalent to the effective thermal expansivity method of Christensen and Yuen (1984). The buoyancy associated with the deflection due to the phase transition is added to the momentum equation (Equation 2). A consequence of the sheet mass anomaly is that this is visually represented as a lens of anomalously low density material at 660 km depth. The density jump associated with the phase change is ~ 10%, assuming an olivine mantle and a slab age at 660 km depth of 100 Myr with a density of ~ 3,380 kgm−3, this would be approximately equivalent to 340 kgm−3. As required by the Boussinesq approximation, no effects due to the phase change are added to the energy equation (Christensen, 1995). We refer the reader to Table 1 for values of the Clapeyron slope and other parameters.
The components of the viscosity have the form:
where ηb(P) contains the viscosity jumps at 660 and 1,000 km, E* and V* are the activation energy and volume, respectively, R is the gas constant, and n is the stress exponent. Subscripts i refer to the two different deformation mechanisms: diffusion or dislocation creep. σTS is the stress value above which dislocation creep is activated. For diffusion creep, the power law exponent is n = 1.
The viscosity at any pressure and temperature in the model is given by
where the limiting plastic viscosity ηy combines a Drucker-Pager yield criterion for brittle failure and a homogeneous ductile yield stress limit S which is applied everywhere throughout our model with the exception of the sticky-air layer;
with cohesion C, strain rate ϵ and friction coefficient μ. Finally, for numerical stability, the viscosity is bounded such that: .
The models include a weak hydrated crustal layer on top of the subducting plate. This develops on the surface of ~10 Myr old portions of the lithospheric plate away from the ridge, and is allowed to form a freely evolving weak subduction channel once the plate subducts (Crameri and Tackley, 2015). The weak crustal layer differs from the mantle material by its lower yield stress, and has a thickness of 15 km. It is converted to regular mantle material once it is subducted below a depth d > 400 km. To simulate a low-viscosity asthenosphere underneath the overriding and subducting plates, we implement a melting viscosity reduction (MVR). The MVR describes the decrease in viscosity by a factor of 10 in regions where the temperature exceeds a simple linear, depth-dependent solidus (Tackley, 2000). It has been shown that the MVR aids in maintaining plate like behavior (see e.g., Tackley, 2000; Crameri and Tackley, 2015, 2016). Finally, all our models include a low viscosity layer (LVL), between 660 and 1,000 km depth (see Figure 3) that is 10 times less viscous than the upper mantle, and an increase of an order of magnitude with respect to the upper mantle at 1,000 km (Rudolph et al., 2015). Table 1 also provides further physical parameter details and Figure 3 provides a visual representation of the physical model setup used in this study complete with an average 1D viscosity profile illustrating the root-mean-square, horizontally averaged viscosity of our models (see left hand side of Figure 3).
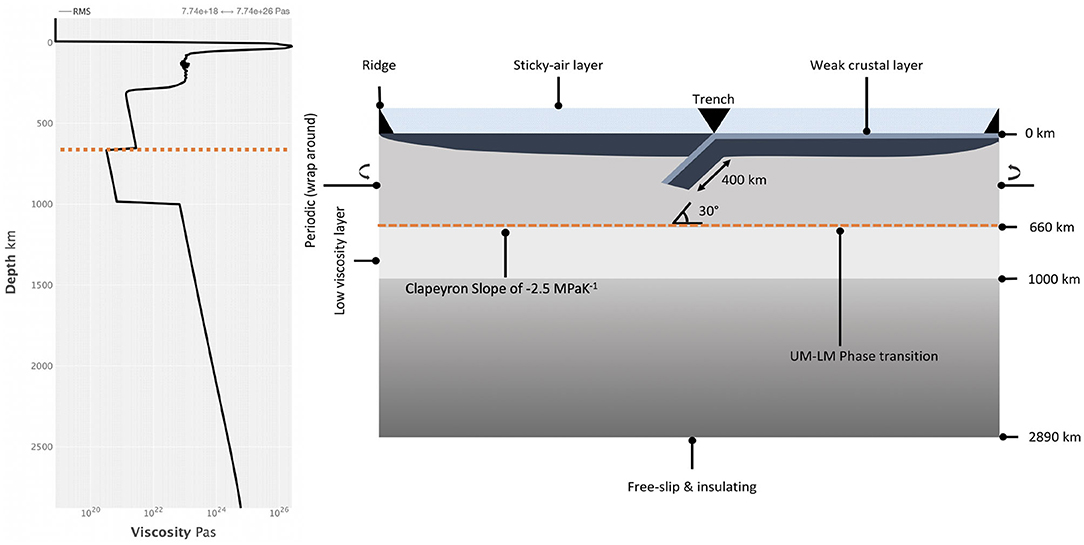
Figure 3. Schematic showing a 1-D root-mean-square, horizontally averaged viscosity profile of our model on the left. The high viscosity at the top-most upper mantle is the result of the high viscosity of the initial slab, which adds to the average viscosity at this depth and overprints the viscosity of the asthenosphere that is present in all our models. The minimum and maximum values of the viscosity are included at the top right of the RMS profile. On the right we show our model setup where changes in the background viscosity follow from Equations (7)–(9). Viscosity increases are indicated by darker shades of gray.
2.2. Numerical Model
Our numerical simulations are implemented in a two-dimensional Cartesian box with an aspect ratio of 2:1 (x:z). The model is discretized to 512 × 256 grid points. The horizontal grid spacing is constant and the resolution in the box is approximately 11 km. The vertical grid spacing is refined toward the rock-air interface, yielding a maximum vertical resolution of 4 km. On average, 100 Lagrangian tracers per grid cell are used to track the composition (i.e., mantle, weak crust, continent, and air) and physical interfaces (e.g., the free surface) in sub-grid resolution. The extensive tests carried out in previous studies such as Crameri and Tackley (2015) and Crameri and Lithgow-Bertelloni (2018) indicate that our simulations have the required resolution to capture the dynamics presented here. However, we have further verified that there are no under-resolved numerical issues, through resolution tests specifically performed for orphaning. The latter are described in detail in the Supplementary Material.
2.3. Boundary and Initial Conditions
The top boundary, including the sticky air layer after Crameri et al. (2012a), is set to a constant 300 K, while the bottom boundary is insulating with a zero heat flux condition. The bottom boundary is free slip and the top simulates a free surface. The side boundaries are periodic to prevent unnatural effects during the model's longer time evolution (Chertova et al., 2012).
The initial condition of our model is one of on-going subduction, with a down-going 400 km long, straight slab (see Figure 3). The slab initially has a constant thickness corresponding to the surface plate thickness at the trench. The slab dip angle is initially defined at the shallow depth range of around 150 − 250 km and subsequently evolves freely. During model evolution, slab tip angles are measured at a depth of 175 km, to account for effects of mantle phase- and/or viscosity transitions.
The initial model setup features a spreading plate boundary at the edge of the box, which self-consistently evolves into a divergent plate boundary during subsequent model evolution. The initial temperature field consists of a standard -law to account for a thickening plate from the ridge toward the subduction trench. The initial plate thickness , where wBL, 0 is a constant controlling the maximum thickness of the plate, x is the horizontal coordinate and Δxsc is the distance from the spreading center at any given position x. The initial temperature is related to plate age as Tz(x) = T0 · erf[(1 − z)/wBL(x)], with T0 = 0.64 the initial, non-dimensional mantle temperature and z the vertical coordinate ranging between 0 at the bottom to 1 at the top boundary. The plate's non-dimensional initial thickness at the trench is chosen to be ~ 0.04D based on the observation that this is a typical boundary layer thickness with the chosen Ra = 107 and H = 18.08 (Crameri and Tackley, 2015). The resulting buoyancy contrast across the plate with variable thickness naturally supports the subsequent movement of the plate away from the ridge. The plate, as everything else in our model, is allowed to evolve freely out of this initial condition within the given boundary conditions and no artificial forcing is imposed (i.e., the model can evolve freely, and what goes out on one side of the domain, comes in on the other side of the domain). No weakening is imposed at the ridge and spreading occurs naturally due to the half space cooling law that we implement as an initial condition, and the subsequent internal dynamics.
While the model setup remains unchanged throughout our various implementations, we do vary key parameters to map out the slab orphaning regime space. We vary the slab yield stress (a measure of slab strength) via the ductile yield stress limit (see Equation 9), the Clapeyron slope, the initial subduction angles and the overriding plate type. When implemented, the continent is 2,000 km wide and 200 km deep, such that its roots extend to the bottom of the asthenosphere into the high viscosity upper mantle. The continental geometry is rectangular with an angled edge facing the trench similar to Crameri and Lithgow-Bertelloni (2018) and Grima et al. (submitted). The continental overriding plate also varies from its oceanic counterpart, due to its lighter density, higher viscosity, and friction coefficient, meaning that continental lithosphere is both lighter and stronger than oceanic lithosphere. Model parameters can be found in Table 1. Details of the model variants and the associated key parameter modifications are detailed in Table 2 below.
Finally, all our data and results are post processed and analyzed using the geodynamic diagnostic, post-processing, and visualization software StagLab 3.0 (Crameri, 2018) (http://doi.org/10.5281/zenodo.1199037).
3. Results
3.1. Orphaning Regimes
We explore a range of subduction parameters (see Table 2) to delimit the conditions under which slabs can orphan. The orphaning regime space for our standard ocean-ocean convergence models is mapped out in Figure 4. Figure 4 clearly highlights how orphaning is an intermediary, transitional stage occupying an optimal space between the two major slab end-member morphologies (i.e., flattened and penetrative slabs) as illustrated in Figure 5.
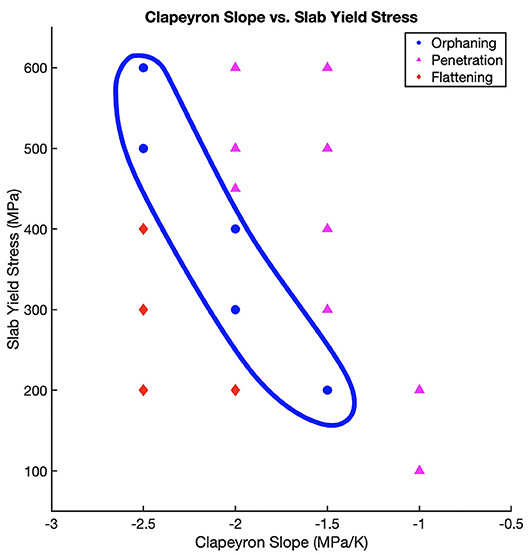
Figure 4. Regime diagram for orphaning (blue circles), penetrating (magenta triangles), and deflected (red diamonds) slab morphologies in an ocean-ocean convergence setting. The orphaning regime space is highlighted in blue and shows that orphaning is prevalent for a range of slab yield stresses/slab strengths and Clapeyron slope values. Slab orphaning describes an intermediary space in the regime diagram between deflected and penetrating morphologies, indicating that orphaning as shown in Figure 9, Videos S1, S2, can be one way for slabs to switch from one mode to the other.
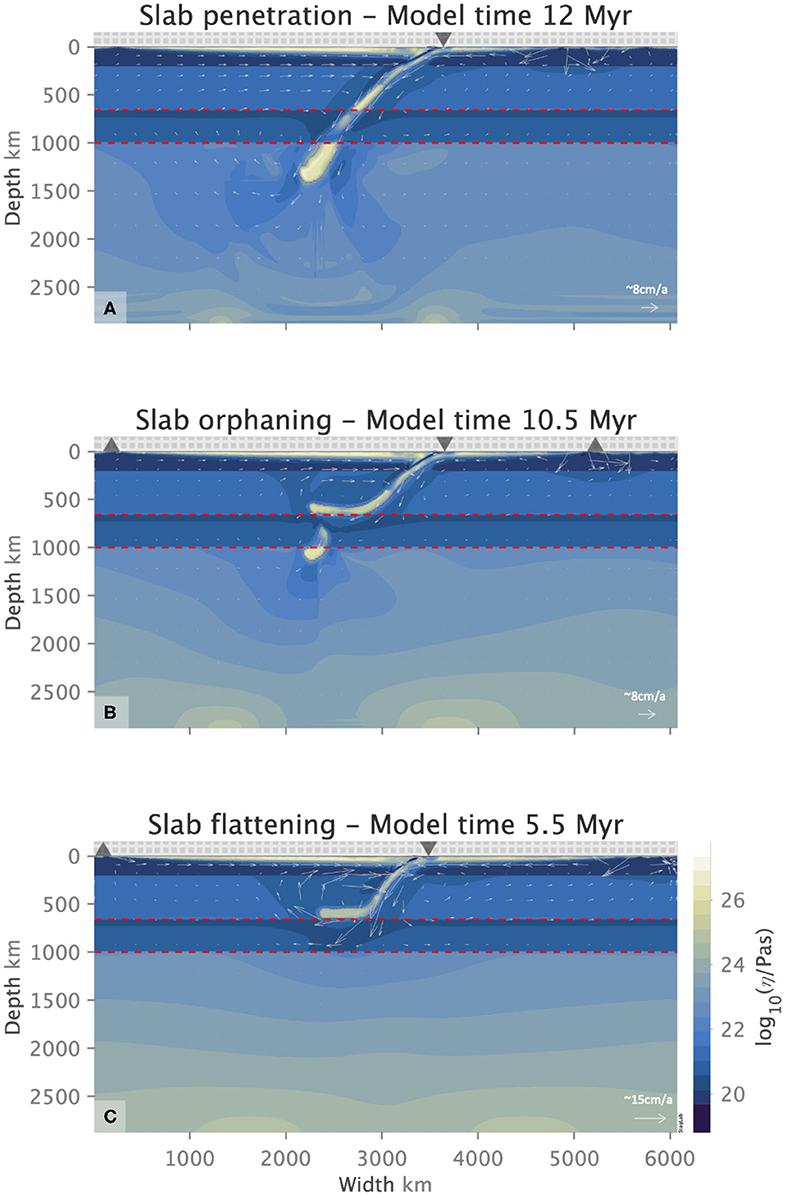
Figure 5. Penetrative (A), orphaning (B), and flattening (C) behavior for a slab with a yield stress value of 400 MPa, the subduction of which is being offset by Clapeyron slope values of −1.5, −2.0 and −2.5 MPaK−1, respectively. Sharp changes in the lower mantle viscosity underneath the slab tip are caused by sudden changes in the stress field. This is due to a heavy slab that is cold and therefore very viscous, subducting into the lower mantle where the viscosity is still stress-dependent due to dislocation creep. Orphaning occurs at the top of the lower mantle and is unaffected by the deeper lower mantle behavior. Flow arrows indicate the sense of flow direction and its relative magnitude for each figure.
We find that slab orphaning is a pervasive slab behavior that is independent of the initial conditions or the model setup. Our results highlight the prevalence of slab orphaning and show that orphaning can occur for a wide range of subduction parameters. We observe that slab orphaning behavior is common to all slabs regardless of their yield stress, indicating that orphaning can occur for both strong and weak slabs (see Figure 6). This is not to say the slab behavior and orphaning are entirely independent of the plate age. Provided that the slab's strength is offset by the appropriate resistance at the depth of the perovskite forming reaction, orphaning will persist. Figure 4 highlights this point further and illustrates slab orphaning occurring for a variety of Clapeyron slope values ranging from −2.5 to −1.5 MPaK −1. Slab orphaning is largely independent of the overriding plate type and occurs in simulations with both oceanic and continental overriding plate types (see Table 4 and Figures 7, 8). Finally, we test the effect of steepening the subduction angle of the slab at the trench and find that in our models, steeper subducting slabs will still orphan at the top of the lower mantle (see Figures 7B–D).
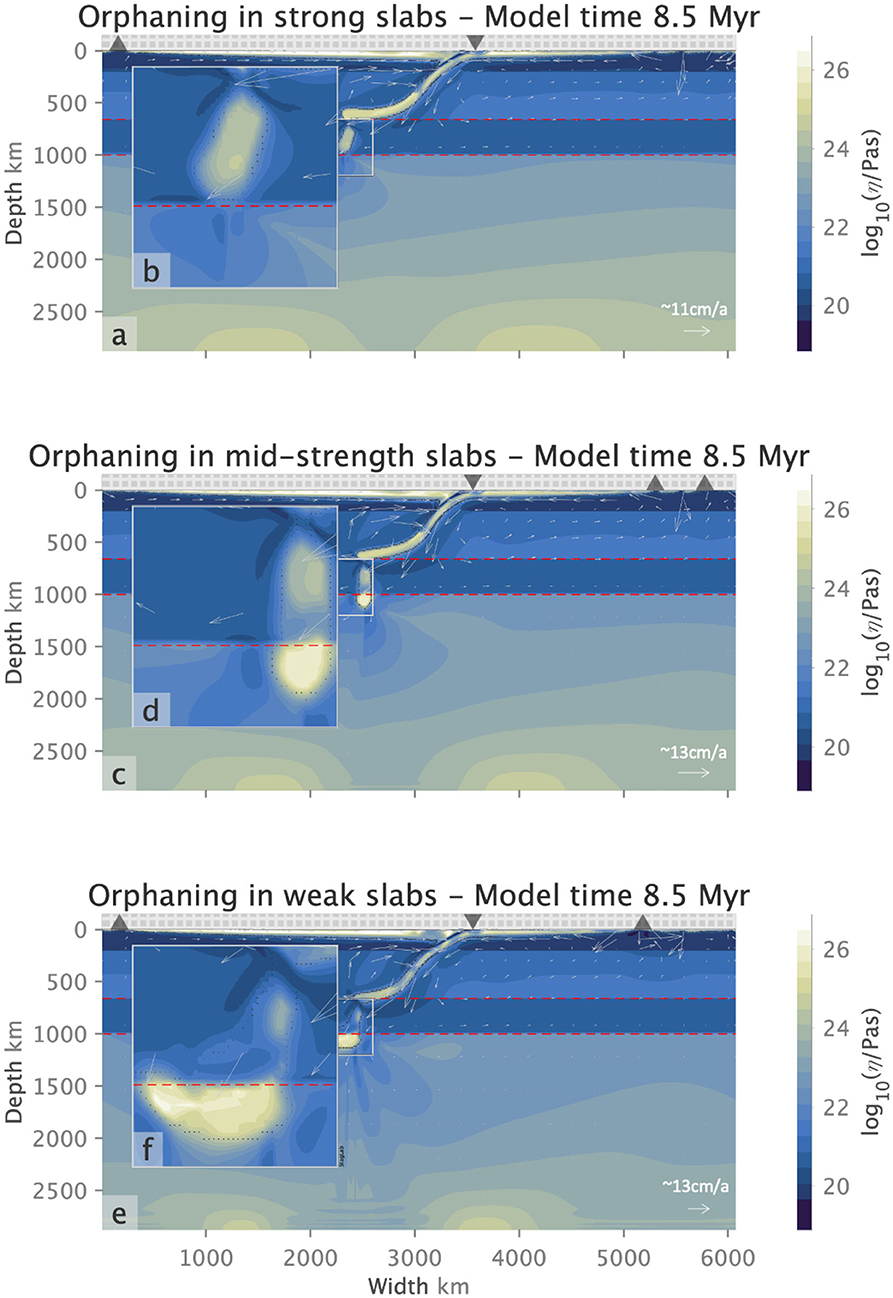
Figure 6. Slab orphaning for slab yield stress values of 600 MPa (a,b), 400 MPa (c,d), and 200 MPa (e,f) with respective Clapeyron slope values of −1.5, −2.0, −2.5 MPaK−1. Variations in orphan slab viscosity across (a–e) reflect the variations in the slab yield stress. Slabs with lower yield stresses produce weaker orphans that deform more [compare (b,d) with (f)]. (c–f) Show penetration of the orphan slab tip into the lower mantle due to the large size of the proto-orphan. In both cases the proto-orphan slab tip penetration occurs before orphaning and does not influence it. Flow arrows indicate the sense of flow direction and its relative magnitude for each figure.
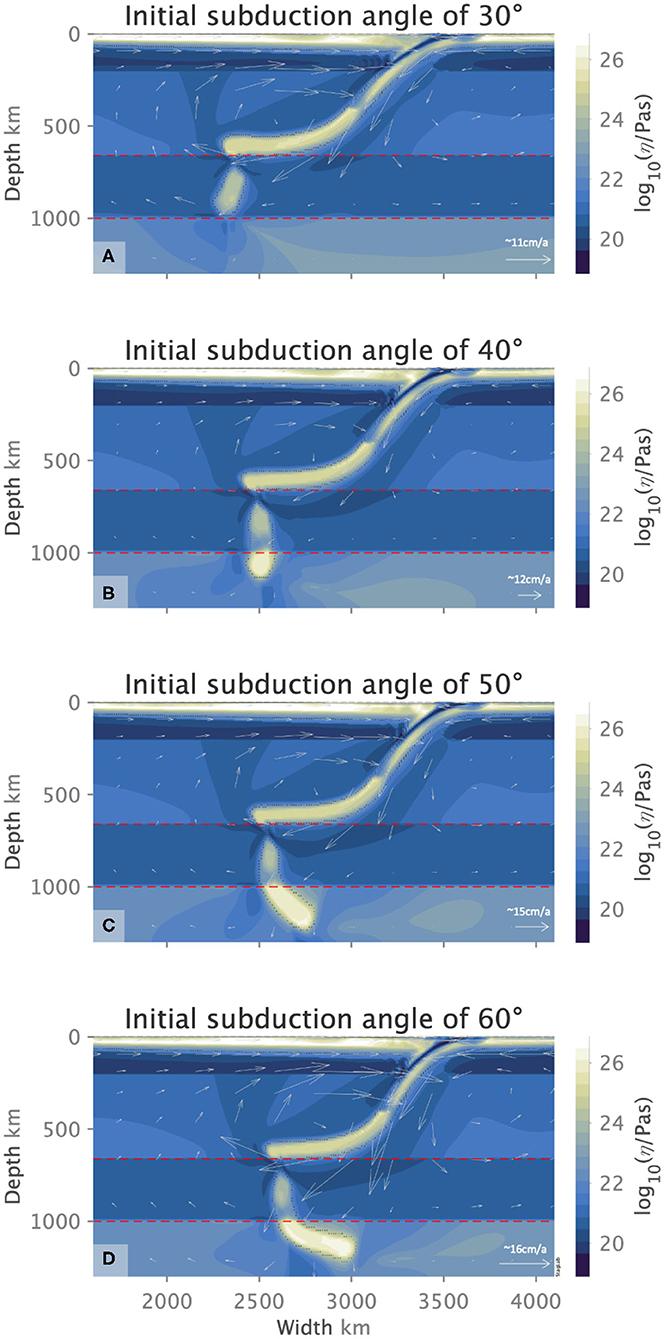
Figure 7. Slab orphaning at 8.5 Myr for initial subduction angle of 30° (A), at 9 Myr for 40° (B), and 10 Myr for 50° and 60° (C,D), respectively, in ocean-ocean settings. Flow arrows indicate the sense of flow direction and its relative magnitude for each figure.
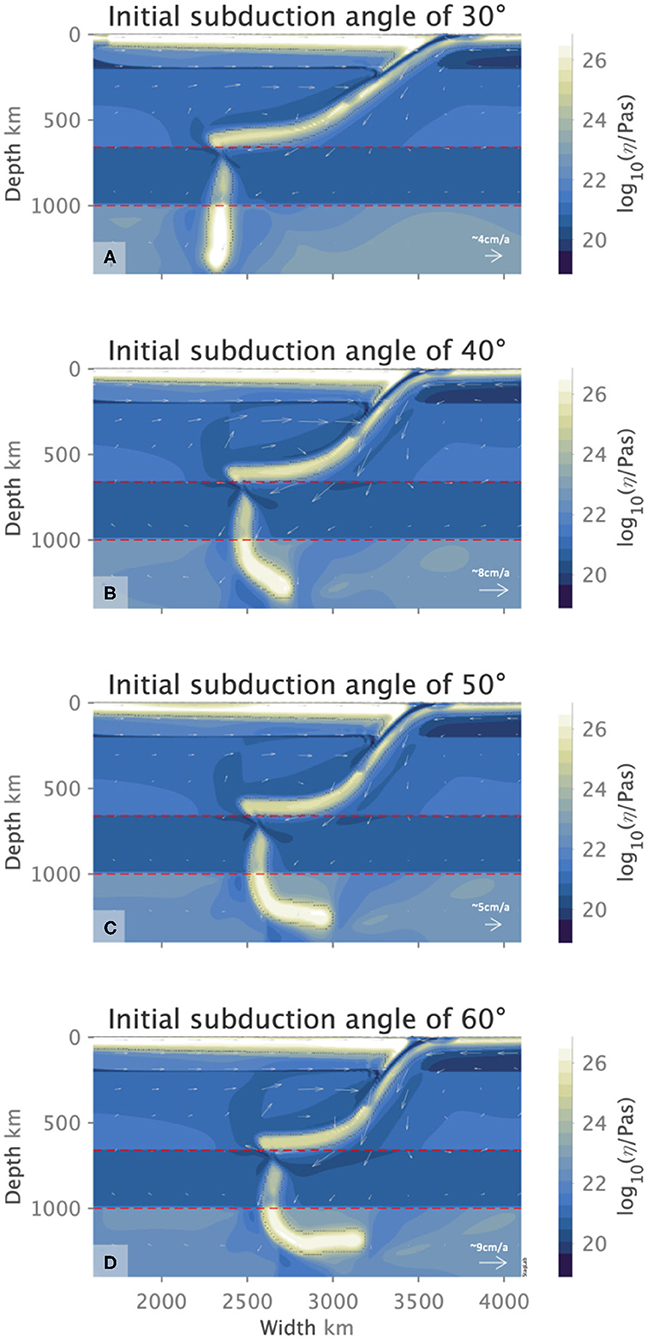
Figure 8. Slab orphaning at 22.5 Myr (A), 16.5 Myr (B), 17 Myr (C), and 18 Myr (D) for initial subduction angles of 30°, 40°, 50°, and 60°, respectively in the presence of a continental overriding plate, showing steep, curved, and overturned orphan slabs. The deep continental roots of the overriding plate reduces the overall subduction velocities due to increased coupling between the overriding plate and the uppermost-upper mantle. This encourages longer orphaning periods. Flow arrows indicate the sense of flow direction and its relative magnitude for each figure.
3.1.1. Slab Yield Stress and Orphaning
The subset of cases in Figure 4 and Table 3 illustrate that slab orphaning is a persistent phenomenon, common to both slabs with high yield stress (i.e., strong slabs) and low yield stress (i.e., weak slabs) observed for a range of Clapeyron slope values (see Figure 6). Figure 4 also indicates that for strong slabs to orphan, a considerably negative Clapeyron slope value of −2.5 MPaK−1 is necessary. Introducing less negative Clapeyron slope values for strong slabs, with yield stress values of 600 and 500 MPa, pushes the slab behavior out of the orphaning regime into a penetrative one. On the other hand, maintaining the same Clapeyron slope value of −2.5 MPaK −1 but reducing the slab yield stress to 400 MPa and below, firmly places the slab into a flattened regime.
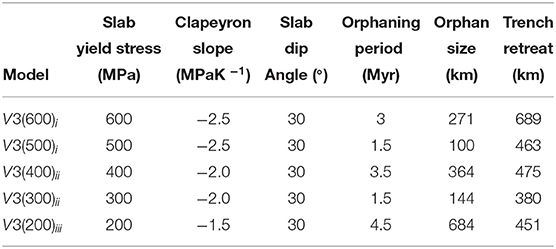
Table 3. Orphan sizes, orphaning periods, and their associated trench retreats compared across orphan variants with different slab yield stresses and Clapeyron slopes for ocean-ocean convergence models.
Slab orphaning is possible across all slab yield stress values between 600 and 200 MPa under the condition that this is offset by the right amount of resistance, allowing for the relationship between strength of the slab and that of the mantle to remain in balance. Slabs only orphan when the anomalous buoyancy associated with the delayed endothermic phase reaction in the cold slab core is large enough to resist the subduction of the slab into the LVL but not large enough to prevent the slab's initial sinking into the LVL. Strong slabs (yield stress 500–600 MPa) therefore only orphan at a Clapeyron slope value of −2.5 MPaK −1. Weaker slabs (yield stresses of 400 MPa or less) require less negative Clapeyron slopes values to orphan (−1.5 and −2.0 MPaK −1). When the slab yield stress is <200 MPa, the slab behavior is drastically altered. Slabs with yield stress values of 100 MPa are too weak to reproduce any of the morphologies observed in seismic tomography models. Clapeyron slope values of −1.0 MPaK −1 and lower do not offer enough resistance to either flatten or orphan slabs, even at a yield stress of 200 MPa.
For a Clapeyron slope of −2.0 MPaK −1 slabs are equally inclined to flatten, deflect, or orphan depending on their strength. At this Clapeyron slope and using yield stress as a proxy for age, it seems the slab age determines whether the slab will penetrate into the lower mantle, orphan or deflect and flatten across the top of the lower mantle. While orphaning generally does not preferentially occur in older (stronger) or younger (weaker) slabs, we find that for this value of the Clapeyron slope the age of the subducting slab plays a role in determining which mode it will adopt at the upper to lower mantle interface, in agreement with previous studies (e.g., van der Hilst and Seno, 1993; Goes et al., 2011, 2017; Garel et al., 2014; Agrusta et al., 2017).
Variations in the slab yield stress produce variations in the length of the orphaning period. We define the orphaning period as the time it takes for the proto-orphan to be completely separated from the parent. It encompasses the period of time from the initial weakening of the proto-orphan at the top of the lower mantle to the time of complete abandonment by its parent. Longer orphaning periods, not surprisingly, produce bigger orphan sizes. The slab with the lowest yield stress from model V3(200)iii produces the largest orphan sizes, exhibits the longest orphaning period (Table 3) and the tip of its orphan undergoes the most folding and deformation (Figure 6f). Models with higher slab yield stresses [e.g., V3(500)i and V3(300)ii] are associated with smaller orphan sizes and shorter orphaning periods.
We compare the amount of trench retreat that occurred during the individual orphaning periods for each model. The amount of trench retreat across all models from the initiation of orphaning at 660 km depth to complete separation of parent and orphan is similar across models. For three of the five models presented the trench retreat is on the order of 460 km for an average orphaning period of 1.9 Myr. Model V3(600)i exhibits significantly larger retreat of 689 km over orphaning periods of 3 Myr. The orphaning period is comparable to other cases and does not explain the larger retreat values. It seems in this case the resistance to subduction is accommodated through significant trench roll-back during the orphaning period. Why for this combination of parameters and not others? In the case of model V3(600)i the strong slab is able to both sink into the lower mantle to produce a considerably larger orphan (Table 3) and continue to act as a coherent stress guide (Conrad and Lithgow-Bertelloni, 2002) transmitting the stresses felt by the slab up to the surface pushing the trench back. In model V3(300)ii we see the most restricted trench retreat out of all the orphaning simulations. In this case the slab's yield stress is a factor of two lower and the slab is not able to transmit stresses up the plate as efficiently. The weaker slab has the second smallest orphan, the shortest orphaning period and the least trench retreat. Out of all our simulations, model V3(200)iii has the lowest possible slab yield stress that can still reproduce the slab morphologies observed in seismic tomography. In this case the slab's ability to transmit stresses to the surface is greatly reduced. The resistance to the slab's subduction is reflected in the deformation of the proto-orphan slab tip/toe and later on as the slab orphans, in the orphan slab tip, as it piles up at 1000 km depth before it sinks into the deeper lower mantle (see Figure 6f). Concurrently to orphaning the parent slab flattens at the depth of the endothermic phase change.
While a comprehensive correlation for all the orphaning behaviors described in Table 3 is difficult, it is possible to tease out some important trends. The most obvious of these is the relationship between the orphan size and the amount of time it takes for the orphan to be separated from its parent (i.e., the orphaning period). The longer the orphaning period, the bigger the orphan. This is because extended orphaning periods allow for more slab material to sink into the lower mantle before the orphan slab is completely abandoned by its parent. The largest orphaning sizes and longest orphaning periods are associated with those slabs of medium and weakest strengths [models V3(400)ii and V3(200)iii]. On the other hand, there seems to be no correlation between the amount of trench retreat and the length of the orphaning period, orphan sizes, the slab yield stress or any other variable. This seems to indicate that trench retreat during orphaning and in general is a complex process (Jarrard, 1986; Tagawa et al., 2007; Torii and Yoshioka, 2007), shaped by many interacting factors such as slab stiffness and strength, arc deformation and upper mantle flow, amongst others (e.g., Funiciello et al., 2003; Schellart, 2004; Faccenna et al., 2007; Di Giuseppe et al., 2008; Boutelier and Cruden, 2013; Čížková and Bina, 2013) most of which are not taken into account here.
3.1.2. Subduction Angles
Slab orphaning is also independent of the initial subduction angle of the slab at the trench. Our results show that varying the initial, shallow-depth angle of subduction from 30° to 60° does not in anyway act as a deterrent to orphaning. We note that the steeper the initial, shallow-depth slab angle, the bigger the orphans which also tend to be highly curved and overturned (see Figure 7).
3.1.3. Orphaning and the Overriding Plate Type
As an upper-lower mantle process, slab orphaning occurs regardless of the nature of the overriding plate. Orphaning occurs both in ocean-ocean and continent-ocean convergence. However, our results indicate that there are small, subtle differences between the two. A continental overriding plate encourages longer orphaning periods and bigger orphans than its oceanic counterpart (Table 4). Slab orphans in a continent-ocean setting also exhibit steeper angles and overturning, characteristics that are less pronounced in the orphan slabs of ocean-ocean settings (see Figures 7, 8).
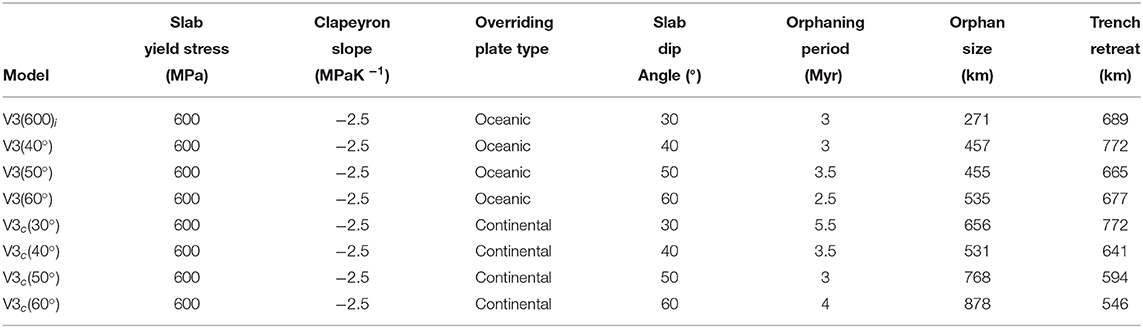
Table 4. Orphan sizes, orphaning periods, and their associated trench retreat compared across all orphan variants in intra-oceanic and continent-ocean subductions.
Table 4 details the orphaning statistics for both overriding-plate types and the associated subduction angles. The time it takes for a slab to orphan (i.e., the orphaning period) in our models ranges between 5.5 and 2.5 Myr. Models with a continental overriding plate exhibit longer orphaning periods with model V3c(30°) exhibiting the longest orphaning period. For models with an oceanic overriding plate, the longest slab orphaning periods are those for V3(50°) where the slab orphans over 3.5 Myr. In this case the longest orphaning periods do not necessarily correspond to the largest orphan sizes. Comparing the results from Table 4 with those in Table 3, we observe that the relationship between slab yield stress, orphan size, and orphaning periods is disrupted once we introduce variations in overriding plate type and initial subduction angles. This indicates that changes in these subduction parameters introduce additional forcing to the system with consequences to the relationship between the forces driving subduction and those resisting it.
The amount of trench retreat measured during the orphaning period varies across models, from 546 to 772 km over orphaning periods of 3–5.5 Myrs. The most conservative trench retreat is recorded for models with a continental overriding plate and an initial subduction angle of 60° for an orphaning period of 4 Myr. The largest trench retreats overall are measured for models with a continental overriding plate and an initial subduction angle of 30° and models with an oceanic overriding plate and an initial subduction angle of 40°, over orphaning periods of 5.5 and 3 Myr, respectively. Similar to our results presented in Table 3 in section 3.1.1, we note that there is no obvious correlation between the amount of trench retreat during orphaning and any orphaning variable recorded in Table 4.
4. Discussion
4.1. Variations in Orphaning
Slab orphaning is a new morphological feature that similar to slab flattening and penetration, prevails under a wide range of subduction parameters and initial model setups. We present examples of slab orphaning occurring for a wide variety of subduction angles, slab yield stresses, Clapeyron slope values and different overriding plate types. Key to orphaning is the presence of an LVL below 660 km and above 1,000 km depth (cf. Supplementary Section 1.4 and Figures S15, S16). This choice of the mantle viscosity structure is motivated by geophysical data and mineral physics studies that suggest the presence of an LVL directly below the upper mantle (Karato et al., 1995, 2001; Mitrovica and Forte, 2004; Rudolph et al., 2015) and a viscosity increase at 1,000 km depth (King and Masters, 1992; Kido and Čadek, 1997; Forte and Mitrovica, 2001; Mitrovica and Forte, 2004; Marquardt and Miyagi, 2015; Rudolph et al., 2015). Our choice of viscosity structure does not exclude penetrative or flattened slab morphologies in favor of slab orphaning, all three slab morphologies can be observed, depending on the slab yield stress and the Clapeyron slope value. The different slab behaviors for the same viscosity structure highlights the role of the dynamic relationship between the strength and buoyancy of the slab and those of the surrounding ambient mantle. We thus, bring to focus a more expansive role for the ambient mantle beyond that of a semi-permeable barrier to one where the deeper mantle directly affects and shapes slab behavior (Yoshioka et al., 2010).
The variations in subduction parameters give rise to a diversity of orphan slab sizes and orphaning periods. Compared to their shallower counterparts, slabs with initial shallow-depth steep subduction angles of 50° and 60° encourage steeper slab angles at the top of the lower mantle. Steeper slab angles at 660 km depth restrict the amount of untransformed, anomalous buoyant material at this depth, which reduces the resistance to the slab's subduction into the LVL and allows for more material to sink into the lower mantle to produce bigger orphans (see Figures 7C,D, 8B–D). We also observe that for steeper subduction angles particularly in the presence of a continental overriding plate, the subducted slab displays an acutely concave geometry (Figure 8) similar to that observed in previous work (e.g., Schellart, 2005; Arredondo and Billen, 2016, 2017; Billen and Arredondo, 2018) and produces overturned, upside-down slab orphans. The concave slab geometry attests to a strong slab that is forced into an acute bend before it is abandoned by its parent. The presence of a continental overriding plate slows down the subduction velocities and induces a strong shear drag in the topmost lower mantle. This introduces additional forcing to the system and encourages slab steepening, yielding larger orphan slabs over longer orphaning periods (see Figure 8 vs. Figure 7).
Slab orphaning is inherently an upper-lower mantle interface process, intrinsically tied to the internal buoyancy changes in the slab. It is entirely independent of surface plate dynamics, or specific conditions at the trench. The diversity of orphan slabs is intimately linked to the orphaning regime space and represents the dynamic balance between the slab strength vis − a − vis that of the ambient, surrounding mantle. As the relationship between the slab and mantle strength varies with depth, the subducting slab is forced to switch from a penetrative mode to a flattened one, leaving a fragmented orphan behind. Orphaning allows a slab to adjust to this evolving ratio of slab and mantle strength without causing any interruptions to the surface kinematics. In this way slab orphaning provides a transitional pathway for a slab mode switch and illustrates one example of how penetrative morphologies can be linked to flattened ones (Figure 9). Figure 4 clearly illustrates how strong, mid-strength and weak slabs can all orphan as long as the negative buoyancy of the slab is offset by an appropriate amount of anomalous buoyancy that resists the slab's subduction into the lower mantle.
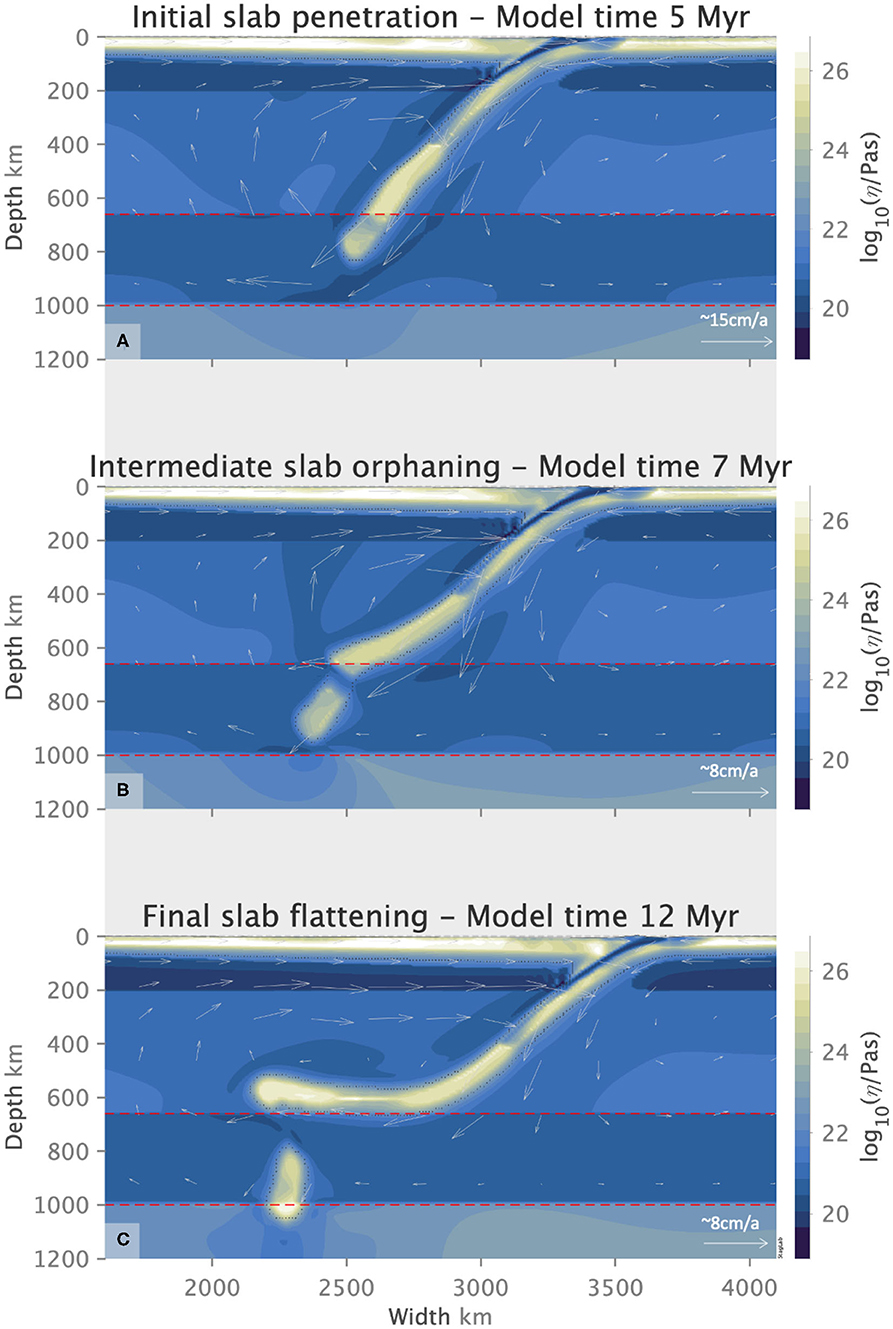
Figure 9. A slab with yield stress of 600 MPa transitions from an initial penetrative behavior (A) to a flattened morphology (C) through orphaning (B), showing how orphaning allows a slab to mode switch and transition from one morphology to the other. Flow arrows indicate the sense of flow direction and its relative magnitude for each figure.
Our results suggests that the slab orphaning process is not dependent on one particular case of subduction dynamics and can theoretically occur at most subduction zones for most slabs. The persistence of orphaning at different Clapeyron slopes indicates that orphaning should still occur for slabs in the mantle, which are not entirely made of olivine, and will have effectively less negative Clapeyron slopes. The Clapeyron slope for the ringwoodite to bridgmanite and periclase transition given in the literature, has evolved over time from −6 to −1 MPaK −1 (Anderson, 1987; Van Hunen et al., 2001; Katsura et al., 2003; Ye et al., 2017; Ishii et al., 2019). In the presence of other elements and other phases it is likely to be less negative than −3 MPaK −1. To cover the range in values, geodynamic studies tend to test for slopes between 0 and −2.5 MPaK −1 (e.g., Billen, 2008; Yoshioka et al., 2010; Honda, 2016; Mao and Zhong, 2018). We illustrate here that orphaning does happen at less negative Clapeyron slope values and is not tied to one pre-determined slab yield stress.
4.2. Orphan Slabs as an Intermediate Slab Morphology
Our results show that there is no simple and direct correlation between subduction angles, slab strength/age, and slab orphaning periods, orphan sizes and the trench retreat throughout the orphaning period. This is in agreement with the work of Jarrard (1986), who has also argued that there is no direct correlation between flattened or penetrative slab morphologies and any one subduction parameter. However, we do note that for Clapeyron slopes values of −2.0 MPaK −1 all three major slab behaviors are equally possible. This is the only case we observe where, provided all subduction parameters remain constant, slab age can determine whether the slab deflects, orphans or penetrates. At a Clapeyron slope value of −2.0 MPaK −1, if the slab has high yield stress values, then it is strong enough to overcome the resistance to its sinking. If the slab has low yield stress values then the anomalous buoyancy due to the delayed endothermic phase transition in the cold slab core will force it to flatten and deflect. Intermediary slab strengths result in orphaning (c.f. Figure 4). However, a change in the Clapeyron slope, to reflect a change in the resistance to sinking, quickly upsets this balance and leads to slab penetration or deflection. This indicates that the slab behavior at deeper mantle depths is more complex than a simple reflection of the slab age and is interdependent on both variations in slab and mantle strength.
It is clear that orphaning morphologies are representative of an intermediary slab behavior between deflected, flattened slabs and deep, penetrative ones (Figure 9). Orphaning fills the gap in the subduction regime diagram between these two end member slab behaviors. Slab orphaning also provides a possible answer to two important questions in slab dynamics: “Can slabs switch from one behavior to the other?” and “How can this transition in slab dynamics be accomplished?” A slab that has split into a parent and orphan is one that has undergone intrinsic buoyancy changes and metamorphosed through all three slab morphologies (see Figure 9). Prior to orphaning the slab adopts a penetrative morphology. Changes in the force balance within the slab in the uppermost-lower mantle force the slab to undergo orphaning, which allows it to adjust from a steep, penetrative morphology to a flattened, deflected one. Orphaning, therefore, provides one pathway through which slabs can switch modes and is available to all slabs, irrespective of their strength, the nature of the overriding plate, or the subduction angle, provided that they reach the top of the lower mantle.
5. Conclusion
We have added a new and potentially transformative element to understanding the slab morphologies observed in seismic tomography by exploring the effects of a new background mantle viscosity structure, different from the traditional viscosity increase at 660 km depth. The new viscosity structure is motivated by new geophysical and mineral physics studies (Marquardt and Miyagi, 2015; Rudolph et al., 2015; Mohiuddin et al., 2020). Slab orphaning presents for the first time, a dynamic link between penetrating and deflecting slab behaviors, and fills a gap in the subduction regime space. We propose that slab orphaning is an important facet in deep slab dynamics, and one that allows slabs to evolve from one morphology to the other as a result of slab intrinsic buoyancy changes at depth. Similar to deflected and penetrating morphologies, slab orphaning ensues for a variety of slab strengths, slab dip angles, and overriding plate types. We note that slab strength is not the only major deciding factor in shaping orphan slabs. Slab morphologies in the lower mantle are an interplay between the slab yield stress and the Clapeyron slope value, where a less negative Clapeyron slope necessitates a lower slab yield stress for orphaning to take place. This signifies that it is the relationship between the forces driving subduction and those resisting it at any given depth, which is far more important than any one single slab/subduction parameter. The new orphaning morphology and its appearance in the presence of a low viscosity layer at the top of the lower mantle, brings to the forefront the importance of determining the viscosity structure of the mantle to understand slab dynamics and interpreting seismic tomography.
Orphan slabs clearly fill the gap in the subduction regime diagram between flattened and penetrating slabs and are the intermediary between these two extensively studied slab morphologies. Seismic tomography models confirm the presence of fragmented slabs at the upper mantle lower mantle interface (e.g., Sigloch et al., 2008; Yoshida et al., 2012; Honda, 2014, 2016; Yoshida, 2017). Our results suggest that the presence of orphan slabs beneath subduction systems such as the Farallon, Tonga, Japan, Tethys, and under NE China could indicate a slab behavior switch from penetrative to flattened morphology, leaving an abandoned orphan in its wake (Grima et al., submitted). For a detailed comparison with seismic tomography we refer the reader to Grima et al. (submitted).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation. The post-processing diagnostic tool StagLab is available from https://zenodo.org/record/3783701#.X1DNSS2w2B0.
Author Contributions
AG performed the research, analyzed the results, and wrote the manuscript. FC provided the numerical model and post processing tools as well as guidance and advice. CL-B supervised the project, provided guidance, and support. All authors contributed to the article and approved the submitted version.
Funding
AG was supported by the Commonwealth Scholarship Commission and the Slichter endowed chair to CL-B, and FC was supported by the Research Council of Norway Centers of Excellence (223272). Computational support was provided by ARCHER (NE/M00046X/1) and sigma2 (NN9283K).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank the editor and reviewers for their constructive and helpful comments that greatly improved the manuscript. We also thank Lars Stixrude, Jeroen van Hunen, and John Brodholt for their fruitful discussions.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2020.00374/full#supplementary-material
Video S1. Orphaning in ultra high resolution.
Video S2. Orphaning in standard high resolution.
Data Sheet 1. Tests and evaluations.
References
Agrusta, R., Goes, S., and Hunen, J. V. (2017). Subducting-slab transition-zone interaction : stagnation, penetration and mode switches. Earth Planet. Sci. Lett. 464, 10–23. doi: 10.1016/j.epsl.2017.02.005
Anderson, D. L. (1987). Thermally induced phase changes, lateral heterogeneity of the mantle, continental roots, and deep slab anomalies. J. Geophys. Res. 92, 13968–13980. doi: 10.1029/JB092iB13p13968
Arredondo, K. M., and Billen, M. I. (2016). The effects of phase transitions and compositional layering in two-dimensional kinematic models of subduction. J. Geodyn. 100, 159–174. doi: 10.1016/j.jog.2016.05.009
Arredondo, K. M., and Billen, M. I. (2017). Coupled effects of phase transitions and rheology in 2D dynamical models of subduction. J. Geophys. Res. 122, 5813–5830. doi: 10.1002/2017JB014374
Billen, M. (2010). Slab dynamics in the transition zone. Phys. Earth Planet. Inter. 183, 296–308. doi: 10.1016/j.pepi.2010.05.005
Billen, M. I. (2008). Modeling the dynamics of subducting slabs. Annu. Rev. Earth Planet. Sci. 36, 325–356. doi: 10.1146/annurev.earth.36.031207.124129
Billen, M. I., and Arredondo, K. M. (2018). Decoupling of plate-asthenosphere motion caused by non-linear viscosity during slab folding in the transition zone. Phys. Earth Planet. Inter. 281, 17–30. doi: 10.1016/j.pepi.2018.04.011
Billen, M. I., and Hirth, G. (2007). Rheologic controls on slab dynamics. Geochem. Geophys. Geosyst. 8, 1–24. doi: 10.1029/2007GC001597
Boutelier, D., and Cruden, A. (2013). Slab rollback rate and trench curvature controlled by arc deformation. Geology 41, 911–914. doi: 10.1130/G34338.1
Buiter, S. J., Govers, R., and Wortel, M. J. (2002). Two-dimensional simulations of surface deformation caused by slab detachment. Tectonophysics 354, 195–210. doi: 10.1016/S0040-1951(02)00336-0
Burkett, E. R., and Billen, M. I. (2009). Dynamics and implications of slab detachment due to ridge-trench collision. J. Geophys. Res. 114, 1–16. doi: 10.1029/2009JB006402
Burkett, E. R., and Billen, M. I. (2010). Three-dimensionality of slab detachment due to ridge-trench collision: laterally simultaneous boudinage versus tear propagation. Geochem. Geophys. Geosyst. 11, 1–21. doi: 10.1029/2010GC003286
Chertova, M. V., Geenen, T., Van Den Berg, A., and Spakman, W. (2012). Using open sidewalls for modelling self-consistent lithosphere subduction dynamics. Solid Earth 3, 313–326. doi: 10.5194/se-3-313-2012
Christensen, U. R. (1995). Effects of phase transitions on mantle convection. Annu. Rev. Earth Planet. Sci. 23, 65–88. doi: 10.1146/annurev.ea.23.050195.000433
Christensen, U. R. (1996). The influence of trench migration on slab penetration into the lower mantle. Earth Planet. Sci. Lett. 140, 27–39. doi: 10.1016/0012-821X(96)00023-4
Christensen, U. R., and Yuen, D. (1984). The interaction of a subducting lithospheric slab with a chemical or phase boundary. J. Geophys. Res. 89, 4389–4402. doi: 10.1029/JB089iB06p04389
Christensen, U. R., and Yuen, D. (1985). Layered convection induced by phase transitions. J. Geophys. Res. 90, 10,291–10,300. doi: 10.1029/JB090iB12p10291
Čížková, H., and Bina, C. R. (2013). Effects of mantle and subduction-interface rheologies on slab stagnation and trench rollback. Earth Planet. Sci. Lett. 379, 95–103. doi: 10.1016/j.epsl.2013.08.011
Čížková, H., and Bina, C. R. (2019). Linked influences on slab stagnation: Interplay between lower mantle viscosity structure, phase transitions, and plate coupling. Earth Planet. Sci. Lett. 509, 88–99. doi: 10.1016/j.epsl.2018.12.027
Čížková, H., van Hunen, J., and van den Berg, A. (2007). Stress distribution within subducting slabs and their deformation in the transition zone. Phys. Earth Planet. Inter. 161, 202–214. doi: 10.1016/j.pepi.2007.02.002
Čížková, H., Van Hunen, J., Van den Berg, A. P., and Vlaar, N. J. (2002). The influence of rheological weakening and yield stress on the interaction of slabs with the 670 km discontinuity. Earth Planet. Sci. Lett. 199, 447–457. doi: 10.1016/S0012-821X(02)00586-1
Conrad, C. P., and Lithgow-Bertelloni, C. (2002). How mantle slabs drive plate tectonics. Science 298, 207–209. doi: 10.1126/science.1074161
Crameri, F. (2018). Geodynamic diagnostics, scientific visualisation and StagLab 3.0. Geosci. Model Dev. 11, 2541–2562. doi: 10.5194/gmd-11-2541-2018
Crameri, F., and Lithgow-Bertelloni, C. (2018). Abrupt upper-plate tilting during slab-transition-zone collision. Tectonophysics 746, 199–211 doi: 10.1016/j.tecto.2017.09.013
Crameri, F., Schmeling, H., Golabek, G. J., Duretz, T., Orendt, R., Buiter, S. J. H., et al. (2012a). A comparison of numerical surface topography calculations in geodynamic modelling: an evaluation of the sticky air method. Geophys. J. Int. 5, 38–54. doi: 10.1111/j.1365-246X.2012.05388.x
Crameri, F., and Tackley, P. J. (2015). Parameters controlling dynamically self-consistent plate tectonics and single-sided subduction in global models of mantle convection. J. Geophys. Res. 3, 1–27. doi: 10.1002/2014JB011664
Crameri, F., and Tackley, P. J. (2016). Subduction initiation from a stagnant lid and global overturn: new insights from numerical models with a free surface. Prog. Earth Planet. Sci. 3:30. doi: 10.1186/s40645-016-0103-8
Crameri, F., Tackley, P. J., Meilick, I., Gerya, T. V., and Kaus, B. J. P. (2012b). A free plate surface and weak oceanic crust produce single-sided subduction on Earth. Geophys. Res. Lett. 39, 1–7. doi: 10.1029/2011GL050046
Dal Zilio, L., Faccenda, M., and Capitanio, F. (2018). The role of deep subduction in supercontinent breakup. Tectonophysics 746, 312–324. doi: 10.1016/j.tecto.2017.03.006
Di Giuseppe, E., Van Hunen, J., Funiciello, F., Faccenna, C., and Giardini, D. (2008). Slab stiffness control of trench motion: insights from numerical models. Geochem. Geophys. Geosyst. 9, 1–19. doi: 10.1029/2007GC001776
Duretz, T., Gerya, T. V., and May, D. A. (2011). Numerical modelling of spontaneous slab breakoff and subsequent topographic response. Tectonophysics 502, 244–256. doi: 10.1016/j.tecto.2010.05.024
Duretz, T., Schmalholz, S. M., and Gerya, T. V. (2012). Dynamics of slab detachment. Geochem. Geophys. Geosyst. 13, 1–17. doi: 10.1029/2011GC004024
Faccenna, C., Heuret, A., Funiciello, F., Lallemand, S., and Becker, T. W. (2007). Predicting trench and plate motion from the dynamics of a strong slab. Earth Planet. Sci. Lett. 257, 29–36. doi: 10.1016/j.epsl.2007.02.016
Forte, A. M., and Mitrovica, J. X. (2001). Deep-mantle high-viscosity flow and thermochemical structure inferred from seismic and geodynamic data. Nature 410, 1049–1056. doi: 10.1038/35074000
Fukao, Y., and Obayashi, M. (2013). Subducted slabs stagnant above, penetrating through, and trapped below the 660 km discontinuity. J. Geophys. Res. 118, 5920–5938. doi: 10.1002/2013JB010466
Fukao, Y., Obayashi, M., and Nakakuki, T. (2009). Stagnant slab: a review. Annu. Rev. Earth Planet. Sci. 37, 19–46. doi: 10.1146/annurev.earth.36.031207.124224
Fukao, Y., Widiyantoro, S., and Obayashi, M. (2001). Stagnant slabs in the upper and lower mantle transition region. Rev. Geophys. 39, 291–323. doi: 10.1029/1999RG000068
Funiciello, F., Faccenna, C., Giardini, D., and Regenauer-Lieb, K. (2003). Dynamics of retreating slabs: 2. Insights from three-dimensional laboratory experiments. J. Geophys. Res. 108, 1–16. doi: 10.1029/2001JB000896
Garel, F., Goes, S., Davies, D. R., Davies, J. H., Kramer, S. C., and Wilson, C. R. (2014). Interaction of subducted slabs with the mantle transition-zone: a regime diagram from 2-D thermo-mechanical models with a mobile trench and an overriding plate. Geochem. Geophys. Geosyst. 15, 1739–1765. doi: 10.1002/2014GC005257
Goes, S., Agrusta, R., van Hunen, J., and Garel, F. (2017). Subduction-transition zone interaction: a review. Geosphere 13:GES01476.1. doi: 10.1130/GES01476.1
Goes, S., Capitanio, F. A., Morra, G., Seton, M., and Giardini, D. (2011). Signatures of downgoing plate-buoyancy driven subduction in Cenozoic plate motions. Phys. Earth Planet. Inter. 184, 1–13. doi: 10.1016/j.pepi.2010.10.007
Hafkenscheid, E., Wortel, M. J. R., and Spakman, W. (2006). Subduction history of the Tethyan region derived from seismic tomography and tectonic reconstructions. J. Geophys. Res. 111, 1–26. doi: 10.1029/2005JB003791
Hager, B. H., Clayton, R. W., Richards, M. A., Comer, R. P., and Dziewonski, A. M. (1985). Lower mantle heterogeneity, dynamic topography and the geoid. 313, 541–545. doi: 10.1038/314752a0
Hager, B. H., and Richards, M. A. (1984). Geoid anomalies in a dynamic Earth. J. Geophys. Res. 89, 5987–6002. doi: 10.1029/JB089iB07p05987
Hager, B. H., and Richards, M. A. (1989). Long-wavelength variations in Earth's geoid: physical models and dynamical implications. Philos. Trans. R. Soc. Lond. Ser. A 328, 309–327. doi: 10.1098/rsta.1989.0038
Honda, S. (2014). Strength of the slab inferred from the seismic tomography and geologic history around the Japanese Islands. Geochem. Geophys. Geosyst. 1333–1347. doi: 10.1002/2014GC005225
Honda, S. (2016). Slab stagnation and detachment under northeast China. Tectonophysics 671, 127–138. doi: 10.1016/j.tecto.2016.01.025
Ishii, T., Huang, R., Myhill, R., Fei, H., Koemets, I., Liu, Z., et al. (2019). Sharp 660-km discontinuity controlled by extremely narrow binary post-spinel transition. Nat. Geosci. 12, 869–872. doi: 10.1038/s41561-019-0452-1
Jarrard, R. D. (1986). Relations among subduction parameters. Rev. Geophys. 24, 217–284. doi: 10.1029/RG024i002p00217
Karato, S., Riedel, M. R., and Yuen, D. A. (2001). Rheological structure and deformation of subducted slabs in the mantle transition zone: implications for mantle circulation and deep earthquakes. Phys. Earth Planet. Inter. 127, 83–108. doi: 10.1016/S0031-9201(01)00223-0
Karato, S.-i., Shuqing, Z., and Hans-Rudolf, W. (1995). Superplasticity in Earth's lower mantle: evidence from seismic anisotropy and rock physics. Science 270:458. doi: 10.1126/science.270.5235.458
Katsura, T., Yamada, H., Shinmei, T., Kubo, A., Ono, S., Kanzaki, M., et al. (2003). Post-spinel transition in Mg2SiO4 determined by high P - T in situ X-ray diffractometry. Phys. Earth Planet. Inter. 136, 11–24. doi: 10.1016/S0031-9201(03)00019-0
Kido, M., and Čadek, O. (1997). Inferences of viscosity from the oceanic geoid: Indication of a low viscosity zone below the 660-km discontinuity. Earth Planet. Sci. Lett. 151, 125–137. doi: 10.1016/S0012-821X(97)81843-2
King, S. D., and Masters, G. (1992). Scott D. King x and guy masters. Geophys. Res. Lett. 19, 1551–1554. doi: 10.1029/92GL01700
Machetel, P., and Weber, P. (1991). Intermittent layered convection in a model mantle with an endothermic phase change at 670 km. Nature 350, 55–57. doi: 10.1038/350055a0
Mao, W., and Zhong, S. (2018). Slab stagnation due to a reduced viscosity layer beneath the mantle transition zone. Nat. Geosci. 11, 876–881. doi: 10.1038/s41561-018-0225-2
Marquardt, H., and Miyagi, L. (2015). Slab stagnation in the shallow lower mantle linked to an increase in mantle viscosity. Nat. Geosci. 8, 311–314. doi: 10.1038/ngeo2393
Mitrovica, J. X., and Forte, A. M. (2004). A new inference of mantle viscosity based upon joint inversion of convection and glacial isostatic adjustment data. Earth Planet. Sci. Lett. 225, 177–189. doi: 10.1016/j.epsl.2004.06.005
Mohiuddin, A., ichiro Karato, S., and Girard, J. (2020). Slab weakening during the olivine to ringwoodite transition in the mantle. Nat. Geosci. 13, 170–174. doi: 10.1038/s41561-019-0523-3
Nakakuki, T., Tagawa, M., Iwase, Y., Suetsugu, D., Bina, C., Inoue, T., et al. (2010). Dynamical mechanisms controlling formation and avalanche of a stagnant slab. Phys. Earth Planet. Inter. 183, 309–320. doi: 10.1016/j.pepi.2010.02.003
Richards, M. A., and Lenardic, A. (2018). The Cathles Parameter (Ct): a geodynamic definition of the asthenosphere and implications for the nature of plate tectonics. Geochem. Geophys. Geosyst. 19, 4858–4875. doi: 10.1029/2018GC007664
Richards, S., Holm, R., and Barber, G. (2011). When slabs collide: a tectonic assessment of deep earthquakes in the Tonga-Vanuatu region. Geology 39, 787–790. doi: 10.1130/G31937.1
Rudolph, M. L., Lekić, V., and Lithgow-Bertelloni, C. (2015). Viscosity jump in Earth's mid-mantle. Science 350, 1349–1352. doi: 10.1126/science.aad1929
Schellart, W. P. (2004). Kinematics of subduction and subduction-induced flow in the upper mantle. J. Geophys. Res. B 109, 1–19. doi: 10.1029/2004JB002970
Schellart, W. P. (2005). Influence of the subducting plate velocity on the geometry of the slab and migration of the subduction hinge. Earth Planet. Sci. Lett. 231, 197–219. doi: 10.1016/j.epsl.2004.12.019
Schellart, W. P., and Spakman, W. (2012). Mantle constraints on the plate tectonic evolution of the Tonga-Kermadec-Hikurangi subduction zone and the South Fiji Basin region. Austr. J. Earth Sci. 59, 933–952. doi: 10.1080/08120099.2012.679692
Sigloch, K. (2011). Mantle provinces under North America from multifrequency P wave tomography- Supplement. Geochem. Geophys. Geosyst. 12, 1–27. doi: 10.1029/2010GC003421
Sigloch, K., and Mihalynuk, M. G. (2013). Intra-oceanic subduction shaped the assembly of Cordilleran North America. Nature 496, 50–56. doi: 10.1038/nature12019
Sigloch, K., Mihalynuk, M. G., McQuarrie, N., and Nolet, G. (2008). Two-stage subduction history under North America inferred from multiple-frequency tomography. Nature 1, 458–462. doi: 10.1038/ngeo231
Tackley, P. J. (1994). Three-dimensional models of mantle convection : influence of phase transitions and temperature-dependent viscosity (Ph.D. thesis). Caltech, Pasadena, CA, United States.
Tackley, P. J. (1996). Effects of strongly variable viscosity on three-dimensional compressible convection in planetary mantles. J. Geophys. Res. 101, 3311–3331. doi: 10.1029/95JB03211
Tackley, P. J. (2000). Self-consistent generation of tectonic plates in time dependent, three-dimensional mantle convection simulations 1. Pseudoplastic yielding. Geochem. Geophys. Geosyst. 1, 2002–2006. doi: 10.1029/2000GC000036
Tackley, P. J. (2008). Modelling compressible mantle convection with large viscosity contrasts in a three-dimensional spherical shell using the yin-yang grid. Phys. Earth Planet. Inter. 171, 7–18. doi: 10.1016/j.pepi.2008.08.005
Tackley, P. J. (2011). Living dead slabs in 3-D: The dynamics of compositionally-stratified slabs entering a “slab graveyard” above the core-mantle boundary. Phys. Earth Planet. Inter. 188, 150–162. doi: 10.1016/j.pepi.2011.04.013
Tackley, P. J., Stevenson, D. J., Glatzmaier, G. A., and Schubert, G. (1993). Effects of an endothermic phase transition at 670 km depth on spherical mantle convection. Nature 361, 699–704. doi: 10.1038/361699a0
Tagawa, M., Nakakuki, T., and Tajima, F. (2007). Dynamical modeling of trench retreat driven by the slab interaction with the mantle transition zone. Earth Planets Space 59, 65–74. doi: 10.1186/BF03352678
Torii, Y., and Yoshioka, S. (2007). Physical conditions producing slab stagnation: constraints of the Clapeyron slope, mantle viscosity, trench retreat, and dip angles. Tectonophysics 445, 200–209. doi: 10.1016/j.tecto.2007.08.003
Turcotte, D., and Schubert, G. (2014). Geodynamics. Cambridge: Cambridge University Press. doi: 10.1017/CBO9780511843877
van der Hilst, R. (1995). 1995_Van der Hilst_ Complex morpholohy of subducted lithoshpere in the mantle beneath the Tonga Trench.pdf. Lett. Nat. 374, 154–157. doi: 10.1038/374154a0
van der Hilst, R., and Seno, T. (1993). Effects of relative plate motion on the deep structure and penetration depth of slabs below the Izu-Bonin and Mariana island arcs. Earth Planet. Sci. Lett. 120, 395–407. doi: 10.1016/0012-821X(93)90253-6
van der Meer, D. G., Spakman, W., van Hinsbergen, D. J. J., Amaru, M. L., and Torsvik, T. H. (2010). Towards absolute plate motions constrained by lower-mantle slab remnants. Nat. Geosci. 3, 36–40. doi: 10.1038/ngeo708
van der Meer, D. G., Torsvik, T. H., Spakman, W., van Hinsbergen, D. J. J., and Amaru, M. L. (2012). Intra-Panthalassa Ocean subduction zones revealed by fossil arcs and mantle structure. Nat. Geosci. 5, 215–219. doi: 10.1038/ngeo1401
van der Meer, D. G., van Hinsbergen, D. J., and Spakman, W. (2017). Atlas of the underworld: Slab remnants in the mantle, their sinking history, and a new outlook on lower mantle viscosity. Tectonophysics. 723, 309–484 doi: 10.1016/j.tecto.2017.10.004
van Hunen, J., and Allen, M. B. (2011). Continental collision and slab break-off: a comparison of 3-D numerical models with observations. Earth Planet. Sci. Lett. 302, 27–37. doi: 10.1016/j.epsl.2010.11.035
Van Hunen, J., Van den Berg, A. P., and Vlaar, N. J. (2001). Latent heat effects of the major mantle phase transitions on low-angle subduction. Earth Planet. Sci. Lett. 190, 125–135. doi: 10.1016/S0012-821X(01)00383-1
Wortel, M. J. R. (2000). Subduction and slab detachment in the Mediterranean-Carpathian region. Science 290, 1910–1917. doi: 10.1126/science.290.5498.1910
Ye, Y., Prakapenka, V., Meng, Y., and Shim, S. H. (2017). Intercomparison of the gold, platinum, and MgO pressure scales up to 140 GPa and 2500 K. J. Geophys. Res. 122, 3450–3464. doi: 10.1002/2016JB013811
Yoshida, M. (2017). Trench dynamics: Effects of dynamically migrating trench on subducting slab morphology and characteristics of subduction zones systems. Phys. Earth Planet. Inter. 268, 35–53. doi: 10.1016/j.pepi.2017.05.004
Yoshida, M., Tajima, F., Honda, S., and Morishige, M. (2012). The 3D numerical modeling of subduction dynamics: Plate stagnation and segmentation, and crustal advection in the wet mantle transition zone. J. Geophys. Res. 117, 1–24. doi: 10.1029/2012JB009391
Yoshioka, S., Naganoda, A., Suetsugu, D., Bina, C., Inoue, T., Wiens, D., et al. (2010). Effects of trench migration on fall of stagnant slabs into the lower mantle. Phys. Earth Planet. Inter. 183, 321–329. doi: 10.1016/j.pepi.2010.09.002
Yoshioka, S., Yuen, D. A., and Larsen, T. B. (1995). Slab weakening: mechanical and thermal-mechanical consequences for slab detachment. Island Arc 4, 89–103. doi: 10.1111/j.1440-1738.1995.tb00134.x
Keywords: slab orphaning, slab dynamics, slab orphaning regimes, deep slab morphologies, deep slab breakoff, subduction dynamics, slab fragmentation, remnant slabs
Citation: Grima AG, Lithgow-Bertelloni C and Crameri F (2020) Orphaning Regimes: The Missing Link Between Flattened and Penetrating Slab Morphologies. Front. Earth Sci. 8:374. doi: 10.3389/feart.2020.00374
Received: 01 April 2020; Accepted: 10 August 2020;
Published: 18 September 2020.
Edited by:
Marina Manea, National Autonomous University of Mexico, MexicoReviewed by:
Masanori Kameyama, Ehime University, JapanLuca Dal Zilio, California Institute of Technology, United States
Bernhard Maximilian Steinberger, Helmholtz Center Potsdam, Germany
Copyright © 2020 Grima, Lithgow-Bertelloni and Crameri. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Antoniette Greta Grima, YS5ncmltYS4xMUB1Y2wuYWMudWs=
 Antoniette Greta Grima
Antoniette Greta Grima Carolina Lithgow-Bertelloni
Carolina Lithgow-Bertelloni Fabio Crameri
Fabio Crameri