Seismo-Acoustic Characterization of Mount Cleveland Volcano Explosions

Volcanic explosions can produce large, ash-rich plumes that pose great hazard to aviation, yet may often have few precursory geophysical signals. Mount Cleveland is one of the most active volcanoes in the Aleutian Arc, Alaska (United States) with at least 65 explosions between December 2011 and June 2020. We characterize the seismo-acoustic signals from explosions at Mount Cleveland over a period of 4 years starting in 2014 when the permanent local instrumentation was installed. While the seismic explosion signals are similar, the acoustic signals vary between explosions. Some explosion acoustic waveforms exhibit a single main compressional phase while other waveforms have multiple compressions. The time lag between seismic and acoustic arrivals varies considerably (up to 2.20 s) at a single station ∼3 km from the vent, suggesting a change in propagation path for the signals between explosions. We apply a variety of methods to explore the potential contributions to this variable time lag from atmospheric conditions, nonlinear propagation, and source depth within the conduit. This variable time lag has been observed elsewhere, but explanations are often unresolved. Our results indicate that while changes in atmospheric conditions can explain some of the variation in acoustic arrival time relative to the seismic signal arrivals, substantial residual time lag variations often still exist. Additionally, nonlinear propagation modeling results do not yield a change in the onset time of the acoustic arrival with source amplitudes comparable to (and larger) than Cleveland explosions. We find that a spectrum of seismic cross-correlation values between events and particle motion dip angles suggests that a varying explosion source depth within the conduit likely plays a dominant role in the observed variations in time lag. Explosion source depths appear to range from very shallow depths down to ∼1.5–2 km. Understanding the seismo-acoustic time lag and the subsequent indication of a variable explosion source depth may help inform explosion source modeling for Mount Cleveland, which remains poorly understood. We show that even with a single co-located seismic and acoustic sensor that does not always remain on scale, it is possible to provide meaningful interpretations of the explosion source depth which may help monitoring agencies understand the volcanic system.

1. Introduction

Coupled seismic and acoustic analyses can be used to help understand shallow to subaerial explosion sources, including buried chemical explosions (e.g., Arrowsmith et al., 2010; Jones et al., 2015; Blom et al., 2020) and volcanic eruptions (e.g., Johnson and Aster, 2005; Petersen and McNutt, 2007; Wech et al., 2018). While some volcanoes are heavily instrumented and monitored, many eruptions occur in remote regions where minimal local monitoring equipment exists. Therefore, the ability to characterize a volcanic system with limited equipment (e.g., a single seismo-acoustic pair of sensors, McKee et al., 2018) is valuable to the volcano monitoring community.

Vulcanian eruptions tend to be violent in nature due to the formation of a dome or plug at the top of the conduit allowing for a buildup of pressure beneath (Clarke et al., 2015). The explosive destruction of this plug and subsequent fragmentation of magma in the conduit results in ash-rich volcanic plumes that are hazardous to aviation and pyroclastic fallout that can impact local communities or observers. Infrasound recordings of Vulcanian eruptions are typically characterized by short duration, high-amplitude signals with the potential for jetting or sustained tremor to occur for several minutes after the initial blast (Fee and Matoza, 2013). Sakurajima volcano, Japan is often viewed as a classic example of a Vulcanian system and its seismic and infrasonic explosion signals have been well studied over many years (e.g., Tameguri et al., 2002; Yokoo et al., 2009; Fee et al., 2014; Kim et al., 2015; Fee et al., 2017). Tameguri et al. (2002) describe the “bottom-up” explosion source model of Sakurajima as beginning with an isotropic expansion at a few kilometers depth, whose pressure waves propagate up the conduit, inducing an expansion of the lava cap or plug (viewed as a small increase in pressure on the infrasound sensor) followed by the main acoustic explosion signal. In contrast, a “top-down” model is sometimes considered, where the explosion initiates near the surface due to the pressurized build-up and failure of the plug or lava dome. This model also causes a very long period earthquake (VLP) at depth (Lyons and Waite, 2011).

Mount Cleveland, Alaska, is one of the most active volcanoes in the Aleutian Arc, with recent activity characterized by nearly continuous degassing and elevated surface temperatures, punctuated by short-lived ash-rich explosions that destroy small domes (De Angelis et al., 2012; Dixon et al., 2017; Werner et al., 2017) (www.avo.alaska.edu). The explosion signals at Mount Cleveland appear to be Vulcanian in nature (De Angelis et al., 2012), yet due to its remote setting, the volcanic system is not well-understood. Prompt and accurate characterization of explosions is essential due to the ash hazard to aviation. Satellite observations of ash plume heights resulting from these explosions can be limited because of meteorological clouds as well as latency issues, so geophysical instrumentation is often used for explosion characterization. The first local seismo-acoustic instrumentation included two stations installed at Mount Cleveland in the summer of 2014, so permanent local monitoring data are limited. Temporary, non-telemetered deployments help better understand the volcanic system, such as the installation of six broadband sensors from 2015 to 2016 (Werner et al., 2020; Haney et al., 2019; Power et al., in review). Remote infrasound recordings supplement the local instrumentation for monitoring large explosions (e.g., De Angelis et al., 2012; Iezzi et al., 2019b). While the Alaska Volcano Observatory (AVO) reports observations of Mount Cleveland at the time of each explosion, detailed characterization of the seismo-acoustic signals from Cleveland has not been performed. Here we use local seismo-acoustic instrumentation to better understand and characterize the Mount Cleveland explosions and volcanic system by taking a holistic look at trends in a variety of analysis techniques from numerous explosions. By analyzing Mount Cleveland explosions, we not only will enhance our knowledge of that particular volcano, but our investigations may illuminate similarities to analogous volcanoes worldwide.

A notable feature of the seismo-acoustic observations from Mount Cleveland explosions over the 4-year time period between 2014 and 2018 is that the difference between the acoustic arrival time in relation to the seismic arrival at station CLES (Figure 1, referred to as the “seismo-acoustic time lag”) is found to vary by up to 2.20 s. If the path and propagation conditions between the explosion source and the receiver are the same, the relative timing between the seismic and acoustic arrivals are expected also to be the same. However, a variable time delay between seismic and acoustic arrivals is observed at many volcanoes similar to Cleveland, implying that the path effects between the explosion source and the receiver may also change. The relative timing between the seismic and acoustic arrivals at co-located seismo-acoustic sensors has been used to help constrain the explosion source location within the conduit of Strombolian and Vulcanian systems, although full explanations are still elusive. Yamada et al. (2016) found that the arrival time differences between seismic and acoustic waveforms vary between 0.5 and 2.1 s at a distance of 5.1 km from the vent of Lokon-Empung volcano, Indonesia. They propose that the cause of the discrepancies does not appear solely to be the atmosphere based on a simple calculation of sound speed given realistic temperature and wind conditions (T = 293 K, winds ±5 m/s), and therefore may be due to source depth changes within the conduit. Ruiz et al. (2006) noted varying time lags of ∼9.3–12.6 s (3.516 km from vent) at Tungurahua volcano, Ecuador, which they contend supports a model where explosions occur at different depths within the shallow portion of the conduit (<200 m depth). Ruiz et al. (2006) presented a model consisting of a spatially fixed point source with a variable velocity of the pressure wave in the conduit, but deemed it less likely than the spatially varying source depth. Sahetapy-Engel et al. (2008) used the thermo-acoustic delay times to calculate explosion source depths between 100 and 600 m below the vent at Santiaguito volcano, Guatemala. More recently, Wallace et al. (2020) observed single station seismo-acoustic time lags between ∼6 and 17 s (2.1 km from the vent) at Santiaguito over a four-year study, and concluded that the larger time differences suggests a potentially deeper fragmentation source, which is consistent with their petrologic analyses. However, Wallace et al. (2020) do not explore the variability further to calculate corresponding depths of the seismo-acoustic time lag and assumed fragmentation depth. While these studies explore a few of the factors that may affect the seismo-acoustic time delay, none combine the three effects we assume most plausible.

FIGURE 1

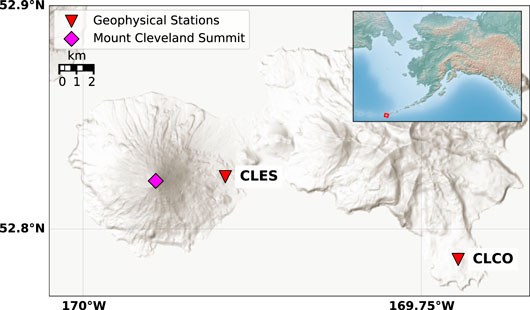
FIGURE 1. Map of Mount Cleveland and the surrounding area. The summit is denoted by a pink diamond, while the two geophysical stations CLES (3.5 km from summit) and CLCO (15.6 km from summit) are denoted by inverted red triangles. Inset map shows location of Mount Cleveland (red square) in relation to the state of Alaska.

In this manuscript, we perform the first local seismic and acoustic analyses and characterization of explosions at Mount Cleveland between 2014 and 2018. We identify three main factors that may affect the seismo-acoustic time lag, and explore their relative contributions: atmospheric conditions, nonlinear propagation, and source depth within the conduit. We apply a variety of methods on acoustic, seismic, and coupled seismo-acoustic observations aimed at extracting as much information as possible about Mount Cleveland using a single co-located seismo-acoustic station. We then combine the methods to interpret their meaning for the volcanic system and how it may be evolving through time.

2. Mount Cleveland

Mount Cleveland is a stratovolcano located in the central Aleutians on Chuginadak Island that is roughly 8.5 km in diameter near its base and 1.73 km in elevation above sea level (Miller et al., 1998). As of June 2020, Cleveland has exploded at least 65 times since December 25, 2011, making it one of the most frequently active volcanoes in Alaska and the United States. Recent activity is characterized by nearly continuous degassing and elevated surface temperatures, as well as short-lived ash-rich explosions that destroy small domes (Dixon et al., 2017; Werner et al., 2017) (www.avo.alaska.edu). The closest inhabited community is the village of Nikolski, located 75 km to the east of the volcano on Umnak Island. Due to its remote location, the main hazards from Mount Cleveland explosions are to aviation and scientists visiting the island, with at least ten explosions since 2014 resulting in detectable ash plumes to an altitude surpassing 15,000 ft (4.572 km) (www.avo.alaska.edu). Explosions occur with little to no known precursory activity suggesting explosion sources to be shallow and/or aseismic.

Previous studies on Mount Cleveland include those using satellite observations (Simpson et al., 2002; Dean et al., 2004; Gu et al., 2005; Worden et al., 2014; Wang et al., 2015; Werner et al., 2017), sparse summit gas flights (Werner et al., 2017; Werner et al., 2020), temporary seismic deployments (Janiszewski et al., 2020; Power et al., in review; Haney et al., 2019), and long range infrasound recordings (De Angelis et al., 2012; Iezzi et al., 2019b). Janiszewski et al. (2020) used receiver functions to find a low seismic velocity zone below Cleveland with a minimum vertical extent of 10–17.5 km below sea level that is <5 km in diameter. This suggests a vertically extensive magma storage region with a lack of sharp horizontal boundaries at the top and bottom of this region (Janiszewski et al., 2020). Janiszewski et al. (2020) note that their results are consistent with a well-developed open volcanic conduit system, which may help explain the general lack of precursory seismicity at Cleveland. A recent study by Werner et al. (2020) used a combination of volcanic gas emission rates and melt inclusion compositions from 2016 and found evidence that magma may be residing and degassing in a vertically extensive conduit region ranging in depth between 0.5 and 3.0 km below the summit. Power et al. (in review) focused on characterizing the general seismicity at Mount Cleveland and located hypocenters of volcano-tectonic earthquakes using a temporary seismic deployment in 2015–2016. Haney et al. (2019) performed moment tensor inversions on the three explosions that occurred during the same 2015–2016 deployment, finding a volumetric source in the VLP band (0.25–0.5 Hz) located 400–640 m above sea level (depths of ∼1.090–1.330 km beneath the summit). Werner et al. (2017) utilized gas emissions, thermal output, and lava extrusion rates to inform their interpretations on the Cleveland volcanic system. They suggest that the lack of precursory geophysical signals are due to small magma volumes, slow ascent rates, and low magma viscosity. Werner et al. (2017) also note that the persistently high thermal output of Mount Cleveland, even in inter-eruptive periods, is indicative of hot magma high in the conduit and suggest that convection causes the continued presence of shallow magma in the upper conduit. Previous studies such as De Angelis et al. (2012) and Iezzi et al. (2019b) have analyzed infrasound signals from Cleveland explosions. However, these previous studies were based on long-range signals where source observations are complicated by propagation in the atmosphere.

2.1. Monitoring Data

Prior to the installation of the local instruments at Mount Clevelend, the closest seismic station was ∼75 km away (Nikolski) and infrasound monitoring was predominantly done using the Dillingham infrasound array (992 km away, De Angelis et al., 2012; Iezzi et al., 2019b) as well as ground-coupled airwaves (GCAs) on nearby seismic networks (De Angelis et al., 2012; Fee et al., 2016). Cleveland is also monitored by AVO using satellite imagery, both in the visible and infrared bands, but the region is regularly cloudy which often obscures smaller explosion plumes below the cloud deck. Temporary seismic deployments, such as a year-long deployment from 2015 to 2016 (Janiszewski et al., 2020; Haney et al., 2019; Power et al., in review), have also been used to gain information about Mount Cleveland, though they were not telemetered in real time.

The first permanent telemetered local instrumentation was installed in the summer of 2014, allowing for more detailed studies of the volcano than previously possible. This instrumentation currently consists of two stations, each with multiple geophysical instruments. Station CLES (52.8235°N, 169.8951°W) is located 3.5 km east of the summit (Figure 1) and consists of a Trillium Compact (120 s period) broadband seismometer sampled at 50 Hz as well as an infrasound sensor. Beginning in August 2014, the infrasound sensor was a USGS VDP-5 sampled at 50 Hz which was replaced in July 2016 by a Chaparral 60UHP sensor sampled at 100 Hz. Station CLCO, located on Concord Point 15.6 km east–southeast of the summit, has a broadband and short period seismometer, web camera, and a 5-element infrasound array (Figure 1). In this study we focus on explosion signals recorded by the closest station (CLES) with co-located seismic and infrasound sensors. We do not use station CLCO for most of the analyses due to the increased influence of path effects over the longer distance, lower signal-to-noise ratio, and the station being roughly in line with station CLES and the summit, thereby not increasing azimuthal coverage around the explosion source. Additionally, part of the purpose of this study is to determine how much information about the explosion mechanism can be extracted from a single co-located seismic and infrasound sensor pair, which can sometimes be the only local instrumentation at remote volcanoes.

3. Explosion Characterization

AVO began consistently counting Mount Cleveland explosions on December 25, 2011 with monitoring capabilities consisting of remote infrasound arrays, GCAs detected by regional seismic networks, and satellite imagery (De Angelis et al., 2012). From 2011 onward, most of the activity at Cleveland consisted of cycles of dome building and subsequent dome destruction via explosive eruptions. This study focuses on 22 explosions between November 2014 and May 2018 which corresponds to Explosions 37 through 59 in the current AVO catalog. The explosion numbers considered here are limited by the installation of the first permanent local instrumentation in the summer of 2014 and a long term data outage that began in September 2018 (ending in August 2019). Detailed information on the explosions used in this study are found in Table 1. The seismic and infrasound traces at station CLES (Figure 1) for these explosions are shown in Figures 2A,B, respectively. Explosions are, in general, short-duration Vulcanian blasts, sometimes with infrasonic tremor occurring for several minutes after the initial explosion signal. The characteristics of the seismic signal produced by explosions consists of a low amplitude compressional first motion on the vertical component (Figure 2A) and positive first motion on the radial component (outward). The peak velocity for the first 9 s of the explosion signal on the vertical component ranges between 109 and 376 μm/s at a distance of 3.5 km from the vent (Table 1). For most explosions, the higher frequency GCA shows up on the seismometer after >9.5 s from the initial arrival, also showing the same variable seismo-acoustic time lag observed by the infrasound sensor. Unlike the similar nature of the seismic signals, the characteristics of the infrasound signal vary substantially between explosions. Peak pressures of the explosion infrasound waveforms at 3.5 km distance range between 21 and 260+ Pa (Table 1) and were generally short-duration. Note that 260 Pa represents the maximum pressure range of the infrasound sensor for much of the time period, thus numerous signals are saturated (clipped) and are higher than 260 Pa at a range of 3.5 km. Some explosions exhibit a single main compressional phase (e.g., Explosions 44, Figure 2B and Supplementary Figure S1A), while other explosions have multiple compressions in a row (e.g., Explosion 42, Figure 2B and Supplementary Figure S1B). A few explosions have a preceding low amplitude infrasound phase <0.5 s prior to the main explosion onset (e.g., Explosion 40, Figure 2B and Supplementary Figure S1C).

TABLE 1

TABLE 1. Mount Cleveland seismo-acoustic time lag investigation results.

FIGURE 2

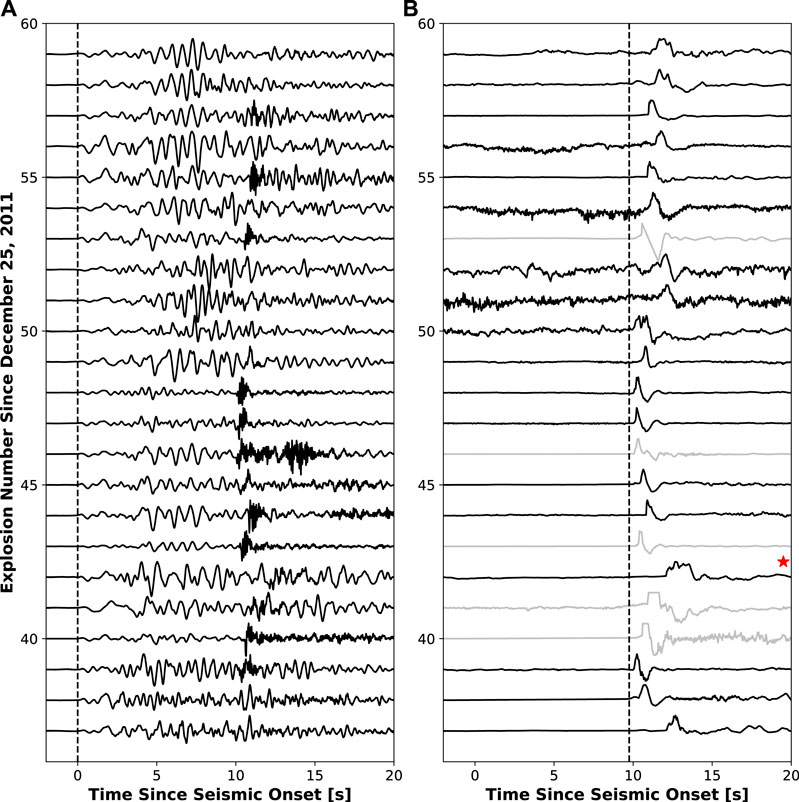
FIGURE 2. Normalized, unfiltered (A) seismic and (B) infrasound waveforms at station CLES for explosions used in this study (Explosions 37–59). Waveforms are aligned where time zero corresponds to the onset of the explosion signal on the seismometer. The infrasound waveforms that clipped are shown in gray in (B) and the date of the infrasound sensor change in July 2016 is shown by a red star. The higher frequency ground-coupled airwave can be seen for most explosions arriving after ∼9.75 s in (A). Vertical line in (B) represents the earliest acoustic arrival of 9.75 s.

The state of dome emplacement in Vulcanian systems affects the pressurization in the shallow conduit system (Clarke et al., 2015) and thus influences the explosion process. The repose time (number of days since previous explosion), as calculated from explosion dates provided by AVO (www.avo.alaska.edu), varied between 2 and 257 days over the 4-year study period but generally decreased with time (Figure 3A). During some intervals, for example between Explosions 45–49 and 56–59, the repose time remained relatively consistent at less than 54 and 22 days, respectively. AVO reported that at least ten of the 22 explosions resulted in eruption plumes visible in satellite imagery greater than 15,000 ft (4.572 km) in altitude (www.avo.alaska.edu), reinforcing the need and importance of characterizing Mount Cleveland explosions. When possible, AVO records observations of the lava dome in Cleveland’s crater using satellite imagery. There appears to be no clear relationship between whether there is no visible dome at the bottom of the crater, dome growth, or a static dome (i.e., dome that has stopped growing) and an explosion occurring (Figure 3B). For the 14 explosions for which we have reliable satellite observations before and after the explosion, 8 explosions destroyed an existing dome, 2 explosions left at least part of the dome intact, and 4 explosions occurred with no confirmed dome prior to the explosion. Dome observations, including whether there was no dome, a growing dome, or a static dome prior to explosion, as well as the dome area (and therefore height estimate) used in the propagation calculations, are subject to the availability of clear satellite imagery. Explosions 37–59 (November 2014 to May 2018) are also plotted in Figure 3B, showing the varying repose time over the course of the study period.

FIGURE 3

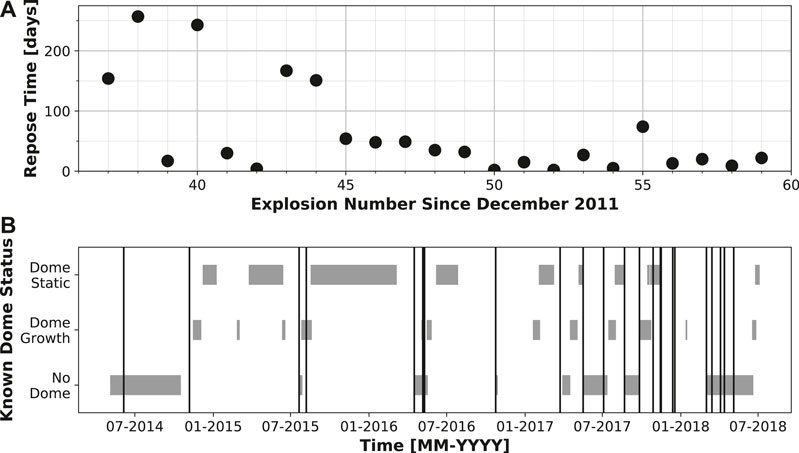
FIGURE 3. Dome emplacement and explosion relationship from mid-2014 to mid-2018. (A) Repose time (in days) prior to each explosion as a function of explosion number. (B) Dome status confirmed by satellite imagery. Categories consist of (i) “no dome”: when there was no visible dome within the crater, (ii) “dome growth”: when a dome was actively growing in size, and (iii) “dome static”: when there was a dome that had ceased growing. Vertical lines denote explosions, which vary in repose time over the course of the study period.

We note two important caveats for CLES data analysis. The first is that amplitude- and frequency-based analysis can only be used for some of the explosions due to clipping of the CLES infrasound sensor for larger explosions (5 explosions, see Figure 2B). Additionally, a GCA appears on CLES seismic data for most explosions (see Figure 2A), so some analyses are limited to the first ∼9 s of the explosion signal recorded by the seismometer. Station CLCO is farther away from the source than station CLES, so propagation effects to CLCO would likely be more substantial and harder to accurately determine than to CLES. Therefore, arrival time-based analysis of Cleveland acoustic signals at station CLES provides the most complete and reliable assessment, more so than amplitude- or frequency-based calculations at either station.

4. Seismo-Acoustic Time Lag Investigation

The observed variable seismo-acoustic time lag (tt_obs) is defined as the time difference between the infrasound travel time (tt_infra) and the seismic travel time (tt_seis)

$t{t}_{\mathrm{o}\mathrm{b}\mathrm{s}}=t{t}_{\text{infra}}-t{t}_{\text{seis}}(1)$

The acoustic arrival time in relation to the seismic arrival of the explosion signal at station CLES is found to vary up to 2.20 s for the 22 explosions investigated, as shown by Figure 2B where traces are aligned to the seismic arrival. The seismic and acoustic arrival times are picked on unfiltered vertical seismic and infrasound data, respectively, first using a short term average long term average algorithm (STA/LTA, STA length = 0.01 s, LTA length = 0.3 s) before values are manually refined. These seismo-acoustic time lags vary with explosion number (Figure 4A) and span a range of 9.75–11.95 s at a distance of 3.5 km from the vent. The distribution of seismo-acoustic time lags for the 22 explosions investigated is skewed towards shorter time lags, with a mean time lag of 10.53 s and median of 10.20 s (Figure 4B).

FIGURE 4

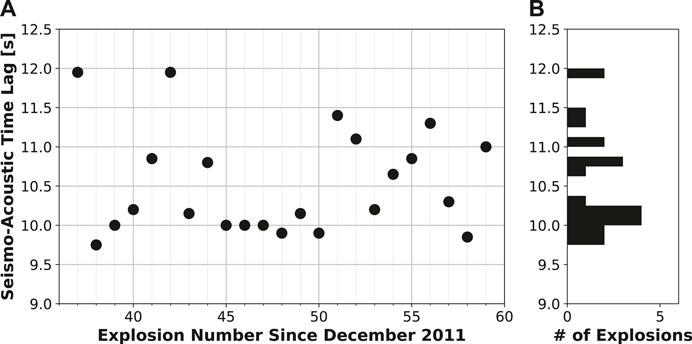
FIGURE 4. Seismo-acoustic time lag for Mount Cleveland explosions (A) as a function of explosion number, and (B) as a histogram of the time lag distribution. Histogram bins are 0.125 s in width.

A schematic of the seismo-acoustic propagation paths is shown by Figure 5. The seismic wave travels directly from the explosion source (Figure 5, Location 1) to station CLES (Figure 5, Location 4). This distance is dependent on the explosion source depth. However, because the seismic velocity is an order of magnitude greater than the acoustic velocity (∼2,500 m/s compared to ∼340 m/s) and the source-receiver distance is small (∼3.5 km), the exact distance does not have a major effect on the seismic travel time (tt_seis). We also assume that the seismic velocity is constant and does not change between explosions or along the path. The calculation of tt_seis is shown by the following equation.

$t{t}_{\text{seis}}=\frac{d_{\text{seis}}}{{\upsilon }_{\text{seis}}}(2)$

FIGURE 5

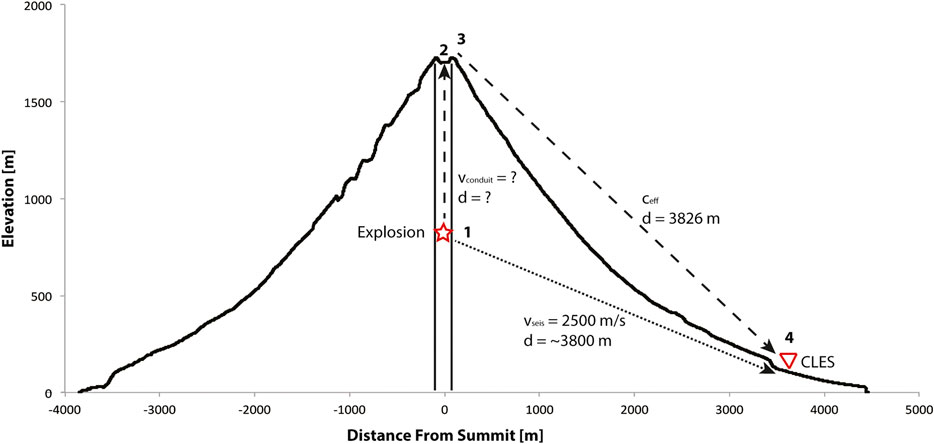
FIGURE 5. Breakdown of propagation segments for the seismic and infrasound paths. Location 1 is the explosion, Location 2 is the bottom of the crater (dome surface), Location 3 is the summit, and Location 4 is station CLES. The signal recorded by the infrasound sensor (dashed line) propagates from Location 1 through Locations 2, 3, and 4, while the initial signal recorded by the seismometer (dotted line) travels directly from Location 1 to Location 4. Elevation profile from the Polar Geospatial Center ArcticDEM (Porter et al., 2018). Vertical exaggeration is ∼2.5.

Using values of υ_seis = 2,500 m/s and d_seis = 3,800 m (assuming an explosion source near the summit), the seismic travel-time between the explosion and receiver (tt_seis) is 1.52s. The wave recorded by the infrasound sensor has a more complex propagation path. It propagates from the explosion source in the conduit (Figure 5, Location 1) to the bottom of the crater and vent location (Figure 5, Location 2) at acoustic velocity within the conduit (υ_conduit) over a distance equivalent to the source depth (d_source). Then, the wave propagates from the bottom of the crater (Figure 5, Location 2) to the top of the crater (Figure 5, Location 3) then to station CLES (Figure 5, Location 4) at the effective sound speed (c_eff) (“Atmospheric Effects” section).

The travel time of the pressure wave that is recorded by the infrasound sensor (tt_infra), and therefore variable observed acoustic time lag (tt_obs), is most likely affected by the following factors: the atmosphere (tt_atm, “Atmospheric Effects” section), potential nonlinear propagation (tt_nonlinear, “Nonlinear Propagation” section), and distance from the crater floor to the source in the conduit (d_source) coupled with potentially varying conduit material velocities (tt_conduit, “Source Depth Within the Conduit” section). We summarize the various contributions on the arrival time recorded by the infrasound sensor (tt_infra) as follows, and discuss them in subsequent sections:

$t{t}_{\text{infra}}=t{t}_{\text{atm}}-\Delta t{t}_{\text{nonlinear}}+t{t}_{\text{conduit}}(3)$

4.1. Atmospheric Effects

Variations in wind and temperature affect the propagation velocity of infrasound. These effects have been the source of multiple recent studies of volcanic explosions in Alaska (e.g., De Angelis et al., 2012; Iezzi et al., 2019b; Schwaiger et al., 2019; Schwaiger et al., 2020). Infrasound propagates in the atmosphere at the speed of sound, defined as

$c=\sqrt{\gamma RT}(4)$

where γ is the specific heat ratio, R is the universal gas constant, and T is the temperature (Pierce, 1981). In a realistic moving atmosphere, this adiabatic sound speed (Eq. 4) is modified by the vector component of the horizontal wind velocity in a particular direction ($\overrightarrow{u}\cdot \overrightarrow{v}$) and is termed the effective sound speed (c_eff), defined as (Salomons, 2001; Fee and Matoza, 2013)

$c_{\text{eff}}=c+\overrightarrow{u}\cdot \overrightarrow{v}(5)$

For Cleveland explosions registered at station CLES, the shortest observed time lag is 9.75 s (requiring a c_eff of 0.392 km/s over a range of 3.826 km) while the longest time lag is 11.95 s (requiring a c_eff of 0.320 km/s over a range of 3.826 km). This spread in effective sound speeds is unlikely, even considering the range of extreme wind and temperatures at Cleveland, as it would require winds of approximately 70 m/s sustained along the entire travel path. This would create very high noise levels at the site. We apply two different methods for inferring the contribution of the atmosphere on acoustic arrival time at CLES (i.e., estimating a unique c_eff for each explosion).

The first method to better understand the possibility of the atmosphere causing the variable observed seismo-acoustic time lags uses an atmospheric reconstruction model, AVO-G2S (Schwaiger et al., 2019), as no local weather stations or in-situ atmospheric data are available. The atmospheric conditions at Mount Cleveland are reconstructed at the closest 6-h interval for each explosion. Within AVO-G2S we use the National Centers for Environmental Prediction (NCEP) Reanalysis data (Kistler et al., 2001) for the lower atmosphere with resolution of 2.5° spatially and 6 h temporally. Once the atmosphere is reconstructed, a 1D stratified atmospheric profile at the location of Mount Cleveland (52.822°N, 169.945°W) is extracted from the reconstruction. The scalar value for effective sound speed (c_eff) above the vent (z = 1.8 km asl) in the direction of CLES (86.6° from N) is used to calculate the predicted acoustic travel time from the summit to CLES based on atmospheric conditions at the time of each explosion:

$t{t}_{\text{atm}}=\frac{d}{c_{\text{eff}}}(6)$

where d = 3.826 km (the hypotenuse distance from the summit to station CLES) plus the hypotenuse distance from the top of the dome to the crater rim (Figure 5, Locations 2–3). This distance is calculated by converting the dome area observed in satellite imagery by AVO to a dome height above the crater floor, using the ArcticDEM digital elevation model (Porter et al., 2018) for crater shape. We note that the presence or absence of a dome only changed the infrasonic path length by ∼40 m at most (depending on the size of the dome), which at a reasonable acoustic speed corresponds to 0.12 s.

The second method leverages the use of the explosion signal arrival time at one of the elements from the infrasound array (CLCO, element 1) that is at a similar azimuth from the vent as station CLES. The azimuths from the Cleveland summit to stations CLES and CLCO are 86.6° and 109.5°, respectively, so the azimuthal difference between the two stations is 22.9°. The infrasound arrival time of the explosion at station CLCO is picked and the two acoustic arrival times are subtracted. Using the distance between the stations (12.33 km) and the difference in arrival times, the effective sound speed based on station arrival times is calculated using Eq. 6.

Our results indicate that AVO-G2S-derived c_eff values are systematically lower than c_eff values found using the acoustic arrival time difference between CLES and CLCO by 0–25 m/s (Figure 6A). The observed travel time is calculated as the time lag between the seismic and infrasound arrivals at CLES, plus seismic travel time from the conduit to CLES (tt_seis, Eq. 2). Both the observed and predicted (tt_atm) travel times as a function of explosion number are shown in Figure 6B. It is clearly seen that the relatively large variation in observed acoustic travel times is not well predicted by either the atmospheric conditions of global reanalysis files (model-based) or calculations between CLES and CLCO arrivals (data-based). For the rest of our analyses, we choose the second method for effective sound speed (c_eff) calculation. If the seismo-acoustic time lags were solely due to changes in the atmosphere, we would expect a very strong correlation with the effective sound speed. However, there is only a weak negative relationship between the two values (Figure 6C). From these analyses, we conclude that while changing atmospheric conditions may partially contribute to the variable seismo-acoustic time lag observed at Cleveland, there is a lack of evidence that it is the main cause for the observed variations.

FIGURE 6

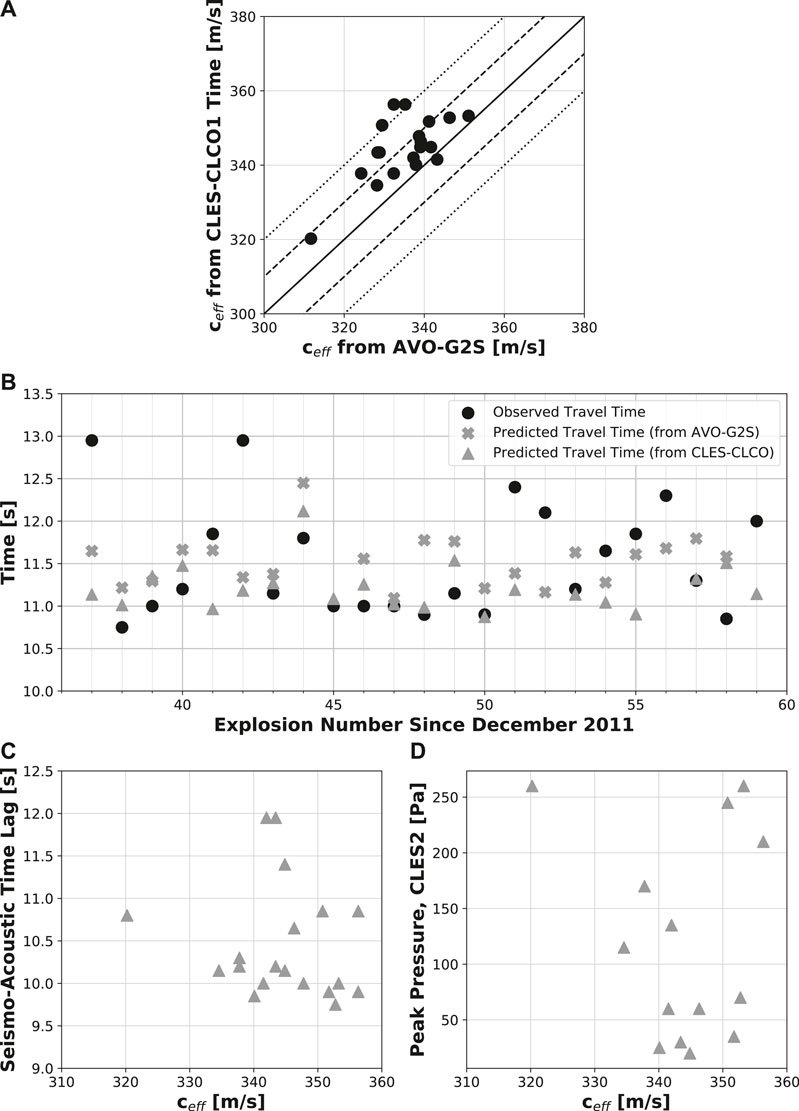
FIGURE 6. Predicted acoustic travel time based on atmospheric effects. (A) Derived c_eff from the two methods, 1) using AVO-G2S and 2) the acoustic arrival time difference between stations CLES and CLCO1. The solid line is 1:1 (values are exactly the same), with dotted lines being successively offset by 10 m/s. (B) Observed (tt_obs, black dots) acoustic travel time, predicted (tt_atm) acoustic travel time from the summit to station CLES using AVO-G2S (gray crosses), and predicted (tt_atm) acoustic travel time from the acoustic arrival time difference between stations CLES and CLCO1 (gray triangles). (C) Seismo-acoustic time lag vs effective sound speed (c_eff) using the CLES/CLCO arrival times for each explosion, showing a weak negative relationship. (D) Peak pressure at station CLES vs effective sound speed (c_eff) for each explosion that did not clip the infrasound sensor. No correlation indicates that the larger amplitude explosions did not happen to occur during times of higher effective sound speeds.

4.2. Nonlinear Propagation

A second factor that may contribute to a change in acoustic propagation time is nonlinear propagation, which is often neglected in local infrasound studies but mentioned as a potential source of error and uncertainty (e.g., Fee et al., 2017; Iezzi et al., 2019a). However, the potential impact of nonlinear propagation on the arrival time (tt_nonlinear) should be quantified, as nonlinear waves with supersonic sound speeds have been observed for volcanic explosions (e.g., Yokoo and Ishihara, 2007; Marchetti et al., 2013).

For very high amplitude acoustic sources such as some Vulcanian explosions, the sound waves produced may travel faster than the speed of sound (i.e., supersonic) and propagate nonlinearly. In nonlinear propagation, the waveform distorts as it travels, where the compressional phase travels faster than the rarefaction, potentially steepening into a shock wave (Atchley, 2005; Reichman et al., 2016; Maher et al., 2020). This shock wave is often described by the Friedlander equation (Friedlander, 1946), which defines the pressure of a shock wave (p(t)) as

$p\left(t\right)=P_s{e}^{-\frac{t}{t^{\ast }}}\left(1-\frac{t}{t^{\ast }}\right)(7)$

where P_s is the source overpressure and t* is the relaxation time (time when the rarefaction begins after the compression returns the ambient pressure). This equation for a theoretical blast wave using t* = 0.75 (value chosen to resemble data from Cleveland explosions) is shown as Figure 7A, along with the waveform for Explosion 44 from Cleveland. A recent study by Maher et al. (2020) performed a detailed analysis of local infrasound data from Sakurajima volcano and the potential impact of spectral energy transfer to higher frequencies due to nonlinear propagation. They find that the effects of nonlinear propagation have a second-order impact on source quantification, whereas the effects of wind and topography may be more influential on the recorded waveform. de Groot-Hedlin (2016) find that nonlinearity has a greater effect on the frequency of the waveform as compared to the amplitude as infrasound propagates away from the source. To our knowledge, there has not been a thorough study on the impact on arrival time due to nonlinear propagation for volcanic explosions.

FIGURE 7

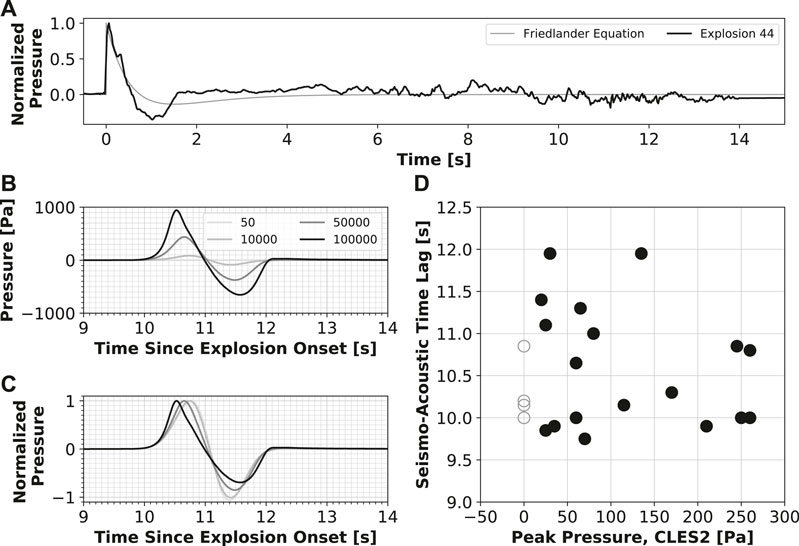
FIGURE 7. Potential contributions to the seismo-acoustic time lag from nonlinear propagation. (A) Friedlander Equation for a blast wave (gray) with normalized Explosion 44 waveform (black). (B) FDTDWave simulation results over a flat plane for source pressures between 50 Pa and 100 kPa at a range of 3.8 km from the source. (C) Normalized FDTDWave simulation results from the previous subplot. (D) Seismo-acoustic time lag vs peak pressure at CLES for explosions that did not clip the infrasound sensor. Open circles represent the time lag for explosions that clipped the infrasound sensor, plotted at a peak pressure of zero.

We note that peak pressures at CLES do not appear to strongly correlate with seismo-acoustic time lags (Figure 7D), indicating that nonlinear propagation (if present) has minimal effect on the seismio-acoustic time lag for Cleveland explosions. This is consistent with the findings of Maher et al. (2020), where nonlinear propagation was found to be a secondary effect on the observed waveform. However, it does appear that the highest peak pressures and those that clipped the infrasound sensor (Figure 7D, open circles) had lower seismo-acoustic time lags. Additionally, we investigate the connection between higher amplitude explosions and the atmospheric conditions. The lack of correlation between the peak pressure at station CLES (for events that did not clip the sensor) and the effective sound speed (Figure 6D), indicates that the larger amplitude explosions did not occur during times of higher effective sound speeds.

We use a 2D finite-difference time-domain (FDTD) code, FDTDWave (de Groot-Hedlin, 2016), to model the potential impact of nonlinear propagation on the acoustic arrival time. Our simulations involve propagating a source with a maximum frequency of 2.0 Hz over a flat plane to a range of 20 km with synthetic receivers spaced every 100 m. We set the transition from nonlinear to linear propagation at 1% ambient pressure (de Groot-Hedlin, 2016), though we note that testing was performed varying this parameter between 0.5 and 5% with no change in our results. We input source pressures ranging from 50 Pa to 100 kPa and note that current modeling capabilities using this code are limited to a linear, Gaussian input source.

Nonlinear propagation modeling results for a synthetic receiver at 3.8 km from the source (slant distance from the Cleveland summit to station CLES) show the expected distortion due to increasingly nonlinear propagation (Figures 7B,C). As the source pressure increases, the compression travels faster while the rarefaction travels relatively slower, similar to results in Maher et al. (2020). Therefore, the arrival time of the peak compression decreases with higher source pressure (Figure 7C). However, even using extreme values of source peak overpressures (Figure 7C, approximately 1,000 Pa at the range of CLES), we are not able to form a full shock front or detect a noticeable change in arrival time of the initial explosion signal recorded by the infrasound sensor. Therefore, we do not find a quantifiable impact on tt_infra from nonlinear propagation effects.

4.3. Source Depth Within the Conduit

The effects of the atmosphere and nonlinear propagation can be reasonably approximated using available data and modeling. Therefore, in previous sections we constrained these values first and assume all residual time discrepancies are due to a variable explosion source depth (d_source) within the conduit and/or conduit velocity (υ_conduit). Explosion source depth and conduit conditions are less well-understood than other aforementioned factors affecting the seismo-acoustic time lag.

The travel time of a pressure wave in the conduit from the explosion depth to the bottom of the crater can be estimated by:

$t{t}_{\text{conduit}}=\frac{d_{\text{source}}}{{\upsilon }_{\text{conduit}}}(8)$

Due to the poorly understood conditions within the conduit and limited seismo-acoustic data, we investigate the potential variable explosion source depth using three techniques: volcano acoustic seismic ratio (VASR), seismic cross-correlation between explosions, and seismic particle motion analysis. We also tried methods of investigating the arrival time of various seismic frequency components and CLES/CLCO seismic amplitude ratio. We include those analyses in the Supplemental Material, as they were not found to be as useful as the three methods in this section (see Supplementary Figures S2 and S3 along with associated text). We are not able to estimate the actual source depth due to the limited data.

4.3.1. Volcano Acoustic Seismic Ratio

Volcanic explosion energy couples into both the atmosphere as acoustic energy and ground as seismic energy. We follow the methods of Johnson and Aster (2005) to calculate the relative partitioning of the energy that is recorded as acoustic and seismic waves, termed Volcano Acoustic Seismic Ratio (VASR). Lower VASR may suggest a deeper explosion source within the conduit; however, caution should be exercised in this interpretation as there are many other factors that can affect the energy partitioning. Note, this can only be used for explosions that did not clip the infrasound sensor.

The acoustic energy (E_acoustic) radiated can be calculated by integrating over a hemispherical surface, assuming a monopole source and homogeneous atmosphere (e.g., Firstov and Kravchenko, 1996; Johnson, 2003; Vergniolle et al., 2004; Johnson and Aster, 2005)

$E_{\text{acoustic}}=\frac{2\pi r^2}{{\rho }_{\text{atmos}}{c}_{\text{atmos}}}{\displaystyle \int \Delta P{\left(t\right)}^2\mathrm{d}t}(9)$

where ρ_atmos is the air density, c_atmos is the speed of sound, and ΔP is the excess pressure. Similarly, the seismic energy (E_seismic) for an isotropic source located at the top of a homogeneous halfspace can be calculated using (Boatwright, 1980; Johnson and Aster, 2005)

$E_{\text{seismic}}=2\pi r^2{\rho }_{\text{earth}}{\upsilon }_{\text{seis}}\frac{1}{A}{\displaystyle \int S^{2}U{\left(t\right)}^2\text{d}t}(10)$

where r is the distance between source and receiver, S is the seismic site response, A is the attenuation, ρ_earth is the volcano density, and U² is the squared particle velocity.

We follow suggestions of Johnson and Aster (2005) and use a bandpass filter between 0.5 and 12 Hz for both acoustic and seismic traces, ρ_atmos = 1.2 kg/m³, c_atmos = 340 m/s, ρ_earth = 2,000 kg/m³, and υ_seis = 2,500 m/s. Note since we do not have good estimates of the seismic attenuation or site response, the values we calculate are only relative to other Cleveland explosions (termed “relative VASR”, VASR_rel) since we set S and A equal to one (i.e., the seismic portion is not true “energy”) and should therefore not be compared with values from other studies. A similar method was used in Fee et al. (2020). Energies are calculated over the first 9 s of the explosion signal onset (infrasound calculation is delayed by the seismo-acoustic time lag) since GCAs appear for most explosions on the seismic data after this time.

VASR_rel is variable for the explosions investigated here (Figure 8A), with Explosions 45, 47–48 having the highest VASR_rel and the rest of the explosions being lower. While there is no trend observed between low values of VASR_rel and the seismo-acoustic time lag (Figure 8B), the three explosions with the highest VASR_rel values (Explosions 45, 47–48) have low seismo-acoustic time lags and none of the explosions with higher seismo-acoustic time lags exhibited high values of VASR_rel.

FIGURE 8

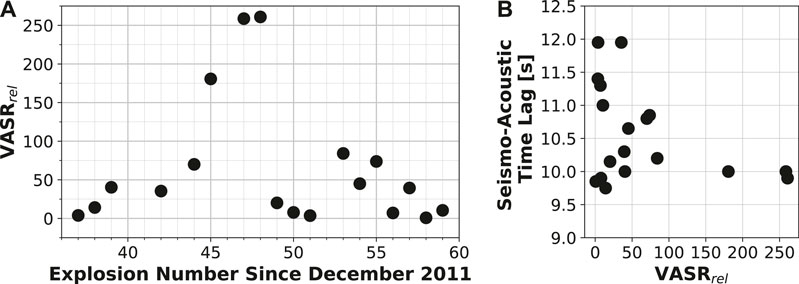
FIGURE 8. Relative VASR (VASR_rel) for explosions that did not clip the infrasound sensor (A) as a function of explosion number and (B) compared to the seismo-acoustic time lag.

4.3.2. Seismic Cross-Correlation

Correlation between seismic waveforms can be used to help determine precise seismic source locations and identify similar source properties from the recorded waveforms. The premise is that seismicity that occurs in the same location may have very similar waveforms due to the seismicity experiencing the same propagation effects over the same path between the source and receiver (Waldhauser and Ellsworth, 2000; Green and Neuberg, 2006; Varley et al., 2010). Using each explosion as a template, we cross-correlate the vertical trace with the rest of the explosions. The seismic data are trimmed to a 10.5 s window surrounding each explosion, starting 1.5 s prior to the explosion onset and ending 9 s after to avoid the GCAs. The data are bandpass filtered between 0.1 and 1.0 Hz.

The correlation of the seismic waveforms between explosions is variable. An example of the similarity between the highly correlated Explosions 45 and 46 (correlation value of 0.91) in this frequency band is shown by Figure 9A. Cross-correlation results for all explosions are shown in Figure 9B, where the diagonal line represents each event correlated with itself (cross-correlation value of 1). There is a section of higher correlation values in the center of Figure 9B (Explosions 43–48), which not only occur sequentially in time, but also have a fairly stable time lag around 10.0 s (Figure 4A). We discuss this further in the “General Characterization of Explosions” section. Explosions 53–59 also have high correlation values (Figure 9B), but in contrast to the previous cluster, the corresponding seismo-acoustic time lags are not similar (Figure 4A). Explosion 45 appears to have higher correlation values with the other explosions (Figure 9B) as well as a time lag close to the median (Figure 4A). The cross-correlation values between Explosion 45 and all other explosions are compared with the seismo-acoustic time lag of each explosion (Figure 9C). The relationship has a “V” shape, where the cross-correlation value increases slightly/remains constant from the lowest time lag, reaches a maximum correlation value at the time lag associated with Explosion 45 (time lag = 10.00 s, cross-correlation value = 1), then the cross-correlation value decreases again as the time lag continues to increase. This indicates that explosion waveforms become more similar as they approach the time lag of Explosion 45. This pattern occurs, to some extent, for most of the explosions with time lags around 10 s. Therefore, explosions with similar seismic waveforms, as measured by the cross-correlation value between them, may occur at similar depths within the conduit, assuming that the seismo-acoustic time lag is related to the source depth.

FIGURE 9

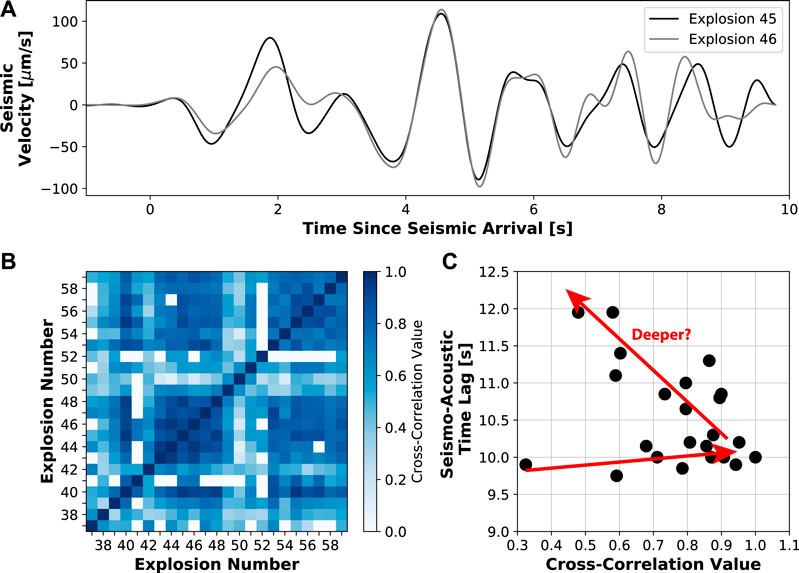
FIGURE 9. Seismic cross-correlation analysis in the 0.1–1.0 Hz frequency band. (A) Waveforms for Explosions 45 and 46 with a cross-correlation value of 0.91. (B) Seismic cross-correlation values for all explosions. (C) Seismo-acoustic time lag vs cross-correlation value for example Explosion 45 compared to other explosions. As the time lag increases, the cross-correlation value increases to a maximum and then decreases again (red arrows).

4.3.3. Seismic Particle Motion

Analysing the particle motion of the three-component seismic data may help understand the explosion source depth within the conduit (e.g., Rowe et al., 1998), or at least the source depth relative to other explosions at Mount Cleveland. Here we examine the particle motion and dip angle for each explosion to get an estimate of the depth. Seismic data at station CLES are integrated from velocity to displacement. Then they are bandpass filtered between 0.25–0.5 Hz and rotated from North (N) and East (E) components to Radial (R) and Transverse (T) components with respect to the vent location (Figures 10A,B). Particle motion analysis is performed for the first 6 s of the seismic explosion signals, which generally shows stable particle motion.

FIGURE 10

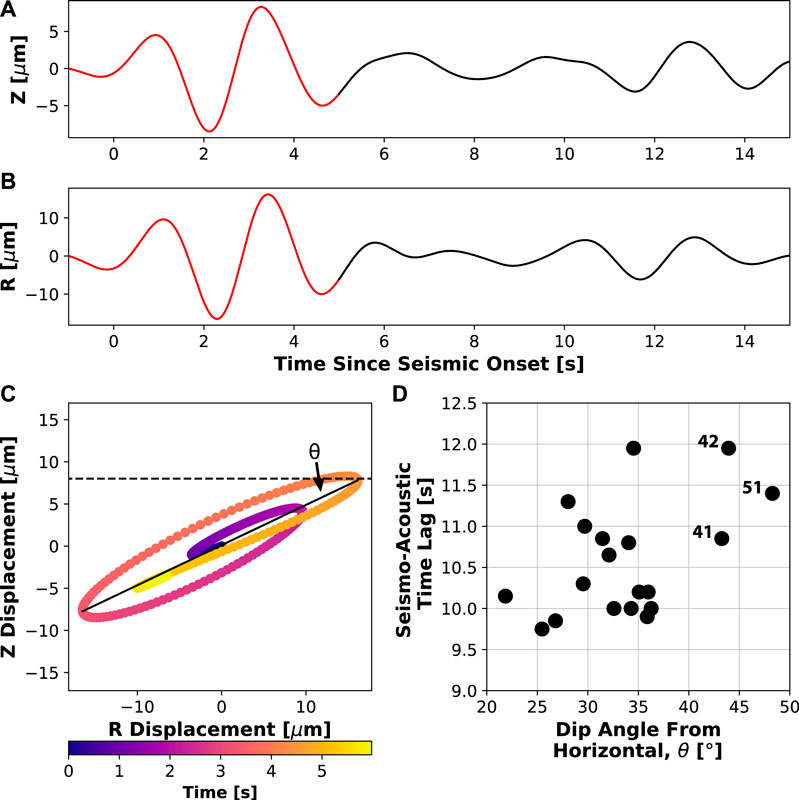
FIGURE 10. Particle motion analysis for example Explosion 38 in the 0.25–0.5 Hz frequency band. (A) Vertical seismic displacement. (B) Radial seismic displacement. (C) Particle motion for the first 6 s of the explosion (red section in panels (A) and (B)), colored as a function of time. The solid black line is the least-squares fit, allowing for the computation of dip angle from horizontal (θ) (D) Time lag vs. dip angle from horizontal (θ), generally showing a trend where larger time lags tend to have larger dip angles (R-squared value of 0.22).

The dip angle (θ) is defined as the angle below the horizontal of the least squares fit to the first 6 s of the R and Z components of the displacement (Figure 10C). Dip angles range from 21.8–48.3° and are distributed fairly uniformly across this range. Explosions with larger dip angles from horizontal tend to correspond to larger seismo-acoustic time lags (Figure 10D). Four explosions are excluded from this analysis (Explosions 39, 49, 50, and 52) for not having rectilinear motion in the first 6 s of the explosion, and therefore no clear dip angle. We caution that near-surface effects (e.g., Neuberg and Pointer, 2000) may affect the absolute dip angle so a direct conversion to depth is not taken here. However, these near surface effects are assumed to be constant over time and minimal in this low frequency band, therefore the relative changes in dip angle between explosions indicate a changing source depth. The three events with dip angles >40° are Explosions 41, 42, and 51, all of which have large differences (>1 s) between the observed and predicted arrival time based on atmospheric conditions (Figure 6B). This suggests relatively deeper sources for explosions with larger time lags than those with shorter time lags. Thus, the pressure wave travels a longer distance prior to reaching CLES, therefore having a larger time delay compared with the seismic arrival.

5. Discussion

5.1. General Characterization of Explosions

The activity of Mount Cleveland has fluctuated through time and it remains one of Alaska’s most historically active volcanoes. The time period analyzed in this study (2014–2018) contains the transient dome building and destruction styles that Cleveland has been known to produce. In 2001, Cleveland exhibited higher eruptive activity with large volcanic plumes (Dean, 2002; Simpson et al., 2002; Dean et al., 2004; Gu et al., 2005). After this time, the volcano was relatively quiet until December 2011, when activity was again heightened and AVO began recording their current explosion catalog. While most of the activity from 2011 to the time of writing was Vulcanian in nature, two explosions in 2013 book-ended a continuous eruption lasting 44 h that was recorded by the infrasound array and as GCAs by the seismic network at Okmok volcano (Power et al., 2020). Additionally, we note that the repose time prior to the most recent explosion at the time of writing (June 2, 2020), was 510 days, the longest repose time in 9 years so it appears the volcano may have entered a new eruptive phase. Explosion dynamics may still be similar though.

Repose time prior to explosions within the study period varied between 2 and 257 days and appeared to occur irrespective of whether a lava dome extruded and was visible on the crater floor (Figure 3B). This is surprising, as we expected the existence and size of a dome to have an impact on the amount of pressure that can be built up in the shallow conduit system prior to the explosion. Therefore, we assume that the observation of “no dome” visible on the crater floor in satellite imagery still means that some form of hardened plug occurs at the top of the conduit that causes pressure to build within the conduit and create the next Vulcanian explosion. We note that permanent gas instrumentation may help better understand this relationship between the dome and subsequent build up of pressure, due to the nearly continuous degassing from fractures within the dome surface.

Unlike the similar nature of the seismic explosion signals, the characteristics of the infrasound signal varied substantially between explosions. Peak pressures at 3.5 km distance from the summit ranged between 20 and 260+ Pa for short-duration Vulcanian explosions, sometimes with acoustic tremor occurring for several minutes after the initial blast. The waveforms of some explosions were similar to a typical blast wave (e.g., Explosion 44, Figure 7A) where the onset is very sharp, and potentially propagated faster than the expected speed of sound. Some explosions have a preceding low amplitude infrasound phase <0.5 s prior to the main explosion onset that may be attributed to a minor increase in pressure due to the swelling or “uncorking” of the lava plug within the crater (e.g., Explosion 40, Figure 2B). This has been seen at other similar volcanoes such as Lokon-Empung (Yamada et al., 2016), Sakurajima (Yokoo et al., 2009), and Suwanosejima (Yokoo and Iguchi, 2010). Some explosions exhibit a single main compressional phase (e.g., Explosion 44, Figure 2B and Supplementary Figure S1A) while other explosions have multiple compressions in a row, which may correspond to a “slow” or complex destruction of the dome (e.g., Explosion 42, Figure 2B and Supplementary Figure S1B). These explosions with multiple compressions have been seen at Sakurajima volcano (e.g., Fee et al., 2014) as well. These observations suggest the surficial component of the explosions, including dome destruction, is complex and variable at Mount Cleveland. We note that some of these features may be obscured in the signals that clipped the infrasound sensor. AVO installed an infrasound sensor in July 2018 with a higher dynamic range that should not clip at station CLES for future explosions of Mount Cleveland.

A notable period of activity is the cluster of Explosions 45–48 (May 2017 to September 2017, see Figure 11). These events had repose intervals between 35 and 54 days (Figure 3A), similar seismo-acoustic time lags of ∼10.00 s (Figure 4A), similar seismic cross-correlation values (Figure 9B), and dip angles tightly clustered between 32.5° and 36.3° (Figure 10D). Given the plethora of similarities, we conclude that Cleveland was in a relatively stable and regular state of activity during this time period.

FIGURE 11

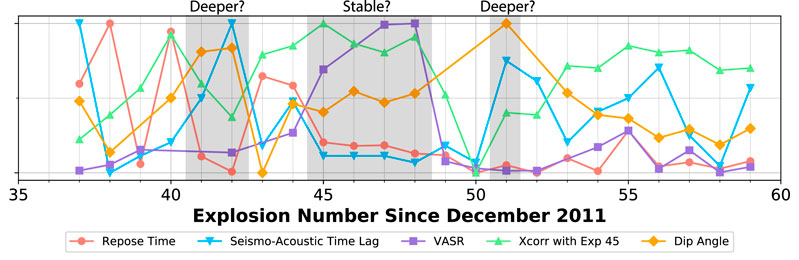
FIGURE 11. Summary figure of trends as a function of explosion number. The five parameters plotted have each been normalized between 0 and 1 and consist of repose time (days), seismo-acoustic time lag (s), VASR_rel, cross-correlation value with Explosion 45, and dip angle from horizontal (θ) (°). The period of apparent stability in the volcanic system (Explosions 45–48) and explosions that are believed to be initiated deeper within the conduit (Explosions 41, 42, and 51) are highlighted with gray shading.

5.2. Implications for Source Depth Within the Conduit

Our results indicate that the explosion depth varied notably between different events and is likely responsible for the variable seismo-acoustic time lag. While an absolute calculation of explosion depth for all 22 explosions in this study does not appear feasible due to our limited data, some trends exist that allow for inferences on relative explosion source depths. Results from the seismo-acoustic time lag investigation are summarized in Table 1 and Figure 11, where Figure 11 shows the repose time, seismo-acoustic time lag, VASR_rel, cross-correlation with Explosion 45, and dip angle from horizontal, each normalized between 0 and 1. It is also clear, from analyses of the atmospheric effect on travel time using two independent methods, that the atmosphere is not the sole cause of the observed variable seismo-acoustic time lags (Figure 6B). Additionally, nonlinear propagation modeling did not yield a change in the onset time of the acoustic arrival at 3.8 km range and source amplitudes comparable (and larger) to those of Cleveland explosions, just a change in the arrival time of the peak pressure. Therefore, we conclude that something else must play a critical role in the variable seismo-acoustic time lags observed, which we argue is a change in explosion source depth within the conduit.

Explosions with shorter seismo-acoustic time lags (<∼10.2 s) may have shallower source depths within the conduit. This is evidenced by small residuals between observed and predicted travel times based on atmospheric effects (<0.5 s) (Figure 6B), higher VASR_rel in some cases (Explosions 45, 47, and 48, Figure 8A), higher seismic-cross correlation values in general (Figure 9B) and in relation to Explosion 45 (Figure 9C), and lower-to-average dip angles based on seismic particle motion (Figure 10D). These results are also summarized in Table 1 and Figure 11. The low residuals between observed and predicted travel times based on atmospheric effects mean that the atmospheric predictions for the entire acoustic propagation path (Locations 1 through 4, Figure 5) are well predicted by the path length within the atmosphere (Locations 2 through 4, Figure 5). Therefore, the distance between Locations 1 and 2 in Figure 5 (i.e., explosion source depth) may be small. Explosions 45, 47, and 48 have high VASR_rel values, which indicates that a higher fraction of the explosion energy coupled into the atmosphere as compared with other explosions, also suggesting a shallow source or change in coupling from the conduit to the conduit wall. The seismic signatures of these events have high correlation, suggesting they may occur in a similar location and thus have the same propagation path to the seismic sensor. Finally, the dip angles of the seismic particle motion analysis for these events are smaller than explosions with larger time lags (e.g., Explosions 41, 42, and 51, dip angles >40°), suggesting a shallower source. While the dip angles seem to point to a source lower than station CLES for all explosions (e.g., Figure 10C), the travel time residuals are low (i.e., the observed time lag seems to be explained well by the predicted acoustic travel time based on the effective sound speed) and may therefore have a short path within the conduit. This is likely related to the surface displacement for P-waves incident at a sloped free surface (e.g., Ben-Menahem and Singh, 2012, their Figure 3), which causes the observed motion to be upward and outward even though the explosion source may be shallower than station CLES. The combination of these observations suggests these events with shorter seismo-acoustic time lags have a shallower source than other explosions at Mount Cleveland.

Explosions with larger seismo-acoustic time lags are likely associated with deeper explosions. This is evidenced by the higher travel time residuals between observed values and those predicted using the effective sound speed (Figure 6B), low cross-correlation values with respect to Explosion 45 (Figure 9C), and larger dip angles from particle motion analysis (>40°, Figure 10D) (Table 1, Figure 11). The three events with dip angles greater than 40° are Explosions 41, 42, and 51, all of which have large differences between the observed and predicted arrival time based on atmospheric conditions (>0.88 s, Figure 6B). We use these three likely deeper explosions to perform calculations on maximum source depths for explosions at Mount Cleveland where the residual travel times (after accounting for atmospheric effects) are 0.88, 1.77, and 1.21 s, respectively. Tameguri et al. (2002) find a reasonable conduit propagation velocity for Sakurajima to be in the range of 1,400–1,900 m/s and Yamada et al. (2016) estimate the velocity of the pressure wave to be > 1,000 m/s at Lokon-Empung. If we use a lower conduit velocity of υ_conduit = 1,000 m/s, explosion depths would be 880, 1770, and 1,210 m, respectively. If we choose a higher conduit velocity of υ_conduit = 1,500 m/s, explosion depths would be 1,320, 2,655, and 1,815 m, respectively. Haney et al. (2019) finds volumetric source locations using moment tensor inversions in the VLP band from 0.25 to 0.5 Hz for the first 2 s of the waveform of 400–640 m above sea level (depths of ∼1,090–1,330 m beneath the summit), which appear to be in the range of our results and favor the lower υ_conduit. We note that moment tensor inversions for explosions from the analogous Tungurahua volcano, Ecuador, point to a source region 1.5 km below the summit (Kim et al., 2014), comparable to estimates for deeper explosions at Mount Cleveland. Additionally, the range of potential source depths we calculate is consistent with the proposed vertically extensive region of magma degassing between 0.5 and 3.0 km beneath the summit at Mount Cleveland in 2016 (Werner et al., 2020).

While changing the depth of the seismic explosion source would affect the time the pressure wave propagates up the conduit, the conduit propagation velocity may also vary due to changing composition and density of the conduit material between explosions. This has been hypothesized in previous studies of analogous volcanoes, including Tungarahua (Ruiz et al., 2006) and Santiaguito (Sahetapy-Engel et al., 2008). While this may occur to some extent at Mount Cleveland, we believe that a changing source depth potentially occurs for Mount Cleveland due to the positive relationship between increasing seismo-acoustic time lag with increasing dip angle from seismic particle motion analysis (Figure 10D), which suggests a changing source location.

Explosion 37 has a similarly large residual between the observed and predicted arrival time based on atmospheric conditions (1.81 s) but lacks the large dip angle observed for other explosions with large residuals (Explosions 41, 42, and 51, explained above). Upon closer inspection of the infrasound waveform, a small compression is noted ∼1.8 s prior to the main onset. This feature is likely not noise, as it shows up at the infrasound array CLCO as well. Therefore, we conclude that the small compression may be an arrival from movement of the dome surface, and that the dome did not completely rupture until ∼1.8 s later, causing a larger delay in the main acoustic onset.

5.3. Other Potential Impacts on Seismo-Acoustic Time Lag

Uncertainties can be introduced when picking the seismic and infrasound onset times. The seismic onsets are low-amplitude compressions which are consistent with studies of similar volcanoes such as Sakurajima (Tameguri et al., 2002), Tungurahua (Ruiz et al., 2006), and Lokon-Empung (Yamada et al., 2016). We chose to pick seismic arrivals on unfiltered waveforms to obtain the first sign of signal onset, as filtering in certain bands may obscure the subtle onset. The infrasound arrival is generally signified by a rapid increase in pressure. However, some explosions have a slow compressional onset (<0.5 s) prior to the rapid onset, which may introduce a small (few tenths of a second) error (e.g., Explosion 40, Supplementary Figure S1C). Both of these potential onset time errors do not change the fact that large variations (up to 2.20 s) in seismo-acoustic time lag exist between explosions at Mount Cleveland.

Two methods were used to determine the impact of the atmosphere on the propagation velocity of the infrasound signal, both of which have pros and cons. The first method used an atmospheric reconstruction model, AVO-G2S (Schwaiger et al., 2019). Using models such as this to obtain atmospheric information is known to not fully capture the exact atmospheric conditions at the time and location of the event (e.g., Iezzi et al., 2019b; Schwaiger et al., 2020). For example, these models have been found to be inadequate for the local atmospheric and boundary layer properties for propagation distances similar to that explored in this study (e.g., Kim et al., 2018). Therefore, atmospheric conditions may not capture smaller-scale changes such as variations within the 6 h increments, transient wind gusts, or flow around topography (i.e., a volcanic edifice). These inaccuracies and simplifications (both spatially and temporally) can be due to using coarse resolution input windfiles (NCEP reanalysis files, 2.5° and 6 h, respectively), as well as smoothing and interpolation during the reconstruction process in order to obtain a 1D atmospheric profile above the volcano. This may explain why the AVO-G2S derived effective sound speed values were systematically lower than those from our second method by 0–25 m/s (Figure 6A). The second method used to obtain effective sound speeds took advantage of the infrasound array CLCO, located 12.33 km further and 22.9° south of the CLES-summit azimuth. While 22.9° is a relatively low azimuthal deviation, if winds were strong the effective sound speed comparison would have error. However, we use this value because it is likely a more accurate representation of the atmospheric conditions at the time of each explosion.

To further investigate the potential effect of wind noise that may remain unresolved by both methods for determining the impact of the atmosphere on the propagation velocity, we look at the low frequency (0.02–0.3 Hz) component of infrasound for each explosion, as the spectral amplitude in this frequency band can sometimes be used as a proxy for wind noise (e.g., Fee and Garces, 2007). We include the infrasound power spectral density (PSD) for the 60 min prior to each explosion in Supplemental Figure S4, and note that the magnitude of the noise levels in this frequency band varies between explosions and does not show a clear correlation with time lag. However, it is not possible to fully interpret wind-related travel time effects on the time lag analysis because the noise conditions captured by the PSD do not account for directionality of the wind. For future studies that may be interested in obtaining explosion source depth from the seismo-acoustic time lag, we suggest adding an in-situ measurement of wind speed and direction using an anemometer along with the co-located seismic and infrasound sensors in order to more thoroughly capture the influence of the atmosphere.

The nonlinear FDTD modeling results in this study did not produce a measurable difference in the onset time of the explosion signal, nor the formation of a shock front. We note that our interpretations are limited by current modeling capabilities only using a linear source. Some of the waveforms at CLES show similarities to shock waves, which we believe would impact the acoustic arrival time observed at CLES due to the shock front overtaking the gradual onset observed for many of the Cleveland explosions. We surmise that future simulations performed that include a nonlinear source may produce a more realistic acoustic travel time. While the simulations performed here did not reproduce nonlinear impacts to the explosion arrival times, we believe there still may be a small contribution due to the highest peak pressures and those that clipped (Figure 7D, open circles) having lower seismo-acoustic time lags. This could be a coincidence, but should be explored further. Building upon a study on Bromo volcano, Indonesia, by Gottschämmer and Surono (2000), Kim et al. (2014) corrected their infrasound onset times for explosions at Tungurahua volcano, Ecuador, using a constant shock velocity of 560 m/s within 2 km of the source, then 340 m/s beyond 2 km. However, we do not feel confident enough to include this type of sound speed assumption in our study with data from only a single station. Due to the uncertainties from a variety of features of potential nonlinear propagation, we chose to not include the potential contribution to our calculations on explosion source depth.

Observing nonlinear propagation near the source is difficult because infrasound sensors are generally placed far enough away from the source in order to decrease hazard to the field team and equipment. Therefore, interpretations often integrate multidisciplinary observations of pressure waves in order to better understand near source pressure dynamics. The propagation of pressure waves or “flashing arcs” has been observed and studied using image luminance techniques (e.g., Genco et al., 2014) and thermal imagery (e.g., Marchetti et al., 2013) then connected to the acoustic propagation velocity of volcanic explosions. Genco et al. (2014) find that explosions at Stromboli volcano propagate at the expected speed of sound, not faster. Marchetti et al. (2013) find that acoustic waves from explosions at Yasur volcano propagate supersonically, along with the observation of blast wave shapes in the infrasound traces. Recall that in nonlinear propagation every point on the waveform travels with a different speed (compression faster than rarefaction), which begs the question of exactly which part of the acoustic waveform this supersonic propagation speed corresponds to, the initial onset (which we are exploring in this study) or the peak compression (which has been shown to arrive faster in both this study and in others)? This remains unclear and should be investigated more thoroughly in the future.

6. Conclusion

Multi-year studies of volcanic activity provide observations of trends. Deviations from those trends prove useful for volcano monitoring that may not be apparent for studies using temporary deployment data that may only catch a few explosions (e.g., Lamb et al., 2019; Wallace et al., 2020). Here we examined the activity at Mount Cleveland from 2014 to 2018 and put it in context of recent work focused on shorter-term, dense observations. We find that Mount Cleveland generally followed a pattern of dome building and subsequent Vulcanian explosions, but parameters including repose time, explosion amplitude, and explosion characteristics varied substantially over the 4 years. In general, seismo-acoustic data from these explosions consisted of typical Vulcanian eruption signals. The seismic arrival for all explosions is a low-amplitude, compressional onset with a GCA often visible on the trace. The acoustic signal generally consists of a high-amplitude compressional onset, followed by a long duration coda. Some acoustic signals resemble high-amplitude, sharp-onset shock waves, while others have a complicated onset indicating a slower, multi-stage destruction of the lava dome. Notably, a variable seismo-acoustic time lag of up to 2.20 s is observed by co-located seismo-acoustic sensors at a station 3.5 km from the summit. Similarly variable seismo-acoustic time lags have been observed at analogous volcanoes such as Santiaguito and Tungurahua, though their precise cause is not well understood. We attribute the variable seismo-acoustic time lags to be due to a combination of varying atmospheric conditions (e.g., winds and temperature), nonlinear propagation, conduit velocity variations, and varying source depth within the conduit. Atmospheric effects were examined using two independent measurements, neither of which could entirely explain the variation observed. Nonlinear propagation impacts were determined to be minimal in relation to the onset time of the infrasound arrival, though they were difficult to quantify and model completely. We find that results from seismic cross-correlation and particle motion analysis suggest that a varying explosion source depth within the conduit may play a role in the observed variations in seismo-acoustic time lag. These results suggest explosion source depths ranging from near the surface down to ∼1.5–2 km beneath the summit. This range in explosion depths is consistent with the evidence of magma potentially residing and degassing in a vertically extensive conduit region ranging in depth between 0.5 and 3.0 km below the summit found by Werner et al. (2020). We stress that no one method provides a complete depiction of the observed variance for all explosions, but a combination of methods is required to help understand the observations. Additionally, we note that combining observations of repose time, seismo-acoustic time lag, seismic cross-correlation values, and seismic particle motion dip angles illuminated periods of stable volcanic activity for Mount Cleveland. This may be useful for the future monitoring of the volcano, such as inferring the potential repose time before another explosion occurs if the system appears to be in a stable period (e.g., Explosions 45–48).

This study was performed primarily using a single co-located seismic and acoustic station. We suggest that similar analyses may be performed at other volcanoes worldwide that have sparse monitoring networks. Even with a single co-located seismic and acoustic sensor that clips sometimes, we show that it is possible to provide meaningful interpretations on the explosion source depth which may help understand the volcanic system during times of unrest. In future years, we anticipate more geophysical and geochemical instrumentation to be installed at Mount Cleveland, which will increase our understanding of the volcanic system, build upon the results of this study, and increase the ability of AVO to monitor and forecast future eruptions of the volcano. Additionally, while this study focuses on volcanic explosions, the goal of finding depth from coupled seismic and acoustic observations is not unique to volcanic studies and can be applied to other disciplines such as the study of buried chemical explosions.

Data Availability Statement

Seismic and infrasound data used in this study are available from the Incorporated Research Institutions for Seismology Data Management Center (https://ds.iris.edu/ds/nodes/dmc/) under network code AV.

Author Contributions

AI led the analysis and writing of the manuscript under the supervision of DF. All authors provided critical feedback and helped shape the research, analysis, and structure of the manuscript.

Funding

The authors acknowledge support from the Alaska Volcano Observatory through the U.S. Geological Survey Volcano Hazards Program.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The reviewer (SDA) declared a past co-authorship with the authors to the handling editor.

Acknowledgments

The authors thank Sean Maher and Catherine de Groot-Hedlin for helpful discussion on nonlinear propagation and the use of the FDTDWave code. We are also grateful to Pavel Izbekov, Carl Tape, and Michael West for discussions on the analyses as well as David Green for discussion on the use of seismic cross-correlation. We would also like to thank Taryn Lopez, Cheryl Searcy, Cheryl Cameron, and Rick Wessels for their help with gathering dome observations and discussions on Mount Cleveland. Helpful reviews were done by Silvio De Angelis, Stephen McNutt, and Rebecca Kramer. Observations of volcanic activity were made by AVO and are detailed on its website (avo.alaska.edu/volcanoes/volcact.php?volcname=Cleveland). Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2020.573368/full#supplementary-material

References

Arrowsmith, S. J., Johnson, J. B., Drob, D. P., and Hedlin, M. A. H. (2010) The seismoacoustic wavefield: a new paradigm in studying geophysical phenomena. Rev. Geophys. 48, RG4003. doi:10.1029/2010RG000335

CrossRef Full Text | Google Scholar

Atchley, A. A. (2005). Not your ordinary sound experience: a nonlinear-acoustics primer. Acoust. Today. 1, 19–24. doi:10.1121/1.2961122

CrossRef Full Text | Google Scholar

Ben-Menahem, A., and Singh, S. J. (2012). Seismic waves and sources. Berlin: Springer Science & Business Media.

Google Scholar

Blom, P., Iezzi, A., and Euler, G. (2020). Seismoacoustic analysis of underground explosions using the Rayleigh integral. Geophys. J. Int. 223, 1069–1085. doi:10.1093/gji/ggaa363

CrossRef Full Text | Google Scholar

Boatwright, J. (1980). A spectral theory for circular seismic sources; simple estimates of source dimension, dynamic stress drop, and radiated seismic energy. Bull. Seismol. Soc. Am. 70, 1–27. doi:10.1785/0120000932

CrossRef Full Text | Google Scholar

Clarke, A. B., Esposti Ongaro, T., and Belousov, A. (2015). Vulcanian eruptions. Encycl. Volcanoes. 10, 505–518. doi:10.1016/b978-0-12-385938-9.00028-6

CrossRef Full Text | Google Scholar

De Angelis, S., Fee, D., Haney, M., and Schneider, D. (2012). Detecting hidden volcanic explosions from Mt. Cleveland Volcano, Alaska with infrasound and ground-coupled airwaves. Geophys. Res. Lett. 39. 19–24. doi:10.1029/2012GL053635

CrossRef Full Text | Google Scholar

de Groot-Hedlin, C. D. (2016). Long-range propagation of nonlinear infrasound waves through an absorbing atmosphere. J. Acoust. Soc. Am. 139, 1565–1577. doi:10.1121/1.4944759

PubMed Abstract | CrossRef Full Text | Google Scholar

Dean, K. G., Dehn, J., Papp, K. R., Smith, S., Izbekov, P., Peterson, R., et al. (2004). Integrated satellite observations of the 2001 eruption of Mt. Cleveland, Alaska. J. Volcanol. Geoth. Res. 135, 51–73. doi:10.1016/j.jvolgeores.2003.12.013

CrossRef Full Text | Google Scholar

Dean, K. G. (2002). Satellite imagery proves essential for monitoring erupting aleutian volcano. Eos 83, 19–21. doi:10.1029/2002eo000168

CrossRef Full Text | Google Scholar

Dixon, J., Cameron, C., Iezzi, A., and Wallace, K. (2017). Report 2017-5104. 2015 Volcanic activity in Alaska-Summary of events and response of the Alaska Volcano Observatory. U.S. Geological Survey Scientific Investigations. doi:10.3133/sir20175104

CrossRef Full Text | Google Scholar

Fee, D., and Garces, M. (2007). Infrasonic tremor in the diffraction zone. Geophys. Res. Lett. 34, 24–42. doi:10.1029/2007GL030616

CrossRef Full Text | Google Scholar

Fee, D., Haney, M., Matoza, R., Szuberla, C., Lyons, J., and Waythomas, C. (2016). Seismic envelope-based detection and location of ground-coupled airwaves from volcanoes in Alaska. Bull. Seismol. Soc. Am. 106, 72–85. doi:10.1785/0120150244

CrossRef Full Text | Google Scholar

Fee, D., Izbekov, P., Kim, K., Yokoo, A., Lopez, T., Prata, F., et al. (2017). Eruption mass estimation using infrasound waveform inversion and ash and gas measurements: evaluation at Sakurajima Volcano, Japan. Earth Planet Sci. Lett. 480, 42–52. doi:10.1016/j.epsl.2017.09.043

CrossRef Full Text | Google Scholar

Fee, D., Lyons, J., Haney, M., Wech, A., Waythomas, C., Diefenbach, A. K., et al. (2020). Seismo-acoustic evidence for vent drying during shallow submarine eruptions at Bogoslof volcano, Alaska. Bull. Volcanol. 82, 1–14. doi:10.1007/s00445-019-1326-5

CrossRef Full Text | Google Scholar

Fee, D., and Matoza, R. S. (2013). An overview of volcano infrasound: from hawaiian to plinian, local to global. J. Volcanol. Geoth. Res. 249, 123–139. doi:10.1016/j.jvolgeores.2012.09.002

CrossRef Full Text | Google Scholar

Fee, D., Yokoo, A., and Johnson, J. B. (2014). Introduction to an open community infrasound dataset from the actively erupting Sakurajima Volcano, Japan. Seismol Res. Lett. 85, 1151–1162. doi:10.1785/0220140051

CrossRef Full Text | Google Scholar

Firstov, P., and Kravchenko, N. (1996). Estimation of the amount of explosive gas released in volcanic eruptions using air waves. Volcanol. Seismol. 17, 547–560

Google Scholar

Friedlander, F. (1946). The diffraction of sound pulses. I. Diffraction by a semi-infinite plate. Proc. Roy. Soc. Lond. 186, 322–344. doi:10.1098/rspa.1946.0046

PubMed Abstract | CrossRef Full Text | Google Scholar

Genco, R., Ripepe, M., Marchetti, E., Bonadonna, C., and Biass, S. (2014). Acoustic wavefield and Mach wave radiation of flashing arcs in strombolian explosion measured by image luminance. Geophys. Res. Lett. 41, 7135–7142. doi:10.1002/2014GL061597

CrossRef Full Text | Google Scholar

Gottschämmer, E., and Surono, I. (2000). Locating tremor and shock sources recorded at Bromo Volcano. J. Volcanol. Geoth. Res. 101, 199–209. doi:10.1016/S0377-0273(00)00171-2

CrossRef Full Text | Google Scholar

Green, D. N., and Neuberg, J. (2006). Waveform classification of volcanic low-frequency earthquake swarms and its implication at Soufrière Hills Volcano, Montserrat. J. Volcanol. Geoth. Res. 153, 51–63. doi:10.1016/j.jvolgeores.2005.08.003

CrossRef Full Text | Google Scholar

Gu, Y., Rose, W. I., Schneider, D. J., Bluth, G. J. S., and Watson, I. M. (2005). Advantageous GOES IR results for ash mapping at high latitudes: cleveland Eruptions 2001. Geophys. Res. Lett. 32, 1–5. doi:10.1029/2004GL021651

CrossRef Full Text | Google Scholar

Haney, M., Lyons, J., Power, J., and Roman, D. (2019). “Moment tensors of small vulcanian explosions at Mount Cleveland, Alaska,” in AGU Fall Meeting, San Fransisco, CA, 2019, V41A-05.

Google Scholar

Iezzi, A. M., Fee, D., Kim, K., Jolly, A. D., and Matoza, R. S. (2019a). Three-dimensional acoustic multipole waveform inversion at Yasur volcano, Vanuatu. J. Geophys. Res.: Solid Earth. 124, 8679–8703. doi:10.1029/2018JB017073

CrossRef Full Text | Google Scholar

Iezzi, A. M., Schwaiger, H. F., Fee, D., and Haney, M. M. (2019b). Application of an updated atmospheric model to explore volcano infrasound propagation and detection in Alaska. J. Volcanol. Geoth. Res. 371, 192–205. doi:10.1016/j.jvolgeores.2018.03.009

CrossRef Full Text | Google Scholar

Janiszewski, H. A., Wagner, L. S., and Roman, D. C. (2020). Aseismic mid-crustal magma reservoir at Cleveland Volcano imaged through novel receiver function analyses. Sci. Rep. 10, 1–9. doi:10.1038/s41598-020-58589-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnson, J. B., and Aster, R. C. (2005). Relative partitioning of acoustic and seismic energy during Strombolian eruptions. J. Volcanol. Geoth. Res. 148, 334–354. doi:10.1016/j.jvolgeores.2005.05.002

CrossRef Full Text | Google Scholar

Johnson, J. B. (2003). Generation and propagation of infrasonic airwaves from volcanic explosions. J. Volcanol. Geoth. Res. 121, 1–14. doi:10.1016/S0377-0273(02)00408-0

CrossRef Full Text | Google Scholar

Jones, K. R., Whitaker, R. W., and Arrowsmith, S. J. (2015). Modelling infrasound signal generation from two underground explosions at the Source Physics Experiment using the Rayleigh integral. Geophys. J. Int. 200, 779–790. doi:10.1093/gji/ggu433

CrossRef Full Text | Google Scholar

Kim, K., Fee, D., Yokoo, A., and Lees, J. M. (2015). Acoustic source inversion to estimate volume flux from volcanic explosions. Geophys. Res. Lett. 42, 5243–5249. doi:10.1002/2015GL064466

CrossRef Full Text | Google Scholar

Kim, K., Lees, J. M., and Ruiz, M. C. (2014). Source mechanism of Vulcanian eruption at Tungurahua Volcano, Ecuador, derived fromseismic moment tensor inversions. J. Geophys. Res.: Solid Earth. 119, 1145–1164. doi:10.1002/2013JB010590

CrossRef Full Text | Google Scholar

Kim, K., Rodgers, A., and Seastrand, D. (2018). Local infrasound variability related to in situ atmospheric observation. Geophys. Res. Lett. 45, 2954–2962. doi:10.1002/2018GL077124

CrossRef Full Text | Google Scholar

Kistler, R., Kalnay, E., Collins, W., Saha, S., White, G., Woollen, J., et al. (2001). The NCEP-NCAR 50-year reanalysis: Monthly means CD-ROM and documentation. Bull. Am. Meteorol. Soc. 82, 247–267. doi:10.1175/1520-0477(2001)082<0247:TNNYRM>2.3.CO;2

CrossRef Full Text | Google Scholar

Lamb, O. D., Lamur, A., Díaz-Moreno, A., De Angelis, S., Hornby, A. J., von Aulock, F. W., et al. (2019). Disruption of long-term effusive-explosive activity at Santiaguito, Guatemala. Front. Earth Sci. 6, 1–14. doi:10.3389/feart.2018.00253

CrossRef Full Text | Google Scholar

Lyons, J. J., and Waite, G. P. (2011). Dynamics of explosive volcanism at Fuego volcano imaged with very long period seismicity. J. Geophys. Res. Solid Earth. 116, 1–18. doi:10.1029/2011JB008521

CrossRef Full Text | Google Scholar

Maher, S. P., Matoza, R. S., Groot-Hedlin, C. D., Gee, K. L., Fee, D., and Yokoo, A. (2020). Investigating spectral distortion of local volcano infrasound by nonlinear propagation at Sakurajima volcano, Japan. J. Geophys. Res. Solid Earth. 125, 19–27. doi:10.1029/2019JB018284

CrossRef Full Text | Google Scholar

Marchetti, E., Ripepe, M., Delle Donne, D., Genco, R., Finizola, A., and Garaebiti, E. (2013). Blast waves from violent explosive activity at Yasur Volcano, Vanuatu. Geophys. Res. Lett. 40, 5838–5843. doi:10.1002/2013GL057900

CrossRef Full Text | Google Scholar

McKee, K., Fee, D., Haney, M., Matoza, R. S., and Lyons, J. (2018). Infrasound signal detection and back azimuth estimation using ground-coupled airwaves on a seismo-acoustic sensor pair. J. Geophys. Res. Solid Earth. 123, 6826–6844. doi:10.1029/2017JB015132

CrossRef Full Text | Google Scholar

Miller, T., McGimsey, R., Richter, D., Riehle, J., Nye, C., Yount, M., et al. (1998). Catalog of historically active volcanoes in Alaska. U.S. Geological Survey Open- File Report. 98–582

Google Scholar

Neuberg, J., and Pointer, T. (2000). Effects of volcano topography on seismic broad-band waveforms. Geophys. J. Int. 143, 239–248. doi:10.1046/j.1365-246X.2000.00251.x

CrossRef Full Text | Google Scholar

Petersen, T., and McNutt, S. R. (2007). Seismo-acoustic signals associated with degassing explosions recorded at Shishaldin Volcano, Alaska, 2003-2004. Bull. Volcanol. 69, 527–536. doi:10.1007/s00445-006-0088-z

CrossRef Full Text | Google Scholar

Pierce, A. (1981). Acoustics: an introduction to its physical principles and applications. New York, NY: McGraw-Hill.

Google Scholar

Porter, C., Morin, P., Howat, I., Noh, M.-J., Bates, B., Peterman, K., et al. (2018). Arctic. [Dataset]. doi:10.7910/DVN/OHHUKH

CrossRef Full Text | Google Scholar

Power, J. A., Haney, M. M., Botnick, S. M., Dixon, J. P., Fee, D., Kaufman, A. M., et al. (2020). Goals and development of the Alaska Volcano Observatory seismic network and application to forecasting and detecting volcanic eruptions. Seismol Res. Lett. 91, 647–659. doi:10.1785/0220190216

CrossRef Full Text | Google Scholar

Power, J., Roman, D., Lyons, J., Haney, M., Werner, C., Rasmussen, D., et al. , A seismic investigation of Mount Cleveland volcano and pre-historic volcanic vents on Chuginadak Island, Alaska and implications for forecasting eruptions at open-vent volcanoes. J. Volcanol. Geoth. Res., in review.

Google Scholar

Reichman, B. O., Gee, K. L., Neilsen, T. B., and Miller, K. G. (2016). Quantitative analysis of a frequency-domain nonlinearity indicator. J. Acoust. Soc. Am. 139, 2505–2513. doi:10.1121/1.4945787

CrossRef Full Text | Google Scholar

Rowe, C. A., Aster, R. C., Kyle, P. R., Schlue, J. W., and Dibble, R. R. (1998). Broadband recording of Strombolian explosions and associated very-long-period seismic signals on Mount Erebus volcano, Ross Island, Antarctica. Geophys. Res. Lett. 25, 2297–2300. doi:10.1029/98GL01622

CrossRef Full Text | Google Scholar

Ruiz, M. C., Lees, J. M., Johnson, J. B., Hall, M., Box, C., and Hill, C. (2006). Source constraints of Tungurahua volcano explosion events. Bull. Volcanol. 68, 480–490. doi:10.1007/s00445-005-0023-8

CrossRef Full Text | Google Scholar

Sahetapy-Engel, S. T., Harris, A. J., and Marchetti, E. (2008). Thermal, seismic and infrasound observations of persistent explosive activity and conduit dynamics at Santiaguito lava dome, Guatemala. J. Volcanol. Geoth. Res. 173, 1–14. doi:10.1016/j.jvolgeores.2007.11.026

CrossRef Full Text | Google Scholar

Salomons, E. (2001). Computational atmospheric acoustics. Dordrecht, The Netherlands: Kluwer Academic Publishers.

Google Scholar

Schwaiger, H. F., Lyons, J. J., Iezzi, A. M., Fee, D., and Haney, M. M. (2020). Evolving infrasound detections from Bogoslof volcano, Alaska: insights from atmospheric propagation modeling. Bull. Volcanol. 82, 27. doi:10.1007/s00445-020-1360-3

CrossRef Full Text | Google Scholar

Schwaiger, H., Iezzi, A., and Fee, D. (2019). AVO-G2S: a modified, open-source Ground-to-Space atmospheric specification for infrasound modeling. Comput. Geosci. 125, 90–97. doi:10.1016/j.cageo.2018.12.013

CrossRef Full Text | Google Scholar

Simpson, J., Hufford, G., Pieri, D., Servranckx, R., Berg, J., and Bauer, C. (2002). The february 2001 eruption of Mount Cleveland, Alaska: case study of an aviation hazard. Am. Meteorol. Soc. 17, 691–704. doi:10.1175/1520-0434(2002)017

CrossRef Full Text | Google Scholar

Tameguri, T., Iguchi, M., and Ishihara, K. (2002). Mechanism of explosive eruptions from moment tensor analyses of explosion earthquakes at Sakurajima volcano, Japan. Bull. Volcanol. Soc. Jpn. 47, 197–215. doi:10.1186/bf03352363

CrossRef Full Text | Google Scholar

Varley, N., Arámbula-Mendoza, R., Reyes-Dávila, G., Sanderson, R., and Stevenson, J. (2010). Generation of vulcanian activity and long-period seismicity at volcán de colima, Mexico. J. Volcanol. Geoth. Res. 198, 45–56. doi:10.1016/j.jvolgeores.2010.08.009

CrossRef Full Text | Google Scholar

Vergniolle, S., Boichu, M., and Caplan-Auerbach, J. (2004). Acoustic measurements of the 1999 basaltic eruption of Shishaldin volcano, Alaska 1. Origin of Strombolian activity. J. Volcanol. Geoth. Res. 137, 109–134. doi:10.1016/j.jvolgeores.2004.05.003

CrossRef Full Text | Google Scholar

Waldhauser, F., and Ellsworth, W. L. (2000). A double-difference earthquake location algorithm: method and application to the Northern Hayward fault, California. Bull. Seismol. Soc. Am. 90, 1353–1368. doi:10.1785/0120000006

CrossRef Full Text | Google Scholar

Wallace, P. A., Lamb, O. D., Angelis, S. D., Kendrick, J. E., Hornby, J., Díaz-moreno, A., et al. (2020). Integrated constraints on explosive eruption intensification at Santiaguito dome complex , Guatemala. Earth Planet Sci. Lett. 536, 116139. doi:10.1016/j.epsl.2020.116139

CrossRef Full Text | Google Scholar

Wang, T., Poland, M. P., and Lu, Z. (2015). Dome growth at Mount Cleveland, Aleutian Arc, quantified by time series TerraSAR-X imagery. Geophys. Res. Lett. 42, 10614–10621. doi:10.1002/2015GL066784

CrossRef Full Text | Google Scholar

Wech, A., Tepp, G., Lyons, J., and Haney, M. (2018). Using earthquakes, T waves, and infrasound to investigate the eruption of bogoslof volcano, Alaska. Geophys. Res. Lett. 45, 6918–6925. doi:10.1029/2018GL078457

CrossRef Full Text | Google Scholar

Werner, C., Kern, C., Coppola, D., Lyons, J. J., Kelly, P. J., Wallace, K. L., et al. (2017). Magmatic degassing, lava dome extrusion, and explosions from Mount Cleveland volcano, Alaska, 2011–2015: insight into the continuous nature of volcanic activity over multi-year timescales. J. Volcanol. Geoth. Res. 337, 98–110. doi:10.1016/j.jvolgeores.2017.03.001

CrossRef Full Text | Google Scholar

Werner, C., Rasmussen, D. J., Plank, T., Kelly, P. J., Kern, C., Lopez, T., et al. (2020). Linking subsurface to surface using gas emission and melt inclusion data at Mount Cleveland volcano, Alaska. G-cubed 21, 141–167. doi:10.1029/2019GC008882

CrossRef Full Text | Google Scholar

Worden, A., Dehn, J., and Webley, P. (2014). Frequency based satellite monitoring of small scale explosive activity at remote North Pacific volcanoes. J. Volcanol. Geoth. Res. 286, 1–14. doi:10.1016/j.jvolgeores.2014.08.019

CrossRef Full Text | Google Scholar

Yamada, T., Aoyama, H., Nishimura, T., Yakiwara, H., Nakamichi, H., Oikawa, J., et al. (2016). Initial phases of explosion earthquakes accompanying Vulcanian eruptions at Lokon-Empung volcano , Indonesia. J. Volcanol. Geoth. Res. 327, 310–321. doi:10.1016/j.jvolgeores.2016.08.011

CrossRef Full Text | Google Scholar

Yokoo, A., and Iguchi, M. (2010). Using infrasound waves from eruption video to explain ground deformation preceding the eruption of Suwanosejima volcano, Japan. J. Volcanol. Geoth. Res. 196, 287–294. doi:10.1016/j.jvolgeores.2010.08.008

CrossRef Full Text | Google Scholar

Yokoo, A., and Ishihara, K. (2007). Analysis of pressure waves observed in Sakurajima eruption movies. Earth Planets Space. 59, 177–181. doi:10.1186/BF03352691

CrossRef Full Text | Google Scholar

Yokoo, A., Tameguri, T., and Iguchi, M. (2009). Swelling of a lava plug associated with a Vulcanian eruption at Sakurajima Volcano, Japan, as revealed by infrasound record: case study of the eruption on January 2, 2007. Bull. Volcanol. 71, 619–630. doi:10.1007/s00445-008-0247-5

CrossRef Full Text | Google Scholar