Solar Radiation Prediction Using Different Machine Learning Algorithms and Implications for Extreme Climate Events

Huang, Liexing; Kang, Junfeng; Wan, Mengxue; Fang, Lei; Zhang, Chunyan; Zeng, Zhaoliang

doi:10.3389/feart.2021.596860

ORIGINAL RESEARCH article

Front. Earth Sci., 30 April 2021

Sec. Environmental Informatics and Remote Sensing

Volume 9 - 2021 | https://doi.org/10.3389/feart.2021.596860

This article is part of the Research Topic Compound Climate Extremes in the Present and Future Climates: Machine Learning, Statistical Methods and Dynamical Modelling View all 16 articles

Solar Radiation Prediction Using Different Machine Learning Algorithms and Implications for Extreme Climate Events

$\r\nLiexing Huang,&#x;$ Liexing Huang^1,2†

Junfeng Kang^2,4*

Mengxue Wan^5,6

Lei Fang⁷

Chunyan Zhang⁸

Zhaoliang Zeng^3*†

¹Ganzhou National Territory Spactial Investigation and Planning Research Center, Ganzhou, China
²School of Civil and Surveying and Mapping, Jiangxi University of Science and Technology, Ganzhou, China
³Chinese Antarctic Center of Surveying and Mapping, Wuhan University, Wuhan, China
⁴Department of Geography, University of Connecticut, Storrs, CT, United States
⁵State Key Laboratory of Environmental Criteria and Risk Assessment, Chinese Research Academy of Environmental Sciences, Beijing, China
⁶National Joint Research Center for Yangtze River Conservation, Beijing, China
⁷Department of Environmental Science and Engineering, Fudan University, Shanghai, China
⁸Chongqing Wanzhou District Planning and Design Institute, Chongqing, China

Solar radiation is the Earth’s primary source of energy and has an important role in the surface radiation balance, hydrological cycles, vegetation photosynthesis, and weather and climate extremes. The accurate prediction of solar radiation is therefore very important in both the solar industry and climate research. We constructed 12 machine learning models to predict and compare daily and monthly values of solar radiation and a stacking model using the best of these algorithms were developed to predict solar radiation. The results show that meteorological factors (such as sunshine duration, land surface temperature, and visibility) are crucial in the machine learning models. Trend analysis between extreme land surface temperatures and the amount of solar radiation showed the importance of solar radiation in compound extreme climate events. The gradient boosting regression tree (GBRT), extreme gradient lifting (XGBoost), Gaussian process regression (GPR), and random forest models performed better (poor) prediction capabilities of daily and monthly solar radiation. The stacking model, which included the GBRT, XGBoost, GPR, and random forest models, performed better than the single models in the prediction of daily solar radiation but showed no advantage over the XGBoost model in the prediction of the monthly solar radiation. We conclude that the stacking model and the XGBoost model are the best models to predict solar radiation.

Introduction

Solar radiation is the Earth’s main source of energy and the amount of solar radiation reaching the Earth’s surface is affected by the atmosphere, hydrosphere and biosphere (Budyko, 1969; Islam et al., 2009). Solar radiation also has a vital role in the global climate, and even small changes in the output of energy from the Sun will cause considerable changes in the Earth’s climate (Beer et al., 2010; Siingh et al., 2011). Variations in solar radiation affect global temperatures, global mean sea-level, and compound extreme climate events (Bhargawa and Singh, 2019). Accurate observations and analyses of the temporal and spatial variability of solar radiation are therefore essential in research on solar energy, building materials, and extreme weather and climate events (Garland et al., 1990; Cline et al., 1998; Hoogenboom, 2000; Grant and Tuohimaa, 2004; Wild, 2009; Beer et al., 2010; Besharat et al., 2013; Ohunakin et al., 2015). Many methods have been developed to predict solar radiation, including theoretical parameter models, empirical models, artificial intelligence models, and satellite retrieval data (Iziomon and Mayer, 2002; Mellit, 2008; Lu et al., 2011; Li et al., 2012; Halabi et al., 2018; Makade et al., 2019). Angstrom (1924) and Prescott (1940) first proposed the A–P model, which is widely used to predict solar radiation. Bristow and Campbell (1984) constructed the BCM model by analyzing the relationship between solar radiation and daily maximum and minimum temperatures. Yang et al. (2001) developed a hybrid model (YHM), improving the A–P model by exploring the effects of meteorological parameters and then validating the model’s accuracy in Japan. Salazar (2011) compared the YHM and a climatological solar radiation model to estimate the horizontal direct and diffuse components of solar radiation to generate a corrected version of the YHM (CYHM). Gueymard (2003) selected 19 solar radiation models to investigate solar irradiance predictions, concluding that detailed transmittance models perform better than bulk models. The development of machine learning has inspired many researchers to use machine learning algorithms to develop solar radiation prediction models (Azadeh et al., 2009; Jiang, 2009; Chen et al., 2011; Voyant et al., 2012). Fadare (2009) and Linares-Rodríguez et al. (2011) adopted artificial neural network (ANN) technology to construct solar radiation prediction models to test their predictive ability. Xue (2017) used a back-propagation algorithm to develop a solar radiation prediction model and showed that the predictive accuracy depended on the combination and configuration of the input parameters. Chen et al. (2011) used the support vector machine (SVM) method to construct a solar radiation prediction model and showed that the SVM-based algorithm had a differential predictive accuracy when using different kernel functions. Olatomiwa et al. (2015) and Shamshirband et al. (2016) both optimized the SVM algorithm and achieved good prediction results. Tree algorithms, such as the random forest algorithm and the gradient boosting regression tree (GBRT) algorithm, have been used to construct solar radiation prediction models with encouraging results (Sun et al., 2016; Persson et al., 2017; Fan et al., 2018; Zeng et al., 2020). In recent years, some scholars have carried out the comparative analysis of a variety of machine learning algorithms (Meenal and Selvakumar, 2018; Pang et al., 2020; Shamshirband et al., 2020), and all these works show that the ANN algorithm does not realize good prediction results but provides a direction for algorithm improvement. Some studies use deep learning techniques to predict solar radiation. For example, Shamshirband et al. (2019) discuss different types of deep learning algorithms applied in the field of solar, and results show hybrid networks have better performance compared with single networks. Mishra et al. (2020) proposed a short-term solar radiation prediction model using WT-LSTM and achieved good results, showing that deep learning technology has great potential in solar radiation. A CEEMDAN–CNN–LSTM model is proposed by Gao et al. (2020) for hourly multi-region solar irradiance forecasting, and the results present that the model can achieve more accurate prediction performance than other models.

As an investigative technique, machine learning has achieved noteworthy success in many areas, including natural language processing and image recognition (Angra and Ahuja, 2017). The use of machine learning has come to the forefront of the construction of solar radiation models and is a popular direction of research. However, many researchers have focused on the construction of one or several machine learning methods, and there are few in-depth considerations of the differences among these models. Therefore, we used a daily dataset of meteorological elements and basic radiation elements for Ganzhou, China, for the time period 1980–2016 to explore the differences between models of solar radiation prediction. After data processing, we applied the random forest algorithm to selected variables and extracted a monthly dataset based on the daily dataset. We selected 12 machine learning methods to construct a solar radiation prediction model. By comparing the prediction results of these 12 machine learning models, we found the solar radiation prediction models with the best prediction ability. The models with the best prediction ability were then stacked in a linear model. A stacking model was obtained and the predicted results were analyzed.

Data and Machine Learning Algorithms

Study Area and Datasets

Ganzhou city (24.48–30.06° N, 113.57–118.46° E) lies in the south of Jiangxi province in the southern subtropical zone of China and is characterized by a subtropical monsoon climate. It is bordered to the south by Guangdong province, to the east by Fujian province, and to the west by Hunan province. Ganzhou has a mild climate with four distinct seasons and both winter and summer monsoons, with precipitation concentrated in the spring and summer seasons. The annual average temperature is 19.1–20.8°C and the annual rainfall is 1152.2–1554.9 mm. There is a solar radiation monitoring station (No. 57993) in Ganxian County (25.51° N, 114.57° E, 137.5 m above sea-level) (Figure 1).

FIGURE 1

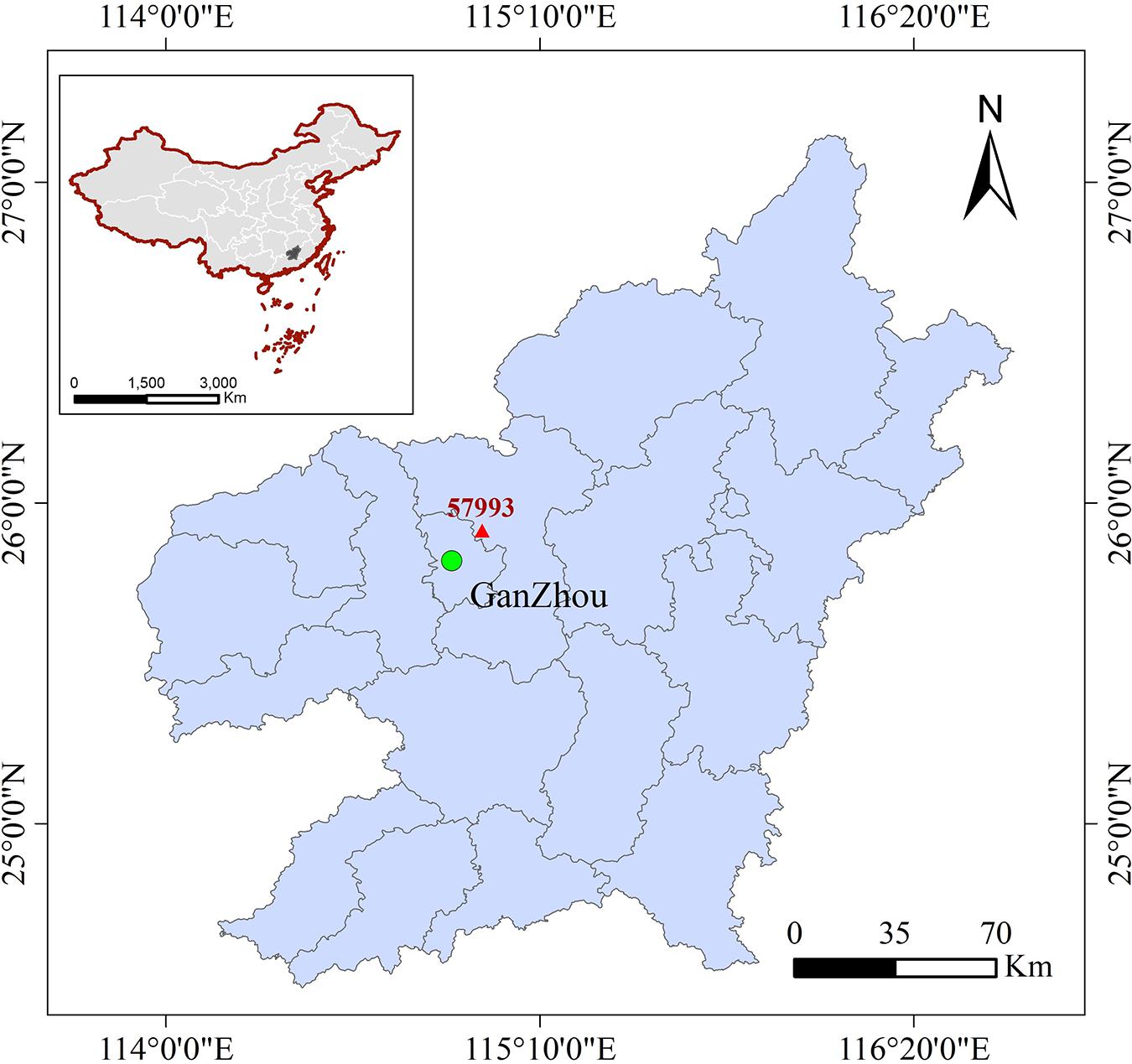
Figure 1. The geographical location of solar radiation monitoring station in Ganzhou County (red triangle).

Experimental data were gathered from the China Meteorological Information Center website, including a dataset (V3.0) of daily climate data (temperature, precipitation, air pressure, humidity, temperature, visibility, wind speed, and sunshine duration) from surface stations in China and a daily radiation dataset from Ganzhou’s surface solar radiation monitoring station. After referring to relevant research (Will et al., 2013; Mohammadi et al., 2016) and analyzing the quality of the collected data, we selected the data from 1980 to 2016 to estimate solar radiation. The data were selected including the visibility (VIS), the mean relative humidity (RHU-mean), the minimum relative humidity (RHU-min), the mean wind speed (WIN-mean), the mean precipitation (PRE-mean), the mean pressure (PRS-mean), the maximum pressure (PRS-max), the minimum pressure (PRS-min), the sunshine duration (SSD), the mean temperature (TEM-mean), the maximum temperature (TEM-max), the minimum temperature (TEM-min), the mean ground temperature (GST-mean), and the total solar radiation (RAD).

Quality control of the data was essential considering the length of the study period and the inherent errors in the instrument-based observations. We excluded missing and abnormal values in the meteorological data from the final dataset and then applied the requirements for solar radiation data quality control proposed by Younes et al. (2005). In total, 13,100 daily data records and 432 monthly average data records were obtained. The dataset was further divided into training and test sets and then normalized, with the training set accounting for 90% and the test set accounting for 10% of all data. Our final sample consisted of 11,790 daily training sets, 1,310 daily test sets, 388 monthly training sets, and 44 monthly test sets.

Machine Learning Predictive Algorithms and Stacking Techniques

Machine Learning Algorithms

With the development of machine learning technology, an increasing number of researchers are using machine learning to predict solar radiation. We investigated 12 different machine learning predictive algorithms: multiple linear regression (Baczek et al., 2005; Nathans et al., 2012), the radial basis function neural network (Mahanty and Dutta Gupta, 2004; Li M. et al., 2008), the K-nearest neighbor model (Shen and Chou, 2005; Deng et al., 2016), the decision tree (Brodley and Friedl, 1997; Quinlan, 1999), the back-propagation neural network (Van Ooyen and Nienhuis, 1992; Trappey et al., 2006), the extreme learning machine (Deng et al., 2015; Huang G. et al., 2015), SVM regression (Burges, 1998; Shamshirband et al., 2016), Gaussian process regression (GPR) (Nguyen-Tuong et al., 2009; Ebden, 2015), the GBRT (Zhang and Haghani, 2015; Johnson et al., 2018), adaptive boosting (Adaboost) (Zhu et al., 2006; Li X. et al., 2008; Wang, 2012), extreme gradient lifting (XGBoost) (Nielsen, 2016; Torlay et al., 2017), and random forest (Kapwata and Gebreslasie, 2016; Sun et al., 2016) algorithms. A detailed description of machine learning methods can be found in Supplementary Text S1.

Stacking Model

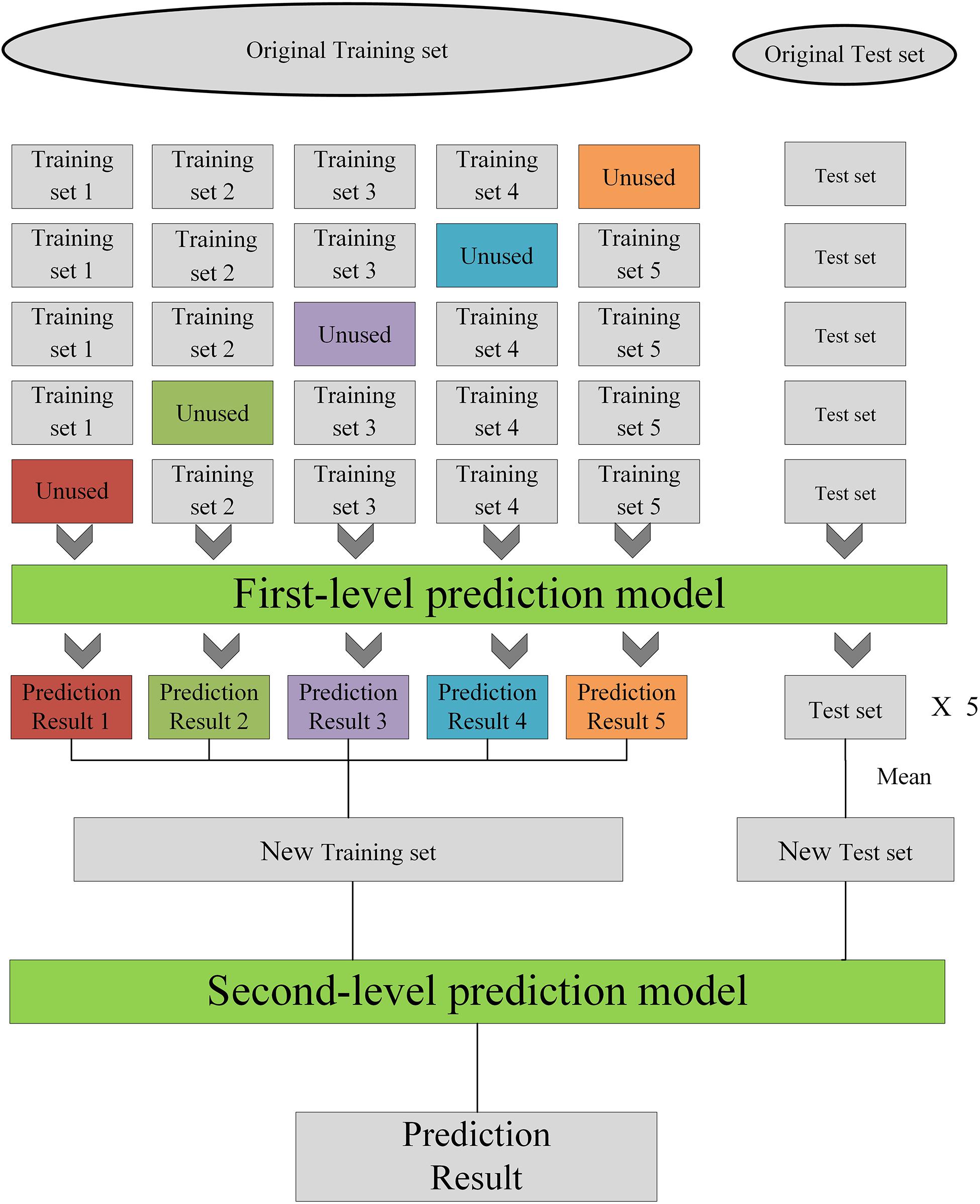
Stacking technology is a general integration algorithm that integrates advanced learners by using multiple lower-level learners to achieve higher performance (Agarwal and Chowdary, 2020). In general, the K-fold cross-validation method is used to train and test these models and then output the prediction results. The prediction results output by each model is then combined into a stacking model, which is built to reduce the generalization errors. The stacking model usually consists of two layers. The first layer is the base learner, and the input is the initial training set. The second layer is trained with the output data from the first layer as the input data and gives the final results.

The steps of the stacking model construction are as Figure 2. Each model is trained using five-fold cross-validation. The training set is divided into five parts, and four parts are selected as the training data and one set as the test data. The test data in each of the four training sets is predicted to obtain a prediction result (a) and the test set data are predicted by the trained model to obtain the test set prediction result (b). After five training runs, the prediction result a of each of the five runs is combined into one column as A and the prediction result b is averaged as B. The new datasets A and B are obtained, in which the number in A is the same as the number of training sets, but A is one-dimensional data. After constructing N single models, N A and N B are generated, then the N A and N B data are combined into a new training set and a new test set. A simple linear model is used as the second layer to train using the new training set and test with the new test set.

FIGURE 2

Figure 2. The framework of the stacking model.

Materials and Methods

Prediction of the Flow of Solar Radiation

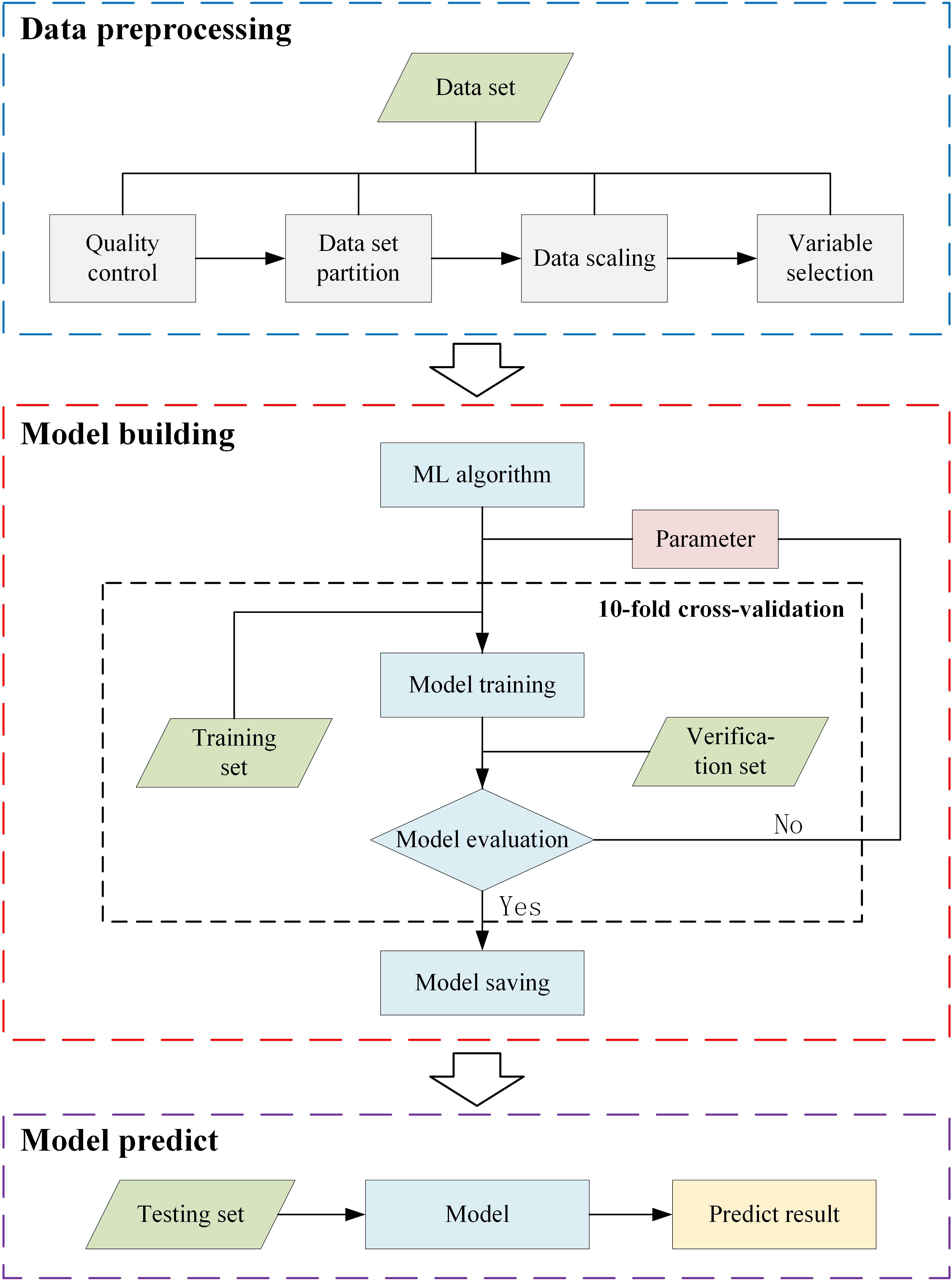
Our experiment consisted of three parts (Figure 3): data preprocessing, model building, and model prediction. The data preprocessing involved four steps: data quality control, dataset partitioning, data scaling, and variable selection. Among them, data quality control, dataset partitioning, and data scaling are described in Section “Study Area and Datasets,” and variable selection is described in Section “Variable Selection.” The main processes of the model building were as follows: the selection of the machine learning algorithm, parameter selection, model construction, and model saving. We used the 10-fold cross-validation method (Jiang and Wang, 2017) in the parameter selection step. We can get a detailed description of the model building in Section “Model Building.” In the model prediction step, the saved model from the model building step was used to predict the solar radiation using the test dataset. Then, we save the predicted results and analysis. The specific experimental steps proceeded as follows:

FIGURE 3

Figure 3. Flow chart of the machine learning models used to estimate solar radiation.

(1) data collection and data preprocessing;

(2) choose a machine learning algorithm from the 12 algorithms to predict solar radiation;

(3) compare solar radiation predictive ability based on different parameters;

(4) if the best predictive ability is achieved, save the model;

(5) return to step (2) and choose another machine learning algorithm until all 12 algorithms have been subjected to machine learning model building;

(6) input the preprocessing dataset (we prepared datasets on two timescales—daily and monthly—to estimate the solar radiation predictive performance of the 12 machine learning models) and use the 12 saved machine learning models to predict solar radiation and obtain the predicted results;

(7) save predicted results and analyze.

Variable Selection

The variable selection step is important in constructing machine learning models. The current mainstream variable selection algorithms include the genetic algorithm (Huang and Chiu, 2006), the Tabu search (Corazza et al., 2013), particle swarm optimization (Khatibi Bardsiri et al., 2013), and the random forest algorithm (Kapwata and Gebreslasie, 2016). We used the random forest algorithm to select data variables (Zeng et al., 2020). Normalized daily data were used to construct and train the random forest model and to calculate the model’s importance. The data preprocessing experiment was intended to verify the importance of variables in a given model and to analyze the impact of changes in the variables on the model’s predictive performance. The experiment proceeded as follows:

(1) divide the dataset into a training set and test set after completing the data quality control process;

(2) use the training set to train and save the model, then calculate the correlation coefficient (R²) and the root mean square error (RMSE) of the saved model;

(3) based on the order of importance of the variables in the model, eliminate the least important variable;

(4) repeat steps (2) and (3) until only two variables remain (the minimum required for calculation).

Figure 4 shows that when the model contained <10 variables, R² tended to decrease and the RMSE tended to increase. Between 12 and 10 variables, R² reached 0.921 and the RMSE was 2.042 MJ/m². With four variables, R² decreased sharply from 0.904 to 0.895 and the RMSE decreased from 2.19 to 2.28 MJ/m². Therefore, the prediction of solar radiation can achieve the best performance when using 10 variables, then the subsequent model experiments were trained with these 10 variables.

FIGURE 4

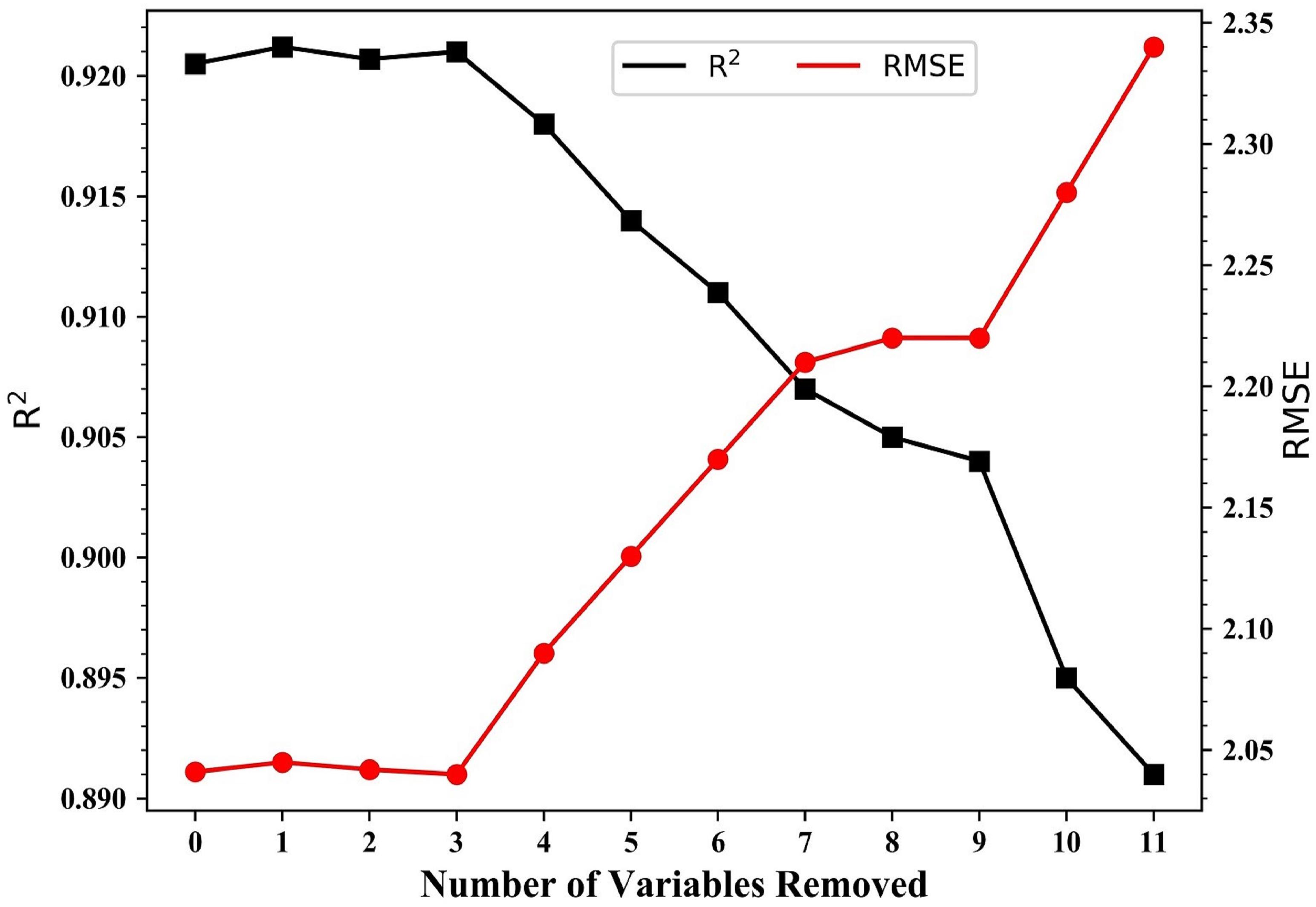
Figure 4. Predictive performance (R² and RMSE) of the random forest model during variable selection. Variables were removed in the order PRS-min, PRS-max, RHU-min, PRE-mean, TEM-mean, WIN-mean, TEM-max, TEM-min, RHU-mean, PRS-mean, and VIS.

Model Building

Experiments were performed in Python 3.6 using third-party libraries such as Pandas, NumPy, the scikit-learn machine learning library (Sklearn), and the Xgb library. Twelve machine learning algorithms were chosen to build the models. The initial parameter settings of each algorithm were determined according to the algorithm’s characteristics. For example, for a neural network model, the number of hidden layers and the number of neurons were determined based on empirical formulas and neural network design principles (Basheer and Hajmeer, 2000). The respective selection ranges of the adjustment parameters and other parameters were then set according to the parameter adjustment methods for different machine learning algorithms. We used Sklearn’s GridSearchCV method to select parameters for each of the 12 machine learning models, ultimately saving the best model. The first layer of the stacking model consists of those multiple models with excellent predictive power. The parameters of the first layer model are the parameters selected previously and the second layer is constructed by multiple linear regression. After obtaining the best parameters, the train set was used to train the model and the final model was saved. The time spent training the model is the model construction time, and the final model size is the model memory. When the model was constructed, input the test set was input to get the prediction result.

Statistical Metrics

The models were evaluated using four indicators: R², RMSE, MAE, and BIAS:

R^{2} = \frac{{(\sum_{t = 1}^{n} (y o_{t} - \bar{y o}) (y m_{t} - \bar{y m}))}^{2}}{\sum_{t = 1}^{n} {(y o_{t} - \bar{y o})}^{2} \cdot \sum_{t = 1}^{n} {(y m_{t} - \bar{y m})}^{2}} (1)

R M S E = \sqrt{\frac{1}{n} \sum_{t = 1}^{n} {(y o_{t} - y m_{t})}^{2}} (2)

M A E = \frac{1}{n} \sum_{t = 1}^{n} || (y o_{t} - y m_{t}) || (3)

B I A S = (y o_{t} - y m_{t}) (4)

where n indicates the amount of data, ym_t is the predicted solar radiation, yo_t is the observed solar radiation, and $\bar{y m}$ and $\bar{y o}$ represent the average of the predicted and observed results, respectively.

If R² is close to 1, then the observed and predicted values are closely correlated. The closer the RMSE/MAE values are to 0, the better the predicted value fits the observed value. A combination of metrics, including, but not limited to, the RMSE and MAE, are often required to assess the performance of the model.

Results

Description and Selection of Variables

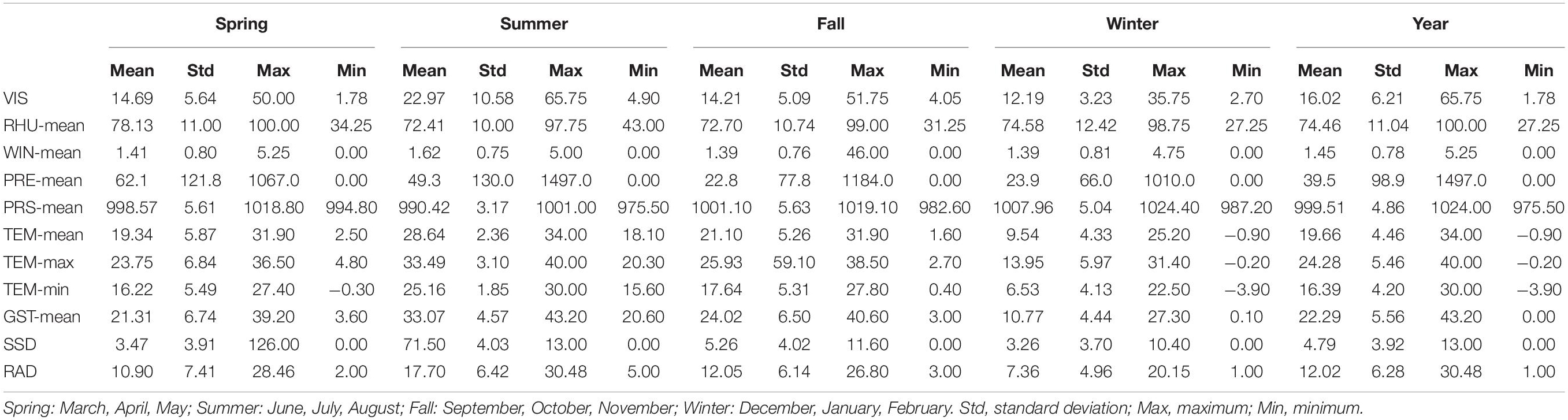
The average annual range of the RAD was 1–30.48 MJ/m², with a mean value of 12.02 MJ/m² and a standard deviation of 6.28 MJ/m² (Table 1). The annual mean (standard deviation) values were VIS 16.02 (6.21) km, RHU-mean 74.46 (11.04)%, WIN-mean 1.45 (0.78) m/s, PRE-mean 39.5 (98.9) mm, PRS-mean 999.51 (4.86) hPa, TEM-mean 19.66 (4.46)°C, TEM-max 24.28 (5.46)°C, TEM-min 16.39 (4.2)°C, GST-mean 22.29 (5.56)°C, and SSD 4.79 (3.92) h. Apart from the RHU-mean, PRE-mean, and PRS-mean, the mean values of the variables were highest in summer, followed by spring and autumn, and were lowest in winter. Supplementary Figure 1 shows the annual maximum GST-mean and the corresponding solar radiation from 1980 to 2016. The trend of GTS-max and the corresponding solar radiation values were generally consistent and increased with the solar radiation, confirming the importance of solar radiation in compound climate extreme events (Ohunakin et al., 2015).

TABLE 1

Table 1. Descriptive statistics of the modeling variables in the training dataset.

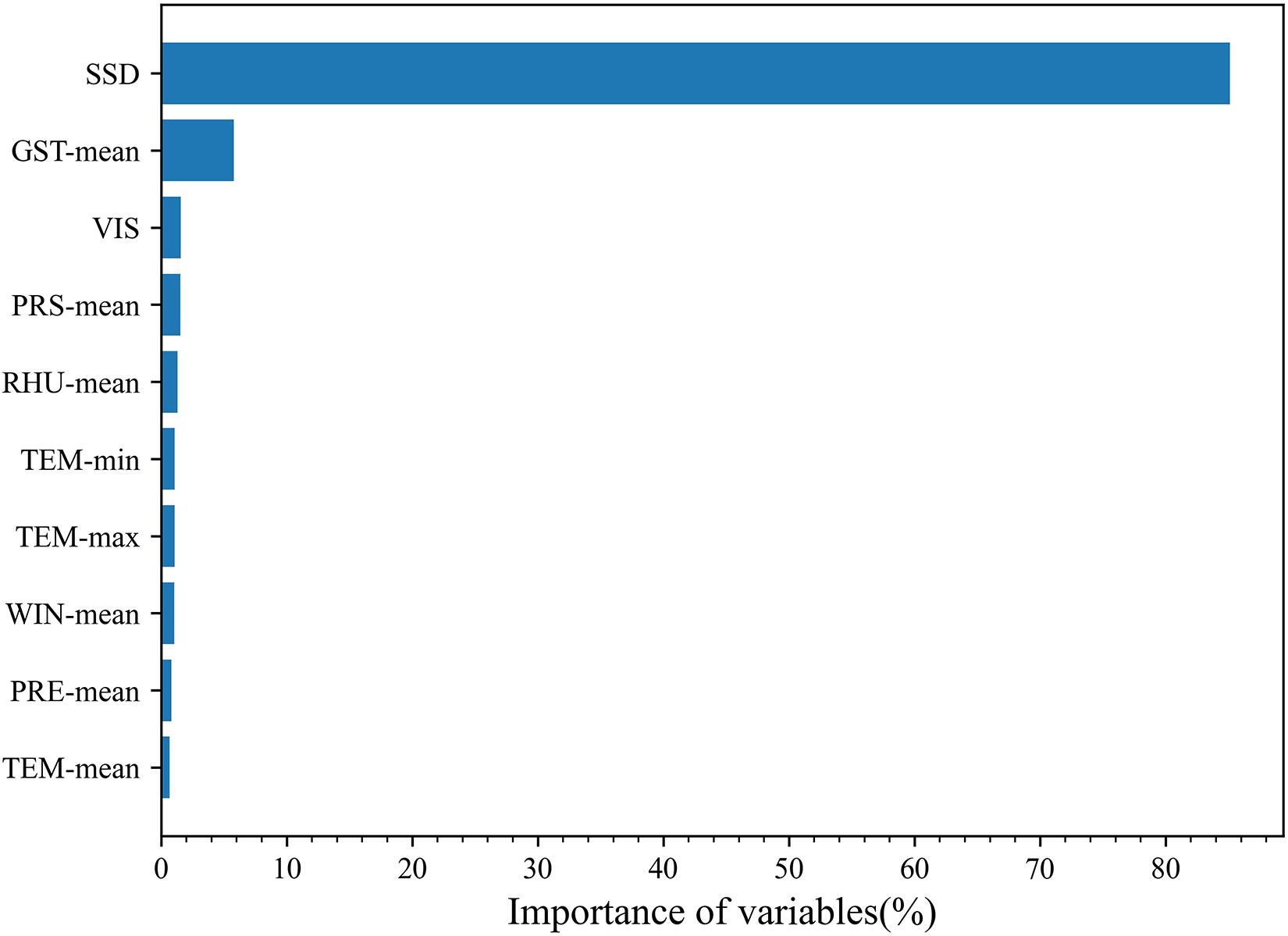
Figure 5 shows the importance of the input variables as predictors in the final random forest model. SSD was identified as the most critical variable, followed in descending order by GST-mean, VIS, PRS-mean, RHU-mean, TEM-min, TEM-max, WIN-mean, TEM-mean, PRE-mean, RHU-min, PRS-max, and PRS-min. The importance of SSD was 85%, which agrees with the results of earlier studies (Chen et al., 2013; Suehrcke et al., 2013; Zeng et al., 2020). The importance of GST-mean was 6% and the importance of all other variables was <5%.

FIGURE 5

Figure 5. Importance of variables in predicting solar radiation using the random forest model.

Predictive Performance for Daily Solar Radiation

Figure 6 shows the performance of the 12 machine learning models in predicting solar radiation for the given daily dataset. The statistical results show that most of the machine learning models used to predict solar radiation yielded satisfactory results. The R² values of the 12 machine learning models ranged from 0.838 to 0.925. The GBRT, GPR, XGBoost, and random forest models were the best machine learning models to predict solar radiation with R² values of 0.925, 0.923, 0.922, and 0.921, respectively. The R² values of the extreme learning machine and decision tree models were 0.874 and 0.838, respectively, which indicated that these models had the poorest precision for the prediction of solar radiation. The RMSE values of the 12 machine learning models were in the range 1.987–2.999 MJ/m². The RMSE value of the GBRT model was the lowest (1.987 MJ/m²), indicating that this model was the best for predicting solar radiation. By contrast, the RMSE value of the decision tree model was the largest (2.999 MJ/m²), suggesting that this model was the poorest predictor of solar radiation. The MAE values of the 12 machine learning models ranged from 1.498 to 2.266 MJ/m², with the GBRT model returning the smallest value (MAE = 1.498 MJ/m²), meaning that the deviation between the predicted and measured values was also the smallest. The MAE value of the decision tree model was the largest (MAE = 2.266 MJ/m²), demonstrating that this model had the largest prediction bias. The MAE values of the other machine learning models were both <2.0 MJ/m².

FIGURE 6

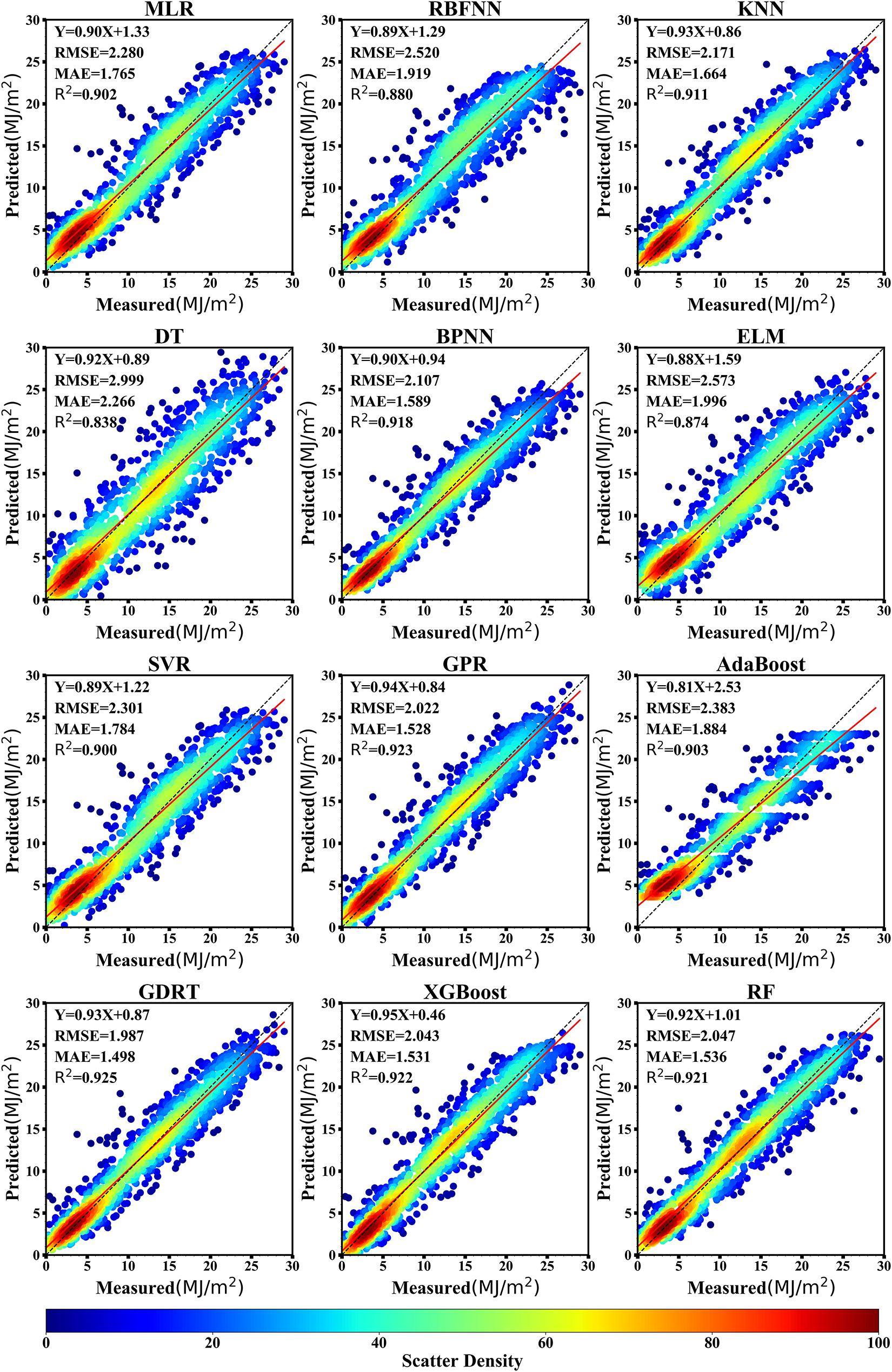
Figure 6. Scatter plots of the cross-validation results for 12 machine learning models in predicting daily solar radiation at Ganzhou from 1980 to 2016.

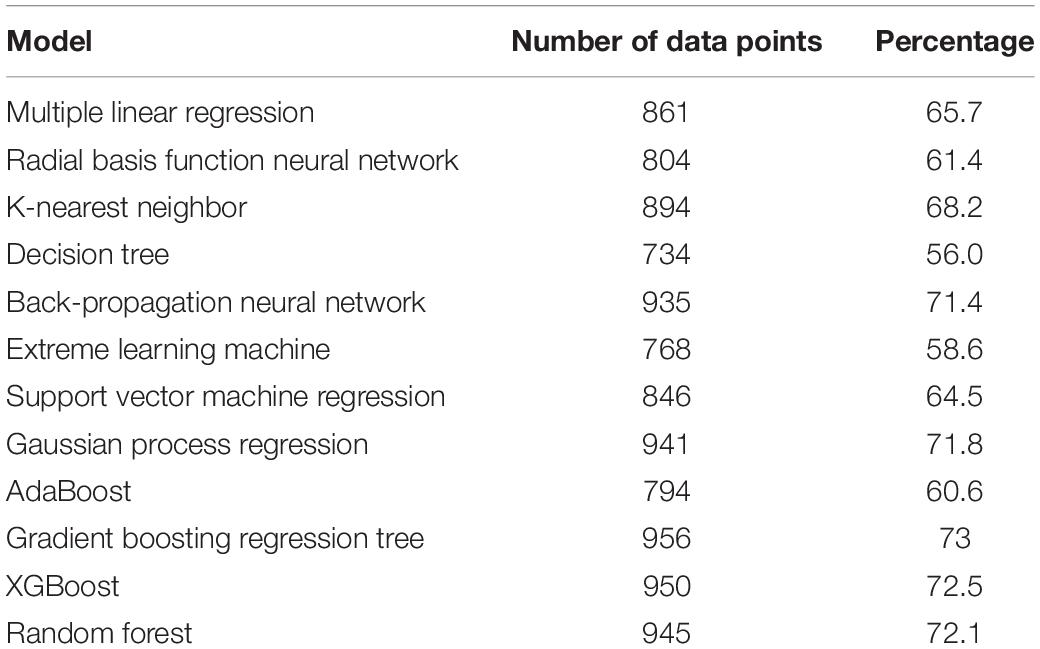
Figure 7 shows distribution maps of the daily deviation probability to further explore the distribution of the deviation of solar radiation prediction for the 12 machine learning models. The results showed that the bias of the GBRT and the decision tree models both were 0.01 MJ/m², followed by the RBNN model (−0.02 MJ/m²). The bias of the AdaBoost model for solar radiation prediction was −0.32 MJ/m². The deviation values of most models were mainly distributed between −6 and +6 MJ/m², whereas those of the decision tree and extreme learning machine models were mainly distributed between −8 and +8 MJ/m². Table 2 shows the number of deviation values that fell within the range ±2 MJ/m² in the prediction of solar radiation for the 12 models. The deviation in solar radiation prediction for the GBRT, GPR, XGBoost, and random forest models each exceeded 940, compared with only 734 for the decision tree model.

TABLE 2

Table 2. Statistics for the amount of daily data for each model deviation within ±2 8 MJ/m².

FIGURE 7

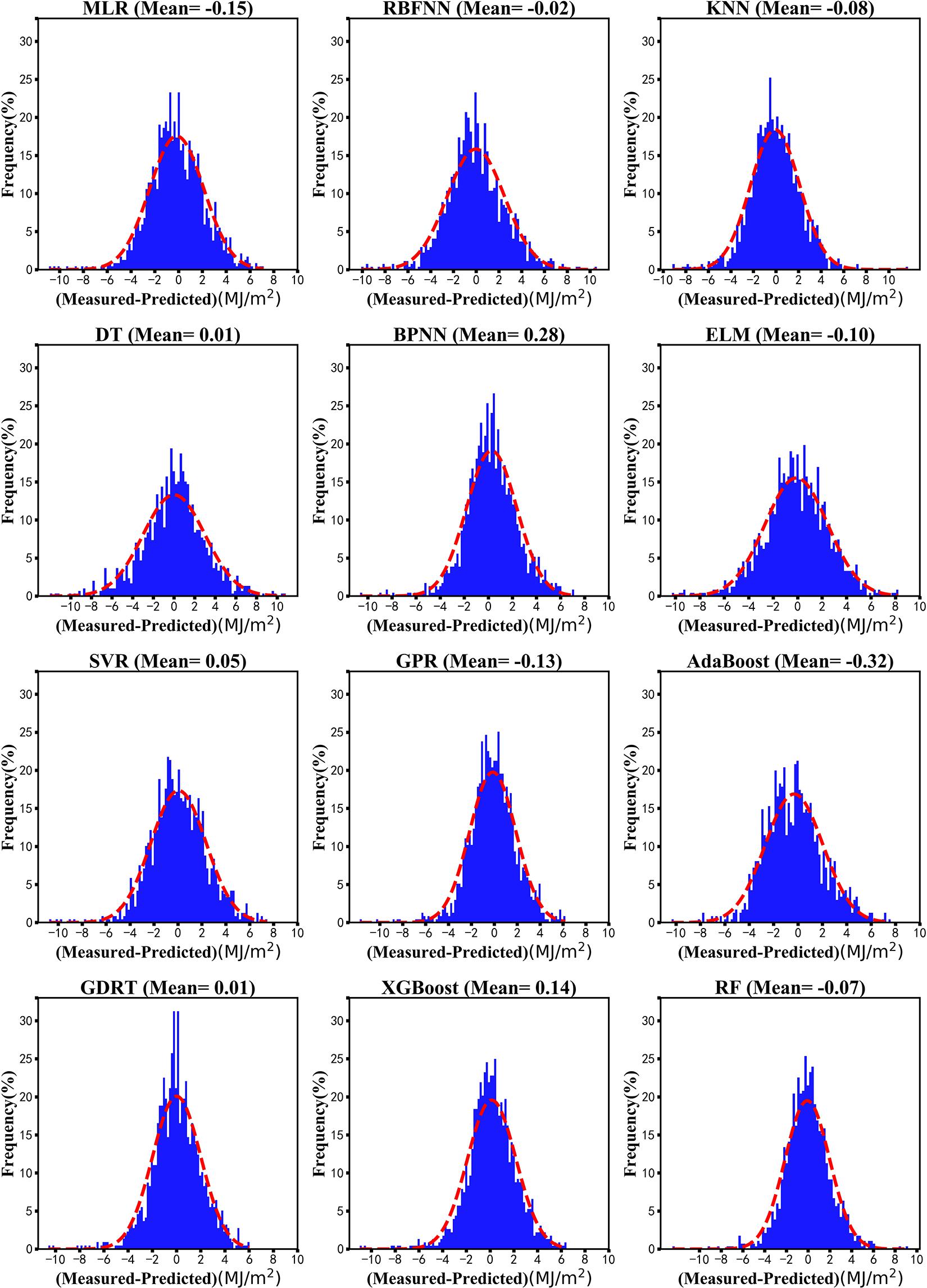
Figure 7. Deviation distribution of machine learning models in predicting daily solar radiation at Ganzhou from 1980 to 2016.

The prediction results from the daily value data indicate that the GBRT, XGBoost, GPR, and random forest models had a relatively good predictive ability, whereas the extreme learning machine and decision tree models performed poorly. The random forest model had the longest construction time, followed by the GBRT and the GPR models; the XGBoost model had the shortest construction time. This is related to the model principle—for example, to obtain better training results, the random forest model needs more CART-based models, which increases the training time. By contrast, XGBoost uses parallel processing to increase the operational speed and therefore requires less time.

Predictive Performance for Monthly Solar Radiation

Figure 8 presents a scatter plot of the monthly predicted and measured values for different models. The R² values for the 12 machine learning models ranged from 0.900 to 0.944 and were > 0.9 for all models. The XGBoost model gave the best prediction result, with an R² value of 0.944; the GPR (R² = 0.941), GBRT (R² = 0.938), and random forest (R² = 0.936) models also demonstrated a good prediction performance. The K-nearest neighbor (R² = 0.900) and decision tree (R² = 0.901) models gave relatively poor prediction results. The RMSE of each model fell between 1.131 and 1.580 MJ/m². The XGBoost model returned the lowest RMSE of 1.131 MJ/m², reflecting the highest precision of all the models. The decision tree model had the lowest precision (RMSE = 1.580 MJ/m²). The MAE values for all models ranged from 0.870 to 1.174 MJ/m². The MAE of the XGBoost model was the smallest (MAE = 0.870 MJ/m²), indicating that the predicted value was close to the observed value.

FIGURE 8

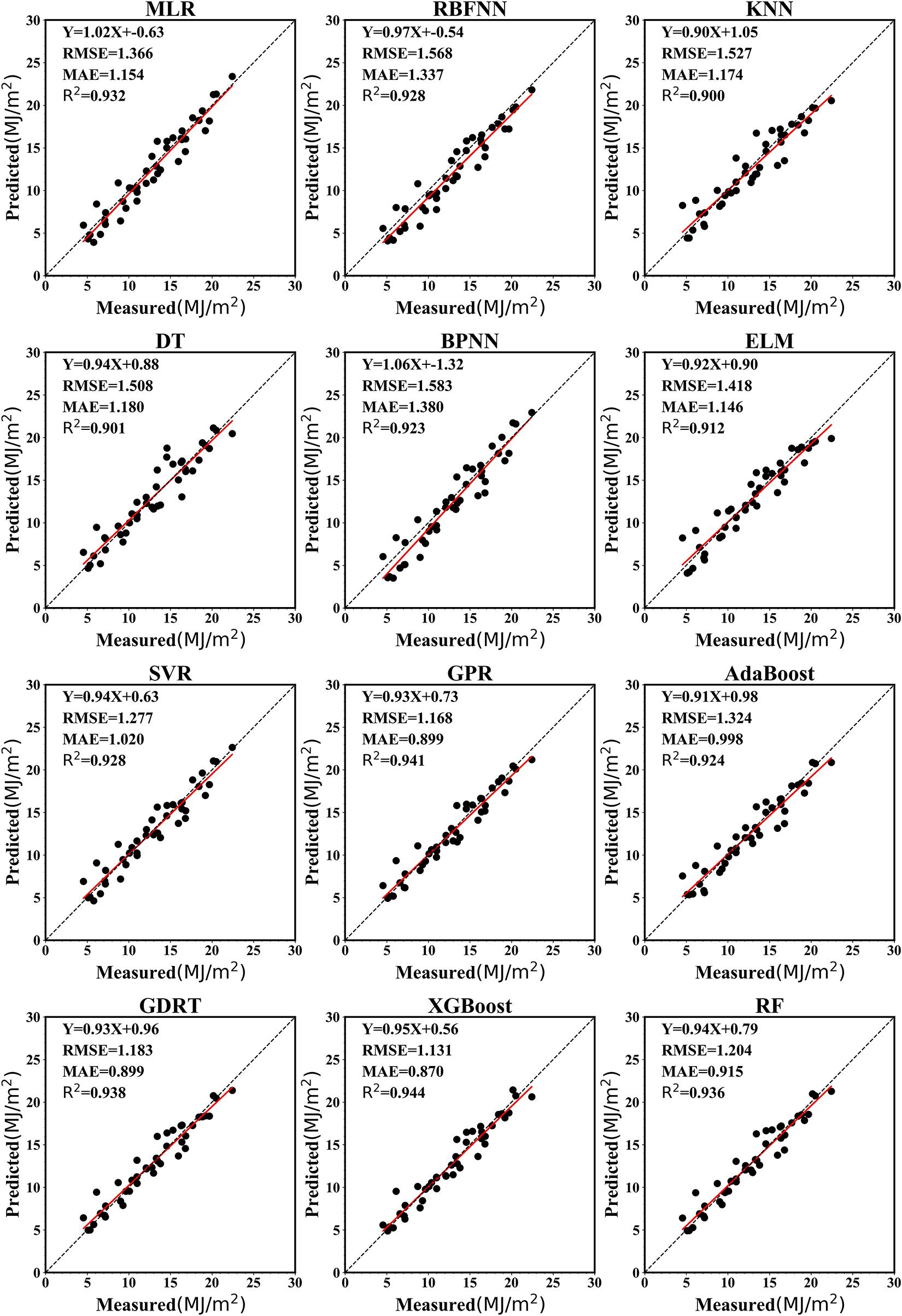
Figure 8. Scatter plots of the results of machine learning models in predicting monthly average solar radiation at Ganzhou from 1980 to 2016.

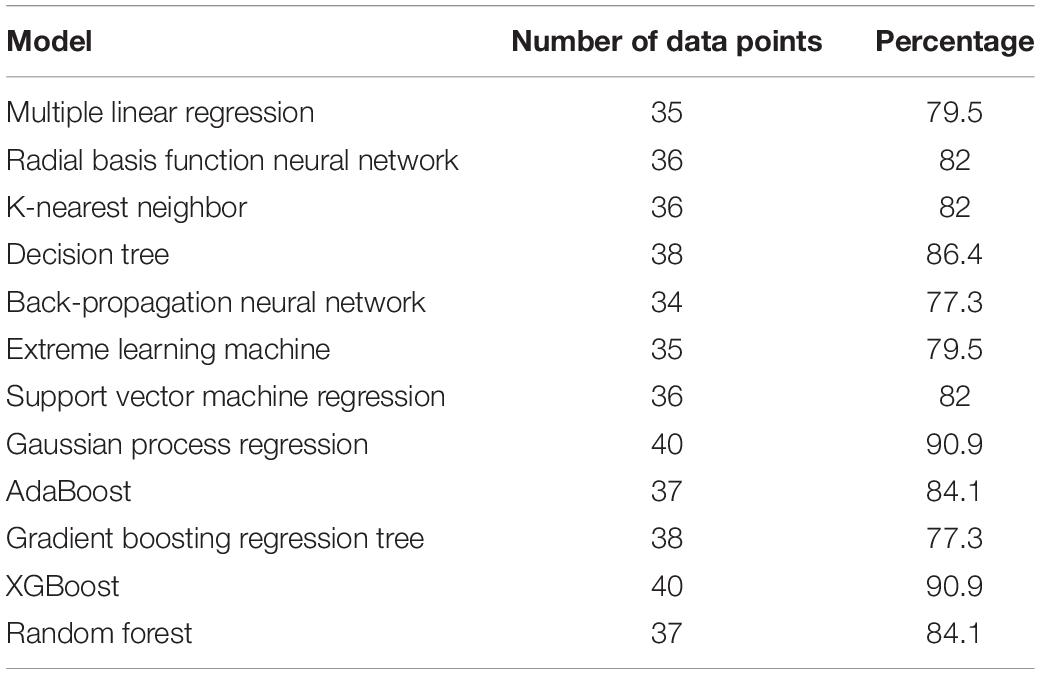
For the monthly average data, Figure 9 shows the largest deviation in the RBNN model (bias 0.88 MJ/m²), followed by random forest (bias −0.02 MJ/m²) and SVM regression (bias 0.08 MJ/m²) models and the lowest deviation in the GBRT model (bias −0.01 MJ/m²). In contrast with the deviation in the daily data, the monthly average prediction bias of most models was positive, although the decision tree, GBRT, and random forest models showed a negative deviation. According to the monthly mean deviation probability distribution, the main distribution interval of the model deviation was within ±4. Table 3 gives the statistical results for the monthly data with a predicted deviation between −2 and +2 MJ/m², with 37 data points in the random forest model and 40 data points in the GBR model.

TABLE 3

Table 3. Statistics for the amount of monthly data in each model deviation within ±2.

FIGURE 9

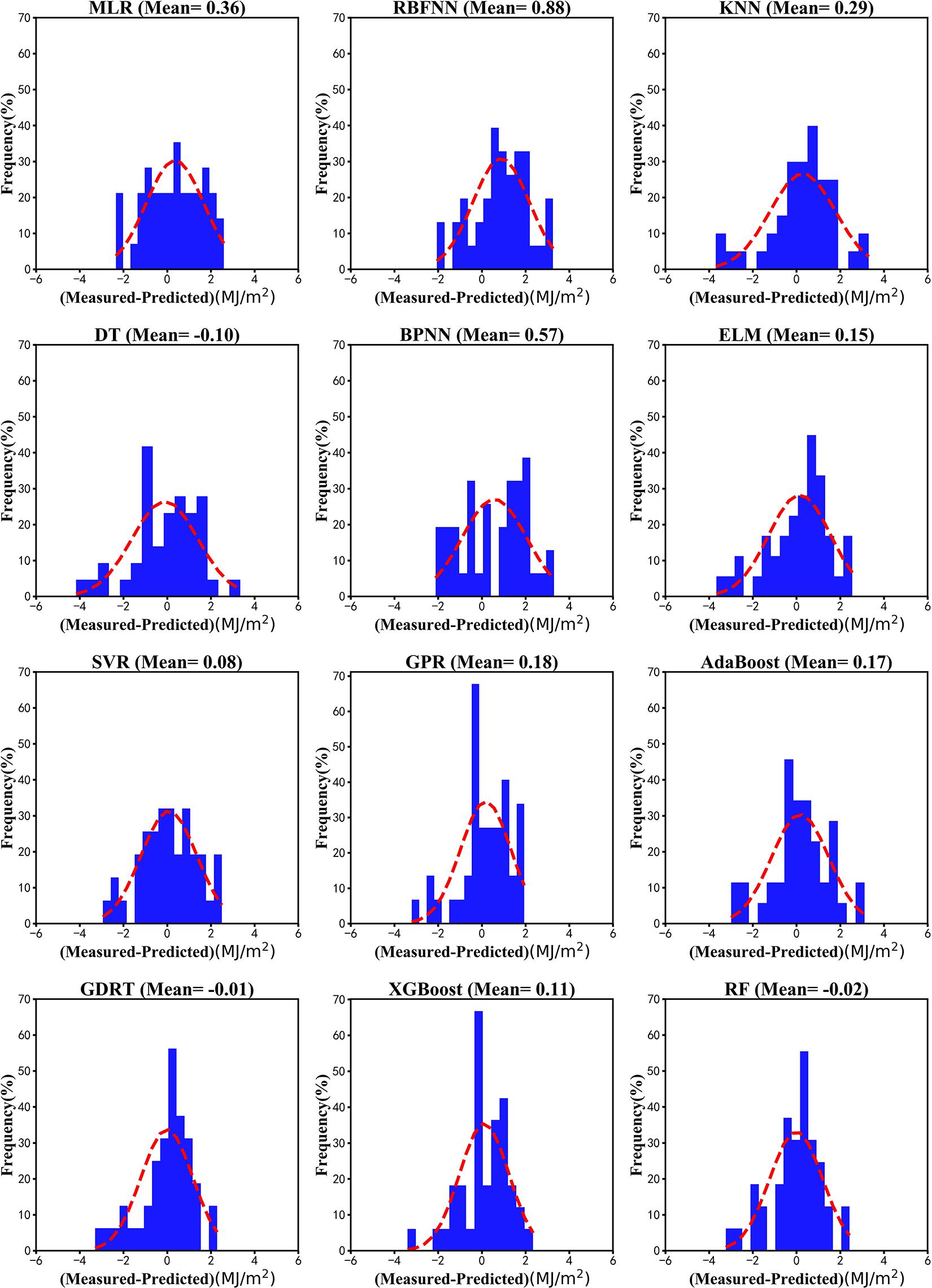
Figure 9. Deviation distribution of machine learning models in predicting the monthly average solar radiation at Ganzhou from 1980 to 2016.

The XGBoost, GPR, GBRT, and random forest models showed better predictive ability on the monthly average data, whereas the K-nearest neighbor and decision tree models performed poorly. When the amount of data is small, the XGBoost, GPR, GBRT, and random forest models are all built very quickly, but the XGBoost model is the fastest with the highest prediction accuracy. Besides, XGBoost has strong anti-overfitting and generalization abilities. This is advantageous for the construction of the monthly radiation value in models with a small number of data points, which is an advantage over the other machine learning models. The XGBoost model is therefore recommended when there is only a small number of data points.

Predictive Performance of the Stacking Model

The XGBoost, GPR, GBRT, and random forest single models showed excellent prediction capabilities. These four models were therefore used as the first layer model and multiple linear regression was used as the second layer model to build a stacking model. Figures 10A,B show the predicted results and bias probability distributions. Figure 10A shows that the R² of the stacking model is 0.929, the RMSE is 1.940 MJ/m², and the MAE is 1.457 MJ/m². Compared with the 12 single models, the stacking model has the highest R² value, but the lowest RMSE and MAE. Figure 10B shows that the average deviation of the stacking model is 0 MJ/m² and the deviation of the distribution is more uniform than that of the single models. The stacking model predicts 74.8% of the data with a bias distribution in [−2, 2]. The stacking model has a better prediction ability for the daily data than the single models. Figure 10C shows that the R² value of the stacking fusion model is 0.943, the RMSE is 1.142 MJ/m², and the MAE is 0.884 MJ/m², all lower than the XGBoost model (R² 0.944, RMSE 1.131 MJ/m², and MAE 0.870 MJ/m²). Figure 10D shows that the average value of the stacking deviation of the stacking model is 0.13 MJ/m² and there are only 39 deviations between [2, −2]. The stacking model has no advantage over the XGBoost model in terms of construction time.

FIGURE 10

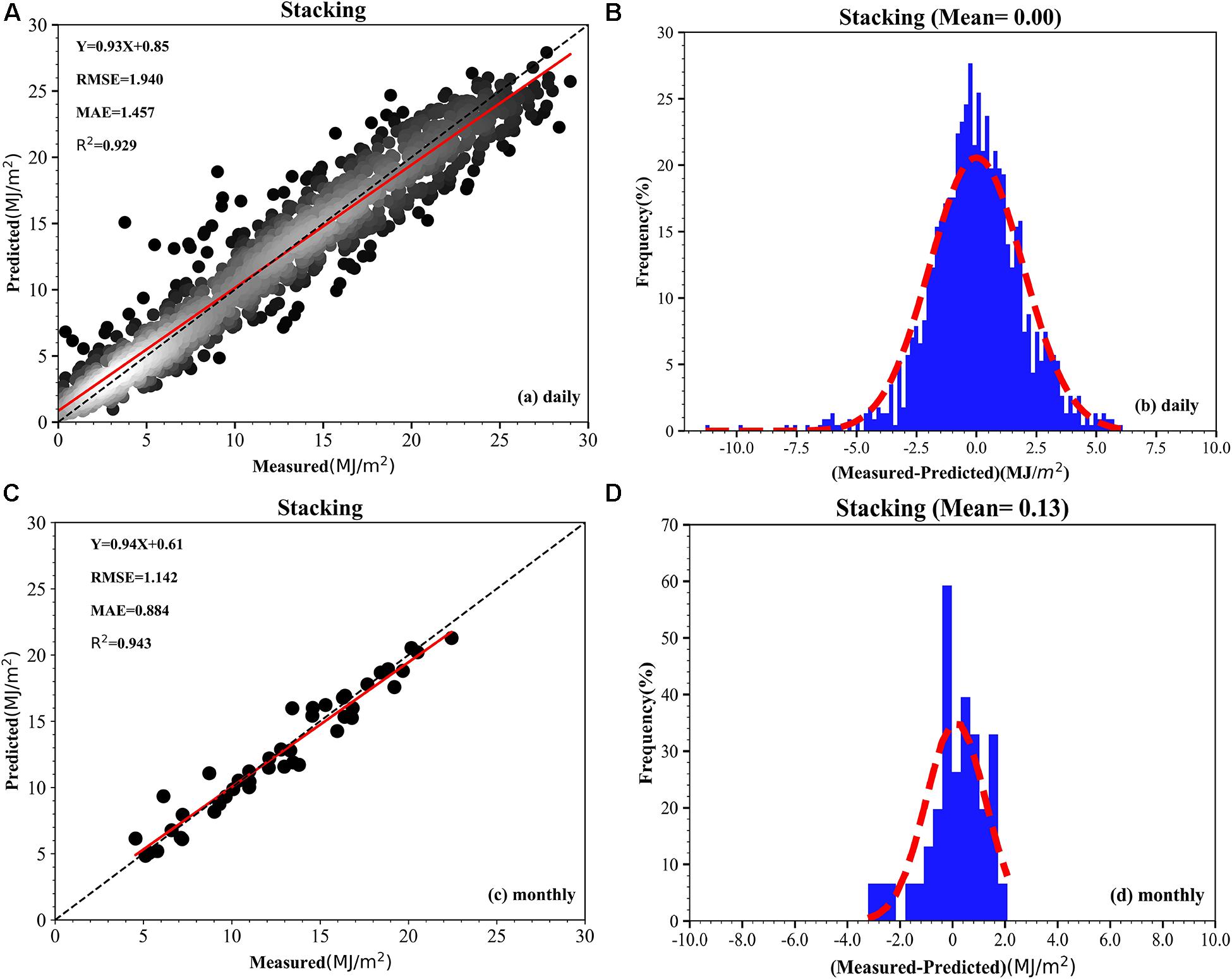
Figure 10. (A–D) Scatter plot and distribution of deviation of the prediction results of the stacking model.

Discussion

Many studies have compared the ability of machine learning algorithms to predict solar radiation (Supplementary Table 1). Moreno et al. (2011) used an ANN and generalized regression to build models separately, positing that an ANN has the same predictive power as generalized regression. Yang et al. (2014) applied ANN-SVM, SVM, and ANN to construct separate models, giving a model performance in the order ANN-SVM > SVM > ANN. Wang et al. (2016) compared the MLP, RBNN, and GRNN models and noted RBNN > GRNN > MLP in terms of performance. We used daily and monthly data to predict the performance of 12 machine learning models and showed that the GBRT, GPR, XGBoost, and random forest models had better prediction capabilities than the other models. We also combined the XGBoost, GBRT, GPR, and random forest models using stacking technology. The performance of the stacking model in predicting the daily solar radiation set was better than that of the 12 single models, but the performance using the monthly dataset gave no advantage over the XGBoost model.

We found that the input of a small measured value of solar radiation returned a large predicted output value, whereas the input of a large value of solar radiation returned a small predicted output value after machine learning processing. This phenomenon may be linked to data that were relatively concentrated and contained fewer, but higher, measured values. The data scaling method greatly influences the performance of machine learning models (Huang J. et al., 2015; García et al., 2016). Normal processing methods include no processing, normalization, standardization, and regularization. We adopted four different data processing methods to build 12 different machine learning models with daily or monthly data. The results are shown in Supplementary Tables 2, 3.

Conclusion

We performed data preprocessing and variable selection based on meteorological elements and solar radiation data from 1980 to 2016 for Ganzhou station, China. Then, 12 machine learning models were developed using Sklearn and the Xgb library. By comparing and evaluating the predictive ability of the 12 machine learning models using R², the RMSE, the MAE and BIAS indices, the XGBoost, GPR, GBRT, and random forest models were selected as the first layer, and multiple linear regression was selected as the second layer to construct a stacking model to predict solar radiation.

Using the random forest algorithm to select the variables, the SSD was identified as the most important variable. The time series of the annual maximum GST-mean and the corresponding solar radiation value from 1980 to 2016 showed that the maximum GTS-max increases with the solar radiation, which confirms the importance of solar radiation in compound extreme climate events. The GBRT, XGBoost, random forest, and GPR models performed better than the other models for the daily and monthly datasets. The GBRT model had the best predictive ability for the daily datasets, whereas the XGBoost model had the best predictive ability for the monthly datasets. The random forest model had the longest construction time, followed by the GBRT and GPR models, whereas the XGBoost model had the shortest construction time. This phenomenon is related to the principles of the models.

The prediction ability of the stacking model was improved in the daily solar radiation prediction model, but the monthly model performed poorly, which may be related to too little monthly training data. We concluded that the XGBoost model is the best solar radiation value prediction model, although when the amount of data is large, we suggest using the stacking fusion or XGBoost model to build the model.

Data Availability Statement

All meteorological data were obtained from the China Meteorological Data Service Center (CMDC, http://data.cma.cn/en/?r=data/index&cid=6d1b5efbdcbf9a58), which requires an authorized log-in or via off-line data processing and product tailoring services. Specifically, daily observations are found at http://data.cma.cn/en/?r=data/detail&dataCode=SURF_CLI_CHN_MUL_DAY_CES_V3.0.

Author Contributions

JK and ZZ conceived the idea of the study. LH analyzed the data and wrote the initial draft of the manuscript. The remaining authors contributed to refining the ideas, carrying out additional analyses, and finalizing this manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Key Research and Development Program of China (Grant No. 2016YFC0803105), National Natural Science Foundation of China (Grant No. 41301423), China Postdoctoral Science Foundation (Grant No. 2018M641926), Projects supported by the National Fund for Study Abroad (Grant No. 201808360065), and Jiangxi Provincial Department of Education Science and Technology Research Projects (Grant No. GJJ150661).

Disclaimer

Frontiers Media SA remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer YY declared a past co-authorship with one of the authors ZZ to the handling editor.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.596860/full#supplementary-material

References

Agarwal, S., and Chowdary, C. R. (2020). A-stacking and A-bagging: adaptive versions of ensemble learning algorithms for spoof fingerprint detection. Expert Syst. Appl. 146:113160. doi: 10.1016/j.eswa.2019.113160