Reconstructing Past Elevations From Triple Oxygen Isotopes of Lacustrine Chert: Application to the Eocene Nevadaplano, Elko Basin, Nevada, United States

Introduction and Geologic Setting

Reconstructing the topographic history of mountain belts relies heavily upon the oxygen (δ¹⁸O) and hydrogen (δD) isotopes of authigenic minerals in paleosols and paleolake sediments (e.g., Chamberlain et al., 1999; Poage and Chamberlain, 2002; Takeuchi and Larson, 2005; Ghosh et al., 2006a; Garzione et al., 2006; Davis et al., 2009; Takeuchi et al., 2010; Mulch et al., 2010, 2015; Gébelin et al., 2013; Schwartz et al., 2019; Pingel et al., 2020; Ingalls et al., 2020a; Quade et al., 2020; San Jose et al., 2020; Kukla et al., 2021). Rainout causes systematic monotonic depletion in δ¹⁸O and δD with elevation (e.g., Rowley et al., 2001), which can be exploited to reconstruct past elevations of ancient mountain belts. However, the interpretation of these isotopic data as signals of past elevation is often complicated by evaporation in soils and lakes that will enrich waters in ¹⁸O and D (e.g., Abruzzese et al., 2005; Davis et al., 2009; Mulch et al., 2015; Mulch, 2016; Ingalls et al., 2020a). These evaporitic effects are particularly problematic in semi-arid to arid settings that often form in the rain shadow of uplifting mountains. Thus, methods to determine the pre-evaporative isotopic composition of meteoric waters are needed to isolate the signal of surface uplift from progressive drying.

One way of assessing evaporative trends is to use combined δD and δ¹⁸O values of chert deposits in the paleolake sediments. Abruzzese et al. (2005) used this approach in their study of the Eocene chert found in foreland lake deposits of the Rocky Mountains. Despite recording strong evaporitic signals, the trends in δD and δ¹⁸O values of chert were used to extrapolate to the isotopic composition of original un-evaporative meteoric waters (Abruzzese et al., 2005). Oxygen isotope ratios of the hydroxyl ions of chert are likely a robust indicator of waters from which they form (Knauth, 1973) since hydroxyl ions appear to resist post-depositional exchange (Micheelsen, 1966). However, it is strongly material dependent how resilient hydrogen isotopes are to later diagenesis and exchange particularly given that other minerals (clays and micas) can exhibit some degree of later exchange of hydrogen (O’Neil and Kharaka, 1976; Chamberlain et al., 2020). For this reason, we explore the triple oxygen system (¹⁶O, ¹⁷O, and ¹⁸O) of chert to determine meteoric water compositions. Complementary to triple oxygen isotopes, carbonate clumped isotope analyses are needed to constrain the effect of evaporation on the δ¹⁸O values of the minerals by assessing the carbonate formation temperatures and the δ¹⁸O values of (evaporatively enriched) lake water from which the carbonate mineral formed.

In this study we present the first lacustrine chert triple oxygen isotope dataset from a Cenozoic basin in western North America and use this data set, with carbonate clumped isotope measurements from overlying strata, to derive an elevation estimate for the Eocene Nevadaplano. Our study site in the vicinity of Elko, Nevada (United States) hosts well-studied sections from the Eocene eastern Nevadaplano. We focused on the Eocene sections in the Elko Basin because of the controversy concerning the timing and extent of surface uplift in this region [contrasting Smith et al. (2017) and Cassel et al. (2018) with Mulch et al. (2015) as well as Lund Snee et al. (2016)]. In essence the controversy revolves around the timing and amount of surface uplift of this region that was first discovered through the stable isotopic studies of Horton et al. (2004). These authors argued that ∼2 km of surface uplift occurred between the middle Eocene and the early Oligocene based on oxygen isotope changes in paleosol and lacustrine carbonate. These data are important as they are one of the few basins with somewhat continuous Cenozoic sedimentation providing a key datum on the progressive north to south topographic response associated with the removal of the Farallon slab or piecemeal remove of the mantle lithosphere (Carroll et al., 2008; Mix et al., 2011; Chamberlain et al., 2012). However, at the time of the Horton et al. (2004) paper there was insufficient age control to know with any certainty when this uplift occurred. New ages and stable isotope data provided by Mulch et al. (2015) suggested that the surface uplift of 2 km occurred in the late Eocene between 43 and 38 Ma. Yet, this has recently been challenged by Smith et al. (2017) who argues that the Mulch et al. (2015) data for pre-uplift isotope values are from lacustrine samples that have been strongly affected by evaporation and they argue that surface uplift likely occurred after the formation of the Eocene lakes, possibly during the Oligocene (Cassel et al., 2018). However, very low δ¹⁸O values in the full isotopic record are consistent with high elevations occurring during the Eocene (Mulch et al., 2015). To place new constraints on this issue we focused on the Eocene lacustrine cherts because the triple oxygen isotopes allow us to quantitatively assess evaporative effects and previous work demonstrated significant spread in the δ¹⁸O of the chert samples from the Elko Formation (Abruzzese et al., 2005).

Our findings suggest that paleoelevation estimates using volcanic glass δD values (Smith et al., 2017; Cassel et al., 2018) give higher elevations than the data derived here from the basin depocenter indicating lower hypsometric mean elevations. Nonetheless, the findings presented below suggest a >2.5 km elevation in the Elko Basin region during the middle Eocene and surface uplift of about 1–1.5 km between deposition of the Cherty Limestone at 42–43.5 Ma and the late Eocene, ∼38–40 Ma.

Isotope Notation and Systematics

We summarize the isotope notation used in this study and define the nomenclature and fractionation factors used for the triple oxygen and carbonate clumped isotope measurements as well as the subsequent calculations. Isotopic abundance ratio is reported here in both standard and linear notation. The standard δ-notation is defined as (McKinney et al., 1950):

$${\mathrm{\delta }}^{x}Y=\left(\frac{{}^{x}R_{sample}}{{}^{x}R_{standard}}-1\right)\times 1000(1)$$

where x is the heavier mass of interest, Y is oxygen (O), carbon (C) and R is the ratio of interest (i.e., ¹⁸O/¹⁶O, ¹⁷O/¹⁶O, ¹³C/¹²C). We report chert oxygen isotopes (δ¹⁸O and δ¹⁷O) relative to the VSMOW2-SLAP2 scale via primary standards (Wostbrock et al., 2020; see section “Materials and Methods”), and the carbonate oxygen and carbon isotopes (δ¹⁸O and δ¹³C) relative to the VSMOW and VPDB standards, respectively, normalized via carbonate standards. Equilibrium fractionation (α) between two phases (A and B) is:

$${\mathrm{\alpha }}_{A-B}\equiv \frac{R_A}{R_B}=\frac{{\mathrm{\delta }}_A-1000}{{\mathrm{\delta }}_B-1000}(2)$$

We are interested in oxygen isotope fractionation between water and minerals (CaCO₃-H₂O and SiO₂-H₂O), as well as oxygen isotope fractionation between liquid and vapor water during lake water evaporation.

Following the recent triple oxygen isotope literature (e.g., Pack and Herwartz, 2014; Passey et al., 2014; Sharp et al., 2018; Barkan et al., 2019; Passey and Ji, 2019; Liljestrand et al., 2020; Bindeman, 2021; Herwartz, 2021; Zakharov et al., 2021), we report our oxygen isotope data using linear notation, which removes curvature when comparing δ¹⁸O and δ¹⁷O variations (Hulston and Thode, 1965; Miller, 2002):

$$\mathrm{\delta }^{\prime }{}^{x}O\equiv 1000ln\left(\frac{{\mathrm{\delta }}^{x}O}{1000}+1\right)(3)$$

where x is either 17 or 18 (as in ¹⁷O or ¹⁸O). In linearized notation the equilibrium fractionation equation between two phases (A and B) is:

$$1000ln\left({\mathrm{\alpha }}_{A-B}\right)=\mathrm{\delta }^{\prime }{}^x{O}_A-\mathrm{\delta }^{\prime }{}^x{O}_B(4)$$

The fractionation of ¹⁷O relative to ¹⁸O is given by the following equations [standard (eq. 5) and linearized (eq. 6) forms]:

$${\mathrm{\alpha }}^{17}{O}_{A-B}={({\mathrm{\alpha }}^{18}{O}_{A-B})}^{\mathrm{\theta }}(5)$$

$$ln\left({\mathrm{\alpha }}^{17}{O}_{A-B}\right)=\mathrm{\theta }\times ln({\mathrm{\alpha }}^{18}{O}_{A-B})(6)$$

where θ is ∼0.5 and is defined, for the triple oxygen isotopes, as

$${\mathrm{\theta }}_{A-B}=\frac{\mathrm{\delta }^{\prime }{}^{17}{O}_A-\mathrm{\delta }^{\prime }{}^{17}{O}_B}{\mathrm{\delta }^{\prime }{}^{18}{O}_A-\mathrm{\delta }^{\prime }{}^{18}{O}_B}(7)$$

representing the mass law associated with physical processes (e.g., mineral precipitation, evaporation, etc.). Originally, variations in θ were observed to be close to ∼0.5, and thus it was thought that the measurement of δ¹⁷O provided no new additional information (Craig, 1957). Recent high-precision work and theory demonstrates measurable (10 s of ppm level) variations in θ for Earth-surface processes like the temperature dependence of equilibrium fractionation during mineral precipitation (θ = 0.5237–0.5255 for SiO₂-H₂O fractionation from 0 to 100°C; Cao and Liu, 2011; Sharp et al., 2016; Hayles et al., 2017; Wostbrock et al., 2018), equilibrium condensation and evaporation of water vapor (θ = 0.529; Barkan and Luz, 2005), and water vapor diffusion (θ = 0.5185; Barkan and Luz, 2007; θ = 0.5194; Yeung et al., 2018), all of which are lower than the theoretical infinite-temperature end-member (θ = 0.5305; Matsuhisa et al., 1978; Young et al., 2002). To visualize variations graphically and normalize to a specific process (Meijer and Li, 2006; Passey et al., 2014; Sharp et al., 2016, 2018; Barkan et al., 2019; Passey and Ji, 2019; Sha et al., 2020; Bindeman, 2021; Herwartz, 2021; Miller and Pack, 2021; Zakharov et al., 2021) we define a reference slope λ_RL to look at small deviations in δ′¹⁷O relative to δ′¹⁸O using Δ′¹⁷O notation (sometimes also denoted ¹⁷O-excess):

$$\mathrm{△}^{\prime }{}^{17}O=\mathrm{\delta }^{\prime }{}^{17}O-{\mathrm{\lambda }}_{RL}\times \mathrm{\delta }^{\prime }{}^{18}O+\mathrm{\gamma }(8)$$

where γ is the y-intercept (zero in this and most work) in δ′¹⁷O vs. δ′¹⁸O space.

We choose a λ_RL value of 0.528 to normalize for variations related to meteoric water processes (Luz and Barkan, 2010). Passey and Ji (2019) recently demonstrated modern waters in western North America also fall along this slope (see also Li et al., 2015) with an intercept of Δ′¹⁷O = 0.032 ± 0.015‰. This choice is similar to using a global or local slope of ∼8 for δD vs. δ¹⁸O measurements (i.e., the “Global Meteoric Water Line”; Craig, 1961; Rozanski et al., 1993). Water vapor diffusion from evaporation into an undersaturated atmosphere (i.e., relative humidity below 100%) yields a slope between 0.529 and 0.5185, thus negative deviations from our reference slope of 0.528 can indicate evaporative lacustrine processes like those observed in modern and Quaternary lake systems (e.g., Passey et al., 2014; Surma et al., 2015, 2018, 2021; Herwartz et al., 2017; Gázquez et al., 2018; Evans et al., 2018; Passey and Ji, 2019; Aron et al., 2020). For the calculations carried out in this work we use the model presented by Passey and Ji (2019) (see their Table 1 and “Materials and Methods” section “Back-Calculation of Unevaporated Waters and Paleoaltimetry Calculations” below). Further, we use here the temperature-dependent equilibrium oxygen isotope fractionation (α) and mass law exponent (θ) for SiO₂ (quartz or opaline phases) and water derived empirically by Sharp et al. (2016) and Wostbrock et al. (2018).

Carbonate clumped isotope thermometry on lacustrine deposits allow for the deconvolution of temperature (via carbonate mineral formation temperatures determined by Δ₄₇, defined below) and water δ¹⁸O values (from which carbonate minerals form) (e.g., Ghosh et al., 2006a; Affek et al., 2008; Passey et al., 2010; Huntington et al., 2010; Eiler, 2011; Lechler et al., 2013; Huntington and Lechler, 2015; Petryshyn et al., 2015; Methner et al., 2016). Given isotopic equilibrium, the tendency of heavier isotopes to “clump” together is only temperature dependent (Eiler, 2007, 2011), and requires only a single mineral phase that can be accurately and precisely measured as Δ₄₇, defined as (Ghosh et al., 2006b; Huntington et al., 2009):

$${\mathrm{\Delta }}_{47}=\left[\left(\frac{{}^{47}R}{{}^{47}R^{*}}-1\right)-\left(\frac{{}^{46}R}{{}^{46}R^{*}}-1\right)-\left(\frac{{}^{45}R}{{}^{45}R^{*}}-1\right)\right]\times 1000(9)$$

where ^xR is for CO₂ relative to mass 44 (i.e., ⁴⁷R = [⁴⁷CO₂]/[⁴⁴CO₂]), and the superscript * is the R value for a system with a stochastic distribution (i.e., high-temperature) for the same bulk composition calculated from the abundance of ¹³C and ¹⁸O in the sample.

Lastly, combinations of temperatures derived from Δ₄₇ values along with the δ¹⁸O values of carbonates allow the δ¹⁸O of the formation fluid, in this case lake water, to be calculated (e.g., Came et al., 2007; Huntington et al., 2010; Lechler et al., 2013). For the calculations carried out here we use the temperature-dependent equilibrium oxygen isotope fractionation of Kim and O’Neil (1997) (and updated by Kim et al., 2007) for inorganic calcite and the temperature calibration of Petersen et al. (2019).

Materials and Methods

Chert Triple Oxygen Isotope Measurements

Chert samples analyzed in this study were 2–4 mg chips of hand samples from Horton et al. (2004) and Abruzzese et al. (2005). Chips were tested for carbonate using HCl, and only those without carbonate were analyzed. We performed triple oxygen isotope measurements using a Thermo Scientific^TM 253 Plus 10kV Isotope Ratio Mass Spectrometer (IRMS) on chert samples at Stanford University with O₂ as the analyte. We generated O₂ gas from silicates using the laser fluorination method after Sharp (1990), on the setup described in Chamberlain et al. (2020) (see also Sharp et al., 2016; Wostbrock et al., 2018, 2020; Lowe et al., 2020; Kukla et al., 2021). This setup is similar to recent studies from other labs producing triple oxygen isotope measurements of chert and silica (Pack and Herwartz, 2014; Levin et al., 2014; Liljestrand et al., 2020; Sengupta et al., 2020; Zakharov et al., 2021). Two to four micrograms of samples are loaded into the vacuum line sample chamber. For a given set of analyses, we generally load 2–3 standards and 3–4 samples. Following loading, samples were pumped down to <10 mbar using a turbopump and then pre-fluorinated with 30 Torr BrF₅ in order to remove absorbed water before analysis. This pre-fluorination step is repeated until it generates <2 mbar of non-condensible gas in a liquid nitrogen trap. When possible, the samples and standards were loaded and vacuumed by turbopump overnight or over several days prior to pre-fluorination.

Following pre-fluorinations, we add 130 mbar BrF₅ to the sample chamber and heat the sample using a 50 W CO₂ infrared laser (Elemental Scientific Lasers/New Wave Research MIR10-25). Consistent with the results of Sharp (1990), we found that we achieve better reproducibility for isotopic measurements and sample yields if the laser fluorination of samples is completed within 5 min. Following laser fluorination, excess BrF₅ is frozen into a liquid nitrogen trap and the evolved O₂ gas is passed over a heated NaCl trap to remove produced waste gases (such as F₂) and then frozen onto a 5 Å mol sieve immersed in liquid nitrogen. The sample is then thawed at room temperature, entrained in a high purity He stream, and passed through a through a GC column to remove NF₃ and other contaminants and refrozen in another 5 Å mole sieve trap immersed in liquid nitrogen. Helium is then pumped away (with the trap still immersed in liquid nitrogen) and the 5 Å mol sieve is heated using heat tape and a heat gun to release the trapped O₂. This purified O₂ is then introduced to and equilibrated with the IRMS sample-side bellow for 6 min. During this equilibration step, the bellow is cycled from 25 and 75% compression ∼6 times.

Samples are measured against an O₂ reference tank (δ¹⁸O = 24.067) with an oxygen isotope composition similar to air and chert samples analyzed in this study. Mass 32, 33, and 34 ion beams are collected on faraday cups, slit widths of 4.5, 1.5, and 4.5 mm, respectively, with a 3 × 10¹³ Ω amplifier for mass 33. Samples are measured at a mass 32 ion-beam intensity of 5–7 volts in blocks that consistent of 10 sample-standard brackets with 36 second integrations and 30 s of equilibration. Between 4 and 7 acquisitions are measured per sample (1.5–3 h) until Δ′¹⁷O precision is <0.01‰ (SE) for an individual dual inlet measurement on gas from a single fluorination. We applied a pressure baseline correction following methods similar to Yeung et al. (2018) to account for Δ′¹⁷O variations due to mass spectrometer and source conditions (see also Yeung and Hayles, 2021). Specifically, we measured the negative voltage to the left of the mass 33 peak and calibrated this baseline correction (additional or missing voltage) against the mass ³²O₂ intensity every session (2 weeks to 1 month). All of our reported sample and standard analyses are relative to the mean published high-precision L1/UNM_Q (δ¹⁸O = 18.070; Δ′¹⁷O = −0.076) values reported in Wostbrock et al. (2020) on the VSMOW2-SLAP2 scale adjusted for a new calibration of SCO, UWG-2, and NBS 28 (Sharp and Wostbrock, 2020), which are also measured regularly in our laboratory (Chamberlain et al., 2020; Lowe et al., 2020). Both δ¹⁸O and Δ′¹⁷O values are measured here relative to L1/UNM_Q. For δ¹⁸O measurements, we correct the data to the measured standards from a given day’s batch of measured samples. For Δ′¹⁷O, values were standardized based on the average values of standards measured in a given session. In this case all samples were measured during one session over several weeks in 2019 that amounted to 10 total analysis days. Two samples were measured in replicate and we report the number of acquisitions measured as well as the (SE) for each individual dual inlet measurement on gas from a single fluorination.

During the session of analyses presented here, we also measured two secondary SiO₂ standards. One of these is a low δ¹⁸O quartz (Sandia quartz; δ¹⁸O = 0.72 ± 0.05, n = 3) also used as an internal standard at University of New Mexico, and the other secondary standard is an in-house chert standard (CH-1; δ¹⁸O = 22.87 ± 0.04, n = 2) previously analyzed in the Stanford laboratory (e.g., Abruzzese et al., 2005; Hren et al., 2009). CH-1 has not been previous measured for Δ′¹⁷O. The Sandia quartz has previously been measured at the University of New Mexico (δ¹⁸O = 0.78 and Δ′¹⁷O = −0.016; Personal Communication, Wostbrock et al., 2018), within error of our measurements (Δ′¹⁷O = −0.012 ± 0.022, n = 3; Table 1).

TABLE 1

Table 1. Lacustrine chert triple oxygen isotope measurements.

Carbonate Clumped Isotope Measurements

Carbonate clumped (Δ₄₇) and stable (δ¹³C, δ¹⁸O) isotope measurements from the Elko Formation were performed on three lake carbonate samples originally reported in Mulch et al. (2015). Carbonate clumped isotope analyses were conducted at the Goethe University-Senckenberg BiK-F Stable Isotope Facility Frankfurt, Germany, following methods outlined in detail in Wacker et al. (2013) and Fiebig et al. (2016). Carbonate powder (8–12 mg) was digested in >106% phosphoric acid at 90°C ± 0.1°C for 30 min in a common acid bath. In brief, the evolved CO₂ gas was purified through cryogenic traps before and after passing through a Porapak Q-packed gas chromatography column with He carrier gas. Measurements of the cleaned CO₂ gas were made in dual inlet on a Thermo Scientific^TM MAT 253 IRMS for 10 acquisitions consisting of 10 cycles with an ion integration time of 20 s per cycle. CO₂ gases equilibrated at 1,000 and 25°C were measured along with the samples to establish the empirical transfer function and the Δ₄₇ values reported here are in the “absolute reference frame” (ARF) (Dennis et al., 2011), also referred to in the literature as the “carbon dioxide equilibrated scale” (CDES). All data was processed using the IUPAC parameters (Daëron et al., 2016). We applied the 25−90°C acid fractionation factor of 0.088‰ and the temperatures calibration of Petersen et al. (2019).

One or two carbonate reference materials were analyzed each measurement day, including Carrara marble, Arctica islandica (also referred to as MuStd, a well-homogenized shell material of an aragonitic cold water bivalve), ETH-1, and ETH-3. During the measurement period, we obtained a mean Δ₄₇ value of 0.205‰ ± 0.004‰ (SE, n = 6) for ETH-1 and of 0.614‰ ± 0.005‰ (SE, n = 7) ETH-3, which are similar to the long-term values reported in Bajnai et al. (2020). We use the Gonfiantini parameters and apply a 25−90°C acid fractionation factor of 0.069‰ to the Δ₄₇ measurements of Carrara marble and Arctica islandica in order to compare them to previously reported Δ₄₇ values of these carbonates. The mean Δ₄₇ value of Carrara marble is 0.390‰ ± 0.005‰ (SE, n = 6), which is just greater than the long-term in-house mean Δ₄₇ value of Carrara marble of 0.376‰ ± 0.002‰ (SE, n = 58) (Methner et al., 2020). The mean Δ₄₇ value of Arctica islandica is 0.722‰ ± 0.007‰ (SE, n = 7), which is indistinguishable from the 0.724‰ ± 0.004‰ (SE, n = 28) reported by Wacker et al. (2013). All carbonate clumped data are provided in a comprehensive clumped isotope results and calculations Supplementary Material.

In addition to the new carbonate clumped isotope data we report the complete δ¹³C values associated with the legacy δ¹⁸O measurements (n = 15) originally made by Abruzzese et al. (2005) (see their Table 1 and “Materials and Methods” section for details), some of which (n = 6) were also remeasured in the dataset reported in Mulch et al. (2015).

Back-Calculation of Unevaporated Waters and Paleoaltimetry Calculations

In this study we follow the approach of Passey and Ji (2019) to back-calculate the unevaporated source water δ¹⁸O value. Passey and Ji (2019) use a simple steady state model for throughflow and closed basin (terminal) lakes first developed by Criss (1999) modified for triple oxygen isotopes (e.g., Herwartz et al., 2017; Gázquez et al., 2018; Surma et al., 2018; Aron et al., 2020) to describe the isotopic composition of the lake water (R_W):

$$R_W=\frac{{\mathrm{\alpha }}_{eq}{\mathrm{\alpha }}_{diff}\left(1-h\right)R_{I}h{X}_E{R}_A}{X_E+{\mathrm{\alpha }}_{eq}{\mathrm{\alpha }}_{diff}\left(1-h\right)(1-X_E)}(10)$$

where R_I and R_A are the isotope ratios of inflowing river water and ambient atmospheric water, respectively, h is the relative humidity, α_eq and α_diff are the equilibrium and kinetic fraction factors associated with lake water evaporation, and X_E is the volumetric fraction of inflowing water lost to evaporation. Applying this model to triple oxygen isotopes, and calibrating using four Quaternary lake systems in the western United States, Passey and Ji (2019) derive a model-based approach for inferring the isotopic composition of the incoming source water (δ′¹⁸O_source) as a function of lake water δ′¹⁸O and Δ′¹⁷O:

$${\mathrm{\delta }}^{{}^{\prime }18}{O}_{source}=\frac{\mathrm{\Delta }{}^{{}^{\prime }17}O_{MWL}-{\mathrm{\Delta }}^{{}^{\prime }17}{O}_{lake}+({\mathrm{\lambda }}_{lake}-{\mathrm{\lambda }}_{RL}){\mathrm{\delta }}^{{}^{\prime }18}{O}_{l}ake}{{\mathrm{\lambda }}_{lake}-{\mathrm{\lambda }}_{RL}}(11)$$

$${\mathrm{\lambda }}_{lake}=1.985\times {(\mathrm{\Delta }{}^{{}^{\prime }17}O_{lake})}^3+0.5730\times {(\mathrm{\Delta }{}^{{}^{\prime }17}O_{lake})}^2+0.0601\times {\Delta }^{\prime 17}{O}_{lake}+0.5236(12)$$

where Δ′¹⁷O_MWL is the intercept of the meteoric water line (0.032 ± 0.015), δ′¹⁸O_lake and Δ′¹⁷O_lake are the isotopic composition of the lake, λ_RL is the reference slope (defined above as 0.528) and λ_lake was determined empirically using Monte Carlo simulations of all parameters in Eq. 10 to determine the polynomial shown in Eq. 12 (see Passey and Ji (2019), their Figure 2 and Table 1). The intercept of the meteoric water line may not be stationary in time due to changes in climate (e.g., humidity, moisture recycling over continents, etc.: Aron et al., 2020; Surma et al., 2021), though modeling studies suggest that Eocene δ¹⁸O-δD have been relatively stationary with respect to slope and intercept, with a significantly compressed global range (Speelman et al., 2010), though it is still unknown how δ¹⁸O-δD relationships map onto δ′¹⁸O–Δ′¹⁷O in space and time, and as constrained by modern datasets (Passey and Levin, 2021). In our primary calculations we fix the Δ′¹⁷O_MWL intercept; however, because this is an uncertainty and factors controlling the Δ′¹⁷O_MWL intercept today are still to be worked out in subsequent sensitivity tests we demonstrate the effect of this assumption to our calculations across the full range of plausible meteoric water line intercepts for the western United States (see Figure 3B). In this study, following transfer of chert δ′¹⁸O and Δ′¹⁷O measurements to δ′¹⁸O_lake and Δ′¹⁷O_lake values using the appropriate empirically derived SiO₂-H₂O fractionation factors (Sharp et al., 2016; Wostbrock et al., 2018; Wostbrock and Sharp, 2021; see also theoretical fractionation factors derived by: Cao and Liu, 2011; Hayles et al., 2018; Schauble and Young, 2021; Yeung and Hayles, 2021) we directly apply Eqs. 11 and 12 to calculate the unevaporated source water when reconstructed lake waters are evaporative (i.e., Δ′¹⁷O_lake values less than the MWL). We then assume that this δ′¹⁸O_source value represents the basin’s hypsometric mean elevation (i.e., the elevation hypsometry upslope of the basin) and apply the model of Rowley et al. (2001) to calculate Eocene paleoelevation of the deposits, similar to our approach recently employed in Chamberlain et al. (2020) for Eocene hydrothermal alteration of the Idaho Batholith.

Results

Chert Oxygen Isotopes

Our triple oxygen isotope external reproducibility (1σ) during the session of analyses based on the primary standard used to correct δ¹⁸O and Δ′¹⁷O data (hydrothermal quartz standard L1/UNM_Q) is ±0.073‰ for δ¹⁸O and 0.016‰ for Δ′¹⁷O (± 1σ; n = 13). Replicates of two samples (CL05 and CL23) indicate similar reproducibility for Δ′¹⁷O (±0.011 and ±0.022‰, respectively) but larger δ¹⁸O variation (±0.295 and ±0.662‰). Comparison to previous measurements made on powders from Horton et al. (2004) and Abruzzese et al. (2005) indicate good agreement [δ¹⁸O difference between the datasets of −0.1 ± 1.3‰ (n = 14)] though we note that we analyzed chips from the same hand samples, not the same sample powders as in the original studies.

Our dataset span 6.5‰ in δ¹⁸O (16.9–23.4‰) and we observe a negative correlation with Δ′¹⁷O ranging from −0.066 to −0.111‰ (Figure 1A and Table 1). We calculate an empirical slope (λ_chert, δ′¹⁷O vs. δ′¹⁸O) of 0.5236, a value between the slopes expected for processes related to meteoric water and SiO₂ precipitation (0.528–0.524), and kinetic fractionation associated with evaporating water (>0.5185) (see section “Isotope Notation and Systematics”).

FIGURE 1

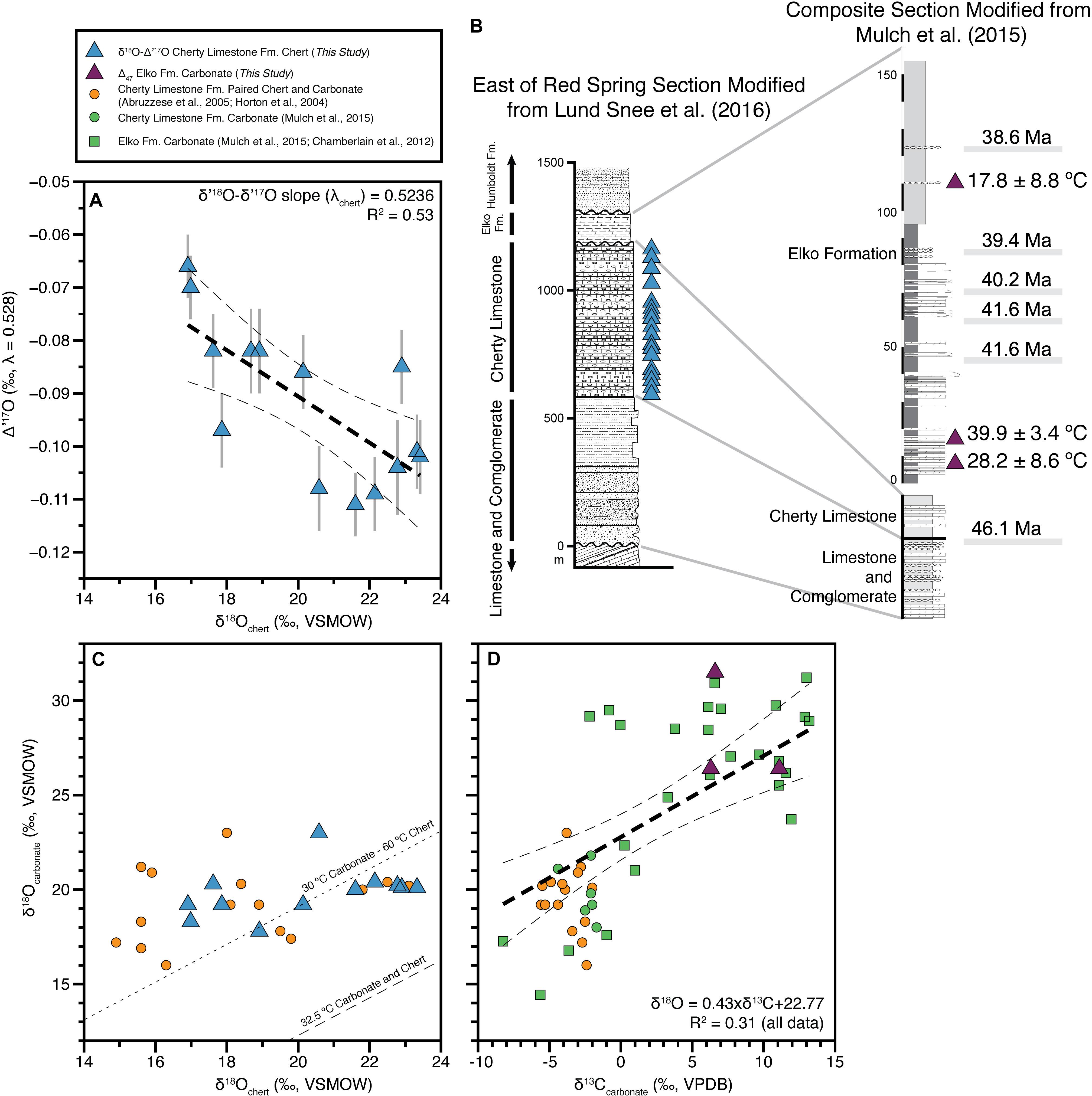
Figure 1. Cross plots of isotope datasets from the Elko Basin. (A) δ¹⁸O and Δ′¹⁷O of chert from the Cherty Limestone (This Study). The λ_chert slope of 0.5236 was calculated in δ′¹⁸O vs. δ′¹⁷O space (not shown). Δ′¹⁷O error bars are 1 SE of the analytical measurements (see section “Materials and Methods”). (B) Stratigraphic sections simplified from Lund Snee et al. (2016) and modified from Mulch et al. (2015) summarizing the Elko Basin stratigraphy and sample locations (vs. stratigraphic height) within the Cherty Limestone and Elko Formations. Ages are from ⁴⁰Ar/³⁹Ar geochronology (Mulch et al., 2015). The reader is referred to Lund Snee et al. (2016) for sampling localities (see their Figure 1B). (C) δ¹⁸O of chert vs. carbonate in the Cherty Limestone Formation [This Study, Horton et al. (2004) and Abruzzese et al. (2005)]. Contours are for assumed co-equilibrium at 32.5°C [carbonate formation temperature (Δ₄₇) weighted mean = 32.5 ± 3.8°C (1σ, MSWD = 3.9)] and 30°C carbonate paired with 60°C chert using the fractionation factors of Kim and O’Neil (1997) and Sharp et al. (2016) (following Abruzzese et al., 2005). (D) Carbonate δ¹⁸O and δ¹³C in both the Cherty Limestone and Elko Formations [This Study (n = 3×Δ₄₇ measurements), Horton et al. (2004), Abruzzese et al. (2005), Chamberlain et al. (2012) and Mulch et al. (2015)]. The linear regression and confidence intervals are calculated through all data from both formations. As shown in the legend triangles are new measurements from this study, circles are previous measurements of paired carbonate and chert samples from the Cherty Limestone Fm. and squares are previous carbonate measurements from the Elko Fm.

Carbonate Oxygen, Carbon, and Clumped Isotopes

New carbonate clumped isotope measurements from the Elko Formation yielded Δ₄₇ values of 0.680–0.710‰, corresponding to temperatures (following Petersen et al., 2019) of 17.8 ± 8.8 °C to 39.9 ± 3.4°C (1σ, Table 2). The Elko Formation carbonates are younger than the Cherty Limestone chert. However, as described below, given the existing age constraints, and the overlap in carbonate δ¹⁸O and δ¹³C values, the Elko Formation measurements provide a useful constraint on the triple oxygen isotope chert dataset. We calculate an error weighted mean temperature of 32.5 ± 3.8°C (MSWD = 3.9; Table 2). The error of this mean temperature is propagated in our subsequent calculations (see Scenario 1 in the section “Discussion”). Our calculated MSWD value for the error weighted mean temperature greater than 1 indicates over-dispersion of the dataset unrelated to analytical precision, which is likely a result of geologic scatter. These values are similar to the average temperatures (28.5 and 35°C) to Early Eocene stromatolites from the Rife Bed, Tipton Shale Member of the Green River Formation reported by Frantz et al. (2014). Similar to carbonate clumped isotope datasets from Quaternary lake systems (e.g., Hudson et al., 2017; Santi et al., 2020) this spread is indicative of a seasonally evaporitic lake system forming carbonates year around, though the climate system (e.g., the seasonality of temperature, precipitation and humidity) was likely quite different in the Eocene (e.g., Hyland et al., 2018). Based on modern lapse rates (Huntington et al., 2010) these temperatures would put our lake basin and the Green River Formation in Wyoming (Frantz et al., 2014) at <500 m, much lower than the oxygen and hydrogen isotope-based methods would suggest (see section “Discussion”). We propose that these temperatures are likely biased toward seasonal summer/warm month carbonate formation, evidenced by a reduced range in the carbonate δ¹⁸O values relative to the chert δ¹⁸O values (Figure 1C). Given the hotter mean annual temperature, and a proposed similar seasonality in temperature in the continental interior during the Eocene (Hyland et al., 2018), the temperature range and magnitude are reasonable, though clearly further work is necessary to better constrain temperatures via clumped isotopes in the Elko Basin and possibly, in combination with other sites, constrain and adjust the Eocene lapse rate for the western United States.

TABLE 2

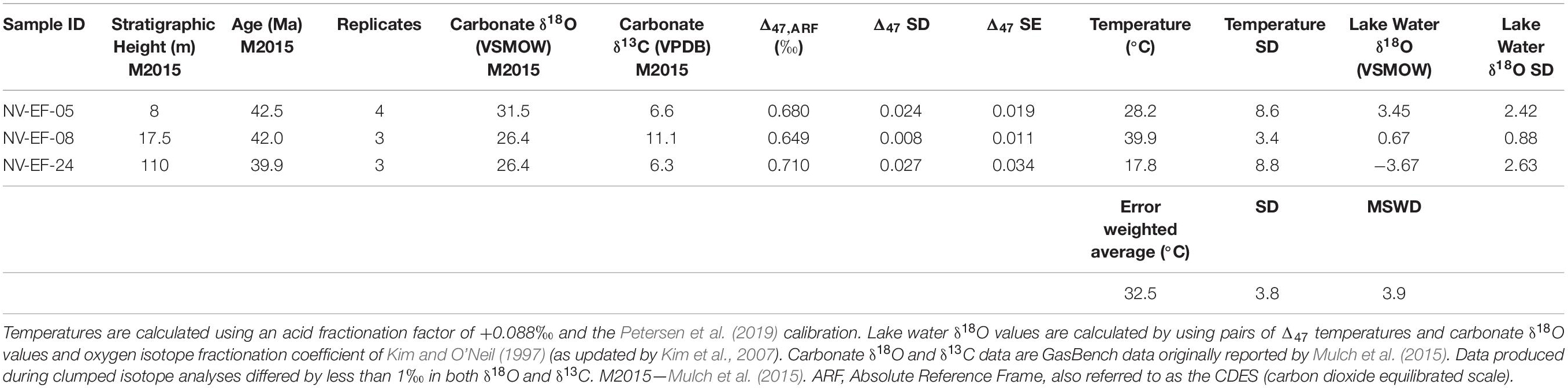
Table 2. Carbonate stable (δ¹⁸O and δ¹³C) and clumped isotope (Δ₄₇) results and calculated oxygen isotopic ratios of lake water (δ¹⁸O).

For the purposes of this work and because of our limited sample set, we use the carbonate clumped isotope data to interpret the triple oxygen isotope results from the lacustrine chert, since the chert formation temperature is itself unknown. Further, the carbonate clumped isotope data, in combination with the more extensive previous oxygen isotope measurements of both the Elko and Cherty Limestone Formations (Horton et al., 2004; Abruzzese et al., 2005; Chamberlain et al., 2012; Mulch et al., 2015), provide a target range for the plausible lake water δ¹⁸O from which the carbonate formed assuming equilibrium fractionation and applying the CaCO₃-H₂O fractionation factor of Kim and O’Neil (1997). The target lake water δ¹⁸O range is then a constraint on the lake water δ¹⁸O from which the chert in the Cherty Limestone Formation may have formed.

The δ¹⁸O and δ¹³C values (δ¹⁸O of 26.4–31.5‰ VSMOW, δ¹³C of 6.3–11.1‰ VPDB) of the three clumped isotope measurements from the Elko Formation reflect evaporatively enriched values relative to the δ¹⁸O and δ¹³C values of incoming source water and dissolved inorganic carbon. These values are relatively high for Cenozoic lake basins in the western US, which range from approximately 10 to 32‰ VSMOW in δ¹⁸O and approximately −6 to +12‰ VPDB in δ¹³C values [see lacustrine samples in compilations by Davis et al. (2009) and Chamberlain et al. (2012)]. Further, these measurements are comparable to previous measurements from the Elko and Cherty Limestone Formations compiled in the box and whisker plots in Figure 2B (Horton et al., 2004; Abruzzese et al., 2005; Chamberlain et al., 2012; Mulch et al., 2015; with legacy δ¹³C data reported for the first time in Table 1). Lake water δ¹⁸O values derived from the three lacustrine carbonate clumped isotope measurements range from −3.7 to +3.5‰ VSMOW (Table 1 and Figure 2). Applying the weighted mean formation temperature (32.5°C) to all samples from the Elko Formation and the Cherty Limestone Formation yields formation water δ¹⁸O of approximately −13 to +5‰ VSMOW. In the δ¹³C-δ¹⁸O crossplot shown in Figure 1C the stable isotope data of the two formations define a robust positive correlation, typical of evaporation trends for lacustrine systems (Li and Ku, 1997; Davis et al., 2009; Horton and Oze, 2012; Chamberlain et al., 2013; Ibarra et al., 2014; Ibarra and Chamberlain, 2015; Horton et al., 2016; Ingalls et al., 2020b). We note that in this limited carbonate dataset we do not see a systematic relationship between the enrichment of δ¹⁸O and δ¹³C in the positive evaporation trend and the carbonate clumped isotope derived temperatures.

FIGURE 2

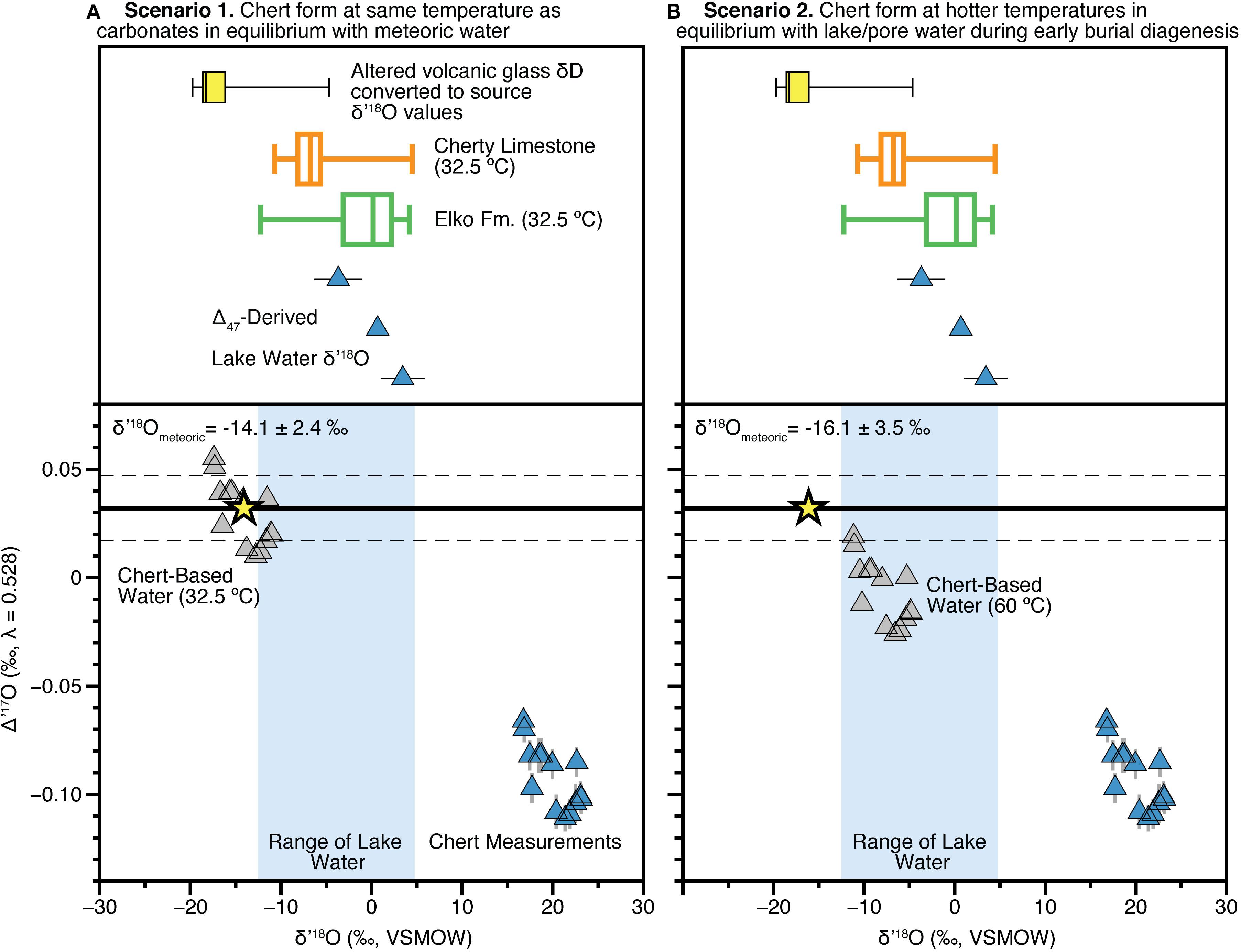
Figure 2. Scenarios for interpreting chert triple oxygen isotope data. (A) In the upper panel we show the individual Δ₄₇-derived lake water δ¹⁸O values (Table 1) from this study, as well as all data from the Elko (green) and Cherty Limestone (orange) Formations shown in Figure 1 as box and whisker plots (Horton et al., 2004; Abruzzese et al., 2005; Chamberlain et al., 2012; Mulch et al., 2015). Yellow box and whisker plots are all Eocene volcanic glass δD data from the Elko Basin region measured by Cassel et al. (2014, 2018) assuming the glass-water fractionation factor determined by Friedman et al. (1993) and conversation to δ¹⁸O using the global meteoric water line. The bottom panel shows the calculations assuming cherts formed at average carbonate formation temperature of 32.5°C (based on Δ₄₇ measurements). Blue triangles are measurements, gray triangles are reconstructed lake water values (Table 1) and using the model equations of Passey and Ji (2019) with the reconstructed average meteoric source water value shown as a yellow star. The thick black line is the regional meteoric water (λ_mwl = 0.528, intercept = 0.032 ± 0.015) determined by Passey and Ji (2019), with the gray hashed horizontal lines representing the error. (B) As in (A) but using a chert formation temperature of 60°C, assumed to be in equilibrium with lake pore waters during early diagenesis.

FIGURE 3

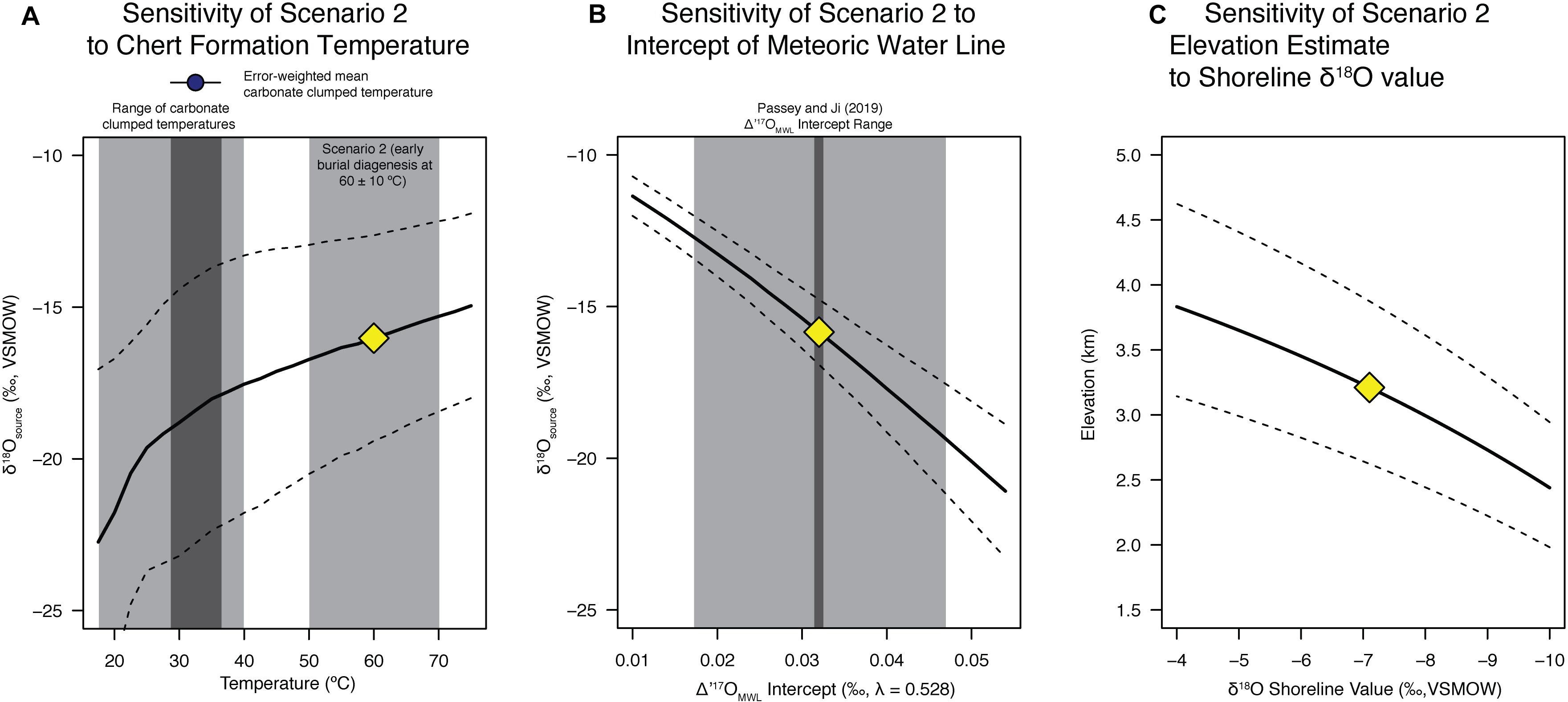
Figure 3. Sensitivity of calculations to modeling assumptions. (A) Sensitivity of our scenario 2 results to the assumed chert formation temperature spanning 17.5–75°C in 2.5°C increments. The result for 60°C shown in Figure 2B is the yellow diamond. Monte Carlo uncertainty propagation (n = 50,000 iterations) using the measurement error (Table 1) and modeling uncertainty (Passey and Ji, 2019) is shown as dashed lines as 1σ uncertainty. (B) As in panel (A) but the sensitivity of our scenario 2 results to the assumed Δ′¹⁷O_MWL intercept values. (C) Sensitivity of the calculated paleoelevation for scenario 2 based on the coastal shoreline precipitation δ¹⁸O value, errors are the 95% confidence using the model of Rowley et al. (2001), as in Figure 4.

FIGURE 4

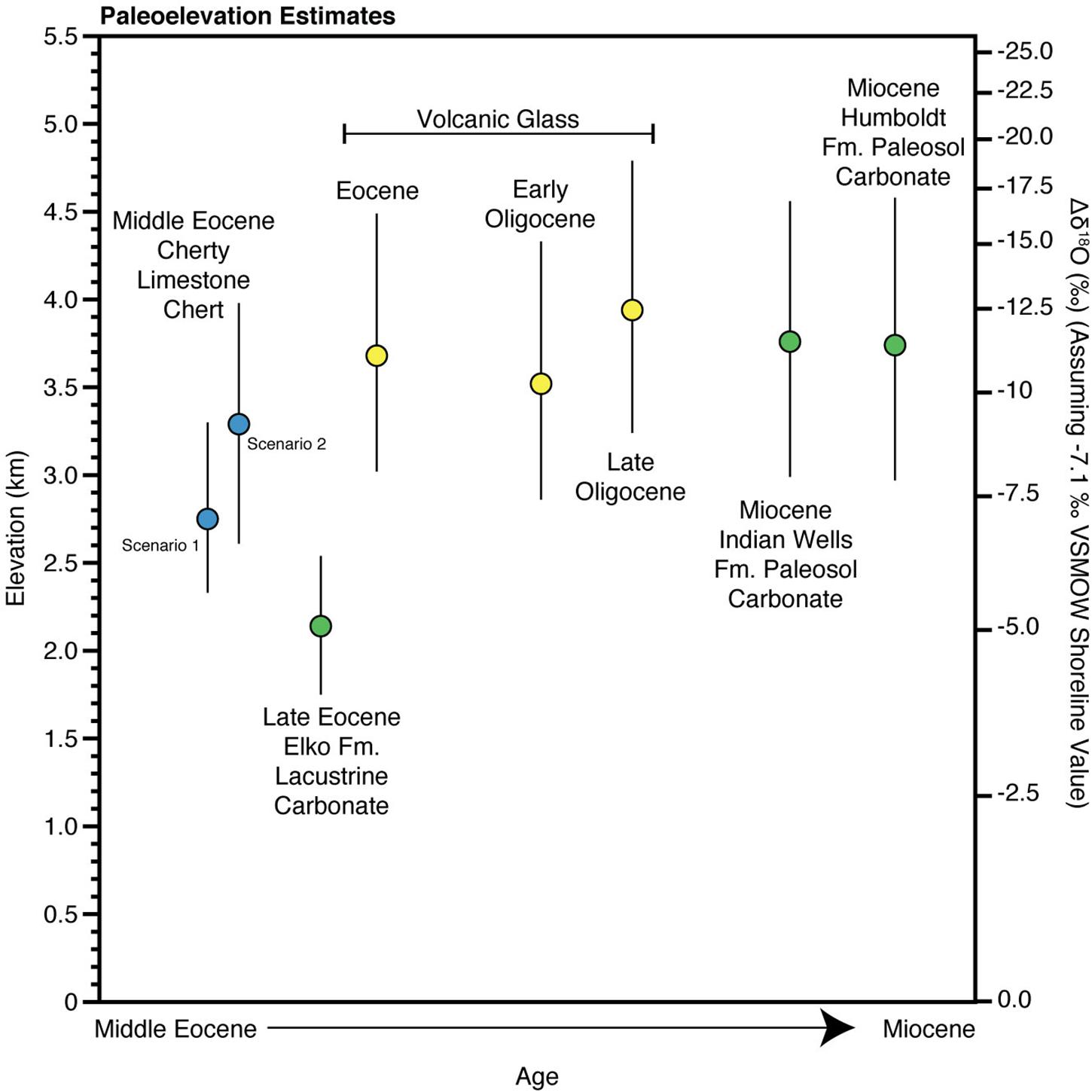
Figure 4. Paleoelevations for this study and previous datasets (Horton et al., 2004; Mix et al., 2011; Chamberlain et al., 2012; Cassel et al., 2014, 2018; Mulch et al., 2015; Smith et al., 2017) as tabulated and calculated in Table 3 using the model of Rowley et al. (2001). The volcanic glass samples include all samples east of the Eocene drainage divide to the west of the Elko Basin (Henry, 2008). Error bars are the 95% confidence (see Table 3).

Discussion

Comparison of Oxygen Isotopes of Chert and Associated Carbonate

In the original work of Abruzzese et al. (2005) the oxygen isotope data of the chert nodules, the same samples as those re-measured here for δ¹⁸O and Δ′¹⁷O, and their associated carbonate (carbonate and chert < 2 cm apart in hand sample) indicated a positive correlation. We pair our measurements with the associated carbonate measurements, as well as plot all data from the original study, and find the resulting trend is relatively unchanged (Figure 1B), though Abruzzese et al. (2005) did report some lower chert δ¹⁸O values not measured here. Additionally, we rederive the temperature contours shown in Abruzzese et al. (2005) (see their Figure 6) by equating the fractionation factors from Kim and O’Neil (1997) and Sharp et al. (2016) assuming the samples formed from the same formation water (i.e., exhibiting identical δ¹⁸O values) and in isotopic equilibrium. Importantly, the original fractionation factor for SiO₂-H₂O used by Abruzzese et al. (2005) from Knauth and Epstein (1976) has changed substantially at low (Earth surface) temperatures (see Sharp et al., 2016 for details), leading to a greater temperature sensitivity of chert δ¹⁸O (a greater 1,000 lnα value). The 32.5°C contour (average Δ₄₇-temperature) does not pass through the samples shown on Figure 1B (lower right long dashed contour in the corner of Figure 1B). Assuming a ∼30°C carbonate formation temperature, the best fit through our new data suggests a chert formation temperature of ∼ 60°C (see dashed contour on Figure 1B), likely during early burial diagenesis, as originally suggested by Abruzzese et al. (2005). The total maximum overburden in the basin is less than 3,250 m; whereas the Eocene overburden is likely less than 1,250 m (Smith and Ketner, 1976; Abruzzese et al., 2005). The latter of which, given regional heat flow estimates (∼65 mW/m²) and thermal conductivities of similar sediments implemented in basin-scale modeling (e.g., Tong et al., 2017), makes 60°C a reasonable temperature estimate during early burial diagenesis. Using the old SiO₂-H₂O fractionation factors from Knauth and Epstein (1976) described above the paired δ¹⁸O-δD measurements of Abruzzese et al. (2005) originate from an equilibrium chert line of 40°C (see their Figure 7). As such, the new fractionation factors drive home the original interpretation that chert nodules and chert laminations of this type, with silica sourced from the weathering of volcanic glass and/or diatom blooms, commonly form from early burial diagenesis and/or dehydration of Opal A to microquartz. In marine settings the Opal A to microquartz transition has been found to occur between 50 and 70°C (Yanchilina et al., 2020), consistent with our estimate of Elko Basin chert formation at ∼60°C. However, given the freshwater nature of this system and the limited δ¹³C-δ¹⁸O spread within the Cherty Limestone Formation, it also remains possible that the chert and coeval/associated carbonate did not form from waters of the same δ¹⁸O value. To account for these alternative interpretations of our dataset, we propose two scenarios for deriving the δ¹⁸O value of the basin source water. Both, however, allow for similar interpretations with respect to Eocene meteoric source water feeding the Elko Basin.

Estimates for Unevaporated Source Water δ¹⁸O From Three Chert Formation Scenarios

First (Scenario 1), we evaluate the possibility that the Cherty Limestone Formation cherts precipitated at (Earth surface) temperatures similar to those suggested by Δ₄₇ results from the overlying Elko Formation (Figure 2). This scenario is plausible given that the carbonate in the Cherty Limestone associated with the chert samples do overlap in δ¹⁸O composition with some of the carbonate samples from the Elko Formation. This assumes that the climatic and hydrologic conditions were similar (i.e., a balance filled to overfilled lake system; Davis et al., 2009), though as described in the Results above, based on the absolute range of δ¹⁸O values in the co-occurring Cherty Limestone carbonate vs. the chert (smaller vs. larger range, respectively in Figure 1C), it may be the case that the carbonates are warm season biased and chert formation is more annually distributed. Using the weighted mean clumped isotope derived temperature of 32.5°C and applying the SiO₂-H₂O triple oxygen isotope fractionation factor of Sharp et al. (2016) and Wostbrock et al. (2018) (θ = 0.5244 and α = 1.0348), we calculate from our chert samples water Δ′¹⁷O values of 0.010–0.055‰ and an average source water value of δ′¹⁸O of −14.1 ± 2.4‰ VSMOW (Figure 2A). These datapoints (gray triangles on Figure 2A) overlap the range of the meteoric water line for the western United States (Li et al., 2015; Passey and Ji, 2019), suggesting negligible evaporation of lake waters since evaporation leads to lower Δ′¹⁷O values. Further, these δ′¹⁸O values are significantly lower than those from coeval carbonate of the Cherty Limestone (shown as an orange box and whisker plot; Figure 2A). Thus, in this scenario we estimate a source δ′¹⁸O of −14.1 ± 2.4‰ assuming that source and lake waters are isotopically indistinguishable.

Applying one single formation temperature is highly unlikely, given that we observe a spread of 6.5‰ in chert δ¹⁸O values, and a negative correlation with Δ′¹⁷O ranging from −0.066 to −0.111‰ with an empirical slope (λ_chert, δ′¹⁷O vs. δ′¹⁸O) of 0.5236 (Figure 1A). As such, the negative correlation and spread would have to be explained by temperatures (assuming the mean value of 32.5°C) ranging from 21 to 47°C, a range comparable but larger than the range measured by the individual carbonate clumped isotope samples (note that this range is asymmetric because 1,000lnα is a function of 1/T with the largest fractionation factor at the coldest temperatures). However, the empirical slope of 0.5236 of our data set (λ_chert) is lower than the theoretical slopes for SiO₂-H₂O fractionation at this temperature range (0.5242–0.5247), suggestive that evaporative processes must still influence a portion of the samples (lower Δ′¹⁷O and higher δ¹⁸O) if this scenario was correct. Additionally, new measurements of carbonates presented by Passey and Ji (2019) from Quaternary lake systems, including the nearby Great Salt Lake, gave λ_lake ranging from 0.5219 to 0.5239, similar to that of the Cherty Limestone Formation chert samples analyzed here.

Thus, the alternative (Scenario 2) is that the chert formed during early diagenesis at higher temperatures from waters of a similar oxygen isotopic composition to the carbonates (Figure 2), as originally suggested by Abruzzese et al. (2005). Assuming 60 ± 10°C as the formation temperature places the primary (lake) water δ¹⁸O recorded by the cherts in the range of expected values based on the carbonate clumped isotope constraints (blue vertical bar in Figure 2B), and with Δ′¹⁷O values lower than the meteoric water line (as expected for evaporative systems). Thus, we take this population of data points (gray triangles) and calculate the unevaporated source water for the Cherty Limestone Formation chert samples using the equations present and derived by Passey and Ji (2019) (see also section “Back-Calculation of Unevaporated Waters and Paleoaltimetry Calculations”), accounting for the measurement uncertainty and the meteoric water line uncertainty. Doing so, and fully propagating errors via a distribution-based Monte Carlo sampling routine following that outlined in the original Matlab code of Passey and Ji (2019), we calculate a source water δ′¹⁸O of −16.3 ± 3.5‰ VSMOW (Figure 2B), lower but within error of that that derived above in scenario 1.

This result is non-unique because the precise temperature of chert formation is (still) unknown despite the added constraint of carbonate clumped isotope temperatures and the third isotope of oxygen. In a sensitivity test we assume chert formation under a wide range of temperatures. Following the same methodology as scenario 2 (Figure 2B), we carried out Monte Carlo simulations at temperatures ranging from 17.5 to 75°C, with the full range of the clumped isotope measurements, the error-weighted mean carbonate clumped temperature and the scenario 2 range shown as gray bars (Figure 3A). Because the SiO₂-H₂O fractionation factor is greater at lower temperatures, the derived source water values are lower at lower temperatures (Figure 3A). Source water δ′¹⁸O values across this broad temperature range span ∼−18 to −15‰. In addition, in Figure 3B we show the sensitivity of our calculations to the intercept of the meteoric water line (i.e., the Δ′¹⁷O_MWL intercept), a key uncertainty given the paucity of triple oxygen isotope data from modern settings and the question of whether the Eocene intercept was within the range used from Passey and Ji (2019) in our calculations. This sensitivity test shows that the source water δ′¹⁸O value decreases with increasing Δ′¹⁷O_MWL intercept (Figure 3B), a relationship that should be expected given that a higher Δ′¹⁷O_MWL intercept places the reconstructed lake water δ′¹⁸O and Δ′¹⁷O points (gray points in Figure 2) further from the meteoric water line (i.e., a greater spacing between the MWL and the data points in the y-axis). In the next section we discuss the implications of this for the paleoelevation reconstruction if the Δ′¹⁷O_MWL intercept was in fact higher.

Previously presented sedimentological data suggested that the chert nodules formed during early diagenesis at higher temperatures (Abruzzese et al., 2005; Davis et al., 2009), which likely lead to the shallow δ¹⁸O-δD slope of 2.7 for these samples (balance to underfilled evaporatively influenced lake systems typically have δ¹⁸O-δD slopes that fall between ∼4 and ∼7; Gonfiantini, 1986). As such, given the systematics explored above, including the empirical negative relationship of the chert data following a plausible evaporation trend, we prefer the results of scenario 2 as the most realistic and parsimonious. This includes the assumption that chert formed at temperatures greater than those recorded by the carbonate clumped isotope measurements of the overlying Elko Formation from lake water incorporated into the sediment pore water of a similar δ¹⁸O composition range (light blue band in Figure 2) as both the coeval carbonate in the Cherty Limestone and the overlying Elko Formation.

Implications for Eocene Nevadaplano Paleoaltimetry and Comparison to Other Datasets

To determine the paleoelevation of the deposits in the Elko Basin we use the model of Rowley et al. (2001). This model assumes Rayleigh distillation whereby water parcel rainout is proportional to lifting due to orography producing a monotonic relationship between elevation and Δδ¹⁸O or ΔδD (defined as coastal precipitation δ¹⁸O value minus the inland δ¹⁸O value). Assuming a shoreline (i.e., zero elevation) δ¹⁸O value and that the air-mass lifting is proportional to the elevation difference between the coast and basin’s hypsometric mean elevation, meteoric (source) δ¹⁸O estimates can be converted to elevations (e.g., Rowley et al., 2001; Mulch et al., 2006). In Figure 3 and Table 3 we do so assuming the mean estimates for our new data accounting only for uncertainty in the Rayleigh distillation model of Rowley et al. (2001). A key limitation of this assumption is that upstream rainout due to orography higher than the study area of interest or due to continentality, which both lead to lower δ¹⁸O values (Kukla et al., 2019), is negligible. Recent regional mapping work by Lund Snee et al. (2016) supports this assumption. Lund Snee et al. (2016) inferred that the Cretaceous to Eocene deposits in the Elko Basin represents a lake basin covered with volcanic rocks situated in relatively subdued topography, with regional rugged Basin and Range style topography only forming in the Miocene. However, upstream rainout could be due to either Eocene topography and associated rainout through the Sierra Nevada further west inferred by hydrogen and oxygen paleoaltimetry (Mulch et al., 2006; Cassel et al., 2009; Hren et al., 2010; Mix et al., 2016), or a drainage divide just west of the Elko Basin inferred from ash-flow tuffs (Henry, 2008), which are both likely and thus this possibility cannot be ruled out.

TABLE 3

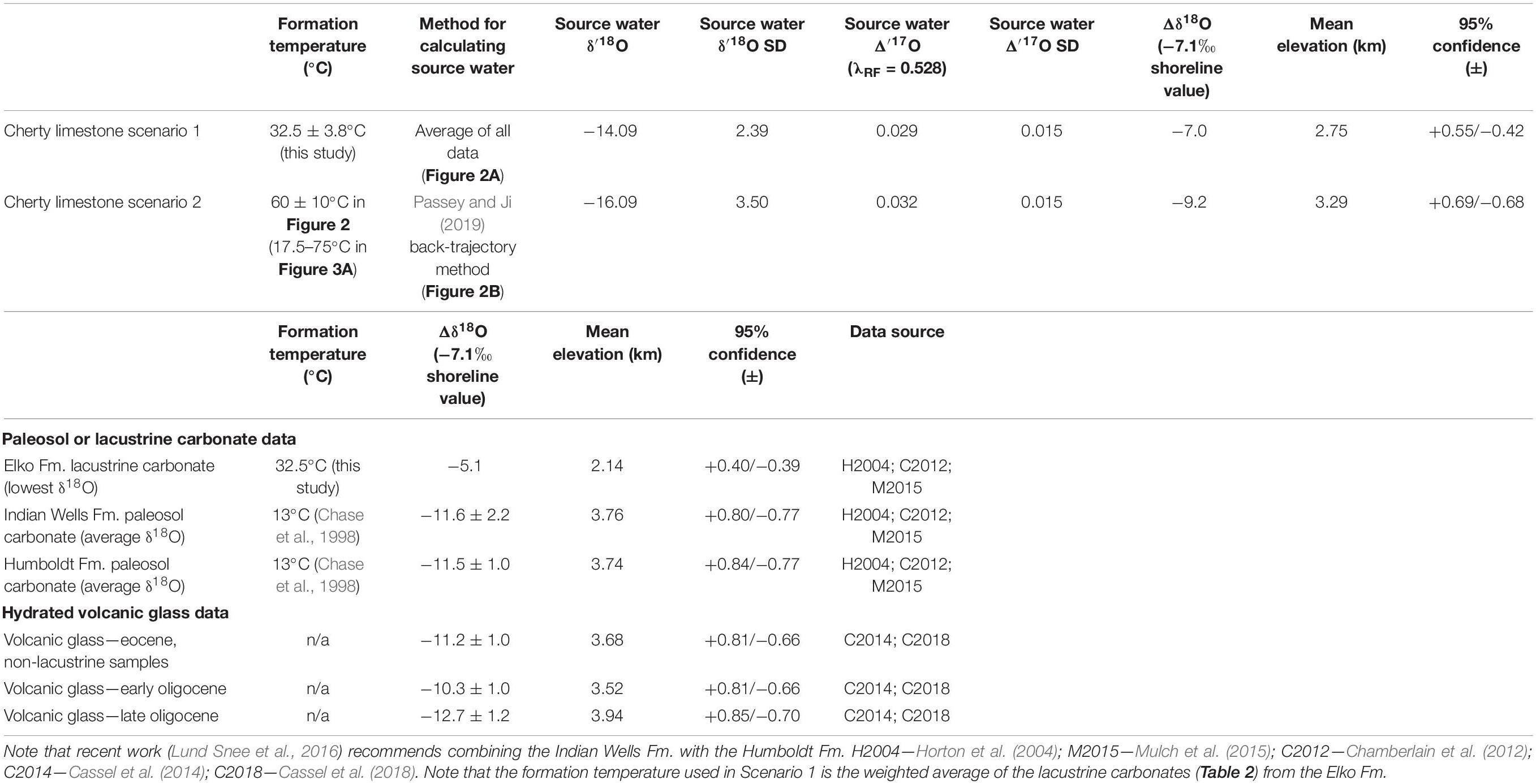
Table 3. Paleoelevation calculations for Scenarios 1 and 2 based on the Rowley et al. (2001) model and previous estimates recalculated.

Assuming a coastal Eocene precipitation δ¹⁸O value of −7.1‰ equivalent to previous studies (e.g., Mulch et al., 2006; Cassel et al., 2009; Hren et al., 2010; Mix et al., 2016), we calculate paleoelevation using the thermodynamic model of Rowley et al. (2001). The Δδ¹⁸O for scenario 1 is −7.0‰, which for Eocene model results for the western United States give a mean elevation of 2.75 +0.55/−0.42 km (95% confidence). Alternatively, for scenario 2, the Δδ¹⁸O value is −9.2‰, giving a mean elevation of 3.29 +0.69/−0.68 km. These estimates, not accounting for uncertainty in the meteoric water line shown in Figure 3 are within error, indicating elevations of ∼3 km. In Figure 3C we show the sensitivity of our assumed coastal Eocene precipitation δ¹⁸O value of −7.1‰, over a range of −4 to −10‰. Previous work in the Pacific Northwest and Idaho Batholith has suggested shoreline Eocene precipitation values of −6‰ (Methner et al., 2016; Chamberlain et al., 2020), which for scenario 2 would increase our elevation estimate to ∼2.9–4.2 km.

These estimates are within error of those derived by previous volcanic glass δD measurements made by Cassel et al. (2014, 2018) and Smith et al. (2017) (see Cassel et al., 2018; their Figure 2). However, putting the δD glass data into equivalent δ¹⁸O values indicates a discrepancy. In Figures 2A,B we show a box and whisker plot (yellow) of all glass δD data from the Late Eocene sediments in and near the Elko Basin previously reported and converted to δ¹⁸O using the fractionation factor of Friedman et al. (1993) to convert to environmental water values and the assumption that waters fall along the global meteoric water line. This approach is similar to assumptions relating δD and δ¹⁸O data in clays (e.g., Poage and Chamberlain, 2002; Sjostrom et al., 2006; Mix and Chamberlain, 2014; Mix et al., 2016). The average δ¹⁸O of the unevaporatively enriched samples reported by volcanic glass δD studies (Cassel et al., 2014, 2018; Smith et al., 2017), converted to δ¹⁸O, is −18.4 ± 1.0‰. This mean value is significantly (Student’s t-test p < 0.05) lower than both estimates presented above in scenarios 1 and 2. We note however, that based on our sensitivity tests in Figure 3, associated with both formation temperature and the Δ′¹⁷O_MWL intercept, it remains possible that the δD glass data and the chert-carbonate derived values presented here are actually in close agreement. For the latter, it would require that the mean value of the Δ′¹⁷O_MWL intercept be higher, by 0.01–0.02‰ (i.e., approximately +1σ of the current modern water data), than the modern data from the western United States (Li et al., 2015; Passey and Ji, 2019).

An alternative possible reason for this discrepancy is hydrogen exchange in volcanic glass (noted previously by Chamberlain et al. (2020) for hydrothermally altered granite). Alternatively, and perhaps most parsimoniously, there are true differences in the depositional setting and thus elevation between the lower elevation lacustrine depocenter, where the thick Chery Limestone Formation (Figure 1B) was deposited, and the syn- and/or post-deposition Eocene fluvial sites of volcanic ash deposition associated with higher elevations. We note that Cassel et al. (2018) explicitly removed samples from their regional dataset from basin depocenters in lacustrine settings because they recorded δD values higher than other (nearby) samples from the same age and fluvial depositional settings. Further work to disentangle and systematically document the depositional settings, paleoelevations and geochronologic control of the individual localities for all of the proxies in the Elko Basin and regionally in northeastern Nevada is clearly necessary. One additional line of evidence is the δ¹⁸O data of four chert samples from the Miocene Humboldt Formation ranging from 17.2 to 23.7‰ (Knauth and Epstein, 1976), thus, exhibiting a similar range to those of the Eocene Cherty Limestone Fm. (15.6–23.1‰) (Table 1; Horton et al., 2004; Abruzzese et al., 2005). Assuming similar formation temperatures, the Humboldt Formation chert data from Knauth and Epstein (1976) would yield similar paleoelevations to the Cherty Limestone Fm., but lower than nearby time equivalent (Miocene) volcanic glass data from Cassel et al. (2018), similar to our observations for the Eocene.

In Figure 3 we summarize the paleoelevation estimates based on this work on triple oxygen isotopes of chert and those from other studies on younger rocks based on carbonates from paleolakes and paleosols and volcanic glasses of the Elko Basin. These data suggest a relatively simple uplift history of the Elko Basin with high elevations (∼3 km) in the mid to late Eocene in the oldest lake unit in the Elko Basin. Surface uplift of this region occurred at some point during the late Eocene to early Oligocene to elevations around 4 km and remained high throughout the Miocene. We do not think that the elevation estimates for the late Eocene Elko Formation reflect true low elevations as even the lowest δ¹⁸O of carbonate have most likely been influenced by evaporation, as pointed out by Smith et al. (2017), and observed here in the positive correlation of δ¹⁸O and δ¹³C among even the lowest δ¹⁸O samples (green squares in Figure 1C; see also discussion in Mulch et al., 2015). In addition, we see no evidence for the more complicated surface uplift history given in Cassel et al. (2018) who suggest high elevation in the Late Eocene to lower elevations in the Early Oligocene to the highest elevation in the Late Oligocene. However, this elevation history is largely based on rocks exposed just west of the Elko Basin as there are few to no substantial Oligocene sedimentary rocks exposed in the Elko Basin that allow paleoelevation constraints, based on the most recent mapping that indicates an angular unconformity (spanning ∼31–24 Ma) between the units mapped previously as the Indian Well Fm. and the Miocene Humboldt Fm (Lund Snee et al., 2016).

Conclusion

In this study we presented the first lacustrine chert triple oxygen isotope dataset from a Cenozoic basin in western North America and used this data, in conjunction with carbonate clumped isotope measurements to derive an elevation estimate for the eastern Eocene Nevadaplano. Future measurements on carbonates (e.g., Passey et al., 2014; Bergel et al., 2020; Fosu et al., 2020; Voarintsoa et al., 2020; Wostbrock et al., 2020) from the Elko Basin, specifically on the Elko Formation, would benefit from paired measurement of the carbonates from the Eocene to Miocene strata for both triple oxygen isotopes and carbonate clumped isotopes, allowing for issues for formation temperature associated with chert formation to be overcome. Nevertheless, state-of-the-art data sets presented here indicate that:

1. The empirical negative relationship in triple oxygen isotopes among the dataset is suggestive of evaporative enrichment of δ¹⁸O values spanning 6.5‰.

2. Cherts in the Cherty Limestone Formation likely formed during early diagenesis at temperatures hotter than those recorded by coeval carbonate and carbonates in the overlying lacustrine portion of the Elko Formation as recorded by our new carbonate clumped isotope dataset.

3. Comparison to δD datasets (converted to water δ¹⁸O values) from volcanic glass of similar age from the Elko Basin demonstrate that either the lacustrine carbonates and chert represent a lower hypsometric mean elevation of the basin depocenter or there exists later hydrogen exchange in the volcanic glass.

4. We calculate a relatively simple surface uplift history for Elko Basin with original deposition of lake sediments (Cherty Limestone Formation) at ∼3 km in the mid-Eocene. When compared to other paleoelevation studies in this area, we suggest that the was surface uplift of ∼1 km in the late Eocene to early Oligocene with elevations remaining high into the Miocene.

Data Availability Statement

All datasets generated for this study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

DI wrote the initial draft of the manuscript with input from CC. DI made the figures. CC, TK, and DI made the triple oxygen isotope measurements. KM made the carbonate clumped isotope measurements. CC and AM provided the samples. DI and TK constructed the modeling framework. All authors provided input on the dataset interpretation and analysis and contributed to writing the manuscript.

Funding

This research was funded by NSF EAR-1322084 and Heising Simons grants to CC. KM and AM acknowledge support through the LOEWE funding program of the Hessen State Ministry of Higher Education, Research, and the Arts as part of the LOEWE VeWa project. DI was supported by the UC Berkeley Miller Institute for Basic Research and UC President’s Postdoctoral Fellowships, and KM was supported by the Feodor-Lynen-Fellowship of the Alexander von Humboldt Foundation.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank NL and JK for thorough reviews and comments, and MH for handling our manuscript. We thank Peter Blisniuk for help with the isotope measurements at the Stanford University Stable Isotope Biogeochemistry Laboratory, Kristina Butler for providing feedback on a previous version of this manuscript, Max K. Lloyd with triple oxygen isotope data handling, as well as Yuan Gao, Zachary D. Sharp, Jordan A.G. Wostbrock, Max K. Lloyd, and Daniel A. Stolper for detailed discussions. We thank both reviewers of this manuscript for thorough and helpful comments and suggestions.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.628868/full#supplementary-material

References

Abruzzese, M. J., Waldbauer, J. R., and Chamberlain, C. P. (2005). Oxygen and hydrogen isotope ratios in freshwater chert as indicators of ancient climate and hydrologic regime. Geochim. Cosmochim. Acta 69, 1377–1390. doi: 10.1016/j.gca.2004.08.036

CrossRef Full Text | Google Scholar

Affek, H. P., Bar-Matthews, M., Ayalon, A., Matthews, A., and Eiler, J. M. (2008). Glacial/interglacial temperature variations in Soreq cave speleothems as recorded by “clumped isotope” thermometry. Geochim. Cosmochim. Acta 72, 5351–5360. doi: 10.1016/j.gca.2008.06.031

CrossRef Full Text | Google Scholar

Aron, P. G., Levin, N. E., Beverly, E. J., Huth, T. E., Passey, B. H., Pelletier, E. M., et al. (2020). Triple oxygen isotopes in the water cycle. Chem. Geol. doi: 10.1016/j.chemgeo.2020.120026 [Epub ahead of print].

CrossRef Full Text | Google Scholar

Bajnai, D., Guo, W., Spötl, C., Coplen, T. B., Methner, K., Löffler, N., et al. (2020). Dual clumped isotope thermometry resolves kinetic biases in carbonate formation temperatures. Nat. Commun. 11, 1–9.

Google Scholar

Barkan, E., Affek, H. P., Luz, B., Bergel, S. J., Voarintsoa, N. R. G., and Musan, I. (2019). Calibration of δ17O and 17Oexcess values of three international standards: IAEA-603, NBS19 and NBS18. Rapid Commun. Mass Spectrom. 33:737. doi: 10.1002/rcm.8391

PubMed Abstract | CrossRef Full Text | Google Scholar

Barkan, E., and Luz, B. (2005). High precision measurements of 17O/16O and 18O/16O ratios in H2O. Rapid Commun. Mass Spectrom. 19, 3737–3742. doi: 10.1002/rcm.2250

PubMed Abstract | CrossRef Full Text | Google Scholar

Barkan, E., and Luz, B. (2007). Diffusivity fractionations of H216O/H217O and H218O/H218O in air and their implications for isotope hydrology. Rapid Commun. Mass Spectrom. 21, 2999–3005. doi: 10.1002/rcm.3180

PubMed Abstract | CrossRef Full Text | Google Scholar

Bergel, S. J., Barkan, E., Stein, M., and Affek, H. P. (2020). Carbonate 17O-excess as a paleo-hydrology proxy: Triple oxygen isotope fractionation between H2O and biogenic aragonite, derived from freshwater mollusks. Geochim. Cosmochim. Acta 275, 36–47. doi: 10.1016/j.gca.2020.02.005

CrossRef Full Text | Google Scholar

Bindeman, I. N. (2021). Triple oxygen isotopes in evolving continental crust, granites, and clastic sediments. Rev. Mineral Geochem. 86, 241–290.

Google Scholar

Came, R. E., Eiler, J. M., Veizer, J., Azmy, K., Brand, U., and Weidman, C. R. (2007). Coupling of surface temperatures and atmospheric CO₂ concentrations during the Palaeozoic era. Nature 449, 198–201. doi: 10.1038/nature06085

PubMed Abstract | CrossRef Full Text | Google Scholar

Cao, X., and Liu, Y. (2011). Equilibrium mass-dependent fractionation relationships for triple oxygen isotopes. Geochim. Cosmochim. Acta 75, 7435–7445. doi: 10.1016/j.gca.2011.09.048

CrossRef Full Text | Google Scholar

Carroll, A. R., Doebbert, A. C., Booth, A. L., Chamberlain, C. P., Rhodes-Carson, M. K., Smith, M. E., et al. (2008). Capture of high altitude precipitation by a low-altitude Eocene lake, western U.S. Geology 36, 791–794. doi: 10.1130/g24783a.1

CrossRef Full Text | Google Scholar

Cassel, E. J., Breecker, D. O., Henry, C. D., Larson, T. E., and Stockli, D. F. (2014). Profile of a paleo-orogen: High topography across the present-day Basin and Range from 40 to 23 Ma. Geology 42, 1007–1010. doi: 10.1130/g35924.1

CrossRef Full Text | Google Scholar

Cassel, E. J., Graham, S. A., and Chamberlain, C. P. (2009). Cenozoic tectonic and topographic evolution of the northern Sierra Nevada, California, through stable isotope paleoaltimetry in volcanic glass. Geology 37, 547–550. doi: 10.1130/g25572a.1

CrossRef Full Text | Google Scholar

Cassel, E. J., Smith, M. E., and Jicha, B. R. (2018). The impact of slab rollback on earth’s surface: uplift and extension in the hinterland of the North American Cordillera. Geophys. Res. Lett. 45, 996–911.

Google Scholar

Chamberlain, C. P., Ibarra, D. E., Lloyd, M. K., Kukla, T., Sharp, Z. D., Gao, Y., et al. (2020). Triple oxygen isotopes of meteoric hydrothermal system – implications for paleoaltimetry. Geochem. Perspect. Lett. 15, 6–9. doi: 10.7185/geochemlet.2026

PubMed Abstract | CrossRef Full Text | Google Scholar

Chamberlain, C. P., Mix, H. T., Mulch, A., Hren, M. T., Kent-Corson, M. L., Davis, S. J., et al. (2012). The Cenozoic climatic and topographic evolution of the western North American Cordillera. Am. J. Sci. 312, 213–262.

Google Scholar

Chamberlain, C. P., Poage, M. A., Craw, D., and Reynolds, R. C. (1999). Topographic development of the Southern Alps recorded by the isotopic composition of authigenic clay minerals, South Island, New Zealand. Chem. Geol. 155, 279–294. doi: 10.1016/s0009-2541(98)00165-x

CrossRef Full Text | Google Scholar

Chamberlain, C. P., Wan, X., Graham, S. A., Carroll, A. R., Doebbert, A. C., Sageman, B. B., et al. (2013). Stable isotopic evidence for climate and basin evolution of the Late Cretaceous Songliao basin, China. Palaeogeogr. Palaeoclimatol. Palaeoecol. 385, 106–124. doi: 10.1016/j.palaeo.2012.03.020

CrossRef Full Text | Google Scholar

Chase, C. G., Gregory-Wodzicki, K. M., Parrish-Jones, J. T., and DeCelles, P. (1998). “Topographic history of the western Cordillera of North America and controls on climate”, in Tectonic Boundary Conditions for Climate Model Simulations, eds T. J. Crowley and K. Burke (Oxford, UK: Oxford University Press, Oxford Monographs on Geology and Geophysics), 73–99.

Google Scholar

Craig, H. (1957). Isotopic standards for carbon and oxygen and correction factors for mass-spectrometric analysis of carbon dioxide. Geochim. Cosmochim. Acta 12, 133–149. doi: 10.1016/0016-7037(57)90024-8

CrossRef Full Text | Google Scholar

Craig, H. (1961). Isotopic variations in meteoric waters. Science 133, 1702–1703. doi: 10.1126/science.133.3465.1702

PubMed Abstract | CrossRef Full Text | Google Scholar

Criss, R. E. (1999). Principles of Stable isotope Distribution. Oxford: Oxford University Press.

Google Scholar

Daëron, M., Blamart, D., Peral, M., and Affek, H. P. (2016). Absolute isotopic abundance ratios and the accuracy of Δ47 measurements. Chem. Geol. 442, 83–96. doi: 10.1016/j.chemgeo.2016.08.014

CrossRef Full Text | Google Scholar

Davis, S. J., Mulch, A., Carroll, A. R., Horton, T. W., and Chamberlain, C. P. (2009). Paleogene landscape evolution of the central North American Cordillera: Developing topography and hydrology in the Laramide foreland. Geol. Soc. Am. Bull. 121, 100–116.

Google Scholar

Dennis, K. J., Affek, H. P., Passey, B. H., Schrag, D. P., and Eiler, J. M. (2011). Defining an absolute reference frame for ‘clumped’ isotope studies of CO2. Geochim. Cosmochim. Acta 75, 7117–7131. doi: 10.1016/j.gca.2011.09.025

CrossRef Full Text | Google Scholar

Eiler, J. M. (2007). “Clumped-isotope” geochemistry—The study of naturally-occurring, multiply-substituted isotopologues. Earth Planet. Sci. Lett. 262, 309–327. doi: 10.1016/j.epsl.2007.08.020

CrossRef Full Text | Google Scholar

Eiler, J. M. (2011). Paleoclimate reconstruction using carbonate clumped isotope thermometry. Quat. Sci. Rev. 30, 3575–3588. doi: 10.1016/j.quascirev.2011.09.001

CrossRef Full Text | Google Scholar

Evans, N. P., Bauska, T. K., Gázquez-Sánchez, F., Brenner, M., Curtis, J. H., and Hodell, D. A. (2018). Quantification of drought during the collapse of the classic Maya civilization. Science 361, 498–501. doi: 10.1126/science.aas9871

PubMed Abstract | CrossRef Full Text | Google Scholar

Fiebig, J., Hofmann, S., Löffler, N., Lüdecke, T., Methner, K., and Wacker, U. (2016). Slight pressure imbalances can affect accuracy and precision of dual inlet-based clumped isotope analysis. Isotop. Environ. Health Stud. 52, 12–28. doi: 10.1080/10256016.2015.1010531

PubMed Abstract | CrossRef Full Text | Google Scholar

Fosu, B. R., Subba, R., Peethambaran, R., Bhattacharya, S. K., and Ghosh, P. (2020). Developments and applications in triple oxygen isotope analysis of carbonates. ACS Earth Space Chem. 4, 702–710. doi: 10.1021/acsearthspacechem.9b00330

CrossRef Full Text | Google Scholar

Frantz, C. M., Petryshyn, V. A., Marenco, P. J., Tripati, A., Berelson, W. M., and Corsetta, F. A. (2014). Dramatic local environmental change during the Early Eocene Climatic Optimum detected using high resolution chemical analyses of Green River Formation stromatolites. Palaeogeogr. Palaeoclimatol. Palaeoecol. 405, 1–15. doi: 10.1016/j.palaeo.2014.04.001

CrossRef Full Text | Google Scholar

Friedman, I., Gleason, J., and Warden, A. (1993). “Ancient climate from deuterium content of water in volcanic glass: climate change in continental isotopic records,” in Climate Change in Continental Isotopic Records: American Geophysical Union Geophysical Monograph, Vol. 78, eds P. K. Swart, K. C. Lohmann, J. Mckenzie, and S. Savin, (Washington, DC: American Geophysical Union), 309–319. doi: 10.1029/gm078p0309

CrossRef Full Text | Google Scholar

Garzione, C. N., Molnar, P., Libarkin, J. C., and MacFadden, B. J. (2006). Rapid late Miocene rise of the Bolivian Altiplano: Evidence for removal of mantle lithosphere. Earth Planet. Sci. Lett. 241, 543–556. doi: 10.1016/j.epsl.2005.11.026

CrossRef Full Text | Google Scholar

Gázquez, F., Morellón, M., Bauska, T., Herwartz, D., Surma, J., Moreno, A., et al. (2018). Triple oxygen and hydrogen isotopes of gypsum hydration water for quantitative paleo-humidity reconstruction. Earth Planet. Sci. Lett. 481, 177–188. doi: 10.1016/j.epsl.2017.10.020

CrossRef Full Text | Google Scholar

Gébelin, A., Mulch, A., Teyssier, C., Jessup, M. J., Law, R. D., and Brunel, M. (2013). The Miocene elevation of Mount Everest. Geology 41, 799–802. doi: 10.1130/g34331.1

CrossRef Full Text | Google Scholar

Ghosh, P., Adkins, J., Affek, H., Balta, B., Guo, W., Schauble, E. A., et al. (2006b). 13C–18O bonds in carbonate minerals: a new kind of paleothermometer. Geochim. Cosmochim. Acta 70, 1439–1456. doi: 10.1016/j.gca.2005.11.014

CrossRef Full Text | Google Scholar

Ghosh, P., Garzione, C. N., and Eiler, J. M. (2006a). Rapid uplift of the altiplano revealed through 13C-18O bonds in paleosol carbonates. Science 311, 511–515. doi: 10.1126/science.1119365

PubMed Abstract | CrossRef Full Text | Google Scholar

Gonfiantini, R. (1986). Environmental isotopes in lake studies. Handb. Environ. Isotop. Geochem. 2, 113–168. doi: 10.1016/b978-0-444-42225-5.50008-5

CrossRef Full Text | Google Scholar

Hayles, J., Gao, C., Cao, X., Liu, Y., and Bao, H. (2018). Theoretical calibration of the triple oxygen isotope thermometer. Geochim. Cosmochim. Acta 235, 237–245. doi: 10.1016/j.gca.2018.05.032

CrossRef Full Text | Google Scholar

Hayles, J. A., Cao, X., and Bao, H. (2017). The statistical mechanical basis of the triple isotope fractionation relationship. Geochem. Perspect. Lett. 3, 1–11. doi: 10.7185/geochemlet.1701

PubMed Abstract | CrossRef Full Text | Google Scholar

Henry, C. D. (2008). Ash-flow tuffs and paleovalleys in northeastern Nevada: implications for Eocene paleogeography and extension in the Sevier hinterland, northern Great Basin. Geosphere 4, 1–35. doi: 10.1130/ges00122.1

CrossRef Full Text | Google Scholar

Herwartz, D. (2021). Triple oxygen isotope variations in Earth’s crust. Rev. Mineral Geochem. 86, 291–322. doi: 10.2138/rmg.2021.86.09

CrossRef Full Text | Google Scholar

Herwartz, D., Surma, J., Voigt, C., Assonov, S., and Staubwasser, M. (2017). Triple oxygen isotope systematics of structurally bonded water in gypsum. Geochim. Cosmochim. Acta 209, 254–266. doi: 10.1016/j.gca.2017.04.026

CrossRef Full Text | Google Scholar

Horton, T. W., Defliese, W. F., Tripati, A. K., and Oze, C. (2016). Evaporation induced 18O and 13C enrichment in lake systems: A global perspective on hydrologic balance effects. Quat. Sci. Rev. 131, 365–379. doi: 10.1016/j.quascirev.2015.06.030

CrossRef Full Text | Google Scholar

Horton, T. W., and Oze, C. (2012). Are two elements better than one? Dual isotope-ratio detrending of evaporative effects on lake carbonate paleoelevation proxies. Geochem. Geophys. Geosyst. 13:Q0AK05.

Google Scholar

Horton, T. W., Sjostrom, D. J., Abruzzese, M. J., Poage, M. A., Waldbauer, J. R., Hren, M., et al. (2004). Spatial and temporal variation of Cenozoic surface elevation in the Great Basin and Sierra Nevada. Am. J. Sci. 304, 862–888. doi: 10.2475/ajs.304.10.862

PubMed Abstract | CrossRef Full Text | Google Scholar

Hren, M. T., Pagani, M., Erwin, D. M., and Brandon, M. (2010). Biomarker reconstruction of the early Eocene paleotopography and paleoclimate of the northern Sierra Nevada. Geology 38, 7–10. doi: 10.1130/g30215.1

CrossRef Full Text | Google Scholar

Hren, M. T., Tice, M. M., and Chamberlain, C. P. (2009). Oxygen and hydrogen isotope evidence for a temperate climate 3.42 billion years ago. Nature 462, 205–208. doi: 10.1038/nature08518

PubMed Abstract | CrossRef Full Text | Google Scholar

Hudson, A. M., Quade, J., Ali, G., Boyle, D., Bassett, S., Huntington, K. W., et al. (2017). Stable C, O and clumped isotope systematics and 14C geochronology of carbonates from the Quaternary Chewaucan closed-basin lake system, Great Basin, USA: Implications for paleoenvironmental reconstructions using carbonates. Geochim. Cosmochim. Acta 212, 274–302. doi: 10.1016/j.gca.2017.06.024

CrossRef Full Text | Google Scholar

Hulston, J. R., and Thode, H. G. (1965). Variations in the S33, S34, and S36 contents of meteorites and their relation to chemical and nuclear effects. J. Geophys. Res. 70, 3475–3484. doi: 10.1029/jz070i014p03475

CrossRef Full Text | Google Scholar

Huntington, K. W., Eiler, J. M., Affek, H. P., Guo, W., Bonifacie, M., Yeung, L. Y., et al. (2009). Methods and limitations of “clumped” CO2 isotope (Δ47) analysis by gas-source isotope ratio mass spectrometry. J. Mass Spectrom. 44, 1318–1329. doi: 10.1002/jms.1614

PubMed Abstract | CrossRef Full Text | Google Scholar

Huntington, K. W., and Lechler, A. R. (2015). Carbonate clumped isotope thermometry in continental tectonics. Tectonophysics 64, 1–20. doi: 10.1016/j.tecto.2015.02.019

CrossRef Full Text | Google Scholar

Huntington, K. W., Wernicke, B. P., and Eiler, J. M. (2010). Influence of climate change and uplift on Colorado Plateau paleotemperatures from carbonate clumped isotope thermometry. Tectonics 29:1129.

Google Scholar

Hyland, E. G., Huntington, K. W., Sheldon, N. D., and Reichgel, T. (2018). Temperature and seasonality in the North American continental interior during the Early Eocene Climatic Optimum. Clim. Past 14, 1391–1404. doi: 10.5194/cp-14-1391-2018

CrossRef Full Text | Google Scholar

Ibarra, D. E., and Chamberlain, C. P. (2015). Quantifying closed-basin lake temperature and hydrology by inversion of oxygen isotope and trace element paleoclimate records. Am. J. Sci. 315, 781–808. doi: 10.2475/09.2015.01

CrossRef Full Text | Google Scholar

Ibarra, D. E., Egger, A. E., Weaver, K. L., Harris, C. R., and Maher, K. (2014). Rise and fall of late Pleistocene pluvial lakes in response to reduced evaporation and precipitation: evidence from Lake Surprise, California. Bull. Geol. Soc. Am. 126, 1387–1415. doi: 10.1130/b31014.1

CrossRef Full Text | Google Scholar

Ingalls, M., Frantz, C. M., Snell, K. E., and Trower, E. J. (2020b). Carbonate facies specific stable isotope data record climate, hydrology, and microbial communities in Great Salt Lake, UT. Geobiology 18, 566–593. doi: 10.1111/gbi.12386

PubMed Abstract | CrossRef Full Text | Google Scholar

Ingalls, M., Rowley, D. B., Currie, B. S., and Colman, A. S. (2020a). Reconsidering the uplift history and peneplanation of the northern Lhasa terrane, Tibet. Am. J. Sci. 320, 479–532. doi: 10.2475/06.2020.01

CrossRef Full Text | Google Scholar

Kim, S. T., and O’Neil, J. R. (1997). Equilibrium and nonequilibrium oxygen isotope effects in synthetic carbonates. Geochim. Cosmochim. Acta 61, 3461–3475. doi: 10.1016/s0016-7037(97)00169-5

CrossRef Full Text | Google Scholar

Kim, S. T., O’Neil, J. R., Hillaire-Marcel, C., and Mucci, A. (2007). Oxygen isotope fractionation between synthetic aragonite and water: influence of temperature and Mg2+ concentration. Geochim. Cosmochim. Acta 71, 4704–4715. doi: 10.1016/j.gca.2007.04.019

CrossRef Full Text | Google Scholar

Knauth, L. P. (1973). Oxygen and Hydrogen Isotope Ratios in Cherts and Related Rocks. 378. Ph.D. Thesis, California Institute of Technology, Pasadena, CA.

Google Scholar

Knauth, L. P., and Epstein, S. (1976). Hydrogen and oxygen isotope ratios in nodular and bedded cherts. Geochim. Cosmochim. Acta 40, 1095–1108. doi: 10.1016/0016-7037(76)90051-x

CrossRef Full Text | Google Scholar

Kukla, T., Ibarra, D. E., Rugenstein, J. K. C., Gooley, J. T., Mullins, C. E., Kramer, S., et al. (2021). High-resolution stable isotope paleotopography of the John Day Region, Oregon, United States. Front. Earth Sci. 9:635181.

Google Scholar

Kukla, T., Winnick, M. J., Maher, K., Ibarra, D. E., and Chamberlain, C. P. (2019). The sensitivity of terrestrial δ18O gradients to hydroclimate evolution. J. Geophys. Res. Atmos. 124, 563–582. doi: 10.1029/2018jd029571

CrossRef Full Text | Google Scholar

Lechler, A. R., Niemi, N. A., Hren, M. T., and Lohmann, K. C. (2013). Paleoelevation estimates for the northern and central proto–Basin and Range from carbonate clumped isotope thermometry. Tectonics 32, 295–316. doi: 10.1002/tect.20016

CrossRef Full Text | Google Scholar

Levin, N. E., Raub, T. D., Dauphas, N., and Eiler, J. M. (2014). Triple oxygen isotope variations in sedimentary rocks. Geochim. Cosmochim. Acta 139, 173–189. doi: 10.1016/j.gca.2014.04.034

CrossRef Full Text | Google Scholar

Li, H. C., and Ku, T. L. (1997). δ13C–δ18C covariance as a paleohydrological indicator for closed-basin lakes. Palaeogeogr. Palaeoclimatol. Palaeoecol. 133, 69–80. doi: 10.1016/s0031-0182(96)00153-8

CrossRef Full Text | Google Scholar

Li, S., Levin, N. E., and Chesson, L. A. (2015). Continental scale variation in 17O-excess of meteoric waters in the United States. Geochim. Cosmochim. Acta 164, 110–126. doi: 10.1016/j.gca.2015.04.047

CrossRef Full Text | Google Scholar

Liljestrand, F. L., Laakso, T. A., Macdonald, F. A., Schrag, D. P., and Johnston, D. T. (2020). Isotopically anomalous organic carbon in the aftermath of the Marinoan snowball Earth. Geobiology 18, 476–485. doi: 10.1111/gbi.12383

PubMed Abstract | CrossRef Full Text | Google Scholar

Lowe, D. R., Ibarra, D. E., Drabon, N., and Chamberlain, C. P. (2020). Constraints on surface temperature 3.4 billion years ago based on triple oxygen isotopes of cherts from the Barberton Greenstone Belt, South Africa, and the problem of sample selection. Am. J. Sci. 320, 790–814. doi: 10.2475/11.2020.02

CrossRef Full Text | Google Scholar

Lund Snee, J.-E., Miller, E. L., Grove, M., Hourigan, J. K., and Konstantinou, A. (2016). Cenozoic paleogeographic evolution of the Elko Basin and surrounding region, northeast Nevada. Geosphere 12, 464–500. doi: 10.1130/ges01198.1

CrossRef Full Text | Google Scholar

Luz, B., and Barkan, E. (2010). Variations of 17O/16O and 18O/16O in meteoric waters. Geochim. Cosmochim. Acta 74, 6276–6286. doi: 10.1016/j.gca.2010.08.016

CrossRef Full Text | Google Scholar

Matsuhisa, Y., Goldsmith, J. R., and Clayton, R. N. (1978). Mechanisms of hydrothermal crystallization of quartz at 250 C and 15 kbar. Geochim. Cosmochim. Acta 42, 173–182. doi: 10.1016/0016-7037(78)90130-8

CrossRef Full Text | Google Scholar

McKinney, C. R., McCrea, J. M., Epstein, S., Allen, H. A., and Urey, H. C. (1950). Improvements in mass spectrometers for the measurement of small differences in isotope abundance ratios. Rev. Sci. Instrum. 21, 724–730. doi: 10.1063/1.1745698

CrossRef Full Text | Google Scholar

Meijer, H. A. J., and Li, W. J. (2006). The use of electrolysis for accurate δ17O and δ18O isotope measurements in water. Isotop. Environ. Health Stud. 34, 349–369.

Google Scholar

Methner, K., Campani, M., Fiebig, J., Löffler, N., Kempf, O., and Mulch, A. (2020). Middle Miocene long-term continental temperature change in and out of pace with marine climate records. Sci. Rep. 10, 1–10.

Google Scholar

Methner, K., Fiebig, J., Wacker, U., Umhoefer, P., Chamberlain, C. P., and Mulch, A. (2016). Eocene-Oligocene proto-Cascades topography revealed by clumped (Δ47) and oxygen isotope (δ18O) geochemistry (Chumstick Basin, WA, USA). Tectonics 35, 546–564. doi: 10.1002/2015tc003984

CrossRef Full Text | Google Scholar

Micheelsen, H. (1966). The structure of dark flint from Stevns Denmark. Medd. Fra Dansk Geol. 16, 285–368.

Google Scholar

Miller, M. F. (2002). Isotopic fractionation and the quantification of 17O anomalies in the oxygen three-isotope system: an appraisal and geochemical significance. Geochim. Cosmochim. Acta 66, 1881–1889. doi: 10.1016/s0016-7037(02)00832-3

CrossRef Full Text | Google Scholar

Miller, M. F., and Pack, A. (2021). Why measure 17O? Historical perspective, triple-isotope systematics and selected applications. Rev. Mineral Geochem. 86, 1–34. doi: 10.2138/rmg.2021.86.01

CrossRef Full Text | Google Scholar

Mix, H. T., and Chamberlain, C. P. (2014). Stable isotope records of hydrologic change and paleotemperature from smectite in Cenozoic western North America. Geochim. Cosmochim. Acta 141, 532–546. doi: 10.1016/j.gca.2014.07.008

CrossRef Full Text | Google Scholar

Mix, H. T., Ibarra, D. E., Mulch, A., Graham, S. A., and Chamberlain, C. P. (2016). A hot and high Eocene Sierra Nevada. Bull. Geol. Soc. Am. 128, 531–542. doi: 10.1130/b31294.1

CrossRef Full Text | Google Scholar

Mix, H. T., Mulch, A., Kent-Corson, M. L., and Chamberlain, C. P. (2011). Cenozoic migration of topography in the North American Cordillera. Geology 39, 87–90. doi: 10.1130/g31450.1

CrossRef Full Text | Google Scholar

Mulch, A. (2016). Stable isotope paleoaltimetry and the evolution of landscapes and life. Earth Planet. Sci. Lett. 433, 180–191. doi: 10.1016/j.epsl.2015.10.034

CrossRef Full Text | Google Scholar

Mulch, A., Chamberlain, C. P., Cosca, M. A., Teyssier, C., Methner, K., and Graham, S. A. (2015). Rapid change in western North American high-elevation rainfall patterns during the Mid Eocene Climatic Optimum (MECO). Am. J. Sci. 315, 317–336. doi: 10.2475/04.2015.02

CrossRef Full Text | Google Scholar

Mulch, A., Graham, S. A., and Chamberlain, C. P. (2006). Hydrogen isotopes in Eocene river gravels and paleoelevation of the Sierra Nevada. Science 313, 87–89. doi: 10.1126/science.1125986

PubMed Abstract | CrossRef Full Text | Google Scholar

Mulch, A., Uba, C. E., Strecker, M. R., Schoenberg, R., and Chamberlain, C. P. (2010). Late Miocene climate variability and surface elevation in the central Andes. Earth Planet. Sci. Lett. 290, 173–182. doi: 10.1016/j.epsl.2009.12.019

CrossRef Full Text | Google Scholar

O’Neil, J. R., and Kharaka, Y. K. (1976). Hydrogen and oxygen isotope exchange reactions between clay minerals and water. Geochim. Cosmochim. Acta 40, 241–246. doi: 10.1016/0016-7037(76)90181-2

CrossRef Full Text | Google Scholar

Pack, A., and Herwartz, D. (2014). The triple oxygen isotope composition of the Earth mantle and understanding ΔO17 variations in terrestrial rocks and minerals. Earth Planet. Sci. Lett. 390, 138–145.

Google Scholar

Passey, B. H., Hu, H., Ji, H., Montanari, S., Li, S., Henkes, G. A., et al. (2014). Triple oxygen isotopes in biogenic and sedimentary carbonates. Geochim. Cosmochim. Acta 141, 1–25. doi: 10.1016/j.gca.2014.06.006

CrossRef Full Text | Google Scholar

Passey, B. H., and Ji, H. (2019). Triple oxygen isotope signatures of evaporation in lake waters and carbonates: A case study from the western United States. Earth Planet. Sci. Lett. 518, 1–12. doi: 10.1016/j.epsl.2019.04.026

CrossRef Full Text | Google Scholar

Passey, B. H., and Levin, N. E. (2021). Triple oxygen isotopes in meteoric waters, carbonates, and biological apatites: implications for continental paleoclimate reconstruction. Rev. Mineral Geochem. 86, 429–462. doi: 10.2138/rmg.2021.86.13

CrossRef Full Text | Google Scholar

Passey, B. H., Levin, N. E., Cerling, T. E., Brown, F. H., and Eiler, J. M. (2010). High-temperature environments of human evolution in East Africa based on bond ordering in paleosol carbonates. Proc. Natl. Acad. Sci. U.S.A. 107, 11245–11249. doi: 10.1073/pnas.1001824107

PubMed Abstract | CrossRef Full Text | Google Scholar

Petersen, S. V., Defliese, W. F., Saenger, C., Daëron, M., Huntington, K. W., John, C. M., et al. (2019). Effects of improved 17O correction on interlaboratory agreement in clumped isotope calibrations, Estimates of mineral-specific offsets, and temperature dependence of acid digestion fractionation. Geochem. Geophys. Geosyst. 20, 3495–3519. doi: 10.1029/2018gc008127

CrossRef Full Text | Google Scholar

Petryshyn, V. A., Lim, D., Laval, B. L., Brady, A., Slater, G., and Tripati, A. K. (2015). Reconstruction of limnology and microbialite formation conditions from carbonate clumped isotope thermometry. Geobiology 13, 53–67. doi: 10.1111/gbi.12121

PubMed Abstract | CrossRef Full Text | Google Scholar

Pingel, H., Strecker, M. R., Mulch, A., Alonso, R. N., Cottle, J., and Rohrmann, A. (2020). Late Cenozoic topographic evolution of the Eastern Cordillera and Puna Plateau margin in the southern Central Andes (NW Argentina). Earth Planet. Sci. Lett. 535:116112. doi: 10.1016/j.epsl.2020.116112

CrossRef Full Text | Google Scholar

Poage, M. A., and Chamberlain, C. P. (2002). Stable isotopic evidence for a Pre-Middle Miocene rain shadow in the western Basin and Range: Implications for the paleotopography of the Sierra Nevada. Tectonics 21, 16–11. doi: 10.1029/2001tc001303

CrossRef Full Text | Google Scholar

Quade, J., Leary, R., Dettinger, M. P., Orme, D., Krupa, A., DeCelles, P. G., et al. (2020). Resetting Southern Tibet: The serious challenge of obtaining primary records of Paleoaltimetry. Glob. Planet. Change 191:103194. doi: 10.1016/j.gloplacha.2020.103194

CrossRef Full Text | Google Scholar

Rowley, D. B., Pierrehumbert, R. T., and Currie, B. S. (2001). A new approach to stable isotope-based paleoaltimetry: implications for paleoaltimetry and paleohypsometry of the High Himalaya since the Late Miocene. Earth Planet. Sci. Lett. 188, 253–268. doi: 10.1016/s0012-821x(01)00324-7

CrossRef Full Text | Google Scholar

Rozanski, K., Araguás-Araguás, L., and Gonfiantini, R. (1993). Isotopic patterns in modern global precipitation. GMS 78, 1–36. doi: 10.1029/gm078p0001

CrossRef Full Text | Google Scholar

San Jose, M., Rugenstein, J. K. C., Cosentino, D., Faccenna, C., Fellin, M. G., Ghinassi, M., et al. (2020). Stable isotope evidence for rapid uplift of the central Apennines since the late Pliocene. Earth Planet. Sci. Lett. 544:116376. doi: 10.1016/j.epsl.2020.116376

CrossRef Full Text | Google Scholar

Santi, L. M., Arnold, A. J., Ibarra, D. E., Whicker, C. A., Mering, J. A., Lomarda, R. B., et al. (2020). Clumped isotope constraints on changes in latest Pleistocene hydroclimate in the northwestern Great Basin: Lake Surprise, California. Geol. Soc. Am. Bull. 132, 2669–2683. doi: 10.1130/b35484.1

CrossRef Full Text | Google Scholar

Schauble, E. A., and Young, E. D. (2021). Mass dependence of equilibrium oxygen isotope fractionation in carbonate, nitrate, oxide, perchlorate, phosphate, silicate, and sulfate minerals. Rev. Mineral Geochem. 86, 137–178. doi: 10.2138/rmg.2021.86.04

CrossRef Full Text | Google Scholar

Schwartz, T. M., Methner, K., Mulch, A., Graham, S. A., and Chamberlain, C. P. (2019). Paleogene topographic and climatic evolution of the Northern Rocky Mountains from integrated sedimentary and isotopic data. Bulletin 131, 1203–1223. doi: 10.1130/b32068.1

CrossRef Full Text | Google Scholar

Sengupta, S., Peters, S. T., Reitner, J., Duda, J. P., and Pack, A. (2020). Triple oxygen isotopes of cherts through time. Chem. Geol. 554:119789. doi: 10.1016/j.chemgeo.2020.119789

CrossRef Full Text | Google Scholar

Sha, L., Mahata, S., Duan, P., Luz, B., Zhang, P., Baker, J., et al. (2020). A novel application of triple oxygen isotope ratios of speleothems. Geochim. Cosmochim. Acta 270, 360–378. doi: 10.1016/j.gca.2019.12.003

CrossRef Full Text | Google Scholar

Sharp, Z. D. (1990). A laser-based microanalytical method for the in situ determination of oxygen isotope ratios of silicates and oxides. Geochim. Cosmochim. Acta 54, 1353–1357. doi: 10.1016/0016-7037(90)90160-m

CrossRef Full Text | Google Scholar

Sharp, Z. D., Gibbons, J. A., Maltsev, O., Atudorei, V., Pack, A., Sengupta, S., et al. (2016). A calibration of the triple oxygen isotope fractionation in the SiO2–H2O system and applications to natural samples. Geochim. Cosmochim. Acta 186, 105–119. doi: 10.1016/j.gca.2016.04.047

CrossRef Full Text | Google Scholar

Sharp, Z. D., and Wostbrock, J. A. G. (2020). Standardization for the triple oxygen isotope system: waters, silicates, carbonates, air, and sulfates. Rev. Mineral. Geochem. 86, 179–196. doi: 10.2138/rmg.2021.86.05

CrossRef Full Text | Google Scholar

Sharp, Z. D., Wostbrock, J. A. G., and Pack, A. (2018). Mass-dependent triple oxygen isotope variations in terrestrial materials. Geochem. Perspect. Lett 7, 27–31. doi: 10.7185/geochemlet.1815

PubMed Abstract | CrossRef Full Text | Google Scholar

Sjostrom, D. J., Hren, M. T., Horton, T. W., Waldbauer, J. R., and Chamberlain, C. P. (2006). Stable isotopic evidence for a pre–late Miocene elevation gradient in the Great Plains–Rocky Mountain region, USA. Geol. Soc. Am. Spec. Pap. 398, 309–319.

Google Scholar

Smith, J. F. Jr., and Ketner, K. B. (1976). Stratigraphy of Post-Paleozoic Rocks and Summary of Resources in the Carlin-Pinon Range Area, Nevada. United States Geological Survey Professional Paper 867-B. Washington, DC: United States Government Printing Office.

Google Scholar

Smith, M. E., Cassel, E. J., Jicha, B. R., Singer, B. S., and Canada, A. S. (2017). Hinterland drainage closure and lake formation in response to middle Eocene Farallon slab removal, Nevada. Earth Planet. Sci. Lett. 479, 156–169. doi: 10.1016/j.epsl.2017.09.023

CrossRef Full Text | Google Scholar

Speelman, E. N., Sewall, J. O., Noone, D., Huber, M., von, der Heyt, A., et al. (2010). Modeling the influence of a reduced equator-to-pole sea surface temperature gradient on the distribution of water isotopes in the Early/Middle Eocene. Earth Planet. Sci. Lett. 298, 57–65. doi: 10.1016/j.epsl.2010.07.026

CrossRef Full Text | Google Scholar

Surma, J., Assonov, S., Bolourchi, M. J., and Staubwasser, M. (2015). Triple oxygen isotope signatures in evaporated water bodies from the Sistan Oasis, Iran. Geophys. Res. Lett. 42, 8456–8462. doi: 10.1002/2015gl066475

CrossRef Full Text | Google Scholar

Surma, J., Assonov, S., Herwartz, D., Voigt, C., and Staubwasser, M. (2018). The evolution of 17O-excess in surface water of the arid environment during recharge and evaporation. Sci. Rep. 8, 1–10.

Google Scholar

Surma, J., Assonov, S., and Staubwasser, M. (2021). Triple oxygen isotope systematics in the hydrologic cycle. Rev. Mineral Geochem. 86, 401–428. doi: 10.2138/rmg.2021.86.12

CrossRef Full Text | Google Scholar

Takeuchi, A., Hren, M. T., Smith, S. V., Chamberlain, C. P., and Larson, P. B. (2010). Pedogenic carbonate carbon isotopic constraints on paleoprecipitation: evolution of desert in the Pacific Northwest, USA, in response to topographic development of the Cascade Range. Chem. Geol. 277, 323–335. doi: 10.1016/j.chemgeo.2010.08.015

CrossRef Full Text | Google Scholar

Takeuchi, A., and Larson, P. B. (2005). Oxygen isotope evidence for the late Cenozoic development of an orographic rain shadow in eastern Washington, USA. Geology 33, 313–316. doi: 10.1130/g21335.1

CrossRef Full Text | Google Scholar

Tong, Y., Ibarra, D. E., Caves, J. K., Mukerji, T., and Graham, S. A. (2017). Constraining basin thermal history and petroleum generation using palaeoclimate data in the Piceance Basin. Colorado 29, 542–553. doi: 10.1111/bre.12213

CrossRef Full Text | Google Scholar

Voarintsoa, N. R. G., Barkan, E., Bergel, S., Vieten, R., and Affek, H. P. (2020). Triple oxygen isotope fractionation between CaCO3 and H2O in inorganically precipitated calcite and aragonite. Chem. Geol. 539:119500. doi: 10.1016/j.chemgeo.2020.119500

CrossRef Full Text | Google Scholar

Wacker, U., Fiebig, J., and Schoene, B. R. (2013). Clumped isotope analysis of carbonates: comparison of two different acid digestion techniques. Rapid Commun. Mass Spectrom. 27, 1631–1642. doi: 10.1002/rcm.6609

PubMed Abstract | CrossRef Full Text | Google Scholar

Wostbrock, J. A., Cano, E. J., and Sharp, Z. D. (2020). An internally consistent triple oxygen isotope calibration of standards for silicates, carbonates and air relative to VSMOW2 and SLAP2. Chem. Geol. 533:119432. doi: 10.1016/j.chemgeo.2019.119432

CrossRef Full Text | Google Scholar

Wostbrock, J. A., and Sharp, Z. D. (2021). Triple oxygen isotopes in silica–water and carbonate–water systems. Rev. Mineral Geochem. 86, 367–400. doi: 10.2138/rmg.2021.86.11

CrossRef Full Text | Google Scholar

Wostbrock, J. A., Sharp, Z. D., Sanchez-Yanez, C., Reich, M., van den Heuvel, D. B., and Benning, L. G. (2018). Calibration and application of silica-water triple oxygen isotope thermometry to geothermal systems in Iceland and Chile. Geochim. Cosmochim. Acta 234, 84–97. doi: 10.1016/j.gca.2018.05.007

CrossRef Full Text | Google Scholar

Yanchilina, A. G., Yam, R., Kolodny, Y., and Shemesh, A. (2020). From diatom opal-A δ18O to chert δ18O in deep sea sediments. Geochim. Cosmochim. Acta 268, 368–382. doi: 10.1016/j.gca.2019.10.018

CrossRef Full Text | Google Scholar

Yeung, L. Y., and Hayles, J. A. (2021). Climbing to the top of mount fuji: uniting theory and observations of oxygen triple isotope systematics. Rev. Mineral Geochem. 86, 97–135. doi: 10.2138/rmg.2021.86.03

CrossRef Full Text | Google Scholar

Yeung, L. Y., Hayles, J. A., Hu, H., Ash, J. L., and Sun, T. (2018). Scale distortion from pressure baselines as a source of inaccuracy in triple-isotope measurements. Rapid Commun. Mass Spectrom. 32, 1811–1821. doi: 10.1002/rcm.8247

PubMed Abstract | CrossRef Full Text | Google Scholar

Young, E. D., Galy, A., and Nagahara, H. (2002). Kinetic and equilibrium mass-dependent isotope fractionation laws in nature and their geochemical and cosmochemical significance. Geochim. Cosmochim. Acta 66, 1095–1104. doi: 10.1016/s0016-7037(01)00832-8

CrossRef Full Text | Google Scholar

Zakharov, D. O., Marin-Carbonne, J., Alleon, J., and Bindeman, I. N. (2021). Triple oxygen isotope trend recorded by Precambrian cherts: a perspective from combined bulk and in situ secondary ion probe measurements. Rev. Mineral Geochem. 86, 323–366. doi: 10.2138/rmg.2021.86.10

CrossRef Full Text | Google Scholar