The Growth of Earthquake Clusters

Migration of hypocenters is a common attribute of induced injection seismicity and of earthquake swarms, which distinguishes them from aftershock sequences. Spreading of the triggering front is often examined by fitting the time dependence of hypocenter distances from the origin by the pore pressure diffusion model. The earthquake migration patterns however often exhibit not only spreading envelopes but also fast-growing streaks embedded in the overall migration trends. We review the observed migration patterns and show that in the case of earthquake-driven migration, where the new ruptures are triggered at the edge of previous ruptures, it is more suitable to examine the cluster growth as a function of the event index instead of time. We propose a model that relates the speed of seismicity spreading to the average rupture area and the effective magnitude of the hypocenter cluster. Application of the model to selected linearly growing clusters of the 2008 West Bohemia swarm gives an almost linear increase of the measured total rupture area with the event index, which fits the proposed model. This is confirmed by a self-similar scaling of the average rupture area with the effective magnitude for stress drops ranging from 0.1 to 1 MPa. The relatively small stress drop level indicates the presence of voids along the fault plane and a possible role of aseismic deformation.

1 Introduction

The spreading of earthquake hypocenters is generally considered to be characteristic of earthquake swarms, which distinguishes them from aftershock sequences. While swarms typically show a clear hypocenter migration starting from a single point of the fault plane, aftershocks usually occur immediately all over the fault plane and along the edges of mainshock rupture. First aftershocks are located close to the rupture plane of the mainshock, while later aftershocks sometimes seem to migrate away from the mainshock (Rydelek and Sacks, 2001) at velocities smaller than 1 km/h. A significant expansion of aftershock clouds is only expected in the presence of aseismic processes such as mainshock-induced afterslip (Peng and Zhao, 2010; Perfettini et al., 2019), while coseismic stress transfer of the aftershocks itself can only explain a minor spreading (Helmstetter et al., 2003).

Hypocenter migration of earthquake swarms is generally attributed to fluid flow along the fault plane. Number of examples of swarms from various tectonic environments show this feature, e.g. in Iceland (Woods et al., 2019), Japan (Yoshida and Hasegawa, 2018a), Afar Rift (Wright et al., 2012), Yellowstone (Massin et al., 2013), or West Bohemia/Vogtland (Fischer et al., 2014). Different migration scenarios are observed from monotonous migration in the horizontal or vertical direction or migration with direction changes within the evolution of the seismic cluster. The migration is often attributed to dyke intrusion, hydrofracture propagation, slow slip events, or pore pressure diffusion. Those models will be discussed below.

Monotonous hypocenter migration is also observed for microearthquakes accompanying hydraulic fracturing, which is commonly used in the industry to create a permeable channel in tight rocks in order to increase the production of oil and gas or facilitate water circulation in the geothermal heat exchanger. The hydraulic fracture is formed by massive water injection at pressures exceeding the minimum principal stress. The growth of the edge of the hydrofracture (so-called rupture triggering front) can be explained by the conservation law relating the injected fluid volume to the volume of the fracture (Fischer et al., 2008; Shapiro, 2015). Accordingly, depending on the hydrofracture geometry, either linear or parabolic growth is observed.

Pronounced migration of epicenters of nonvolcanic tremors, the weak seismic signals associated with slow slip on fault planes, has been observed in subduction zones along distances above 100 km, e.g. (Houston et al., 2011). The observed hypocenter patterns are explained by slow slip initiated by pressurization by fluids interacting with small asperities, which is reproduced by model simulations (Luo and Ampuero, 2017). In many cases, the coordinate-time plots of the migrating hypocenters show two features: slow nonlinear growth of the overall envelope and rapid growth of linear streaks during bursts of activity as observed e.g. within the 2008 West Bohemia swarm (Figure 1A). Here, a streak is defined as a narrow linear belt of points in the coordinate-time plot, which is usually embedded in the overall large-scale migration of the seismic cloud. We identified similar rapidly propagating streaks also in other swarms from West Bohemia and other areas as Yellowstone (Shelly et al., 2016) or Corinth Rift (Kapetanidis et al., 2015). Interestingly, similar streaks also occur during the nonvolcanic tremors showing both forward and reverse motion of epicenters at velocities from 7 to 100 km/day (Ghosh et al., 2010; Houston et al., 2011) (see Figure 2 in Ghosh et al., 2010). In contrast to the natural earthquakes, the seismicity evolution with time is quite smooth and in most cases no streaks of hypocenters are apparent for the injection-induced seismicity (Figure 1G). The only observation of a feature similar to the rapid streaks is that of Shapiro and Dinske, 2009, who attributed the linear fronts in the distance-time plots to hydraulic fracture opening.

FIGURE 1

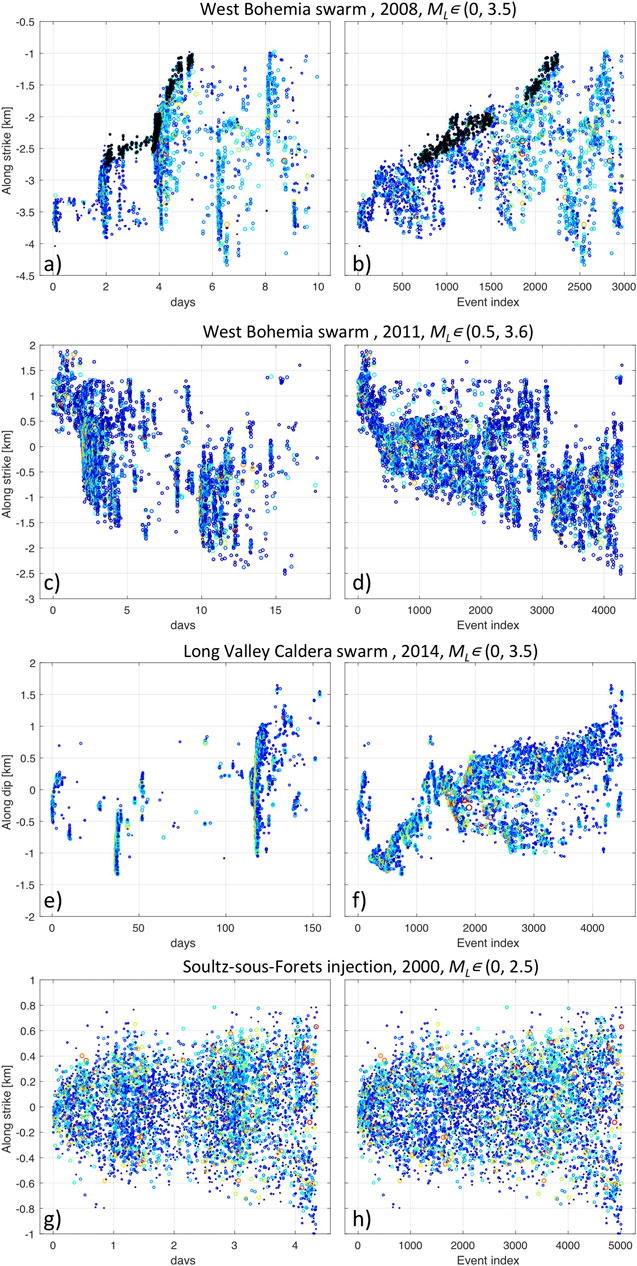
FIGURE 1. Migration of various types of seismicity for three cases of swarm activity (A–C) and one case of injection-induced seismicity (D). Coordinate-time plots (left panels) and coordinate–event-index plots (right panels) for the West-Bohemian swarm in 2008 (A), in 2011 (B), Long-Valley Caldera swarm in 2014 (C) and Soultz-sous-Forets injection in 2000. Note the episodic occurrence of activity in the coordinate-time plots compared to the overall continuous spreading of activity in the coordinate-event-index plots. Note also that fast propagating streaks of hypocenters are observed in swarms but are missing in the injection induced seismicity. The color of symbols from dark blue to dark red is proportional to the event magnitude. In (A) two spreading episodes are highlighted in black in both coordinate-time and coordinate-event-index plots.

In summary, seismic swarms and nonvolcanic tremors show migration patterns on two scales: 1) an (asymmetric) overall growth over days to weeks 2) rapid migration on small spatial and temporal scales, partially with reversed trends. While the overall growth is to be explained either by pore pressure diffusion or hydraulic fracture growth (possibly also by slow slip, but not analyzed in detail yet), the embedded rapid migration have been studied only rarely in detail. Yoshida and Hasegawa (2018b) analyzed the triggering of the Sendai-Okura earthquake swarm by the 2011 Tohoku-Oki earthquake. And recently, Dublanchet and Barros (2020) proposed a model that reproduces the dual migration speeds observed in real swarms by coupling rate-and-state friction, non-linear diffusivity and elasticity along the fault.

Regarding the control of seismicity migration, two end-member cases can be distinguished: externally (aseismic) and internally (seismic) controlled propagation. In the first case an external physical process drives and controls the migration, where earthquakes are only passive markers of this usually time-dependent process. This could be pore-pressure diffusion (Shapiro et al., 1997), hydraulic fracture growth (Dahm et al., 2010), or slow slip (Schwartz and Rokosky, 2007). In the second case, the migration is self-controlled by the earthquake ruptures themselves in the way that the ruptures allow or facilitate nucleation of adjacent new ruptures. Such an earthquake-induced effect can be related to coseismically induced elastic stress changes as well as postseismic effects such as creation of pore-space enabling subsequent fluid flow. Both increase the stress state at the rupture borders facilitating subsequent adjacent ruptures. In such a case, the internal processes and conditions control the “time” and no general time dependence of the seismicity migration is necessarily expected.

In this paper, we review the existing approaches to understanding the earthquake migration. We show examples of migration of earthquake swarms, where both the slow growth of the triggering front and the fast propagation of streaks occur, in particular when displayed using the coordinate - event order plot. Provided that every rupture opens the way for nucleation of the further rupture, we develop a theoretical model of the seismicity spreading related to the source parameters of the earthquakes suitable for the physical interpretation of the observed migration patterns.

2 Models and Interpretation of Earthquake Migration

In the following, we review the existing approaches for interpreting and employing the spreading of earthquake hypocenters.

2.1 Pore Pressure Diffusion

The observed hypocenter migration shows, in many cases, a non-linear growth of envelope in the distance-time plot, which is commonly interpreted by pore pressure diffusion in a homogeneous isotropic medium. The model was originally proposed to interpret the spreading of hypocenters of injection-induced seismicity (Shapiro et al., 1997). It is based on the assumption that earthquakes map the advance of the pore pressure front. It is also assumed that the diffusivity of the rock is constant and that the pore pressure field is decoupled from seismic rupturing and related stress changes. This is in contrast to, for example, the model of Yamashita (1999) where the effect of dynamic pore creation is considered. Ignoring such coupling effects, the evolution of the pore-pressure field can be described by the diffusion equation whose solution for a point pressure source gives the distance r of the propagating pore pressure front as $r=\sqrt{4\pi Dt}$ (Shapiro et al., 1997), where t is the time since the first contact of the pore pressure source with the host rock and D is the hydraulic diffusivity. Observations of injection-induced seismicity also show that after stopping the injection the induced earthquakes close to the injection point gradually cease to occur. A triggering backfront is being formed that becomes more distant from the injection point; its distance is also proportional to $\sqrt{Dt}$ (Parotidis et al., 2004).

Rock properties are, however, anisotropic because of strong heterogeneities like faults acting as permeable channels on the one hand, or as impermeable barriers on the other hand. Furthermore, the stress field is heterogeneous due to the stress gradients originating from density contrasts between fluid and rock or heterogeneous tectonic stress. The combination of both types of heterogeneities necessarily results in the preferred orientation of the fluid flow. Consequently, the seismicity front is expected to depend on the direction. The data of West-Bohemia/Vogtland swarms show a clear directional dependence of earthquake migration. In the case of the 2008 swarm the migration in dip-direction could be very well fitted by the pore pressure front curves. However, it requires different hydraulic diffusivities for up-dip and down-dip directions. The estimated down-dip diffusivity ($D=0.1{\text{m}}^2{\text{s}}^{-1}$) is only one-third of the up-dip value ($D=0.3{\text{m}}^2{\text{s}}^{-1}$) (Hainzl et al., 2012). Furthermore, in the down-dip direction, the migration stops completely after approximately nine days, whereas the migration continues in the up-dip direction. These discrepancies indicate that the diffusion model is often not able to explain earthquake migration in more detail and reveals the need for an alternative model in the case of tectonic earthquakes.

2.2 Hydraulic Fracture Growth

The pore pressure diffusion model is only appropriate in the limit of poroelasticity, which means, if non-linear effects such as the creation of pore-volume can be neglected and hydraulic properties remain unchanged. If the involved fluid pressure exceeds the minimum confining pressure, hydrofracturing of intact rock takes place. This leads locally to open channels for fluid transport and thus strongly changes the local permeability and hydraulic properties. As a result, instead of pore pressure diffusion in isotropic intact medium, the high-pressure fluid injection results in a subsequent opening of the fault zone and related fluid flows that are driven, in addition to the injection itself, by stress gradients. In a homogeneous rock a hydraulic fracture should open against the direction of the minimum stress component ${\sigma }_3$. The model of hydrofracture growth of Fischer et al., (2009) and Dahm et al., (2010) can be then used to fit the migration pattern of the swarm activity. The resulting relation between the distance r of the triggering front and the time t since the start of the injection depends on the fracture geometry. Using the mass conservation of the injected fluid and assuming a constant injection rate and thickness of the hydraulic fracture without fluid penetration in the rock matrix, a linear relation of r and t is predicted for fracture propagation in a single dimension (1D). Similarly, for unlimited two-dimensional fracture propagation, a square-root growth of r with t is predicted. If asymmetric growth similar to that shown in Figures 1A, 2 is observed, the relation between the length of the shorter and longer wing can be used to estimate the driving stress gradient responsible for the asymmetry as presented in our previous studies (Fischer et al., 2009; Hainzl et al., 2012; Mls and Fischer, 2017).

FIGURE 2

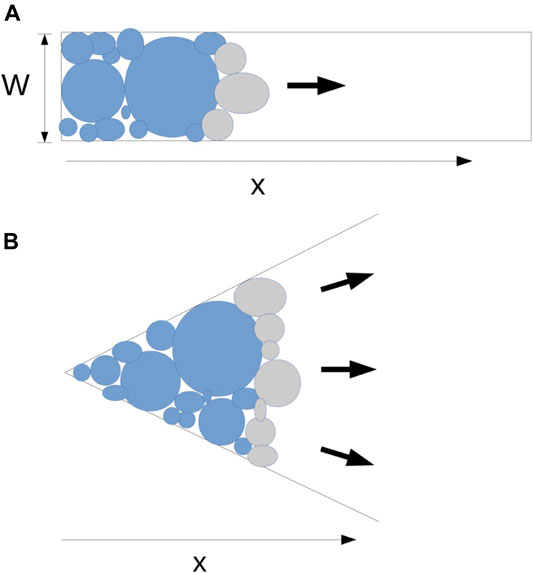
FIGURE 2. Schematic illustration of seismicity model growth supposing that a new rupture is initiated at the edge of the previous rupture. (A) The channel growth (model C) is related to a unidirectional or bidirectional 1-D advance of the rupture front. (B) The sector growth (model S) considers a 2-D advance of the rupture front.

2.3 Slow Slip Driven Seismicity

In contrast to the two other mechanisms, slow slip describes transient aseismic shear dislocation (slip) on faults. By means of new geodetic instrumentation, slow slip events have been identified to occur frequently on faults (Schwartz and Rokosky, 2007). Particularly, it is expected to occur in fault zones, where frictional behavior is partly characterized by velocity strengthening. However, it can also occur in velocity weakening zones, if the nucleation dimension exceeds the asperity size. The nucleation size is itself inversely proportional to the effective normal stress, thus the evaluated pore pressure favors aseismic vs. coseismic slip (Dieterich, 2007). While aseismic slip events can nucleate spontaneously, they can also be triggered by fluid injection (Guglielmi et al., 2015) or coseismic slip. The latter is known as afterslip which is believed to be one of the main drivers for aftershocks (Perfettini et al., 2019). In particular, a $\log \left(t\right)$ expansion of the aftershock zone has been forecasted for faults governed by rate-state-dependent friction, where the rupture of the mainshock asperity triggers postseismic creep in the surrounding velocity-strengthening region (creep zone). Simulations show that this creep leads to a $\log \left(t\right)$ migration front of aftershocks which are triggered in smaller embedded asperities (Kato, 2007). Such a $r\propto \log \left(t\right)$ expansion of the aftershock zone has been observed for the early aftershocks of the 2014 M6 Parkfield event (Peng and Zhao, 2010) and for the aftershocks of the 2014 mainshock in Western Bohemia (Hainzl et al., 2016).

2.4 Effective Stress Drop Concept

Fischer and Hainzl (2017) proposed to employ the spreading of hypocenters of earthquake clusters for interpreting the stress release of the involved seismicity. The basic idea is that if a large earthquake rupture is replaced by numerous small ruptures, which is the mainshock on the one hand and the earthquake swarm on the other hand, similar strain should be released in both cases. Then the total seismic moment of the cluster should equal the seismic moment of a single large event and the familiar formula for seismic moment of a circular rupture $M_0=7/16\Delta \sigma R^3$ could be used to relate the total seismic moment $\Sigma M_0$, radius of the cluster R and stress drop $\Delta \sigma$. To distinguish it from the static stress drop, we name it the effective stress drop. The validity of this approach however depends on the fact that all stress has been released during the sequence, which is pronounced in the power of $M_0\left(R\right)$ scaling. For this purpose, we compare the spatiotemporal evolution of the seismic moment release by projecting the hypocenters to a best-fitted plane and measuring the radius of the convex envelope of the cluster. By analyzing the uncertainties of the estimated effective stress drops it was found that the effective stress drop is only comparable to earthquake stress drops in specific cases. In particular, the effective stress-drop values underestimate the earthquake stress drops in the presence of aseismic deformation significantly. The values are only scale-independent if pre-stress and post-stress conditions are uniform in space. The analysis of data from injection-induced seismicity, natural earthquake swarms, and aftershock sequences showed that in most cases the effective stress-drop estimate is rather stable during the cluster evolution. The effective stress drop concept, however, explores only the overall growth of the earthquake cluster. It does not explore the preferred direction of the triggering front advance. We hypothesize that the advance of the overall cluster envelope and, in particular, of the embedded rapid migration patterns are closely related to the triggering forces and can be possibly used for discrimination of the underlying mechanism. In particular, we aim at modifying the effective stress drop concept in order to reflect the specific character of rapidly propagating streaks to learn more about their origin.

3 Identification of Migration Patterns

Typically, migration patterns are analyzed in the distance-time domain, where the form of observed migration patterns also depends on definition of distance. Traditionally, the dependence of unsigned distance on time, $r\left(t\right)$, is explored, which masks however the possible asymmetry of the cluster growth. Such type of plot is suitable for determining the hydraulic diffusivity, which is independent of direction. To explore the asymmetry of the fracture propagation a coordinate-time plot $x\left(t\right)$, where the coordinates x are taken including their sign, is more suitable (left panels of Figure 1). Concerning the independent variable, it is usually the time, which is used. This however postulates that it is the time, which controls the seismogenic process. Such plots are suitable to identify and characterize the external driving force, such as e.g. to estimate the hydraulic diffusivity D in the case of seismicity driven by pore-pressure diffusion.

An additional analysis tool is to use the event order as the independent variable, which is also termed natural time (Rundle et al., 2018). In such a case, a coordinate-event-index plot $x\left(N\right)$ is produced. This postulates that the seismogenic process itself controls the seismicity. In other words, every rupture opens the way for nucleation of the further rupture, which is also the basis of the Yamashita (1999) model where the effect of dynamic pore creation is considered. Exploring the seismicity spreading dependent on the event order ignores the influence of time on the seismicity and allows for investigating the dynamics of the cluster formation. As a result, it is the seismogenic process that measures the new natural time; the pendulum stops in the period of quiescence and restarts with the new onset of seismic activity. Thus, the combined analysis of both plots, the coordinate-time and the coordinate-event-index plot, offers the possibility to understand the processes in more detail.

The form of migration diagrams using the coordinate-time plot and coordinate-event-index plot is compared in the left and right panels of Figure 1 for selected swarm activities. In the coordinate-event-index plots the periods of quiescence disappear and the original temporal clusters apparent in the coordinate-time plot merge into a continuous seismicity sequence migrating in a single dominating direction. The triggering front shows a linear envelope whose slope (migration velocity measured in meters per event) stays almost constant for longer periods. Note the continuous seismicity growth of the 2008 West-Bohemia swarm in the event-index plot (Figure 1B) compared to the heavily interrupted spreading in the time plot (Figure 1A) of the same activity. The change of growth character is highlighted in two rupture front clusters, which are continuous in the coordinate-event-index plot, but strongly discontinuous in the coordinate-time plot. Similar characteristics are illustrated in Figures 1E,F for the 2014 swarm in the Long Valley Caldera (Shelly et al., 2016), which showed, compared to the 2008 West-Bohemia swarm, almost simple unilateral spreading. The plots in Figure 1 also illustrate the two aforementioned phenomena: the overall growth of the seismic clouds manifested in the triggering front envelope and embedded rapid streaks that propagate both in the same and opposite directions as the triggering envelope.

4 Theoretical Model

One end-member model considers earthquakes only as a passive result of an underlying driving force, e.g. pore-pressure diffusion or slow slip which is not influenced by the triggered earthquakes. In this case, the analysis of the distance-time or coordinate-time plots is sufficient to characterize the migration pattern and the underlying process. However, in the other end-member model, earthquake migration is only possible due to the occurrence of earthquakes, e.g. by the creation of pore-space during ruptures. The presence of clear triggering fronts and embedded linear streaks in the coordinate-event-index plots, while no clear migration pattern can be observed in the coordinate-time plot, points to the latter case. In particular, in such a case, the speed of growth should increase with the size of the event ruptures. Developing a theoretical model for the earthquake generation in the case of a self-driven seismicity migration would help understand the generation mechanism of earthquake swarms.

In accordance with the Yamashita (1999) model we suppose that every rupture facilitates the nucleation of adjacent ruptures. This can be simplified by assuming that subsequent events are without overlap initiated at the outer border of the previous rupture. In two dimensions, two geometrical concepts are considered, the channel (C) model describing a unilateral growth along a channel of width W and the sector (S) model describing a two-dimensional sectorial growth with angle θ (Figure 2).

The speed of the cluster growth is then related to the average position x of the rupture front, which is after the occurrence of N events (as observed in Figure 1) simply given by

$x\left(N\right)=\{\begin{array}{ll}\frac{\langle A\rangle }{W}N=\nu N,\hfill & \text{model} C,\hfill \\ \sqrt{\frac{360}{\pi \theta }\langle A\rangle }\sqrt{N}=\sqrt{DN},\hfill & \text{model}S,\hfill \end{array}(1)$

where both constants ν and D are proportional to the average rupture area $\langle A\rangle$ of the earthquakes in the cluster. In particular, model C predicts a linear growth of the rupture front x with increasing event index N according to a velocity $\nu =\langle A\rangle /W$, which is consistent to a constant average advance per observed event. On the other hand, model S predicts a square-root growth of the rupture front x with event index N, with a local velocity $0.5\sqrt{D/N}=0.5\sqrt{360/\pi \theta \langle A\rangle /N}$ per event. In both cases, the total rupture area grows linearly with event index as

$A=\langle A\rangle \cdot N.(2)$

In order to express $\langle A\rangle$ we suppose that the frequency-magnitude distribution of the events follows a doubly truncated Gutenberg-Richter distribution with exponent b and truncations at a minimum magnitude $M_1$ and maximum magnitude $M_2$. The corresponding probability density function for the event magnitudes is in this case given by Marzocchi and Sandri (2003).

$p\left(m\right)=\ln \left(10\right)b\frac{{10}^{-bm}}{{10}^{-b{M}_1}-{10}^{-b{M}_2}}.(3)$

We also use the relation between the area A of a circular rupture and seismic moment $M_0=f\Delta \sigma A^{3/2}$ (see, e.g., review of Madariaga and Ruiz (2016)). Rearranging this relation and using the scaling between the seismic moment $M_0$ and the magnitude m in the form of

$\log M_0=c+dm(4)$

leads to

$A\left(m\right)={\left(\frac{{10}^{c+dm}}{f\Delta \sigma }\right)}^{2/3},(5)$

where f is a geometric factor of the source model, $\Delta \sigma$ is the static stress drop, c and d are 9.1 and 1.5, respectively, for the moment magnitude $m_W$ (Hanks and Kanamori, 1979).

Then, the average rupture area $\langle A\rangle$ can be determined (see Appendix) by

$\langle A\rangle =\{\begin{array}{ll}{\left(\frac{{10}^c}{f\Delta \sigma }\right)}^{23}\frac{b}{\left(23\right)d-b}{10}^{b{M}_1}\left({10}^{\left(\left(23\right)d-b\right)M_2}-{10}^{\left(\left(23\right)d-b\right)M_1}\right),\hfill & \text{if}b\ne \left(23\right)d,\hfill \\ {\left(\frac{{10}^c}{f\Delta \sigma }\right)}^{23}b\ln \left(10\right){10}^{b{M}_1}\left(M_2-M_1\right),\hfill & \text{if}b=\left(2/3\right)d.\hfill \end{array}(6)$

In the above equations, $M_1$ is the true physical minimum magnitude of the earthquakes, while we usually have a larger observational cutoff magnitude $M_c$ (completeness magnitude). Assuming that magnitude correlations do not exist (magnitudes are random within the sequence), the observed $m\ge M_c$ events are mapping the true advance, but missing on average ${10}^{b\left(M_c-M_1\right)}$ events between two successive $m\ge M_c$ events. Consequently, the event index is

$N_{\text{obs}}={10}^{-b\left(M_c-M_1\right)}N.(7)$

Then Eq. 1 describes the average position of the seismicity as a function of observed events $N_{\text{obs}}$, if the parameters

$\begin{array}{l}\tilde{\nu }={10}^{b\left(M_c-M_1\right)}\nu ,\\ \tilde{D}={10}^{b\left(M_c-M_1\right)}D,\end{array}(8)$

are used instead of ν and D, respectively.

5 Application to the Seismicity Data

Equation (6) predicts the average rupture area $\langle A\rangle$ from the seismicity parameters $\left(b,M_1,M_2\right)$. These parameters can be related to the average seismic moment per event $\langle M_0\rangle$ and its corresponding effective magnitude $M_{\text{eff}}$ using Eqs. 4, 5. The empirical value of $\langle M_0\rangle$ can easily be calculated for an observed sequence, while the theoretical value is given by Zakharova et al., (2013).

$\langle M_0\rangle ={10}^{c+d{M}_1}\frac{b}{d-b}\frac{{10}^{\left(d-b\right)\left(M_2-M_1\right)}-1}{1-{10}^{-b\left(M_2-M_1\right)}},\text{if}b\ne d.(9)$

Based on $\langle M_0\rangle$, the effective magnitude of the average seismic moment can be determined by

$\langle M_{\text{eff}}\rangle =\frac{\left(\log \left(\langle M_0\rangle \right)-c\right)}{d}.(10)$

As follows from Eq. 6, the average rupture $\langle A\rangle$ area depends on the stress drop and the magnitude distribution of the analyzed sequence reflected in its effective magnitude. This dependence is illustrated in Figure 3 showing the average rupture area as a function of the maximum and effective magnitude for a set of b-values ranging from 0.8 to 1.2 and stress drops between 0.1 and 100 MPa.

FIGURE 3

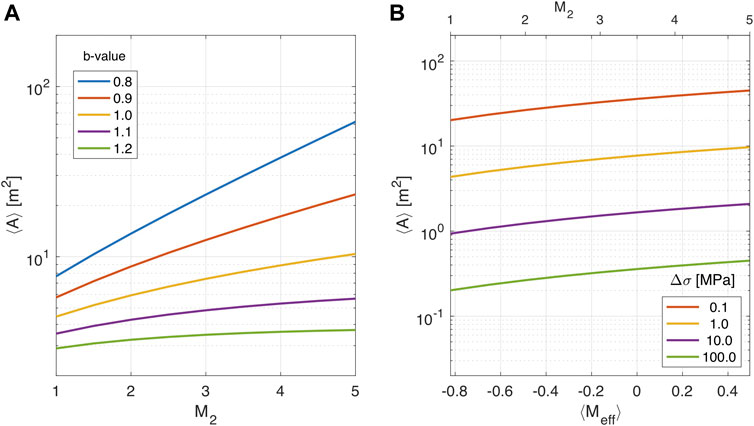
FIGURE 3. Average rupture area $\langle A\rangle$ obtained by Eq. 6 for b-values 0.8, 0.9, 1.0, 1.1, 1.2 with stress drop 1 MPa in (A) and for stress drops 0.1, 1, 10, and 100 MPa with $b=1.0$ in (B). The following constants were used: $c=9.1,d=1.5$ and $f=1$. The plots were generated for minimum magnitude $M_1=-2$ and maximum magnitude $M_2$ in the range from 1 to 5. The corresponding effective magnitude $\langle M_{eff}\rangle$ on the horizontal axis in (B) was obtained by Eq. 4. Both plots show nonlinear increase of $\langle A\rangle$ with the maximum magnitude $M_2$.

As predicted by Eq. 6, except the case $b=2/3d$, the average rupture area $\langle A\rangle$ increases non-linearly with the maximum magnitude $M_2$. The growth rate decreases with increasing b-value (Figure 3A), which is related to the decreasing number of large events. Similarly, larger $\langle A\rangle$-values are observed for smaller stress drops (Figure 3B). Equation 6 further predicts that the slope increases with the moment-magnitude scaling factor d and that the curves shift up with the constant c.

The curves in Figure 3 predict the average rupture area $\langle A\rangle$ growth in the case that the seismic activity is driven internally by the earthquake ruptures themselves. Then, $\langle A\rangle$ equals the average advance of the cluster growth per event (Eq. 1) directly. For real data, comparing the observed average rupture area $\langle A\rangle$ with the theoretical rupture area for the same effective magnitude would allow us to compare the scaling of the growth velocity with magnitude and verify the validity of our model for real data. Additionally, an estimate of the average stress drop of the cluster could be obtained.

To test the validity of the presented models on data we measure the growth of selected clusters of the 2008 swarm in West Bohemia, whose migration patterns are presented in Figure 1 and compare it with theoretical $\langle A\rangle$ obtained using Eq. 6. The strike and dip coordinates are obtained by projecting the hypocenters to the best-fitting plane, which is justified by the planar character of the activated area (Figure 4C). As follows from the diagrams, the 2008 swarm experienced prevailing upward and strike-ward (south-north) migration interrupted by several short reverse trends. The same clusters as indicated in Figures 1A,B were chosen for the analysis; both occurred at the migration front in the middle of the swarm, see also two projections of the $x\left(N\right)$ diagram in Figure 4 and panels a and e of Figure 5. The earlier cluster resembles the sector type and the later one the channel type. The events close to the rupture front (the envelope of hypocenters) were selected in the strike projection; outliers in the other projection were removed using the criterion that at least 10% neighboring hypocenters have to occur within the distance equal to the length of the rupture front.

FIGURE 4

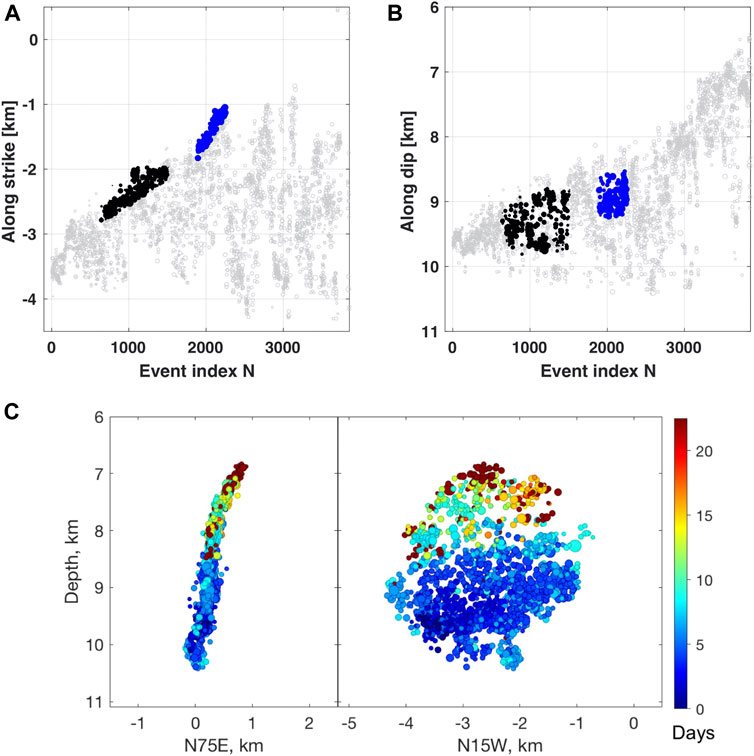
FIGURE 4. The 2008 earthquake swarm in West-Bohemia showed prevailing unidirectional growth of the seismicity front in the strike-ward (A) and upward (B) directions. Two linearly growing clusters were selected in the strike direction for the analysis. The triggering front of the earlier cluster (black) growed slower than that of the later cluster (blue). To measure the distance between the points needed for removing outliers, the event index was transformed into a distance in km so that the aspect ratio of the diagram was 1:1. In (C), two vertical sections show the planar character of the swarm activity; the symbol color is proportional to the event origin time.

FIGURE 5

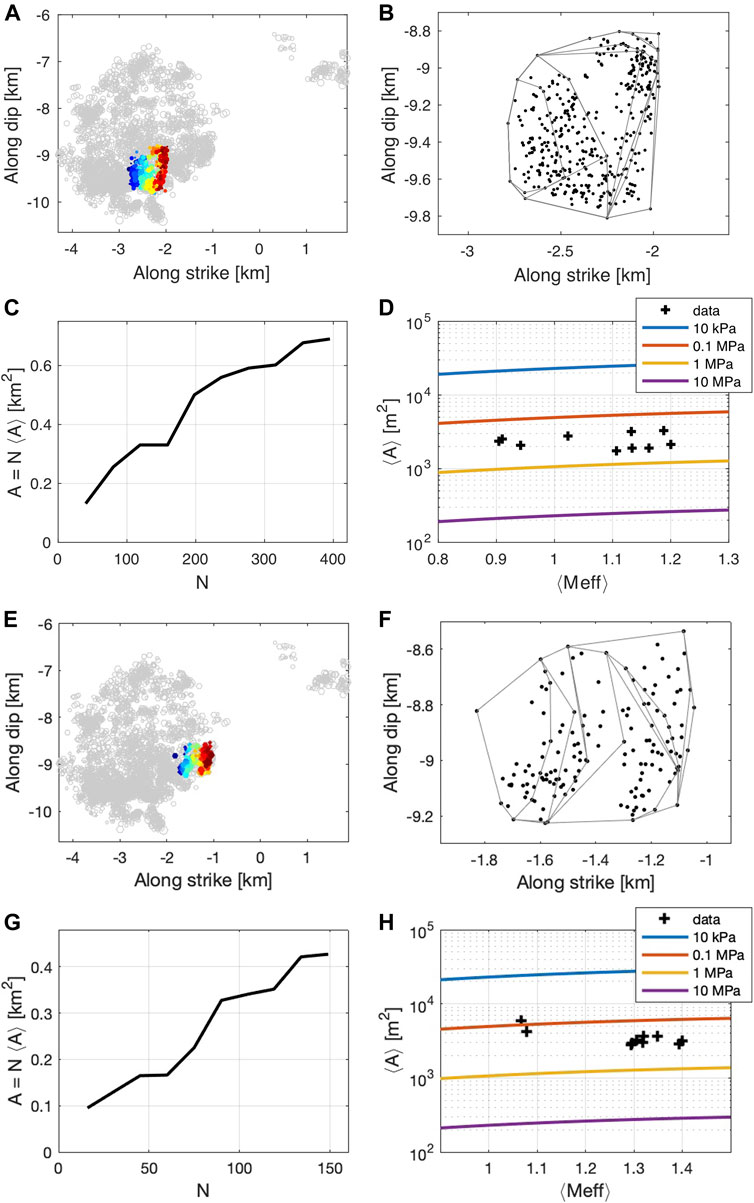
FIGURE 5. Growth analysis of the two clusters of the 2008 West-Bohemia swarm identified in Figure 4: The activated area is marked in colors, which are proportional to the event index (A,E); its convex hull was determined (B,F) for extending equidistant windows that included from 10 to 100% of events; the scaling of the total rupture area with the number of events is almost linear (C,D). The dependence of the average rupture area per event $\langle A\rangle$ on the average observed effective magnitude $\langle M_{\text{eff}}\rangle$ is examined (D,H).

The total rupture area was measured by the convex envelope algorithm (convhull) implemented in Matlab, which determines the smallest total area A that contains the hypocenter projections within a convex hull. To track the cluster growth, we determine the ruptured area for an increasing number of events; 10 equidistant steps were used. The panels b and f of Figure 5 show the growing convex hull of the clusters indicating a mixed channel and sector growth. The dependence of the measured total rupture area on the number of included events is shown in panels c and g of Figure 5 indicating an approximately linear increase of the area with event index, which is in agreement with the model prediction in Eq. 2. The average rupture area per event $\langle A\rangle$ is 1750 m² for the earlier cluster and 2,870 m² for the later cluster. Considering the approximate width $W=740\pm 100\text{m}$ for the earlier and $630\pm 100\text{m}$ for the later cluster, this corresponds to the speed of 2.4 and 4.6 m per event for the earlier and later clusters, respectively. The difference of $\langle A\rangle$ and of the growth speeds is clearly related to the different $\langle M_{\text{eff}}^{\text{obs}}\rangle$, which amount to 1.1 for the earlier and 1.4 for the later cluster. Using Eq. 6 to estimate the theoretical ratio of $\langle A\rangle$ of events with 0.3 magnitude difference gives 1.64, which equals the ratio of measured $\langle A\rangle$ amounting to 1.66.

Scaling between the average rupture area and the measured average effective magnitude of the two clusters is analyzed in panels d and h of Figure 5. The measured $\langle A\rangle$ is shown (crosses) in dependence on the $\langle M_{\text{eff}}^{\text{obs}}\rangle$ of each subset of events defined by the expanding window mentioned above. Curves of theoretical $\langle A\rangle$ are shown for comparison with the measured $\langle A\rangle$ (Eq. 6). We used $b=0.9$ as determined by Hiemer et al., (2012) for the 2008 swarm, $M_1=0$ according to the empirical cutoff magnitude minimum, and varied $M_2$ so that the $\langle M_{\text{eff}}\rangle$ (Eq. 10) covers the measured $\langle M_{\text{eff}}^{\text{obs}}\rangle$ range. It is worth to note that the choice of both $M_1$ and $M_2$ influences the theoretical curves. While the range of $M_2$ -values (for given $M_1$) only determine the $\langle M_{\text{eff}}\rangle$-interval of each theoretical curve but not its shape, $M_1$ slightly affects the vertical shift and curvature of the lines (see Supplementary Figure S1). Accordingly, $M_1$ should be chosen with care to correspond to the real minimum magnitude.

For the moment-magnitude relation (Eq. 4) we used constants $c=10.09,d=1.1$ obtained for the West Bohemian swarms by Jakoubkova et al., (2017) and $f=\left(7/16\right){\pi }^{3/2}$ for the circular rupture. It turns out that for the earlier cluster (Figure 5D), $\langle A\rangle$ scales with $\langle M_{\text{eff}}^{\text{obs}}\rangle$ with rather constant stress drop $\text{Δ}\sigma$ in the range 0.2–0.8 MPa. Similar behavior is found for the later cluster with a slightly smaller stress drop from 0.1 to 0.5 MPa (Figure 5H).

6 Discussion and Conclusions

Our analysis shows that the usage of coordinate-event-index plots can yield valuable insights into the earthquake triggering process. However, it is important to note that this analysis should always be performed in conjunction with an analysis of traditional coordinate-time plots. A linear growth with the event-index does not necessarily mean that the migration process is internally driven. In the case that earthquakes are triggered in a homogeneously pre-stressed brittle fault segment by external forcing such as pore-pressure diffusion, the earthquake number would be expected to increase with the pressurized area. Thus, even if the events do not influence each other, this would lead to a linear or square-root growth with earthquake index, similarly to the case of self-driven migration. However, in the case of diffusion-driven seismicity, the space-time plots would also show a clear and continuous migration pattern. In contrast, the space-time plots are expected to show a less clear picture with discontinuous spreading in the case of self-driven migration, as observed for our analyzed cases (see Figure 1). Only the combined analysis of space-time and space-index plots together can resolve this issue.

The graphs in Figure 5 show that the total ruptured area grows almost linearly with the event index, as expected for the suggested model supposing that every rupture facilitates the nucleation of a new adjacent rupture making the seismogenic process self-organized. The local shape of the $x\left(N\right)$ curve is however influenced by the actual magnitude distribution of the running activity; increased magnitudes will also increase the average rupture area and raise the slope of the curve. In general, the linearity of the migration in the coordinate-event-index plots might be distorted by the occurrence of single earthquakes with large magnitudes departing from the trend of the Gutenberg-Richter distribution. However, this is usually only observed in mainshock-aftershock sequences, but not in swarm activity as considered here.

Another worth-noting point is the estimated stress drop of less than 1 MPa, which appears rather small compared to the estimated static stress drops of individual events of the West-Bohemia swarms in the order of 10 MPa (Michalek and Fischer, 2013). It is of interest to note that using the concept of effective stress drop (Fischer and Hainzl (2017)), we arrived at a similar value of $\Delta {\sigma }_{\text{eff}}$ = 0.23 MPa for the whole 2008 swarm. Both approaches are of similar nature and exploit the relation between the rupture area and the seismic moment. The difference to the static stress drop estimates of more than one order of magnitude could be partially related to the usage of the Madariaga’s model (Madariaga (1976)) for the static stress drop values, which gives five times higher estimates than the alternative Brune’s model (Brune (1970)). Another reason might be related to our assumption that subsequent events are without overlap initiated at the outer border of the previous rupture. If the deformation process involves triggered aseismic afterslip, void areas will remain among adjacent ruptures and the resulting stress drop estimate would decrease accordingly. A direct proof is difficult because of the large uncertainties involved in the estimation of hypocenters, stress drops, and rupture geometries. For illustration, Supplementary Figure S2 shows the estimated rupture extensions for the two analyzed clusters assuming circular ruptures centered at the estimated and projected hypocenters, where the rupture radius depends on the stress drop. Using a constant stress drop of 1 MPa for all events leads to a significant overlap of the activity, while a stress drop of 10 MPa leads to adjacent ruptures with some void areas.

Migration characteristics are used to typify seismic activity. In contrast to the random occurrence of aftershock hypocenters along the mainshock fault plane, earthquake swarms and injection-induced seismicity outstand by monotonous migration resulting in the spreading of the hypocenter cloud. This is usually attributed to fluid flow along the fault plane, which could be modeled by pore-pressure diffusion or by a propagating hydraulic fracture. In this end-member case, the aseismic load leads to an increase of the effective stress in an expanding volume which triggers the earthquake migration as function of time, independently of precursory seismicity. Earthquakes are assumed to be triggered in this case in critically loaded areas, where stresses or pore pressure is elevated due to the aseismic driving process. As a result, void areas may occur in the diffusion model, which are bridged by the aseismic pore pressure diffusion or hydrofracture growth. Accordingly, the event coordinates would grow non-linear, respectively jump with increasing event index, which would also apply to the growth of average rupture area with the event index. This would result in low values of the estimated stress drop due to the large activated area and small strain released in a brittle way, as discussed in detail in our previous study (Fischer and Hainzl, 2017). However, the suggested analysis of the coordinate-event-index plots would indicate that aseismic deformation is present in this case due to the non-linear, jump-type shape of the rupture front.

In contrast to the models where the seismicity is externally controlled by the underlying time-dependent aseismic process, the seismicity is self-controlled by the rupture occurrences in the other end-member case of self-driven migration. In that case, fluid flow is only a secondary process where seismic slip allows the fluid to migrate into the reactivated fracture through dilatancy, and once the pressure gets high enough on the rupture edge, the subsequent rupture occurs. Consequently, it is the rupture occurrence that measures the time and, hence, it is more suitable to use the event index as an independent variable when exploring the seismicity migration. A continuous, and in most cases linear advance of rupture front is predicted in the coordinate-event-index plot in the case of self-driven earthquake migration.

For several examples of seismic swarms, we show how the form of migration plots changes when the event index is used instead of time. Discontinuous activities convert to continuous ones and nonlinear growth with time becomes linear when the event index is displayed on the horizontal axis. We interpret this behavior by a model supposing that every rupture opens the way for nucleation of the further one. Then the speed of growth is proportional to the average rupture area of the earthquakes that is related to the magnitude-frequency distribution of the events and the stress drop.

Our test using relocations of the 2008 earthquake swarm in West-Bohemia confirms the validity of the presented model. The two selected clusters, which represent the linearly spreading triggering front in the coordinate-event-index plot, show an almost linear growth of the total rupture area with the event index. Based on the envelopes of the observed hypocenters, the estimated speed of growth is 2.4 and 4.6 m per event and the average rupture area of the cluster events is 1750 m² and 2,870 m² for the two clusters, respectively. The observed difference in the spatial spreading speed is explained by differences in the frequency-magnitude distribution, which is expressed by the different effective magnitudes of 1.1 and 1.4 for the two clusters, respectively. The average speed measured in time domain is 340 m/day for the first cluster and 720 m/day for the second cluster. The dependence of average rupture areas on the effective magnitude points to self-similar scaling with stress drops ranging between 0.1 and 1 MPa. Although our analysis indicates a self-driven cluster growth, the low stress drops might indicate that parts of the rupture area deformed aseismically either by pore-pressure induced or seismically triggered creep and did not contribute to the seismic moment release. In future studies, we will address the role of fluids and earthquake ruptures for specific migration patterns such as triggering fronts and embedded linear streaks in the case of various seismic activities in more detail.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://zenodo.org/record/4294887.

Author Contributions

TF and SH developed the idea of linear streaks and wrote the manuscript. TF contributed to the theory developed by SH and carried out the data analysis.

Funding

The work of TF was supported by the Czech Funding Agency under the grant 20-26018S.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.638336/full#supplementary-material.

Acknowledgments

We are grateful to Josef Vlček for help with preparing the code for the cluster identification and Martin Bachura for providing the relocated hypocenters. We also thank the editor Pascal Audet and two reviewers for their very helpful comments.

Appendix

Average rupture area

Given the probability density function of the Gutenberg-Richter distribution (Eq. 3) and the relation between rupture area A and earthquake magnitude m (Eq. 5), the average rupture area can be determined as

$\langle A\rangle ={\displaystyle {\int }_{M_1}^{M_2}p\left(m\right)A\left(m\right)dm}=\{\begin{array}{ll}{\left(\frac{{10}^c}{f\Delta \sigma }\right)}^{23}\frac{b}{\left(23\right)d-b}\frac{{10}^{\left(\left(23\right)d-b\right)M_2}-{10}^{\left(\left(23\right)d-b\right)M_1}}{{10}^{-b{M}_1}-{10}^{-b{M}_2}},\hfill & \text{if}b\ne \frac{2}{3}d,\hfill \\ {\left(\frac{{10}^c}{f\Delta \sigma }\right)}^{23}\ln \left(10\right)b\frac{M_2-M_1}{{10}^{-b{M}_1}-{10}^{-b{M}_2}},\hfill & \text{if}b=\frac{2}{3}d.\hfill \end{array}(11)$

For $M_2\gg M_1$, the denominator ${10}^{-b{M}_1}-{10}^{-b{M}_2}$ can be approximated by ${10}^{-b{M}_1}$ and the equations simplify to

$\langle A\rangle =\{\begin{array}{ll}{\left(\frac{{10}^c}{f\Delta \sigma }\right)}^{23}\frac{b}{\left(23\right)d-b}{10}^{b{M}_1}\left({10}^{\left(\left(23\right)d-b\right)M_2}-{10}^{\left(\left(23\right)d-b\right)M_1}\right),\hfill & \text{if}b\ne \frac{2}{3}d,\hfill \\ {\left(\frac{{10}^c}{f\Delta \sigma }\right)}^{23}\ln \left(10\right)b{10}^{b{M}_1}\left(M_2-M_1\right),\hfill & \text{if}b=\frac{2}{3}d.\hfill \end{array}$

References

Brune, J. N. (1970). Tectonic stress and the spectra of seismic shear waves from earthquakes. J. Geophys. Res. 75, 4997–5009. doi:10.1029/jb075i026p04997

CrossRef Full Text | Google Scholar

Dahm, T., Hainzl, S., and Fischer, T. (2010). Bidirectional and unidirectional fracture growth during hydrofracturing: role of driving stress gradients. J. Geophys. Res. 115, B12322. doi:10.1029/2009jb006817

CrossRef Full Text | Google Scholar

Dieterich, J. H. (2007). Applications of rate- and state-dependent friction to models of fault-slip and earthquake occurrence. Treatise Geophys. (Elsevier) 4, 93–110. doi:10.1016/b978-0-444-53802-4.00075-0

CrossRef Full Text | Google Scholar

Dublanchet, P., and Barros, L. D. (2020). Stress‐dependent b value variations in a heterogeneous rate‐and‐state fault model. Geophys. Res. Lett. 47, e2020GL090025. doi:10.1029/2020gl087434

CrossRef Full Text | Google Scholar

Fischer, T., Hainzl, S., and Dahm, T. (2009). The creation of an asymmetric hydraulic fracture as a result of driving stress gradients. Geophys. J. Int. 179, 634–639. doi:10.1111/j.1365-246x.2009.04316.x

CrossRef Full Text | Google Scholar

Fischer, T., and Hainzl, S. (2017). Effective stress drop of earthquake clusters. Bull. Seism. Soc. Am. 107, 2247–2257. doi:10.1785/0120170035

CrossRef Full Text | Google Scholar

Fischer, T., Hainzl, S., Eisner, L., Shapiro, S. A., and Le Calvez, J. (2008). Microseismic signatures of hydraulic fracture growth in sediment formations: observations and modeling. J. Geophys. Res. 113, B02307. doi:10.1029/2007JB005070

CrossRef Full Text | Google Scholar

Ghosh, A., Vidale, J. E., Sweet, J. R., Creager, K. C., Wech, A. G., Houston, H., et al. (2010). Rapid, continuous streaking of tremor in cascadia. Geochem. Geophys. Geosyst. 11. doi:10.1029/2010GC003305

CrossRef Full Text | Google Scholar

Guglielmi, Y., Cappa, F., Avouac, J. P., Henry, P., and Elsworth, D. (2015). INDUCED SEISMICITY. Seismicity triggered by fluid injection-induced aseismic slip. Science 348, 1224–1226. doi:10.1126/science.aab0476

PubMed Abstract | CrossRef Full Text | Google Scholar

Hainzl, S., Fischer, T., Čermáková, H., Bachura, M., and Vlček, J. (2016). Aftershocks triggered by fluid intrusion: evidence for the aftershock sequence occurred 2014 in West Bohemia/Vogtland. J. Geophys. Res. Solid Earth 121, 2575–2590. doi:10.1002/2015jb012582

CrossRef Full Text | Google Scholar

Hainzl, S., Fischer, T., and Dahm, T. (2012). Seismicity-based estimation of the driving fluid pressure in the case of swarm activity in western bohemia. Geophys. J. Int. 191, 271–281. doi:10.1111/j.1365-246x.2012.05610.x

CrossRef Full Text | Google Scholar

Hanks, T. C., and Kanamori, H. (1979). A moment magnitude scale. J. Geophys. Res. 84, 2348–2350. doi:10.1029/jb084ib05p02348

CrossRef Full Text | Google Scholar

Helmstetter, A., and Sornette, D. (2003). Diffusion of epicenters of earthquake aftershocks, Omori's law, and generalized continuous-time random walk models. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 66, 061104. doi:10.1103/PhysRevE.66.061104

CrossRef Full Text | Google Scholar

Hiemer, S., Roessler, D., and Scherbaum, F. (2012). Monitoring the west bohemian earthquake swarm in 2008/2009 by a temporary small-aperture seismic array. J. Seismol. 16, 169–182. doi:10.1007/s10950-011-9256-5

CrossRef Full Text | Google Scholar

Houston, H., Delbridge, B. G., Wech, A. G., and Creager, K. C. (2011). Rapid tremor reversals in cascadia generated by a weakened plate interface. Nat. Geosci. 4, 404–409. doi:10.1038/ngeo1157

CrossRef Full Text | Google Scholar

Jakoubková, H., Horálek, J., and Fischer, T. (2017). 2014 mainshock-aftershock activity versus earthquake swarms in west bohemia, Czech republic. Pure Appl. Geophys. 175, 109–131. doi:10.1007/s00024-017-1679-7

CrossRef Full Text | Google Scholar

Kapetanidis, V., Deschamps, A., Papadimitriou, P., Matrullo, E., Karakonstantis, A., Bozionelos, G., et al. (2015). The 2013 earthquake swarm in helike, Greece: seismic activity at the root of old normal faults. Geophys. J. Int. 202, 2044–2073. doi:10.1093/gji/ggv249

CrossRef Full Text | Google Scholar

Kato, N. (2007). Expansion of aftershock areas caused by propagating post-seismic sliding. Geophys. J. Int. 168, 797–808. doi:10.1111/j.1365-246x.2006.03255.x

CrossRef Full Text | Google Scholar

Le Calvez, T., Horálek, J., Hrubcová, P., Vavryčuk, V., Bräuer, K., and Kämpf, H. (2014). Intra-continental earthquake swarms in west-bohemia and vogtland: a review. Tectonophysics 611, 1–27. doi:10.1016/j.tecto.2013.11.001

CrossRef Full Text | Google Scholar

Luo, Y., and Ampuero, J. P. (2017). Tremor migration patterns and the collective behavior of deep asperities mediated by creep. Preprint. doi:10.17605/OSF

CrossRef Full Text | Google Scholar

Madariaga, R. (1976). Dynamics of an expanding circular fault. Bull. Seismol. Soc. Am. 66, 639–666.

Google Scholar

Madariaga, R., and Ruiz, S. (2016). Earthquake dynamics on circular faults: a review 1970-2015. J. Seismol. 20, 1235–1252. doi:10.1007/s10950-016-9590-8

CrossRef Full Text | Google Scholar

Marzocchi, W., and Sandri, L. (2003). A review and new insights on the estimation of the b-value and its uncertainty. Ann. Geophys. 46, 1271–1282. doi:10.4401/ag-3472

CrossRef Full Text | Google Scholar

Massin, F., Farrell, J., and Smith, R. B. (2013). Repeating earthquakes in the yellowstone volcanic field: implications for rupture dynamics, ground deformation, and migration in earthquake swarms. J. Volcanol. Geoth. Res. 257, 159–173. doi:10.1016/j.jvolgeores.2013.03.022

CrossRef Full Text | Google Scholar

Michálek, J., and Fischer, T. (2013). Source parameters of the swarm earthquakes in west bohemia/vogtland. Geophys. J. Int. 195, 1196–1210. doi:10.1093/gji/ggt286

CrossRef Full Text | Google Scholar

Mls, J., and Fischer, T. (2017). A new mathematical model of asymmetric hydraulic fracture growth. Geophys. Prospect. 66, 549. doi:10.1111/1365-2478.12590

CrossRef Full Text | Google Scholar

Parotidis, M., Shapiro, S. A., and Rothert, E. (2004). Back front of seismicity induced after termination of borehole fluid injection. Geophys. Res. Lett. 31, L02612. doi:10.1029/2003gl018987

CrossRef Full Text | Google Scholar

Peng, Z., and Zhao, P. (2009). Migration of early aftershocks following the 2004 parkfield earthquake. Nat. Geosci. 2, 877–881. doi:10.1038/NGEO697

CrossRef Full Text | Google Scholar

Perfettini, H., Frank, W. B., Marsan, D., and Bouchon, M. (2019). Updip and along‐strike aftershock migration model driven by afterslip: application to the 2011 tohoku‐oki aftershock sequence. J. Geophys. Res. Solid Earth 124, 2653. doi:10.1029/2018JB016490

CrossRef Full Text | Google Scholar

Rundle, J. B., Luginbuhl, M., Giguere, A., and Turcotte, D. L. (2018). Natural time, nowcasting and the physics of earthquakes: estimation of seismic risk to global megacities. Pure Appl. Geophys. 175, 647–660. doi:10.1007/s00024-017-1720-x

CrossRef Full Text | Google Scholar

Rydelek, P. A., and Sacks, I. S. (2001). Migration of large earthquakes along the san jacinto fault; stress diffusion from the 1857 fort tejon earthquake. Geophys. Res. Lett. 28, 3079–3082. doi:10.1029/2001gl013005

CrossRef Full Text | Google Scholar

Schwartz, S. Y., and Rokosky, J. M. (2007). Slow slip events and seismic tremor at circum-pacific subduction zones. Rev. Geophys. 45, a. doi:10.1029/2006RG000208

CrossRef Full Text | Google Scholar

Shapiro, S. (2015). Fluid-induced seismicity. Cambridge, United Kingdom: Cambridge University Press.

Shapiro, S. A., and Dinske, C. (2009). Fluid-induced seismicity: pressure diffusion and hydraulic fracturing. Geophys. Prospect. 57, 301–310. doi:10.1111/j.1365-2478.2008.00770.x

CrossRef Full Text | Google Scholar

Shapiro, S. A., Huenges, E., and Borm, G. (1997). Estimating the crust permeability from fluid-injection-induced seismic emission at the ktb site. Geophys. J. Int. 131, F15–F18. doi:10.1111/j.1365-246x.1997.tb01215.x

CrossRef Full Text | Google Scholar

Shelly, D. R., Ellsworth, W. L., and Hill, D. P. (2016). Fluid-faulting evolution in high definition: connecting fault structure and frequency-magnitude variations during the 2014 long valley caldera, California, earthquake swarm. J. Geophys. Res. Solid Earth 121, 1776–1795. doi:10.1002/2015jb012719

CrossRef Full Text | Google Scholar

Woods, J., Winder, T., White, R. S., and Brandsdóttir, B. (2019). Evolution of a lateral dike intrusion revealed by relatively-relocated dike-induced earthquakes: the 2014-15 Bárðarbunga-Holuhraun rifting event, Iceland. Earth Planet. Sci. Lett. 506, 53–63. doi:10.1016/j.epsl.2018.10.032

CrossRef Full Text | Google Scholar

Wright, T. J., Sigmundsson, F., Pagli, C., Belachew, M., Hamling, I. J., Brandsdóttir, B., et al. (2012). Geophysical constraints on the dynamics of spreading centres from rifting episodes on land. Nat. Geosci, 5, 242. doi:10.1038/NGEO1428

CrossRef Full Text | Google Scholar

Yamashita, T. (1999). Pore creation due to fault slip in a fluid-permeated fault zone and its effect on seismicity: generation mechanism of earthquake swarm. Pure Appl. Geophys. 155, 625–647. doi:10.1007/978-3-0348-8677-2_19

CrossRef Full Text | Google Scholar

Yoshida, K., and Hasegawa, A. (2018a). Hypocenter migration and seismicity pattern change in the yamagata-fukushima border, NE Japan, caused by fluid movement and pore pressure variation. J. Geophys. Res. Solid Earth 123, 5000–5017. doi:10.1029/2018jb015468

CrossRef Full Text | Google Scholar

Yoshida, K., and Hasegawa, A. (2018b). Sendai-okura earthquake swarm induced by the 2011 tohoku-oki earthquake in the stress shadow of ne Japan: detailed fault structure and hypocenter migration. Tectonophysics 733, 132–147. doi:10.1016/j.tecto.2017.12.031

CrossRef Full Text | Google Scholar

Zakharova, O., Hainzl, S., and Bach, C. (2013). Seismic moment ratio of aftershocks with respect to main shocks. J. Geophys. Res. Solid Earth 118, 5856–5864. doi:10.1002/2013jb010191

CrossRef Full Text | Google Scholar