A Numerical Study of the Critical Threshold for Landslide Dam Formation Considering Landslide and River Dynamics

Introduction

Landsides occurring in river valleys have the potential to block river channels by forming dams, and a cascade of negative consequences, such as dam-break floods and debris flows, can be induced if a dam forms (Romeo et al., 2017; Liang et al., 2019). Such a chain effect can greatly enlarge the broad scope and destructive power of disasters, resulting in serious economic loss and high casualties. Recent examples include the 2014 Bujumbura floods resulting from the failure of a landslide dam in Burundi, which caused 64 casualties and destroyed more than 940 houses Nibigira et al. (2018), and the 2018 Baige landslide dam in Southwest China, which caused economic losses of approximately RMB 74.3 billion (Deng et al., 2019). Finding the critical condition for forming a landslide dam has become a key issue that needs solution in landslide dam disaster prevention.

Numerous studies have demonstrated that geomorphological features Korup (2004); Fan et al. (2012); Chen and Chang (2016); Chen et al. (2021) and hydrological conditions Zhao et al. (2017); Chen et al. (2019a); Liao et al. (2019) jointly determine whether a landslide dam can be formed. Based on these studies, the following three conditions are essentially mandatory to form a landslide dam: first, the landslide needs to cross the river channel; second, the erosive rate of river flow must be smaller than the depositional rate of the landslide; and three, the thickness of landslide deposits in the river channel must be greater than the water depth (Fan et al., 2014; Chen and Chang, 2016; Chen et al., 2019b). To find the threshold, (e.g. landslide runout distance and dam height) for satisfying these conditions, empirical database analysis Fan et al. (2012); Chen and Chang (2016) and experimental measurements Okada and Uchida (2014); Chen and Orense (2020) are widely used, and several dimensionless critical indexes that are composed of variables characterizing the different elements involved, (e.g. landslide and river) have been proposed; these indexes have high significance (Ermini and Casagli, 2003; Fan et al., 2012; Dal Sasso et al., 2014). However, although the indexes can be used to forecast and discriminate between possible dam evolutions, they cannot quantitatively describe the formation process of landslide dam. From this point of view, numerical modeling in recent years has been devoted to studying landslide dam formation by using different physical models (Liu and He, 2016; Zhao et al., 2017; Chen and Wu, 2018; Zhao et al., 2019; Li et al., 2020). In summary, these models apply two distinct equations with corresponding rheological properties to describe the dynamics of the landslide and the river. Furthermore, some behaviours of the landslides, such as the high mobility of landslide Pastor et al. (2014), the entrainment induced by landslide Liu and He (2016), and the interactions between river flow and submerged landslide Zhao et al. (2017), are also investigated by these models since these behaviours may have appreciable impacts on the process of landslide dam formation. However, most of the existing studies focus on the first and three conditions mentioned above, and works related to the second condition are still rare.

The erosive capacity of the river and the deposition rate of the landslide determine whether a dam can be formed when a landslide reaches a river. The former factor is significantly influenced by river conditions, including flow depth, flow velocity and river slope (Whipple et al., 1998; Carroll et al., 2004; Zhang et al., 2009; Chen et al., 2019a). The latter factor depends mostly on the characteristics, (e.g. mass volume, velocity and material composition) of the landslide (Fan et al., 2014; Pastor et al., 2014; Liu et al., 2016). Although some studies have investigated the mechanism of granular deposition in fluid and its influence on dam formation Shan and Zhao (2014); Zhao et al. (2019); Li et al. (2020), they do not consider the impacts of the erosive capacity of river flow on dam formation. Recently, Chen et al. (2019a) suggested a critical threshold that reflects the influence of river erosive capacity on dam formation in a quantitative way. However, one drawback of this threshold is that it does not consider the dynamic characteristics of the landslide. This factor determines the coverage area and deposition rate of a landslide in a river. In addition, in most field cases, the landslides enter river in an orthogonal (or oblique) direction, which may have an influence on dam formation and needs to be considered.

Because only average river erosive capacity can be observed in the experiment performed by Chen et al. (2019a), there are no way to quantify dynamic processes and dynamic change of different enter river direction (between the river channel and landslide movement direction). Therefore, we need to use numerical simulation to clarify the dynamic process of landslide movement, landslide dam formation and river erosive capacity. At the same time we also observe the dynamic effects of different river entry directions and thus more accurately capture the block point of landslide dam based on river erosive capacity.

In this study, focusing on the second condition, we attempt to determine a critical threshold that incorporates the dynamic characteristics of both landslide and river, in order to reflect the erosive capacity of river flow and its effect on dam formation more reasonably. To describe the dynamics of a landslide and a river during the process of landslide dam formation, a two-layer model based on the depth-averaged theory is used, which incorporates the erosion term between the landslide and the water flow. By analyzing the existing laboratory experimental data and numerical simulation results in combination, a critical threshold value is determined. Finally, the variation in the critical threshold value is discussed by simulating several numerical cases that consider different landslide dynamic characteristics.

Critical Threshold for Landslide Dam Formation

Several works have demonstrated that the formation of a landslide dam is determined by the erosive capacity of the river and the deposition rate of the landslide, both of which are related to the landslide and river discharges, particle diameter and river slope (Yan et al., 2009; Zhao et al., 2017; Chen et al., 2019a). Based on experiments, Chen et al. (2019a) suggest that landslide-generated dams form once the ratio of the erosion rate of river flow to the deposition rate of the landslide exceeds a threshold value. As a matter of fact, these rates represent the discharges of eroded mass and intruding landslide per unit time and therefore, the dimensionless critical discharge can be written in the form of discharge as

$q_{\ast }=\frac{q_e}{q_s\sqrt{\frac{{\rho }_s-{\rho }_f}{{\rho }_f}g{D}_{50}^3}},(1)$

where q_e is the discharge of mass eroded by river flow with a discharge q_w, q_s is the discharge of landslide intrusion into river, ρ_f is the flow density, ρ_s is the landslide density, D₅₀ is the median grain size of the landslide, and g represents the gravitational acceleration. As mentioned above, the experiments by Chen et al. (2019a) were performed with a constant discharge of sediment into the flow channel. In general, during the process of landslide intrusion into a river, the landslide discharge changes over time in practical cases, as reflected by the variations in the depth and velocity of the sliding mass. This in turn affects the flow erosive capacity, which depends on the interactions between the landslide and the river. Thus, the dimensionless discharge also changes with time and a time-averaged value of this variable may be more suitable for predicting landslide dam formation. To achieve this, instantaneous discharges of the landslide and the river are required, which are relative to their dynamic characteristics.

Physical Model Framework

Governing Equations

The dynamics of the landslide and river are influenced by many different factors, including initial and boundary conditions, material properties, and topography (Chen and Chang 2016). This means that a reliable method of predicting both landslide and river dynamics is needed. From this point of view, a two-layer model that describes the landslide and river dynamics simultaneously has been developed and widely used (Capart and Young, 2002; Chen and Peng, 2006; Liu and He, 2016; Li et al., 2020). Thus, a two-layer model incorporating the erosion term between the landslide and river flow is presented here, following Adduce et al. (2012) and Liu and He (2016). A detailed derivation of the model equations is presented in Supplmentary Appendix A. Since we focus on studying the erosive capacity of river flow and its effect on dam formation, bed entrainment is not considered. By assuming that both layers are incompressible, the mass and momentum equations in a Cartesian coordinate system for each layer can be written as

$\begin{array}{l}\frac{\partial h_1}{\partial t}+\frac{\partial \left(h_1{u}_1\right)}{\partial x}+\frac{\partial \left(h_1{v}_1\right)}{\partial y}=E,\\ \frac{\partial \left(h_1{u}_1\right)}{\partial t}+\frac{\partial }{\partial x}\left(h_1{u}_1^2+\frac{1}{2}g{h}_1^2\right)+\frac{\partial \left(h_1{u}_1{v}_1\right)}{\partial y}=u_{1m}E-g{h}_1\frac{\partial \left(z_b+h_2\right)}{\partial x}-C_{fs}\left(u_1–u_2\right)\left|{\mathbf{u}}_1-{\mathbf{u}}_2\right|,\\ \frac{\partial \left(h_1{v}_1\right)}{\partial t}+\frac{\partial \left(h_1{u}_1{v}_1\right)}{\partial x}+\frac{\partial }{\partial y}\left(h_1{v}_1^2+\frac{1}{2}g{h}_1^2\right)=v_{1m}E-g{h}_1\frac{\partial \left(z_b+h_2\right)}{\partial y}-C_{fs}\left(v_1–v_2\right)\left|{\mathbf{u}}_1-{\mathbf{u}}_2\right|,\end{array}(2)$

$\begin{array}{l}\frac{\partial h_2}{\partial t}+\frac{\partial \left(h_2{u}_2\right)}{\partial x}+\frac{\partial \left(h_2{v}_2\right)}{\partial y}=-E\\ \frac{\partial \left(h_2{u}_2\right)}{\partial t}+\frac{\partial }{\partial x}\left(h_2{u}_2^2+\frac{1}{2}{k}_{ap}g{h}_2^2\right)+\frac{\partial \left(h_2{u}_2{v}_2\right)}{\partial y}=-u_{2m}E-k_{ap}\gamma g{h}_2\frac{\partial h_1}{\partial x}-k_{ap}g{h}_2\frac{\partial z_b}{\partial x}+\gamma C_{fs}\left(u_1–u_2\right)\left|{\mathbf{u}}_1-{\mathbf{u}}_2\right|-\frac{u_2}{\left|{\mathbf{u}}_2\right|}g{h}_2\left(1-\gamma \right)\tan {\phi }_{bed},\\ \frac{\partial \left(h_2{v}_2\right)}{\partial t}+\frac{\partial \left(h_2{u}_2{v}_2\right)}{\partial x}+\frac{\partial }{\partial y}\left(h_2{v}_2^2+\frac{1}{2}{k}_{ap}g{h}_2^2\right)=-v_{2m}E-k_{ap}\gamma g{h}_2\frac{\partial h_1}{\partial y}-k_{ap}g{h}_2\frac{\partial z_b}{\partial y}+\gamma C_{fs}\left(v_1–v_2\right)\left|{\mathbf{u}}_1-{\mathbf{u}}_2\right|-\frac{v_2}{\left|{\mathbf{u}}_2\right|}g{h}_2\left(1-\gamma \right)\tan {\phi }_{bed},\end{array}(3)$

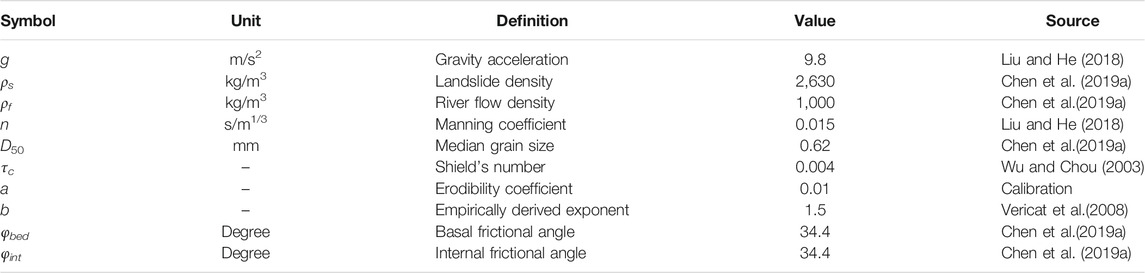
where t is the time; h₁ is the river flow depth; and h₂ is the landslide depth. The two flowing layers, river and landslide, are assumed to have distinct densities ρ_f and ρ_s, with corresponding velocities u₁ = (u₁, v₁) and u₂ = (u₂, v₂), respectively. γ = ρ_f/ρ_s is the density ratio; z_b is the fixed bed surface; E is the erosion rate; k_ap is the earth-pressure coefficient, which reflects the state of stress when a material element deforms Gray et al. (1999); and φ_bed is the basal frictional angle. The term C_fs(u₁–u₂)|u₁–u₂| represents the shear stress at the interface when the landslide moves underneath the water flow, where C_fs = gn²/h₁^1/3Li et al. (2020) and n is the Manning roughness coefficient. In other cases, this term for water flow can be reduced to C_fsu₁|u₁|. u_1m = (u_1m, v_1m) and u_2m = (u_2m, v_2m) are the velocities for the landslide and water flow at the interface boundary, respectively. In simplified situations, as suggested by Adduce et al. (2012), u_(1m,2m) is considered simply as u_{(1, 2)}.

To close the model, the quantity E must be expressed in terms of variables such as river flow depth, flow velocity and solid density. Currently, researchers have gradually reached an agreement that the erosion rate results from the inequality between the shear stress imparted by water flow and the shear resistance by sediment material (Fraccarollo and Capart, 2002; Spinewine, 2005; Zech et al., 2008). Thus, hydraulic erosion rates are quantified by using a Meyer-Peter and Muller (1948)-style equation that can be empirically fitted to each shear stress-bed load relation (Vericat et al., 2008; Darby et al., 2010).

$E=a{\left({\tau }_s-{\tau }_b\right)}^b(4)$

where a is an erodibility coefficient and b is an empirically derived exponent; the shear stress τ_s can be expressed as τ_s = ρ_fC_fs|u₁–u₂|²; the critical shear stress τ_b is calculated using Shields (1936) equation, τ_b = τ_cD₅₀g (ρ_s–ρ_f) Vericat et al. (2008), in which τ_c is the dimensionless shear stress or Shield’s number modified for sediment materials.

In summary, Eqs. 2, 3 control the state of river flow and landslide, respectively. The first Eqs. 2, 3 represent mass conservation. The second and third Eq 2 represent the momentum conservation in the x and y directions, and the terms on the right-hand side represent the effects of momentum production due to erosion, the gradient induced by the river bed and landslide, and the interface shear stress. Similarly, the terms on the right-hand side of the momentum conservation Eqs. 3 represent the effects of momentum production generated by erosion, buoyancy-related force, gradient induced by the river bed, interface shear stress and friction loss. By coupling (2)–(4), the process of dam formation can be quantitatively described while considering the dynamic characteristics of the river and the landslide. To verify the feasibility of the presented model, the numerical case proposed by Fernández-Nieto et al. (2008) and further used by Kurganov and Miller (2014) is calculated (see Supplmentary Appendix B).

Computational Scheme

In this paper, the Godunov-type scheme based on the finite volume method is adopted to solve the presented model equations. The Godunov-type scheme is a conservative numerical scheme which solves exact or approximate Riemann problems at each inter-cell boundary (Brufau et al., 2004). Here, the Riemann problem at the cell interface is solved by using Harten–Lax–van Leer contact (HLLC) approximation as a robust and efficient solver (Benkhaldoun et al., 2012). In convenience, the model equations can be written in vector format as following:

$\frac{\partial \text{U}}{\partial t}+\frac{\partial \text{F}}{\partial x}+\frac{\partial \text{G}}{\partial y}=\text{S}+\text{T,}(5)$

where,

$\mathbf{U}\mathit{=}\left(\begin{array}{l}{h}_1\\ h_1{u}_1\\ h_1{v}_1\\ h_2\\ h_2{u}_2\\ h_2{v}_2\end{array}\right),\mathbf{F}\mathit{=}\left(\begin{array}{l}{h}_1{u}_1\\ h_1{u}_1^2+\frac{1}{2}g{h}_1^2\\ h_1{u}_1{v}_1\\ h_2{u}_2\\ h_2{u}_2^2+\frac{1}{2}{k}_{ap}g{h}_2^2\\ h_2{u}_2{v}_2\end{array}\right),\mathbf{G}\mathit{=}\left(\begin{array}{l}{h}_1{v}_1\\ h_1{u}_1{v}_1\\ h_1{v}_1^2+\frac{1}{2}g{h}_1^2\\ h_2{v}_2\\ h_2{u}_2{v}_2\\ h_2{v}_2^2+\frac{1}{2}{k}_{ap}g{h}_2^2\end{array}\right),$

$\mathbf{S}=\left(\begin{array}{l}E\\ u_{1m}E-g{h}_1\frac{\partial \left(z_b+h_2\right)}{\partial x}-C_{fs}\left(u_1–u_2\right)\left|{\mathbf{u}}_1-{\mathbf{u}}_2\right|\\ 0\\ -E\\ -u_{2m}E-k_{ap}\gamma g{h}_2\frac{\partial h_1}{\partial x}-k_{ap}g{h}_2\frac{\partial z_b}{\partial x}+\gamma C_{fs}\left(u_1–u_2\right)\left|{\mathbf{u}}_1-{\mathbf{u}}_2\right|-\frac{u_2}{\left|{\mathbf{u}}_2\right|}g{h}_2\left(1-\gamma \right)\tan {\phi }_{bed}\\ 0\end{array}\right),$

$\mathbf{T}=\left(\begin{array}{l}0\\ 0\\ v_{1m}E-g{h}_1\frac{\partial \left(z_b+h_2\right)}{\partial y}-C_{fs}\left(v_1–v_2\right)\left|{\mathbf{u}}_1-{\mathbf{u}}_2\right|\\ 0\\ 0\\ -v_{2m}E-k_{ap}\gamma g{h}_2\frac{\partial h_1}{\partial y}-k_{ap}g{h}_2\frac{\partial z_b}{\partial y}+\gamma C_{fs}\left(v_1–v_2\right)\left|{\mathbf{u}}_1-{\mathbf{u}}_2\right|-\frac{v_2}{\left|{\mathbf{u}}_2\right|}g{h}_2\left(1-\gamma \right)\tan {\phi }_{bed}\end{array}\right).$

A simplest space-splitting type has also been used for dividing the model equations into two 1-D problems as following (Liang and Marche, 2009; Liu and He, 2016).

$\{\begin{array}{l}\frac{\partial \mathbf{U}}{\partial t}+\frac{\partial \mathbf{F}}{\partial x}=\mathbf{S}\\ \frac{\partial \mathbf{U}}{\partial t}+\frac{\partial \mathbf{G}}{\partial y}=\mathbf{T}\end{array}(6)$

After that, the solution at next time step can be obtained by an efficient step as following:

${\mathbf{U}}^{n+1}=L_x\left(\frac{dt}{2}\right)L_y\left(\frac{dt}{2}\right)L_y\left(\frac{dt}{2}\right)L_x\left(\frac{dt}{2}\right){\mathbf{U}}^n(7)$

where n represents the time level; L_x and L_y represent the operator in x and y directions, respectively. For L_x, the internal flux, e.g., F_w, is computed as follows:

${\mathbf{F}}_w=\{\begin{array}{c}{\mathbf{F}}_{l}if0\le S_l\\ {\mathbf{F}}_{\ast l}if{S}_l\le 0\le S_m\\ {\mathbf{F}}_{\ast r}if{S}_m\le 0\le S_r\\ {\mathbf{F}}_{r}if{S}_r\le 0\end{array}(8)$

where F_l and F_r are the interface fluxes on both sides of a cell interface; F_*l and F_*r represent the left and right sides of the contact wave, respectively. Both of them are calculated from the left and right Riemann states U_l and U_r. S_l, S_m, and S_r represent the speeds of the left, middle, and right waves, respectively, for a local Riemann problem. The fluxes F_* in the middle region are needed to calculate F_*l and F_*r, which is obtained from the Harten–Lax–van Leer (HLL) formula (Harten et al., 1983).

${\mathbf{F}}_{\ast }=\frac{S_r{\mathbf{F}}_l-S_l{\mathbf{F}}_r+S_r{S}_l\left({\mathbf{U}}_r-{\mathbf{U}}_l\right)}{S_r-S_l}(9)$

Considering the dry-bed condition from the two-rarefaction approximate Riemann solver, the wave speeds are calculated as follows (Fraccarollo and Toro, 1995; Soares-Frazão and Zech, 2011).

$\begin{array}{l}{S}_l=\{\begin{array}{c}{u}_r-2c_{r}if{h}_l=0\\ \min \left(u_l-c_l,u_{\ast }-c_{\ast }\right)if{h}_l>0\end{array}\\ S_r=\{\begin{array}{c}{u}_l+2c_{l}if{h}_r=0\\ \max \left(u_r+c_r,u_{\ast }+c_{\ast }\right)if{h}_r>0\end{array}\\ S_m=\frac{S_l{h}_r\left(u_r-S_r\right)-S_r{h}_l\left(u_l-S_l\right)}{h_r\left(u_r-S_r\right)-h_l\left(u_l-S_l\right)}\end{array}(10)$

where c is the speed of gravity waves; u_l, u_r, h_l, h_r are the components of the left and right Riemann states for a local Riemann problem; u_* and h_* are the components of the middle Riemann states, which are calculated as follows:

$u_{\ast }=\frac{1}{2}\left(u_l+u_r\right)+c_l-c_r;h_{\ast }=\frac{1}{g_z}{\left(\frac{1}{2}\left(c_l+c_r\right)+\frac{1}{4}\left(u_l-u_r\right)\right)}^2,(11)$

In order to obtain high-order of accuracy and avoid spurious oscillations, we couple the monotonic upstream-centered scheme for conservation laws (MUSCL) with HLLC scheme to reconstruct the interface data. The reconstruction form can be expressed as

${\mathbf{U}}_l={\mathbf{U}}_i^n+\frac{1}{2}\left({\mathbf{U}}_i^n-{\mathbf{U}}_{i-1}^n\right)\cdot \mathit{M}\left({\mathbf{q}}_i^{-}\right);{\mathbf{U}}_r={\mathbf{U}}_{i+1}^n-\frac{1}{2}\left({\mathbf{U}}_{i+1}^n-{\mathbf{U}}_i^n\right)\cdot \mathit{M}\left({\mathbf{q}}_i^{+}\right)(12)$

where,

$\{\begin{array}{l}{\mathbf{q}}_i^{-}=\frac{{\mathbf{U}}_{i+1}^n-{\mathbf{U}}_i^n}{{\mathbf{U}}_i^n-{\mathbf{U}}_{i-1}^n}\\ {\mathbf{q}}_i^{+}=\frac{{\mathbf{U}}_{i+2}^n-{\mathbf{U}}_{i+1}^n}{{\mathbf{U}}_{i+1}^n-{\mathbf{U}}_i^n}\end{array}$

The function M is a Roe’ Superbee flux limiter and can be written as

$M\left(x\right)=max\left(0,min\left(\mathrm{1,2}x\right),min\left(2,x\right)\right)(13)$

The time step ∆t that satisfies the demand of two layers dynamic computing simultaneously can be calculated by the stability criterion (Simpson and Castelltort, 2006).

$\Delta t=\min \left(\begin{array}{cc}\Delta t_{layer1},& \Delta t_{layer2}\end{array}\right);\text{which}\Delta t_{layer1/2}\le \min \left(\frac{cfl\cdot \eta }{\max \left(\left|{\mathbf{u}}_{\left(1/2\right)}\right|+\sqrt{g{h}_{\left(\mathrm{1,2}\right)}}\right)}\right)(14)$

where cfl is the Courant number and its value should be less than one; η is the ratio of the area of the grid to its perimeter.

Computing Dimensionless Discharge

Landslide and river dynamics and mass exchange between two layers are simulated for each of the cases under different conditions, which allows us to compute the dimensionless discharge as a function of time for every channel location in the basin. Since we are interested in the value of q_* within channel areas at the times when a landslide intrusion enters the river, we compute time-averaged values of q_e and q_s (which allows us to calculate q_*) with the channel network over a length of time from the moment when the landslide reaches the river to the moment when the landslide dam forms. The reasons why we compute time-averaged values of q_* rather than instantaneous values or final values are that the formation of a landslide dam is a gradual process and the erosive capacity of river flow changes over time.

Results

The present model is first applied to simulate laboratory experiments on landslide dam formation over a fixed bed. Then, based on numerical case studies, the value changes in the dimensionless critical discharge for landslide dam formation are presented by considering different dynamic conditions for the landslide.

The setup of the laboratory experiments by Chen et al. (2019a) consisted of two acrylic flumes: one for transporting water and the other for transporting sediment. The water channel was rectangular, 200 cm long, 15.5 cm wide and 20 cm high, with an adjustable slope and a flow valve. The sediment flume was located above the water channel with a longitudinally adjustable gate and was used to supply sediment to simulate a landslide mass entering a river channel. A water reservoir at the upstream end of the flume was used to provide water. The flow valve was attached to the water supply line behind the reservoir. The slope of the water channel was adjusted by attaching a shaft to the upstream end of the flume and a height-adjustable cross-bar at the downstream end. The sediment flume was 180 cm long, 14 cm wide, and 20 cm high, positioned in parallel above the water channel and inclined at a 40° angle, (i.e. the slope angle was always greater than the internal friction angle of the sediment). This arrangement ensured that the deposited sediments were evenly distributed along the width of the water channel. The rate of sediment supply discharge was controlled through an adjustable gate and an acrylic panel at the upstream end of the sediment flume (see Figure 1). Based on experimental results of Chen et al. (2019a), a dimensionless velocity index $v_{de}$ equation was proposed. If $v_{de}\mathrm{<}54$, the landslide mass would block the river channel and form a landslide dam; if $v_{de}\mathrm{<47}$, the landslide mass would not be able to block the river flow; and if $v_{de}$ was between 47 and 54, the formation of a landslide dam would be inconclusive. The experimental results showed an 89% accuracy when the dimensionless velocity index ($v_{de}$) was used to evaluate conditions for which a landslide dam forms. As suggested by Wu and Chou (2003), the empirical value of τ_c for pure sand materials was found to be 0.004 for grain sizes larger than 0.5 mm. The value of q_s for each case was in the Chen et al. (2019a) experiments. Values of other parameters were adjusted in a trial-and-error procedure until empirical adequacy was reached. An overview of the required parameters for the model is shown in Table 1.

FIGURE 1

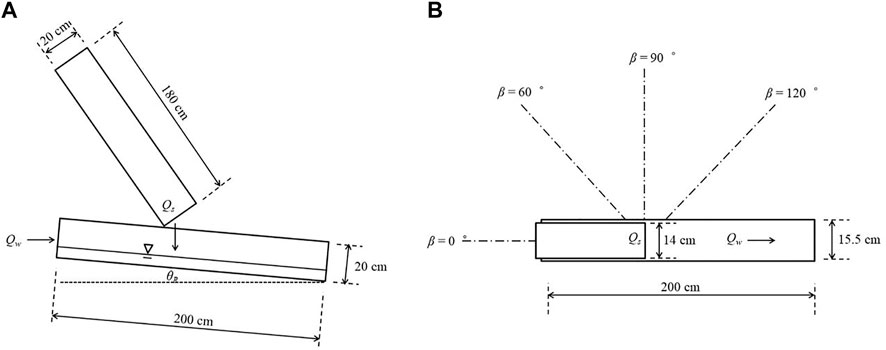
FIGURE 1. Diagram of the experimental setup on front view (A) and top view (B), modified from Chen et al. (2019a).

TABLE 1

TABLE 1. Model parameter values used in numerical simulations of landslide dam formation.

Figure 2 shows the computed erosion discharge q_e and dimensionless discharge q_* obtained by simulating the processes of 46 experiments in which landslide dams formed in 20 experimental runs and did not form in 26 runs. The dynamic processes of the landslide and river for some cases (1, 3, and 40) are provided in Supplementary Figures S1–S3 (see Supplementary Material). The results show that the mass of the landslide obstructs flow in the river channel and forms a landslide dam when the ratio of q_e and q_s is larger than a certain value (Figure 2B). This trend is similar to the results from Chen et al. (2019a) (Figure 2A), which verifies the feasibility of using our numerical approach to investigate the variations in the dam formation process under different conditions. Simulations indicate that for some cases (especially for the cases that form a dam), there is a large difference between values of q_e calculated by Chen et al. (2019a) and values of q_e calculated by our approach. On the one hand, this contrast is due to the different formula for the erosion rate that we employed. The erosion rate derived by Chen et al. (2019a) is an average value, and that obtained in this study is derived by a process-based method. On the other hand, this difference may result from the fact that the erosion rate gradually decreases to zero during the process of dam formation; thus, a small average value of q_e is obtained. Moreover, the critical threshold of dimensionless discharge q_* as a function of river slope θ is also presented. This threshold clearly shows that q_* is lower for cases where a landslide dam forms than for cases that form no dam (Figures 2C,D). With steeper river slopes, the discharge of the landslide has to be relatively high to form a dam since the erosive capacity of river flow is enhanced by slope.

FIGURE 2

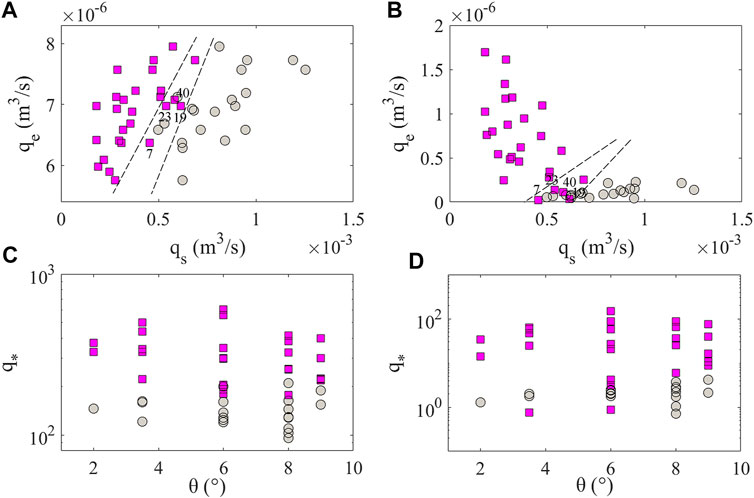
FIGURE 2. Relationship between depositional capacity of landslides q_s and erosive capacity of river flows q_e obtained from Chen et al. (2019a)(A) and numerical simulation (B); critical threshold of dimensionless discharge q_* derived from Chen et al. (2019a)(C) and experimental simulations (D) as a function of river slope θ. Red squares represent the experimental runs with no dam, and gray dots represent the experimental runs with dams. The values of these variables are obtained as an average from the time that the landslide starts entering the river until the time that the landslide dam forms.

Next, the processes of dam formation under different dynamic conditions for the river and landslide are simulated. In general, the dynamic condition of surface flow can be reflected by flow velocity and flow depth; thus, these two variables are considered in our simulation. In addition, field surveys indicate that landslide debris always enters river in an oblique (or orthogonal) direction Tang et al. (2011); Xu et al. (2018), so the angle β between the river channel and landslide movement direction is considered another variable. Based on this consideration, the simulation setups for all the numerical cases are set as h₁ = 1.03 cm, u₁ = 62.8 cm/s, h₂ = 3–25 cm (an interval of one between two adjacent cases), u₂ = 5–35 cm/s (an interval of 15 between two adjacent cases), and θ = 2–9° (an interval of one between two adjacent cases). The sizes of river and landslide channels in the simulation are the same as those in Chen et al. (2019a), except that the two channels are linked at an angle (see Figure 1B). Three values of β are chosen as β = 60, 90, and 120°. For the sake of simplicity, we ran these simulations by using the same model parameter values applied in the prior runs. It should be noted that the value of q_s is not constant in this simulation and calculated at the contact surface between two channels at each time step as well as q_e. The dynamic processes of the landslide and river with different values of β are also provided in Supplementary Material (see Supplementary Figures S4–S6). Using the threshold based on dimensionless discharges (Figure 3), we find that the dynamic characteristics of the landslide have significant impacts on dam formation. In general, typical values of q_* for dam formation are high compared with q_* obtained from flume experiment simulations. With the same angle β, the values of q_* decrease when the landslide velocity increases, and the gap between the values of q_* under different landslide velocity conditions increases as the river slope increases. This means that the erosive capacity of river flow plays a key role in dam formation when the discharge of landslide intrusion into the river is not very large. If the ratio of landslide discharges to river discharges is large, the river channel is blocked quickly, and the effects of flow erosion and river slope on dam formation become less visible. In addition, there is a gap between the values of q_* obtained with different intrusion directions of landslides into rivers. The interesting point is that the value of q_* is largest when β = 90°. One potential explanation for this trend is that the river erosive capacity is enhanced due to the intensified interaction between landslide and river flows when the landslide moves against the river (β = 120°). A larger discharge of landslide intrusion into the river is needed to form a dam; thus, a smaller value of q_* is generated.

FIGURE 3

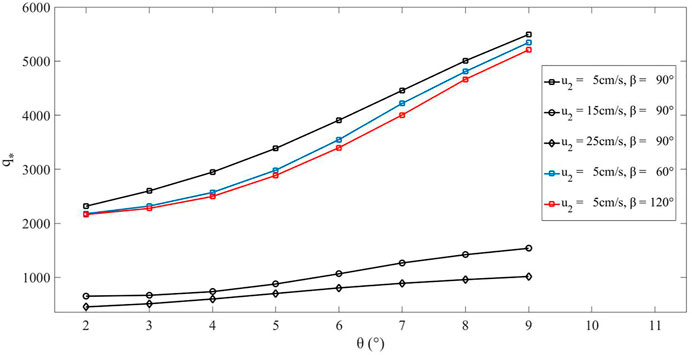
FIGURE 3. Critical threshold of dimensionless discharge q_* derived from numerical simulations as a function of river slope θ, by considering different dynamic conditions for the river and the landslide. Values of q_* are obtained as an average from the time that the landslide starts entering the river until the time that the landslide dam forms.

Discussion

The results demonstrate that the thresholds for dimensionless discharge obtained in our experimental simulations are smaller than the thresholds for dimensionless discharge suggested by Chen et al. (2019a) (Figures 2C,D). Moreover, there are large differences between the erosion rates derived here and the values suggested by Chen et al. (2019a). As a consequence, the threshold proposed by Chen et al. (2019a) may lead to underestimates of the erosive capacity of river flow required to produce landslide dam under a given hydrodynamic condition. The apparent discrepancy between thresholds derived here and those derived previously may arise from the fact that the previous study focused on a threshold over the whole time period (from landslide entry into river to the end of landslide movement). Whether landslides will continue to be eroded by river flow after dam formation is unclear since they require adequate hydrodynamic conditions. In addition, both our results and those of Chen et al. (2019a) show transitional conditions under which several dam formed and no dams formed (see Figures 2A,B). This is principally because the cases that form no dam have small values of q_e and the cases that form a dam have large values of q_e. Experimental observations indicate that these cases are in (or close to) the critical state of dam formation (see Supplementary Videos S3–S6, which refer to groups 7, 19, 23, and 40, respectively, in Chen et al., 2019a). This means that the erosion rate caused by river flow experiences major changes over the whole time period. Variation histories of erosion rates in these cases calculated by our approach are shown in Figure 4A, which illustrates that the rates of erosion increase first and then decrease (close to zero) and finally increase again. This trend is in line with that observed from the experiments. The changing trend of q_* calculated by our approach is similar with that of q_e (Figure 4B). By comparing the time averaged and Chen et al. (2019a) values of q_* (refer to q_*sa and q_*e), it can be found that q_*sa can reflect the state of dam more accurately. For example, the dam in experiment case seven is more close to the critical state of dam formation than that in experiment case 23, so the value of q_* for experiment case seven should be less than that for experiment case 23. However, the value of q_*e for experiment case seven is greater than that for experiment case 23, which do not reflect this trend. Thus, the dimensionless critical discharge calculated by our approach can reflect the characteristics of dam evolution that is determined by the dynamics of landslide and river, and make it possible to more accurately capture the block point of landslide dam. However, some behaviours, (e.g. local collapses of debris and hydraulic jumps) cannot be considered here due to the limitations of the applied model, and these behaviours may influence the value of the erosion rate. Nevertheless, the proposed approach for generating dimensionless discharge thresholds based on model simulations provides a promising alternative to empirical methods for assessing the potential for dam formation.

FIGURE 4

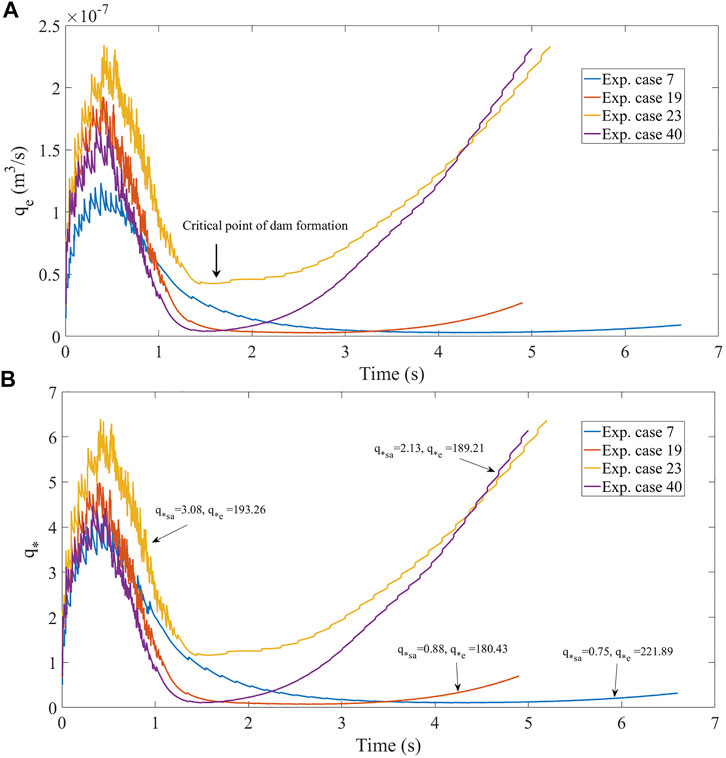
FIGURE 4. Variation histories of (A) erosion rates and (B) dimensionless critical discharge for the experiment simulation cases 7, 19, 23, and 40. The arrow in the figure represents the critical point of dam formation. q_*sa and q_*e represent the average value of q_* calculated with the data from the simulation and Chen et al. (2019a), respectively.

The choice to average values of dimensionless discharge over a length of time from when the landslide starts entering the river until a dam forms is based on past observations in laboratory experiments that no landslide mass is transported after dam formation (see Supplementary Videos S1). Simulations indicate similar trends between the results obtained by Chen et al. (2019a) and the results obtained from our approach (see Figure 2). Based on the physical model, averaging q_e and q_* over time periods appears reasonable and produces similar results. An additional consideration is whether including landslide and river dynamics in the simulations is necessary to obtain dimensionless thresholds. Our results show that dimensionless thresholds derived from the physical model are larger than those estimated using an empirical formula that cannot consider landslide and river dynamics. The primary reason is that the landslide velocity and the direction of landslide intrusion into river can change the erosion capacity of river flow due to the enhanced or weakened interaction between the landslide and the flowing river. The dimensionless critical threshold in conjunction with numerical simulations potentially reflects the dynamic characteristics of both landslide and river flow. This result is encouraging since landslide and river dynamics may be poorly considered in many applications. An additional benefit of deriving the dimensionless discharge based on model simulation for landslide dam formation is that the erosion rate varies due to the instantaneous states of the landslide and the river. For example, landslide velocity, river flow height, and riverbed elevation change with time following sediment transport (Liu and He, 2016; Zhao et al., 2017; Li et al., 2020). The erosive capacity of river flow therefore changes with time, but thresholds based on dimensionless discharge remain constant. Thus, given data that constrain the initial conditions of the landslide and the river, the variables (q_e and q_s) derived here can be applied to determine how dimensionless discharge changes with time and can be used to identify the landslide-induced terrain changes that have great impacts on dam formation potential. The applicability of the dimensionless discharge threshold, however, assumes that the difference between the discharges of the landslide and the river is not too large.

On the other hand, the presented model assumes that landslide materials are uniform, which is simple if more complex scenarios are considered e.g., different grain size distributions of landslide material. Some complex behaviours that may influence the value of the erosion rate are also not considered. Thus, further research is needed to improve the physical model for providing more accurate results that are closer to reality.

Conclusion

In this study, we derive critical thresholds for the formation of a landslide dam based on slope-dependent values of dimensionless discharge. Furthermore, we present a method for estimating dimensionless discharge thresholds using a process-based two-layer model and the proposed physically based thresholds. The erosion rate and dimensionless discharge derived from the present method indicate trends similar to those estimated by the empirical formula for the experimental cases. The results establish a new method to estimate the thresholds for dam formation focusing on the relationship between the erosive rate of river flow and the deposition rate of a landslide. Several dynamic conditions for the landslide are considered to study their influences on the dimensionless discharge threshold. The physically based dam formation thresholds derived here also make it possible to incorporate the effects of changes in dynamic conditions on the landslide and the river, which could be particularly valuable in addressing landslide dam hazards when landslides and river flow have small differences in discharge.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

WL and YH did a lot of work in numerical data analysis; SH and JZ helped perform the analysis with constructive discussions; WL and KC performed the data analyses, wrote the manuscript, made all figures and approved the final version.

Funding

This work was supported by the National Natural Science Foundation of China (Grant Nos. 41907241, U19A2049, and U20A20111), Open Project of State Key Laboratory of Hydraulics and Mountain River Engineering (Grant No. SKHL 2025), the Soil and Water Conservation Innovation Research Projects in 2021 (SWCB-110–026), the CAS “Light of West China” Program and the Foundation for Young Scientists of the Institute of Mountain Hazards and Environment, CAS (Grant No. SDS-QN-1912, No. SDS-QN-1901).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors wish to thank the Editor (Mark Bebbington) and two anonymous reviewers for their constructive comments which helped to improve the manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.651887/full#supplementary-material

References

Adduce, C., Sciortino, G., and Proietti, S. (2012). Gravity Currents Produced by Lock Exchanges: Experiments and Simulations with a Two-Layer Shallow-Water Model with Entrainment. J. Hydraul. Eng. 138 (2), 111–121. doi:10.1061/(asce)hy.1943-7900.0000484

CrossRef Full Text | Google Scholar

Benkhaldoun, F., Sari, S., and Seaid, M. (2012). A Flux-Limiter Method for Dam-Break Flows over Erodible Sediment Beds. Appl. Math. Model. 36 (10), 4847–4861. doi:10.1016/j.apm.2011.11.088

CrossRef Full Text | Google Scholar

Brufau, P., García-Navarro, P., and Vázquez-Cendón, M. E. (2004). Zero Mass Error Using Unsteady Wetting-Drying Conditions in Shallow Flows over Dry Irregular Topography. Int. J. Numer. Meth. Fluids 45 (10), 1047–1082. doi:10.1002/fld.729

CrossRef Full Text | Google Scholar

Capart, H., and Young, D. L. (2002). “Two-layer Shallow Water Computations of Torrential Geomorphic Flows,” in Proceedings of the International Conference on Fluvial Hydraulics (Belgium: Louvain-la-Neuve), 1003–1012.

Google Scholar

Carroll, R. W. H., Warwick, J. J., James, A. I., and Miller, J. R. (2004). Modeling Erosion and Overbank Deposition during Extreme Flood Conditions on the Carson River, Nevada. J. Hydrol. 297 (1-4), 1–21. doi:10.1016/j.jhydrol.2004.04.012

CrossRef Full Text | Google Scholar

Chen, C.-Y., and Chang, J.-M. (2016). Landslide Dam Formation Susceptibility Analysis Based on Geomorphic Features. Landslides 13 (5), 1019–1033. doi:10.1007/s10346-015-0671-5

CrossRef Full Text | Google Scholar

Chen, K.-T., Chen, X.-Q., Hu, G.-S., Kuo, Y.-S., and Chen, H.-Y. (2019a). Effects of River Flow Velocity on the Formation of Landslide Dams. J. Mt. Sci. 16 (11), 2502–2518. doi:10.1007/s11629-018-5319-1

CrossRef Full Text | Google Scholar

Chen, K.-T., Chen, X.-Q., Niu, Z.-P., and Guo, X.-J. (2019b). Early Identification of River Blocking Induced by Tributary Debris Flow Based on Dimensionless Volume index. Landslides 16, 2335–2352. doi:10.1007/s10346-019-01221-8

CrossRef Full Text | Google Scholar

Chen, K.-T., and Wu, J.-H. (2018). Simulating the Failure Process of the Xinmo Landslide Using Discontinuous Deformation Analysis. Eng. Geology. 239, 269–281. doi:10.1016/j.enggeo.2018.04.002

CrossRef Full Text | Google Scholar

Chen, K. T., Chen, T. C., Chen, X. Q., Chen, H. Y., and Zhao, W. Y. (2021). An Experimental Determination of the Relationship between the Minimum Height of Landslide Dams and the Run-Out Distance of Landslides. Landslides, 1–14. doi:10.1007/s10346-020-01605-1

Chen, S.-C., and Peng, S.-H. (2006). Two-dimensional Numerical Model of Two-Layer Shallow Water Equations for confluence Simulation. Adv. Water Resour. 29 (11), 1608–1617. doi:10.1016/j.advwatres.2005.12.001

CrossRef Full Text | Google Scholar

Chen, X., and Orense, R. P. (2020). Investigating the Mechanisms of Downslope Motions of Granular Particles in Small-Scale Experiments Using Magnetic Tracking System. Eng. Geology. 265, 105448. doi:10.1016/j.enggeo.2019.105448

CrossRef Full Text | Google Scholar

Dal Sasso, S. F., Sole, A., Pascale, S., Sdao, F., Pinzon, A. B., and Medina, V. (2014). Assessment Methodology for the Prediction of Landslide Dam hazard. Nat. Hazards Earth Syst. Sci. 14 (3), 557–567. doi:10.5194/nhess-14-557-2014

Google Scholar

Darby, S. E., Trieu, H. Q., Carling, P. A., Sarkkula, J., Koponen, J., Kummu, M., et al. (2010). A Physically Based Model to Predict Hydraulic Erosion of fine-grained Riverbanks: The Role of Form Roughness in Limiting Erosion. J. Geophys. Res. 115, F04003. doi:10.1029/2010JF001708

CrossRef Full Text | Google Scholar

Deng, J. H., Gao, Y. J., Yu, Z. Q., and Xie, H. P. (2019). Analysis on the Formation Mechanism and Process of Baige Landslides Damming the Upper Reach of Jinsha River, China. Adv. Eng. Sicences 51 (1), 9–16. doi:10.15961/j.jsuese.201801438 (In Chinese).

Google Scholar

Ermini, L., and Casagli, N. (2003). Prediction of the Behaviour of Landslide Dams Using a Geomorphological Dimensionless index. Earth Surf. Process. Landforms 28 (1), 31–47. doi:10.1002/esp.424

CrossRef Full Text | Google Scholar

Fan, X., Rossiter, D. G., van Westen, C. J., Xu, Q., and Görüm, T. (2014). Empirical Prediction of Coseismic Landslide Dam Formation. Earth Surf. Process. Landforms 39 (14), 1913–1926. doi:10.1002/esp.3585

CrossRef Full Text | Google Scholar

Fan, X., van Westen, C. J., Xu, Q., Gorum, T., and Dai, F. (2012). Analysis of Landslide Dams Induced by the 2008 Wenchuan Earthquake. J. Asian Earth Sci. 57, 25–37. doi:10.1016/j.jseaes.2012.06.002

CrossRef Full Text | Google Scholar

Fernández-Nieto, E. D., Bouchut, F., Bresch, D., Castro Díaz, M. J., and Mangeney, A. (2008). A New Savage-Hutter Type Model for Submarine Avalanches and Generated Tsunami. J. Comput. Phys. 227 (16), 7720–7754. doi:10.1016/j.jcp.2008.04.039

CrossRef Full Text | Google Scholar

Fraccarollo, L., and Capart, H. (2002). Riemann Wave Description of Erosional Dam-Break Flows. J. Fluid Mech. 461, 183–228. doi:10.1017/s0022112002008455

CrossRef Full Text | Google Scholar

Fraccarollo, L., and Toro, E. F. (1995). Experimental and Numerical Assessment of the Shallow Water Model for Two-Dimensional Dam-Break Type Problems. J. Hydraulic Res. 33 (6), 843–864. doi:10.1080/00221689509498555

CrossRef Full Text | Google Scholar

Gray, J. M. N. T., Wieland, M., and Hutter, K. (1999). Gravity-driven Free Surface Flow of Granular Avalanches over Complex Basal Topography. Proc. R. Soc. Lond. A. 455, 1841–1874. doi:10.1098/rspa.1999.0383

CrossRef Full Text | Google Scholar

Harten, A., Lax, P. D., and Leer, B. v. (1983). On Upstream Differencing and Godunov-type Schemes for Hyperbolic Conservation Laws. SIAM Rev. 25, 35–61. doi:10.1137/1025002

CrossRef Full Text | Google Scholar

Iverson, R. M. (2012). Elementary Theory of Bed-Sediment Entrainment by Debris Flows and Avalanches. J. Geophys. Res. Earth Surf. 117, 117. doi:10.1029/2011JF002189

CrossRef Full Text | Google Scholar

Korup, O. (2004). Geomorphometric Characteristics of New Zealand Landslide Dams. Eng. Geology. 73 (1-2), 13–35. doi:10.1016/j.enggeo.2003.11.003

CrossRef Full Text | Google Scholar

Kurganov, A., and Miller, J. (2014). Central-upwind Scheme for Savage-Hutter Type Model of Submarine Landslides and Generated Tsunami Waves. Comput. Methods Appl. Math. 14 (2), 177–201. doi:10.1515/cmam-2014-0003

CrossRef Full Text | Google Scholar

Li, J., Cao, Z., Cui, Y., and Borthwick, A. G. L. (2020). Barrier lake Formation Due to Landslide Impacting a River: A Numerical Study Using a Double Layer-Averaged Two-phase Flow Model. Appl. Math. Model. 80, 574–601. doi:10.1016/j.apm.2019.11.031

CrossRef Full Text | Google Scholar

Liang, G., Wang, Z., Zhang, G., and Wu, L. (2019). Two Huge Landslides that Took Place in Quick Succession within a Month at the Same Location of Jinsha River. Landslides 16, 1059–1062. doi:10.1007/s10346-019-01165-z

CrossRef Full Text | Google Scholar

Liang, Q., and Marche, F. (2009). Numerical Resolution of Well-Balanced Shallow Water Equations with Complex Source Terms. Adv. Water Resour. 32 (6), 873–884. doi:10.1016/j.advwatres.2009.02.010

CrossRef Full Text | Google Scholar

Liao, H.-m., Yang, X.-g., Lu, G.-d., Tao, J., and Zhou, J.-w. (2019). Experimental Study on the River Blockage and Landslide Dam Formation Induced by Rock Slides. Eng. Geology. 261, 105269. doi:10.1016/j.enggeo.2019.105269

CrossRef Full Text | Google Scholar

Liu, W., and He, S. (2016). A Two-Layer Model for Simulating Landslide Dam over mobile River Beds. Landslides 13 (3), 565–576. doi:10.1007/s10346-015-0585-2

CrossRef Full Text | Google Scholar

Liu, W., and He, S. (2018). A Two-Layer Model for the Intrusion of Two-phase Debris Flow into a River. Q. J. Eng. Geology. Hydrogeology 51 (1), 113–123. doi:10.1144/qjegh2017-071

CrossRef Full Text | Google Scholar

Liu, W., He, S., Li, X., and Xu, Q. (2016). Two-dimensional Landslide Dynamic Simulation Based on a Velocity-Weakening Friction Law. Landslides 13 (5), 957–965. doi:10.1007/s10346-015-0632-z

CrossRef Full Text | Google Scholar

Meyer-Peter, E., and Müller, R. (1948). “Formulas for Bed-Load Transport,” in IAHSR 2nd Meeting, Stockholm, Appendix 2 (Stockholm, Sweden: IAHR).

Google Scholar

Nibigira, L., Havenith, H.-B., Archambeau, P., and Dewals, B. (2018). Formation, Breaching and Flood Consequences of a Landslide Dam Near Bujumbura, Burundi. Nat. Hazards Earth Syst. Sci. 18, 1867–1890. doi:10.5194/nhess-18-1867-2018

CrossRef Full Text | Google Scholar

Okada, Y., and Uchida, I. (2014). Dependence of Runout Distance on the Number of Rock Blocks in Large-Scale Rock-Mass Failure Experiments. J. For. Res. 19 (3), 329–339. doi:10.1007/s10310-013-0425-y

CrossRef Full Text | Google Scholar

Pastor, M., Blanc, T., Haddad, B., Petrone, S., Sanchez Morles, M., Drempetic, V., et al. (2014). Application of a SPH Depth-Integrated Model to Landslide Run-Out Analysis. Landslides 11 (5), 793–812. doi:10.1007/s10346-014-0484-y

CrossRef Full Text | Google Scholar

Romeo, S., Di Matteo, L., Melelli, L., Cencetti, C., Dragoni, W., and Fredduzzi, A. (2017). Seismic-induced Rockfalls and Landslide Dam Following the October 30, 2016 Earthquake in Central Italy. Landslides 14 (4), 1457–1465. doi:10.1007/s10346-017-0841-8

CrossRef Full Text | Google Scholar

Savage, S. B., and Hutter, K. (1989). The Motion of a Finite Mass of Granular Material Down a Rough Incline. J. Fluid Mech. 199, 177–215. doi:10.1017/s0022112089000340

CrossRef Full Text | Google Scholar

Shan, T., and Zhao, J. (2014). A Coupled CFD-DEM Analysis of Granular Flow Impacting on a Water Reservoir. Acta Mech. 225 (8), 2449–2470. doi:10.1007/s00707-014-1119-z

CrossRef Full Text | Google Scholar

Shields, A. (1936). Anwendung der Aehnlichkeitsmechanik und der Turbulenzforschung auf die Geschiebebewegung. Berlin: PhD Thesis Technical University.

Simpson, G., and Castelltort, S. (2006). Coupled Model of Surface Water Flow, Sediment Transport and Morphological Evolution. Comput. Geosciences 32 (10), 1600–1614. doi:10.1016/j.cageo.2006.02.020

CrossRef Full Text | Google Scholar

Soares-Frazão, S., and Zech, Y. (2011). HLLC Scheme with Novel Wave-Speed Estimators Appropriate for Two-Dimensional Shallow-Water Flow on Erodible Bed. Int. J. Numer. Meth. Fluids 66 (8), 1019–1036. doi:10.1002/fld.2300

CrossRef Full Text | Google Scholar

Spinewine, B. (2005). Two-layer Flow Behaviour and the Effects of Granular Dilatancy in Dam-Break Induced Sheet-Flow (Doctoral Dissertation, PhD Thesis. Belgium: Univerisité de Louvain.

Tang, C., Zhu, J., Ding, J., Cui, X. F., Chen, L., and Zhang, J. S. (2011). Catastrophic Debris Flows Triggered by a 14 August 2010 Rainfall at the Epicenter of the Wenchuan Earthquake. Landslides 8 (4), 485–497. doi:10.1007/s10346-011-0269-5

CrossRef Full Text | Google Scholar

Vericat, D., Batalla, R. J., and Gibbins, C. N. (2008). Sediment Entrainment and Depletion from Patches of fine Material in a Gravel-Bed River. Water Resour. Res. 44 (11). doi:10.1029/2008wr007028

CrossRef Full Text | Google Scholar

Whipple, K. X., Parker, G., Paola, C., and Mohrig, D. (1998). Channel Dynamics, Sediment Transport, and the Slope of Alluvial Fans: Experimental Study. J. Geology. 106 (6), 677–694. doi:10.1086/516053

CrossRef Full Text | Google Scholar

Wu, F., and Chou, Y. (2003). Simulation of Gravel-Sand Bed Response to flushing Flows Using a Two-Fraction Entrainment Approach: Model Development and Flume experiment. Water Resour. Res. 39 (8). doi:10.1029/2003wr002184

CrossRef Full Text | Google Scholar

Xu, Q., Zheng, G., Li, W. L., He, C. Y., Dong, X. J., Guo, C., et al. (2018). Study on Successive Landslide Damming Events of Jinsha River in Baige Village on Octorber 11 and November 3. J. Eng. Geology. 26 (6), 1534–1551. doi:10.13544/j.cnki.jeg.2018-406 (In Chinese).

Google Scholar

Yan, J., Cao, Z.-x., Liu, H.-h., and Chen, L. (2009). Experimental Study of Landslide Dam-Break Flood over Erodible Bed in Open Channels. J. Hydrodyn 21 (1), 124–130. doi:10.1016/s1001-6058(08)60127-4

CrossRef Full Text | Google Scholar

Zech, Y., Soares-Frazão, S., Spinewine, B., and Le Grelle, N. (2008). Dam-break Induced Sediment Movement: Experimental Approaches and Numerical Modelling. J. Hydraulic Res. 46 (2), 176–190. doi:10.1080/00221686.2008.9521854

CrossRef Full Text | Google Scholar

Zhang, G.-h., Liu, Y.-m., Han, Y.-f., and Zhang, X. C. (2009). Sediment Transport and Soil Detachment on Steep Slopes: I. Transport Capacity Estimation. Soil Sci. Soc. Am. J. 73 (4), 1291–1297. doi:10.2136/sssaj2008.0145

CrossRef Full Text | Google Scholar

Zhao, G.-W., Jiang, Y.-J., Qiao, J.-P., Yang, Z.-J., and Ding, P.-P. (2019). Numerical and Experimental Study on the Formation Mode of a Landslide Dam and its Influence on Dam Breaching. Bull. Eng. Geol. Environ. 78 (4), 2519–2533. doi:10.1007/s10064-018-1255-0

CrossRef Full Text | Google Scholar

Zhao, T., Dai, F., and Xu, N.-w. (2017). Coupled DEM-CFD Investigation on the Formation of Landslide Dams in Narrow Rivers. Landslides 14 (1), 189–201. doi:10.1007/s10346-015-0675-1

CrossRef Full Text | Google Scholar