Probabilistic Assessment of Slip Rates and Their Variability Over Time of Offshore Buried Thrusts: A Case Study in the Northern Adriatic Sea

Introduction

Buried and blind active faults pose one of the major challenges for understanding seismotectonics in many regions worldwide (Yeats and Lillie, 1991; Stein and Ekström, 1992; Berberian, 1995; Shaw and Shearer, 1999; Walker and Jackson, 2002). When such faults are located offshore, there is an additional challenge because they can be investigated only using geophysical subsurface data (Fisher et al., 2004; Sorlien et al., 2006; Hayes et al., 2010; Wolfe et al., 2019). Blind thrusts can be determined by inelastic deformation ahead of fault tip (Roering et al., 1997) that contributes to dissipate the strain in the overlying cover by backthrusting, coupling, and forethrusting (Dunne and Ferrill, 1988). Analog models also show that the upward propagation of thrust faults can be slowed down or even halted by the presence of pre-existing frictional discontinuity (e.g., decollements) above the fault propagating tip (Bonanno et al., 2017). However, they can also be determined by the relatively young inception of fault activity within the current regional stress state or by the interplay between fault activity and sedimentation rates in the cases in which the second one is significantly higher than the first one (Pueyo Anchuela et al., 2016). Blind thrusts are documented as to be the cause of several significant earthquakes and tsunami worldwide (Hauksson et al., 1995; Lettis et al., 1997; Borrero et al., 2001; Hayes et al., 2010; Burrato et al., 2012; McAuliffe et al., 2015) thus significantly contributing to seismic and tsunami hazard.

One of the key parameters for describing a fault system evolution is the rate of activity (slip-rate) and its variability through time. The slip-rate assessment is very sensitive to the scale and the methodological approach to its calculation (see Morell et al., 2020, for an overview). The different approaches to slip rate calculation and the variability of the results can be treated considering all the uncertainties involved and providing a probabilistic approach to the results (Zechar and Frankel, 2009; Styron, 2019). The determination of slip rates of blind faults is mostly based on the analysis of deformed syn-tectonic markers either on surface exposures (Ward and Valensise, 1996; Vannoli et al., 2004; Gunderson et al., 2013, 2018; Livio et al., 2014; Tiberti et al., 2014) or in the subsurface (Dolan et al., 2003; Wang et al., 2014; Maesano et al., 2015, 2020; Bergen et al., 2017), and requires a good three-dimensional geometrical definition of the underlying fault (Shaw et al., 2002).

The Po Plain and the northern Adriatic seafloor (northern Italy) is a flat elongated depression extended for more than 400–600 km (Figure 1), hosting the buried active thrust fronts of the Southern Alps, the Northern Apennines, and the Dinarides, as well as their correlative foredeep-foreland sectors. Our study area spans a sector in the offshore (Northern Adriatic Sea) of the Northern Apennines foredeep basin, located between the Po River delta to the north and Mount Conero to the south (Figure 1B). Here, the outermost buried thrust faults of the Northern Apennines chain have mainly been investigated through the interpretation of seismic reflection profiles, either onshore and offshore (Pieri and Groppi, 1981; Castellarin et al., 1985; Cassano et al., 1986; Bigi et al., 1992; Fantoni and Franciosi, 2010). The present-day tectonic activity of the Northern Apennines chain has been dramatically testified by the significant seismic sequence (Mw 5.9–6.1) that in 2012 involved the reactivation of two main blind thrusts (Burrato et al., 2012; Scognamiglio et al., 2012; Pezzo et al., 2013; Tizzani et al., 2013; Bonini et al., 2014; Nespoli et al., 2017). The rates of thrust activity in this region have been estimated using geology-geomorphology, subsurface geophysics, geodesy, and instrumental seismology (e.g., Burrato et al., 2003; Basili and Barba, 2007; Scrocca et al., 2007; Boncio and Bracone, 2009; Wegmann and Pazzaglia, 2009; Devoti et al., 2011; Michetti et al., 2012; Maesano et al., 2013, 2015; Bresciani and Perotti, 2014; Livio et al., 2014; Maesano and D’Ambrogi, 2016; Maestrelli et al., 2018; Palano et al., 2020; Zuffetti and Bersezio, 2020).

FIGURE 1

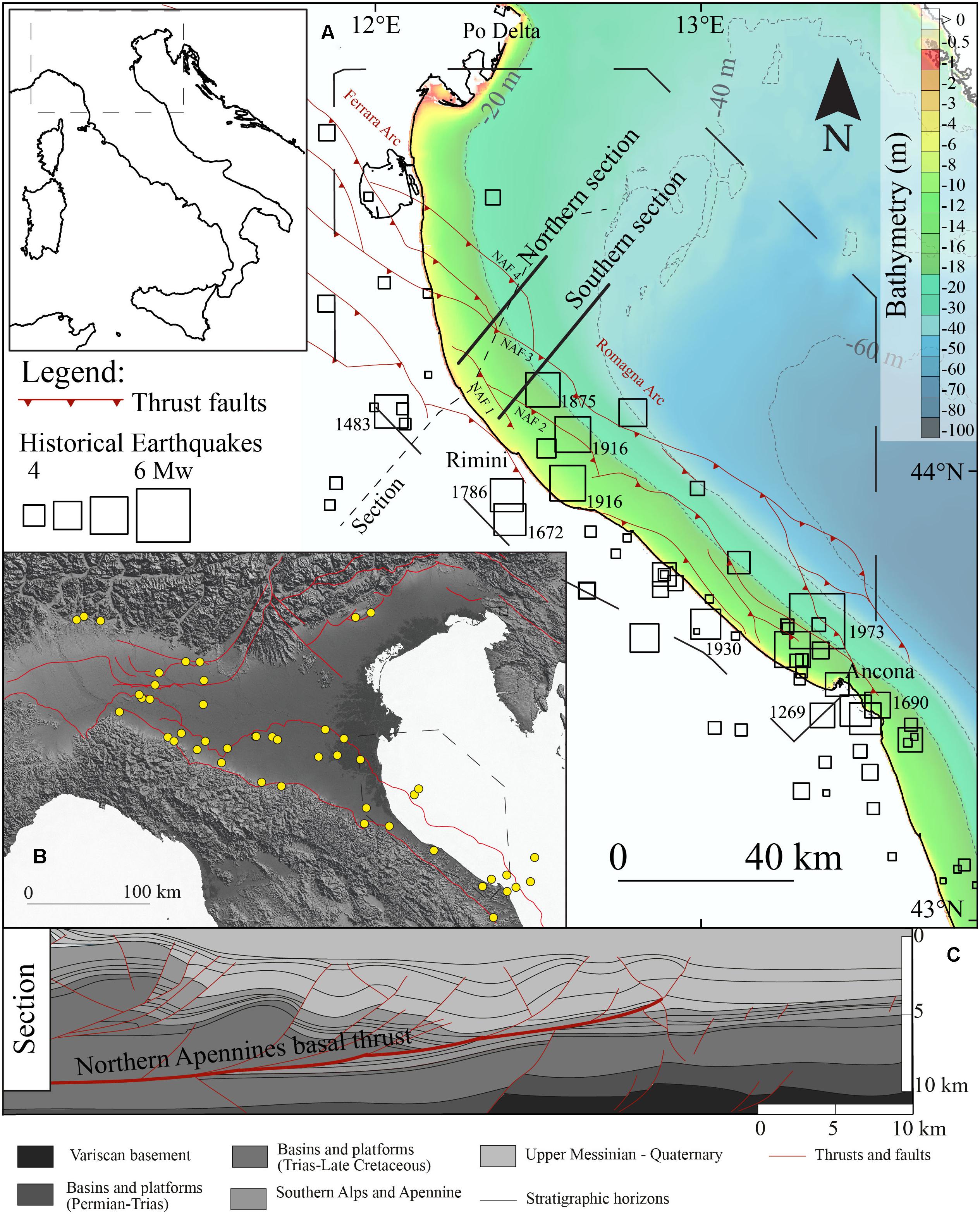
Figure 1. (A) Simplified structural map of the Eastern Po Plain and Northern Adriatic Sea. Thrust fronts analyzed in this study are modified after Ghielmi et al. (2013). The color-coded bathymetry, also represented by dashed gray contour lines (every 20 m), is derived from the EMODnet Bathymetry Consortium (2020). Historical earthquakes (Mw > 4) are from Rovida et al. (2020), with labels indicating the year for the largest ones. The traces of the Northern Section and the Southern Section refer to two 2D seismic reflection profiles used in this study to compute the slip rates (see Figures 6–8). (B) Map showing the locations where slip rate values (yellow circles) are available from literature data in the Po Plain and Northern Adriatic Sea (see Supplementary Figure 1 for details and references). (C) Regional cross-section showing the structural arrangement of the main thrusts and detachment from Fantoni and Franciosi (2010). See the section trace in panel (A) for the location.

Inland, recent or ongoing tectonic activity and fault reactivation in individual seismic events can be studied by analyzing geologic exposures (Bresciani and Perotti, 2014; Livio et al., 2014; Amorosi et al., 2016, 2020; Zuffetti and Bersezio, 2020), or by detecting river drainage anomalies (Burrato et al., 2003), or by inspecting GPS and remote-sensing data (Serpelloni et al., 2012; Pezzo et al., 2013, 2020; Nespoli et al., 2016, 2017). Instead, the just mentioned approaches cannot be used in the marine environment, especially where the Pleistocene sedimentation rate exceeds the tectonic signal leading to a completely undisturbed and almost flat bathymetry. In such cases, the contribution of detailed geophysical investigations is always needed. Noteworthily, the tectonic activity in the Northern Adriatic Sea has recently been estimated from the analysis of Continuous GPS data combined with the analysis based on publicly available seismic reflection profiles and analytical models (Pezzo et al., 2020).

Our study area (Figure 1) has a long record of both instrumental and historical seismicity; in particular, the offshore area near Rimini was affected by severe seismic sequences in 1875 (Mw 5.7) and 1916 (Mw 5.8) (Guidoboni et al., 2018; Rovida et al., 2020). The largest earthquake recorded in the instrumental era is the Mw 5.9, 1930 Senigallia earthquake, associated with a reverse fault running along the coast and controlling the deformation of Quaternary coastal terraces (Vannoli et al., 2004, 2015). Small tsunami effects were also observed following the 1916 and 1930 earthquakes (Guidoboni et al., 2018, 2019). However, the tsunami potential associated with active faults in the region remains relatively small (Tiberti et al., 2008), and the tsunami hazard in the Northern Adriatic Sea is generally lower than the rest of the Mediterranean region (Basili et al., 2021). Nonetheless, considering the region’s built environment, an advanced analysis of the tectonic activity is important to evaluate better and mitigate the risks derived from earthquake and tsunami hazards (Di Bucci et al., 2017; Antoncecchi et al., 2020).

This background information motivated us to investigate two key aspects of active faults that contribute to formulating better estimates of earthquake-related hazards. One aspect is the fault geometry that controls the ground-motion distribution with significant effects in the fault near field (Passone and Mai, 2017) and the tsunami wave height distribution in the fault near field and the far-field (Tonini et al., 2020). The other aspect is the slip rate that controls the maximum amount of tectonic moment converted into seismic moment release (Morell et al., 2020). To this end, we reconstructed the 3D geometries of the blind thrusts and a regional unconformity at the base of Pliocene deposits taking advantage of a wide dataset of 2D seismic reflection profiles (provided by ENI; Figure 2). Then, focusing on two high-quality regional seismic reflection profiles (Ghielmi et al., 2013), we performed a probabilistic assessment of the slip rates of four major thrusts by restoring the deformation of several key-horizons after removing the differential compaction effect. We adopted the trishear inversion method (Cardozo et al., 2011; Figure 3) for recovering the fault-propagation folding and incorporated the uncertainty on both displacement and age in the slip-rate calculations using the formulation of Zechar and Frankel (2009). We calculated multiple slip rates and associated uncertainties on eight stratigraphic horizons, spanning the last 5.33 Ma, from the Pliocene to the present, supporting recent findings that suggest an ongoing activity of the Northern Apennines basal thrust (Barba et al., 2008; Carafa et al., 2015a; Pezzo et al., 2020) and detailing the previous work on this topic performed in adjacent areas but with coarser temporal resolution (Maesano et al., 2013, 2015). The reconstructed fault 3D geometries together with the computed slip-rates can be of help in better defining the tectonic evolution of coastal and near-offshore active faults in the Northern Adriatic Sea and provide data that can be integrated into databases of seismogenic sources (Basili et al., 2008) and seismic and tsunami hazard studies.

FIGURE 2

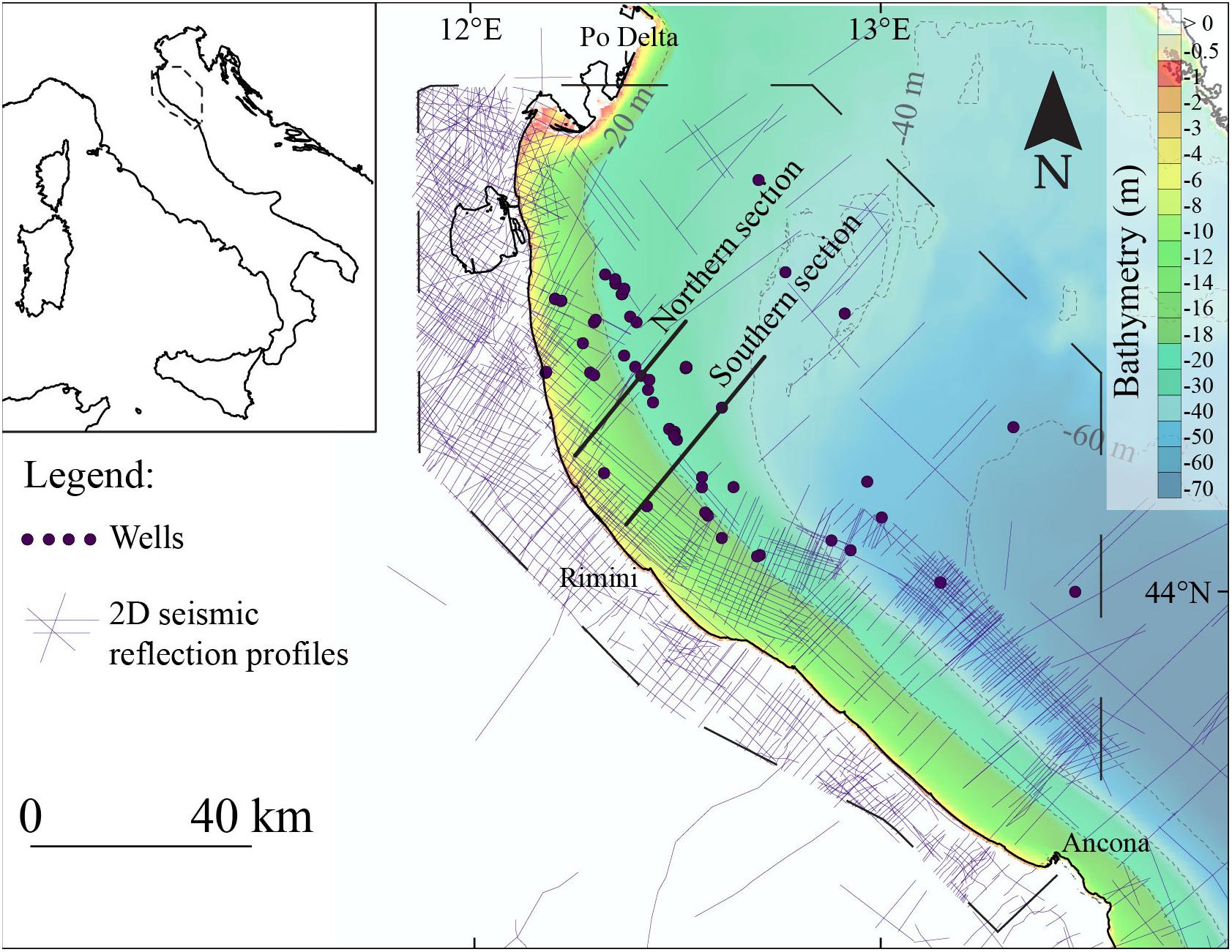
Figure 2. Dataset of 2D seismic reflection profiles and wells (courtesy of ENI) used in this study to reconstruct the fault 3D geometries and the hor-PL1 regional unconformity (Figure 5), the cross-sections (Figures 6–8), and to derive the slip rate values (Table 3). The bathymetry, as in Figure 1, is derived from the EMODnet Bathymetry Consortium (2020).

FIGURE 3

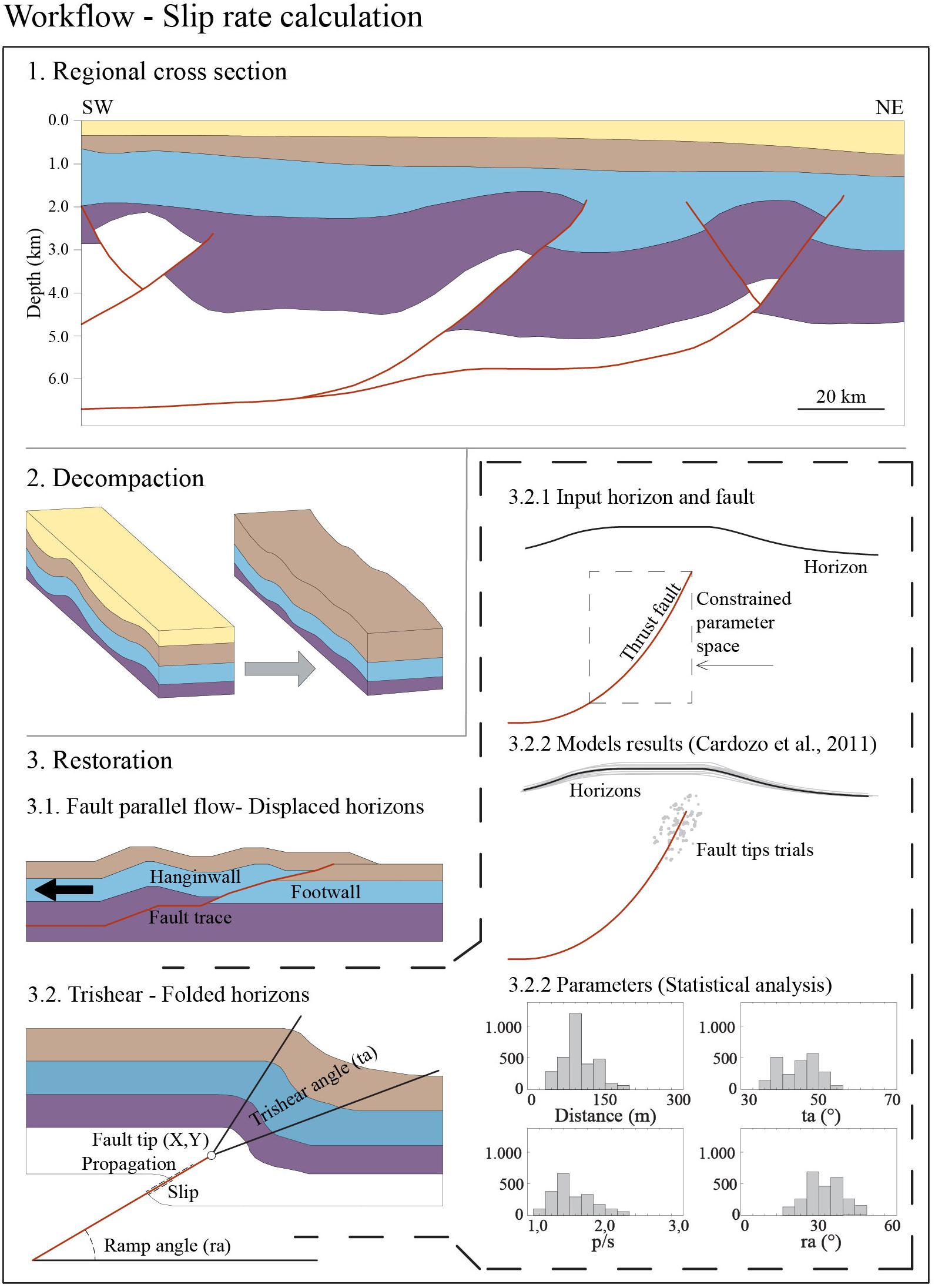
Figure 3. Workflow adopted in this study to decompact and restore the regional cross-sections (Figures 7, 8) and derive the slip rate values (Table 3) using a combination of the fault-parallel flow algorithm for displaced horizons and the trishear algorithm for folded horizons. The trishear parameters have been defined through statistical analysis shown in Figure 9 and Supplementary Data 1.

The Po Plain-Northern Adriatic Sea Foredeep Basin

The Northern Apennines is part of the system of fold-and-thrust belts (Northern Apennines, Southern Alps, and Dinarides) that wraps around the northern part of the Adria microplate, which is a promontory of the African plate (Malinverno and Ryan, 1986; Dewey et al., 1989), in the general framework of the Africa-Eurasia convergence. Starting from the late Mesozoic time, Adria was involved in multiple tectonic phases that led through times to the development of the Dinarides to the east (Handy et al., 2010), the Southern Alps to the north (Carminati and Siletto, 1997), and the Northern Apennines to the Southeast (Patacca et al., 1990; Carminati et al., 2012). Adria is presently overridden to the northeast by the outermost fronts of the Dinarides and the Southern Alps in the Veneto-Friulian Basin (Fantoni et al., 2002; Caputo et al., 2010; Toscani et al., 2016), to the west by the Southern Alps and Northern Apennines in the Po Plain (Fantoni and Franciosi, 2010; Toscani et al., 2014), and to the south by the Northern Apennines and Dinarides confronting to each other in the central Adriatic Sea (Argnani, 1998; Di Bucci and Mazzoli, 2002; Scrocca, 2006; Scrocca et al., 2007; Scisciani and Calamita, 2009; Kastelic et al., 2013; Finocchio et al., 2016).

The Po Plain and Northern Adriatic Foreland basin subsurface architecture resulted from a Mesozoic extensional tectonic phase developed in the western Tethys realm related to Upper Triassic-Lower Jurassic rifting, with evidence for Cretaceous-to-Paleogene structural inversion during Alpine pre- and syn-collisional tectonic phases (Bertotti et al., 1993; Masetti et al., 2012 and reference therein). Since the late Miocene, contraction affected the foreland and the surrounding orogenic belts due to Apennine north-to-northeast migration (Barchi et al., 1998; Basili and Barba, 2007; Fantoni and Franciosi, 2008, 2010; Ghielmi et al., 2013; Turrini et al., 2014). The buried thrusts and related fault-propagation folds have been investigated mainly using seismic reflection profiles and deep well logs taking advantage of hydrocarbon exploration activities in the region (Pieri and Groppi, 1981; Barchi et al., 1998; Regione Emilia-Romagna and ENI-AGIP, 1998; Regione Lombardia and ENI-AGIP, 2002; Fantoni et al., 2004; Fantoni and Franciosi, 2010; Ghielmi et al., 2010, 2013; Toscani et al., 2014; Turrini et al., 2014; Maesano et al., 2015; Amadori et al., 2019). The outermost fronts of the Northern Apennines buried in the southern Po Plain and the central Adriatic Sea are organized in structural arcs separated by recesses (Figure 1; Livani et al., 2018; Amadori et al., 2019). These arcs show an eastward increase in shortening and tectonic activity, consistent with their emplacement processes, while the Northern Apennines underwent a counterclockwise rotation within oblique convergence (Carminati et al., 2012; Maino et al., 2013). More specifically, the easternmost structural arcs were activated during the Pliocene, and their tectonic activity continued throughout the late Pliocene until the present, as demonstrated by the age of syn-tectonic deposits and the associated growth strata geometries (Boccaletti et al., 2011; Bonini et al., 2014, Maesano et al., 2015).

The blind thrusts in our study area (Figure 1), which are part of the Romagna Arc and the eastern termination of the Ferrara Arc, are rooted on two regional decollement levels, at the bottom and on the top of the Mesozoic carbonates, respectively (Barchi et al., 1998; Fantoni and Franciosi, 2010), and deform Early Pliocene and Pleistocene deposits (Maesano et al., 2015). All thrust fronts and related anticlines show an arcuate shape with a general NW–SE trend and NE vergence (Bigi et al., 1992; Casero, 2004; Fantoni and Franciosi, 2010).

The Adriatic basin infill is organized in large-scale tectono-eustatic driven sequences defined as unconformity-bounded units whose boundaries correspond to abrupt major changes in the type and gross distribution of depositional systems, angular unconformities due to high-magnitude basin-wide tectonic phases or eustatic changes that occurred during the Plio-Pleistocene. From the bottom up (i.e., from the Zanclean base to the present-day seafloor), these sequences are referred to as PL1, PL2, and PL3 for the Pliocene, and PS1, PS2, PS3a, PS3b, and PS3c for the Pleistocene (Figure 4). To discriminate between seismic horizons (i.e., the sequence boundary unconformity and correlative conformity) and the stratigraphic unit or sequence they bound at the base, we use the prefixes “hor-” and “seq-” for horizon and sequence, respectively, before the age name abbreviation (Figure 4). Note that the unconformities always lie at the base of a sedimentary unit. The accurate determination of chronostratigraphic ages relies on micropaleontologic and magnetostratigraphic analyses (Table 1; Muttoni et al., 2003; Ghielmi et al., 2010, 2013), which were used to support and verify the correlations between well-logs and seismic horizons, as well as to aid the interpretation of the sedimentation environment. From a sedimentological perspective, the Plio-Pleistocene sedimentary infill of the Po Plain and Northern Adriatic Foreland represents an overall regressive cycle (sensu Catuneanu, 2004).

FIGURE 4

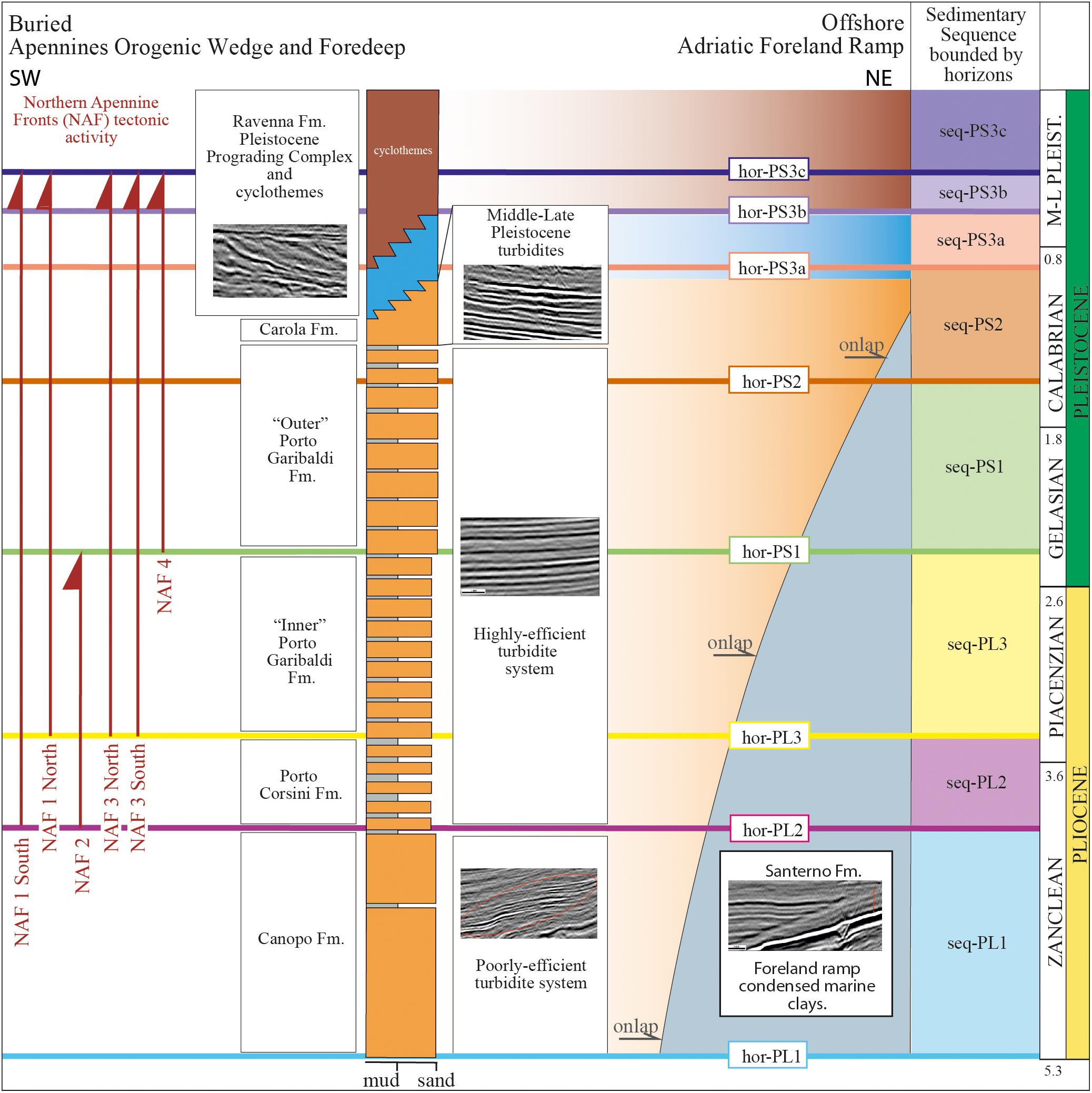
Figure 4. Simplified Plio-Pleistocene tectonostratigraphic scheme of the Northern Adriatic Sea (after Fantoni and Franciosi, 2010; Ghielmi et al., 2010, 2013). The regional unconformities/stratigraphic horizons used in this work and related ages (see Table 3) are indicated. A brief description of the sedimentological characteristics and seismic facies is provided for each geologic formation (for details, see Ghielmi et al., 2013; Amadori et al., 2020). Vertical red arrows on the left-hand panel indicate the inception and duration of tectonic activity of the thrust faults detected on the Northern Section and Southern Section, as derived from decompaction and restoration (see Figure 1 for trace locations and Figures 6–8) and used to derive the fault slip values.

TABLE 1

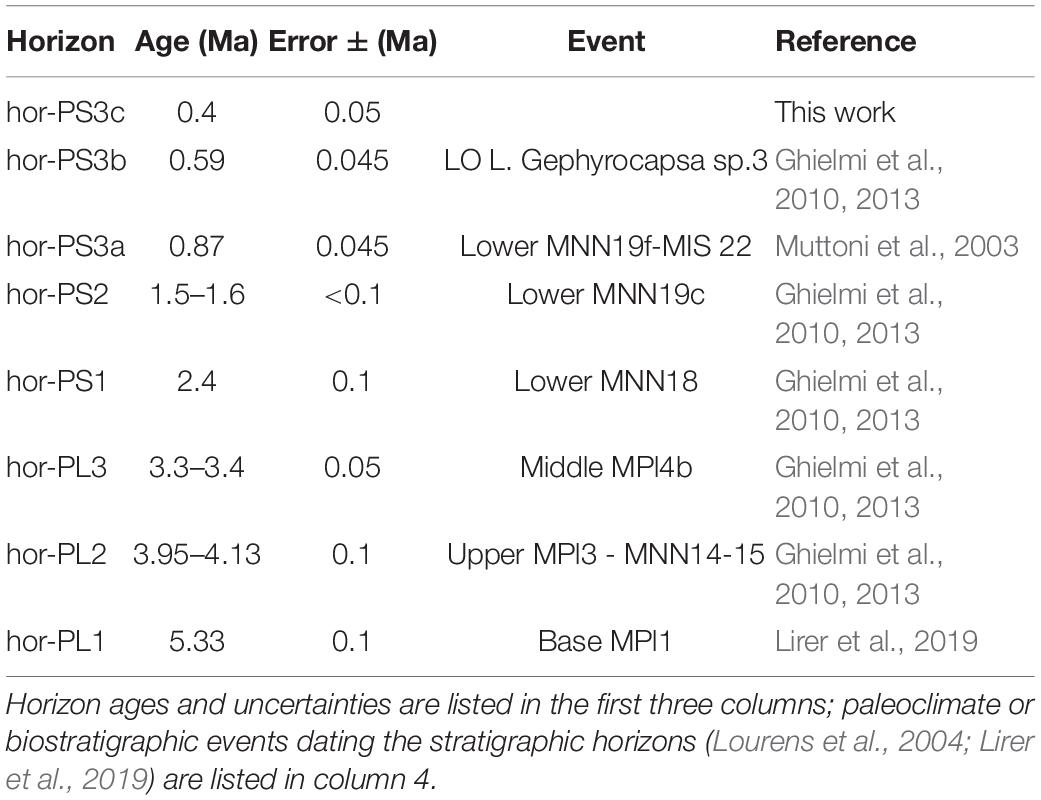
Table 1. Ages and related uncertainties of the stratigraphic horizons that were used for restoring the cross-sections of Figure 6 and for calculating the slip rates (Table 3).

The Pliocene sequence is mostly represented by thick turbidites deposited in a deep marine environment (during the underfilled phase), upwardly and eastwardly evolving into shallow water (slope, shelfal, and coastal) and continental (fluvial) sequences during the Pleistocene (filled and overfilled phases). After the abrupt transgression that ended the Messinian Salinity Crisis (Amadori et al., 2018; Micallef et al., 2018), Pliocene marine clays were deposited on the Adriatic foreland and foreland-ramp at the base of the turbiditic succession (Ghielmi et al., 2013; Rossi et al., 2015). These turbidites onlap the substantially undeformed SW-dipping Adriatic foreland ramp. In the study area, Pliocene-to-Calabrian clastic deposits (seq-PL1 to seq-PS2) are present with thin sequences of marls intercalated with thin- to thick-bedded fine-grained sandstones, interpreted as “highly-efficient” turbidite systems (according to Mutti et al., 1999; Ghielmi et al., 2010, 2013, 2019).

The thickness of these sequences is highly variable due to the different depositional settings (from the Northern Adriatic foredeep depocenter to the shallower foreland ramp toward the northeast) and the coeval tectonic activity. Based on the works by Ghielmi et al. (2013) and Ghielmi et al. (2019), the maximum thickness for the early Pliocene sequence of the Canopo Formation (seq-PL1) is about 600 m, whereas for the first Pleistocene sequence of the Porto Corsini and Porto Garibaldi Formations (from seq-PL2 to seq-PS1) the maximum thickness is about 1,200 m each. These systems show remarkable lateral continuity in seismic reflection profiles. They are overlain by a maximum of 800 m of Middle-Late Pleistocene sand-rich turbidites of the Carola Formation (seq-PS2) and 1,500 m of the north-eastward progradational geometries of the Pleistocene Progradation Complex and Cyclothemes of the Ravenna Formation (seq-PS3).

Despite the tectonic uplift and exhumation of the Northern Apennines range to the southwest, the main area of sediment provenance for the Pliocene and Pleistocene sequences was located to the northwest, as shown by southeast-directed paleocurrents (Ghielmi et al., 2010, 2013). Therefore, the sediment supply’s main direction during the Pliocene and Pleistocene was almost perpendicular to the fold-and-thrust vergence and propagation.

Datasets and Methods

Here we briefly illustrate the subsurface dataset (Figure 2) used to reconstruct the fault planes and the Pliocene unconformity (hor-PL1) in the study area. Since the area is almost completely offshore, the ground-surface reference dataset includes the bathymetric data from the EMODnet Bathymetry Consortium (2020). We also present the methodological approach we followed to (1) depth convert and restore two regional seismic reflection profiles representative of the structural setting and (2) calculate the Probability Density Function (PDF) of the slip rate for each fault, for each deformed horizon within these sections.

Seismic Dataset

The subsurface datasets comprise public and confidential 2D seismic reflection profiles, all acquired in TWT units. Specifically, we collected (1) all the seismic reflection profiles available in the VIDEPI project,¹ (2) published sections and subsurface maps (Fantoni and Franciosi, 2010; Amadori et al., 2018, 2019), and (3) confidential 2D seismic reflection profiles kindly provided by ENI in the framework of the SPOT project (Antoncecchi et al., 2020). This data collection resulted in a dense grid of seismic reflection profiles covering the entire study area (Figure 2).

Public data available in the VIDEPI project consist of 112 deep wells with associated stratigraphies and about 100 seismic reflection profiles, for a total length of almost 2,000 km. These well and seismic data were drilled and acquired at different times and with different techniques, resulting in an overall inhomogeneous dataset. The dataset quality and resolution permit to depict the general structural setting, but it is not suitable for detailed structural or stratigraphic reconstructions. Nevertheless, some of these data have been considered together with the confidential high-resolution dataset provided by ENI. This dataset includes more than 900 seismic reflection profiles for a total length of over 10,000 km. All data have the same datum plane and maintain a good quality up to 4,000–5,000 ms. Over an extended portion of the study area, the Pliocene succession and the youngest Messinian deposits are usually separated by a marked contrast of acoustic impedance, creating a strong and well recognizable high-amplitude reflector, also identified in neighboring onshore and offshore sectors of the Po Plain—Northern Adriatic basin (Ghielmi et al., 2013; Amadori et al., 2018, 2020; Mancinelli and Scisciani, 2020).

To detect possible evidence of recent/ongoing tectonic activity, one needs to analyze seismic reflection profiles with a good resolution in the first 4–500 ms. We thus selected two of the best seismic reflection profiles running SW–NE through the study area to perform the structural restoration and slip rate analysis. These profiles originally belong to the ENI “Adria” 3D seismic survey and are interpreted and described in detail by Ghielmi et al. (2013).

Depth Conversion

The reconstruction of fault geometries, the structural restoration, and the following slip and slip-rate calculation necessitate depth-converted cross-sections. To this end, we took advantage of the well-log stratigraphies and TWT-velocity tables associated with the wells available in the study area, which survey the entire Plio-Pleistocene sequences (Figure 2). We derived the trendline and the related function for each time-depth table, selecting the one with the highest coefficient of determination (R²), using an approach similar to that adopted for more complex 3D depth conversions (Maesano and D’Ambrogi, 2017). The obtained velocity function is linear [see also section “Fault surface and PL1 unconformity (hor-PL1)”], in agreement with velocity models recently carried out for neighboring sectors in the Adriatic Sea (Mancinelli and Scisciani, 2020), and fully comparable with other velocity models used for the same stratigraphic sequence in the Po Plain-Northern Adriatic Sea (Amadori et al., 2019).

Decompaction and Restoration

To carry out the complete restoration of the interpreted and depth-converted cross-sections, we used the MOVE Software (Petroleum Experts) (Figure 3). Different algorithms were adopted to appropriately restore geological structures, depending on the observed deformation style and related kinematics. For a correct restoration of the regional cross-sections, all deformation due to differential sediment compaction effects must be considered and excluded from the tectonic-related component before the slip calculation. Restoration can then effectively be carried out step by step after having decompacted the sedimentary body above the target stratigraphic horizon. In this view, decompaction is needed to remove the effect of sediment volume change over time-related with porosity reduction, and it represents a crucial operation to avoid an overestimation of fault slip and, consequently, the slip-rate. Sediment compaction can be driven both by natural (Teatini et al., 2011) and human activities (Stramondo et al., 2007). By removing the load associated with a layer of sediments, the residual deformation of the underlying levels can safely be ascribed to tectonic processes. The applied decompaction algorithm is based on principles described by Sclater and Christie (1980). The original sediment porosity and elastic properties were assumed homogeneous, and an equal mixture of shale and sand was also assumed (Scrocca et al., 2007; Maesano et al., 2013, 2015). In the Northern Adriatic foreland basin sedimentary succession, the sediment thickness can change from 10 to 40%, with an average change of 25% (Maesano et al., 2015). Despite sediments can reduce their thickness up to 55%, the associate fault displacement loss varies between 5 and 15% (Taylor et al., 2008). After each decompaction step, we progressively recovered each key stratigraphic horizon residual deformation, from the youngest to the oldest, by calculating the fault slip amount needed to restore the selected stratigraphic horizons to the original horizontal depositional geometry.

Different deformation styles associated with faults and folds require different restoration procedures. The study area is characterized by fault-propagation folding controlled by buried thrusts. The trishear algorithm (Erslev, 1991; Allmendinger, 1998) is suitable for studying complex fault propagation folds geometries and allows for reproducing some features commonly observed in natural folds, such as footwall synclines and thickness and dip variations in the forelimbs (Allmendinger et al., 2011). The trishear algorithm was thus adopted to restore the folding ahead of the fault tip. Since the trishear transfers the fault slip in a triangular shear zone emanating from the fault upper tip, the resulting fault and fold geometries depend on the fault tip location, the fault ramp dip, the amount of slip, the ratio between the propagation of the fault and the slip (p/s), and the angle of the trishear zone.

Trishear can be used for both forward and inverse modeling of fault displacement. In the case of inverse modeling, due to the number of variables in the trishear formulation, there is no univocal solution in the restoration (Cardozo et al., 2011; Oakley and Fisher, 2015). We thus adopted the formulation of trishear proposed by Cardozo et al. (2011), which solves the inverse problem by minimizing an objective function, representing the least-squared linear regression of the restored horizons, by using an optimization method (simulated annealing). The optimization algorithm does not systematically test the parameter space (which is an inefficient approach from the computational side) but traverses the space searching for the best-fit model. Even if the optimization procedure proposed by Cardozo et al. (2011) is less affected by local minima compared to earlier versions (Cardozo and Aanonsen, 2009), we performed multiple runs for each model, particularly for the cases in which the amplitude of folding was small to have a more robust assessment of the stability of the inversion.

For each structure and each horizon, we performed between 10,000 and 50,000 inversions in each model run. In setting up the model, we decided to restrict the parameter space for the variables that are well constrained by the seismic data interpretation. We thus limited the boundary area for the tip position by the upper and lower coordinates of the fault ramp in the cross-section. According to seismic interpretation, the fault ramp dip was searched in a narrow range of variability (±5°) around the measured values. We left search limits for the other parameters (slip, trishear angle, and p/s) wider (slip between 0 and 2 km; trishear angle between 20 and 80°; p/s between 0 and 3). Since the parameter exploration space is a rectangular area between the upper and lower endpoints of the fault, we have several final solutions located at various distances from the fault trace. We assigned a weight to each solution obtained from the inversion to incorporate the epistemic uncertainty related to the restoration performed with the trishear method. The highest weight was assigned to the solutions with smaller residuals from the inversion and the fault tip position near the fault traces. The weight decreases linearly with increasing distance (inverse distance weighting method) and for the solutions with high residual. Note that the value of slip is independent of the criteria adopted for the weighting of the results. The slip of the best-fit solution was used to restore each horizon before the successive decompaction step.

The Fault Parallel Flow is an algorithm designed for kinematic modeling of the hanging wall blocks where deformation is accommodated by fault-parallel shear (Egan et al., 1997). This algorithm moves all the material within the hanging wall parallel to the fault trace along virtual flow paths and can be applied to a wide range of fault geometries, and it is better suited for compressional faults (Ziesch et al., 2014). Therefore, we restored the observed on-fault deformation with the Fault Parallel Flow method, where the displacement could be directly estimated from the cut-off of faulted horizons. However, the Fault Parallel Flow restoration does not completely recover the folding associated with off-fault deformation. This residual deformation was thus recovered using the Trishear, and the final slip amount associated with the fault is given by summing the results of both methods.

Probabilistic Slip Rate Assessment

Slip rate is a derived quantity that bears the epistemic uncertainty of both variables needed to calculate them: the amount of slip and the age of the reference horizon. To this end, we adopted the probabilistic approach for the slip rate calculation and reporting proposed by Zechar and Frankel (2009), which has been already applied in different tectonic contexts, continental and offshore faults, as well as at different spatial and temporal scales (Frankel et al., 2011; Gold and Cowgill, 2011; Chevalier et al., 2012; Maesano et al., 2020).

We first considered the age and uncertainty of eight Plio-Pleistocene horizons (Table 1) and used a boxcar PDF with not-null probability in the time interval covered by the horizon age uncertainty.

If t₁ and t₂ are the minimum and maximum ages, respectively, for a given sequence, the probability for the slip to occur at any time during this interval, p(t), is expressed by

$$p(t)=\{\begin{array}{c}\hfill 0,t\notin [t_1,t_2]\hfill \\ \hfill {(t_2-t_1)}^{-1},t\in [t_1,t_2]\hfill \end{array}$$

Then, considering the slip obtained from the restoration of each horizon for each fault, we used a Gaussian PDF around the weighted mean displacement values.

If μ_d is the mean displacement and σ_d is the associated standard deviation, the Gaussian displacement uncertainty, p(d) is expressed by:

$$p\left(d\right)=\frac{1}{{\mathrm{\sigma }}_d\sqrt{2\mathrm{\pi }}}\text{exp}\left[-\frac{{\left(d-{\mathrm{\mu }}_d\right)}^2}{2{\left({\mathrm{\sigma }}_d\right)}^2}\right]$$

Finally, we combined these PDFs to report the probability of the slip rate estimates. The maximum possible slip rate is given by the maximum displacement divided by the minimum age and vice versa for the minimum slip rate.

Results

Stratigraphic Ages and Their Uncertainty

High-resolution geological information on the youngest sedimentary units is needed to assess details of recent tectonics. The seismo-stratigraphic, sedimentologic, and bio-chronostratigraphic characterization of the Plio-Pleistocene sequence reached in the Po Plain and Northern Adriatic Foreland area (Muttoni et al., 2003; Ghielmi et al., 2010, 2013; Amadori et al., 2019, 2020) provides an effective tool to constrain the inception age of thrust faults and their activity age ranges, as well as to estimate displacement and slip rates for the Middle-Late Pleistocene time interval (Figure 4 and Table 1). Given the available temporal resolution, the probability of slip rate estimates is computed considering errors on the identified key-horizon age intervals. Here, we introduce the uncertainty associated with each of them based on bio-chronostratigraphic zones and subzones, paleomagnetism, or the tuning to Milankovitch astronomical cycles [e.g., astronomically tuned Neogene time scale (ATNTS2004) Lourens et al., 2004].

From the older to the younger, the first horizon in the Pliocene part of the sequence is hor-PL1, which corresponds to the beginning of the Zanclean Stage, calibrated at the base of the planktonic foraminiferal biozone MPl1, dated 5.33 Ma (Lirer et al., 2019). This reflector can be easily tracked in the seismic profiles because it was generated during an overall general reorganization of the Po Plain and Northern Adriatic Foreland basin at the end of the Messinian Salinity Crisis. During the Zanclean time, the study area was the foredeep deep-water depocenter of the Northern Apennines; therefore, we can exclude hiatuses within seq-PL1. The uncertainty associated with hor-PL1 age determination is ∼0.1 Myr, tied to the base of the Sphaeroidinellopsis s.l. biozone, and it cannot be older than the MPl1 biozone (Lourens et al., 2004; Lirer et al., 2019).

The next horizon is hor-PL2. Although its age is intra-Zanclean, its determination is very accurate. It falls within the upper MPl3 planktonic foraminiferal biozone, within MNN14-15 nannofossil biozones, dated between 4.13 and 3.95 Ma (Ghielmi et al., 2010, 2013), resulting in an age error smaller than ±0.1 Myr.

The third horizon is the Piacenzian hor-PL3, dated between 3.3 and 3.4 Ma and falling within the MPl4b biozone with a considered uncertainty of ±0.1 Myr (Ghielmi et al., 2010, 2013).

The first horizon in the Pleistocene part of the sequence, hor-PS1, is close to the Gelasian base, constrained in the lower part of MNN18 nannofossil biozones dated 2.4 Ma (Ghielmi et al., 2010, 2013). In the absence of specific studies on this age determination uncertainty but considering hor-PS1 to have similar stratigraphic detectability and importance as hor-PL3, we assigned an error of ±0.1 Myr even though the younger age would let suppose a smaller uncertainty.

The second is the hor-PS2 unconformity, which is dated at 1.5–1.6 Ma because it falls within the lower MNN19c nannofossil biozones before the first occurrence of the Hyalinea balthica, dated at ∼1.5 Ma (Sprovieri et al., 1998). According to the age determination accuracy, we retain an error of ±0.1 Myr also in this case.

The Middle-Late Pleistocene is characterized by the region-wide Pleistocene Progradation Complex, within which we identified three main unconformities, namely hor-PS3a, hor-PS3b, and hor-PS3c.

At the regional scale, the hor-PS3a unconformity is highly diachronic and falls into the MNN19f biozone, so that its age ranges in a large interval between 0.98 and 0.47 Ma (Lirer et al., 2019). However, in the Po Plain region, hor-PS3a is well tied at 0.87 Ma, which corresponds to the glacio-eustatic minimum peak MIS 22, through calibration using pollen and paleomagnetic inclinations (Muttoni et al., 2003). Based on the unconformity mapped by Amadori et al. (2019), we can safely attribute the age of 0.87 Ma to the hor-PS3a identified in our study area. The associated error can be estimated to be ±0.045 Myr based on the temporal range in which the MIS 22 peak can be defined according to the position of the two next midpoints of the sea-level curve.

The hor-PS3b unconformity is dated after the last occurrence of L. Gephyrocapsa sp. 3 at 0.597 Ma (Lourens et al., 1998). Based on the uncertainty usually attributed to the glacial-interglacial cycle absolute timing (less than ∼0.5 Myr; Lourens, 2004), and to keep consistency with the older horizon in the sequence, we assigned to hor-PS3b an error of ±0.045 Ma.

The uppermost unconformity, hor-PS3c, is the top lap of the Pleistocene Progradation Complex in the study area and does not correspond to any previously defined stratigraphic event. Hence, the hor-PS3c age determination had to be indirectly estimated by considering the sediment thickness deposited above PS3b and the average depositional rate, known to be slightly lower than 1.0 mm/year (Amadori et al., 2020). Given the average thickness of seq-PS3c and its average depositional rate, we estimate the age of hor-PS3c at 0.4 Ma. To validate this estimate, we compared the sedimentary setting and seismic facies association of the study area with the high-resolution chronostratigraphic correlation available for the neighboring Venetian-Northern Adriatic region (Massari et al., 2004; Amadori et al., 2020). In both cases, the first 500 ms of the seismic sequence corresponds to the topset portion of the Pleistocene Progradation Complex. According to the depth-converted position of hor-PS3c in the study area, the estimated age-depth relationship, and the correlation with dated horizons in the Po Delta area (Amadori et al., 2020), we assume an age of 0.4 and an error of ±0.05 Ma based on the age and scale of individual Milankovitch cycles.

Fault Surface and PL1 Unconformity (hor-PL1)

The interpretation of the seismic reflection profiles (Figure 2) allowed for a detailed 3D reconstruction of the hor-PL1 unconformity and 11 fault surfaces, referred to as NAF, for Northern Apennines Fault, followed by a progressive number (Figure 5). To produce this reconstruction in the depth domain, both 3D fault surfaces and the two interpreted seismic reflection profiles (Figure 6) have been depth converted following the same approach recently proposed for neighboring sectors of the Adriatic Sea by Mancinelli and Scisciani, 2020. Considering the Plio-Pleistocene sequence time-depth values, the function better representing the velocity increase with increasing depth is linear and is v = 0.3557d + 1945, where v is velocity and d is depth, with an R² = 0.881. Since all the faults mapped in the area are detached below hor-PL1, the velocity model validity domain includes the depth-converted fault geometries and the hor-PL1 surface entirely.

FIGURE 5

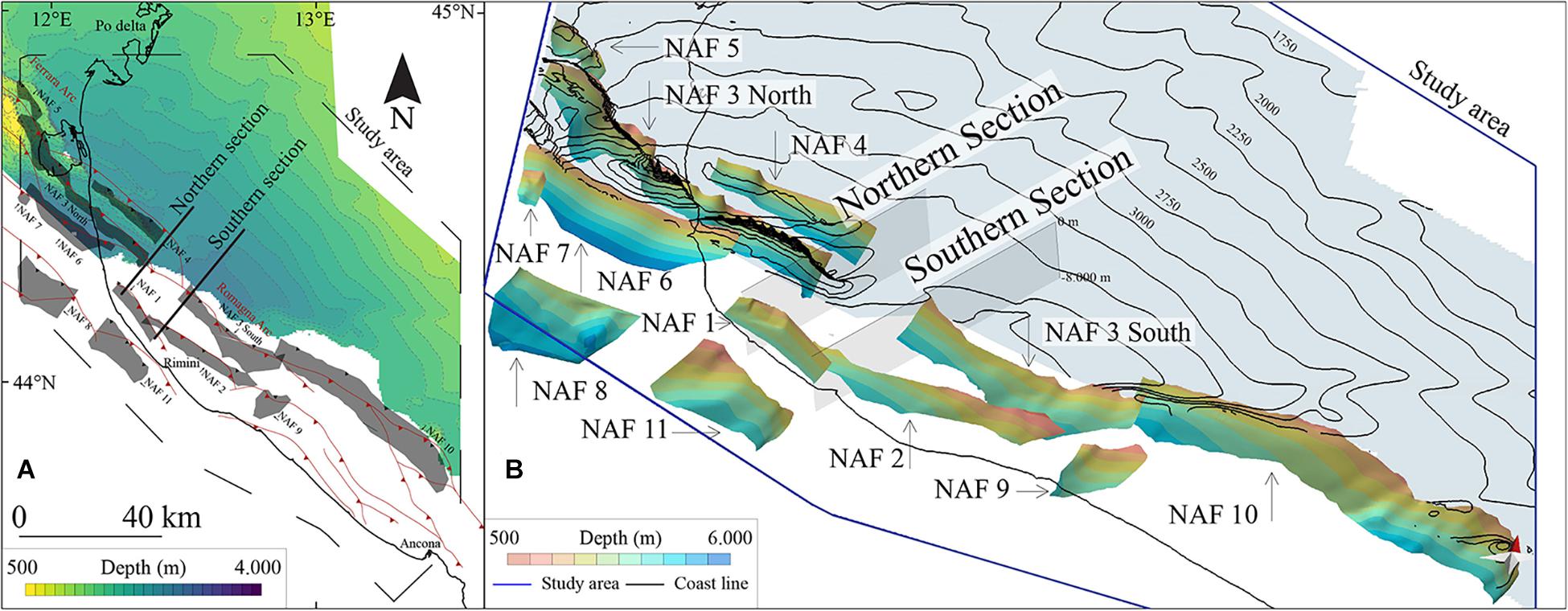
Figure 5. (A) Map of the study area showing the reconstructed fault planes (in gray) and the hor-PL1 contour map. (B) Oblique view (looking toward northeast) of the 3D fault geometries (color-coded with depth) and the hor-PL1 regional unconformity. Fault parameters are detailed in Table 2.

FIGURE 6

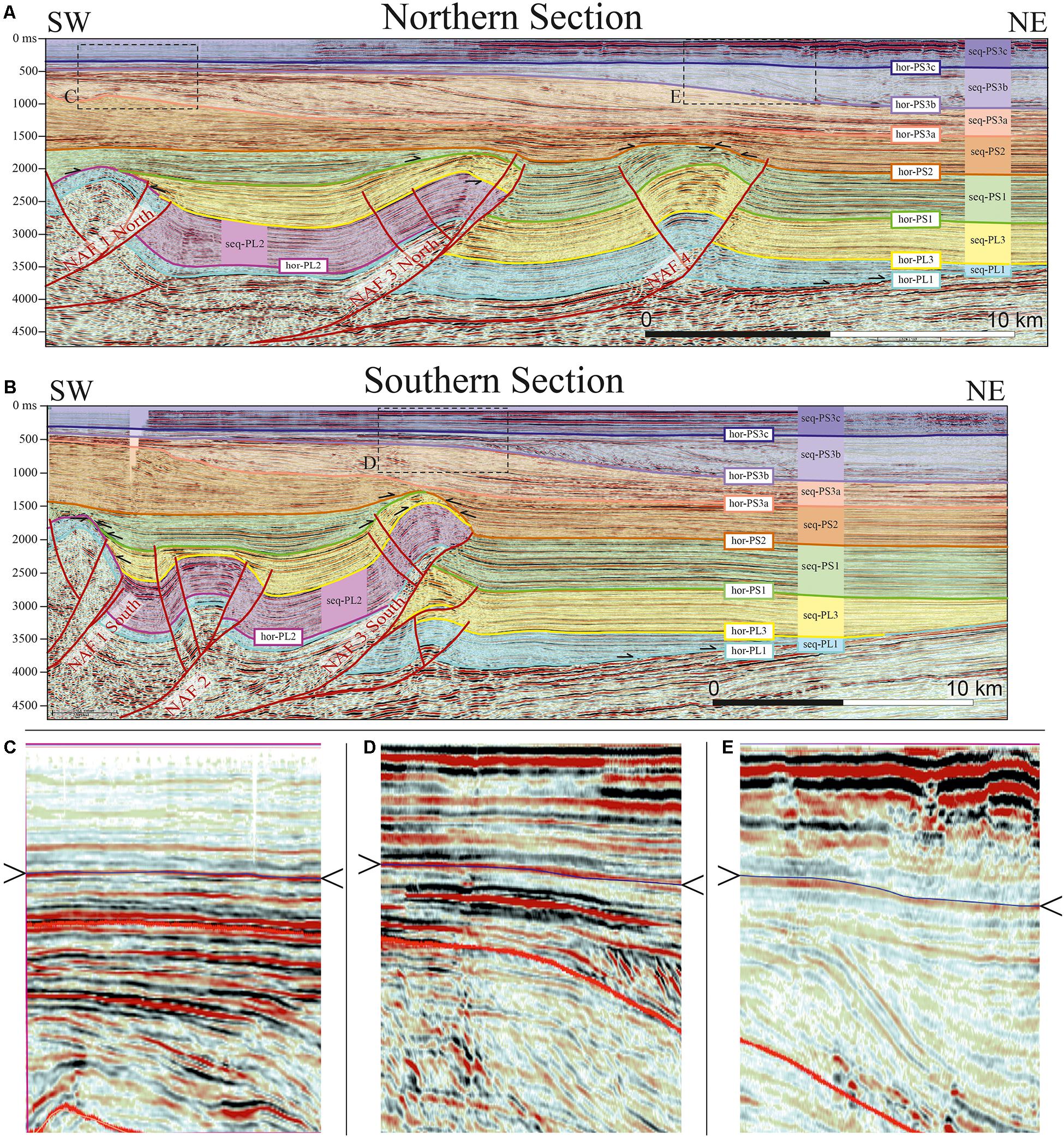
Figure 6. Seismic reflection profiles (see Figure 1 for location) adopting the interpretation by Ghielmi et al. (2013). (A) Northern Section; (B) Southern Section; (C–E) close-up views of the uppermost 1,000 ms above the studied structures [see boxes in panels (A,B)]. Vertical pseudo-exaggeration ∼10 times at 1,500 m/s default uniform velocity. Slight deformations of hor-PS3c are visible (marked by a thin blue line indicated by arrows on either side of the image).

The hor-PL1 unconformity was reconstructed at a regional scale to provide a first-order geometrical constraint on the folding related to the underlying thrust activity and is particularly detailed in northeastern and foreland sectors. The hor-PL1 reconstruction was integrated with the available information from the literature (Bigi et al., 1992; Amadori et al., 2018) where the seismic dataset was not dense enough to provide an accurate interpolation (Figure 2). The depth contours depict a rather monotonous southwestward gently dipping monocline in the foreland area interrupted by a deformation pattern dominated by arc-shaped NW–SE oriented anticlines.

The fault geometries were initially obtained from interpreting the 2D seismic reflection profiles and interpolating the points sampled along the traces. Then, the final fault surfaces were obtained by an overall depth conversion. Coming from an industrial dataset, the seismic reflection profiles are not homogeneously distributed over the study area, but they are more concentrated in the correspondence of selected geological structures. For this reason, the fault reconstructions are not always laterally continuous and needed to be interrupted where the distribution of the seismic profiles did not permit their recognition. However, their continuity could be inferred by the anticline geometry detected in the hor-PL1, which aided the interpolation in zones of scarce data coverage or seismic profile poor quality.

All the faults strike NW–SE and dip SW coherently with the Northern Apennines thrust belt and are buried under Plio-Pleistocene deposits. For this reason, none of them has any clear seafloor evidence of activity that could be deduced from an inspection of the bathymetry. Instead, their overall structural arrangement could be characterized by analyzing the regional cross-sections (Figure 6), which show that they offset the Pliocene horizons and deform the Pleistocene horizons. They also show that minor backthrusts contribute to accommodate the deformation produced by the identified major thrusts.

A summary of the main geometric characteristics of the mapped faults is presented in Table 2. Dealing with arc-shaped concave-up faults, the internal variability in strike, dip, and depth is represented by percentiles (10th, 50th, and 90th) of the encountered values. Overall, these faults range in size from 12 to over 400 km² and cut through the crust between 2 and 6 km depth. Note that the lower depth values do not necessarily correspond to the detachment level depth but only to the depth where a reliable reconstruction was possible.

TABLE 2

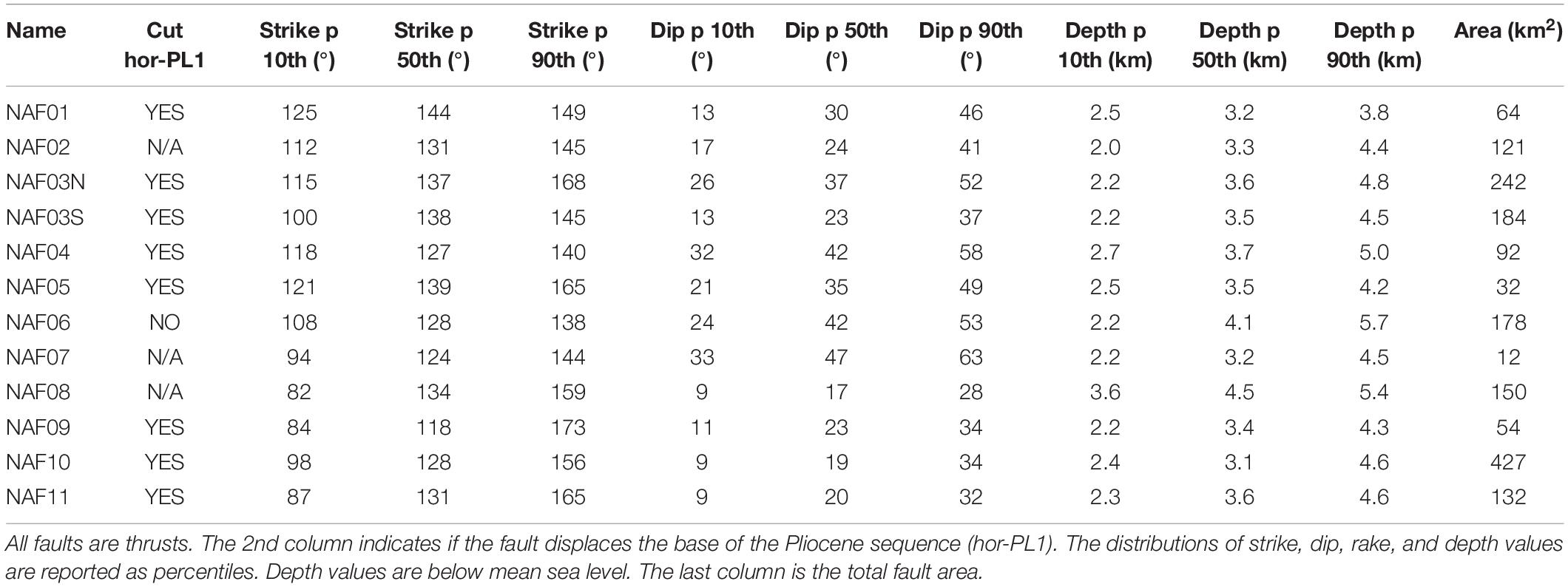
Table 2. Geometric parameters of the faults shown in Figure 5.

Regional Cross-Sections and Chronology of Thrust Activity

The seismic reflection profiles that are shown in Figure 6 (location in Figure 5) have a high-enough resolution for observing growth strata on top of the main thrusts and recognizing the horizon geometries within the Pleistocene Progradation Complex (hor-PS3a, hor-PS3b, and hor-PS3c; Figure 4 and Table 1) in the first 500 ms. The Northern Section (Figure 6A) is 27 km long, whereas the Southern Section (Figure 6B) is an excerpt of a more than 70 km long seismic reflection profile and was cut where it intersects our study area (at 36 km in Figure 25 in Ghielmi et al., 2013). Overall, they intersect and provide insights for four of the 11 thrust ramps in the study area and their related secondary features. For some of them, the fault geometry can be followed down to their basal detachment (∼4,500 ms) and the bottom Pliocene unconformity. Detailed line-drawings of the tectonic structures and depositional sequence boundaries have been possible in the entire depth range spanned the profiles, allowing for estimating their inception age.

According to the structural map shown in Figure 5, the structures intersected by the two cross-sections are as follows. NAF1 is the innermost structure and is intersected by both cross-sections close to its structural culmination. NAF2 is intersected only by the Southern Section near its northern termination. NAF3 is composed of a series of NW–SE thrusts correlated from the onshore Ferrara Arc to the offshore Romagna Arc. The lack of seismic profiles between the two cross-sections prevents imaging the along-strike features; therefore, we keep the NAF3North and NAF3South geometric reconstructions separate. However, based on the structural trend deduced from other profiles, we can consider NAF3North and NAF3South as part of the same geological structure. NAF4, the outermost structure in this sector, is intersected only by the Northern Section, although it terminates just north of the Southern Section.

By analyzing these seismic reflection profiles, it was possible to infer the inception age of each structure by comparing the stratigraphic succession thickness in the hanging wall and footwall on each of them and verifying the presence of onlap geometries or growth strata in correspondence of fault-related anticlines. The presence of possible recent and ongoing tectonic deformation, albeit less evident than that affecting the Zanclean to Gelasian sequences, can be noted in the close-up views of the upper sectors of the seismic stratigraphy (Figures 6C–E).

NAF1 is made up of the main forethrust, with a deep splay visible only in the Northern Section and an associated backthrust. This structure clearly offsets hor-PL1 and hor-PL2. Above NAF1, seq-PL1 has the same thickness in both the hanging wall and footwall, whereas seq-PL2 is completely absent and seq-PL3 onlaps on the anticline forelimb. The main thrust activity can then be set at the beginning of seq-PL2. Later activity is testified by the warping of hor-PL3 and hor-PS1 on top of the anticline. The stratigraphic sequence above hor-PS1 shows only hints to elusive deformation, difficult to be traced. However, the stratigraphic markers are well detectable, and the weak signs of deformation appear more clearly through vertical exaggeration, as shown in the close-up view of Figure 6C.

NAF2 includes a forethrust splayed into two branches and two separate backthrusts. The seq-PL2 thickness differences between the hanging wall and footwall suggest that NAF2 inception age can be set at the sequence base. This structure slightly deforms the bottom of the seq-PS1, whereas hor-PS2 is flat and undeformed, thereby marking the ceased activity.

NAF3North is constituted by a main forethrust and a few associated secondary backthrusts with very limited displacement. The main thrust shows a flat-ramp geometry and is rooted within the Plio-Pleistocene deposits. Above NAF3-North, seq-PL1 has the same thickness in the hanging wall and footwall. The main thrust inception age can be identified within the deposition of seq-PL3 that is strongly thinned on top of the related thrust anticline. Hor-PS2 is warped but not offset by the thrust, and signs of thrust activity are also detectable in the lower levels/reflectors of seq-PS2.

NAF3South is a rather complex structure in which the main forethrust with a flat-ramp geometry is associated with splay faults and backthrusts. This structure offsets and deforms both Pliocene and Pleistocene successions. Its tectonic activity starts at the base of seq-PL3, as evidenced by the sequence reduced thickness on the top of the related thrust anticline. The main fault slightly offset hor-PS2 at the base of the sequence, and growth strata near the main anticline demonstrate its activity carried on during the whole seq-PS2 deposition. Above the anticline, looking at the seismic reflection profiles, no clear evidence of tectonic activity is detectable for seq-PS3a and seq-PS3b due to the presence of clinoforms and prograding strata. However, the effects of tectonic activity can be detected for the overlying seq-PS3c (Figure 6D), suggesting that the tectonic process remained active during the entire sequence emplacement.

NAF4 is a flat-ramp-shaped thrust with an associated backthrust. The ramp connects downward with a basal flat that merges with NAF3North. Seq-PL1 and seq-PL3 have the same thickness at the hanging wall and footwall of the main thrust, and reflectors are always parallel and coherent with the stratigraphic boundaries so that the hor-PS1 unconformity dates the thrust inception age. The thickness of seq-PS1 shows strong variations on the top of the anticline and significant differences relative to the undeformed layers in front of it. Hor-PS2, instead, is only slightly offset by the main thrust. On top of the anticline, seq-PS2 growth strata are present on both limbs, and the hor-PS3a and the reflectors immediately above it shows weak signs of deformation (Figure 6E).

Restoration and Slip Rates

The two seismic reflection profiles shown in Figure 6 were depth converted to obtain two regional cross-sections suitable for restoration and concurrent calculation of the total slip and subsequent estimation of the slip rate on each fault. These two cross-sections intersect four structures: NAF1, NAF2, NAF3, NAF4. The depth-converted versions of the two cross-sections are shown in Figures 7, 8. The line drawing in the depth-converted sections is rather simplified relative to the original interpretation of the seismic profiles in Figure 6 to avoid numerical instabilities in the restoration process.

FIGURE 7

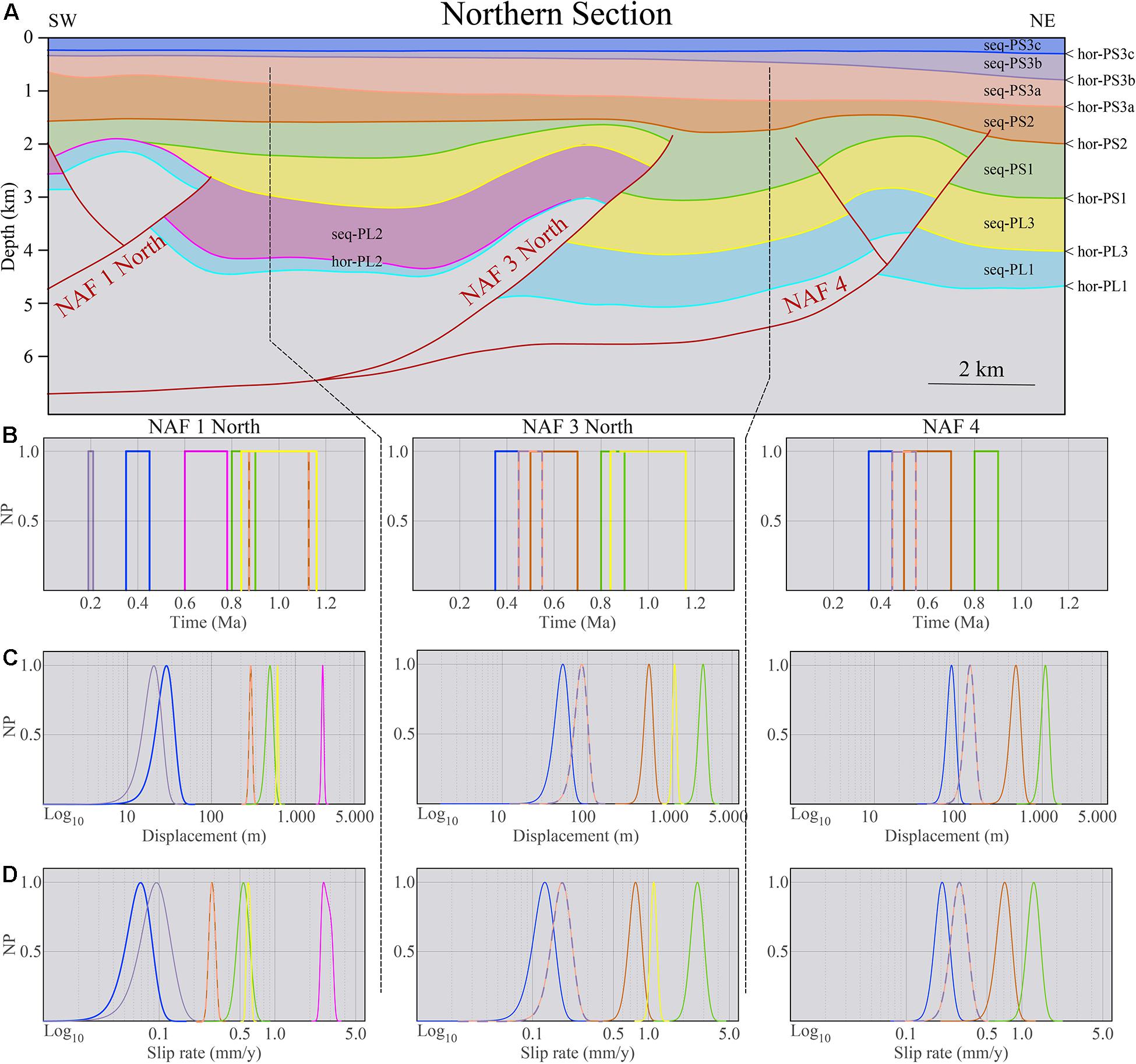
Figure 7. (A) Depth-converted version of the Northern Section. Some minor faults (e.g., backthrusts) were not included in the restoration after having verified that their contribution to the total displacement was two orders of magnitude smaller. The main restoration steps are provided in Supplementary Figure 2. A summary of the slip-rate calculation results for the studied structures is shown by plots of the time-interval ages (B), the recovered slips (C), and the slip rates (D) for each fault. A boxcar distribution describes the interval-age uncertainty Probability Density Functions (PDF), whereas a Gaussian distribution describes the slip and slip-rate uncertainty PDFs. X-axes are in logarithmic scale for displacement and slip-rate values. Only the horizons considered for the slip rate calculations are represented (see Table 3 and Supplementary Data 2 for numerical information).

FIGURE 8

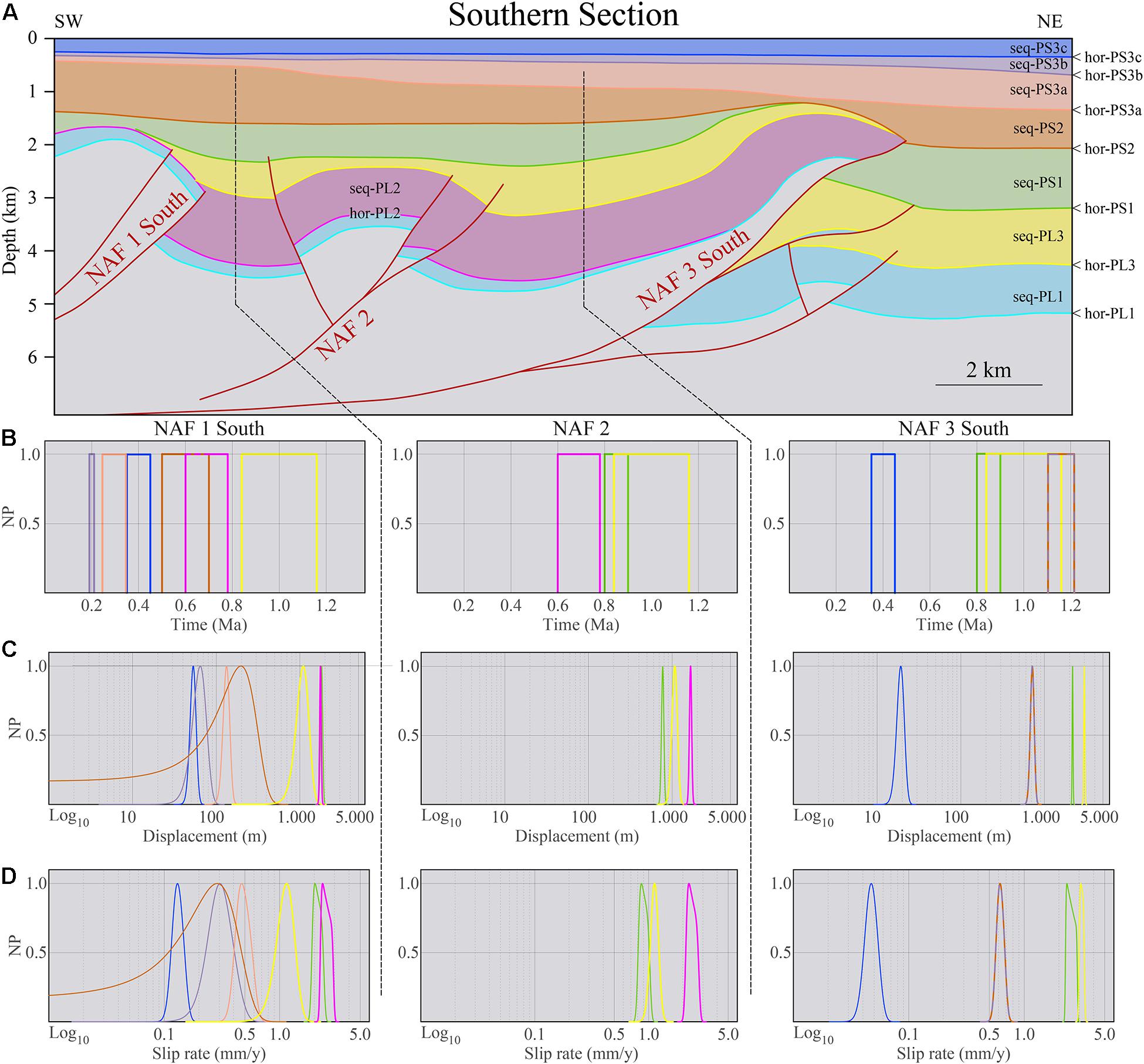
Figure 8. Same as Figure 7 for the Southern Section.

We performed the horizon restoration and fault-slip calculation from the younger to older horizons and from the outer to inner structures. The hor-PS3c is the shallowest horizon, placed around 300 m depth. Hor-PL1 reaches almost 6 km depth. We excluded from the restoration procedure the horizons located within the Pleistocene Progradation Complex since their clinoformal deposition prevents the correct discrimination of the tectonic component in determining their present geometry. The shallowest horizons were affected only by folding and were thus restored using the trishear method only. Deeper horizons were restored, combining the Fault Parallel Flow and the trishear methods. The step-by-step restoration progression is shown in Supplementary Figure 2.

We then selected the slip value that best represents the restored deformation by weighing each inversion component (p/s ratio, trishear angle, and ramp-dip angle). Figure 9 shows an example of the trishear inversion results, while the full model inversion results are provided in Supplementary Figures 3, 4 (numerical information in Supplementary Data 1). For the shallower horizons (hor-PS3a, hor-PS3b, and hor-PS3c), we made 50,000 trials to test better the stability of results associated with the very low slip values. This effect is represented by the high dispersion of the fault tips used for the trishear inversion. It is worth noting that for some of the shallow horizons (NAF1-South hor-PS3a, NAF1-South hor-PS3b, NAF3 hor-PS3a, NAF3 hor-PS3c, NAF4 hor-PS3a, NAF4 hor-PS3c), the resulting slip values are not null, and the position of the solution is in good agreement with the fault geometry even considering a large number of trials with a significant dispersion around the faults. We considered the weighted average and standard deviation of the slip values to incorporate these results in the slip rate calculations. The trishear restoration produced a larger uncertainty than the Fault Parallel Flow restoration because, in the latter, the uncertainty is limited to the accuracy of the offset measured at the fault cut-off. Overall, the slip values obtained from the trishear inversions have limited variability around the values with the highest weight, showing some dispersion only for the solutions with lower weights. In most cases, the solutions are located on the mapped faults or within a 500 m distance from the faults. The slip values are coherent with the amount of deformation of the relevant horizon, being small (<100 m) for the younger and less deformed horizons and higher for older and more deformed horizons.

FIGURE 9

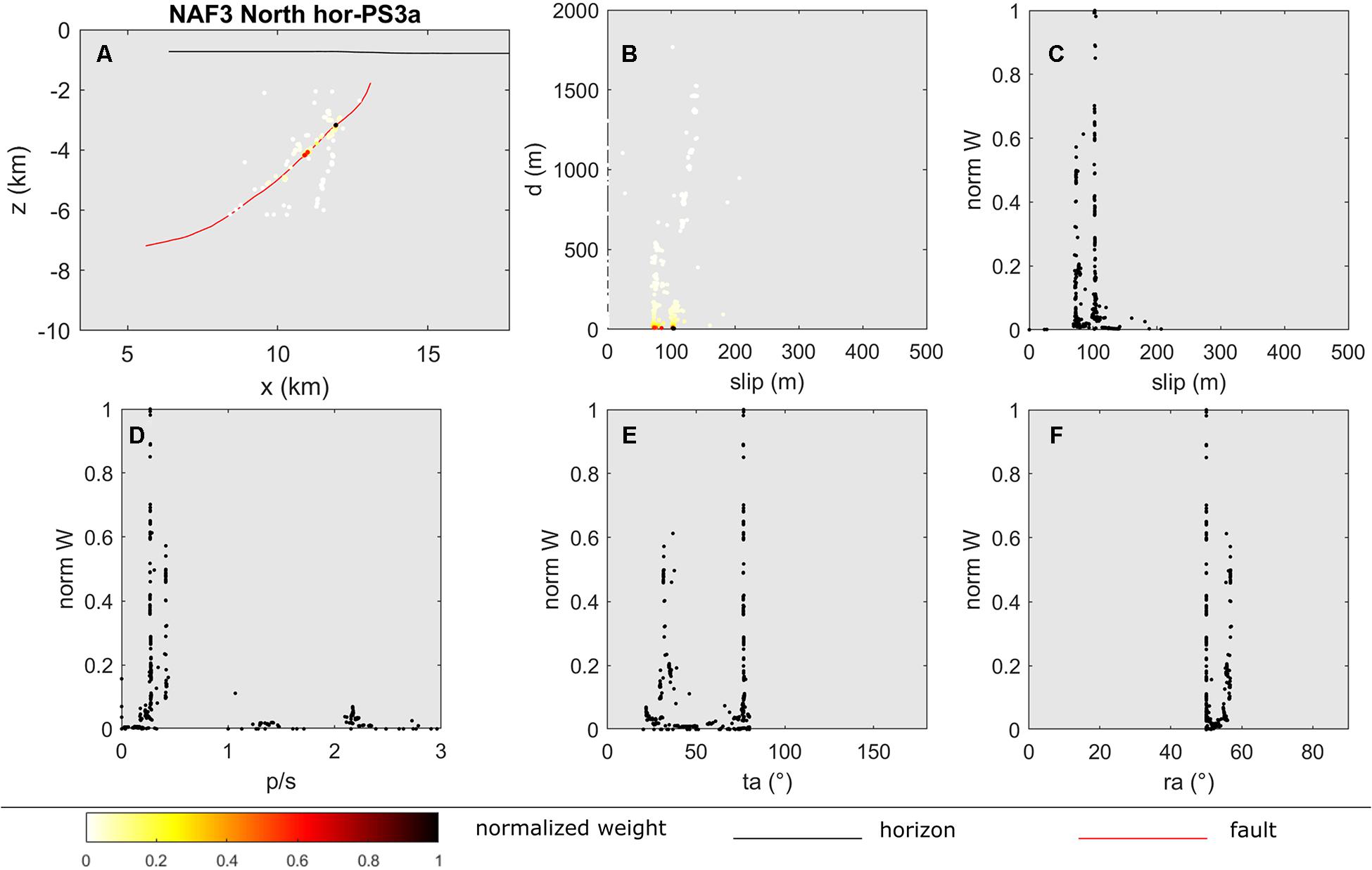
Figure 9. Example of trishear inversion referred to hor-PS3a above NAF3 North thrust. (A) Position of the fault-tip trial points. The fault and horizon geometries are shown for comparison. The color scale represents the normalized weight of each trial. (B) Slip of inversion trial plotted against the distance of the trial from the actual fault. The color scale represents the normalized weight of each trial. (C) Distribution of the slip values and relative normalized weight. (D) Distribution of the propagation versus slip ratio (p/s) and relative normalized weight. (E) Distribution of the trishear angle (ta) values and relative normalized weight. (F) Distribution of dip ramp angle (ra) and relative normalized weight. Full model inversion results and numerical results are available in Supplementary Figures 3, 4 and Supplementary Data 1.

The slip rate calculations results, along with their uncertainty PDFs, for each fault and each restored horizon are graphically shown in Figures 7, 8 for the Northern Section and the Southern Section, respectively. Table 3 summarizes the horizon age, restoration method and restored slip, and slip rate results. In five cases, the displacement cannot be calculated because the relevant horizon is part of the Pleistocene Progradation Complex. For these five cases, we retained the slip associated with the underlying horizon. This missing information seems not to affect the general trend of the investigated structures.

TABLE 3

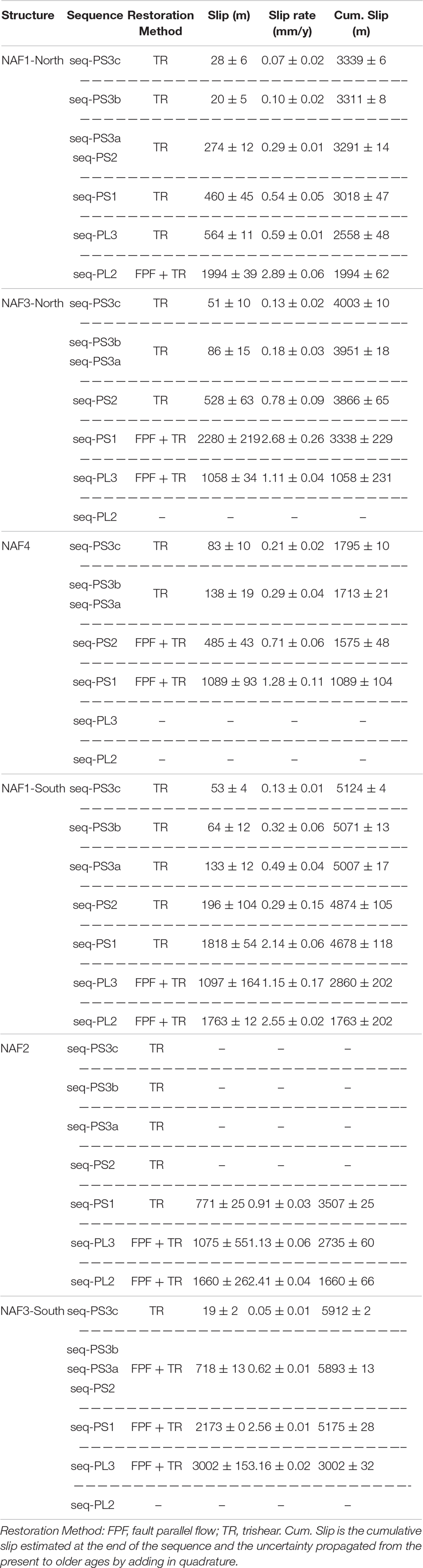
Table 3. Slip and slip rate for the various restored horizons, and cumulative slip with associated uncertainties (1σ standard deviation).

Overall, the progressive restoration showed that the inception age is different for different faults in agreement with the inception age visual estimations based on the seismic stratigraphy. Considering the structural relative positions, the inception age is progressively younger from the inner toward the outer structures. NAF1, NAF2, and NAF3 start in the Pliocene. The former two during seq-PL2 and the latter during seq-PL3. NAF2 remained active until the end of seq-PS1 or slightly afterward. NAF4 is the younger structure, starting its activity in the Pleistocene with the onset of seq-PS1 and has only a short period of activity overlap with NAF2 lasting about 1 Myr (2.5–1.5 Ma). The total cumulative slip is differently distributed on the different structures along the two regional cross-sections and varies from about 1,800 m for NAF4 to about 6,000 m for NAF3-South. This structure shows the highest structural elevation and amount of slip, probably due to the limited or almost null tectonic activity on the NAF2 structure after seq-PS1. The distribution of the cumulative slip over time is shown in Figure 10. Note that because of the adopted restoration methods (Figure 3), each discrete displacement increment is attained by each restored horizon at the bottom of each decompacted sequence or group of sequences (in the presence of clinoforms). Therefore, in Figure 10, the cumulative displacement distribution is attributed to the sequence termination age, regardless of the possibly finer internal displacement variations that could have occurred within the sequence or, in other words, between two successive horizons. This distribution can be approximated with an exponential function whose local slope and slope changes represent the slip rate and its decay over time. The fit parameters, along with some function features, are reported in Table 4.

FIGURE 10

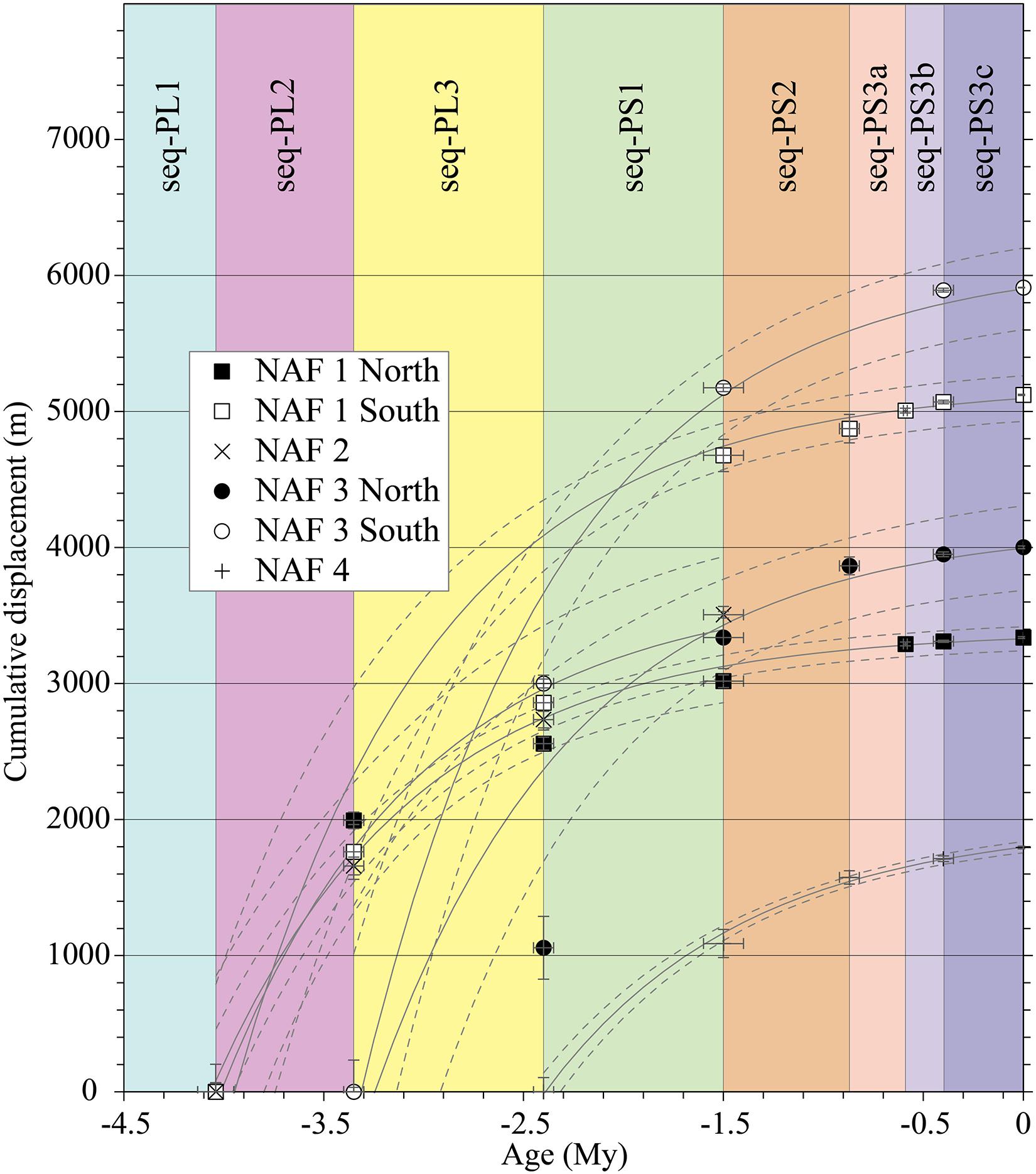
Figure 10. Cumulative displacement distribution versus age obtained from data listed in Table 3. Based on the adopted method, the displacement is attributed to each restored horizon at the bottom of each sequence, regardless of the displacement distribution during the sequence deposition. Error bars on the y-axis represent the error of interval displacement propagated from the present to older ages by adding in quadrature. Error bars on the x-axis represent the error on the age determination at the end of the interval. All datasets are fitted by an exponential function in the form y = a + be^−x (solid line) shown along with their 95% confidence interval (dashed lines). See Table 4 for the fit parameters.

TABLE 4

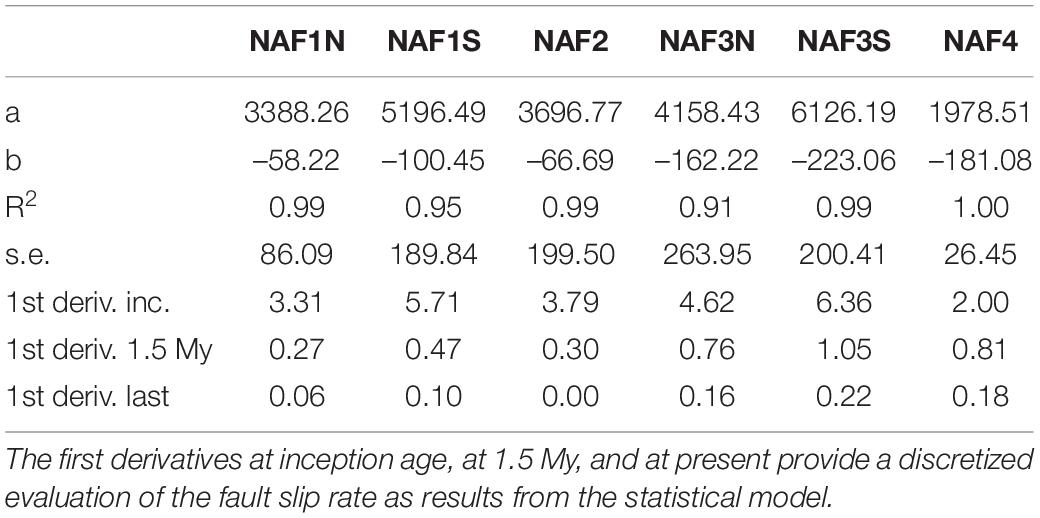
Table 4. Parameters of the fitted curves y = a + be^−x along with their coefficient of determination and the fit standard error.

The obtained slip rates for the various horizons span two orders of magnitude, from a few millimeters to a few hundredths of millimeters per year. The faster slip rates characterize the earlier stage of activity (Pliocene and Gelasian) and slower slip rates in the more recent times (Pleistocene), with the main rate change around 1.5 Ma within the deposition of seq-PS2. All faults retain some activity level until the present except for NAF2 that ceased its activity sometime after 1.5 Ma. Within the Pliocene (seq-PL1 to seq-PL3), NAF2 has rates of activity similar to those of the other structures. However, it must be noted that the Southern Section intersects NAF2 very close to its northern termination.

Further analyses are necessary to verify its activity to the south. Both cross-sections intersect NAF1 near the structural culmination; therefore, the deduced activity could be a good proxy to its maximum. NAF3 is a very long structure, and because of the lack of data between the two cross-sections, the two slip rate determinations NAF3North and NAF3South may represent the activity of two separate strands. NAF4, the youngest and outermost structure, has an onset slip rate slower than that of the older structures. However, its slip rate since hor-PS3c is almost twice as faster as the other faults in the same period.

Discussion

We analyzed a large dataset of 2D seismic profiles to perform a structural reconstruction of an offshore sector of the Northern Apennines thrust front. The reconstructed faults generally agree with the tectonic lineaments and main faults identified in previous studies (Bigi et al., 1992; Fantoni and Franciosi, 2010; DISS Working Group, 2018; Pezzo et al., 2020). Nevertheless, the quality, density, and spatial distribution of the dataset used here allowed us to improve the 3D definition of the fault geometries. Relative to the DISS Working Group’s (2018) fault compilation in the area, we characterized some new faults, such as NAF1, NAF3, NAF4, and NAF6, to be considered and provided data to improve some of the already mapped. Overall, our reconstructions provide a better definition, especially of the fault upper edges, whereas the deeper parts of the faults still require extrapolation unless data with deeper penetration become available. These improved fault geometries can help develop a new generation of seismotectonic models and earthquake hazards applications at the local scale.

As regards the seismotectonics of the area, the elusiveness of geomorphic signatures of tectonic activity in the bathymetry makes it difficult to assess the recent activity of the thrusts that has remained a matter of debate for years (e.g., Di Bucci and Mazzoli, 2002; Pezzo et al., 2020). The prevalence of sedimentary accumulation relative to the frontal anticline growth during the Pleistocene, as already observed within the Po Plain (Maesano and D’Ambrogi, 2016), causes the complete burial of the fault upper ends and the fault-related folds, thereby challenging the direct recognition of tectonic activity.

The present-day stress field acting in the Northern Adriatic Sea is also a matter of debate. Mazzoli et al. (2015) proposed maximum horizontal stress with orientation variable from NE–SW to NW–SE within a dominant transcurrent tectonic regime, based on minor seismic sequences in the area. Nonetheless, considering the distribution and clustering of stress data in the region, robust stress inversions indicate NE–SW to ENE–WSW directions of the maximum horizontal stress, which are almost orthogonal to the strike of the major contractional structures in the area (Carafa and Barba, 2013; Carafa et al., 2015b). The analysis of the seismological data of the largest past earthquake in the region (Senigallia, 1930, Mw 5.9) is consistent with a compressive stress field (Vannoli et al., 2015), as also confirmed by the focal mechanisms of the smaller seismic sequence (max Ml 5.0) recorded in the offshore of Porto San Giorgio (south of the study area) in 1987 (Riguzzi et al., 1989; Battimelli et al., 2019). This evidence suggests that the mechanism that produced the weak but not negligible deformation observed for the post-hor-PS3c (0.4 Ma) period is coherent with the current stress regime.

The structures with a 5–10 km wavelength of the outer Northern Apennines share a common basal thrust located on the top of the Meso-Cenozoic carbonatic succession (Barchi et al., 1998; Fantoni and Franciosi, 2010; Maesano et al., 2015). The flat thrust geometry is favored by the presence of a regional detachment level corresponding to the Gallare marls (upper Eocene to lower Miocene), a highly plastic formation locally characterized by overpressure zones (Livani et al., 2018). The presence of an Eocene-Miocene detachment level is a common characteristic of the entire Po Plain and Northern Adriatic Foreland (Fantoni et al., 2004; Massoli et al., 2006; Toscani et al., 2006; Maesano and D’Ambrogi, 2016; Turrini et al., 2016) and, together with a deeper decollement level located in the Triassic evaporites, is a key factor in controlling the structural style of the whole region. Basili and Barba (2007) estimated an average long-term (17 Myr) shortening rate of 2.9 mm/year of the structures above this basal thrust. Numerical modeling fitting GPS recordings and horizontal stress directions, both onshore and offshore, demonstrated the necessity of basal tractions to justify the observed ongoing deformation (Barba et al., 2008), which requires slip-rates between 0.6 and 2.5 mm/year on the basal thrust (Carafa et al., 2015a; Pezzo et al., 2020). The deformation along the common detachment should be transferred and distributed onto the outer frontal ramps. Our work focused on improving the geometric definition of these fault ramps to provide a numerical representation of how the deformation is distributed in both space and time.

As highlighted by the analysis of two regional cross-sections, we documented the asynchronous activation of four thrusts (NAF1, NAF2, NAF3, and NAF4), with a younger inception age for the outer faults as already observed in other sectors of the Northern Apennines, the Po Plain, and the Adriatic foredeep (Barchi et al., 1998; Scrocca, 2006; Scisciani and Calamita, 2009; Fantoni and Franciosi, 2010). Our findings thus confirm a general trend that characterizes the Northern Apennines fold-and-thrust belt in its entirety.

Importantly, the recent and ongoing tectonic activity can be effectively examined only after having decompacted and restored the depth-converted horizons. The removal of the differential compaction effect is necessary for the correct estimates of the deformation of fault-related folds and growth strata. The impact of differential compaction in this type of structural setting could lead to an overestimation of the slip required to restore the fault geometry (Scrocca et al., 2007; Maesano et al., 2013, 2015). After the decompaction and restoration procedure, all the analyzed structures showed evidence of activity throughout the Pleistocene. NAF2 is the only structure for which we did not find deformation evidence after the early Calabrian (hor-PS2). This result could either be due to the Southern Section position that crosses NAF2 near its northern lateral termination where its slip is minimum or to a migration of activity determining an accommodation of the deformation by the outermost structures (NAF3South).

We underline the importance of two main requirements when dealing with inverse problems for fault slip assessment, implying a non-unique solution (Cardozo et al., 2011). The first requirement is the use of horizons that need to extend across both walls of the fault. The effect of using incomplete datasets has already been evaluated and tested by comparing results in natural and analog experiments, showing that a lower spread of the results is obtained when the restored horizon includes a significant portion located on both the hanging wall and footwall of the underlying fault (Cardozo et al., 2011). The second requirement is the use of well-constrained and accurate fault geometries. During the inverse restoration with the trishear method, we observed that some of the solutions with a good performance from a numerical viewpoint (i.e., low residuals) require a fault tip located far from the actual fault (Figure 9). Since seismic reflection profiles very well constrain the fault position and geometry, we adopted a solution that weighs both the distance from the fault and the residuals on the necessary slip. The solutions closer to the actual fault trace are preferred in the slip evaluation. One of our inversion results is that the spread of slip values is quite limited, showing some dispersion only for low-weighed solutions.

The treatment of slip-rate uncertainties in tectonic contexts involving slow-moving, blind or buried, faults is one of the major outcomes of this work. In our case study, we adopted age constraints provided by literature data in most cases (Table 1), and their uncertainties were related to the dating method. The age of the most recent horizon, hor-PS3c, instead was based on a detailed interpretation of the most recent reflectors, then correlated and compared with the interpretations and mean sedimentation rates calculated in neighboring sectors of the Adriatic Sea (Amadori et al., 2020). Although this horizon does not have a strong stratigraphic constraint from previous literature, it was important to confirm the recent tectonic activity. We thus recommend using more data on sedimentation rates because they can provide further constraints to the horizon definitions that could not be performed in this work. With the data at hand, we had to treat the age uncertainty as maximum and minimum values, in which all values within that range are equally likely (boxcar PDF). Combining the age boxcar PDF with the slip Gaussian PDF resulted in a probabilistic distribution of the slip rates, representing a significant improvement in treating this epistemic uncertainty relative to previous works in the area. However, the possibility of incorporating more horizons with peaked uncertainty distributions, like a Gaussian, also for the age term would lead to narrower uncertainty in the slip rate determination and a further potential improvement. When these improvements regard the most recent fault activity stages, they can have compelling implications when such data are used as input in earthquake hazard applications because the slip rate parameter controls the tectonic moment rate that is then converted into annual earthquake rates (see Morell et al., 2020, for an overview of these relationships).

In this work, we also estimated the slip rate variations over time. Slip rates calculated for different time intervals provide evidence for an exponential decrease over time for all the investigated structures. Over the Plio-Pleistocene, such variation spans two orders of magnitude (Table 3), from a few millimeters per year during the Pliocene to early Pleistocene, coincident with the early stages of fault activity depending on the inception age, to only a few hundredths of millimeters per year during the Middle-Late Pleistocene. For example, NAF3-South is the structure with the largest slip-rate variation through time, starting its activity at more than 3 mm/year during seq-PL3, then slowing down to 0.05 mm/year during seq-PS3. NAF4, which is much younger, starts its activity at a much slower rate of ∼1.3 mm/yr during seq-PS1 and then slows down to ∼0.2 mm/year while remaining the faster structure during seq-PS3 (Table 3). The amount of restored deformation for seq-PS3c (post 0.4 Ma) is very small but not negligible in all cases. One must be aware, though, that these values are nearly in the same order of magnitude as the resolution limits of the adopted methodology, which is affected by the inherent limitations due to various factors, such as the manual picking of the seismic reflectors and the homogeneous decompaction parameters of the deposits.

For all the analyzed structures, we observed a marked slip rate reduction occurred during the Calabrian (seq-PS2), evidenced by the slope change of the fitted curves shown in Figure 10, in agreement with a general reduction of the Northern Apennines thrust fronts activity observed during the Pleistocene (Gunderson et al., 2013; Maesano et al., 2013, 2015; Bresciani and Perotti, 2014; Maesano and D’Ambrogi, 2016) coincident with the overfilling of the Po Plain - Northern Adriatic foredeep beginning in the Early Pleistocene (Gunderson et al., 2018). On average, slip rates obtained here are consistent with previous works and findings in adjacent areas (Maesano et al., 2013, 2015) and represent, in most cases, a finer temporal scan of thrust activity. However, although this trend seems to characterize most Northern Apennines thrusts, we must be aware of the exceptions such as the Mirandola Thrust, buried under the Po Plain, whose slip rates might have increased during the Middle-Late Pleistocene (Maesano et al., 2015) and be cautious in generalizing these results. Discriminating between decelerating and accelerating thrusts is key to understanding the recent Northern Apennines evolution and providing elements for mindful comparison with activity rates derived from modeling decadal geodetic (GPS and InSAR) observations and estimates of seismic efficiency (Carafa et al., 2017; Caporali et al., 2018). In this perspective, we note that the slip rates measured on the most recent horizon (hor-PS3c), and thus representing the last 0.4 Myr, for all the thrust ramps intersected by the two regional sections, collectively account for a fraction (25–50%) of the slip rates on the basal detachment (Carafa et al., 2015a; Pezzo et al., 2020). This apparent discrepancy can be explained considering that part of the basal detachment strain can be distributed on the innermost coastal or onshore active thrust (Maesano et al., 2015). The slip partition between disconnected faults and their common detachment may shed light on the mechanism that drives the slip-rate variability in the million-year timescale and contribute to better understanding the relative roles of the different factors controlling this process (Roy et al., 2016; Gunderson et al., 2018), including exogenous forcing due to the competition between erosion and deposition of the rock volume above the blind faults. In our study area, the main sediment supply comes from an axial system in an almost NW–SE elongated foredeep (Ghielmi et al., 2010, 2013; Amadori et al., 2019) where the Pleistocene sedimentation rates are fast enough to conceal the tectonic signature. The kinematic relationships between a fold-and-thrust belt and syntectonic sedimentation are crucial in controlling the thrust geometries and activity (e.g., Storti and McClay, 1995; Duerto and McClay, 2009; Fillon et al., 2013). Syntectonic sedimentation could likely play an important role also in our case study by acting as an exogenous forcing in affecting the thrust kinematics. Indeed, the Pleistocene foredeep sediments mainly come from the northwest, i.e., from outside the thrust belt and foreland system. Looking at the regional cross-sections (Figure 6) and the slip-rate values (Table 3 and Figure 10), one may notice that the clinoform deposition occurs while the tectonic signal dramatically decreases, suggesting a chronological correspondence between the high sedimentation rates and the low slip-rate values. While the increasing synkinematic sedimentation rate delays the development of frontal contractional structures and favors the formation and reactivation of more internal thrusts and backthrusts (Pla et al., 2019, and references therein), the presence of clinoforms typically indicates periods with reduced tectonic activity when new accommodation space in the basin is not created. Therefore, our data do not allow us to discriminate if the reduced tectonic activity after 1.5 Ma is the cause or the consequence of the sedimentation rate increase, but it is worth to be noted that these two processes have already been observed in large parts of the Northern Apennine outermost fronts (Maesano et al., 2013, 2015; Amadori et al., 2020).

Conclusion

In this work, we emphasized the critical role played by subsurface data in characterizing the activity of buried faults, where sedimentation rates overtake tectonic rates, counteracting the geomorphic signature development at the ground surface or the seafloor.

Using a dense dataset of 2D seismic reflection profiles and wells, we performed a 3D structural reconstruction of eleven buried thrusts of the Northern Apennines chain in a near-offshore sector of the northern Adriatic Sea. The investigated structures are consistent with previously published studies, but a well-constrained 3D reconstruction of the fault surfaces provided elements for improving the local structural setting description that can be useful for further seismotectonics and earthquake hazard analyses. The study area location is also a key factor in creating the opportunity to homogenize the results of thrust tectonics studies across the onshore-offshore transition of the Northern Apennines frontal part.

For four of the mapped thrusts, we documented the slip history over the last 4 Myr, revealing an exponential slip reduction implying a decelerating slip-rate pattern from a few millimeters to a few hundredths of millimeters per year with a major slip-rate change around 1.5 Ma. The slip histories revealed an asynchronous activation proceeding from the inner to the outer thrusts and that the youngest structure is also the fastest during the last 0.4 Myr interval. Comparing these findings with region-wide literature data confirms that, beyond the observed slip-rate variations within each fault, the strong slip-rate deceleration after 1.5 Ma is a widespread behavior of the Northern Apennines thrust faults. Yet, we are aware that also accelerating faults might exist in the thrust belt. Therefore, further studies should better address this occurrence to answer the remaining open questions on whether we can consider the deceleration due to a common regional forcing or just aleatory fluctuations of individual fault behavior.

The eight stratigraphic horizons with well-constrained age determinations (Zanclean to Middle Pleistocene) provided a slip-rate history reconstruction spanning a temporal scale that suits various geodynamic model needs. Slip rate values obtained through the analysis of older geologic markers could lead to apparent discrepancies when compared with deformation rates derived through geodetic data analyses. The slip-rate values in the most recent interval are the most appropriate to reconcile such possible discrepancies and would be useful to highlight how the geodetically derived basal thrust strain can be partitioned on different structures.

Data Availability Statement

The datasets presented in this article are not readily available because the well-log and 2D seismic reflection profiles data analyzed in this study were obtained from ENI E&P, under a non-exclusive confidentiality agreement (https://www.eni.com/en-IT/contacts.html). The VIDEPI dataset can be found online at www.videpi.com. Requests to access the datasets should be directed to https://www.eni.com/en-IT/contacts.html.

Author Contributions

YP: restoration of regional cross sections, trishear analysis, slip rate calculations, and figure preparation. FM: conceptualization, performed seismic interpretation, 3D reconstructions, trishear analysis, and slip rate calculation. CA: stratigraphic horizon age definitions, reconstruction of the 3D model, stratigraphic setting, and preparation of related figures and tables. JF: seismic interpretation and 3D reconstructions. GT: conceptualization, performed seismic interpretation, 3D fault reconstruction, restoration of regional cross sections, and managed part of the funding. RB: conceptualization, slip rates calculation, supervised the work, revised the final version of the manuscript, and managed part of the funding. All authors actively contributed to writing various parts of the manuscript according to their individual specialty and agreed with the final content.

Funding

This research was developed in the framework the SPOT project funded by the Italian Ministry of Economic Development (MISE), Directorate General for Safety-National Mining Office for Hydrocarbons and Georesources (DGS–UNMIG) under the umbrella of the offshore safety network “Clypea”—Innovation Network for Future Energy and received additional resources by PRIN 2017 (2017KT2MKE) funding by the Italian Ministry of Education, University and Research (P.I.: Giusy Lavecchia; R.U at University of Pavia: responsible Giovanni Toscani).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank ENI for the permission to consult the reflection seismic profiles and wells datasets; Manlio Ghielmi for the fruitful discussions which contributed to constrain the seismic profile interpretation, the stratigraphic horizon age definitions, and the geological reconstruction, as well as for the feedback on an earlier version of the manuscript. We also thank Mauro Coltelli for coordinating the INGV team of the SPOT project and the SPOT consortium members for insightful discussions on fault activity and related earthquake hazards. Our views, opinions, and results expressed herein do not necessarily state or reflect MISE’s and MIUR’s or any agency thereof. Petroleum Experts are acknowledged for the donation of MOVE academic licenses to the University of Pavia. We are grateful to Nestor Cardozo for his suggestions and help on the use of his code. FM and RB acknowledge the resources made available by the SISMOLAB-3D at INGV.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.664288/full#supplementary-material

Supplementary Figure 1 | Po Plain and Northern Adriatic Sea slip rates. Red lines are the main tectonic lineaments, colored circles show the location of the slip rate datasets available in literature (see Supplementary References).

Supplementary Figure 2 | Main steps of the regional cross sections’ restoration process. Colors are the same as those in Figures 6–8 of the article. The terms “fault” and “fold” near the passages indicate the restoration of the shortening associated to either fault displacement or to folding, respectively.

Supplementary Figure 3 | (A–O) Plots of trishear inversion for Northern Section. Legend: d (m): distance from fault; norm W: normalized weight (1-fval)^∗(1/d); fval is the normalized value of the regression function (Cardozo et al., 2011); p/s: ratio of fault propagation (p) versus slip on fault (s); ta (°): trishear angle; ra (°): ramp dip angle.

Supplementary Figure 4 | (A–M) Plots of trishear inversion for Southern Section. Legend: d (m): distance from fault; norm W: normalized weight (1-fval)^∗(1/d); fval is the normalized value of the regression function (Cardozo et al., 2011); p/s: ratio of fault propagation (p) versus slip on fault (s); ta (°): trishear angle; ra (°): ramp dip angle.

Footnotes

1. ^ www.videpi.com

References

Allmendinger, R. W. (1998). Inverse and forward numerical modeling of trishear fault-propagation folds. Tectonics 17, 640–656. doi: 10.1029/98TC01907

CrossRef Full Text | Google Scholar

Allmendinger, R. W., Cardozo, N., and Fisher, D. M. (2011). Structural Geology Algorithms: Vectors and Tensors. Cambridge: Cambridge University Press, 1–289.

Google Scholar

Amadori, C., Garcia-Castellanos, D., Toscani, G., Sternai, P., Fantoni, R., Ghielmi, M., et al. (2018). Restored topography of the po plain-northern adriatic region during the messinian base-level drop—implications for the physiography and compartmentalization of the palaeo-Mediterranean basin. Basin Res. 30, 1247–1263. doi: 10.1111/bre.12302

CrossRef Full Text | Google Scholar

Amadori, C., Ghielmi, M., Mancin, N., and Toscani, G. (2020). The evolution of a coastal wedge in response to Plio-Pleistocene climate change: the Northern Adriatic case. Mar. Pet. Geol. 122:104675. doi: 10.1016/j.marpetgeo.2020.104675

CrossRef Full Text | Google Scholar

Amadori, C., Toscani, G., Di Giulio, A., Maesano, F. E., D’Ambrogi, C., Ghielmi, M., et al. (2019). From cylindrical to non-cylindrical foreland basin: pliocene–pleistocene evolution of the Po Plain–Northern Adriatic basin (Italy). Basin Res. 31, 991–1015. doi: 10.1111/bre.12369

CrossRef Full Text | Google Scholar

Amorosi, A., Bruno, L., Campo, B., Costagli, B., Hong, W., Picotti, V., et al. (2020). Deformation patterns of upper quaternary strata and their relation to active tectonics, Po Basin, Italy. Sedimentology 68:sed.12784. doi: 10.1111/sed.12784

CrossRef Full Text | Google Scholar

Amorosi, A., Bruno, L., Facciorusso, J., Piccin, A., and Sammartino, I. (2016). Stratigraphic control on earthquake-induced liquefaction: a case study from the Central Po Plain (Italy). Sediment. Geol. 345, 42–53. doi: 10.1016/j.sedgeo.2016.09.002

CrossRef Full Text | Google Scholar

Antoncecchi, I., Ciccone, F., Dialuce, G., Grandi, S., Terlizzese, F. M. A., Tinti, S., et al. (2020). Progetto SPOT - Sismicità Potenzialmente Innescabile Offshore e Tsunami: Report Integrato di Fine Progetto. Roma: Ministero dello Sviluppo Economico. doi: 10.5281/zenodo.3732887

CrossRef Full Text | Google Scholar

Argnani, A. (1998). Structural elements of the adriatic Foreland. Mem. Soc. Geol. It. 52, 647–654.

Google Scholar

Barba, S., Carafa, M. M. C., and Boschi, E. (2008). Experimental evidence for mantle drag in the Mediterranean. Geophys. Res. Lett. 35:L06302. doi: 10.1029/2008GL033281

CrossRef Full Text | Google Scholar

Barchi, M. R., De Feyter, A., Magnani, M. B., Minelli, G., Pialli, G., and Sotera, B. M. (1998). The structural style of the Umbria-Marche fold and thrust belt. Mem. Soc. Geol. Ital. 52, 557–578.

Google Scholar

Basili, R., and Barba, S. (2007). Migration and shortening rates in the northern Apennines, Italy: implications for seismic hazard. Terra Nova 19, 462–468. doi: 10.1111/j.1365-3121.2007.00772.x

CrossRef Full Text | Google Scholar

Basili, R., Brizuela, B., Herrero, A., Iqbal, S., Lorito, S., Maesano, F. E., et al. (2021). The making of the NEAM Tsunami Hazard Model 2018 (NEAMTHM18). Front. Earth Sci. 8:616594. doi: 10.3389/FEART.2020.616594

CrossRef Full Text | Google Scholar

Basili, R., Valensise, G., Vannoli, P., Burrato, P., Fracassi, U., Mariano, S., et al. (2008). The Database of Individual Seismogenic Sources (DISS), version 3: summarizing 20 years of research on Italy’s earthquake geology. Tectonophysics 453, 20–43. doi: 10.1016/j.tecto.2007.04.014

CrossRef Full Text | Google Scholar

Battimelli, E., Amoroso, O., Capuano, P., and Adinolfi, G. M. (2019). Seismic activity in the central adriatic offshore of Italy: a review of the 1987 ML 5 Porto San Giorgio earthquake. Seismol. Res. Lett. 90, 1889–1901. doi: 10.1785/0220190048

CrossRef Full Text | Google Scholar

Berberian, M. (1995). Master “blind” thrust faults hidden under the zagros folds: active basement tectonics and surface morphotectonics. Tectonophysics 241, 193–224. doi: 10.1016/0040-1951(94)00185-c

CrossRef Full Text | Google Scholar

Bergen, K. J., Shaw, J. H., Leon, L. A., Dolan, J. F., Pratt, T. L., Ponti, D. J., et al. (2017). Accelerating slip rates on the Puente Hills blind thrust fault system beneath metropolitan Los Angeles, California, USA. Geology 45, 227–230. doi: 10.1130/g38520.1

CrossRef Full Text | Google Scholar

Bertotti, G., Picotti, V., Bernoulli, D., and Castellarin, A. (1993). From rifting to drifting: tectonic evolution of the South-Alpine upper crust from the Triassic to the Early Cretaceous. Sediment. Geol. 86, 53–76. doi: 10.1016/0037-0738(93)90133-P

CrossRef Full Text | Google Scholar

Bigi, G., Cosentino, D., Parotto, M., Sartori, R., and Scandone, P. (1992). Structural Model of Italy and Gravity Map, 1:500,000. Quad. Ric. Sci. 114, 3, S.EL.CA Florence.

Google Scholar

Boccaletti, M., Corti, G., and Martelli, L. (2011). Recent and active tectonics of the external zone of the Northern Apennines (Italy). Int. J. Earth Sci. 100, 1331–1348. doi: 10.1007/s00531-010-0545-y

CrossRef Full Text | Google Scholar

Bonanno, E., Bonini, L., Basili, R., Toscani, G., and Seno, S. (2017). How do horizontal, frictional discontinuities affect reverse fault-propagation folding? J. Struct. Geol. 102, 147–167. doi: 10.1016/j.jsg.2017.08.001

CrossRef Full Text | Google Scholar

Boncio, P., and Bracone, V. (2009). Active stress from earthquake focal mechanisms along the Padan-Adriatic side of the Northern Apennines (Italy), with considerations on stress magnitudes and pore-fluid pressures. Tectonophysics 476, 180–194. doi: 10.1016/j.tecto.2008.09.018

CrossRef Full Text | Google Scholar

Bonini, L., Toscani, G., and Seno, S. (2014). Three-dimensional segmentation and different rupture behavior during the 2012 Emilia seismic sequence (Northern Italy). Tectonophysics 630, 33–42. doi: 10.1016/j.tecto.2014.05.006

CrossRef Full Text | Google Scholar

Borrero, J. C., Dolan, J. F., and Synolakis, C. E. (2001). Tsunamis within the Eastern Santa Barbara Channel. Geophys. Res. Lett. 28, 643–646. doi: 10.1029/2000GL011980

CrossRef Full Text | Google Scholar

Bresciani, I., and Perotti, C. R. (2014). An active deformation structure in the Po Plain (N Italy): the Romanengo anticline. Tectonics 33, 2059–2076. doi: 10.1002/2013TC003422

CrossRef Full Text | Google Scholar

Burrato, P., Ciucci, F., and Valensise, G. (2003). An inventory of river anomalies in the Po Plain, Northern Italy: evidence for active blind thrust faulting. Ann. Geophys. 46, 865–882. doi: 10.4401/ag-3459

CrossRef Full Text | Google Scholar

Burrato, P., Vannoli, P., Fracassi, U., Basili, R., and Valensise, G. (2012). Is blind faulting truly invisible? Tectonic-controlled drainage evolution in the epicentral area of the May 2012, Emilia-Romagna earthquake sequence (northern Italy). Ann. Geophys. 55, 525–531. doi: 10.4401/ag-6182

CrossRef Full Text | Google Scholar

Caporali, A., Braitenberg, C., Montone, P., Rossi, G., Valensise, G., Viganò, A., et al. (2018). A quantitative approach to the loading rate of seismogenic sources in Italy. Geophys. J. Int. 213, 2096–2111. doi: 10.1093/gji/ggy112

CrossRef Full Text | Google Scholar

Caputo, R., Poli, M. E., and Zanferrari, A. (2010). Neogene-Quaternary tectonic stratigraphy of the eastern Southern Alps, NE Italy. J. Struct. Geol. 32, 1009–1027. doi: 10.1016/j.jsg.2010.06.004

CrossRef Full Text | Google Scholar

Carafa, M. M. C., and Barba, S. (2013). The stress field in Europe: optimal orientations with confidence limits. Geophys. J. Int. 193, 531–548. doi: 10.1093/gji/ggt024

CrossRef Full Text | Google Scholar

Carafa, M. M. C., Barba, S., and Bird, P. (2015a). Neotectonics and long-term seismicity in Europe and the Mediterranean region. J. Geophys. Res. Solid Earth 120, 5311–5342. doi: 10.1002/2014JB011751

CrossRef Full Text | Google Scholar

Carafa, M. M. C., Tarabusi, G., and Kastelic, V. (2015b). SHINE: web application for determining the horizontal stress orientation. Comput. Geosci. 74, 39–49. doi: 10.1016/j.cageo.2014.10.001

CrossRef Full Text | Google Scholar

Carafa, M. M. C., Valensise, G., and Bird, P. (2017). Assessing the seismic coupling of shallow continental faults and its impact on seismic hazard estimates: a case-study from Italy. Geophys. J. Int. 209, 32–47. doi: 10.1093/gji/ggx002

CrossRef Full Text | Google Scholar

Cardozo, N., and Aanonsen, S. (2009). Optimized trishear inverse modeling. J. Struct. Geol. 31, 546–560. doi: 10.1016/j.jsg.2009.03.003

CrossRef Full Text | Google Scholar

Cardozo, N., Jackson, C. A.-L., and Whipp, P. S. (2011). Determining the uniqueness of best-fit trishear models. J. Struct. Geol. 33, 1063–1078. doi: 10.1016/j.jsg.2011.04.001

CrossRef Full Text | Google Scholar

Carminati, E., and Siletto, G. B. (1997). The effects of brittle-plastic transitions in basement-involved foreland belts: the Central Southern Alps case (N Italy). Tectonophysics 280, 107–123. doi: 10.1016/S0040-1951(97)00135-2

CrossRef Full Text | Google Scholar

Carminati, E., Lustrino, M., and Doglioni, C. (2012). Geodynamic evolution of the central and western Mediterranean: tectonics vs. igneous petrology constraints. Tectonophysics 579, 173–192. doi: 10.1016/j.tecto.2012.01.026

CrossRef Full Text | Google Scholar

Casero, P. (2004). “Structural setting of petroleum exploration plays in Italy,” in Special Volume of the Italian Geological Society for the IGC 32 Florence-2004, eds U. Crescenti, S. D’Offizi, S. Merlino, and L. Sacchi (Rome: Italian Geological Society), 189–199.

Google Scholar

Cassano, E., Anelli, L., Fichera, R., and Cappelli, V. (1986). “Pianura Padana: interpretazione integrata di dati geofisici e geologici,” in Paper presented at 73° Congr. della Soc. Geol. Ital, (Roma: AGIP), 27.

Google Scholar

Castellarin, A., Eva, C., Giglia, G., and Vai, G. B. (1985). Analisi strutturale del fronte appenninico padano. Giomale Geol. 47, 47–75.

Google Scholar

Catuneanu, O. (2004). Basement control on flexural profiles and the distribution of foreland facies: the Dwyka Group of the Karoo Basin, South Africa. Geology 32, 517–520. doi: 10.1130/G20526.1

CrossRef Full Text | Google Scholar

Chevalier, M.-L., Tapponnier, P., Van der Woerd, J., Ryerson, F. J., Finkel, R. C., and Li, H. (2012). Spatially constant slip rate along the southern segment of the Karakorum fault since 200ka. Tectonophysics, 530– 531, 152–179. doi: 10.1016/j.tecto.2011.12.014

CrossRef Full Text | Google Scholar

Devoti, R., Esposito, A., Pietrantonio, G., Pisani, A. R., and Riguzzi, F. (2011). Evidence of large scale deformation patterns from GPS data in the Italian subduction boundary. Earth Planet. Sci. Lett. 311, 230–241. doi: 10.1016/j.epsl.2011.09.034

CrossRef Full Text | Google Scholar

Dewey, J. F., Helman, M. L., Knott, S. D., Turco, E., and Hutton, D. H. W. (1989). Kinematics of the western Mediterranean. Geol. Soc. Spec. Publ. 45, 265–283. doi: 10.1144/GSL.SP.1989.045.01.15

CrossRef Full Text | Google Scholar

Di Bucci, D., and Mazzoli, S. (2002). Active tectonics of the Northern Apennines and Adria geodynamics: new data and a discussion. J. Geodyn. 34, 687–707. doi: 10.1016/S0264-3707(02)00107-2

CrossRef Full Text | Google Scholar

Di Bucci, D., Antoncecchi, I., Ciccone, F., Teofilo, G., Terlizzese, F., Argnani, A., et al. (2017). The SPOT project (Potentially triggerable offshore seismicity and tsunamis): a first appraisal of the possible impact of oil and gas platforms on the seismic and tsunami risks along the Italian coasts. Geoingegneria Ambientale e Mineraria 152, 61–68.

Google Scholar

DISS Working Group (2018). Database of Individual Seismogenic Sources (DISS), Version 3.2.1: A Compilation of Potential Sources for Earthquakes Larger than M 5.5 in Italy and Surrounding Areas. Italian: Istituto Nazionale di Geofisica e Vulcanologia. doi: 10.6092/INGV.IT-DISS3.2.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Dolan, J. F., Christofferson, S. A., and Shaw, J. H. (2003). Recognition of paleoearthquakes on the Puente Hills blind thrust fault, California. Science 300, 115–118. doi: 10.1126/science.1080593

PubMed Abstract | CrossRef Full Text | Google Scholar

Duerto, L., and McClay, K. (2009). The role of syntectonic sedimentation in the evolution of doubly vergent thrust wedges and foreland folds. Mar. Pet. Geol. 26, 1051–1069. doi: 10.1016/j.marpetgeo.2008.07.004

CrossRef Full Text | Google Scholar

Dunne, W. M., and Ferrill, D. A. (1988). Blind thrust systems. Geology 16, 33–36. doi: 10.1130/0091-76131988016<0033:BTS<2.3.CO;2

CrossRef Full Text | Google Scholar

Egan, S. S., Buddin, T. S., Kane, S., and Williams, G. D. (1997). Three-dimensional modelling and visualisation in structural geology: new techniques for the restoration and balancing of volumes. proceedings of the 1996 geoscience information group conference on geological visualisation. Electron. Geol. 1, 67–82.

Google Scholar

EMODnet Bathymetry Consortium (2020). EMODnet Digital Bathymetry (DTM). Available online at: https://doi.org/10.12770/bb6a87dd-e579-4036-abe1-e649cea9881a. (Accessed March 20, 2021).

Google Scholar

Erslev, E. A. (1991). Trishear fault-propagation folding. Geology 19, 617–620. doi: 10.1130/0091-76131991019<0617:TFPF>2.3.CO;2

CrossRef Full Text | Google Scholar

Fantoni, R., and Franciosi, R. (2008). 8 geological sections crossing Po Plain and Adriatic foreland. Rend. Online Soc. Geol. It. 3, 367–368.

Google Scholar

Fantoni, R., and Franciosi, R. (2010). Tectono-sedimentary setting of the Po Plain and adriatic Foreland. Rend. Lincei 21, S197–S209. doi: 10.1007/s12210-010-0102-4

CrossRef Full Text | Google Scholar

Fantoni, R., Bersezio, R., and Forcella, F. (2004). Alpine structure and deformation chronology at the Southern Alps-Po Plain border in Lombardy. Boll. Della Soc. Geol. Ital. 123, 463–476.

Google Scholar

Fantoni, R., Catellani, D., Merlini, S., Rogledi, S., and Venturini, S. (2002). La registrazione degli eventi deformativi cenozoici nell’avampaese Veneto-Friulano. Mem. Della Soc. Geol. Ital. 57, 301–313.

Google Scholar

Fillon, C., Huismans, R. S., Van Der Beek, P., and Muñoz, J. A. (2013). Syntectonic sedimentation controls on the evolution of the southern Pyrenean fold-and-thrust belt: inferences from coupled tectonic-surface processes models. J. Geophys. Res. Solid Earth 118, 5665–5680. doi: 10.1002/jgrb.50368

CrossRef Full Text | Google Scholar

Finocchio, D., Barba, S., and Basili, R. (2016). Slip rate depth distribution for active faults in Central Italy using numerical models. Tectonophysics 687, 232–244. doi: 10.1016/j.tecto.2016.07.031

CrossRef Full Text | Google Scholar

Fisher, M. A., Normark, W. R., Langenheim, V. E., Calvert, A. J., and Sliter, R. (2004). The offshore Palos Verdes fault zone near San Pedro, Southern California. Bull. Seismol. Soc. Am. 94, 506–530. doi: 10.1785/0120030042

CrossRef Full Text | Google Scholar

Frankel, K. L., Dolan, J. F., Owen, L. A., Ganev, P., and Finkel, R. C. (2011). Spatial and temporal constancy of seismic strain release along an evolving segment of the Pacific–North America plate boundary. Earth Planet. Sci. Lett. 304, 565–576. doi: 10.1016/j.epsl.2011.02.034

CrossRef Full Text | Google Scholar

Ghielmi, M., Minervini, M., Nini, C., Rogledi, S., and Rossi, M. (2013). Late miocene-middle pleistocene sequences in the Po Plain - Northern Adriatic Sea (Italy): the stratigraphic record of modification phases affecting a complex foreland basin. Mar. Pet. Geol. 42, 50–81. doi: 10.1016/j.marpetgeo.2012.11.007

CrossRef Full Text | Google Scholar

Ghielmi, M., Minervini, M., Nini, C., Rogledi, S., Rossi, M., and Vignolo, A. (2010). Sedimentary and tectonic evolution in the eastern Po-Plain and northern Adriatic Sea area from Messinian to Middle Pleistocene (Italy). Rend. Lincei 21, 131–166. doi: 10.1007/s12210-010-0101-5

CrossRef Full Text | Google Scholar

Ghielmi, M., Serafini, G., Artoni, A., Di Celma, C., and Pitts, A. (2019). “From Messinian to Pleistocene: tectonic evolution and stratigraphic architecture of the central Adriatic foredeep (Abruzzo and Marche, Central Italy),” in Field Trips - Guide Book, eds M. Viglio, M. Tropeano, V. Pascucci, D. Ruber, and L. Sabato (Rome: IAS).

Google Scholar

Gold, R. D., and Cowgill, E. (2011). Deriving fault-slip histories to test for secular variation in slip, with examples from the Kunlun and Awatere faults. Earth Planet. Sci. Lett. 301, 52–64. doi: 10.1016/j.epsl.2010.10.011

CrossRef Full Text | Google Scholar

Guidoboni, E., Ferrari, G., Mariotti, D., Comastri, A., Tarabusi, G., Sgattoni, G., et al. (2018). CFTI5Med, Catalogo dei Forti Terremoti in Italia (461 a.C.-1997) e nell’area Mediterranea (760 a.C.-1500). Italy: Istituto Nazionale di Geofisica e Vulcanologia (INGV).

Google Scholar

Guidoboni, E., Ferrari, G., Tarabusi, G., Sgattoni, G., Comastri, A., Mariotti, D., et al. (2019). CFTI5Med, the new release of the catalogue of strong earthquakes in Italy and in the Mediterranean area. Sci. Data 6:80. doi: 10.1038/s41597-019-0091-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Gunderson, K. L., Anastasio, D. J., Pazzaglia, F. J., and Kodama, K. P. (2018). Intrinsically variable blind thrust faulting. Tectonics 37, 1454–1471. doi: 10.1029/2017TC004917

CrossRef Full Text | Google Scholar

Gunderson, K. L., Anastasio, D. J., Pazzaglia, F. J., and Picotti, V. (2013). Fault slip rate variability on 104-105yr timescales for the Salsomaggiore blind thrust fault, Northern Apennines, Italy. Tectonophysics 608, 356–365. doi: 10.1016/j.tecto.2013.09.018

CrossRef Full Text | Google Scholar

Handy, M. R., Schmid, S. M., Bousquet, R., Kissling, E., and Bernoulli, D. (2010). Reconciling plate-tectonic reconstructions of Alpine Tethys with the geological-geophysical record of spreading and subduction in the Alps. Earth Sci. Rev. 102, 121–158. doi: 10.1016/j.earscirev.2010.06.002

CrossRef Full Text | Google Scholar

Hauksson, E., Jones, L. M., and Hutton, K. (1995). The 1994 Northridge earthquake sequence in California: seismological and tectonic aspects. J. Geophys. Res. 100, 12335–12355. doi: 10.1029/95jb00865

CrossRef Full Text | Google Scholar

Hayes, G. P., Briggs, R. W., Sladen, A., Fielding, E. J., Prentice, C., Hudnut, K., et al. (2010). Complex rupture during the 12 January 2010 Haiti earthquake. Nat. Geosci. 3, 800–805. doi: 10.1038/ngeo977

CrossRef Full Text | Google Scholar

Kastelic, V., Vannoli, P., Burrato, P., Fracassi, U., Tiberti, M. M., and Valensise, G. (2013). Seismogenic sources in the adriatic domain. Mar. Pet. Geol. 42, 191–213. doi: 10.1016/j.marpetgeo.2012.08.002

CrossRef Full Text | Google Scholar

Lettis, W. R., Wells, D. L., and Baldwin, J. N. (1997). Empirical observations regarding reverse earthquakes, blind thrust faults, and quaternary deformation: are blind thrust faults truly blind? Bull. Seismol. Soc. Am. 87, 1171–1198.

Google Scholar

Lirer, F., Foresi, L. M., Iaccarino, S. M., Salvatorini, G., Turco, E., Cosentino, C., et al. (2019). Mediterranean neogene planktonic foraminifer biozonation and biochronology. Earth Sci. Rev. 196:102869. doi: 10.1016/j.earscirev.2019.05.013

CrossRef Full Text | Google Scholar

Livani, M., Scrocca, D., Arecco, P., and Doglioni, C. (2018). Structural and Stratigraphic control on salient and recess development along a thrust belt front: the Northern Apennines (Po Plain, Italy). J. Geophys. Res. Solid Earth 123, 4360–4387. doi: 10.1002/2017JB015235

CrossRef Full Text | Google Scholar

Livio, F. A., Berlusconi, A., Zerboni, A., Trombino, L., Sileo, G., Michetti, A. M., et al. (2014). Progressive offset and surface deformation along a seismogenic blind thrust in the Po Plain foredeep (Southern Alps, Northern Italy). J. Geophys. Res. Solid Earth 119, 7701–7721. doi: 10.1002/2014JB011112

CrossRef Full Text | Google Scholar

Lourens, L. J. (2004). Revised tuning of Ocean Drilling Program Site 964 and KC01B (Mediterranean) and implications for the δ18O, tephra, calcareous nannofossil, and geomagnetic reversal chronologies of the past 1.1 Myr. Paleoceanography 19:PA3010. doi: 10.1029/2003PA000997

CrossRef Full Text | Google Scholar

Lourens, L. J., Hilgen, F. J., and Raffi, I. (1998). “Base of large Gephyrocapsa and astronomical calibration of early Pleistocene sapropels in Site 967 and Hole 969D: solving the chronology of the Vrica section (Calabria, Italy),” in Proc. Ocean Drill. Progr. Sci. Results, eds A.H.F. Robertson, K.-C. Emeis, C. Richter, and A. Camerlenghi (College Station, TX: Ocean Drilling Program), 191–198.

Google Scholar

Lourens, L., Hilgen, F. J., Shackleton, N. J., Laskar, J., and Wilson, D. (2004). “The Neogene period,” in A Geologic Time Scale 2004, eds F. M. Gradstein, J. Ogg, and A. Smith (Cambridge: Cambridge University Press), 409–440. doi: 10.1017/CBO9780511536045.022

CrossRef Full Text | Google Scholar

Maesano, F. E., and D’Ambrogi, C. (2016). Coupling sedimentation and tectonic control: pleistocene evolution of the central Po Basin. Ital. J. Geosci. 135, 394–407. doi: 10.3301/IJG.2015.17

CrossRef Full Text | Google Scholar

Maesano, F. E., and D’Ambrogi, C. (2017). Vel-IO 3D: a tool for 3D velocity model construction, optimization and time-depth conversion in 3D geological modeling workflow. Comput. Geosci. 99, 171–182. doi: 10.1016/j.cageo.2016.11.013

CrossRef Full Text | Google Scholar

Maesano, F. E., D’Ambrogi, C., Burrato, P., and Toscani, G. (2015). Slip-rates of blind thrusts in slow deforming areas: examples from the Po Plain (Italy). Tectonophysics 643, 8–25. doi: 10.1016/j.tecto.2014.12.007

CrossRef Full Text | Google Scholar

Maesano, F. E., Toscani, G., Burrato, P., Mirabella, F., D’Ambrogi, C., and Basili, R. (2013). Deriving thrust fault slip rates from geological modeling: examples from the Marche coastal and offshore contraction belt, Northern Apennines, Italy. Mar. Pet. Geol. 42, 122–134. doi: 10.1016/j.marpetgeo.2012.10.008

CrossRef Full Text | Google Scholar

Maesano, F. E., Volpi, V., Civile, D., Basili, R., Conti, A., Tiberti, M. M., et al. (2020). Active extension in a Foreland trapped between two contractional chains: the South Apulia Fault System (SAFS). Tectonics 39:e2020TC006116. doi: 10.1029/2020TC006116

CrossRef Full Text | Google Scholar

Maestrelli, D., Benvenuti, M., Bonini, M., Carnicelli, S., Piccardi, L., and Sani, F. (2018). The structural hinge of a chain-foreland basin: quaternary activity of the Pede-apennine thrust front (Northern Italy). Tectonophysics 723, 117–135. doi: 10.1016/j.tecto.2017.12.006

CrossRef Full Text | Google Scholar

Maino, M., Decarlis, A., Felletti, F., and Seno, S. (2013). Tectono-sedimentary evolution of the tertiary piedmont basin (NW Italy) within the oligo-miocene central mediterranean geodynamics. Tectonics 32, 593–619. doi: 10.1002/tect.20047

CrossRef Full Text | Google Scholar

Malinverno, A., and Ryan, W. B. F. (1986). Extension in the tyrrhenian sea and shortening in the apennines as result of arc migration driven by sinking of the lithosphere. Tectonics 5, 227–245. doi: 10.1029/TC005i002p00227

CrossRef Full Text | Google Scholar

Mancinelli, P., and Scisciani, V. (2020). Seismic velocity-depth relation in a siliciclastic turbiditic foreland basin: a case study from the Central Adriatic Sea. Mar. Pet. Geol. 120:104554. doi: 10.1016/j.marpetgeo.2020.104554

CrossRef Full Text | Google Scholar

Masetti, D., Fantoni, R., Romano, R., Sartorio, D., and Trevisani, E. (2012). Tectonostratigraphic evolution of the Jurassic extensional basins of the eastern southern Alps and Adriatic foreland based on an integrated study of surface and subsurface data. Am. Assoc. Pet. Geol. Bull. 96, 2065–2089. doi: 10.1306/03091211087

CrossRef Full Text | Google Scholar

Massari, F., Rio, D., Serandrei Barbero, R., Asioli, A., Capraro, L., Fornaciari, E., et al. (2004). The environment of venice area in the past two million years. Palaeogeogr. Palaeoclimatol. Palaeoecol. 202, 273–308. doi: 10.1016/S0031-0182(03)00640-0

CrossRef Full Text | Google Scholar

Massoli, D., Koyi, H. A., and Barchi, M. R. (2006). Structural evolution of a fold and thrust belt generated by multiple décollements: analogue models and natural examples from the Northern Apennines (Italy). J. Struct. Geol. 28, 185–199. doi: 10.1016/j.jsg.2005.11.002

CrossRef Full Text | Google Scholar

Mazzoli, S., Santini, S., Macchiavelli, C., and Ascione, A. (2015). Active tectonics of the outer northern Apennines: adriatic vs. po plain seismicity and stress fields. J. Geodyn. 84, 62–76. doi: 10.1016/j.jog.2014.10.002

CrossRef Full Text | Google Scholar

McAuliffe, L. J., Dolan, J. F., Rhodes, E. J., Hubbard, J., Shaw, J. H., and Pratt, T. L. (2015). Paleoseismologic evidence for large-magnitude (MW 7.5-8.0) earthquakes on the Ventura blind thrust fault: implications for multifault ruptures in the transverse ranges of southern California. Geosphere 11, 1629–1650. doi: 10.1130/GES01123.1

CrossRef Full Text | Google Scholar

Micallef, A., Camerlenghi, A., Garcia-Castellanos, D., Cunarro Otero, D., Gutscher, M. A., Barreca, G., et al. (2018). Evidence of the Zanclean megaflood in the eastern Mediterranean Basin. Sci. Rep. 8:1078. doi: 10.1038/s41598-018-19446-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Michetti, A. M., Giardina, F., Livio, F., Mueller, K., Serva, L., Sileo, G., et al. (2012). Active compressional tectonics, quaternary capable faults, and the seismic landscape of the po plain (northern Italy). Ann. Geophys. 55, 969–1001. doi: 10.4401/ag-5462

CrossRef Full Text | Google Scholar

Morell, K. D., Styron, R., Stirling, M., Griffin, J., Archuleta, R., and Onur, T. (2020). Seismic hazard analyses from geologic and geomorphic data: current and future challenges. Tectonics 39:e2018TC005365. doi: 10.1029/2018TC005365

CrossRef Full Text | Google Scholar

Mutti, E., Tinterri, R., Remacha, E., Mavilla, N., Angella, S., and Fava, L. (1999). An Introduction To the Analysis of Ancient Turbidite Basins From an Outcrop Perspective: Aapg Continuing Education Course Note Series #39. AAPG Contin. Educ. Course Note Series, 93. Tulsa, OK: AAPG.

Google Scholar

Muttoni, G., Carcano, C., Garzanti, E., Ghielmi, M., Piccin, A., Pini, R., et al. (2003). Onset of major pleistocene glaciations in the alps. Geology 31, 989–992. doi: 10.1130/G19445.1

CrossRef Full Text | Google Scholar

Nespoli, M., Belardinelli, M. E., Anderlini, L., Bonafede, M., Pezzo, G., Todesco, M., et al. (2017). Effects of layered crust on the coseismic slip inversion and related CFF variations: hints from the 2012 Emilia Romagna earthquake. Phys. Earth Planet. Inter. 273, 23–35. doi: 10.1016/j.pepi.2017.10.011

CrossRef Full Text | Google Scholar

Nespoli, M., Todesco, M., Serpelloni, E., Belardinelli, M. E., Bonafede, M., Marcaccio, M., et al. (2016). Modeling earthquake effects on groundwater levels: evidences from the 2012 Emilia earthquake (Italy). Geofluids 16, 452–463. doi: 10.1111/gfl.12165

CrossRef Full Text | Google Scholar

Oakley, D. O. S., and Fisher, D. M. (2015). Inverse trishear modeling of bedding dip data using markov chain Monte Carlo methods. J. Struct. Geol. 80, 157–172. doi: 10.1016/j.jsg.2015.09.005

CrossRef Full Text | Google Scholar

Palano, M., Pezzo, G., Serpelloni, E., Devoti, R., D’Agostino, N., Gandolfi, S., et al. (2020). Geopositioning time series from offshore platforms in the Adriatic Sea. Sci. Data 7:373. doi: 10.1038/s41597-020-00705-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Passone, L., and Mai, P. M. (2017). Kinematic earthquake ground-motion simulations on listric normal faults. Bull. Seism. Soc. Am. 107, 2980–2993. doi: 10.1785/0120170111

CrossRef Full Text | Google Scholar

Patacca, E., Sartori, R., and Scandone, P. (1990). Tyrrhenian basin and apenninic arcs: kinematic relations since late tortonian times. Mem. Soc. Geol. It. 45, 425–451.

Google Scholar

Pezzo, G., Boncori, J. P. M., Tolomei, C., Salvi, S., Atzori, S., Antonioli, A., et al. (2013). Coseismic deformation and source modeling of the May 2012 Emilia (Northern Italy) earthquakes. Seismol. Res. Lett. 84, 645–655. doi: 10.1785/0220120171

CrossRef Full Text | Google Scholar

Pezzo, G., Petracchini, L., Devoti, R., Maffucci, R., Anderlini, L., Antoncecchi, I., et al. (2020). Active fold-thrust belt to Foreland transition in Northern Adria, Italy, tracked by seismic reflection profiles and GPS offshore data. Tectonics 39:e2020TC006425. doi: 10.1029/2020TC006425

CrossRef Full Text | Google Scholar

Pieri, M., and Groppi, G. (1981). Subsurface Geological Structure of the Po Plain, Italy. C.N.R. (Ed.), Progett. Final. Geodin. 414, 1–13.

Google Scholar

Pla, O., Roca, E., Xie, H., Izquierdo-Llavall, E., Muñoz, J. A., Rowan, M. G., et al. (2019). Influence of syntectonic sedimentation and décollement rheology on the geometry and evolution of orogenic wedges: analog modeling of the Kuqa fold-and-thrust belt (NW China). Tectonics 38, 2727–2755. doi: 10.1029/2018TC005386

CrossRef Full Text | Google Scholar

Pueyo Anchuela, Ó, Lafuente, P., Arlegui, L., Liesa, C. L., and Simón, J. L. (2016). Geophysical characterization of buried active faults: the concud fault (Iberian Chain, NE Spain). Int. J. Earth Sci. 105, 2221–2239. doi: 10.1007/s00531-015-1283-y

CrossRef Full Text | Google Scholar

Regione Emilia–Romagna, and ENI-AGIP (1998). in Riserve Idrichesotterranee Nella Regione Emilia–Romagna, ed. G. Di Dio (Firenze: S.EL.CA), 119.

Google Scholar

Regione Lombardia, and ENI-AGIP (2002). in Geologia Degli Acquiferi Padani della Regione Lombardia, eds C. Carcano and A. Piccin (Firenze: S.EL.CA), 130.

Google Scholar

Riguzzi, F., Tertulliani, A., and Gasparini, C. (1989). Study of the seismic sequence of Porto San Giorgio (Marche)-3 July 1987. I1 Nuovo Cim. C 12, 453–466. doi: 10.1007/BF02525078

CrossRef Full Text | Google Scholar

Roering, J. J., Cooke, M. L., and Pollard, D. D. (1997). Why blind thrust faults do not propagate to the Earth’s surface: numerical modeling of coseismic deformation associated with thrust-related anticlines. J. Geophys. Res. B Solid Earth 102, 11901–11912. doi: 10.1029/97jb00680

CrossRef Full Text | Google Scholar

Rossi, M., Minervini, M., Ghielmi, M., and Rogledi, S. (2015). Messinian and Pliocene erosional surfaces in the Po Plain-Adriatic Basin: insights from allostratigraphy and sequence stratigraphy in assessing play concepts related to accommodation and gateway turnarounds in tectonically active margins. Mar. Pet. Geol. 66, 192–216. doi: 10.1016/j.marpetgeo.2014.12.012

CrossRef Full Text | Google Scholar

Rovida, A., Locati, M., Camassi, R., Lolli, B., and Gasperini, P. (2020). The Italian earthquake catalogue CPTI15. Bull. Earthq. Eng. 18, 2953–2984. doi: 10.1007/s10518-020-00818-y

CrossRef Full Text | Google Scholar

Roy, S. G., Koons, P. O., Upton, P., and Tucker, G. E. (2016). Dynamic links among rock damage, erosion, and strain during orogenesis. Geology 44, 583–586. doi: 10.1130/G37753.1

CrossRef Full Text | Google Scholar

Scisciani, V., and Calamita, F. (2009). Active intraplate deformation within Adria: examples from the Adriatic region. Tectonophysics 476, 57–72. doi: 10.1016/j.tecto.2008.10.030

CrossRef Full Text | Google Scholar

Sclater, J. G., and Christie, P. A. F. (1980). Continental stretching: an explanation of the Post-Mid-Cretaceous subsidence of the central North Sea Basin. J. Geophys. Res. Solid Earth 85, 3711–3739. doi: 10.1029/jb085ib07p03711

CrossRef Full Text | Google Scholar

Scognamiglio, L., Margheriti, L., Mele, F. M., Tinti, E., Bono, A., De Gori, P., et al. (2012). The 2012 Pianura Padana Emiliana seimic sequence: locations, moment tensors and magnitudes. Ann. Geophys. 55, 549–559. doi: 10.4401/ag-6159

PubMed Abstract | CrossRef Full Text | Google Scholar

Scrocca, D. (2006). Thrust front segmentation induced by differential slab retreat in the Apennines (Italy). Terra Nov. 18, 154–161. doi: 10.1111/j.1365-3121.2006.00675.x

CrossRef Full Text | Google Scholar

Scrocca, D., Carminati, E., Doglioni, C., and Marcantoni, D. (2007). “Slab retreat and active shortening along the central-northern apennines,” in Thrust Belts and Foreland Basins: from Fold Kinematics to Hydrocarbon Systems, eds O. Lacombe, J. Lavé, F. Roure, and J. Verges (Berlin: Springer), 471–487. doi: 10.1007/978-3-540-69426-7_25

CrossRef Full Text | Google Scholar

Serpelloni, E., Anderlini, L., Avallone, A., Cannelli, V., Cavaliere, A., Cheloni, D., et al. (2012). GPS observations of coseismic deformation following the May 20 and 29, 2012, Emilia seismic events (northern Italy): data, analysis and preliminary models. Ann. Geophys. 55, 759–766. doi: 10.4401/ag-6168

CrossRef Full Text | Google Scholar

Shaw, J. H., and Shearer, P. M. (1999). An elusive blind-thrust fault beneath metropolitan Los Angeles. Science 283, 1516–1518. doi: 10.1126/science.283.5407.1516

PubMed Abstract | CrossRef Full Text | Google Scholar

Shaw, J. H., Plesch, A., Dolan, J. F., Pratt, T. L., and Fiore, P. (2002). Puente Hills blind-thrust system, Los Angeles, California. Bull. Seismol. Soc. Am. 92, 2946–2960. doi: 10.1785/0120010291

CrossRef Full Text | Google Scholar

Sorlien, C. C., Kamerling, M. J., Seeber, L., and Broderick, K. G. (2006). Restraining segments and reactivation of the Santa Monica-Dume-Malibu Coast fault system, offshore Los Angeles, California. J. Geophys. Res. Solid Earth 111:B11402. doi: 10.1029/2005JB003632

CrossRef Full Text | Google Scholar

Sprovieri, R., Di Stefano, E., Howell, M., Sakamoto, T., Di Stefano, A., and Marino, M. (1998). Integrated calcareous plankton biostratigraphy and cyclostratigraphy at Site 964. Proc. Ocean Drill. Progr. Sci. Results 160, 155–166. doi: 10.2973/odp.proc.sr.160.010.1998

CrossRef Full Text | Google Scholar

Stein, R. S., and Ekström, G. (1992). Seismicity and geometry of a 110-km-long blind thrust fault 2. synthesis of the 1982–1985 California earthquake sequence. J. Geophys. Res. 97:4865. doi: 10.1029/91jb02847

CrossRef Full Text | Google Scholar

Storti, F., and McClay, K. (1995). Influence of syntectonic sedimentation on thrust wedges in analogue models. Geology 23, 999–1002. doi: 10.1130/0091-7613(1995)023<0999:IOSSOT>2.3.CO;2

CrossRef Full Text | Google Scholar

Stramondo, S., Saroli, M., Tolomei, C., Moro, M., Doumaz, F., Pesci, A., et al. (2007). Surface movements in Bologna (Po Plain - Italy) detected by multitemporal DInSAR. Remote Sens. Environ. 110, 304–316. doi: 10.1016/j.rse.2007.02.023

CrossRef Full Text | Google Scholar

Styron, R. (2019). The impact of earthquake cycle variability on neotectonic and paleoseismic slip rate estimates. Solid Earth 10, 15–25. doi: 10.5194/se-10-15-2019

CrossRef Full Text | Google Scholar

Taylor, S. K., Nicol, A., and Walsh, J. J. (2008). Displacement loss on growth faults due to sediment compaction. J. Struct. Geol. 30, 394–405. doi: 10.1016/j.jsg.2007.11.006

CrossRef Full Text | Google Scholar

Teatini, P., Tosi, L., and Strozzi, T. (2011). Quantitative evidence that compaction of Holocene sediments drives the present land subsidence of the Po Delta, Italy. J. Geophys. Res. Solid Earth 116:B08407. doi: 10.1029/2010JB008122

CrossRef Full Text | Google Scholar

Tiberti, M. M., Basili, R., and Vannoli, P. (2014). Ups and downs in western Crete (Hellenic subduction zone). Sci. Rep. 4:5677. doi: 10.1038/srep05677

PubMed Abstract | CrossRef Full Text | Google Scholar

Tiberti, M. M., Lorito, S., Basili, R., Kastelic, V., Piatanesi, A., and Valensise, G. (2008). Scenarios of earthquake-generated tsunamis for the Italian coast of the Adriatic Sea. Pure Appl. Geophys. 165, 2117–2142. doi: 10.1007/s00024-008-0417-6

CrossRef Full Text | Google Scholar

Tizzani, P., Castaldo, R., Solaro, G., Pepe, S., Bonano, M., Casu, F., et al. (2013). New insights into the 2012 Emilia (Italy) seismic sequence through advanced numerical modeling of ground deformation InSAR measurements. Geophys. Res. Lett. 40, 1971–1977. doi: 10.1002/grl.50290

CrossRef Full Text | Google Scholar

Tonini, R., Basili, R., Maesano, F. E., Tiberti, M. M., Lorito, S., Romano, F., et al. (2020). Importance of earthquake rupture geometry on tsunami modelling: the Calabrian Arc subduction interface (Italy) case study. Geoph. J. Intern. 233, 1805–1819. doi: 10.1093/gji/ggaa409

CrossRef Full Text | Google Scholar

Toscani, G., Bonini, L., Ahmad, M. I., Bucci, D., Di Giulio, A., Di, et al. (2014). Opposite verging chains sharing the same foreland: kinematics and interactions through analogue models (Central Po Plain, Italy). Tectonophysics 633, 268–282. doi: 10.1016/j.tecto.2014.07.019

CrossRef Full Text | Google Scholar

Toscani, G., Marchesini, A., Barbieri, C., Di Giulio, A., Fantoni, R., Mancin, N., et al. (2016). The friulian-venetian basin I: architecture and sediment flux into a shared foreland basin. Ital. J. Geosci. 135, 444–459. doi: 10.3301/IJG.2015.35

CrossRef Full Text | Google Scholar

Toscani, G., Seno, S., Fantoni, R., and Rogledi, S. (2006). Geometry and timing of deformation inside a structural arc; the case of the western Emilian folds (Northern Apennine front, Italy). Boll. Soc. Geol. Ital. 125, 59–65.

Google Scholar

Turrini, C., Lacombe, O., and Roure, F. (2014). Present-day 3D structural model of the Po Valley basin, Northern Italy. Mar. Pet. Geol. 56, 266–289. doi: 10.1016/j.marpetgeo.2014.02.006

CrossRef Full Text | Google Scholar

Turrini, C., Toscani, G., Lacombe, O., and Roure, F. (2016). Influence of structural inheritance on foreland-foredeep system evolution: an example from the Po valley region (northern Italy). Mar. Pet. Geol. 77, 376–398. doi: 10.1016/j.marpetgeo.2016.06.022

CrossRef Full Text | Google Scholar

Vannoli, P., Basili, R., and Valensise, G. (2004). New geomorphic evidence for anticlinal growth driven by blind-thrust faulting along the northern Marche coastal belt (central Italy). J. Seismol. 8, 297–312. doi: 10.1023/B:JOSE.0000038456.00574.e3

CrossRef Full Text | Google Scholar

Vannoli, P., Vannucci, G., Bernardi, F., Palombo, B., and Ferrari, G. (2015). The source of the 30 october 1930 Mw 5.8 senigallia (Central Italy) earthquake: a convergent solution from instrumental, macroseismic, and geological data. Bull. Seismol. Soc. Am. 105, 1548–1561. doi: 10.1785/0120140263

CrossRef Full Text | Google Scholar

Walker, R., and Jackson, J. (2002). Offset and evolution of the Gowk fault, S.E. Iran: a major intra-continental strike-slip system. J. Struct. Geol. 24, 1677–1698. doi: 10.1016/s0191-8141(01)00170-5

CrossRef Full Text | Google Scholar

Wang, M., Jia, D., Shaw, J. H., Hubbard, J., Plesch, A., Li, Y., et al. (2014). The 2013 Lushan earthquake: implications for seismic hazards posed by the range front blind thrust in the Sichuan Basin, China. Geology 42, 915–918. doi: 10.1130/g35809.1

CrossRef Full Text | Google Scholar

Ward, S. N., and Valensise, G. (1996). Progressive growth of San Clemente Island, California, by blind thrust faulting: implications for fault slip partitioning in the California Continental Borderland. Geoph. J. Intern. 126, 712–734. doi: 10.1111/j.1365-246x.1996.tb04699.x

CrossRef Full Text | Google Scholar

Wegmann, K. W., and Pazzaglia, F. J. (2009). Late Quaternary fluvial terraces of the romagna and marche apennines, Italy: climatic, lithologic, and tectonic controls on terrace genesis in an active orogen. Quat. Sci. Rev. 28, 137–165. doi: 10.1016/j.quascirev.2008.10.006

CrossRef Full Text | Google Scholar

Wolfe, F. D., Shaw, J. H., Plesch, A., Ponti, D. J., Dolan, J. F., and Legg, M. R. (2019). The wilmington blind-thrust fault: an active concealed earthquake source beneath Los Angeles, California. Bull. Seismol. Soc. Am. 109, 1890–1906. doi: 10.1785/0120180335

CrossRef Full Text | Google Scholar

Yeats, R. S., and Lillie, R. J. (1991). Contemporary tectonics of the Himalayan frontal fault system: folds, blind thrusts and the 1905 Kangra earthquake. J. Struct. Geol. 13, 215–225. doi: 10.1016/0191-8141(91)90068-t

CrossRef Full Text | Google Scholar

Zechar, J. D., and Frankel, K. L. (2009). Incorporating and reporting uncertainties in fault slip rates. J. Geophys. Res. Solid Earth 114:B12407. doi: 10.1029/2009JB006325

CrossRef Full Text | Google Scholar

Ziesch, J., Tanner, D. C., and Krawczyk, C. M. (2014). Strain associated with the fault-parallel flow algorithm during kinematic fault displacement. Math Geosci. 46, 59–73. doi: 10.1007/s11004-013-9464-3

CrossRef Full Text | Google Scholar

Zuffetti, C., and Bersezio, R. (2020). Morphostructural evidence of late quaternary tectonics at the Po Plain-Northern Apennines border (Lombardy, Italy). Geomorphology 364:107245. doi: 10.1016/j.geomorph.2020.107245

CrossRef Full Text | Google Scholar