What Can Thermal Imagery Tell Us About Glacier Melt Below Rock Debris?

Rock debris on the surface of a glacier can dramatically reduce the local melt rate, where the primary factor governing melt reduction is debris layer thickness. Relating surface temperature to debris thickness is a recurring approach in the literature, yet demonstrations of reproducibility have been limited. Here, I present the results of a field experiment conducted on the Canwell Glacier, Alaska, United States to constrain how thermal data can be used in glaciology. These datasets include, 1) a measured sub-daily “Østrem curve” time-series; 2) a time-series of high resolution thermal images capturing several segments of different debris thicknesses including the measurements from 1); 3) a thermal profile through a 38 cm debris cover; and 4) two Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) satellite thermal images acquired within 2 and 3 min of a field-based thermal camera image. I show that, while clear sky conditions are when space-borne thermal sensors can image a glacier, this is an unfavorable time, limiting the likelihood that different thicknesses of debris will have a unique thermal signature. I then propose an empirical approach to estimate debris thickness and compare it to two recently published methods. I demonstrate that instantaneous calibration is essential in the previously published methods, where model parameters calibrated only 1 h prior to a repeat thermal image return diminished debris thickness estimates, while the method proposed here remains robust through time and does not appear to require re-calibration. I then propose a method that uses a time-series of surface temperature at one location and debris thickness to estimate bare-ice and sub-debris melt. Results show comparable cumulative melt estimates to a recently published method that requires an explicit/external estimate of bare ice melt. Finally, I show that sub-pixel corrections to ASTER thermal imagery can enable a close resemblance to high resolution, field-based thermal imagery. These results offer a deeper insight into what thermal data can and cannot tell us about surface debris properties and glacier melt.

1 Introduction

Most large-scale glacier models consider a glacier to be composed solely of ice and snow. However, eroded rock debris from surrounding bedrock can enter a glacier and is either sequestered within the ice or rafts on the glacier surface (Goodsell et al., 2005). A layer of rock debris at the surface causes a modulation of the net atmospheric energy flux that reaches the sub-debris ice surface. A debris layer that is less than a few centimeters thick can enhance the local melt rate, while a debris layer with a thickness greater than a few centimeters causes an exponential decrease in the local melt rate, scaling with increasing debris thickness (Østrem, 1959; Mattson, 1993; Evatt et al., 2015). Englacial debris is exhumed to the surface through glacier melt causing an increased accumulation of surface debris towards the terminus of a glacier where melt rates would be the highest in a debris-free setting (Anderson, 2000).

Earth’s mountain glaciers are 7.3% debris-covered (Herreid and Pellicciotti, 2020), yet estimates of debris thickness, the key variable governing sub-debris melt rates, are only now being derived at large scales (Kraaijenbrink et al., 2017; Rounce et al., 2021) and their accuracy will benefit from further validation. Debris thickness can be derived from a high density network of excavation point measurements (e.g., Anderson et al., 2021), naturally occurring cross sections (e.g., Nicholson and Mertes, 2017) or ground penetrating radar (e.g., Nicholson et al., 2018); however, these methods are time and resource intensive and impractical at large spatial scales. Proposed methods to derive debris thickness at wider spatial scales are 1) empirical relations between debris thickness and satellite thermal data (e.g., Ranzi et al., 2004; Mihalcea et al., 2008a; Kraaijenbrink et al., 2017); 2) debris thickness derived from satellite thermal data as the residual of a physically-based surface temperature inversion (Foster et al., 2012; Rounce and McKinney, 2014; Schauwecker et al., 2015); 3) a sub-debris melt inversion (Ragettli et al., 2015; Rounce et al., 2018); and 4), a combination of both a sub-debris melt inversion and a surface temperature inversion (Rounce et al., 2021). While studies using moderate/coarse resolution thermal data acquired from satellites is common, the use of field-based oblique or airborne/unmanned aerial vehicle (UAV) acquired high resolution thermal data is surprisingly rare in glaciology (Hopkinson et al., 2010; Aubry-Wake et al., 2015, 2018; Herreid and Pellicciotti, 2018; Kraaijenbrink et al., 2018), and none of these studies used their thermal data to explicitly solve for debris thickness and/or glacier melt rates.

A thermal data approach to derive debris thickness is based on a relation first described by Lougeay (1974). Lougeay (1974) established the shallow, ∼0.5 m, debris thickness detection limit as the surface temperature signal from thick debris cover decouples from the cooling effect of the ice below. This limitation persists through modern methods, yet thermal data remain a recurring central component of new methods to derive debris thickness. While debris thicknesses that exceed 0.5 m are common, an argument can be made that the required debris thickness estimate accuracy decreases as the debris thickness increases and the sub-debris melt rate asymptotically approaches 0, or a low rate of melt (Kraaijenbrink et al., 2017). Because debris thickness is a relatively stable quantity over short timescales (months to years), scientists can, optimally, be selective with the acquisition timing of the data used to derive a debris thickness estimate. More realistically, the data acquisition will be limited by satellite pass frequency, snow cover and cloud cover constraints. Mihalcea et al. (2008a) considered the strength of the relation between debris thickness and in-field surface temperature data as a function of time of day. Their results suggested the early morning hours optimize the correlation, while the weakest correlation was observed in the afternoon. To my knowledge, this experiment has not been repeated and a deeper understanding of the variable meteorological conditions and diurnal/seasonal timing of data acquisition would help optimize debris thickness estimate methodologies as well as better inform what information can be feasibly extracted from thermal data. Here, I use a high spatiotemporal resolution time-series of thermal imagery over variable debris thicknesses to consider the time of day and meteorological conditions that are most favorable for acquiring an optimal thermal image to derive debris thickness.

The stability of debris thickness over months to years also posits the main challenge for researchers attempting to derive debris thickness from surface temperature measurements: a constantly changing independent variable needs to repeatedly return a constant dependent variable. While solving for debris thickness is a nontrivial challenge in its own right, apart from mountain erosion rate problems and the study of peri/supraglacial landforms, the explicit volume of rock debris rafting on a glacier is a largely inconsequential quantity. For research centered around water resources and sea level rise, it is strictly the impact this layer of rock has on sub-debris melt rates that is significant. To this point, a debris thickness estimate that succeeds in extracting a constant and correct value from surface temperature data is also removing information coupled to the energy flux that is driving sub-debris melt. While a thermal image time-series of bare-glacier ice at the pressure-melting point will reveal nothing about the melt rate occurring in frame, a thermal time-series of neighboring supraglacial debris that is sufficiently thick to thermally decouple from a melting ice heat sink below, or possibly a thermal time-series of a local valley wall that can be considered a debris cover of infinite thickness, can presumably be used to derive the melt rate at both bare glacier ice locations and below a debris cover of any thickness. In this study, I explore both of these propositions: 1) can a simple function relate variable surface temperatures to stable debris thicknesses while retaining model stability through time where parameter calibration is not required for each thermal image? And 2), can surface temperature collected at a location with thick debris, or of a neighboring glacier valley wall, be used to solve for glacier melt below any known thickness of debris?

To evaluate these questions, I use data from a carefully orchestrated field experiment that includes an Østrem curve time-series (sub-debris melt rates collected at neighboring locations of variable debris thickness at a sub-daily interval) that is coincident in time with, and captured within the frame of, a high resolution thermal camera time-series. This enables a field-based derivation of the mirrored relation between surface temperature and sub-debris melt rates as a function of debris thickness that has been established through modeling (Nicholson et al., 2018). While this analysis relies on a carefully chosen field site and data that are not feasibly acquired at wide scales, I present a set of methods where each field-based thermal image can essentially be treated as if it were a moderate resolution thermal satellite image. Following these methods, input data to solve for debris thickness and sub-debris melt can be extracted from the thermal image itself with an optional alternative input from a thermistor deployed at the surface of local and thick debris cover. I quantify the success of the proposed methods and consider factors that cause method failure, specifically, by indirectly solving for debris layer saturation. I then compare these results to two recently proposed/published methods from Rowan et al. (2021) and Rounce et al. (2021).

Finally, to further bridge the gap between fine-scale, in-field studies and moderate-scale satellite based methodologies, I propose a sub-pixel signal correction for satellite thermal data. I evaluate this correction using two Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) satellite images, one acquired during the day and one at night, where both were acquired within minutes of high resolution field-based thermal images.

2 Study Site

Canwell Glacier (Figure 1) is a 60 km² glacier in the Delta Mountains, a sub-range of the eastern Alaska Range (63°19.8′N, 145°32′W). The lower-middle ablation zone of Canwell Glacier was a carefully selected field site for the experiment conducted in this study, meeting a specific set of conditions packed tightly into one location. Several prior field seasons were spent developing and testing field methods and surveying debris thicknesses for an ideal field site and thermal camera vantage point (Supplementary Figure S1). Looking orthogonal to glacier flow, from the higher elevation and more thickly debris-covered southern half of the ablation zone, there are seven swaths of near-homogeneous surface types in one field of view. Medial moraine bands at different stages of englacial exhumation and/or with different source-point erosion rates are visible, either as a discrete band surrounded by bare glacier ice, or connected to neighboring moraines as they coalesce down glacier, while still retaining their near-homogeneous rock composition and thickness (Supplementary Figure S1). The presence of relatively thick (∼38 cm) debris cover next to swaths of thinner debris cover and bare ice provides an ideal natural setting to measure the Østrem curve, normalized to bare glacier melt rates, under effectively homogeneous meteorological conditions, as well as allowing this field experiment to be conducted with only one thermal camera. Further, the off-glacier valley wall is also within the frame of view adding one more potentially useful point of reference that I explore further in this study.

FIGURE 1

FIGURE 1. (A) thermal camera in position to capture (B). (B) one (unprocessed) frame of the thermal time-series with black lines defining image segments (1–7) described in Section 3.1. (8) is the corner of a weather station structure and (9) is an aluminum ablation stake, both were cut out of each thermal image to not influence segment statistics. (10) is the side of a medial moraine with a thinly debris-covered, or proto, ice cliff visible. The nadir footprint of (B) is shown in (C) and one to seven correspond to their respective image segments. The line of sight distance is shown between the thermal camera [10 m away from (1)] and the seven segments. Ablation was measured at (1)–(5) where the atmospheric classification pie is centered over the ablation measurement location.

3 Data and Methods

3.1 Field-Based Thermal Infrared Camera Data

Between July 30, 2016 23:42 AKDT (Alaska daylight time) and August 30, 2016 20:14 AKDT, a field experiment monitoring sub-debris glacier melt and temperature at an array of locations was conducted (data gaps will limit different experiments in this study to subsets of this time range). Using a FLIR T620 camera (uncooled microbolometer, 640 × 480 resolution, spectral range 7.5–14.0 μm, accuracy ±2°C, thermal sensitivity <0.04°C at 30°C), surface temperature was monitored at a 15 min interval for 164 h, broken into six observations periods under different meteorological conditions. Due to data gaps, there were 102 h, split between four observation periods (1 August 11:42 AKDT to 3 August 10:57; 3 August 3:45 to 4 August 16:13; 10 August 21:47 to 11 August 8:02; and, 16 August 23:15 to 17 August 19:45) where measurements from all data sources were collected simultaneously. The thermal camera was mounted on a surveying tripod and deployed at the same coordinate location for each of the six periods. Emissivity was set to one and distance set to 0 to facilitate post-processing. Within each oblique thermal image, seven distinct image segments were captured, each with a near-homogeneous debris thickness (Supplementary Figure S1). The segments, ordered in distance from the thermal camera and corresponding to locations shown in Figure 1, are:

1. 38 cm (average) debris thickness (10 m from sensor)

2. 8 cm debris thickness (110 m)

3. Debris-free glacier ice (225 m)

4. 4 cm debris thickness (275 m)

5. Debris-free glacier ice (490 m)

6. 10 cm debris thickness (620 m)

7. Off glacier, southwest facing valley wall (1,000 m)

3.2 Meteorological Data to Process Thermal Imagery

Air temperature and relative humidity are required input to solve for surface temperature from a thermal image. Measurements of 1.5 m air temperature and relative humidity were collected at a 10 min interval throughout the duration of this study at site 1 (on top of structure 8) labeled in Figure 1. The measurements were made using an ONSET HOBO U23 Pro v2 Temperature/Relative Humidity Data Logger housed in a radiation shield. A second, identical structure and sensor configuration was deployed to the same debris-covered location as well as a bare ice location (Figure 1, site 5) in 2012 spanning the same period of time as the data collected in 2016 (31 July 23:42 AKDT to 30 August 20:14 AKDT). These 2012 data are used in this study to amend a 2016 sensor deployment deficiency, providing hourly correction factors to quantify the difference in air temperature over debris cover and bare ice which is notably different (Supplementary Figure S2). To provide context to analysis of debris saturation, precipitation was also measured at site 1 (on top of structure 8) labeled in Figure 1, using a HOBO tipping bucket Rain Gauge Data Logger.

3.3 Solving for Surface Temperature

Thermal infrared cameras are often sold along with integrated software packages that facilitate post processing. There is nothing inherently wrong with using proprietary software packages, but given the complexities and scales that glacier research is conducted on, it is helpful to have oversight/control of the equations used to decompose the several entangled signals present in at-sensor radiance values. In contrast to other geophysical applications of thermal imagery, e.g., volcanology where dramatic thermal anomalies (+100s of degrees) are the signal of interest (Spampinato et al., 2011), applications in glaciology mainly use absolute temperature values that have a relatively low deviation (∼10–30°C over varying debris thicknesses), thus further increasing the importance of careful image processing. Here, I present a method to process field-based, oblique time-lapse thermal imagery which poses unique difficulties from, 1) variable atmospheric attenuation that can be present in one frame imaging several surfaces at different distances (in this study, ranging from a few meters to a kilometer away from the sensor); 2) variable atmospheric attenuation through time; and 3), image shift and rotation from both imaging an unstable landscape and, in the case of this study, acquiring the image time-series from an unstable location on the glacier surface. The method uses Thermimage (Tattersall, 2017) to automate the extraction of raw values from FLIR images and (Tỳč and Gohlke, 2015) to co-register images in the series. This processing routine was developed specifically for a glacier setting by including atmospheric corrections accounting for variability in near-surface conditions over bare and debris-covered ice surfaces present along the line of sight distance from the thermal camera sensor to the target surface. Aside from this correction, which can be omitted, the image processing routine is suitable for any Earth science application with a few meters to a few kilometers line of sight surface to sensor distance. The code uses both R and Python packages combined in one open-source Jupyter Notebook available at (https://github.com/samherreid/ThermalTimelapse).

The value assigned to each pixel in a thermal image is a quantization of the net radiant intensity, W_tot (Wm⁻²), received at the sensor within a set, sensor specific, spectral range (7.5–14.0 μm for the camera used in this study). Following the formulation from Usamentiaga et al. (2014), the surface temperature of an object, T_s (K), can be calculated by:

$T_s=\sqrt[4]{\frac{W_{tot}-(1-{\epsilon }_{obj})*{\tau }_{atm}*\sigma *{(T_{refl})}^4-(1-{\tau }_{atm})*\sigma *{(T_{atm})}^4}{{\epsilon }_{obj}*{\tau }_{atm}*\sigma }}(1)$

where ɛ_obj is the emissivity of the object, τ_atm is the transmittance of the atmosphere between the sensor and the object, σ is the Stefan-Boltzmann constant (5.67 × 10^–8 Wm⁻²K⁻⁴), T_refl (K) is the reflected temperature and T_atm (K) is the temperature of the atmosphere.

None of these quantities (apart from σ) are constant in time or space. However, variability in ɛ_obj through time, e.g., from rock surfaces becoming wet, was assumed to be negligible. In this study, ɛ_obj was varied in space based on site specific values extracted from an ASTER image, acquired on August 30th, 2016 at 13:25 AKDT, that was processed to estimate surface emissivity (AST05) (following Gillespie et al., 1998; Abrams et al., 2002). These values averaged to a debris cover emissivity of 0.94 and an ice emissivity of 0.97. T_refl was assigned for each thermal image by extracting the mean temperature of the aluminum poles of the weather station structure visible in the field of view of each image (Figure 1). This loosely follows the reflector method described in Usamentiaga et al. (2014); however, variation from vectors normal to a smooth cylindrical aluminum surface rather than normal to a complex, randomly oriented crumpled and then flattened aluminum surface (a more favorable configuration) was not quantified. Atmospheric temperature (T_atm, Section 3.2) measurements coincident in time with each thermal image were extracted, and a correction (derived from local data collected 4 years earlier in 2012) was applied to account for air temperature variability for the portions of each thermal image that were debris-free. A set of correction factors were computed for each hour of the day by finding the difference between hourly averaged 1.5 m air temperature collected at location Figure 1 1) and the same measurement recorded at location Figure 1 5) (Supplementary Figure S2).

The final parameter needed to solve Eq. 1, τ_atm, can be formulated as the product of the two main quantities that cause signal attenuation received at the thermal camera,

${\tau }_{atm}={\tau }_m{\tau }_s,(2)$

where τ_m is molecular absorption by constituent gases and τ_s is scattering by particles in the atmosphere (Gaussorgues, 1994). Following Gaussorgues (1994), τ_m is simplified to account for the two dominant constituent gases of the atmosphere, water vapor and gaseous carbon dioxide:

${\tau }_m={\tau }_{H_{2}O}{\tau }_{C{O}_2}.(3)$

As electromagnetic radiation travels through the atmosphere from the target glacier surface to the infrared sensor, some of the radiation is absorbed by atmospheric water vapor molecules (Gaussorgues, 1994). Discrete volumes of interest requiring a solution for atmospheric water vapor content can be approximated as a solid angle or ellipse-based cone, where the point of the cone is at the sensor and the ellipse base approximates the glacier surface radiation source area surrounding each (rectangular) pixel in a thermal image. The number of water vapor molecules present within this cone is a function of the local partial pressure of water vapor and the presences of gaseous water vapor molecules (Gaussorgues, 1994). These quantities are governed both by predictable factors (e.g., elevation, diurnal and seasonal cycles) and chaotic factors (e.g., wind and weather systems). Considering these factors, ${\tau }_{H_{2}O}$ cannot be considered static even at sub-hourly time scales. For this study, the volume of the ellipse-based cone was simplified to a one-dimensional distance, x, from the object surface to the infrared sensor. This is a practical simplification even in an oblique setting because objects that are close to the sensor have a sufficiently disproportionate pixel resolution to the length of x scale ratio of millimeters to meters and objects imaged in the distance have a scale ratio of centimeters to 100s of meters. The quantity of water vapor along x is most commonly expressed as a height of precipitable water, which is the amount of liquid water that would result from the condensation of all of the present water vapor molecules (Gaussorgues, 1994). Precipitable water, h, can be expressed as

$h={\int }_0^x{q}_v\rho dx,(4)$

where q_v (dimensionless) is specific humidity, the mass mixing ratio of water vapor to the total mass of the moist air along x, and ρ (kg m⁻³) is the density of the moist air. h has units of kg m⁻² which is equal to a one-dimensional height of water in mm. h is frequently solved for over a vertical column from the ground to the top of the atmosphere. Many parameterizations exist for this quantity (e.g., Maghrabi and Al Dajani, 2013), but are not applicable to a horizontal x with a variable length and also where pressure and temperature profiles cannot be approximated as simple functions of elevation. h is therefore estimated using measured relative humidity, RH (dimensionless), T_atm (K) and sensor to surface distance, x (m).

The longest x over which h was solved for was 1 km with variable ground-surface types (alternating between debris cover and bare glacier ice, Figure 1C) where RH and T_atm cannot be assumed constant. For this study, the landscape imaged repeatedly was broken into segments where each segment contains area with a near constant debris thickness (Supplementary Figure S1) and a similar ground to sensor distance, x (Figure 1; 1–7). For each segment, h is approximated from the quadrature of Eq. 4 by

$h={q_v}_{ice}{\rho }_{ice}{x}_{ice}+{q_v}_{deb}{\rho }_{deb}{x}_{deb},(5)$

where the distance, x, is the sum of two components accounting for variability in the atmosphere above two distinct surfaces, bare ice, x_ice, and debris cover, x_deb (Figure 1). Using a set of standard equations, T_atm and RH can be used to solve for q_v and ρ over bare ice (${q_v}_{ice}$, ρ_ice) and over debris cover (${q_v}_{deb}$, ρ_deb) (Supplementary Appendix). With a solution for h from Eq. 5, spectral transmittance through the atmosphere considering molecular absorption of water vapor, ${\tau }_{H_{2}O}$, can be estimated as a function of wavelength (λ, μm) (Passman and Larmore, 1956; Gaussorgues, 1994) (Supplementary Appendix). Numerical integration of ${\tau }_{H_{2}O}(\lambda )$ over the specific thermal camera spectral range (in this study 7.5–14.0 μm) enables a solution of ${\tau }_{H_{2}O}$.

Solving for spectral transmittance through the atmosphere considering molecular absorption of gaseous carbon dioxide, ${\tau }_{C{O}_2}$ and signal attenuation from scattering by particles in the atmosphere, τ_s, can be estimated more simply as functions of λ and sensor to object distance, x (Gaussorgues, 1994) (Supplementary Appendix). Together, these calculations of ${\tau }_{H_{2}O}$, ${\tau }_{C{O}_2}$ and τ_s enable an estimate of τ_atm for each image segment that accounts for the specifications of the thermal camera, the physical setting of the experiment and the instantaneous near-surface atmosphere.

The unique setting of imaging a glacier surface with simultaneous measurements of non-zero melt means that bare glacier ice can be expected to be at the pressure melting point. While small impurities are present on even bare ice surfaces with the potential to raise the surface temperature slightly above 0°C, I used this setting of a known, in-frame temperature to identify and correct an assumed linear −2°C sensor bias for all of the images used in this study.

The procedure described here forms the basis of a thermal image processing routine that considers variable surface types, variable line of sight distances and variable near-surface atmosphere along the line of sight distance within a single thermal image. This routine was applied to 684 images acquired over a total span of 164 h. This process was fully automated including automated rotation, translation and scaling data shifts (Tỳč and Gohlke, 2015) to co-register images to match manually defined image segments (black lines in Figure 1B). Locations in the image where unnatural objects were present (e.g., an ablation stake and the corner of a weather station) were removed to not disrupt the mean, median and percentile values computed for each segment.

3.4 Sub-daily Ablation Measurements

Contemporaneous with the thermal image time-series, sub-daily melt measurements were made within four of the seven segments defined in Figure 1: Segments 1, 2, 4, and 5 with debris thicknesses 38, 8, 4, and 0 cm, respectively. Melt measurements were made using a “glacier selfie stick” approach where a graduated, rigid aluminum ablation stake was drilled into bare, or sub-debris ice with a visible spectrum time-lapse camera loosely attached and floating on the surface to photograph the progressive exposure of graduations 5 times per day (Figure 2, Supplementary Video S1). For the ablation stake located closest to the thermal camera [Figure 1 (8), 38 cm debris thickness], the visible spectrum time-lapse camera was fixed to the floating meteorological station. These measurements enabled a sub-daily measurement of melt and were validated against periodic, field-based manual measurements. The presence of the camera assembly at the ablation stake also impacted melt, which was most visible at the bare ice location. Instances where the camera assembly caused clear excess lowering were corrected for by adding back the height of an unnatural (few cm) trench, yet these instances were rare and the assembly remained largely flush with the visible surrounding surface (Supplementary Video S1). Each of the four image time-series were post-processed to derive melt rates by manually measuring the graduation exposure rate. While the cameras acquired five images per day, the frequency of melt measurements were also a function of melt. If the melt rate between images was low, e.g., for the locations with a thicker debris cover, measurements intervals were lengthened until a discernible change could be confidently measured. This makes selecting a meaningful common dt for the computed melt rate difficult. For the purposes of the modeling effort described in Section 3.6 below, where high frequency (10 or 15 min) measurements were downsampled to a 1 h frequency, these melt measurements were resampled to 1 h. This resampling produces error in the melt model validation, but preserves the diurnal variation in the melt rate below thin debris cover and at bare ice. This diurnal variation is a unique signal since most melt measurements of bare glacier ice or sub-debris melt are averaged over days to weeks or months. The bare ice ablation stake, with the highest melt rate, needed to be occasionally re-drilled to maintain a continuous record. These disruptions to the melt record and subsequent post processing proved difficult to mitigate, where disruptions to the melt rate only causes obvious momentary unrealistic values, while a large and more subtle error can accrue in the cumulative melt signal. Large errors were manually smoothed by taking an average between the surrounding days melt measurements at the same time of day. Finally, to have all of the ablation records begin at the same time, linear regression was used to solve for melt over the hours needed to be subtracted from earlier emplaced ablation stakes to align with the initial measurement of the last emplaced ablation stake.

FIGURE 2

FIGURE 2. (A,B) glacier selfie stick configuration used to collect a sub-daily record of surface lowering at locations (2), (4), and (5) in Figure 1. Location (1) had its ablation time-lapse camera fixed to the floating weather station structure. Errors in this style of measurement can be estimated by observing offset in the surrounding landscape compared with the melt signal. (C,D) an example of a particularly large camera movement between two successive images (the camera was set to turn off during the night) where a simple reading of the graduations exposed would suggest glacier accumulation (red bar) but is clearly an error of upward camera rotation based on the lowering of the background landscape. An additional advantage of this method to record ablation is the background imaging of the local sky and cloud fraction.

Melt measurement error was estimated at 0.12 cm per measurement, which sums to 0.6 cm per day if all five images were suitable for use. This value is the result of watching the landscape shift in the background of each image which is caused by movement of the camera assembly unrelated to melt-driven surface lowering. Figures 2C,D shows an extreme shift event where the camera tilted backwards overnight giving the impression of glacier accumulation. While the distance to the background landscape is unknown as well as the angle of rotation, it is still a clear indication of when the measurement will contain an error, requiring a correction factor that will carry through the remaining melt measurements when solving for cumulative melt. A video (Supplementary Video S1) of the complete visible time-lapse datasets from the four locations shows that while events like the one shown in Figures 2C,D do occur, through much of the time-series, the camera position (and background landscape) remains stable, facilitating meaningful melt measurements.

3.5 Thermal Diffusivity

For the three locations of measured ablation with debris cover [Figure 1(1,2,4)], temperatures were recorded within the debris layer in 4 cm increments from the debris-ice interface to the surface. These measurements were collected using ONSET U23 Pro v2 External Temperature Data Loggers at a 10 min increment (resampled to 1 h for the modeling effort, described in Sections 3.4, 3.6). At the location of the thickest debris cover [Figure 1(1), 38 cm debris thickness], further analysis was conducted to investigate the energy transfer within the debris layer concurrently with the ablation and thermal time-lapse measurements. Thermal diffusivity, in a strictly conductive energy transfer setting, can be solved for using the finite-difference method to approximate the Biot-Fourier diffusion equation,

$\frac{\partial T}{\partial t}={\kappa }_c\frac{{\partial }^{2}T}{\partial h_d^2}(6)$

where T is temperature (°C), h_d is depth (mm), t is time and κ_c is thermal diffusivity (mm²s⁻¹) (Hinkel et al., 1990; Conway et al., 2000; Rowan et al., 2021). The subscript, c, denotes the exclusion of any heat transfer mechanism besides conduction.

A second approach was used to solve for thermal diffusivity from diurnal amplitude decay with depth, incorporating all heat transfer mechanisms. In order to automate the selection of diurnal maximum and minimums, a Savitzky-Golay filter was applied (polynomial order 3, window length 51) to smooth the jagged nature of a surface, or near-surface temperature profile as clouds pass overhead. Considering the change in temperature amplitude with depth for each day, amplitude derived thermal diffusivity, κ_a can be calculated,

${\kappa }_a=\frac{\omega {(h_1-h_2)}^2}{2{(\ln (A(h_1))-\ln (A(h_2)))}^2}(7)$

where A(h₁) and A(h₂) are temperature amplitudes at depths h₁ and h₂, respectively Wang et al. (2020). ω is the radial frequency,

$\omega =\frac{2\pi }{\varphi }(8)$

where ϕ is the period of the diurnal cycle set to 86,400 s (24 h).

Using the smoothed temperature profiles, phase shift was calculated at each measurement depth by finding the lag in time between the maximum temperature at depth and the maximum temperature at the surface for each day. The slope of phase shift with depth is also proportional to thermal diffusivity (Anderson, 1998).

3.6 Methods to Estimate Debris Thickness and Sub-debris Melt

The simultaneous hourly measurements of sub-debris melt under variable debris thicknesses and the corresponding surface temperatures offer an ideal framework to evaluate, and possibly improve upon, methods to solve for debris thickness and sub-debris melt.

Exponential scaling is often used to describe the nonlinear relation between surface temperature and debris thickness (e.g., Mihalcea et al., 2008b), yet local variability intrinsic to the relation are embedded within the model parameters, limiting transferability. Here, I propose a method similar to Kraaijenbrink et al. (2017) that draws on information present in the same thermal image used to estimate debris thickness to constrain the exponential scaling. The approach here differs from Kraaijenbrink et al. (2017) by 1) introducing one model parameter that I hypothesize will be stable through time and for other locations on Earth; and 2) looking both within the glacier domain as well as outside the glacier domain, to the local valley walls, to constrain a realistic relation between debris thickness and surface temperature even if there is no thick debris cover present within a thermal image (or no debris cover at all).

I define ${T_s}^{*}$ as the “warmest local temperature” extracted from the thermal image. ${T_s}^{*}$ is used as a reference surface temperature representing the local radiative forcing without heat sinks. For any location with little or no prior knowledge of the setting, for example, a routine iterating through all glaciers on Earth, ${T_s}^{*}$ can be defined as ${T_s}^{*}=\text{max}(\text{max}(T_s),\text{max}({T_s}_{buffer}))$, where T_s is surface temperature across the glacier domain and ${T_s}_{buffer}$ is off-glacier surface temperature within a set buffer distance outside of the glacier domain to capture the local valley walls. The assumption behind looking off-glacier is that the maximum temperature in close proximity, and at a similar elevation, will be from a rock surface with a similar emissivity and surface roughness to a thick debris cover that is decoupled from heat sinks regardless of whether there is thick, thin or no supraglacial debris present at that location. The maximum function is used to discard less ideal, e.g., vegetated, surfaces that will likely be cooler than till or bedrock. Measurements from this study show the surface temperature of thick debris cover can exceed even south facing valley wall temperature, but the two quantities, thick debris T_s and valley wall T_s, are correlated (Figure 3). Since the field experiment presented here is conducted with the knowledge that there is thick debris cover, ${T_s}^{*}$ is set to max(T_s) which, for this time-series, is equivalent to T_s at the 38 cm debris thickness segment. If using only max(T_s) or $\text{max}({T_s}_{buffer})$, it is possible for T_s to exceed ${T_s}^{*}$ which can be accommodated by using a piecewise function. Where available, ${T_s}^{*}$ is taken from the thermal camera data. For the sub-debris melt analysis expanding beyond the thermal camera observation windows, ${T_s}^{*}$ is set to the temperature measured by the contact thermistor at the top of the thermal profile at the 38 cm debris thickness segment (Section 3.5).

FIGURE 3

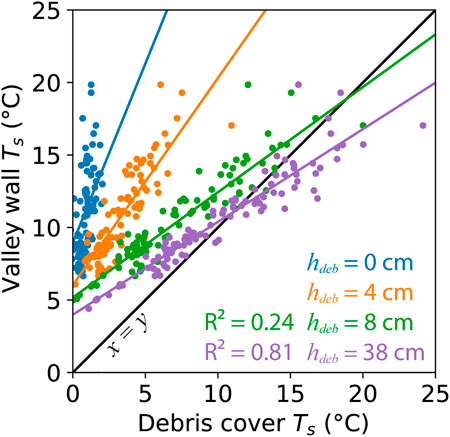
FIGURE 3. Thermal camera derived surface temperatures over the observation period shown in Figure 5. Debris cover surface temperatures approach the warm valley wall temperature as debris thickness increases. Where debris is sufficiently thick, it is possible surface temperature from these two surfaces could be used interchangeably to force a model of local sub-debris melt, giving preference to whichever is easier to collect in a given field setting. Model coefficients should be able to accommodate any valley wall aspect. Imaging rock surfaces, preferably till, rather than vegetation is likely critical to maintain a similar emissivity. These data suggest an off-plot, non-zero convergence, likely due to differences in emissivity/aspect/surface angle, or the temperature at the surface of a 38 cm debris cover may not be entirely free from close proximity temperature modulation from glacier ice below.

With ${T_s}^{*}$ established, a relation to solve for debris thickness, h_deb, can be expressed as,

$h_{deb}(T_s)=\left\{\begin{array}{cc}\text{min}\left(a_9\exp \left(\frac{{T_s}^{*}}{{T_s}^{*}-T_s}\right),h_{max}\right),\hfill & 0\le T_s<{T_s}^{*}\hfill \\ h_{max},\hfill & T_s\ge {T_s}^{*}\hfill \end{array}\right.(9)$

where a₉ is the single model coefficient (subscript referring to the equation number in this paper, subsequently developed model coefficients, a_x, b_x and c_x, will follow the same, subscript to the equation number, notation) that I hypothesize will be stable through space and time because much of the local and regional variability, both in terms of micrometeorology and broad geographical/orographical effects, will be captured in ${T_s}^{*}$. h_max is a user defined value of “thick” debris cover where associated sub-debris melt rates can be assumed to have asymptotically approached a stable, low value. Here, I set h_max to 40 cm. While an exponential function is generally successful at capturing the relation between surface temperature and debris thickness for debris thicknesses around 40 cm or less, towards thicker debris cover, it is unrealistic that small, incremental increases in surface temperature should return exponentially thicker debris cover. Lacking data to support, for example, a third-order polynomial fit that would smoothly transition to a constant debris thickness while surface temperature continues to increase, I have opted to flat-line debris thickness to make clear that what can be safely resolved is that the debris is thick, but the model is unable to predict an absolute thickness. This method also cannot predict debris thicknesses when temperatures are below freezing.

I compare this approach to two recently proposed/published methods from Rowan et al. (2021) and Rounce et al. (2021). Analysis by Rowan et al. (2021) shows a power-law relation between debris thickness and near-surface temperature which they invoke to suggest solving for sub-debris melt from surface temperature data. Following this framework, I evaluate the inverse of the power-law from (Rowan et al., 2021, Figure 7A), where

$h_{deb}(T_s)=a_{10}{T}_s^{b_{10}}.(10)$

I also evaluate the approach used by Rounce et al. (2021) where debris thickness is estimated using the Hill equation,

$h_{deb}(T_s)={\left(\frac{T_s{b}_{11}^{c_{11}}}{a_{11}-T_s}\right)}^{\frac{1}{c_{11}}}.(11)$

With h_deb either known or estimated from one of the methods described above, it becomes feasible to estimate sub-debris melt rate, $\dot{b}$. For the method I propose here, I continue to use ${T_s}^{*}$ as defined above, but now use it to first solve for debris cover surface temperature. This may sound redundant, since ${T_s}^{*}$ was derived from distributed surface temperature data. However, the above method was developed to solve for stable (over the timescale considered here) debris thickness. To solve for debris thickness, especially over large spatial scales, there are at best a few suitable (cloud and snow free) satellite-based thermal images acquired per year. To force a method to derive $\dot{b}$, ${T_s}^{*}$ is not discovered, as above, but rather measured (or derived) continuously from a fixed location. For this study, ${T_s}^{*}$ is again set to T_s at the “thick” 38 cm debris thickness segment from thermal camera data where available, and from the contact thermistor at the debris surface for the longer time-scale analysis. In future applications, ${T_s}^{*}$ can be measured from either a contact thermistor at the surface of thick debris (which is an exceptionally easy sensor to deploy in the field) or by taking repeat thermal images below as much of the cloud canopy as possible which could be possible from a vantage point off-glacier where a power source might be more readily available.

Using ${T_s}^{*}$ and one model coefficient, distributed debris surface temperature, T_s, can be estimated at the same temporal interval as ${T_s}^{*}$ where debris thickness is known,

$T_s({T_s}^{*},h_{deb})={T_s}^{*}-({T_s}^{*}\exp (-a_{12}{h}_{deb})).(12)$

With distributed T_s derived through time, $\dot{b}$ can be estimated as,

$\dot{b}({T_s}^{*},h_{deb})=\left\{\begin{array}{cc}{a}_{13}(1-b_{13})({T_s}^{*}-T_s({T_s}^{*},h_{deb}))+a_{13}{b}_{13}{T_s}^{*},\hfill & {T_s}^{*}\ge 0\hfill \\ 0,\hfill & {T_s}^{*}<0\hfill \end{array}\right.(13)$

where $a_{13}={\dot{b}}_0/{T_s}^{*}$, the ratio of bare ice melt rate, ${\dot{b}}_0$, and ${T_s}^{*}$. This term scales the relation to melt. I hypothesize a₁₃ will remain relatively stable through space and time because it is a ratio of two physically related quantities. If true, this would mean that ${\dot{b}}_0$ would not need to be explicitly derived from other melt modeling methods to solve for bare ice and sub-debris melt rates. a₁₃ will likely need to be recalibrated between geographic regions where the energy balance terms are not similarly weighted and the hypothesis may be rejected where the weighting is locally variable, e.g., where turbulent fluxes are an important component of the energy balance (Steiner et al., 2018). b₁₃ is a term that accounts for the thermal inertia of a debris cover, where melt below thick debris is forced by energy transfer occurring over a period longer than the 24 h diurnal cycle. Here, I parameterize b₁₃ as $b_{13}=\text{median}({\dot{b}}_{38})/\text{median}({\dot{b}}_0)$, where ${\dot{b}}_{38}$ is the melt rate below a “thick” 38 cm debris cover (note ${\dot{b}}_{38}$ is a melt rate, while b₁₃ is a model parameter). This ratio is the empirical middle value of a fairly difficult to obtain set of measurements. It scales the empirical asymptotic convergence of the full (in time) melt rate dataset collected for this study and is possibly stable through space and time. If stable, this would facilitate transferability and reduce the frequency these cumbersome measurements would need to be repeated. With the two model parameters expressed in their expanded ratio form and explicitly solved for (meaning without taking the median values), the last term of Eq. 13 reduces from $\frac{{\dot{b}}_0}{{T_s}^{*}}\frac{{\dot{b}}_{38}}{{\dot{b}}_0}{T_s}^{*}$, to ${\dot{b}}_{38}$. This sets the melt rate for the region of the curve after the exponential decay approaches the asymptote. Because the parameterized form is scaled by ${T_s}^{*}$, melt will not continue throughout the winter as surface temperature drops to 0°C, or below, from the piecewise case of sub-freezing temperatures.

While Eq. 12 has the same arguments as Eq. 13 and could thus be easily written into Eq. 13, it is worthwhile to consider it as a separate step because surface temperature measurements are easier to obtain than sub-debris melt measurements for the purposes of method validation.

The analysis presented in this study is over a small portion of one glacier where factors like elevation dependent temperature lapse rates can be neglected. In order to derive distributed results from the new methods presented here, ${T_s}^{*}$ will need to be extracted at elevation bins to solve for h_deb, and corrected for elevation to solve for $\dot{b}$.

Finally, I evaluate the method proposed above against the approach used by Rounce et al. (2021) where $\dot{b}$ is estimated using a second-order reaction rate equation,

$\dot{b}({\dot{b}}_0,h_{deb})=\frac{{\dot{b}}_0}{1+a_{14}{\dot{b}}_0{h}_{deb}}.(14)$

While Rounce et al. (2021) used an energy balance model to solve for ${\dot{b}}_0$ and a₁₄, for this study, I simply fit Eq. 14 to measured ${\dot{b}}_0$, thus evaluating the expression as if bare ice melt was externally modeled perfectly (under the assumption that my bare ice melt measurements are correct). To evaluate the methods used in this study, the coefficient of determination was found between instantaneous measurements (debris thickness, surface temperature or glacier melt rates) and the respective instantaneous modeled values.

3.7 Sub-pixel Correction for ASTER Thermal Data

Three ASTER thermal images were acquired under clear sky conditions that were coincident in space and time (2 min, 3 min, and 3 h separation) with the terrestrial based, high resolution thermal images collected within this study. Of the two ASTER images with a separation of minutes, one was acquired during the night (August 28, 2016 23:16 AKDT) and the other during the day (August 30, 2016 13:25 AKDT) about 1.5 days later. These images were processed on-demand by NASA to surface kinetic temperature (AST08) which has a spatial resolution of 90 m and a temperature accuracy and precision of about 1.5 K (Gillespie et al., 1998; Abrams et al., 2002).

Due to the high spatial variability in surface characteristics that can occur over very short length scales within a debris cover (Kraaijenbrink et al., 2018), a correction was applied to the ASTER thermal pixels that were coincident with this study. While acknowledging the ASTER processing algorithm is not linear, the most simplistic approach to applying any correction at all is through linear spatial averaging. Using the high resolution, manually digitized bare glacier ice and ice cliff map used as a validation dataset in Herreid and Pellicciotti (2018), the fraction of bare glacier ice within each ASTER pixel was found. Assuming the temperature value assigned to the ASTER pixel is an area weighted average of the true temperature distribution within the pixel area and assuming the area mapped as bare ice or ice cliff has a surface temperature of 273.15 K, the surface temperature of the remaining debris-covered fraction of the pixel can be computed. This debris area only temperature, ${T_s}_{cor}$, can be defined as

${T_s}_{cor}=\frac{{T_s}_{sat}{L_{sat}}^2-(273.15{\beta }_{ice}{L_{sat}}^2)}{(1-{\beta }_{ice}){L_{sat}}^2}(15)$

where ${T_s}_{sat}$ (K) is the raw satellite temperature for the whole pixel, L_sat is the length of one edge of a satellite pixel (90 m for ASTER) and β_ice is the fraction of a pixel that can be assumed to have a surface temperature of 273.15 K.

4 Results and Discussion

The field data collected in this study provide an Østrem curve time-series, capturing the diurnal variation in melt rates below different thicknesses of debris cover, which are all spatially contained within the field of view of a high resolution thermal image time-series. A record of temperature within a 38 cm thick debris layer is also coincident in time and space. These data are best shown as a video time-series (Supplementary Video S2).

4.1 Optimal Timing for Thermal Image Acquisition

For each thermal image segment with a near-homogeneous debris thickness (Figure 1, Supplementary Figure S1), median and percentile statistics were computed (Figure 4). The time-evolution of the median and spread of temperatures within each segment illustrate when it is most feasible to automate the differentiation of these segments and assign a debris thickness. The ideal setting is when there is near-homogeneous temperatures within a segment (narrow individual ranges, Figure 4F), heterogeneous temperatures across segments (high stacked spread, Figure 4G) and even, un-clustered distribution of the spread (swaths equal in magnitude, Figure 4H).

FIGURE 4

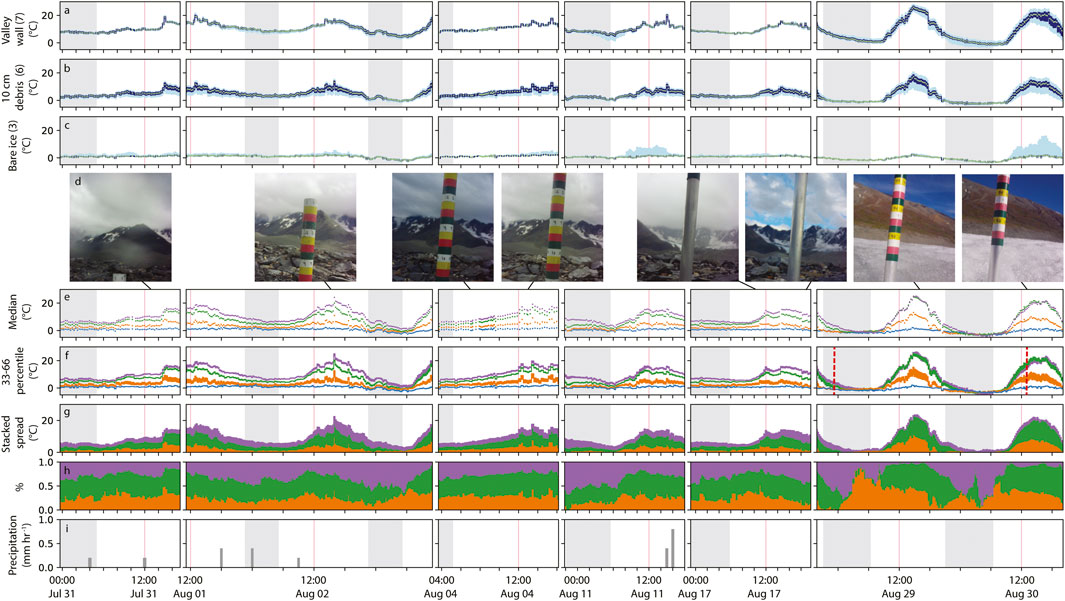
FIGURE 4. (A–C) segments where glacier melt was not measured. Location from Figure 1 is given on the y-axis label. Light and dark blue are the 10–90 and 33–66 percentile temperature range, respectively. The green dot is the segment median temperature. (D) select images from the glacier selfie sticks. Ignoring the ablation stake in the center frame, cloudiness and the local weather can be observed. Segment median temperature (E) and 33–66 percentile range (F) for the four segments where ablation was measured. The colors correspond to: blue, bare glacier ice at Figure 1 location (5); orange, 4 cm debris thickness (4); green, 8 cm debris thickness (2); and purple, 38 cm debris thickness (1). (G) spread of median values for segments in (E) by stacking the gap, in °C, between two neighboring segments. The difference swath is assigned the color of the upper segment. (H) same as (G), normalized to 100%. (I) precipitation of liquid water. Solid red vertical lines show noon of each day, and grey swaths show the local night (corrected for local latitude). The two vertical red dashed lines in (F) show the timing of two ASTER thermal images that were acquired concurrently with this time-series.

While satellites can only acquire surface temperature data when the surface is not obstructed by clouds, Figure 4 suggests that the two cloud-free days (August 29 and August 30) were the least optimal of the collected time-series. During these clear sky conditions, the percentile spread in individual segments is high, and the spread between segments is uneven to nonexistent. The warmest two segments (with debris thicknesses of 38 and 8 cm) became nearly isothermic during the peak heat of the day. On the contrary, it appears that overcast days without precipitation offer the most ideal conditions for deriving debris thickness from surface temperature (some rain occurred during this time-series but no major rain events were recorded). While this could be useful for small scale studies using terrestrial or airborne/UAV imaging platforms that can operate under a cloud ceiling, it adds to the challenge of using thermal satellite data to derive debris thickness.

There are reasonable arguments to use thermal data from both night and day-time imagery to derive debris thickness. During the night the near-isothermic state described above would be avoided, and, drawing on the stored heat signal of a thick debris cover, or its absence for a thin debris cover, the surface temperature may scale well with debris thickness. On the other hand, during the day, direct short-wave radiation will warm thick debris cover surfaces while thin layers remain cool, even under direct incoming short-wave radiation. Both approaches seem reasonable and possibly a combination will be most successful. The key circumstances to avoid are a night isothermic state when debris cover of all thicknesses cool off, or during peak heat of a clear day when most rock surfaces are heated to a high temperature and decouple from a predictable relation with the ice below. Within the data acquired in this study, there is evidence of all four states: an optimal night setting, an optimal daytime setting, isothermic nights and isothermic days. Both isothermic states (for all segments at night and the two segments with the thickest debris cover during the day) occur during the clear sky days, August 29 and 30. The remaining measurement days have variable degrees of spread but differentiation seems feasible at any time of day. Based solely on the spread of the full thermal histogram over the observation period (Supplementary Video S2), daytime offers a more broad spectrum of temperature to discretize.

4.2 Solving for Debris Thickness From Surface Temperature Data

Three empirical equations relating surface temperature to debris thickness were evaluated using the same input data over the same 102 h of observation (Figure 5). Each approach was evaluated in four ways: 1) the number of required model coefficients and their stability through time; 2) the optimal performance of the method where a new set of model coefficients were calibrated for each hourly instance in the 102 h time-series; 3) method performance when holding the model coefficients stable through time as the median values of the model coefficient set derived in 2); and 4) using the model coefficients that were best fit one and 2 h prior.

FIGURE 5

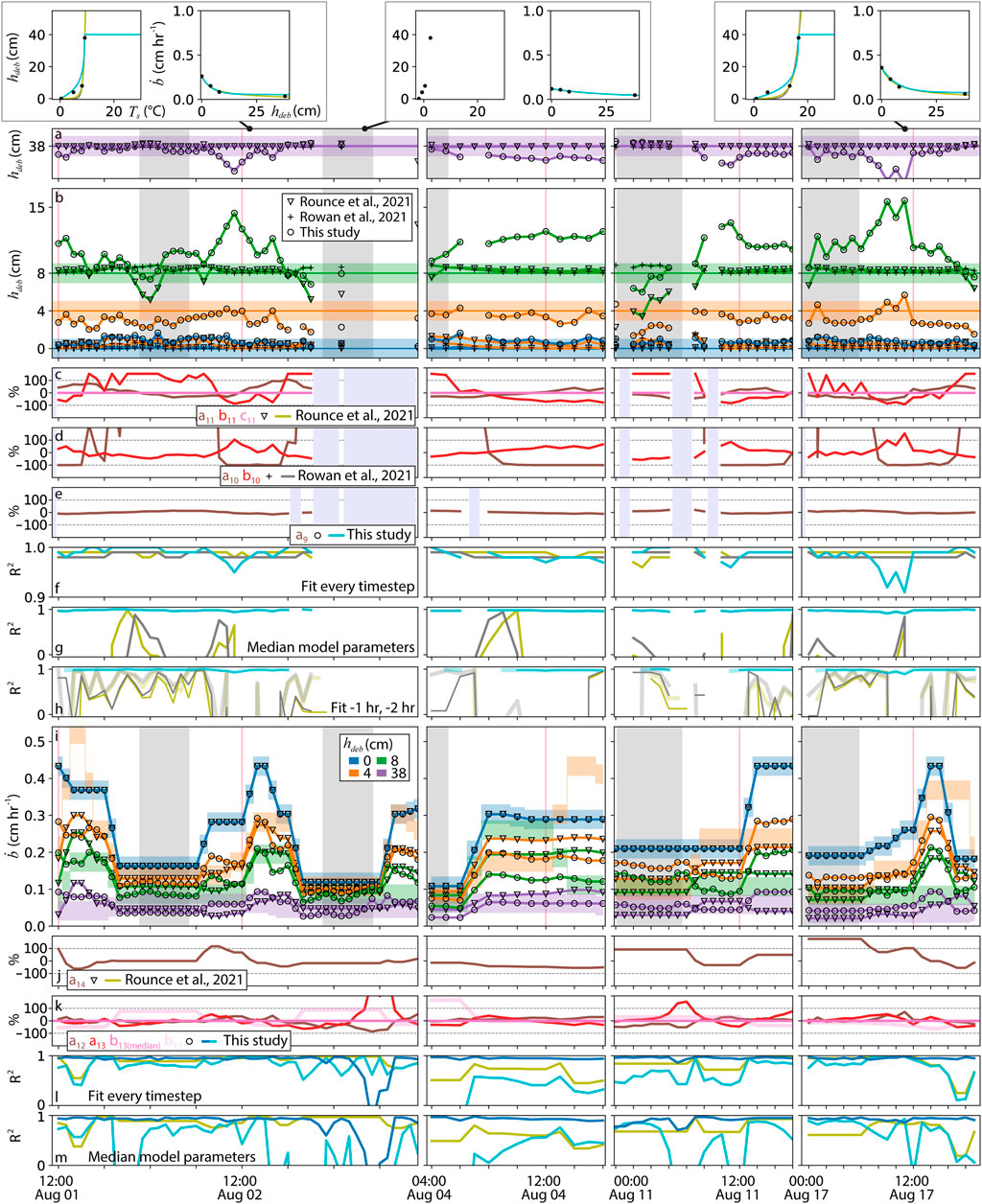
FIGURE 5. (A,B) measured debris thickness, solid flat lines with a ±1 cm error buffer; and modeled debris thickness, forced with T_s from thermal camera segment medians over the measured debris thicknesses. Model coefficients were calibrated for every timestep. A successful model would match the flat line debris thickness of the same color for every timestep. Different models are denoted by shape at each timestep. Debris thickness colors are the same as (I) and Figures 3, 4, 6: blue, bare glacier ice at Figure 1 location (5); orange, 4 cm debris thickness (4); green, 8 cm debris thickness (2); and purple, 38 cm debris thickness (1). Solid red vertical lines show noon of each day, and grey swaths show the local night [same in (I)]. (C–E) Normalized [(x −median(x))/median(x)] variability in model coefficients calibrated at every timestep for the three methods used. Legend gives the model coefficient name, subscript with equation number, and color coded to the plot of its variability through time. Dashed lines are ±100% deviation from the median value. Vertical lavender swaths are where the model failed, e.g., log of a negative. (F–H) R² for each model, color defined in legends (C–E), where: (F) calibrated at every timestep; (G) constant median model coefficients, derived over this time-series (C–E), applied at every timestep; and (H) using model coefficients calibrated 1 h prior (wide, transparent line) and 2 h prior (thin solid line). (I) same figure configuration as (A,B) but for bare ice and sub-debris melt, comparing only two methods. Measurements are colored swaths, model results are solid lines. For this experiment, both methods were prescribed measured bare ice melt and therefore match it perfectly. (J,K) same figure configuration as (C–E) but for sub-debris melt. b_13(median) is derived from median melt data spanning the whole time-series in Figure 6 and used for the calculations here and in Figure 6. b₁₃, light pink, is the same data ratio but using the explicit solution for each timestep, not medians, to show its relative stability, it is not used elsewhere. (L,M) R² for each model, color defined in legends (J,K) where dark blue is Eq. 12, solving for surface temperature; and light blue is Eq. 13, solving for sub-debris melt. (L) calibrated at every timestep; (M) constant median model coefficients, derived over this time-series (J,K), applied at every timestep. Three timestep examples are shown at the top of the Figure illustrating (A,B,I). Model color coding follows the legends in (C–E); measurements are black dots.

General results from this analysis show that the methods from Rowan et al. (2021) and Rounce et al. (2021) (Eqs. 10, 11, respectively) easily translate variable surface temperatures through time into stable and correct debris thicknesses when calibrated at every timestep (Figures 5A,B). A notable exception for both methods is an under estimation of debris that is 4 cm thick, both methods returned a near-zero debris thickness for every timestep. The method presented here (Eq. 9), is notably less stable, especially at 8 cm debris thickness, where, at its worst, the debris thickness estimate is off by nearly a factor of 2. A visible advantage of this method is the ability to better estimate the 4 cm thick debris cover. Given these visible shortcomings and advantages, when calibrated at every timestep, all three methods have a high (>0.90) coefficient of determination for every timestep (Figure 5F).

The equations from Rowan et al. (2021) and Rounce et al. (2021) produce a nearly identical curve (Supplementary Video S3, frame examples at the top of Figure 5), yet Eq. 11 from Rounce et al. (2021) requires one additional model coefficient (c₁₁) that appears to remain constant and does not absorb any temporal variability (Figure 5C). The remaining two model coefficients in Eq. 11 (a₁₁ and b₁₁) and the two in Eq. 10 from Rowan et al. (2021) (a₁₀ and b₁₀) show considerable variability through time with varying adherence to a diurnal pattern (Figures 5C,D). The two parameter sets are most stable during mid-day on August 4th, which for Eq. 11, means the values are constrained within the ±100% deviation from median bounds, which is still considerable variability. For the rest of the series, both approaches deviate outside of these bounds to absorb the surface temperature variability. While these two methods are very accurate when instantaneously calibrated, their coefficients of determination are rarely above zero when the median model coefficient values were used (Figure 5G, Supplementary Table S1). Rounce et al. (2021) implemented a clever methodology to derive, and optimize a parameter set for each surface temperature instance within a dataset covering all mountain glaciers on Earth. In this case, temporal transferability is not necessarily relevant, but even a short dt between neighboring thermal images might cause a depreciation of results. To explore this, I used each method to solve for debris thickness with the current timestep surface temperature, but used the best fit model coefficients from one and 2 h prior (Figure 5H). Results from this experiment show a dramatic loss of performance, where R² averaged across the time-series decreased from 0.99 (no lag), 0.53 (−1 h) and 0.37 (−2 h) for Eq. 11 (Rounce et al., 2021); and 0.98 (no lag), 0.54 (−1 h) and 0.41 (−2 h) for Eq. 10 (Rowan et al., 2021).

While the method proposed here, Eq. 9, carries more variability than the other two methods when calibrated at every timestep, it has some key advantages when used in less ideal conditions. Nearly all of the local variability in surface temperature is accounted for by ${T_s}^{*}$, which means the single model coefficient is simply scaling a physical relation and not needing to vary itself to accommodate different thermal distributions. The parameter stability apparent in Figure 5E carries through both experiments, of a constant median value and −1 and −2 h, with a notably high coefficient of determination. For the hours lag experiment, average R² remains constant at 0.98 (no lag), 0.98 (−1 h) and 0.98 (−2 h). While these results show more variability from Eq. 9 around the 8 cm debris thickness, it is a quantifiable variability. Because evidence suggest the method is stable, an appropriate error can be assigned and assumed also stable enabling confident and constrained estimates of debris thickness through time.

4.3 Solving for Bare Ice and Sub-debris Melt from Surface Temperature Data

Following the same framework used to evaluate debris thickness methods above, I propose a method to solve for bare ice and sub-debris melt from debris thickness and surface temperature and compare it to the method from Rounce et al. (2021). The method used by Rounce et al. (2021) (Eq. 14) is not forced by surface temperature, but is a similar simple parameterization of sub-debris melt. For the 102 h time-series, where hourly sub-debris melt is known, measured bare ice melt, ${\dot{b}}_0$, and constant, known debris thicknesses were used as input to Eq. 14 and a least squares fit was used to optimized a₁₄, the single model coefficient, for each timestep. Similarly, the 102 h time-series was used to fit the sub-debris melt method presented in this study for each timestep, but instead of melt data, Eq. 12, solving for debris surface temperature, was forced with thermal camera derived surface temperature over thick debris (${T_s}^{*}$) and the same constant, known debris thicknesses. The model coefficient, a₁₂, was fit using thermal camera derived surface temperature for the known debris thicknesses. This solution of debris surface temperature was then used in Eq. 13 to solve for sub-debris melt where a₁₃ was set to the ratio of ${\dot{b}}_0$ and ${T_s}^{*}$, adjusted for each timestep, and b₁₃ was set to the ratio of median melt rate measured below 38 cm of debris and median melt rate of bare ice (both medians computed from the entire time-series in this study, shown in Figure 6). This means that for this limited 102 h time-series, both methods are prescribed measured bare ice melt rates and will fit the (identical) bare ice validation time-series perfectly. This enables the evaluation of how each method resolves sub-debris melt starting from a perfect solution of bare ice melt, and enables an evaluation of model coefficient stability.

FIGURE 6

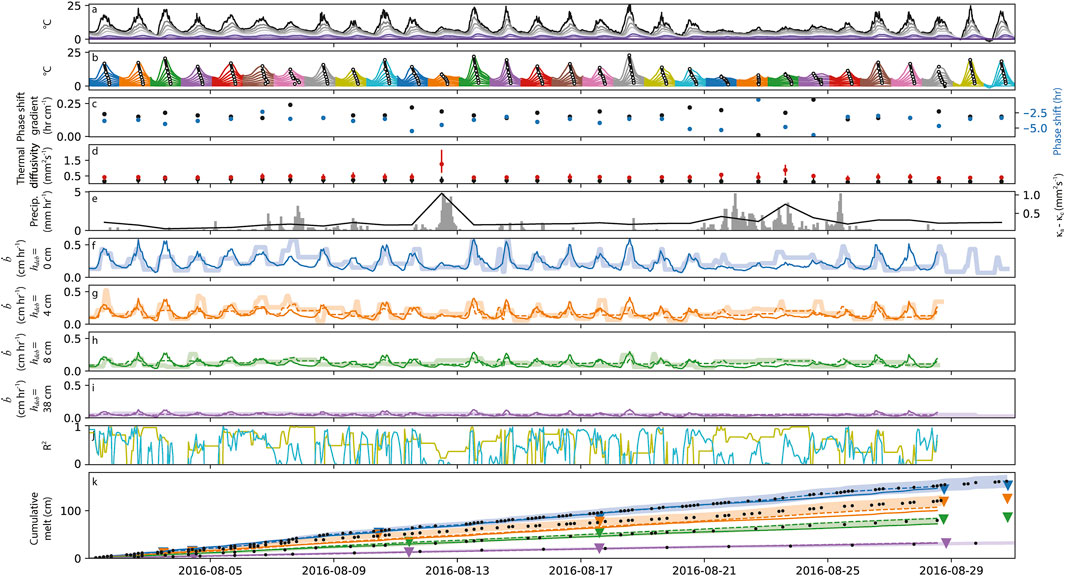
FIGURE 6. Time-series showing data and model results at locations (1)–(5) in Figure 1. (A) raw temperature profile data where each line is a temperature record from within the debris cover (4 cm spacing). Black is the surface and dark purple is the debris-ice interface. (B) same as (A) but smoothed to automate the selection of diurnal maxima and amplitude values. The series is segmented per day (colors). The phase shift gradient is shown: white dots are diurnal maxima and the black line is a least squares linear fit of these points. These gradients are plotted in temperature over time space, but due to the linear spacing of the sensors, is proportional to the time over debris depth gradient (C) (black dots). Blue dots in (C) are the maximum phase shift in hours between the top surface layer and the bottom of the debris layer. Both values in (C) are computed for each day. (D) median (dot) and 33–66 percentile range (bar) of apparent thermal diffusivities calculated for each day from two methods: diurnal amplitudes (κ_a, red) and the Biot-Fourier diffusion equation considering only conductive heat transfer (κ_c, black). (E) local precipitation rate (grey vertical bars) measured at location (8) in Figure 1. The black line scaled by the second y-axis is the difference between κ_a and κ_c. (F–I) ablation modeled from Eq. 13 (this study) solid lines; and from Eq. 14 (Rounce et al., 2021) dashed lines. Measured melt is wide transparent. Colors are the same as Figures 3–5: blue, bare glacier ice at Figure 1 location (5); orange, 4 cm debris thickness (4); green, 8 cm debris thickness (2); and purple, 38 cm debris thickness (1). (J) R² between the measured and modeled Østrem curve for each time step; turquoise, this study; yellow-green, Rounce et al. (2021). The model following Rounce et al. (2021) was forced with measured bare ice melt and is therefore omitted from (F) and not included in the R² calculation (J). (K) cumulative melt. Selfie stick sub-daily measurements are shown as black dots. Error bounds around measured melt are colored, transparent; and traditional, manual ablation stake measurements are shown as colored triangles. Model results are shown as a solid line (this study), and dashed (Rounce et al., 2021). All colors in (K) match (F–I).

The general results of this experiment are shown in Figure 5I and the Supplementary Video S3 (where three frames are shown at the top of Figure 5. Error within the melt measurements make model validation less robust. I do not have complete confidence that instances of notable deviation, for example, measured sub-debris melt being higher below 8 cm of debris than below 4 cm of debris in the morning of August 4th, are correct. Still, both methods preform reasonably well with average R² values of 0.85 for Eq. 14 (Rounce et al., 2021) and 0.71 for Eq. 13 (Figure 5L). Repeating the experiment with the median model coefficient, average R² reduces to 0.77 for Eq. 14 and is 0.50, notably less for Eq. 13 (Figure 5M). Using median model coefficients seems to cause Eq. 13 to fail dramatically during nights when melt is nearly shut off for all debris thicknesses. Interestingly, these nighttime failures are not necessarily caused by a failure of the surface temperature estimates from Eq. 12, which remain stable and accurate for most of the time-series (Figures 5L,M). During the night of August 3rd, R² of estimated surface temperature crashes, but appears independent of when sub-debris melt is unable to be resolve, for example, the evening of August 1st, afternoon of August 2nd (preceding the surface temperature crash) and the morning of August 11th. Model coefficients appear to remain mostly stable for both methods (Figures 5J,K), which is encouraging for the method presented here because this means that the ratios contained within a₁₃ and b₁₃ are stable, physical relations that can now be prescribed as constants, eliminating the need for an explicit solution of ${\dot{b}}_0$, which Eq. 14 will always need. By prescribing these ratios as constants, I next apply both approaches to a wider time-series of measurements and evaluate the loss of performance from my method forced with surface temperature and debris thickness alone, against Eq. 14 forced with measured ${\dot{b}}_0$.

For the time interval August 1st 2:00 AKDT to August 28th 13:00 AKDT 2016, thermal camera images were not continuously collected, so ${T_s}^{*}$ was set to contact thermistor data collected at the surface of the 38 cm debris cover temperature profile (Sections 3.5, 3.6). Using ${T_s}^{*}$, debris thickness and median values of a₁₂, a₁₃, and b₁₃ derived above (Supplementary Table S1), Eqs. 12, 13 were used to estimate sub-debris melt below 0, 4, 8 and 38 cm of debris, where sub-debris was simultaneously measured for validation (Figures 6F–I; Supplementary Video S4). Forced with measured ${\dot{b}}_0$ and the median value of a₁₄ derived above, Eq. 14 was also used to estimate sub-debris melt, but only below 4, 8, and 38 cm of debris since melt at 0 cm (${\dot{b}}_0$) was used as model input. Eq. 14 from Rounce et al. (2021) out performs the method presented here (Figure 6J) with averaged R² values of 0.50 and 0.38 for the two methods, respectively. While the instantaneous fit to Østrem curve measurements have a relatively low R², estimated melt summed over the 28 days observation period was close to the measured value (Figure 6K; Table 1). The largest error was modeled melt falling 11 cm below the lower error bound for summed measured melt at 4 cm debris thickness. Summed melt at the lower error bound was 111 cm, indicating the least accurate melt measurement from the method presented in this study had a 10% error. The bare ice estimate was off by only 5 cm, indicating 3% error from the middle measured value (the estimate fell within the error bounds). Some instances where one, or both, methods performed poorly appear to be non-random, correlating with rainfall (Figures 6E,J). The next section considers moisture entering the system and how it could disrupt sub-debris melt estimates.

TABLE 1

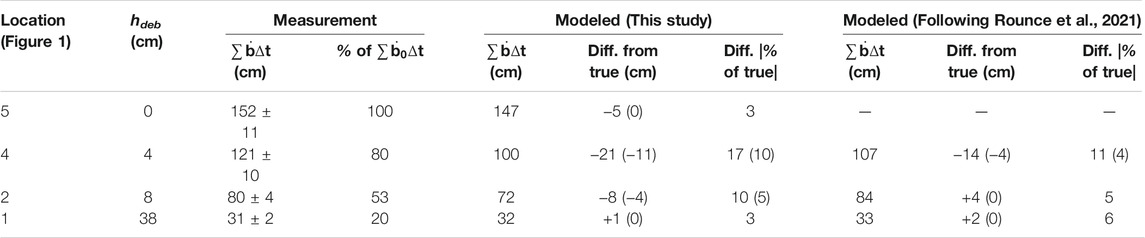
TABLE 1. Cumulative melt ($\sum \dot{b}\mathrm{\Delta }t$) from August 1st 2:00 AKDT to August 28th 13:00 AKDT 2016. Difference, in parentheses, is the difference relative to the nearest (±) error bound, where “(0)” means the sum fell within the error bounds.

4.4 Solving for Debris Layer Saturation to Isolate a Source of Sub-debris Melt Estimate Failure

For a statistical glacier melt model framework emphasizing simplicity, minimal input and transferability, there will always be a trade off in performance relative to more sophisticated approaches with more comprehensive input data. Still, it is worthwhile to consider additional data when available to look for patterns of when the simple method fails and if there might be a simple fix, or an approach to infer method confidence as a function of some variable. From the melt modeling experiment conducted in this study, there are numerous instances where the method fails, yet there is an apparent pattern of failure around rain events (Figures 6E,J). Evaporative cooling of the debris and interstitial water modifying the thermal properties of the debris layer (Collier et al., 2014) are two possible explanations for the phase shift gradient variability visible in Figures 6B,C. While at least one rainy day shows a phase shift gradient that is reduced to near zero, it seems more common that introducing moisture into the debris layer causes more thermal resistance, a more gradual phase shift gradient and an increase in the number of hours it takes diurnal surface warming to reach a depth of 38 cm. During days of heavy rain, apparent thermal diffusivity formulated to include all energy transfer mechanisms, κ_a, spikes while apparent thermal diffusivity considering only conduction, κ_c remains essentially static (Figure 6D). Drawing on this observation, the difference between κ_a and κ_c appears to have the potential to be a proxy measure of precipitation, where relative precipitation rate may even be inferred (Figure 5E). Emphasizing again a methodology favoring simplicity and minimal field sensor deployment, it might be advantageous to establish a network of surface and sub-debris thermistor strings rather than one or two costly and cumbersome weather stations.

4.5 Improving ASTER Thermal Data for Wide-scale Applications

While I provide evidence in Section 4.1 suggesting clear days are the least favorable for deriving debris thickness from thermal data (Figure 4, August 28 to August 30), it was during these days that two ASTER scenes were acquired concurrently within minutes (a third within hours) of a high resolution, field-based thermal image. The timing of the ASTER images are shown in Figure 4F (red dashed vertical lines) and show that the August 28th acquisition narrowly missed the nighttime isothermic state, and captured the August 30th warming limb of the diurnal cycle. The sub-pixel bare ice correction described in Section 3.7 was applied to each image (Figure 7) and a comparison between ASTER and field-based thermal camera surface temperature data is shown in Figure 8 where the ASTER data is draped over a local DEM [from Herreid and Pellicciotti (2018)] and obliquely angled to mimic the field of view of the field-based thermal image. While acquired under less favorable conditions, the relation between the ASTER pixels contained within the field of view of the field-based thermal camera image agree with R² values of 0.70 and 0.78 for the nighttime August 28 and daytime August 30 images, respectively. The near isothermic state during the night is apparent, yet a thermal delineation can still be made between the near-field 38 cm thick debris cover and the adjacent 8 cm thick debris (segment boundaries are shown in Figure 1). The ability of these two ASTER images to replicate high resolution field-based data during less than ideal conditions is promising for satellite based methodologies to derive debris thickness.

FIGURE 7

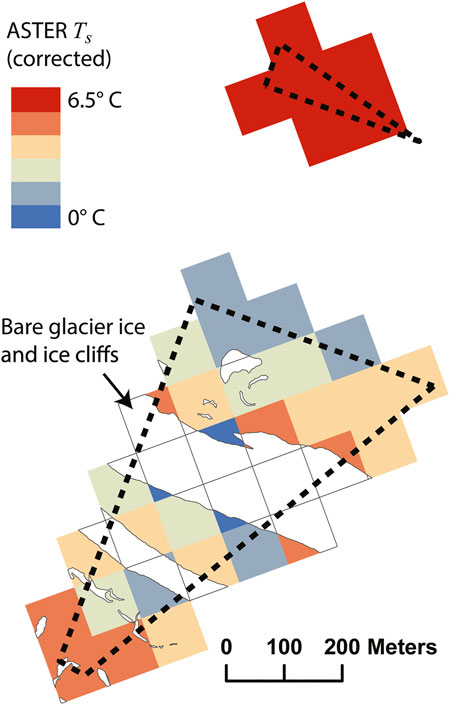
FIGURE 7. Example of the linear spatial averaging (Eq. 15) applied to ASTER surface temperature data. The sub-pixel area and thermal signal of locations known to be bare glacier ice, or ice cliff area, are removed. The dashed line outlines the study site (Figure 1C).

FIGURE 8

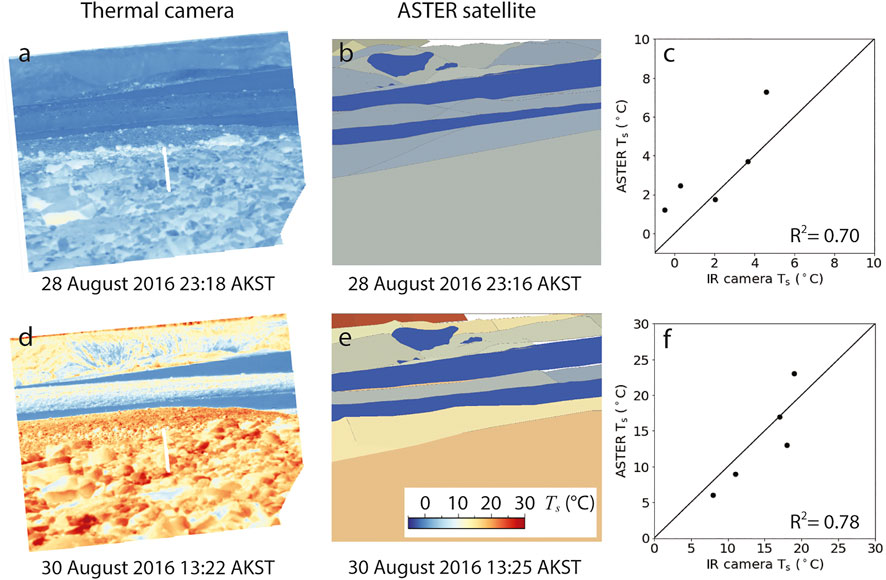
FIGURE 8. Two image pairs of oblique field-based thermal camera data coupled with space-borne ASTER thermal data that are coincident in time. The ASTER data is draped over a DEM and displayed obliquely to match the view angle of the thermal camera image. The image pair (A,B) are coincident in time by 2 min and (D,E) are coincident in time by 3 min. Surface temperatures were averaged over the image segments shown in Figure 1A,B; regression is shown between the infrared (here shortened to “IR”) camera and ASTER thermal data. Bare ice segments were excluded from the regression because the ASTER values were unnaturally set to 0°C from Eq. 15. The 1:1 line is plotted for reference. (C) corresponds to image pair (A,B); (F) corresponds to image pair (D,E). Temperatures in (A,B,D,E) are all scaled to the temperature scale in (E).

5 Conclusion

Thermal imagery, particularly from field-based or airborne sensors, have been under utilized in glaciology. In an effort to bring attention to thermal image applications, I have established a series of methods and field experiments using surface temperature data to solve for glacier melt below rock debris in a mountain glacier setting. I begin with a decomposition of the many factors that are entangled within a raw thermal image and describe a method to solve for surface temperature from a field-based, oblique thermal image time-series. My hope is that, instead of appearing discouragingly complicated, future glaciolgists can use this paper, and the accompanying annotated Jupyter notebook as a way to bypass industry focused literature that rarely addresses the specific problems (environmental factors, line of sight distances) encountered in glacier, or more generally, Earth science applications.

The series of field experiments explored in this study build upon one another with standalone methods and results. The first used the tight (dt = 15 min) time-series of thermal imagery, encompassing seven segments with different debris thicknesses, to determine the ideal time of day and meteorological conditions to acquire a thermal image for the purpose of deriving debris thickness. This is a relevant question when designing a field campaign that will collect thermal imagery, in a situation where it is possible to task a satellite or when it would be helpful to know what information can be extracted from the one good image that exists over a particularly cloudy field site. Results from this analysis suggest thermal images acquired below a cloud cover at most times of day, apart from cold nights when all surfaces become isothermal, are best suited to derive high confidence debris thickness estimates. The least favorable time appears to be clear sunny days with cool nights, which is unfortunately the late ablation season conditions when satellite data is the most useful for many applications in glaciology. The closing section of this paper, however, applies a sub-pixel correction to two ASTER thermal images that fall within this least favorable window and the resulting images are promisingly similar to high resolution field-based thermal imagery captured within minutes of the satellite data.

Building on the conceptual framework of when a thermal image would be best suited to derive debris thickness, I applied two methods, and proposed a third, to solve for debris thickness from surface temperature, validated against known debris thickness segments. This approach makes use of the unique, low and consistent dt (relative to satellite data) between thermal images to evaluate how the three methods mitigate diurnal and meteorological variability in order to return a stable-through-time debris thickness output. The method I propose treats part of the thermal image like a model coefficient that is able to absorb the temperature variability and allow the one model coefficient to remain stable through time. The other two established methods perform well when calibrated for each instance, yet have diminished results, by almost 50%, if the set of model coefficients used were optimized only 1 h earlier. Where instantaneous calibration is feasible, all of the methods can confidently capture the relation between an instance of surface temperature and stable debris thicknesses, however, the stability demonstrated in the method proposed here opens new avenues for easy transferability in space and time.

Finally, I build on the application of surface temperature data in glaciology by solving for one of the key unknowns remaining in mountain glacier research, sub-debris melt rates. For this analysis, I partially diverge from using thermal imagery in order to consider a wider time interval where data were available. I use a contact thermistor at the surfaces of a “thick” debris cover and known distributed debris thickness to solve for both bare ice and sub-debris melt. While the sensor is different, the key quantity remains surface temperature which can be measured using either approach. Debris thicknesses were prescribed from measurements, but in future applications at wider scales or where less prior knowledge is available, debris thickness can be derived from one of the methods described in this paper. The method was evaluated alongside an alternative parameterization of sub-debris melt forced, in part, with externally modeled bare ice melt rates, or, for the controlled method evaluation experiment conducted in this study, forced with directly measured bare ice melt rates. Both methods were evaluated against a time-series of sub-daily Østrem curve measurements. While the approach described here using only surface temperature and debris thickness as input was outperformed by the method forced with bare ice melt measurements, this is fairly predictable trade-off of performance for simplicity, and, perhaps surprisingly, the divergence between the two methods and the measured validation data was on the order of a few to 10 cm for summed melt values over a 28 days observation period, equivalent to a maximum error of 10%. Further development and evaluation of this, or a similar approach will likely be able to reduce this error term further. As first steps towards this, I present some approaches to identify instances of debris cover saturation where a temporary alternative parameterization of sub-debris might better fit the apparent altered energy transfer state.

The methods proposed in this study can be implemented at any location on Earth with one good satellite thermal image to derive debris thickness and one local time-series of surface temperature collected at either a location of “thick” debris or a neighboring valley wall. The surface temperature data can be collected either via thermal camera or a contact thermistor which is a notably cheap, small and easy sensor to deploy in the field, relative to a traditional weather station, and runs a very low risk of being damaged from wind, bears or other factors that hamper glacier data collection. Further, by burying a thermistor string within the debris layer, it may be possible to solve indirectly for precipitation from apparent thermal diffusivity calculations which further simplifies field sensor deployment. For the next few implementations, model coefficients should be again empirically derived from a network of coincident measurements of debris thickness, surface temperature and sub-debris melt, but if the set of model coefficients prove to remain stable and transferable, especially at different locations on Earth, this will support wider application in space and time with fewer validating measurements.

The methods and comparative results presented in this study offer a new evaluation of what thermal imagery and surface temperature measurements can tell us about a glacier setting. Future studies may be better equipped to make informed methodological choices and have a greater understanding of what information can and possibly cannot be extracted from surface temperature measurements. This study emphasizes simplistic, empirical methods that require minimal input and field data. The intent is to bring method stability and constrained confidence to large-scale problems. Next steps would be to successfully distribute these methods accounting for elevation and constraining a field sensor array that is minimal but adequate. With several well resolved full glaciers, it would become easier to evaluate new and existing methods to derive debris thickness and sub-debris melt from remote sensing data alone and arrive at confident global scale solutions that will aid water resource management and reduce error in glacier sourced eustatic sea level rise estimates.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the author, without undue reservation.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This project, including the publishing fee, was self-funded. A successful proposal to the University of Alaska Fairbanks Technology Advisory Board written during my undergraduate in 2012 provided funding for the FLIR thermal camera. An earlier version of this study was included in my PhD thesis at Northumbria University.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

I would like to thank Rebekah Tsigonis Helkenn for her invaluable help in the field and Francesca Pellicciotti for her helpful suggestion on how to appropriately use 2012 data to make up for a 2016 field data deficiency. I would also like to thank Liza Ershova, Lauren Moulder and Ned Rozell for their support of this work. Two reviewers and the Editor, LN, provided very constructive feedback that helped me bring this work to its potential. Finally, I would like to thank Maeberrie Market in Avon-By-The-Sea, New Jersey for providing me with gainful employment as a barista during the pandemic which enabled me to write this paper.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.681059/full#supplementary-material

References

Abrams, M., Hook, S., and Ramachandran, B. (2002). Aster User Handbook, Version 2. Jet propulsion Lab. 4800, 135.

Google Scholar

Anderson, L. S., Armstrong, W. H., Anderson, R. S., and Buri, P. (2021). Debris Cover and the Thinning of Kennicott Glacier, alaska: In Situ Measurements, Automated Ice Cliff Delineation and Distributed Melt Estimates. The Cryosphere 15, 265–282. doi:10.5194/tc-15-265-2021

CrossRef Full Text | Google Scholar

Anderson, R. S. (2000). A Model of Ablation-Dominated Medial Moraines and the Generation of Debris-Mantled Glacier Snouts. J. Glaciol. 46, 459–469. doi:10.3189/172756500781833025

CrossRef Full Text | Google Scholar

Anderson, R. S. (1998). Near-surface thermal Profiles in alpine Bedrock: Implications for the Frost Weathering of Rock. Arctic Alpine Res. 30, 362–372. doi:10.2307/1552008

CrossRef Full Text | Google Scholar

Aubry-Wake, C., Baraer, M., McKenzie, J. M., Mark, B. G., Wigmore, O., Hellström, R. Å., et al. (2015). Measuring Glacier Surface Temperatures with Ground-Based thermal Infrared Imaging. Geophys. Res. Lett. 42, 8489–8497. doi:10.1002/2015GL065321

CrossRef Full Text | Google Scholar

Aubry-Wake, C., Zéphir, D., Baraer, M., McKenzie, J. M., and Mark, B. G. (2018). Importance of Longwave Emissions from Adjacent Terrain on Patterns of Tropical Glacier Melt and Recession. J. Glaciol. 64, 49–60. doi:10.1017/jog.2017.85

CrossRef Full Text | Google Scholar

Collier, E., Nicholson, L. I., Brock, B. W., Maussion, F., Essery, R., and Bush, A. B. G. (2014). Representing Moisture Fluxes and Phase Changes in Glacier Debris Cover Using a Reservoir Approach. The Cryosphere 8, 1429–1444. doi:10.5194/tc-8-1429-2014

CrossRef Full Text | Google Scholar

Conway, H., Rasmussen, L., and Nakawo, M. (2000). Summer Temperature Profiles within Supraglacial Debris on Khumbu Glacier. Nepal: IAHS PUBLICATION, 89–98.

Evatt, G. W., Abrahams, I. D., Heil, M., Mayer, C., Kingslake, J., Mitchell, S. L., et al. (2015). Glacial Melt under a Porous Debris Layer. J. Glaciol. 61, 825–836. doi:10.3189/2015jog14j235

CrossRef Full Text | Google Scholar

Foster, L. A., Brock, B. W., Cutler, M. E. J., and Diotri, F. (2012). A Physically Based Method for Estimating Supraglacial Debris Thickness from thermal Band Remote-Sensing Data. J. Glaciol. 58, 677–691. doi:10.3189/2012jog11j194

CrossRef Full Text | Google Scholar

Gaussorgues, G. (1994). Infrared Thermography. Berlin/Heidelberg, Germany: Springer.

Gillespie, A., Rokugawa, S., Matsunaga, T., Cothern, J. S., Hook, S., and Kahle, A. B. (1998). A Temperature and Emissivity Separation Algorithm for Advanced Spaceborne thermal Emission and Reflection Radiometer (Aster) Images. IEEE Trans. Geosci. Remote Sensing 36, 1113–1126. doi:10.1109/36.700995

CrossRef Full Text | Google Scholar

Goodsell, B., Hambrey, M. J., and Glasser, N. F. (2005). Debris Transport in a Temperate valley Glacier: Haut Glacier d'Arolla, Valais, Switzerland. J. Glaciol. 51, 139–146. doi:10.3189/172756505781829647

CrossRef Full Text | Google Scholar

Herreid, S., and Pellicciotti, F. (2018). Automated Detection of Ice Cliffs within Supraglacial Debris Cover. The Cryosphere 12, 1811–1829. doi:10.5194/tc-12-1811-2018

CrossRef Full Text | Google Scholar

Herreid, S., and Pellicciotti, F. (2020). The State of Rock Debris Covering Earth's Glaciers. Nat. Geosci. 13, 621–627. doi:10.1038/s41561-020-0615-0

CrossRef Full Text | Google Scholar

Hinkel, K. M., Outcalt, S. I., and Nelson, F. E. (1990). Temperature Variation and Apparent thermal Diffusivity in the Refreezing Active Layer, Toolik lake, alaska. Permafrost Periglac. Process. 1, 265–274. doi:10.1002/ppp.3430010306

CrossRef Full Text | Google Scholar

Hopkinson, C., Barlow, J., Demuth, M., and Pomeroy, J. (2010). Mapping Changing Temperature Patterns over a Glacial Moraine Using Oblique thermal Imagery and Lidar. Can. J. Remote Sensing 36, S257–S265. doi:10.5589/m10-053

CrossRef Full Text | Google Scholar

Kraaijenbrink, P. D. A., Bierkens, M. F. P., Lutz, A. F., and Immerzeel, W. W. (2017). Impact of a Global Temperature Rise of 1.5 Degrees Celsius on Asia's Glaciers. Nature 549, 257–260. doi:10.1038/nature23878

PubMed Abstract | CrossRef Full Text | Google Scholar

Kraaijenbrink, P. D. A., Shea, J. M., Litt, M., Steiner, J. F., Treichler, D., Koch, I., et al. (2018). Mapping Surface Temperatures on a Debris-Covered Glacier with an Unmanned Aerial Vehicle. Front. Earth Sci. 6, 64. doi:10.3389/feart.2018.00064

CrossRef Full Text | Google Scholar

Lougeay, R. (1974). “Detection of Buried Glacial and Ground Ice with thermal Infrared Remote Sensing,” in Advanced Con-Cepts and Techniques in the Study of Snow and Ice Resources (Washington, DC, USA: National Academy of Sciences).

Google Scholar

Maghrabi, A., and Al Dajani, H. M. (2013). Estimation of Precipitable Water Vapour Using Vapour Pressure and Air Temperature in an Arid Region in central saudi arabia. J. Assoc. Arab Universities Basic Appl. Sci. 14, 1–8. doi:10.1016/j.jaubas.2012.11.001

CrossRef Full Text | Google Scholar

Mattson, L. (1993). Ablation on Debris Covered Glaciers: an Example from the Rakhiot Glacier, punjab, Himalaya. Intern. Assoc. Hydrol. Sci. 218, 289–296.

Google Scholar

Mihalcea, C., Brock, B. W., Diolaiuti, G., D'Agata, C., Citterio, M., Kirkbride, M. P., et al. (2008a). Using Aster Satellite and Ground-Based Surface Temperature Measurements to Derive Supraglacial Debris Cover and Thickness Patterns on Miage Glacier (Mont Blanc Massif, italy). Cold Regions Sci. Tech. 52, 341–354. doi:10.1016/j.coldregions.2007.03.004

CrossRef Full Text | Google Scholar

Mihalcea, C., Mayer, C., Diolaiuti, G., D’Agata, C., Smiraglia, C., Lambrecht, A., et al. (2008b). Spatial Distribution of Debris Thickness and Melting from Remote-Sensing and Meteorological Data, at Debris-Covered Baltoro Glacier, Karakoram, pakistan. Ann. Glaciol. 48, 49–57. doi:10.3189/172756408784700680

CrossRef Full Text | Google Scholar

Nicholson, L. I., McCarthy, M., Pritchard, H. D., and Willis, I. (2018). Supraglacial Debris Thickness Variability: Impact on Ablation and Relation to Terrain Properties. The Cryosphere 12, 3719–3734. doi:10.5194/tc-12-3719-2018

CrossRef Full Text | Google Scholar

Nicholson, L., and Mertes, J. (2017). Thickness Estimation of Supraglacial Debris above Ice Cliff Exposures Using a High-Resolution Digital Surface Model Derived from Terrestrial Photography. J. Glaciol. 63, 989–998. doi:10.1017/jog.2017.68

CrossRef Full Text | Google Scholar

Østrem, G. (1959). Ice Melting under a Thin Layer of Moraine, and the Existence of Ice Cores in Moraine Ridges. Geografiska Annaler 41, 228–230. doi:10.1080/20014422.1959.11907953

CrossRef Full Text | Google Scholar

Passman, S., and Larmore, L. (1956). Atmospheric Transmission. Santa Monica, CA: Tech. rep., Rand Corp Santa Monica CA.

Ragettli, S., Pellicciotti, F., Immerzeel, W. W., Miles, E. S., Petersen, L., Heynen, M., et al. (2015). Unraveling the Hydrology of a Himalayan Catchment through Integration of High Resolution In Situ Data and Remote Sensing with an Advanced Simulation Model. Adv. Water Resour. 78, 94–111. doi:10.1016/j.advwatres.2015.01.013

CrossRef Full Text | Google Scholar

Ranzi, R., Grossi, G., Iacovelli, L., and Taschner, S. (2004). “Use of Multispectral Aster Images for Mapping Debris-Covered Glaciers within the Glims Project,” in Geoscience and Remote Sensing Symposium, 2004. IGARSS’04. Proceedings. 2004 IEEE International (IEEE), 1144–1147.

Google Scholar

Rounce, D., and McKinney, D. (2014). Debris Thickness of Glaciers in the everest Area (nepal Himalaya) Derived from Satellite Imagery Using a Nonlinear Energy Balance Model. The Cryosphere 8, 1317–1329. doi:10.5194/tc-8-1317-2014

CrossRef Full Text | Google Scholar

Rounce, D. R., Hock, R., McNabb, R. W., Millan, R., Sommer, C., Braun, M. H., et al. (2021). Distributed Global Debris Thickness Estimates Reveal Debris Significantly Impacts Glacier Mass Balance. Geophys. Res. Lett. 48, e2020GL091311. doi:10.1029/2020GL091311

PubMed Abstract | CrossRef Full Text | Google Scholar

Rounce, D. R., King, O., McCarthy, M., Shean, D. E., and Salerno, F. (2018). Quantifying Debris Thickness of Debris-Covered Glaciers in the everest Region of nepal through Inversion of a Subdebris Melt Model. J. Geophys. Res. Earth Surf. 123, 1094–1115. doi:10.1029/2017JF004395

CrossRef Full Text | Google Scholar

Rowan, A. V., Nicholson, L. I., Quincey, D. J., Gibson, M. J., Irvine-Fynn, T. D. L., Watson, C. S., et al. (2021). Seasonally Stable Temperature Gradients through Supraglacial Debris in the everest Region of nepal, central Himalaya. J. Glaciol. 67, 170–181. doi:10.1017/jog.2020.100

CrossRef Full Text | Google Scholar

Schauwecker, S., Rohrer, M., Huggel, C., Kulkarni, A., Ramanathan, A., Salzmann, N., et al. (2015). Remotely Sensed Debris Thickness Mapping of Bara Shigri Glacier, Indian Himalaya. J. Glaciol. 61, 675–688. doi:10.3189/2015jog14j102

CrossRef Full Text | Google Scholar

Spampinato, L., Calvari, S., Oppenheimer, C., and Boschi, E. (2011). Volcano Surveillance Using Infrared Cameras. Earth-Science Rev. 106, 63–91. doi:10.1016/j.earscirev.2011.01.003

CrossRef Full Text | Google Scholar

Steiner, J. F., Litt, M., Stigter, E. E., Shea, J., Bierkens, M. F. P., and Immerzeel, W. W. (2018). The Importance of Turbulent Fluxes in the Surface Energy Balance of a Debris-Covered Glacier in the Himalayas. Front. Earth Sci. 6, 144. doi:10.3389/feart.2018.00144

CrossRef Full Text | Google Scholar

Tattersall, G. (2017). Thermimage: Thermal Image Analysis.

Tỳč, M., and Gohlke, C. (2015). Imreg Dft.

Usamentiaga, R., Venegas, P., Guerediaga, J., Vega, L., Molleda, J., and Bulnes, F. (2014). Infrared Thermography for Temperature Measurement and Non-destructive Testing. Sensors 14, 12305–12348. doi:10.3390/s140712305

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J., Lee, W. F., and Ling, P. P. (2020). Estimation of thermal Diffusivity for Greenhouse Soil Temperature Simulation. Appl. Sci. 10, 653. doi:10.3390/app10020653

CrossRef Full Text | Google Scholar