Softening of Temperate Ice by Interstitial Water

Ice at depth in ice-stream shear margins is thought to commonly be temperate, with interstitial meltwater that softens ice. Models that include this softening extrapolate results of a single experimental study in which ice effective viscosity decreased by a factor of ∼3 over water contents of ∼0.01–0.8%. Modeling indicates this softening by water localizes strain in shear margins and through shear heating increases meltwater at the bed, enhancing basal slip. To extend data to higher water contents, we shear lab-made ice in confined compression with a large ring-shear device. Ice rings with initial mean grain sizes of 2–4 mm are kept at the pressure-melting temperature and sheared at controlled rates with peak stresses of ∼0.06–0.20 MPa, spanning most of the estimated shear-stress range in West Antarctic shear margins. Final mean grain sizes are 8–13 mm. Water content is measured by inducing a freezing front at the ice-ring edges, tracking its movement inward with thermistors, and fitting the data with solutions of the relevant Stefan problem. Results indicate two creep regimes, below and above a water content of ∼0.6%. Comparison of effective viscosity values in secondary creep with those of tertiary creep from the earlier experimental study indicate that for water contents of 0.2–0.6%, viscosity in secondary creep is about twice as sensitive to water content than for ice sheared to tertiary creep. Above water contents of 0.6%, viscosity values in secondary creep are within 25% of those of tertiary creep, suggesting a stress-limiting mechanism at water contents greater than 0.6% that is insensitive to ice fabric development in tertiary creep. At water contents of ∼0.6–1.7%, effective viscosity is independent of water content, and ice is nearly linear-viscous. Minimization of intercrystalline stress heterogeneity by grain-scale melting and refreezing at rates that approach an upper bound as grain-boundary water films thicken might account for the two regimes.

Introduction

Over the last few decades, flow of marine-terminating ice streams has accounted for most of the mass lost from the Antarctic Ice Sheet (Rignot et al., 2019). Owing to low effective stress at the beds of ice streams, their driving stresses tend to be resisted mainly at their margins (e.g., Raymond et al., 2001). Resultant high rates of shear strain at ice-stream margins dissipate sufficient heat to overcome effects of cold ice advection from the glacier surface and from adjacent slow-moving ice to cause many margins to be temperate at depth (Meyer and Minchew, 2018; Hunter et al., 2021). Resultant water that resides at grain boundaries reduces the effective viscosity of the ice (Duval, 1977). When incorporated in a numerical model of an ice-stream shear margin that also includes routing of interstitial water, this ice softening by water reduces the width of the temperate zone and steepens velocity gradients in the margin (Haseloff et al., 2019). Resultant focusing of heat dissipation increases the meltwater discharge delivered to the bed, which affects the distribution of basal effective stress and slip velocity (Suckale et al., 2014; Perol and Rice, 2015; Meyer et al., 2018; Haseloff et al., 2019). Strain localization at ice-stream margins also creates troughs on the surfaces of shear margins that precondition ice shelves for ocean-driven break-up (Alley et al., 2019).

The softening effect of a melt phase on rock at its pressure-melting temperature (PMT) usually depends non-linearly on the melt content (e.g., Hirth and Kohlstedt, 1995; Rosenberg and Handy, 2005), so defining the range of water content in temperate ice is likely to be important for assessing the softening effect. The intergranular water in temperate ice is thought to reside in veins at three-grain intersections, at nodes where these veins meet, and in lenses along grain boundaries oriented optimally with respect to deviatoric stress in the ice (Nye and Mae, 1972; Nye and Frank, 1973; Nye, 1989). Careful microscopic study of temperate ice at atmospheric pressure bears this out (Nye and Mae, 1972; Mader, 1992). Measurements of the resultant water content of temperate ice—equivalent to the ice porosity if voids are saturated—are few. Water contents of cores from two temperate glaciers in the French Alps did not generally exceed about 3% and much more commonly were less than 2%, with an average value of ∼0.7% (Vallon et al., 1976; Lliboutry and Duval, 1985). In situ measurement of ice water content at the bed of the Norwegian temperate glacier, Engabreen, yielded values of ∼1% to slightly greater than 2% (Cohen, 2000). No data exist on the water content of temperate ice in ice-stream shear margins. The model results of Haseloff et al. (2019) for idealized shear margins included spatially averaged water contents of less than 0.5 to up to ∼8%. This wide range resulted from model sensitivity to the ice permeability, which was poorly known.

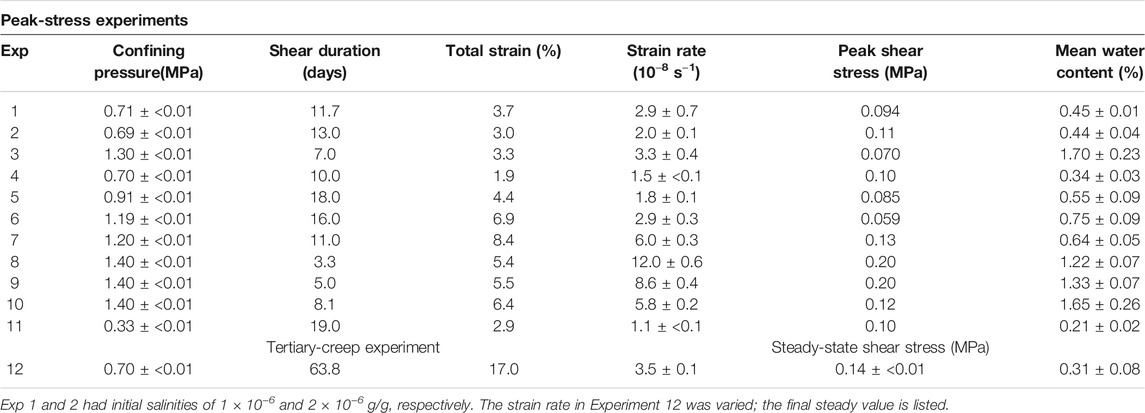
Effects of interstitial water on ice viscosity were apparent to early field workers and experimentalists who did not measure water content but noted its likely effect on their observations. Carol (1947), while studying ice from a cavity beneath a temperate glacier, noted that where water “exuded from countless capillaries” in basal ice it was more “plastic” than ice elsewhere and “had almost the consistency of cheese.” Many experimental studies have indicated that creep rates of ice at or close to its PMT are greatly enhanced (Glen, 1955; Mellor and Testa, 1969; Barnes et al., 1971; Colbeck et al., 1973; Morgan, 1991) relative to softening expected from a simple Arrhenius dependence on temperature (e.g., Cuffey and Paterson, 2010, p. 64). Extreme sensitivity of strain rate to temperature very close to the PMT (Figure 1) has led to the conclusion that water at grain boundaries either introduces new deformation mechanisms or enhances existing ones (e.g., Mellor and Testa, 1969; Barnes et al., 1971; Morgan 1991; Hooke, 2020). This strain-rate sensitivity to grain-boundary processes is reinforced by no comparable temperature sensitivity observed in experiments on single crystals of ice near the PMT (Jones and Brunet, 1978). The widely adopted constitutive relation of Goldsby and Kohlstedt (2001), with grain-boundary sliding limiting deformation rate over most glacially relevant stresses, also cannot explain severe enhancement of strain rates very near the PMT (Figure 1).

FIGURE1

FIGURE1. High-temperature creep data from uniaxial compression experiments on laboratory-made polycrystalline ice, replotted from Morgan (1991). The octahedral stress was 0.1 MPa. Strain rates are minimum values of secondary creep. A fit to Morgan’s (1991) data gathered at lower temperatures (−32.5 to −5°C) yields an activation energy in the Arrhenius relation that underestimates the measured strain rate at −0.01°C by a factor of ∼10. Exponential thickening of pre-melted water films at grain boundaries with increasing temperature is thought to be responsible for enhanced strain rates (Hooke, 2020).

In only the study of Duval (1977) was water content measured during creep experiments on ice kept at or close the PMT. Hollowed-out cores of natural ice containing impurities (Vallon et al., 1976) were sheared to tertiary creep. Water content of ice samples varied with temperature and impurity content. The variation of grain sizes among ice samples was 8–19 mm (Vallon et al., 1976). Ice samples were sheared at a constant stress of 0.29 MPa, above shear stresses measured in ice-stream shear margins of West Antarctica and leading to strain rates 10–50 times larger than the largest strain rates measured there, as compiled by Raymond et al. (2001). Water content was measured by tracking with thermistors in the ice the speed of a freezing front induced at the boundaries of the ice specimen (Duval, 1976a). Strain rate was sensitive to water content, and increased linearly by a factor of ∼3 across water contents of 0.008–0.8%.

Barnes et al. (1971) believed, based on experimental data collected at temperatures above −1°C, that grain-scale pressure melting and refreezing and grain boundary sliding were important micro-deformation mechanisms. Stress heterogeneity around grains at the PMT will create thermal gradients across grains that drive grain-scale melting, movement of water through grain-boundary melt films, and refreezing of water. Melt films may also enhance grain-boundary sliding (e.g., Hooke, 2020).

Duval (1977), however, excluded these possibilities. His high-temperature experiments (Duval, 1976b) indicated a stress exponent in Glen’s flow law equal to 3.0, inconsistent with deformation limited by either grain-scale melting and refreezing or grain-boundary sliding. Although Duval thought that water would be created by melting where stress concentrations between grains locally lower the melting temperature, he thought this water would absorb dislocations that pile up at stressed grain boundaries and cause strain hardening. More specifically the water creates a free surface that attracts dislocations by reducing strain energy in their vicinity and thereby absorbs them, relieving their pile-ups at grain boundaries. He thought that this water also likely facilitated grain-boundary migration (Duval, 1977).

Herein, we present the first measurements of the relationship between effective ice viscosity and liquid water content in temperate ice since Duval’s (1977) pioneering study. Rings of polycrystalline laboratory ice with different water contents are sheared at controlled rates in confined compression, with mean final grain diameters of 8.3–12.6 mm and hence within the range considered by Duval (1977). Except for one high-strain experiment conducted to tertiary creep, ice is sheared only to peak stresses associated with secondary creep and total strains less than ∼8. This approach avoids the complicating influence of softening by ice fabric development that accompanies the transition from secondary to tertiary creep (e.g., Hooke, 2020) and allows experiments at low strain rates. Most importantly, these experiments extend the range of water content considered to 1.7%, more than twice the highest value considered by Duval (1977). We find that at about the upper limit of the water-content range he considered, the relationship between ice softening and water content changes markedly, yielding an ice rheology above that limit that is seemingly not controlled by either grain boundary sliding or dislocation creep.

Materials and Methods

Apparatus

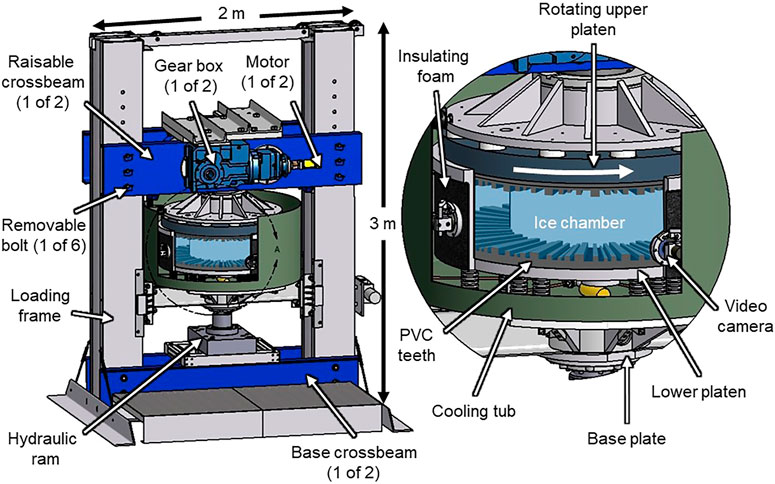
These experiments are conducted using a ring-shear device housed in a cold room and designed and used previously to study glacier slip (Iverson and Petersen, 2011; Thompson et al., 2020; Zoet and Iverson, 2020). The device’s ice chamber is adjusted to study ice rheology by installing a toothed platen that grips the ice at the base of the chamber (Figure 2). This modification transforms the chamber into a viscometer that deforms a large ice ring (outside diameter of 0.9 m diameter, width of 0.2 m, and a maximum thickness of ∼0.17 m) confined on its sides and held in compression between the rotating upper platen and the stationary lower platen. The platens are made of PVC plastic; its low thermal conductivity inhibits regelation past the platen teeth and promotes internal deformation of the ice ring. The upper platen rotates at a controlled speed while a vertical stress, which fluctuates less than 2%, is applied to the ice ring by a servo-controlled hydraulic ram (Figure 2). The resistance to platen rotation is measured with a torque sensor in the drive assembly and used to compute shear stress, averaged over the area of the ice ring. The vertical stress is measured with a load cell on the hydraulic ram. Rotation and downward motion of the upper platen resulting from melting are measured to the nearest 0.01 mm. Video cameras that image tracers in the ice can help describe strain patterns (Figure 2).

FIGURE 2

FIGURE 2. Schematic of the ring-shear device, configured as a viscometer.

The ice chamber resides in a bath (cooling tub of Figure 2) consisting of a mixture of ethylene glycol and water. Its temperature is regulated to the nearest 0.01°C with an external heating/cooling circulator that pumps the fluid through the cooling tub. This system holds the ice at the PMT without melting it too quickly so experiments of durations up to several months can be conducted. Temperature is measured with glass-bead thermistors, calibrated to a precision of ∼0.01°C with high-precision reference thermistor and embedded at various points flush within the inside surfaces of the ice chamber walls to measure temperature at the sides of the ice ring. Owing to the ice being at its PMT, movement of the ice ring along the lateral walls of the aluminum chamber during shear results in negligible drag because of the water film that divides the smooth aluminum from the ice. Meltwater drains to atmospheric pressure from ports in the base of the ice chamber. More details about the apparatus can be found in Iverson and Petersen (2011).

Procedure

Ice rings are built within the ice chamber incrementally, with ice layers 15–20 mm in thickness. To build each layer, chilled and distilled or deionized water is added to the ice chamber and then saturated with sieved snow (2 mm sieve) to promote the growth of randomly oriented crystals as the water freezes. Water for two of these experiments was doped with low concentrations of pure sodium chloride (10⁻⁶ g/g) to experiment with the effect of solutes in controlling water content. At mid-height in the ice ring, two horizontal transects of thermistors are frozen into place (Figure 3). These transects are oriented radially, along the width if the ring and in-line with thermistors in the inner and outer walls. During ring construction ice samples are collected so initial grain sizes can be measured. Once a ring is built to its full height (∼0.17 m), four vertical, 12 mm holes are drilled through the ice ring along its radial centerline. To serve as strain indicators, weighted threads are suspended vertically in each of the drilled holes to just above the lower platen. Chilled water is then added to the holes to freeze the threads in position.

FIGURE 3

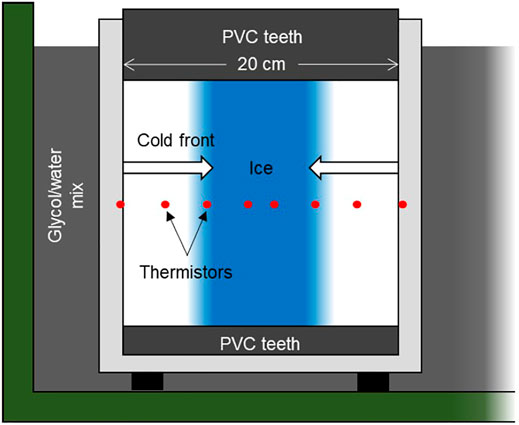
FIGURE 3. Schematic cross-section through the ice chamber along a radius with a thermistor transect, showing freezing fronts induced by lowering the temperature of the glycol/water mixture surrounding the ice chamber.

After a final water layer, seeded with snow, is added to the top of the ice ring, it is raised into contact with the upper platen, which during freezing fully couples to the ice ring under a low applied normal stress (∼0.3 MPa). The cold room is then warmed to 1 ± 0.8°C, and the external circulator is set so that glycol/water mixture in the cooling tub is just above freezing (+0.015 ± 0.010°C). The ice ring warms to the PMT for approximately three days. Normal stress on the ice is then increased to the value chosen for shearing. The increased pressure results in an abrupt decrease in ice temperature that confirms the ice is at the PMT.

Shear of the ice is initiated by rotating the upper platen at a steady speed of 0.1–1.5 m a⁻¹ at the centerline of the ring, depending on the strain rate desired in the experiment. Stresses are measured at 40 Hz, averaged, and saved every 20 s. In some experiments the time to reach a peak stress is reduced by allowing up to one-third of the anticipated peak stress to accrue (at a strain less than 0.25%) and then reducing the speed to target a lower desired strain rate; development of ice microstructural properties that reflect the higher initial strain rate and that might affect peak stresses is not expected in the early stages of primary creep. In 11 experiments ice rings were sheared until shear stress reached a peak value and then either remained steady or began to decrease consistently. Durations of shear were 3–18 days. The single experiment carried out to tertiary creep lasted 64 days.

Efforts to systematically vary water content evolved with trial and error. Varying of ice salinity yielded inconsistent water contents, at least partly because of preferential release of salt early in experiments, as measured in meltwater draining from the ice chamber. A more successful method for varying water content was to systematically vary the confining pressure. Water content tended to increase with increasing confining pressure (0.3–1.4 MPa) and less so with increasing experimental duration when the effects of these variables could be adequately isolated (Adams, 2021). The former dependence reflects the thermodynamic requirement to melt ice with increasing pressure to attain the lower PMT. The latter dependence likely reflects progressive heat transfer into the ice from the boundaries of the ice ring, owing to the slightly lower PMT at curved water vein walls relative to the boundaries of the ice ring (Nye, 1991).

At the ends of experiments, after the peak stress is attained, the water content of the ice is measured. To do this, over less than a two-hour period the glycol/water mixture in the cooling tub is cooled to −0.5°C, initiating freezing fronts that move radially into the ice ring from the inner and outer walls (Figure 3). The insulating PVC platens inhibit heat conduction across the upper and lower surfaces of the ice ring, promoting dominantly horizontal heat flow through the ice as the temperature of the glycol/water mixture decreases. The speed at which freezing fronts advance through the ice is measured by the thermistors embedded in the walls, which track temperature at the inner and outer edges of the ice ring, and by the thermistors frozen into ice along radial transects (Figure 3). Freezing-front arrival times are selected for each thermistor when temperature begins to sustainably decrease at a rate commensurate with the rate of the wall-temperature decrease (Supplementary Figure 1). The speed of freezing fronts is sensitive to interstitial water content of the ice owing to the high latent heat of fusion of water. Water contents are determined by fitting numerical solutions of the relevant Stefan heat-conduction model (Asaithambi, 1988; Cohen, 1999) to the arrival times of the freezing fronts (see Supplementary Material, including Supplementary Figure 2). Four determinations of water content are made for each experiment and averaged, with one determination for each half-transect of thermistors on either side of the ice-ring centerline. Freezing-front movement on one side of the interior temperate zone is independent of that on the other side because temperate ice cannot serve as a heat sink (i.e., all heat conduction is toward the walls of the ice ring). From the variability of the water-content determinations, error bars are computed as plus or minus one standard deviation. These multiple measurements, as opposed to a single determination along one transect (e.g., Duval, 1976, 1977), help compensate for uncertainty in identifying arrival times of freezing fronts.

After freezing fronts have advanced past the innermost thermistor, ice is warmed back to the PMT, and the ice ring is extracted from the ice chamber. Initially vertical threads in the ice are carefully photographed and measured to determine their deflection from the vertical and thereby determine total shear strain at the centerline of the ice ring. This value, if compared to the total rotation of the upper platen, allows the internal deformation of the ice ring to be isolated from movement focused at the platens (i.e., slip). This tactic is similar to that of Kamb (1972) who conducted torsion experiments on warm ice and drew lines on ice rings to isolate slip at platen surfaces. Strain rates are computed from the measured platen rotation with time, using the proportion of platen rotation by ice deformation indicated by thread deflection.

To evaluate ice softening by water, we make no assumption regarding the stress exponent in the power-law flow rule for ice and plot effective ice viscosity,

$\eta =\frac{\tau }{2\dot{\epsilon }}(1)$

as a function of water content, where τ is the measured peak shear stress and $\dot{\epsilon }=\frac{1}{2}\frac{\delta u}{\delta z}$ is the shear strain rate, as determined from thread deflection, based on the variation with height, z, in circumferential ice velocity at the ice-ring centerline, u. In the context of Glen’s flow law (e.g., Cuffey and Paterson, 2010), $\dot{\epsilon }=A{\tau }^n$, effective ice viscosity depends in the constants A and n:

$\eta =\frac{1}{2}{\left(A{\tau }^{n-1}\right)}^{-1}(2)$

The prefactor, A, contains all effects on viscosity other than stress.

To measure final grain sizes, thin sections in the longitudinal flow plane are made from ice samples of sheared ice. Photographs are analyzed in ImageJ, open-source image processing software (Schneider et al., 2012). The mean planimetric grain area for each thin section is calculated by dividing the sum of planimetric grain areas by the total number of grains (Fitzpatrick, 2013). The mean planimetric diameter is then determined as the diameter of a circle of equivalent area and up-scaled to estimate the mean volumetric diameter from the two-dimensional image (Durand, 2004). Grains truncated at edges of thin sections are not considered, and a minimum of 100 grains is counted in each section so that mean diameters are not underestimated (Durand, 2004).

Results

Strain rates varied from ∼1.0 to 12.0 × 10⁻⁸ s⁻¹ (Table 1), a factor of ∼1.2–15 higher than the highest strain rates measured in the margins of Whillan’s Ice Stream (Whillans and van der Veen, 1997; Raymond et al., 2001). As noted, motion resulting from slip near the platen surfaces was not included in strain-rate determinations and varied roughly with confining pressure: an experiment at abnormally low confining pressure (0.33 MPa) yielded slip that accounted for 62% of the platen motion, whereas the average motion by slip was much lower, 27%. Despite slip at the platens, no discontinuity at the tips of platen teeth was visible in any experiment, unlike in Kamb’s (1972) torsion experiments in which slip was recorded at slightly subfreezing temperatures and discontinuities were visible after experiments.

TABLE 1

TABLE 1. Summary of experimental parameters. Reported errors are ± one standard deviation.

Peak shear stresses during secondary creep were attained at strains of 1.7–6.8% (Figure 4 and Supplementary Figures 3, 4) and varied from ∼0.06 to 0.20 MPa. These values of stress span most of the range of shear stress in West Antarctic shear margins, as computed by Raymond et al. (2001) from measurements and force-balance calculations. In the one experiment conducted to tertiary creep, a steady stress was measured over a total strain of ∼15–17%. Water contents of ice in experiments varied from 0.21 to 1.70% (Table 1), exceeding the upper limit of the water-content range measured by Duval (1977) (0.008–0.80%). Stress-strain plots usually contained a few isolated stress drops of up to ∼4 kPa (Figure 4 and Supplementary Figure 3).

FIGURE 4

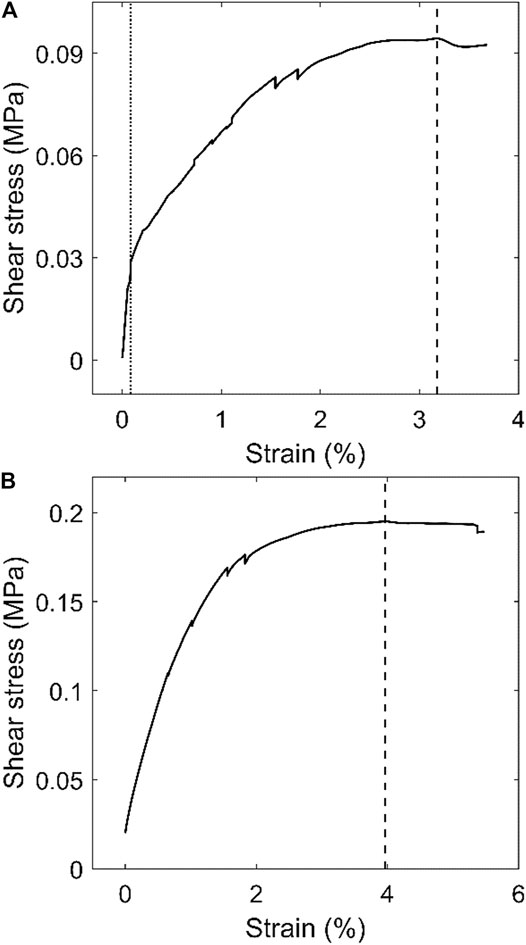
FIGURE 4. Representative stress-strain curves from (A) Experiment 1, one of five experiments in which strain rate was initially high, to accelerate the experiment, and then reduced (dotted line) to a lower value; strain rate at the peak stress (dashed line) was 2.9 ± 0.7 × 10⁻⁸ s⁻¹, and (B) Experiment 9, conducted at a single strain rate of 8.6 ± 0.4 × 10⁻⁸ s⁻¹.

Mean grain diameters during the experiments conducted to secondary creep increased by a factor of 2.7–4.2 (Figure 5). Initial mean grain diameters were 2.8–3.9 mm, with standard deviations of 1.0–1.6 mm. Mean grain diameters measured at the ends of experiments conducted to secondary creep averaged 8.3–12.5 mm, with standard deviations of 4.2–8.0 mm. Grain size increased slightly with decreasing strain rate (∼30%) and increasing experimental duration, but correlations were weak (Adams, 2021).

FIGURE 5

FIGURE 5. Initial and final ice textures (A,B) from Experiment 5 and (C,D) from Experiment 11 viewed under polarized light. Initial ice textures (A,C) are from the plane of shear; final ice textures (B,D) are in a longitudinal flow plane. Grid squares are 10 mm × 10 mm. Arrows indicate the orientation of shear.

The character of grain boundaries differed before and after shearing to secondary creep (Figure 5). Un-sheared ice had grains that were relatively equant with mostly straight, smooth boundaries. Grain boundaries of large crystals (>∼10 mm diameter) after shearing were highly irregular, and boundaries of large grains in some cases intruded into adjacent grains. The shapes of smaller crystals in sheared ice were more like crystals of the un-sheared ice, but boundaries were more irregular.

Plotting effective viscosity as a function of the mean water content of the ice ring indicates two regimes of sensitivity to water content (Figure 6). At water contents below ∼0.6%, effective viscosity decreases markedly with increasing water content, but at higher values viscosity is essentially independent of water content and centered on a value of about 1 × 10⁻¹² Pa s. Effective viscosity values computed from Duval’s (1977) data, collected in experiments conducted to tertiary creep with glacier ice, are a factor of 3.6–1.3 lower than effective viscosities measured in this study in secondary creep over the equivalent water-content range. Interestingly, the viscosity values of the two data sets more or less converge at a water content of ∼0.6%. Duval’s (1977) data indicate a factor of ∼2 less viscosity sensitivity to water content than observed in this study. The one tertiary-creep viscosity value from this study plots between the two data sets but closer to the trend of Duval’s tertiary-creep data (Figure 6).

FIGURE 6

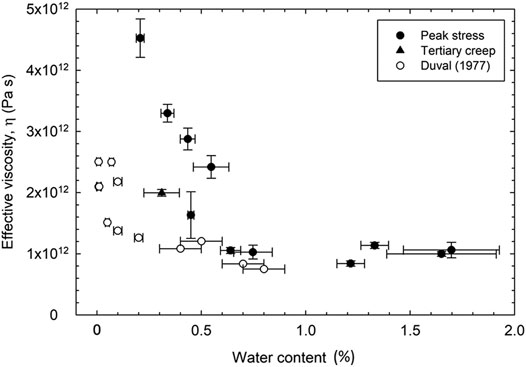
FIGURE 6. Effective ice viscosity as a function of water content, as measured in the 11 experiments to peak stresses and one tertiary-creep experiment of this study, compared with the tertiary-creep results of Duval (1977). Duval’s rotary experiments were conducted at a constant shear stress of 0.29 MPa.

The lack of a systematic change in effective ice viscosity at water contents greater than ∼0.6% implies that viscosity did not depend on the magnitude of the stress or strain rate, which each varied through roughly a factor of 3 among the relevant six experiments. Indeed, the lack of viscosity dependence on water content allows strain rate to be plotted as a function of stress, with a tight power-law fit yielding a stress exponent of n = 1.1 (Figure 7). Thus, it would appear, unexpectedly, that above a threshold water content of ∼0.6% the ice is essentially linear-viscous. Only two of Duval’s (1977) experiments included water contents above 0.6%, but those data plot close to the trend of the data of this study (Figure 7). Unfortunately, at water contents less than ∼0.6%, determining the value of n is not possible from our data, owing to the lack of multiple experiments at a single water content, which precludes inferring a controlling deformation mechanism based on the value of n.

FIGURE 7

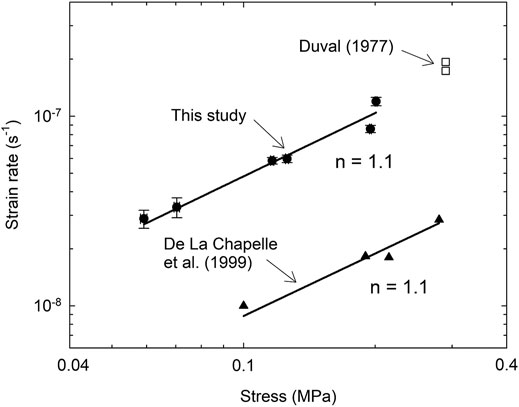
FIGURE 7. Strain rate as a function of stress for experiments at water contents of 0.6–1.7%, compared with data from uniaxial compression tests on saline ice (2 mm grain size) with a water content of 7% and at a temperature of −13°C (De La Chapelle et al., 1999). Also shown are the two strain rates measured in Duval’s (1977) study at water contents greater than 0.6% (the fitted line excludes these points and implies A = 6.21 × 10⁻⁷ Pa^−1.1 s⁻¹ in Eq. 2).

Discussion

Some aspects of these results, when compared with those of Duval (1977), are unsurprising. The higher effective viscosity values of the present study are expected, given their basis on peak stresses of secondary creep rather than on lower flow stresses of tertiary creep that reflect the development of crystalline fabric. Enhancement of A in Eq. 2 due to fabric development is thought to be 1–12 in simple shear, with both laboratory and field-based values spanning most of this range (Cuffey and Paterson, 2010; Hooke, 2020). However, values in the lower half of this range are expected here owing to the relatively low stresses of these experiments (Treverrow et al., 2012). Experiments on shallow ice from a shear margin pointed to enhancement of less than 2 (Jackson and Kamb, 1997). Modest enhancement (1.3–3.6) is indeed consistent with the comparison of our results with Duval’s (1977) (Figure 6). As noted, viscosity from the one experiment here conducted to tertiary creep plots close to but above the trend of Duval’s (1977) data. The additional softening from Duval’s study could derive from his use of glacier ice, which contained soluble impurities; in contrast, the ice of the tertiary-creep experiment here was made from deionized water. Also expected in these experiments at the PMT is the observed rapid grain growth and development of interlocking, irregular grains that likely indicates grain boundary migration as peak stresses were attained (e.g., Duval and Castelnau, 1995; Montagnat et al., 2015; Journaux et al., 2019). Longer experiments at low strain rates may account for the slightly larger grains observed at low strain rates. Also, grain growth during experiments, as well as melting by heat dissipation during shear, probably resulted in water content that evolved as stress, strain, and grain size increased. The measured values of water content, therefore, reflect those when peak stresses were attained but not necessarily water contents earlier in experiments.

More unexpected is the observation that viscosity values from these two studies converge at a water content of ∼0.6%; at higher water contents effective viscosity values from the Duval (1977) study are only ∼25% lower than in this study (Figure 6). If fabric development is indeed responsible for the softer ice of Duval’s experiments, then the effect of this fabric-related softening is progressively reduced as water content increases toward ∼0.6%, above which the softening associated with ice fabric is minimal.

Equally intriguing is the apparent linear-viscous behavior of ice in this study at water contents above ∼0.6% (Figure 7). We are aware of only one study of ice rheology, other than this one, in which ice contained more interstitial water than in the study of Duval (1977). De La Chapelle et al. (1999) reported results of compression creep tests conducted to secondary creep on cold (−13°C), saline ice with a water content of 7%. Four of these experiments were conducted at low shear stresses (<0.3 MPa) comparable to those of the present study. Although these authors fit their low-stress data based on n = 1.8 (their Figure 4), power-law regression of their data leaving the value of n free yields n = 1.1, as in the present study (Figure 7). This value of n cannot be explained by invoking basal slip accommodated by grain boundary sliding (n = 1.8), dislocation creep (n = 4) or a combination of the two at intermediate stresses (n = 3) (Goldsby and Kohlstedt, 2001).

Before considering further ice softening by water, the small stress drops that occurred in some experiments (Figure 4) require discussion. These stress drops may point to isolated brittle events, such as microcracking, despite the warm ice and confining pressures exceeding deviatoric stresses by a factor of 3–20. The water pressure within veins in the ice was unknown and if sufficiently large could have reduced the effective confining pressure to values less than deviatoric stresses, promoting microcracking. However, unlike studies in which microcracks enhanced creep (Sinha, 1989), microcracks were not visible in thin sections at the grain scale (Figures 5B,D), and continuous strain markers (weighted threads) across the thickness of the ice ring displayed no discontinuities. In contrast, some slip occurred at the platens that gripped the ice ring at its top and bottom, and very near the teeth of the platens deviatoric stresses would have locally attained maximum values. Thus if crack growth occurred, it likely happened near the platens, and was excluded in the measurement of total shear strain used to compute strain rate. Microcracking was less likely in this study than in the rotary experiments of Duval (1977), in which deviatoric stresses were higher by a factor of 1.5–4.9, and the ice was not confined radially.

The starting point of the leading hypothesis for ice softening by water (Duval, 1977; De La Chapelle et al., 1999; Schulson and Duval, 2009) is that where stresses are concentrated between adjacent crystals made “soft” and “hard” by their respectively favorable and unfavorable alignments with the macroscopic stress, dislocations pile up in tangles. These tangles cause the progressive strengthening associated with primary creep in rate-controlled tests. Water at grain boundaries is thought to reduce these tangles by absorbing dislocations, thereby softening ice by redistributing stresses and allowing activation of easy slip on basal planes (i.e., basal glide). However, if basal glide controlled peak stresses in our experiments, effective viscosity values with increasing water content would not have converged with those of Duval’s (1977) experiments conducted to tertiary creep. Rather, if the experiments here had been carried out to tertiary creep, the weakening associated with recrystallization and alignment of basal planes would have made flow stresses in tertiary creep significantly smaller than peak stresses in secondary creep, regardless of the water content. Moreover, the observed transition to nearly linear viscous behavior cannot be explained by basal glide limiting peak stresses at water contents greater than ∼0.6%.

To try to account for this near linear viscous behavior, we now consider the old idea that grain-boundary melting and refreezing, as a linear diffusive process, contributes to deformation of ice at the PMT (Barnes and Tabor, 1966; 1967; Barnes et al., 1971). As noted, extreme sensitivity of strain rate to temperature very near the PMT—observed in several studies of polycrystalline ice but absent in experiments with single crystals—clearly highlights the importance of processes at grain boundaries for ice at the PMT (Figure 1). The experiments of Barnes et al. (1971) provided evidence for grain boundary migration accompanying melting and the movement of liquid water at grain boundaries. Although Duval (1977) rejected melting and refreezing as possibly controlling ice deformation because his data collected at low water contents indicated n = 3 (Duval, 1976b), he acknowledged, nevertheless, that grain-scale stress heterogeneity would lead to temperature gradients across crystals that would cause local melting and refreezing at grain boundaries. This hypothesis is supported by observations of melting and refreezing in ice subjected to non-hydrostatic stress (Nye and Mae, 1972). Melting and refreezing is also a central process in theories aimed at describing the permeability of ice at its PMT (e.g., Lliboutry, 1996). Thus, a reasonable expectation is that melting and refreezing, in response to stress heterogeneity at grain boundaries and with associated movement of water in films along grain boundaries, contributed to the transfer of mass required for deformation and continuity among grains.

We next tentatively consider whether melting and refreezing (e.g., Barnes et al., 1971), if evaluated in the context of water films at grain boundaries, might limit peak stresses, given our observations that at water contents greater than 0.6% n ≈ 1 and viscosity values are similar in secondary and tertiary creep (Figure 6). Melting would reduce stress concentrations at grain boundaries, in concert with absorption of dislocations by water films at those locations, as suggested by Duval (1977), and with grain boundary migration (e.g., Montagnat and Duval, 2000). Rempel and Meyer (2019), who adapted classical regelation theory to account for effects of premelting, have shown how temperature gradients between zones of melting and refreezing and associated regelation speeds can be proportional to the permeability of films that transfer water between such zones. The permeability associated with Poiseuille flow through a film depends on its thickness squared, so film permeability and the rate of melting and refreezing are likely sensitive to water content. If so, the stress-limiting role of basal glide (e.g., De La Chapelle et al., 1999) may diminish with increasing water content as melting and refreezing redistribute mass with increasing efficiency, such that effective viscosity values in secondary creep decrease to nearly those of tertiary creep, as observed. Rempel and Meyer (2019, their equation 9) also showed that for sufficiently permeable (i.e., thick) water films, pressure gradients within them become negligible, so the speed of regelation approaches an upper bound that is linearly proportional to ice stress differences between melting and refreezing zones. This upper bound attained at a sufficiently high water content might account for the lack of viscosity sensitivity to water content and for linear-viscous behavior, assuming melting and refreezing can become principally responsible for minimizing stress heterogeneity among grains at water contents greater than 0.6%.

The value n ≈ 1 at water contents greater than 0.6% implies diffusional creep, possibly somewhat analogous to that studied in finely crystalline olivine with varying percentages of basaltic melt (Hirth and Kohlstedt, 1995; Kohlstedt and Zimmerman, 1996). In these studies sensitivity of effective viscosity to melt content was attributed to differences in the degree of wetting by melt along grain boundaries, which was thought to control diffusive transport of mass there. On the other hand, the relevant physics for the ice-water system could be significantly different than in other rock-melt systems. Processes in ice would indeed need to be different to allow a diffusive creep mechanism to control peak stresses at high melt contents despite the large grain sizes of the present study. A quantitative model, which should include relevant physics of water films at grain boundaries, is necessary to evaluate our suggestion that melting and refreezing might help account for the results of this study.

More experiments, particularly at water contents greater than 0.6% and to values beyond those of this study (>1.7%), need to be conducted to provide definitive guidance for ice-stream modelers who require a relationship between the effective viscosity of temperate ice and its water content. Nevertheless, our results should, at a minimum, be cautionary: extrapolating Duval’s (1977) data or the data herein to water contents higher than those studied experimentally will require a leap of faith until a tested, micromechanical model of the effect of interstitial water on ice rheology is available.

Conclusion

By exploring a greater range of water content than previously studied in experiments with pure ice, we have identified two distinct creep regimes above and below a threshold interstitial meltwater content of ∼0.6%. Across water contents of 0.2–0.6%, ice effective viscosity decreases by a factor of 4.4—a sensitivity that is ∼2.0 times greater than for the case of ice sheared to tertiary creep (Duval, 1977), although the sensitivity in tertiary creep is more relevant to ice-stream shear margins. Over increasing water content in this regime, effective viscosity values in secondary creep decrease to nearly those of tertiary creep (Duval, 1977), implying that development of ice crystal fabric during tertiary creep has little effect on softening ice at water contents above ∼0.6%. At water contents of ∼0.6–1.7%, ice effective viscosity does not change systematically with water content, and n = 1.1. A working hypothesis to account for the two regimes is that grain-scale stress heterogeneity can become limited by grain-boundary melting and refreezing, at rates that approach an upper bound as water films at grain boundaries thicken with increasing water content.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, with additional data archived at the U.S. Antarctic Program Data Center (https://www.usap-dc.org/view/dataset/601460). Further inquiries can be directed to the corresponding author.

Author Contributions

CA executed most of the experiments and wrote the thesis upon which the manuscript is based. NI supervised the project, secured funding for the research, and condensed the thesis for publication. CH contributed to the analysis for determining water content and helped write the manuscript. LZ helped secure funding for the research and write the manuscript. CB conducted one experiment and contributed to the analysis for determining water content.

Funding

This work was supported by a grant to NI and LZ from the United States National Science Foundation (NSFGEO-NERC-1643120).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank the two reviewers, H. Löwe, and M. Ranganathan, for their useful comments, R. B. Alley for helpful discussion of ice softening by water, and the United States National Science Foundation for supporting this study (NSFGEO-NERC-1643120).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.702761/full#supplementary-material

References

Adams, C. J. C. (2021). “Sensitivity of the Effective Viscosity of Temperate Ice to its Water Content,”. Master’s thesis (Ames, IA: Iowa State University).

Google Scholar

Alley, K. E., Scambos, T. A., Alley, R. B., and Holschuh, N. (2019). Troughs Developed in Ice-Stream Shear Margins Precondition Ice Shelves for Ocean-Driven Breakup. Sci. Adv. 5, eaax2215. doi:10.1126/sciadv.aax2215

PubMed Abstract | CrossRef Full Text | Google Scholar

Asaithambi, N. S. (1988). On a Variable Time-step Method for the One-Dimensional Stefan Problem. Comp. Methods Appl. Mech. Eng. 71, 1–13. doi:10.1016/0045-7825(88)90092-8

CrossRef Full Text | Google Scholar

Barnes, P., and Tabor, D. (1966). Plastic Flow and Pressure Melting in the Deformation of Ice I. Nature 210, 878–882. doi:10.1038/210878a0

CrossRef Full Text | Google Scholar

Barnes, P., and Tabor, D. (1967). Plastic Flow and Pressure Melting in the Deformation of Ice I. IASH Publ. 79, 303–315.

Google Scholar

Barnes, P., Tabor, D., and Walker, J. C. F. (1971). The Friction and Creep of Polycrystalline Ice. Proc. Roy. Soc. Lond. A. 324, 127–155. doi:10.1098/rspa.1971.0132

CrossRef Full Text | Google Scholar

Carol, H. (1947). The Formation Of Roches Moutonnées. J. Glaciol. 1 (2), 57–59. doi:10.3189/S0022143000007589

Cohen, D. (1999). Rheology of Basal Ice at Engabreen, Norway. Minneapolis, MN: University of Minnesota.

Cohen, D. (2000). Rheology of Ice at the Bed of Engabreen, Norway. J. Glaciol. 46, 611–621. doi:10.3189/172756500781832620

CrossRef Full Text | Google Scholar

Colbeck, S. C., and Evans, R. J. (1973). A Flow Law for Temperate Glacier Ice. J. Glaciol. 12, 71–86. doi:10.3189/S0022143000022711

CrossRef Full Text | Google Scholar

Cuffey, K. M., and Paterson, W. S. B. (2010). The Physics of Glaciers. Fourth Edition. London: Butterworth-Heinemann.

De La Chapelle, S., Milsch, H., Castelnau, O., and Duval, P. (1999). Compressive Creep of Ice Containing a Liquid Intergranular Phase: Rate-Controlling Processes in the Dislocation Creep Regime. Geophys. Res. Lett. 26, 251–254. doi:10.1029/1998gl900289

CrossRef Full Text | Google Scholar

Durand, G. (2004). Microstructure, recristallisation et déformation des glaces polaires de la carotte EPICA, Dôme Concordia, Antarctique. Grenoble, France: Université Joseph-Fourier.

Duval, P., and Castelnau, O. (1995). Dynamic Recrystallization of Ice in Polar Ice Sheets. J. Phys. IV 05, C3-C197–C3-205. doi:10.1051/jp4:1995317

CrossRef Full Text | Google Scholar

Duval, P. (1976a). Fluage et recristallisation des glaces polycristallines. Grenoble, France: Université Scientifique et Médicale de Grenoble.

Duval, P. (1976b). Lois du fluage transitoire ou permanent de la glace polycristalline pour divers états de contrainte. Ann. Geophysicae 32, 355–360.

Google Scholar

Duval, P. (1977). The Role of the Water Content on the Creep Rate of Polycrystalline Ice. Proc. Grenoble Symposium, 1975, IAHS 118, 29–33.

Google Scholar

Fitzpatrick, J. J. (2013). Digital-image Processing and Image Analysis of Glacier Ice. U.S. Geol. Surv. Tech. Methods 7, 1–21. doi:10.3133/tm7D1

CrossRef Full Text | Google Scholar

Glen, J. W. (1955). The Creep of Polycrystalline Ice. Proc. Roy. Soc. Lond. A. 228, 519–538. doi:10.1098/rspa.1955.0066

CrossRef Full Text | Google Scholar

Goldsby, D. L., and Kohlstedt, D. L. (2001). Superplastic Deformation of Ice: Experimental Observations. J. Geophys. Res. 106, 11017–11030. doi:10.1029/2000jb900336

CrossRef Full Text | Google Scholar

Haseloff, M., Hewitt, I. J., and Katz, R. F. (2019). Englacial Pore Water Localizes Shear in Temperate Ice Stream Margins. J. Geophys. Res. Earth Surf. 124, 2521–2541. doi:10.1029/2019JF005399

CrossRef Full Text | Google Scholar

Hirth, G., and Kohlstedt, D. L. (1995). Experimental Constraints on the Dynamics of the Partially Molten Upper Mantle: Deformation in the Diffusion Creep Regime. J. Geophys. Res. 100, 1981–2001. doi:10.1029/94jb02128

CrossRef Full Text | Google Scholar

Hooke, R. Le. B. (2020). Principles of Glacier Mechanics. Third Edition. Cambridge, UK: Cambridge University Press.

Hunter, P., Meyer, C., Minchew, B., Haseloff, M., and Rempel, A. (2021). Thermal Controls on Ice Stream Shear Margins. J. Glaciol. 67, 435–449. doi:10.1017/jog.2020.118

CrossRef Full Text | Google Scholar

Iverson, N. R., and Peterson, B. B. (2011). A New Laboratory Device for Study of Subglacial Processes: First Results on Ice–Bed Separation during Sliding. J. Glaciol. 57, 1135–1146. doi:10.3189/002214311798843458

CrossRef Full Text | Google Scholar

Jackson, M., and Kamb, B. (1997). The Marginal Shear Stress of Ice Stream B, West Antarctica. J. Glaciol. 43, 415–426. doi:10.1017/s0022143000035000

CrossRef Full Text | Google Scholar

Jones, S. J., and Brunet, J.-G. (1978). Deformation of Ice Single Crystals Close to the Melting point. J. Glaciol. 21, 445–455. doi:10.3189/s0022143000033608

CrossRef Full Text | Google Scholar

Journaux, B., Chauve, T., Montagnat, M., Tommasi, A., Barou, F., Mainprice, D., et al. (2019). Recrystallization Processes, Microstructure and Crystallographic Preferred Orientation Evolution in Polycrystalline Ice during High-Temperature Simple Shear. The Cryosphere 13, 1495–1511. doi:10.5194/tc-13-1495-2019

CrossRef Full Text | Google Scholar

Kamb, B. (1972). “Experimental Recrystallization of Ice under Stress,” in Flow and Fracturing of Rocks. Editors H. C. Heard, I. Y. Borg, N. L. Carteret al. (Washington, DC: Geophysical Monograph 16, American Geophysical Union).

Google Scholar

Kohlstedt, D. L., and Zimmerman, M. E. (1996). Rheology of Partially Molten Mantle Rocks. Annu. Rev. Earth Planet. Sci. 24, 41–62. doi:10.1146/annurev.earth.24.1.41

CrossRef Full Text | Google Scholar

Lliboutry, L., and Duval, P. (1985). Various Isotropic and Anisotropic Ices Found in Glaciers and Polar Ice Caps and Their Corresponding Rheologies. Ann. Geophysicae 3, 207–224.

Google Scholar

Lliboutry, L. (1996). Temperate Ice Permeability, Stability of Water Veins and Percolation of Internal Meltwater. J. Glaciol. 42, 201–211. doi:10.3189/s0022143000004068

CrossRef Full Text | Google Scholar

Mader, H. M. (1992). Observations of the Water-Vein System in Polycrystalline Ice. J. Glaciol. 38, 333–347. doi:10.1017/s0022143000002227

CrossRef Full Text | Google Scholar

Mellor, M., and Testa, R. (1969). Effect of Temperature on the Creep of Ice. J. Glaciol. 8, 131–145. doi:10.1017/s0022143000020803

CrossRef Full Text | Google Scholar

Meyer, C. R., and Minchew, B. M. (2018). Temperate Ice in the Shear Margins of the Antarctic Ice Sheet: Controlling Processes and Preliminary Locations. Earth Planet. Sci. Lett. 498, 17–26. doi:10.1016/j.epsl.2018.06.028

CrossRef Full Text | Google Scholar

Meyer, C. R., Yehya, A., Minchew, B., and Rice, J. R. (2018). A Model for the Downstream Evolution of Temperate Ice and Subglacial Hydrology along Ice Stream Shear Margins. J. Geophys. Res. Earth Surf. 123, 1682–1698. doi:10.1029/2018jf004669

CrossRef Full Text | Google Scholar

Montagnat, M., Chauve, T., Barou, F., Tommasi, A., Beausir, B., and Fressengeas, C. (2015). Analysis of Dynamic Recrystallization of Ice from EBSD Orientation Mapping. Front. Earth Sci. 3, 81. doi:10.3389/feart.2015.00081

CrossRef Full Text | Google Scholar

Montagnat, M., and Duval, P. (2000). Rate Controlling Processes in the Creep of Polar Ice, Influence of Grain Boundary Migration Associated with Recrystallization. Earth Planet. Sci. Lett. 183, 179–186. doi:10.1016/s0012-821x(00)00262-4

CrossRef Full Text | Google Scholar

Morgan, V. I. (1991). High-temperature Ice Creep Tests. Cold Regions Sci. Tech. 19, 295–300. doi:10.1016/0165-232x(91)90044-h

CrossRef Full Text | Google Scholar

Nye, J. F., and Frank, F. C. (1973). Hydrology of the Intergranular Veins in a Temperate Glacier. Symposium on the Hydrology of Glaciers. Cambridge, IASH 95, 157–161.

Google Scholar

Nye, J. F., and Mae, S. (1972). The Effect of Non-hydrostatic Stress on Intergranular Water Veins and Lenses in Ice. J. Glaciol. 11, 81–101. doi:10.3189/s0022143000022528

CrossRef Full Text | Google Scholar

Nye, J. F. (1989). The Geometry of Water Veins and Nodes in Polycrystalline Ice. J. Glaciol. 35, 17–22. doi:10.3189/002214389793701437

CrossRef Full Text | Google Scholar

Nye, J. F. (1991). The Rotting of Temperate Ice. J. Cryst. Growth 113, 465–476. doi:10.1016/0022-0248(91)90081-f

CrossRef Full Text | Google Scholar

Perol, T., and Rice, J. R. (2015). Shear Heating and Weakening of the Margins of West Antarctic Ice Streams. Geophys. Res. Lett. 42, 3406–3413. doi:10.1002/2015gl063638

CrossRef Full Text | Google Scholar

Raymond, C. F., Echelmeyer, K. A., Whillans, I. M., and Doake, C. S. M. (2001). “Ice Stream Shear Margins,”. The West Antarctic Ice Sheet: Behaviour and Environment. Editors R. B. Alley, and R. A. Bindschadler (Washington, DC: American Geophysical Union Antarctic Research Series), 137–155.

Google Scholar

Rempel, A. W., and Meyer, C. R. (2019). Premelting Increases the Rate of Regelation by an Order of Magnitude. J. Glaciol. 65, 518–521. doi:10.1017/jog.2019.33

CrossRef Full Text | Google Scholar

Rignot, E., Mouginot, J., Scheuchl, B., van den Broeke, M., van Wessem, M. J., and Morlighem, M. (2019). Four Decades of Antarctic Ice Sheet Mass Balance from 1979-2017. Proc. Natl. Acad. Sci. USA 116, 1095–1103. doi:10.1073/pnas.1812883116

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosenberg, C. L., and Handy, M. R. (2005). Experimental Deformation of Partially Melted Granite Revisited: Implications for the continental Crust. J. Metamorph Geol. 23, 19–28. doi:10.1111/j.1525-1314.2005.00555.x

CrossRef Full Text | Google Scholar

Schneider, C. A., Rasband, W. S., and Eliceiri, K. W. (2012). NIH Image to ImageJ: 25 Years of Image Analysis. Science 9 (7), 671–675. doi:10.1038/nmeth.2089

Schulson, E. M., and Duval, P. (2009). Creep and Fracture of Ice. Cambridge, UK: Cambridge University Press. doi:10.1017/cbo9780511581397

CrossRef Full Text

Sinha, N. K. (1989). Microcrack-enhanced Creep in Polycrystalline Material at Elevated Temperature. Acta Metallurgica 37 (11), 3107–3118. doi:10.1016/0001-6160(89)90346-5

CrossRef Full Text | Google Scholar

Suckale, J., Platt, J. D., Perol, T., and Rice, J. R. (2014). Deformation-induced Melting in the Margins of the West Antarctic Ice Streams. J. Geophys. Res. Earth Surf. 119, 1004–1025. doi:10.1002/2013JF003008

CrossRef Full Text | Google Scholar

Thompson, A. C., Iverson, N. R., and Zoet, L. K. (2020). Controls on Subglacial Rock Friction: Experiments with Debris in Temperate Ice. J. Geophys. Res. Earth Surf. 125. doi:10.1029/2020JF005718

CrossRef Full Text | Google Scholar

Treverrow, A., Budd, W. F., Jacka, T. H., and Warner, R. C. (2012). The Tertiary Creep of Polycrystalline Ice: Experimental Evidence for Stress-dependent Levels of Strain-Rate Enhancement. J. Glaciol. 58, 301–314. doi:10.3189/2012jog11j149

CrossRef Full Text | Google Scholar

Vallon, M., Petit, J. R., and Fabre, B. (1976). Study of an Ice Core to the Bedrock in the Accumulation Zone of an alpine Glacier. J. Glaciol. 17, 13–28. doi:10.3189/S0022143000030677

CrossRef Full Text | Google Scholar

Whillans, I., and van der Veen, C. (1997). The Role of Lateral Drag in the Dynamics of Ice Stream B, Antarctica. J. Glaciol. 43 (144), 231–237. doi:10.3189/S0022143000003178

Zoet, L. K., and Iverson, N. R. (2020). A Slip Law for Glaciers on Deformable Beds. Science 368, 76–78. doi:10.1126/science.aaz1183

PubMed Abstract | CrossRef Full Text | Google Scholar