Contributions to Polar Amplification in CMIP5 and CMIP6 Models

As a step towards understanding the fundamental drivers of polar climate change, we evaluate contributions to polar warming and its seasonal and hemispheric asymmetries in Coupled Model Intercomparison Project phase 6 (CMIP6) as compared with CMIP5. CMIP6 models broadly capture the observed pattern of surface- and winter-dominated Arctic warming that has outpaced both tropical and Antarctic warming in recent decades. For both CMIP5 and CMIP6, CO₂ quadrupling experiments reveal that the lapse-rate and surface albedo feedbacks contribute most to stronger warming in the Arctic than the tropics or Antarctic. The relative strength of the polar surface albedo feedback in comparison to the lapse-rate feedback is sensitive to the choice of radiative kernel, and the albedo feedback contributes most to intermodel spread in polar warming at both poles. By separately calculating moist and dry atmospheric heat transport, we show that increased poleward moisture transport is another important driver of Arctic amplification and the largest contributor to projected Antarctic warming. Seasonal ocean heat storage and winter-amplified temperature feedbacks contribute most to the winter peak in warming in the Arctic and a weaker winter peak in the Antarctic. In comparison with CMIP5, stronger polar warming in CMIP6 results from a larger surface albedo feedback at both poles, combined with less-negative cloud feedbacks in the Arctic and increased poleward moisture transport in the Antarctic. However, normalizing by the global-mean surface warming yields a similar degree of Arctic amplification and only slightly increased Antarctic amplification in CMIP6 compared to CMIP5.

Introduction

Observations (Serreze et al., 2009; Screen and Simmonds, 2010a) and climate model projections (Manabe and Stouffer, 1980; Holland and Bitz, 2003) consistently exhibit a pattern of enhanced surface warming in the Arctic compared to the rest of the globe. This so-called Arctic amplification peaks during winter and is at its minimum during summer (Manabe and Stouffer, 1980; Holland and Bitz, 2003; Screen and Simmonds, 2010b; Deser et al., 2010). There is also a strong warming asymmetry between the poles: Antarctic amplification has yet to be observed and is projected to be much weaker than Arctic amplification (Marshall et al., 2015; Smith et al., 2019). Multiple processes contribute to polar amplification, making it a robust feature of the long-term climate response to forcing while at the same time making polar warming inherently more uncertain than global-mean warming (e.g., Holland and Bitz, 2003; Roe et al., 2015; Bonan et al., 2018; Stuecker et al., 2018). Further investigation into the causes of polar warming and its seasonal and hemispheric asymmetry is thus needed to develop reliable projections of future polar change.

Studies examining a suite of climate models in the Coupled Model Intercomparison Project phase 5 (CMIP5; Block et al., 2020; Goosse et al., 2018; Pithan and Mauritsen, 2014) have quantified key contributors to the magnitude and intermodel spread of polar amplification, motivating the direction of further research with a refined focus. These studies suggest that the largest contributor to Arctic-amplified warming is the lapse-rate feedback, which is more positive in the Arctic than elsewhere. Unlike in the tropics, where deep convection causes surface warming to be amplified with height, in polar regions, a stable lower troposphere inhibits vertical mixing and contributes to stronger warming near the surface than aloft (Cronin and Jansen, 2015; Payne et al., 2015; Hahn et al., 2020). This surface-trapped warming leads to a positive lapse-rate feedback by producing less longwave emission to space than a vertically uniform heating of the atmospheric column.

While the positive surface albedo feedback associated with sea-ice loss plays a key role in polar warming (e.g., Hall, 2004; Dai et al., 2019), Pithan and Mauritsen (2014) suggest that its contribution to Arctic amplification is secondary to that of the lapse-rate feedback. However, the strength of the lapse-rate feedback itself is highly dependent on the degree of surface warming and sea-ice loss (Graversen et al., 2014; Feldl et al., 2017; Feldl et al., 2020; Boeke et al., 2021). The albedo feedback additionally contributes most to intermodel spread in polar warming among CMIP5 models, followed by the lapse-rate feedback (Pithan and Mauritsen, 2014).

Another substantial contribution to Arctic amplification is made by the Planck feedback (Pithan and Mauritsen, 2014). Following the Stefan-Boltzmann law, a given surface warming at initially colder temperatures produces a weaker increase in emitted longwave radiation, causing a less-negative Planck feedback in the Arctic than the tropics. Finally, poleward atmospheric heat transport (AHT) into the Arctic increases only a small amount under climate warming within CMIP5 models, suggesting that AHT makes only a small contribution to Arctic amplification (Pithan and Mauritsen, 2014; Goosse et al., 2018). However, many studies highlight increased latent heat transport into the Arctic as a primary driver of polar warming and note that the small change in total AHT reflects compensating changes in latent and dry heat transports (e.g., Alexeev et al., 2005; Armour et al., 2019). Other processes such as water-vapor and cloud feedbacks, Arctic surface heat fluxes (i.e., ocean heat uptake), and the meridional structure of CO₂ forcing contribute more to tropical than polar warming (Pithan and Mauritsen, 2014; Goosse et al., 2018).

Assessments of polar warming in CMIP5 highlight key drivers not only of Arctic amplification, but also of seasonal and hemispheric asymmetry in polar warming. Summer ocean heat storage and its release to the atmosphere in winter contributes most to the winter peak in Arctic warming, and drives substantial intermodel spread in Arctic amplification (Pithan and Mauritsen, 2014; Boeke and Taylor, 2018). As a result of enhanced vertical stability in winter, the winter-peaking lapse-rate feedback makes an additional contribution to the winter maximum in Arctic warming (Pithan and Mauritsen, 2014). The lapse-rate feedback is also the largest contributor to greater warming in the Arctic than Antarctic in CMIP5 models (Goosse et al., 2018) due to the elevation of the Antarctic ice sheet and resulting shallower and weaker base-state Antarctic inversions (Salzmann, 2017; Hahn et al., 2020). Goosse et al. (2018) also confirm a large role for Southern Ocean heat uptake (Marshall et al., 2015; Armour et al., 2016) and a more-negative cloud feedback in weakening transient Antarctic warming compared to the Arctic.

The Coupled Model Intercomparison Project phase 6 (CMIP6) offers an opportunity to reexamine the processes contributing to polar amplification in a new model ensemble and evaluate the evolution of relevant processes between model generations. The higher effective climate sensitivity in CMIP6 than CMIP5, on average, has been traced to less-negative extratropical cloud feedbacks within many CMIP6 models (Zelinka et al., 2020), suggesting that extratropical cloud feedbacks may also contribute more to polar warming in CMIP6. To explore how cloud and other feedbacks contribute to polar amplification in CMIP6 models, we apply a ‘warming contribution’ analysis (Pithan and Mauritsen, 2014; Goosse et al., 2018) to CMIP6 and compare with the same analysis applied to CMIP5. We evaluate the drivers of Arctic amplification, weaker Antarctic amplification, and seasonal asymmetry in polar warming, considering also the spread in warming contributed by model differences. We note that Cai et al. (2021) have previously examined Arctic and Antarctic warming contributions in CMIP6, but here we expand this analysis from 15 to 42 CMIP6 models (Supplementary Table S1), add a comparison to CMIP5, consider climate feedback sensitivity to the choice of radiative kernel, and consider more closely the role of AHT in driving polar amplification by partitioning its changes into moist and dry components. We also apply the warming contribution analysis to Atmospheric Model Intercomparison Project phase 6 (AMIP6) models to estimate contributions to historical modelled warming in comparison to warming projected by fully-coupled CMIP6 models. By quantifying key contributors to polar warming and its asymmetries in CMIP6, we hope to assess previously established mechanisms of Arctic amplification as well as identify open questions in support of future polar research.

Historical Polar Amplification in Observations and Models

Before quantifying contributions to projected surface warming in CMIP6, we compare historical near-surface and atmospheric temperature trends over 1979–2014 from fully-coupled CMIP6 models with reanalysis data and observations (Figures 1, 2). We use the European Centre for Medium-Range Weather Forecasts Interim Re-Analysis (ERA-Interim; Dee et al., 2011) which, in an evaluation of seven reanalyses over the Arctic, has been found to perform best in simulating observations of near-surface air temperature, surface radiative fluxes, precipitation, and wind speed (Lindsay et al., 2014). Limitations of this and other reanalyses in the Arctic include a positive near-surface temperature bias over sea ice in winter, with a slightly smaller bias for ERA-Interim than its successor, ERA5 (Graham et al., 2019; Wang et al., 2019). Although ERA-Interim also overestimates the lowest observed near-surface temperatures over Antarctica, it correlates relatively well with Antarctic observations of near-surface temperatures (Gossart et al., 2019) and their trends (Wang et al., 2016). We also show historical near-surface temperature trends for HadCRUT5, an observational dataset which combines CRUTEM5 near-surface air temperature over land with HadSST4 sea-surface temperatures, with statistical infilling where observations are unavailable (Morice et al., 2021). Throughout this study, we define the Arctic as 60 to 90˚N and the Antarctic as 60 to 90˚S, and define polar amplification as the near-surface warming poleward of 60° in a given hemisphere divided by global-mean near-surface warming.

FIGURE 1

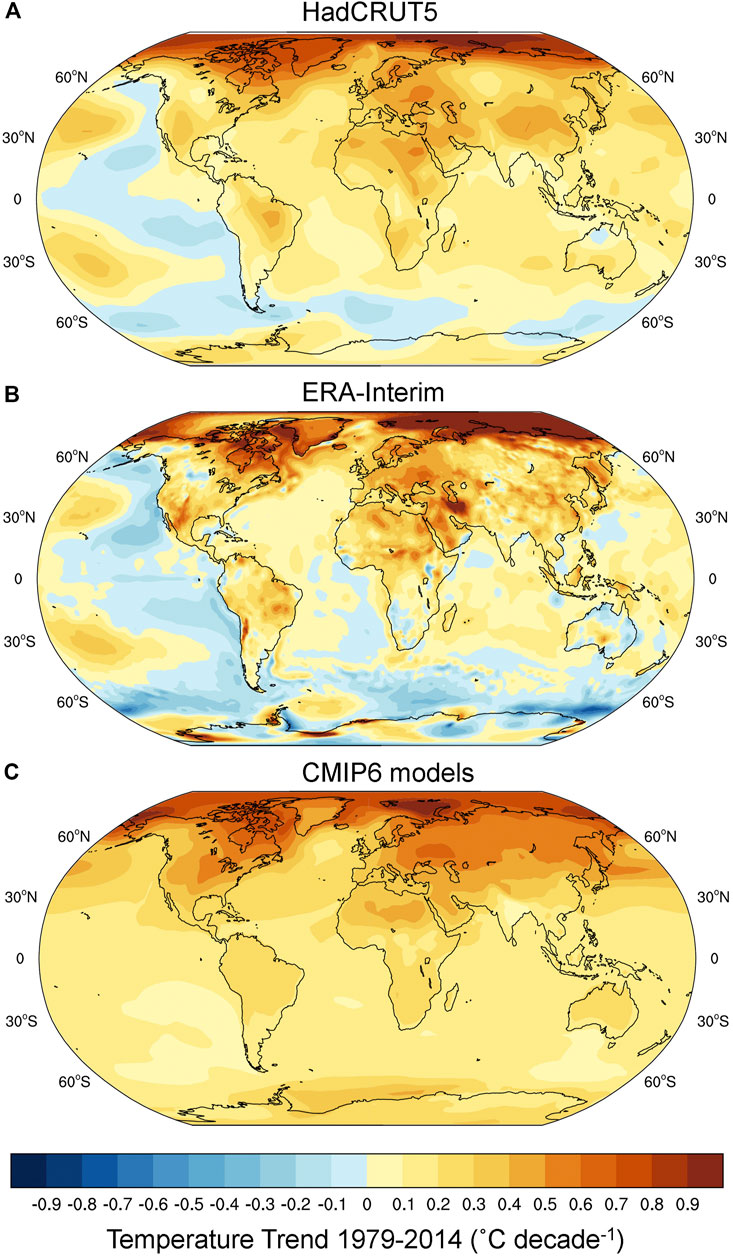
FIGURE 1. Annual-mean near-surface temperature trends (˚C decade⁻¹) for 1979–2014 from (A) HadCRUT5 observations, (B) the ERA-Interim reanalysis, and (C) the historical CMIP6 multimodel mean.

FIGURE 2

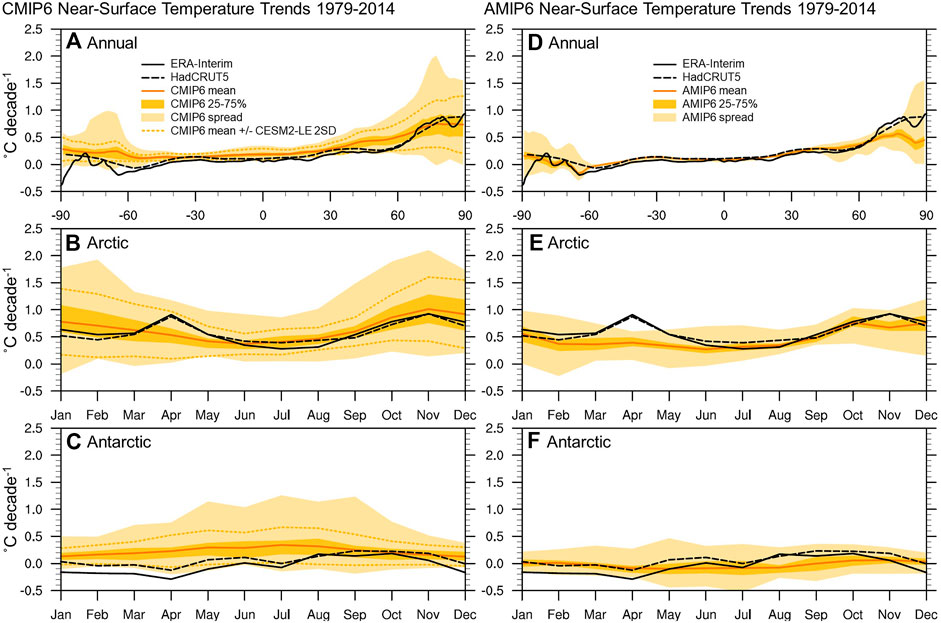
FIGURE 2. Near-surface temperature trends (˚C decade⁻¹) for 1979–2014 for (A,D) the annual- and zonal-mean, (B,E) the Arctic seasonal cycle, and (C,F) the Antarctic seasonal cycle in the ERA-Interim reanalysis (solid black line), HadCRUT5 observations (dashed black line), and the historical CMIP6 (A–C) and AMIP6 (D–F) multimodel means (solid orange line). The dark orange shading shows the 25th to 75th percentiles, and the light orange shading shows the full intermodel spread. The dashed orange lines (A–C) show the CMIP6 mean ± 2 standard deviations across ensemble members in the CESM2-LE.

The ensemble mean of fully-coupled CMIP6 models (hereafter called the CMIP6 mean) for historical simulations reproduces the observed pattern of amplified Arctic warming and weaker warming in the Antarctic, but exceeds the observed warming at all latitudes except in the Arctic (Figures 1, 2A). As a result, the CMIP6 mean produces too little Arctic amplification and too much Antarctic amplification over this historical period: the degree of Arctic and Antarctic amplification in the CMIP6 mean is 2.6 and 0.9, respectively, compared to 3.5 and 0.4 in HadCRUT5 observations. Figure 2 also shows the CMIP6 mean near-surface temperature trend with ± 2 standard deviations of trends calculated across the first 90 ensemble members of the Community Earth System Model version 2 Large Ensemble (CESM2-LE) as a reference for the range of internal variability within a single climate model in CMIP6. The CESM2-LE uses identical time-varying external forcing for its ensemble members, but begins each with a combination of different oceanic and atmospheric initial conditions (Rodgers et al., 2021). With the exception of the Southern Hemisphere mid-latitudes, zonal-mean warming trends in HadCRUT5 fall within the range of CMIP6 intermodel spread and the range of internal variability for CESM2-LE, suggesting that CMIP6 models may be largely consistent with observations when internal variability is taken into account.

CMIP6 models capture the seasonality of near-surface warming in the Arctic, with a peak in warming during early winter (Figure 2B). While the CMIP6 multimodel mean excludes a second peak in warming in April found in observations and reanalyses (Screen et al., 2012), this April maximum falls within the intermodel spread for CMIP6 and the ensemble spread for CESM2-LE, suggesting that it may be explained by internal variability. Model underestimation of observed reductions in spring snow cover extent over land may also contribute to a low bias in modeled Arctic springtime warming (Screen et al., 2012; Brutel-Vuilmet et al., 2013). In the Antarctic, CMIP6 models on average simulate year-round warming with a winter maximum (Figure 2C) whereas the observations and reanalysis show near-zero warming or slight cooling. Both the intermodel spread and spread due to internal variability in historical near-surface warming are largest in polar regions and during winter.

In addition to considering historical trends from fully coupled models in CMIP6, we show historical near-surface and atmospheric temperature trends from models in the Atmospheric Model Intercomparison Project phase 6 (AMIP6; Supplementary Table S1). These models prescribe time-varying monthly sea-surface temperatures and sea-ice concentrations based on observations, while still including atmosphere-land coupling, along with time-varying historical forcing agents (Eyring et al., 2016). The ensemble mean of AMIP6 models aligns more closely than the CMIP6 mean with observed near-surface atmospheric temperature trends in the tropics and Antarctic (Figures 2D–F). Despite having prescribed observational sea-surface temperature and sea-ice concentration changes, the AMIP6 mean underestimates observed Arctic warming over both land and sea-ice surfaces. This may result from differences between models and observations in sea-ice thickness and the near-surface air temperature response to sea-ice loss. Underestimated Arctic amplification in both the CMIP6 and AMIP6 means is also shown in Supplementary Figure S1, with historical temperature trends normalized by global-mean near-surface warming.

Consistent with previous modelling and observational studies, the vertical and seasonal pattern of Arctic warming for both ERA-Interim and CMIP6 is amplified near the surface during winter and is more vertically-uniform during summer (Figures 3A,C). For both summer and winter, mid-tropospheric warming trends are stronger for CMIP6 than ERA-Interim, which may reflect stronger increased poleward AHT due to overestimated mid-latitude surface warming (Fajber et al., 2018; Feldl et al., 2020; Kosaka and Xie, 2013). Consistent with this hypothesis, AMIP6 models, which simulate mid-latitude near-surface temperature trends closer to observations, show weaker warming aloft than CMIP6 (Figure 3E). AMIP6 models still demonstrate stronger mid-tropospheric summer warming than ERA-Interim, which may be related to AHT differences contributed by surface temperatures over land, or to enhanced atmospheric shortwave absorption by water vapor in these models (Donohoe and Battisti, 2013).

FIGURE 3

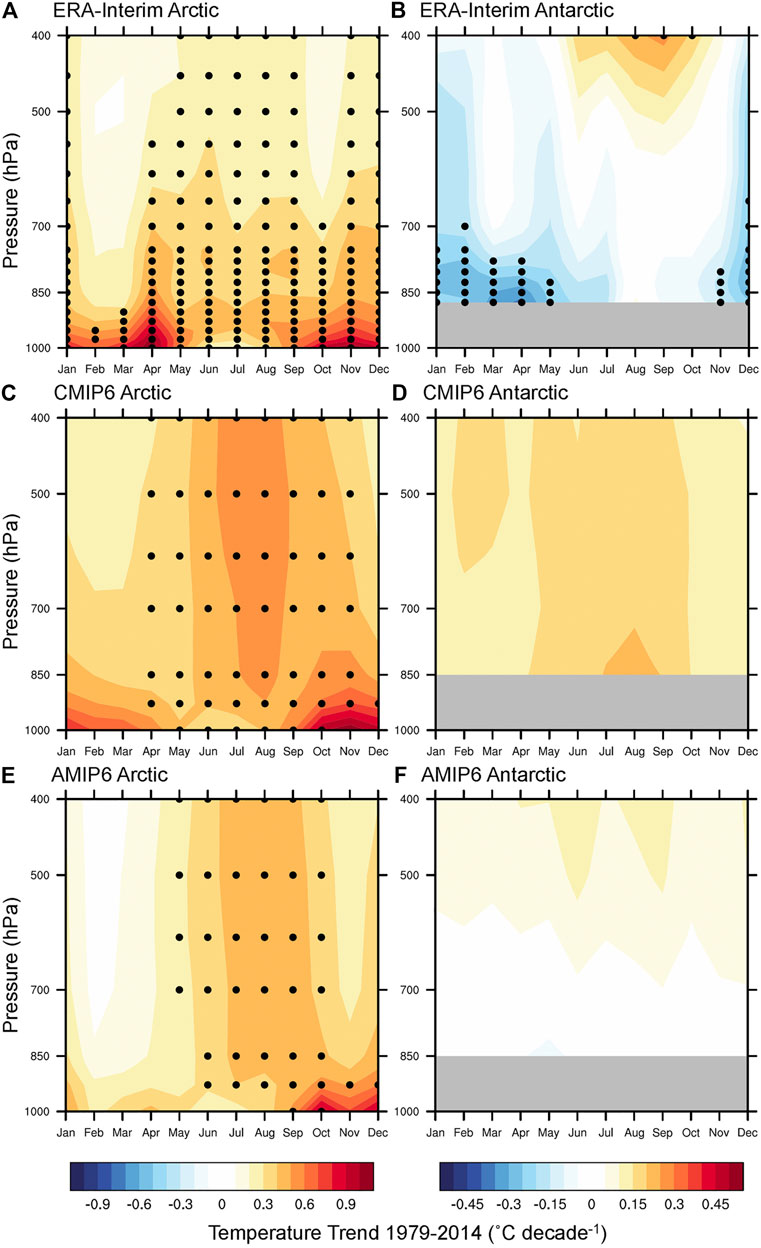
FIGURE 3. Atmospheric temperature trends (˚C decade⁻¹) for 1979–2014 for (A,C,E) the Arctic and (B,D,F) the Antarctic in the ERA-Interim reanalysis (A,B), and historical CMIP6 (C,D) and AMIP6 (E,F) multimodel mean trends. Black dots in (A,B) show statistically significant trends at the 95% level based on a two-tailed Student’s t-test, and black dots in (C,D) and (E,F) show where 75% of models meet these criteria for significant trends. For the reanalysis and models, temperature data is first masked at pressures greater than the surface pressure, and trends are only shown where more than 50% of area-averaged grid points are non-missing.

In contrast to CMIP6 models, which propagate Arctic winter surface warming further aloft than the ERA-Interim reanalysis, CMIP3 and CMIP5 models simulate excessively surface-trapped Arctic warming as a result of overestimating mean-state inversion strength (Medeiros et al., 2011; Pithan et al., 2014; Screen et al., 2012). This overestimated stability in earlier models has been attributed to a low bias in the supercooled liquid fraction of mixed-phase clouds, which allows for too much surface radiative cooling (Pithan et al., 2014). While CMIP6 models also tend to overestimate winter surface inversion strength in the Arctic (Supplementary Figure S2), increased supercooled liquid fraction in some CMIP6 models may have reduced these biases in inversion strength and surface-trapped warming compared to earlier models. A weaker ice-to-liquid transition in CMIP6 models with more mean-state supercooled liquid may also lead to a smaller increase in downward longwave radiation under warming, additionally causing weaker surface-trapped warming in CMIP6 (Tan and Storelvmo., 2019).

In both models and observations, Antarctic temperature trends are much weaker than those in the Arctic (Figures 3B,D,F; note the reduced colorbar range for the Antarctic). CMIP6 models demonstrate a small surface-amplified warming during winter, while ERA-Interim shows surface-amplified cooling particularly for December-May, as observed in near-surface temperature trends. In summary, although differences exist between observed and modeled Antarctic temperature trends, CMIP6 models generally agree with observations in producing winter- and surface-amplified warming in the Arctic, with much weaker trends in the Antarctic. Next we investigate the drivers of this Arctic-amplified warming and its hemispheric and seasonal asymmetry in CMIP5 and CMIP6 models.

Contributions to Polar Warming in CMIP5 and CMIP6 Models

Warming Contribution Methodology

Following previous studies (Lu and Cai, 2009; Crook and Forster 2011; Feldl and Roe 2013; Taylor et al., 2013; Pithan and Mauritsen, 2014; Goosse et al., 2018), we calculate contributions to projected polar warming based on an energy budget analysis. To do so, we use CMIP5 and CMIP6 output from pre-industrial control (piControl) and abrupt CO₂ quadrupling (abrupt4xCO2) experiments, in which CO₂ concentrations are quadrupled from piControl conditions and then held fixed for 150 years. As in Zelinka et al. (2020) and Caldwell et al. (2014), we apply a 21-year running average to piControl experiments to account for model drift before computing anomalies between abrupt4xCO2 and piControl during corresponding time periods (i.e., after branching to abrupt4xCO2, year-100 in piControl is compared to year-100 in abrupt4xCO2). With the assumption of similar model drift in the abrupt4xCO2 and piControl experiments, this approach isolates anomalies due to CO₂ forcing rather than model drift. We calculate the effective radiative forcing (ERF) as the y-intercept of the regression between top-of-atmosphere (TOA) radiation anomalies at each grid point against the global-mean near-surface temperature anomalies for the first 20 years after CO₂ quadrupling (Gregory et al., 2004). Smith et al. (2020) demonstrate that this 20-year regression yields ERF values which closely match methods using fixed sea-surface temperatures (Hansen et al., 2005) under CO₂ quadrupling in CMIP6 models, while regression over the full 150-year abrupt4xCO2 period instead underestimates ERF as a result of time-varying feedbacks in models (Andrews et al., 2015; Dong et al., 2020).

To calculate temperature anomalies, climate feedbacks, and heat transport anomalies under CO₂ quadrupling, we use monthly climate variable anomalies averaged over 31 years centered on year-100 of the abrupt4xCO2 experiments. We calculate climate feedbacks using the radiative kernel method (Shell et al., 2008; Soden et al., 2008), in which relevant climate variable anomalies are multiplied by monthly- and spatially-resolved radiative kernels, which quantify the change in radiative flux per unit change in a given climate variable. Vertically integrating this product throughout the troposphere gives the contribution of each feedback to TOA radiation anomalies. Temperature feedbacks are separated into the effect of surface temperature changes propagated throughout the troposphere (the Planck feedback) and the effect of departures from this vertically uniform temperature change (the lapse-rate feedback). Cloud feedbacks are calculated using the change in cloud radiative forcing (ΔCRF), equal to the change in all-sky minus clear-sky TOA radiation, minus a cloud masking term. This cloud masking term is defined as the effect of noncloud variables (temperature, water vapor, and surface albedo) on ΔCRF, calculated using all-sky and clear-sky radiative kernels. While our method is consistent with Goosse et al. (2018), one caveat of using year-100 feedback energetic contributions divided by year-100 temperature anomalies as opposed to linear regression of these fields (as in Zelinka et al. (2020)) is that the resulting feedbacks include both the true temperature-mediated feedbacks and rapid adjustments that occur immediately upon quadrupling CO₂. Resulting differences from the regression method used in Zelinka et al. (2020) for cloud feedbacks are discussed at the end of the section Warming Contributions in CMIP5 and CMIP6.

We primarily show feedbacks calculated using the Huang et al. (2017) kernels, which are based on ERA-Interim reanalysis data and give the smallest residual terms between the modelled TOA radiation anomalies and the sum of feedback and forcing radiative contributions (Zelinka et al., 2020). However, we additionally consider sensitivity to kernel choice, including kernels from Soden et al. (2008) (based on GFDL AM2), Shell et al. (2008) (based on NCAR CAM3), Block and Mauritsen (2013) (based on MPI ECHAM6), Pendergrass et al. (2018) (based on NCAR CAM5), and Smith et al. (2018) (based on HadGEM2). For comparison with the kernel-derived surface albedo feedback, we also compute the surface albedo feedback using the approximate partial radiative perturbation (APRP) method (Taylor et al., 2007).

As in Pithan and Mauritsen (2014), we calculate the annual AHT convergence as the difference between surface and net TOA fluxes. We further partition this into a moist component using the difference between precipitation and evaporation multiplied by the latent heat of vaporization (with the latent heat of fusion for solid precipitation neglected), and a dry component calculated as the residual between total and moist AHT convergence. To calculate the seasonal cycle of AHT convergence, we additionally subtract atmospheric energy and moisture storage terms following Donohoe et al. (2020a). Anomalous surface heat fluxes (referred to here as ocean heat uptake) implicitly include both ocean heat transport and ocean heat storage, on both seasonal and annual timescales.

We use a local energy budget (Eq. 1 below) to convert these energetic contributions of climate feedbacks and heat transport anomalies surrounding year-100 of the abrupt4xCO2 experiments into contributions to near-surface warming ($\Delta T$) in the tropics, Arctic, and Antarctic, as in previous studies (Lu and Cai, 2009; Crook and Forster, 2011; Feldl and Roe, 2013; Taylor et al., 2013; Pithan and Mauritsen, 2014; Goosse et al., 2018). Equation 1 includes the ERF, energetic contributions of climate feedbacks (${\lambda }_i\text{Δ}T)$ and the Planck response (${\lambda }_p\text{Δ}T)$, anomalies in AHT convergence ($\Delta AHT$) and ocean heat uptake ($\Delta O)$, and a residual term ($\Delta R_{res})$, all in units of Wm⁻²:

$ERF+\left({\lambda }_p+{\displaystyle \sum }_i{\lambda }_i \right)\text{Δ}T+\text{Δ}AHT+\text{Δ}O + \Delta R_{res}=0(1)$

In addition to computing annual-mean warming contributions, we calculate contributions during winter (December-January-February for the Arctic and June-July-August for the Antarctic) and summer (June-July-August for the Arctic and December-January-February for the Antarctic) seasons. For each region and season, warming contributions are defined by dividing each term in Eq. 1 by the global- and annual-mean Planck feedback ($\overline{{\lambda }_p}$) in Wm⁻² K⁻¹:

$\text{Δ}T= -\frac{ERF}{\overline{{\lambda }_p}}-\frac{{\lambda }_p^{\prime }\text{Δ}T}{\overline{{\lambda }_p}}-\frac{{{\displaystyle \sum }}_i{\lambda }_i\text{Δ}T}{\overline{{\lambda }_p}}-\frac{\text{Δ}AHT}{\overline{{\lambda }_p}}-\frac{\text{Δ}O}{\overline{{\lambda }_p}}-\frac{\Delta R_{res}}{\overline{{\lambda }_p}}(2)$

where ${\lambda }_p^{\prime }={\lambda }_p-\overline{{\lambda }_p}$ is the difference between the regional, seasonal Planck feedback, ${\lambda }_p,$ and its annual- and global-mean value, $\overline{{\lambda }_p}$.

Warming Contributions in CMIP5 and CMIP6

Near-surface temperature anomalies centered around year-100 of the abrupt4xCO2 simulations in CMIP5 and CMIP6 are shown in Figure 4A. Consistent with observed and modelled historical temperature trends (Figures 1, 2), both CMIP5 and CMIP6 models project transient warming under CO₂ quadrupling that is amplified in the Arctic compared to the tropics, with weaker Antarctic amplification. CMIP6 models exhibit large intermodel spread in the Arctic, with an interquartile range of up to 8°C in Arctic warming compared to about 4°C in the Antarctic and 2°C in the tropics. In the multimodel mean, Arctic warming has increased from 10.1°C in CMIP5 to 11.5°C in CMIP6, while Antarctic warming has increased from 5.1°C in CMIP5 to 6.4°C in CMIP6. This increase in polar warming is greater than the increase in tropical warming from 4.3°C in CMIP5 to 4.8°C in CMIP6. However, normalizing by the global-mean surface warming in each model (Figure 4B) demonstrates a similar degree of Arctic amplification and only slightly increased Antarctic amplification in CMIP6 compared to CMIP5.

FIGURE 4

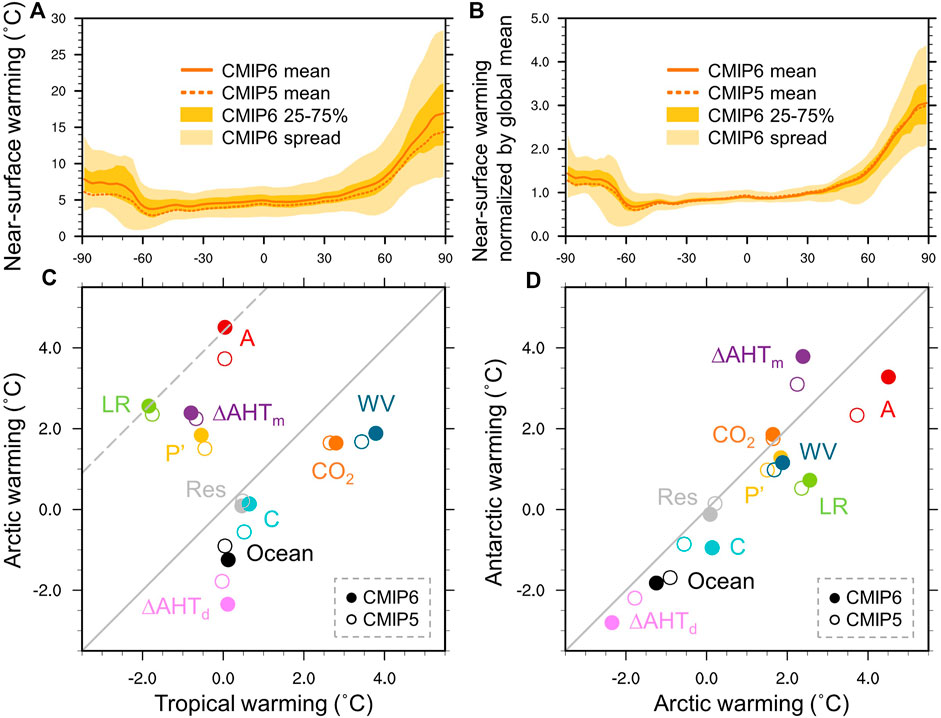
FIGURE 4. (A) Annual- and zonal-mean near-surface warming (˚C) averaged over 31 years centered on year-100 after CO₂ quadrupling for the CMIP6 (solid orange line) and CMIP5 (dashed orange line) multimodel means. The dark orange shading shows the 25th to 75th percentiles, and the light orange shading shows the full intermodel spread for CMIP6. (B) As in (A), but with zonal-mean near-surface warming normalized by global-mean near-surface warming within each model. (C,D) Contributions of each feedback and atmospheric forcing to warming (˚C) centered around year-100 of abrupt CO₂ quadrupling in CMIP6 (filled circles) and CMIP5 (hollow circles) for (C) the tropics relative to the Arctic and (D) the Arctic relative to the Antarctic. Warming contributions are shown for the lapse-rate (LR), surface albedo (A), water-vapor (WV), and cloud (C) feedbacks, the variation in the Planck response from its global-mean value (P’), effective radiative forcing (CO₂), change in moist and dry AHT convergence (ΔAHT_m; ΔAHT_d) and ocean heat uptake (Ocean), and residual term (Res). Dashed grey line shows a 1-to-1 slope through the lapse-rate feedback warming contribution.

To investigate the drivers of polar amplification and hemispheric asymmetry in CMIP6 as compared to CMIP5, we calculate contributions to polar warming from feedbacks, AHT changes, and ocean heat uptake following Eq. 2. We use the Huang et al. (2017) kernels for climate feedbacks in Figures 4C,D, and investigate the sensitivity to kernel choice in Figure 5. Consistent with Pithan and Mauritsen (2014) and Goosse et al. (2018), key contributors to Arctic amplification in both CMIP5 and CMIP6 are the lapse-rate, albedo, and Planck feedbacks (Figure 4C). In contrast to the secondary role of the albedo feedback found in Pithan and Mauritsen (2014) using the Block and Mauritsen (2013) radiative kernels, use of the Huang et al. (2017) kernels yields lapse-rate and albedo feedbacks of almost equal importance for polar amplification in CMIP5, and equivalent importance in CMIP6. Partitioning AHT into moist and dry components illustrates that while reduced dry AHT opposes Arctic amplification, increased moist AHT is a large contributor to Arctic amplification.

FIGURE 5

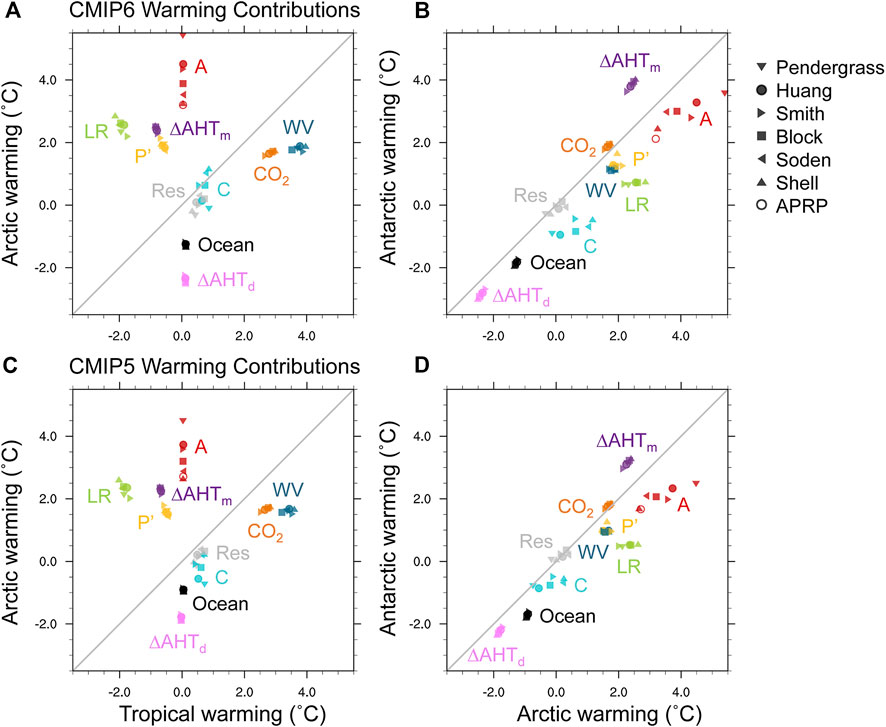
FIGURE 5. Sensitivity of warming contributions (˚C) to radiative kernels in (A,B) CMIP6 and (C,D) CMIP5 centered around year-100 of abrupt CO₂ quadrupling for (A,C) the tropics relative to the Arctic and (B,D) the Arctic relative to the Antarctic. Warming contributions are shown for the lapse-rate (LR), surface albedo (A), water-vapor (WV), and cloud (C) feedbacks, the variation in the Planck response from its global-mean value (P’), effective radiative forcing (CO₂), change in moist and dry AHT convergence (ΔAHT_m; ΔAHT_d) and ocean heat uptake (Ocean), and residual term (Res). The warming contribution for the albedo feedback is additionally calculated using the APRP method.

Stronger Arctic warming in CMIP6 than CMIP5 is mainly contributed by more-positive albedo and less-negative cloud feedbacks. Less-negative Arctic cloud feedbacks in CMIP6 result from less-negative shortwave low cloud amount and scattering feedbacks, likely due to updated treatment of supercooled liquid fraction in mixed phase clouds (Zelinka et al., 2020). The lapse-rate feedback, Planck response, and moist AHT changes also contribute to stronger Arctic warming in CMIP6, while increased ocean heat uptake and equatorward dry AHT more strongly oppose Arctic warming in CMIP6. Normalizing Arctic warming contributions by the global-mean warming yields contributions which sum to the total Arctic amplification in CMIP5 and CMIP6 (Supplementary Figure S3A, vertical axis): less-negative cloud and more-positive albedo feedbacks support greater Arctic amplification in CMIP6, while most other contributions support weaker Arctic amplification in CMIP6 due to normalizing by the larger global-mean warming in CMIP6 than CMIP5. This results in a similar degree of Arctic amplification in CMIP5 and CMIP6 (Figure 4B).

Consistent with Goosse et al. (2018), the largest contributor to stronger warming in the Arctic than Antarctic is the lapse-rate feedback for both CMIP5 and CMIP6 (Figure 4D). In fact, all factors except for CO₂ forcing and moist AHT changes support greater warming in the Arctic than Antarctic, with an additionally large contribution from the albedo feedback in CMIP5 and CMIP6. This feedback asymmetry between the poles is supported by the elevation of the Antarctic ice sheet (Salzmann, 2017), which primarily weakens the Antarctic lapse-rate feedback through reducing the average strength of mean-state inversions (Hahn et al., 2020). We note that the Planck feedback (in W m⁻² K⁻¹) is slightly less negative in the Antarctic than Arctic, likely due to colder and drier initial conditions, but that the Planck warming contribution is larger in the Arctic due to a larger Arctic $\text{Δ}T$resulting in a larger contribution ${\lambda }_p^{\text{'}}\text{Δ}T$ in Eq. 2. This illustrates one limitation of the warming contribution framework: a warming contribution from one feedback is influenced by all other feedbacks through their influence on $\text{Δ}T$.

Moist AHT is the largest contributor to Antarctic warming in both CMIP5 and CMIP6. Combined with initially colder Antarctic temperatures and Clausius-Clapeyron nonlinearity, weaker warming in the Antarctic under CO₂ quadrupling produces a weaker moisture increase compared to the Arctic. As a result, the equator-to-Antarctic latent heat gradient increases more than the equator-to-Arctic gradient, contributing to a stronger increase in moist AHT to the Antarctic (Supplementary Figure S4). Moist AHT changes are also sensitive to climate feedbacks which alter the equator-to-pole moist static energy gradient, particularly shortwave cloud feedbacks (Hwang and Frierson, 2010; Zelinka and Hartmann, 2012; Shaw and Voigt, 2016; Chen et al., 2021). More-negative shortwave cloud feedbacks in the Antarctic may therefore also contribute to larger increased moist AHT to the Antarctic than Arctic by enhancing the equator-to-pole moist static energy gradient in the Southern Hemisphere.

Most warming contributions change similarly for the Arctic and Antarctic from CMIP5 to CMIP6 (i.e., on a one-to-one slope in Figure 4D), including the lapse-rate, water-vapor, Planck, and albedo feedbacks, as well as ocean heat uptake and dry AHT. The two warming contributions that change differently for the Arctic and Antarctic from CMIP5 to CMIP6 are the cloud and moist AHT contributions. While the cloud contribution primarily increases in the Arctic, the moist AHT contribution primarily increases in the Antarctic. Stronger Arctic than Antarctic changes in cloud feedbacks result from shortwave cloud feedback changes (Supplementary Figure S5), and this polar difference appears to be amplified by the use of year-100 feedbacks rather than the 150-year regression method of Zelinka et al. (2020). Still, the year-100 feedbacks are generally consistent with the 150-year regression method in demonstrating less-negative polar cloud feedbacks in CMIP6 compared to CMIP5 (Supplementary Figure S5).

Dependence on Choice of Kernel and Feedback Definition

While most feedbacks are relatively insensitive to the choice of radiative kernel, polar surface albedo and cloud feedbacks particularly for the Arctic show substantial kernel sensitivity in both CMIP5 and CMIP6 (Figure 5). This is consistent with evidence that the radiative sensitivity to albedo changes (the albedo radiative kernel) varies by a factor of two across climate models in the Arctic and Southern Ocean due to intermodel differences in mean-state cloudiness (Donohoe et al., 2020b). Kernel sensitivity in the albedo feedback also contributes to kernel sensitivity in the cloud feedback, which is calculated using radiative kernels to compute and subtract the cloud masking effect of noncloud variables, including surface albedo, from the total ΔCRF. The APRP method gives an albedo feedback near the bottom of the range in kernel-derived albedo feedbacks. This may result from using the average of a forward- and backward-radiative substitution in the APRP method, whereas the kernels rely solely on a forward calculation. The surface albedo feedback derived from the APRP method versus radiative kernels are thus conceptually different quantities, as the APRP method allows cloud changes to impact the surface albedo feedback while the kernel method does not.

Of the model-derived surface albedo kernels, the Smith et al. (2018) kernels come closest to simulating the radiative sensitivity to albedo changes derived from satellite observations in the Arctic (Donohoe et al., 2020b). The Smith et al. (2018) kernels also produce an Arctic albedo feedback similar to the Huang et al. (2017) observationally-derived kernels (Figure 5A). This suggests that the observed mean state is consistent with a stronger Arctic albedo feedback than previously found, on par with the lapse rate feedback in its contribution to Arctic amplification.

An important result of kernel sensitivity in the albedo feedback is that the relative importance of the albedo versus lapse-rate feedback depends on the choice of kernel. However, for all kernels the lapse-rate and albedo feedbacks remain key contributors to Arctic amplification and hemispheric asymmetry in polar warming. Additionally, because the albedo and cloud feedbacks have compensating sensitivity to kernel choice, the total polar feedback remains relatively insensitive to kernel choice, as evidenced by the small kernel sensitivity in the residual term.

In addition to the traditional feedback framework applied here, alternative feedback definitions can be used, including a framework which quantifies the effect of warming and moistening at constant relative humidity (RH) separately from the effect of RH changes (Held and Shell, 2012). We compare the traditional feedback framework with the fixed-RH method, where the lapse-rate and Planck feedbacks are calculated at constant RH, an RH feedback is calculated, and all other feedbacks are identical to the traditional feedbacks (Supplementary Figure S6). Consistent with Held and Shell (2012), the magnitude of the fixed-RH Planck, fixed-RH lapse-rate, and RH feedbacks is reduced compared to the traditional Planck, lapse-rate, and water-vapor feedbacks. Although the other feedbacks are unchanged, division by a weaker global Planck feedback contributes to larger fixed-RH warming contributions for these feedbacks. Applied to the tropics, the fixed-RH framework gives a less-negative lapse-rate feedback than in the traditional framework: while amplified warming aloft promotes a large, negative lapse-rate feedback, amplified moistening aloft to maintain constant relative humidity offsets this negative feedback. In the Arctic, the fixed-RH framework produces a less-positive lapse-rate feedback: while weaker warming aloft compared to the surface supports a large, positive lapse-rate feedback, weaker moistening aloft to maintain constant relative humidity reduces the magnitude of the positive fixed-RH lapse-rate feedback. As a result, the relative contribution of the lapse-rate feedback to Arctic amplification is weakened in the fixed-RH framework, with stronger contributions from the albedo feedback and poleward moisture transport. While feedback definition choice can impact the relative roles of contributions to Arctic warming, we note that moist AHT and the albedo and lapse-rate feedbacks remain important contributors to Arctic amplification for both the traditional and fixed-RH frameworks.

Intermodel Spread

Following Pithan and Mauritsen (2014), we also investigate what factors contribute to substantial intermodel spread in polar warming by analyzing intermodel spread in CMIP6 warming contributions in both the Arctic and Antarctic (Figure 6). The albedo feedback is the single largest contributor to increased intermodel spread in both Arctic and Antarctic warming. While the dry AHT term itself exhibits substantial intermodel spread, it contributes more cooling to models with stronger polar warming and thus reduces intermodel spread in polar warming, as shown in Hwang et al. (2011). In contrast, changes in moist AHT generally increase with total polar warming and contribute to intermodel spread. Relationships between total polar warming and each warming contribution are similar for CMIP6 and CMIP5 (Supplementary Figure S7) with the exception of ocean heat uptake changes. In CMIP5, the ocean term becomes more negative (greater ocean heat uptake) in models with greater Arctic warming, while in CMIP6, models with weaker ocean heat uptake simulate greater Arctic warming. In the Antarctic, CMIP5 models with weaker ocean heat uptake simulate greater warming, while there is no correlation between ocean heat uptake and Antarctic warming across different models in CMIP6.

FIGURE 6

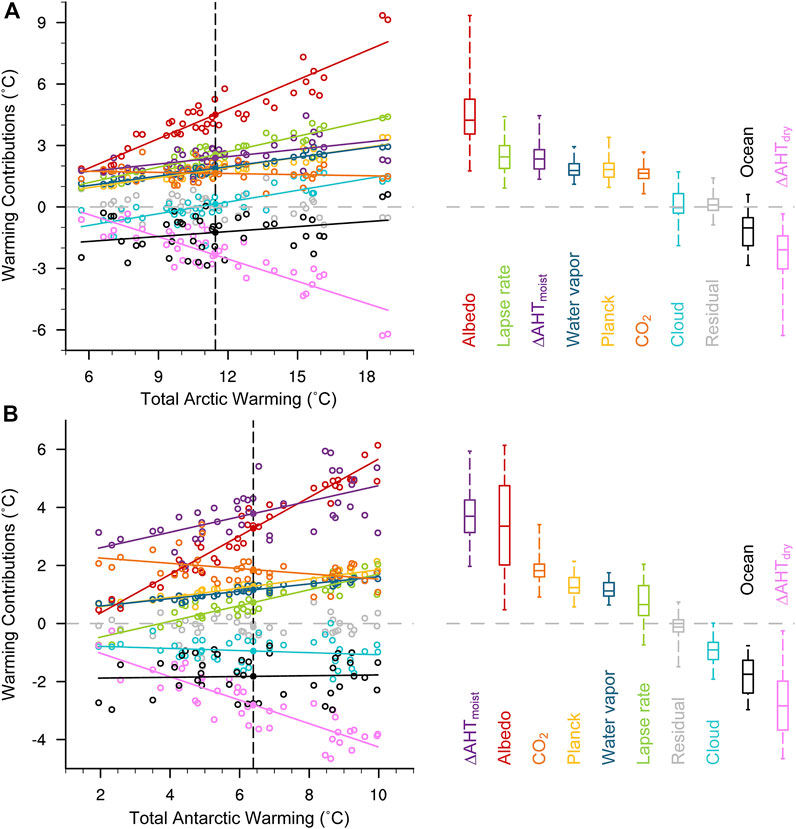
FIGURE 6. Intermodel spread of warming contributions versus total warming (˚C) in individual models for (A) the Arctic and (B) the Antarctic in CMIP6. Solid lines show linear regressions of feedback contributions against total warming at each pole. Filled circles on the black dashed line show the CMIP6 multimodel mean. In the right-hand panel, boxes indicate the median and 25th and 75th percentiles, and whiskers show the full intermodel spread of polar warming contributions.

Intermodel spread in polar warming is contributed not only by individual warming contributions, but also by their covariances; to quantify both, we show covariance matrices of the contributions to Arctic and Antarctic warming in Figure 7, following Caldwell et al. (2014). Each term has been normalized by the total warming variance (10.2 K² in the Arctic; 4.9 K² in the Antarctic) to illustrate fractional contributions to warming variance in each region. To avoid showing redundant information in these symmetric matrices, covariance terms below the diagonal are omitted and those above the diagonal are multiplied by two. Consistent with Figure 6, the main diagonal in Figure 7 shows large variances contributed by the albedo feedback and dry AHT at both poles. However, strong negative covariance between these two terms leads to a large damping of intermodel spread. Negative covariances between dry AHT and almost every other warming contribution suggest that dry AHT responds to polar warming, with stronger polar warming weakening the equator-to-pole temperature gradient and reducing dry AHT to polar regions. In contrast, large positive covariance between the albedo and lapse-rate feedbacks magnifies the intermodel spread in polar warming. In the Antarctic, variance in moist AHT and its covariance with the albedo feedback also contribute strongly to total warming variance. Although the total warming variance is smaller in the Antarctic than the Arctic, the albedo feedback constitutes a larger fraction of the total variance in Antarctic warming. These results support previous suggestions that constraining the albedo feedback may reduce intermodel spread in polar warming contributed both directly by this feedback and by covariances with other feedbacks (e.g., Feldl et al., 2020; Boeke et al., 2021).

FIGURE 7

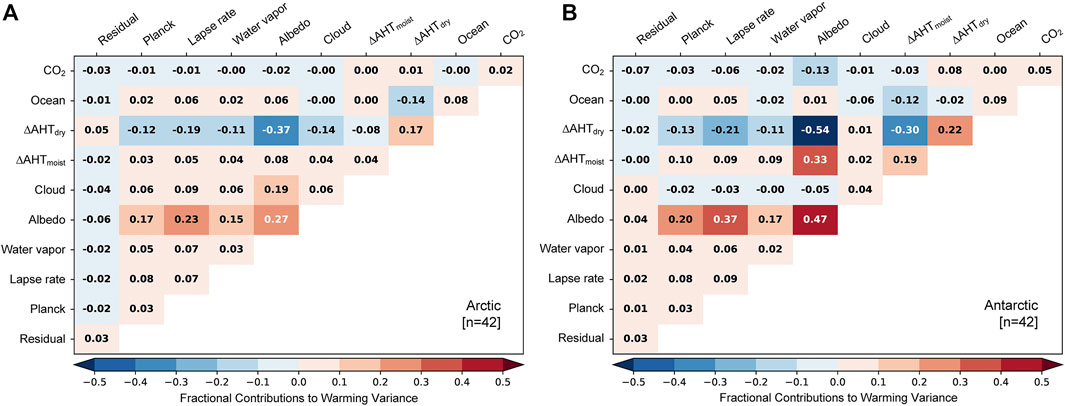
FIGURE 7. Fractional contributions of each warming contribution term to intermodel variance in (A) Arctic and (B) Antarctic warming in CMIP6.

Seasonality in Polar Warming Contributions

Lastly, we consider what drives seasonality in warming for the Arctic and Antarctic. As seen in historical CMIP6 trends, polar warming under CO₂ quadrupling peaks during winter (Figures 8A,B). Compared to the Antarctic, stronger seasonality in Arctic warming largely stems from stronger winter warming, while summer warming is more similar between the poles. Contributions to Arctic seasonality in warming in CMIP6 are consistent with CMIP5 results (Supplementary Figure S8 and Pithan and Mauritsen, 2014): while the albedo and water-vapor feedbacks support stronger summer warming, summer ocean heat storage and its release to the atmosphere in winter contributes to stronger winter warming. In addition, the lapse-rate and Planck feedbacks contribute to winter-amplified Arctic warming. While similar factors contribute to Antarctic seasonality in warming, weaker winter warming in the Antarctic compared to the Arctic results from weaker temperature feedbacks and seasonal ocean heat storage.

FIGURE 8

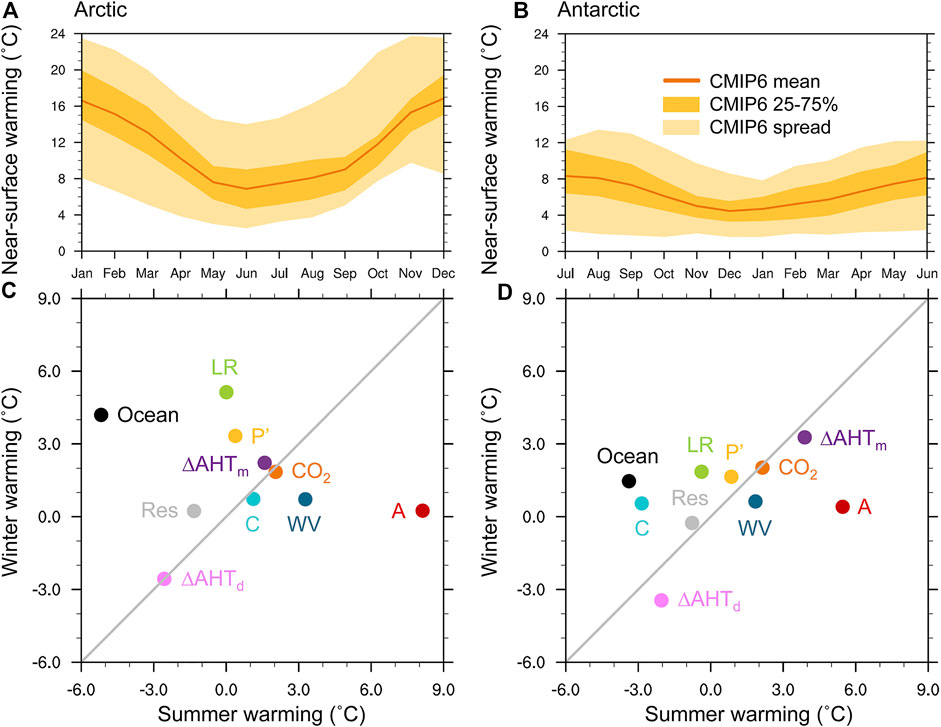
FIGURE 8. Monthly near-surface warming (˚C) centered around year-100 of abrupt CO₂ quadrupling for the CMIP6 multimodel mean (orange line), the 25th to 75th percentile (dark orange shading), and the full intermodel spread (light orange shading) in (A) the Arctic and (B) the Antarctic. (C,D) Contributions to winter and summer warming (˚C) centered around year-100 of abrupt CO₂ quadrupling in CMIP6 for (C) the Arctic and (D) the Antarctic. Warming contributions are shown for the lapse-rate (LR), surface albedo (A), water-vapor (WV), and cloud (C) feedbacks, the variation in the Planck response from its global-mean value (P’), effective radiative forcing (CO₂), change in moist and dry AHT convergence (ΔAHT_m; ΔAHT_d) and ocean heat uptake (Ocean), and residual term (Res).

Comparison With Historical Warming Contributions in AMIP6

Applying the above methodology to historical AMIP6 simulations allows us to evaluate polar warming contributions within models that use the observed patterns of sea-surface temperatures and sea-ice concentrations as boundary conditions, which may produce some differences from the fully-coupled CMIP6 results under CO₂ quadrupling shown above. To calculate feedbacks in AMIP6, we compute monthly anomalies in climate variables with respect to the 1979–2014 climatology, and regress radiative contributions of feedbacks against near-surface air temperature anomalies for this period. We then calculate warming contributions again using Eq. 2, where $\text{Δ}$ now indicates the trend in each variable from 1979 to 2014, multiplied by the period of 36 years.

Unlike the idealized CO₂ quadrupling experiments, AMIP simulations have time-evolving effective radiative forcing (ERF) that must be accounted for. Previous studies have derived the historical ERF in AMIP6 models using experiments from the Radiative Forcing Model Intercomparison Project (RFMIP, Pincus et al., 2016) with time-varying forcing applied on top of constant pre-industrial sea-surface temperature and sea-ice concentrations (e.g.,Zhang et al., 2020). However, these RFMIP experiments are only available for 7 CMIP6 models. To increase our model sample size, we estimate ERF using kernels in each model as follows. Because clear-sky TOA radiation anomalies are equal to the sum of clear-sky feedback energetic contributions, the clear-sky ERF, and a residual term arising from errors in the kernel approach, we estimate the clear-sky ERF as the difference between TOA radiation anomalies and the sum of kernel-derived clear-sky feedback energetic contributions. The neglect of kernel residual terms is justified by the fact that 1) kernel-derived and RFMIP-derived estimates of clear-sky ERF are in excellent agreement and 2) kernel residuals are very close to zero in amip-piForcing experiments from the Cloud Feedback Model Intercomparison Project (CFMIP, Webb et al., 2017) in which forcings are held constant at pre-industrial levels while sea-surface temperature and sea-ice concentration fields are prescribed to follow time-varying observations (not shown). Following standard practice, we then estimate the all-sky ERF by dividing clear-sky ERF by 1.16 (Soden et al., 2008). This method allows us to include 38 AMIP6 models in this analysis (Supplementary Table S1).

As in CMIP6 CO₂-quadrupling experiments, historical AMIP6 experiments show strong contributions to Arctic amplification from increased moist AHT and the lapse-rate, Planck, and albedo feedbacks, while the water-vapor feedback, Arctic ocean heat uptake, longwave forcing, and changes in dry AHT oppose Arctic amplification (Figure 9A). Despite differences in the vertical structure of warming between CMIP6 and AMIP6 models, their lapse-rate contributions to Arctic amplification appear relatively similar and consistently on par with respective surface albedo contributions. As suggested by Boeke et al. (2021), this may indicate the strong dependence of the lapse-rate feedback on the surface albedo feedback and surface temperature changes, more so than the vertical structure of warming. Differences in warming contributions between AMIP6 and CMIP6 include a relatively larger Planck contribution to Arctic amplification in AMIP6 and an Arctic-amplified SW ERF contribution in AMIP6. This positive SW forcing may be driven by reduced European sulfate emissions since 1980, which disproportionately warmed the Arctic compared to the rest of the globe (Acosta Navarro et al., 2016).

FIGURE 9

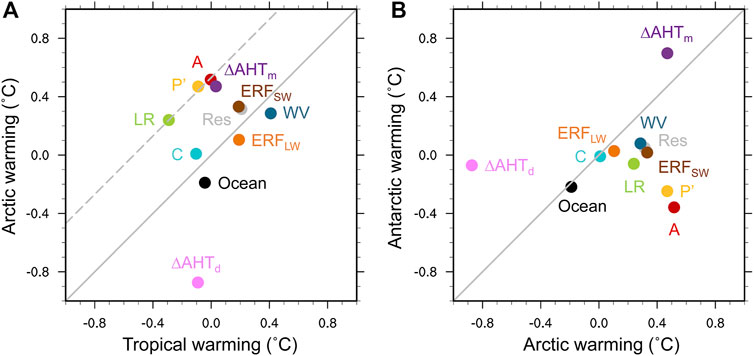
FIGURE 9. Contributions to warming (˚C) for 1979–2014 in AMIP6 models for (A) the tropics relative to the Arctic and (B) the Arctic relative to the Antarctic. Warming contributions are shown for the lapse-rate (LR), surface albedo (A), water-vapor (WV), and cloud (C) feedbacks, the variation in the Planck response from its global-mean value (P’), longwave and shortwave effective radiative forcing (ERF_LW; ERF_SW), change in moist and dry AHT convergence (ΔAHT_m; ΔAHT_d) and ocean heat uptake (Ocean), and residual term (Res). Dashed grey line shows a 1-to-1 slope through the lapse-rate feedback warming contribution.

In both AMIP6 and CMIP6, the lapse rate, water vapor, Planck, and albedo feedbacks contribute to weaker warming in the Antarctic than Arctic, while increased poleward moisture transport contributes more strongly to Antarctic warming (Figure 9B). In contrast to CMIP6 projections, negative Antarctic warming contributions in AMIP6 for the albedo feedback and Planck feedback deviation from its global-mean value reflect historical cooling and sea-ice expansion over the Southern Ocean. As a result, the albedo feedback contributes most to stronger Arctic than Antarctic warming in AMIP6, while the lapse-rate feedback makes the largest contribution to this hemispheric asymmetry in CMIP6 projections. Weaker historical than projected Antarctic warming also weakens the equatorward dry AHT opposing Antarctic warming in AMIP6. These differences between AMIP6 and CMIP6 illustrate the strong dependence of Antarctic feedbacks on changes in Southern Ocean sea-surface temperature and sea ice.

Even with identical prescribed sea-surface temperature and sea-ice concentration changes for all models in AMIP6, there is still considerable intermodel spread in polar warming contributions (Supplementary Figure S9). Consistent with Crook and Forster (2011), intermodel spread in polar ocean heat uptake outweighs intermodel spread in most polar feedbacks for this modelled historical period, while intermodel spread in the albedo feedback plays a relatively larger role under CO₂ quadrupling.

Discussion

Analysis of polar warming in CMIP6 reveals key contributors to polar amplification and their changes from CMIP5. While CMIP6 models overestimate historical Antarctic warming, they generally capture the observed pattern of strong Arctic amplification and weaker Antarctic warming. As in reanalysis data, Arctic warming in CMIP6 models is both surface- and winter-amplified, although CMIP6 shows stronger mid-tropospheric warming than the ERA-Interim reanalysis and previous climate models.

Our quantification of contributions to polar warming in CMIP6 is largely consistent with previous results for CMIP5 (e.g., Pithan and Mauritsen, 2014; Goosse et al., 2018). As in CMIP5, abrupt CO₂ quadrupling experiments in CMIP6 demonstrate that the lapse-rate and albedo feedbacks are the largest contributors to both Arctic amplification and weaker warming in the Antarctic than Arctic. The albedo feedback also contributes most to intermodel spread in polar warming, while the lapse-rate feedback and seasonal ocean heat storage contribute most to seasonal asymmetry in warming at both poles.

Novel results in comparison to existing literature include our assessment of the sensitivity of polar warming contributions to the choice of radiative kernel. While most feedbacks are relatively insensitive to kernel choice, the Arctic albedo warming contribution in CMIP6 varies by almost a factor of two for different kernels. This yields an Arctic albedo warming contribution in CMIP6 of equal or greater importance than the lapse-rate feedback for half of the kernels considered, while the other half suggest that the lapse-rate feedback contributes more to polar amplification. However, the kernels most consistent with observations produce a stronger Arctic albedo feedback than previously found, on par with the lapse-rate feedback in its contribution to Arctic amplification. We also add a partitioning of AHT changes into moist and dry components, which demonstrates that increased moist AHT contributes to stronger Arctic amplification, and is the largest contributor to warming in the Antarctic. We find that increased polar warming in CMIP6 versus CMIP5 is explained by a stronger albedo feedback at both poles, combined with a less-negative cloud feedback in the Arctic and a larger increase in moist AHT to the Antarctic. Lastly, similar factors contribute to historical Arctic amplification in AMIP6 models compared to CMIP6 CO₂-quadrupling experiments, although the albedo feedback plays a larger role in weakening Antarctic warming in AMIP6 compared to CMIP6.

A limitation of using warming contribution methods to diagnose the mechanisms of polar amplification is that it implicitly includes interactions between feedbacks, making mechanistic interpretation difficult. For example, the strength of the lapse-rate feedback may be impacted by the amount of surface warming contributed by the albedo feedback (Graversen et al., 2014; Feldl et al., 2017) and mixed-phase cloud changes (Tan and Storelvmo, 2019), but the warming contribution method diagnoses the contributions of surface albedo, cloud, and lapse-rate changes separately. Others have argued that a strong winter lapse-rate feedback additionally requires seasonal ocean heat storage and sea-ice insulation loss in order to increase surface turbulent heat fluxes and upward longwave radiation, promoting warming in the lower-troposphere (Dai et al., 2019; Feldl et al., 2020; Chung et al., 2021). As demonstrated by these studies, experiments isolating specific mechanisms in climate models are needed to fully address the interconnected feedbacks promoting polar amplification.

While this study applies a TOA feedback framework, analysis from a surface perspective (e.g., Lu and Cai, 2009; Taylor et al., 2013; Pithan and Mauritsen, 2014; Boeke and Taylor, 2018) can provide additional insight on warming mechanisms in polar regions, where the surface and tropospheric responses to forcing are decoupled. Surface albedo and temperature feedbacks remain important contributors to Arctic amplification from a surface perspective in CMIP5 models, while the water vapor feedback and ocean heat uptake continue to oppose Arctic amplification (Pithan and Mauritsen, 2014). One key difference between surface and TOA frameworks in CMIP5 is that cloud feedbacks oppose Arctic amplification from a TOA perspective but slightly promote Arctic amplification from a surface perspective: changes in low-level clouds increase longwave radiation to the surface but have little impact on TOA longwave radiation, yielding a negative TOA cloud feedback due to shortwave radiative effects (Pithan and Mauritsen, 2014). Further analysis from a surface perspective may also be useful for understanding physical drivers of the surface-trapped warming that supports the positive Arctic lapse-rate feedback (Boeke et al., 2021).

Our analysis both confirms and updates previous results in consideration of CMIP6, while also highlighting several open questions about the mechanisms driving polar amplification, such as: 1) What controls the vertical profile of Arctic warming in CMIP6 models? Compared to reanalyses, stronger mid-tropospheric warming in CMIP6 models may be driven by shortwave atmospheric absorption (Donohoe and Battisti, 2013) or by overestimated midlatitude surface temperatures and poleward AHT (Laliberté and Kushner, 2013; Fajber et al., 2018; Feldl et al., 2020). Weaker surface-trapped warming in the lower troposphere may also be influenced by updated mixed-phase clouds and surface inversions in CMIP6 (Tan and Storelvmo, 2019). 2) Which kernels or other methods should be used to calculate the albedo feedback? Our kernel sensitivity analysis demonstrates the importance of evaluating and standardizing radiative kernels or alternative methods used to compare albedo and cloud feedbacks across models and studies. 3) Why does increased moist AHT contribute more to Antarctic than Arctic warming? While this may be explained by Clausius-Clapeyron nonlinearity and more-negative Antarctic cloud feedbacks, other possible mechanisms include any process (e.g., ocean heat uptake, water vapor feedback) that leads to a stronger equator-to-pole moist static energy gradient in the Southern Hemisphere than Northern Hemisphere under CO₂ quadrupling. Further investigation of these polar warming asymmetries may highlight key processes for constraining both Arctic and Antarctic amplification.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: All CMIP and AMIP data analyzed for this study can be found in the Earth System Grid Federation (ESGF) repository at https://esgf-node.llnl.gov/projects/esgf-llnl/. ERA-Interim data was provided by the ECMWF Data Archive at https://apps.ecmwf.int/datasets/data/interim-full-moda/levtype=pl/. The HadCRUT5 Analysis is available from the University of East Anglia Climatic Research Unit at https://crudata.uea.ac.uk/cru/data/temperature/.

Author Contributions

All authors contributed to the study design. MZ calculated the climate feedbacks and AMIP forcing, and LH computed the warming contributions and remaining analysis. LH wrote the original draft, and all authors contributed to the final manuscript.

Funding

LH was supported by the National Science Foundation (NSF) Graduate Research Fellowship Grant DGE-1762114 and the ARCS Foundation Fellowship. KA was supported by National Science Foundation Grants AGS-1752796 and OCE-1850900 and an Alfred P. Sloan Research Fellowship. MZ was supported by the Regional and Global Model Analysis Program of the Office of Science at the U.S. Department of Energy. CB was supported by NOAA MAPP NA18OAR4310274. AD was supported by the NSF Antarctic Program Grant PLR-1643436 and NOAA MAPP Grant eGC1#A127135.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We acknowledge computing resources (doi:10.5065/D6RX99HX) provided by NCAR’s Computational and Information Systems Laboratory (2019), sponsored by the National Science Foundation. The work of MZ was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.710036/full#supplementary-material

References

Acosta Navarro, J. C., Varma, V., Riipinen, I., Seland, Ø., Kirkevåg, A., Struthers, H., et al. (2016). Amplification of Arctic Warming by Past Air Pollution Reductions in Europe. Nat. Geosci 9, 277–281. doi:10.1038/ngeo2673

CrossRef Full Text | Google Scholar

Alexeev, V. A., Langen, P. L., and Bates, J. R. (2005). Polar Amplification of Surface Warming on an Aquaplanet in “Ghost Forcing” Experiments without Sea Ice Feedbacks. Clim. Dyn. 24, 655–666. doi:10.1007/s00382-005-0018-3

CrossRef Full Text | Google Scholar

Andrews, T., Gregory, J. M., and Webb, M. J. (2015). The Dependence of Radiative Forcing and Feedback on Evolving Patterns of Surface Temperature Change in Climate Models. J. Clim. 28 (4), 1630–1648. doi:10.1175/jcli-d-14-00545.1

CrossRef Full Text | Google Scholar

Armour, K. C., Marshall, J., Scott, J. R., Donohoe, A., and Newsom, E. R. (2016). Southern Ocean Warming Delayed by Circumpolar Upwelling and Equatorward Transport. Nat. Geosci 9 (7), 549–554. doi:10.1038/ngeo2731

CrossRef Full Text | Google Scholar

Armour, K. C., Siler, N., Donohoe, A., and Roe, G. H. (2019). Meridional Atmospheric Heat Transport Constrained by Energetics and Mediated by Large-Scale Diffusion. J. Clim. 32 (12), 3655–3680. doi:10.1175/JCLI-D-18-0563.1

CrossRef Full Text | Google Scholar

Block, K., and Mauritsen, T. (2013). Forcing and Feedback in the MPI-ESM-LR Coupled Model under Abruptly Quadrupled CO2. J. Adv. Model. Earth Syst. 5, 676–691. doi:10.1002/jame.20041

CrossRef Full Text | Google Scholar

Block, K., Schneider, F. A., Mülmenstädt, J., Salzmann, M., and Quaas, J. (2020). Climate Models Disagree on the Sign of Total Radiative Feedback in the Arctic. Tellus A: Dynamic Meteorology and Oceanography 72 (1), 1–14. doi:10.1080/16000870.2019.1696139

CrossRef Full Text | Google Scholar

Boeke, R. C., and Taylor, P. C. (2018). Seasonal Energy Exchange in Sea Ice Retreat Regions Contributes to Differences in Projected Arctic Warming. Nat. Commun. 9, 5017. doi:10.1038/s41467-018-07061-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Boeke, R. C., Taylor, P. C., and Sejas, S. A. (2021). On the Nature of the Arctic's Positive Lapse‐Rate Feedback. Geophys. Res. Lett. 48, e2020GL091109. doi:10.1029/2020GL091109

CrossRef Full Text | Google Scholar

Bonan, D. B., Armour, K. C., Roe, G. H., Siler, N., and Feldl, N. (2018). Sources of Uncertainty in the Meridional Pattern of Climate Change. Geophys. Res. Lett. 45, 9131–9140. doi:10.1029/2018GL079429

CrossRef Full Text | Google Scholar

Brutel-Vuilmet, C., Ménégoz, M., and Krinner, G. (2013). An Analysis of Present and Future Seasonal Northern Hemisphere Land Snow Cover Simulated by CMIP5 Coupled Climate Models. The Cryosphere 7, 67–80. doi:10.5194/tc-7-67-2013

CrossRef Full Text | Google Scholar

Cai, S., Hsu, P.-C., and Liu, F. (2021). Changes in Polar Amplification in Response to Increasing Warming in CMIP6. Atmos. Oceanic Sci. Lett. 14, 100043–102834. doi:10.1016/j.aosl.2021.100043

CrossRef Full Text | Google Scholar

Caldwell, P. M., Bretherton, C. S., Zelinka, M. D., Klein, S. A., Santer, B. D., and Sanderson, B. M. (2014). Statistical Significance of Climate Sensitivity Predictors Obtained by Data Mining. Geophys. Res. Lett. 41, 1803–1808. doi:10.1002/2014GL059205

CrossRef Full Text | Google Scholar

Chen, Y.-J., Hwang, Y.-T., and Ceppi, P. (2021). The Impacts of Cloud-Radiative Changes on Poleward Atmospheric and Oceanic Energy Transport in a Warmer Climate. J. Clim., 1–63. published online ahead of print 2021. doi:10.1175/JCLI-D-20-0949.1

CrossRef Full Text | Google Scholar

Chung, E. S., Ha, K. J., Timmermann, A., Stuecker, M. F., Bodai, T., and Lee, S. K. (2021). Cold‐Season Arctic Amplification Driven by Arctic Ocean‐Mediated Seasonal Energy Transfer. Earth's Future 9, e2020EF001898. doi:10.1029/2020EF001898

CrossRef Full Text | Google Scholar

Computational and Information Systems Laboratory (2019). Cheyenne: HPE/SGI ICE XA System. Boulder, CO: University Community Computing)National Center for Atmospheric Research. doi:10.5065/D6RX99HX

CrossRef Full Text

Cronin, T. W., and Jansen, M. F. (2016). Analytic Radiative‐advective Equilibrium as a Model for High‐latitude Climate. Geophys. Res. Lett. 43, 449–457. doi:10.1002/2015GL067172

CrossRef Full Text | Google Scholar

Crook, J. A., and Forster, P. M. (2011). A Balance between Radiative Forcing and Climate Feedback in the Modeled 20th century Temperature Response. J. Geophys. Res. 116, D17108. doi:10.1029/2011JD015924

CrossRef Full Text | Google Scholar

Dai, A., Luo, D., Song, M., and Liu, J. (2019). Arctic Amplification Is Caused by Sea-Ice Loss under Increasing CO2. Nat. Commun. 10, 121. doi:10.1038/s41467-018-07954-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., et al. (2011). The ERA-Interim Reanalysis: Configuration and Performance of the Data Assimilation System. Q.J.R. Meteorol. Soc. 137, 553–597. doi:10.1002/qj.828

CrossRef Full Text | Google Scholar

Deser, C., Tomas, R., Alexander, M., and Lawrence, D. (2010). The Seasonal Atmospheric Response to Projected Arctic Sea Ice Loss in the Late Twenty-First Century. J. Clim. 23 (2), 333–351. doi:10.1175/2009JCLI3053.1

CrossRef Full Text | Google Scholar

Dong, Y., Armour, K. C., Zelinka, M. D., Proistosescu, C., Battisti, D. S., Zhou, C., et al. (2020). Intermodel Spread in the Pattern Effect and its Contribution to Climate Sensitivity in CMIP5 and CMIP6 Models. J. Clim. 33 (18), 7755–7775. doi:10.1175/JCLI-D-19-1011.1

CrossRef Full Text | Google Scholar

Donohoe, A., Armour, K. C., Roe, G. H., Battisti, D. S., and Hahn, L. (2020a). The Partitioning of Meridional Heat Transport from the Last Glacial Maximum to CO2 Quadrupling in Coupled Climate Models. J. Clim. 33 (10), 4141–4165. doi:10.1175/JCLI-D-19-0797.1

CrossRef Full Text | Google Scholar

Donohoe, A., and Battisti, D. S. (2013). The Seasonal Cycle of Atmospheric Heating and Temperature. J. Clim. 26, 4962–4980. doi:10.1175/JCLI-D-12-00713.1

CrossRef Full Text | Google Scholar

Donohoe, A., Blanchard-Wrigglesworth, E., Schweiger, A., and Rasch, P. J. (2020b). The Effect of Atmospheric Transmissivity on Model and Observational Estimates of the Sea Ice Albedo Feedback. J. Clim. 33 (13), 5743–5765. doi:10.1175/JCLI-D-19-0674.1

CrossRef Full Text | Google Scholar

Eyring, V., Bony, S., Meehl, G. A., Senior, C. A., Stevens, B., Stouffer, R. J., et al. (2016). Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) Experimental Design and Organization. Geosci. Model. Dev. 9, 1937–1958. doi:10.5194/gmd-9-1937-2016

CrossRef Full Text | Google Scholar

Fajber, R., Kushner, P. J., and Laliberté, F. (2018). Influence of Midlatitude Surface Thermal Anomalies on the Polar Midtroposphere in an Idealized Moist Model. J. Atmos. Sci. 75 (4), 1089–1104. doi:10.1175/JAS-D-17-0283.1

CrossRef Full Text | Google Scholar

Feldl, N., Bordoni, S., and Merlis, T. M. (2017). Coupled High-Latitude Climate Feedbacks and Their Impact on Atmospheric Heat Transport. J. Clim. 30, 189–201. doi:10.1175/JCLI-D-16-0324.1

CrossRef Full Text | Google Scholar

Feldl, N., Po-Chedley, S., Singh, H. K. A., Hay, S., and Kushner, P. J. (2020). Sea Ice and Atmospheric Circulation Shape the High-Latitude Lapse Rate Feedback. Npj Clim. Atmos. Sci. 3 (41). doi:10.1038/s41612-020-00146-7

CrossRef Full Text | Google Scholar

Feldl, N., and Roe, G. H. (2013). Four Perspectives on Climate Feedbacks. Geophys. Res. Lett. 40, 4007–4011. doi:10.1002/grl.50711

CrossRef Full Text | Google Scholar

Goosse, H., Kay, J. E., Armour, K. C., Bodas-Salcedo, A., Chepfer, H., Docquier, D., et al. (2018). Quantifying Climate Feedbacks in Polar Regions. Nat. Commun. 9, 1919. doi:10.1038/s41467‐018‐04173‐0

PubMed Abstract | CrossRef Full Text | Google Scholar

Gossart, A., Helsen, S., Lenaerts, J. T. M., Broucke, S. V., van Lipzig, N. P. M., and Souverijns, N. (2019). An Evaluation of Surface Climatology in State-Of-The-Art Reanalyses over the Antarctic Ice Sheet. J. Clim. 32 (20), 6899–6915. doi:10.1175/JCLI-D-19-0030.1

CrossRef Full Text | Google Scholar

Graham, R. M., Cohen, L., Ritzhaupt, N., Segger, B., Graversen, R. G., Rinke, A., et al. (2019). Evaluation of Six Atmospheric Reanalyses over Arctic Sea Ice from Winter to Early Summer. J. Clim. 32 (14), 4121–4143. doi:10.1175/JCLI-D-18-0643.1

CrossRef Full Text | Google Scholar

Graversen, R. G., Langen, P. L., and Mauritsen, T. (2014). Polar Amplification in CCSM4: Contributions from the Lapse Rate and Surface Albedo Feedbacks. J. Clim. 27, 4433–4450. doi:10.1175/JCLI-D-13-00551.1

CrossRef Full Text | Google Scholar

Gregory, J. M., Ingram, W. J., Palmer, M. A., Jones, G. S., Stott, P. A., Thorpe, R. B., et al. (2004). A New Method for Diagnosing Radiative Forcing and Climate Sensitivity. Geophys. Res. Lett. 31, L03205. doi:10.1029/2003GL018747

CrossRef Full Text | Google Scholar

Hahn, L. C., Armour, K. C., Battisti, D. S., Donohoe, A., Pauling, A. G., and Bitz, C. M. (2020). Antarctic Elevation Drives Hemispheric Asymmetry in Polar Lapse Rate Climatology and Feedback. Geophys. Res. Lett. 47, e2020GL088965. doi:10.1029/2020GL088965

CrossRef Full Text | Google Scholar

Hall, A. (2004). The Role of Surface Albedo Feedback in Climate. J. Clim. 17 (7), 1550–1568. doi:10.1175/1520-0442(2004)017%3C1550:TROSAF%3E2.0.CO;2

CrossRef Full Text | Google Scholar

Hansen, J., Sato, M., Ruedy, R., Nazarenko, L., Lacis, A., Schmidt, G. A., et al. (2005). Efficacy of Climate Forcings. J. Geophys. Res. 110, d18104. doi:10.1029/2005JD005776

CrossRef Full Text | Google Scholar

Held, I. M., and Shell, K. M. (2012). Using Relative Humidity as a State Variable in Climate Feedback Analysis. J. Clim. 25 (8), 2578–2582. doi:10.1175/JCLI-D-11-00721.1

CrossRef Full Text | Google Scholar

Holland, M. M., and Bitz, C. M. (2003). Polar Amplification of Climate Change in Coupled Models. Clim. Dyn. 21, 221–232. doi:10.1007/s00382-003-0332-6

CrossRef Full Text | Google Scholar

Huang, Y., Xia, Y., and Tan, X. (2017). On the Pattern of CO2 Radiative Forcing and Poleward Energy Transport. J. Geophys. Res. Atmos. 122, 10578–10593. doi:10.1002/2017JD027221

CrossRef Full Text | Google Scholar

Hwang, Y.-T., and Frierson, D. M. W. (2010). Increasing Atmospheric Poleward Energy Transport with Global Warming. Geophys. Res. Lett. 37, L24807. doi:10.1029/2010GL045440

CrossRef Full Text | Google Scholar

Hwang, Y.-T., Frierson, D. M. W., and Kay, J. E. (2011). Coupling between Arctic Feedbacks and Changes in Poleward Energy Transport. Geophys. Res. Lett. 38, L17704. doi:10.1029/2011GL048546

CrossRef Full Text | Google Scholar

Kosaka, Y., and Xie, S.-P. (2013). Recent Global-Warming Hiatus Tied to Equatorial Pacific Surface Cooling. Nature 501, 403–407. doi:10.1038/nature12534

PubMed Abstract | CrossRef Full Text | Google Scholar

Laliberté, F., and Kushner, P. J. (2013). Isentropic Constraints by Midlatitude Surface Warming on the Arctic Midtroposphere. Geophys. Res. Lett. 40, 606–611. doi:10.1029/2012GL054306

CrossRef Full Text | Google Scholar

Lindsay, R., Wensnahan, M., Schweiger, A., and Zhang, J. (2014). Evaluation of Seven Different Atmospheric Reanalysis Products in the Arctic*. J. Clim. 27, 2588–2606. doi:10.1175/JCLI-D-13-00014.1

CrossRef Full Text | Google Scholar

Lu, J., and Cai, M. (2009). A New Framework for Isolating Individual Feedback Processes in Coupled General Circulation Climate Models. Part I: Formulation. Clim. Dyn. 32, 873–885. doi:10.1007/s00382-008-0425-3

CrossRef Full Text | Google Scholar

Manabe, S., and Stouffer, R. J. (1980). Sensitivity of a Global Climate Model to an Increase of CO2concentration in the Atmosphere. J. Geophys. Res. 85 (C10), 5529–5554. doi:10.1029/JC085iC10p05529

CrossRef Full Text | Google Scholar

Marshall, J., Scott, J. R., Armour, K. C., Campin, J.-M., Kelley, M., and Romanou, A. (2015). The Ocean's Role in the Transient Response of Climate to Abrupt Greenhouse Gas Forcing. Clim. Dyn. 44, 2287–2299. doi:10.1007/s00382-014-2308-0

CrossRef Full Text | Google Scholar

Medeiros, B., Deser, C., Tomas, R. A., and Kay, J. E. (2011). Arctic Inversion Strength in Climate Models. J. Clim. 24, 4733–4740. doi:10.1175/2011JCLI3968.1

CrossRef Full Text | Google Scholar

Morice, C. P., Kennedy, J. J., Rayner, N. A., Winn, J. P., Hogan, E., Killick, R. E., et al. (2021). An Updated Assessment of Near‐Surface Temperature Change from 1850: The HadCRUT5 Data Set. Geophys. Res. Atmos. 126, e2019JD032361. doi:10.1029/2019JD032361

CrossRef Full Text | Google Scholar

Payne, A. E., Jansen, M. F., and Cronin, T. W. (2015). Conceptual Model Analysis of the Influence of Temperature Feedbacks on Polar Amplification. Geophys. Res. Lett. 42, 9561–9570. doi:10.1002/2015GL065889

CrossRef Full Text | Google Scholar

Pendergrass, A. G., Conley, A., and Vitt, F. M. (2018). Surface and Top-Of-Atmosphere Radiative Feedback Kernels for CESM-CAM5. Earth Syst. Sci. Data 10 (1), 317–324. doi:10.5194/essd-10-317-2018

CrossRef Full Text | Google Scholar

Pithan, F., and Mauritsen, T. (2014). Arctic Amplification Dominated by Temperature Feedbacks in Contemporary Climate Models. Nat. Geosci 7, 181–184. doi:10.1038/ngeo2071

CrossRef Full Text | Google Scholar

Pithan, F., Medeiros, B., and Mauritsen, T. (2014). Mixed-phase Clouds Cause Climate Model Biases in Arctic Wintertime Temperature Inversions. Clim. Dyn. 43, 289–303. doi:10.1007/s00382-013-1964-9

CrossRef Full Text | Google Scholar

Pincus, R., Forster, P. M., and Stevens, B. (2016). The Radiative Forcing Model Intercomparison Project (RFMIP): experimental protocol for CMIP6. Geosci. Model Dev. 9, 3447–3460. doi:10.5194/gmd-9-3447-2016

Rodgers, K., Lee, S.-S., Rosenbloom, N., Timmermann, A., Danabasoglu, G., Deser, C., et al. (2021). Ubiquity of Human-Induced Changes in Climate Variability. Submitted Earth Syst. Dyn.. doi:10.31223/X5GP79

CrossRef Full Text | Google Scholar

Roe, G. H., Feldl, N., Armour, K. C., Hwang, Y.-T., and Frierson, D. M. W. (2015). The Remote Impacts of Climate Feedbacks on Regional Climate Predictability. Nat. Geosci 8, 135–139. doi:10.1038/ngeo2346

CrossRef Full Text | Google Scholar

Salzmann, M. (2017). The Polar Amplification Asymmetry: Role of Antarctic Surface Height. Earth Syst. Dynam. 8, 323–336. doi:10.5194/esd-8-323-2017

CrossRef Full Text | Google Scholar

Screen, J. A., Deser, C., and Simmonds, I. (2012). Local and Remote Controls on Observed Arctic Warming. Geophys. Res. Lett. 39, L10709. doi:10.1029/2012GL051598

CrossRef Full Text | Google Scholar

Screen, J. A., and Simmonds, I. (2010b). Increasing Fall-winter Energy Loss from the Arctic Ocean and its Role in Arctic Temperature Amplification. Geophys. Res. Lett. 37, L16707. doi:10.1029/2010GL044136

CrossRef Full Text | Google Scholar

Screen, J. A., and Simmonds, I. (2010a). The central Role of Diminishing Sea Ice in Recent Arctic Temperature Amplification. Nature 464, 1334–1337. doi:10.1038/nature09051

PubMed Abstract | CrossRef Full Text | Google Scholar

Serreze, M. C., Barrett, A. P., Stroeve, J. C., Kindig, D. N., and Holland, M. M. (2009). The Emergence of Surface-Based Arctic Amplification. The Cryosphere 3, 11–19. doi:10.5194/tc-3-11-2009

CrossRef Full Text | Google Scholar

Shaw, T. A., and Voigt, A. (2016). What Can Moist Thermodynamics Tell Us about Circulation Shifts in Response to Uniform Warming?. Geophys. Res. Lett. 43, 4566–4575. doi:10.1002/2016GL068712

CrossRef Full Text | Google Scholar

Shell, K. M., Kiehl, J. T., and Shields, C. A. (2008). Using the Radiative Kernel Technique to Calculate Climate Feedbacks in NCAR's Community Atmospheric Model. J. Clim. 21, 2269–2282. doi:10.1175/2007JCLI2044.1

CrossRef Full Text | Google Scholar

Smith, C. J., Kramer, R. J., Myhre, G., Alterskjær, K., Collins, W., Sima, A., et al. (2020). Effective Radiative Forcing and Adjustments in CMIP6 Models. Atmos. Chem. Phys. 20, 9591–9618. doi:10.5194/acp-20-9591-2020

CrossRef Full Text | Google Scholar

Smith, C. J., Kramer, R. J., Myhre, G., Forster, P. M., Soden, B. J., Andrews, T., et al. (2018). Understanding Rapid Adjustments to Diverse Forcing Agents. Geophys. Res. Lett. 45, 12023–12031. doi:10.1029/2018GL079826

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, D. M., Screen, J. A., Deser, C., Cohen, J., Fyfe, J. C., García-Serrano, J., et al. (2019). The Polar Amplification Model Intercomparison Project (PAMIP) Contribution to CMIP6: Investigating the Causes and Consequences of Polar Amplification. Geosci. Model. Dev. 12, 1139–1164. doi:10.5194/gmd-12-1139-2019

CrossRef Full Text | Google Scholar

Soden, B. J., Held, I. M., Colman, R., Shell, K. M., Kiehl, J. T., and Shields, C. A. (2008). Quantifying Climate Feedbacks Using Radiative Kernels. J. Clim. 21, 3504–3520. doi:10.1175/2007JCLI2110.1

CrossRef Full Text | Google Scholar

Stuecker, M. F., Bitz, C. M., Armour, K. C., Proistosescu, C., Kang, S. M., Xie, S.-P., et al. (2018). Polar Amplification Dominated by Local Forcing and Feedbacks. Nat. Clim Change 8, 1076–1081. doi:10.1038/s41558-018-0339-y

CrossRef Full Text | Google Scholar

Tan, I., and Storelvmo, T. (2019). Evidence of Strong Contributions from Mixed‐Phase Clouds to Arctic Climate Change. Geophys. Res. Lett. 46, 2894–2902. doi:10.1029/2018GL081871

CrossRef Full Text | Google Scholar

Taylor, K. E., Crucifix, M., Braconnot, P., Hewitt, C. D., Doutriaux, C., Broccoli, A. J., et al. (2007). Estimating Shortwave Radiative Forcing and Response in Climate Models. J. Clim. 20 (11), 2530–2543. doi:10.1175/JCLI4143.1

CrossRef Full Text | Google Scholar

Taylor, P. C., Cai, M., Hu, A., Meehl, J., Washington, W., and Zhang, G. J. (2013). A Decomposition of Feedback Contributions to Polar Warming Amplification. J. Clim. 26 (18), 7023–7043. doi:10.1175/JCLI-D-12-00696.1

CrossRef Full Text | Google Scholar

Wang, C., Graham, R. M., Wang, K., Gerland, S., and Granskog, M. A. (2019). Comparison of ERA5 and ERA-Interim Near-Surface Air Temperature, Snowfall and Precipitation over Arctic Sea Ice: Effects on Sea Ice Thermodynamics and Evolution. The Cryosphere 13, 1661–1679. doi:10.5194/tc-13-1661-2019

CrossRef Full Text | Google Scholar

Wang, Y., Zhou, D., Bunde, A., and Havlin, S. (2016). Testing Reanalysis Data Sets in Antarctica: Trends, Persistence Properties, and Trend Significance. J. Geophys. Res. Atmos. 121, 839–12855. doi:10.1002/2016JD024864

CrossRef Full Text | Google Scholar

Webb, M. J., Andrews, T., Bodas-Salcedo, A., Bony, S., Bretherton, C. S., Chadwick, R., et al. (2017). The Cloud Feedback Model Intercomparison Project (CFMIP) Contribution to CMIP6. Geosci. Model. Dev. 10, 359–384. doi:10.5194/gmd-10-359-2017

CrossRef Full Text | Google Scholar

Zelinka, M. D., and Hartmann, D. L. (2012). Climate Feedbacks and Their Implications for Poleward Energy Flux Changes in a Warming Climate. J. Clim. 25 (2), 608–624. doi:10.1175/JCLI-D-11-00096.1

CrossRef Full Text | Google Scholar

Zelinka, M. D., Myers, T. A., McCoy, D. T., Po‐Chedley, S., Caldwell, P. M., Ceppi, P., et al. (2020). Causes of Higher Climate Sensitivity in CMIP6 Models. Geophys. Res. Lett. 47, e2019GL085782. doi:10.1029/2019GL085782

CrossRef Full Text | Google Scholar

Zhang, R., Wang, H., Fu, Q., and Rasch, P. J. (2020). Assessing Global and Local Radiative Feedbacks Based on AGCM Simulations for 1980–2014/2017. Geophys. Res. Lett. 47, e2020GL088063. doi:10.1029/2020GL088063