Numerical Study of Reactive Flow in Fractured Carbonate Rock

Acidizing technology is an effective reformation method of oil and gas reservoirs. It can also remove the reservoir pollution near wellbore zones and enhance the fluid transmissibility. The optimal injection rate of acid is one of the key factors to reduce cost and improve the effect of acidizing. Therefore, the key issue is to find the optimal injection rate during acid corrosion in fractured carbonate rock. In this work, a novel reactive flow mathematical model based on two-scale model and discrete fracture model is established for fractured carbonate reservoirs. The matrix and fracture are described by a two-scale model and a discrete fracture model, respectively. Firstly, the two-scale model for matrix is combined with the discrete fracture model. Then, an efficient numerical scheme based on the finite element method is implemented to solve the corresponding dimensionless equations. Finally, several important aspects, such as the influence of the injection rate of acid on the dissolution patterns, the influence of fracture aperture and fracture orientations on the dissolution structure, the breakthrough volume of injected acid, and the dynamic change of fracture aperture during acidizing, are analyzed. The numerical simulation results show that there is an optimal injection rate in fractured carbonate rock. However, the fractures do not have an impact on the optimal acid injection rate, they only have an impact on the dissolution structure.

Introduction

Since the 1980s, many scholars have conducted systematic research on matrix acidizing. Hoefner (Hoefner and Fogler, 1989; Fredd et al., 1997) and (Fredd et al., 1997) first undertook studies on the dissolution patterns of porous media. They injected the inorganic acid into limestone, then, injected the low melting point alloy into limestone after acid etching. They studied the dissolution structure of porous media by observing the shape of the alloy. (Hoefner and Fogler, 1988) used the network model to study the wormhole propagation and formation in the porous media and performed a series of experiments to analyze the mechanism of wormhole formation and many numerical simulations to study the characteristics of the mass-transfer limited regime and reaction-limited regime. These results suggested that the branch length of the main channel will never exceed the distance between the branch and the main channel. Next, based on this mathematical model, (Budek and Szymczak, 2012) improved the extended pore network model to qualitatively characterize the dissolution patterns at different Damköhler numbers and analyze optimal injection velocity. (Kim and Santamarina, 2015) explored how CO₂ dissolves into water and flows into the reservoir with a 2-D pore network model. (Wang et al., 1993) adopted the core displacement method to study the influence of temperature, acid concentration, and the velocity of the injected acid on the wormhole. Finally, (Frick et al., 1994) also found the optimal injection rate at different acid concentrations and temperatures in the radial core. These analysis result consistent with their mathematical model, which can predict the wormhole diameter and the permeability influences the breakthrough time in the cross-section of the core.

(Bazin et al., 1995) proposed a pressure drop function based on morphology after acidizing. (Daccord et al., 1989) used water flowing on gypsum to simulate wormhole formation, three dissolution patterns were obtained: compaction, wormhole, and uniform. (Bazin, 2001) studied the optimal injection rate of injected acid using CT scanning technology and (Ziauddin and Bize, 2007) discusses the influence of the heterogeneity of porous media on the dissolution patterns based on CT scanning technology, NMR, and SEM technologies. (Zhang et al., 2017) studied the dissolution structure of acid-etched core by CT scanning technology, undertaking (He, 2009) an acid erosion experiment on carbonate rocks with undeveloped fractures, but the permeability is so low that the injected acid struggles to form a wormhole and break through the core end. (Yang and Pan, 2000) studied the influence of the injection rate and type of acid on dolomite based on the mechanism of acid filtration. (Daccord et al., 1989) described the dissolution structure based on fractal theory. (Golfier et al., 2001) studied the reactive flow combined with Brinkman. They found that the optimal condition was related to the acid concentration and the length of the core. This was the first confirmation that the acid capacity number affects the breakthrough time of injected acid.

A.D.Hill (Hill et al., 2009) built a model of wormhole formation considering acid filtration theory. (Liu et al., 1997) developed a simulator to describe the dissolution patterns. (Chen and Ying, 2006) deduced the equations of acid diffusion and acid surface reaction rate of reactive flow. (Catherine, 2004) injected the CO2-enriched water into the limestone to study the relationship between porosity and permeability, which are distinct at different dissolution stages in the core. (Andersen and Evje, 2016) considered flow through a fracture coupled with diffusion to the surrounding matrix, where the reaction occurring presented a reactive flow model in the fractured medium. (Nierode and Williams, 1971) established description equation for reactive flow based on the reaction kinetics, indicating that the mass transfer coefficient of solute in acid affects the result of acidizing treatment, and the effect of matrix acidizing was related to the injection rate of acid in the ground.

The above physical experiments and numerical simulation experiments did not consider the influence of natural complex fractures on the dissolution patterns and the dynamic change of fracture aperture during acid-rock reaction time. In response, this paper established a novel mathematical model of reactive flow in a fractured medium based on the two-scale model and the discrete fracture model. The numerical simulation of reactive flow in the fractured medium was realized.

In The Mathematical Model for Matrix of this paper, the two-scale mathematical model in matrix is presented. The Mathematical Model for Fracture outlines the mathematical model of reactive flow in a fractured medium based on the discrete fracture model. Then, in Dimensionless the governing equations and boundary conditions are written in a dimensionless formula. Validation of the Model verifies the theoretical model by examining the conclusions of previous studies. In Numerical Results and Discussion, the numerical simulation of reactive flow is studied in different conditions. Finally, the paper is summarized by conclusions in Conclusion.

The Mathematical Model for Matrix

Darcy Scale Model

The flow equation of injected acid in a porous medium is described by Darcy’s law, the formula is written as:

$\mathit{v}=-\frac{\mathit{K}}{\mu }\nabla P$(1.1)

Where, v is the vector of Darcy’s velocity, m/s; K is the tensor of permeability in study region, m²; μ is fluid viscosity, mPa·s; P is fluid pressure, Pa. The continuity equation is derived from the law of mass conservation, the formula is as follows:

$\frac{\partial \varphi }{\partial t}+\nabla \cdot \mathit{v}+Q_{\mathrm{m}\mathrm{f}}=0$(1.2)

Where, ϕ is the porosity of carbonate rock; t is reaction time, s. Q_mf is the normal flow rate through the interface between the matrix system and the fracture system.

Generally, when the acid is injected into the carbonate rock, the equation of acid transport in the rock is described by the following mass balance equation.

$\frac{\partial \left(\varphi C_{\mathrm{f}}\right)}{\partial t}+\nabla \cdot \left(\mathit{v}{C}_{\mathrm{f}}\right)=\nabla \cdot \left(\varphi {\mathit{D}}_{\mathrm{e}}\cdot \nabla C_{\mathrm{f}}\right)+R+{\mathit{\Phi }}_{\mathrm{m}\mathrm{f}}$(1.3)

Where, C_f is acid concentration in a liquid phase, mol/m³; D_e is the tensor of the diffusion coefficient, m/s²; Φ_mf is solute mass transmitted into the matrix system through the interface between matrix medium and fracture medium. R is reaction term, its physical significance is that the amount of acid transferred to the liquid-solid surface is equal to the consumption of surface reaction, the formula of reaction term is expressed as:

$\mathit{R}=-a_{\mathrm{v}}\cdot k_{\mathrm{c}}\left(C_{\mathrm{f}}-C_{\mathrm{s}}\right)$(1.4)

Where, a_v is specific surface area, m⁻¹; k_c is local transport coefficient of acid, m/s; C_s is the acid concentration of liquid-solid surface in core pore, mol/m³, it is calculated by:

$C_s=\frac{C_{\mathrm{f}}}{\left(1+\raisebox{1ex}{$k_{\mathrm{s}}$}\!\left/ \!\raisebox{-1ex}{$k_{\mathrm{c}}$}\right.\right)}$(1.5)

The porosity will change as acid corrodes carbonate rock. The calculation formula of dynamic change of porosity is as follows:

$\frac{\partial \mathit{\varphi }}{\partial t}=\frac{a_{\mathrm{v}}\cdot \alpha \cdot k_{\mathrm{c}}\left(C_{\mathrm{f}}-C_{\mathrm{s}}\right)}{{\mathit{\rho }}_{\mathit{s}}}$(1.6)

Where, α is the dissolving power of acid, kg/mol; ρ_s is the density of carbonate rock, kg/m³.

Pore Scale Model

The porosity, radius of the pore, and specific surface area of rock are decided by pore structure. It is a dynamic process and the injected acid changes the pore structure of rock when it continuously erodes porous media. This means that the different kinds of physical parameters of carbonate rock will change dynamically. There are two methods to compute the physical parameters of carbonate rock in reactive flow (Panga et al., 2005; Kalia and Balakotaiah, 2009; Maheshwari et al., 2013; Ghommem et al., 2015; Liu et al., 2020). In the first method, these various physical parameters are computed based on the dynamic change of pore structure obtained through the laboratory. Another method is to calculate the various physical parameters of rock according to empirical or semi-empirical formulas. This paper adopts the modified Carman Kozeny equation to describe the dynamic change of porosity and permeability, the formulas are as follows:

$\{\begin{array}{c}\frac{k}{k_0}=\frac{\varphi }{{\varphi }_0}{\left(\frac{\varphi \left(1-{\varphi }_0\right)}{{\varphi }_0(1-\varphi )}\right)}^{2\mathrm{\beta }}\\ \frac{r_{\mathrm{p}}}{{\overline{r}}_0}=\sqrt{\frac{k{\varphi }_0}{k_0\varphi }}\\ \frac{a_{\mathrm{v}}}{{\overline{a}}_0}=\frac{\varphi {\overline{r}}_0}{{\varphi }_0{r}_{\mathrm{p}}}\end{array}$(1.7)

Where, r_p is pore radius, m; ${\overline{a}}_0$ is initial specific surface area, m-1; k₀ is initial permeability, m²; ϕ₀ is initial porosity; β is a constant that depends on the structure of the medium.

When solute of liquid phase flows in the pores, the velocity of solute in the acid through the pore flows from liquid phase to pore surface and contact with the pore surface is expressed by the rate of the mass transfer. It can be seen from Eq. 1.5 that the effect of the rate of mass transfer on reactive flow cannot be ignored when the acid system is certain, because its magnitude makes a difference to the chemical reaction. (Panga et al., 2010) defined a dimensionless number to the analysis of the associated factors, it is referred to the Sherwood number and represents the dimensionless mass transfer coefficient, it is given by:

$Sh=\frac{2k_{\mathrm{c}}{\overline{r}}_{\mathrm{p}}}{D_{\mathrm{m}}}=S{h}_{\infty }+b{\mathrm{Re}}_{\mathrm{p}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}S{c}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}$(1.8)

Where, r_p is the average pore radius of porous media, m; D_m is the molecular diffusion coefficient, m/s²; Sh_∞ is asymptotic Sherwood number of the pore, b is a constant number related to the structure of porous media, b = 0.7/m^1/2, where, the m is the ratio of pore length to pore radius, Re_p is pore Reynolds number, Re_p = 2ur_p/ν, where, ν is hydrodynamic viscosity; Sc is Schmidt number, Sc = ν_k/D_m, ν_k is hydrodynamic viscosity.

Diffusion Coefficient

When the acid is transported in the homogeneous and anisotropic matrix, in 2D, the diffusion tensor is characterized by axial diffusion coefficient D_eX and transverse diffusion coefficient D_eT. There is only solute molecular diffusion in the liquid phase and the transverse diffusion coefficient equals the axial diffusion coefficient when the fluid does not flow, the formula is as follows:

$D_{\mathrm{e}\mathrm{X}}=D_{\mathrm{e}\mathrm{T}}={\alpha }_{\mathrm{o}\mathrm{s}}{D}_{\mathrm{m}}$(1.9)

Where, D_m is the molecular diffusion coefficient, m/s²; α_os is a constant related to the structure of porous media (such as tortuosity or connectivity between pores). The two-dimensional diffusion coefficient of acid relates to the geometry of porous media, the flow pattern of pore scale, and the properties of acid. Researchers usually define a dimensionless Peclet number to describe the contrast between convection and diffusion. The expression formula of the Peclet number is found to be

$P{\mathit{e}}_{\mathrm{p}}=\frac{\left|\mathit{v}\right|d_{\mathrm{h}}}{\varphi D_{\mathrm{m}}}$(1.10)

Where, |v| describes the magnitude of Darcy’s velocity, m/s; d_h is pore diameter of porous media, m.

The formula of diffusion coefficient derived by Panga (Panga et al., 2010) is used to describe the diffusion of acid in porous media in this paper. the diffusion coefficient can be computed as:

$D_{\mathrm{e}\mathrm{X}}={\alpha }_{\mathrm{o}\mathrm{s}}{D}_{\mathrm{m}}+{\lambda }_{\mathrm{X}}{D}_{\mathrm{m}}P{e}_{\mathrm{p}}$(1.11)

$D_{\mathrm{e}\mathrm{T}}={\alpha }_{\mathrm{o}\mathrm{s}}{D}_{\mathrm{m}}+{\lambda }_{\mathrm{T}}{D}_{\mathrm{m}}P{e}_{\mathrm{p}}$(1.12)

Where, the subscript of X and T denotes the injection direction and vertical transverse direction of acid injection; α_os, λ_T, and λ_x are constants that have typical values of 0.5, 0.5,0.1 for a packed-bed of spheres (Kalia, 2008; Kalia and Balakotaiah, 2009; Liu et al., 2017), respectively.

Initial Conditions and Boundary Conditions

The pressure at the outlet is constant and the outlet boundary is a constant pressure boundary. The upper and down boundaries are closed boundaries. The specific expression of boundary conditions is given by:

$P=0,C_{\mathrm{f}}=0,att=0$(1.13)

$u_0=-\frac{k_x}{v}\frac{\partial P}{\partial x},\frac{\partial P}{\partial y}=0,C_{\mathrm{f}}=C_0,atx=0$(1.14)

$u_0=-\frac{k_x}{v}\frac{\partial P}{\partial x},\frac{\partial P}{\partial y}=0,C_{\mathrm{f}}=C_0,atx=0$(1.15)

$\frac{\partial C_{\mathrm{f}}}{\partial x}=0,P=P_e,atx=L$(1.16)

$\frac{\partial P}{\partial y}=0,\frac{\partial C_{\mathrm{f}}}{\partial y}=0,aty=0andy=L$(1.17)

Where, u₀ is initial injection velocity, m/s; C₀ is a concentration of injected acid at the inlet, mol/m³; P_e is a constant, it is boundary pressure at the outlet, Pa.

A random function $\widehat{f}$ is defined to simulate the heterogeneity of rock. Its value varies from -Δϕ₀ to +Δϕ₀ and satisfies the random function of uniform distribution, the generated initial porosity field is shown in Figure 1. The heterogeneity of fracture aperture is defined in this way.

FIGURE 1

FIGURE 1. Initial porosity field.

The Mathematical Model for Fracture

The governing equation of the fracture system is written as:

$d\frac{\partial \left(\mathit{\rho }{\mathit{\varphi }}_{\mathrm{f}}\right)}{\partial t}+\nabla \cdot \left(d\rho {\mathit{v}}_{\mathrm{f}}\right)+Q_{\mathrm{f}\mathrm{m}}=0$(1.18)

Where, v_f is the velocity vector of injected acid in the fracture system, the subscript f denotes fracture, d is fracture aperture, ϕ_f is fracture porosity; Q_mf is the flow exchange between the matrix system and fracture system. According to the cubic law, the flow velocity of injected acid in fracture system is expressed by the Poiseuille equation, the expression equation of flow velocity is given as:

${\mathit{v}}_{\mathrm{f}}=-\frac{d^2}{12\mathit{\mu }}\nabla P$(1.19)

The expression equation of permeability in fracture system is derived as:

$K_{\mathrm{f}}=\frac{d^2}{12}$(1.20)

Similarly, the convection-diffusion equation in fracture system is obtained as:

$d\left(\frac{\partial \left({\varphi }_{\mathrm{f}}{C}_{\mathrm{f}}\right)}{\partial t}+\nabla \cdot \left({\mathit{v}}_{\mathrm{f}}{C}_{\mathrm{f}}\right)-\nabla \cdot \left({\varphi }_{\mathrm{f}}{D}_{\mathrm{e},\mathrm{f}}\cdot \nabla C_{\mathrm{f}}\right)\right)+{\mathit{\Phi }}_{\mathrm{f}\mathrm{m}}=0$(1.21)

Where, C_f is the concentration of injected acid in the fracture system, D_e,f is the effective diffusion coefficient of solute in acid in the fracture system. Φ_mf is solute mass transmitted into the fracture system through the interface between matrix medium and fracture medium. Fracture aperture changes when the acid flow in the fracture system alters. The dynamic change process of fracture aperture can be obtained as:

$\frac{\partial d}{\partial t}=\frac{2R_{\mathrm{c},\mathrm{f}}\left(C_{\mathrm{f}}-C_{\mathrm{s}}\right)\alpha }{{\rho }_{\mathrm{s}}}$(1.22)

The effective diffusion coefficient (Steefel and Lichtner, 1998) of solute in acid in fracture system is as follows:

$D_{\mathrm{e},\mathrm{f}}={\alpha }_{\mathrm{f}}\cdot \left|{\mathit{v}}_{\mathrm{f}}\right|+D_{\mathrm{m}}$(1.23)

Where α_f is constant, which is equal to 0.5 in this paper.

Dimensionless

Many factors affect the process of reactive flow. The above governing equations and boundary conditions are written in a dimensionless formula to make the numerical solution of reactive flow easier and numerical simulation results more clear. The expression equations are defined:

$\begin{array}{l}{x}^{\ast }=\frac{x}{L},y^{\ast }=\frac{y}{L},{\mathit{U}}^{\ast }=\frac{\mathit{v}}{u_0},t^{\ast }=\frac{t}{\left(L/u_0\right)},r_{\mathrm{p}}^{\ast }=\frac{r_{\mathrm{p}}}{{\overline{r}}_0},\\ a_{\mathrm{v}}^{\ast }=\frac{a_{\mathrm{v}}}{{\overline{a}}_0},{\mathit{K}}^{\ast }=\frac{\mathit{K}}{k_0},{\mathit{D}}^{\ast }=\frac{{\mathit{D}}_{\mathrm{e}}}{D_{\mathrm{m}}},C_{\mathrm{f}}^{\ast }=\frac{C_{\mathrm{f}}}{C_0},\\ P^{\ast }=\frac{P-P_{\mathrm{e}}}{\left(\mu u_{0}L\right)/K_0},h_{\mathrm{T}}^2=\frac{2k_{\mathrm{s}}{\overline{r}}_0}{D_{\mathrm{m}}},Da=\frac{k_{\mathrm{s}}{\overline{a}}_{0}L}{u_0},P{e}_{\mathrm{L}}=\frac{u_{0}L}{D_{\mathrm{m}}},\\ N_{\mathrm{a}\mathrm{c}}=\frac{\alpha C_0}{{\rho }_{\mathrm{s}}},{\mathit{\Phi }}^2=\frac{k_{\mathrm{s}}{\overline{a}}_0{L}^2}{D_{\mathrm{m}}},\eta =\frac{2r_0}{L},{\mathit{U}}_{\mathrm{f}}^{\ast }=\frac{{\mathit{v}}_{\mathrm{f}}}{u_0},B=\frac{d}{L},K_{\mathrm{f}}^{\ast }=\frac{K_{\mathrm{f}}}{k_0},D_{\mathrm{f}}^{\ast }=\frac{D_{\mathrm{e},\mathrm{f}}}{D_{\mathrm{m}}}\end{array}$

Where the superscript ∗ denotes dimensionless; L is a characteristic length of the research area of the mathematical model; x,y are parameters of the coordinate system; U^∗ indicates that velocity vector is dimensionless; K^∗ indicates that the permeability vector is dimensionless; k₀ is initial permeability of porous media; ${\overline{r}}_0$ is average pore radius of porous media; ${\overline{a}}_0$ is initial specific surface area, B indicates that fracture aperture is dimensionless; the subscript f denotes fracture; D_f^∗ indicates diffusion coefficient is dimensionless; K^∗ indicates that permeability vector of fracture is dimensionless. Da represents the rate of reaction velocity to convection velocity at the core scale.

Based on the expression of the above-mentioned variables, dimensionless variables are substituted into governing equation. The dimensionless equations are obtained:

${\mathit{U}}^{\ast }=-{\mathit{K}}^{\ast }\cdot \nabla P_D$(1.24)

$\frac{\partial \varphi }{\partial t^{\ast }}+\nabla \cdot {\mathit{U}}^{\ast }+Q_{\mathrm{m}\mathrm{f}}^{\ast }=0$(1.25)

$\frac{\partial \left(\varphi C_{\mathrm{f}}^{\ast }\right)}{\partial t^{\ast }}+\nabla \cdot \left({\mathit{U}}^{\ast }{C}_{\mathrm{f}}^{\ast }\right)=\nabla \cdot \left({\mathit{D}}^{\ast }\cdot \nabla C_{\mathrm{f}}^{\ast }\right)-\frac{Da\cdot a_{\mathrm{v}}^{\ast }\cdot C_{\mathrm{f}}^{\ast }}{\left(1+\frac{h_{\mathrm{T}}^{\mathit{2}}\cdot r_{\mathrm{p}}^{\mathrm{\ast }}}{Sh}\right)}+{\mathit{\Phi }}_{\mathrm{m}\mathrm{f}}^{\ast }$(1.26)

The dimensionless equation of porosity changing is

$\frac{\partial \varphi }{\partial t^{\ast }}=\frac{Da\cdot N_{\mathit{a}\mathit{c}}\cdot a_{\mathrm{v}}^{\ast }\cdot C_{\mathrm{f}}^{\ast }}{\left(1+\frac{h_T^2\cdot r_p^{\ast }}{Sh}\right)}$(1.27)

The dimensionless equation of diffusion coefficient is rewritten as:

${\mathit{D}}^{\ast }=\left(D_x,D_y\right)={\left(\begin{array}{c}\frac{{\alpha }_{\mathrm{o}\mathrm{s}}\varphi Da}{{\mathit{\Phi }}^2}+{\lambda }_{\mathit{X}}\left|U\right|r_{\mathrm{p}}^{\ast }\eta \\ \frac{{\alpha }_{\mathrm{o}\mathrm{s}}\varphi Da}{{\mathit{\Phi }}^2}+{\lambda }_{\mathit{T}}\left|U\right|r_{\mathrm{p}}^{\ast }\eta \end{array}\right)}^T$(1.28)

The above equations are mathematical models of matrix systems for reactive flow. The dimensionless mathematical equations in the fracture system for reactive flow are

${\mathit{U}}_{\mathrm{f}}^{\ast }=-K_{\mathrm{f}}^{\ast }\cdot \nabla P^{\ast }$(1.29)

$\nabla \cdot \left(B{\mathit{U}}_{\mathrm{f}}^{\ast }\right)+Q_{\mathrm{f}\mathrm{m}}^{\ast }=0$(1.30)

$B\left(\frac{\partial \left(\varphi C_{\mathrm{f}}^{\ast }\right)}{\partial t^{\ast }}+\nabla \cdot \left({\mathit{U}}_{\mathrm{f}}^{\ast }{C}_{\mathrm{f}}^{\ast }\right)-\nabla \cdot \left(D_{\mathrm{f}}^{\ast }\cdot \nabla C_{\mathrm{f}}^{\ast }\right)\right)+{\mathit{\Phi }}_{\mathrm{f}\mathrm{m}}^{\ast }=0$(1.31)

Where, the expression equation of diffusion coefficient D_f^∗ is

$D_{\mathrm{f}}^{\ast }=\frac{{\alpha }_{\mathrm{o}\mathrm{s}}}{L}\left|{\mathit{U}}_{\mathrm{f}}^{\ast }\right|+\frac{1}{P{e}_{\mathrm{L}}}$(1.32)

The dimensionless boundary conditions and initial conditions are arranged as:

$\{\begin{array}{c}{U^{\ast }|}_{injectionboundary}=1\\ {P^{\ast }|}_{outerboundary}=0\\ {\frac{\partial P^{\ast }}{\partial \overrightarrow{n}}|}_{outerboundary}=0\\ {C_{\mathrm{f}}^{\ast }|}_{injectionboundary}=1\\ {\frac{\partial C_{\mathrm{f}}^{\ast }}{\partial \overrightarrow{n}}|}_{outerboundary}=0\\ {\frac{\partial P^{\ast }}{\partial \overrightarrow{n}}|}_{horizontalboundary}=0\end{array}$(1.33)

$\{\begin{array}{c}{C^{\ast }|}_{{\mathit{t}}^{\ast }=0}=0\\ {U^{\ast }|}_{{\mathit{t}}^{\ast }=0}=0\end{array}$(1.34)

Validation of the Model

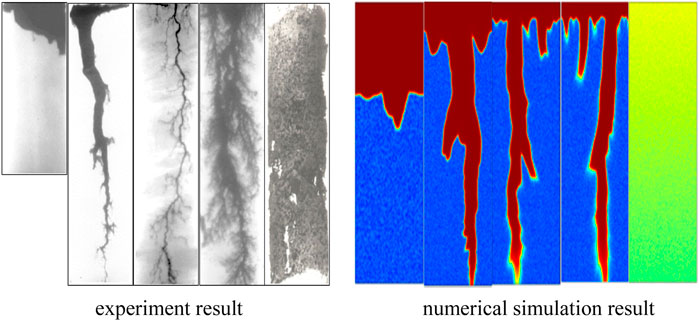
In this section, the correctness of the mathematical model of the matrix is verified. The numerical simulation results are compared with (Fredd and Fogler, 1999) physical experiment results. In the physical experiment, the diameter of the core is 3.8 cm and the length of the core is 10.2 cm. The comparison results of numerical simulation and physical experiment are shown in Figure 2.

FIGURE 2

FIGURE 2. Comparison of physical experiment and numerical simulation.

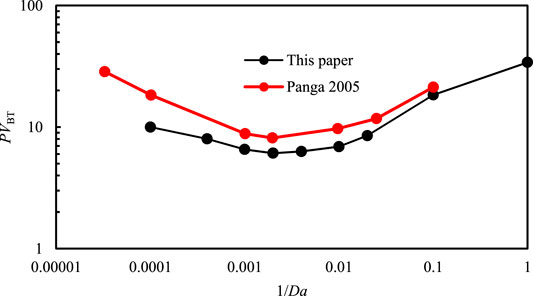
Through the comparison results, there are five different dissolution patterns. The results of numerical simulation in this paper are consistent with physical experiment in Fredd’s paper. A numerical example is used to test the accuracy of the mathematical model in Panga’s paper (Panga et al., 2010). The length and width of the model are 5 and 2 cm, separately. The initial porosity is 0.2, the fluctuation range is 0.05, Ф² = 10^5, N_ac = 0.1, h_T² = 0.07. The comparison cures are shown in Figure 3. It shows that the two cures are not coincident. The reasons are the difference between accurate value and solving algorithm.

FIGURE 3

FIGURE 3. Comparsion chart of fitting cure.

Numerical Results and Discussion

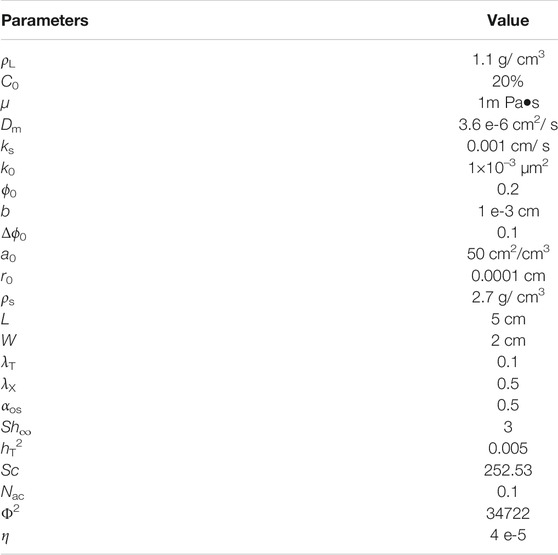
In this section, the numerical simulation of reactive flow in the fractured medium is implemented based on the above dimensionless mathematical model. The parameters and values in the numerical simulation are shown in Table 1. Unless otherwise specified, all parameters remain unchanged. The corresponding dissolution patterns in complex fractured media are studied, then, the effect of fracture aperture and the fracture orientation on dissolution structure and breakthrough volume of injected acid are studied in a single fracture system. The effect of heterogeneity of initial fracture aperture and dynamic variation of fracture aperture with dissolution on dissolution patterns, dissolution structure, and breakthrough volume of injected acid are studied. In this case, Da = 250.

TABLE 1

TABLE 1. The parameters and values in numerical simulation.

The definition equation of the breakthrough volume of injected acid is as follows:

$P{V}_{\mathrm{B}\mathrm{T}}=\frac{V_{\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{d}}}{V_{\mathrm{i}\mathrm{p}}}=\frac{Q_{\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{d}}{T}_{\mathrm{b}\mathrm{t}}}{V_{\mathrm{i}\mathrm{p}}}$(1.35)

Where, V_acid is the consumption volume of injected acid; V_ip is the initial pore volume of the core; Q_acid is the flow rate of injected acid, T_bt is waste time that injected acid breaks through core when the pressure rate of inlet end to outlet end is 0.01 at each time point.

Dissolution Patterns at Different Damköhler Number

The results of the numerical simulation are shown in Figure 4. There are five different dissolution patterns with Damköhler number changing. They are face dissolution, conical dissolution, wormhole, branch dissolution, and uniform dissolution. Figure 4A is the concentration field, Figure 4B is the porosity field. Column (A) is the concentration field and porosity field in the initial phase. (B) is the concentration field and porosity field when injected acid breaks through the core. It can be seen that there is a big difference among dissolution patterns. The reason is that the dissolution patterns are determined by the combined effect of convection velocity and reaction velocity of the solute in acid. When the convection velocity is smaller than the diffusion velocity and reaction velocity, the reaction between acid and rock is mainly controlled by the diffusion and reaction velocity of solute in acid. Therefore, the hydrogen ions transferred from the center of the pore to the surface of the pore will be completely consumed by the chemical reaction, and the rate of injected acid cannot promote the injected acid to penetrate the core deeper. In this case, the dissolution of acid in the core is named surface dissolution. As the rate of injected acid gets higher, so does the convection velocity of solute in acid, and the convection velocity is dominant for diffusion velocity and reaction velocity.

FIGURE 4

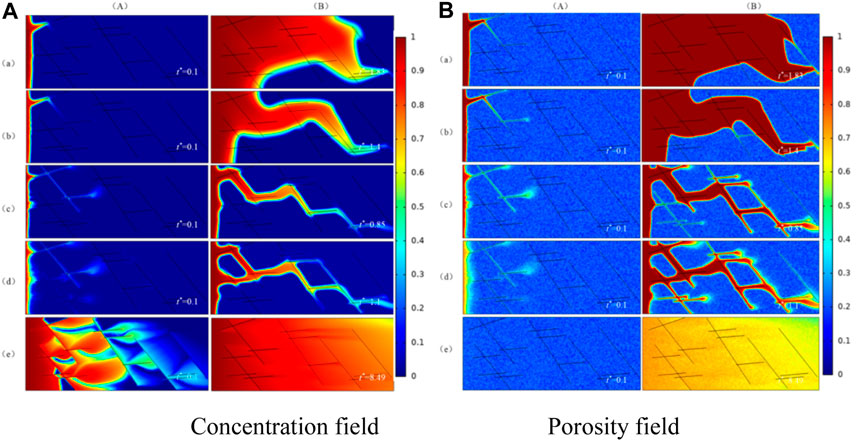
FIGURE 4. Dissolution patterns of different Damkohler numbers. (a) Face dissolution, Da = 2,000; (b) Concial dissolution, Da = 1,000; (c) Wormhole, Da = 250; (d) Branching dissolution, Da = 100; (e) Uniform dissolution, Da = 1. (A) The initial phase; (B) The dissolution structure when injected acid breaks through the core.

The solute in the acid flows away before it reacts on the pore surface of carbonate rock. This results in the core pores being filled with acid and leads to a uniform variation in pore porosity. There is no dominant channel in the core like wormhole, and the dissolution pattern is called uniform dissolution.

As can be seen from Eq. 1.4, the reaction rate is determined by the properties of acid and rock, and have nothing to do with the existence of fractures in the matrix. In this case, we can draw an important conclusion: in the case of the same acid-rock reaction system, whether there are fractures in the matrix has no effect on the dissolution patterns of the fractured medium.

In addition, the comparison results of numerical simulation show that the fracture is equivalent to the main advantage channel in the matrix. An injection rate that is too high or too low will not substantially change the dissolution patterns. This is because the injected acid has already reacted with the rock completely when the acid is injected into the core at a low injection rate and there is no excess acid to flow into the fracture. In the case of high injection velocity, the dominant role of fracture in the flow is negligible and may even play a negative role. In the above situations, the existence of fractures does not affect the dissolution patterns, however, the dissolution structure will change when the injection rate of acid is between the two. This is because the flow of injected acid is controlled by fracture conductivity, and the ultimate dissolution pattern is closely related to the distribution of fracture in the fractured medium.

The Effect of Fracture Orientations

In this section, the effect of fracture orientations on the wormhole structure is studied when Damkohler number is 250. Firstly, a fracture is located in the matrix and then the dissolution structure is obtained by numerical simulation. The results of numerical simulation are compared with the results obtained in a matrix without fracture. The numerical simulation results of a porosity field and concentration field are shown in Figure 5.

FIGURE 5

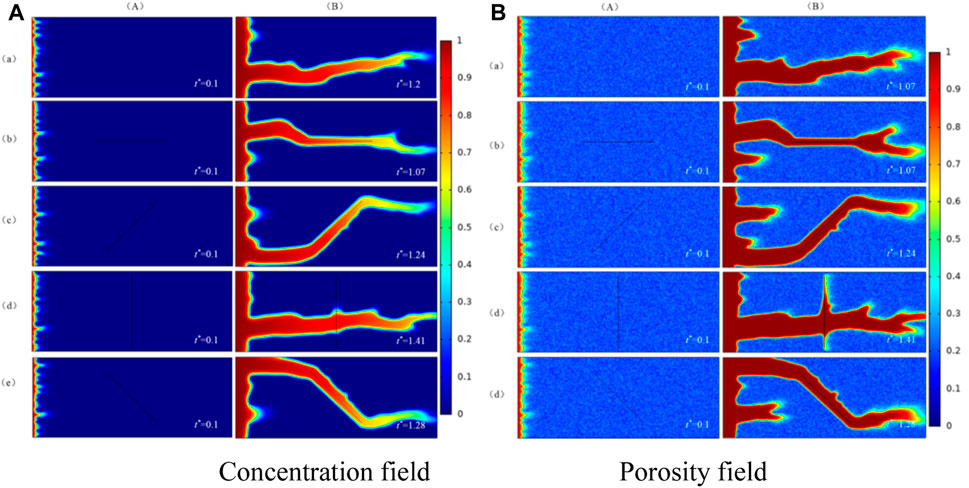
FIGURE 5. Wormhole structure in the presence of different fracture orientations. (a) No fracture; (b) Fracture orientation is 0°; (c) Fracture orientation is 45°; (d) Fracture orientation is 90°; (e) Fracture orientation is 135°; (A) The initial phase; (B) The dissolution structure when injected acid breaks through core.

(A) is concentration field and porosity field of numerical simulation in the initial phase and (B) is the concentration field and porosity field of numerical simulation when injected acid breaks through the core. In Figure 5, it can be obtained from column (A), the existence and orientations of fracture in the matrix do not affect the formation of the initial wormhole, but the direction of wormhole formation is consistent with the injected port of fractures. (B) shows that the fracture orientations influence the orientation of the wormhole and the fracture gradually becomes the part of the wormhole. The generation trend of the wormhole is random and branching in the matrix without fracture. When the orientation of fracture and injection direction of acid is at an angle of 90°, as shown in row (d) of Figure 5, the formation direction of the wormhole is not controlled by the orientation of the fracture. Instead, it is consistent with the direction of injected acid. Different from the wormhole in the matrix without fractures, the wormhole radius has increased and the direction of the wormhole has also changed in the fractured medium. This shows that the influence mechanism of fracture orientation on the formation direction of the wormhole is like to a high permeability zone.

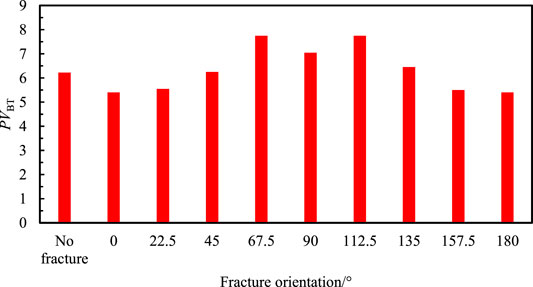
The breakthrough volume of injected acid in a matrix with different fracture orientations is drawn in Figure 6. It shows that when the orientation of fracture is consistent with the injection direction of acid or the orientation of fracture is similar with horizontal direction, the breakthrough volume of injected acid is smaller than the breakthrough volume in the matrix without fracture, the branching randomness of the wormhole is also getting weaker. When the direction of fracture is bigger than a certain angle, the breakthrough volume of injected acid becomes larger, and so does the consumption of acid. At this time, the effect of fracture inhibits the flow of acid in the fractured medium. The waiting time in the fractured medium becomes larger and then consumes more acid. When the direction of fracture is between 67.5° and 112.5°, the breakthrough volume of injected acid increases first and then decreases. It is because the conductivity of fracture has a smaller impact on the development and formation of the wormhole. When the direction of fracture is bigger than 90°, the breakthrough volume of acid is similar to volume when the angle is less than 90°, the slight difference is due to the heterogeneity of the core.

FIGURE 6

FIGURE 6. The breakthrough volume of injected acid at different fracture orientations.

In this example, the breakthrough volume of injected acid is largest in the core with a single fracture and the orientation of fracture is 67.5. The consumption of injected acid is even larger than the matrix without fracture.

The Effect of Fracture Aperture

In this section, the effect of fracture aperture on wormhole structure is studied when Damkohler number is 250. This model contains a fracture. The numerical simulation results are compared with the matrix without fracture, and the result of the numerical simulation is shown in Figure 7.

FIGURE 7

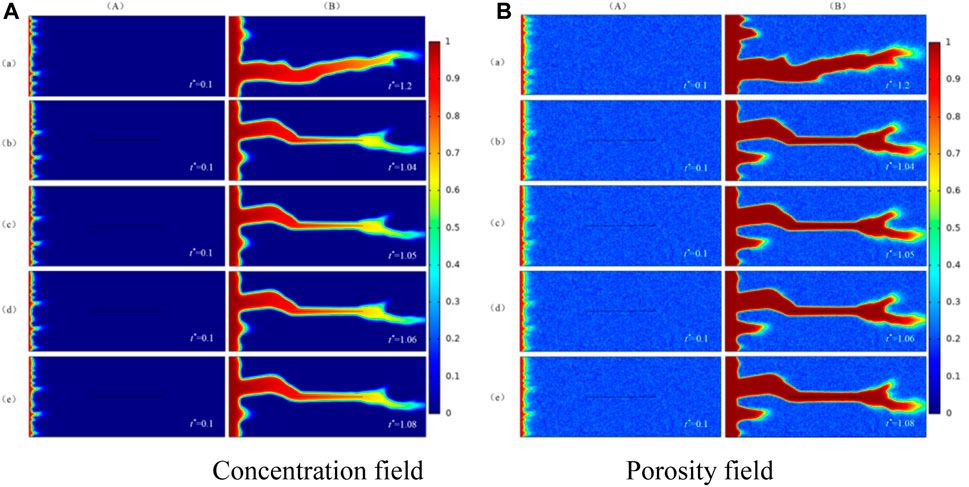
FIGURE 7. Wormhole structure in the presence of different fracture aperture. (a) No fracture; (b) b = 5e-4 m; (c) b = 1e-4 m; (d) b = 5e-5 m; (e) b = 1e-5 m; (A) The initial phase; (B) The dissolution structure when injected acid breaks through core.

(A) is concentration field and porosity field of numerical simulation in the initial phase and (B) is the concentration field and porosity field of numerical simulation when injected acid breaks through the core in Figure 7. In column (A) of the concentration field and porosity field in Figure 7, whether the fracture exists or not and no matter how the fracture aperture changes, it does not affect the initial wormhole structure.

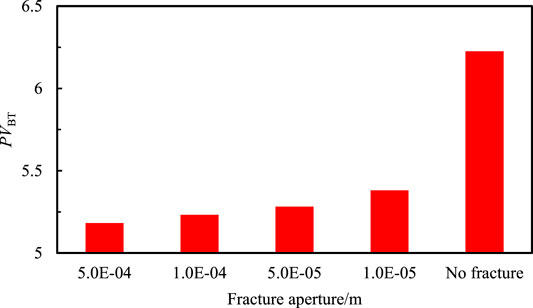
From column (B), it can be concluded that fracture aperture don't affect the formation trend of the wormhole and the fracture gradually becomes a part of the wormhole. The fracture aperture has no significant effect on the dissolution structure. The relationship between the breakthrough volume of injected acid and the fracture aperture is plotted as a columnar graph shown in Figure 8.

FIGURE 8

FIGURE 8. Effect of the fracture aperture on the breakthrough volume of injected acid.

Figure 8 shows that the breakthrough volume of injected acid is the smallest when the fracture aperture is largest. In the mathematical model of this paper, the calculation equation of permeability is obtained by the cubic law: the larger the fracture aperture and the higher the fracture permeability, the conductivity of fracture will become stronger. This means that the fracture has a stronger impact on the formation of the wormhole. As a result, the breakthrough volume of injected acid will become smaller and the consumption of acid will become less. In the same way, the smaller the fracture aperture, the lower the fracture permeability. The efforts of fracture on the formation of the wormhole are weaker and the breakthrough volume and consumption of injected acid are less than before. When the fracture aperture equals 5e-5m, the breakthrough volume of injected acid is the smallest in the study.

The Effect of Heterogeneity of Initial Fracture Aperture and Dynamic Variation of Fracture Aperture

The numerical simulation results are shown in Figure 9. With the increase of injected acid and the Damköhler number, there are five different dissolution patterns in fractured medium: face dissolution, conical dissolution, wormhole, branch dissolution, uniform dissolution.

FIGURE 9

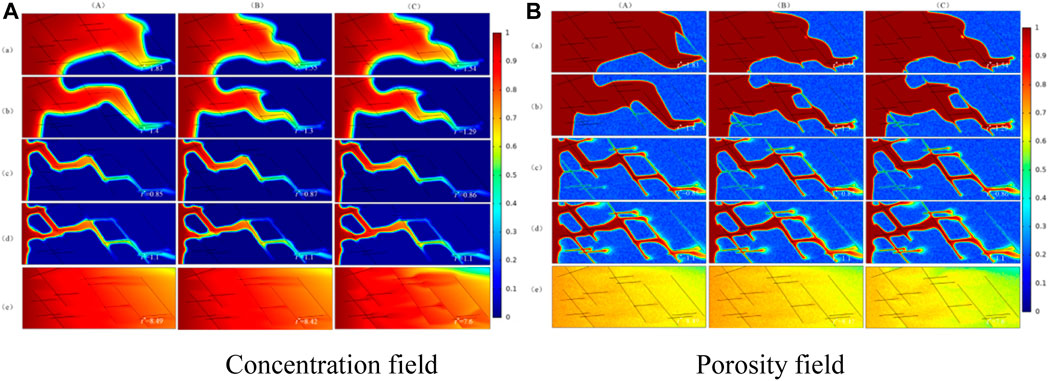
FIGURE 9. Dissolution patterns of homogeneity of initial fracture aperture, heterogeneity of initial fracture aperture, and dynamic change of fracture aperture in fractured medium. (a) Face dissolution, Da = 2000; (b) Concial dissolution, Da = 1,000; (c) Wormhole, Da = 250; (d) Branch dissolution, Da = 100; (e) Uniform dissolution, Da = 1. (A) The initial phase; (B) The dissolution structure when injected acid breaks through core.

The breakthrough volume curve of injected acid is plotted in Figure 10. It depicts the effect of homogeneity of the initial fracture aperture, the heterogeneity of initial fracture aperture, and the dynamic change of fracture aperture to the breakthrough volume of injected acid.

FIGURE 10

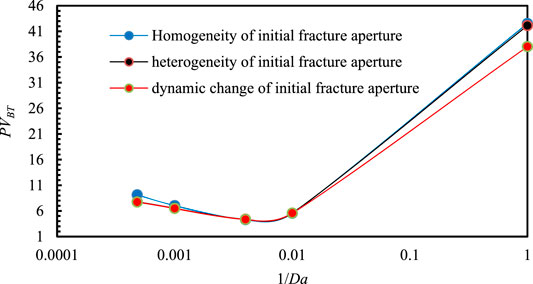
FIGURE 10. Influence of homogeneity of initial fracture aperture, of the heterogeneity of initial fracture aperture, and the changing of fracture aperture on the breakthrough volume of injected acid.

As shown in Figure 10, The dissolution patterns are unchangeable regardless of whether the initial fracture aperture is homogeneous, heterogeneous or fracture aperture is dynamic change with the acid etching fracture wall, the optimal injection rate of acid solution will not change when Da = 250.

Conclusion

A mathematical model of reactive flow in a fractured medium based on the two-scale model and discrete fracture model is built in this paper. This paper uses studies by predecessors, including physical experiments and numerical simulation experiments, to verify the correctness of the theoretical model of reactive flow in a matrix.

The discrete fracture model is solved numerically under the condition of two-dimensional linear flow. There are five different kinds of dissolution patterns according to the velocity of injected acid: face dissolution, conical dissolution, wormhole, branch dissolution, and uniform dissolution.

In the fractured medium, the existence of fracture does not affect the dissolution patterns of the matrix. The homogeneity and heterogeneity of fracture aperture and dynamic change of fracture aperture do not affect the optimal injection rate of injected acid.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

ZX: Conceptuation, Methodology, Software,Writing-Draft preparation ZF:Data curation, Validation, Writing-Reviewing and Editing HQ:Investigation, software. LR:Funding acquisition. SB:supervision. XC:Investigation.

Funding

This study received funding from the National Nature Science Foundation of China (52074336) and the Major Science and Technology Projects of China National Petroleum Corporation (ZD2019-183-008).

Conflict of Interest

Authors ZX, LR, and SB were employed by the company Xinjiang Oilfield Company, PetroChina. Author ZF was employed by the company Shengli Oilfield Company, SINOPEC.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.765139/full#supplementary-material

References

Andersen, P. Ø., and Evje, S. (2016). A Model for Reactive Flow in Fractured Porous media. Chem. Eng. Sci. 145, 196–213. doi:10.1016/j.ces.2016.02.008

CrossRef Full Text | Google Scholar

Bazin, B. (2001). From Matrix Acidizing to Acid Fracturing: A Laboratory Evaluation of Acid/Rock Interactions. SPE Prod. Facil. 16 (01), 22–29. doi:10.2118/66566-pa

CrossRef Full Text | Google Scholar

Bazin, B., Roque, C., and Bouteca, M. (1995). “A Laboratory Evaluation of Acid Propagation in Relation to Acid Fracturing: Results and Interpretation[A],” in Proceedings of the SPE European Formation Damage Conference[C], Hague, Netherlands, May 15–16, 1995 (Society of Petroleum Engineers).

Google Scholar

Budek, A., and Szymczak, P. (2012). Network Models of Dissolution of Porous Media. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 86 (5), 056318. doi:10.1103/PhysRevE.86.056318

PubMed Abstract | CrossRef Full Text | Google Scholar

Catherine, N. (2004). Investigation of Porosity and Permeability Effects from Microstructure Changes during limestone Dissolution[J]. Geophys. Res. Lett. 31 (24). doi:10.1029/2004GL021572

CrossRef Full Text | Google Scholar

Chen, G., and Ying, H. (2006). An Analysis of Acidizing Reaction Mechanism of Carbonates[J]. Nat. Gas Industry 26 (1), 104–108.

Google Scholar

Daccord, G., Touboul, E., and Lenormand, R. (1989). Carbonate Acidizing: Toward a Quantitative Model of the Wormholing Phenomenon. Spe Prod. Eng. 4 (01), 63–68. doi:10.2118/16887-pa

CrossRef Full Text | Google Scholar

Fredd, C. N., and Fogler, H. S. (1999). Optimum Conditions for Wormhole Formation in Carbonate Porous Media: Influence of Transport and Reaction. SPE J. 4 (03), 196–205. doi:10.2118/56995-pa

CrossRef Full Text | Google Scholar

Fredd, C., Tjia, R., and Fogler, H. (1997). “The Existence of an Optimum Damkohler Number for Matrix Stimulation of Carbonate Formations[A],” in Proceedings of the SPE European Formation Damage Conference[C], Hague, Netherlands, June 2–3, 1997 (OnePetro).

Google Scholar

Frick, T., Mostofizadeh, B., and Economides, M. (1994). “Analysis of Radial Core Experiments for Hydrochloric Acid Interaction with Limestones[A],” in Proceedings of the SPE Formation Damage Control Symposium[C]Lafayette, Louisiana, February 7–10, 1994 (Society of Petroleum Engineers).

Google Scholar

Ghommem, M., Zhao, W., Dyer, S., Qiu, X., and Brady, D. (2015). Carbonate Acidizing: Modeling, Analysis, and Characterization of Wormhole Formation and Propagation. J. Pet. Sci. Eng. 131, 18–33. doi:10.1016/j.petrol.2015.04.021

CrossRef Full Text | Google Scholar

Golfier, F., Bazin, B., and Zarcone, C. (2001). Acidizing Carbonate Reservoirs: Numerical Modelling of Wormhole Propagation and Comparison to Experiments[C]. SPE European Formation Damage Conference, Hague, May 21–22, 2001. doi:10.2118/68922-MS

CrossRef Full Text | Google Scholar

He, C. (2009). Study on Acidizing Wormhole of Tight Carbonate Reservoir[J]. Fault-Block Oil & Gas Field.

Google Scholar

Hill, A. D., Zhu, D., and Wang, Y. (2009). The Effect of Wormholing on the Fluid Loss Coefficient in Acid Fracturing. SPE Prod. Facil. 10 (04), 257–264. doi:10.2118/27403-pa

CrossRef Full Text | Google Scholar

Hoefner, M. L., and Fogler, H. S. (1989). Fluid-Velocity and Reaction-Rate Effects During Carbonate Acidizing: Application of Network Model. Spe Prod. Eng. 4 (01), 56–62. doi:10.2118/15573-pa

CrossRef Full Text | Google Scholar

Hoefner, M. L., and Fogler, H. S. (1988). Pore Evolution and Channel Formation during Flow and Reaction in Porous media. Aiche J. 34 (1), 45–54. doi:10.1002/aic.690340107

CrossRef Full Text | Google Scholar

Kalia, N. (2008). Modeling and Analysis of Reactive Dissolution of Carbonate Rocks[J]. Dissertations & Theses - Gradworks 8 (2), 67–151.

Google Scholar

Kalia, N., and Balakotaiah, V. (2009). Effect of Medium Heterogeneities on Reactive Dissolution of Carbonates. Chem. Eng. Sci. 64 (2), 376–390. doi:10.1016/j.ces.2008.10.026

CrossRef Full Text | Google Scholar

Kim, S., and Santamarina, J. C. (2015). Reactive Fluid Flow in CO 2 Storage Reservoirs: A 2‐D Pore Network Model Study. Greenhouse Gas Sci. Technol. 5 (4), 462–473. doi:10.1002/ghg.1487

CrossRef Full Text | Google Scholar

Liu, P., Li, J., and Sun, S. (2020). Numerical Investigation of Carbonate Acidizing with Gelled Acid Using a Coupled Thermal-Hydrologic-Chemical Model[J]. Int. J. Therm. Sci. 160 (106700), 23955–26900. doi:10.1016/j.ijthermalsci.2020.106700

CrossRef Full Text | Google Scholar

Liu, P., Yao, J., Couples, G. D., Huang, Z., Sun, H., and Ma, J. (2017). Numerical Modelling and Analysis of Reactive Flow and Wormhole Formation in Fractured Carbonate Rocks. Chem. Eng. Sci. 172, 143–157. doi:10.1016/j.ces.2017.06.027

CrossRef Full Text | Google Scholar

Liu, X., Ormond, A., and Bartko, K. (1997). A Geochemical Reaction-Transport Simulator for Matrix Acidizing Analysis and Design[J]. J. Pet. Sci. Eng. 17 (1-2), 181–196. doi:10.1016/s0920-4105(96)00064-2

CrossRef Full Text | Google Scholar

Maheshwari, P., Ratnakar, R. R., Kalia, N., and Balakotaiah, V. (2013). 3-D Simulation and Analysis of Reactive Dissolution and Wormhole Formation in Carbonate Rocks. Chem. Eng. Sci. 90, 258–274. doi:10.1016/j.ces.2012.12.032

CrossRef Full Text | Google Scholar

Nierode, D. E., and Williams, B. B. (1971). Characteristics of Acid Reaction in Limestone Formations. Soc. Pet. Eng. J. 11 (04), 406–418. doi:10.2118/3101-pa

CrossRef Full Text | Google Scholar

Panga, M. K. R., Ziauddin, M., and Balakotaiah, V. (2005). Two-Scale Continuum Model for Simulation of Wormholes in Carbonate Acidization. Aiche J. 51 (12), 3231–3248. doi:10.1002/aic.10574

CrossRef Full Text | Google Scholar

Panga, M., Ziauddin, M., and Ba Lakotaiah, V. (2010). Two-Scale Continuum Model for Simulation of Wormholes in Carbonate Acidization[J]. AIChE J. 51 (12), 3231–3248. doi:10.1002/aic.10574

CrossRef Full Text | Google Scholar

Steefel, C. I., and Lichtner, P. C. (1998). Multicomponent Reactive Transport in Discrete Fractures: I. Controls on Reaction Front Geometry[J]. J. Hydrol. 209 (1-4), 186–199. doi:10.1016/s0022-1694(98)00146-2

CrossRef Full Text | Google Scholar

Wang, Y., Hill, A., and Schechter, R. (1993). “The Optimum Injection Rate for Matrix Acidizing of Carbonate Formations[A],” in Proceedings of the SPE Annual Technical Conference and Exhibition[C], Houston, Texas, October 3–6, 1993 (Society of Petroleum Engineers).

Google Scholar

Yang, X., and Pan, Q. (2000). Acidizing Fluid Leakoff Mechanism Studying on Dolomite Reservoir[J]. Drilling Prod. Technol.

Google Scholar

Zhang, H., Zou, H., and Liu, S. (2017). Dual Fractal Model of Carbonate Acidizing Wormholes[J]. Nat. Gas Geosci. 28 (3), 466–472. doi:10.11764/j.issn.1672-1926.2017.01.010

CrossRef Full Text | Google Scholar

Ziauddin, M. E., and Bize, E. (2007). “The Effect of Pore Scale Heterogeneities on Carbonate Stimulation Treatments[A],” in Proceedings of the SPE Middle East Oil and Gas Show and Conference[C], Kingdom of Bahrain, March 11–14, 2007 (Society of Petroleum Engineers).

Google Scholar