- 1Department of Earth Sciences, Faculty of Geosciences, Utrecht University, Utrecht, Netherlands
- 2Univ Rennes, CNRS, Geósciences Rennes ‐ UMR, Rennes, France
- 3Institut Universitaire de France (IUF), Paris, France
- 4Institut für Geowissenschaften, Goethe-Universität Frankfurt, Frankfurt, Germany
We perform numerical modelling to simulate the shortening of an oceanic basin and the adjacent continental margins in order to discuss the relationship between compressional stresses acting on the lithosphere and the time dependent strength of the mid-oceanic ridges within the frame of subduction initiation. We focus on the role of stress regulating mechanisms by testing the stress–strain-rate response to convergence rate, and the thermo-tectonic age of oceanic and continental lithospheres. We find that, upon compression, subduction initiation at passive margin is favoured for thermally thin (Palaeozoic or younger) continental lithospheres (<160 km) over cratons (>180 km), and for oceanic basins younger than 60 Myr (after rifting). The results also highlight the importance of convergence rate that controls stress distribution and magnitudes in the oceanic lithosphere. Slow convergence (<0.9 cm/yr) favours strengthening of the ridge and build-up of stress at the ocean-continent transition allowing for subduction initiation at passive margins over subduction at mid-oceanic ridges. The results allow for identifying geodynamic processes that fit conditions for subduction nucleation at passive margins, which is relevant for the unique case of the Alps. We speculate that the slow Africa–Europe convergence between 130 and 85 Ma contributes to the strengthening of the mid-oceanic ridge, leading to subduction initiation at passive margin 60–70 Myr after rifting and passive margin formation.
Highlights
• Numerical models are used to investigate the kinematic and stress conditions for subduction initiation to occur at passive margins or amid the oceanic plate.
• Slow convergence rate favours subduction initiation at passive margins over subduction at mid-oceanic ridges.
• Distribution of deformation is key to regulate levels of stress in the lithosphere.
Introduction
Studies of subduction systems show that oceanic subduction either nucleates at passive margins or within oceanic plates (Gurnis et al., 2004; Stern, 2004; Stern and Gerya, 2018; Crameri et al., 2020). Over the past decades several analogue, numerical and analytical modelling studies have been conducted to infer the preferred locus and suitable geometric, kinematic and mechanical conditions for the initiation of subduction zones (e.g., Cloetingh et al., 1989; Faccenna et al., 1999; Gurnis et al., 2004; Mart et al., 2005; Goren et al., 2008; Nikolaeva et al., 2010; Maffione et al., 2015; Zhong and Li, 2019; Auzemery et al., 2020; Candioti et al., 2020; Kiss et al., 2020). These studies have shown that subduction zones develop at passive margin through the lateral propagation from pre-existing subduction (Ulvrova et al., 2019; Crameri et al., 2020) or from the formation of new subduction fault at the ocean-continent transition (Kiss et al., 2020; McCarthy et al., 2020). In the latest scenario, subduction initiation at passive continental margins critically depends on the buoyancy of the oceanic lithosphere as well as density and strength contrasts across the ocean-continent transition and the stratification of the passive margin lithosphere (Goren et al., 2008; Nikolaeva et al., 2010; Auzemery et al., 2020). Intra-oceanic subduction initiation is favoured for oceanic lithosphere younger than 50 Myr, whereas subduction nucleation occurs at the ocean-continent transition for cases of intermediate age (50–110 Myr) oceanic lithosphere and when the margin crust is decoupled from the underlying mantle lithosphere. The latter condition is particularly important because it facilitates strain localization and subsequent strain propagation within weak layers of the passive margin crust (Nikolaeva et al., 2010; Auzemery et al., 2020; Kiss et al., 2020). Although the above quoted modelling studies successfully simulate the initiation of subduction zones at passive margins upon vertical or horizontal loading, the stress levels required for the nucleation of subduction are usually significantly higher than plate tectonic forces (England and Wortel, 1980; Cloetingh et al., 1989; Mueller and Phillips, 1991; Gerbault, 2000; Gurnis et al., 2004; Zhong and Li, 2019). In fact, the stress needed for subduction initiation at passive margins is in general one order of magnitude larger than the horizontal component of stress generated by ridge push (Mahatsente and Coblentz, 2015). From a mechanical perspective, it is important to note that the critical stress for subduction initiation is also higher by ∼5 TN than the lithospheric yield strength at (slow spreading) mid-ocean ridges (Luttrell and Sandwell, 2012). This suggests that upon contraction, deformation should predominantly affect the mid-ocean ridge, the weakest part of the system, where subduction would then initiate. Although active compressional tectonics is well-documented in several oceanic basins (e.g., Forsyth, 1973; Wysession et al., 1991; Stein and Stein, 1993), recent and past examples of subduction initiation at or close to mid-ocean ridges as suggested for the Tethys or Pacific realms, are less well documented and subject to debate (Agard et al., 2016; Crameri et al., 2020), suggesting that mechanisms such as the dissipation of mechanical energy into heat regulates the stress level in the oceanic lithosphere (Brun and Cobbold, 1980; Schmalholz et al., 2009). How such mechanisms then contribute to favour subduction initiation at passive margins over subduction at mid-oceanic ridges remain unclear.
As stress regulation mechanism is linked to the strength of the lithosphere and thermo-mechanical feedback mechanism leading to strain localization, we argue that 1) convergence rate and the 2) thermo-tectonic age of oceanic and continental lithospheres are key parameters controlling the stress levels in the lithosphere. We test this hypothesis through thermo-mechanical modelling to infer the stress–strain-rate response to different kinematic and stress conditions eventually leading to subduction initiation at passive margins over subduction at mid-oceanic ridges. We conclude, by discussing how the interplay between far-field tectonic forcing and the strength of oceanic lithosphere impacts on the time-scales of subduction initiation and highlight similarities of modelling results to subduction initiation in the European Alps.
Stress Magnitudes in Oceanic Basins
On earth, the magnitudes of depth-integrated compressive differential stress is in the order of 3–15 TN/m (Cloetingh and Wortel, 1986; Coblentz and Richardson, 1996; Ghosh et al., 2013; Naliboff et al., 2009; Richardson et al., 1979). We emphasise here that this value can vary from one study to another because some used the integral of the maximum horizontal deviatoric stress which is half of the differential stress used in this study (
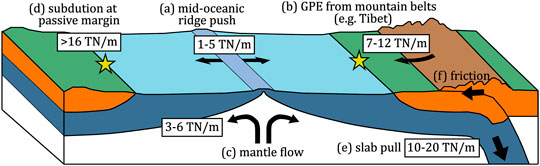
FIGURE 1. Simplified sketch illustrating magnitudes of integrated differential stress observed on earth arising from: (A) ridge push (Mahatsente, 2017), (B) gravitational potential energy (GPE, Schmalholz et al., 2019) and (C) shear tractions generated by mantle flow (Kendall and Lithgow-Bertelloni, 2016). (D) In comparison, minimum differential stress required for subduction initiation at a passive margin is 16–20 TN/m (Zhong and Li, 2020) (E) slab pull (Turcotte and Schubert, 2014) (F) frictional resistance at plate interface. The orange and dark blue layers represent the crust and the mantle lithosphere, respectively.
As loads of 16 TN/m are needed to initiate subduction at passive margins (Zhong and Li, 2020) additional forces are required next to ridge push for the formation of a new subduction zone. It is, therefore, expected that stress levels in excess of ridge push would be relaxed through deformation of the mid-oceanic ridge, where the lithospheric strength is low. The strength of spreading ridges is subject to considerable uncertainty because the magma supply mechanisms are not sufficiently well understood and quantified (Luttrell and Sandwell, 2012). However, inferences from geochemical (Beaussier et al., 2019), geophysical (Luttrell and Sandwell, 2012) and numerical modelling (Husson, 2012) studies suggest that there is a strong correlation between spreading rate and thermal thickness of the lithosphere at mid-ocean ridges. When spreading rates are lower than ca. 1.5 cm yr−1, the melt concentration is particularly low, and the thermal thickness of oceanic lithosphere (isotherm 1,300°C) at the mid-ocean ridges can be as large as 55 km (Husson, 2012). Therefore, an ultra-slow spreading ridge is of similar strength than a 5–8 Myr old oceanic lithosphere. This is in agreement with stress predictions associated with oceanic lithospheric folding suggesting that an ultra-slow mid-oceanic ridge could support horizontal loads of 8 TN/m (e.g., Indian ocean, Gerbault, 2000).
Numerical Model
To investigate stress-controlled mechanisms for subduction initiation at passive margins, 2D numerical thermo-mechanical models with a visco-elasto-plastic rheology were used. The finite-difference, marker-in-cell code (MDoodz; Duretz et al., 2016b) was used to solve the equations of momentum 1), mass conservation and the heat Equation 3.
where v is the velocity vector, T is the temperature, k is the thermal conductivity,
Modelling Approach
In order to test our hypothesis, we perform numerical modelling simulating shortening of an oceanic basin and the adjacent continental margins. These models do not include melt production processes at mid-ocean ridges but are designed to capture the essential deformation features that characterize the shortening of an oceanic basin of a given age, as a consequence of the interplay between plate cooling and stresses arising from far-field forcing. Ultimately, they serve as a basic model to determine the stress and strain-rate boundary conditions required for subduction initiation at passive margins or within the oceanic domain.
The modelling approach of this study is two-fold (Figures 2A,B). We first run a simplified model setup that adopts a laterally uniform distribution of physical properties within the oceanic lithosphere, where the age of the oceanic lithosphere is everywhere the same (Figure 2A).
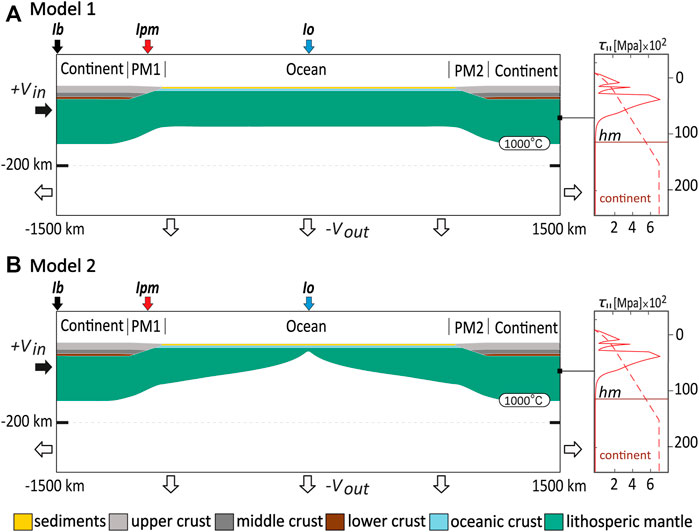
FIGURE 2. Model setup for (A) a uniform thickness of oceanic lithosphere; and (B) a model incorporating a mid-oceanic ridge.
In step two, we incorporate the age dependent thickening and lengthening of the oceanic lithosphere from an extinct spreading center to the passive margin (Figure 2B). Hereafter, the extinct spreading center will be referred to as the “ridge”. The results of the parametric study (step 1) facilitate obtaining favourable boundary conditions for subduction initiation at passive margins in step 2, where the role of lithosphere thickness variation which varies through time with cooling was investigated.
Model Geometry and Rheology
The model domain is a section of 3,000 × 500 km and the numerical resolution is 1 × 1 km in both dimensions. The model top boundary is represented by a true free surface (Duretz et al., 2016b). Erosion and sedimentation have been implemented following a kinematic approach (e.g., Candioti et al., 2020) where erosion and sedimentation are implemented above or below a base level fixed at 0 km. In all models, the accommodation space is filled with a sedimentary material composed of calcite, which is a rheologically weak lithology.
Models of step 1 comprise a 2000 km wide oceanic plate flanked by two continental plates on either side (Figure 2A and Table 1). The continental lithosphere consists of an 18 km thick granitic upper crust, a 12 km thick feldspathic middle crust, a 5 km thick granulitic lower crust and a lithospheric mantle with a fixed thermal thickness (hl). The oceanic lithosphere entails an 8 km thick crust and a lithospheric mantle with a thermal thickness that depends on its age following the plate cooling model used in Auzemery et al. (2020). The passive margin is characterized by a crust that thins progressively towards the ocean over a distance of 150 km. The thermal base of the lithosphere at the passive margin is defined by a linear interpolation between the ocean and the continent. Deformation is governed by frictional, dislocation, diffusion and Peierls creep equations, with parameters displayed in Table 1. Following previous studies (Zhong and Li, 2019; Candioti et al., 2020; Kiss et al., 2020) we account for thermal softening instead of pre-defined strain softening mechanisms to allow for shear localization leading to subduction initiation. The initial geotherm is computed assuming steady-state conditions and accounts for different radiogenic heat productions in each layer and a constant asthenosphere temperature of 1,330°C.
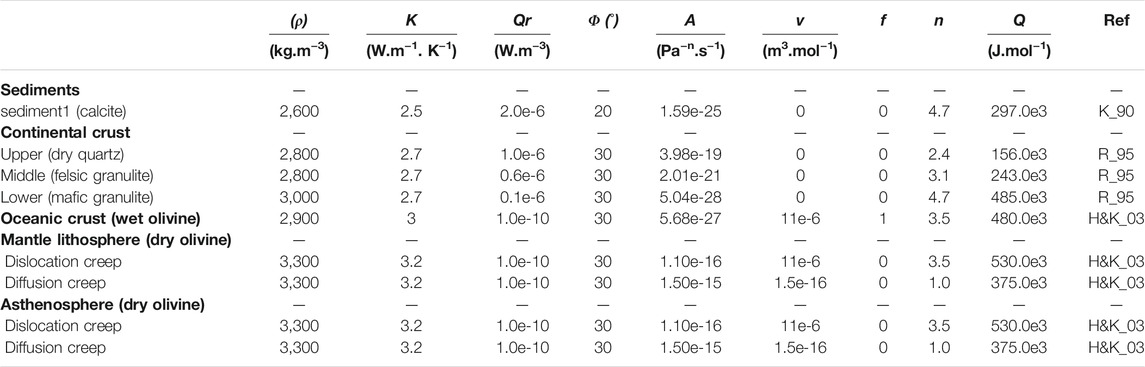
TABLE 1. Rheological and thermal parameters used for the reference numerical models. Here ρ is the density, k is the thermal conductivity, Qr is the radiogenic heat production, ϕ is the friction angle, A is a pre-factor, f is a correction factor, n is the stress exponent, Q is the activation energy. The shear modulus G is set to 6e 1010 Pa. References for rheology are H&K_03: Hirth and Kohlstedt (2003); K_90: Kronenberg et al. (1990); R_95: Ranalli (1995).
Investigated Parameters
For each model, we varied the thermal thickness of the oceanic lithosphere and the convergence rate at the boundary, which both influence the stress level within the oceanic lithosphere. The first model setup (uniform thickness) comprises a 2,000 km wide oceanic plate flanked by two continental plates on either side (Figure 2A). 14 ages of oceanic lithosphere were tested, at 10 Myr intervals, counting from 0 to 140 Myr. For each age of oceanic lithosphere, a wide range of convergence rates were tested to arrive at a threshold value for which we observe a change from intra-oceanic subduction to subduction at the passive margin. We carried-out two sets of numerical experiments with two different thermal thicknesses (160 and 180 km) of continental lithosphere fixed in time, representing continental lithosphere of Palaeozoic and Proterozoic age, respectively (Artemieva, 2009).
Based on the results of step one, the thermal thickness of the continental lithosphere has been fixed at 160 km in stage two, as this thickness facilitates subduction initiation at passive margins. The thermal thickness and the length of the oceanic domain depend on the age of the lithosphere along the x-axis, as functions of distance from the former ridge. Therefore, by assuming that the ocean was formed at an average half-spreading rate of 1 cm yr−1 (in accordance with a slow spreading rate, e.g. Dick et al., 2003), the oceanic lithosphere gets 10 Myr older every 100 km (counting from the ridge) and the width of a 30 Myr oceanic basin is 600 km. We carried out three sets of numerical experiments with three different ages of oceanic basin namely 30 and 60 and 90 Myr. For each, the tested parameters include the duration of the cooling period at the start of the experiment and the convergence rate at the boundary during subsequent shortening. The implementation of a cooling period prior to shortening is necessary in order to obtain scenarios where subduction nucleates at the passive margin.
Boundary and Loading Conditions
The model top boundary is a true free surface (Duretz et al., 2016b). A constant inward normal velocity (
These models with different thermal ages of the oceanic lithosphere have been subject to horizontal velocity boundary conditions. For each age of oceanic lithosphere, a wide range of convergence rates were tested to arrive at a threshold value for which we observe a change from intra-oceanic subduction to subduction at the passive margin.
Model Output and Stress Analysis
With the aim of monitoring stress magnitude through time, at every location along the models, we compute for each time step the total integrated stress in the lithosphere
where
A stress analysis is performed by computing the integrated differential stress as a function of time (Figure 3) at three positions: the model boundary, the passive margin, and the oceanic lithosphere (Figure 2A). The integrated stress for the oceanic lithosphere is an averaged value over the oceanic domain. At each position, subduction initiation is assumed to start at the time where the integrated stress has reached the highest value and is followed by a sudden stress drop at ts, the time of subduction initiation (Figure 3). Figure 3 is an example of how the integrated stress
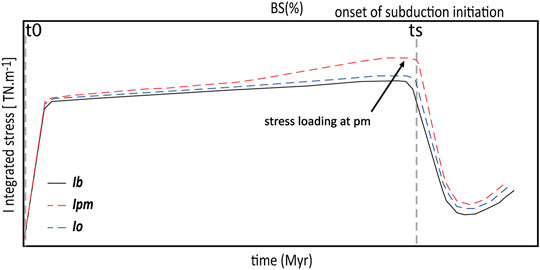
FIGURE 3. Schematic example of integrated stress evolution through time and amount of convergence expressed as bulk shortening (BS) for an experiment where subduction initiates at the passive margin. The steep increase in the early stage represents elastic loading. The stress values presented in Figure 4 are stresses integrated over the whole lithosphere for the three locations indicated by the coloured arrows in Figure 2A (model boundary Ib, passive margin Ipm, oceanic basin Io). t0 and ts refers to the time at the start of the model and the time of subduction initiation, respectively.
Models were run for a range of convergence velocities, ages of oceanic lithosphere, and thicknesses of continental lithosphere. In each model, the integrated stress at the model boundary was calculated and plotted in various domain diagrams (Figure 4). We also use the evolution of integrated stress through time to explain how it controls the lithosphere dynamics (Figure 5C). A total of 150 models were run in order to establish a robust stress transfer model for the oceanic basin.
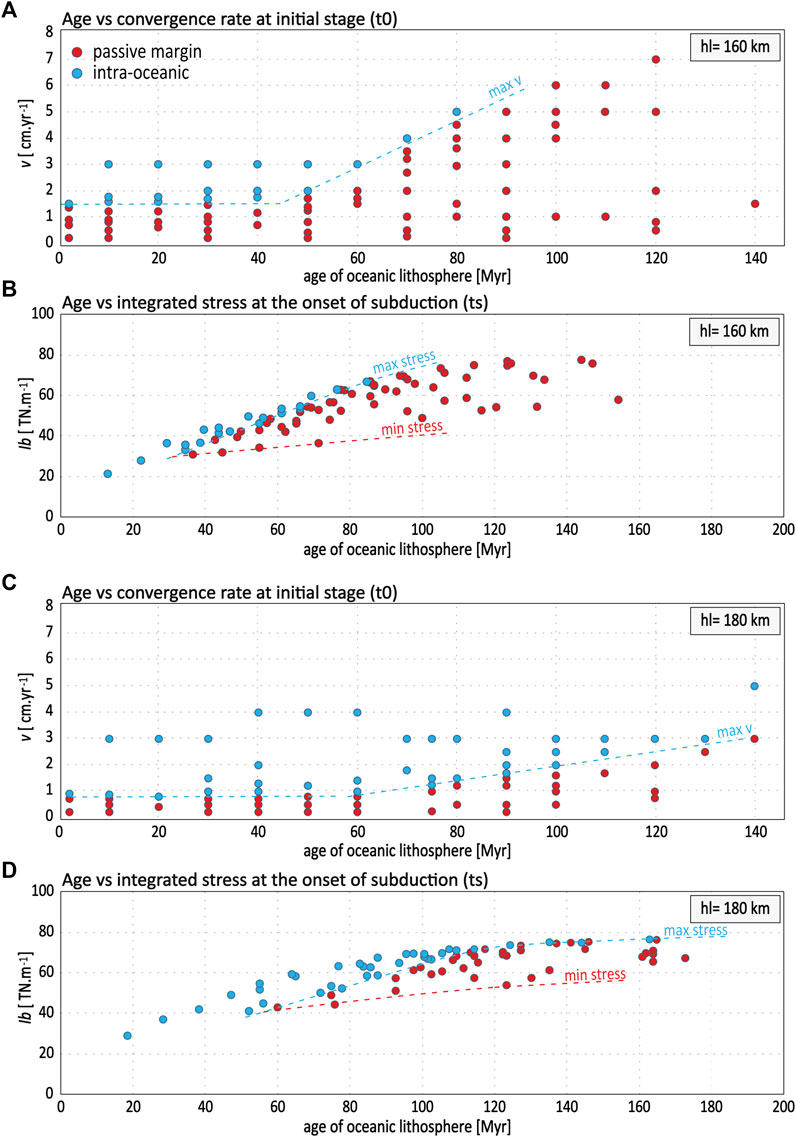
FIGURE 4. Results of model series 1 with laterally uniform thickness of oceanic lithosphere: role of stress and convergence rate on the locus of subduction initiation for two thermal thicknesses of continental lithosphere, 160 and 180 km. (A, C) Age of oceanic lithosphere vs convergence rate at model boundary at the onset of convergence (t0). (B, D) Age of subduction vs integrated stress at model boundary at the onset of subduction initiation. The red and blue dot lines represent the minimum and maximum integrated stress for subduction at passive margin.
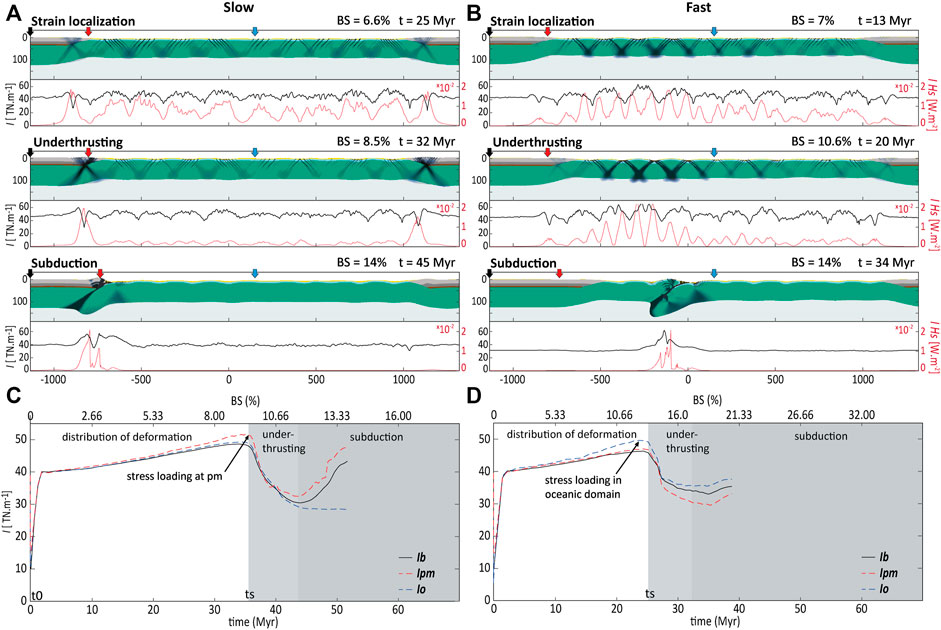
FIGURE 5. Effect of convergence rate on mode of subduction initiation in model series 2. Inversion of a 30 Myr old oceanic basin at convergence rate of 0.8 cm yr-1 (left) and 1.6 cm yr-1 (right). (A, B) Model evolution, displayed in terms of composition of the lithosphere overlain by the second invariant of the strain rate tensor to show strain localization mechanism (top panel), and integrated stress I (black curve) and integrated heat production by visco-plastic dissipation IHs (red curve) over the thickness of the lithosphere (bottom panels). (C, D) Evolution integrated stress for three locations indicated by the coloured arrows (model boundary Ib, passive margin Ipm, oceanic basin Io). Note that Io is an averaged value of integrated stress over the oceanic domain. BS is bulk shortening.
Modelling Results
Series 1: Oceanic Lithosphere with Laterally Uniform Thickness
In this section, we present the results of the first set of experiments that shows the relationship of convergence rate and the locus of subduction initiation as a function of the age of the oceanic basin (Figures 4A,C). Throughout this study we define t0 as the age of the oceanic lithosphere at the start of the model and ts as the age of the oceanic basin when subduction initiates. For each experiment, we calculate the value of integrated stress
Figures 4A,C indicate that for young oceanic lithospheres (age < 50 Myr) subduction initiation at a passive margin is only feasible at low convergence rates. The upper bound value of convergence rate for subduction at passive margin (max v) is relatively constant (∼v = 1.5 cm yr−1, Figure 4A) and thus independent of the age of the oceanic lithosphere. Moreover, this limit is relatively lower for 180 km thick continental lithosphere (∼v = 0.9 cm yr−1, Figure 4C).
In contrast, for oceanic lithosphere older than 50–60 Myr, the upper bound values of convergence rate for subduction initiation at passive margin varies with the age of oceanic lithosphere at the start of the model as well as the thickness of the continental lithosphere. Intra-oceanic subduction is consistently observed for higher convergence rates across all tested ages of oceanic lithosphere (Figures 4A,C). Moreover, the range of velocities leading to subduction initiation at a passive margin is much larger in case of a 160 km thick continental lithosphere (Figure 4A), than for a 180 km thick continental lithosphere (Figure 4C), suggesting that subduction at passive margin is less likely in case of thick continental lithospheres. It shows again that for similar kinematic conditions, strain localization at passive margins is controlled by the strength of the continental lithosphere, regulated through its thermal thickness.
From the distribution of modelling results, we delineate upper and lower bounds of stress levels for subduction initiation (max. and min stress, Figures 4B,C). The results show that, overall, subduction at passive margins requires less stress than intra-oceanic subduction suggesting that subduction at passive margins is possible for stress levels lower than that within the oceanic plate (Figure 4B, blue dash-dot line), which is predicted for oceanic lithospheres older than ∼40 Myr (Figure 4B). Consequently, with cooling of the oceanic lithosphere, intra-oceanic subduction becomes particularly intricate and requires large amounts of integrated stress.
The minimum integrated differential stress necessary for subduction nucleation at a passive margin (red dashed line at 60 Myr, Figure 4B) is in the order of 30 TN/m, which corresponds to an age of 40–50 Myr for the oceanic lithosphere at the time of subduction. The stress magnitude required for subduction at passive margins is sensitive to the thermal thickness hl of the continental lithosphere. The minimum stress for subduction initiation at passive margins ranges from 30 to 36 TN/m for hl = 160 km and from 40 to 50 TN/m for hl = 180 km (Figures 4B,D), which corresponds to age limits of oceanic lithosphere of 40 Myr for hl = 160 km and 60 Myr for hl = 180 km. This result shows that among all the parameters analysed in this study, the thermal thickness of the continental lithosphere is probably most important. For similar ages of subduction initiation at passive margins, the disparity in stress is due to a variation in convergence rate, with low convergence rate models requiring lower stress levels for subduction initiation at passive margins (red dashed line, Figure 4B).
Mechanisms for Subduction Initiation
Subduction initiation at passive margins requires high loading level of shear stress acting on the margin but also low levels of shear stress in the oceanic lithosphere. Our modelling results show that convergence velocity is an important parameter that regulates stress in the lithospheric layers and therefore controls the locus of deformation. Models with low convergence rate (∼0.8 cm yr−1) predict strain localization and subsequent subduction initiation at the passive margin (Figure 5A, 6.6%BS), whereas models with high convergence rate predict intra-oceanic subduction (Figure 5B, 7%BS). These results show that stress loading preferentially occurs at passive margins for cases of low convergence rate (Figure 5C), because deformation is distributed over many small structures within the brittle layer that accommodate low amounts of strain and is even more distributed within the ductile layers of the models. Consequently, distributed deformation (black curve) leads to low shear rates and low heat production (Figure 5A). The heat produced by viscoplastic dissipation (Hs, Figure 5A) is then efficiently diffused within the viscous layer (red curve, Figure 5A, 6.6%BS). Therefore, homogeneous distribution of deformation and shear heating at low strain-rate limits the magnitude of stress in the oceanic domain and thus prevents stress loading and failure during cooling of the lithosphere (Figure 5C). When the oceanic lithosphere reaches a certain thickness (after t = 30–35 Myr), it barely deforms, but acts as a buttress and shortening leads to deformation of the passive margin until subduction initiates (Figure 5A, 8.5%BS).
The passive margin lithosphere consists of brittle layers in the crust and the underlying lithospheric mantle where deformation localises in shear bands, which eventually link-up to form a through-going shear structure (Figure 5A). This moment of formation of the incipient subduction plate boundary allowing for underthrusting of the oceanic plate correlates with a significant stress drop as shown in Figure 5C.
In contrast, for models with relatively high convergence rate deformation is localized in the oceanic domain (Figure 5B, between -500-0 km). The increase of integrated stress is largest within oceanic lithosphere for both young and old oceanic basins (Figure 5D, t = 20 Myr). Higher strain rates within shear band type-structures lead to localised shear heating (Hs) triggering shear-localization by thermal softening in the ductile layer and the formation of a subduction plate boundary (Figure 5B).
Series 2: Oceanic Lithosphere with Age Dependent Thickness
In this section we present the results for three sets of experiments defined by the age of the oceanic basin (30 Myr, 60 Myr and 90 Myr; Figures 6A–C) that include age dependent thickness variations within the oceanic lithosphere (Figure 2B). Figure 6 delineates the mode of subduction as function of the cooling period implemented at the start of the experiments and the convergence rate during the subsequent shortening period. Overall, these modelling results show that a cooling period of at least 5 Myr before the start of shortening (Figure 6A) is necessary to prevent underthrusting at the position where the thermal thickness of the oceanic lithosphere is smallest, representing in simplified forma former ridge. Consistent with results derived from step 1, we infer that subduction initiation at a passive margin is only feasible for low convergence rates (v < 0.9 cm yr−1, Figure 6A). However, different to the models with a uniform oceanic lithosphere, Figure 6 shows that subduction initiation is more favourable in case of a young oceanic basin rather than an old one (Figures 6A vs Figures 6B,C). To understand this result, we present in Figure 7 two modelling results with similar boundary conditions (tc = 5 Myr, v = 0.3 cm yr−1) but with different ages of the oceanic basin (age = 30 and 60 Myr; Figures 6A,B) at the onset of shortening.
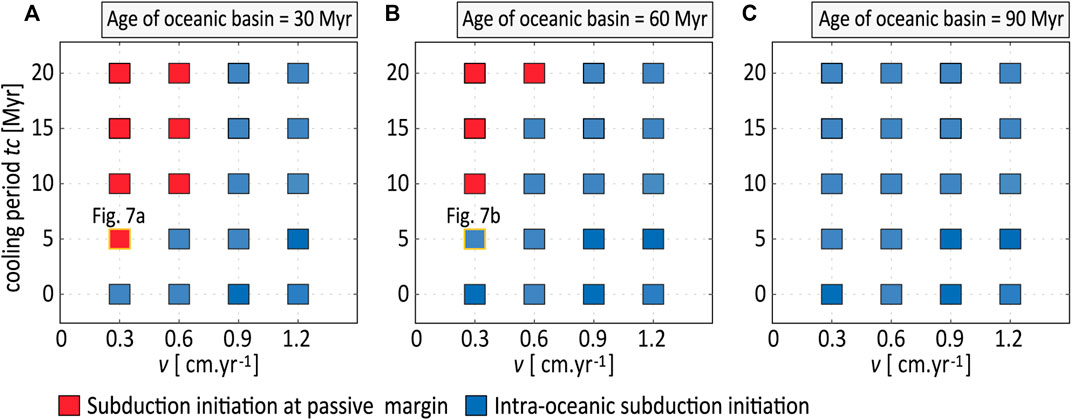
FIGURE 6. Results of model series 2 with an age dependent thickness of oceanic lithosphere: Domain diagrams mapping the location of subduction initiation against the cooling time (tc) and the convergence velocity (v) during the subsequent shortening period. Each diagram represents a different age of the oceanic basin (age of the oceanic lithosphere at the margin) before the start of the experiment.
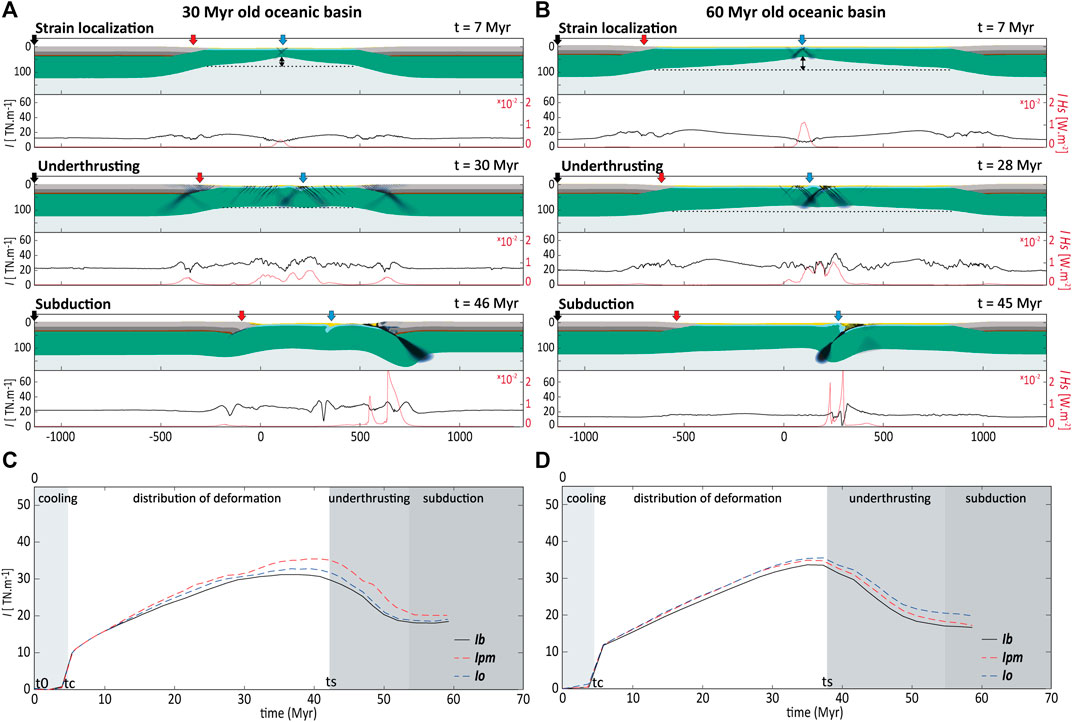
FIGURE 7. Effect of oceanic basin age on subduction initiation in model series 2. Shortening of a 30 Myr old (left) and a 60 Myr old (right) oceanic basin at convergence rate of 0.3 cm yr−1 (left) after a cooling period of 5 Myr. (A–C) Model evolution, illustrated through plots of model composition overlain by plots of strain-rate (top panels) and through plots of integrated stress I (black curve) and integrated heat production by visco-plastic dissipation IHs (red curve) over the thickness of the lithosphere (lower panels). (C,D) Evolution of integrated stress for three locations: the model boundary, the passive margin, and in the oceanic basin.
For both models, the oceanic lithosphere shows an increase in thickness and integrated stress from the basin centre to the continental lithosphere (Figures 7A,B), which is largest for the older (60 Myr) oceanic basin (Figures 7A,B). In case of a 30 Myr oceanic basin, the level of integrated stress at the ridge is close to the value at the margin (∼16–18 TN/m, black curve in Figure 7A). Shortening of such young lithosphere at a slow rate of 0.3 cm yr−1 leads to strain localization at the former ridge early in the deformation history (Figures 7A, 7 Myr). However, in the later stage (Figure 7A, 30 Myr), strain is rather distributed, because lateral thermal thickness variations get reduced as the oceanic lithosphere cools faster at the ridge compared to the passive margin. Under such conditions, the subsequent development of a shear-zone at the base of the continental crust leads to underthrusting of the oceanic plate under the margin (Fig. 7a, 46 Myr). In comparison, in case of a 60 Myr old oceanic basin the level of integrated stress at the ridge is significantly lower than at the passive margin (ΔI = 10 TN, Figures 7B, 7 Myr).
Consequently, strain localises at the mid-oceanic boundary which is much thinner (Fig. 7b, 45 Myr), resulting in intra-oceanic under-thrusting (Fig. 7b, 45 Myr). These results suggest that the strength contrast (expressed in this section by the thermal thickness) between the lithospheres at the centre of the oceanic basin and the passive margin controls the locus of subduction initiation. Therefore, a young oceanic basin with minor variation in strength between the extinct ridge and the margin requires only 5 Myr of cooling prior to convergence to permit subduction at a passive margin. In contrast, an old oceanic basin would require a significant period of cooling (tc > 20 Myr) to reduce the strength differences between the lithosphere at the ridge and at the passive margin to allow for subduction initiation at the passive margin (Figure 6B).
Discussion
Favourable Conditions for Subduction Initiation at Passive Margins
We have set to investigate what conditions and mechanisms lead to intra-oceanic subduction vs passive margin subduction (Figure 8). Because mid-oceanic ridges have a thinner and weaker lithosphere compared to passive margins, they represent a priori preferential locations for subduction initiation (e.g. Maffione et al., 2015; Agard et al., 2016). Moreover, the large difference between ridge push force (∼1–5 TN) and stresses arising from tectonics, or topography related gravitational potential energy (5–10 TN) suggests that subduction should predominantly initiate at mid-oceanic ridges, which is consistent with our modelling predictions for fast convergence rates. Additionally, this modelling study suggests that subduction initiation at passive margin is physically feasible under restricted conditions.
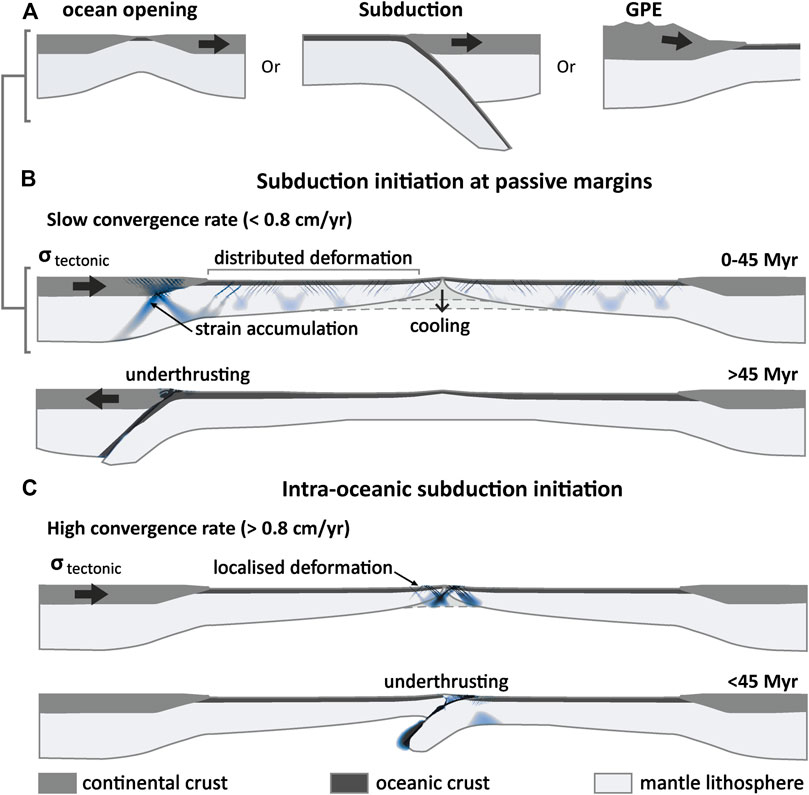
FIGURE 8. Strain-rate dependent mechanisms for subduction initiation at passive margins. (A) Geodynamic processes that potentially contribute to the transfer of stress to a passive margin. (B) Subduction at passive margin for slowly converging ocean-continent systems: the formation of a subduction plate boundary at the passive margin critically depends on the stability of the mid-ocean ridge, which is controlled by the distributed style of deformation. 0–45 Myr after the onset of shortening: strain accumulation at passive margin under low convergence rate. >45 Myr: strain localization and subduction. (C) Subduction amid oceanic plates for fast converging ocean-continent systems: Rapid closure of the oceanic basin leads to localized deformation and underthrusting near the ridge crest. Black arrows represent stress arising from mid-oceanic ridge and far-field forcing.
First, subduction initiation at a passive margin requires processes that regulate stress levels in the oceanic lithosphere. Our modelling results show that rheological conditions and processes favouring distributed deformation within the ductile part of the oceanic lithosphere is key for reducing stress levels and de-localising deformation (Figure 8B). As such localised deformation within the brittle layer, expressed as shear band type structures, fail to propagate into and through the ductile layer to form a subduction plate boundary. This behaviour is tied to low convergence rates, i.e., below 0.9 cm yr-1 (Figure 8B). Similar results have been obtained by Gülcher et al. (2019) and Qing et al. (2021), who observed in their numerical models, reactivation of multiple detachment faults upon their inversion but did not produce intra-oceanic subduction. When deformation does not localized in oceanic domain, the vertical rheological decoupling at the margin allows for the development of a long-lasting shear zone where stresses are relaxed through the formation of a decollement that propagate through the mantle. Our results predict that even young (5 Myr old) oceanic lithospheres can support tectonic stress of up to 12 TN/m underlining its long-term stability. As such, subduction initiation along spreading ridges is largely favored by warm ridge and fast convergence rate (Figure 8C, see also Qing et al., 2021) and/or the implementation of lithosphere-scale pre-existing weak zones (Maffione et al., 2015) to localize deformation in the mantle lithosphere.
Second, subduction initiation at a passive margin also entails the transfer of deformation from the ridge to the margin during the cooling of the oceanic lithosphere (Figure 7A). Previous studies have emphasized that deformation at the passive margin through spontaneous margin collapse is an unlikely mechanism for subduction initiation, because stresses acting on the passive margin lithosphere are never at yield (Cloetingh et al., 1984; Mueller and Phillips, 1991). It is thus more likely that the nucleation of a subduction zone at a passive margin occurs upon additional external forcing to reach stress levels of at least 16 TN/m (Zhong and Li, 2020) to induce failure of the passive margin lithosphere. Numerical modelling studies simulating the shortening of an oceanic basin (Auzemery et al., 2020; Candioti et al., 2020; McCarthy et al., 2020; Zhong and Li, 2020) emphasise that such stress levels can only be supported by thick oceanic lithospheres, suggesting that subduction initiation is only feasible in case of shortening of an old oceanic basin. Therefore, subduction at a passive margin could only happen after a relatively long period of cooling at an extinct ridge prior to plate convergence (>60 Myr, Candioti et al., 2020; McCarthy et al., 2020). In comparison, our models simulating the effects of an extinct and cooling mid-oceanic ridge suggest that subduction initiation at passive margins is also possible in case of slow shortening of a young oceanic basin (<30 Myr), following a short period of cooling (>5 Myr). Although our approach assumes an initial short period (5 Myr) of cooling where no external forcing (convergence) is applied, the results predict a more reasonable time scale for the development of a subduction zone at a passive margin, which amounts to 45 Myr from the moment that shortening is applied.
Third, subduction initiation at continental margins does not only depend on the age of the oceanic lithosphere (e.g. Auzemery et al., 2020; Zhong and Li, 2020) but also on the thermo-tectonic age of the rifted continental lithosphere (Figure 4, see also Nikolaeva et al., 2010). We show that subduction initiation is favoured for thermally thin (Palaeozoic or younger) continental lithospheres (<160 km) over cratons (>180 km) (Artemieva, 2009). This could explain why subduction does not exist along the north and south Atlantic margin, where the continental lithosphere is particularly thick (Tesauro et al., 2013) and might also be the reason for the proposed transference of subduction from the paleo-Tethys, to the neo-Tethys, along the margin of the thinned Cimmerian micro-continent (Wan et al., 2019).
Driving and Resisting Factors
Similar to Candioti et al. (2020) and Kiss et al., 2020, the stress levels obtained in our study are larger than plate boundary forces and represent upper bonds. Thus, other pre-existing lithospheric structures or weakening mechanism are generally suggested to explain subduction initiation at a passive margin (e.g., Stern and Gerya, 2018).
First we note that, the level of integrated stress required for subduction initiation depends mainly on the strength of the continental lithosphere that depends largely on its composition, thermal regime and the presence of weakening mechanisms (Cloetingh et al., 2005) and fluids (Regenauer-Lieb et al., 2001). In our study, the stress limit also varies with rheological layering and thermal state at the margin (Auzemery et al., 2021) and the earlier mentioned 20 TN/m limit is only valid for a 4 layer-160 km thick-continental lithosphere. This explains differences with similar studies (e.g., Zhong and Li, 2019), in which the crust is weaker and thermal thickness at the margin is significantly smaller than in our models.
Second, in our models, the sensitivity of deformation pattern to the choice of softening parameters is too high. Therefore, to not prescribed the locus of deformation, the magmatic (Gerya and Meilick, 2011), hydro-mechanical (Dymkova and Gerya, 2013; Schmalholz et al., 2020) and grain boundary weakening (Bercovici and Ricard, 2014) were not implemented. Parameterized strain softening was also not used because it is not a transient mechanism and the strain-dependent weakening limits are not well calibrated (Jaquet and Schmalholz, 2018). In addition, our models do not include inherited structures such as detachment faults that are prone to reactivation at stress levels (Maffione et al., 2015) that are well below those required for the development of new faults. Furthermore, a very thin oceanic lithosphere is used to simulate an extinct mid-ocean ridge. As such, melt- and fluid-related processes at mid-oceanic ridges, which are yet poorly constrained because of scars high resolution observations and rheology data from natural systems (Bickert et al., 2021) are not taken into account. These have been discussed in models deploying lithosphere extension (e.g. Ligi et al., 2008; Dannberg et al., 2019), which is different to our setup, which focuses on contraction of an oceanic ridge and its continental margins. The mechanisms discussed above could greatly reduce the stress limits after deformation localize at a passive margin or at a mid-oceanic ridge. However, the doubts and uncertainties associated with the choice of the weakening parameters would affect too much the results of the parametric study and a less complex approach was adopted.
Lastly, the discrepancy between analytical and numerical models could be explained by the very high uncertainties about the levels of integrated stress present within the lithosphere. Traditionally, the magnitudes of integrated stress used to explain plate tectonic processes are compared with analytical calculations made on plate boundaries (subduction, ridge-push; e.g., England and Wortel, 1980). However, these models are extremely unclear as they ignore multi-scale and multi-physics processes such as magmatic accretion or mantle dynamics (e.g., Husson et al., 2015). Besides, in nature, additional stress sources are necessary in order to explain regional-to local-scale stress (e.g. Heidbach et al., 2007) and deformation patterns (Gerbault, 2000; Cloetingh et al., 2005). Furthermore, it is common that forces are calculated using the integral of the horizontal deviatoric stresses (Ghosh et al., 2006; Mahatsente and Coblentz, 2015) that are lower by a factor of two (see Schmalholz et al., 2019) than the differential stress usually used to calculate lithosphere forces.
Subduction Initiation in the Wilson Cycle
Our modelling results together with previous modelling studies (Cloetingh et al., 1989; Gurnis et al., 2004; Hall, 2019; Nikolaeva et al., 2011; Stern and Gerya, 2018) suggest a mechanism that favors forced subduction initiation at passive margins. In particular, we find that slow convergence (<0.9 cm yr−1) over a long period of time (∼40 Myr) is critical in this context. Forces at play may include ridge push (e.g., Forsyth, 1973; Vlaar and Wortel, 1976) GPE from adjacent high areas (Ghosh et al., 2006; Marques et al., 2013; Pascal and Cloetingh, 2009), transference from an existing subduction zone (Baes et al., 2018; Duarte et al., 2013) or mantle flow (Candioti et al., 2020 and references therein). Associated with this far-field tectonics (Figure 8A), the partial starvation of basaltic melt underneath an ultraslow spreading ridge can lead to the gradual increase in thermal thickness of the oceanic lithosphere by 40–50 km (Husson, 2012) resulting in a period where stresses transmitted from the extinct ridge affect the passive margin (Figure 7).
In the frame of the above, the Alpine Tethys is a particular good analogue where the geological record demonstrates ultra-slow spreading (Lagabrielle and Cannat, 1990) and subduction initiated at the passive margin (Manzotti et al., 2014b; Marroni et al., 2017; Schmid et al., 2004). The latter process was probably associated with low convergence rates affecting the Adriatic crust of Palaeozoic (∼320 Ma) tectono-thermal age (Castellarin and Cantelli, 2010). The actual age of subduction initiation in the Alps is debated, but high pressure rocks found in the Adriatic margin constrain an age for underthrusting of ca 90–80 Ma (Manzotti et al., 2014a and references therein). However, several authors suggest an earlier subduction initiation at ca. 130 Ma, related to the change in Africa-Europe convergence controlled by the opening of the south Atlantic Ocean (Handy et al., 2010; van Hinsbergen et al., 2020; Le Breton et al., 2021). Based on our modelling results, we argue that subduction initiation in the Alps was a long-lasting (40–50 Myr) process that required a long period of very slow convergence allowing for strengthening of the ridge and the stress build-up at the ocean-continent transition. We note that the latter is achieved for times when Africa did not move head-on relative to Europe. During this period from 130 to 85 Ma, referred as “Cretaceous Quiet Zone” by van Hinsbergen et al. (2020), plate reorganisation leads to a quasi-absence of convergence between Africa and Europe (c.a. 0.6 cm yr−1 based on Figure 9). We suggest that such configuration would favour a reduction of the spreading rate, the strengthening of the mid-oceanic ridge as well as strain accumulation at the margin, until subduction finally initiates due to an increase in plate convergence rate 90 Ma (Capitanio and Goes, 2006). This scenario implies that at the onset of slow convergence at 130 Ma, the Piemonte-Liguria ocean is 30–40 Myr old, which falls within the range of “favourable” conditions for SI at passive margins (Figure 6A). We furthermore remark that exhumed and serpentinised mantle lithosphere of the Alpine Tethys provided additional favourable mechanical conditions for subduction initiation at stress levels that are compatible with plate tectonic forces (e.g. Candioti et al., 2020).
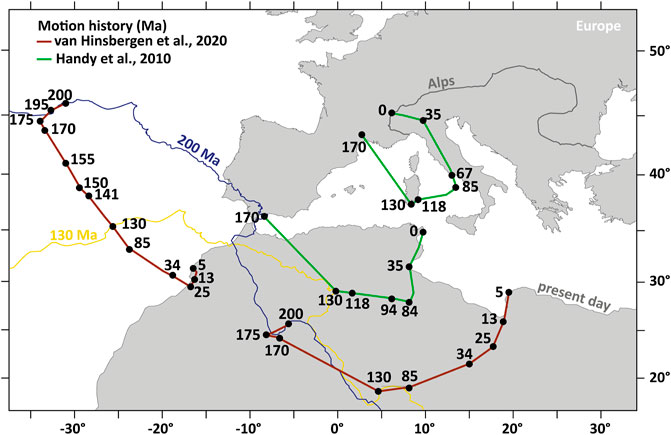
FIGURE 9. Plate motion history of Africa with respect to Europe from the Triassic to present day modified after van Hinsbergen et al. (2020). Red and green lines represents the motions path calculated by van Hinsbergen et al. (2020) and Handy et al. (2010), respectively. Numbers are ages in Ma. The yellow and blue lines represent the outline of Africa and illustrate its position at 200 Ma and 130 Ma (van Hinsbergen et al., 2020). The motion paths highlight a period of slow Africa-Europe convergence between 130 and 90 Ma, which is key for the future development of a subduction zone along the Adriatic passive margin.
Conclusion
Subduction initiation at passive continental margins is function of a complex interplay between horizontal forcing and the strength of the lithosphere, which acts as a stress guide. Both can vary depending on the thermal thickness of the continental lithosphere at the margin, the age of the oceanic lithosphere and the convergence rate. Strain accumulation at the passive margin during a long period of time with very slow convergence enables the development of a long-lasting shear-zone in the lower crust as well as the strengthening of the oceanic lithosphere at the mid-oceanic ridge. At the same time, this shear zone is critical for connecting localised deformation within the brittle crust to deformation in the mantle lithosphere. This evolution leading to the formation of a subduction plate boundary at the passive margin critically depends on the stability of the mid-ocean ridge, which is controlled by the distributed style of deformation within the ductile oceanic lithosphere. This has a de-localising effect, which prevents the formation of a throughgoing shear zone and maintains a low level of stress in the lithosphere. Under these conditions, oceanic plate cooling together with gravitational stresses and far-field tectonic forces provide suitable driving forces for subduction nucleation at passive margins. In contrast, models with high convergence rate favour strain localization also within the ductile oceanic lithosphere, because shear heating is more efficient, predicting the formation of a subduction plate boundary at the weakest spot of the system, the mid-oceanic ridge.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
Credit Author Statement AA First author: Conceptualization, investigation, formal analysis, validation, writing. EW Funding acquisition, supervision, writing, review and editing. PY Software, validation, review and editing. TD Software, conceptualization, methodology, review and editing. FB Writing, validation, review and editing.
Funding
The research project was funded by the European Union’s EU Framework Programme for Research and Innovation Horizon 2020 “Subitop” under Grant Agreement No 674899.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We are indebted to the editor and two reviewers for their valuable comments and suggestions.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.765893/full#supplementary-material
References
Agard, P., Yamato, P., Soret, M., Prigent, C., Guillot, S., Plunder, A., et al. (2016). Plate Interface Rheological Switches during Subduction Infancy: Control on Slab Penetration and Metamorphic Sole Formation. Earth Planet. Sci. Lett. 451, 208–220. doi:10.1016/j.epsl.2016.06.054
Artemieva, I. M. (2009). The continental Lithosphere: Reconciling thermal, Seismic, and Petrologic Data. Lithos 109 (1-2), 23–46. doi:10.1016/j.lithos.2008.09.015
Auzemery, A., Willingshofer, E., Sokoutis, D., Brun, J. P., and Cloetingh, S. A. P. L. (2021). Passive Margin Inversion Controlled by Stability of the Mantle Lithosphere. Tectonophysics 817, 229042. doi:10.1016/j.tecto.2021.229042
Auzemery, A., Willingshofer, E., Yamato, P., Duretz, T., and Sokoutis, D. (2020). Strain Localization Mechanisms for Subduction Initiation at Passive Margins. Glob. Planet. Change 195, 103323. doi:10.1016/j.gloplacha.2020.103323
Baes, M., Sobolev, S. V., and Quinteros, J. (2018). Subduction Initiation in Mid-ocean Induced by Mantle Suction Flow. GeoJI 215 (3), 1515–1522. doi:10.1093/gji/ggy335
Beaussier, S. J., Gerya, T. V., and Burg, J.-P. (2019). Near-ridge Initiation of Intraoceanic Subduction: Effects of Inheritance in 3D Numerical Models of the Wilson Cycle. Tectonophysics 763, 1–13. doi:10.1016/j.tecto.2019.04.011
Bercovici, D., and Ricard, Y. (2014). Plate Tectonics, Damage and Inheritance. Nature 508 (7497), 513–516. doi:10.1038/nature13072
Bessat, A., Duretz, T., Hetényi, G., Pilet, S., and Schmalholz, S. M. (2020). Stress and Deformation Mechanisms at a Subduction Zone: Insights from 2-D Thermomechanical Numerical Modelling. GeoJI 221 (3), 1605–1625. doi:10.1093/gji/ggaa092
Bickert, M., Cannat, M., Jammes, S., Tommasi, A., and Lavier, L. (2021). Strain Localization in the Root of Detachment Faults at a Melt-Starved Mid-Ocean Ridge: A Microstructural Study of Abyssal Peridotites From the Southwest Indian Ridge. Geochem. Geophys. Geosyst. 22, e2020GC009434. doi:10.1029/2020GC009434
Bird, P. (2017). Stress Field Models from Maxwell Stress Functions: Southern California. GeoJI 210 (2), 951–963. doi:10.1093/gji/ggx207
Brun, J., and Cobbold, P. (1980). Strain Heating and thermal Softening in continental Shear Zones: a Review. J. Struct. Geology. 2 (1-2), 149–158. doi:10.1016/0191-8141(80)90045-0
Candioti, L. G., Schmalholz, S. M., and Duretz, T. (2020). Impact of Upper Mantle Convection on Lithosphere Hyperextension and Subsequent Horizontally Forced Subduction Initiation. Solid Earth 11 (6), 2327–2357. doi:10.5194/se-11-2327-2020
Capitanio, F. A., and Goes, S. (2006). Mesozoic Spreading Kinematics: Consequences for Cenozoic Central and Western Mediterranean Subduction. GeoJI 165 (3), 804–816. doi:10.1111/j.1365-246x.2006.02892.x
Castellarin, A., and Cantelli, L. (2010). Geology and Evolution of the Northern Adriatic Structural triangle between Alps and Apennine. Rendiconti Lincei 21 (1), 3–14. doi:10.1007/s12210-010-0086-0
Cloetingh, S. A. P. L., Wortel, M. J. R., and Vlaar, N. J. (1984). Passive margin evolution, initiation of subduction and the Wilson cycle. Tectonophysics, 109(1-2), 147–163. doi:10.1016/0040-1951(84)90175-6
Cloetingh, S., and Wortel, R. (1986). Stress in the Indo-Australian Plate. Tectonophysics 132 (1-3), 49–67. doi:10.1016/0040-1951(86)90024-7
Cloetingh, S., Wortel, R., and Vlaar, N. J. (1989). “On the Initiation of Subduction Zones,” in Subduction Zones Part II. Editors L. J. Ruff, and H. Kanamori (Birkhäuser Basel), 7–25. doi:10.1007/978-3-0348-9140-0_2
Cloetingh, S., Ziegler, P. A., Beekman, F., Andriessen, P. A. M., Hardebol, N., and Dèzes, P. (2005). Intraplate Deformation and 3D Rheological Structure of the Rhine Rift System and Adjacent Areas of the Northern Alpine Foreland. Int. J. Earth Sci. (Geol Rundsch) 94 (4), 758–778. doi:10.1007/s00531-005-0502-3
Coblentz, D. D., and Richardson, R. M. (1996). Analysis of the South American Intraplate Stress Field. J. Geophys. Res. 101 (B4), 8643–8657. doi:10.1029/96jb00090
Crameri, F., Magni, V., Domeier, M., Shephard, G. E., Chotalia, K., Cooper, G., et al. (2020). A Transdisciplinary and Community-Driven Database to Unravel Subduction Zone Initiation. Nat. Commun. 11 (1), 3750–3814. doi:10.1038/s41467-020-17522-9
Dannberg, J., Gassmöller, R., Grove, R., and Heister, T. (2019). A New Formulation for Coupled Magma/mantle Dynamics. GeoJI 219 (1), 94–107. doi:10.1093/gji/ggz190
Dick, H. J. B., Lin, J., and Schouten, H. (2003). An Ultraslow-Spreading Class of Ocean ridge. Nature 426 (6965), 405–412. doi:10.1038/nature02128
Duarte, J. C., Rosas, F. M., Terrinha, P., Schellart, W. P., Boutelier, D., Gutscher, M.-A., et al. (2013). Are Subduction Zones Invading the Atlantic? Evidence from the Southwest Iberia Margin. Geology 41 (8), 839–842. doi:10.1130/g34100.1
Duretz, T., Petri, B., Mohn, G., Schmalholz, S. M., Schenker, F. L., and Müntener, O. (2016b). The Importance of Structural Softening for the Evolution and Architecture of Passive Margins. Sci. Rep. 6 (1), 38704–38707. doi:10.1038/srep38704
Duretz, T., Agard, P., Yamato, P., Ducassou, C., Burov, E. B., and Gerya, T. V. (2016a). Thermo-mechanical Modeling of the Obduction Process Based on the Oman Ophiolite Case. Gondwana Res. 32, 1–10. doi:10.1016/j.gr.2015.02.002
Dymkova, D., and Gerya, T. (2013). Porous Fluid Flow Enables Oceanic Subduction Initiation on Earth. Geophys. Res. Lett. 40 (21), 5671–5676. doi:10.1002/2013gl057798
England, P., and Wortel, R. (1980). Some Consequences of the Subduction of Young Slabs. Earth Planet. Sci. Lett. 47 (3), 403–415. doi:10.1016/0012-821x(80)90028-x
Faccenna, C., Giardini, D., Davy, P., and Argentieri, A. (1999). Initiation of Subduction at Atlantic-type Margins: Insights from Laboratory Experiments. J. Geophys. Res. 104 (B2), 2749–2766. doi:10.1029/1998jb900072
Flesch, L. M., Haines, A. J., and Holt, W. E. (2001). Dynamics of the India-Eurasia Collision Zone. J. Geophys. Res. 106 (B8), 16435–16460. doi:10.1029/2001jb000208
Forsyth, D. (1973). Compressive Stress between Two Mid-ocean Ridges. Nature 243 (5402), 78–79. doi:10.1038/243078a0
Fowler, C. M. R., Fowler, C. M. R., and Fowler, M. (1990). The Solid Earth: An Introduction to Global Geophysics. Cambridge: Cambridge University Press.
Gerbault, M. (2000). At what Stress Level Is the central Indian Ocean Lithosphere Buckling? Earth Planet. Sci. Lett. 178 (1-2), 165–181. doi:10.1016/s0012-821x(00)00054-6
Gerya, T. V., and Meilick, F. I. (2011). Geodynamic Regimes of Subduction under an Active Margin: Effects of Rheological Weakening by Fluids and Melts. J. Metamorphic Geology. 29 (1), 7–31. doi:10.1111/j.1525-1314.2010.00904.x
Ghosh, A., Holt, W. E., Flesch, L. M., and Haines, A. J. (2006). Gravitational Potential Energy of the Tibetan Plateau and the Forces Driving the Indian Plate. Geol 34 (5), 321–324. doi:10.1130/g22071.1
Ghosh, A., Holt, W. E., and Wen, L. (2013). Predicting the Lithospheric Stress Field and Plate Motions by Joint Modeling of Lithosphere and Mantle Dynamics. J. Geophys. Res. Solid Earth 118 (1), 346–368. doi:10.1029/2012JB009516
Goren, L., Aharonov, E., Mulugeta, G., Koyi, H. A., and Mart, Y. (2008). Ductile Deformation of Passive Margins: A New Mechanism for Subduction Initiation. J. Geophys. Res. 113, B08411. doi:10.1029/2005JB004179
Gülcher, A. J. P., Beaussier, S. J., and Gerya, T. V. (2019). On the Formation of Oceanic Detachment Faults and Their Influence on Intra-oceanic Subduction Initiation: 3D Thermomechanical Modeling. Earth Planet. Sci. Lett. 506, 195–208. doi:10.1016/j.epsl.2018.10.042
Gurnis, M., Hall, C., and Lavier, L. (2004). Evolving Force Balance during Incipient Subduction. GGG 5, Q07001. doi:10.1029/2003gc000681
Hall, R. (2019). The Subduction Initiation Stage of the Wilson Cycle. Geol. Soc. Lond. Spec. Publications 470 (1), 415–437. doi:10.1144/sp470.3
Handy, M. R., Schmid, S. M., Bousquet, R., Kissling, E., and Bernoulli, D. (2010). Reconciling Plate-Tectonic Reconstructions of Alpine Tethys with the Geological–Geophysical Record of Spreading and Subduction in the Alps. Earth-sci. Rev. 102 (3-4), 121–158. doi:10.1016/j.earscirev.2010.06.002
Heidbach, O., Reinecker, J., Tingay, M., Müller, B., Sperner, B., Fuchs, K., et al. (2007). Plate Boundary Forces Are Not Enough: Second‐and Third‐order Stress Patterns Highlighted in the World Stress Map Database. Tectonics 26, TC6014. doi:10.1029/2007tc002133
Hirth, G., and Kohlstedt, D. (2003). Rheology of the Upper Mantle and the Mantle Wedge: A View from the Experimentalists. Geophys. monograph-american Geophys. union 138, 83–105. doi:10.1029/138gm06
Husson, L., Yamato, P., and Bezos, A. (2015). Ultraslow, Slow, or Fast Spreading Ridges: Arm Wrestling Between Mantle Convection and Far-Field Tectonics. Earth Planet. Sci. Lett. 429, 205–215.
Husson, L. (2012). Trench Migration and Upper Plate Strain over a Convecting Mantle. Phys. Earth Planet. Interiors 212-213, 32–43. doi:10.1016/j.pepi.2012.09.006
Jaquet, Y., and Schmalholz, S. M. (2018). Spontaneous Ductile Crustal Shear Zone Formation by thermal Softening and Related Stress, Temperature and Strain Rate Evolution. Tectonophysics 746, 384–397. doi:10.1016/j.tecto.2017.01.012
Kendall, J.-M., and Lithgow-Bertelloni, C. (2016). Why Is Africa Rifting? Geol. Soc. Lond. Spec. Publications 420 (1), 11–30. doi:10.1144/sp420.17
Kiss, D., Candioti, L. G., Duretz, T., and Schmalholz, S. M. (2020). Thermal Softening Induced Subduction Initiation at a Passive Margin. GeoJI 220 (3), 2068–2073. doi:10.1093/gji/ggz572
Kronenberg, A. K., Kirby, S. H., and Pinkston, J. (1990). Basal Slip and Mechanical Anisotropy of Biotite. J. Geophys. Res. 95 (B12), 19257–19278. doi:10.1029/jb095ib12p19257
Lagabrielle, Y., and Cannat, M. (1990). Alpine Jurassic Ophiolites Resemble the Modern central Atlantic Basement. Geol 18 (4), 319–322. doi:10.1130/0091-7613(1990)018<0319:ajortm>2.3.co;2
Le Breton, E., Brune, S., Ustaszewski, K., Zahirovic, S., Seton, M., and Müller, R. D. (2021). Kinematics and Extent of the Piemont-Liguria Basin–implications for Subduction Processes in the Alps. Solid Earth 12, 885–913. doi:10.5194/se-12-885-2021
Ligi, M., Cuffaro, M., Chierici, F., and Calafato, A. (2008). Three-dimensional Passive Mantle Flow beneath Mid-ocean Ridges: an Analytical Approach. GeoJI 175 (2), 783–805. doi:10.1111/j.1365-246x.2008.03931.x
Luttrell, K., and Sandwell, D. (2012). Constraints on 3‐D Stress in the Crust from Support of Mid‐ocean ridge Topography. J. Geophys. Res. 117, B04402. doi:10.1029/2011JB008765
Maffione, M., Thieulot, C., Van Hinsbergen, D. J. J., Morris, A., Plümper, O., and Spakman, W. (2015). Dynamics of Intraoceanic Subduction Initiation: 1. Oceanic Detachment Fault Inversion and the Formation of Supra-subduction Zone Ophiolites. Geochem. Geophys. Geosyst. 16 (6), 1753–1770. doi:10.1002/2015gc005746
Mahatsente, R., and Coblentz, D. (2015). Ridge-push Force and the State of Stress in the Nubia-Somalia Plate System. Lithosphere 7 (5), 503–510. doi:10.1130/l441.1
Mahatsente, R. (2017). Global Models of ridge-push Force, Geoid, and Lithospheric Strength of Oceanic Plates. Pure Appl. Geophys. 174 (12), 4395–4406. doi:10.1007/s00024-017-1647-2
Manzotti, P., Ballevre, M., Zucali, M., Robyr, M., and Engi, M. (2014a). The Tectonometamorphic Evolution of the Sesia–Dent Blanche Nappes (Internal Western Alps): Review and Synthesis. Swiss J. Geosci. 107 (2-3), 309–336. doi:10.1007/s00015-014-0172-x
Manzotti, P., Le Carlier De Veslud, C., Le Bayon, B., and Ballèvre, M. (2014b). Petro-structural Map of the Money Unit (Gran Paradiso Massif, Valnontey valley, Western Alps). J. Maps 10 (2), 324–340. doi:10.1080/17445647.2013.866912
Marques, F. O., Nikolaeva, K., Assumpção, M., Gerya, T. V., Bezerra, F. H. R., do Nascimento, A. F., et al. (2013). Testing the Influence of Far-Field Topographic Forcing on Subduction Initiation at a Passive Margin. Tectonophysics 608, 517–524. doi:10.1016/j.tecto.2013.08.035
Marroni, M., Meneghini, F., and Pandolfi, L. (2017). A Revised Subduction Inception Model to Explain the Late Cretaceous, Double-Vergent Orogen in the Precollisional Western Tethys: Evidence from the Northern Apennines. Tectonics 36 (10), 2227–2249. doi:10.1002/2017tc004627
Mart, Y., Aharonov, E., Mulugeta, G., Ryan, W., Tentler, T., and Goren, L. (2005). Analogue Modelling of the Initiation of Subduction. GeoJI 160 (3), 1081–1091. doi:10.1111/j.1365-246X.2005.02544.x
McCarthy, A., Tugend, J., Mohn, G., Candioti, L., Chelle-Michou, C., Arculus, R., et al. (2020). A Case of Ampferer-type Subduction and Consequences for the Alps and the Pyrenees. Am. J. Sci. 320 (4), 313–372. doi:10.2475/04.2020.01
Molnar, P., England, P. C., and Jones, C. H. (2015). Mantle Dynamics, Isostasy, and the Support of High Terrain. J. Geophys. Res. Solid Earth 120 (3), 1932–1957. doi:10.1002/2014jb011724
Molnar, P., and Lyon-Caen, H. (1988). Some Simple Physical Aspects of the Support, Structure, and Evolution of Mountain Belts. Process. continental lithospheric deformation 218, 179–208. doi:10.1130/spe218-p179
Mueller, S., and Phillips, R. J. (1991). On the Initiation of Subduction. J. Geophys. Res. 96 (B1), 651–665. doi:10.1029/90jb02237
Naliboff, J., Conrad, C., and Lithgow‐Bertelloni, C. (2009). Modification of the Lithospheric Stress Field by Lateral Variations in Plate‐mantle Coupling. Geophys. Res. Lett. 36 (22). doi:10.1029/2009gl040484
Nikolaeva, K., Gerya, T. V., and Marques, F. O. (2011). Numerical Analysis of Subduction Initiation Risk along the Atlantic American Passive Margins. Geology 39 (5), 463–466. doi:10.1130/g31972.1
Nikolaeva, K., Gerya, T. V., and Marques, F. O. (2010). Subduction Initiation at Passive Margins: Numerical Modeling. J. Geophys. Res. 115, B03406. doi:10.1029/2009JB006549
Pascal, C., and Cloetingh, S. A. (2009). Gravitational Potential Stresses and Stress Field of Passive continental Margins: Insights from the South-Norway Shelf. Earth Planet. Sci. Lett. 277 (3-4), 464–473. doi:10.1016/j.epsl.2008.11.014
Qing, J., Liao, J., Li, L., and Gao, R. (2021). Dynamic Evolution of Induced Subduction through the Inversion of Spreading Ridges. JGRB: Solid Earth 126 (3), e2020JB020965. doi:10.1029/2020jb020965
Regenauer-Lieb, K., Yuen, D. A., and Branlund, J. (2001). The Initiation of Subduction: Criticality by Addition of Water? Science 294 (5542), 578–580. doi:10.1126/science.1063891
Richardson, R. M., Solomon, S. C., and Sleep, N. H. (1979). Tectonic Stress in the Plates. Rev. Geophys. 17 (5), 981–1019. doi:10.1029/rg017i005p00981
Schmalholz, S. M., Duretz, T., Hetényi, G., and Medvedev, S. (2019). Distribution and Magnitude of Stress Due to Lateral Variation of Gravitational Potential Energy between Indian lowland and Tibetan Plateau. GeoJI 216 (2), 1313–1333. doi:10.1093/gji/ggy463
Schmalholz, S. M., Kaus, B. J. P., and Burg, J.-P. (2009). Stress-strength Relationship in the Lithosphere during continental Collision. Geology 37 (9), 775–778. doi:10.1130/g25678a.1
Schmalholz, S. M., Moulas, E., Plümper, O., Myasnikov, A. V., and Podladchikov, Y. Y. (2020). 2D Hydro‐Mechanical‐Chemical Modeling of (De) Hydration Reactions in Deforming Heterogeneous Rock: The Periclase‐Brucite Model Reaction. GGG 21 (11), e2020GC009351. doi:10.1029/2020gc009351
Schmid, S. M., Fügenschuh, B., Kissling, E., and Schuster, R. (2004). Tectonic Map and Overall Architecture of the Alpine Orogen. Eclogae Geol. Helv. 97 (1), 93–117. doi:10.1007/s00015-004-1113-x
Stein, C. A., and Stein, S. (1993). Constraints on Pacific Midplate Swells from Global Depth-Age and Heat Flow-Age Models. Mesozoic Pacific: Geology. Tectonics, Volcanism, Geophys. Monogr. Ser. 77, 53–76. doi:10.1029/gm077p0053
Stern, R. J. (2004). Subduction Initiation: Spontaneous and Induced. Earth Planet. Sci. Lett. 226 (3-4), 275–292.
Stern, R. J., and Gerya, T. (2018). Subduction Initiation in Nature and Models: A Review. Tectonophysics 746, 173–198. doi:10.1016/j.tecto.2017.10.014
Swedan, N. H. (2015). Ridge Push Engine of Plate Tectonics. Geotecton. 49 (4), 342–359. doi:10.1134/s0016852115040081
Tesauro, M., Kaban, M. K., and Cloetingh, S. A. P. L. (2013). Global Model for the Lithospheric Strength and Effective Elastic Thickness. Tectonophysics 602, 78–86. doi:10.1016/j.tecto.2013.01.006
Ulvrova, M. M., Coltice, N., Williams, S., and Tackley, P. J. (2019). Where Does Subduction Initiate and Cease? A Global Scale Perspective. Earth Planet. Sci. Lett. 528, 115836. doi:10.1016/j.epsl.2019.115836
van Hinsbergen, D. J. J., Torsvik, T. H., Schmid, S. M., Maţenco, L. C., Maffione, M., Vissers, R. L. M., et al. (2020). Orogenic Architecture of the Mediterranean Region and Kinematic Reconstruction of its Tectonic Evolution since the Triassic. Gondwana Res. 81, 79–229. doi:10.1016/j.gr.2019.07.009
van Summeren, J., Conrad, C. P., and Lithgow‐Bertelloni, C. (2012). The Importance of Slab Pull and a Global Asthenosphere to Plate Motions. GGG 13 (2). doi:10.1029/2011gc003873
Vlaar, N., and Wortel, M. (1976). Lithospheric Aging, Instability and Subduction. Tectonophysics 32 (3-4), 331–351. doi:10.1016/0040-1951(76)90068-8
Wan, B., Wu, F., Chen, L., Zhao, L., Liang, X., Xiao, W., et al. (2019). Cyclical One-Way continental Rupture-Drift in the Tethyan Evolution: Subduction-Driven Plate Tectonics. Sci. China Earth Sci. 62 (12), 2005–2016. doi:10.1007/s11430-019-9393-4
Wysession, M. E., Okal, E. A., and Miller, K. L. (1991). Intraplate Seismicity of the Pacific Basin, 1913?1988. Pageoph 135 (2), 261–359. doi:10.1007/bf00880241
Zhong, X., and Li, Z. H. (2019). Forced Subduction Initiation at Passive Continental Margins: Velocity‐Driven versus Stress‐Driven. Geophys. Res. Lett. 46 (20), 11054–11064. doi:10.1029/2019gl084022
Keywords: subduction initiation, passive margins, convergence rate, mid-oceanic ridge, Alps
Citation: Auzemery A, Willingshofer E, Yamato P, Duretz T and Beekman F (2021) Kinematic Boundary Conditions Favouring Subduction Initiation at Passive Margins Over Subduction at Mid-oceanic Ridges. Front. Earth Sci. 9:765893. doi: 10.3389/feart.2021.765893
Received: 27 August 2021; Accepted: 05 November 2021;
Published: 02 December 2021.
Edited by:
Fabio Crameri, University of Oslo, NorwayReviewed by:
Zhong-Hai Li, University of Chinese Academy of Sciences, ChinaJie Liao, Sun Yat-sen University, China
Copyright © 2021 Auzemery, Willingshofer, Yamato, Duretz and Beekman. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: A. Auzemery, YS5hdXplbWVyeUB1dS5ubA==
 A. Auzemery
A. Auzemery E. Willingshofer
E. Willingshofer P. Yamato
P. Yamato T. Duretz2,4
T. Duretz2,4 F. Beekman
F. Beekman