Flow Field Description and Simplification Based on Principal Component Analysis Downscaling and Clustering Algorithms

The flow field obtained from streamline simulation reflects key properties of the reservoir, such as the distribution of the remaining oil and the location of channels. However, in the three-dimensional streamline field, the advantages of streamline simulation are limited. Because numerous streamlines interfere with each other and distribute in a sophisticated way, it is really difficult to infer the connectivity between wells and the flow characteristics of the reservoir. To make a more effective and visualizable description of the flow field, the three-dimensional streamline field has to be simplified. In this paper, principal component analysis (PCA) is applied to parameterize the streamline attributes and reduce the dimensionality of the flow field. After dimension reduction, the principal components of the streamline field can be analyzed by the clustering method. In the clustering procedure, the mainstream lines are selected according to the clustering center, thereby intuitively illustrating the properties of the reservoir. Through experimental verification, the proposed method can characterize the streamlines of the flow field more efficiently and reflect the inter-well connectivity more clearly than the commercial numerical simulator.

Introduction

At present, most onshore oil fields in China have entered the later development stage after long-term water injection development. The average comprehensive water cut of oil fields is high, and the oil production rate decreases gradually. Therefore, the development effect deteriorates year by year, making it difficult to meet the requirements of stable production. Besides that, most offshore oil fields are in the stage with a low water-oil ratio, which is the golden period of injection–production adjustment to increase the production potential. Hence, it is necessary to adjust the spreading coefficient of the flow field to control water and oil production. The streamline simulation is one of the most feasible methods for dominant flow characterization. In recent years, streamline simulation has attracted more and more attention (Mesbah et al., 2019; Wang et al., 2020; Morse and Mahesh, 2021; Namdari et al., 2021; Zhang et al., 2021). However, discrete streamline distribution cannot accurately represent the actual flow field, limiting its effective application to the oil field. Therefore, it is urgent to develop a flow field description technology to realize the visualization of the main flow area, thus improving the effectiveness of the streamline simulation method.

The features of the streamline field for actual reservoirs are more complex than other fields, since the number of streamlines is large and these lines cross together. Thus, the simplification of the streamlines is of vital importance for the clear visualization of the flow field. The main methods to simplify the streamline field are feature analysis and classification, which group the streamlines based on similar attributes of streamlines. Nevertheless, due to the large number of streamline features generated by the streamline numerical simulator, it is difficult to give an effective evaluation of these features. Currently, the evaluation of streamline similarity is mainly based on Euclidian distance, while the characterization of the flow field is still difficult by only using the selected geometric features. A new visualization method was proposed, which is for streamlining in Euclidean three-dimensional space (Rossl and Theisel, 2011). The AHC clustering method (Yu et al., 2011) was used to cluster the streamline and evaluated its clustering efficiency, which pointed out that the AHC method is more efficient than the Euclidean distance-based clustering method for streamline clustering. Streamline similarity, evaluated based on streamline curvature and bending characteristics, was more comprehensive than the previous distance evaluation (McLoughlin et al., 2012). Considering the curvature and other factors of the curve, accurate and fast clustering methods should be developed. The streamline data were analyzed by the clustering method, and the streamline sets with the same geometric characteristics were divided into a class. Three clustering methods, namely K-means, hierarchical clustering, and spectral clustering, were used to effectively classify the chaotic streamline, which provided a favorable reference for further visualization of the streamline (Qi, 2015). The dynamic time regularization algorithm and the mean minimum distance between adjacent points were used to measure the similarity of streamlines, simplify the flow field, and improve the visualization (Lintao); and through streamline normalization and regular-polyhedron projection, high-dimensional features of each fiber tract are computed and fed to the IDEC clustering algorithm for clustering, which also provide qualitative and quantitative evaluations of the IDEC clustering method and QB clustering method (Xu et al., 2021). A streamline numerical simulation method (Hu and Lihui, 2018) was presented, which calculates the average attribute of streamlines and then applies a clustering method to identify the flow field of the water–drive reservoir. Furthermore, the FlowNet was presented, a single deep learning framework for clustering and selection of streamlines and stream surfaces (Han et al., 2018).[9] The approach based on the idea of cluster centers was proposed, which are characterized by a higher density than their neighbors and by a relatively large distance from points with higher densities. This idea forms the basis of a clustering procedure in which the number of clusters arises intuitively, outliers are automatically spotted and excluded from the analysis, and clusters are recognized regardless of their shape and of the dimensionality of the space in which they are embedded (Rodriguez and Laio, 2014). The flow field characterization indicators were screened based on the logical analysis method, using the analytic hierarchy process (AHP) to evaluate the potential of the flow field (Pandeng; Qi, 2009; Yupei, 2011; Zheng, 2014). It was discovered that multiple displacements are ineffective in the water flooding process of the flow field and the surface flux is defined as the ratio of flux to the area of displacement (Qiaoliang et al., 2014).

The dimension reduction method aims to alleviate the curse of dimensionality in machine learning. The dimension reduction algorithms transform the high-dimensional space of the original data into low-dimensional space by mathematical methods. Generally speaking, the simplest spatial transformation method is the linear transformation. Through the linear projection matrix, d, dimensional samples in high-dimensional space can be transformed into d’′ dimensional samples. When the projection vector of the projection matrix is orthogonal to each other, it is an orthogonal transformation. The transformed data should be a linear combination of the original data. Principal component analysis (PCA) (Mika et al., 1998) is a basic linear dimension reduction method, which is easily implemented to reduce the dimension of the original data. It is an appropriate dimension reduction algorithm for the reservoir flow field.

Cluster analysis is an unsupervised learning algorithm in machine learning, which studies the intrinsic characteristics between samples for classification. The main clustering methods can be divided into three categories: the prototype-based method, the density-based clustering method, and the hierarchical clustering method. The prototype-based clustering method is initialized with a group of prototypes and then optimizes the prototypes through iterations. These algorithms include K-means clustering algorithms and Gaussian mixture model clustering algorithms. Density-based clustering algorithms include the density-based spatial clustering of applications with noise algorithm (DBSCAN). Hierarchical clustering algorithms include the bottom-up approach and the top-down approach. The streamline field can be accurately grouped by these clustering algorithms based on streamline features.

The rest of this paper is organized as follows: Section 2 and Section 3 give detailed information and steps about the proposed method; the experimental results and discussion are given in Section 4, and Section 5 is about the conclusion of this paper.

Streamline feature dimension reduction

In recent years, streamline numerical simulation has gained increasing popularity in the oilfield. Compared with the black oil numerical simulation, the streamline numerical simulation model has faster calculation speed, stronger convergence, and better adaptability of the time step. In addition, in the streamline numerical simulation, the relevant characteristics of the flow field are output in the streamline manner, which is conducive to the visual characterization and quantitative analysis of the flow field. There are three main steps of using three-dimensional streamlines to simulate the reservoir development process. Firstly, use implicit equations to solve the pressure distribution in porous media. Secondly, use explicit equations to obtain the saturation distribution. Finally, obtain streamline trajectory information. Different from the finite difference numerical simulation, the fluid in the streamline numerical simulation moves along the streamline, and the pressure is solved on the basic grid to obtain the pressure equipotential surface, and then the streamline field is solved.

The streamline information directly extracted by the streamline numerical simulator is complex. The three-dimensional streamline field has complex streamline distribution. A streamline field contains multiple streamline lines, while a streamline contains multiple streamline points. Each streamline point also has many attributes. Therefore, a complete description of a streamline field requires many features; but it is not practical to use too many features to describe the streamlines in the actual process. To generate an accurate description of the streamline field, it is necessary to reduce the dimensionality of the streamline properties without losing the main features of the streamline field. Principal component analysis (PCA) [17] is a commonly used linear dimensionality reduction method, which is simple to calculate and can be easily restored from low-dimensional to high-dimensional space. Thus, it is selected to reduce the characteristic dimension of streamline and reconstruct the flow field in this paper. The process of the PCA dimension reduction algorithm used in this paper is as follows:

1) After the standardized processing of the data set, for each evaluation attribute: ${\tilde{x}}_{ij}=\frac{x_{ij}-{\overline{x}}_j}{s_j}$;

2) The characteristic covariance matrix of streamline is calculated according to $\mathrm{cov}\left(X,Y\right)=\frac{1}{n-1}{\displaystyle \sum _{i=1}^n\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}$;

3) The eigenvalue and eigenvector of the covariance matrix are obtained according to $Av=\lambda v$;

4) The eigenvalues are sorted and the principal component contribution is calculated according to the eigenvalues;

5) The first K feature vectors are selected to form the projection matrix: $M=\left[p_1,p_2,p_3\text{,}\mathrm{...},p_{k-1},p_k\right]$;

6) Calculate the principal component vector according to the projection matrix: $Y=\mathrm{MX}Y=\mathrm{MX}$,

where ${\overline{x}}_j$ is the mean of the jth indicator for all samples; $s_j$ is the standard deviation of the jth index; A denotes the characteristic covariance matrix; $\lambda$ and $v$ are the eigenvalues of the covariance matrix and the eigenvectors respectively; M is the projection coefficient matrix composed of the first k eigenvectors; $p_k$ is the transpose vector corresponding to the kth eigenvector; X is the original data; and Y is the data after dimensionality reduction.

In general, if the cumulative contribution of principal components is higher than 95%, the most important dimensions can be transformed without losing too much accuracy; 95% is called the cumulative contribution threshold. The corresponding projection matrix can be constructed based on this threshold. The contribution of principal components of the sample is calculated as follows:

$c=\frac{{\displaystyle {\sum }_{i=1}^{d^{\prime }}{\lambda }_i}}{{\displaystyle {\sum }_{i=1}^d{\lambda }_i}}(1)$

Where c is the contribution of the main components, ${\lambda }_i$ is the ith eigenvalue.

1) Principal component analysis matrix

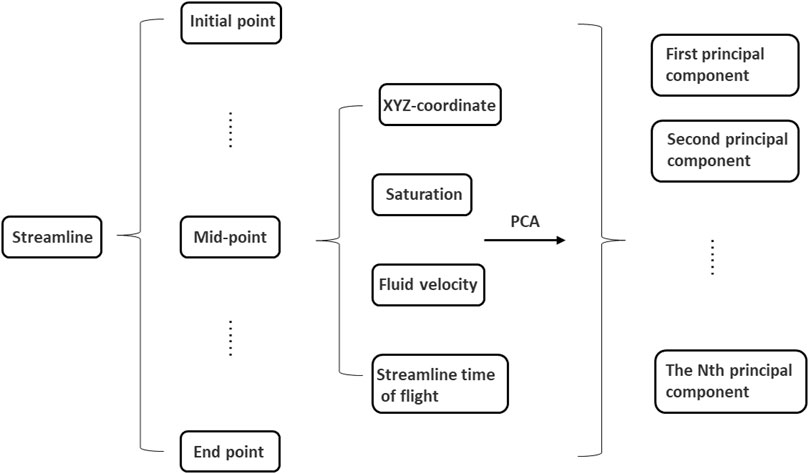
For the streamline field, each streamline can be regarded as a sample with a series of points with different attributes, such as coordinates, saturation, velocity, and so on. The number of features of the streamline is determined by the number of streamline points and the attribute information. The principal component analysis can be used to reduce the dimension of streamline attributes.

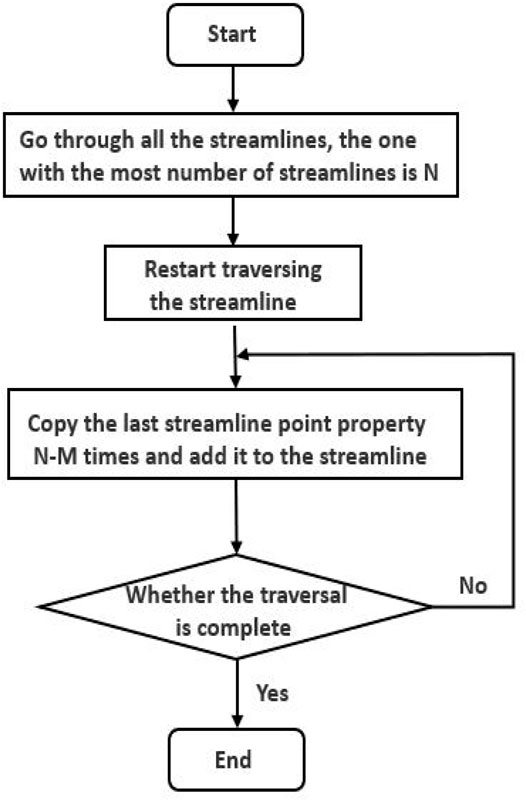
Principal component analysis (PCA) first requires the construction of the matrix of original data. In the process of dimension reduction, each streamline is regarded as a sample. When PCA is applied, the original matrix of samples needs to be constructed. There are N points on the streamline, and each point has its X, Y, and Z coordinates. If considering the saturation and the flying time, each point possesses five attributes. For a streamline, there are 5N characteristics. Because of different points for different streamlines, PCA cannot deal with this kind of sample. The characteristics of all streamlines should be consistent. Therefore, it is necessary to construct the matrix of the sample as shown in Figures 1, 2. After collecting all streamlines, the maximum number of points of all streamlines can be obtained. The number of features of the original matrix is set according to the streamline with the largest features. The covariance matrix of the original sample is obtained after standardization. The eigenvalues are obtained after the Eigen decomposition. The eigenvectors of the largest eigenvalues form the projection matrix, and the transformed matrix can be obtained according to the projection matrix.

2) Streamline field reconstruction and principal component selection

FIGURE 1

FIGURE 1. Streamline attribute dimension reduction.

FIGURE 2

FIGURE 2. Flow chart of the streamline PCA dimension reduction matrix construction.

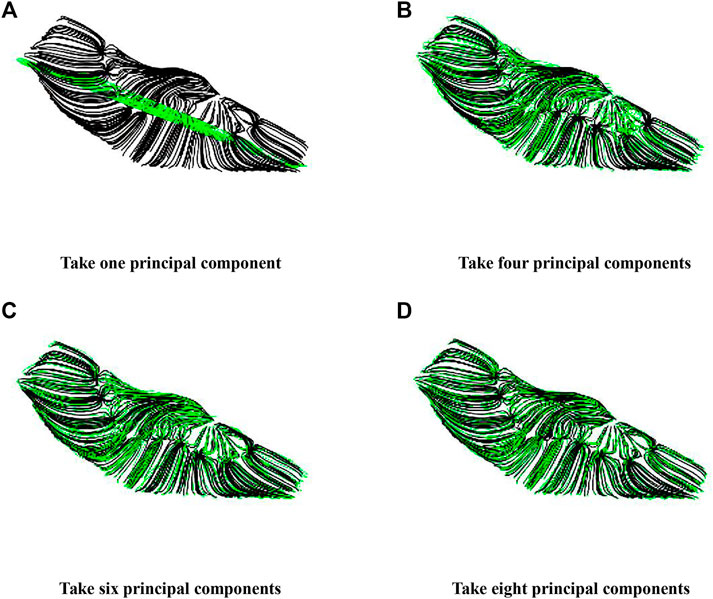
General selection of the number of principal components is determined by the cumulative contribution of the principal components. For the flow field, as shown in Figure 3, the optimal selection of principal components should consider the reconstruction accuracy of the flow field. The reconstruction accuracy is high, which means that the principal components are selected appropriately. According to the selected principal components, the projection matrix maps the high dimensional problem to a low dimensional problem. Generally, when the reconstruction accuracy reaches 90%, the reconstruction of the flow field can be considered accurate. The reconstruction error can be calculated using Eq. 2:

$E={\displaystyle \sum _{i=1}^k\frac{|{p^{\prime }}_i-p_i|}{\left|p_i\right|}}(2)$

where ${p^{\prime }}_i$ is the reconstructed data, and $p_i$ is the original data.

FIGURE 3

FIGURE 3. Principal component selection and flow field reconstruction accuracy.

The optimal number of principal components is selected based on the cumulative contribution of principal components and the accuracy of flow field reconstruction. When the cumulative contribution rate of principal components reaches 95% and the reconstruction accuracy reaches 90%, the number of principal components is considered to be the best, and each streamline can be represented by these characteristics.

Streamline clustering and flow field simplification

Streamlines have many advantages that other conventional reservoir description methods do not have. As mentioned above, streamlines appear complex because they have a large number of features. According to the streamline features selected by PCA, the clustering algorithm and the cluster number are selected to classify different streamlines without losing much accuracy of the streamline field. It can simplify the streamline field and improve the visualization of the flow field. Different clustering methods have different adaptabilities to streamlines in different flow fields, so the effects of the clustering method should be analyzed. Therefore, certain rules are needed to select an appropriate clustering algorithm and the cluster number, which is significant for a reasonable description of the flow field.

1) K-means clustering algorithm: K-means is an iteration algorithm based on Euclidean distance. The calculation speed of K-means is fast. However, the number of clustering must be specified in advance. The iteration of the K-means minimizes the sum of squares of errors. For flow field clustering, K-means has low clustering complexity. The parameters of K-means can be modified based on the clustering result, such as the clustering number (K value). So it has good adaptability in flow field streamline clustering.

2) Gaussian mixture model method: The Gaussian mixture model clustering method adopts mean value and variance and uses the probability model to initialize the prototype. It presents the shape of the cluster as an ellipse, not a circle, to improve the accuracy of clustering. The disadvantage of the Gaussian mixture model method is the complexity of the calculation. Figure 9 shows the streamline field diagram of the Egg model [18] using the Gauss-expectation clustering method. The Egg model is a synthetic reservoir model consisting of 101 relatively small three-dimensional realizations. The model has eight water injectors and four oil producers. It has been applied in numerous publications to demonstrate a variety of aspects related to computer-assisted history matching and production optimization.

3) Density-based clustering method: This clustering algorithm performs clustering based on the sample distribution. The advantage of this algorithm is that it does not need to specify the cluster number. However, to determine the “neighborhood” required by the density-based clustering algorithm, the radius of the circle and the minimum number of points in the circle need to be given.

4) Hierarchical clustering method: The hierarchical clustering algorithm divides samples at different levels and calculates the similarity of each node. Then this algorithm establishes a sample tree and connects each node step by step according to the similarity principle. For example, AGNES bottom-up hierarchical clustering algorithm regards the initial sample as a single cluster and searches for the nearest cluster in each step until the preset cluster number is reached. In the streamline field, the advantage of the hierarchical clustering method is that it does not need a random cluster center at the beginning. As a range-based clustering method, its calculation speed is fast. However, the limitation that the number of clusters cannot be specified restricts its application in flow field clustering.

For the streamline field, the reasonable clustering method and the selection of cluster number plays a decisive role in the clustering of the flow field. It also has an important significance for the description of the flow field. It is necessary to first determine the clustering number according to the elbow method and the contour coefficient method, and then evaluate the best clustering number and the effect of different clustering methods using the contour coefficient value.

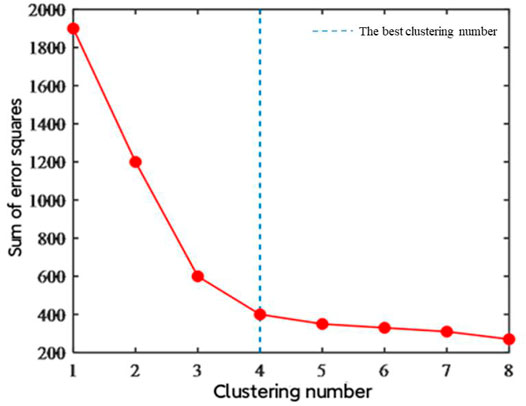
The streamline clustering can effectively improve the visualization of the flow field and accurately describe the flow field. The first step of the clustering of the flow field is the selection of cluster numbers. According to the sum of squared errors (SSE), the clustering effect under different cluster numbers can be determined. With the increase of the cluster number (which is the k value for the K-means clustering method), the sum of squared errors keep decreasing. However, in terms of the purpose of clustering, the number of clusters cannot increase indefinitely. In this paper, the elbow method is used to determine the optimal cluster number combined with the sum of squared errors.

The formula of the sum of squared errors for the streamline clustering is shown in Eq. 3:

$\text{SSE}={\displaystyle \sum _{i=1}^k{\displaystyle \sum _{p\in C_i}|p-m_i{|}^2}}(3)$

where p is the streamline feature belonging to the class C_i; m_i is represented as the average streamline characteristic of the class C_i; and k is the total cluster number of streamlines.

According to the principle of the “elbow method”, the mean square errors for different cluster numbers are calculated. When the sum of squared errors changes significantly, the corresponding cluster number can be regarded as the best cluster number. As shown in Figures 4, 5, when the number of clusters is less than four, the error decreases quickly. When the number of clusters exceeds four, the error decreases very slowly. It is unnecessary to increase the number of clusters; so it can be inferred that the optimal number of clusters is four.

FIGURE 4

FIGURE 4. The flow field in clustering.

FIGURE 5

FIGURE 5. Determining the best cluster number by the Elbow method.

As an important index to measure the dissimilarity among clusters, the contour coefficient is of great significance in evaluating the clustering effect. For each sample involved in clustering, the contour coefficient of the sample can be calculated according to the contour coefficient method. According to the formula of the contour coefficient, the contour coefficient should be between −1 and 1. The closer the contour coefficient is to 1, the higher the clustering accuracy of the sample. Otherwise, the closer it is to −1, the more the sample should be divided into other classes. Therefore, the contour coefficient of the sample reflects the classification effect of the sample. In this paper, the mean value of the contour coefficient is calculated for all samples to measure the effect of clustering according to the formula. The calculation of the streamline clustering contour coefficient is as follows:

1) The average distance between the streamline sample i and other streamline samples in this class is calculated, denoted as $a\left(i\right)$, representing the dissimilarity of this class for the streamline samples i;

2) Calculate the average distance between the streamline sample i and all samples of other classes k, denoted as $b{\left(i\right)}_k$ to represent the degree of dissimilarity between the sample i and the class k, denoted as $b\left(i\right)=\min \left(\left\{b{\left(i\right)}_1,b{\left(i\right)}_2,\cdots ,b{\left(i\right)}_k\right\}\right)$;

3) The contour coefficient of the sample is calculated according to the formula: $s\left(i\right)=\frac{b\left(i\right)-a\left(i\right)}{\max \left\{a\left(i\right),b\left(i\right)\right\}}$;

4) The average contour coefficient of all samples is calculated as the standard to measure the effect of the clustering.

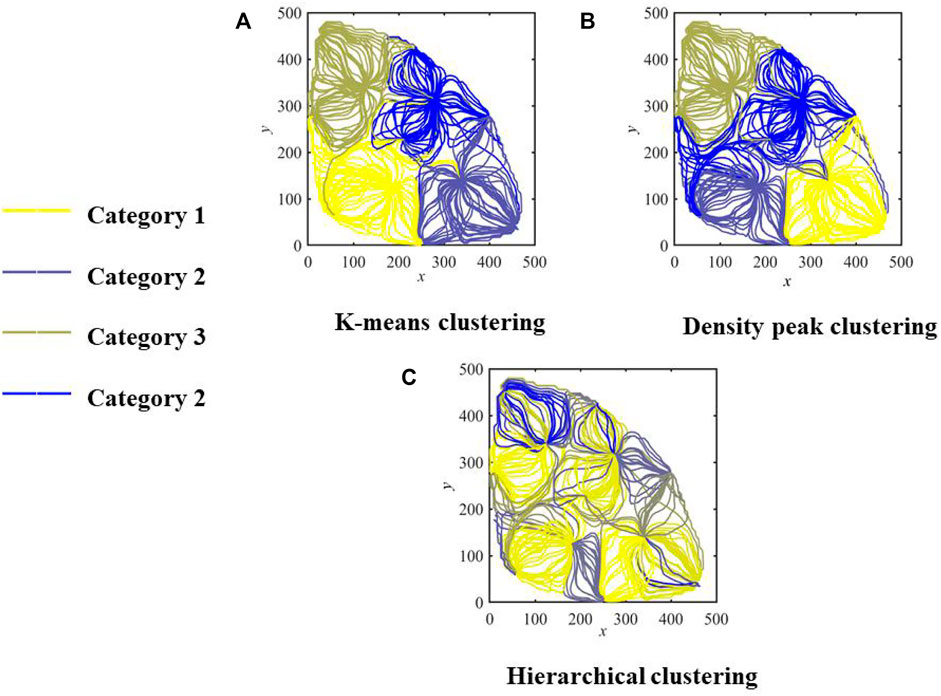
The streamline field of the Egg model is clustered by the K-means algorithm. The average contour coefficient is calculated, which is 0.89. The average contour coefficient of hierarchical clustering is 0.61. The average contour coefficient of the Gaussian mixture model method is 0.84. For simple flow fields with few features, the K-means clustering method is adopted to achieve high computational efficiency; for flow fields with complex features, the Gaussian mixture model method can be adopted to improve the accuracy of clustering.

There is a problem with the reasonable layout of directly extracted streamlines in the flow field. Too few streamlines may cause the visual image that misses the information of a certain part in the flow field space, while too many and too dense streamlines may cause visual confusion. To obtain the streamline with a high degree of visualization and reflect the characteristics of the flow field, we can start with the streamline generation algorithm. Then, we can use mathematical methods to simplify the generated streamline field without losing many features. Through clustering the streamlines, the flow field can be simplified and the main streamlines can be selected.

The main streamlines have long been defined as the dominant streamline of the flow field. However, for flow field description, the main streamlines are not only the dominant streamlines but also the streamlines that can represent the characteristics of the flow field. According to the dimension reduction and clustering results, the streamlines in the cluster center can be selected as the main streamlines of the flow field. The main streamlines represent the streamline field area as the result of flow field simplification.

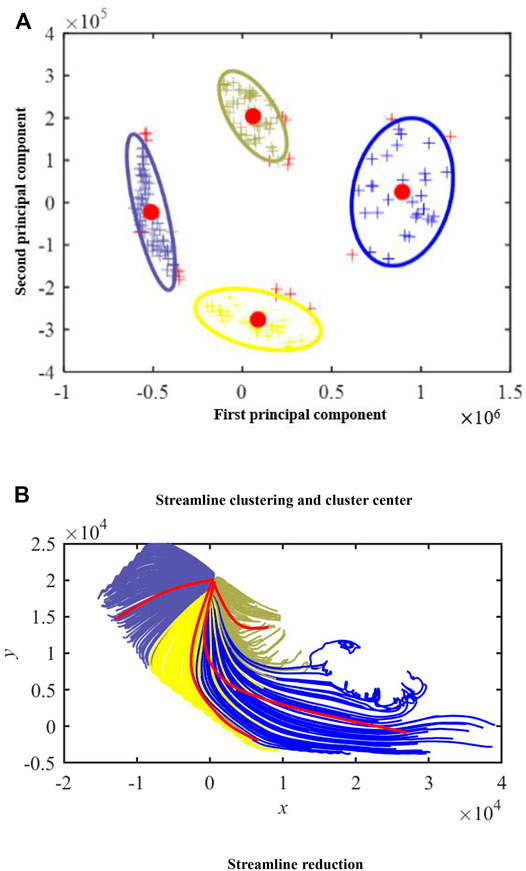
As shown in Figure 6A, according to the result of PCA, a reasonable cluster number and the clustering method are selected for the streamline field. The red dots represent the cluster centers, the plus signs represent different samples, and the ellipses with different colors represent different classes. All samples in the same ellipse belong to the same class. Then, as shown in Figure 6B, streamline points are mapped from low dimension to high dimension to reconstruct streamlines, and the center of the cluster is taken as the main streamline in the flow field. Four red lines are the cluster centers of four categories, and the lines of the same color belong to the same category.

FIGURE 6

FIGURE 6. Mainline selection.

The injection–production unit including injection wells and production wells is the basic unit of reservoir production. The connection relationship reflects the production status of the reservoir. The streamlines between injection and production units are analyzed for feature dimensionality reduction. The description and simplification of the reservoir flow field are of great significance. As shown in Figure 7, the clusters can be analyzed between injection–production units according to streamline characteristics. The main streamlines can be selected from the cluster center, which represents the relationship between injection–production units and simplifies the description of the flow field.

FIGURE 7

FIGURE 7. Main streamline selection of injection and production units.

Reservoir example

The depth of the reservoir of CB22F area is about 1,400 m, the porosity of formation sand is about 33.3%, the permeability of gas measurement is 1,379 × 10^–3 μm², and the viscosity of crude oil is about 30–70 mPa·s at formation pressure and temperature of 65°C. The upper part of the Chengdao Zhuangguan Formation is mainly composed of sand-mudstone; the lower layer is muddy. The thickness is about 450 m. The upper part of Chengdao Oilfield is fluvial sedimentary by analyzing the characteristic morphology of this area.

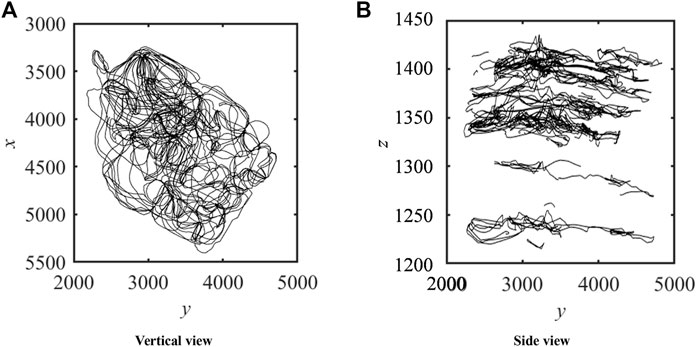
Streamline is the basis of the flow field, and streamline points constitute the streamline. By extracting the coordinates of streamline points after the streamline simulation, the reconstructed streamline field diagram can be drawn. As shown in Figure 8, data is extracted from the results of the streamline simulation of the CB22F area, and the three-dimensional flow field can be redrawn according to the location attributes of the extracted streamlines.

FIGURE 8

FIGURE 8. The redrawn streamline field.

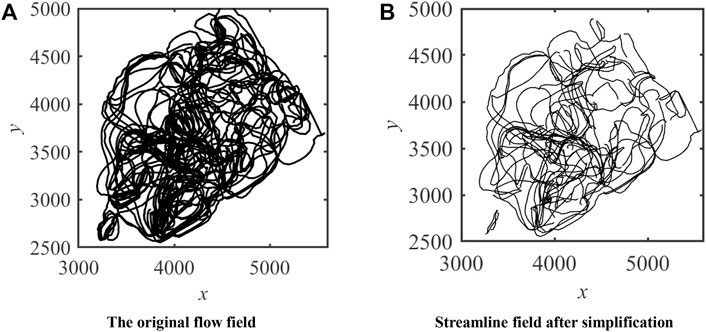
All streamlines of the CB22F streamline field are extracted, and cluster analysis is carried out according to streamline attributes. All similar streamlines are clustered into one category. As shown in Figure 9, the cluster center of this class is taken as the selection standard for the main streamlines. For the complex flow field, only the main streamlines are retained to simplify the flow field. Before the characterization and simplification of the flow field, the streamline distribution of the streamline field is messy. Meanwhile, the visualization degree is extremely low, and the connection relationship between the injection and production units is not clear. With the help of the dimension reduction and clustering methods, the main streamlines of the chaotic streamline field are selected for simplification. In Figure 9, the connection relationship of the streamline field is much clearer using our method.

FIGURE 9

FIGURE 9. Streamline simplification based on clustering.

Conclusion

The flow field can reflect many important attributes that affect the production of the reservoir, such as the remaining oil distribution, oil displacement energy distribution, and high-permeability channels. Therefore, research on the changes of the flow field is important for reservoir development. However, the flow field of actual reservoirs is extremely complicated and it is difficult to effectively characterize the flow field. These challenges motivate the research of this paper. In this paper, PCA is used to reduce the dimension of streamline features, which achieves an accurate representation of streamlines without losing many features. Based on the streamline features from the dimension reduction, the clustering method is applied to simplify the flow field. The streamlines with different characteristics in the flow field are divided, and the main streamlines are selected among the injection–production units. The visualization of the streamline field is greatly improved and the interference phenomenon of the complicated streamlines is relieved.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

FL and BL developed the theoretical formalism, performed the analytic calculations, and performed the numerical simulations. All authors contributed to the final version of the manuscript. KZ supervised the project.

Funding

This work is supported by the Open Fund Project of State Key Laboratory of Offshore Oil Exploitation.

Conflict of Interest

Author BL was employed by the company Wave Software Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Han, J., Tao, J., and Wang, C. (2019). FlowNet: A Deep Learning Framework for Clustering and Selection of Streamlines and Stream Surfaces. IEEE Trans. Vis. Comput. Graphics 26 (4), 1. doi:10.1109/TVCG.2018.2880207

PubMed Abstract | CrossRef Full Text | Google Scholar

Hongfeng Yu, H., Chaoli Wang, C., Ching-Kuang Shene, C.-K., and Chen, J. H. (2012). Hierarchical Streamline Bundles. IEEE Trans. Vis. Comput. Graphics 18 (8), 1353–1367. doi:10.1109/TVCG.2011.155

CrossRef Full Text | Google Scholar

Hu, J., and Lihui, D. (2018). Identification of Water Drive Reservoir Flow Field Based on Streamline Clustering Artificial Intelligence Method. Pet. Exploration Dev. 45 (2), 8. doi:10.11698/PED.2018.02.14

CrossRef Full Text | Google Scholar

Lintao, Z. Research and Implementation of Streamline Selection Algorithm Based on Flow Field Characteristics. Chang Sha: National University of Defense Technology.

McLoughlin, T., Jones, M. W., Laramee, R. S., Malki, R., Masters, I., and Hansen, C. D. (2013). Similarity Measures for Enhancing Interactive Streamline Seeding. IEEE Trans. Vis. Comput. Graphics 19 (8), 1342–1353. doi:10.1109/TVCG.2012.150

PubMed Abstract | CrossRef Full Text | Google Scholar

Mesbah, M., Vatani, A., Siavashi, M., and Doranehgard, M. H. (2019). Parallel Processing of Numerical Simulation of Two-phase Flow in Fractured Reservoirs Considering the Effect of Natural Flow Barriers Using the Streamline Simulation Method. Int. J. Heat Mass Transfer 131, 574–583. doi:10.1016/j.ijheatmasstransfer.2018.11.097

CrossRef Full Text | Google Scholar

Mika, S., Schölkopf, B., Smola, A. J., Müller, K.-R., Scholz, M., and Rätsch, G. (1998). “Kernel PCA and De-noising in Feature Spaces,” in Neural Information Processing Systems, 536–542.

Google Scholar

Morse, N., and Mahesh, K. (2021). Large-eddy Simulation and Streamline Coordinate Analysis of Flow over an Axisymmetric hull. J. Fluid Mech. 926, 714. doi:10.1017/jfm.2021.714

CrossRef Full Text | Google Scholar

Namdari, S., Baghbanan, A., and Hashemolhosseini, H. (2021). Investigation of the Effect of the Discontinuity Direction on Fluid Flow in Porous Rock Masses on a Large-Scale Using Hybrid FVM-DFN and Streamline Simulation. Rudarsko-geološko-naftni zbornik 36 (4), 49–59. doi:10.17794/rgn.2021.4.5

CrossRef Full Text | Google Scholar

Pandeng, X. Study on Flow Field Characterization Technology of Gudong Oilfield at the Late Stage of Extra High Water Cut. Qing Dao: China University of Petroleum. (East China).

Qi, L. (2009). Numerical Simulation of Reservoir Based on Streamline. Qing Dao: China University of Petroleum. (East China).

Google Scholar

Qi, W. (2015). Study on Streamline Clustering Analysis and Visualization Method. Hang Zhou: Zhejiang University.

Google Scholar

Qiaoliang, Z., Ruizhong, J., and Ping, J. (2014). Establishment and Application of Reservoir Flow Field Evaluation System [J]. Pet. Geology. Oilfield Dev. Daqing 33 (3), 86–89. doi:10.3969/J.ISSN.1000-3754.2014.03.018

CrossRef Full Text | Google Scholar

Rodriguez, A., and Laio, A. (2014). Clustering by Fast Search and Find of Density Peaks. Science 344 (6191), 1492–1496. doi:10.1126/science.1242072

PubMed Abstract | CrossRef Full Text | Google Scholar

Rossl, C., and Theisel, H. (2012). Streamline Embedding for 3D Vector Field Exploration. IEEE Trans. Vis. Comput. Graphics 18 (3), 407–420. doi:10.1109/TVCG.2011.78

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, L., Zuo, L., and Zhu, C. (2020). Tracer Test and Streamline Simulation for Geothermal Resources in Cuona of Tibet. Fluids 5 (3), 128. doi:10.3390/fluids5030128

CrossRef Full Text | Google Scholar

Xu, C., Sun, G., Liang, R., and Xu, X. (2021). “Vector Field Streamline Clustering Framework for Brain Fiber Tract Segmentation,” in IEEE Transactions on Cognitive and Developmental Systems (IEEE), 1. doi:10.1109/TCDS.2021.3094555

CrossRef Full Text | Google Scholar

Yupei, H. (2011). Numerical Simulation of Flow Field Reforming for Enhanced Oil Recovery in Integrated Reservoirs. Qing Dao: China University of Petroleum. (East China).

Google Scholar

Zhang, N., Cao, J., James, L. A., and Johansen, T. E. (2021). High-order Streamline Simulation and Macro-Scale Visualization Experimental Studies on Waterflooding under Given Pressure Boundaries. J. Pet. Sci. Eng. 203, 108617. doi:10.1016/j.petrol.2021.108617

CrossRef Full Text | Google Scholar

Zheng, Y. (2014). Establishment of Reservoir Flow Field Evaluation System and Research on Enhanced Oil Recovery. Qing Dao: China University of Petroleum. (East China)

Google Scholar