Constraining Arctic Climate Projections of Wintertime Warming With Surface Turbulent Flux Observations and Representation of Surface-Atmosphere Coupling

Introduction

Sea ice and its overlying snowpack shape energy flows through the Arctic by reflecting the majority of the solar radiation in the sunlit months and inhibiting the Arctic Ocean and atmosphere from exchanging heat, moisture and momentum year-round (e.g., Screen et al., 2013; Vihma, 2014; Boisvert et al., 2015b; Taylor et al., 2018). As global temperatures rise due to climate change, the Arctic is warming faster than anywhere else on the Earth (IPCC, 2013), known as Arctic Amplification (Serreze et al., 2009; Screen and Simmonds, 2010a; Screen and Simmonds, 2010b). In response, Arctic sea ice has melted and satellite monitoring of sea ice extent has shown that the summer minimum has decreased at a rate of ∼14% per decade over the past 4 decades (Cavalieri and Parkinson, 2012; Stroeve and Notz, 2018). From 2009 to 2020, the Arctic saw 11 out of the lowest 13 September sea ice extents of the satellite record. Arctic sea ice extent is decreasing in all months, with the most rapid declines occurring since the early 2000s (Parkinson and DiGirolamo, 2016). In addition to declining sea ice extent, the totality of the changing conditions in the Arctic, including a warming of SSTs and a lengthening of the sea ice melt season, contribute to increases in evaporation and turbulent fluxes (e.g. Steele et al., 2008; Markus et al., 2009; Stroeve et al., 2014; Boisvert et al., 2015a; Taylor et al., 2018; Boeke et al., 2021).

Increased sensible (SHF) and latent (LHF) heat fluxes play an important role in the Arctic Amplification process. Although the Arctic sea ice albedo feedback is largest in the summer months, the strongest warming has occurred in fall and winter (Deser et al., 2010). This wintertime warming maximum has been linked to sea ice loss using observations, meteorological reanalysis, and climate model simulations (Boeke and Taylor, 2018; Screen and Simmonds, 2010a; Screen et al., 2012; Serreze et al., 2009). One way in which sea ice influences the winter warming maximum is that reduced sea ice cover promotes increased turbulent fluxes from the ocean surface to the lower atmosphere and drives atmospheric warming (Screen and Simmonds, 2010b).

Given the multiple mechanisms through which surface-atmosphere coupling processes influence Arctic climate system evolution, one may be surprised to find that the representation of surface turbulent flux parameterizations has not kept up with our understanding. Bourassa et al. (2013) indicate that modern understanding of the physics behind the bulk formula parameterizations and their application over highly stable and heterogeneous sea ice surfaces has not been incorporated into surface flux parameterizations (e.g., Brunke et al., 2006; Grachev et al., 2007; Andreas et al., 2010a; Andreas et al., 2010b; Reeves Eyre et al., 2021). While there have been changes to these parameterizations globally that have produced more accurate surface turbulent fluxes in the mid-latitudes; these changes have not significantly improved estimates in the Arctic (Bourassa et al., 2013). As a result, turbulent fluxes in the Arctic from reanalyses and climate models are inaccurate and often get the magnitude and sign of the fluxes incorrect when compared to in situ and satellite-derived data (Boisvert et al., 2015b; Taylor et al., 2018; Graham et al., 2019; Renfrew et al., 2021).

The large disparities between modeled and observed turbulent fluxes (Cullather and Bosilovich, 2011; Boisvert et al., 2015b; Graham et al., 2019; Taylor et al., 2018; Bourassa et al., 2013) are caused by multiple factors: 1) the specific parameterizations and assumptions used in the bulk formula, 2) discrepancies in sea ice properties, which drive the surface temperature and humidity and drag coefficients, 3) the representation of near surface-air temperature and humidity gradients, and 4) the spatial and temporal resolution. Currently, climate models and reanalyses apply mid-latitude boundary layer parameterizations in the Arctic (Bourassa et al., 2013). However, the boundary layer over sea ice is more stable than the nocturnal boundary layer over land, resulting in substantial flux errors (Grachev et al., 2007). The basic difference between these stable boundary layers is that the surface boundary layer in the Arctic is long-lived. Hence, there is usually no residual layer separating the Arctic surface boundary layer from the free atmosphere, making it more responsive to the influence of gravity waves, an additional source of turbulence (Zilitinkevich and Esau, 2007). Boisvert et al., (2015a) demonstrate that the magnitude of the fluxes in these stable boundary layers in the winter produced with the Grachev et al. (2007) algorithm are on average 24% larger than those calculated with Holtslag and de Bruin (1988), which is widely used in climate models.

Accurate roughness lengths for wind speed, humidity and temperature profiles over the ice are required to determine the transfer coefficients and to calculate the fluxes (Andreas, 2002; Andreas et al., 2010a). These have often been difficult to estimate and there are large inaccuracies especially over the sea ice due to its complex and heterogeneous topography, consisting of ridges and leads. Climate models often represent Arctic sea ice simplistically and cannot reproduce the sea ice extent, thickness and loss from observations and lack arepresentation of surface topography (Schweiger et al., 2011; Stroeve J. et al., 2014; Holland et al., 2010; Jahn et al., 2012). While there have been improvements in representing sea ice properties and seasonality in recent climate models, there are still significant biases compared to observations and a range in future predictions (SIMIP Community, 2020; Smith et al., 2020; Crawford et al., 2021; Watts et al., 2021). These errors in the sea ice can feedback on the near surface atmospheric variables, for example, in a large-eddy simulation model, a 1% variation in sea ice concentration was found to change the surface air temperature by 3.5 K in winter (Lüpkes et al., 2008a). Models and reanalyses also struggle to capture near surface temperature, humidity, and wind speeds and suffer from a lack of available in situ observations for assimilation (Jakobson et al., 2012; Graham et al., 2019; Davy and Outten, 2020). Finally, models have different temporal, spatial and vertical resolutions and do not resolve changes in the fluxes due to small scale changes in the atmospheric and surface conditions.

It is likely that the patchwork manner in which Arctic surface turbulent schemes have been developed and the incomplete integration of modern understanding are behind some of the substantial inter-model differences in surface turbulent fluxes. Graham et al. (2019) compared six reanalyses with in-situ observations and found that reanalyses do not represent turbulent fluxes correctly in any season over sea ice and consistently have the direction of the SHF wrong and the order of magnitude incorrect for LHF. Taylor et al. (2018) found substantial differences in the mean surface turbulent fluxes in the Arctic across Coupled Model Intercomparison Project 5 (CMIP5) models indicating that they did not appropriately simulate that the central Arctic tends to be a heat sink to the Arctic atmosphere. Further, Taylor et al. (2018) found the largest inter-model spread occurring in winter and in regions of the most rapid sea ice retreat. Given the substantial inter-model differences in the representation of surface turbulent fluxes found across recent multi-model ensembles (e.g., Taylor et al., 2018), additional work is needed to evaluate the next generation of climate models from the Coupled Model Intercomparison Project 6 (CMIP6) (Eyring et al., 2016) and better understand the sources of model discrepancies.

The large discrepancies between the model representation of surface-atmospheric coupling processes indicates that this area is prime for the use of observations to understand and constrain the influence of these processes on projected Arctic warming--a goal of this paper. These differences are thought to be caused by how models handle the evolution of the surface albedo and the properties of the sea ice pack (e.g. extent, concentration, thickness, snow) and their representation of surface turbulent fluxes. Previous work suggests that atmospheric coupling processes and in particular surface turbulent fluxes may serve as a meaningful constraint on projected Arctic warming. For example, Boeke and Taylor (2018) indicate that the magnitude of projected Arctic Amplification strongly correlates with the seasonal heat transfer from summer to fall/winter, of which the surface turbulent flux response plays a substantial role. Physically, surface turbulent fluxes directly contribute to Arctic warming via the ice insulation effect and can influence the atmospheric circulation variability (Burt et al., 2016; Zheng et al., 2019). Thus, there is a need to evaluate models and understand the causes of differences with observations.

This study is designed to address two knowledge gaps: 1) continued evaluation of surface turbulent flux representation and inter-model spread across contemporary climate models and 2) exploration of the use of observational constraints of surface turbulent fluxes to constrain projected Arctic warming during the winter, which we define as October-January. To do this we use the observation-derived turbulent flux dataset produced using NASA’s Atmospheric Infrared Sounder (AIRS) (Boisvert et al., 2013; Boisvert et al., 2015a; Boisvert et al., 2015b; Taylor et al., 2018) together with CMIP6 models to perform the model evaluation and assess inter-model spread. From the outset, we knew that this comparison would be challenging due to the substantial natural variability in the Arctic not being synced in models and observations, which has not been fully considered in previous assessments of climate model representation of surface turbulent fluxes. To account for this, we adopt a sea ice regime compositing approach to control for the inter-model differences in the natural variability of sea ice (Section 3a). By controlling for sea ice trend differences, this approach gives insights into the physical reasons for the errors in the parameterizations and input variables which are driving the intermodal differences. Guided by previous studies (Screen and Simmonds, 2010a; Sejas and Cai, 2016; Boeke and Taylor, 2018), we also hypothesize that models that more efficiently produce larger surface turbulent fluxes produce more winter warming and sea ice loss.

Data and Models

Atmospheric InfraRed Sounder Surface Turbulent Fluxes

The Atmospheric Infrared Sounder (AIRS) onboard NASA’s Aqua satellite was launched in May 2002 and has been collecting twice daily, global data ever since. AIRS has 2,378 infrared channels and a 13.5 km spatial resolution. The AIRS instrument was designed to produce highly accurate temperature and humidity profiles globally (Susskind et al., 2014), which is important in the Arctic where data is sparse and clouds are prevalent. We use version 7, level 3 daily skin temperatures, 925–1,000 hPa air temperatures, 925–1,000 hPa relative humidity and 925–1,000 hPa geopotential heights to derive SHF and LHF. Level 3 data is produced on a 1° × 1° grid with retrievals from data quality control flagged as best and good quality (Susskind et al., 2014). Unfortunately, the Advanced Microwave Sounding Unit-A2 (AMSU-A2) instrument, used in the creation of AIRS/AMSU combined data products, lost power in September 2016 causing these data products to no longer be produced, thus we use the AIRS-only products for October-January 2002–2020 for consistency. AIRS temperatures and humidity products have been compared with a variety of in-situ data and have shown to have modest uncertainty in skin temperature (±2.3 K), 2-m air temperature (±3.41 K) and specific humidity (±0.54 g kg⁻¹) (Boisvert et al., 2015a; Taylor et al., 2018).

Daily 10-m wind speeds are taken from NASA’s Modern Era-Retrospective Analysis for Research and Applications, version 2 (MERRA-2) (Gelaro et al., 2017) and are used in the calculations of the surface turbulent fluxes. MERRA-2 winds perform well when compared to radiosonde sounding data over the Arctic Ocean and are deemed reliable for turbulent flux computations over sea ice (Graham et al., 2019).

Sea ice concentrations (I_C) are produced using the Defense Meteorological Satellite Program (DMSP) Special Sensor Microwave Imager (SSMI) on board the F-13 satellite (31 January 2003-31 December 2007), the Special Sensor Microwave Imager/Sounder (SSMI/S) on board the F-17 satellite (1 January 2008- April 1, 2016), and SSMI/S on board the F-18 satellite (April 1, 2016—present). The daily I_C is derived from the NASA Team sea ice algorithm (Cavalieri et al., 1996, updated 2020) and is used in the calculations of the surface turbulent fluxes. Accuracy of the I_C product is between 5 (winter)-15 (summer)% (Cavalieri et al., 1992).

The SHF and LHF are calculated via the bulk method using the Monin Obukhov Similarity Theory and are given by

$\text{SHF }={\mathit{c}}_{\mathit{p}}{\mathit{S}}_{\mathit{r}}\left[{\mathit{C}}_{\mathit{Sz,i}}{\mathit{ I}}_{\mathit{C}}\left({\mathit{T}}_{\mathit{S,i}}-{\mathit{T}}_{\mathit{A}}\right)+{\mathit{C}}_{\mathit{Sz,w}}\left(1-{\mathit{I}}_{\mathit{C}}\right)\left({\mathit{T}}_{\mathit{S,w}}-{\mathit{T}}_{\mathit{A}}\right)\right](1)$

$\text{LHF }=\rho {\mathit{S}}_{\mathit{r}}\left[{\mathit{C}}_{\mathit{Ez,i}}\mathit{ }{\mathit{L}}_{\mathit{i}}\mathit{ }{\mathit{I}}_{\mathit{C}}\left({\mathit{q}}_{\mathit{S,i}}-{\mathit{q}}_{\mathit{A}}\right)+{\mathit{C}}_{\mathit{Ez,w}}\mathit{ }{\mathit{L}}_{\mathit{w}}\left(1-{\mathit{I}}_{\mathit{C}}\right)\left({\mathit{q}}_{\mathit{S,w}}-{\mathit{q}}_{\mathit{A}}\right)\right](2)$

where ρ is the air density, c_p is the specific heat of air, L_i (L_w) is the latent heat of sublimation (vaporization) over ice (water), C_Sz (C_Ez) is the sensible (latent) heat transfer coefficient over ice (i) and water (w), I_C is the sea ice concentration, S_r is the effective wind speed at 10 m (m s⁻¹) (Andreas et al., 2010b), T_S (q_S) is the surface temperature (specific humidity) of either sea ice (i) or water (w), and T_A (q_A) is the air temperature (specific humidity) at 2 m. Extensive in situ measurements were made over the Arctic sea ice during the Surface Heat Budget of the Arctic Ocean Experiment (SHEBA) campaign in 1997–1998 and Grachev et al. (2007) used these to create a highly accurate flux profile algorithm for stable conditions over the ice. This algorithm better fits the very stable boundary layer conditions in the Arctic and are used in our calculations over sea ice. Andreas et al. (2010a), Andreas et al., 2010b used roughness lengths measured from the SHEBA campaign to create an algorithm over the sea ice in the winter when the ice is covered with compact, dry snow and in the summer when the ice is covered with wet snow, melt ponds and leads. As these are the most accurate estimates made for the sea ice in different seasons, these new roughness lengths are used in our turbulent flux scheme.

The updated flux profile algorithm from Launiainen and Vihma (1990) includes these changes, which improve the accuracy of the turbulent flux calculations over grid points that contain sea ice (Boisvert et al., 2015a). This method also allows for the input parameters of temperature, humidity and wind speed to be taken at various heights above the surface and uses an iterative calculation that accounts for the stability of the boundary layer in calculating the values at a predetermined reference height (e.g., 2 m) (Launiainen and Vihma, 1990). Readers are referred to Boisvert et al., 2013, Boisvert et al., (2015a) for a full description of the model used to calculate the turbulent fluxes over the sea ice. These Arctic sea ice specific changes made to this algorithm, to the best of our knowledge, have not been adopted in any other climate models or reanalysis products. This algorithm is better suited to simulate turbulent fluxes over the Arctic Ocean and when compared with in situ data from the N-ICE2015 campaign, AIRS-derived LHF (SHF) had a root mean square error of 0.74 W m⁻² (5.32 W m⁻²) (Taylor et al., 2018). Overall, these comparisons indicate an uncertainty of ∼20% in the AIRS-derived surface turbulent fluxes, however we can’t say for certain that this uncertainty is the same over all sea ice types and seasons with a lack of in situ data. The native resolution of this data set is 25 × 25 km, however these fluxes have been interpolated onto a common 1° × 1° grid for this study.

Coupled Model Intercomparison Project 6

Model results are calculated from 18 CMIP6 models (Table 1) participating in the historical and SSP5-8.5 (shared socioeconomic pathway) scenarios (Eyring et al., 2016). To cover the entire 2002–2020 observational time period, monthly data from the historical simulations for the period 2002–2015 is merged with the first 5 years of the SSP5-8.5 future scenario (2015–2020). We just use one ensemble member per model. Model-simulated surface turbulent flux differences are poorly understood due to insufficient observational datasets; further, substantial across-model spread in turbulent fluxes has remained consistent from CMIP5 to CMIP6 (Wild, 2020). Models often lack the complexity required to represent the processes affecting the simulation of surface turbulent fluxes (e.g. evaporation/precipitation, sea ice/snow cover, wind speed) (Wild, 2020). All CMIP6 model output has been interpolated onto a common 1° × 1° grid.

TABLE 1

TABLE 1. Summary of CMIP6 models used in this study.

Methodology

Sea Ice Regimes

Models and observations represent unique perspectives of the climate system, such that differences between them cannot always be interpreted as model error. Meaningful observation-model comparisons require the rectification of these different perspectives. Common challenges include rectifying differences in quantity definitions (e.g., cloud fraction; Bodas-Salcedo et al., 2011) and differences in spatial and temporal resolution. When comparing trends, natural variability differences must also be accounted for.

Coupled, free running atmosphere-ocean models used to simulate the recent climate (Table 1) produce their own natural variability that is not synced with observed variability. Thus, a direct comparison of the spatial patterns of modeled and observed trends does not provide a meaningful evaluation. This is a substantial challenge in the Arctic where natural variability is especially large (e.g., Kay et al., 2012). We adopt a sea ice regime compositing approach to control for the effects of Arctic sea ice variability on our comparison.

The sea ice regime compositing approach defines four regimes based upon trends in I_C: persistent sea ice, and slow, moderate, and fast sea ice loss. The four sea ice regimes are defined by the quartiles of observed I_C trends:

● Persistent regime: I_C trends > −0.27% decade⁻¹

● Slow sea ice loss: −0.27% decade⁻¹ > I_C trends > −2.4% decade⁻¹

● Moderate sea ice loss: −2.4% decade⁻¹ > I_C trends > −7.5% decade⁻¹

● Fast sea ice loss: I_C trends < −7.5% decade⁻¹

Figure 1 depicts the sea ice regimes for passive microwave observations and four CMIP6 models. These models highlight the inter-model range in sea ice loss trends. While ACCESS-CM2 (Figure 1B) simulates sea ice retreat regimes similar to observations (Figure 1A), the other models vary drastically (Figures 1C–E). These differences in I_C trends across the models indicate that the location and number of grid boxes in each sea ice loss regime also differ. Overall, the observed I_C trends are found within the model range. Our approach is to compare SHF and LHF from models and observations within these sea ice loss regimes to control for the large differences in I_C trends.

FIGURE 1

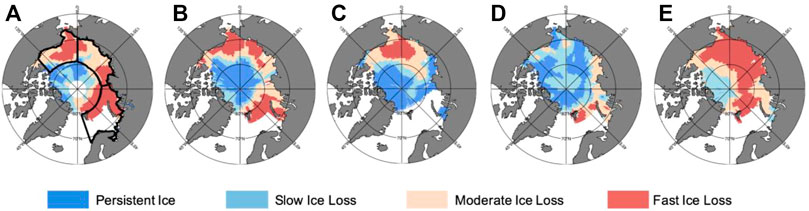
FIGURE 1. Winter (October-January) sea ice loss regimes for observations (A) and four CMIP6 models (B–E) ACCESS-CM2, CESM2-WACCM, INM-CM4-8 and MRI-ESM2-0. White and grey (land) portions are areas not included in our discussion. Black lines denote regions of interest (clockwise): Beaufort-Chukchi seas, Laptev-East Siberian seas, Barents-Kara seas and the Central Arctic in the areas around the North Pole.

Diagnostic Approach Assessing Sensitivity of Surface Turbulent Fluxes to Controlling Factors

A multi-linear regression approach is developed to determine the most impactful variables on surface turbulent fluxes (namely, air-sea temperature (T_S−T_A) and moisture (q_S−q_A) gradients, 10-m wind speed (Ū), I_C) and to provide a means of consistently intercomparing models without knowing the specific model bulk formula. The full regression equation below is fit to observations and models.

$SHF={\beta }_0+{\beta }_{T_S-T_A}\cdot \left(T_S-T_A\right)+{\beta }_{I_C}\cdot I_C+{\beta }_{\overline{U}}\cdot \overline{U}+{\beta }_{I_C\cdot T_S-T_A}\cdot \left[I_C\cdot \left(T_S-T_A\right)\right]+{\beta }_{\overline{U}\cdot T_S-T_A}\cdot \left[\overline{U}\cdot \left(T_S-T_A\right)\right](3)$

$LHF={\beta }_0+{\beta }_{q_S-q_A}\cdot \left(q_S-q_A\right)+{\beta }_{I_C}\cdot I_C+{\beta }_{\overline{U}}\cdot \overline{U}+{\beta }_{I_C\cdot q_S-q_A}\cdot \left[I_C\cdot \left(q_S-q_A\right)\right]+{\beta }_{\overline{U}\cdot q_S-q_A}\cdot \left[\overline{U}\cdot \left(q_S-q_A\right)\right](4)$

For CMIP6 models, Ū was calculated as $Ū=\sqrt{(u^2+v^2)}$ where u and v are the 10-m Ū components. All other variables were obtained from the CMIP6 archive except for q_S, which was calculated using the Clausius-Clapeyron equation and model temperature output. Before performing the regression, the linear trend at each grid box was removed for each variable and it was normalized by its standard deviation over the time period of the study. This step is performed to account for the differences in the variability of each of these terms across models. Further, the multi-linear regression model was applied using all available grid boxes within a regime to create a set of Arctic domain coefficients for each model and for observations.

The slopes β_TS-TA, -β_Ic, and -β_U represent the linear response of SHF (LHF) to T_S-T_A (q_S-q_A), I_C, and Ū. Two covariance terms [${\beta }_{I_C\cdot T_S-T_A}$ $\left({\beta }_{I_C\cdot q_S-q_A}\right)$ and ${\beta }_{\overline{U}\cdot T_S-T_A}$ $\left({\beta }_{\overline{U}\cdot q_S-q_A}\right)$] are included in the regression due to the strong covariation between T_S-T_A (q_S-q_A) with both I_C and Ū. The relationship between T_S-T_A (q_S-q_A) and I_C is because less sea ice coverage potentially allows for a larger air-sea temperature (moisture) gradient; incorporating a product term [I_C*(T_S-T_A); I_C*(q_S-q_A)] approximates this interaction. T_S-T_A (q_S-q_A) also covaries with Ū, whereby higher Ū tends to occur with a larger air-sea temperature (moisture) gradient. The significance of these terms is tested for each model and in observations by computing the extra sum of squares (ESS) and performing an F-test (Ramsey and Schafer, 2012). ESS is a measure of how much the unexplained variance in SHF (LHF) decreases with the addition of the covariance terms and is calculated as, ESS = Sum of squared residuals in reduced model−Sum of squared residuals in the full model, where the reduced model is the regression equation without the covariance term and the full model is the regression equation including the covariance term. The full model variance is used in the denominator of Eq. 5 because the purpose of this test is to evaluate the statistical significance of adding covariance terms to the regression model. The significance test was performed for observations and each model individually for each ice loss regime.

The F-statistic based on the ESS is defined in Equation 5 and is used to obtain a p-value at the desired level of confidence.

$F-statistc=\frac{\left[\frac{ESS}{\# of {\beta }^{\prime }s being tested}\right]}{{\sigma }^{2}from full model}(5)$

If the p-value is small then we can conclude that the reduced model without the covariance terms is incorrect and accept the full model. In Equation (5), σ² is the variance from the full model including covariance terms. The full model is appropriate for all ice regimes for the SHF and LHF regressions. The significance of each term (β) for CMIP6 models and observations are found in Supplementary Table S1.

Results

Models that produce a stronger increase in SHF and LHF for the same sea ice loss are hypothesized to warm more over the Arctic. We address this hypothesis by 1) evaluating the SHF and LHF climatological distribution in CMIP6 models against observations, 2) comparing observed and simulated SHF and LHF trends within sea ice retreat regimes, 3) analyzing SHF and LHF sensitivities to controlling factors, and 4) analyzing relationships with projected Arctic warming. We separate the discussion of observed and model-simulated trends deliberately to reduce the temptation to directly compare observed and model-simulated trends and limit observation-model comparison to the appropriate circumstances when the influence of sea ice natural variability is controlled for or small: 20-year mean state and sea ice loss regimes. In the discussion below, positive (negative) fluxes denote energy exchange from the surface to the atmosphere (atmosphere to the surface).

Observed Surface Turbulent Flux Mean State and Trends

The Arctic surface is a net heat sink to the Arctic atmosphere during winter with the strongest sink in the central Arctic and a heat source in the Barents-Kara (B-K) seas region (Figure 2). The central Arctic is characterized by a broad region of negative SHF and LHF values that contribute to the Arctic average SHF and LHF values: −31.8 ± 5.19 W m⁻² and −3.1 ± 1.88 W m⁻², respectively (Table 2 and 3). The primary mechanism of turbulent heat transfer from the atmosphere to the surface is the SHF; central Arctic LHF values are an order of magnitude smaller than SHF. The magnitude of the heat sink is reduced by the positive SHF and LHF fluxes in the B-K seas, providing a narrow area of surface heat source to the atmosphere. The contributions to the B-K sea heat source are roughly equally distributed between SHF and LHF.

FIGURE 2

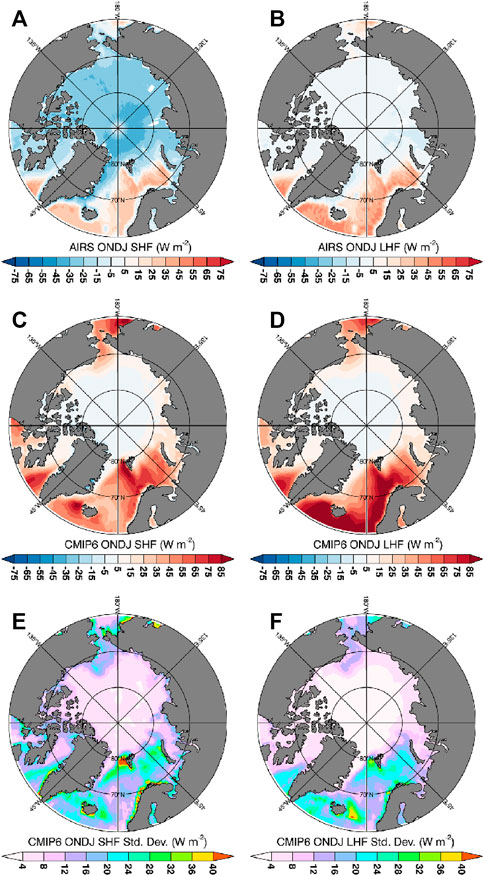
FIGURE 2. Average winter (ONDJ) SHF and LHF from 2002 to 2020 for AIRS-derived (A,B) and CMIP6 (C,D) and across-model spread represented as the standard deviation (E,F).

TABLE 2

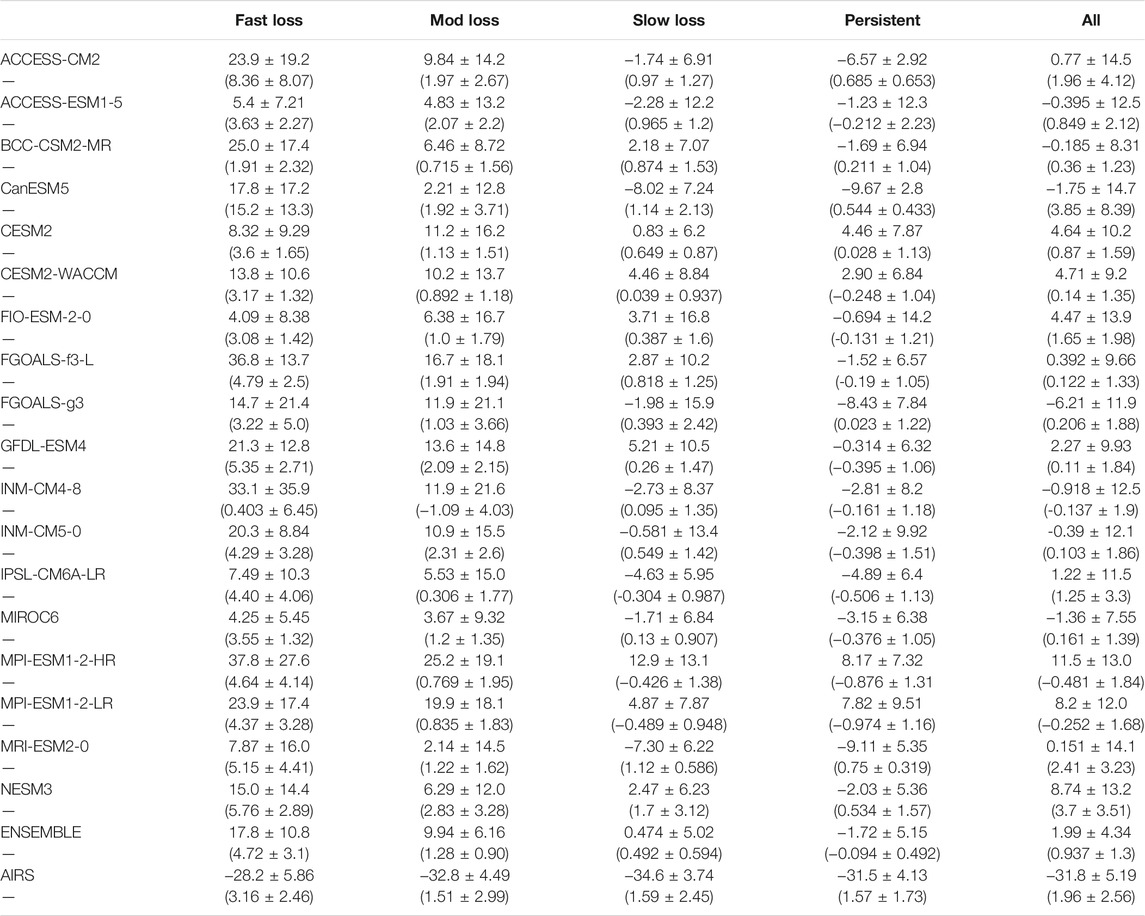
TABLE 2. Summary of mean values and their standard deviation (decadal trends and their standard deviations in parenthesis) for AIRS-derived and CMIP6 models SHF for October-January 2002–2020. Values are stratified by Arctic sea ice loss regimes.

TABLE 3

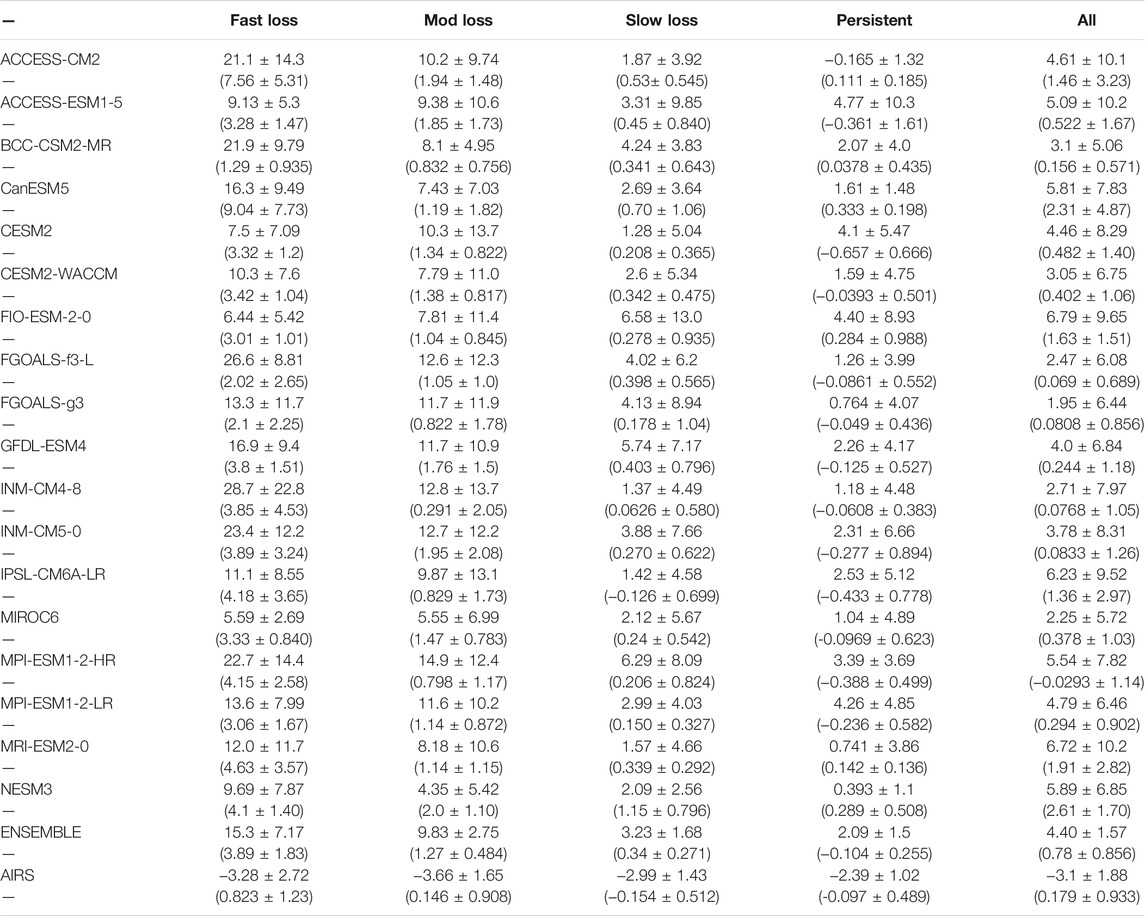
TABLE 3. Summary of mean values and their standard deviation (decadal trends and their standard deviations in parenthesis) for AIRS-derived and CMIP6 models LHF for October-January 2002–2020. Values are stratified by Arctic sea ice loss regimes regions.

The observed SHF and LHF trends suggest that the changing Arctic surface is altering the character of the atmosphere’s heat sink in the winter (Figure 3). Turbulent flux trends (Figure 3F) show increases across much of the central Arctic, weakening the heat sink. SHF trends, rather than LHF, account for most of this weakening and are driven by a thinning of the multi-year sea ice (Kwok, 2018), which allows for more conduction through the sea ice from the ocean and warming surface temperatures, along with a potential weakening of the surface-based temperature inversion. Additionally, there is a strengthening surface heat source near the sea ice edge in the B-K seas region, roughly evenly distributed between SHF and LHF trends (Figure 3). There is also a weakening of the heat source farther south in the North Atlantic potentially related to surface cooling from Greenland melt water (Allan and Allan, 2019). These SHF and LHF trends are consistent with the AIRS-observed changes in T_S−T_A and q_S−q_A (Figures 3C,D), and are largest in regions of substantial sea ice loss (Figure 3E).

FIGURE 3

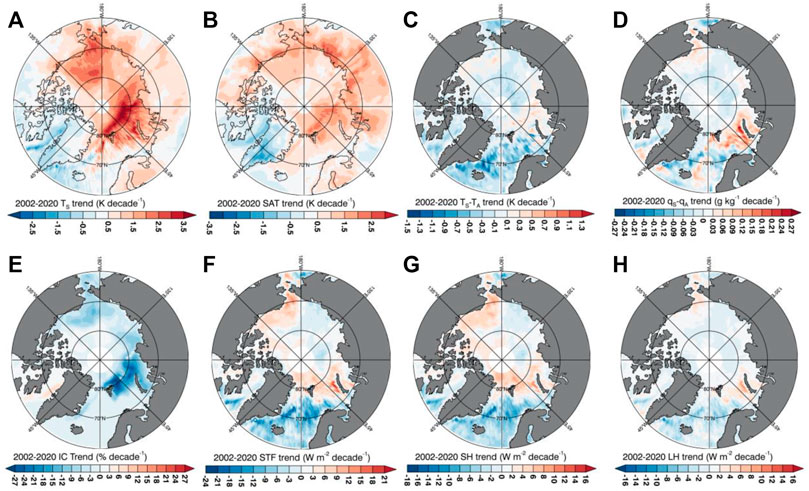
FIGURE 3. Winter (ONDJ) decadal trends in (A) AIRS surface skin temperature, (B) AIRS surface air temperature, (C) AIRS T_S−T_A, (D) AIRS q_S−q_A, (E) observed I_C, (F) AIRS-derived surface turbulent flux, (G) AIRS-derived SHF and (H) AIRS-derived LHF.

Analysis of trends within the sea ice loss regimes shows that the fast sea ice loss regime exhibits the largest trends, further highlighting the relationship between sea ice and SHF and LHF (Figure 4). LHF trends increase from the slow to fast sea ice loss regime (Figure 4). The regime-to-regime differences in SHF trends from observations are constant in all regimes and increase for the fast sea ice retreat regime. The SHF trends are positive in all sea ice loss and persistent regimes, whereas the LHF trends are slightly negative in the slow sea ice retreat and persistent regimes. The trends in SHF and LHF are consistent with the trends in T_S−T_A and q_S−q_A. Overall, in the entire Arctic, the SHF and LHF trends in the observations are positive.

FIGURE 4

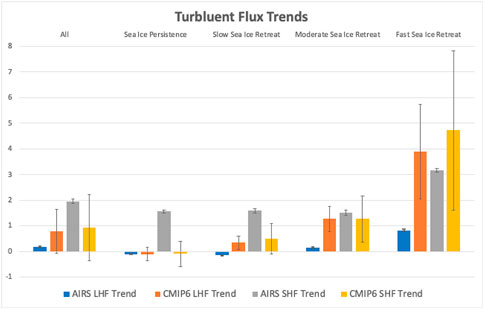
FIGURE 4. Bar plot summarizing the Arctic winter (ONDJ) surface turbulent flux trends (Wm⁻² per decade) by sea ice loss regime. Average trends for both AIRS-derived and CMIP6 ensemble-means are shown in the bars. The standard error of the AIRS-derived turbulent flux trends are shown in the error bars and the error bars for the CMIP6 ensemble-mean turbulent flux trends represent the inter-model spread.

The presence of sea ice modifies the SHF and LHF frequency distributions (Figure 5). The mode of the AIRS-derived LHF is slightly negative and the SHF is more negative. The SHF distribution shows a broader distribution than LHF. All sea ice regimes have a similar slightly negative mode of the SHF and LHF, however regions of faster sea ice loss exhibit a broader distribution of SHF and LHF (Figure 5). The frequency of slightly negative SHF and the frequency of moderate and strong positive LHF increases as sea ice loss becomes stronger. The fast sea ice loss regime has a much higher frequency of positive LHF values compared to any of the other sea ice regimes. Changes in the SHF and LHF distributions by sea ice regime correspond to differences in the T_S−T_A and q_S−q_A distributions (Figures 5E,G) showing that faster sea ice loss regimes correspond to greater T_S−T_A and q_S−q_A values. Thus, faster wintertime sea ice loss corresponds with larger T_S−T_A and q_S−q_A gradients and positive SHF and LHF trends.

FIGURE 5

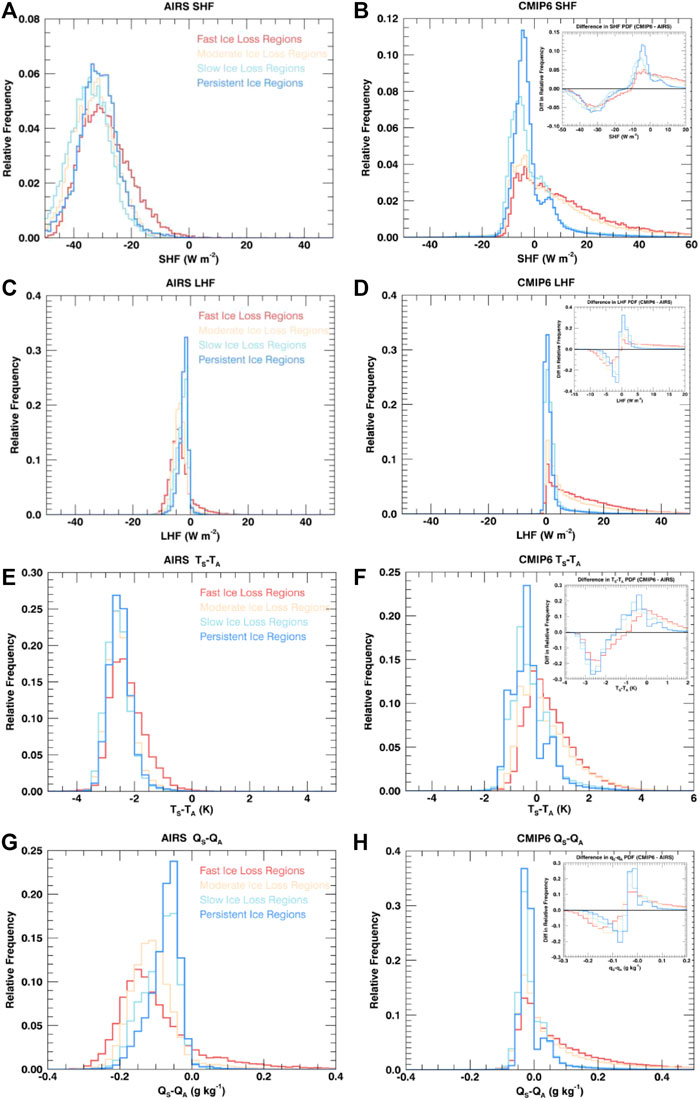
FIGURE 5. PDFs of surface turbulent fluxes and surface-air temperature and moisture gradients for AIRS (A,C,E,G) and CMIP6 (B,D,F,H) for the four ice loss regimes for the Arctic winter (ONDJ). Insets represent difference plots (CMIP6—AIRS).

CMIP6 Models Surface Turbulent Flux Mean State and Trends

While capturing key features of the observed spatial variations in SHF and LHF (Figures 2A,B), models represent the Arctic surface as a heat source, not a heat sink, to the winter Arctic atmosphere (Figures 2C,D). The model ensemble shows weak negative SHF and LHF across much of the central Arctic and strong positive SHF and LHF in the B-K seas region. The ensemble mean also shows similar magnitudes of the SHF and LHF across the Arctic suggesting that the two flux terms are of equal importance to the central Arctic surface energy budget, different from observations. The B-K seas region heat source is approximately 34 times stronger than in observations (CMIP6 ensemble average SHF + LHF: 70.1 W m⁻²; AIRS-derived SHF + LHF: 2.1 W m⁻²). While Table 2 indicates that the magnitude of the surface heat source varies strongly, most models simulate the winter Arctic surface as a heat source to the atmosphere indicating a different role of surface-atmospheric coupling in the simulations compared to observations.

CMIP6 SHF and LHF trends indicate a narrowing area of the surface atmospheric heat sink and a broadening of the heat source, as observed, in concert with the declining sea ice cover (Figure 6). Surface temperature, SHF, and LHF trends are strongest in the Beaufort-Chukchi (B-C) and B-K seas regions with the most rapid sea ice decline. While the ensemble mean and observed patterns in the SHF and LHF trends are similar, the magnitudes are weaker than observations due to the averaging over multiple models. Moreover, the correspondence between the observed and ensemble mean spatial patterns of SHF and LHF trends may be misleading as the observations represent only a single realization of natural variability. The inter-model spread of these trends is substantial (Figures 6F–J) and is also strongest in the regions of the largest sea ice loss. As a result, the degree of sea ice loss and the resulting surface energy budget changes may serve as a useful observational constraint (Section 4d).

FIGURE 6

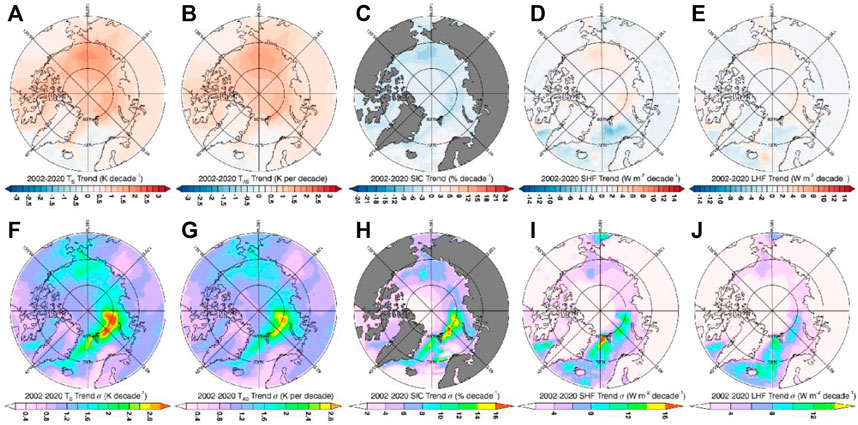
FIGURE 6. Winter (ONDJ) decadal trends for CMIP6 for (A) T_S, (B) T_A, (C) I_C, (D) SHF and (E) LHF, and the across model spread for (F) T_S, (G) T_A, (H) I_C, (I) SHF and (J) LHF.

Model SHF and LHF trends within sea ice loss regimes tell a story consistent with observations, highlighting the sea ice influence on the inter-model trend differences (Figure 4). Model simulated SHF and LHF trends increase with greater sea ice loss and increases in T_S-T_A. The largest discrepancies between models and observations occur in the fast sea ice loss regime. For all sea ice loss regimes, the model ensemble LHF trends are always greater and more than double the observed value. With respect to SHF, there is a large observed trend in the persistent regime not found in models indicating that the models are struggling to capture the observed increase in T_S-T_A. This difference could also result from differences in the conductive heat flux through sea ice in the presence of thinning. The inter-model differences in SHF and LHF trends (Figure 4, error bars) are smaller within the sea ice loss regime framework than within the spatial distribution indicating that much of the inter-model differences in SHF and LHF flux trends correspond to differences in sea ice loss.

The SHF and LHF distributions within sea ice regimes indicate that the character of model-observational differences stems in part from different distributions of T_S−T_A and q_S−q_A (Figure 5). Model simulated SHF and LHF distributions show similar high frequencies of slightly negative SHF values and near zero LHF values as observations, however do not capture the frequency of negative SHF or LHF values. The dependence of the model-simulated SHF and LHF distributions on the sea ice loss rate exhibits similar behavior as observations. However, the model SHF distributions show moderate negative values for all sea ice regimes, but do not show values that reach < −20 W m⁻² as in observations. These differences stem from models not simulating as strongly negative T_S−T_A values. The mode of the observed T_S−T_A distribution is ∼ −3 K which is not found in the model simulated range (Figure 5E). Similarly, the model LHF distributions for all sea ice regimes show a larger frequency of positive values than observed and rarely produce negative values. These model-observation differences in the LHF distribution are driven by the differences in the q_S-q_A distributions; observations indicate frequent negative q_S−q_A values (Figure 5G), whereas the models rarely simulate negative q_S−q_A gradients. Radiosondes taken during the SHEBA campaign showed that specific humidity and temperature consistently increased with height near the surface due to frequent wintertime inversions (Yu., 2019; Yu et al., 2019) and q_S−q_A measurements taken during the Tara drifting station in spring and summer 2007 showed slight negative differences (Boisvert et al., 2015a) when surface-based inversions are weaker than the winter. Thus, these negative gradients in satellite-derived q_S−q_A appear realistic and are not captured in CMIP6 models. The underlying model-observations differences in the SHF and LHF values are related to the differences in the T_S−T_A and q_S−q_A distributions.

Since it appears that the source of the model and observational differences in SHF and LHF are largely driven by the difference in T_S−T_A and q_S−q_A, the turbulent fluxes are stratified by T_S−T_A, q_S−q_A for each sea ice regime (Figure 7). Qualitatively, the dependence of the mean SHF and LHF stratified by T_S−T_A and q_S−q_A is similar between models and observations; however quantitatively, the models show larger SHF values for the same T_S−T_A and much larger values for LHF for the same q_S−q_A. Especially surprising in Figure 7, is that models substantially differ from observed SHF and LHF values when the T_S−T_A and q_S−q_A values are the same. Especially troubling is that for negative q_S-q_A gradients, models are largely unable to produce a negative (atmosphere-to-surface) LHF. Figures 5, 7 together indicate that the larger SHF and LHF for models is from both more frequent T_S−T_A and q_S−q_A positive values and the larger SHF and LHF values at the same T_S−T_A and q_S−q_A values.

FIGURE 7

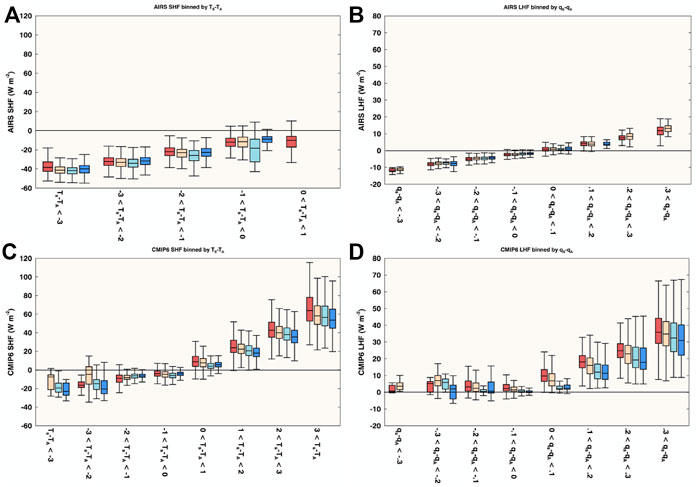
FIGURE 7. Arctic winter (ONDJ) SHF (LHF) binned by T_S−T_A (q_S−q_A) for AIRS (A,B) and CMIP6 (C,D). Data is further separated into the four ice loss regimes, denoted by color: fast loss (red), moderate loss (yellow), slow loss (light blue), and persistent regimes (royal blue). If a given T_S−T_A (q_S−q_A) bin lacked sufficient data points to compute a box and whisker, the bin was omitted (e.g, AIRS SHF for the largest T_S−T_A bin for moderate, slow and persistent ice loss regimes).

Surface Turbulent Flux Controlling Factors

Understanding which factors are most important for controlling surface turbulent flux variability and which factors contribute most strongly to the differences with observations is needed to improve the model representations of Arctic surface turbulent fluxes. We first considered applying a sensitivity study methodology to surface turbulent flux parameterizations from individual models to quantify the contributions of the component terms. However, compiling a complete set of STF parameterizations used by CMIP6 models would be complex and is beyond the scope of this study. Instead, we develop a multi-linear regression approach (Section 3b) to quantify the contributions from individual factors to SHF and LHF variability that can be consistently applied across models.

The multi-linear regression approach reasonably captures the variance in SHF and LHF for observations and models at the monthly mean timescale. The method is applied consistently to observations and models using 1° × 1° monthly mean fields to create a single, Arctic-wide set of coefficients. The root mean square error of the multi-linear regression (Figures 8F, 9F) shows a range in reliability; root mean square error values range from 5 to ∼60% depending upon the model and sea ice regime. In most cases, the root mean square error values are <30% and the approach is better at representing LHF than SHF. While imperfect, the root mean square errors indicate that this approach captures the majority of SHF and LHF variability and captures physically-valid relationships.

FIGURE 8

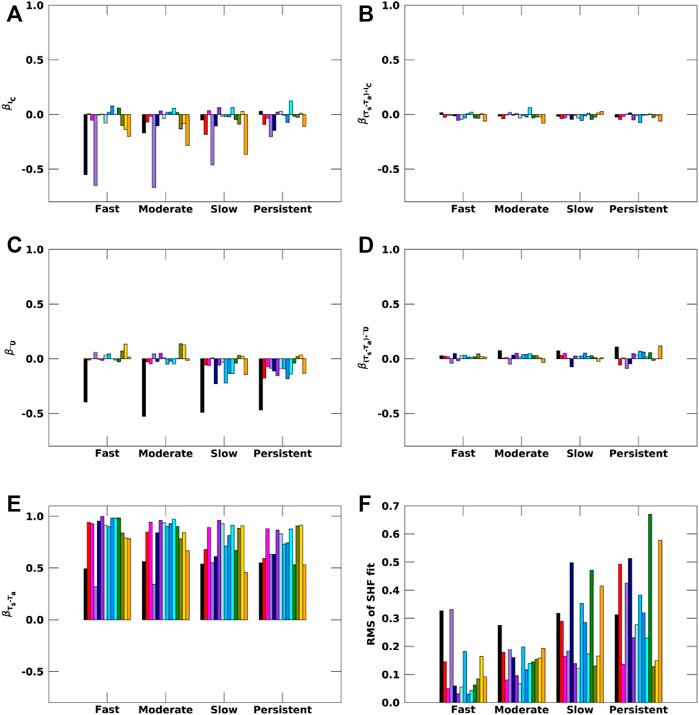
FIGURE 8. Slopes obtained from the multi-linear regression on SHF (A–E) for observations (black) and CMIP6 models (colored) for the four ice loss regimes during Arctic winter (ONDJ). RMS for the fit is shown in (F).

FIGURE 9

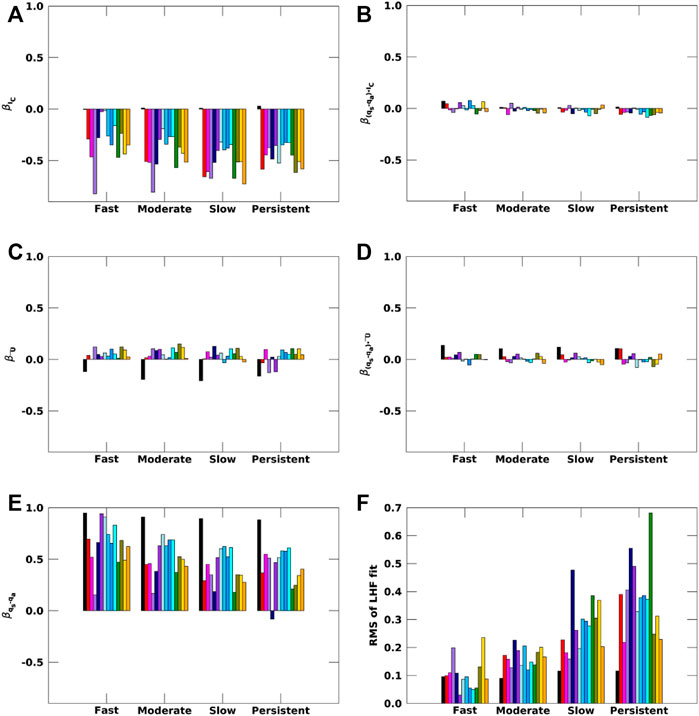
FIGURE 9. Slopes obtained from the multi-linear regression on LHF (A–E) for observations (black) and CMIP6 models (colored) for the four ice loss regimes during Arctic winter (ONDJ). RMS for the fit is shown in (F).

Regression model robustness is also supported by the consistency in sign and magnitude across the CMIP6 model results (Figures 8, 9). Error bars are not included in Figures 8, 9 since the accurate statistical error analysis is not considered trustworthy enough given the potential for spatial autocorrelation in the residuals. However, the overall consistency across the 18 CMIP6 models in the sign and magnitude of the dominant coefficients (β_Ts−_Ta, β_IC, and β_qs−qa; Figures 8, 9) provides confidence that the regression model approach is robust and indicates substantial model-observational disagreements in the importance of specific terms.

Applying the approach yields some expected features, such as the importance of T_S−T_A, and some unexpected features, such as the strong negative sign of the wind term for observations. β_Ts−Ta is the largest term in the majority of models with values from 0.3 to nearly 1.0 W m⁻² per unit anomaly (Figure 8E). This is the case across all sea ice regimes. β_Ts−Ta is also an important term for observed SHF variability; however, most climate models possess a β_Ts−Ta nearly double the observational value.

β_IC, the largest magnitude observational slope, and β_Ū terms are associated with negative SHF anomalies. The β_IC represents the influence of sea ice surface properties and atmospheric conditions, such as stability, that correlate with I_C. The models show a wider range of β_IC and β_Ū values compared to β_Ts−Ta (Figure 8). For β_IC, the large spread in the values suggests that sea ice surface properties that influence SHF (e.g., surface roughness, atmospheric stability, sea ice topography, etc.) are either represented differently by models and/or their effects on SHFs are parameterized differently. The importance of β_IC in producing SHF variability is much larger in observations than in most models.

The observational β_Ū value may seem slightly counterintuitive when not considering the mean state context. The majority of observational grid boxes have negative mean T_S−T_A values such that months with anomalously strong winds drive a more negative SHF. Stated plainly, this result indicates that a positive monthly mean wind anomaly drives a more negative SHF anomaly. The model β_Ū values are similarly tied to the background mean SHF value and stronger winds reinforce the background SHF. This explains the model behavior in the overall progression of β_Ū values to be generally positive over fast loss regime and generally negative over the persistent regime due to the smaller and negative mean state SHF values (Table 2).

As opposed to the SHF, observed variability of LHF is dominated by a single term, β_qs−qa. The observed β_qs−qa exceeds 0.9 W m⁻² per unit anomaly for all sea ice regimes (Figure 9E). All models show a consistent sign of β_qs−qa, in line with observations, with a substantial inter-model spread in the magnitude. β_IC and β_Ū (Figures 9A,C) are substantially weaker than β_qs−qa in observations; specifically, observed β_IC is near zero. However, β_IC is of equal importance as β_qs−qa to explaining variability of LHF in models. β_Ū is of similar magnitude as β_IC and β_qs−qa for a few models, but overall accounts for small contributions to LHF variability.

Lastly, the inclusion of covariance terms is compelled by the statistical analysis and improves the explained variance of the model. Figures 8B,D, 9B,D indicate, however, that most of these values are less than 0.1 Wm⁻² per unit anomaly. The slopes of the covariance terms are small, show a narrower inter-model spread, and contribute little to the variance in SHF and LHF.

As shown in Figures 5, 7, a portion of the discrepancy with the observed and model mean SHF and LHF results from different distributions of surface-air temperature and moisture gradients in models. In this section, we learn that substantial differences exist between the sensitivity of SHFs and LHFs to perturbations in relevant controlling factors (e.g., Eqs. 1, 2. Models are much more efficient, by ∼50%, at turning a T_S−T_A anomaly into a SHF anomaly relative to observations. Further, the influence of I_C on SHF is more important in observations than in models. The opposite is found for LHF variability in models; LHF is more sensitive to an I_C anomaly. Thus, the sea ice surface property influence on variability in SHF and LHF are inconsistent with observations and with each other. These results (Figures 8, 9) illustrate that the most important terms for the model SHF and LHF flux variability are T_S−T_A and q_S−q_A.

Relationships With Projected Arctic Warming

There is a great deal of interest around constraining Arctic projections with observations to reduce uncertainty and make projections more actionable. We address the possibility of the above analyses being applied in this manner. Boeke and Taylor (2018) found that seasonal energy exchanges in sea ice retreat regions contribute significantly to the spread in model projections of Arctic amplification, whereby models that more efficiently disperse the energy stored in the ocean from summer via surface turbulent fluxes warm more. Dai et al. (2019) also found that increased turbulent heat fluxes from ice-free ocean in sea ice retreat regimes contributes to Arctic amplification. Given the importance of turbulent heat fluxes in recent literature, the SHF (LHF) regression slopes from Figures 8, 9 are tested as a possible emergent constraint (EC)--an approach that uses an ensemble of models to connect an observable process from present-day to future climate projections to narrow the uncertainty.

Given the dominance of the β_Ts-Ta (β_qs−qa) terms in determining SHF (LHF), we hypothesized that model capability in turning a strong surface-air temperature (moisture) gradient into SHF (LHF) would correlate with projected Arctic warming and could make a suitable EC. While significant correlations with projected Arctic winter warming are found for some of the regression slopes, none of the regression slopes are good ECs because the observed regression slopes typically fall outside the model range. Despite this, we found that present-day trends in surface turbulent fluxes, I_C and T_S in ice-retreat regions correlate strongly with projected winter warming and could serve as a useful EC (Figure 10); for these quantities the observed trends fall within the model range, and the range in model values is large relative to the observational uncertainty (grey shading in Figure 10). To ensure that CanESM5 is not driving these relationships, we computed the regression again, removing CanESM5. The slopes and y-intercept values are very similar to those obtained using all the models, and while the correlation coefficient is smaller, it is still significant at the 95% level, therefore this relationship is robust. The relationships in Figure 10 indicate a constrained Arctic winter warming range of ∼14–17 K, substantially smaller than the 10–21 K inter-model range in warming.

FIGURE 10

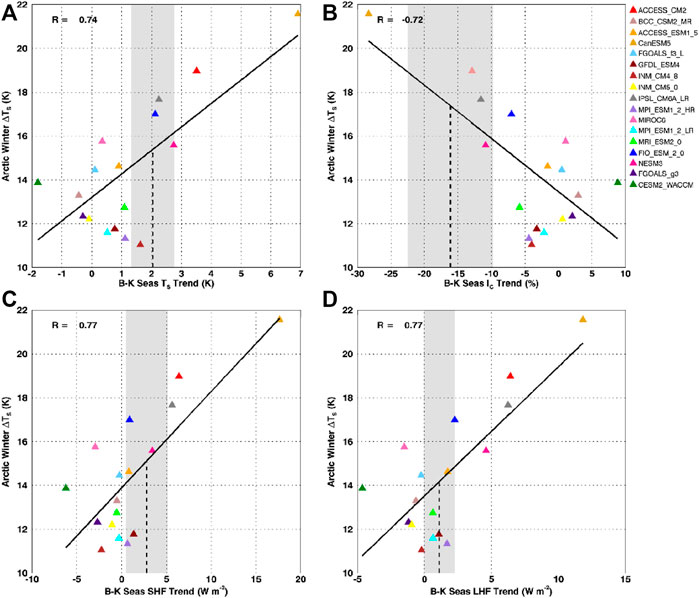
FIGURE 10. Barents-Kara Seas present-day trends for sea ice gridboxes (>15% I_C) in (A) T_S, (B) I_C, (C) SHF and (D) LHF correlated with projected Arctic winter (ONDJ) warming. CMIP6 models are colored triangles while the dashed line indicates the present-day trend found for observations with the grey shading ± the observational standard deviation.

Discussion

The results presented in this study are not unique to the current generation of climate models. In fact, the previous generation of climate models and current reanalyses both have turbulent flux biases when compared with observations in the Arctic. For instance, Taylor et al. (2018) show substantial model-observational differences between CMIP5 models and the previous version of the AIRS-derived SHF and LHF dataset that also indicate that the magnitude of the central Arctic surface heat sink is too weak. However, in situ observations show that negative fluxes in the winter over sea ice are a realistic phenomenon (e.g. SHEBA: Persson et al., 2017; N-ICE2015: Walden et al., 2017), and SHF were found to range between −20 and −30 W m⁻², consistent with the AIRS-derived SHF magnitudes. Here, we have shown that the unrealistically weak heat sink also persists in the current generation of CMIP6 models and could in part be driven by the poor representation of the stable boundary layer over ice in winter, which can underestimate the magnitude of the fluxes (Grachev et al., 2007; Boisvert et al., 2015a). These results are also consistent with comparisons of reanalyses and in situ data. For example, Graham et al. (2019) compared six widely used reanalysis products with in situ flux measurements taken during the N-ICE2015 campaign during winter, summer and spring of 2015. They found that the reanalyses got similar magnitudes for SHF and an order of magnitude difference in LHF, however the direction of the fluxes were often wrong. Thus, the inability to represent the sign and magnitude of the SHF and LHF is also present in reanalysis.

Our results have also shown that models have a positive bias in T_S-T_A and q_S-q_A when compared to observations, which may be related to the model representation of the strong wintertime surface-based inversions over sea ice. Arctic temperature inversions and associated near-surface variables are poorly represented in climate models (CMIP3: Medeiros et al., 2011; CMIP5: Pithan et al., 2014) and reanalyses (Serreze et al., 2012), and are influenced by how they simulate the stable boundary layer turbulence, surface energy budget, clouds, radiative transfer, and their vertical resolution (Lammert et al., 2010; Kilpeläinen et al., 2012). However, the accurate representation of these temperature and humidity inversions have important implications for the magnitude and sign of the turbulent fluxes (Bintanja et al., 2011; Devasthale et al., 2011; Vihma, 2014). These misrepresented temperature and humidity inversions could be contributing to biases in T_A and q_A, and would mean that the magnitude of T_S-T_A and q_S-q_A would be smaller and/or greater than zero depending on the situation, thus affecting the direction and magnitude of the fluxes in the Arctic.

Sea ice cover also influences the thermodynamic structure of the Arctic atmosphere by promoting more frequent temperature inversions, particularly in winter (Pavelsky et al., 2011; Taylor et al., 2015). Once sea ice forms in fall and winter, its lower effective heat capacity means the surface can cool more rapidly than the air above it leading to the development of temperature inversions, indicating a downward turbulent flux. Thus, how climate models represent the sea ice is very important, not just for the surface-based inversions, but also T_S and q_S and the boundary layer structure. However, climate models continue to struggle to represent sea ice cover extent and recent decline compared to observations (Schweiger et al., 2011; Stroeve J. et al., 2014; Holland et al., 2010; Jahn et al., 2012; SIMIP Community, 2020, Smith et al., 2020; Crawford et al., 2021; Watts et al., 2021; Figure 1), let alone the snow and ice thickness and surface characteristics. These sea ice and snow properties (e.g. location, compactness, roughness, and thickness) affect T_S and q_S, and the drag coefficients and roughness lengths, all which influence the boundary layer representation, and in turn the magnitude of the fluxes.

Observations are not free from bias, and the current limitations of satellite retrievals might contribute to the apparent model biases. For example, the vertical resolution of AIRS is 1 km and the instrument is therefore not able to resolve near surface variables (Susskind et al., 2014). In order to get the 2-m T_A and q_A variables, an iterative technique is used following Launiainen and Vihma (1990) to estimate these values from standard pressure levels using various boundary layer stability assumptions. These estimated T_A and q_A have been compared previously with in situ observations and have root mean square errors of 3.41 K and 0.54 g kg⁻¹, respectively, demonstrating that this iterative technique produces realistic results (Boisvert et al., 2015a; Taylor et al., 2018). Future satellite missions, as part of the Decadal Survey Planetary Boundary Layer, will work on having better resolution near the surface (Teixeira et al., 2021), which would improve the near surface temperature and humidity retrievals and reduce some of the errors in the fluxes.

Additionally, the observations might be biased towards clear sky or heterogeneous cloud cover conditions. Accurate retrievals can be derived for all channels under most cloud conditions, except for overcast or near-overcast conditions within the AIRS footprint Susskind et al. (2003), Susskind et al. (2014). Pithan et al. (2014) have shown that surface-based inversions were weaker during cloudy wintertime conditions than during clear conditions, and because under some extreme cloud conditions AIRS cannot retrieve variables, occurrences of smaller gradients in T_S-T_A and q_S-q_A might sometimes be missed. Regardless of these potential biases, AIRS captures wintertime Arctic temperature and humidity inversions well Devasthale et al. (2010), Devasthale et al. (2011).

While some CMIP6 ensemble member modeling groups have not made any changes to the turbulent flux scheme over sea ice (e.g. CESM2, Danabasoglu et al., 2020), others like the BCC-CSM2-MR have specifically made changes to improve these fluxes (Wu et al., 2019). Like the AIRS-derived scheme, they incorporate a gustiness parameterization, have updated the bulk parameterizations, changed the roughness lengths to be different based on season, and adopted the scalar roughness as a function of the Reynolds number. However, the gustiness parameterization used in BCC-CSM2-MR is one computed over the Western Pacific and tropical North Atlantic oceans (Zeng et al., 2002) and is not an Arctic sea ice specific parameterization that is different in stable and unstable conditions (Andreas et al., 2010b), which is adopted in the AIRS-derived scheme. The bulk parameterizations are taken from Zeng et al. (1998), which were produced using data from the tropical ocean, whereas in the AIRS-derived scheme, the bulk parameterizations are taken from Grachev et al. (2007), which were produced using SHEBA data and are specifically for Arctic sea ice. The roughness lengths do change according to T_S being < or > −2°C in BCC-CSM2-MR, but are fixed numbers and are the same for heat and moisture. The AIRS-derived scheme has varying roughness lengths by season, by ice concentration, and differs for heat and moisture following Andreas et al. (2010a), Andreas et al. (2010b). The sea ice thickness and concentration are simulated using a sea ice simulator (Winton, 2000) in BCC-CSM2-MR, which might not reproduce the same sea ice cycle and trends that are observed in observations. While these adjustments to the BCC-CSM2-MR turbulent flux scheme are an example of climate models trying to improve the flux estimates over sea ice, large differences between BCC-CSM2-MR and the AIRS-derived fluxes still exist (e.g. BCC-CSM2-MR LHF: 3.1 ± 5.06 W m⁻², SHF: −0.185 ± 8.31 W m²; AIRS-derived LHF: −3.1 ± 1.85, SHF: −31.8 ± 5.19 W m⁻²).

While there are some diagnostic analyses of the sensitivity of surface turbulent fluxes (e.g. Reeves Eyre et al., 2021), multiple studies have compared bulk algorithms over the global oceans (Zeng et al., 1998; Brunke et al., 2002; Brunke et al., 2006; Brodeau et al., 2016), and some bulk algorithm parameterizations have been compared over Arctic sea ice (Andreas, 2002; Brunke et al., 2006; Grachev et al., 2008; Lu et al., 2013), there does not appear to be large-scale sensitivity analysis of these fluxes undertaken specifically over the Arctic sea ice. The multi-linear regression approach described here appears to be a first attempt to consistently evaluate the causes of inter-model differences in the surface turbulent flux calculations. While the approach provides a means of intercomparing models, we think that it represents just the ‘tip of the iceberg’ and we encourage and are pursuing additional techniques.

Conclusion

The Arctic is rapidly warming; this warming is most pronounced near the surface and during the winter months and is expected to continue in the future. Recent works have attributed this surface-based warming to a loss in sea ice cover and an increase in surface turbulent fluxes. Currently, there are large inter-model spreads in present day sea ice loss, turbulent fluxes and wintertime warming. This uncertainty hinders our ability to predict the magnitude of future wintertime warming. Here we use observational AIRS-derived turbulent fluxes computed from an Arctic-specific turbulent flux scheme to assess CMIP6 models in the winter months (October-January) between 2002 and 2020 to constrain future projections of wintertime warming.

The results show that CMIP6 models represent the surface turbulent fluxes in the central Arctic differently from observations, as a heat source rather than a heat sink to the winter Arctic atmosphere like observations. CMIP6 models produce mostly positive fluxes (from the surface to the atmosphere) in winter, meaning that the surface temperature and humidity is consistently larger than that of the overlying air, even in areas of persistent sea ice cover. These biases are likely driven by the models’ inability to reproduce the strong surface-based inversions over the sea ice in the winter. The poor representation of these fluxes by climate models is a severe limitation to reducing uncertainties in projected Arctic warming. To evaluate model surface turbulent fluxes, a sea ice loss regime approach was used to account for the natural variability differences between climate models and observations. Both observations and models show that the turbulent fluxes have increased the most in areas of fast ice loss, whereas in areas of persistent ice cover there has been relatively little change.

When using a multiple regression approach to diagnose the influence of various controlling factors on surface turbulent flux variability, it was found that models exhibit much stronger sensitivities to a T_S-T_A anomaly than is found in observations. Models also exhibit a much weaker I_C damping effect than observations, suggesting that specific surface properties and characteristics associated with the sea ice surface type (e.g. strong stability) are represented differently between models compared to observations. Hence, the differences in observed and modeled surface turbulent fluxes is not solely due to parameterization differences. Differences in the air-sea temperature and moisture gradient distributions make a substantial contribution.

The magnitudes of differences of air-sea temperature and moisture gradients between observations and models is large, and is likely a driving factor in the magnitude of differences seen in the turbulent fluxes. One hypothesis for these differences is that models struggle to produce strong surface-based inversions over the sea ice in winter. Another hypothesis is that the models can not accurately parameterize the stable boundary layer characteristics over sea ice. While it remains difficult to pinpoint the exact causes of the differences between the models themselves and observations, due to the different turbulent flux schemes and representation of sea ice, future work should focus on understanding the driving factors for the differences.

There is a clear relationship between modeled trends in turbulent fluxes and sea ice loss with projected wintertime Arctic warming. Models that simulate larger surface turbulent flux trends and more sea ice loss show larger amounts of winter warming. Using trends in the observations to constrain these models, our results indicate that Arctic winter warming could fall within the range of ∼14–17 K in the Barents-Kara seas, compared to the unconstrained ∼10–21 K intermodel spread.

There is still a long road ahead to improve turbulent flux representation in the Arctic, especially over sea ice. These include: 1) turbulent flux schemes need to use more parameterizations that are ‘Arctic specific’ in order to represent the very stable boundary layer conditions over sea ice, particularly during the winter, 2) the representation of sea ice and snow properties and characteristics (e.g. snow and ice thickness, roughness, concentration, floe size distribution) need to be improved so that the surface drag coefficients and roughness lengths can be accurately assessed and surface and near surface variables can more closely match observed values, 3) spatial and vertical resolution of climate models and satellite observations need to increase so that the boundary layer and sub-grid scale processes that are not currently resolved can be simulated, and 4) better collaboration between those taking the measurements and those who produce the models.

Recent field campaigns, such as MOSAiC, provide valuable measurements for use in improving these turbulent flux parameterizations in the Arctic. We can use these measurements to build upon what was learned from the SHEBA campaign more than 20 years ago. The future Decadal Survey mission, aimed to improve our understanding of the planetary boundary layer, will increase the vertical resolution from satellites, thus enhancing our retrievals of these near surface variables. These current and future measurements could significantly improve the representation of surface turbulent fluxes in the Arctic and hence Arctic wintertime warming.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author. AIRS data can be downloaded from https://airs.jpl.nasa.gov/data/get-data/standard-data/. MERRA-2 data can be downloaded from https://gmao.gsfc.nasa.gov/reanalysis/MERRA-2/data_access/. ERA-5 data can be downloaded from https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era5. AIRS-derived turbulent heat fluxes can be distributed upon request to L. Boisvert. CMIP6 data can be downloaded from https://esgfnode.llnl.gov/.

Author Contributions

LB wrote the paper, edited the paper and provided analysis of the data, RB helped to write and edit the paper, and produce the figures. PT helped in idea development, writing and editing of the manuscript. CP helped in writing and editing of the paper.

Funding

The work of LB, RB, PT, and CP was funded by NASA IDS Project “Investigating the Fate of Sea Ice and its Interaction with the Atmosphere in the New Arctic” (grant number 80NSSC21K0264).

Conflict of Interest

RB was employed by the company Science Systems and Applications, Inc.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would also like to thank the two reviewers for their feedback and suggestions.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.765304/full#supplementary-material

References

Allan, D., and Allan, R. P. (2019). Seasonal Changes in the North Atlantic Cold Anomaly: The Influence of Cold Surface Waters from Coastal Greenland and Warming Trends Associated with Variations in Subarctic Sea Ice Cover. J. Geophys. Res. Oceans 124 (12), 9040–9052. doi:10.1029/2019JC015379

CrossRef Full Text | Google Scholar

Andreas, E. L., Horst, T. W., Grachev, A. A., Persson, P. O. G., Fairall, C. W., Guest, P. S., et al. (2010a). Parametrizing Turbulent Exchange over Summer Sea Ice and the Marginal Ice Zone. Q.J.R. Meteorol. Soc. 136, 927–943. doi:10.1002/jq.61810.1002/qj.618

CrossRef Full Text | Google Scholar

Andreas, E. L. (2002). Parameterizing Scalar Transfer over Snow and Ice: A Review. J. Hydrometeor 3, 417–432. doi:10.1175/1525-7541(2002)003<0417:pstosa>2.0.co;2

CrossRef Full Text | Google Scholar

Andreas, E. L., Persson, P. O. G., Grachev, A. A., Jordan, R. E., Horst, T. W., Guest, P. S., et al. (2010b). Parameterizing Turbulent Exchange over Sea Ice in Winter. J. Hydrometeorology 11, 87–104. doi:10.1175/2009JHM1102.1

CrossRef Full Text | Google Scholar

Bintanja, R., Graversen, R. G., and Hazeleger, W. (20112011). Arctic winter Warming Amplified by the thermal Inversion and Consequent Low Infrared Cooling to Space. Nat. Geosci 4, 758–761. doi:10.1038/ngeo1285

CrossRef Full Text | Google Scholar

Bodas-Salcedo, A., Webb, M. J., Bony, S., Chepfer, H., Dufresne, J.-L., Klein, S. A., et al. (2011). COSP: Satellite Simulation Software for Model Assessment. Bull. Am. Meteorol. Soc. 92 (8), 1023–1043. doi:10.1175/2011BAMS2856.1

CrossRef Full Text | Google Scholar

Boeke, R. C., and Taylor, P. C. (2018). Seasonal Energy Exchange in Sea Ice Retreat Regions Contributes to Differences in Projected Arctic Warming. Nat. Commun. 9, 5017. doi:10.1038/s41467-018-07061-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Boeke, R. C., Taylor, P. C., and Sejas, S. A. (2021). On the Nature of the Arctic's Positive Lapse-Rate Feedback. Geophys. Res. Lett. 48, e2020GL091109. doi:10.1029/2020GL091109

CrossRef Full Text | Google Scholar

Boisvert, L. N., Markus, T., and Vihma, T. (2013). Moisture Flux Changes and Trends for the Entire Arctic in 2003-2011 Derived from EOS Aqua Data. J. Geophys. Res. Oceans 118, 5829–5843. doi:10.1002/jgrc.20414

CrossRef Full Text | Google Scholar

Boisvert, L. N., Wu, D. L., and Shie, C.-L. (2015b). Increasing Evaporation Amounts Seen in the Arctic between 2003 and 2013 from AIRS Data. J. Geophys. Res. Atmos. 120, 6865–6881. doi:10.1002/2015JD023258

CrossRef Full Text | Google Scholar

Boisvert, L. N., Wu, D. L., Vihma, T., and Susskind, J. (2015a). Verification of Air/surface Humidity Differences from AIRS and ERA-Interim in Support of Turbulent Flux Estimation in the Arctic. J. Geophys. Res. Atmos. 120, 945–963. doi:10.1002/2014JD021666

CrossRef Full Text | Google Scholar

Boucher, O., Denvil, S., Levavasseur, G., Cozic, A., Caubel, A., Foujols, M.-A., et al. (2021). IPSL IPSL-Cm6a-LR-INCA Model Output Prepared for CMIP6 CMIP Historical. Version r1i1p1f1 [1]. Earth System Grid Federation. doi:10.22033/ESGF/CMIP6.13601

CrossRef Full Text | Google Scholar

Bourassa, M. A., Gille, S. T., Bitz, C., Carlson, D., Cerovecki, I., Clayson, C. A., et al. (2013). High-Latitude Ocean and Sea Ice Surface Fluxes: Challenges for Climate Research. Bull. Amer. Meteorol. Soc. 94 (3), 403–423. doi:10.1175/BAMS-D-11-00244.1

CrossRef Full Text | Google Scholar

Brodeau, L., Barnier, B., Gulev, S. K., and Woods, (2017). Climatologically Significant Effects of Some Approximations in the Bulk Parameterizations of Turbulent Air-Sea Fluxes. J. Phys. Oceanogr. 47, 5–28. doi:10.1175/JPO-D-16-0169.1

CrossRef Full Text | Google Scholar

Brunke, M. A., Zeng, X., and Anderson, S. (2002). Uncertainties in Sea Surface Turbulent Flux Algorithms and Data Sets. J. Geophys. Res. 107, 5–1–5–21. doi:10.1029/2001JC000992

CrossRef Full Text | Google Scholar

Brunke, M. A., Zhou, M., Zeng, X., and Andreas, E. L. (2006). An Intercomparison of Bulk Aerodynamic Algorithms Used over Sea Ice with Data from the Surface Heat Budget for the Arctic Ocean (SHEBA) experiment. J. Geophys. Res. 111. doi:10.1029/2005JC002907

CrossRef Full Text | Google Scholar

Burt, M. A., Randall, D. A., and Branson, M. D. (2016). Dark Warming. J. Clim. 29 (2), 705–719. doi:10.1175/JCLI-D-15-0147.1

CrossRef Full Text | Google Scholar

Cao, J., and Wang, B. (2019). NUIST NESMv3 Model Output Prepared for CMIP6 CMIP Historical. Version r1i1p1f1[1]. Earth System Grid Federation. doi:10.22033/ESGF/CMIP6.8769

CrossRef Full Text | Google Scholar

Cavalieri, D. J., Crawford, J., Drinkwater, M., Emery, W. J., Eppler, D. T., Farmer, L. D., et al. (1992). NASA Sea Ice Validation Program for the DMSP SSM/I: Final Report, NASA Technical Memorandum 104559. Washington, D. C.: National Aeronautics and Space Administration, 126.

Google Scholar

Cavalieri, D. J., and Parkinson, C. L. (2012). Arctic Sea Ice Variability and Trends, 1979-2010. The Cryosphere 6, 881–889. doi:10.5194/tc-6-881-2012

CrossRef Full Text | Google Scholar

Cavalieri, D. J., Parkinson, C. L., Gloersen, P., and Zwally, H. (1996). Sea Ice Concentrations from Nimbus-7 SMMR and DMSP SSM/I-SSMIS Passive Microwave DataNASA DAAC at the Natl. Snow and Ice Data Cent. Boulder, Colo. [Updated yearly.

Google Scholar

Community, D. S. (2020). Arctic Sea Ice in CMIP6. Geophys. Res. Lett. 47. doi:10.1029/2019gl086749

CrossRef Full Text | Google Scholar

Crawford, A., Stroeve, J., Smith, A., and Jahn, A. (2021). Arctic Open-Water Periods Are Projected to Lengthen Dramatically by 2100. Commun. Earth Environ. 2, 109. doi:10.1038/s43247-021-00183-x

CrossRef Full Text | Google Scholar

Cullather, R. I., and Bosilovich, M. G. (2012). The Energy Budget of the Polar Atmosphere in MERRA. J. Clim. 25, 5–24. doi:10.1175/2011JCLI4138.1

CrossRef Full Text | Google Scholar

Dai, A., Luo, D., Song, M., and Liu, J. (2019). Arctic Amplification Is Caused by Sea-Ice Loss under Increasing CO2. Nat. Commun. 10, 121. doi:10.1038/s41467-018-07954-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Danabasoglu, G., Lamarque, J. F., Bacmeister, J., Bailey, D. A., DuVivier, A. K., Edwards, J., et al. (2020). The Community Earth System Model Version 2 (CESM2). J. Adv. Model. Earth Syst. 12 (2). doi:10.1029/2019MS001916

CrossRef Full Text | Google Scholar

Danabasoglu, G. (2019). NCAR CESM2 Model Output Prepared for CMIP6 CMIP Amip. Earth System Grid Federation. doi:10.22033/ESGF/CMIP6.7522

CrossRef Full Text | Google Scholar

Davy, R., and Outten, S. (2020). The Arctic Surface Climate in CMIP6: Status and Developments since CMIP5. J. Clim. 33 (18), 8047–8068. doi:10.1175/JCLI-D-19-0990.1

CrossRef Full Text | Google Scholar

Deser, C., Tomas, R., Alexander, M., and Lawrence, D. (2010). The Seasonal Atmospheric Response to Projected Arctic Sea Ice Loss in the Late Twenty-First Century. J. Clim. 23, 333–351. doi:10.1175/2009JCLI3053.1

CrossRef Full Text | Google Scholar

Devasthale, A., Sedlar, J., and Tjernström, M. (2011). Characteristics of Water-Vapour Inversions Observed over the Arctic by Atmospheric Infrared Sounder (AIRS) and Radiosondes. Atmos. Chem. Phys. 11, 9813–9823. doi:10.5194/acp-11-9813-2011

CrossRef Full Text | Google Scholar

Devasthale, A., Willén, U., Karlsson, K.-G., and Jones, C. G. (2010). Quantifying the clear-sky Temperature Inversion Frequency and Strength over the Arctic Ocean during Summer and winter Seasons from AIRS Profiles. Atmos. Chem. Phys. 10, 5565–5572. doi:10.5194/acp-10-5565-2010

CrossRef Full Text | Google Scholar

Dix, M. (2019). CSIRO-ARCCSS ACCESS-CM2 Model Output Prepared for CMIP6 CMIP Historical. Version r1i1p1f1[1]. Earth System Grid Federation. doi:10.22033/ESGF/CMIP6.4271

CrossRef Full Text | Google Scholar

Eyring, V., Bony, S., Meehl, G. A., Senior, C. A., Stevens, B., Stouffer, R. J., et al. (2016). Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) Experimental Design and Organization. Geosci. Model. Dev. 9, 1937–1958. doi:10.5194/gmd-9-1937-2016

CrossRef Full Text | Google Scholar

Gelaro, R., Suárez, W. M. J., Todling, R., Molod, A., Takacs, L., Randles, C. A., et al. (2017). The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 30, 5419–5454. doi:10.1175/JCLI-D-16-0758.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Grachev, A. A., Andreas, E. L., Fairall, C. W., Guest, P. S., and Persson, P. O. G. (2007). SHEBA Flux-Profile Relationships in the Stable Atmospheric Boundary Layer. Boundary-layer Meteorol. 124, 315–333. doi:10.1007/s10546-007-9177-6

CrossRef Full Text | Google Scholar

Grachev, A. A., Andreas, E. L., Fairall, C. W., Guest, P. S., and Persson, P. O. G. (2008). Turbulent Measurements in the Stable Atmospheric Boundary Layer during SHEBA: Ten Years after. Acta Geophys. 56 (1), 142–166. doi:10.2478/s11600-007-0048-9

CrossRef Full Text | Google Scholar

Graham, R. M., Cohen, L., Ritzhaupt, N., Segger, B., Graversen, R. G., Rinke, A., et al. (2019). Evaluation of Six Atmospheric Reanalyses over Arctic Sea Ice from Winter to Early Summer. J. Clim. 32 (14), 4121–4143. doi:10.1175/JCLI-D-18-0643.1

CrossRef Full Text | Google Scholar

Holland, M. M., Serreze, M. C., and Stroeve, J. (2010). The Sea Ice Mass Budget of the Arctic and its Future Change as Simulated by Coupled Climate Models. Clim. Dyn. 34, 185–200. doi:10.1007/s00382-008-0493-4

CrossRef Full Text | Google Scholar

Holtslag, A. A. M., and de Bruin, H. A. R. (1988). Applied Modeling of the Nighttime Surface Energy Balance over Land. J. Appl. Meteorol. 27, 689–704. doi:10.1175/1520-0450(1988)027<0689:amotns>2.0.co;2

CrossRef Full Text | Google Scholar

Intergovernmental Panel on Climate Change (IPCC) (2013). Annex I: Atlas of Global and Regional Climate Projections.

Google Scholar

Jahn, A., Sterling, K., Holland, M. M., Kay, J. E., Maslanik, J. A., Bitz, C. M., et al. (2012). Late-Twentieth-Century Simulation of Arctic Sea Ice and Ocean Properties in the CCSM4. J. Clim. 25 (5), 1431–1452. doi:10.1175/JCLI-D-11-00201.1

CrossRef Full Text | Google Scholar

Jakobson, E., Vihma, T., Palo, T., Jakobson, L., Keernik, H., and Jaagus, J. (2012). Validation of Atmospheric Reanalyses over the central Arctic Ocean. Geophys. Res. Lett. 39, a–n. doi:10.1029/2012GL051591

CrossRef Full Text | Google Scholar

Jungclaus, J. (2019). MPI-M MPI-ESM1.2-HR Model Output Prepared for CMIP6 CMIP Historical. Version r1i1p1f1[1]. Earth System Grid Federation. doi:10.22033/ESGF/CMIP6.6594

CrossRef Full Text | Google Scholar

Kay, J. E., Holland, M. M., Bitz, C. M., Blanchard-Wrigglesworth, E., Gettelman, A., Conley, A., et al. (2012). The Influence of Local Feedbacks and Northward Heat Transport on the Equilibrium Arctic Climate Response to Increased Greenhouse Gas Forcing. J. Clim. 25 (16), 5433–5450. doi:10.1175/JCLI-D-11-00622.1

CrossRef Full Text | Google Scholar

Kilpeläinen, T., Vihma, T., Manninen, M., Sjöblom, A., Jakobson, E., Palo, T., et al. (2012). Modelling the Vertical Structure of the Atmospheric Boundary Layer over Arctic Fjords in Svalbard. Q.J.R. Meteorol. Soc. 138, 1867–1883. doi:10.1002/qj.1914

CrossRef Full Text | Google Scholar

Krasting, J. P., John, J. G., Blanton, C., McHugh, C., Nikonov, S., Radhakrishnan, A., et al. (2018). NOAA-GFDL GFDL-ESM4 Model Output Prepared for CMIP6 CMIP Historical. Version YYYYMMDD[1]. Earth System Grid Federation. doi:10.22033/ESGF/CMIP6.8597

CrossRef Full Text | Google Scholar

Kwok, R. (2018). Arctic Sea Ice Thickness, Volume, and Multiyear Ice Coverage: Losses and Coupled Variability (1958-2018). Environ. Res. Lett. 13 (10), 105005. doi:10.1088/1748-9326/aae3ec

CrossRef Full Text | Google Scholar

Lammert, A., Brümmer, B., Haller, M., Müller, G., and Schyberg, H. (2010). Comparison of Three Weather Prediction Models with Buoy and Aircraft Measurements under Cyclone Conditions in Fram Strait. Tellus A 62, 361–376. doi:10.1111/j.1600-0870.2010.00460.x

CrossRef Full Text | Google Scholar

Launiainen, J., and Vihma, T. (1990). Derivation of Turbulent Surface Fluxes - an Iterative Flux-Profile Method Allowing Arbitrary Observing Heights. Environ. Softw. 5, 113–124. doi:10.1016/0266-9838(90)90021-W

CrossRef Full Text | Google Scholar

Li, L. (2019). CAS FGOALS-G3 Model Output Prepared for CMIP6 CMIP Historical. Version YYYYMMDD[1]. Earth System Grid Federation. doi:10.22033/ESGF/CMIP6.3356

CrossRef Full Text | Google Scholar

Lu, Y., Zhou, M., and Wu, T. (2013). Validation of Parameterizations for the Surface Turbulent Fluxes over Sea Ice with CHINARE 2010 and SHEBA Data. Polar Res. 32, 20818. doi:10.3402/polar.v32i0.20818

CrossRef Full Text | Google Scholar

Lüpkes, C., Vihma, T., Birnbaum, G., and Wacker, U. (2008a). Influence of Leads in Sea Ice on the Temperature of the Atmospheric Boundary Layer during Polar Night. Geophys. Res. Lett. 35, L03805. doi:10.1029/2007GL032461

CrossRef Full Text | Google Scholar

Markus, T., Stroeve, J. C., and Miller, J. (2009). Recent Changes in Arctic Sea Ice Melt Onset, Freezeup, and Melt Season Length. J. Geophys. Res. 114 (C12). doi:10.1029/2009JC005436

CrossRef Full Text | Google Scholar

Medeiros, B., Deser, C., Tomas, R. A., and Kay, J. E. (2011). Arctic Inversion Strength in Climate Models. J. Clim. 24 (17), 4733–4740. doi:10.1175/2011JCLI3968.1

CrossRef Full Text | Google Scholar

Parkinson, C. L., and DiGirolamo, N. E. (2016). New Visualizations Highlight New Information on the Contrasting Arctic and Antarctic Sea-Ice Trends since the Late 1970s. Remote Sensing Environ. 183, 198–204. doi:10.1016/j.rse.2016.05.020

CrossRef Full Text | Google Scholar

Pavelsky, T. M., Boé, J., Hall, A., and Fetzer, E. J. (2011). Atmospheric Inversion Strength over Polar Oceans in winter Regulated by Sea Ice. Clim. Dyn. 36, 945–955. doi:10.1007/s00382-010-0756-8

CrossRef Full Text | Google Scholar

Persson, P. O. G., Shupe, M. D., and Solomon, A. (2017). Linking Atmospheric Synoptic Transport, Cloud Phase, Surface Energy Fluxes, and Sea-Ice Growth: Observations of Midwinter SHEBA Conditions. Clim. Dyn. 49, 1341–1364. doi:10.1007/s00382-016-3383-1

CrossRef Full Text | Google Scholar

Pithan, F., Medeiros, B., and Mauritsen, T. (2014). Mixed-phase Clouds Cause Climate Model Biases in Arctic Wintertime Temperature Inversions. Clim. Dyn. 43 (1-2), 289–303. doi:10.1007/s00382-013-1964-9

CrossRef Full Text | Google Scholar

Ramsey, F., and Schafer, D. (2012). The Statistical Sleuth: A Course in Methods of Data Analysis. 2nd Edition. Pacific Grove: Wadsworth Group.

Google Scholar

Reeves Eyre, J. E. J., Zeng, X., and Zhang, K. (2021). Ocean Surface Flux Algorithm Effects on Earth System Model Energy and Water Cycles. Front. Mar. Sci. 8. doi:10.3389/fmars.2021.642804

CrossRef Full Text | Google Scholar

Renfrew, I. A., Barrell, C., Elvidge, A. D., Brooke, J. K., Duscha, C., King, J. C., et al. (2021). An Evaluation of Surface Meteorology and Fluxes over the Iceland and Greenland Seas in ERA5 Reanalysis: The Impact of Sea Ice Distribution. Q. J. R. Meteorol. Soc. 147, 691–712. doi:10.1002/qj.3941

CrossRef Full Text | Google Scholar

Schweiger, A., Lindsay, R., Zhang, J., Steele, M., Stern, H., and Kwok, R. (2011). Uncertainty in Modeled Arctic Sea Ice Volume. J. Geophys. Res. 116 (C8). doi:10.1029/2011JC007084

CrossRef Full Text | Google Scholar

Screen, J. A., Deser, C., and Simmonds, I. (2012). Local and Remote Controls on Observed Arctic Warming. Geophys. Res. Lett. 39 (10), a–n. doi:10.1029/2012GL051598

CrossRef Full Text | Google Scholar

Screen, J. A., Simmonds, I., Deser, C., and Tomas, R. (2013). The Atmospheric Response to Three Decades of Observed Arctic Sea Ice Loss. J. Clim. 26 (4), 1230–1248. doi:10.1175/JCLI-D-12-00063.1

CrossRef Full Text | Google Scholar

Screen, J. A., and Simmonds, I. (2010b). Increasing Fall-winter Energy Loss from the Arctic Ocean and its Role in Arctic Temperature Amplification. Geophys. Res. Lett. 37 (16), a–n. doi:10.1029/2010GL044136

CrossRef Full Text | Google Scholar

Screen, J. A., and Simmonds, I. (2010a). The central Role of Diminishing Sea Ice in Recent Arctic Temperature Amplification. Nature 464, 1334–1337. doi:10.1038/nature09051

PubMed Abstract | CrossRef Full Text | Google Scholar

Sejas, S. A., and Cai, M. (2016). Isolating the Temperature Feedback Loop and its Effects on Surface Temperature. J. Atmos. Sci. 73 (8), 3287–3303. doi:10.1175/JAS-D-15-0287.1

CrossRef Full Text | Google Scholar

Serreze, M. C., Barrett, A. P., Stroeve, J. C., Kindig, D. N., and Holland, M. M. (2009). The Emergence of Surface-Based Arctic Amplification. The Cryosphere 3, 11–19. doi:10.5194/tc-3-11-2009

CrossRef Full Text | Google Scholar

Serreze, M. C., Barrett, A. P., and Stroeve, J. (2012). Recent Changes in Tropospheric Water Vapor over the Arctic as Assessed from Radiosondes and Atmospheric Reanalyses. J. Geophys. Res. 117, a–n. doi:10.1029/2011jd017421

CrossRef Full Text | Google Scholar

Shiogama, H., Abe, M., and Tatebe, H. (2019). MIROC MIROC6 Model Output Prepared for CMIP6 ScenarioMIP Ssp585. Earth System Grid Federation. doi:10.22033/ESGF/CMIP6.898

CrossRef Full Text | Google Scholar

Smith, A., Jahn, A., and Wang, M. (2020). Seasonal Transition Dates Can Reveal Biases in Arctic Sea Ice Simulations. The Cryosphere 14, 2977–2997. doi:10.5194/tc-14-2977-2020

CrossRef Full Text | Google Scholar

Song, Z., Qiao, F., Bao, Y., Shu, Q., Song, Y., and Yang, X. (2019). FIO-QLNM FIO-ESM2.0 Model Output Prepared for CMIP6 CMIP piControl. Version YYYYMMDD[1]. Earth System Grid Federation. doi:10.22033/ESGF/CMIP6.9205

CrossRef Full Text | Google Scholar

Steele, M., Ermold, W., and Zhang, J. (2008). Arctic Ocean Surface Warming Trends over the Past 100 Years. Geophys. Res. Lett. 35 (2). doi:10.1029/2007GL031651

CrossRef Full Text | Google Scholar

Stroeve, J., Barrett, A., Serreze, M., and Schweiger, A. (2014a). Using Records from Submarine, Aircraft and Satellites to Evaluate Climate Model Simulations of Arctic Sea Ice Thickness. The Cryosphere 8, 1839–1854. doi:10.5194/tc-8-1839-2014

CrossRef Full Text | Google Scholar

Stroeve, J. C., Markus, T., Boisvert, L., Miller, J., and Barrett, A. (2014). Changes in Arctic Melt Season and Implications for Sea Ice Loss. Geophys. Res. Lett. 41 (4), 1216–1225. doi:10.1002/2013GL058951

CrossRef Full Text | Google Scholar

Stroeve, J., and Notz, D. (2018). Changing State of Arctic Sea Ice across All Seasons. Environ. Res. Lett. 13 (10), 103001. doi:10.1088/1748-9326/aade56

CrossRef Full Text | Google Scholar

Susskind, J., Barnet, C. D., and Blaisdell, J. M. (2003). Retrieval of Atmospheric and Surface Parameters from AIRS/AMSU/HSB Data in the Presence of Clouds. IEEE Trans. Geosci. Remote Sensing 41 (2), 390–409. doi:10.1109/TGRS.2002.808236

CrossRef Full Text | Google Scholar

Susskind, J., Blaisdell, J. M., and Iredell, L. (2014). Improved Methodology for Surface and Atmospheric Soundings, Error Estimates, and Quality Control Procedures: The Atmospheric Infrared Sounder Science Team Version-6 Retrieval Algorithm. J. Appl. Remote Sens 8 (1), 084994. doi:10.1117/1.JRS.8.084994

CrossRef Full Text | Google Scholar

Swart, N. C., Cole, J. N. S., Kharin, V. V., Lazare, M., Scinocca, J. F., Gillett, N. P., et al. (2019). CCCma CanESM5 Model Output Prepared for CMIP6 ScenarioMIP Ssp126. Version YYYYMMDD[1]. Earth System Grid Federation. doi:10.22033/ESGF/CMIP6.3683

CrossRef Full Text | Google Scholar

Taylor, P. C., Kato, S., Xu, K. M., and Cai, M. (2015). Covariance between Arctic Sea Ice and Clouds within Atmospheric State Regimes at the Satellite Footprint Level. J. Geophys. Res. Atmos. 120 (24), 12656–12678. doi:10.1002/2015JD023520

CrossRef Full Text | Google Scholar

Taylor, P., Hegyi, B., Boeke, R., and Boisvert, L. (2018). On the Increasing Importance of Air-Sea Exchanges in a Thawing Arctic: A Review. Atmosphere 9 (2), 41. doi:10.3390/atmos9020041

CrossRef Full Text | Google Scholar

Teixeira, J., Piepmeier, J. R., Nehrir, A. R., Ao, C. O., Chen, S. S., Clayson, C. A., et al. (2021). Toward a Global Planetary Boundary Layer Observing System: The NASA PBL Incubation Study Team Report. NASA PBL Incubation Study Team, 134.

Google Scholar

Vihma, T. (2014). Effects of Arctic Sea Ice Decline on Weather and Climate: A Review. Surv. Geophys. 35 (5), 1175–1214. doi:10.1007/s10712-014-9284-0

CrossRef Full Text | Google Scholar

Volodin, E., Mortikov, E., Gritsun, A., Lykossov, V., Galin, V., Diansky, N., et al. (2019). INM INM-CM4-8 Model Output Prepared for CMIP6 CMIP piControl. Version YYYYMMDD[1]. Earth System Grid Federation. doi:10.22033/ESGF/CMIP6.5080

CrossRef Full Text | Google Scholar

Walden, V. P., Hudson, S. R., Cohen, L., Murphy, S. Y., and Granskog, M. A. (2017). Atmospheric Components of the Surface Energy Budget over Young Sea Ice: Results from the N-Ice2015 Campaign. J. Geophys. Res. Atmos. 122 (16), 8427–8446. doi:10.1002/2016JD026091

CrossRef Full Text | Google Scholar

Watts, M., Maslowski, W., Lee, Y. J., Kinney, J. C., and Osinski, R. (2021). A Spatial Evaluation of Arctic Sea Ice and Regional Limitations in CMIP6 Historical Simulations. J. Clim., 1–54. doi:10.1175/jcli-d-20-0491.1

CrossRef Full Text | Google Scholar

Wieners, K.-H. (2019). MPI-M MPI-ESM1.2-LR Model Output Prepared for CMIP6 CMIP Historical. Version r1i1p1f1[1]. Earth System Grid Federation. doi:10.22033/ESGF/CMIP6.6595

CrossRef Full Text | Google Scholar

Wild, M. (2020). The Global Energy Balance as Represented in CMIP6 Climate Models. Clim. Dyn. 55, 553–577. doi:10.1007/s00382-020-05282-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Winton, M. (2000). A Reformulated Three-Layer Sea Ice Model. J. Atmos. Oceanic Technol.CO 17 (4), 5252–5531. doi:10.1175/1520-0426(2000)017<0525:ARTLSI>2.010.1175/1520-0426(2000)017<0525:artlsi>2.0.co;2

CrossRef Full Text | Google Scholar

Wu, T., Chu, M., Dong, M., Fang, Y., Jie, W., Li, J., et al. (2018). BCC BCC-Csm2mr Model Output Prepared for CMIP6 CMIP Historical. Version r1i1p1f1 [1]. Earth System Grid Federation. doi:10.22033/ESGF/CMIP6.2948

CrossRef Full Text | Google Scholar

Wu, T., Lu, Y., Fang, Y., Xin, X., Li, L., Li, W., et al. (2019). The Beijing Climate Center Climate System Model (BCC-CSM): the Main Progress from CMIP5 to CMIP6. Geosci. Model. Dev. 12, 1573–1600. doi:10.5194/gmd-12-1573-2019

CrossRef Full Text | Google Scholar

Yu, L., Yang, Q., Zhou, M., Zeng, X., Lenschow, D. H., Wang, X., et al. (2019). The Intraseasonal and Interannual Variability of Arctic Temperature and Specific Humidity Inversions. Atmosphere 10 (4), 214. doi:10.3390/atmos10040214

CrossRef Full Text | Google Scholar

Yu, Y. (2019). CAS FGOALS-F3-L Model Output Prepared for CMIP6 CMIP Historical. Version YYYYMMDD[1]. Earth System Grid Federation. doi:10.22033/ESGF/CMIP6.3355

CrossRef Full Text | Google Scholar

Yukimoto, , Koshiro, S. T., Kawai, H., Oshima, N., Yoshida, K., Urakawa, S., et al. (2019). MRI MRI-ESM2.0 Model Output Prepared for CMIP6 CMIP Historical. Version r1i1p1f1 [1]. Earth System Grid Federation. doi:10.22033/ESGF/CMIP6.6842

CrossRef Full Text | Google Scholar

Zeng, X., Zhang, Q., Johnson, D., and Tao, W.-K. (2002). Parameterization of Wind Gustiness for the Computation of Ocean Surface Fluxes at Different Spatial Scales. Mon. Wea. Rev. 130 (8), 2125–2133. doi:10.1175/1520-0493(2002)130<2125:powgft>2.0.co;2

CrossRef Full Text | Google Scholar

Zeng, X., Zhao, M., and Dickinson, R. E. (1998). Intercomparison of Bulk Aerodynamic Algorithms for the Computation of Sea Surface Fluxes Using TOGA COARE and TAO Data. J. Clim. 11 (10), 2628–2644. doi:10.1175/1520-0442(1998)011<2628:iobaaf>2.0.co;2

CrossRef Full Text | Google Scholar

Zheng, J., Zhang, Q., Li, Q., Zhang, Q., and Cai, M. (2019). Contribution of Sea Ice Albedo and Insulation Effects to Arctic Amplification in the EC-Earth Pliocene Simulation. Clim. Past 15, 291–305. doi:10.5194/cp-15-291-2019

CrossRef Full Text | Google Scholar

Ziehn, T., Chamberlain, M., Lenton, A., Law, R., Bodman, R., Dix, M., et al. (2019). CSIRO ACCESS-ESM1.5 Model Output Prepared for CMIP6 ScenarioMIP Ssp245. Version YYYYMMDD[1]. Earth System Grid Federation. doi:10.22033/ESGF/CMIP6.4322

CrossRef Full Text | Google Scholar

Zilitinkevich, S. S., and Esau, I. N. (2007). “Similarity Theory and Calculation of Turbulent Fluxes at the Surface for the Stably Stratified Atmospheric Boundary Layer,” in Atmospheric Boundary Layers. Editors A. Baklanov, and B. Grisogono (New York, NY: Springer). doi:10.1088/0143-0807/27/4/007

CrossRef Full Text | Google Scholar