Constraining Morphologies of Soft Tissues in Extinct Vertebrates Using Multibody Dynamic Simulations: A Case Study on Articular Cartilage of the Sauropod Dreadnoughtus

Rarity of soft tissue preservation, including of articular cartilage, in the fossil record hinders creation of biologically-realistic mechanical models. Previous studies of articular cartilage in extant taxa have documented important aspects of cartilage shapes and thicknesses, but these insights remain generalized and have yet to see systematic implementation in biomechanical modeling. Herein, we present a new method for modeling joints that allows for testing of hypotheses about articular cartilage morphology in extinct taxa. Our case study examines the left elbow joint of the sauropod dinosaur Dreadnoughtus schrani using articular cartilage reconstructions constrained by extant phylogenetic bracketing (EPB). EPB investigations of alligator and chicken articular cartilage revealed the presence of a spherical anterior projection of cartilage on the distal humerus which articulates with the radius during flexion. Importantly, this shape does not directly mirror the underlying bone. Using multibody dynamic models created in Adams™ without a priori restrictions on joint degrees of freedom, we simulated the effects of three alternative cartilage reconstructions based on these EPB findings which differ in mediolateral placement of a cartilage sphere and its anteroposterior thickness, encompassing a range of possibilities for the condition in Dreadnoughtus. Bone kinematics and contact area (calculated in Geomagic^®) were tracked. Additionally, we modeled the elbow of an alligator and turkey using the same methodology and compared the results to XROMM (X-ray Reconstruction of Moving Morphology) analysis of the same limbs. Each model produced distinct results but were generally similar supporting our modeling methodology. Based on these findings, we predict that Dreadnoughtus, and presumably other extinct archosaurs, had a spherical projection of cartilage on the anterior face of the distal end of the humerus for articulation with the radius. Though many valuable insights have been gained by existing modeling methodologies, we chose a different approach that focused on joint contact surfaces. Moreover, applying our methods within a quantitative hypothesis-testing framework can advance the field of paleobiology by testing hypotheses relating shape and kinematics that are not possible with prescribed joint motions.

Introduction

Reconstructing the paleobiology of extinct organisms is difficult due to a frequent lack of preserved soft tissues (Schweitzer, 2011) and, by definition, living specimens. One such type of soft tissue that is rarely preserved in the fossil record but of critical importance toward understanding the functional morphology and biomechanics of extinct vertebrates is articular cartilage. Except for a few noteworthy specimens (e.g., Schwarz et al., 2007; Mallison, 2010b; Bailleul et al., 2020; de Cerff et al., 2020), the vast majority of dinosaurian articular cartilage does not preserve in the fossil record (Chinsamy-Turan, 2005). This is problematic for locomotion studies on these organisms as the articulating joint surfaces are thus not preserved and fossilized bones do not necessarily retain the same morphology as original articulating surfaces of the joint cartilage (Bonnan et al., 2010; Holliday et al., 2010). On the rare occasion of cartilage preservation, the effects of fossilization on its material properties (Rayfield, 2007) and morphology (Mallison, 2010b) are likely be substantial. Despite these challenges, previous attempts to reconstruct the articular cartilage of dinosaurs have drawn comparisons with both taxa comprising the Extant Phylogenetic Bracket (EPB; sensu Witmer, 1995) of dinosaurs (e.g., Bonnan et al., 2010, 2013; Fujiwara et al., 2010; Holliday et al., 2010; Tsai et al., 2018; Senter and Sullivan, 2019) and mammals (Coombs, 1975; Bonnan et al., 2013).

One aspect of articular cartilage morphology that has received significant attention is its thickness (Bonnan et al., 2010, 2013; Holliday et al., 2010). Specifically, Holliday et al. (2010) reported percent change in dimensions before and after the removal of articular cartilage from various limb bones belonging to several extant taxa. They reported numerous instances of significant change for various measurements of the same element, which are important because they suggest that the examined cartilage is not of a uniform thickness across the bone. Of additional importance to our study, Holliday et al. (2010) found a significant difference between the anteroposterior breadth of the distal humeral condyles when articular cartilage was present versus when only the underlying bone was measured in three of the five archosaurian taxa they investigated. Similarly, Bonnan et al. (2010) found greater variation in the general shape of articular cartilage compared to the underlying bone surface (as identified with two-dimensional morphometrics) in humeri than femora, and suggested this may result from greater stresses being placed on the femur, causing its bony and cartilaginous surfaces to become more similar in shape. Together, these finding suggest that articular cartilage does not exhibit a consistent thickness over the entire epiphyseal ends of all limb bones, especially for the humerus. In other words, simply modeling a specific thickness of articular cartilage in the same shape as the epiphyseal end of a bone may be an inaccurate surface to predict factors such as range of motion and joint kinematics.

Fujiwara et al. (2010) investigated in-detail the articular cartilage shape of the elbow in 18 non-mammalian species of terrestrial vertebrates (crocodilians, avian dinosaurs, squamates, and turtles) and its relation to elbow range of motion (ROM). These authors suggested it might be difficult to estimate ROM in non-avian dinosaurs because of the predicted discrepancy between articular cartilage shape and calcified cartilage (bony) surfaces. Additionally, Fujiwara et al. (2010) reported the presence of a meniscus in the elbow of crocodilians and birds. Hutson and Hutson, (2012, 2014, 2015) investigated these potential discrepancies by examining the effect of sequential removal of soft tissues from the elbow and shoulder joints of crocodilians. Their repeated measures studies found that the presence of some soft tissues (e.g., muscles) decreases potential joint ROM, whereas the presence of articular cartilage frequently increases ROM relative to bone-only ROM. This implies that the accuracy of ROM studies which do not account for articular cartilage in extinct taxa (e.g., Senter and Robins, 2005; Mallison, 2010a; Snively et al., 2013; Lefebvre et al., 2020; Manafzadeh and Gatesy 2021) are likely underestimated due to this missing soft tissue (Senter and Sullivan, 2019). Some researchers have attempted to compensate for missing articular cartilage by adding a consistent thickness at each joint (e.g., Otero et al., 2017; Fahn-Lai et al., 2018; Jannel et al., 2019; Demuth et al., 2020; Molnar et al., 2021); however, as noted above, this also may not be sufficient to replicate the soft-tissue morphology nor joint motions of extinct organisms (cf., Holiday et al., 2010).

Herein, we present a case study examining the kinematic effects of various potential morphologies of articular cartilage in the elbow of the titanosaurian sauropod dinosaur Dreadnoughtus schrani (Lacovara et al., 2014), in which we adapted a novel methodology for the biomechanical modeling of human ankles (Imhauser et al., 2008; Palazzi et al., 2020). Our method does not restrict joint degrees of motion or define the sequence of joint rotation and translations a priori (as many prior studies have; e.g., Pierce et al., 2012; Snively et al., 2013; Sellers et al., 2017, Nyakatura et al., 2019; Bishop et al., 2021) and instead allows the anatomy of the joint (i.e., articular cartilage shape, muscles, etc.) and the forces applied (i.e., muscle and contact forces) to dictate joint motion. This case study demonstrates the utility of our method, which, importantly, expands the range of biomechanical investigations about extinct organisms to include anatomies with complex or difficult to decipher motion that is not easily simplified a priori. Combining quantitative methods (e.g., Bonnan et al., 2010; Holliday et al., 2010; Hutson and Hutson, 2012) with detailed investigations of specific shape features of articular cartilage (e.g., Fujiwara et al., 2010; Tsai et al., 2020) will facilitate future reconstructions of cartilaginous structures that can then be further analyzed for their effect on joint kinematics by our method described herein. In short, Holliday et al. (2010) stated that the consequences of not modeling articular cartilage in dinosaurs were yet to be investigated: we are taking a step toward understanding such consequences with this study.

Materials and Methods

Specimen Selection

The holotype individual of Dreadnoughtus schrani (MPM-PV 1156) is a mostly complete, well-preserved, giant lithostrotian titanosaurian sauropod dinosaur (Lacovara et al., 2014). Unlike many dinosaurs which are only known from fragmentary remains (Weishampel et al., 2004; Cashmore and Butler, 2019, and references therein), 70% of the postcranial skeleton of Dreadnoughtus is preserved, including every major bone in the forelimb. Dreadnoughtus was selected for use in this case study because of its overall skeletal completeness, minimal taphonomic deformation to the shoulder girdle and forelimb bones, and because of the wealth of well-preserved osteological correlates that are readily identifiable on most of its appendicular skeletal elements (Voegele et al., 2020, 2021). Additionally, this dinosaur is the heaviest yet discovered to preserve all bones forming the elbow joint from the same individual. The left elbow was specifically chosen because: 1) elbow and knee morphologies are more evolutionarily conserved in tetrapods than the hip and shoulder joints (Hogervorst et al., 2009); 2) all bones forming this joint are preserved as complete specimens in this individual of Dreadnoughtus, and; 3) the humerus, radius, and ulna of this individual of Dreadnoughtus exhibit less taphonomic deformation and better surface bone preservation than its femur, tibia, and fibula, including the presence of well-defined osteological correlates for muscle attachment (Voegele et al., 2020, 2021). Specifically, the radius and ulna exhibit little to no visible deformation and the humerus is only minorly anteroposteriorly compressed with a twisted offset of its proximolateral corner (Ullmann and Lacovara, 2016), which is insignificant to this study as none of the modeled muscles attach to this region of the humerus (and we are not investigating movement at the shoulder).

Reasonable conditions of the soft tissues of Dreadnoughtus were reconstructed and modeled based on EPB comparisons with crocodilian and avian dinosaurs (birds), the closest living relatives of non-avian dinosaurs. To reconstruct the ligaments of Dreadnoughtus we followed Baumel et al. (1993) and dissected three juvenile (body mass unknown) American alligator forelimbs (Alligator mississippiensis) to complete the EPB (Figure 1B). Additional dissections were completed on adult alligator forelimbs (body mass unknown) and chicken wings (Gallus; body mass unknown) to investigate any deviations in the shape of articular cartilage vs. bone morphology. Contrasts in cartilage vs. bone morphology were identified by dissection in order to first isolate bones and articular cartilage from other surrounding soft tissues, followed by digitization using a NextEngine Desktop 3D Laser Scanner with 0.05 inch precision. All cartilage was then removed and each bone was rescanned. The difference between these two scans represents the location and spatial extent of articular cartilage over the end of each bone, which were visualized as a semi-transparent overlay in Autodesk^® Maya^® over the bone-only file (Figure 2). Finally, adult wild alligator (humerus proximodistal length of 13.8 cm) and domestic turkey (humerus proximodistal length 12.2 cm) forelimbs were used in the XROMM (X-ray Reconstruction of Moving Morphology) analysis (see below).

FIGURE 1

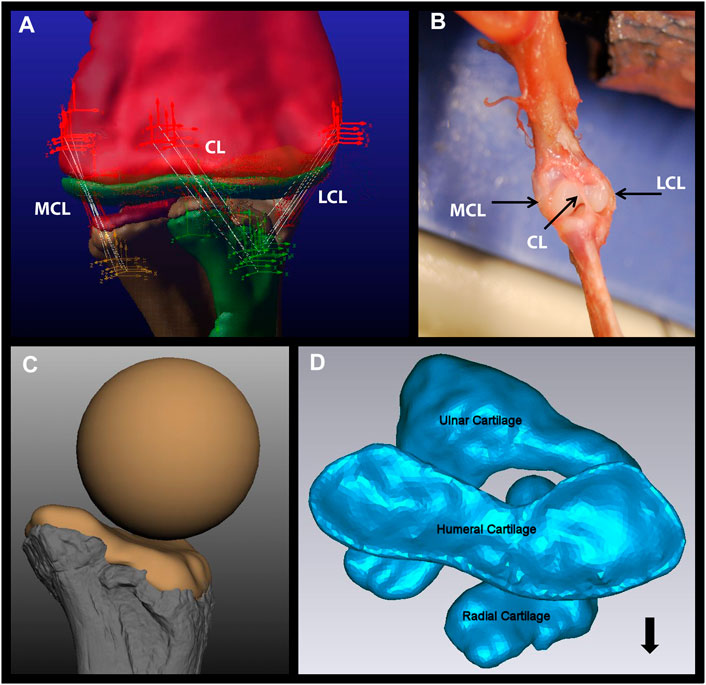
FIGURE 1. Components of the Dreadnoughtus model. (A) The five strands of each of the three ligaments modeled in the elbow of Dreadnoughtus schrani. The orthogonal, tripartite icons mark the locations of attachment of each ligament strand, which are shown as white lines. The red icons mark attachment locations on the humerus, the yellow icons mark attachment locations on the ulna, and the green icons mark attachment locations on the radius. All objects (bones, articular cartilage) are shown as semi-transparent to allow all ligament strands to be visible. (B) Dissection of a juvenile alligator left forelimb with black arrows pointing to the three ligaments identified. (C)The proximal end of the radius of Dreadnoughtus in anterior view with a 2% thick articular cartilage shape, along with the sphere (of diameter matching the curvature of the proximal end of the radius) used to create the anterior spherical articular cartilage on the humerus for our three ensuing biomechanical models. Bone is shown in shades of gray, cartilage in tan. (D) The 2% articular cartilages in their equilibrated positions (after the model was simulated to establish equilibrium), shown in proximal view. The humeral cartilage is seen overlaying the radial and ulnar articular cartilages. The radius is located in an anterolateral position, allowing the ulnar articular cartilage to articulate with both distal condyles of the humerus. The black arrow points anteriorly. Abbreviations: CL, central ligament; LCL, lateral collateral ligament; MCL, medial collateral ligament.

FIGURE 2

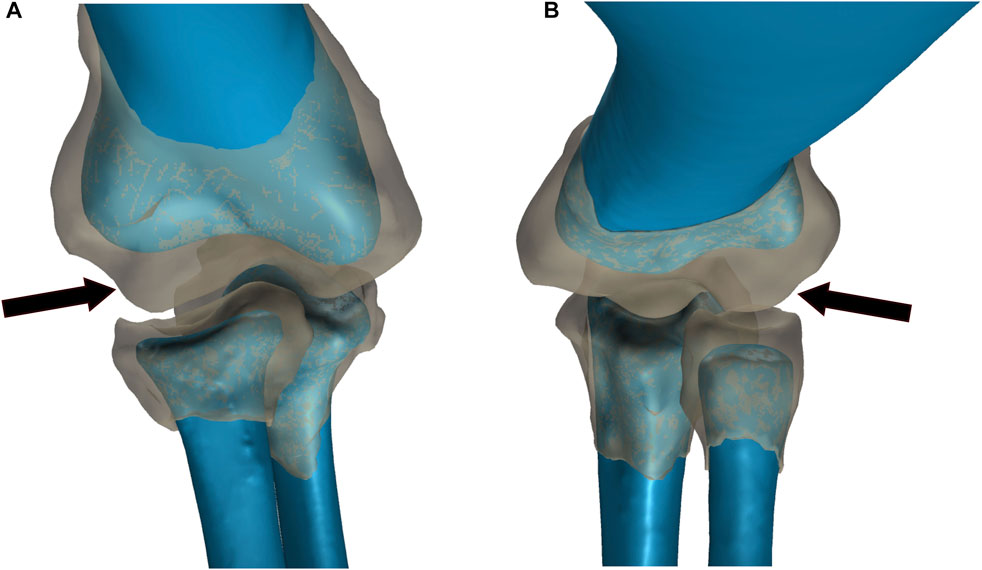
FIGURE 2. Comparison of bone and articular cartilage morphologies in extant taxa. (A) American Alligator right elbow. (B) Chicken left elbow. Bone morphology is displayed in blue and articular cartilage morphology is displayed as a semi-transparent gray overlay. The black arrows denote the anterior spherical projection of articular cartilage on the lateral distal condyle of the humerus.

Material Properties

Material property data were collected from the literature for taxa comprising the EPB of dinosaurs. An average bone density of 1,780.0 kg/m³, derived by averaging values for extant American alligator (Alligator mississippiensis: 1,770.0 kg/m³; Zapata et al., 2010) and chicken (Gallus: 1,790.0 kg/m³; Rath et al., 1999), was used to calculate the mass of all bones modeled. Following Rayfield et al. (2001), mammalian material properties were also used in our analyses. The mass of each cartilage element was based on Yamada’s (1973) average estimate of 1,300 kg/m³ for extant mammals, as reports on archosaur cartilage material properties are scant.

Extant XROMM Analysis

We used XROMM (X-ray Reconstruction of Moving Morphology) to reconstruct the movements of the radius and ulna at the elbow of one intact alligator and turkey cadaver to test the accuracy of our dinosaur forelimb model. XROMM is now a widely utilized method for reconstructing skeletal movements: see Brainered et al. (2010) and Gatesy et al. (2010) for an overview and specifics of the method. Briefly, XROMM creates three-dimensional animations of the skeleton by registering (matching) bone models from experimental animals against calibrated cineradiographic videos of their movements. We used radiopaque markers embedded in the bones of one alligator and one turkey specimen to automate the registration and animation of the bones. Because the resulting animations are reconstructed in real world space, translational and rotational movements between bones can be quantified and used to illuminate skeletal range of movement.

Cineradiographic videos were captured using two modified ComEd KMC-950CM C-arm fluoroscopes with 30 cm image intensifiers housed in the XROMM lab at Stockton University. During each trial, X-ray emission was continuous at 65–75 kVp (the settings on each fluoroscope were adjusted for each specimen to provide the best images) and 5 mA. Each fluoroscope was modified to hold a Photron Fastcam Mini UX50 camera that captured cineradiographic videos for each trial at 250 frames per second (fps) using a 1/1,000 shutter speed at high resolution (1,024 × 1024). At the start and end of each set of trials we imaged a Lego calibration object press-fit with 48 steel spheres (5 mm diameter) spaced 64 mm apart in a 4 × 4 × 3 matrix of 192 mm × 192 mm x 128 mm dimensions to calibrate our cineradiographic videos. The calibration object was modified from specifications in Knörlein et al. (2016). To generate three-dimensional bone models, the alligator and turkey specimens were placed in a Fidex Animage veterinary CT scanner housed in the XROMM lab at Stockton University. All CT scans were performed at 110 kVp and 0.08 mAs at a resolution of 0.183–0.312 mm slice intervals with a voxel size of 0.17 mm³. All reported trials and CT scans including relevant calibration files and metadata are available on the XMA Portal at Brown University (https://xmaportal.org/webportal/).

The intact forelimb of the alligator and turkey (including skin) were carefully dissected at the shoulder (glenoid) so that the head of the humerus was freed from the scapulocoracoid. Incisions were made along the skin and muscle superficial to the humerus, radius, and ulna on the alligator and turkey specimens to implant 3-4 0.8 mm spherical tantalum markers into each bone. These markers were later tracked in the XMA program (see below). Next, each specimen was temporarily secured at the upper arm to an inclined plexiglass plane using plastic zip ties such that the forearm was naturally, maximally extended at the elbow due to the force of gravity. Fishing line was secured around the wrist of each specimen and pulled until the elbow reached maximum flexion during each cineradiographic trial (Supplementary Figure S1). Compared to mammals, the elbows of alligators and especially birds have multiple degrees of freedom that make consistent, comparable movements difficult to replicate. Therefore, the inclined plane ensured that when the forearm was pulled into flexion it was always restricted to the same plane and angle of motion to improve the consistency and interpretation of our results. Given that no known non-avian dinosaur possessed a patagium (the fleshy and muscular portion of the wing that spans the elbow joint in extant avians), to make our comparisons more applicable to a non-avian dinosaur we cut the patagium on our turkey at its widest transverse section.

Fluoroscope videos were calibrated and marker sets tracked using XMA Lab software (www.xromm.org) for each trial. DICOM files from CT scans of each specimen were imported into Slicer3D (Fedorov et al., 2012) to create OBJ mesh bone models and marker sets which were subsequently refined in OpenFlipper (Mobius and Kobbelt, 2010) and MeshLab (Cignoni et al., 2008). We used Autodesk^® Maya^® and the XROMM MAYA Tools (xromm.org) to animate the bone models and calculate the joint angles as is standard for other XROMM studies (e.g., Baier and Gatesy, 2013; Bonnan et al., 2016).

To quantify the range of motion of the radius and ulna at the elbow relative to the humerus, we created an elbow joint coordinate system (JCS) with six degrees of freedom (6 DOF). For consistency, each forelimb model was oriented into a reference pose (zero position) against which all joint translations and rotations are measured. The radius and ulna were flexed until they were aligned in parallel with the long-axis of the humerus, and thereafter translated until they were each in direct articulation with the distal articular surface of the humerus. The reference pose does not represent a biologically realistic orientation for an alligator or turkey forelimb or elbow (in this position the bones overlap one another) but instead serves as a convenient, repeatable, and standard reference from which to interpret and discuss movements of the radius and ulna in relation to the humerus. Following other XROMM studies, each JCS was based on a right-hand rule Euler angle ZYX rotation order (e.g., Bonnan et al., 2016). This is figured in Supplementary Figure S2 for the alligator which represents the alignment of all models. This is very similar to the method recently proposed by Gatesy et al. (2022). Each JCS was created with six DOF because we did not want to bias or restrict possible joint movements a priori.

Model Construction

Our two extant taxa, alligator and turkey, were modeled with two cartilage conditions for each taxon; one with the digitized bones and cartilage from the XROMM analyses and one with the digitized bones from the XROMM analyses but cartilage constructed in the same way as in the dinosaur models (see below). In addition, four models of the elbow of Dreadnoughtus were constructed. However, the initial model with strictly pad like articular cartilage was not considered further at it was anatomically dissimilar to the cartilage conditions in the EPB taxa. The remaining three Dreadnoughtus models and the four extant models were constructed and analyzed as described below (Table 1). See Model Construction for details on the digitization of the extant bones.

TABLE 1

TABLE 1. Summary of the models constructed for simulations in this study. Adams™ files available at [https://doi.org/10.6084/m9.figshare.c.6022103.v1 figshare link once accepted].

Fossils were digitized using a NextEngine Desktop 3D Laser Scanner and then imported into in Geomagic^® (3DSystems). The immense original point clouds, ranging from over 7.5 million for the humerus to just under three million triangles for the radius, for each bone necessitated reduction to allow for reasonable model simulation times (following Imhauser, 2004). To retain relevant morphology of the epiphyseal ends of each bone, in Geomagic^® the point cloud density of each shaft was reduced more then point density of the articular ends (because the geometry of the shaft is less crucial to the kinematics of the joint). This final density of triangles ranged from over twenty two thousand for the radius to roughly fifty thousand for the humerus.

Articular cartilage was constructed in Geomagic^® by duplicating and displacing each respective bone geometry by the desired thickness. This straight displacement yielded a pad-like cartilage of a consistent thickness to simulate previous cartilage reconstructions (e.g., Senter and Robins, 2005; Pierce et al., 2012; Molnar et al., 2021). As it is simpler to model less material and iteratively add more, we chose the minimum estimated articular cartilage thickness in prior literature of 2% of total bone length (based on the 4% of total bone length for both the proximal and distal articular cartilage observed by Bonnan et al., 2010 in extant archosaurs). We acknowledge that this minimum value may underestimate the true thickness of articular cartilage in the elbow of Dreadnoughtus; furthermore, the subadult status of the holotype (Schroeter, 2013; Lacovara et al., 2014) suggests that thicker and less congruent (with underlying bone morphology) articular cartilage may have been present than if it was a full adult (Bonnan et al., 2010; Holliday et al., 2010). However, as our goal was to test the effects of articular cartilage morphology on joint kinematics, modeling thicker articular cartilage with the same morphology would be unlikely to result in a different kinematic solution (because the only dimension increasing would be the length of each segment, not their shapes). This is supported by the differences in the articular cartilage modeled in our extant taxa that result in general similar motion. Boolean operators were used to subtract the overlapping geometries of the duplicated and displaced bones to create articular cartilage that has the same articular surface morphology of its corresponding bone. This process created thin, excess points leftover around the cartilage-bone interface. After removing these sharp edge artifacts, all elements were imported into Adams™.

The modeling software employed in this study, Adams™ by MSC Software Corporation, is a multi-body dynamics simulation program. Objects, such as bones, are modeled as rigid bodies which move according to the forces applied to them (including inertia) along paths which are constrained by the motion of other rigid bodies in contact with them (MSC Software Corporation, 2013). As reviewed by Imhauser, (2004) and McConville, (2015), Adams™ calculates the motion of objects through time by solving non-linear ordinary differential equations for each single time step by using the previous time step to predict the next time step. Then corrector formulae are applied using an implicit method of difference relationships to estimate error in the solution. If the error is above a threshold, the solution is rejected and recalculated with a smaller time step. Once a solution for a time step is accepted, the program moves to the next time step, until all are time-step solutions are completed.

Geomagic^®, Adams™, and Maya^® use the same coordinate system, allowing seamless transfer of rigid body files which retain the same axis orientations and reference pose, permitting use of the same Euler rotation order. Because manipulation of bone models is more easily accomplished in Geomagic^®, this program was used to identify the coordinates for muscle and ligament attachments (again, based on attachment locations from Baumel et al., 1993; Meers, (2003); Voegele et al., 2020 and our EPB dissections). Marker sites chosen in Geomagic^® were then added to the relevant rigid body at the same coordinates in Adams™. Operationally, the humerus and scapula were locked to ground (meaning they were frozen in position), the radius and ulna were locked together (allowing no relative motion between them), and the articular cartilage shapes were locked to their respective bones. A turkey scapula was acquired from the Virtual Creation Lab on Sketchfab and an alligator scapula was acquired from Boucher (2010) and scaled to size. These elements served only to correctly align the biceps force. Since sauropods are hypothesized to have had limited pronation/supination abilities (Bonnan, 2003), keeping the radius and ulna as separate bodies but fixed together allowed easier adjustment of their individual properties and morphologies while simultaneously simplifying the model (by not investigating any motion that may have occurred between these zeugopodial elements). The corresponding material properties listed above were then applied to the appropriate rigid body. Contact forces, using the built in feature in Adams™ were added between the articular cartilage shapes and between the cartilage shapes and bones with an Exponent value of 0.7, Stiffness value of 1,000, Penetration Depth of 0.1, and Damping value of 10 to account for the fact that cartilage is not a rigid body and would be expected to deform slightly during joint flexion (following Imhauser et al., 2008). As all of our models included 3D translations of the antebrachium relative to the humerus, in addition to rotations, there is not a fixed center of rotation.

Muscles were each modeled as a single force from the center of one preserved osteological correlate to the other using the One Body Fixed in Space force type. Specifically, the Mm. biceps brachii, brachialis inferior, and humeroradialis were modeled and their attachment locations follow Voegele et al. (2020). To reduce the number of assumptions regarding the contribution and magnitude of each muscle to elbow movement, the amount of force applied by a muscle was not calculated based on any attribute(s) of preserved osteological correlates or fossil morphology (as in, e.g., Mallison, 2011; Lautenschlager, 2020). Instead, muscle forces were modeled as the minimum magnitude applied equally to all muscles required to flex the elbow until maximum flexion was reached (i.e., when the zeugopodium contacted the stylopodium). This force value was identified by sequential permutations from a hypothetical starting value. If a smaller magnitude force was simulated, the limb could not overcome the force of gravity and would not flex to this maximum degree. To be clear, we drew no assumptions as to whether or not the elbow flexed to this degree during normal gait, and we did not attempt to answer such a question either, because such a determination is beyond the anatomical focus of this investigation. Rather, we investigated the kinematic consequences of various plausible articular cartilage morphologies in the elbow of Dreadnoughtus. We acknowledge that these modeling parameters did or could result in motion beyond what was possible for all organisms modeled as we did not model the soft tissues that assuredly would contact prior to bone-on-bone contact nor did we model additional constraints by tissues such as skin (or the patagium in the turkey). Additionally, it is unlikely that all muscles applied equal force throughout flexion. Therefore, whereas we acknowledge the potential limitations of our model, we stress that we chose this approach because it requires the least number of assumptions. Moreover, helpfully, it is also similar to how we approached our XROMM reconstructions: using a string to pull the forearm in a single vector relative to the elbow without considering individual muscle forces. Muscle and ligament forces were modeled with a temporally-building function to reduce simulation errors (resulting in no solution) from any aberrant spike(s) in force values (following Imhauser, 2004).

Ligaments were modeled as a Force Between Two Bodies force type. Each of the three ligaments in the elbow (as documented by Baumel et al. (1993) and found in our dissections, see Results) was modeled as five forces in Adams™ to encompass the total hypothesized area of the ligament attachments (Figure 1A). Modeling each ligament as five individual forces was found to be the lowest number of “strands” necessary to stabilize the forelimb. Though more strands would better mimic the histologic structure of a ligament, we found that they would increase computational time for negligible stability improvements. The force of each ligament was calculated as a function of how much it stretched from its original length multiplied by a spring constant (i.e., using the equation of a spring) which acted to provide pretension to account for the force they apply to hold the joint in congruence under gravity. This constant was initially estimated for each ligament strand as if it was the only strand of the ligament and then averaged for each ligament. This average value was then divided by the number of ligament strands (five) and the same value was used for each ligament strand. To account for any potential sensitivities related to initial ligament length, if the ligament length changed after the equilibrium simulation, then the K values were recalculated with the new length.

Forelimb bones of Dreadnoughtus were initially manually articulated in a fully-upright orientation. For extant taxa the position of the bone geometries were preserved from the XROMM analysis and used as the starting location for our simulations. The extant dinosaur-like reconstruction of articular cartilage models required manual manipulation of the radius and ulna to reduce the gap between the articular cartilages. An equilibrium starting articulation was found for each model by simulating with only gravity (normal Earth gravity acting proximodistally down the shaft of the humerus), contact, and ligament forces activated. This allowed any pretention slack in the ligaments (length longer than what is needed to maintain joint articulation) and/or articulation error(s) imposed by manual alignment (e.g., slight overlapping of rigid bodies) to be removed. The final position found by this equilibrium simulation was saved and used as the starting position for all further modeling simulations.

Since our dissections revealed that both taxa comprising the EPB of dinosaurs possess an anterior spherical projection of cartilage on the lateral distal condyle of the humerus, we added this cartilage to our initial 2% thickness model of Dreadnoughtus and we simulated each of the EPB taxa in a model with cartilage constructed as in the dinosaur. It must be noted that our analyses of extant taxa identified that some species-specific variations in the morphology and position of this cartilage around the lateral condyle of the humerus are probable. Unfortunately, the surface of the anterior face of the humerus of Dreadnoughtus (MPM-PV 1156-49) is disrupted and does not preserve any original surface or osteological correlates; however, even the presence of an osteological correlate on this surface would still be insufficient to confidently resolve the morphology (i.e., thickness and shape) of this articular cartilage. Given these causes of uncertainty, we created three models to encompass a range of expression of an anterior spherical projection of cartilage on the lateral distal condyle of the humerus, simulations of which were then cross-compared to constrain the probable morphological and positional attributes of this additional, EPB-supported cartilage structure in Dreadnoughtus (Table 1). Specifically, our three models varied the placement of a cartilage sphere whose diameter was set to match that of the preserved concave proximal articular surface of the radius (Figure 1C, 3). In the first model, the cartilage sphere was positioned slightly lateral to the distal apex of the lateral distal condyle of the humerus and protruding more anteriorly than in either of our other two models. The second model served as our other endmember, with the cartilage sphere positioned slightly medial to the distal apex of the lateral distal condyle of the humerus and protruding less anteriorly than either of our other models. The cartilage sphere in our third model occupies a comparatively intermediate mediolateral position and moderate anterior protrusion compared to the first two models. This sphere of cartilage was also positioned to grade smoothly into the 2% thick cartilage on the distal end of the humerus. Other than the differences in placement of the cartilage sphere, all three models were identical to one another and the original 2% model.

FIGURE 3

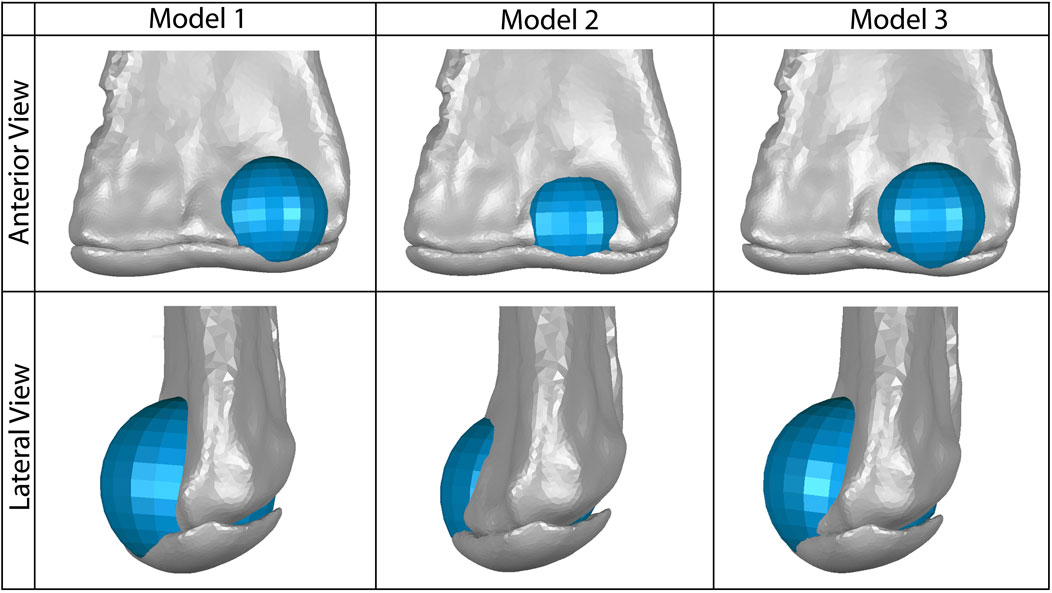
FIGURE 3. Our three models of possible placement of the anterior spherical projection of articular cartilage (shown in blue) on the lateral distal condyle of the humerus, which would articulate with the proximal end of the radius. Model one represents the greatest anteroposterior breadth of this cartilage and the most lateral placement of the sphere. Model two represents the least anteroposterior breadth of this cartilage and the most medial placement of the sphere. Model three represents a moderate breadth and position of this cartilage sphere. The 2% thick articular cartilage on the distal end of the humerus is also shown in gray; the cartilage sphere was also positioned proximodistally to align smoothly with the curve of this humeral cartilage in lateral view.

To better compare to our extant XROMM models, we exported the bone geometry and their accompanying positional metadata from frames across each simulations, imported them into Maya^®, and followed the standard XROMM protocols summarized above to calculate rotations and translation. For the extant simulations, the same reference position was used as with the XROMM analyses. For the dinosaur simulations frame one was used as the reference frame to calculate the magnitude of displacements and the coordinate system was aligned such that the “Z" axis passes through the widest points of the distal condyles of the humerus and the “Y" axis passes through the center of the radius/ulna unit. The “X” axis is oriented so that it is always orthogonal to the other two. With this arrangement, the joint motions reported correspond to abduction/adduction, long axis rotation, and flexion/extension, about X, Y, and Z axes, respectively. These were analyzed to compare the kinematics among all models. Bone and cartilage files exported to Maya^® were also used to create proximity maps of overlapping rigid bodies (the 0.1 mm of penetration allowed by the contact force parameters described above) in Geomagic^® which display the area of overlap of the radial and humeral articular cartilages and thus the minimum area of contact between this tissue. Proximity maps were made which display the area of physical contact at each time point between the radial and humeral articular cartilage. As the spherical cartilage was created to match the curvature of the proximal radius, it is likely that contact but not penetration is occurring in these models that is not being captured by this technique, hence we refer to this as the minimum area of contact.

Results

EPB Dissections

Though archosaur knee ligaments have received detailed study (e.g., Suzuki et al., 2021), archosaur elbow ligaments have yet to be documented as thoroughly. Our dissections of three juvenile alligator forelimbs from two individuals each revealed the presence of three ligaments: a left and right collateral ligament and a central ligament. The two collateral ligaments appear to be figured by, but not labeled in, Meers (2003, Figures 6, 7). The medial and lateral collateral ligaments attach near the distal margin of the medial and lateral aspects of the distal end of the humerus (Figure 1B). The lateral collateral ligament attaches near the proximal margin of the lateral face of the proximal end of the radius. Similarly, the medial collateral ligament attaches near the proximal margin of the medial face of the proximal end of the ulna. The central ligament traverses from an attachment between the ulnar and radial condyles near the distal end of the anterior face of the humerus to the proximal margin of the anterior face of the proximal end of the radius (Figure 1B). According to Baumel et al. (1993), the elbow ligaments of birds are similar to those we describe in the alligator. At least for the archosaurs investigated herein, having three ligaments appears to potentially be a conserved trait. There are no definitive osteological correlates for any of these ligaments on the fossil forelimb bones of Dreadnoughtus, so they were modeled as attaching to similar morphological locations on each respective limb bone.

The articular cartilage and epiphyseal bone end morphologies are similar for both the extant chicken and alligator (Figure 2) and confirm previous examinations of these regions by others (Holliday et al., 2010; Bonnan et al., 2010; Fujiwara et al., 2010). In both the alligator and in the chicken (as well as in the turkey used in the XROMM experiments), the distal epiphysis of the humerus and the proximal epiphyses of the radius and ulna are greatly expanded and contain more complex geometries than the underlying bony surfaces. Figure 2 clearly shows that the gently curving bony surfaces of the lateral (radial) and medial (ulnar) condyles of the humerus are enhanced by expanded and bulbous articular cartilages. In particular, the lateral condyle is more expanded than that of the medial condyle. This thicker articular cartilage forms a generally spherical shape anterior to the lateral condyle of the humerus which mirrors the shape of a depression in the proximal articular cartilage of the radius, which is deeper in the chicken (and observed to be deeper in the turkey from CT scans). The medial distal condyle and overlying articular cartilage of the alligator humerus exhibit a superficially similar geometry, including slightly thicker cartilage over the condyle than in the intercondylar region, but to a substantially-lesser degree than on the lateral distal condyle. This pattern is very similar but more pronounced in the chicken (and observed in the CT scans of the turkey), which exhibits an anterior spherical projection of cartilage on the lateral distal condyle for articulation with the radius and a thinner, separate spherical projection of cartilage for articulation with the ulna. The ulna and radius each have a clear depression in their articular cartilage on their proximal end to form a congruent joint with each humeral condyle (as would be expected). The substantially-thicker articular cartilage over the lateral condyle of the humerus than the medial condyle results from the presence of a subtle depression on the anterior face of the underlying bone forming the lateral condyle in combination with a thick anterior projection of cartilage at that same location. Thus, both taxa exhibit a spherical anterior projection of cartilage on the lateral condyle of the humerus for articulation with the radius.

XROMM Comparisons

All three alligator XROMM trials produce more consistent rotation and translation results than the three turkey trials (Supplementary Videos S1, 2; Supplementary Figure S3). This was not surprising: 1) given that avian elbow joints are less constrained - in fact, elbow luxation is a common injury in living birds (Ackerman and Redig, 1997); and 2) the patagium of our specimen was cut which likely increased variation in elbow movements trial to trial. All translations in the alligator trials were under a magnitude of 0.5 cm (3.6% of humerus length); whereas in the turkey trials, translations in the X and Z axes were roughly equal to or greater than 0.5 cm (4.1% of humerus length), with a maximum of nearly 1.5 cm (12.3% of humerus length). The alligator elbow flexed roughly 30° with the turkey flexing roughly three times that magnitude. A similar pattern in seen in abduction and long axis rotation as the alligator only rotated approximately six and five degrees, respectively, and the turkey rotated between 30 and 15° in these directions. The alligator rotations also display a consistent trend. In contrast, rotations in the turkey trials have more complex trends, for example, in the Y plane the turkey sequentially displays both adduction and abduction.

Simulation Results

As mentioned previously, it is easier to iteratively add material to a model, so we initially ran a simulation with just the articular cartilage of 2% thickness (based on Bonnan et al., 2010) mirroring the epiphyseal ends of the bones. All other parameters of this simulation were the same as in our other models. In this initial 2% thickness model, at moderate flexion the radial articular cartilage does not contact either the humerus or the humeral articular cartilage. This is not due to dislocation of the elbow joint as the morphology and thickness of the articular cartilage does not account for the incongruent morphologies of the boney surfaces. For the radius to remain articulated with the humerus during moderate to maximum flexion of the elbow the cartilage must be thicker on the lateral (radial) condyle compared to the rest of the bone (indicated by the white outlined space on Figure 4). Additionally, when this initial model was equilibrated prior to flexion simulations, the process pulled the radius and ulna slightly medially, such that the anterolateral lobe of the head of the ulna was centered under the lateral distal condyle of the humerus. This initial 2% model, after equilibrium, formed the base model to which we added three possible forms of a cartilage sphere over the lateral distal condyle (as discussed above).

FIGURE 4

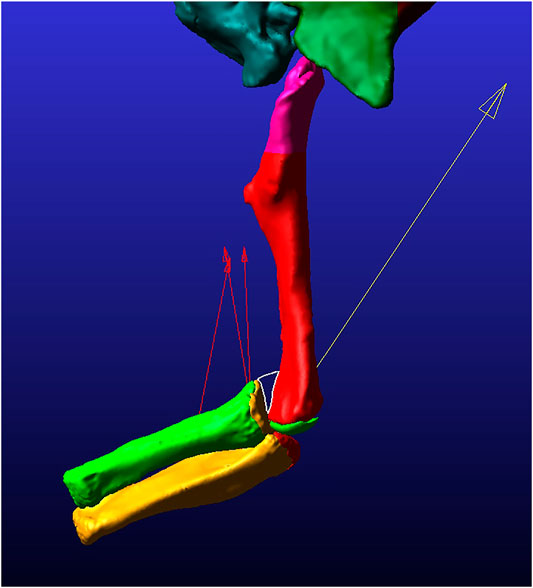
FIGURE 4. Still image of frame 45 from the 2% thickness model simulation in lateral view. The white-outlined triangle surrounds the area of lack of contact between the radial and humeral cartilages. The red arrows pointing mostly proximally display the magnitude and direction of the muscle forces for each of three modeled muscles. The yellow arrow pointing proximally from the ulna/radius unit displays the contact force magnitude and direction present at this time point in the simulation.

All analyses terminated once each simulation reached maximum flexion (in other words, when the forearm began to extend as each model ‘rebounded’ toward reaching equilibrium at a flexed position). The EPB simulations all display greater flexion than reported from the XROMM of the extant forelimbs, again likely due to the absence of other constraining soft tissues (Figures 5, 6; Supplementary Videos S1, 2). The general pattern of motion in the EPB simulations follows that of the extant XROMM analysis. The simulations of Dreadnoughtus are almost identical in flexion, both in magnitude and timing (Figure 7; Supplementary Video S3). Similarly, long axis rotation differs little between the three simulations with increasing twisting laterally. However, models one and two oscillate between abduction and adduction with increasing abduction. Model 3 has much less oscillation and more consistent abduction. The mediolateral translations for models one and two are also more similar, as they both translate medially then laterally, than the pattern for model 3, which only translates laterally. This pattern is also almost identical for dorsoventral and anteroposterior translations.

FIGURE 5

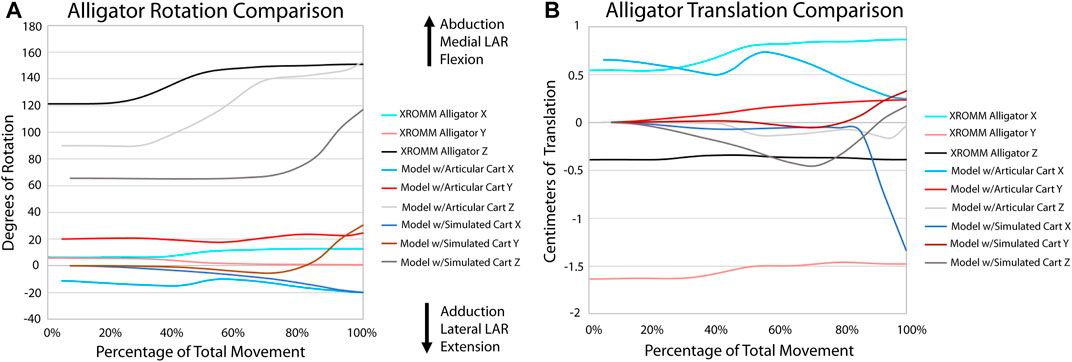
FIGURE 5. Comparison of kinematic data of the alligator simulations and XROMM analysis. (A) Comparison of rotational data. (B) Comparison of translational data.

FIGURE 6

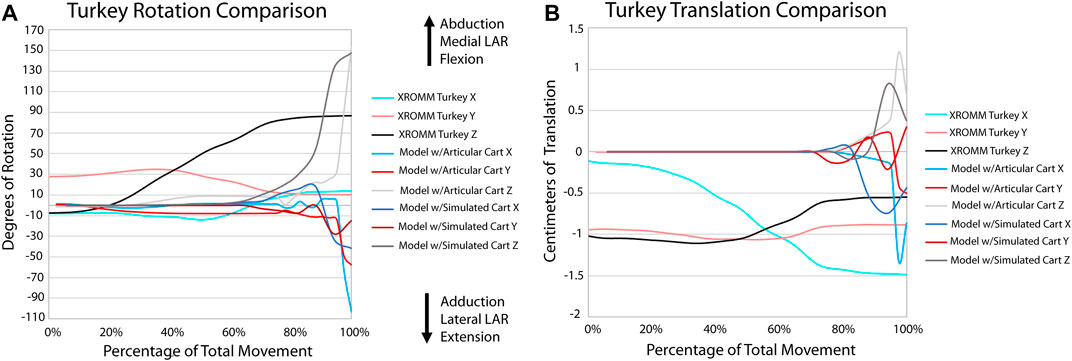
FIGURE 6. Comparison of kinematic data of the turkey simulations and XROMM analysis. (A) Comparison of rotational data. (B) Comparison of translational data.

FIGURE 7

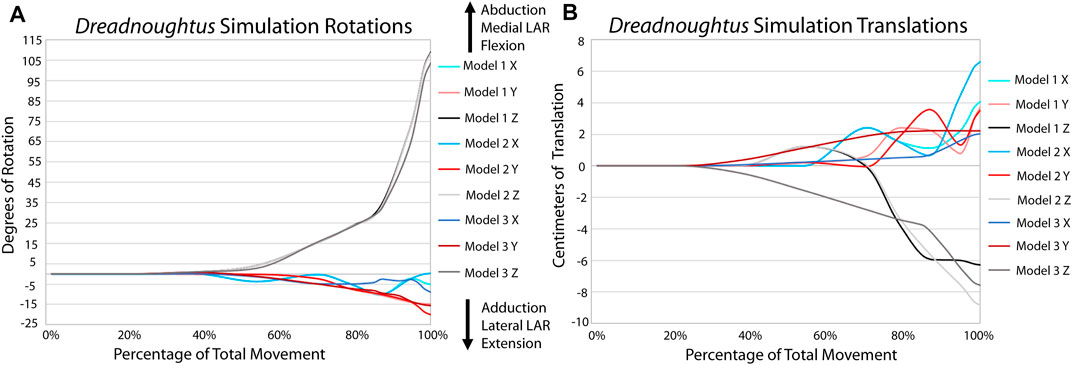
FIGURE 7. Comparison of kinematic data of the three simulations of the Dreadnoughtus elbow. (A) Comparison of rotational data. (B) Comparison of translational data.

Proximity Maps

To better understand kinematic differences among our models, we exported the model geometry from Adams™ at specific time points and created proximity maps of each of these frames in Geomagic^® to assess the minimum area of articular cartilage in contact between the humerus and radius during flexion (Figure 8) in the simulations. Analysis of the XROMM trials resulted in limited areas of contact (Supplementary Figures S3, 4), which is unsurprising as the fat pad and meniscus are present and no penetration of articular cartilage occurs in vivo. Therefore, these minimum contact area maps instead portray where the cartilage may be deforming during flexion due to the contact forces of the joint. The small area of contact that is only present at low angles of flexion in our simulations of the extant taxa also suggest that the lack of a fat pad and meniscus are not significantly affecting the overall kinematics of the simulations. Similarly, minimal contact is also observed in all three of the Dreadnoughtus models. As evidenced by the similarities of all simulations, the cartilage of the models differs little if at all until the elbow is flexed sufficiently to bring the radius in contact with the cartilage sphere, at which point all three models diverge. In general, our third model exhibits the largest area of contact between the radial and humeral articular cartilages at all degrees of flexion, and the radial cartilage articulates with the spherical projection of cartilage on the medial half of the sphere in all three models.

FIGURE 8

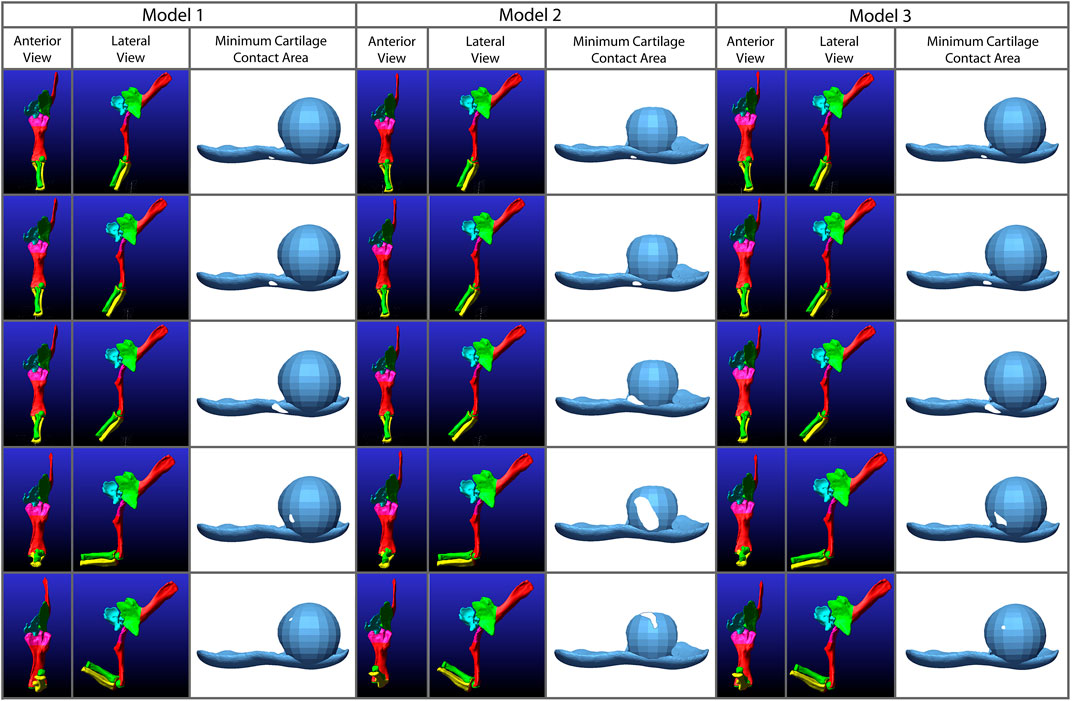
FIGURE 8. Comparison of the minimum areas of contact (between the radial cartilage and combined 2% thickness and spherical cartilages of the humerus) generated from the simulations of our three Dreadnoughtus models in anterior view. Five time points from each simulation are shown that correspond to increasing degrees of flexion. Minimum area of contact is always represented by white shapes. Model 2 has the largest area of minimal contact and model 1 has the smallest. Model two also contacts the cartilage sphere the earliest during flexion.

Specifically, in our first model the radial cartilage articulates essentially entirely with the medial side of the spherical cartilage projection of the humeral cartilage and never approaches the midline of the spherical cartilage (Figure 8). Model three is similar to model 1, however, it has a larger area of contact once the radius is in contact with the humerus and the contact area is closer to the midline of the cartilage sphere. The area of contact in model two migrates dorsolaterally across the humeral cartilage sphere through flexion.

Discussion

Our XROMM analysis displays more variation in motion among the turkey trials than the alligator. It is possible that some of this variation could be caused by the cutting of the patagium whereas the alligator forelimb skin remained mostly intact. As the skin still remained attached to the forelimb, this suggests that the elbow of turkeys is likely a more loosely constrained joint compared to the elbow of alligators. This is documented in the results as the differences between individual turkey specimens and their more complex patterns of motion. The turkey forelimb also exhibits a greater magnitude of rotation and translation than the alligator elbow. This nearly 1 cm (8.2% of proximodistal length of the turkey humerus) of translation down the long axis of the forearm should be considered in future modeling of complex motion in avian forelimbs and, in some instances, it is possible that modeling this joint as a simple hinge may be insufficient to capture all relevant motion. Additionally, our current data predicts that future studies may reveal more motion available to theropod elbows than previously predicted.

A portion of this complex motion exhibited by the turkey elbow is likely explained by the additional complexity of this joint compared to that of alligators. The larger cartilage sphere on the lateral humeral condyle and the spherical cartilage on the medial condyle both have the ability to act as pivot points during flexion. Additionally, more relative motion occurs between the radius and ulna of the turkey than in the alligator and none of this motion is modeled in our simulations. This last finding was not too surprising given that it is known the radius and ulna translate relative to one another along their long axes (Vazquez, 1994; Stowers et al., 2017). The comparison of our extant simulations to XROMM supports this as there is greater convergence for the alligator than the turkey (Supplementary Figure S4). These anatomical features in the turkey elbow joint that are not modeled in our simulations (the spherical cartilage on the medial condyle and translation between the radius and ulna), in addition to other known factors, such as a fat pad and a meniscus (Fujiwara et al., 2010), likely explain the greater divergence of the simulation from the XROMM data for the turkey. Greater convergence in the alligator is likely a result of the more constrained joint.

In general, even though our models are simplifications of the extant morphology, these models exhibit the same patterns of motion as seen in the XROMM trials. The motion of these models are exaggerated compared to the extant data most likely because of a lack of additional constraints on motion, such as muscle tissue and skin. However, because 1) sauropods are not predicted to have much relative movement occurring between the radius and ulna, 2) the overall morphology of a sauropod humerus is more similar to that of an alligator, and 3) our methodology reasonably predicts the kinematics of an alligator (and turkey) elbow compared to our XROMM trials, we predict that our modeling technique reasonably approximates the kinematics of the elbow of Dreadnoughtus. Any future improvements in our understanding of articular cartilage in the elbow of dinosaurs would further improve our predictions of joint kinematics. In addition, future studies may also elucidate the importance of addition of soft-tissues currently not modeled.

Equilibrating our Dreadnoughtus model with gravity, contact, and ligament forces prior to the addition of muscle forces established a kinematically-neutral starting articulation. This initial simulation rotated the radius and ulna more medially than our manually-estimated initial starting articulation, thereby allowing the anterolateral lobe of the proximal head of the ulna to become centered under the lateral distal condyle of the humerus (Figure 1D). This articulation geometry is more similar to those proposed for sauropod dinosaurs by Bonnan, (2003), Gilmore, (1936), and Hatcher, (1902) than those proposed by Wilson and Sereno, (1998) and Wilson and Carrano, (1999). Our results from this initial equilibration simulation suggest that there may have been some stabilizing kinematic advantages to a more anteroposteriorly aligned radius and ulna (as opposed to the traditional mediolateral placement); however, our models do not factor in a ground reaction force which would be necessary to fully explore the biomechanical effects of such different articulations.

Based on dissections of taxa comprising the EPB of dinosaurs, we predict the presence of thick cartilage forming an overall-spherical shape on the anterior face of the lateral condyle of the humerus of Dreadnoughtus. This spherical projection was found in both extant archosaurs (Figure 2), though it was more pronounced in the chicken than the alligator. Our initial modeling of articular cartilage as a thickness of 2% of total bone length resulted in no contact between the radial and humeral cartilages, implying that there should be additional cartilage at this location to preclude dislocation during flexion. Klinkhamer et al. (2019, Figure 3) also diagrammed a representation of the elbow joint cartilage as generally spherical in another sauropod, Diamantinasaurus, in general agreement with our findings. Presence of an anterior spherical projection of cartilage on the humerus for articulation with the concave proximal end of the radius would form a congruent joint that would be predicted to be biomechanically advantageous in terms of weight support and stability, especially for large terrestrial vertebrates such as sauropods (Bonnan et al., 2013). A more congruent joint would be predicted, based on our XROMM analysis, to be more similar to the alligator than the turkey results. Our findings are also consistent with previous studies which found that the articular cartilage of archosaurs is generally thicker than that of mammals to achieve congruent joints (Bonnan et al., 2013) and that articular cartilage does not always form a covering of consistent thickness over the end of a given limb bone (Bonnan et al., 2010; Holliday et al., 2010). Furthermore, Holliday et al. (2010) suggested that some features of joint congruence may be cartilaginous and therefore lost during fossilization. Given these considerations, our EPB taxa dissections, and our simulation results, we conclude that additional cartilage was present on the lateral condyle of the humerus of Dreadnoughtus beyond a simple bone-mirroring articular cartilage over its distal end, and that this additional cartilage was likely spherical in form.

It is difficult to determine the exact morphology and placement of this sphere of articular cartilage in Dreadnoughtus as no direct fossil evidence of it is preserved. However, our modeling technique allowed us to explore various hypothesized conditions (Figure 3). Since the articular cartilage surfaces are in contact during joint articulation, it is important that we understand as much as possible about these surfaces in extinct organisms because it is their geometry that directly constrains joint motion, not the morphology of the underlying bones. Our goal was to explore the possible kinematics of the elbow of Dreadnoughtus as affected by different cartilage reconstructions. Our comparison of simulations and XROMM data for taxa comprising the EPB of dinosaurs supports our ability to model the anatomy and simulate motion similar to the observed motion (Figures 5, 6; Supplementary Videos S1, 2). These alignments between XROMM observations and the simulation results of our extant models imply that if the in vivo structural anatomy of the elbow of Dreadnoughtus was similar to the conditions modeled herein, then our results provide reasonably-close estimations of the kinematics of this joint in the living dinosaur. This conclusion is also supported by the differences among the simulations and the XROMM data, likely being connected to anatomical simplifications made during model construction.

The same input muscle forces generated the same degree of flexion of the elbow in each model, indicating that none of the articular cartilage morphologies we modeled created any additional biologically-imposed forces that impeded flexion. Though the ability of the Dreadnoughtus elbow to only flex to roughly one hundred degrees could be a physical limitation, it is just as likely a result of the cartilage reconstruction. There are almost infinite additional alterations that could be made to the cartilage reconstruction and simulation (e.g., proximodistal position of the sphere or larger/smaller diameter sphere). However, the high degree of consistency among the three models simulated herein leads us to predict that such additional alterations of the modeled parameters are unlikely to drastically affect the modeled kinematics of the elbow. Future studies may find merit in continued simulation to potentially identify specific relationships between alterations in the cartilage reconstruction and kinematics, as this is beyond the scope of this study. It is of note that model 3 has smooth, unidirectional rotation and translation compared to models one and 2 (Figure 7, Supplementary Video S3). For example, model three consistently increases in adduction over the course of the simulation, whereas following a similar path to each other, models one and 2 ‘wobble’ slightly between adduction and abduction while overall increasing in adduction. This pattern is more distinct in all translations. The consistent motion path of model three suggests this morphology results in a more constrained joint, similar to that of the alligator observed in XROMM. Even the kinematic pattern of the less constrained turkey elbow is more similar to model three than models one or 2.

Model two stands out with a larger area of minimum contact area in the proximity maps and the proximity maps of both models two and three show the radius travel dorsolaterally across the cartilage sphere. As these proximity maps show only the minimum area of contact, and articular cartilage is not a rigid body (as it is modeled in Adams™), it is possible the area of contact is greater than that depicted in these maps. It must be noted that these maps do not show when the surfaces of the articular cartilages are touching but do not pass through each other, this area is not included on these maps. Therefore, they are minimum areas of contact and contact is likely occurring without penetration as the curve of the spherical cartilage was constructed to match the curvature of the radius. However, this also means that the larger area exhibited by model two might not reflect more contact area but rather a poorer alignment to the cartilage sphere. When the area of contact between the XROMM trials and the extant simulations is compared (Supplementary Figures S2, 3), there is also only a small area of contact displayed in these minimum area contact maps. This contact is only present for a portion of flexion as, presumably, the fat pad and meniscus is in direct contact with the bone during the rest of flexion. If Dreadnoughtus, had a fat pad and/or a meniscus, we would also expect a smaller area of minimum contact in these contact maps. We predict this would be more similar to what is shown in models one and 3. Future investigations are required to fully interpret if this larger area would indicate joint stability as model 2 has more ‘wobble’ than model three but displays a larger area in the proximity maps.

Although it will almost always be difficult to determine the precise morphology of articular cartilage in any extinct organism, our modeling results suggest a plausible arrangement of such tissues in the elbow of Dreadnoughtus that is supported by the EPB of non-avian dinosaurs. By applying a modeling technique that uses the morphology of articular cartilage to characterize joint kinematics, we were able to test multiple articular cartilage reconstructions, which in turn improves our reconstructions of this organism that can be used in future studies to better understand broader aspects of its paleobiology (e.g., functional morphology, locomotion). Additionally, identifying and using the minimum magnitude of force to achieve full range of motion (i.e., flexion until the forelimb and humerus come into contact) provides an alternative approach independent of estimates of muscular attributes not preserved in the majority of fossils (such as muscle cross-sectional area, muscle mass, and muscle fiber length [e.g., Sellers and Manning, 2007; Sellers et al., 2013; Snively et al., 2013]). No further speculations are made as to whether this force magnitude was within those used by the animal during locomotion as herein we are not investigating locomotion. We emphasize we chose this approach simply to minimize a priori assumptions. Additionally, without our novel method for modeling joints without a priori restrictions on the degrees of freedom we would not have been able to evaluate the kinematic effects of these different articular cartilage reconstructions (i.e., if all reconstructions were modeled as a simple hinge).

Conclusion

Previous studies have investigated the differences between articular cartilage shape and that of the underlying bone and found the differences to be significant (e.g., Bonnan et al., 2010, 2013; Holliday et al., 2010). Researchers examining extant taxa have found the presence (or absence) of soft tissues can affect biomechanical aspects of a given joint, such as the presence of articular cartilage altering the ROM of a joint (e.g., Hutson and Hutson, 2012, 2014, 2015). Therefore, being able to test the effects of articular cartilage thickness and morphology on kinematics, as demonstrated by our case study herein, is important to understanding the overall kinematics of extinct organisms. In this study, the morphology of soft tissues in taxa comprising the EPB of non-avian dinosaurs predicts the presence of thick cartilage with an overall spherical shape on the anterior face of the lateral distal condyle of the humerus of Dreadnoughtus. Without this additional cartilage predicted by our EPB analyses, an articular cartilage thickness of 2% of total bone length resulted in no contact between the radial and humeral cartilages. When a sphere of cartilage was placed over the lateral distal condyle of the humerus, contact was achieved. Our three models of the elbow of Dreadnoughtus differed in the placement and degree of anterior protrusion of the additional spherical articular cartilage on the anterior face of the lateral condyle of the humerus of Dreadnoughtus. However, the arrangement of articular cartilages in our third model is considered to afford the greatest stability as simulations of this model produced the most consistent motion with the least amount of oscillating between both directions of movement. However, model two produced the greatest area of minimum contact during flexion. Our case study also suggests that the radius occupied a more anterior than medial position relative to the ulna, such that the anterolateral lobe of the proximal head of the ulna was centered under the lateral distal condyle of the humerus. This finding agrees with the previous reconstructions of sauropod forelimb structure by Bonnan, (2003), Gilmore, (1936), and Hatcher, (1902).

Herein, we employed an iterative modeling process which allowed easy alteration of modeling conditions and facilitated rapid re-running of simulations. Despite the simplified myological parameters, our simulation results compare favorably (i.e., produce similar forearm motions) with ex vivo XROMM data of our EPB example taxa, indicating that our method of modeling of joints without a priori constraints on degrees of freedom is a viable means of examining joint kinematics. Although we only modeled one joint of one organism, future applications and adaptations of our method could be used to explore numerous biomechanical questions about extinct organisms (i.e., reconstructing articular cartilage shape and thickness, predicting muscle functions, locomotion studies) because we have developed a powerful modeling method that can be applied to systems more complex than those tested herein. In the future, drawing comparisons between quantitative and qualitative outputs from Adams™ with many other techniques commonly used in biomechanical studies (e.g., video analysis, force plates, ROM studies) could facilitate independent hypothesis testing, which in turn would provide greater understanding of the biomechanics of extinct organisms.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.

Author Contributions

KV, SS, and KL designed the study. KV, CL, and MB completed all portions of this research involving extant animals. KV and SS generated and analyzed all the computer simulation data. CL and MB processed and analyzed all XROMM data. The first draft of the manuscript was prepared by KV, which then received input from all coauthors.

Funding

This work was supported by Rowan University (to KV), Stockton University Research & Professional Development Grant (to MB), and the National Science Foundation (Graduate Research Fellowship (DGE Award 1002809) to KV). The XROMM equipment was purchased through a New Jersey Equipment Lease Fund (ELF) grant to Stockton University.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank G.F. Barbato, R. Elsey and P. Dodson for assistance in acquisition of extant specimens, and J. Tangorra, D. Seth, M. Powers, G. Voegele, N. Brace, and D. McDevitt for fruitful discussions and reviewers J.R. Hutchinson, P.J. Bishop for constructive comments which improved the manuscript. We also thank J. Ciraolo for her help on multiple fronts, including the procurement of the XROMM equipment and for assistance and oversight in maintaining the XROMM lab at Stockton University.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.786247/full#supplementary-material

References

Ackerman, J., and Redig, P. (1997). Surgical Repair of Elbow Luxation in Raptors. J. Avian Med. Surg. 11, 247–254. Available at: https://www.jstor.org/stable/30135161.

Google Scholar

Baier, D. B., and Gatesy, S. M. (2013). Three-dimensional Skeletal Kinematics of the Shoulder Girdle and Forelimb in walkingAlligator. J. Anat. 223, 462–473. doi:10.1111/joa.12102

PubMed Abstract | CrossRef Full Text | Google Scholar

Bailleul, A. M., Zheng, W., Horner, J. R., Hall, B. K., Holliday, C. M., and Schweitzer, M. H. (2020). Evidence of Proteins, Chromosomes and Chemical Markers of DNA in Exceptionally Preserved Dinosaur Cartilage. Natl. Sci. Rev. 7, 815–822. doi:10.1093/nsr/nwz206

PubMed Abstract | CrossRef Full Text | Google Scholar

Baumel, J. J., King, S. A., Breasile, J. E., Evans, H., and Berge, J. C. V. (1993). Handbook of Avian Anatomy: Nomina Anatomica Avium, 23. Cambridge, Massachusetts: Nuttall Ornithological Club.

Google Scholar

Bishop, P. J., Falisse, A., de Groote, F., and Hutchinson, J. R. (2021). Predictive Simulations of Running Gait Reveal a Critical Dynamic Role for the Tail in Bipedal Dinosaur Locomotion. Sci. Adv. 7, eabi7348. doi:10.1126/sciadv.abi7348

PubMed Abstract | CrossRef Full Text | Google Scholar

Bonnan, M. F., Sandrik, J. L., Nishiwaki, T., Wilhite, D. R., Elsey, R. M., and Vittore, C. (2010). Calcified Cartilage Shape in Archosaur Long Bones Reflects Overlying Joint Shape in Stress-Bearing Elements: Implications for Nonavian Dinosaur Locomotion. Anat. Rec. 293, 2044–2055. doi:10.1002/ar.21266

PubMed Abstract | CrossRef Full Text | Google Scholar

Bonnan, M. F., Shulman, J., Varadharajan, R., Gilbert, C., Wilkes, M., Horner, A., et al. (2016). Forelimb Kinematics of Rats Using XROMM, with Implications for Small Eutherians and Their Fossil Relatives. PLoS ONE 11, e0149377. doi:10.1371/journal.pone.0149377

PubMed Abstract | CrossRef Full Text | Google Scholar

Bonnan, M. F. (2003). The Evolution of Manus Shape in Sauropod Dinosaurs: Implications for Functional Morphology, Forelimb Orientation, and Phylogeny. J. Vertebrate Paleontology 23, 595–613. doi:10.1671/a1108

CrossRef Full Text | Google Scholar

Bonnan, M. F., Wilhite, D. R., Masters, S. L., Yates, A. M., Gardner, C. K., and Aguiar, A. (2013). What Lies beneath: Sub-articular Long Bone Shape Scaling in Eutherian Mammals and Saurischian Dinosaurs Suggests Different Locomotor Adaptations for Gigantism. PLoS ONE 8, e75216. doi:10.1371/journal.pone.0075216

PubMed Abstract | CrossRef Full Text | Google Scholar

Boucher, E. M. (2010). Digital Paleoart: Reconstruction and Restoration from Laser Scanned Fossils. Philadelphia (PA)]: Drexel University. [dissertation].

Google Scholar

Brainered, E. L., Baier, D. B., Gatesy, S. M., Hedrick, T. L., Metzger, K. A., Gilber, S. L., et al. (2010). X-ray Reconstruction of Moving Morphology (XROMM): Precision, Accuracy and Applications in Comparative Biomechanics Research. J. Experiemental Zoology Part A Ecol. Genet. Physiology 313A, 262–279. doi:10.1002/jez.589

CrossRef Full Text | Google Scholar

Cashmore, D. D., and Butler, R. J. (2019). Skeletal Completeness of the Non‐avian Theropod Dinosaur Fossil Record. Palaeontology 62, 951–981. doi:10.1111/pala.12436

CrossRef Full Text | Google Scholar

Chinsamy-Turan, A. (2005). The Microstructure of Dinosaur Bone: Deciphering Biology with Fine-Scale Techniques. Baltimore, MD: The John Hopkins University Press, 1–195.

Google Scholar

Cignoni, P., Callieri, M., Corsini, M., Dellepiane, M., Ganovelli, F., and Ranzuglia, G. (2008). MeshLab: an Open-Source Mesh Processing Tool. Eurogr. Ital. Chapter Conf., 129–136.,

Google Scholar

Coombs, W. P. (1975). Sauropod Habits and Habitats. Palaeogeogr. Palaeoclimatol. Palaeoecol. 17, 1–33. doi:10.1016/0031-0182(75)90027-9

CrossRef Full Text | Google Scholar

de Cerff, C., Krupandan, E., and Chinsamy, A. (2020). Paleobiological Implications of the Osteohistology of a Basal Sauropodomorph Dinosaur from South Africa. Hist. Biol. 33 (11), 2865–2877. doi:10.1080/08912963.2020.1833000

CrossRef Full Text | Google Scholar

Demuth, O. E., Rayfield, E. J., and Hutchinson, J. R. (2020). 3D Hindlimb Joint Mobility of the Stem-Archosaur Euparkeria Capensis with Implications for Postural Evolution within Archosauria. Sci. Rep. 10, 15357. doi:10.1038/s41598-020-70175-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Fedorov, A., Beichel, R., Kalpathy-Cramer, J., Finet, J., Fillion-Robin, J.-C., Pujol, S., et al. (2012). 3D Slicer as an Image Computing Platform for the Quantitative Imaging Network. Magn. Reson. Imaging 30, 1323–1341. doi:10.1016/j.mri.2012.05.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Fujiwara, S., Taru, H., and Suzuki, D. (2010). Shape of Articular Surface of Crocodilian (Archosauria) Elbow Joints and its Relevance to Sauropsids. J. Morphol. 271, 883–896. doi:10.1002/jmor.10846

PubMed Abstract | CrossRef Full Text | Google Scholar

Gatesy, S. M., Kambic, R. E., and Roberts, T. (2010). Beyond Hinges: 3-D Joint Function in Erect Bipeds. J. Vertebrate Paleontology 30, 94A.

Google Scholar

Gatesy, S. M., Manafzadeh, A. R., Bishop, P. J., Turner, M. L., Kambic, R. E., Cuff, A. R., et al. (2022). A Proposed Standard for Quantifying 3‐D Hindlimb Joint Poses in Living and Extinct Archosaurs. J. Anatomy. Online ahead of print. doi:10.1111/joa.13635

CrossRef Full Text | Google Scholar

Gilmore, C. W. (1936). Osteology of Apatosaurus with Special Reference to Specimens in the Carnegie Museum. Memoirs Carnegie Mus. 11, 175–300. doi:10.5962/p.234849

CrossRef Full Text | Google Scholar

Hatcher, J. B. (1902). Structure of the Forelimb and Manus of Brontosaurus. Ann. Carnegie Mus. 1, 356–376. doi:10.5962/p.234819

CrossRef Full Text | Google Scholar

Hogervorst, T., Bouma, H. W., and de Vos, J. (2009). Evolution of the Hip and Pelvis. Acta Orthop. 80, 1–39. doi:10.1080/17453690610046620

PubMed Abstract | CrossRef Full Text | Google Scholar

Holliday, C. M., Ridgely, R. C., Sedlmayr, J. C., and Witmer, L. M. (2010). Cartilaginous Epiphyses in Extant Archosaurs and Their Implications for Reconstructing Limb Function in Dinosaurs. PLoS ONE 5, e13120. doi:10.1371/journal.pone.0013120

PubMed Abstract | CrossRef Full Text | Google Scholar

Hutson, J. D., and Hutson, K. N. (2014). A Repeated-Measures Analysis of the Effects of Soft Tissues on Wrist Range of Motion in the Extant Phylogenetic Bracket of Dinosaurs: Implications for the Functional Origins of an Automatic Wrist Folding Mechanism in Crocodilia. Anat. Rec. 297, 1228–1249. doi:10.1002/ar.22903

PubMed Abstract | CrossRef Full Text | Google Scholar

Hutson, J. D., and Hutson, K. N. (2012). A Test of the Validity of Range of Motion Studies of Fossil Archosaur Elbow Mobility Using Repeated-Measures Analysis and the Extant Phylogenetic Bracket. J. Exp. Biol. 215, 2030–2038. doi:10.1242/jeb.069567

PubMed Abstract | CrossRef Full Text | Google Scholar

Hutson, J. D., and Hutson, K. N. (2015). Inferring the Prevalence and Function of Finger Hyperextension in A Rchosauria from Finger‐joint Range of Motion in the A Merican alligator. J. Zool. 296, 189–199. doi:10.1111/jzo.12232

CrossRef Full Text | Google Scholar

Imhauser, C. W., Siegler, S., Udupa, J. K., and Toy, J. R. (2008). Subject-specific Models of the Hindfoot Reveal a Relationship between Morphology and Passive Mechanical Properties. J. Biomechanics 41, 1341–1349. doi:10.1016/j.jbiomech.2007.12.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Imhauser, C. W. (2004). The Development and Evaluation of a 3-dimensional, Image-Based, Patient-specific, Dynamic Model of the Hindfoot. PhD Dissertation. Philadelphia: Drexel University.

Google Scholar

Jannel, A., Nair, J. P., Panagiotopoulou, O., Romilio, A., and Salisbury, S. W. (2019). "Keep Your Feet on the Ground": Simulated Range of Motion and Hind Foot Posture of the Middle Jurassic Sauropod Rhoetosaurus Brownei and its Implications for Sauropod Biology. J. Morphol. 280, 849–878. doi:10.1002/jmor.20989

PubMed Abstract | CrossRef Full Text | Google Scholar

Klinkhamer, A. J., Mallison, H., Poropat, S. F., Sloan, T., and Wroe, S. (2019). Comparative Three‐Dimensional Moment Arm Analysis of the Sauropod Forelimb: Implications for the Transition to a Wide‐Gauge Stance in Titanosaurs. Anat. Rec. 302, 794–817. doi:10.1002/ar.23977

PubMed Abstract | CrossRef Full Text | Google Scholar

Knörlein, B. J., Baier, D. B., Gatesy, S. M., Laurence-Chasen, J. D., and Brainerd, E. L. (2016). Validation of XMALab Software for Marker-Based XROMM. J. Exp. Biol. 219, 3701–3711. doi:10.1242/jeb.145383

PubMed Abstract | CrossRef Full Text | Google Scholar

Lacovara, K. J., Lamanna, M. C., Ibiricu, L. M., Poole, J. C., Schroeter, E. R., Ullmann, P. V., et al. (2014). A Gigantic, Exceptionally Complete Titanosaurian Sauropod Dinosaur from Southern Patagonia, Argentina. Sci. Rep. 4, 6196. doi:10.1038/srep06196

PubMed Abstract | CrossRef Full Text | Google Scholar

Lai, P. H., Biewener, A. A., and Pierce, S. E. (2018). Three-dimensional Mobility and Muscle Attachments in the Pectoral Limb of the Triassic Cynodont Massetognathus Pascuali (Romer, 1967). J. Anat. 232, 383–406. doi:10.1111/joa.12766

PubMed Abstract | CrossRef Full Text | Google Scholar

Lautenschlager, S. (2020). Multibody Dynamics Analysis (MDA) as a Numerical Modelling Tool to Reconstruct the Function and Palaeobiology of Extinct Organisms. Palaeontology 63, 703–715. doi:10.1111/pala.12501

CrossRef Full Text | Google Scholar

Lefebvre, R., Allain, R., Houssaye, A., and Cornette, R. (2020). Disentangling Biological Variability and Taphonomy: Shape Analysis of the Limb Long Bones of the Sauropodomorph Dinosaur Plateosaurus. PeerJ 8, e9359. doi:10.7717/peerj.9359

PubMed Abstract | CrossRef Full Text | Google Scholar

Mallison, H. (2010b). CAD Assessment of the Posture and Range of Motion of Kentrosaurus Aethiopicus Hennig 1915. Swiss J. Geosci. 103, 211–233. doi:10.1007/s00015-010-0024-2

CrossRef Full Text | Google Scholar

Mallison, H. (2011). Defense Capabilities of Kentrosaurus Aethiopicus Henning, 1915Palaeontologia Electronica 14: Palaeo-Electronica, .org/2011_2/255/index.html.

Google Scholar

Mallison, H. (2010a). The DigitalPlateosaurusII: An Assessment of the Range of Motion of the Limbs and Vertebral Column and of Previous Reconstructions Using a Digital Skeletal Mount. Acta Palaeontol. Pol. 55, 433–458. doi:10.4202/app.2009.0075

CrossRef Full Text | Google Scholar

Manafzadeh, A. R., and Gatesy, S. M. (2021). Paleobiological Reconstructions of Articular Function Require All Six Degrees of Freedom. J. Anat. 239, 1516–1524. doi:10.1111/joa.13513

PubMed Abstract | CrossRef Full Text | Google Scholar

McConville, J. B. (2015). Introduction to Mechanical System Simulation Using Adams. Mission, KS: SDC Publications, 1–148.

Google Scholar

Meers, M. B. (2003). Crocodylian Forelimb Musculature and its Relevance to Archosauria. Anat. Rec. 274A, 891–916. doi:10.1002/ar.a.10097

PubMed Abstract | CrossRef Full Text | Google Scholar

Mobius, J., and Kobbelt, L. (2010). OpenFlipper: An Open Source Geometry Processing and Rendering Framework. Proc. Curves Surf., 1–13.

Google Scholar

Molnar, J. L., Hutchinson, J. R., Diogo, R., Clack, J. A., and Pierce, S. E. (2021). Evolution of Forelimb Musculoskeletal Function across the Fish-To-Tetrapod Transition. Sci. Adv. 7, eabd7457. doi:10.1126/sciadv.abd7457

PubMed Abstract | CrossRef Full Text | Google Scholar

MSC Software Corporation (2013). Adams: The Multibody Dynamic Simulation Solution. June 9, 2013, Available at: http://www.mscsoftware.com/product/adams.

Google Scholar

Nyakatura, J. A., Melo, K., Horvat, T., Karakasiliotis, K., Allen, V. R., Andikfar, A., et al. (2019). Reverse-engineering the Locomotion of a Stem Amniote. Nature 565, 351–355. doi:10.1038/s41586-018-0851-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Otero, A., Allen, V., Pol, D., and Hutchinson, J. R. (2017). Forelimb Muscle and Joint Actions in Archosauria: Insights from Crocodylus Johnstoni (Pseudosuchia) and Mussaurus Patagonicus (Sauropodomorpha). PeerJ 5, e3976. doi:10.7717/peerj.3976

PubMed Abstract | CrossRef Full Text | Google Scholar

Palazzi, E., Siegler, S., Balakrishnan, V., Leardini, A., Caravaggi, P., and Belvedere, C. (2020). Estimating the Stabilizing Function of Ankle and Subtalar Ligaments via a Morphology-specific Three-Dimensional Dynamic Model. J. Biomechanics 98, 109421. doi:10.1016/j.jbiomech.2019.109421

PubMed Abstract | CrossRef Full Text | Google Scholar

Pierce, S. E., Clack, J. A., and Hutchinson, J. R. (2012). Three-dimensional Limb Joint Mobility in the Early Tetrapod Ichthyostega. Nature 486, 523–526. doi:10.1038/nature11124

PubMed Abstract | CrossRef Full Text | Google Scholar

Rath, N., Balog, J., Huff, W., Huff, G., Kulkarni, G., and Tierce, J. (1999). Comparative Differences in the Composition and Biomechanical Properties of Tibiae of Seven- and Seventy-Two-Week-Old Male and Female Broiler Breeder Chickens. Poult. Sci. 78, 1232–1239. doi:10.1093/ps/78.8.1232

PubMed Abstract | CrossRef Full Text | Google Scholar

Rayfield, E. J. (2007). Finite Element Analysis and Understanding the Biomechanics and Evolution of Living and Fossil Organisms. Annu. Rev. Earth Planet. Sci.Science 35, 541–576. doi:10.1146/annurev.earth.35.031306.140104

CrossRef Full Text | Google Scholar

Rayfield, E. J., Norman, D. B., Horner, C. C., Horner, J. R., Smith, P. M., Thomason, J. J., et al. (2001). Cranial Design and Function in a Large Theropod Dinosaur. Nature 409, 1033–1037. doi:10.1038/35059070

PubMed Abstract | CrossRef Full Text | Google Scholar

Schroeter, E. R. (2013). The Morphology, Histology, and Molecular Preservation of an Exceptionally Complete Titanosaur from Southernmost Patagonia. Philadelphia (PA)]: Drexel University. [dissertation].

Google Scholar

Schwarz, D., Wings, O., and Meyer, C. A. (2007). Super Sizing the Giants: First Cartilage Preservation at a Sauropod Dinosaur Limb Joint. J. Geol. Soc. 164, 61–65. doi:10.1144/0016-76492006-019

CrossRef Full Text | Google Scholar

Schweitzer, M. H. (2011). Soft Tissue Preservation in Terrestrial Mesozoic Vertebrates. Annu. Rev. Earth Planet. Sci. 39, 187–216. doi:10.1146/annurev-earth-040610-133502

CrossRef Full Text | Google Scholar

Sellers, W. I., and Manning, P. L. (2007). Estimating Dinosaur Maximum Running Speeds Using Evolutionary Robotics. Proc. R. Soc. B 274, 2711–2716. doi:10.1098/rspb.2007.0846

PubMed Abstract | CrossRef Full Text | Google Scholar

Sellers, W. I., Margetts, L., Coria, R. A., and Manning, P. L. (2013). March of the Titans: the Locomotor Capabilities of Sauropod Dinosaurs. PLoS ONE 8, e78733. doi:10.1371/journal.pone.0078733

PubMed Abstract | CrossRef Full Text | Google Scholar

Sellers, W. I., Pond, S. B., Brassey, C. A., Manning, P. L., and Bates, K. T. (2017). Investigating the Running Abilities ofTyrannosaurus Rexusing Stress-Constrained Multibody Dynamic Analysis. PeerJ 5, e3420. doi:10.7717/peerj.3420

PubMed Abstract | CrossRef Full Text | Google Scholar

Senter, P., and Robins, J. H. (2005). Range of Motion in the Forelimb of the Theropod Dinosaur Acrocanthosaurus Atokensis , and Implications for Predatory Behaviour. J. Zoology 266, 307–318. doi:10.1017/s0952836905006989

CrossRef Full Text | Google Scholar

Senter, P., and Sullivan, C. (2019). Forelimbs of the Theropod Dinosaur Dilophosaurus Wetherilli: Range of Motion, Influence of Paleopathology and Soft Tissues, and Description of a Distal Carpal Bone. Palaeontol. Electron 222.2.30A, 1–19. doi:10.26879/900

CrossRef Full Text | Google Scholar

Snively, E., Cotton, J. R., Ridgely, R., and Witmer, L. M. (2013). Multibody Dynamics Model of Head and Neck Function in Allosaurus (Dinosauria, Theropoda). Paleontol. Electron. 16, 1–29. doi:10.26879/338

CrossRef Full Text | Google Scholar

Stowers, A. K., Matloff, L. Y., and Lentink, D. (2017). How Pigeons Couple Three-Dimensional Elbow and Wrist Motion to Morph Their Wings. J. R. Soc. Interface. 14, 20170224. doi:10.1098/rsif.2017.0224

PubMed Abstract | CrossRef Full Text | Google Scholar

Suzuki, D., Yamakawa, S., Iijima, M., and Fujie, H. (2021). Function of the Crocodilian Anterior Cruciate Ligaments. J. Morphol. 282, 1514–1522. doi:10.1002/jmor.21401

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsai, H. P., Middleton, K. M., Hutchinson, J. R., and Holliday, C. M. (2018). Hip Joint Articular Soft Tissues of Non-dinosaurian Dinosauromorpha and Early Dinosauria: Evolutionary and Biomechanical Implications for Saurischia. J. Vertebrate Paleontology 38, e1427593. doi:10.1080/02724634.2017.1427593

CrossRef Full Text | Google Scholar

Tsai, H. P., Turner, M. L., Manafzadeh, A. R., and Gatesy, S. M. (2020). Contrast‐enhanced XROMM Reveals In Vivo Soft Tissue Interactions in the Hip of Alligator mississippiensis. J. Anat. 236, 288–304. doi:10.1111/joa.13101

PubMed Abstract | CrossRef Full Text | Google Scholar

Ullmann, P. V., and Lacovara, K. J. (2016). Appendicular Osteology of Dreadnoughtus Schrani, a Giant Titanosaurian (Sauropoda, Titanosauria) from the Upper Cretaceous of Patagonia, Argentina. J. Vertebrate Paleontology 36, e1225303. doi:10.1080/02724634.2016.1225303

CrossRef Full Text | Google Scholar

Vazquez, R. J. (1994). The Automating Skeletal and Muscular Mechanisms of the Avian Wing (Aves). Zoomorphology 114, 59–71. doi:10.1007/bf00574915

CrossRef Full Text | Google Scholar

Voegele, K. K., Ullmann, P. V., Lamanna, M. C., and Lacovara, K. J. (2020). Appendicular Myological Reconstruction of the Forelimb of the Giant Titanosaurian Sauropod Dinosaur Dreadnoughtus Schrani. J. Anat. 237, 133–154. doi:10.1111/joa.13176

PubMed Abstract | CrossRef Full Text | Google Scholar

Voegele, K. K., Ullmann, P. V., Lamanna, M. C., and Lacovara, K. J. (2021). Myological Reconstruction of the Pelvic Girdle and Hind Limb of the Giant Titanosaurian Sauropod Dinosaur Dreadnoughtus Schrani. J. Anat. 238, 576–597. doi:10.1111/joa.13334

PubMed Abstract | CrossRef Full Text | Google Scholar

Weishampel, D. B., Dodson, P., and Osmólska, H. (2004). The Dinosauria. second edition. Berkeley, CA: University of California Press, 1–3. Introduction. doi:10.1525/california/9780520242098.003.0001

CrossRef Full Text | Google Scholar

Wilson, J. A., and Carrano, M. T. (1999). Titanosaurs and the Origin of "Wide-Gauge" Trackways: a Biomechanical and Systematic Perspective on Sauropod Locomotion. Paleobiology 25, 252–267. doi:10.1017/s0094837300026543

CrossRef Full Text | Google Scholar

Wilson, J. A., and Sereno, P. C. (1998). Early Evolution and Higher-Level Phylogeny of Sauropod Dinosaurs. J. Vertebrate Paleontology 18, 1–79. doi:10.1080/02724634.1998.10011115

CrossRef Full Text | Google Scholar

Witmer, L. M. (1995). “The Extant Phylogenetic Bracket and the Importance of Reconstructing Soft Tissues in Fossils,” in Functional Morphology in Vertebrate Paleontology. Editor J. Thompson (London, England: Cambridge University Press), 19–33.

Google Scholar

Yamada, H. (1973). “Ratios for Age Changes in the Mechanical Properties of Human Organs and Tissues,” in Strength of Biological Materials. Editor F. G. Evans (Hutington, NY: Robert E. Kriger Publishing Co.), 255–271.

Google Scholar

Zapata, U., Metzger, K., Wang, Q., Elsey, R. M., Ross, C. F., and Dechow, P. C. (2010). Material Properties of Mandibular Cortical Bone in the American alligator, Alligator mississippiensis. Bone 46, 860–867. doi:10.1016/j.bone.2009.11.010

PubMed Abstract | CrossRef Full Text | Google Scholar