Effects of Plate Velocity Slowdown on Altering Continental Collision Patterns and Crustal-Lithospheric Deformation During the Collision Process

Introduction

Continental collision is an important process for regional tectonic evolution. It is widely distributed across the earth, ranging from the Mediterranean Sea to southwestern China (Figure 1A) (Li et al., 2011; Handy et al., 2010, 2015; Roda et al., 2010, 2012), significantly affecting the climate, resource reallocation, surface topography construction process, and deep mantle spatial–temporal evolution (Wang et al., 2014; Li et al., 2015). Complex discrepant tectonic evolution exists among different continental convergence zones (Negredo et al., 2007; Chertova et al., 2014; Spakman et al., 2018), and even the same collision zone also shows evident lateral variations of tectonic characters along its strike direction (Chen et al., 2015; Liang et al., 2016); in particular, along the Himalaya orogen, tomographic images have recognized distinct east–west inhomogeneous subducting angles and horizontal slip distances (Figures 1B,C) there. For example, Nabelek et al. (2009) used the receiver function method to construct an image of the crust and upper mantle beneath the Himalayas and the southern Tibetan Plateau; they argued that the Indian mantle lithosphere has not extended significantly beyond 31°N. Mechie et al. (2011a, 2011b, 2012) also adopted receiver function method to identify Moho characters across Tibet Plateau and recognized that Indian lithospheric mantle extends northwards until about the Banggong-Nujiang suture, where it steeply sinks to 350–400 km depth. Based on seismic anisotropy characters, Chen et al. (2015) suggested that the geometry of Indian lithosphere underthrusting beneath South Tibet is characterized by lateral variations. Kufner et al. (2021) presented finite-frequency tomography in Hindu Kush; they interpreted their high-velocity anomalies as crustal subduction on top of a northwards-subducting Indian lithosphere, and its penetration depth increases along-strike while thinning and steepening. By contrast, Alpine orogen exhibits several distinct lithospheric mantle deformation features (Kissling et al., 2006; Roda et al., 2010, 2012; Handy et al., 2015; Zhao et al., 2015); e.g., under the central and eastern Alps, subductions operate in an opposite polarity (Figure 1D, profile CC′), while in the western Alps, the overriding Adriatic lithospheric mantle seemed to delaminate and was dragged down by the subducting European lithosphere (Figure 1E, profile DD’).

FIGURE 1

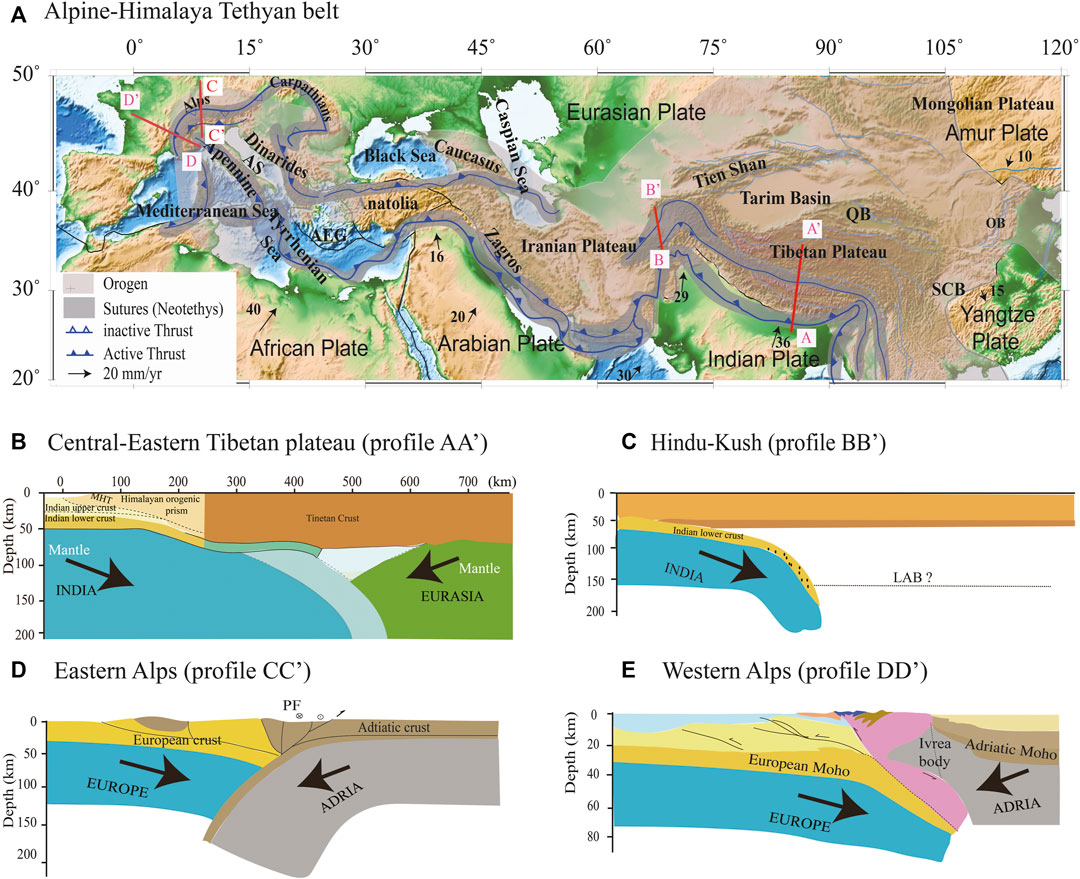
FIGURE 1. (A) The Alpine–Himalayan Tethyan belt and main tectonic units along the collisional orogens. White and black lines outline the orogens and plate convergence boundary, respectively. Gray shadows mark the continental sutures since Cenozoic. Dark sawtooth blue lines show the main thrust belts, and light blue lines delineate the first-order block boundaries around Tibet. Black arrows refer to the plate convergence direction with numbers denoting plate velocity. AS: Adria Sea, AEG: Aegean Sea, QB: Qaidam Basin, SCB: Sichuan Basin, OB: Ordos Basins (Bird, 2003; Li et al., 2011; Saein and Afzal 2017). A simplified schematic diagram of the lithospheric structure of the collisional orogens is shown across (B) central-eastern Tibetan Plateau (AA′) (Owens and Zandt, 1997; Tilmann and Ni, 2003; Nabelek et al., 2009; Mechie et al., 2012; Mechie and Kind, 2013; Ye et al., 2015; Huangfu et al., 2018), (C) Hindu Kush (BB′) (Liang et al., 2020; Kufner et al., 2021), (D) eastern Alps (CC′) (Lippitsch et al., 2003; Kissling et al., 2006; Handy et al., 2015), and (E) Austroalpine of the western Alps (DD′) (Lippitsch et al., 2003; Kissling et al., 2006; Handy et al., 2010; Roda et al., 2010, 2012; Zhao et al., 2015).

In recent years, a number of numerical simulations have been conducted to investigate the essential process and controlling parameters of different continental convergence processes, and prominent progress has been achieved in our understanding of these dynamic processes. Although previous studies have recognized kinematic characters (like subducting angle and plate velocity) and plate rheology can highly influence the fate of plates when they do meet each other, further efforts are still needed to better understand the geodynamic controls and styles of post-subduction collisional orogenic processes (Faccenda et al., 2008). According to the differential dynamic processes controlled by different plate kinematic characters and lithospheric deformation among the various continental convergent boundaries, conceptual models that account for the behavior of continental lithospheric mantle, proposed thus far, can be summarized as follows: (1) pure shear thickening, (2) folding and buckling, (3) one-sided underthrusting or subduction (steep/flat), (4) two-sided/ablative plate consumption, and (5) subducting slab break-off (Pysklywec, 2001; Li et al., 2011; Li, 2014; Yang et al., 2019; Chen, 2021). Pysklywec et al. (2000) suggested that according to their modeling results, continental convergence is such a complicated process that it needs to be illustrated through a combination of several modes, rather than using a single model. Little work, however, has focused on such a combined effect.

Slowdown of plate motion after continental collision, following the oceanic subduction, is a common process that has already been recognized by previous geological and geophysical measurements. For example, plate reconstruction has shown that the convergence velocity between India and Asia experienced a dramatic decrease from ∼18 to ∼3.5 cm/year (Patriat and Achache, 1984; Wang et al., 2001, 2014; Copley et al., 2010) at 50–35 Ma, started from the initial contact of margins between Indian and Asian continents, and continued as the Himalayan orogeny developed and the Tibetan Plateau uplifted (Guillot et al., 2003; Copley et al., 2010). Although numerous numerical simulations have been conducted to study the evolution of continental collision, most of them have adopted a constant plate velocity through the plate convergence process (oceanic subduction and continental collision) for simplification (Burg and Gerya, 2005; Warren et al., 2008; Yamato et al., 2008; Duretz et al., 2012; Liao and Gerya, 2017), and little attention has been given to the influence of plate velocity slowdown (Faccenda et al., 2008; Li et al., 2013; Capitanio et al., 2015).

In this study, we conducted a series of two-dimensional (2D) numerical experiments that integrated both oceanic subduction and the following continental convergence process to systematically investigate differences between a constant velocity system (CVS; a constant plate velocity is incorporated through oceanic subduction and continental convergence) and a velocity-dropping system (VDS; plate velocity decreases after continental collision), as well as the influences of various kinematic characters (e.g., convergence velocity and subducting angle) and continental crustal rheological strength on diverse continental convergence styles in VDS, by following the evolutionary trajectory of plates, analyzing the results of different model series, exploring the potential relationships, or even transitions, among the various continental collision modes to better understand the evolution of continental convergence, and, finally, applying it to explain dynamic processes of related natural cases. This study shed new light on the study of continental collision differentiation.

Materials and Methods

Governing Equation

We conducted numerical experiments with a 2D finite element code [Advanced Solver for Problems in Earth’s ConvecTion (ASPECT); Kronbichler et al., 2012]. ASPECT is an extensible code of the C++ program library deal.ii (Differential Equations Analysis Library, https://www.dealii.org/) targeted at the computational solution of partial differential equations using adaptive finite elements (Arndt et al., 2021). It solves regional thermal convection problems and incorporates the use of complex boundary conditions, large variations in rheological parameters, and localized mesh refinement. The viscous-plastic rheology used in this study satisfied the equations of the conservation of mass (Eq. 1), momentum (Eq. 2), and internal energy (Eq. 3) for an incompressible medium and adopted the Boussinesq approximation.

$-\nabla \cdot 2\mathrm{\eta }\mathrm{\epsilon }\left(\mathbf{u}\right)+ \nabla p = \rho \mathbf{g}in \mathrm{\Omega },(1)$

$\nabla \cdot \mathbf{u} = 0in \mathrm{\Omega },(2)$

$\begin{array}{l}{\mathrm{\rho }}_0{C}_p\left(\frac{\partial T}{\partial t} + \mathbf{u} \cdot \nabla T\right)-\nabla \cdot k\nabla T = {\mathrm{\rho }}_{0}H\\ + 2\mathrm{\eta } \mathrm{\epsilon }\left(\mathbf{u}\right) : \epsilon \left(\mathbf{u}\right)\\ + \alpha T (\mathbf{u} \cdot \nabla p)in \mathrm{\Omega }\end{array}(3)$

The right-hand-side terms of Eq. 3 correspond to internal heat production, for example, due to radioactive decay, friction heating, and adiabatic compression of material. $\eta$ is the viscosity, $\text{ε}\left(\mathbf{u}\right)=\frac{1}{2}\left(\nabla \mathbf{u}+\nabla {\mathbf{u}}^{\text{T}}\right)$ is the symmetric gradient of the velocity (often called the strain rate), $\mathbf{u}$ is the velocity, $p$ is the pressure, g is the gravitational acceleration, $\text{Ω}$ is the interesting domain, $C_p$ is the heat capacity, $k$ is heat conductivity, H is the intrinsic specific heat production, $\alpha$ is the thermal expansion coefficient, and ${\text{ρ}}_0$ is the adiabatic reference density. We consider that the density satisfies the equation

$\rho = {\mathrm{\rho }}_0\left(1 – \mathrm{\alpha } \left(T - T_0 \right)\right) (4)$

where ${\rho }_0$ is the reference density at reference temperature $T_0$ (293 K).

Eq. 5 is used to describe the evolution of a set of variables $c_i$ (X, t), I = C named compositional fields here. Compositional fields were designed to track the chemical composition of the convecting medium. Thus, the composition is a non-diffusive quantity (Kronbichler et al., 2012).

$\frac{\partial \mathit{c}}{\partial t}+\mathit{u}\cdot \nabla \mathit{c=}0(5)$

Rheology

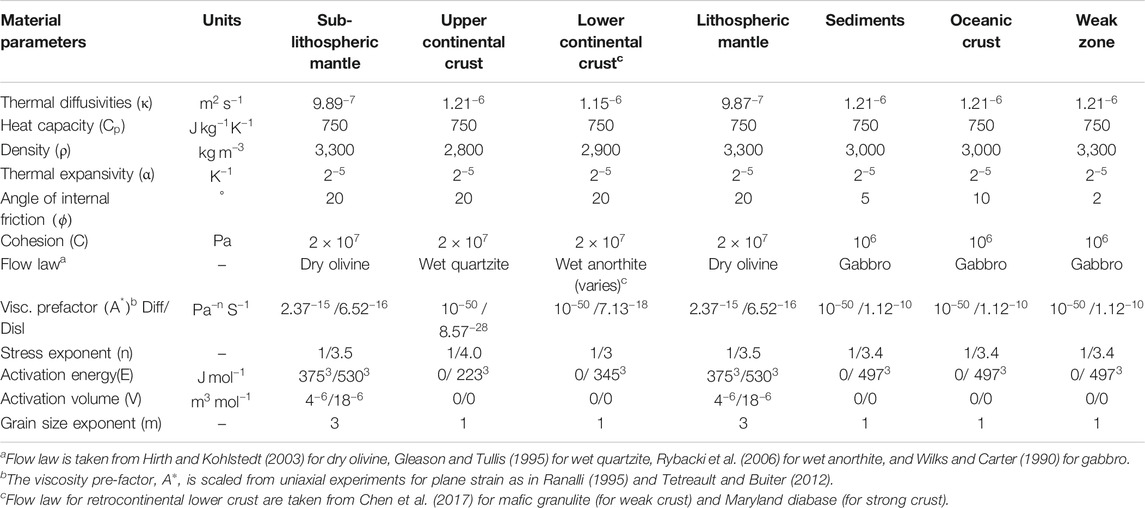
Like other geodynamics codes, ASPECT assumes that the solid Earth materials can be treated as a highly viscous fluid, its deformation is predominantly defined by brittle fracture or viscous creep; thus, we apply three basic rheological characters: plastic yielding, diffusion creep, and dislocation creep. Diffusion and dislocation creep can be conveniently formulated with Eq. 6 (Karato and Wu, 1993; Karato, 2008).

${\mathrm{\eta }}_{diff/disl}= \frac{1}{2}{A}^{-\frac{1}{n}} {\mathrm{d}}^{\frac{m}{n} }{\dot{{\epsilon }_e}}^{\frac{1-n}{n}}exp\left(\frac{Q+PV}{nRT}\right)(6)$

Where the effective deviatoric strain rate is defined as ${\dot{\epsilon }}_e$ = $\sqrt{\frac{1}{2}{\dot{\epsilon }}_{ij}^{\text{'}} {\dot{\epsilon }}_{ij}^{\text{'}}}$. For diffusion creep, n = 1, m > 0, while in the case of dislocation creep n > 1, m = 0. Definition and values of other symbols are shown in Table 1. Surface erosion and sedimentation are neglected.

TABLE 1

TABLE 1. Parameter list of the numerical experiments.

We implemented composite viscosity combining diffusion creep ($\mathrm{\eta }$_diff) and dislocation creep ($\mathrm{\eta }$_disl) for both lithospheric mantle and sub-lithospheric mantle as shown in Eq. (7).

${\mathrm{\eta }}_{\mathrm{comp}}={\left(\frac{1}{{\mathrm{\eta }}_{\mathrm{diff}}}+\frac{1}{{\mathrm{\eta }}_{\mathrm{disl}}}\right)}^{-1}(7)$

The effective viscosity in the viscous stress is defined for the power law creep based on the temperature and the strain rate tensor (Glerum et al., 2018; Karato, 2008). The plastic yielding is defined by the Drucker–Prager criterion Eq. 8 (Davis and Selvadurai, 2002):

${\sigma }_{yield} = C\cos \left(\varphi \right)+ P\sin \left(\varphi \right)(8)$

When the viscous stress 2 $\mathrm{\eta }$_{diff/disl/comp} $\dot{\epsilon }$_ii exceeds the yield stress, the viscosity is rescaled to the yield surface:

${\mathrm{\eta }}_{yield }= \frac{ {\sigma }_{yield}}{2\cdot {\dot{\mathrm{\epsilon }}}_e }(9)$

After giving the maximum ($\mathrm{\eta }$_max) and minimum ($\mathrm{\eta }$_min) viscosity cutoffs, the viscosity is then given by Eq. (10):

${\mathrm{\eta }}_{\mathrm{eff}}=\min \left(\max \left({\mathrm{\eta }}_{\mathrm{i}},{\mathrm{\eta }}_{\min }\right),{\mathrm{\eta }}_{\max }\right)(10)$

where i is one of the subscripts among diff, disl, comp, and yield.

Initial Model Configuration and Boundary Conditions

The model is 2,000 km long and 660 km deep in the x- and z-directions, respectively. The resolution of finite element mesh consists of three parts, in the upper 2,000 km $\times$ 200 km domain is 2 km $\times$ 2 km, then it is decreased to 4 km $\times$ 4 km in the following 2,000 km $\times$ 100 km, while resolution of the rest domain is 8 km $\times$ 8 km. In the context, we adopted terminology from Jamieson et al. (1998) to distinguish different parts of the adjacent convergent plates, a plate with an initial oceanic subduction on the left is defined as the “pro” side, an overriding plate on the right is defined as the “retro” side. The initial model consists of three plates: procontinental plate (length of 600 km), oceanic plate (length of 400 km), and retrocontinental plate (length of 1,000 km). An inclined 10-km-width weak zone (Table 1) sits between the retro and pro sides, and various angles (30°, 45°, and 60°) are designed to test their effects on model evolutions. The continental lithosphere is 140 km thick, with an upper crust (20 km thick), a lower crust (20 km thick), and a 100-km-thick lithospheric mantle, while the oceanic lithosphere (∼80 Ma) comprises of a sediment layer (4 km thick), crust (8 km thick), and lithospheric mantle of 68 km thick (Figure 2). Continental upper crustal and procontinental lower crustal rheological properties are defined as wet quartzite (Gleason and Tullis, 1995) and wet anorthite (Rybacki et al., 2006), respectively, while different flow laws for retrocontinental lower crust are applied to explore their effects on model results, mafic granulite (Chen et al., 2017) for a relatively weak lower crust compared to wet anorthite, and Maryland diabase (Chen et al., 2017) for a relatively strong one. In addition, sediment and oceanic crust are both represented by gabbro (Wilks and Carter, 1990). Dry olivine (Hirth and Kohlstedt, 2003) is used for lithospheric mantle and sub-lithospheric mantle (see Tables 1, 2 for more details).

FIGURE 2

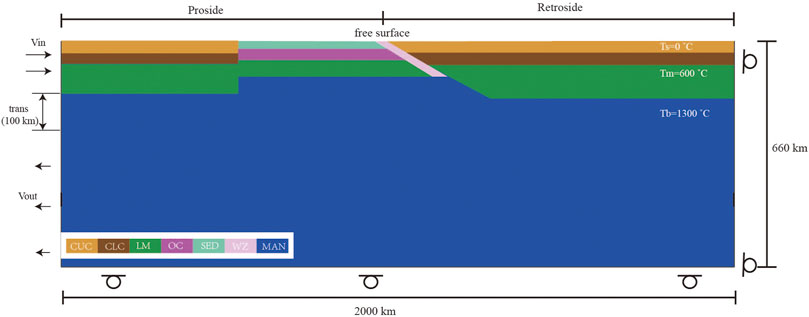
FIGURE 2. Configuration of the reference model. The size of the numerical box is 2000 × 660 km, and an oceanic plate is integrated with a continental plate on the proside (left). The retroside (right) is an overriding continental plate. Various colors reflect to different lithologies, CUC: continental upper crust, CLC: continental lower crust, LM: lithospheric mantle, OC: oceanic crust, SED: sediment, WZ: weak zone, and MAN: sub-lithospheric mantle. Ts is surface temperature, Tmn is the Moho temperature of normal continent, Tmc stands for the Moho temperature of continental Craton, Tb is the bottom temperature of lithosphere. V_in and V_out denote where material flow in and out, and V_trans denotes the transition zone from flow in to flow out.

TABLE 2

TABLE 2. Viscous flows used for retrocontinental lower crust.

The initial surface temperature is 0°C, the initial Moho temperature of the oceanic lithosphere and retrocontinent is 600°C, while it is 400°C for the procontinent. The initial Lithosphere–Asthenosphere Boundary (LAB) temperature is defined as 1,300°C, below which an adiabatic thermal gradient of 0.5°C/km is assumed. Both side walls are thermal insulated boundaries.

The initial temperature structure of continental lithosphere follows a steady-state geotherm from Chapman (1986) that considers the thickness of each compositional layer, shown as Eqs. (11), (12), and (13). The initial oceanic lithospheric temperature distribution follows the plate cooling model (Turcotte and Schubert, 2002).

${\mathrm{T}}_{\mathrm{Z}}={\mathrm{T}}_{\mathrm{T}}-\frac{q_T}{k} \times Z-\frac{A \times Z^2}{2k}(11)$

${\mathrm{T}}_{\mathrm{B}}={\mathrm{T}}_{\mathrm{T}}+\frac{q_T}{k} \times \mathrm{\Delta }Z-\frac{A \times \mathrm{\Delta }{Z}^2}{2k}(12)$

${\mathrm{q}}_{\mathrm{B}}={\mathrm{q}}_{\mathrm{T}}-\mathrm{A}\times \mathrm{\Delta }\mathrm{Z}(13)$

Where T_Z denotes the temperature of the depth Z, T_T is the top surface temperature of each layer, T_B denotes the bottom temperature of each layer, and the heat flows at the top and bottom of each layer are denoted as q_T and q_B, respectively. $\Delta$Z is the thickness of the layer, A is volumetric heat production, and k is thermal conductivity.

Mechanical boundary conditions are free slip at both the retroside and bottom boundaries; the top boundary used a true free-surface condition to account for topography evolution. Inflow velocity at the procontinental lithosphere wall, it is the approximation of an integration of three major forces in nature, i.e., slab pull, ridge push, and convection drag, and equivalently balanced outflow velocity on the same sidewall across the sub-lithospheric mantle. Besides, there is a velocity transition zone between flow-in and flow-out zones (thickness of 100 km) (Figure 2).

Results

Comparison of CVS and VDS

Previous studies have indicated that the force equilibrium state and thermal structure of plate, and lithospheric deformation styles during subduction, are related to the convergence velocity (Li et al., 2002). It has also been recognized that dramatic plate velocity slowdown after continental collision following oceanic subduction is a general phenomenon, but little work has been done using numerical modeling to systematically investigate how such a convergence velocity drop influences the spatial–temporal evolution of crustal-lithospheric deformation during continental collision. Thus, we started with the comparison of CVS and VDS.

First, we constructed two series of numerical models using (1) MSII-ca1, -ca2, and -ca3 and (2) MSI-v1a1, -v2a1, and -v3a1 that belong to CVS and VDS, respectively (Table 3). All models shared the same initial subducting angle ($\alpha$ = 30°) and continental crustal rheological strength (medium).

TABLE 3

TABLE 3. Model list of parametric tests.

Take MSII-ca1 as an example (Figure 3). In this model, we push from the proside with a constant velocity. This velocity during oceanic subduction is equal to that in the continental convergence phase, and both are constant (V_os = V_cc = 3 cm/year) (Figure 3E). During the initial stage of oceanic subduction, relatively dense oceanic plate subducted along a prescribed slope weak zone, and little sediment and oceanic crust was scraped off and rested in site (Figure 3A1). Excess negative buoyancy is attributed to the prior oceanic plate subduction and then dragged the trailing continental plate downward though it is buoyant, accompanied by the steepening of subducting angle. Note that, as procontinent arrived at trench, collision started, characterized by a notable upbending of the leading edge of retrocontinent. Besides, slow pushing led to a slow proplate motion, which resulted in relatively strong coupling between plates, as a portion of the retrocontinental lithospheric mantle was dragged down and sank together with the subducting slab (Figure 3A2). At the early stage of continental collision, combined effects from continuous pushing from the proside trailing edge and slab downward dragging maintained the downward movement of the continental lithospheric mantle. However, as more buoyant continental crust resisted sinking, it accumulated at shallow. Later, pushing from prescribed velocity competed with the crust’s buoyance. The process gave rise to strain localization (Figure 3C3), especially in the proside ocean-continent transition zone, and then generated a rupture there, along which temperature abnormally increased (Figure 3A3). In addition, we can recognize significant uplift of both plates adjacent to the collision zone, especially the retroside that formed a narrow and almost stationary orogen (Figure 3F).

FIGURE 3

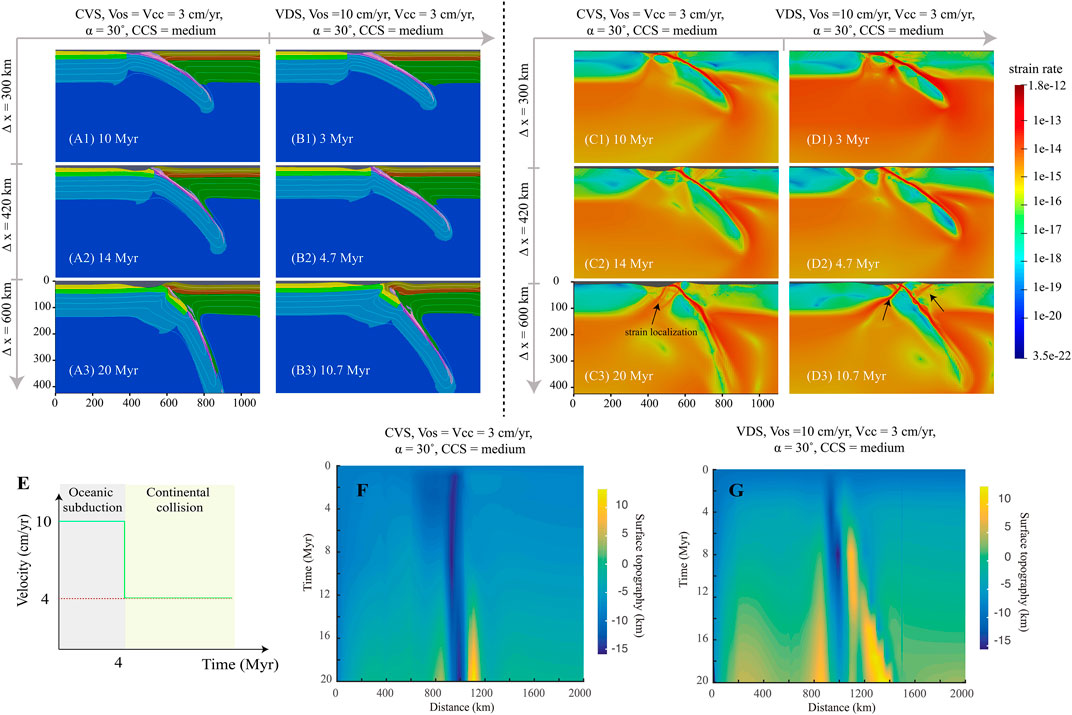
FIGURE 3. The upper left panel shows the snapshots of compositional fields from models MSII-ca1 (CVS) (A1–A3) and MSI-v1a1 (VDS) (B1–B3), respectively. Different colors denote different lithologies (see Figure 2). White lines denote isotherm with 200°C increment that start from 200°C to 1,200°C. The upper right panel shows the snapshots of strain rate from models MSII-ca1 (C1–C3) and MSI-v1a1 (D1–D3). ∆x is the amount of convergence. (E) shows the velocity boundary conditions of CVS (red dotted line) and VDS (green dotted line). (F) and (G) show the topography evolution of both models.

MSI-v1a1 from VDS, on the other hand, was applied with a 10 cm/year plate velocity during oceanic subduction (V_os = 10 cm/year) for ∼4 Myr, followed by a much slower continental convergence (V_cc = 3 cm/year). Though a higher V_os was applied to MSI-v1a1 than to MSII-ca1, the main process of oceanic subduction proceeded in a similar way except for two differences: (1) Little material from the retrocontinental lithospheric mantle was dragged down by the slab due to plates’ relative weaker coupling resulting from fast subduction (Figure 3B1). (2) The subducting angle was slightly gentle (Figures 3A2,3B2). After the continents’ initial contact, convergence velocity decreased to 3 cm/year. Similar to the process in MSI-ca1, accumulation of buoyant continental crust at the plate interface occurred, and local crustal rupture developed in the proplate through which an anomalous temperature increasing occurred (Figure 3B3). At shallow depth, dramatic strain localization developed in the proside ocean-continent transition zone (Figure 3D3). Besides, under the increased pulling from the slab in depth, the subducting angle gradually steepened (Figures 3D2,3D3). It is worth noting that the subducting angle in model MSI-ca1 is much steeper than the one in MSI-v1a1. We supposed that, as the prior oceanic subduction was prescribed a higher plate convergence velocity in the latter model, during the early stage of continental collision, plates were still weakly coupled. The subducting plate could keep cold and maintain its strength, which facilitated the lithosphere sinking integrally with a nearly steady dipping angle. At the same time, prior fast plate convergence velocity could cause tense compression in the collision zone and result in severe deformation at the front edge of the retrocontinent. A new shear zone at shallow was then formed retroside (Figures 3D2,3D3). Finally, compared with the nearly fixed narrow orogen in the MSII-ca1, orogen in MSI-v1a1 showed a prominent retroward advance, and eventually developed into a relatively wider orogen (Figures 3F,G).

To further investigate the effects of plate velocity on the continental collision pattern in both systems, we varied the continental convergence velocity (V_cc) (Table 3). As is shown in Figure 4: (1) Increasing V_cc could get a relatively gentle subducting angle in both series of models (Figures 4A,B). (2) All models tended to generate plate polarity reversal, while the time of slab break-off and polarity alteration was initiated earlier in the VDS than in the CVS (Figure 4C). In addition, fast V_cc always causes severe deformation of both plates adjacent to the collision zone.

FIGURE 4

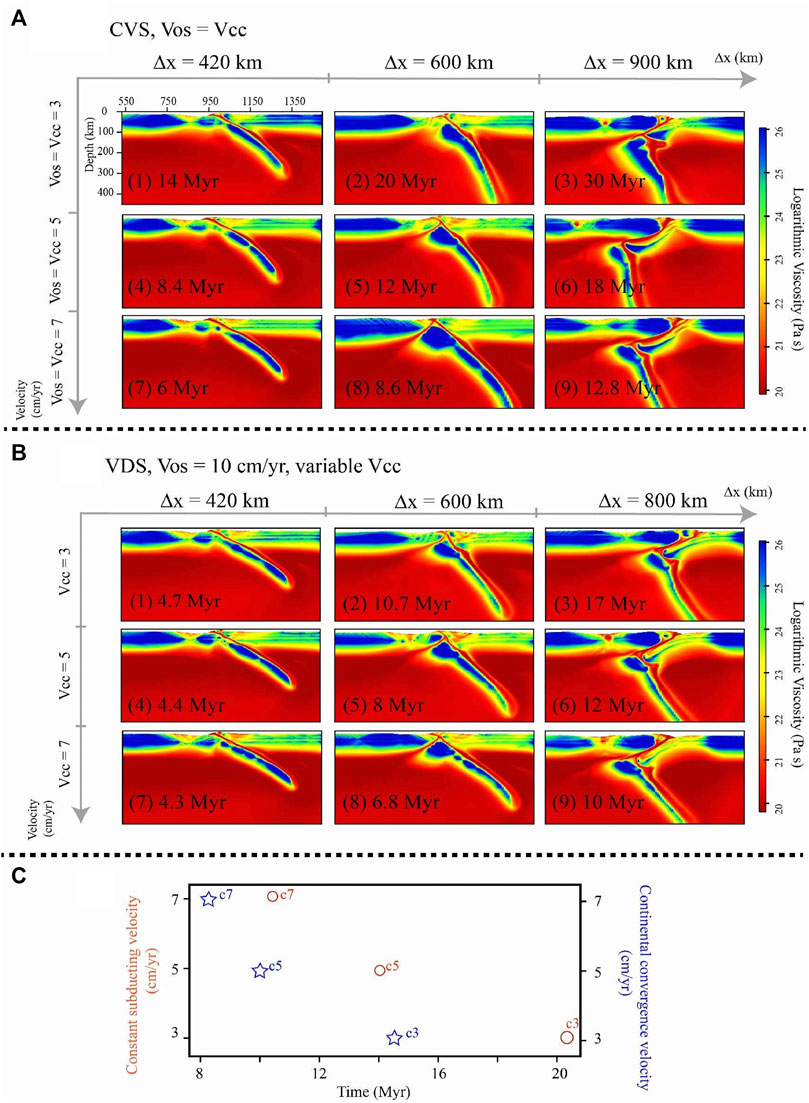
FIGURE 4. (A) shows the viscosity field of models with variable plate velocity in CVS (V_os = V_cc), (1)–(3) are the snapshots of model with a 3 cm/year constant plate velocity, and (4)–(9) correspond to the snapshots of models with 5 cm/year and 7 cm/year constant plate velocity, respectively. (B) shows the viscosity field of models with variable plate velocity in VDS (V_os > V_cc), (1)–(3) show the snapshots of model with a 3 cm/year continental convergence velocity (V_cc), and (4)–(9) correspond to the snapshots of the model with 5 cm/year and 7 cm/year continental convergence velocity, respectively. Δx is the amount of convergence. (C) The start time of slab break-off. Red notes and circles denote the results of CVS; blue notes and stars denote the VDS results.

Controlling Parameters of Altering the Continental Collision Mode in VDS

According to the foregoing numerical experiment results, VDS showed conspicuous differences from the normally used CVS. By varying the continental convergence velocity, the dip angle of the initial weak zone, and retrocontinental crustal rheological strength, we then examined how these parameters influence the spatial−temporal evolution of the continental collision process in VDS. Three end members of the continental collision mode can be obtained according to the model results from parametric sensitive tests: (1) polarity reversed mode, (2) oceanic-type stable mode, and (3) two-sided/ablative mode

The polarity reversed continental collision mode is not a new concept model. Numerous geological and geophysical records have recognized this type of collision mode and referred to these collisions between volcanic arcs and ocean−continent subduction zones or those with subducting ridges (Clift et al., 2003; Brown et al., 2011; Handy et al., 2015; von Hagke et al., 2016). Take the model MSI-v1a1 as an example (Figure 5). The whole evolution process includes oceanic subduction (OS) and continental collision (CC). Considering the negative buoyance of cool oceanic plate, fast plate convergence velocity (10 cm/year) was prescribed during the whole OS. At the early stage, little sediment and crust material was scraped off from the lower plate because of weak coupling between plates under fast plate convergence. The scraped-off material then rested in site, accumulated, and accreted to the adjoining retroplate. Meanwhile, distinct subsidence occurred as slab bended and promoted to the formation of a foreland basin (Figure 5A). When the ocean closed (during CC), the prescribed plate convergence velocity slowed down (3 cm/year). Continuous compression, along with the accumulation of scraped-off material at shallow, uplifted the collision zone rapidly, producing a narrow orogen, underneath which the slab dipping angle gradually steepened (Figures 5B,C). The model results also showed that a small portion of the retrocontinental lithospheric mantle was dragged down by the slab as plates’ strong coupling under slow convergence (Figure 5C). As continental convergence continued, on the retroside around orogen, a slight subsidence happened at almost the symmetric place to the proside foreland basin with respect to the axis of orogenic belt. On the proside, foreland basin broadened slightly, with its proside flank slightly uplifted. It is worth noting that temperature increased abnormally at the retroplate leading edge (Figure 5C). The reasons for this may come from two aspects: (1) The compression from continental collision resulted in crustal thickening (Figure 5D), which may increase the radioactive heat from the continental crust. (2) A portion of hot retrocontinental lithospheric material moved upward along the plates’ interface (Figure 5D). Following that, procontinental crust ruptured, leaving the surface crust indented to the orogenic wedge and causing the wedge to grow retroward along the reversed shear zone on the retroplate (Figure 5E). Eventually, the procontinent plate obducted onto the retroplate. The retrocontinent then delaminated, accompanied by parts of the lower crust and lithospheric mantle underthrusted beneath the procontinent, leaving a gentle uplift and widening of the foreland basin on the proside. Meanwhile, a new narrow retroside subsidence generated behind orogenic wedge (Figure 5F). To conclude, from OS to the early stage of CC, topography building up was relatively concentrated on the collision zone, followed by a broad surface uplift and a retroward movement of the orogenic wedge.

FIGURE 5

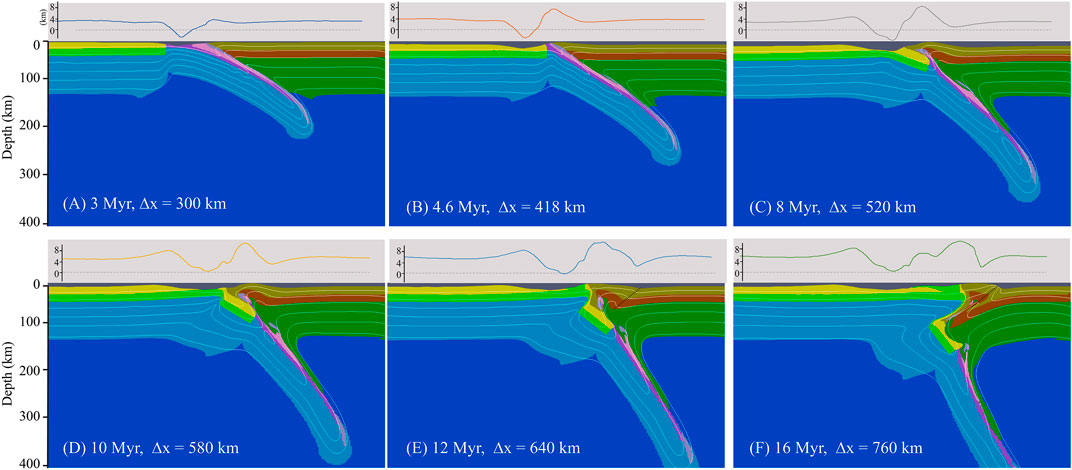
FIGURE 5. Evolution of polarity reversed mode. Panels above each snapshot with gray shading show the corresponding topography. Δx is the amount of convergence. Different colors in (A–F) denote different lithologies (same as Figure 2).

The most common mode is the stable continental collision mode, which has been confirmed by geological and geophysical observations as well as numerical models (Chemenda et al., 2000; Yin and Harrison, 2000; Li et al., 2011; Huangfu et al., 2018). It has a one-sided asymmetric type with a stable plate polarity and can be further divided into flat and steep subtypes.

The model MSI-s2a3 was an example of a steep subtype (Figure 6). The general process of OS in this model was similar to that in model MSI-v1a1 (Figure 5), while much more sediment and oceanic crust were scraped off (Figure 6A). During CC, a relative slow continental convergence velocity of 3 cm/year compared to the OS was prescribed. Initially, accumulated oceanic crust at shallow detached from its deeper part. After that, temperature abnormally increased along the gap. The accumulation then contributed to the growth of the orogen wedge and the notable uplift (Figure 6B). As the procontinental lithosphere arrived at the collision zone, the subducting angle gradually steepened, accompanied by a slight slab roll-over. At ∼8 Myr, a second proside crustal rupture happened at the place where slab necking occurred. During this period, both the proside and the retroside around the collision zone experienced uplift (Figures 6C,D). Meanwhile, the break-off procontinental crust moved downward, persisted at approximately 130–180 km because of its intrinsic buoyancy, and partly intruded into the bottom of the adjacent retrocontinental lithosphere. Contemporary decoupling between the procontinental upper and lower crust occurred, leaving the upper crust stacked at the surface, while the lower crust started to sink with the lithospheric mantle. The retrocontinental leading end near the surface was warped slightly upward, followed by a proward advance of the orogeny wedge (Figures 6E,F).

FIGURE 6

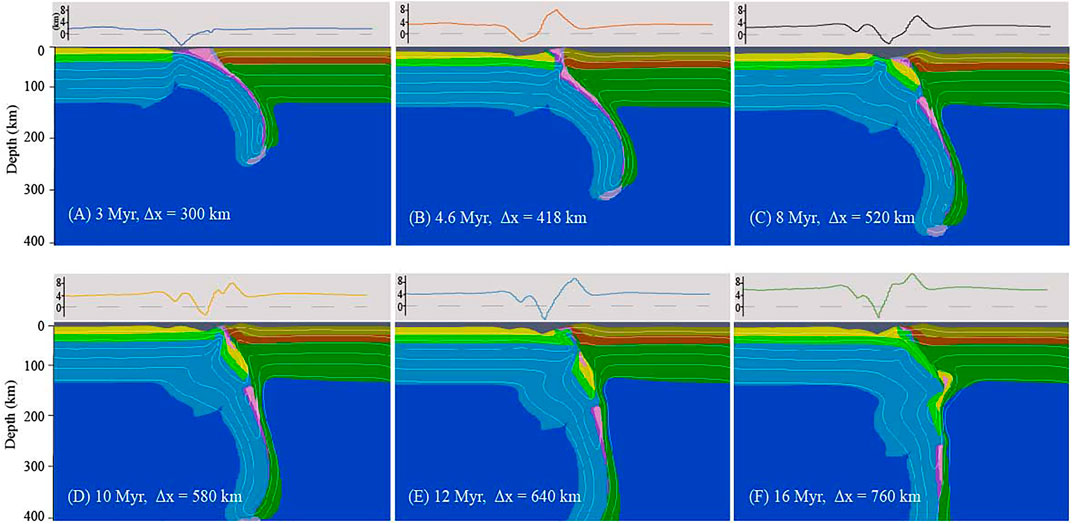
FIGURE 6. Evolution of the stable continental collision mode. Panels above each snapshot with gray shading show the corresponding topography. Δx is the amount of convergence. Different colors in (A–F) denote different lithologies (same as Figure 2).

The ablative/two-sided continental collision mode (Tao and O’connell, 1992; Faccenda et al., 2008; Warren et al., 2008) was the third mode obtained from the model results. This mode can be further divided into symmetric and polarity-reversed subtypes. The model MSI-s1a2 consisted of a weaker retrocontinental lower crust and a 45° subducting angle. It yielded a similar oceanic subduction process as MSI-v1a1 (Figure 5) did. However, it generated a relatively gentle topographic uplift (Figures 7A,B). Thereafter, it became extremely distinct as the continents ran into each other. As the retrocontinental lower crust was designed to be rheologically weak, the sediment and procrustal rocks accumulated at shallow could easily cause an indention without creating significant orogen wedge rising. In contrast, under the obstruction from a buttress that consisted of the scraped-off material and the upward retrolithospheric mantle, the procontinental leading edge uplifted instead (Figure 7C). Continuous horizontal proside pushing gave rise to a thick and quasi-symmetric collision zone with a thickened crust, which caused a wide retroside topographic growth. As the procontinental crust is intrinsically buoyant, it resisted going downward. The competition between continuous proside pushing and the resistance from the retrocontinent then resulted in strain localization of the proplate leading edge, after which the procontinental crust ruptured (Figures 7D,E). Later on, the subducting slab gradually turned over and changed its polarity, indented into the retrocontinent, peeled off the retrocontinental upper crust, and started to subduct with the delaminated retrocontinental lithospheric mantle, leaving a retrocrustal fold at the surface (Figure 7F).

FIGURE 7

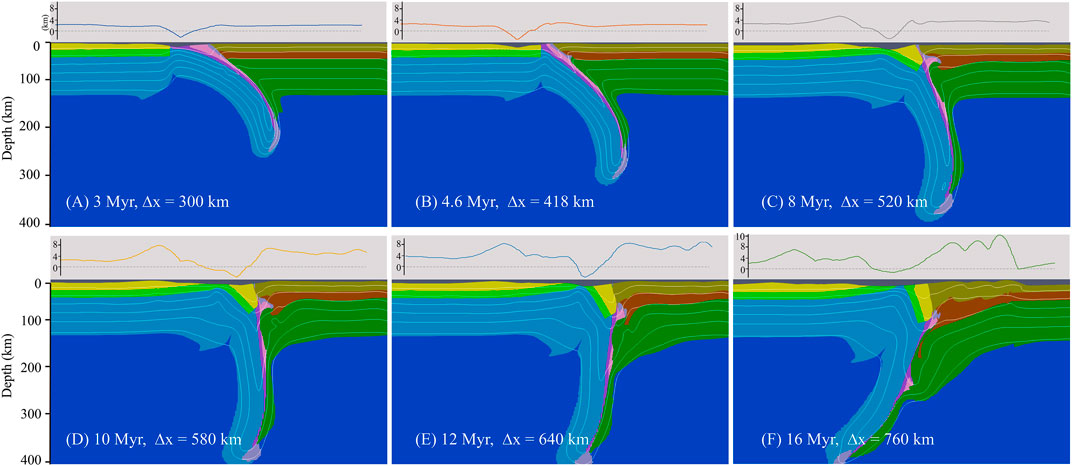
FIGURE 7. Evolution of the ablative/two-sided continental collision mode. Panels above each snapshot with gray shading show the corresponding topography. $\text{Δ}$ x is the amount of convergence. Different colors in (A–F) denote different lithologies (same as Figure 2).

In this study, an important aspect of our effort to differentiate the models from previous experiments was conducting a parametric study in VDS. Three distinct end members of continental collision modes were obtained. The regime diagram (Figure 8, Supplementary Material) shows the dependence of continental collision evolution on the continental convergence rate, initial subducting angle, and continental crustal rheological strength.

FIGURE 8

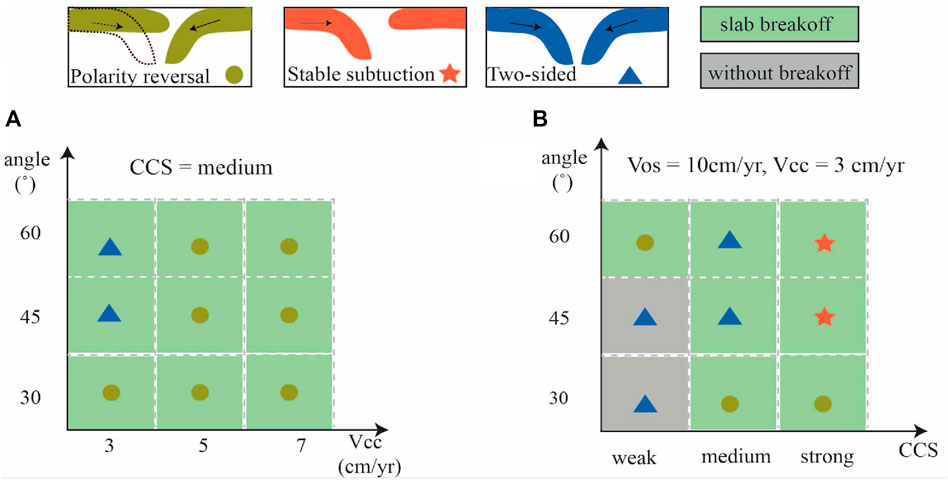
FIGURE 8. Schematic figures of continental collision modes depending on (A) subducting angle and plate velocity, and (B) subducting angle and crustal rheological strength. Different symbols denote different collision modes.

Among models that used a medium retrocontinental crustal strength, the ones with a gentle subducting angle (30°) always exhibited polarity-reversed mode. In the same time frame, increasing continental convergence velocity resulted in an earlier break-off of the proplate as well as a longer retrocontinental delamination (Figure 4B). In contrast, models with a slightly steeper subducting angle (45°) and slow continental convergence (3 cm/year) evolved into the ablative continental collision mode, whereas models with fast convergence velocity ($\ge$5 cm/year) evolved into the two-sided mode (Figure 8A). Although increasing the subducting angle to a steeper degree (60°) has little influence on the tendency of continental convergence modes transition, fast continental convergence may result in a second or even multiple fractures in procontinental forepart adjacent to the collision zone, as Model v3a2 (Table 1) indicated.

In the weak continental crustal regime (CCS = weak), the retrocontinental lower crust had relatively low viscosity in favor of the decoupling between the retrocontinental crust and the underlying mantle lithosphere. Such models were more liable to evolve polarity reversals. Differences existed, however, between models with a relatively gentle subducting angle ($\le$45°) and those with a steep angle (>45°). The former corresponded to the two-sided mode, while the latter refers to the process that occurred as the slab first broke off, and then the detached retro lithospheric mantle began to sink and formed a one-sided polarity reversed mode (Figure 8B).

As we applied a strong retrocontinental crustal strength (CCS = strong), the retroplate seemed to be strong enough to resist intense deformation and delamination. It was then more inclined to deform as an integrated plate, which produced a stable continental collision mode (Figure 8B).

To conclude, these numerical results indicate that continental convergence velocity, initial subducting angle, and retrocontinental crustal rheological strength are three crucial first-order controlling parameters that have significant influences on the continental collision process in VDS, and the crustal strength is especially important for the alteration of continental collision patterns among them. As illustrated in Figure 8, in models with medium crustal strength, slow convergence velocity and steep subducting angle tended to evolve into a two-sided/ablative continental collision mode. Fast convergence and gentle subducting angles always developed into a polarity reversal mode. Models with a weak continental lower crust were more likely to form a two-sided reversed mode. Further enhancing crustal strength contributed to a strong, coherent retrocontinental lithosphere and tended to evolve into a stable mode. Note that a weak retrocontinental lower crust with a gentle subducting angle accommodated continental convergence with a two-sided reversed mode characterized by rolling over of the proplate, rather than breaking off.

Discussion

The Effects of Plate Velocity Slowdown on the Continental Collision Process

The most crucial setup that differentiates VDS models from CVS is decreasing plate convergence velocity from 10 cm/year during oceanic subduction to the slower ones (3/5/7 cm/year) after the onset of continental collision. Figure 4 shows that the polarity reversal mode dominated the continental collision style in both VDS and CVS, while the time of polarity reversal in VDS is always earlier than in CVS. This phenomenon arises from the change of both net force and temperature field in VDS: On one hand, during oceanic subduction, fast plate convergence velocity caused fast slab sinking that led to an increase in negative buoyancy. When sharply decreasing the continental convergence velocity after the continental collision, surface lithospheric motion notably slowed down, with slab in depth continuing its downward dragging. The net effect from the forces acting in opposite directions could trigger tension and localized strain in the slab interior. In addition, the foregoing fast oceanic subduction could aggravate the plates’ relative motion and increase shear heating on the plates’ interface, which may also warm and weaken the plates from the surface. As a consequence, the subducting slab may weaken in certain zones. On the other hand, fast plate convergence velocity corresponded to high horizontal compression. Intense compression between plates could result in severe deformation in and around the collision zone, providing ideal conditions for the formation of a new fault, along which a new subduction may develop.

Besides, slab break-off always results in a sudden removal of downward slab pulling. After that, the following continental forepart could rebound upward due to its buoyancy. In our models, such a process may facilitate the obduction of procontinent along the newly developed fault, and contribute to the evolution of plate polarity reversal (Figure 5).

Continental Collision Modes in the Plate Velocity Slowdown Model

Parametric sensitive tests revealed that kinematic characteristics (including plate convergence velocity and subducting angle), as well as the rheological strength of continental crust, had strong influences on continental collision evolution in a plate velocity slowdown model, which has also been confirmed by previous studies that adopted a constant plate velocity model (Pysklywec, 2001; Faccenda et al., 2008; Yang et al., 2019). However, it has its own characteristics. Except for models with slow continental convergence velocity (3 cm/year) and steep subducting angles (>45°), which result in a quasisymmetric ablative mode, the polarity-reversed mode dominated the continental collision style in models with medium overriding crustal strength. When we fixed the plate convergence velocity but altered the subducting angle and retrocontinental crustal strength, three end members of the collision modes were observed under specific parameter ranges: Models with a weak crust and low subducting angles (<45°) showed a reversed ablative mode whereas models with a strong crust always demonstrated a stable mode. In addition, with the exception of a weak crust group, the others evolved into slab necking or slab break-off. Thus, we can infer that plate velocity slowdown after continents meet can break the force equilibrium of the slab by increasing resistance to subduction and then intensifying the extension of the slab, especially in the transition zone between the oceanic and continental plates. This extension is responsible for the local weakening and subsequent break-off of the subducting plate. The shallower the slab that breaks off, the much easier it is for the adjacent overriding plate to switch its polarity. Overriding crustal strength is crucial to altering continental collision modes among these three parameters. A weak overriding continental crust could partially or completely decouple the crust from the lithospheric mantle and facilitate the proplate’s indention, resulting in the sinking of the delaminated lithospheric mantle. On the contrary, a strong overriding crust could hamper further deformation and maintain its polarity to form a stable mode inherited from the foregoing oceanic subduction.

Geological Implications for Different Continental Collision Modes

Plate convergence involving oceanic lithosphere is always characterized by one plate that descends beneath the other at the plate’s boundary (namely, subduction). The nature of lithospheric deformation during continental plate convergence, however, is still ambiguous. Continental crust generally resists subduction because of its buoyancy, and consequently, it is more liable to deform, thicken, and uplift at a collision zone. These orogenic events significantly contribute to cover up the nature of the underlying lithospheric mantle dynamics. Evidence supports the subduction of the lithospheric mantle at continental collision boundaries. This process is not as steady or coherent as it is in oceanic subduction; instead, it is characterized by diverse tectonic complexities. Our numerical experiments are not prescribed to certain specific orogeny; thus, snapshots mainly show the general process of lithospheric scale deformation at collisional margins. However, numerous seismic images conducted in the active continental collision zones enable the division of continental collision modes into three end members.

Hindu Kush

The Hindu Kush region, located in the western syntaxis of the Tibetan plateau, is the westernmost part of the India-Eurasia collision system and a prominent site to study ongoing continental collision. The comparison of the geodynamic conditions and evolution of Hindu Kush with the stable continental collision mode exhibited good consistency (Figures 1C, 6F). In the Hindu Kush region, the lower plate has been interpreted to be the Indian craton lithosphere, and the overriding plate as the Tajik Basin (TB). The TB is formed by accreted continental terrane during the late Carboniferous to Early Permian, and its crust experienced limited extension. Thus, it is reasonable to presume TB to be a strong overriding lithosphere, which is the favored condition to develop a stable continental collision mode according to the model predictions (Figure 8). Seismic tomographic and seismological studies indicated a steep northward dipping High Velocity Zone (HVZ) underneath the HK. The HVZ was interpreted as the subducting Indian lithosphere, along the surface of which is a thin intermediate-depth seismic belt that was interpreted as the subducting lower crust; these slab geometry and lithospheric deformation features are well consistent with the results of stable collision models (Figure 6F). In addition, a slab necking was observed in seismic images, the structure of which was also indicated by the model results (Figure 6F).

Eastern Alps

Geophysical and geologic evidence has suggested that switches in subduction polarity, either in time (at a given location) or in space, along the plate convergent boundaries are ubiquitous (von Hagke et al., 2016). Polarity reversed mode has been recognized in both subduction orogenies (e.g., Taiwan) and collisional mountain belts (e.g., Pamir-Hindu-Kush, circum-Mediterranean Alpine mountain belt) (Faccenna et al., 2004; Handy et al., 2015; von Hagke et al., 2016). Teleseismic tomographic images have indicated that two + VP anomalies with disparate orientations exist beneath the Alps (Handy et al., 2015): one of them beneath the western and central parts subducts southeastward to ∼200 km (Schmid et al., 1996), and the other one beneath the eastern part directs to the opposite side for European subduction and inclines northward to $\ge$210 km (Kissling et al., 2006; Dando et al., 2011). Mitterbauer et al. (2011) considered the high-velocity anomaly beneath the Eastern Alps to be a vertical to steeply northeast-dipping subducting plate that represented European lithosphere, which originally subducted southward and then steepened and overturned. Handy et al. (2015) have described the polarity reversal process in detail through plate reconstruction based on measurements. According to their concept model, in the late Cretaceous time, the eastern part of the Alpine orogeny underwent Alpine Tethys subduction. During this period, scraped-off oceanic crust from the downward slab accumulated in the collision zone, followed by the entering of the margin of the European plate into the Alpine trench at ∼45 Ma, which was recorded by Priabonian flysch in distal Ultra-helvetic units. Calc-alkaline magmatism along the Periadriatic Fault System indicated that the European slab subducts beneath the Alps ruptured in the Oligocene, and the slab gap between the recent Central and Eastern parts of the Alps experienced a vertical tear in the downward European slab that nucleated during Early Oligocene–Early Miocene (Kissling et al., 2006). They proposed that when collision happened in the Alps, the convergence rate between Adria and Europe then dropped from 15 mm/year (before 35 Ma) to 6 mm/year; lateral decoupling occurred between the Eastern Alps and adjacent Adriatic lithosphere. This process led to the subduction of Adriatic slab fragments beneath the Eastern Alps in early Miocene. In this study, we observed similar processes in the models that belong to the polarity reversal continental collision mode (Figure 5): They both experienced an oceanic subduction stage, accompanied by oceanic material scraped off, moving upward, and then accreting. The continental collision was followed by slab necking and detachment. A temperature anomaly resulted from asthenosphere upwelling from the slab tearing window. Eventually, polarity reversal was realized.

Furthermore, the evolution of surface topography in our model is coincidental with the results of analogue modeling (Willingshofer and Sokoutis, 2009), as well as the evolution of the eastern Alps based on geological data (Genser et al., 2007). Willingshofer and Sokoutis (2009) once pointed out that plates experienced weakly coupling during the consumption of Alpine Tethys as calcareous clays and silts from sediment and oceanic crust worked as decoupling materials, after which the European continental margin started underthrusting (late Eocene). During the late Eocene–early Oligocene, strong subsidence occurred to form a foreland basin (Genser et al., 2007). The above process is compatible with our polarity-reversed models (Figures 5A–C) with fast oceanic subduction. From Oligocene to Miocene, strong internal deformation and vertical motion occurred in the wedge, followed by the switch of thrusting of the orogenic wedge from north-directed onto the European plate to south-directed. During Middle-late Miocene, cooling of the orogenic wedge strengthened it to facilitate the transmission of stress to the northern plate, which may have led to the late-stage uplift of foreland basin. First-order characteristics of topographic evolution from our model with slow convergence (Figures 5C–F) are also consistent with the evolution of the above continental collision stage.

On the basis of model results, we can conclude that the following conditions are favorable for the development of the polarity reversed mode: (1) slab break-off at shallow, after which the remaining strong surface proplate moves upward; and (2) newly developed reversed fault (in this case, the Periadriatic Fault System) working as a weak zone in the leading edge of the overriding plate contiguous to the collision zone, along which the pre-subducting plate would readily slide and facilitate its obduction (Figure 9A).

FIGURE 9

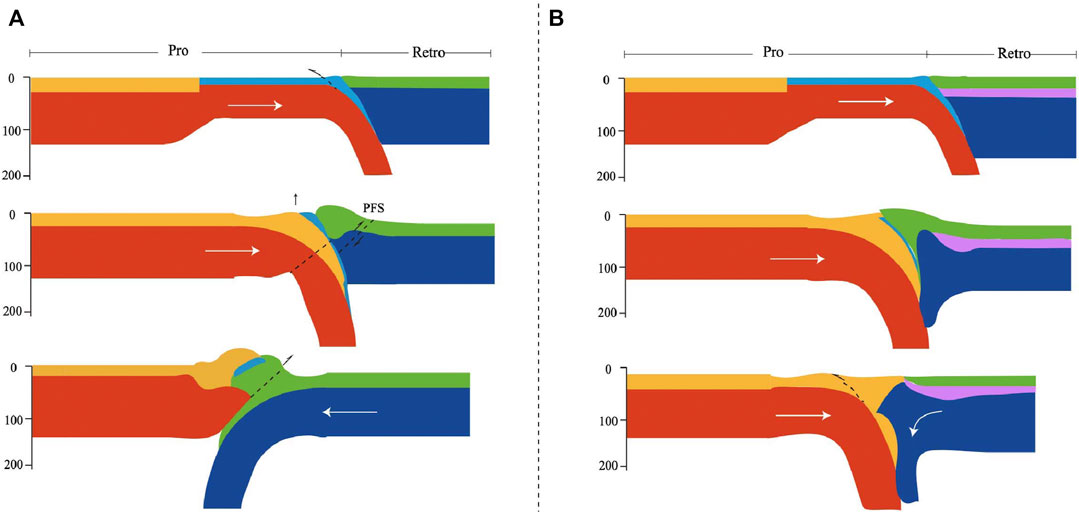
FIGURE 9. Schematic diagram of the evolution of (A) polarity reversed mode in eastern Alps and (B) ablative mode in the Austroalpine of the western Alps. PFS is Periadriatic Fault System (Handy et al., 2015; Zhao et al., 2015).

The Austroalpine of the Western Alps

Ablative/two-sided plate consumption model was first introduced by Tao and O'Connell (1992), they interpreted the process based on the dynamics of fluids, which suggests that the viscous lower lithosphere flows downward, and the brittle upper lithosphere deforms in a passive response as it is dragged downward by a dense, descending neighbor. Roda et al. (2012) once verified that the statistical data of the natural P–T peak assemblages coming from the Austroalpine of the Western Alps and the simulated P-T data from the continental upper and lower crust are in good agreement; they proposed that the structural, metamorphic setting, and exhumation of HP/UHP rocks in the Austroalpine Domain could be interpreted as episodic oceanic subduction and orogenic processes that might be manifested by an ablative mode induced by strong coupling of adjacent converged plates. As in model MSI-s1a2, continuous indention of the prolithosphere peeled off the upper crust from the weaker lower lithosphere, leaving a notable shallow converge deformation and an uplift of the collision zone; meanwhile retrocrust accreted to the orogenic wedge (Figure 9B). These features are in accordance with certain tectonic characters of the western Austroalpine, for example, the double-verged accretion in the region (Handy et al., 2010; Roda et al., 2012). Although it might not totally explain tectonic evolution of the Austroalpine, the results of our ablative model could shed new light on our understanding of the tectonic evolution of this region.

Ivrea body, once recognized as a slice of the Adriatic mantle exhumed during Mesozoic extension (Nicolas et al., 1990; Zhao et al., 2015), is a special tectonic unit that shapes the recent orogenic structure and crust–mantle deformation pattern of the western Alps. It can work as a buttress between lower and upper plates, impedes pro-upper crustal material from retroward advancing, constrains crustal shortening in the subducting plate, and generates high surface elevation (Liao et al., 2018). Our ablative models also showed the similar characteristics of a lithospheric structure and topography evolution (Figure 7C).

Model Limitations

Though our models can reconcile important first-order continental collision characteristics, as well as topographic responses, limitations still exist and hamper the reproduction of detailed orogenic process. Because it is based on a 2D model, it cannot reproduce tectonic processes, such as extrusion tectonics and highly curved collision front and lateral mantle flow; however, the formation of the natural orogens is intrinsically 3D; therefore, 3D modeling approach is required in the future for a better simulation. Figure 3F exhibited a surface uplift of ∼10 km, which is not observed on earth. This extremely high value in 2D models may be due in part to the lateral extrusion deformation. Besides, in the models, the flow-in and flow-out were prescribed on the same wall, which is not strictly consistent with the mantle flow pattern, and may introduce differences in the model results.

To simplify the model, we neglected mineral phase changes. However, it would modify density. For example, eclogitization in subducted oceanic crust can influence the slab pull and help change the continental collision regime, and control slab break-off. Partial melting is not included either, which can reduce the effective viscosity (strength) of crustal rocks. Besides, no plastic weakening occurs, which is related to the strength of lithosphere, topography evolution, and slab break-off.

Conclusion

Plate velocity slowdown between the transition from oceanic subduction to continental convergence, along with continental convergence velocity, subducting angle, and continental crustal rheological strength, are first-order controlling parameters that have significant influences on the fate of the oceanic and continental lithosphere, as well as on the whole evolution of the continental convergence system.

Three different deformation modes of the lithospheric mantle can be obtained through conducting a series of numerical experiments: polarity-reversed mode, two-sided/ablative mode, and stable mode. In addition, by comparing models with distinct configurations, we can conclude the following:

1) A dramatic decrease in plate convergence velocity when continents meet facilitated the extension in the interior of the subducting plate, as the surface plate’s motion was slower than the slab’s downward sinking, which may have resulted in the slab break-off after certain localized strain accumulation.

2) Fast continental convergence velocity in VDS helps the acceleration of continental collision processes and results in earlier slab break-off. In contrast, in models with a slow continental convergence velocity and a steep subducting angle, the overriding lithospheric mantle tended to delaminate and was dragged down by the subducting plate.

3) Increasing overriding crustal strength produces a stable collision zone. Such a strong crust can limit the development of strain localization in the overriding plate, making the model more likely to evolve into a stable continental convergence mode. Applying a medium or even weak overriding continental crust may more easily produce crust–mantle decoupling, after which the lithospheric mantle may sink in either a reversed mode or a two-sided mode.

4) Favorable conditions for the development of a polarity reversed mode are as follows: (i) a shallow slab break-off, after which the remaining surface subducting plate would move upward, and (ii) a newly developed reversed fault (in this case, the Periadriatic Fault System) contiguous to the collision zone would act as a weak zone at the leading edge of the overriding plate, along which the presubducting plate would readily slide and facilitate its obduction. Decoupling between the upper and middle/lower crust could decrease the influence of downward slab pull and facilitate the scrape-off and accumulation of crustal material at surface. Continuous pulling down of the deeper slab can then dragged the delaminated overriding lithospheric mantle downward.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

ML performed numerical modeling and wrote the manuscript. DY contributed to the writing and revision of the manuscript. PH contributed to the revision of the manuscript. All authors contributed to scientific interpretations and commented on the manuscript.

Funding

This work is supported by the National Key Research and Development Program on Monitoring, Early Warning and Prevention of Major Natural Disaster (No. 2017YFC1500301) and the National Natural Science Foundation of China (Grant Nos. U1839206 and 42104097). The figures in this paper are produced by the Generic Mapping Tools V5.4.2 (Wessel et al., 2013), Python V3.6.7, and Paraview V5.7.0, and then compiled by Adobe Illustrator.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank the Computational Infrastructure for Geodynamics for supporting the development of ASPECT (https://aspect.geodynamics.org).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.814710/full#supplementary-material

Supplementary Figure S1 | Viscosity fields of models in VDS with variable subducting angle (30˚, 45˚, 60˚) and continental convergence velocity (3 cm/year, 5 cm/year, 7 cm/year) correspond to Figure 8.

Supplementary Figure S2 | Viscosity fields of models in VDS with variable retrocontinental lower crustal strength (weak, medium, strong) and dip angle (30˚, 45˚, 60˚) correspond to Figure 8.

References

Arndt, D., Bangerth, W., Blais, B., Fehling, M., Gassmöller, R., Heister, T., et al. (2021). The deal.II Library, Version 9.3. J. Numer. Math. 29, 171–186. doi:10.1515/jnma-2021-0081

CrossRef Full Text | Google Scholar

Bird, P. (2003). An Updated Digital Model of Plate Boundaries. Geochem. Geophys. Geosyst. 4 (3), 1027. doi:10.1029/2001GC000252

CrossRef Full Text | Google Scholar

Brown, D., Ryan, P. D., Afonso, J. C., Boutelier, D., Burg, J. P., Byrne, T., et al. (2011). “Arc–Continent Collision: The Making of an Orogen,” in Arc-Continent Collision (Berlin, Heidelberg: Springer Berlin Heidelberg), 477–493. doi:10.1007/978-3-540-88558-0_17

CrossRef Full Text | Google Scholar

Burg, J.-P., and Gerya, T. V. (2005). The Role of Viscous Heating in Barrovian Metamorphism of Collisional Orogens: Thermomechanical Models and Application to the Lepontine Dome in the Central Alps. J. Metamorph. Geol. 23 (2), 75–95. doi:10.1111/j.1525-1314.2005.00563.x

CrossRef Full Text | Google Scholar

Capitanio, F. A., Replumaz, A., and Riel, N. (2015). Reconciling Subduction Dynamics during Tethys Closure with Large-Scale Asian Tectonics: Insights from Numerical Modeling. Geochem. Geophys. Geosyst. 16, 962–982. doi:10.1002/2014gc005660

CrossRef Full Text | Google Scholar

Chapman, D. S. (1986). Thermal Gradients in the continental Crust. Geol. Soc. Lond. Spec. Publ. 24 (1), 63–70. doi:10.1144/GSL.SP.1986.024.01.07

CrossRef Full Text | Google Scholar

Chemenda, A. I., Burg, J. P., and Mattauer, M. (2000). Evolutionary Model of the Himalaya–Tibet System: Geopoembased on New Modelling, Geological and Geophysical Data. Earth Planet. Sci. Lett. 174 (3-4), 397–409. doi:10.1016/S0012-821X(99)00277-0

CrossRef Full Text | Google Scholar

Chen, Y., Li, W., Yuan, X., Badal, J., and Teng, J. (2015). Tearing of the Indian Lithospheric Slab beneath Southern Tibet Revealed by SKS-Wave Splitting Measurements. Earth Planet. Sci. Lett. 413, 13–24. doi:10.1016/j.epsl.2014.12.041

CrossRef Full Text | Google Scholar

Chen, L., Capitanio, F. A., Liu, L., and Gerya, T. V. (2017). Crustal Rheology Controls on the Tibetan Plateau Formation during India-Asia Convergence. Nat. Commun. 8, 15992–15998. doi:10.1038/ncomms15992

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, L. (2021). The Role of Lower Crustal Rheology in Lithospheric Delamination during Orogeny. Front. Earth Sci. 9. doi:10.3389/feart.2021.755519

CrossRef Full Text | Google Scholar

Chertova, M. V., Spakman, W., Geenen, T., Van Den Berg, A. P., and Van Hinsbergen, D. J. J. (2014). Underpinning Tectonic Reconstructions of the Western Mediterranean Region with Dynamic Slab Evolution from 3-D Numerical Modeling. J. Geophys. Res. Solid Earth 119 (7), 5876–5902. doi:10.1002/2014JB011150

CrossRef Full Text | Google Scholar

Clift, P. D., Schouten, H., and Draut, A. E. (2003). A General Model of Arc-Continent Collision and Subduction Polarity Reversal from Taiwan and the Irish Caledonides. Geol. Soc. Lond. Spec. Publ. 219, 81–98. doi:10.1144/GSL.SP.2003.219.01.04

CrossRef Full Text | Google Scholar

Copley, A., Avouac, J.-P., and Royer, J.-Y. (2010). India-Asia Collision and the Cenozoic Slowdown of the Indian Plate: Implications for the Forces Driving Plate Motions. J. Geophys. Res. 115 (B3). doi:10.1029/2009JB006634

CrossRef Full Text | Google Scholar

Dando, B. D. E., Stuart, G. W., Houseman, G. A., Hegedüs, E., Brückl, E., and Radovanović, S. (2011). Teleseismic Tomography of the Mantle in the Carpathian-Pannonian Region of central Europe. Geophys. J. Int. 186 (1), 11–31. doi:10.1111/j.1365-246X.2011.04998.x

CrossRef Full Text | Google Scholar

Davis, R. O., and Selvadurai, & A. P. S. (2002). Plasticity and Geomechanics. Cambridge: Cambridge University Press.

Google Scholar

Duretz, T., Schmalholz, S. M., and Gerya, T. V. (2012). Dynamics of Slab Detachment. Geochem. Geophys. Geosyst. 13 (3), a–n. doi:10.1029/2011GC004024

CrossRef Full Text | Google Scholar

Faccenda, M., Gerya, T. V., and Chakraborty, S. (2008). Styles of post-subduction Collisional Orogeny: Influence of Convergence Velocity, Crustal Rheology and Radiogenic Heat Production. Lithos 103 (1-2), 257–287. doi:10.1016/j.lithos.2007.09.009

CrossRef Full Text | Google Scholar

Faccenna, C., Piromallo, C., Crespo-Blanc, A., Jolivet, L., and Rossetti, F. (2004). Lateral Slab Deformation and the Origin of the Western Mediterranean Arcs. Tectonics 23. doi:10.1029/2002tc001488

CrossRef Full Text | Google Scholar

Genser, J., Cloetingh, S. A. P. L., and Neubauer, F. (2007). Late Orogenic Rebound and Oblique Alpine Convergence: New Constraints from Subsidence Analysis of the Austrian Molasse basin. Glob. Planet. Change 58, 214–223. doi:10.1016/j.gloplacha.2007.03.010

CrossRef Full Text | Google Scholar

Gleason, G. C., and Tullis, J. (1995). A Flow Law for Dislocation Creep of Quartz Aggregates Determined with the Molten Salt Cell. Tectonophysics 247, 1–23. doi:10.1016/0040-1951(95)00011-b

CrossRef Full Text | Google Scholar

Glerum, A., Thieulot, C., Fraters, M., Blom, C., and Spakman, W. (2018). Nonlinear Viscoplasticity in ASPECT: Benchmarking and Applications to Subduction. Solid Earth 9, 267–294. doi:10.5194/se-9-267-2018

CrossRef Full Text | Google Scholar

Guillot, S., Garzanti, E., Baratoux, D., Marquer, D., Mahéo, G., and de Sigoyer, J. (2003). Reconstructing the Total Shortening History of the NW Himalaya. Geochem. Geophys. Geosyst. 4 (7). doi:10.1029/2002GC000484

CrossRef Full Text | Google Scholar

Handy, M. R., M. Schmid, S. S., Bousquet, R., Kissling, E., and Bernoulli, D. (2010). Reconciling Plate-Tectonic Reconstructions of Alpine Tethys with the Geological-Geophysical Record of Spreading and Subduction in the Alps. Earth-Science Rev. 102 (3-4), 121–158. doi:10.1016/j.earscirev.2010.06.002

CrossRef Full Text | Google Scholar

Handy, M. R., Ustaszewski, K., and Kissling, E. (2015). Reconstructing the Alps-Carpathians-Dinarides as a Key to Understanding Switches in Subduction Polarity, Slab Gaps and Surface Motion. Int. J. Earth Sci. (Geol Rundsch) 104 (1), 1–26. doi:10.1007/s00531-014-1060-3

CrossRef Full Text | Google Scholar

Hirth, G., and Kohlstedt, D. (2003). “Rheology of the Upper Mantle and the Mantle Wedge: A View from the Experimentalists,” in Geophysical Monograph Series (Washington DC: American Geophysical Union), 138, 83–105. doi:10.1029/138gm06

CrossRef Full Text | Google Scholar

Huangfu, P., Li, Z.-H., Gerya, T., Fan, W., Zhang, K.-J., Zhang, H., et al. (2018). Multi-terrane Structure Controls the Contrasting Lithospheric Evolution beneath the Western and central-eastern Tibetan Plateau. Nat. Commun. 9 (1), 3780. doi:10.1038/s41467-018-06233-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Jamieson, R. A., Beaumont, C., Fullsack, P., and Lee, B. (1998). Barrovian Regional Metamorphism: Where's the Heat? Geol. Soc. Lond. Spec. Publ. 138 (1), 23–51. doi:10.1144/GSL.SP.1996.138.01.03

CrossRef Full Text | Google Scholar

Karato, S.-i., and Wu, P. (1993). Rheology of the Upper Mantle: A Synthesis. Science 260, 771–778. doi:10.1126/science.260.5109.771

PubMed Abstract | CrossRef Full Text | Google Scholar

Karato, S.-i. (2008). Deformation of Earth Materials: An Introduction to the Rheology of Solid Earth. Cambridge: Cambridge University Press.

Google Scholar

Kissling, E., Schmid, S. M., Lippitsch, R., Ansorge, J., and Fügenschuh, B. (2006). Lithosphere Structure and Tectonic Evolution of the Alpine Arc: New Evidence from High-Resolution Teleseismic Tomography. Geol. Soc. Lond. Mem. 32 (1), 129–145. doi:10.1144/GSL.MEM.2006.032.01.08

CrossRef Full Text | Google Scholar

Kronbichler, M., Heister, T., and Bangerth, W. (2012). High Accuracy Mantle Convection Simulation through Modern Numerical Methods. Geophys. J. Int. 191 (1), 12–29. doi:10.1111/j.1365-246X.2012.05609.x

CrossRef Full Text | Google Scholar

Kufner, S.-K., Kakar, N., Bezada, M., Bloch, W., Metzger, S., Yuan, X., et al. (2021). The Hindu Kush Slab Break-Off as Revealed by Deep Structure and Crustal Deformation. Nat. Commun. 12, 1685. doi:10.1038/s41467-021-21760-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, L., Liao, X., and Fu, & R. (2002). Slab Breakoff Depth: A Slowdown Subduction Model. Geophys. Res. Lett. 29 (3), 11–111113. doi:10.1029/2001GL013420

CrossRef Full Text | Google Scholar

Li, Z. H., Xu, Z. Q., and Gerya, T. V. (2011). Flat versus Steep Subduction: Contrasting Modes for the Formation and Exhumation of High- to Ultrahigh-Pressure Rocks in continental Collision Zones. Earth Planet. Sci. Lett. 301 (1-2), 65–77. doi:10.1016/j.epsl.2010.10.014

CrossRef Full Text | Google Scholar

Li, Z.-H., Xu, Z., Gerya, T., and Burg, J.-P. (2013). Collision of continental Corner from 3-D Numerical Modeling. Earth Planet. Sci. Lett. 380, 98–111. doi:10.1016/j.epsl.2013.08.034

CrossRef Full Text | Google Scholar

Li, Y., Wang, C., Dai, J., Xu, G., Hou, Y., and Li, X. (2015). Propagation of the Deformation and Growth of the Tibetan-Himalayan Orogen: A Review. Earth-Sci. Rev. 143, 36–61. doi:10.1016/j.earscirev.2015.01.001

CrossRef Full Text | Google Scholar

Li, Z. (2014). A Review on the Numerical Geodynamic Modeling of continental Subduction, Collision and Exhumation. Sci. China Earth Sci. 57 (1), 47–69. doi:10.1007/s11430-013-4696-0

CrossRef Full Text | Google Scholar

Liang, X., Chen, Y., Tian, X., Chen, Y. J., Ni, J., Gallegos, A., et al. (2016). 3D Imaging of Subducting and Fragmenting Indian continental Lithosphere beneath Southern and central Tibet Using Body-Wave Finite-Frequency Tomography. Earth Planet. Sci. Lett. 443, 162–175. doi:10.1016/j.epsl.2016.03.029

CrossRef Full Text | Google Scholar

Liang, Y., Li, L., Liao, J., and Gao, R. (2020). Interaction of the Indian and Asian Plates under the Pamir and Hindu-Kush Regions: Insights from 3-D Shear Wave Velocity and Anisotropic Structures. Geochem. Geophys. Geosyst. 21, e2020GC009041. doi:10.1029/2020gc009041

CrossRef Full Text | Google Scholar

Liao, J., and Gerya, T. (2017). Partitioning of Crustal Shortening during continental Collision: 2‐D Thermomechanical Modeling. J. Geophys. Res. Solid Earth 122 (1), 592–606. doi:10.1002/2016JB013398

CrossRef Full Text | Google Scholar

Liao, J., Gerya, T., and Malusà, M. G. (2018). 3D Modeling of Crustal Shortening Influenced by Along-Strike Lithological Changes: Implications for continental Collision in the Western and Central Alps. Tectonophysics 746, 425–438. doi:10.1016/j.tecto.2018.01.031

CrossRef Full Text | Google Scholar

Lippitsch, R., Kissling, E., and Ansorge, J. (2003). Upper Mantle Structure beneath the Alpine Orogen from High-Resolution Teleseismic Tomography. J. Geophys. Res. 108. doi:10.1029/2002JB002016

CrossRef Full Text | Google Scholar

Mechie, J., and Kind, R. (2013). A Model of the Crust and Mantle Structure Down to 700 Km Depth beneath the Lhasa to Golmud Transect across the Tibetan Plateau as Derived from Seismological Data. Tectonophysics 606, 187–197. doi:10.1016/j.tecto.2013.04.030

CrossRef Full Text | Google Scholar

Mechie, J., Kind, R., and Saul, J. (2011a). The Seismological Structure of the Tibetan Plateau Crust and Mantle Down to 700 Km Depth. Geol. Soc. Lond. Spec. Publ. 353, 109–125. doi:10.1144/sp353.7

CrossRef Full Text | Google Scholar

Mechie, J., Yuan, X., Schurr, B., Schneider, F., Sippl, C., Ratschbacher, L., et al. (2011b). Crustal and Uppermost Mantle Velocity Structure along a Profile across the Pamir and Southern Tien Shan as Derived from Project TIPAGE Wide-Angle Seismic Data. Geophys. J. Int. 188, 385–407. doi:10.1111/j.1365-246x.2011.05278.x

CrossRef Full Text | Google Scholar

Mechie, J., Zhao, W., Karplus, M., Wu, Z., Meissner, R., Shi, D., et al. (2012). Crustal Shear (S) Velocity and Poisson's Ratio Structure along the INDEPTH IV Profile in Northeast Tibet as Derived from Wide-Angle Seismic Data. Geophys. J. Int. 191, 716. doi:10.1111/j.1365-246x.2012.05616.x

CrossRef Full Text | Google Scholar

Mitterbauer, U., Behm, M., Brückl, E., Lippitsch, R., Guterch, A., Keller, G. R., et al. (2011). Shape and Origin of the East-Alpine Slab Constrained by the ALPASS Teleseismic Model. Tectonophysics 510 (1), 195–206. doi:10.1016/j.tecto.2011.07.001

CrossRef Full Text | Google Scholar

Nábelek, J., Hetényi, G., Vergne, J., Sapkota, S., Kafle, B., Jiang, M., et al. (2009). Underplating in the Himalaya-Tibet Collision Zone Revealed by the Hi-CLIMB experiment. Science 325, 1371–1374. doi:10.1126/science.1167719

PubMed Abstract | CrossRef Full Text | Google Scholar

Negredo, A. M., Replumaz, A., Villaseñor, A., and Guillot, S. (2007). Modeling the Evolution of continental Subduction Processes in the Pamir-Hindu Kush Region. Earth Planet. Sci. Lett. 259 (1-2), 212–225. doi:10.1016/j.epsl.2007.04.043

CrossRef Full Text | Google Scholar

Nicolas, A., Hirn, A., Nicolich, R., and Polino, R. (1990). Lithospheric Wedging in the Western Alps Inferred from the ECORS-CROP Traverse. Geol 18, 587–590. doi:10.1130/0091-7613(1990)018<0587:lwitwa>2.3.co;2

CrossRef Full Text | Google Scholar

Owens, T. J., and Zandt, G. (1997). Implications of Crustal Property Variations for Models of Tibetan Plateau Evolution. Nature 387, 37–43. doi:10.1038/387037a0

CrossRef Full Text | Google Scholar

Patriat, P., and Achache, J. (1984). India-Eurasia Collision Chronology Has Implications for Crustal Shortening and Driving Mechanism of Plates. Nature 311 (5987), 615–621. doi:10.1038/311615a0

CrossRef Full Text | Google Scholar

Pysklywec, R. N., Beaumont, C., and Fullsack, P. (2000). Modeling the Behavior of the continental Mantle Lithosphere during Plate Convergence. Geology 28 (7), 655. doi:10.1130/0091-7613(2000)028<0655:mtbotc>2.3.co;2

CrossRef Full Text | Google Scholar

Pysklywec, R. N. (2001). Evolution of Subducting Mantle Lithosphere at a continental Plate Boundary. Geophys. Res. Lett. 28 (23), 4399–4402. doi:10.1029/2001gl013567

CrossRef Full Text | Google Scholar

Roda, M., Marotta, A. M., and Spalla, M. I. (2010). Numerical Simulations of an Ocean-Continent Convergent System: Influence of Subduction Geometry and Mantle Wedge Hydration on Crustal Recycling. Geochem. Geophys. Geosyst. 11 (5). doi:10.1029/2009GC003015

CrossRef Full Text | Google Scholar

Roda, M., Spalla, M. I., and Marotta, A. M. (2012). Integration of Natural Data within a Numerical Model of Ablative Subduction: a Possible Interpretation for the Alpine Dynamics of the Austroalpine Crust. J. Metamorph. Geol. 30 (9), 973–996. doi:10.1111/jmg.12000

CrossRef Full Text | Google Scholar

Rybacki, E., Gottschalk, M., Wirth, R., and Dresen, G. (2006). Influence of Water Fugacity and Activation Volume on the Flow Properties of fine-grained Anorthite Aggregates. J. Geophys. Res. Solid Earth 111. doi:10.1029/2005jb003663

CrossRef Full Text | Google Scholar

Saein, L. D., and Afzal, P. (2017). Correlation between Mo Mineralization and Faults Using Geostatistical and Fractal Modeling in Porphyry Deposits of Kerman Magmatic Belt, SE Iran. J. Geochem. Explor. 181, 333–343. doi:10.1016/j.gexplo.2017.06.014

CrossRef Full Text | Google Scholar

Schmid, S. M., Pfiffner, O. A., Froitzheim, N., Schönborn, G., and Kissling, E. (1996). Geophysical-geological Transect and Tectonic Evolution of the Swiss-Italian Alps. Tectonics 15 (5), 1036–1064. doi:10.1029/96TC00433

CrossRef Full Text | Google Scholar

Spakman, W., Chertova, M. V., van den Berg, A. P., and van Hinsbergen, D. J. J. (2018). Publisher Correction: Puzzling Features of Western Mediterranean Tectonics Explained by Slab Dragging. Nat. Geosci. 11 (5), 374. doi:10.1038/s41561-018-0096-6

CrossRef Full Text | Google Scholar

Tao, W. C., and O'connell, R. J. (1992). Ablative Subduction: A Two-Sided Alternative to the Conventional Subduction Model. J. Geophys. Res. 97 (B6), 8877–8904. doi:10.1029/91JB02422

CrossRef Full Text | Google Scholar

Tetreault, J. L., and Buiter, S. J. H. (2012). Geodynamic Models of Terrane Accretion: Testing the Fate of Island Arcs, Oceanic Plateaus, and continental Fragments in Subduction Zones. J. Geophys. Res. 117 (B8). doi:10.1029/2012JB009316

CrossRef Full Text | Google Scholar

Tilmann, F., and Ni, J. (2003). Seismic Imaging of the Downwelling Indian Lithosphere Beneath Central Tibet. Science 300, 1424–1427. doi:10.1126/science.1082777

PubMed Abstract | CrossRef Full Text | Google Scholar

Turcotte, D. L., and Schubert, G. (2002). Geodynamics. Cambridge: Cambridge University Press. doi:10.1017/CBO9780511807442

CrossRef Full Text | Google Scholar

von Hagke, C., Philippon, M., Avouac, J.-P., and Gurnis, M. (2016). Origin and Time Evolution of Subduction Polarity Reversal from Plate Kinematics of Southeast Asia. Geology 44 (8), 659–662. doi:10.1130/G37821.1

CrossRef Full Text | Google Scholar

Wang, Q., Zhang, P.-Z., Freymueller, J. T., Bilham, R., Larson, K. M., Lai, X. a., et al. (2001). Present-Day Crustal Deformation in China Constrained by Global Positioning System Measurements. Science 294 (5542), 574–577. doi:10.1126/science.1063647

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, C., Dai, J., Zhao, X., Li, Y., Graham, S. A., He, D., et al. (2014). Outward-growth of the Tibetan Plateau during the Cenozoic: A Review. Tectonophysics 621, 1–43. doi:10.1016/j.tecto.2014.01.036

CrossRef Full Text | Google Scholar

Warren, C. J., Beaumont, C., and Jamieson, R. A. (2008). Modelling Tectonic Styles and Ultra-high Pressure (UHP) Rock Exhumation during the Transition from Oceanic Subduction to continental Collision. Earth Planet. Sci. Lett. 267 (1-2), 129–145. doi:10.1016/j.epsl.2007.11.025

CrossRef Full Text | Google Scholar

Wessel, P., Smith, W. H. F., Scharroo, R., Luis, J., and Wobbe, F. (2013). Generic Mapping Tools: Improved Version Released. Eos Trans. AGU 94, 409–410. doi:10.1002/2013eo450001

CrossRef Full Text | Google Scholar

Wilks, K. R., and Carter, N. L. (1990). Rheology of Some continental Lower Crustal Rocks. Tectonophysics 182, 57–77. doi:10.1016/0040-1951(90)90342-6

CrossRef Full Text | Google Scholar

Willingshofer, E., and Sokoutis, D. (2009). Decoupling along Plate Boundaries: Key Variable Controlling the Mode of Deformation and the Geometry of Collisional Mountain Belts. Geology 37, 39–42. doi:10.1130/g25321a.1

CrossRef Full Text | Google Scholar

Yamato, P., Burov, E., Agard, P., Le Pourhiet, L., and Jolivet, L. (2008). HP-UHP Exhumation during Slow continental Subduction: Self-Consistent Thermodynamically and Thermomechanically Coupled Model with Application to the Western Alps. Earth Planet. Sci. Lett. 271 (1), 63–74. doi:10.1016/j.epsl.2008.03.049

CrossRef Full Text | Google Scholar

Yang, T., Huangfu, P., and Zhang, Y. (2019). Differentiation of Continental Subduction Mode: Numerical Modeling. J. Earth Sci. 30 (4), 809–822. doi:10.1007/s12583-017-0946-y

CrossRef Full Text | Google Scholar

Ye, Z., Gao, R., Li, Q., Zhang, H., Shen, X., Liu, X., et al. (2015). Seismic Evidence for the North China Plate Underthrusting beneath Northeastern Tibet and its Implications for Plateau Growth. Earth Planet. Sci. Lett. 426, 109–117. doi:10.1016/j.epsl.2015.06.024

CrossRef Full Text | Google Scholar

Yin, A., and Harrison, T. M. (2000). Geologic Evolution of the Himalayan-Tibetan Orogen. Annu. Rev. Earth Planet. Sci. 28, 211–280. doi:10.1146/annurev.earth.28.1.211

CrossRef Full Text | Google Scholar

Zhao, L., Paul, A., Guillot, S., Solarino, S., Malusà, M. G., Zheng, T., et al. (2015). First Seismic Evidence for continental Subduction beneath the Western Alps. Geology 43, 815–818. doi:10.1130/g36833.1

CrossRef Full Text | Google Scholar