How Aseismic Ridges Modify the Dynamics of Free Subduction: A 3-D Numerical Investigation

Suchoy, Lior; Goes, Saskia; Chen, Fangqin; Davies, D. Rhodri

doi:10.3389/feart.2022.852742

ORIGINAL RESEARCH article

Front. Earth Sci., 05 May 2022

Sec. Solid Earth Geophysics

Volume 10 - 2022 | https://doi.org/10.3389/feart.2022.852742

This article is part of the Research Topic Subduction and Collision Dynamics of Tectonic Plates View all 15 articles

How Aseismic Ridges Modify the Dynamics of Free Subduction: A 3-D Numerical Investigation

Lior Suchoy¹*

Saskia Goes¹*

Fangqin Chen²

D. Rhodri Davies²

¹Department of Earth Science and Engineering, Imperial College London, London, United Kingdom
²Research School of Earth Sciences, Australian National University, Canberra, ACT, Australia

The subduction of positively buoyant features has been implicated in the development of flat and shallow dipping slabs, the formation of cusps in trench geometry, and the cessation of associated arc magmatism. However, how such buoyant anomalies influence subduction dynamics to produce these different tectonic expressions remains debated. In this paper, using a series of multi-material 3-D simulations of free subduction, we investigate how linear buoyant ridges modify subduction dynamics, in particular downgoing plate velocities, trench motions and slab morphology. We examine the sensitivity of results to downgoing plate age (affecting buoyancy and strength), ridge buoyancy and ridge location along the trench, finding that buoyant ridges can locally change slab sinking and trench retreat rates, in turn modifying the evolution of slab morphology at depth and trench shape at the surface. In all cases examined, trench retreat is reduced, or switches to trench advance, where the ridge subducts. These effects depend strongly on downgoing plate age: on young, weak plates, the change in trench shape is more localised than on old, strong plates. Slab shallowing at the ridge only occurs for young plates, while the stronger and more negatively buoyant older plates pull down the ridge at a steeper angle than the rest of the slab. On old plates, ridges located near regions of trench stagnation or advance, which typically develop in wide slabs, have a stronger effect on trench and slab shape. The combined effects of buoyant feature location, subducting plate age and overriding plate properties can result in a range of responses: from mainly trench deformation, through local slab shallowing, to the formation of a flat slab, a variation in expressions also observed on Earth.

1 Introduction

Buoyant features are thickened ridges and plateaus on the ocean floor that mark the surface expression of excess mantle melting. Ridges are typically elongated features with a specific orientation, whilst plateaus are often more uniform in their dimensions. Owing to their composition and thickness, they add a component of positive buoyancy to the associated lithosphere and will typically resist the subduction of this lithosphere. As a result, the subduction of buoyant features has been implicated in many irregularities of subduction tectonics, including the interruption of arc volcanism on the corresponding overriding plate (e.g., Vogt et al., 1976; Nur and Ben-Avraham, 1983; Mahlburg Kay and Mpodozis, 2002; Hu et al., 2016), uplift and compression in the overriding plate (e.g., Humphreys, 1995; Espurt et al., 2007; O’Driscoll et al., 2009) and either enhancement or suppression of seismic activity (e.g., Nur and Ben-Avraham, 1983; Gutscher et al., 1999, 2000; Kumar et al., 2016).

Although they have been widely studied, there is currently no consensus on how the subduction of buoyant features modulates subduction dynamics. It was first proposed that buoyant-feature subduction alters the shape of the trench (Vogt, 1973). The main evidence was the proximity of many features to trench cusps (e.g., the Emperor Chain at the intersection of the Aleutian and Kuril trenches, the Caroline Ridge between the Mariana and Yap trenches and the Ogasawara Ridge between the Mariana and Bonin arcs: Vogt, 1973; Vogt et al., 1976; Miller et al., 2006c; Mason et al., 2010; Rosenbaum and Mo, 2011). A proposed consequence of subduction of buoyant features is the association with low angle (i.e., “flat”), subduction (Sacks, 1983; Gutscher et al., 2000). The main examples of flat slab subduction are where the Nazca plate subducts beneath South America: the Nazca ridge is associated with the Peruvian flat slab (Gutscher et al., 2000), the Juan Fernandez ridge with the Chilean flat slab (Mahlburg Kay and Mpodozis, 2002) and the Carnegie ridge with the Ecuadorian flat slab (Gutscher et al., 1999). The Northeast Pacific hosts an example of a present-day flat slab which is associated with subduction of the plateau-like Yakutat Terrane beneath Alaska (e.g., Gulick et al., 2007). Subduction of the Palau-Kyushu ridge under Japan (Xia et al., 2021) has also been associated with low-angle subduction along the Nankai Trench, and subduction of the Emperor chain with shallow subduction under Kamchatka (Davaille and Lees, 2004). Finally, the subduction of the Shatsky Rise conjugate has been linked to past flat subduction below North America leading to the Laramide Orogeny (Atwater, 1989; Liu et al., 2010).

It is proposed that when a buoyant feature subducts, its buoyancy counteracts downgoing motion of the surrounding negatively buoyant plate, keeping it afloat (Sacks, 1983; Gutscher et al., 1999). When a full flat slab matures and develops a horizontal section that extends several hundred kilometres from the trench, the lack of mantle wedge flow between the slab and overriding plate might cause a shut-down in arc volcanism (Nur and Ben-Avraham, 1981; Isacks, 1988; Atwater, 1989). Furthermore, the release of slab fluids into the thin coupling layer between the plates may reduce seismic activity (Nur and Ben-Avraham, 1983; Kim et al., 2012; Manea et al., 2013) and the induced slab bathymetry may limit the size of large ruptures (Sparkes et al., 2010). Other studies propose that a wide upper-lower plate contact area above a shallow slab increases the potential for large inter-plate earthquakes (Corbi et al., 2017; Muldashev and Sobolev, 2020).

Although there are a number of observations supportive of a link between the subduction of buoyant features and shallow-angle or flat slab subduction (Vogt et al., 1976; Nur and Ben-Avraham, 1983; Gutscher et al., 1999; Van Hunen et al., 2002), there are also buoyant ridges and plateaus that subduct without affecting slab dip. Skinner and Clayton (2013) observed that some of the largest features subducting in the Pacific (e.g., the Magellan seamounts, Louisville ridge, Caroline ridge) are not correlated with any lower-angle subducting slab. Moreover, for some flat slab segments (most notably, Mexico, and past subduction below the Altiplano-Puna region) no candidate buoyant features have been identified to explain the anomalous subduction angle (Rosenbaum and Mo, 2011; Skinner and Clayton, 2011). In addition, a number of numerical and analogue subduction models indicate that although the subduction of buoyant features may lead to slab shallowing, by themselves they are insufficient to generate a flat slab (Van Hunen et al., 2002; Martinod et al., 2005; Gerya et al., 2009; Manea et al., 2017).

Several other mechanisms have been suggested to cause or contribute to the formation of flat or low-angle slabs. One mechanism is the active overthrusting of the upper plate, which results in forced trench retreat and can lead to a flat slab if the plate is unable to increase its sinking velocity accordingly (van Hunen et al., 2004; Currie and Beaumont, 2011; Liu and Currie, 2016). Episodes of fast convergence ( $>$ 10 cm/yr; Currie and Beaumont, 2011; Manea et al., 2017) have been proposed to have a similar flattening effect. Suction forces in the mantle wedge, although unlikely to lead to flat subduction on their own, generate an upwards force above the slab and can be enhanced by a higher viscosity mantle wedge or thick (cratonic) upper plate (van Hunen et al., 2004; Manea and Gurnis, 2007; O’Driscoll et al., 2009; Roda et al., 2011; Manea et al., 2012; Taramón et al., 2015; Schellart and Strak, 2021), thus encouraging the evolution from a low-angle to a flat slab. Another mechanism suggested to contribute to low-angle subduction is the presence of buoyant mantle support below the slab, as would be expected from a hot upwelling plume (Betts et al., 2009; Bishop et al., 2017), or as a result of slab tearing (Liu and Stegman, 2012), although this effect may be relatively small (Schellart, 2020). Finally, it has been suggested that long-lived, very wide subduction zones for which the slab is anchored in the lower mantle, can develop a shallow-dipping segment in their centre (e.g., Farallon plate) (Schellart, 2020). Most studies suggest that varying combinations of mechanisms, likely involving buoyant features, may be required to explain the observed range of low-angle and flat slab cases (van Hunen et al., 2004; Skinner and Clayton, 2013; Antonijevic et al., 2015; Hu et al., 2016).

While previous studies have modelled the subduction of buoyant features, the majority have done so in 2-D (e.g., Van Hunen et al., 2002; van Hunen et al., 2004; Gerya et al., 2009; Arrial and Billen, 2013; Schellart and Strak, 2021), which is most appropriate for simulating features with a large lateral extent. Of the 3-D studies undertaken, some focus on modelling specific subduction zones (Espurt et al., 2008; Mason et al., 2010; Hu et al., 2016). Only a few, analogue modelling, studies have systematically explored how variations in the shape and position of buoyant features affect subduction dynamics with and without an overriding plate (Martinod et al., 2005, 2013; Flórez-Rodríguez et al., 2019). These show that the relative buoyancy of a buoyant feature compared to the rest of the slab affects the extent to which it modulates subduction. Several other, numerical, 3-D models, which did not include buoyant features, examined how overriding plate thickness (Capitanio et al., 2011; Manea et al., 2012; Rodríguez-González et al., 2014; Taramón et al., 2015) and the width of the subducting plate (Schellart et al., 2007; Schellart, 2020; Chen et al., 2022) influence slab dip and can possibly cause flat subduction. In this study, we build on and complement previous work, using 3-D numerical models to investigate the effects of the relative buoyancy of buoyant features and their position along the trench. It is the first to study the effect of the age-dependent buoyancy and strength of the background subducting slabs. This study uses fully dynamic numerical simulations to simulate a subset of buoyant features, i.e., elongated, trench-perpendicular buoyant ridges, on single-plate subduction (i.e., “free subduction”) to evaluate effects on trench shape and the slab dip angle. We find that the different modes of ridge subduction exhibited by our models help to explain the different expressions of subducting buoyant features around the Pacific and on the Indo-Australian plate.

2 Methods

2.1 Modelling System

We design a series of simulations in a 3-D Cartesian domain. We use a multi-material approach to simulate subduction of a composite visco-plastic plate into a viscous mantle, with no upper plate (i.e., “free subduction”). While numerous studies demonstrate that the upper plate can affect subduction dynamics significantly (e.g. van Hunen et al., 2004; Espurt et al., 2008), its absence allows us to analyse the dynamic forcing by the subducting plate which is widely agreed to be the main driver of subduction dynamics and diversity (e.g. Forsyth and Uyeda, 1975; Goes et al., 2017). Our approach neglects the thermal evolution of the slab and associated feedbacks on density and viscosity (e.g., Garel et al., 2014; Suchoy et al., 2021). This simplification enhances numerical efficiency, allowing us to perform a systematic 3-D study across a wide parameter space. Previous studies have demonstrated that the multi-material, mechanical approach used herein captures the first-order dynamics of subduction (e.g. Bellahsen et al., 2005; Capitanio et al., 2007; Stegman et al., 2010; Chen et al., 2022).

We use Fluidity, an adaptive, unstructured mesh, finite-element, control-volume computational modelling framework (e.g., Wilson, 2009; Davies et al., 2011; Kramer et al., 2012, 2021), to solve the conservation equations of mass and momentum for an incompressible fluid under the infinite Prandtl number and Boussinesq approximations:

\nabla \cdot u = 0 (1)

\nabla \cdot [η (\vec{\nabla} u + {(\vec{\nabla} u)}^{T})] - \vec{\nabla} p = - g Δ ρ Γ \hat{y} (2)

\frac{\partial Γ}{\partial t} + u \cdot \vec{\nabla} Γ = 0 (3)

where u is the velocity, η is the dynamic viscosity, p is the pressure, g is the acceleration due to gravity, Δρ is the difference in density between different materials, Γ is the material volume fraction (Γ = 1 within a given material and Γ = 0 elsewhere) and $\hat{y}$ is a unit vector in the direction of gravity. We utilise an adaptive unstructured mesh of tetrahedral elements, with minimum and maximum element sizes of 3 and 300 km, respectively. This allows us to resolve fine-scale features where the gradients of velocity and viscosity are strong, whilst maintaining computational efficiency (see Davies et al., 2007, 2011, for further detail).

2.2 Reference Models

Our reference young and old “no-ridge” models (Table 1) follow two Cartesian model designs from Chen et al. (2022) (models W2400_young and W2400_ref, respectively). We use a domain of 4,000 × 2890 × 4,000 km³ (length×depth×width) to simulate half the subducting plate, assuming symmetry at the centre of the plate along the long axis (z = 0) (Figure 1).

TABLE 1

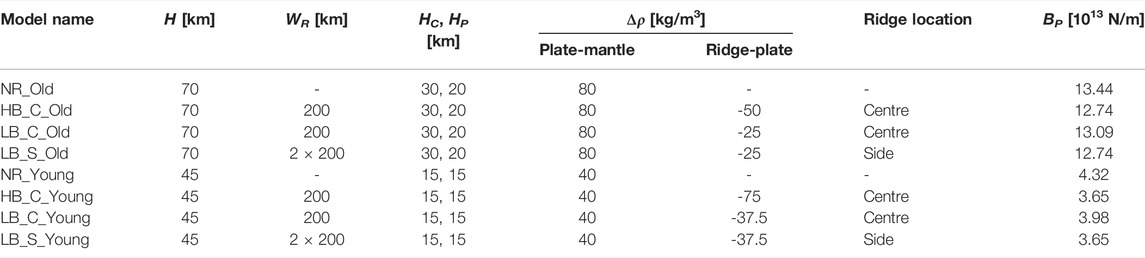
TABLE 1. Parameters for all model cases. H—plate thickness, W_R - ridge width (cases with side ridges effectively contain two symmetrical ridges of this width), H_C—thickness of high-viscosity core, H_P—thickness of visco-plastic layers above and below the plate core, Δρ—excess density of plate or ridge, B_P—buoyancy of the plate per unit length, calculated as (Δρ_P-M ⋅ W_P + Δρ_R-P ⋅ W_R) ⋅ H ⋅ g, and which is positive in the direction of gravity. Model name abbreviations: NR—no-ridge, HB—high positive buoyancy, LB—low positive buoyancy, C—central ridge, S—side ridge. High and low positive buoyancy refer to ridge buoyancy relative to the rest of the plate. Central and side ridge locations pertain to a ridge at the symmetry boundary or at the centre of the half-plate, respectively (see also Figure 1B). Old and young refer to the age of the plate, which is assumed to affect both density and thickness (and thereby strength and buoyancy) of the plate.

FIGURE 1

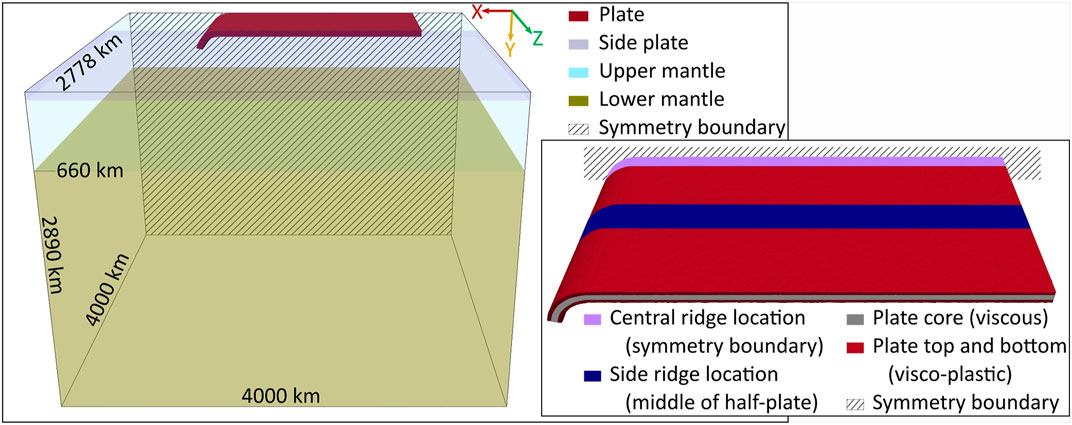
FIGURE 1. Initial conditions of (A) our computational domain and (B) the subducting plate. See text and Tables 1,2 for material properties and dimensions. We apply a free-surface boundary condition at the top of the domain, and free-slip boundary conditions elsewhere.

We apply a free-surface boundary condition at the top of the domain and free-slip boundary conditions at all other boundaries. The initial half-plate is 2,200 km long (in the direction of subduction), 1,200 km wide (along strike) and 45 or 70 km thick, for young or old plates, respectively. We limit lateral flow from the mantle to the section below the plate by adding a side plate with an initial gap of 22 km away from the edge of the subducting plate (e.g., Holt and Becker, 2017). A 600 km gap was prescribed between the trailing edge of the subducting plate and the domain boundary at x = 0. The initial slab morphology follows an arc with a radius of 250 km along the top surface, to a dip of 77° (as in Garel et al., 2014; Suchoy et al., 2021), extending to an initial depth of 200 km.

The subducting plate is composed of 3 layers with a strong isoviscous core in the centre, and visco-plastic layers at the top and bottom. The core has a viscosity 100 times η_UM. The visco-plastic layers have this same initial viscosity, but follow a von Mises yield criterion (e.g., OzBench et al., 2008) so that:

η_{P} = \{\begin{cases} \frac{τ_{I I}}{2 \cdot {\dot{ε}}_{I I}}, & if τ_{I I} < τ_{y} \\ \frac{τ_{y}}{2 \cdot {\dot{ε}}_{I I}}, & if τ_{I I} \geq τ_{y} \end{cases} (4)

where the second invariant of the stress tensor $τ_{I I} = 2 η \cdot {\dot{ε}}_{I I}$ , with ${\dot{ε}}_{I I}$ the second invariant of the strain-rate tensor and τ_y the yield stress. This rheological layering captures the concentration of slab strength in the centre of the dense plate, as expected from temperature and strain-rate dependent mantle rheology (OzBench et al., 2008; Capitanio et al., 2009; Buffett and Becker, 2012). For the old reference plate, the core is 30 km thick and the top and bottom layers are each 20 km thick, while for the young plate each layer is 15 km thick. The density of the older plate is set to be higher than that of the young plate, such that the combined densities and thicknesses of the two background plates yield a range of plate buoyancies similar to that expected for 20 and 120 Myr lithosphere from plate cooling models (e.g., McKenzie et al., 2005). We applied the same density contrast to the full thickness of the plate, i.e., only considering joint buoyancy effects of the crust and mantle lithosphere. This results in the old plate being more negatively buoyant and effectively stronger than the young plate. The upper-lower mantle boundary (ULMB) is implemented as a viscosity jump at 660 km depth, with an upper mantle viscosity, η_UM, of 2 ⋅ 10²⁰ Pa ⋅ s and a lower mantle viscosity, η_LM, of 50 times η_UM. The side plate has a viscosity of 1,000 times η_UM. Material properties common to all simulations are summarised in Table 2.

TABLE 2

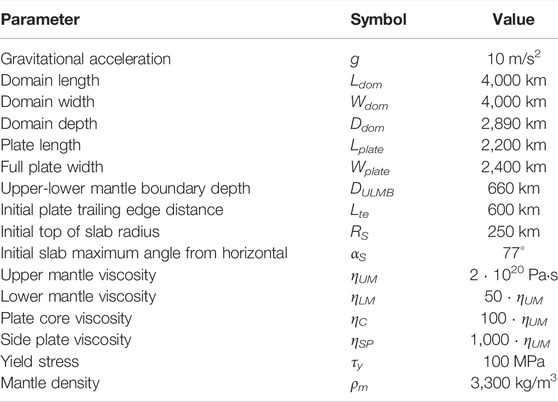
TABLE 2. Parameters common to all simulations. Plate length, L_plate, is in the direction of subduction and plate width, W_plate, is along strike. Note the simulated width is half the full plate width, assuming symmetry at the centre.

2.3 Cases With Ridges

To examine the effect of buoyant ridges (see Table 1), we decrease the density in a trench-perpendicular strip of the subducting plate (Figure 1B). We ran cases with a ridge positioned either at the centre of the plate (i.e., the symmetry edge of the half-plate, at z = 0) or positioned offset from the centre, in the centre of the half plate (initially centred at z = 600 km). The off-centre ridge cases effectively include two ridges (mirrored across the symmetry plane). The distance between these ridges is sufficiently large to allow us to investigate the effect of a single offset ridge. For off-centre ridges, we use a 200 km wide segment. For the central ridges, we use a 100 km wide segment of the plate, to represent half of a 200 km wide symmetrical ridge.

We consider 8 cases (Table 1). For each reference plate type (old and young), we ran a case without any ridges (“NR” or “no-ridge” models, Table 1), as well cases with a central ridge of high and low excess positive buoyancy (“HB” and “LB” models) relative to the buoyancy of the plate (i.e., counteracting the negative buoyancy of the downgoing plate). We also ran simulations for each plate type with a low positive buoyancy (“LB” cases) ridge at the side of the plate. Based on the topography of buoyant ridges on Earth today, we chose cases that yield a typical excess relief of 0.75 and 1.5 km (relative to background plate bathymetry) to define the parameters for our low and high buoyancy ridges, respectively. We calculated what difference in buoyancy for each ridge type relative to surrounding lithosphere would yield this excess relief assuming isostatic equilibrium (following Cloos, 1993; Gutscher et al., 2000; McKenzie et al., 2005, see supplementary material for further details). We then determined the corresponding density difference over the thickness of our modelled plates and reduced it accordingly. Since the modelled young plate is thinner than the old plate, this resulted in much greater density contrast between the ridge and the young plate, compared with the old plate.

When calculating subduction diagnostics, the plate-mantle interface was delineated as the iso-surface where the mantle material volume fraction is 0.5. Snapshots of slab morphologies for all 8 cases, following interaction with the ULMB, are displayed in Figure 2. The trench is defined as the front edge of the plate at 20 km depth (Figure 3). We measure the motion and velocity of the trench and the tip of the slab at 3 points along strike: 15 km from the symmetry boundary, 50 km from the edge of the plate and at a point half way along the trench (denoted as “symmetry,” “edge” and “middle,” respectively). The location of the edge and the middle was calculated throughout the simulations to account for temporal changes in trench shape (red diamonds in Figure 3).

FIGURE 2

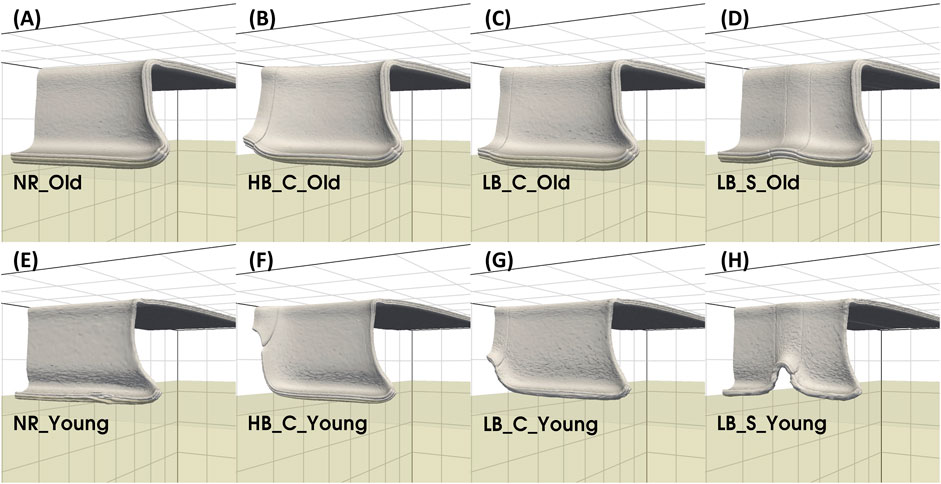
FIGURE 2. Representative slab geometries after plates start interacting with the ULMB for all model cases. Old plate cases are presented in panels (A–D) at 10 Myr and young plate cases in panels (E–H) at 30 Myr. The lower mantle is depicted by green semi-transparent box. For scale, grey grid cells of 400 km by 400 km are shown on domain boundaries.

FIGURE 3

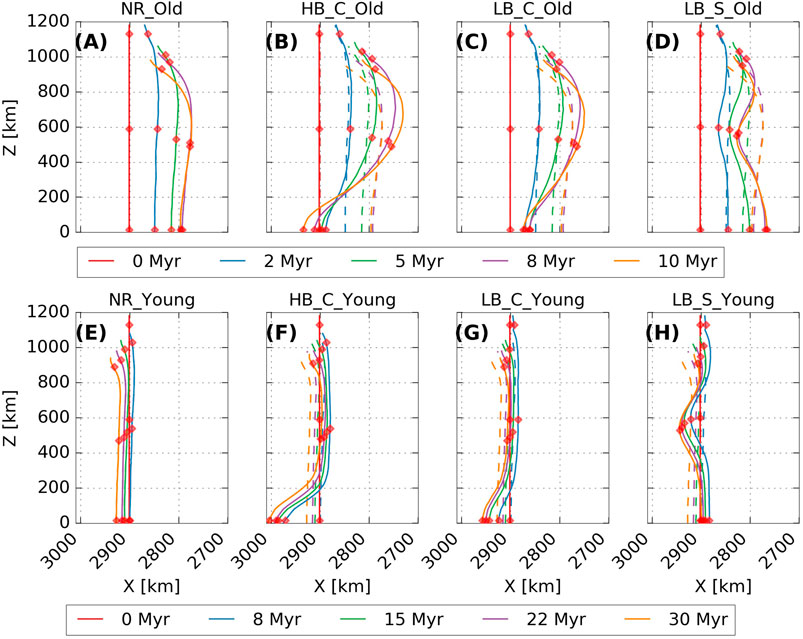
FIGURE 3. Temporal evolution of trench shape, corresponding to the front of the plate measured at 20 km depth, for Old (A–D) and Young (E–H) models. Dashed lines in panels (B–D) and (F–H) represent the location of the trench in the corresponding reference models without a ridge (cases NR_Old and NR_Young). Red diamonds mark the location where motion of the trench and slab were measured, with results displayed in Figures 4,5. Note that the X and Z axes are differently scaled.

3 Results

3.1 No Ridge Behaviour

We first discuss the behaviour of the two reference “no-ridge” models (NR_Old and NR_Young). The evolution of both is consistent with similar 2-D and 3-D models in previous studies (Funiciello et al., 2003; Schellart, 2005; Capitanio et al., 2007; Stegman et al., 2010) and includes two phases: initial sinking of the slab through the upper mantle and subsequent interaction of the slab with the lower mantle. We refer to the time of the first slab-ULMB interaction as t660.

In case NR_Old, the slab sinks through the upper mantle at an increasing rate, reaching the ULMB after ∼7 Myr (Figure 4A). Over the same period, the trench retreats at rates between 1 and 3 cm/yr, depending on the position along the trench. The highest cumulative trench retreat occurs at the middle of the half-plate (∼120 km in 7 Myr), with a lower value at the symmetry plane (∼100 km in 7 Myr) and the lowest value at the slab edge (∼70 km in 7 Myr; Figures 3A, 5A). As the slab approaches the ULMB, it flattens due to interaction with the more viscous lower mantle, which reduces the sinking velocity from an average rate of ∼6.5 cm/yr before t660 to ∼2.7 cm/yr after t660 (Figure 4A). Upon interaction with the ULMB, the trench stagnates and even advances slightly at the edge and at the symmetry boundary (Figures 3A, 5A). As a result, the trench develops a “W”-shape with a stagnation point, where trench motion tends to zero, at the centre (i.e., at the symmetry boundary) surrounded by faster retreating segments, with a maximum in retreat at the middle point of the half-plate (and its symmetrical equivalent).

FIGURE 4

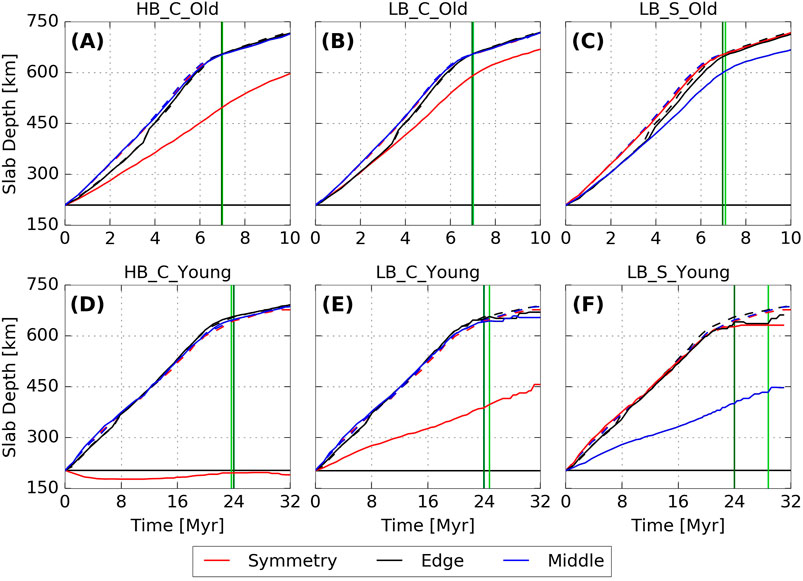
FIGURE 4. Slab depth as a function of time for old plate models in panels (A–C) and young plate models in panels (D–F). Dashed lines represent motions of the corresponding reference model without a ridge (cases NR_Old and NR_Young). Red lines are for measurements at the symmetry boundary [also ridge location in (A,B, D,E)], blue lines are for measurements in the middle of the half-plate [also ridge location in (C,F)] and black lines for measurements at the edge of the plate. Z-positions (along strike) where sinking was measured are marked on Figure 3. Vertical lines mark the time that the slab reaches ULMB (i.e. t660) for the ridge model (light green) and the reference cases (dark green). Solid horizontal black line corresponds to the initial depth of the slab tip at 200 km.

FIGURE 5

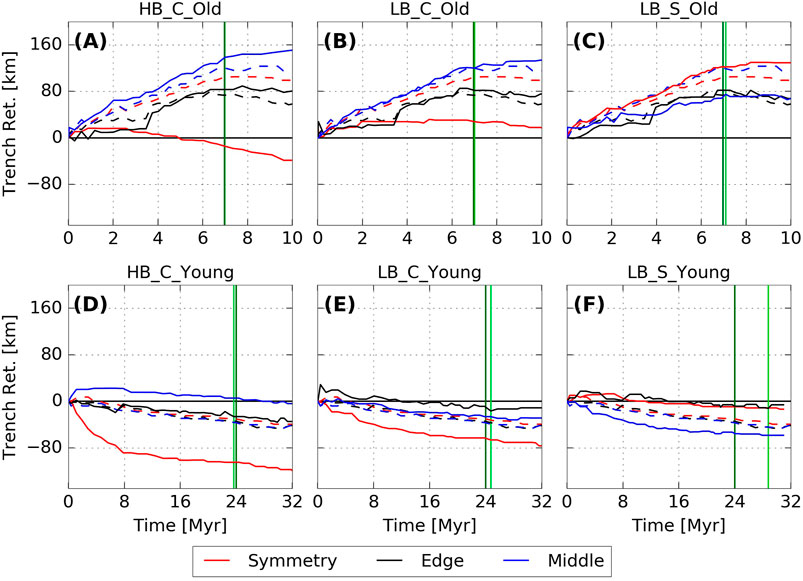
FIGURE 5. Trench motion evolution for old plate models in panels (A–C) and young plate models in panels (D–F), at the locations marked on Figure 3. Lines styles are as in Figure 4, i.e., solid lines are for the ridge models, and dashed lines for the corresponding reference cases. Vertical lines mark t660 for the ridge (light green) and no-ridge (dark green) cases. The initial location of the trench, i.e. 0 km, is marked with solid black horizontal lines.

In case NR_Young, the slab has less negative buoyancy and, accordingly, sinks at a slower rate of ∼2 cm/yr, reaching the ULMB after 24 Myr. Owing to its reduced thickness, the NR_Young plate is also weaker and, consequently, as the slab approaches the ULMB, it buckles (Figure 2E), as its sinking velocity reduces to ∼0.5 cm/yr (Figure 4E). Both before and after t660, the trench slowly advances at a steady rate of 0.1–0.5 cm/yr (Figure 5E). The rate of trench advance is similar everywhere along the trench, resulting in a reasonably straight “I”-shaped trench (Figure 3E).

In both the young and old reference models, the shape of the trench is determined by slab-mantle interactions (Schellart et al., 2007). The difference in trench retreat along strike for the old plate is due to return flow caused by slab rollback, which creates toroidal flow cells in the mantle near the edges of the plate. When the toroidal cell is smaller than the width of the half-plate, a stagnation point emerges at the centre of the trench (Schellart et al., 2007; Schellart, 2020). Our reference old plate is wide enough for such a central stagnation point to develop (Chen et al., 2022), thereby providing an excellent basis for evaluating the effect of ridge position. Narrower old plates develop a “C”-shaped trench instead, where the centre of the slab retreats more than its sides. The young plate sinks slower, which provides more time for deformation and bending at the trench. As a result, the young plate sinks almost vertically and drives very little trench motion (e.g., Capitanio et al., 2007). The slight curvature at the edge of the plate is the result of the weak toroidal cell caused by the displacement of mantle material due to plate sinking, and overall the trench stays reasonably straight (Chen et al., 2022).

3.2 Ridge Buoyancy Effects

Next, we examine cases with ridges at the centre of the plate (i.e., at the symmetry plane), with low and high positive buoyancy relative to the downgoing plate: cases HB_C and LB_C. In all cases, the addition of a buoyant ridge results in less trench retreat, or even trench advance, at the location where the ridge impacts the trench. Compared with the NR_Old reference case, trench retreat at the centre of the plate in case LB_C_Old is reduced from ∼100 km to ∼30 km by t660 (Figure 5B), while in case HB_C_Old, the centre of the trench advances ∼15 km by t660 (Figure 5A). In the NR_Young reference case, the centre of the trench is already advancing, and the addition of the ridge enhances this advance. For case LB_C_Young, the trench at the centre of the plate advances by ∼70 km by the reference t660 compared with ∼30 km in NR_Young case (Figure 5E). For the HB_C_Young case, the trench advances ∼110 km by the reference t660 (Figure 5D). In both young and old plate models, trench retreat at locations away from the ridge is increased or trench advance is decreased compared to the corresponding NR case.

The sinking velocity of the slab carrying the ridge is reduced locally due to the added positive buoyancy of the ridge. Particularly in the young plate models, the local plate sinking velocity at the ridge is significantly lower than in the rest of the plate. In model HB_C_Young, the ridge has not sunk at all by the reference t660 (Figure 4D). The differential sinking rate in this model is accommodated through thinning of the slab at the side of the ridge, which could facilitate slab tearing under certain rheological parameterisations. In comparison, the less buoyant ridge in model LB_C_Young has sunk ∼200 km, from its initial depth, by the reference t660 (Figure 4E). For older plate models, sinking velocity at the ridge deviates less from that in the rest of the plate. The part of the slab with the ridge has sunk ∼300 km for the HB_C_Old case and ∼400 km for LB_C_Old case (Figures 4A,B). Elsewhere along the slab, the sinking velocity remains similar to the reference case for both young and old plate models.

Previous 2-D models have demonstrated that, in free-subduction, higher slab pull and increased resistance to bending at the trench encourage trench retreat (Capitanio et al., 2007; Ribe, 2010). In our 3-D models, it is the difference between slab pull at the ridge and in the rest of the plate that drives the variable trench retreat, hindered at the ridge and enhanced elsewhere. This differential trench motion increases trench curvature, leading to the formation of a “W”-shaped trench in the young plate models and a more pronounced “W”-shape in the old plate, with more retreat at the edge of the plate than at the symmetry boundary (Figures 3B,C,F,G). Due to the low resistance to bending in young plates, such a “W”-shaped trench is difficult to generate by young plate subduction without along-strike buoyancy variations (Chen et al., 2022). The differential sinking between the ridge and rest of the plate also creates along-strike tension in the plate. The higher plate strength of the old plates facilitates stress transmission along strike. As a result, old plates can pull the ridge more effectively into the mantle, resulting in less along-strike variations in sinking and a smoother trench and slab shape in comparison to the corresponding young plates with ridges (Figures 2B,C,F,G and Figures 3B,C,F,G).

3.3 Ridge Location Effects

We evaluate the impact of ridge location by comparing results from models LB_C and LB_S. As for the models with a central ridge, subduction of a ridge on the side of the plate results in locally reduced trench retreat and, sometimes, induces a small amount of trench advance (Figures 3D,H). Although the side ridge cases effectively contain two ridges, there is no indication from the resulting trench shapes (Figures 3D,H) that there is an interference due to superposition of the influence of the two ridges, so these models can be used to study the effect of the subduction of a ridge offset from the slab centre.

The along-strike changes in trench motion compared to the reference cases are less for the cases with a side ridge than for the cases with a central ridge. For case LB_S_Old, the reduction in trench retreat by t660 is ∼50 km, compared to a reduction of ∼80 km for case LB_C_Old (Figures 5B,C). This is likely because the impact of the ridge in LB_S_Old is concentrated at the point where a ridge-free trench (case NR_Old) would retreat the most. Therefore, in this case, ridge subduction reduces the overall lateral deflection of the trench in comparison to the reference case (Figures 3A,D). For case LB_S_Young, the increase in trench advance relative to case NR_Young by the reference t660 is ∼20 km, compared with ∼35 km for case LB_C_Young (Figures 5E,F). All young plate cases with a ridge deform the trench from the straight reference shape of the NR_Young case to a curved trench with a cusp (Figures 3E,G,H).

As for cases with central ridges, the sinking velocity is reduced relative to the corresponding NR cases where the side ridge is subducted. The local reduction in sinking velocity is smaller for the LB_S cases than for the LB_C cases. The ridge in case LB_S_Old has sunk ∼400 km by the reference t660, compared with ∼390 km for case LB_C_Old (Figures 4B,C). Similarly, in LB_S_Young, the ridge has subducted ∼10 km deeper by the reference t660 than case LB_C_Young at the same time (Figures 4E,F). The side-ridge cases, that effectively contain two ridges, also demonstrate that a subducting buoyant ridge can lower the overall sinking velocity of the plate if the ridge adds enough positive buoyancy. The reduction in overall sinking velocity is small, resulting in a delay of ∼0.2 Myr in t660 in model LB_S_Old. In LB_C_Old, where the change in buoyancy is only half of that in the LB_S_Old case, the t660 delay is half as small, ∼0.1 Myr. The effect is somewhat larger for the LB_S_Young case, where t660 is delayed by ∼5 Myr compared with the reference NR_Young case (Figure 4F).

As in the cases with central ridges, a side ridge’s main effect is to locally reduce trench retreat and sinking velocity. These effects are both diminished when the ridge subducts along a part of the trench that is, otherwise strongly retreating. When the ridge impacts at the side, the composite trends of the plate’s tendency to retreat and the reduced trench retreat of the ridge leads to less along-strike variation in trench shape. The lower amount of along-strike bending in the LB_S cases may explain the slightly higher sinking velocities for the side ridges compared to the central ridges, as less potential energy is lost in plate deformation. Thus, our results imply that ridges that subduct along parts of the trench where trench motion is already hampered by other factors impact subduction more.

4 Discussion

4.1 Buoyant Feature Subduction and the Morphology of the Trench and Slab

While 2-D models can elucidate some of the effects of buoyant feature subduction, they overestimate the buoyancy force exerted by the feature, due to the implicit assumption of infinite feature width. The full effects of the subduction of buoyant features of limited along-strike extent can therefore only be investigated using 3-D models.

All our ridge-subduction cases lead to trench deformation, with decreased trench retreat, trench stagnation or increased trench advance where the buoyant ridges subduct. Previous 3-D models that investigated the effect of buoyant feature subduction (Martinod et al., 2005; Mason et al., 2010; Flórez-Rodríguez et al., 2019) also found that trench retreat was impeded where the buoyant feature subducts, leading to differential retreat along strike. This observation was independent of size, shape and orientation and applied to both buoyant ridges and plateaus (Martinod et al., 2005, 2013). The resulting formation of trench cusps can be offset from the position of ridge impact at the trench if the feature subducts obliquely (Martinod et al., 2013). We show that significant trench deformation occurs in both old and young plates. Plate strength and the relative buoyancy of the ridges compared to the underlying plate determine how pronounced trench deformation is. That is, trenches where a weaker young plate subducts are deformed more locally than those where a stronger old plate subducts, for the same excess ridge buoyancy.

We also find that the position of buoyant ridges along the trench affects the response of the trench and resulting slab morphology. In older plates, ridges near intrinsic trench stagnation points accentuate along-strike variations in trench shape while ridges impacting the trench at other locations lead to less pronounced curvature. Schellart (2020), in 3-D models without buoyant features, found that the central trench stagnation point can, at a late stage of subduction zone evolution, facilitate local slab shallowing. Our results suggest that the subduction of a buoyant ridge at or near such a stagnation point would further enhance such behaviour. We note that trench stagnation points can also form in response to other factors, for example, at the edge of a subducting plate, due to interaction with a side plate or existence of a triple junction, and by interaction with a thick upper plate (Capitanio et al., 2011; Jadamec and Billen, 2012).

Although it is commonly assumed that the subduction of buoyant ridges leads to a decreased slab dip (e.g., Gutscher et al., 2000), our models display a range of behaviour (Figure 6). In old plate cases (Figures 6A–D), the slab is steepened where the ridge subducts, while the dip of the slab along the rest of the plate is slightly lower than in the reference case without a ridge. Although buoyant ridges act to inhibit sinking, the older subducting plates are sufficiently strong that the pull from the rest of the plate leads to a steeper slab where the buoyant feature enters the subduction zone. In this case, the lowest dips occur where the trench retreats most. In contrast, ridges on young plates develop shallower dip angles than the surrounding plate, and the shallowing is stronger for ridges with a higher positive buoyancy (Figures 6E–H). In these cases, the rest of the plate is weak, and is not negatively buoyant enough to pull down the segment with the ridge. Martinod et al. (2005) found that their slabs shallowed where the buoyant feature was subducting but steepened below. Flórez-Rodríguez et al. (2019) found yet another variation in their 3-D analogue models of subduction of buoyant ridges on relatively narrow plates, where the slab shallows in the centre of the ridge but steepens on its sides. In a spherical geometry, effective resistance to plate bending at the trench is higher than in equivalent Cartesian plates (Morra et al., 2006; Mahadevan et al., 2010; Chamolly and Ribe, 2021; Chen et al., 2022). Models of spherical plates display trench and slab deformation in response to along-strike variations in slab buoyancy comparable to Cartesian models (Morra et al., 2006), and are therefore likely to respond to subduction of buoyant ridge similarly. The differences in model behaviour illustrate that the effect of buoyant features on slab dip varies depending on plate strength and relative feature buoyancy, and a range of responses are possible.

FIGURE 6

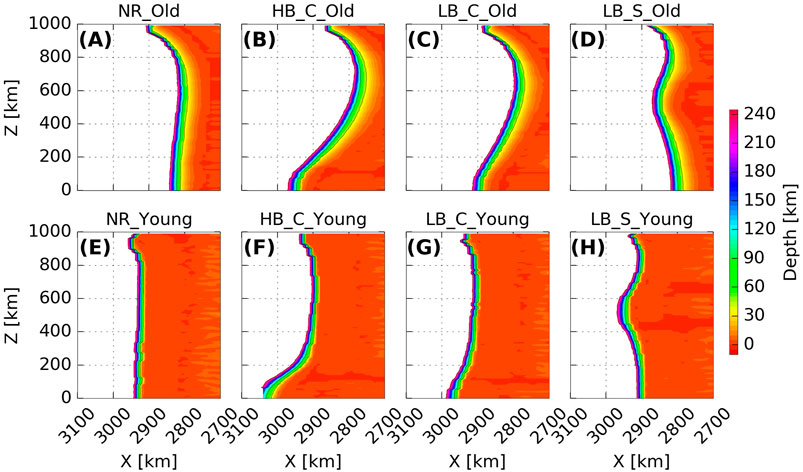
FIGURE 6. Top-down view of final plate top surface depth above 250 km for Old (A-D) and Young (E-H) models. Coloured by depth, thereby providing an illustration of the along-strike variations in slab dip. Note that the X and Z axes are scaled differently.

4.2 Buoyant Ridges and Low-Angle Subduction

Our results confirm that ridge subduction alone is insufficient to generate a flat slab, a finding that is, consistent with other 3-D free-subduction models (Martinod et al., 2005; Flórez-Rodríguez et al., 2019). Even in 2-D models (van Hunen et al., 2004; Gerya et al., 2009), where the buoyant features are essentially infinite in their along-strike dimension, the subduction of buoyant features alone does not generate a fully flattened slab. Instead, a number of studies have now confirmed that slab flattening requires additional mechanisms such as an upper plate that (by external forcing) overrides the lower plate faster than it can subduct (Van Hunen et al., 2002; Arcay et al., 2008; Currie and Beaumont, 2011; Martinod et al., 2013; Liu and Currie, 2016) or a thick upper plate that generates an upward suction force in the relatively high viscosity mantle wedge, which can pull a shallow-angle slab into a flat-slab geometry (Gerya et al., 2009; O’Driscoll et al., 2009; Manea et al., 2012; Rodríguez-González et al., 2012, 2014; Taramón et al., 2015; Schellart and Strak, 2021).

While upper plate forcing or thickness can result in a flat slab in the absence of buoyant feature subduction, these mechanisms have clear limitations (Hu et al., 2016). Overthrusting requires a highly forced upper plate velocity (3–5 cm/yr, e.g. van Hunen et al., 2004; Currie and Beaumont, 2011) and would usually apply to the entire upper plate, failing to localise flat subduction in bounded regions of several hundred kilometres, as is observed on Earth at present. A similar issue arises for a thickened upper plate which needs to be of a craton-like thickness (O’Driscoll et al., 2009; Manea et al., 2012; Taramón et al., 2015). While cratons comprise limited parts of the upper plate (e.g. Wyoming craton in North America; Amazonian craton in South America), they extend over scales of 1,000 km (e.g. Kusky et al., 2014, and references therein) and, therefore, can only explain very wide flat slabs. Conversely, modelling studies demonstrate that the subduction of buoyant features can aid flat slab formation, by locally reducing trench motion and slab dip (van Hunen et al., 2004; Gerya et al., 2009; Martinod et al., 2013). Thus the contribution of buoyant feature subduction can help to explain the limited lateral extent and temporal duration of flat slabs.

4.3 Buoyant Feature Subduction Styles on Earth

Together with published dynamic models, our results illustrate a number of different responses to buoyant feature subduction, both ridges and plateaus, are possible. These include three types: 1) a “trench deforming” response is an end-member in which subduction of a buoyant feature mainly deforms the trench with minor slab steepening or contortion. Our results demonstrate that this occurs when the positive buoyancy force of a buoyant ridge is low compared with overall plate strength. The upper plate in a “trench deforming” subduction style is typically thin or weak and therefore does not impede trench deformation; 2) a “slab deforming” response, in which subduction of the buoyant feature reduces slab dip locally whilst also deforming the trench. This happens when the buoyancy force associated with the feature is strong enough to locally decrease slab dip while any forcing by the upper plate does not play a significant role; 3) a “slab flattening” response, an end-member in which the slab is flattened at shallow depth over a distance of up to several hundred kilometres. This response occurs when the positive buoyancy of a feature is substantial, and it subducts under a thick, possibly advancing, upper plate. Observations of buoyant features subducting at the plate boundaries of the Pacific and Indian Oceans reflect these different expressions (see Figure 7 and Table 3), although many subduction zones do have additional complexities.

FIGURE 7

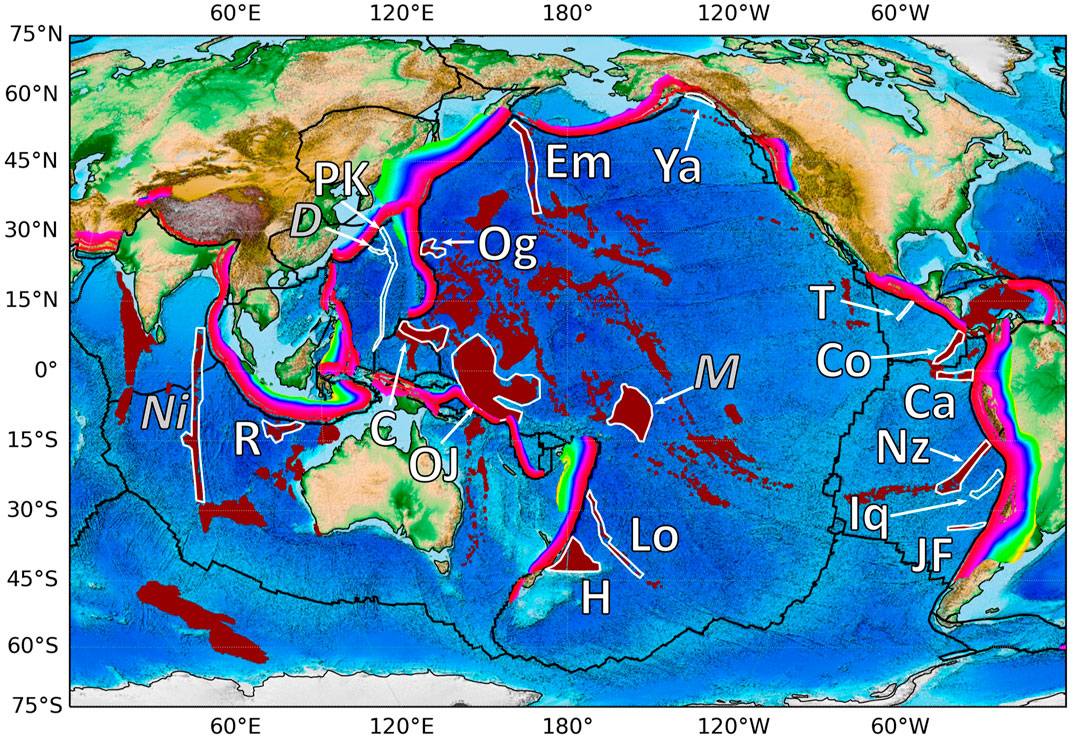
FIGURE 7. Map of buoyant features (white outlined polygons) interacting with subduction zones in the Pacific and Indian oceans. Maroon surfaces indicate oceanic large igneous provinces (LIPs) and volcanic island chains. Slab depth contours are marked in RBG colours. Black lines indicate plate boundaries. Abbreviations for buoyant features discussed in the main text (white text): C—Caroline ridge, Ca—Carnegie ridge, Co—Cocos ridge, Em—Emperor ridge, H—Hikurangi plateau, Iq—Iquique ridge, JF—Juan-Fernandez ridge, Lo—Louisville ridge, Nz—Nazca ridge, OJ—Ontong Java plateau, Og—Ogasawara plateau, PK—Palau-Kyushu ridge, R—Roo rise, T—Tehuantepec ridge, Ya—Yakutat block. Other features (italic grey text): D—Daito ridge, M—Manihiki plateau, Ni—Ninetyeast ridge. Data from Coffin et al. (2006); Skinner and Clayton (2011); Tetreault and Buiter (2014), plate boundaries after Bird (2003), bathymetric data from Amante and Eakins (2008) and slab depth data from Hayes et al. (2018).

TABLE 3

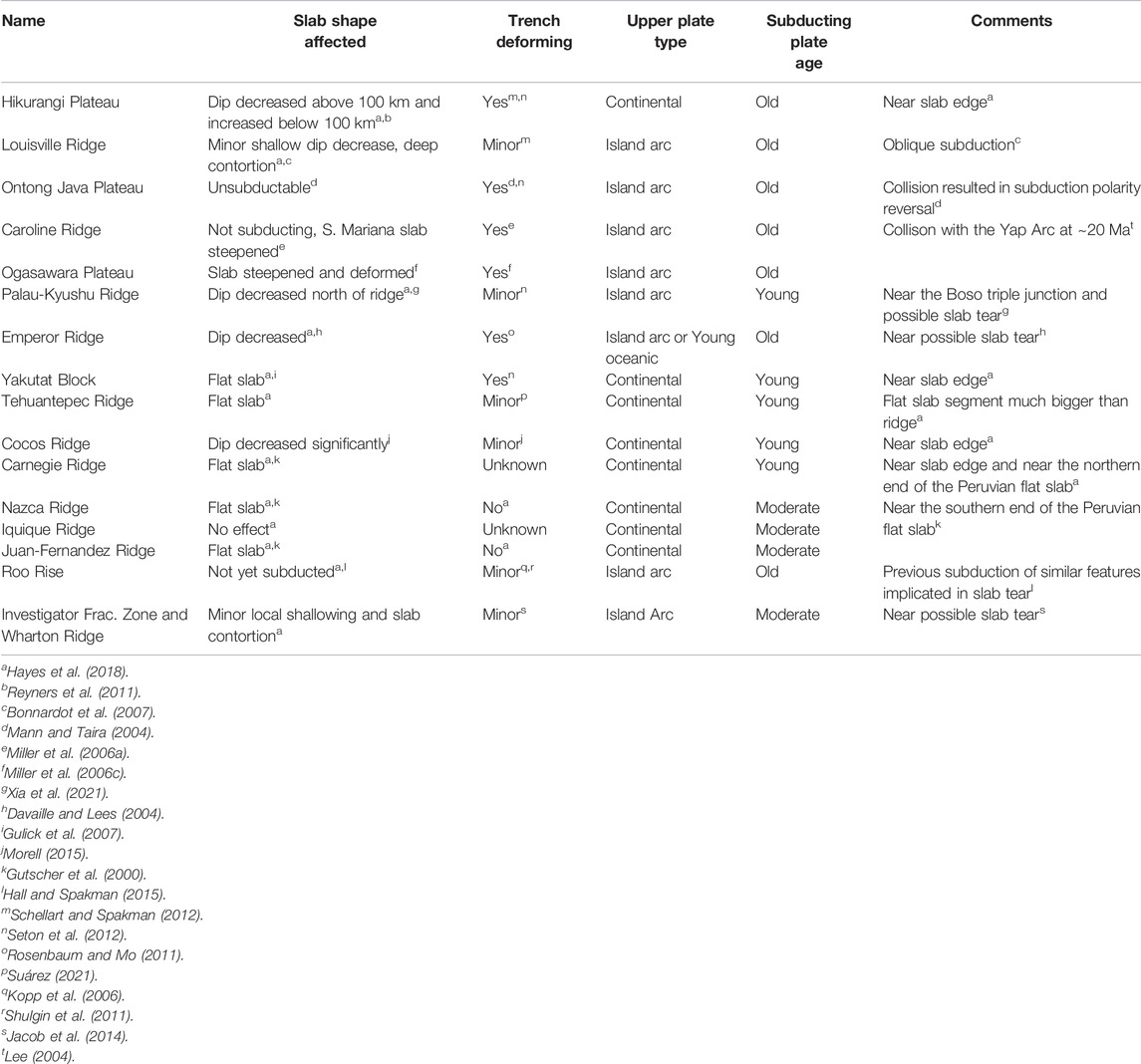
TABLE 3. Properties of buoyant features discussed in the main text. Superscripts refer to information source.

The best example of “trench-deforming” buoyant-feature subduction occurs along the Izu-Bonin-Mariana (IBM) system. The two main buoyant features interacting with the IBM subduction system and impeding retreat of the Mariana trench are both located near major cusps (i.e. the Caroline ridge near the Mariana-Yap junction and the Ogasawara ridge near Bonin-Mariana junction) and these cusps are inferred to have developed when these buoyant features began interacting with the trench (Miller et al., 2006a,c; Seton et al., 2012; Xia et al., 2020). The slab below the Ogasawara Plateau is slightly steeper than adjacent slab segments subducting north and south of it (Miller et al., 2006c; Hayes et al., 2018). The Caroline Island Ridge at the southern end of Mariana is located at a clear cusp where it has reduced convergence velocity significantly and blocked subduction (Miller et al., 2006a; Xia et al., 2021). The slab on the side of the Caroline Ridge, subducting below the southern Mariana trench (Miller et al., 2006a; Zhu et al., 2019) is steep, while the part of the slab along the Yap trench may have detached in response to impingement of the Caroline Ridge (Zhang and Zhang, 2020). Another example of “trench-deforming” buoyant-feature subduction is at the southern end of the Tonga trench, where the Hikurangi Plateau appears to have served as a pivot for the rotation and migration of the Tonga-Kermadec system (Schellart and Spakman, 2012; Seton et al., 2012). Although there is some shallowing of the Hikurangi-southern Kermedec slab above 100 km, this shallowing occurs mainly north of the plateau, while below 100 km depth, the slab is steeper than further north (Reyners et al., 2011; Hayes et al., 2018). These examples all display the expected behaviour for old plates with sufficient slab pull to carry buoyant features into the trench. Rosenbaum and Mo (2011) previously noted that this behaviour is typical of the western Pacific, where subduction of buoyant features often leads to locally hampered trench retreat and to slab steepening rather than slab shallowing.

Several other buoyant features in the Pacific and Indian Oceans are associated with “slab deforming” subduction, in which both a cusp in the trench and local shallowing of the slab dip is observed. Some cases correspond to smaller features on plates of young or intermediate age (as in our young plate models), and others to larger features on older plates (similar to the models of Flórez-Rodríguez et al., 2019). The most straightforward example of “slab deforming” buoyant-feature subduction may be the Cocos ridge, which coincides with a cusp and shallowing of the slab (Morell, 2015). Subduction of the Louisville Ridge below the Tonga trench introduces a minor cusp and some slab shallowing and contortion along the downdip projection of the obliquely subducting ridge (Bonnardot et al., 2007; Hayes et al., 2018). The Tonga-Kermadec trench is of moderate length, and might be expected to evolve to a “C” shaped trench (Schellart et al., 2007). However, the present-day shape of the Tonga-Kermadec trench is relatively straight, which may be due to early interaction between the middle of the trench, where it would have had the largest curvature, and the Louisville Ridge. This process would also account for the small size of the observed cusp where the ridge currently interacts with the Tonga-Kermadec trench. The cusp between the Japan and Kurile trench near Hokkaido is also associated with shallow slab below the island (Miller et al., 2006b; Kennett and Furumura, 2010; Hayes et al., 2018). Although there is no buoyant feature evident on the incoming plate, it has all the signatures of a recently subducted feature.

The interaction of the Ontong Java Plateau (OJP) with the South Pacific Trench is probably an extreme example of “slab deforming” style of interaction. The OJP separated from the Hikurangi plateau at ∼120 Myr and from the Manihiki plateau at ∼100 Myr (Taylor, 2006; Chandler et al., 2012; Seton et al., 2012) to reach the South Pacific trench at ∼20 Myr (Mann and Taira, 2004; Seton et al., 2012). The impinging of the OJP on the trench hampered trench retreat and deformed the trench which, until that time, had a typical concave shape similar to the present-day Japan trench (Mann and Taira, 2004; Seton et al., 2012). The large extent of the OJP made it too buoyant to subduct, perhaps acting similarly to the ridge in model HB_C_Young. As a result, subduction in the region ceased and eventually reversed polarity (Mann and Taira, 2004).

Slab deformation due to buoyant-feature subduction may expose parts of the slab to increased stresses, which result in slab tears (e.g. models by Mason et al., 2010). This may be the case for the subduction of the Emperor ridge at the cusp between the Kamchatka and Aleutian trench, which is associated with a low slab dip angle and a possible tear (Davaille and Lees, 2004). However, this cusp may predate subduction of the Emperor chain (Seton et al., 2012), and its formation may instead have been associated with the subduction of previous, arc-related, buoyant features (e.g., Vaes et al., 2019). Another example is the Palau-Kyushu ridge, located at the cusp between the Ryukyu and Nankai trenches, which has been proposed to contribute to shallow subduction along Nankai trench, possibly with a tear near the subducting ridge (Wu et al., 2016; Pownall et al., 2017; Xia et al., 2021). The low dip of the Nankai slab may also be affected by the fact that its northern end lies at the Boso triple junction, where trench motion is limited by interaction between the Nankai, Izu and Japan trenches. In the Indian ocean, subduction of the Investigator Fracture Zone and the extinct Wharton spreading ridge coincide with a cusp in the Sumatra trench, a local slab “kink” and possible slab tear (Hall and Spakman, 2015). The excess buoyancy is likely due to subduction of the Wharton ridge, as oceanic fracture zones like Investigator are not usually associated with changes to plate buoyancy (e.g., Jacob et al., 2014). Along the Java trench, where the Roo rise is starting to deform the trench (Kopp et al., 2006; Shulgin et al., 2011), it has been suggested that past subduction of similar buoyant features is responsible for a slab tear within the Java slab (Hall and Spakman, 2015).

Flat subduction is currently observed in several subduction zones in the Eastern Pacific, under Alaska, Mexico, and South America. In all cases, the strong westward motion of the Americas over the subducting Pacific, Cocos and Nazca plates may facilitate slab flattening (Van Hunen et al., 2002; Manea et al., 2017). In Alaska, the subduction of the Yakutat terrane occurs at a major cusp at the eastern end of the Aleutian trench and is associated with subduction of a narrow flat slab segment (Gulick et al., 2007). The Yakutat terrane subducts under a continental plate, although not of cratonic thickness, with a possible tear on the side (e.g., Daly et al., 2021). In South America, the Ecuador-Peru flat slab is associated with the subduction of the Carnegie and Nazca Ridges (which bound it from north and south) and the Chilean flat slab is associated with subduction of the Juan-Fernandez Ridge (Gutscher et al., 1999, 2000; Skinner and Clayton, 2013; Kumar et al., 2016; Bishop et al., 2017; Manea et al., 2017). The upper South American plate comprises several old platforms which may all have had thick roots, although not all persist to the present day (Feng et al., 2007). Although the Carnegie ridge interacts with the edge of the trench, where the trench motion is expected to be limited (Schellart et al., 2007), the associated Ecuador-Peru flat slab is located closer to the centre of the trench, as is the Chilean flat slab. Below the major cusp in the Andean trench, at the Bolivian Orocline, the slab is relatively steep. Although the cusp is in front of the subducting Iquique Ridge at present, it was formed before the arrival of the ridge to the trench, at 40–25 Ma (Allmendinger et al., 1997; Schepers et al., 2017). It may have formed above a previous flat slab segment which has been proposed to have existed between 40–20 Ma (Ramos and Folguera, 2009; Skinner and Clayton, 2013). A previously subducted buoyant feature may have formed the older flat slab and, aided by its location close to the centre of a long trench, have induced slab flattening. Capitanio et al. (2011) proposed that, in contrast to most trenches whose shape appears to be determined by subducting plate forcing, the recent ( $<$ 20 Ma) rise of the Andes and corresponding shape of the South American trench may be controlled by variations in thickness of the upper plate. Finally, flat subduction below Mexico is generally thought to be too wide to be induced by the buoyant Tehuantepec ridge that subducts at its southern end (Gutscher et al., 2000; Skinner and Clayton, 2011). Factors that may contribute to the formation of the Mexican flat slab include the subduction of a spreading ridge near the northern end of the plateau, a continental overriding plate, and the flat slab location just north of the boundary between the North and South American plates, where shearing due to differential movement between the Americas may result in fast moving upper plate over slow and young subducting plate.

5 Conclusion

We performed a set of 3-D multi-material numerical models of free subduction carrying a buoyant ridge, to investigate the role of plate age, ridge buoyancy and ridge location on trench shape and slab morphology for lower-plate controlled subduction (i.e., cases where the upper plate is young, thin or weak). Our models are the first to illustrate systematically that age-dependent slab density and viscosity can lead to different expressions of the subduction of buoyant features.

Our old-plate cases with buoyant ridges induce significant trench deformation and some steepening (rather than shallowing) of the dip angle of the subducting slab at the ridge. A similar type of “trench-deforming” response is observed in several Western Pacific subduction zones (e.g., Ogasawara Plateau on the old Pacific plate). Our young-plate cases with buoyant features generate both trench deformation and local shallowing of the subducting plate. This style of “slab-deforming” response is observed at several other locations around the Pacific, where the buoyant features are substantial enough that the background plate’s pull and strength is insufficient to override the effect of local buoyancy (e.g., Cocos Ridge on the young Cocos plate). Finally, the position of the buoyant features relative to the natural slab shape, which is governed by slab width (Schellart et al., 2007; Schellart, 2020), may lead to a stronger or more subdued expression of ridge subduction. For example, the subduction of the Louisville ridge near the centre of the Tonga-Kermadec trench may explain the relatively mild expression of this ridge in slab dip and the relative straightness of the Tonga trench.

Our results, considered alongside previously published 3-D models that investigated other combinations of subducting plate buoyancy, strength and width, as well as buoyant features of various sizes and densities (Martinod et al., 2005; Mason et al., 2010; Flórez-Rodríguez et al., 2019), illustrate that a range of responses are possible for different subducting plate ages, and it is not expected that all subducting features lead to a shallowing of slab dip (Rosenbaum and Mo, 2011; Skinner and Clayton, 2011). Other studies have shown that the upper plate, if comprised of sufficiently thick continental lithosphere, can lead to further modulation of the expressions of buoyant feature subduction including the formation of flat slab segments (Manea et al., 2012; Rodríguez-González et al., 2012; Taramón et al., 2015). Our results suggest that buoyant features can play an important and varied role in shaping subduction dynamics and, particularly, on the evolution of plate boundaries, where local hampering of trench motion can induce boundary rotations and segmentation.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: Zenodo repository; DOI: 10.5281/zenodo.5833712; URL: https://doi.org/10.5281/zenodo.5833712.

Author Contributions

The ideas for this research were developed by all co-authors. Models were developed, validated and run by LS, FC and DRD. The paper was written by LS and SG, with input from DRD and FC.

Funding

LS was supported by the Engineering and Physical Sciences Research Council (EPSRC) (grant no. EP/N509486/1). FC was supported by an Australian Government Research Training Program (RTP) Scholarship. SG received support from Natural Environment Research Council (NERC grant NE/G004749/1). DRD acknowledges support from the Australian Research Council (ARC), under DP170100058.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The MSci projects of Luke Jenkins and Kamile Rudaviciute, in collaboration with Loic Fourel, seeded the ideas developed in this paper. Numerical simulations were undertaken on the NCI National Facility in Canberra, Australia, which is supported by the Australian Commonwealth Government. The Fluidity computational modelling framework, including source code and documentation, is available from https://fluidityproject.github.io/. Authors would like to thank Stephan Kramer, Cian Wilson and Angus Gibson for support with the development and maintenance of Fluidity and two reviewers for constructive comments that helped to clarify important parts of the manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.852742/full#supplementary-material

References

Allmendinger, R. W., Jordan, T. E., Kay, S. M., and Isacks, B. L. (1997). The Evolution of the Altiplano-Puna Plateau of the Central Andes. Annu. Rev. Earth Planet. Sci. 25, 139–174. doi:10.1146/annurev.earth.25.1.139