Combined Effect of Pore Water Overpressure, Far-Field Stresses, and Strength Parameters in Wellbore Stability

1 Introduction

Wellbores drilled to access reservoirs go through different rocks affected by different pore pressures (Deangeli and Omwanghe, 2018). Consequently, unexpected or unknown behavior of rock and overpressures are often the cause of drilling problems, resulting in an expensive loss of time, sometimes in a loss of part or the entire borehole (Nmegbu and Ohazuruike, 2014; Ambati et al., 2021). The role of geomechanics in wellbore stability has grown over the years, although there are still uncovered areas because of the variable and uncertain character of rocks at depth. The limited availability of relevant data is also part of the problem (Fjaer et al., 2008).

Mud weights are usually kept in balance with or at slightly greater pressure than pore-fluid pressure to avoid kicks or losses. Ideally, mud weights are commonly used as a guide to predict maximum pore pressure (Liu et al., 2016). Nevertheless, drilling in overpressured basins is a challenging task. In this framework, Zhang (2011) reviewed the fracture gradient prediction and proposed a theoretical pore pressure-porosity model to predict overpressures. A comprehensive geomechanical model can critically address these issues by assessing the far-field stresses. At the same time, information such as rock strength and pore pressures are used together to minimize the risks associated with drilling (Ganguli and Sen, 2020). Reference mud weights based on post drilling experience help manage wellbore instability at large depths in complex basins (Tan and Willoughby, 1999; Sen et al., 2018). The coupling between post-drilling experience and stability analysis aids the designer in avoiding or mitigating the risks of catastrophic hole collapse and lost circulation (McLellan and Hawkes, 1999).

The Mohr–Coulomb criterion is the most widely used method in geomechanical/geotechnical applications and, in particular, wellbore stability analysis due to its simple formulation. This criterion is linear and needs a fixed cutoff to predict the tensile strength. Other criteria used in wellbore stability are the Mogi–Coulomb and modified Lade criteria, which account for the intermediate principal stress, and Drucker–Prager criterion (Kristiansen, 2004; Al-Ajmi and Zimmerman, 2006; Zhang et al., 2010; Gholami et al., 2014; Manshad et al., 2014; Ma et al., 2015; Singh et al., 2019). In particular, the Lade and Drucker–Prager criteria have been developed for the plastic deformation of soils and were modified to include materials such as concrete and rocks (da Fontoura, 2012). The Hoek–Brown criterion (1980–2019) has been developed specifically for rock materials and rock masses (Priest, 2005). It has been updated by the authors based on over 40 years of experience in several geological and engineering contexts. This criterion is nonlinear and well predicts rock failure in the compression zone. Cai (2010) suggested a modification of this criterion with two different frictional strength parameters to define the compression and tension zone better. The Hoek–Brown criterion is generally used for wellbore stability in shales and fractured formations (Ottesen, 2010; Zhang et al., 2010; Gholami et al., 2014; Deangeli and Omwanghe, 2018; Ma et al., 2018; Parkash and Deangeli, 2019; Deangeli et al., 2021).

The analytical prediction of mud pressures to maintain wellbore stability is achieved by coupling the strength criterion with the Kirsch solution, which is based on the theory of elasticity. Nevertheless, this approach predicts the initiation of borehole failure and does not indicate the consequences of this occurrence. For this, Abdelghany et al. (2021) proposed a procedure based on the depth of damage to the estimation of the rock volume that displaces into the wellbore. Failure can occur in successive steps (Zoback et al., 1985), and the generation of local failure planes causes stress redistribution in the surrounding intact rock. The rock failure is related to the transition from elastic to elastoplastic deformations. Elastoplastic numerical modeling of wellbores allows analyzing the consequences of rock failure (McLellan and Hawkes, 2001). In particular, numerical simulations of wellbore instability in underbalanced conditions allow the determination of a safe drilling mud window based on the extent of the area of the yielded rock around the borehole (McLellan and Hawkes, 2001; Salehi et al., 2010). The numerical simulations are generally set up with the Mohr–Coulomb, Mogi–Coulomb, and modified Lade criteria (Salehi et al., 2010; Manshad et al., 2014; Yousefian et al., 2018).

Nevertheless, comparative analyses of wellbore stability with different criteria indicate that the predicted mud weights are different (Zhang et al., 2010; Rahimi and Nygaard 2015; Meng et al., 2021), and some criteria do not match the post drilling evidence. These results demonstrate that selecting an appropriate strength criterion is a key step in mud weight prediction. However, the uncertainties related to rock strength parameters have not been properly investigated in these studies. The mechanical parameters of the rock are generally obtained from log correlations and, in some cases, from laboratory tests carried out on outcropping similar formations because the core material from wells can be rather limited (Risnes, 2001).

The mechanical response of rocks in some specific conditions requires a dedicated study to unravel the uncertainties related to failure during drilling operations. In particular, unexpected overpressures can induce tensile stresses around the wellbore, and identifying the most suitable strength criterion is crucial. Furthermore, the accuracy in selecting the strength parameters represents a key component of the stability analysis. The lack of direct measurements of rock strength and the uncertainties of the parameters derived with log correlations makes it difficult to achieve accurate results.

This study focuses on analyzing the failure of isotropic porous rocks in overpressured basins during drilling operations. We investigated the difficulties that can arise in estimating strength properties from laboratory tests and log correlations. In order to highlight the importance of an accurate choice of the input parameters, we performed sensitivity analyses, with the Mohr–Coulomb and Hoek–Brown criteria, by varying the uniaxial compressive and tensile strength, the frictional component of the strength, the far-field stresses, and the pore pressure (overpressure). As this study aims at investigating the occurrence of mechanisms of failure as a function of the strength parameters and in-site conditions, we performed the analyses at specific depths. Finally, we also performed numerical simulations with the code FLAC (ver. 8.1) using the Hoek–Brown criterion to investigate the extent of plasticity, the borehole convergence, and the occurrence of collapse.

2 Methods

Sedimentary rocks are porous materials generally affected by the pore-fluid pressure p_f in hydrocarbon basins. The presence of a fluid in a porous rock modifies its mechanical response (Detournay and Cheng, 1993). Hoek and Brown (1997) and Brady and Brown (2004) found that the solution to some rock engineering problems requires an effective stress approach. Sedimentary rocks show a significant strength decrease with increasing moisture content. The theory of poroelasticity indicates that the deformation of the porous medium is proportional to the effective stress (Detournay and Cheng, 1993):

$\mathit{\sigma }{\mathrm{\prime }}_{\mathit{ij}}={\mathit{\sigma }}_{\mathit{ij}}-\mathit{\alpha }{\mathit{p}}_{\mathit{f}}{\mathit{\delta }}_{\mathit{ij}},(1)$

where σ′_ij and σ_ij are the effective and total stress tensors, respectively; α is the Biot coefficient, which is a function of the compressibility of rock skeleton and rock grains; p_f is the pore pressure of the formation; and δ_ij is the Kronecker function.

The pore pressure p_f at a point of a continuum medium has the same magnitude in all directions.

The effective stress concept in Eq. 1 was derived under the assumption that the rock is linearly elastic, and it is not directly applicable for a rock at failure (Fjaer et al., 2008). Moreover, Terzaghi’s (1936) formulation of effective stress developed for soils (α = 1) appears to be the most relevant definition to be used in failure criteria (Detournay and Cheng, 1988; Guéguen and Boutéca, 2004; Fjaer et al., 2008).

The wellbore stability analysis is related to rock failure and has to be performed in terms of effective stresses.

2.1 Strength Criteria

Two strength criteria are selected among those widely used in geomechanics: Mohr–Coulomb (M-C) and Hoek–Brown (H&B).

The Mohr–Coulomb (M-C) criterion is linear and can be expressed in terms of effective principal stresses (Terzaghi, 1936) as follows:

$\mathit{\sigma }{\mathrm{\prime }}_{\mathbf{1}}={\mathit{\sigma }}_{\mathit{c}}+\mathit{\sigma }{\mathrm{\prime }}_{\mathbf{3}}{\mathit{N}}_{\mathit{\varphi }},(2)$

where σ_c is the uniaxial compressive strength of the intact rock and N_ϕ is the slope of the strength envelope.

The term N_ϕ is a constant, which affects the strength in the compression zone (high and low confinement) and in the tension zone and is a function of the friction angle ϕ′ of the rock: N_ϕ=(1+sinϕ′)/(1−sinϕ′). The uniaxial compressive strength σ_c can be expressed in terms of cohesion c′ and friction angle ϕ′, as 2c′cosϕ′/(1−sinϕ′).

Despite its simplicity, the constant slope of the M-C criterion cannot account for the transition from shear to ductile failure in the compression zone and predicts a very high uniaxial tensile strength σ_t, which is not in agreement with the experimental data. Figure 1A shows the variation of the tension and compression zone with the friction angle ϕ′, displayed through N_ϕ.

FIGURE 1

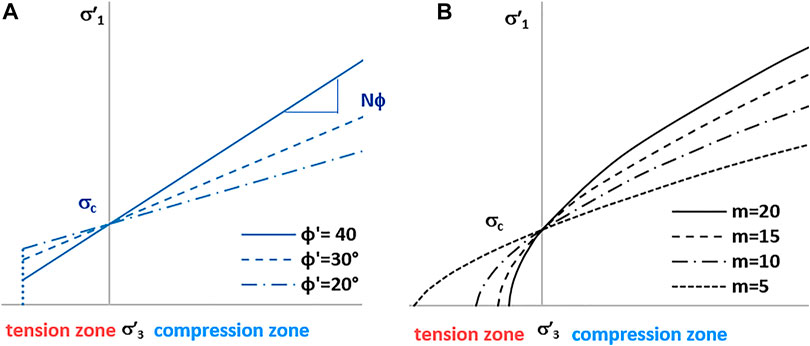
FIGURE 1. (A) The Mohr–Coulomb criterion calculated with different N_ϕ. (B) The Hoek–Brown criterion calculated with different m.

The Hoek–Brown (H&B) criterion was introduced in 1980 for applications in the underground excavation in hard, brittle rocks and has been updated by the authors based on over 40 years of experience in several geological and engineering contexts. The general nonlinear criterion for intact rock is

$\mathit{\sigma }{\mathrm{\prime }}_{\mathbf{1}}=\mathit{\sigma }{\mathrm{\prime }}_{\mathbf{3}}+{\left(\mathit{m}{\mathit{\sigma }}_{\mathit{c}}\mathit{\sigma }{\mathrm{\prime }}_{\mathbf{3}}+\mathit{s}{\mathit{\sigma }}_{\mathit{c}}^{\mathit{2}}\right)}^{\mathit{a}},(3)$

where σ_c is the uniaxial compressive strength of the intact rock obtained from data fitting and m and s are empirical dimensionless constants. For intact rock, the parameter s equals 1 and the constant a = 0.5 (Hoek and Brown, 2019).

The parameter m defines the slope of the strength envelope, and its value influences the strength in both the compression zone (high and low confinement) and the tension zone. The applicability range of the criterion is determined by the transition from shear to ductile failure in the compression zone. Furthermore, tensile failure is not dealt with by the H&B criterion. However, the H&B criterion gives a more reasonable value to the uniaxial tensile strength σ_t. Figure 1B shows the variation of the tension and compression zone with parameter m.

The nonlinearity of the H&B criterion shows, in general, a better agreement with the experimental data than the M-C criterion for both the tensile and the compression zones. However, the uniaxial compressive strength estimated with data fitting with both criteria can be higher than the experimental value when high confinements are considered. In contrast, the tensile strength obtained with data fitting with the H&B criterion can be underestimated for strong and brittle rocks and overestimated for soft rocks (Cai, 2010).

To solve this issue, Fairhurst (1964) proposed the Griffith crack theory to set the ratio of compressive strength σ_c to tensile strength σ_t for hard rocks: σ_c/σ_t ≈ 8. The original Griffith’s theory was extended by Murrell (1963) into three dimensions, resulting in σ_c/σ_t ≈ 12. The use of this ratio results in the introduction of a tensile cutoff. Practitioners in rock engineering set ratio σ_c/σ_t ≈ 10. Sheorey (1997) analyzed a data set of uniaxial compressive and tensile strengths for different types of rocks. The ratio σ_c/σ_t ranges from ≈4 to ≈40. This large variation of the ratio poses uncertainties in selecting the uniaxial tensile strength. In the strength criteria, the overestimation of the tensile strength with the M-C criterion is practically solved with the introduction of a fixed tensile cutoff, whereas Hoek and Brown (2019) suggested an empirical relationship, for the definition of the tensile cutoff: σ_c/σ_t = 0.81 m + 7. This relationship indicates that the tensile cutoff depends on the slope of the strength envelope (frictional component).

Based on experimental data fitting carried out by Carter et al. (1991) and Alber and Heiland (2001), Cai (2010) concluded that the m value is not a constant but confining pressure-dependent. Consequently, he introduced two parameters, one for the compression zone m_c and the other for the tension zone m_t. For porous/weak rocks, a practical estimate of m_t can be obtained through the experimental value of the uniaxial compressive strength σ_{c_exp}, the crack initiation stress level σ_ci, and a constant α that ranges 3 < α < 8 for porous/weak rocks. Deangeli (2021) adopted this procedure to analyze the stability of an unsupported excavation subject to radial tensile failure in a sandstone.

2.2 Strength Parameters From Lab Tests and Log Correlations

Once selecting the strength criterion, the rock failure analysis around a wellbore needs a determination of the rock strength properties. The most appropriate characterization of the rock is under controlled conditions, that is, in laboratory, through uniaxial and triaxial compressive tests and direct or indirect tensile tests.

The test interpretation requires knowledge of the effective principal stresses at failure, which are measured during the test. The strength parameters are hence obtained with data fitting procedures. In particular, the uniaxial and triaxial tests are used to obtain the strength parameters in the compression zone. The uniaxial compression test results give the uniaxial compressive strength σ_c, which is undoubtedly an important parameter. However, these tests cannot determine the frictional component of the strength (ϕ′ or m), and triaxial tests are necessary. Considering specifically the field of application, the triaxial tests are not routinely conducted for most oil and gas projects.

The Brazilian test is an indirect estimation of the tensile strength of the rock. This test is one of the most popular because of the simplicity in specimen preparation, resulting in low scattering of the results (Coviello et al., 2005). However, it is not routinely conducted in oil and gas applications. Several debates were developed in the interpretation of the Brazilian tests and the features of the apparatus (Deangeli and Omwanghe, 2018). Indirect tests generally overestimate the uniaxial tensile strength, but their easy setup makes them widely used. In this context, Perras and Diederichs (2014) proposed correction factors of the Brazilian strength. This test’s result is undoubtedly a measure of the rock tensile strength that avoids an automatic setting of the ratio σ_c/σ_t and helps in defining the tension zone. As the tensile strength is lower than the compressive strength, a rock material is more likely to fail in tension than in compression. A simple program of lab tests for a minimal characterization of the rock strength in the tension zone can be based on the results of the uniaxial compressive test and Brazilian test, and a rough data fitting with trials of m in the H&B criterion can give a reasonable definition of the tension zone.

Despite the data accuracy obtainable by controlled tests, the difficulty in the sample retrieval at large depths, core preservation (especially for shales), and damage induced during specimen preparation (Josh et al., 2012) can make the test results uncertain. Alternatively, the tests can be carried out on outcropping similar formation.

Furthermore, extensive coring is expensive and time-consuming. As an alternative, rock mechanical properties are often obtained from correlations with log data (Abousleiman et al., 2007; Woehrl et al., 2010). Empirical equations are then used to have a continuous profile of the strength parameters with the depth (Mandal et al., 2021). For a given wellbore, log-derived petrophysical data, such as acoustic slowness, porosity, and bulk density, are correlated with laboratory-derived rock mechanical properties. However, these empirical relations may be specific to the geological setting of the region from where they were developed. An alternative log-based approach is the use of microscopic rock models that calculate deformation behavior (Woehrl et al., 2010). A comprehensive overview of published empirical relations is given by Chang et al. (2006) and Khaksar et al. (2009). New correlations for deepwater reservoirs and shale oil and shale gas formations are proposed by Zhang (2019). Nevertheless, mechanical properties obtained by log and microscopic models not only have large uncertainty but also are insufficient for a complete characterization of the rock material (Abousleiman et al., 2007). Finally, correlations for estimating the rock’s friction angle have not been well defined yet (Horsrud, 2001; Woehrl et al., 2010; Mandal et al., 2021). In addition, Abousleiman et al. (2007) argued that there are no suitable correlations for estimating the tensile strength. Consequently, the estimation of rock strength properties is still a matter of concern.

Concerning the adopted criterion, most triaxial test results reported in the technical/scientific literature in the oil and gas field are interpreted with the M-C criterion. Often, the rock testing results are directly presented in terms of friction angle ϕ′, cohesion c′, or uniaxial compressive strength σ_c. The cohesion and friction angle are not directly measured because they are obtained from data fitting. Even where the Mogi–Coulomb and modified Lade criteria are adopted, the friction angle and cohesion are derived. The log correlations are also based on the M-C criterion.

Figures 1A,B show how frictional parameters are fundamental in both the tension and compression zones. The lower the frictional component, the larger the tension zone and vice versa for the compression zone. Furthermore, using a cutoff (e.g., σ_c/σ_t ≈ 10) with the M-C criterion is independent of the frictional strength (Figure 1A). Similarly, using a high m constrains the predicted uniaxial tensile strength at low values (Figure 1B), and the tension zone area is reduced because of the nonlinearity of the H&B criterion.

These considerations indicate that using the M-C with a cutoff is a simple and effective solution. However, a more appropriate criterion is required in some field cases if the mud weight window is small.

The previous discussions highlighted the shortcomings of rock strength characterization in the oil and gas field, particularly at large depths. Section 3 interprets and discusses the available strength data of the rocks in two overpressured basins and highlights their impact on limit mud pressures.

2.3 Stability Analysis of Wellbores in Overpressured Basins

With the choice of the strength criterion and the estimation of the mechanical parameters, the first step of wellbore stability analysis is calculating the induced state of stress during drilling. Figure 2 shows a sketch of a wellbore drilled along a principal direction, with the convention used to calculate the induced state of stress. At the wall of the borehole, the Kirsch solution in plane strain conditions and in terms of effective stresses is

$\begin{array}{l}\mathit{\sigma }{\mathrm{\prime }}_{\mathit{r}}={\mathit{P}}_{\mathit{w}}-{\mathit{p}}_{\mathit{f}}\\ \mathit{\sigma }{\mathrm{\prime }}_{\vartheta }=\mathit{S}-{\mathit{P}}_{\mathit{w}}-{\mathit{p}}_{\mathit{f}}\\ \mathit{\sigma }{\mathrm{\prime }}_{\mathit{axis}}={\mathit{S}}_{\mathit{z}}-{\mathit{p}}_{\mathit{f}}\\ \mathit{S}={\mathit{\sigma }}_{\mathit{MAX}}+{\mathit{\sigma }}_{\mathit{min}}-\mathbf{2}\left({\mathit{\sigma }}_{\mathit{MAX}}-{\mathit{\sigma }}_{\mathit{min}}\right)\mathbf{cos}\left(\mathbf{2}\mathit{\theta }\right)\\ {\mathit{S}}_{\mathit{z}}={\mathit{\sigma }}_{\mathit{z}}-\mathbf{2}\mathit{\nu }\left({\mathit{\sigma }}_{\mathit{MAX}}-{\mathit{\sigma }}_{\mathit{min}}\right)\mathbf{cos}\left(\mathbf{2}\mathit{\theta }\right)\end{array}(4)$

where σ_min and σ_MAX are the far-field stresses, σ′_r is the radial stress, σ′_ϑ is the tangential stress, σ′_axis is the axial stress, S and S_z are the induced state of stress, P_w is the mud pressure, ϑ is the azimuth, and ν is the Poisson ratio.

FIGURE 2

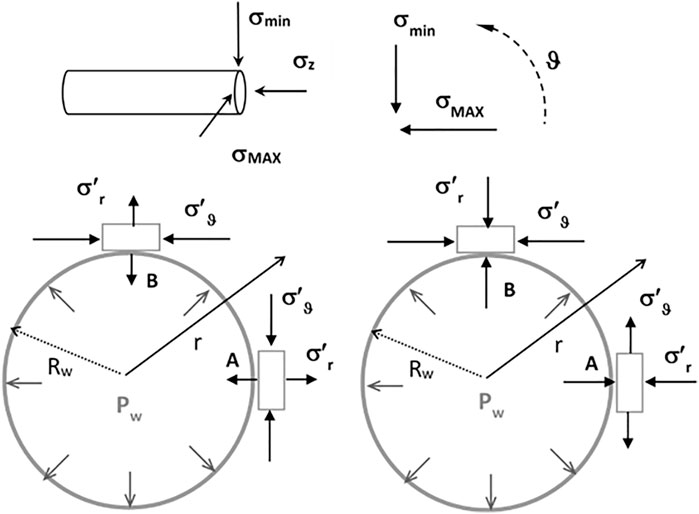
FIGURE 2. Sketch of a wellbore drilled along a principal direction. Far-field stresses are σ_min, σ_MAX, and σ_z. The rock is saturated and the pore pressure p_f at a point of the continuum medium has the same magnitude in all directions. The induced stresses are the radial stress σ′_r, tangential stress σ′_ϑ, and the axial stress σ′_axis that acts normal to the cross section of the wellbore. The cross sections of the wellbore report the possible positive and negative radial σ′_r and tangential stress σ′_ϑ.

The analyses focus on the effective tangential stress σ′_ϑ and radial stress σ′_r that are both affected by P_w (we disregarded the occurrence of failure with σ′_z) and their combination. These effective stresses are principal stresses at the wall of the borehole. Figure 2 shows the sign of the effective stresses that can occur with different values of S, P_w, and p_f, when the far-field stresses are anisotropic.

The far-field stress anisotropy R = σ_MAX/σ_min affects the effective tangential stress σ′_ϑ. At ϑ = 0° (@A), the induced state of stress is minimum S_min = 3σ_min−σ_MAX = σ_min(3−R) and the far-field stress anisotropy opens some scenarios: σ′_ϑ can be positive or negative. At ϑ = 90° (@B), the induced state of stress is maximum S_MAX = 3σ_MAX−σ_min = σ_min (3R−1) and is always positive in practical cases.

The stress state at the wall of the borehole is described as follows:

$\mathit{\sigma }{\mathrm{\prime }}_{\mathbf{1}}=\mathit{\sigma }{\mathrm{\prime }}_{\vartheta }=\mathit{S}-{\mathit{P}}_{\mathit{w}}-{\mathit{p}}_{\mathit{f}}\mathit{\sigma }{\mathrm{\prime }}_{\mathbf{3}}=\mathit{\sigma }{\mathrm{\prime }}_{\mathit{r}}={\mathit{P}}_{\mathit{w}}-{\mathit{p}}_{\mathit{f}}(5)$

$\mathit{\sigma }{\mathrm{\prime }}_{\mathbf{1}}=\mathit{\sigma }{\mathrm{\prime }}_r={\mathit{P}}_{\mathit{w}}-{\mathit{p}}_{\mathit{f}}\mathit{\sigma }{\mathrm{\prime }}_{\mathbf{3}}=\mathit{\sigma }{\mathrm{\prime }}_{\vartheta }=\mathit{S}-{\mathit{P}}_{\mathit{w}}-{\mathit{p}}_{\mathit{f}}(6)$

which indicate that the mud pressure can be assumed as the only adjustable factor during drilling operations. Three types of condition are identified:

• Overbalanced drilling (OBD): P_w > p_f.

• Underbalanced drilling (UBD): P_w < p_f.

• Drilling in balance: P_w = p_f.

The most common type of drilling is OBD, for which σ′_r > 0. However, in overpressured basins, unexpected high pore pressure can occur, or the site conditions do not allow OBD. The case P_w = p_f (drilling in balance) occurs when σ′_r = 0. In contrast, the effective radial stress can be negative σ′_r <0 at all azimuths (ϑ = 0°–90°) if the mud pressure is lower than the pore pressure (or overpressure) p_f, which results in UBD.

Conventional wellbore stability analyses identify two main types of rock failure: shear failure (breakouts) and tensile failure (hydraulic fracturing, HF). The term “shear failure” is conventionally used to indicate compressive failure. If possible, the wellbore pressure P_w should be set higher than the formation pore pressure p_f, to avoid “radial tensile failure” that can occur in UBD.

Unexpected overpressures reduce the effective stresses, according to the Terzaghi principle (Eq. 1). Consequently, the strength of the material decreases. Furthermore, overpressures can move the analysis to the tension zone by inducing negative effective stresses (Figure 3).

FIGURE 3

FIGURE 3. Effect of pore pressure increase on the effective stresses.

The occurrence of compressive failure is evaluated through the comparison of the strength criterion and the induced state of stress σ′_ϑ and σ′_r. In contrast, the occurrence of tensile failure (hydraulic fracturing HF and radial tensile failure) is described through a limit function, derived from the equality of the effective tangential stress σ′_ϑ or radial stress σ′_r with the uniaxial tensile strength σ_t. This simplified approach is used routinely and successfully in most practical cases.

A rock element at the boundary of a wellbore is generally subject to σ′_r ≠ 0 and σ′_ϑ ≠ 0. Figure 4A shows the Mohr circles of a general state of stress with positive (violet circle) and negative-positive principal stresses (green circle). Figure 4B shows the Mohr circles at failure in uniaxial compression (turquoise circle) and tension (pink circle).

FIGURE 4

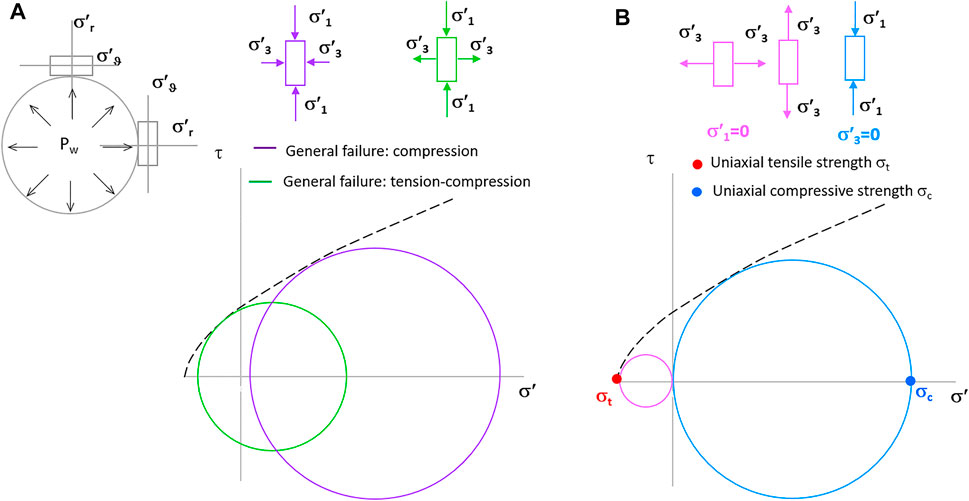
FIGURE 4. Stress states at failure. (A) General case with positive and negative principal stresses (green circle) and positive principal stresses (violet circle). (B) Uniaxial tension (pink circle); uniaxial compression (turquoise circle).

The strength envelope of Figures 4A,B is the same. Consequently, geomaterials fail in shear. In fact, it is possible to draw a Mohr circle in uniaxial compression (turquoise circle) and tension (pink circle). “Tensile failure” can occur when σ′_r < 0 and |σ′_r | < |σ_t | (green circle) because the stress state is not uniaxial (Figure 4A). Definitely, rock failure is completely described by a shear strength criterion (in the tension and compression zone), and the split between compressive failure (often called shear failure) and tensile failure verification is unnecessary.

The coupling between Eq. 5 (σ′₁ = σ′_ϑ and σ′₃ = σ′_r) and M-C and H&B criteria (Eqs 2, 3 ) gives the limit mud pressure P_w:

${\mathit{P}}_{\mathit{w}\_\mathit{M}-\mathit{C}}=\frac{\mathit{S}-{\mathit{\sigma }}_{\mathit{c}}+{\mathit{p}}_{\mathit{f}}\left({\mathit{N}}_{\mathit{\varphi }}-\mathbf{1}\right)}{\left({\mathit{N}}_{\mathit{\varphi }}+\mathbf{1}\right)}(7)$

${\mathit{P}}_{\mathit{w}\_\mathit{H}\&\mathit{B}}=\frac{\mathbf{4}\mathit{S}+\mathit{m}{\mathit{\sigma }}_{\mathit{c}}-{\left[{\mathit{\sigma }}_{\mathit{c}}^{\mathbf{2}}\left({\mathit{m}}^{\mathbf{2}}+\mathbf{16}\right)+\mathbf{8}\mathit{m}{\mathit{\sigma }}_{\mathit{c}}\mathit{S}-\mathbf{16}\mathit{m}{\mathit{\sigma }}_{\mathit{c}}{\mathit{p}}_{\mathit{f}}\right]}^{\mathbf{0.5}}}{\mathbf{8}}(8)$

Equation 7 is widely used in routine wellbore stability analyses and is implemented in commercial software. Equation 8 was proposed by Deangeli and Omwanghe (2018) to analyze wellbore stability in saturated transversely isotropic shales and by Deangeli (2021) to investigate tensile failure around an unsupported excavation in a saturated sandstone. Both equations can be used in the compression and tension zone and account for the tensile strength and the extent of the tension zone. In order to avoid failure, the mud pressure must be set higher than P_w of Eq. 7 or Eq. 8, which represents the pressure in the limit state.

In contrast, if the stress state is represented by Eq. 6 (σ′₁ = σ′_r and σ′₃ = σ′_ϑ), the mud pressure becomes

${\mathit{P}}_{\mathit{w}\_\mathit{M}-\mathit{C}}=\frac{\mathit{S}+{\mathit{\sigma }}_{\mathit{c}}+{\mathit{p}}_{\mathit{f}}(\mathbf{1}-{\mathit{N}}_{\mathit{\varphi }})}{\left({\mathit{N}}_{\mathit{\varphi }}+\mathbf{1}\right)}(9)$

${\mathit{P}}_{\mathit{w}\_\mathit{H}\&\mathit{B}}=\frac{\mathbf{4}\mathit{S}-\mathit{m}{\mathit{\sigma }}_{\mathit{c}}+{\left[{\mathit{\sigma }}_{\mathit{c}}^{\mathit{2}}\left({\mathit{m}}^{\mathbf{2}}+\mathbf{16}\right)+\mathbf{8}\mathit{m}{\mathit{\sigma }}_{\mathit{c}}\mathit{S}-\mathbf{16}\mathit{m}{\mathit{\sigma }}_{\mathit{c}}{\mathit{p}}_{\mathit{f}}\right]}^{\mathbf{0.5}}}{\mathbf{8}}(10)$

Equations 9, 10 hold for tangential tensile failure (HF) and consider the tensile strength and the tension zone extent. In order to avoid failure, the mud pressure P_w must be set lower than P_w calculated in Eqs 9, 10.

As emerged in Eqs 7–10, the constants N_ϕ and m, discussed in the previous sections, should be evaluated for the compression and tension zones.

It is worth observing that the rotation of principal stresses occurs from Eqs 7, 8 to Eqs 9, 10. Consequently, the couples of principal stresses have the same values because the strength envelope is unique for a given set of parameters.

The effective state of stress acting at the borehole boundary can be uniaxial in three cases. By imposing the limit state of the rock in tension and compression, we found the three pore pressures leading to failure in uniaxial conditions:

(1) σ′_r = P_w−p_f = 0. The uniaxial compressive failure occurs when σ′_ϑ = S−2p_f = σ_c:

${\mathit{p}}_{\mathit{fA}}=\frac{\mathit{S}-{\mathit{\sigma }}_{\mathit{c}}}{\mathbf{2}}(11)$

In a practical case, the minimum p_fA is calculated at ϑ = 0° with S_min = 3σ_min−σ_MAX = σ_min (3−R) with R > 1 and defines the critical condition when drilling in balance (turquoise Mohr circle in Figure 4B).

(2) σ′_r = P_w−p_f = 0. The uniaxial tensile failure occurs when σ′_ϑ = S−2p_f = −σ_t:

${\mathit{p}}_{\mathit{fB}}=\frac{\mathit{S}+{\mathit{\sigma }}_{\mathit{t}}}{\mathbf{2}}(12)$

In a practical case with R > 1, the p_fB calculated at ϑ = 0° with S_min = 3σ_min−σ_MAX = σ_min (3−R) defines the critical condition when drilling in balance. Failure occurs at ϑ = 0° (HF) (pink Mohr circle in Figure 4B). If R = 1, the uniaxial tensile failure does not hold.

(3) σ′_ϑ = S−P_w−p_f = 0. The uniaxial tensile failure occurs when σ′_r = P_w−p_f = −σ_t:

${\mathit{p}}_{\mathit{fC}}=\frac{\mathit{S}+{\mathit{\sigma }}_{\mathit{t}}}{\mathbf{2}}(13)$

In a practical case with R > 1, the p_fC calculated at ϑ = 0° with S_min = 3σ_min−σ_MAX = σ_min (3−R) defines the critical condition when drilling in UBD. Failure is radial and occurs at any azimuth ϑ (pink Mohr circle in Figure 4B). If R = 1, the uniaxial tensile failure does not hold.

The comparison between case B and case C indicates that p_fB = p_fC, but the principal stresses are rotated. Equation 12 refers to rock failure ruled by the equality σ′_ϑ = −σ_t; hence, P_w = S−p_fB + σ_t which is the conventional approach used in wellbore stability for HF. In contrast, Eq. 13 refers to rock failure ruled by the equality σ′_r = −σ_t; hence, P_w = p_fC−σ_t which is the conventional approach used in wellbore stability for radial tensile failure. The critical pore pressure is the same, but the mud pressure is different. These two conditions are the lower and the upper limits in the tension zone. The Mohr circle (pink circle in Figure 4B) of cases B and C is the same because the uniaxial tensile strength is unique σ_t = σ′₃ and the maximum principal stress is σ′₁ = 0.

In case B, drilling is in balance (σ′_r = 0) P_wB = p_fB, and in case C, drilling is UBD (with σ′_r < 0) P_wC < P_wB. This outcome indicates that a preliminary check of the condition p_fB = p_fC gives some preliminary information on the stability of wellbores in overpressured fields.

Equations 7–10 provide the analytical solutions to define the failure limit in wellbore stability analysis at the excavation boundary. Moreover, the prediction of the area extent of the yielded rock around the borehole in tension and compression is of interest. To this end, we carried out numerical modeling with the code FLAC 2D (ver. 8.10, Itasca). Given the symmetry of the hole with respect to its axis and assuming isotropic behavior of the rock, the numerical model represents one-quarter of the full section of a borehole and the surrounding rock, with a radial grid of 60 × 60 elements. The borehole radius is R_w = 0.5 m, and the radial dimension r = 5 m. Figure 5 shows the grid used in the numerical simulations.

FIGURE 5

FIGURE 5. Grid used in the numerical simulations with FLAC.

Plasticity occurrence is obtained by decreasing the pressure at the excavation boundary until a plasticity pattern is reached. The magnitude of the mud pressure P_w can be slightly different from the analytical solution because of the numerical finite difference procedure. The code defines plasticity in shear (compression zone) and tension (tension zone). It is possible to plot two types of plasticity. “Plasticity past” occurs during the numerical convergence and results in a distressed weakened zone at the end of the calculation cycles. The occurrence of “Plasticity new” at the end of the numerical convergence means that the elements are at failure.

The local occurrence of plasticity (past) results in stress redistribution during the numerical convergence. The weakened rock transfers the load to the zones that are still in the elastic field. Furthermore, the results of numerical simulations give the magnitude of the rock deformation that can result in borehole collapse. The analytical solutions cannot calculate this effect.

3 Results and Discussion

We selected two overpressured basins characterized by different far-field stress regimes and types of rock: the Valhall field in the North Sea basin and the Ichthys field in the Browse basin. The setup of wellbore stability in these fields requires an estimation of the far-field stresses, overpressure, and strength properties of the rock.

In the first case (i.e., the Valhall field), the mechanical behavior of the chalk has been extensively investigated for the problem of subsidence that affects this formation in the North Sea. The mechanical response of the chalk is affected by pore collapse, but this effect is beyond the scope of this study. Risnes (2001) observed that the reservoir chalk formations appear on the surface of many places in Europe. Consequently, as core material from chalk wells is rather limited, outcrop chalk, available in large quantities, can be adopted as an interesting substitute. We selected the results of laboratory tests, carried out on specimens of an outcrop chalk with properties similar to the reservoir chalks. These tests were carried out for the mechanical characterization of the chalk in the North Sea basin (Risnes and Flaageng, 1999; Risnes 2001; Risnes et al., 2003).

On the contrary, in the second case (i.e., the Ichthys field), the available mechanical properties of the overpressured shaly formation, found in the literature, are estimated by log correlations. Only the reservoir formation (sandstone) was characterized by compression tests. The strength parameters derived from these correlations are the uniaxial compressive strength σ_c and the friction angle ϕ′.

The following sections interpret and discuss the rock data of the two fields and present sensitivity analyses of a vertical wellbore by varying the rock strength, the far-field stresses, and the overpressure. In order to understand the influence of the estimation of a given parameter on the mud pressure prediction, the analyses refer to a specific depth.

The results can be extended to depth intervals with almost the same far-field stresses, overpressure, and formation type.

3.1 Sensitivity Analysis of Wellbores Drilled in the Valhall Field

The Valhall oilfield is a large chalk reservoir in the Norwegian sector of the North Sea. The reservoir consists of highly overpressured chalk. The high overpressure and early oil migration resulted in very well preserved porosity n = 40%–50%, exceeding 50% in parts of the field. This highly porous chalk is extremely weak, and during appraisal drilling, the first issues with soft chalk and solids production were experienced (Pattillo et al., 1998; Fjaer et al., 2008; Barkved et al., 2003).

Fjaer et al. (2008), Pattillo et al. (1998), and Kristiansen (2004) indicated that, in the Valhall field, the vertical stress is σ_v = 49 MPa and the pore pressure is p_f = 44.7 MPa at a depth z = 2,500 m. Several techniques have been used to indicate the amount of stress anisotropy at the Valhall field. The conclusion is that the magnitude of the horizontal stress anisotropy in the Valhall area is fairly low: less than 5% and about 0% in the flank of the field (Kristiansen, 2004). Hence, we considered the horizontal stress anisotropy R = 1. Pattillo et al. (1998) estimated a constant effective stress ratio (ESR) in the Tor layer: R_o = σ′_h/σ′_v = 0.735. At the same depth, considered as the reference in this study, the total horizontal stress results equal σ_h = 47.86 MPa, in agreement with the in situ initial condition determined by Kristiansen (2004): σ_h ≈ 50 MPa. Table 1 reports the far-field stresses, the induced state of stress S, the pore pressure p_f in site condition, and two lower values p_fX and p_fY.

TABLE 1

TABLE 1. Far-field stresses, pore pressures of the Valhall field.

As mentioned before, due to the large availability of chalk outcrops, several investigations have been performed on this material, assuming it is representative of the wellbore material.

Havmøller and Foged (1996) established correlations between mechanical properties and porosity of North Sea chalk. They found the following equation for the estimation of the uniaxial compressive strength:

${\mathit{\sigma }}_{\mathit{c}}=\mathbf{174}{\mathit{e}}^{-\mathbf{7.57}\mathit{n}}(14)$

where $n$ is the porosity.

The friction angle ϕ′ of the chalk typically ranges between 10° and 30° (Fjaer et al., 2008) up to 40° (Risnes and Flaageng, 1999; Risnes, 2001; Risnes et al., 2003). Bell (1977) performed undrained triaxial tests on upper chalk of Kent and found an undrained friction angle ϕ_u = 17°. However, Risnes and Flaageng (1999) carried out compressional and extensional triaxial tests and Brazilian tests on outcrop chalk (Liège chalk, Belgium) specimens saturated with water and methanol. The average porosity of the specimens was $n$ = 40%. They reported the following strength parameters: 1) c′ = 0.9 MPa, ϕ′ = 30°, and σ_t = 0.8 MPa for water-saturated specimens and 2) c′ = 1.3 MPa, ϕ′ = 40°, and σ_t = 1.2 MPa for methanol saturated specimens. Unfortunately, the measured data of these triaxial tests are not reported, and only the strength parameters obtained by data fitting with the M-C criterion are available. Consequently, with the M-C criterion, we calculated the uniaxial compressive strengths: σ_c ≈ 3 MPa (water) σ_c ≈ 6 MPa (methanol). The authors observed that methanol and oil-saturated specimens turned out to be 2–3 times as strong as water-saturated samples. Although the chalk was a weak rock, the tensile strength became higher than the common prediction from compressive strength: σ_c/σ_t ≈ 4 (water) σ_c/σ_t ≈ 5 (methanol).

Risnes (2001) reported the results of six triaxial tests and one Brazilian test, in terms of σ′₃ and σ′₁, on the outcrop Aalborg chalk (Denmark) oil-saturated specimens with n = 45% and indicated ϕ′ = 38.5°, c′ = 1.76 MPa, and σ_t = 1.02 MPa. These data were obtained in the fitting procedure by using σ′₃ and σ′₁ of the Brazilian test. The calculation of the uniaxial compressive strength from this data gives σ_c = 7.4 MPa. Consequently, the ratio is σ_c/σ_t ≈ 7.

In contrast, Bell (1977) performed uniaxial compression tests and Brazilian tests on three types of outcrop chalk specimens retrieved in the United Kingdom. The author tested at least five cores from the same bulk sample. This was done for ten bulk samples from each area. The average uniaxial compressive strength for the three chalks ranges from σ_c = 28 MPa (n = 25%) to σ_c = 5.5 MPa (n = 46%). The moderately strong to moderately weak chalks ratio became constant σ_c/σ_t ≈ 10.

The uniaxial compressive test results reported above are quite in agreement with those of Eq. 14. Uncertainties are mainly related to the Brazilian tensile strength, with the ratio σ_c/σ_t ranging from 4 to 10. As observed in the previous section, the Brazilian tensile strength is often higher than the uniaxial tensile strength in sedimentary rocks. Perras and Diederichs (2014) found a reduction factor equal to 0.7 to obtain the uniaxial tensile strength from the Brazilian tests in sedimentary rocks.

Figure 6A shows the strength envelopes for the Liège and Aalborg chalks with the Risnes and Flaageng (1999) and Risnes (2001) parameters. Figure 6A indicates that a small increase in friction angles causes the strength envelope to intersect the horizontal axis before the cutoff for the Liège chalk. The figure also shows the Brazilian strengths reduced by 0.7 and the Brazilian data used by Risnes (2001) to obtain the strength parameters of the Aalborg chalk. The reduced Brazilian strengths give the ratio σ_c/σ_t ≈ 10 for the Aalborg chalk and σ_c/σ_t ≈ 5−7 for the Liège chalk. Risnes (2001) also reported a set of Mohr circles of triaxial and Brazilian tests carried out on Aalborg chalk in [σ′−τ] diagram. From this diagram, we fitted the test data in [σ′₃−σ′₁] diagram with the H&B criterion. We used the Brazilian strength as a uniaxial strength for two cases: σ_t = 1.02 MPa (green dotted line) and reduced σ_t = 1.02*0.7 = 0.7 MPa (brown line). Figure 6B shows the H&B strength envelopes and the envelope with Risnes properties (yellow dash-dotted line). The comparison between the H&B envelope with σ_t = 1.02 MPa (green dotted line) and Risnes M-C envelope criterion (yellow dash-dotted line) indicates that the tension zone predicted with the H&B criterion is smaller. This fact makes the H&B criterion conservative for analyzing wellbore stability in the tension zone.

FIGURE 6

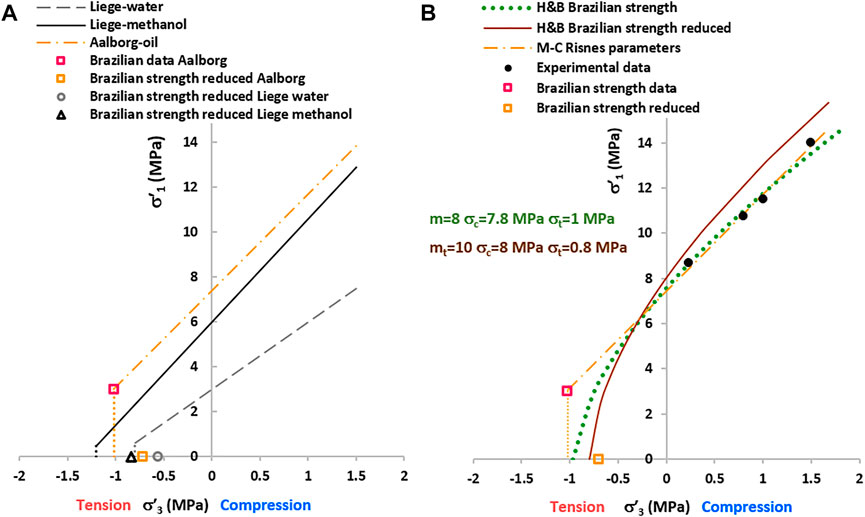
FIGURE 6. (A) M-C strength envelopes of Liège and Aalborg chalks, calculated with the strength data of Risnes and Flaageng (1999) and Risnes (2001), respectively. The dotted lines are the cutoff. The red symbol represents the data of the Brazilian test. The other open symbols represent the Brazilian strength reduced by a factor of 0.7. (B) Data fitting of Aalborg chalk tests and comparison with Risnes (2001) data fitting.

We calculated the limit mud pressures with Eqs 7, 8 for compressive failure and radial tensile failure. The results of these analyses are reported in [σ′₃−σ′₁] diagrams where σ′_r = P_w−p_f = σ′₃ and σ′_ϑ = S−P_w−p_f =σ′₁.

Based on the porosity of the chalk in the Valhall field and the analysis of experimental data, we considered three cases (V1, V2, V3) with σ_c = 4–12 MPa; σ_c/σ_t ≈ 10; ϕ′ = 20°-30°-40°; m_t = 10. Table 2 reports the selected strength parameters.

TABLE 2

TABLE 2. Strength properties of the chalk.

Figure 7A shows the limit conditions of failure for the three cases (V1, V2, and V3) with p_f = 44.7 MPa. The points representing the rock failure lie on the straight failure line, which is the effective stress path (ESP) at the wall of the borehole, for different strength parameters. This ESP has a slope equal to −1. Figure 7A also shows the intercept with the vertical axis that defines the tension-compression threshold (yellow symbol), which is the condition of Eq. 11 (turquoise Mohr circle in Figure 4B). The strength parameters determine if the limit condition of failure occurs in the tension zone or in the compression zone along this ESP. The ESP has limits constrained by rock properties. In fact, the M-C analysis in Case V3 needs the cutoff correction for ϕ′ = 20°–30° because these points are beyond the tensile strength. The cutoff correction is calculated from P_w−p_f = −σ_t by factoring out P_w. The value of P_w is substituted in S−P_w−p_f = S−2p_f+σ_t. In other words, the correction for failure in tension is set up on the ESP failure line. The H&B analysis directly constrains the failure points to belong to the strength envelope. The limit mud pressure P_w, calculated with Eqs 7, 8, increases along the ESP from the tension to the compression zone (black arrow in Figure 7A). Figure 7A shows that the simple use of the conventional uniaxial analysis with the uniaxial tensile strength does not appropriately describe the occurrence of failure in the tension zone. For instance, the failure points of Case V2 have |σ′₃| < |σ_t|, but these points indeed indicate the occurrence of failure in the tension zone because they belong to the strength envelopes. These points belong to a Mohr circle with a positive and a negative principal stress (green circle in Figure 4A).

FIGURE 7

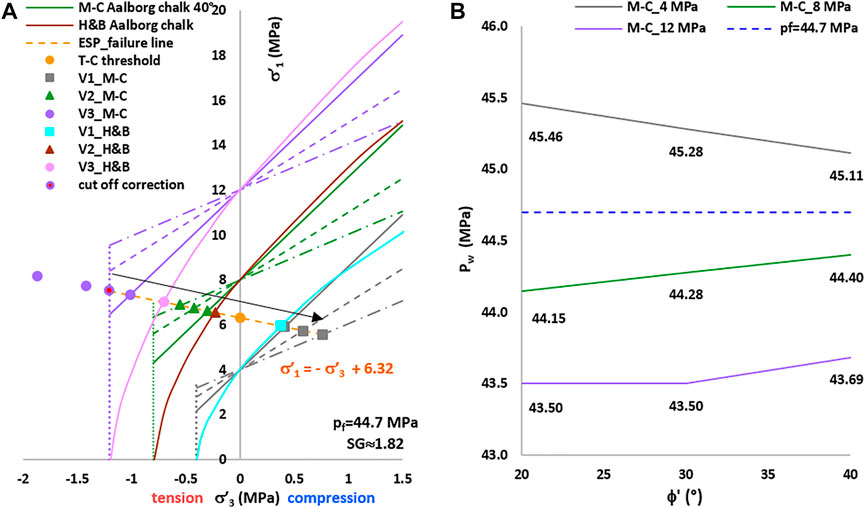
FIGURE 7. (A) Strength envelopes of the chalk with σ_c = 4-8-12 MPa, and σ_c/σ_t ≈ 10. The pink, brown, and turquoise lines represent the H&B strength envelopes with m_t = 10. The violet, green, and grey lines represent the M-C strength envelopes with ϕ′ = 20°-30°-40°. The principal stresses are σ′_r = P_w–p_f = σ′₃ and σ′_ϑ = S−P_w−p_f =σ′₁. The cutoff correction is reported when σ′₃ < σ_t. The black arrow indicates the direction of P_w increase. (B) Variation of the mud pressures P_w (Eq. 8) with ϕ′ for Cases V1, V2, and V3. The violet line has the cutoff correction for ϕ′ = 20°–30° (P_w = 43.5 MPa).

Case V1, with the lowest uniaxial compressive strength σ_c = 4 MPa, predicts a failure limit in the compression zone. These points belong to a Mohr circle with positive principal stresses (violet Mohr circle in Figure 4A). Cases V2 and V3 belong to a Mohr circle with positive and negative principal stresses (green Mohr circle in Figure 4A).

Cases V2_M-C and V3_M-C indicate that low friction angles predict a larger tension zone and slightly lower mud pressures P_w. Figure 7B shows the variation of the mud pressure P_w with ϕ′. The predicted mud pressure P_w increases with increasing the friction angle ϕ′ in the tension zone. This result seems counterintuitive but is consistent with the shape of the tension zone and the ESP failure line.

We carried out an analysis with the same conditions of Figure 7A but with reduced uniaxial tensile strengths: σ_c/σ_t ≈ 12. This uniaxial tensile strength is obtained with the H&B criterion by setting m_t = 12. In this case, there is an increase of the frictional component of the strength and a reduction of the tension zone. Figure 8A shows that the failure points lie on the same ESP failure line of Figure 7A, and the mud pressure P_w is slightly higher for the case σ_c/σ_t ≈ 12, as expected.

FIGURE 8

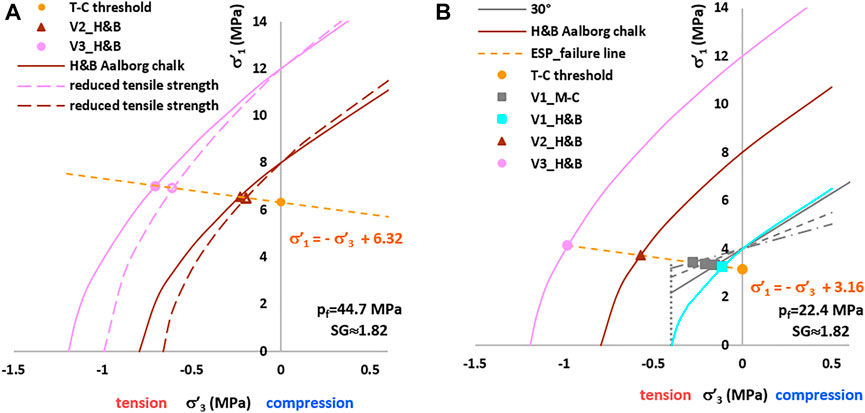
FIGURE 8. (A) Comparison of the strength envelopes of the chalk with σ_c = 8–12 MPa; m_t = 10 and σ_c/σ_t ≈ 10; σ_c/σ_t ≈ 12 and m_t = 12 (reduced tensile strength). (B) Cases V1, V2, and V3 at a depth z = 1,250 m: σ_h = 23.93 MPa, p_f = 22.35 MPa.

We carried out a further analysis at a depth z = 1,250 m (i.e., half of the previous case), where σ_h = 23.93 MPa and the pore pressure is p_f = 22.35 MPa. Figure 8B shows that the ESP failure line moves downwards, as expected, and all the cases (V1, V2, and V3) are in the tension zone. The lowest σ_c = 4 MPa (Case V1) reaches the failure limit in the tension zone at a depth half of in Figure 7.

Figures 9A,B show the analysis results carried out with p_fX = 43 MPa and p_fY = 42 MPa, respectively. Case V2 moves the failure limit to the compression zone, and only Case V3 remains in the tension zone. Figure 9B shows that the failure points V3 are close to the tension-compression threshold (yellow symbol). We noted that Case V3 is at failure in the tension zone with |σ′₃| < |σ_t|, as already indicated in Figure 7A.

FIGURE 9

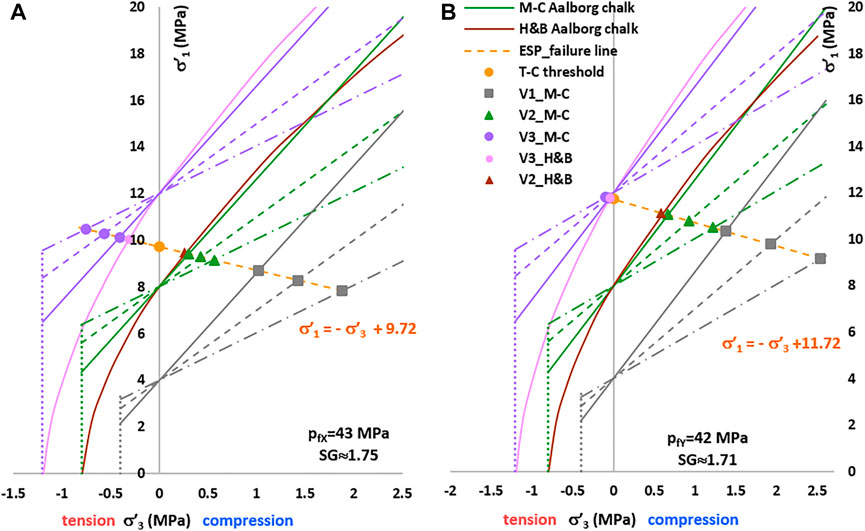
FIGURE 9. Strength envelopes of the chalk with σ_c = 4-8-12 MPa, and σ_c/σ_t ≈ 10. The pink, brown, and turquoise lines represent the H&B strength envelopes with m_t = 10. The violet, green, and grey lines represent the M-C strength envelopes with ϕ′ = 20°-30°-40°. The principal stresses are σ′_r = P_w−p_f = σ′₃ and σ′_ϑ = S−P_w−p_f =σ′₁. Depth z = 2,500 m. (A) Reduced pore pressure p_fX = 43 MPa. (B) Reduced pore pressure p_fY = 42 MPa.

The comparison between Figure 7A and Figures 9A,B indicates that the ESP failure line moves upwards, with an increasing intercept when p_f is reduced.

The discussion of the results of wellbore stability analysis in terms of [σ′₃−σ′₁] allows appreciating the position of the failure points in the tension-compression zone. An automatic calculation of P_w with software can predict the absence of failure with the M-C criterion if implementing the check of uniaxial tensile failure.

Furthermore, we analyzed the results of the mud pressure P_w in terms of specific gravity (SG = pressure/9.81/depth). Figures 10A,B show the variation of SG with the uniaxial compressive strength σ_c and hence with the uniaxial tensile strength σ_t with two different p_f. In these calculations, we used σ_c = 4–12 MPa, ϕ′ = 40°, m_t = 10, and σ_c/σ_t ≈ 10. Figures 10A,B show that the SG calculated with the M-C criterion in the tension zone is lower because of the linearity of the envelope and the extent of the tension zone. They show the SG of the pore pressure p_f and the SG of the uniaxial radial tensile failure: σ′_r = P_w−p_f = −σ_t and σ′_ϑ = 0 (purple line). The results indicate that the simple approach used in the conventional uniaxial radial tensile failure analysis underestimates the mud pressure in the tension zone, as discussed previously. The difference between the SG for radial tensile failure, calculated with Eqs 7, 8, and the uniaxial tensile approach seems small. However, this SG margin can be detrimental to the wellbore stability in overpressured formations and UBD.

FIGURE 10

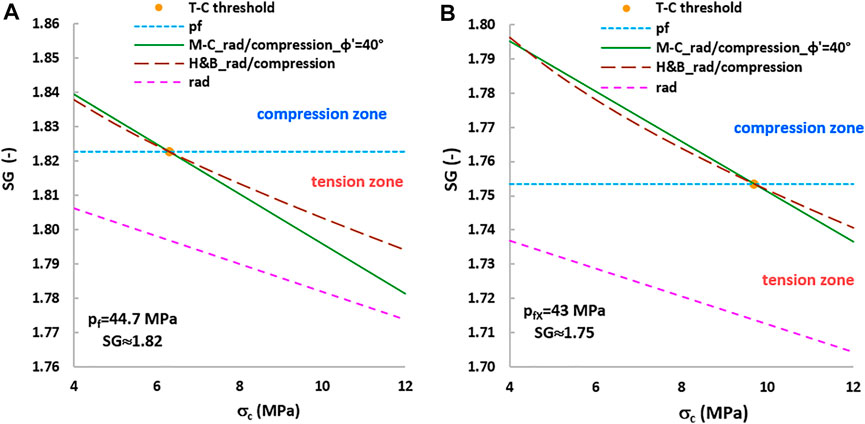
FIGURE 10. Variation of the limit mud weight (SG) with the uniaxial compressive strength calculated with σ_c = 4–12 MPa, ϕ′ = 40°, m_t = 10, and σ_c/σ_t ≈ 10. (A) Compressive failure and radial tensile failure with p_f = 44.7 MPa. (B) Compressive failure and radial tensile failure with p_f = 43 MPa.

Figure 11 shows the case of tangential tensile failure (HF) calculated with Eqs 9, 10 and with the uniaxial analysis: σ′_ϑ =S−P_w−p_f = −σ_t and σ′_r = 0 (red line). The comparison shows that the uniaxial analysis slightly overestimates the SG for HF, and the lower SG is obtained with the H&B criterion. The mud weight windows calculated with H&B are ΔSG = 0.23 at σ_c = 4 MPa and ΔSG = 0.31 at σ_c = 12 MPa. The results of these analyses clearly indicate that tensile failure prediction is undoubtedly more conservative with the H&B criterion.

FIGURE 11

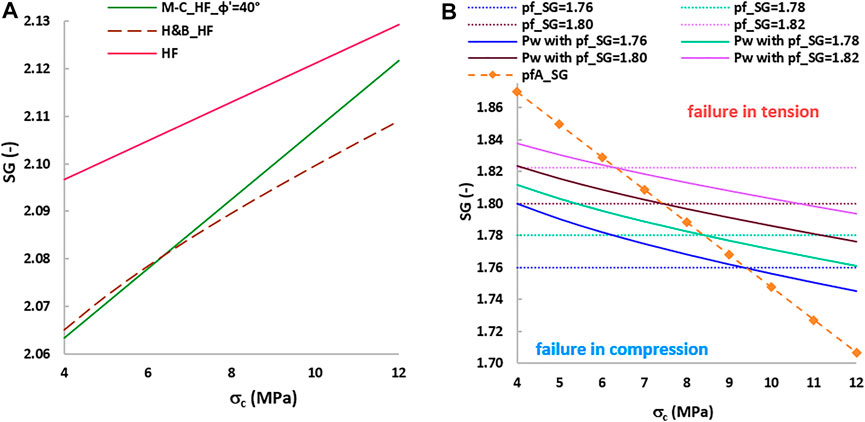
FIGURE 11. (A) Variation of the limit mud weight (SG) with the uniaxial compressive strength σ_c = 4–12 MPa, ϕ′ = 40°, m_t = 10, and σ_c/σ_t ≈ 10. p_f = 44.7 MPa. The red line is the uniaxial tangential tensile failure HF calculated with σ′_ϑ = S−P_w−p_f = −σ_t and σ′_r = 0. (B) Comparison between p_fA_SG and the P_w_SG calculated with Eq. 8 with the four overpressures p_f_SG. σ_c = 4–12 MPa, m_t = 10, and σ_c/σ_t ≈ 10.

The previous discussions highlighted the difficulty in managing the mud weight because of the uncertainties related to both p_f and σ_c. Figures 7–9 indicate that S and p_f determine the ESP failure line and the intercept with the vertical axis, a uniaxial compressive strength σ′₁ = σ_c that refers to drilling in balance. In practical applications, the condition of drilling in balance refers to P_w = p_f and does not consider the values of σ_c.

Equation 11 predicts a threshold pore pressure p_fA in a formation. By substituting Eq. 11 in Eqs 7, 8, we obtain

${\mathit{P}}_{\mathit{w}\_\mathit{M}-\mathit{C}}={\mathit{P}}_{\mathit{w}\_\mathit{H}\&\mathit{B}}=\frac{\mathit{S}-{\mathit{\sigma }}_{\mathit{c}}}{\mathbf{2}}={\mathit{p}}_{\mathit{fA}}(15)$

Equation 15 is a failure condition when drilling in balance and indicates that the mud pressure P_w does not depend on the frictional component of the strength (ϕ′ or m). The estimation of the uniaxial compressive strength σ_c is hence important for the prediction of rock failure when drilling in balance. The pore pressure (or overpressure) and the state of stress S in a site are estimated before drilling operations. Using Eq. 15, it is possible to determine the required magnitude of σ_c for drilling in balance. A comparison with the lab/log correlated σ_c of the rock indicates the mud weight required in the site. The orange straight line in Figure 11B shows the trend of p_fA with σ_c in the Valhall field. Any point of the p_fA_SG line corresponds to a threshold of p_f coupled with σ_c in the rock. The p_fA_SG line also defines the possible failure scenarios, as failure occurs in tension or compression if the region is above or below this line, respectively. Figure 11B also shows the P_w_SG calculated with the H&B criterion (Eq. 8) and four different overpressures p_f_SG = 1.76–1.82. These p_f can reproduce the uncertainties related to estimating the magnitude of the overpressure in the site. A comparison between the p_fA line and the P_w_SG calculated with the estimated p_f and σ_c indicates the limit failure condition calculated with Eq. 8.

The variation of σ_c in Figure 11B is wide and considers different formation conditions to outline a general scenario. The highest predicted P_w_SG = 1.84 occurs at p_f_SG ≈ 1.82 (violet line) for the lowest σ_c = 4 MPa, as expected, and the predicted failure occurs in the compression zone (OBD). At the same σ_c, the limit condition for failure in balance requires p_fA_SG = 1.87 = P_w.

These results refer to the wall of the borehole r = R_w and are calculated by coupling the elastic solution with the strength criterion. A numerical analysis can indicate if the failure is local or borehole collapse occurs.

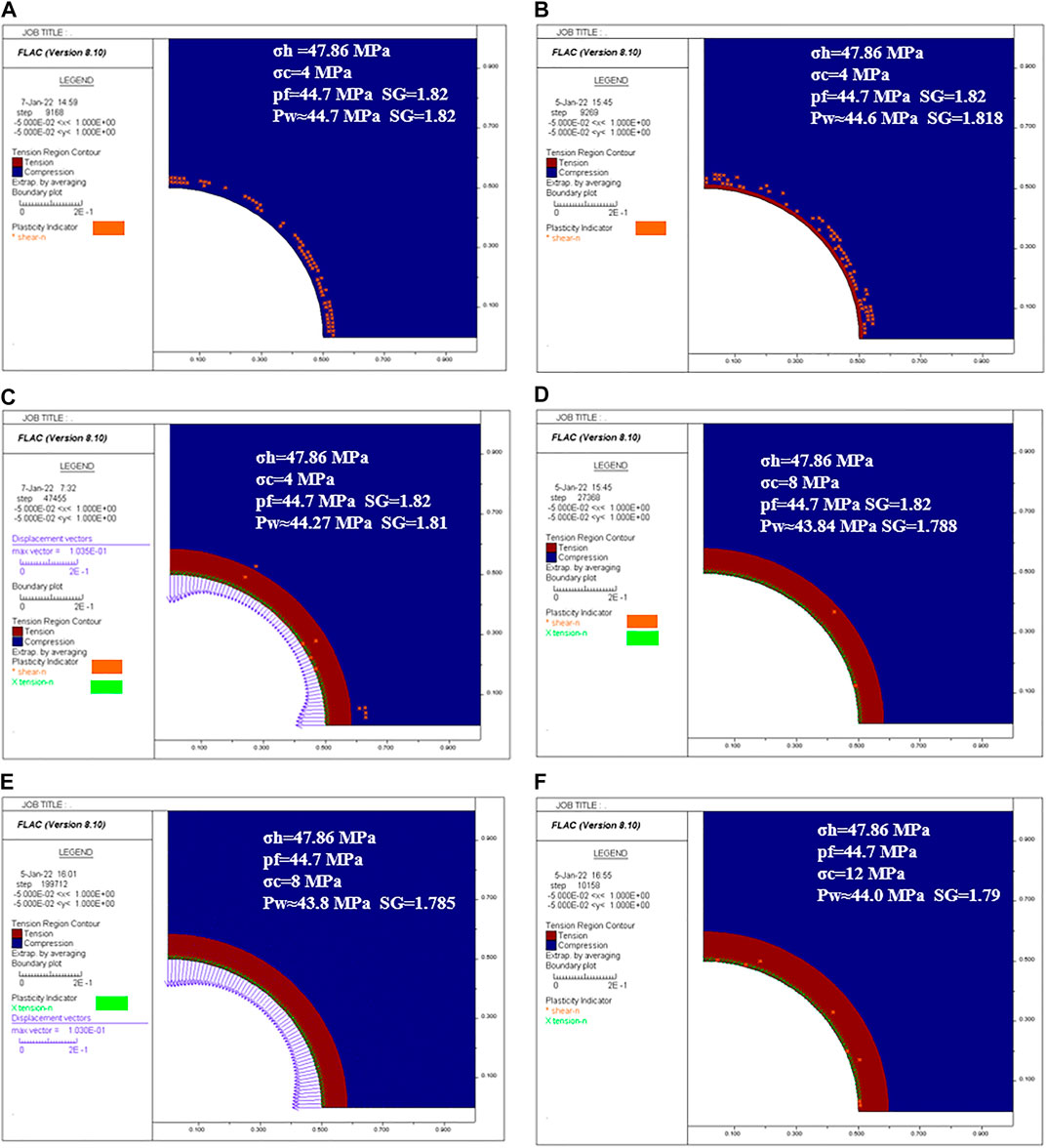
For this reason, we analyzed the onset and the extent of plasticity with numerical simulations carried out with the H&B criterion with σ_c = 4–12 MPa, m_t = 10, σ_c/σ_t ≈ 10, shear modulus G = 1.1 GPa, and bulk modulus K = 1.84 GPa. The pore pressure is p_f_SG = 1.82 (p_f = 44.7 MPa). The analyses are set in drained conditions, with constant overpressure during the excavation. Figure 12 shows the results of the numerical simulations.

FIGURE 12

FIGURE 12. Results of the numerical simulations performed with FLAC2D.

The case with σ_c = 4 MPa has the failure limit in compression with P_w_SG = 1.84 (P_w = 45.05 MPa) (OBD) in the analytical solution. The first simulation was set up with P_w_SG = 1.82 = p_f_SG (drilling in balance). In this case, the state of stress is in compression (blue), and there is the occurrence of plasticity in compression (shear: orange symbol), as expected (Figure 12A). A very small decrease in mud weight P_w_SG = 1.818 results in the generation of a state of stress in tension (red) at any azimuth (Figure 12B). However, plasticity occurs in compression (shear: orange symbol) because the tensile stresses are small. In these two cases, the convergence of the wellbore is a few millimeters. A further reduction of the mud weight P_w_SG = 1.81 induces an increase in the zone with a state of stress in tension (thickness of ≈8 cm) and UBD (Figure 12C). Plasticity occurs essentially in tension (tension: green symbol) at any azimuth. Figure 12C shows that the convergence of the wellbore is 10 cm. These high displacements lead to a catastrophic failure. The margin is ΔP_w_SG = 1.84–1.81 = 0.03.

For comparison we set up a numerical simulation with σ_c = 5 MPa and P_w_SG = 1.81. In this case, the zone with a state of stress in tension is smaller than the previous case (thickness of ≈6 cm). Plasticity occurs in compression with a thickness of ≈9 cm. The convergence is ≈1 mm. The situation seems unrelated to borehole collapse, but it is undoubtedly very critical. These results indicate that a rock with low σ_c at large depth and high overpressure moves from plasticity in compression to plasticity in tension with a margin of mud weight ΔP_w_SG = 0.01. This margin is undoubtedly very low. A small underestimation of the overpressure can cause the borehole collapse.

The case with σ_c = 8 MPa has the failure limit in compression with P_w_SG = 1.81 (P_w = 44.47 MPa) (UBD) in the analytical solution. The first simulation was set up with P_w_SG = 1.80 (UBD). The zone with a state of stress in tension has a thickness of ≈5 cm, and there is an occurrence of plasticity in compression (shear: orange symbol) because the tensile stresses are small. Figure 12D shows that a decrease in mud weight P_w_SG = 1.788 increases the state of stress in tension (red) ≈ 8 cm and the occurrence of tensile failure (green symbol) at any azimuth. A further reduction of the mud weight P_w_SG = 1.785 causes the borehole collapse (Figure 12E). The margin is ΔP_w_SG = 1.81–1.79 = 0.02.

We also carried out a simulation with σ_c = 8 MPa and the correspondent p_fA_SG = 1.79 (P_w = 43.86 MPa). This condition was discussed in Figure 11 with the analytical solution, referring to drilling in balance. The onset of plasticity occurs at P_w_SG ≈ 1.78 in agreement with the analytical solution.

The case with σ_c = 12 MPa has the failure limit in tension with P_w_SG = 1.79 (P_w = 44.00 MPa) (UBD) in the analytical solution. Figure 12F shows that tensile plasticity at any azimuth occurs at P_w_SG = 1.773. The zone with a state of stress in tension has a thickness of ≈10 cm. A further reduction of the mud weight P_w_SG = 1.77 causes the borehole collapse. The margin is ΔP_w_SG = 1.79–1.77 = 0.02 and is equal to the case with σ_c = 8 MPa.

Figure 13A shows the variation of the mud weights of borehole collapse with σ_c, calculated with FLAC with the overpressures in the range p_f_SG = 1.76–1.82. The difference between the mud weights calculated with the highest and the lowest overpressure is almost constant ΔP_w_SG ≈ 0.06–0.07 for all σ_c. The maximum variation of overpressures is Δp_f_SG = 0.06. Consequently, there is a one-to-one correspondence between p_f and P_w-collapse. Figure 13A indicates that a small underestimation of the overpressure (i.e., Δp_f_SG = 0.04) can induce borehole collapse.

FIGURE 13

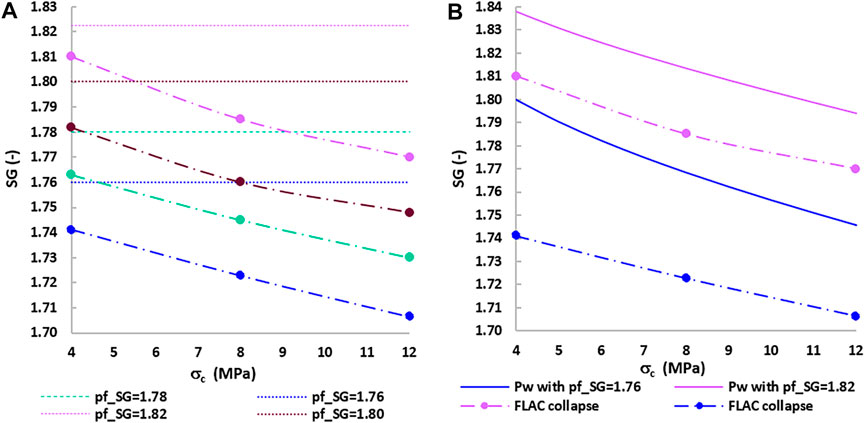
FIGURE 13. (A) Comparison between the mud weight of borehole collapse calculated with FLAC at different overpressures p_f_SG = 1.76–1.82 and the uniaxial compressive strength σ_c = 4–12 MPa. (B) Comparison between the limit mud weight calculated analytically and the mud weight corresponding to wellbore collapse calculated with FLAC.

Figure 13B shows the comparison between the mud weight at the failure limit calculated analytically (in agreement with the numerical solution) and the mud weight that corresponds to wellbore collapse (FLAC analysis) when p_f_SG = 1.82 and p_f_SG = 1.76. It indicates that borehole collapse is attained closer to the failure limit at the higher overpressure.

3.2 Sensitivity Analysis of Wellbores Drilled in the Browse Basin

The Browse Basin in the North West Shelf of Australia is one of the most prolific areas in terms of hydrocarbon accumulation (Asaka et al., 2016). The basin is subject to high overpressure and a strike-slip regime with significant stress anisotropy (Khaksar, 2011; Asaka et al., 2016; Asaka and Holt, 2021; Mandal et al., 2021). The pressure ramp starts within the Jamieson shaly formation (z ≈ 2,200 m), reaching a maximum at the top of the Aptian shaly formation (z ≈ 3,200 m) and then regresses to the hydrostatic condition in the sand reservoir (z = 3,900 m) (Hansen et al., 2014; Mandal et al., 2021).

Asaka et al. (2016) and Asaka and Holt (2021) reported the data of a field (field AH) in the Browse basin: σ_v_SG ≈ 2.00, σ_h_SG ≈ 1.77, σ_H_SG ≈ 2.39, p_f_SG ≈ 1.51.

Mandal et al. (2021) reported the far-field stress and pore pressure profiles in the gas condensate Ichthys field (Ichthys-Deep-1 vertical well drilled in 2003) in the Browse Basin. The data indicate that the vertical stress σ_v and minimum horizontal stress σ_h are in agreement with those indicated by Asaka and Holt (2021) in the depth interval z = 3,080–3,520 m. However, the maximum horizontal stress is higher σ_H_SG ≈ 3.29. The overpressure starts from the top of Jamieson formation (shale unit), reaching a maximum gradient of p_f_SG ≈ 1.25 at the middle of the layer and then regressed. At a depth z = 3,100 m, the pore pressure is p_f = 38 MPa and is lower than in field AH. Mandal et al. (2021) used these outcomes to validate the 3D proposed model in the Prelude-1A discovery well (near vertical) in the same field.

Khaksar (2011) reported the data of the Ichthys field at depths z ≈ 4,000–4,900 m in the reservoir. The maximum horizontal stress is σ_H_SG ≈ 2.64. This value is consistent with Asaka et al.’s (2016) data.

Hansen et al. (2014) carried out a predrill pore-pressure and borehole-stability prediction for potential well locations close to the Prelude-1A discovery well. The overburden stress and the minimum horizontal stress agree with Asaka and Holt’s (2021)data. The overpressure at z = 3,100 m results in p_f = ≈40 MPa (SG = 1.32) close to Mandal et al.’s (2021) value. The estimation of the maximum horizontal stress was set up in the reservoir sand units and transferred to the shaly formations. The upper limit is σ_H_SG ≈ 2, lower than the value predicted by Asaka and Holt (2021).

Asaka et al. (2016) and Asaka and Holt (2021) reported the strength parameters of a transversely isotropic shale at depth z = 3,100 m in the AH field within the Browse Basin. The uniaxial compressive strength of the rock matrix is σ_c = 55 MPa, and the friction angle is ϕ′ = 30°. The authors did not describe if lab tests or log correlations were used to obtain these rock properties.

Mandal et al. (2021) estimated by log correlations the uniaxial compressive strength profile along with burial depth of the Ichthys-Deep-1 vertical well at z ≈ 0–4,900 m (Figure 14A). The log correlations are based on empirical formulas developed by McNally (1987) and Horsrud (2001). The results indicate that the uniaxial compressive strength of the shaly formations (depth interval z = 2,200–3,900 m) ranges from σ_c = 15 MPa to σ_c = 25 MPa. A sharp increase/decrease in the uniaxial compressive strength occurs in the Aptian formation (silty shale) with σ_c ≈ 50 MPa at z = 3,300. The Jamieson shaly formation has a constant σ_c ≈ 15 MPa (z ≈ 2,200–3,200 m). This constant σ_c is lower than the value indicated by Asaka and Holt (2021).

FIGURE 14

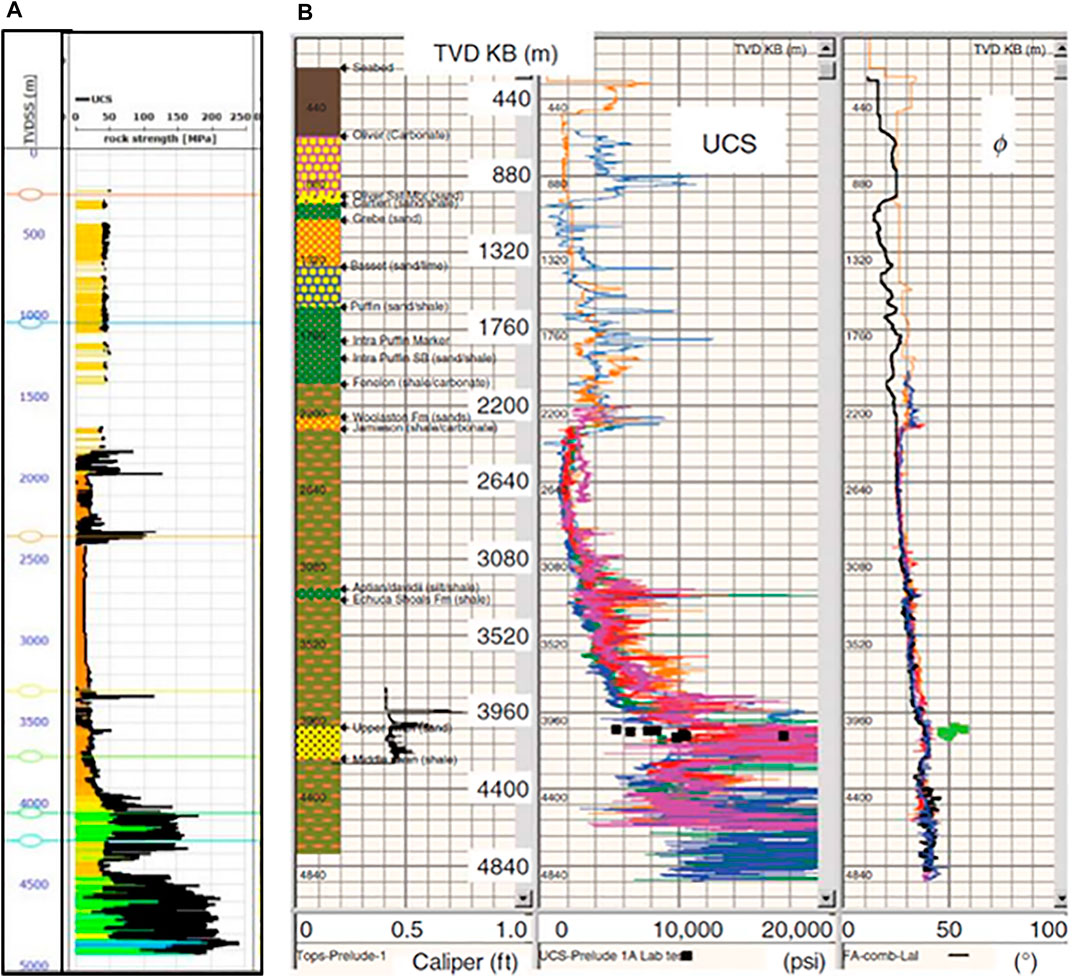
FIGURE 14. Uniaxial compressive strength (UCS) and friction angle ϕ′ profiles. (A) Ichthys deep-1 well (modified from Mandal et al., 2021). (B) Prelude wells (modified from Hansen et al., 2014).

Hansen et al. (2014) estimated, with log correlations, the profile of the uniaxial compressive strength and friction angle of Prelude 1 A well (Figure 14B). The uniaxial compressive strength in the shaly formations, depth interval z = 2,200–3,960 m, is σ_c = 15–55 MPa, and the friction angle is practically constant ϕ′ ≈ 30°. The uniaxial compressive strength in the depth interval z = 3,080–3,520 m is σ_c ≈ 30–40 MPa.

The comparison between the estimated uniaxial strength by Hansen et al. (2014) and Mandal et al. (2021) in the depth range z ≈ 3,080–3,520 m indicates a large difference. In contrast, the uniaxial strength reported by Asaka and Holt (2021) is the upper limit.

The available data in this basin resulted in a wide scattering of the parameters that must be used in wellbore stability analysis. We set up stability analyses with the available data to obtain different scenarios and highlighted the more uncertain data.

The analysis depth is set at z = 3,100 m. At first, we calculated the mud pressure P_w with σ_H ≈ 110 MPa, p_f = 38 MPa, and ϕ′ = 30°. The mud pressure at ϑ = 90° (compression zone) results in P_w = 1.56 σ_h when σ_c = 15 MPa and P_w = 1.38 σ_h when σ_c = 55 MPa. Asaka and Holt (2021) and Mandal et al. (2021) did not report the mud weight of the post-drilling experience. We evaluated the maximum horizontal stress in the Browse Basin with the frictional limit (ϕ′ ≈ 30°). The maximum horizontal stress is constrained to be below σ_H_SG ≈ 3, agreeing with the estimation reported by Rollet et al. (2016). In the end, the maximum horizontal stress σ_H ≈ 73 MPa can be used in the analysis. Table 3 reports the field data that we considered in the stability analyses.

TABLE 3

TABLE 3. Field data in the Ichthys field, Browse Basin.

We considered a range of uniaxial compressive strength σ_c = 15–55 MPa, with a friction angle of ϕ′ = 30°. We roughly fitted with the H&B criterion σ_c with m_t = 10 (σ_c/σ_t ≈ 10) for the tension zone and with m_c = 5 (which is similar to the M-C criterion with ϕ′ = 30°) for the compression zone. We selected two different m because at ϑ = 0° and ϑ = 90° two well-defined tension and compression zones can occur. These different slopes of the criterion are conservative for the two zones. The strength parameters selected for the shale are reported in Table 4. Figure 15 shows the strength envelopes of the shale calculated with the M-C criterion and H&B criterion.

TABLE 4

TABLE 4. Strength properties of the shaly formations.

FIGURE 15

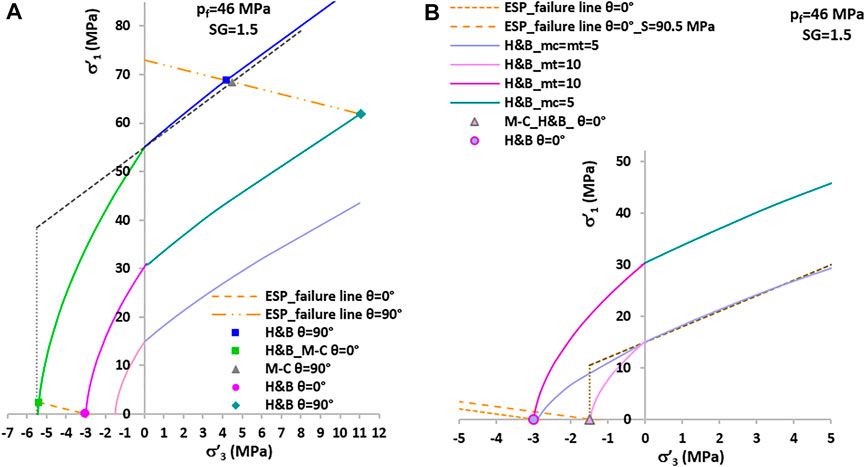
FIGURE 15. Strength envelopes of the shale and limit failure condition with H&B and M-C criterion, points at failure and ESP failure lines. p_f = 46 MPa. (A) Parameters of the H&B criterion: σ_c = 15-30.3-55 MPa, m_c = 5, m_t = 10, and σ_c/σ_t ≈ 10; parameters of the M-C criterion: σ_c = 30 MPa, σ_c/σ_t ≈ 10, and ϕ′ = 30°. (B) Comparison between σ_c = 15 MPa and m_t = m_c = 5; σ_c = 30 MPa and m_t = 10; σ_c = 15 MPa and ϕ′ = 30°.

At first, we analyzed the tension zone. We calculated with Eqs 12, 13 the limit pore pressures for the uniaxial tensile failure (radial and tangential) p_fB = p_fC in the range σ_c = 15–55 MPa with m_t = 10 (σ_c/σ_t ≈ 10). The limit pore pressure is p_fB = p_fC = 46 MPa at σ_c = 30.3 MPa. Consequently, the prediction of the limit mud pressures with the overpressure p_f = 46 MPa, reported by Asaka and Holt (2021), must be carried out by setting σ_c ≥ 30.3 MPa (with m_t = 10 and σ_c/σ_t ≈ 10). We interpreted this issue with the ESP failure lines. Figure 15A shows the strength envelopes calculated with H&B and M-C criteria, the points calculated with Eqs 7, 8 for compressive failure and radial tensile failure and Eqs 9, 10 for tangential tensile failure (HF). The points at failure are at the limit conditions at ϑ = 0° and ϑ = 90° (because of stress anisotropy R > 1). The purple symbol represents the uniaxial tensile failure, occurring at σ_c = 30.3 MPa.

Hence, there are two ESP failure lines at the two azimuths. If the uniaxial compressive strength is σ_c = 15 MPa, as predicted by Mandal et al. (2021), a solution can be set to m_t = m_c = 5, equivalent to the conventional approach used with the M-C criterion with a constant friction angle (in the compression and tension zone). This m_t = m_c predicts σ_t = −3.08 MPa that corresponds to a ratio σ_c/σ_t ≈ 5, which is nearly the lower limit for the set of rocks investigated by Sheorey (1997). This σ_t is close to the σ_t of the case σ_c = 30.3 MPa (σ_c/σ_t ≈ 10 and m_t = 10). Figure 15B shows the results of this analysis. The purple-violet symbol refers to the case of σ_c = 15 MPa m_t = m_c = 5 and σ_c/σ_t ≈ 5 and to the case of σ_c = 30.3 MPa m_t = 10 and σ_c/σ_t ≈ 10. This point belongs to the ESP failure line calculated with S_min = 89 MPa and p_f = 46 MPa, the basin data reported in Table 3. However, the strength envelope with σ_c/σ_t ≈ 5 is probably not appropriate for the rock under study.

Figure 15B also shows the analysis with the M-C criterion with σ_c = 15 MPa, ϕ′ = 30°, and the conventional cutoff at σ_c/σ_t ≈ 10. The point at failure in the tension zone with the M-C criterion needs a cutoff correction. This correction cannot belong to the ESP failure line at ϑ = 0° because this line stops at σ_t = −3.08 MPa. The constraint must refer to another ESP line determined by a different S_min = 90.5 MPa, represented by the pink-grey symbol.

The simple calculation of the mud pressures for HF in conventional stability analysis gives P_w = S_min−p_f + σ_t = 89–46 + 1.5 ≈ 44.5 MPa, which corresponds to S_min−P_w−p_f = −1.5 MPa (pink-grey symbol in Figure 15B). However, the stress state is not uniaxial because P_w−p_f = −1.5 MPa.

In the end, the prediction of the limit of failure results in a fully tensile state of stress (σ′₃ < 0, σ′₁ < 0) along the two principal directions, when σ_c < 30.3 MPa (with σ_c/σ_t ≈ 10). This state of stress is incompatible with the strength criteria of the rock, as observed above.

Supplementary Figure S1A shows the variation of the mud weights when p_f = 46 MPa (SG = 1.51) with σ_c = 15–55 MPa. The SG calculated for tangential HF and radial tensile failure is not compatible with the strength criterion in the range σ_c = 15–30.3 MPa. In the range of σ_c = 30.3–42 MPa, the mud weight in the compression zone at ϑ = 90° (green line) is higher than σ_h (brown line). On the contrary, the mud weight for tangential tensile failure HF (red line) is always lower than the mud weight in compression (green line).

Supplementary Figure S1B shows the variation of the mud weights when p_f = 38 MPa (SG = 1.25). The mud weight in the compression zone at ϑ = 90° (green line) is higher than σ_h (brown line), in the range of σ_c = 15–30 MPa. The mud weight for tangential tensile failure HF (red line) becomes lower than the mud weight in the compression zone (green line) at σ_c > 32.5 MPa.

The previous discussion indicates that drilling in this formation is troublesome with the overpressures in the range of p_f_SG = 1.25–1.51 for a wide range of uniaxial compressive strengths.

The comparison between Supplementary Figures S1A,B indicates that the overpressure p_f = 46 MPa (SG = 1.51) reported by Asaka and Holt (2021) is probably overestimated.

Khaksar (2011) analyzed the post drilling data at depths of z = 4,000–4,900 m and the pore pressure derived from the conventional compaction trend-based analysis with sonic log in the Vulcan shale (z = 4,300–4,450 m), which separates the two reservoir units. The predicted pore pressure was SG = 1.27. Khaksar (2011) observed that mud weights of SG = 1.12–1.14 were used to drill the hole section, implying that the 4,300–4,450 m section was drilled underbalanced if the sonic-derived pore pressure profile is accurate. Instances of a tight hole, overpull, and drag and reaming did not occur at the z = 4,300–4,450 m section, which was drilled trouble-free. The predicted breakout angle with high overpressure SG = 1.27 was 100°, inconsistent with log and drilling data. The strength parameters of this rock were quite high σ_c = 100 MPa and ϕ′ = 50° and were not modified in the new stability analysis. The author proposed a revised normal pore pressure gradient SG = 1.02 at these depths and concluded that the prediction method might lead to inaccurate pore pressure estimates.

Hansen et al. (2014) noticed instances of circulation losses in well Concerto 2 (in the same area) at depths of z ≈2,300–4,000 m (shaly formations), with an estimated pore pressure SG = 1.32. Furthermore, they noticed the absence of any observed breakouts in shales. This post-drilling experience gives some input in the selection of the overpressure.

The uniaxial compressive strength reported by Mandal et al. (2021) σ_c = 15 MPa is probably underestimated. The data reported by Hansen et al. (2014) for the shaly formation indicate that a value σ_c > 30 MPa is reasonable, agreeing with the discussion of Supplementary Figure S1A.

In order to unravel the uncertainties related to the overpressure and the strength of the rock, given that the Ichthys Deep-1 well, Prelude 1A well, and Concerto 2 well were already drilled, we selected p_f_SG = 1.32 and σ_c = 35 MPa. Supplementary Figure S1C shows the results of the stability analyses in the range ϑ = 0°–90°. The limit mud weight is undoubtedly high in the compression zone (ϑ = 35°–90°) and the limit mud weight of HF is low in the range ϑ = 0°–10°. Mandal et al. (2021) reported that the existence of overpressure in the overburden Jamieson layer required a higher mud weight to balance out any potential drilling hazard. We also noted that the limit mud weight for radial tensile failure is not constant with ϑ in an anisotropic far-field stress state and is overcome by the limit of failure in compression at ϑ ≈ 35°.

Supplementary Figure S1D, a zoom of Supplementary Figure S1C, shows that local failures are expected to occur. In fact, the setting of the mud weight SG > 1.74 results in tensile failure at least in the range of ϑ = 0°–10° (as well as ϑ = 170°–180°), in agreement with the instances of circulation losses reported by Hansen et al. (2014). On the contrary, the setting of the mud weight SG < 1.70 results in a breakout angle of at least ≈30°.

The results of the previous analyses indicate that the uncertainties related to the estimation of the strength parameters and pore pressure could lead to erroneous mud weight prediction.

The sensitivity analyses aided in the exclusion of some data. This procedure can be considered a sort of guideline for stability analyses of wellbores drilled in overpressured basins.

The results of the sensitivity analyses evidenced that further research to improve the estimation of the strength parameters from log data is crucial.

4 Conclusion

This study analyzed the wellbores’ stability in two overpressured basins differing in far-field stress regimes and rock types.

The influence of variation of the strength parameters of the rock, overpressure, and far-field stresses was investigated with analytical and numerical analyses using the Mohr Coulomb criterion and the Hoek–Brown criterion.

The results indicated that the Hoek–Brown criterion better describes the conditions of rock failure in tension and compression because it is nonlinear.

The induced state of stress and the pore pressure at the wellbore boundary define an ESP failure line. The wellbore pressure calculated with the strength parameters of the rock determines the radial and tangential stresses and the points at failure along the ESP. The limit condition of failure is calculated in the tension and compression zones because the occurrence of unexpected overpressures can result in underbalanced drilling (UBD) or hydraulic fracture (HF).

The analysis of tensile failure indicated that selecting a high frictional component of the strength in the tension zone is conservative because it reduces the extent of this zone. On the contrary, a low frictional component of the strength in the compression zone is conservative, as expected. This outcome suggested using two different frictional components of the strength for the tension zone and the compression zone in the overpressured basin.

The conventional approach used for tensile failure (uniaxial radial and tangential HF) gives a different failure limit with respect to the complete coupling between the strength criterion and the Kirsch solution, herein suggested. These differences are low, but in overpressured basins, the margin of the mud weight can be low. The failure limit for the radial and tangential uniaxial tensile condition occurs with the same pore pressure but with two different mud pressures because of the rotation of principal stresses.

Drilling in balance cannot be considered a threshold for drilling in safe conditions. In fact, when drilling in balance, the stability is ruled by the uniaxial compressive strength.

The results of the numerical simulations carried out with FLAC indicated that the margin of mud weight from local failure to borehole collapse is low and increases with a decrease in overpressure.

The sensitivity analyses allowed highlighting how the uncertainties in the estimation of strength parameters can considerably affect mud weights.

The geomechanical analysis of wellbore stability in overpressured basins indicated the need for improving the log correlations to determine the strength parameters of the rock.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors without undue reservation.

Author Contributions

Conceptualization, CD; methodology, CD; formal analysis, CD and MM; writing—original draft preparation, CD; writing—review and editing, CD and MM.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.860818/full#supplementary-material

Supplementary Figure S1 | Variation of the limit mud weight SG with σ_c = 15–55 MPa, m_c = 5, m_t = 10, and σ_c/σ_t ≈ 10. Compression zone (green line); tangential tensile failure HF (red line); radial tensile failure (blue line). (A) p_f = 46 MPa (SG = 1.51) at ϑ = 0° and ϑ = 90°. (B) p_f = 38 MPa (SG = 1.25) at ϑ = 0° and ϑ = 90°. (C) σ_c = 35 MPa, p_f = 40 MPa (SG = 1.32) ϑ = 0–90°. (D) Zoom of panel (C).

References

Abdelghany, W. K., Radwan, A. E., Elkhawaga, M. A., Wood, D. A., Sen, S., and Kassem, A. A. (2021). Geomechanical Modeling Using the Depth-Of-Damage Approach to Achieve Successful Underbalanced Drilling in the Gulf of Suez Rift basin. J. Pet. Sci. Eng. 202, 108311. doi:10.1016/j.petrol.2020.108311

CrossRef Full Text | Google Scholar

Abousleiman, Y. N., Tran, M. H., Hoang, S., Bobko, C. P., Ortega, A., and Ulm, F. J. (2007). “Geomechanics Field and Laboratory Characterization of the Woodford Shale: The Next Gas Play,” in SPE Annual Technical Conference and Exhibition. OnePetro. doi:10.2118/110120-MS

CrossRef Full Text | Google Scholar

Al-Ajmi, A. M., and Zimmerman, R. W. (2006). Stability Analysis of Vertical Boreholes Using the Mogi-Coulomb Failure Criterion. Int. J. Rock Mech. Mining Sci. 43 (8), 1200–1211. doi:10.1016/j.ijrmms.2006.04.001

CrossRef Full Text | Google Scholar

Alber, M., and Heiland, J. (2001). Investigation of a limestone Pillar Failure Part 1: Geology, Laboratory Testing and Numerical Modeling. Rock Mech. Rock Eng. 34 (3), 167–186. doi:10.1007/s006030170007

CrossRef Full Text | Google Scholar

Ambati, V., Mahadasu, N. B., and Nair, R. R. (2021). Reservoir Wellbore Stability Analysis and Weak Zones Identification Using the 1D MEM, Swelling Tests and UCS: A Case Study From Mumbai Offshore, India. Arab J. Sci. Eng., 1–23. doi:10.1007/s13369-021-05530-w

CrossRef Full Text | Google Scholar

Asaka, M., and Holt, R. M. (2021). Anisotropic Wellbore Stability Analysis: Impact on Failure Prediction. Rock Mech. Rock Eng. 54 (2), 583–605. doi:10.1007/s00603-020-02283-0

CrossRef Full Text | Google Scholar

Asaka, M., Sekine, T., and Furuya, K. (2016). Geologic Cause of Seismic Anisotropy: a Case Study from Offshore Western Australia. The Leading Edge 35, 662–668. doi:10.1190/tle35080662.1

CrossRef Full Text | Google Scholar

Bell, F. G. (1977). A Note on the Physical Properties of the Chalk. Eng. Geology. 11 (3), 217–225. doi:10.1016/0013-7952(77)90003-5

CrossRef Full Text | Google Scholar

Brady, B., and Brown, E. (2004). Rock Mechanics for Underground Mining. Dorrecht, The Netherlands; Boston, MA, USA; London, UK: Kluwer academic Publishers.

Google Scholar

Cai, M. (2010). Practical Estimates of Tensile Strength and Hoek-Brown Strength Parameter M I of Brittle Rocks. Rock Mech. Rock Eng. 43 (2), 167–184. doi:10.1007/s00603-009-0053-1

CrossRef Full Text | Google Scholar

Carter, B. J., Scott Duncan, E. J., and Lajtai, E. Z. (1991). Fitting Strength Criteria to Intact Rock. Geotech Geol. Eng. 9 (1), 73–81. doi:10.1007/bf00880985

CrossRef Full Text | Google Scholar

Chang, C., Zoback, M. D., and Khaksar, A. (2006). Empirical Relations between Rock Strength and Physical Properties in Sedimentary Rocks. J. Pet. Sci. Eng. 51 (3-4), 223–237. doi:10.1016/j.petrol.2006.01.003

CrossRef Full Text | Google Scholar

Coviello, A., Lagioia, R., and Nova, R. (2005). On the Measurement of the Tensile Strength of Soft Rocks. Rock Mech. Rock Engng. 38, 251–273. doi:10.1007/s00603-005-0054-7

CrossRef Full Text | Google Scholar

da Fontoura, B. (2012). Lade and Modified Lade 3D Rock Strength Criteria. Rock Mech. Rock Eng. 45 (6), 1001–1007. doi:10.1007/s00603-012-0279-1

CrossRef Full Text | Google Scholar

Deangeli, C., Cardu, M., and Martinelli, D. (2021). “Analysis of the Stability of Openings Excavated in Anisotropic Rocks,” in Proceedings of the International Conference of the International Association for Computer Methods and Advances in Geomechanics, Turin, Italy, 5–8 May 2021 (Cham, Switzerland: Springer), 361–368. doi:10.1007/978-3-030-64518-2_43

CrossRef Full Text | Google Scholar

Deangeli, C. (2021). Failure in the Tension Zone Around a Circular Tunnel Excavated in Saturated Porous Rock. Appl. Sci. 11 (18), 8384. doi:10.3390/app11188384

CrossRef Full Text | Google Scholar

Deangeli, C., and Omwanghe, O. (2018). Prediction of Mud Pressures for the Stability of Wellbores Drilled in Transversely Isotropic Rocks. Energies. 11, 1944. doi:10.3390/en11081944

CrossRef Full Text | Google Scholar

Detournay, E., and Cheng, A. D. (1988). Poroelastic Response of a Borehole in a Non-hydrostatic Stress Field. Int. J. Rock Mech. Mining Sci. Geomechanics Abstr. 25, 171–182. doi:10.1016/0148-9062(88)92299-1

CrossRef Full Text | Google Scholar

Detournay, E., and Cheng, A. H.-D. (1993). “Fundamentals of Poroelasticity,” in Analysis and Design Methods (Pergamon), 113–171. doi:10.1016/b978-0-08-040615-2.50011-3

CrossRef Full Text | Google Scholar

Fairhurst, C. (1964). On the Validity of the 'Brazilian' Test for Brittle Materials. Int. J. Rock Mech. Mining Sci. Geomechanics Abstr. 1, 535–546. doi:10.1016/0148-9062(64)90060-9

CrossRef Full Text | Google Scholar

Fjaer, E., Holt, R. M., Horsrud, P., and Raaen, A. M. (2008). Petroleum Related Rock Mechanics. Amsterdam: Elsevier.

Google Scholar

Ganguli, S. S., and Sen, S. (2020). Investigation of Present-Day In-Situ Stresses and Pore Pressure in the South Cambay Basin, Western India: Implications for Drilling, Reservoir Development and Fault Reactivation. Mar. Pet. Geology. 118, 104422. doi:10.1016/j.marpetgeo.2020.104422

CrossRef Full Text | Google Scholar

Gholami, R., Moradzadeh, A., Rasouli, V., and Hanachi, J. (2014). Practical Application of Failure Criteria in Determining Safe Mud Weight Windows in Drilling Operations. J. Rock Mech. Geotechnical Eng. 6 (1), 13–25. doi:10.1016/j.jrmge.2013.11.002

CrossRef Full Text | Google Scholar

Guéguen, Y., and Boutéca, M. (2004). Mechanics of Fluid-Saturated Rocks. Amsterdam: Elsevier.

Google Scholar

Havmøller, O., and Foged, N. (1996). “Review of Rock Mechanics Data for Chalk,” in Proceeding of North Sea Chalk Symposium, Reims/France, October 7–9, 1–26.

Google Scholar

Hansen, K. S. S., Wang, G., Adeleye, O., McNeil, K. V. V., Couzens-Schultz, B. A. A., and Tare, U. (2014). Integrated Predrill Pore-Pressure and Borehole-Stability Prediction for Prelude Development. SPE Drilling & Completion. 29 (04), 418–430. doi:10.2118/173179-pa

CrossRef Full Text | Google Scholar

Hoek, E., and Brown, E. T. (1980). Empirical Strength Criterion for Rock Masses. J. Geotech. Engrg. Div. 106 (9), 1013–1035. doi:10.1061/ajgeb6.0001029

CrossRef Full Text | Google Scholar

Hoek, E., and Brown, E. T. (1997). Practical Estimates of Rock Mass Strength. Int. J. rock Mech. mining Sci. 34 (8), 1165–1186. doi:10.1016/s1365-1609(97)80069-x

CrossRef Full Text | Google Scholar

Hoek, E., and Brown, E. T. (2019). The Hoek-Brown Failure Criterion and GSI - 2018 Edition. J. Rock Mech. Geotechnical Eng. 11 (3), 445–463. doi:10.1016/j.jrmge.2018.08.001

CrossRef Full Text | Google Scholar

Horsrud, P. (2001). Estimating Mechanical Properties of Shale From Empirical Correlations. J. SPE Drilling Completion. 16 (2), 68–73. doi:10.2118/56017-pa

CrossRef Full Text | Google Scholar

Josh, M., Esteban, L., Delle Piane, C., Sarout, J., Dewhurst, D. N., and Clennell, M. B. (2012). Laboratory Characterisation of Shale Properties. J. Pet. Sci. Eng. 88, 107–124. doi:10.1016/j.petrol.2012.01.023

CrossRef Full Text | Google Scholar

Khaksar, A. (2011). “Depth Limit of Velocity-Effective Stress Relationships for Pore Pressure Prediction, Implications for Wellbore Stability Analysis,” in 45th US Rock Mechanics/Geomechanics Symposium. OnePetro.

Google Scholar

Khaksar, A., Taylor, P. G., Fang, Z., Kayes, T. J., Salazar, A., and Rahman, K. (2009). “Rock Strength from Core and Logs, where We Stand and Ways to Go,” in EUROPEC/EAGE Conference and Exhibition. OnePetro. doi:10.2118/121972-ms

CrossRef Full Text | Google Scholar

Kristiansen, T. G. (2004). “March). Drilling Wellbore Stability in the Compacting and Subsiding Valhall Field,” in IADC/SPE drilling conference. OnePetro.

Google Scholar

Liu, Y., Qiu, N., Xie, Z., Yao, Q., and Zhu, C. (2016). Overpressure Compartments in the central Paleo-Uplift, Sichuan Basin, Southwest China. Bulletin 100 (5), 867–888. doi:10.1306/02101614037

CrossRef Full Text | Google Scholar

Ma, T., Chen, P., Yang, C., and Zhao, J. (2015). Wellbore Stability Analysis and Well Path Optimization Based on the Breakout Width Model and Mogi-Coulomb Criterion. J. Pet. Sci. Eng. 135, 678–701. doi:10.1016/j.petrol.2015.10.029

CrossRef Full Text | Google Scholar

Ma, T., Yang, Z., and Chen, P. (2018). Wellbore Stability Analysis of Fractured Formations Based on Hoek-Brown Failure Criterion. Ijogct 17 (2), 143–171. doi:10.1504/ijogct.2018.089934

CrossRef Full Text | Google Scholar

Mandal, P. P., Essa, I., Saha, S., and Rezaee, R. (2021). “Multi-purpose Utility of Constructing 3D Static Geomechanical Model in the Ichthys Field, Browse Basin,” in Australian Exploration Geoscience Conference AEGC (Brisbane, Australia.

Google Scholar

Manshad, A. K., Jalalifar, H., and Aslannejad, M. (2014). Analysis of Vertical, Horizontal and Deviated Wellbores Stability by Analytical and Numerical Methods. J. Petrol. Explor Prod. Technol. 4 (4), 359–369. doi:10.1007/s13202-014-0100-7

CrossRef Full Text | Google Scholar

McLellan, P., and Hawkes, C. (2001). Borehole Stability Analysis for Underbalanced Drilling. J. Can. Pet. Technology. 40 (05). doi:10.2118/01-05-01

CrossRef Full Text | Google Scholar

McLellan, P., and Hawkes, C. (1999). “User-friendly Borehole Stability Software for Designing Horizontal and Deviated wells,” in CADE/CAODC Spring Drilling Conference. Calgary, Alberta Canada, 31–38.

Google Scholar

McNally, G. H. (1987). Estimation of Coal Measures Rock Strength Using Sonic and Neutron Logs. Geoexploration. 24 (4-5), 381–395. doi:10.1016/0016-7142(87)90008-1

CrossRef Full Text | Google Scholar

Meng, M., Baldino, S., and Miska, S. (2021). Evaluation of Failure Criteria under Dynamic Loading of the Wellbore with Strain Rates between 10−6 and 100/s. J. Pet. Sci. Eng. 201, 108448. doi:10.1016/j.petrol.2021.108448

CrossRef Full Text | Google Scholar

Murrell, S. A. F. (1963). “A Criterion for Brittle Fracture of Rocks and concrete under Triaxial Stress and the Effect of Pore Pressure on the Criterion,” in Proceedings of the 5th Symposium on Rock Mechanics (University of Minnesota. Oxford Pergamon Press), 563–577.

Google Scholar

Nmegbu, C. J., and Ohazuruike, L. (2014). Wellbore Instability in Oil Well Drilling: a Review. Int. J. Eng. Res. Development. 10 (5), 11–20.

Google Scholar

Ottesen, S. (2010). “Wellbore Stability in Fractured Rock,” in IADC/SPE drilling conference and exhibition. OnePetro. doi:10.2118/128728-ms

CrossRef Full Text | Google Scholar

Parkash, D., and Deangeli, C. (2019). “Wellbore Stability Analysis in Anisotropic Shale Formations,” in Proceedings of the SPE/PAPG Pakistan Section Annual Technical Symposium and Exhibition, Society of Petroleum Engineers PATS 2019-201183-MS-SPE. Islamabad, Pakistan. doi:10.2118/201183-ms

CrossRef Full Text | Google Scholar

Pattillo, P. D., Kristiansen, T. G., Sund, G. V., and Kjelstadli, R. M. (1998). “Reservoir Compaction and Seafloor Subsidence at Valhall,” in SPE/ISRM rock mechanics in petroleum engineering. OnePetro.

CrossRef Full Text | Google Scholar

Perras, M. A., and Diederichs, M. S. (2014). A Review of the Tensile Strength of Rock: Concepts and Testing. Geotech Geol. Eng. 32 (2), 525–546. doi:10.1007/s10706-014-9732-0

CrossRef Full Text | Google Scholar

Priest, S. D. (2005). Determination of Shear Strength and Three-Dimensional Yield Strength for the Hoek-Brown Criterion. Rock Mech. Rock Engng. 38 (4), 299–327. doi:10.1007/s00603-005-0056-5

CrossRef Full Text | Google Scholar

Rahimi, R., and Nygaard, R. (2015). Comparison of Rock Failure Criteria in Predicting Borehole Shear Failure. Int. J. Rock Mech. Mining Sci. 79, 29–40. doi:10.1016/j.ijrmms.2015.08.006

CrossRef Full Text | Google Scholar

Risnes, R. (2001). Deformation and Yield in High Porosity Outcrop Chalk. Phys. Chem. Earth, A: Solid Earth Geodesy. 26 (1-2), 53–57. doi:10.1016/s1464-1895(01)00022-9

CrossRef Full Text | Google Scholar

Risnes, R., and Flaageng, O. (1999). Mechanical Properties of Chalk with Emphasis on Chalk-Fluid Interactions and Micromechanical Aspects. Oil Gas Sci. Technology - Rev. IFP. 54 (6), 751–758. doi:10.2516/ogst:1999063

CrossRef Full Text | Google Scholar

Risnes, R., Haghighi, H., Korsnes, R. I., and Natvik, O. (2003). Chalk–fluid Interactions with Glycol and Brines. Tectonophysics. 370 (1-4), 213–226. doi:10.1016/s0040-1951(03)00187-2

CrossRef Full Text | Google Scholar

Rollet, N., Abbott, S. T., Lech, M. E., Romeyn, R., Grosjean, E., Edwards, D. S., et al. (2016). A Regional Assessment of CO2 Storage Potential in the Browse Basin: Results of a Study Undertaken as Part of the National CO2 Infrastructure Plan. Record 2016/17. Canberra: Geoscience Australia. doi:10.11636/Record.2016.017

CrossRef Full Text | Google Scholar

Salehi, S., Hareland, G., and Nygaard, R. (2010). Numerical Simulations of Wellbore Stability in Under-balanced-drilling wells. J. Pet. Sci. Eng. 72 (3-4), 229–235. doi:10.1016/j.petrol.2010.03.022

CrossRef Full Text | Google Scholar

Sen, S., Kundan, A., and Kumar, M. (2018). “Post-drill Analysis of Pore Pressure and Fracture Gradient from Well Logs and Drilling Events—An Integrated Case Study of a High Pressure Exploratory Well from Panna East, Mumbai Offshore Basin, India,” in Pore pressure and geomechanics from exploration to abandonment, AAPG geosciences technology workshop (Perth, Australia, 6–7.

Google Scholar

Shen, J., and Karakus, M. (2014). Simplified Method for Estimating the Hoek-Brown Constant for Intact Rocks. J. Geotech. Geoenviron. Eng. 140 (6), 04014025. doi:10.1061/(asce)gt.1943-5606.0001116

CrossRef Full Text | Google Scholar

Sheorey, P. R. (1997). Empirical Rock Failure Criteria. Rotterdam: AA Balkema.

Google Scholar

Singh, A., Rao, K. S., and Ayothiraman, R. (2019). An Analytical Solution to Wellbore Stability Using Mogi-Coulomb Failure Criterion. J. Rock Mech. Geotechnical Eng. 11 (6), 1211–1230. doi:10.1016/j.jrmge.2019.03.004

CrossRef Full Text | Google Scholar

Tan, C. P., and Willoughby, D. R. (1999). “A Pragmatic Approach to Managing Wellbore Instability in Extended Reach wells in the Goodwyn Field,” in SPE Annual Technical Conference and Exhibition. OnePetro. doi:10.2118/56565-ms

CrossRef Full Text | Google Scholar

Terzaghi, K. (1936). “The Shearing Resistance of Saturated Soils and the Angle between the Planes of Shear,” in First International Conference of soil mechanics and Foundation Engineering, 54–56.

Google Scholar

Woehrl, B., Wessling, S., Bartetzko, A., Pei, J., and Renner, J. (2010). “Comparison of Methods to Derive Rock Mechanical Properties from Formation Evaluation Logs,” in 44th US Rock Mechanics Symposium and 5th US-Canada Rock Mechanics Symposium. OnePetro.

Google Scholar

Yousefian, H., Soltanian, H., Marji, M. F., Abdollahipour, A., and Pourmazaheri, Y. (2018). Numerical Simulation of a Wellbore Stability in an Iranian Oilfield Utilizing Core Data. J. Pet. Sci. Eng. 168, 577–592. doi:10.1016/j.petrol.2018.04.051

CrossRef Full Text | Google Scholar

Zhang, J. J. (2019). Applied Petroleum Geomechanics. Cambridge, MA: Gulf Professional Publishing, Imprint of Elsevier. doi:10.1016/C2017-0-01969-9

CrossRef Full Text | Google Scholar

Zhang, J. (2011). Pore Pressure Prediction from Well Logs: Methods, Modifications, and New Approaches. Earth-Science Rev. 108 (1-2), 50–63. doi:10.1016/j.earscirev.2011.06.001

CrossRef Full Text | Google Scholar

Zhang, L., Cao, P., and Radha, K. C. (2010). Evaluation of Rock Strength Criteria for Wellbore Stability Analysis. Int. J. rock Mech. mining Sci. 47 (8), 1304–1316. doi:10.1016/j.ijrmms.2010.09.001

CrossRef Full Text | Google Scholar

Zoback, M. D., Moos, D., Mastin, L., and Anderson, R. N. (1985). Well Bore Breakouts and In Situ Stress. J. Geophys. Res. 90 (B7), 5523–5530. doi:10.1029/jb090ib07p05523

CrossRef Full Text | Google Scholar