Identification of Rock Properties of Rock Wall Cut by Roadheader Based on PSO-VMD-LSSVM

Introduction

Coal mining mainly involves underground mining, and several underground roadways are required to ensure continuous and efficient coal production. As the key technology of coal mine roadway, rapid roadway digging is directly related to the economy and safety of coal mine production, an important guarantee for high and stable coal production. Yin studied the damage characteristics of rocks, mainly based on semi-rock or whole rock, under the action of dynamic and static coupling to improve the safety of deep mining (Yin et al., 2019). Methods to avoid the overlying rock layers being affected by mining to prevent accidents were studied by analyzing mining techniques and the mechanical properties of rocks (Du et al., 2020a). Extensive research has been conducted to minimize the impact of mining and ensure the safety and efficiency of coal production (Yin et al., 2012). However, reducing the impact of mining using roadway boring machines must be studied to minimize blasting vibrations and ensure a high degree of safety even with continuous rapid digging. Roadheader excavation has gradually become the main method of roadway mining, but safe and efficient roadheading technology is still in the exploration stage. In the process of excavation, cut-off rock wall properties change drastically. However, the roadheader driver cannot promptly adjust the cut-off speed, cantilever swing speed, and other conditions according to the cut-off lithology because of limited vision due to excessive coal and rock dust. These limitations lead to unstable output of cutting motor, excessive wear of cut-off teeth, abnormal collapse of working face, thus significantly impacting mining, accelerating the damage and aging of the digging equipment, and affecting the safety of digging the working face. Therefore, if the rock properties can be identified in the excavation, the efficiency of excavation can be improved, the service life of the excavator can be prolonged, the safety of excavation can be guaranteed, and the impact on the working face can be reduced.

The problem of rock identification has been extensively studied since it was introduced in the 1960s (Li and Ouyang, 2017; Yang et al., 2020). There are two main methods classified according to the means used: direct detection and indirect detection. The direct detection methods are as follows: 1. The natural ray method (Wang S. et al., 2021) uses the ray intensity remaining after the ray penetrates the coal seam and determines the thickness of the top and bottom coal seams according to the attenuation law to achieve the purpose of identifying lithology. However, this method is difficult to operate and has a small adaptation range (K., H, Sampath et al., 2019); 2. The radar detection method (Wang et al., 2016) determines the top coal thickness based on the characteristics of the speed, phase, propagation time of the reflected electromagnetic wave and the frequency of the emitted wave. This method is applicable only if large differences exist in the coal and rock properties as the recognition rate is low if the coal and rock properties are similar. 3. Infrared detection method (Zhang et al., 2022) uses a highly sensitive infrared temperature sensor to measure the temperature difference change of the truncated part. The lithology is identified after applying algorithm classification and artificial ray detection methods (Zhang et al., 2017). In addition to these methods, there are terahertz spectroscopy methods (Wang et al., 2018). Direct detection methods are susceptible to environmental, terrain, and working conditions due to direct contact with different lithologies. These methods are also limited by low tolerance, small application range, minimal feature extraction effects, and low recognition accuracy.

Indirect electric parametric detection is an indirect detection method. It uses image detection (Gao et al., 2021; Wang and Zhang, 2020; Wang X. et al., 2021) and was used in the early 20th century in the United Kingdom and the United States. It has re-emerged now due to the development of artificial intelligence and lithology recognition methods. Different lithology pictures are analyzed using modern image detection techniques to identify the lithology. However, the method is susceptible to working surface dust, light, and other conditions. Rocks exhibit certain electrical properties such as cutting force (Dai, 2020), current (He et al., 2020), and working voltage (Wang et al., 2018). The acceleration sensor (Zhang et al., 2020) and acoustic emission sensor (Du et al., 2020b) also show different readings. These properties can form the basis for distinguishing different lithologies. This method has the advantages of strong anti-interference ability, wide application range, clear feature extraction, and fast recognition. Moreover, current acquisition requires only the placement of the current sensor at the truncation motor, which is easy to perform with little modification to the machine. In this paper, the current signal is processed and used to identify rock lithology.

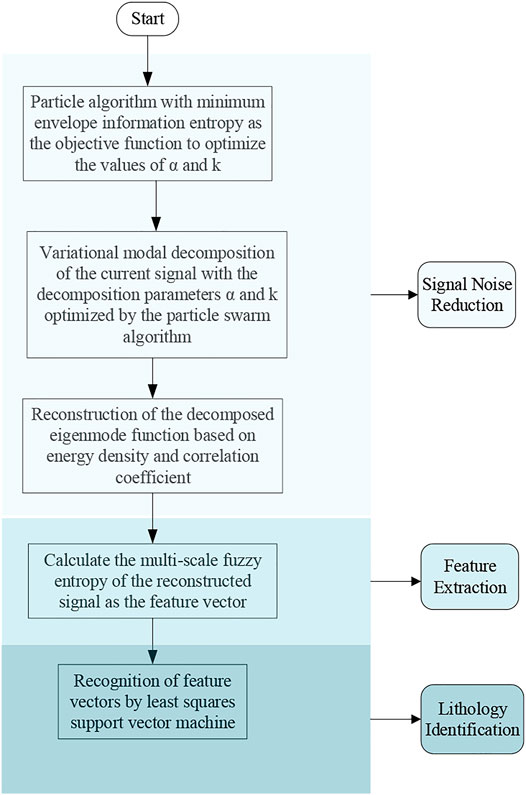
A simulated excavation experiment platform is built to simulate the cutting process and obtain the current sensor data of the excavator working on different lithologies to realize the identification of rock properties while cutting rock walls to improve the excavation efficiency. The current data are firstly decomposed by adaptive variational modal decomposition and the components are reconstructed according to the energy density and correlation coefficient criterion, Next, the multi-scale fuzzy entropy is used as the current signal feature vector. Finally, the least-squares support vector machine (LSSVM) is used to classify the features to achieve the purpose of identifying different lithologies.

Research on Lithology Identification Methods

Variational Modal Decomposition

Variational modal decomposition (VMD) is a nonlinear signal processing method that determines the center frequency and bandwidth of each component by iteratively searching the variational model in the optimal solution to achieve the effective separation of each signal component. VMD can highlight the local characteristics of the data.

The constrained variational model constructed by the VMD algorithm is (Dragomiretskiy and Zosso, 2013):

$\{\begin{array}{l}\underset{\left\{u_k\right\},\left\{{\omega }_k\right\}}{\min }\{{{\displaystyle \sum _k\Vert d_t\left[\left(\delta \left(t\right)+\frac{j}{\pi t}\right)\cdot u_k\left(t\right)\right]e^{-j{\omega }_{k}t}\Vert }}_2^2\\ s_{\cdot }{t}_{\cdot }{\displaystyle \sum _k{u}_k=f}\end{array}(1)$

Where $u_k$ is the component of each mode, ${\omega }_k$ is the central frequency of each mode component, $\delta \left(t\right)$ is the pulse function, and $k$ is the number of modes obtained by decomposition.

To solve the variational problem, the model is converted into an unconstrained variational solution by introducing Lagrange multipliers $\lambda$ and multiplicative factors $\alpha$, where the extended Lagrange operator equation is:

$L\left(\left\{u_k\right\},\left\{{\omega }_k\right\},\lambda \right)=\alpha {\displaystyle \sum _k{\Vert {\partial }_t\left[\left(\delta \left(t\right)+\frac{j}{\pi t}\right)\cdot u_k\left(t\right)\right]e^{-j{\omega }_{k}t}\Vert }_2^2+{\Vert f\left(t\right)-{\displaystyle \sum _k{u}_k\left(t\right)}\Vert }_2^2}+\langle \lambda \left(t\right),f\left(t\right)-{\displaystyle \sum _k{u}_k\left(t\right)}\rangle (2)$

Then the multiplier alternating direction method is used to search for the extended Lagrangian expression, and the updated equation for each modal component $u_k$, central frequency ${\omega }_k$, and Lagrangian operator is:

${\widehat{u}}_k^{n+1}\left(\omega \right)=\frac{\widehat{f}\left(\omega \right)-{\displaystyle \sum _{i\ne k}\widehat{u}\left(\omega \right)}+\frac{\lambda \left(\omega \right)}{2}}{1+2\alpha {\left(\omega -{\omega }_k\right)}^2}(3)$

${\omega }_k^{n+1}=\frac{{\displaystyle {\int }_0^{\infty }\omega {\left|{\widehat{u}}_k\left(\omega \right)\right|}^{2}d\omega }}{{\displaystyle {\int }_0^{\infty }{\left|{\widehat{u}}_k\left(\omega \right)\right|}^{2}d\omega }}(4)$

${\widehat{\lambda }}^{n+1}\left(\omega \right)=\widehat{\lambda }\left(\omega \right)+\tau \left(\widehat{f}\left(\omega \right)-{\displaystyle \sum _{k=1}^K{\widehat{u}}^{n+1}\left(\omega \right)}\right)(5)$

If the following equation, with $e>0,$ is satisfied for a given discriminant accuracy, then VMD can be achieved.

${\displaystyle \sum _k{\Vert {\widehat{u}}_{k,n+1}-{\widehat{u}}_{k,n}\Vert }_2^2}/{\Vert {\widehat{u}}_{k,n}\Vert }_2^2<e(6)$

Combined with the above VMD decomposition process, there are four main parameters: decomposition mode number $k$, penalty factor $\alpha$, noise tolerance $\tau$, and convergence error $e$. Among them, the decomposition mode number $k$ and penalty factor $\alpha$ significantly influence the decomposition performance; the decomposition signal will be incomplete if the value of $k$ is too small, while too large a value will lead to over-decomposition and modal mixing. $\alpha$ will be large when the bandwidth of decomposition mode is small, and the bandwidth of decomposition mode will be small if $\alpha$ is too large. Therefore, the key to determining the decomposition modes is to determine the decomposition mode number $k$ and penalty factor $\alpha$ correctly.

Particle Swarm Algorithm Optimized Variational Modal Decomposition

The particle swarm algorithm (Kennedy and Eberhart, 1995; Eberhart and Kennedy, 2002) is a population-based evolutionary algorithm. The core idea of the algorithm is that each feasible solution is considered a “particle” and all solutions are scales of particles, each of which has an adaptation value determined by the fitness function. Each particle also has a velocity that determines its position and direction. These particles are updated iteratively in the solution space following the optimal particle value gbest and the individual extreme value pbest, and finally converge to the optimal solution. The velocity and position update is performed as follows:

$v_{id}\left(t+1\right)=\lambda v_{id}\left(t\right)+{\kappa }_1{r}_1\left(pbest\left(t\right)-x_{id}\left(t\right)\right)+{\kappa }_2{r}_2\left(gbest\left(t\right)-x_{id}\left(t\right)\right)(7)$

$x_{id}\left(t+1\right)=x_{id}\left(t\right)+\alpha v_{id}\left(t\right)(8)$

where $d$ is the dimension of the particle; $\lambda$ is the inertia weight, ${\kappa }_1$ and ${\kappa }_2$ are the learning factors, usually chosen between [0, 2], $r_1$ and $r_2$ are random values, and $\alpha$ is the constraint factor, which controls the weight of the velocity. The position change and velocity change should be constrained according to the actual situation so that they do not exceed the boundary values.

The number of decomposition modes $k$ and the penalty factor $\alpha$ for VMD decomposition can be determined quickly using the particle swarm algorithm; however, this optimization process requires an objective function to qualify the optimization. The information entropy can well reflect the sparsity of the decomposition signal, and the magnitude of its value can reflect the uniformity of the probability distribution. The most uncertain distribution will have the largest entropy value. Information entropy is based on this concept. The envelope signal obtained after applying the demodulation operation on the signal gets processed into a series of probability distributions $p_i$, and the entropy value calculated from it reflects the sparsity of the original signal. After the noise reduction process, the more the information contained, the smaller the minimum envelope information entropy is. In this paper, the minimum envelope information entropy is used as the fitness function of the PSO algorithm.

$p_i=\frac{a_i}{{\displaystyle {\sum }_{i=1}^N{a}_i}},i=\mathrm{1,2},\dots \dots ,N(9)$

$a_i$ is the envelope amplitude of the $i$ th point of the modal signal after VMD decomposition, $N$ is the length of the modal signal after VMD decomposition, and $p_i$ is the normalized envelope of the modal signal.

$IMF{F}_{EE}\left(k\right)=-{\displaystyle \sum _{j=1}^N{p}_i{\log }_2\left(p_j\right)}(10)$

$IMF{F}_{EE}\left(k\right)$ is the entropy of the envelope information of the k modal signals.

$MEE=\min \left\{IMF{F}_{EE}\left(1\right),\dots \dots ,IMF{F}_{EE}\left(k\right)\right\}(11)$

The minimum value of envelope information entropy of $k$ modal signals is chosen as the minimum envelope information entropy, which is the adaptation function MEE. When the adaptation function reaches the minimum value, i.e., the minimum envelope information entropy reaches the minimum, the best decomposition modal number $k$ and penalty factor $\alpha$ are determined to achieve adaptive decomposition.

Signal Reconstruction

When decomposing the current signal using PSO-optimized VMD, the sampling rate may be insufficient, and spurious intrinsic mode function (IMF) components may occur. This problem is addressed by combining energy density and correlation coefficient to reconstruct the components of the current signal truncated from different lithology acquisitions. The steps are as follows.

1) Perform energy analysis on the four components obtained and calculate the energy density of each IMF:

$E_k=\frac{1}{K}{\displaystyle \int {\left|C_k\left(t\right)\right|}^2}dt=\frac{1}{K}{\displaystyle \sum _{d=1}^K{\left[x_k\left(d\right)\right]}^2}(12)$

where E_k is the energy density of the $k$^th energy mode, $k$ is the length of the IMF, and $x_k\left(d\right)$ is the amplitude of the $k$^th IMF component.

2) Analysis of the correlation between the IMF component and the cutting current signal.

$R_k=\frac{E\left[\left(C_k-{\mu }_k\right)\left(y-\mu \right)\right]}{{\sigma }_k\sigma }(13)$

$R_k$ denotes the mathematical expectation, ${\mu }_k$ is the mean of the IMF components, $\mu$ is the mean of the original signal y, ${\sigma }_k$ is the standard deviation of the IMF components, and $\sigma$ is the standard deviation of the original current signal.

The average energy of the IMF components of the intercepted current signals of the four lithologies multiplied by the correlation coefficient. The three IMF components with the largest product are selected and superimposed to reconstruct the simulated current signals of the four lithologies.

Feature Extraction

The relevant features, such as the input for recognition, need to be extracted from the reconstructed current signal. Multi-scale fuzzy entropy is based on fuzzy entropy with the addition of scale factors. The fuzzy entropy value of the same time series under different scale factors, which can effectively overcome the defects of single-scale fuzzy entropy value, is used to measure the possible abrupt changes of time series to effectively measure the nonlinearity and complexity changes of the current signal. The algorithm description of multi-scale fuzzy entropy is:

1) Construct a new coarse-grained vector $y_j\left(\tau \right)$ for the reconstructed current signal $X_i=\left\{x_1,x_2,\dots ,x_n\right\}$, where $N$ denotes the sequence length

$y_j\left(\tau \right)=\frac{1}{\tau }{\displaystyle \sum _{i=\left(j-1\right)\tau +1}^{j\tau }{x}_i},1\le j\le \frac{N}{\tau }(14)$

Where $\tau =\mathrm{1,2},\dots ,n$ denotes the scale factor. When $\tau =1,$ $\left\{y_1\left(1\right),y_2\left(1\right),\cdots ,y_n\left(1\right)\right\}=X_i$ is the original time series.

2) Fuzzy entropy solutions of all time series $y_j\left(\tau \right)$ are converted into the corresponding scale factor function.

Rockiness Identification

The LSSVM is an improvement of the support vector machine, using equations instead of inequality constraints, and applying the linear least-squares criterion to the optimization of the loss function to improve the convergence efficiency, with the following process (Fu et al., 2021):

1) The training data set $\left\{\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots ,\left(x_n,y_n\right)\right\}$ in which x_i is the $i$^th input sample and $y_i$ is the output variable, and the kernel function mapping is used to construct the regression function in the high-dimensional space as follows:

$y\left(x\right)=\omega \cdot \phi \left(x\right)+b(15)$

where $\omega$ is the weight vector and $\phi \left(x\right)$ is the normal vector and b is the intercept of the hyperplane in the high-dimensional space.

2) According to the structural risk minimization criterion, $\omega$ and $b$ must be optimized. The optimization equations are:

$\{\begin{array}{c}\min J\left(\omega ,\zeta \right)=\frac{1}{2}{\Vert \omega \Vert }^2+\frac{\gamma }{2}{\displaystyle \sum _{i=1}^n{\xi }_i^2}\\ s.t.y_i={\omega }^T\cdot \phi \left(x_i\right)+b+{\xi }_i\end{array}(16)$

Where $\gamma$ is the regularization parameter and ${\xi }_i$ is the relaxation variable.

3) Construction of Lagrangian function

$L\left(\omega ,b,\xi ,\alpha \right)=\frac{1}{2}{\Vert \omega \Vert }^2+\frac{\gamma }{2}{\displaystyle {\sum }_{i=1}^n{\xi }_i^2}-{\displaystyle {\sum }_{i=1}^n{\alpha }_i\left(\omega \cdot \phi \left(x_i\right)+b-y_i+{\xi }_i\right)}(17)$

Here ${\alpha }_i$ is the Lagrangian multiplier corresponding to $x_i$.

4) Find the partial differential for $\omega$, $b$, $\xi$, $\alpha$, get the optimal value, and establish the regression function

$y\left(x\right)={\displaystyle \sum _{i=1}^n{\alpha }_{i}K\left(x,x_i\right)+b}(18)$

where $K\left(x_i,x_j\right)$ is the kernel function.

In lithology identification with LSSVM, the choice of kernel function significantly influences the identification performance of LSSVM. It is known from the literature that the prediction accuracy of radial basis kernel function is higher (Jiang et al., 2016); hence, the radial basis kernel function is chosen as the kernel function of LSSVM in this paper.

$K\left(x_i,x_j\right)=\exp \left(-\frac{{\Vert x_i,x_j\Vert }^2}{2{\sigma }^2}\right)(19)$

Where $\sigma$ is the kernel width.

The flow chart of PSO-VMD-LSSVM based lithology identification method is shown in Figure 1.

FIGURE 1

FIGURE 1. Flow chart of PSO-VMD-LSSVM algorithm.

Cut-Off Motor Current Signal Acquisition

Experimental Platform for Simulating Roadheading

As shown in Figure 2, the roadheading experimental platform, mainly comprising the propulsion system, the cutting system, and the signal acquisition system, was built to obtain the current sensor data of the roadheader under different lithology cutting work. The propulsion system comprises a 0.75 kW servo motor as the cutting propulsion motor and two slide rails as the walking guide. The cutting system uses a 1.5 kW, 60:1 reduction ratio gear motor with a frequency converter to control the cutting drilling speed. A cutting head of the roadheader with equal proportional reduction is used as the cutting tool for cutting different rock properties. The signal acquisition system uses 1.4 J LT series three-phase AC sensor; the output is analog with a range: 0 ∼ 5 V and response time is under 1 ms. LabJack T7-PRO data acquisition card, used to collect the analog output of the current sensor, is connected to the upper computer; the upper computer processes and analyzes the collected current data.

FIGURE 2

FIGURE 2. Diagram of the tunneling experiment platform.

Lithology Specimen Production

When studying the damage process, the damage of rocks is related to the force and the different rock properties (Du et al., 2020c), and the difference of compressive strength, density, and elastic modulus of similar materials can be used as a basis for different lithologies (Liu et al., 2020). In this paper, four specimen blocks with four different lithologies were prepared with four different ratios to realize the identification of lithology in the process of cutting off rocks wall using a roadheader. We selected quartz sand as the aggregate, cement and gypsum as the cementing material, and borax as an additive, collectively in four ratios (Shi et al., 2015). After weighing, mixing, compacting, resting, and air-drying, four similar simulated specimens with different lithologies were prepared as shown in Figure 3; the ratios of the four lithologies and rock mechanical properties are shown in Table 1.

FIGURE 3

FIGURE 3. Four similar simulated specimens.

TABLE 1

TABLE 1. Four types of ratios and rock mechanical properties.

As seen from Table 1, the mastic sand ratio plays a major role in controlling the uniaxial compressive strength and elastic modulus of similar materials; these quantities decrease significantly with the increase of the mastic sand ratio. The density, compressive strength, and elastic modulus of similar materials made with the selected four ratios are uniformly large and different. Thus, the simulated specimens can represent four kinds of lithologies.

Digging Simulation Experiment

After the four pieces of specimens were left to air-dry and stabilize, the tunneling simulation experiment was carried out for the four specimen blocks with different lithologies by controlling the reducer motor parameters; the cutting head was rotated at a speed of 10 r/min and the propulsion motor at a propulsion speed of 0.5 m/min, as shown in Figure 4.

FIGURE 4

FIGURE 4. Diagram of tunneling simulation experiment.

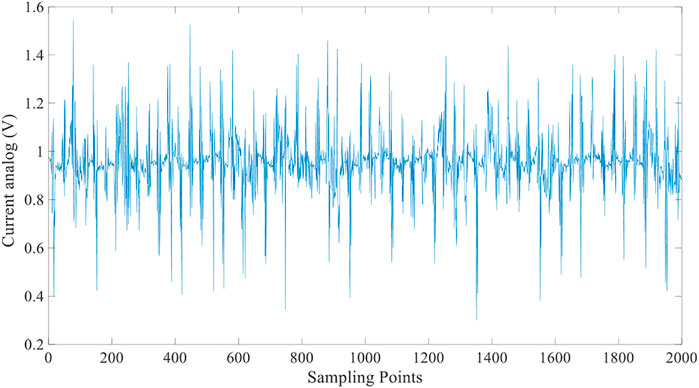
As shown in Figure 4, the four roadheader cut-off motor currents were obtained by conducting the tunneling simulation experiments on the four simulated rock specimens of different lithologies, using 2048 sampling points. The results of the cut-off motor current sampling for cut-off lithology 1 are shown in Figure 5.

FIGURE 5

FIGURE 5. Cut-off lithology 1 cut-off motor current sampling graph.

Experimental Results and Discussion

To verify the effectiveness of adaptive modal decomposition, the current signal of the truncated motor on lithology 1 working steadily for 4s, is first subjected to variable modal decomposition with custom decomposition parameters. The input parameters are chosen as follows: decomposition modal number $k$ = 3, penalty factor under $\alpha$ = 3000, noise tolerance $\tau$ = 0 and convergence error $e$ = 10⁻⁷, to obtain the decomposition results shown in Figure 6.

FIGURE 6

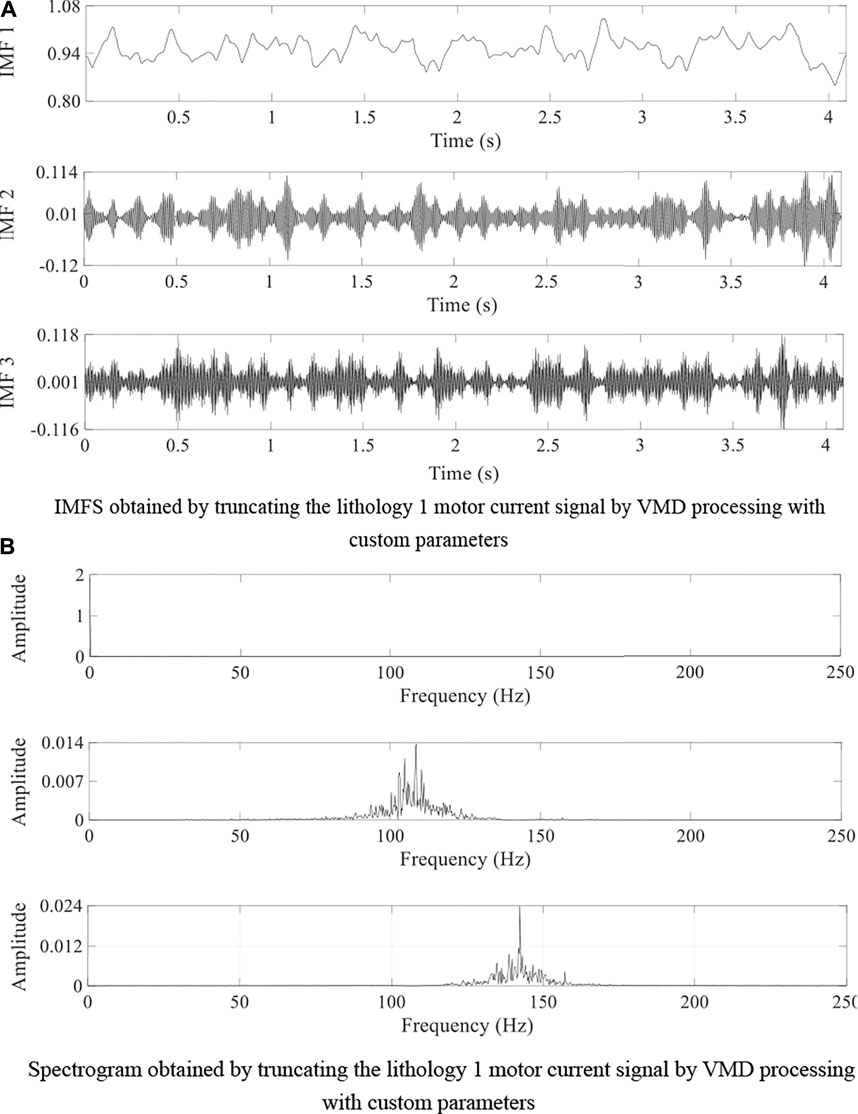
FIGURE 6. VMD with custom parameters to process the truncated lithology 1 motor current signal graph. (A) IMFs obtained by truncating the lithology 1 motor current signal by VMD processing with custom parameters (B) Spectrogram obtained by truncating the lithology 1 motor current signal by VMD processing with custom parameters.

As seen in Figure 6, using VMD with custom decomposition parameters will lead to no decomposition results at frequencies 0–70 Hz, incomplete signal decomposition, modal mixing at 114–138 Hz as the main frequency separation is not complete because the signal mainly contains the frequency signal and is not completely decomposed. Therefore, the particle swarm algorithm with the minimum envelope information entropy as the fitness function is used to optimize the selection of the parameters of the variational modal decomposition. The parameters of the particle swarm algorithm are initialized to the following values: dimension of particles, $d$ = 2; r $\lambda$ = 0.8; learning factors ${\kappa }_1$ and ${\kappa }_2$ are 1 and 2, respectively; number of iterations = 15; particle population size = 30. The selection of VMD parameters is optimized, and the penalty factors of the four lithologies and the number of decomposition layers corresponding to the envelope entropy part of the selection point iteration curve are shown in Figure 7.

FIGURE 7

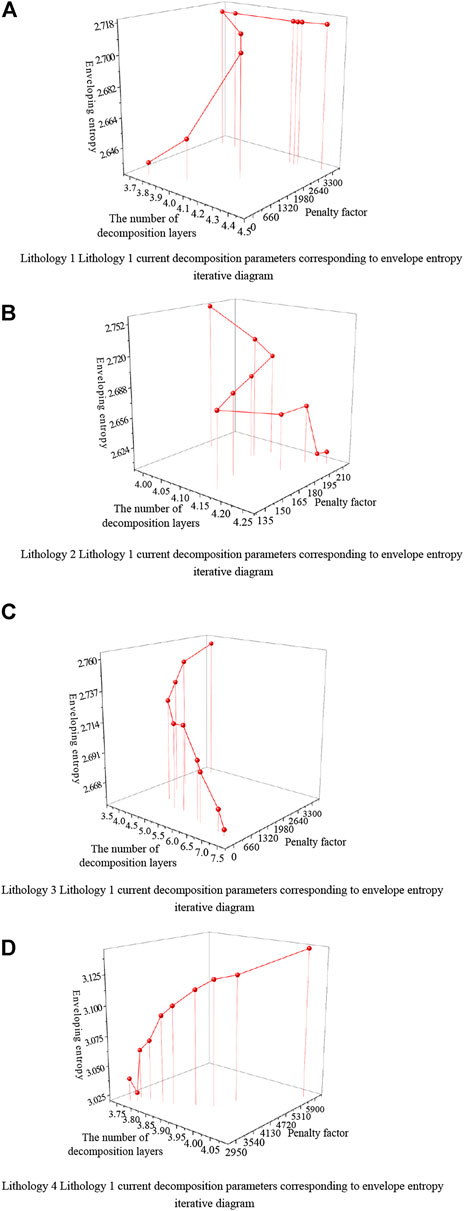
FIGURE 7. Truncation current decomposition parameters corresponding to the iterative process of envelope entropy. (A) Lithology 1 Lithology 1 current decomposition parameters corresponding to envelope entropy iterative diagram (B) Lithology 2 Lithology 1 current decomposition parameters corresponding to envelope entropy iterative diagram (C) Lithology 3 Lithology 1 current decomposition parameters corresponding to envelope entropy iterative diagram (D) Lithology 4 Lithology 1 current decomposition parameters corresponding to envelope entropy iterative diagram.

As seen in Figure 7, using PSO to optimize the VMD parameter selection first uses the envelope entropy as the objective function to randomly select the decomposition modal number $k$ and penalty factor $\alpha$ as the initial positions of the particles, and then calculates the envelope entropy value corresponding to each particle position. Next, the optimization function continuously compares the envelope entropy values and selects the minimum value of the envelope entropy for each update and determines the parameters $k$ and $\alpha$ at this minimum position as the local extremes. Finally, the global minimum as the final decomposition modal number $k$ and penalty factor $\alpha$ are selected. The lithologies of the four truncated motor current simulation signals are determined by the particle swarm algorithm as the best decomposition parameters with different penalty factors, wit the number of decomposition layers set to 4. Under these parameters, the fitness function of the particle swarm algorithm, i.e., the envelope entropy, reaches the minimum.

The variable modal decomposition of the cutter motor current signal after the particle swarm algorithm optimizes the value of the excavator under the four different lithologies is shown in Figure 8.

FIGURE 8

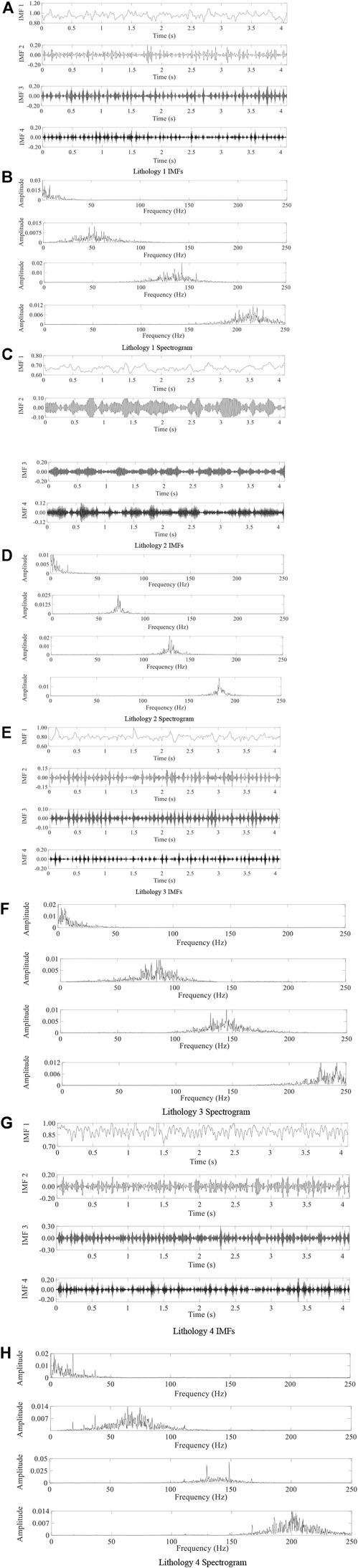
FIGURE 8. Results of truncated motor current signal decomposition of PSO-VMD for four lithologies. (A) Lithology 1 IMFs (B) Lithology 1 Spectrogram (C) Lithology 2 IMFs (D) Lithology 2 Spectrogram (E) Lithology 3 IMFs (F) Lithology 3 Spectrogram (G) Lithology 4 IMFs (H) Lithology 4 Spectrogram.

As seen from the above figure, the PSO-VMD determines the optimal decomposition parameters modal number $k$ and penalty factor $\alpha$. The VMD decomposition of the truncated currents of the four lithologies achieves an adaptive and completely non-recursive decomposition, effectively separating each modal component of the four current signals and overcoming the problems of endpoint effects and modal component mixing, with a good decomposition effect.

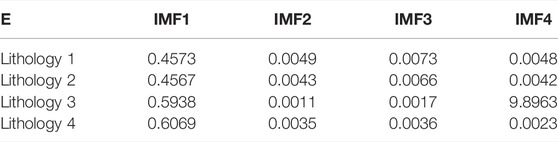
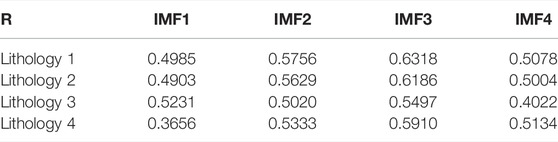
The results of calculating the average energy density and correlation coefficient for the decomposed current signal eigenmode function are shown in Tables 2, 3.

TABLE 2

TABLE 2. Truncated motor current signal IMF component average energy density table.

TABLE 3

TABLE 3. Truncated motor current signal IMF component correlation coefficient table.

The average energy of the IMF components of the current signals of the four lithologies are correspondingly multiplied by the average energy. The three IMF components with the largest product are superimposed to reconstruct the current analog signals of the four lithologies. The signal-to-noise ratio before and after signal reconstruction is shown in Table 4.

TABLE 4

TABLE 4. Signal-to-noise ratio comparison before and after signal reconstruction.

The PSO-VMD reconstructs the eigenmodes based on the correlation coefficient and energy density to reduce the noise of the original truncated current signal (Liang et al., 2021).

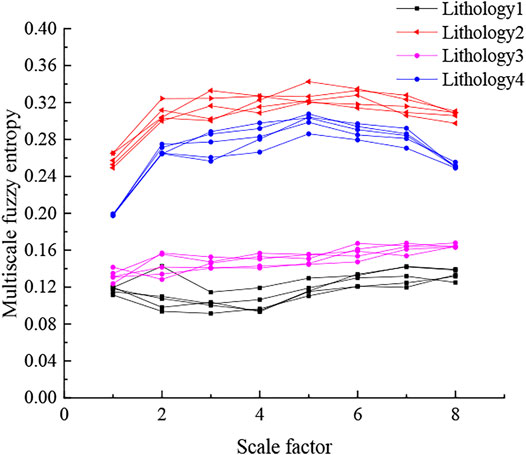
After noise reduction of the current signal, multi-scale fuzzy entropy is calculated, with the scale factor set to 8 and the similarity tolerance limit of 0.15. Fifty sets of 8-scale fuzzy entropy are taken for each of the current signals truncated on the four lithologies to obtain a total of 200 sets of 8-scale fuzzy entropy. Part of the 8-scale fuzzy entropy is shown in Figure 9.

FIGURE 9

FIGURE 9. Fuzzy entropy values of the four current reconstruction signals with scale factor.

As seen from Figure 9, the fuzzy entropy values of lithology 1 and lithology 3 overlap when the scale factor is 2. When the scale factors are 3, 4, and 5, the scale factors of lithology 2 and lithology 4 do not differ much. Finally, when the scale factors are 5, 6 and 7, the scale factors of lithology 1 and lithology 3 are closer, but they do not overlap. In general, the multi-scale fuzzy entropy of each lithology is distinguishable and can be used as a feature vector for identifying these four lithologies.

Forty sets of 50 sets of multiscale fuzzy entropy for each lithology were randomly selected as the training set and 10 sets as the test set. Finally, the four lithologies are classified using a least squares support vector machine with kernel function as the radial basis function. Considering the regularization parameter $\gamma$ as 3.1 and the kernel width $\sigma$ as 10, the lithology was identified using LSSVM for the eigenvectors of the current signal with VMD of custom parameters; the recognition rate was 87.%. Further, the lithology was identified for the current signal optimized using PSO-VMD, and the final recognition rate was 97.5%. The recognition results are shown in Figure 10.

FIGURE 10

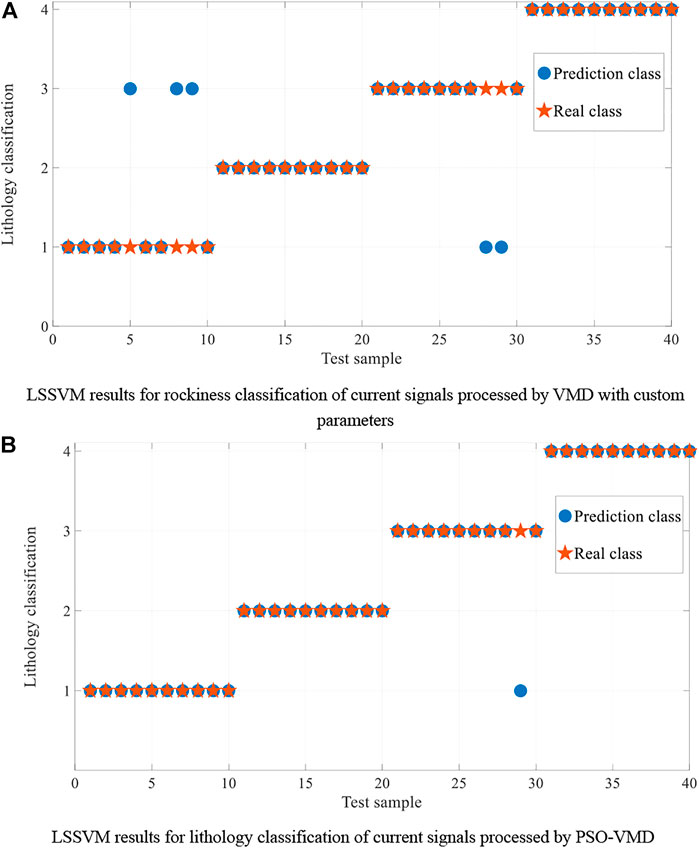
FIGURE 10. LSSVM recognition result graph. (A) LSSVM results for rockiness classification of current signals processed by VMD with custom parameters (B) LSSVM results for lithology classification of current signals processed by PSO-VMD.

As seen from Figure 10, using LSSVM to identify the lithology of the current signal processed by VMD with custom decomposition parameters, three of the ten test groups of lithology 1 failed to identify lithology 1 as lithology 3, and two of the test groups of lithology 3 identified lithology 3 as lithology 1, possibly due to the inconspicuous difference between the features of lithology 1 and 3 by multi-scale fuzzy entropy. While identifying the PSO-VMD processed current signals using LSSVM, only lithology 3 was identified as lithology 1 in one test group; the identification effect was better, and the recognition rate was improved by 10% relative to the custom parameter processed VMD.

In this study, we first obtained the eigenmode function by PSO-VMD, and then obtained the reconstructed current signal by summing the eigenmode function with energy density and correlation coefficient criterion. Multi-scale fuzzy entropy was used as the feature vector, and finally, the LSSVM was used to identify different lithologies. Further improvement of the recognition efficiency could be realized by applying other methods to improve the signal-to-noise ratio before and after noise reduction, or feature vectors with better differentiation between different lithologies.

Conclusion

Aiming to resolve the lithology identification problem of cut-off rock walls during excavation, we obtained current sensor data by building an excavation experiment platform and proposed an intelligent lithology identification method of PSO-VMD-LSSVM. The following conclusions are mainly obtained.

1) The particle swarm algorithm using the minimum envelope information entropy as the fitness function can optimize the parameter selection of the variational modal function of the current signal, ensuring that the parameters of the VMD can be selected adaptively.

2) The energy density and correlation coefficient criteria are used to reconstruct the modal components of the current signal after the VMD to increase the signal-to-noise ratio of the current signal.

3) Multi-scale fuzzy entropy is used as a feature vector for truncating the reconstructed current signal of different lithologies. It can be used as a feature vector for recognition because it has better differentiation for different lithologies under different scale factors.

4) The lithology classification by the LSSVM is performed for the VMD with custom decomposition parameters and the PSO-VMD; the recognition results are 87.5 and 97.5%, respectively. Thus, the PSO-VMD can improve the recognition rate of the LSSVM.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

PQ: Conceptualization, Methodology, Software, Data curation, Validation, Writing-original draft. JC: Writing-review and editing, Funding acquisition. XC: Supervision, Writing-review and editing, Funding acquisition. TW: Writing-review and editing. XZ: Writing-review. MW: Data curation.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No.52174105), Collaborative Innovation Project of Anhui University(GXXT-2019-029), University-level key projects of Anhui University of science and technology (xjzd2020-14), the Key Projects of Natural Science Research in Anhui Universities (KJ2021A0426).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Dai, B. (2020). Coal-rock Identification Method Based on Load Data Fusion of Shearer Rocker Axle. China: Liaoning Technical University. doi:10.27210/d.cnki.glnju.2020.000032

CrossRef Full Text | Google Scholar

Dragomiretskiy, K., and Zosso, D. (2013). Variational Mode Decomposition. IEEE Transactions Signal. Processing 62 (3), 531–544.

Google Scholar

Du, K., Li, X.-f., Yang, C.-z., Zhou, J., Chen, S.-j., and Manoj, K. (2020a). Experimental Investigations on Mechanical Performance of Rocks under Fatigue Loads and Biaxial Confinements. J. Cent. South. Univ. 27 (10), 2985–2998. doi:10.1007/s11771-020-4523-7

CrossRef Full Text | Google Scholar

Du, K., Li, X., Tao, M., and Wang, S. (2020b). Experimental Study on Acoustic Emission (AE) Characteristics and Crack Classification during Rock Fracture in Several Basic Lab Tests. Int. J. Rock Mech. Mining Sci. 133, 104411. doi:10.1016/j.ijrmms.2020.104411

CrossRef Full Text | Google Scholar

Du, K., Yang, C., Su, R., Tao, M., and Wang, S. (2020c). Failure Properties of Cubic Granite, marble, and sandstone Specimens under True Triaxial Stress. Int. J. Rock Mech. Mining Sci. 130, 104309. doi:10.1016/j.ijrmms.2020.104309

CrossRef Full Text | Google Scholar

Eberhart, R., and Kennedy, J. (2002). “A New Optimizer Using Particle Swarm Theory,” in Mhs95 Sixth International Symposium on Micro Machine & Human Science, Nagoya, Japan, 4-6 Oct. 1995 (IEEE).

Google Scholar

Fu, L., Li, P., and G ao, L. (2021). Improved LSSVM Algorithm Considering Sample Outliers. Chin. J. Scientific Instrument 42 (06), 179–190. doi:10.19650/j.cnki.cjsi.J2107724

CrossRef Full Text | Google Scholar

Gao, F., Yin, X., Liu, Q., Huang, X., Bo, Y., Zhang, T., et al. (2021). Coal-rock Image Recognition Method for Mining and Heading Face Based on Spatial Pyramid Pooling Structure. J. China Coal Soc. 46 (12), 4088–4102. doi:10.13225/j.cnki.jccs.2021.0624

CrossRef Full Text | Google Scholar

He, Y., Tian, M., Song, J., Feng, J., and Dong, Z. (2020). Rock Hardness Identification Based on Cutting Motor Current of Roadheader. Saf. Coal Mines 138 (12), 159–162. doi:10.13347/j.cnki.mkaq.2020.12.032

CrossRef Full Text | Google Scholar

Jiang, Y., Yang, X., He, F., Chen, L., and He, Z. (2016). Super-short-time Wind Power Forecasting Based on EEMD-IGSA-LSSVM[J]. J. Hunan University(Natural Sciences) 43 (10), 70–78. doi:10.16339/j.cnki.hdxbzkb.2016.10.009

CrossRef Full Text | Google Scholar

Kennedy, J., and Eberhart, R. (1995). “Particle Swarm Optimization,” in Icnn95-international Conference on Neural Networks, Perth, WA, Australia, 27 Nov.-1 Dec. 1995 (IEEE).

Google Scholar

Li, L., and Ouyang, C. (2017). Research on Coal-Rock Interface Recognition Based on Ultrasonic Phased Array. J. China Univ. Mining Tech. 46 (03), 485–492. doi:10.13247/j.cnki.jcumt.000668

CrossRef Full Text | Google Scholar

Liang, Y., Tiegen, L., Kun, L., Junfeng, J., and Yafan, L. (2021). Optimized Gas Detection Method Based on Variational Mode-Decomposition Algorithm. Chin. J. Lasers 48 (7), 0706003–706011. doi:10.3788/CJL202148.0706003

CrossRef Full Text | Google Scholar

Liu, Y., Zhou, W., Guo, B., Ma, Q., and Xiao, H. (2020). Study on Similar Materials in Similar Simulation Test. Chin. J. Rock Mech. Eng. 39 (S1), 2795–2803. doi:10.13722/j.cnki.jrme.2019.0885

CrossRef Full Text | Google Scholar

Sampath, K. H. S. M., Perera, M. S. A., Li, D., Ranjith, P. G., and Matthai, S. K. (2019). Characterization of Dynamic Mechanical Alterations of Supercritical Co2-Interacted Coal through Gamma-ray Attenuation, Ultrasonic and X-ray Computed Tomography Techniques - Sciencedirect. J. Pet. Sci. Eng. 174, 268–280. doi:10.1016/j.petrol.2018.11.044

CrossRef Full Text | Google Scholar

Shi, X., Liu, B., and Xiao, J. (2015). A Method for Determining the Ration of Similar Materials with Cement and Plaster as Bonding Agents. Rock Soil Mech. 36 (05), 1357–1362. doi:10.16285/j.rsm.2015.05.017

CrossRef Full Text | Google Scholar

Wang, C., and Zhang, Q. (2020). Coal Rock Image Feature Extraction and Recognition Method Based on LBP and GLCM. Saf. Coal Mines 51 (04), 129–132. doi:10.13347/j.cnki.mkaq.2020.04.028

CrossRef Full Text | Google Scholar

Wang, H., and Zhang, Q. (2018). Dynamic Identification of Coal-Rock Interface Based on Adaptive Weight Optimization and Multi-Sensor Information Fusion. Inf. Fusion 51, 114–128. doi:10.1016/j.inffus.2018.09.007

CrossRef Full Text | Google Scholar

Wang, S., Wang, S., and Liu, W. (2021a). The Measurement Model and Error Analysis for Shearer Cutting Height. Chin. J. Sci. Instrument 42 (04), 140–149. doi:10.19650/j.cnki.cjsi.J2107324

CrossRef Full Text | Google Scholar

Wang, X., Ding, E., Hu, K., and &Zhao, R. (2016). Effects of Coal-Rock Scattering Characteristics on the GPR Detection of Coal-Rock Interface. J. China Univ. Mining Tech. 45 (01), 34–41. doi:10.13247/j.cnki.jcumt.000455

CrossRef Full Text | Google Scholar

Wang, X., Gao, F., Chen, J., He, P., and Jing, Z. (2021b). Generative Adversarial Networks Based Sample Generation of Coal and Rock Images. J. China Coal Soc. 46 (09), 3066–3078. doi:10.13225/j.cnki.jccs.2020.1718

CrossRef Full Text | Google Scholar

Wang, X., Zhao, D., and Ding, E. (2018). Coal-rock Identification Method Based on Terahertz Spectroscopy Technology. Coal Mining Tech. (01), 13–17+91. doi:10.13532/j.cnki.cn11-3677/td.2018.01.004

CrossRef Full Text | Google Scholar

Yang, J., Zhang, Q., Wang, C., Chang, B., Wang, X., Ge, S., et al. (2020). Status and Development of Robotization Research on Roadheader for Coal Mines. J. China Coal Soc. (08), 2995–3005. doi:10.13225/j.cnki.jccs.2019.1452

CrossRef Full Text | Google Scholar

Yin, Z., Chen, W., Hao, H., Chang, J., Zhao, G., Chen, Z., et al. (2019). Dynamic Compressive Test of Gas-Containing Coal Using a Modified Split Hopkinson Pressure Bar System. Rock Mech. Rock Eng. 53, 815–829. doi:10.1007/s00603-019-01955-w

CrossRef Full Text | Google Scholar

Yin, Z. Q., Xi-Bing, L. I., Jin, J. F., Xian-Qun, H. E., and Kun, D. U. (2012). Failure Characteristics of High Stress Rock Induced by Impact Disturbance under Confining Pressure Unloading. Chin. J. Mech. Eng. 22, 175–184.

CrossRef Full Text | Google Scholar

Zhang, J., Han, X., and Cheng, D. (2022). Improving Coal/gangue Recognition Efficiency Based on Liquid Intervention with Infrared Imager at Low Emissivity. Measurement 189, 110445. doi:10.1016/j.measurement.2021.110445

CrossRef Full Text | Google Scholar

Zhang, Q., Liu, Z., and Qiu, J. (2017). Design of Cutting Vibration Signal Acquisition and Recognition System for a New Type of Shearer. Colliery Mech. Electr. Tech. (06), 1–4+8. doi:10.16545/j.cnki.cmet.2017.06.001

CrossRef Full Text | Google Scholar

Zhang, Q., Sun, S., Zhang, K., Zhang, X., and Guo, T. (2020). Coal and Rock Interface Identification Based on Active Infrared Excitation. J. China Coal Soc. (09), 3363–3370. doi:10.13225/j.cnki.jccs.2019.0748

CrossRef Full Text | Google Scholar