- 1School of Resources and Safety Engineering, Central South University, Changsha, China
- 2Department of Mechanical and Industrial Engineering, Norwegian University of Science and Technology, Trondheim, Norway
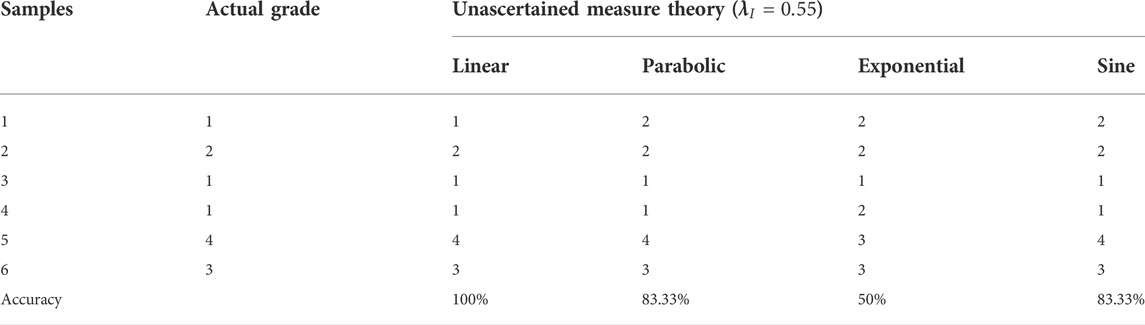
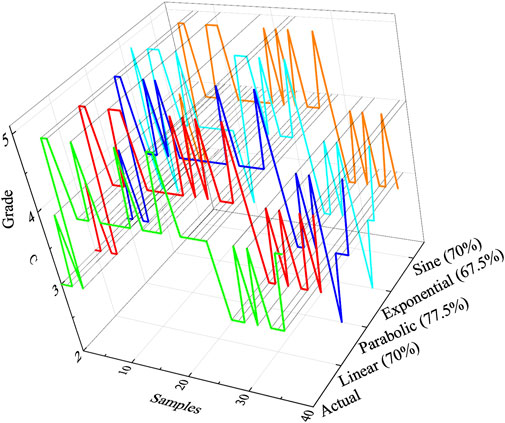
Tunnel squeezing brought great difficulties to the construction and severely threatened the safety of on-site operators. The researches regarding large deformation evaluation have been widely developed, but actual conditions of tunnels are considerably complex, producing a large variety of uncertainty information existing in the evaluation process. Therefore, we constructed an unascertained measurement model incorporating four membership functions for evaluation of tunnel squeezing based on the collected datasets. Simultaneously, information entropy was introduced to objectively calculate the index importance for each index. For the first group data (GPI), the accuracy associated with four membership functions are 100%, 83.33%, 50%, and 83.33%, respectively, while the accuracy of GPII are 70%、77.5%、67.5%, and 70%, respectively. Linear function and parabolic function show better performance on uncertainty information interpretation according to the classification results. The results revealed that the uncertainty model constructed in this study can enrich the available uncertainty evaluation system.
Introduction
Various technologies related to tunnel engineering have been greatly developed, such as ventilation technology, support technology, excavation technology, operation management, rock characteristics (Wang et al., 2021b; Du et al., 2022; Wang et al., 2022; Yu et al., 2022), prediction and prevention of geological disasters (Feng et al., 2015; Wang et al., 2021a; Feng et al., 2022; Zhou et al., 2021a; Zhou et al., 2021b), among which geological disasters are the main risk factors in engineering. In recent years, with the excavation of various tunnels in underground at great depth, the hazards regarding large deformation of surrounding rock frequently occurred. Currently, the scientific community gradually focused on the large deformation of excavated tunnels (Zhang et al., 2003; Singh et al., 2007; Chen, 2008; Lai et al., 2018; Sharma et al., 2020). Large deformation of surrounding rock can be divided into extrusion and expansion (Wood, 1972; Barton et al., 1974; Jethwa et al., 1984; Barla, 1995; Barla, 2001; He et al., 2002). The former occurs in soft rocks with high geostress, while the latter mainly occurs in rock mass with strong expansion properties. The stress redistribution caused by excavation exceeds the ultimate shear stress, resulting in a large-scale plastic failure zone in the surrounding rock of the tunnel (Gioda and Cividini, 1996; Panet, 1996; Barla, 2001; Singh et al., 2007; Dwivedi et al., 2013). Most of the large deformation of surrounding rock occurs in deep and long soft rock tunnels, e.g., in China, Zhegushan Highway Tunnel, Guanjiao Tunnel, Jiazhuqing Tunnel, Dazhailing Tunnel, the China-Laos railway tunnel, etc. The above-mentioned tunnels all suffered from large deformation to some extent, which brought great difficulties to the construction. In addition, the weak surrounding rock is more prone to squeeze and occur large deformation under the action of high in-situ stress. At this time, the surrounding rock ruptures and squeezes out of the tunnel boundary and further damages the supporting structure, which will seriously lead to tunnel collapse even cause damage to construction workers (Liu, 2004; Chen, 2008; Liu et al., 2008; Yu, 2020; Ren et al., 2021). The large deformation of surrounding rock is gradually accelerated with the development of time (Bhasin and Grimstad, 1996; Barla, 2001; Singh et al., 2007; Azizi et al., 2019). Therefore, the evaluation of tunnel squeezing is of great significance for improving the construction efficiency, reducing the cost, and ensuring the safety of the construction personnel (Aydan et al., 1993; Aydan et al., 1996; Hoek, 2001; Ghiasi et al., 2012; Panthi, 2013; Azizi et al., 2019).
The tunnel squeezing is a major engineering problem that needs to be solved urgently in this field. Many scholars tried to use different methods to evaluate the severity of large extrusion deformation (Dube et al., 1986; Jiang et al., 2004; Fatemi Aghda et al., 2016; Azizi et al., 2019; Liao et al., 2020). For example, Singh et al. (2007) evaluated the tunnel squeezing based on burial depth (H) and rock quality index (Q). Then, Goel et al. (1995) introduced the rock mass number N (the Q value of SRF = 1) into the fitting curve equation. Additionally, Liu et al. (2019) proposed an improved cloud model for the prediction of large deformation of surrounding rock in Mila Mountain Tunnel in Tibet based on the uncertainty and randomness of tunnel squeezing prediction. Although various methods associated with tunnel squeezing evaluation has been widely explored, the mechanism of this geological hazard is considerably complex, leading to a large variety of uncertainty exists in the evaluation of tunnel squeezing. (ISRM, 1995; Steiner, 1996; Malan and Basson, 1998; Palmstrom and Broch, 2006; Williams, 2010; Dwivedi et al., 2014; Farhadian and Nikvar-Hassani, 2020; Zhang et al., 2020).
In view of the wide application and robust uncertainty information interpretation of unascertained measurement theory in this field, e,g., stability evaluation, scheme optimization, risk assessment, and performance evaluation. This study aims to develop a hybrid model based on information entropy and unascertained measurement incorporating four membership functions to evaluate the tunnel squeezing, which is able to enrich the available risk evaluation methods for underground excavation projects.
Method description
There are n samples in the evaluation object space
Single-index measurement matrix
According to the above
The above Eq. 4
The single index measurement judgment matrix is calculated by the membership function. In this paper, we will use four types membership functions (Zhou et al., 2020b; Zhou et al., 2021a): linear, parabolic, exponential and sine functions, as shown in Eqs 5–8 respectively.
Where,
Information entropy theory
Based on the above single-index measurement matrix (Eq. 4), a more objective method is applied to determine the index weight in this paper, i.e., information entropy (Ruan et al., 2021).
Where,
Then, the index weight vector of the
Comprehensive measurement matrix
The multi-index comprehensive measurement matrix is calculated as follows (Jia et al., 2019; Ma et al., 2021).
Where,
Where,
Credible identification principle
In order to determine the grade of individual sample, the credible identification principle was utilized. The grade of samples can be calculated through Eq. 13 based on the above-mentioned comprehensive multi-index measurement vectors (Shi et al., 2010).
Where,
Sample score
Although the risk level of samples is judged through credible identification principle, it is difficult to further distinguish the severity of the tunnel deformation, that is, the large deformation cannot be quantitatively analyzed. There, each sample can be scored by the following equation.
where,
Squeezing evaluation using unascertained measurement
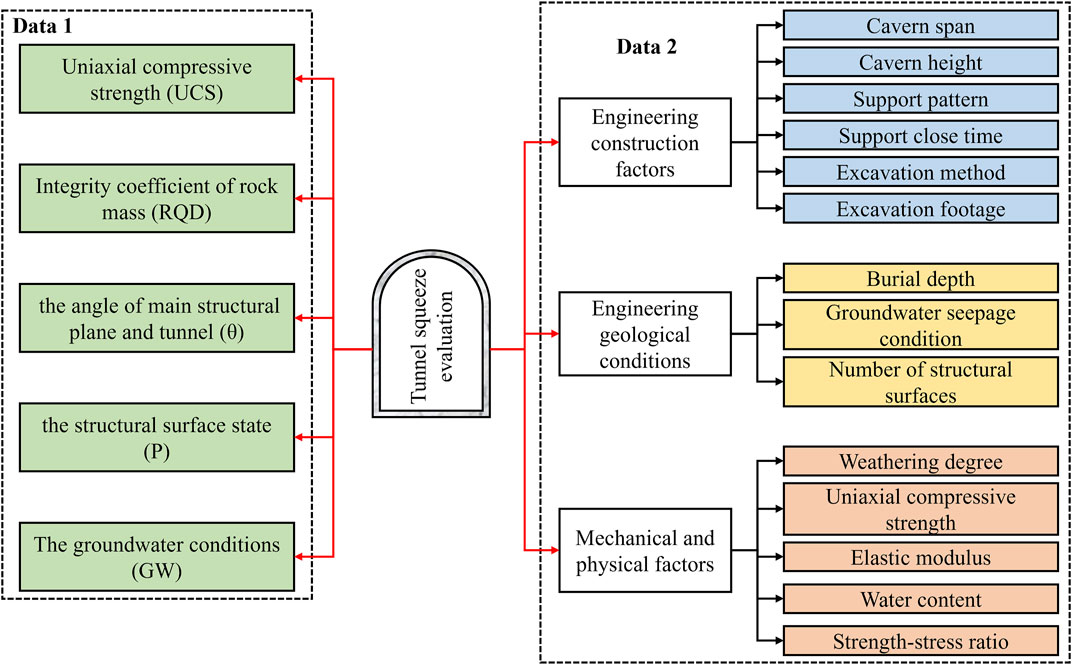
The influencing factors of tunnel squeezing are divided into objective and subjective factors, the former includes geological conditions, such as rock mass conditions, engineering geological conditions, and geo-hydrologic conditions; the latter refers to construction technology, survey and design. Studies shown that poor geological conditions are the main factors for tunnel squeezing, such as the strength of surrounding rock, in-situ stress, and groundwater. This study employed two sets of data collected from the literature to evaluate tunnel squeezing. For the first group of data, the construction of index system considers geological factors and construction technology, while only geological factors are taken into consideration for the second one. Simultaneously, we use
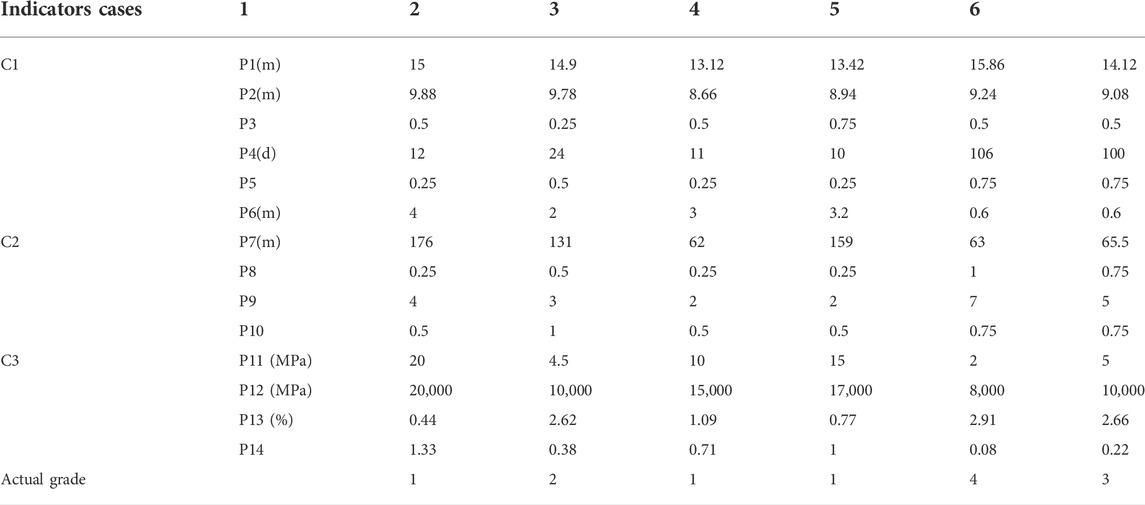
The first group data is composed of six research samples, simultaneously, the evaluation results are categorized into four grades
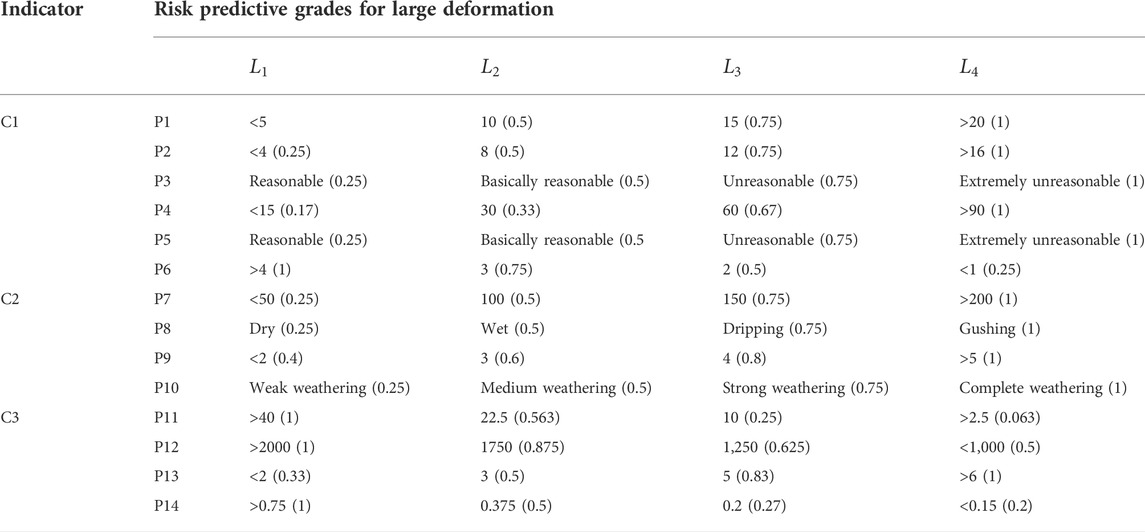
The second group was obtained from the Telmo Tunnel in the Chengdu-Kunming Railway double track (Wang, 2019), which is a deep-buried tunnel with poor surrounding rock conditions. Combine the current railway tunnel deformation classification standard and previous tunnel deformation research, five factors, i.e., the rock uniaxial compressive strength (Rc), the integrity coefficient of rock mass (RQD), the groundwater condition (GW), the angle between the main structural plane and the axis of the tunnel (θ), and the structural surface state (P) are considered as the evaluation indexes, as shown in Figure 2. The evaluation set
Single index measurement of samples
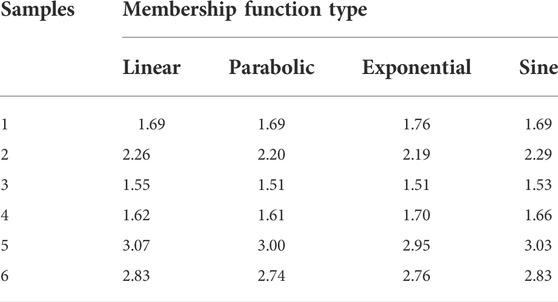
Firstly, based on the four different membership functions shown in Eqs 5–8, the index measurement matrix calculated by different membership functions are obtained. In Figures 3A,B, different membership functions, corresponding to profit and cost index, respectively, are displayed, which can easily calculate the index membership incorporating Eqs 5–8. The single-index measurement matrix of the first and second group data can be represented by
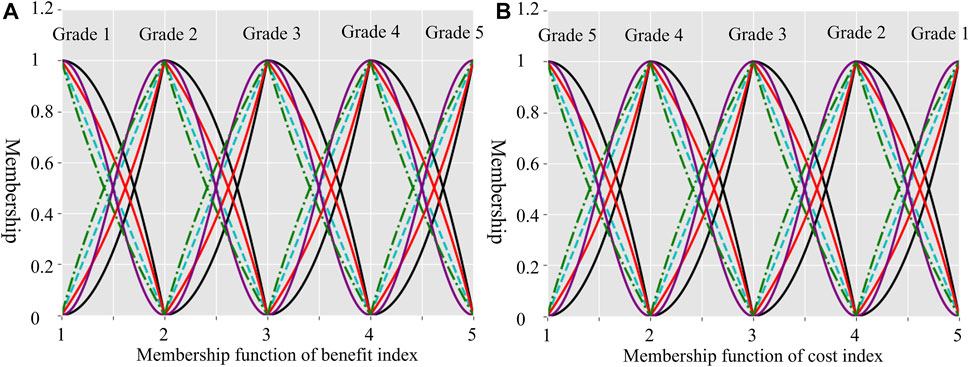
FIGURE 3. Membership function for different indexes. (A) Membership function of benefit index, and (B) Membership function of cost index.
Finally, taking sample 1 (
Index weight of squeezing evaluation
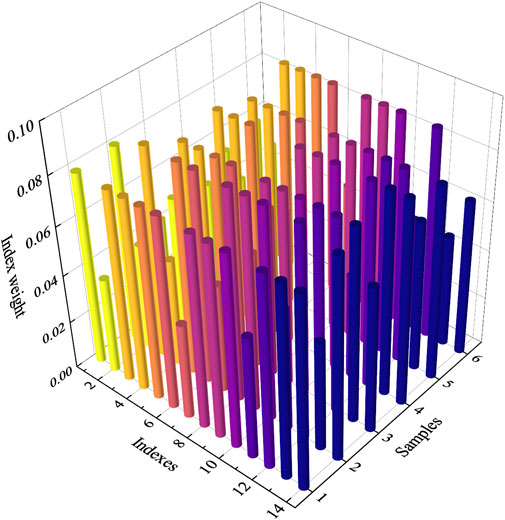
In this study, information entropy is introduced to calculate the index weight coefficients of each sample referring to Eqs 9, 10. There, only the weights calculated by linear function are visualized, as shown in Figure 4.
Determination of squeezing grade
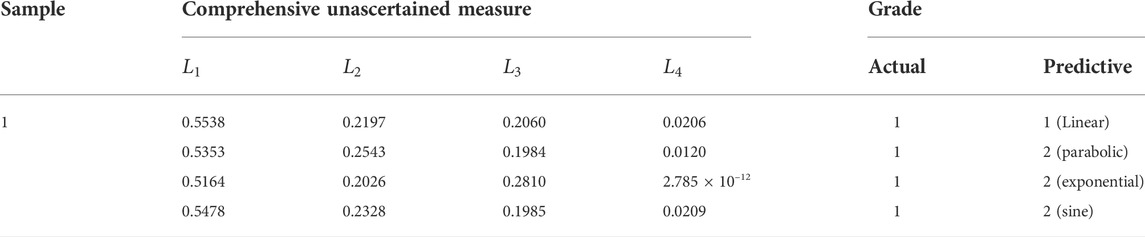
For the first sample of first group, the multi-index comprehensive measurement vectors calculated through the linear function are listed
Sample score for tunnel squeezing
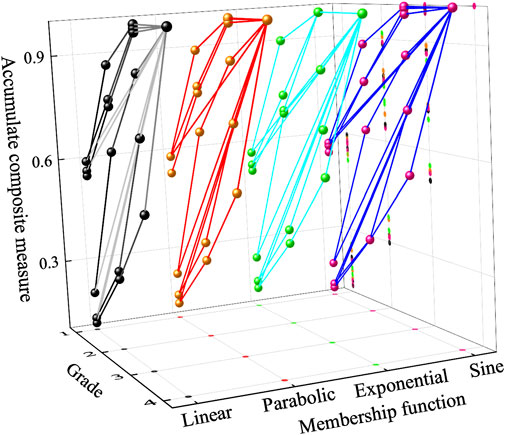
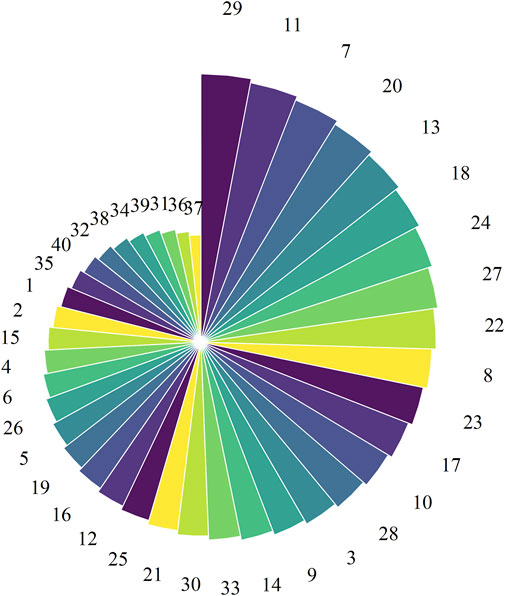
For most comprehensive evaluation models, risk level judgment of samples can be high-efficiently calculated, however, few models are able to quantify the samples simultaneously. Sample score can easily distinguish the risk state of samples at the same grade, which is beneficial to take more accurate measures to prevent geological hazards for on-site engineering issues. There, the scores of samples existing in the two groups data are shown in Table 7; Figure 7, making it possible to identify the most dangerous sample in the dataset. In Figure 7, the score of sample 29 is highest in comparison with other samples, that is, this sample is more likely to occur large deformation.
Conclusion
In this paper, two sets of data with different evaluation index system are collected, and the unascertained measurement theory is used to comprehensively evaluate the tunnel squeezing. The calculation of this hybrid model includes single-index measurement matrix, index weight coefficient and comprehensive measurement matrix. Ultimately, credible identification principle is used to evaluate the risk level. The main conclusions are listed as following:
(1) Four membership functions are used in this paper: linear, parabolic, exponential, and sine function. The accuracy of the first datasets are: 100%, 83.33%, 50%, and 83.33%, respectively, while the accuracy of second dataset are: 70%, 77.5%, 67.5%, and 70%, respectively.
(2) Two groups of data evaluate the tunnel squeezing through constructing different dataset. For the first dataset, sample five is the most dangerous sample while sample 29 is the most dangerous one for the other dataset.
(3) The factors affecting the large deformation of surrounding rock are complex, not only related to the mechanical properties of rock and engineering geological factors, but also related to the construction conditions. There is high uncertainty in the evaluation of large deformation of surrounding rock, more models should be explored to remove various uncertainty existing in the evaluation process in the next research.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Author contributions
Writing—original draft preparation, CW, JZ, CC, and SZ; Modelling, CC and CW; Writing—review and editing, CW, JZ, and CC. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Foundation of China (42177164 and 41807259) the Distinguished Youth Science Foundation of Hunan Province of China (2022JJ10073) and the Innovation-Driven Project of Central South University (No. 2020CX040). The authors gratefully acknowledge financial support from the China Scholarship Council (Grant No. 202206370030).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aydan, Ö., Akagi, T., and Kawamoto, T. (1996). The squeezing potential of rock around tunnels: theory and prediction with examples taken from Japan. Rock Mech. Rock Eng. 29 (3), 125–143. doi:10.1007/bf01032650
Aydan, Ö., Akagi, T., and Kawamoto, T. (1993). The squeezing potential of rocks around tunnels; theory and prediction. Rock Mech. Rock Eng. 26 (2), 137–163. doi:10.1007/bf01023620
Azizi, F., Koopialipoor, M., and Khoshrou, H. (2019). Estimation of rock mass squeezing potential in tunnel route (case study: Kerman water conveyance tunnel). Geotech. Geol. Eng. (Dordr). 37 (3), 1671–1685. doi:10.1007/s10706-018-0714-5
Bai, C., Xue, Y., Qiu, D., Yang, W., Su, M., Ma, X., et al. (2021). Real-time updated risk assessment model for the large deformation of the soft rock tunnel. Int. J. Geomech. 21 (1), 04020234. doi:10.1061/(asce)gm.1943-5622.0001887
ISRM (1995). Editor G. Barla (Tokyo: Proc.Workshop 8th ICRM). [A].Commission on squeezing rocks in tunnels tunneling in difficult ground
Barla, G. (2001). Tunnelling under squeezing rock conditions. Innsbruck: Eurosummer-school in tunnel mechanics, 169–268.
Barton, N., Lien, R., and Lunde, J. (1974). Engineering classification of rock masses for the design of tunnel support. Rock Mech. 6 (4), 189–236. doi:10.1007/bf01239496
Bhasin, R., and Grimstad, E. (1996). The use of stress-strength relationships in the assessment of tunnel stability. Tunn. Undergr. Space Technol. 11 (1), 93–98. doi:10.1016/0886-7798(95)00047-x
Chen, C., Zhou, J., Zhou, T., and Yong, W. (2021). Evaluation of vertical shaft stability in underground mines: comparison of three weight methods with uncertainty theory. Nat. Hazards (Dordr). 109 (2), 1457–1479. doi:10.1007/s11069-021-04885-5
Chen, Yu. (2008). Study on large deformation mechanism and prevention technique of the wall rock in Gong He tunnel. Chongqing, China: Chongqing University. [D].
Du, K., Li, X., Su, R., Tao, M., Lv, S., Luo, J., et al. (2022). Shape ratio effects on the mechanical characteristics of rectangular prism rocks and isolated pillars under uniaxial compression. Int. J. Min. Sci. Technol. 32 (2), 347–362.
Dube, A. K., Singh, B., and Singh, B. (1986). Study of squeezing pressure phenomenon in a tunnell—II. Tunn. Undergr. space Technol. 1 (1), 41–48. doi:10.1016/0886-7798(86)90126-4
Dwivedi, R. D., Singh, M., Viladkar, M. N., and Goel, R. K. (2014). Estimation of support pressure during tunnelling through squeezing grounds. Eng. Geol. 168, 9–22. doi:10.1016/j.enggeo.2013.10.020
Dwivedi, R. D., Singh, M., Viladkar, M. N., and Goel, R. K. (2013). Prediction of tunnel deformation in squeezing grounds. Eng. Geol. 161, 55–64. doi:10.1016/j.enggeo.2013.04.005
Farhadian, H., and Nikvar-Hassani, A. (2020). Development of a new empirical method for tunnel squeezing classification (TSC). Q. J. Eng. Geol. Hydrogeology 53 (4), 655–660. doi:10.1144/qjegh2019-108
Fatemi Aghda, S. M., Ganjalipour, K., and Esmaeil Zadeh, M. (2016). Comparison of squeezing prediction methods: a case study on nowsoud tunnel. Geotech. Geol. Eng. (Dordr). 34 (5), 1487–1512. doi:10.1007/s10706-016-0056-0
Feng, G. L., Chen, B. R., Xiao, Y. X., Jiang, Q., Li, P. X., Zheng, H., et al. (2022). Microseismic characteristics of rockburst development in deep tbm tunnels with alternating soft–hard strata and application to rockburst warning: A case study of the neelum–jhelum hydropower project. Tunn. Undergr. Space Technol. 122, 104398. doi:10.1016/j.tust.2022.104398
Feng, G. L., Feng, X. T., Chen, B. R., Xiao, Y. X., and Yu, Y. (2015). A microseismic method for dynamic warning of rockburst development processes in tunnels. Rock Mech. Rock Eng. 48 (5), 2061–2076. doi:10.1007/s00603-014-0689-3
Ghiasi, V., Ghiasi, S., and Prasad, A. (2012). Evaluation of tunnels under squeezing rock condition. J. Eng. Des. Technol. 10, 168–179. doi:10.1108/17260531211241167
Gioda, G., and Cividini, A. (1996). Numerical methods for the analysis of tunnel performance in squeezing rocks. Rock Mech. Rock Eng. 29 (4), 171–193. doi:10.1007/bf01042531
Goel, R. K., Jethwa, J. L., and Paithankar, A. G. (1995). Tunnelling through the young himalayas—a case history of the maneri-uttarkashi power tunnel. Eng. Geol. 39 (1-2), 31–44. doi:10.1016/0013-7952(94)00002-j
He, M. C., Jing, H., and Sun, X. (2002). Soft rock engineering Mechanics. Beijin: Science Press. [M].
Hoek, E. (2001). Big tunnels in bad rock. J. Geotech. Geoenviron. Eng. 127 (9), 726–740. doi:10.1061/(asce)1090-0241(2001)127:9(726)
Jethwa, J. L., Singh, B., and Singh, B. (1984). “28 estimation of ultimate rock pressure for tunnel linings under squeezing rock conditions—a new approach,” in Design and Performance of Underground Excavations: ISRM Symposium, Cambridge UK, 3–6 September 1984 (Thomas Telford Publishing), 231–238.
Jia, Q., Wu, L., Li, B., Chen, C., and Peng, Y. (2019). The comprehensive prediction model of rockburst tendency in tunnel based on optimized unascertained measure theory. Geotech. Geol. Eng. (Dordr). 37 (4), 3399–3411. doi:10.1007/s10706-019-00854-9
Jiang, Y., Li, Y., Li, T., and Wang, L. (2004). Study of the classified system of types and mechanism of great distortion in tunnel and underground engineering. J. Geol. Hazards Environ. Preserv. 15 (4), 46–51.
Jing, Y., and Hua, J. (2008). “Study on the evaluation of community informatization level based on unascertained measure model,” in 2008 international workshop on modelling, simulation and optimization (New York, US: IEEE), 69–73.
Lai, J., Wang, X., Qiu, J., Chen, J., Hu, Z., Wang, H., et al. (2018). Extreme deformation characteristics and countermeasures for a tunnel in difficult grounds in southern Shaanxi, China. Environ. Earth Sci. 77 (19), 706. doi:10.1007/s12665-018-7888-2
Liao, Y., Guo, D., Liu, Z., and Chen, D. (2020). Application of peripheral strain and squeezing factor methods in the prediction of large deformation of tunnel surrounding rocks. Mod. Tunn. Technol. 57 (04), 20–26. doi:10.13807/j.cnki.mtt.2020.04.003
Liu, Q. S. (2004). The study of control technique for great deformation tunnels in soft surrounding rock of press. Chengdu, China: Southwest Jiaotong University. [D].
Liu, Z., Xie, Q., Xu, S., and Yang, W. (2019). Improved cloud model for evaluation of large deformation of tunnel surrounding rock and its application[J]. Water Resour. Hydropower Eng. 50 (09), 108–113.
Liu, Z. C., Zhu, Y. Q., Li, W. J., and Liu, P. X. (2008). Mechanism and classification criterion for large deformation of squeezing ground tunnels. Chin. J. Geotechnical Eng. 30 (5), 690–697.
Ma, H., Zhou, Y., Rao, B., Ma, Q., and Chen, S. (2021). Optimization of qualified lump size of ore based on undetermined measure theory. Min. Technol. 21 (06), 176–179. doi:10.13828/j.cnki.ckjs.2021.06.046
Malan, D. F., and Basson, F. R. P. (1998). Ultra-deep mining: the increased potential for squeezing conditions. J. South. Afr. Inst. Min. Metallurgy 98 (7), 353–363.
Palmstrom, A., and Broch, E. (2006). Use and misuse of rock mass classification systems with particular reference to the Q-system. Tunn. Undergr. space Technol. 21 (6), 575–593. doi:10.1016/j.tust.2005.10.005
Panet, M. (1996). Two case histories of tunnels through squeezing rocks. Rock Mech. Rock Eng. 29 (3), 155–164. doi:10.1007/bf01032652
Panthi, K. K. (2013). Predicting tunnel squeezing: a discussion based on two tunnel projects. Hydro Nepal. 12, 20–25. doi:10.3126/hn.v12i0.9027
Ren, H., Zhang, B., Bian, P., Wang, S., and Wang, L. (2021). Case analysis and technical countermeasures of tunnelling in squeezing surrounding rocks. Mod. tunneling Technol. 58 (S2), 165–171. doi:10.13807/j.cnki.mtt.2021.S2.025
Ruan, C., Zhang, Y., Li, H., Hou, W., Dong, D., and Tian, H. (2021). Construction risk assessment of urban wastewater deep-buried tunnel under passing existing railway based on the improved entropy weight unascertained measurement model. Saf. Environ. Eng. 28 (06), 84–90. doi:10.13578/j.cnki.issn.1671-1556.20201160
Sharma, S., Muthreja, I. L., and Yerpude, R. R. (2020). Application and comparison of squeezing estimation methods for Himalayan tunnels. Bull. Eng. Geol. Environ. 79 (1), 205–223. doi:10.1007/s10064-019-01530-1
Shi, X., Zhou, J., Dong, L., Hu, H., Wang, H., and Chen, S. (2010). Application of unascertained measurement model to prediction of classifiation of rockburst intensity. Chin. J. Mech. Eng. 29 (S1), 2720–2726.
Singh, M., Singh, B., and Choudhari, J. (2007). Critical strain and squeezing of rock mass in tunnels. Tunn. Undergr. space Technol. 22 (3), 343–350. doi:10.1016/j.tust.2006.06.005
Steiner, W. (1996). Tunnelling in squeezing rocks: case histories. Rock Mech. Rock Eng. 29 (4), 211–246. doi:10.1007/bf01042534
Tu, S. W., Guo, X. C., and He, J. M. (2008). “Safety evaluation for first class Highway design based on unascertained measure model,” in 2008 workshop on power electronics and intelligent transportation system (New York, US: IEEE), 511–514.
Wang, L. (2019). Research on nonlinear prediction of large deformation drade of mountain railway tunnel and supporting measures. Jinan, China: Shan Dong University.
Wang, S. M., Zhou, J., Li, C. Q., Armaghani, D. J., Li, X. B., and Mitri, H. S. (2021a). Rockburst prediction in hard rock mines developing bagging and boosting tree-based ensemble techniques. J. Cent. South Univ. 28 (2), 527–542.
Wang, S. F., Yu, T. A. N. G., Li, X. B., and Kun, D. U. (2021b). Analyses and predictions of rock cuttabilities under different confining stresses and rock properties based on rock indentation tests by conical pick. Trans. Nonferrous Metals Soc. China 31 (6), 1766–1783. doi:10.1016/s1003-6326(21)65615-7
Wang, S., Sun, L., Li, X., Zhou, J., Du, K., Wang, S., et al. (2022). Experimental investigation and theoretical analysis of indentations on cuboid hard rock using a conical pick under uniaxial lateral stress. Geomech. Geophys. Geo. Energy. Ge. Resour. 8 (1), 34. doi:10.1007/s40948-022-00345-x
Williams, A. S. (2010). “Estimating the squeeze potential for long, deep tunnels beneath the santa mountains of southern California,” in 44th US Rock Mechanics Symposium and 5th US-Canada Rock Mechanics Symposium, Salt Lake City, Utah, June 27–30, 2010. OnePetro.
Wood, A. M. M. (1972). Tunnels for roads and motorways. Q. J. Eng. Geol. Hydrogeology 5 (1-2), 111–126. doi:10.1144/gsl.qjeg.1972.005.01.12
Yu, X., and Zhang, W. (2020). Study on control technique for large deformation of soft rocks in huifulai tunnel of China-Laos raiway[J]. Int. J. Equity Health 11 (03), 12. doi:10.1186/s12939-020-1128-6
Yu, Y., Zhao, D. C., Feng, G. L., Geng, D. X., and Guo, H. S. (2022). Energy evolution and acoustic emission characteristics of uniaxial compression failure of anchored layered sandstone. Front. Earth Sci. (Lausanne). 10, 841598. doi:10.3389/feart.2022.841598
Zhang, J., Li, D., and Wang, Y. (2020). Predicting tunnel squeezing using a hybrid classifier ensemble with incomplete data. Bull. Eng. Geol. Environ. 79 (6), 3245–3256. doi:10.1007/s10064-020-01747-5
Zhang, Z. (2003). Discussion and study on large deformation of tunnel in squeezing ground. Mod. Tunn. Technol. (2), 5–12+40. doi:10.13807/j.cnki.mtt.2003.02.002
Zhou, J., Chen, C., Armaghani, D. J., and Ma, S. (2020a). Developing a hybrid model of information entropy and unascertained measurement theory for evaluation of the excavatability in rock mass. Eng. Comput. 38, 247–270. doi:10.1007/s00366-020-01053-4
Zhou, J., Chen, C., Du, K., Jahed Armaghani, D., and Li, C. (2020b). A new hybrid model of information entropy and unascertained measurement with different membership functions for evaluating destressability in burst-prone underground mines. Eng. Comput. 38, 381–399. doi:10.1007/s00366-020-01151-3
Zhou, J., Chen, C., Khandelwal, M., Tao, M., and Li, C. (2021a). Novel approach to evaluate rock mass fragmentation in block caving using unascertained measurement model and information entropy with flexible credible identification criterion. Eng. Comput., 1–21. doi:10.1007/s00366-020-01230-5
Zhou, J., Chen, C., Wang, M., and Khandelwal, M. (2021b). Proposing a novel comprehensive evaluation model for the coal burst liability in underground coal mines considering uncertainty factors. Int. J. Min. Sci. Technol. 31 (5), 799–812. doi:10.1016/j.ijmst.2021.07.011
Zhou, J., Chen, C., Wei, C., and Du, K. (2022a). An improved connection cloud model of an updated database: A multicriteria uncertainty model for coal burst liability evaluation. Nat. Resour. Res. 31 (3), 1687–1704.
Keywords: Squeezing, Unascertained measurement, Information entropy, Classification, Risk evaluation
Citation: Wei C, Zhu S, Chen C and Zhou J (2022) Developing an evaluation model based on unascertained measurement for evaluation of tunnel squeezing. Front. Earth Sci. 10:967328. doi: 10.3389/feart.2022.967328
Received: 12 June 2022; Accepted: 05 July 2022;
Published: 04 August 2022.
Edited by:
Guang-Liang Feng, Institute of Rock and Soil Mechanics (CAS), ChinaReviewed by:
Tao Zhou, Shenzhen University, ChinaLishuai Jiang, Shandong University of Science and Technology, China
Copyright © 2022 Wei, Zhu, Chen and Zhou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shuangli Zhu, MTk1NTEyMDc4QGNzdS5lZHUuY24=; Chao Chen, Y3N1Y2hlbmNoYW9AY3N1LmVkdS5jbg==, Y2hhb19jaGVuX2Jlc3RAaG90bWFpbC5jb20=
 Cong Wei
Cong Wei Shuangli Zhu1*
Shuangli Zhu1* Chao Chen
Chao Chen Jian Zhou
Jian Zhou