A comprehensive evaluation method for the site selection of new healthcare facilities in geological hazard-prone areas

1 Introduction

Healthcare facilities are closely related to social development and health (Bahadori et al., 2017). With the rapid development of urbanization and the improvement of residents’ living standards, the demand for medical services is increasing. China has a large number of mountainous areas where geological hazard activities are frequent (Lin, Chen, Qi, & Hou, 2021). Geological hazards seriously threaten the life and property safety of residents and affect socioeconomic development (Ma & Mei, 2021). Healthcare facilities in geological hazard-prone areas are not only responsible for providing basic medical services (Tripathi, Agrawal, & Gupta, 2021), but also a key part of the post-hazard emergency rescue management. Nevertheless, China suffers from an imbalance between the supply and demand of medical resources, especially in mountainous regions, where the population distribution and economic development are heterogeneous. Scientific and reasonable site selection of healthcare facilities is essential to meet residents’ medical needs, improve the efficiency of the regional medical system, and enhance hazard prevention and mitigation (Dell'Ovo et al., 2017; Sara & Abbas, 2014). The geological hazard factors should be considered in the site selection study of healthcare facilities (Gul & Guneri, 2021). Therefore, this paper examined the scientific and rational site selection of new healthcare facilities in geological hazard-prone areas to improve the safety of healthcare facility sites and make the spatial layout more reasonable.

The site selection of new healthcare facilities requires consideration of criteria such as geological hazard susceptibility, construction land suitability, accessibility, and medical equalization, which is a multidimensional and complex multicriteria decision-making (MCDM) problem in nature (Eldemir & Onden, 2016; Senvar, Otay, & Bolturk, 2016; Wang, Shi, & Gan, 2018). MCDM is a method for solving decision-making and planning problems involving multiple criteria by evaluating alternatives based on a set of decision criteria (Tyagi & Singh, 2019). The MCDM method is used to select healthcare facility sites in many studies, and the criteria and methods used in some of these studies are shown in Supplementary Table S9. Scholars generally consider the criteria for healthcare facility site selection in terms of accessibility, competition, cost, demand, and environment, with the accessibility criterion being used by all scholars, indicating that the proximity of healthcare facilities to the transportation road network is one of the criteria that must be considered. Meanwhile, GIS is widely used in the site selection of healthcare facilities (Tripathi et al., 2021) because it can create a problem-solving environment for spatially referenced data. The integration of MCDM methods and GIS enables the manipulation and presentation of spatial data, providing effective ranking of alternatives based on multiple criteria (Sara & Abbas, 2014), as well as reducing errors and increasing the efficiency of the decision-making process (Eghtesadifard, Afkhami, & Bazyar, 2020). Some researchers have identified areas suitable for the site selection of healthcare facilities in the study areas based on GIS (Ajaj et al., 2019; Dell'Ovo, Capolongo, & Oppio, 2018; Dulin et al., 2010; Halder, Bandyopadhyay, & Banik, 2020), but did not prioritize suitable locations for site selection, leading to decision-makers’ own judgment for selection. Zolfani, Yazdani, Torkayesh, and Derakhti (2020), Adali and Tus (2021), and Yilmaz and Atan (2021) used the MCDM method to identify the ranking of the advantages and disadvantages of healthcare facility site alternatives based on the corresponding criteria but lacked a basis for selection when determining the site alternatives. Based on the above analysis, this paper will combine GIS and MCDM methods to study the site selection of new healthcare facilities in geological hazard-prone areas, identify site alternatives in the study area and comprehensively evaluate and rank them to help decision-makers make appropriate choices.

Judging from the research content of this paper, the types of evaluation indices required in this paper are extensive and the data are diverse. Therefore, the MCDM method was chosen in the study, which required less data processing and could reflect various index information. Of course, the MCDM method must be applicable to siting selection research. Based on relevant researches (Chai, Liu, & Ngai, 2013; Wu et al., 2020b; Guo, Gao, Men, Fan, & Liu, 2021), the advantages and disadvantages of common MCDM methods are summarized as Supplementary Table S10. Preference Ranking Organization Methods for Enrichment Evaluations (PROMETHEE) is a ranking method among multicriteria decision-making methods that can rank and select a limited set of alternatives among conflicting criteria (Behzadian, Kazemzadeh, Albadvi, & Aghdasi, 2010). As shown in Supplementary Table S10, it has the advantages of no need to process raw data, little missing information, and the ability to reflect various characteristics of indicator attributes, which meets the research requirements of this paper and can better solve the ranking problem of site alternatives. Sennaroglu and Celebi (2018), Wu, Zhang, Wu, Zhang, and Liu (2019), Wu et al., 2020a, and Guo et al. (2021) all applied the PROMETHEE method to facility site studies and successfully ranked and selected the site alternatives, reducing the difficulty for decision-makers to identify the best alternative. To sum up, the PROMETHEE method is selected for comprehensive evaluation of site selection alternatives. The PROMETHEE method has many derivative versions, among which the PROMETHEE II method can obtain a complete ranking of the alternatives instead of a partial ranking by improving the PROMETHEE I method.

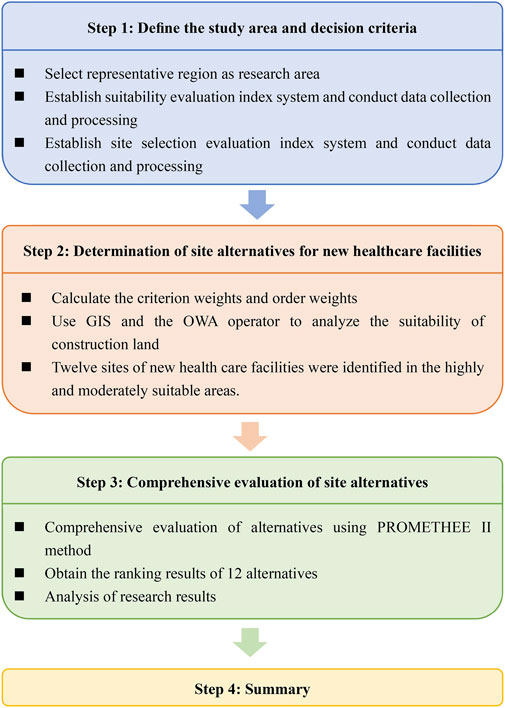
In summary, this paper proposes a comprehensive evaluation method for the site selection of new healthcare facilities based on GIS and PROMETHEE Ⅱ methods in geological hazard-prone areas. The flowchart of the methodology in this paper is shown in Figure 1. The study area is Shimian County, Ya’an City, Sichuan Province, which is prone to geological hazards. The suitability map for construction and site alternatives for new healthcare facilities are determined based on GIS and OWA methods in the study area. The PROMETHEE II method is used to comprehensively evaluate the alternatives and obtain the ranking results of the alternatives. The method proposed in this paper can take full advantage of the combination of GIS and PROMETHEE II, which can ensure the safety and suitability of the site and consider the comprehensive and developmental aspects of new healthcare facilities. Thus, the purpose of reasonable and scientific site selection for new healthcare facilities in geological hazard-prone areas can be achieved.

FIGURE 1

FIGURE 1. Flowchart of the methodology.

The rest of the paper is organized as follows: Section 2 briefly introduces the research methodology, Section 3 details the process of determining the study area and the evaluation index system, Section 4 details the results of the site alternative identification and comprehensive evaluation of new healthcare facilities, Section 5 discusses the study results and concludes the paper, and Section 6 proposes future research directions.

2 Methods

2.1 Ordered Weighted Averaging operator

In methods of combining GIS with multicriteria decision-making, the linear weighted combination approach can result in some criteria compensating for other criteria that have obvious constraints (Bagheri, Sulaiman, & Vaghefi, 2013; Kapoor & Bansal, 2021; Aghmashhadi, Azizi, Zahedi, Hoseinkhani, & Cirella, 2022) since the selection of evaluation indices is usually interrelated. Thus, it may make the obtained results not as restrictive as intended by the evaluator (Liu Y. et al., 2014). The ordered weighted averageing (OWA) operator involves two types of weights: criterion weights and order weights (Yager, 1988). First, the weighting method is used to calculate the weight of the criterion, and the criterion is ranked according to the weight. Then, different order weights are assigned to the criterion according to the order. The OWA operator can reduce the influence of extreme values on the results and increase the influence of central values and the importance of the weighted measure values (in relation to other values) while maintaining independence from the original information source (Csiszar, 2021). Moreover, the OWA operator can simulate scenarios that indicate the suitability of construction land under different decision-making preferences by setting the decision preference coefficient α. The OWA operator has been widely used in land suitability studies (Liu R. et al., 2014; Kumar & Kumar, 2014; Billaud, Soubeyrand, Luque, & Lenormand, 2020; Cosimo, Martins, & Gleriani, 2021; Luan, Liu, & Peng, 2021; Yang, Tang, & Li, 2021). Thus, this paper uses the OWA operator to analyze construction land suitability and determine the suitable sites of new healthcare facilities in the study areas. The calculation process is as follows:

$\begin{array}{c}OW{A}_i={\displaystyle \sum _{j=1}^n}\left(\frac{u_j{v}_j}{{\displaystyle \sum }_{j=1}^n{u}_j{v}_j}\right)Z_{ij}\end{array}(1)$

In the formula, OWA_i is the suitability analysis result of the ith pixel; j is the rank; n is the number of evaluation indices; Z_ij is the attribute value corresponding to the jth index of the ith pixel; u_j is the criterion weight; and v_j is the order weight.

The Analytic Hierarchy Process (AHP) is used to calculate the criterion weights of the evaluation indices, the quantitative method of Regular Increasing Monotone (RIM) is used to determine the order weights (Yager, 1996), and v_j is calculated as follows:

$\begin{array}{c}{v}_j=Q_{RIM}\left(\frac{j}{n}\right)-Q_{RIM}\left(\frac{j-1}{n}\right)\end{array}(2)$

$\begin{array}{c}{Q}_{RIM}\left(r\right)=r^{\alpha }\end{array}(3)$

where r is the independent variable and α is the decision-makers’ preference coefficient. When α=1, the order weights are equal, and the calculation turns into a linear weighted combination of criterion weights; when 0<α<1, the greater the criterion weights of the indices are, the greater their order weights. At this time, the evaluation results can visually show the most important attributes of the index system. When α>1, the order weights of indices with larger criterion weights are smaller, and the less important indices at the back receive more attention. The study area is prone to geological hazards; therefore, the impact of geological hazards is the most important factor and must be considered. Finally, we take α=0.5.

2.2 PROMETHEE Ⅱ

The PROMETHEE II method compares each attribute of the alternatives in pairs to obtain the ranking of the alternatives according to certain criteria (recognized criterion). The specific computational process is as follows:

1) Construction of decision matrix

Suppose a multicriteria decision problem with m alternatives A={a₁,a₂, $\dots$ a_m}, each corresponding to n evaluation indices, the set of evaluation indices C={c₁,c₂, $\dots$ c_n}, and the weight vector w= (w₁, w₂, $\dots$, w_n) corresponding to the evaluation indices and satisfying w_j ∈ [0,1] and ∑w_j = 1, (j = 1,2, $\dots$ n).

2) Construction of preference functions

$\begin{array}{c}{P}_j\left(a_p,a_q\right)=F_j\left[d_j\left(a_p,a_q\right)\right]\end{array}(4)$

$\begin{array}{c}{d}_j\left(a_p,a_q\right)=f_j\left(a_p\right)-f_j\left(a_q\right)\end{array}(5)$

where P_j (a_p,a_q) (0≤P_j (a_p,a_q)≤1) is a preference function that is used to describe the priority of alternative a_p relative to a_q for indicator c_n; f_j (a_p) is the value of evaluation index c_j for alternative a_p, and f_j (a_q) is the same.

3) Calculation of the overall preference indices G (ap,aq) and G (aq,ap)

$\begin{array}{c}G\left(a_p,a_q\right)={\displaystyle \sum _{j=1}^n}{w_{j}P}_j\left(a_p,a_q\right)\end{array}(6)$

$\begin{array}{c}G\left(a_q,a_p\right)={\displaystyle \sum _{j=1}^n}{w_{j}P}_j\left(a_q,a_p\right)\end{array}(7)$

where G (a_p,a_q) indicates that alternative a_p is superior to alternative a_q and G (a_p,a_q) indicates that alternative a_q is superior to alternative a_p.

4) Calculation of the positive flow φ+(ap) and negative flow φ-(ap) of alternative a_p

$\begin{array}{c}{\phi }^{+}\left(a_p\right)=\frac{1}{m-1}{\displaystyle \sum _{x\in A}}G\left(a_p,x\right)\end{array}(8)$

$\begin{array}{c}{\phi }^{-}\left(a_p\right)=\frac{1}{m-1}{\displaystyle \sum _{x\in A}}G\left(x,a_p\right)\end{array}(9)$

5) Calculation of net flow φ(ap)

$\begin{array}{c}\phi \left(a_p\right)={\phi }^{+}\left(a_p\right)-{\phi }^{-}\left(a_p\right)\end{array}(10)$

The net flow reflects the priority of alternative a_p. The alternative is ranked according to the net flow of each alternative, and the higher the net flow value, the higher the priority of the alternative and the ranking.

3 Determination of study area and decision criteria

3.1 Study area

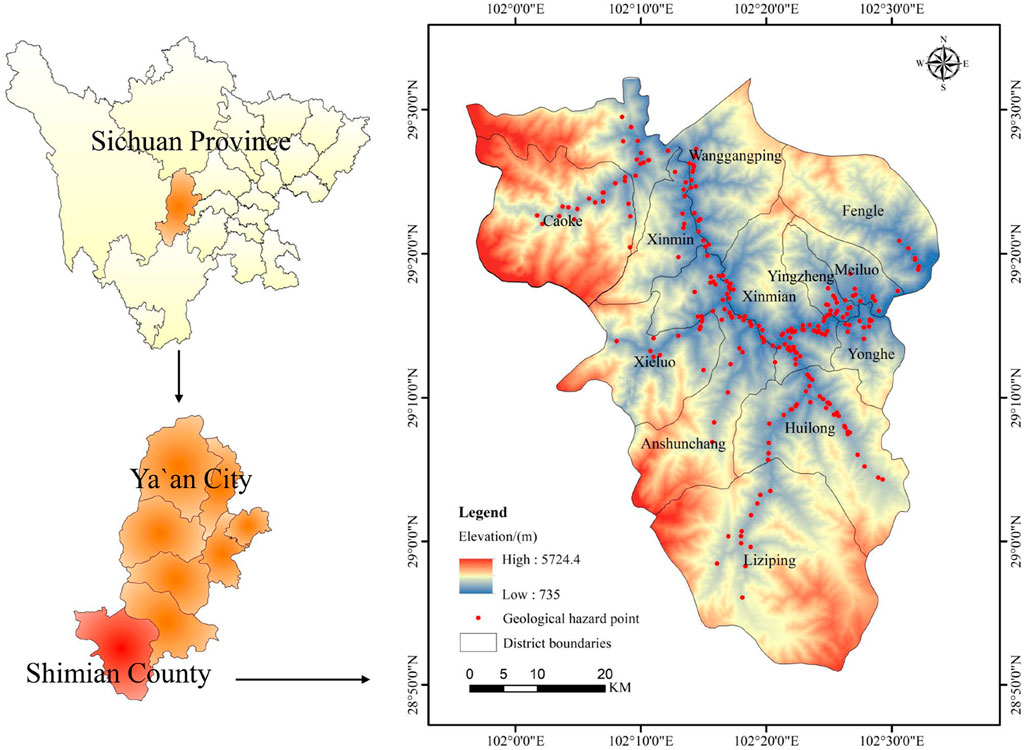
Rational planning of the site layout of new healthcare facilities in the county is a strategic need for national development. Geological hazards are frequent in Shimian County, Ya’an City, Sichuan Province. According to data from the Geospatial Data Cloud platform, there were 442 geological hazard sites in Shimian County from 1949 to 2018, accounting for 24.26% of the total geological hazard sites in Sichuan Province. Shimian County is one of the most prominent hazard prevention and mitigation areas in Sichuan Province. Therefore, the selection of Shimian County as the study area has practical significance and representativeness.

Shimian County is located in the eastern part of the Hengduan Mountains on the Qinghai-Tibet Plateau in the middle reaches of the Dadu River. The geographical coordinates are 101°55′-102°34′E and 28°51′-29°32′N (Figure 2). The maximum horizontal distance from east to the west in Shimian County is 60 km, and the maximum vertical distance from north to south is 76.5 km. It is a typical mountainous county with an elevation of more than 1,000 m accounting for approximately 90% of the total area, while the river valley and flat areas only account for 2%.

FIGURE 2

FIGURE 2. Study area overview.

3.2 Establishment of the evaluation index system

3.2.1 Establishment of the suitability evaluation index system

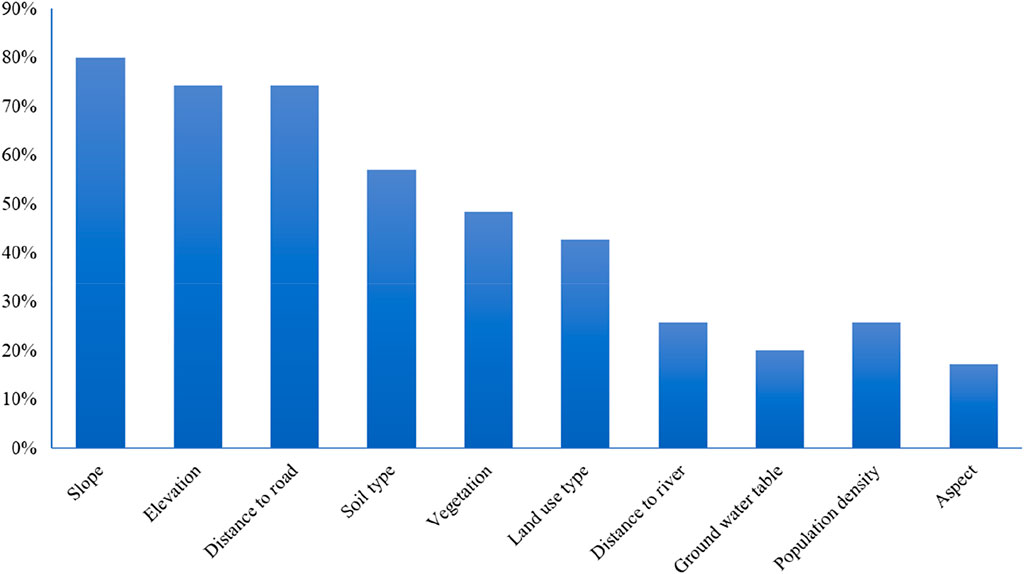
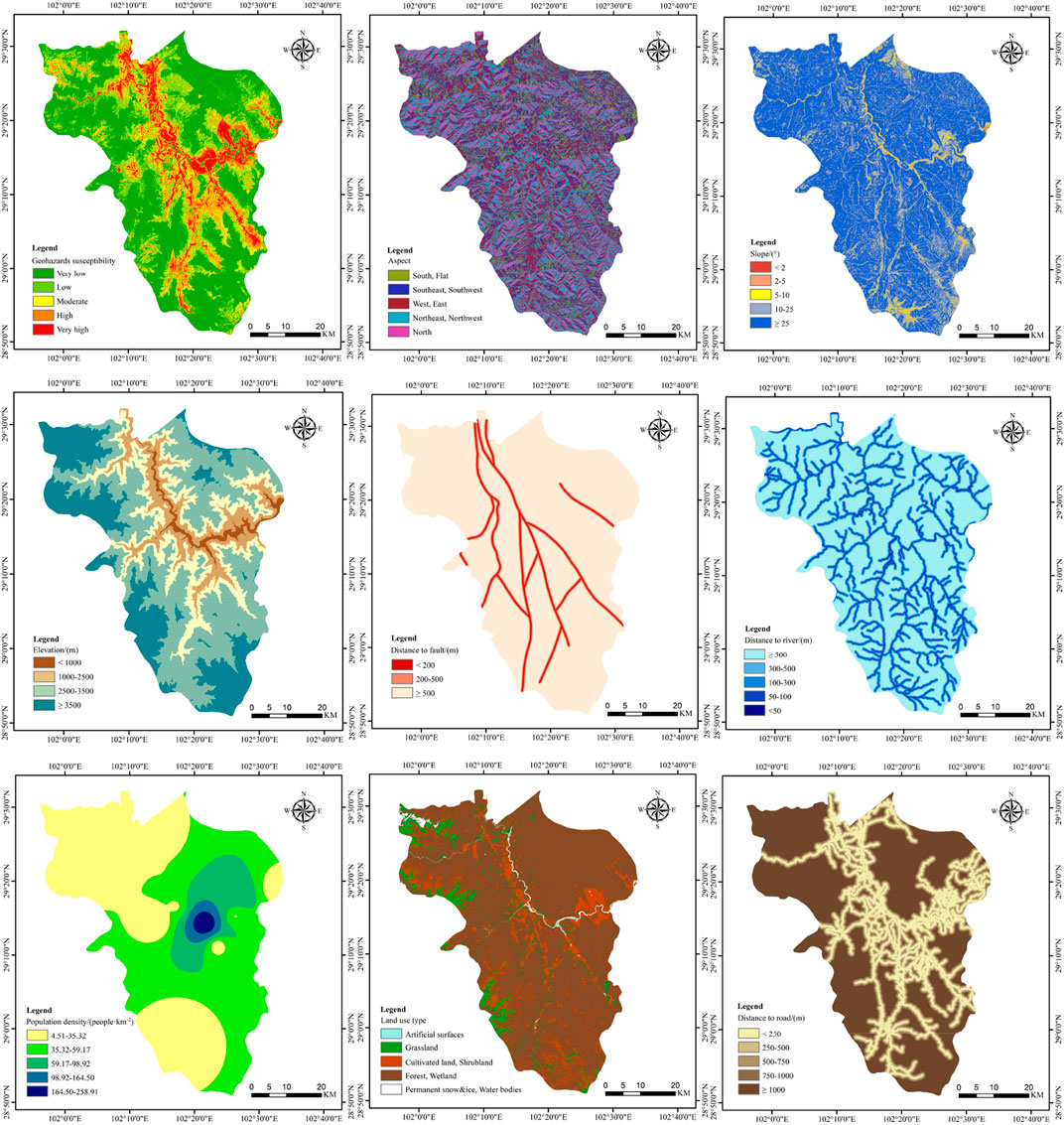
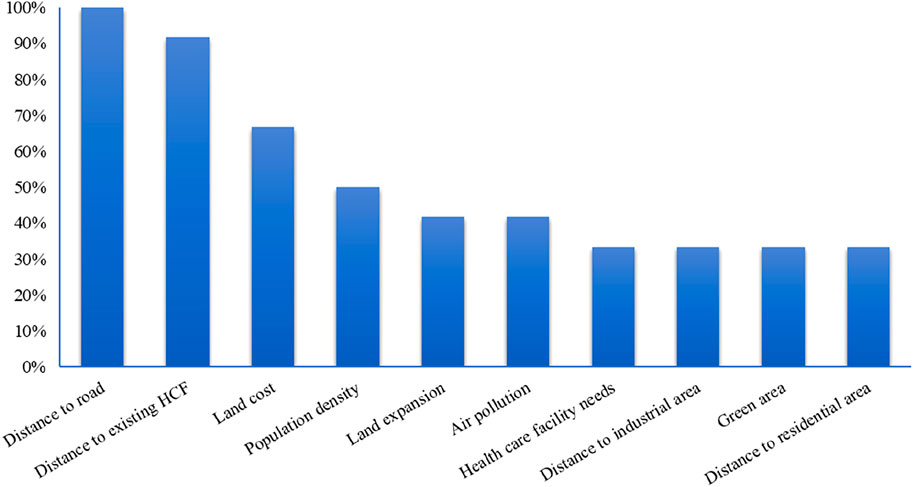
Based on the principles of scientificity, comprehensiveness, accessibility and comparability, literature analysis are used to identify and filter indices for construction land suitability analysis, and the final evaluation index system is established by making corrections in the context of the study area. According to Kapoora and Bansalb’s study, we compile a total of 35 papers on the topics of “Spatial suitability”, “Land use suitability”, “Urban land suitability” and “Construction land suitability”, which involve a total of 29 evaluation indices (Kapoor & Bansal, 2021). After eliminating the irrelevant indices, the frequency statistics of the indices were conducted, and the indices that appear≥6 times are selected as the initial evaluation indices. The frequency diagram of the initial evaluation indices is shown in Figure 3.

FIGURE 3

FIGURE 3. Frequency diagram of initial evaluation indices for construction land suitability.

The initial filtering process could potentially result in two situations. One is that the indices with strong relevance to construction land suitability in geological hazard-prone areas are not selected due to insufficient frequency, and the other is that the evaluation indices do not conform to the selection principles of this study. To ensure that the indices could accurately evaluate construction land suitability in geological hazard-prone areas, the indices in Figure 3 are adjusted as follows: 1) The geological hazard-prone index is added to ensure the safety of the site selection. 2) The distance to fault is added because Shimian County is located at the compound intersection of three fault zones, namely, Xianshui River, Anning River and Longmen Mountain, and thus the strata in the territory are fragmented and earthquake prone, so the buildings should not be built close to the fault. 3) The vegetation is excluded because it has been considered in the geological hazard susceptibility index and thus is not repeatedly selected here. 4) The groundwater table data do not conform to the principle of availability, hence, the evaluation index is excluded. 5) The precision and comparability of the soil type in the study area is not high, and the land use type can replace the soil type to a certain extent; thus, the soil type is also excluded.

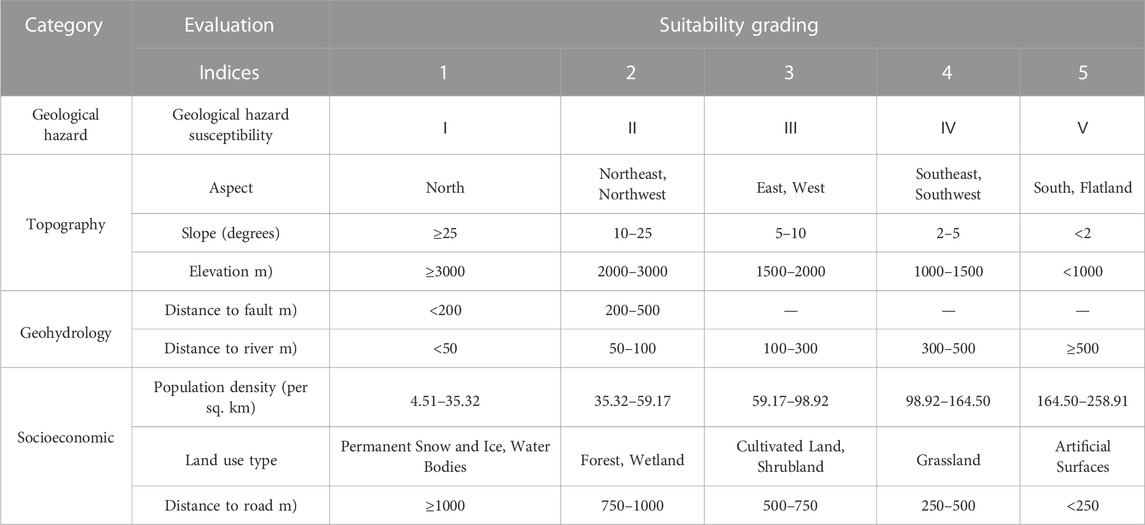
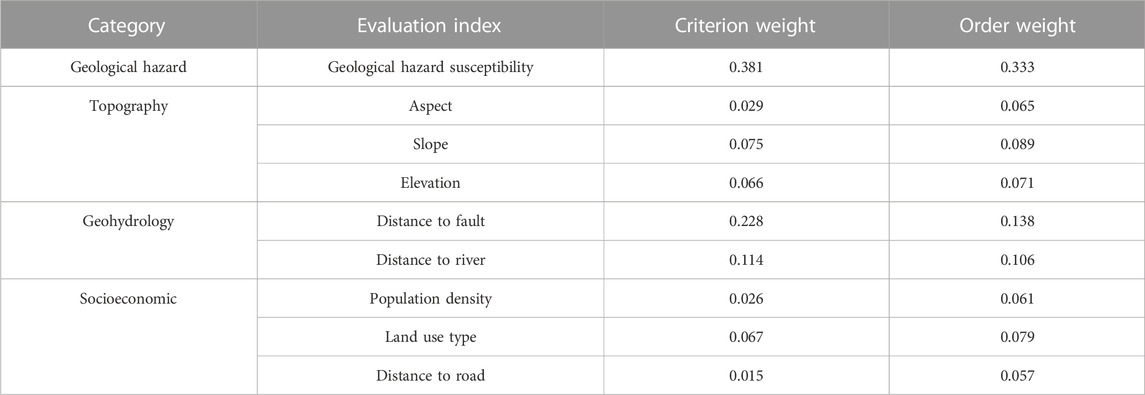
Based on the above analysis, nine indices of geological hazard susceptibility, slope, aspect, elevation, distance to fault, distance to river, population density, distance to road and land use type are determined as the suitability evaluation index system for construction land. These indices are classified from four aspects: geological hazards, topography, geohydrology and socioeconomics. Based on previous studies (Kapoor & Bansal, 2021; Luan et al., 2021; Yang et al., 2021) and the situation of Shimian County, the grading standard of the suitability evaluation index is determined. The results are shown in Table 1. Grades 1–5 correspond to unsuitable, barely suitable, generally suitable, moderately suitable and highly suitable, i.e., the suitability gradually increases with increasing grade. The Jenks natural breaks classification method is a data clustering method that determines how values are optimally arranged in different classes by reducing within-class variance and maximizing between-class variance. Therefore, this paper used the Jenks natural breaks classification method to classify the population density index.

TABLE 1

TABLE 1. Suitability evaluation index system and grading criteria.

The geological hazard susceptibility is obtained by calculating and correcting 11 evaluation indices of elevation, aspect, distance to fault, lithology, river system density, NDVI, road network density, population density, slope, mean annual precipitation, and land use type using the information value-logistic regression coupled model (Yu, Xing, & Hu, 2021). The data sources and processing of the remaining indices are shown in Table 2.

TABLE 2

TABLE 2. Evaluation index data sources and preprocessing.

The Multiple Ring Buffer and Reclassifies Tool of ArcGIS are used for grading processing, and the evaluation indices are all raster data with a size of 30 m*30 m; a detailed map of the evaluation index grading is shown in Figure 4.

FIGURE 4

FIGURE 4. Detailed diagram of suitability evaluation index classification.

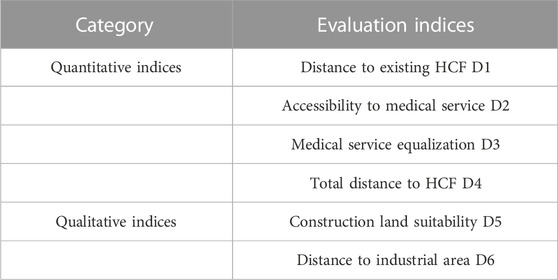
3.2.2 Establishment of the site selection evaluation index system

1) Selection of site selection evaluation indices

The frequency of evaluation indices is counted in the literature of Supplementary Appendix SA. The indices that appear ≥4 times are selected as the preliminary evaluation indices, whose frequency diagram is shown in Figure 5.

FIGURE 5

FIGURE 5. Frequency diagram of the preliminary evaluation indices.

The indices are adjusted in Figure 5 via the following: 1) indices for construction land suitability are increased and the alternative with the highest suitability level is selected as often as possible; 2) the evaluation index of medical service equalization is increased. Improving the level of equalization of basic public services is a clear requirement in China’s 14th Five-Year Plan period. 3) The distance to roads and population density have been considered in construction land suitability, so they are excluded. 4) The data for land cost, land expansion and green area do not conform to the principle of accessibility, so they are excluded. 5) The study area has better air quality, and the air pollution data do not meet the principle of comparability, so the air pollution data are excluded. 6) The demand for healthcare facilities are characterized by medical service accessibility. If the new healthcare facility in a certain place has the largest sum of medical service accessibility at the demand points of the residents in the study area, then the demand for healthcare facilities in that place is the largest. 7) The total distance to healthcare facilities is used to characterize the distance to residential points. Based on the above analysis, the site selection evaluation index system of the new healthcare facility is determined as shown in Table 3, which contains two categories of quantitative and qualitative evaluation indices.

2) Data sources

1) Resident demand point data. Most of the population demand data take streets, communities and other residential surfaces as a whole and extract the geometric center as the resident demand point. However, this practice will cause certain errors in the calculation results of travel impedance for mountainous cities with uneven population distribution. In this paper, the median center of natural villages in each township and street is calculated, and the median center of natural villages is used as the resident demand point, as shown in Figure 6A.

2) Healthcare facility data. The healthcare facilities in Shimian County include 4 hospitals, 15 rural township health centers, 1 community health service center, 1 disease control and prevention center, and 1 maternal and child healthcare hospital. The data are obtained from Gao De Map POI interest points, as shown in Figure 6B. Since the internal data of some healthcare facilities are not available, the following healthcare facilities refer to hospitals.

3) Traffic road network data. Based on the Open Streets Map, the carriageway is drawn with reference to the road data in the National Catalog Service for Geographic Information and Google Earth. After topologically processing the road network data, the travel impedance between resident demand points and healthcare facilities is calculated. According to the road types in Shimian County, Technical code for urban road engineering GB51286-2018 and Regulation on the Implementation of the Road Traffic Safety Law of the People’s Republic of China, the vehicle travel speed is assigned to the traffic road network, where the vehicle travel speeds of Class I, Class II, Class III and Class IV are set to 60 km/h, 45 km/h, 40 km/h and 30 km/h, respectively, as shown in Figure 6C.

3) Data calculation

1) Distance to existing HCF (D1). To make the distribution of healthcare resources more balanced, the distance between the new healthcare facilities and the existing healthcare facilities should be as far as possible. Therefore, the following equation is used to calculate the distance between the two kinds of healthcare facilities:

$D_k=AVERAGE\sum d_{jk}(11)$

where D_k is the average distance from the new healthcare facility k to the existing healthcare facility j and d_jk is the distance from the new healthcare facility k to the existing healthcare facility j. The network analysis function of ArcGIS is used to calculate d_jk.

2) Accessibility to medical service (D2). Accessibility refers to the sum of the accessibility to medical services at resident demand points in the study area, including the sum of the original accessibility to medical services at resident demand points and the increased accessibility after the addition of healthcare facilities. The greater the accessibility to medical services in the study area is, the better. The specific equation is as follows:

$A_k^{*}={\displaystyle \sum }_{i=1}^m{OA}_i+{\displaystyle \sum }_{i=1}^m{A}_{ik}(12)$

where A_k^* is the medical service accessibility at resident demand points in the study area after the addition of healthcare facility k, OA_i is the original medical service accessibility at resident demand point i, and A_ik is the medical service accessibility increased by resident demand point i after the addition of healthcare facility k. An improved potential model is used to calculate the accessibility to medical service (Joseph & Bantock, 1982).

3) Medical service equalization (D3). The fairness of accessibility to medical services is used to measure medical service equalization in the study area, which is represented by the deviation degree (variance) of accessibility (Zhang, Cao, Liu, & Huang, 2016). The smaller the variance of accessibility is, the better. The specific equation is as follows:

$E_k=Var\left\{A_i\right\}(13)$

$A_i={pop}_i\ast \left[\frac{\left({OA}_i+A_{ik}\right)}{A_k^{*}}\right],i=\mathrm{1,2},\dots \dots n(14)$

where E_k is the medical service equalization in the study area after the addition of healthcare facility k, Var(A_i) is the variance of the sequence A_i of the accessibility at resident demand point i, and pop_i is the population at resident demand point i.

4) Total distance to HCF (D4). Total distance to HCFs is calculated by the sum of the weighted distance between resident demand points and their nearest healthcare facilities (existing and new). The smaller the total distance to HCFs is, the more suitable the site. The weight of demand points is the population of the site, and the specific equation is as follows:

${TD}_k={\displaystyle \sum }_i^m{pop}_i\ast \mathit{Min}\left(d_{ij`}\right)(15)$

where TD_k is the total distance to the HCF at resident demand points after the addition of new healthcare facility k, Min(d_ij’) is the shortest distance from resident demand point i to healthcare facility j`, and j` includes existing and new healthcare facilities. The calculation process of d_ij’ is the same as Eq. 11.

5) Construction land suitability (D5). The evaluation results of construction land suitability are used to measure the suitability of alternative sites for new healthcare facilities. The multivalue extraction to points function of ArcGIS is utilized to extract the suitability rating to the alternative, which is considered the evaluation value of this index.

6) Distance to industrial area (D6). There are two industrial parks in Shimian County, the Sichuan Shimian Industrial Park and the Xiaoshui Industrial Complex. To avoid possible damage to healthcare facilities caused by unexpected environmental events under special circumstances in industrial parks, healthcare facilities should be as far away from industrial parks as possible. The distance to the industrial area is classified with reference to “Basic requirements of safety technology for enterprise handing hazardous chemicals business GB18265-2019” (Table 4).

TABLE 3

TABLE 3. New healthcare facility site selection evaluation index system.

FIGURE 6

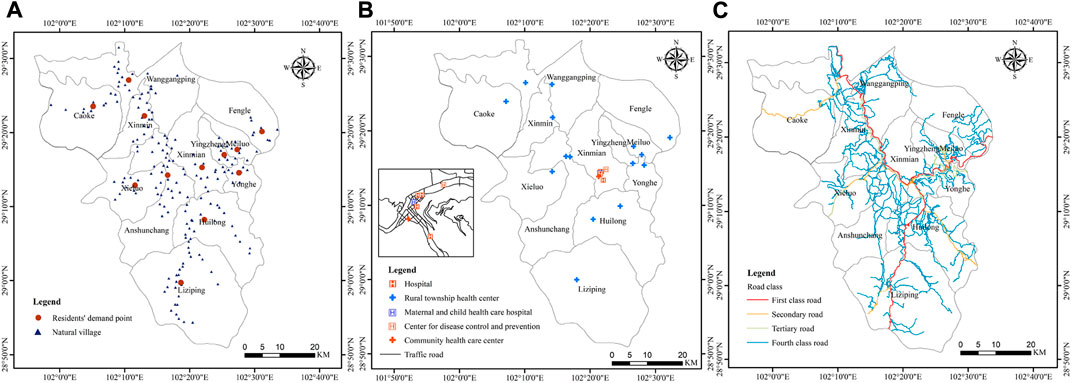
FIGURE 6. (A) resident demand point distribution map; (B) healthcare facilities distribution map; (C) traffic road network distribution map.

TABLE 4

TABLE 4. Distance classification to industrial area.

4 Results

4.1 Determination of site alternatives for new healthcare facilities

4.1.1 Suitability results

The Analytic Hierarchy Process (AHP) is used to calculate the criterion weights of the evaluation indices. The evaluation indices are ranked according to the values of criterion weights from large to small, and then the order weights of the evaluation indices are calculated according to Eqs 2, 3. The results of the criterion and order weights are shown in Table 5.

TABLE 5

TABLE 5. Weights of suitability evaluation indices.

According to the criterion and order weights of evaluation indices, the suitability of construction land in geological hazard-prone areas is evaluated in ArcGIS using the raster calculator combined with suitability grading values and Eq. 1. The results of the suitability analysis range from 1.01 to 4.90. Then, the results are classified as highly suitable, moderately suitable, generally suitable, barely suitable, and unsuitable by using the natural breakpoint method (Figure 7).

FIGURE 7

FIGURE 7. Results of the construction land suitability analysis.

4.1.2 Determination of the site alternatives for new healthcare facilities

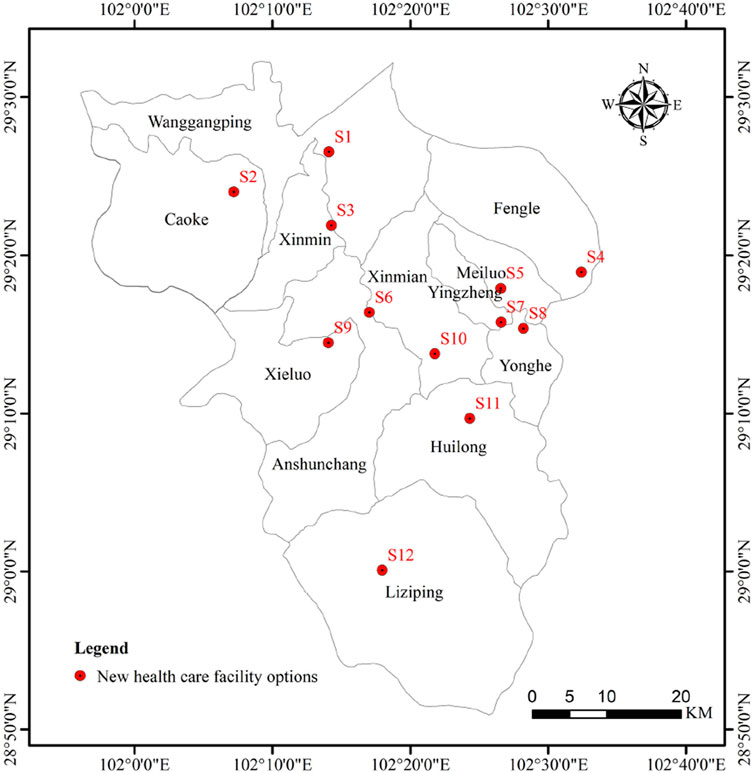
According to the suitability analysis results and the resident point data of Shimian County, the highly suitable and moderately suitable sites are selected as the site alternatives for new healthcare facilities in the residential surface layer coverage area of each township and street in Shimian County (Figure 8).

FIGURE 8

FIGURE 8. The site alternatives for new healthcare facilities.

4.2 Comprehensive evaluation of site alternatives based on PROMETHEE II

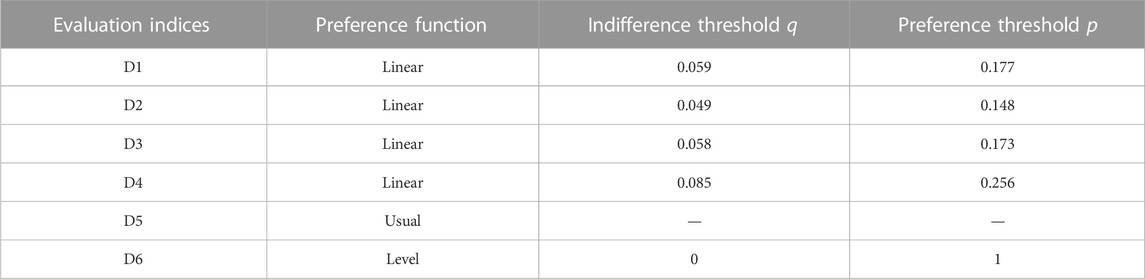
Based on the characteristics of 6 common preference functions in PROMETHEE Ⅱ, the linear preference is the best choice for quantitative criteria when needing a Q indifference threshold. Therefore, the linear preference function is selected for the four quantitative evaluation indices of distance to existing HCFs, accessibility to medical services, medical service equalization, and total distance to HCFs. The indice of construction land suitability has only two grades, and the alternatives with large values have absolute advantages, so the usual preference function is selected. Distance to industrial area is a qualitative indice and has multiple levels. The level preference function is better suited to qualitative criteria when the decision-maker wants to modulate the preference degree according to the deviation between evaluation levels. Hence, the level preference function is selected for the evaluation index of distance to industrial areas.

The indifference and preference thresholds of the linear preference functions are determined based on the average absolute deviation of the quantitative evaluation indices. The detailed equation is as follows:

1) Determine the mean absolute deviation S of index j.

$S=\frac{{\displaystyle \sum }_{i=1}^m\left|a_{ij}-{\overline{a}}_{ij}\right|}{m}(16)$

where a_ij is the value of the jth evaluation index for alternative i, and m is the number of alternatives.

2) If the preference function requires only a single indifference threshold or preference threshold, the threshold equals 0.5S.

3) If the preference function requires both an indifference threshold and a preference threshold, the indifference threshold q equals 0.25S and the preference threshold p equals 0.75S.

The level preference function of the evaluation index of distance to industrial area defines the indifference threshold q as 0 and the preference threshold p as 1.

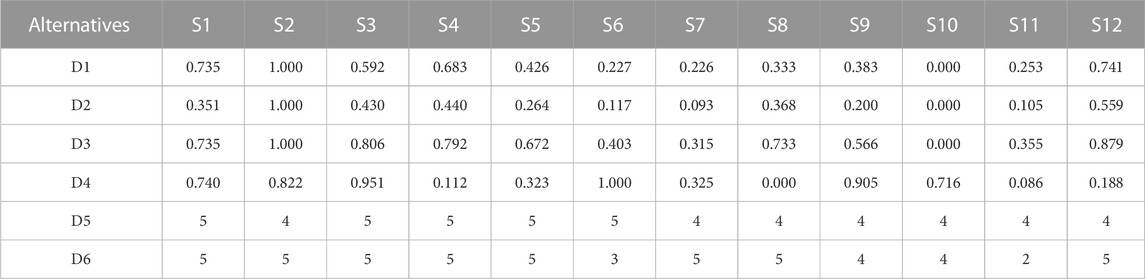
The quantitative evaluation indices for 12 alternatives are calculated using Eqs 11–15 and standardized. The higher the value of these indices, the higher the degree of preference. According to the results of construction land suitability analysis, different grades of construction land suitability are assigned. The grades of unsuitable, barely suitable, generally suitable, moderately suitable and highly suitable are assigned 1, 2, 3, 4 and 5, respectively. The numerical results of the distance to industrial area are obtained by extracting the value of the distance to industrial area grading chart into the alternatives (Figure 7). The numerical results of the evaluation indices for 12 alternatives are shown in Table 6.

TABLE 6

TABLE 6. Results of evaluation indices for alternatives.

Based on the calculation results in Table 6, the indifferent and preference thresholds for each quantitative index are calculated using Eq. 16, as shown in Table 7.

TABLE 7

TABLE 7. Preference functions and thresholds of evaluation indices.

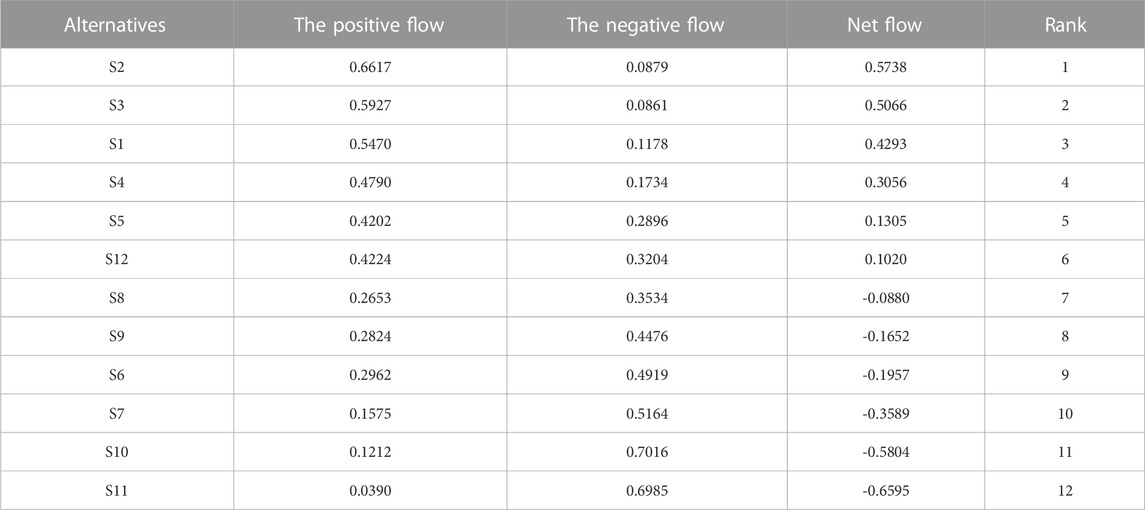
The results in Tables 6 and 7 are input into Visual PROMETHEE software, and then the positive flow, negative flow, net flow and ranking results of 12 site alternatives for new healthcare facilities in geological hazard-prone areas are shown in Table 8.

TABLE 8

TABLE 8. Flow scores of site alternatives.

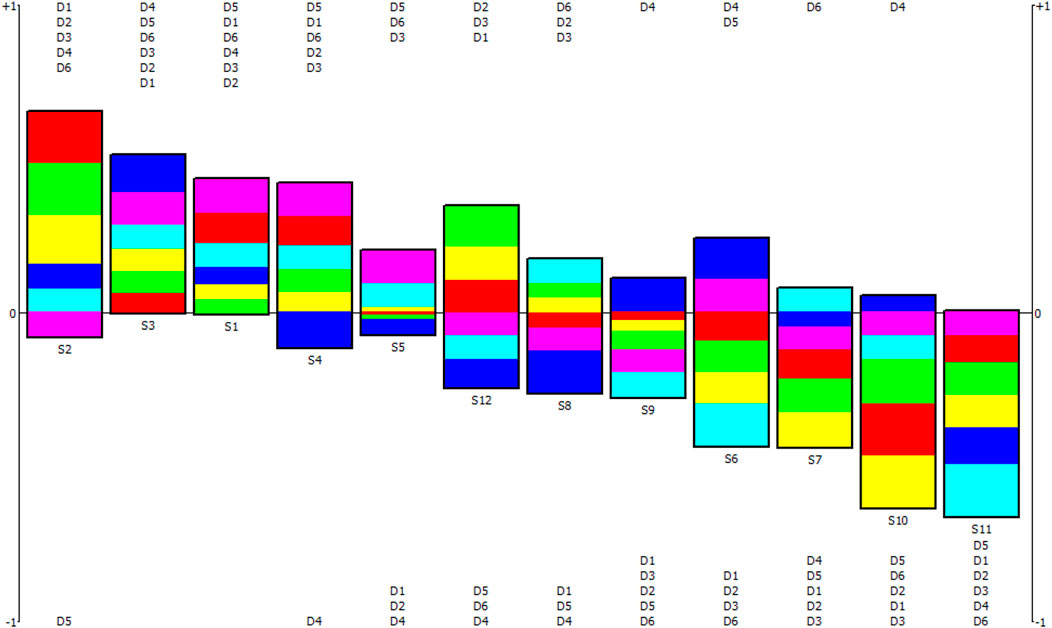
The net flow values of the alternatives are S2, S3, S1, S4, S5, S12, S8, S9, S6, S7, S10 and S11 in descending order, as shown in Table 8. S2, with a net flow value of 0.5738, is the best site for a new healthcare facility. S11, with a net flow value of -0.6595, is the most unfavorable site for a new healthcare facility.

5 Discussion

5.1 Analysis of suitability results

As shown in Figure 7, the barely suitable and unsuitable construction land areas are distributed in the longitudinal central and central-eastern parts of Shimian County, which are mostly areas with high geological hazard susceptibility. The highly suitable and moderately suitable areas are mainly distributed in western, northeastern and southeastern Shimian County. Generally, suitable areas are mixed at the junction of suitable and unsuitable areas. There is a high consistency between the results of construction land suitability and geological hazard susceptibility. This situation occurs because the OWA operator is chosen for the suitability analysis with an “optimistic” attitude and the decision preference coefficient is small, which gives more weights to indices with a high degree of importance. Therefore, the geological hazard susceptibility indices have the greatest weights, and their influences on the suitability results are most significant. Comparing the results of the construction land suitability analysis with the land use type map of Shimian County (Figure 4), it can be found that almost all the construction land with the highest suitability rating in the land use type map is located in the highly suitable areas in Figure 7. This finding indicates that the suitability analysis of construction land is reasonable in this study.

5.2 Analysis of comprehensive evaluation results of site selection

After obtaining the ranking of site alternatives, the PROMETHEE Rainbow and Graphical Analysis for Interactive Aid (GAIA) functions in Visual PROMETHEE software are used to further analyze the comprehensive evaluation results of the site selection of new healthcare facilities.

1) Subindex analysis of site alternatives

The rainbow chart is generated by the function of PROMETHEE Rainbow, as shown in Figure 9. A bar chart is drawn for each site alternative, with different fragments representing different evaluation indices. The size of the fragments is proportional to the net flow of the index and is ordered from top to bottom by the size of the net flow of the index. The names of evaluation indices corresponding to the sequence of fragments are marked on the upper and lower sides of the bar chart. The site alternatives are also ranked from left to right according to the numerical magnitude of their net flows. Figure 9 shows the subindex scores for the site alternatives. As an example, S2 scores higher on indices D1, D2, D3, D4, and D6 and lower on D5. The results show that compared to other alternatives, the new healthcare facility at S2 can be located as far away from existing healthcare facilities as possible, which can balance the layout of medical resources, increase accessibility to medical services, and improve the level of medical service equalization in the study area. Meanwhile, a new healthcare facility at S2 can also reduce the total distance to healthcare facilities for residents and be located away from industrial areas. However, the net flow value of the construction land suitability for S2 is negative, indicating that the construction land suitability rating of S2 is moderately suitable. Although the score of S2 is lower compared to other site alternatives, the site meets the requirements for construction suitability. The Rainbow figure can also be used to compare different alternatives. For example, compared with S3 and S2, the net flow of all indices in S3 is positive, but the fragments size of D1, D2, D3, and D6 indices is smaller than S2. It shows that the new healthcare facility at S3 can increase the accessibility to medical services and improve the level of medical service equalization to a certain extent. And it is far from the existing healthcare facilities and industrial areas, which can basically meet the requirements of balanced distribution and competitiveness of medical resources. However, the effect of the new healthcare facility at S3 is far worse than that at S2. In addition, it is better than S2 in terms of the total distance to healthcare facilities for residents and construction land suitability. Based on the above methods, the analysis of the subindexes of other site alternatives can also be obtained. The decision-maker can choose the site alternative according to his personal preference.

2) Graphical Analysis for Interactive Aid (GAIA)

FIGURE 9

FIGURE 9. PROMETHEE Rainbow figure.

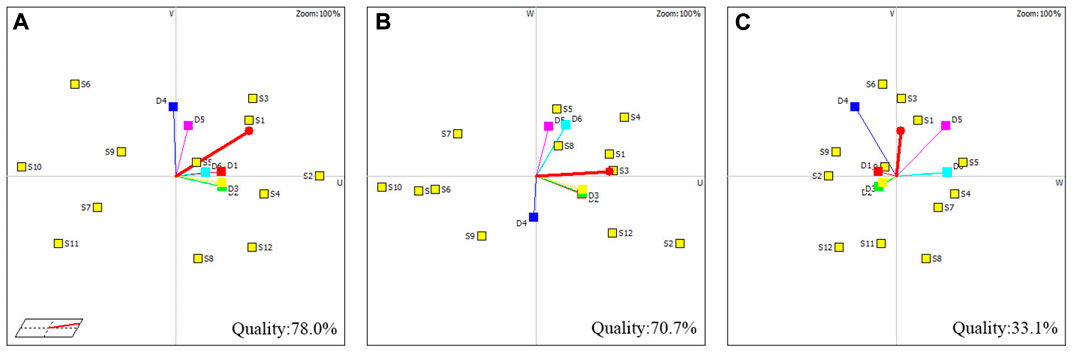
GAIA is used to carry out an interaction-aided graphical analysis of the site alternatives. Three-dimensional space is used to visualize the proximity of evaluation indices and alternatives by GAIA, which is expressed in three planes: U-V, U-W and W-V (Figure 10). As shown in Figure 10, the red lines at the end of the circles represent the decision axes; the longer the decision axis is, the more information the plane expresses and the more accurate the decision. Thus, Figures 10A expresses the most information, representing 78.0% of the 3D spatial information. In Figures 10A, when the decision-maker uses D1, D5, and D6 as the main evaluation indices, S1, S3, S4, and S2 will be the final decision targets. When D2 and D3 are defined as the main evaluation indices, S3, S2, S12, and S8 will be the optimal solutions. If an evaluation index is in the same or similar direction as the decision axis, then the index meets the current evaluation criteria. Therefore, all 6 evaluation indices meet the current evaluation criteria in Figures 10A–C can all be analyzed according to the above methods and will not be repeated here. The decision-maker can analyze whether the current results are the same as their expectations using GAIA to make timely adjustments.

FIGURE 10

FIGURE 10. Interaction-assisted graphic: (A) U-V plane, (B) U-W plane, (C) W-V plane.

6 Conclusion

Healthcare is a matter of national economy and people’s livelihood. This paper aims to reduce the losses caused by geological hazards and to achieve equalization of medical services and balanced allocation of medical resources in mountainous areas with heterogeneous population distribution and economic development. Thus, this paper proposes a GIS and PROMETHEE II-based method for determining the site selection of new healthcare facilities in geological hazard-prone areas. First, GIS and OWA operator are used to identify site alternatives for new healthcare facilities. Second, based on the identification of site alternatives, the PROMETHEE II method is used to conduct a comprehensive evaluation of the alternatives. This comprehensive evaluation method has the following advantages: 1) four criteria of geohazard, topography, geohydrology and socioeconomic are fully considered; 2) the importance of each index is measured using the α value set by the OWA operator; and 3) both qualitative and quantitative evaluation indices are considered, meeting the requirement of multiple criteria to be considered in the site selection study for new healthcare facilities. The paper fully measures the suitability of the site and the competition, accessibility, equalization, environment, and demand for new healthcare facilities, effectively ensuring the safety, suitability and development of the site and achieving a reasonable and scientific site selection for new healthcare facilities in geological hazard-prone areas. The results of the study show that the GIS and PROMETHEE II-based evaluation method has the ability and advantage of solving the site selection of new healthcare facilities in geological hazard-prone areas and other similar complex site selection problems, which can provide some references for similar studies.

In addition, the method allows the decision-making process for suitability analysis to be more flexible by setting the α value according to the decision-makers’ attitudinal preferences. The α value can represent the mutual restriction relationship between geological hazards and construction land development. At the same time, decision-makers can assign weights to indices in Visual PROMETHEE software to intuitively obtain the changes in weights on ranking results. Decision-makers can also conduct detailed analysis on the relationship between the subindexes of the ranking results and the alternatives to improve the accuracy of decision-making according to rainbow graph and GAIA.

With the development of society and economy, other standards should be considered for the site selection of new healthcare facilities in geological hazard-prone areas to improve the comprehensiveness and accuracy of the indices, such as land cost, land expansion, green area, air pollution and so on. Other multicriteria decision-making methods or fuzzy multicriteria decision-making methods, such as ANP, ELECTRE, TOPSIS, Fuzzy-TOPSIS, VIKOR, Fuzzy-VIKOR, TODIM, Fuzzy-SAW, and EDAS, can also be used to study site selection. Follow-up research can use a variety of MCDM tools for comparative research. The transparency of the decision-making process and the robustness of the decision-making results can be improved by comparing the advantages and disadvantages of different decision-making methods. In addition, machine learning methods, such as LSSVM, MPA, PSO, GA, GWO, SVR, LSSVR, and RBFNN, can also be tried to solve the site selection problems in the future.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

MY, formal analysis, investigation, methodology, writing—original draft; S-YH, investigation, formal analysis, data curation; J-MC, investigation, resources; P-NG, investigation, software, formal analysis; H-BL, investigation, formal analysis, visualization; H-GX, conceptualization, funding acquisition, writing—review and editing.

Funding

This work was supported by the National Natural Science Foundation of China (U20A20111).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2023.1121690/full#supplementary-material

References

Adali, E. A., and Tus, A. (2021). Hospital site selection with distance-based multi-criteria decision-making methods. Int. J. Healthc. Manag. 14 (2), 534–544. doi:10.1080/20479700.2019.1674005

CrossRef Full Text | Google Scholar

Aghmashhadi, A. H., Azizi, A., Zahedi, S., Hoseinkhani, M., and Cirella, G. T. (2022). Land suitability mapping using GIS-based ANP for residential zoning: Case research from central Iran. Trans. GIS 26 (2), 1017–1039. doi:10.1111/tgis.12896

CrossRef Full Text | Google Scholar

Ajaj, Q. M., Shareef, M. A., Jasim, A. T., Hasan, S. F., Noori, A. M., and Hassan, N. D. (2019). “An AHP-based GIS for a new hospital site selection in the kirkuk governorate,” in Proceedings of the 2nd International Conference on Electrical, Communication, Computer, Power and Control Engineering (ICECCPCE), Iraq, February 2019.

CrossRef Full Text | Google Scholar

Bagheri, M., Sulaiman, W. N. A., and Vaghefi, N. (2013). Application of geographic information system technique and analytical hierarchy process model for land-use suitability analysis on coastal area. J. Coast. Conservation 17 (1), 1–10. doi:10.1007/s11852-012-0213-4

CrossRef Full Text | Google Scholar

Bahadori, M., Hosseini, S. M., Teymourzadeh, E., Ravangard, R., Raadabadi, M., and Alimohammadzadeh, K. (2017). A supplier selection model for hospitals using a combination of artificial neural network and fuzzy VIKOR. Int. J. Healthc. Manag. 13 (4), 286–294. doi:10.1080/20479700.2017.1404730

CrossRef Full Text | Google Scholar

Behzadian, M., Kazemzadeh, R. B., Albadvi, A., and Aghdasi, M. (2010). Promethee: A comprehensive literature review on methodologies and applications. Eur. J. Operational Res. 200 (1), 198–215. doi:10.1016/j.ejor.2009.01.021

CrossRef Full Text | Google Scholar

Billaud, O., Soubeyrand, M., Luque, S., and Lenormand, M. (2020). Comprehensive decision-strategy space exploration for efficient territorial planning strategies. Comput. Environ. Urban Syst. 83, 101516. doi:10.1016/j.compenvurbsys.2020.101516

CrossRef Full Text | Google Scholar

Boyaci, A. C., and Sisman, A. (2022). Pandemic hospital site selection: A GIS-based MCDM approach employing pythagorean fuzzy sets. Environ. Sci. Pollut. Res. 29 (2), 1985–1997. doi:10.1007/s11356-021-15703-7

CrossRef Full Text | Google Scholar

Chai, J., Liu, J. N. K., and Ngai, E. W. T. (2013). Application of decision-making techniques in supplier selection: A systematic review of literature. EXPERT Syst. Appl. 40 (10), 3872–3885. doi:10.1016/j.eswa.2012.12.040

CrossRef Full Text | Google Scholar

Cosimo, L. H. E., Martins, S. V., and Gleriani, J. M. (2021). Suggesting priority areas in the buffer zone of Serra do Brigadeiro State Park for forest restoration compensatory to bauxite mining in Southeast Brazil. Ecol. Eng. 170, 106322. doi:10.1016/j.ecoleng.2021.106322

CrossRef Full Text | Google Scholar

Csiszar, O. (2021). Ordered weighted averaging operators: A short review. IEEE Syst. Man, Cybern. Mag. 7 (2), 4–12. doi:10.1109/msmc.2020.3036378

CrossRef Full Text | Google Scholar

Dell'Ovo, M., Capolongo, S., and Oppio, A. (2018). Combining spatial analysis with MCDA for the siting of healthcare facilities. Land Use Policy 76, 634–644. doi:10.1016/j.landusepol.2018.02.044

CrossRef Full Text | Google Scholar

Dell'Ovo, M., Frej, E. A., Oppio, A., Capolongo, S., Morais, D. C., and de Almeida, A. T. (2017). “Multicriteria decision making for healthcare facilities location with visualization based on FITradeoff method,” in Proceedings Of The Decision Support Systems Vii: Data, Information And Knowledge Visualization In Decision Support Systems, Namur, Belgium, May 2017.

Google Scholar

Dulin, M. F., Ludden, T. M., Tapp, H., Blackwell, J., de Hernandez, B. U., Smith, H. A., et al. (2010). Using geographic information systems (GIS) to understand a community's primary care needs. J. Am. Board Fam. Med. 23 (1), 13–21. doi:10.3122/jabfm.2010.01.090135

PubMed Abstract | CrossRef Full Text | Google Scholar

Eghtesadifard, M., Afkhami, P., and Bazyar, A. (2020). An integrated approach to the selection of municipal solid waste landfills through GIS, K-Means and multi-criteria decision analysis. Environ. Res. 185, 109348. doi:10.1016/j.envres.2020.109348

PubMed Abstract | CrossRef Full Text | Google Scholar

Eldemir, F., and Onden, I. (2016). Geographical information systems and multicriteria decisions integration approach for hospital location selection. Int. J. Inf. Technol. Decis. Mak. 15 (5), 975–997. doi:10.1142/s0219622016500218

CrossRef Full Text | Google Scholar

Gul, M., and Guneri, A. F. (2021). Hospital location selection: A systematic literature review on methodologies and applications. Math. Problems Eng. 2021, 1–14. doi:10.1155/2021/6682958

CrossRef Full Text | Google Scholar

Guo, F., Gao, J., Men, H., Fan, Y., and Liu, H. (2021). Large-scale group decision-making framework for the site selection of integrated floating photovoltaic-pumped storage power system. J. Energy Storage 43, 103125. doi:10.1016/j.est.2021.103125

CrossRef Full Text | Google Scholar

Halder, B., Bandyopadhyay, J., and Banik, P. (2020). Assessment of hospital sites' suitability by spatial information technologies using AHP and GIS-based multi-criteria approach of Rajpur-Sonarpur Municipality. Model. EARTH Syst. Environ. 6 (4), 2581–2596. doi:10.1007/s40808-020-00852-4

CrossRef Full Text | Google Scholar

Joseph, A. E., and Bantock, P. R. (1982). Measuring potential physical accessibility to general practitioners in rural areas: A method and case study. Soc. Sci. Med. 16 (1), 85–90. doi:10.1016/0277-9536(82)90428-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Kapoor, N., and Bansal, V. K. (2021). Spatial suitability assessment for planning infrastructure facilities at site level in hill areas. J. Urban Manag. 10 (1), 27–45. doi:10.1016/j.jum.2021.02.003

CrossRef Full Text | Google Scholar

Kumar, S., and Kumar, R. (2014). Site suitability analysis for urban development of a hill town using GIS based multicriteria evaluation technique: A case study of nahan town, Himachal Pradesh, India. Int. J. Adv. Remote Sens. GIS 3 (1), 516–524.

Google Scholar

Lin, J., Chen, W., Qi, X., and Hou, H. (2021). Risk assessment and its influencing factors analysis of geological hazards in typical mountain environment. J. Clean. Prod. 309, 127077. doi:10.1016/j.jclepro.2021.127077

CrossRef Full Text | Google Scholar

Liu, R., Zhang, K., Zhang, Z., and Borthwick, A. G. L. (2014a). Land-use suitability analysis for urban development in Beijing. J. Environ. Manag. 145, 170–179. doi:10.1016/j.jenvman.2014.06.020

CrossRef Full Text | Google Scholar

Liu, Y., Peng, J., Han, Y., Wei, H., and Du, Y. (2014b). Suitability assessment for building land consolidation on gentle hillside based on OWA operator: A case in dali Bai nationality borough in yunnan, China. Acta Ecol. Sin. 34 (12), 3188–3197.

Google Scholar

Luan, C., Liu, R., and Peng, S. (2021). Land-use suitability assessment for urban development using a GIS-based soft computing approach: A case study of ili valley, China. Ecol. Indic. 123, 107333. doi:10.1016/j.ecolind.2020.107333

CrossRef Full Text | Google Scholar

Ma, Z., and Mei, G. (2021). Deep learning for geological hazards analysis: Data, models, applications, and opportunities. Earth-Science Rev. 223, 103858. doi:10.1016/j.earscirev.2021.103858

CrossRef Full Text | Google Scholar

Sahin, T., Ocak, S., and Top, M. (2019). Analytic hierarchy process for hospital site selection. HEALTH POLICY Technol. 8 (1), 42–50. doi:10.1016/j.hlpt.2019.02.005

CrossRef Full Text | Google Scholar

Sara, B., and Abbas, A. (2014). A multi-objective optimization approach for location-allocation of clinics. Int. Trans. Operational Res. 22 (2), 313–328. doi:10.1111/itor.12088

CrossRef Full Text | Google Scholar

Sennaroglu, B., and Celebi, G. V. (2018). A military airport location selection by AHP integrated PROMETHEE and VIKOR methods. Transp. Res. PART D-TRANSPORT Environ. 59, 160–173. doi:10.1016/j.trd.2017.12.022

CrossRef Full Text | Google Scholar

Senvar, O., Otay, I., and Bolturk, E. (2016). Hospital site selection via hesitant fuzzy TOPSIS. IFAC Pap. 49 (12), 1140. doi:10.1016/j.ifacol.2016.07.656

CrossRef Full Text | Google Scholar

Tripathi, A. K., Agrawal, S., and Gupta, R. D. (2021). Comparison of GIS-based AHP and fuzzy AHP methods for hospital site selection: A case study for prayagraj city. GeoJournal 28. doi:10.1007/s10708-021-10445-y

CrossRef Full Text | Google Scholar

Tyagi, A., and Singh, P. (2019). Hospital performance management: A multi-criteria decision-making approach. Int. J. Healthc. Manag. 12 (4), 286–291. doi:10.1080/20479700.2017.1337606

CrossRef Full Text | Google Scholar

Wang, L., Shi, H., and Gan, L. (2018). Healthcare facility location-allocation optimization for China's developing cities utilizing a multi-objective decision support approach. Sustainability 10 (12), 4580. doi:10.3390/su10124580

CrossRef Full Text | Google Scholar

Wu, Y., Liu, F., Huang, Y., Xu, C., Zhang, B., Ke, Y., et al. (2020a). A two-stage decision framework for inland nuclear power plant site selection based on GIS and type-2 fuzzy PROMETHEE II: Case study in China. Energy Sci. Eng. 8 (6), 1941–1961. doi:10.1002/ese3.640

CrossRef Full Text | Google Scholar

Wu, Y., Tao, Y., Zhang, B., Wang, S., Xu, C., and Zhou, J. (2020b). A decision framework of offshore wind power station site selection using a PROMETHEE method under intuitionistic fuzzy environment: A case in China. Ocean Coast. Manag. 184, 105016. doi:10.1016/j.ocecoaman.2019.105016

CrossRef Full Text | Google Scholar

Wu, Y., Zhang, B., Wu, C., Zhang, T., and Liu, F. (2019). Optimal site selection for parabolic trough concentrating solar power plant using extended PROMETHEE method: A case in China. Renew. Energy 143, 1910–1927. doi:10.1016/j.renene.2019.05.131

CrossRef Full Text | Google Scholar

Yager, R. R. (1988). On ordered weighted averaging aggregation operators in multicriteria decisionmaking. IEEE Trans. Syst. Man, Cybern. 18 (1), 183–190. doi:10.1109/21.87068

CrossRef Full Text | Google Scholar

Yager, R. R. (1996). Quantifier guided aggregation using OWA operators. Int. J. Intelligent Syst. 11 (1), 49–73. doi:10.1002/(SICI)1098-111X(199601)11:1<49:AID-INT3>3.0.CO;2-Z

CrossRef Full Text | Google Scholar

Yang, Y., Tang, X-l., and Li, Z-h. (2021). Land use suitability analysis for town development planning in nanjing hilly areas: A case study of tangshan new town, China. J. Mt. Sci. 18 (2), 528–540. doi:10.1007/s11629-020-6037-z

CrossRef Full Text | Google Scholar

Yilmaz, M., and Atan, T. (2021). Hospital site selection using fuzzy EDAS method: Case study application for districts of Istanbul. J. INTELLIGENT FUZZY Syst. 41 (2), 2591–2602. doi:10.3233/jifs-201757

CrossRef Full Text | Google Scholar

Yu, M., Xing, H., and Hu, S. (2021). Debris flow susceptibility assessment based on information value and logistic regression coupled model: Case of shimian county, sichuan Province. Yangtze River 52 (12), 107–114.

Google Scholar

Zhang, W., Cao, K., Liu, S., and Huang, B. (2016). A multi-objective optimization approach for health-care facility location-allocation problems in highly developed cities such as Hong Kong. Comput. Environ. Urban Syst. 59, 220–230. doi:10.1016/j.compenvurbsys.2016.07.001

CrossRef Full Text | Google Scholar

Zolfani, S. H., Yazdani, M., Torkayesh, A. E., and Derakhti, A. (2020). Application of a gray-based decision support framework for location selection of a temporary hospital during COVID-19 pandemic. SYMMETRY 12 (6), 886. doi:10.3390/sym12060886

CrossRef Full Text | Google Scholar