- 1School of Geosciences and Info-Physics, Central South University, Changsha, China
- 2Key Laboratory of Petroleum Resource Research, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing, China
- 3College of Geophysics, Chengdu University of Technology, Chengdu, China
- 4Energy and Deep Earth Exploration Laboratory, Institute of Geophysical and Geochemical Exploration, China Geological Survey, Langfang, China
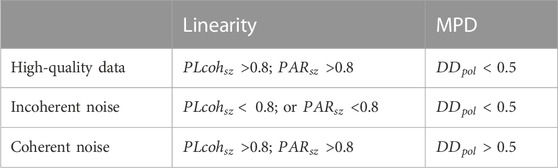
The magnetotelluric response function can be severely disturbed by cultural electromagnetic noise. The preselection strategy is one of the effective ways to remove the influence of noise when calculating the response function. This study proposed three new parameters (the amplitude ratio predicted amplitude ratio and linear coherence (PLcoh) between the predicted and observed electric fields and the dispersion degree of the magnetic polarization direction (
1 Introduction
The magnetotelluric (MT) method is an electromagnetic (EM) geophysical method used to infer the subsurface electrical conductivity from the natural geomagnetic and geoelectric fields obtained at the Earth’s surface (Tikhonov, 1950; Cagniard, 1953). There is a linear relationship between the geoelectric and geomagnetic fields in the frequency domain, and it can be expressed as follows (Tikhonov and Berdichevsky, 1966):
where E and H are the horizontal electric and magnetic field components at a specific frequency, respectively,
Methods to remove these disturbances are mainly based on robust statistical algorithms, remote reference processing, multistation analyses or time series modification. The robust statistical methods are based on data-adaptive weighting schemes, which aim to detect and reject outliers from a majority of well-behaved samples (Egbert and Booker, 1986; Chave and Thomson, 2004; 2003; 1989; Jones et al., 1989). These methods require reasonable proportions of normal data to yield reliable results, e.g., data with no more than 50% contamination (Smirnov, 2003). If a noise source is more persistent, it can easily result in a distribution of the majority of the data, which is wrong (Weckmann et al., 2005). The remote reference method requires simultaneously recorded EM fields from at least two sites. Remote reference processing uses cross-power spectra instead of auto-power spectra when performing regression based on the least-squares estimator (Goubau et al., 1978; Gamble et al., 1979). The remote reference method cannot always improve the results, as a successful application requires a horizontal magnetic field at a remote site without correlated noise. It is difficult to find a suitable reference site because cultural noise signals can be widespread and coherent over large areas (Weckmann et al., 2005), and we are faced with single-site robust processing. Moreover, MT researchers have proposed multistation analyses. Larsen et al. (1996) and Oettinger et al. (2001) proposed the signal-noise separation (SNS) method. SNS uses the remote magnetic field to estimate the interstation transform function as the separation tensor; they separated the local magnetic field into signal and noise parts and then calculated the impedance. Egbert (1997) proposed a robust multivariate errors-in-variables estimator (RMEV) to separate field data into signal and noise components using principal component analysis. A more recent application of the method is shown in Smirnov and Egbert (2012). Both the RMEV and SNS methods use a robust approach to their data processing. Those methods may be biased when the majority of the data are contaminated and the noise is coherent between the local and remote sites. In a strong noise environment, the time series modification method is also effective in suppressing the influence of noise (Chen et al., 2022; Li et al., 2022; Li et al., 2023; Li et al., 2018; Zhang et al., 2022; Zhang et al., 2021; Zhou et al., 2022; Wang et al., 2017; Kappler, 2012). These methods identify abnormal waveforms in the time domain and modify the original time series, and they are useful for data contaminated by strong noise with an abnormal waveform.
In a noisy EM environment, as an alternative method, it is practical to use a preselection strategy (Jones and Jödicke, 1984; Travassos and Beamish, 1988; Smirnov, 2003; Chave and Thomson, 2004; Weckmann et al., 2005; Platz and Weckmann, 2019) to reduce the EM noise to a level that the robust statistic method can handle. All of the studies, e.g., Platz and Weckmann (2019), Weckmann et al. (2005), and Garcia and Jones (2002), demonstrated substantially better performance for data-adaptive weighting schemes after prescreening. In theory, if the noise does not contaminate the local site all the time, we can extract high signal-to-noise ratio (SNR) data and obtain a reliable result. The multiple coherence (Jones and Jödicke, 1984; Travassos and Beamish, 1988; Egbert and Livelybrooks, 1996; Bendat and Piersol, 2011) and bivariate coherence (Ritter et al., 1998; Weckmann et al., 2005) are widely used to evaluate the data quality under the assumption that the dataset follows a linear relationship. In this research, we propose a new method, which performs similarly with multiple coherence and is superior to the bivariate coherence, to evaluate the linearity by comparing the similarity between the observed and predicted electric fields. The parameters based on the linearity are effective for detecting incoherent noise, but coherent noise may also have high linearity (Weckmann et al., 2005). In addition, Weckmann et al. (2005) showed the effectiveness of magnetic polarization direction (MPD) in visualizing coherent noise. However, their preselection strategy cannot be performed automatically. Platz and Weckmann (2019) attempted to perform data preselection automatically and used statistical information on the magnetic polarization direction (SMPD) to constrain coherent noise with strong polarization direction. They removed all the data whose polarization directions fall in a bin which is much higher than the threshold. However, the data fall in out of the bin also may correspond to the coherent noise. We proposed a new parameter based on the dispersion degree of the magnetic polarization direction (
The following sections are organized as follows. Section 2 introduces the new parameters proposed to detect noise. Section 3 shows the effectiveness of the parameters to detect noise and compares the new parameters with the previous study.
2 Parameters proposed for the preselection strategy
The method to obtain the spectra of EM fields in different frequencies is similar to the method used in the bounded influence remote reference processing (BIRRP) code (Chave and Thomson, 1989; Chave and Thomson, 2004; 2003). The time series is prewhited and divided into adjacent segments. These segments are cosine tapered before the Fourier transformation. Then, the Fourier coefficients are corrected for the influence of the instrument response. Next, selected frequencies within each segment are extracted to calculate the impedance tensor and uncertainty followed by the robust estimator created by Neukirch and García (2014). At last, the segment length is variable, the previous steps are repeated to calculate the impedance in different frequencies. During data processing, one segment corresponds to one data in the frequency domain. In the following, we refer to one data as one event in the frequency domain. The key to obtaining a reliable impedance from the noisy site is detecting and removing the noise before the impedance estimation. This section introduces the parameters used to detect noisy events from the perspective of linearity and MPD.
2.1 Noise detection based on linearity
From the perspective of whether the data follow the linear relationship in Eq. 1, the field data (E and H) can be subdivided into three parts as follows:
where the superscript HLN denotes the data dominated by noise with high linearity, the superscript LLN denotes the data dominated by noise with low linearity, and the superscript MT denotes the high-quality data with high linearity. Noise with low linearity can be identified from the similarity between the observed electric field and that predicted by the linear relationship. It is similar to the single-input/single-output linear model to evaluate the linearity, as shown in Figure 1. The difference between the data with high linearity and low linearity is that most of the predicted and observed values of the output are similar.
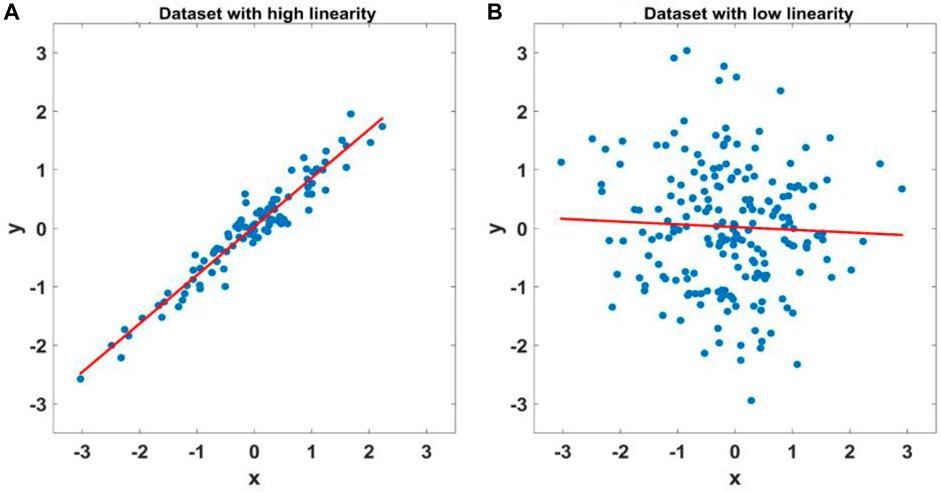
FIGURE 1. Single-input/single-output linear model y=a*x+b. x is the input, and y is the output. The blue points denote the observed data, and the red line is the model calculated by regression. The difference between the data with high linearity and low linearity is that most of the predicted values (a*x+b) calculated by the model and the output (y) are similar, as shown in (A) and (B).
Assuming the data are highly linear related, the observed electric field (E) should be similar to the predicted electric field (
The linear coherence (Lcoh) between two spectra
where
where
The high predicted linear coherence can ensure the phase similarity. We also use the predicted amplitude ratio (PAR) to ensure the amplitude similarity, and it is defined as follows:
The PAR ranges from 0 to 1; the higher PAR is, the higher the similarity between the two spectra in terms of the amplitude.
There is a problem that the energy of the signal and noise changes with time, and the linearity may change. Suppose we perform regression with all the available data; the linearity may be low in the presence of a large amount of noise and provide misleading information. It is similar to the single-input/single-output linear model, as shown in Figure 2. There are six datasets, and only dataset 1 has high linearity. When we perform regression with all the available data, the linearity is low, and we cannot extract data with high linearity. To solve this problem, we subdivide the data into small groups and calculate the PAR and PLcoh values separately. We rename the predicted linear coherence and amplitude ratio as
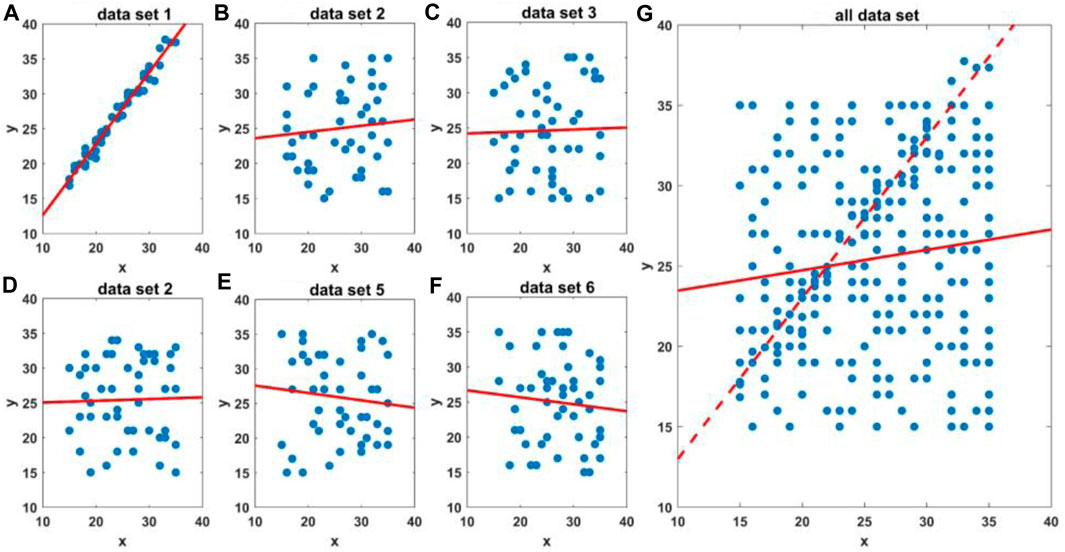
FIGURE 2. Single-input/single-output linear model y=a*x+b. (A–F) show the regression results for six datasets separately; each dataset has 50 points, and only dataset 1 has high linearity. The blue points denote the observed data, and the red line is the model calculated by regression. (G) shows the regression results for all the available data, including 300 points. The red solid line denotes the model calculated by all the available data, and the dashed line denotes the model calculated by dataset 1.
2.2 Noise detection based on the magnetic polarization directions
Fowler et al. (1967) proposed the polarization direction, and Weckmann et al. (2005) showed the effectiveness of MPD in detecting coherent noise. The MPD (
where i (=1,2, … , N) is the number index of the event,
To quantify the dispersion degree of MPD, the dispersion degree of the polarization directions (
where
When the polarization direction has a preferred direction,
3 Case studies for the preselection strategy
Usually, data dominated by incoherent noise do not have a stable relationship; therefore, the linearity should be low. We can identify the incoherent noise using the parameters
The preselection strategy based on linearity and the MPD is tested on approximately 500 site data from the USArray project (Schultz et al., 2018; Kelbert, 2019) and data collected in China. It can improve the quality of the impedance tensor when intermittent noise contaminates the field data. Two typical field datasets are chosen to demonstrate the effectiveness of those parameters to identify noisy events. The location map is shown in Figure 3. The first data are contaminated by incoherent noise, which contains a geomagnetic storm, the energy from the natural EM signal increases significantly, and high signal-to-noise ratio (SNR) data appear during the storm. The second dataset is contaminated by coherent noise and incoherent noise simultaneously, the noise decreases during the local nighttime, and high SNR data appear.
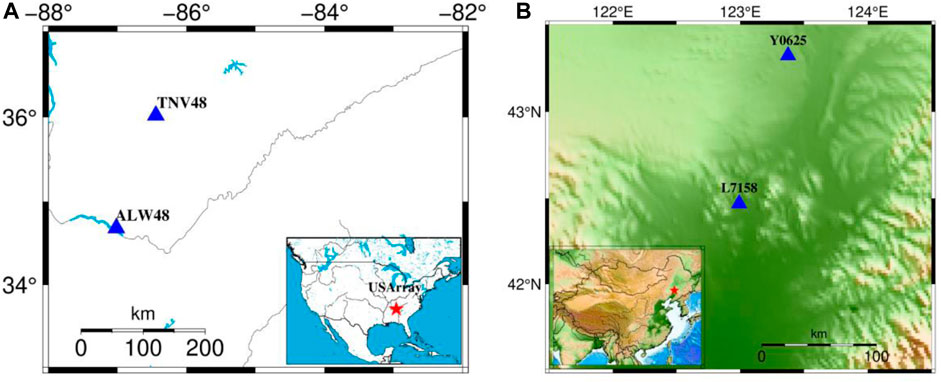
FIGURE 3. Location map of the field data. (A) shows the location of the first field data; the blue triangles denote the observation site. TNV48 is used as the locale site, and ALW48 is set as the remote reference site. The lower right corner in (A) shows the survey location of the USArray, and the red star denotes the location of site TNV48. (B) shows the location map of the second field data observed in China. Y0625 is the remote reference site, and L7-158 is the local site. The lower left corner in (B) shows the survey area in China, and the red star denotes the local site.
3.1 Case study 1: Data contaminated by intermittent incoherent noise
The first case study used the data observed at TVN48 from the USArray project. The time-series data can be downloaded from the Incorporated Research Institutions for Seismology (IRIS) website. The data sampling period is 1 s, and the used times-series data are observed from July 19 to 24 July 2015. First, we examine the variation in the parameters at different frequencies. Figure 4 shows the parameter variation in the period of 13.1 s. Figures 4A, B show the variation in
where H represents N by two matrices of the horizontal magnetic field (
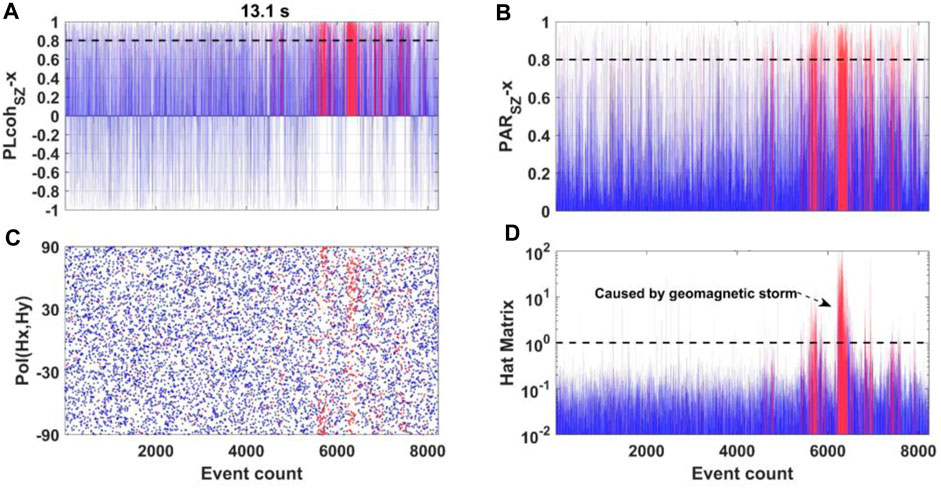
FIGURE 4. Parameters variation at TVN48 in the period of 13.1 s. The horizontal axis denotes the event count. Panels (A, B) show the variation in
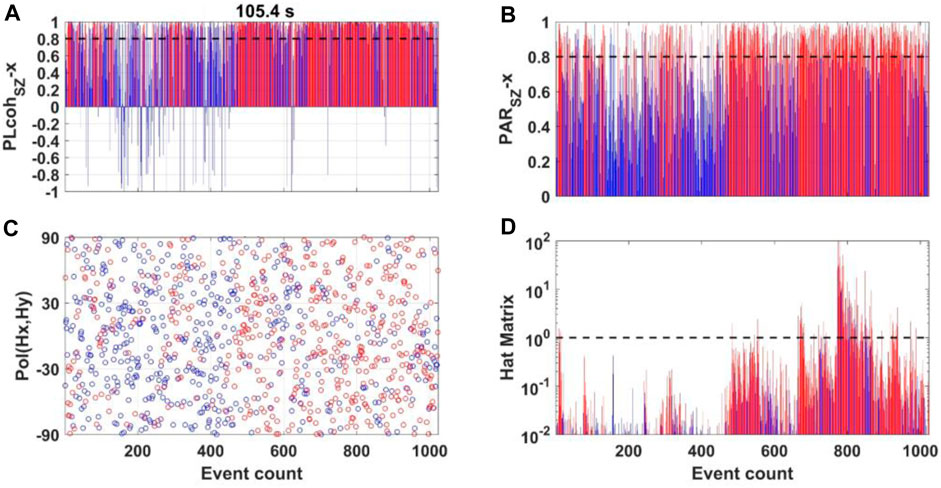
FIGURE 5. Parameters variation at TVN48 in the period of 105.4 s. (A, B) show the variation in
Then, we compare the MT sounding curves calculated by the different methods, as shown in Figure 6. All of those responses are estimated by M-estimator (Egbert and Booker, 1986; Neukirch and García, 2014; Maronna et al., 2019). The result using the data preselection strategy with
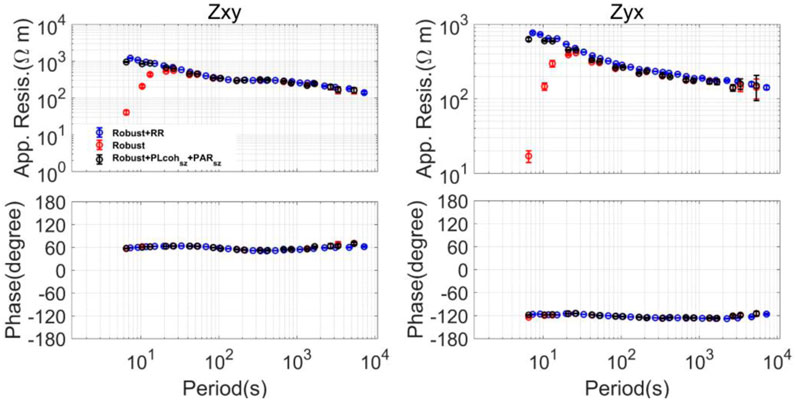
FIGURE 6. MT sounding curves calculated by the different methods using the data observed at site TNV48. The upper figures show the apparent resistivity, and the lower figures show the impedance phase. All the responses are estimated by a M-estimator. The blue curves denote the remote reference results. The red curves denote the single-site robust result. The black curves are calculated by the preselection strategy using
3.2 Comparison of the parameters used to evaluate the linearity
This subsection compares the performance of the related parameters used to evaluate linearity, e.g., multiple coherence (Travassos and Beamish, 1988; Egbert and Livelybrooks, 1996; Bendat and Piersol, 2011) and bivariate coherence (Ritter et al., 1998; Weckmann et al., 2005). All of those parameters can be indicators of the data quality under the assumption that the dataset follows a linear relationship.
Multiple coherence is defined as the ratio of the ideal output spectrum due to the measured inputs in the absence of noise to the total output spectrum, which includes the noise (Bendat and Piersol, 2011). In equation form, the multiple coherence associated with
where
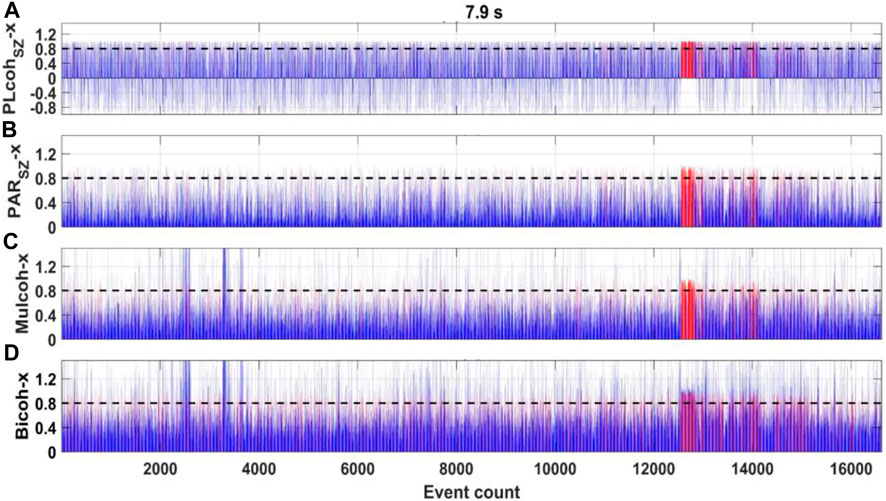
FIGURE 7. Parameters variation at TVN48 in the period of 7.9 s. The red color denotes the events in high linearity based on different parameters, and the other events are shown in blue. All the parameters are determined from the bivariate equations whose dependent variable is the
Bivariate coherence is defined as a function of the amplitude ratio and phase difference between the predicted and the observed electric field. In equation form, bivariate coherence associated with
where
The comparison of the parameters used to evaluate the linearity is shown in Figure 7. First, the events are divided into groups that contain N samples, e.g., 20 samples. We calculate the predicted electric field for each group, separately. If the data quality is high, all of the parameters should be close to one under the assumption that the data follow a linear relationship. All of the parameters can identify the high-quality data corresponding to the magnetic storm. However, the parameters (
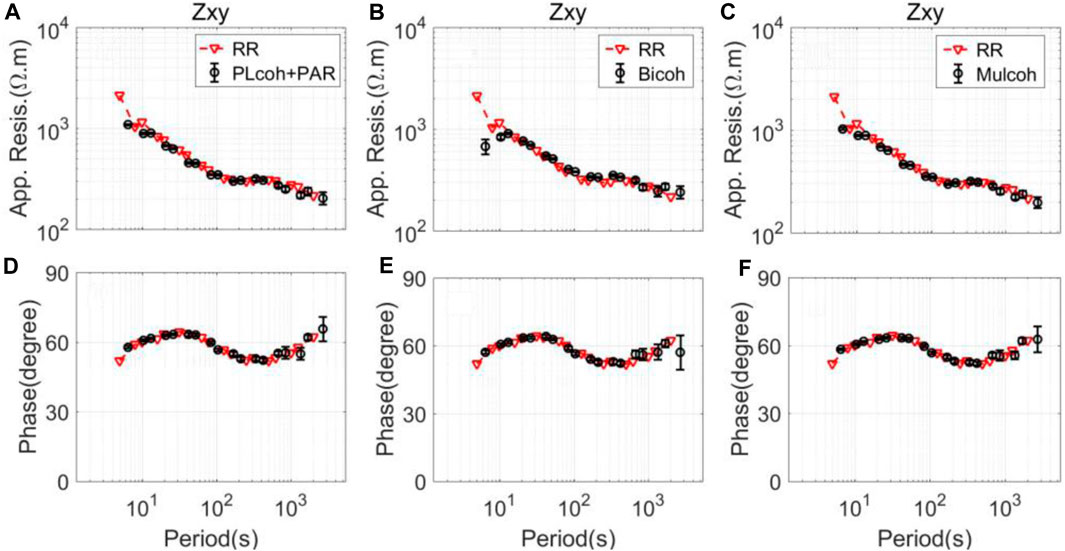
FIGURE 8. MT sounding curves calculated by the different preselection strategies corresponding to
3.2 Case study 2: Data contaminated by intermittent coherent Noise and incoherent noise
The second case study uses data observed in northeastern China on 26 June 2020. Phoenix Geophysics Instruments were used to collect the MT time-series data. These data are provided by the Institute of Geophysical and Geochemical Exploration, China Geological Survey. Time-series data from 3:00 to 22:00 UTC were used in this case study. The sampling rate is 15 Hz. The observation area is in the GMT+8 time zone, and the local midnight time is approximately 16:00.
First, we examine the variation in the parameters at different frequencies. Figure 9 shows the variation in the period of 6.7 s. Red denotes events with high linearity, and blue denotes events with low linearity. The previous 2,500 events in the daytime have a preferred polarization direction of approximately −30
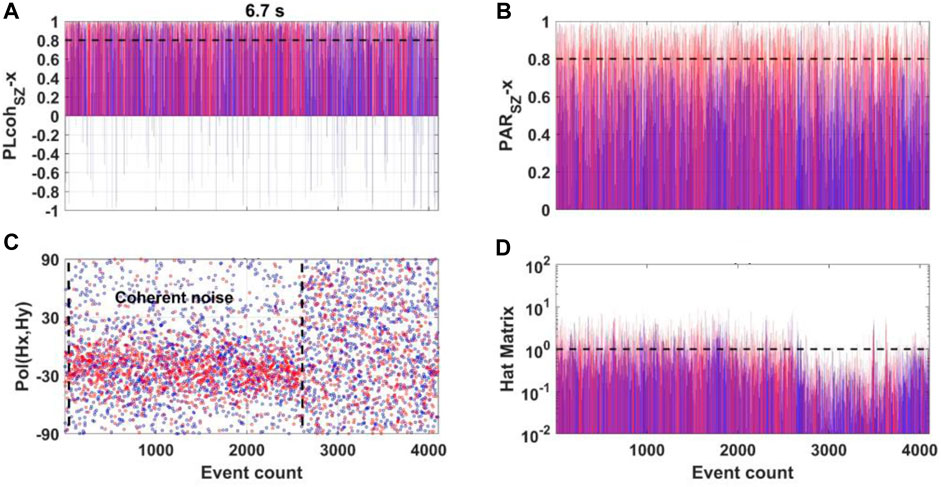
FIGURE 9. Parameters variation at L7-158 in the period of 6.7 s. (A, B) show the variation in
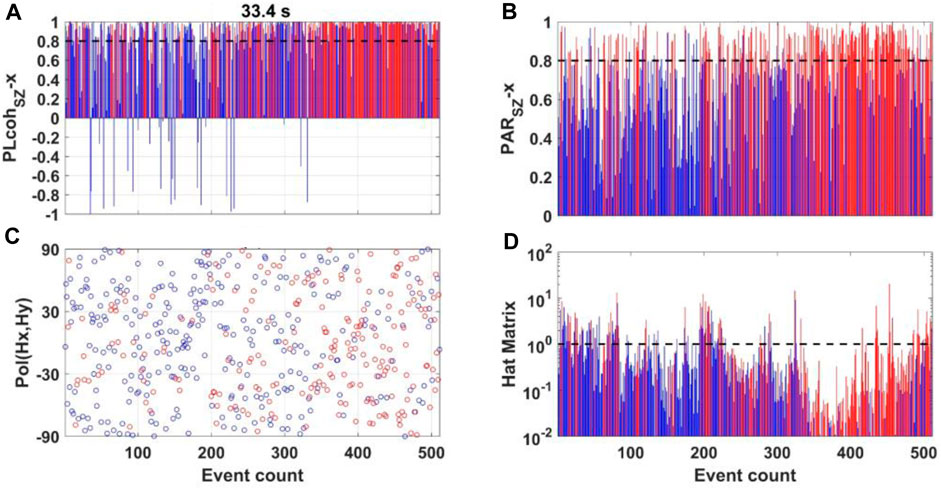
FIGURE 10. Parameters variation at L7-158 in the period of 33.4 s. (A, B) show the variation in
Then, we compare the MT sounding curves calculated by the different methods. First, we compare the result calculated by the SSMT-2000 and the results with and without the preselection strategy based on linearity, as shown in Figure 11. SSMT-2000 is one of the standard Phoenix software sets. After comparing all the results, we think all the impedance results are biased between 2 and 20 s, and there is a rapid rise and fall in the apparent resistivities. The SSMT-2000 result coincides with the preselection strategy result between 20 and 100 s and changes smoothly. The single-site robust result is improved between 20 and 100 s after using the preselection strategy with
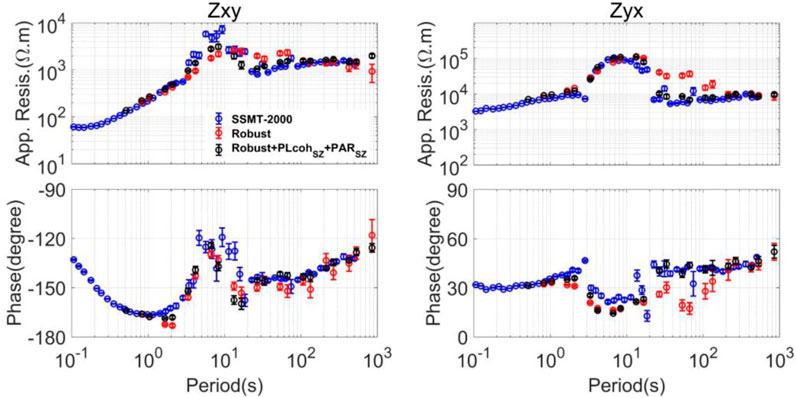
FIGURE 11. MT sounding curves calculated by the different methods using the data observed at site L7-158. SSMT-2000 is used to calculate the blue curves. SSMT-2000 is one of the standard Phoenix software sets. The robust single-site processing approach is used to calculate the red curves. The preselection strategy using
Next, we try to use the information on MPD to constrain the coherent noise. Figure 12 shows the variation in the MPD and the corresponding variation in
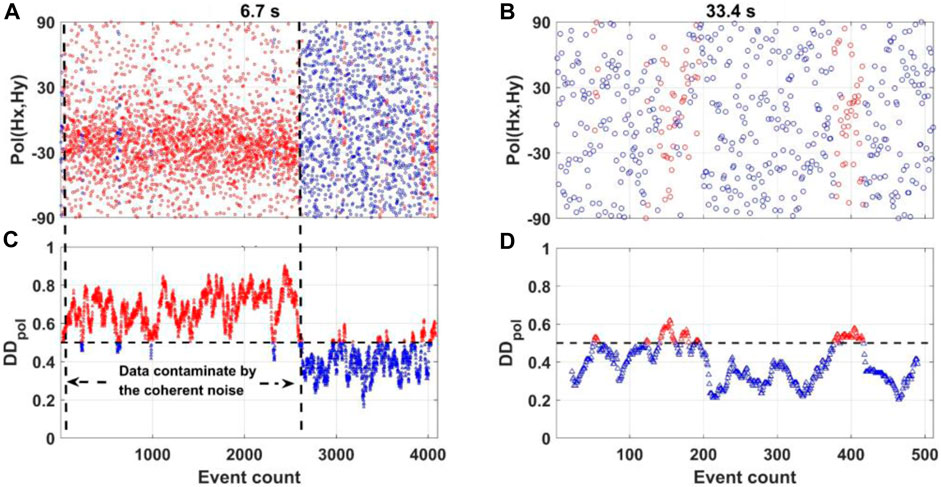
FIGURE 12. Variation in the polarization direction and the corresponding variation in
We also compare the criteria proposed by Platz and Weckmann (2019) which is based on the statistical information on magnetic polarization direction (SMPD). They subdivided the polarization direction into 180 bins with a bin width of 1
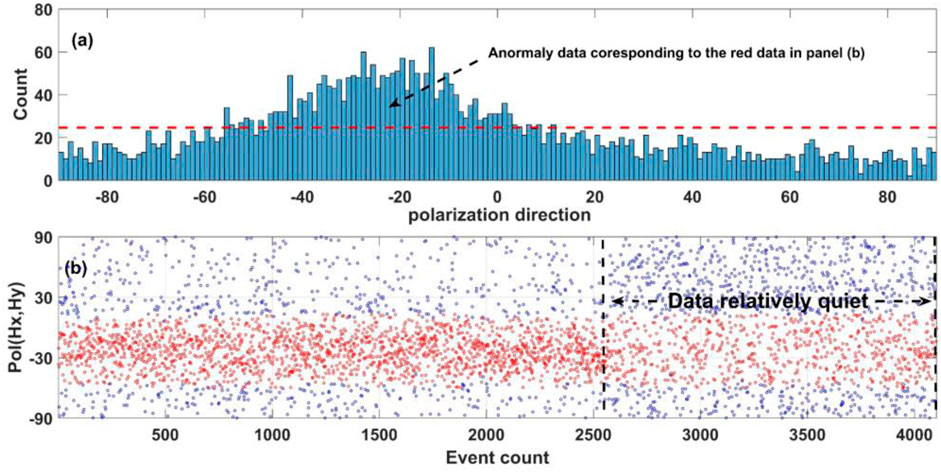
FIGURE 13. Histogram of the MPD and the corresponding variation in the MPD at site L7-158 in the period of 6.7 s. (A) shows the histogram of the MPD; the horizontal axis denotes the bins of the MPD, the vertical axis denotes the number falling in the corresponding bin, and the red dashed line denotes the threshold. (B) shows the variation in the MPD. The horizontal axis denotes the event count. The red color denotes the events that fall into a bin with a higher than expected value, and the other events are shown in blue. The quiet event may be removed at nighttime (the event from 2,500 to 4,000) and many of the events in the daytime remain based on the criteria of SMPD.
At last, we compare the MT sounding curves calculated by the different preselection strategies based on the information on MPD, as shown in Figure 14. The robust estimator combining
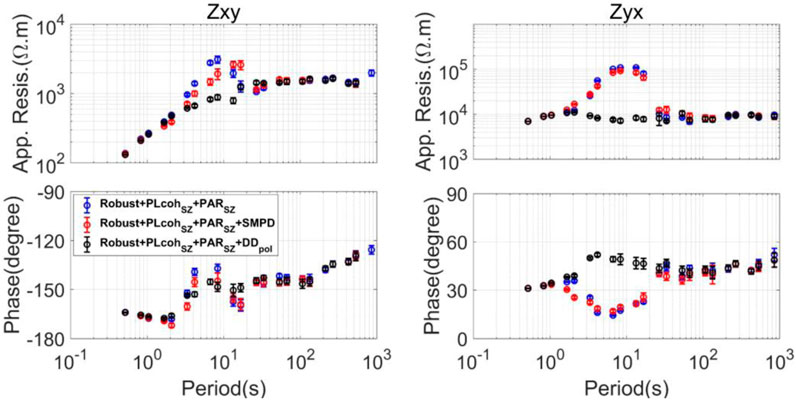
FIGURE 14. MT sounding curves calculated by the different preselection strategies using the data observed at site L7-158. The robust estimator combining
4 Conclusion
Robust single-site data processing may work well unless a large fraction of the data is quiet. On the other hand, the remote reference method may also fail to obtain a reliable result when the noise is correlated between local and remote sites. In a noisy EM environment, it is practical to use a preselection strategy to extract high signal-to-noise ratio (SNR) data, and a reliable response function can be obtained if the noise does not contaminate the local site all the time.
We proposed three new parameters for the preselection strategy from the perspectives of linearity and magnetic polarization, making the preselection process automatic. The predicted linear coherence (
Data availability statement
The time-series data from the USArray project are available from IRIS (http://ds.iris.edu/gmap/#network=_US-MT&planet=earth).
Author contributions
HaC processed the time-series data, created the results, and wrote the paper. HaC contributed approximately 50%. ZR, LZ, and HuC reviewed the paper and contributed approximately 30%; GW provided the MT field data and processed the time-series data with SSMT-2000 software. GW contributed approximately 20% to this work.
Funding
This research is financially supported by the National Natural Science Foundation of China (grants 41774086, 41930430), the Major Research plan of the National Natural Science Foundation of China (grant 92262303), and the Key Research Program of the Institute of Geology and Geophysics, Chinese Academy of Sciences (IGGCAS-201901).
Acknowledgments
We are grateful to the Institute of Geophysical and Geochemical Exploration, China Geological Survey, and USArray team members for providing the time-series data used in this study. The valuable comments and suggestions by three reviewers have greatly improved the manuscript. Finally, we thank Ruan Shuai and Hao Zhou for making meaningful comments on the paper’s content.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer XZ declared a shared affiliation with the authors HC, ZR to the handling editor at time of review,
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2023.1230071/full#supplementary-material
References
Bendat, J. S., and Piersol, A. G. (2011). Random data: Analysis and measurement procedures. Hoboken, NJ, United States: John Wiley & Sons.
Cagniard, L. (1953). Basic theory of the magneto-telluric method of geophysical prospecting. Geophysics 18, 605–635. doi:10.1190/1.1437915
Chave, A. D., and Jones, A. G. (2012). The magnetotelluric method: Theory and practice. Cambridge, United Kingdom: Cambridge University Press.
Chave, A. D., and Thomson, D. J. (2003). A bounded influence regression estimator based on the statistics of the hat matrix. J. R. Stat. Soc. Ser. C Appl. Stat. 52, 307–322. doi:10.1111/1467-9876.00406
Chave, A. D., and Thomson, D. J. (2004). Bounded influence magnetotelluric response function estimation. Geophys. J. Int. 157, 988–1006. doi:10.1111/j.1365-246x.2004.02203.x
Chave, A. D., and Thomson, D. J. (1989). Some comments on magnetotelluric response function estimation. J. Geophys. Res. Solid Earth 94, 14215–14225. doi:10.1029/jb094ib10p14215
Chen, H., Mizunaga, H., and Tanaka, T. (2022). Influence of geomagnetic storms on the quality of magnetotelluric impedance. Earth Planets Space 74, 111–117. doi:10.1186/s40623-022-01659-6
Egbert, G. D., and Booker, J. R. (1986). Robust estimation of geomagnetic transfer functions. Geophys. J. Int. 87, 173–194. doi:10.1111/j.1365-246x.1986.tb04552.x
Egbert, G. D., and Livelybrooks, D. W. (1996). Single station magnetotelluric impedance estimation: coherence weighting and the regression M-estimate. Geophysics 61, 964–970. doi:10.1190/1.1444045
Egbert, G. D. (1997). Robust multiple-station magnetotelluric data processing. Geophys. J. Int. 130, 475–496. doi:10.1111/j.1365-246x.1997.tb05663.x
Fowler, R. A., Kotick, B. J., and Elliott, R. D. (1967). Polarization analysis of natural and artificially induced geomagnetic micropulsations. J. Geophys. Res. 72, 2871–2883. doi:10.1029/jz072i011p02871
Gamble, T. D., Goubau, W. M., and Clarke, J. (1979). Magnetotellurics with a remote magnetic reference. Geophysics 44, 53–68. doi:10.1190/1.1440923
Garcia, X., and Jones, A. G. (2002). Atmospheric sources for audio-magnetotelluric (AMT) sounding. Geophysics 67, 448–458. doi:10.1190/1.1468604
Goubau, W. M., Gamble, T. D., and Clarke, J. (1978). Magnetotelluric data analysis: removal of bias. Geophysics 43, 1157–1166. doi:10.1190/1.1440885
Jones, A. G., Chave, A. D., Egbert, G., Auld, D., and Bahr, K. (1989). A comparison of techniques for magnetotelluric response function estimation. J. Geophys. Res. Solid Earth 94, 14201–14213. doi:10.1029/jb094ib10p14201
Jones, A. G., and Jödicke, H. (1984). “Magnetotelluric transfer function estimation improvement by a coherence-based rejection technique,” in SEG technical program expanded abstracts 1984 (Houston, Texas, United States: Society of Exploration Geophysicists), 51–55.
Junge, A. (1996). Characterization of and correction for cultural noise. Surv. Geophys. 17, 361–391. doi:10.1007/bf01901639
Kappler, K. N. (2012). A data variance technique for automated despiking of magnetotelluric data with a remote reference. Geophys. Prospect. 60, 179–191. doi:10.1111/j.1365-2478.2011.00965.x
Kelbert, A. “Taking magnetotelluric data out of the drawer,” in Proceedings of the AGU Fall Meeting Abstracts, San Franciso, CA, USA, December 2019, IN21A–01.
Larsen, J. C., Mackie, R. L., Manzella, A., Fiordelisi, A., and Rieven, S. (1996). Robust smooth magnetotelluric transfer functions. Geophys. J. Int. 124, 801–819. doi:10.1111/j.1365-246x.1996.tb05639.x
Li, G., Gu, X., Ren, Z., Wu, Q., Liu, X., Zhang, L., et al. (2022). Deep learning optimized dictionary learning and its application in eliminating strong magnetotelluric noise. Minerals 12, 1012. doi:10.3390/min12081012
Li, G., Wu, S., Cai, H., He, Z., Liu, X., Zhou, C., et al. (2023). IncepTCN: A new deep temporal convolutional network combined with dictionary learning for strong cultural noise elimination of controlled-source electromagnetic data. Geophysics 88, E107–E122. doi:10.1190/geo2022-0317.1
Li, J., Zhang, X., Gong, J., Tang, J., Ren, Z., Li, G., et al. (2018). Signal-noise identification of magnetotelluric signals using fractal-entropy and clustering algorithm for targeted de-noising. Fractals 26, 1840011. doi:10.1142/s0218348x1840011x
Maronna, R. A., Martin, R. D., Yohai, V. J., and Salibián-Barrera, M. (2019). Robust statistics: Theory and methods (with R). Hoboken, NJ, United States: John Wiley & Sons.
Neukirch, M., and García, X. (2014). Nonstationary magnetotelluric data processing with instantaneous parameter. J. Geophys. Res. Solid Earth 119, 1634–1654. doi:10.1002/2013jb010494
Oettinger, G., Haak, V., and Larsen, J. C. (2001). Noise reduction in magnetotelluric time-series with a new signal–noise separation method and its application to a field experiment in the Saxonian Granulite Massif. Geophys. J. Int. 146, 659–669. doi:10.1046/j.1365-246x.2001.00473.x
Platz, A., and Weckmann, U. (2019). An automated new pre-selection tool for noisy Magnetotelluric data using the Mahalanobis distance and magnetic field constraints. Geophys. J. Int. 218, 1853–1872. doi:10.1093/gji/ggz197
Ritter, O., Junge, A., and Dawes, G. J. (1998). New equipment and processing for magnetotelluric remote reference observations. Geophys. J. Int. 132, 535–548. doi:10.1046/j.1365-246x.1998.00440.x
Schultz, A., Egbert, G. D., Kelbert, A., Peery, T., Clote, V., Fry, B., et al. (2018). Staff of the National Geoelectromagnetic Facility and their contractors (2006–2018). USArray TA magnetotelluric Transf. Funct., doi:10.17611.DP/EMTF/USARRAY/TA
Simpson, F., and Bahr, K. (2005). Practical magnetotellurics. Cambridge, United Kingdom: Cambridge University Press.
Sims, W. E., Bostick, F. X., and Smith, H. W. (1971). The estimation of magnetotelluric impedance tensor elements from measured data. Geophysics 36, 938–942. doi:10.1190/1.1440225
Smirnov, M. Y., and Egbert, G. D. (2012). Robust principal component analysis of electromagnetic arrays with missing data. Geophys. J. Int. 190, 1423–1438. doi:10.1111/j.1365-246x.2012.05569.x
Smirnov, M. Y. (2003). Magnetotelluric data processing with a robust statistical procedure having a high breakdown point. Geophys. J. Int. 152, 1–7. doi:10.1046/j.1365-246x.2003.01733.x
Szarka, L. (1988). Geophysical aspects of man-made electromagnetic noise in the earth—a review. Surv. Geophys. 9, 287–318. doi:10.1007/bf01901627
Tikhonov, A. N., and Berdichevsky, M. N. (1966). Experience in the use of magnetotelluric methods to study the geological structures of sedimentary basins. Izv. Acad. Sci. USSR Phys. Solid Earth 2, 34–41.
Tikhonov, A. N. (1950). On determining electrical characteristics of the deep layers of the Earth’s crust. Dokl. Citeseer, 295–297.
Travassos, J. M., and Beamish, D. (1988). Magnetotelluric data processing—a case study. Geophys. J. Int. 93, 377–391. doi:10.1111/j.1365-246x.1988.tb02009.x
Wang, H., Campanyà, J., Cheng, J., Zhu, G., Wei, W., Jin, S., et al. (2017). Synthesis of natural electric and magnetic Time-series using Inter-station transfer functions and time-series from a Neighboring site (STIN): applications for processing MT data. J. Geophys. Res. Solid Earth 122, 5835–5851. doi:10.1002/2017jb014190
Weckmann, U., Magunia, A., and Ritter, O. (2005). Effective noise separation for magnetotelluric single site data processing using a frequency domain selection scheme. Geophys. J. Int. 161, 635–652. doi:10.1111/j.1365-246x.2005.02621.x
Zhang, L., Ren, Z., Xiao, X., Tang, J., and Li, G. (2022). Identification and suppression of magnetotelluric noise via a deep residual network. Minerals 12, 766. doi:10.3390/min12060766
Zhang, X., Li, J., Li, D., Li, Y., Liu, B., and Hu, Y. (2021). Separation of magnetotelluric signals based on refined composite multiscale dispersion entropy and orthogonal matching pursuit. Earth Planets Space 73, 76–18. doi:10.1186/s40623-021-01399-z
Keywords: magnetotelluric impedance, linearity, polarization direction, data processing, preselection
Citation: Chen H, Zhang L, Ren Z, Cao H and Wang G (2023) An automatic preselection strategy for magnetotelluric single-site data processing based on linearity and polarization direction. Front. Earth Sci. 11:1230071. doi: 10.3389/feart.2023.1230071
Received: 28 May 2023; Accepted: 08 August 2023;
Published: 23 August 2023.
Edited by:
Cong Zhou, East China University of Technology, ChinaReviewed by:
Xian Zhang, Central South University, ChinaYoshiya Usui, The University of Tokyo, Japan
Ikuko Fujii, Meteorological College, Japan
Copyright © 2023 Chen, Zhang, Ren, Cao and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lili Zhang, bGlseXpoYW5nQG1haWwuaWdnY2FzLmFjLmNu
 Hao Chen
Hao Chen Lili Zhang2*
Lili Zhang2* ZhengYong Ren
ZhengYong Ren Hui Cao
Hui Cao Gang Wang
Gang Wang