- Research Methods and Information Science, University of Denver, Denver, CO, United States
In educational research, the amount of learning opportunities that students receive may be conceptualized as either an attribute of the context or climate in which that student attends school, or as an individual difference in perception of opportunity among students, driven by individual factors. This investigation aimed to inform theory-building around student learning opportunities by systematically comparing 11 theoretically plausible latent and doubly latent measurement models that differed as to the locus (i.e., student- or school-level) and dimensional structure of these learning opportunities. A large (N = 963) and diverse sample of high school students, attending 15 different high schools, was analyzed. Results suggested that student learning opportunities are best conceptualized as distinct but positively correlated factors, and that these doubly latent factors occurred at the student level, although with a statistical correction for school-based clustering. In this way, student learning opportunities may be best described as individual perceptions, rather than an indicator of school climate or context. In general, these results are expected to inform current conceptualizations of student learning opportunities within schools, and function as an example of the substantive inferences that can be garnered from multi-level measurement modeling.
Students attend school, in large part, in order to receive opportunities to learn. This fundamental premise undergirds much of modern educational thought (e.g., Dewey, 1902/2010; Cromley et al., 2016; Alexander, 2017). Presumably, however, some schools or teachers offer more or less opportunity for learning to their students, and certain students, for a variety of reasons, have greater or less ability to seek out and benefit from those opportunities (Dinsmore et al., 2014; Wilhelm et al., 2017). Given this generally complex conceptualization of student learning opportunities, is this construct better hypothesized as a context- or climate-driven attribute of schools, or is it more appropriately conceived of as an individual difference among students? In other words, are learning opportunities something that wholly occur within a school climate such that students within those schools receive relatively interchangeable learning opportunities, or are student learning opportunities heterogeneous at the individual level in a way that should define the construct as occurring within students, and not schools? In this article, this conceptual question is empirically investigated through the systematic comparison of “doubly latent” (Marsh et al., 2012; Morin et al., 2014) measurement models that posit differing dimensional structures and school- or student-level specifications of student learning opportunities.
The Locus of Learning Opportunities
It is often overlooked within the educational psychology literature that conceptualizing a construct as occurring at the individual student or school level is predicated upon a number of theoretical decisions concerning the nature of the constructs being analyzed (Stapleton et al., 2016b). For instance, in educational psychology it is typical to engage in theory-building investigations in which the latent structure of a given construct is examined (e.g., Finch et al., 2016), and rich discussions about the dimensionality of various cognitive (e.g., Dumas and Alexander, 2016) and motivational (Muenks et al., 2018) constructs are ongoing in the field. However, it is not yet typical to conduct analogous inquiries into the locus, or level specification (e.g., student or school level), of any given construct (Morin et al., 2014).
Currently in the field, measured constructs, such as those quantified through item-response or factor analytic models, are typically assumed to exist at the individual student level, and investigations that formerly posit classroom- or school-level measurement models are comparatively rare, and those that do exist are very recent (e.g., Oliveri et al., 2017). In contrast, researchers interested in explaining student outcomes through the analysis of data collected across multiple schools or classrooms tend to assume that the outcomes they are predicting have a multi-level structure and therefore the construct of interest exists separately at the individual and aggregate level (Coelho and Sousa, 2017). However, recent methodological work with educational data (e.g., Morin et al., 2014; Stapleton et al., 2016a) has shown that both of these typical frameworks in educational research rest on tenuous assumptions about the locus of the construct of interest. Specifically, whether a particular construct occurs, for example, at the individual student level, at the school level, or both, is an empirical question that should be answered before further theorizing or analysis. For example, it may be that, within educational research, multi-level modeling is currently “unnecessarily ubiquitous” (McNeish et al., 2017) because many of the constructs being modeling principally occur at the student-level. In contrast, because the multi-level loci of latent constructs are rarely considered as part of theory building in the field, it may be that the contextual and climatic aspects of learning environments are also being systematically overlooked in the field (Lüdtke et al., 2009). This investigation seeks to address both of these simultaneous issues by incorporating multi-level measurement modeling into a theory-building enterprise, therefore potentially identifying the most meaningful conceptualization of student learning opportunities.
Understanding the learning opportunities in which students participate in school lies close to the heart of educational research (e.g., Dewey, 1902/2010), however, the level (e.g., individual student or school level) at which those opportunities actually occur has never been systematically investigated. Although such a gap is currently not uncommon among social-science research, areas, it may be particularly problematic for educational psychology because it means that it is not currently known, for example, whether the learning experiences of students within schools are heterogeneous such that learning opportunities should only be measured or described at the individual, and not aggregate, level. Conversely, it may also be that school-level efforts to engage students in learning opportunities create student learning opportunities that are an attribute of the school, not of individual students. Still, learning opportunities may be meaningfully conceptualized at both the individual student and school levels, but the meaning of the construct across those levels may differ in important ways. In this way, the actual locus of the construct of student learning opportunities is an open theoretical and empirical question. Here, three loci at which student learning opportunities may theoretically occur are posited: (a) the individual student (b) the level of school context, and (c) the level of school climate. Each of these possible loci are now further discussed.
Student Level Construct
Following in-step with typical latent variable research (e.g., Dumas and Alexander, 2016), student learning opportunities may be conceptualized as occurring at the individual student level, and not at any aggregated level above that. This conceptualization rests on a belief (or an empirical observation) that student heterogeneity within schools is too great to validly aggregate student-level opportunities to the school level (Stapleton et al., 2016a). There are a number of literature-based reasons why student learning opportunities may be conceptualized at the student level. For example, learning opportunities may be principally driven by psychological individual differences among students such as motivation (Muenks et al., 2018), cognitive functioning (Fiorello et al., 2008), or mindset (Lin-Siegler et al., 2016). Additionally, heterogeneity in student prior knowledge, parental involvement, or other individual differences could create a situation in which student learning opportunities can only be understood at the individual, rather than aggregate level.
Moreover, if student learning opportunities are conceptualized as wholly occurring at the student level, multi-level modeling of the effects of such opportunities at the school level, or even simply averaging measured quantities associated with the construct within a school, may be invalid (Marsh et al., 2012). Explanations of what outside variables (e.g., student motivation) effect learning opportunities would also need to be forwarded at the individual student, and not aggregate, level. Currently, for those researchers engaged in structural-equation-modeling of student psychological attributes, such a theoretical landscape is familiar, because these theory-building investigations typically, although not always, take place at the student level (e.g., Ardasheva, 2016).
It should also be noted that a theoretical conceptualization of learning opportunities as an individual student level construct does not preclude the use of some methodological adjustments (e.g., linearization; Binder and Roberts, 2003) that are designed to correct for sampling error brought on by a cluster-based research design. Currently, measurement models that simultaneously account for measurement error through the use of multiple observed indicators to estimate latent variables, as well as account for sampling error through the use of either statistical adjustments or a multi-level design are referred to as doubly latent (e.g., Marsh et al., 2012; Morin et al., 2014; Mahler et al., 2017). This terminology reflects the fact that these models account for two major sources of error in construct estimation: measurement and sampling error. In this way, student learning opportunities may be modeled in a doubly latent way at either the student (using a linearization correction) or school (using a two-level model) level.
School Contextual Construct
If student learning opportunities were conceptualized as a school contextual construct, this would indicate that the construct exists at both the individual student and school level, and that the school-level construct represents the aggregation (e.g., average) of individual level measurements (Stapleton et al., 2016b). Existing literature suggests that such a conceptualization may be meaningful, in that many student level individual differences drive variance in learning opportunities, but students within schools tend to be homogenous enough on those individual differences that the learning opportunities students experience within any one school can be validly aggregated (e.g., Mahler et al., 2017). Within current research practice (e.g., Muthén and Satorra, 1995; Zhonghua and Lee, 2017), this pattern of variance within- and between-schools typically results in an intraclass correlation coefficient [ICC(1)] above 0.05, implying that the use of multi-level models may be warranted.
In addition, methodological researchers sometimes refer to such a construct as configural because this theoretical conceptualization implies that the measurement properties (e.g., loadings) associated with the construct at the school level are equivalent to those at the student level (Stapleton et al., 2016a). In this way, the school contextual construct has the same theoretical meaning as the student level construct, except that it is capable of being measured at the school-level as well. Therefore, aggregation procedures such as multi-level models or simply averaging quantities across students within the same school are valid for contextual constructs.
School Climate Construct
In contrast to school contextual constructs, which have the same meaning as student level constructs but represent an aggregation, school climate constructs have a distinctly different theoretical meaning at the school level than at the student level (Marsh et al., 2012). For example, some existing literature suggests that student learning opportunities may be best conceptualized as a climate construct, because schools may make concerted efforts to provide particular learning opportunities to all students, and those opportunities therefore exist within the school climate and not at the individual level (McGiboney, 2016).
Indeed, for a climate construct, individual students within the same school should be entirely interchangeable in terms of their learning opportunities, because they attend school within the same learning climate (Cronbach, 1976). Such a belief may seem intuitively unlikely to be true; however, it is a commonly held belief in educational research. For example, research endeavors that attempt to quantify effects on student performance or beliefs that are wholly attributable to teachers or schools (e.g., Fan et al., 2011) either implicitly or explicitly posit climate constructs at the aggregated level. Methodologically, climate constructs are often referred to as shared constructs, because they represent an aspect of experience that is shared equally by individuals within that climate (i.e., individuals are interchangeable), and require that the measurement parameters of the shared construct be freely estimated at the school level, and not be equivalent to those at the student level (Stapleton et al., 2016b). A climate construct is differentiated from a contextual construct such that a climate construct is defined as a separate attribute than what is being modeled at the student-level: an attribute that is shared, or experienced equally, among members of a particular group (e.g., school), and not a more general second-level aggregation of a student-level attribute (i.e., a contextual construct). In a theoretical way, contextual, and climate constructs may be distinguished in that a contextual construct is an aggregate of the student-level attributes, while a climate construct is an attribute of the environment (e.g., school) itself. Given this different definition, it may be hypothesized that the existence of a salient climate construct would result in a higher intraclass correlation coefficient (ICC) than would a contextual construct [e.g., ICC(1) >0.25 for a large effect; Schneider et al., 2013]. However, given the relative novelty of such investigations in the literature, it may not be possible at this point to forward a particular value of ICC that differentiates a contextual from a climate construct: instead the two conceptualizations must be distinguished by a more nuanced examination of measurement parameters (i.e., loadings) at second-level of a latent measurement model.
It is critical to note here that none of these different loci of student learning opportunities—student level, school context, or school climate—specifically formulate the construct of learning opportunities as either stable or variable across time. Although the loci of the constructs tested here (e.g., context vs. climate) hold critical implications for understanding student learning opportunities, it is not possible based on a comparison of these theoretical models to determine how stable learning opportunities may be (or students may perceive them to be) across years, semesters, or even smaller time increments such as weeks or days. In this way, the analysis presented within this investigation is capable of informing an understanding of student learning opportunities at a single measurement time-point, but is not capable of supporting inferences about how those opportunities change over time. For such inferences to be supported, data would need to be collected with alternative methodologies such as experience sampling (Zirkel et al., 2015), and modeling paradigms that are capable of handling multi-level and longitudinal data [e.g., dynamic measurement modeling (DMM); Dumas and McNeish, 2017] would need to be applied.
With these three possible loci of student learning opportunities described, it is also necessary to specifically delineate the areas of learning in which student opportunities are of interest within this study. Although the actual latent structure of student learning opportunities is considered an empirical question in this examination, the following section specifically describes the conceptual specification of the construct utilized here.
Specifying the Construct of Student Perceived Learning Opportunities
In specifying the general construct of perceived opportunities for learning, nine general areas in which student opportunities for learning typically occur were identified: a) relational thinking, (b) creative thinking, (c) communication, (d) collaboration, (e) learning to learn, (f) teacher feedback, (g) meaningful assessments, (h) interdisciplinary learning, and (i) real-world connections. This list is not intended to be an entirely exhaustive sampling of every learning opportunity students receive in school. Instead, it is intended to provide a reasonable sampling of the learning opportunities that high school students may perceive themselves to be receiving in school. Each of these general areas are now reviewed in more detail.
Relational Thinking
Student opportunities to engage in cognitive activities in which they analyze ideas by examining their component parts, relate or combine multiple ideas, or solve novel problems with existing skills, were here deemed to be learning opportunities. Such cognitive activities are termed here opportunities for relational thinking, because they are designed to allow for the development of relational ability in students. Indeed, a rich understanding of the development and relevance of relational thinking already exists within the educational and psychological literature (e.g., Dumas et al., 2013, 2014), with the proximal link between such relational skills and higher-order thinking skills being well-established (Goswami and Brown, 1990; Richland and Simms, 2015).
Creative Thinking
In-class opportunities for students to pose original solutions to existing problems, create new ideas, or generally use their imagination—opportunities for creative thinking—have been linked to the development of future creativity and divergent thinking ability (Sternberg, 2015; Gajda et al., 2017). Indeed, links between student creative thinking and success in a number of complex cognitive tasks have been described in the literature (e.g., Clapham et al., 2005; Dumas et al., 2016). Therefore, the degree to which students have the opportunity to engage in creative thinking in school was considered an indicator of learning opportunities in this study.
Communication
Opportunities for communication require students to interact with one another to give presentations, share opinions, or discuss ideas (Farrell, 2009). Moreover, asynchronous interaction among students through expository or persuasive writing may also be considered an opportunity for communication (Drew et al., 2017). Because communicative abilities are widely regarded as critical for future school and career success across a number of domains of learning (e.g., Beaufort, 2009; Roscoe and McNamara, 2013), opportunities to practice and develop such abilities were included here.
Collaboration
Differentiated from communication, in which students share or discuss ideas, collaboration refers to activities in which multiple students share responsibility for the quality of the work produced, or work together to achieve a goal (Pegrum et al., 2015). The contributions of opportunities for collaboration to student learning, as evidenced by existing literature, are two-fold. First, collaborative opportunities such as working with other students on an experiment or assignment have been shown to aid students in developing specific skills related to collaboration and the coordinating of activities among individuals (e.g., turn-taking, division of labor; Cortez et al., 2009; Wilder, 2015). Second, collaboration among students, including the reviewing and discussing of shared work, has also been shown to improve individual students' conceptual understanding of knowledge being learned within the class domain (e.g., science; Murphy et al., 2017).
Learning How to Learn
While the four of student perceived learning opportunities already identified tend to be predicated on students' use of cognitive strategies, opportunities to engage in scaffolded metacognitive thinking—as when a teacher asks a student to reflect on their thinking processes—are also linked to learning outcomes in the literature (Peters and Kitsantas, 2010; Pilegard and Mayer, 2015). Here, such metacognitive activities are referred to as indicators of student opportunities to learn how to learn.
Receiving Feedback
Although it is likely that some kind of teacher contribution would be involved in each of the other components of learning opportunities so-far specified, evidence also suggests that teachers who give more specific feedback across learning contexts may better support the development of higher-order thinking in students, and therefore better facilitate learning (Burnett, 2003; Van den Bergh et al., 2014). So, it may be prudent to include the specificity of teacher feedback about student work, the regularity with which students receive feedback, and students' chances to revise their work in response to that feedback, generally termed opportunity to receive feedback as an aspect of the student perceived learning opportunity construct. Moreover, peer (e.g., Patchan et al., 2016) or parental (e.g., Vandermaas-Peeler et al., 2016) feedback on student work has also been shown to support learning, and therefore was deemed relevant here.
Assessments
In contrast to the components of perceived learning opportunity already identified, which tend to occur during instructional time, student opportunities for meaningful assessment, occur while a student is being assessed. Importantly, evidence suggests that assessments that prioritize rote memorization of class material may discourage higher-order thinking among students (Geisinger, 2016), but regular assessments that require students to explain their thinking, evaluate sources of information, or even build a portfolio of different types of work, may do more to encourage learning (Schraw and Robinson, 2011; Greiff and Kyllonen, 2016).
Interdisciplinary Learning
Also implicated as an opportunity for learning is the degree to which teachers combine ideas or concepts from different domains or disciplines into their teaching and assignments (Robles-Rivas, 2015). For example, instances where science and mathematics, or literature and history, are explicitly taught together indicate student opportunities for interdisciplinary learning. Further, instances where students are prompted to use knowledge previously learned in one domain (e.g., algebra) to solve problems in another (e.g., chemistry), are also considered instances of interdisciplinary learning (Zimmerman et al., 2011).
Real-World Connections
One historical critique of educational practice is that it tends to be divorced from the out-of-school contexts in which students are expected to later apply their knowledge gained in school (e.g., Dewey, 1902/2010). Indeed, in the research literature, much has been written about the authenticity of school-work (Swaffield, 2011; Ashford-Rowe et al., 2014), with a growing body of empirical research demonstrating that utilizing real-world examples, encouraging students to draw information from sources outside of school, and allowing students to pursue topics that interest them and that relate to their outside-of-school life, all positively influence student learning outcomes (e.g., Hazari et al., 2010; Yadav et al., 2014). Therefore, student opportunities for real-world connections is here considered to be a component of student learning opportunities.
Dimensionality of Student Perceived Learning Opportunities
Although current literature supports the inclusion of each of the previously reviewed areas of student learning opportunities, it does little to suggest the actual underling latent structure of these components, especially in high school students. For example, each of the reviewed areas of student learning all generally pertain to learning opportunities, and therefore they may represent a single underlying latent dimension. Indeed, previous theory suggests that younger students, such as those in a k-12 setting, are more likely than higher education students to indicate latent constructs that are undifferentiated, or unidimensional (Lonigan and Burgess, 2017). In contrast, students may indicate that each of the areas of learning opportunity represent a separate factor of a multidimensional learning opportunity construct. Such a result may seem reasonable, given that the various areas of learning opportunity included here may be perceived as occurring separately in schools. However, if each of the areas of student learning opportunity represents a distinct latent factor, the further question remains: are those dimensions unrelated, or correlated at some particular strength? If the underlying latent factors of student learning opportunity are related, than the strength of those latent correlations (or doubly latent correlations if sampling error is taken into account) may offer clues as to the co-occurance of the various learning opportunities within schools. Further, a combination of these dimensional specifications, in which a single general learning opportunity dimension is present in the data as well as specific dimensions pertaining to each learning opportunity area, is also a possibility. Such a latent structure would allow for the inference that the areas of opportunity co-occur enough so as to form a single perception of learning, but also retain an individualized aspect such that students perceive the areas to be specifically differentiated in important ways.
Goals of the Current Study
Given the existing gaps in the field's understanding of student perceived learning opportunities already reviewed here, this investigation aimed to address a number of specific empirical research questions regarding the conceptualization of the construct. Specifically, the following research questions are posited:
1. At the observed variable level, can student perceived learning opportunities be quantified reliably?
2. At the observed variable level, how much variance in student perceived learning opportunities is accounted for at the school, rather than individual student, level?
3. What is the appropriate latent dimensionality of student perceived learning opportunities?
4. What is the appropriate doubly latent locus, or level specification, of student perceived learning opportunities?
5. Using a doubly latent measurement model, can student perceived learning opportunities be quantified in a reliable and valid way?
Method
Participants
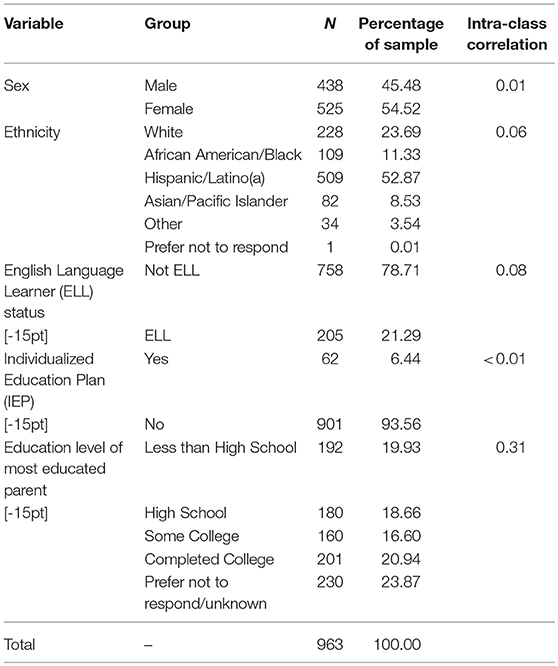
Participants were 963 11th and 12th grade students attending fifteen public high schools in Southern California. Please see Table 1 for a full demographic breakdown of the sample, aggregated across schools. In overview, the overall sample featured a slight majority of females (54.52%), and Hispanic/Latino(a) students (52.87%). Participants were highly diverse in terms of the educational attainment of their parents (see Table 1 for details). In addition, 62.80% of this sample qualified for free/reduced price lunch, and 21.29% were classified as English Language Learners (ELLs). The response rate for this study was 76.00%, indicating that a heavy majority of eligible students returned parental consent forms and chose to participate on the day of data collection. Also appearing in Table 1 are the intraclass correlations coefficients (ICCs) corresponding to each demographic variable. This statistic describes the portion of total variance in the demographic variable that is occurring at the school, rather than individual student level, and is analogous to an R-square value but typically slightly lower (Bartko, 1976). As can be seen, nearly all of these demographic variables featured relatively weak ICCs, indicating the schools sampled in this study were not overly homogenous within-school in terms of student demographics. One possibly unsurprising exception is parental education level, which displayed an ICC of moderate strength (ICC = 0.31), indicating that, of the demographic variables collected here, parental education level was the most unevenly distributed among the schools.
Measure
In order to address the research questions present in this investigation, a measure of student perceived learning opportunities was created for this study. Importantly, if an item existed on an established and publically usable measure of student learning opportunities that the research-team was aware of that suited the purposes of this study, then that item was used to inform the development of this measure. Existing measures from which items were adapted were the National Survey of Student Engagement (NSSE; Tendhar et al., 2013), Measures of Effective Teaching (MET; Kane et al., 2013), and the Consortium on Chicago School Research's Survey of Chicago Public Schools (Chicago Consortium on School Research, 2015). After an initial pool of items was created or identified, a preliminary content validation pilot study was utilized to further inform the development of items and scales.
Content Validation and Preliminary Pilot
With a corpus of possible items adapted or composed by the research team, a small content validation pilot study was pursued in order to preliminarily ascertain the suitability of the items. It should be noted that this pilot study is not the main focus of this article, but it is briefly described here as it pertains to the development of the measure. In this preliminary pilot study, a small number (N = 60) of high school students attending public school in Southern California completed the set of initially conceived items. Those students who participated in the pilot study were given the opportunity to voice concerns about the content, wording, and directions for the items. After pilot data were collected, initial checks of classical difficulty and reliability statistics were utilized with these pilot data in order to identify items that were clearly not functioning well. The main useful aspect of this preliminary pilot study was in the dropping, adding, or rewording of items in order to maximize the content validity (based on student feedback) of the measure.
After these edits to items were completed, this measure contained a total of 62 polytomously scored Likert-type items organized into 9 scales, each designed to tap self-reported student perceived opportunities for a different dimension of learning. Each of the polytomously scored items featured four response categories. The scales of the measure were as follows: Student opportunities for (a) relational thinking, (b) creative thinking, (c) communication, (d) collaboration, (e) learning to learn, (f) teacher feedback, (g) meaningful assessment, (h) interdisciplinary learning, and (i) real-world connections. Numbers of items on each individual scale ranged from 4 to 12 (median = 6). Please see Table 2 for specific numbers of items within each scale. It should be noted that, regardless of the psychometric properties that a given item displayed on previous scales, in other published work, or in the this pilot study, in order to ensure that every item functioned well in this particular context, with this target population, and among the other items on the scale, the functioning of all of the items included on the measure were here investigated afresh within the full sample, and those findings are presented as a first phase within the Results section of this paper. Moreover, the fully developed measure, with complete citation information as to the sources of individual items, is included with this article as an Supplementary Materials.
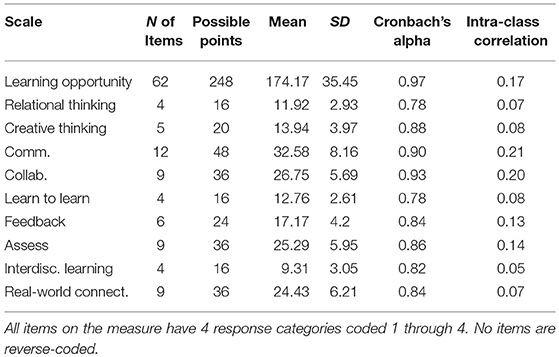
Table 2. Mean, standard deviation, internal consistency, and intraclass correlation of measure scales.
Exemplar Items
In most of the developed scales, students were directed to “Think about your English, Math, Science, and Social Studies classes this school year. For how many of these classes is each statement true” Response categories then represented the number of classes: none, one, two, three or more. In other cases (i.e., the feedback and assessment scales) students were specifically directed to think of their teachers in each given class, and the Likert response categories then represented numbers of teachers for which students judged the statement to be true. In yet other cases (i.e., interdisciplinary learning), students were directed to think of how often they engaged in certain learning activities across multiple classes, and the response categories were therefore a frequency scale consisting of: never, some, most or all of the time.
As previously mentioned, specific items were composed to tap various identified dimensions of student learning opportunities. Although the full measure is included as an Supplementary Materials, some exemplar items are presented here. For instance, on the relational thinking scale, questions like I combine many ideas and pieces of information into something new and more complex, were featured. For creative thinking, items such as I am encouraged to come up with new and different ideas, were included. Items such as I share my opinions in class discussion, and I work with other students on projects during class, were included on the communication and collaboration scales, respectively. For the learning to learn scale, items like My teacher asks me to think about how I learn best, were used to tap the construct, while on the feedback scale, items such as My teacher gives me specific suggestions about how I can improve my work, were utilized. Items like My teacher gives us points on a test or homework for how we solved a problem, not just whether we got the right answer, were used to tap student opportunities for meaningful assessment. Moreover, items such as I work on a project that combines more than one subject (for example, science and literature), were utilized on the interdisciplinary learning scale, while the real-world connections scale included items like We connect what we are learning to life outside the classroom.
Procedures
As part of a larger on-going research endeavor, the learning opportunity measure was administered to students within their regularly scheduled class time. This study was approved by institutional-review-board (IRB) of the institution where the study took place, and followed all ethical guidelines of the American Psychological Association (APA). Parents of all students for whom data were collected in this study signed informed consent forms, and informed assent was also provided by participating students on the day of data collection. During data collection, students' teachers were present, as well as a member of the research team. In order to be sure students understood the nature of Likert-type items, an example item not included on the measure was demonstrated to students before they began. Because class-time was being utilized to facilitate data collection, all students whose parents had provided consent completed the study materials. However, data on this learning opportunity measure was only analyzed for students who were enrolled in at least three core courses (i.e., English, math, social studies, and science). Ninety-four percent of the consenting participants met this requirement, and formed the analytic sample within this study.
The measure was typically administered using pencil and paper survey forms, but in a small minority of classrooms (i.e., 4) in which computers were available to students, the measure was administered electronically. Such a procedural choice was intended to alleviate data collection tasks for teachers participating in this study, and previous findings in the educational research literature (e.g., Alexander et al., 2016) suggest surveys being electronically administered during class time does not unduly alter student responses as compared to paper and pencil surveys. In addition, students who were absent on the data collection day were offered an online make-up survey which could be completed in school or from a home computer (but not from a smartphone or tablet). Flexible data collection strategies such as this one have been shown to improve survey response rates, especially of low-income and minority students (Stoop, 2005), therefore improving the validity of statistical inferences drawn from survey data with diverse populations of students. After students completed the measure, they supplied demographic information and submitted their survey packets, either on paper or electronically.
Results
Observed Score Description
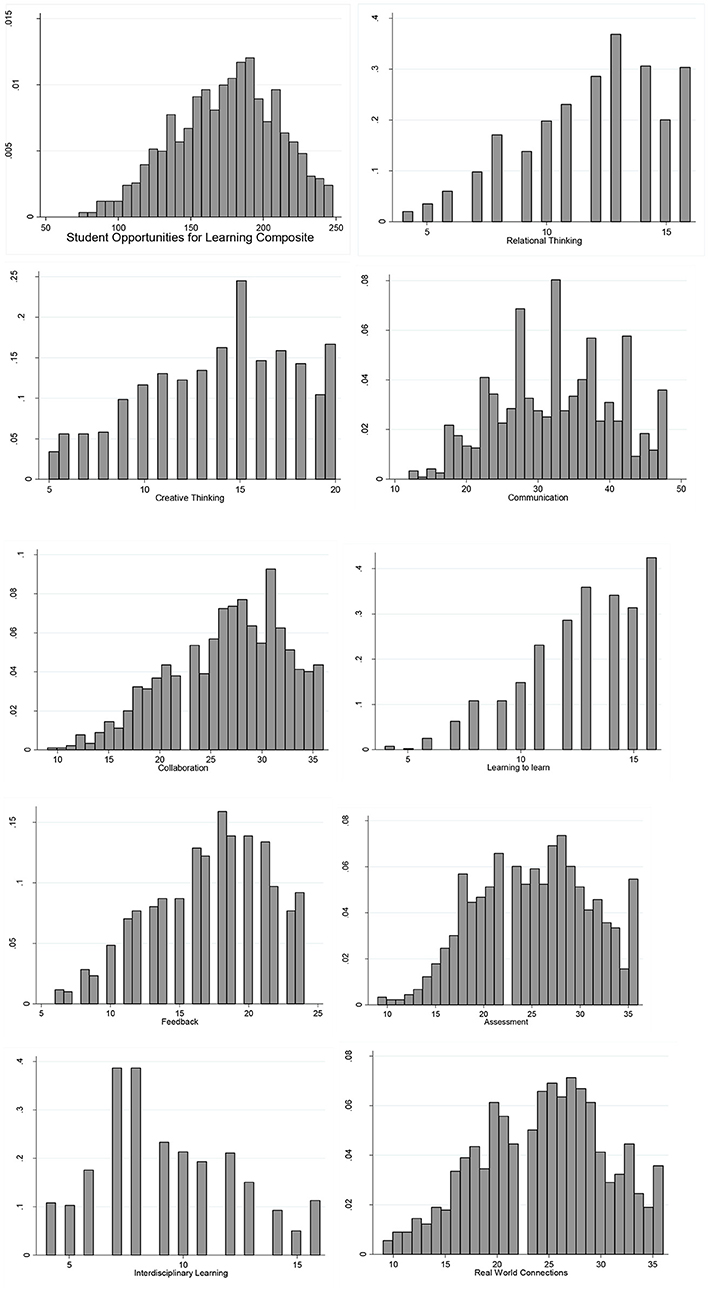
At the composite level, the average score in this sample was 174.17, out of a possible 248 points. Because the four polytomous response categories for each item were coded 1–4 in the dataset, this possible total number of points is calculated by multiplying the number of items on the measure (i.e., 62) by the number of response categories (i.e., 4) on the items. Moreover, composite learning opportunity scores appear to be approximately normally distributed (See histogram in Figure 1), although perhaps with a slight ceiling effect constricting variability at the upper end of the composite distribution. Histograms for the composite scores from each of the nine scales of the measure are also available in Figure 1.
Reliability
At the composite level, scores exhibited a high level of classical reliability (α = 0.97). Such a high level of classical reliability at the composite level indicates that the items tended to correlate positively with one another, but does not indicate unidimensionality (Cho and Kim, 2015). Numbers of items, total possible points, average scores, standard deviations, and Cronbach's alpha reliability coefficients for each of the scales of the perceived learning opportunity measure are available in Table 2. In general, each of these scales exhibited a satisfactory level of classical reliability, with the least reliable scales (i.e., Creative thinking and Learning to Learn) exhibiting a Cronbach's alpha of 0.78. Not surprisingly, these scales are also those with the smallest number of items (i.e., 4 items). In contrast, the two scales with the highest classical reliability were Collaboration (α = 0.93; 9 items) and Communication (α = 0.90; 12 items). Classical reliability statistics for each of the other scales fell in the range of 0.80–0.90.
Intraclass Correlations
Also depicted in Table 2 are ICCs corresponding to each of the scales of the measure. As with the demographic variables in Table 1, the ICCs describe the proportion of variance in the scale that occurs at the school, as opposed to the student, level. Because these data will form the basis of substantive inferences in this investigation, the scale ICCs are highly relevant to the research questions. For example, one currently utilized rule-of-thumb (e.g., Muthén and Satorra, 1995; Zhonghua and Lee, 2017) is that measures that exhibit an ICC >0.05 are possible candidates for multilevel measurement modeling, and may be tapping constructs at a level above the individual (i.e., school level). As can be seen, every scale of the measure has an ICC of at least 0.05, and some (e.g., Opportunities for Communication, ICC = 0.21) have ICCs that are much stronger. Importantly however, these ICCs do not necessarily indicate that the locus of the construct being tapped in this study is indeed at the school level, only that there is empirical reason to investigate such a possibility (both statistically and theoretically) at this point.
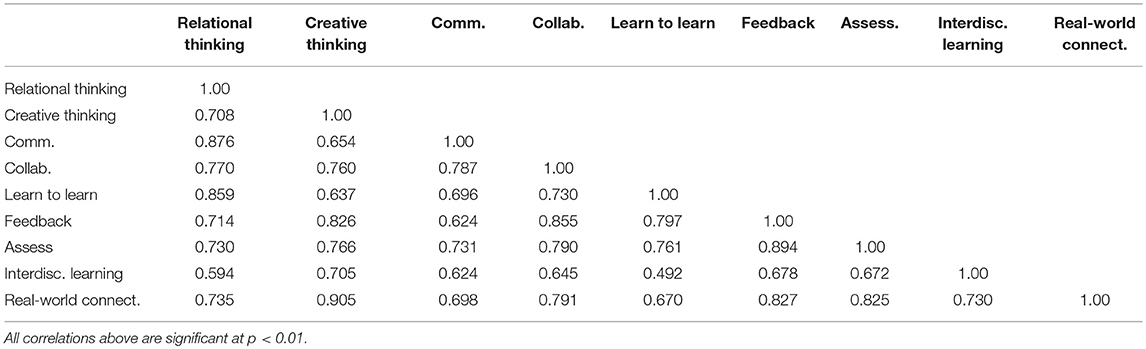
Scale Correlations
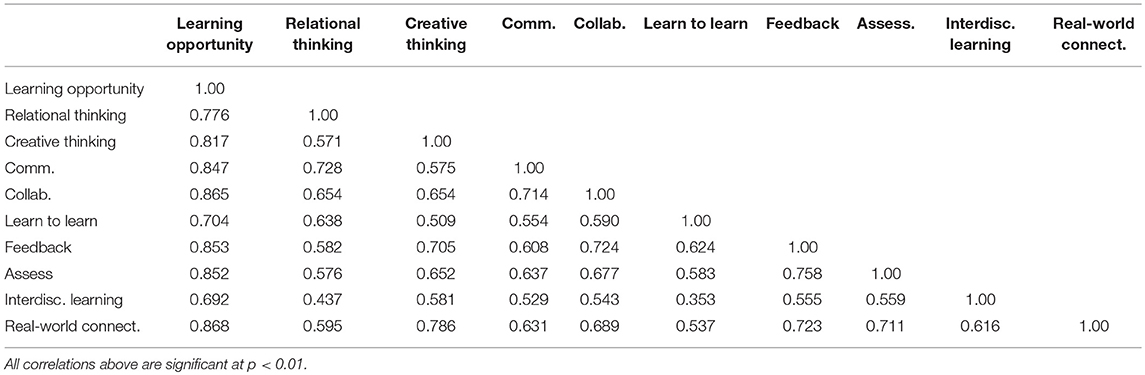
Scores on each of the nine scales of the measure correlated positively and statistically significantly with scores for every other scale, as well as with total learning opportunity composite scores. A full matrix of these correlations is available in Table 3. As can be seen, correlations among the scales range from r = 0.35 between Learning to Learn and Interdisciplinary Learning to r = 0.78 between Creative Thinking and Real-world Connections, with most of the inter-scale correlations falling between 0.50 and 0.70. In general, the correlations between the scales and the composite scores (i.e., scale level discrimination coefficients) are higher than the inter-scale correlations and range from 0.69 between Interdisciplinary Learning and the Learning Opportunity composite, and 0.86 between Real-world Connections and the Learning Opportunity composite.
Conceptual Model Comparison
In order to ascertain both the dimensionality and appropriate level-specification of student perceived learning opportunities, 11 different multilevel and multidimensional item-response theory models were fit. As previously explained, latent-variable measurement models that simultaneously feature multiple dimensions and a multilevel structure are referred to in extant literature as “doubly latent” (Marsh et al., 2012; Morin et al., 2014; Khajavy et al., 2017; Mahler et al., 2017) because these models account for both the measurement error present in the items given to participants, as well as the sampling error produced by clustered data. The 11 theoretically plausible models compared here are organized into three groups, depending on their multilevel specification. First, models that only account for measurement error at the student level, and do not include any mechanism to account for clustering, are referred to as naïve analyses because they ignore the clustered nature of the data (i.e., are singly latent). Second, models that use a linearization method to provide cluster-robust estimates of model fit statistics as well as model parameter variances in order to account for cluster-based sampling error are referred to as design-based analyses (Muthén and Satorra, 1995; Binder and Roberts, 2003; Stapleton et al., 2016a). Third, in this investigation, models that feature a two-level specification to estimate latent variables at the school level and latent variables or a saturated covariance structure at the student level are referred to as two-level analyses (Stapleton et al., 2016b). Importantly, regardless of the level-specification and dimensionality of each of these models, they all accounted for the polytomous nature of item responses using a graded-response modeling framework, modeling three threshold parameters and one loading for each of the items. It should be noted that all latent variable modeling for this analysis was conducted using Mplus 8, using a robust diagonally-weighted least squares estimator using a diagonal weight matrix (ESTIMATOR = WLSMV in Mplus) to account for the categorical nature of the polytomous item responses (DiStefano and Morgan, 2014). Example Mplus code utilized in this study is also available with this article as Supplemental Material.
Naïve Analysis
Within a single-level framework, the model-data fit of theoretically plausible models that differed on their dimensional specifications was systematically compared. Conceptual path diagrams of each of these models are depicted in Figures 2A–D. The first model that was fit to the data was an uncorrelated model (Figure 2A), in which each of the scales of the learning opportunity measure was represented by its own latent dimension, and these dimensions did not covary. If this model fit best, learning opportunities would be best described as consisting of nine orthogonal factors, each representing an unrelated aspect of student opportunities for learning. The second model that was fit to these data was a correlated model (Figure 2B), in which each of the scales was represented by its own latent dimension, but those dimensions were free to covary. If this model were to fit best, student learning opportunities would be thought of as comprising nine related scales, each conceptually distinct but overlapping with the others.
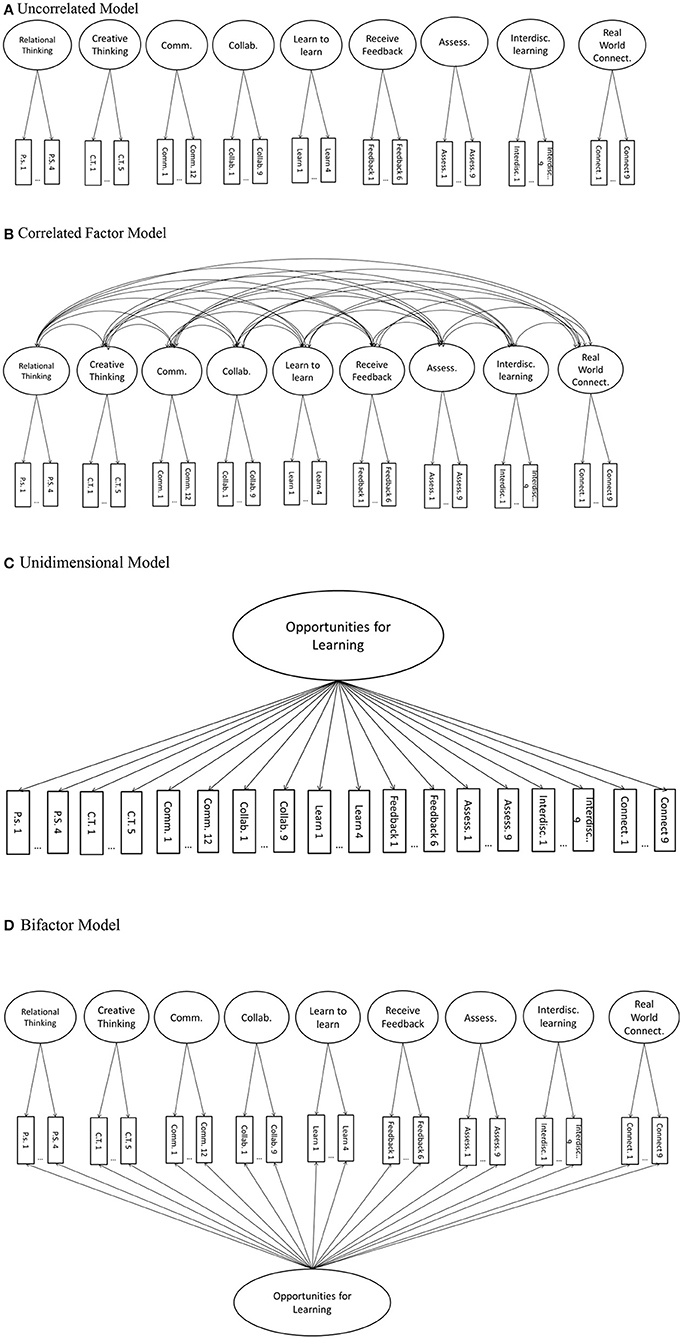
Figure 2. Theoretically plausible models systematically compared at the student-level: (A) Uncorrelated; (B) Correlated; (C) Unidimensional and, (D) Bifactor models. These dimensional specifications hold for both naïve and design-based analyses. Error terms are not depicted here for simplicity.
The third model fit to these data was unidimensional (Figure 2C). Conceptually antithetical to the uncorrelated model, this model posits that all the latent dimensions of student perceived learning opportunity are perfectly correlated, or conceptually that each of the scales measures a single student attribute: general opportunities for learning. In contrast to the first three models fit, in which each individual item loaded on a single dimension, the fourth model (Figure 2D) posits that each item loads on two separate dimensions: a general opportunities for learning dimension and a scale-specific residualized dimension. If this model, termed the bifactor model, were to fit best, student responses to any given item would be best described as indicating both a general opportunity for learning and a specific opportunity in the dimension measured by that particular item.
Further, if any of the naïve analysis models were to fit best of all the models fit in this investigation (including the design-based and two-level models) that would indicate that the clustered nature of these data was not relevant to the measurement models, and that opportunities for learning should not be conceptualized as occurring at the school level. Instead, the constructs being measured would be tapped entirely at the individual student level, with no need to account for school clustering.
Design-Based Adjusted Analysis
Four different design-based adjusted models were fit in this investigation, following the same dimensional specifications as the naïve analysis. However, these models featured a linearization technique (TYPE = COMPLEX in Mplus 8) to produce robust model estimates (Stapleton et al., 2016a). In this way, these models are also conceptually depicted in Figures 2A–D, and when estimated had the same number of degrees of freedom as the naïve models. However, because the estimation is adjusted to account for the sampling error arising from the clustered data, the fit statistics associated with each model differed from the naïve models. If a design-based adjusted model fit best of all the models compared in this investigation, than—over and above the inferences made about construct dimensionality—it will be clear that school-based clustering does affect the way learning opportunities are distributed across students. However, because these adjusted models do not specify the measurement of separate constructs at the student and school level, should a design-based model fit best (as opposed to a two-level model), the inference could be drawn that the variance in learning opportunities that was due to schools was not so great that school-level measurement ias meaningful as student-level measurement. However, the school-level cluster effect would have been strong enough to require a modeling adjustment on the standard errors, but not strong enough to require the modeling of a separate school-level construct. In general, a design-based adjusted model supports the inference that individual student experience drives their perceived learning opportunities, but that the estimation of that construct requires an adjustment for school-based clustering.
Two-Level Analysis
Because the two-level models were fit after the naïve and adjusted models, three two-level models were fit based on the previous results. Conceptual path diagrams for these models are depicted in Figures 3A–C. First, a configural correlated factor model (Figure 3A) was fit to the data. In this configural model, nine correlated factors (one for each scale of the measure) were fit to the data at both the student and school level, and the loadings were constrained to be equal across levels. For identification purposes, the latent factors were standardized across both the levels in the configural model. If this configural model were to fit best, the constrained loadings allow for a particular substantive inference: that school-level learning opportunities should be conceptualized not as a separately defined construct from student-level learning opportunities, but simply as an aggregate (e.g., average) of the student-level responses (Stapleton et al., 2016b). Some in the literature (e.g., Marsh et al., 2012; Morin et al., 2014) have described such configural models as measuring context constructs, in which the higher level (i.e., school) measurement is an aggregation of individual measurement at a lower (i.e., individual) level.
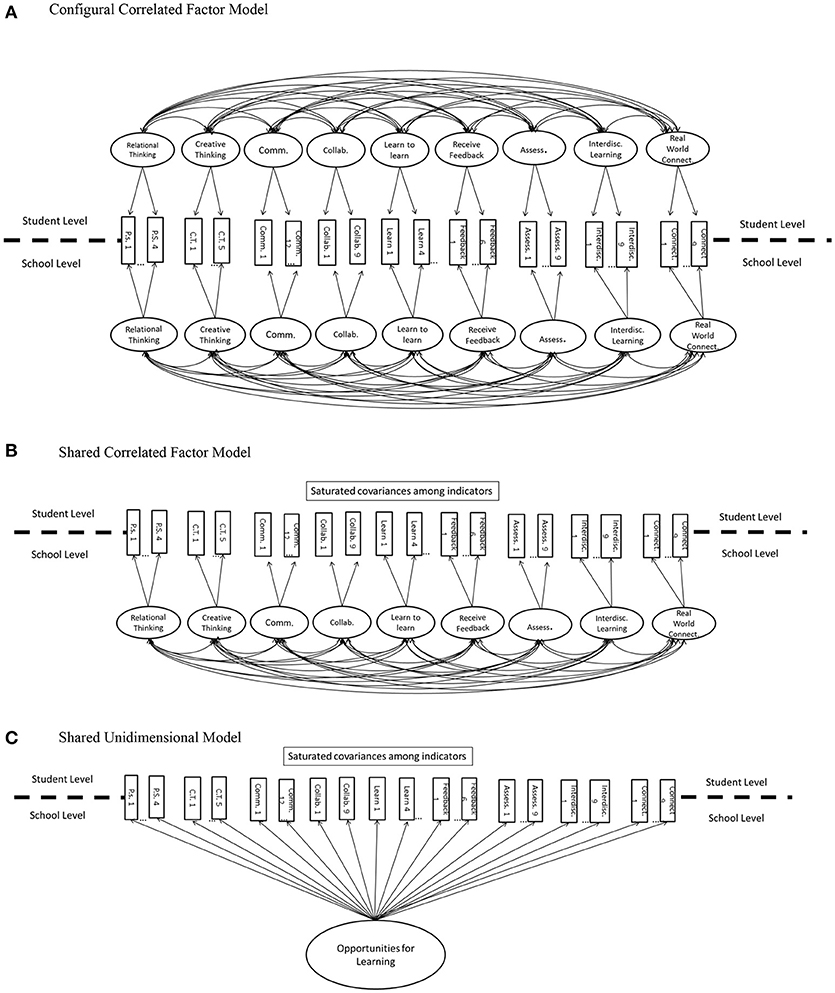
Figure 3. Theoretically plausible systematically compared at both student and school levels: (A) Configural Correlated; (B) Shared Correlated; and (C) Shared Unidimensional Factor Model. Error terms are not depicted here for simplicity.
Next, a shared correlated factor model was fit to the data (Figure 3B). Such a model featured saturated covariances among the items at the student level, and nine correlated factors at the school level. In this way, this shared model implies that student learning opportunities are best conceptualized as occurring at the school level, without meaningful measurement at the student level. Such a conceptualization reflects what has been termed a climate construct (Morin et al., 2014), in which students within a cluster (i.e., school) have homogenous experiences such that they are essentially interchangeable regarding the measurement of their learning opportunities. Finally, another shared climate construct model was fit, that posited a single dimension—general opportunities for learning—at the school level (Figure 3C). Such a model follows current findings that school level constructs may be more likely than student level constructs to exhibit a unidimensional structure (Marsh et al., 2012). Therefore, if this unidimensional shared model were to fit best, student learning opportunities would best be conceptualized as occurring at the school-level, in a way that was undifferentiated by the dimension of those learning opportunities.
Additionally, another critical difference in the two-level models fit in this investigation (whether configural or shared), in comparison to the naïve and design-based analyses, is that the model mean structure (i.e., item thresholds) was fit only to the school-level portion of the model, not to the student level. This methodological feature is a necessity for two-level measurement model identification (Stapleton et al., 2016a), but also holds substantive considerations. For example, two-level measurement models are not useful for modeling latent means at the individual student level. Instead, if one of the two-level models were to fit best in this study, then research questions about “how much” of a particular learning opportunity is present must be posed at the school, rather than the student level. Indeed, research questions about quantitative differences in learning opportunities among individual students within schools would be nonsensical from a two-level perspective, because, if one of these models were to fit best, this finding would indicate that within-school homogeneity in student learning opportunity was high enough so as to make comparisons only meaningful at the school level.
Model FIT Comparison
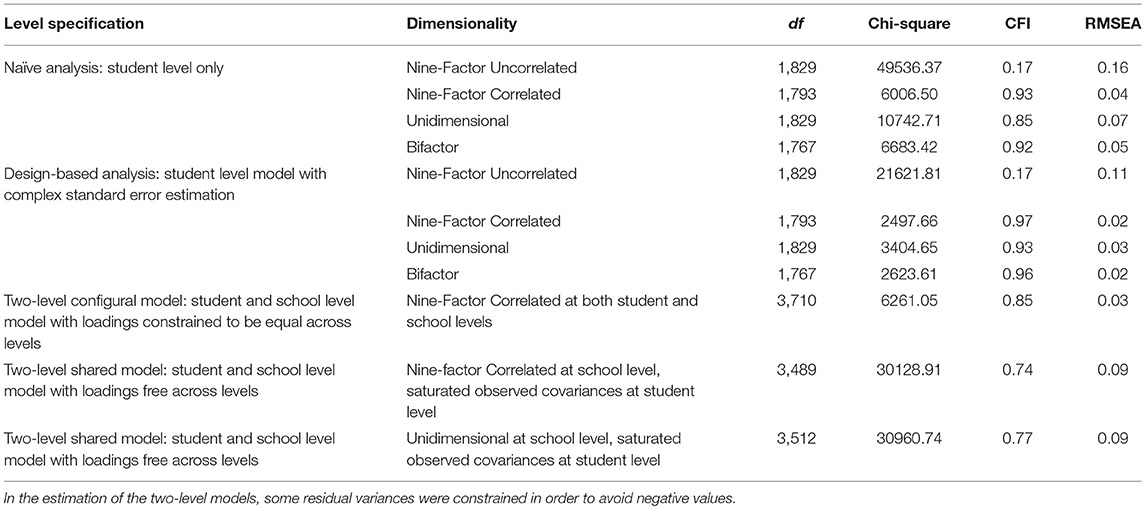
Relevant fit statistics corresponding to each of the 11 tested models are available in Table 4, organized first by their level specification (i.e., naïve, design-based, or two-level) and dimensionality. Specifically, chi-square values, degrees of freedom, comparative fit index (CFI), and root mean square error of approximation (RMSEA) are depicted in this table. It should be noted that because the robust diagonally-weighted least squares estimator was utilized for this analysis, the model chi-square is not calculated in the traditional way used with other estimators, and therefore the chi-square statistic cannot be directly compared across models, regardless of model nestedness. In evaluating the fit of each of these models, the empirical model-data fit was compared to commonly utilized standards for adequate fit (e.g., Hu and Bentler, 1999), which generally recommend CFIs above 0.95 and RMSEAs below 0.06. Moreover, the strength of the model loadings were also taken into account, because strong loadings increase statistical power to detect model-data mis-fit (Kang et al., 2016).
Beginning with the naïve analysis models, as can be seen in Table 4, the uncorrelated factor model fit the data very poorly, making it clear that the relatedness of the dimensions of these learning opportunities must be taken into account by the best-fitting model. The next best fitting model was the unidimensional model, although this model also did not fit the data adequately. Based on commonly utilized fit criteria, both the correlated factor model and the bifactor model appear to have adequate fit. However, by every measure (i.e., chi-square, CFI, RMSEA) the correlated factor model fit the data better than the bifactor model. Also relevant, the correlated factor model retained more degrees of freedom than the bifactor model, making it a more statistically parsimonious explanation of student learning opportunities.
Within the design-based adjusted models, a similar pattern emerged: the correlated factor model fit slightly better than the bifactor model, while also retaining more degrees of freedom, marking it as the best-fitting dimensional specification. However, it is crucial to note that all of the design-based adjusted models fit better than their dimensional counterparts in the naïve analysis, making it clear that the school-based clustering of these data must be taken into account when measuring student learning opportunities. In particular, the adjusted correlated factor model displayed very good fit, very much within widely used standards for good model-data-fit (e.g., Hu and Bentler, 1999).
Among the two-level models, the configural model, which featured constrained loadings across the student and school level in order to depict school level measurement as an aggregate of individual level data, displayed reasonable fit. However, both of the shared models, which assume student level responses to be interchangeable in order to quantify a school level climate construct, fit relatively poorly. Indeed, each of the shared two-level models fit worse than all of the naïve models, except for the naïve uncorrelated model. This finding makes it clear that, in these data at least, opportunities for learning are not school climate or context variables, but can be more correctly described as individual student perceptions. This substantive finding stems from the statistical observation that student level heterogeneity is too great to meaningfully quantify an entirely school-level climate construct. Given this fit comparison, student learning opportunities are best modeled with nine correlated factors at the student level, featuring a design-based linearization adjustment for school level clustering. Above and beyond the fit indices previously discussed, the design-based adjusted correlated model also featured small residual correlations (i.e., the difference between observed and model predicted correlations among the items). The vast majority of the residual correlations resulting from this best-fitting model were below an absolute value of 0.05, with many being below 0.01. In rare cases, residual correlations were higher (e.g., 108 between items Real-world connections 1 and 8), implying that, among a small minority of the item-responses being modeled here, some of their covariance may be due to factors unexplained in the current modeling framework. Such a finding implies that student learning opportunities are very heterogeneous within schools, and therefore that construct should best be understood through individual level measurement of a school contextual construct.
Doubly Latent Model Parameters
After selecting the design-based adjusted correlated factor model as the best fitting model, it is necessary to look closely at the parameters estimated in the model, in order to ascertain whether such a model may be a reliable and valid tool for making inferences about student perceived opportunities for learning.
Factor Correlations
Because the best fitting correlated factor model features substantively interesting latent variable correlations, they are presented in Table 5. Across the board, these correlations are stronger than those at the observed variable level (Table 3), although it should be noted that the composite score correlations are not in this table because full-measure scores are not present in the correlated factor model. At the lowest, correlations among latent dimensions of were r = 0.492 between Learning to Learn and Interdisciplinary Learning (as compared to r = 0.353 at the observed variable level). At the highest, latent correlations were r = 0.894 between both Feedback and Assessments as well as Feedback and Collaboration. In general, latent correlations among dimensions in the model were mostly between 0.60 and 0.90, indicating a relatively strong level of relation among the constructs.
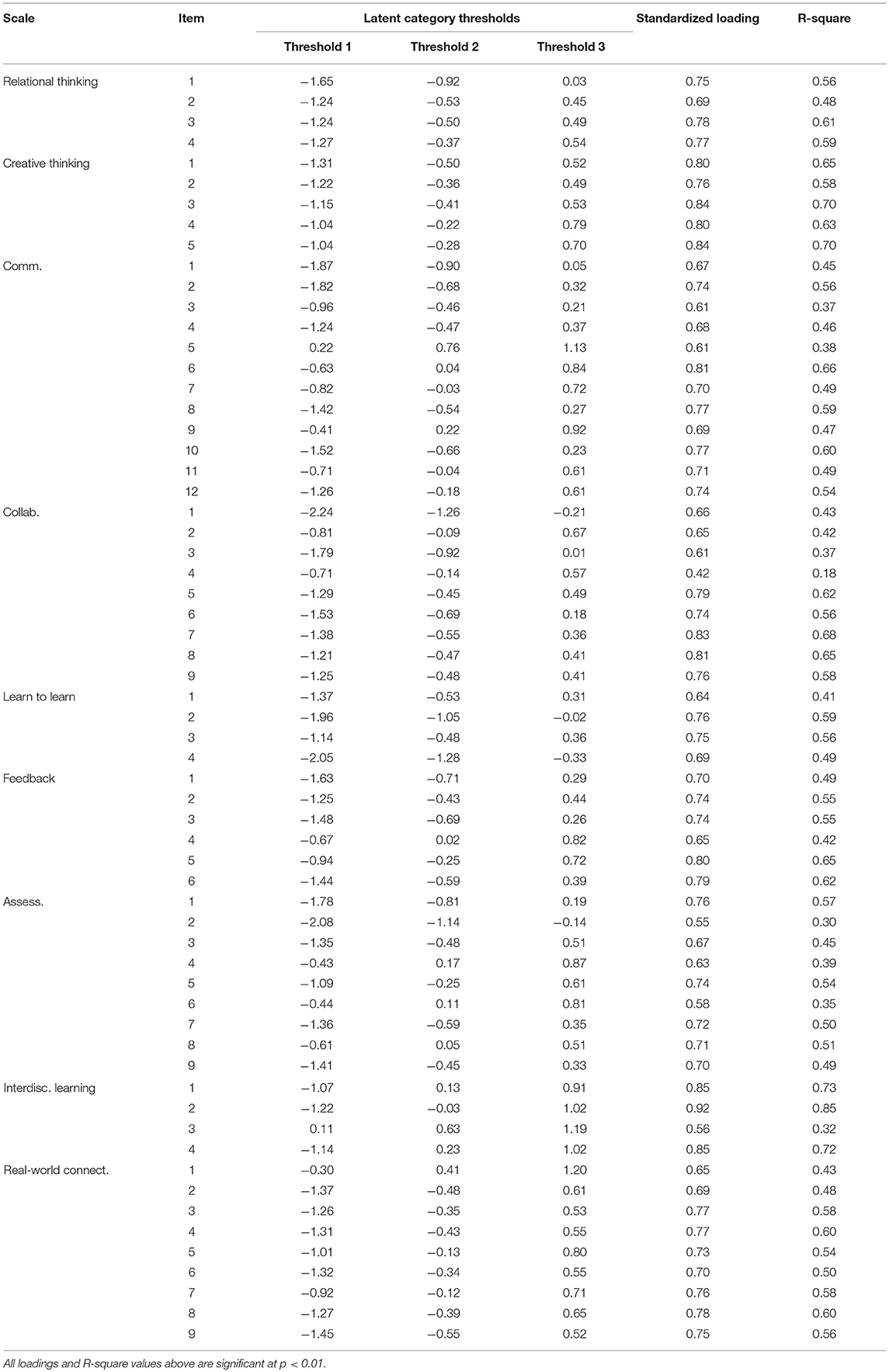
Response Category Thresholds
To account for the polytomous nature of item responses, three separate threshold parameters were modeled for each item. These thresholds, which are presented in Table 6, can be conceptualized as the point on the underlying latent distribution in which students become likely to respond to a particular polytomous response category. As such, threshold parameters are on a standardized scale in which a value of zero depicts the mean level of a given underlying distribution. As can be seen in Table 6, most of the administered items have a negative value for their first threshold parameter, indicating that students are likely to choose the second response category when they are below average on the latent attribute. In contrast, most items have a positive value for their third threshold, indicating that students are likely to be above average on the latent attribute when they choose to endorse the fourth response category. For the middle threshold parameter, values close to average (i.e., 0) appear to be typical, indicating that students move to endorse the third response category, as opposed to the second, around the average of the latent attribute distribution. Such a spread of threshold estimates may be ideal, because it suggests that the items may be generally worded in such a way as to capture the full range of each latent attribute (Ostini and Nering, 2006).
Item Loadings and R-Squares
Standardized loadings and r-square parameters for each item are also available in Table 6. As can be seen, most items load on their corresponding latent dimension strongly and positively, with the weakest being 0.42 (Collaboration 4) and the strongest being 0.92 (Interdisciplinary learning 2). Although this complete range is relatively wide, the large majority of item loadings fell between 0.65 and 0.85. Such strong-positive loadings suggest that the items are generally strongly related to the latent constructs on which they load. Also importantly, the r-square value associated with each item depicts the amount of variance in the item that is explained by the latent factors. The generally strong r-square values presented in Table 6 imply that the correlated factor model is explaining a statistically and practically significant amount of item variance. Therefore, the constructs depicted in the correlated factor model may be considered internally valid representations of the underlying latent attributes being tapped (Lissitz and Samuelsen, 2007).
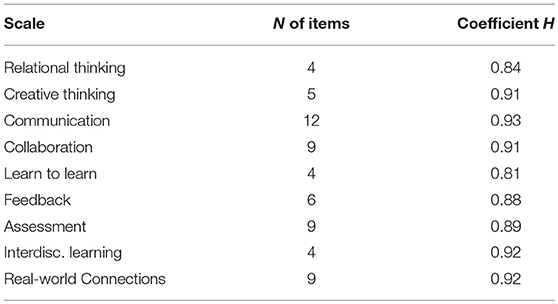
Construct Reliability
While item loadings and r-squares provide evidence of the reliability of the administered items to tap latent constructs, these functions do not encapsulate the reliability or reproducibility of the latent constructs themselves. For this, coefficient H (Gagne and Hancock, 2006), is needed. Coefficient H indicates the degree to which a latent construct could be reproduced from its measured indicators, and can be conceptualized as analogous to an r-square value, if a latent variable were regressed on each of its indicators (Dumas and Dunbar, 2014). Here, values of H for each of the latent dimensions are presented in Table 7. As can be seen, the construct reliability of each of the latent constructs measured in this study is strong, with the lowest being H = 0.82 (Relational Thinking) and the highest being H = 0.92 (Interdisciplinary learning). It should be noted that, because H does not require any strict assumptions about tau-equivalence of the measurement model (as Cronbach's alpha does), it is likely a more accurate depiction of the reliability of these constructs than other available reliability measures (Gagne and Hancock, 2006; Cho and Kim, 2015). Importantly, alternative reliability metrics for non-tau-equivalent measurement models do exist in the literature (e.g., Omega; McDonald, 1999) however, H is particularly suited for the current context because the estimation of the item loadings in this study allows the latent variables to be optimally weighted, meaning that each item contributes information to the latent variable in accordance with its loading. In contrast, other modern reliability indices such as Omega assume a unit weighted composite score in which each item contributes the same amount of information to the composite score, but lower loading items detract from the reliability (McNeish, 2017).
Implications and Conclusion
This investigation has been a systematic comparison of a number of theoretically plausible latent and doubly latent models for conceptualizing high school students' learning opportunities. Associated with these models have been research questions associated with both the underlying dimensionality of this construct, as well as the locus of the construct at the individual or aggregate level. As such, the results of this investigation are able to offer a number of principal findings that may deeply inform the conceptualization of student learning opportunities—and specifically high school student perceptions of these opportunities—in the future. Three specific principal findings are offered here: (a) perceived learning opportunities are multidimensional, (b) perceived learning opportunities occur at the student-level, and (c) despite this individual student-level locus, school-based clustering should still be statistically taken into account when modeling these perceptions across multiple schools.
Perceived Learning Opportunities Are Multidimensional
As is seen from the fit of the various models to these study data, perceived learning opportunities have a distinct multidimensional latent structure. Specifically, given the study results, the nine areas of perceived student learning opportunities measured in this study should be conceptualized as separate but related latent dimensions. Such a finding, at first blush, may appear to be unsurprising given the diverse areas of learning that were tapped by the measure utilized in this study. However, it should be highlighted that in previous studies of learning opportunities available to students, scores are sometimes aggregated across areas of academic learning (e.g., Song et al., 2017), a methodological choice that may not be valid given the results of this study. Of course, although the latent structure of the data in this study was multidimensional, this does not mean that those latent dimensions are not positively, and even strongly, related. Indeed, the nine-factor uncorrelated factor model, which formally posited that each area of learning opportunity was unrelated, fit the worst of any of the models included here. In this way, it may be that examining only a single perceived learning opportunity, without reference to the other diverse opportunities available to students, would not provide a meaningful picture of student learning opportunity.
Such a finding may be explained by the observation that students who are more likely than others to receive more opportunities for a given area of learning (e.g., opportunities for relational thinking) are also more likely to receive opportunities for other areas of learning (e.g., opportunities for creative thinking). Moreover, it may also be that the perception of such opportunities effect one another within students, or even that the actual provision of these opportunities to specific students are correlated. Indeed, there is evidence to suggest that students who receive more opportunities for learning in one area are also more likely to receive other opportunities as well (Wilhelm et al., 2017). But, also given the modeling results here, the correlations among these learning opportunities are far from one, indicating that students perceive critical differences in the opportunities they receive across the areas measured here.
Perceived Learning Opportunities Occur at the Student-Level
Another critical research question posed in this investigation concerned the actual locus of learning opportunities. In brief, the question was posed: are student learning opportunities an attribute of the school that provides those opportunities (i.e., a school context or climate construct), or are they an attribute of the students that perceive those opportunities and receive them? This question may be conceptualized as critically relevant to understanding the educational endeavor within schools: are individual learners the locus of learning opportunities, or are the learning opportunities that those learners engage in determined by schools? Such a conceptual question may be traced back to educational thinkers such as Dewey (1902/2010), who grappled with the issue of learning opportunity by positing an interaction between students and the curriculum they experience.
At least in this particular investigation, the results strongly implied that learning opportunities occur within students and not at the school-level. This finding is predicated on the observation that student level models (the design-based analysis), on the whole, fit better than the two-level models in this examination. However, it should be noted that the two-level configural model—that is formulated to indicate a school contextual construct that represents the aggregated (i.e., averaged) student level measurements—did display somewhat satisfactory fit to the data (although not as good of fit as the student level models). However, the two-level shared models, that are formulated to indicate school climate constructs in which individual students are considered interchangeable indicators of school climate, fit poorly. Taken together, these observed results indicate that the learning opportunities that are provided to students should not be conceptualized as wholly an attribute of a school, but rather an individual student level perception.
Perhaps, for those educational psychologists deeply engaged in the study of individual differences in learning, this finding will appear intuitive, because students' ability to benefit from learning opportunities in schools have been shown to be driven by a number of student level attributes including cognitive (Dinsmore et al., 2014), motivational (Muenks et al., 2018), and metacognitive skills (Peters and Kitsantas, 2010). However, within the larger literature of educational research, learning opportunities do often appear to be conceptualized as occurring wholly at the school, or possibly classroom (e.g., Wilhelm et al., 2017), level. Indeed, many existing lines of argument concerning the need for school level reform (McGiboney, 2016) or the current imperative to evaluate schools or teachers through the analysis of student level data (e.g., Ballou and Springer, 2015), either explicitly or implicitly posit student learning as a construct occurring within schools or classrooms (i.e., a context or climate construct). Another common arena in which student level learning perceptions are utilized to make inferences at the classroom or school level is in the general field of instructor educational evaluations, such as those typically completed by university students. Although the current study was completed high schools, it is clear that these data should not be utilized to evaluate the learning climate of any of the high schools in the dataset. If, as could be hypothesized, similar results to the current study were to be found with university data, than the current use of learning perception measures to evaluate instructors, departments, or colleges, would be entirely invalid because the critical assumption associated with climate construct measurement—that students within the same climate are fully interchangeable in their learning opportunities—would not be met.
In general, the current practice in educational research of modeling effects at both the individual student level, as well as a higher level such as the classroom or school, assumes that the constructs being modeled actually exist at both of those levels (McNeish et al., 2017). In this way, the constructs may be “split” into both an attribute of individual students as well as a school level attribute, sometimes without much explanation as to the construct meaning across these two levels. The results of this investigation imply that, at least for the multidimensional construct of student learning opportunity measured here, such a theoretical conceptualization would be inappropriate.
School-Based Clustering Must be Taken Into Account
Despite the principal finding that student learning opportunities appear to be a student-level, rather than school level construct, it is also apparent from the findings of this study that, in cases such as the present study in which student learning opportunities are measured across a number of schools, that school level clustering should be taken into account statistically. In this study, a linearization method (TYPE = COMPLEX in Mplus 8) was utilized to account for the school level clustering in these data within the design-based adjusted models. In contrast, the naïve analysis did not take the school level clustering into account in any way. Although both the naïve and adjusted models conceptualize learning opportunities at the student level, the adjusted analyses fit much better, on the whole, than the naïve analysis, and the best fitting model was the design-based adjusted correlated factor model.
It may seem that the combination of findings in this study—that learning opportunities occur at the student level, but school-based clustering should be accounted for statistically—contradict one another because one finding implies student level measurement while the other implies school-based effects. However, such a pattern of findings can be conceptually explained in that, according to the results of this study, school clustering does have an effect on student perceived opportunities for learning, but the effect is not accounted for in the measurement model utilized here. That is to say that all of the latent variables posited in the correlated factor model occur at the student level, but some other aspect of student responses, external to the model, may occur at the school level. In the nine factor model that was found to be best fitting, the school-based clustering essentially appears to effect the error variance in responses, which conceptually represent the reasons, other than the latent variables in the model, why a student may perceive a particular opportunity for learning.
Some general hypotheses for what these school-based effects may represent include: a school based climate construct not specified in the model such as faculty approachability or school resource availability, or an individual difference among students that is disproportionately distributed on average among schools. For example, it is clear from this analysis (i.e., intraclass correlations) that substantial differences on students' parents' education level existed across the schools present in this dataset, and in addition, that variable was relatively homogenous within schools. So, it may well have been that systematic differences across schools on such socio-economic variables resulted in the need to adjust the student-level models for cluster-based sampling error (i.e., make them doubly latent). However, because the student-level adjusted models fit better than the two-level models, it is likewise clear that these across school differences were not salient enough to negate the heterogeneity in student perceived learning opportunities within schools.
Future Directions
As in nearly any published investigation in the social sciences, the particular methodological and analytical choices made in this study preclude some relevant and interesting inferences from being made about student learning opportunities. Therefore, a number of specific future directions may be forwarded to address the issues that this study, with its particular delimitations, could not. These future directions, to be discussed in detail in the coming sections of this article include: (a) investigation of a classroom effect on student learning opportunities, (b) investigation of intra-individual variance in reported opportunities for learning, and (c) taking a person-centered approach to the investigation of patterns of learning opportunities within and between students.
Classroom Effect
Throughout the entirety of this investigation, from the initial formulation and selection of items to administer to students, to the analysis of the resulting data using doubly latent measurement models, the second-level of this analysis (above individual students) was always considered to be the school those students attended. This choice is reflected in the manner in which the items specifically prompted students to consider multiple of their courses or teachers when responding, making a specific analysis of learning opportunity differences within each of those subject-area classrooms outside the scope of this study. In essence, the measure administered to participants in this study may be thought of as specifically attempting to tap a school-level context or climate construct: something which the results of this analysis make clear was not achieved. However, it may have been an equally reasonable methodological choice to construct a measure that prompted students to think and respond about multiple scenarios within the same classroom or subject-area, which would have created the logical need to model classrooms as the second-level variable in this study. Given such an alternative methodological and measurement direction, it is not yet known whether the detection and quantification of a classroom level climate or context construct would have been possible with these particular participating students, teachers, and schools. At this point, such an investigation into the possible classroom-level locus of student learning opportunities, such as they are operationally defined here, necessarily remains a future direction. However, a number of classroom-level doubly latent investigations are currently extant in the educational psychology literature (e.g., Marsh et al., 2012; Morin et al., 2014), allowing for the inference that such a future direction may be tenable and interesting going forward.
Stability of Learning Opportunity Over-time
As previously mentioned in the introduction to this study, all of the analysis presented here considered only a single-time point of student response data, and did not consider possible intra-individual differences across time within students on their perceived learning opportunities. Of course, it seems very reasonable to hypothesize that students' perceptions of their learning opportunities would vary substantially as those opportunities were presented to them, made motivationally salient, or taken away as a possibility over time. Therefore, such an analysis of time-varying intra-individual differences in learning opportunity seem warranted and interesting as a future direction to this research. From a methodological perspective, such a data collection would necessitate utilizing time-point as a second-level clustering variable in which to nest individual students, possibly using a mixed-effects modeling framework (e.g., McNeish and Dumas, 2017). Using such a framework, interesting research questions could be answered—especially if combined with the collection and modeling of other psychological attributes such as motivational or emotional states—about when and why student perceived learning opportunities increased and decreased within students. Indeed, it could very possibly be the case that the variance in student perceived learning opportunities due to time would be greater than the variance due to classroom or school, although such a statement must remain a hypothesis for the time being, until such a question can be investigated within a longitudinal investigation.
Person-Centered Approach
In addition to future directions that investigate the effect of classroom- and time-nestedness on student perceptions of their learning opportunities, it may also be interesting and fruitful to take a person-centered approach to the analysis of student response data in order to determine how learning opportunities co-occur within individual or groups of students, even within a single school. Such a person-centered approach is inherently different form the construct-centered approach taken in this study, because rather than identifying the relations among the latent constructs across levels of the model, such an analysis (e.g., cluster analysis) would seek to identify sub-groups of students who report differing patterns of learning opportunities. Then, through the careful examination of the make-up of these groups of students (especially if other psychological variables are also measured), inferences could be made about the source of these patterns of perceived opportunities. Given that person-centered perspectives on learning-related variables have been previously fruitful in the educational psychology literature (Harring and Hodis, 2016), it is reasonable to expect that such an analysis may be an interesting next step in this line of inquiry as well. Indeed, such a mixture-modeling approach may also be combined with classroom- or time-clustered models as well, in order to create the richest possible understanding of student perceptions of their learning opportunities in the future.
In general, the results of this study suggest that high school students' perceptions of their learning opportunities can be described as a nine-dimensional construct that occurs within students, and is not principally an aspect of their school. However, given some systematic average student level differences among schools (e.g., average student socioeconomic status) it is necessary to statistically adjust student level measurement models based on school based clustering, in order to most reliably and validly quantify the construct. Given the critical role that schools play in student academic development and learning, this understanding is expected to be relevant to future theorizing and empirical investigations wherever student perceptions of their learning opportunities play a role. Moreover, this study may contribute to a burgeoning awareness in the field that theorizing constructs that occur across different loci (e.g., student, school context, and school climate) requires careful empirical consideration in order to inform theoretical construct conceptualization.
Author Contributions
The author confirms being the sole contributor of this work and approved it for publication.
Funding
This research was supported by the American Educational Research Association Deeper Learning Fellowship, funded by the William and Flora Hewlett Foundation.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2018.00076/full#supplementary-material
References
Alexander, P. A. (2017). Issues of constructs, contexts, and continuity: commentary on learning in higher education. Educ. Psychol. Rev. 29, 345–351. doi: 10.1007/s10648-017-9409-3
Alexander, P. A., Dumas, D., Grossnickle, E. M., List, A., and Firetto, C. M. (2016). Measuring relational reasoning. J. Exp. Educ. 84, 119–151. doi: 10.1080/00220973.2014.963216
Ardasheva, Y. (2016). A structural equation modeling investigation of relationships among school-aged ELs' individual difference characteristics and academic and second language outcomes. Learn. Individ. Differ. 47, 194–206. doi: 10.1016/j.lindif.2016.02.010
Ashford-Rowe, K., Herrington, J., and Brown, C. (2014). Establishing the critical elements that determine authentic assessment. Assess. Evalu. Higher Educ. 39, 205–222. doi: 10.1080/02602938.2013.819566
Ballou, D., and Springer, M. G. (2015). Using student test scores to measure teacher performance: some problems in the design and implementation of evaluation systems. Educ. Res. 44, 77–86. doi: 10.3102/0013189X15574904
Bartko, J. J. (1976). On various intraclass correlation reliability coefficients. Psychol. Bull. 83, 762–765. doi: 10.1037/0033-2909.83.5.762
Beaufort, A. (2009). “Preparing adolescents for the literacy demands of the 21st-century workplace,” in Handbook of Adolescent Literacy Research, eds L. Christenbury, R. Bomer, and P. Smargorinsky (New York, NY: Guilford Publications), 239–355.
Binder, D. A., and Roberts, G. R. (2003). “Design-based and model-based methods for estimating model parameters,” in Analysis of Survey Data, eds R. L. Chambers and C. J. Skinner (Chichester: Wiley & Sons), 29–48. doi: 10.1002/0470867205.ch3
Burnett, P. C. (2003). The impact of teacher feedback on student self-talk and self-concept in reading and mathematics. J. Classroom Inter. 38, 11–16.
Chicago Consortium on School Research (2015). Survey Measure Statistics. Available online at: http://consortium.uchicago.edu/page/2015-survey-documentation
Cho, E., and Kim, S. (2015). Cronbach's coefficient alpha: well-known but poorly understood. Organ. Res. Methods 18, 207–230. doi: 10.1177/1094428114555994
Clapham, M. M., Cowdery, E. M., King, K. E., and Montang, M. A. (2005). Predicting work activities with divergent thinking tests: a longitudinal study. J. Creat. Behav. 39, 149–167. doi: 10.1002/j.2162-6057.2005.tb01256.x
Coelho, V. A., and Sousa, V. (2017). Comparing two low middle school social and emotional learning program formats: a multilevel effectiveness study. J. Youth Adolesc. 46, 656–667. doi: 10.1007/s10964-016-0472-8
Cortez, C., Nussbaum, M., Woywood, G., and Aravena, R. (2009). Learning to collaborate by collaborating: a face-to-face collaborative activity for measuring and learning basics about teamwork. J. Comput. Assist. Learn. 25, 126–142. doi: 10.1111/j.1365-2729.2008.00298.x
Cromley, J. G., Weisberg, S. M., Dai, T., Newcombe, N. S., Schunn, C. D., Massey, C., et al. (2016). Improving middle school science learning using diagrammatic reasoning. Sci. Educ. 100, 1184–1213. doi: 10.1002/sce.21241
Cronbach, L. J. (1976). Research on Classrooms and Schools: Formulation of Questions, Design and Analysis. Stanford Evaluation Consortium, School of Education, Stanford University, Stanford, CA. Available online at: https://eric.ed.gov/?id=ED135801
Dewey, J. (1902/2010). “Selected writings of John Dewey,” in American Educational Thought: Essays from 1640–1940, 2nd Edn, eds A. J. Milson, C. H. Bohan, P. L. Glanzer, and J. W. Null (Charlotte, NC: IAP Information Age Publishing), 361–399.
Dinsmore, D. L., Baggetta, P., Doyle, S., and Loughlin, S. M. (2014). The role of initial learning, problem features, prior knowledge, and pattern recognition on transfer success. J. Exp. Educ. 82, 121–141. doi: 10.1080/00220973.2013.835299
DiStefano, C., and Morgan, G. B. (2014). A comparison of diagonal weighted least squares robust estimation techniques for ordinal data. Struct. Equ. Model. 21, 425–438. doi: 10.1080/10705511.2014.915373
Drew, S. V., Olinghouse, N. G., Faggella-Luby, M., and Welsh, M. E. (2017). Framework for disciplinary writing in science grades 6–12: a national survey. J. Educ. Psychol. 109, 935–955. doi: 10.1037/edu0000186
Dumas, D., and Alexander, P. A. (2016). Calibration of the test of relational reasoning. Psychol. Assess. 28, 1303–1318. doi: 10.1037/pas0000267
Dumas, D., Alexander, P. A., Baker, L. M., Jablansky, S., and Dunbar, K. N. (2014). Relational reasoning in medical education: patterns in discourse and diagnosis. J. Educ. Psychol. 106, 1021–1035. doi: 10.1037/a0036777
Dumas, D., Alexander, P. A., and Grossnickle, E. M. (2013). Relational reasoning and its manifestations in the educational context: a systematic review of the literature. Educ. Psychol. Rev. 25, 391–427. doi: 10.1007/s10648-013-9224-4
Dumas, D., and Dunbar, K. N. (2014). Understanding fluency and originality: a latent variable perspective. Think. Skills Creat. 14, 56–67. doi: 10.1016/j.tsc.2014.09.003
Dumas, D., and McNeish, D. M. (2017). Dynamic measurement modeling: using nonlinear growth models to estimate student learning capacity. Educ. Res. 46, 284–292. doi: 10.3102/0013189X17725747
Dumas, D., Schmidt, L. C., and Alexander, P. A. (2016). Predicting creative problem solving in engineering design. Think. Skills Creat. 21 50–66. doi: 10.1016/j.tsc.2016.05.002
Fan, W., Williams, C. M., and Corkin, D. M. (2011). A multilevel analysis of student perceptions of school climate: the effect of social and academic risk factors. Psychol. Sch. 48, 632–647. doi: 10.1002/pits.20579
Farrell, T. S. C. (2009). Talking, listening, and Teaching: A Guide to Classroom Communication. Thousand Oaks, CA: Corwin Press.
Finch, W. H., Cassady, J. C., and Jones, J. A. (2016). Investigation of the latent structure for the learning and study strategies inventory. J. Psychoeduc. Assess. 34, 73–84. doi: 10.1177/0734282915588443
Fiorello, C. A., Hale, J. B., Snyder, L. E., Forrest, E., and Teodori, A. (2008). “Validating individual differences through examination of converging psychometric and neuropsychological models of cognitive functioning,” in Applied cognitive research in K−3 classrooms, eds S. K. Thurman and C. A. Fiorello (New York, NY: Routledge/Taylor & Francis Group), 151–186.
Gagne, P., and Hancock, G. R. (2006). Measurement model quality, sample size, and solution propriety in confirmatory factor models. Multivariate Behav. Res. 41, 65–83. doi: 10.1207/s15327906mbr4101_5
Gajda, A., Beghetto, R. A., and Karwowski, M. (2017). Exploring creative learning in the classroom: a multi-method approach. Think. Skills Creat. 24, 250–267. doi: 10.1016/j.tsc.2017.04.002
Geisinger, K. F. (2016). 21st century skills: what are they and how do we assess them? Appl. Measur. Educ. 29, 245–249. doi: 10.1080/08957347.2016.1209207
Goswami, U., and Brown, A. L. (1990). Higher-order structure and relational reasoning: contrasting analogical and thematic relations. Cognition 36, 207–226. doi: 10.1016/0010-0277(90)90057-Q
Greiff, S., and Kyllonen, P. (2016). Contemporary assessment challenges: the measurement of 21st century skills. Appl. Measur. Educ. 29, 243–244. doi: 10.1080/08957347.2016.1209209
Harring, J. R., and Hodis, F. A. (2016). Mixture modeling: applications in educational psychology. Educ. Psychol. 51, 354–367. doi: 10.1080/00461520.2016.1207176
Hazari, Z., Sonnert, G., Sadler, P. M., and Shanahan, M.-C. (2010). Connecting high school physics experiences, outcome expectations, physics identity, and physics career choice: a gender study. J. Res. Sci. Teach. 47, 978–1003. doi: 10.1002/tea.20363
Hu, L., and Bentler, P. M. (1999). Cutoff criteria for fit indexes in covariance structure analysis: conventional criteria versus new alternatives. Struct. Equ. Model. 6, 1–55. doi: 10.1080/10705519909540118
Kane, T. J., McCaffrey, D. F., Miller, T., and Staiger, D. O. (2013). Have We Identified Effective Teachers? Validating Measures of Effective Teaching Using Random Assignment. Research Paper. MET Project. Bill & Melinda Gates Foundation. Available online at: https://eric.ed.gov/?id=ED540959
Kang, Y., McNeish, D. M., and Hancock, G. R. (2016). The role of measurement quality on practical guidelines for assessing measurement and structural invariance. Educ. Psychol. Meas. 76, 533–561. doi: 10.1177/0013164415603764
Khajavy, G. H., MacIntyre, P. D., and Barabadi, E. (2017). Role of the emotions and classroom environment in willingness to communicate: applying doubly latent multilevel analysis in second language acquisition research. Stud. Sec. Langu. Acquis. doi: 10.1017/S0272263117000304. [Epub ahead of print].
Lin-Siegler, X., Dweck, C. S., and Cohen, G. L. (2016). Instructional interventions that motivate classroom learning. J. Educ. Psychol. 108, 295–299. doi: 10.1037/edu0000124
Lissitz, R. W., and Samuelsen, K. (2007). A suggested change in terminology and emphasis regarding validity and education. Educ. Res. 36, 437–448. doi: 10.3102/0013189X07311286
Lonigan, C. J., and Burgess, S. R. (2017). Dimensionality of reading skills with elementary-school-age children. Sci. Stud. Read. 21, 239–253. doi: 10.1080/10888438.2017.1285918
Lüdtke, O., Robitzsch, A., Trautwein, U., and Kunter, M. (2009). Assessing the impact of learning environments: how to use student ratings of classroom or school characteristics in multilevel modeling. Contemp. Educ. Psychol. 34, 120–131. doi: 10.1016/j.cedpsych.2008.12.001
Mahler, D., Großschedl, J., and Harms, U. (2017). Using doubly latent multilevel analysis to elucidate relationships between science teachers' professional knowledge and students' performance. Int. J. Sci. Educ. 39, 213–237. doi: 10.1080/09500693.2016.1276641
Marsh, H. W., Lüdtke, O., Nagengast, B., Trautwein, U., Morin, A. J. S., Abduljabbar, A. S., et al. (2012). Classroom climate and contextual effects: conceptual and methodological issues in the evaluation of group-level effects. Educ. Psychol. 47, 106–124. doi: 10.1080/00461520.2012.670488
McGiboney, G. W. (2016). The Psychology of School Climate. Newcastle upon Tyne: Cambridge Scholars Publishing.
McNeish, D. (2017). Thanks coefficient alpha, we'll take it from here. Psychol. Methods. doi: 10.1037/met0000144. [Epub ahead of print].
McNeish, D., and Dumas, D. (2017). Nonlinear growth models as measurement models: a second-order growth curve model for measuring potential. Multiv. Behav. Res. 52, 61–85. doi: 10.1080/00273171.2016.1253451
McNeish, D., Stapleton, L. M., and Silverman, R. D. (2017). On the unnecessary ubiquity of hierarchical linear modeling. Psychol. Methods 22, 114–140. doi: 10.1037/met0000078
Morin, A. J. S., Marsh, H. W., Nagengast, B., and Scalas, L. F. (2014). Doubly latent multilevel analyses of classroom climate: an illustration. J. Exp. Educ. 82, 143–167. doi: 10.1080/00220973.2013.769412
Muenks, K., Yang, J. S., and Wigfield, A. (2018). Associations between grit, motivation, and achievement in high school students. Motivat. Sci. 4, 158–176. doi: 10.1037/mot0000076
Murphy, P. K., Firetto, C. M., and Greene, J. A. (2017). Enriching students' scientific thinking through relational reasoning: seeking evidence in texts, tasks, and talk. Educ. Psychol. Rev. 29, 105–117. doi: 10.1007/s10648-016-9387-x
Muthén, B. O., and Satorra, A. (1995). “Complex ample data in structural equation modeling,” in Sociological Methodology, ed P. V. Marsden (Washington, DC: American Sociological Association), 267–316.
Oliveri, M., McCaffrey, D., Ezzo, C., and Holtzman, S. (2017). A multilevel factor analysis of third-party evaluations of noncognitive constructs used in admissions decision making. Appl. Measur. Educ. 30, 297–313. doi: 10.1080/08957347.2017.1353989
Patchan, M. M., Schunn, C. D., and Correnti, R. J. (2016). The nature of feedback: how peer feedback features affect students' implementation rate and quality of revisions. J. Educ. Psychol. 108, 1098–1120. doi: 10.1037/edu0000103
Pegrum, M., Bartle, E., and Longnecker, N. (2015). Can creative podcasting promote deep learning? The use of podcasting for learning content in an undergraduate science unit. Br. J. Educ. Technol. 46, 142–152. doi: 10.1111/bjet.12133
Peters, E. E., and Kitsantas, A. (2010). Self-regulation of student epistemic thinking in science: the role of metacognitive prompts. Educ. Psychol. 30, 27–52. doi: 10.1080/01443410903353294
Pilegard, C., and Mayer, R. E. (2015). Adding judgments of understanding to the metacognitive toolbox. Learn. Individ. Differ. 41, 62–72. doi: 10.1016/j.lindif.2015.07.002
Richland, L. E., and Simms, N. (2015). Analogy, higher order thinking, and education. WIREs Cognit. Sci. 6, 177–192. doi: 10.1002/wcs.1336
Robles-Rivas, E. (2015). “Higher order thinking skills: an arts-infused core curriculum for English learners and their peers,” in Effective Educational Programs, Practices, and Policies for English Learners, ed L. Minaya-Rowe (Charlotte, NC: IAP Information Age Publishing), 107–135.
Roscoe, R. D., and McNamara, D. S. (2013). Writing pal: feasibility of an intelligent writing strategy tutor in the high school classroom. J. Educ. Psychol. 105, 1010–1025. doi: 10.1037/a0032340
Schneider, B., Ehrhart, M. G., and Macey, W. H. (2013). Organizational climate and culture. Annu. Rev. Psychol. 64, 361–388. doi: 10.1146/annurev-psych-113011-143809
Schraw, G., and Robinson, D. R. (eds.) (2011). Assessment of Higher Order Thinking Skills. Charlotte, NC: IAP Information Age Publishing.
Song, L., Golinkoff, R. M., Stuehling, A., Resnick, I., Mahajan, N., Hirsh-Pasek, K., et al. (2017). Parents' and experts' awareness of learning opportunities in children's museum exhibits. J. Appl. Dev. Psychol. 49(Suppl. C), 39–45. doi: 10.1016/j.appdev.2017.01.006
Stapleton, L. M., McNeish, D. M., and Yang, J. S. (2016a). Multilevel and single-level models for measured and latent variables when data are clustered. Educ. Psychol. 51, 317–330. doi: 10.1080/00461520.2016.1207178
Stapleton, L. M., Yang, J. S., and Hancock, G. R. (2016b). Construct meaning in multilevel settings. J. Educ. Behav. Stat. 41, 481–520. doi: 10.3102/1076998616646200
Sternberg, R. J. (2015). Teaching for creativity: the sounds of silence. Psychol. Aesthet. Creat. Arts 9, 115–117. doi: 10.1037/aca0000007
Stoop, I. A. L. (2005). The Hunt for the Last Respondent: Nonresponse in Sample Surveys. The Hague: Sociaal en Cultureel Planbureau.
Swaffield, S. (2011). Getting to the heart of authentic assessment for learning. Assess. Educ. Princ. Policy Pract. 18, 433–449. doi: 10.1080/0969594X.2011.582838
Tendhar, C., Culver, S. M., and Burge, P. L. (2013). Validating the national survey of student engagement (NSSE) at a research-intensive university. J. Educ. Train. Stud. 1, 182–193. doi: 10.11114/jets.v1i1.70
Van den Bergh, L., Ros, A., and Beijaard, D. (2014). Improving teacher feedback during active learning: effects of a professional development program. Am. Educ. Res. J. 51, 772–809. doi: 10.3102/0002831214531322
Vandermaas-Peeler, M., Massey, K., and Kendall, A. (2016). Parent guidance of young children's scientific and mathematical reasoning in a science museum. Early Child. Educ. J. 44, 217–224. doi: 10.1007/s10643-015-0714-5
Wilder, S. (2015). Impact of problem-based learning on academic achievement in high school: a systematic review. Educ. Rev. 67, 414–435. doi: 10.1080/00131911.2014.974511
Wilhelm, A. G., Munter, C., and Jackson, K. (2017). Examining relations between teachers' explanations of sources of students' difficulty in mathematics and students' opportunities to learn. Elem. Sch. J. 117, 345–370. doi: 10.1086/690113
Yadav, A., Vinh, M., Shaver, G. M., Meckl, P., and Firebaugh, S. (2014). Case-based instruction: improving students' conceptual understanding through cases in a mechanical engineering course. J. Res. Sci. Teach. 51, 659–677. doi: 10.1002/tea.21149
Zhonghua, Z., and Lee, J. C. K. (2017). Students' behavioral and emotional participation in academic activities in the mathematics classroom: a multilevel confirmatory factor analysis. J. Exp. Educ. doi: 10.1080/00220973.2017.1335684. [Epub ahead of print].
Zimmerman, S. D., Short, G. F. L., Hendrix, E. M., and Timson, B. F. (2011). Impact of interdisciplinary learning on critical thinking using case study method in allied health care graduate students. J. Allied Health 40, 15–18.
Keywords: high school students, classroom climate, multi-level measurement models, perceptions of learning, creative thinking
Citation: Dumas D (2018) Understanding High School Students' Perceptions of Their Learning Opportunities: A Doubly Latent Approach. Front. Educ. 3:76. doi: 10.3389/feduc.2018.00076
Received: 21 May 2018; Accepted: 20 August 2018;
Published: 10 September 2018.
Edited by:
Michael S. Dempsey, Boston University, United StatesReviewed by:
Maciej Karwowski, University of Wrocław, PolandPeter Adriaan Edelsbrunner, ETH Zürich, Switzerland
Copyright © 2018 Dumas. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Denis Dumas, ZGVuaXNnZHVtYXNAZ21haWwuY29t
 Denis Dumas
Denis Dumas