Connected or compartmentalized knowledge use: Two views of MKT with implications

Howell, Heather; Lai, Yvonne; Suh, Heejoo

doi:10.3389/feduc.2025.1611169

ORIGINAL RESEARCH article

Front. Educ., 08 October 2025

Sec. Teacher Education

Volume 10 - 2025 | https://doi.org/10.3389/feduc.2025.1611169

This article is part of the Research TopicMathematics teachers' construction and enactment of disciplinary knowledgeView all 5 articles

Connected or compartmentalized knowledge use: Two views of MKT with implications

Heather Howell^1*

Yvonne Lai²

Heejoo Suh³

¹The Socratic Experience, Austin, TX, United States
²Department of Mathematics, University of Nebraska-Lincoln, Lincoln, NE, United States
³College of Education, Seoul National University, Seoul, Republic of Korea

One common approach to assessing mathematical knowledge for teaching (MKT) is designing items to measure individual subdomains of MKT as specified by a theoretical framework, with factor analyses confirming, or disconfirming, hypothesized subdomains. We interpret this approach as adhering to a “compartmentalized” view of MKT, as opposed to a “connected” view of MKT. We argue in this paper that a compartmentalized view of MKT is embedded in the ways that frameworks are represented, discussed, and used in the field. However, a compartmentalized view of MKT may unintentionally undermine understanding of MKT, and in turn, how to measure and cultivate it in teachers. We support this argument with an empirical analysis of nine typical practice-based items designed to assess MKT at the secondary level, categorized according to dimensions of five prominent frameworks for MKT. A key finding is that all of the items capture multiple subdomains, suggesting they are not measuring compartmentalized knowledge well. This finding held across all five frameworks, suggesting that it is more a characteristic of practice-based item design than of the frameworks used. We suggest that viewing MKT from a connected view can open potential lines of research that can impact assessment, learning, and teacher education.

1 Introduction

The 18th and 19th centuries heralded great advances in scientific theory. The pursuit of indivisible substances supported the development of stoichiometry and the systematic classification of elements, ultimately leading to the periodic table. However, classification of elements could not explain how organic compounds, such as glucose and formaldehyde, could comprise similar proportions of the same elements, yet behave in dramatically different ways. To make progress in this problem, scientists needed to ask different kinds of questions. They needed to expand their focus to the implications of how atoms connected to each other, rather than only on whether elements could be isolated. Theory building in mathematical knowledge for teaching (MKT) may now be in an analogous position, with questions and apparent conflicts arising in attempts to classify and compartmentalize theorized subdomains of MKT.

In broad terms, MKT is the content knowledge used in recognizing, understanding, and responding to mathematical situations, considerations, and challenges that arise in the course of teaching mathematics (e.g., Ball et al., 2008; Baumert et al., 2010; Thompson and Thompson, 1996). As interest in both the construct of MKT and its measurement has increased, a number of competing frameworks to describe MKT and its constituent components have proliferated, and so has debate about the utility, meaning, and observability of domains of MKT (e.g., Baumert et al., 2010; Beswick et al., 2012; Depaepe et al., 2013; Hill et al., 2008; Kaarstein, 2014).

There has been some progress in distinguishing subdomains of MKT, particularly at a high level between purely mathematical knowledge and knowledge applied in pedagogical contexts (e.g., Baumert et al., 2010). But researchers have also found that the same terms are interpreted in multiple and sometimes incompatible ways across different projects (Depaepe et al., 2013; Kaarstein, 2014), and some domains have proven difficult to assess directly (Hill et al., 2008).

The purpose of this manuscript is to argue that a focus on isolating domains of MKT is embedded in the way that various (though not all) frameworks for MKT are represented, discussed, and used in the field. Moreover, in adopting a compartmentalized view, we may unintentionally limit the kinds of questions we ask about the nature and use of MKT. Consequently, we may undermine our understanding of MKT, and in turn our understanding of how to measure and cultivate teachers’ MKT. In the first portion of the paper, where we discuss conceptual perspective and background, we describe evidence from the literature that supports our argument, as well as where there are exceptions. In the second portion of the paper, we illustrate our argument through a study of nine cases of items designed to assess MKT. The questions guiding our analysis were: In what compartmentalized or connected ways do practice-based items (i.e., items that situate the respondent in a teaching scenario) elicit evidence of MKT? How do connectedness or compartmentalization appear to differ or be similar when viewing MKT through different frameworks proposed for MKT?

2 Background

2.1 Conceptual perspective on MKT as knowledge and knowing

Following Cook and Brown (1999), we take knowledge to be possessed by individuals and groups, such as facts or procedures or schemas. We take knowing to be actions performed, such as analyzing student work. Following Ball (2017) and Ghousseini (2017), we take MKT to encompass professional knowledge and knowing. In this sense, knowing uses, demands, and may cultivate knowledge. This conceptual perspective helps us make sense of commonalities underlying existing work on MKT (e.g., Charalambous et al., 2020; Copur-Gencturk and Tolar, 2022; Kersting et al., 2012; McCrory et al., 2012; Hill et al., 2004; Hill and Chin, 2018; Krauss et al., 2008; Rowland, 2013). Across work that conceptualizes MKT and its constituent domains, researchers have attended to possessed mathematical and pedagogical knowledge, while also identifying the “work of teaching, and in particular the mathematical work of teaching” (Ball, 2017, p. 17, emphasis in the original).

As Ball (2017) observed, MKT initially addressed a “quest to uncover how mathematics is used in teaching” (p. 13). However, she argued,

What we need to be talking more clearly about is mathematical knowing and doing inside the mathematical work of teaching. This change from nouns — “knowledge” and “teachers” — to verbs — “knowing and doing” and “teaching” — is not mere rhetorical flourish. These words can support a focus on the dynamics of a revised fundamental question: what is the mathematical work of teaching? (p. 14).

The work of teaching refers to instructional practices and how teachers perceive ongoing interactions to shape these practices. In response to students’ discourse and products, teachers may determine the mathematical validity of multiple approaches, or how and whether task features support students’ mathematical trajectory (National Council of Teachers of Mathematics, 2014; Office for Standards in Education, 2021). Generally, teacher educators may privilege an image of instructional practices where students participate in the creation of mathematics (Österling, 2021). In enacting instructional practices, teachers make sense of the context, see what can be done, and make reasoned judgments for how to respond (Ball, 2017; Blömeke et al., 2022; Österling, 2021).

Hence, in examining MKT and how the field has conceptualized it, we follow the roots of MKT as premised on the work of both mathematics and teaching (e.g., Ball et al., 2008; Thompson and Thompson, 1996). MKT encompasses knowledge and knowing, because it is brought to bear in the practice of teaching.

2.2 A critical distinction between compartmentalized and connected views

To problematize the purposes of frameworks for MKT, as well as the purposes driving efforts made by scholars to validate the accuracy of these proposed frameworks, we differentiate between two views: compartmentalized and connected. By compartmentalized, we refer to orientations toward finding measurable distinctions among uses of theorized domains of MKT. We argue that this view is supported by the ways in which many framework authors and other scholars have presented and used the frameworks.

Consider that frameworks are often represented in graphics as area models in which non-overlapping sets are joined together to make up the whole of MKT. Such graphics epitomize a compartmentalized view. Perhaps the most well-known such representation is the Learning Mathematics for Teaching (LMT) model (see Ball et al., 2008, p. 403). We note that the authors of the representation called careful attention in textual descriptions to what they call the “boundary problem” (p. 403), in which knowledge and knowing domains are often closely coordinated in the work of teaching in ways that make it difficult to discern the precise division between domains. However, the powerful heuristic of the graphical representation by Ball et al. (2008) with its unambiguous divisions, tends to be the reader’s main impression, rather than fuzzy overlap among domains. The representation strongly suggests mutually exclusive categories with clear divisions.

Moreover, the LMT group’s work in the 2000’s sought to empirically validate these divisions as descriptive of teacher performance (Hill et al., 2004), implicitly endorsing the notion that theorization is flawed if theorized constructs cannot be independently measured. Confirmatory factor analysis approaches used in this work, when taken as a means to validate the structure of frameworks, also adhere to a compartmentalized view, taking as given the logic of mapping individual items to subdomains of frameworks. In this line of work, test forms are assembled intended to assess the subdomains distinctly from other components of MKT. Validity studies conducted by the LMT project, Cognitively Activating Instruction (COACTIV; Baumert et al., 2010); Knowledge for Algebra Teaching (KAT; McCrory et al., 2012) and Teacher Education Study in Mathematics (TEDS-M; Tatto et al., 2008), fall into this model. Such approaches, as described in the next section, have not always confirmed theorized divisions.

In contrast to compartmentalized views, a connected view holds that MKT is usefully thought of as having domains that may necessarily overlap in teaching; in other words, that the domains are not distinctly visible in teachers’ use or development of MKT. This view may be implicit in the notion of practice-based item design that underlies many MKT assessments (cf. Forzani, 2014). We discuss the notion of practice-based in more detail in the next section. For now, we note that assessments using practice-based item design generally provide context intended to present a test-taker with a problem of teaching practice, the solving of which may invoke multiple knowledge demands. Under such a view, a failure of factor analyses to confirm a division among theorized subdomains is less fatal to the theory than might be imagined; drawing on multiple domains in complex decision making in the moment need not be taken as evidence that the distinctions between those domains are not theoretically useful or meaningful.

We contend that a connected view is less prominent in scholarship on MKT than a compartmentalized view, though there are some projects aligned with the connected view. For example, Thompson and Thompson (1996) analyzed a case of instruction to illustrate how teachers’ images of mathematics “cuts across the types of knowledge typically embraced by phrases such as content knowledge or pedagogical content knowledge” (p. 19). Scholars working on the Mathematical Understandings for Secondary Teaching (MUST) project identified “perspectives,” rather than domains of knowledge and knowing, and emphasized that these perspectives “are interactive” (Heid et al., 2015, p. 12). The MUST perspectives come closest to a purely knowing perspective, rather than knowledge and knowing.

Hill (2016) argued that assessment design is productively based on domains of teaching practices, rather than domains of possessed knowledge. A number of lines of work resonate with this argument, including Rowland’ (2013) work on the Knowledge Quartet, which uses analyses of classroom instruction to classify teaching practices that leverage mathematical knowledge, Kersting et al. (2012) instrument in which teachers respond to videos, and Thompson’s (2016) framework for teachers’ development of mathematical meaning.

2.3 Searching for a “periodic table” of professional knowledge

In a presidential address to the American Educational Research Association, Shulman (1986) foregrounded the need for a “coherent theoretical framework” for examining professional knowledge and knowing for teaching, including the “domains and categories of content knowledge in the minds of teachers” (p. 9, italics ours). In the two decades since Shulman’s call, multiple groups have responded by developing frameworks that decompose MKT into theorized domains and sought to generate validity evidence to support those frameworks. These efforts have yielded mixed success and largely illustrate a compartmentalized view of knowledge use.

2.3.1 The learning mathematics for teaching (LMT) framework

The Learning Mathematics for Teaching (LMT) group was among the first to respond to Shulman’s call; this group hypothesized and tested a structure they characterized as a “rudimentary periodic table of teacher knowledge” (Ball et al., 2008, p. 396). This “periodic table” included content knowledge and pedagogical knowledge as distinguished by Shulman, and hypothesized further sub-components of each, distinguishing, under the umbrella of content knowledge, common content knowledge from specialized content knowledge; and under the umbrella of pedagogical content knowledge (PCK), knowledge of content and students from knowledge of content and teaching.

In efforts to validate their framework the LMT group developed an assessment instrument. The items in this instrument spanned their theorized components and situated the use of mathematical knowledge in teaching scenarios (Hill et al., 2004). The LMT group conducted a series of studies to determine whether the knowledge and knowing assessed with their instrument in fact was mathematical knowledge used in teaching, and whether the theorized components were measurably distinct from one another (e.g., Schilling and Hill, 2007; Hill et al., 2007; Schilling, 2007).

The LMT’s evaluation of their own work aligns with a compartmentalized view of knowledge use. Although the LMT group found compelling evidence that their instrument did assess mathematical knowledge used in skillful teaching (e.g., Hill et al., 2005), they cited shortcomings of their work to identify distinct domains of MKT, especially subdomains of PCK. Speaking to the results of their factor analyses, Hill et al. (2004) commented, “there remain some significant problems with multidimensionality with these items, particularly in the areas of knowledge of students and content [a component of pedagogical content knowledge] and, for those who choose to use this construct, the specialized knowledge of content” (p. 26). In this way, the knowledge components are “imperfectly discerned” (Hill et al., 2008, p. 385). Due to these issues, the LMT instrument does not distinguish between common content knowledge and specialized content knowledge; and subsequent iterations of their instrument do not contain any items intended to represent PCK (e.g., Hill, 2007). In other words, a compartmentalized view of knowledge, which positions multidimensionality as a problem, led to excluding a type of item on subsequent versions of this assessment. This exclusion happened despite evidence in qualitative studies that these kind of items represented knowledge distinctive to mathematics teaching as compared to knowledge use in other professions using mathematics (Hill et al., 2007).

2.3.2 The cognitively activating instruction (COACTIV) framework

Another group taking up the challenge of differentiating hypothesized components of MKT through assessments is the COACTIV group (Baumert et al., 2010), whose stated goal was to “conceptualize and measure content knowledge and pedagogical content knowledge separately” (p. 142, italics ours). This group examined MKT at the secondary level.

The COACTIV framework is summarized in Baumert and Kunter (2013). Their framework differs from that of the LMT group both in degree of reification and in fundamental definitions. In contrast to the work of the LMT group, COACTIV’s framework focuses on the larger grain size distinctions between content knowledge, PCK, and general pedagogical knowledge, but their definition of PCK includes ideas that the LMT framework would classify under specialized content knowledge.

The COACTIV group, like LMT, interpreted their main result from a compartmentalized view. By comparing data from 181 teachers of 194 secondary mathematics classes, they found that teachers’ scores on the PCK measure predicted 39% of the variance in achievement between classes (with β = 0.42) and impacted teachers’ capacity to design learning opportunities (β = 0.24 for appropriate cognitive level and β = 0.24 for individual learning support), whereas content knowledge assessment results had much lower predictive power (β = 0.32 versus β = 0.42) and had nearly trivial impact on the structure of learning opportunities (β = 0.01 for cognitive level and β = −0.06 for individual learning support) (Baumert et al., 2010). In this way, “in contrast to Hill et al. (2008) the COACTIV group has succeeded in distinguishing [content knowledge] and [pedagogical content knowledge] of secondary mathematics teachers conceptually and empirically” (p. 166).

2.3.3 The knowledge of algebra for teaching (KAT) framework

Another framework for MKT used to design assessment is the KAT framework, developed at Michigan State University (McCrory et al., 2012).

While broadly grounded in the LMT group’s notion of MKT, this framework differs significantly on a number of points. It is limited to algebra, making it a more targeted framework than those that pre-dated it. Its organizing principle is also markedly different, as it divides knowledge into categories delineated by whether a teacher might have been expected to acquire it during their own K-12 schooling, through more advanced university coursework, or through courses oriented toward teacher preparation. While the category titled “algebra for teaching” overlaps with the LMT framework’s construct of “specialized content knowledge” (Ball et al., 2008, p. 390), “algebra for teaching” is defined less by the professional context in which the knowledge is expected to be used and more by the context in which it is to be learned by novice teachers.

This line of work did not produce a larger-scale set of assessments but shared some characteristics with other efforts described here. Most saliently, they were guided by an aim consistent with a compartmentalized view of knowledge use: to identify and describe “distinct factors” of knowledge (Knowledge of Algebra for Teaching [KAT], n.d.). Similar to the results of LMT, subsequent factor analyses did not support the hypothesis that their instrument measured distinct subdomains of knowledge (Howell, 2012).

Teacher Education Study in Mathematics (TEDS-M). The international TEDS-M study also used Shulman’s categories for assessment development. The TEDS-M framework is described in Tatto et al. (2008). Similar to the COACTIV work, this framework draws a high-level distinction between “mathematical content knowledge (MCK)” and “mathematical pedagogical content knowledge (MPCK).” Their framework differs from that of COACTIV and LMT in that it explicitly operationalizes content knowledge with a matrix with curricular areas (e.g., number, geometry) and cognitive domains (knowing, reasoning, and applying). The TEDS-M framework draws directly on the LMT group’s operational definitions for PCK (and to some extent their assessment items), so while the level of reification is more like COACTIV’s, their definitional structure is more like LMT’s. Their definition for MPCK includes “Analyzing or evaluating students’ mathematical solutions” (p. 45).

There are two main ways in which the TEDS-M exemplify a compartmentalized view. First, validation efforts took the distinction between MCK and MPCK as a starting point. Expert reviews at the item level evaluated the “clarity and the extent to which it was consistent with its classification” within their framework (Tatto et al., 2012, p. 131). Second, the results of prospective teachers’ MCK and MPCK are reported separately, without any comparison or inferred relationships among the two (Tatto et al., 2012). There are no statistical results reported to confirm or disconfirm the distinction between content knowledge and PCK.

2.3.4 Teacher education study in mathematics (TEDS-M)

The international TEDS-M study also used Shulman’s categories for assessment development. The TEDS-M framework is described in Tatto et al. (2008). Similar to the COACTIV work, this framework draws a high-level distinction between “mathematical content knowledge (MCK)” and “mathematical pedagogical content knowledge (MPCK).” Their framework differs from that of COACTIV and LMT in that it explicitly operationalizes content knowledge with a matrix with curricular areas (e.g., number, geometry) and cognitive domains (knowing, reasoning, and applying). The TEDS-M framework draws directly on the LMT group’s operational definitions for PCK (and to some extent their assessment items), so while the level of reification is more like COACTIV’s, their definitional structure is more like LMT’s. Their definition for MPCK includes “Analyzing or evaluating students’ mathematical solutions” (p. 45).

2.3.5 The mathematical understandings for secondary teaching (MUST) framework

In contrast to the work already described, the MUST project embraced the potential interaction among aspects of knowledge for teaching. Moreover, they recognized that this stance differentiated their work from prior efforts to conceptualize MKT. As Heid et al. (2015) noted, “rather than seeking primarily to identify the knowledge and specific understandings of mathematics useful in secondary teaching,” the MUST project chose instead to “highlight the dynamic nature of secondary teachers’ mathematical understandings” (p. 5).

The three perspectives described in the MUST framework are mathematical proficiency, mathematical activity, and mathematical context of teaching. Mathematical proficiency describes understandings and orientations that students need in their grade and beyond, such as conceptual understanding, procedural fluency, and productive disposition. Mathematical activity describes actions of “doing mathematics,” such as noticing mathematical structure and generalizing mathematical findings. Mathematical context of teaching enables teachers to use and develop their personal mathematical knowledge and knowing to help advance students’ mathematical understandings. This perspective involves accessing and understanding the mathematical thinking of learners, knowing and using the curriculum, and reflecting on the mathematics of teaching practice.

The MUST project exemplifies a connected view in their approach to describing mathematical knowledge for teaching. While they identify theoretically different aspects of mathematical knowledge for teaching that “together form a robust picture of the mathematics required of a teacher of secondary mathematics,” they do not shy away from the idea that “the three perspectives of MUST are interactive” (Heid et al., 2015, p. 12). Their examples of knowing and using mathematics use consistently encompass all three perspectives. Their examples of using the framework to design formative assessments leverage all three perspectives, and they do not attempt to differentiate the contributions from each perspective.

2.4 MKT frameworks, practice-based teacher education, and assessment

The development of the above frameworks coincided with a widespread focus in the field on practice-based teacher education (Forzani, 2014; McDonald et al., 2013): the idea that teacher learning should be focused on the instructional practices that teachers will be engaged in. Instructional practices are a form of engagement rather than a form of propositional knowledge (Sykes and Wilson, 2015). Hence, from this perspective, teacher education should be organized to provide opportunities for teachers to learn instructional practices and that those opportunities should be embedded earlier and more frequently than may have been the case in prior decades. For example, Grossman et al.’s (2009) seminal work on pedagogies of practice delineates different ways of engaging teachers around practice during teacher preparation. An associated focus on core instructional practices (Forzani, 2014; Core Practices Consortium, n.d.) sought during these years to identify the instructional practices most worthy of focus, often relying on factors such as how commonly a practice is used or how likely its fluent use is to impact student learning.

The theory also informed assessment item design, with the LMT group and those following their model focusing strongly on the use of practice-based items: those that use scenarios to engage the participant in a sample of an instructional practice, such as analyzing student work, or selecting an example (Hill et al., 2004). These groups followed the underlying logic that responding to mathematical prompts in the context of instruction is more likely to elicit knowledge use specialized to teaching (Gitomer et al., 2014). In the years since, these approaches have become the standard for assessing MKT. For example, the Praxis CKT assessments, now administered across multiple subjects and grade spans for teacher certification are organized with items focused on instructional practices (ETS, n.d.) and most research-based instruments that measure MKT use this item design to some extent.

2.5 Framework purposes, and impacts, and critiques

Shulman’s (1986) call to map the domains of knowledge for teaching were grounded in a concern for the professionalization of teachers. The resulting conversation around MKT and its components has played an important role in shifting the discourse around mathematical requirements for teacher education from simply more math to identifying and developing mathematical knowledge and knowing that is distinctively used in teaching (e.g., Conference Board of the Mathematical Sciences, 2001, 2012; Association of Mathematics Teacher Educators, 2017).

Alongside this evolution, the use of frameworks has shifted away from defending the existence of professional knowledge and knowing toward using them as an intellectual resource for the work of teacher education. Frameworks for MKT are now used to design assessments (e.g., Herbst and Kosko, 2012; Tatto et al., 2008), including some high-stakes tests (ETS, n.d.), clarify the nature and development of MKT (e.g., Baumert et al., 2010; Bair and Rich, 2011; Beswick et al., 2012), and facilitate teacher education and professional development (e.g., Elliott et al., 2009; Heid et al., 2015; Rowland, 2013).

However, some researchers who used instruments designed from a compartmentalized view have suggested that a connected view of MKT use may better support productive inquiry. For example, Beswick et al.’s (2012) factor analysis of knowledge and belief assessment results from 62 middle-school teachers found that one construct fit the data better than multiple constructs. They concluded, “analysing and categorizing their knowledge, although useful in many respects, risks losing an appreciation of the complexity of the work of teaching mathematics and may never be possible with complete clarity” (p. 154). Although they were not the first to provide evidence that assessments of MKT may suggest only a single underlying construct, they went farther than previous scholars by arguing explicitly that the assessment of MKT as a single uni-dimensional construct may be more fruitful than focusing on domain distinctions. Similarly, Copur-Gencturk et al. (2019)’s study of upper elementary teachers concluded that MKT as measured by the assessment was best conceptualized as unidimensional and suggested that more work is needed to disentangle the extent to which this reflects the underlying construct rather than item design. And while we know from other work that seamless extension of the underlying frameworks from elementary to secondary teaching cannot necessarily be assumed (Speer et al., 2015), we believe that the underlying question raised by this analysis is as worth asking for secondary teachers as for elementary teachers. The COACTIV group also concluded that content knowledge influences the development of pedagogical content knowledge (Kleickmann et al., 2013) suggesting an underlying connection not quite aligned to their assessment framework. These scholars concluded that a connected view could benefit research into comparing teachers’ MKT with student outcomes, as well as assessing the effectiveness of professional development.

Other scholars have called into question the utility of decompositions of MKT, particularly outside of the assessment domain. As Silverman and Thompson (2008) argued, even if MKT were composed of independent knowledge bases, MKT is more than the union of its parts. Moreover, decompositions of MKT, especially those that focus even in part on declarative knowledge, may obscure underlying practices of teaching and learning that are critical to MKT use and its development (Heid et al., 2015; Rowland, 2013; Silverman and Thompson, 2008; Thompson, 2016; Watson, 2008). Rocha (2025) contrasts two epistemological perspectives on MKT, notes that more static views of knowledge such as those represented in the above frameworks are fundamentally different from views that approach teacher knowledge from the perspective of development. They argue that these differences must be better understood for the field to move forward productively and note in particular the inadequacy of static views in supporting teacher education. Other scholars, similarly critiquing extant frameworks, seek to reify them further, adding different perspectives (e.g., Pansell, 2023). From this perspective, it is unsurprising that scholars take a connected view of knowledge use or seek to design entirely different frameworks when their purpose is facilitating experiences in teacher education and professional development (e.g., Heid et al., 2015; Rowland, 2013).

In summary, the purposes of framework development may explain whether scholars take a compartmentalized or connected view of knowledge use. Inquiry from a compartmentalized view focuses on identifying empirically distinguishable domains, and success is evaluated by evidence for differentiating domains. A connected view may better support inquiry into teachers’ development of MKT along their professional trajectory, because it avoids delineation problems and embraces the inherent overlap in knowledge use. Finally, considering evidence from research initially designed with a compartmentalized view of knowledge use, there may be a role for a connected view of knowledge use even for assessment purposes. And while the field largely persists in holding compartmentalized views of MKT and organizing around those views, there is some emergent evidence, both empirical and theoretical, calling into question the dominance of that view, which served to motivate the present study.

3 Materials and methods

We turn now to an empirical study that we use to illustrate the ways in which MKT, as represented in assessment items, may align more with a connected than compartmentalized view. Our study takes a novel approach to the issue of whether subdomains are distinguishable. Rather than asking how many factors there are, or whether there are distinguishable factors, we instead ask:

• (RQ1) In what compartmentalized or connected ways do practice-based items elicit evidence of MKT?

• (RQ2) How does connectedness or compartmentalization appear to differ or be similar when viewing MKT through different frameworks proposed for MKT?

While the study produces findings with respect to the studied items, our purpose in presenting this empirical work is less to draw strong conclusions about the items and more to use the exercise of applying frameworks to a common set of items as a lens for exploring the implications of framework choice. In doing so, we hope to raise critical questions about what each framework and the set of frameworks taken together make less or more visible about the nature of MKT.

We begin with an example item from the study, shown in Figure 1, in order to familiarize the reader with the item type and to make more salient the thinking that provoked the study. Then we discuss methods used, item and framework selection, and our coding process. Following this, we discuss results and implications.

FIGURE 1

During a lesson on writing equations of linear functions from tables, students find a linear equation from a table of values: x = 1, 2, 3, 4 and y = 6, 11, 16, 21. Students A and B provide explanations. Student A explains using changes in x and y to find the slope and y-intercept, concluding with the equation y = 5x + 1. Student B observes consistent changes in y to determine the slope and calculates the y-intercept, also concluding with y = 5x + 1. The task is to evaluate whether each explanation is mathematically valid.

Figure 1. The Morgan item. Note that for brevity a third student’s work sample is omitted and the item format adjusted. Item copyright @2013 Educational Testing Service, publicly released item.

3.1 A framing example

The Morgan item, like those produced by multiple projects cited previously, is scenario-based, placing the test-taker in Ms. Morgan’s shoes in asking for an evaluation of work her students have produced. This item represents typical classroom interaction on multiple levels. These students have been asked to find an equation that fits a set of bivariate data, a type of content problem ubiquitous to algebra curricula. Every day, teachers attend to and interpret student work. The intended answers are that Student A’s work demonstrates a mathematically valid approach and Student B’s work does not. Of course, it is difficult to interpret Student B’s work in the absence of information of what Student B might do when the x-values change by values other than + 1. In the context of actual instruction, we would expect a skilled teacher to ask follow up questions to better inform their understanding of this student’s thinking. In the context of the assessment item, we simply hope that a teacher notes that the given evidence leaves it unclear whether Student B’s work shows evidence of understanding the role of the change in x.

We hypothesize a teacher responding to this item needs to proceed through a series of reasoned steps, including recognizing, making sense of, and noting any mathematically relevant features of the student level task, making sense of the student explanations, inferring from the explanation a generalized method for each student, and deciding whether the method as inferred relies on a systematic and sufficiently generalizable logic.

However, this is simply a hypothesis, and as such raises questions about what reasoning teachers might use in responding to such an item and what the implications might be for claims about what the item measures. For example, a teacher who attends strongly to the student-level mathematics might solve the student-level problem. In doing so, this teacher might notice that it is necessary to account for the changes in x-values, that consecutive changes are always 1 in the given table, and that differences need not be always 1. These observations might prime the teacher to note the key difference between the two students’ approaches: Student A does explicitly account for differences in x-values, and Student B does not. A second teacher, familiar with student thinking, might recognize the approach that student B takes as a common student conception. A third teacher might be able to infer the issue from the explanations given by the students and recognize that Student B’s reasoning might not generalize.

It is precisely the deep contextualized reasoning that is required that makes items like this one elicit evidence of MKT. But does this mean that this item assesses student-level mathematics for the first test-taker, knowledge of student error patterns for the second, and interpretative skill for the third? If so, has it somehow failed as an assessment item by not drawing out evidence of precisely one MKT sub-domain? And what are we to make of a test-taker who takes some of each of these actions and draws on various domains in a connected and fluid way?

3.2 Research design

As a foundation to our study, we observe that the literature suggests two reasons that practice-based item design may be incompatible with a compartmentalized view. First, different domains may be applied to draw similar conclusions (e.g., Lai and Jacobson, 2018), and second, facility in one domain may be dependent on facility in others (e.g., Baumert et al., 2010). We also note that this incompatibility, while evinced by results of the literature, is also not well-understood. To examine this phenomenon, we do a version of a comparative case study (Yin, 2009), in which the cases are items and accompanying idealized response patterns, where the items exemplify practice-based item design, and the object is to explore and explain how such items draw on multiple theorized subdomains. We now summarize the steps of this case study.

Before addressing the main research questions directly, we first sought to evaluate the empirical accuracy of the cases, guided by the question:

• (RQ0) Do teachers’ responses to each item align or not align with the idealized response patterns for that item?

We introduce this research question here and not previously, because addressing this research question is not the main focus of our study. However, it was a prerequisite to addressing the main research questions, hence numbering it as “RQ0.”

To address the main research questions, we selected a set of frameworks for MKT to examine, and we operationalized the identification of each component of each framework in a description of elicited MKT. To address our RQ1 (In what compartmentalized or connected ways do practice-based items elicit evidence of MKT?), we identified the components of each framework elicited by enacting the idealized response patterns to the components of each framework elicited by enacting the idealized response patterns to that item.

To address RQ2 (How does connectedness or compartmentalization appear to differ or be similar when viewing MKT through different frameworks proposed for MKT?), we compared component identification across items and across frameworks.

Our design is illustrated in Figure 2.

FIGURE 2

Flowchart describing a process for selecting MKT assessment items across frameworks. Steps include item selection as a comparison point, analyzing response patterns, identifying components from frameworks, and comparing component identification. Each step is linked with arrows and labeled with research questions such as RQ0, RQ1, and RQ2.

Figure 2. Study design: relationship between methods to address each research question.

3.3 Item selection and rationale

We selected a set of nine practiced-based items designed to elicit MKT, including the Morgan item. Items were paired with idealized response patterns (IRPs), idealized descriptions of typical correct responses to items as a proxy for actual responses; and our RQ0 guides a separate analysis to confirm the adequacy of the proxies. We call these descriptions patterns rather than pattern because IRPs can account for multiple possible responses to the item. We now discuss the selection of items and their associated data as cases (Yin, 2009).

The items used in this study and their idealized response patterns were developed as part of a systematic effort to extend practice-based item design principles to upper-secondary content areas and had undergone extensive expert review prior to the start of the present analysis (Howell et al., 2013b). We selected these nine items from a pool of 51 items designed to assess MKT at the secondary level. This item pool contained items in the areas of linear, quadratic, and exponential expressions and functions, content topics originally chosen to represent broadly the most critical components of a typical algebraically focused secondary curriculum. Among the nine items, eight were closed-ended items (e.g., Morgan, which asks the teacher to evaluate whether each of Student A’s and Student B’s responses demonstrates a mathematically valid approach), one (Swain) was open-ended. Two of the eight closed-ended items were testlets (e.g., Morgan) with multiple subparts (e.g., Morgan Student A, Morgan Student B). An advisory panel consisting of three external experts in secondary mathematics education reviewed potential sets of items for use in this study as well as pilot interview transcripts with teachers about the items. Based on their recommendations, we narrowed our selection to three items in each topic area, with attention to maintaining diversity among item types, content areas, and representation, and to selecting items with no previously identified design flaws. The list of selected items and descriptions is provided in Supplementary Appendix B. By selecting a variety of MKT assessment items, we create a common comparison point across multiple MKT frameworks. We anticipated that the diversity of item types would provide the potential to exemplify components of different frameworks for MKT.

3.4 Evaluating the accuracy of idealized response patterns: analysis for RQ0

We describe here the method we used to evaluate the accuracy of the idealized response patterns (IRPs). Because we wished to treat these descriptions as representing typical correct responses, a preliminary step was to evaluate empirical evidence for support or lack of alignment of IRP to teachers’ actual responses. We operationalized the IRPs by identifying essential elements of the reasoning represented by each IRP, resulting in 3–5 elements per IRP. We compared the operationalized IRPs to responses from think-aloud interviews of secondary teachers across the items. Figure 3 shows an IRP, operationalization, and sample teacher reasoning for Morgan Student B.

FIGURE 3

A three-column table titled “IRP,” “Operationalization,” and “Sample teacher reasoning.” The IRP column critiques a student’s approach to identifying changes in a linear function, noting a lack of evidence and clarity regarding changes in x and y. The Operationalization column defines specific abilities like determining rate of change, writing equations from tables, evaluating explanations, and constructing mathematically valid methods. The Sample teacher reasoning column contains excerpts from teachers explaining these concepts, emphasizing the need for understanding both x and y changes and the risks of overgeneralization.

Figure 3. Idealized response patterns (IRP), operationalization, and sample teacher reasoning for Morgan student B.

We compared IRPs to reasoning in 171 responses from 23 teachers, whose years of experience ranged from student teaching to 16 years of experience, with a median of 5 years and average of 5.7 years. Participants were recruited via email lists to alumni of two teaching programs, one in a metropolitan area and one in a suburban area. All teachers who expressed interest in participating were selected to participate.

We used block assignment so that each participant responded to a subset of approximately six items, with each item collecting between 13 and 15 participants’ reasoning. When an item was a testlet (e.g., Morgan), we counted each subpart as a distinct response (e.g., assessing Student A’s response and assessing Student B’s response are separate), resulting in 171 responses.

We coded each teacher’s response against the IRP for that item in two ways. First, we coded each response as aligning or not aligning to the reasoning in the IRPs. Responses were coded as aligning with the IRPs if the response represented all essential elements of IRPs (allowing for some degree of variation in the exact wording participants used). Second, we coded the interviewee’s answer as aligning or not aligning to the item’s intended answer (e.g., he the response “Student B does not demonstrate enough evidence for a mathematically valid approach” was coded as aligning).

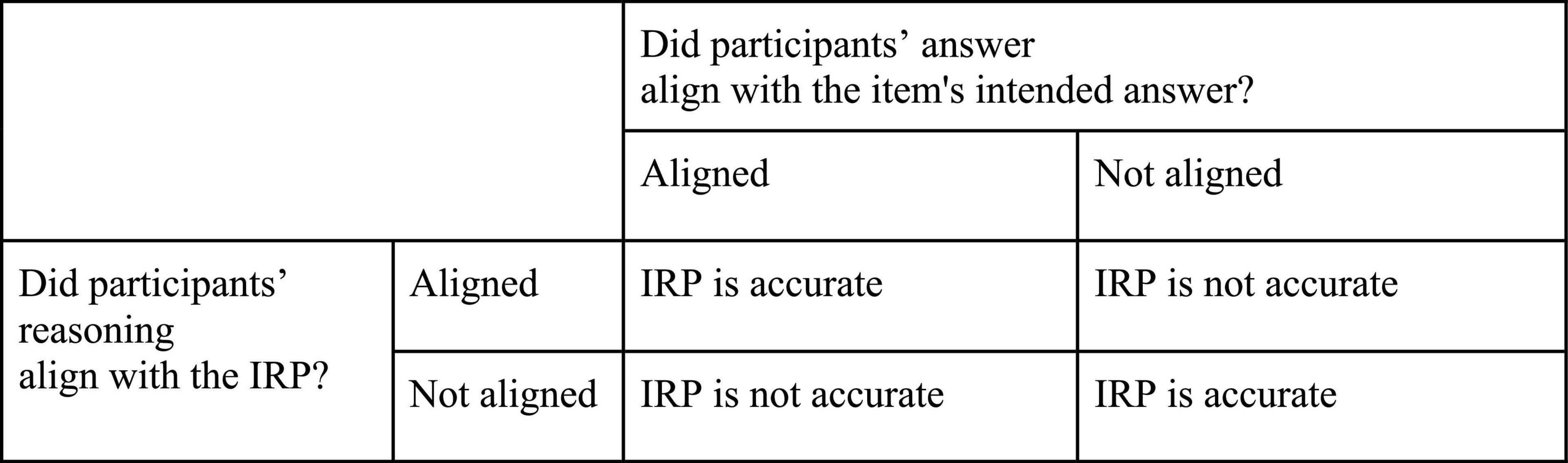
The purpose of this coding was to account for whether the presence of what we hypothesized as essential elements of the IRPs actually led to items’ intended answers and whether absence of at least one essential element of the IRPs would lead to unaligned answers. Note that this coding is binary (aligned or did not align with IRP reasoning, aligned or did not align with item’s intended answer) precisely because we are examining the accuracy of IRPs (whether they describe teachers’ reasoning in empirical data).

For each participant’s response, four possibilities result, as shown in Figure 4. We interpret the item/IRP pair as accurate when intended answers result from the presence of all proposed essential elements of the IRP and unintended answers result from the absence of even one proposed essential element. We interpret the item/IRP pair to be inaccurate otherwise. In other words, a not accurate code represents false positives or false negatives.

FIGURE 4

Table evaluating alignment between participants’ reasoning and answers with IRP (interpretive reasoning process) accuracy. Rows assess reasoning alignment: “Aligned” and “Not aligned.” Columns assess answer alignment: “Aligned” and “Not aligned.” Cells indicate IRP accuracy: “IRP is accurate” or “IRP is not accurate.”

Figure 4. Coding logic for addressing RQ0.

We then computed the percentage of accurate codes across responses per item. Certainly having 100% accurate codes is most desirable, but the possibility of reaching a correct answer with flawed reasoning by guessing is simply a reality in any selected response item format, making it unlikely that the number of false positive responses would ever approach zero. To gauge whether the percentage of accurate codes was reasonable, we compared the distribution and percentage of accurate codes to the findings of a prior study that utilized a similar methodology and was conducted in elementary-level mathematics and English Language Arts (Howell et al., 2013a). We took the results of that study as a reasonable estimate of results that could be expected for such measures.

As discussed below, our findings suggest that the accuracy of the IRPs was sufficient for study purposes. We mention this result now so that the reader can assume the accuracy of the IRPs in reading the remainder of this methods section, where we address framework selection and describe coding processes.

3.5 Analysis for RQ1 and RQ2

To address RQ1, we use IRPs to examine whether practice-based items elicit evidence of MKT in connected or compartmentalized ways. We consider an item to elicit evidence of MKT in a connected way if its IRP requires the coordination of multiple domains in a particular framework. For instance, consider the IRP for the Morgan item (Figure 3) and the TEDS-M definitions of mathematical content knowledge (MCK) and mathematical pedagogical content knowledge (MPCK). We see B1 and B2 as eliciting MCK, because they are about applying the definition of slope and intercept to a table. We also see B3 as MCK, because it is about reasoning. We consider B4 to elicit MPCK because one component of MPCK is “Analyzing or evaluating students’ mathematical solutions or arguments” (p. 45). The Morgan IRP then elicits MKT in a connected way when using the TEDS-M framework, because both MCK and MPCK were needed to reason through the item. However, just because one item elicits MKT in a connected way by one framework does not mean that practice-based items in general do so. Hence, we examine our sample of practice-based items relative to multiple frameworks, and to address RQ2, we compare how connectedness and compartmentalization appear to differ or be similar when viewing MKT through different frameworks. We now discuss how we selected frameworks for this analysis.

3.5.1 Framework selection

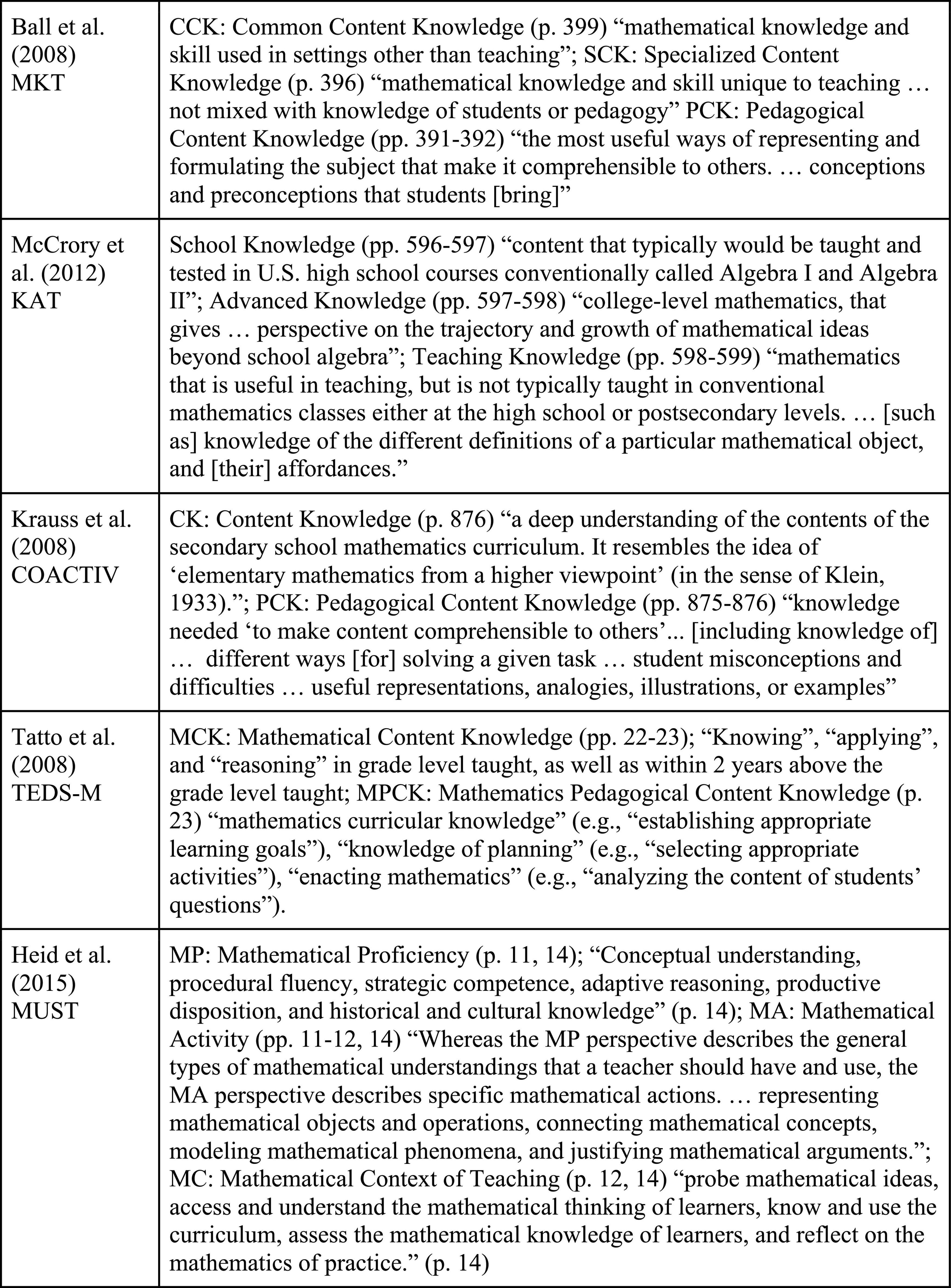
We sought theoretical frameworks for MKT that were fully developed in available documents, and that directly claimed to describe the entire MKT construct. We performed searches for literature on MKT in various databases, including the VM²ED repository (Krupa et al., 2024). Ultimately, we considered five theoretical frameworks for MKT: Ball et al. (2008) MKT framework; KAT (McCrory et al., 2012); COACTIV (Krauss et al., 2008); TEDS-M (Tatto et al., 2008); and MUST (Heid et al., 2015). We did not restrict framework selection to those explicitly designed to describe secondary level MKT but did exclude those that could not reasonably be taken to describe the MKT measured in our item set. For example, we excluded the GAST (Mohr-Schroeder et al., 2017) and DTMR (Izsák et al., 2019) frameworks because our item set did not include geometry items or focus on fraction arithmetic.

Each examined framework proposed 2–3 subdomains, as summarized in Figure 5 and with additional description of sources in Supplementary Appendix A. The frameworks generally delineate “purely” mathematical knowledge and its use from amalgams of mathematical and pedagogical knowledge and its use. However, interpretations differed across the frameworks. These variations seemed amenable to our design: if, even across frameworks that sliced MKT differently, we generally found that IRPs were not isolated in any domain, this supports the argument for a connected rather than compartmentalized view of MKT. On the other hand, if IRPs could be cleanly placed into single subdomains, then this would lend support to a compartmentalized view of MKT.

FIGURE 5

A table compares various studies on mathematical knowledge for teaching. It includes the researchers’ names, publication years, and key concepts. The studies focus on different types of mathematical knowledge, such as common, specialized, and pedagogical content knowledge, as well as mathematical proficiency and teaching context. Each entry provides descriptions and page numbers for further reference, highlighting how mathematics education is conceptualized and the skills emphasized in each framework.

Figure 5. Proposed subdomains of MKT in examined frameworks.

3.5.2 Operational descriptions of framework component

To develop a usable set of codes that could be applied to our IRPs for each framework, our first step was to extract operational definitions of key subdomain. We did so using seminal documents listed in Figure 5 by quoting descriptions directly from the source. We added clarifications throughout the coding process where authors’ original language in the source document or other reports was insufficient to inform coding decisions. For instance, we operationalized “conventional mathematics classes” (from KAT) to mean courses taught by mathematics departments that do not primarily enroll teachers.

We note here that early in this process we were faced with the need to make a choice about coding subdomains of pedagogical content knowledge (PCK). Several frameworks included a domain with the phrase “pedagogical content knowledge,” making explicit reference to Shulman’s (1986) definition of the term, but two of these frameworks (COACTIV and TEDS-M) elected not to differentiate subdomains of PCK in their assessment design. While the Ball et al. (2008) framework does define subdomains of PCK, and at least one study describes efforts to assess one of those subdomains directly (Hill et al., 2008), most assessment efforts based on this framework have focused on differentiating between common and specialized knowledge, with less focus overall on measuring PCK and its subdomains. Given these considerations, we elected not to code subdomains of PCK.

3.5.3 Coding

Once an initial code list was developed from seminal documents of each framework, researchers coded essential elements of the item’s IRP for the domain(s) of the framework that the piece represented. To do so, we assessed to what degree an IRP element was an instance of each domain of each framework, keeping open the possibility that an IRP element may not correspond to any domain of a framework, or that it may correspond to multiple elements. For instance, when considering the COACTIV framework, we coded B4 in the Morgan IRP (Figure 3) to be both CK and PCK, because the notion of mathematical generalization is consistent with mathematics from a higher standpoint (CK) and B4 concerns student misconceptions (PCK); and we coded B1 and B2 to not correspond to CK or PCK, because they are not about working with students or tasks, and applying a standard procedure to a standard task does not constitute deep knowledge of the secondary curriculum.

A codebook was created and used in order to maintain adequate rigor (MacQueen et al., 1998; Saldaña, 2012), and, following Creswell’s (2009) suggestion to document as many analysis steps as possible, the coding sheet included a note section for the coders to keep a record of their reasoning for assigning certain codes to an item, any questions they had, the decisions made, and additional observations worthy of attention.

Coding was done independently, with two coders per item, and a third coder brought in to arbitrate discrepancies as needed. At least one author coded each item. Two colleagues familiar with research on MKT served as additional coders as needed. Inter-rater reliabilities between the pairs of initially assigned raters were calculated as simple percent agreement and were generally adequate, ranging from 0.69 to 0.97, but our goal in this coding was less to establish reliability in coding and more to produce a consensus around accurate final coding. Because we drew on codes extracted from the selected frameworks, we were limited in how far we could develop our code list without compromising fidelity to each framework’s authors’ intentions. Given this, the inter-rater reliability in this study may reflect more than anything else the degree to which each framework’s provided definitions were specified in ways that made them amenable to use as codes.

What is more salient to our study is the intercoder agreement, a term introduced by Creswell (2009) to represent the final agreement among researchers after reconciling discrepancies in initial coding. Gibbs (2007) suggested that researchers can minimize bias by first individually coding the same set of data using the same codes and then discussing the results of the coding with a goal of reaching a common agreement about the meaning and application of each code. Following this method, we were able to reach consensus on the final code application. We then counted, for each item under each framework, the number of domains of that framework represented in the IRP for that item, to represent quantitatively the number of compartments that item could be taken to measure under the given framework.

4 Results

4.1 Analysis of idealized response patterns: results for RQ0

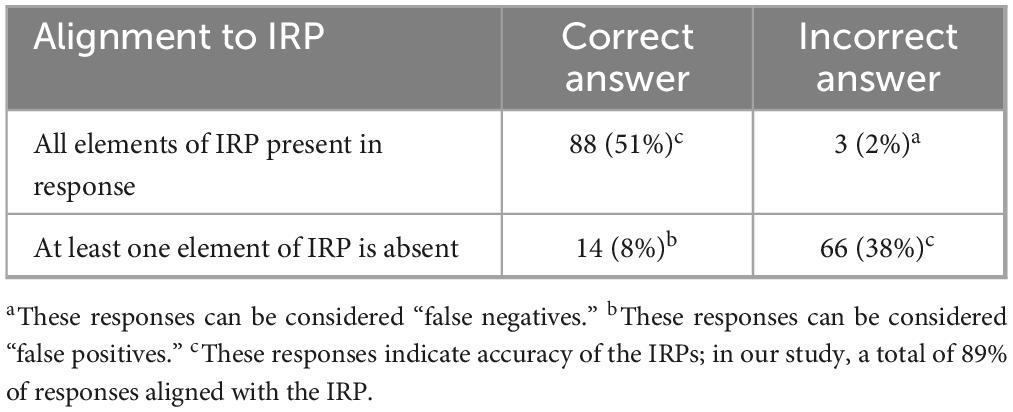
Results from the analysis of IRP accuracy are shown in Table 1. Our results indicate that the idealized response pattern is supported in most cases, with 89% of responses falling on diagonal (We note that all responses to the Morgan item were on diagonal; all participants but one selected “Student B does not demonstrate a mathematically valid approach,” and these participants all note that there was lack of evidence of Student B’s attending to change in x; the one participant that selected “Student B demonstrates a mathematically valid approach” did not mention anything about Student B’s attention to change in x.).

TABLE 1

Table 1. Alignment between ideal response patterns (IRPs) and selected answers.

As for comparison to prior studies (Howell et al., 2013a), we noted that the on-diagonal percentage (89%) compared favorably to those found in similar studies of elementary mathematics (88%) and elementary level English Language Arts (90%). We interpret this result as providing evidence that the IRPs can be taken as a proxy for the teacher reasoning drawn on in responding correctly to the items analyzed in this study.

4.2 Number of domains assessed by framework and item: results for RQ1 and RQ2

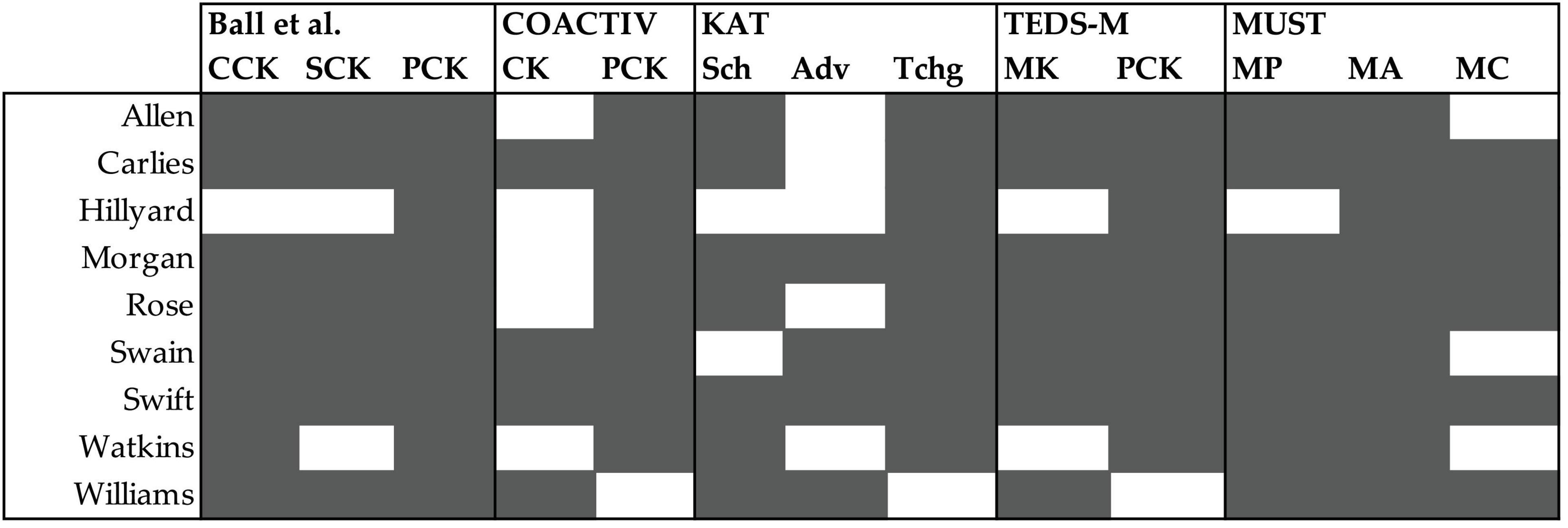
Table 2 shows the number of domains of each framework assessed by each of the nine items, with Figure 6 specifying the specific domains. There was some variation in the degree to which individual item elicited evidence of multiple domains. The Hillyard item represented one extreme, eliciting evidence of a single subdomain (PCK) under four of the five frameworks, and evidence of multiple subdomains under only one, the MUST framework (Heid et al., 2015), where it was coded as eliciting evidence of both mathematical activity and mathematical context. By way of contrast, the Morgan item elicited evidence of multiple subdomains under all five frameworks, indicating that it may elicit evidence of a blend of domains regardless of which framework is selected. Variation by framework was less pronounced, with all frameworks except COACTIV showing all available domains coded to a significant subset of the items; we note that the COACTIV framework only contained two domains. All frameworks were represented across all items and all items elicited something from each framework, confirming, as expected, that the frameworks were reasonable ways to describe the MKT elicited across the set of items.

TABLE 2

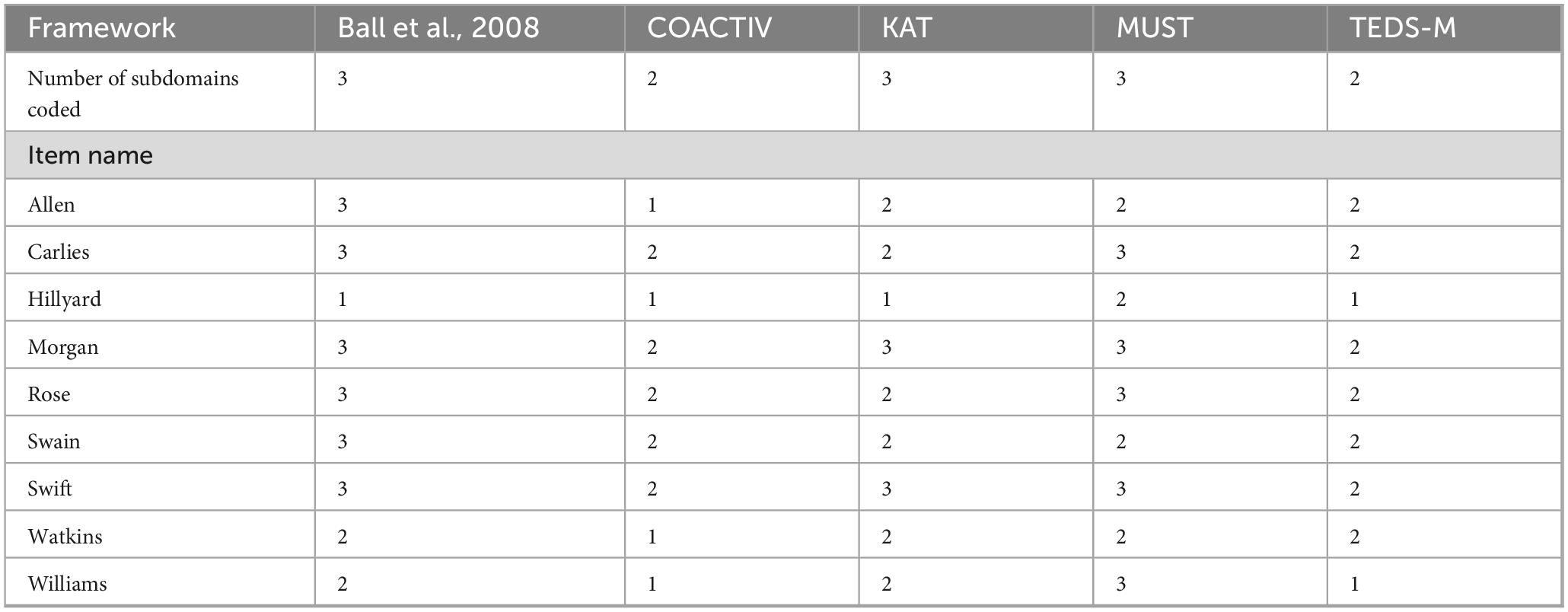
Table 2. Number of subdomains measured by item by framework, with frameworks and item listed in alphabetical order.

FIGURE 6

Comparison chart of various educational studies and assessments, including Ball et al., COACTIV, KAT, TEDS-M, and MUST. Columns represent different knowledge types like CCK, SCK, PCK, CK, MK, MA, with rows listing researchers’ names: Allen, Carlies, Hillyard, etc. White blocks indicate intersections where specific knowledge components are linked to each study or researcher.

Figure 6. Subdomains captured by IRPs.

5 Discussion

5.1 Discussion of findings

In the first portion of the paper, we advanced an argument that the reification of MKT in frameworks has led to the field’s adoption of a compartmentalized view of MKT, with a potentially disproportionate representation in the literature of studies focused on defining, measuring, and defending a given decomposition of the whole. We complemented that argument with a description of a two-part study of MKT items. In the first part of this study, we compared hypothesized idealized response patterns to teachers’ interview responses to those items. We found that these idealized response patterns do represent teachers’ actual reasoning. In the second part of this study, we used these idealized response patterns to code each item for the domains measured using five different frameworks for MKT. Our results illustrate that reasoning for most items, as represented by the idealized response patterns, rely on multiple elements of domains of multiple frameworks, suggesting that for most items, knowledge is used in connected ways. Additionally, as a set, these items did not measure domains of any of these frameworks distinctly, suggesting that sets of items are insufficient to distinguish among components that are theorized to be important.

One explanation for our results is that this set of items was designed to capture MKT by following a practice-based item design theory. From a practice-based perspective, what makes an assessment task effective in measuring MKT is how closely it represents the work of teaching and, hence, the item is considered successful based on how well it represents “the actual practices we hope teachers will successfully master, rather than the more slippery notion of the kinds of knowledge teachers should possess” (Hill, 2016, p. 5). And because these tasks of teaching are designed to approximate the work of teaching, it stands to reason that, like teaching, a strong assessment item might call on multiple types of knowledge use and ask the test taker to coordinate them in application to the work of teaching. Because the set of items we examined were designed to be practice-based, we cannot claim that our findings are likely to generalize to assessment items that follow a different design. However, as Hill (2016) points out, many current assessments (and all of those explicitly based on the frameworks we examined) follow some degree of this practice-based design in which an item focuses on engaging the test taker in key tasks of teaching mathematics. This suggests that the findings may generalize, at least in part, to many current MKT assessment efforts.

Overall, a potential interpretation of our results is that these frameworks, each designed with different and particular intent and potentially useful with respect to that purpose, may not be useful for distinguishing measurable subdomains of MKT. Our study illustrates that the tendency for practice-based items to capture multiple subdomains is a common issue across frameworks and perhaps one that is a necessary result of practice-based item design. To some degree this is a divide between approaches to theory and approaches to assessment. If one takes a compartmentalized view of an MKT framework, assuming that subdomains must be distinctly measurable in isolation from the larger construct to establish the value of the theory, this result could be viewed as problematic, or as refuting the theory. We also note that there are various measurement techniques that to our knowledge have not been applied to the study of MKT, that may give estimates for subdomain knowledge even when multiple subdomains are drawn upon (e.g., Tatsuoka, 1983, Copur-Gencturk et al., 2019). We hold, however, that identification of distinctly measurable subdomains, or estimation of knowledge of such subdomains, is not the only or even the most desirable purpose of theory; a theorized subdomain need not be distinctly measurable in isolation from the larger construct to be useful in informing the field’s thinking, designing policy, or as a heuristic for organizing teacher supports. Our analysis adds depth to previous arguments for the utility of a connected view of MKT (e.g., Beswick et al., 2012; Watson, 2008) by directly demonstrating the co-occurrence of theorized subdomains, and by showing that it occurs across multiple frameworks used in the field and is not simply an attribute of one of them.

An alternate interpretation of the same results might point to the finding as a weakness of practice-based item design, in that MKT items written to this design, even if found to be reasonable measures of MKT writ large, may not be a productive method for the assessment of more refined components. We caution, however, that while this may be a reasonable critique, practice-based items have a long and established place in the literature and a stronger evidentiary base to date than other approaches to measuring MKT, so it would be unwise to dismiss them on this basis. There is clear evidence that assessments written to this model are measuring MKT, which represents remarkable progress made over several decades of research and development work. We would prefer to foreground in this conversation the need to decide, given a particular assessment use case, whether it is necessary or desirable to measure subdomains of MKT in isolation, or whether a general measure of MKT suffices.

5.2 Limitations

We caution here against potential overgeneralizations of our results, which we would characterize as more illustrative than generalizable. The set of items analyzed is small, and while we intentionally selected items to represent strong examples of practice-based item design theory for which we had evidence of success in capturing MKT, our observations may not generalize to all practice-based items and almost certainly do not generalize to differently designed assessment items. That a practice-based approach is prevalent in the field provides some evidence that it is a fruitful design method, but other approaches may emerge that are equally able to measure MKT and better able to capture its domains, or more careful domain analysis and framework development might produce a set of distinctions in knowledge and knowing that can be measured in clear isolation from one another.

We also note a variability across the cases analyzed, calling attention to the two cases that seemed to measure distinct domains best: the Hillyard item, which was coded as measuring only one domain under most frameworks, and the Williams item, which was coded as measuring only one domain under three frameworks. These cases illustrate that is clearly possible, even within the set of items we analyzed, for an item to measure a single subdomain under a framework. In fact, the results for the Hillyard item, which were coded with the single domain of PCK in all frameworks with a PCK component, corroborates the suggestion of Lai and Jacobson (2018) that it may be possible to write a pure PCK item when the reasoning requires pedagogical warrant. It is not our claim that practice-based items measure multiple subdomains, with no exception. We simply note that measuring isolated subdomains does not appear to be a typical pattern.

We also note that the critique of frameworks on the basis of our numerical results is inappropriate given the purpose and method of the coding. Frameworks did not have equal numbers of categories to begin with, and our coding decisions may have exaggerated these differences or obscured them. Some frameworks afforded clearer coding decisions than others, but none were designed with this type of coding in mind, and many of the authors of the frameworks acknowledge some ambiguity in the boundary cases between domains. Not all the frameworks were explicitly designed to support assessment design, and it is also worth noting that none were utilized to design the set of items we analyzed, and it is possible, therefore, that our items may distinguish subdomains less well than items designed for that purpose under a particular framework might do.

Finally, we note the necessary limitation of having utilized a small set of frameworks that explicitly focus on MKT, which limits the implications of our findings. There are, as noted in the background section, scholars who critique not just particular frameworks for knowledge, but the broader approach, including for example underlying idea that describing knowledge in static ways is useful (e.g., Rocha, 2025). While some of these critiques may complement our findings about connectedness, neither the critiques nor alternate framings such as Thompson (2016) were the subject of our inquiry and therefore our empirical results cannot speak directly to those.

5.3 Implications

We note that the true takeaway from our results is simple: there is not a clear mapping between MKT subdomains and assessment items. Whether this is seen as a weakness of the theory or of the item design is somewhat irrelevant to our larger point, which is just that compartmentalized views of MKT may be inadequate to describe the way that MKT is drawn on and used by teachers. We suggest that research would benefit from stepping back from debates about individual frameworks and theorized domains of MKT and instead consider what it would mean to design research and practice around a more connected view of knowledge use. In this view, theoretically distinguishable uses of knowledge may necessarily overlap during the work of teaching.

In this study, we asked: In what compartmentalized or connected ways do practice-based items elicit MKT? How does connectedness or compartmentalization appear to differ or be similar when viewed through different frameworks proposed for MKT? Our study provides evidence that practice-based items may tend to elicit MKT in connected ways because uses of knowledge domains co-occur, regardless of which framework is used to parse MKT. In our results, the only framework to not isolate any domains in any idealized response pattern was MUST, which was also the only framework we used that was developed from a connected view.

One way in which our study is novel is that we sought to take up directly the question of the compartmentalized nature of MKT. And while other scholars observe a finding of unidimensionality as reflecting a flaw in conceptualizations of MKT, we interpret such findings in a more nuanced way by observing that connectedness among and between subdomains in use may manifest in assessment as unidimensionality while still leaving room for considerable complexity in how we understand the domain and organize instruction around it. It is not that the conceptualized sub-domains are somehow “wrong” because they are not well supported by assessment evidence, but rather that we need better ways of understanding sub-domains that are both non-isomorphic and deeply intertwined. The present study takes an initial step toward a more connected view of MKT, but the results suggest that there is much more to study and to understand, questions that we unintentionally overlook if adopting a compartmentalized view of MKT. For example, our analysis provides evidence that reasoning through teaching problems can draw on multiple knowledge domains, but co-occurrence is a limited descriptor of connections, and we could imagine lines of research that explore the nature of these connections, the directionality of dependence where there is such directionality, the cognitive demands associated with coordination of these knowledge domains, and how those domains and the connections among them are more or less salient under different use cases such as assessment, learning, and application in teaching. In other words, we acknowledge that this is just a start toward addressing the questions that led us down this path, and we hope that the field will consider the potential affordances of a connected perspective on MKT and engage in work to better understand those connections moving forward. To return to the periodic table metaphor of Ball et al. (2008), we suggest moving beyond studies that seek to isolate rudimentary elements and toward ones that explore the nature and properties of compounds and how different conditions may elicit different behavior by the same molecule.

Data availability statement

The data analyzed in this study is subject to the following licenses/restrictions: Data can be obtained by contacting the first or second author directly. Requests to access these datasets should be directed to HH, aGVhdGhlcmhvd2VsbEBpY2xvdWQuY29t; YL, eXZvbm5leGxhaUB1bmwuZWR1.

Ethics statement

The studies involving humans were approved by the ETS Institutional Review Board. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation was not required from the participants or the participants’ legal guardians/next of kin in accordance with the national legislation and institutional requirements.

Author contributions

HH: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. YL: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Supervision, Visualization, Writing – original draft, Writing – review & editing. HS: Formal analysis, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This material is supported in part by the National Science Foundation under Grant No. (1445630/1445551). Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

Conflict of interest

HH was employed by Educational Testing Service.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2025.1611169/full#supplementary-material

References

Association of Mathematics Teacher Educators. (2017). Standards] for mathematics teacher preparation. Available online at: https://amte.net/sites/default/files/SPTM.pdf (accessed August 30, 2025).

Google Scholar

Bair, S. L., and Rich, B. S. (2011). Characterizing the development of specialized mathematical content knowledge for teaching in algebraic reasoning and number theory. Math. Thinking Learn. 13, 292–321. doi: 10.1080/10986065.2011.608345