Novel Multiplicity and Stability Criteria for Non-Isothermal Fixed-Bed Reactors

Introduction

Currently, we see many incentives for more sustainable chemicals and energy carrier production based on ${\text{CO}}_2$ and ${\text{H}}_2$. Chemical reactors for ${\text{CO}}_2$ hydrogenation play a crucial role in setting up sustainable production chains (e.g., via Fischer–Tropsch synthesis, ${\text{CO}}_2$ methanation, CO methanation, methanol synthesis, reverse water-gas shift). Especially for chemical energy conversion systems, as currently evaluated in the context of Power-to-X, these reactors are decisive for the overall process efficiency. Moreover, sustainable production increasingly demands for more flexible usage of chemical reactors accessing broader operation ranges and faster load changes. Encountering these new challenges demands a reassessment of former perspectives on reactor design and operation.

Due to the exothermic nature of most ${\text{CO}}_2$ hydrogenations, strong heat releases may result in harmful temperature excursions within the reactor interior, influencing catalyst lifetime, process safety, and performance. Cooled fixed-bed reactors allow for effective heat management and better controllability (Bremer and Sundmacher, 2019). These polytropic reactor concepts are often the first choice for the hydrogenation of ${\text{CO}}_2$ (Kopyscinski et al., 2010; Wood et al., 2012; Biollaz and Schildhauer, 2016).

However, designing and operating polytropic fixed-bed reactors is a rather challenging task, due to a variety of possible physiochemical phenomena (e.g., runaway, parametric sensitivity), which can lead to performance losses or critical process failures (see e.g., Kreitz et al., 2019; Kiewidt and Thöming, 2019; Moioli et al., 2019; Theurich et al., 2019; Fache et al., 2020; Fischer and Freund, 2020; Zimmermann et al., 2020). Such instances correlate with features from systems theory, i.e., uniqueness, multiplicity, and stability. Much work has been done in this direction for ideal plug flow tubular reactors (PFTRs) and continuous stirred tank reactors (CSTRs), providing explicit criteria based on fundamental reactor parameters (Zaldívar et al., 2003; Szeifert et al., 2007; Dochain, 2018). However, real polytropic reactors with finite back-mixing are yet inaccessible for these criteria and are therefore usually subject to qualitative descriptions.

This work intends to review the current perspective on uniqueness and multiplicity of real polytropic reactors under non-isothermal conditions and demonstrates their close connection to stability. Therefore, we perform a bifurcation analysis on a cascade of CSTRs with unlimited stage numbers. As a result, novel criteria for uniqueness and multiplicity are derived that underline the importance of back-mixing within fixed-bed reactors, even at an industrial scale. The theoretical discussions are exemplified for ${\text{CO}}_2$ methanation — a highly exothermic reaction that is currently under intensive investigation for future energy storage.

Carbon Dioxide Methanation

The key reaction for methanation of ${\text{CO}}_2$ and ${\text{H}}_2$ reads

${\text{CO}}_2+4{\text{H}}_2\rightleftharpoons {\text{CH}}_4+2{\text{H}}_2\text{O},{\Delta }_R{\tilde{\text{H}}}^0=-164.9\text{\hspace{0.17em}\hspace{0.17em}kJ}{\text{mol}}^{-1}.(1)$

Methanation is one of several possibilities to activate the inert carbon dioxide. Further reactions are, for instance, dry reforming, reverse water-gas shift (RWGS), and methanol synthesis. Among these reactions, ${\text{CO}}_2$ methanation is thermodynamically the most favored, as it exhibits the lowest Gibbs free energy of reaction in a temperature range from ambient to 900 K $\left({\text{Δ}}_R{\tilde{G}}^0=-142\text{\hspace{0.17em}kJ}{\text{mol}}^{-1}\right)$ (Wenzel, 2018). As depicted in Reaction1, ${\text{CO}}_2$ methanation also features a strong exothermicity, such that lower temperatures shift the chemical equilibrium to the product side. This fact is supported by Figure 1, which shows the result of chemical equilibrium calculations assuming stoichiometric feed over a wide temperature range and for technical relevant pressures (thermochemistry data taken from Lemmon et al., 1998; Haynes, 2017).

FIGURE 1

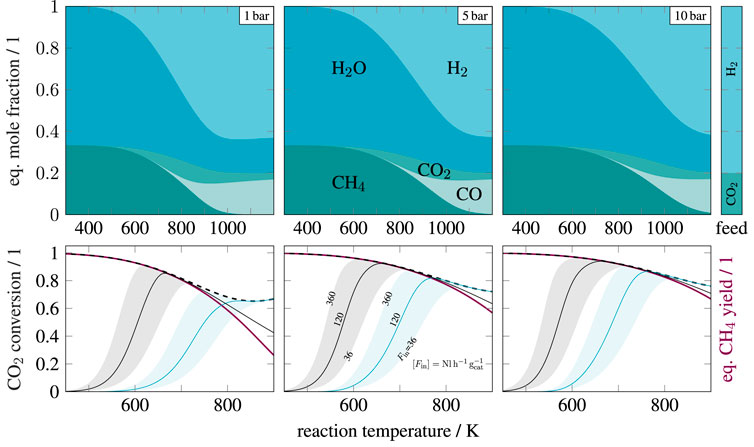
FIGURE 1. Mole fractions at chemical equilibrium (top row) and kinetic conversion (bottom row) over temperature for pure, stoichiometric feed (${\text{H}}_2/{\text{CO}}_2$ = 4) at different pressures and flows, computed via Gibbs-free-energy minimization, kinetic model according to Koschany et al. (2016) (——) and Xu and Froment (1989) (——), equilibrium ${\text{CO}}_2$ conversion (⁃ ⁃ ⁃ ⁃ ⁃), equilibrium CH${}_4$ yield (———).

Figure 1 also illustrates two relevant kinetic models for nickel catalysts. The model from Koschany et al. (2016) differs significantly at temperatures above 700 K and shows higher methane contents due to the exclusion of carbon monoxide. Xu and Froment (1989), in contrast, considered the CO methanation and RWGS reaction to account for carbon monoxide. This was certainly motivated by the lower activity, which achieves sufficient conversions only at higher temperatures where CO formation becomes relevant. Although CO methanation and RWGS reaction certainly occur, they are not favored at elevated pressures and temperatures below 800 K. An analysis of thermodynamic limitations is comprehensively illustrated by Gao et al. (2012), who also showed possible amounts of solid carbon under ${\text{CO}}_2$ excess. More detailed calculations are presented by Kiewidt (2017), who identified considerable amounts of solid carbon at feed ratios ${\text{H}}_2/{\text{CO}}_2<3.2$.

Regardless of the many details on chemistry, this work considers methanation mainly as a well-studied and highly relevant reference reaction. However, the presented results and criteria are easily applicable to other exothermic reactions.

Reactor Concepts for Exothermic Reactions

Reactor concepts for exothermic reactions are mainly determined by the expected temperature rise and the corresponding heat generation. In order to assess the temperature increase, the adiabatic temperature rise (ATR) is considered as an appropriate worst-case estimate. The ATR is defined as

$\text{Δ}{T}_{\text{ad}}=\frac{c_{{\text{CO}}_2}\left(-{\text{Δ}}_R\tilde{H}\right)}{{\rho }_{\text{gas}}{c}_{p,\text{gas}}}=\frac{w_{{\text{CO}}_2}\left(-{\text{Δ}}_R\tilde{H}\right)}{M_{{\text{CO}}_2}{c}_{p,\text{gas}}},(2)$

and exemplary evaluated for methanation at standard, stoichiometric feed conditions

$\text{Δ}{T}_{\text{ad}}^0=\frac{0.845\left(\mathrm{164\text{'}900}\text{\hspace{0.17em}J}{\text{mol}}^{-1}\right)}{0.044\text{\hspace{0.17em}kg}{\text{mol}}^{-1}\mathrm{2\text{'}950}\text{\hspace{0.17em}J}{\text{kg}}^{-1}{\text{K}}^{-1}}=1073.5\text{\hspace{0.17em}K}.$

Looking at Eq. 2 reveals that the ATR is pressure-independent, since ${\text{Δ}}_R\tilde{H}$ and $c_{p,\text{gas}}$ depend exclusively on temperature under ideal gas conditions. Although a higher pressure leads to more reactants and thus more heat generation, the gas heat capacity increases simultaneously and compensates for a further temperature rise. The temperature dependence of the ATR is also rather negligible.

Technologically, this large temperature increase is answered with a series of adiabatic or polytropic fixed-bed reactors (with or without product recycles). Figure 2 illustrates exemplary state-space diagrams for both concepts. Which concept is used for a particular application is often driven by several aspects (e.g., plant size, product quality, costs, safety, reliability, flexibility). However, for modern hydrogenation, we see an increasing application of polytropic fixed-bed reactors (Kopyscinski et al. 2010).

FIGURE 2

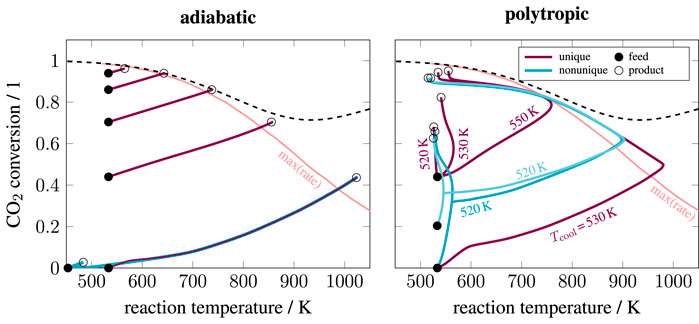
FIGURE 2. State-space diagram for adiabatic and polytropic reactors with exemplary reaction pathways, reactor length: 2 m, pressure: 5 bar, reaction: ${\text{CO}}_2$ methanation according to Koschany et al. (2016), equilibrium ${\text{CO}}_2$ conversion (⁃ ⁃ ⁃ ⁃).

Switching the reactor concept from adiabatic to polytropic (e.g., by cooled multi-tubular bundle reactors) potentially enables a lower catalyst volume, fewer reactor stages, better heat management, and the elimination of gas recycling. Nevertheless, such reactors are more difficult to construct and maintain (e.g., in case of catalyst replacements), which is, in particular, difficult for process scale-up. Hence, the performance benefit must outweigh the increased complexity of the reactor. In the context of gas-to-liquids, Fischer–Tropsch synthesis is an example of the successful use of multi-tubular reactors on a large scale (Wood et al., 2012).

Figure 2 also highlights the relevance of uniqueness. Under certain conditions, both adiabatic and polytropic reactor concepts allow for nonunique operating states (here illustrated for ${\text{CO}}_2$ methanation with respect to cooling or inlet temperature). Especially for polytropic reactors, these nonunique states allow for large conversions and reduced peak temperatures in one single reactor stage, even for undiluted feeds (Bremer and Sundmacher, 2019). Furthermore, uniqueness is very much related to potential reactor runaways and is, thus, relevant to guarantee safe operation. Consequently, a clear determination of uniqueness is of great value for the design and operation of real non-isothermal fixed-bed reactors but has not been sufficiently addressed in the literature yet. This work shall contribute to close this gap and proceeds with a brief literature overview on state-space multiplicity.

State-Space Multiplicity

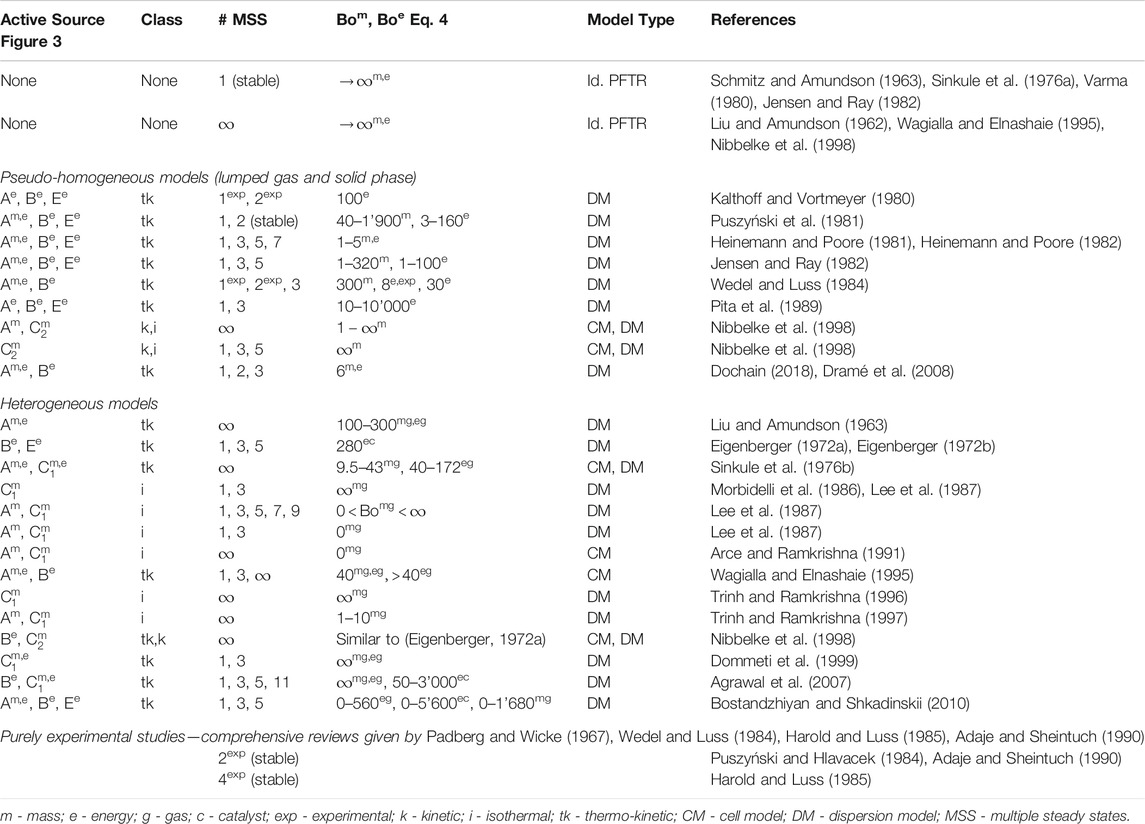
State-space multiplicity of fixed-bed reactors is differentiated in extrinsic and intrinsic (Bremer and Sundmacher, 2019), whereas this work exclusively deals with the intrinsic version. There are numerous sources for intrinsic state-space multiplicity. Three scales are in particular of interest: the scale of the active site, the catalyst pellet (including pores), and the reactor (Sheintuch, 1987). Figure 3 illustrates all three scales and the corresponding multiplicity sources (A to E) that have been most discussed in the literature.

FIGURE 3

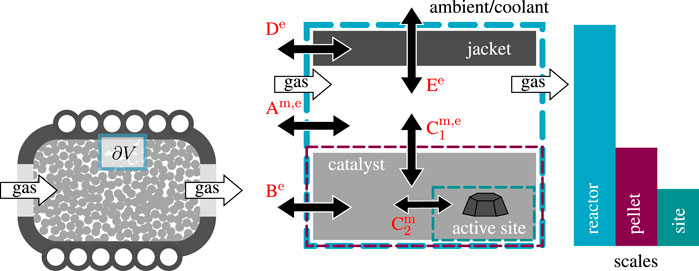
FIGURE 3. Flux network and sources A to E for intrinsic multiplicity within fixed-bed reactors, double arrows indicate mass (m) and/or energy (e) fluxes to be part of the respective source.

These sources typically relate to mass and energy fluxes within a reactor control volume ($\partial V$) and their natural drive to equalize temperature and concentration differences caused by reactive sources and sinks. All fluxes are determined by corresponding transport resistances and linked in a network connecting scales and phases. Depending on inlet and surrounding conditions of the control volume, some resistances are rate-determining for the overall mass and energy transport. According to conservation laws, at steady state all fluxes, sources, and sinks are in equilibrium. A change of inlet and surrounding conditions disturbs the entire network, and a new flux equilibrium emerges. At reactor scale, there exists a unique flux equilibrium if all individual fluxes are unique and if inlet and surrounding of the control volume are not influenced by the control volume itself. If the control volume influences its inlet and/or surrounding (e.g., due to back-mixing), multiple flux equilibria, and, thus, multiple steady states are possible. This interaction is typically denoted as feedback at reactor scale. Similarly, these feedbacks may also occur at catalyst and site scale due to the interaction with neighboring scales.

When steady-state multiplicities in fixed-bed reactors are observed (either numerically or experimentally), they often result from several sources simultaneously. In order to assign the observed multiplicity to the correct source, careful evaluation of each source is required. Therefore, Sheintuch (1987) divided intrinsic multiplicity sources from Figure 3 into three classes:

• purely kinetic (${\mathrm{C}}_2^{\text{m}}$),

• isothermal (A^m, ${\text{C}}_1^{\text{m}}$),

• thermo-kinetic (A^e, B^e, ${\mathrm{C}}_1^{\text{e}}$, D^e, E^e).

Purely kinetic sources belong to mass transport at the active site induced by nonlinear kinetics (e.g., adsorption vs. reaction) (Nibbelke et al., 1998), concurrent reactions/reaction networks (Balakotaiah and Luss, 1983; Elnashaie and Elshishini, 1993; Nibbelke et al., 1998; Mohl et al., 2001), or catalyst deactivation (Gilles, 1977; Eigenberger, 1983). Isothermal sources arise from mass transport at catalyst (diffusion) (Morbidelli et al., 1986; Lee et al., 1987) or reactor scale (convection, dispersion). Thermo-kinetic sources are mainly caused by nonisothermicities, which influence the nonlinear reaction rate coefficients according to the Arrhenius relation (Eigenberger, 1972a; Heinemann and Poore, 1982; Wagialla and Elnashaie, 1995).

Furthermore, multiplicities are also able to propagate through different scales and along with spatial directions. As a result, a large amount of multiple steady states (in theory up to infinity) at reactor scale can be produced by only a few (typically three) multiple steady states at pallet or site scale (Lee et al., 1987; Arce and Ramkrishna, 1991; Nibbelke et al., 1998). Due to the variety of different sources and their ability to propagate through scales, literature (going back to the early 60s) reports very differently or even controversially about total number, relevant sources, and necessary conditions of multiple steady states in fixed-bed reactors. This aspect is demonstrated by a brief literature review in Table 1.

TABLE 1

TABLE 1. Review on multiplicity sources within fixed-bed reactor models and experiments.

As shown in Table 1, the investigation of steady-state multiplicity is mainly performed via cell models and dispersion models (see Materials and Methods). Both model types have been used to outline the two theoretical limiting cases: a reactor without and with an infinite number of multiple steady states. The dominating opinion is that the ideal PFTR is free of any state-space multiplicity due to the absence of transport in countercurrent direction (feedback). However, some studies opposed that the ideal PFTR is rather characterized by an infinite number of steady states (Liu and Amundson, 1962; Wagialla and Elnashaie, 1995; Nibbelke et al., 1998). These studies refer to the fact that the continuum description of an ideal PFTR corresponds to a series of infinite CSTRs. Assuming that the ignition can occur at any CSTR within the series gives rise to an ignition possible at any position along the reactor axis. This thought experiment allows for discontinuous solutions in packed-beds, which is often correlated to multiple steady states of single particles (Arce and Ramkrishna, 1991) or active sites (Nibbelke et al., 1998). Although the confusing concept of infinite solutions was discussed very controversially, it was certainly the main driver behind many investigations. Thereby, two objectives became the most relevant for technical applications: Firstly, the ability to operate at various states promises performance improvements. Secondly, state-space uniqueness is of great value for safety reasons (e.g., to avoid runaways).

Apart from ideal reactors, many studies in Table 1 also focus on real reactors considering finite Bodenstein numbers (see definition in Materials and Methods) within dispersion models or finite numbers n of representative CSTRs within cell models. As shown in Levenspiel (1999), both concepts are interchangeable due to the relation

$\frac{1}{n}=\frac{2}{\text{Bo}}-\frac{2}{{\text{Bo}}^2}(1-\text{exp}(-\text{Bo})),\text{\hspace{1em}and\hspace{1em}}n=\frac{\text{Bo}}{2}(\text{if\hspace{0.5em}Bo}>100).(3)$

Besides the different model concepts, various assumptions are made in order to uncover the influence of specific sources of steady-state multiplicity. Therefore, the studies in Table 1 differ in many aspects of the model constitution (e.g., heterogeneous vs. homogeneous, isothermal vs. non-isothermal, first-order reaction vs. Langmuir-Hinshelwood Hougen-Watson-type reaction, with vs. without radial dispersion). For instance, the use of isothermal reactor models eliminates all thermo-kinetic multiplicities and allows for investigations on purely kinetic and/or isothermal multiplicities. On the contrary, the study of purely thermo-kinetic multiplicities is preferably done in the absence of kinetic and isothermal multiplicities.

Most studies dealing with thermo-kinetic multiplicity sources agree that axial dispersion of heat plays a vital role in the existence of multiple steady states in fixed-bed reactors. Eigenberger (1972b), in particular, argued that heat conduction through the solid phase (source B^e) must reduce an infinite multiplicity to a finite number of multiple steady states. The author also identified a maximum number of three or five multiple steady states, depending on the boundary conditions of the solid phase. It took about 20 years before this finding was revised. Therefore, Nibbelke et al. (1998) extended the model of Eigenberger (1972b) and considered a reaction kinetic with multiplicities at the active site (source C${}_2^{\text{m}}$). The authors could prove that an infinite number of steady states is maintained even if axial heat dispersion through the solid phase is incorporated. Unfortunately, this research direction is still very narrow, which is certainly due to the fact that the required heterogeneous model is a rather sophisticated numerical tool for such analyses. The use of pseudo-homogeneous models provides a possible remedy. Although pseudo-homogeneous models are not able to distinguish between energy transport in source A and B, their results point in the same direction. By making use of dimensionless model formulations and bifurcation techniques Heinemann and Poore (1981), Jensen and Ray (1982), Heinemann and Poore (1982) classified several aspects that also contribute to the existence of multiplicity. Both stated that a nonadiabatic reactor with unequal Bodenstein numbers for heat and mass dispersion shows a unique solution, either for sufficiently high values of the Bodenstein numbers, large heat transfer coefficients, or small values of the Damköhler number. These conditions also hold for industrial fixed-bed reactors; such that multiplicity was found to be relevant even for technical configurations (Puszyński et al., 1981; Pita et al., 1989). This is reflected in Table 1 by the broad range of Bodenstein numbers in which multiple steady states are observed. In most investigations, the number of three multiple steady states is confirmed. Beyond that, some studies report up to eleven multiple steady states. However, experimental evidence above four multiple steady states was not found. For instance, Wedel and Luss (1984) validated their results with an experimental setup for CO and CO${}_2$ methanation in a fixed-bed of 25 cm in length and 2.5 cm in diameter. The authors could reproduce predicted model solutions of one ignited and one extinguished state with identical feed concentration. Therefore, a one-dimensional axial dispersion model, which accounts for the diffusion-reaction interactions within the pellets, was found to be well suited for multiplicity analysis. Since their experimental setup has a low bed length and, thus, a low Bodenstein number (Bo^e = 8), conclusions for industrial reactors are rather limited. Nevertheless, the good agreement between model and experiment verified and proved that state-space multiplicity is of significance within fixed-bed reactors. More recently, Agrawal et al. (2007) pointed out that the often reported high number of multiple solutions originates from the assumption of constant transport coefficients, which leads to many fragile solutions that emerge from unstable branches. Accounting for the variation of heat and mass transfer coefficients with local flow and reaction properties eliminates these nonphysical solutions. For this reason, recent works are often motivated to add more physical meaning to their models. This allows to additionally focus on effects of secondary order (e.g., flow maldistributions, localized hot-spots, spatial and spatiotemporal patterns) (Sheintuch, 1997; Trinh and Ramkrishna, 1997; Jaree et al., 2001; Papadias et al., 2001; Marwaha and Luss, 2003; Agrawal et al., 2007; Viswanathan et al., 2008; Nekhamkina and Sheintuch, 2012), which is, however, not object of this work. Similarly, stable oscillatory solutions are also disregarded in this work, since they are unlikely to occur in fixed-bed reactors on an industrial scale due to their high thermal inertia (Jensen and Ray, 1982).

In order to identify the full operating range of fixed-bed reactors, this work considers state-space multiplicity as a crucial feature. Therefore, thermo-kinetic sources are of major interest, since purely kinetic and isothermal multiplicities are reported to be rather fragile. The literature survey from above reveals that axial dispersion, as well as the diffusion-reaction interaction, are essential model components to obtain consistent results. However, for specific applications, these studies rather provide trends than generally valid correlations and criteria. The impact of several simultaneously interacting features is certainly the main reason for this obstacle. Furthermore, the operation at unstable states is also underrepresented in the literature and needs further elaboration (see e.g., Bremer and Sundmacher, 2019). Therefore, the following sections intend to provide more insights and propose general criteria that unifies the aspects uniqueness, multiplicity, and stability.

Materials and Methods

Analyzing chemical fixed-bed reactors requires to incorporate a variety of physicochemical interactions and is often motivated by models from first-principles. Solving these models can lead to a challenging computational task due to the complex coupling of mass, energy, and momentum transport. However, putting all available details into consideration is not always necessary. For instance, the basic phenomena described in this work are fully representable by mass and energy transport alone, which agrees well with previous works (see Table 1). In addition to physical assumptions, the considered control volume boundary also determines the relevant balance components. This differentiation meets the two ideal reactor concepts for continuously operated reactors:

• the ideal CSTR,

• the ideal PFTR.

The CSTR concept often considers a control volume around the entire reactor volume (integral balance). In contrast, the control volume for the ideal PFTR typically refers to an infinitesimally small volume segment within the reactor volume (differential balance). The PFTR allows to describe in detail spatial distributions of the reactors state variables (e.g., temperature and mass fraction), but also requires higher numerical efforts. Both ideal reactors also represent the two limiting cases for back-mixing/axial dispersion, which is typically measured by the axial Bodenstein number for mass and energy according to

${\text{Bo}}^{\text{m}}=\frac{v_{z}L}{{\mathcal{D}}_z},{\text{Bo}}^{\text{e}}=\frac{v_z{\rho }_{\text{gas}}{c}_{p,\text{gas}}L}{{\lambda }_z},(4)$

which are essential for later discussions. In case of an ideal CSTR the reactive volume is fully mixed (${\mathcal{D}}_z={\lambda }_z\to \infty$, ${\text{Bo}}^{\text{m}}={\text{Bo}}^{\text{e}}\to 0$), whereas in case of the ideal PFTR no back-mixing/dispersion exists (${\mathcal{D}}_z={\lambda }_z\to 0$, ${\text{Bo}}^{\text{m}}={\text{Bo}}^{\text{e}}\to \infty$) (Levenspiel, 1999).

Real reactors, as considered in this work, are allocated right in between these two limiting cases. The corresponding model approaches are

• the CSTR cascade (tanks-in-series model, cell model),

• the tubular reactor model with axial dispersion (dispersion model, continuous model).

In order to represent real reactors more accurately, the control volume might also differentiate between bulk gas phase and catalyst phase. Two model concepts are commonly applied:

• the pseudo-homogeneous model (no phase distinction),

• the heterogeneous model (phase distinction with interfacial and intraparticle mass and energy transport).

Depending on the considered model, the energy dispersion coefficient in Eq. 4 is considered differently. The pseudo-homogeneous model lumps solid and gas phase, which requires an effective energy dispersion term (${\lambda }_z={\lambda }_z^{\text{eff}}$). On the contrary, the heterogeneous model allows for the distinction between gas and catalyst-phase dispersion and, thus, accounts for two separate energy-based Bodenstein numbers (${\text{Bo}}^{\text{eg}},{\text{Bo}}^{\text{ec}}$). For real fixed-bed reactors, the mass-based Bodenstein number is reported to be three to ten times higher than the energy-based Bodenstein number (Puszyński et al., 1981; Bostandzhiyan and Shkadinskii, 2010). Thus, energy back-mixing is the dominating axial dispersion mechanism within fixed-bed reactors (Mears, 1976). Note that some studies define the here stated Bodenstein number as Péclet number. In this work, these numbers are distinguished by the characteristic length, which is the reactor length L for the Bodenstein number and the particle diameter $d_{\text{p}}$ for the Péclet number.

Both model concepts offer different levels of sophistication, e.g., one-, two-, or three-dimensional spatial resolution, stationary or dynamic, with or without axial dispersion. How sophisticated a model needs to be is often rated by criteria (e.g., Mears’ criterion), which incorporate dominating transport phenomena and reactor design. A comprehensive overview is provided by Pérez-Ramírez (2000). Besides these criteria, distinct model or transport components may be examined separately. This decoupling approach is well-established to identify and analyze, for instance, different sources of state-space multiplicity. In this context, Nibbelke et al. (1998) emphasized that the identification of multiplicity sources is inevitable for a correct interpretation of numerical and also experimental results. This observation is crucial for the construction of adequate reactor models as well as for optimal reactor operation and control.

In the following, a single pseudo-homogeneous CSTR model is used to represent fully mixed reactive conditions and to illustrate its implications on uniqueness, multiplicity and stability. Afterward, the single CSTR is extended to a series of CSTRs (cell model) in order to approach conditions as they prevail in real fixed-bed reactors. All investigations are exemplified for methanation under realistic reactive conditions.

Results

As indicated by the previous section, back-mixing is an essential feature that determines multiplicity. In order to show how this applies to real reactors, the following derivations shall serve as a guideline for multiplicity analysis, exemplified for catalytic methanation. Beginning with the well-known limiting case of a fully mixed reactive volume illustrates the fundamental parameters that characterize the range and intensity of multiplicity.

CSTR Analogy

The technical relevance of this limiting case can be found, for instance, with Berty reactors, which are widely used for catalyst characterization. Although the relationships presented here are already state of knowledge, they are crucial for later excursions toward industrial-scale fixed-bed reactors. Further on, a CSTR model as described in Supplementary Section S1 is used. The required mass and energy balances read accordingly:

$\text{mass\hspace{0.17em}balance}:X_{{\text{CO}}_2}=\frac{\tau }{\epsilon }\frac{{\text{R}}_{\text{meth}}\left(T,p,w_{\alpha }\right)}{c_{{\text{CO}}_2,\text{in}}},(5)$

$\text{energy\hspace{0.17em}balance}:X_{{\text{CO}}_2}=\frac{\left(1+\text{St}\right)}{\text{Δ}{T}_{\text{ad}}}\left(T-T_{\text{op}}\right).(6)$

Consequently, steady-state operation of a single CSTR is governed by the equality of Eqs. 5 and 6. In order to evaluate unique and non-unique operating points, Supplementary Table S1 provides a reference setting that corresponds to carbon dioxide methanation in a fixed-bed reactor including realistic parameter ranges.

The six key parameters in Supplementary Table S1 are highlighted in bold and result in Figure 4 for variations of the operating temperature and Figure 5 for variations of the Stanton number. The operating temperature is given in Supplementary Eq. S19 and reflects changes in coolant and inlet temperature, whereas the Stanton number mainly results from changes in the coolant heat transfer. The left side of both figures shows that under realistic conditions, multiple equilibrium (or operating) points are indeed attainable, similar to the theoretical discussions in State-Space Multiplicity. The right side in both figures illustrates how hysteresis emerges when the operating temperature varies within realistic ranges. Apart from variations in operating temperature and Stanton number, one might also consider variations of the residence time τ. Higher residence times correspond to higher Damköhler numbers and increase the curvature of the mass balance operating curve (Eq. 5) and, thus, increase the hysteresis.

FIGURE 4

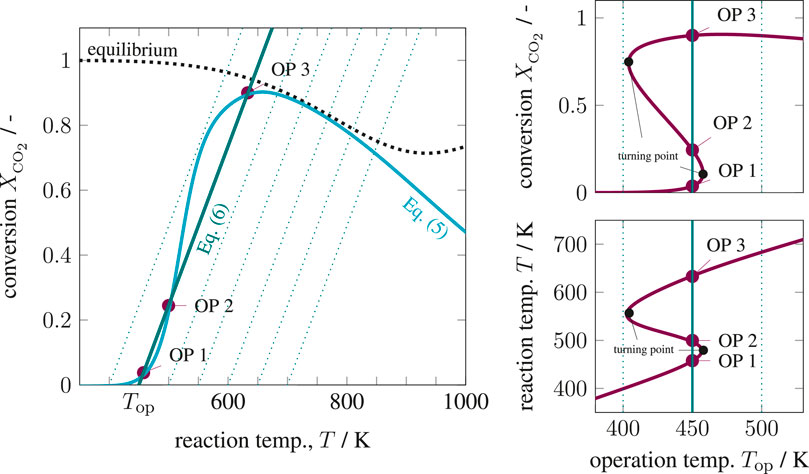
FIGURE 4. State-space diagram for mass and energy balance (left) and for all equilibrium points (right) under variation of the operating temperature, reference setting taken from Supplementary Table S1.

FIGURE 5

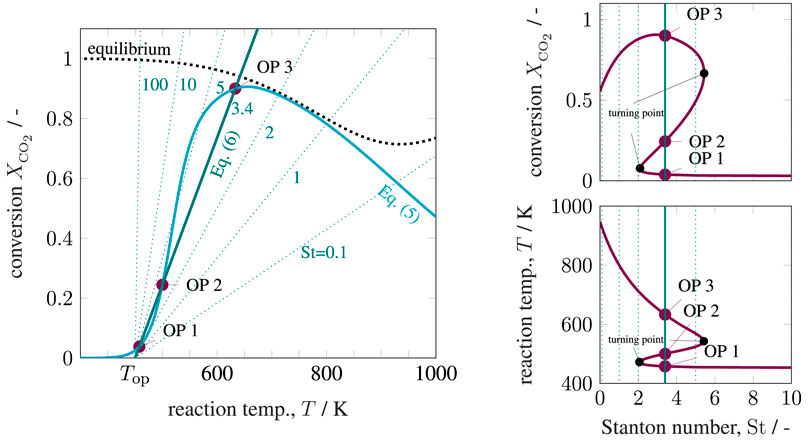
FIGURE 5. State-space diagram for mass and energy balance (left) and for all equilibrium points (right) under variation of the Stanton number, reference setting taken from Supplementary Table S1.

These results explicitly show that under perfect back-mixing at most three operating points are attainable, whereas two are stable (OP 1 and OP 3) and one is unstable (OP 2). As seen in the upper right figures, the unstable operating points are always surrounded by stable ones and cover a significant part of the attainable conversion range. If these unstable states are ignored for reactor design and operation, a significant potential might get lost. This clearly demonstrates the close connection between multiplicity and stability. Here, the generalized criterion for stability of a CSTR at a certain operating point is known to result from mass and energy-based sensitivities according to

${\frac{\mathrm{d}X}{\mathrm{d}T}|}_{\text{OP}}=\frac{\tau }{\epsilon c_{\text{in}}}{\frac{\mathrm{d}\text{R}}{\mathrm{d}T}|}_{\text{OP}}<\frac{1+\text{St}}{\text{Δ}{T}_{\text{ad}}},(7)$

which is equivalent to the criteria proposed by van Heerden (1953) and Gilles and Hofmann (1961). Note that sensitivities might also be considered with respect to other parameters than temperature. However, this work focuses primarily on thermo-kinetic multiplicities, for which temperature sensitivities are the most relevant. The mass-based sensitivity may be further evaluated by resolving the total differential at constant τ and $c_{\text{in}}$, such that

$0=\frac{\mathrm{d}X}{\mathrm{d}T}-\frac{\tau }{\epsilon c_{\text{in}}}\frac{\mathrm{d}\text{R}}{\mathrm{d}T}=\frac{\mathrm{d}X}{\mathrm{d}T}-\frac{\tau }{\epsilon c_{\text{in}}}\left(\frac{\partial \text{R}}{\partial T}+\frac{\partial \text{R}}{\partial X}\frac{\mathrm{d}X}{\mathrm{d}T}\right)\Rightarrow \frac{\mathrm{d}X}{\mathrm{d}T}=\frac{\frac{\tau }{\epsilon c_{\text{in}}}\frac{\partial \text{R}}{\partial T}}{1-\frac{\tau }{\epsilon c_{\text{in}}}\frac{\partial \text{R}}{\partial X}}.$

Plugging this into Eq. 7 leads to the rate-based CSTR stability criterion

$\text{CSTR}\text{stability}:\frac{\frac{\tau }{\epsilon c_{\text{in}}}\frac{\partial \text{R}}{\partial T}}{1-\frac{\tau }{\epsilon c_{\text{in}}}\frac{\partial \text{R}}{\partial X}}<\frac{1+\text{St}}{\text{Δ}{T}_{\text{ad}}}.(8)$

In comparision, Szeifert et al. (2007) comprehensibly reviewed available criteria for reactor stability, runaway, and parametric sensitivity. Among those, the authors recommend using the Ljapunov stability criterion for a PFTR in space (or for a batch reactor in time), which is very similar to the upper CSTR stability criterion. In case of an equimolar reaction the PFTR stability criterion accordingly reads

$\text{PFTR\hspace{0.17em}\hspace{0.17em}stability}:\frac{\frac{\tau }{\epsilon c_{\text{in}}}\frac{\partial \text{R}}{\partial T}}{\text{St}-\frac{\tau }{\epsilon c_{\text{in}}}\frac{\partial \text{R}}{\partial X}}<\frac{1}{\text{Δ}{T}_{\text{ad}}}.$

Both criteria reveal that reactor stability is supported under intensive cooling conditions ($\text{St}\to \infty$) and suppressed under reduced cooling conditions ($\text{St}\to 0$). As explained in State-Space Multiplicity the PFTR is primarily considered to have a unique solution for fixed parameters. Hence, the features stability, runaway, and parametric sensitivity need to be separated from multiplicity, which was already highlighted by (Bilous and Amundson, 1956). Until today, this separation is often considered to be generally valid. However, in the CSTR case a strong coupling of these features is clearly given. From the above explanations, generalized criteria for uniqueness and multiplicity within the operating range $\mathcal{O}$ derive very similar to the stability criterion and read

$\text{CSTR\hspace{0.17em}\hspace{0.17em}uniqueness}:\underset{T\in \mathcal{O}}{\text{max}}\frac{\mathrm{d}X}{\mathrm{d}T}=\frac{\mathrm{d}X}{\mathrm{d}T}{|}_{T^{\text{*}}}\le \frac{1+\text{St}}{\text{Δ}{T}_{\text{ad}}},(9)$

$\text{CSTR\hspace{0.17em}\hspace{0.17em}multiplicity}:\underset{T\in \mathcal{O}}{\text{max}}\frac{\mathrm{d}X}{\mathrm{d}T}=\frac{\mathrm{d}X}{\mathrm{d}T}{|}_{T^{\text{*}}}>\frac{1+\text{St}}{\text{Δ}{T}_{\text{ad}}}.(10)$

On the left side, the mass-based sensitivity corresponds to the steepest conversion gradient at the inflection point $T=T^{\text{*}}$ of Eq. 5. On the right side, the energy-based sensitivity corresponds to the constant conversion gradient of Eq. 6. Although the uniqueness criterion applies to all operating points in $\mathcal{O}$ (sufficient condition for uniqueness), the multiplicity criterion only indicates the existence of some operating points with multiple steady states in $\mathcal{O}$ (necessary condition for multiplicity). Thus, even if the multiplicity criterion holds, unique solutions in $\mathcal{O}$ might still exist. Furthermore, discontinuous jumps at the turning points from a stable extinguished to a stable ignited branch ‐ and vice versa ‐ is also solely induced by the existence of multiplicity. These jumps coincide with what is generally denoted as parametric sensitivity and reactor runaway (Morbidelli and Varma, 1982). Moreover, the equivalence strikingly demonstrates the close connection between stability, runaway, parametric sensitivity, and multiplicity when back-mixing is present. However, commonly accepted criteria for reactor runaway and stability do not consider back-mixing at all (Szeifert et al., 2007; Kummer and Varga, 2019). To close this gap, the next section applies the upper correlations for mass and energy to a series of CSTRs, where a finite number of stages corresponds to finite back-mixing.

CSTR Cascade Analogy

In order to approach a more realistic description of industrial-scale fixed-bed reactors, this section extends the previous relations to a CSTR cascade with multiple stages. Note that such cascades also mimic finite volume schemes, which are widely used to solve dispersion models numerically. Supplementary Section S2 provides the entire cascade model notation, mass and energy balances, as well as the solution strategy. The resulting equations of each CSTR stage {i} are

$\text{mass\hspace{0.17em}\hspace{0.17em}balance}:\hspace{1em}{X}_{{\text{CO}}_2}^{\left\{i\right\}}=\frac{1}{n}\frac{\tau }{\epsilon c_{{\text{CO}}_2,\text{in}}}{\text{R}}_{\text{meth}}^{\left\{i\right\}}=C_n{\text{R}}_{\text{meth}}^{\left\{i\right\}},(11)$

$\text{energy\hspace{0.17em}\hspace{0.17em}balance}:\hspace{1em}{X}_{{\text{CO}}_2}^{\left\{i\right\}}=\frac{\left(1+{\text{St}}_n\right)}{\text{Δ}{T}_{\text{ad}}^{\left\{i\right\}}}\left(T^{\left\{i\right\}}-T_{\text{op}}^{\left\{i\right\}}\right).(12)$

In order to separate different multiplicity sources, isothermal and non-isothermal cascades are discussed in the following.

Two Isothermal CSTRs

Under intensive cooling conditions ($\text{St}\to \infty$) or negligible heat effects ($\text{Δ}{T}_{\text{ad}}^{\left\{i\right\}}\to 0$) the CSTR cascade becomes isothermal, meaning that $T_{\text{in}}=T_{\text{cool}}=T^{\left\{i\right\}}$. The corresponding implicit nonlinear equation system results from Eq. 11 and reads

$\begin{array}{c}0=X_{{\text{CO}}_2}^{\left\{1\right\}}-C_2{\text{R}}_{\text{meth}}^{\left\{1\right\}},\\ 0=X_{{\text{CO}}_2}^{\left\{2\right\}}-C_2{\text{R}}_{\text{meth}}^{\left\{2\right\}},\end{array}(13)$

which can be solved consecutively (stage-wise) or simultaneously for $X_{{\text{CO}}_2}^{\left\{1\right\}}$ and $X_{{\text{CO}}_2}^{\left\{2\right\}}$ by root-finding algorithms (e.g., Newton–Raphson method). The solution of Eq. 13 is illustrated in Figure 6.

FIGURE 6

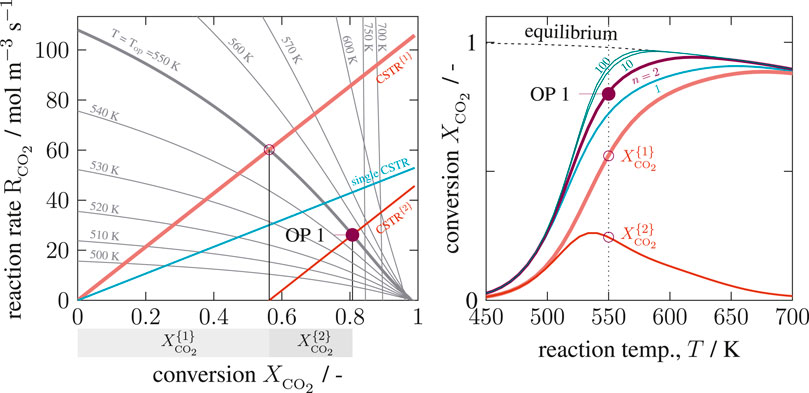
FIGURE 6. State-space diagram for a cascade of two isothermal Continuous Stirred Tank Reactors (CSTRs) in the R–X(left) and X–T(right) plane, reference setting taken from Supplementary Table S1 but $T_{\text{op}}$ = 550 K.

As seen on the left side of Figure 6, the operating point (depicted by bullets) of each CSTR lies on a straight line in the R-X diagram. The unique intersection at any temperature proves, that no purely kinetic multiplicity (C${}_2^{\text{m}}$ in Figure 3) exists for the rate expressions used in this work. Since intraparticle and interfacial transport resistances are neglected (${\eta }_{\text{meth}}=1$), the multiplicity sources C${}_1^{\text{m}}$ and C${}_1^{\text{e}}$ are also absent. This graphical analysis is also applicable to other reactions in order to check for these multiplicity sources. The right side of Figure 6 depicts the stage operating range as well as the overall operating range for two CSTRs in series and compares it to scenarios with 1, 10, and 100 stages. The comparison shows the well-known tendency that the higher the stage number, the higher the conversion.

Two Non-Isothermal CSTRs

The operating points for a series of non-isothermal CSTRs are additionally determined by individual stage temperatures deviating from inlet and cooling temperature $T_{\text{in}}=T_{\text{cool}}\ne T^{\left\{i\right\}}$. Thus, the nonlinear equation System13 needs to be extended by the stage energy balances in Eq. 12 such that

$\begin{array}{c}0=X_{{\text{CO}}_2}^{\left\{1\right\}}-C_2{\text{R}}_{\text{meth}}^{\left\{1\right\}},\\ 0=X_{{\text{CO}}_2}^{\left\{1\right\}}\text{Δ}{T}_{\text{ad}}^{\left\{1\right\}}+\left(1+{\text{St}}_2\right)\left(T_{\text{op}}^{\left\{1\right\}}-T^{\left\{1\right\}}\right),\\ 0=X_{{\text{CO}}_2}^{\left\{2\right\}}-C_2{\text{R}}_{\text{meth}}^{\left\{2\right\}},\\ 0=X_{{\text{CO}}_2}^{\left\{2\right\}}\text{Δ}{T}_{\text{ad}}^{\left\{2\right\}}+\left(1+{\text{St}}_2\right)\left(T_{\text{op}}^{\left\{2\right\}}-T^{\left\{2\right\}}\right).\end{array}(14)$

This system can be solved again stage-wise or simultaneously for $X_{{\text{CO}}_2}^{\left\{1\right\}}$, $X_{{\text{CO}}_2}^{\left\{2\right\}}$, $T^{\left\{1\right\}}$, and $T^{\left\{2\right\}}$ by root-finding algorithms. The previous section showed that one single stage allows for up to three multiple solutions, which indicates that the CSTR cascade in Eq. 14 also generates multiple steady states. In theory, if each stage exhibits up to three multiple steady states (OP 1, 2, and 3), a total number of 3ⁿ state combinations arise for the entire cascade. Standard root-finding algorithms, however, converge only to one local solution of System 14. Thus, finding all solutions requires further efforts, which is part of the following discussions.

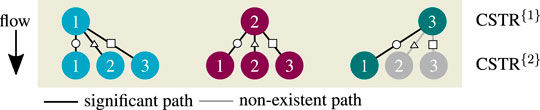
The graphical solution of System 14 is shown in Figure 7 considering three of nine possible combinations ([1–1], [2–1], [3–1]). This figure comprehensively shows how the first operating point influences its downstream stage. The more conversion is achieved within the first stage, the less remains within the next stage. Furthermore, the energy-based operating line (green) of the second stage becomes steeper due to the reduced ATR. Both effects simultaneously reduce the occurrence for multiplicities within the second stage, if the first stage operates at an ignited state (OP 2 or 3). Later, this will be an essential aspect to interpret solutions of multi-stage CSTRs. Enumerating all possible solutions within the relevant coolant temperature range leads to the results in Figure 8.

FIGURE 7

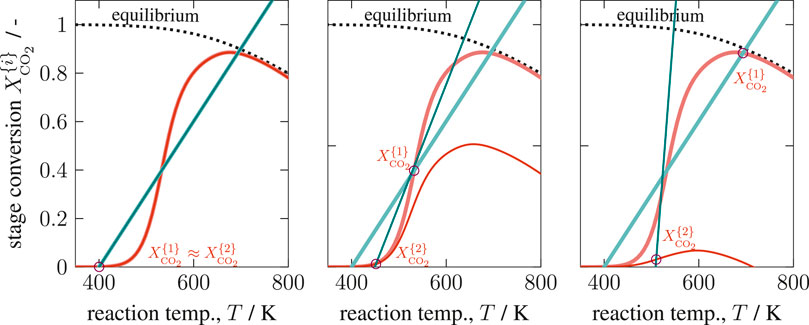
FIGURE 7. Graphical solution of a two-stage CSTR series with state combination [1-1], [2–1], and [3–1], reference setting taken from Supplementary Table S1 but $T_{\text{op}}^{\left\{1\right\}}$ = 400 K and $T_{\text{in}}=T_{\text{cool}}$.

FIGURE 8

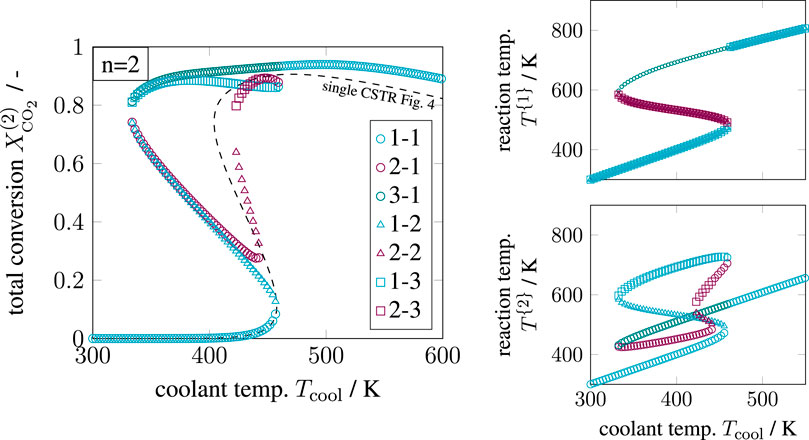
FIGURE 8. Enumerative solution of significant operating points in a two-stage CSTR series, reference setting taken from Supplementary Table S1 but $T_{\text{in}}=T_{\text{cool}}$. Note: $T_{\text{cool}}$ is constant over the entire cascade, whereas $T_{\text{op}}$ changes in each CSTR stage.

Compared to the single CSTR, the hysteresis is more pronounced, and intermediate solutions emerge. Although combinatorics allows nine multiple steady states, only seven remain significant after enumeration. The combinations [3–2] and [3–3] cancel out, due to the previous discussions on Figure 7. In addition, combinations [2–2] and [2–3] are rather seen as fragile because they exist in a very narrow operating range. In consequence, multiplicity driven by combinatorics is divided into significant and non-existing paths, as illustrated in Figure 9. These findings indicate that multiplicity in a CSTR cascade attributes only to a few stages. In order to confirm this hypothesis, a multi-stage cascade is analyzed in the following.

FIGURE 9

FIGURE 9. Possible state combinations for a two-stage CSTR cascade.

Multi-Stage CSTR Cascade

The enumeration effort of a multi-stage CSTR cascade increases exponentially with the number of stages if all possible combinations are taken into account. With six stages, there exist already 3⁶ = 729 state combinations for all coolant temperature increments (here 300), leading to over 200'000 solver runs. Although a brute force enumeration would provide all solutions, many of them will be insignificant, due to missing physical constraints. Thus, a more elegant way is the use of bifurcation theory and numerical continuation techniques, which track solution branches according to slight parameter changes (e.g., coolant temperature) within a predefined range. During these changes, the eigenvalues of the linearized system equations may change such that the system becomes unstable. The shift to instability occurs if some eigenvalues cross the imaginary axis. At this point, bifurcation can take place from which new branches spread. However, this method also suffers from extensive computational efforts due to the eigenvalue calculation and possible inaccuracies of the systems Jacobian close to the bifurcation point. Furthermore, there is no guarantee that this method obtains all solutions. More details on bifurcation theory and numerical continuation techniques can be found in (Heinemann and Poore, 1981; Jensen and Ray, 1982; Kubíček and Marek, 1983; Wagialla and Elnashaie, 1995).

In this work, the enumeration of all solutions was found to be the more convenient and illustrative approach. It will be shown that the non-existent solutions can be excluded already in advance. Together with efficient nonlinear computation techniques (here provided by CasADi; Andersson et al., 2018) the enumeration of all solutions with reasonable computational effort becomes feasible. Accordingly, the results for three to six CSTRs in series are illustrated in Figure 10.

FIGURE 10

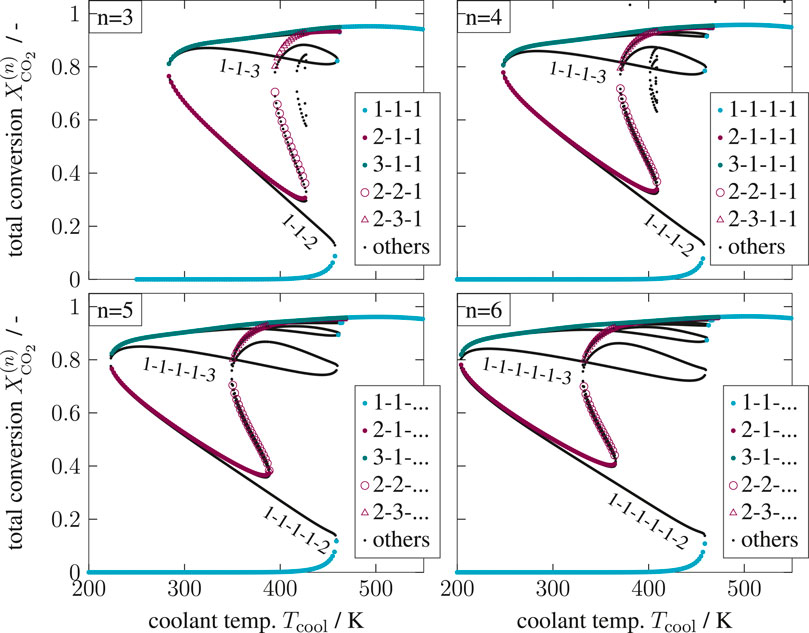
FIGURE 10. Enumerative solution of operating points (OPs) in a multi-stage CSTR cascade, color—OPs of two key stages at the inlet, black—OPs of subordinate branches, reference setting taken from Supplementary Table S1 but $T_{\text{in}}=T_{\text{cool}}$.

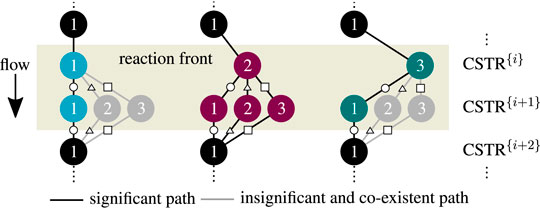
Most importantly, the solutions in Figure 10 aggregate in three main clusters forming ‐ similar to a single CSTR ‐ a stable ignition and extinction branch, as well as an unstable intermediate branch. The number of multiple steady states increases with increasing stage number n, but most solutions persistently converge to the three main clusters. Once again, each relevant solution has not more than two stages exhibiting multiplicity. Cascades with more stages as represented by Figure 11 confirm that two stages are sufficient to map the dominating state clusters. These two stages are further on denoted as key stages, which may exist at any position within the cascade. The key stage solutions directly at the inlet are colored in Figure 10. Solutions with the same key stage combination but different locations along the cascade aggregate within the same cluster. For instance, the upper ignition branch is covered by n [$\cdots$1–3–1$\cdots$] combinations, the middle unstable branch is covered by n [$\cdots$1–2–1$\cdots$] combinations, and the lower extinction branch is covered by n [$\cdots$1–1–1$\cdots$] combinations. Again $n-1$ [$\cdots$1–2–2–1$\cdots$] and $n-1$ [$\cdots$1–2–3–1$\cdots$] fragile combinations exist but appear only in a narrow operating range. This clustering can be explained by the insignificance of previous stages at the extinguished state [$\cdots$1$\cdots$]. The insignificance partly eliminates if the inlet and coolant temperature of the cascade differ, which is, however, not considered here. Beyond that, subordinate branches (in black) develop from the last stage ([$\cdots$1–2] [$\cdots$1–3]). These observations are summarized in the pathway structure of Figure 12, showing the relevant state combinations of a multi-stage CSTR cascade.

FIGURE 11

FIGURE 11. Possible state combinations of a multi‐stage CSTR cascade with two key stages.

FIGURE 12

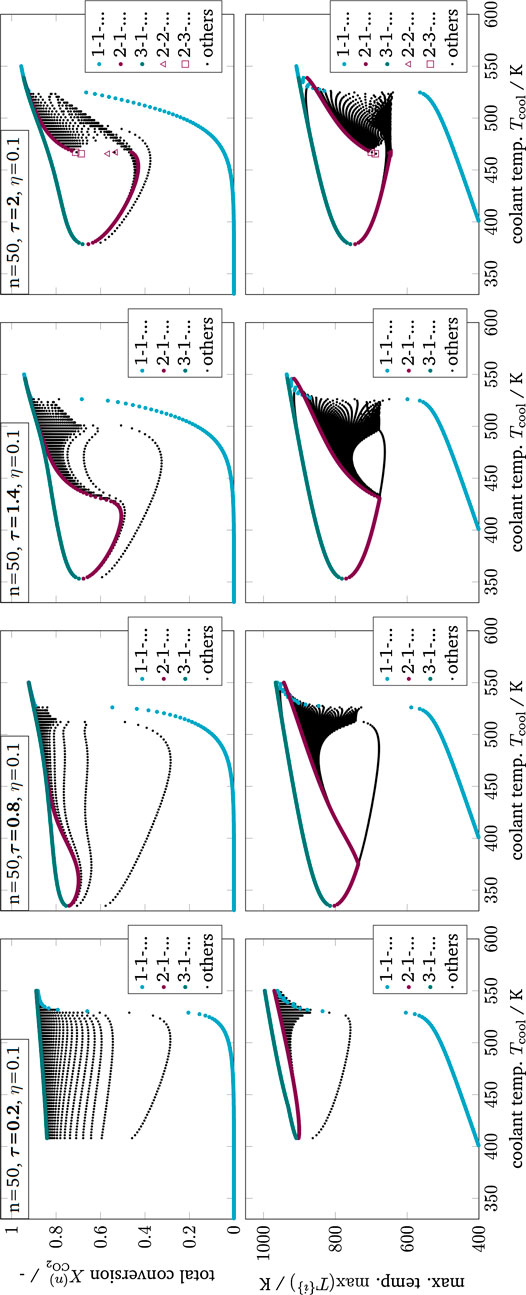
FIGURE 12. Enumerative solution of operating points (OP) in a multi-stage CSTR cascade with varying residence time, color - OPs of two key stages at the inlet, black - OPs of subordinate branches, reference setting taken from Supplementary Table S1 but T_in = T_cool.

As illustrated in Figure 11, the clustering of all key stage solutions still remains for higher stage numbers. It was found that the hysteresis loop widens significantly with increasing stage number. However, after reaching a certain stage number, the hysteresis loop degenerates again until it finally disappears. Furthermore, different shapes of the unstable intermediate branch emerge, depending on the parameter setting. The unstable branch evolves more or less pronounced, as indicated by variations of the residence time in Figure 11. This is in particular relevant if an operation at these unstable branches is aspired (Bremer and Sundmacher, 2019).

Technically, key stages are the analogy of narrow reaction fronts in real fixed-bed reactors. Those fronts often develop within a very short reactor segment, preferably close to the reactor inlet. Considering this, the key stages become less likely if they are located further downstream, which curtails the relevance of the black subordinate branches associated with the last stage. In real reactors, the actual reaction front position is typically determined by second-order effects (e.g., preheating, dispersion, flow maldistribution, heat conduction within the reactor jacket).

From all this, the following three-level hierarchy of thermo-kinetic multiplicity in fixed-bed reactors can be drawn:

$\begin{array}{llllll}\mathbf{Assumption}\hfill & \hfill \text{Multiplicity in }\text{all stages}\hfill & \hfill \hfill & \hfill \text{Two key stages }\left(\text{reaction front}\right)\hfill & \hfill \hfill & \hfill \mathrm{Cluster formation}\hfill \\ \mathbf{Max}\#\mathbf{MSS}\hfill & \hfill 3^n\hfill & \hfill \Rightarrow \hfill & \hfill 4n-1\hfill & \hfill \Rightarrow \hfill & \hfill 3\mathrm{to}5\hfill \end{array}$

Moving from left to right considers more physical details and approaches the situation in real fixed-bed reactors. This three-level hierarchy compromises many different and controversial opinions found in the literature (see State-Space Multiplicity). For instance, the findings of Eigenberger (1972a), and Eigenberger (1972b) reporting only three to five multiple steady states are mainly associated with cluster formation, whereas studies that report an infinite number of multiple steady states (for $n\to \infty$) neglect clustering and count each state separately.

So far, state clustering and its connection to reaction fronts and multiplicity in real reactors is rather disregarded in literature. One reason might be the missing availability for efficient numerical tools, which have only been accessible in recent years. Since the previous considerations mainly address multiplicity trends, it remains to be shown under which conditions uniqueness applies.

Until today, an exact uniqueness criterion for non-isothermal fixed-bed reactors largely remains an open question (Dochain, 2018). The axial dispersion model has been a favorite target for extensive mathematical analyses but often limited to first-order reactions under isothermal conditions (Schmitz, 1975; Varma, 1980; Arce and Ramkrishna, 1991). However, numerous studies provide qualitative trends pointing in similar directions. For instance, Jensen and Ray (1982) summarized, that the solution will be unique for sufficiently high Bodenstein numbers, large heat transfer coefficients, or small Damköhler numbers. The previous results are very much in line with these qualitative trends, but moreover, they reveal generalized criteria for stability, uniqueness, and multiplicity of non-isothermal fixed-bed reactors. These criteria are derived in the following.

Stability, Uniqueness, and Multiplicity Criteria for Real Non-Isothermal Reactors

The observations from above show that the thermo-kinetic multiplicity feature of the first stage is entirely capable of representing the three main state clusters. Consequently, if the first stage is free of multiplicity, then all following stages are also free of multiplicity. This key feature enables the criteria of the first CSTR stage (see Eqs 8‐10) to be assigned to the entire CSTR cascade (cell model) according to

$\begin{array}{c}\text{stability}\left(\text{CM}\right):\hspace{1em}\frac{\mathrm{d}{X}^{\left\{1\right\}}}{\mathrm{d}T}<\frac{1+\frac{\text{St}}{\text{n}}}{\text{Δ}{T}_{\text{ad}}^{\left\{1\right\}}},\\ \text{uniqueness}\left(\text{CM}\right):\hspace{1em}\underset{T\in \mathcal{O}}{\text{max}}\frac{\mathrm{d}{X}^{\left\{1\right\}}}{\mathrm{d}T}={\frac{\mathrm{d}{X}^{\left\{1\right\}}}{\mathrm{d}T}|}_{T=T^{\text{*}}}\le \frac{1+\frac{\text{St}}{\text{n}}}{\text{Δ}{T}_{\text{ad}}^{\left\{1\right\}}},\\ \text{multiplicity}\left(\text{CM}\right):\hspace{1em}\underset{T\in \mathcal{O}}{\text{max}}\frac{\mathrm{d}{X}^{\left\{1\right\}}}{\mathrm{d}T}={\frac{\mathrm{d}{X}^{\left\{1\right\}}}{\mathrm{d}T}|}_{T=T^{\text{*}}}>\frac{1+\frac{\text{St}}{\text{n}}}{\text{Δ}{T}_{\text{ad}}^{\left\{1\right\}}},\end{array}$

with $T=T^{\text{*}}$ as inflection point of Eq. 11 corresponding to the steepest conversion gradient. For simplicity, the index CO${}_2$ is omitted here and in the following.

Consequently, in the absence of purely kinetic and isothermal multiplicity, uniqueness in non-isothermal CSTR cascades boils down to very few key parameters, lumped together as mass and energy-based thermal sensitivity. Both sensitivities are evaluated in Figure 13 with respect to the methanation reference setting of Supplementary Table S1.

FIGURE 13

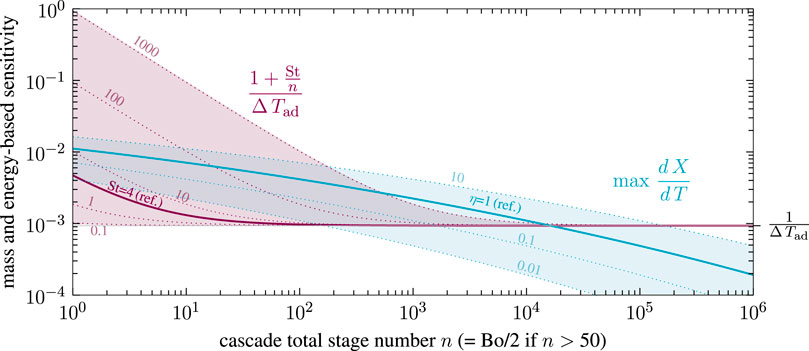
FIGURE 13. First stage mass and energy-based sensitivity for non-isothermal CSTR cascades with various stage number, effectiveness factor and Stanton number, reference setting taken from Supplementary Table S1.

According to the reference setting in Figure 13, uniqueness can only be guaranteed for cascades with several thousand stages. This fact still applies to a wide range of heat transfer and catalyst activity, as indicated by variations of the Stanton number and effectiveness factor. Intensified heat transfer mainly affects cascades with higher back-mixing and leads to reduced multiplicity regions. In some scenarios, uniqueness is guaranteed for low and high back-mixing conditions, but not for the intermediates (e.g., for St = 100 and η = 1). In contrast, reducing the ATR (e.g., via product gas recycling) always leads to diminished multiplicity regions. At adiabatic conditions ($\text{St}\to 0$), back-mixing does not influence the energy-based thermal sensitivity, and uniqueness becomes solely determined by the mass-based thermal sensitivity and the ATR. Not shown is the influence of the remaining key parameters, pressure, and residence time. However, both are indirectly incorporated into the Stanton number and effectiveness factor.

The equivalence of stage and Bodenstein number in Eq. 3 at low back-mixing (Bo $>$ 100) allows for the transition from cell to dispersion models.^a Therefore, we introduce a surrogate conversion$\tilde{X}$ which allows for applying the first stage mass balance from Eq. 11 to dispersion models according to

$0=\tilde{X}-\frac{2}{\text{Bo}}\frac{\tau }{\epsilon c_{\text{in}}}\text{R}=\tilde{X}-C_{\text{Bo}}\text{R},(15)$

which is then used to calculate the mass-based thermal sensitivity of a fixed-bed reactor. Together with the adapted energy-based thermal sensitivity from Eq. 12 at elevated Bodenstein numbers (Bo $>$ 100) the previous criteria read as

$\text{stability}\left(\text{DM}\right):\hspace{1em}\frac{\mathrm{d}\tilde{X}}{\mathrm{d}T}<\frac{1+\frac{2\text{St}}{\text{Bo}}}{\text{Δ}{T}_{\text{ad},\text{in}}},(16)$

$\text{uniqueness}\left(\text{DM}\right):\hspace{1em}\underset{T\in \mathcal{O}}{\text{max}}\frac{\mathrm{d}\tilde{X}}{\mathrm{d}T}={\frac{\mathrm{d}\tilde{X}}{\mathrm{d}T}|}_{T=T^{\text{*}}}\le \frac{1+\frac{2\text{St}}{\text{Bo}}}{\text{Δ}{T}_{\text{ad},\text{in}}},(17)$

$\text{multiplicity}\left(\text{DM}\right):\hspace{1em}\underset{T\in \mathcal{O}}{\text{max}}\frac{\mathrm{d}\tilde{X}}{\mathrm{d}T}={\frac{\mathrm{d}\tilde{X}}{\mathrm{d}T}|}_{T=T^{\text{*}}}>\frac{1+\frac{2\text{St}}{\text{Bo}}}{\text{Δ}{T}_{\text{ad},\text{in}}},(18)$

with $T=T^{\text{*}}$ as inflection point of Eq. 11 corresponding to the steepest conversion gradient. The evaluation of the reference setting from Supplementary Table S1 leads to the same results as in Figure 13 with $n=\text{Bo}/2$.

The generalized Criteria16-18 have not been found in literature yet. They can be used as an a priori estimate for any exothermic reaction and reactors at any scale, only requiring apparent rate expression, coolant heat transfer coefficient, inlet condition, and back-mixing intensity. Note that no expensive computation of the entire dispersion model is required, which makes it easy to use for reactor design, operation, and safety analysis. The criteria, however, demand for a representative Bodenstein number either mass or energy-based. As illustrated in State-Space Multiplicity, the energy feedback is of major interest for thermo-kinetic multiplicity, which indicates that the three to ten times smaller energy-based Bodenstein number is the most reasonable choice. Furthermore, the here proposed criteria recommends considering axial dispersion even for high Bodenstein numbers beyond 400. This is contrary to commonly accepted criteria of Hlaváček and Marek (1966), Mears (1976), Young and Finlayson (1973), and Mederos et al. (2009), which did neither consider multiplicity nor reactor stability.

In order to access the mass-based sensitivity on the left, the total differential applied to the implicit Eq. 15 may help:

$0=\frac{\mathrm{d}\tilde{X}}{\mathrm{d}T}-C_{\text{Bo}}\frac{\mathrm{d}\text{R}}{\mathrm{d}T}=\frac{\mathrm{d}\tilde{X}}{\mathrm{d}T}-C_{\text{Bo}}\left(\frac{\partial \text{R}}{\partial T}+\frac{\partial \text{R}}{\partial \tilde{X}}\frac{\mathrm{d}\tilde{X}}{\mathrm{d}T}\right).$

Consequently, the sensitivity is represented by

$\frac{\mathrm{d}\tilde{X}}{\mathrm{d}T}=\frac{C_{\text{Bo}}\frac{\partial \text{R}}{\partial T}}{1-C_{\text{Bo}}\frac{\partial \text{R}}{\partial \tilde{X}}}.(19)$

Thus, the mass-based sensitivity only requires valid reaction rates, their partial derivatives and the main reactor parameters used in Eq. 15. For first-order, equimolar reactions, the first Damköhler number from Supplementary Eq. S7 can be used to further simplify Eq. 19 via

$\begin{array}{c}\tilde{X}=\frac{2}{\text{Bo}}{\text{Da}}_{\text{I}}(1-\tilde{X})=\frac{\frac{2}{\text{Bo}}{\text{Da}}_{\text{I}}}{1+\frac{2}{\text{Bo}}{\text{Da}}_{\text{I}}},\\ \frac{\mathrm{d}\tilde{X}}{\mathrm{d}T}=\frac{\frac{2}{\text{Bo}}{\text{Da}}_{\text{I}}}{1+\frac{2}{\text{Bo}}{\text{Da}}_{\text{I}}}(1-\tilde{X})\frac{E_{\text{A}}}{\mathcal{R}{T}^2}=\frac{\frac{2}{\text{Bo}}{\text{Da}}_{\text{I}}}{{\left(1+\frac{2}{\text{Bo}}{\text{Da}}_{\text{I}}\right)}^2}\frac{E_{\text{A}}}{\mathcal{R}{T}^2}.\end{array}(20)$

With Eq. 20, the mass-based sensitivity can be evaluated within the relevant temperature range to identify the maximum gradient at $T^{\text{*}}$ and ${\text{Da}}_{\text{I}}^{\text{*}}$. Thus, there is no further need to solve the implicit Eq. 15. Note that the here used Damköhler number remains as a function of temperature such that the above criteria condense to

$\text{stability}\left(1^{\text{st}}-\text{order},\text{equimolar}\right):\frac{\frac{2}{\text{Bo}}{\text{Da}}_{\text{I}}}{{\left(1+\frac{2}{\text{Bo}}{\text{Da}}_{\text{I}}\right)}^2}\frac{E_{\text{A}}}{\mathcal{R}{T}^2}<\frac{1+\frac{2\text{St}}{\text{Bo}}}{\text{Δ}{T}_{\text{ad},\text{in}}},(21)$

$\text{uniqueness}\left(1^{\text{st}}-\text{order},\text{equimolar}\right):\frac{\frac{2}{\text{Bo}}{\text{Da}}_{\text{I}}^{\text{*}}}{{\left(1+\frac{2}{\text{Bo}}{\text{Da}}_{\text{I}}^{\text{*}}\right)}^2}\frac{E_{\text{A}}}{\mathcal{R}{T}^{\text{*}2}}\le \frac{1+\frac{2\text{St}}{\text{Bo}}}{\text{Δ}{T}_{\text{ad},\text{in}}},(22)$

$\text{multiplicity}\left(1^{\text{st}}-\text{order},\text{equimolar}\right):\frac{\frac{2}{\text{Bo}}{\text{Da}}_{\text{I}}^{\text{*}}}{{\left(1+\frac{2}{\text{Bo}}{\text{Da}}_{\text{I}}^{\text{*}}\right)}^2}\frac{E_{\text{A}}}{\mathcal{R}{T}^{\text{*}2}}>\frac{1+\frac{2\text{St}}{\text{Bo}}}{\text{Δ}{T}_{\text{ad},\text{in}}},(23)$

with $T^{\text{*}}$ and ${\text{Da}}_{\text{I}}^{\text{*}}$ as arguments of the maximum gradient of Eq. 20. Although these simplified criteria are not adequately applicable for methanation due to the strong influence of the thermodynamic equilibrium, they comprehensively show how the key parameters affect multiplicity. At the beginning of this section, the current state in the literature was highlighted to be rather qualitative. The statement of Jensen and Ray (1982) saying that the solution will be unique for sufficiently high Bodenstein numbers ($\text{Bo}\to \infty$), large heat transfer coefficients ($\text{St}\to \infty$), or small Damköhler numbers ($\text{Da}\to 0$) is perfectly represented by the Criteria22and23. Furthermore, the limiting case of an adiabatic CSTR ($\text{St}\to 0$, $\text{Bo}/2\to 1$) applied to Criteria21 is equivalent to the stability criterion presented by Kimura and Levenspiel (1977).

In extension to the infinite back-mixing case in CSTR Analogy, it can be confirmed that stability and uniqueness are closely related under finite back-mixing conditions. However, the finite back-mixing case ($1<\text{Bo}/2<\infty$) is typically not considered in the literature (Szeifert et al., 2007; Kummer and Varga, 2019), or was found to be insignificant (Balakotaiah et al., 1995) for stability analysis. In contrast, this work shows a distinct relevance of multiplicity for real reactors, so that back-mixing must also be highly relevant for stability, runaway, and parametric sensitivity. In this regard, the quantitative description of all features results in the here proposed Criteria17and22.

Discussions

In summary, uniqueness and multiplicity of real non-isothermal reactors have proven to be decisive characteristics. In addition to the qualitative descriptions prevailing in the literature, the criteria proposed here represent a novel quantitative measure applicable to any exothermic reaction and reactors at any scale. This work also shows that mass and energy back-mixing represents the essential link between uniqueness, multiplicity, stability, runaway, and parametric sensitivity, which are usually treated independently in the literature. The observation that back-mixing remains relevant for these characteristics even at high Bodenstein numbers implies that generally accepted back-mixing criteria of Hlaváček and Marek (1966), Mears (1976), Young and Finlayson (1973), and Mederos et al. (2009) are insufficient for real non-isothermal reactors.

In addition, the CSTR cascade model indicates that a narrow reaction front, not larger than two representative CSTR stages (key stages), mainly determines uniqueness and multiplicity in real non-isothermal fixed-bed reactors. The illustrated state-clustering of the cascade model accounts for the fact that this reaction front may occur at any position within the fixed-bed. From this, a three-level hierarchy is derived, which unifies controversial opinions that still exist in the literature.

In summary, the presented methodology, as well as the derived criteria, shall allow for easier accessibility of fundamental reactor characteristics. This is particularly useful for the future objective of operating chemical reactors more flexible and within larger operating ranges. Therefore the derived criteria may be used for reactor design, control, and safety purposes. Ignoring uniqueness and multiplicity would disregard a broad operating range and thus a substantial reactor performance potential.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

JB and KS contributed conception and design of the study. JB organized the content, ran the computational experiments, and derived the criteria. KS motivated the detailed bifurcation analysis and supervised the project. JB wrote the first draft of the manuscript. All authors contributed to manuscript revision, read and approved the submitted version.

Funding

This research work was partly supported by the DFG Priority Program SPP 2080 “Catalysts and reactors under dynamic conditions for energy storage and conversion”, funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Grant Number 406914011. The author Jens Bremer is also affiliated to the International Max Planck Research School (IMPRS) for Advanced Methods in Process and Systems Engineering, Magdeburg, Germany. Open Access funding provided by the Max Planck Society.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2020.549298/full#supplementary-material.

Glossary

Latin

A surface (m²)
Bo Bodenstein number
c concentration (mol/m³)
$c_p$ heat capacity (J/(kgK))
C constant (various)
${\text{Da}}_{\text{I}}$ first Damköhler number
$\mathcal{D}$ diffusion coefficient (m²/s)
$E_{\text{A}}$ activation energy (kJ/mol)
F specific gas flow ($\text{NL}/\left({\text{hg}}_{\text{cat}}\right)$)
$\text{k}$ heat transport coefficient (W/(mK))
k reaction rate constant $\left(\text{mol}/\left(\text{bar\hspace{0.17em}}{\text{g}}_{\text{cat}}\text{s}\right)\right)$
K adsorption and equilibrium constant (various)
L reactor length (m)
$\dot{\mathit{m}}$ mass flow (kg/s)
M molar mass (kg/mol)
n total stage number in CSTR cascade
$\text{Pe}$ Péclet number
p pressure (bar)
$\text{r}$ mass-based reaction rate $\left(\text{mol}/\left({\text{g}}_{\text{cat}}\text{s}\right)\right)$
$\tilde{\text{r}}$ molar reaction rate $\left(\text{mol}/\left({\text{m}}_{\text{cat}}^3\text{s}\right)\right)$
R inner radius of tubular reactor (m)
$\text{R}$ reactive source term $\left(\text{mol}/\left({\text{m}}^3\text{s}\right)\right)$
$\mathcal{R}$ universal gas constant $\left(\mathrm{J}/\left(\text{mol\hspace{0.17em}K}\right)\right)$
$\text{St}$ Stanton number
T temperature $\left(\text{K}\right)$
v superficial velocity (m/s)
V reactor volume (m³)
$\dot{\mathit{V}}$ volume flow (m³/s)
w mass fraction
X conversion
x molar fraction

Greek

$\text{Δ}H$ adsorption enthalpy (J/mol)
${\text{Δ}}_R{\tilde{G}}^0$ Gibbs free energy of reaction (STP) (J/mol)
${\text{Δ}}_R{\tilde{H}}^0$ Reaction enthalpy (STP) (J/mol)
$\text{Δ}{T}_{\text{ad}}$ adiabatic temperature rise (K)
$\mathbf{\varepsilon }$ fixed-bed void fraction
η catalyst effectiveness factor
λ thermal conductivity (W/(mK))
ν stoichiometric coefficient
$\mathit{\rho }$ density (kg/m³)
$\mathit{\tau }$ residence time (s)

Subscripts

_α component $\left\{\mathrm{C}{\mathrm{H}}_4,\mathrm{C}{\mathrm{O}}_2,{\mathrm{H}}_{\mathrm{2}}\mathrm{O},{\mathrm{H}}_{\mathrm{2}}\right\}$
${}_{\text{Bo}}$ Bodenstein number
${}_{\text{cat}}$ catalyst phase
${}_{\text{cool}}$ cooling
${}_{\text{eq}}$ equilibrium
${}_{\text{gas}}$ gas phase
${}_{\text{in}}$ inlet
${}_{\text{meth}}$ methanation reaction
${}_{\text{mix}}$ mixture
${}_{\text{n}}$ total stage number
${}_{\text{op}}$ operation
${}_{\text{OP}}$ operation point
${}_{\text{out}}$ outlet
${}_{\text{ref}}$ reference
${}_{\text{P}}$ particle
${}_{\text{z}}$ axial

Superscripts

${}^0$ STP
^c catalyst
^e energy
^eff effective
^exp experimental
^g gas
^m mass
$\text{*}$ arg max value

Abbreviations

ATR adiabatic temperature rise
CM cell model
DM dispersion model
DEN denominator
CSTR continuously stirred tank reactor
PFTR plug flow tubular reactor
RWGS reverse water-gas shift
STP standard temperature and pressure

Footnotes

^aThis equivalence is exploited when the finite volume upwind scheme is used to solve dispersion models numerically. In this case, the corresponding number of finite volumes in flow direction inherently contains a certain degree of back-mixing. If the number of finite volumes is too low, an artificial dispersion (so-called numerical diffusion) will superimpose other dispersion components included in the model.

References

Adaje, J., and Sheintuch, M. (1990). Comparison of multiplicity patterns of a single catalytic pellet and a fixed catalytic bed for ethylene oxidation. Chem. Eng. Sci. 45, 1331–1342. doi:10.1016/0009-2509(90)87125-C

CrossRef Full Text | Google Scholar

Agrawal, R., West, D. H., and Balakotaiah, V. (2007). Modeling and analysis of local hot spot formation in down-flow adiabatic packed-bed reactors. Chem. Eng. Sci. 62, 4926–4943. doi:10.1016/j.ces.2006.11.057

CrossRef Full Text | Google Scholar

Andersson, J. A. E., Gillis, J., Horn, G., Rawlings, J. B., and Diehl, M. (2018). CasADi—A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 11(3), 1–36.

Google Scholar

Arce, P., and Ramkrishna, D. (1991). Pattern formation in catalytic reactors: the role of fluid mixing. AIChE J. 37, 98–110. doi:10.1002/aic.690370109

CrossRef Full Text | Google Scholar

Balakotaiah, V., Kodra, D., and Nguyen, D. (1995). Runaway limits for homogeneous and catalytic reactors. Chem. Eng. Sci. 50, 1149–1171. doi:10.1016/0009-2509(94)00463-2

CrossRef Full Text | Google Scholar

Balakotaiah, V., and Luss, D. (1983). Multiplicity features of reacting systems. Chem. Eng. Sci. 38, 1709–1721. doi:10.1016/0009-2509(83)85028-3

CrossRef Full Text | Google Scholar

Bilous, O., and Amundson, N. R. (1956). Chemical reactor stability and sensitivity: II. Effect of parameters on sensitivity of empty tubular reactors. AIChE J. 2, 117–126. doi:10.1002/aic.690020124

CrossRef Full Text | Google Scholar

S. M. Biollaz, and T. J. Schildhauer (Editors) (2016). Synthetic natural gas from coal, dry biomass, and power-to-gas applications. Hoboken, NJ: John Wiley & Sons, Inc.

Google Scholar

Bostandzhiyan, S. A., and Shkadinskii, K. G. (2010). Multiple steady states and transitional regimes in a cylindrical fixed-bed catalytic reactor. Theor. Found. Chem. Eng. 44, 119–125. doi:10.1134/S0040579510020016

CrossRef Full Text | Google Scholar

Bremer, J., and Sundmacher, K. (2019). Operation range extension via hot-spot control for catalytic CO₂ methanation reactors. React. Chem. Eng. 4, 1019. doi:10.1039/C9RE00147F

CrossRef Full Text | Google Scholar

Dochain, D. (2018). Analysis of the multiplicity of steady-state profiles of two tubular reactor models. Comput. Chem. Eng. 114, 318–324. doi:10.1016/j.compchemeng.2017.10.028

CrossRef Full Text | Google Scholar

Dommeti, S. M. S., Balakotaiah, V., and West, D. H. (1999). Analytical criteria for validity of pseudohomogeneous models of packed-bed catalytic reactors. Ind. Eng. Chem. Res. 38, 767–777. doi:10.1021/ie980365g

CrossRef Full Text | Google Scholar

Dramé, A. K., Lobry, C., Harmand, J., Rapaport, A., and Mazenc, F. (2008). Multiple stable equilibrium profiles in tubular bioreactors. Math. Comput. Model. 48, 1840–1853. doi:10.1016/j.mcm.2008.05.008

CrossRef Full Text | Google Scholar

Eigenberger, G. (1972a). On the dynamic behavior of the catalytic fixed-bed reactor in the region of multiple steady states-I. The influence of heat conduction in two phase models. Chem. Eng. Sci. 27, 1909–1915. doi:10.1016/0009-2509(72)87049-0

CrossRef Full Text | Google Scholar

Eigenberger, G. (1972b). On the dynamic behavior of the catalytic fixed-bed reactor in the region of multiple steady states-II. The influence of the boundary conditions in the catalyst phase. Chem. Eng. Sci. 27, 1917–1924. doi:10.1016/0009-2509(72)87050-7

CrossRef Full Text | Google Scholar

Eigenberger, G. (1983). Dynamik und stabilität verfahrenstechnischer prozesse. Chem. Ing. Tech. 55, 503–515. doi:10.1002/cite.330550702

CrossRef Full Text | Google Scholar

Elnashaie, S., and Elshishini, S. S. (1993). “Modelling, simulation and optimization of industrial fixed bed catalytic reactors,” in Topics in chemical engineering. Philadelphia, Pa: Gordon and Breach, Vol. 7.

Google Scholar

Fache, A., Marias, F., and Chaudret, B. (2020). Catalytic reactors for highly exothermic reactions: steady-state stability enhancement by magnetic induction. Chem. Eng. J. 390, 124531. doi:10.1016/j.cej.2020.124531

CrossRef Full Text | Google Scholar

Fischer, K. L., and Freund, H. (2020). On the optimal design of load flexible fixed bed reactors: integration of dynamics into the design problem. Chem. Eng. J. 393, 124722. doi:10.1016/j.cej.2020.124722

CrossRef Full Text | Google Scholar

Gao, J., Wang, Y., Ping, Y., Hu, D., Xu, G., Gu, F., et al. (2012). A thermodynamic analysis of methanation reactions of carbon oxides for the production of synthetic natural gas. RSC Adv. 2, 2358–2368. doi:10.1039/c2ra00632d

CrossRef Full Text | Google Scholar

Gilles, E. D. (1977). Dynamisches verhalten von Festbettreaktoren. Chem. Ing. Tech. 49, 142–149. doi:10.1002/cite.330490211

CrossRef Full Text | Google Scholar

Gilles, E. D., and Hofmann, H. (1961). Bemerkung zu der Arbeit: “an analysis of chemical reactor stability and control”. Chem. Eng. Sci. 15, 328–331. doi:10.1016/0009-2509(61)85038-0

CrossRef Full Text | Google Scholar

Harold, M. P., and Luss, D. (1985). An experimental study of steady-state multiplicity features of two parallel catalytic reactions. Chem. Eng. Sci. 40, 39–52. doi:10.1016/0009-2509(85)85045-4

CrossRef Full Text | Google Scholar

W. M. Haynes (Editor) (2017). CRC handbook of chemistry and physics: a ready-reference book of chemical and physical data. 97th Edn. Boca Raton, London and New York: CRC Press.

Google Scholar

Heinemann, R. F., and Poore, A. B. (1981). Multiplicity, stability, and oscillatory dynamics of the tubular reactor. Chem. Eng. Sci. 36, 1411–1419. doi:10.1016/0009-2509(81)80175-3

CrossRef Full Text | Google Scholar

Heinemann, R. F., and Poore, A. B. (1982). The effect of activation energy on tubular reactor multiplicity. Chem. Eng. Sci. 37, 128–131. doi:10.1016/0009-2509(82)80079-1

CrossRef Full Text | Google Scholar

Hlaváček, V., and Marek, M. (1966). Axialer stoff- und Wärmetransport im adiabatischen Rohrreaktor—II. Numerische Untersuchung—ablauf einer einfachen Reaktion bezw. einer Folgereaktion. Chem. Eng. Sci. 21, 501–513. doi:10.1016/0009-2509(66)85064-9

CrossRef Full Text | Google Scholar

Jaree, A., Budman, H. M., Hudgins, R. R., Silveston, P. L., Yakhnin, V., and Menzinger, M. (2001). Temperature excursions in reactors packed with segregated layers of catalyst and inert solids. Chem. Eng. Sci. 56, 5719–5726. doi:10.1016/S0009-2509(01)00285-8

CrossRef Full Text | Google Scholar

Jensen, K. F., and Ray, W. H. (1982). The bifurcation behavior of tubular reactors. Chem. Eng. Sci. 37, 199–222. doi:10.1016/0009-2509(82)80155-3

CrossRef Full Text | Google Scholar

Kalthoff, O., and Vortmeyer, D. (1980). Ignition/extinction phenomena in a wall cooled fixed bed reactor. Chem. Eng. Sci. 35, 1637–1643. doi:10.1016/0009-2509(80)80056-X

CrossRef Full Text | Google Scholar

Kiewidt, L. (2017). Solid sponges as support for heterogeneous catalysts in gas-phase reactions. PhD thesis. Bremen: University of Bremen.

Google Scholar

Kiewidt, K., and Thöming, J. (2019). Pareto-optimal design and assessment of monolithic sponges as catalyst carriers for exothermic reactions. Chem. Eng. J., 359, 496–504. doi:10.1016/j.cej.2018.11.109

Kimura, S., and Levenspiel, O. (1977). Temperature excursions in adiabatic packed bed reactors. Ind. Eng. Chem. Proc. Des. Dev. 16, 145–148. doi:10.1021/i260061a610

CrossRef Full Text | Google Scholar

Kopyscinski, J., Schildhauer, T. J., and Biollaz, S. M. A. (2010). Production of synthetic natural gas (SNG) from coal and dry biomass—a technology review from 1950 to 2009. Fuel 89, 1763–1783. doi:10.1016/j.fuel.2010.01.027

CrossRef Full Text | Google Scholar

Koschany, F., Schlereth, D., and Hinrichsen, O. (2016). On the kinetics of the methanation of carbon dioxide on coprecipitated NiAl(O). Appl. Catal. B Environ. 181, 504–516. doi:10.1016/j.apcatb.2015.07.026

CrossRef Full Text | Google Scholar

Kreitz, B., Wehinger, G. D., and Turek, T. (2019). Dynamic simulation of the CO₂ methanation in a micro-structured fixed-bed reactor. Chem. Eng. Sci. 195, 541–552. doi:10.1016/j.ces.2018.09.053

CrossRef Full Text | Google Scholar

Kubíček, M., and Marek, M. (1983). “Computational methods in bifurcation theory and dissipative structures,” in Springer series computational physics. Berlin, Heidelberg and New York, NY: Springer. doi:10.1007/978-3-642-85957-1

CrossRef Full Text | Google Scholar

Kummer, A., and Varga, T. (2019). Completion of thermal runaway criteria: two new criteria to define runaway limits. Chem. Eng. Sci. 196, 277–290. doi:10.1016/j.ces.2018.11.008

CrossRef Full Text | Google Scholar

Lee, C. K., Morbidelli, M., and Varma, A. (1987). Steady state multiplicity behavior of an isothermal axial dispersion fixed-bed reactor with nonuniformly active catalyst. Chem. Eng. Sci. 42, 1595–1608. doi:10.1016/0009-2509(87)80164-1

CrossRef Full Text | Google Scholar

Lemmon, E. W., McLinden, M. O., and Friend, D. G. (1998). “Thermophysical properties of fluid systems,” in NIST chemistry webbook, NIST standard reference database. Editors P. J. Linstrom, and W. G. Mallard (Gaithersburg, MD: National Institute of Standards and Technology), Vol. 69. doi:10.18434/T4D303

CrossRef Full Text | Google Scholar

Levenspiel, O. (1999). Chemical reaction engineering. 3rd Edn. Hoboken, NJ: Wiley.

Google Scholar

Liu, S.-L., and Amundson, N. R. (1962). Stability of adiabatic packed bed reactors. an elementary treatment. Ind. Eng. Chem. Fund. 1, 200–208. doi:10.1021/i160003a008

CrossRef Full Text | Google Scholar

Liu, S.-L., and Amundson, N. R. (1963). Stability of adiabatic packed-bed reactors. effect of axial mixing. Ind. Eng. Chem. Fund. 2, 183–189. doi:10.1021/i160007a004

CrossRef Full Text | Google Scholar

Marwaha, B., and Luss, D. (2003). Hot zones formation in packed bed reactors. Chem. Eng. Sci. 58, 733–738. doi:10.1016/S0009-2509(02)00602-4

CrossRef Full Text | Google Scholar

Mears, D. E. (1976). On criteria for axial dispersion in nonisothermal packed-bed catalytic reactors. Ind. Eng. Chem. Fund. 15, 20–23. doi:10.1021/i160057a004

CrossRef Full Text | Google Scholar

Mederos, F. S., Ancheyta, J., and Chen, J. (2009). Review on criteria to ensure ideal behaviors in trickle-bed reactors. Appl. Catal. Gen. 355, 1–19. doi:10.1016/j.apcata.2008.11.018

CrossRef Full Text | Google Scholar

Mohl, K. D., Kienle, A., Sundmacher, K., and Gilles, E. D. (2001). A theoretical study of kinetic instabilities in catalytic distillation processes: influence of transport limitations inside the catalyst. Chem. Eng. Sci. 56, 5239–5254. doi:10.1016/S0009-2509(01)00243-3

CrossRef Full Text | Google Scholar

Moioli, E., Gallandat, N., and Züttel, A. (2019). Parametric sensitivity in the Sabatier reaction over Ru/Al₂O₃—theoretical determination of the minimal requirements for reactor activation. React. Chem. Eng. 4, 100–111. doi:10.1039/C8RE00133B

CrossRef Full Text | Google Scholar

Morbidelli, M., Servida, A., and Varma, A. (1986). Optimal catalyst activity profiles in pellets. 4. Analytical evaluation of the isothermal fixed-bed reactor. Ind. Eng. Chem. Fund. 25, 307–313. doi:10.1021/i100023a001

CrossRef Full Text | Google Scholar

Morbidelli, M., and Varma, A. (1982). Parametric sensitivity and runaway in tubular reactors. AIChE J. 28, 705–713. doi:10.1002/aic.690280502

CrossRef Full Text | Google Scholar

Nekhamkina, O., and Sheintuch, M. (2012). Are 3-D models necessary to simulate packed bed reactors? Analysis and 3-D simulations of adiabatic and cooled reactors. AIChE J. 58, 3494–3503. doi:10.1002/aic.13752

CrossRef Full Text | Google Scholar

Nibbelke, R. H., Hoebink, J. H. B. J., and Marin, G. B. (1998). Kinetically induced multiplicity of steady states in integral catalytic reactors. Chem. Eng. Sci. 53, 2195–2210. doi:10.1016/S0009-2509(98)00055-4

CrossRef Full Text | Google Scholar

Padberg, G., and Wicke, E. (1967). Stabiles und instabiles Verhalten eines adiabatischen Rohrreaktors am Beispiel der katalytischen CO-Oxydation. Chem. Eng. Sci. 22, 1035–1051. doi:10.1016/0009-2509(67)80167-2

CrossRef Full Text | Google Scholar

Papadias, D., Edsberg, L., and Björnbom, P. (2001). Effect of eccentricity and interaction between kinetics and mass transfer on the behaviour of catalytic annular reactors: a comparison between lumped and distributed models. Chem. Eng. Sci. 56, 4863–4878. doi:10.1016/S0009-2509(01)00132-4

CrossRef Full Text | Google Scholar

Pérez-Ramírez, J. (2000). The six-flow reactor technology: a review on fast catalyst screening and kinetic studies. Catal. Today. 60, 93–109. doi:10.1016/S0920-5861(00)00321-7

CrossRef Full Text | Google Scholar

Pita, J., Balakotaiah, V., and Luss, D. (1989). Thermoflow multiplicity in a packed-bed reactor: conduction and cooling effects. AIChE J. 35, 373–384. doi:10.1002/aic.690350305

CrossRef Full Text | Google Scholar

Puszyński, J., and Hlavacek, V. (1984). Experimental study of ignition and extinction waves and oscillatory behavior of a tubular nonadiabatic fixed bed reactor for the oxidation of carbon monoxide. Chem. Eng. Sci. 39, 681–692. doi:10.1016/0009-2509(84)80175-X

CrossRef Full Text | Google Scholar

Puszyński, J., Šnita, D., Hlaváček, V., and Hofmann, H. (1981). A revision of multiplicity and parametric sensitivity concepts in nonisothermal nonadiabatic packed bed chemical reactors. Chem. Eng. Sci. 36, 1605–1609. doi:10.1016/0009-2509(81)80004-8

CrossRef Full Text | Google Scholar

Schmitz, R. A. (1975). “Multiplicity, stability, and sensitivity of states in chemically reacting systems—a review,” in Chemical reaction engineering reviews, Editor H. M. Hulburt (Washington, DC: American Chemical Society), Vol. 148, 156–211. doi:10.1021/ba-1975-0148.ch007

CrossRef Full Text | Google Scholar

Schmitz, R. A., and Amundson, N. R. (1963). An analysis of chemical reactor stability and control-VII. Chem. Eng. Sci. 18, 447–456. doi:10.1016/0009-2509(63)80033-0

CrossRef Full Text | Google Scholar

Sheintuch, M. (1987). The determination of global solutions from local ones in catalytic systems showing steady-state multiplicity. Chem. Eng. Sci. 42, 2103–2114. doi:10.1016/0009-2509(87)85031-5

CrossRef Full Text | Google Scholar

Sheintuch, M. (1997). Dynamics of catalytic reactions and reactors. Catal. Today. 36, 461–476. doi:10.1016/S0920-5861(96)00237-4

CrossRef Full Text | Google Scholar

Sinkule, J., Hlaváček, V., and Votruba, J. (1976a). Modeling of chemical reactors-ΧΧΧI. Chem. Eng. Sci. 31, 31–36. doi:10.1016/0009-2509(76)85005-1

CrossRef Full Text | Google Scholar

Sinkule, J., Votruba, J., Hlaváček, V., and Hofmann, H. (1976b). Modeling of chemical reactors-ΧΧΧ. Chem. Eng. Sci. 31, 23–29. doi:10.1016/0009-2509(76)85004-X

CrossRef Full Text | Google Scholar

Szeifert, F., Chován, T., Nagy, L., Abonyi, J., and Árva, P. (2007). Runaway of chemical reactors: parametric sensitivity and stability. Hungar. J. Ind. Chem. 35. doi:10.1515/127

CrossRef Full Text | Google Scholar

Theurich, S., Rönsch, S., and Güttel, R. (2019). Transient flow rate ramps for methanation of carbon dioxide in an adiabatic fixed‐bed recycle reactor. Energy Technol. 8, 1901116. doi:10.1002/ente.201901116

CrossRef Full Text | Google Scholar

Trinh, S., and Ramkrishna, D. (1996). Pattern formation in fixed bed catalytic reactors-I. Chem. Eng. Sci. 51, 4887–4901. doi:10.1016/0009-2509(96)00298-9

CrossRef Full Text | Google Scholar

Trinh, S., and Ramkrishna, D. (1997). Pattern formation in fixed-bed catalytic reactors-II. Chem. Eng. Sci. 52, 3561–3578. doi:10.1016/S0009-2509(97)00148-6

CrossRef Full Text | Google Scholar

van Heerden, C. (1953). Autothermic processes. Ind. Eng. Chem. 45, 1242–1247. doi:10.1021/ie50522a030

CrossRef Full Text | Google Scholar

Varma, A. (1980). On the number and stability of steady states of a sequence of continuous-flow stirred tank reactors. Ind. Eng. Chem. Fund. 19, 316–319. doi:10.1021/i160075a016

CrossRef Full Text | Google Scholar

Viswanathan, G. A., Sheintuch, M., and Luss, D. (2008). Transversal hot zones formation in catalytic packed-bed reactors. Ind. Eng. Chem. Res. 47, 7509–7523. doi:10.1021/ie8005726

CrossRef Full Text | Google Scholar

Wagialla, K. M., and Elnashaie, S. S. E. H. (1995). Bifurcation and complex dynamics in fixed-bed catalytic reactors. Chem. Eng. Sci. 50, 2813–2832. doi:10.1016/0009-2509(95)00042-4

CrossRef Full Text | Google Scholar

Wedel, S., and Luss, D. (1984). Steady-state multiplicity features of an adiabatic fixed-bed reactor with Langmuir-Hinshelwood kinetics; carbon monoxide or carbon dioxide methanation. Ind. Eng. Chem. Fund. 23, 280–288. doi:10.1021/i100015a003

CrossRef Full Text | Google Scholar

Wenzel, M. (2018). Reverse water-gas shift chemical looping for syngas production from CO₂. PhD thesis. Magdeburg: Otto-von-Guericke-Universität Magdeburg. doi:10.25673/13421

CrossRef Full Text | Google Scholar

Wood, D. A., Nwaoha, C., and Towler, B. F. (2012). Gas-to-liquids (gtl): a review of an industry offering several routes for monetizing natural gas. J. Nat. Gas Sci. Eng. 9, 196–208. doi:10.1016/j.jngse.2012.07.001

CrossRef Full Text | Google Scholar

Xu, J., and Froment, G. F. (1989). Methane steam reforming, methanation and water-gas shift: I. Intrinsic kinetics. AIChE J. 35, 88–96. doi:10.1002/aic.690350109

CrossRef Full Text | Google Scholar

Young, L. C., and Finlayson, B. A. (1973). Axial dispersion in nonisothermal packed bed chemical reactors. Ind. Eng. Chem. Fund. 12, 412–422. doi:10.1021/i160048a004

CrossRef Full Text | Google Scholar

Zaldívar, J. M., Cano, J., Alós, M. A., Sempere, J., Nomen, R., Lister, D., et al. (2003). A general criterion to define runaway limits in chemical reactors. J. Loss Prev. Process. Ind. 16, 187–200. doi:10.1016/S0950-4230(03)00003-2

CrossRef Full Text | Google Scholar

Zimmermann, R. T., Bremer, J., and Sundmacher, K. (2020). Optimal catalyst particle design for flexible fixed-bed CO2 methanation reactors. Chem. Eng. J. 387, 123704. doi:10.1016/j.cej.2019.123704

CrossRef Full Text | Google Scholar