An Eulerian Single-Phase Transport Model for Solid Fission Products in the Molten Salt Fast Reactor: Development of an Analytical Solution for Verification Purposes

Nuclear reactor modeling has been shifting, over the last decades, towards full-core multiphysics analysis due to the ever-increasing safety requirements and complexity of the designs of innovative systems. This is particularly true for liquid-fuel reactor concepts such as the Molten Salt Fast Reactor (MSFR), given their strong intrinsic coupling between thermal-hydraulics, neutronics and fuel chemistry. In the MSFR, fission products (FPs) are originated within the liquid fuel and are carried by the fuel flow all over the reactor core and through pumping and heat exchange systems. Some of FP species, in the form of solid precipitates, can represent a major design and safety challenge, e.g., due to deposition on solid boundaries, and their distribution in the core is relevant to the design and safety analysis of the reactor. In this regard it is essential, both for the design and the safety assessment of the reactor, the capability to model the transport of solid FPs and their deposition to the boundary (e.g., wall or heat exchanger structures). To this aim, in this study, models of transport of solid FPs in the MSFR are developed and verified. An Eulerian single-phase transport model is developed and integrated in a consolidated multiphysics model of the MSFR based on the open-source CFD library OpenFOAM. In particular, general mixed-type deposition boundary conditions are considered, to possibly describe different kinds of particle-wall interaction mechanisms. For verification purposes, analytical solutions for simple case studies are derived ad hoc based on the extension of the classic Graetz problem to linear decay, distributed source terms and mixed-type boundary conditions. The results show excellent agreement between the two models, and highlight the effects of decay and deposition phenomena of various intensity. The resulting approach constitutes a computationally efficient tool to extend the capabilities of CFD-based multiphysics MSFR calculations towards the simulation of solid fission products transport.

1 Introduction

Liquid-fuel reactor concepts have gained renewed interest over the last years. Among them, the Molten Salt Reactor (MSR) and, in particular, the fast-spectrum MSFR (Molten Salt Fast Reactor) has obtained a prominent role thanks to the selection as one of the Generation IV reference technologies (Serp et al., 2014). The adoption of a circulating liquid fuel, in conjunction with the fast neutron spectrum, makes the MSFR system unique from the design and modeling viewpoints. Internal heat generation, fuel thermal feedback and transport of delayed neutron precursors and fission products lead to a strong intrinsic coupling between thermal-hydraulics, neutronics and fuel chemistry. Reactor modeling efforts have therefore shifted towards full-core and multiphysics analysis to meet the requirements and complexity of physical and computational models for the MSFR. A comprehensive account of state-of-the-art multiphysics modeling tools for the MSFR can be found in the work of Tiberga et al. (2020).

In the MSFR, fission products (FPs) that are originated within the fuel as the result of fission reactions are not retained by solid fuel elements and are therefore free to be carried by the liquid fuel flow within the primary circuit. The presence of mobile FPs represents a major design and safety challenge, as some of them are not expected to form stable compounds with the constituents of the fuel salt mixture (Grimes, 1970; Baes, 1974) and therefore give rise to separate phases, either in the form of solid precipitates or gas bubbles. In the case of solid FPs, precipitates are likely to deposit on reactor solid surfaces (Kedl, 1972; Compere et al., 1975) with potential issues such as formation of localized decay heat sources as well as deterioration of heat exchanger performance. Surface deposits might also pose a serious radiological threat in inspection/maintenance operations. Despite the analysis of FPs transport in recent MSFR studies is still limited, information on their distribution over the reactor core has great relevance for the design of the reactor, and in particular for the analysis of removal/reprocessing (Delpech et al., 2009) and bubbling (Cervi et al., 2019b) units. In this regard, there has been focus on modelling the behavior and effects of Xenon transport in MSRs (Price et al., 2020). Concerning metallic FPs, their analysis in the context of a multiphysics system code for the study of the Molten Salt Reactor Experiment has been recently addressed by Walker and Ji (2021). The aim of this work is the development of models of transport of solid FPs and their integration in state-of-the-art multiphysics tools adopted for MSFR analysis. To this aim, a single-phase Eulerian transport modeling approach is chosen, which represents a common and versatile choice for particle transport modeling in complex turbulent flows, and allows for the direct implementation in consolidated MSFR codes. A similar approach has been recently employed for the coupling of CFD and equilibrium chemistry calculations with application to localized-corrosion modeling in lead-cooled reactors (Marino et al., 2020). The development platform is the C++ open-source finite-volume CFD library OpenFOAM (OpenFOAM, 2021).

A preliminary implementation is here described and verified against analytical solutions for simplified test cases. The analytical solutions are derived from the well-known Graetz problem, which is here formulated for a general case with distributed source terms, linear decay and mixed-type boundary conditions. To the authors knowledge, such form of the Graetz problem has not been addressed in detail in the literature, and therefore the complete derivation is here reported. The influence of some key model parameters is discussed, and corresponding solutions from the OpenFOAM and analytical models are presented and compared.

The paper is organized as follows. The adopted multiphysics approach is briefly described in Section 2.1. In Section 2.2, the proposed FPs transport model implemented in the OpenFOAM solver is described in detail. The analytical solution against which the OpenFOAM FPs transport model is verified is presented in Section 2.3. Section 3 presents the results of the verification together with some discussion. Conclusive remarks are finally reported in Section 4.

2 Materials and Methods

2.1 The Multiphysics Model

The OpenFOAM library, based on standard finite-volume methods for CFD calculations, is used to develop the numerical solver used in the present work. Originally developed for the transient analysis of the MSFR (Aufiero et al., 2014), the adopted multiphysics solver was recently extended to allow for the study of compressibility effects during super-prompt-critical transients (Cervi et al., 2019b) and of the bubbling system (Cervi et al., 2019a). The version employed in this work features single-phase incompressible thermal-hydraulics, multi-group neutron diffusion and transport equations for delayed neutron and decay heat precursors. Transport equations for fission products are solved alongside the other physical modules, to provide a fully-coupled multiphysics simulation. All model equations are solved by means of finite-volume discretization, following an iterative segregated coupling approach.

2.1.1 Thermal-Hydraulics Model

Continuity, momentum and energy (in temperature form) conservation equations are expressed in a single-phase incompressible formulation:

$\nabla \cdot \mathbf{u}=0(1)$

$\begin{array}{l}\frac{\partial \mathbf{u}}{\partial t}+\nabla \cdot \left(\mathbf{u}{\mathbf{u}}^T\right)=-\frac{1}{\rho }\nabla p+\left[1-{\beta }_T\left(T-T_0\right)\right]\mathbf{g}\\ +\nabla \cdot \left[{\nu }_{eff}\left(\nabla \mathbf{u}+{\left(\nabla \mathbf{u}\right)}^T\right)\right]\end{array}(2)$

$\frac{\partial T}{\partial t}+\nabla \cdot \left(\mathbf{u}T\right)=\nabla \cdot \left({\alpha }_{eff}\nabla T\right)+\frac{q}{\rho c_p}(3)$

where the quantities $\mathbf{u}$, p and T, which correspond to velocity, pressure and temperature, respectively, are intended as averaged in the sense of Reynolds-Averaged Navier-Stokes modeling. It follows that turbulence modeling is performed by means of standard eddy-viscosity based closure models, such as the well-known k-ε model (Launder and Spalding, 1974), for which effective momentum and thermal diffusivities can be expressed as the sum of a laminar and a turbulent contribution:

${\nu }_{eff}=\nu +{\nu }_t(4)$

${\alpha }_{eff}=\alpha +{\alpha }_t=\frac{\nu }{Pr}+\frac{{\nu }_t}{P{r}_t}(5)$

where $Pr$ and $P{r}_t$ are the Prandtl and turbulent Prandtl numbers, respectively. Momentum and energy equations are coupled thanks to the Boussinesq approximation, for which the density value driving the buoyancy term in Eq 2 is linearized around a reference temperature $T_0$ and ${\beta }_T$ represents the volumetric thermal expansion coefficient of the fluid. Except for what concerns density in the linearized buoyancy term, constant average values are used for thermophysical properties to keep the numerics and the coupling between different physics as simple as possible. Finally, q represents a volumetric energy source which includes internal heat generation (both prompt and delayed) and optionally other energy sinks to model heat removal systems.

Pressure-velocity coupling is performed through the standard SIMPLE/PISO algorithms (Patankar and Spalding, 1972; Issa, 1986).

2.1.2 Neutronics Model

The multi-group diffusion model is adopted for neutron flux calculations (Hébert, 2010). Despite some limitations, it is widely employed in standard nuclear reactor analysis. Thanks to its relative simplicity and limited computational effort, it has found several successful applications especially for multiphysics analysis (Aufiero et al., 2014; Fiorina et al., 2016). More recent works have also proposed the extension of OpenFOAM-based multiphysics codes to more advanced neutron transport approaches, e.g. the SP3 model (Fiorina et al., 2017; Cervi et al., 2019b). The diffusion equation for the gth group-integrated neutron flux ${\phi }_g$ reads:

$\frac{1}{v_g}\frac{\partial {\phi }_g}{\partial t}=\nabla \cdot \left(D_{n,g}\nabla {\phi }_g\right)-{\text{Σ}}_{a,g}{\phi }_g-{\displaystyle \sum }_{h\ne g}{\text{Σ}}_{s,g\to h}{\phi }_g+\left(1-{\beta }_d\right){\chi }_{p,g}\frac{{\overline{\nu }}_g}{k_{eff}}{\text{Σ}}_{f,g}{\phi }_g+S_{n,g}(6)$

where $S_{n,g}$ is the explicit neutron source of the gth group, constituted by prompt fission and scattering neutrons from other groups and delayed neutron precursors decay:

$S_{n,g}=\left(1-{\beta }_d\right){\displaystyle \sum }_{h\ne g}{\chi }_{p,h}\frac{{\overline{\nu }}_h}{k_{eff}}{\text{Σ}}_{f,h}{\phi }_h+{\displaystyle \sum }_{h\ne g}{\text{Σ}}_{s,h\to g}{\phi }_h+{\chi }_{d,h}{\displaystyle \sum }_k{\lambda }_k{c}_k(7)$

The presence of ${\phi }_h$ in the explicit source term $S_{n,g}$ couples the transport equations for different energy groups, which are therefore dealt with following a segregated iterative approach. Most symbols have straightforward meaning and are listed in the Nomenclature section. It is worth mentioning that $k_{eff}$ acts as a tunable multiplication factor to model a prescribed reactivity insertion. A power-iteration routine based on the k-eigenvalue method is also included for steady-state simulation, which allows for the iterative adjustment of $k_{eff}$ to attain criticality at a specified power level.

Due to the circulating nature of the fuel, transport equations are formulated also for delayed neutron and decay heat precursors. The transport equation for the concentration of delayed neutron precursors of the kth family $c_k$ reads:

$\frac{\partial c_k}{\partial t}+\nabla \cdot \left(\mathbf{u}{c}_k\right)=\nabla \cdot \left(D_{eff}\nabla c_k\right)-{\lambda }_k{c}_k+{\beta }_{d,k}{\displaystyle \sum }_g{\overline{\nu }}_g{\text{Σ}}_{f,g}{\phi }_g(8)$

A discussion on the diffusion coefficient $D_{eff}$ is given in Section 2.2. We omit here for brevity the transport equation for the decay heat precursors, which is entirely analogous.

Group constants are adjusted as functions of local temperature around reference values to account for Doppler and fuel density effects. For a generic neutron reaction r occurring in the gth energy group:

${\text{Σ}}_{r,g}=\left({\text{Σ}}_{r,g}^0+A_{r,g}^0\text{log}\frac{T}{T_0^{\text{Σ}}}\right)\frac{1-{\beta }_T\left(T-T_0\right)}{1-{\beta }_T\left(T_0^{\text{Σ}}-T_0\right)}(9)$

where Doppler effects are modeled by means of a logarithmic term where ${\text{Σ}}_{r,g}^0$ and $A_{r,g}^0$, respectively represent the cross-section and a corresponding logarithmic coefficient at a reference temperature $T_0^{\text{Σ}}$, whereas density effects are taken into account through a linear correction consistently with the buoyancy term. The reference temperature for cross-sections can be chosen independently from $T_0$. An analogous approach is employed for the correction of the intra-group neutron diffusion coefficient $D_{n,g}$. The quantities ${\text{Σ}}_{r,g}^0$ and $A_{r,g}^0$ are evaluated by means of the Monte Carlo reactor physics and burnup code SERPENT 2 (Leppänen et al., 2015).

2.2 Fission Products Transport Model

Similarly to other transported scalar quantities, each fission product specie is modelled as a continuous scalar concentration field subject to advection, dispersion and decay mechanisms:

$\frac{\partial c}{\partial t}+\nabla \cdot \left(\mathbf{u}c\right)=\nabla \cdot \left(D_{eff}\nabla c\right)-\lambda c+S(10)$

where c is the concentration of the species under consideration, expressed in number of particles per unit volume. $D_{eff}$ is the total particle diffusivity, $\mathbf{u}$ is the carrier velocity field and λ and S represent the decay constant and source of a fission product specie, respectively. When chemical interactions between species and formation of separate phases are neglected, the source term can be simply related to the fission rate through a suitable yield coefficient $y_f$:

$S=y_f{\displaystyle \sum }_g{\text{Σ}}_{f,g}{\phi }_g(11)$

As previously mentioned, this modeling choice is motivated by the need to limit the overall complexity and computational requirements of the MSFR, and to easily integrate such models in state-of-the-art MSFR codes. The single-phase Eulerian approach can still represent a valid approximation, provided that some conditions are met. Theoretical and experimental analysis has suggested that Fick’s diffusion law only applies when inertial effects are negligible, and that particles inertia plays an increasingly dominant role in transport mechanisms as particles size increases (Liu and Agarwal, 1974; Guha, 2008). Little information is known about the expected size of fission product particles in the MSFR, but previous experience with MSRs suggests formation of colloidal suspensions (i.e., with particle diameters approx. between 10^–9 and 10^–6 m) should be expected (Compere et al., 1975) and that simple diffusion laws may apply, at least as a first approximation. The other main condition requires the particle concentration in the carrier fluid to be sufficiently low to make all interactions between each particle and the fluid, or among particles themselves, negligible. Provided that such conditions are met, the adoption of more sophisticated approaches, e.g., Eulerian-Eulerian multiphase or Eulerian-Lagrangian, may prove little benefit at the expense of a much more complex modeling framework.

As regards the particle diffusivity, it is commonly assumed that the diffusivity coefficient $D_{eff}$ may be separated in a laminar and a turbulent contribution, analogously to Eq 5:

$D_{eff}=D+D_t=\frac{\nu }{Sc}+\frac{{\nu }_t}{S{c}_t}(12)$

where $Sc$ and $S{c}_t$ are Schmidt and turbulent Schmidt numbers, respectively. An alternative expression for the laminar diffusivity D is given by the so-called Einstein equation:

$D=\frac{k_{B}T}{3\pi \rho \nu d_p}(13)$

which is derived under the assumption of large Schmidt number $Sc$ (Balboa Usabiaga et al., 2013). $k_B$ is the Boltzmann constant and $d_p$ is the particle diameter. For monodisperse particles in isothermal bulk flow, D can therefore be regarded as a constant. As already stated, the inverse proportionality from Eq 13 between the particle flux and $d_p$ only holds for small values of $d_p$, even in full-laminar flows.

2.2.1 Deposition Modeling

Besides particle transport in the bulk flow, transport mechanisms which lead to deposition need to be addressed separately. First of all, when particle-wall interaction in the boundary layer is considered, a variable diffusion coefficient can be introduced to model hydrodynamic interactions between particles and solid walls (Brenner, 1961). In such case, $D_{eff}$ is assumed as a function of the particle-wall distance:

$D_{eff}=D_{eff}\left(y\right)(14)$

where y denotes the wall-distance in the normal direction in a boundary layer flow. Moreover, it is commonly accepted that $D_{eff}$ is mostly constant in the bulk of the flow and abruptly decreases in a very small layer close to walls. For this reason it can be assumed

$D_{eff}\left(y\right)=F_D\left(y\right)D_{eff}^{\infty }(15)$

where $D_{eff}^{\infty }$ is a constant bulk diffusivity and $F_D\left(y\right)$ a correction factor which is always comprised within 0 and 1 (Brenner, 1961).

Moreover, to model deposition mechanisms and formulate appropriate boundary conditions for the particle concentration field, one possible approach is the inclusion in the transport equation of a particle-wall interaction forcing term based on an interaction potential energy ϕ (Ruckenstein and Prieve, 1973; Bowen et al., 1976). Since boundary layer flows are inherently two-dimensional, close to a generic wall the steady-state transport equation reads

$D_{eff}\left(y\right)\frac{{\partial }^{2}c}{\partial x^2}+\frac{\partial }{\partial y}\left(D_{eff}\left(y\right)\frac{\partial c}{\partial y}+\frac{D_{eff}\left(y\right)}{kT}\frac{\text{d}\varphi }{\text{d}y}c\right)-u\left(y\right)\frac{\partial c}{\partial x}-\lambda c+S=0(16)$

where x and y here denote the longitudinal and transversal directions. This approach is general but introduces significant complication in the general problem. It is therefore beneficial, when possible, to decouple the advection-diffusion and deposition problems.

When the energy potential ϕ and the hydrodynamic interaction effects are significant only over distances of the order of the particle size, this can be effectively achieved by dividing the boundary layer in two regions (Figure 1): the bulk region, where advection occurs and interactions are negligible, and a very thin wall region, where advection is negligible and deposition processes take place. The two regions are subject to an interface condition, which equates the particle concentration $c\left({\delta }_{\varphi }\right)$ and its flux at a certain distance ${\delta }_{\varphi }$ from the wall (with ${\delta }_{\varphi }$ chosen such that $\varphi \left({\delta }_{\varphi }\right)$ is arbitrarily small). It has been shown that, under fairly general hypotheses on ϕ, the coupled solution of the two regions may be approximated such that the wall region influence is collapsed in a first-order reaction boundary condition for the bulk region (Ruckenstein and Prieve, 1973; Prieve and Ruckenstein, 1976):

$D_{eff}^{\infty }\frac{\partial c}{\partial y}=\gamma c,y=0(17)$

where

$\gamma =D_{eff}^{\infty }{\left[{{{\displaystyle \int }}^{\text{}}}_0^{{\delta }_{\varphi }}\left(F_D{\left(y\right)}^{-1}{e}^{\varphi \left(y\right)/kT}-1\right)\text{d}y\right]}^{-1}(18)$

FIGURE 1

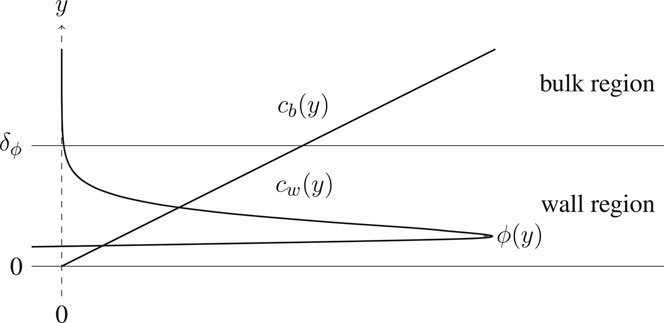
FIGURE 1. Decoupling of the transport and deposition problems: solutions for the wall region ($c_w$) and the bulk region ($c_w$) are obtained separately and joined by imposing interface continuity on particle concentration and particle flux at $y={\delta }_{\varphi }$. The wall region thickness ${\delta }_{\varphi }\ll H$ is defined as the distance at which $\varphi \left({\delta }_{\varphi }\right)$ becomes arbitrarily small.

The coefficient γ is therefore a constant depending on F and ϕ. In principle its value might also depend on the integration limit ${\delta }_{\varphi }$, but it has been shown that in many circumstances its influence on the value of the integral is relatively small over a relatively broad range (Prieve and Ruckenstein, 1976). It should be noted that these results are derived under the assumption of negligible axial diffusion (which is commonly the case) and in absence of source terms and decay. They are, however, representative of a broad class of particle-wall interaction problems and it is here assumed that internal sources or decay phenomena do not alter significantly such behavior.

In the general three-dimensional case, the wall boundary condition can be written as

$-D_{eff}^{\infty }\nabla c\cdot \mathbf{n}=\gamma c(19)$

for any point on the wall boundary, where $\mathbf{n}$ denotes the outward pointing wall-normal direction. Since particle-wall interactions are modeled with a simple first-order boundary condition, the deposited quantities can easily be tracked by solving

$\frac{\partial c_d}{\partial t}=-\lambda c_d+\gamma c(20)$

where $c_d$ represents the surface concentration of deposited particles on the wall boundary, expressed in number of particles per unit area. In this simple model, wall adsorption of FP particles is modeled through a single deposition parameter γ, which has the physical dimensions of a velocity. Desorption mechanisms can be included as well by adding a corresponding term Eq 20,

$\frac{\partial c_d}{\partial t}=-\left(\lambda +\delta \right)c_d+\gamma c(21)$

with δ being the desorption rate constant (Wood et al., 2004).

2.3 Test Case

In this Section the results of the verification of the implemented FP transport model are described. A simple test case with an analytical solution has been chosen. A two-dimensional channel between parallel plates is considered (Figure 2). The particle transport model is decoupled from neutronics and heat transfer models. The source term S from Eq 10 is therefore specified explicitly, and a steady-state isothermal laminar flow is considered.

FIGURE 2

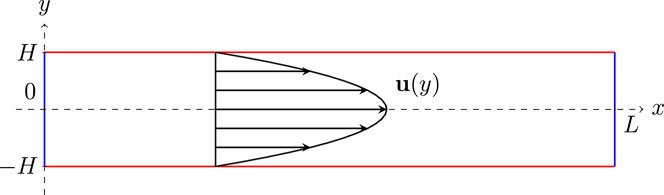
FIGURE 2. Parallel plates geometry: with respect to the flow, the x and y coordinates denote the longitudinal and transversal directions. Inlet and outlet boundaries are located at $x=0$ and $x=L$ respectively, while wall boundaries are located at $y=\pm H$.

The problem here considered resembles the well-known Graetz problem, for which different solutions are available in the literature. An exhaustive treatment of the Graetz theory applied to particle transport problems is given by Bowen et al. (1976), although it doesn’t consider linear decay or distributed source terms. It is indeed difficult to find, in the literature, realistic applications which consider simultaneously, as in the case under consideration, distributed internal sources, decay reactions and mixed type boundary conditions. Corresponding analytical solutions for this specific problem are not found in the literature, and are therefore derived in the following.

2.3.1 Momentum Equation

Analytical solutions of the momentum equation can be found only for simple steady-state fully-developed laminar flow problems. In such a case, the well known parabolic solution reads

$\mathbf{u}=\left[\begin{array}{c}u\left(y\right)\\ 0\end{array}\right](22)$

with

$u\left(y\right)=u_m\left(1-\frac{y^2}{H^2}\right)(23)$

where $u_m$ is the maximum profile velocity and H is half the channel width as depicted in Figure 2.

2.3.2 Particle Concentration Equation

The boundary value problem then becomes, in explicit cartesian coordinates,

$\{\begin{array}{l}D\left(\frac{{\partial }^{2}c}{\partial x^2}+\frac{{\partial }^{2}c}{\partial y^2}\right)-u\left(y\right)\frac{\partial c}{\partial x}-\lambda c+S=0\hfill \\ -\left(\lambda +\delta \right)c_d+\gamma c=0,y=\pm H\hfill \\ \mp D\frac{\partial c}{\partial y}=\gamma c-\delta c_d,y=\pm H\hfill \end{array}(24)$

where D is used, from now on, to denote the constant bulk diffusivity. Boundary conditions for the x-direction are discussed later. The problem is conveniently re-scaled by defining appropriate non-dimensional quantities:

$\widehat{x}=\frac{x}{L}$

$\widehat{y}=\frac{y}{H}$

$\widehat{u}\left(\widehat{y}\right)=\frac{u\left(H\widehat{y}\right)}{u_m}=1-{\widehat{y}}^2$

$\widehat{c}\left(\widehat{x},\widehat{y}\right)=\frac{c\left(L\widehat{x},H\widehat{y}\right)}{c_0}$

${\widehat{c}}_d\left(\widehat{x}\right)=\frac{c_d\left(L\widehat{x}\right)}{H{c}_0}$

$\widehat{S}\left(\widehat{x},\widehat{y}\right)=\frac{H^2}{D}\frac{S\left(L\widehat{x},H\widehat{y}\right)}{c_0}$

where $c_0$ is a concentration value typical of the problem. The equations are then rewritten as

$\{\begin{array}{l}{f}^2\frac{{\partial }^2\widehat{c}}{\partial {\widehat{x}}^2}+\frac{{\partial }^2\widehat{c}}{\partial {\widehat{y}}^2}-fPe\widehat{u}\left(\widehat{y}\right)\frac{\partial \widehat{c}}{\partial \widehat{x}}-Da\widehat{c}+\widehat{S}=0\hfill \\ {\widehat{c}}_d=\frac{Sh}{Da+\text{Δ}}\widehat{c},\widehat{y}=\pm 1\hfill \\ \mp \frac{\partial \widehat{c}}{\partial \widehat{y}}=\frac{DaSh}{Da+\text{Δ}}\widehat{c},\widehat{y}=\pm 1\hfill \end{array}(25)$

where non-dimensional groups are defined as

$Re=\frac{u_{m}H}{\nu }\left(\text{Reynolds number}\right)$

$Sc=\frac{\nu }{D}\left(\text{Schmidt number}\right)$

$Pe=ReSc=\frac{u_{m}H}{D}\left(\text{P}\mathrm{é}\text{clet number}\right)$

$Da=\frac{\lambda H^2}{D}\left(\text{Damk}\mathrm{ö}\text{hler number}\right)$

$Sh=\frac{\gamma H}{D}\left(\text{Sherwood number}\right)$

$\text{Δ}=\frac{\delta H^2}{D}\left(\text{desorption number}\right)$

$f=\frac{H}{L}\left(\text{aspect ratio}\right)$

Longitudinal diffusion is neglected to allow for separation of variables. This assumption is reasonable in all cases where diffusion is negligible compared to advection, i.e., if $Pe\gg f$. Since the order of the equation with respect to x is now reduced, a single (inlet) boundary condition for x is required. As a further simplification, full symmetry of the problem with respect the x-axis is assumed. The full problem now reads

$\{\begin{array}{l}\frac{{\partial }^2\widehat{c}}{\partial {\widehat{y}}^2}-fPe\widehat{u}\left(\widehat{y}\right)\frac{\partial \widehat{c}}{\partial \widehat{x}}-Da\widehat{c}+\widehat{S}=0\hfill \\ {\widehat{c}}_d=\frac{Sh}{Da+\text{Δ}}\widehat{c},\widehat{y}=\pm 1\hfill \\ -\frac{\partial \widehat{c}}{\partial \widehat{y}}=\frac{DaSh}{Da+\text{Δ}}\widehat{c},\widehat{y}=1\hfill \\ \frac{\partial \widehat{c}}{\partial \widehat{y}}=0,\widehat{y}=0\hfill \\ \widehat{c}={\widehat{c}}_{in}=\frac{c_{in}}{c_0},\widehat{x}=0\hfill \end{array}(26)$

where $c_{in}$ specifies a uniform inlet condition for $c\left(0,y\right)$.

For the following discussion, it is convenient to assume that the distributed source can be expressed as

$S\left(x,y\right)=\overline{S}\tilde{S}\left(x,y\right)(27)$

where $\overline{S}$ is a representative value of the source, e.g., its average value over the domain. The choice of $c_0$ is purely a matter of convenience. A meaningful definition, however, is not trivial to find in the general case, given the interplay of several physical phenomena. In the simplest case with no internal source, concentration profiles become self-similar far from the inlet but no fully-developed solutions can be attained (in presence of removal mechanisms such as deposition and decay). In such case, the definition is straightforward:

$c_0=c_{in}(28)$

On the other hand, when a distributed source is present, the inlet contribution is forgotten as the fully-developed concentration profile is attained and therefore a more meaningful choice should be based on the relative intensity of generation and removal mechanisms. When radioactive decay is dominant, a good definition reads

$c_0=\frac{\overline{S}}{\lambda }(29)$

When decay is negligible, the reference concentration $c_0$ can be chosen as

$c_0=\{\begin{array}{cc}\frac{H^2\overline{S}}{D},& Sh\gg 1\\ \frac{H\overline{S}}{\gamma },& Sh\ll 1\end{array}(30)$

These values are useful to identify correct scaling with respect to the dominant removal mechanisms. Similar expressions are easily found when solving for the centerline concentration in fully-developed profiles with uniform source.

Solutions of the boundary value problem Eq 26 can be found by separation of variables:

$\widehat{c}\left(\widehat{x},\widehat{y}\right)={\displaystyle \sum }_{n=1}^{\infty }{X}_n\left(\widehat{x}\right)Y_n\left(\widehat{y}\right)(31)$

2.3.3 Derivation of the Analytical Solution

The functions $Y_n\left(\widehat{y}\right)$ coincide with the eigenfunctions of the associated Sturm-Liouville problem found by isolating the $\widehat{y}$ part of the equation. This can be highlighted by inserting Eq 31 in Eq 26 and after some manipulation:

${\displaystyle \sum }_{n=1}^{\infty }[fPe{Y}_n\frac{\text{d}{X}_n}{\text{d}\widehat{x}}-\frac{1}{\widehat{u}\left(\widehat{y}\right)}\left(\frac{{\text{d}}^2{Y}_n}{\text{d}{\widehat{y}}^2}-Da{Y}_n\right)X_n]=\frac{\widehat{S}\left(\widehat{x},\widehat{y}\right)}{\widehat{u}\left(\widehat{y}\right)}(32)$

The eigenvalue problem is therefore stated as

$\mathrm{ℒ}{Y}_n={\beta }_n^2{Y}_n(33)$

where

$\mathrm{ℒ}=-\frac{1}{\widehat{u}\left(\widehat{y}\right)}\left(\frac{{\text{d}}^2}{\text{d}{\widehat{y}}^2}-Da\right)(34)$

and ${\beta }_n^2$ being the eigenvalue associated to the eigenfunction $Y_n$. The problem must be equipped with the corresponding boundary conditions:

$\{\begin{array}{l}\frac{{\text{d}}^2{Y}_n}{\text{d}{\widehat{y}}^2}+\left({\beta }_n^2-Da-{\beta }_n^2{\widehat{y}}^2\right)Y_n=0\hfill \\ -\frac{\text{d}{Y}_n}{\text{d}\widehat{y}}=\frac{DaSh}{Da+\text{Δ}}{Y}_n,\widehat{y}=1\hfill \\ \frac{\text{d}{Y}_n}{\text{d}\widehat{y}}=0,\widehat{y}=0\hfill \end{array}(35)$

It is easily verified that ${\beta }_n=0$ is not an eigenvalue. Then, through the simple change of variable $\eta =\sqrt{2{\beta }_n}\widehat{y}$, Eq 35 can be recast into one form of the parabolic cylinder equation (DLMF, 2020, Ch. 12):

$\frac{{\text{d}}^2{Y}_n}{\text{d}{\eta }^2}-\left[\frac{{\eta }^2}{4}-\frac{{\beta }_n}{2}\left(1-\frac{Da}{{\beta }_n^2}\right)\right]Y_n=0(36)$

$Y_n\left(\widehat{y}\right)=A_{1,n}{Y}_{1,n}\left(\widehat{y}\right)+A_{2,n}{Y}_{2,n}\left(\widehat{y}\right)(37)$

where

$Y_{1,n}\left(\widehat{y}\right)=e^{-{\beta }_n{\widehat{y}}^2/2}M\left(\frac{1-{\beta }_n}{4}+\frac{Da}{4{\beta }_n},\frac{1}{2};{\beta }_n{\widehat{y}}^2\right)(38)$

$Y_{2,n}\left(\widehat{y}\right)=\sqrt{2{\beta }_n}\widehat{y}{e}^{-{\beta }_n{\widehat{y}}^2/2}M\left(\frac{3-{\beta }_n}{4}+\frac{Da}{4{\beta }_n},\frac{3}{2};{\beta }_n{\widehat{y}}^2\right)(39)$

are two linearly independent solutions. $M(\cdot ,\cdot ;\cdot )$ is the confluent hypergeometric function of the first kind (DLMF, 2020, Ch. 13), which can be expressed as the following power series expansion:

$M\left(a,b;z\right)=1+\frac{a}{b}z+\frac{a\left(a+1\right)}{b\left(b+1\right)}\frac{z^2}{2!}+\dots ={\displaystyle \sum }_{k=0}^{\infty }\frac{{\left(a\right)}_k}{{\left(b\right)}_k}\frac{z^k}{k!}(40)$

where

${\left(a\right)}_k=a\left(a+1\right)\cdots \left(a+k-1\right)={\displaystyle \prod }_{s=1}^k\left(a+s-1\right)(41)$

denotes the so-called Pochhammer symbol, or rising factorial. The eigenvalue problem must be solved by imposing the associated boundary conditions. By means of the following properties of $M\left(a,b;z\right)$,

$M\left(a,b;0\right)=1(42)$

$\frac{\text{d}}{\text{d}z}M\left(a,b;z\right)=\frac{a}{b}M\left(a+1,b+1;z\right),(43)$

it can be easily shown that the symmetry condition at $\widehat{y}=0$ implies $A_{2,n}=0$. The wall boundary condition requires

$\frac{DaSh}{Da+\text{Δ}}{Y}_{1,n}\left(1\right)+{Y^{\prime }}_{1,n}\left(1\right)=0(44)$

which gives the ${\beta }_n$ values that correspond to the non-trivial solutions of the eigenvalue problem. Solutions of Eq 44 have to be found numerically; more detailed numerical considerations can be found in the Supplementary Appendix. The eigenfunctions are therefore determined (up to an arbitrary multiplicative constant) as

$Y_n\left(\widehat{y}\right)=Y_{1,n}\left(\widehat{y}\right)(45)$

whose general solution (back in terms of $\widehat{y}$) can be expressed as

The separated Eq 32 now reads

${\displaystyle \sum }_{n=1}^{\infty }\left(\frac{\text{d}{X}_n}{\text{d}\widehat{x}}+\frac{{\beta }_n^2}{fPe}{X}_n\right)Y_n=\frac{1}{fPe}\frac{\widehat{S}\left(\widehat{x},\widehat{y}\right)}{\widehat{u}\left(\widehat{y}\right)}(46)$

The eigenfunctions $Y_n$ are orthogonal with respect to the scalar product defined as

$\langle f,g\rangle ={{{\displaystyle \int }}^{\text{}}}_{-1}^{+1}\widehat{u}\left(\widehat{y}\right)fg\text{d}\widehat{y}(47)$

with

$\langle Y_m,Y_n\rangle ={{{\displaystyle \int }}^{\text{}}}_{-1}^{+1}\widehat{u}\left(\widehat{y}\right)Y_m{Y}_n\text{d}\widehat{y}=C_n{\delta }_{m,n}(48)$

$C_n=\langle Y_n,Y_n\rangle ={{{\displaystyle \int }}^{\text{}}}_{-1}^{+1}\widehat{u}\left(\widehat{y}\right)Y_n^2\text{d}\widehat{y}(49)$

This is exploited to transform Eq 46 into

$\frac{\text{d}{X}_n}{\text{d}\widehat{x}}+\frac{{\beta }_n^2}{fPe}{X}_n=\frac{1}{fPe}{S}_n\left(\widehat{x}\right)(50)$

whose general solution is

$X_n\left(\widehat{x}\right)=\text{exp}\left(-\frac{{\beta }_n^2}{fPe}\widehat{x}\right)\left[X_n\left(0\right)+\frac{1}{fPe}{{{\displaystyle \int }}^{\text{}}}_0^{\widehat{x}}\text{exp}\left(\frac{{\beta }_n^2}{fPe}\xi \right)S_n\left(\xi \right)\text{d}\xi \right](51)$

To obtain this last form, $\widehat{S}$ has been expanded as

$\widehat{S}\left(\widehat{x},\widehat{y}\right)=\widehat{u}\left(\widehat{y}\right)\stackrel{\infty }{{\displaystyle \sum }_{n=1}}{S}_n\left(\widehat{x}\right)Y_n(52)$

$S_n\left(\widehat{x}\right)=\frac{1}{C_n}{{{\displaystyle \int }}^{\text{}}}_{-1}^{+1}\widehat{S}\left(\widehat{x},\widehat{y}\right)Y_n\text{d}\widehat{y}(53)$

and the arbitrary constants $X_n\left(0\right)$ have been determined from the remaining inlet boundary condition (expanded as well):

$X_n\left(0\right)=\frac{1}{C_n}{{{\displaystyle \int }}^{\text{}}}_{-1}^{+1}\widehat{u}\left(\widehat{y}\right){\widehat{c}}_{in}{Y}_n\text{d}\widehat{y}=\frac{D_n}{C_n}{\widehat{c}}_{in}(54)$

where

$D_n=\langle 1,Y_n\rangle ={{{\displaystyle \int }}^{\text{}}}_{-1}^{+1}\widehat{u}\left(\widehat{y}\right)Y_n\text{d}\widehat{y}(55)$

The normalization constants $C_n$ and $D_n$ can be found by numerical integration of Eqs 49, 55, respectively. More details on their computation are reported in the Supplementary Appendix.

3 Results and Discussion

In this Section, results of the verification of the implemented models against the analytical solutions are presented. In Section 2.3.3 it is shown that, if the effect of desorption is negligible compared to decay, the ${\beta }_n$ are the roots of

$Sh{Y}_n\left(1\right)+{Y^{\prime }}_n\left(1\right)(56)$

with

$Y_n\left(\widehat{y}\right)=e^{-{\beta }_n{\widehat{y}}^2/2}M\left(\frac{1-{\beta }_n}{4}+\frac{Da}{4{\beta }_n},\frac{1}{2};{\beta }_n{\widehat{y}}^2\right)(57)$

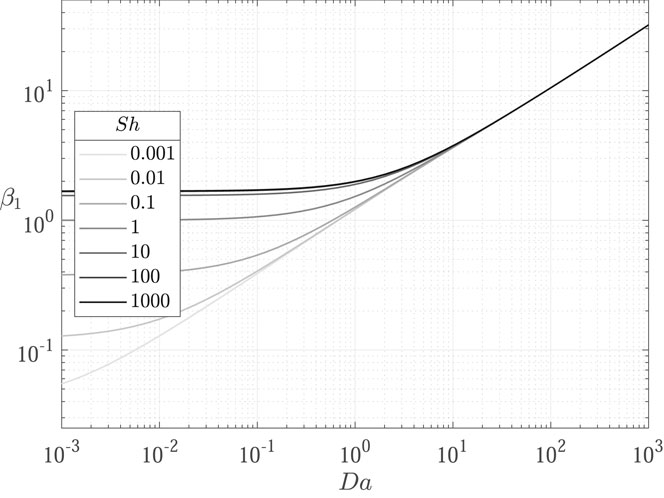
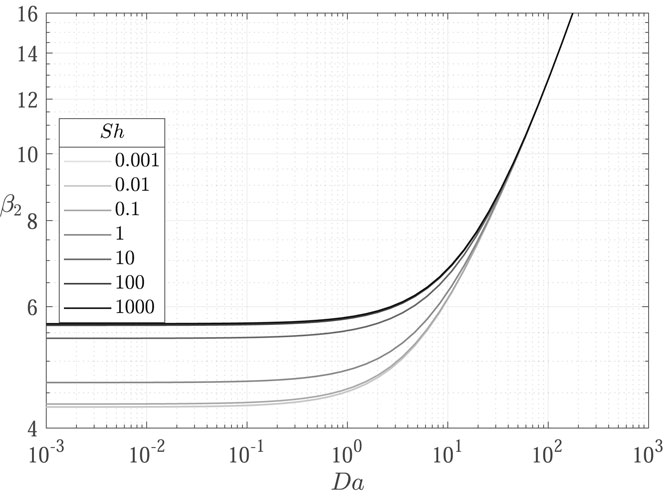
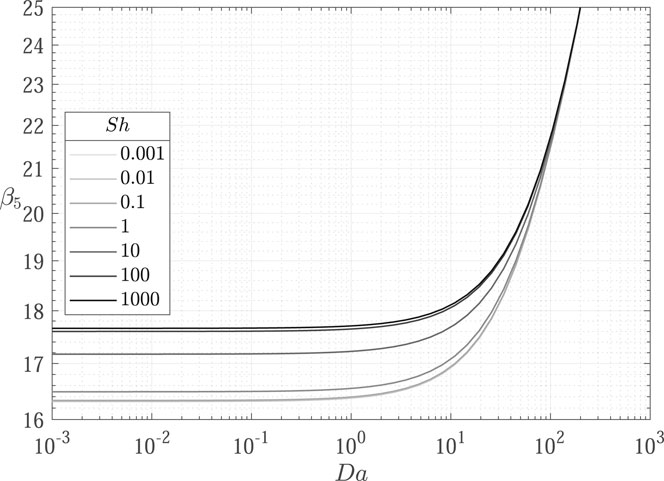
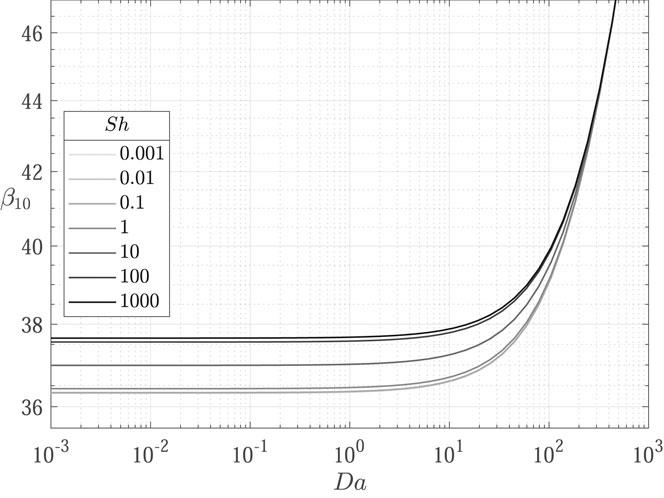
It is therefore evident that the inclusion of a linear decay term in the transport equation affects the concentration profiles shape by shifting the eigenvalues. As shown in Figures 3–6, the influence of the decay parameter $Da$ is significant. For dominant modes, the increase of $Da$ tends to flatten the ${\beta }_n$ curves, resulting in a vanishing influence of $Sh$ in determining the shape of the concentration field. On the contrary, higher-order modes are less affected, with the eigenvalue shift due to linear decay decreasing as n increases.

FIGURE 3

FIGURE 3. Dependence of the 1st eigenvalue ${\beta }_1$ on model parameters $Sh$ and $Da$.

FIGURE 4

FIGURE 4. Dependence of the 2nd eigenvalue ${\beta }_5$ on model parameters $Sh$ and $Da$.

FIGURE 5

FIGURE 5. Dependence of the 5th eigenvalue ${\beta }_5$ on model parameters $Sh$ and $Da$.

FIGURE 6

FIGURE 6. Dependence of the 10th eigenvalue ${\beta }_{10}$ on model parameters $Sh$ and $Da$.

In the following, results from the comparison between the OpenFOAM model described in Section 2.2 and the corresponding analytical solutions are discussed. To highlight the role of decay and deposition phenomena, the selected parameters are $Da$ and $Sh$, with values ranging in [0.1,1,10] for both. Case study parameter values are listed in Table 1, while other relevant parameters of the problem are listed in Table 2.

TABLE 1

TABLE 1. Values of $Da$ and $Sh$ selected for verification cases.

TABLE 2

TABLE 2. Model parameters used in all verification cases.

To simplify the analysis, the inlet concentration is set to zero ($c_{in}=0$). Furthermore, to allow for a direct comparison between different test cases, the reference concentration value has been selected as

$c_0=\frac{H^2\overline{S}}{D}(58)$

It follows that

$\widehat{S}\left(\widehat{x},\widehat{y}\right)=\frac{S\left(L\widehat{x},H\widehat{y}\right)}{\overline{S}}=\tilde{S}\left(L\widehat{x},H\widehat{y}\right)(59)$

Therefore in dimensionless form the solution does not depend on the source term average value, but only on its shape. For the present analysis, a cosine-shaped source term has been selected to resemble the typical shape of fission rate profiles in simplified reactor geometries such as the one here considered:

$\tilde{S}\left(L\widehat{x},H\widehat{y}\right)=\frac{\pi }{2}\text{cos}\left(\frac{\pi }{2}\widehat{y}\right)(60)$

Concentration profiles obtained for the nine test cases (Table 1) are shown in Figures 7–9.

FIGURE 7

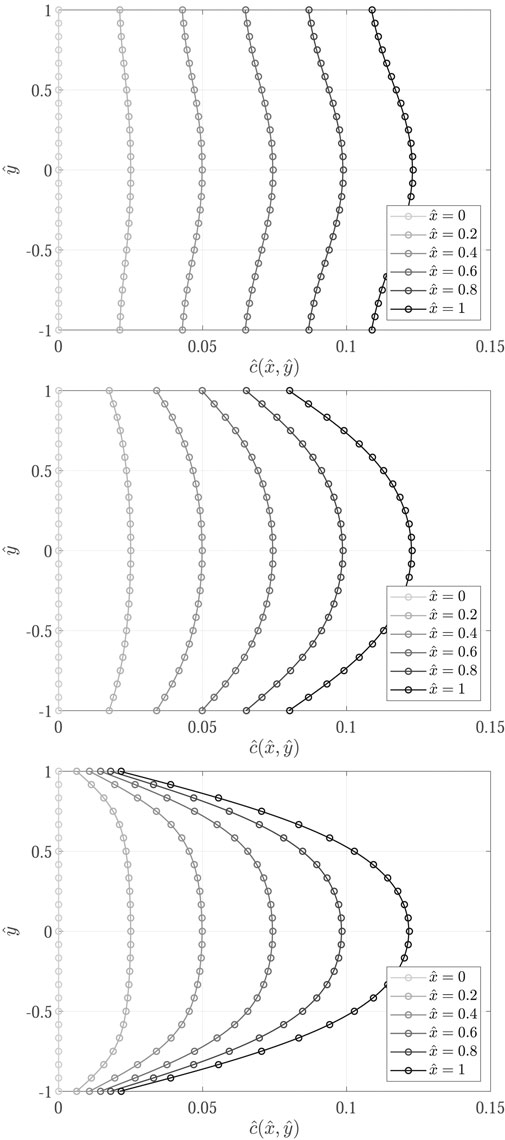
FIGURE 7. Comparison of concentration profiles obtained with the proposed transport model implemented in OpenFOAM ($\circ$) and the corresponding analytical solutions ($-$) for cases 1, 2 and 3 (from top to bottom).

FIGURE 8

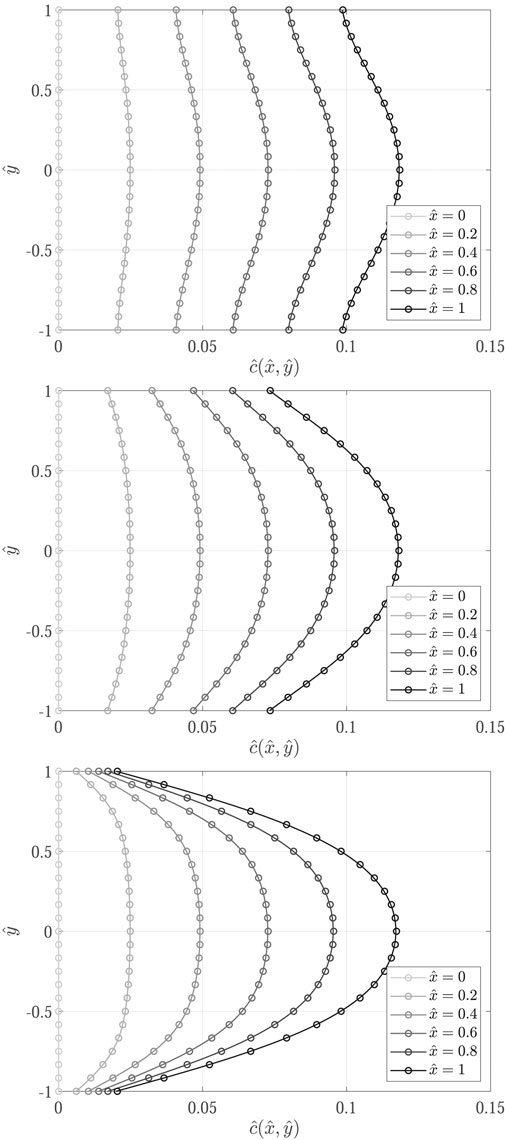
FIGURE 8. Comparison of concentration profiles obtained with the proposed transport model implemented in OpenFOAM ($\circ$) and the corresponding analytical solutions ($-$) for cases 4, 5 and 6 (from top to bottom).

FIGURE 9

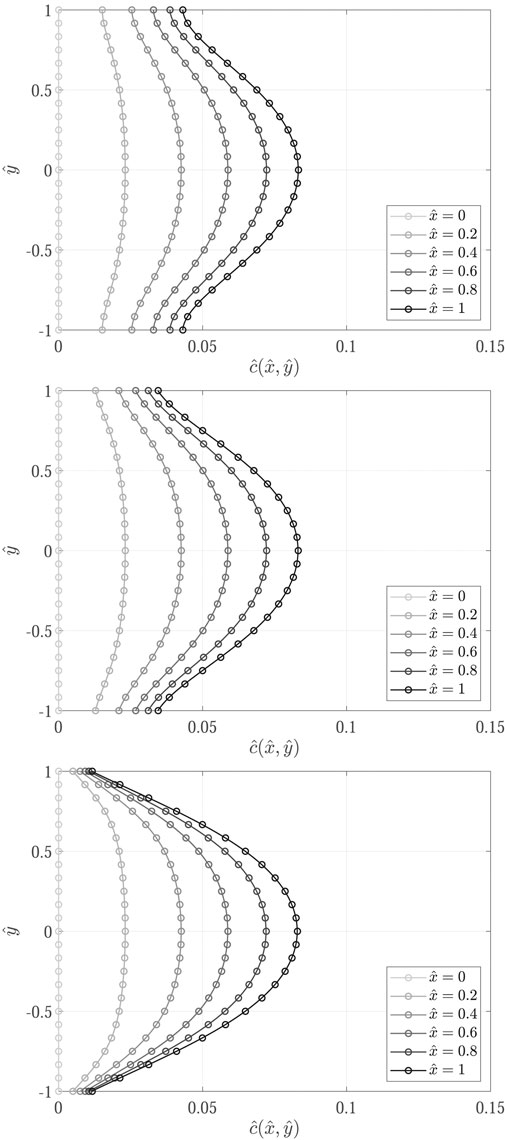
FIGURE 9. Comparison of concentration profiles obtained with the proposed transport model implemented in OpenFOAM ($\circ$) and the corresponding analytical solutions ($-$) for cases 7, 8 and 9 (from top to bottom).

Results show excellent agreement between the proposed transport model and the analytical solutions, proving a successful verification of the implemented transport models in OpenFOAM. The influence of decay is evidenced from the decrease in concentration profiles from $Da=0.1$ to $Da=10$. Besides the average value, the effect of decay is also evident on the shape itself as also pointed out by the analysis of the eigenvalues. With increasing $Da$, particles can diffuse less before decaying, and therefore the concentration profiles tend to resemble more the shape of the source term. The same effect can be seen on the combined effect of deposition: as previously said, the effect of $Sh$ on the profiles is more evident for smaller values of $Da$, while profiles tend to become more similar as $Da$ increases.

We finally report here some brief computational information regarding the verification. All simulations were performed on a structured orthogonal mesh, constituted by 5 × 10⁴ hexahedral volumes, with respectively 500 and 100 divisions on the longitudinal and transversal directions. All 9 cases shown similar convergence behavior, with approximately 5 × 10⁴ pseudo-transient iterations needed to ensure tight convergence for the particle concentration field. Computational times are comparable among all cases, showing no significant dependence on the physical parameters within the selected range (Table 3).

TABLE 3

TABLE 3. Computational times for the verification cases. 5 × 10⁴ iterations are performed on 5 × 10⁴ volumes with eight CPUs.

4 Conclusion

In this paper, the preliminary development of transport models for the solid fission products in the MSFR was discussed. Simplified transport models based on a Eulerian single-phase framework were implemented in consolidated MSFR multiphysics simulation tools based on the open-source finite-volume library OpenFOAM. The resulting model has been verified against analytical solutions for simplified test cases, based on an extended version of the Graetz problem. Results show the good agreement between the two models, proving the correct implementation of the transport and deposition mechanisms considered and the capability of OpenFOAM in treating coupled deposition and decay phenomena of different relative intensities, albeit on a simplified reference problem. The proposed approach constitutes a computationally efficient framework to extend the capabilities of CFD-based multiphysics MSFR calculations towards the simulation of solid fission products transport.

The analytical model used for verification has been developed specifically for this application. The simultaneous presence of distributed internal generation, radioactive decay and mixed deposition boundary condition in a Graetz problem represents an original contribution, and the resulting analytical model could therefore constitute a useful benchmark for future developments of the FPs migration model and for other similar MSFR applications. Future work will include the analysis of the integration of FPs transport in a full reactor simulation. In this regard, turbulent transport in more complex geometries may lead to large concentration gradients close to walls, with the need for mesh refinement. The extension to reactor simulation might therefore lead to numerical and/or computational issues to be addressed. Among other possible limitations of the current modelling approach, we highlight the adoption pure concentration-driven diffusive transport. As already mentioned, such approximation is strictly valid only for particles of very small size. Further study will be needed to assess the validity of such assumption for MSFR applications and to possibly extend the methodology to more advanced particle transport models.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material. The data that support the findings of this study are openly available in Zenodo at http://doi.org/10.5281/zenodo.4557568.

Author Contributions

All authors contributed to conception and design of the study. AD performed the theoretical and technical analysis and wrote the first draft of the manuscript. SL, FG and AC supervised the analysis. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This project has received funding from the Euratom research and training programme 2014–2018 under grant agreement no. 847527.

Disclaimer

The content of this paper does not reflect the official opinion of the European Union. Responsibility for the information and/or views expressed therein lies entirely with the authors.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.692627/full#supplementary-material

References

Aufiero, M., Cammi, A., Geoffroy, O., Losa, M., Luzzi, L., Ricotti, M. E., et al. (2014). Development of an OpenFOAM Model for the Molten Salt Fast Reactor Transient Analysis. Chem. Eng. Sci. 111, 390–401. doi:10.1016/j.ces.2014.03.003

CrossRef Full Text | Google Scholar

Baes, C. F. (1974). The Chemistry and Thermodynamics of Molten Salt Reactor Fuels. J. Nucl. Mater. 51, 149–162. doi:10.1016/0022-3115(74)90124-X

CrossRef Full Text | Google Scholar

Balboa Usabiaga, F., Xie, X., Delgado-Buscalioni, R., and Donev, A. (2013). The Stokes-Einstein Relation at Moderate Schmidt Number. J. Chem. Phys. 139, 214113. doi:10.1063/1.4834696

PubMed Abstract | CrossRef Full Text | Google Scholar

Bowen, B. D., Levine, S., and Epstein, N. (1976). Fine Particle Deposition in Laminar Flow through Parallel-Plate and Cylindrical Channels. J. Colloid Interf. Sci. 54, 375–390. doi:10.1016/0021-9797(76)90317-9

CrossRef Full Text | Google Scholar

Brenner, H. (1961). The Slow Motion of a Sphere through a Viscous Fluid towards a Plane Surface. Chem. Eng. Sci. 16, 242–251. doi:10.1016/0009-2509(61)80035-3

CrossRef Full Text | Google Scholar

Cervi, E., Lorenzi, S., Cammi, A., and Luzzi, L. (2019a). Development of a Multiphysics Model for the Study of Fuel Compressibility Effects in the Molten Salt Fast Reactor. Chem. Eng. Sci. 193, 379–393. doi:10.1016/j.ces.2018.09.025

CrossRef Full Text | Google Scholar

Cervi, E., Lorenzi, S., Cammi, A., and Luzzi, L. (2019b). Development of an SP3 Neutron Transport Solver for the Analysis of the Molten Salt Fast Reactor. Nucl. Eng. Des. 346, 209–219. doi:10.1016/j.nucengdes.2019.03.001

CrossRef Full Text | Google Scholar

Compere, E., Kirslis, S., Bohlmann, E., Blankenship, F., and Grimes, W. (1975). “Fission Product Behavior in the Molten Salt Reactor experiment.”. Tech. Rep. ORNL–, 4865, 4077644 (Oak Ridge National Laboratory) Oak Ridge (TN). doi:10.2172/4077644

CrossRef Full Text | Google Scholar

Delpech, S., Merle-Lucotte, E., Heuer, D., Allibert, M., Ghetta, V., Le-Brun, C., et al. (2009). Reactor Physic and Reprocessing Scheme for Innovative Molten Salt Reactor System. J. Fluorine Chem. 130, 11–17. doi:10.1016/j.jfluchem.2008.07.009

CrossRef Full Text | Google Scholar

Fiorina, C., Hursin, M., and Pautz, A. (2017). Extension of the GeN-Foam Neutronic Solver to SP3 Analysis and Application to the CROCUS Experimental Reactor. Ann. Nucl. Energ. 101, 419–428. doi:10.1016/j.anucene.2016.11.042

CrossRef Full Text | Google Scholar

Fiorina, C., Kerkar, N., Mikityuk, K., Rubiolo, P., and Pautz, A. (2016). Development and Verification of the Neutron Diffusion Solver for the GeN-Foam Multi-Physics Platform. Ann. Nucl. Energ. 96, 212–222. doi:10.1016/j.anucene.2016.05.023

CrossRef Full Text | Google Scholar

DLMF (2020). “NIST Digital Library of Mathematical Functions. Release 1.1.0 of 2020-12-15,”. Editors F. W. J. Olver, A. B. Olde Daalhuis, D. W. Lozier, B. I. Schneider, R. F. Boisvert, C. W. Clarket al.

Google Scholar

Grimes, W. R. (1970). Molten-salt Reactor Chemistry. Nucl. Appl. Tech. 8, 137–155. doi:10.13182/NT70-A28621

CrossRef Full Text | Google Scholar

Guha, A. (2008). Transport and Deposition of Particles in Turbulent and Laminar Flow. Annu. Rev. Fluid Mech. 40, 311–341. doi:10.1146/annurev.fluid.40.111406.102220

CrossRef Full Text | Google Scholar

Hébert, A. (2010). “Multigroup Neutron Transport and Diffusion Computations,” in Handbook of Nuclear Engineering. Editor D. G. Cacuci (Boston, MA: Springer US), 751–911. doi:10.1007/978-0-387-98149-9_8

CrossRef Full Text | Google Scholar

Issa, R. I. (1986). Solution of the Implicitly Discretised Fluid Flow Equations by Operator-Splitting. J. Comput. Phys. 62, 40–65. doi:10.1016/0021-9991(86)90099-9

CrossRef Full Text | Google Scholar

Johansson, F. (2017). Arb: Efficient Arbitrary-Precision Midpoint-Radius Interval Arithmetic. IEEE Trans. Comput. 66, 1281–1292. doi:10.1109/TC.2017.2690633

CrossRef Full Text | Google Scholar

Johansson, F. (2019). Computing Hypergeometric Functions Rigorously. ACM Trans. Math. Softw. 45, 1–26. doi:10.1145/3328732

CrossRef Full Text | Google Scholar

Kedl, R. J. (1972). “Migration of a Class of Fission Products (Noble Metals) in the Molten-Salt Reactor experiment,”. Tech. Rep. ORNL-TM–3884, 4471292(Oak Ridge National Laboratory) Oak Ridge (TN). doi:10.2172/4471292

CrossRef Full Text | Google Scholar

Launder, B. E., and Spalding, D. B. (1974). The Numerical Computation of Turbulent Flows. Comp. Methods Appl. Mech. Eng. 3, 269–289. doi:10.1016/0045-7825(74)90029-2

CrossRef Full Text | Google Scholar

Leppänen, J., Pusa, M., Viitanen, T., Valtavirta, V., and Kaltiaisenaho, T. (2015). The Serpent Monte Carlo Code: Status, Development and Applications in 2013. Ann. Nucl. Energ. 82, 142–150. doi:10.1016/j.anucene.2014.08.024

CrossRef Full Text | Google Scholar

Liu, B. Y. H., and Agarwal, J. K. (1974). Experimental Observation of Aerosol Deposition in Turbulent Flow. J. Aerosol Sci. 5, 145–155. doi:10.1016/0021-8502(74)90046-9

CrossRef Full Text | Google Scholar

Marino, A., Peltomäki, M., Lim, J., and Aerts, A. (2020). A Multi-Physics Computational Tool Based on CFD and GEM Chemical Equilibrium Solver for Modeling Coolant Chemistry in Nuclear Reactors. Prog. Nucl. Energ. 120, 103190. doi:10.1016/j.pnucene.2019.103190

CrossRef Full Text | Google Scholar

OpenFOAM (2021). The OpenFOAM Foundation. Online; (accessed 20 January. 2021).

Google Scholar

Patankar, S., and Spalding, D. (1972). A Calculation Procedure for Heat, Mass and Momentum Transfer in Three-Dimensional Parabolic Flows. Int. J. Heat Mass Transfer 15, 1787a–1806. doi:10.1016/0017-9310(72)90054-3

CrossRef Full Text | Google Scholar

Pearson, J. W., Olver, S., and Porter, M. A. (2017). Numerical Methods for the Computation of the Confluent and Gauss Hypergeometric Functions. Numer. Algorithms 74, 821–866. doi:10.1007/s11075-016-0173-0

CrossRef Full Text | Google Scholar

Price, T., Chvala, O., and Bereznai, G. (2020). A Dynamic Model of Xenon Behavior in the Molten Salt Reactor Experiment. Ann. Nucl. Energ. 144, 107535. doi:10.1016/j.anucene.2020.107535

CrossRef Full Text | Google Scholar

Prieve, D. C., and Ruckenstein, E. (1976). Rates of Deposition of Brownian Particles Calculated by Lumping Interaction Forces into a Boundary Condition. J. Colloid Interf. Sci. 57, 547–550. doi:10.1016/0021-9797(76)90232-0

CrossRef Full Text | Google Scholar

Ruckenstein, E., and Prieve, D. C. (1973). Rate of Deposition of Brownian Particles under the Action of london and Double-Layer Forces. J. Chem. Soc. Faraday Trans. 2 69, 1522–1536. doi:10.1039/F29736901522

CrossRef Full Text | Google Scholar

Serp, J., Allibert, M., Beneš, O., Delpech, S., Feynberg, O., Ghetta, V., et al. (2014). The Molten Salt Reactor (MSR) in Generation IV: Overview and Perspectives. Prog. Nucl. Energ. 77, 308–319. doi:10.1016/j.pnucene.2014.02.014

CrossRef Full Text | Google Scholar

Tiberga, M., de Oliveira, R. G. G., Cervi, E., Blanco, J. A., Lorenzi, S., Aufiero, M., et al. (2020). Results from a Multi-Physics Numerical Benchmark for Codes Dedicated to Molten Salt Fast Reactors. Ann. Nucl. Energ. 142, 107428. doi:10.1016/j.anucene.2020.107428

CrossRef Full Text | Google Scholar

Walker, S. A., and Ji, W. (2021). Species Transport Analysis of noble Metal Fission Product Transport, Deposition, and Extraction in the Molten Salt Reactor experiment. Ann. Nucl. Energ. 158, 108250. doi:10.1016/j.anucene.2021.108250

CrossRef Full Text | Google Scholar

Wood, B. D., Quintard, M., and Whitaker, S. (2004). Estimation of Adsorption Rate Coefficients Based on the Smoluchowski Equation. Chem. Eng. Sci. 59, 1905–1921. doi:10.1016/j.ces.2003.12.021

CrossRef Full Text | Google Scholar

Nomenclature

Latin symbols

${\mathit{A}}_{\mathit{r},\mathit{g}}^0$ reference gth group, rth neutron reaction cross-section log. coeff.

c particle (vol.) concentration

$\widehat{\mathit{c}}$ non-dim. particle (vol.) concentration

${\widehat{\mathit{c}}}_{\mathit{d}}$ non-dim. deposited particle (surf.) conc.

${\widehat{\mathit{c}}}_{\mathit{i}\mathit{n}}$ non-dim. inlet particle (vol.) concentration

c₀ ref. particle (vol.) concentration

c_d deposited particle (surf.) concentration

c_k kth family del. neutron prec. (vol.) concentration

c_p specific heat capacity

c_in inlet particle (vol.) concentration

D laminar particle diffusivity

d_p particle diameter

D_t turbulent particle diffusivity

D_eff effective particle diffusivity

${\mathit{D}}_{\mathit{e}\mathit{f}\mathit{f}}^{\infty }$ bulk effective particle diffusivity

${\mathit{D}}_{\mathit{n},\mathit{g}}$ gth group neutron diffusion coefficient

Da Damköhler number

f channel aspect ratio

F_D particle diffusivity correction factor

g gravitational acceleration

H channel half-width

k_B Boltzmann constant

k_eff effective multiplication factor

L channel length

M confluent hypergeometric function

p pressure

Pe Péclet number

Pr Prandtl number

Pr_t turbulent Prandtl number

q vol. energy source

Re Reynolds number

S particle (vol.) source

$\overline{\mathit{S}}$ average particle (vol.) source

$\widehat{\mathit{S}}$ non-dim. particle (vol.) source

$\tilde{\mathit{S}}$ unit-average particle (vol.) source

Sc Schmidt number

Sc_t turbulent Schmidt number

Sh Sherwood number

T temperature

T₀ reference temperature (buoyancy)

${\mathit{T}}_0^{\text{Σ}}$ reference temperature (cross-sections)

u longitudinal velocity comp. velocity

$\widehat{\mathit{u}}$ non-dim. longitudinal velocity comp.

u longitudinal velocity comp. velocity

u_m maximum profile velocity

${\mathit{v}}_{\mathit{g}}$ avg. gth group neutron velocity

x longitudinal coordinate

$\widehat{\mathit{x}}$ non-dim. longitudinal coord.

y transversal coord.

$\widehat{\mathit{y}}$ non-dim. transversal coord.

${\mathit{y}}_{\mathit{f}}$ fission yield of transported fission product

Greek symbols

α laminar thermal diffusivity

α_t turbulent thermal diffusivity

α_eff effective thermal diffusivity

${\mathit{\beta }}_{\mathit{d}}$ total delayed neutrons fraction $\left({\displaystyle {\sum }_k{\beta }_{d,k}}\right)$

${\mathit{\beta }}_{\mathit{d},\mathit{k}}$ kth family delayed neutrons fraction

${\mathit{\beta }}_{\mathit{n}}$ (square root of) nth eigenvalue

${\mathit{\beta }}_{\mathit{T}}$ vol. thermal expansion coeff.

$\text{Δ}$ desorption number

δ desorption rate constant

${\mathit{\delta }}_{\mathit{\varphi }}$ wall region thickness

γ deposition velocity

λ particle decay constant

${\mathit{\lambda }}_{\mathit{k}}$ kth family del. neutron prec. decay constant

ρ fluid density

${\Sigma }_{\mathit{a},\mathit{g}}$ gth group absorption cross-section

${\Sigma }_{\mathit{f},\mathit{g}}$ gth group fission cross-section

${\Sigma }_{\mathit{r},\mathit{g}}$ gth group, rth neutron reaction cross-section

${\Sigma }_{\mathit{r},\mathit{g}}^0$ reference gth group, rth neutron reaction cross-section

${\Sigma }_{\mathit{s},\mathit{g}\to h}$ g-to-h-th group scattering cross-section

${\mathit{\chi }}_{\mathit{d},\mathit{g}}$ gth energy group delayed neutron spectrum

${\mathit{\chi }}_{\mathit{p},\mathit{g}}$ gth energy group prompt neutron spectrum

${\overline{\mathit{\nu }}}_{\mathit{g}}$ avg. gth group neutrons emitted per fission

ν laminar kinematic viscosity

${\mathit{\nu }}_{\mathit{e}\mathit{f}\mathit{f}}$ effective kinematic viscosity

${\mathit{\nu }}_{\mathit{t}}$ turbulent kinematic viscosity

ϕ particle-wall interaction potential

${\mathit{\phi }}_{\mathit{g}}$ gth group integrated neutron flux