- Center for Regional Environmental Research, National Institute for Environmental Studies, Tsukuba, Japan
Predicting the environmental fate of Cs radionuclides in forest ecosystems is important for the effective management and assessment of radioactively contaminated forest areas. A large proportion of the radioactively contaminated areas in Japan consist of forest ecosystems, and most of these areas are artificial forests that are used for timber production [e.g., Japanese cedar (Cryptomeria japonica) and red pine (Pinus densiflora)]. Determining the long-term redistribution of 137Cs in forest ecosystems is important for estimating human doses and understanding the ecological impacts and challenges associated with managing contaminated forests. To facilitate the management and 137Cs decontamination of these forests, we developed a new open-source 137Cs cycling model, ForRothCs, that considers C cycling within forests, as well as biomass production and soil decomposition processes. For the 137Cs inventory, this model estimates the dynamics (Bq m−2) and activity (Bq kg−2) of 137Cs on a decadal time scale, primarily in the leaves, branches, stems, litter layer, and the soil. This model is based on the biomass production and the dynamics of the C cycle models. We tested the model by considering a simple scenario of forest management, i.e., thinning and harvesting, for the first five years following a fallout event. The results showed that these activities have a limited impact on the 137Cs inventory due to the rapid migration of 137Cs from vegetation to soil. Our projections also showed the examined forest management practices resulted in reduced litterfall, which in turn reduced C input to the forest floor and increased the concentration of 137Cs in the litterfall and soil organic layer. Although further validation of the ForRothCs model is required using field observation data, the model can be used to evaluate long-term 137Cs dynamics associated with commonly used forest and decontamination management scenarios.
Introduction
As a result of the March 2011 accident at the Fukushima Daiichi Nuclear Power Plant (FDNPP), large quantities of radionuclides were released into the atmosphere and distributed over terrestrial environments in Japan (Morino et al., 2011). The dominant land use type affected by the FDNPP event was forest, which comprises approximately 70% of the affected area and 11 Mm3 of the above-ground biomass in the region (Hashimoto et al., 2012). Although the total amount of 137Cs released into the atmosphere was estimated to be 1.2 × 1016 Bq (Chino et al., 2011), the extent of radioactive contamination in the forests (up to 24 Sv h−1) produced an air dose that was well below the lethal dose for living plants (Geras'kin et al., 2008; Steinhauser et al., 2014). Consequently, no direct radiation damage, such as necrosis of plant tissues, was reported in the region.
In the case of the Chernobyl nuclear power plant (ChNPP) accident, decontamination management of forests was not conducted over a wide area and little export of radioactive substances from these ecosystems has been observed (e.g., Tikhomirov et al., 1993; Ueda et al., 2013). Therefore, a large proportion of the radionuclides derived from fallout tend to remain in these ecosystems for extended periods of time; for example, 137Cs has a slow rate of decay (the half-life of 137Cs is 30.2 years). Previous studies have shown that some of the ecosystem components in the region affected by the ChNPP event still have high levels of 137Cs contamination due to the long effective half-life of itself or the active accumulation of 137Cs; examples include the litter layer (Thiry and Myttenaere, 1993), wild boar (Semizhon et al., 2009), and mushrooms (Yoshida et al., 1994). Recycling of 137Cs within the forest ecosystem is a dynamic processes in which reciprocal transfers occur between biotic and abiotic components of the ecosystem on a seasonal (or longer-term) basis (Tikhomirov and Shcheglov, 1994). Accumulation, retention, and internal cycling of radionuclides in a forest ecosystem are dependent on a variety of different compartments, each of which has different turnover rates and phenologies. It is therefore considered necessary to develop radioecological models capable of accurately clarifying 137Cs cycling dynamics in order to support forest management and radioactive decontamination activities. Such models could also be applied to predict ecological impacts on decadal timescales and characterize the migration of radioactive substances in forest ecosystems.
In Fukushima prefecture, 50% of the forested land is artificial forest, and this amounts to an area of about 120,000 ha; the trees range from 20 to 45 years old, and thus it might be necessary to manage them with thinning and pruning in order to maintain growth (Forestry Agency, 2014). In Japan, a special management measure had been planned to promote improvement of the forest, by thinning and pruning about 58,000 ha in the Fukushima area by 2020. However, after the fallout, the forest management area in Fukushima prefecture rapidly decreased (from 12,000 ha in 2010 to 7800 ha in 2012). From the point of view of ecosystem services (MEA, 2005), plantation forests that are not well managed (relatively low thinning and harvesting activities) tend to have a reduced amount of ecosystem services, such as slower C accumulation, lower runoff, and higher leaching of N (Ooba et al., 2010). In addition, plantation forests with less than a moderate amount of management have high levels of soil erosion (e.g., Onda et al., 2010), and this might promote the migration via stream flow of 137Cs from the forest ecosystem to other ecosystems. Thus, for an artificial forest contaminated with radioactive Cs, it is important to maintain the natural ecosystem services in order to reduce the human dose and to promote sustainable forest management.
Approximately 50% of the forested area in Fukushima Prefecture comprises artificial forest (Forestry Agency, 2014). The trees in a 120,000 ha area range from 20 to 45 years old, which means that it is necessary to manage them by thinning and pruning in order to maintain growth. The act on special measures concerning advancement of implementation of forest thinning were drafted by the Japanese government to thin and prune about 58,000 ha of forest in the prefecture by 2020. However, after the accident at the FDNPP, the area of forest under management decreased from 12,000 ha in 2010 to 7800 ha in 2012. From a view of ecosystem services (MEA, 2005), this is a problem because poorly managed plantation forests tend provide fewer ecosystem services and are characterized by slower rates of C accumulation and runoff, and higher rates of N leaching (Ooba et al., 2010). In addition, forest plantations with less than moderate amounts of management have high levels of soil erosion (e.g., Onda et al., 2010), which can promote the migration of 137Cs from the contaminated forest to other ecosystems via stream flow. It is therefore considered important to maintain natural ecosystem services in artificial forests that have been contaminated with radioactive Cs, as doing so can reduce the potential for human exposure, and to promote sustainable forest management.
Given the persistence of radioactive Cs in forest ecosystems, it is necessary to use operational models that can predict the exposure dose and to assess the risk of exposure; this information can also be used to assess the effectiveness of countermeasures and to develop remediation strategies (Riesen, 2002). Fesenko et al. (2005) emphasized the importance of optimizing the long-term radioactive Cs dynamics prior to implementing countermeasures. Process models are important management tools for limiting exposure to radioactivity and for increasing forest production. There currently are several models that could potentially be used to predict 137Cs cycling in forest ecosystems, including FORESTPATH (Schell et al., 1996), RIFE (Shaw and Belli, 1999), and FORSUN (Konoplev et al., 2002). The International Atomic Energy Agency's BIOMASS Forest Working Group (IAEA, 2002; Shaw et al., 2005) has already evaluated more than ten radioecological models for forest 137Cs cycling, by performing simulations with standardized inputs. All of the models were found to be practicable and appropriate for evaluating remedial policies. However, most of the models did not explicitly implement tree dynamics (IAEA, 2002) or the C dynamics of soils, which meant that they were unable to comprehensively forecast the 137Cs dynamics, especially under non-steady-state conditions (e.g., due to natural disturbances or forest management activities). In terms of radioecology, the C:Cs ratio is important for herbivores and decomposers of litterfall (i.e., soil animals) as they feed on plant material (Witkamp and Frank, 1970). Consequently, the ability to implement both C and Cs cycling in a radioecological model would allow managers to more accurately comprehend the migration of 137Cs in forest ecosystems.
In this paper, we present the forest Roth-C and Cs cycling model (FoRothCs), a new open-source model for predicting the 137Cs dynamics in artificial forest ecosystems and for evaluating the effects of forest management practices and decontamination activities on 137Cs cycling. The model couples a forest growth model with the Rothamsted carbon model (Jenkinson et al., 1990) and uses 137Cs transfer factors as parameters. Therefore, our model can predict the C dynamics in forest environments, by simultaneously considering trees, the litter layer, and soils. We introduce the model structure and its behavior by presenting a sensitivity analysis for a forest of Japanese cedar (Cryptomeria japonica).
Materials and Methods
The model presented in this study is based on the Rothamsted Carbon (Roth-C) model (Jenkinson et al., 1990; Coleman and Jenkinson, 1999) and the diameter distribution prediction system (DDPS; Hayashi et al., 2002; Hayashi and Yamamoto, 2006). The Roth-C model is a carbon-cycling model for soil organic C decomposition, and the DDPS is a self-thinning growth model for artificial forest biomass prediction. Our model is coupled to these two models, and it incorporates the Cs dynamics into the C cycling by using transfer factor parameters based on the dynamics of both C and biomass.
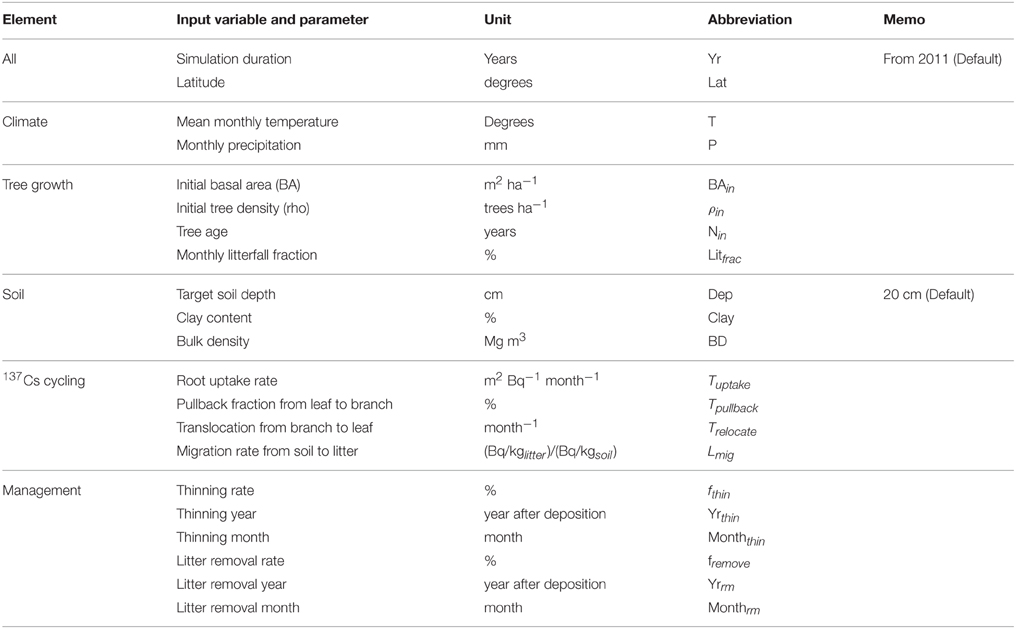
Based on the studies of Avila et al. (2001) and IAEA (2002), we used a matrix representation to summarize the overall model structure and transfer processes (Figure 1). Our model has seven compartments, of which three are for aboveground biomass, and the others are for soil components (litter layer, organic soil fraction, and mineral soil fraction). Table 1 summarizes all of the input variables and parameters that are used in the simulation. The model requires monthly climate data (temperature and precipitation), initial forest condition (age, density, and basal area), soil properties, and parameters related to 137Cs dynamics (such as 137Cs deposition, initial 137Cs inventory in each component, tree uptake constant, pullback rate, and retranslocation rate). The code for the FoRothCs model is provided in the Supplementary Materials.
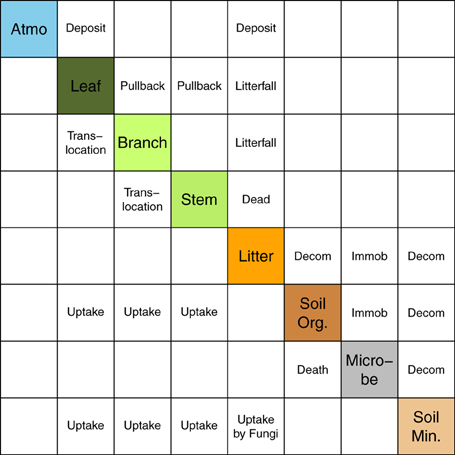
Figure 1. Representation matrix of the FoRothCs model. Diagonal components (shaded) indicate variables in the model. The other components indicate processes that are explicitly included in the model.
Forest Growth Model
For the tree growth model, we used the DDPS (Hayashi et al., 2002; Hayashi and Yamamoto, 2006) for basal area prediction and the allometry equations for estimating aboveground biomass (leaves, branches, and stems) in an artificial forest stand in which all of the trees are of the same age. The DDPS calculates the annual tree density, tree height, and total basal area in a forest stand, based on the self-thinning theory. Using this model, we estimated tree growth and implemented forest management practices, such as thinning. The model is stated as follows:
where G(n) indicates the basal area of the stand at age n (m2 ha−1), ρ(n) is the density of the stand at age n (trees ha−1), and a1, a2, and a3 are parameters for the shape of the growing trees.
To estimate the maximum density, we used following equation:
where ρmax(n) indicates the maximum density of the stand at age t (trees ha−1). This equation indicates maximum density line, which determines self-thinning rate at year n. If ρmax(n) is lower than ρ(n), then ρ(n) decreases to the previous level and G(n + 1) is recalculated with an updated ρ(n).
To estimate the tree height [H(n)], we used the following empirical equation:
where c0, c1, c2, and c3 are empirical coefficients; the values used in this study are for Japanese cedar forests (Hayashi and Yamamoto, 2006). Hmax is the maximum height allowed for the forest stand, which is determined by the conditions at the study site.
To estimate the aboveground biomass (kg ha−1), we used the allometry relationships for the diameter, height, leaves (branches and stems), and the basal area and density:
where DBH(n) is the diameter at breast height (cm) at stand age n, which is calculated from the basal area G(n) and tree density ρ(n). The parameters for the allometry equations (dl0, dl1, db0, db1, ds0, and ds1) were obtained from a national survey conducted for general allometric equations for Japanese cedar in Japan (Tanouchi and Utsugi, 2004). Lind, Bind, and Sind all give the biomass of a typical tree (kg tree−1). Using the biomass multiplied by the tree density ρ(n), we can then calculate the biomass in each compartment for each stand (i.e., Lms, Bms, and Sms; kg m−2). Finally, we summed the compartments to calculate the total above-ground biomass Allms (kg m−2), as follows:
Carbon Cycling in Soils (Roth-C)
For carbon cycling in soils, we used the Roth-C model (Coleman and Jenkinson, 1996), which can be formulated as the following transition matrix equation:
where the time step t is 1 month. In this model, there are four different active compartments for C: decomposable plant material (cDPM), resistant plant material (cRPM), microbial biomass (cBIO), and humus (cHUM). In this study, cDPM and cRPM are considered as part of the litter layer, with factors a1 = 0.46 and a2 = 0.54, respectively. At and Bt are the monthly inputs from vegetation litterfall. D is the clay content, which is determined by the partitioning ratio between CO2 in the atmosphere and the (cBIO + cHUM) formed during decomposition. The fi are defined as the decomposition functions for the monthly step in each compartment of the soil C. All compartments (cDPM, cRPM, cHUM, cBIO) can be described by first-order kinetics decomposition equations with limitation functions, as follows:
where the decay constant ki (month−1) for each compartment corresponds to the degree of decomposition, as follows: DPM, 10.0/12; RPM, 0.3/12; BIO, 0.66/12; and HUM, 0.02/12. fT, fM, and fC are regulation functions for the monthly average air temperature, monthly average soil moisture, and the soil coverage, respectively. fT is an exponential function. fM is the precipitation and potential evaporation rate, which was estimated using the Thornthwaite equation (Thornthwaite, 1948). fC is the soil cover factor, which has only two states: bare or covered. Details on the formulation of the regulation functions employed in the Roth-C model are presented in Coleman and Jenkinson (1996).
Dint and Rint are the C inputs from tree compartments to the forest floor as litterfall, which is formulated as follows:
where FS is the monthly litterfall rate, which represents the fraction of each biomass component at the corresponding increment for each year (n). The carbon content of each of the tree compartments (cL, cB, cS) is set to be 50% of each of the biomass compartments (Lms, Bms, Sms; Noguchi et al., 2009). FD and FR are the fractions of DPM and RPM in the litterfall, respectively. For the DPM/RPM ratio of forest vegetation, we used a value of 0.25 (Coleman and Jenkinson, 1996). In FoRothCs, the litter layer is assumed to be the sum of DPM and RPM. Mt is the mortality rate caused by self-thinning.
Cesium-137 Cycling
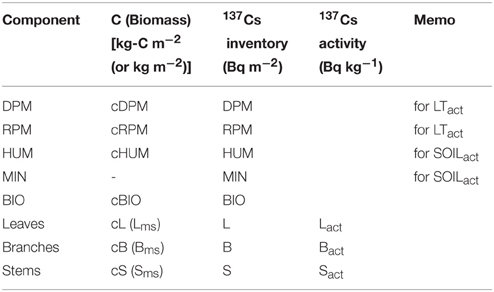
In FoRothCs, the components have different descriptions for 137Cs (see Table 2); these are based on an area inventory (Bq m−2) and activity, which is a mass-based concentration (Bq kg−1) (i.e., the activity of each compartment was divided by the mass weight). The 137Cs activity of each compartment is indicated by a subscript, e.g., Lact.
In FoRothCs, the 137Cs cycling in the soil and tree compartments is formulated as follows:
where the transition matrix in Equation (13) almost corresponds to the matrix in Figure 1, even though the order and the number of components are different (e.g., DPM and RPM). The dynamics of Cs in soil organic matter were based on the decomposition dynamics of the Roth-C model, and the parameters and functions related to the decomposition processes in Cs cycling are the same as those used in the Roth-C model (e.g., f1 – f4). In our model, the 137Cs in the fraction of decomposed organic materials to CO2 migrates mineral soils. In addition to decomposition processes, Brückmann and Wolters (1994) and Fukuyama and Takenaka (2004) described the upward migration of radioactive Cs from the soil layer into the litter layer through litterfall decomposition and translocation by fungi. To account for this process, we introduced a migration parameter Lmig ((Bq/kglitter)/(Bq/kgsoil)), which is based on the findings of Fukuyama and Takenaka (2004).
Tuptake (m2 kg−1 month−1) is a parameter that determines the uptake rate of 137Cs relative to the 137Cs in soil (HUM and the soil mineral compartments). Tpullback is the translocation parameter that determines the fraction of 137Cs that is recycled by green leaves prior to them becoming litterfall.
RBtoL, RLtoB, RLtoS, and RStoB are the translation rates between tree compartments and can be defined as follows:
Trelocate determines the retranslocation rate from branches to leaves. Thus, RBtoL is proportional to the 137Cs activity of a branch (Bq kg−1), but not to the 137Cs inventory of a branch.
RLtoB and RLtoS are the translocation rates due to the pullback of 137Cs from leaves to branches and leaves to stems, respectively. The distribution of pullback 137Cs is determined by biomass.
For translocation from stems to branches (RStoB), we used the following equations:
We incorporated the deposition of 137Cs from the atmosphere on March 2011 at t = 3; the initial time t0 was defined as December 2010. In this study, the fallout of 137Cs was assumed to have been deposited onto tree leaves and the litter layer, as follows:
where Fint is the interception ratio of 137Cs deposited in the canopy layer. Based on Kato et al. (2012), the interception ratio for the forest canopy of Japanese cedar is set to 62%. The 137Cs intercepted by the forest crown is assumed to have remained in or on the tree or its surfaces for at least a year (Nishikiori et al., 2015). In addition, we assumed that the captured 137Cs was chemically and biologically absorbed into the leaf tissue.
Finally, we summed the components of DPM and RPM to form a litter layer (LT), and the components of HUM and MIN to form a soil layer (SOIL), which we calculated based on the 137Cs activity of each compartment, as follows:
Simulation Settings and Sensitivity Analysis
The initial forest and climate condition were set to match those of the Mt. Tsukuba site, which is located approximately 160 km southwest of the FDNPP (Nishikiori et al., 2015). The stand age was 50 years, the mean tree height was 21.6 m, the mean DBH was 25.3 cm, and the stand density was 1600 trees ha−1. The initial values of the soil organic C (SOC) components were calculated by inverse estimation technique (Jenkinson et al., 1999). We assumed that SOC was in equilibrium at the beginning of the experiment. To achieve this, we ran the FoRothCs model for 200 years. Inert organic matter (IOM) was estimated using the equation of Falloon et al. (1998) with an initial total SOC at a depth of 0–20 cm in 2011. We used the monthly average temperature and precipitation conditions for the 30-year period between 1981 and 2010, which we obtained from the closest meteorological observation station. The 137Cs fallout was taken as 11,000 Bq m−2, based on a reference level for the Mt. Tsukuba site (Nishikiori et al., 2015).
To explore feasible transfer parameters for tree 137Cs cycling, sensitivity analyses were conducted with different settings for the tree uptake constant Tuptake, the pullback rate Tpullback, and the retranslocation rate Trelocate by grid searching method. All of the parameters were specified by range, with maximum and minimum values, in order to ensure that the parameters were appropriately framed. We calculated the aggregated transfer factors TFag (m2 Bq−1) for the leaves at 30 years after the fallout event, as follows:
at t = 30 years with no forest management.
The reason why we used TFag instead of the concentration-based transfer factor (kg Bq−1) was the availability of appropriate values for different forest ecosystems. Importantly, in FoRothCs, the concentration of 137Cs in the soil compartment is arbitrary and depends on the soil depth. It is thus necessary to carefully consider the activity of 137Cs in soils, but the model gave a robust estimate for TFag.
In order to evaluate the impact of thinning and litterfall removal on decontamination 30 years after the fallout event, we conducted base-case scenario analyses with different timings and intensities of management activities and using appropriate parameters. In the thinning analysis, we assumed that entire trees were removed and we considered an extreme and unrealistic case of over 70% thinning (100% thinning is equal to clearcutting). For the removal of litterfall, we assumed that all of the litter layers (Ol, Of, and Oh) were removed at the same rate. For both scenarios, management activities were performed in October of each year.
Results and Discussion
General Behavior of FoRothCs and a Sensitivity Test for the Tree Transfer Parameters
The model presented in this paper can simulate the monthly dynamics of the 137Cs inventory in a Japanese cedar forest over a decadal time scale. Figures 2, 3 show the simulations that were performed to determine the behavior of FoRothCs. The model successfully estimated forest biomass production (kg m−2) in Figure 2A, soil C (kg-C m−2) in Figure 2B, 137Cs inventory (Bq m−2) in Figure 2C, and their activities (Bq kg−1) in Figure 2D in the various forest ecosystem compartments (Figure 1). These are the general output variables of FoRothCs. In addition, the dynamics of tree density (trees ha−1) and mean basal area of each individual tree (cm2) were estimated in FoRothCs according to the self-thinning power law (Hayashi et al., 2002). Late in each of the simulation periods, the unmanaged above-ground biomass fluctuated due to self-thinning (Figure 2). As can be seen for 137Cs in the RIFE simple compartment model (Hashimoto et al., 2013), our model also showed rapid migration of 137Cs inventory from leaves to the forest floor (i.e., to litterfall and soil compartments), even though the migration via litterfall was represented as biomass- or C-based mass flow. This rapid migration was also comparable with field observations of Japanese cedar in Fukushima, where the 137Cs inventory in the litter layer doubled from the autumn of 2011 to the autumn of 2012 (Kaneko et al., 2014).
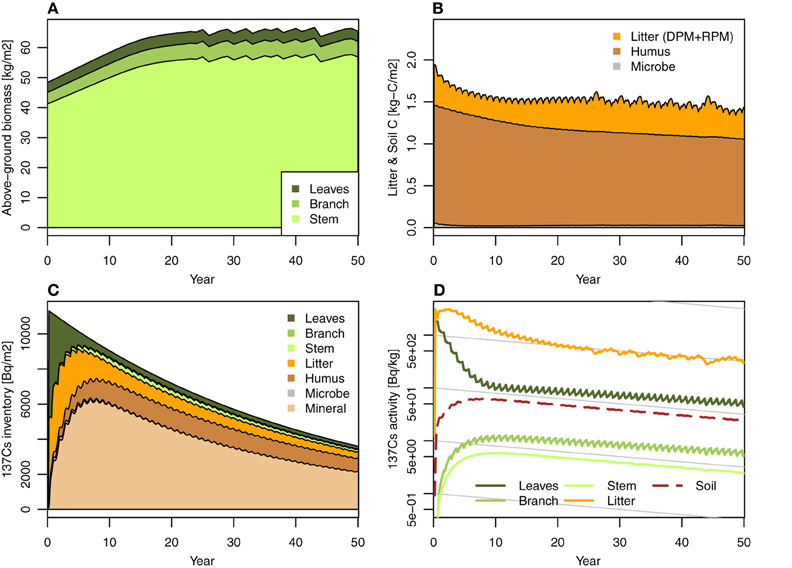
Figure 2. Simulation case 1: No forest management. (A) Forest biomass (annual), (B) litter layer and soil C, (C) 137Cs inventory, and (D) 137Cs activity.
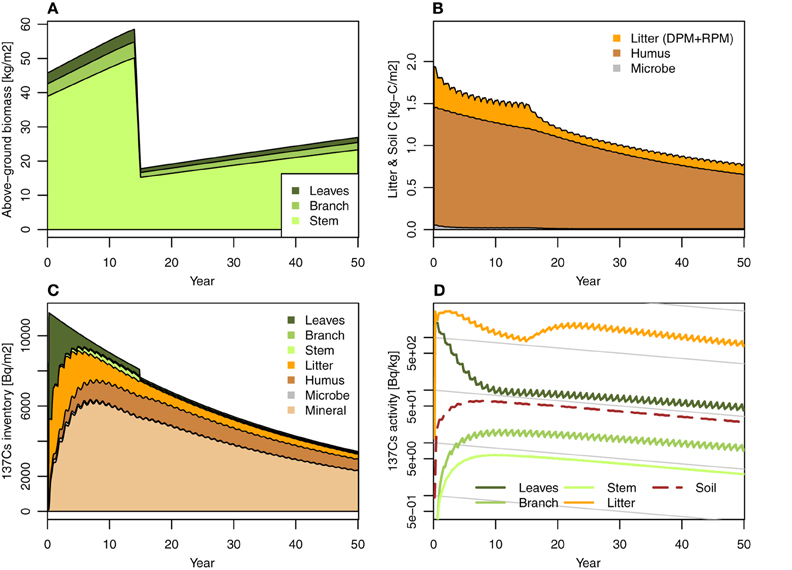
Figure 3. Simulation case 2: Intensity thinning (70%) management, at 15 years after fallout event. (A) Forest biomass (annual), (B) litter layer and soil C, (C) 137Cs inventory, and (D) 137Cs activity.
The 137Cs in the litter layer showed relatively high radioactivity and long persistence during the entire simulation period (Figure 2D). In most forest types, most of the radioactive Cs was observed in the fragmented litter (Of) and humus (Oh) layers (Thiry and Myttenaere, 1993; Karadeniz et al., 2015). In the definition of FoRothCs, the litter layer is comprised of litter at different stages of decomposition: Ol (fresh litter), Of, and Oh. Therefore, the high amount of 137Cs in the litter layer that was predicted by FoRothCs is considered reasonable. Stemmer et al. (2005) reported that the fraction of soil microbial biomass to total 137Cs inventory ranged from 2 to 3% at six forest sites in Austria. The microbial compartments in our results are comparable with that study, particularly in the early phase shortly after the fallout event.
We tested the impact of 70% thinning management at 15 years after the fallout on 137Cs dynamics in FoRothCs (Figure 3). Figure 3D show that the reduction in litterfall after intensive thinning reduced the litter layer and consequently enriched the concentration of 137Cs in the litter layer, even though the inventory of 137Cs in the litter layer was not markedly different from that in the no-thinning condition (Figure 2). This enrichment in the concentration of 137Cs in the litter layer is due to the low 137Cs activity in litter, its upward migration from the soil into the litter layer, and immobilization by microbes during decomposition (Witkamp and Barzansky, 1968; Rafferty et al., 1997). Thus, by simulating C cycling in conjunction with Cs cycling, FoRothCs enables us to evaluate the disturbance in the 137Cs dynamics in a forest ecosystem. However, this simulation was restricted to the case in which all of the trees were removed. A previous field study (Berthelsen et al., 1999) showed that clearcutting resulted in leaf and branch slash that caused an increase of 137Cs on the forest floor. It is considered that future studies need to verify this phenomenon in the field during an actual forest thinning operation.
Since little data exists for the transfer factors of 137Cs for trees, we first reconciled the parameters associated with the internal cycling of 137Cs in trees (Tuptake, Tpullback, and Trelocate) by searching them against published values for the mean aggregated transfer factor TFag (m2 g−1) of old needles in conifers (Calmon et al., 2009) in Figure 4. The sensitivity tests revealed that these parameters were sensitive to the TFag in FoRothCs (Figure 4), which determines the ecological half-life of 137Cs in whole trees. Since we avoid the effect of surface absorption of fallout occurred in the canopy, we used the values of the 137Cs inventory and activities for 30 years after the fallout event to estimate TFag. Calmon et al. (2009) summarizes the TFag values published to date, although these values were likely to be for steady-state conditions some years after a fallout event. Figure 4 shows TFag for various ranges of Tuptake and Tpullback. In ForRothCs, instead of mathematically fitting the data, we used a rounded figure (see Figure 4) for estimating the average TFag for coniferous trees; the values obtained for Tuptake, Tpullback, and Trelocate were 4.0 × 10−5, 0.30, and 5.0 × 10−3, respectively. TFag is not an exact match for Japanese cedar and might vary depending on environmental factors. The values of TFag for coniferous needles in the literature vary widely, ranging from 2.4 × 10−4 to 1.8 × 10−3 (m2 g−1) (Calmon et al., 2009). However, some comparable data to be found for Tpullback in previous field observations; for example, the percentage of N and P pullback in coniferous trees (Pinus Radiate) from senescence before litterfall was estimated to range from 20 to 40% (Sadanandan Nambiar and Fife, 1991). On the other hand, because of the high mobility of 137Cs ions inside tree compartments (Goor and Thiry, 2004; Thiry et al., 2009), 60–70% of the annual supply of 137Cs was pulled-back into nonphotosynthetic tissues (stems and branches) before litterfall from Scots pines contaminated by the Chernobyl accident. Compared to that study, our values for Tpullback were relatively small. Since more than 60% of the 137Cs in Japanese cedar needles remains in the epicuticular wax (Nishikiori et al., 2015), which might not contribute to the inter-tree cycling of 137Cs, the magnitude of Tpullback employed in this study is not considered unreasonable. However, more intensive field validation is required in order to better clarify these aspects of 137Cs dynamics.
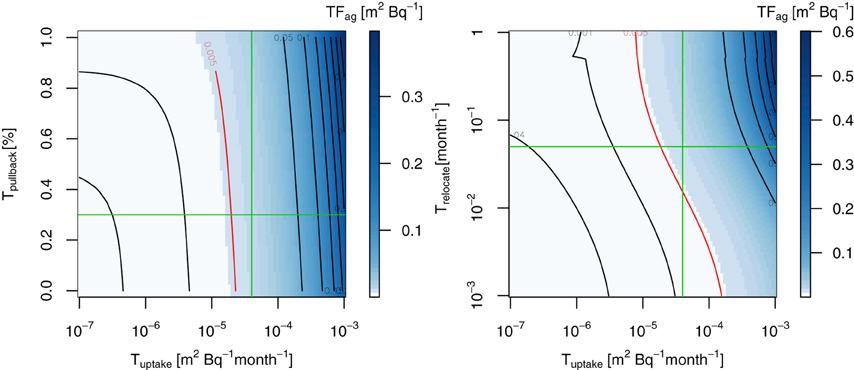
Figure 4. Sensitivity test of Tuptake, Tpullback, and Trelocate for TFag (m2 kg−1) of unmanaged forest, 30 years after the FDNPP fallout event. Red lines indicates the averaged TFag values in the literature for coniferous forest (Calmon et al., 2009). Green lines indicates the values used in this study.
Impact of Thinning and Litter Removal on the Cesium-137 Inventory of a Forest Stand
As mentioned in the introduction, thinning of the forest trees is considered necessary for extensive areas in Fukushima. In addition, the removal of trees and litter layers are other important countermeasures for decontaminating forest ecosystems (Guillitte et al., 1993, 1994), and both have been conducted in the regions affected by the FDNPP accident. However, the extent and timing of such countermeasures and their effect on the long-term 137Cs dynamics remains unclear. In this study, we used the total 137Cs inventory at 30 years after the fallout event as a reference point for the reduction effects of the countermeasures in 137Cs inventory. Figures 5, 6 show the reduction of total 137Cs inventory by the thinning and litter removal timings and intensities in FoRothCs simulation. The reduction rate under the no-management scenario was still nearly 50%, and this was attributable to physical decay (see Figures 5, 6).
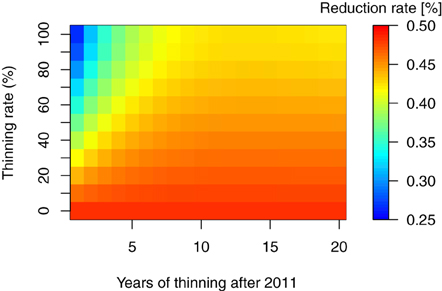
Figure 5. Reduction rate in percent total 137Cs inventory, 30 years after the fallout event, for thinning at various rates and timing.
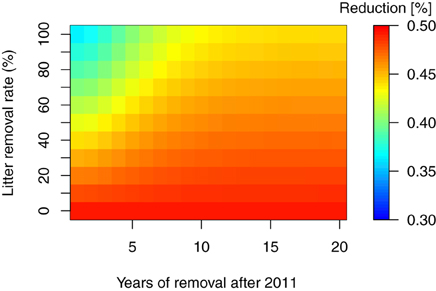
Figure 6. Reduction rate in percent total 137Cs inventory, 30 years after the fallout event, for litter removal at various rates and timing.
The simulation revealed that, five years after the fallout event, forest management practices such as thinning and harvesting has a limited effect on 137Cs inventories, as the migration of 137Cs from the vegetation to the soil is so rapid. This migration rate is comparable to the values obtained in field observations at various sites (e.g., Calmon et al., 2009) and from modeling studies (e.g., Hashimoto et al., 2013). However, when intensive thinning or harvesting is undertaken in an area, the reduction of C input via litterfall to the forest floor leads to an increase in 137Cs activity in the litter and soil organic layer (Figure 3).
For the litter removal management, as suggested in previous studies (Linkov et al., 1997; Hashimoto et al., 2012), our simulation results showed that the efficiency of litter removal as a means of reducing the total 137Cs inventory is only effective in the first few years after a fallout event, mainly because the 137Cs rapidly migrates to the soil organic and mineral layers by decomposing litter layer (Figure 2). Our result also showed that the 137C migration initially interrupted by the canopy via litterfall lasted for at least 10 years. So, the timing depends on the fraction of 137Cs interrupted by the canopy. The magnitude of the reduction due to these management activities is thus highly dependent on the vertical distribution of the initial deposition onto the forest crown (leaves).
Uncovered Processes in FoRothCs and Upcoming Challenges
FoRothCs does not explicitly incorporate 137Cs migration due to throughfall precipitation. Especially during the first half year after the fallout event, throughfall processes contributed to the migration of 137Cs from the canopy to the forest floor at a rate that was comparable to litterfall migration in the area affected by the FDNPP accident (Teramage et al., 2014; Nishikiori et al., 2015). On the other hand, in a Japanese cedar forest, throughfall migration of 137Cs was negligible after only a single year, even though a considerable amount of 137Cs remained in the leaves. The low rates of throughfall were attributed to most of the 137Cs being captured (Koizumi et al., 2013), absorbed, and cycled within the internal tissues of the trees (Tagami et al., 2012; Mahara et al., 2014; Nishikiori et al., 2015). Thus, in this model, the initial deposition onto the forest crown (leaf compartment) should be reduced, and the actual crown interception should consider throughfall migration.
Goor and Thiry (2004) suggested from the field observations that the root uptake rate and translocation of 137Cs circulated within a plant varies as a function of tree age and other environmental factors. In addition, immobilization of 137Cs in soils could affect uptake rate of 137Cs by the tree over the long term (Goor and Thiry, 2004; Takeda et al., 2013). Thus, the parameters affecting the transfer factors for the tree uptake rate Tuptake may also change for trees of different ages (Rantavaara et al., 2012); the parameters used in our model are constants. Regarding the mobility of 137Cs in soils, it is possible that soil organic matter may affect the radiocesium interception potential (RIP) (Takeda et al., 2014), and consequently, the availability of 137Cs in soils (Rigol et al., 2002; Rantavaara et al., 2012). In addition, changes in the vertical profile of 137Cs by factors such as bioturbation and the vertical distribution of roots may also affect the uptake of 137Cs by the roots (Velasco et al., 1993, 1997).
In ForRothCs, the distribution of 137Cs in each tree compartment was assumed to be homogeneous. However, parts of the stem (i.e., bark, sapwood, and heartwood) showed different levels of 137Cs activity, especially early in the contamination period (Rantavaara et al., 2012; Ohashi et al., 2014). Although the proportion of bark biomass to stem is about 5% in Japanese cedar (Lim et al., 2013), the 137Cs concentration in bark was much higher due to sorption of the initial fallout on the bark surface (Kuroda et al., 2013; Ohashi et al., 2014). A refinement of the model should consider 137Cs activity in the tree to be heterogeneous, as in the other compartments. Further, the slope of the reference site in a forested catchment on Mount Tsukuba was 0.3% (NIES, 2012), and if our model is applied to a steep forest stands or to a regional catchment, the soil erosion rate should be implemented using models such as the Revised Universal Soil Loss Equation (RUSLE; Renard et al., 1991).
Although we did not show the results for 134Cs, because the ratio of 134Cs to 137Cs is approximately unity in the affected region (Tagami et al., 2011), the use of the 134Cs decay constant in FoRothCs enables us to simulate 134Cs cycling in the forest ecosystem affected by the FDNPP accident.
Finally, we need to validate our model with various field observations and data for different tree species—for both the inventory and transfer processes—in order to fully understand the mid- to long-term 137Cs projections of the model. FoRothCs is highly parameterized, whereas our knowledge is limited, especially for the transfer processes (Linkov and Burmistrov, 2003; Rantavaara et al., 2012; Nishikiori et al., 2015). For this reason, parameterization for the various transfer processes is essential. To reduce the uncertainties in the parameters in process models, data assimilation is widely used in many fields. For the 137Cs dynamics, the FORESTPATH model was applied using Bayesian calibration for the time series analysis of 137Cs activity in the soil organic layer (Linkov et al., 1999). As a consequence of the parameter calibration, the uncertainties in the prediction are expected to be reduced. However, structural uncertainties associated with the model cannot be determined by a single model inversion. To evaluate these uncertainties and to make valid management decisions, it will be necessary to use multiple models to assimilate data, especially chronosequence observations. As shown in this study, the effects of disturbances due to management and decontamination activities on the 137Cs dynamics have not been sufficiently considered in field observations and previous model studies. Meeting this challenge will improve our capacity to predict 137Cs dynamics in forest ecosystems, and take us one step closer to the actual application of these models.
Conclusion
We developed a new open-source model, FoRothCs, to facilitate forest management and decontamination decisions in radioactively contaminated artificial forest environments. Although further validation of FoRothCs using field observation data is necessary, the results presented here are a preliminary step toward applying this model to evaluate and project the long-term 137Cs dynamics in artificial forests in conjunction with forest management and decontamination activities. An advanced forest management plan using a process-based model is recommended for comprehending the effects of management activities on the 137Cs dynamics of forest ecosystems. The findings of this study will be applied to a series of future field studies in which the projections of 137Cs behavior in different forest ecosystems will be explored.
Funding
This study was performed in part as a project contracted by the Ministry of the Environment, Government of Japan.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The author is grateful for the assistance and advice of Dr. M. Koshikawa, Dr. M. Watanabe, Dr. K Nishikori, and Dr. H. Tsuji, all of whom are members of the Soils Environmental Laboratory at the National Institute for Environmental Studies (NIES), Japan. Dr. M. Ooba of NIES is thanked for his feedback on the manuscript, and Dr. T. Fukuyama at Shinshu University for providing the value for the upward migration rate of the litter layer.
Supplementary Material
The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fenvs.2015.00061
The R code of FoRothCs used in this study is in supplementary material.
References
Avila, R., Bergman, R., Scimone, M., Fesenko, S., Sancharova, N., and Moberg, L. (2001). A comparison of three models of 137Cs transfer in forest ecosystems. J. Environ. Radioact. 55, 315–327. doi: 10.1016/S0265-931X(00)00199-5
Berthelsen, B., Steinnes, E., and Næumann, R. (1999). Distribution of 137Cs in surface soils as affected by forest clear-cutting. J. Environ. Radioact. 42, 39–49.
Brückmann, A., and Wolters, V. (1994). Microbial immobilization and recycling of 137Cs in the organic layers of forest ecosystems: relationship to environmental conditions, humification and invertebrate activity. Sci. Total Environ. 157, 249–256.
Calmon, P., Thiry, Y., Zibold, G., Rantavaara, A., and Fesenko, S. (2009). Transfer parameter values in temperate forest ecosystems: a review. J. Environ. Radioact. 100, 757–766. doi: 10.1016/j.jenvrad.2008.11.005
Chino, M., Nakayama, H., Nagai, H., Terada, H., Katata, G., and Yamazawa, H. (2011). Preliminary estimation of release amounts of 131I and 137Cs accidentally discharged from the fukushima daiichi nuclear power plant into the atmosphere. J. Nuclear Sci. Technol. 48, 1129–1134. doi: 10.1080/18811248.2011.9711799
Coleman, K., and Jenkinson, D. (1996). “Rothc-26.3-a model for the turnover of carbon in soil,” in Evaluation of Soil Organic Matter Models, eds D. S. Powlson, P. Smith, and P. J. U. Smith (Heidelberg: Springer), 237–246.
Coleman, K., and Jenkinson, D. (1999). ROTHC-26.3. A Model for the Turnover of Carbon in Soil: Model Description and Users Guide. Berlin; Heidelberg: Springer. 237–246.
Falloon, P., Smith, P., Coleman, K., and Marshall, S. (1998). Estimating the size of the inert organic matter pool from total soil organic carbon content for use in the Rothamsted carbon model. Soil Biol. Biochem. 30, 1207–1211.
Fesenko, S. V., Voigt, G., Spiridonov, S. I., and Gontarenko, I. A. (2005). Decision making framework for application of forest countermeasures in the long term after the chernobyl accident. J. Environ. Radioact. 82, 143–166. doi: 10.1016/j.jenvrad.2004.10.014
Forestry Agency. (2014). Annual Report on Trends in Forests and Forestry (in Japanese). Forestry Agency, Ministry of Agriculture Forestry and Fisheries of Japan, Tokyo.
Fukuyama, T., and Takenaka, C. (2004). Upward mobilization of 137Cs in surface soils of Chamaecyparis obtusa sieb. et zucc.(hinoki) plantation in japan. Sci. Total Environ. 318, 187–195. doi: 10.1016/S0048-9697(03)00366-8
Geras'kin, S. A., Fesenko, S. V., and Alexakhin, R. M. (2008). Effects of non-human species irradiation after the chernobyl npp accident. Environ. Int. 34, 880–897. doi: 10.1016/j.envint.2007.12.012
Goor, F., and Thiry, Y. (2004). Processes, dynamics and modelling of radiocaesium cycling in a chronosequence of chernobyl-contaminated scots pine (Pinus sylvestris L.) plantations. Sci. Total Environ. 325, 163–180. doi: 10.1016/j.scitotenv.2003.10.037
Guillitte, O., Tikhomirov, F., Shaw, G., Johanson, K., Dressler, A., and Melin, J. (1993). Decontamination methods for reducing radiation doses arising from radioactive contamination of forest ecosystemsa summary of available countermeasures. Sci. Total Environ. 137, 307–314.
Guillitte, O., Tikhomirov, F., Shaw, G., and Vetrov, V. (1994). Principles and practices of countermeasures to be carried out following radioactive contamination of forest areas. Sci. Total Environ. 157, 399–406.
Hashimoto, S., Matsuura, T., Nanko, K., Linkov, I., Shaw, G., and Kaneko, S. (2013). Predicted spatio-temporal dynamics of radiocesium deposited onto forests following the fukushima nuclear accident. Sci. Rep. 3:2564. doi: 10.1038/srep02564
Hashimoto, S., Ugawa, S., Nanko, K., and Shichi, K. (2012). The total amounts of radioactively contaminated materials in forests in fukushima, japan. Sci. Rep. 2:416. doi: 10.1038/srep00416
Hayashi, T., and Yamamoto, K. (2006). A system to predict diameter distribution in pure even-aged hinoki (Chamaecyparis obtusa sieb.) plantations (ii): application to sugi (Cryptomeria japonica d. don) plantations. J. For. Plan. 11, 67–76.
Hayashi, T., Yamamoto, K., and Umemura, T. (2002). A system to predict diameter distribution in pure even-aged hinoki (chamaecyparis obtusa sieb.) plantations (i): diameter distribution prediction system. J. For. Plan. 8, 31–39.
IAEA. (2002). Modelling the Migration and Accumulation of Radionuclides in Forest Ecosystems: Report of Division of Radiation and Waste Safety. Waste Safety Section and Biosphere Modelling and Assessment (Program). International Atomic Energy Agency, IAEA-BIOMASS, Vienna.
Jenkinson, D., Andrew, S., Lynch, J., Goss, M., and Tinker, P. (1990). The turnover of organic carbon and nitrogen in soil [and discussion]. Philos. T. R. Soc. B. 329, 361–368.
Jenkinson, D., Meredith, J., Kinyamario, J., Warren, G., Wong, M., Harkness, D., et al. (1999). Estimating net primary production from measurements made on soil organic matter. Ecology 80, 2762–2773.
Kaneko, S., Takahashi, M., Ikea, S., and Akama, A. (2014). The pollution and dynamics of radiocesium in forest ecosystem due to the accident of fukushima nuclear power plant (in japansese). Jpn. J. Soil Sci. Plant Nutr. 85, 86–89.
Karadeniz, Ö., Karakurt, H., Çak1r, R., Çoban, F., Büyükok, E., and Akal, C. (2015). Persistence of 137Cs in the litter layers of forest soil horizons of mount ida/kazdagi, turkey. J. Environ. Radioact. 139, 125–134. doi: 10.1016/j.jenvrad.2014.10.004
Kato, H., Onda, Y., and Gomi, T. (2012). Interception of the fukushima reactor accident-derived 137Cs, 134Cs and 131I by coniferous forest canopies. Geophys. Res. Let. 39:20403. doi: 10.1029/2012GL052928
Koizumi, A., Niisoe, T., Harada, K. H., Fujii, Y., Adachi, A., Hitomi, T., et al. (2013). 137Cs trapped by biomass within 20 km of the Fukushima daiichi nuclear power plant. Environ. Science Technol. 47, 9612–9618. doi: 10.1021/es401422g
Konoplev, A., Avila, R., and Bulgakov, A. (2002). Model of radiocesium transfer from soil to understorey in forest ecosystems. Radioprotection 37, C1–25. doi: 10.1051/radiopro/2002049
Kuroda, K., Kagawa, A., and Tonosaki, M. (2013). Radiocesium concentrations in the bark, sapwood and heartwood of three tree species collected at fukushima forests half a year after the fukushima dai-ichi nuclear accident. J. Environ. Radioact. 122, 37–42. doi: 10.1016/j.jenvrad.2013.02.019
Lim, H., Lee, K.-H., Lee, K. H., and Park, I. H. (2013). Biomass expansion factors and allometric equations in an age sequence for japanese cedar (Cryptomeria japonica) in southern korea. J. For. Res. 18, 316–322. doi: 10.1007/s10310-012-0353-2
Linkov, I., and Burmistrov, D. (2003). Model uncertainty and choices made by modelers: lessons learned from the international atomic energy agency model intercomparisons. Risk Anal. 23, 1297–1308. doi: 10.1111/j.0272-4332.2003.00402.x
Linkov, I., Burmistrov, D., Kandlikar, M., and Schell, W. (1999). “Reducing uncertainty in the radionuclide transport modeling for the chernobyl forests using bayesian updating,” in Contaminated Forests, eds L. Linkov and W. R. Schell (Dordrecht: Springer Netherlands), 143–150.
Linkov, I., Morel, B., and Schell, W. R. (1997). Remedial policies in radiologically-contaminated forests: environmental consequences and risk assessment. Risk Anal. 17, 67–75.
Mahara, Y., Ohta, T., Ogawa, H., and Kumata, A. (2014). Atmospheric direct uptake and long-term fate of radiocesium in trees after the fukushima nuclear accident. Sci. Rep. 4:7121. doi: 10.1038/srep07121
MEA. (2005). Millennium Ecosystem Assessment. Ecosystems and Human Well-being. Synthesis. Washington, DC: Island Press.
Morino, Y., Ohara, T., and Nishizawa, M. (2011). Atmospheric behavior, deposition, and budget of radioactive materials from the fukushima daiichi nuclear power plant in march 2011. Geophys. Res. Let. 38:D06307. doi: 10.1029/2011GL048689
NIES. (2012). “Radioactive materials and environmental disaster research,” in NIES Annual Report 2012 (Tsukuba: National Institute for Environemental Studies). Available online at: http://www.nies.go.jp/kanko/annual/ae18.pdf
Nishikiori, T., Watanabe, M., Koshikawa, M. K., Takamatsu, T., Ishii, Y., Ito, S., et al. (2015). Uptake and translocation of radiocesium in cedar leaves following the fukushima nuclear accident. Sci. Total Environ. 502, 611–616. doi: 10.1016/j.scitotenv.2014.09.063
Noguchi, K., Hirai, K., Takahashi, M., Aizawa, S., Itoh, Y., Shigenaga, H., et al. (2009). Effects of thinning on aboveground carbon and nitrogen dynamics at a sugi (Cryptomeria japonica) plantation in northern kanto region, eastern japan. Bull. FFPRI 8, 205–214.
Ohashi, S., Okada, N., Tanaka, A., Nakai, W., and Takano, S. (2014). Radial and vertical distributions of radiocesium in tree stems of Pinus densiflora and Quercus serrata 1.5 y after the fukushima nuclear disaster. J. Environ. Radioact. 134, 54–60. doi: 10.1016/j.jenvrad.2014.03.001
Onda, Y., Gomi, T., Mizugaki, S., Nonoda, T., and Sidle, R. C. (2010). An overview of the field and modelling studies on the effects of forest devastation on flooding and environmental issues. Hydrol. Process. 24, 527–534. doi: 10.1002/hyp.7548
Ooba, M., Wang, Q., Murakami, S., and Kohata, K. (2010). Biogeochemical model (bgc-es) and its basin-level application for evaluating ecosystem services under forest management practices. Ecol. Model. 221, 1979–1994. doi: 10.1016/j.ecolmodel.2010.05.008
Rafferty, B., Dawson, D., and Kliashtorin, A. (1997). Decomposition in two pine forests: the mobilisation of 137Cs and k from forest litter. Soil Biol. Biochem. 29, 1673–1681.
Rantavaara, A., Vetikko, V., Raitio, H., and Aro, L. (2012). Seasonal variation of the 137Cs level and its relationship with potassium and carbon levels in conifer needles. Sci. Total Environ. 441, 194–208. doi: 10.1016/j.scitotenv.2012.09.045
Renard, K. G., Foster, G. R., Weesies, G. A., and Porter, J. P. (1991). Rusle: revised universal soil loss equation. J. Soil Water Conserv. 46, 30–33.
Riesen, T. K. (2002). Radiocaesium in forests a review on most recent research. Environ. Rev. 10, 79–90. doi: 10.1139/a02-001
Rigol, A., Vidal, M., and Rauret, G. (2002). An overview of the effect of organic matter on soil–radiocaesium interaction: implications in root uptake. J. Environ. Radioact. 58, 191–216. doi: 10.1016/S0265-931X(01)00066-2
Sadanandan Nambiar, E. K., and Fife, D. N. (1991). Nutrient retranslocation in temperate conifers. Tree Physiol. 9, 185–207.
Schell, W., Linkov, I., Myttenaere, C., and Morel, B. (1996). A dynamic model for evaluating radionuclide distribution in forests from nuclear accidents. Health Phys. 70, 318–335.
Semizhon, T., Putyrskaya, V., Zibold, G., and Klemt, E. (2009). Time-dependency of the 137Cs contamination of wild boar from a region in southern germany in the years 1998 to 2008. J. Environ. Radioact. 100, 988–992. doi: 10.1016/j.jenvrad.2009.06.023
Shaw, G., and Belli, M. (1999). “The rife models of radionuclide fluxes in european forests,” in Contaminated Forests, eds L. Linkov and W. R. Schell (Dordrecht: Springer Netherlands), 161–171.
Shaw, G., Venter, A., Avila, R., Bergman, R., Bulgakov, A., Calmon, P., et al. (2005). Radionuclide migration in forest ecosystems–results of a model validation study. J. Environ. Radioact. 84, 285–296. doi: 10.1016/j.jenvrad.2003.09.006
Steinhauser, G., Brandl, A., and Johnson, T. E. (2014). Comparison of the chernobyl and fukushima nuclear accidents: a review of the environmental impacts. Sci. Total Environ. 470, 800–817. doi: 10.1016/j.scitotenv.2013.10.029
Stemmer, M., Hromatka, A., Lettner, H., and Strebl, F. (2005). Radiocesium storage in soil microbial biomass of undisturbed alpine meadow soils and its relation to 137Cs soil–plant transfer. J. Environ. Radioact. 79, 107–118. doi: 10.1016/j.jenvrad.2004.04.010
Tagami, K., Uchida, S., Ishii, N., and Kagiya, S. (2012). Translocation of radiocesium from stems and leaves of plants and the effect on radiocesium concentrations in newly emerged plant tissues. J. Environ. Radioact. 111, 65–69. doi: 10.1016/j.jenvrad.2011.09.017
Tagami, K., Uchida, S., Uchihori, Y., Ishii, N., Kitamura, H., and Shirakawa, Y. (2011). Specific activity and activity ratios of radionuclides in soil collected about 20km from the fukushima daiichi nuclear power plant: radionuclide release to the south and southwest. Sci. Total Environ. 409, 4885–4888. doi: 10.1016/j.scitotenv.2011.07.067
Takeda, A., Tsukada, H., Nakao, A., Takaku, Y., and Hisamatsu, S. (2013). Time-dependent changes of phytoavailability of Cs added to allophanic andosols in laboratory cultivations and extraction tests. J. Environ. Radioact. 122, 29–36. doi: 10.1016/j.jenvrad.2013.02.005
Takeda, A., Tsukada, H., Yamaguchi, N., Takeuchi, M., Sato, M., Nakao, A., et al. (2014). Relationship between the radiocesium interception potential and the transfer of radiocesium from soil to soybean cultivated in 2011 in Fukushima prefecture, japan. J. Environ. Radioact. 137, 119–124. doi: 10.1016/j.jenvrad.2014.06.022
Tanouchi, H., and Utsugi, G. (2004). National survey on forest productivity in various growth environment (in japanese). Stud. Grant. For. For. Product Res. Instit. 3, 24–28.
Teramage, M. T., Onda, Y., Kato, H., and Gomi, T. (2014). The role of litterfall in transferring fukushima-derived radiocesium to a coniferous forest floor. Sci. Total Environ. 490, 435–439. doi: 10.1016/j.scitotenv.2014.05.034
Thiry, Y., Colle, C., Yoschenko, V., Levchuk, S., Hees, M. V., Hurtevent, P., and Kashparov, V. (2009). Impact of scots pine (Pinus sylvestris L.) plantings on long term 137Cs and 90Sr recycling from a waste burial site in the chernobyl red forest. J. Environ. Radioact. 100, 1062–1068. doi: 10.1016/j.jenvrad.2009.05.003
Thiry, Y., and Myttenaere, C. (1993). Behaviour of radiocaesium in forest multilayered soils. J. Environ. Radioact. 18, 247–257.
Thornthwaite, C. W. (1948). An approach toward a rational classification of climate. Geogr. Rev. 38, 55–94.
Tikhomirov, F. A., and Shcheglov, A. I. (1994). Main investigation results on the forest radioecology in the kyshtym and chernobyl accident zones. Sci. Total Environ. 157, 45–57.
Tikhomirov, F. A., Shcheglov, A. I., and Sidorov, V. P. (1993). Forests and forestry: radiation protection measures with special reference to the chernobyl accident zone. Sci. Total Environ. 137, 289–305.
Ueda, S., Hasegawa, H., Kakiuchi, H., Akata, N., Ohtsuka, Y., and Hisamatsu, S. (2013). Fluvial discharges of radiocaesium from watersheds contaminated by the fukushima dai-ichi nuclear power plant accident, japan. J. Environ. Radioact. 118, 96–104. doi: 10.1016/j.jenvrad.2012.11.009
Velasco, R. H., Belli, M., Sansone, U., and Menegon, S. (1993). Vertical transport of radiocesium in surface soils: model implementation and dose-rate computation. Health Phys. 64, 37–44.
Velasco, R., Toso, J., Belli, M., and Sansone, U. (1997). Radiocesium in the northeastern part of Italy after the chernobyl accident: vertical soil transport and soil-to-plant transfer. J. Environ. Radioact. 37, 73–83.
Witkamp, M., and Barzansky, B. (1968). Microbial immobilization of 137Cs in forest litter. Oikos. 19, 392–395.
Witkamp, M., and Frank, M. L. (1970). Effects of temperature, rainfall, and fauna on transfer of 137Cs, K, Mg, and mass in consumer-decomposer microcosms. Ecology. 51, 465–474.
Keywords: rCs and C modeling, 137Cs inventory, forest management, decontamination, 137Cs dynamics
Citation: Nishina K and Hayashi S (2015) Modeling radionuclide Cs and C dynamics in an artificial forest ecosystem in Japan -FoRothCs ver1.0-. Front. Environ. Sci. 3:61. doi: 10.3389/fenvs.2015.00061
Received: 08 March 2015; Accepted: 26 August 2015;
Published: 11 September 2015.
Edited by:
Xuan Zhu, Monash University, AustraliaCopyright © 2015 Nishina and Hayashi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kazuya Nishina, Center for Regional Environmental Research, National Institute for Environmental Studies, 16-2, Onogawa, Tsukuba 305-8506, Japan,bmlzaGluYS5rYXp1eWFAbmllcy5nby5qcA==
 Kazuya Nishina
Kazuya Nishina Seiji Hayashi
Seiji Hayashi