pH as a Primary Control in Environmental Microbiology: 1. Thermodynamic Perspective

pH influences the occurrence and distribution of microorganisms. Microbes typically live over a range of 3–4 pH units and are described as acidophiles, neutrophiles, and alkaliphiles, depending on the optimal pH for growth. Their growth rates vary with pH along bell- or triangle-shaped curves, which reflect pH limits of cell structural integrity and the interference of pH with cell metabolism. We propose that pH can also affect the thermodynamics and kinetics of microbial respiration, which then help shape the composition and function of microbial communities. Here we use geochemical reaction modeling to examine how environmental pH controls the energy yields of common redox reactions in anoxic environments, including syntrophic oxidation, iron reduction, sulfate reduction, and methanogenesis. The results reveal that environmental pH changes energy yields both directly and indirectly. The direct change applies to reactions that consume or produce protons whereas the indirect effect, which applies to all redox reactions, comes from the regulation of chemical speciation by pH. The results also show that energy yields respond strongly to pH variation, which may modulate microbial interactions and help give rise to the pH limits of microbial metabolisms. These results underscore the importance of pH as a control on microbial metabolisms and provide insight into potential impacts of pH variation on the composition and activity of microbial communities. In a companion paper, we continue to explore how the kinetics of microbial metabolisms responds to pH variations, and how these responses control the outcome of microbial interactions, including the activity and membership of microbial consortia.

Introduction

Microorganisms are widespread in natural environments, from hot springs to deep aquifers, and to ocean floors (Chapelle et al., 1995; Ward et al., 1998; Edwards et al., 2012). They drive a series of biogeochemical processes, from redox reactions, to weathering, and to the global cycling of carbon and other elements (Bennett et al., 2001; Falkowski et al., 2008; Maguffin et al., 2015). In return, their metabolisms are controlled by a wide range of environmental variables, including pH, temperature, salinity, nutrient availability, and geographic locations (Lennon and Jones, 2011; Amend et al., 2013). Among these factors, pH emerges as a primary control (Chen et al., 2004; Kemmitt et al., 2006; Bethke et al., 2011; Zhalnina et al., 2015). pH correlates strongly with microbial communities across a wide range of biogeochemical conditions (Thompson et al., 2017). In addition, variations in environmental pH also induce significant responses of metabolic activities of natural communities (Kotsyurbenko et al., 2004; Ye et al., 2012).

pH shapes microbial metabolisms in different ways. First, it affects the environmental conditions that are relevant to microbial growth and survival. pH describes the chemical activity of protons, a key player in redox reactions, mineral dissolution and precipitation, surface complexation, and other geochemical reactions (Stumm and Morgan, 1996; Bethke et al., 2011). These reactions determine the salinity and composition of aqueous solutions and control the bioavailability of nutrients and trace elements. In addition, pH also affects the activities of extracellular enzymes, and the reactivity of natural organic matter (Leprince and Quiquampoix, 1996; Paul et al., 2006). In this way, pH becomes an indicator of overall environmental settings that shape the composition and activity of microbial communities (Lauber et al., 2009).

Second, pH may interfere with microbial metabolisms. Most laboratory cultures live within a pH range of 3–4 units—that is 3–4 orders of magnitude difference in the chemical activity of protons (Rosso et al., 1995). The pH of maximum growth rate is called the optimal growth pH. Based on optimal growth pH, microbes can be separated into three groups: acidophiles grow best at pH < 5, neutrophiles grow optimally at pH between 5 and 9, and alkaliphiles grow fastest above pH 9 (Horikoshi, 1999; Baker-Austin and Dopson, 2007). Where environmental pH deviates from optimal pH levels, microbial growth rates decrease (Rosso et al., 1995). For a microbe with a pH range spanning 4 pH units, assuming that its optimal pH is near the middle point of the pH range, a deviation of one unit from this pH optimal can reduce its growth rate by about 50% (see Maestrojuan and Boone, 1991; O'Flaherty et al., 1998, and others). In natural environments, decreasing or increasing the environmental pH by one unit can also lower the metabolic activity of microbial communities by up to 50% (Kotsyurbenko et al., 2004; Fernández-Calviño and Bååth, 2010).

pH may also affect microbial metabolisms and hence microbial community structures by modulating the thermodynamics and kinetics of redox reactions. Microbial respiration catalyzes redox reactions in order to synthesize ATPs. Respiration rates thus depend on thermodynamic drives, the differences between the energy available from redox reactions and the energy conserved by respiration (Jin and Bethke, 2002, 2003). Many redox reactions produce or consume protons, and thus, their free energy yields vary with pH (Bethke et al., 2011). Where the available energies equal or fall below the conserved energies, respiration reactions become thermodynamic unfavorable (Jin and Bethke, 2005, 2007, 2009). In this way, environmental pH helps control the progress of microbial respiration and growth, which in turn shapes the community composition.

The goal of this study is to illustrate how environmental pH influences the thermodynamics of redox reactions, and how these influences may shape microbial metabolisms and interactions. We focus on syntrophic oxidation, iron reduction, sulfate reduction, and methanogenesis, common microbial redox reactions in anoxic environments (Lovley and Chapelle, 1995; Bethke et al., 2011). We evaluate their thermodynamic responses to environmental pH using geochemical reaction modeling. In a companion paper (Jin and Kirk, under review), we continue to explore how the pH-induced thermodynamic responses affect the kinetics of microbial metabolisms and the outcome of microbial interactions.

Methods

Microbes catalyze different redox reactions and, accordingly, can be separated into fermenters and respirers (Jin and Roden, 2011). Fermenting microbes degrade natural organic matter to a series of products, including short-chain fatty acids (e.g., acetate, lactate, and propionate), and primary alcohols (e.g., methanol and ethanol) (Schink and Stams, 2013). Some respirers oxidize short-chain fatty acids and primary alcohols to acetate and CO₂, and transfer the released electrons to the reduction of protons to dihydrogen (H₂). Others oxidize the products of organic matter degradation, and transfer the released electrons to the reduction of O₂, ferric minerals, sulfate, bicarbonate, and other electron acceptors.

Table 1 lists the stoichiometric equations for microbial redox reactions commonly found in anoxic environments. Following standard practice in biochemistry and low-temperature geochemistry, we write these reactions using dominant chemical species at neutral pH. For example, at pH 7, short-chain fatty acids occur mainly as their conjugate bases, and most dissolved inorganic carbon (DIC) appears as bicarbonate (Figure 1). In contrast, sulfide occurs in nearly equal proportions as dihydrogen sulfide (H₂S) and monohydrogen sulfide (HS⁻). We choose dihydrogen sulfide, instead of both dihydrogen sulfide and monohydrogen sulfide in writing the equations for sulfate reduction (reaction 14–20 in Table 1). Following previous practice (Bethke et al., 2011; Jin, 2012), we write reaction equations that transfer 8 electrons, or the consumption of one acetate or four dihydrogen molecules.

TABLE 1

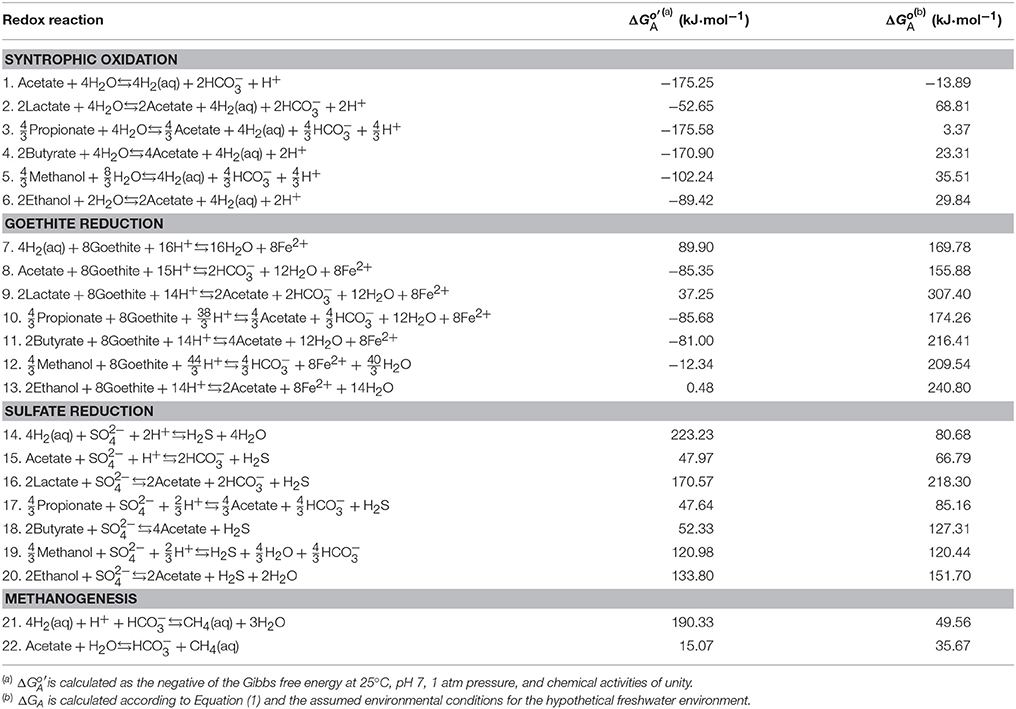
Table 1. Redox reactions, standard available energy$\Delta G_A^{o^{\prime }}$, and the energy ΔG_A available in the assumed environment.

FIGURE 1

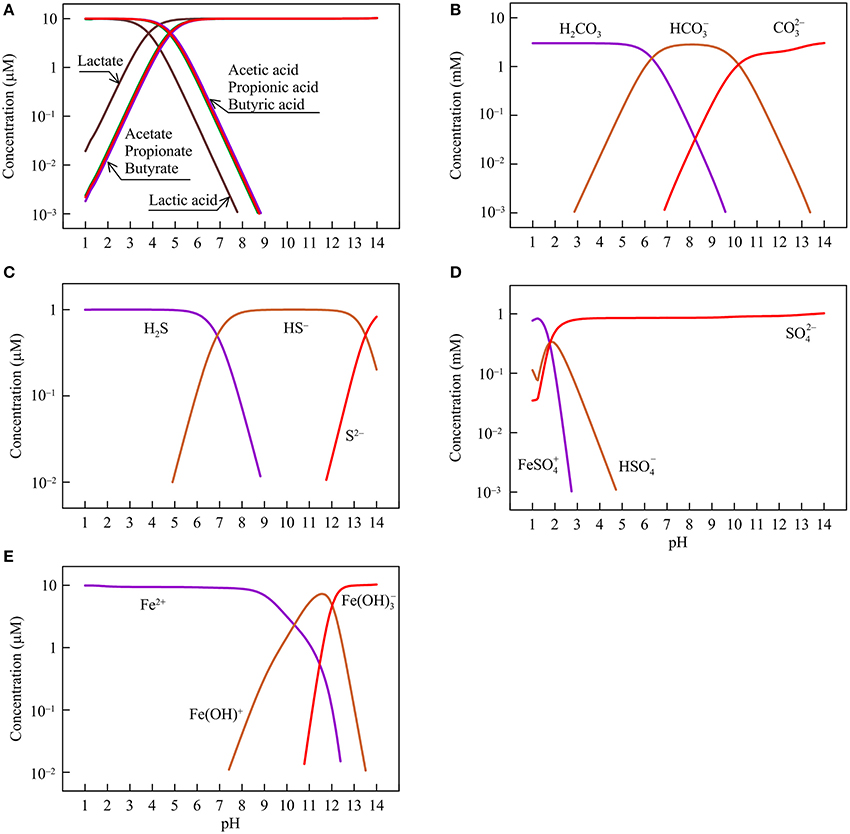
Figure 1. Variations with pH in the concentrations of short-chain fatty acids and their conjugate bases (A), dissolved inorganic carbon (carbonic acid H₂CO₃, bicarbonate HCO${}_3^{-}$, and carbonate CO${}_3^{2-}$) (B), sulfide (dihydrogen sulfide H₂S, monohydrogen sulfide HS⁻, and sulfide S²⁻) (C), sulfate (ferric iron-sulfate complex FeSO${}_4^{+}$, hydrogen sulfate HSO${}_4^{-}$, and sulfate SO${}_4^{2-}$) (D), and ferrous iron (ferrous iron Fe²⁺, and ferrous iron-hydroxide complex Fe(OH)⁺ and Fe(OH)${}_3^{-}$) (E) in the hypothetical solution.

Energy available from a redox reaction, ΔG_A [J·(mol reaction)⁻¹, or J·mol⁻¹], is calculated as the negative of its Gibbs free energy change,

$\begin{array}{cc}\Delta G_A=-\Delta G^o-RT\left[\ln \left({\displaystyle \prod _{\text{P}}{a}_{\text{P}}^{{\nu }_{\text{P}}}}\right)-\ln \left({\displaystyle \prod _{\text{S}}{a}_{\text{S}}^{{\nu }_{\text{S}}}}\right)\right],& (1)\end{array}$

where ΔG° is the standard Gibbs free energy change, a_P and a_S are the activities of products and reactants, respectively, ν_P and ν_S are the stoichiometric coefficients, R is the gas constant (J·mol⁻¹·K⁻¹), and T is the temperature in kelvin (K). Chemical activity is calculated as the product of activity coefficients (M⁻¹) and molal concentrations of chemical species. The activity coefficients are calculated according to an extended form of the Debye-Hückel equation (Helgeson, 1969). Table 1 lists the available energy calculated under the biochemical standard conditions of pH 7, 25°C, 1 atm, and chemical activities of unity.

We compute available energies ΔG_A for a hypothetical solution in contact with goethite. The composition of the solution is consistent with dilute groundwater. The solution has 1 atm pressure and a temperature of 25°C and contains 10 mM Na⁺, 10 mM Cl⁻, 2.0 mM Ca²⁺, and 3 mM DIC. The solution also contains 1 mM sulfate, 10 μM acetate, lactate, propionate, butyrate, methanol, ethanol, and ferrous iron, 1 μM sulfide and methane, and 0.1 μM H₂.

Chemical compounds dissolved in water may react with water molecules, acquire or give up protons and hydroxide, and combine with other molecules and ions. As a result, they appear in different forms or chemical species—a process called chemical speciation. To calculate available energies, we simulate the speciation of dissolved chemical compounds and compute the activities of chemical species using the program React of the software package Geochemist's Workbench version 9.0 (Bethke, 2008). The simulation assumes that chemical speciation is at thermodynamic equilibrium, and describes these reactions on the basis of the updated LLNL Thermodynamic Database (Delany and Lundeen, 1990). The simulation also assumes that goethite and ferrihydrite dissolution are at equilibrium. We added into the thermodynamic database the entries for natural goethite and ferrihydrite (Lindsay, 1979; Bigham et al., 1996). The input script and the modeling output are available in the Supplementary Material.

To investigate the impact of pH, we take the available energies at pH 7 as references, and compute the changes in the available energies at pH ranging from 1 to 14. We consider changes in available energies, rather than absolute values, in order to highlight the relative responses of different microbial redox reactions to pH variations. This approach also simplifies the discussion of ferric mineral reduction. Different ferric minerals, such as ferrihydrite, goethite, hematite, and lepidocrocite, have different chemical potentials (Cornell and Schwertmann, 2003), but their potentials respond in the same fashion to pH, because the reduction of these ferric minerals consumes the same number of protons per electron. Here we take goethite as an example, but the results are applicable to ferrihydrite, hematite, and lepidocrocite.

We use the thermodynamic potential factor F_T to quantify the control of the available energy on the rate of microbial respiration,

$\begin{array}{cc}{F}_T=1-\exp \left(-\frac{f}{\chi RT}\right),& (2)\end{array}$

where f is the thermodynamic drive (J·mol⁻¹), and χ is the average stoichiometric number (Jin and Bethke, 2007, 2009). The χ value is 8 per reaction for syntrophic oxidation of organic compounds and the reduction of goethite (reaction 1–13 in Table 1), 6 per reaction for the reduction of sulfate (reaction 14–20), and 2 per reaction for methanogenesis (reaction 21 and 22) (Jin and Bethke, 2005; Jin and Roden, 2011). The thermodynamic drive is

$\begin{array}{cc}f=\Delta G_{\text{A}}-\Delta G_{\text{C}},& (3)\end{array}$

the difference between the energy ΔG_A available in the environment and the energy ΔG_C conserved by respiration (Jin and Bethke, 2002, 2003). For microbial iron reduction, sulfate reduction, and methanogenesis, we calculate the conserved energy,

$\begin{array}{cc}\Delta G_{\text{C}}={\nu }_{\text{P}}·\Delta G_{\text{P}},& (4)\end{array}$

as the product of the ATP yield ν_P–the number of ATPs synthesized per reaction–and the phosphorylation energy ΔG_P–the energy required by ATP synthesis from ADP and phosphate in the cytoplasm. Based on Jin (2012), we take the ΔG_P value as 45 kJ·(mol ATP)⁻¹, and the ATP yields ν_P as 1, 0.75, and 0.5 ATPs per 8 electron transfer (or per acetate or 4 H₂) for iron reducers, sulfate reducers, and methanogens, respectively.

Results

Respiring microbes harvest energy from a wide range of redox reactions. Here we focus on the electron donors generated from organic matter degradation, including dihydrogen (H₂), acetate, lactate, propionate, butyrate, methanol, and ethanol, and consider the common electron acceptors in anoxic environments, such as goethite, sulfate, bicarbonate, and protons (Lovley and Chapelle, 1995; Bethke et al., 2011).

Available Energy

Table 1 lists the energies available from different redox reactions in the assumed freshwater environment. Among the different redox reactions, goethite reduction provides the largest available energies, followed by sulfate reduction, methanogenesis, and syntrophic oxidation of organic compounds. This order in energy yield follows the well-known redox tower in microbiology (Bethke et al., 2011). Under acidic or alkaline conditions, however, the redox tower is not applicable anymore because pH affects the available energies of different redox reactions to different extents, as described in the subsections that follow.

Proton Reaction

Most redox reactions in Table 1 consume or produce protons. Therefore, pH variations, or in other words, changes in the chemical activity of protons, affect the energy yields of the reactions. The slope L of the change in available energy depends on how many protons participate in the reaction,

$\begin{array}{cc}L=RT\ln \left(10\right)·{\nu }_H.& (5)\end{array}$

Here ν_H is the stoichiometric coefficient for protons in the reaction, which is positive where protons are produced.

Equation (5) predicts that energy available from syntrophic oxidation reactions increases linearly with pH because syntrophic reactions generate protons (Figure 2). For reactions that consume protons, their energies decrease linearly with increasing pH. These reactions include iron reduction, hydrogenotrophic methanogenesis, and sulfate reduction by oxidizing H₂, acetate, propionate, and methanol (Figures 3, 4A–C, 5A). No proton appears in acetoclastic methanogenesis or sulfate reduction by oxidizing lactate, butyrate, and ethanol. As such, pH variation does not directly influence their energy yields (Figures 4D, 5B).

FIGURE 2

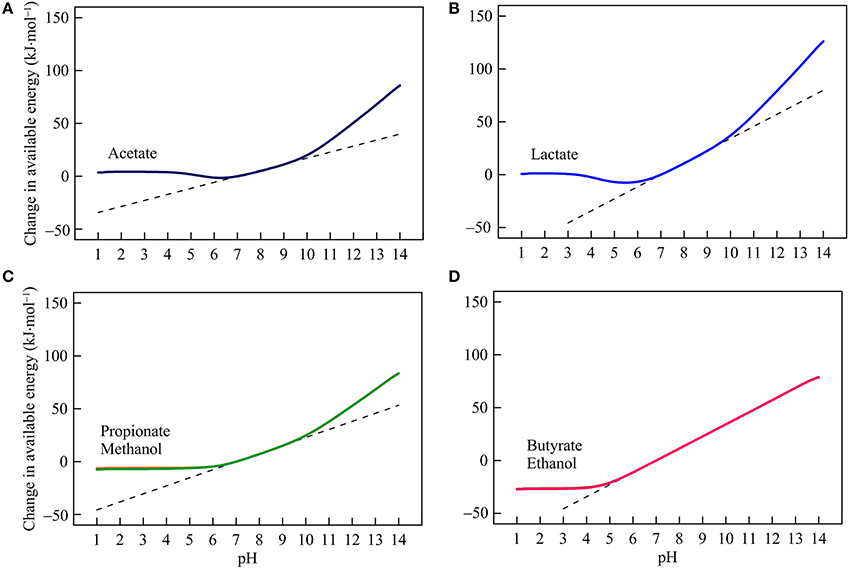
Figure 2. Variations with pH in the energy available from syntrophic oxidation of acetate (A), lactate (B), propionate, methanol (C), butyrate, and ethanol (D) in the hypothetical solution. Solid lines are results of geochemical modeling, and dashed lines are calculated according to Equation (5). The variations are calculated in reference to the available energies at pH 7.

FIGURE 3

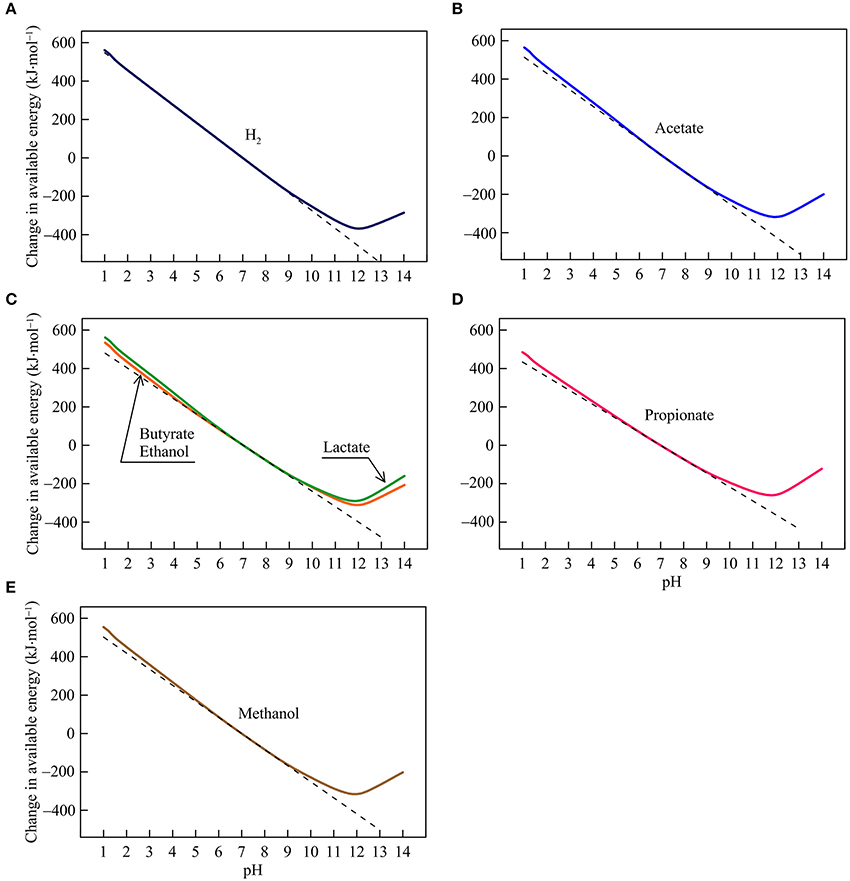
Figure 3. Variations with pH in the energy available from the reduction of goethite coupled to the oxidation of H₂ (A), acetate (B), lactate, butyrate, ethanol (C), propionate (D), and methanol (E) in the hypothetical solution. Solid lines are results of geochemical modeling, and dashed lines are calculated according to Equation (5). The variations are calculated in reference to the available energies at pH 7.

FIGURE 4

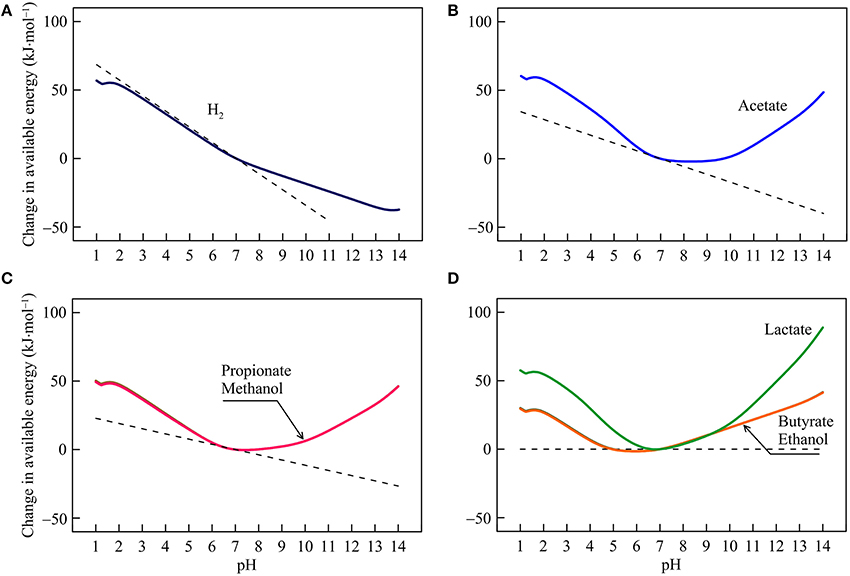
Figure 4. Variations with pH in the energy available from the reduction of sulfate coupled to the oxidation of H₂ (A), acetate (B), propionate, methanol (C), lactate, butyrate, and ethanol (D) in the hypothetical solution. Solid lines are results of geochemical modeling, and dashed lines are calculated according to Equation (5). The variations are calculated in reference to the available energies at pH 7.

FIGURE 5

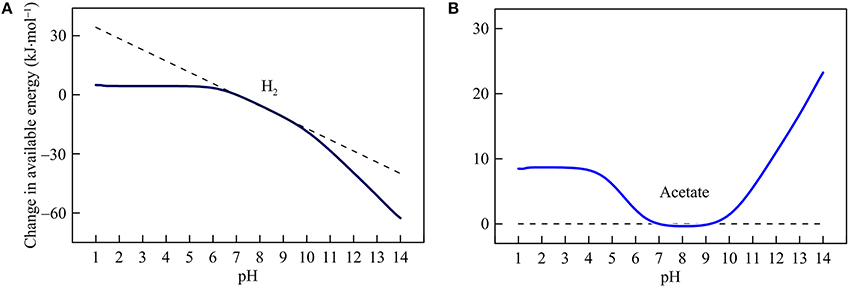
Figure 5. Variations with pH in the energy available from hydrogenotrophic (A) and acetoclastic methanogenesis (B) in the hypothetical solution. Solid lines are results of geochemical modeling, and dashed lines are calculated according to Equation (5). The variations are calculated in reference to the available energies at pH 7.

Chemical Speciation

We also compute available energies at different pHs using the results of geochemical reaction modeling. Figures 2–5 compare the simulation results to those predicted by Equation (5). For most microbial redox reactions, the modeling results overlap with the equation predictions only over a limited range around neutral pH. The differences between the two predictions arise from the speciation of dissolved mass, which determines the activities of chemical species and hence the energy available from redox reactions.

Figure 1 shows, according to the simulation results, how the concentrations of different chemical species change with pH. Specifically, short-chain fatty acids occur in the solution as both acids and their conjugate bases (Figure 1A). The relative abundances of the two chemical species depend on acidity constants. Lactate has the smallest logarithmic acidity constant (pKa) of 3.9, and acetate, propionate, and butyrate have pKa values of 4.8–4.9 (Lide, 2003). Where pH is smaller than the pKa values, the acids are dominant. At pH > the pKa values, the conjugate bases take over.

DIC occurs mainly as carbonic acid, bicarbonate, and carbonate (Figure 1B). At pH between 6 and 10.5, bicarbonate dominates. Carbonic acid and carbonate are the main forms at pH below 6 and above 10.5, respectively. Dissolved sulfide also has three main species—dihydrogen sulfide, monohydrogen sulfide, and sulfide (S²⁻), which appear as the dominant species at pH < 7, between 7 and 13.5, and above 13.5, respectively (Figure 1C). Sulfate occurs mainly as sulfate anion at pH > 2.5, and as ferric iron/sulfate-complex at lower pH (Figure 1D). We assume that the hypothetical solution is in contact with goethite and as such, ferric iron in the sulfate complex species comes from the dissolution of goethite.

Ferrous iron occurs as a free cation (Fe²⁺) and two hydroxide-complexes (Figure 1E). The free cation dominates the solution at pH below 9. At pH around 11, ferrous monohydroxide Fe(OH)⁺ is the main species whereas at pH above 13, ferrous trihydroxide Fe(OH)${}_3^{-}$ becomes dominant.

Syntrophic Oxidation

Syntrophic oxidation reactions can be separated into two groups, depending on whether bicarbonate is produced (reaction 1–6 in Table 1). The group that produces bicarbonate includes the oxidations of acetate, lactate, propionate, and methanol. Figures 2A–C show according to the modeling results how the energies available from these reactions respond to pH variations. Below pH 6, available energies remain roughly constant. Above pH 7, the energies increase with pH with the highest rate of increase above pH 10.

This variation in available energy reflects changes in DIC speciation. Below pH 6, bicarbonate concentration declines with decreasing pH, which works to raise available energies (Figure 1B). At the same time, however, decreasing pH works to reduce available energies because the reactions generate protons. The thermodynamic effects of DIC speciation and proton generation cancel each other and, as a result, the available energies remain relatively constant. pH also affects the speciation of acetate, lactate, and propionate (Figure 1A), but the concentrations of these chemical species co-vary with pH, and their thermodynamic effects are either balanced by each other (such as in the oxidation of lactate and propionate) or by the speciation of DIC (acetate oxidation).

Between pH 7 and 10, bicarbonate concentration varies relatively little with pH (Figure 1B). As such, the thermodynamic effect of DIC speciation dissipates, and the thermodynamic effect of proton production causes energies to rise with increasing pH. Above pH 10, bicarbonate concentration falls with increasing pH, which further raises the available energies.

Reactions that do not generate bicarbonate include the oxidations of butyrate and ethanol. Their available energies depend on pH and the speciation of acetate—a product of the two reactions. Below pH 4, acetate concentration falls with decreasing pH (Figure 1A). While pH decreases work to lower the available energies, falling acetate concentration works to raise the available energies. The two effects balance each other, and hold the available energies constant. At pH above 5, the available energies depend primarily on pH, and increase linearly with increasing pH.

Iron Reduction

The available energies of iron reduction respond strongly to changes in pH (Figure 3). Between pH 1 and 9, the available energies fall almost linearly with rising pH. The slopes of the fall depend on the number of protons consumed in the reactions, and range from 72 to 91 kJ·mol⁻¹ per pH unit (reaction 7–13 in Table 1). Speciation of short-chain fatty acids and DIC also responds to pH (Figures 1A,B). However, their thermodynamic effects are relatively insignificant compared to the energy variations induced directly by proton consumption.

Between pH 9 and 12, the available energies continue to decline with increasing pH but the slopes of the decline are smaller than those between pH 1 and 9. Here, the speciation of ferrous iron starts to take effect—ferrous iron concentration drops with increasing pH, due to the formation of ferrous iron/hydroxide-complexes (Figure 1E). The diminished concentration works to raise the available energies, which counteracts the thermodynamic effect of proton consumption. Ultimately, above pH 12, the speciation effect becomes dominant, leading to the rising available energies with increasing pH.

Sulfate Reduction

The response of sulfate reduction to pH varies between reactions. For hydrogenotrophic sulfate reduction (reaction 14 in Table 1), available energy declines at varying rates with increasing pH (Figure 4A). The energy change reflects proton consumption by the reaction but other factors also contribute. For example, at pH < 2, the sulfate ion is a secondary species of dissolved sulfate, and its concentration rises with increasing pH (Figure 1D), which partially counteracts the thermodynamic effect of proton consumption and slows down the decline in the available energy. At pH > 7, dihydrogen sulfide concentration starts to fall with increasing pH (Figure 1C), which also slows down the energy decline.

For sulfate reduction by the oxidation of acetate, propionate, and methanol (reaction 15, 17, and 19), energy variations separate into two phases (Figures 4B,C). Below pH 7, available energies largely fall with increasing pH, reflecting proton consumption and bicarbonate production by the reactions. Above pH 7, available energies rise with increasing pH, because the thermodynamic effect of proton consumption is counteracted by those of the speciation of DIC and sulfide. As pH increases, bicarbonate and dihydrogen sulfide concentrations diminish (Figures 1B,C).

For sulfate reductions by the oxidation of lactate, butyrate, and ethanol (reaction 16, 18, and 20), Equation (5) predicts that pH variations have no impact on the available energies, because no protons participate in the reactions. But the modeling results show that the available energies do respond considerably to pH changes (Figure 4D). These responses reflect variation with pH in the speciation of acetate, bicarbonate, sulfate, and sulfide (Figure 1). Between pH 1 and 7, an increase in pH raises the concentrations of acetate and bicarbonate, thereby lowering the available energies. In contrast, above pH 7, an increase in pH lowers the concentrations of bicarbonate and dihydrogen sulfide, which raises the available energies.

Methanogenesis

Hydrogenotrophic and acetoclastic methanogenesis respond differently to pH variation (Figure 5). Hydrogenotrophic pathway consumes proton and bicarbonate (reaction 21 in Table 1). Below pH 6, its available energy remains largely unchanged because the thermodynamic effects of proton consumption and DIC speciation counteract each other (see Figure 1B). Above pH 6, increases in pH cause available energy to decline because of proton consumption by the reaction. Above pH 9, the slope of the decrease becomes steeper because pH increases also lower the concentration of bicarbonate.

For acetoclastic methanogenesis (reaction 22), Equation (5) predicts no response in the available energy with pH. However, the simulation results show that this prediction only applies between pH 7 and 9. Above pH 9, pH increases raise the available energy by lowering bicarbonate concentrations. Below pH 7, a decrease in pH also decreases bicarbonate concentration and hence raises available energy. Below pH 4, however, acetate concentration begins to decrease with decreasing pH, which counteracts the thermodynamic effect of decreasing bicarbonate concentration. Hence, the available energy varies little below pH 4.

Thermodynamic Drive

Microbes conserve a part of the energy available in the environment by making ATP, and spend the other part to drive respiration reactions. By changing the energy available in the environment, pH also changes the thermodynamic drive, which in turn changes the rate of respiration (Equations 2, 3).

For the purpose of this analysis, we focus on syntrophic oxidation of butyrate, and acetotrophic and hydrogenotrophic iron reduction, sulfate reduction, and methanogenesis, and compute how their thermodynamic drives respond to pH in the assumed environment. Butyrate is a key product of organic matter degradation, and acetate and H₂ are common electron donors in subsurface environments (Monokova, 1975; Molongoski and Klug, 1980; Lovley and Klug, 1982).

Environmental Conditions

Like energy availability, microbial energy conservation also depends on environmental conditions. For example, the amount of energy conserved by syntrophs depends on dihydrogen of the environment. Jin (2007) constructed a kinetic model for syntrophic butyrate oxidation. This model considers reverse electron transfer, a key step in the pathway of syntrophic oxidation (Schink, 1992), and describes the energy conserved by microbes, ΔG_C [J·(mol butyrate)⁻¹], as a function of molal concentration of dissolved dihydrogen m_H2,

$\begin{array}{cc}\Delta G_{\text{C}}=-3.55\times {10}^4-RT·\ln \left(m_{{\text{H}}_2}\right).& (6)\end{array}$

According to this model, the conserved energy equals 15.8 kJ·mol⁻¹ at 1 nM H₂ and decreases with increasing H₂ concentration. In the assumed environment, the conserved energy takes a value of 4.5 kJ·(mol butyrate)⁻¹. At H₂ concentration of more than 0.6 μM, the conserved energy decreases to 0.

pH also affects microbial energy conservation. Respiring microbes conserve energy by translocating protons across their cytoplasmic membrane to create proton motive force. Proton motive force includes electrical potential difference and the gradient in proton activity across the membrane. Changes in environmental pH directly affect the proton gradient as well as the electrical potential difference across the membrane (Sprott et al., 1985). In addition, microbes also respond to pH changes by changing the number of protons translocated across the membrane (Steigmiller et al., 2008).

Currently, no model is available to quantitatively predict how conserved energy changes with pH. Thus the impact of pH on conserved energies cannot be evaluated as rigorously as we have done for energy availability. For this reason, we follow the current practice, and calculate the conserved energy of syntrophic butyrate oxidizers according to Equation (6). For iron reducers, sulfate reducers, and methanogens, we calculate the conserved energies using Equation (4).

Thermodynamic Control

Figure 6 shows how thermodynamic drives respond to changes in pH. By fixing conserved energies, variations in thermodynamic drives follow the same patterns of the available energies. In the assumed environment, the thermodynamic drive of butyrate syntrophic oxidation is 14.3 kJ mol⁻¹ at pH 7 and decreases with decreasing pH. Below pH 5.7, the drive becomes negative, and thus butyrate syntrophic oxidation becomes thermodynamically unfavorable. Hydrogenotrophic and acetotrophic iron reducers have a thermodynamic drive of 125 and 111 kJ·mol⁻¹, respectively, at pH 7. Their thermodynamic drives decrease with increasing pH and become negative above pH 7.9.

FIGURE 6

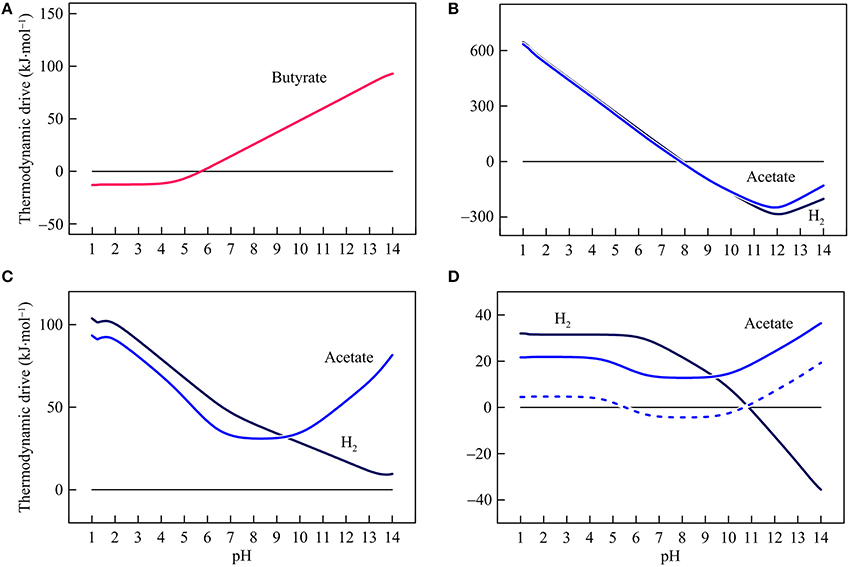
Figure 6. Variations with pH in the thermodynamic drives of syntrophic butyrate oxidation (A), hydrogenotrophic and acetotrophic goethite reduction (B), sulfate reduction (C), and methanogenesis (D). Solid lines are results of the hypothetical solution, and dashed line is the result of acetoclastic methanogenesis by raising methane concentration in the hypothetical solution to 1 mM.

In the assumed environment, hydrogenotrophic and acetotrophic sulfate reducers have positive thermodynamic drives over the pH range of 1–14. Acetoclastic methanogen also has positive thermodynamic drives over the entire pH range but its thermodynamic drives fall to a minimum level around pH 8. On the other hand, hydrogenotrophic methanogens have a relatively large drive at low pH. Above pH 6, the thermodynamic drive begins to decrease and becomes negative above 10.9.

Figure 7 shows how the thermodynamic potential factors F_T vary with pH. The thermodynamic potential factor quantifies the significance of thermodynamic limitation on respiration rate (Equation 2). This factor approaches unity where available energy is much larger than conserved energy. In this case, thermodynamic control is considered insignificant; respiration rate is relatively large, and varies little with the thermodynamic drive. However, where available energy approaches conserved energy, the thermodynamic drive and hence the thermodynamic potential factor approach zero. Under this condition, respiration rate increases linearly with the thermodynamic drive, and the thermodynamic control is significant. Where the thermodynamic drive is negative, microbial respiration reaction is thermodynamically unfavorable. Here, respiration reaction ceases and the thermodynamic potential factor is set to 0.

FIGURE 7

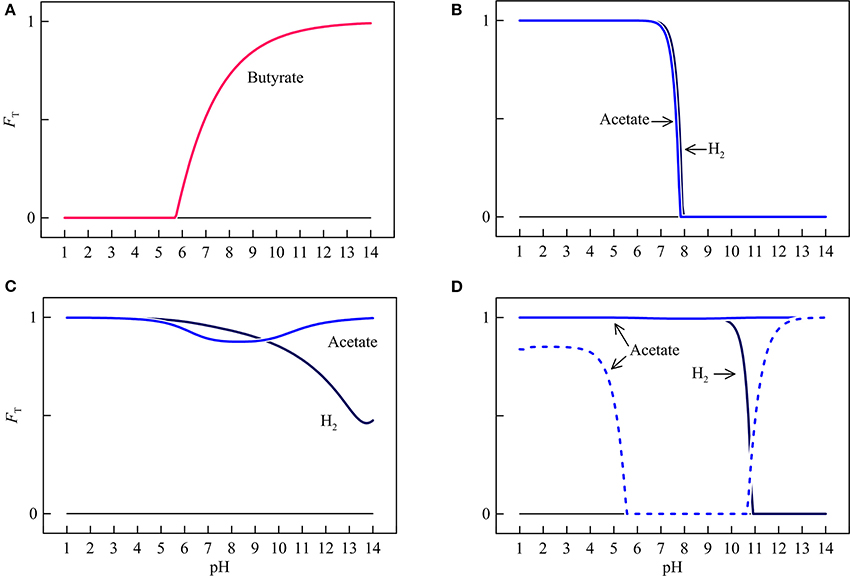
Figure 7. Variations with pH in the thermodynamic factors F_T of syntrophic butyrate oxidation (A), hydrogenotrophic and acetotrophic goethite reduction (B), sulfate reduction (C), and methanogenesis (D). Solid lines are results of the hypothetical solution, and dashed line is the result of acetoclastic methanogenesis by raising methane concentration in the hypothetical solution to 1 mM.

In the assumed environment, the thermodynamic factors of different microbial respiration reactions respond differently to pH. For syntrophic butyrate oxidation, the thermodynamic factor is positive above pH 5.7 and increases nonlinearly with pH. At pH above 9.8, the thermodynamic factor increases to over 0.9.

The thermodynamic factors of hydrogenotrophic and acetotrophic iron reduction remain close to unity below pH 7.3. Above pH 7.3, increases in pH decrease sharply the thermodynamic factors for both reactions. At a pH of 7.9, the factors decrease to 0.

The thermodynamic factor of hydrogenotrophic sulfate reduction stays close to unity at pH < 5.0. Above pH 5.0, increases in pH gradually decrease the thermodynamic factor to a value of 0.48 at pH 14. The thermodynamic factor of acetotrophic sulfate reduction remains relatively large over the entire pH range, with a minimum of 0.88 at pH 8.3.

The thermodynamic factor of hydrogenotrophic methanogenesis stay close to unity below pH 10.3. Above that level, the thermodynamic factor decreases sharply to 0 at pH 10.9. The thermodynamic factor of acetoclastic methanogenesis stays close to unity across the entire pH range because of its relatively large thermodynamic drive. Taking together the variations of the thermodynamic potential factors, we see that pH variations are capable of modifying the thermodynamic states of respiration reactions between favorable and unfavorable, and regulating the progress of the reactions, from relatively fast pace to complete rest.

Discussion

We used geochemical reaction modeling and analyzed the thermodynamic and kinetic responses of microbial redox reactions to environmental pH. The results illustrate how pH can act as a key controlling parameter on microbial activities and interactions.

Thermodynamic Response

We first analyzed how the thermodynamics of microbial redox reactions respond to pH variations. Bethke et al. (2011) analyzed how the energies available from acetotrophic and hydrogenotrophic iron reduction, sulfate reduction, and methanogenesis respond to variation in pH between 4 and 10. We expand their analyses by varying pH from 1 to 14 and by including additional microbial redox reactions involved in the degradation of natural organic matter. These reactions include the oxidation of short-chain fatty acids and primary alcohols by proton reduction, iron reduction, and sulfate reduction. Our analyses confirm the previous conclusion that changes in environmental pH directly alter energy available from redox reactions that produce or consume protons, and the significances of the changes depend on the numbers of protons produced or consumed (Bethke et al., 2011).

Our simulation results also resonate with the previous studies that emphasize the indirect thermodynamic role of pH—pH affects chemical energies in the environment indirectly by affecting chemical speciation and thereby the concentrations of chemical species involved in microbial redox reactions (Windman et al., 2007; Dolfing et al., 2010; Shock et al., 2010; Hedrich et al., 2011; Johnson et al., 2012). We often write stoichiometric reaction equations and compute their Gibbs free energy changes using the main chemical species at pH 7 (Table 1 and Equation 1). By doing so, we implicitly account for the speciation effect at pH 7.

But chemical speciation depends on pH, which impacts chemical reactions and their energies in two ways. First, chemical species participating in protonation and deprotonation have different concentrations at different pHs. As a result, the main chemical species of pH 7 may give way to alternative forms at other pHs. Second, the stoichiometries of proton consumption and production are not fixed, but vary with pH. At a given pH, proton consumption and production depend on the relative significances of acids and their conjugate bases. In response to pH variations, the concentrations of acids and their conjugate bases change (Figure 1) and thus so do the stoichiometries of proton reactions. Consequently, for reactions that include proton consumption and production, the direct pH effect is not set but varies in magnitude with pH.

The indirect thermodynamic impact of pH is most notable for sulfate reduction by the oxidation of lactate, butyrate, and ethanol, and for acetoclastic methanogenesis (reaction 16, 18, 20, and 22 in Table 1). At pH 7, no proton would be produced or consumed by these reactions, and the available energies are not affected directly by pH. But according to the simulation results, their available energies vary significantly with the pH of the environment (Figures 4D, 5B). We account for the variations using pH-dependent chemical speciation—these reactions involve bicarbonate, sulfide, and other chemical species, whose concentrations vary significantly with pH.

Figures 2–5 compare the direct and the total thermodynamic impacts of pH (the dashed and solid lines, respectively). The differences between the two lines highlight the indirect energy contribution by chemical speciation. Two patterns arise from these figures.

First, microbial thermodynamic responses are not uniform. The available energies of syntrophic oxidation reactions increase with increasing pH. For hydrogenotrophic sulfate reduction and methanogenesis, their available energies decrease with increasing pH. For other microbial redox reactions, in response to pH increases, available energies first decrease and then, after reaching minimum values, begin to increase.

These heterogeneous responses arise in part from the indirect speciation impact of pH. The speciation impact is not consistent throughout the entire pH range of 1–14. For example, for redox reactions that produce bicarbonate, energy available always increases as pH moves away from 7, regardless of whether pH is increasing or decreasing. As a second example, the speciation of ferrous iron only affects significantly the available energy of iron reduction at pH above 9. At lower pHs, the speciation impact is negligible.

Second, microbial iron reduction stands out from the other reactions in its strong response to pH. Energy available from the reduction of iron oxides and hydroxides depends significantly on pH. This sensitivity reflects consumption of relatively large numbers of protons, from 12.7 to 16 protons per reaction (8 electron transfer). As a result, a one-unit change in pH can lead to a change of 72–91 kJ·(mol reaction)⁻¹ in the available energy. In comparison, thermodynamic responses are relatively modest for other microbial redox reactions—a one-unit change in pH can lead to up to 20 kJ·(mol reaction)⁻¹ of change in the available energies of these reactions.

Kinetic Response

Microbial thermodynamic responses to pH lead to a cascade of metabolic effects, including impacts to the thermodynamic drives of respiration. We took butyrate syntrophic oxidation, and acetotrophic and hydrogenotrophic iron reduction, sulfate reduction, and methanogenesis as examples, and analyzed how environmental pH controls the thermodynamic drives and hence the rates of these reactions in the assumed freshwater environment.

Like the energies available in the environment, the thermodynamic drives of different microbial respiration reactions respond differently to changes in pH. Specifically, a pH increase from 1 to 14 raises the thermodynamic drive of syntrophic butyrate oxidation from negative to positive and hence moves the reaction from thermodynamically unfavorable to favorable. On the other hand, increasing pH changes iron reduction and hydrogenotrophic methanogenesis from thermodynamically favorable to unfavorable. pH variation can also push hydrogenotrophic sulfate reduction close to thermodynamic equilibrium but this reaction always remains thermodynamically favorable in the assumed environment across the pH range considered.

It should be made clear that our thermodynamic drive calculations are specific for the assumed environment. In an environment of different geochemical conditions, thermodynamic drives may be different, and hence pH variations may modify respiration rates to different extents. For example, in the hypothetical solution, pH variation does not change much the thermodynamic potential factor of acetoclastic methanogenesis, and hence has little influence on the rate of the process (Figure 7D). However, if we raise methane concentration in the solution from 1 μM to 1 mM, we would decrease the thermodynamic drive by 17.1 kJ·mol⁻¹ (Figure 6D). At pH between 5.7 and 10.6, the thermodynamic drive decreases below 0, and methanogenesis stops (Figure 7D). But the pattern in the responses of the thermodynamic drive should be similar, regardless of the concentration of methane or other chemical compounds. As shown in Figure 6D, the thermodynamic drive always increases as pH moves away from 7.

Microbial pH Response

The pH limits of microbial metabolisms are a classical physiological parameter. Previous studies have attributed these pH limits to different physiological mechanisms, including cellular structures and metabolisms. First, both acidophiles and alkaliphiles need to employ unique surface structures to develop acid or alkaline tolerance. For example, the cell walls of alkaliphiles have acidic polymers, which may protect cells from hydroxide ions (Horikoshi, 1999). Acidophiles, such as the members of Ferroplasma, mix caldarchaetidylglycerol tetraether lipids into their membranes to make a barrier to protons in the environment (Golyshina and Timmis, 2005).

Acidic or alkaline conditions also present a challenge to cell metabolism. For both acidophiles and alkaliphiles, cytoplasmic pH is often closer to neutral pH than the environments (Lowe et al., 1993). Maintaining a pH gradient across the membrane consumes energy (Booth, 1985). In addition, under acidic conditions, conjugate acids become significant in the environment, and diffuse through the cell membrane, which destabilizes the membrane and dissipates proton motive force (Russell, 1992). Very low or high pH levels also interfere with solute transport across the membrane and energy conservation by respiration (Matin, 1990; Krulwich et al., 1998).

Our thermodynamic analyses show that environmental pH affects the thermodynamics of microbial redox reactions, and determines whether microbial respiration reactions are thermodynamically favorable or not. Therefore, in addition to microbial physiology, the pH limits may arise, at least in part, from the response of reaction thermodynamics to pH.

For example, reaction thermodynamics sets the lower pH limit for syntrophic butyrate oxidizers. In the assumed environment, syntrophic butyrate oxidation becomes thermodynamically unfavorable and thus stops at pH below 5.7. In laboratory experiments, both butyrate and acetate have relatively large concentrations (Dwyer et al., 1988; Schmidt and Ahring, 1993). We repeat the calculation by taking their concentrations as 5 mM, and setting H₂ partial pressures at 10⁻⁴ atm (or dissolved H₂ at 77 nM), and find that butyrate oxidation would stop at pH < 6.3.

The predicted pH limits are consistent with previous laboratory observations. For example, S. wolfei is one of the first isolates that can grow syntrophically on butyrate, and it can grow at pH above 6.5 (Wu et al., 2007). Its close relatives, including S. bryantii, also have pH limit above 6.0 (Zhang et al., 2004, 2005).

As a second example, the thermodynamics of iron reduction sets the upper limit for microbes reducing ferric oxides and oxyhydroxides. In the assumed environment, at pH above 7.9, both hydrogenotrophic and acetotrophic reduction of goethite become thermodynamically unfavorable. In laboratory reactors, H₂, acetate, and ferrous iron often have concentrations orders magnitude above the concentrations in the assumed environment. If we take acetate concentration at 5 mM and ferrous iron at 1 mM, the reduction of goethite would remain thermodynamically favorable only at pH < 7.6.

The upper pH limit for iron reduction depends on ferric minerals (Postma and Jakobsen, 1996). For example, if we choose natural ferrihydrite as an electron acceptor, acetotrophic reduction of ferrihydrite becomes thermodynamically unfavorable at pH 8.3. This upper limit is consistent with the value determined using laboratory experiments. Straub et al. (1998) reported that by reducing ferrihydrite, two Geobacter strains grow optimally at pH around 7, and can grow at pH up to 7.5.

Implications for Environmental Microbiology

By promoting or inhibiting microbial redox reactions, environmental pH is capable of shaping the interactions between microbial groups. For example, previous studies of microbial syntrophy have emphasized the importance of H₂ levels of the environment—a key parameter that dictates the thermodynamics and occurrence of syntrophic degradation (Schink, 1997). The above results show that like H₂ levels, pH can change the thermodynamic status and rates of syntrohic oxidation of short-chain fatty acids and primary alcohols, and hence determine the occurrence and significance of these processes in the environment.

By promoting or inhibiting microbial respiration, environmental pH is also capable of shaping microbial community composition. Microbial iron reduction and sulfate reduction, for example, occur widely in subsurface environments and compete against each other for the common electron donors of H₂ and acetate. The current paradigm describing their interactions follows the tragedy of commons and assumes that iron reducers hold either a thermodynamic or kinetic advantage and as a result, always win the competition against sulfate reducers (Chapelle and Lovley, 1992; Bethke et al., 2008).

Our modeling results show that the competitive advantage of iron reducers is pH dependent. Specifically, the thermodynamic drive of microbial iron reduction responds significantly to pH. In the assumed environment, that response lowers iron reduction rates from maximum values to 0 over a narrow pH range of 1 unit. In comparison, sulfate reduction responds relatively modestly to pH and stays thermodynamically favorable over the entire pH range between 1 and 14. These results suggest iron reducers can win the competition against sulfate reducers under acidic conditions but might lose the competition under alkaline conditions. Thus, changes in pH have the potential to alter the proportions of iron reducers relative to sulfate reducers in an environment.

Results of laboratory experiments by Kirk et al. (2013) are consistent with this possibility. In their study, microbial consortia from a freshwater aquifer grew on acetate under two different pHs, 7.2 and 5.7, and the microbial community that developed in each reactor was sampled at the end of the study and analyzed by sequencing 16S rRNA gene amplicons. The relative abundance of sequences that grouped within Geobacteraceae and Myxococcaceae was twice as high in pH 5.7 reactors than pH 7.2 reactors. Members of Geobacteraceae and Myxococcaceae, such as Geobacter and Anaeromyxobacter, are capble of iron reduction (Lonergan et al., 1996; Treude et al., 2003). Conversely, sequences that grouped within taxa commonly associated with sulfate reduction, such as Desulfobulbaceae, Desulfovibrionaceae, Desulfuromonadaceae, and Desulfobacteraceae, were primarly only present in pH 7.2 reactors.

These differences in relative abundance are consistent with contributions of iron reduction and sulfate reduction to acetate oxidation evaluated using mass-balance calculations. According to their results, in pH 7.2 reactors, sulfate reduction overwhelmed iron reduction; sulfate reduction consumed 85% of acetate, and the rest is accounted for by iron reduction. At pH 5.7, iron reduction consumed at least 90% of acetate while sulfate reduction consumed a negligible amount (<1%). In agreement with these findings, furthermore, Kirk et al. (2016) found that broad-scale patterns in groundwater geochemistry in U.S. aquifers are also consistent with an increase in the significance of iron reduction relative to sulfate reduction as pH decreases.

Concluding Comments

We applied geochemical reaction modeling, and explored the thermodynamic responses of microbial redox reactions to environmental pH. Our modeling focused on the energy yields of redox reactions, and neglected other impacts brought upon cell metabolisms by pH. For example, low pH conditions promotes the diffusion of formic acid, acetic acid, and other short-chain fatty acids across the membrane, which dissipates proton motive force across the membrane and inhibits microbial growth (Russell, 1992). Low pH also helps dissolve ferric and ferrous minerals, which makes available ferric iron to iron reducers and ferrous iron to iron oxidizers, and promotes the biogeochemical cycling of iron (Coupland and Johnson, 2008; Emerson et al., 2010).

Our work represents a step forward toward a mechanistic view of the pH control on microbial metabolisms and community structures. Current studies rely on phenomenological models to describe the apparent microbial responses to pH. Here we focused on microbial respiration, and illustrated that environmental pH influences the thermodynamics of microbial redox reactions and that this influence can be strong enough to cause significant changes in respiration kinetics.

The simulation results illustrate that environmental pH can impact the energies of microbial redox reactions in two ways. Chemical energies are a direct function of pH—the chemical activity of protons—for reactions that consume and produce protons. In addition, pH also controls the speciation and concentrations of electron donors, acceptors, and reaction products, which in turn determine the energy yields of redox reactions. For microbial reduction of goethite and other ferric oxyhydroxides, the effect of proton consumption is dominant. For other reactions, the indirect speciation effect is of similar magnitude as the proton activity effect. These thermodynamic responses are strong enough that they can switch the thermodynamic states of microbial respiration between favorable and unfavorable and change microbial rates from 0 to their maximum values. Thermodynamic responses also help give rise to the lower or upper pH limits of microbial respiration reactions and pH-dependent changes in microbial community composition. By changing the thermodynamics of individual microbial redox reactions, pH variations are capable of shifting microbial community structures and modulating the interactions among microbes.

Taken together, our results provide a mechanistic understanding of how environmental pH regulates microbial respiration and affects the community composition of natural microbes. They expand our view on the evaluation of microbial processes using routine environmental parameters, such as pH and chemical energies. In addition to microbial respiration, microbial growth, and maintenance are also influenced by environmental pH (Russell and Dombrowski, 1980). Future efforts should explore the pH impact on growth and maintenance in order to achieve a holistic view of microbial response to environmental pH.

Author Contributions

QJ and MK designed the research. QJ carried out the simulation, and wrote the first draft of the manuscript, and MK revised the manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This research was funded by the National Science Foundation under Award EAR-1636815 and by National Aeronautics and Space Administration under Grant NNX16AJ59G.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2018.00021/full#supplementary-material

References

Amend, A. S., Oliver, T. A., Amaral-Zettler, L. A., Boetius, A., Fuhrman, J. A., Horner-Devine, M. C., et al. (2013). Macroecological patterns of marine bacteria on a global scale. J. Biogeogr. 40, 800–811. doi: 10.1111/jbi.12034

CrossRef Full Text | Google Scholar

Baker-Austin, C., and Dopson, M. (2007). Life in acid: pH homeostasis in acidophiles. Trends Microbiol. 15, 165–171. doi: 10.1016/j.tim.2007.02.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Bennett, P. C., Rogers, J. R., Choi, W. J., and Hiebert, F. K. (2001). Silicates, silicate weathering, and microbial ecology. Geomicrobiol. J. 18, 3–19. doi: 10.1080/01490450151079734

CrossRef Full Text | Google Scholar

Bethke, C. M. (2008). Geochemical and Biogeochemical Reaction Modeling, 2nd Edn. Cambridge: Cambridge University Press.

Google Scholar

Bethke, C. M., Ding, D., Jin, Q., and Sanford, R. A. (2008). Origin of microbiological zoning in groundwater flows. Geology 36, 739–742. doi: 10.1130/G24859A.1

CrossRef Full Text | Google Scholar

Bethke, C. M., Sanford, R. A., Kirk, M. F., Jin, Q., and Flynn, T. M. (2011). The thermodynamic ladder in geomicrobiology. Am. J. Sci. 311, 183–210. doi: 10.2475/03.2011.01

CrossRef Full Text | Google Scholar

Bigham, J. M., Schwertmann, U., Traina, S. J., Winland, R. L., and Wolf, M. (1996). Schwertmannite and the chemical modeling of iron in acid sulfate waters. Geochim. Cosmochim. Acta 60, 2111–2121. doi: 10.1016/0016-7037(96)00091-9

CrossRef Full Text | Google Scholar

Booth, I. R. (1985). Regulation of cytoplasmic pH in bacteria. Microbiol. Rev. 49, 359–378.

PubMed Abstract | Google Scholar

Chapelle, F. H., and Lovley, D. R. (1992). Competitive exclusion of sulfate reduction by Fe(lll)-reducing bacteria: a mechanism for producing discrete zones of high-iron ground water. Ground Water 30, 29–36. doi: 10.1111/j.1745-6584.1992.tb00808.x

CrossRef Full Text | Google Scholar

Chapelle, F. H., McMahon, P. B., Dubrovsky, N. M., Fujii, R. F., Oaksford, E. T., and Vroblesky, D. A. (1995). Deducing the distribution of terminal electron-accepting processes in hydrologically diverse groundwater systems. Water Resour. Res. 31, 359–371. doi: 10.1029/94WR02525

CrossRef Full Text | Google Scholar

Chen, G., He, Z., and Wang, Y. (2004). Impact of pH on microbial biomass carbon and microbial biomass phosphorus in red soils. Pedosphere 14, 9–15.

Google Scholar

Cornell, R. M., and Schwertmann, U. (2003). The Iron Oxides: Structure, Properties, Reactions, Occurrences and Uses, 2nd Edn. Weinheim: Wiley-VCH.

Coupland, K., and Johnson, D. B. (2008). Evidence that the potential for dissimilatory ferric iron reduction is widespread among acidophilic heterotrophic bacteria. FEMS Microbiol. Lett. 279, 30–35. doi: 10.1111/j.1574-6968.2007.00998.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Delany, J. M., and Lundeen, S. R. (1990). The LLNL Thermodynamical Database. Lawrence Livermore National Laboratory Report UCRL-21658, 150.

Dolfing, J., Xu, A., and Head, I. M. (2010). Anomalous energy yields in thermodynamic calculations: importance of accounting for pH-dependent organic acid speciation. ISME J. 4, 463. doi: 10.1038/ismej.2010.14

PubMed Abstract | CrossRef Full Text | Google Scholar

Dwyer, D. F., Weeg-Aerssens, E., Shelton, D. R., and Tiedje, J. M. (1988). Bioenergetic conditions of butyrate metabolism by a syntrophic, anaerobic bacterium in coculture with hydrogen-oxidizing methanogenic and sulfidogenic bacteria. Appl. Environ. Microbiol. 54, 1354–1359.

PubMed Abstract | Google Scholar

Edwards, K. J., Becker, K., and Colwell, F. (2012). The deep, dark energy biosphere: intraterrestrial life on Earth. Annu. Rev. Earth Planet. Sci. 40, 551–568. doi: 10.1146/annurev-earth-042711-105500

CrossRef Full Text | Google Scholar

Emerson, D., Fleming, E. J., and McBeth, J. M. (2010). Iron-Oxidizing bacteria: an environmental and genomic perspective. Annu. Rev. Microbiol. 64, 561–583. doi: 10.1146/annurev.micro.112408.134208

PubMed Abstract | CrossRef Full Text | Google Scholar

Falkowski, P. G., Fenchel, T., and Delong, E. F. (2008). The Microbial engines that drive earth's biogeochemical cycles. Science 320, 1034–1039. doi: 10.1126/science.1153213

PubMed Abstract | CrossRef Full Text | Google Scholar

Fernández-Calviño, D., and Bååth, E. (2010). Growth response of the bacterial community to pH in soils differing in pH. FEMS Microbiol. Ecol. 73, 149–156. doi: 10.1111/j.1574-6941.2010.00873.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Golyshina, O. V., and Timmis, K. N. (2005). Ferroplasma and relatives, recently discovered cell wall-lacking archaea making a living in extremely acid, heavy metal-rich environments. Environ. Microbiol. 7, 1277–1288. doi: 10.1111/j.1462-2920.2005.00861.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Hedrich, S., Schlömann, M., and Johnson, D. B. (2011). The iron-oxidizing proteobacteria. Microbiology 157, 1551–1564. doi: 10.1099/mic.0.045344-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Helgeson, H. C. (1969). Thermodynamics of hydrothermal systems at elevated temperatures and pressures. Am. J. Sci. 267, 729–804. doi: 10.2475/ajs.267.7.729

CrossRef Full Text | Google Scholar

Horikoshi, K. (1999). Alkaliphiles: some applications of their products for biotechnology. Microbiol. Mol. Biol. Rev. 63, 735–750.

PubMed Abstract | Google Scholar

Jin, Q. (2007). Control of hydrogen partial pressures on the rates of syntrophic microbial metabolisms: a kinetic model for butyrate fermentation. Geobiology 5, 35–48. doi: 10.1111/j.1472-4669.2006.00090.x

CrossRef Full Text | Google Scholar

Jin, Q. (2012). Energy conservation of anaerobic respiration. Am. J. Sci. 312, 573–628. doi: 10.2475/06.2012.01

CrossRef Full Text | Google Scholar

Jin, Q., and Bethke, C. M. (2002). Kinetics of electron transfer through the respiratory chain. Biophys. J. 83, 1797–1808. doi: 10.1016/S0006-3495(02)73945-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, Q., and Bethke, C. M. (2003). A new rate law describing microbial respiration. Appl. Environ. Microbiol. 69, 2340–2348. doi: 10.1128/AEM.69.4.2340-2348.2003

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, Q., and Bethke, C. M. (2005). Predicting the rate of microbial respiration in geochemical environments. Geochim. Cosmochim. Acta 69, 1133–1143. doi: 10.1016/j.gca.2004.08.010

CrossRef Full Text | Google Scholar

Jin, Q., and Bethke, C. M. (2007). The thermodynamics and kinetics of microbial metabolism. Am. J. Sci. 307, 643–677. doi: 10.2475/04.2007.01

CrossRef Full Text | Google Scholar

Jin, Q., and Bethke, C. M. (2009). Cellular energy conservation and the rate of microbial sulfate reduction. Geology 36, 739–742. doi: 10.1130/G30185A.1

CrossRef Full Text | Google Scholar

Jin, Q., and Roden, E. E. (2011). Microbial physiology-based model of ethanol metabolism in subsurface sediments. J. Contam. Hydrol. 125, 1–12. doi: 10.1016/j.jconhyd.2011.04.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnson, D. B., Kanao, T., and Hedrich, S. (2012). Redox transformations of iron at extremely low pH: fundamental and applied aspects. Front. Microbiol. 3:96. doi: 10.3389/fmicb.2012.00096

PubMed Abstract | CrossRef Full Text | Google Scholar

Kemmitt, S. J., Wright, D., Goulding, K. W. T., and Jones, D. L. (2006). pH regulation of carbon and nitrogen dynamics in two agricultural soils. Soil Biol. Biochem. 38, 898–911. doi: 10.1016/j.soilbio.2005.08.006

CrossRef Full Text | Google Scholar

Kirk, M. F., Jin, Q., and Haller, B. R. (2016). Broad-scale evidence that pH influences the balance between microbial iron and sulfate reduction. Groundwater 54, 406–413. doi: 10.1111/gwat.12364

PubMed Abstract | CrossRef Full Text | Google Scholar

Kirk, M. F., Santillan, E. F. U., Sanford, R. A., and Altman, S. J. (2013). CO2-induced shift in microbial activity affects carbon trapping and water quality in anoxic bioreactors. Geochim. Cosmochim. Acta 122, 198–208. doi: 10.1016/j.gca.2013.08.018

CrossRef Full Text | Google Scholar

Kotsyurbenko, O. R., Chin, K.-J., Glagolev, M. V., Stubner, S., Simankova, M. V., Nozhevnikova, A. N., et al. (2004). Acetoclastic and hydrogenotrophic methane production and methanogenic populations in an acidic West-Siberian peat bog. Environ. Microbiol. 6, 1159–1173. doi: 10.1111/j.1462-2920.2004.00634.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Krulwich, T. A., Ito, M., Hicks, D. B., Gilmour, R., and Guffanti, A. A. (1998). pH homeostasis and ATP synthesis: studies of two processes that necessitate inward proton translocation in extremely alkaliphilic Bacillus species. Extremophiles 2, 217–222. doi: 10.1007/s007920050063

PubMed Abstract | CrossRef Full Text | Google Scholar

Lauber, C. L., Hamady, M., Knight, R., and Fierer, N. (2009). Pyrosequencing-based assessment of soil pH as a predictor of soil bacterial community structure at the continental scale. Appl. Environ. Microbiol. 75, 5111–5120. doi: 10.1128/AEM.00335-09

PubMed Abstract | CrossRef Full Text | Google Scholar

Lennon, J. T., and Jones, S. E. (2011). Microbial seed banks: the ecological and evolutionary implications of dormancy. Nat. Rev. Microbiol. 9, 119–130. doi: 10.1038/nrmicro2504

PubMed Abstract | CrossRef Full Text | Google Scholar

Leprince, F., and Quiquampoix, H. (1996). Extracellular enzyme activity in soil: effect of pH and ionic strength on the interaction with montmorillonite of two acid phosphatases secreted by the ectomycorrhizal fungus Hebeloma cylindrosporum Activité enzymatique extracellulaire dans Ie sol: effet du pH et de la force ionique sur l'interaction avec la montmorillonite de deux phosphates acides sécrdteés par le champignon ectomycorhizien Hebeloma cylindrosporum. Eur. J. Soil Sci. 47, 511–522. doi: 10.1111/j.1365-2389.1996.tb01851.x

CrossRef Full Text | Google Scholar

Lide, D. R. (2003). Handbook of Chemistry and Physcis, 83rd Edn. Boca Raton, FL: CRC Press.

Lindsay, W. L. (1979). Chemical Equilibria in Soils. New York, NY: John Wiley and Sons Ltd.

Google Scholar

Lonergan, D. J., Jenter, H. L., Coates, J. D., Phillips, E. J., Schmidt, T. M., and Lovley, D. R. (1996). Phylogenetic analysis of dissimilatory Fe(III)-reducing bacteria. J. Bacteriol. 178, 2402–2408. doi: 10.1128/jb.178.8.2402-2408.1996

PubMed Abstract | CrossRef Full Text | Google Scholar

Lovley, D. R., and Chapelle, F. H. (1995). Deep subsurface microbial processes. Rev. Geophys. 33, 365–382. doi: 10.1029/95RG01305

CrossRef Full Text | Google Scholar

Lovley, D. R., and Klug, M. J. (1982). Intermediary metabolism of organic matter in the sediments of a eutrophic lake. Appl. Environ. Microbiol. 43, 552–560.

PubMed Abstract | Google Scholar

Lowe, S. E., Jain, M. K., and Zeikus, J. G. (1993). Biology, ecology, and biotechnological applications of anaerobic bacteria adapted to environmental stresses in temperature, pH, salinity, or substrates. Microbiol. Rev. 57, 451–509.

Google Scholar

Maestrojuan, G. M., and Boone, D. R. (1991). Characterization of Methanosarcina barkeri MST and 227, Methanosarcina mazei S-6T, and Methanosarcina vacuolata Z-761T. Int. J. Syst. Evol. Microbiol. 41, 267–274. doi: 10.1099/00207713-41-2-267

CrossRef Full Text | Google Scholar

Maguffin, S. C., Kirk, M. F., Daigle, A. R., Hinkle, S. R., and Jin, Q. (2015). Substantial contribution of biomethylation to aquifer arsenic cycling. Nat. Geosci. 8, 290–293. doi: 10.1038/ngeo2383

CrossRef Full Text | Google Scholar

Matin, A. (1990). Bioenergetics parameters and transport in obligate acidophiles. Biochim. Biophys. Acta Bioenerg. 1018, 267–270. doi: 10.1016/0005-2728(90)90264-5

CrossRef Full Text | Google Scholar

Molongoski, J. J., and Klug, M. J. (1980). Anaerobic metabolism of particulate organic matter in the sediments of hypereutrophic lake. Freshwater Biol. 10, 507–518.

Google Scholar

Monokova, S. V. (1975). Volatile fatty acids in bottom sediments of the Rybinsk reservoir. Hydrobiol. J. 11, 45–48.

O'Flaherty, V., Mahony, T., O'Kennedy, R., and Colleran, E. (1998). Effect of pH on growth kinetics and sulphide toxicity thresholds of a range of methanogenic, syntrophic and sulphate-reducing bacteria. Process Biochem. 33, 555–569. doi: 10.1016/S0032-9592(98)00018-1

CrossRef Full Text | Google Scholar

Paul, A., Stösser, R., Zehl, A., Zwirnmann, E., Vogt, R. D., and Steinberg, C. E. W. (2006). Nature and abundance of organic radicals in natural organic matter: effect of pH and irradiation. Environ. Sci. Technol. 40, 5897–5903. doi: 10.1021/es060742d

PubMed Abstract | CrossRef Full Text | Google Scholar

Postma, D., and Jakobsen, R. (1996). Redox zonation: equilibrium constraints on the Fe(III)/SO4-reduction interface. Geochim. Cosmochim. Acta 60, 3169–3175. doi: 10.1016/0016-7037(96)00156-1

CrossRef Full Text | Google Scholar

Rosso, L., Lobry, J. R., Bajard, S., and Flandrois, J. P. (1995). Convenient model to describe the combined effects of temperature and pH on microbial growth. Appl. Environ. Microbiol. 61, 610–616.

PubMed Abstract | Google Scholar

Russell, J. B. (1992). Another explanation for the toxicity of fermentation acids at low pH: anion accumulation versus uncoupling. J. Appl. Bacteriol. 73, 363–370. doi: 10.1111/j.1365-2672.1992.tb04990.x

CrossRef Full Text | Google Scholar

Russell, J. B., and Dombrowski, D. B. (1980). Effect of pH on the efficiency of growth by pure cultures of rumen bacteria in continuous culture. Appl. Environ. Microbiol. 39, 604–610.

PubMed Abstract | Google Scholar

Schink, B. (1992). “Syntrophism among prokaryotes,” in The Prokaryotes, eds A. Balows, H. Trüper, M. Dworkin, W. Harder, and K. Schleifer (New York, NY: Springer-Verlag), 276–299.

Google Scholar

Schink, B. (1997). Energetics of syntrophic cooperation in methanogenic degradation. Microbiol. Mol. Biol. Rev. 61, 262–280.

PubMed Abstract | Google Scholar

Schink, B., and Stams, A. J. M. (2013). “Syntrophism among prokaryotes,” in The Prokaryotes: Prokaryotic Communities and Ecophysiology, eds E. Rosenberg, E. F. DeLong, S. Lory, E. Stackebrandt, and F. Thompson (Heidelberg; Berlin: Springer), 471–493.

Google Scholar

Schmidt, J. E., and Ahring, B. K. (1993). Effects of hydrogen and formate on the degradation of propionate and butyrate in thermophilic granules from an upflow anaerobic sludge blanket reactor. Appl. Environ. Microbiol. 59, 2546–2551.

PubMed Abstract | Google Scholar

Shock, E. L., Holland, M., Meyer-Dombard, D. A., Amend, J. P., Osburn, G. R., and Fischer, T. P. (2010). Quantifying inorganic sources of geochemical energy in hydrothermal ecosystems, Yellowstone National Park, USA. Geochim. Cosmochim. Acta 74, 4005–4043. doi: 10.1016/j.gca.2009.08.036

CrossRef Full Text | Google Scholar

Sprott, G. D., Bird, S. E., and McDonald, I. J. (1985). Proton motive force as a function of the pH at which Methanobacterium bryantii is grown. Can. J. Microbiol. 31, 1031–1034. doi: 10.1139/m85-194

CrossRef Full Text | Google Scholar

Steigmiller, S., Turina, P., and Gräber, P. (2008). The thermodynamic H+/ATP ratios of the H+-ATPsynthases from chloroplasts and Escherichia coli. Proc. Natl. Acad. Sci. U.S.A. 105, 3745–3750. doi: 10.1073/pnas.0708356105

PubMed Abstract | CrossRef Full Text | Google Scholar

Straub, K. L., Hanzlik, M., and Buchholz-Cleven, B. E. E. (1998). The use of biologically produced ferrihydrite for the isolation of novel iron-reducing bacteria. Syst. Appl. Microbiol. 21, 442–449. doi: 10.1016/S0723-2020(98)80054-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Stumm, W., and Morgan, J. J. (1996). Aquatic Chemistry. Chemical Equilibria and Rates in Natural Waters, 3rd Edn. New York, NY: John Wiley and Sons, Inc.

Google Scholar

Thompson, L. R., Sanders, J. G., McDonald, D., Amir, A., Ladau, J., Locey, K. J., et al. (2017). A communal catalogue reveals Earth's multiscale microbial diversity. Nature 551, 457. doi: 10.1038/nature24621

PubMed Abstract | CrossRef Full Text | Google Scholar

Treude, N., Rosencrantz, D., Liesack, W., and Schnell, S. (2003). Strain FAc12, a dissimilatory iron-reducing member of the Anaeromyxobacter subgroup of Myxococcales. FEMS Microbiol. Ecol. 44, 261–269. doi: 10.1016/S0168-6496(03)00048-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Ward, D. M., Ferris, M. J., Nold, S. C., and Bateson, M. M. (1998). A natural view of microbial biodiversity within hot spring cyanobacterial mat communities. Microbiol. Mol. Biol. Rev. 62, 1353–1370.

PubMed Abstract | Google Scholar

Windman, T., Zolotova, N., Schwandner, F., and Shock, E. L. (2007). Formate as an energy source for microbial metabolism in chemosynthetic zones of hydrothermal ecosystems. Astrobiology 7, 873–890. doi: 10.1089/ast.2007.0127

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, C., Dong, X., and Liu, X. (2007). Syntrophomonas wolfei subsp. methylbutyratica subsp. nov., and assignment of Syntrophomonas wolfei subsp. saponavida to Syntrophomonas saponavida sp. nov. comb. nov. Syst. Appl. Microbiol. 30, 376–380. doi: 10.1016/j.syapm.2006.12.001

PubMed Abstract | CrossRef Full Text

Ye, R., Jin, Q., Bohannan, B., Keller, J. K., McAllister, S. A., and Bridgham, S. D. (2012). pH controls over anaerobic carbon mineralization, the efficiency of methane production, and methanogenic pathways in peatlands across an ombrotrophic–minerotrophic gradient. Soil Biol. Biochem. 54, 36–47. doi: 10.1016/j.soilbio.2012.05.015

CrossRef Full Text | Google Scholar

Zhalnina, K., Dias, R., de Quadros, P. D., Davis-Richardson, A., Camargo, F. A. O., Clark, I. M., et al. (2015). Soil pH determines microbial diversity and composition in the park grass experiment. Microb. Ecol. 69, 395–406. doi: 10.1007/s00248-014-0530-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, C., Liu, X., and Dong, X. (2004). Syntrophomonas curvata sp. nov., an anaerobe that degrades fatty acids in co-culture with methanogens. Int. J. Syst. Evol. Microbiol. 54, 969–973. doi: 10.1099/ijs.0.02903-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, C., Liu, X., and Dong, X. (2005). Syntrophomonas erecta sp. nov., a novel anaerobe that syntrophically degrades short-chain fatty acids. Int. J. Syst. Evol. Microbiol. 55, 799–803. doi: 10.1099/ijs.0.63372-0

PubMed Abstract | CrossRef Full Text