Comparison of Types and Amounts of Nanoscale Heterogeneity on Bacteria Retention

Introduction

Colloids are particles with diameters of around 10 nm to 10 μm and include microorganisms, dissolved and particulate organic matter, clays and mineral precipitates, and nanoparticles (DeNovio et al., 2004). An understanding of factors that control colloid retention and release from surfaces is important for many environmental and industrial applications (Salata, 2004; Molnar et al., 2015; Stark et al., 2015). Conventional filtration theory considers that retention depends on the mass transfer rate of colloids to the solid-water-interface (SWI) and immobilization on the surface (Yao et al., 1971). The relative magnitude of the forces and torques that act on a colloid adjacent to the SWI will determine whether a colloid will be immobilized or released from a surface (Cushing and Lawler, 1998). Filtration theory considers that the adhesive force dominates colloid retention and release (Tufenkji and Elimelech, 2004).

The adhesive force is typically determined from interaction energy calculations (Bergendahl and Grasso, 1999). The interaction energy between a colloid and the SWI usually considers electrostatic double layer and van der Waals interactions but has also been increasingly extended to include Lewis acid-base, steric, and Born interactions (Grasso et al., 2002). However, many experimental observations of colloid retention and release have not been consistent with such interaction energy calculations (Suresh and Walz, 1996; Huang et al., 2009; Bendersky and Davis, 2011). Traditional interaction energy calculations have been limited to smooth, chemically homogeneous surfaces (Grasso et al., 2002). Conversely, natural surfaces always exhibit some degree of nanoscale roughness (NR) and chemical heterogeneity (CH) (Vaidyanathan and Tien, 1991; Suresh and Walz, 1996). A number of researchers have therefore extended interaction energy calculations to include NR and/or CH as a means to explain colloid retention and release (e.g., Suresh and Walz, 1996; Bhattacharjee et al., 1998; Hoek et al., 2003; Hoek and Agarwal, 2006; Huang et al., 2009; Bendersky and Davis, 2011; Henry et al., 2011).

Consideration of NR and surface charge heterogeneity (CH1) in interaction energy calculations can account for many observed colloid retention and release behavior that were previously unexplained (Shen et al., 2011; Bradford and Torkzaban, 2012, 2013, 2015; Bradford et al., 2017); e.g., a small fraction of the surface contributing to colloid retention on net electrostatically unfavorable and favorable surfaces. Increasing CH1 locally reduces the energy barrier height and increases the depth of the primary minimum under net electrostatically unfavorable conditions, especially for more positively charged and larger sized heterogeneities under higher ionic strength (IS) conditions (Bendersky and Davis, 2011; Bradford and Torkzaban, 2012; Shen et al., 2013; Pazmino et al., 2014). Small NR fractions locally decreases the height of the energy barrier (Suresh and Walz, 1996; Bhattacharjee et al., 1998; Hoek et al., 2003; Hoek and Agarwal, 2006; Huang et al., 2009; Bendersky and Davis, 2011; Shen et al., 2011) and the magnitude of the primary minimum (Shen et al., 2012; Bradford and Torkzaban, 2013), especially for roughness on both the surface of the colloid and the SWI (Bradford et al., 2017). Roughness properties that contribute to colloid retention and release change with the solution IS, the colloid size, and the surface chemical properties (e.g., Bradford et al., 2017). Small NR fractions have been shown to control the shape of the interaction energy profile when surfaces contain both NR and CH1 (Bradford and Torkzaban, 2013, 2015; Bradford et al., 2017).

In addition to CH1 and NR, natural subsurface environments may also exhibit heterogeneity arising from the presence of microorganisms and the degradation of soil organic matter (SOM). A diversity of types and numbers of soil microorganisms may occur in soils and sediments (Stevenson, 1994). SOM is usually divided into fulvic acid, humic acid, and humin fractions (Huang et al., 2003). Fulvic acid has higher contents of carboxylic and phenolic groups than humic acid (Aiken, 1985). Humin is a complex mixture of variably degraded biopolymers such as lignin and polysaccharides (Aiken, 1985), mineral-bound lipids and humic acid-like materials (Rice and MacCarthy, 1990), and kerogen and black carbon (Song et al., 2002).

Although the organic fraction of soils and sediments is usually small in comparison to the inorganic fraction, it can coat large portions of the exposed mineral surface (Doerr et al., 2000). The physical and chemical properties of organic coatings can be vastly different from the underlying mineral surface. For example, NR of microbes and SOM are expected to be very different than pure mineral surfaces (Wilkinson et al., 1999), and to change with the water content (Ma'shum and Farmer, 1985), and the solution pH, IS, and ionic composition (Stevenson, 1994; Sposito, 2008). SOM consists of both hydrophobic and hydrophilic components (Ellerbrock et al., 2005). The wettability of soils and sediments is highly impacted by the types and amounts of SOM (Doerr et al., 2000). Humic acids and humins are reported to contain hydrophobic surfaces (de Blas et al., 2010) such as polyalkyl molecules (e.g., free fatty acids and wax esters) (Ma'Shum et al., 1988; Hudson et al., 1994; Franco et al., 2000). This hydrophobicity can be enhanced in fire-affected soils because of thermal decarboxylation of the humic matter (Almendros et al., 1990), and in dry soils due to conformational changes of the SOM (Ma'shum and Farmer, 1985). In addition, microorganism species are known to exhibit wide variations in hydrophobicity (Van Loosdrecht et al., 1987). The hydrophobicity of a surface is known to have a strong influence on the Lewis acid-base interaction (Bergendahl and Grasso, 1999). In addition, an increase in the presence of organic coatings is expected to reduce the Hamaker constant and the van der Waals interaction (Drummond and Chan, 1997; Tong et al., 2011).

Adsorbed organics on surfaces have frequently been reported to create a brush-like surface that diminishes colloid retention and/or increases colloid stability (Kretzschmar and Sticher, 1997; Yang et al., 2010, 2011, 2013, 2014; Flynn et al., 2012). This diminished colloid retention or increased stability in the presence of adsorbed organics has typically been attributed to steric repulsion which creates a large energy barrier to interaction in a primary minimum (Espinasse et al., 2007; Han et al., 2014). The large energy barrier from steric repulsion predicts no colloid retention on a surface, whereas limited amounts of colloid retention are commonly observed even in the presence of absorbed SOM (Jiang et al., 2012; Han et al., 2014). Furthermore, steric repulsion cannot account for enhanced retention of hydrophobic colloids on SOM surfaces (Amirbahman and Olson, 1993). Alternatively, the brush-like surface of absorbed SOM may be explicitly accounted for in interaction energies calculations through NR heights and fractions parameters. In contrast to the influence of steric repulsion, NR creates colloid stability and low amounts of retention by producing shallow primary minima that are subject to diffusive or hydrodynamic release (Morales et al., 2011). Spatial differences in roughness parameters on natural surfaces will alter the depth of the primary minimum to produce colloid retention only in some locations (Bradford et al., 2017).

Previous research that has examined the influence of CH on colloid interactions have focused on CH1 (e.g., from metal oxides, mineral defects, and protonation and deprotonation of surface functional groups) (Pazmino et al., 2014; Park and Kim, 2015). No research to date has systematically examined the influence of SOM heterogeneity on the van der Waals and Lewis acid-base components of the interaction energy. Furthermore, the relative importance of various types and amounts of CH (e.g., charge, Hamaker, and contact angle), separately or in combination, has not yet been studied on a single surface let alone on both interacting surfaces. The influence of all of these chemical heterogeneities in the presence of NR on one or both surfaces is also a question that has not yet been addressed.

Bradford et al. (2017) previously presented an approach to simultaneously account for the influence of NR and CH1 on colloid and solid (or another colloid) surfaces on interaction energies. In this case, the interaction energies only considered constant potential double layer electrostatics (Hogg et al., 1966), retarded London-van der Waals attraction (Gregory, 1981), and Born repulsion (Ruckenstein and Prieve, 1976; Oliveira, 1997) for sphere-plate and sphere-sphere geometries. In this work, these equations were further extended to include Lewis acid-base interactions (Van Oss, 1994), and CH arising from Hamaker constants (van der Waals interactions) and contact angles (Lewis acid-base interactions). These changes allow us to consider a wide variety of types, amounts, and combinations of NR and/or CH (charge, Hamaker, and/or contact angle) on one or both surfaces. This tool provides us with valuable information and insight to determine the relative importance of the various heterogeneity types and combinations on colloid retention, release, and stability. A special focus of this research was to better understand the influence of SOM coatings on interactions with mineral surfaces and bacteria.

Materials and Methods

Interaction Energies for Homogeneous Surfaces

The total interaction energy between a colloid and the SWI (Φ_ij, ML²T⁻² where M, L, and T denote units of mass, length, and time, respectively) is associated with a smooth and chemically homogeneous surface. The value of Φ_ij was considered to be the sum of electrostatic, van der Waals, Lewis acid-base, and Born repulsion interaction energies as:

$\begin{array}{ll}{\Phi }_{ij}(h)={\Phi }^{el}(h)+{\Phi }^{vdW}(h)+{\Phi }^{AB}(h)+{\Phi }^{Born}(h)& (1)\end{array}$

where ${\Phi }^{el}$ [ML²T⁻²], ${\Phi }^{vdW}$[ML²T⁻²], ${\Phi }^{AB}$[ML²T⁻²] and ${\Phi }^{Born}$[ML²T⁻²] are the electric double layer, van der Waals, Lewis acid-base, and Born interaction energies, respectively. The value of ${\Phi }_{ij}$ was made dimensionless by dividing by the product of the Boltzmann constant (k_B = 1.38 × 10⁻²³ J K⁻¹) and the absolute temperature (T_K).

The value of ${\Phi }^{el}$ was determined using the constant surface potential interaction expression of Hogg et al. (1966) for a sphere-plate interaction as:

$\begin{array}{l}{\Phi }^{el}\left(h\right)=\pi \epsilon {\epsilon }_o{r}_c\{2{\zeta }_{ci}{\zeta }_{sj}\ln \left[\frac{1+\exp \left(-\kappa h\right)}{1-\exp \left(-\kappa h\right)}\right]\\ +\left({{\zeta }_{ci}}^2+{{\zeta }_{sj}}^2\right)\ln \left[1-\exp \left(-2\kappa h\right)\right]\}& (2)\end{array}$

where ε (dimensionless) is the dielectric constant of the medium, ε₀ [M⁻¹L⁻³T⁴A⁻², where A denotes ampere] is the permittivity in a vacuum, r_c [L] is the colloid radius, ζ_ci is the zeta potential of the colloid, ζ_sj is the zeta potential of the solid, and κ [L⁻¹] is the Debye-Huckel parameter.

The value of ${\Phi }^{vdW}$ for a retarded sphere-plate interaction was determined using the expression by Gregory (1981) as:

$\begin{array}{ll}{\Phi }^{vdW}\left(h\right)=-\frac{A_{cws}{r}_c}{6h}{\left[1+\frac{14h}{\text{λ}}\right]}^{-1}& (3)\end{array}$

where A_cws [ML²T⁻²] is the combined Hamaker constant, and λ is a characteristic wavelength that was taken as 100 nm (Gregory, 1981). The value of A_cws can be estimated from Hamaker constants for the various materials (Israelachvili, 1992) as:

$\begin{array}{ll}{A}_{cws}=\left(\sqrt{A_{ci}}-\sqrt{A_w}\right)\left(\sqrt{A_{sj}}-\sqrt{A_w}\right)& (4)\end{array}$

where A_ci [ML²T⁻²], A_sj [ML²T⁻²], and A_w [ML²T⁻²] are the Hamaker constants for the colloid, the solid, and water, respectively. The value of A_w is commonly taken as 3.7 × 10⁻²⁰ J (Israelachvili, 1992). Values of A_sj were estimated from literature values of their surface energies in the air (γ_sj) as (Israelachvili, 1992):

$\begin{array}{ll}{A}_{sj}=24\pi {\gamma }_{sj}{h_0}^2& (5)\end{array}$

where h₀ [L] is the value of closest approach taken to be 0.157 nm (Van Oss, 1994). The value of A_ci was estimated in an analogous fashion from γ_ci.

The value of ${\Phi }^{AB}$ was determined using the approach of Van Oss (1994) as:

$\begin{array}{ll}{\Phi }^{AB}\left(h\right)=2\pi r_c{\lambda }_{AB}{\Phi }_{AB\left(h=h_0\right)}\exp \left[\frac{h_o-h}{{\lambda }_{AB}}\right]& (6)\end{array}$

where λ_AB [L] is the characteristic decay length of acid-base interactions in water taken as 1 nm (Israelachvili, 1992), and ${\Phi }_{AB(h=h_0)}$ [MT⁻²] is the Lewis acid-base free interaction energy per area between the two surfaces when h = h₀. The value of ${\Phi }_{AB(h=h_0)}$ in Equation (6) was determined using the approach of Bergendahl and Grasso (1999) and Yoon et al. (1997) as:

$\begin{array}{ll}{\Phi }_{AB\left(h=h_0\right)}=-\frac{K}{2\pi h_0{\lambda }_{AB}}& (7)\end{array}$

$\begin{array}{ll}\log \left(K\right)=-7.0\left(\frac{\cos \left({\theta }_{ci}\right)+\cos \left({\theta }_{sj}\right)}{2}\right)-18.0& (8)\end{array}$

where θ_sj [degrees] and θ_ci [degrees] are the contact angles for the air-water-solid and air-water-colloid systems, respectively, and K [ML²T⁻²] is the hydrophobic force constant.

It should be mentioned that values of θ_sj and/or θ_ci can be theoretically related to A_sj and/or A_ci, respectively, for dispersive liquids and solids (Drummond and Chan, 1997). However, in the presence of water, this theoretical relationship does not hold because non-dispersive interactions dominate (Hough and White, 1980). In this work, individual material Hamaker constants and contact angles were therefore considered to be independent from each other. This approach is consistent with the assumption that Φ^vdw and Φ^AB terms account for separate processes.

The value of ${\Phi }^{Born}$ was calculated from Ruckenstein and Prieve (1976) for sphere-plate interactions as:

$\begin{array}{ll}{\Phi }^{Born}\left(h\right)=\frac{A_{cws}{\sigma }_c^6}{7560}\left[\frac{8r_c+h}{{\left(2r_c+7\right)}^7}+\frac{6r_c-h}{h^7}\right]& (9)\end{array}$

where σ_c [L] is the collision diameter that was taken as 0.26 nm in order to achieve a primary minimum depth at 0.157 nm.

Interaction Energies for Heterogeneous Surfaces

An approach of Bradford et al. (2017) to account for the influence of NR and CH on interaction energy calculations between a spherical colloid suspended in a monovalent electrolyte solution and a planar solid surface or another colloid is extended below. Both interacting surfaces may exhibit binary NR and CH within the area of the electrostatic zone of influence (A_z). The zone of electrostatic influence (e.g., proportional to the colloid radius and the Debye length) on the SWI is assumed to contain a NR fraction (f_sr) with a height equal to h_sr, and the complementary fraction (1-f_sr) correspond to a smooth surface. Similar NR parameters were defined within the electrostatic zone of influence for the colloid as for the SWI. In this case, parameters f_sr and h_sr for the SWI correspond to f_cr and h_cr for the colloid, respectively. The mean dimensionless interaction energy between a colloid and SWI that contains NR on both surfaces (Φ) can be determined as a linear combination of interaction energies for the various NR components as (Bradford et al., 2017):

$\begin{array}{l}\Phi (h)=a_{r1}{\Phi }_S(h+h_{sr}+h_{cr})+a_{r2}{\Phi }_S(h+h_{sr})\hfill \\ +a_{r3}{\Phi }_S(h+h_{cr})+a_{r4}{\Phi }_S(h)\hfill & (10)\end{array}$

where h [L] is the separation distance from the center of the electrostatic zone of influence at a height h_sr from the SWI to the leading face of the colloid center at a height h_cr, and a_r1 [–], a_r2 [–], a_r3 [–], and a_r4 [–] are constants that determine the contributions of the various possible roughness combinations that are equal to:

$\begin{array}{l}{a}_{r1}=\left(1-f_{sr}\right)\left(1-f_{cr}\right)\hfill \\ a_{r2}=\left(1-f_{sr}\right)f_{cr}\hfill \\ a{r}_3=f_{sr}\left(1-f_{cr}\right)\hfill \\ a{r}_4=f_{sr}{f}_{cr}\hfill & (11)\end{array}$

Equations (10) and (11) assume that h > 0 such that roughness on the colloid and SWI do not overlap, and that lateral components of the interaction energy are insignificant or cancel out.

The value of parameter Φ_S in Equation (10) is the mean dimensionless interaction energy between a smooth colloid and SWI that contains binary CH on both surfaces. Similar to Equation (10), Φ_S can be determined as a linear combination of interaction energies for the various CH components as (Bradford and Torkzaban, 2012).

$\begin{array}{ll}{\Phi }_S(h)={\displaystyle \underset{j=1}{\overset{2}{{\sum }^{\text{}}}}\underset{i=1}{\overset{2}{{\sum }^{\text{}}}}}{f}_{sj}{f}_{ci}{\Phi }_{ij}(h)& (12)\end{array}$

where f_sj [–] and f_ci [–] are fractions of the electrostatic zone of influence that are associated with binary CH classes on the SWI (j = 1, 2) and colloid (i = 1, 2), respectively, and Φ_ij was defined by Equations (1)–(8) for the various possible CH combinations. It should be mentioned that f_s1 = (1-f_s2) and f_c1 = (1-f_c2). Note that Equations (10)–(12) are consistent with previous studies that have demonstrated that the mean interaction energy for heterogeneous surfaces can be determined as a linear combination of interaction energies associated with the various heterogeneity combinations (Huang et al., 2009; Bendersky and Davis, 2011; Bradford and Torkzaban, 2013).

Note that our approach for NR in Equations (10) and (11) is independent of the type of CH. Consequently, many types and combinations of CH can be considered using the same approach. For example, the combined CH arising from differences in charge, Hamaker, and contact angle can be simultaneously considered when accounting for separate interaction parameters for each CH class on the SWI and colloid. Alternatively, heterogeneity in charge (CH1), Hamaker constant (CH2), or contact angle (CH3) can be separately determined by only varying these interaction parameters for each CH class. In this case, CH1, CH2, and CH3 reflect the influence of heterogeneity on ${\Phi }^{el}$, ${\Phi }^{vdW}$ (and ${\Phi }^{Born}$), and ${\Phi }^{AB}$ components of the total interaction energy (Equation 1), respectively, whereas other interaction energy terms consider homogeneous conditions.

Equations (1)–(12) therefore allow the influence of NR and CH, NR and CH1, NR and CH2, and NR and CH3 to be systematically investigated for various heterogeneity parameters when considering double layer, van der Waals, Lewis acid-base, and Born interactions. All interaction energy profiles were analyzed to determine the energy barrier height (Φ_max), and the depths of the secondary (Φ_2min) and primary (Φ_1min) minima.

Energy Balance

The probability (ε_k) that a colloid interacting in a primary (k = 1) or secondary (k = 2) minimum would be immobilized in the presence of random kinetic energy fluctuations of a diffusing colloid may be estimated using the Boltzmann factor and Maxwellian kinetic energy models as (Simoni et al., 1998; Shen et al., 2007; Bradford and Torkzaban, 2015; Bradford et al., 2017):

$\begin{array}{cc}{\epsilon }_k=\exp (-A)-\exp (-B)& (13)\end{array}$

$\begin{array}{l}{\epsilon }_k=\left(erf(\sqrt{B})-\sqrt{\frac{4B}{\pi }}\exp (-B)\right)\\ -\left(erf(\sqrt{A})-\sqrt{\frac{4A}{\pi }}\exp (-A)\right)& (14)\end{array}$

where A and B are equal to the dimensionless interaction energies to enter and escape from a minimum, respectively (Bradford and Torkzaban, 2015; Bradford et al., 2017). Note that an infinite depth of the primary minimum has frequently been assumed by setting B = ∞ (Bradford and Torkzaban, 2015). Predicted values of ε₁ as a function of A (with B = ∞) are shown in Figure S1. Results demonstrate that values of ε₁ are quite similar when using Equations (13) and (14), and we, therefore, choose to employ Equation (14). It should be mentioned that Equations (13) and (14) may also be used to determine the probability that an interacting colloid will be released from a secondary and primary minima (ε_rk) by diffusion. In this case, A is equal to the minimum kinetic energy to escape from the minimum and B = ∞ (e.g., the maximum kinetic energy) (Bradford and Torkzaban, 2015; Bradford et al., 2017).

The values ε_k and ε_rk determine whether a diffusing colloid will interact in a minimum and the reversibility of this interaction, respectively. No colloid interaction in the minimum occurs if ε_k is below a critical threshold (ε_c) that was taken to be 0.01 (Bradford et al., 2017). Reversible interaction occurs when ε_k > ε_c and ε_c < ε_rk, and irreversible interaction occurs when ε_k > ε_c and ε_c > ε_rk. The condition for irreversible colloid interaction can, therefore, be expressed mathematically using β_k terms as (Bradford and Torkzaban, 2015; Bradford et al., 2017):

$\begin{array}{ll}{\beta }_k=H_o({\epsilon }_k-{\epsilon }_c)H_o({\epsilon }_c-{\epsilon }_{rk})& (15)\end{array}$

where H_o is a Heaviside function that is equal to 1 or 0 depending on whether the quantity in parentheses is greater than or equal to 0 or less than 0, respectively. A value of β_k = 1 indicates a location of irreversible retention, whereas β_k = 0 denotes no or reversible retention. In this work, if β₁ = 1 or β₂ = 1 we define a parameter β equal to 1 otherwise 0. It should be mentioned that this approach may also be extended to account for the role of hydrodynamics and the spatial distributions of NR and/or CH on colloid immobilization (Bradford and Torkzaban, 2015), but this was not the focus of this study.

Numerical Experiments

Numerical experiments were conducted to examine interaction energy parameters and irreversible retention of hydrophilic and hydrophobic bacteria on quartz surfaces with different types and amounts of CH and/or NR under different IS conditions. Results were presented as interpolated contour graphs which were generated using the marching square graphics algorithm in Plotly (Plotly, Canada).

The individual Hamaker constants for water, pure quartz, and the bacteria were taken as 3.7 × 10⁻²⁰ J (Israelachvili, 1992), 8.86 × 10⁻²⁰ J (Bergström, 1997), and 6.46 × 10⁻²⁰ J, respectively. This yields a commonly employed value for the combined Hamaker constant for bacteria-water-quartz equal to 6.5 × 10⁻²¹ J (Rijnaarts et al., 1995a,b). The zeta potential of pure quartz was taken to be −22, −12, and −11.2 mV in 10, 50, and 100 mM NaCl solution, respectively (Torkzaban et al., 2008). The zeta potential of the bacteria in 10, 50, and 100 mM NaCl solution was taken to be −49, −32, and −21 mV, respectively (Torkzaban et al., 2008).

The influence of different amounts and types of organic matter and metal oxide coatings on the quartz surface was considered by systematically changing values of A_s2, θ_s2, ζ_s2, and f_s2 over hypothetical ranges. The various types of CH (Hamaker, contact angle, or zeta potential) were separately examined to better understand their individual contributions and relative importance. The solid phase Hamaker constant and fraction on site 2 were varied from A_s2 = 2.5 × 10⁻²⁰ to 10 × 10⁻²⁰ J and f_s2 = 0 to 1 when considering heterogeneity in van der Waals interactions. This range in individual Hamaker constants encompassed reported values for humic acid, extracellular polymeric substances, and carbon black that are equal to 4.85 × 10⁻²⁰, 7.78 × 10⁻²⁰, 1 × 10⁻¹⁹ J, respectively (Tong et al., 2011; Han et al., 2017). The solid phase contact angle and fraction on site 2 were varied from θ_s2 = 0 to 125° and f_s2 = 0 to 1 when considering heterogeneity in Lewis acid-base interactions. This range in contact angles includes reported values for humic acid and fulvic acid of around 20° (Lin et al., 2006), and a upper limit similar to black carbon which is equal to 136.6° (Hwang et al., 2018). The solid phase zeta potential and fraction on site 2 were varied from ζ_s2 = −20 to +30 mV and f_s2 = 0 to 1 when considering heterogeneity in electrostatic double layer interactions. This range in zeta potentials encompasses a wide range of minerals, metal oxide coatings, and humic materials (Fuerstenau and Pradip, 2005; Tong et al., 2011).

Some calculations considered roughness on the bacteria and solid surfaces. In this case, values of h_cr and f_cr on the bacteria surface were set to 25 nm and 0.2, respectively, to be consistent with reported values in the literature (King et al., 2014). Tunneling Electron Microscopy of the surface of various bacteria species has also revealed that their macromolecules extend between 5 and 100 nm into solution (Rijnaarts et al., 1995a). Heterogeneity on bacteria cell surface lipopolysaccharides and extracellular polysaccharides have been found to have a role in bacterial adhesion (Camesano and Abu-Lail, 2002; Abu-Lail and Camesano, 2003). The value of h_sr and f_sr on the solid surface varied from 0 to 80 nm and 0 to 1, respectively, when considering only the influence of NR. When the combined influence of CH and solid phase roughness was considered values of h_sr = 50 nm and f_sr = 0.1 (IS = 50 or 100 mM) or 0.05 (IS = 10 mM). These roughness parameters values were selected to be consistent with published studies that have employed Atomic Force Microscopy to measure the roughness properties on quartz or glass bead surfaces (Han et al., 2016; Rasmuson et al., 2017) or examined the influence of roughness on interaction energies (Bradford et al., 2017).

Results and Discussion

Chemical Heterogeneity

Figure 1 shows contour plots of Φ_2min (Figure 1A), Φ_max (Figure 1B), Φ_1min (Figure 1C), β₁ (Figure 1D), β₂ (Figure 1E), and β (Figure 1F) for a hydrophilic bacteria when the IS = 100 mM NaCl and heterogeneity in the van der Waals interaction was considered; e.g., the solid phase Hamaker constant and fraction on site 2 were varied from A_s2 = 2.5 × 10⁻²⁰ to 10 × 10⁻²⁰ J and f_s2 = 0 to 1. Heterogeneity in double layer and Lewis acid-base interactions was neglected (Table 1). The Hamaker constant on solid phase site 1 was A_s1 = 8.86 × 10⁻²⁰ J to be consistent with quartz (Bergström, 1997). When A_s2 is less than A_s1 and f_s2> 0 the combined Hamaker is smaller than that of quartz. In this case, the relative importance of the van der Waals interaction is diminished relative to quartz, and conditions for bacteria retention become less favorable. Consequently, a decrease in A_s2 produces an increase in Φ_2min, Φ_max, and Φ_1min, especially for higher values of f_s2. Bacteria release or reversible retention (β = 0 in Figure 1F) only occurs for smaller A_s2 and for larger f_s2. Both primary (Figure 1D) and secondary (Figure 1E) minima contributed to irreversible retention for the complementary conditions. It should be mentioned that the interaction energy profiles were similarly influenced by variability in A_s2 and f_s2 under lower IS conditions (Figure S2). However, these changes were not sufficient to eliminate the energy barrier because the influence of the repulsive electrostatic double layer interaction is greater under lower IS conditions. In this case, irreversible retention therefore only occurred in a secondary minimum. Consequently, the influence of variability in the Hamaker constant increased the relative importance of secondary to primary minima retention under lower IS conditions.

FIGURE 1

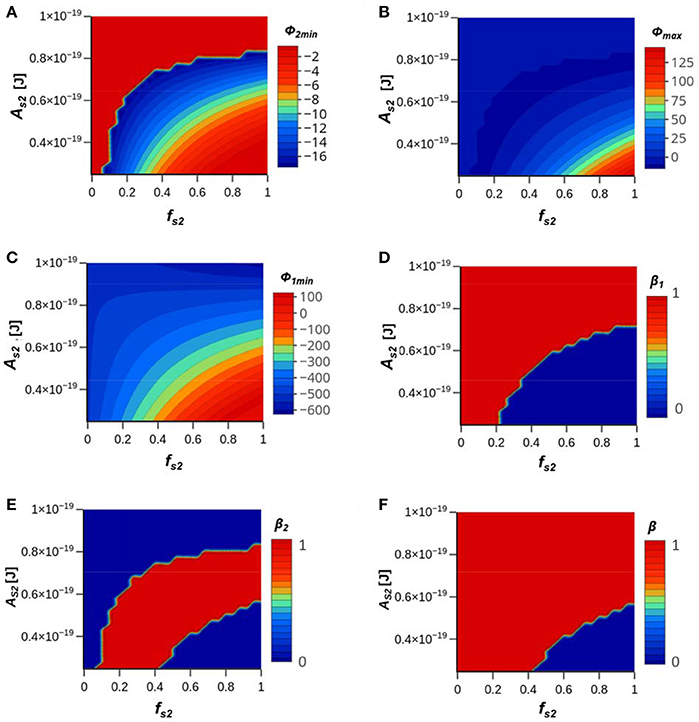
Figure 1. Contour plots of (A) Φ_2min, (B) Φ_max, (C) Φ_1min, (D) β₁, (E) β₂, and (F) β for a hydrophilic bacterium when the IS = 100 mM NaCl and heterogeneity in the van der Waals interaction was considered. The solid phase Hamaker constant and fraction on site 2 were varied from A_s2 = 2.5 × 10⁻²⁰ to 10 × 10⁻²⁰ J and f_s2 = 0 to 1. Table 1 gives a summary of all parameters.

TABLE 1

Table 1. A summary of all model parameters employed in the figures that were varied.

Figure 2 shows contour plots of Φ_2min (Figure 2A), Φ_max (Figure 2B), Φ_1min (Figure 2C), and β (Figure 2D) for a hydrophilic bacteria when the IS = 50 mM NaCl and heterogeneity in Lewis acid-base interaction on the solid phase was considered. In this case, the solid phase contact angle and fraction on site 2 were varied from θ_s2 = 0 to 125° and f_s2 = 0 to 1, and values of θ_s1 and θ_c1were both set to zero. Heterogeneity in double layer and van der Waals interactions was neglected (Table 1). An increase in θ_s2 produces an increase in the attractive Lewis acid-base interaction that reduced Φ_2min, Φ_max, and Φ_1min, especially for larger values of f_s2. Higher values of θ_s2 and f_s2 created conditions that were favorable for irreversible retention (β = 1 in Figure 2D) in either a primary or secondary minima. The influence of variations in Lewis acid-base interactions similarly reduced the energy barrier when the IS = 10 mM, but were insufficient to eliminate that energy barrier and produce irreversible retention in a primary minimum (Figure S3). Variations in Lewis acid-base interaction only influenced the depth of the primary minimum when the IS = 100 mM because the energy barrier was already eliminated (Figure S4). Similar, calculations were conducted for hydrophobic bacteria (Figure S5). In this case, the influence of Lewis acid-base interactions on interaction energy parameters followed the same trends as for the hydrophilic bacteria, but became even more pronounced (e.g., irreversible retention occurred at lower θ_s2, f_s2, and IS conditions). It should be mentioned that increasing f_s2 produced greater amounts of irreversible retention with heterogeneity in θ_s2, whereas the opposite trend was observed for heterogeneity in A_s2 in Figure 1.

FIGURE 2

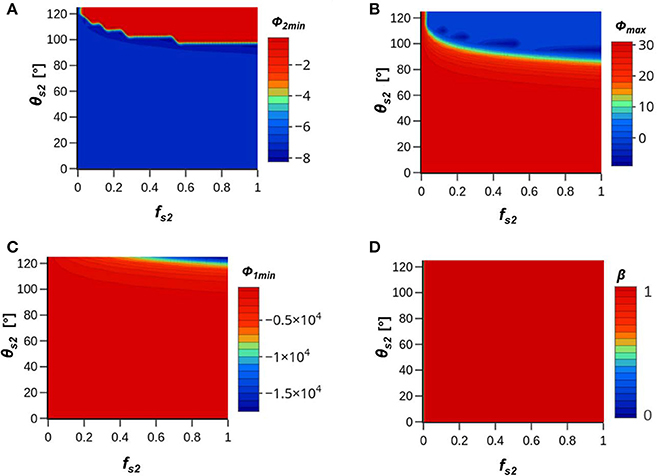
Figure 2. Contour plots of (A) Φ_2min, (B) Φ_max, (C) Φ_1min, and (D) β for a hydrophilic bacterium when the IS = 50 mM NaCl and heterogeneity in Lewis acid-base interaction on the solid phase was considered. The solid phase contact angle and fraction on site 2 were varied from θ_s2 = 0 to 125° and f_s2 = 0 to 1, and values of θ_s1 and θ_c1were both set to zero. Table 1 gives a summary of all parameters.

Figure 3 shows contour plots of Φ_2min (Figure 3A), Φ_max (Figure 3B), Φ_1min (Figure 3C), and β₁ (Figure 3D) for a hydrophilic bacteria when the IS = 10 mM NaCl and heterogeneity in electrostatic double layer interaction on the solid phase was considered. In this case, the solid phase zeta potential and fraction on site 2 were varied from ζ_s2 = −20 to 30 mV and f_s2 = 0 to 1, and values of ζ_s1 and ζ_c1were equal to −22 and −49, respectively. Heterogeneity in van der Waals and Lewis acid-base interactions was neglected (Table 1). Electrostatic repulsion was decreased as ζ_s2 and f_s2 were increased, and this produced a decrease in Φ_2min, Φ_max, and Φ_1min. Eventually, the values of ζ_s2 and f_s2 were sufficiently large to create an electrostatic attraction which eliminated the energy barrier and produced irreversible retention (β₁ = 1 in Figure 3D) in a primary minimum. Other researchers have systematically examined the influence of CH1 on interaction energy profiles under different IS conditions and have observed similar trends (Bendersky and Davis, 2011; Bradford and Torkzaban, 2012; Shen et al., 2013; Pazmino et al., 2014). This information is presented in this work to facilitate the comparison with other CH arising from van der Waals (Figure 1) and Lewis acid-base (Figure 2) interactions. Comparison of Figures 1–3 indicates that CH1 can produce irreversible hydrophilic bacteria retention under lower IS conditions than heterogeneity in the solid phase Hamaker constant or contact angle. However, Lewis acid-base interactions become more important for hydrophobic bacteria and this may produce even greater amounts of irreversible retention than CH1 under some solution chemistry conditions (Figure 3 and Figure S5).

FIGURE 3

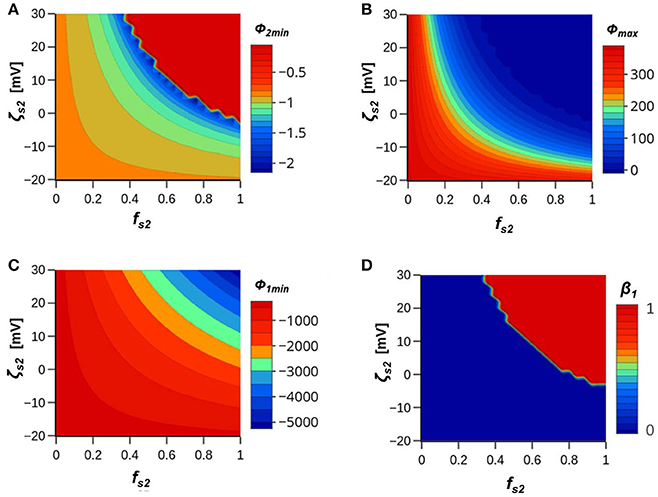
Figure 3. Contour plots of (A) Φ_2min, (B) Φ_max, (C) Φ_1min, and (D) β₁ for a hydrophilic bacterium when the IS = 10 mM NaCl and heterogeneity in electrostatic double layer interaction on the solid phase was considered. The solid phase zeta potential and fraction on site 2 were varied from ζ_s2 = −20 to 30 mV and f_s2 = 0 to 1, and values of ζ_s1 and ζ_c1were equal to −22 and −49, respectively. Table 1 gives a summary of all parameters.

Roughness Heterogeneity

Figure 4 shows contour plots of Φ_2min (Figure 4A), Φ_max (Figure 4B), Φ_1min (Figure 4C), and β₁ (Figure 4D) for a hydrophilic bacteria when the IS = 10 mM NaCl and roughness heterogeneity on the bacteria and the solid phase was considered. In this case, the bacteria had f_cr = 0.2 and h_cr = 25 nm, and the roughness height (h_sr = 0–80 nm) and fraction (f_sr = 0–1) on the solid phase were varied. The different types of CH were neglected in these calculations (Table 1). Roughness on the solid surface had a dramatic influence on interaction energy parameters. In particular, values of Φ_max were significantly reduced or eliminated because of differences in van der Waals and electrostatic double layer interactions with separation distance, and Φ_2min and Φ_1min became shallower for small values of f_sr because of diminished van der Waals attraction from the underlying surfaces (Torkzaban and Bradford, 2016). Only a small fraction of the solid phase roughness conditions produced irreversible bacteria retention (β₁ = 1 in Figure 4D) in a primary minimum; e.g., when f_sr = 0.05. Other researchers have previously observed similar trends for solid phase roughness parameters on interaction energies (Suresh and Walz, 1997; Bhattacharjee et al., 1998; Hoek et al., 2003; Hoek and Agarwal, 2006; Huang et al., 2009; Bendersky and Davis, 2011; Shen et al., 2011, 2012; Bradford and Torkzaban, 2013; Bradford et al., 2017). In this research, we compare this behavior to various CH conditions. In particular, small amounts of NR reduces the energy barrier height to a much greater extent than similar amounts of heterogeneity in charge (Figure 3), Hamaker constant (Figure 1), or contact angle (Figure 2) on the solid phase. Furthermore, NR produced shallower Φ_2min and Φ_1min, whereas heterogeneity in charge (increasing ζ_s2 and f_s2), Hamaker constant (increasing A_s2 and decreasing f_s2), and contact angle (increasing θ_s2 and f_s2) on the solid increased the depth of Φ_2min and Φ_1min. In the next section, we investigate the combined influence of NR and the various CH types.

FIGURE 4

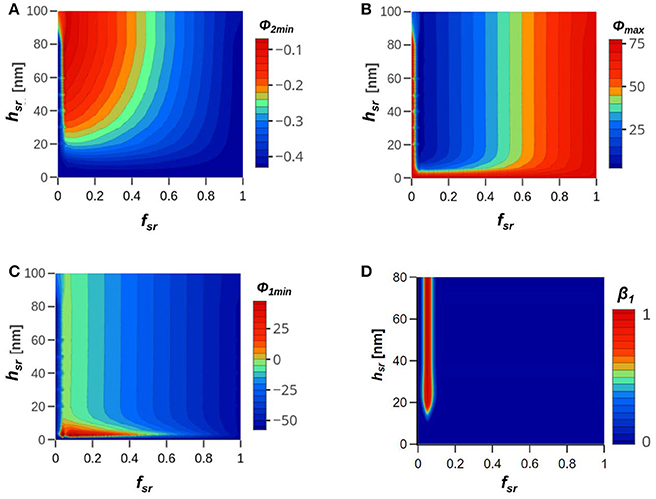
Figure 4. Contour plots of (A) Φ_2min, (B) Φ_max, (C) Φ_1min, and (D) β₁ for a hydrophilic bacterium when the IS = 10 mM NaCl and roughness heterogeneity on the bacteria and the solid phase was considered. The bacteria had f_cr = 0.2 and h_cr = 25 nm, and the roughness height (h_sr = 0 to 80 nm) and fraction (f_sr = 0 to 1) on the solid phase were varied. Table 1 gives a summary of all parameters.

Roughness and Chemical Heterogeneity

Figure 5 shows contour plots of Φ_2min (Figure 5A), Φ_max (Figure 5B), Φ_1min (Figure 5C), and β₁ (Figure 5D) for a hydrophilic bacteria when the IS = 100 mM NaCl, the bacteria (f_cr = 0.2 and h_cr = 25 nm) and solid phase (f_sr = 0.1 and h_cr = 50 nm) have roughness, and the solid phase has the same Hamaker constant heterogeneity conditions as in Figure 1. Table 1 summarizes all parameter values. Note that values of Φ_max in Figure 5 were significantly reduced or eliminated, and Φ_2min and Φ_1min became shallower in comparison to Figure 1. The net effect of these changes was to decrease the amount of irreversible bacteria retention and to increase the relative importance of the primary to the secondary minima. These observations clearly reveal that these roughness conditions dominated the interaction energy profile parameters in the presence of heterogeneity in solid phase Hamaker constants. However, heterogeneity in solid phase Hamaker constants will control the profile parameters when f_sr becomes large and approaches 1 (Figure S6).

FIGURE 5

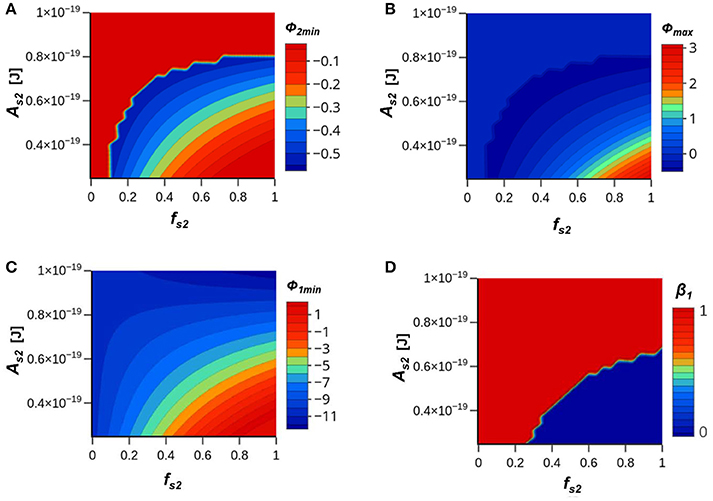
Figure 5. Contour plots of (A) Φ_2min, (B) Φ_max, (C) Φ_1min, and (D) β₁ for a hydrophilic bacterium when the IS = 100 mM NaCl, the bacteria (f_cr = 0.2 and h_cr = 25 nm) and solid phase (f_sr = 0.1 and h_sr = 50 nm) have roughness. The solid phase Hamaker constant and fraction on site 2 were varied from A_s2 = 2.5 × 10⁻²⁰ to 10 × 10⁻²⁰ J and f_s2 = 0 to 1 (Figure 1). Table 1 gives a summary of all parameters.

Figure 6 shows contour plots of Φ_2min (Figure 6A), Φ_max (Figure 6B), Φ_1min (Figure 6C), and β₁ (Figure 6D) for a hydrophilic bacteria when the IS = 10 mM NaCl, the bacteria (f_cr = 0.2 and h_cr = 25 nm) and solid phase (f_sr = 0.05 and h_cr = 50 nm) have roughness, and the solid phase has the same CH3 conditions as in Figure S3. Comparison of Figure S3 and Figure 6 reveals that roughness reduced or eliminated Φ_max for the considered CH3 conditions. In addition, the depths of Φ_2min and especially Φ_1min were reduced in the presence of roughness. CH3 produced no irreversible retention on the smooth surface when the IS = 10 mM (Figure S3). In contrast, the combined influence of roughness and CH3 created irreversible retention in a primary when the IS = 10 mM for all conditions (Figure 6D). These same trends were observed for hydrophobic bacteria when the IS = 10 mM (Figure S7). However, the depth of the primary minimum was much deeper for the hydrophobic than the hydrophilic bacteria. These observations indicate that roughness had a controlling influence on eliminating the energy barrier, but that Lewis acid-base interactions had a significant influence on the depth of the primary minima and may be used to offset some of the influence on roughness. The relative contributions of NR and CH3 are therefore expected to change with the physical and CH parameters, as well as the solution IS.

FIGURE 6

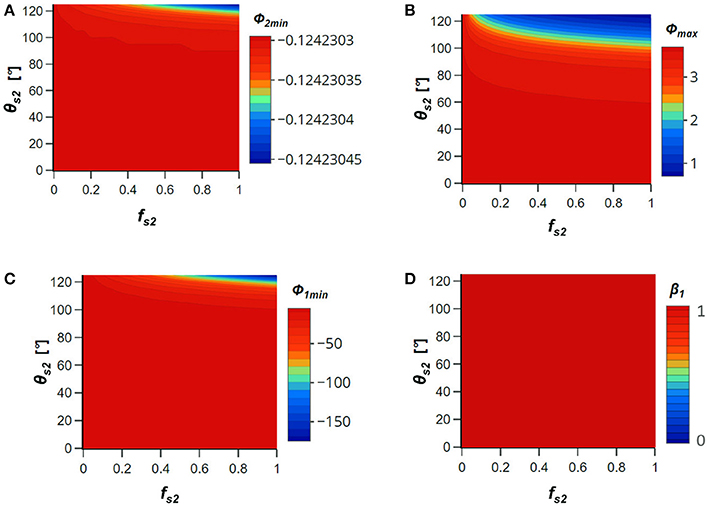
Figure 6. Contour plots of (A) Φ_2min, (B) Φ_max, (C) Φ_1min, and (D) β₁ for a hydrophilic bacterium when the IS = 10 mM NaCl, the bacteria (f_cr = 0.2 and h_cr = 25 nm) and solid phase (f_sr = 0.05 and h_sr = 50 nm) have roughness. The solid phase contact angle and fraction on site 2 were varied from θ_s2 = 0 to 125° and f_s2 = 0 to 1, and values of θ_s1 and θ_c1were both set to zero (Figure 2). Table 1 gives a summary of all parameters.

The combined influence of CH1 and NR on interaction energies has been previously investigated (e.g., Bradford and Torkzaban, 2013; Bradford et al., 2017). However, for completeness Figure S8 shows contour plots of Φ_2min (Figure S8A), Φ_max (Figure S8B), Φ_1min (Figure S8C), and β₁ (Figure S8D) for a hydrophilic bacteria when the IS = 10 mM NaCl, the bacteria (f_cr = 0.2 and h_cr = 25 nm) and solid phase (f_sr = 0.05 and h_cr = 50 nm) have roughness, and the solid phase has the same CH1 conditions as in Figure 3. Similar to Figure 6 (NR with CH3), bacteria retention was enhanced in the presence of roughness in comparison to a smooth surface with the same CH1 conditions (Figure 3 and Figure S8). This occurred because roughness readily reduced the energy barrier, and the combination of roughness and CH1 produced a sufficiently deep primary minimum for retention. It should be mentioned that if f_cr and f_sr are further decreased that the primary minimum will become shallower and bacteria will be subject to diffusive release even in the presence of CH1 (Bradford et al., 2017).

Conclusions

An approach was developed to determine interaction energies between a colloid and the solid water interface when both surfaces have binary NR and CH. These interaction energies considered constant potential double layer electrostatics, retarded London-van der Waals attraction, Lewis acid-base interactions, and Born repulsion for a sphere-plate geometry. CH from variability in Hamaker constants (van der Waals interactions), contact angles (Lewis acid-base interactions), and zeta potentials (electrostatic double layer interactions) can be considered separately or in combination with other heterogeneities. Calculated interaction energy parameters were used in conjunction with an energy balance model to determine conditions for irreversible retention in the presence of random fluctuations in kinetic energy of a diffusing colloid.

SOM coatings on mineral surfaces are expected to create heterogeneity by altering their Lewis acid-base (contact angle) and van der Waals (Hamaker constant) interactions. Charge heterogeneity may also occur as a result of SOM as well as metal oxide coatings. Numerical experiments were conducted to investigate the influence of various heterogeneity types, amounts, and combinations on bacteria interaction energy parameters and irreversible retention. Heterogeneity in the solid phase Hamaker constant over expected ranges for SOM produced a combined Hamaker constant that was smaller than quartz. Increasing Hamaker constant heterogeneity, therefore, tended to increase the relative importance of repulsive double layer interactions over attractive van der Waals interactions and produced a more repulsive surface with less bacteria retention. This effect became more apparent under higher IS conditions when the double layer was compressed, and the energy barrier was smaller.

In contrast to heterogeneity in the Hamaker constant, variability in the solid phase contact angle over expected ranges for SOM produced enhanced attractive Lewis acid-base interactions. This decreased the height of the energy barrier, and increased the depths of the secondary and primary minima and the amount of irreversible bacteria retention under lower IS conditions. These effects were magnified for greater contact angles and fractions on the solid surface, and for more hydrophobic bacteria.

Heterogeneity in the solid phase zeta potential behaved in a similar manner to heterogeneity in the contact angle. In particular, increasing the fraction and zeta potential of site 2 decreased the energy barrier height and increased the depths of the secondary and primary minima and the amount of irreversible retention. In general, increasing CH1 was more effective at reducing the energy barrier height and creating irreversible retention at lower IS conditions than increasing CH3 for hydrophilic bacteria. However, CH3 tended to produce deeper secondary and primary minima than CH1.

Small fractions of NR always significantly reduced and/or eliminated the energy barrier under lower IS conditions. Furthermore, NR tended to control the energy barrier height in the presence of CH in Hamaker constant, contact angle, or zeta potential. Small amounts of NR also significantly decreased the depths of the secondary and primary minima in comparison to a smooth surface. However, the depths of the secondary and primary minima tended to be deeper in the presence of zeta potential and especially CH3, and this made bacteria retention more irreversible.

Collectively, our results demonstrate the critical role of CH and NR in controlling interaction energy parameters and irreversible bacteria retention. In particular, spatial variations in SOM, metal oxide coatings, and especially NR will have important roles in determining bacteria retention on natural surfaces. The relative importance of the various heterogeneity types was found to change with the solution IS and specific ranges in considered heterogeneity parameters. NR tended to be dominant for small roughness fractions. In contrast, SOM and metal oxide coatings are expected to play more important roles on smooth surfaces. In this case, CH1 and CH3 were more important under lower IS conditions, whereas CH2 started to play a role at a higher IS.

Author Contributions

SB, SS, HK, and GH contributed to the conceptual processes described in the paper, description of interaction energies, determination of simulation parameters, and discussion of findings.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This research was supported by the USDA, ARS, National Program 212. The abstract for this paper was based on an oral presentation (online abstract found at https://events.interpore.org/event/2/contributions/923/) that was given by SB at the Interpore 2018 meeting, on May 15, 2018 in New Orleans, LA.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2018.00056/full#supplementary-material

References

Abu-Lail, N. I., and Camesano, T. A. (2003). The role of lipopolysaccharides in the adhesion, retention, and transport of Escherichia coli JM109. Environ. Sci. Technol. 37, 2173–2183. doi: 10.1021/es026159o

PubMed Abstract | CrossRef Full Text | Google Scholar

Aiken, G. R. (1985). Humic Substances in Soil, Sediment, and Water: Geochemistry, Isolation, and Characterization. New York, NY: Wiley.

Google Scholar

Almendros, G., González-Vila, F., and Martin, F. (1990). Fire-induced transformation of soil organic matter from an oak forest: an experimental approach to the effects of fire on humic substances. Soil Sci. 149, 158–168.

Google Scholar

Amirbahman, A., and Olson, T. M. (1993). Transport of humic matter-coated hematite in packed beds. Environ. Sci. Technol. 27, 2807–2813.

Google Scholar

Bendersky, M., and Davis, J. M. (2011). DLVO interaction of colloidal particles with topographically and chemically heterogeneous surfaces. J. Colloid Interface Sci. 353, 87–97. doi: 10.1016/j.jcis.2010.09.058

PubMed Abstract | CrossRef Full Text | Google Scholar

Bergendahl, J., and Grasso, D. (1999). Prediction of colloid detachment in a model porous media: thermodynamics. AIChE J. 45, 475–484. doi: 10.1002/aic.690450305

CrossRef Full Text | Google Scholar

Bergström, L. (1997). Hamaker constants of inorganic materials. Adv. Colloid Interface Sci. 70, 125–169.

Google Scholar

Bhattacharjee, S., Ko, C. H., and Elimelech, M. (1998). DLVO interaction between rough surfaces. Langmuir 14, 3365–3375.

Google Scholar

Bradford, S. A., Kim, H., Shen, C., Sasidharan, S., and Shang, J. (2017). Contributions of nanoscale roughness to anomalous colloid retention and stability behavior. Langmuir 33, 10094–10105. doi: 10.1021/acs.langmuir.7b02445

PubMed Abstract | CrossRef Full Text | Google Scholar

Bradford, S. A., and Torkzaban, S. (2012). Colloid adhesive parameters for chemically heterogeneous porous media. Langmuir 28, 13643–13651. doi: 10.1021/la3029929

PubMed Abstract | CrossRef Full Text | Google Scholar

Bradford, S. A., and Torkzaban, S. (2013). Colloid interaction energies for physically and chemically heterogeneous porous media. Langmuir 29, 3668–3676. doi: 10.1021/la400229f

PubMed Abstract | CrossRef Full Text | Google Scholar

Bradford, S. A., and Torkzaban, S. (2015). Determining parameters and mechanisms of colloid retention and release in porous media. Langmuir 31, 12096–12105. doi: 10.1021/acs.langmuir.5b03080

PubMed Abstract | CrossRef Full Text | Google Scholar

Camesano, T. A., and Abu-Lail, N. I. (2002). Heterogeneity in bacterial surface polysaccharides, probed on a single-molecule basis. Biomacromolecules 3, 661–667. doi: 10.1021/bm015648y

PubMed Abstract | CrossRef Full Text | Google Scholar

Cushing, R. S., and Lawler, D. F. (1998). Depth filtration: fundamental investigation through three-dimensional trajectory analysis. Environ. Sci. Technol. 32, 3793–3801. doi: 10.1021/es9707567

CrossRef Full Text | Google Scholar

de Blas, E., Rodríguez-Alleres, M., and Almendros, G. (2010). Speciation of lipid and humic fractions in soils under pine and eucalyptus forest in northwest Spain and its effect on water repellency. Geoderma 155, 242–248. doi: 10.1016/j.geoderma.2009.12.007

CrossRef Full Text | Google Scholar

DeNovio, N. M., Saiers, J. E., and Ryan, J. N. (2004). Colloid movement in unsaturated porous media. Vadose Zone J. 3, 338–351. doi: 10.2113/3.2.338

CrossRef Full Text | Google Scholar

Doerr, S., Shakesby, R., and Walsh, R. (2000). Soil water repellency: its causes, characteristics and hydro-geomorphological significance. Earth Sci. Rev. 51, 33–65. doi: 10.1016/S0012-8252(00)00011-8

CrossRef Full Text | Google Scholar

Drummond, C. J., and Chan, D. Y. (1997). van der Waals interaction, surface free energies, and contact angles: dispersive polymers and liquids. Langmuir 13, 3890–3895.

Google Scholar

Ellerbrock, R., Gerke, H., Bachmann, J., and Goebel, M.-O. (2005). Composition of organic matter fractions for explaining wettability of three forest soils. Soil Sci. Soc. Am. J. 69, 57–66. doi: 10.2136/sssaj2005.0057

CrossRef Full Text | Google Scholar

Espinasse, B., Hotze, E. M., and Wiesner, M. R. (2007). Transport and retention of colloidal aggregates of C60 in porous media: Effects of organic macromolecules, ionic composition, and preparation method. Environ. Sci. Technol. 41, 7396–7402. doi: 10.1021/es0708767

PubMed Abstract | CrossRef Full Text | Google Scholar

Flynn, R. M., Yang, X., Hofmann, T., and von der Kammer, F. (2012). Bovine serum albumin adsorption to iron-oxide coated sands can change microsphere deposition mechanisms. Environ. Sci. Technol. 46, 2583–2591. doi: 10.1021/es202048c

PubMed Abstract | CrossRef Full Text | Google Scholar

Franco, C., Clarke, P., Tate, M., and Oades, J. (2000). Hydrophobic properties and chemical characterisation of natural water repellent materials in Australian sands. J. Hydrol. 231, 47–58. doi: 10.1016/S0022-1694(00)00182-7

CrossRef Full Text | Google Scholar

Fuerstenau, D. W. (2005). Zeta potentials in the flotation of oxide and silicate minerals. Adv. Colloid Interface Sci. 114–115, 9–26. doi: 10.1016/j.cis.2004.08.006

CrossRef Full Text | Google Scholar

Grasso, D., Subramaniam, K., Butkus, M., Strevett, K., and Bergendahl, J. (2002). A review of non-DLVO interactions in environmental colloidal systems. Rev. Environ. Sci. Biotechnol. 1, 17–38. doi: 10.1023/a:1015146710500

CrossRef Full Text | Google Scholar

Gregory, J. (1981). Approximate expressions for retarded van der waals interaction. J. Colloid Interface Sci. 83, 138–145. doi: 10.1016/0021-9797(81)90018-7

CrossRef Full Text | Google Scholar

Han, P., Wang, X., Cai, L., Tong, M., and Kim, H. (2014). Transport and retention behaviors of titanium dioxide nanoparticles in iron oxide-coated quartz sand: effects of pH, ionic strength, and humic acid. Colloids Surfaces A Physicochem. Eng. Aspects 454, 119–127. doi: 10.1016/j.colsurfa.2014.04.020

CrossRef Full Text | Google Scholar

Han, Y., Hwang, G., Kim, D., Bradford, S. A., Lee, B., Eom, I., et al. (2016). Transport, retention, and long-term release behavior of ZnO nanoparticle aggregates in saturated quartz sand: role of solution pH and biofilm coating. Water Res. 90, 247–257. doi: 10.1016/j.watres.2015.12.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, Y., Hwang, G., Park, T., Gomez-Flores, A., Jo, E., Eom, I-C., et al. (2017). Stability of carboxyl-functionalized carbon black nanoparticles: the role of solution chemistry and humic acid. Environ. Sci. Nano 4, 800–810. doi: 10.1039/C6EN00530F

CrossRef Full Text | Google Scholar

Henry, C., Minier, J.-P., Lefevre, G., and Hurisse, O. (2011). Numerical study on the deposition rate of hematite particle on polypropylene walls: role of surface roughness. Langmuir 27, 4603–4612. doi: 10.1021/la104488a

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoek, E. M. V., and Agarwal, G. K. (2006). Extended DLVO interactions between spherical particles and rough surfaces. J. Colloid Interface Sci. 298, 50–58. doi: 10.1016/j.jcis.2005.12.031

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoek, E. M. V., Bhattacharjee, S., and Elimelech, M. (2003). Effect of membrane surface roughness on colloid-membrane DLVO interactions. Langmuir 19, 4836–4847. doi: 10.1021/la027083c

CrossRef Full Text | Google Scholar

Hogg, R., Healy, T. W., and Fuerstenau, D. W. (1966). Mutual coagulation of colloidal dispersions. Trans. Faraday Soc. 62:1638. doi: 10.1039/tf9666201638

CrossRef Full Text | Google Scholar

Hough, D. B., and White, L. R. (1980). The calculation of Hamaker constants from Lifshitz theory with applications to wetting phenomena. Adv. Colloid Interface Sci. 14, 3–41. doi: 10.1016/0001-8686(80)80006-6

CrossRef Full Text | Google Scholar

Huang, W., Peng, P. A., Yu, Z., and Fu, J. (2003). Effects of organic matter heterogeneity on sorption and desorption of organic contaminants by soils and sediments. Appl. Geochem. 18, 955–972. doi: 10.1016/S0883-2927(02)00205-6

CrossRef Full Text | Google Scholar

Huang, X., Bhattacharjee, S., and Hoek, E. M. V. (2009). Is surface roughness a “scapegoat” or a primary factor when defining particle–substrate interactions? Langmuir 26, 2528–2537. doi: 10.1021/la9028113

PubMed Abstract | CrossRef Full Text | Google Scholar

Hudson, R., Traina, S., and Shane, W. (1994). Organic matter comparison of wettable and nonwettable soils from bentgrass sand greens. Soil Sci. Soc. Am. J. 58, 361–367.

Google Scholar

Hwang, G., Gomez-Flores, A., Bradford, S. A., Choi, S., Jo, E., Kim, S. B., et al. (2018). Analysis of stability behavior of carbon black nanoparticles in ecotoxicological media: Hydrophobic and steric effects. Colloids Surf. A Physicochem. Eng. Aspects.

Google Scholar

Israelachvili, J. N. (1992). Intermolecular and Surface Forces. London; San Diego, CA: Academic Press.

Google Scholar

Jiang, X., Tong, M., and Kim, H. (2012). Influence of natural organic matter on the transport and deposition of zinc oxide nanoparticles in saturated porous media. J. Colloid Interface Sci. 386, 34–43. doi: 10.1016/j.jcis.2012.07.002

PubMed Abstract | CrossRef Full Text | Google Scholar

King, J. D., Berry, S., Clarke, B. R., Morris, R. J., and Whitfield, C. (2014). Lipopolysaccharide O antigen size distribution is determined by a chain extension complex of variable stoichiometry in Escherichia coli O9a. Proc. Natl. Acad. Sci. U.S.A. 111, 6407–6412. doi: 10.1073/pnas.1400814111

PubMed Abstract | CrossRef Full Text | Google Scholar

Kretzschmar, R., and Sticher, H. (1997). Transport of humic-coated iron oxide colloids in a sandy soil: influence of Ca²⁺ and trace metals. Environ. Sci. Technol. 31, 3497–3504.

Google Scholar

Lin, C.-Y., Chou, W.-C., Tsai, J.-S., and Lin, W.-T. (2006). Water repellency of Casuarina windbreaks (Casuarina equisetifolia Forst.) caused by fungi in central Taiwan. Ecol. Eng. 26, 283–292. doi: 10.1016/j.ecoleng.2005.10.010

CrossRef Full Text | Google Scholar

Ma'shum, M., and Farmer, V. (1985). Origin and assessment of water repellency of a sandy South Australian soil. Soil Res. 23, 623–626.

Google Scholar

Ma'Shum, M., Tate, M., Jones, G., and Oades, J. (1988). Extraction and characterization of water–repellent materials from Australian soils. Eur. J. Soil Sci. 39, 99–110.

Google Scholar

Molnar, I. L., Johnson, W. P., Gerhard, J. I., Willson, C. S., and O'Carroll, D. M. (2015). Predicting colloid transport through saturated porous media: a critical review. Water Resour. Res. 51, 6804–6845. doi: 10.1002/2015WR017318

CrossRef Full Text | Google Scholar

Morales, V. L., Zhang, W., Gao, B., Lion, L. W., Bisogni, J. J., McDonough, B. A., et al. (2011). Impact of dissolved organic matter on colloid transport in the vadose zone: deterministic approximation of transport deposition coefficients from polymeric coating characteristics. Water Res. 45, 1691–1701. doi: 10.1016/j.watres.2010.10.030

PubMed Abstract | CrossRef Full Text | Google Scholar

Oliveira, R. (1997). Understanding adhesion: a means for preventing fouling. Exp. Therm. Fluid Sci. 14, 316–322. doi: 10.1016/S0894-1777(96)00134-3

CrossRef Full Text | Google Scholar

Park, J.-A., and Kim, S.-B. (2015). DLVO and XDLVO calculations for bacteriophage MS2 adhesion to iron oxide particles. J. Contam. Hydrol. 181:131–140. doi: 10.1016/j.jconhyd.2015.01.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Pazmino, E., Trauscht, J., Dame, B., and Johnson, W. P. (2014). Power law size-distributed heterogeneity explains colloid retention on soda lime glass in the presence of energy barriers. Langmuir 30, 5412–5421. doi: 10.1021/la501006p

PubMed Abstract | CrossRef Full Text | Google Scholar

Rasmuson, A., Pazmino, E., Assemi, S., and Johnson, W. P. (2017). Contribution of nano- to microscale roughness to heterogeneity: closing the gap between unfavorable and favorable colloid attachment conditions. Environ. Sci. Technol. 51, 2151–2160. doi: 10.1021/acs.est.6b05911

PubMed Abstract | CrossRef Full Text | Google Scholar

Torkzaban, S., and Bradford, S. A. (2016). Critical role of surface roughness on colloid retention and release in porous media. Water Res. 88, 274–284. doi: 10.1016/j.watres.2015.10.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Rice, J. A., and MacCarthy, P. (1990). A model of humin. Environ. Sci. Technol. 24, 1875–1877.

Google Scholar

Rijnaarts, H. H., Norde, W., Bouwer, E. J., Lyklema, J., and Zehnder, A. J. (1995a). Reversibility and mechanism of bacterial adhesion. Colloids Surfaces B Biointerfaces 4, 5–22.

Google Scholar

Rijnaarts, H. H., Norde, W., Lyklema, J., and Zehnder, A. J. (1995b). The isoelectric point of bacteria as an indicator for the presence of cell surface polymers that inhibit adhesion. Colloids Surfaces B Biointerfaces 4, 191–197.

Google Scholar

Ruckenstein, E., and Prieve, D. C. (1976). Adsorption and desorption of particles and their chromatographic separation. AIChE J. 22, 276–283. doi: 10.1002/aic.690220209

CrossRef Full Text | Google Scholar

Salata, O. V. (2004). Applications of nanoparticles in biology and medicine. J. Nanobiotechnology 2:3. doi: 10.1186/1477-3155-2-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Shen, C., Lazouskaya, V., Zhang, H., and Wang, F. (2012). Theoretical and experimental investigation of detachment of colloids from rough collector surfaces. Colloids Surfaces A Physicochem. Eng. Aspects 410, 98–110. doi: 10.1016/j.colsurfa.2012.06.025

CrossRef Full Text | Google Scholar

Shen, C., Lazouskaya, V., Zhang, H., Li, B., Jin, Y., and Huang, Y. (2013). Influence of surface chemical heterogeneity on attachment and detachment of microparticles. Colloids Surfaces A Physicochem. Eng. Aspects 433, 14–29. doi: 10.1016/j.colsurfa.2013.04.048

CrossRef Full Text | Google Scholar

Shen, C., Li, B., Huang, Y., and Jin, Y. (2007). Kinetics of coupled primary- and secondary-minimum deposition of colloids under unfavorable chemical conditions. Environ. Sci. Technol. 41, 6976–6982. doi: 10.1021/es070210c

PubMed Abstract | CrossRef Full Text | Google Scholar

Shen, C., Li, B., Wang, C., Huang, Y., and Jin, Y. (2011). Surface roughness effect on deposition of nano- and micro-sized colloids in saturated columns at different solution ionic strengths. Vadose Zone J. 10:1071. doi: 10.2136/vzj2011.0011

CrossRef Full Text | Google Scholar

Simoni, S. F., Harms, H., Bosma, T. N. P., and Zehnder, A. J. B. (1998). Population heterogeneity affects transport of bacteria through sand columns at low flow rates. Environ. Sci. Technol. 32, 2100–2105. doi: 10.1021/es970936g

CrossRef Full Text | Google Scholar

Song, J., Peng, P., and Huang, W. (2002). Black carbon and kerogen in soils and sediments. 1. Quantification and characterization. Environ. Sci. Technol. 36, 3960–3967. doi: 10.1021/es025502m

PubMed Abstract | CrossRef Full Text | Google Scholar

Sposito, G. (2008). The Chemistry of Soils. New York, NY: Oxford university press.

Google Scholar

Stark, W. J., Stoessel, P. R., Wohlleben, W., and Hafner, A. (2015). Industrial applications of nanoparticles. Chem. Soc. Rev. 44, 5793–5805. doi: 10.1039/C4CS00362D

PubMed Abstract | CrossRef Full Text | Google Scholar

Stevenson, F. J. (1994). Humus Chemistry: Genesis, Composition, Reactions. New York, NY: John Wiley & Sons.

Google Scholar

Suresh, L., and Walz, J. Y. (1996). Effect of surface roughness on the interaction energy between a colloidal sphere and a flat plate. J. Colloid Interface Sci. 183, 199–213.

Google Scholar

Suresh, L., and Walz, J. Y. (1997). Direct measurement of the effect of surface roughness on the colloidal forces between a particle and flat plate. J. Colloid Interface Sci. 196, 177–190.

PubMed Abstract | Google Scholar

Tong, M., Zhu, P., Jiang, X., and Kim, H. (2011). Influence of natural organic matter on the deposition kinetics of extracellular polymeric substances (EPS) on silica. Colloids and Surfaces B: Biointerfaces 87, 151–158. doi: 10.1016/j.colsurfb.2011.05.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Torkzaban, S., Tazehkand, S. S., Walker, S. L., and Bradford, S. A. (2008). Transport and fate of bacteria in porous media: Coupled effects of chemical conditions and pore space geometry. Water Resources Res. 44:W0440. doi: 10.1029/2007wr006541

CrossRef Full Text | Google Scholar

Tufenkji, N., and Elimelech, M. (2004). Correlation equation for predicting single-collector efficiency in physicochemical filtration in saturated porous media. Environ. Sci. Technol. 38, 529–536. doi: 10.1021/es034049r

PubMed Abstract | CrossRef Full Text | Google Scholar

Vaidyanathan, R., and Tien, C. (1991). Hydrosol deposition in granular media under unfavorable surface conditions. Chem. Eng. Sci. 46, 967–983.

Google Scholar

Van Loosdrecht, M., Lyklema, J., Norde, W., Schraa, G., and Zehnder, A. (1987). The role of bacterial cell wall hydrophobicity in adhesion. Appl. Environ. Microbiol. 53, 1893–1897.

PubMed Abstract | Google Scholar

Van Oss, C. (1994). Interfacial forces in aqueous media, 1. Marcel Dekker. New York, NY.

Wilkinson, K. J., Balnois, E., Leppard, G. G., and Buffle, J. (1999). Characteristic features of the major components of freshwater colloidal organic matter revealed by transmission electron and atomic force microscopy. Colloids Surfaces A Physicochem. Eng. Aspects 155, 287–310.

Google Scholar

Yang, X., Deng, S., and Wiesner, M. R. (2013). Comparison of enhanced microsphere transport in an iron-oxide-coated porous medium by pre-adsorbed and co-depositing organic matter. Chem. Eng. J. 230, 537–546. doi: 10.1016/j.cej.2013.06.122

CrossRef Full Text | Google Scholar

Yang, X., Flynn, R., Von der Kammer, F., and Hofmann, T. (2010). Quantifying the influence of humic acid adsorption on colloidal microsphere deposition onto iron-oxide-coated sand. Environ. Pollut. 158, 3498–3506. doi: 10.1016/j.envpol.2010.03.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, X., Flynn, R., Von Der Kammer, F., and Hofmann, T. (2011). Influence of ionic strength and pH on the limitation of latex microsphere deposition sites on iron-oxide coated sand by humic acid. Environ. Pollut. 159, 1896–1904. doi: 10.1016/j.envpol.2011.03.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, X., Lin, S., and Wiesner, M. R. (2014). Influence of natural organic matter on transport and retention of polymer coated silver nanoparticles in porous media. J. Hazard. Mater. 264, 161–168. doi: 10.1016/j.jhazmat.2013.11.025

PubMed Abstract | CrossRef Full Text | Google Scholar

Yao, K.-M., Habibian, M. T., and O'Melia, C. R. (1971). Water and wastewater filtration. Concepts Appl. Environ. Sci. Technol. 5, 1105–1112. doi: 10.1021/es60058a005

CrossRef Full Text | Google Scholar

Yoon, R.-H., Flinn, D. H., and Rabinovich, Y. I. (1997). Hydrophobic interactions between dissimilar surfaces. J. Colloid Interface Sci. 185, 363–370.

PubMed Abstract | Google Scholar