Prediction of Soil Formation as a Function of Age Using the Percolation Theory Approach

Recent modeling and comparison with field results showed that soil formation by chemical weathering, either from bedrock or unconsolidated material, is limited largely by solute transport. Chemical weathering rates are proportional to solute velocities. Nonreactive solute transport described by non-Gaussian transport theory appears compatible with soil formation rates. This change in understanding opens new possibilities for predicting soil production and depth across orders of magnitude of time scales. Percolation theory for modeling the evolution of soil depth and production was applied to new and published data for alpine and Mediterranean soils. The first goal was to check whether the empirical data conform to the theory. Secondly we analyzed discrepancies between theory and observation to find out if the theory is incomplete, if modifications of existing experimental procedures are needed and what parameters might be estimated improperly. Not all input parameters required for current theoretical formulations (particle size, erosion, and infiltration rates) are collected routinely in the field; thus, theory must address how to find these quantities from existing climate and soil data repositories, which implicitly introduces some uncertainties. Existing results for soil texture, typically reported at relevant field sites, had to be transformed to results for a median particle size, d₅₀, a specific theoretical input parameter. The modeling tracked reasonably well the evolution of the alpine and Mediterranean soils. For the Alpine sites we found, however, that we consistently overestimated soil depths by ~45%. Particularly during early soil formation, chemical weathering is more severely limited by reaction kinetics than by solute transport. The kinetic limitation of mineral weathering can affect the system until 1 kyr to a maximum of 10 kyr of soil evolution. Thereafter, solute transport seems dominant. The trend and scatter of soil depth evolution is well captured, particularly for Mediterranean soils. We assume that some neglected processes, such as bioturbation, tree throw, and land use change contributed to local reorganization of the soil and thus to some differences to the model. Nonetheless, the model is able to generate soil depth and confirms decreasing production rates with age. A steady state for soils is not reached before about 100 kyr to 1 Myr

Introduction

Setting

The importance of quantifying chemical weathering and soil formation rates has as its basis their relevance across a wide range of fields of study, from agricultural engineering (Montgomery, 2007a,b; Lal, 2010) through climate change (Berner, 1992; Raymo, 1994; Algeo and Scheckler, 1998; Molnar and Cronin, 2015) and geochemistry (White and Brantley, 2003; Anderson and Anderson, 2010) to geomorphology (Heimsath et al., 1997, 1999; Burke et al., 2006; Dixon et al., 2009; Egli et al., 2012, 2014; Amundson et al., 2015). This relevance can be traced to the location of the soil in the middle of what is called the “Critical Zone” at the Earth's surface (Brantley et al., 2007; Richter and Mobley, 2009; Lin, 2010), where interactions between the solid Earth and the atmosphere are most rapid, as well as to the presence of humans at this boundary, and the many uses we have for, as well as burdens we place on, soil (Hillel, 2005).

Concepts in soil formation have been developed since the nineteenth century (Darwin, 1881; Dokuchaev, 1948). Soil is formed from bedrock by a complex interaction of biochemical and physical processes (Jenny, 1941; Huggett, 1998). The role of physical fractures in soil formation, by allowing water penetration of bedrock, was recognized as long ago as Gilbert (1877). Soil also forms in unconsolidated sediments developed through processes such as alluvial deposition (White et al., 1996) tree-throw (Borman et al., 1995), landslides (Trustrum and de Rose, 1988; Smale et al., 1997), mining, (Frouz et al., 2006), and exposure of glacial sediments by glacial retreat (Mavris et al., 2010; Egli et al., 2014). In the latter, the role of any gradual physical weathering processes is correspondingly reduced, since water penetration is guaranteed.

The perception of the importance of chemical weathering to soil formation and geology in general has been steadily climbing for decades (Anderson and Anderson, 2010), partly on the basis of the experimentally determined proportionality between soil production rates, erosion and chemical weathering (Burke et al., 2006; Dixon et al., 2009; Egli et al., 2014; Hunt and Ghanbarian, 2016), and partly through the increased attention to its role in past climate change (Berner, 1992; Raymo, 1994; Algeo and Scheckler, 1998). In the latter, it is only the weathering of silicates that is relevant, as, e.g., weathering of carbonates has no effect on the atmospheric carbon content (e.g., Berner, 1992). Here the simplification offered by the representation of silicate weathering in the Urey reaction (Urey, 1952) CaSiO₃ + CO₂ ↔ CaCO₃ + SiO₂ demonstrates the universality of its impact on climate; each mole of silicate mineral weathered draws down one mole of carbon dioxide from the atmosphere, with only the CO₂ present as a gas. The often-cited Urey reaction describes the weathering of wollastonite. A general reaction for the more common plagioclase is (White et al., 1999):

$\begin{array}{l}{\text{Ca}}_{\text{x}}{\text{Na}}_{(\text{1-x})}{\text{Al}}_{(\text{1+x})}{\text{Si}}_{(\text{3-x})}{\text{O}}_{\text{8}}\text{+}(\text{1+x}){\text{CO}}_{\text{2}}\text{+}(\text{2+2x}){\text{H}}_{\text{2}}\text{O }\leftrightarrow \\ {\text{xCa}}^{\text{2+}}\text{+}(\text{1-x}){\text{Na}}^{\text{+}}\text{+}(\text{3-x}){\text{SiO}}_{\text{2}}\text{+}(\text{1+x}){\text{HCO}}_{\text{3}}^{-}\text{+}\\ (\text{1+x})\text{Al}{(\text{OH})}_{\text{3}}.\end{array}$

The Urey representation by itself or the dissolution of plagioclase do not explicitly give form to the known role of water fluxes in the geochemistry, which is typically, according to both experiment (Maher, 2010) and theory (Hunt et al., 2015), the limiting factor. Identification of this particular limitation then places the science of hydrology right at the center of study.

While one can focus on any one of a number of the individual components of the entire process of weathering, such as: (1) the necessity for vegetation to deliver CO₂ fluxes above equilibrium values as derived from atmospheric CO₂ levels, (2) the importance of fractures in facilitating water penetration into bedrock, (3) the interactions of the various components of biota in the porous medium that contribute the respiration necessary to produce the CO₂, other research is currently providing grounds for focusing one's attention on chemical weathering processes. For example, it has been shown (Eppes and Keanini, 2017) that crack formation in bedrock under subcritical conditions is chiefly a result of chemical weathering, which changes mineral volumes, thus producing the stress that continues the fracturing. The particular phenomenon of fracture formation, traditionally viewed as predominantly physical, consequently turns out to be often, at its core, a chemical process. At the same time, however, theoretical and experimental studies of chemical weathering indicate that the rate at which this process occurs is very often limited by solute transport (Maher, 2010; Braun et al., 2016; Hunt and Ghanbarian, 2016; Yu and Hunt, 2017c), that is to say, the rate at which reaction products may be removed from the weathering front. A quasi-universal description of soil formation and production could answer a question first posed by Dokuchaev at the turn of the twentieth century (the translation into English, however, did not arrive until 1948; Dokuchaev, 1948), regarding how to frame soil formation in terms of a set of consistent (soil forming) factors: Climate, organisms, relief, parent material, and time (Yu et al., 2017).

In summary, while it is important to keep in mind that weathering phenomena may not be easily separable into, e.g., chemical and physical processes, for interpretation it is still important to be able to identify the rate-limiting input into the soil formation process. The evidence summarized briefly above places an importance on the development of a model of soil formation, based on chemical weathering, that can deliver specific predictions for soil depth in a general framework, with results that can be applied across boundaries defining geological, climatological, and biogeochemical variability.

Relationship of Chemical Weathering to Solute Transport

In order to understand properly the limits on chemical weathering placed by solute transport, it turns out that it is necessary to use a modern solute transport theory for heterogeneous porous media, which generates non-Gaussian predictions (Hunt and Skinner, 2008; Hunt et al., 2011; Ghanbarian-Alavijeh et al., 2012). Here, non-Gaussian means several things: (1) the solute velocity (or flux) is only proportional to the water flow rate, not equal to it, (2) the solute velocity decays according to a power of the time, (3) the dispersivity is linear in the time (Scher et al., 1991). In the present case, condition (2) is most important, since the predicted power-law decay of the solute velocity in time (Hunt and Ghanbarian, 2016) matches the experimentally observed power in both soil formation (Friend, 1992; Egli et al., 2014) and for chemical weathering (White and Brantley, 2003). Condition (1) is also relevant, since soil formation and chemical weathering rates are also typically proportional to water fluxes, and thus to precipitation. This simple statement is in accord with a great deal of data on soil production and/or chemical weathering (Maher, 2010; Owen et al., 2010, 2013; Amundson et al., 2015; Hunt and Ghanbarian, 2016). It is important that solute transport in heterogeneous porous media is so often non-Gaussian, rather than Gaussian, (Cushman and O'Malley, 2015) that the non-Gaussian condition is becoming recognized as the norm, rather than the anomaly. It is also important that the non-Gaussian transport results used are derived from network models (Hunt and Manzoni, 2016), which places a premium on identifying network properties not always investigated in the field, such as a fundamental length scale, and which generate results fundamentally different from continuum models of solute transport.

In treatments of solute transport limitations on chemical weathering by non-Gaussian solute transport, it has been shown that the solute flux is an excellent proxy for reaction rates (Hunt et al., 2017) as, aside from a factor equal to molar density, the weathering rate (expressed in moles m⁻² s ⁻¹) is equivalent to a solute velocity. The more rapid the Urey reaction or the plagioclase dissolution reaction occurs, the more likely it is that solute transport is the limiting factor over the entire period of soil formation. The fundamental length scale brings in the most important single parameter from the parent material. The flow rate brings in climate variables.

The theory of solute transport limited weathering (“percolation theory”; Hunt and Ghanbarian, 2016; Hunt, 2017; Yu et al., 2017) that explains the observed overall dependence of chemical weathering rates and soil formation on (1) time (or soil depth), (2) climate, i.e., the dominant influence on flow rates, (3) substrate heterogeneity scale, (4) erosion rates (thus relief), is based on a percolation theoretical treatment of solute transport. The erosion rate depends on the relief, or topography, and the time is expressed explicitly, thus accounting for all five of Dokuchaev's original soil forming factors. Our analytical formulas, as well as the numerical routine that have been derived in initial publications, with their closer correspondence to chemistry, rather than geology, do not contain variability over time in such important input parameters as flow rates, or particle size. It is known that in the field these quantities vary over time, both systematically and randomly, and over all time scales, and some of these effects will ultimately need to be considered.

This theoretical description has been thoroughly reviewed in some recent books (Hunt et al., 2013; Hunt and Manzoni, 2016), as well as in Reviews of Geophysics (Hunt and Sahimi, 2017). This theoretical treatment so far does not incorporate directly changes in the medium associated with changing density, changing particle size (network scale), or changing depth due either to deposition or erosion, but such changes can, in principle, be introduced into the equation describing changes in soil depth as calculated from the erosion and soil production rates, a topic deferred to later.

Relationship Between Chemical Weathering and Soil Formation

A range of studies over the past decade has shown empirically (Burke et al., 2006; Dixon et al., 2009; Egli et al., 2014), at least, that the processes of soil formation (and thus soil upbuilding and therefore thickness) and chemical weathering are highly correlated. Since the “w” in Bw horizon indicates the development of color or structure, or both (Soil Survey Division Staff, 2014), and thus weathering, using the bottom of the Bw for calculating the soil depth would mean that such a correlation is partly a result of definition. But some of these studies (Burke et al., 2006; Dixon et al., 2009) have also indicated that the correlation between the two processes is rather loose. Sources of discrepancy can be that total soil thickness may include an organic layer (O horizon), for example, which is deposited on top of the weathered soil, or that aeolian dust deposition or alluvial deposits, that are disconnected from the parent material, may be significant, neither of which is directly connected to soil production from weathering. At many of the sites discussed in the present study the correlation has already been shown to be robust (Hunt and Ghanbarian, 2016; Yu and Hunt, 2017b,c). Furthermore, it has also been shown (Hunt and Ghanbarian, 2016) that the time dependence of the soil formation rates of these particular studies corresponds closely to the time dependence of chemical weathering from completely different sources (White and Brantley, 2003), and over time scales from years to millions of years. Determination that chemical weathering and soil formation rates are proportional across a range of field experiments lends support to the assumption that such a proportionality holds more universally, but does not constitute a proof that extension to all sites under all conditions will be valid.

Present Study

Our present study applies systematically this recent model of soil formation derived from the chemical weathering depth as limited mainly by solute transport (percolation theory) to two suites of soils; i.e., alpine and Mediterranean soils. What distinguishes this particular work is in its more systematic approach to the analysis, an improvement which is appropriate for the greater richness of the data analyzed. Such an approach also allows an increase in the corresponding richness of interpretation. The purpose of the study is fundamentally two-fold. The first goal is to check whether the data conform generally to the theory as published heretofore. The second purpose, if the first should be verified, is to use any discrepancies between theory and observation to draw inferences regarding (1) in what ways the theory may be incomplete or inadequate, (2) what modifications of typical existing experimental procedure may be necessary to test the theoretical results properly, and (3) what parameters may have been estimated improperly. The field data were drawn from alpine sites as well as from sites with Mediterranean climate. Data collected include what is required to calculate (or estimate) such relevant parameters as the infiltration rate, the erosion rate, and a characteristic particle size, d₅₀. In order to incorporate any temporal variability in length and time scales into predictions, it will be necessary to make some straightforward extensions of the theoretical model and, possibly, to collect additional data as well.

Theory

Solute Transport and Reaction Kinetics: Damköhler Number

Chemical weathering rates in the field decline according to a power-law by orders of magnitude over time (White and Brantley, 2003). Such weathering rates are also demonstrated to be proportional to fluid flow rates (Maher, 2010). Understanding this particular pair of results has posed problems for workers in this field. In particular, progress in understanding reactive solute transport has been limited (Hunt and Ewing, 2016; Hunt and Manzoni, 2016; Hunt et al., 2017) by modeling based on the advection-dispersion equation (ADE), which treats ultimately a mean flow rate in the advection term, with diffusion-like dispersion superimposed (for example, Neuman and Di Federico, 2003).

The Peclet number, P_e, a ratio of diffusion to advection times (Saffman, 1959; Pfannkuch, 1963), was developed to distinguish regimes where either advective (P_e > 1) or diffusive (P_e < 1) solute transport might dominate. If the ADE is valid, dominance of advection, P_e > 1, implies a solute velocity equal to the flow velocity; in the latter case, which reproduces a diminishing solute velocity with time, no proportionality to the flow rate can be developed, since P_e < 1 and the diffusion term dominates (Hunt and Ewing, 2016). Although the ADE can be applied to predicting solute transport at the scale of a single pore (e.g., Neuman and Di Federico, 2003), scaling up the application of the ADE to larger length scales produces serious problems. The only way the ADE can relate the observed reduction in reaction rates to a diminishing solute transport capability in time (rather diffusion like) is to abandon the observed proportionality to the flow rates. In other words, one cannot have it both ways with the continuum approach.

The solute velocity is obtained from a known scaling relationship between transit time and system length (Lee et al., 1999), plus the identification of the fundamental length and time scales (Hunt, 2017). The Damköhler number, Da_I, which is the ratio (Salehikhoo et al., 2013) of a solute advection time to a reaction time under well-mixed conditions (Yu and Hunt, 2017a), measures the importance of solute transport relative to reaction kinetics on chemical weathering rates. When Da_I is larger than 1, the transport limitation for the chemical weathering rate is expected to be valid; for smaller values of Da_I, reaction kinetics will dominate. With increasing time of soil evolution soil depth usually increases. Because the Damköhler number is a ratio of transport time to reaction time and because the solute transport time increases more rapidly than linearly in system length, Da_I increases during soil evolution from its initial value (Yu and Hunt, 2017a). At shorter time scales, when Da_I is small and the kinetics of the particular weathering reaction dominant at each specific site dominates, more structure is expected to be visible in the time-dependence of the weathering rates.

It is necessary at the outset to be clear that the solute transport limitations discussed here arise from advective solute transport, not from diffusion, as has been argued by Bandopadhyay et al. (2017). Arguments based on the Peclet number as calculated from characteristic instantaneous flow velocities at the scale of a single pore were used to justify this a priori (Hunt and Manzoni, 2016). However, this may be criticized on the grounds that one should use a yearly average velocity, since diffusion may be relevant throughout the year, even in the vadose zone. The structure of advective solute transport paths in heterogeneous porous media is fractal, though not, in general, related to any structure of the medium, and it is this fractality, which leads to the power-law decay in solute transport fluxes with time (Hunt and Ewing, 2016). In applying percolation theory, it is assumed that the flow paths of least resistance can be calculated using the critical percolation probability. As long as the optimal flow paths can be described using such critical paths, their fractal dimensionality is as given in percolation theory, explaining why the particular characteristics of the medium have reduced importance to flow path characteristics.

Percolation theory generates a suite of properties relevant to flow, diffusion, and dispersion, as well as to structure, although it is sometimes necessary to choose which percolation results are appropriate, or whether an alternate formulation, such as the effective medium approximation (EMA), may be more suited to generating an accurate prediction in any specific case (Hunt and Sahimi, 2017). Nevertheless, the general theory of percolation is best discussed in terms of its topological implications first. Also, although its application need not be restricted to a regular grid, it is much easier to discuss under such restrictions, so only regular grids, also known as lattices, are considered here in the theory review.

The best review for understanding the basics of percolation theory is by Stauffer and Aharony (1994), from which much of the following discussion ultimately comes. Consider a square lattice, on which sites may be occupied by either plastic or steel spheres of the same size. The choice, metal or plastic, at any given site is randomly generated, though the conclusions do not change fundamentally if spatial correlations are added. Nearest neighbor spheres touch at one point. If sufficiently many of the spheres are metallic, a continuously connected infinitely long path through metallic spheres is produced. This transition occurs, for any given medium, at a specific value of the fraction of spheres that is metallic, called p_c. In general, the connections between two such sites are called bonds, allowing definition of what is called “bond percolation,” based on the minimum fraction of connected bonds necessary for percolation. In the particular case of the square lattice site percolation problem, p_c = 0.59. All other common systems have smaller values of p (Hunt et al., 2013; Hunt and Sahimi, 2017). Bond percolation values are smaller than site percolation values on the same lattice. In order for a bond percolation problem to be relevant to real systems, the (hydraulic or electric) conductance values connecting sites (i.e., pores) must vary widely (Hunt and Sahimi, 2017). In a procedure called critical path analysis (CPA) the percolation probability can then be used in a way that generates the connected path of lowest total resistance (to flow), i.e., the preferential flow paths (Pollak, 1972; Hunt, 2001). This is particularly relevant here, as Sahimi (1994) has emphasized how the topological structure of the critical paths will dominate solute transport whenever they describe such flow concentration as are observed. In natural 3D systems p_c values tend to be around 15% (Scher and Zallen, 1970) or, as a consequence of correlations, even less (Garboczi et al., 1995). The small values of p_c in bond percolation in natural media imply that only a relatively small portion of the medium generates nearly all the fluid flow. It thus also means that percolation theory may generate connected flow paths that look like what hydrogeologists refer to as preferential flow. It is quite generally believed that such preferential flow paths are important to solute transport (National Research Council, 1996). Here, and in previous work, we have made this assumption regarding the relevance of such paths, as medium flow paths were assumed compatible with CPA. Then the percolation descriptions of, e.g., the tortuosity or fractal dimensionality, of such paths should correspond to observation (Hunt and Sahimi, 2017).

Once one has an infinitely large interconnected cluster of sites (or bonds), it is possible to define the percolation backbone as that part of the infinite connected cluster which remains when all sites (bonds) that can be connected to it through only one point have been removed (Stanley, 1977). All sites that connect through two points are retained. Sites that connect only through one point are called dead-ends, since they do not support flow. The remaining structure has mass fractal dimensionality D_b, a quantity which is relevant for solute transport (Lee et al., 1999).

Importantly, for a wide range of conditions, the value of D_b remains the same, but it differs fundamentally depending on the dimensionality of the system studied (Sheppard et al., 1999). Flow in fractures as well as in strongly layered (anisotropic) soils may be fundamentally 2D, but, more generally, 3D conditions are observed. The value of D_b does depend sensitively on the saturation condition, i.e., whether the medium is fully saturated, or whether imbibition or drainage is occurring (Sheppard et al., 1999). The latter two processes are known as invasion percolation (Wilkinson and Willemsen, 1983). Most other medium variations, such as the particular lattice type chosen, or the particle size values, do not change the value of D_b. However, under certain long-range correlations in the positions of highly conducting bonds, such paths can be straighter than in random percolation (Sahimi and Mukhopadhyay, 1996), for which values of D_b are closer to 1 (a value of D_b = 1 corresponds rather closely to Gaussian transport). However, in the present work, complications from such correlations are not addressed. Moreover, evidence for the relevance of such correlations, though demonstrated for such frequently measured quantities as the electrical conductivity (Hunt and Sahimi, 2017), has not yet been found for problems of chemical weathering or soil formation.

Scaling, Chemical Weathering, and Soil Production

In the following, the scaling relationships relating time, distance, and velocity of solute transport are reproduced from known results for systems near the percolation threshold (Sheppard et al., 1999). What can make their applicability universal, however, is the tendency for water flow in disordered media to follow paths of least resistance, as defined in CPA. Then the solute transport is controlled by paths near the percolation threshold, as quantified by using percolation theory.

In Figure 1, the concept of the percolation theory is schematically drawn and compared with a soil mass balance. Soil depth depends on mass input and output. Soil production includes all mass and volume changes due to the transformation of the parent material into soil (by chemical and physical weathering processes, mineral transformation), the lowering of the bedrock/parent material—soil boundary (Heimsath et al., 1997), but also atmospheric deposition and net organic matter input:

$\begin{array}{cc}\begin{array}{r}{P}_{Soil}=T_{Soil}+A+(O-G)\end{array}& (1)\end{array}$

FIGURE 1

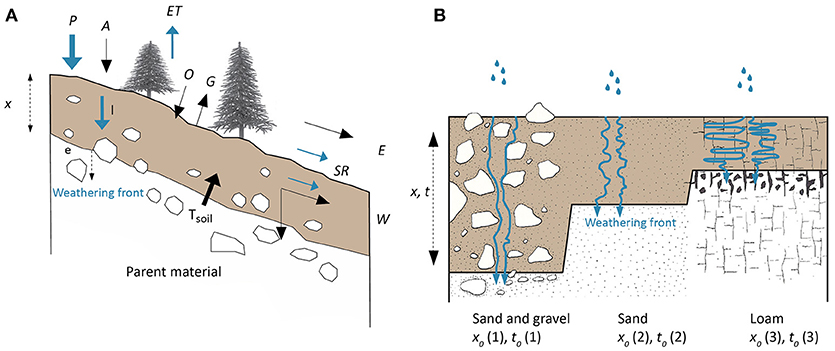
Figure 1. Schematic overview of the applied concept. (A) The black arrows show the mass fluxes into and out of a soil with T_Soil = the transformation of the parent material or rock into soil, A = atmospheric deposition, O = net organic matter input, G = organic matter decay, E = Erosion and W = chemical weathering (solute output). Water fluxes into and out of the soil are given by the blue arrows with P = precipitation, ET = evapotranspiration, SR = surface and subsurface runoff, I = infiltration. The weathering front e is intimately linked to these water fluxes. (B) Soil depth (x) as a function of the median granulometry (x₀ as fundamental length scale) of the soil (scheme modified after Birkeland, 1984). Time constraints are given by the fundamental length scale, x₀, and the corresponding time scale, t₀, and x and the related time scale t. The ratio of x₀/t₀ = v₀, is assumed to represent the pore-scale fluid flow rate (see Equation 2).

where T_Soil = the transformation of the parent material or rock into soil; according to Equation (1), A = atmospheric deposition and O = net organic matter input, G = organic matter decay (Zollinger et al., 2017). Erosion (E) and chemical leaching (W) contribute to mass losses. Besides P_Soil and the parameters E and W, soil depth is strongly related to the hydrologic water balance, granulometry of the medium and time (or velocity).

The specific role of percolation theory in describing solute transport is now discussed. When solute enters a medium at a point (Lee et al., 1999), say a site on a grid that corresponds to a particle with a particular mineralogy, the time, t, it takes for the solute to travel a distance x, is proportional to x^Db. This proportionality can be represented as an equation, if appropriate values of constants representing a fundamental length scale, x₀, and corresponding time scale, t₀, can be identified,

$\begin{array}{cc}\begin{array}{r}t=t_0{\left(\frac{x}{x_0}\right)}^{D_b}\end{array}& (2)\end{array}$

The ratio of x₀/t₀ ≡ v₀, having units of velocity, is assumed to represent the pore-scale fluid flow rate, which is the only externally imposed velocity in the physical system. We refer to v₀ as a pore-scale flow rate. In the context of the following discussion, it will become clear that v₀ must be a value that characterizes the mean of the local vertical flow rate. Determination of one additional parameter, either x₀ or t₀, completes the parameter determination in Equation (2).

If the network representation is applied to a porous medium, essential suggestive choice for x₀ is a pore separation (Hunt and Manzoni, 2016), which should be more or less equal to a particle diameter, because this length scale defines the separations of the local connections between flow pathways.

In a highly disordered network, where particle sizes can vary widely, we have proposed (Yu and Hunt, 2017b,c) that the best choice for x₀ is d₅₀, the median particle size. Although temporal mean values of v₀ are on the order of 1 m yr⁻¹, the instantaneous flow rates are much higher, either during storms or seasonal snowmelt. The larger instantaneous flow rates, which are limited primarily by the hydraulic conductivity, can often be on the order of 0.1 m day⁻¹, a value typical for saturated conditions (Blöschl and Sivapalan, 1995), and used to provide the rationale for neglecting diffusion.

While the instantaneous flow rates must be large enough to neglect diffusion, the time-averaged flow rates must be small enough to limit reaction. Otherwise, reaction kinetics can be the limiting factor. In order to diagnose the relative importance of these two factors, one can apply the Damköhler number, defined as (Yu and Hunt, 2017a):

$\begin{array}{cc}D{a}_I=\frac{{\tau }_{\text{ad}}}{{\tau }_{\text{r}}}\text{=}\frac{\frac{\text{L}}{{\text{v}}_{\text{0}}}{}^{\ast }{\left(\frac{\text{L}}{{\text{x}}_{\text{0}}}\right)}^{\text{0}.\text{87}}}{\frac{{\text{V}}_{\text{p}{}^{\ast }{\text{C}}_{\text{0}}}}{{\text{R}}_{\text{0}}{}^{\ast }{\text{A}}_{\text{T}}}}& (3)\end{array}$

Here τ_ad is the advection time, τ_r the reaction time, L the column length, v₀ the fluid flow velocity, V_p the pore volume description of fluid flow rate, C an equilibrium concentration, R₀ the well-mixed reaction rate normalized by surface area, and A_T the surface area. Note that this definition corrects inconsistencies in Salehikhoo et al. (2013), while we do not agree with choosing a Da_I based on diffusion, as in Bandopadhyay et al. (2017). Reasons for our distinct opinion are that: (1) weathering rates are proportional to flow rates over four orders of magnitude (Maher, 2010), as are soil production rates (Hunt, 2017), and (2) the known dominance of advective solute transport over diffusive transport (Hunt and Manzoni, 2016) at typical instantaneous subsurface flow rates (Blöschl and Sivapalan, 1995). The tendency for Da_I to increase with column length is evident in Equation (3). The pore volume is proportional to length, canceling the linear factor in L in the numerator, but the more rapid than linear increase in transport time with length leaves a second factor in length to the 0.87 power, which is not canceled in the denominator. As long as Da_I < 1, reaction rates are time-independent, if the only limiting factor considered explicitly is solute transport. When Da_I > 1, reaction rates decline over time. In the previously analyzed case of MgCO₃ dissolution (Yu and Hunt, 2017a), for all field conditions the value of Da_I was never smaller than tens of thousands. However, reaction rates of silicate minerals, even under well-mixed conditions, can be orders of magnitude smaller (Stumm and Morgan, 1996) than for MgCO₃, as treated by Salehikhoo et al. (2013), and further analyzed by Yu and Hunt (2017a).

Inverting the relationship Equation (2) for t(x) leads to

$\begin{array}{cc}{\text{x=x}}_{\text{0}}{\left(\frac{\text{t}}{{\text{t}}_{\text{0}}}\right)}^{\frac{\text{1}}{{\text{D}}_{\text{b}}}}& (4)\end{array}$

The time derivative of x(t) yields the solute velocity, argued above to be a proxy for a chemical weathering rate, v

$\begin{array}{cc}\text{v=}\frac{\text{1}}{{\text{D}}_{\text{b}}}\frac{{\text{x}}_{\text{0}}}{{\text{t}}_{\text{0}}}{\left(\frac{\text{t}}{{\text{t}}_{\text{0}}}\right)}^{\frac{\text{1}}{{\text{D}}_{\text{b}}}-\text{1}}& (5)\end{array}$

Equation (5) can be rewritten in a form that depends only on the distance, x. Since the introduction of erosion can, in principle, make it impossible to define a unique time for a given transport distance, it is more useful to write Equation (5) in a form that eliminates time from the equation:

$\begin{array}{cc}\text{R=v=}\frac{\text{1}}{{\text{D}}_{\text{b}}}{\text{v}}_{\text{0}}{\left(\frac{\text{x}}{{\text{x}}_{\text{0}}}\right)}^{\text{1}-{\text{D}}_{\text{b}}}& (6)\end{array}$

Here, the soil production function, R, was equated with v, and v₀ was substituted for x₀/t₀ as well. In the absence of erosion, it is a reasonable hypothesis that the total solute transport distance is equal to the soil depth. Then, the temporal derivative of the soil depth, v, is the soil production function (in units of depth divided by time), as also given by Equation (5), making the soil production function proportional to the chemical weathering rate. The proportionality constant is equal to the ratio of the (bulk) density of the chemically weathered material to its molecular mass.

Equation (4) for the soil depth can hold only as long as erosion can be neglected, which is very rarely the case. Since the soil production rate (Equation 5) declines with age (or depth, Equation 6), the period of time when erosion can be neglected is always limited.

Erosion and Soil Depth Evolution

When erosion, E, must be considered, one can construct an equation for the soil depth based on the concept of mass balance,

$\begin{array}{cc}\frac{dx}{dt}=R-E& (7)\end{array}$

Here, R is given by Equation 6 and E is, for constant erosion rates, a parameter. In general, however, E is a function of time. The term E in fact is equaled to denudation that includes besides the output of solid material also chemical leaching of silicate particles. Compared to erosion, this type of leaching and, therefore, loss is in most cases fully subordinate (Dixon and von Blanckenburg, 2012). In three dimensions with moisture conditions corresponding either to wetting or full saturation, D_b has the value 1.87 in a wide range of conditions (Sheppard et al., 1999), and has, up to now, been treated as universal. Note that 1/1.87 = 0.53, which is very close to the exponent for diffusion, which explains in a single relationship both the proportionality of weathering rates to flow rates, and the resemblance of their time-dependence to diffusion.

Substituting in R from Equation (6) yields,

$\begin{array}{cc}\begin{array}{l}\frac{dx}{dt}=R-E\left(t\right)=\frac{1}{1.87}\frac{x_0}{t_0}{\left(\frac{t}{t_0}\right)}^{-0.87}\\ -E(t)=\frac{1}{1.87}\frac{I(t)}{\varphi }{\left(\frac{x}{x_0}\right)}^{-0.87}-E(t)\end{array}& (8)\end{array}$

with I(t)/ϕ as the net infiltration rate that varies over time and ϕ = pore volume.

Owing to the fractional exponent of x introduced by R, Equation (7) does not have an analytical solution, but it may be readily solved numerically. One simply solves Equation (4) for some initial (sufficiently small) time and then calculates R from Equation (6). Using the calculated value of R and the field value for E as well as an arbitrary time step one can calculate the change in soil depth and add it to the initial value. Then one calculates R from Equation (6) using the new soil depth. This procedure is then simply followed until the total time elapsed is equal to the age of the soil, or until the depth no longer changes in time, at which point a steady-state soil depth has been generated. As long as no significant changes in parameters occur, steady-state conditions will then prevail. In steady state, dx/dt = 0, and the soil depth x may be obtained by solution of E = R as,

$\begin{array}{cc}x=x_0{\left(\frac{v_0}{1.87E}\right)}^{1.1494}& (9)\end{array}$

At the opposite (short time) end of the time spectrum, an important complication can arise when chemical weathering is not solute transport-limited. In particular, there is the theoretical possibility that for some ranges of experimental, or field conditions, Da_I < 1. In this case, a constant rate of weathering would ensue, reaction kinetics provide a limitation which is unchanging in time. Since the limits imposed by kinetics are stronger in this case, at least at short time scales, than those due to solute transport, data would lie below the percolation predictions. Further, a constant reaction rate would imply a linear increase in soil depth with increasing time up until the point that the predicted and observed depths were equal, at which time the transport-limited result would become valid.

Theoretical sensitivity of soil thickness to various parameters may be estimated from Equation (4) for short times (when erosion might be neglected), or at long times from Equation (9). Owing to the power-law forms of these equations, the sensitivity relationships relate simply to the exponents. At intermediate times, sensitivities, like depths, must be obtained numerically. From Equation (4), a 1% increase in x₀ produces a 0.47% increase in x, while a 1% increase in either t or v₀, produces a 0.53% increase in x. From Equation (9), a 1% increase in x₀ produces a 1.14% change in x, while a 1% change in either v₀ or E produces a 1.14% change in x, though an increase in v₀ (E) produces an increase (decrease) in x. On account of the gradual evolution of the overall behavior from Equation (4) to Equation (9) through time, and the variable time period over which this change occurs due to variation in actual parameter values, actual sensitivities will exhibit somewhat more complex behavior as a function of time.

Materials and Methods

Regions Studied: Alpine and Mediterranean

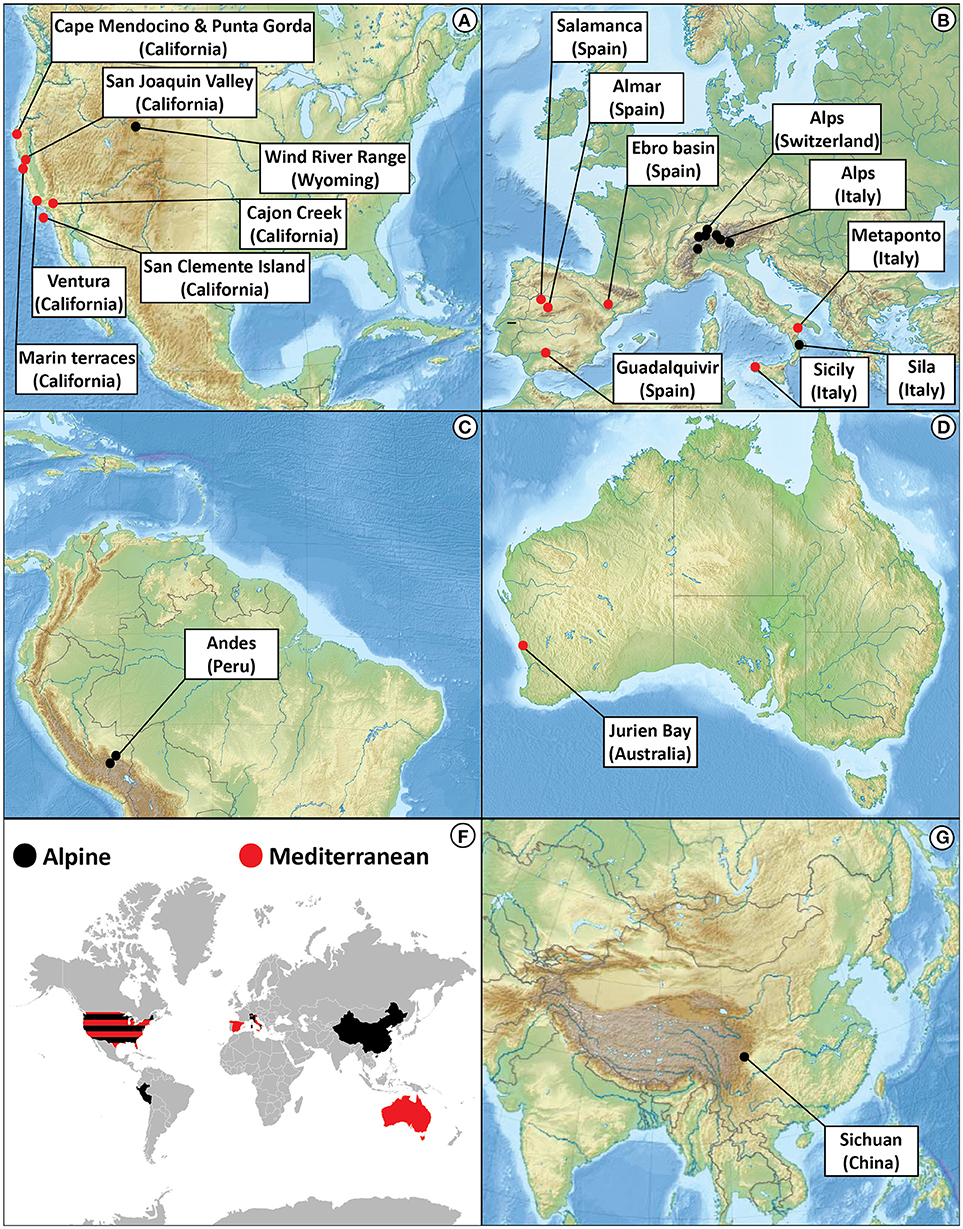
Data for soil depth as a function of age have been collected for a large number of sites in two distinct geographic environments: Alpine (148 sites; Supplementary Table S1), and Mediterranean (94 sites; Supplementary Table S2). Most of these data have already been published, but some of the Wind River Range, Wyoming, USA, are new. Other data have been accessed from the literature. All soils have developed from unconsolidated material. The sites are distributed on five continents, as shown in Figure 2.

FIGURE 2

Figure 2. Overview of the sites (alpine and Mediterranean).

To solve Equation (8) the parameters E(t), I(t), ϕ, t, and x_{t = i} need to be known. Some of these parameters are more or less easily accessible (e.g., soil depth) and others need to be estimated (e.g., E(t)). Accompanying data relevant to assess actual evapotranspiration, AET, and soil particle sizes, which are necessary to make concrete predictions, have also been collected for each site within these regions. All data, together with their sources, are given in the Supplementary Tables S1–S6.

Determination of Parameters

Soil Depth

Soil depths are determined mostly through a process of excavation and measurement. We used datasets where information was available about soil horizons designation and thickness. In addition, data was collected (where available) about soil density, coarse fragment content and grain size distribution. According to Sauer et al. (2010) and Egli et al. (2014), transitional horizons to the parent material (AC, CA, BC, CB) were counted as horizon thickness × 0.5. Further, particle size distributions at the time of original exposure of the medium are assumed to be preserved in the C layer.

Soil mass was determined using the thickness of the horizons, their corresponding bulk density and summed up over the entire profile. This mass was calculated with and without coarse fragments (soil mass and mass of fine earth FE). For the stocks of FE we have:

$\begin{array}{cc}F{E}_{stock}={\displaystyle \sum _{a=1}^{n}F}{E}_i\Delta z_i{\rho }_i\text{ and similarly }M={\displaystyle \sum _{a=1}^n\Delta z_i{\rho }_i}& (10)\end{array}$

where FE_stock (calculated as kg m⁻²) = the fine earth stock summed over all soil horizons, FE_i = the proportion or concentration of fine earth, Δz_i (m) = the thickness of layer i and ρ (t m⁻³) = soil density, M = soil mass including coarse fragments (calculated as kg m⁻²).

Dating and Erosion

Sites were selected where numerical indication about the surface and its soils was available (e.g., ¹⁴C, ¹⁰Be, etc.) or where soils could be correlated to terraces, moraines or geologic events that were dated. Erosion rates are sensitive to local vegetation, relief and slope angle, aspect, climate, and topographic curvature, as well as substrate. Not all of these influences can be quantified. In situ measurements of erosion or denudation were available only for a few sites (e.g., the sites “Sila,” several sites in the European Alps and some of the Wind River Range). Otherwise, present-day erosion rates had to be estimated from published maps (e.g., Bosco et al., 2008, 2015; Panagos et al., 2015) where relatively detailed information was accessible for alpine sites (and natural conditions such as grassland or forest cover). Furthermore, related information was also available from specific investigations, e.g., such as Norton et al. (2010). Time-averaged (over the entire soil evolution) rates of soil erosion were measured for a few alpine sites (some sites of the Wind River Range and European Alps). For the other sites, erosion rates had to be estimated over the entire soil evolution. Soils on terraces (many Mediterranean sites) with a flat position have a very low to almost negligible water erosion rate (Panagos et al., 2015). According to Raab et al. (2018) and Schaller et al. (2016), erosion rates show a particular fluctuation over time that is related to major climate changes. The transition from the Pleistocene to the Holocene was accompanied by distinctly higher rates. Raab et al. (2018) showed that the erosion rates can be up to 10 times higher when climate very distinctly changes (transition Pleistocene to Holocene). These fluctuations, which occurred during the evolution of many of the soils considered, are shown in Figure 3 and had to be considered for sites where erosion values were derived from the previously mentioned maps (mostly alpine sites). We assumed that the maps provide an average and relatively reliable erosion rate value for undisturbed sites for the entire Holocene. The erosion rate of soils having an older age had to be corrected using the average trend given in Figure 3.

FIGURE 3

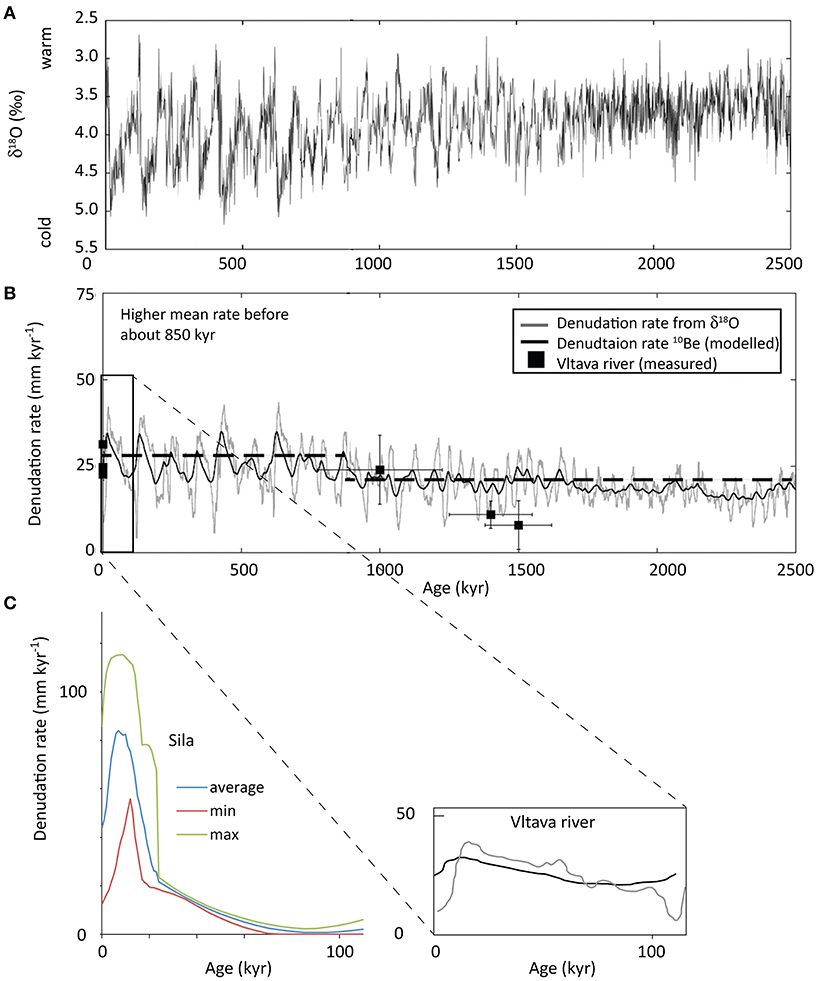
Figure 3. (A) Climate oscillations over the last 2.5 Myr. The δ¹⁸O values indicate warm and cold stages (Zachos et al., 2001); (B) modeled denudation rates (together with some empirical data of the Vltava river in Central Europe; Schaller et al., 2016) for the same period; (C) variability of the denudation (erosion) rates for the last 100 kyr (data from Schaller et al., 2016 and Raab et al., 2018). Note, similarly to (B) that erosion increases at the transition from cold to warm periods.

Particle Size: d₅₀ and x₀

The experimental procedures to determine the particle size fractions were mostly determined using the techniques of wet sieving, for particles greater in diameter than 32 μm, and at smaller sizes, by hydrometry or by using X-ray techniques. Using these data it was possible to determine directly d₅₀. Since the fraction of coarse sand is less relevant for soil formation when compared to smaller fractions d₅₀ was calculated for the fractions <500 μm. A mechanical disintegration of the rock material into small units facilitates chemical decay by increasing the total area of particle surfaces and surface reactive sites that are in contact with the solutions (Stumm and Wollast, 1990; Lageat et al., 2001). The d₅₀ value was then multiplied by 0.83, since the product of this factor and a bond length is used in expressions of the percolation correlation length (Stauffer and Aharony, 1994). Tortuosity models for porous media (Ghanbarian-Alavijeh et al., 2013) confirm that this multiplicative factor for the correlation length generates expressions for the tortuosity of flow paths which match results from numerical simulations over the entire range of porosity. We therefore used a length factor of 0.83 times d₅₀ to best represent the fundamental length scale. Data for many sites, however were not sufficient for the determination of d₅₀. Previously published data, for example, often give only the percentages of the three fundamental size classes: sand, silt, and clay. Since it is necessary to know d₅₀ in order to make a concrete prediction of soil depths, we developed a regression routine over well-characterized soils for this purpose, using the percentages of sand, silt, and clay to calculate a mean diameter for the input, and the observed d₅₀ as an output. Since we expected, at the very least, key differences in regression parameters between Alpine and Mediterranean sites, these regressions were performed separately. The results are given in Figures 4A,B. Once these relationships are established, we can use the appropriate regression relationship to generate automatically a reasonable median particle size for any soil in these two environments, as long as the sand, silt, and clay fractions are available. Note that the particle size distribution is a function of height in the soil column. This result implies that the soil texture is changing over time. Specific results indicate that the studied soils either become finer over time, or do not change perceptibly (Figure 5). The smallest values of d₅₀ diminish from an initial value of about 100 μm to around 10 μm at about 20,000 years, a factor 10, while the largest value remains constant at about 200 μm over the same interval. These results are rather comparable in both Mediterranean and Alpine regions. From the theoretical sensitivity analysis, one should expect that those soils most severely impacted by diminishing particle sizes could be a factor 10^0.53 = 3.4 thinner than what the predictions using a constant value of d₅₀ would generate. Even use of a median grain size in such soils, rather than the final value, could still overpredict the depth by a factor roughly as high as the square root of 3.4, or about 80%.

FIGURE 4

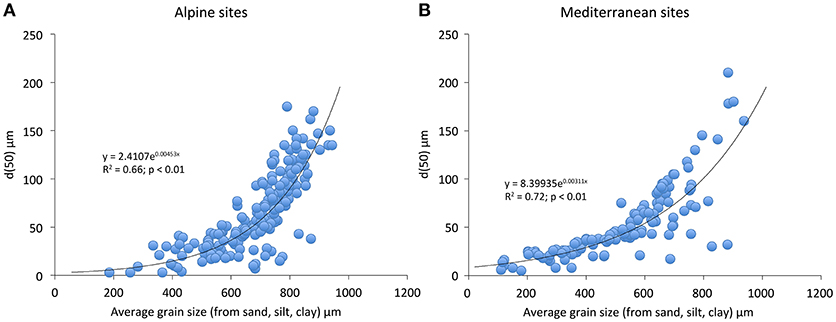
Figure 4. Transfer functions to calculate d₅₀ for sites having only indications about the three fundamental grain size classes (sand, silt, clay) based on detailed grain size data for (A) the alpine (Supplementary Table S3) and (B) Mediterranean type of sites (Supplementary Table S4).

FIGURE 5

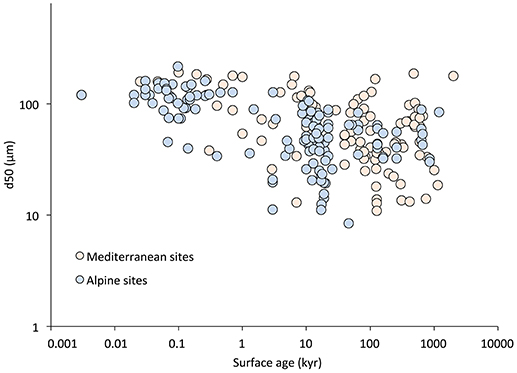
Figure 5. Evolution of the median grain size (d₅₀) of the soils (alpine or Mediterranean environment) over time. This detectable decrease is significant for both series of soils. It is, however, more significant (R² = 0.47; p < 0.01; power law function) for the alpine region than for the Mediterranean sites (R² = 0.26; p < 0.05; power law function).

Infiltration

Infiltration is the parameter that is most difficult to obtain accurately, while it is also demonstrated below to be the parameter, to which the predicted soil depth responds most sensitively. Strictly speaking, the infiltration rate required here, the fraction of precipitation actually relevant for soil weathering, is what penetrates to the bottom of the soil layer, and is the difference between precipitation and (actual) evapotranspiration plus whatever surface water runs on to the site less the amount that runs off. Infiltration is seldom measured. Some combination of stream flow data, base and storm, can be used to estimate mean regional infiltration values, as long the fraction can be excluded (as “weathering inefficient”) that travels exclusively by overland flow. It is furthermore difficult to estimate the local variability in this variable. Evapotranspiration data, (surface) runoff and infiltration rates were obtained from Sanford and Selnick (2013), Commonwealth of Australia (2005), BAFU (2015), Sboarina and Cescatti (2004), PRISM Climate Group (2014), US Climate Data (climatedata.eu), Massatti (2007) and related publications where the soil data were taken.

These datasets, however, provide only an overview. The infiltration rate, however, might have varied considerably over the period of soil evolution. Consequently, an estimate of the hydrologic mass balance had to be estimated for the duration of soil development. For this purpose, information about palaeoclimate had to be accessed. Basic data about climate variability were obtained from the following sources:

Middle Europe, USA: Brugger (2010), Makos (2015), Guiot et al. (1989), Van Andel and Tzedakis (1996), Petit et al. (1999), Minnich (2007), Mulch et al. (2008), Reheis et al. (2012), Oster et al. (2009), Stokes and García (2009), Kirby et al. (2013), Peryam et al. (2011), Meyer et al. (2009), Riedel (2017), Winograd et al. (1992), Arppe and Karhu (2010), Heyman et al. (2013)

Asia:                          Kigoshi et al. (2017), Shchetnikov et al. (2016)

Southern Europe:       Peyron (1998), Blain et al. (2016), Burke et al. (2014)

Andes:                      Graf (1992), Schauwecker et al. (2014)

others:                       Zachos et al. (2001)

During the cold (glacial) periods, climate in Central Europe and the northern USA was much colder (4–14°C) and often drier (25–75% of present-day's precipitation). In southern Europe and mid to southern USA, the climate was distinctly colder and precipitation rates varied from slightly lower to higher, depending on the area.

The present-day hydrologic mass balance was used for soils that started to form during the Holocene. For older soils, climatic conditions also of the Pleistocene had to be considered. Because the percolation theory approach uses the hydrologic mass balance, precipitation, overland flow, and evapotranspiration had to be estimated also for periods prior to the Holocene. Even though the climatic conditions were cold to very cold at the alpine sites, it does not mean that no weathering has occurred during this period. Zollinger et al. (2017), Egli et al. (2014), d 'Amico et al. (2014) and others clearly showed that even under very cold conditions, a high rate of soil formation is possible, provided that water is available. The hydrologic mass balance is relevant for the percolation theory approach—temperature is therefore at first sight less important. The present-day and averaged precipitation, evapotranspiration, and infiltration rates over the entire soil formation period are given in the Supplementary Tables S1, S2.

Damköhler Number Estimations

Our present procedure for determining Da_I is less an independent calculation, and more of a scaling estimate. We use the above referenced formula from Yu and Hunt (2017) as our starting point. In that calculation, all the parameters were given in the publication describing the experiments (Salehikhoo et al., 2013). These experiments were performed on MgCO₃, a mineral with dissolution rate that can easily be orders of magnitude faster (Stumm and Morgan, 1996) than for the silicate minerals predominantly responsible for the soil formation in the studies considered here. In fact, Figure 13.9 from Stumm and Morgan (1996) shows that, for dolomite, the reaction rate ratio can vary from around 3.5 orders of magnitude at pH near 8 to more nearly 5 orders of magnitude at pH = 6. This is the range of pH values expected for conditions with, or without, carbonate present as a solid phase. Such a contrast makes it important to estimate a value of Da_I relevant for the field conditions relevant to this study.

Under field conditions, parameters for surface area and equilibrium solution concentration are simply not available over the entire range of sites investigated, as the surface area depends on the particle morphology, and the equilibrium concentrations on their mineralogy. Consequently, we do not attempt to represent any distinction in their values from those of the experiments of Salehikhoo et al. (2013). Further, although surface area is a strong function of particle size; in the alpine regions studied here, at least, their relatively coarse particle sizes make the soils a fairly reasonable physical analog to the media of Salehikhoo et al. (2013) where the typical particle size was 400 μm, allowing us to estimate this parameter by its experimental value as well. We thus concentrate on the contrasts between field and experimental values for flow rates and well-mixed reaction rates. In the case of MgCO₃, the reaction rate used was R_m = 10⁻⁹ mol m⁻² s⁻¹. Four orders of magnitude slower for silicates leaves R_m = 10⁻¹³ mol m⁻² s⁻¹. The slower flow rates in the field, i.e., on the order of meters per year, instead of experimental values measured in meters per day, will tend to mitigate the impact of the slower reaction rates.

If we keep unknown parameters including the equilibrium concentration and the Brunauer-Emmet-Teller BET surface area at the same values as those in the MgCO₃ experiment of Salehikhoo et al. (2013), but substitute in a well-mixed reaction rate, of 10⁻¹³ mol m⁻² s⁻¹ for R_m, and a yearly average infiltration rate of I = 0.7 m yr⁻¹ for the flow rate, it is found that Da_I = 1 at about 11 cm. For smaller length scales, chemical weathering should be limited by reaction kinetics, instead of transport.

Note that the calculated value of Da_I is sensitive to the particular choice of particle length scale; smaller lengths increase the numerator but decrease the denominator, since the total surface area increases with diminishing particle size. Thus, the impact of reaction kinetics in limiting chemical weathering diminishes rapidly with diminishing particle sizes. Except for the Alpine sites, most sites have d₅₀ values well under 500 μm, and such a complication from a kinetic-limited regime is much less likely. However, considering only the range of particle sizes observed in the field, we estimate that there is probably close to an order of magnitude uncertainty in our estimation of Da_I in the alpine sites, and incorporating variability expressed in the geographic regions investigated would probably tend to increase Da_I from our calculated value, even for alpine sites. A similar range of uncertainty may result from considerations of effects of variations in pH on R_m, while field pH conditions here may tend to reduce Da_I from our calculated value. Note that R_m and d₅₀ are quantities for which some guidance for estimating the site-to-site uncertainty, at least, exists.

Computations

Programming and calculations were done using the software R (R 3.3.2.). In order to facilitate reproducibility, all R code and the required input data is made available under https://github.com/curdon/soilDepth.

Results and Discussion

Alpine Sites

Soil depth and, therefore, also soil mass increase with time (Figure 6). The rate of change, however, decreases considerably with time. The factor time is a very strong predictor of soil mass but it does not provide any further process specific details. Our model, which reduces chemical weathering of solute transport in soils to a few physical parameters such as infiltration rate, particle size, erosion rate, and surface age, consistently overestimates soil depths at alpine sites by a factor approximately 1.45 (Figure 7A). The Mediterranean sites are shown in Figure 7B, but are discussed below, except to note that their depths are modeled quite precisely. Although soil mass and soil depth are two different parameters, their overall trend over time is similar.

FIGURE 6

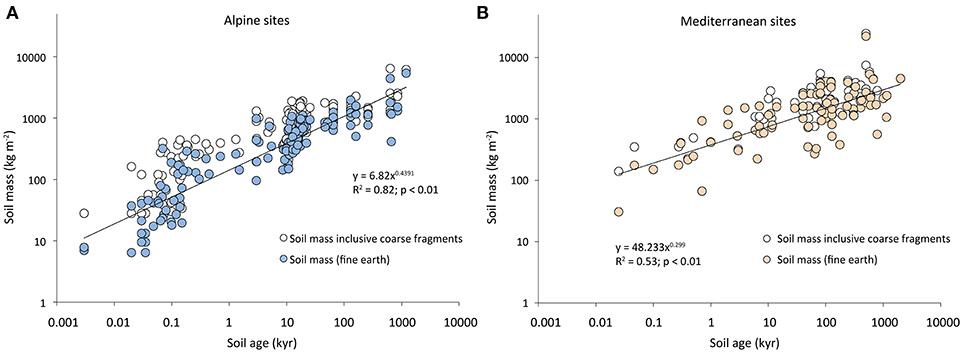
Figure 6. Temporal development of the soil mass (fine earth and whole soil mass that includes coarse fragments) for the alpine and Mediterranean sites. Temporal development of the soil mass (fine earth and whole soil mass that includes coarse fragments) for the (A) alpine and (B) Mediterranean sites.

FIGURE 7

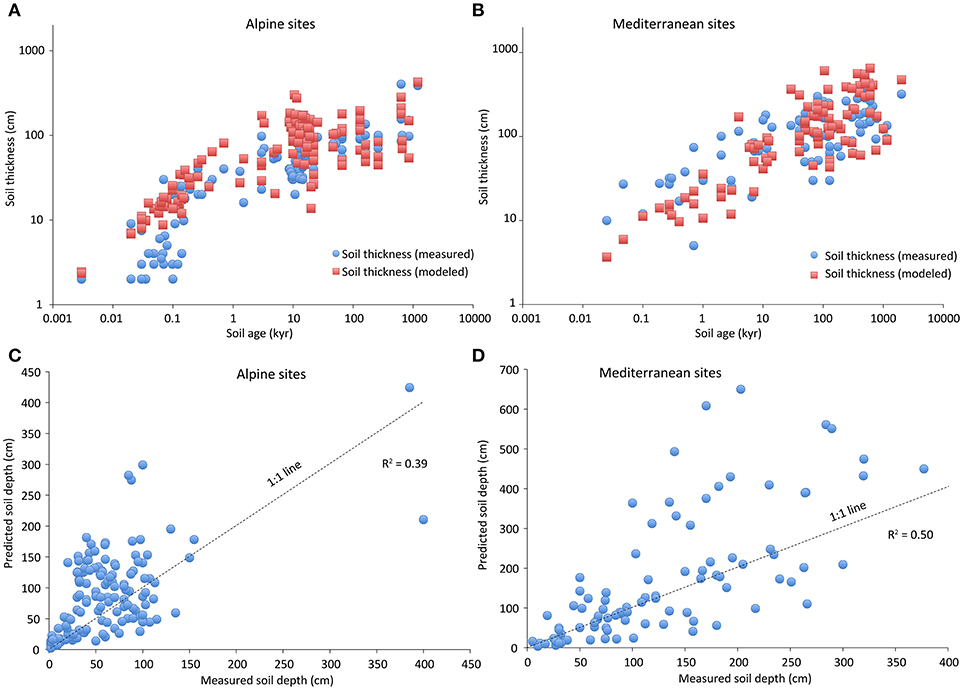
Figure 7. Time trends of modeled and measured soil thickness for the distinct geographic regions, (A) alpine soils, (B) Mediterranean soils, and correlation between predicted and measured soil depth for (C) alpine and (D) Mediterranean sites.

At short time intervals, the overestimation of alpine soil depths is particularly severe, as is also apparent. Noting that the slope of the early (in time) data appears also to be steeper than predicted, we suggest that one of the problems in applying Equation 8 to find the soil depths of alpine sites is that at early times, the chemical weathering is more severely limited by reaction kinetics than by solute transport. Indeed, our most basic calculation (section Damköhler Number Estimations) of the complications of alpine sites in calculating Da_I, suggested that for distances less than about 10 cm (corresponding to times of less than about 100 years), chemical weathering is kinetic-limited. Comparing the predictions of a constant rate of soil development in the case of kinetic-limited weathering leads to a linear dependence of soil depth on time at early times, consistent with the trend of the data in Figure 7A, for which a number of sites lie well below the predicted depths at times less than 100 years. Further, the trend of these data is nearly linear, as evidenced by the approximate thickness of 1 cm at 10 years to about 10 cm at 100 years. The later slowing in the increase of soil thickness with increasing age is compatible with a cross-over to transport-limited soil formation at later times. Thus, the linear increase in depth with increasing time, while predicting a thinner soil than what would be due to transport limitations at short times, would predict a deeper soil than is observed at longer times. Soil depth is, however, reasonably well predicted for the Wind River Range sites. No data for very young soils (<100 yr) were available. The Wind River Range soils have, in contrast to the other alpine sites, a small loess layer. The relatively small grain size of loess leads to slower infiltration rates, longer contact time with minerals so that transport is limiting from the beginning of soil formation (what can be better predicted with our model).

An alternate, but related, framework to address the overprediction of soil depths at short times is discussed in the literature (e.g., Dixon and von Blanckenburg, 2012), and is based on the description of the trend curves, the interrelation of erosion and mineral weathering and the designation of certain “speed limits” in soil production. In regions with solid bedrock as soil parent material, discussions of the possible relevance of a “humped” soil production function can help provide an introduction to this topic, though discussion of a humped soil production function also brings in additional complications.

Gilbert (1877) was the first to propose the existence of a “humped” soil production function, with rates of bedrock to soil conversion diminishing both for thinner soils and thicker ones and, thus, a maximum at intermediate depths. Such a soil production function can lead to two modes of stability depending on initial conditions, one with, and one without soil mantle, making this also an environmentally relevant model. There are two proposed causes, of which one is relevant here. The first owes to Gilbert (1877) and was later discussed by Heimsath et al. (2009). If the soil is too thin, the difficulty in establishing plants reduces the impact of fracture formation in the bedrock, limiting infiltration on account of the low water storage in the thin soil, thus promoting run-off and erosion compared with chemical weathering of the bedrock. Once vegetation is established in deeper soils, roots are considered to provide a physical mechanism for fracturing bedrock, with increase in vertical infiltration rates and associated increase in weathering rates. Heimsath et al. (2009) appear to have verified this model. However, this particular explanation, though it is the original one, has no obvious relevance for the present difficulty.

In the second perspective, (Egli et al., 2014), it is not the physical fracturing process that is expressed in the humped soil production function. These authors find that the cause relates to the increase in the available surface area of primary mineral grains over time until a certain maximum (Dixon et al., 2012) is reached. With time, weathering rates decrease again producing the “humped” time-trend (Humphreys and Wilkinson, 2007). This decrease is due to the gradually advancing consumption of fresh and reactive minerals. The texture of the parent rock, and thus the available surface area, is an important factor in controlling the reaction rates (Taboada and García, 1999). If however a moraine or other sediment layer is present, not a humped but rather an exponential, power law or logistic function over time is observed (Egli et al., 2014). Both types of function usually predict a maximum soil production rate under thin soils, and an inverse relationship between soil thickness and soil production. Based on this, some speed limits were derived. Transport limitation and kinetic limitation are often considered processes that determine the speed of silicate weathering. A transport-limited weathering regime exists then when the supply of water, inorganic and organic acids and ligands is large relative to the supply of silicate (West et al., 2005). The supply of fresh minerals limits the weathering rates. Old and flat topographies typically are in this category. A kinetic limitation is then given when the main control on chemical weathering, silicate weathering ω depends on the kinetic rate of mineral dissolution W, the supply of material (e.g., by erosion) e, and the time t available for reaction (West et al., 2005).

$\begin{array}{cc}\begin{array}{r}\omega =W·e·t\end{array}& (11)\end{array}$

Mineral dissolution (W) depends on environmental conditions such as temperature and runoff (or precipitation). The weathering rate of a mineral or rock decreases with the time that the mineral spends in the weathering environment, as ${\omega }_V⋉t^{\lambda }$ with ω_V = instantaneous volumetric weathering rate, λ = (erosion) exponent (White and Brantley, 2003; West et al., 2005). Apparently, young surfaces or surfaces exhibiting a high erosion rate (leading to a continuous rejuvenation of the surface and soils) are in this category.

Our model overestimates soil production rates for young soils. The kinetic limitation of mineral weathering, that is particularly effective at young sites, is most likely the cause for this. This seems to be the case up to about 100 years but sometimes up to 1,000 or more years of soil formation. Alpine soils often have a coarse soil structure (Egli et al., 2001) that gives rise to a high hydraulic conductivity, minimizing the opportunity for overland flow, and decreasing the reactive surface area. The model predicts soil production rates (Figure 8) for very young soils of about 10⁻² m yr⁻¹. In terms of soil mass (using an average soil coarse fragment content of young soils of about 60% and soil density about 1.4 t m⁻³; Figure 6), this would lead to a maximum soil production rate of ca. 5,600 t km⁻² yr⁻¹. Particles > 2 mm (coarse fragments) are usually considered “chemically inert” for plant growth, although they can very well be the source of nutrients such as Ca, Mg, and K (Ugolini et al., 2001). The obtained maximum rate is an extremely high value, but not fully impossible. Dixon and von Blanckenburg (2012) estimated a soil production speed limit of between 320 and 450 t km⁻² yr⁻¹. Later, Larsen et al. (2014), Egli et al. (2014) and Alewell et al. (2015) derived a speed limit of about 2,000 t km⁻² yr⁻¹ or even higher (the largest measurements of Larsen et al. (2014) are 2,400 m Myr⁻¹, which corresponds to ca. 6,000 t km⁻² yr⁻¹). Alpine soils with an age of 1 to 10 kyr have, according to our calculations, a production rate of about 150 to 230 t km⁻² yr⁻¹ which is quite close to those given in Alewell et al. (2015) with 119–248 t km⁻² yr⁻¹.

FIGURE 8

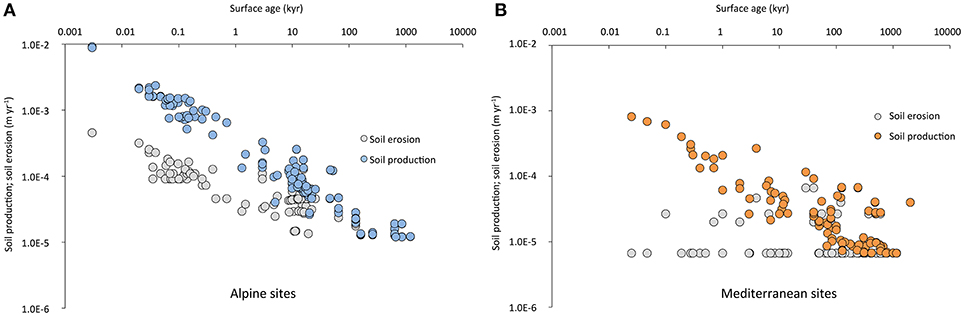
Figure 8. Soil production rates (modeled) and erosion (or denudation) rates (measured or estimated) over time for the distinct geographic regions: (A) alpine and (B) Mediterranean sites.

We can also consider maximum soil production rates in the present and related models. An exponentially declining soil production function, such as those considered by the Heimsath group, introduce an obvious “speed limit” equal to the value of the pre-exponential factor, as found by substituting a soil depth of zero into the exponential function. The inverse power-law formulation here generates a maximum conceivable speed of soil formation equal to the infiltration rate, I. But that value is obtained for a soil thickness of only a single particle. For typical infiltration rates (on the order of 1 m yr⁻¹), I is about 400 times greater than the largest soil formation rates observed to date, around 2400 m/M yr (Larsen et al., 2014), which are found in areas of precipitation with more nearly 10 m yr⁻¹ in New Zealand. Clearly, if such a thin soil could be defined, most precipitation rates around the world would effectively “cleanse” the bedrock of the soil, rather than forming additional soil. For a soil with a thickness of one thousand particle diameters, however, according to Equation (6), with x/x₀ = 1000, the soil production rate has already dropped by a factor 1000 ^−0.87, or ca. 400 to about 2,500 m Myr⁻¹. So, if layers thinner than some hundreds of particles are not considered soils, the excessive “speed limits” implied by the model do not disqualify it generally from being relevant, but may help to explain limitations on its relevance at very short time scales, when weathering reactions are more likely to be kinetic-limited. Consider that a thickness of 10 cm for particles of 500 μm size represents a total of only 200 particles. Finally, since percolation theory is a statistical theory, for soils much thinner than a few hundred particles, its quantitative predictions will not be accurate anyway. This implies that for, say media less than 10 particles thick, percolation concepts would not be relevant at all. In the range 10 to a few hundred particles, percolation predictions of soil formation rates may be too high, especially when weathering may be kinetic-limited.

The minor over-prediction at larger time scales must also be addressed. Within our theoretical framework, the three most likely candidates to explain this discrepancy are: (1) the systematic decrease in particle size over time (Figure 5), (2) the possibility that our estimations of infiltration are inaccurate, (3) the use of a too small erosion rate. We consider these possible factors separately.

In constructing Figure 7A, we used site-to-site variability in a median particle size, which incorporates information on this distribution throughout the soil column, including the original material. This particular value represents likewise an approximation to a dominant particle size over the temporal evolution of the soil. For some sites, the implication of the vertical cross-section is that the median particle size did not change over time. For others, it apparently decreased, in some cases by as much as a factor 10. Trying to reconstruct a history of particle size evolution for each of the 147 alpine soils in the database is unpractical, but we did construct an amalgamated history of a typical such site and an extreme site. A variability for a typical site was determined by a power-law regression on the entire data set represented as a function of time, and yielded d₅₀ = 165 μm t^−0.123, where t is measured in years. Use of this function of t for d₅₀ for all sites yielded an R² value of 0.2 instead of 0.39 (Figure 7C), and did not visually improve the agreement in the trend. A similar investigation of the extreme of using the smallest particle size as a function of time was even less satisfying. Thus, it appears that temporal variability in median particle sizes averaged across a wide range of sites is less important information than the site-to-site variability in the vertically averaged profile at the observed time, at least for this study. If the Wind River sites (many of them having very old surfaces ages) are excluded, then the predicted and modeled values correlate better (R² = 0.48). One difficulty therefore might be due to less precise estimation of the hydrologic mass balance over very long time periods. We, therefore, cannot exclude the possibility that the discrepancy between theory and observation would be reduced if the temporal history of each soil could be reconstructed by careful analysis of the vertical profile and environmental conditions. In this context, it may be pointed out that Yu and Hunt (2017b,c) used current values of the soil particle sizes, corresponding to the smallest in the profile, and did not generate an overestimation.

Consider next the effects of uncertainty in AET. The global average actual evapotranspiration (AET) rate is roughly 65% of precipitation (Lvovitch, 1973; Schlesinger and Jasechko, 2014), and can be considerably higher. A 10% underestimation of AET, when its actual value is 80% can lead to a nearly 50% overestimation of the net infiltration rate I.

We expect that erosion rates are less likely to be the cause. While erosion rates higher than those used in the model could also produce a reduction in predicted soil depth at longer times, we found no support for choosing higher erosion rates. Further, the largest effect of a higher erosion rate would be to shorten the time scale at which steady-state conditions (unchanging depth) are approached. Cursory examination of the data suggests that the given suite of erosion rate values is in relative accord with this time scale.

The magnitude of the observed scatter at any given time is reasonably well accounted for by the variability in predicted values that arises from the variations in the input parameters. However, comparison of all individual predicted and observed depths yields a somewhat unimpressive R² value of about 0.39. Thus, we conclude that, in Alpine soils, it is possible that for small scale predictions local soil rearrangement from such processes such as bioturbation need to be incorporated into our model of soil production. For somewhat larger scales, a statistical correspondence could suffice.

Mediterranean Sites

For the Mediterranean sites, predicted soil depths match quite well observed soil depths (Figure 7B). There is no obvious trend toward greater or smaller underestimation at longer time intervals. The scatter in experimental data is also well captured by the scatter in predictions, as seen in Figure 7B. However, direct representation of the individual predictions as a function of observed depths reveals a relatively large scatter, and an R² value of only about 0.50 (Figure 7D). All sites have a predominantly silicate geology. If the sites having some carbonate additions are excluded, then this scatter is slightly reduced and R² increases to 0.59. Therefore, the diversity of the geology also seems to affect to a minor extent the performance of the model. Furthermore, it is to be presumed that: (1) there is considerable uncertainty in the determination of the parameters, which could be due to incompletely guessed surface flow routing, or (2) other influences on soil depth that are important have been omitted. Since the mean depth as a function of age is relatively well predicted, in the case of (2), we suggest that the best candidates for neglected processes should be those that contribute to local reorganization of the soil, such as bioturbation, tree throw (Šamonil et al., 2017), eaolian deposits (after the start of soil formation), petrography, other hillslope processes or unconsidered human impact. The Mediterranean soils have a typical soil density of about 1.6 t m⁻³ and a soil coarse fragment content of about 20%. Production rates for soils having an age between 1 and 10 kyr are in the range of about 70 to 380 t km⁻² yr⁻¹. Very young soils (age of 10 to 100 yr) have rates of up to 1,000 t km⁻² yr⁻¹. Although the climate is warmer (but not moister), weathering and soil production are not significantly faster than in alpine areas.

It is, furthermore, interesting to note from examination of Figures 7A,B that the model better reflects the variability of the data of both systems, Mediterranean and alpine soils. Furthermore, soil erosion (output) and soil production (input) appear to be in a similar range after about 100 kyr to 1 Myr as seen in Figures 8A,B. We therefore hypothesize that soils tend to a quasi steady-state after about 100 kyr to 1 Myr. We however have to underline that soils are dynamic and that a change in the settings may cause a distinct shift away from steady-state conditions. As already Phillips (2010) mentioned, steady state soil thickness is only there applicable, where sufficient time has elapsed for regolith accumulation, and where effects of processes other than weathering and surface removals on thickness are negligible.

Sensitivity Analysis

Owing to the simplifications made to run the model, it is necessary to know which effect a change in these parameters has on the results. The influence of the parameters on soil depth and soil production (Equation 8) was checked by a sensitivity analysis. A convenient way to express the sensitivity of a system to changes in parameters is the normalized sensitivity coefficient, Q_{i, m}, that is defined by

$\begin{array}{cc}\begin{array}{r}{Q}_{i,m}=\frac{\partial ln{C}_i}{\partial ln{P}_m}\end{array}& (12)\end{array}$

where C_i is the dependent variable (in this case, it can be either soil production or soil depth) and P is the value of parameter m (Furrer et al., 1990). This formula expresses a partial derivative based on the percent change in the dependent variable caused by a 1% change in the value of the parameter m. Sensitivity coefficients are negative for parameters in processes that lead to a reduction and positive for parameters that cause an increase in variables of interest (Table 1). Processes that lead to a deeper soil exhibit positive values: a greater particle size, a higher infiltration rate and, not surprisingly, a longer soil evolution. Due to the fact that the rate of soil depth increase decreases with soil evolution, an increase in age has a negative effect on the soil production rate, both for the alpine and Mediterranean sites. The strongest influence of a change in the infiltration rate on soil depth and production rate is particularly noteworthy. The estimation of the water fluxes and infiltration rates becomes particularly difficult for old surfaces (having an age >20 kyr). Although the paleoclimate studies give some hints about the hydrological conditions over time, they are all not precise enough and only enable a rough, regional estimate at its best (Minnich, 2007; Reheis et al., 2012; Heyman et al., 2013; Blain et al., 2016; Kigoshi et al., 2017). In our model, a misjudgement of the infiltration rate has, thus, the greatest effect on a change in soil depth. However, the sensitivity even for the infiltration rate I is still < 1.

TABLE 1

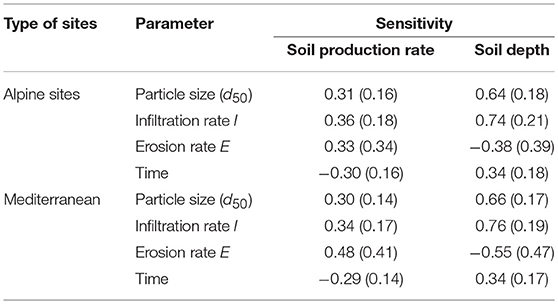
Table 1. Normalized sensitivity coefficients in response to the site type (average and standard deviation).

Most Closely Related Model

We have discussed the exponential soil production model in several contexts above. We have also mentioned some of the difficulties of models of chemical weathering based on the advection-dispersion equation under conditions of full saturation. However, there is one related model due to Braun et al. (2016), that is rather closely related to ours, and that deserves separate mention. These authors investigate regolith production from chemical weathering in the context of unsaturated flow, which, in turn, is addressed using Philip infiltration theory (Philip, 1967, 1969). The Philip theory indeed delivers a net infiltration that has a term proportional to the square root of the time; thus it would be possible to generate a time-dependence for chemical weathering more or less equal to what is typically observed, while preserving the proportionality of weathering to the flow rate. This publication has been criticized by Harman et al. (2017) who found that the specific flow paths envisioned by Braun et al. (2016) were not realistic. Since we do not specify the flow paths in the same level of detail, we do not find this criticism compelling. However, the Philip infiltration theory applied by Braun et al. (2016) is nominally for an ordered medium, and is based on a solution of the Richards' equation. Hunt et al. (2017) have shown that in disordered media, the precise form of the time-dependent infiltration term can be verified to be t ^0.53 rather than t ^0.5. Such verification was possible by using a scaling analysis from Sharma et al. (1980) for which data in agreement with the Philip infiltration result would necessarily scale precisely to the same curve, whereas this is not observed. But a more serious objection is that the experiments of chemical weathering and related surface reactions performed by White and Brantley (2003) and by Pacific Northwest National Laboratory scientists (Zhong et al., 2005; Liu et al., 2008, 2009, etc.) under saturated conditions show the same time-dependent scaling and proportionality to flow rates as observed in the field. Thus, the percolation scaling theory yields the same time-dependence for unsteady flow under unsaturated conditions as for solute transport under either saturated or wetting conditions, but the validity of the Philip infiltration model explanation is restricted to unsaturated conditions and is incompatible with identical results obtained under saturated conditions.

Conclusions

We applied a theoretical model of soil formation rates as limited by chemical weathering to prediction of the evolution of soil depths at about 250 sites in two climate regimes, Mediterranean and alpine. The chemical weathering was assumed to be limited by advective solute transport, a result which made relevant the rate of the mean vertical flow through the soil column over time. These rates were estimated using the difference between precipitation and evapotranspiration, but without accounting for the effects of topography on the divergence of surface water flow. The model requires, as a second input parameters, a characteristic particle size, which we assumed could be equated with d₅₀, equivalent to a fundamental soil network spatial scale. In most cases this value had to be obtained from a regression function relating observed soil sand, silt, and clay fractions to observed d₅₀ values in the same climatic region. The other two input parameters are the erosion rate and the time. The output depth, generated from the model was then compared with the observed depth on a site-by-site basis. We found that the model matched soil depths in the Mediterranean climate zone, but overpredicted depths in alpine regions by ~45%. The results suggest that it is possible to model soil formation rates with our analytical formula and generate the major trends. Further, the range of predicted soil depths, at any given time is generally in accord with our predicted variability. If this variation could be traced to an accurate representation of the actual variability in the net infiltration rate I, erosion rate E, and the characteristic particle size d₅₀ at these times, one would expect a very high R² value. Unfortunately, our two direct comparisons between predicted and observed soil depth yielded R² values of 0.39 for the Alpine soils and 0.50 for the Mediterranean soils. Such relatively low values of R² indicate the presence of a significant discrepancy. While there are a number of possible implications, including that the theoretical model leaves out important local redistributions of soils, such as due to bioturbation, we think that the first place to check for a source for the discrepancy is in the estimation of the parameters. Systematic overestimation of soil depths at later times will arise from exclusion of, or only partial accounting for, the fining of particle size with time. But systematic overestimation of soil depth can also arise from random errors in actual evapotranspiration (AET) estimation, when AET is significantly larger than 50% of the precipitation. For example, if AET is 80% of the total precipitation, an underestimation of AET 10% can make an almost 50% overestimation of the value of I, while an overestimation of AET of the same magnitude leads to a 100% underestimation of I. Beyond systematic errors, neglect of surface water routing will fail to generate any patchiness of soil depth due to differences in local infiltration rates.

In the future, we would like most importantly to improve the model performance with respect to its ability to generate the actual variability in soil depths of a given age, not just the envelope of such soil depths. We think that a logical means to address this issue is to solve for the variations of soil depth along hillslopes and within individual basins. To accomplish this, we must first develop a protocol that yields a more accurate value of I, which is possible only through integration with models that accurately describe surface water routing. Although it would be useful as well to couple with hillslope subsurface flow models, including dependences on surface topography, this particular improvement has a lower priority. A goal is to be able to apply our soil production model at regional and larger scales using maps of relevant data. Describing the subsurface hydrologic processes requires another level of input data, including hydraulic conductivity variability, more difficult to access and predict. It will also be important to incorporate into the numerical routine information regarding any known time dependence of parameters, such as precipitation or erosion. With these advances, it is hoped that we can meet the ultimate goal of the research, to transform mapped data regarding climate, erosion rates, and soil characteristics and so forth into a reliable and compatible representation of predicted soil depths.

Author Contributions

AH theoretical development, writing the article. ME data collection and analysis, R-coding, writing the article. DD data collection, writing the article. GR preparation of figure, writing the article. CD R-coding, writing the article. SR data collection, writing the article. FY geochemical calculations, writing the article.

Funding

The funding supported AH's stay at the University of Zurich.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This research was supported by the Swiss National Science Foundation (SNSF) project grant no. IZSEZ0_180377/1. We furthermore would like to thank the reviewers for their useful comments on an earlier version of the manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2018.00108/full#supplementary-material

References

Alewell, C., Egli, M., and Meusburger, K. (2015). An attempt to estimate tolerable soil erosion rates by matching soil formation with denudation in Alpine grasslands. J. Soils Sediments 15, 1383–1399. doi: 10.1007/s11368-014-0920-6

CrossRef Full Text | Google Scholar

Algeo, T. J., and Scheckler, S. E. (1998). Terrestrial-marine teleconnections in the Devonian: links between the evolution of landplants, weathering processes, and marine anoxic events. Philos. Trans. Roy. Soc. Lond. Ser. B-Biol. Sci. 353, 113–128. doi: 10.1098/rstb.1998.0195

CrossRef Full Text | Google Scholar

Alonso, P., Dorronsoro, C., and Egido, J. A. (2004). Carbonatation in palaeosols formed on terraces of the Tormes river basin (Salamanca, Spain). Geoderma 118, 261–276. doi: 10.1016/S0016-7061(03)00211-8

CrossRef Full Text | Google Scholar

Amundson, R., Heimsath, A., Owen, J., Yoo, K., and Dietrich, W. E. (2015). Hillslope soils and vegetation. Geomorphology 234, 122–132. doi: 10.1016/j.geomorph.2014.12.031

CrossRef Full Text | Google Scholar

Anderson, R. S., and Anderson, S. P. (2010). Geomorphology: The Mechanics and Chemistry of Landscapes. New York, NY: Cambridge Press. doi: 10.1017/CBO9780511794827

CrossRef Full Text | Google Scholar

Aniku, J. R. F., and Singer, M. J. (1990). Pedogenic iron oxide trends in a marine terrace chronosequence. Soil Sci. Soc. Am. J. 54, 147–152. doi: 10.2136/sssaj1990.03615995005400010023x

CrossRef Full Text | Google Scholar

Arppe, L., and Karhu, J. A. (2010). Oxygen isotope values of precipitation and the thermal climate in Europe during the middle to late Weichselian ice age. Quat. Sci. Rev. 29, 1263–1275. doi: 10.1016/j.quascirev.2010.02.013

CrossRef Full Text | Google Scholar

Badía, D., Martí, C., Palacio, E., Sancho, C., and Poch, R. M. (2009). Soil evolution over the Quaternary period in a semiarid climate (Segre river terraces, northeast Spain). Catena 77, 165–174. doi: 10.1016/j.catena.2008.12.012

CrossRef Full Text | Google Scholar

BAFU (Bundesamt für Umwelt) (2015). Hydrologischer Atlas der Schweiz. Geographisches Institut der Universität Bern, Bern. Available online at: http://hydrologischeratlas.ch/

Bandopadhyay, A., Le Borgne, T., Meheust, Y., and Dentz, M. (2017). Enhanced reaction kinetics and reactive mixing scale dynamics in mixing fronts under shear flow for arbitrary Damköhler numbers. Adv. Water Resour. 100, 78–95. doi: 10.1016/j.advwatres.2016.12.008

CrossRef Full Text | Google Scholar

Berner, R. A. (1992). Weathering, plants, and the long-term carbon-cycle. Geochim. Cosmochim. Acta 56, 3225–3231. doi: 10.1016/0016-7037(92)90300-8

CrossRef Full Text | Google Scholar

Birkeland, P. (1984). Soils and Geomorphology. New York, NY: Oxford University Press.

Google Scholar

Blain, H.-A., Lozano-Fernández, I., Agustí, J., Bailon, S., Menéndez Granda, L., Espígares Ortiz, M. P., et al. (2016). Refining upon the climatic background of the Early Pleistocene hominid settlement in western Europe: Barranco León and Fuente Nueva-3 (Guadix-Baza Basin, SE Spain). Quat. Sci. Rev. 144, 132–144. doi: 10.1016/j.quascirev.2016.05.020

CrossRef Full Text | Google Scholar

Blöschl, G., and Sivapalan, M. (1995). Scale issues in hydrological modelling: a review. Hydrol. Process. 9, 251–290. doi: 10.1002/hyp.3360090305

CrossRef Full Text | Google Scholar

Böhlert, R., Mirabella, A., Plötze, M., and Egli, M. (2011). Landscape evolution in Val Mulix, eastern Swiss Alps – Soil chemical and mineralogical analyses as age proxies. Catena 87, 313–325. doi: 10.1016/j.catena.2011.06.013

CrossRef Full Text | Google Scholar

Borman, P. T., Spaltensein, H., McClellan, M. H., Ugolini, F. C., Cromack, K., and Nay, S. M. (1995). Rapid soil development after windthrow disturbance in pristine forests. J. Ecol. 83, 747–757. doi: 10.2307/2261411

CrossRef Full Text | Google Scholar

Bosco, C., de Rigo, D., Dewitte, O., Poesen, J., and Panagos, P. (2015). Modelling soil erosion at European scale: towards harmonization and reproducibility. Nat. Hazards Earth Syst. Sci. 15, 225–245. doi: 10.5194/nhess-15-225-2015

CrossRef Full Text | Google Scholar

Bosco, C., Montanarella, L., Rusco, E., Oliveri, S., and Panagos, P. (2008). Soil Erosion in the Alps. Luxembourg: Office of Official Publications of the European Communities.

Brantley, S. L., Goldhaber, M. B., and Vala-Ragnarsdottir, K. (2007). Crossing disciplines and scales to understand the critical zone. Elements 3, 307–314. doi: 10.2113/gselements.3.5.307

CrossRef Full Text | Google Scholar

Braun, J., Mercier, J., Gullocheau, F., and Robin, C. (2016). A simple model for regolith formation by chemical weathering. J. Geophys. Res. Earth Surf. 121, 2140–2171. doi: 10.1002/2016JF003914

CrossRef Full Text | Google Scholar

Brugger, K. A. (2010). Climate in the Southern Sawatch Range and Elk Mountains, Colorado, U.S.A., during the Last Glacial Maximum: Inferences Using a Simple Degree-Day Model. Arct Antarc. Alp. Res. 42, 164–178. doi: 10.1657/1938-4246-42.2.164

CrossRef Full Text | Google Scholar

Burke, A., Levavasseur, G., James, P. M., Guiducci, D., Izquierdo, M. A., Bourgeon, L., et al. (2014). Exploring the impact of climate variability during the Last Glacial Maximum on the pattern of human occupation of Iberia. J. Hum. Evol. 73, 35–46. doi: 10.1016/j.jhevol.2014.06.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Burke, B. C., Heimsath, A. M., and White, A. F. (2006). Coupling chemical weathering with soil production across soil-mantled landscapes. Earth Surf. Proc. Landf. 32, 853–873. doi: 10.1002/esp.1443

CrossRef Full Text | Google Scholar

Calero, J. (2005). Génesis de la Fracción Mineral y de la Ultramicrofábrica en una Cronosecuencia de Suelos Sobre Terrazas del río Guadalquivir. dissertation. Spain: Universidad de Granada.

Calero, J., Delgado, R., Delgado, G., and Martín-García, J. M. (2008). Transformation of categorical field soil morphological properties into numerical properties for the study of chronosequences. Geoderma 145, 278–287. doi: 10.1016/j.geoderma.2008.03.022

CrossRef Full Text | Google Scholar

Commonwealth of Australia (2005). Australian Climate Averages., Evapotranspiration (Climatology 1961-1990). Available online at: www.bom.gov.au

Curatolo„, G, Pedone, P., Raimondi, S., Sarno, M., Sciortino, A., and Scuderi, G. (2000). Giardino alofilo nelle Saline Ettore Infersa di Marsala. Workshop “Il verde come strumento di riqualificazione e recupero di aree degradate e dissestate.” Italus Hortus 7, 45–49.

Google Scholar

Cushman, J. H., and O'Malley, D. (2015). Fickian dispersion is anomalous. J. Hydrol. 531, 161–167. doi: 10.1016/j.jhydrol.2015.06.036

CrossRef Full Text | Google Scholar

Dahms, D., and Egli, M. (2016). Carbonate and elemental accumulation rates in arid soils of mid-to-late Pleistocene outwash terraces, southeastern Wind River Range, Wyoming, USA. Chem. Geol. 446, 147–162. doi: 10.1016/j.chemgeo.2015.12.006

CrossRef Full Text | Google Scholar

Dahms, D. E. (2002). Glacial stratigraphy of stough creek basin, wind river range, wyoming. Geomorphology 42, 59–83. doi: 10.1016/S0169-555X(01)00073-3

CrossRef Full Text | Google Scholar

Dahms, D. E. (2004). Relative and numeric age data for Pleistocene glacial deposits and diamictons in and near Sinks Canyon, Wind River Range, Wyoming, U.S.A. Arct. Antarct. Alp. Res. 36, 59–77. doi: 10.1657/1523-0430(2004)036[0059:RANADF]2.0.CO;2

CrossRef Full Text | Google Scholar

d'Amico, M. E., Freppaz, M., Filippa, G., and Zanini, E. (2014). Vegetation influence on soil formation rate in a proglacial chronosequence (Lys Glacier, NW Italian Alps). Catena 113, 122–137. doi: 10.1016/j.catena.2013.10.001

CrossRef Full Text | Google Scholar

Darwin, C. (1881). The Formation of Vegetable Mould through the Action of Worms, with Observations on Their Habits. London: John Murray. doi: 10.5962/bhl.title.107559

CrossRef Full Text | Google Scholar

Dixon, J. L., Hartshorn, A. S., Heimsath, A. M., DiBiase, R. A., and Whipple, K. X. (2012). Chemical weathering response to tectonic forcing: a soils perspective from the San Gabriel Mountains, California. Earth Planet. Sci. Lett. 323–324, 40–49. doi: 10.1016/j.epsl.2012.01.010

CrossRef Full Text | Google Scholar

Dixon, J. L., Heimsath, A. M., Kaste, J., and Amundson, R. (2009). Climate-driven processes of hillslope weathering. Geology 37, 975–978. doi: 10.1130/G30045A.1

CrossRef Full Text | Google Scholar

Dixon, J. L., and von Blanckenburg, F. (2012). Soils as pacemakers and limiters of global silicate weathering. Comptes Rendus. Geosci. 344, 596–609. doi: 10.1016/j.crte.2012.10.012

CrossRef Full Text | Google Scholar

Dokuchaev, V. V. (1948). “Russian Chernozem,” in Selected Works, ed S. Monson (Moscow: Israel Program for Scientific Translations Ltd), 14–419.

Google Scholar

Dorronsoro, C., and Alonso, P. (1994). Chronosequence in Almar River, fluvial terrace soil. Soil Sci. Soc. Am. J. 58, 3, 910–925.doi: 10.2136/sssaj1994.03615995005800030039x

CrossRef Full Text | Google Scholar

Egli, M., Brandová, D., Böhlert, R., Favilli, F., and Kubik, P. (2010). ¹⁰Be inventories in Alpine soils and their potential for dating land surfaces. Geomorphology, 119, 62–73. doi: 10.1016/j.geomorph.2010.02.019

CrossRef Full Text | Google Scholar

Egli, M., Dahms, D., and Norton, K. (2014). Soil formation rates on silicate parent material in alpine environments: different approaches–different results? Geoderma 213, 320–333. doi: 10.1016/j.geoderma.2013.08.016

CrossRef Full Text | Google Scholar

Egli, M., Favilli, F., Krebs, R., Pichler, B., and Dahms, D. (2012). Soil organic carbon and nitrogen accumulation rates in cold and alpine environments over 1 Ma. Geoderma 183–184, 109–123. doi: 10.1016/j.geoderma.2012.03.017

CrossRef Full Text | Google Scholar

Egli, M., Fitze, P., and Mirabella, A. (2001). Weathering and evolution of soils formed on granitic, glacial deposits: results from chronosequences of Swiss alpine environments. Catena 45, 19–47. doi: 10.1016/S0341-8162(01)00138-2

CrossRef Full Text | Google Scholar

Egli, M., Mirabella, A., and Fitze, P. (2003). Formation rates of smectites derived from two Holocene chronosequences in the Swiss Alps. Geoderma 117, 81–98. doi: 10.1016/S0016-7061(03)00136-8

CrossRef Full Text | Google Scholar

Egli, M., Zanelli, R., Kahr, G., Mirabella, A., and Fitze, P. (2002). Soil evolution and development of the clay mineral assemblage of a Podzol and Cambisol in “Meggerwald” (Switzerland). Clay Miner. 37, 351–366. doi: 10.1180/0009855023720039

CrossRef Full Text | Google Scholar

Eppes, M. C., and Keanini, R. (2017). Peering into the cracks. Eos 98:78321. doi: 10.1029/2018EO078321

CrossRef Full Text | Google Scholar

Fabel, D., Harbor, J., Dahms, D., James, A., Elmore, D., Horn, L., et al. (2004). Spatial patterns of glacial erosion at a valley scale derived from terrestrial cosmogenic ¹⁰Be and ²⁶Al concentrations in rock. Ann. Assoc. Am. Geogr. 94, 241–255. doi: 10.1111/j.1467-8306.2004.09402001.x

CrossRef Full Text | Google Scholar

Favilli, F., Egli, M., Brandová, D., Ivy-Ochs, S., Kubik, P. W., Cherubini, P., et al. (2009). Combined use of relative and absolute dating techniques for detecting signals of Alpine landscape evolution during the late Pleistocene and early Holocene. Geomorphology 112, 48–66. doi: 10.1016/j.geomorph.2009.05.003

CrossRef Full Text | Google Scholar

Friend, J. A. (1992). Achieving soil sustainability. J. Soil Water Conserv. 47, 156–157.

Google Scholar

Frouz, J., Elhottova, D., Kuraz, V., and Sourkova, M. (2006). Effects of soil macrofauna on other soil biota and soil formation in reclaimed and unreclaimed post mining sites: results of a field microcosm experiment. Appl. Soil Ecol. 33, 308–320. doi: 10.1016/j.apsoil.2005.11.001

CrossRef Full Text | Google Scholar

Furrer, G., Sollins, P., and Westall, J. C. (1990). The study of soil chemistry through quasi-steady-state models: II. acidity of soil solution. Geochim. Cosmochim. Acta 54, 2363–2374. doi: 10.1016/0016-7037(90)90225-A

CrossRef Full Text | Google Scholar

Garboczi, E. J., Snyder, K. A., Douglas, J. F., and Thorpe, M. F. (1995). Geometrical percolation threshold of overlapping ellipsoids. Phys. Rev. E 52, 819–828. doi: 10.1103/PhysRevE.52.819

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghanbarian-Alavijeh, B., Hunt, A. G., Sahimi, M., Ewing, R. P., and Skinner, T. E. (2013). Percolation theory generates a physically based description of tortuosity in saturated and unsaturated porous media. Soil Sci. Soc. Am. J. 77, 1920–1929. doi: 10.2136/sssaj2013.01.0089

CrossRef Full Text | Google Scholar

Ghanbarian-Alavijeh, B., Skinner, T. E., and Hunt, A. G. (2012). Saturation dependence of dispersion in porous media. Phys. Rev. E 86:066316. doi: 10.1103/PhysRevE.86.066316

PubMed Abstract | CrossRef Full Text | Google Scholar

Gilbert, G. K. (1877). Report on the Geology of the Henry Mountains, U.S. Washington, DC: Geological Survey.

Google Scholar

Goodman, A. Y., Rodbell, D. T., Seltzer, G. O., and Mark, B. G. (2001). Subdivision of glacial deposits in southeastern Peru based on pedogenetic development and radiometric ages. Quat. Res. 56, 31–50. doi: 10.1006/qres.2001.2221

CrossRef Full Text | Google Scholar

Graf, K. (1992). Pollendiagramme aus den Anden: Eine Synthese zur Klimageschichte und Vegetationsentwicklung seit der letzten Eiszeit. Phys. Geogr. 34, 1–138.

Google Scholar

Guiot, J., Pons, A., de Beaulieu, J. L., and Reille, M. (1989). A 140,000-year continental climate reconstruction from two European pollen records. Nature 338, 309–313. doi: 10.1038/338309a0

CrossRef Full Text | Google Scholar

Harden, J. W., Sarna-Wojcicki, A. M., and Dembroff, G. R. (1986). Soils Developed on Coastal and Fluvial Terraces Near Ventura, California. U.S. Geological Bulletin, 1590-B, Series: Soil Chronosequences in the Western United States. Washington, DC: United States Government Printing Office.

Google Scholar

Harman, C. J., Cosans, C. L., and Putnam, S. M. (2017). Comment on “A simple model for regolith formation by chemical weathering,” by Braun et al. Contradictory concentrations and a tale of two velocities. J. Geophys. Res. 122, 2033–2036. doi: 10.1002/2016JF004151

CrossRef Full Text | Google Scholar

He, L., and Tang, Y. (2008). Soil development along primary succession sequences on moraines of Hailuogou Glacier, Gongga Mountain, Sichuan, China. Catena 72, 259–269. doi: 10.1016/j.catena.2007.05.010

CrossRef Full Text | Google Scholar

Heimsath, A. M., Dietrich, W. E., Nishiizumi, K., and Finkel, R. C. (1997). The soil production function and landscape equilibrium. Nature 388, 358–361. doi: 10.1038/41056

CrossRef Full Text | Google Scholar

Heimsath, A. M., Dietrich, W. E., Nishiizumi, K., and Finkel, R. C. (1999). Cosmogenic nuclides, topography, and the spatial variation of soil depth. Geomorphology 27, 151–172. doi: 10.1016/S0169-555X(98)00095-6

CrossRef Full Text | Google Scholar

Heimsath, A. M., Fink, D., and Hancock, G. R. (2009). The ‘humped' soil production function: eroding Arnhem Land, Australia. Earth Surf. Process. Landf. 34, 1674–1684. doi: 10.1002/esp.1859

CrossRef Full Text | Google Scholar

Heyman, B. M., Heyman, J., Fickert, T., and Harbor, J. M. (2013). Paleo-climate of the central European uplands during the last glacial maximum based on glacier mass-balance modeling. Quat. Res. 79, 49–54. doi: 10.1016/j.yqres.2012.09.005

CrossRef Full Text | Google Scholar

Hillel, D. (2005). Soil: crucible of life. J. Nat. Resour. Life Sci. Educ. 34, 60–61.

Google Scholar

Huggett, R. (1998). Soil chronosequences, soil development, and soil evolution: a critical review. Catena 32, 155–172. doi: 10.1016/S0341-8162(98)00053-8

CrossRef Full Text | Google Scholar

Humphreys, G. S., and Wilkinson, M. T. (2007). The soil production function: a brief history and its rediscovery. Geoderma 139, 73–78. doi: 10.1016/j.geoderma.2007.01.004

CrossRef Full Text | Google Scholar

Hunt, A. G. (2001). Applications of percolation theory to porous media with distributed local conductances. Adv. Water Res. 24, 279–307. doi: 10.1016/S0309-1708(00)00058-0

CrossRef Full Text | Google Scholar

Hunt, A. G. (2017). Spatio-temporal scaling of vegetation growth and soil formation: explicit predictions. Vadose Zone J. doi: 10.2136/vzj2016.06.0055

CrossRef Full Text | Google Scholar

Hunt, A. G., Alavijeh, B., Skinner, T. E., and Ewing, R. P. (2015). Scaling of geochemical reaction rates via advective solute transport. Chaos 25:075403. doi: 10.1063/1.4913257

PubMed Abstract | CrossRef Full Text | Google Scholar

Hunt, A. G., and Ewing, R. P. (2016). “Scaling,” in Handbook of Groundwater Engineering, 3rd edn, eds J. H. Cushman and D. Tartakovsky (Boca Raton, FL: Taylor & Francis).

Google Scholar

Hunt, A. G., Ewing, R. P., and Ghanbarian-Alavijeh, B. (2013). Percolation Theory for Flow in Porous Media (3rd edition), Lecture Notes in Physics 880, Berlin: Springer.

Google Scholar

Hunt, A. G., and Ghanbarian, B. (2016). Percolation Theory for Solute Transport in Porous Media: Geochemistry, Geomorphology, and Carbon Cycling. Water Resour. Res. 52, 7444–7459. doi: 10.1002/2016WR019289

CrossRef Full Text | Google Scholar

Hunt, A. G., and Manzoni, S. (2016). Networks on Networks: The Physics of Geobiology and Geochemistry. (Bristol UK: Morgan & Claypool Publishers). 176.

Hunt, A. G., and Sahimi, M. (2017). Flow, transport, and reaction in porous media: percolation scaling, critical path analysis and effective-medium approximation. Rev. Geoph. 55, 993–1078. doi: 10.1002/2017RG000558

CrossRef Full Text | Google Scholar

Hunt, A. G., and Skinner, T. E. (2008). Longitudinal dispersion of solutes in porous media solely by advection. Philos. Mag. 88, 22, 2921–2944. doi: 10.1080/14786430802395137

CrossRef Full Text | Google Scholar

Hunt, A. G., Skinner, T. E., Ewing, R. P., and Ghanbarian-Alavijeh, B. (2011). Dispersion of solutes in porous media. Eur. Phys. J. B 80, 4, 411–432. doi: 10.1140/epjb/e2011-10805-y

CrossRef Full Text | Google Scholar

Hunt, A. G., Skinner, T. E., Ewing, R. P., and Ghanbarian-Alavijeh, B. (2017). Percolation Theory to Reaction and Flow in Geochemical Systems in Soil and Rock, Encyclopedia of Complexity and Systems Science, 2nd Edn. (Berlin: Springer).

Google Scholar

Jenny, H. (1941). Factors of Soil Formation: A System of Quantitative Pedology. New York, NY: Dover.

Google Scholar

Kigoshi, T., Kumon, F., Kawai, S., and Kanauchi, A. (2017). Quantitative reconstruction of paleoclimate in central Japan for the past 158,000 years based on a modern analogue technique of pollen composition. Quat. Int. 455, 126–140. doi: 10.1016/j.quaint.2017.05.015

CrossRef Full Text | Google Scholar

Kirby, M. E., Feakins, S. J., Bonuso, N., Fantozzi, J. M., and Hiner, C. A. (2013). Latest pleistocene to holocene hydroclimates from lake elsinore, California. Quat. Sci. Rev. 76, 1–15. doi: 10.1016/j.quascirev.2013.05.023

CrossRef Full Text | Google Scholar

Lageat, Y., Lagasquie, J. J., Coque-Delhuille, B., Martin, C., Penven, M. J., and Simon-Coinçon, R. (2001). “Chemical weathering, regolith and climate in metamorphic and igneous terrains,” in Basement Regions, eds A. Godard, J. J. Lagasquie, and Y. Lageat (Berlin, Heidelberg: Springer), 117–145. doi: 10.1007/978-3-642-56821-3_6

CrossRef Full Text | Google Scholar

Lal, R. (2010). Enhancing Eco-efficiency in agro-ecosystems through soil carbon sequestration. Crop Sci. 50, S120–S131. doi: 10.2135/cropsci2010.01.0012

CrossRef Full Text | Google Scholar

Larsen, I. J., Almond, P. C., Eger, A., Stone, J. O., Montgomery, D. R., and Malcolm, B. (2014). Rapid soil production and weathering in the Southern Alps, New Zealand. Science 343, 637–640. doi: 10.1126/science.1244908

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, Y., Andrade, J. S., Buldyrev, S. V., Dokholoyan, N. V., Havlin, S., King, P. R., et al. (1999). Traveling time and traveling length in critical percolation clusters. Phys. Rev. E 60, 3425–3428. doi: 10.1103/PhysRevE.60.3425

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, H. (2010). Earth's Critical Zone and hydropedology: concepts, characteristics, and advances. Hydrol. Earth Syst. Sci. 14, 25–45. doi: 10.5194/hess-14-25-2010

CrossRef Full Text | Google Scholar

Liu, C., Shi, Z., and Zachara, J. M. (2009). Kinetics of Uranium(VI) desorption from contaminated sediments: effect of geochemical conditions and model evaluation. Environ. Sci. Technol. 43, 6560–6566. doi: 10.1021/es900666m

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, C., Zachara, J. M., Qafoku, N. P., and Wang, Z. (2008). Scale-dependent desorption of uranium from contaminated subsurface sediments. Water Resour. Res. 44:W08413. doi: 10.1029/2007WR006478

CrossRef Full Text | Google Scholar

Lvovitch, M. I. (1973). The global water balance: U.S. National Committee for the International Hydrological Decade. Natl. Acad. Sci. Bull. 23, 28–42

Google Scholar

Maher, K. (2010). The dependence of chemical weathering rates on fluid residence time. Earth Plan. Sci. Lett. 294, 101–110. doi: 10.1016/j.epsl.2010.03.010

CrossRef Full Text | Google Scholar

Makos, M. (2015). Deglaciation of the high Tatra mountains. Cuadernos Invest. Geogr. 41, 317–335. doi: 10.18172/cig.2697

CrossRef Full Text | Google Scholar

Massatti, R. T. (2007). A Floristic Inventory of the East Slope of the Wind River Mountain Range and Vicinity,Wyoming. dissertation. Wyoming, University of Wyoming.

Mavris, C., Egli, M., Plötze, M., Blum, J., Mirabella, A., et al. (2010). Initial stages of weathering and soil formation in the Morteratsch proglacial area (Upper Engadine, Switzerland). Geoderma 155, 359–371. doi: 10.1016/j.geoderma.2009.12.019

CrossRef Full Text | Google Scholar

McFadden, L. D., and Weldon, R. J. (1987). Rates and processes of soil development on Quaternary terraces in Cajon Pass, southern California. Geol. Soc. Am. Bull. 98, 280–293. doi: 10.1130/0016-7606(1987)98<280:RAPOSD>2.0.CO;2

CrossRef Full Text | Google Scholar

Meixner, R. E., and Singer, M. J. (1981). Use of a field morphology rating system to evaluate soil formation and discontinuities. Soil Sci. 131, 2, 114–123. doi: 10.1097/00010694-198102000-00008

CrossRef Full Text | Google Scholar

Merritts, D. J., Chadwick, O. A., and Hendricks, D. M. (1991). Rates and processes of soil evolution on uplifted narine terraces, Northern California. Geoderma 51, 241–275. doi: 10.1016/0016-7061(91)90073-3

CrossRef Full Text | Google Scholar

Meyer, M. C., Cliff, R. A., Spötl, C., Knipping, M., and Gagini, A. (2009). Speleothems from the earliest Quaternary: snapshots of paleoclimate and landscape evolution at the northern rim of the Alps. Quat. Sci. Rev. 28, 1374–1391. doi: 10.1016/j.quascirev.2009.01.010

CrossRef Full Text | Google Scholar

Minnich, R. A. (2007). “Terrestrial vegetation of California,” in Climate, Paleoclimate, and Paleovegetation, eds M. G. Barbour, T. Keeler-Wolf, and A. A. Schoenherr (Berkeley, CA: University of California Press), 43–70.

Google Scholar

Molnar, P., and Cronin, T. W. (2015). Growth of the Maritime Continent and its possible contribution to recurring ice ages. Paleoceanography 30, 196–225. doi: 10.1002/2014PA002752

CrossRef Full Text | Google Scholar

Montgomery, D. (2007a). Soil erosion and agricultural sustainability. Proc. Natl. Acad. Sci. 104, 13268–13272. doi: 10.1073/pnas.0611508104

PubMed Abstract | CrossRef Full Text | Google Scholar

Montgomery, D. (2007b). Dirt, The Erosion of Civilization. (Los Angeles, CA: University of California Press).

Google Scholar

Muhs, D. (1982). A soil chronosequence on Quaternary marine terraces, San Clemente Island, California. Geoderma 28, 257–283. doi: 10.1016/0016-7061(82)90006-4

CrossRef Full Text | Google Scholar

Mulch, A., Sarna-Wojcicki, A. M., Perkins, M. E., and Chamberlain, C. P. (2008). A Miocene to Pleistocene climate and elevation record of the Sierra Nevada (California). Proc. Natl. Acad. Sci. 105, 6819–6824. doi: 10.1073/pnas.0708811105

PubMed Abstract | CrossRef Full Text | Google Scholar

National Research Council (1996). Rock Fractures and Fluid Flow. Washington, DC: National Academy Press.

Neuman, S. P., and Di Federico, V. (2003). Multifaceted nature of hydrogeologic scaling and its interpretation. Rev. Geophys. 41:1014. doi: 10.1029/2003RG000130

CrossRef Full Text | Google Scholar

Norton, K. P., von Blanckenburg, F., and Kubik, P. W. (2010). Cosmogenic nuclide-derived rates of diffusive and episodic erosion in the glacially sculpted upper Rhone Valley, Swiss Alps. Earth Surf. Process. Landf. 35, 651–662. doi: 10.1002/esp.1961

CrossRef Full Text | Google Scholar

Oster, J. L., Montañez, I. P., Sharp, W. D., and Cooper, K. M. (2009). Late Pleistocene droughts during deglaciation and Arctic warming. Earth Planet. Sci. Lett. 288, 434–443. doi: 10.1016/j.epsl.2009.10.003

CrossRef Full Text | Google Scholar

Owen, J. J., Amundson, R., Nishiizumi, K., Sutter, B., and Chong, G. (2010). The sensitivity of hillslope soil production to precipitation. Earth Surf. Process. Landf. 36, 1, 117–135. doi: 10.1002/esp.2083

CrossRef Full Text | Google Scholar

Owen, J. J., Nishiizumi, K., Chong, G., and Amundson, R. (2013). Zebra stripes in the Atacama Desert: fossil evidence for overland flow. Geomorphology 182, 157–172. doi: 10.1016/j.geomorph.2012.11.006

CrossRef Full Text | Google Scholar

Panagos, P., Borrelli, P., Poesen, J., Ballabio, C., Lugato, E., Meusburger, K., et al. (2015). The new assessment of soil loss by water erosion in Europe. Environ. Sci. Policy 54, 438–447. doi: 10.1016/j.envsci.2015.08.012

CrossRef Full Text | Google Scholar

Peryam, T. C., Dorsey, R. J., and Bindeman, I. (2011). Plio-Pleistocene climate change and timing of Peninsular Ranges uplift in southern California: evidence from paleosols and stable isotopes in the Fish Creek–Vallecito basin. Palaeogeogr. Palaeocl. 305, 65–74. doi: 10.1016/j.palaeo.2011.02.014

CrossRef Full Text | Google Scholar

Petit, J. R., Jouzel, J., Raynaud, D., Barkov, N. I., Barnola, J.-M., Basile, I., et al. (1999). Climate and atomspheric history of the past 420,000 years from the Vostok ice core, Antarctica. Nature 399, 429–436. doi: 10.1038/20859

CrossRef Full Text | Google Scholar

Peyron, O. (1998). Was the climate of the Eemian stable? A quantitative climate reconstruction from seven European pollen records. Palaeogeogr. Palaeocl. 143, 73–85. doi: 10.1016/S0031-0182(98)00067-4

CrossRef Full Text | Google Scholar

Pfannkuch, H. (1963). Contribution à l'étude des déplacements de fluides miscibles dans un milieu poreux [Contribution to the study of the displacement of miscible fluids in a porous medium]. Rev. Inst. Fr. Pétr. 2, 215–270.

Google Scholar

Philip, J. R. (1967). Sorption and infiltration in heterogeneous media. Aust. J. Soil Res. 5, 1–10. doi: 10.1071/SR9670001

CrossRef Full Text | Google Scholar

Philip, J. R. (1969). Moisture equilibrium in the vertical in swelling soils. I. Basic theory. Aust. J. Soil Res. 7, 99–120 doi: 10.1071/SR9690099

CrossRef Full Text | Google Scholar

Phillips, J. D. (2010). The convenient fiction of steady-state soil thickness. Geoderma 156, 389–398. doi: 10.1016/j.geoderma.2010.03.008

CrossRef Full Text | Google Scholar

Pollak, M. (1972). A percolation treatment of dc hopping conduction. J. Non Cryst. Solids 11, 1–24. doi: 10.1016/0022-3093(72)90304-3

CrossRef Full Text | Google Scholar

Portes, R, Dahms, D., Brandová, D., Raab, G., Christl, M., Kühn, P., et al. (2018). Evolution of soil erosion rates in alpine soils of the Central Rocky Mountains using fallout Pu and δ13C. Earth Planet. Sci. Lett. 496, 257–269. doi: 10.1016/j.epsl.2018.06.002

CrossRef Full Text | Google Scholar

PRISM Climate Group (2014). Annual Average Precipitation (1981–2010). Oregon State University.

Raab, G., Halpern, D., Scardiglia, F., Raimondi, S., Norton, K., et al. (2017). Linking tephrochronology and soil characteristics in the Sila and Nebrodi Mountains, Italy. Catena 158, 266–285. doi: 10.1016/j.catena.2017.07.008

CrossRef Full Text | Google Scholar

Raab, G., Scarciglia, F., Norton, K., Dahms, D., de Castro Portes, R., Christl, M., et al. (2018). Denudation variability of the Sila upland massif (Italy) from decades to millennia using 10Be and 239+240Pu. Land. Degrad. Dev. doi: 10.1002/ldr.3120

CrossRef Full Text | Google Scholar

Raimondi, S. (1993). “Il clima ed il pedoclima dei suoli siciliani durante il trentaduennio 1951-1982,” in Quaderni di Agronomia n. 13, eds Istituto di Agronomia Generale e Coltivazioni Erbacee di Palermo (Palermo: Bonfardino Editore), 24–51.

Google Scholar

Raimondi, S., and Lupo, M. (1998). Il clima ed il pedoclima dei suoli della Sicilia occidentale. Sicilia Foreste 19/20, 59–64.

Google Scholar

Raymo, M. E. (1994). The Himalayas, organic-carbon burial, and climate in the Miocene. Paleoceanography 9, 399–404. doi: 10.1029/94PA00289

CrossRef Full Text | Google Scholar

Reheis, M. C., Bright, J., Lund, S. P., Miller, D. M., Skipp, G., and Fleck, R. J. (2012). A half-million-year record of paleoclimate from the Lake Manix Core, Mojave Desert, California. Palaeogeogr. Palaeocl. 365–366, 11–37. doi: 10.1016/j.palaeo.2012.09.002

CrossRef Full Text | Google Scholar

Richter, D. d., and Mobley, M. L. (2009). Monitoring Earth's critical zone. Science 326, 1067–1068. doi: 10.1126/science.1179117

PubMed Abstract | CrossRef Full Text | Google Scholar

Riedel, J. L. (2017). Deglaciation of the North Cascade Range, Washington and British Columbia, from the last glacial maximum to the Holocene. Cuadernos Invest. Geogr. 43, 467–496. doi: 10.18172/cig.3236

CrossRef Full Text | Google Scholar

Saffman, P. G. (1959). A theory of dispersion in a porous medium. J. Fluid Mech. 6, 321–349. doi: 10.1017/S0022112059000672

CrossRef Full Text | Google Scholar

Sahimi, M. (1994). Applications of Percolation Theory. London: Taylor & Francis.

Google Scholar

Sahimi, M., and Mukhopadhyay, S. (1996). Scaling properties of a percolation model with long-range correlations. Phys. Rev. E 54:3870. doi: 10.1103/PhysRevE.54.3870

PubMed Abstract | CrossRef Full Text | Google Scholar

Salehikhoo, F., Li, L., and Brantley, S. (2013). Magnesite dissolution rates at different spatial scales: the role of mineral spatial distribution and flow velocity. Geochim, Cosmochim. Acta 108, 91–106. doi: 10.1016/j.gca.2013.01.010

CrossRef Full Text | Google Scholar

Šamonil, P., Daněk, P., Adam, D., and Phillips, J.D. (2017). Breakage or uprooting: how tree death affects hillslope processes in old-growth temperate forests. Geomorphology 299, 76–84. doi: 10.1016/j.geomorph.2017.09.023

CrossRef Full Text | Google Scholar

Sanford, W. E., and Selnick, D. L. (2013). Estimation of evapotranspiration across the conterminous United States using a regression with climate and land-cover data. J. Am. Water Res. Assoc. 49, 217–230. doi: 10.1111/jawr.12010

CrossRef Full Text | Google Scholar

Sauer, D., Wagner, S., Brückner, H., Scarciglia, F., Mastronuzzi, G., and Stahr, K. (2010). Soil development on marine terraces near Metaponto (Gulf of Taranto, southern Italy). Quat. Int. 222, 48–63. doi: 10.1016/j.quaint.2009.09.030

CrossRef Full Text | Google Scholar

Sboarina, C., and Cescatti, A. (2004). Il Clima del Trentino – Distribuzione Spaziale delle Principali Variabili Climatiche. Report 33, Centro di Ecologia Alpina Monte Bondone, Trento.

Schaller, M., Ehlers, T. A., Stor, T., Torrent, J., Lobato, L., Christl, M., et al. (2016). Spatial and temporal variations in denudation rates derived from cosmogenic nuclides in four European fluvial terrace sequences. Geomorphology 274, 180–192. doi: 10.1016/j.geomorph.2016.08.018

CrossRef Full Text | Google Scholar

Schauwecker, S., Rohrer, M., Acuña, D., Cochachin, A., Dávila, L., Frey, H., et al. (2014). Climate trends and glacier retreat in the Cordillera Blanca, Peru, revisited. Glob. Planet. Change 119, 85–97. doi: 10.1016/j.gloplacha.2014.05.005

CrossRef Full Text | Google Scholar

Scher, H., Shlesinger, M., and Bendler, J. (1991). Time-scale invariance in transport and relaxation. Physics Today 44, 26–34. doi: 10.1063/1.881289

CrossRef Full Text | Google Scholar

Scher, H., and Zallen, R. (1970). Critical density in percolation processes. J. Chem. Phys. 53, 3759–3761. doi: 10.1063/1.1674565

CrossRef Full Text | Google Scholar

Schlesinger, W. H., and Jasechko, S. (2014). Transpiration in the global water cycle. Agric. For. Meteorol. 189, 115–117. doi: 10.1016/j.agrformet.2014.01.011

CrossRef Full Text | Google Scholar

Sharma, M. L., Gander, G. A., and Hunt, C. G. (1980). Spatial variability of infiltration in a watershed. J. Hydrol. 1980, 45, 101–122. doi: 10.1016/0022-1694(80)90008-6

CrossRef Full Text | Google Scholar

Shchetnikov, A. A., Bezrukova, E. V., Maksimov, F. E., Kuznetsov, V. Y., and Filinov, I. A. (2016). Environmental and climate reconstructions of the Fore-Baikal area during MIS 5-1: Multiproxy record from terrestrial sediments of the Ust-Oda section (Siberia, Russia). J. Asian Earth Sci. 129, 220–230. doi: 10.1016/j.jseaes.2016.08.015

CrossRef Full Text | Google Scholar

Sheppard, A. P., Knackstedt, M. A., Pinczewski, W. V., and Sahimi, M. (1999). Invasion percolation: new algorithms and universality classes. J. Phys. A Math. Gen. 32, L521–L529. doi: 10.1088/0305-4470/32/49/101

CrossRef Full Text | Google Scholar

Smale, M. C., McLeod, M., and Smale, P. N. (1997). Vegetation and soil recovery on shallow landslide scars in tertiary hill country, East Cape region, New Zealand. N. Zeal. J. Ecol. 21, 31–41.

Google Scholar

Soil Survey Division Staff (2014). Keys to Soil Taxonomy. US Department of Agriculture (USDA) and National Resource Conservation Service (NRCS). 12th edn. Washington, DC.

Stanley, H. E. (1977). Cluster shapes at the percolation threshold and effective cluster dimensionality and it connection with critical point exponents. J. Phys. A: Math. Gen 10:L211. doi: 10.1088/0305-4470/10/11/008

CrossRef Full Text | Google Scholar

Stauffer, D., and Aharony, A. (1994). Introduction to Percolation Theory. London: Taylor and Francis.

Google Scholar

Stokes, M., and García, A. F. (2009). Late Quaternary landscape development along the Rancho Marino coastal range front (southcentral Pacific Coast Ranges, California, USA). J. Quat. Sci. 24, 728–746. doi: 10.1002/jqs.1243

CrossRef Full Text | Google Scholar

Stumm, W., and Morgan, J. J. (1996). Aquatic Chemistry. 3rd edn. New York, NY: John Wiley & Sons.

Google Scholar

Stumm, W., and Wollast, R. (1990). Coordination chemistry of weathering: kinetics of the surface-controlled dissolution of oxide minerals. Rev. Geophys. 28, 53–69. doi: 10.1029/RG028i001p00053

CrossRef Full Text | Google Scholar

Taboada, T., and García, C. (1999). Pseudomorphic transformation of plagioclase during the weathering of granitic rocks in Galicia (NW Spain). Catena 35, 293–304. doi: 10.1016/S0341-8162(98)00108-8

CrossRef Full Text | Google Scholar

Trustrum, N. A., and de Rose, R. C. (1988). Soil depth-age relationships of landslides on deforested hillsides, Taranaki, New Zealand, Geomorphology 1, 143–160. doi: 10.1016/0169-555X(88)90012-8

CrossRef Full Text | Google Scholar

Turner, B. L., and Laliberté, E. (2015). Soil development and nutrient availability along a 2 million-year coastal dune chronosequence under species-rich Mediterranean shrubland in southwestern Australia. Ecosystems 18, 287–309. doi: 10.1007/s10021-014-9830-0

CrossRef Full Text | Google Scholar

Ugolini, F. C., Corti, G., Dufey, J. E., Agnelli, A., and Certini, G. (2001). Exchangeable Ca, Mg, and K of rock fragments and fine earth from sandstone and siltstone derived soils and their availability to grass. J. Plant Nutr. Soil Sci. 164, 309–315. doi: 10.1002/1522-2624(200106)164:3<309::AID-JPLN309>3.0.CO;2-8

CrossRef Full Text | Google Scholar

Urey, H. C. (1952). On the early chemical history of the earth and the origin of life. Proc. Nat. Acad. of Sci. 38, 351–363. doi: 10.1073/pnas.38.4.351

PubMed Abstract | CrossRef Full Text | Google Scholar

Van Andel, T. H., and Tzedakis, P. C. (1996). Palaeolithic landscapes of Europe and environs, 150,000-25,000 years ago: an overview. Quat. Sci. Rev. 15, 481–500. doi: 10.1016/0277-3791(96)00028-5

CrossRef Full Text | Google Scholar

West, A. J., Galy, A., and Bickle, M. (2005). Tectonic and climatic controls on silicate weathering. Earth Planet. Sci. Lett. 235, 211–228. doi: 10.1016/j.epsl.2005.03.020

CrossRef Full Text | Google Scholar

White, A. F., and Brantley, S. L. (2003). The effect of time on the weathering rates of silicate minerals. why do weathering rates differ in the lab and in the field? Chem. Geol. 202, 479–506. doi: 10.1016/j.chemgeo.2003.03.001

CrossRef Full Text | Google Scholar

White, A. F., Bullen, T. D., Vivit, D. V., Schulz, M. S., and Clow, D. W. (1999). The role of disseminated calcite in the chemical weathering of granitoid rocks. Geochim. Cosmochim. Acta 63, 1939–1953. doi: 10.1016/S0016-7037(99)00082-4

CrossRef Full Text | Google Scholar

White, A. G., Blum, A. E., Schulz, M. C., Bullen, T. D., Harden, J. W., and Peterson, M. L. (1996). Chemical weathering rates of a soil chronosequence on granitic alluvium: I. quantification of mineralogical and surface area changes and calculation of primary silicate reaction rates. Geochim. Cosmochim. Acta 60, 2533–2550. doi: 10.1016/0016-7037(96)00106-8

CrossRef Full Text | Google Scholar

Wilkinson, D., and Willemsen, J. (1983). Invasion percolation: a new form of percolation theory. J. Phys. A Math. Gen. 16, 3365–3376. doi: 10.1088/0305-4470/16/14/028

CrossRef Full Text | Google Scholar

Winograd, I. J., Coplen, T. B., Landwehr, J. M., Riggs, A. C., Ludwig, K. R., Szabo, B. J., et al. (1992). Continuous 500,000-year climate record from vein calcite in devils hole, nevada. Science 258, 255–260. doi: 10.1126/science.258.50

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, F., Faybishenko, B., Hunt, A. G., and Ghanbarian, B. (2017). A simple model of the variability of topsoil depths. Water 9:460. doi: 10.3390/w9070460

CrossRef Full Text | Google Scholar

Yu, F., and Hunt, A. G. (2017a). Damköhler number input to transport-limited chemical weathering and soil production calculations. ACS Earth Space Chem. 1,1, 30–38. doi: 10.1021/acsearthspacechem.6b00007

CrossRef Full Text | Google Scholar

Yu, F., and Hunt, A. G. (2017b). An examination of the steady-state assumption in certain soil production models with application to landscape evolution. Earth Surf. Process. Landf. 42, 2599–2610. doi: 10.1002/esp.4209

CrossRef Full Text | Google Scholar

Yu, F., and Hunt, A. G. (2017c). Predicting soil formation on the basis of transport-limited chemical weathering. Geomorphology 301, 21–27. doi: 10.1016/j.geomorph.2017.10.027

CrossRef Full Text | Google Scholar

Zachos, J., Pagani, M., Sloan, L., Thomas, E., and Billups, K. (2001). Trends, rhythms, and aberrations in global climate 65 Ma to present. Science 292, 686–693. doi: 10.1126/science.1059412

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhong, L., Liu, C., Zachara, J. M., Kennedy, D. W., Scezcody, J. E., and Wood, B. (2005). 1180 Oxidative remobilization of biogenic Uranium(IV) precipitates: Effects of Iron(II) 1181 and pH. J. Environ. Qual. 34, 1763–1771. doi: 10.2134/jeq2005.0057

CrossRef Full Text | Google Scholar

Zollinger, B., Alewell, C., Kneisel, C., Brandova, D., Petrillo, M., Plötze, M., et al. (2017). Soil formation and weathering in a permafrost environment of the Swiss Alps: a multi-parameter and a non-steady-state approach. Earth Surface Processes and Landforms 42, 814–835. doi: 10.1002/esp.4040

CrossRef Full Text | Google Scholar