Groundwater Contaminant Transport: Prediction Under Uncertainty, With Application to the MADE Transport Experiment

Transport of solutes in porous media at the laboratory scale is governed by an Advection Dispersion Equation (ADE). The advection is by the fluid velocity U and dispersion by D_dL = Uα_dL, where the longitudinal dispersivity α_dL is of the order of the pore size. Numerous data revealed that the longitudinal spreading of plumes at field scale is characterized by macrodispersivity α_L, larger than α_dL by orders of magnitude. This effect is attributed to heterogeneity of aquifers manifesting in the spatial variability of the logconductivity Y. Modeling Y as a stationary random field and for mean uniform flow (natural gradient), α_L could be determined in an analytical form by a first order approximation in ${\sigma }_Y^2$ (variance of Y) of the flow and transport equations. Recently, models and numerical simulations for solving transport in highly heterogeneous aquifers (${\sigma }_Y^2>1$), primarily in terms of the mass arrival (the breakthrough curve BTC), were advanced. In all cases ergodicity, which allows to exchange the unknown BTC with the ensemble mean, was assumed to prevail for large plumes, compared to the logconductivity integral scale. Besides, the various statistical parameters characterizing the logconductivity structure as well as the mean flow were assumed to be known deterministically. The present paper investigates the uncertainty of the non-ergodic BTC due to the finiteness of the plume size as well as due to the uncertainty of the various parameters on which the BTC depends. By the use of a simplified transport model we developed in the past (which led to accurate results for ergodic plumes), we were able to get simple results for the variance of the BTC. It depends in an analytical manner on the flow parameters as well as on the dimension of the initial plume relative to the integral scale of logconductivity covariance. The results were applied to the analysis of the uncertainty of the plume spatial distribution of the MADE transport experiment. This was achieved by using the latest, recent, analysis of the MADE aquifer conductivity data.

1. Introduction

Aquifers pollution by various contaminants constitutes a major threat to fresh water resources all over the world. Unlike the accessible surface water bodies, groundwater pollution is detectable by wells which cover a limited zone and often respond after a large portion of the aquifer is already contaminated. Furthermore, the process is slow, occurring over periods of tens of years and cleaning by natural attenuation or remediation, whenever possible, is also slow. Under these circumstances, transport mathematical models, which may help analyzing field findings on one hand and predicting solute future spreading on the other, are of crucial importance.

There are various modes of quantification of transport. In this study we focus on characterization of solute plumes longitudinal spreading by the BTC (breakthrough curve) M(x, t) at vertical control planes located at longitudinal distance x = const, normal to the mean flow direction. An alternative and related measure is the longitudinal mass distribution m(x, t) as function of distance x, for a given time t. We limit the scope to inert solutes (tracers) and to constant mean head gradient J (natural gradient flow), a setup of interest for many applications and an essential first step toward analysis of more complex configurations. For the benefit of the reader not familiarized with the groundwater transport theory, we recapitulate in the following a few essential developments.

The traditional modeling of transport was based on column laboratory experiments (Bear, 1979) for which the macroscopic (at the pore, Darcy, scale) concentration C(x, t) satisfies the advection dispersion equation (ADE)

$\begin{array}{ll}\frac{\partial C}{\partial t}+U\frac{\partial C}{\partial x}=D_{dL}\frac{{\partial }^{2}C}{\partial x^2}& (1)\end{array}$

where U = q/n is the macroscopic flow velocity (q-specific discharge, n-effective porosity) at the Darcy's scale and D_dL is the longitudinal dispersion coefficient. For the large Peclet number Pe₀ = Ud/D₀ (d-pore scale, D₀-molecular diffusion coefficient) encountered in applications it was found that D_dL = α_dLU, where α_dL is the pore scale dispersivity, of order d (Bear, 1979).

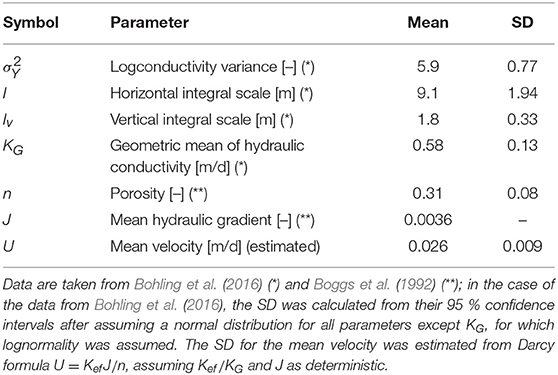
Field findings (for a recent compendium see Zech et al., 2015) have revealed that the longitudinal α_L (derived for instance with the aid of the spatial moments of aquifer plumes) is larger than α_dL by orders of magnitude; α_L was coined as longitudinal macrodispersivity in the literature. The contrast has been attributed to the impact of aquifers heterogeneity, manifesting primarily in the spatial variation of the hydraulic conductivity K(x). For illustration we present in Figure 1 the spatial distribution of Y = ln K in a cross section of the Columbus Air Force Base aquifer, where the MAcro Disperion Experiment (MADE) took place (Boggs and Rehfeldt, 1990; Boggs et al., 1992). It was obtained by interpolating among the measured values provided by Bohling et al. (2012) at a relatively dense set of points. A few significant features of the aquifer in Figure 1 are worth mentioning: (i) K varies by orders of magnitude, (ii) the spatial distribution of K is seemingly erratic and difficult to be captured by smooth interpolators, (iii) the zones of different K are elongated in the horizontal direction, the aquifer being coined as anisotropic at the field scale (notice that for clarity of representation the scale of reduction is smaller in the vertical direction with respect to the horizontal one, such that these zones are more elongated than how they appear in the figure).

FIGURE 1

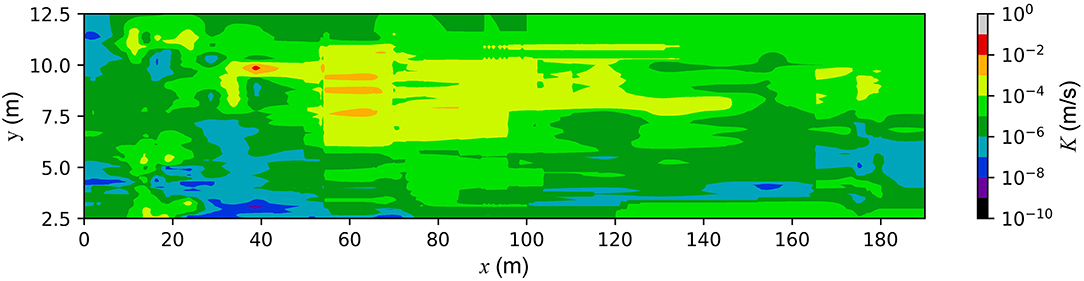
Figure 1. The spatial distribution of Y = ln K in a cross section of the Columbus Air Force Base aquifer, where the MADE transport experiment took place (Boggs and Rehfeldt, 1990; Boggs et al., 1992). It is seen that K = exp(Y) has anisotropic structure and varies by several orders of magnitude.

The above features have a dramatic impact upon the spreading of plumes of solutes. For illustration we represent in Figure 2 the concentration spatial distribution obtained by a numerical solution of the advective transport equation (in 2D). The velocity field V(x) was derived by a numerical solution of the flow equation for a K field statistically similar to that of Figure 1, with logconductivity variance ${\sigma }_Y^2=6$, under conditions of constant mean head gradient J. The transport equation was solved by using a Smooth Particle Hydrodynamic (SPH) scheme, which is virtually free of numerical diffusion (Boso et al., 2013), for Pe = I/α_dL = 1000 (I is the longitudinal integral scale of logconductivity).

FIGURE 2

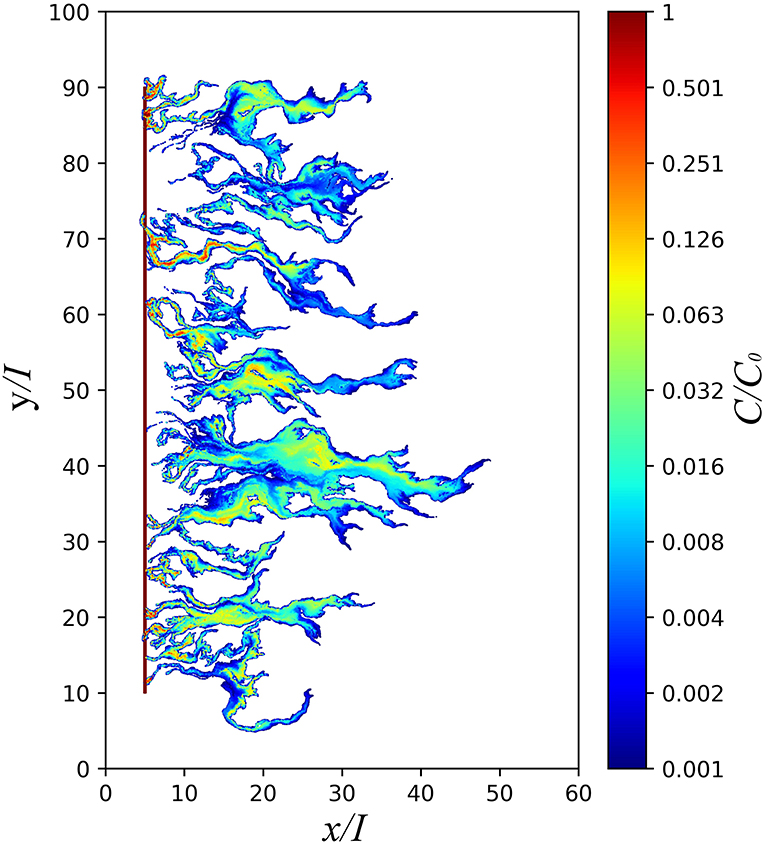
Figure 2. Numerically simulated concentration field (in 2D) after an instantaneous injection within a thin (linear) source perpendicular to mean flow (indicated by a red vertical line at x/I = 5, with I the longitudinal integral scale of logconductivity), of dimensions L_y = 80 I and L_x = 0.25 I at time tU/I = 10; the other parameters are ${\sigma }_Y^2=6$ and Pe = I/α_dL = 1000. The plume is seemingly erratic, with clear fingering patterns and stagnant regions.

A few qualitative features of distribution of C in Figure 2 are: (i) for an initial rectangular pulse of constant C = C₀, the plume becomes highly fragmented with time and of progressive spreading, (ii) the plume splits, with quicker advancing “fingers” in zones of high K , and practically stagnant solute in regions of low K, (iii) like the K field (see Figure 1) the plume is seemingly erratic and defies a representation by smooth functions but, at the same time, it makes the identification of point concentration at a given location an elusive goal, (iv) in contrast, global measures like the mass arrival at vertical planes over the entire domain (the BTC M) smooth out the variations and the extent of spreading can be quantified for instance by α_L, (v) it was found that the presence of the pore scale dispersion (primarily the vertical one) causes mixing which affects the local C, but has a minor effect on M (Fiori and Dagan, 2000) and (vi) space averages like M are the ones of interest in many applications, e.g., those in which the goal is to determine the mass of solute pumped by wells which intercept the plume (Fiori et al., 2016).

This state of affairs has motivated the emergence around 40 years ago (for a review see for instance the books by Dagan, 1989; Gelhar, 1993; Rubin, 2003) of a new discipline, namely stochastic subsurface hydrology. In its frame the hydraulic logconductivity field Y(x) is modeled as a stationary random space function whose univariate distribution and two point covariance are characterized by a few parameters: the geometric mean K_G, the variance ${\sigma }_Y^2$ and the horizontal I and the vertical I_v < I integral scales, respectively. As a consequence, the steady Eulerian velocity V(x), is also a random space function, of constant mean U(U, 0, 0). The statistics of V are obtained by solving the flow equations for conditions of constant mean head gradient J(J, 0, 0) and random K(x). Similarly the concentration field C(x,t) is random and so are its global measures like the BTC M(x, t). The latter is obtained by solving the transport equation with advection by the random V and dispersion by the local pore scale dispersion tensor. Unfortunately, heterogeneity renders point concentration C(x, t) highly uncertain with a coefficient of variation that is controlled by pore-scale dispersion and reduces slowly with time (Fiori and Dagan, 2000). Uncertainty reduces considerably when global measures are used, such as M(x, t), or the sampling volume has dimensions comparable with the integral scales of Y, thereby making the ensemble mean 〈C(x, t)〉 a reliable and robust measure, similarly to M (Bellin et al., 1994; Tonina and Bellin, 2008). If the point concentration is of interest, such as in risk assessment for example, uncertainty can be reduced by focusing on the probability that a given concentration threshold is exceeded, irrespective of the position where this occurs, rather than focusing on a given fixed location where the ensemble mean concentration provided a unreliable estimate (Bellin and Tonina, 2007). Another option is by conditioning on available data (e.g., Y, head, concentration etc), for which, however, several conditioning points are needed in order to significantly reduce uncertainty. In any case, as previously stated our study focuses on the BTC M which is relevant to many applications and is quite robust and less prone to uncertainty than point concentration.

A common adopted assumption is that transport is ergodic in the sense that M (or similar global attributes) in a realization can be exchanged with the ensemble mean 〈M〉. This is a basic tenet in many branches of physics and engineering, e.g., molecular diffusion driven by Brownian motion or effective properties of composite materials. It is justified by the large contrast between the microscopic length scales and the macroscopic ones of interest in applications. For groundwater transport ergodicity implies that the solute plume samples a sufficiently large aquifer volume compared to the integral scales so as to encounter zones of various K, representative of the entire population. Since typically I and I_v are of the order of meters and solute plumes of tens of meters, the contrast is not so large and ergodicity may be not obeyed and prediction of M by models is subjected to uncertainty. This feature differentiates transport by groundwater from the traditional pursuit of the effective properties solely, prevalent in the literature on heterogeneous media.

Similarly, it is common to assume in applications that the various parameters and variables like J, U, K_G, ${\sigma }_Y^2$, I are known. In reality, in the field they are only estimated and subjected to uncertainty as well, impinging on the uncertainty of M.

The aim of the present study is to provide a discussion of uncertainty in modeling transport in three-dimensional heterogeneous aquifers, with application to the MADE transport experiment (Zheng et al., 2011) as a platform for discussion; we summarize what we have learned in the last two decades or so, in view of applications, with a particular focus on uncertainty due to plume sampling (i.e., non-ergodicity) and incomplete knowledge of parameters that are both important for MADE. A novel analytical formulation is also proposed for assessing uncertainty due to lack of ergodicity by the plume. It is emphasized that this is not a review paper and we build primarily on our developments in modeling flow and transport in three-dimensional heterogeneous formations.

The plan of the paper is as follows: section 2 provides an overview of concepts development and paper aims, recapitulating some of our recent developments in transport of ergodic plumes; section 3 addresses the modeling of uncertainty in the prediction of the BTC, the main topic of the paper; section 4 presents the application of the uncertainty analysis to the MADE-1 experiment, relying on the latest published data; finally, section 5 summarizes and concludes the study.

2. Background and Mathematical Preliminaries

2.1. The K Structure

As already mentioned above, we limit the study to stationary random Y(x). For sedimentary formations of concern here, the histogram of Y = ln K was found to fit a normal univariate distribution f(Y), of mean 〈Y〉 = ln K_G and variance ${\sigma }_Y^2$ (see for instance the analysis of MADE data by Fiori et al., 2015; Bohling et al., 2016) which we adopt here. At the lowest order, the spatial structure is captured by the two point covariance $C_Y({\text{x}}_1,{\text{x}}_2)={\sigma }_Y^2\rho (\text{r})$ where ρ is the autocorrelation and r = x₁ − x₂ is the distance vector between the two points respect to which the covariance is computed. In turn, the assumed axisymmetric ρ is characterized by the finite horizontal I and vertical I_v integral scales, respectively. The Y field is often assumed to be multivariate normal (multi-Gaussian), and then the structure is completely characterized by 〈Y〉 and C_Y. This is a very convenient representation which is commonly adopted in numerical simulations or analytical approximations. For other types of structures higher multipoint correlations are required for a complete statistical characterization. Thus, in our past numerical simulations of 3D flow and transport (see for a summary our recent paper Jankovic et al., 2017) we have generated a few fields which share the same f(Y) and I, I_v but differ at higher order as manifested for instance by the spatial connectivity of zones defined by classes of K. Thus, we considered besides the multivariate normal (multi-Gaussian) one, two Y fields devised by Zinn and Harvey (2003), obtained by transformations which led to more connected or disconnected zones of large conductivity. Besides, we investigated extensively flow and transport in a structure we coined as MIM (Multi-Indicator-Model): rectangular blocks which tessellate the space or spheroidal inclusions of dimensions 2I in the horizontal and 2I_v in the vertical directions, respectively, and are of independent K = exp(Y). Unlike the three previous ones, the connectivity of different classes of K values is the same.

It is worthwhile to note that even for thoroughly monitored aquifers like that of MADE, field data do not generally allow for determining statistical parameters beyond f(Y) and ρ, i.e., K_G, ${\sigma }_Y^2$, I, and I_v and even those are estimated within ranges of values.

2.2. Flow

We consider here steady flow governed by

$\begin{array}{l}q=-K\nabla h(\text{Darcy’s law}),\\ \nabla ·q=0(\text{continuity})\to \nabla ·(K\nabla h)=\text{0}& (2)\end{array}$

where h(x) is the head. With the assumed constant porosity n (which is much less variable than K), the velocity V also satisfies ∇ · V = 0. The boundary condition of interest here is the one of constant head, such that the head gradient has components J(J, 0, 0). Consequently the mean velocity U(U, 0, 0) is also constant and its fluctuation u(x) is stationary. The relationship U = K_efJ/n defines the effective conductivity and its dependence on the structural parameters is the subject of a vast literature (see e.g., Renard and De Marsily, 1997).

Analytical approximate solutions of the statistics of the h and V fields, as well as K_ef, were obtained in the literature (e.g., Dagan, 1989; Rubin, 2003) by a first order approximation in ${\sigma }_Y^2$, presumably valid for weak heterogeneity. In contrast, based on numerical simulations, with values of the logconductivity variance up to ${\sigma }_Y^2=8$, we have recently presented (Zarlenga et al., 2018) the dependence of the K_ef components on ${\sigma }_Y^2$ for different e = I_v/I and for the above different structures, as well as by the first order approximation. A striking result is that the first order approximation of the horizontal component K_efh is quite accurate for ${\sigma }_Y^2<2$, which reinforces what already observed for the velocity covariance function and the spatial plume moments in an early works by Bellin et al. (1992) and Salandin and Fiorotto (1998).

2.3. Transport (General)

We consider injection of a solute over an area A₀ in the plane at x = 0. A thin plume with total mass M₀ is modeled as a Dirac pulse of infinitesimal duration δ(t) at x = 0 (extension to arbitrary spatial or temporal initial distributed plumes is straightforward); following the definitions of Kreft and Zuber (1978) injection may be in resident or flux proportional mode. Thus, the initial mass density m₀ = dM₀/db is constant and equal to M₀/A₀ for uniform initial resident concentration while it is given by the variable and random m₀(b) = [V₀(b)/${\overline{V}}_0$](M₀/A₀) for the flux proportional one. Here b(b_y, b_z) is a coordinate in A₀, V₀(b) = V_x(0, b_y, b_z) and ${\bar{V}}_0=(1/A_0){\int }_{A_0}{V}_0(\text{b})d\text{b}$ is the mean velocity over A₀, which for sufficiently large A₀ is equal to the mean velocity U.

We adopt the boundary condition of flux proportional initial condition which applies to many cases e.g., injection by wells as it was the case for field experiments including MADE. It simply states that solutes initially occupy preferential zones of high conductivity. We also adopt the detection in the flux proportional mode (Kreft and Zuber, 1978), i.e., the BTC defined by $M(x,t)=M_0-{\int }_0^x\int \int nC(x,y,z,t)dxdydz={\int }_0^{t}dt\int \int n{V}_x(x,y,z)C(x,y,z,t)dydz$, where integration in y, z is over the cross section of the domain. The issue related to injection and detection conditions and their impact on transport was extensively discussed in past work (see e.g., Kreft and Zuber, 1978; Dagan, 2017; Fiori et al., 2017). If it satisfies the ADE (1) with initial condition M(0, t) = M₀H(t) (where H is the Heaviside step function), the solution for the semi-bounded domain is given by the CDF of the Inverse Gaussian (IG) distribution (Kreft and Zuber, 1978):

$\begin{array}{ll}\frac{M(x,t)}{M_0}=\frac{1}{2}\left\{\text{erfc }\left[\frac{x-Ut}{2{(D_{L}t)}^{1/2}}\right]+\text{exp }\left(\frac{Ux}{D_L}\right)\text{ erfc }\left[\frac{x+Ut}{2{(D_{L}t)}^{1/2}}\right]\right\}& (3)\end{array}$

with D_L the longitudinal macrodispersion coefficient, whereas the relative mass flux is given by the Inverse Gaussian (hereinafter IG) distribution

$\begin{array}{ll}\frac{\mu (x,t)}{M_0}=\frac{1}{M_0}\frac{\partial M}{\partial t}=\frac{x}{2{(\pi D_L{t}^3)}^{1/2}}\text{exp }\left[\frac{{(x-Ut)}^2}{4D_{L}t}\right]& (4)\end{array}$

In the frame of random walk transport theory, the Inverse Gaussian distribution pertains to a first arrival process (see, e.g., Redner, 2001), i.e., the detection plane at x serves as an absorbing boundary. Note that IG is a special case of the more general Tempered One-Sided Stable distribution (TOSS) with exponent 1/2 (Cvetkovic, 2011).

We proceed now with reviewing the results we obtained recently for ergodic transport in heterogeneous aquifers.

2.4. Transport (Summary of Results for Ergodic Plumes)

The starting point for our recent developments are the systematic accurate numerical simulations (see Jankovic et al., 2017, and reference therein) of flow and transport in 3D; they are recapitulated in the Appendix of Jankovic et al. (2017) and only briefly here. The K field was generated for a lognormal univariate distribution and two point covariances C_Y of integral scales I and I_v, with different values of the anisotropy coefficient e = I_v/I. The complete characterization of the structures was achieved by a variety of different models: multi-Gaussian, the previously mentioned connected and disconnected fields, spheroidal inclusions and rectangular blocks tessellating the space (MIM). The BTC was finally calculated by large-scale numerical simulations, for a variety of parameters (logconductivity variance, Peclet number, control plane distances etc.).

A striking result (Jankovic et al., 2017, Figure 3) was that for the various structures the bulk of M (say M/M₀ < 0.95) did not differ significantly among structures, proving indeed that M is a very robust measure. Furthermore, the simple model (3), with the macrodispersivity given by the well-known first-order approximation D_L = α_LU, ${\alpha }_L={\sigma }_Y^{2}I$, agreed well with the bulk of the BTC derived numerically (Fiori et al., 2017) while it underestimated the late arrival time of the tail of a few percents of M. However, the tail prediction is anyway quite imprecise. In particular, it was found that the IG model behaves similar to the MIMSCA (Multi Indicator Model Self Consistent Approximation) that we developed in the last 20 years (e.g., Dagan et al., 2003; Fiori et al., 2007), that is more accurate for the prediction of late mass arrival.

FIGURE 3

Figure 3. Comparison of the proposed solution (11) with the results of Cvetkovic et al. (1992) (Figure 5C), for ${\sigma }_Y^2=0.5$, x/I = 20 and a few values of the size of the initial plume (L_y/I = L_z/I = ${H}$). The figure displays the cumulative mass M and the bands M ± σ_M predicted by the present approach (blue lines) over the original Figure 5C of Cvetkovic et al. (1992).

Thus, the IG model (3) is quite effective in capturing the behavior of the bulk of the BTC, for a wide range of flow and transport parameters; the model depends on a few parameters characterizing the permeability structure (${\sigma }_Y^2,I$) and the flow (J, K_ef). It is emphasized that the first-order approximation was applied to deriving the longitudinal macrodispersivity α_L while M(x, t) (3) itself depends non-linearly on ${\sigma }_Y^2$ and is different from the Gaussian distribution; the two coalesce for small ${\sigma }_Y^2$ or large tU/I.

Summarizing, the simple formula (3), with D_L given by the first-order approximation, is a very robust model that can be safely used in applications, e.g., as a screening tool for a preliminary assessment of the BTC. We note that a similar, simple approach, although with parameters based on numerical simulations, was proposed by Hansen et al. (2018).

We move now to the central topic of the present study, the uncertainty of prediction of the BTC.

3. Uncertainty of BTC Predictive Modeling

3.1. A Few Sources of Uncertainty

Transport predictions by the above modeling approach is prone to several sources of uncertainty, the major ones being:

(i) Uncertainty in medium characterization, and its representation in general. Field data are generally scarce and even the identification of fundamental and basic quantities like K_G (geometric mean of K) and ${\sigma }_Y^2$ is difficult and error prone. This is even more true for higher order measures, like e.g., the covariance (or variogram) and I, based on the assumption of stationarity which is also hard to validate. As a matter of fact, multipoint correlations are needed for a full characterization of K, which is a prohibitive task for applications (Boso and Tartakovsky, 2016). Alternative models like facies identification by using the indicator variogram (Ritzi, 2000) requires identification of zones of connectivity of K classes, which again is feasible only for highly monitored aquifers. Fortunately, global measures like 〈M〉 are quite robust in 3D and adopting for instance the common multi-Gaussian structure model does not affect significantly the bulk of the BTC (Bianchi and Pedretti, 2017, 2018).

(ii) Uncertainty due to the limited domain sampled by the plume. Thus, the initial plume may not be so large, as discussed in the previous section, and non-ergodicity issues may emerge (Kitanidis, 1988; Dagan, 1990; Andričević and Cvetković, 1998; Attinger et al., 1999). As a consequence, the quantities of interest, including M, are random, and uncertain due to non-ergodic behavior emerges. As it was found in the past and confirmed by the developments of the following section, uncertainty for small plumes can be quite large. Instead, the uncertainty related to the size of the sampling volume (Fiori et al., 2002; Bellin and Tonina, 2007; Severino et al., 2010) is not relevant for the transport scenario investigated here in which solute is detected at a large control plane at distance x from the source.

(iii) Uncertainty in the modeling approach. This is a highly debated issue in the literature, and various models have been advanced during the years. However, our recent developments summarized in the previous section, based on accurate and systematic 3D numerical simulations which were not available in the literature for the high ${\sigma }_Y^2$ values, show that for global, upscaled, measures like 〈M〉, the ADE with upscaled first-order longitudinal macrodispersivity ${\alpha }_L={\sigma }_Y^{2}I$, solved under the conditions of flux proportional injection and detection, offers a simple and quite accurate, physically based solution.

(iv) Parametric uncertainty. Besides the uncertainty of the adopted K model, the same is true for the other hydrological parameters controlling transport, like e.g., the mean velocity. Parametric uncertainty is expected to have an important impact on predictions because of the limitations of measurements and the significant impact of parameters, like U.

(v) Additional uncertainty may stem from unsteadiness, spatial non-uniformity of the mean head gradient, partial knowledge of the plume initial condition etc. These sources of uncertainty are rather case specific and less prone to a general analysis (see e.g., Bellin et al., 1996; see e.g., Dagan et al., 1996).

According to the above discussion, the major sources of uncertainty for transport in mean uniform flow are likely (ii) and (iv), i.e., possible non-ergodicity of the plume and parametric uncertainty; this is particularly true for the MADE experiment, as shown in the sequel. Thus, in the following we shall focus on the uncertainty quantification originating from (ii) and (iv). Furthermore, we shall apply the uncertainty analysis to MADE, that is a well-known benchmark, very useful for a thorough discussion on uncertainty in applications.

3.2. Quantifying Uncertainty Due to Non-ergodic Effect

3.2.1. General

We follow here the theoretical framework and the notations of Cvetkovic et al. (1992) and Dagan et al. (1992). Focusing on the BTC M we may write for flux proportional injection over an area A₀

$\begin{array}{ll}\frac{M(t;x)}{M_0}=\frac{1}{A_0}{\displaystyle {\int }_{A_0}\frac{V_0(b)}{{\overline{V}}_0}}H[t-\tau (x,b)]db& (5)\end{array}$

where we remind that V₀ is the local velocity at the location b within A₀ and ${\bar{V}}_0=(1/A_0){\int }_{A_0}{\bar{V}}_0(\text{b})d\text{b}$ ≈ U. It is also reminded that in (5) H is the Heaviside step function and τ(x, b) is the random travel time to the control plane at x of a fluid particle injected at x = 0 within A₀. The travel time is related to the random velocity field by dτ/dx = ${(V_x\left[x,\eta (x),\zeta (x)\right])}^{-1}$ where y = η(x, b), z = ζ(x, b) are the equations of a streamline originating at b within the plane A₀ at x = 0. In words, (V₀(b)/${\overline{V}}_0$) H[t − τ(x, b)](db/A₀) in Equation (5) marks the contribution of the particle originating at b to the mass that crossed the control section at x until the time t = τ.

The expected mass 〈M(t; x)〉 is easily calculated from (5), yielding

$\begin{array}{ll}\frac{\langle M(t;x)\rangle }{M_0}=\frac{1}{A_0}{\displaystyle \langle {\displaystyle {\int }_{A_0}\frac{V_0(b)}{{\overline{V}}_0}}H[t-\tau (x,b)]db\rangle }=G_1\left(t;x\right)& (6)\end{array}$

where $G_1={\int }_0^{t}f(\tau )d\tau$, is the cumulative travel time distribution, where τ is weighted by the injection velocity V₀ (Cvetkovic and Dagan, 1994). Here f(τ) = ∫ (V₀) f (τ, V₀)d(V₀) is the marginal pdf of τ, with f (τ, V₀) being the joint pdf of τ and V₀.

Formula (6) is the well-known result (Shapiro and Cvetkovic, 1988) that the mean mass arrival is the CDF of travel time. Furthermore, in view of the findings of section 2.3, it is seen that G₁(τ) is the CDF of the Inverse Gaussian distribution Equation (3) and the pdf g₁ = dG₁/dτ is the Inverse Gaussian (4).

After recapitulating these preparatory steps we move now, along Dagan et al. (1992), to the derivation of the variance of M

$\begin{array}{ll}\frac{{\sigma }_M^2(t;x)}{M_0^2}=\langle \frac{M^2(t;x)}{M_0^2}\rangle -\frac{{\langle M(t;x)\rangle }^2}{M_0^2}& (7)\end{array}$

Considering the expression (5) for the mass M we may write

$\begin{array}{l}\langle \frac{M^2(t;x)}{M_0^2}\rangle =\frac{1}{A_0^2}\langle {\displaystyle {\int }_{A_0}{\displaystyle {\int }_{A_0}\frac{V_0(b)V_0(b^{\prime })}{{\overline{V}}_0^2}}}\\ H[t-\tau (x,b)]H[t-\tau (x,b^{\prime })]dbd{b}^{\prime }\rangle & (8)\end{array}$

Thus, by taking advantage of the linearity of the ensemble mean operator and considering Equation (6) we arrive at

$\begin{array}{ll}\frac{{\sigma }_M^2(t;x)}{M_0^2}=\frac{1}{A_0^2}{\displaystyle {\int }_{A_0}{\displaystyle {\int }_{A_0}{G}_2}}\left(t;x,b-b^{\prime }\right)dbd{b}^{\prime }-G_1^2\left(t;x\right)& (9)\end{array}$

where G₂ is the bivariate travel time CDF, which is given by $G_2(t;x,\text{b}-{\text{b}}^{\prime })$ = ${\int }_0^t{\int }_0^t{g}_2(\tau ,{\tau }^{\prime };x,{\text{b}-\text{b}}^{\prime })d\tau d{\tau }^{\prime }$, with $g_2(\tau ,{\tau }^{\prime };x,\text{b}-{\text{b}}^{\prime })$ being the marginal joint pdf of travel times τ, τ′of two particles injected at b and b′, respectively.

The general result (9) by Dagan et al. (1992) has served Cvetkovic et al. (1992) to effectively compute ${\sigma }_M^2(x,t)$ by adopting a few assumptions: the bivariate g₂ is lognormal, the travel time moments were derived from the velocity field by a first order approximation in ${\sigma }_Y^2$, A₀ is a square. Two quadratures, which were carried out numerically, were needed to complete the derivation.

The above approach can be generalized to compute the covariance of M (C_M) at two different times t₁, t₂, leading to

$\begin{array}{l}\frac{C_M\left(t_1,t_2;x\right)}{M_0^2}=\frac{1}{A_0^2}{\displaystyle {\int }_{A_0}{\displaystyle {\int }_{A_0}{G}_2}}\left(t_1,t_2;x,b^{\prime }-b^{″}\right)d{b}^{\prime }d{b}^{″}\\ -G_1(t_1;x)G_1(t_2;x)& (10)\end{array}$

with $G_2(t_1,t_2;x,\text{b}-{\text{b}}^{\prime })={\int }_0^{t_1}{\int }_0^{t_2}{g}_2(\tau ,{\tau }^{\prime };x,{\text{b}-\text{b}}^{\prime })d\tau d{\tau }^{\prime }$.

3.2.2. Simplified Derivation of ${\sigma }_M^2(x,t)$ and Comparison With Numerical Simulations

The derivation of the two particles covariance needed in (9) is complex and requires additional information, like e.g., the shape of the two particles covariance and its moments. Also, the calculation of ${\sigma }_M^2$ along (9) requires a few numerical quadratures, as done by Cvetkovic et al. (1992). We simplify the calculations by using the basic properties of the MIMSCA model which, as mentioned above, led to very good agreement with the numerical solution of 〈M〉.

Consider the covering of the input area A₀ by rectangles of sides 2I and 2I_v in the y and z directions, respectively. Following the MIMSCA model, the travel time of particles originating within an areal element in A₀ is the same whereas they are statistically independent for particles originating from different elements. This is the only property we use in the present derivation.

With the above assumption, the calculation of (9) can be considerably simplified. The detailed derivations are given in Appendix A, leading to the final result (A.8), that is reproduced here

$\begin{array}{ll}{\sigma }_M^2=M_0^2\omega \left(L\right)G_1\left(t;x\right)\left[1-G_1\left(t;x\right)\right]& (11)\end{array}$

where the weight function ω is given by

$\begin{array}{ll}\omega \left(L\right)=\Omega \left(\frac{L_y}{I}\right)\Omega \left(\frac{L_z}{I_v}\right)& (12)\end{array}$

with L_y, L_z the sides of the rectangular injection area, i.e., A₀ = L_yL_z and

$\begin{array}{ll}\Omega \left(\ell \right)=\{\begin{array}{c}\left(1-\frac{\ell }{6}\right)\text{ for }\ell <2\\ \frac{1}{\ell }\left(2-\frac{4}{3\ell }\right)\text{ for }\ell >2\end{array}& (13)\end{array}$

In particular ω ≃ 1 for A₀/(II_v) ≪ 1 (maximal uncertainty for small source) and ω ≃ (II_v/A₀) for A₀/(II_v) ≫ 1 (ergodic, practically deterministic).

Thus, ${\sigma }_M^2$ is given by an analytical expression supposed to apply to highly heterogeneous formations which separates the effect of spreading represented by the IG G₁ (3) with $D_L={\sigma }_Y^{2}IU$, one hand, and the weight function ω accounting for the size of the injection area on the other hand.

As a first test of (11) we compare it in Figure 3 with the results of Cvetkovic et al. (1992) described above (${\sigma }_Y^2=0.5$, x/I = 20, L_y/I = L_z/I = ${H}$) and it is seen that the agreement if very good in spite of the different methodologies. A more stringent test is carried out by comparison with the numerical simulations of Jankovic et al. (2017), which were carried out for single realizations for the large ${H}$ = L_y/I = L_z/I = 90. This was achieved by dividing A₀ in subdomains of ${H}\simeq 2,5,10,15,30$ regarded as independent realizations, a proxy for Monte Carlo simulations. The results are displayed in Figure 4, where both the BTC and its standard deviation (SD) for the multivariate normal field at two Control Plane distances (6I and 18I) are represented. The SD predictions by the simplified model (11) are also displayed (dashed lines). It is seen that, in spite of the limited number of realizations for some cases (9 for L_y = L_z = 30I) the agreement is quite good, even for the largest ${\sigma }_Y^2=8$. The behavior is very similar for other K structures examined (e.g., connected/disconnected and blocks, as described in section 2.4; not shown in the figure). Thus, the simple model proposed here can be an effective tool for the prediction of the BTC uncertainty due to the non-ergodic effect (i.e., finite size of the plume compared to the heterogeneity length scales).

FIGURE 4

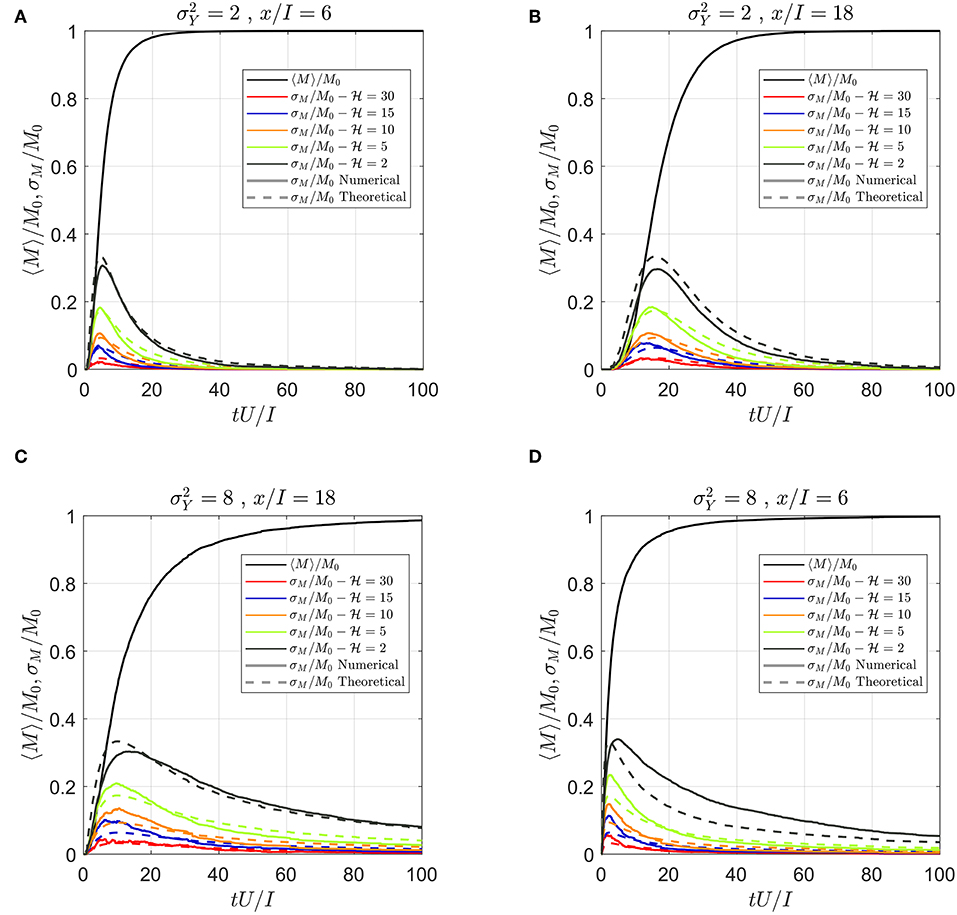
Figure 4. Comparison of solution (11) with the numerical simulations of Jankovic et al. (2017), which were carried out for single realizations and a large source ${H}$ = L_y/I = L_z/I = 90. The comparison is achieved by dividing the initial plume in subdomains of ${H}=2,5,10,15,30$ regarded as independent realizations, a proxy for Monte Carlo simulations. The BTC M and its standard deviation (SD) for the multivariate normal field at two Control Plane distances (6I and 18I) and two degrees of heterogeneity (${\sigma }_Y^2=2$ and ${\sigma }_Y^2=8$) are represented. The SD predictions by the simplified model (11) are represented by the dashed lines.

It is worthwhile noting that for a small plume (ω close to unity) uncertainty affects its time of arrival at the control plane (de Barros et al., 2011; de Barros, 2018). In contrast, for a large plume the practically deterministic prediction reflects the spreading of the BTC. For intermediate cases the two effects are combined, and they are incorporated in the simple function ω (12).

3.3. Impact of Parametric Uncertainty

Even under the basic assumptions of stationarity, steadiness and mean flow uniformity the mean BTC (Equation 3 with $D_L={\sigma }_Y^{2}IU$) depends on a few parameters. Thus, U = JK_ef/n depends, besides the mean gradient J, on K_G and ${\sigma }_Y^2$ since K_ef/K_G depends on ${\sigma }_Y^2$ as well as on the structure (Renard and De Marsily, 1997). Of course the knowledge of these parameters is not needed if K_ef is determined for instance directly by pumping tests and/or U by flowmeters. In all cases these parameters are affected by uncertainty due to measurement errors, insufficient data etc. The same is true for the parameters influencing the mean BTC namely ${\sigma }_Y^2$ and I besides U. Finally, the uncertainty quantified by ${\sigma }_M^2$ (11) depends on the additional parameter A₀, reflecting the initial size of the plume.

The uncertainty of these parameters impacts that of M in addition to the non-ergodic effect. However, the magnitude depends on the availability of data and their precision, which is aquifer specific. In the following section we shall examine the impact of parametric uncertainty for the Columbus Air Force Base aquifer where the MADE experiment took place and for which a relatively large amount of data is available.

Nevertheless, we may make a few statements on the relative impact of various parameters based on the numerical simulations and theoretical developments. Thus, as mentioned above, Fiori et al. (2017) and Jankovic et al. (2017) have already found that 〈M〉 is quite insensitive to the structure (as characterized by connectivity), whereas U, and to a lesser extent heterogeneity ${\sigma }_Y^2$, has a larger impact. Rather than a general discussion we defer the analysis to the MADE case in the following.

4. Analysis of the Mass Distribution at the MADE-1 Experiment

The first experiment conducted at the Columbus Air Force Base (MADE-1) represents the ideal platform for discussing the above issues regarding uncertainty of solute transport predictions in aquifers. In terms of the quantity and quality of investigations, regarding both aquifer characterization and plume monitoring, the MADE-1 experiment represents a benchmark for analyzing groundwater transport; it has motivated a large body of research work, from the testing of innovative measuring techniques to the development of novel theoretical frameworks. For such reasons, after more than 30 years, MADE is still providing insight and topics of discussion in the scientific community, as witnessed for instance by the recent 2015 AGU Chapman conference (Gómez-Hernández et al., 2016). Before discussing uncertainty, along the previous lines, we briefly recapitulate in the following the main features of the MADE-1 experiment, as well as the flow and transport parameters that shall be used in the present work, together with their uncertainty measures. More details can be found in the original papers (Boggs and Rehfeldt, 1990; Boggs et al., 1992) and the review (Zheng et al., 2011).

The experiment took place in a highly heterogeneous sedimentary aquifer at Columbus, Ohio (USA). A plume was injected in a relatively small area of the domain, and the plume movement, along the natural gradient, was continuously monitored for about 2 years by a dense network of multilevel samplers. The relevant transport quantity that was analyzed at the MADE-1 experiment is the longitudinal mass distribution m(x; t), which was first analyzed and presented by Adams and Gelhar (1992). Six snapshots were analyzed, at t = 49, 126, 202, 279, 370, 503 days since injection. The mass distribution was derived by calculating the solute mass (after interpolation of concentration measurements) within a moving window of 10 m length, at spatial intervals of 5 m. The striking feature of m is its skewed shape, very much different from the presumed symmetrical Gaussian behavior, that was mainly caused by the highly heterogeneous velocity field induced by the complex aquifer system; such feature has motivated subsequently a flurry of theoretical developments to explain it. Despite this dense grid of samplers, mass recovery was incomplete, except for the snapshot at t = 126 d, and the mass recovery continuously decreased after it, down to 43% in the last snapshot at t = 503 d [the topic is discussed by Fiori (2014)].

In the following, the longitudinal mass distribution at MADE is modeled by the aid of the model (3). Following Adams and Gelhar (1992), the mass distribution is calculated within a moving window of Δ = 10m, i.e., m(x; t) = (M(x + Δ/2; t) − M(x − Δ/2; t))/Δ, with space intervals of 5m (x = 0, 5, 10, 15, …). The parameters to be used in the model were inferred from different studies and are presented in Table 1; the standard deviation (SD) is also reproduced, when available. Of particular relevance is the analysis of Bohling et al. (2016) of the K values based on DPIL measurements, that superseded a previous analysis by same authors (Bohling et al., 2012). This study analyzed the conductivity field at an unprecedented detail and resolution, and constitute the best available conductivity analysis of MADE data so far.

TABLE 1

Table 1. Mean and standard deviation (SD) for the MADE-1 parameters employed in the present work.

The mean velocity is calculated by U = K_GJϵ/n, with K_G, J, n, ϵ the geometric mean of K, the mean hydraulic gradient, the mean porosity and the effective conductivity ratio ϵ = K_ef/K_G, respectively. Unfortunately, ϵ cannot be measured and it is variable, as a function of the particular conductivity structure at hand (the matter is discussed in Zarlenga et al., 2018). An estimate of ϵ was provided by the formula (5) derived by Zarlenga et al. (2018) based on extensive 3D numerical simulations, obtaining ϵ = 3.93; this results in the estimated U = 0.026 m/d. The SD of U is calculated by a perturbation approach over the parameters K_G, n, hence assuming J and ϵ as deterministic; as a consequence, the standard deviation of U appearing in Table 1 is likely underestimated.

4.1. Prediction of Mass Distribution and Uncertainty Due to Non-ergodic Effects

Before embarking on the analysis of the spatial mass distribution (the snapshots), it is worthwhile to estimate the non-ergodic effect on the uncertainty of the BTC M(x, t), although the latter was not determined experimentally. According to Equation (11) the maximal value of σ_M/M₀ is obtained by differentiating with respect to t and is reached for G₁ = 1/2. This leads to (σ_M/M₀)_max = ω^1/2/2. We show in the sequel that for MADE plume initial size the estimate is ω = 0.148, i.e., (σ_M/M₀)_max = 0.19. Thus, the width of the band 〈M〉/M₀ ± σ_M/M₀ reaches its maximum at the time for which 〈M〉/M₀ = 1/2 and its size is ±0.19. diminishing to zero for 〈M〉/M₀ → 0, 1. However, a direct comparison with the experimental results (the snapshots) needs reformulation in terms of spatial distribution.

Along the lines of section 4, the longitudinal mass distribution at MADE is given by

$\begin{array}{ll}m\left(x;t\right)=\frac{M\left(x+\Delta /2;t\right)-M\left(x-\Delta /2;t\right)}{\Delta }& (14)\end{array}$

where m is the longitudinal mass distribution aggregated over the spatial interval Δ = 10 m.

The expected value and variance of m for non-ergodic plumes can be derived with the same procedure of section 3.2.2 , and detailed in Appendix A. The detailed derivations are given in Appendix B, and we reproduce here the final result

$\begin{array}{l}\frac{\langle m\left(x;t\right)\rangle }{M_0}=\frac{G_1\left(x+\Delta /2;t\right)-G_1\left(x-\Delta /2;t\right)}{\Delta }\\ {\sigma }_m^2(x;t)=\omega \left(L\right)\langle m(x;t)\rangle \left(\frac{M_0}{\Delta }-\langle m(x;t)\rangle \right)& (15)\end{array}$

In (15), G₁ is given by (3), as previously explained, although any alternative model can be used. As discussed in Fiori et al. (2017), the time of the snapshots at the MADE experiment was very small in dimensionless terms, namely tU/I = 0.15 − 1.0, posing doubts regarding the use of a constant D_L in (3). Therefore, the pre-asymptotic D_L, as predicted by the first order approximation, was employed here; the issue is discussed in Fiori et al. (2017) and it is further elaborated in Appendix C, leading to the revised formula (C.3), for the travel time CDF G₁ that shall be used in the present analysis.

The formula (15) for ${\sigma }_m^2$ requires the vertical and transverse dimensions of the initial plume, L_y and L_z. The distances between the injection wells and the width of the screens in the wells are not reliable estimates of L_y and L_z as the plume underwent a significant expansion in all directions soon after the injection, as visible in the early snapshots. Figure 6a of Adams and Gelhar (1992) shows that after 9 days the vertical size of the plume was around 8 m, much larger than the vertical size of the screen of the wells. Also, Figure 4a from the same paper suggests that, again after 9 days from the injection event, the size of the plume was already about 40 m wide. Thus, in the following we assume L_y = 40 m and L_z = 8 m as the initial sizes of the plume; such estimates are rather rough and uncertain, but there is no other way to accurately assess them. With those estimates of L_y, L_z, and those of I, I_v of (1), the variance reduction factor due to the finite size of the plume appearing in (15) is ω(L) = 0.148 (Equations 12, 13).

Figure 5 displays the experimental longitudinal mass distribution at the MADE-1 experiment for the six snapshots presented by Adams and Gelhar (1992); black lines); the blue solid line depicts the theoretical m(x; t) (Equation 15), while the dashed lines represent the bounds m + σ_m (green) and m − σ_m (orange). It is seen that the theoretical model captures quite well the experimental mass distribution at MADE; the result is not entirely new as a similar comparison was made in Fiori et al. (2017), although the updated estimates of Bohling et al. (2016) and the more accurate spatial aggregation over the Δ interval was made here for the first time. The direct comparison between experiment and theory is made difficult by the overestimation of mass in the first snapshot (around 200% of the injected mass was recovered) and the incomplete mass recovery for increasing time. Still, the model captures the peak and its timing quite accurately in most of the snapshots, all the approximations and uncertainties notwithstanding.

FIGURE 5

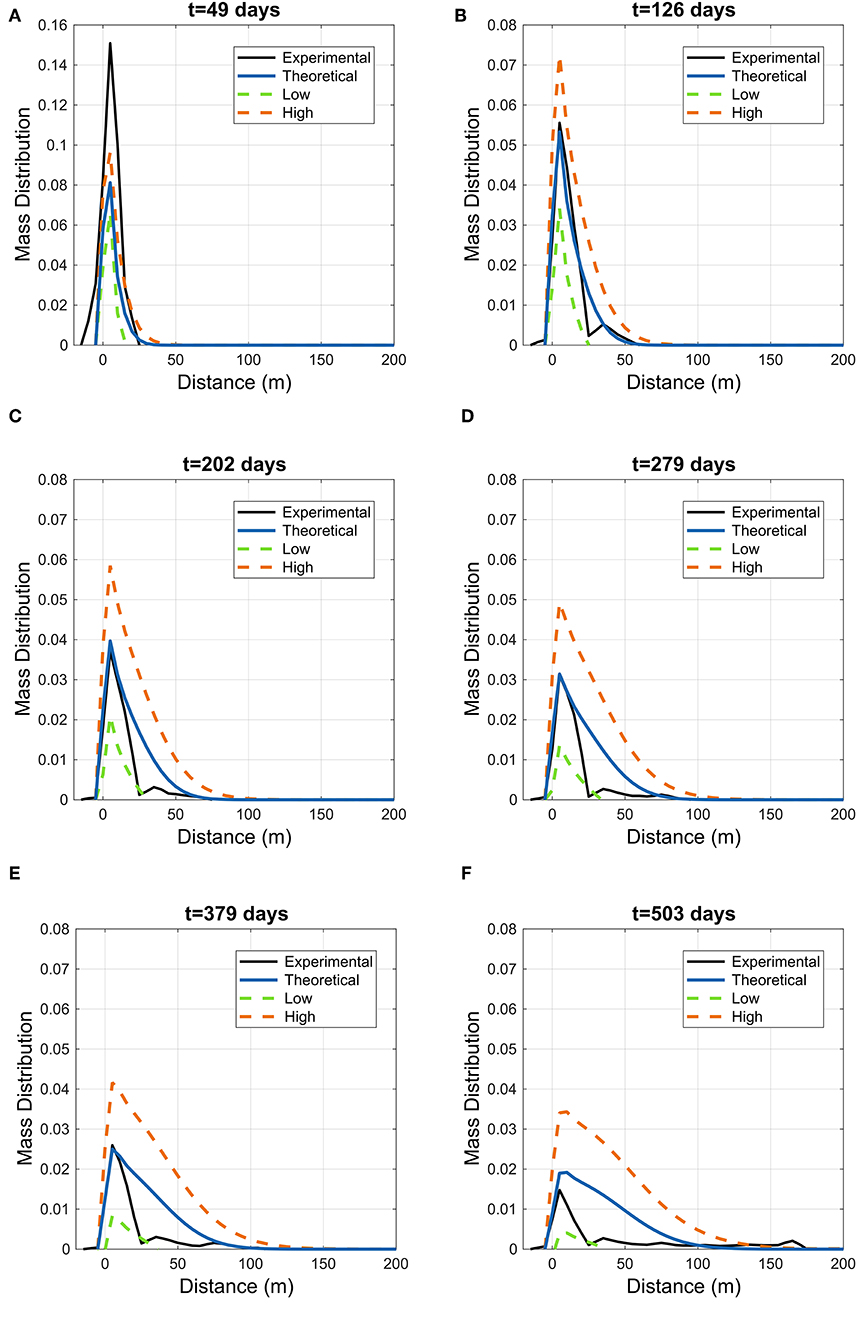
Figure 5. Uncertainty due to non-ergodic effects: the experimental longitudinal mass distribution at the MADE-1 experiment for the six snapshots presented by Adams and Gelhar (1992); black lines); the blue solid line depicts the theoretical m(x; t) (15), while the dashed lines represent the bounds for non-ergodicity uncertainty m + σ_m (orange dashed line, “High”) and m − σ_m (green dashed line, “Low”). G₁ in solutions (15) is given by (C.3). Mass recovery in the experiments was 206, 99, 68, 62, 54, and 43% at snapshots t = 49, 126, 202, 279, 370, 503 days, respectively.

It is seen that the bands of uncertainty, described by the bounds m±σ_m (dashed lines), are rather wide for all snapshots (note that m is subject to the constraint ${\int }_0^{\infty }m(t)dt=1$). The bounds tend to increase with time; as a matter of fact the behavior is quite expected in view of the nature of the analytical solution (15): the broader is the distribution, the larger is the uncertainty. The wide bounds of uncertainty pose doubts regarding the applicability of analytical solutions, based on stochastic approaches, that implicitly assume ergodicity; in such cases, it is advisable to present results together with the bands of uncertainty, as done here. Although the bands can be rather wide, like the present MADE case, the representation of Figure 5 in terms of prediction and bands of uncertainty may be of definite help in applications, for instance the case of risk assessment and plume management.

Uncertainty can in principle be constrained by some conditioning of the solution, e.g., based on available K data. Still, the impact of conditioning permeability at a point is generally limited to a domain of the order of the integral scales of Y (see e.g., Dagan, 1985), which has a minor effect on M for a large plume unless the grid of measurements is dense and covers the advancing plume. For small plumes conditioning may be more effective in reducing uncertainty if the measurements grid covers the trajectory. In any case, conditioning requires a theoretical model more complex that (3), posing additional computational burden that may not be otherwise required for simple preliminary (screening) analysis.

The relative good agreement of m (solid blue line) with experiments is quite surprising in view of the large uncertainty, as represented by the upper and lower limits (the dashed lines) of the figures; it may suggest that the initial size of the plume was indeed large enough to adequately sample the range of velocity variations in the aquifer, hence more in favor of ergodicity, and the estimates of L_y and L_z (that we recall were roughly estimated from the profiles of Adams and Gelhar, 1992) might perhaps be too conservative.

4.2. Parameter Uncertainty

Parameter uncertainty impact is assessed here by a simple first order analysis, that provides the variance of mass distribution m due to parametric uncertainty

$\begin{array}{ll}{\sigma }_m^2={\displaystyle \sum _{i=1}^{N_p}{\left(p_i\frac{\partial m}{\partial p_i}\right)}^2}C{V}_{p_i}^2={\displaystyle \sum _{i=1}^{N_p}{s}^2}\left(p_i\right)C{V}_{p_i}^2& (16)\end{array}$

where the function s is the sensitivity, and it represents the relative variation of the solution to changes in the generic parameter p_i (i = 1, …, N_p). The procedure is justified by the relatively small coefficient of variation of the parameters, that is below 0.35 for all parameters (see Table 1).

It is instructive to analyze first the sensitivity function s(p_i), (Equation 16), as function of the generic parameter p_i. Figure 6 illustrates the sensitivity pertaining to the relevant parameters ${\sigma }_Y^2,U,I,I_v$ for the snapshot t = 202 d (the sensitivities for the other snapshots are similar). It is seen that the sensitivity displays an antisymmetric behavior, which is determined by the constraint that the area underneath the curve m is unitary. Hence, increasing a parameter has opposite effects in different segments of the mass distribution. The behavior is similar for all parameters except I_v, that contributes through the anisotropy ratio (see Appendix C) and hence has opposite effects with respect to I. The curves of Figure 6 indicate that the most relevant parameter for uncertainty is the mean velocity U, followed by the logconductivity variance ${\sigma }_Y^2$ and the horizontal integral scale I; the impact of the vertical scale I_v is rather small. This finding already suggests what are the parameters requiring a more careful and precise estimate in order to reduce uncertainty, with the mean velocity playing an important role; the issue was also mentioned in section 3.1.

FIGURE 6

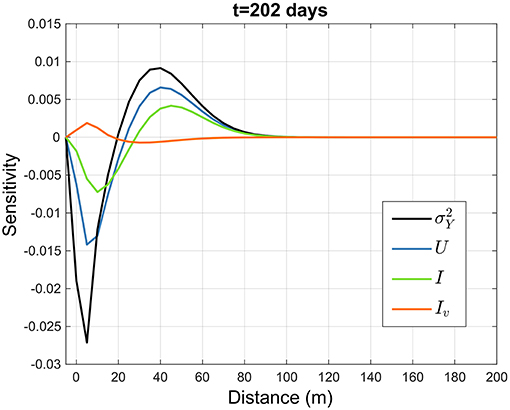
Figure 6. The sensitivity function s, Equation (16), as function of the parameters ${\sigma }_Y^2,U,I,I_v$ for the snapshot at t = 202 days, MADE-1 experiment.

The bands of parametric uncertainty m ± σ_m, along the model (16), are represented in Figure 7 for the six snapshots of the MADE-1 experiment. Comparison with Figure 5 indicates that the parametric uncertainty effect is smaller than the one due to non-ergodic behavior (section 3.2). We remind, however, that the bands may be wider as the variance of the mean velocity U is expected to be larger than the one estimated here, and reproduced in Table 1; this issue was discussed in section 4.1. The behavior of the uncertainty bands observed in Figure 7, with a central area where the bands shrink, is easily explained by the antisymmetric shape of the sensitivity, as previously discussed. The width of the uncertainty bands increases with time, just like the case illustrated in Figure 5.

FIGURE 7

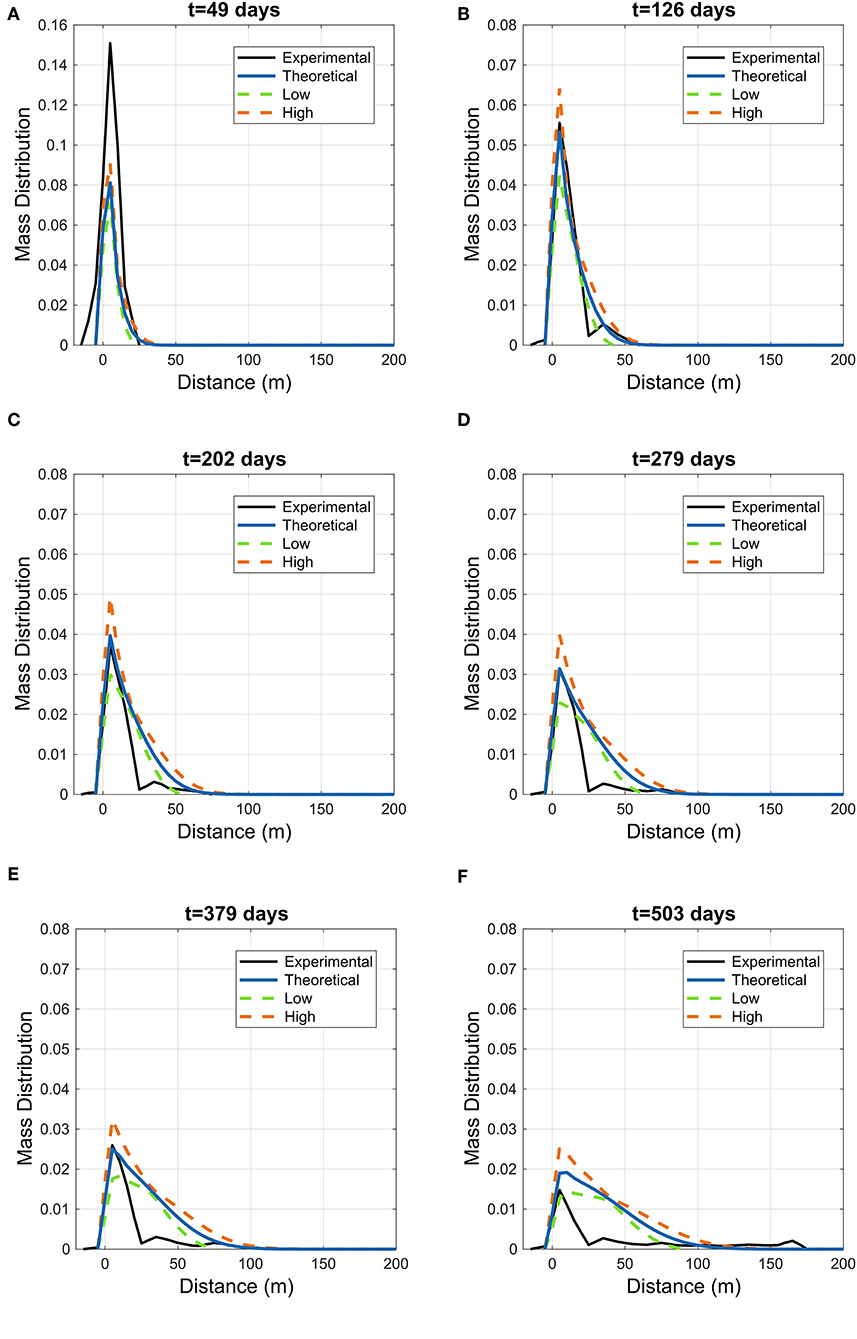
Figure 7. Parametric uncertainty: the experimental longitudinal mass distribution at the MADE-1 experiment for the six snapshots presented by Adams and Gelhar (1992), black lines; the blue solid line depicts the theoretical m(x; t) (15), while the dashed lines represent the bounds for parametric uncertainty m + σ_m (orange dashed line, “High”) and m − σ_m (green dashed line, “Low”). G₁ in solutions (15) is given by (C.3).

The analysis of parametric uncertainty is indeed a first and relative easy (if data are available) estimate of possible prediction errors. However, as shown here, it may be not the main source of uncertainty. It is worth noting that Cvetkovic et al. (2015) discussed the global sensitivity including mass transfer reactions.

5. Summary and Conclusions

Spreading of solute plumes in aquifers, as quantified for instance by the longitudinal macrodispersivity α_L, is much larger than the one observed in laboratory experiments (pore scale dispersion). This enhancement is caused by the spatial variability of the conductivity K, which in the context of stochastic subsurface hydrology, is modeled as a random space function. The paper considers flow which is uniform in the mean (natural gradient flow of velocity U) and inert solutes. Transport is quantified by the BTC M(t, x) at control planes at x as well as the associated spatial longitudinal mass distribution m(x, t). The logconductivity Y = ln K is modeled as stationary, of normal univariate pdf (parameters K_G and ${\sigma }_Y^2$) and axisymmetric covariance of horizontal I and vertical I_v integral scales. The latter are much larger than the pore scale, which explains the above findings. Flow and transport variables, solutions of the flow and transport equations, are consequently random as well.

Most of the transport models developed in the past, aiming at prediction of M, were underlain by the ergodic hypothesis, valid for plumes of large extent at the I, I_v scales. As a consequence, the one realization M is approximately equal to the ensemble mean 〈M〉.

The paper investigates the uncertainty of M (or m) in three dimensional formations, as quantified by the variance ${\sigma }_M^2$. Among the various sources of uncertainty, we deal with two: primarily with the non-ergodic effect present for finite plumes, as encountered in many applications. Besides we consider the impact of uncertainty of parameters like U, K_G, ${\sigma }_Y^2$, I. Indeed, the latter are affected by measurement errors even in extensively monitored aquifers.

The non-ergodic effect on transport was investigated in the past by adopting the first-order approximation in ${\sigma }_Y^2$ in solving the flow and transport equations (weakly heterogeneous formations). One of our main aims here is to extend the analysis to highly heterogeneous aquifers for which ${\sigma }_Y^2\le 8$. The investigation is based on our work in the last 15 years on ergodic transport, both by extensive and accurate numerical simulations not available in the past for three-dimensional configurations, as well as by simplified models. This was done for a few types of heterogeneous structures, differing in the connectivity of K classes. One of our main results was that 〈M〉 is a very robust predictor whose bulk can be modeled by the Inverse Gaussian CDF, with travel time variance given by the first order approximation.

The main novel theoretical contribution is the development of a simple analytical model to compute ${\sigma }_M^2$. It combines the above Inverse Gaussian distribution with an analytical function of the size of the injected plume relative to the integral scale, covering the spectrum from small plumes to ergodic ones. The result is illustrated by depicting the bands of uncertainty delimited by 〈M〉 ± σ_M (Figure 4) as dependent on ${\sigma }_Y^2$. While the present contribution is limited to non-reactive transport, the methodology can be easily extended to reactive solutes, along the lines of Cvetkovic and Dagan (1994) and Fiori et al. (2002).

A major part of the paper is devoted to application of the concepts to the MADE aquifer (${\sigma }_Y^2\simeq 6$) transport experiment, which has become a platform for groundwater contaminant transport modeling in the last 30 years. We present the observed snapshots of m(x, t), functions of x for a few values of t, as well as the bands of uncertainty related both to non-ergodic effects and uncertainty of parameters. The analysis relies on published recent analysis of field data, based on renewed characterization campaigns, and it represents a major overhaul of our previous analyses of the MADE-1 experiment. The results indicate that the most relevant parameter for uncertainty is the mean velocity U, followed by the logconductivity variance ${\sigma }_Y^2$ and the horizontal integral scale I. This finding suggests what are the parameters requiring a more careful and precise estimate in order to reduce uncertainty.

The main conclusion of the study is that, even for thoroughly characterized aquifers (like MADE) prediction of transport is affected by uncertainty; in particular, the major source of uncertainty for the MADE-1 experiment seems to be the non-ergodic behavior, i.e., the finite size of the plume with respect to the directional correlation scales of hydraulic conductivity. Uncertainty is prone to be even greater for the common, less detailed, sites data available in practice.

The above finding, and the general argumentation brought by the present work, enforces the conclusions from past work that estimating uncertainty of prediction should become an integral part of solving aquifer contamination problems, toward risk analysis. To that aim, characterization efforts should be directed toward reducing uncertainty of most influential parameters like the mean velocity U. Due to the prevailing scarcity of data in practice, it is advisable to use simple models, at least for screening scenarios.

The envisaged main future developments which may contribute to uncertainty and risk reduction are 2-fold. On one hand improvement of characterization technology may provide a detailed and large volume of data which may need analysis relying on Big Data treatment approach. On the other hand, numerical models of flow and transport in which the detailed aquifer architecture is based on conditioning on the large number of data should also be devised. At present, simple models like the ones presented here may serve for preliminary and screening analysis.

Author Contributions

AF: derivation of the new analytical expression of variance reduction due to non-ergodic effects; application to the MADE transport experiment using updated field data; exploration of the impact of parameters uncertainty on that of the MADE experiment plume snapshots. AZ: calculation of the variance reduction and related figures; computation of the comparisons of the BTC variance; detailed computation of the updated solution of the mean mass spatial distribution at MADE Site and comparison with the experimental snapshots. AB: computation of the logconductivity profiles at the MADE (Figure 1); numerical simulation of a 2D flow and transport with MADE parameters values (Figure 2); discussion of Figures 1, 2 to serve as starting point for the new developments of the paper. VC: establishing the connection of the results of the present study with those derived previously in the literature; comparison of the new results with the previous ones in the literature; relating the methodology of the paper to random walk theory. GD: coordination of the preparation of the study; establishing and description of the connection with previous work of the authors; formulation and writing of the final text while blending the various contributions of the team members and formulating the conclusions.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors are grateful to Francesca Boso for the numerical simulations of Figure 2. AB, AF, and AZ acknowledge funding from the Italian Ministry of Education, University and Research (MIUR) in the frame of the Departments of Excellence Initiative 2018–2022 granted to DICAM of the University of Trento (AB) and the Department of Engineering of Roma Tre University (AF and AZ).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2019.00079/full#supplementary-material

References

Adams, E. E., and Gelhar, L. W. (1992). Field study of dispersion in a heterogeneous aquifer: 2. Spatial moments analysis. Water Resour. Res. 28, 3293–3307.

Google Scholar

Andričević, R., and Cvetković, V. (1998). Relative dispersion for solute flux in aquifers. J. Fluid Mech. 361, 145–174.

Google Scholar

Attinger, S., Dentz, M., Kinzelbach, H., and Kinzelbach, W. (1999). Temporal behaviour of a solute cloud in a chemically heterogeneous porous medium. J. Fluid Mech. 386, 77–104.

Google Scholar

Bear, J. (1979). Hydraulics of Groundwater. New York, NY: McGraw-Hill, Inc.

Google Scholar

Bellin, A., Dagan, G., and Rubin, Y. (1996). The impact of head gradient transients on transport in heterogeneous formations: application to the borden site. Water Resour. Res. 32, 2705–2713.

Google Scholar

Bellin, A., Rubin, Y., and Rinaldo, A. (1994). Eulerian-lagrangian approach for modeling of flow and transport in heterogeneous geological formations. Water Resour. Res. 30, 2913–2924.

Google Scholar

Bellin, A., Salandin, P., and Rinaldo, A. (1992). Simulation of dispersion in heterogeneous porous formations: Statistics, first order theories, convergence of computations. Water Resour. Res. 28, 2211–2227.

Google Scholar

Bellin, A., and Tonina, D. (2007). Probability density function of non-reactive solute concentration in heterogeneous porous formations. J. Contamin. Hydrol. 94, 109–125. doi: 10.1016/j.jconhyd.2007.05.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Bianchi, M., and Pedretti, D. (2017). Geological entropy and solute transport in heterogeneous porous media. Water Resour. Res. 53, 4691–4708. doi: 10.1002/2016WR020195

CrossRef Full Text | Google Scholar

Bianchi, M., and Pedretti, D. (2018). An entrogram-based approach to describe spatial heterogeneity with applications to solute transport in porous media. Water Resour. Res. 54, 4432–4448. doi: 10.1029/2018WR022827

CrossRef Full Text | Google Scholar

Boggs, J., and Rehfeldt, K. R. (1990). Field Study of Macrodispersion in a Heterogeneous Aquifer. 2. Observations of Hydraulic Conductivity Variability. Technical Report 10308. Available online at: https://inis.iaea.org/collection/NCLCollectionStore/_Public/25/009/25009041.pdf?r=1&r=1

Google Scholar

Boggs, J. M., Young, S. C., Beard, L. M., Gelhar, L. W., Rehfeldt, K. R., and Adams, E. E. (1992). Field study of dispersion in a heterogeneous aquifer: 1. Overview and site description. Water Resour. Res. 28, 3281–3291.

Google Scholar

Bohling, G. C., Liu, G., Dietrich, P., and Butler, J. J. (2016). Reassessing the MADE direct-push hydraulic conductivity data using a revised calibration procedure. Water Resour. Res. 52, 8970–8985. doi: 10.1002/2016WR019008

CrossRef Full Text | Google Scholar

Bohling, G. C., Liu, G., Knobbe, S. J., Reboulet, E. C., Hyndman, D. W., Dietrich, P., et al. (2012). Geostatistical analysis of centimeter-scale hydraulic conductivity variations at the MADE site. Water Resour. Res. 48:2525. doi: 10.1029/2011WR010791

CrossRef Full Text | Google Scholar

Boso, F., Bellin, A., and Dumbser, M. (2013). Numerical simulations of solute transport in highly heterogeneous formations: a comparison of alternative numerical schemes. Adv. Water Resour. 52, 178–189. doi: 10.1016/j.advwatres.2012.08.006

CrossRef Full Text | Google Scholar

Boso, F., and Tartakovsky, D. M. (2016). The method of distributions for dispersive transport in porous media with uncertain hydraulic properties. Water Resour. Res. 52, 4700–4712. doi: 10.1002/2016WR018745

CrossRef Full Text | Google Scholar

Cvetkovic, V. (2011). The tempered one-sided stable density: a universal model for hydrological transport? Environ. Res. Lett. 6:034008. doi: 10.1088/1748-9326/6/3/034008

CrossRef Full Text | Google Scholar

Cvetkovic, V., and Dagan, G. (1994). Transport of kinetically sorbing solute by steady random velocity in heterogeneous porous formations. J. Fluid Mech. 265, 189–215.

Google Scholar

Cvetkovic, V., Shapiro, A. M., and Dagan, G. (1992). A solute flux approach to transport in heterogeneous formations: 2. Uncertainty analysis. Water Resour. Res. 28, 1377–1388.

Google Scholar

Cvetkovic, V., Soltani, S., and Vigouroux, G. (2015). Global sensitivity analysis of groundwater transport. J. Hydrol. 531, 142–148. doi: 10.1016/j.jhydrol.2015.07.035

CrossRef Full Text | Google Scholar

Dagan, G. (1985). Stochastic modeling of groundwater flow by unconditional and conditional probabilities: the inverse problem. Water Resour. Res. 21, 65–72. doi: 10.1029/WR021i001p00065

CrossRef Full Text | Google Scholar

Dagan, G. (1989). Flow and Transport in Porous Formations. Berlin: Springer-Verlag.

Google Scholar

Dagan, G. (1990). Transport in heterogeneous porous formations: spatial moments, ergodicity, and effective dispersion. Water Resour. Res. 26, 1281–1290.

Google Scholar

Dagan, G. (2017). Solute plumes mean velocity in aquifer transport: impact of injection and detection modes. Adv. Water Resour. 106, 6–10. doi: 10.1016/j.advwatres.2016.09.014

CrossRef Full Text | Google Scholar

Dagan, G., Bellin, A., and Rubin, Y. (1996). Lagrangian analysis of transport in heterogeneous formations under transient flow conditions. Water Resour. Res. 32, 891–899.

Google Scholar

Dagan, G., Cvetkovic, V., and Shapiro, A. (1992). A solute flux approach to transport in heterogeneous formations: 1. The general framework. Water Resour. Res. 28, 1369–1376.

Google Scholar

Dagan, G., Fiori, A., and Janković, I. (2003). Flow and transport in highly heterogeneous formations: 1. Conceptual framework and validity of first-order approximations. Water Resour. Res. 39. doi: 10.1029/2002WR001717

CrossRef Full Text | Google Scholar

de Barros, F. P. (2018). Evaluating the combined effects of source zone mass release rates and aquifer heterogeneity on solute discharge uncertainty. Adv. Water Resour. 117, 140–150. doi: 10.1016/j.advwatres.2018.05.010

CrossRef Full Text | Google Scholar

de Barros, F. P. J., Fiori, A., and Bellin, A. (2011). A simple closed-form solution for assessing concentration uncertainty. Water Resour. Res. 47:W12603. doi: 10.1029/2011WR011107

CrossRef Full Text | Google Scholar

Fiori, A. (2014). Channeling, channel density and mass recovery in aquifer transport, with application to the MADE experiment. Water Resour. Res. 50, 9148–9161. doi: 10.1002/2014WR015950

CrossRef Full Text | Google Scholar

Fiori, A., Berglund, S., Cvetkovic, V., and Dagan, G. (2002). A first-order analysis of solute flux statistics in aquifers: the combined effect of pore-scale dispersion, sampling, and linear sorption kinetics. Water Resour. Res. 38, 121–1215. doi: 10.1029/2001WR000678

CrossRef Full Text | Google Scholar

Fiori, A., Cvetkovic, V., Dagan, G., Attinger, S., Bellin, A., Dietrich, P., et al. (2016). Debates-stochastic subsurface hydrology from theory to practice: the relevance of stochastic subsurface hydrology to practical problems of contaminant transport and remediation. What is characterization and stochastic theory good for? Water Resour. Res. 52, 9228–9234. doi: 10.1002/2015WR017525

CrossRef Full Text | Google Scholar

Fiori, A., and Dagan, G. (2000). Concentration fluctuations in aquifer transport: a rigorous first-order solution and applications. J. Contam. Hydrol. 45, 139–163. doi: 10.1016/S0169-7722(00)00123-6

CrossRef Full Text | Google Scholar

Fiori, A., Janković, I., Dagan, G., and Cvetković, V. (2007). Ergodic transport through aquifers of non-gaussian log conductivity distribution and occurrence of anomalous behavior. Water Resour. Res. 43. doi: 10.1029/2007WR005976

CrossRef Full Text | Google Scholar

Fiori, A., Volpi, E., Zarlenga, A., and Bohling, G. C. (2015). Gaussian or non-gaussian logconductivity distribution at the MADE site: is its impact on the breakthrough curve? J. Contam. Hydrol. 179, 25–34. doi: 10.1016/j.jconhyd.2015.05.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Fiori, A., Zarlenga, A., Jankovic, I., and Dagan, G. (2017). Solute transport in aquifers: the comeback of the advection dispersion equation and the first order approximation. Adv. Water Resour. 110, 349–359. doi: 10.1016/j.advwatres.2017.10.025

CrossRef Full Text | Google Scholar

Gelhar, L. W. (1993). Stochastic Subsurface Hydrology. Englewood Cliffs, NJ: Prentice Hall.

Google Scholar

Gómez-Hernández, J. J., Butler, J. J., Fiori, A., Bolster, D., Cvetkovic, V., Dagan, G., et al. (2016). Introduction to special section on modeling highly heterogeneous aquifers: lessons learned in the last 30 years from the MADE experiments and others. Water Resour. Res. 53, 2581–2584. doi: 10.1002/2017WR020774

CrossRef Full Text | Google Scholar

Hansen, S. K., Haslauer, C. P., Cirpka, O. A., and Vesselinov, V. V. (2018). Direct breakthrough curve prediction from statistics of heterogeneous conductivity fields. Water Resour. Res. 54, 271–285. doi: 10.1002/2017WR020450

CrossRef Full Text | Google Scholar

Jankovic, I., Maghrebi, M., Fiori, A., and Dagan, G. (2017). When good statistical models of aquifer heterogeneity go right: the impact of aquifer permeability structures on 3d flow and transport. Adv. Water Resour. 100, 199–211. doi: 10.1016/j.advwatres.2016.10.024

CrossRef Full Text | Google Scholar

Kitanidis, P. K. (1988). Prediction by the method of moments of transport in a heterogeneous formation. J. Hydrol. 102, 453–473.

Google Scholar

Kreft, A., and Zuber, A. (1978). On the physical meaning of the dispersion equation and its solutions for different initial and boundary conditions. Chem. Eng. Sci. 33, 1471–1480.

Google Scholar

Redner, S. (2001). A Guide to First-Passage Processes. Cambridge: Cambridge University Press.

Google Scholar

Renard, P., and De Marsily, G. (1997). Calculating equivalent permeability: a review. Adv. Water Resour. 20, 253–278.

Google Scholar

Ritzi, R. W. (2000). Behavior of indicator variograms and transition probabilities in relation to the variance in lengths of hydrofacies. Water Resour. Res. 36, 3375–3381. doi: 10.1029/2000WR900139

CrossRef Full Text | Google Scholar

Rubin, Y. (2003). Applied Stochastic Hydrogeology. Oxford: Oxford University Press.

Google Scholar

Salandin, P., and Fiorotto, V. (1998). Solute transport in highly heterogeneous aquifers. Water Resour. Res. 34, 949–961.

Google Scholar

Severino, G., Comegna, A., Coppola, A., Sommella, A., and Santini, A. (2010). Stochastic analysis of a field-scale unsaturated transport experiment. Adv. Water Resour. 33, 1188–1198. doi: 10.1016/j.advwatres.2010.09.004

CrossRef Full Text | Google Scholar

Shapiro, A. M., and Cvetkovic, V. D. (1988). Stochastic analysis of solute arrival time in heterogeneous porous media. Water Resour. Res. 24, 1711–1718.

Google Scholar

Tonina, D., and Bellin, A. (2008). Effects of pore-scale dispersion, degree of heterogeneity, sampling size, and source volume on the concentration moments of conservative solutes in heterogeneous formations. Adv. Water Resour. 31, 339–354. doi: 10.1016/j.advwatres.2007.08.009

CrossRef Full Text | Google Scholar

Zarlenga, A., Janković, I., Fiori, A., and Dagan, G. (2018). Effective hydraulic conductivity of three-dimensional heterogeneous formations of lognormal permeability distribution: the impact of connectivity. Water Resour. Res. 54, 2480–2486. doi: 10.1002/2017WR022141

CrossRef Full Text | Google Scholar

Zech, A., Attinger, S., Cvetkovic, V., Dagan, G., Dietrich, P., Fiori, A., et al. (2015). Is unique scaling of aquifer macrodispersivity supported by field data? Water Resour. Res. 51, 7662–7679. doi: 10.1002/2015WR017220

CrossRef Full Text | Google Scholar

Zheng, C., Bianchi, M., and Gorelick, S. M. (2011). Lessons learned from 25 years of research at the MADE site. Groundwater 49, 649–662. doi: 10.1111/j.1745-6584.2010.00753.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Zinn, B., and Harvey, C. F. (2003). When good statistical models of aquifer heterogeneity go bad: a comparison of flow, dispersion, and mass transfer in connected and multivariate gaussian hydraulic conductivity fields. Water Resour. Res. 39. doi: 10.1029/2001WR001146

CrossRef Full Text | Google Scholar