- 1Vitrociset Belgium SPRL, A Leonardo Company, Darmstadt, Germany
- 2Institute of Polar Sciences, National Research Council of Italy (ISP-CNR), Venice, Italy
- 3Earth and Environmental Sciences Department, University of Milano-Bicocca, Piazza Della Scienza, Milan, Italy
In this paper, we present a simplified algorithm to retrieve snow grain size, dust mass absorption coefficient and dust mass concentration from spectral diffuse reflectance measurements at three wavelengths located in the visible and near infrared. The theoretical model is then compared with field spectroscopy data collected in different days from an automated spectrometer in the Alps.
Introduction
The spectral reflectance of snow depends on several variables related both to the observation system (e.g., view zenith angle, diffuse or direct radiation etc.) and the physical properties of the surface (Warren, 1982). These latter can be summarized as: snow grain size (Nolin and Dozier, 1993), snow liquid water content (Green et al., 2006), snow density (Dadic et al., 2013) and presence and type of light-absorbing impurities (also referred as light-absorbing particles) (Di Mauro et al., 2015; Dumont et al., 2017; Skiles et al., 2018). Therefore, respective parameters can be derived from snow spectral reflectance measurements obtained both from field spectroscopy, airborne and satellite data, as shown in various studies (Nolin and Dozier, 1993; Green et al., 2006; Negi and Kokhanovsky, 2011; Di Mauro et al., 2015; Seidel et al., 2016). The retrieval of these parameters from remote sensing data is an active field of research (Bohn et al., 2020) and it is useful for assessing the state of the snowpack for hydrological and climatic-related applications. In particular, the development of algorithms for the quantitative retrieval of snow parameters is relevant in the context of current and future space imaging spectroscopy missions.
When snow is mixed with various impurities, its optical properties are modified (Warren and Wiscombe, 1980; Warren, 1982). This process leads to an increase in the absorption of solar radiation and an enhancement of surface melting (Di Mauro et al., 2019). The retrieval of the abundance and optical properties of impurities in snow is still an open issue in the remote sensing of the cryosphere. Furthermore, the timing and intensity of impurities depositions can be directly assimilated in snow hydrology models for runoff prediction (Cluzet et al., 2020).
The determination of snow properties from reflectance measurements has been discussed in a previous study (Kokhanovsky et al., 2018). In this paper, we present a simplified algorithm to retrieve snow grain size, dust mass absorption coefficient and dust mass concentration from spectral diffuse reflectance measurements at three wavelengths located in the visible and near infrared (NIR). The theoretical model is then compared with field spectroscopy data collected in different days from an automated spectrometer in the Alps.
Theory
The spherical albedo r of a semi-infinite plane - parallel snow is defined as
where
By definition, it follows that
where
where
are volumetric absorption coefficients of ice and pollutants, respectively,
The second term in Eq. 6 can be ignored in the visible. Then it follows:
An important point is that
where
where
where
Therefore, it follows for the polluted snow spectral spherical albedo:
or
where
is the effective transport length (ETL). One can conclude from Eq. 12 that the soot - polluted snow spherical albedo spectrum in the visible and near infrared is determined by just two constants:
where
where
where
Let us consider the physical meaning of the second spectrally invariant parameter
where we have accounted for the fact that the snow extinction coefficient can be derived from the following geometrical optics equation (Kokhanovsky and Zege, 2004):
where d is the effective ice grain size and
It follows that the value of
where
Taking into account that the ratio B/(1-g) is close to 9 (Kokhanovsky et 2019), we derive:
We have assumed that impurity particles are much smaller than the wavelength of incident light. This is often not the case. Let us assume now that the volumetric absorption coefficient of impurities can be presented as (Kokhanovsky et al., 2018):
where
or
where
and
where
Determination of Polluted Snow Properties From Spectral Reflectance Measurements
The theory presented above has been used to process the spectral reflectance measurements collected in the field at the Torgnon experimental site (Valle d’Aosta, Italy, 45.845012N, 7.578517E) on May 16, 17, 18, 2018, in the presence of dust - loaded snow. Mineral dust deposited on seasonal snow at this site has probably a Saharan origin (Di Mauro et al., 2019), as reported by other studies in the Alps (Dumont et al., 2017).
In Figure 1, we show an example of a picture of the site acquired on the 17th of May (2018) from a webcam (namely Phenocam Network) installed at the site (see Di Mauro et al., 2019 for further details).

FIGURE 1. The photo of the Torgnon site in Italian Alps (45.845012N, 7.578517E) taken on May 17, 2018. Dust is visible on the surface of snow.
This experimental site is equipped with several instruments for snow modeling and snow hydrology (Colombo et al., 2019; Di Mauro et al., 2019). The site is seasonally covered by snow from October to May and it is located at the altitude of 2,160 m in the Italian European Alps. Since November 2017, a RoX spectrometer (JB Hyperspectral Devices, Düsseldorf, Germany) is installed at the site, and it continuously acquires spectral data each 3 min. The spectrometer collects incident and reflected radiation in the wavelengths between 400 and 900 nm. This makes it possible to derive the spectral plane (or spherical for the overcast sky) albedo. The instrument features a full width at half maximum of 1.5 nm, and a spectral sampling of 0.65 nm (JB Hyperspectral devices). Albedo is calculated as the ratio between the reflected and incident fluxes. Following previous studies (Picard et al., 2016a; Dumont et al., 2017), the automatic system is equipped with a cosine diffusor both for the upwelling and downwelling fluxes in order to measure the Bi-Hemispherical Reflectance factor (BHR) (here referred as spectral plane albedo). For this study, 30 measurements collected at the minimum of the solar zenith angle have been averaged. In order to remove noise from data, spectra were smoothed with a Savitzky-Golay filter by using a third order polynomial and a kernel of 99 data points. Albedo spectra were corrected for a constant slope (10 degrees) and aspect (230 degrees) of the snow surface, as proposed in Weiser et al. (2016). Slope and aspect values were calculated from a digital surface model obtained from a drone survey of the snow-covered area. The measurements above 865 nm appear still noisy and, therefore, are not present in the subsequent analysis.
The field data provides the plane albedo. The spherical albedo is estimated from the plane albedo using Eq. 26. Namely, it follows:
The parameter α has been derived from Eq. 24 using BHR measurements at two wavelengths in the visible (
where
The parameter
Then it follows:
The relative volumetric concentration of dust particles can be estimated from Eq. 25:
The relative mass concentration
where
One can see that one needs the value of
where
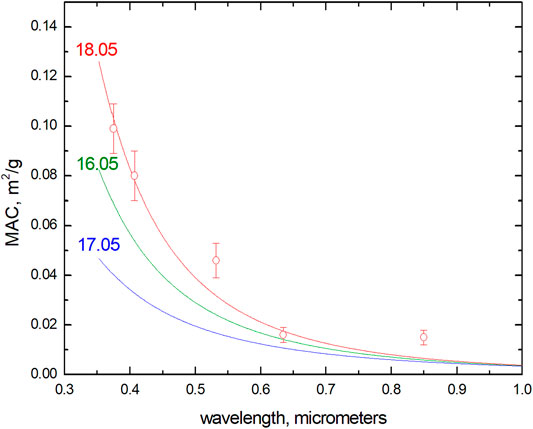
FIGURE 2. The derived dust mass absorption coefficients for the three days. Symbols represent experimental measurement of the mass absorption coefficient in the CESAM simulation chamber (Caponi et al., 2017).
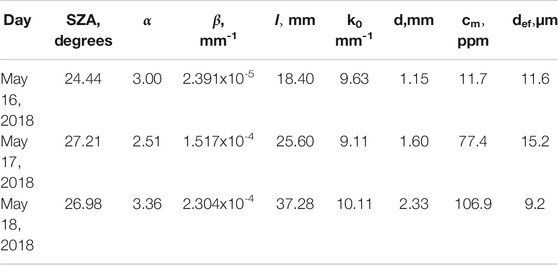
The solar zenith angle at the time of measurements needed for the determination of spherical plane albedo and results of calculation of various snow parameters for May 16, 17, 18, 2018 at the Torgnon site are given in Table 1. They are based on theory presented above and also on the plane albedo measurements performed at three wavelengths: 410, 500, and 865 nm.The plane albedo was modelled using the following simple analytical equation derived from Eqs 24, 26:
with the parameters shown in Table 1. The function
We show the spectral albedo measured on site and the results of calculations using Eq. 36 with the parameters (α, β,
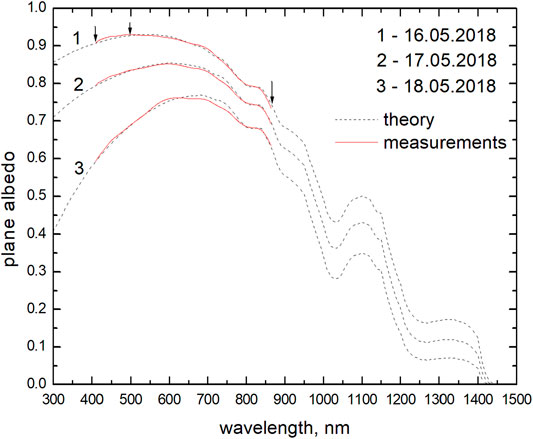
FIGURE 3. The spectral snow albedo: measurements–solid lines, calculations using Eq. 36–dashed lines. Dates refer to the acquisitions of the albedo spectra. Arrows show the wavelengths used in the inversion procedure (410, 500, and 865 nm).
Regarding the data collected on 18th May, we noticed a mismatch between observed and modeled spectra between 650 and 750 nm. Since this spectral range is particularly sensitive to chlorophyll concentration, the mismatch can be due to other impurities not accounted for in our study, such as cryospheric algae (Di Mauro et al., 2020). Further analysis is needed to decouple the effect of organic and inorganic impurities in snow at this experimental site in the European Alps.
During the three days considered in this study, we observe a steady increase of dust load (11.7–106.9 ppm) in surface snow. This is explained by the resurfacing of impurity layers during the melting season (Di Mauro et al., 2019; Skiles and Painter, 2019; Tuzet et al., 2020), a well-known process in the Alpine region. The reinforcing albedo feedback induced by the concentration of impurities in surface snow strongly accelerates the melting and represent an important application for remote sensing and snow hydrology studies.
The possibility of directly estimating dust concentration and snow grain size represents a breakthrough in the remote sensing of the cryosphere. In fact, this will allow to map the spatial and temporal variability of impurities in snow at global scale and to evaluate the role of impurities on the melting processes of snow and ice.
Conclusion
In this paper, we present a technique for the simultaneous determination of the size of ice grains and size of dust grains and also mass concentration of pollutants in snow. The technique to determine the mass absorption coefficient of impurity particles deposited in snow is also proposed. The technique is valid for the case of plane–parallel semi-infinite vertically homogeneous snow layers illuminated by a plane parallel direct solar light (or by the diffuse light from the overcast sky). The proposed method has been tested on field spectroscopy data and can be extended to account multiple pollutants in snowpack and to remote sensing data with different spectral resolution. Also, one can account for the fact that in reality the measured albedo is a mixture of white sky and blue sky albedo determined by the diffuse to direct light ratio. Although no validation data are available for this study, the modeling results obtained with the proposed model are comparable with previous literature focusing on the impact of dust in snow. The validation of the proposed technique will be a subject of our future study. This will lead to the simple and robust technique needed for the quantitative estimations of various polluted snow intrinsic characteristics from multispectral and hyperspectral data. The technique could be also applied to the analysis of snow reflectance spectra
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
AK: theory, conceptualization. BDM, RC, and RG: experimental measurements. AK, BDM, RC, and RG: writing of the paper. All authors reviewed and approved the final version.
Conflict of Interest
Author AK was employed by company Vitrociset Belgium SPRL, A Leonardo Company.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The data shown in Figure 2 by symbols have been supplied by Adriana Rocha-Lima. This is acknowledged with many thanks. AK acknowledges the support of the ESRIN/ESA contract 4000125043-ESA/AO/1-9101/17/I-NB EO SCIENCE FOR SOCIETY. BDM, RG, and RC acknowledge the support of the MUSICA project (Multiband Ultrawide SpectroImager for Cryosphere Analysis, contract: 2019-NAZ-0045) funded by the Italian Space Agency (ASI). BD, RG, and RC would like also to thank Tommaso Julitta (JB Hyperspectral Devices) for the help in pre-processing the Rox data, and Edoardo Cremonese and the personnel of the Environmental Protection Agency of Aosta Valley (ARPA-VDA) for maintaining the experimental site in Torgnon (AO, Italy). The hyperspectral data was processed from raw digital numbers to calibrated radiances using the FieldSpectroscopyDP (https://github.com/tommasojulitta/FieldSpectroscopyDP) and FieldSpectroscopyCC (https://github.com/tommasojulitta/FieldSpectroscopyCC) packages in R (R Core Team, 2017).
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2021.644551/full#supplementary-material
Appendix 1
Escape Function
We shall assume that the snow phase function is described by the Henyey – Greenstein phase function with the asymmetry parameter g=0.75 (Henyey and Greenstein, 1941; Kokhanovsky et al., 2019). The escape function has been numerically calculated for this specific case in Yanovitskij (1997). The corresponding dependence is shown in Figure A1.1 together with approximation derived by us from the fit of numerical values:
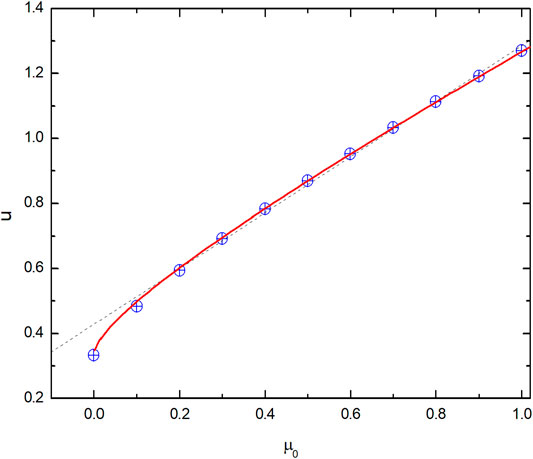
FIGURE A1.1. The dependence of the escape function on the cosine of the solar zenith angle for the Henyey – Greenstein phase function at g=0.75 calculated using exact radiative transfer theory (symbols), and Eq. (A1.1) (solid line) and Eq. (A1.2) (dashed line).
It follows from Fig. A1.1 that a linear approximation for the escape function (Sobolev, 1972; Kokhanovsky et al., 2019):
can be also used (at μ0>0.2).
References
Bohn, N., Guanter, L., Kuester, T., Preusker, R., and Segl, K. (2020). Coupled retrieval of the three phases of water from spaceborne imaging spectroscopy measurements. Remote Sens. Environ. 242, 111708. doi:10.1016/j.rse.2020.111708
Caponi, L., Formenti, P., Massabó, D., Di Biagio, C., Cazaunau, M., Pangui, E., et al. (2017). Spectral- and size-resolved mass absorption efficiency of mineral dust aerosols in the shortwave spectrum: a simulation chamber study. Atmos. Chem. Phys. 17, 7175–7191. doi:10.5194/acp-17-7175-2017
Cluzet, B., Revuelto, J., Lafaysse, M., Tuzet, F., Cosme, E., Picard, G., et al. (2020). Towards the assimilation of satellite reflectance into semi-distributed ensemble snowpack simulations. Cold. Regions. Sci. Tech. 170, 102918. doi:10.1016/j.coldregions.2019.102918
Colombo, R., Garzonio, R., Di Mauro, B., Dumont, M., Tuzet, F., Cogliati, S., et al. (2019). Introducing thermal inertia for monitoring snowmelt processes with remote sensing. Geophys. Res. Lett. 46, 4308–4319. doi:10.1029/2019gl082193
Dadic, R., Mullen, P. C., Schneebeli, M., Brandt, R. E., and Warren, S. G. (2013). Effects of bubbles, cracks, and volcanic tephra on the spectral albedo of bare ice near the Transantarctic Mountains: implications for sea glaciers on Snowball Earth. J. Geophys. Res. Earth Surf. 118 (3), 1658–1676. doi:10.1002/jgrf.20098
Dalzell, W. H., and Sarofim, AP (1969). Optical constants of soot and their application to heat-flux calculations. ASME J. Heat. Transf. 91 (1), 100–104. doi:10.1115/1.3580063
Dang, C., Brandt, R. E., and Warren, S. G. (2015). Parameterizations for narrowband and broadband albedo of pure snow and snow containing mineral dust and black carbon. J. Geophys. Res. Atmos. 120, 5446–5468. doi:10.1002/2014JD022646
Di Mauro, B., Fava, F., Ferrero, L., Garzonio, R., Baccolo, G., Delmonte, B, and Colombo, R (2015). Mineral dust impact on snow radiative properties in the European Alps combining ground, UAV, and satellite observations. J. Geophys. Res. Atmos. 120, 6080–6097. doi:10.1002/2015JD023287
Di Mauro, B., Garzonio, R., Baccolo, G., et al. (2020). Glacier algae foster ice-albedo feedback in the European Alps. Sci. Rep. 10, 4739. doi:10.1038/s41598-020-61762-0
Di Mauro, B., Garzonio, R., Rossini, M., Filippa, G., Pogliotti, P., Galvagno, M., et al. (2019). Saharan dust events in the European Alps: role in snowmelt and geochemical characterization. Cryosphere 13, 1147–1165. doi:10.5194/tc-13-1147-2019
Dumont, M., Arnaud, L., Picard, G., Libois, Q., Lejeune, Y., Nabat, P., et al. (2017). In situ continuous visible and near-infrared spectroscopy of an alpine snowpack. Cryosphere 11, 1091–1110. doi:10.5194/tc-11-1091-2017
Green, R. O., Painter, T. H., Roberts, D. A., and Dozier, J. (2006). Measuring the expressed abundance of the three phases of water with an imaging spectrometer over melting snow. Water Resour. Res. 42 (10). doi:10.1029/2005wr004509
Kokhanovsky, A. A., Lamare, M., Danne, O., Brockmann, C, Dumont, M., Picard, G., et al. (2019). Retrieval of snow properties from the sentinel-3 ocean and land colour instrument. Remote Sens. 11, 2280. doi:10.3390/rs11192280
Kokhanovsky, A. A., Lamare, M., Di Mauro, B., Picard, G., Arnaud, L., Dumont, M., et al. (2018). On the reflectance spectroscopy of snow. Cryosphere 12, 2371–2382. doi:10.5194/tc-12-2371-2018
Kokhanovsky, A. A., and Macke, A. (1997). Integral light-scattering and absorption characteristics of large, nonspherical particles. Appl. Opt. 36, 8785–8790. doi:10.1364/ao.36.008785
Kokhanovsky, A. A., and Zege, E. P. (2004). Scattering optics of snow. Appl. Opt. 43, 1589–1602. doi:10.1364/ao.43.001589
Libois, Q., Picard, G., Dumont, M., Arnaud, L., Sergent, C., Pougatch, E., et al. (2014). Experimental determination of the absorption enhancement parameter of snow. J. Glaciol. 60, 714–724. doi:10.3189/2014jog14j015
Negi, H. S., and Kokhanovsky, A. (2011). Retrieval of snow grain size and albedo of western Himalayan snow cover using satellite data. Cryosphere 5 (4), 831–847. doi:10.5194/tc-5-831-2011
Nolin, A. W., and Dozier, J. (1993). Estimating snow grain size using AVIRIS data. Remote Sens. Environ. 44 (2–3), 231–238. doi:10.1016/0034-4257(93)90018-s
Picard, G., Libois, Q., and Arnaud, L. (2016b). Refinement of the ice absorption spectrum in the visible using radiance profile measurements in Antarctic snow. Cryosphere 10, 2655–2672. doi:10.5194/tc-10-2655-2016
Picard, G., Libois, Q., Arnaud, L., Verin, G., and Dumont, M. (2016a). Development and calibration of an automatic spectral albedometer to estimate near-surface snow SSA time series. Cryosphere 10, 1297–1316. doi:10.5194/tc-10-1297-2016
Seidel, F. C., Rittger, K., Skiles, M, Molotch, N. P., and Painter, T. H. (2016). Case study of spatial and temporal variability of snow cover, grain size, albedo and radiative forcing in the Sierra Nevada and Rocky Mountain snowpack derived from imaging spectroscopy. Cryosphere 10, 1229–1244. doi:10.5194/tc-10-1229-2016
Skiles, S. M., Flanner, M., Cook, J. M., Dumont, M., and Painter, T. H. (2018). Radiative forcing by light-absorbing particles in snow. Nature Clim Change 8 (11), 964–971. doi:10.1038/s41558-018-0296-5
Skiles, S. M. K., and Painter, T. H. (2019). Toward understanding direct absorption and grain size feedbacks by dust radiative forcing in snow with coupled snow physical and radiative transfer modeling. Water Resour. Res. 55, 7362–7378. doi:10.1029/2018wr024573
Tuzet, F., Dumont, M., Picard, G., Lamare, M., Voisin, D., Nabat, P., et al. (2020). Quantification of the radiative impact of light-absorbing particles during two contrasted snow seasons at Col du Lautaret (2058 m a.s.l., French Alps). Cryosphere 14, 4553–4579. doi:10.5194/tc-14-4553-2020
Warren, S. G. (1982). Optical properties of snow. Rev. Geophys. 20 (1), 67–89. doi:10.1029/rg020i001p00067
Warren, S. G., and Brand, R. E. (2008). Optical constants of ice from the ultraviolet to the microwave: a revisited compilation. J. Geophys. Res. 113, D14220. doi:10.1029/2007JD009744
Warren, S. G., and Wiscombe, W. J. (1980). A model for the spectral albedo of snow. II: snow containing atmospheric aerosols. J. Atmos. Sci. 37 (12), 2734–2745. doi:10.1175/1520-0469(1980)037<2734:amftsa>2.0.co;2
Weiser, U., Olefs, M., Schöner, W., Weyss, G., and Hynek, B. (2016). Correction of broadband snow albedo measurements affected by unknown slope and sensor tilts. Cryosphere 10, 775–790. doi:10.5194/tc-10-775-2016
Keywords: snow, dust, albedo, remote sensing, snow grain size
Citation: Kokhanovsky A, Di Mauro B, Garzonio R and Colombo R (2021) Retrieval of Dust Properties From Spectral Snow Reflectance Measurements. Front. Environ. Sci. 9:644551. doi: 10.3389/fenvs.2021.644551
Received: 21 December 2020; Accepted: 01 February 2021;
Published: 30 April 2021.
Edited by:
Dmitry Efremenko, Helmholtz Association of German Research Centers (HZ), GermanyReviewed by:
Sergey Korkin, Universities Space Research Association (USRA), Columbia, MD, United StatesJian Xu, Helmholtz Association of German Research Centers (HZ), Germany
Copyright © 2021 Kokhanovsky, Di Mauro, Garzonio and Colombo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alexander Kokhanovsky, YS5rb2toYW5vdnNreUB2aXRyb2Npc2V0YmVsZ2l1bS5jb20=
 Alexander Kokhanovsky
Alexander Kokhanovsky Biagio Di Mauro
Biagio Di Mauro Roberto Garzonio
Roberto Garzonio Roberto Colombo
Roberto Colombo