Modelling the Fate of Pesticide Transformation Products From Plot to Catchment Scale—State of Knowledge and Future Challenges

Transformation products (TP) of pesticides are found everywhere in the aquatic environment. Their dynamic formation and subsequent transport from agricultural fields to adjacent water bodies can be estimated by using environmental fate models, which is done in the registration process for plant protection products in the European Union. In this study, peer-reviewed applications of such models, the model complexity and their structure are documented and analysed. In total, 20 publications of 10 models – eight leaching models (GLEAMS, MACRO, RZWQM2, PEARL, PRZM, Pelmo, LEACHM, HYDRUS 1-D) and two catchment scale models (Zin-AgriTra, FRM) – were identified. The reviewed models greatly differ in their process complexity regarding the formation rate and the formation pathways of TPs.The major reason given for models failing to reproduce sampled TP concentrations in case studies was an erroneous substance transport, especially missing preferential flow simulation in soil. However, the contribution of TP formation processes to simulation uncertainty was not analysed at all in most of the studies. By comparing the structure of existing models, the state of knowledge on TP fate and requirements of TP fate assessment, the following recommendations were drawn: i) It is suggested that the models should be updated to reflect the current state of knowledge in process research, especially more complex transformation schemes and the formation of different TPs in different compartments, which was not included in most of the models. ii) Even though there are pesticide parent compound fate models at the catchment scale with a temporal resolution of one day, none of these models is able to simulate TP fate. Such models would enable scientists and authorities to estimate the environmental fate of TPs at the larger catchment scale or the regional scale. iii) To get over the assessment of the huge number of TPs formed in the environment, an integration of Quantitative Structure Properties Relationship models predicting TP fate characteristics, TP pathway prediction models and environmental fate models is suggested. This would allow for a largely automated and comprehensive assessment of the fate of a pesticide parent compound and all its TPs for regulatory purposes.

Introduction

Pesticides applied to agricultural fields dissipate with time. The major processes of dissipation are transport and degradation. However, large parts of the pesticide mass are not fully degraded, but are transformed into transformation products (TPs), which are often also called metabolites, degradates or daughter compounds. TPs are often more stable and more mobile than their parent compounds (Boxall et al., 2004), which is why they are frequently detected in rivers (Olsson et al., 2013) and groundwater (McManus et al., 2017; Kiefer at al., 2019). Transformation processes relevant in the environment are microbial transformation, photolysis and hydrolysis (Fenner et al., 2013). Microbial processes mainly take place in the soil and are influenced by soil moisture, soil temperature, organic carbon content and soil pH (Gavrilescu, 2005). Photolysis may occur directly via UV radiation or catalysed by reactants in water (Bustos et al., 2019). Hydrolysis is mainly influenced by the pH value of the solvent. The number of stable TPs varies between compounds and processes. Often, pesticides have 2–4 major stable TPs and various less important degradates (regarding formation fractions, the fraction of degraded substance emerging as a specific TP). In the E.U. regulation for plant protection products, TPs are deemed relevant, if the formation fraction is 10% or more (Regulation (EC) No 1107/2009). The sheer number of possible TPs per parent compound (PC) hampers research on single TP compounds. Thus, often, physico-chemical characteristics of TPs are not even known (Lewis et al., 2016). Reaction pathways between the parent and its daughters are generally different for different transformation processes. Thus, TPs built in the soil may be different to the TPs built at the plant surface (Roberts et al., 1999; Fenner et al., 2013). Additionally, reaction kinetics usually vary between processes (Lewis et al., 2016).

For several decades, the environmental fate of pesticide residues has been simulated at different spatial and temporal scales. Fate processes in these models cover the whole range of known transport, transfer and transformation processes (Gavrilescu, 2005) in different complexity. Multimedia Multifate models, coming from the community of environmental chemistry, cover transfer and transformation with relatively high complexity, but simulate transport in a simplified manner (Mackay, 2001). These models include steady-state models (Level I–III) and continuous models (level IV). The range of spatial scales reaches from catchment scale (Kern et al., 2011) to global scale (Schenker et al., 2007). The downside of these models is that they are often not compared to sampled environmental concentrations. One explanation may be that in some cases not concentrations, but indices are calculated. Thus, the use of these models is rather restricted to identification of processes or expected environmental concentrations for emerging contaminants. Without model validation, an application for regulation purposes is hardly possible.

A different type of models for simulating pesticide fate are models based on physical or conceptual descriptions of water fluxes. For this purpose, models from hydrology/hydraulics were supplemented by a mass transport and environmental fate module. This type of models is by default continuous with time steps ranging from minutes to days and spatial scales from soil columns to river basins. Since water fluxes are explicitly calculated, concentrations can be simulated directly. In most cases, their simulation results are directly compared to environmental concentrations. In the European Union, pesticide leaching models (soil column to field scale) are part of the assessment of the environmental fate of pesticides and their TPs during the registration procedure.

There are several reviews available on the modelling of pesticide parent compounds in agricultural settings (Petit et al., 1995; Siimes and Kämäri, 2003; Holvoet et al., 2007; Köhne et al., 2009; Payraudeau and Gregoire, 2012; Mottes et al., 2014; Ippolito and Fait, 2019). However, to the best of our knowledge, the only prior review about modelling approaches for the simulation of TPs in the environment was provided by Fenner et al. (2009). Still, the focus of the former review was slightly different to this work, since not only pesticide TPs were considered but all TPs from micropollutants. Furthermore, the main emphasis was on Multispecies Multimedia Models. In contrast, this review concentrates on models predicting time-variable concentrations of TPs in the environment; ranking methods or relative behaviour models are not considered. This review is also restricted to models which were actually applied for the simulation of TPs. The application must be documented by peer-reviewed articles or scientific reports. To find literature satisfying these needs, the scientific literature service Web of Science (https://apps.webofknowledge.com) was employed using the keywords “pesticide” and “modelling” in combination with “transformation product”, “degradate” or “metabolite” and “leaching”, “soil”, “subsurface” or “catchment”. All literature up to the year 2020 was examined. This resulted in 396 potential studies. In a second step, the search results fulfilling the above-mentioned needs were picked manually, resulting in 17 studies. A final search was undertaken by combining the names of the identified models with “transformation product”, “degradate” or “metabolite”. Since the model names “MACRO” and “PEARL” are not unique identifiers, the additional keyword ‘pesticide’ was added for these models. As a result, another 74 studies were identified, of which three fulfilled the criteria. Thus, 20 studies were included in the analysis.

In the following, first, details about transformation processes and pathways implemented in considered models are provided (Transformation Equations and Pathways in Current Models). A brief model description of each model, aided by application cases, is presented in Overview of Models and Model Applications Considering Transformation Products. In Analysis and Discussion, the strength and weaknesses of the approaches are discussed and future directions for the simulation of pesticide TPs in the environment are given.

Transformation Equations and Pathways in Current Models

The major difference between the environmental fate simulation of TPs and their PCs is the input function of the substance into the environment. While PCs are applied at discrete time steps, TPs emerge at every time step from PC degradation. Therefore, TP transport and transfer process conceptualizations such as adsorption/desorption, volatilization and root uptake are the same compared to PC processes. In their application domain, all models discussed in this study address these processes, with differences in their level of detail.

While all considered models use a first-order approach for degradation, the formation of TPs is implemented differently. In most models the method of formation fractions (ff), which are fractions of the decayed PC emerging as a TP, is implemented (Leonard et al., 1990). Formation fractions can be obtained from the Pesticide Properties Database (PPDB, Lewis et al., 2016). However, it is important to note that in some cases formation fractions are weight-based and in some cases, they are molar-based. Weight-based formation fractions may draw fractions from the range of [0.0; ∞] since the molar weight of a TP may be lower or larger than that of a PC. In contrast, molar-based formation fractions are between 0.0 and 1.0 and all ff of a PC add up to a maximum of 1.0. The corresponding formation equations for two TPs (subscripts 1 and 2) in a time increment $dt$ are:

$\frac{d{m}_{PC}}{dt}=m_{app}-\left(k_{PC}\cdot m_{PC}\right)(1)$

$\frac{d{m}_{TP1}}{dt}=\left(f{f}_1\cdot k_{PC}\cdot m_{PC}\right)-\left(k_{TP1}\cdot m_{TP1}\right)(2)$

$\frac{d{m}_{TP2}}{dt}=\left(f{f}_2\cdot k_{PC}\cdot m_{PC}\right)-\left(k_{TP2}\cdot m_{TP2}\right)(3)$

$m_{PC}$ and $m_{TP}$ are the masses of the PC and TP, respectively, and $k_{PC}$ and $k_{TP}$ the decay rates (t⁻¹) of the PC and TP. A slightly different approach is the usage of a separate parent decay rates ($k_{PC-TP})$ towards each TP (Webb et al., 2011). In case of two TPs (TP1 and TP2), the corresponding transformation equations are:

$\frac{d{m}_{PC}}{dt}=m_{app}-\left(\left(k_{PC-TP1}+k_{PC-TP2}\right)\cdot m_{PC}\right)(4)$

$\frac{d{m}_{TP1}}{dt}=\left(k_{PC-TP1}\cdot m_{PC}\right)-\left(k_{TP1}\cdot m_{TP1}\right)(5)$

$\frac{d{m}_{TP2}}{dt}=\left(k_{PC-TP2}\cdot m_{PC}\right)-\left(k_{TP2}\cdot m_{TP2}\right)(6)$

Both methods are connected by $k_{PC}=k_{PC-TP1}+k_{PC-TP2}$ and $ff=\frac{k_{PC-TP1}}{k_{PC}}$ and thus they are equivalent. However, the overall PC degradation rate $k_{PC}$ and the formation fraction are better available from the literature than single degradation rates.

Microbial degradation in soil is influenced by various environmental factors affecting microbial activities such as soil moisture $\theta$, soil temperature $T_S$, soil depth, pH, clay content (cl) and organic matter (OC) content. Often, the influences of soil moisture, soil temperature and soil depth are calculated by multiplying a reference transformation rate $k_{ref}$, which was measured under known moisture and temperature conditions, by three factors:

$k=f_{Ts}\cdot f_{\theta }\cdot f_z\cdot k_{ref}(7)$

$f_{Ts}$ and $f_{\theta }$ are the factors (-) for the influence of soil temperature and soil moisture, respectively. $f_z$ considers the influence of soil depth, i.e., microbial activity. The dependence of $k$ on soil moisture is calculated by:

$f_{\theta }={\theta }^b(8)$

$\theta$ (-) is the current relative soil moisture and $b$ is an empirical exponent which has an average of 0.7 for many pesticides (Boesten and van der Linden, 1991). The soil temperature factor $f_{Ts}$ usually consists of an approximation to the Arrhenius equation, modified for low soil temperatures:

$f_{Ts}=\{\begin{array}{l}exp\left(\alpha \cdot \left(T_S-T_{ref}\right)\right) \forall T_S>5°C\hfill \\ \left(\frac{T_S}{5}\right)exp\left(\alpha \cdot \left(5-T_{ref}\right)\right) \forall 0\le T_S\le 5°C\hfill \\ 0 \forall T_S<0°C\hfill \end{array}(9)$

$T_{ref}$ (°C) is the soil temperature at which the $k_{ref}$ has been measured. $\alpha$ (K⁻¹)is a factor considering the gas constant and the molar activation energy and can be set to 0.08 for many pesticides (Boesten and van der Linden, 1991).

The reduction factor $f_z$ considers the reduction of microbial activity with soil depth. It was implemented by Boesten and van der Linden (1991) as a discrete reduction from $f_z$ = 1.0 at the soil surface to $f_z$ = 0.0 in 1 m depth. In a study by Gassmann et al. (2013), $f_z$ was set to 0.5 in about 40 cm depth and to 0.1 in about 90 cm depth.

The influence of pH, OC and cl on the degradation half-live $DT50=\frac{\ln \left(2\right)}{k}$ was simulated by van der Linden et al. (2009) in the GeoPEARL model. The shape of the equations was the same for all three factors:

$DT50=DT{50}_{ref}+f\cdot \left(i-i_{ref}\right)(10)$

Where $ref$ denotes reference conditions, $f$ (-) a specific factor and $i$ the influence of interest, i.e., OC (-), cl (-) or pH (-). The factors $f$ are empirical and might be taken from the literature.

Transformation pathways between pesticides and TPs or between TPs are often complex in reality, including several “there and back”—reactions. The investigated models, however, all use simplifications, starting from simple chain reactions to more complex interactions (Figure 1).

FIGURE 1

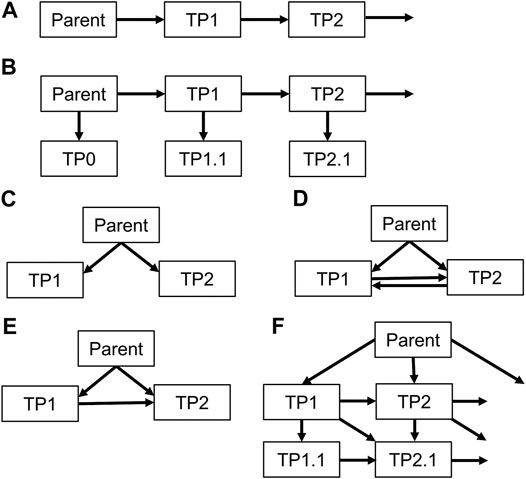
FIGURE 1. Fixed transformation schemes implemented in investigated models. A: MACRO, RZWQM, LEACHM; B: GLEAMS, HYDRUS 1D, C: RZWQM; D: Zin-AgriTra; E: PRZM, FRM; F: Pelmo. PEARL and GeoPEARL contain totally flexible schemes.

Overview of Models and Model Applications Considering Transformation Products

Generally, two types of models differing in their spatial and temporal resolution and their general representation of mass fluxes and chemical fate were developed for an estimation of pesticide TPs and their transfer to water bodies in agricultural areas:

(i) Leaching models considering vertical transport of substances towards tile drains or groundwater, some of them also considering horizontal transport to the river via overland flow. These models are available at the field scale or at regional scale which is basically a raster of field scale applications.

(ii) Catchment models considering vertical and lateral transport in soil and at the land surface towards groundwater or surface waters. The spatial scale reaches from headwaters to mesoscale catchments.

Field Scale Leaching Models

GLEAMS

The original GLEAMS (Groundwater Loading Effects of Agricultural Management Systems) model was published in the late 1980s (Leonard et al., 1987) and was one of the first mathematical pesticide leaching models. It was extended by Leonard et al. (1990) for the simulation of TP fate. It has a conceptual water flux implementation, is able to handle multiple TPs per pesticide in a fixed transformation scheme (B in Figure 1) and uses formation fractions.

The model was applied for the simulation of the fate of the insecticide fenamiphos and two of its TPs, fenamiphos sulfoxide and fenamiphos sulfone, in soil during a time span of 7 months at the Coastal Plain Experiment Station near Tifton, Georgia (Leonard et al., 1990). Due to a lack of experimental data, ff were estimated from experimental data of the insecticide aldicarb and its sulfoxide and sulfone TPs. Adding laboratory data for half-lives, the model simulated the time series of total substance masses in soil and the concentrations with depth at two time points in the range of sampling data. No information is provided for adsorption parameterization. Further validation was recommended, which was provided by Truman et al. (1998) using sampling data of two more years. Half-lives and ff were calibrated for each of the six applications and provided reasonable results for the time series of total masses of each substance in the field. However, the timing and amount of lateral subsurface substance export was not predicted well, which might be a result of incorrect water flux predictions. Over time, both, DT50 and ff decreased, which was explained by increased microbial degradation due to adaptation to the substances.

MACRO

MACRO is a dual-permeability model using a numerical solution of the Richards Equation for soil matrix transport and a kinematic wave approximation for preferential flow (Larsbo and Jarvis, 2003). It can handle the simulation of one pesticide and one of its TPs subsequently, but not in the same run. Formation of the TPs can be at the canopy or/and in soil where it is influenced by soil temperature, soil moisture and soil depth. Half-lives can be specified for the liquid and the adsorbed phase in micropores and macropores separately. MACRO is currently used in the E.U. registration procedure for plant protection products.

Rosenbom et al. (2009) tested the ability of the MACRO model for long-term leaching simulations of the herbicide metribuzin and one of its key TPs towards a sandy aquifer in Denmark. Even after calibration, the model was not able to simulate TP concentrations using sorption concepts recommended by the E.U. Only after using a more sophisticated sorption concept, the model simulated the leaching of both, metribuzin and its TP, close to sampled values (R² = 0.24).

RZWQM(2)

The Root Zone Water Quality Model 2 (RZWQM2; Ahuja, 2000) is a numerical dual-permeability leaching model with, compared to the MACRO model, the additional ability to simulate overland flow. The model can handle two TPs in transformation schemes A or C (Figure 1). TPs can be formed at the canopy by microbial, photolytic or abiotic processes or in soil by photolytic, microbial, aerobic, anaerobic and abiotic processes or a lumped half-life is given. Different TPs can be formed at the canopy, plant residues, soil surface and in the subsoil. In soil, microbial transformation depends on temperature, soil moisture and depth.

The RZWQM model was tested for pesticide and TP simulation using fenamiphos, fenamiphos sulfoxide and fenamiphos sulfone sampling data from a two-year rainfall simulation experiment with 12 events by Ma et al. (2004). Surface crusting was calibrated, and the surface transformation rate roughly adjusted. This resulted in good event runoff predictions. Event loads of fenamiphos species were generally over-estimated, especially for the parent compound. The authors concluded that calibration of soil surface half-lives between years might improve predictions largely.

In two studies Fox et al. (2007b) and Fox et al. (2007a) applied the RZWQM model for the simulation of the herbicide isoxaflutole and its TP RPA202248 at 10–30 ha fields underlain by tile drains in Indiana. The calibrated model underestimated sampled peak concentrations and falling limbs of parent and daughter compounds even though the model code was extended for direct macropore loss to tile drains. Still, deviations were within one order of magnitude and the general declining trend was captured. A long-term 30-years simulation suggested that tile drain loss of substances was similar to surface runoff losses. The model was further applied for an investigation of the effects of rainfall time step input on model results. For both substances, an hourly time step brought superior model results for short-term simulation compared to 5 and 24 h time steps. Especially peak concentrations, presumably resulting from macropore flow, could be simulated more accurately. However, for long-term simulations, the rainfall timestep had no significant effect.

PEARL

A numerical solution of the Richards Equation and two domains of macropores are the governing transport processes underlying the PEARL (Pesticide Emission Assessment at Regional and Local) model (Leistra et al., 2001). Multiple TPs can be simulated in a flexible transformation scheme. TPs are formed in soil using lumped first-order transformation affected by soil temperature, soil moisture and depth. In combination with other models, the PEARL model is used for leaching assessment in the E.U. registration process for pesticides.

Farlin et al. (2013) used PEARL for an inverse modelling of atrazine and its TP desethylatrazine in a sandy soil aquifer system in Luxembourg. The model was able to reproduce spring mass flux ranges. Identified transformation rates and $ff$ of both substances were close to experimental literature values.

In a three-year lysimeter experiment in Austria, Schuhmann et al. (2016) tracked the fate of the herbizide chloridazon (CLZ) and its TPs desphenyl-CLZ and methyl-desphenyl-CLZ. They applied PEARL successfully for the simulation of water fluxes but had some problems with fitting pesticide residues: even after calibration, an early break-through of the parent and desphenyl-CLZ could not be simulated. The authors explained the mismatch by preferential flow, which, although PEARL generally is able to consider preferential flow, was not simulated in this study. Later events were simulated just fine in terms of mass flux, timing and magnitude.

Metolachlor and its TP Metolachlor-ESA were simulated in a lysimeter by Kupfersberger et al. (2018) as part of a study investigating substance fate in an aquifer. Again, water fluxes were successfully simulated with PEARL. An early breakthrough of the parent compound could not be captured, but the main breakthrough was simulated adequately. The onset of the TP simulation was correctly estimated, but the mass fluxes were largely overestimated in the following months. The authors assumed that different agricultural management practices during the two subsequent parent applications were causing these erroneous TP simulations.

PRZM

The Pesticide Root Zone Model (PRZM) has been evolved to version 5 (Young and Fry, 2014) after its introduction in 1985 (Carsel et al., 1985). It combines a conceptual hydrological “tipping bucket” approach for water transfer in soil with the possibility for the simulation of one pesticide and two TPs following transformation scheme E (Figure 1). Different TPs can be formed at plant canopy and/or in soil by adjusting $ff$ in soil and formation rate constants at plants. TP formation rate in soil is influenced by soil temperature only. The model is part of the registration process for pesticides in the European Union.

PRZM has been applied to simulate the leaching of Glyphosate and AMPA in a soil of an experimental site located in Eastern France (Mamy et al., 2008). PRZM could describe the general behaviour of the substance masses in the soil profile and of concentrations in the topsoil but overestimated the parent and underestimated AMPA persistence. The authors concluded that PRZM results are satisfactory, especially since no calibration was applied, but the absence of preferential flow might have led to an underestimation of AMPA mobility.

Marín-Benito et al. (2015) investigated the leaching of the fungicide metalaxyl and its TP CGA-62826 in laboratory soil columns filled with vineyard soils, which were differently treated with spent mushroom substrates. They tested the ability of the PRZM model to simulate the breakthrough curves of the substances in the soil columns. The model was parameterized by experimental data and literature values. After calibration of diffusion coefficients and sorption parameters, model performance was reasonable for the parent breakthrough curves and most depth-distributions of soil residues. However, simulations of CGA-62826 were poorer than for the parent compound. Breakthrough curves were too wide, and depth-distributions of soil concentrations were largely overestimated.

Pelmo

The Pesticide Leaching Model (PELMO) is a model based on conceptual calculations (tipping bucket) of water fluxes (Klein, 1995). The model is able to simulate the formation of TPs at canopy and in soil with the option of simulating different TPs in each compartment. Transformation in the soil solution or the adsorbed phase is affected by soil temperature, soil moisture and soil depth. The transformation scheme is relatively flexible following scheme F in Figure 1. PELMO is also used as one of the models in the E.U. registration procedure for plant protection products.

The only scientific PELMO publication including TPs was provided by Guzzella et al. (2006) simulating the leaching of the herbicides diuron and linuron, which can both be transformed to DCPMU, DCPU, and DCA, in a series of ten small (20–40 cm depth) field lysimeters. Without calibration, the model overestimated biodegradation rates and leaching of the parent compounds and DCPMU. DCPU persistence was overestimated and simulated DCA persistence too low. Still, persistence simulations were generally in the correct order of magnitude. The authors mentioned that there was a large heterogeneity in the sampling results of leaching and soil persistence between the ten lysimeters.

LEACHM/LEACHP

The LEACHM (Leaching Estimation and Chemistry Model) model describes water fluxes according to a finite-differences numerical solution of the Richards equation neglecting preferential flow in soil (Hutson and Wagenet, 1992; Hutson, 2005). LEACHP is the pesticide-version of the model. Multiple TPs can be considered in the model in a chain reaction (type A, Figure 1). Instead of $ff$, a degradation rate is implemented for the formation of each TP and another rate for degradation of each substance. LEACHM adjusts soil transformation (in dissolved and/or adsorbed species), which is the only transformation compartment, according to soil temperature, soil moisture and soil depth. In contrast to other models, Michaelis-Menten transformation kinetics can be used in addition to first-order kinetics.

In an early study, Pennell et al. (1990) applied the LEACHM model for leaching simulations of the insecticide aldicarb and two of its TPs, aldicarb sulfoxide and aldicarb sulfone, in the soils of an orange grove in Florida. The model was set up using experimental data for sorption and degradation of substances. Substance masses remaining in the field were calculated for each species and compared to sampling data. LEACHM predictions were close to sampled values for the parent and the sulfoxide. The persistence of the sulfone TP was overestimated. Soil concentrations with depth were not compared to each species but to the parent compound and to total residues, including TPs (TR). Parent concentrations were largely overestimated at the beginning of the experiment while, at the same time, vertical leaching was underestimated. Later on, the overestimation was consistent in the whole soil profile. TR were overestimated in the topsoil at the beginning and underestimated during the experiment. At the end of the experiment, the model underestimated the depth of TR leaching which might have been an effect of missing preferential pathways.

The same substances were simulated by Vink et al. (1997) in a large lysimeter filled with clay soil. Experimental substance breakthrough was fast, indicating a high importance of preferential flow pathways. Breakthrough of aldicarb and its TPs was simulated much too late (100 days) by LEACHM. It was concluded that the absence of a preferential flow module might be responsible for the unsuccessful model application.

To overcome the limitations of the LEACHM model regarding the serial transformation scheme, Webb et al. (2011) implemented a branched transformation scheme into the code of the model. They applied the modified model for the simulation of the herbicide atrazine and three of its first-order TPs: deethylatrazine, deisopropylatrazine and hydroxyatrazine. For model testing, soil samples from several locations in the United States were mixed with atrazine and stored in the dark at different temperatures. The calibrated model was able to reproduce microbial transformation behaviour of all species as affected by soil temperature. Analysing optimized parameters, the authors found that there was a significant difference between degradation half-lifes of atrazine in adapted (5 days) to non-adapted (42 days) soil.

HYDRUS 1-D

HYDRUS 1-D was developed as a finite element numerical model for vertical water and solute fluxes in dual-porosity soils (Šimůnek et al., 1998). It can handle up to five TPs in a chain reaction with side products (type B, Figure 1). TPs are formed in soil using a temperature and moisture-dependent first-order rate per TP.

Papiernik et al. (2007) applied HYDRUS 1-D for simulating the fate of the herbicide isoxaflutole and its TP diketonitrile (DKN) in field soils. The model was able to fit sampled depth distributions of the summarized concentrations of isoxaflutole and DKN. By analysing processes in the model, the authors concluded that plant uptake is an important process in pesticide fate modelling.

A coupling of HYDRUS 1-D with the groundwater model MODFLOW was done by Bergvall et al. (2011) to track the fate of the 2,6-dichlorobenzoamide (BAM), a TP of the herbicide dichlobenil, in a drinking water supply well. The model combination was able to simulate BAM concentrations, but the HYDRUS simulations of the vadose zone were biased. The authors discussed possible reasons among which heterogeneity of preferential transport, which was not included in the model, was most likely responsible.

Large-Scale Leaching Models

GeoPEARL

GeoPEARL (Tiktak et al., 2002) is a spatially distributed version of the PEARL leaching model and thus shares all the transformation equations of the PEARL model. Even though it is distributed, the model is restricted to vertical water transfer. Thus, there is no lateral connection between soil profiles.

van der Linden et al. (2009) extended the model for the influences of organic matter, clay content and pH on degradation and simulated the leaching of Mesotrione and two of its TPs in Netherlands. The influence of the dependencies could clearly be shown in the results, but the model was neither calibrated nor validated using field data.

LEACHM

The LEACHM model was applied in a semi-distributed way to estimate the leaching of different pesticides and TPs in soil with different unsaturated zone thickness in a meso-scale watershed (Webb et al., 2008). Soil moisture of different depths and bromide tracer concentrations were calibrated, but not the organic chemical concentrations. Thus, similar to the GeoPEARL applications, the results are used as hypotheses about the fate of pesticides and TPs in soil.

Catchment Scale Models

ZIN-AgriTra

The catchment scale reactive transport model ZIN-AgriTra aims at providing information about pesticides and their transformation products in agricultural catchments (Gassmann, 2013). The model is fully distributed and has time steps between a few minutes and one hour. Based on an explicit simulation of the mass balance per cell, it is able to simulate up to three substances of which two can be TPs (scheme D, Figure 1). The transformation half-live can independently be specified for the mixing layer and three soil layers. TPs might be formed at the canopy, but the half-live and the formation fractions cannot be specified separately from soil.

The model was applied in a Swiss headwater catchment for the simulation of three pre-emergence herbicides with one TP each (Gassmann et al., 2013). The peak mass fluxes and the spatial distribution of parent compounds and TPs could be successfully reproduced. However, there were peaks during small rainfall events after application which could not be reproduced. One reason was that even the 10 m spatial resolution was too coarse to include paved roads and that drift of pesticides during application was not considered. It could be shown that the export pathways of the TPs were different from the PCs, which was attributed to the physico-chemical characteristics and the large tile-drained area in the catchment. The model was further used to estimate the critical source areas of pesticides and TP loss based on 55 agricultural fields in the catchment (Gassmann et al., 2015). 144 simulations of different physico-chemical characteristics showed that critical source areas of TPs were on average larger than PCs.

Field Release Model (FRM)

In a lumped parameter model based on linear reservoirs, Gassmann et al. (2014) investigated simulation uncertainties associated with TP simulations. The model was set up to simulate the transformation of chlorpyrifos (CP) to chlorpyrifos oxon (CPO) and trichlorpyridinol (TCP) (scheme E, Figure 1) in a Mediterranean catchment. It was shown that the estimation of TCP was consistent in two subsequent rainfall events, but that CPO concentrations and masses were highly uncertain and failed in the second event. This was attributed to changing transformation processes since CP was applied during the dry period with surface transformation processes, which prevailed before the first event. During the first event substances were flushed to the soil where degradation was then controlled by soil microbes forming TCP.

Analysis and Discussion

Spatio-Temporal Classification

The models reviewed were restricted to field scale leaching models, catchment scale models and regional-scale leaching models. These models are all process-based and thus their time step is one day or lower (Figure 2). This degree of detail is required for the assessment of non-linear processes such as pesticide fate (Tiktak et al., 2003; Gassmann et al., 2012). Both investigated catchment scale models operate at a time step of one hour or lower, since the catchments in focus were rather small and thus the consideration of fast processes such as overland flow was required. In contrast, many of the field scale leaching models operate at a daily time step, which is often suitable for the relatively slow leaching process. Still, it needs to be mentioned that numerical models often internally reduce the calculation time step in case of fast flow events (e.g., Larsbo and Jarvis, 2003; Gassmann et al., 2013). Figure 2 shows, that, even though there are models simulating pesticide parent compounds at the large catchment scale with a time step of one day (e.g., SWAT (Arnold et al., 1998) or AnnAGNPS (Bingner et al., 2011), none of these models is able to simulate TPs. Thus, a spatio-temporal gap exists at the one-day—catchment scale combination.

FIGURE 2

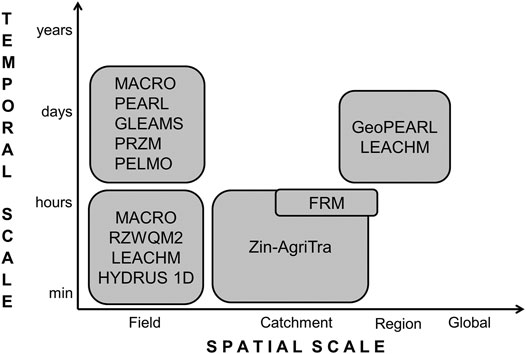
FIGURE 2. Spatio-temporal resolution of investigated models. The temporal scale depicts the minimum output time step possible.

Modelling Aim and Model Performance

The major aim of the above cited 20 TP model applications was model testing (50%). 30% of the studies performed process analysis and 20% did both. Most of the above cited studies (except the spatial leaching models) compared the TP simulations to sampling data. However, many model applications were unsuccessful or did not capture the full behaviour of TPs. One reason may be, that only 70% of the applications were calibrated while the rest performed no calibration. Others, such as Marín-Benito et al. (2015) did not calibrate the transformation parameters but only sorption parameters. The question whether a model should be calibrated or not depends on the aim of the modelling exercise: all model applications without calibration were performed for testing their ability to simulate the environmental fate of TPs. On the other hand, all applications done for process analysis were calibrated first. Generally, parameterization of TP fate modules is hampered by the fact, that studies investigating environmental fate characteristics such as transformation kinetics or adsorption of TPs are rare (Lewis et al., 2016). Thus, deriving parameter ranges for model calibration from the literature is often not possible. Without any fate studies for Chlorpyrifos Oxon, Gassmann et al. (2014) gained parameter values using Quantitative Structure Property Relationships (QSPR) from BIOWIN (Boethling et al., 1994) and KOCWIN (Meylan et al., 1992). Since experimental fate studies are hampered by the high number of TPs in the environment and the fact that pure standards are often not available for lab analytics, such in silico methods may gain importance in the future.

The simulation of preferential flow is a critical topic for water and substance fluxes in soil, since they largely influence the transit time distributions of water (Weiler, 2017). This is reflected in the large number of studies (35%) in this review stating that missing (PEARL, PRZM, LEACHM, HYDRUS) or unsatisfactorily simulated (RZWQM) preferential flow was the main problem. However, one might ask why models without the possibility to simulate preferential flow are applied at all, if they fail in reproducing the chemograph? One reason might be the difficulties of simulating preferential flow: even if there is a module for preferential flow, the parameterisation (number of macropores, radius, etc.) may not be possible without comprehensive field studies. One way forward may be the implementation of pedotransfer functions deriving main parameters from basic physical soil properties as it is done in the MACRO model (Larsbo and Jarvis, 2003).

Another source of failure for TP modelling (20%) were the implemented environmental fate concepts such as transformation schemes, long-term sorption and transformation dynamics in the models MACRO, RZWQM, PEARL, and FRM. This reflects a mismatch between known environmental fate processes from experimental studies and model implementation of these processes. It should also be noted that transformation processes were only given twice as reasons for model failure. Thus, either the implemented transformation processes were well suited in all other studies, or these equations were not even evaluated for their influence on model performance.

Less often (10%), parent compound application conditions, which could not be mimicked in the model, were given as reasons for model failure (PEARL, Zin-AgriTra). Especially spray drift and deposition on non-target surfaces during application are hard to capture in pesticide and TP fate models. Even though there are methods for an assessment of spray drift from meteorological and technical variables (e.g., Butler Ellis and Miller, 2010), short-term wind variations (wind gusts) and farmers’ behaviour (best management practices) are often unknown. Thus, the error introduced into the simulation of PCs is transferred to the simulation of TPs.

Model Complexity

The investigated models highly differ in their transformation process representation (Table 1). While most of the models have equations for the influence of soil moisture, soil temperature and soil depth on transformation rates, only the spatially distributed model GeoPEARL considers the influence of pH, organic carbon content and clay content. Half of the models are able to calculate the transformation of substances in the dissolved form, in the adsorbed domain or both. Only three models (RZWQM, PRZM, Pelmo) can form different TPs in different environmental compartments such as soil, plant surface or water body. In two models (RZWQM, Pelmo) different transformation rates can be attributed to different transformation processes such as microbial transformation or photolysis.

TABLE 1

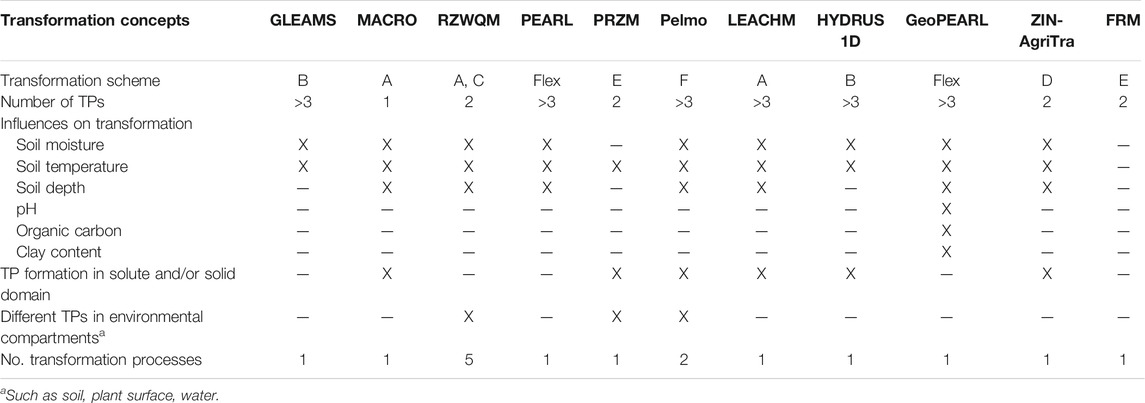
TABLE 1. Reviewed models and their model structures regarding pesticide transformation/TP formation. “Transformation scheme” refers to Figure 1. “flex” means a totally flexible scheme. X means the feature is included in a model.

To compare the models’ process representation numerically, their transport-related (hydrological) processes were rated in four classes and their transformation-related processes using a finer graduation (Figure 3). The method used for rating can be found in the supplement. The leaching models Pelmo and RZWQM2 are the models with the highest process complexity regarding transformation calculations. While RZWQM2 also has a high detail of hydrological process representation, Pelmo is more simplified in this respect. Generally, most leaching models have a moderate to high transformation process complexity. The MACRO model is the least detailed leaching model regarding transformation representation owing to its lumped processes approach, the simulation of only one TP and thus its simple transformation scheme (Table 1).

FIGURE 3

FIGURE 3. Level of detail of transformation and transport (i.e. hydrological) processes implemented in the models. For better visibility, models may have been shifted on the Transport axis (black: leaching models; green: catchment models).

Among the two catchment scale models, ZIN-AgriTra is by far the most detailed model in both, hydrological and transformation process representation. However, compared to leaching models, ZIN-AgriTra only has a medium level of transformation process complexity. The conceptual FRM model has both, a low transformation process complexity and a low transport process complexity. Thus, it might rather be seen as a quick overview tool than as a tool for the estimation of TP concentrations.

The choice of model complexity is always a balance between process representation and parameterisation effort. While the implementation of some process complexity such as the impact of soil moisture, soil temperature and soil depth on transformation rates is state-of-the-art (see Table 1), other process details may only be required in specific case studies. The differentiation between photolysis at plant surfaces and microbial transformation in soil, for example, might not be relevant for pre-emergent herbicides in Central Europe, but for fungicides or insecticides in Mediterranean orchards (Gassmann et al., 2014). Since experimental environmental fate information about TPs is rare, a higher degree of process representation in models might not even be desirable.

Number and Pathways of TPs

Many of the investigated models deal with one or two TPs at the same time. However, it became more and more obvious in the last decades, that there may rather be several dozen of TPs for each parent compound (e.g., Roberts et al., 1999). Even though it would be possible to simulate all these TPs in various runs, the complex interactions between TPs could not be considered. Thus, future models should be able to simulate a dynamic number of parent compounds and degradates and their interactions. While computational limits may have been an argument in the past, parallel computing and advanced computer hardware break these limits nowadays.

One approach to overcome the limitations of a simplistic transformation scheme outside the actual modelling software was implemented in LEACHM, which is only able to simulate a linear decay series (Webb et al., 2011). Input and output data of individual model runs were processed to fit the next PC-TP series. With this approach, a dynamic transformation scheme could be simulated. Similarly, a first approach for a more dynamic pathway calculation was implemented for MACRO. The model can be externally controlled by an R script called “MACRO unchained” (https://julienmoeys.github.io/macrounchained/), developed by Julien Moeys. The script adds the possibility of simulating n-th order TPs in MACRO, including TPs which are formed by several other TPs.

Comparing all the transformation schemes (Figure 1), it is apparent, that there is no model considering the pathway from a TP back to the parent. Only one model provides the possibility to have a two-way transformation between TPs (ZIN-AgriTra). A case where this transformation scheme would be needed is, for example, the insecticide endosulfan, where its two stereoisomers can transform into each other (Mukherjee and Gopal, 1994). Closely connected is the possibility of models to form different TPs by different transformation processes, which is currently only included in RZWQM, PRZM, and Pelmo with different levels of detail. Given that transformation processes may change in space and time, it seems necessary to implement the formation of TPs originating from different transformation processes in environmental fate models at all discussed scales.

Future Directions: Integrated Modelling

One major obstacle in moving forward in environmental fate estimation of TPs may be that different scientific communities work on this topic: environmental chemists rather investigating substance behaviour at the molecular level and build models for their prediction (QSPR models). Hydrologists rather work at the transport and fate in soil and at the surface and create leaching models and catchment models as discussed above. Taking the results of both communities, a future integrated modelling approach for pesticide TPs would be a fusion of models predicting transformation pathways of pesticides and TPs (e.g. Eawag-Soil in enviPath, Latino et al., 2017), models predicting environmental parameters such as sorption coefficients or degradation of TPs (e.g. the models included in the US-EPA EPI Suite, Card et al., 2017) and models predicting the dynamic transport and environmental fate (see above). With such integrated models, the environmental fate of pesticides could be estimated in a comprehensive way by only knowing the molecular structure of the parent compound and the environmental conditions. However, since all three types of models still have huge uncertainties, an expert application of each model is currently required. Thus, an interdisciplinary collaboration is currently the only way a comprehensive environmental fate assessment of pesticides including its multiple TPs can be achieved.

Conclusion

After more than two decades of research, pesticide TPs can no longer be called “emerging substances”, but they still pose a threat to many aquatic ecosystems. Thus, one might expect, that TP models are still being developed further, as is the case for pesticide parent compounds. However, research activity in TP model development and application was found to be surprisingly low in the last years. Even though there are eight leaching models and two catchment scale models described in the literature for the assessment of TP fate, only 20 individual studies have been published in which these models were tested or applied. According to the simulation problems stated in the investigated studies, the reason for the low number is rather not that all problems have been solved. Most of the studies did not even critically discuss implemented TP fate equations and concepts, but the predominating reasons given for model failure were transport processes, especially preferential flow. By comparing the structure of existing models, the state of knowledge on TP fate and requirements of TP fate assessment, the following recommendations can be drawn from this review:

(i) Advancement of environmental fate concepts: existing TP fate models should be extended to simulate flexible PC-TP transformation schemes; the formation of TPs originating from different transformation processes, such as phototransformation or microbial transformation, should be included.

(ii) Spatio-temporal structure: well-developed and applied catchment-scale models for pesticide fate assessment at 1-day temporal resolution should be extended by a TP module. This would enable a regional-scale river-concentration assessment.

(iii) The fusion of models predicting substance fate characteristics from the molecular structure (QSPR models) with environmental fate models should be advanced to get over the assessment of the huge number of TPs being built in the environment. The major benefit of these improvements would be tools for an easier and more comprehensive regulatory environmental exposure assessment of pesticides including most of their TPs in various compartments and climates.

Author Contributions

MG performed all the work included in this article.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2021.717738/full#supplementary-material

References

L. R. Ahuja (Editors) (2000). Root Zone Water Quality Model. Modeling Management Effects on Water Quality and Crop Production (Highlands Ranch Colo: Water Resources Publ).

Arnold, J. G., Srinivasan, R., Muttiah, R. S., and Williams, J. R. (1998). Large Area Hydrologic Modeling and Assessment Part I: Model Development. J. Am. Water Resour. Assoc 34 (1), 73–89. doi:10.1111/j.1752-1688.1998.tb05961.x

CrossRef Full Text | Google Scholar

Bergvall, M., Grip, H., Sjöström, J., and Laudon, H. (2011). Modeling Subsurface Transport in Extensive Glaciofluvial and Littoral Sediments to Remediate a Municipal Drinking Water Aquifer. Hydrol. Earth Syst. Sci. 15 (7), 2229–2244. doi:10.5194/hess-15-2229-2011

CrossRef Full Text | Google Scholar

Bingner, R. L., Theurer, F. D., and Yuan, Y. (2011). AnnAGNPS TECHNICAL PROCESSES Documentation, Version 5.2, December 2011. Oxford, Mississippi: USDA-ARS, National Sedimentation Laboratory.

Boesten, J. J. T. I., and Linden, A. M. A. (1991). Modeling the Influence of Sorption and Transformation on Pesticide Leaching and Persistence. J. Environ. Qual. 20 (2), 425–435. doi:10.2134/jeq1991.00472425002000020015x

CrossRef Full Text | Google Scholar

Boethling, R. S., Howard, P. H., Meylan, W., Stiteler, W., Beauman, J., and Tirado, N. (1994). Group Contribution Method for Predicting Probability and Rate of Aerobic Biodegradation. Environ. Sci. Technol. 28 (3), 459–465. doi:10.1021/es00052a018

PubMed Abstract | CrossRef Full Text | Google Scholar

Boxall, A. B., Sinclair, C. J., Fenner, K., Kolpin, D., and Maund, S. J. (2004). When Synthetic Chemicals Degrade in the Environment. Environ. Sci. Technol. 38 (19), 368A–375A. doi:10.1021/es040624v

PubMed Abstract | CrossRef Full Text | Google Scholar

Bustos, N., Cruz-Alcalde, A., Iriel, A., Fernández Cirelli, A., and Sans, C. (2019). Sunlight and UVC-254 Irradiation Induced Photodegradation of Organophosphorus Pesticide Dichlorvos in Aqueous Matrices. Sci. Total Environ. 649, 592–600. doi:10.1016/j.scitotenv.2018.08.254

PubMed Abstract | CrossRef Full Text | Google Scholar

Butler Ellis, M. C., and Miller, P. C. H. (2010). The Silsoe Spray Drift Model: A Model of spray Drift for the Assessment of Non-target Exposures to Pesticides. Biosyst. Eng. 107 (3), 169–177. doi:10.1016/j.biosystemseng.2010.09.003

CrossRef Full Text | Google Scholar

Card, M. L., Gomez-Alvarez, V., Lee, W.-H., Lynch, D. G., Orentas, N. S., Lee, M. T., et al. (2017). History of EPI Suite and Future Perspectives on Chemical Property Estimation in US Toxic Substances Control Act New Chemical Risk Assessments. Environ. Sci. Process. Impacts 19 (3), 203–212. doi:10.1039/c7em00064b

PubMed Abstract | CrossRef Full Text | Google Scholar

Carsel, R. F., Mulkey, L. A., Lorber, M. N., and Baskin, L. B. (1985). The Pesticide Root Zone Model (PRZM). A Procedure for Evaluating Pesticide Leaching Threats to Groundwater. Ecol. Modell. 30 (1-2), 49–69. doi:10.1016/0304-3800(85)90036-5

CrossRef Full Text | Google Scholar

C. C. Truman, C. C., R. A. Leonard, R. A., and A. W. Johnson, A. W. (1998). Fenamiphos Transport, Transformation, and Degradation in a Highlyweathered Soil. Trans. Am. Soc. Agric. Eng. 41, 663–671. doi:10.13031/2013.17234

CrossRef Full Text | Google Scholar

Farlin, J., Gallé, T., Bayerle, M., Pittois, D., Braun, C., El Khabbaz, H., et al. (2013). Using the Long-Term Memory Effect of Pesticide and Metabolite Soil Residues to Estimate Field Degradation Half-Life and Test Leaching Predictions. Geoderma 207-208, 15–24. doi:10.1016/j.geoderma.2013.04.028

CrossRef Full Text | Google Scholar

Fenner, K., Canonica, S., Wackett, L. P., and Elsner, M. (2013). Evaluating Pesticide Degradation in the Environment: Blind Spots and Emerging Opportunities. Science 341 (6147), 752–758. doi:10.1126/science.1236281

PubMed Abstract | CrossRef Full Text | Google Scholar

Fenner, K., Schenker, U., and Scheringer, M. (2009). “Modelling Environmental Exposure to Transformation Products of Organic Chemicals,” in Transformation Products of Synthetic Chemicals in the Environment. Editor A. Boxall (Heidelberg: Springer Berlin), 121–149.

Google Scholar

Fox, G. A., Pulijala, S. H., and Sabbagh, G. J. (2007a). Influence of Rainfall Distribution on Simulations of Atrazine, Metolachlor, and Isoxaflutole/metabolite Transport in Subsurface Drained fields. J. Agric. Food Chem. 55, 5399–5407. doi:10.1021/jf063753z

PubMed Abstract | CrossRef Full Text | Google Scholar

Fox, G. A., Sabbagh, G. J., Malone, R. W., and Rojas, K. (2007b). Modeling Parent and Metabolite Fate and Transport in Subsurface Drained Fields with Directly Connected Macropores1. J. Am. Water Resour. Assoc 43 (6), 1359–1372. doi:10.1111/j.1752-1688.2007.00116.x

CrossRef Full Text | Google Scholar

Gassmann, M., Khodorkovsky, M., Friedler, E., Dubowski, Y., and Olsson, O. (2014). Uncertainty in the River export Modelling of Pesticides and Transformation Products. Environ. Model. Softw. 51, 35–44. doi:10.1016/j.envsoft.2013.09.021

CrossRef Full Text | Google Scholar

Gassmann, M., Lange, J., and Schuetz, T. (2012). Erosion Modelling Designed for Water Quality Simulation. Ecohydrol 2012 (5), 269–278. doi:10.1002/eco.207

CrossRef Full Text | Google Scholar

Gassmann, M., Olsson, O., Stamm, C., Weiler, M., and Kümmerer, K. (2015). Physico-chemical Characteristics Affect the Spatial Distribution of Pesticide and Transformation Product Loss to an Agricultural brook. Sci. Total Environ. 532, 733–743. doi:10.1016/j.scitotenv.2015.06.068

PubMed Abstract | CrossRef Full Text | Google Scholar

Gassmann, M., Stamm, C., Olsson, O., Lange, J., Kümmerer, K., and Weiler, M. (2013). Model-based Estimation of Pesticides and Transformation Products and Their export Pathways in a Headwater Catchment. Hydrol. Earth Syst. Sci. 17 (12), 5213–5228. doi:10.5194/hess-17-5213-2013

CrossRef Full Text | Google Scholar

Gavrilescu, M. (2005). Fate of Pesticides in the Environment and its Bioremediation. Eng. Life Sci. 5 (6), 497–526. doi:10.1002/elsc.200520098

CrossRef Full Text | Google Scholar

Guzzella, L., Capri, E., Di Corcia, A., Barra Caracciolo, A., and Giuliano, G. (2006). Fate of Diuron and Linuron in a Field Lysimeter experiment. J. Environ. Qual. 35 (1), 312–323. doi:10.2134/jeq2004.0025

PubMed Abstract | CrossRef Full Text | Google Scholar

Holvoet, K. M. A., Seuntjens, P., and Vanrolleghem, P. A. (2007). Monitoring and Modeling Pesticide Fate in Surface Waters at the Catchment Scale. Ecol. Model. 209 (1), 53–64. doi:10.1016/j.ecolmodel.2007.07.030

CrossRef Full Text | Google Scholar

Hutson, J. L. (2005). LEACHM: Leaching Estimation and Chemistry Model: A Process-Based Model of Water and Solute Movement, Transformations, Plant Uptake and Chemical Reactions in the Unsaturated Zone: Model Description and User’s Guide, Version 4.1 Research Series R03-1. Ithaca, NY, USA: Cornell University.

Hutson, J. L., and Wagenet, R. J. (1992). LEACHM, Leaching Estimation and Chemistry Model, a Process-Based Model of Water and Solute Movement, Transformations, Plant Uptake and Chemical Reactions in the Unsaturated Zone, Version 3, Research Series No. 92-3. NY, USA: Department of Soil, Crop and Atmospheric Sciences, Cornell University.

Ippolito, A., and Fait, G. (2019). Pesticides in Surface Waters: from Edge-Of-Field to Global Modelling. Curr. Opin. Environ. Sustainability 36, 78–84. doi:10.1016/j.cosust.2018.10.023

CrossRef Full Text | Google Scholar

Kern, S., Singer, H., Hollender, J., Schwarzenbach, R. P., and Fenner, K. (2011). Assessing Exposure to Transformation Products of Soil-Applied Organic Contaminants in Surface Water: Comparison of Model Predictions and Field Data. Environ. Sci. Technol. 45 (7), 2833–2841. doi:10.1021/es102537b

PubMed Abstract | CrossRef Full Text | Google Scholar

Kiefer, K., Müller, A., Singer, H., and Hollender, J. (2019). New Relevant Pesticide Transformation Products in Groundwater Detected Using Target and Suspect Screening for Agricultural and Urban Micropollutants with LC-HRMS. Water Res. 165, 114972. doi:10.1016/j.watres.2019.114972

PubMed Abstract | CrossRef Full Text | Google Scholar

Klein, M. (1995). Pesticide Leaching Model, User Manual Version 2.01. Schmallenberg, Germany: Fraunhofer-Institut für Umweltchemie und Ökotoxikogie.

Köhne, J. M., Köhne, S., and Šimůnek, J. (2009). A Review of Model Applications for Structured Soils: B) Pesticide Transport. J. contaminant Hydrol. 104 (1–4), 36–60. doi:10.1016/j.jconhyd.2008.10.003

CrossRef Full Text | Google Scholar

Kupfersberger, H., Klammler, G., Schumann, A., Brückner, L., and Kah, M. (2018). Modeling Subsurface Fate of -Metolachlor and Metolachlor Ethane Sulfonic Acid in the Westliches Leibnitzer Feld Aquifer. Vadose Zone J. 17 (), 1–12. doi:10.2136/vzj2017.01.0030

CrossRef Full Text | Google Scholar

Larsbo, M., and Jarvis, N. (2003). MACRO 5.0. A Model of Water Flow and Solute Transport in Macroporous soilTechnical Description. Uppsala, Sweden: Swedish University of Agricultural Sciences.

Latino, D. A. R. S., Wicker, J., Gütlein, M., Schmid, E., Kramer, S., and Fenner, K. (2017). Eawag-Soil in enviPath: a New Resource for Exploring Regulatory Pesticide Soil Biodegradation Pathways and Half-Life Data. Environ. Sci. Process. Impacts 19 (3), 449–464. doi:10.1039/c6em00697c

PubMed Abstract | CrossRef Full Text | Google Scholar

Leistra, M., van der Linden, A., Boesten, J., Tiktak, A., and van den Berg, F. (2001). “PEARL Model for Pesticide Behaviour and Emissions in Soil-Plant Systems. Description of Processes,”. Alterra report 13, RIVM report 711401009 (Wageningen: Alterra), 107.

Google Scholar

Leonard, R. A., Knisel, W. G., Davis, F. M., and Johnson, A. W. (1990). Validating GLEAMS with Field Data for Fenamiphos and its Metabolites. J. Irrigation Drainage Eng. 116, 24–35. doi:10.1061/(asce)0733-9437(1990)116:1(24)

CrossRef Full Text | Google Scholar

Lewis, K. A., Tzilivakis, J., Warner, D. J., and Green, A. (2016). An International Database for Pesticide Risk Assessments and Management. Hum. Ecol. Risk Assess. Int. J. 22 (4), 1050–1064. doi:10.1080/10807039.2015.1133242

CrossRef Full Text | Google Scholar

Ma, Q., Don Wauchope, R., Ma, L., Rojas, K. W., Malone, R. W., and Ahuja, L. R. (2004). Test of the Root Zone Water Quality Model(RZWQM) for Predicting Runoff of Atrazine, Alachlor and Fenamiphos Species from Conventional-Tillage Corn Mesoplots. Pest Manag. Sci. 60, 267–276. doi:10.1002/ps.846

PubMed Abstract | CrossRef Full Text | Google Scholar

Mackay, D. (2001). Multimedia Environmental Models. The Fugacity Approach. Hoboken: CRC Press.

Mamy, L., Gabrielle, B., and Barriuso, E. (2008). Measurement and Modelling of Glyphosate Fate Compared with that of Herbicides Replaced as a Result of the Introduction of Glyphosate-Resistant Oilseed Rape. Pest Manag. Sci. 64 (3), 262–275. doi:10.1002/ps.1519

PubMed Abstract | CrossRef Full Text | Google Scholar

Marín-Benito, J. M., Rodríguez-Cruz, M. S., Sánchez-Martín, M. J., and Mamy, L. (2015). Modeling Fungicides Mobility in Undisturbed Vineyard Soil Cores Unamended and Amended with Spent Mushroom Substrates. Chemosphere 134, 408–416. doi:10.1016/j.chemosphere.2015.04.103

PubMed Abstract | CrossRef Full Text | Google Scholar

McManus, S.-L., Coxon, C. E., Mellander, P.-E., Danaher, M., and Richards, K. G. (2017). Hydrogeological Characteristics Influencing the Occurrence of Pesticides and Pesticide Metabolites in Groundwater across the Republic of Ireland. Sci. Total Environ. 601-602, 594–602. doi:10.1016/j.scitotenv.2017.05.082

PubMed Abstract | CrossRef Full Text | Google Scholar

Meylan, W., Howard, P. H., and Boethling, R. S. (1992). Molecular Topology/fragment Contribution Method for Predicting Soil Sorption Coefficientsficients. Environ. Sci. Technol. 26 (8), 1560–1567. doi:10.1021/es00032a011

CrossRef Full Text | Google Scholar

Mottes, C., Lesueur-Jannoyer, M., Le Bail, M., and Malézieux, E. (2014). Pesticide Transfer Models in Crop and Watershed Systems: a Review. Agron. Sustain. Dev. 34 (1), 229–250. doi:10.1007/s13593-013-0176-3

CrossRef Full Text | Google Scholar

Mukherjee, I., and Gopal, M. (1994). Interconversion of Stereoisomers of Endosulfan on Chickpea Crop under Field Conditions. Pestic. Sci. 40 (2), 103–106. doi:10.1002/ps.2780400203

CrossRef Full Text | Google Scholar

Olsson, O., Khodorkovsky, M., Gassmann, M., Friedler, E., Schneider, M., and Dubowski, Y. (2013). Fate of Pesticides and Their Transformation Products: First Flush Effects in a Semi-arid Catchment. Clean. Soil Air Water 41 (2), 134–142. doi:10.1002/clen.201100545

CrossRef Full Text | Google Scholar

Papiernik, S. K., Yates, S. R., Koskinen, W. C., and Barber, B. (2007). Processes Affecting the Dissipation of the Herbicide Isoxaflutole and its Diketonitrile Metabolite in Agricultural Soils under Field Conditions. J. Agric. Food Chem. 55 (21), 8630–8639. doi:10.1021/jf071256s

PubMed Abstract | CrossRef Full Text | Google Scholar

Payraudeau, S., and Gregoire, C. (2012). Modelling Pesticides Transfer to Surface Water at the Catchment Scale: a Multi-Criteria Analysis. Agron. Sustain. Dev. 32 (2), 479–500. doi:10.1007/s13593-011-0023-3

CrossRef Full Text | Google Scholar

Pennell, K. D., Hornsby, A. G., Jessup, R. E., and Rao, P. S. C. (1990). Evaluation of Five Simulation Models for Predicting Aldicarb and Bromide Behavior under Field Conditions. Water Resour. Res. 26 (11), 2679–2693. doi:10.1029/wr026i011p02679

CrossRef Full Text | Google Scholar

Petit, V., Cabridenc, R., Swannell, R. P. J., and Sokhi, R. S. (1995). Review of Strategies for Modelling the Environmental Fate of Pesticides Discharged into Riverine Systems. Environ. Int. 21 (2), 167–176. doi:10.1016/0160-4120(95)00006-2

CrossRef Full Text | Google Scholar

R. A. Leonard, R. A., W. G. Knisel, W. G., and D. A. Still, D. A. (1987). GLEAMS: Groundwater Loading Effects of Agricultural Management Systems. Trans. Am. Soc. Agric. Eng. 30 (5), 1403–1418. doi:10.13031/2013.30578

CrossRef Full Text | Google Scholar

Roberts, T. R., Hutson, D. H., Lee, P. W., Nicholls, P. H., and Plimmer, J. R. (1999). Metabolic Pathways of Agrochemicals. Cambridge: Royal Society of Chemistry.

Rosenbom, A. E., Kjær, J., Henriksen, T., Ullum, M., and Olsen, P. (2009). Ability of the MACRO Model to Predict Long-Term Leaching of Metribuzin and Diketometribuzin. Environ. Sci. Technol. 43 (9), 3221–3226. doi:10.1021/es802752x

PubMed Abstract | CrossRef Full Text | Google Scholar

Schenker, U., Scheringer, M., and Hungerbühler, K. (2007). Including Degradation Products of Persistent Organic Pollutants in a Global Multi-media Box Model. Env Sci. Poll Res. Int. 14 (3), 145–152. doi:10.1065/espr2007.03.398

CrossRef Full Text | Google Scholar

Schuhmann, A., Gans, O., Weiss, S., Fank, J., Klammler, G., Haberhauer, G., et al. (2016). A Long-Term Lysimeter experiment to Investigate the Environmental Dispersion of the Herbicide Chloridazon and its Metabolites-Comparison of Lysimeter Types. J. Soils Sediments 16 (3), 1032–1045. doi:10.1007/s11368-015-1311-3

CrossRef Full Text | Google Scholar

Siimes, K., and Kämäri, J. (2003). A Review of Available Pesticide Leaching Models: Selection of Models for Simulation of Herbicide Fate in Finnish Sugar Beet Cultivation. Boreal Environ. Res. 8 (1), 31–51.

Google Scholar

Šimůnek, J., Huang, K., and van Genuchten, M. T. (1998). “The HYDRUS Code for Simulating the One-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated media,” . version 6.0. Research Report 144 (Riverside, CA: US Salin. Lab., USDA-ARS).

Google Scholar

Tiktak, A., Nie, D. D., Van Der LindenTon, Kruijne, T., and Kruijne, R. (2002). Modelling the Leaching and Drainage of Pesticides in the Netherlands: the GeoPEARL Model. Agronomie 22 (4), 373–387. doi:10.1051/agro:2002022

CrossRef Full Text | Google Scholar

Tiktak, A., van der Linden, A., and Boesten, J. J. T. I. (2003). “The GeoPEARL Model. Model Description, Applications and Manual,”. RIVM report 716601007/2003.

Google Scholar

van der Linden, A. M. A., Tiktak, A., Boesten, J. J. T. I., and Leijnse, A. (2009). Influence of pH-dependent Sorption and Transformation on Simulated Pesticide Leaching. Sci. Total Environ. 407 (10), 3415–3420. doi:10.1016/j.scitotenv.2009.01.059

PubMed Abstract | CrossRef Full Text | Google Scholar

Vink, J. P. M., Gottesbüren, B., Diekkrüger, B., and van der Zee, S. E. A. T. M. (1997). Simulation and Model Comparison of Unsaturated Movement of Pesticides from a Large clay Lysimeter. Ecol. Model. 105 (1), 113–127. doi:10.1016/s0304-3800(97)00147-6

CrossRef Full Text | Google Scholar

Webb, R. M. T., Sandstrom, M. W., Krutz, L. J., and Shaner, D. L. (2011). Simulation of Branched Serial First-Order Decay of Atrazine and Metabolites in Adapted and Nonadapted Soils. Environ. Toxicol. Chem. 30 (9), 1973–1981. doi:10.1002/etc.597

PubMed Abstract | CrossRef Full Text | Google Scholar

Webb, R. M. T., Wieczorek, M. E., Nolan, B. T., Hancock, T. C., Sandstrom, M. W., Barbash, J. E., et al. (2008). Variations in Pesticide Leaching Related to Land Use, Pesticide Properties, and Unsaturated Zone Thickness. J. Environ. Qual. 37 (3), 1145–1157. doi:10.2134/jeq2007.0245

PubMed Abstract | CrossRef Full Text | Google Scholar

Weiler, M. (2017). Macropores and Preferential Flow-A Love-Hate Relationship. Hydrol. Process. 31 (1), 15–19. doi:10.1002/hyp.11074

CrossRef Full Text | Google Scholar

Young, D., and Fry, M. (2014). PRZM5 A Model for Predicting Pesticide in Runoff, Erosion, and Leachate: User Manual. Washington DC: US-EPA.