Pollutant Flux Estimation of the Lijiang River Based on an Improved Prediction-Correction Method

Introduction

Globally, water pollution is one of the most important environmental issues. In rivers, various pollutants, impacted by physical, chemical, biological, ecological, climatic, and other factors, can cause eutrophication, acidification, or alkalization, posing a threat to river ecosystem health (Aparicio et al., 2016; Steward et al., 2018). Pollutants in rivers can be rapidly transported through surface and subsurface routes, directly influencing the landscape water quality and regional water safety (Zhang et al., 2017; Qin et al., 2019). The river pollutant flux can directly reflect the total pollution load in the watershed above the river section, representing the production and transportation characteristics of pollutants in the watershed, which is the basis for formulating pollution control plans and measures (Halliday et al., 2014). However, low-frequency and discrete water quality monitoring data series pose great challenges to the reliable quantification of river pollutant fluxes (Li and Guo, 2017).

In China, water quality is routinely monitored once a month in most rivers. The monthly representative value method (i.e., assuming that the water quality monitoring data represent the monthly average water quality concentration) and the linear interpolation method (i.e., assuming that the water quality concentration changes linearly between two measured data) are conventional pollutant flux calculation methods suitable for rivers that are not subjected to considerable human activities (Valero, 2012; Gnann et al., 2018). However, when human activities are intensified, this has an obvious influence on water quality. Since river pollutant flux estimations are mainly based on the above two conventional methods, the actual situation is mostly not reflected, impeding the development of refined water management strategies. Therefore, to obtain more accurate simulation results, a method of pollutant flux estimation based on watershed pollution load modeling (e.g., SWAT model and HSPF model) is developed (Chang and Li, 2017; Bui et al., 2019). As such an approach requires numerous data types (e.g., terrain, meteorological, land use, soil, and vegetation data), which are difficult to obtain, it is necessary to develop a method which not only reasonably describes the water quality fluctuation characteristics but also has simple requirements for data and can be easily used (Murphy and Sprague, 2019; Terskii et al., 2019).

Based on previous studies, there are good statistical correlations between river pollutant flux and discharge (Li and Guo, 2017; Kim et al., 2018). Therefore, by establishing the regression relationship between pollutant flux and discharge, high-frequency discharge monitoring data can be used to interpolate the pollutant flux between two measured water quality values, facilitating the determination of the fluctuation process between two measured values. In this paper, the Load Estimator (LOADEST) model can establish the regression equation between pollutant flux and daily discharge and can subsequently estimate the river pollutant flux at different time and space scales using daily discharge monitoring data and low-frequency water quality monitoring data (Runkel et al., 2004). Some authors have applied the LOADEST model to estimate pollutant fluxes in the North Jiulong River, the Three Gorges Reservoir Area, the Peru Creek, the Mississippi River, and the Ishikari River (Duan et al., 2013; Runkel et al., 2013; Pellerin et al., 2014; Gao et al., 2018; Zhu et al., 2019). However, affected by incomplete data and non-optimal parameters, there are inevitable errors between estimated and measured values, resulting in deviation during pollutant flux estimation. Therefore, to reduce the error and improve the calculation accuracy, an effective data correction method is crucial.

As an optimal autoregressive data-processing algorithm, Kalman filtering has the advantages of a small calculation workload and a short computing time. The main processes of Kalman filtering are prediction and correction (Cammalleri and Ciraolo, 2012). The prediction process mainly uses the time renewal equation to establish an a-priori estimation for the current state and calculates the values of state variable and error covariance to establish an a-priori estimation for the next time state. In the correction process, the measurement renewal equation is used to establish an improved posterior estimation of the current state based on the prior estimation of the prediction process and the measured variables (Evensen, 2003). It can improve the rationality and reliability of the estimation results, and is widely used in the real-time correction of hydrological and hydrodynamic models (Goncalves and Costa, 2013; Javaheri et al., 2019; Xiong et al., 2019).

This paper combines the LOADEST model and the Kalman filtering algorithm to improve the reliability of river pollutant flux estimation results. Based on low-frequency water quality monitoring data and daily discharge data collection, the optimal pollutant flux regression equation was selected by the LOADEST model, and the daily pollutant flux process was predicted based on the regression equation. Subsequently, the predicted pollutant flux was corrected by the Kalman filtering algorithm, thus obtaining the estimated pollutant flux.

Materials and Methods

Prediction of Pollutant Flux Based on the LOADEST Model

The LOADEST model estimates the river pollutant flux using multiple linear regression. The optimal flux regression equation of the corresponding pollutant is established based on continuous daily discharge monitoring data, the low-frequency water pollutant concentration monitoring data, and subsequently, the daily pollutant flux at different time scales is estimated, which makes up for the deficiency that conventional statistical methods cannot describe the fluctuation characteristics of water pollutant concentration (Kim et al., 2018).

Regression Equation of Pollutant Flux

Taking the water pollutant concentration monitoring data and the daily discharge monitoring data as input, the optimal regression equation between pollutant flux and discharge is selected by the LOADEST model to determine the daily pollutant flux (Gao et al., 2021). The LOADEST model provides 11 regression equations, as shown in Table 1.

TABLE 1

TABLE 1. Regression equations to determine the river pollutant flux by the LOADEST model.

In Table 1, L refers to the pollutant flux, kg/day; a₀ to a₆ represent the regression equation parameters to be estimated; lnQ equals ln (streamflow) minus the center of ln (streamflow); D equals the decimal time minus the center of decimal time in the research period; per is used to identify the duration of the estimation sequence (Runkel et al., 2004).

Parameter Estimation and Test

Due to limited observation times and the inaccuracy of historical information, the data frequently contain non-specific values, which fall in a specific observation interval, or values greater (less) than a certain threshold rather than a specific value. In statistics, such data are called censored data. The LOADEST model uses different parameter estimation methods based on whether the residual error of pollutant flux follow normal distribution and whether censored data occur. When residual error values are normally distributed, the censored data are estimated by adjusted maximum likelihood estimation (AMLE), whereas uncensored data are estimated by minimum variance unbiased estimation (MVUE) (Cohn et al., 1989, 1992). The specific algorithms are shown in Eqs 1, 2, respectively. When the residual error does not meet the requirements of normal distribution, the least absolute deviation (LAD) is used whether the data are censored or not, as shown in Eq. 3 (Powell, 1984):

$\begin{array}{c}{L}_{\mathbf{AMLE}}=\mathrm{e}\mathrm{x}\mathrm{p}\left(a_0+{\displaystyle \sum _{j=1}^{NV}{a}_j{X}_j}\right)\times H\left(a,b,s^2,\alpha ,\kappa \right)\end{array}(1)$

$\begin{array}{c}{L}_{\text{MVUE}}=\mathrm{e}\mathrm{x}\mathrm{p}\left(a_0+{\displaystyle \sum _{j=1}^{NV}{a}_j{X}_j}\right)\times g_m\left(m,s^2,V\right)\end{array}(2)$

$\begin{array}{c}{L}_{\text{LAD}}=\mathrm{e}\mathrm{x}\mathrm{p}\left(a_0+{\displaystyle \sum _{j=1}^{NV}{a}_j{X}_j}\right)\times \frac{{\displaystyle {\sum }_{k=1}^{n}exp\left(e_k\right)}}{n}\end{array}(3)$

where L_AMLE, L_MVUE, and L_LAD are the estimated pollutant fluxes calculated by AMLE, MVUE, and LAD methods, respectively; H (a, b, s², α, κ) represents the likelihood approximation function of infinite series; g_m (m, s², V) represents the Bessel function; α and κ represent the function of gamma distribution; a, b, and V represent the dependent variables; m represents the degree of freedom; s² represents the residual variance; e_k represents the residual error; and n represents the number of data points for equation calibration.

For the parameters of pollutant flux regression equation a₀ to a₆, the LOADEST model mainly tests the validity by the following methods:

1) Determination coefficient (R²) testing method. The determination coefficient is used to test the data fitness of the regression equation. According to the theory of mathematical statistics, R² > 80% indicates that the regression equation has a preferable fitting degree, and R² > 90% indicates that the regression equation fits well (Menard, 2000; Runkel et al., 2004).

2) Nash-Sutcliffe efficiency (NSE) testing method. The NSE represents the relationship between the calculated value and the average measured value of the model, which ranges from -∞ to 1. The larger the NSE value, the higher the coincidence between the simulated value and the measured value (Wu et al., 2019). The NSE value is calculated as follows:

$\begin{array}{c}NSE=1-\frac{{{\displaystyle \sum }}_{i=1}^n{\left(Q_{mea,i}-Q_{sim,i}\right)}^2}{{{\displaystyle \sum }}_{i=1}^n{\left(Q_{mea,i}-\overline{Q_{mea}}\right)}^2}\end{array}(4)$

where Q_mea,i and Q_sim,i represent the measured and simulated values, respectively, and $\overline{Q_{obs}}$ represents the average of the total measured value.

3) Serial correlation of residuals (SCR) testing method. The SCR is used to test whether there is sequence correlation in the residuals (Verbeke et al., 1998). The smaller the SCR value, the more independent the residual of the equation. For uncensored data, the probability plot correlation coefficient (PPCC) is used to test whether the residual of the regression equation is in accordance with normal distribution, and PPCC > 0.9 indicates that the residual meets the requirements of normal distribution (Vogel, 1986; Runkel et al., 2004). For censored data, the Turnbull-Weiss statistic method is used to test whether the residual of the regression equation is in accordance with normal distribution, and P < 0.05 indicates normal distribution (Turnbull and Weiss, 1978).

4) T-ratio testing method. As multicollinearity affects the result of regression analysis, the regression model uses the correlation coefficient to determine whether there is a correlation between independent variables. In the case of multicollinearity correlation, it can be eliminated by centralizing independent variables (Cohn et al., 1992). The equations are as follows:

$\begin{array}{c}\tilde{T}=\overline{T}+\frac{{\displaystyle {\sum }_{k=1}^N{\left(T_i-\overline{T}\right)}^3}}{2{\displaystyle {\sum }_{k=1}^N{\left(T_i-\overline{T}\right)}^2}}\end{array}(5)$

$\begin{array}{c}\overline{T}=\frac{1}{N}{\displaystyle \sum _{i=1}^N{T}_i}\end{array}(6)$

where $\tilde{T}$ represents the centering value; N represents the number of observation data used for parameter calibration; $\overline{T}$ is the mean value of the observation data.

Regression Equation Optimization

The regression equation is optimized by the Akaike Information Criterion (AIC) and the Schwarz Posterior Probability Criterion (SPPC) (Akaike, 1974; Schwarz, 1978). Both AIC and SPCC are standards to measure the complexity and the fitting accuracy of statistical models. They can be used to select the model with good fitness and least free parameters. When optimizing the regression equation, the AIC and SPCC values of each regression equation can be calculated by Eqs 7, 8, respectively. The equation with the minimum values is the optimum:

$\begin{array}{c}AIC=m\ln \left(\frac{SSR}{m}\right)+2k\end{array}(7)$

$\begin{array}{c}SPPC=m\ln \left(\frac{SSR}{m}\right)+k\ln \left(m\right)\end{array}(8)$

where SSR is the residual sum of squares; k represents the number of equation parameters; m represents the number of data groups for parameter estimation.

Pollutant Flux Correction Based on Kalman Filtering

The basic idea of the Kalman filtering algorithm is taking the minimum mean square error as the best estimation criterion, establishing the space model of signal and noise states, and using estimates of the previous time and observations of the present time to update the estimation of state variables, followed by obtaining the optimal estimates of the present time (Kalman, 1960; Campestrini et al., 2016). In this study, taking the measured pollutant flux values and the corresponding predicted pollutant flux values by the LOADEST model as inputs, the optimal pollutant flux estimates at the measured time are calculated based on the Kalman filtering algorithm. The difference between the optimal estimates and the measured values is the error at the measured time. Assuming that the errors follow linear distribution, the daily pollutant flux errors are obtained by extending the interpolation of the measured error values to the daily values (Aulenbach, 2013). Therefore, the corrected pollutant flux values are obtained by adding the daily flux pollutant error values to the predicted daily pollutant flux values.

According to the Kalman filtering theory, the state equation needs to be established and is as follows:

$\begin{array}{c}{X}_0=A{X}_L+\omega ,\cdots ,{\widehat{X}}_k=A{X}_{k-1}+\omega \end{array}(9)$

where X₀ is the initial iteration value by Kalman filtering; X_L represents the pollutant flux estimated by the LOADEST model; A represents the state transition parameter, which is equal to the linear correlation coefficient between the measured and the predicted value using the LOADEST model; w is the model noise that meets the requirements of normal distribution with mean value of 0 and a variance of D. The value of D can be determined based on the estimated flux error by the LOADEST model. ${\widehat{X}}_k$ represents the predicted value of the pollutant flux for the kth iteration; X_k-1 represents the corrected value of the pollutant flux for the k-1st iteration.

The updated equation of the state estimation error covariance is as follows:

$\begin{array}{c}{\widehat{P}}_k=A{P}_{k-1}{A}^T+D\end{array}(10)$

where ${\widehat{P}}_k$ represents the predicted error covariance for the kth iteration; P_k-1 represents the corrected error covariance for the k-1st iteration, and the initial value P₀ refers to the predicted error covariance by the LOADEST model.

The Kalman gain can be calculated as follow:

$\begin{array}{c}{\widehat{K}}_k=\frac{{\widehat{P}}_k{H}^T}{H{\widehat{P}}_k{H}^T+B}\end{array}(11)$

where K_k represents the Kalman gain for the kth iteration; H is the transformation parameter matrix with the determinant value of 1; and B represents the variance of measured noise.

The equation used for the filtering correction is as follows:

$\begin{array}{c}{X}_k={\widehat{X}}_k+K_k\left(Y-H{\widehat{X}}_k\right)\end{array}(12)$

where X_k represents the corrected pollutant flux value for the kth iteration, and Y represents the measured pollutant flux value.

The updated equation of the state filtering error covariance is as follows:

$\begin{array}{c}{P}_k=\left(I-K_{k}H\right){\widehat{P}}_k\end{array}(13)$

where P_k represents the state filtering error covariance, and I is the identity matrix. The autoregressive iterative calculation is performed sequentially according to Eqs 9–13. The optimal corrected pollutant flux value in the measured time is obtained when P_k converges to a constant value.

Study Area and Data

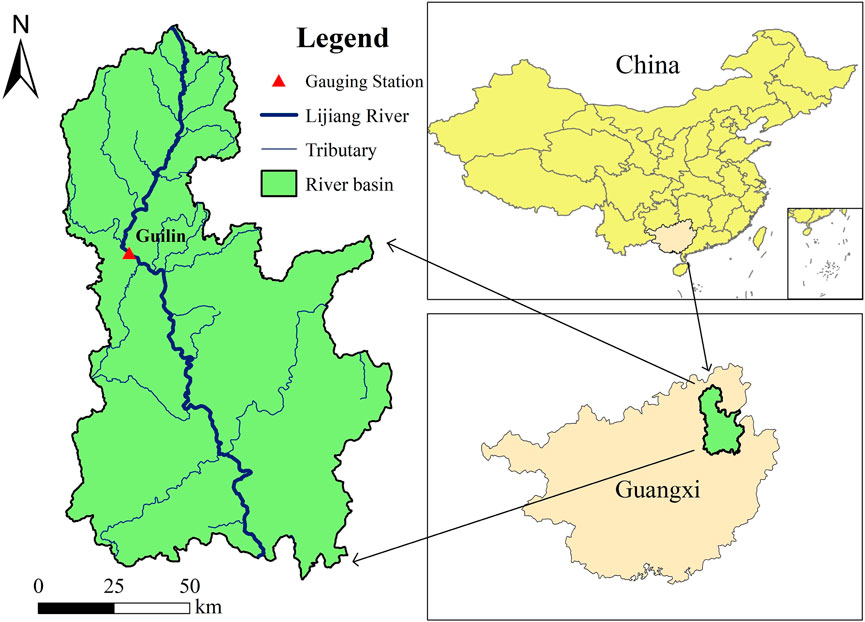
In this study, the improved method was applied to the Lijiang River (Figure 1) which is a tourist attraction of world-wide interest and belongs to the Pearl River basin. It is located in the northeast of the Guangxi Zhuang Autonomous Region, China. The Lijiang River originates from the northeast of the Mao’er Mountain and is famous for its picturesque scenery of mountains on the riverbanks, with a karst topography. The total length of the Lijiang River is 214 km, with a drainage area of 12,285 km² (24°18′–25°41′ N, 109°45′–110°40′ E). The climate of the Lijiang River basin is subtropical monsoonal climate, with warm, humid summers and cool, wet winters. The annual average temperature is 19.3°C, with an annual average precipitation of about 2,200 mm. Flooding mostly occurs in June and July, and the dry period is from October to March (Li et al., 2015).

FIGURE 1

FIGURE 1. Location of the lijiang river basin and gauging station.

The overall water quality of the Lijiang River is good. The rapid population growth, coupled with accelerated economic development, has gradually led to a deterioration of the water quality during the last few years (Deng et al., 2021). The discharge of wastewater from factories and the increase in industrial and domestic pollution discharge have resulted in water pollution risk. As it is difficult to control diffuse pollution from agricultural sources, the protection of the basin is challenging. Currently, water pollution is threatening the safety of water resources from the Lijiang River.

This paper estimated the river pollutant flux from 2010 to 2019 at the Guilin section of the Lijiang River. Due to nitrogen pollution caused by the extensive use of chemical fertilizers and pesticides on farmland, coupled with wastewater discharge from households and restaurants on both sides of the Lijiang River, chemical oxygen demand (COD), ammonia nitrogen (NH₃-N), and total phosphorus (TP) were selected as characteristic pollutants (Ye et al., 2010). Simultaneous observed precipitation data were obtained from the National Meteorological Information Center of China. Monitoring data of daily average discharge and low-frequency monitoring water pollutant concentration data for the Guilin section from 2010 to 2019 were provided by the Guilin Hydrology Bureau. These data were examined and calibrated to test whether they were homogeneous, extreme, and temporally consistent. Therefore, the data were considered to be reliable (Huang et al., 2019). The statistics of measured data, such as maximum, minimum, and mean of discharge and pollutant concentration parameters were seen in Table 2.

TABLE 2

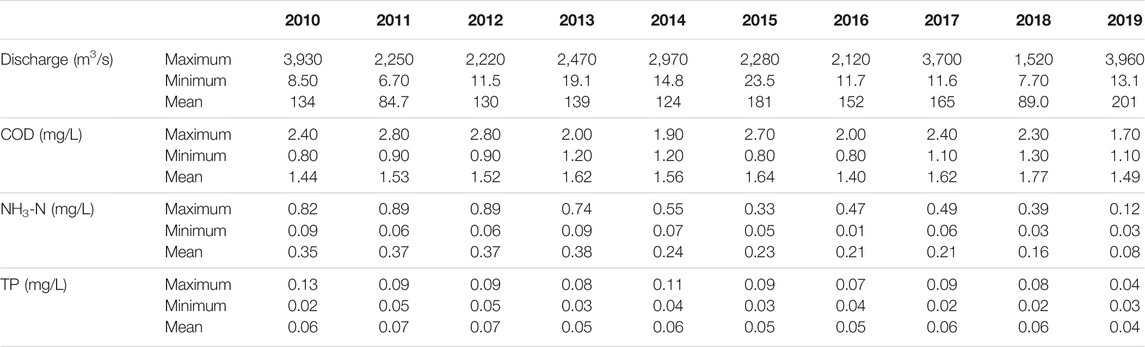
TABLE 2. Statistics of discharge, chemical oxygen demand (COD), ammonia nitrogen (NH₃-N), and total phosphorus (TP) data.

Results and Discussion

Regression Model

The pollutant flux regression Eqs 14–16 were obtained by using the daily average discharge, measured time, and water pollutant concentration data at the Guilin section of the Lijiang River; the parameters were calibrated by the optimization of AIC and SPCC. The results of the LOADEST model show that the optimal regression models for both NH₃-N and TP fluxes were seven-parameter equations, whereas the optimal regression model for COD was a three-parameter equation. The regression model analyses of COD, ammonia nitrogen, and TP are shown in Table 3.

$\begin{array}{c}\mathrm{COD}003A;\begin{array}{c}\ln L=9.3694+0.9166\ln Q+0.0104D\\ \left(AIC=0.02;SPCC=-0.17\right)\end{array}\}\end{array}(14)$

$\begin{array}{c}{\text{NH}}_3-\mathrm{N}003A;\begin{array}{c}\ln L=7.4448+0.7228\ln Q+0.0471{\left(\ln Q\right)}^2+0.3766\sin \left(2\pi D\right)\\ -0.0749\cos \left(2\pi D\right)-0.1318D-0.0229D^2\\ \left(AIC=1.88;SPCC=-122.63\right)\end{array}\}\end{array}(15)$

$\begin{array}{c}\mathrm{TP}003A;\begin{array}{c}\ln L=6.0083+0.8268\ln Q+0.0530{\left(\ln Q\right)}^2+0.0981\sin \left(2\pi D\right)\\ -0.1304\cos \left(2\pi D\right)-0.0249D-0.0086D^2\\ \left(AIC=0.72;SPCC=-52.89\right)\end{array}\}\end{array}(16)$

TABLE 3

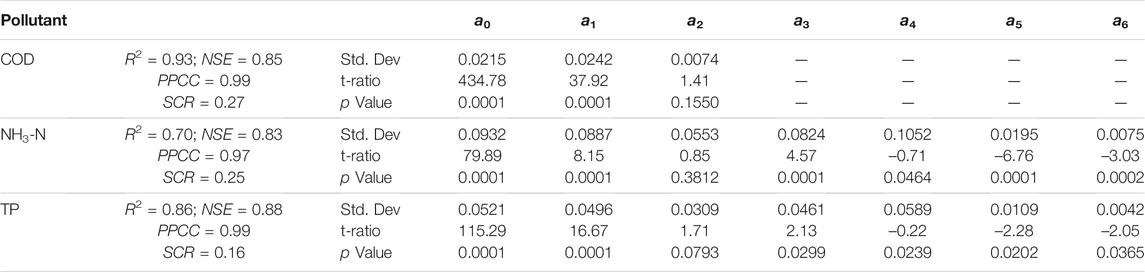
TABLE 3. Regression model analyses of chemical oxygen demand (COD), ammonia nitrogen (NH₃-N), and total phosphorus (TP). Std. Dev, standard deviation; NSE, Nash-Sutcliffe efficiency value; PPCC, probability plot correlation coefficient; SCR, serial correlation of residuals.

As shown in Table 3, the pollutant flux regression equations for COD, NH₃-N, and TP fit well for the study period, with R² values ranging from 0.70 to 0.93. The highest R² value was obtained for COD; a large R² value indicates that the pollutant flux, daily discharge, and time are well correlated. When comparing the simulated pollutant flux to the measured one, the NSE values were 0.85 (COD), 0.83 (NH₃-N), and 0.88 (TP), indicating that the numerical results for the Lijiang River and the monitoring results were similar, with a small error, and the LOADEST model is highly reliable. The p values obtained for COD, ammonia nitrogen, and TP were below 0.05, indicating that the equation coefficients were statistically significant. The SCR values were 0.27 (COD), 0.25 (NH₃-N), and 0.16 (TP), indicating that the residuals were independent. Furthermore, the PPCC values were 0.99 (COD), 0.97 (NH₃-N), and 0.99 (TP), indicating that the residuals meet the requirements of normal distribution. Based on the results, the regression equation optimized based on the LOADEST model can be used to predict the pollutant flux in the Lijiang River.

Pollutant Flux Estimation

In this study, the improved prediction-correction method was used to estimate the pollutant flux of the Lijiang River. The predicted pollutant flux based on the LOADEST model was corrected by applying the Kalman filtering algorithm. Generally, pollution flux depends on river discharge and water pollutant concentration. However, based on the results of the correlation analysis, the fluxes of COD, NH₃-N, and TP were only correlated with river discharge, with R² values of 0.92, 0.73, and 0.89, respectively (Figure 2). Although the pollution flux is a product of river discharge and water pollutant concentration, here, the fluxes of COD, NH₃-N, and TP mainly depended on the variation of river discharge during the study period, whereas the influence of water pollutant concentration was weak. These results indicate that there is a significant correlation between pollution flux and river discharge, which is consistent with the results of previous studies (Park and Engel, 2016; Kim et al., 2018). The correlation between pollutant flux and concentration largely depends on the hydrological conditions; in rivers with stable discharge, it is higher than in those with large flow fluctuations (Li and Guo, 2017).

FIGURE 2

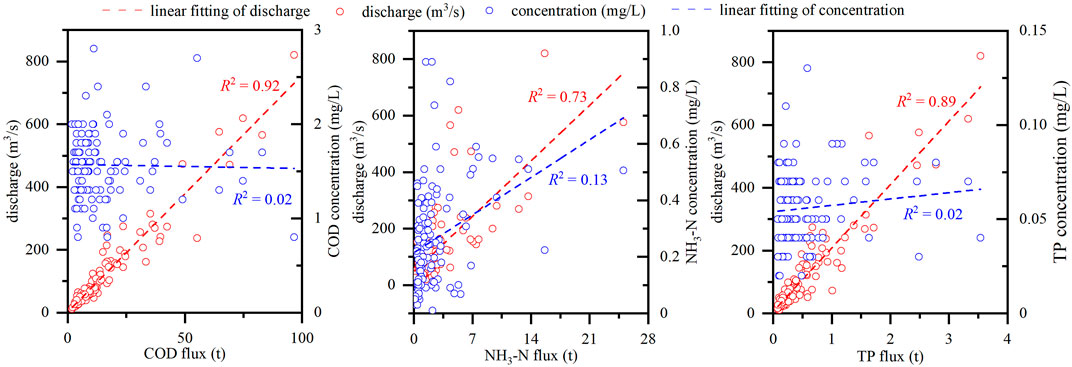
FIGURE 2. Correlations of measured of COD, NH₃-N, and TP fluxes with discharge and water pollutant concentration of the Lijiang River.

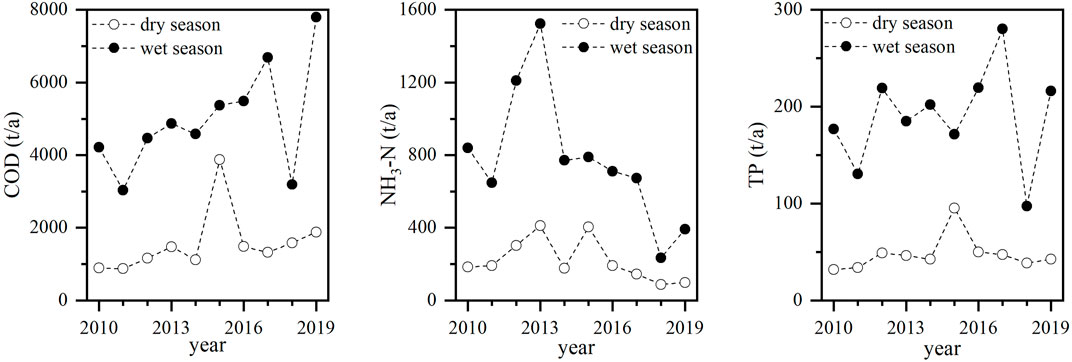
The annual and seasonal variations of pollutant fluxes are shown in Figures 3, 4. Throughout the study period, the annual average fluxes of COD, NH₃-N, and TP were 6,523.35, 997.53, and 237.21 t, respectively. As shown in Figure 3, the annual pollutant fluxes of both COD and TP exhibited an increasing trend from 2010 to 2019, with growth rates of 5.18 and 0.94%, respectively. This increase was mainly due to the economic and industrial development and the population increase in the Lijiang River Basin. The scouring on sediment causes more phosphorus to be released into the river, which may increase the pollutant flux of TP. The NH₃-N flux increased from 2010 to 2013, followed by a decrease until 2019, with an overall decline rate of 6.79%. Most likely, this is a result of the reduction of non-point source pollution input (e.g., pesticides, livestock manure, and fertilizer) and the decreased rural wastewater discharge (Xu et al., 2020).

FIGURE 3

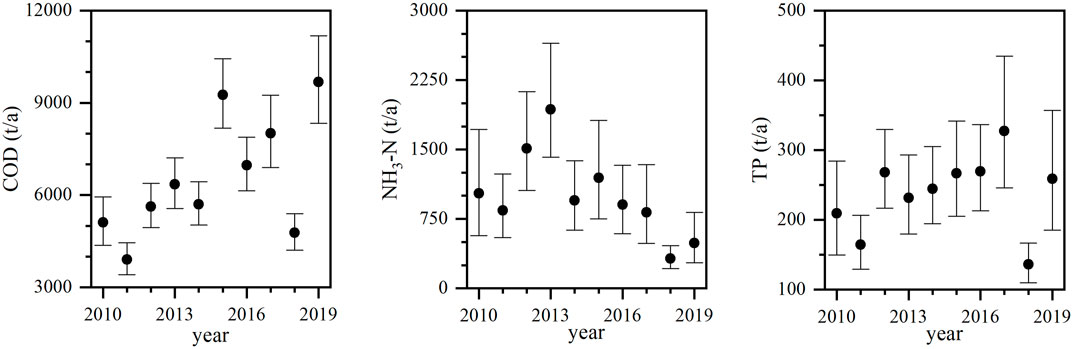
FIGURE 3. Estimated annual fluxes of COD, NH₃-N, and TP from 2010 to 2019. (Symbols represent annual fluxes; lines represent 95% confidence intervals).

FIGURE 4

FIGURE 4. Estimated seasonal fluxes of COD, NH₃-N, and TP from 2010 to 2019.

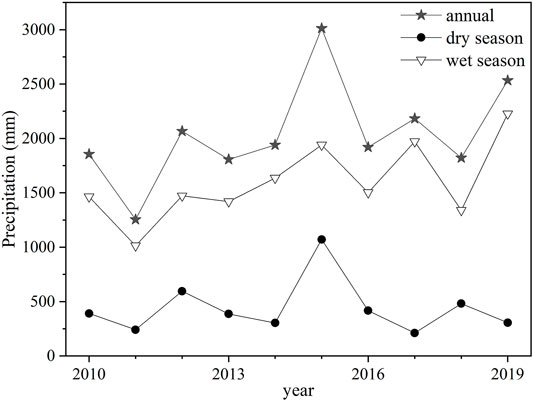
As shown in Figures 4, 5, annual fluxes of COD, NH₃-N, and TP showed considerable seasonality, corresponding with variations in discharge and rainfall (Li and Guo, 2017). All pollutants showed larger fluxes in the wet season (from March to August) compared to the dry season (from September to February). The annual average fluxes of COD, NH₃-N, and TP in the wet season were 4,970.98, 779.35, and 189.86 t throughout the study period, accounting for 76.20, 78.13, and 80.04% of the annual average fluxes, respectively. In the wet season, precipitation in the Lijiang River Basin is heavy, accounting for about 80% of the annual precipitation, which explains the large seasonal variations in pollutant fluxes (Figure 4). Pollutants are discharged into the river by runoff scouring after precipitation, resulting in increased pollutant loads. Therefore, precipitation is the main driving factor for the increase of runoff pollution in the river basin, and attention should be paid to the control of pollutant fluxes in the wet season. However, the NH₃-N flux in the wet season decreased from 2014 to 2019, which is basically consistent with the change in pollutant concentration, indicating that concentration is another factor affecting the NH₃-N flux.

FIGURE 5

FIGURE 5. Annual and seasonal precipitation of the Lijiang River Basin from 2010 to 2019.

Comparison With Other Methods

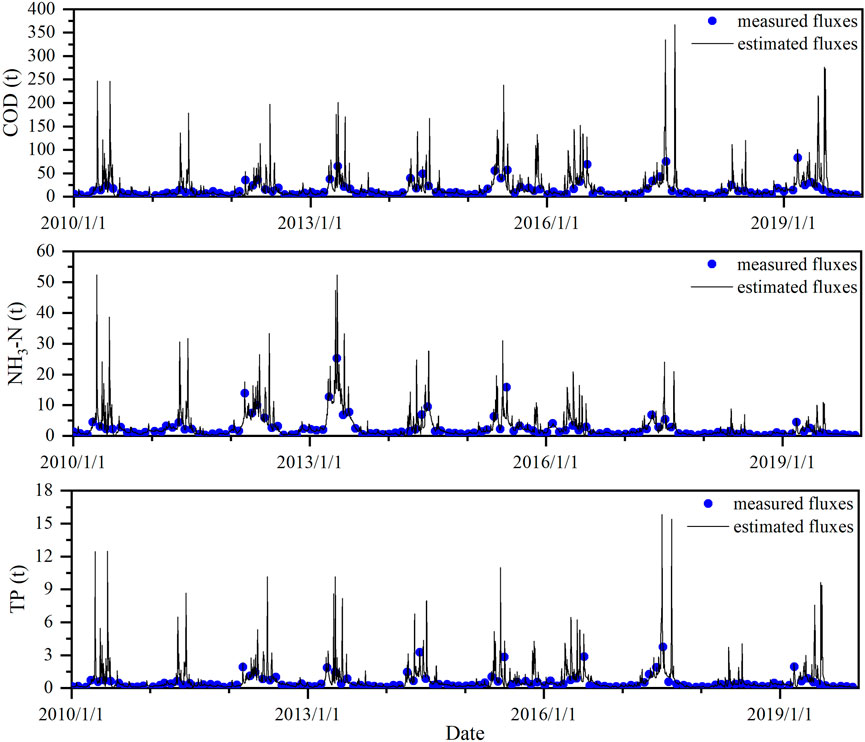
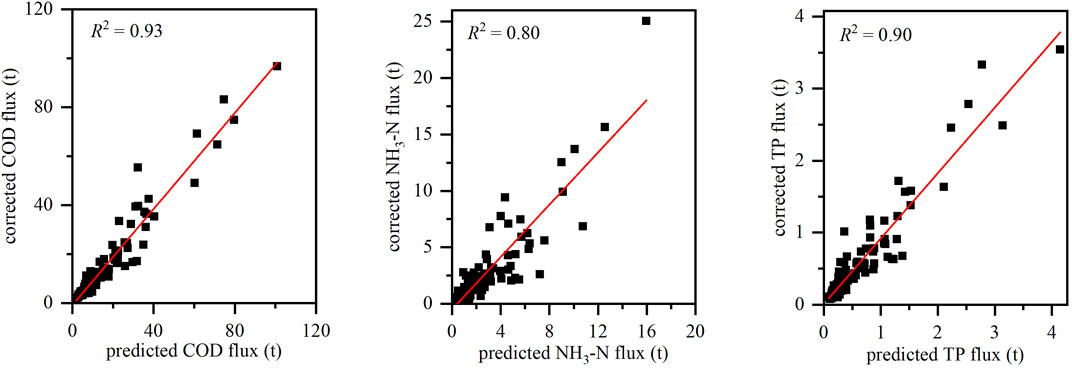
To verify the rationality of the pollutant flux estimation results based on the improved prediction-correction method, the estimated fluxes of COD, NH₃-N, and TP were compared with the measured fluxes and the simulated ones based on the LOADEST model. As shown in Figures 6, 7, the estimated daily fluxes largely coincided with the measured pollutant fluxes. Linear regression analysis was carried out on 120 predicted and corrected flux values and showed that the correlation coefficients of COD, NH₃-N, and TP were 0.93, 0.80, and 0.90, respectively. The cumulative COD fluxes of the total 120 measured values and their corresponding estimated values were 1,756.43 and 1,796.25 t, respectively. The relative deviation between estimated and measured fluxes of COD was reduced from 10.01 to 2.27% after pollutant flux correction. The cumulative NH₃-N fluxes of the total 120 measured values and their corresponding estimated values were 283.75 and 292.83 t, respectively. The relative deviation between estimated and measured fluxes of NH₃-N reduces from 7.18 to 3.20% after pollutant flux correction. The cumulative TP fluxes of the measured values and their corresponding estimated values were 63.52 and 64.40 t, respectively. The relative deviation between estimated and measured fluxes of TP was reduced from 9.76 to 1.39% after pollutant flux correction. These results indicate that the fluxes of COD, NH₃-N, and TP of the Lijiang River from 2010 to 2019, estimated by using the improved prediction-correction method based on the LOADEST model and the Kalman filtering algorithm, are reasonable and reliable.

FIGURE 6

FIGURE 6. Pollutant flux estimation with measured values.

FIGURE 7

FIGURE 7. Correlation of predicted COD, NH₃-N, and TP fluxes with corrected fluxes.

The fluxes of COD, NH₃-N, and TP at Guilin Section were calculated for 2010 to 2019, using the monthly representative value method (MRVM) and the linear interpolation method (LIM), and subsequently compared with the fluxes estimated by the improved prediction-correction method. As shown in Tables 4, 5, the values obtained by the different methods largely varied. For periods with small fluctuations in water quality (e.g., 2013–2015), the annual pollutant fluxes calculated via MRVM, LIM, and in the present study only slightly differed, with a deviation ranging from 0.21 to 18.60%. On the contrary, for periods with large fluctuations (e.g., 2010, 2011, 2016, and 2019), the annual pollutant fluxes differed largely depending on the applied method, with deviation ranging from 20.94 to 41.78%. Because of the slight fluctuations in monthly COD, NH₃-N, and TP concentrations at Guilin Section in the dry season, the variation in pollutant flux was mainly determined via discharge, resulting in only slight differences depending on the method. In the wet season, the opposite was observed. The pollutant flux deviation in separate months exceeded 100% (Supplementary Tables S1–S10). In addition, there was no significant difference in the processes and total COD flux estimated by the different methods. The main reason is that the monthly change of COD concentration is small, ranging between 1 and 2 mg/L in most months, and its flux is mainly determined by river discharge. In summary, for water pollutant concentration within a narrow range, the LIM and the MRVM can be used for pollutant flux estimation, whereas in the case of large fluctuations, these conventional methods should be used with caution. Here, the improved prediction-correction method, combining the LOADEST model and the Kalman filter algorithm, is a better choice for pollutant flux estimation.

TABLE 4

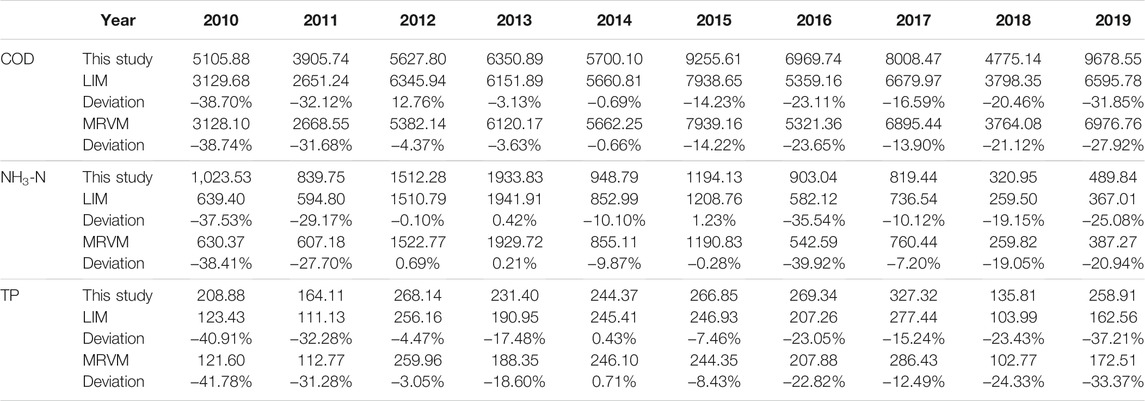
TABLE 4. Comparison of annual pollutant flux estimates obtained by different methods (LIM represents linear interpolation method, MRVM represents monthly representative value method).

TABLE 5

TABLE 5. Comparison of monthly pollutant flux estimates obtained by different methods.

Conclusion

To further develop the currently used river pollutant flux estimation methods, an improved prediction-correction method is proposed, including two steps: pollutant flux prediction based on the LOADEST model and pollutant flux correction using the Kalman filter algorithm. In the first step, the regression equation between pollutant flux and daily discharge is established to reflect the fluctuation characteristics of pollutants to compensate for the shortcomings of conventional calculation methods. In the second step, the predicted pollutant fluxes are corrected by the Kalman filter algorithm to reduce the error between the corrected and the measured values and to increase the reliability of the estimated results. The improved method has the advantages of simple data requirements and low technical complexity, making it the method of choice in large-scale applications. The results showed that the estimated fluxes of COD, NH₃-N, and TP were in good agreement with the measured values, indicating that the results based on the combination of the LOADEST model and the Kalman filtering algorithm are reliable. Compared with the results of the LIM and the MRVM, the improved prediction-correction method can be used as a better choice for pollutant flux estimation.

The improved method requires a good statistical regression relationship between pollutant flux and river discharge and is therefore suitable for rivers subjected to non-point source pollution. With the increase in the proportion of point source pollution, its application effect will decrease. The pollutant flux estimation method for rivers dominated by point source pollution should be further investigated.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

JC: conceptualization; data curation; methodology; validation; formal analysis; writing–original draft preparation; writing–review and editing; funding acquisition. WS: conceptualization; data curation; methodology; formal analysis; investigation; writing–original draft. XJ: supervision; writing–review and editing.

Funding

This research was financially supported by the Specific Research Project of Guangxi for Research Bases and Talents (GuiKe-AD21220106), and the National Natural Science Foundation of China (42101270).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Special thanks to Liangang Chen and Gang Wang for providing instructions and suggestion on this work. In addition, we thank the reviewers for their useful comments and suggestions.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2022.868404/full#supplementary-material

References

Akaike, H. (1974). A New Look at the Statistical Model Identification. IEEE Trans. Automat. Contr. 19 (6), 716–723. doi:10.1109/tac.1974.1100705

CrossRef Full Text | Google Scholar

Aparicio, F. L., Nieto-Cid, M., Borrull, E., Calvo, E., Pelejero, C., Sala, M. M., et al. (2016). Eutrophication and Acidification: Do They Induce Changes in the Dissolved Organic Matter Dynamics in the Coastal Mediterranean Sea? Sci. Total Environ. 563-564, 179–189. doi:10.1016/j.scitotenv.2016.04.108

PubMed Abstract | CrossRef Full Text | Google Scholar

Aulenbach, B. T. (2013). Improving Regression-Model-Based Streamwater Constituent Load Estimates Derived from Serially Correlated Data. J. Hydrol. 503, 55–66. doi:10.1016/j.jhydrol.2013.09.001

CrossRef Full Text | Google Scholar

Bui, H. H., Ha, N. H., Nguyen, T. N. D., Nguyen, A. T., Pham, T. T. H., Kandasamy, J., et al. (2019). Integration of SWAT and QUAL2K for Water Quality Modeling in a Data Scarce basin of Cau River basin in Vietnam. Ecohydrol. Hydrobiol. 19 (2), 210–223. doi:10.1016/j.ecohyd.2019.03.005

CrossRef Full Text | Google Scholar

Cammalleri, C., and Ciraolo, G. (2012). State and Parameter Update in a Coupled Energy/hydrologic Balance Model Using Ensemble Kalman Filtering. J. Hydrol. 416-417, 171–181. doi:10.1016/j.jhydrol.2011.11.049

CrossRef Full Text | Google Scholar

Campestrini, C., Heil, T., Kosch, S., and Jossen, A. (2016). A Comparative Study and Review of Different Kalman Filters by Applying an Enhanced Validation Method. J. Energ. Storage 8, 142–159. doi:10.1016/j.est.2016.10.004

CrossRef Full Text | Google Scholar

Chang, C.-L., and Li, M.-Y. (2017). Predictions of Diffuse Pollution by the HSPF Model and the Back-Propagation Neural Network Model. Water Environ. Res. 89 (8), 732–738. doi:10.2175/106143017x14902968254665

PubMed Abstract | CrossRef Full Text | Google Scholar

Cohn, T. A., Delong, L. L., Gilroy, E. J., Hirsch, R. M., and Wells, D. K. (1989). Estimating Constituent Loads. Water Resour. Res. 25 (5), 937–942. doi:10.1029/wr025i005p00937

CrossRef Full Text | Google Scholar

Cohn, T. A., Gilroy, E. J., and Baier, W. G. (1992). “Estimating Fluvial Transport of Trace Constituents Using a Regression Model with Data Subject to Censoring,” in Proceedings of the Joint Statistical Meeting (Boston), 142–151.

Google Scholar

Deng, L., Shahab, A., Xiao, H., Li, J., Rad, S., Jiang, J., et al. (2021). Spatial and Temporal Variation of Dissolved Heavy Metals in the Lijiang River, China: Implication of Rainstorm on Drinking Water Quality. Environ. Sci. Pollut. Res. 28, 68475–68486. doi:10.1007/s11356-021-15383-3

CrossRef Full Text | Google Scholar

Duan, W., Takara, K., He, B., Luo, P., Nover, D., and Yamashiki, Y. (2013). Spatial and Temporal Trends in Estimates of Nutrient and Suspended Sediment Loads in the Ishikari River, Japan, 1985 to 2010. Sci. Total Environ. 461-462, 499–508. doi:10.1016/j.scitotenv.2013.05.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Evensen, G. (2003). The Ensemble Kalman Filter: Theoretical Formulation and Practical Implementation. Ocean Dyn. 53, 343–367. doi:10.1007/s10236-003-0036-9

CrossRef Full Text | Google Scholar

Gao, J., White, M. J., Bieger, K., and Arnold, J. G. (2021). Design and Development of a Python-Based Interface for Processing Massive Data with the LOAD ESTimator (LOADEST). Environ. Model. Softw. 135, 104897. doi:10.1016/j.envsoft.2020.104897

CrossRef Full Text | Google Scholar

Gao, X., Chen, N., Yu, D., Wu, Y., and Huang, B. (2018). Hydrological Controls on Nitrogen (Ammonium versus Nitrate) Fluxes from River to Coast in a Subtropical Region: Observation and Modeling. J. Environ. Manage. 213, 382–391. doi:10.1016/j.jenvman.2018.02.051

CrossRef Full Text | Google Scholar

Gnann, S. J., Allmendinger, M. C., Haslauer, C. P., and Bárdossy, A. (2018). Improving Copula-Based Spatial Interpolation with Secondary Data. Spat. Stat. 28, 105–127. doi:10.1016/j.spasta.2018.07.001

CrossRef Full Text | Google Scholar

Gonçalves, A. M., and Costa, M. (2013). Predicting Seasonal and Hydro-Meteorological Impact in Environmental Variables Modelling via Kalman Filtering. Stoch Environ. Res. Risk Assess. 27, 1021–1038. doi:10.1007/s00477-012-0640-7

CrossRef Full Text | Google Scholar

Halliday, S., Skeffington, R., Bowes, M., Gozzard, E., Newman, J., Loewenthal, M., et al. (2014). The Water Quality of the River Enborne, UK: Observations from High-Frequency Monitoring in a Rural, Lowland River System. Water 6, 150–180. doi:10.3390/w6010150

CrossRef Full Text | Google Scholar

Huang, D., Wang, D., and Ren, Y. (2019). Using Leaf Nutrient Stoichiometry as an Indicator of Flood Tolerance and Eutrophication in the Riparian Zone of the Lijang River. Ecol. Indicators 98, 821–829. doi:10.1016/j.ecolind.2018.11.064

CrossRef Full Text | Google Scholar

Javaheri, A., Babbar-Sebens, M., Miller, R. N., Hallett, S. L., and Bartholomew, J. L. (2019). An Adaptive Ensemble Kalman Filter for Assimilation of Multi-Sensor, Multi-Modal Water Temperature Observations into Hydrodynamic Model of Shallow Rivers. J. Hydrol. 572, 682–691. doi:10.1016/j.jhydrol.2019.03.036

CrossRef Full Text | Google Scholar

Kalman, R. E. (1960). A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 82 (1), 35–45. doi:10.1115/1.3662552

CrossRef Full Text | Google Scholar

Kim, J., Lim, K. J., and Park, Y. S. (2018). Evaluation of Regression Models of LOADEST and Eight-Parameter Model for Nitrogen Load Estimations. Water Air Soil Pollut. 229, 179. doi:10.1007/s11270-018-3844-8

CrossRef Full Text | Google Scholar

Li, N., and Guo, H. (2017). Estimation of Long-Term Trends and Loads with Low-Frequency Water Quality Sampling in the Baoxiang River, One Tributary to Dianchi Lake. Acta Sci. Natur. Univ. Pekinensis 53 (2), 378–386. doi:10.13209/j.0479-8023.2017.019

CrossRef Full Text | Google Scholar

Li, R., Chen, Q., Tonina, D., and Cai, D. (2015). Effects of Upstream Reservoir Regulation on the Hydrological Regime and Fish Habitats of the Lijiang River, China. Ecol. Eng. 76, 75–83. doi:10.1016/j.ecoleng.2014.04.021

CrossRef Full Text | Google Scholar

Menard, S. (2000). Coefficients of Determination for Multiple Logistic Regression Analysis. Am. Statist. 54 (1), 17–24. doi:10.1080/00031305.2000.10474502

CrossRef Full Text | Google Scholar

Murphy, J., and Sprague, L. (2019). Water-quality Trends in US Rivers: Exploring Effects from Streamflow Trends and Changes in Watershed Management. Sci. Total Environ. 656, 645–658. doi:10.1016/j.scitotenv.2018.11.255

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, Y., and Engel, B. (2016). Identifying the Correlation between Water Quality Data and LOADEST Model Behavior in Annual Sediment Load Estimations. Water 8 (9), 368. doi:10.3390/w8090368

CrossRef Full Text | Google Scholar

Pellerin, B. A., Bergamaschi, B. A., Gilliom, R. J., Crawford, C. G., Saraceno, J., Frederick, C. P., et al. (2014). Mississippi River Nitrate Loads from High Frequency Sensor Measurements and Regression-Based Load Estimation. Environ. Sci. Technol. 48 (21), 12612–12619. doi:10.1021/es504029c

PubMed Abstract | CrossRef Full Text | Google Scholar

Powell, J. L. (1984). Least Absolute Deviations Estimation for the Censored Regression Model. J. Econom. 25 (3), 303–325. doi:10.1016/0304-4076(84)90004-6

CrossRef Full Text | Google Scholar

Qin, W., Han, D., Song, X., and Engesgaard, P. (2019). Effects of an Abandoned Pb-Zn Mine on a Karstic Groundwater Reservoir. J. Geochem. Explor. 200, 221–233. doi:10.1016/j.gexplo.2018.09.007

CrossRef Full Text | Google Scholar

Runkel, R. L., Crawford, C. G., and Cohn, T. A. (2004). Load Estimator (LOADEST): A FORTRAN Program for Estimating Constituent Loads in Streams and Rivers. Center for Integrated Data Analytics Wisconsin Science Center. Available at: http://pubs.usgs.gov/tm/2005/tm4A5 (Accessed December 1, 2004).

Google Scholar

Runkel, R. L., Walton-Day, K., Kimball, B. A., Verplanck, P. L., and Nimick, D. A. (2013). Estimating Instream Constituent Loads Using Replicate Synoptic Sampling, Peru Creek, Colorado. J. Hydrol. 489, 26–41. doi:10.1016/j.jhydrol.2013.02.031

CrossRef Full Text | Google Scholar

Schwarz, G. (1978). Estimating the Dimension of a Model. Stat. 6 (2), 461–464. doi:10.1214/aos/1176344136

CrossRef Full Text | Google Scholar

Steward, A. L., Negus, P., Marshall, J. C., Clifford, S. E., and Dent, C. (2018). Assessing the Ecological Health of Rivers when They Are Dry. Ecol. Indicators 85, 537–547. doi:10.1016/j.ecolind.2017.10.053

CrossRef Full Text | Google Scholar

Terskii, P., Kuleshov, A., Chalov, S., Terskaia, A., Belyakova, P., Karthe, D., et al. (2019). Assessment of Water Balance for Russian Subcatchment of Western Dvina River Using SWAT Model. Front. Earth Sci. 7, 241. doi:10.3389/feart.2019.00241

CrossRef Full Text | Google Scholar

Turnbull, B. W., and Weiss, L. (1978). A Likelihood Ratio Statistic for Testing Goodness of Fit with Randomly Censored Data. Biometrics 34 (3), 367–375. doi:10.2307/2530599

PubMed Abstract | CrossRef Full Text | Google Scholar

Valero, E. (2012). Characterization of the Water Quality Status on a Stretch of River Lérez Around a Small Hydroelectric Power Station. Water 4, 815–834. doi:10.3390/w4040815

CrossRef Full Text | Google Scholar

Verbeke, G., Lesaffre, E., and Brant, L. J. (1998). The Detection of Residual Serial Correlation in Linear Mixed Models. Statist. Med. 17 (12), 1391–1402. doi:10.1002/(sici)1097-0258(19980630)17:12<1391::aid-sim851>3.0.co;2-4

CrossRef Full Text | Google Scholar

Vogel, R. M. (1986). The Probability Plot Correlation Coefficient Test for the Normal, Lognormal, and Gumbel Distributional Hypotheses. Water Resour. Res. 22 (4), 587–590. doi:10.1029/wr022i004p00587

CrossRef Full Text | Google Scholar

Wu, Z., Mei, Y., Chen, J., Hu, T., and Xiao, W. (2019). Attribution Analysis of Dry Season Runoff in the Lhasa River Using an Extended Hydrological Sensitivity Method and a Hydrological Model. Water 11, 1187. doi:10.3390/w11061187

CrossRef Full Text | Google Scholar

Xiong, M., Liu, P., Cheng, L., Deng, C., Gui, Z., Zhang, X., et al. (2019). Identifying Time-Varying Hydrological Model Parameters to Improve Simulation Efficiency by the Ensemble Kalman Filter: A Joint Assimilation of Streamflow and Actual Evapotranspiration. J. Hydrol. 568, 758–768. doi:10.1016/j.jhydrol.2018.11.038

CrossRef Full Text | Google Scholar

Xu, B., Dai, J., Yu, C., Xie, X., Su, Y., Zhang, L., et al. (2020). Responses of Nitrogen and Phosphorus Emissions to Water and Fertilizer Management and Underlying Surface Property Changes in Lijiang River Basin. Trans. Chin. Soc. Agr. Eng. 36 (2), 245–254. (in Chinese with English abstract). doi:10.11975/j.issn.1002-6819.2020.02.029

CrossRef Full Text | Google Scholar

Ye, F., Chen, Q., and Li, R. (2010). Modelling the Riparian Vegetation Evolution Due to Flow Regulation of Lijiang River by Unstructured Cellular Automata. Ecol. Inform. 5 (2), 108–114. doi:10.1016/j.ecoinf.2009.08.002

CrossRef Full Text | Google Scholar

Zhang, L., Qin, X., Tang, J., Liu, W., and Yang, H. (2017). Review of Arsenic Geochemical Characteristics and its Significance on Arsenic Pollution Studies in Karst Groundwater, Southwest China. Appl. Geochem. 77, 80–88. doi:10.1016/j.apgeochem.2016.05.014

CrossRef Full Text | Google Scholar

Zhu, Y., Chen, L., Wei, G., Li, S., and Shen, Z. (2019). Uncertainty Assessment in Baseflow Nonpoint Source Pollution Prediction: The Impacts of Hydrographic Separation Methods, Data Sources and Baseflow Period Assumptions. J. Hydrol. 574, 915–925. doi:10.1016/j.jhydrol.2019.05.010

CrossRef Full Text | Google Scholar